GENIE Fysica GO! 3 leerschrift 2u (editie 2024)

Fysica GO!

©VANIN

GENIE 3.2 Fysica GO! ©VANIN

Via www.diddit.be heb je toegang tot het onlineleerplatform bij GENIE Activeer je account aan de hand van de onderstaande code en accepteer de gebruiksvoorwaarden.

GENIE

3.2 Fysica GO!

LET OP: ACTIVEER DEZE LICENTIE PAS VANAF 1 SEPTEMBER; DE LICENTIEPERIODE START VANAF ACTIVATIE EN IS 365 DAGEN GELDIG.

Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën. Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.

In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen. Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.

Ook voor het digitale lesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www.diddit.be.

© Uitgeverij VAN IN, Wommelgem, 2024

De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen. Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.

Credits

©VANIN

p. 25 kaart trajectcontroles © Het Nieuwsblad, created with Datawrapper, p. 30 kaart © CC BY OpenStreetMap Foundation (OSMF), p. 37 kaart filemelding © Vlaams Verkeerscentrum, p. 81 raket © BELGA/AFP, p. 82 meisje met ballon © Imageselect, p. 99 zwemmer © Imageselect, p. 120 Belgian Bullets © BELGA, p. 145 applet © CC BY PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu, p. 146 valpartij © BELGA, tegenwindfietsen © ANP, p. 176 applet © CC BY PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu, p. 229 shadowology © Vincent Bal, p. 240 shadowology © Vincent Bal, p. 244 spiegel op bergtop © MAXPPP, publiek bij spiegel © REUTERS

Eerste druk 2024 Vormgeving en ontwerp cover: Shtick ISBN 978-94-647-0678-9 Tekeningen: Geert Verlinde, Tim Boers (Studio B) D/2024/0078/228 Zetwerk: Vrijdag Grafis

Art. 606731/01

NUR 126

THEMA 02: KRACHTEN

HOOFDSTUK 1: Wat is zwaartekracht?

1 Welke kenmerken heeft de zwaartekracht?

2 Hoe groot is de zwaartekracht?

3 Wat is het verband tussen massa, gewicht en zwaartekracht?

` HOOFDSTUK 3: Hoe kun je krachten samenstellen of ontbinden?

1 Hoe stel je krachtvectoren met dezelfde richting samen?

2 Hoe stel je krachtvectoren met een verschillende richting samen?

` HOOFDSTUK 4: Welke verband bestaat er tussen kracht en evenwicht?

1 Hoe groot is de resulterende kracht bij een voorwerp in rust?

2 Wanneer is een voorwerp in evenwicht?

` HOOFDSTUK 5: Welke verband bestaat er tussen

1 Bij welke kracht beweegt een voorwerp aan een constante snelheid?

2 Bij welke kracht

` HOOFDSTUK 1: Hoe ontstaan kleur en schaduw?

1 Hoe plant licht zich voort?

Hoe ontstaan kleuren?

2 Hoe ontstaat schaduw?

` HOOFDSTUK 2: Welke eigenschappen hebben spiegelbeelden?

1 Hoe weerkaatst licht?

2 Welke eigenschappen heeft een spiegelbeeld bij een vlakke spiegel?

3 Welke eigenschappen heeft een spiegelbeeld bij een gekromde spiegel?

` HOOFDSTUK 3: Welke eigenschappen hebben beelden gevormd door doorzichtige stoffen?

1 Wat gebeurt er met licht dat doorgelaten wordt?

2 Welk beeld ontstaat bij breking aan een vlak scheidingsoppervlak?

3 Welke eigenschappen heeft een beeld gevormd door een lens?

MASSADICHTHEID (UITBREIDING)

LABO’S

STEM-VAARDIGHEDEN (VADEMECUM)

` METROLOGIE

• Grootheden en eenheden

• Machten van 10 en voorvoegsels

• Eenheden omzetten

• Nauwkeurig meten

• Afrondingsregels

` STAPPENPLANNEN

• Grafieken tekenen

• NW-stappenplan

` OPLOSSINGSSTRATEGIE

• Formules omvormen

• Formules uit de wiskunde

• Vraagstukken oplossen

• Vectoren optellen

• Grafieken lezen

STARTEN MET GENIE

1

Opbouw van een thema

CHECK IN

In de CHECK IN maak je kennis met het onderwerp van het thema. In het kadertje onderaan vind je een aantal vragen die je op het einde van het thema kunt beantwoorden.

VERKEN

In de verkenfase zul je merken dat je al wat kennis hebt over het onderwerp dat in het thema aan bod komt. Jouw voorkennis wordt hier geactiveerd.

©VANIN

DE HOOFDSTUKKEN

Na het activeren van de voorkennis volgen een aantal hoofdstukken Een thema bestaat uit meerdere hoofdstukken. Doorheen de hoofdstukken verwerf je de nodige kennis en vaardigheden om uiteindelijk een antwoord te geven op de centrale vraag of het probleem uit de CHECK IN.

SYNTHESE EN CHECKLIST

We vatten de kern van het thema voor je samen in de hoofdstuksynthese en themasynthese Vervolgens willen we graag dat je vorderingen maakt en dat je reflecteert op je taken en leert uit feedback. De checklist is een hulpmiddel om zelf zicht te krijgen of je de leerdoelen al dan niet onder de knie hebt.

CHECK IT OUT

In CHECK IT OUT pas je de vergaarde kennis en vaardigheden toe om terug te koppelen naar de vragan uit de CHECK IN.

AAN DE SLAG

In het onderdeel Aan de slag kun je verder oefenen. Je leerkracht beslist of je de oefeningen op het einde van het thema maakt of doorheen de lessen.

` Per thema vind je op adaptieve oefenreeksen om te leerstof verder in te oefenen.

LABO

©VANIN

LABO’S

Ga zelf op onderzoek! Bij het onlinelesmateriaal staan een aantal labo’s om verder experimenten uit te voeren.

LEREN LEREN

• In de linkermarge naast de theorie is er plaats om zelf notities te maken. Noteren tijdens de les helpt je om de leerstof actief te verwerken.

• Op vind je per themasynthese een kennisclip waarin we alles voor jou nog eens op een rijtje zetten.

2 Handig voor onderweg

In elk thema word je ondersteund met een aantal hulpmiddelen.

Kenniskader

We zetten doorheen het thema de belangrijkste zaken op een rijtje in deze rode kaders.

©VANIN

VEILIGHEIDSVOORSCHRIFT !

Met GENIE ga je zelf experimenteren en op onderzoek. Daarbij moet je natuurlijk een aantal veiligheidsvoorschriften respecteren. Die vind je terug in dit kader.

WEETJE

Een weetjeskader geeft extra verduidelijking of illustreert de leerstof met een extra voorbeeld.

OPDRACHT 11 DOORDENKER

Nood aan meer uitdaging? Doorheen een thema zijn er verschillende doordenkers. Niet altijd even makkelijk om op te lossen, maar het proberen waard!

In de tipkaders vind je handige tips terug bij het uitvoeren van de onderzoeken of opdrachten.

OPLOSSINGSSTRATEGIE

Een oplossingsstrategie maakt je duidelijk hoe je het best aan de slag gaat met bijvoorbeeld een vraagstuk. Heb je daarna nogmaals dezelfde strategie nodig? Dan vind je die in de vorm van QR-codes, om zo de strategie opnieuw op te frissen.

VRAAGSTUKKEN OPLOSSEN

Bij het onlinelesmateriaal vind je een vademecum

Dat vademecum ̒GENIE in STEM-vaardigheden omvat:

• stappenplannen om een grafiek te maken, opstellingen correct te bouwen, metingen uit te voeren …;

• stappenplannen om een goede onderzoeksvraag op te stellen, een hypothese te formuleren …;

• oplossingsstrategieën om formules om te vormen, vraagstukken op te lossen ...;

• een overzicht van grootheden en eenheden, machten van 10 en voorvoegsels, afrondingsregels ...;

• een overzicht van labomateriaal en labotechnieken;

• een overzicht van gevarensymbolen en P- en H-zinnen;

• …

TIP

GENIE EN DIDDIT

HET ONLINELEERPLATFORM BIJ GENIE

©VANIN

Een e-book is de digitale versie van het leerschrift. Je kunt erin noteren, aantekeningen maken, zelf materiaal toevoegen ...

• De leerstof kun je inoefenen op jouw niveau.

• Je kunt vrij oefenen en de leerkracht kan ook voor jou oefeningen klaarzetten.

Hier vind je de opdrachten terug die de leerkracht voor jou heeft klaargezet.

Hier kan de leerkracht toetsen en taken voor jou klaarzetten.

Benieuwd hoever je al staat met oefenen en opdrachten? Hier vind je een helder overzicht van je resultaten.

Meer info over diddit vind je op https://www.vanin.diddit.be/nl/leerling.

• Hier vind je het lesmateriaal per thema.

• Alle instructiefilmpjes, kennisclips en andere video's zijn ook hier verzameld.

Notities ©VANIN

BEWEGING

1 Wat betekent je verplaatsen tussen twee punten?

2

3

2

3 Hoe kun je de positie, de tijd en de snelheid bij een ERB berekenen?

Licht op reis

De aarde leeft op zonne-energie. Door die energie ontstaat er een leefbaar klimaat, kennen we dag en nacht, groeien planten en kunnen we als mens andere energievormen ontwikkelen. De zon zal volgens wetenschappers nog 4,5 miljard jaar bestaan. Hopelijk heeft de mensheid al iets eerder grote verhuisplannen gemaakt!

1 Wanneer bereikt volgens jou het zonlicht de aarde?

Duid je hypothese aan.

onmiddellijk

na ongeveer acht seconden

na ongeveer acht minuten

na ongeveer acht uur

2 Welke gegevens heb je nodig om dat te kunnen berekenen?

©VANIN

Het zonlicht ontstaat doordat er in de zon voortdurend

waterstofkernen samensmelten tot heliumkernen.

(Helios is Grieks voor ‘zon’.) Daarbij komt enorm veel warmte vrij, waardoor de zon een grote vuurbol is met temperaturen tot wel 15 miljoen graden Celsius in de kern.

Op aarde proberen wetenschappers dat proces na te bootsen met een soortgelijke reactie (zie afbeelding).

Mochten we daar ooit in slagen, dan zou dat een vorm van energieproductie zijn zonder schadelijke afvalstoffen.

Helaas zijn de voorwaarden om de samensmelting te veroorzaken, zo moeilijk dat dat voorlopig nog niet gelukt is.

` Hoe kunnen we de beweging van het zonlicht beschrijven met berekeningen en grafieken?

We zoeken het uit!

WEETJE

Rechtlijnige beweging?

OPDRACHT 1

Welke informatie kun je aflezen op een bewegingskaart?

Bestudeer het Strava-kaartje van een hardloopsessie van Bram.

Beantwoord de vragen.

1 Hoe zie je dat Bram bewogen heeft?

2 Wat kun je afleiden uit de getekende weg? Duid aan. Er zijn meerdere antwoorden mogelijk.

Het vertrek- en aankomstpunt vallen niet samen.

De beweging is rechtlijnig.

De beweging is niet rechtlijnig.

De beweging verloopt in wijzerzin.

De beweging verloopt in tegenwijzerzin.

Afb. 1 Avondloop

WINKELSTAP

3 Bram is vertrokken aan Winkelstap. Vervolledig het kaartje met de onderstaande symbolen.

• Noteer de positie in het vertrekpunt A.

• Noteer de positie in het aankomstpunt B.

• Teken een pijl op de baan. Die noem je de bewegingszin.

• Teken een pijl van het vertrekpunt naar het aankomstpunt. Die noem je de verplaatsing.

OPDRACHT 2

Welke informatie kun je berekenen uit een bewegingsrapport?

Bestudeer de gegevens uit het bijbehorende Strava-rapport van een hardloopsessie van Bram. Beantwoord de vragen.

1 Hoe zie je dat Bram gelopen heeft?

2 Je kunt twee soorten tijden (tijdstip en tijdsverloop) aflezen uit het Strava-rapport. Noteer en omschrijf ze in de tabel.

Tijdstip

Tijd

Omschrijving

Hardloopsessie

Bram 14 juli om 18:10

Afstand 5,03 km

Calorieën 309 kcal

Afb. 2 Hardloopsessie

Tijdsverloop

Beweegtijd 30:10

Gem. hartslag 151 bpm

3 Schat met de weergegeven informatie de gemiddelde snelheid van Bram in. a Duid aan.

ongeveer 2,5 km h … ongeveer 5 km h … ongeveer 10 km h … ongeveer 30 km h

b Leg in je eigen woorden uit hoe je die snelheid hebt ingeschat.

c Leg uit waarom je dat de gemiddelde snelheid noemt.

OPDRACHT 3

Wat is een rechtlijnige beweging?

Bestudeer de bewegingen op de pretparkattracties.

1 Maak de uitspraken correct door het juiste antwoord aan te duiden.

• De personen zijn in beweging / in rust ten opzichte van de attractie.

• De personen zijn in beweging / in rust ten opzichte van de aarde.

2 Duid de kenmerken van de beweging aan in de tabel.

1

Je rijdt met een botsauto. Op de vrijevaltoren ga je traag omhoog en val je plotseling naar beneden.

één bewegingsrichting

één bewegingszin

rechtlijnige beweging

één bewegingsrichting

één bewegingszin

rechtlijnige beweging

Je schommelt heen en weer in de piratenboot.

één bewegingsrichting

één bewegingszin

rechtlijnige beweging

Je rijdt omhoog bij de start van de achtbaan.

één bewegingsrichting

één bewegingszin

rechtlijnige beweging

3 Teken op de foto’s in de tabel bij de rechtlijnige bewegingen een rechte volgens de bewegingsrichting.

Bij een rechtlijnige beweging is er een verandering van de positie langs een rechte.

• De oriëntatie van de rechte noem je de bewegingsrichting (bijvoorbeeld horizontaal, verticaal, schuin).

• De kant naar waar je beweegt, noem je de bewegingszin (bijvoorbeeld naar links, naar rechts, naar boven, naar onder).

Welke eigenschappen heeft een rechtlijnige beweging?

LEERDOELEN

Je kunt al:

M omschrijven wat een rechtlijnige beweging is;

M omschrijven wat richting en zin zijn.

Je leert nu:

M de baan van een rechtlijnige beweging voorstellen;

M de afgelegde weg en de verplaatsing aflezen;

M de gemiddelde snelheid berekenen;

M de ogenblikkelijke snelheid voorstellen als een vector. 1

1.1 Baan weergeven

OPDRACHT 4

In het verkeer is iedereen in beweging. Voetgangers, fietsers en automobilisten voeren daarbij willekeurige, maar ook rechtlijnige bewegingen uit.

In dit hoofdstuk gaan we op zoek naar een wetenschappelijke manier om die rechtlijnige bewegingen te beschrijven. Dat doen we door de baan voor te stellen en door de verplaatsing en de snelheid te bepalen.

Wat betekent je verplaatsen tussen twee punten?

©VANIN

Bestudeer de afbeelding op de volgende pagina en stel de beweging voor.

Marco steekt de straat (van 6 m breed) over op het zebrapad.

Hij is halfweg op het moment dat de foto wordt gemaakt.

1 Vul de kenmerken van de beweging aan.

• bewegingsrichting:

• bewegingszin:

2 Teken een positie-as op de afbeelding volgens de kenmerken van de beweging.

a Teken een pijl over de volledige lengte van het zebrapad.

b Benoem de positie-as met x (m).

c Breng de oorsprong en de huidige positie aan op de as.

OPDRACHT 4 (VERVOLG)

3 Teken de baan die Marco heeft afgelegd.

Stel de baan voor als een pijl tussen Marco’s vertrekpunt en zijn huidige positie.

4 Hoe groot is de verplaatsing van Marco?

OPDRACHT 5

Bestudeer de twee verschillende bewegingen.

1 Teken bij beide bewegingen een positie-as (x -as).

2 Stel de bewegende voorwerpen voor door centraal op de voorwerpen een punt te tekenen.

3 Duid in de tabel de bewegingszin aan.

Beweging volgens de positie-as De lift stijgt / daalt.

Beweging tegengesteld aan de positie-as De lift stijgt / daalt.

De mensen wandelen naar links / rechts.

De mensen wandelen naar links / rechts.

Om een beweging te beschrijven, moet je de positie van een voorwerp weergeven in een assenstelsel. Bij een rechtlijnige beweging gebeurt de beweging in één richting en is één as voldoende.

Je noemt die positie-as de x -as

Afb. 3 Marco steekt de straat over op het zebrapad.

Om rechtlijnige bewegingen van een of meerdere voorwerpen te beschrijven, kies je een positie-as. Het bewegende voorwerp stel je voor door een massapunt (= een centraal punt op het voorwerp). De positie stel je voor met de letter x en een onderschrift in de benaming.

Grootheid met symbool SI-eenheid met symbool positie x meter m

Tijdens de beweging kan elk voorwerp op twee verschillende manieren langs de x-as bewegen:

©VANIN

SI is de afkorting van système international. SIeenheid betekent dat het de standaardeenheid is en dat je in formules die eenheid moet gebruiken. Via de QR-code leer je meer over grootheden (wat je meet) en eenheden (de maat waarin je iets uitdrukt).

bewegen volgens de positie-as bewegen tegengesteld aan de positie-as

Voor elke beweging kies je een positie-as die aansluit bij de beweging:

• oorsprong van de x-as: het vertrekpunt,

• richting van de x-as: de rechte waarop de beweging plaatsvindt (horizontaal/verticaal/schuin),

• zin van de x-as: weg van het vertrekpunt (links/rechts/boven/onder).

De baan is weergegeven met de rode lijn. De begin-en eindpositie worden benoemd zodat je duidelijk ziet in welke zin de beweging verloopt. De pijlpunt geeft de bewegingszin aan.

De lengte van de baan noem je de afgelegde weg. Die grootheid heeft als symbool l en als eenheid meter.

Grootheid met symbool SI-eenheid met symbool afgelegde weg l meter m

VOORBEELD AFGELEGDE WEG VAN EEN PIZZABEZORGER

Op afbeelding 5 is de positie-as getekend voor een pizzabezorger die vertrekt aan de pizzeria, om 3,5 km verder in de straat een pizza aan huis te bezorgen.

Na de levering keert hij terug naar de pizzeria om de volgende bestelling op te pikken.

Voor de pizzabezorger is de afgelegde weg:

• heentraject (pizzeria  leveradres): lheen = 3,5 km,

• terugtraject (leveradres  pizzeria): l terug = 3,5 km,

• volledige traject (pizzeria  pizzeria): lvolledig = 7,0 km.

TIP

Het symbool ∆ is de Griekse letter delta. Dat symbool gebruik je in de fysica om een verschil tussen twee meetwaarden aan te geven. Uit de wiskunde ken je dat als het begin- en eindpunt van een interval:

[xbegin, xeind]

volgens de x-as bewegen

xbegin xeind

l > 0

∆x > 0

x

1.2 Verplaatsing berekenen

Bij een rechtlijnige beweging verandert de positie x. Voor elk traject is er een beginpunt (genoteerd als xbegin) en een eindpunt (genoteerd als xeind).

De kortste afstand tussen beide noem je de verplaatsing. Je leest de verplaatsing af met behulp van de baanvoorstelling op de x-as.

Grootheid met symbool SI-eenheid met symbool verplaatsing ∆x = xeind – xbegin meter m

VOORBEELD VERPLAATSING VAN DE PIZZABEZORGER

Voor de pizzabezorger zijn er drie trajecten. Je leest de verplaatsing af op de baanvoorstelling.

Groene pijl: heentraject (pizzeria  huis)

Blauwe pijl: terugtraject (huis  pizzeria)

De verplaatsing is positief en verloopt dus in dezelfde zin als de x-as.

De verplaatsing is negatief en verloopt dus tegengesteld aan de zin van de x-as.

Groene pijl gevolgd door blauwe pijl: volledige traject (pizzeria  pizzeria)

De verplaatsing is nul, omdat het begin- en eindpunt van de beweging samenvallen

Bij een rechtlijnige beweging verandert je positie in één richting (een rechte). Je kiest een positie-as volgens de bewegingsrichting. De opeenvolgende posities noem je de baan. De lengte van de baan noem je de afgelegde weg.

Voor elke deelbeweging kun je de verplaatsing berekenen als

©VANIN

x xbegin xeind

l > 0

∆x < 0 tegengesteld aan de positie-as bewegen

∆x = 0 Afb. 7 heen en terug bewegen

xbegin = xeind

l > 0

x

∆x = xeind – xbegin, waarbij je het begin- en eindpunt (voor die deelbeweging) afleest op de x-as.

Grootheid met symbool SI-eenheid met symbool positie x meter m afgelegde weg l meter m verplaatsing

∆x = xeind – xbegin meter m

` Maak oefening 1 t/m 5 op p. 30 en 31.

PIZZERIA

2 Wat betekent bewegen aan een bepaalde snelheid?

2.1 Snelheid berekenen

De verplaatsing gebeurt in een bepaalde tijd. De tijd tussen het beginpunt (tbegin bij xbegin) en het eindpunt (teind bij xeind) noem je het tijdsverloop.

Grootheid met symbool

SI-eenheid met symbool tijdsverloop ∆t = teind – tbegin seconde s tijdstip t seconde s

WEETJE

Snelheidsmeters zijn meettoestellen die de verplaatsing en het tijdsverloop meten en daarmee de snelheid berekenen.

Voorbeelden:

• snelheidsmeter in de auto

• fietscomputer

• sporthorloge

• flitspaal

• bewegingssensor

©VANIN

Je vindt meer informatie over meetnauwkeurigheid en beduidende cijfers op de steekkaart met formules.

Het tijdsverloop is altijd positief, omdat de tijd nooit achteruitgaat (teind > tbegin).

Om de grootte van de snelheid van een voorwerp te bepalen, meet je de grootte van de verplaatsing ∆x en het tijdsverloop ∆t dat nodig is om die afstand af te leggen.

• Als je de verplaatsing ∆x meet, meet je de grootheid afstand in meter.

Je gebruikt een meetlat, een rolmeter, een laserafstandsmeter …

• Als je het tijdsverloop ∆t meet, meet je een tijd in seconde.

Je gebruikt een chronometer of je smartphone.

• De snelheid v is de verhouding van de verplaatsing ∆x ten opzichte van het tijdsverloop ∆t:

Je gebruikt de opgemeten waarden voor de verplaatsing en het tijdsverloop.

Grootheid met symbool SI-eenheid met symbool snelheid meter per seconde

De afstand, het tijdsverloop en de snelheid zijn gemeten grootheden Je kent ze tot op een bepaalde nauwkeurigheid en met een aantal beduidende cijfers:

• meetnauwkeurigheid: de kleinste schaalverdeling die op het meettoestel af te lezen is;

• beduidende cijfers: de cijfers die je werkelijk hebt afgelezen in een meetresultaat.

Voor de afstand en het tijdsverloop is de meetnauwkeurigheid afhankelijk van de meetnauwkeurigheid van het toestel. Voor de snelheid moet je rekening houden met de beduidende cijfers van de verplaatsing en het tijdsverloop.

Via de ontdekplaat ‘GENIE in STEM-vaardigheden’ bij het onlinelesmateriaal vind je de afspraken daarover terug en kun je dat inoefenen.

OPDRACHT 6 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

Een pizzabezorger levert in 6,00 minuten een pizza bij een huis op 3,5 km van de pizzeria.

Hij heeft geluk: het verkeerslicht op 2,0 km van de pizzeria staat op groen.

1 Welke gemiddelde snelheid heeft de pizzabezorger?

2 Na hoeveel minuten en seconden passeert hij het verkeerslicht?

PIZZERIA

Gegeven: xhuis = 3,5 km

xpizzeria = 0,0 km

xlicht = 2,0 km

Δt = 6,00 min

Gevraagd: a v = ?

b Δtlicht = ?

Oplossing:

a Basisformule: v = ∆x ∆t = xhuis – xpizzeria ∆t = 3,5 km – 0,0 km 6,00 min =

Om een snelheid in m s te bekomen, moet je …

• de verplaatsing omzetten naar meter:

∆x = 3,5 km = 3,5 103 m

BEREKENINGEN AFRONDEN

• het tijdsverloop omzetten naar seconden: ∆t = 6,00 min = 6,00 · 60 s = 360 s

Dat betekent voor de snelheid: v = 3,5 km 6,00 min = 3,5 103 m 360 s = 9,7 m s

b Basisformule: v = ∆x ∆t

• Om het tijdsverloop te berekenen, herschrijf je de basisformule en vul je de waarden in:

∆t = ∆xlicht v = xlicht – xpizzeria v = 2,0 km – 0,0 km 9,7 m s = 2,0 km

• Je zet het tijdsverloop om naar de gevraagde eenheid:

∆t = 206 s = 206 60 min = 3,43 min = 3 min + 0,43 min · 60 s min = 3 min 26 s

Controle: Bestudeer de berekende waarden.

a Kloppen de eenheden? Ja

• m s is een eenheid van snelheid.

• min is een eenheid van tijd.

b Klopt de grootte van de getalwaarde? Ja

• Ongeveer 10 m s (30 tot 40 km h ) is een normale waarde voor een bromfiets.

• De tijd is iets meer dan de helft van de tijd voor het volledige traject.

(we ronden dit niet af op 2 BC omdat dit een tussenresultaat is)

©VANIN

OPDRACHT 6 (VERVOLG)

OPLOSSINGSSTRATEGIE

• Omschrijf in je eigen woorden wat er gebeurt en wat je zoekt.

• Stel de baan voor op een geschikte x-as.

• Noteer de gekende waarden op de baan.

• Denk na over de gegevens die je nodig hebt om de snelheid te berekenen.

• Noteer alles in symbolen bij de gegevens en het gevraagde.

• Werk de oplossing uit.

Noteer de geschikte formule.

Hervorm de formule indien nodig.

Vul de gegevens in.

Vergeet de eenheid niet.

Reken uit.

Rond af.

• Sta stil bij de oplossing.

Klopt de eenheid? Klopt de getalwaarde? EENHEDEN OMZETTEN

OPDRACHT 7

Vorm de basisformule voor snelheid om.

1 Hoe kun je de verplaatsing berekenen, als de snelheid en het tijdsverloop gegeven zijn?

2 Hoe kun je het tijdsverloop berekenen, als de snelheid en de verplaatsing gegeven zijn?

TIP

• Onthoud enkel de basisformule.

• Gebruik de hoofdeigenschap van evenredigheden (kruisproduct) voor de omgevormde formules.

a b = c d a d = b c

Hier is a = v; b = 1; c = ∆x en d = ∆t

OPDRACHT 8

©VANIN

• Gebruik eenvoudige getallen om je omzetting te controleren.

Voorbeeld: 3 = 6 2 , dus 6 = 3 ∙ 2 en 2 = 6 3

Ga op zoek naar de omzettingsfactor tussen m s en km h  .

Vul de omzettingsschema’s aan.

• omzetting m s naar km h

1,0 m s = 1,0 m 1,0 s = 3 600 m = km h = km h

• omzetting km h naar m s

1,0 km h = 1,0 km 1,0 h = m = m s = m s 1,0 m s km h :

Snelheid wordt uitgedrukt in de eenheden km h of m s . Die keuze hangt af van de situatie.

• De eenheid kilometer per uur ( km h ) wordt het meest gebruikt voor alledaagse snelheden, zoals snelheden in het verkeer. Je legt lange afstanden af en bent een lange tijd in beweging.

Voorbeeld: Een auto rijdt aan een snelheid van 70 km h .

• De eenheid meter per seconde ( m s ) wordt gebruikt voor korte en snelle bewegingen

Voorbeelden:

Usain Bolt liep het wereldrecord 100 meter sprint aan 10,4  m s .

De lichtsnelheid is 3,00 ∙ 108 m s .

In de wetenschap is m s de SI-eenheid.

Je kunt een snelheid omzetten van de ene naar de andere eenheid door de omzettingsfactor te gebruiken.

VOORBEELD SNELHEID VAN DE PIZZABEZORGER OMZETTEN

De snelheid van de pizzabezorger is 9,7 m s tijdens de heenrit. Je kunt dat omrekenen naar km h :

v = 9,7 m s = 9,7 3,6 km h = 35 km h

Om de snelheid in een tijdsverloop te berekenen, deel je de verplaatsing door het tijdsverloop waarin de beweging plaatsvindt.

Grootheid met symbool SI-eenheid met symbool snelheid meter per seconde

` Maak oefening 6 t/m 11 op p. 31 t/m 34. v = ∆x ∆t m s

Kilometer per uur ( km h ) is een andere veelgebruikte eenheid van snelheid. 1,0 m s 3,6 km h : 3,6 ∙ 3,6

2.2 Ogenblikkelijke en gemiddelde snelheid

OPDRACHT 9

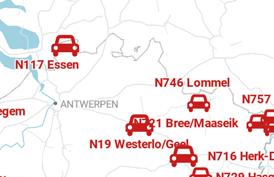
Bestudeer de afbeelding uit de krant.

Bij een trajectcontrole wordt elk voertuig aan het begin en aan het einde van een traject gefotografeerd met een digitale camera. Een computeranalyse is in staat om hetzelfde voertuig bij de tweede post te herkennen en zo het tijdsverloop op het traject te bepalen.

1 Op de Grote Steenweg in Westerlo is de maximumsnelheid 70  km h

a Over welke afstand staat de trajectcontrole?

∆x =

b Welke auto’s worden zeker geflitst? Er zijn meerdere antwoorden mogelijk.

v > 70  km h op een moment

v > 70  km h op elk moment

v > 70  km h gemiddeld over het traject

∆t > 2,0 minuten

∆t < 2,0 minuten

2 Een alternatieve manier van snelheidscontroles zijn de flitspalen. Welke snelheid meet de flitspaal?

3 Waarom investeert de overheid sterk in trajectcontroles?

©VANIN

De snelheid over een lang traject is meestal niet constant. De omstandigheden zorgen ervoor dat een voorwerp vertraagt en versnelt. Er is een onderscheid tussen:

• gemiddelde snelheid: snelheid over een (lang) tijdsverloop. Je berekent de gemiddelde snelheid als v gem = ∆xtot ∆ttot (Het onderschrift ‘gem’ wordt vaak weggelaten)

• ogenblikkelijke snelheid: snelheid op een bepaald tijdstip

De ogenblikkelijke snelheid lees je af op een snelheidsmeter.

VOORBEELD GEMIDDELDE EN OGENBLIKKELIJKE SNELHEID

De pizzabezorger heeft tijdens de heenrit een gemiddelde snelheid van 35  km h . Op de momenten waarop er geen andere weggebruikers zijn, heeft hij een topsnelheid van 40  km h . Op het moment waarop er fietsers zijn, moet hij vertragen tot een snelheid van 24  km h

De pizzabezorger heeft een gemiddelde snelheid van 35  km h over de volledige heenrit.

We kennen de ogenblikkelijke snelheid op twee momenten: 40  km h als topsnelheid en 24  km h wanneer de pizzabezorger fietsers nadert.

Grote Steenweg van km 23,2 tot km 25,4

Afb. 10

De gemiddelde snelheid bereken je als vgem = ∆x ∆t (het onderschrift 'gem' wordt vaak weggelaten).

De ogenblikkelijke snelheid lees je af op een snelheidsmeter.

` Maak oefening 12 t/m 14 op p. 35 en 36.

2.3 Snelheidsvector

OPDRACHT 10

Bestudeer de afbeelding en beantwoord de vragen.

1 Voor elk voertuig is zijn snelheidsmeter weergegeven.

Vervolledig de tabel met de bewegingsrichting en -zin van elk voertuig.

©VANIN

G W

Voertuig gele auto (G) rode auto (R) witte auto (W)

Richting

Zin

2 Stel voor elk voertuig de snelheid voor als een vector. a Teken vanuit het massapunt een pijl, zodat alle kenmerken van de ogenblikkelijke snelheid duidelijk zijn. b Benoem de vector met het vectorsymbool. Bijvoorbeeld voor de gele auto: vG.

3 De gele auto doet 45 minuten over 30 km. Ga na met berekeningen of de gemiddelde snelheid hetzelfde is als de ogenblikkelijke snelheid die je afleest op afbeelding 11.

Gegeven:

Gevraagd: Oplossing:

Controle: Vergelijk de gemiddelde snelheid met de ogenblikkelijke snelheid op afbeelding 11. Verklaar.

Afb. 11

Een vector in de fysica is een pijl met de naam van de grootheid. Om aan te duiden dat het een vector is, staat altijd een klein pijltje naar rechts op de grootheid.

zin grootte richting

aangrijpingspunt v TIP

De ogenblikkelijke snelheid van een voorwerp kun je voorstellen door een snelheidsvector v met vier kenmerken:

• het aangrijpingspunt: een centraal punt (= massapunt) op het voorwerp,

• de richting: de richting van de positie-as (x-as),

• de zin: de bewegingszin, aangegeven door de pijlpunt,

• de grootte: de getalwaarde van de ogenblikkelijke snelheid, aangegeven door de lengte van de pijl. Om de snelheidsgrootte precies weer te geven, is er een schaalverdeling

VOORBEELD SNELHEIDSVECTOREN VAN DE PIZZABEZORGER

©VANIN

Een schaal wordt weergegeven met een symbool: 1 cm

Dat betekent: 1 cm komt overeen met ...

Hieronder zie je de vectorvoorstelling van de ogenblikkelijke snelheid van de pizzabezorger op drie momenten. De kenmerken van de vectoren vind je in de tabel.

Topsnelheid tijdens heenrit v1

Lagere snelheid door hinder van fietsers tijdens heenrit v2

Topsnelheid tijdens terugrit v3

1 cm 20 km h

Aangrijpingspunt massapunt massapunt massapunt

Richting horizontaal horizontaal horizontaal

Zin naar rechts naar rechts naar links

Grootte 40 km h 25 km h 40 km h

Notatie v1 v2 v3

Via de lengteverhouding van de vectoren kun je de snelheden rangschikken volgens hun grootte (v2 < v1 = v3). Voor de pizzabezorger is die 1 cm 40 km h . Dat betekent dat 1 cm overeenkomt met een snelheid van 40 km h :

- v1 = 40 km h , de pijl van v1 heeft een lengte van 1 cm,

- v2 = 25 km h , de pijl van v2 heeft een lengte van 25 40 cm = 0,6 cm.

traag bewegen volgens de positie-as

snel bewegen, tegengesteld aan de positie-as

Afb. 12 x v

De ogenblikkelijke snelheid kun je voorstellen als een vector met het symbool v:

• aangrijpingspunt: het massapunt,

• richting: de bewegingsrichting,

• zin: de bewegingszin,

` Maak oefening 15 t/m 18 op p. 36 en 37. x v

• grootte: de getalwaarde van de ogenblikkelijke snelheid. Om de grootte van de snelheidsvector precies weer te geven, voeg je een schaalverdeling toe.

TIP

In het dagelijks leven voegt men vaak de bewegingsrichting en -zin in woorden toe aan de snelheidsgrootte. Op die manier beschrijft men de snelheidsvector.

Voorbeelden:

• Er waait een strakke zuidenwind met snelheden tot 90  km h

• Door filegolven op de E40 richting de kust is de snelheid beperkt tot 60  km h .

Opgepast: de term ‘richting’ wordt daarbij (meestal) verkeerdelijk gebruikt om de zin aan te geven. In het voorbeeld is ‘E40’ de richting en ‘richting de kust’ de zin van de snelheidsvector.

3 Wat betekent versnellen en vertragen?

OPDRACHT 11 DOORDENKER

Bestudeer de krantenkop.

1 Welke grootheid kun je afleiden uit de krantenkop?

Duid aan.

de totale rijtijd

de maximale snelheid over het hele traject

de versnelling

2 De Ferrari en een stadswagen vertrekken op vol vermogen. Teken de snelheidsvectoren bij het vertrek, op 1 s en op 3 s.

DIT IS DE SNELSTE FERRARI ALLER TIJDEN: IN 2,9 SECONDEN NAAR 100 KM/U

Prijskaartje? 393 971 euro

©VANIN

Voorwerpen versnellen om een bepaalde snelheid te halen. Ze vertragen om tot stilstand te komen of hindernissen te nemen. Ze ondergaan een snelheidsverandering.

Het tempo van de snelheidsverandering wordt uitgedrukt met de grootheid versnelling.

Hoe je de grootheid versnelling berekent en voorstelt, leer je in de derde graad.

Vertrek

Op 1 s

Op 3 s

Bron: www.hln.be

POSITIE

• = verandering van de positie in de tijd

• = plaats waar een voorwerp zich bevindt

• twee grootheden om een verandering in positie voor te stellen: = lengte van de baan = verschil tussen de begin- en eindpositie met symbool met symbool

Teken de verplaatsing op de figuren. x

achteruit bewegen: ∆x 0

vooruit bewegen: ∆x 0 x

SNELHEID

• snelheid = tempo van de verandering

snelheid = snelheid over een tijdsverloop

snelheid = snelheid op één moment

met symbool met symbool v =

meter per seconde / kilometer per uur /

©VANIN

1,0 m s km h

Teken de snelheidsvectoren op de figuren.

traag bewegen volgens de positie-as x

• omzettingsfactor tussen m s en km h x

snel bewegen tegengesteld aan positie-as

zin grootte richting aangrijpingspunt v

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg! EENHEDEN OMZETTEN

1 Geef een voorbeeld van rechtlijnige bewegingen … in de horizontale richting:

in de verticale richting:

in een schuine richting:

2 Op een fietscomputer kun je een afstand aflezen.

a Is dat de verplaatsing of de afgelegde weg?

b Maak duidelijk met een voorbeeld.

3 Bestudeer de onderstaande voorbeelden.

BEREKENINGEN AFRONDEN

GRAFIEKEN LEZEN

a Noteer de afgelegde weg en de verplaatsing in de tabel.

b Stel de baan van de rechtlijnige bewegingen voor op een positie-as (x-as).

Afgelegde weg (l )

Verplaatsing (∆x )

Voorstelling rechtlijnige beweging 1

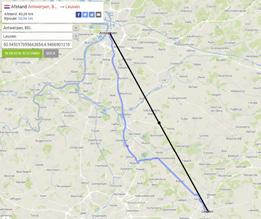
Je rijdt van Antwerpen naar Leuven. De afstand bedraagt 43,26 km en de rijroute 50,56 km.

Een appel valt uit een 2,5 m hoge boom.

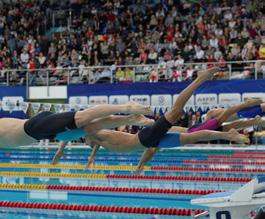
Een zwemmer zwemt 100 m in een olympisch zwembad van 50 m.

4 Maak de onderstaande uitspraken correct door ze te vervolledigen met ‘altijd’, ‘soms’ of ‘nooit’.

• Een beweging is rechtlijnig.

• Een rechtlijnige beweging verloopt in één richting.

• Een rechtlijnige beweging verloopt in één zin.

• De afgelegde weg is korter dan de verplaatsing.

• De afgelegde weg is langer dan de verplaatsing.

• Voor een rechtlijnige beweging in één zin is de verplaatsing even lang als de afgelegde weg.

5 Sarah werkt op de achtste verdieping. Als ze in de lift stapt op de vierde verdieping, heeft Ismael de knop van de tweede verdieping al ingedrukt. De lift werkt de verdiepingen (elk 3,2 m hoog) af volgens de indrukvolgorde.

a Teken de baan die Sarah aflegt op de weergegeven positie-as (x-as).

b Noteer de posities van de tweede, vierde en achtste verdieping op de x-as.

c Splits de beweging op in deelbewegingen en bereken de verplaatsing.

• verplaatsing van de naar de verdieping:

∆x1 =

• verplaatsing van de tweede naar de achtste verdieping:

∆x2 =

• verplaatsing van de vierde naar de achtste verdieping:

∆xtot =

d Waarom is de verplaatsing van de lift tijdens het eerste deeltraject negatief?

©VANIN

e Welke afstand heeft de lift afgelegd over het volledige traject?

6 Bekijk het verkeersbord.

a Welke betekenis heeft het bord?

b Hoeveel m s is 100 km h ?

c Hoeveel km h is 100 m s ? x (m)

7 Voor een verplaatsing in een tijdsverloop is de gemiddelde snelheid gelijk aan v Hoe groot is de snelheid in de volgende situaties? Noteer in symbolen.

a Je legt dezelfde verplaatsing in het dubbel van de tijd af.

b Je legt in dezelfde tijd het dubbel van de verplaatsing af.

c Je legt in het dubbel van de tijd het dubbel van de verplaatsing af.

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen gebruiken als extra ondersteuning.

VRAAGSTUKKEN OPLOSSEN TIP

8 Bestudeer de onderstaande drie wereldrecords en bereken de gemiddelde snelheid (in km h en m s ).

1 100 m sprint bij de mannen: Usain Bolt, in 9,58 s

Gegeven:

Gevraagd:

Oplossing:

2 Werelduurrecord baanrennen: Victor Campenaerts, 55,089 km in 60 min

Gegeven: Gevraagd:

Oplossing:

3 Marathon (42,2 km) bij de vrouwen: Brigid Kosgei, in 2 uur 14 minuten 5 seconden

Gegeven:

Gevraagd:

Oplossing:

9 Bestudeer de vluchten van de verschillende vliegtuigen en bereken de afstand die de ze afleggen.

1 Een F-16 doet een oefenvlucht van 43 min en haalt een snelheid van 2 414 km h

Gegeven:

Gevraagd:

Oplossing:

©VANIN

2 Een Boeiing vliegt in 7 uur 50 minuten naar New York met een snelheid van 988 km h .

Gegeven:

Gevraagd:

Oplossing:

3 Een helikopter van de zeemacht vliegt tijdens een reddingsoperatie gedurende 25 min 15 s aan 260 km h .

Gegeven:

Gevraagd:

Oplossing:

10 Bestudeer de recordhouders uit de natuur.

Bereken de tijd die de dieren nodig hebben om 1,00 km af te leggen.

1 De slechtvalk is het snelste dier ter wereld, met een topsnelheid van 389 km h .

Gegeven:

Gevraagd:

Oplossing:

2 De marlijn kan in het water een topsnelheid bereiken van 129 km h .

Gegeven:

Gevraagd:

Oplossing:

3 Het wereldrecord bij de slakken is 2,75 mm s .

Gegeven:

Gevraagd:

Oplossing:

Vergelijk de tijden. Komen de verschillen overeen met je verwachtingen?

11 Een onweer bevindt zich op 5,3 km. Het geluid van de donder plant zich voort met een snelheid van 340  m s , het licht van de bliksem met een snelheid van ongeveer 3 ∙ 108 m s

a De lichtsnelheid wordt voor de eenvoud bij rekenwerk afgerond. Welke niet afgeronde snelheid geeft de lichtsnelheid correct weer? (meerdere mogelijkheden)

299 792 458  m s … 299 792  m s … 299 792  km s … 299  km s

b Bereken na welke tijd je de bliksem ziet en de donder hoort.

Gegeven:

Gevraagd:

Oplossing:

c Verklaar het trucje dat je kunt gebruiken om de afstand van een onweer tot jezelf te bepalen: ‘Deel de tijd tussen de bliksem en de donder in seconden door drie om de afstand van het onweer tot jou in kilometer te kennen.’

12 Op het moment dat je op je fietscomputer kijkt, heb je een snelheid van 22,1 km h

Als je thuiskomt, heb je 53,6 km afgelegd in 2 h en 33 min.

Maak de uitspraken correct door te schrappen wat niet past.

a De gemiddelde snelheid is precies / lager dan / hoger dan 22,1  km h

b De ogenblikkelijke snelheid is misschien / zeker tijdens een deel van het traject gelijk aan 22,1  km h

c De ogenblikkelijke snelheid is misschien / zeker tijdens een deel van het traject hoger dan 22,1  km h

d De ogenblikkelijke snelheid is misschien / zeker tijdens een deel van het traject lager dan 22,1  km h

13 Een slak heeft een topsnelheid van 1,8  mm s . Na 10 s aan die topsnelheid rust ze 2 s uit.

Vervolgens kruipt ze nog 15 s verder aan haar topsnelheid.

a Stel de baan voor op een positie-as (x-as).

b Bereken de verplaatsing, het tijdsverloop en de gemiddelde snelheid over het hele traject.

Gegeven:

c Vergelijk de gemiddelde snelheid met de topsnelheid. Verklaar het verschil.

14 Los het vraagstuk op. Een vrachtwagen rijdt een halfuur aan 100  km h op de autosnelweg. Door wegenwerken moet hij vertragen en rijdt hij een kwartier aan 50  km h

1 Welke gemiddelde snelheid verwacht je?

2 Bereken de gemiddelde snelheid.

Gegeven:

en

Gevraagd: v = ?

Oplossing:

Controle:

a Vergelijk je uitkomst met je verwachting. Was je juist?

b Waarom is de gemiddelde snelheid niet gelijk aan 75 km h ?

• Stel de gegevens schematisch voor op een x-as: Splits de beweging in deelbewegingen.

Noteer de gegevens in symbolen voor elke deelbeweging.

• Vertrek bij de oplossing vanuit de basisformule voor gemiddelde snelheid.

15 Bestudeer de foto’s van sporters. De skiër en de jetskiër bewegen ongeveer even snel. De parachutespringer is net vertrokken.

a Teken en benoem de snelheidsvector op elke foto.

b Noteer de richting en zin van elke vector.

OPLOSSINGSSTRATEGIE 1 2 3

• Bepaal de totale verplaatsing en het tijdsverloop via de deelbewegingen.

©VANIN

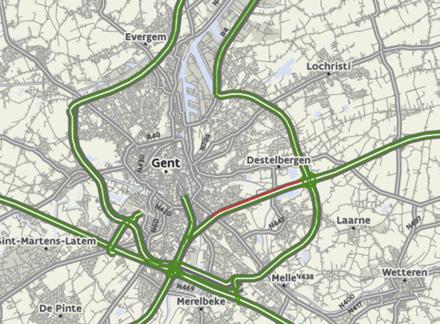
16 Bestudeer de filemelding op de afbeelding.

a Teken en benoem een snelheidsvector voor een auto die in de beschreven file staat.

b Duid de kenmerken van de vector aan.

• richting: E17 / naar Gent

• zin: E17 / naar Gent

c Welk begrip uit de fysica komt overeen met wat men in de spreektaal ‘richting’ noemt?

©VANIN

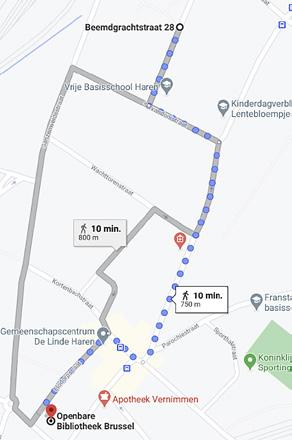
17 Aïsha vertrekt van thuis om een boek te halen in de bibliotheek. Haar weg is weergegeven op het plan. Ze wandelt aan een constante snelheid.

a Bereken Aïsha’s snelheid in m s en km h

b Teken de snelheidsvectoren op de vijf delen van de beweging.

• Benoem elke vector (v1 ... v5).

• Duid de juiste uitspraken aan. Verklaar.

v1 = v2 = v3 = v4 = v5 … v1 = 5,1 km h

v1 = v2 = v3 = v4 = v5 … v1 = 5,1 km h

18 Stel de omschreven bewegingen voor met snelheidsvectoren op drie opeenvolgende tijdstippen.

In een station staat trein A stil, vertrekt trein B naar rechts en rijdt trein C naar links het station binnen om tot stilstand te komen.

` Verder oefenen? Ga naar .

Trein A

Trein B

Trein C

1 Begripskennis

• Ik kan omschrijven wat richting en zin zijn.

• Ik kan de begrippen ‘beweging’ en ‘baan’ in mijn eigen woorden omschrijven

• Ik kan het verschil tussen ‘afgelegde weg’ en ‘verplaatsing’ omschrijven.

• Ik kan de afgelegde weg en de verplaatsing van een rechtlijnige beweging bepalen

• Ik kan de baan, de afgelegde weg en de verplaatsing van een rechtlijnige beweging voorstellen.

• Ik kan het begrip ‘snelheid’ in mijn eigen woorden omschrijven

• Ik kan het verschil tussen ‘gemiddelde snelheid’ en ‘ogenblikkelijke snelheid’ omschrijven

• Ik kan de gemiddelde snelheid van een rechtlijnige beweging bepalen

• Ik kan de ogenblikkelijke snelheid van een rechtlijnige beweging voorstellen als een vector.

2 Onderzoeksvaardigheden

• Ik kan eenheden omzetten

• Ik kan formules omvormen

• Ik kan afrondingsregels toepassen.

• Ik kan informatie in symbolen noteren

• Ik kan rekenvraagstukken gestructureerd oplossen.

` Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

Hoe stel je een rechtlijnige beweging voor op grafieken?

LEERDOELEN

Je kunt al:

M een beweging volgens en tegengesteld aan de positie-as (x-as) herkennen;

M de verplaatsing, het tijdsverloop en de snelheid berekenen.

Je leert nu:

M een beweging linken aan een x(t)-grafiek;

M de verplaatsing, het tijdsverloop en de snelheid aflezen op een x(t)-grafiek;

M een beweging linken aan een v(t)-grafiek;

M de snelheid aflezen op een v(t)-grafiek.

1.1 Positie en tijd afleiden uit waarnemingen

OPDRACHT 12

Bekijk de video van Rocky de hond.

1 Beschrijf de beweging van Rocky.

2 De hond is zichtbaar op 125 beelden. Hoe komt het dat je die foto’s niet apart ziet?

In het dagelijks leven registreer je bewegingen door naar je omgeving of naar videobeelden te kijken. Die waarnemingen kun je delen met woorden. Je kunt ze ook wetenschappelijk voorstellen met grafieken. In dit hoofdstuk zoeken we uit hoe je dat doet en hoe je de verplaatsing en de snelheid kunt aflezen op die grafieken.

3 De video toont dertig foto’s per seconde. Hoeveel tijd is er tussen twee posities?

VIDEO ROCKY

OPDRACHT 12 (VERVOLG)

4 De punten op de schermafdruk stellen het massapunt voor om de vier beelden. Hoe zie je op die schermafdruk het verloop van de beweging?

5 De totale verplaatsing van de hond is 0,80 m. Teken op de schermafdruk een positie-as (x -as) en de baan.

1.2 Positie weergeven op een x (t )-grafiek

OPDRACHT 13

Bestudeer de video. Let op de beweging van de rode auto, de ambulance en de politiewagen.

1 Bestudeer de onderstaande x (t )-grafieken.

a Welke grootheid staat op de horizontale as?

b Welke grootheid staat op de verticale as?

c Omschrijf wat een punt op de grafiek voorstelt.

Afb. 14

OPDRACHT 13 (VERVOLG)

2 Bij welke van de x (t )-grafieken horen de volgende omschrijvingen, als je weet dat de x -as naar rechts is gekozen?

• De rode auto vertrekt naar rechts.

• De politieauto staat stil om de voetgangers over te laten.

• De ambulance rijdt naar links.

3 Bekijk de animatie om je antwoord te controleren.

4 Duid op elke x (t )-grafiek de verplaatsing Δx en het tijdsverloop Δt aan na de volledige beweging.

©VANIN

x (t )-GRAFIEK KRUISPUNT

Een beweging is een verandering van positie in de tijd. Om de beweging te bestuderen, moet je de positie op elk tijdstip kennen. De baan geeft informatie over de positie, maar je kunt er de tijd niet op aflezen. De geschikte manier om aan te geven waar het voorwerp zich bevindt op elk moment, is een x (t )-grafiek waarop de positie van het massapunt voorgesteld wordt in functie van de tijd. Op de horizontale as van een x(t)-grafiek lees je de tijd (t) af, op de verticale as van een x(t)-grafiek lees je de positie (x) af. Met de x(t)-grafiek kun je:

• het verloop van de beweging beschrijven, • de verplaatsing en het tijdsverloop aflezen.

VOORBEELD x(t )-GRAFIEK ROCKY

Op afbeelding 14 op de vorige pagina zie je de baan van Rocky, maar daaruit kun je geen informatie afleiden over hoe Rocky tot dat punt gereden is en hoelang hij daar al stilstaat.

Op de x(t)-grafiek is de positie van Rocky weergegeven op elk tijdstip.

Via de QR-code zie je hoe de verschillende posities van Rocky overeenstemmen met de punten op de x(t)-grafiek.

x(t)-grafiek Rocky beweging naar rechts stilstand

VOORBEELD x(t )-GRAFIEK ROCKY (VERVOLG)

Met de x(t)-grafiek kun je het verloop van de beweging beschrijven.

Je kunt de beweging van Rocky opsplitsen in twee deelbewegingen:

• een beweging naar rechts (volgens de positie-as): de positie neemt toe, de x(t)-grafiek stijgt;

• stilstand: de positie verandert niet, de x(t)-grafiek is horizontaal.

Voor Rocky lees je de volgende informatie over de verplaatsing en het tijdsverloop af.

Beweging naar rechts Stilstand Totale beweging

= 0,86 m – 0,00 m = 0,86 m

= 2,15 s – 0,00 s = 2,15 s

©VANIN

= 0,86 m – 0,86 m = 0,00 m

2 = 3,85 s – 2,15 s = 1,70 s

= 0,86 m – 0,00 m = 0,86 m

= 3,85 s – 0,00 s = 3,85 s

Op een x (t)-grafiek is de positie op elk tijdstip weergegeven.

Je kunt rechtstreeks de kenmerken van de beweging afleiden:

• bewegingszin: stijgende x(t)-grafiek: beweging volgens de positie-as (x -as), dalende x(t)-grafiek: beweging tegengesteld aan de positie-as (x -as), horizontale x(t)-grafiek: geen beweging,

• verplaatsing: de afstand tussen twee punten op de verticale x-as,

• tijdsverloop: de afstand tussen twee punten op de horizontale t-as.

` Maak oefening 1 t/m 4 op p. 49 en 50.

2 Hoe lees je de snelheid af op een x (t )-grafiek?

2.1 Gemiddelde snelheid aflezen op een x (t )-grafiek

OPDRACHT 14

Bepaal voor de voertuigen uit opdracht 13 de gemiddelde snelheid.

1 Welke grootheden heb je nodig om de gemiddelde snelheid te bepalen?

©VANIN

2 Bepaal de gemiddelde snelheid van de drie voertuigen met de gegevens die je afleest uit de grafieken van opdracht 13.

• beweging rode auto: v 1, gem =

• beweging politiewagen: v2, gem =

• beweging ambulance: v3, gem =

Op een x(t)-grafiek kun je de verplaatsing en het tijdsverloop aflezen. Daarmee bereken je de gemiddelde snelheid voor elke (deel)beweging: v gem =

Je kunt ook rechtstreeks informatie over de gemiddelde snelheid aflezen op de x (t )-grafiek. Daarvoor verbind je het beginpunt en het eindpunt van de (deel)beweging met een lijnstuk

De helling van het getekende lijnstuk vertelt je iets over de gemiddelde snelheid van de (deel)beweging: hoe groter de verplaatsing in een tijdsverloop, hoe groter de helling.

Een beweging opsplitsen in deelbewegingen betekent dat je verschillende tijdsintervallen [tbegin, teind] met tijdsverloop ∆t bestudeert.

TIP

VOORBEELD GEMIDDELDE SNELHEID AFLEZEN OP x(t )-GRAFIEK ROCKY

Voor de beweging van Rocky vind je de onderstaande resultaten.

Beweging naar rechts Stilstand Totale beweging

Grafiek 2

• Voor de beweging volgens de positie-as (x-as) (naar rechts) is het groene lijnstuk stijgend. De snelheid is positief.

©VANIN

x(t)-grafiek Rocky beweging naar rechts stilstand totale beweging

• Voor de stilstand is het blauwe lijnstuk horizontaal. De snelheid is nul.

• Voor de totale beweging is het oranje lijnstuk stijgend. De snelheid is positief.

• Voor de totale beweging (oranje lijnstuk) is het lijnstuk minder steil dan voor de eerste deelbeweging (groene lijnstuk). De gemiddelde snelheid tijdens de totale beweging is lager dan de gemiddelde snelheid tijdens de eerste deelbeweging, omdat Rocky tijdens de tweede deelbeweging stilstaat.

2.2

Ogenblikkelijke snelheid aflezen op een x (t )-grafiek

OPDRACHT 15

Welke uitspraak is correct?

De ogenblikkelijke snelheid is altijd gelijk aan de gemiddelde snelheid van de hele beweging.

De ogenblikkelijke snelheid is altijd verschillend van de gemiddelde snelheid van de hele beweging.

De ogenblikkelijke snelheid is altijd de gemiddelde snelheid bij een kort tijdsverloop.

De ogenblikkelijke snelheid is altijd de gemiddelde snelheid bij een lang tijdsverloop.

Om de ogenblikkelijke snelheid af te lezen uit een x(t)-grafiek, bepaal je de gemiddelde snelheid voor een kort deel van de beweging. Je kiest een zo klein mogelijk tijdsverloop

Bij het onlinemateriaal vind je als voorbeeld hoe je de ogenblikkelijke snelheid op de x(t)-grafiek van Rocky kunt aflezen. Bekijk het extra materiaal over ogenblikkelijke snelheid bij het onlinelesmateriaal.

Op de x(t)-grafiek lees je de gemiddelde snelheid af als de helling van het lijnstuk tussen het begin- en eindpunt van de (deel)beweging.

• teken van de snelheid

Bij een stijgend lijnstuk is de snelheid positief (beweging volgens de x-as).

Bij een dalend lijnstuk is de snelheid negatief (beweging tegengesteld aan de x-as).

Bij een horizontaal lijnstuk of een overgang tussen een dalend en een stijgend lijnstuk is de snelheid nul (geen beweging).

• snelheidsgrootte

Hoe steiler het lijnstuk, hoe groter de snelheid.

Een verandering in de helling van een lijnstuk wijst op een versnelling/vertraging.

Op de x(t)-grafiek lees je de ogenblikkelijke snelheid af als de helling van de grafiek bij een lijnstuk tussen twee opeenvolgende tijdstippen.

` Maak oefening 5 t/m 8 op p. 50 en 52.

©VANIN

3 Hoe stel je een beweging voor op een v (t )-grafiek?

OPDRACHT 16

Bestudeer de video. Let op de snelheid van de rode auto, de ambulance en de politiewagen.

1 Bestudeer de onderstaande v (t )-grafieken.

a Welke grootheid staat op de horizontale as?

b Welke grootheid staat op de verticale as?

c Omschrijf wat een punt op de grafiek voorstelt.

©VANIN

2 Bij welke van de v (t )-grafieken horen de volgende omschrijvingen? De positie-as (x -as) is naar rechts gekozen.

• De rode auto vertrekt naar rechts.

• De politieauto staat stil om de voetgangers over te laten.

• De ambulance rijdt naar links.

3 Bekijk de animatie om je antwoord te controleren.

4 Duid op elke v (t )-grafiek de snelheidsverandering Δv en het tijdsverloop Δt aan na de volledige beweging.

v (t )-GRAFIEK KRUISPUNT

Op een x(t)-grafiek kun je informatie aflezen over de verplaatsing, de snelheid en het vertragen of versnellen. Om de ogenblikkelijke snelheid en de snelheidsverandering af te lezen, stel je de beweging voor op een v (t )-grafiek. Op de verticale as staat de ogenblikkelijke snelheid v van het voorwerp voor elk tijdstip t

De ogenblikkelijke snelheid bereken je voor elk tijdstip door de gemiddelde snelheid voor het tijdsverloop dat net voorbij is, te berekenen als: v = ∆x

t

Je kunt de snelheid voorstellen op een v (t )-grafiek door de ogenblikkelijke snelheid op elk tijdstip aan te duiden met een punt.

Op de horizontale as van een v(t)-grafiek lees je de tijd t af, op de verticale as van een v(t)-grafiek lees je de ogenblikkelijke snelheid v

Met de v(t)-grafiek kun je:

• het verloop van de beweging beschrijven,

• de snelheidsverandering en het tijdsverloop aflezen.

VOORBEELD v(t )-GRAFIEK VAN ROCKY

Op grafiek 4 is de v(t)-grafiek van Rocky weergegeven

v(t)-grafiek Rocky

©VANIN

4

Op de v(t)-grafiek kun je informatie over de snelheid van beide deelbewegingen aflezen:

• beweging naar rechts (groen):

De snelheid is positief. De grafiek ligt boven de t-as.

De snelheidsgrootte neemt af. De grafiek daalt naar nul.

• stilstand (blauw):

De snelheid is nul. De grafiek ligt op de t-as.

De snelheidsgrootte is constant. De grafiek is horizontaal.

Op de v(t)-grafiek kun je informatie aflezen over de snelheid van een rechtlijnige beweging.

• Ligt de grafiek boven de tijdsas, dan is de snelheid positief (beweging volgens de positie-as (x-as)).

• Ligt de grafiek onder de tijdsas, dan is de snelheid negatief (beweging tegengesteld aan de positie-as (x-as)).

Grafiek

v (t )-GRAFIEK ROCKY

Verandert de positie van het voorwerp?

Hoe ziet de x (t)-grafiek eruit? Hoe ziet de v (t)-grafiek eruit?

JA

Beweegt het voorwerp volgens de x-as?

Het voorwerp is .

Voorbeeld: Een auto staat stil.

©VANIN

NEE

JA

De verplaatsing van het voorwerp is positief/ negatief.

Voorbeeld: Een hond vertraagt naar , met de as naar rechts gekozen.

De x (t)-grafiek is stijgend/dalend/horizontaal

De v (t)-grafiek is stijgend/dalend/horizontaal

Hoe ziet de x (t)-grafiek eruit? Hoe ziet de v (t)-grafiek eruit?

De verplaatsing van het voorwerp is positief/ negatief.

Voorbeeld: Een ambulance rijdt naar , met de as naar rechts gekozen.

De x (t)-grafiek is stijgend/dalend/horizontaal Hoe groter de ogenblikkelijke snelheid, hoe de grafiek.

De v (t)-grafiek is

• bij een constante ogenblikkelijke snelheid,

• bij een versnelling,

• bij een vertraging.

Hoe groter de ogenblikkelijke snelheid, hoe de grafiek.

Hoe ziet de x (t)-grafiek eruit? Hoe ziet de v (t)-grafiek eruit?

De x (t)-grafiek is stijgend/dalend/horizontaal Hoe groter de ogenblikkelijke snelheid, hoe de grafiek.

De v (t)-grafiek is stijgend/dalend/horizontaal

1 Bestudeer de onderstaande x(t)-grafieken van een auto.

a Welke grafieken zijn niet mogelijk? Verklaar.

b Kleur op de mogelijke x(t)-grafieken deze delen van de grafiek:

• in het groen: De auto rijdt vooruit.

• in het blauw: De auto rijdt achteruit.

• in het rood: De auto staat stil.

2 Soms gebruik je x(m) en soms x(t). Wat is de betekenis van beide?

a x(m):

b x(t):

3 Vier vrienden gaan lopen. Hun beweging is weergegeven op de grafiek.

a Rangschik hun afgelegde weg van kort naar lang.

b Rangschik hun loopduur van kort naar lang.

Katrien vertrekt vanaf de zetel en wandelt naar de tafel. Daar staat ze eventjes stil om haar smartphone te pakken. Ze loopt vervolgens naar het aanrecht en staat daar stil om een glas water te nemen. Ze slentert terug naar de zetel, waar ze blijft. De zetel, de tafel en het aanrecht staan op een rechte lijn, zoals weergegeven op de positie-as (

eken de baan op de positie-as ( oot is de afgelegde weg? oot is de verplaatsing?

©VANIN

x )-grafiek komt overeen met haar beweging?

5 Noa en Suze vertrekken gelijktijdig.

a Wie heeft de grootste gemiddelde snelheid?

b Wie heeft de grootste ogenblikkelijke snelheid?

c Wie heeft de kleinste ogenblikkelijke snelheid?

6 Fatima gaat fietsen. Bestudeer de x(t)-grafieken van verschillende delen van haar fietstocht.

©VANIN

a Welke grafiek past bij de omschrijving?

• Fatima vertrekt:

• Fatima neemt een pauze:

• Fatima is op de terugweg:

• Fatima gaat voluit tijdens een afdaling:

• De vermoeidheid slaat toe, dus Fatima vertraagt:

b Bereken (zonder rekentoestel) de gemiddelde snelheid. Noteer die onder elke grafiek.

7 Wat stellen de punten op een v(t)-grafiek voor?

de positie van het massapunt

de gemiddelde snelheid van de beweging

de gemiddelde snelheid van een afgelopen klein tijdsverloop

de gemiddelde snelheid van een toekomstig klein tijdsverloop

geen van de bovenstaande antwoorden

8 Je laat een bal los bovenaan een helling.

a Beschrijf de beweging van de bal.

b Welke x(t)-grafiek hoort bij de beweging van de bal?

c Welke v(t)-grafiek hoort bij de beweging van de bal?

` Verder oefenen? Ga naar .

©VANIN

1 Begripskennis

• Ik kan een eenvoudige beweging voorstellen op een x(t)-grafiek.

• Ik kan een eenvoudige beweging die voorgesteld is op een x(t)-grafiek, in woorden omschrijven

• Ik kan het tijdsverloop en de verplaatsing aflezen op een x(t)-grafiek.

• Ik kan de gemiddelde snelheid afleiden uit een x(t)-grafiek.

• Ik kan de ogenblikkelijke snelheid afleiden uit een x(t)-grafiek.

• Ik kan een eenvoudige beweging voorstellen op een v(t)-grafiek.

• Ik kan een eenvoudige beweging die voorgesteld is op een v(t)-grafiek, in woorden omschrijven

• Ik kan het tijdsverloop aflezen op een v(t)-grafiek.

2 Onderzoeksvaardigheden

• Ik kan waarnemingen en beschrijvingen verbinden met de wetenschappelijke voorstelling in grafieken.

• Ik kan grafieken nauwkeurig tekenen

• Ik kan grafieken nauwkeurig aflezen.

• Ik kan berekeningen uitvoeren met afgelezen waarden.

` Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

Welke eigenschappen heeft een rechtlijnige beweging met een constante snelheid?

LEERDOELEN

Je kunt al:

M de snelheid berekenen en voorstellen;

M een beweging voorstellen op een x(t)- en een v(t)-grafiek.

Je leert nu:

M de eigenschappen van een eenparig rechtlijnige beweging (ERB) opsommen;

M een ERB grafisch voorstellen aan de hand van een x(t)- en een v(t)-grafiek;

M grafische voorstellingen van een ERB interpreteren;

M voor een ERB de positie, de tijd en de snelheid berekenen.

In het dagelijks leven ben je constant in beweging. Meestal beweeg je je op gekronkelde banen met hoogteverschillen en met snelheden die voortdurend veranderen.

In dit hoofdstuk zoom je in op rechtlijnige bewegingen waarvan de snelheid niet verandert. Je gaat op zoek naar een wetenschappelijke manier om die te beschrijven door de positie, het tijdstip en de snelheid te berekenen en voor te stellen.

1 Wat betekent bewegen aan een constante snelheid?

OPDRACHT 17

Bekijk de dronebeelden van een verkeerskruispunt.

Op de rechte autobaan rijdt een rode auto aan een constante snelheid v = 60 km h .

Op de U-vormige brug rijdt een rode auto aan v’ = 40 km h .

1 Volg op de brug en op de rechte weg de twee rode auto’s die met een cirkel zijn aangeduid.

2 Op de onderstaande afbeeldingen zijn met stippen verschillende posities van de twee rode auto’s aangeduid. Teken en benoem de snelheidsvectoren voor de auto’s op die posities.

3 Bekijk de snelheidsvectoren gedurende de hele opname.

4 Duid voor elk kenmerk van de snelheid aan of het al dan niet constant is tijdens de beweging.

VECTOREN U-BOCHT

Kenmerk Auto op de rechte baan Auto op de U-vormige brug aangrijpingspunt constant / niet constant constant / niet constant bewegingsrichting constant / niet constant constant / niet constant bewegingszin constant / niet constant constant / niet constant snelheidsgrootte constant / niet constant constant / niet constant snelheidsvector v constant / niet constant constant / niet constant

zin grootte richting aangrijpingspunt v

Snelheid is een vectoriële grootheid. Ze bestaat dus niet enkel uit een getalwaarde (de grootte), maar ook uit een richting, een zin en een aangrijpingspunt. Als iemand vraagt ‘Is de snelheid constant?’, dan moet je elke vectoreigenschap bestuderen, en niet enkel de grootte.

We spreken dus van een constante snelheid, als de volgende vier kenmerken constant blijven:

• het aangrijpingspunt,

• de richting,

• de zin,

• de grootte

We noemen dat een eenparig rechtlijnige beweging (ERB).

• eenparig: De snelheid is constant en verschillend van nul.

• rechtlijnige beweging: De beweging verloopt volgens één richting.

Bij een rechtlijnige beweging in één zin is de snelheid(svector) constant zodra de snelheidsgrootte constant is.

VOORBEELD ERB OP DE AUTOSNELWEG

Emma rijdt met de auto tussen de oprit van Sint-Denijs-Westrem (Gent) en de afrit in Aalter aan een constante snelheid.

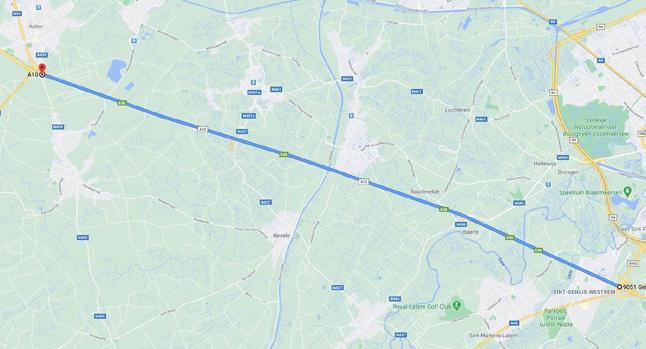
9,00 min 17,4 km v

De snelheidsvector v is getekend op drie momenten en is constant gedurende het volledige traject:

• het aangrijpingspunt: het massapunt,

• de richting: A10 (E40),

• de zin: naar Aalter,

• de grootte v: ingesteld op cruisecontrol.

©VANIN

OPDRACHT 18

Bekijk de gegevens op de kaart van afbeelding 18.

Op welke snelheid (in km h ) is de cruisecontrol ingesteld?

Gegeven: ∆x = ; ∆t =

Gevraagd: v = ?

Oplossing: v =

Controle:

a Is dat een logische waarde? Verklaar.

b Waarom kun je de ogenblikkelijke snelheid (van de cruisecontrol) berekenen als de gemiddelde snelheid over het traject?

De gemiddelde snelheid van een voorwerp dat een ERB uitvoert, is gelijk aan de ogenblikkelijke snelheid van dat voorwerp op elk moment van de beweging. Daarom spreek je bij een ERB kortweg over de snelheid.

In de fysica wordt de werkelijkheid voorgesteld door modellen. Dat zijn ideale voorstellingen waarin bepaalde elementen benaderd worden weergegeven. Een ERB is een voorbeeld van een model.

• Constante snelheid

Vertrekken en aankomen worden verwaarloosd.

We nemen aan dat het voorwerp onmiddellijk de constante snelheid bereikt.

Menselijke bewegingen hebben bijna nooit een perfect constante snelheid.

Voorbeeld: Wanneer je tijdens een fietstocht een stuk aan een constante snelheid fietst, zal de snelheid op je snelheidsmeter of smartphone toch een beetje veranderen.

Bij elektrisch aangestuurde bewegingen kan de snelheid wel perfect constant zijn.

Voorbeelden: cruisecontrol in een auto of een trein, de ingestelde snelheid van skiliften of roltrappen

• Rechtlijnig

Een verkeersweg is zelden een perfecte rechte over een lange afstand. Als de baan benaderd wordt door een rechte, noem je ze rechtlijnig.

Een beweging heeft een constante snelheid als de snelheidsvector v constant is.

Een rechtlijnige beweging met een constante snelheid (verschillend van nul) noem je een eenparig rechtlijnige beweging (ERB):

• eenparig: De snelheid is constant.

• rechtlijnige beweging: De beweging verloopt volgens één richting.

Bij een ERB is de gemiddelde snelheid gelijk aan de ogenblikkelijke snelheid.

` Maak oefening 1 op p. 68.

2 Welke grafieken horen bij een ERB?

OPDRACHT 19 ONDERZOEK

Onderzoek het verloop van een eenparig rechtlijnige beweging aan de hand van het labo bij het onlinelesmateriaal.

De snelheid wijkt een klein beetje af van de ingestelde snelheid. Dat is te wijten aan de afleesnauwkeurigheid op de grafiek.

Je kunt een ERB voorstellen op bewegingsgrafieken:

• x (t )-grafiek: de positie x (op de verticale as) verandert volgens een schuine rechte in functie van de tijd t (op de horizontale as). Hoe steiler de rechte, hoe groter de snelheid.

• v (t )-grafiek: de snelheid v (op de verticale as) verandert niet in functie van de tijd t (op de horizontale as). De grafiek is een horizontale rechte Hoe hoger de rechte, hoe groter de snelheid.

VOORBEELD BEWEGINGSGRAFIEKEN VAN ERB OP AUTOSNELWEG

We bekijken opnieuw de rit tussen Sint-Denijs-Westrem en Aalter. Je kunt de beweging van Emma tijdens haar traject op de autosnelweg voorstellen op grafieken.

De x(t)-grafiek is een stijgende rechte door de oorsprong.

De v(t)-grafiek is een horizontale rechte.

v (km) h v(t)-grafiek met xbegin= 0

5

Grafiek 6

• De x (t)-grafiek is een stijgende rechte door de oorsprong.

We kiezen de oorsprong aan de oprit: xbegin = 0 km.

We starten de tijd aan de oprit: tbegin = 0 min.

We bepalen de positie om de drie minuten (∆t = 3 min = 0,05 h, de schaalverdeling op de grafiek is 0,80 minuut.).

We verbinden de opgemeten punten met een rechte.

Op de x (t)-grafiek kun je de volgende informatie aflezen:

De beweging verloopt volgens de positie-as: een stijgende rechte.

De verplaatsing ∆x na een willekeurig tijdsverloop

Voorbeeld: Bij ∆t = 4,20 min (= 0,0700 h) is ∆x = 8,0 km.

Het tijdsverloop ∆t om een willekeurige verplaatsing af te leggen

Voorbeeld: Bij ∆x = 15,0 km is ∆t = 7,80 min (= 0,130 h).

De snelheid is de helling van de rechte.

©VANIN

Merk op dat de verticale as niet start bij v = 0 km h . In functie van de leesbaarheid van de grafiek kozen we er in dit voorbeeld voor om de as pas te laten starten bij v = 105 km h . We duiden dat aan met twee schuine streepjes. 0 105 110 115 120

t (min) 0,003,006,009,00 v (km) h v(t)-grafiek met xbegin= 0

Voorbeeld: v = ∆x ∆t = 15,0 km 0,130 h = 115 km h

• De v (t)-grafiek is een horizontale rechte.

De ogenblikkelijke snelheid is constant en gelijk aan de gemiddelde snelheid.

Op de v (t)-grafiek kun je de volgende waarden aflezen:

vgemiddeld = vogenblik = ∆x ∆t = 116 km h

Grafiek

OPDRACHT 20

Bestudeer de bewegingsgrafieken van vier voertuigen die voorbij rijden (voor een positie-as die naar rechts gekozen is).

① een auto rijdt naar links met een snelheid van –8 m s ,

② een auto rijdt naar rechts met een snelheid van 10 m s ,

③ een bus rijdt iets later naar rechts met een snelheid van 9 m s en

④ een auto rijdt als laatste voorbij naar rechts met een snelheid van 13 m s

1 Bestudeer de bewegingsgrafieken waarin de beweging van de vier voertuigen weergegeven is.

(t)-grafiek

©VANIN

2 Plaats de nummers van de auto’s bij de juiste rechte op de x (t )-grafiek en v (t )-grafiek.

3 Controleer je antwoord met de video van de x (t )-grafiek en de v (t )-grafiek.

(t )-GRAFIEK

v (t )-GRAFIEK

Bij een ERB is de x (t )-grafiek altijd een rechte met als helling de snelheid De exacte ligging van de rechte is gekoppeld aan de keuzes die je bij de voorstelling van de beweging maakt.

• De rechte snijdt de verticale x-as in de beginpositie x begin

• De rechte snijdt de horizontale t-as in de begintijd t begin (die je kiest als nul als er maar één voorwerp beweegt)

De v (t)-grafiek is een horizontale rechte die door de snelheidswaarde gaat. De beginpositie x begin en de begintijd t begin hebben geen invloed op de v (t)-grafiek.

Grafiek 7

Grafiek 8

VOORBEELD INVLOED VAN DE OORSPRONG OP BEWEGINGSGRAFIEKEN

Tijdens een autorit kun je de beginpositie kiezen. De oprit van een autosnelweg is een logische keuze voor de beweging die je beschrijft, maar het is een vage beschrijving in het algemeen. Om precies te omschrijven waar je je bevindt op een autosnelweg (bijvoorbeeld bij een ongeluk, panne of file), zijn kilometerpalen aangebracht.

De oprit van Sint-Denijs-Westrem bevindt zich bij kilometerpaal 48,3 km. Je kunt de autorit voorstellen op een x (t)-grafiek ten opzichte van de kilometerpalen.

(km)

x(t)-grafiek met xbegin= 48,3 km

©VANIN

• De vorm van de grafiek is hetzelfde: een stijgende rechte met als helling de snelheid.

• De grafiek is verticaal verschoven van de oorsprong naar de nieuwe beginpositie xbegin = 48,3 km.

• Je kunt aflezen dat de afrit zich ongeveer bij kilometerpaal 65,0 km bevindt.

De nieuwe beginpositie heeft geen invloed op de v (t)-grafiek.

Het verloop van een ERB kun je weergeven in bewegingsgrafieken:

• De x (t )-grafiek is een schuine rechte.

• De v (t )-grafiek is een horizontale rechte.

De snelheidsgrootte, de bewegingszin, de beginpositie xbegin en de begintijd tbegin bepalen de grafiek.

` Maak oefening 2, 3 en 4 op p. 68 en 69.

Grafiek 9

Afb. 22

3 Hoe kun je de positie, de tijd en de snelheid bij een ERB berekenen?

3.1 Positie op elk moment

OPDRACHT 21

Bepaal de positie bij een ERB op elk moment.

Op het moment dat Emma (rode auto) de autosnelweg oprijdt aan een constante snelheid v = 116 km h , bevindt er zich een gele taxi 2,0 km voor haar. De taxi rijdt ook aan een constante snelheid. Ze rijden allebei voorbij de afrit in Aalter.

1 Bepaal de positie van de rode auto na een willekeurig tijdsverloop.

a Vul de posities in de tabel verder aan.

b Noteer je werkwijze voor ∆t = 0,50 h

xauto =

c Vervolledig de uitdrukking om de positie na een willekeurig tijdsverloop Δt te berekenen.

xauto =

2 Bepaal de positie van de taxi na een willekeurig tijdsverloop.

a Bereken de snelheid van de taxi.

vtaxi =

b Vul de posities in de tabel verder aan.

c Noteer je werkwijze voor ∆t = 0,50 h

xtaxi =

d Vervolledig de uitdrukking om de positie op een willekeurig moment te berekenen.

xtaxi =

Bij een ERB is de ogenblikkelijke snelheid gelijk aan de gemiddelde snelheid. Vanuit de basisformule voor de gemiddelde snelheid kun je de positie na een willekeurig tijdsverloop berekenen:

(1)

De verplaatsing tussen een willekeurige positie x eind en de beginpositie x begin is gegeven door:

x = xeind – xbegin (2)

Als je uitdrukking (1) en (2) combineert, wordt dat:

©VANIN

VOORBEELD POSITIES BEPALEN VAN TAXI EN AUTO

Positie ten opzichte van de oprit (xbegin = 0,0 km) v

Positie ten opzichte van de kilometerpaal (xbegin = 48,3 km)

Uitdrukking om de positie na tijdsverloop Δt te berekenen

Bij een ERB met snelheid v en beginpositie xbegin bereken je de positie x na een tijdsverloop ∆t als:

x eind = x begin + v · ∆t

(Dit is geen nieuwe formule, maar een omvorming van de definitie van snelheid.)

` Maak oefening 5, 6 en 7 op p. 70 en 71.

3.2 Inhalen

OPDRACHT

22 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

Op het moment dat Emma (rode auto) de autosnelweg oprijdt aan een constante snelheid van 116 km h , bevindt er zich een gele taxi 2,0 km voor haar. De taxi heeft een constante snelheid van 90  km h .

Wanneer en waar haalt de auto de taxi in?

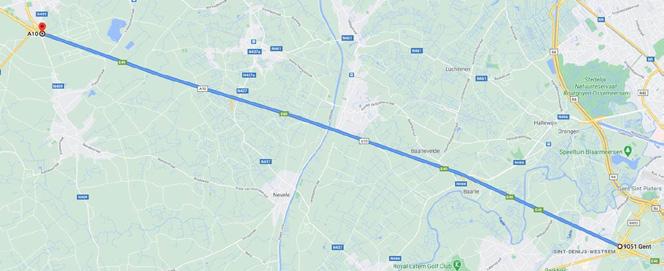
Afb. 24

OPLOSSINGSSTRATEGIE

• Formuleer in je eigen woorden wat ‘inhalen’ betekent.

• Noteer de gegevens en het gevraagde in symbolen.

• Ga op zoek naar de uitdrukking voor de positie van beide voertuigen.

Gegeven: • auto: vauto = 116 km h en xbegin, auto = 0,0 km

• taxi: vtaxi = 90 km h en xbegin, taxi = 2,0 km

Gevraagd: t en x bij inhalen = ?

Oplossing: Uitdrukking voor de positie van de auto:

Uitdrukking voor de positie van de taxi: x

‘Inhalen’ betekent dat de auto en de taxi op hetzelfde moment op dezelfde positie zijn.

= 2,0 km + 90  km

– 90  km h

t = 2,0 km 26  km h ∆t = 2,0 km

∆t =  2,0 km 26 km h = 0,077 h = 4,60 min = 4 min 36 s

• Schrijf de betekenis van ‘inhalen’ wiskundig op.

• Los de vergelijking op om de tijd te vinden.

©VANIN

• Bereken de positie van beide voertuigen op de gevonden tijd.

• Controleer of aan de voorwaarde voor inhalen voldaan is.

Dit is een eerstegraadsvergelijking met als onbekende t: a t = b t + c

De positie vind je door het tijdsverloop ∆t in te vullen in een van beide uitdrukkingen voor de positie: xauto = 116  km h ∆t = 116  km h · 0,077 h = 8,9 km

Controle: Bevindt de taxi zich op dezelfde positie? xtaxi = 2,0 km + 90  km h · ∆t = 2,0 km + 90  km h · 0,077 h = 8,9 km

De afgelezen waarden verschillen een klein beetje van de berekende waarden.

Dat is te wijten aan de afleesnauwkeurigheid op de grafiek. Berekende waarden zijn de meest correcte waarden.

Als twee voorwerpen in dezelfde richting en zin bewegen, kan een snel voorwerp een trager voorwerp dat al voorop is, inhalen. Op het moment van inhalen bevinden het trage en het snelle voorwerp zich op hetzelfde moment op dezelfde plaats:

xsnel = x traag

Door de gegevens in te vullen en een vergelijking op te lossen, vind je de tijd en de positie waarbij de voorwerpen elkaar inhalen.

Je kunt de positie en de tijd ook aflezen op een x (t )-grafiek waarop je de beweging van beide voorwerpen tegelijk voorstelt.

VOORBEELD x(t)-GRAFIEKEN BIJ INHALEN

(km) x(t)-grafiek auto en taxi

©VANIN

Grafiek 11

De auto haalt de taxi in op het snijpunt van beide grafieken.

Dat is na het tijdsverloop ∆t = 0,08 h op de positie x = 9,0 km.

• De auto rijdt sneller dan de taxi (steilere grafiek).

• De auto haalt de taxi in op het snijpunt van beide grafieken.

Dat is bij t = 0,08 h en x = 9,0 km.

Een snel bewegend voorwerp haalt een trager bewegend voorwerp in op een tijdstip t waarop de positie van beide voorwerpen gelijk is (xsnel = xtraag).

` Maak oefening 8 en 9 op p. 72.

TIP

3.3 Kruisen

OPDRACHT 23

Los het vraagstuk op.

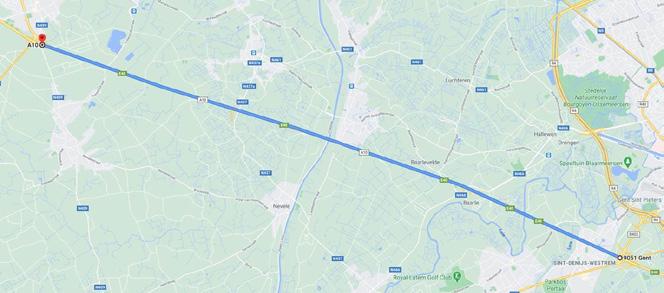
In de richting van Gent rijdt een bus aan een snelheid van 100  km h . De bus bevindt zich ter hoogte van de afrit in Aalter als Emma in Sint-Denijs-Westrem de autosnelweg oprijdt aan een snelheid van 116  km h

Waar en wanneer kruisen ze elkaar?

Tekening:

Teken de vectoren op de kaart (afbeelding 26) en op de voertuigen (afbeelding 27). 9,00 min 17,4 km

(km)

VRAAGSTUKKEN OPLOSSEN

©VANIN

Gegeven:

• auto:

• bus:

Opgelet: de bus beweegt tegengesteld aan de positie-as (x-as).

Gevraagd:

Oplossing:

a Noteer de uitdrukking voor de positie van:

• de auto:

• de bus:

b Leg in je eigen woorden uit wat ‘kruisen’ betekent.

Denk goed na over het teken van de snelheden.

Afb. 26

Afb. 27

TIP

OPDRACHT 23 (VERVOLG)

c Schrijf de betekenis van ‘kruisen’ wiskundig op en werk verder uit om het tijdverloop te bepalen.

©VANIN

d Bepaal de positie door het tijdsverloop Δt in te vullen in een van beide uitdrukkingen voor de positie.

Controle: Bevindt de bus zich op dezelfde positie?

Als twee voorwerpen in dezelfde richting, maar in tegengestelde zin bewegen, zullen ze elkaar op een bepaald tijdstip kruisen. Op het moment van kruisen bevinden beide voorwerpen zich op hetzelfde moment op dezelfde plaats: x voorwerp 1 = xvoorwerp 2 Door de gegevens in te vullen en een vergelijking op te lossen, vind je de tijd en de positie waarbij de voorwerpen elkaar kruisen. Je kunt de positie en de tijd ook aflezen op een x (t )-grafiek waarop je de beweging van beide voorwerpen tegelijk voorstelt.

VOORBEELD x(t)-GRAFIEKEN BIJ KRUISEN

x (km)

Je ziet de x (t)-grafiek voor de rode auto en de bus. De auto kruist de bus op het snijpunt van beide grafieken. Dat is bij t = 0,08 h en x = 9,0 km.

x(t)-grafiek auto en bus

kruisen

Grafiek 12

Twee voorwerpen die in dezelfde richting, maar in tegengestelde zin bewegen, kruisen elkaar wanneer ze zich op een tijdstip t op dezelfde positie bevinden (x voorwerp 1 = xvoorwerp 2).

` Maak oefening 10 en 11 op p. 73 en 74.

BEGRIPPEN

Een beweging heeft een constante snelheid als constant is.

Een rechtlijnige beweging met een constante snelheid (verschillend van nul) noem je een :

• eenparig:

• rechtlijnige beweging:

Voor een ERB is de snelheid gelijk aan de snelheid.

GRAFIEKEN VAN EEN ERB

Grafiek

x ( t )-grafiek

v ( t )-grafiek

Verloop

x De x (t)-grafiek is een rechte.

• De rechte snijdt de x -as in de beginpositie / begintijd / beginsnelheid

• De rechte snijdt de t -as in de beginpositie / begintijd / beginsnelheid.

• De rechte is stijgend als de beweging volgens / tegengesteld aan de positie-as (x-as) verloopt.

• De rechte is dalend als de beweging volgens / tegengesteld aan de positie-as (x-as) verloopt.

v De v (t)-grafiek is een rechte.

• De rechte snijdt de v -as in de beginpositie / begintijd / beginsnelheid.

• De snelheid vergroot / blijft constant / verkleint gedurende het traject.

• De rechte ligt boven de t -as als de beweging volgens / tegengesteld aan de x-as verloopt

• De rechte ligt onder de t -as als de beweging volgens / tegengesteld aan de x-as verloopt.

BEREKENEN

Bij een ERB met snelheid v en beginpositie xbegin bereken je de positie x na een tijdsverloop ∆t als:

©VANIN

1 Duid aan of de bewering juist of fout is. Is de bewering fout, geef dan een tegenvoorbeeld.

a Als de beweging rechtlijnig is, is de snelheidsvector constant.

juist … fout

Tegenvoorbeeld:

b Als de grootte van de snelheid constant is, dan heeft de beweging een constante snelheidsvector.

juist … fout

Tegenvoorbeeld:

©VANIN

c Als de snelheidsvector constant is, dan is de beweging rechtlijnig.

juist … fout

Tegenvoorbeeld:

d Als de snelheidsvector constant is, dan heeft de beweging een constante snelheidsgrootte.

juist … fout

Tegenvoorbeeld:

2 Bestudeer de onderstaande bewegingsgrafieken.

a Omcirkel de letters van de grafieken die een ERB voorstellen.

b De onderstaande beschrijvingen horen bij de grafieken.

Noteer (indien mogelijk) de bijbehorende grafieken in de tabel.

Omschrijving x (t )-grafiek v (t )-grafiek

Finn zit op een bankje te wachten.

Chloé fietst aan een constante snelheid naar school.

Mo keert terug om zijn boekentas op te pikken.

3

Vul aan met ‘soms’, ‘altijd’ of ‘nooit’.

• De x(t)-grafiek van een ERB is een schuine rechte.

• De x(t)-grafiek van een ERB gaat door de oorsprong.

• De v(t)-grafiek van een ERB is een schuine rechte.

4

Vier personen steken een weg van 12 m over: een zakenman, een jogger die loopt, een kind dat snel wandelt en een vrouw die traag wandelt.

Op de v(t)-grafiek is het verloop van hun snelheid tijdens het oversteken weergegeven.

a Vul de legende bij de v(t)-grafiek aan met de personen.

b Teken op de afbeelding hierboven de positie-as (x-as) die overeenstemt met de v(t)-grafiek.

c Zijn de volgende uitspraken juist of fout?

• De afgelegde weg is voor iedereen hetzelfde.

• De verplaatsing is voor iedereen hetzelfde.

• Het tijdsverloop is voor iedereen hetzelfde.

d Teken de bijbehorende x(t)-grafieken.

5 Lees het onderstaande krantenartikel.

STEEKPROEF BEWIJST GEVAAR VAN GSM ACHTER HET STUUR

In ons land sterven per jaar minstens dertig mensen in ongevallen veroorzaakt door iemand die aan het gsm’en was achter het stuur. En dat is nog een voorzichtige schatting. Agenten schrijven constant boetes uit, maar toch blijven duizenden bestuurders het dagelijks doen.

Bron: www.hln.be

Gegeven:

Gevraagd:

Oplossing:

Bereken welke afstand je ‘blind’ aflegt, als je op de snelweg aan een snelheid van 120  km h rijdt en gedurende 2,0 s een berichtje stuurt.

©VANIN

Controle:

6 Bestudeer de x(t)-grafiek van de Thalys naar Parijs met een tussenstop in Brussel-Zuid.

x (km) x(t)-grafiek Thalys

08:3008:5009:1009:3009:50 10:10 10:3010:5011:10 t (h)

a Van Antwerpen-Centraal tot Brussel-Zuid voert de Thalys een ERB uit. Wat zijn de tijdsduur en de afstand tijdens dat traject?

b Welke snelheid heeft de trein in het tijdsinterval [8:30, 9:10]?

Gegeven:

Gevraagd:

Oplossing:

©VANIN

Controle:

c Wat gebeurt er tussen 9:10 en 9:20?

d Bereken de afstand tussen Brussel-Zuid en Parijs.

e Toont de gegeven x(t)-grafiek een realistische voorstelling van de beweging van een trein?

7 Vleermuizen gebruiken echolocatie om hun weg te vinden en eten te verzamelen in het donker.

Ze zenden met hun neus of mond geluidsgolven uit. Die geluidsgolven botsen tegen objecten en weerkaatsen terug naar de oren van de vleermuis.

De snelheid van het geluid bedraagt 340 m s

a Voert het geluid een ERB uit? Verklaar.

b Bereken hoe ver de prooi van de vleermuis verwijderd is, als je weet dat de vleermuis na 6 · 10–4 s het weerkaatste geluid weer opvangt met zijn oren.

Gegeven:

Gevraagd:

Oplossing:

Controle:

8 Mil en Josefien trainen voor de aankomende Run & Bike-wedstrijd. Mil vertrekt om 9:37 en loopt langs de vaart aan een constante snelheid van 12 km h . Josefien vertrekt 10 min later op dezelfde plek met de fiets aan een constante snelheid van 18 km h

a Teken beide bewegingen op de onderstaande x(t)-grafiek.

©VANIN

b Wie haalt wie in?

c Leid uit de grafiek af waar dat gebeurt.

d Mil kijkt op zijn horloge op het moment dat Josefien en hij elkaar tegenkomen. Bereken welk uur zijn horloge aangeeft.

9 Een auto vertraagt, zodat hij aan de start van de wegenwerken aan een constante snelheid van 90  km h rijdt. 300 m na de start van de werken rijdt een wegenwerker (in dezelfde richting en zin) met zijn machine aan een constante snelheid van 36  km h over het nieuwe asfalt.

Bereken na hoeveel seconden de auto de wegenwerker inhaalt.

Gegeven:

Gevraagd:

Oplossing:

:

©VANIN

10 Twee treinen rijden naar elkaar toe op parallelle sporen. De gele trein heeft een snelheid van 95  km h , de rode trein een snelheid van 85  km h . De treinen bevinden zich op 10 km van elkaar. Bereken hoeveel minuten het duurt voordat de twee treinen elkaar passeren.

Gegeven:

Gevraagd:

Oplossing:

Controle:

Controle

11 Een taxichauffeur rijdt op de snelweg en hoort op de radio dat er een spookrijder gesignaleerd is ter hoogte van de volgende afrit, 5,0 km verder. Hij vertraagt tot 100  km h en blijft uiterst rechts rijden.

Na 2,0 min passeert hij de spookrijder.

Bereken hoe snel de spookrijder rijdt en hoeveel afstand hij heeft afgelegd wanneer de taxi voorbijrijdt.

Gegeven:

Gevraagd:

Oplossing:

Controle:

` Verder oefenen? Ga naar

©VANIN

1 Begripskennis

• Ik kan in woorden uitleggen wat een eenparig rechtlijnige beweging (ERB) is.

• Ik kan voorbeelden geven van ERB’s uit het dagelijks leven.

• Ik kan verklaren waarom de gemiddelde snelheid in een ERB gelijk is aan de ogenblikkelijke snelheid.

• Ik kan een ERB voorstellen op een x(t)-grafiek.

• Ik kan een ERB die voorgesteld is op een x(t)-grafiek, in woorden omschrijven

• Ik kan het tijdsverloop en de verplaatsing aflezen op een x(t)-grafiek.

• Ik kan de snelheid afleiden uit een x(t)-grafiek.

• Ik kan een ERB voorstellen op een v(t)-grafiek.

• Ik kan een ERB die voorgesteld is op een v(t)-grafiek, in woorden omschrijven.

• Ik kan het tijdsverloop en de snelheidsverandering aflezen op een v(t)-grafiek.

• Ik kan de positie van een voorwerp dat een ERB uitvoert, op elk moment berekenen.

• Ik kan de snelheid van een voorwerp dat een ERB uitvoert, berekenen

• Ik kan het tijdsverloop van een voorwerp dat een ERB uitvoert, na een bepaalde afstand berekenen.

• Ik kan de positie en het tijdstip van voorwerpen die met een ERB bewegen, berekenen op het moment dat ze elkaar inhalen.

• Ik kan de positie en het tijdstip van voorwerpen die met een ERB bewegen, berekenen op het moment dat ze elkaar kruisen.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek stap voor stap uitvoeren

• Ik kan waarnemingen en beschrijvingen verbinden met de wetenschappelijke voorstelling in grafieken.

• Ik kan het verband tussen grootheden benoemen (recht evenredig / omgekeerd evenredig / niet evenredig).

• Ik kan grafieken nauwkeurig tekenen

• Ik kan grafieken nauwkeurig aflezen.

• Ik kan berekeningen uitvoeren met afgelezen waarden.

` Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

Rechtlijnige beweging

Eigenschappen van een rechtlijnige beweging berekenen

snelheid : v = ∆ x ∆ t

• gemiddelde snelheid: totale (deel)beweging

• ogenblikkelijke snelheid: op één moment, voor te stellen als een vector

v traag bewegen volgens de positie-as ( x -as)

©VANIN

• afgelegde weg : lengte van de baan

• verplaatsing

begin

volgens de positie-as ( x -as) bewegen

tegengesteld aan de positie-as ( x -as) bewegen

v snel bewegen, tegengesteld aan de positie-as ( x -as)

heen en terug bewegen

Eigenschappen aflezen op grafieken

• eenparig: De snelheid is constant.

• rechtlijnige beweging: De beweging verloopt volgens één richting.

• x ( t )-grafiek = schuine rechte

• v ( t )-grafiek = horizontale rechte

Positie: x eind = x begin + v ·

©VANIN

v ( t )-grafiek :

• ogenblikkelijke snelheid: punt op de grafiek

• informatie over de snelheid van een rechtlijnige beweging: Ligt de grafiek boven de tijdsas, dan is de snelheid positief (beweging volgens de x -as).

Ligt de grafiek onder de tijdsas, dan is de snelheid negatief (beweging tegengesteld aan de x -as). Ligt de grafiek op de tijdsas, dan is de snelheid nul (geen beweging).

x ( t )-grafiek :

• verplaatsing (op de verticale as)

• tijdsstip (op de horizontale as)

• snelheid: berekenen met verplaatsing en tijdsverloop helling van lijnstuk tussen beginen eindpositie

Rocky beweging naar rechts stilstand totale beweging

Licht op reis

Kijk terug naar de CHECK IN. Gebruik je kennis om de antwoorden te vinden op de volgende vragen.

1 Welke beweging voert licht uit? Verklaar.

2 Teken en benoem de snelheidsvector op een lichtstraal.

3 Hoelang doet het licht over de reis van de zon tot de aarde? Zoek de nodige gegevens op het internet op.

Gegeven:

Gevraagd:

Oplossing:

Controle: Vergelijk je antwoord met je hypothese in de CHECK IN.

4 Teken een x (t )- en een v (t )-grafiek van het licht tussen de zon en de aarde. Kies een geschikte schaalverdeling.

Zonlicht plant zich voort op een rechte baan met een constante snelheidsgrootte. Licht voert een ERB uit.

De x(t)-grafiek is een stijgende rechte, de v(t)-grafiek een horizontale rechte.

KRACHTEN

2 Hoe groot is de zwaartekracht?

` HOOFDSTUK 3: Hoe kun je krachten samenstellen of ontbinden?

` HOOFDSTUK 4: Welke verband bestaat er tussen kracht en evenwicht?

1 Hoe groot is de resulterende kracht bij een voorwerp in rust?

2 Wanneer is een voorwerp in evenwicht?

` HOOFDSTUK 5: Welke verband bestaat er tussen

en beweging?

1 Bij welke kracht beweegt een voorwerp aan een constante snelheid?

2 Bij welke kracht verandert de snelheid van een voorwerp?

Op naar de ruimte

Bekijk de krantenkop en de video.

1 Wat betekent ‘lanceren’?

LANCERING SPACEX-RAKET

2 Wat is er nodig om de raket te lanceren?

3 Op welke baan beweegt het ruimtestation ISS?

SPACEX-RAKET MET SUCCES GELANCEERD NAAR ISS

Het Amerikaanse ruimtevaartagentschap NASA en SpaceX, het bedrijf van Elon Musk, hebben deze nacht vier astronauten naar het internationale ruimtestation ISS gelanceerd. De lancering vond plaats om 01.27 u. (Belgische tijd) vanaf de Amerikaanse ruimtebasis Cape Canaveral.

Bron: www.hln.be

4 Hoe kan het ISS zo blijven bewegen volgens jou?

Door de zwaartekracht.

Door de motorkracht.

Door de zwaartekracht en de motorkracht.

Er werkt geen kracht op het ISS.

5 De astronauten zijn gewichtloos in het ISS. Kun je hier op aarde ook gewichtloos worden? Zo ja, hoe?

` Welke krachten laten een ruimtetuig bewegen?

` Hoe kun je een ruimtetuig laten versnellen, laten vertragen of in een cirkelbaan laten bewegen?

` En waarom zijn astronauten gewichtloos?

We zoeken het uit!

Krachtvector

OPDRACHT 1

Welke soorten krachten zijn er?

1 Bestudeer de foto’s.

Je kunt al vooruitblikken naar het kenniskader op p.85 als je de begrippen niet meer goed kent! TIP

2 Vul de omschrijvingen aan onder de foto’s. Vul op de invullijnen de voorwerpen in en duid de juiste begrippen aan.

1 2

• Er wordt een kracht uitgeoefend door op

• Er is wel / geen contact nodig.

• De elektrostatische kracht is een veldkracht / contactkracht

3 Geef een ander voorbeeld van een …

• contactkracht:

• veldkracht:

OPDRACHT 2

Wat is het effect van een kracht?

• Er wordt een kracht uitgeoefend door op

• Er is wel / geen contact nodig.

• De spierkracht is een veldkracht / contactkracht

3

1 Bestudeer de foto’s van drie sportievelingen.

• Er wordt een kracht uitgeoefend door op

• Er is wel / geen contact nodig.

• De magnetische kracht is een veldkracht / contactkracht

2 Vul de tabel aan. 1 2 3

©VANIN

Hoe zie je dat er een kracht wordt uitgeoefend?

verandering van bewegingstoestand

vervorming

dynamisch effect … statisch effect

Welk effect heeft de kracht?

verandering van bewegingstoestand

vervorming

dynamisch effect … statisch effect

verandering van bewegingstoestand

vervorming

dynamisch effect … statisch effect

OPDRACHT 3

Wat is de grootheid kracht?

Om de knijpkracht van een patiënt te bepalen, gebruikt een kinesist een krachtmeter.

1 Welke andere benaming heeft een krachtmeter?

2 Welke eenheid kun je aflezen op een krachtmeter?

3 Vul de tabel voor de grootheid kracht aan.

Grootheid met symbool

SI-eenheid met symbool

OPDRACHT 4

Hoe stel je de kracht voor als een vector?

Bestudeer de krachttrainingen.

1 Teken en benoem de spierkracht van Yena en Margot.

2 Noteer de kenmerken van de kracht onder de foto.

Aangrijpingspunt

Richting

Zin

Grootte

Een kracht heeft twee soorten effecten:

• dynamisch effect: een verandering van bewegingstoestand,

• statisch effect: een verandering van vorm.

We kunnen een onderscheid maken tussen:

• een veldkracht: een kracht die op afstand werkt zonder rechtstreeks contact;

• een contactkracht: een kracht die enkel werkt als er contact is tussen twee voorwerpen.

Kracht is een vectoriële grootheid met als symbool F. De grootte van een kracht meet je met een dynamometer of een krachtsensor. De eenheid van kracht is de newton (N). zin grootte richting aangrijpingspunt F

Yena heft de halter op met een kracht van 800 N.

Margot trekt aan het touw met een kracht van 500 N.

Wat is zwaartekracht?

LEERDOELEN

Je kunt al:

M de grootheid kracht voorstellen als een vector;

M het effect van krachten omschrijven.

Je leert nu:

M de vier kenmerken van de zwaartekrachtvector bepalen en weergeven;

M de werking van de zwaartekracht op en rond hemellichamen kennen;

M een kracht meten door gebruik te maken van een dynamometer;

M het verband tussen de grootheden massa, zwaartekracht en gewicht omschrijven.

In de sport draait het vaak om kracht. Een gewichtheffer moet spierkracht gebruiken om halters omhoog te heffen. Hij of zij moet de kracht die wordt uitgeoefend door de aarde, overwinnen.

In dit hoofdstuk bestudeer je hoe je de zwaartekracht die inwerkt op voorwerpen, kunt berekenen en voorstellen. Je gaat op zoek naar de betekenis van ‘gewicht’ en bestudeert gewichtloosheid op verschillende hemellichamen.

1 Welke kenmerken heeft de zwaartekracht?

1.1 Zwaartekracht

OPDRACHT 5

Bestudeer de zwaartekracht en haar effecten.

1 Hoe zie je dat de zwaartekracht inwerkt? Noteer.

2 Welk effect heeft de zwaartekracht? Duid aan.

3 Is er contact tussen de aarde en de sporter? Duid aan.

©VANIN

2 … statisch effect

dynamisch effect

3 … geen contact

contact met de aarde

statisch effect

dynamisch effect

geen contact

contact met de aarde

statisch effect

dynamisch effect

geen contact

contact met de aarde

1.2 Zwaartekrachtvector

OPDRACHT 6

De aarde oefent een kracht uit op alle voorwerpen in haar buurt, ook zonder contact tussen de aarde en het voorwerp zelf. De zwaartekracht is een veldkracht die op alle voorwerpen in het zwaarteveld werkt.

De zwaartekracht is de aantrekkingskracht waarmee de aarde voorwerpen in haar omgeving aantrekt. De zwaartekracht kan twee effecten veroorzaken:

• statisch effect: het voorwerp vervormt;

• dynamisch effect: het voorwerp verandert van bewegingstoestand.

VOORBEELD EFFECTEN VAN DE ZWAARTEKRACHT

Tijdens het gewichtheffen ervaren Kiran en Saar de zwaartekracht:

• Ze worden naar beneden getrokken en staan recht op de fitnessmat. Er is contact tussen hen en de grond. De mat vervormt. Er is een statisch effect van de zwaartekracht.

• Ze gebruiken hun armspieren om de zwaartekracht te overwinnen en de halters omhoog te duwen. Er is geen contact tussen de halters en de aarde, maar toch voelen ze de zwaartekracht, die de halters naar de aarde trekt. Hun handen vervormen (= statisch effect), en als ze de halters lossen, vallen die op de grond (= dynamisch effect).

©VANIN

De zwaartekracht is de kracht waarmee de aarde (en andere hemellichamen) voorwerpen in haar zwaarteveld aantrekt.

Onderzoek de kenmerken van de zwaartekrachtvector.

Otis (27 jaar) en Liam (8 jaar) hangen aan de rekstok.

1 Vul het kenmerk van de vector aan in de tabel.

2 Teken en benoem de zwaartekrachtvector op beide sporters.

Kenmerk vector

Omschrijving

1 Elk deeltje van Otis en Liam, van hun armen tot hun kleine teen, wordt aangetrokken door de aarde. De totale aantrekking stel je voor in het zwaartepunt (Z).

2 Als Otis en Liam stil hangen, heeft hun lichaam een richting loodrecht ten opzichte van het wateroppervlak. Het is verticaal gespannen.

3 Otis en Liam vallen naar beneden, naar het middelpunt van de aarde

4 De aantrekkingskracht op Otis is groter dan die op Liam.

Afb. 1 Kiran en Saar

Afb. 2

Een kracht is een vectoriële grootheid die wordt voorgesteld door het symbool F. Om duidelijk te maken dat het om de zwaartekracht gaat, voeg je de letter z toe: F z

VOORBEELD ZWAARTEKRACHTVECTOREN

Op de halters van Kiran en Saar én op de lichamen van Kiran en Saar zelf werkt de zwaartekracht Fz met deze kenmerken:

Halters Sporters

Aangrijpingspunt zwaartepunt (Z) van de halters zwaartepunt (Z) van de sporters

Richting verticaal verticaal

Zin naar het middelpunt van de aarde naar het middelpunt van de aarde

Grootte Fz,

©VANIN

Je kent het zwaartepunt van regelmatige figuren uit de wiskunde.

• driehoek: snijpunt van de zwaartelijnen

• vierhoek: snijpunten van de diagonalen

Bij de mens ligt het zwaartepunt ter hoogte van de navel.

De zwaartekracht is een vectoriële grootheid:

• aangrijpingspunt: het zwaartepunt (Z) van het voorwerp,

• richting: verticaal (loodrecht op het wateroppervlak),

• zin: naar het middelpunt van de aarde (of ander hemellichaam),

• grootte: Fz, afhankelijk van het voorwerp.

` Maak oefening 1 en 2 op p. 95.

halter S < Fz, halter K Fz, Saar < Fz, Kiran

Fz, halter K

z, halter S

Fz, Kiran Fz, Saar

Z

Afb. 3

TIP

2 Hoe groot is de zwaartekracht?

2.1 Invloed van de massa

OPDRACHT 7 ONDERZOEK

Onderzoek de grootte van de zwaartekracht aan de hand van het labo bij het onlinelesmateriaal.

F z (N)

1 2 3 4

Fz(m )-grafiek N kg

De Fz(m)-grafiek is een halfrechte door de oorsprong. De grootte F z van de zwaartekracht op een voorwerp is recht evenredig met de massa m van dat voorwerp:

FZ m = g dus FZ = m · g

De evenredigheidsconstante g noem je de zwaarteveldsterkte. Nauwkeurige experimenten in onze streken leveren deze waarde op: g = 9,81 N kg

Grootheid met symbool SI-eenheid met symbool zwaarteveldsterkte g newton per kilogram

VOORBEELD GROOTTE VAN DE ZWAARTEKRACHT

We bekijken opnieuw de fitnessoefening van Kiran en Saar. De halter van Saar heeft een massa van 2,0 kg. Je berekent de zwaartekracht op de halter als:

Fz, halter S = m · g = 2,0 kg · 9,81 N kg = 20 N

Uit afbeelding 3 op p. 86 blijkt dat de grootte van de zwaartekracht uitgeoefend op de halter van Kiran groter is dan die uitgeoefend op de halter van Saar. Daaruit leid je af dat de halter van Kiran een grotere massa heeft.

De grootte van de zwaartekracht op een voorwerp met massa m en zwaarteveldsterkte g bereken je als volgt:

F z = m · g

De zwaarteveldsterkte in onze streken is g = 9,81 N kg .

` Maak oefening 3 t/m 7 op p. 96 en 97.

OPDRACHT 8

Los het vraagstuk op.

1 Bereken de grootte van de aantrekkingskracht die de aarde uitoefent op Jimmy, die een massa van 58,0 kg heeft. Werk het vraagstuk uit op een cursusblad.

2 Teken en benoem het zwaartepunt en de zwaartekrachtvector op afbeelding 4 (schaal: 1 cm 200 N).

3 Controleer je antwoord.

Locatie g ( N kg )

Noordpool 9,83 evenaar 9,78

Mount Everest 9,77

Tabel 1

Hemellichaam g ( N kg )

Mercurius 3,78

2.2 Zwaarteveldsterkte

De grootte van de zwaarteveldsterkte op het aardoppervlak in België is gelijk aan g = 9,81 N kg .

Dat betekent dat een massa van 1 kilogram door de aarde wordt aangetrokken met een kracht van 9,81 newton.

Door hoogteverschillen, de aanwezigheid van verschillende soorten gesteenten en de rotatie van de aarde om haar as is de zwaarteveldsterkte op het aardoppervlak niet overal even groot.

©VANIN

Venus 8,87

aarde 9,81

Mars 3,71

Jupiter 24,8

Saturnus 10,4

Uranus 8,87

Neptunus 11,0

maan 1,62

Tabel 2

De zwaartekracht is een veldvector en werkt dus ook op voorwerpen die geen contact hebben met het aardoppervlak. De grootte van de zwaartekracht op een voorwerp vermindert naarmate het voorwerp zich verder van de aarde begeeft. Het gebied waar de zwaartekracht werkzaam is, noem je het zwaarteveld. Het zwaarteveld van de aarde reikt tot buiten de atmosfeer. Daardoor kunnen voorwerpen in de ruimte, zoals de maan, satellieten en het ruimtestation ISS, toch op een baan rond de aarde bewegen.

6

Zwaarteveld van de aarde

Niet enkel de aarde, maar ook andere hemellichamen oefenen een kracht uit op voorwerpen in hun omgeving. Elk hemellichaam oefent een zwaartekracht uit. De grootte van de zwaartekracht hangt af van het hemellichaam, omdat elk hemellichaam een eigen zwaarteveldsterkte heeft.

Op de meeste planeten is de zwaarteveldsterkte kleiner dan op aarde. Enkel op Jupiter, Neptunus en Saturnus is de zwaarteveldsterkte groter.

Afb.

Afb. 4

F Z

F Z

F Z

F z Z

F z Z

Afb. 5

OPDRACHT 9

Bestudeer de zwaarteveldsterkte van andere hemellichamen.

1 Bestudeer tabel 2. Op welk hemellichaam is de zwaartekracht op een halter het kleinst? Verklaar.

VRAAGSTUKKEN OPLOSSEN

2 Bereken de zwaartekracht op een halter (500 g) als een gewichtheffer zich op Jupiter bevindt.

Gegeven: Bestudeer tabel 2 en vul de zwaarteveldsterkte aan.

m = 500 g; g =

Gevraagd: Welke grootheid wordt er gevraagd?

Oplossing: Noteer de formule voor de zwaartekracht.

Vorm de gegeven massa om naar de SI-eenheid.

Vul de formule voor de zwaartekracht in met de gegevens.

Controle: Klopt de eenheid?

3 In de gegevens staan een g en een g . Leg het verschil tussen beide uit.

VOORBEELD ZWAARTEKRACHT OP ANDERE HEMELLICHAMEN

Stel je voor dat Saar haar halter meeneemt naar de maan en naar verschillende planeten. Op de maan zouden de oefeningen vlot moeten gaan, aangezien de zwaarteveldsterkte er zes keer kleiner is dan op aarde. Op Jupiter zou ze harder trainen, want daar is de zwaarteveldsterkte meer dan dubbel zo groot als op aarde.

aarde maan Mars Venus Jupiter

De zwaarteveldsterkte is een maat voor de sterkte van de aantrekkingskracht van een hemellichaam.

Grootheid met symbool SI-eenheid met symbool zwaarteveldsterkte g newton per kilogram

N kg

` Maak oefening 8 t/m 10 op p. 97 en 98.

3 Wat is het verband tussen massa, gewicht en zwaartekracht?

In het dagelijks leven gebruiken we de begrippen massa en gewicht door elkaar. In de fysica zijn dat twee verschillende grootheden

1 g = 0,001 kg = 1 · 10–3 kg

1 ton = 1 · 103 kg EENHEDEN

©VANIN

De massa van een voorwerp is de hoeveelheid materie waaruit dat voorwerp bestaat. De grootheid massa stel je voor met het symbool m. De SI-eenheid van massa is 1 kg (kilogram). Voor kleine en grote massa’s gebruik je afgeleide eenheden, zoals gram en ton.

Aangezien massa enkel een grootte heeft, is het een scalaire grootheid. Een scalaire grootheid heeft, in tegenstelling tot een vectoriële grootheid, geen richting, zin of aangrijpingspunt. De massa van een voorwerp bepaal je aan de hand van een balans.

VOORBEELD MASSA VAN HALTERS

Kiran en Saar heffen elk een verschillende massa. Kiran heeft een halter met een massa van 3 kg, Saar een halter met een massa van 2 kg.

De massa van een voorwerp is de hoeveelheid materie waaruit dat voorwerp is opgebouwd.

Grootheid met symbool SI-eenheid met symbool massa m kilogram kg

OPDRACHT 10

Zoek het gewicht.

1 Leg een pennenzak op je hand.

2 Welke kracht werkt er op de pennenzak?

3 Waar ervaar je de kracht?

4 Hoe groot is de kracht die je voelt?

Kleiner dan/groter dan/gelijk aan de zwaartekracht

5 Teken en benoem zowel de zwaartekracht op de pennenzak als de kracht waarmee er op de hand gesteund wordt.

©VANIN

We definiëren hier de gewichtskracht. Dat is de kracht die ontstaat ten gevolge van de zwaartekracht voor een voorwerp dat op een horizontaal oppervlak staat of opgehangen is, waar geen andere krachten op inwerken. In de derde graad bestudeer je de gewichtskracht in andere situaties.

Elk voorwerp ondervindt een zwaartekracht, die aangrijpt in het zwaartepunt van het voorwerp. Als het voorwerp ondersteund wordt, ontstaat daardoor een kracht op de ondersteuning. Die kracht noem je de gewichtskracht of kortweg het gewicht. Het gewicht is net als de zwaartekracht een vector, voorgesteld door Fg.

Kenmerk vector Zwaartekracht F z Gewicht Fg aangrijpingspunt zwaartepunt Z steunpunt S richting verticaal verticaal zin naar het middelpunt van de aarde naar het middelpunt van de aarde grootte

F z = m g F g = m g

VOORBEELD ZWAARTEKRACHT EN GEWICHT

Een halter van Saar heeft een massa m = 2,0 kg. In de buurt van de aarde werkt er altijd een zwaartekracht Fz, halter S verticaal naar het middelpunt van de aarde met als grootte:

Fz, halter S = m g = 2,0 kg 9,81 N kg = 20 N

Die kracht grijpt aan in het zwaartepunt.

Als Saar de halter vasthoudt, voelt ze de inwerking van de zwaartekracht in haar hand. Het gewicht F g, halter S van het voorwerp veroorzaakt een vervorming (statisch effect) in het steunpunt. Het gewicht werkt verticaal naar het midden van de aarde en heeft dezelfde grootte als de zwaartekracht:

Fg, halter S = Fz, halter S = m · g = 2,0 kg · 9,81 N kg = 20 N

Afb. 9

TIP

Ook op Saar zelf werkt de zwaartekracht Fz, Saar in. Saar staat op de grond en verdeelt haar gewicht over haar beide benen:

Fg, links + Fg, rechts = F g, totaal

Het gewicht heeft dezelfde grootte als de zwaartekracht:

Fz, Saar = Fg, totaal F z, Saar

OPDRACHT 11

Bestudeer de massa, het gewicht en de zwaartekracht van de snowboarder.

Seppe Smits (m = 83,0 kg), Belgisch kampioen snowboarden, maakt een sprong.

1 Bekijk zijn sprong in de video.

2 Vul de tabel aan.

©VANIN

3 Teken en benoem de zwaartekrachtvector en het gewicht.

4 Omschrijf in je eigen woorden wat gewichtloosheid is.

VIDEO SNOWBOARDER

Massa m Grootte van de zwaartekracht Fz Grootte van het gewicht Fg

Als een voorwerp niet ondersteund wordt, oefent het geen kracht uit op de ondersteuning. Het heeft geen gewicht. Het is gewichtloos. De massa en de zwaartekracht veranderen niet.

VOORBEELD MASSA VAN HALTERS

Saar schrikt en laat de halter vallen. Op afbeelding 11 zie je de zwaartekracht F z en het gewicht F g net voor, tijdens en na de val.

©VANIN

Voor het vallen Tijdens het vallen Na het vallen

m = 2,0 kg

F z = m g

= 2,0 kg · 9,81 N kg

= 20 N

F g = m g

= 2,0 kg · 9,81 N kg

= 20 N

m = 2,0 kg

F z = m g = 2,0 kg · 9,81 N kg

= 20 N

F g = 0 N

m = 2,0 kg

F z = m g = 2,0 kg · 9,81 N kg = 20 N

F g = m g = 2,0 kg · 9,81 N kg = 20 N

Het gewicht Fg van een voorwerp is de kracht van dat voorwerp op zijn ondersteuning. Gewicht is een vectoriële grootheid met de kenmerken (voor een voorwerp dat ophangt of horizontaal staat):

• aangrijpingspunt: op de ondersteuning, in het steunpunt,

• richting: verticaal,

• zin: naar het middelpunt van de aarde,

• grootte: Fg = m · g

Als een voorwerp niet ondersteund wordt, oefent het geen kracht uit op de ondersteuning. Het heeft geen gewicht. Het is gewichtloos

` Maak oefening 11, 12 en 13 op p. 99 en 100.

1 massa ( m ) =  de hoe veelheid materie waaruit een voorwerp is opgebouwd

Grootheid met symbool SI-eenheid met symbool

2 zwaarteveldsterkte  ( g ) =  een ma at voor de sterkte van de aantrekkingskracht van een hemellichaam

zwaartekracht

KENMERKEN

Grootheid met symbool SI-eenheid met symbool In België is g = . Hemellichaam g ( N

INVLOEDSFACTOREN

)

©VANIN

F z

zwaartekrachtvector

• aangrijpingspunt :

• richting : • zin : • grootte : teken de zwaartekrachtvector

= de a antrekkingskracht van een hemellichaam op alle voorwerpen in het zwaarteveld gewicht = de kracht van een voorwerp op zijn ondersteuning Als een voorwerp niet ondersteund wordt, oefent het geen kracht uit op de ondersteuning. Het heeft geen gewicht. Het is .

KENMERKEN

gewichtsvector F g

• aangrijpingspunt :

• richting : • zin : • grootte : teken de gewichtsvector

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

GRAFIEKEN LEZEN FORMULES OMVORMEN

VOORVOEGSELS EN MACHTEN

EENHEDEN OMZETTEN

BEREKENINGEN AFRONDEN

1

Bestudeer de voorstelling van de zwaartekrachtvectoren.

a Duid aan welk(e) kenmerk(en) van de zwaartekrachtvector foutief is/zijn.

b Verbeter de foutief getekende zwaartekrachtvectoren.

aangrijpingspunt / richting / zin / grootte

aangrijpingspunt / richting / zin / grootte

aangrijpingspunt / richting / zin / grootte

2 Juist of fout? Verklaar.

a Het zwaartepunt bevindt zich altijd in het midden van een voorwerp.

b Als een gewichtheffer zijn halters stil boven zich houdt, hoeft hij geen kracht uit te oefenen.

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’. Je kunt de oplossingsstrategie en de voorbeeldoefeningen gebruiken als extra ondersteuning.

3 Bekijk de vier grafieken. Welke grafiek geeft het verband weer tussen de zwaarteveldsterkte g en de massa m op aarde?

©VANIN

4 De Falcon Heavy-raket, met een massa van 1 420 ton, wordt vanop de evenaar (g = 9,78 N kg) gelanceerd.

a Bereken de grootte van de zwaartekracht op de raket.

Gegeven: Gevraagd:

Oplossing:

Controle: Hoe verandert je resultaat bij een lancering vanaf België?

b Teken en benoem de zwaartekrachtvector op schaal 1 cm 70 ∙ 105 N.

5 Vorm de basisformule om naar de gevraagde grootheid.

a Hoe kun je de massa berekenen, als de zwaartekracht en de zwaarteveldsterkte gegeven zijn?

b Hoe kun je de zwaarteveldsterkte berekenen, als de massa en de zwaartekracht gegeven zijn?

6

Bereken de gevraagde grootheden.

Voorwerp

emmer water

Massa m Zwaartekracht F z

11,0 kg smartphone

g

7 Tijdens een labo hang je twee identieke blokjes aan een dynamometer. Je leest de waarde 4,9 N af. Bereken de massa van één blokje.

Gegeven:

Gevraagd:

Oplossing:

Controle: Klopt de eenheid?

8 Het onbemande ruimtetoestel Curiosity doet onderzoek naar bodemstalen op een planeet. Het schept een massa van 250 g op en meet met een dynamometer dat de planeet een kracht van 0,928 N uitoefent op het bodemstaal. Onderzoek op welke planeet het ruimtetoestel zich bevindt.

Gegeven:

Gevraagd:

Oplossing:

Controle: Klopt de eenheid?

9 In de grafiek wordt het verband tussen de zwaarteveldsterkte g en de hoogte h ten opzichte van het wateroppervlak weergegeven. Bestudeer de grafiek en beantwoord de vragen.

a Duid aan.

Hoe verder een voorwerp van het wateroppervlak verwijderd is, hoe kleiner / groter de zwaarteveldsterkte op dat voorwerp.

b Op welke hoogte is de grootte van de zwaarteveldsterkte gehalveerd? Duid aan op de grafiek.

c Bereken bij benadering de grootte van de zwaartekracht die inwerkt op het International Space Station (ISS). Het ISS heeft een massa van 420 ton en zweeft op een hoogte van 400 km boven het wateroppervlak.

Gegeven: Gevraagd:

Oplossing:

Controle: Klopt de eenheid?

10 De grafiek geeft het verband weer tussen de massa van en de aantrekkingskracht op verschillende planeten.

a Vul de legende bij de grafiek verder aan.

Gebruik tabel 2 op p. 94.

b Er wordt heel wat onderzoek gedaan naar de bewoonbaarheid van de planeet Mars. In veel opzichten lijkt Mars een veelbelovend alternatief voor de aarde. Beantwoord de vragen.

• Is de aantrekkingskracht op Mars groter of kleiner dan op aarde?

• Bepaal hoeveel keer minder je wordt aangetrokken op Mars dan op aarde.

©VANIN

11 Een zwemmer (m = 73,0 kg) staat op een duikplank.

a Bereken de zwaartekracht die op de zwemmer inwerkt als hij op de duikplank staat.

Gegeven: Gevraagd:

Oplossing: Controle: Hoe verandert de zwaartekracht tijdens de duiksprong?

b Bereken het gewicht van de zwemmer als hij op de duikplank staat.

Gegeven: Gevraagd:

Oplossing:

c Hoe verandert het gewicht tijdens de duiksprong?

d Teken en benoem de zwaartekrachtvector en de gewichtsvector op de duiker voor de duiksprong.

e Teken en benoem de zwaartekrachtvector en de gewichtsvector op de duiker tijdens de duiksprong.

12 Een steen van 1 kg wordt in balans gebracht op aarde. Dezelfde proef wordt herhaald op de maan, waar de zwaarteveldsterkte zes keer kleiner is. Duid aan welke afbeelding de juiste weergave toont.

©VANIN

13 Het ruimtepak van de eerste man op de maan, Neil Armstrong (82,0 kg), wordt tentoongesteld in het nationale lucht- en ruimtevaartmuseum in Washington. Het pak heeft op aarde een massa van 70,0 kg.

a Bereken het totale gewicht van Neil Armstrong in zijn pak voor vertrek én op de maan.

Gegeven: Gevraagd:

Oplossing:

Controle: Hoe verandert het gewicht wanneer de zwaarteveldsterkte kleiner is?

b Hoe verandert de massa van het pak op de maan?

` Verder oefenen? Ga naar .

1 Begripskennis

• Ik kan in mijn eigen woorden uitleggen wat ‘zwaartekracht’ betekent.

• Ik kan het effect van de zwaartekracht bespreken.

• Ik kan de kenmerken van de zwaartekracht opsommen

• Ik kan de zwaartekrachtvector tekenen op voorwerpen.

• Ik kan opsommen welke factoren de grootte van de zwaartekracht beïnvloeden.

• Ik kan het verband tussen de massa en de zwaartekracht onderzoeken

• Ik kan in mijn eigen woorden uitleggen wat de zwaarteveldsterkte betekent.

• Ik kan de zwaarteveldsterkte voorstellen op een Fz(m)-grafiek.

• Ik kan met de massa van een voorwerp de zwaartekracht op dat voorwerp berekenen met behulp van de zwaarteveldsterkte.

• Ik kan het onderscheid tussen massa, zwaartekracht en gewicht toelichten

• Ik kan de gewichtsvector tekenen op voorwerpen.

2 Onderzoeksvaardigheden

• Ik kan een goed wetenschappelijk onderzoek opstellen om een onderzoeksvraag te beantwoorden.

• Ik kan een onderzoek stap voor stap uitvoeren

• Ik kan waarnemingen en beschrijvingen verbinden met de wetenschappelijke voorstelling in grafieken.

• Ik kan het verband tussen grootheden benoemen (recht evenredig / omgekeerd evenredig / niet evenredig).

• Ik kan grafieken nauwkeurig tekenen

• Ik kan grafieken nauwkeurig aflezen

• Ik kan berekeningen uitvoeren met afgelezen waarden.

• Ik kan een kracht meten door gebruik te maken van een dynamometer.

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Wat is veerkracht?

LEERDOELEN

Je kunt al:

M de grootte van de zwaartekracht en een gewicht bepalen;

M het statisch effect van een kracht omschrijven.

Je leert nu:

M plastische en elastische vervorming van elkaar onderscheiden;

M de veerconstante experimenteel bepalen;

M de invloedsfactoren op de veerkracht kwalitatief en kwantitatief toepassen;

M de wet van Hooke formuleren.

In de fitnesszaal kun je niet enkel halters gebruiken om je spieren te trainen. Ook weerstandsbanden en -elastieken zijn handige hulpmiddelen om je spieren te versterken. Je moet je spierkracht namelijk gebruiken om de weerstandsbanden en -elastieken te vervormen.

In dit hoofdstuk bestudeer je welke types vervorming er bestaan. Je gaat op zoek naar de kenmerken van de veerkracht die inwerkt op voorwerpen. Je leert hoe je die kennis kunt gebruiken om een dynamometer te bouwen.

1 Welke kenmerken heeft de veerkracht?

1.1 Vervorming

©VANIN

OPDRACHT 12

Bestudeer het statisch effect van krachten.

1 Bestudeer de drie sportievelingen.

2 Vul de tabel aan. 1 2 3

Op welk voorwerp werkt de kracht?

Is de uitgeoefende kracht een contactkracht of een veldkracht?

contactkracht / veldkracht contactkracht / veldkracht contactkracht / veldkracht

Wanneer is de vervorming door de kracht merkbaar?

voor / terwijl / nadat de kracht werkt

voor / terwijl / nadat de kracht werkt

voor / terwijl / nadat de kracht werkt

Krachten veroorzaken bij contact een vervorming van een voorwerp. Ze hebben een statisch effect. Er zijn twee soorten vervorming:

• Elastische vervorming

De voorwerpen vervormen tijdens het contact en nemen hun oorspronkelijke vorm weer aan nadat de kracht wegvalt

veer wordt tijdens het

©VANIN

• Plastische vervorming

De voorwerpen vervormen tijdens het contact en de vervorming blijft nadat de kracht wegvalt. Sommige elastische vervormingen worden plastische vervormingen als de kracht te groot is of de kracht te vaak uitgeoefend wordt.

Een skiër laat sporen na in de sneeuw. Nadat hij gepasseerd is, zijn de sporen nog altijd zichtbaar.

Voorwerpen die elastisch vervormen, noem je veren. Binnen de elasticiteitsgrenzen neemt een veer haar oorspronkelijke vorm weer aan.

De vervorming van een voorwerp is het statisch effect van een kracht op het voorwerp.

• Een elastische vervorming verdwijnt als de kracht wegvalt.

• Een plastische vervorming is blijvend

Voorwerpen die hun oorspronkelijke vorm weer aannemen nadat de kracht verdwijnt, noem je veren

` Maak oefening 1 en 2 op p. 114.

Een voetbal wordt ingedeukt tijdens het contact met de voet. Na de schop krijgt hij terug zijn ronde vorm.

De

fietsen meer en minder ingedrukt door de verandering in kracht. Daardoor vangt ze de schokken op.

1.2 Veerkracht

OPDRACHT 13

Onderzoek het verband tussen de kracht op de veer en de veerkracht.

1 Open de applet en kies voor ‘Inleiding’.

2 Oefen een trek- en een duwkracht uit op de veer.

3 Bestudeer de grootte van de kracht op de veer Fop en de veerkracht Fv.

4 Vul je waarnemingen aan in de tabel.

a Duid de lengteverandering ∆l aan op de figuur.

b Teken en benoem de krachten in beide situaties.

c Vergelijk de kenmerken van Fop en Fv.

Tekening

©VANIN

Trekkracht

Duwkracht

Kenmerken F op en F v

• Aangrijpingspunt: hetzelfde / verschillend

• Richting: hetzelfde / verschillend

• Zin: hetzelfde / verschillend

• Grootte: hetzelfde / verschillend

• Aangrijpingspunt: hetzelfde / verschillend

• Richting: hetzelfde / verschillend

• Zin: hetzelfde / verschillend

• Grootte: hetzelfde / verschillend

Om een veer te vervormen, is er een kracht nodig op de veer. Je noemt die contactkracht de kracht op de veer, voorgesteld door het symbool F op.

De vervorming van de veer merk je aan een lengteverandering ∆l Een onbelaste veer bevindt zich in de evenwichtspositie en heeft een lengte lbegin. Een belaste veer heeft een lengte leind. De lengteverandering ∆l bereken je als het verschil tussen de begin- en eindlengte.

Grootheid met symbool SI-eenheid met symbool lengteverandering ∆l = leind – lbegin meter m

Bij een uitrekking wordt de veer langer. De lengteverandering ∆l > 0. Bij een indrukking wordt de veer korter. De lengteverandering ∆l < 0.

Uitrekking

Indrukking

De vervormde veer oefent zelf een kracht uit om haar oorspronkelijke vorm weer aan te nemen.

Je noemt dat de veerkracht, voorgesteld door het symbool F v

De kracht op de veer Fop en de veerkracht Fv zijn vectoren die nauw verbonden zijn met elkaar. Ze hebben dezelfde richting en grootte: F v = – F op .

Kenmerk vector Kracht op veer F op Veerkracht F v

Aangrijpingspunt in het contactpunt op de veer in het contactpunt op het voorwerp dat de kracht uitoefent

Richting de richting van de veer

Zin tegengesteld aan elkaar

Grootte even groot

VOORBEELD VEERKRACHT

Julia kiest voor een training van de armspieren, waarbij ze aan een veer moet trekken die aan één kant vasthangt aan de muur.

Uitgeoefend door Uitgeoefend op F op = Fspier

©VANIN

Julia

Julia veer F v veer

Julia oefent met haar arm een spierkracht uit op de veer. Het statisch effect van die kracht is een lengteverandering van de veer: de veer rekt uit.

We kiezen voor een lengteas (l-as) waarbij de oorsprong samenvalt met het een uiteinde van de veer. De onbelaste veer heeft een lengte lbegin = 1,00 m.

Julia oefent een spierkracht Fspier (Fspier = 60 N) uit op de veer, waardoor de veer uitrekt tot een lengte leind = 1,20 m.

Je kunt de lengteverandering van de veer als volgt berekenen:

∆l = leind – lbegin = 1,20 m – 1,00 m = 0,20 m

De opgespannen veer oefent ook een kracht uit op Julia, de veerkracht. De veer wil terug naar haar oorspronkelijke positie en trekt aan de arm van Julia. De grootte van de veerkracht is gelijk aan de grootte van de uitgeoefende kracht op de veer:

F v = Fspier = 60 N

Kenmerk vector Kracht op veer Fspier Veerkracht F v

Aangrijpingspunt veer Julia Richting horizontaal

Zin naar rechts, volgens de uitrekking naar links, tegen de uitrekking in

Grootte

De kracht op de veer F op is een contactkracht, uitgeoefend door een voorwerp op de veer. Het effect van de kracht op de veer is een lengteverandering ∆l

• ∆l > 0: De veer rekt uit.

• ∆l < 0: De veer drukt in.

De veerkracht F v is een contactkracht, uitgeoefend door de opgespannen veer op dat voorwerp.

De kracht op de veer en de veerkracht zijn vectoriële grootheden.

Fspier = F v = 60 N

©VANIN

Kenmerk vector Kracht op veer Veerkracht

Aangrijpingspunt in het contactpunt op de veer in het contactpunt op het voorwerp dat de kracht uitoefent

Richting de richting van de veer

Zin volgens de uitrekking volgens de indrukking tegen de uitrekking in tegen de indrukking in

Grootte F op = F v

Bij een veer in rust is de kracht op de veer even groot als, maar tegengesteld aan de veerkracht.

2 Hoe groot is de veerkracht?

2.1 Veerconstante

OPDRACHT 14 ONDERZOEK

Onderzoek de factoren die een invloed hebben op de grootte van de veerkracht aan de hand van het labo bij het onlinelesmateriaal.

De absolute waarde van een getal is dat getal zonder toestandsteken.

bv. |−5| = 5

v(Δ l )-grafiek

Als een veer uitgerekt is door een kracht F op over een afstand ∆l, oefent de veer een veerkracht F v uit op het voorwerp dat de veer uitrekt. De F(Δl)-grafiek is een halfrechte door de oorsprong. De grootte F v van de veerkracht is recht evenredig met de absolute waarde van de uitrekking ∆

van de veer:

Dat is de wet van Hooke. De evenredigheidsconstante k noem je de veerconstante

Grootheid met symbool SI-eenheid met symbool veerconstante k newton per meter

OPDRACHT 15

Geef betekenis aan de veerconstante.

1 Leg in je eigen woorden uit wat een veerconstante van 8 N m betekent.

2 Zet alle veerconstanten om naar de eenheid N m

k2 = 8 kN m =

k3 = 8 N cm =

k5 = 4 N cm =

3 Rangschik de veren van soepel naar stijf.

k1 = 8 N m ; k2 = 8 kN m ; k3 = 8 N cm ; k4 = 4 N m ; k5 = 4 N cm

EENHEDEN OMZETTEN

VOORBEELD VEERCONSTANTE

De waarde van k is constant voor een bepaalde veer. De veerconstante is een maat voor de stijfheid van de veer. Hoe groter de veerconstante is, hoe meer kracht er nodig is om dezelfde lengteverandering te bekomen.

Julia oefent een kracht uit op een veer met veerconstante k = 300 N m . Door de uitgeoefende kracht op de veer rekt de veer 0,20 m uit. De veerkracht van de veer kun je als volgt berekenen:

F v = k |∆l| = 300 N m |0,20 m| = 60 N

©VANIN

De veer oefent een kracht F v = 60 N uit op Julia’s arm. Julia zelf oefent een even grote, maar tegengestelde kracht uit op de veer: F op = 60 N.

Om haar armspieren nog sterker te maken, vervangt Julia de veer door een stijvere versie met veerconstante k = 450 N m . Om dezelfde lengteverandering ∆l = 0,20 m te bekomen, zal Julia een grotere kracht moeten uitoefenen op de veer:

F v = k |∆l| = 450 N m |0,20 m| = 90 N

OPDRACHT 16 DOORDENKER

Bestudeer een combinatie van veren.

Bart traint met een expander die uit drie veren met veerconstante k bestaat.

1 Welke veerconstante heeft de expander volgens jou?

k

3 · k

1 3 · k

niet te bepalen

2 Ga je voorspelling na met de applet. Kies voor ‘Stelsels’.

a Kies twee veren met veerconstante k1 = k2 = 200 N m .

b Hoe groot is de uitrekking bij een kracht van 100 N?

c Bereken de veerconstante van de samengestelde veer.

Gegeven:

Gevraagd:

©VANIN

Oplossing: Antwoord: Vergelijk de veerconstante van de expander met de veerconstante van de twee veren. Wat stel je vast?

3 Vergelijk je antwoord met je voorspelling.

4 Verklaar de bouw van de expander op afbeelding 15.

Afb. 15

OPEN APPLET

OPDRACHT 17

Los het vraagstuk op.

In een balpen zit een veertje van 2,5 cm lang. Het veertje, met een veerconstante van 800 N m , wordt ingedrukt tot een lengte van 2,0 cm als je op de top van de balpen drukt. Bepaal de kracht waarmee je op de balpen drukt.

1 Bereken de kracht op de veer in de pen. Werk het vraagstuk uit op een cursusblad.

2 Teken en benoem de krachten die inwerken op de pen.

3 Controleer je antwoord.

©VANIN

VRAAGSTUK VEERKRACHT

Als een veer met veerconstante k een lengteverandering ∆l heeft, dan oefent de veer een veerkracht F v uit op het voorwerp dat de veer uitrekt of induwt: F

waarbij k de veerconstante (een maat voor de stijfheid van de veer) is.

Grootheid met symbool

SI-eenheid met symbool veerconstante k newton per meter

Die uitdrukking noem je de wet van Hooke. Die wet is geldig als de veer elastisch vervormt.

` Maak oefening 3 t/m 8 op p. 114 t/m 116.

2.2 Vervorming door de zwaartekracht

OPDRACHT 18

Bestudeer de veerkracht bij een verticale veer.

Na een bungeejump hangt Thijs stil aan de elastiek.

1 Welke kracht oefent Thijs uit op de elastiek?

2 Teken en benoem die kracht in het punt P.

3 Geef de formule voor die kracht in symbolen.

4 Welke kracht oefent de veer uit op Thijs?

5 Teken en benoem die kracht in het punt P.

6 Geef de formule voor die kracht in symbolen.

7 Wat kun je zeggen over de grootte van de inwerkende krachten?

OPDRACHT 19 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

De veren van een zadel hebben elk een veerconstante van 130 N cm .

De massa (m = 54 kg) van de fietser wordt gelijkmatig verdeeld over twee identieke veren. Bereken de lengteverandering van één veer, als de fietser op zijn zadel zit.

Gegeven: k = 130 N cm ; mtotaal = 54 kg; g = 9,81 N kg

Gevraagd: Δl = ?

Oplossing: De fietser oefent een gewichtskracht uit op de veer. F v = F g k · |∆l| = m · g |∆l| = m ∙ g k

De massa van de fietser wordt gelijkmatig verdeeld over twee identieke veren. m = mtotaal 2 = 54 kg 2 = 27 kg

We vervangen de symbolen in de formule voor de veerkracht door de overeenkomstige waarden.

|∆l| = m g k = 27 kg · 9,81 N kg 130 N cm = 2,0 cm

Controle: Klopt de eenheid? Ja, de lengteverandering ∆l wordt uitgedrukt in cm.

Klopt de getalwaarde? Ja, de veer van een zadel is niet lang en kan dus ook niet ver indrukken.

OPDRACHT 20 DOORDENKER

Op een massablokje dat bevestigd is aan een verticale veer, werkt de zwaartekracht.

Het blokje oefent een gewichtskracht uit op de veer

F op = F g

Door het gewicht van het blokje rekt de veer uit over een afstand Δl en is er een veerkracht F v . De veerkracht is in rust even groot als, maar tegengesteld aan het gewicht van het blokje: F v = –F g

Daaruit volgt voor de krachtgroottes:

F v = F g k |∆l| = m g

De veerconstante en de massa bepalen hoeveel de veer uitrekt, want:

|∆l| = m g k

• Hoe groter de massa, hoe groter de lengteverandering (|∆l| ~ m).

• Hoe groter de veerconstante (= hoe stijver de veer), hoe kleiner de lengteverandering (|∆l| ~ 1 k ).

Als een massa m die bevestigd is aan een verticale veer met veerconstante k, een lengteverandering ∆l veroorzaakt, dan oefent die massa een gewichtskracht uit op de veer. In rust geldt:

F v = F g

` Maak oefening 9 t/m 11 op p. 116 t/m 118.

Bestudeer de werking van een dynamometer op verschillende hemellichamen.

Een dynamometer wordt meegenomen op een ruimtereis naar de maan en naar Mars.

1 Noteer boven elke dynamometer het juiste hemellichaam.

2 Welke uitspraak over het meetbereik is correct?

Het meetbereik is op elk hemellichaam hetzelfde.

Het meetbereik is het grootst op de maan.

Het meetbereik is het grootst op aarde.

Het meetbereik is het grootst op Mars.

3 Welke uitspraak is correct?

Op de maan gebruik je het best een dynamometer met dezelfde veerconstante als op aarde.

Op de maan gebruik je het best een dynamometer met een grotere veerconstante dan op aarde.

Op de maan gebruik je het best een dynamometer met een kleinere veerconstante dan op aarde.

1 = het v erschil tussen de lengte van de onbelaste veer  l begin en de lengte van de belaste veer l eind Δ l = Δ l > 0: Δ l < 0: 2 = een maat voor de stijfheid van de veer

Grootheid met symbool SI-eenheid met symbool

©VANIN

vervorming

• : De vervorming verdwijnt als de kracht wegvalt.

• : De vervorming blijft als de kracht wegvalt.

• aangrijpingspunt:

KENMERKEN

INVLOEDSFACTOREN

wet van Hooke

veerkracht = een c ontactkracht, uitgeoefend door de opgespannen veer op een voorwer pteken de krachtvectoren

KENMERKEN

• grootte: = k · |delta l| kracht op de veer = een c ontactkracht, uitgeoefend door een voorwerp op de veer

• richting: • zin: • grootte:

• aangrijpingspunt:

• richting: • zin:

1 Boris schiet tijdens het boogschieten in de roos.

a Welke kracht zorgt voor de vervorming van de boog?

b Welk type vervorming ondergaat de boog?

c Welk type vervorming ondergaat de schietschijf?

d Welk van beide voorwerpen kun je beschouwen als een veer?

2 Los de vragen op.

a Welke uitspraak is correct, als de uitgeoefende kracht toeneemt?

Elke vervormbare stof vervormt eerst plastisch en daarna elastisch.

Elke vervormbare stof vervormt eerst elastisch en daarna plastisch.

Elke veer vervormt eerst plastisch en daarna elastisch.

Elke veer vervormt eerst elastisch en daarna plastisch.

b Geef een tegenvoorbeeld bij de foute antwoorden.

3 Je hebt een soepele en een stijve veer. Vul aan met ‘kleiner dan’, ‘gelijk aan’ of ‘groter dan’.

a De veerconstante van de soepele veer is de veerconstante van de stijve veer.

b Bij eenzelfde kracht is de uitrekking van de soepele veer de uitrekking van de stijve veer.

c Bij eenzelfde uitrekking is de kracht op de soepele veer de kracht op de stijve veer.

4 Bestudeer de grafiek en los de vragen op.

a Duid de juiste bewering(en) aan.

Veer 1 heeft de grootste veerconstante.

Veer 1 is de soepelste veer.

Veer 2 is de langste veer.

©VANIN

Op veer 1 en 3 wordt een even grote kracht uitgeoefend.

De lengteverandering van veer 1 en veer 3 is gelijk.

b Van welke veer kun je de veerconstante rechtstreeks aflezen uit de grafiek?

• Duid het punt aan waar je dat afleest.

• Geef de veerconstante. k =

F v (N) Fv(Δ l )-grafiek

5 Zet de veerconstanten om naar N m .

a k = 2 N cm =

b k = 152 kN m =

c k = 0,05 N cm =

d k = 1,2 kN cm =

6 Vervolledig de tabel met de (omgevormde) formule in symbolen en het eindresultaat.

7 Tommy oefent een kracht van 5,0 N uit op de elastiek van een katapult. De elastiek rekt 2,5 cm uit. Bereken de grootte van de veerconstante van zijn katapult.

Gegeven:

Gevraagd: Oplossing: Controle:

8 Rangschik de volgende veren volgens stijgende veerconstante.

• Veer 1 heeft een veerconstante van 8,0 N m .

• Veer 2 drukt 7,0 cm in als er een kracht van 3,5 N op wordt uitgeoefend.

• Veer 3 rekt 4,5 cm uit als er een blokje met massa 25 g aan wordt gehangen.

9 Arya (m = 64 kg) ligt op een matras, waardoor er 160 veren met een veerconstante van 112 N m indeuken. Bereken voor elke veer … a het gewicht dat Arya erop uitoefent; b de indeuking van de matras.

Gegeven:

Gevraagd:

Oplossing:

Controle:

10 De avontuurlijke familie Peeters doet graag extreme sporten. Op reis in Nieuw-Zeeland staat er een bungeejump van een 112 m hoge brug op de planning.

Dochter Lana (m = 33 kg) heeft zich net aan de sprong gewaagd en hangt stil aan de elastiek (k = 19 N m en beginlengte 70 m).

a Bereken de afstand tot het water als Lana stil hangt.

Gegeven:

Gevraagd:

Oplossing:

©VANIN

Controle:

b Is het een goed idee dat vader Mark (m = 96 kg) met dezelfde elastiek springt als Lana? Staaf je antwoord met een berekening.

Gegeven:

Gevraagd:

Oplossing:

Controle:

(–8 m)

c Wat kan de organisatie doen opdat vader Mark toch een veilige spong kan maken?

11 Julia en Saar komen elkaar tegen in de fitness. Saar houdt een halter (m = 2,0 kg) in de lucht en Julia rekt een veer (k = 300 N m ) uit over een afstand van Δl = 0,20 m. Vergelijk de spierkracht die Saar en Julia uitoefenen om de halter en de veer stil te houden.

a Vul de tabel verder aan.

b Teken en benoem de krachten in beide situaties.

` Verder oefenen? Ga naar . 1 2

Aangrijpingspunt

Richting Zin

Grootte

Fspier, H

Fspier, V

1 Begripskennis

• Ik kan het verschil tussen elastische en plastische vervorming uitleggen

• Ik kan het effect van een kracht op een veer bespreken.

• Ik kan in woorden uitleggen wat ‘veerkracht’ en ‘kracht op een veer’ betekenen.

• Ik kan de kenmerken van de veerkracht en de kracht op een veer opsommen.

• Ik kan de krachtsvectoren van en op een veer tekenen.

• Ik kan opsommen welke factoren de grootte van de veerkracht beïnvloeden.

• Ik kan het verband tussen de lengteverandering en de grootte van de veerkracht onderzoeken

• Ik kan het verband tussen de stijfheid van de veer en de grootte van de veerkracht onderzoeken.

• Ik kan in mijn eigen woorden uitleggen wat de veerconstante betekent.

• Ik kan de veerconstante voorstellen op een Fv(∆l)-grafiek.

• Ik kan de wet van Hooke formuleren.

• Ik kan met de lengteverandering van een veer de veerkracht van de veer berekenen met behulp van de veerconstante.

• Ik kan de lengteverandering van een veer die wordt veroorzaakt door de gewichtskracht op die veer, berekenen

2 Onderzoeksvaardigheden

• Ik kan een goed wetenschappelijk onderzoek opstellen om een onderzoeksvraag te beantwoorden.

• Ik kan een onderzoek stap voor stap uitvoeren

• Ik kan waarnemingen en beschrijvingen verbinden met de wetenschappelijke voorstelling in grafieken.

• Ik kan het verband tussen grootheden benoemen (recht evenredig / omgekeerd evenredig / niet evenredig).

• Ik kan grafieken nauwkeurig tekenen.

• Ik kan grafieken nauwkeurig aflezen

• Ik kan berekeningen uitvoeren met afgelezen waarden.

• Ik kan een kracht meten door gebruik te maken van een dynamometer.

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Hoe kun je krachten samenstellen of ontbinden?

LEERDOELEN

Je kunt al:

M een kracht voorstellen als een vector;

M de zwaartekracht en het gewicht berekenen.

Je leert nu:

M krachten met dezelfde richting samenstellen;

M krachten met een verschillende richting samenstellen;

M krachten ontbinden in componenten.

©VANIN

Op de meeste voorwerpen grijpen verschillende krachten tegelijk in. De Belgische bobsleeatletes duwen hun tweemansbob bij de start. Daarbij gebruiken ze spierkracht. Samen met de zwaartekracht en de wrijvingskracht is dat cruciaal voor hun aankomsttijd.

In dit hoofdstuk bestudeer je de kenmerken van de resulterende kracht van krachten die in dezelfde richting of in verschillende richtingen werken, en ga je op zoek naar de component van een kracht volgens de bewegingsrichting.

1 Hoe stel je krachtvectoren met dezelfde richting samen?

OPDRACHT 21

Bestudeer de video van het vertrek van een bobsleeteam.

1 Waarom duwen de atleten de bobslee met vier teamleden?

Duid alle correcte antwoorden aan.

Om de vertreksnelheid zo klein mogelijk te maken.

Om de vertreksnelheid zo groot mogelijk te maken.

Om de zwaartekracht te overwinnen.

Om de wrijvingskracht zo klein mogelijk te maken.

Om de duwkracht zo groot mogelijk te maken.

Om de resulterende kracht op de slee zo groot mogelijk te maken.

2 Bestudeer afbeelding 20 van het vertrekpunt, waarop de wrijvingskracht F w getekend is.

a Teken en benoem de duwkracht Fduw die elke atleet uitoefent.

b Noteer de richting en de zin van de krachten.

Richting Zin

Duwkrachten

Wrijvingskrachten

OPDRACHT 22 ONDERZOEK

Onderzoek de samenstelling van krachten met eenzelfde richting aan de hand van het labo bij het onlinelesmateriaal.

INSTRUCTIEFILMPJE

De samenstelling van verschillende krachten die op een voorwerp inwerken, noem je de resulterende kracht F res . Het is de som van alle krachten (F1, F2 Fn) die inwerken op een voorwerp.

In symbolen: F res = F 1 + F2 + ... + F n .

Voor krachten met dezelfde richting heeft de resulterende kracht (Fres) dezelfde richting.

De grootte F res van de resulterende kracht bereken je als volgt:

• resulterende krachtgrootte van krachten met dezelfde zin berekenen = som krachtgroottes (F res = F 1 + F2);

• resulterende krachtgrootte van krachten met een tegengestelde zin berekenen = verschil tussen de grootste en kleinste krachtgroottes (F res = F 1 – F2).

OPLOSSINGSSTRATEGIE

F res = F 1 + F2

Krachten met eenzelfde richting en eenzelfde zin

F2 F 1

F res

Krachten met eenzelfde richting en een tegengestelde zin

F2 F 1

F res

©VANIN

Je tekent de resulterende krachtvector met de kop-staartmethode:

• Je tekent de eerste krachtvector F 1

• Je tekent de tweede krachtvector F2 vanaf de pijlpunt van F 1

• Je tekent de resulterende krachtvector F res vanaf het begin van de eerste krachtvector tot aan de pijlpunt van de laatste krachtvector.

• Als er meer dan twee krachten ingrijpen, herhaal je dat: eerst voor krachtvectoren met een gelijke zin, vervolgens voor krachtvectoren met een tegengestelde zin.

De krachten worden vaak getekend in een krachtenschema. Dat is een aparte figuur waarop alle krachten getekend zijn in het massapunt.

VOORBEELD KRACHTEN MET DEZELFDE RICHTING SAMENSTELLEN

We bekijken de resulterende kracht op de bobslee tijdens het afduwen. Er werken zes verschillende krachten in de horizontale richting:

• vier duwkrachten Fduw uitgeoefend door de atleten op de (handvaten van de) bobslee volgens de zin van de beweging, met elk een grootte  Fduw = 500 N;

• twee wrijvingskrachten F w uitgeoefend door het ijs op de (glijders van de) bobslee tegengesteld aan de zin van de beweging, met elk een grootte  F w = 250 N.

Krachtenschema

1 cm 500 N

res, w

De resulterende kracht F res is de som van alle krachten die inwerken op de bobslee:

F res = Fduw + Fduw + Fduw + Fduw + F w + F w = 4 · Fduw + 2 · F w

• Het aangrijpingspunt van de resulterende kracht is het massapunt van de bobslee.

• De richting van de resulterende kracht is horizontaal.

Dat is de richting van de individuele krachten.

• De grootte van de resulterende kracht F res bereken je als volgt:

De duwkrachten zijn gericht volgens de bewegingszin:

Fres, duw = Fduw + Fduw + Fduw + Fduw

= 4 · Fduw = 4 · 500 N = 2 000 N

De wrijvingskrachten zijn gericht tegen de bewegingszin:

F res, w = F w + F w = 2 · Fduw = 2 · 250 N = 500 N

Stap 1: Zoek welke kracht het grootst is.

Fduw, res > F w, res

Stap 2: Bereken het verschil.

F res = Fduw + Fduw + Fduw + Fduw – (F w + Fw)

= Fres, duw – F res, w = 2 000 N – 500 N = 1 500 N

• De zin van de resulterende kracht is de zin van de duwkrachten.

Dat is de zin van de grootste kracht. De pijlpunt van F res wijst volgens de bewegingszin.

©VANIN

De resulterende kracht (Fres) is de som van alle krachten (F1, F2 Fn) die inwerken op een voorwerp.

In symbolen: F res = F 1 + F2 + ... + F n .

Voor krachten in dezelfde richting bepaal je de resulterende kracht met de kop-staartmethode in één richting. De resulterende kracht heeft dezelfde richting als de afzonderlijke krachten.

` Maak oefening 1 t/m 4 op p. 126 en 127.

2 Hoe stel je krachtvectoren met een verschillende richting samen?

OPDRACHT 23 ONDERZOEK

Onderzoek de samenstelling van krachten met een verschillende richting aan de hand van het labo bij het onlinelesmateriaal.

OPLOSSINGSSTRATEGIE

INSTRUCTIEFILMPJE

Je tekent de resulterende krachtvector met de kop-staartmethode:

• Je tekent de eerste krachtvector F1.

• Je tekent de tweede krachtvector F2 vanaf de pijlpunt van F1.

• Je tekent de resulterende krachtvector Fres vanaf het begin van de eerste krachtvector tot aan de pijlpunt van de laatste krachtvector.

Dat is ook hoe je in de wiskunde vectoren optelt. De krachten worden vaak getekend in een krachtenschema.

VOORBEELD KRACHTEN MET VERSCHILLENDE RICHTING SAMENSTELLEN

Op afbeelding 23 zie je het bovenaanzicht van twee atleten die na de wedstrijd hun bobslee voorttrekken met een touw. Ze oefenen twee verschillende krachten met een verschillende richting uit:

• Atleet 1 trekt met een kracht Ftrek, 1 met een richting schuin naar rechts en een grootte Ftrek, 1 = 200 N.

• Atleet 2 trekt met een kracht Ftrek, 2 met een richting schuin naar links en een grootte Ftrek, 2 = 200 N. De resulterende trekkracht F res is de som van beide trekkrachten die inwerken op de touwen aan de bobslee: F res = Ftrek, 1 + Ftrek, 2.

• Het aangrijpingspunt van de resulterende kracht is het massapunt van de bobslee.

• De richting en de zin van de resulterende kracht vind je met de kopstaartmethode.

©VANIN

Gebruik de schaalverdeling nauwkeurig wanneer je de krachten tekent. TIP

• De richting van de resulterende kracht F res is rechtdoor en de zin is naar links.

• De grootte van de resulterende kracht F res wordt bepaald door de lengte van Fres. Je meet de lengte van de vector en gebruikt de schaal om de krachtgrootte te bepalen. De lengte van F res is voor de atleten 3,7 cm. Met een schaalverdeling van 1 cm 100 N betekent dat dat F res = 370 N

Op Diddit vind je verdiepingsmateriaal over hoe je een krachtvector kunt ontbinden in componenten.

De resulterende kracht F res is de diagonaal van het parallellogram gevormd door de vectoren Ftrek, 1 en Ftrek, 2 Op afbeelding 24 zie je de trekkrachten en de resulterende kracht terwijl de atleten de bobslee voorttrekken.

Krachtenschema

©VANIN

Bij krachten in een verschillende richting bepaal je de resulterende kracht met de kop-staartmethode. De resulterende kracht is gericht volgens de diagonaal van het parallellogram gevormd door de krachten.

` Maak oefening 5 en 6 op p. 127.

Je leerde hier hoe je krachten kunt samenstellen. Je kunt krachten ook ontbinden in verschillende componenten volgens een gekozen richting. Je vindt meer over de ontbinding van krachten bij het onlinelesmateriaal.

WEETJE

Kenmerken resulterende kracht : F res = • richting: • zin: • grootte:

Kenmerken resulterende kracht : F res = • richting:

Gegeven : kr achten van 10 N en 20 N naar rechts

Gevraagd : F res = ?

De enige kracht die inwerkt is ook de resulterende kracht.

JA

grootte: NEE

Hebben de krachten dezelfde zin?

Gegeven : kr achten van 10 N naar rechts en 20 N naar links

Gevraagd : F res = ?

zin:

©VANIN

NEE

JA Werkt er meer dan één kracht in op het voorwerp?

Je kunt de resulterende kracht bepalen met de kop-staartmethode.

F res =

JA

Hebben al de krachten dezelfde richting?

NEE

Kenmerken resulterende kracht : F res = • richting: • zin: • grootte:

Stel eerst de krachten per richting samen.

1 Lisa (m = 80 kg) neemt de lift (m = 320 kg) van de gelijkvloerse naar de derde verdieping. Teken en benoem de gevraagde krachten in het massapunt P.

De zwaartekracht op de lege lift De zwaartekracht

• op de lege lift,

• op Lisa,

• op het geheel

2 Rani en Louise houden een wedstrijdje touwtrekken.

Ze trekken beiden met een kracht van 200 N.

Louise kan een kracht van 100 N uitoefenen met haar schoen op de grond, Rani een kracht van 150 N.

a Teken de trekkrachten (Ftrek, L en Ftrek, R) en de krachten op de grond (Fgrond, L en Fgrond, R).

Gebruik de schaal.

b Teken het krachtenschema in het punt P met …

De motorkracht en de zwaartekracht tijdens het vertrek omhoog, zodat de weergegeven resulterende kracht inwerkt

• de resulterende kracht uitgeoefend door Louise (FL) en Rani (FR),

• de resulterende kracht van Rani en Louise samen (Fres).

c Wie wint? Meerdere antwoorden zijn mogelijk.

degene die het hardste trekt

degene die zich het best kan tegenhouden

degene die de grootste resulterende kracht levert

De trekkrachten zijn altijd gelijk. Ga dat na door aan twee dynamometers te trekken, zoals op de afbeelding.

Dat principe staat bekend als de derde wet van Newton: actie-reactie. Als voorwerp A een kracht uitoefent op voorwerp B, dan oefent voorwerp B een even grote, maar tegengestelde kracht uit op voorwerp A.

Het is dus degene die de grootste kracht kan uitoefenen op de grond, die wint bij het touwtrekken.

WEETJE

3 Een raket met een massa van 2 050 ton wordt gelanceerd met een motorkracht van 30 MN.

a Teken de zwaartekracht, de motorkracht en de resulterende kracht in een krachtenschema. Schat de onderlinge groottes.

b Bereken de grootte van de zwaartekracht en de grootte van de resulterende kracht.

Gegeven:

Gevraagd: 1 2

Oplossing: 1 2

c Klopt je voorspelling over de onderlinge groottes?

4 Twee krachten F 1 en F2 werken in dezelfde richting, met F 1 > F2. Vul aan.

Resulterende krachtvector

Resulterende krachtgrootte

Krachten werken in dezelfde zin

res =

res = Krachten werken in tegengestelde zin

res =

5 Twee luchtkussens worden voortgetrokken door een motorboot. De trekkrachten zijn even groot. Teken en benoem in het punt P de trekkrachten en de resulterende kracht.

Krachtenschema

6 Op een rubberbootje worden twee krachten uitgeoefend: een kracht F horizontaal naar rechts en een kleinere kracht F'. De oriëntatie van F verandert. Rangschik de groottes van de resulterende krachten F 1 F6 van klein naar groot.

Verder oefenen?

1 Begripskennis

• Ik kan het begrip ‘resulterende kracht’ omschrijven

• Ik kan de kenmerken van de resulterende kracht van krachten met dezelfde richting bepalen

• Ik kan de kenmerken van de resulterende kracht van krachten met een verschillende richting bepalen.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan een dynamometer aflezen.

• Ik kan de resulterende krachten nauwkeurig tekenen.

• Ik kan de componenten van een kracht nauwkeurig tekenen

• Ik kan nauwkeurig berekeningen uitvoeren.

` Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

Welk verband bestaat er tussen kracht en evenwicht?

LEERDOELEN

Je kunt al:

M de resulterende kracht bepalen;

M het dynamisch effect van een kracht omschrijven;

M de zwaartekracht en het gewicht berekenen.

Je leert nu:

M de normaalkracht omschrijven en voorstellen;

M het verband tussen de resulterende kracht en rust omschrijven;

M het krachtmoment omschrijven en berekenen;

M de voorwaarden voor evenwicht bepalen en toepassen.

Acrobaten gebruiken hun spierkracht om in verrassende poses te gaan staan. Ze zoeken een evenwicht en overwinnen daarbij de zwaartekracht. Ook de meeste voorwerpen rondom ons staan stil en bevinden zich in evenwicht. Welke kracht zorgt ervoor dat ze niet door de ondergrond zakken? Hoe komt het dat ze niet of net wel kantelen?

In dit hoofdstuk bestudeer je de voorwaarden voor evenwicht.

1 Hoe groot is de resulterende kracht bij een voorwerp in rust?

1.1 Normaalkracht

OPDRACHT 24

Bestudeer de afbeeldingen van spelende kinderen.

1 Wat gebeurt er als de kinderen het oppervlak raken? Duid aan onder de afbeeldingen.

2 Hoe komt dat? Duid aan onder de afbeeldingen.

©VANIN

De kinderen kunnen wel / niet op het water staan. De kinderen kunnen wel / niet op het grasveld staan.

De ondersteuning door het water is te klein / groot genoeg / te groot

De ondersteuning door het grasveld is te klein / groot genoeg / te groot

Een voorwerp dat ondersteund wordt, ondervindt een normaalkracht. Als het ondersteunende voorwerp niet stevig genoeg is, is er geen normaalkracht.

De normaalkracht is een contactkracht met als symbool F n en deze kenmerken:

• Het aangrijpingspunt is op het voorwerp dat ondersteund wordt

• De richting is loodrecht op het oppervlak. Daar komt de naam ‘normaalkracht’ vandaan: ‘normaal’ is een ander woord voor ‘loodrecht’.

• De zin van de normaalkracht is van het oppervlak weg.

OPDRACHT 25 DOORDENKER

• De grootte van de normaalkracht is voor horizontale oppervlakken even groot als het gewicht

VOORBEELD NORMAALKRACHT

De breakdancer staat met zijn handen op de grond. Hij oefent een gewicht F g uit op de vloer. Hij zakt niet door de vloer, omdat de vloer hem ondersteunt. Er is een normaalkracht F n in het contactpunt van de hand met de grond.

Als een voorwerp ondersteund wordt door een oppervlak, dan werkt er een normaalkracht F n met deze kenmerken:

• aangrijpingspunt: op het voorwerp dat ondersteund wordt,

• richting: loodrecht op het oppervlak,

• zin: van het oppervlak weg,

• grootte: voor horizontale oppervlakken even groot als het gewicht.

` Maak oefening 1 en 2 op p. 139.

©VANIN

Bestudeer de kenmerken van de normaalkracht.

1 Teken en benoem de normaalkracht op beide afbeeldingen.

1 2

2 Welke uitspraak is correct? Duid aan.

De normaalkracht is altijd even groot als en tegengesteld aan de gewichtskracht.

De normaalkracht is altijd verticaal.

De normaalkracht staat altijd loodrecht op het oppervlak.

1.2 Verband tussen resulterende kracht en rust

OPDRACHT 26

Bestudeer de bewegingstoestand van een baal hooi tijdens het duwen.

1 Welke krachten werken op de baal hooi?

• in de x-richting:

©VANIN

• in de y-richting:

2 Jonas en Lukas duwen even hard tegen een baal hooi in rust. Duid de juiste uitspraken aan in de tabel.

In welke bewegingstoestand bevindt de baal zich?

• De baal hooi blijft altijd / soms / nooit in rust.

• De baal hooi komt altijd / soms / nooit in beweging in de x-richting.

• De baal hooi komt altijd / soms / nooit in beweging in de y-richting.

• De snelheidsvector verandert altijd / soms / nooit

• De baal hooi blijft altijd / soms / nooit in rust.

• De baal hooi komt altijd / soms / nooit in beweging in de x-richting.

• De baal hooi komt altijd / soms / nooit in beweging in de y-richting.

• De snelheidsvector verandert altijd / soms / nooit

Welk verbanden gelden voor de resulterende kracht?

• De baal blijft in rust in de horizontale richting als F res, x = 0 / F res, x ≠ 0

• De baal blijft in rust in de verticale richting als F res, y = 0 / F res, y ≠ 0.

• De baal blijft helemaal in rust als F res = 0 / F res ≠ 0

De bewegingsrichting noem je de x-richting. De richting loodrecht op de beweging noem je de y-richting.

Bij een voorwerp in rust of in evenwicht is er geen beweging in de x - en de y -richting. De snelheid is de hele tijd nul: vbegin = veind = 0 , dus de snelheidsverandering ∆v = 0.

De bewegingstoestand van het voorwerp in rust verandert niet. Er is geen dynamisch effect van de resulterende kracht, omdat de resulterende kracht nul is: F res = 0.

De totale resulterende kracht bestaat uit de resulterende kracht in de bewegingsrichting en de resulterende kracht loodrecht op de bewegingsrichting: F res = F res, x + F res, y

Bij rust geldt: F res, x = 0 en F res, y = 0

VOORBEELD RESULTERENDE KRACHT BIJ RUST

We bekijken de bewegingstoestand van de acrobaten. Ze zijn in rust.

• In de horizontale richting werken er geen krachten. Er is geen resulterende kracht en geen verandering van bewegingstoestand.

• In de verticale richting werken er telkens twee krachten. Krachten bij de hangende acrobate (m = 66,0 kg): zwaartekracht F z en spankracht F s

Rust betekent dat F res = F z + F s = 0. De grootte van de spankracht is:

F s = F z = m · g = 66,0 kg · 9,81 N kg = 647 N

Krachten bij de staande acrobaat die een andere acrobaat optilt (mtot = 172,3 kg): zwaartekracht F z en normaalkracht F n Rust betekent dat F res = F z + F n = 0. De grootte van de normaalkracht is:

©VANIN

F n = F z = m g = 172,3 kg 9,81 N kg = 1,69 kN

Per voet is de grootte van de normaalkracht F n, 1 = F n, 2 = F n 2 = 845 N.

Voor een voorwerp in rust of in evenwicht is de resulterende kracht nul in beide richtingen:

F res, x = 0 en F res, y = 0, dus F res = 0.

` Maak oefening 3 t/m 7 op p. 139 en 140.

Afb. 26

Afb. 27

OPDRACHT 27 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

Simon staat klaar om te schieten met zijn pijl (m = 30 g) en boog. Hij trekt met een kracht van 85 N aan het koord.

1 Teken en benoem de inwerkende krachten op de pijl in een krachtenschema.

2 Bereken de normaalkracht en de veerkracht.

Gegeven: F = 85 N; m = 30 g

Gevraagd: F v = ?; F n = ?

Oplossing: De pijl is in rust, dus F res = 0.

Krachtenschema

©VANIN

n F F z F v

• Er werken twee krachten in de x -richting: de trekkracht uitgeoefend door Simon en de veerkracht uitgeoefend door het koord.

F res, x = F + F v = 0 dus F v = F = 85 N

• Er werken twee krachten in de y -richting: de zwaartekracht en de normaalkracht door de hand en door de boog.

F res, y = F n + F z = 0 dus F n = F z = m · g = 30 · 10–3 kg · 9,81 N kg = 0,29 N

Controle: Klopt de verhouding van de getekende krachten in de x- en de y-richting?

Nee, de krachten in de y-richting moeten veel kleiner getekend worden. Voor de duidelijkheid worden ze vergroot weergegeven. Het is wel belangrijk dat de krachten in één richting even groot getekend zijn.

OPLOSSINGSSTRATEGIE

• Omschrijf in je eigen woorden wat er gebeurt en wat je zoekt.

• Bepaal de krachten die inwerken.

• Teken de krachten. Denk na over de onderlinge groottes.

• Denk na over de gegevens die je nodig hebt om de ontbrekende krachten te berekenen.

• Noteer alles in symbolen bij de gegevens en het gevraagde.

• Werk de oplossing uit.

Noteer de voorwaarde voor rust in de x-richting en de y-richting. Vul de krachtvectoren in voor elke richting.

Bepaal daarmee de grootte van de ontbrekende kracht in elke richting.

• Sta stil bij je antwoord.

Klopt de eenheid? Klopt de grootte?

INSTRUCTIEFILMPJE

F

2 Wanneer is een voorwerp in evenwicht?

2.1 Krachtmoment

OPDRACHT 28

Bestudeer de positie van een deurklink.

Op welke positie kun je een draaideur het makkelijkst openen?

1 Voorspel een rangschikking van de klinken volgens toenemende moeilijkheid.

2 Test je rangschikking uit.

• Ga naar een deur en zet ze op een kier.

• Zet je wijsvinger op de deur op de verschillende posities en open de deur.

3 Schrijf de juiste rangschikking op.

4 Verklaar de positie van een standaarddeurklink.

Het draai-effect van een kracht ten opzichte van een draaipunt kun je beschrijven met de grootheid krachtmoment M

• De grootte van het krachtmoment voor een loodrechte kracht wordt bepaald door de krachtgrootte F en de afstand r tussen het draaipunt en het aangrijpingspunt van de kracht.

©VANIN

Grootheid met symbool SI-eenheid met symbool krachtmoment M = F · r newtonmeter N ∙ m

• De draaizin wordt bepaald door de zin van de kracht. De kracht kan een draaiing veroorzaken: in tegenwijzerzin: het krachtmoment is positief; in wijzerzin: het krachtmoment is negatief

Afb. 29

Om aan te duiden dat een kracht loodrecht inwerkt, voeg je een tekentje toe dat je kent uit de wiskunde: . Als het duidelijk is dat de kracht loodrecht inwerkt, noteer je dat tekentje niet.

In de wiskunde gebruik je een georiënteerde hoek om de draaizin aan te geven:

• draaiing in tegenwijzerzin: AÔB is een positieve hoek.

• draaiing in wijzerzin: BÔA is een negatieve hoek.

In de fysica gebruik je vaak een Griekse letter.

Voorbeelden:

• thèta i

• alfa a

• bèta b

• mu n

VOORBEELD x(t)-GRAFIEKEN BIJ INHALEN

Op afbeelding 31 zie je de bovenkant van een deur, waar op twee plaatsen een even grote kracht wordt uitgeoefend.

• De kracht F 1 zorgt voor een draaiing in tegenwijzerzin

Het krachtmoment is positief, met grootte M 1 = F 1 · r1

• De kracht F2 zorgt voor een draaiing in wijzerzin. Het krachtmoment is negatief, met grootte M2 = F2 · r2

• De kracht F3 wordt schuin (onder een hoek i met de deur) uitgeoefend. De loodrechte component van de kracht zorgt voor een draaiing in wijzerzin. Het krachtmoment is negatief, met grootte M3 = F 3, · r2 = F3 · sin i · r3 = F3 · r3 · sin i.

Aangezien de krachten even groot zijn, veroorzaakt de kracht op het uiteinde van de deur het grootste krachtmoment. Je kunt de deur het makkelijkst openen als je op het uiteinde duwt.

Je duwt het best loodrecht (i = 90°) op de deur om ze te openen. Hoe schuiner je duwt, hoe kleiner het krachtmoment is.

Krachtmoment is een grootheid die het draai-effect beschrijft. Als je een kracht F uitoefent op een afstand r van het draaipunt onder een hoek i, dan is het krachtmoment gegeven door:

M = F r sin i

i

Afb. 32

De eenheid van krachtmoment is N ∙ m.

OPDRACHT 29

Los het vraagstuk op.

Lieselotte is fietsenmaker. Om een bout los te draaien, is er een krachtmoment nodig van M = 5,0 N ∙ m in tegenwijzerzin. Daarvoor gebruikt ze een steeksleutel, zoals op afbeelding 33.

1 Teken en bereken de nodige krachten.

Werk de berekening uit op een cursusblad.

a de nodige kracht die loodrecht uitgeoefend wordt op het uiteinde van de steeksleutel

b de nodige kracht die loodrecht uitgeoefend wordt halverwege de steeksleutel

c de nodige kracht die onder een hoek van 60° uitgeoefend wordt op het uiteinde van de steeksleutel

2 Controleer je antwoord.

VRAAGSTUK KRACHTMOMENT

2.2 Evenwichtsvoorwaarden

OPDRACHT 30 ONDERZOEK

©VANIN

r1 = 10 cm

1 Werk in het sjabloon dat je bij het onlinelesmateriaal vindt, een onderzoek uit om na te gaan wanneer een draaiend voorwerp in evenwicht is.

2 Laat je inspireren door de links bij het onlinelesmateriaal.

3 Sla je onderzoek op in je onderzoeksmap.

Je kent de begrippen ‘translatie’ en ‘rotatie’ uit de wiskunde. Een translatie is een verschuiving van het voorwerp als geheel. Een rotatie beschrijft de draaiing rond een vast punt, het centrum.

NW-METHODE

Een voorwerp is in rust of in evenwicht als er geen verandering van bewegingstoestand is. Er is geen verschuiving en geen draaiing

Daarvoor zijn er twee evenwichtsvoorwaarden:

• translatie-evenwicht: Er is geen verschuiving. De resulterende kracht is nul.

• rotatie-evenwicht: Er is geen draaibeweging. Het resulterende krachtmoment is nul

draaipunt

TIP

• Translatie-evenwicht: De normaalkracht in het draaipunt is even groot als en tegengesteld aan de totale zwaartekracht.

• Rotatie-evenwicht: De zwaartekracht van elke massa veroorzaakt een krachtmoment. Hun zin is tegengesteld: krachtmoment in tegenwijzerzin: M 1 = F z, 1

krachtmoment in wijzerzin: M2 = –F

Er is evenwicht als M tot = M

Dat betekent dat F z,

VOORBEELD EVENWICHTSVOORWAARDEN BIJ ATLEET

Op afbeelding 35 zie je een acrobate in evenwicht. Ze kan in die positie blijven liggen doordat ze het juiste steunpunt gevonden heeft om haar zwaardere bovenlichaam (met zwaartekracht F z, romp ) in evenwicht te brengen met haar lichtere benen (met zwaartekracht Fz, benen ).

Een voorwerp is in rust of in evenwicht als er geen verandering van bewegingstoestand is. Er is geen verschuiving en geen draaiing.

Er zijn twee evenwichtsvoorwaarden:

• translatie-evenwicht: De resulterende kracht is nul. F res = 0 dus F

x = 0 en F res, y = 0

• rotatie-evenwicht: Het resulterende krachtmoment is nul M res = 0 dus F 1 r1 = F2 r2

` Maak oefening 8 t/m 11 op p. 141 en 142.

OPDRACHT 31

Los het vraagstuk op.

Josse (m = 70,0 kg) is in evenwicht op een draaibare plank door zijn gewicht te verdelen over zijn voeten. Het gewicht op zijn rechtervoet is 458 N, op 15 cm van het draaipunt.

©VANIN

Bereken de normaalkracht in het steunpunt en de lengte van de plank.

Werk uit op een cursusblad.

Controleer je antwoord via de QR-code

CONTROLEER JE OPLOSSING

EVENWICHT

Kernbegrippen

normaalkracht

translatie-evenwicht

krachtmoment

Notities

• Het oefent een kracht uit met deze kenmerken:

aangrijpingspunt:

richting: zin:

grootte: voor horizontale oppervlakken

• Als het voorwerp zich niet verschuift, is de

©VANIN

rotatie-evenwicht

In formules: F res, x = en F res, y = , dus F res =

• Een kracht F uitgeoefend onder een hoek i op een afstand r van een

draaipunt veroorzaakt een :

grootte: M =

draaizin:

° positief krachtmoment:

° negatief krachtmoment:

• Als het voorwerp geen draaiing uitvoert, is het

In formules:

Leg uit waarom de acrobate in evenwicht is.

• Translatie-evenwicht:

• Rotatie-evenwicht:

.

1 Bestudeer het spel van Thor en Rosie. Teken de normaalkrachten op de strandbal.

De strandbal rolt over het strand.

De strandbal ligt stil.

De strandbal is net losgekomen van de grond en vliegt omhoog.

2 Waarom moet het ijs dik genoeg zijn om veilig te kunnen schaatsen? Leg uit met de normaalkracht.

3 Bestudeer de bowlingbal. Duid de bewegingstoestand aan.

1 2

• rust / beweging

• rust / beweging in de x-richting

• rust / beweging in de y-richting

4 Welke uitspraak is correct? Duid aan.

• rust / beweging

• rust / beweging in de x-richting

• rust / beweging in de y-richting

Op een voorwerp in rust werken geen krachten.

3

• rust / beweging

• rust / beweging in de x-richting

• rust / beweging in de y-richting

©VANIN

Op een voorwerp in rust werken enkel de zwaartekracht en de normaalkracht.

Op een voorwerp in rust werkt geen resulterende kracht.

Op een voorwerp in rust werken geen krachten volgens de x-richting.

5 Liesbeth (m = 61 kg) hangt onderaan een elastiek (k = 500 N m ) na een bungeesprong.

a Teken een krachtenschema.

b Bereken de uitrekking van de elastiek.

Gegeven:

Gevraagd:

Oplossing:

©VANIN

6 Twee verhuizers verhuizen een sofa (m = 165 kg).

Ze heffen allebei evenveel.

a Teken en benoem de zwaartekracht en de hefkrachten op de sofa in hun aangrijpingspunt.

b Bereken de hefkracht van elke verhuizer.

Gegeven:

Gevraagd:

Oplossing:

7 Leg een kartonnetje met een munt op een glas, zoals op de afbeelding.

a Wat zal er gebeuren als je het kartonnetje plots wegtrekt of ertegen duwt?

b Test het uit.

c Wat stel je vast? Was je voorspelling juist?

d Verklaar.

8

9

Een inbussleutel heeft een korte en een lange arm. Waarom steek je de korte arm in de schroef? Duid aan.

Dat is handiger om vast te pakken.

Dat maakt niet uit.

Je creëert een grote kracht.

Je creëert een groot krachtmoment.

Emilie (m = 18 kg) en Sanne (m = 16 kg) zitten op een wip met stoeltjes op 1,3 m van het draaipunt. Op de afbeelding zie je de situatie in rust.

a Benoem de kinderen.

b Wie moet verschuiven om evenwicht te bekomen?

c Bereken hoeveel ze vooruit moet schuiven.

Gegeven:

Gevraagd:

Oplossing:

10 Karolien draagt haar ski’s (l = 180 cm) over haar schouder, met 100 cm van de ski’s voor haar schouder. De ski’s liggen in evenwicht.

a Hoe is de kracht die haar hand uitoefent, gericht?

verticaal omlaag

verticaal omhoog

horizontaal naar rechts

horizontaal naar links

©VANIN

b Wat zal er veranderen aan de kracht als Karolien de ski’s 40 cm naar achteren schuift? Verklaar.

11 Op een bouwwerf worden lasten verplaatst met kranen en heftrucks. Opdat die machines niet kantelen, mag de last niet te groot zijn. Bestudeer de afbeeldingen. De massa van de heftruck is 2,3 ton.

a Hoeveel last kunnen de kraan en de heftruck optillen? Voer de nodige berekeningen uit.

Gegeven:

Gevraagd:

Oplossing:

b Vervolledig de afbeeldingen met de gewichtskrachten.

c De last van de kraan kan nog verder naar links schuiven. Moet de maximale last dan groter of kleiner zijn om ongelukken te vermijden? Verklaar.

` Verder oefenen? Ga naar .

1 Begripskennis

• Ik kan de normaalkracht omschrijven

• Ik kan het verband tussen kracht en rust omschrijven.

• Ik kan de krachten in rust berekenen

• Ik kan het krachtmoment omschrijven.

• Ik kan de evenwichtsvoorwaarden geven.

• Ik kan de krachten en de krachtmomenten bij evenwicht berekenen

2 Onderzoeksvaardigheden

• Ik kan een onderzoek opstellen en uitvoeren

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan de inwerkende en resulterende krachten weergeven als een vector in een krachtenschema.

• Ik kan nauwkeurig berekeningen uitvoeren.

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Welk verband bestaat er tussen kracht en beweging?

LEERDOELEN

Je kunt al:

M de resulterende kracht bepalen;

M het dynamisch effect van een kracht omschrijven;

M de zwaartekracht, het gewicht en de normaalkracht berekenen.

Je leert nu:

M de wrijvingskracht bepalen en voorstellen;

M het verband tussen de resulterende kracht en een ERB omschrijven;

M het verband tussen de resulterende kracht en een snelheidsverandering omschrijven.

Om als eerste over de meet te komen, steken de sprinters een tandje bij. Ze gebruiken al hun spierkracht om te versnellen. Maar welke rol spelen de wind, de helling en de ondergrond?

In dit hoofdstuk bestudeer je welke krachten werken bij alledaagse bewegingen. Je onderzoekt het verband tussen de resulterende kracht en de eventuele veranderingen van de bewegingstoestand.

1 Bij welke kracht beweegt een voorwerp aan een constante snelheid?

1.1 Wrijvings- en weerstandskrachten

OPDRACHT 32

Bestudeer de wrijvingskracht.

Als je een kast probeert te verschuiven, ondervind je hinder door de ondergrond.

1 Maak de uitspraak correct.

©VANIN

Om een stilstaande kast in beweging te duwen is meer/minder/evenveel kracht nodig dan om een schuivende kast in beweging te houden.

2 Welke kenmerken heeft de wrijvingskracht volgens jou? Duid aan.

Kenmerken wrijvingskracht

aangrijpingspunt

Hypothese

handen / contactpunt met de grond / zwaartepunt

richting volgens / loodrecht op de bewegingsrichting zin volgens de beweging / tegengesteld aan de beweging / omhoog / omlaag

• afhankelijk / onafhankelijk van de ondergrond

grootte

• afhankelijk / onafhankelijk van de massa van het voorwerp

• constant / niet constant tussen het moment dat je begint te duwen, en de beweging

3 Open in de applet het onderdeel ‘Wrijving’.

a Onderzoek de kenmerken van de wrijvingskracht.

b Noteer de kenmerken in de tabel.

c Vergelijk de kenmerken met je hypothese.

WRIJVING

Waarneming

• van de ondergrond

• van de massa van het voorwerp

• tussen het moment dat je begint te duwen, en de beweging

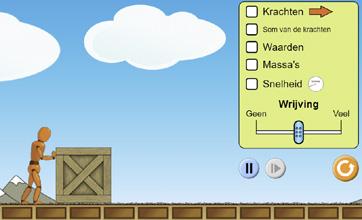
Contactoppervlak

©VANIN

Materiaal n

rubber op asfalt 0,90

ski op sneeuw 0,14

hout op hout 0,42

staal op staal 0,74

rubber op staal 1,20 Tabel 3

Een voorwerp dat beweegt of in beweging gebracht wordt, ondervindt hinder van het oppervlak waardoor het ondersteund wordt. Het oppervlak oefent een wrijvingskracht F w uit op het voorwerp. Wrijving zorgt voor grip op de ondergrond en is nodig om te kunnen bewegen.

De wrijvingskracht F w heeft deze kenmerken:

• De wrijvingskracht is een contactkracht met als aangrijpingspunt het contactpunt

• De wrijvingskracht is gericht volgens de bewegingsrichting.

• De zin van de wrijvingskracht is tegengesteld aan de beweging.

• De grootte van de wrijvingskracht is afhankelijk van de ondergrond en is niet constant tijdens de beweging. De wrijvingskracht is maximaal net voordat een voorwerp in beweging komt.

De maximale wrijvingskracht kun je berekenen als: F w, max = n · F n waarbij n de wrijvingscoëfficiënt is en F n de normaalkracht. Hoe groter de hinder, hoe groter de wrijvingscoëfficiënt.

De wrijvingscoëfficiënt is een onbenoemd getal. In tabel 3 zie je enkele voorbeelden.

F

Oppervlak

OPDRACHT 33 VOORBEELDOEFENING

Bestudeer het vraagstuk.

Mehdi wil een houten kast van 75,0 kg verschuiven op een houten vloer.

1 Teken op afbeelding 37 de krachten net voordat de kast in beweging komt.

2 Hoe hard moet Medhi duwen?

Gegeven: m = 75,0 kg; n = 0,42

Gevraagd: Fduw = ?

Oplossing:

De kast is in rust, dus F res = 0.

• Er werken twee krachten in de x -richting: de duwkracht uitgeoefend door Mehdi en de wrijvingskracht uitgeoefend door de grond.

F res, x = Fduw + F w = 0 dus Fduw = F w = n · F n (1)

• Om de normaalkracht te kennen, moet je de krachten in de y-richting bestuderen.

Er werken twee krachten in de y -richting: de normaalkracht uitgeoefend door de vloer en de zwaartekracht

F res, y = F n + F z = 0 dus F n = F z = m · g = 75,0 kg · 9,81 N kg = 736 N (2)

(2) invullen in (1) geeft: Fduw = F w = n

Controle: Vergelijk de grootte van de zwaartekracht van de kast en de duwkracht. Wat stel je vast?

De duwkracht is kleiner dan de zwaartekracht. Je kunt een kast makkelijker verschuiven dan opheffen.

VOORBEELD INVLOED VAN ONDERGROND OP WRIJVINGSKRACHT

Renners neutraliseren de koers na talloze valpartijen: ‘Die laatste afdaling lag vol olie’

Op droog asfalt is de wrijvingskracht met de dunne rubberen banden van koersfietsen ideaal (afbeelding 38, links). Bij regen (afbeelding 38, rechts) worden de wegen gevaarlijk glad doordat de wrijvingskracht van water en olie veel kleiner is. Renners verliezen dan hun grip op de weg, met valpartijen (zoals in de Tour de France van 2020) tot gevolg.

©VANIN

Bron: www.hln.be

Naast de ondergrond veroorzaakt ook de lucht hinder. De hinder veroorzaakt door een gas of een vloeistof noem je de weerstandskracht. Je leert er meer over bij het onlinemateriaal.

Een voorwerp ondervindt hinder van de omgeving. Er werkt op het voorwerp een wrijvingskracht door de ondergrond en een weerstandkracht door de lucht. De wrijvingskracht worden voorgesteld door F w met deze kenmerken:

• aangrijpingspunt: het contactpunt (voorgesteld in het massapunt),

• richting: de x -as,

• zin: tegengesteld aan de beweging,

• grootte: afhankelijk van materiaal en afhankelijk van de bewegingstoestand

` Maak oefening 1 t/m 4 op p. 158.

1.2 Verband resulterende kracht en ERB

OPDRACHT 34 ONDERZOEK

Onderzoek het verband tussen de resulterende kracht en een ERB aan de hand van het labo bij het onlinelesmateriaal.

©VANIN

Een voorwerp voert een ERB uit als de snelheid(svector) v ≠ 0 constant is: vbegin = veind, dus de snelheidsverandering ∆v = 0.

De bewegingstoestand van het voorwerp dat een ERB uitvoert, verandert niet. Er is geen dynamisch effect van de resulterende kracht, omdat de resulterende kracht nul is: F res = 0.

VOORBEELD KRACHT BIJ ERB VAN DE RENNERS

Tijdens een wedstrijd ondervindt een wielrenner wrijving van de grond en luchtweerstand. Om zijn snelheid constant te houden, moet hij een spierkracht uitoefenen die net even groot is als de weerstandskracht.

De renner voert een ERB met een snelheid van v = 43 km h uit.

• Bij het begin van de wedstrijd is er weinig wind (tijd t1 en t2).

• De renner fietst aan een constante snelheid van 43 km h in eenzelfde richting en zin. De snelheidsvector is constant (∆v = 0, want v1 = v2). Er is geen verandering van bewegingstoestand.

Om aan een constante snelheid te fietsen, oefent de renner een spierkracht (Fspier = 600 N) uit die even groot is als de wrijvingskracht (F w = 600 N). De resulterende kracht is nul.

F res, x = Fspier + F w = 0, dus

F res, x = Fspier – F w = 600 N – 600 N = 0 N

• Na een tijdje steekt de wind op (tijd t3 en t4). Als de renner harder trapt, kan hij aan dezelfde snelheid (v = 43 km h ) blijven fietsen.

©VANIN

De renner fietst aan een constante snelheid van 43 km h in eenzelfde richting en zin. De snelheidsvector is constant (∆v = 0, want v3 = v4).

Er is geen verandering van bewegingstoestand.

Om aan een constante snelheid te blijven fietsen, moet de renner een spierkracht uitoefenen die even groot is als de wrijvingskracht (F w ' = 800 N), zodat de resulterende kracht nul is.

F r ' es, x = F s ' pier + F w ' = 0, dus F s ' pier = F w ' = 800 N

De benodigde spierkracht is groter dan op het rustige stuk.

Zoals besproken in paragraaf 4.1 B, is de renner in de y-richting in rust, omdat de normaalkracht de zwaartekracht compenseert:

F res, y = F z + F n = 0.

Een voorwerp voert een ERB uit als de snelheid constant is:

vbegin = veind ≠ 0, dus ∆v = 0.

Er is geen snelheidsverandering, omdat de resulterende kracht nul is:

F res = 0.

` Maak oefening 5 t/m 8 op p. 159 en 160.

OPDRACHT 35

Los het vraagstuk op.

Een renner (m = 75,6 kg) fietst aan een constante snelheid van 48 km h . Hij trapt met een kracht van 560 N.

1 Teken en benoem alle krachten in een krachtenschema.

2 Bereken alle inwerkende krachten. Werk je berekening uit op een cursusblad.

3 Controleer je antwoord.

Krachtenschema

©VANIN

VRAAGSTUK ERB

OPLOSSINGSSTRATEGIE

• Omschrijf in je eigen woorden wat er gebeurt en wat je zoekt.

• Welke bewegingstoestand is er in de x-richting?

• Welke bewegingstoestand is er in de y-richting?

• Welke krachten werken er in?

• Welk verband is er tussen de bewegingstoestand en de krachten?

• Teken de krachten in de x- en de y-richting.

• Noteer alles in symbolen bij de gegevens en het gevraagde.

• Werk de oplossing uit

Welke krachten kun je rechtstreeks berekenen?

Voor welke krachten heb je een andere kracht nodig?

• Sta stil bij de oplossing.

Klopt de eenheid?

Klopt de getalwaarde?

2 Bij welke kracht verandert de snelheid van een voorwerp?

2.1 Snelheidsverandering

OPDRACHT 36

Bestudeer de snelheid van de renners in de verschillende fasen van een wedstrijd.

1 Teken de snelheidsvectoren op de massapunten op twee verschillende tijdstippen.

2 Noteer onder elke situatie welk kenmerk van de snelheidsvector veranderd is tussen de twee tijdstippen.

©VANIN

De kopgroep komt aan. De renners versnellen naar de eindstreep.

De van de snelheidsvector verandert.

Het peloton neemt een bocht aan 30 km h .

De van de snelheidsvector verandert.

Het peloton rijdt als afsluiter van de rit twee keer het publiek voorbij aan 50 km h

De van de snelheidsvector verandert.

Een voorwerp verandert van bewegingstoestand als de snelheid v verandert. Snelheid is een vectoriële grootheid. Er is een snelheidsverandering ∆v als een van de kenmerken van de snelheid verandert:

• de snelheidsgrootte: de grootte neemt af of neemt toe;

• de snelheidsrichting: de beweging is niet rechtlijnig;

• de snelheidszin: de beweging is rechtlijnig, maar verloopt volgens en tegengesteld aan de x-as.

Tijdens een wielerwedstrijd kan een renner nooit aan een constante snelheid fietsen gedurende de hele rit. De renner verandert voortdurend van bewegingstoestand. We bestuderen de kenmerken van de resulterende kracht bij elke snelheidsverandering ∆v

OPDRACHT 37

Bestudeer de video van een curlingwedstrijd.

1 Waarom gebruiken de atleten een borstel?

2 Boots de situatie na in de applet.

a Open in de applet het onderdeel ‘Wrijving’.

b Klik ‘Krachten’, ‘Som van de krachten’ en ‘Snelheid’ aan.

c Breng een voorwerp in beweging zonder wrijving.

d Bestudeer de resulterende kracht op het moment dat het voorwerp in beweging komt.

e Bestudeer voor een voorwerp dat in beweging gebracht is:

• de resulterende kracht,

• de snelheidsgrootte.

f Herhaal met veel wrijving.

3 Op de x -as is de curlingsteen bij vertrek getekend.

Teken voor een situatie zonder en een situatie met borstelen:

a het massapunt van de curlingpuck bij vertrek, na 1 s en na 2 s,

b de snelheidsvector op de drie tijdstippen,

c de wrijvingskracht en de resulterende kracht na 1 s.

Zonder borstelen

Met borstelen

Als de snelheidsgrootte verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van een voorwerp dat versnelt of vertraagt, verandert Er is een dynamisch effect, omdat de resulterende kracht niet nul is: F res ≠ 0. De resulterende kracht voor een verandering van grootte is gericht volgens de x -as. De zin bepaalt of het voorwerp versnelt of vertraagt.

VOORBEELD KRACHT BIJ VERANDERING VAN SNELHEIDSGROOTTE

BIJ FIETSERS

We bekijken een renner tijdens een wedstrijd.

• Om te vertrekken, moet de renner een grote spierkracht uitoefenen. Hij beweegt vooruit en versnelt, omdat de resulterende kracht een zin heeft volgens de beweging.

w Fspier

De renner vertrekt vanuit stilstand en versnelt tot een snelheid van 35  km h . Zijn snelheidsgrootte neemt toe: ∆v = 35 km h – 0 = 35 km h

De snelheidsvector is niet constant (∆v ≠ 0, want v1 ≠ v2).

Er is een verandering van bewegingstoestand.

Om te versnellen, oefent de renner een spierkracht (Fspier = 1 000 N) uit die groter is dan de wrijvingskracht (F w = 400 N). De resulterende kracht is gericht volgens de 5 -as.

F res, x = Fspier + F w ≠ 0, want Fspier > Fw, dus F res, x = Fspier – F w = 1 000 N – 400 N = 600 N

©VANIN

• Bij de sprint heeft de renner een grote snelheid. Om tot stilstand te komen, moet hij stoppen met trappen en hard remmen. Hij beweegt vooruit, maar vertraagt, omdat de resulterende kracht een zin heeft tegengesteld aan de beweging.

De renner heeft een snelheid van 58 km h   en vertraagt tot stilstand. Zijn snelheidsgrootte neemt af: ∆v = 0 – 58 km h = –58 km h De snelheidsvector is niet constant (∆v ≠ 0, want v3 ≠ v4).

Er is een verandering van bewegingstoestand.

Om te vertragen, stopt de renner met trappen (Fspier = 0 N) en remt hij hard, zodat de wrijvings-, weerstands- en remkracht (F w = 1 200 N) heel groot is. De resulterende kracht is tegengesteld aan de x-as gericht.

F res, x = Fspier + F w ≠ 0, want Fspier = 0, dus F res, x = F w = 1 200 N

In de y-richting is de renner in elke situatie in rust, omdat de normaalkracht de zwaartekracht compenseert: F res, y = F z + F n = 0.

©VANIN

Als de snelheidsgrootte verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van het voorwerp verandert. Er is een dynamisch effect, omdat er een resulterende kracht (F res ≠ 0) is met deze kenmerken:

• aangrijpingspunt: het massapunt,

• richting: volgens de positie-as (x -as),

• zin: volgens de beweging bij een versnelling (∆v > 0), tegengesteld aan de beweging bij een vertraging (∆v < 0),

• grootte: F res ≠ 0.

Hoe groter de resulterende kracht Fres, hoe groter het dynamisch effect.

` Maak oefening 9 t/m 11 op p. 160 en 161.

2.3 Verandering van snelheidsrichting

OPDRACHT 38

Bestudeer de video van de wereldkampioen kogelslingeren.

1 Welke kenmerken van de kogelsnelheid veranderen tijdens het ronddraaien? Verklaar.

VIDEO KOGELSLINGEREN

2 Welk pad volgt de kogel nadat de atleet hem heeft losgelaten? Bestudeer de video en duid aan.

3 Maak de uitspraak correct.

Om een bal op een cirkel te laten bewegen is er geen/wel een resulterende kracht nodig.

45

Als de snelheidsrichting verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0. De bewegingstoestand van een voorwerp dat een bocht maakt, verandert.

Er is een dynamisch effect, omdat de resulterende kracht niet nul is: F res ≠ 0. De resulterende kracht voor een verandering van richting is naar het midden van de bocht gericht.

VOORBEELD RESULTERENDE KRACHT BIJ VERANDERING VAN

SNELHEIDSRICHTING

We bestuderen renners die een bocht nemen. Een renner die rondjes rijdt op een cirkelvormige baan met een constante snelheidsgrootte van v = 25 km h , verandert voortdurend van richting. Zijn snelheidsvector verandert: ∆v = v2 – v1 ≠ 0.

©VANIN

Voor die verandering van bewegingstoestand is een resulterende kracht F res loodrecht op de baan naar het midden nodig. De renner draait aan zijn stuur, en de wrijvingskracht zorgt ervoor dat de wielen niet wegglijden tijdens het draaien.

Op de weg nemen de renners bochten, waarbij hun snelheidsrichting verandert. De koploper op afbeelding 46 heeft een andere richting dan enkele ogenblikken eerder: ∆v = v2 – v1 ≠ 0.

VIDEO BOCHT

Als de snelheidsrichting verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van een voorwerp dat een bocht maakt, verandert. Er is een dynamisch effect, omdat de resulterende kracht niet nul is: F res ≠ 0.

De resulterende kracht voor een verandering van richting is naar het midden van de bocht gericht.

Je kunt een bocht bekijken als een deel van een (denkbeeldige) cirkel (zie afbeelding 48). Om de bocht veilig te kunnen nemen, heb je een resulterende kracht F res nodig. Als die kracht er niet was, zouden de renners rechtdoor gaan.

De resulterende kracht op de weg wordt geleverd door de wrijvingskracht. Als de wrijvingskracht te klein is (bijvoorbeeld bij regenweer of ijzel), kunnen de renners de bocht niet of moeilijk nemen. Ze moeten hun snelheidsgrootte heel klein maken om niet rechtdoor te gaan.

Als de snelheidsrichting verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van het voorwerp verandert. Er is een dynamisch effect, omdat er een resulterende kracht (F res ≠ 0) is met deze kenmerken:

• aangrijpingspunt: het massapunt,

• richting: loodrecht op baan,

• zin: naar het middelpunt van de (denkbeeldige) ingesloten cirkel toe,

• grootte: F res ≠ 0.

2.4 Verandering van snelheidszin

OPDRACHT 39

Bestudeer de video van Amber op een trampoline.

1 Op de foto beweegt Amber naar beneden.

Welke eigenschap van de snelheid verandert als ze de trampoline raakt?

2 Welke uitspraak is correct tijdens de neerwaartse beweging bij het landen op de trampoline (vlak voor het keerpunt)?

De trampoline oefent een kracht uit op Amber volgens de bewegingszin.

De trampoline oefent een kracht uit op Amber tegen de bewegingszin in.

De trampoline oefent geen uit kracht uit op Amber.

VIDEO TRAMPOLINE

Afb. 49

Als de snelheidszin verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van het voorwerp verandert. Er is een dynamisch effect, omdat de resulterende kracht niet nul is: F res ≠ 0.

De resulterende kracht voor een verandering van zin is tegengesteld aan de beweging.

VOORBEELD RESULTERENDE KRACHT BIJ VERANDERING VAN SNELHEIDSZIN BIJ FIETSERS

©VANIN

Als een fietser door een manoeuvre tegen de vangrail terechtkomt aan een snelheid v1, oefent de vangrail een kracht F uit op de fiets. De fiets beweegt achteruit aan een tegengestelde snelheid v2. De snelheidsgrootte na de botsing is veel kleiner geworden, want de fietser oefent geen kracht meer uit en de wrijvingskracht remt de fiets af.

Snelheid van de fiets voor de botsing

Snelheid van de fiets na de botsing

De renner zelf ondervindt de kracht niet.

Zijn resulterende kracht is nul (F res, x = 0), waardoor zijn snelheid niet verandert in de bewegingsrichting.

Hij beweegt verder aan een snelheid v1, komt los van zijn fiets en komt voorbij de vangrail terecht.

Als de snelheidszin verandert, verandert de snelheidsvector: vbegin ≠ veind, dus ∆v ≠ 0.

De bewegingstoestand van het voorwerp verandert. Er is een dynamisch effect, omdat er een resulterende kracht (F res ≠ 0) is met deze kenmerken:

• aangrijpingspunt: het massapunt,

• richting: volgens de x-as,

• zin: tegengesteld aan de beweging,

• grootte: F res ≠ 0.

` Maak oefening 12 t/m 14 op p. 161 en 162.

Afb.

Afb.

Boots de verschillende situaties na in de applet.

Op een voorwerp werken verschillende . Ze bepalen of er een verandering is van bewegingstoestand. Je noemt dat het effect van de resulterende kracht.

©VANIN

beweging is een ERB (in de x-richting)

geen verandering van bewegingstoestand:

∆v 0 en F res 0

beweging is geen ERB in de x-richting

F res, x = 0 in de y-richting

verandering van bewegingstoestand:

∆v 0 en F res 0

F res, y = 0 :

F res heeft dezelfde richting en dezelfde zin als de snelheid v of van zin veranderen:

F res heeft dezelfde richting en een tegengestelde zin als de snelheid v : F res staat loodrecht op de snelheid v

OPEN APPLET

1 Welke uitspraak is correct? Duid aan.

De wrijvingskracht is altijd even groot als en tegengesteld aan de trekkracht.

De wrijvingskracht is altijd verticaal.

De wrijvingskracht is altijd horizontaal.

De wrijvingskracht is altijd gericht volgens de beweging.

De wrijvingskracht is altijd tegengesteld aan de beweging.

2 Je moet een kracht van 530 N uitoefenen om een zetel op een tapijt (n = 0,63) te verschuiven.

a Hoe groot is de normaalkracht?

b Welke massa heeft de zetel?

Gegeven:

Gevraagd:

Oplossing:

©VANIN

3 Een kist staat op de laadbak van een vrachtwagen.

Vanaf een bepaalde hoek schuift de kist naar beneden. Hoe komt dat? Duid alle antwoorden aan.

De zwaartekracht wordt kleiner.

De zwaartekracht wordt groter.

De wrijvingskracht wordt kleiner.

De wrijvingskracht wordt groter.

De normaalkracht wordt kleiner.

De normaalkracht wordt groter.

4 Bestudeer de zwemster tijdens de verschillende fases van haar duiksprong. Teken de weerstandskrachten in de verschillende situaties.

1 2 3

In de lucht voor de duiksprong In de lucht tijdens de duiksprong In het water na de duiksprong

5 De Hyperloop is een revolutionair transportmiddel.

a Bekijk de video

b Welke voordeel heeft de Hyperloop ten opzichte van een gewone trein?

c Teken en benoem in een krachtenschema de snelheids- en krachtvectoren bij een ERB van …

• een klassieke trein,

• de Hyperloop.

6

Een parachutist opent zijn parachute.

a Hoe beweegt hij terwijl de parachute opengaat? Duid aan.

Hij vliegt even omhoog.

Hij hangt even stil.

Hij remt heel hard af.

b Onder welke omstandigheden voert hij een ERB uit? Duid aan.

altijd

nooit

als de zwaartekracht groter is dan de weerstandskracht

als de zwaartekracht even groot is als de weerstandskracht

als de zwaartekracht kleiner is dan de weerstandskracht

©VANIN

7 Een lift (m = 430 kg) beweegt tussen de verdiepingen aan een constante snelheid.

a Teken en bereken de motorkracht tijdens de beweging omhoog.

Gegeven:

Gevraagd:

Oplossing:

b Hoe verandert de motorkracht tijdens de beweging naar beneden? Verklaar.

VIDEO HYPERLOOP

8 Je staat rechtop in een bus die aan een constante snelheid rijdt.

Wat gebeurt er als de bus plots stopt? Verklaar.

9 Bestudeer de bewegingen op de pretparkattracties.

a Welke eigenschap van de snelheidsvector verandert? Duid aan.

b Noteer in symbolen of er al dan niet een snelheidsverandering is.

Je rijdt met een botsauto.

De richting v verandert.

De zin v verandert.

De grootte v verandert.

Op de vrijevaltoren ga je traag omhoog en val je plotseling naar beneden.

De richting v verandert.

De zin v verandert.

De grootte v verandert.

10 Een voetballer trapt een strafschop.

Je schommelt heen en weer in de piratenboot.

De richting v verandert.

De zin v verandert.

De grootte v verandert.

©VANIN

Je rijdt aan 5 m s omhoog bij de start van de achtbaan.

De richting v verandert.

De zin v verandert.

De grootte v verandert.

a Teken en benoem de resulterende kracht in de horizontale x-richting in elk van de volgende situaties. Verwaarloos de luchtweerstand.

b Noteer onder elke situatie de (verandering van) bewegingstoestand van de bal. Kies uit:

rust – ERB – versnelling – vertraging

c Vul de uitdrukking van de resulterende kracht aan met = of ≠.

Bewegingstoestand en resulterende kracht in de x -richting

11 Korneel duwt een slee (m = 32 kg). Om ze aan een constante snelheid te laten bewegen, oefent hij een kracht uit van 160 N.

a Benoem de (verandering van) bewegingstoestand in de drie situaties.

b Teken en benoem alle krachten in een krachtenschema.

c Vul de uitdrukking voor de resulterende kracht aan.

Vertrek

Constante snelheid

Stoppen met duwen

©VANIN

12 Bestudeer de afbeelding van een slijpschijf.

a Welke baan volgt een deeltje op de schijf?

b Welke beweging voert een deeltje uit na het slijpen?

c Verklaar het verschil.

13 De maan beweegt in een bijna cirkelvormige baan rond de aarde.

a Welke kracht zorgt ervoor dat de maan rond de aarde beweegt?

b Welk kenmerk van de snelheidsvector van de maan verandert?

c Teken de kracht die de aarde op de maan uitoefent.

14 Bestudeer de verschillende situaties van de basketbal en de vectorvoorstellingen van de snelheid en de resulterende kracht.

a Verbind elke foto met de overeenkomstige vectorvoorstelling.

b Omschrijf een beweging van de basketbal die past bij de overblijvende vectorvoorstellingen.

` Verder oefenen? Ga naar .

`

1 Begripskennis

• Ik kan de wrijvingskracht en de weerstandskracht omschrijven

• Ik kan het krachtmoment omschrijven.

• Ik kan het verband tussen kracht en een ERB omschrijven

• Ik kan de krachten bij een ERB berekenen.

• Ik kan de verschillende veranderingen van bewegingstoestand omschrijven.

• Ik kan het verband tussen kracht en verandering van bewegingstoestand omschrijven.

• Ik kan de richting en de zin van de resulterende kracht bij een verandering van bewegingstoestand bepalen

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan een onderzoek opstellen en uitvoeren

• Ik kan een dynamometer aflezen

• Ik kan de inwerkende en resulterende krachten weergeven als een vector in een krachtenschema.

• Ik kan nauwkeurig berekeningen uitvoeren.

©VANIN

Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

KRACHTEN

VEELVOORKOMENDE

spier F n F g

Kenmerken

Aangrijpingspunt Richting Zin Grootte

Omschrijving Type

Krachten samenstellen in de x -richting

F w F spier F v F res, x = F v + F w + F spier

F res, x F res, x = F v + F w –F spier

Krachten samenstellen in de y -richting F n F z

Kracht

F z = m · g

zwaartekracht F z aantrekkingskracht door een hemellichaam veldkracht zwaartepunt (Z) verticaal naar middelpunt hemellichaam

F g = m · g

contactkracht steunpunt (S) verticaal naar middelpunt hemellichaam

gewicht F g kracht op de ondersteuning door de aantrekking door een hemellichaam

bewegings- richting tegengesteld aan vervorming F

contactkracht contactpunt

veerkracht F v terugroepkracht door een elastiek of veer

variabel

contactkracht op het voorwerp dat ondersteund wordt loodrecht op oppervlak van oppervlak weg

normaalkracht F n ondersteuningskracht door het oppervlak

variabel

bewegings- richting tegengesteld aan beweging

contactkracht contactpunt

F w kracht door de hinder van de ondergrond en de omgeving

wrijvingsen weerstandskracht

KRACHTEN SAMENSTELLEN EN ONTBINDEN

Krachten samenstellen: kop-staartmethode

Krachten die inwerken volgens een verschillende richting F 2 F 1 F 2 F 1 F 2 F 1 F res

Krachten die inwerken volgens dezelfde richting F res F 2 F 1 F res F 2 F 1

versnellen : F res heeft dezelfde richting en dezelfde zin als de snelheid v vertragen of van zin veranderen: F res heeft dezelfde richting en een tegengestelde zin als de snelheid v een bocht nemen : F res staat loodrecht op de snelheid v zin grootte richting aangrijpingspunt F

Op een voorwerp werken verschillende krachten. Ze bepalen of er een verandering is van bewegingstoestand. Je noemt dat het dynamisch effect van de resulterende kracht.

©VANIN

Veelvoorkomende krachten:

• kracht op de ondersteuning door de aantrekking door de aarde: gewicht

• veerkracht: terugroepende kracht door elastiek of veer

• ondersteuningskracht door het oppervlak: normaalkracht

• ondersteuningskracht door een touw: spankracht

= 0 verandering van bewegingstoestand:

geen verandering van bewegingstoestand:

ERB

constante snelheid in de x -richting F res, x = 0 rust in de y -richting F res, y = 0

translatie -evenwicht:

• geen verschuiving

• F res = 0 rotatie -evenwicht:

• geen draaiing

• M res = 0

• hinder door de ondergrond: wrijvingskracht

• hinder door de lucht: weerstandskracht

BEKIJK DE KENNISCLIP

Op naar de ruimte

We kijken opnieuw naar de SpaceX-raket uit de CHECK IN.

1 Bestudeer de video’s van de lancering en de landing van de SpaceX-raket.

2 Vul voor elke situatie van de raket en het ISS de tabel aan.

a Teken de krachten in een krachtenschema.

b Welke (verandering van) bewegingstoestand is er?

c Hoe groot is de resulterende kracht?

De raket staat klaar voor lancering

a Krachtenschema

Lancering van de raket

Krachtenschema

Beweging van de raket aan een constante snelheid

Krachtenschema b

De parachute van de Crew Dragon-capsule is net geopend om te landen

a Krachtenschema

De capsule nadert aan een constante snelheid de aarde om te landen

Krachtenschema

Ruimtestation ISS

Krachtenschema

b

c F res 0

3 Hoe komt het dat de astronauten gewichtloos zijn?

4 Hoe kun jij gewichtloos zijn?

Op een voorwerp werken meerdere krachten. De zwaartekracht werkt in een groot gebied rond een hemellichaam. In combinatie met de motorkracht, de normaalkracht en de weerstandskrachten bekom je een resulterende kracht. Zodra de resulterende kracht verschilt van nul, verandert een voorwerp (zoals een raket) van bewegingstoestand: het versnelt, vertraagt of maakt een bocht.

Een kleine stap voor de mens ...

De eerste bemande maanlanding gebeurde door de Apollo 11 op 21 juli 1969.

Twee astronauten landden en stegen weer op met de maanlander. De eerste man die voet zette op de maan, was Neil Armstrong.

De maan is bedekt met een metersdikke laag stof. Dat maanstof bestaat uit materiaal dat uit de ruimte op de maan terechtkomt. Het verbrandt niet doordat er geen atmosfeer is. Het maanstof is scherp, statisch geladen en de samenstelling is heel gevarieerd.

Het stof schuurt zo sterk dat het de buitenste lagen van de schoenen van ruimtepakken aantast, instrumenten beschadigt en irritatie veroorzaakt aan de ogen, keel en neus. De gezondheidsrisico’s van langere blootstelling aan fijn maanstof of de precieze samenstelling ervan zijn nog onbekend. Een ambitieus onderzoeksprogramma van de ESA (European Space Agency) met experts van over de hele wereld probeert die vraag te beantwoorden.

1 Op de afbeelding zie je de voetafdruk van Buzz Aldrin tijdens de eerste maanwandeling.

Welke factoren beïnvloeden de voetafdruk volgens jou?

2 De onderzoekers nemen stalen van het maanstof.

Kunnen ze daarvoor een stofzuiger gebruiken?

Duid je hypothese aan.

Ja.

Ja, als de stofzuiger krachtiger is dan op aarde.

Ja, als de stofzuiger minder krachtig is dan op aarde.

Nee.

` Hoe kunnen we de vervorming met een grootheid beschrijven?

` Welke factoren spelen een rol?

` Hoe ontstaat zuigkracht?

We zoeken het uit!

Druk(kracht)

OPDRACHT 1

Waar komt ‘druk’ voor in het dagelijks leven?

1 Bestudeer de foto’s.

2 Vul de tabel aan. 1 2

Welke druk is voorgesteld?

Noteer de aggregatietoestand van elke stof.

• lucht in de fietsband:

• wand van de fietsband:

3 Geef nog een voorbeeld van druk uit het dagelijks leven.

• bloed in de bloedvaten:

• wanden van de bloedvaten:

OPDRACHT 2

Hoe verschillen vaste stoffen, vloeistoffen en gassen?

Duid de eigenschappen van de drie aggregatietoestanden aan in de tabel. vast vloeibaar gas

©VANIN

Welke macroscopische eigenschappen heeft een stof in de aggregatietoestand?

Vorm variabel / vast variabel / vast variabel / vast

Volume variabel / vast variabel / vast variabel / vast

Welke microscopische eigenschappen heeft een stof in de aggregatietoestand?

Kracht tussen de deeltjes klein / redelijk groot /  heel groot klein / redelijk groot /  heel groot klein / redelijk groot /  heel groot

Snelheid van de deeltjes klein / redelijk groot /  heel groot klein / redelijk groot /  heel groot

klein / redelijk groot /  heel groot

OPDRACHT 3

Wat is drukkracht?

Bestudeer de uitgeoefende krachten.

a Teken de beschreven krachtvector voor de verschillende situaties.

b Duid het type kracht aan.

Een vinger klikt op een computermuis. Een hand trekt aan een trainingselastiek. De lamp heeft een gewicht. De bureaulamp heeft een gewicht.

trekkracht / drukkracht trekkracht / drukkracht trekkracht / drukkracht trekkracht / drukkracht

Bekijk de module massadichtheid bij het onlinelesmateriaal.

OPDRACHT 4

Hoe kun je de verschillende grootheden van een voorwerp berekenen?

Een gom, met de afmetingen die weergegeven zijn op de afbeelding, heeft een massadichtheid van 1,3  g cm3 .

Vul de tabel aan met de gevraagde grootheden.

In formules

Oppervlakte grondvlak

©VANIN

Berekende waarde In eenheden van de gegevens In SI-eenheden

Gassen en vloeistoffen veroorzaken een druk als ze begrensd zijn door een vaste stof. Een kracht die uitgeoefend wordt in de richting van een oppervlak, noem je een drukkracht

Wat is druk?

LEERDOELEN

Je kunt al:

M drukkracht en het statisch effect ervan omschrijven;

M het deeltjesmodel van gassen gebruiken;

M het gewicht en de resulterende kracht bepalen.

Je leert nu:

M de druk op een oppervlak omschrijven en berekenen;

M de druk in een gas omschrijven;

M het absolute nulpunt omschrijven;

M het ontstaan van atmosferische druk omschrijven;

M over- en onderdruk gebruiken om stroming te beschrijven.

1 Wat is druk op een oppervlak?

1.1

Maat voor indrukking

OPDRACHT 5

Bestudeer de afbeelding en de uitspraken.

Wie heeft gelijk volgens jou?

©VANIN

Dieren zijn aangepast aan hun omgeving. Hun bek, tanden en ledematen hebben een specifieke vorm, zodat ze zich kunnen voeden en verplaatsen. Hoe kunnen we die aanpassingen beschrijven met grootheden? Welke invloed heeft de omliggende atmosfeer?

In dit hoofdstuk bestudeer je wat druk is en hoe een druk(verschil) voor vervorming en beweging zorgt.

De fakir verdeelt zijn gewicht over de spijkers.

De fakir spant zijn spieren op en verkleint zo zijn gewicht.

Dankzij meditatie voel ik de pijn veroorzaakt door de spijkers niet.

OPDRACHT 6 ONDERZOEK

Onderzoek hoe verschillende factoren de vervorming beïnvloeden.

1 Gebruik het labo bij het onlinelesmateriaal.

2 Verklaar waarom een fakir op een spijkerbed kan liggen.

Als een drukkracht F uitgeoefend wordt op een oppervlak, wordt het oppervlak ingedrukt.

De indrukking hangt af van:

• de grootte van de drukkracht: F

• de grootte van het contactoppervlak: A

De mate van de indrukking wordt weergegeven met de grootheid druk, die wordt voorgesteld met het symbool p .

• De indrukking neemt toe met een toenemende krachtgrootte.

p ~ F

• De indrukking neemt af met een toenemende grootte van het contactoppervlak.

p ~ 1 A

VOORBEELD DRUK DOOR VOGELPOTEN

p = F A

©VANIN

In zand zie je de pootafdrukken van verschillende dieren. Eenden en kippen hebben een vergelijkbare massa. Hun gewicht op de ondergrond is ongeveer gelijk. Toch is de indrukking van de kippenpoot dieper, doordat het contactoppervlak veel kleiner is.

• De massa van de kip en de eend is vergelijkbaar. Ze oefenen een bijna gelijke kracht (gewicht) uit op de grond.

Feend ≈ Fkip

• Het contactoppervlak van de eend is veel groter. Aeend > Akip

De indrukking van de eendenpoot is kleiner: peend < pkip

OPDRACHT 7

Bestudeer de formule voor druk.

1 Is druk een scalaire of een vectoriële grootheid? Verklaar.

2 Welke eenheid van druk kun je afleiden uit de formule?

3 Vorm de formule om, zodat je …

a de kracht kunt berekenen als je het contactoppervlak en de druk kent:

b het contactoppervlak kunt berekenen als je de kracht en de druk kent:

OPDRACHT 8

Los het vraagstuk op.

Een dame steunt op twee naaldhakken, een olifant op zijn vier poten.

1 Wie veroorzaakt de grootste druk volgens jou?

de dame

de olifant

2 Duid de correcte gegevens aan.

• A 4 poten = 80 cm² / 8,0 dm² / 0,80 m²

• molifant = 60 kg / 600 kg / 6 000 kg

• A2 hakken = 40 cm² / 4,0 dm² / 0,40 m²

• mdame = 60 kg / 600 kg / 6 000 kg

3 Ga na wie de grootste druk veroorzaakt.

Werk dat uit op een cursusblad.

4 Controleer je antwoord via de QR-code.

©VANIN

Om de eenheid van een grootheid aan te duiden worden vierkante haakjes gebruikt.

Bijvoorbeeld: eenheid van tijd is seconde en wordt genoteerd als [t] = 1 s.

EENHEDEN OMZETTEN

1 m2 100 g Afb. 6

VRAAGSTUK DRUK

De SI-eenheid van druk is de pascal. Die eenheid is samengesteld uit de eenheden van kracht en oppervlakte (newton gedeeld door vierkante meter):

1 Pa = 1 N m2

Om een druk van 1 pascal te bekomen, oefen je een kracht van 1 N uit op een oppervlakte van 1 m². Dat betekent bijvoorbeeld dat je een massa van (ongeveer) 100 g op een vierkante meter legt. De pascal is dus een heel kleine eenheid.

TIP

Vaak gebruikt men de grotere hulpeenheden hectopascal en kilopascal.

1 hPa = 1 ∙ 10² Pa

1 kPa = 1 ∙ 10³ Pa

Als een kracht F uitgeoefend wordt op een oppervlak met grootte A, wordt het oppervlak ingedrukt.

De grootheid druk p is de maat voor de indrukking en kan berekend worden als: p = F A

Grootheid met symbool SI-eenheid met symbool druk p pascal Pa

1.2 Druk verhogen en verlagen

OPDRACHT 9

Bestudeer het verschil tussen drukkracht en druk.

1 Duw op drie manieren even hard tegen de hand van je buur. 1 2 3

2 Hoe merk je het statisch effect van de drukkracht?

©VANIN

3 Rangschik de situaties volgens …

a toenemende drukkracht:

b toenemend contactoppervlak:

c toenemend statisch effect van de drukkracht:

d toenemende druk:

In het dagelijks leven worden druk en (druk)kracht vaak door elkaar gebruikt. In de fysica is er een heel duidelijk onderscheid:

1 Drukkracht: de kracht die uitgeoefend wordt op een oppervlak.

2 Druk: het statisch effect dat het gevolg is van een drukkracht. De grootte van de drukkracht wordt verdeeld over het contactoppervlak

De grootte van het contactoppervlak bepaalt dus het statisch effect van de uitgeoefende drukkracht.

VOORBEELD GROTE EN KLEINE DRUK IN DE NATUUR

In de natuur is de bouw van dieren aangepast aan hun omgeving.

• Een leeuw is een vleeseter. Dankzij zijn scherpe hoektanden (= klein contactoppervlak) kan hij met een kleine kracht zijn prooien verslinden. Hij veroorzaakt een grote druk.

• Een pinguïn leeft in moerassige en besneeuwde gebieden. Dankzij de vliezen tussen zijn poten (= groot contactoppervlak) zakt hij niet in de sneeuw. Hij veroorzaakt een kleine druk.

• De mens gebruikt zulke inzichten uit de natuur bij de ontwikkeling van voorwerpen. Gebruiksvoorwerpen hebben, afhankelijk van hun doel, een klein of een groot contactoppervlak.

1 Groot statisch effect van de drukkracht: hoge druk Als je met een (kleine) kracht een groot effect wilt bekomen, moet het contactoppervlak zo klein mogelijk zijn.

• Een mes en een schaar worden scherp geslepen, zodat je makkelijk kunt snijden en knippen.

• Een naald heeft een scherpe punt, zodat je niet hard hoeft te duwen.

• Loopschoenen hebben spikes, zodat je meer grip hebt.

2 Klein statisch effect van de drukkracht: lage druk Als je het effect van de uitgeoefende kracht wilt beperken, moet het contactoppervlak zo groot mogelijk zijn.

• Een boekenkast staat niet op pootjes, maar steunt over de volledige breedte.

• Met een snowboard zak je niet weg in de sneeuw.

• Graafmachines hebben rupsbanden, zodat je over de modder kunt rijden.

©VANIN

Om het statisch effect van de drukkracht te beïnvloeden, kies je een geschikt contactoppervlak:

• Bij een klein contactoppervlak is het effect groot.

Er ontstaat een grote druk.

• Bij een groot contactoppervlak is het effect klein.

Er ontstaat een kleine druk

` Maak oefening 1 t/m 7 op p. 186 t/m 188.

2 Wat is druk in een gas?

2.1 Botsingen

OPDRACHT 10

Bestudeer een fietsband die opgepompt wordt.

1 Je leerkracht pompt een fietsband op met een voetpomp. Hoe verandert de band?

2 Wat meet de meter die op een fietspomp staat?

3 In welke eenheid wordt dat gemeten?

4 Hoe verandert de druk tijdens het oppompen?

OPDRACHT 11

Bestudeer het gedrag van gasdeeltjes.

1 Hoe ontstaat de druk in een gas volgens jou? Formuleer een hypothese.

2 Bestudeer het gedrag van de deeltjes met de applet.

• Open ‘Ontdek’.

• Pomp deeltjes in het vat.

• Klik ‘Botsingteller’ aan.

• De tijd is weergegeven als 10 ps = 10 picoseconden (= 10 · 10–12 s). Waarom?

• Bestudeer de druk en het aantal botsingen (voor 10 ps).

• Herhaal met meer deeltjes.

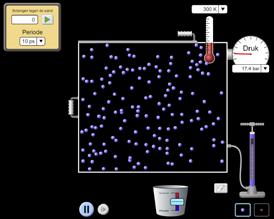
OPDRACHT 11 (VERVOLG)

3 Hoe kun je het ontstaan van druk verklaren met het deeltjesmodel?

Duid de juiste uitspraken aan.

De deeltjes zitten allemaal tegen elkaar en oefenen daardoor een drukkracht uit op de wand.

De deeltjes bewegen heel snel.

De deeltjes botsen tegen de wand.

De deeltjes worden aangetrokken tot de wand.

De druk ontstaat door botsing van de deeltjes tegen de wand.

De druk ontstaat door botsing van de deeltjes tegen elkaar.

4 Vergelijk je hypothese met je besluit.

©VANIN

Gasdeeltjes kunnen in een afgesloten ruimte vrij bewegen. Op elk moment botsen een groot aantal gasdeeltjes tegen de wanden. Tijdens de botsing oefenen ze een kracht uit op de wanden. Er ontstaat een druk op elke wand.

De druk in een gas meet je door het vat waarin het gas zit, aan te sluiten op een drukmeter of manometer Een drukmeter om de luchtdruk te meten, is een barometer.

• Bij een analoge drukmeter lees je de druk af op een wijzerplaat.

• Bij een digitale drukmeter (= druksensor) lees je de druk af als cijfertjes op een scherm.

De druk in een gas is groot. Daarom gebruikt men vaak de hulpeenheden bar en millibar.

1 bar = 1 ∙ 105 Pa

1 mbar = 1 ∙ 10–3 bar = 1 · 10-3 · 105 Pa = 1 ∙ 10² Pa = 1 hPa

Door de druk van de botsende gasdeeltjes ontstaat er een kracht op de wanden. p = F A fi F = p · A

LONGEN

VOORBEELD DRUK VAN GASSEN IN EEN BALLON

• Als de druk groot is, moet het vat uit een stevig materiaal gemaakt zijn om niet te vervormen door die kracht. Gassen worden gestockeerd in metalen gasflessen. Tijdens het vullen wordt een grote hoeveelheid gas samengeperst in een metalen fles. De druk in een pas gevulde gasfles kan oplopen tot 300 bar = 30,0 MPa.

OPDRACHT 12

longblaasjes

• Bij een vervormbaar systeem zorgt de kracht ervoor dat het gas zijn maximale volume inneemt. Een ballon, een fietsband, de longen … zetten uit, totdat de resulterende kracht op de wand nul is. In het menselijk lichaam ontstaat een gasdruk in de ademhalingsorganen, die schommelt rond de 1 bar. Het zuurstofgas van de ingeademde lucht komt terecht in de longblaasjes. In die miniballonnetjes botsen de zuurstofdeeltjes tegen de wanden, waardoor ze hun maximale volume bereiken.

Druk in een gas ontstaat door de botsingen van de gasdeeltjes tegen de wanden. Voor gasdruk gebruikt men vaak de hulpeenheid bar: 1 bar = 105 Pa.

Los het vraagstuk op.

Een duikfles wordt gevuld tot een druk van 230 bar en is afgesloten met een schroefdop (diameter 5,0 cm).

Bepaal het oppervlak van en de kracht op de schroefdop.

1 Welke grootteorde van kracht verwacht je? Duid aan.

1 N … 1 kN … 10 N … 10 kN … 100 N … 100 kN … 1 MN

2 Bereken het oppervlak van en de krachtop de schroefdop. Werk op een cursusblad.

3 Controleer je antwoord via de QR-code.

4 Komt je berekening overeen met je voorspelling?

5 Hoe komt het dat de dop niet van de fles vliegt?

2.2

OPDRACHT 13 DEMO

Bestudeer de invloed van de temperatuur op de gasdruk.

1 Sluit een erlenmeyer af met een dop met drukmeter.

2 Welk gas bevindt zich in de erlenmeyer?

©VANIN

3 Verplaats de erlenmeyer van een bak met koud water naar een bak met kokend water.

a Hoe zal de druk veranderen volgens jou?

b Test uit.

c Verklaar.

4 Ga op zoek naar de temperatuur (in °C) waarbij de druk nul wordt.

a Waar ligt die temperatuur volgens jou?

rond 20 °C

rond 0 °C

veel lager dan 0 °C

b Test uit met de applet.

5 Beantwoord opnieuw de vraag uit opdracht 12.

De gemiddelde snelheid van de deeltjes is een maat voor de temperatuur

• Hoe hoger de temperatuur, hoe sneller de gasdeeltjes bewegen.

Daardoor botsen ze meer en harder tegen de wanden. De druk stijgt.

• Hoe lager de temperatuur, hoe trager de gasdeeltjes bewegen.

Daardoor botsen ze minder vaak en minder hard tegen de wanden.

De druk daalt.

Als de temperatuur –273,15 °C is, bewegen de deeltjes niet meer.

Ze kunnen niet meer botsen tegen de wanden. De druk is nul.

Het punt waarbij de druk nul is, noem je het absolute nulpunt

Het absolute nulpunt wordt gekozen als nulpunt voor een nieuwe temperatuurschaal, de absolute temperatuurschaal of kelvinschaal. Dat is de basisgrootheid, met als symbool T en als SI-eenheid de kelvin.

Grootheid met symbool Eenheid met symbool temperatuur i graad Celsius °C

Basisgrootheid met symbool SI-eenheid met symbool temperatuur T kelvin K

Het verband tussen de temperatuur i in °C en de temperatuur T in K is gegeven door:

i = (T – 273,15) °C en T = (i + 273,15) K Een temperatuurverschil ∆i van 1 °C komt overeen met een temperatuurverschil ∆T van 1 K op de kelvinschaal. Dat is zo omdat ze dezelfde schaalverdeling hebben.

Bij –273,15 °C bewegen deeltjes niet. De gasdruk is nul.

Dat is het absolute nulpunt.

De kelvinschaal is een temperatuurschaal ten opzichte van het absolute nulpunt.

Het verband tussen de temperatuur i in °C en de temperatuur T in K is gegeven door:

i = (T – 273,15) °C en T = (i + 273,15) K

` Maak oefening 8, 9 en 10 op p. 189.

2.3 Atmosferische druk

©VANIN

OPDRACHT 14 DEMO

Bestudeer de kracht van lucht.

1 Voer de volgende experimentjes uit.

a Leg een lat op een tafel. De lat moet over de rand uitsteken. Sla nu op het stuk van de lat dat uitsteekt. Herhaal met een opengevouwen krant op het stuk van de lat dat op de tafel ligt.

b Vul een glas helemaal met water. Leg er een kartonnetje op. Draai het glas voorzichtig om boven een emmer.

2 Waarover ben je verwonderd?

3 Probeer je waarneming te verklaren.

Het zwaarteveld van een planeet trekt gassen naar zich toe, waardoor de planeet omhuld wordt met een dunne laag gassen. Dat is de atmosfeer.

Rondom de aarde bevindt zich een luchtlaag met een dikte van ongeveer 1 000 km. Lucht is een mengsel van gassen (voornamelijk stikstof en zuurstof), en oefent door de botsingen van die gasdeeltjes druk uit op alle voorwerpen in de atmosfeer van de aarde. De druk van de lucht noem je de luchtdruk of de atmosferische druk, met als symbool p atm.

De grootte van de atmosferische druk wordt bepaald door de luchtkolom die zich boven die plaats bevindt. De atmosferische druk op de Mount Everest is kleiner dan op zeeniveau.

©VANIN

luchtkolom boven

Everest

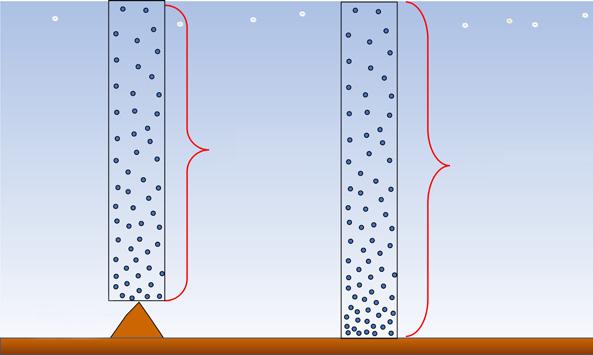
luchtkolom boven zeeniveau

Door de weersomstandigheden treden er variaties op.

De gemiddelde waarde van de atmosferische druk op zeeniveau is:

p0 = 1,013 bar = 1,013 ∙ 105 Pa = 1 013 hPa

Dat noem je de normdruk. In de praktijk rondt men de normdruk vaak af tot 1 bar.

De atmosferische druk ontstaat door de lucht die zich rondom de aarde bevindt. Het gewicht van de bovenliggende luchtdeeltjes bepaalt de grootte van de atmosferische druk.

De normdruk is de gemiddelde atmosfeerdruk op zeeniveau:

p0 = 1,013 bar = 1,013 ∙ 105 Pa = 1 013 hPa

Grafiek 1

Mount

Mount Everest zeeniveau

Afb. 10

OPDRACHT 15

Verklaar waarom je oorpijn voelt als je een steile berg op rijdt of met een vliegtuig opstijgt.

Maak de uitspraken correct.

Bij het oprijden van een steile berg zal de luchtdruk aan de buitenkant van het trommelvlies stijgen / dalen / gelijk blijven. De luchtdruk aan de buitenkant wordt kleiner dan / groter dan / gelijk aan de luchtdruk in je binnenoor. Je trommelvlies zal daardoor naar buiten / naar binnen / niet doorbuigen.

Door zal de buis van Eustachius openen. De luchtdruk in het binnenoor wordt daardoor groter dan / kleiner dan / gelijk aan de atmosferische druk.

2.4 Over- en onderdruk

OPDRACHT 16

Bestudeer de drie afbeeldingen.

je blaast een ballon op je duwt op een spuitbus je zuigt aan een rietje

1 Waar is er een hoge druk (H) en waar een lage druk (L)? Duid aan.

2 Teken met een pijl hoe de deeltjes bewegen.

3 Hoe ontstaat er stroming?

©VANIN

In het luchtledige of vacuüm zijn er geen gasdeeltjes. De druk is nul. Zodra er deeltjes zijn en T > 0 K, ontstaat er een gasdruk.

Absolute druk is gemeten ten opzichte van het absolute luchtledige. De normdruk (p0 = 1 013 hPa) is een absolute druk.

Relatieve druk is de gasdruk in vergelijking met een andere gasdruk.

• overdruk: De gasdruk is groter dan de druk in de omgeving

De relatieve druk is positief.

• onderdruk: De gasdruk is kleiner dan de druk in de omgeving. De relatieve druk is negatief.

trommelvlies

buis van Eustachius

Afb. 11

VIDEO ADEMEN

Vaak wordt de druk vergeleken met de normdruk. Als er een over- of onderdruk is in een systeem en de verbinding open is, ontstaat er stroming.

VOORBEELD ADEMHALING BIJ ZOOGDIEREN

Zoogdieren ademen in door hun borstholte te vergroten en zo in hun longen een onderdruk te creëren ten opzichte van de buitendruk. Uitademen gebeurt door de borstholte kleiner te maken en zo een overdruk te creëren.

INADEMEN

OPDRACHT 17 DOORDENKER

023 1 013

0 luchtledige

uit

UITADEMEN

©VANIN

1 Bekijk het experiment.

0 –1 013 onderdruk overdruk

12 p0 = 1 013 hPa

Bestudeer het historische experiment van de Maagdenburgse halve bollen.

a Sluit de twee halve bollen op elkaar aan, zodat ze luchtdicht zijn afgesloten.

b Sluit een vacuümpomp aan op het voorziene kraantje en zuig de lucht gedurende één minuut uit de bollen.

c Draai het kraantje toe en ontkoppel de pomp.

d Probeer de bollen uit elkaar te trekken.

2 Wat zal er volgens jou gebeuren?

druk (hPa) 995 0 –18

atmosferische druk onderdruk

druk (hPa)

MAAGDENBURGSE

13

OPDRACHT 17 (VERVOLG)

3 Wat stel je vast?

4 Verklaar.

In een vacuüm zijn er geen of weinig gasdeeltjes. Er is een grote onderdruk. Dat zorgt voor een grote kracht met een richting in de zin van de overdruk naar de onderdruk en een grootte  F = ∆p A = pover – ponder A

Die kracht wordt in het dagelijks leven de zuigkracht genoemd (terwijl er eigenlijk een duwkracht wordt uitgeoefend door de omliggende lucht).

Op afbeelding 14 zie je de kracht op een zuignap met oppervlakte A

VOORBEELD KRACHT DOOR EEN ONDERDRUK

• Boomkikkers kunnen zich vasthechten aan oppervlakken en zelfs ondersteboven hangen door de zuignapjes aan hun poten. Diezelfde techniek gebruikt men om zware voorwerpen op te tillen met zuignappen.

• In een stofzuiger (Engels: vacuum cleaner) wordt een grote onderdruk gecreëerd, waardoor je voorwerpen kunt optillen.

1 2 3

Er is overdruk als de gasdruk groter is dan de druk in de omgeving

Er is onderdruk als de gasdruk kleiner is dan de druk in de omgeving. Men vergelijkt de druk vaak met de normdruk.

Als er een over- of onderdruk is, ontstaat er een kracht F = ∆p ∙ A.

Bij een open verbinding ontstaat er stroming.

` Maak oefening 11 t/m 16 op p. 189-191.

Druk

Kernbegrippen

Notities druk drukkracht

• De grootheid druk is de maat voor Grootheid met symbool SI-eenheid met symbool

Als een drukkracht uitgeoefend wordt op een oppervlak met grootte A, wordt het oppervlak ingedrukt.

–

Bij een

contactoppervlak is het effect groot.

Er ontstaat een druk.

– Bij een

druk in een gas

absolute nulpunt

atmosferische druk over- en onderdruk

contactoppervlak is het effect klein.

Er ontstaat een druk.

• De druk in een gas ontstaat door . Voor de gasdruk gebruikt men vaak de hulpeenheid bar: 1 bar =

• Temperatuur is een maat voor de van de deeltjes.

• Bij i = °C bewegen de deeltjes niet. De gasdruk is Dat is het absolute nulpunt.

Grootheid met symbool

Eenheid met symbool temperatuur graad Celsius

Basisgrootheid met symbool SI-eenheid met symbool temperatuur

• De atmosferische druk ontstaat door die zich rondom de aarde bevindt. De is de gemiddelde atmosfeerdruk op zeeniveau: p0 = 1,013 bar = Pa = hPa

De atmosferische druk neemt met de hoogte.

• Er is als de gasdruk groter is dan de druk in de omgeving. Er is als de gasdruk kleiner is dan de druk in de omgeving.

Men vergelijkt de druk vaak met de

Als er een over- of onderdruk is, ontstaat er een kracht F =

©VANIN

Bij een open verbinding ontstaat er . Geef een eigen voorbeeld van de verschillende fenomenen.

Fenomeen

aanpassing om een grote druk te bekomen aanpassing om een kleine druk te bekomen een druk in een gas

lage atmosferische druk

Voorbeeld

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

GRAFIEKEN LEZEN

FORMULES OMVORMEN

VOORVOEGSELS EN MACHTEN

EENHEDEN OMZETTEN

BEREKENINGEN AFRONDEN

©VANIN

1 Je verplaatst een stoel van het terras naar het gras. Welke uitspraak is correct? Duid aan.

De druk van de stoel is in beide situaties even groot.

De druk van de stoel is groter op het gras.

De druk van de stoel is kleiner op het gras.

De stoel oefent geen druk uit op het terras.

2 Trekkersrugzakken hebben bredere schouderriemen dan zwemzakjes. Verklaar.

3 Zet de druk om naar de gevraagde eenheid.

• p = 5,3 Pa = N m2

• p = 40 N cm2 = · N m2 = Pa

• p = 1,8 kN m2 = · N m2 = Pa = kPa = hPa

• p = 3,0 · 10‒5 kN dm2 = N m2 = Pa

• p = 1 013 hPa = Pa = N m2

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen gebruiken als extra ondersteuning.

VRAAGSTUKKEN OPLOSSEN

TIP

4 Op het internet vind je de volgende gegevens over een smartphone terug.

a Verbeter de fout gebruikte grootheid.

b Bereken de druk in kPa wanneer de smartphone plat op tafel ligt.

Gegeven: Gevraagd:

Oplossing:

p = ? p

iPhone 12 specs

Formaat

Lengte 150,9 mm

Breedte 75,7 mm

Dikte 8,3 mm

Gewicht 164 gram

5

Een wagen heeft een massa van 1,20 ton.

De druk van elke band op de weg is 300 kPa.

Bereken de grootte van het contactoppervlak van elke band met de weg. Schrijf het resultaat in cm².

Gegeven: Gevraagd:

Oplossing:

Werk uit zonder rekentoestel.

TIP

6 Jan gaat skiën met ski’s van 1,80 m lang en 11,0 cm breed. Zelf heeft hij een massa van 72,0 kg, inclusief skikledij. Met zijn twee ski’s aan veroorzaakt hij een druk van 1,95 kPa op de sneeuw. Bereken de massa van de twee ski’s.

Gegeven:

Gevraagd:

Oplossing:

©VANIN

7 Een blokje met een constante massa steunt op een oppervlak dat toeneemt van 1,0 cm² tot 10,0 cm².

a Welke grafieklijn stelt de druk in functie van het oppervlak voor?

b Hoe groot is de massa?

8 Rangschik de druk van klein naar groot.

a 100 N cm2 , 5 N dm2 , 20 N m2 , 3 N mm2 , 1 Pa

b 5 N cm2 , 5 kN m2 , 5 Pa, 5 bar, 5 hPa

©VANIN

9 Zijn de volgende beweringen juist of fout? Verbeter indien nodig.

a Tussen gasmoleculen is er lucht.

b Gasmoleculen hebben een kleine massa.

c De luchtdruk neemt toe met de hoogte.

d De druk in een gas neemt toe met de temperatuur.

e Gasmoleculen hebben snelheid nul bij 0 °C

10 Zet de temperatuur om naar de andere eenheid.

a kamertemperatuur: i = 20 °C  T = K

b temperatuur vloeibare zuurstof: T = 155 K  i = °C

c kookpunt alcohol: i = 78,4 °C  T = K

d temperatuur vloeibare stikstof: T = 77,36 K  i = °C

11 Op zeeniveau heerst de normdruk.

a Wat is de massa van een voorwerp dat die druk zou uitoefenen als je het op je hand legde? Duid aan.

ongeveer 10 kg

ongeveer 1 kg

ongeveer 100 g

ongeveer 10 g

b Hoe komt het dat je je hand toch probleemloos op en neer kunt bewegen?

12 Voor een parachutesprong stijgt een vliegtuig naar 2,0 km hoogte. De druk in het vliegtuig is de normdruk. Een parachutist staat klaar in de deuropening om een sprong te maken, met zijn gezicht naar buiten gericht.

a Op welke figuur is de kracht op de parachutist net na het openen van de deur correct weergegeven?

©VANIN

b Bereken de kracht op zijn lichaam, dat een oppervlakte van 0,85 m² heeft.

Zoek de nodige gegevens op (in de theorie).

Gegeven: Gevraagd:

Oplossing:

c Kan de parachutist blijven staan? Vergelijk de berekende kracht met zijn gewicht.

13 Je laat op kamp de gasfles van het kookvuur openstaan nadat het vuur uit is. Wat gebeurt er? Duid aan.

Niets.

De fles loopt leeg, totdat er geen deeltjes meer in de fles zitten.

De fles loopt leeg, totdat de druk de normdruk is.

De fles loopt vol, totdat de druk de normdruk is.

14 Is er over- of onderdruk in de volgende situaties?

a in een quarantaineruimte voor patiënten die herstellen van een kankerbehandeling:

b in een dampkap:

c in een stofvrije kamer (cleanroom) waar micro-elektronica geproduceerd worden:

d in het reactorgebouw van een kerncentrale:

15 Bestudeer de drukmeter op een fietspomp bij een opgepompte band.

a Meet de manometer de absolute of de relatieve druk? Verklaar.

©VANIN

b Hoe groot is de relatieve druk?

c Hoe groot is de absolute druk?

16 Bestudeer de weerkaart.

a Verklaar de betekenis van de volgende symbolen.

• de gesloten zwarte lijnen, die ‘isobaren’ worden genoemd:

• de getalwaarden op de isobaren:

• de letters L en H:

b Duid een gebied met veel wind aan. Verklaar.

` Verder oefenen? Ga naar

Afb.

`

1 Begripskennis

• Ik kan de druk op een oppervlak omschrijven.

• Ik kan de druk op een oppervlak berekenen.

• Ik kan aanpassingen om de druk te verhogen of te verlagen, toelichten

• Ik kan de druk in een gas omschrijven.

• Ik kan het verband tussen de snelheid van de deeltjes en de temperatuur omschrijven

• Ik kan het absolute nulpunt omschrijven.

• Ik kan temperatuur omzetten naar de kelvinschaal.

• Ik kan het ontstaan van atmosferische druk omschrijven

• Ik kan over- en onderdruk omschrijven.

• Ik kan de kracht die ontstaat door over- en onderdruk, berekenen

• Ik kan het ontstaan van stroming omschrijven

2 Onderzoeksvaardigheden

• Ik kan een onderzoek stap voor stap uitvoeren

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan nauwkeurig berekeningen uitvoeren

©VANIN

Je kunt deze checklist ook op invullen bij je Portfolio.

JA NOG OEFENEN

Wat is druk in en op een vloeistof?

LEERDOELEN

Je kunt al:

M de druk op een oppervlak berekenen;

M de atmosferische druk en over- en onderdruk gebruiken;

M rekenen met massadichtheid;

M het gewicht en de resulterende kracht bepalen.

Je leert nu:

M de druk in een vloeistof omschrijven en berekenen;

M de druk op een vloeistof en toepassingen ervan omschrijven;

M de opwaartse kracht op een ondergedompeld voorwerp omschrijven en berekenen;

M de voorwaarden voor zinken, zweven en drijven verklaren.

1 Wat is druk in een vloeistof?

1.1 Druk in een vloeistof

OPDRACHT 18

Bestudeer de afbeelding en de uitspraken.

Wie heeft gelijk volgens jou?

©VANIN

Walvissen kunnen ondanks hun kolossale afmetingen en massa probleemloos op grote dieptes zwemmen, welke kant ze ook uit willen. Hoe komt het dat ze niet platgedrukt worden? Wat zorgt ervoor dat ze de zwaartekracht kunnen overwinnen? En hoe kunnen we die kennis gebruiken om een duikboot te maken?

In dit hoofdstuk bestudeer je hoe druk ontstaat in een vloeistof, welk effect de omgeving heeft op de totale druk en hoe er door de druk in een vloeistof krachten ontstaan.

Je kunt niet diep snorkelen, omdat je longen de druk van het water niet kunnen overwinnen. Als de snorkel lang en stevig genoeg is om de druk van het water te overwinnen, kun je op elke diepte snorkelen.

Je kunt niet diep snorkelen, omdat de snorkel niet zo lang kan worden gemaakt.

OPDRACHT 19 ONDERZOEK

Onderzoek hoe verschillende factoren de druk in een vloeistof beïnvloeden.

1 Voer het labo bij het onlinelesmateriaal uit.

2 Verklaar tot welke diepte je kunt snorkelen.

• De massa van een voorwerp kun je berekenen als m = t ∙ V

• Het volume V van een regelmatig voorwerp kun je berekenen als de oppervlakte van het grondvlak A maal de hoogte h: V = A ∙ h

In een vloeistof ontstaat er een druk door het gewicht van de bovenliggende vloeistoflagen.

Die druk noem je de hydrostatische druk, met als symbool phydro

De grootte van de hydrostatische druk wordt bepaald door de grootte van het gewicht van het bovenliggende water. Uit experimenten blijkt:

• De hydrostatische druk neemt recht evenredig toe met de diepte onder het oppervlak. phydro ~ h

• De hydrostatische druk neemt recht evenredig toe met de massadichtheid van de vloeistof. phydro ~ tvl

• De hydrostatische druk neemt recht evenredig toe met de zwaarteveldsterkte. phydro ~ g

Je kunt de uitdrukking voor de hydrostatische druk ook afleiden uit de definitie van druk.

Een vat heeft een horizontale doorsnede A en is gevuld met een vloeistof met dichtheid tvl. Elke laag vloeistof ervaart een zwaartekracht F z en oefent hierdoor een gewicht F g uit uit op de onderliggende lagen. Dat gewicht (dat even groot is als de zwaartekracht) veroorzaakt een druk.

Op een hoogte h onder het oppervlak is de grootte van de zwaartekracht F z gelijk aan: F

= m

De hydrostatische druk die werkt op een oppervlak A op een hoogte h onder het vloeistofoppervlak, kun je dan berekenen als: phydro = Fg A = F z A = t

Afb.

Afb.

ANIMATIE p hydro

Bekijk in de animatie hoe groot het gewicht en de druk zijn op verschillende dieptes.

VOORBEELD HYDROSTATISCHE DRUK BIJ HET ZWEMMEN

Tijdens het zwemmen en duiken ervaar je effecten van de hydrostatische druk:

• Tijdens het duiken voel je pijn aan je oren door de overdruk op je trommelvlies.

• Om diep onder water te zwemmen, heb je een gasfles nodig. Gasflessen creëren een druk in de longen die bestand is tegen de hydrostatische druk. De gasbellen die opstijgen na het uitademen, worden groter naarmate ze opstijgen, doordat de druk van buitenaf kleiner wordt.

In een vloeistof ontstaat er een druk door het gewicht van de bovenliggende vloeistoflagen. Die druk noem je de hydrostatische druk phydro = tvl ∙ g ∙ h

` Maak oefening 1 t/m 4 op p. 212-213.

OPDRACHT 20

Los het vraagstuk op.

De aderen van giraffen zijn extra stevig, om de grote hydrostatische druk op te vangen.

Een giraf is 5,5 m groot. De massadichtheid van bloed is 1,050 g cm3 .

1 Bereken de hydrostatische druk onderaan de poot.

Gegeven:

Gevraagd:

Oplossing:

©VANIN

2 Controleer je antwoord via de QR-code.

Werk in SI-eenheden.

TIP

VRAAGSTUK p hydro

1.2 Kracht op een oppervlak door de hydrostatische druk

Uit experimenten en de formule voor de hydrostatische druk kun je de volgende eigenschappen afleiden:

1 De hydrostatische druk werkt in alle richtingen De hydrostatische druk ontstaat door de zwaartekracht, een vectoriële grootheid die verticaal naar beneden werkt. De hydrostatische druk is een scalaire grootheid en werkt dus niet in een specifieke richting en zin.

HYDROSTATISCHE

h h h h

2 De hydrostatische druk veroorzaakt op elk oppervlak een (druk)kracht F loodrecht op het oppervlak, met als grootte: F = phydro ∙ A

3 De hydrostatische druk en de bijbehorende kracht zijn niet afhankelijk van de hoeveelheid vloeistof en van de vorm van het vat. Enkel de hoogte is van belang.

VOORBEELD HYDROSTATISCHE DRUK EN KRACHT IN HET ZWEMBAD

De hydrostatische druk in een meer, een vijver of een zwembad is op eenzelfde hoogte hetzelfde.

Voorbeeld op 1,0 m diepte: phydro = tvl g h = 1 000 kg m3 2 9,81 N kg 1,0 m = 9,8 103 N m2 = 9,8 kPa

De hydrostatische druk veroorzaakt een kracht op de wanden. Die kracht staat loodrecht op de wanden en neemt toe met de diepte. De hydrostatische druk en de kracht op de wanden zijn onafhankelijk van de vorm van het zwembad en de hoeveelheid water.

©VANIN

De massadichtheid van water is heel eenvoudig. twater = 1 000 kg m3 = 1 g cm3

Andere waarden kun je opzoeken.

De hydrostatische druk werkt in alle richtingen en is onafhankelijk van de hoeveelheid vloeistof.

De kracht die ontstaat door de hydrostatische druk, staat loodrecht op een oppervlak en heeft als grootte: F = phydro ∙ A

` Maak oefening 5 en 6 op p. 213.

Afb. 24

Afb. 22

Afb. 23

TIP

2 Wat is druk op een vloeistof?

2.1 Wet van Pascal

OPDRACHT 21

Bestudeer het effect van druk op een vloeistof.

1 Welke druk werkt op het sap in een drinkbusje dat halfleeg op tafel staat?

2 Geef twee manieren om uit een drinkbusje te drinken. Noteer in de eerste rij van de tabel.

3 Vul de tabel verder aan voor beide manieren.

1

2

©VANIN

Welke druk verandert er eerst?

De druk op het sap verandert.

De hydrostatische druk verandert.

Door een onderdruk te creëren.

Door een overdruk te creëren.

De druk op het sap verandert.

De hydrostatische druk verandert.

Hoe ontstaat de stroming?

Door een onderdruk te creëren.

Door een overdruk te creëren.

• Duid een punt P aan waar de druk eerst verandert.

• Duid een punt S aan waar de drukverandering een effect heeft (er ontstaat stroming).

• Teken een pijl volgens de stroming.

Een vloeistof is (meestal) omgeven door de atmosfeer. Boven de vloeistof heerst de atmosferische druk. Het effect van de atmosferische druk wordt onverminderd doorgegeven naar elk punt van de vloeistof. Zo ontstaat er in de vloeistof een totale druk:

tot (hPa)

ptot(h)-grafiek

ptot = 1 013 hPa + 98,1 · h = patm + tvl · g · h

©VANIN

Om termen op te tellen, zet je ze eerst in dezelfde eenheid.

Op een kleine diepte is de totale druk vergelijkbaar met de normdruk.

VOORBEELD TOTALE DRUK BIJ HET ZWEMMEN

Als je zwemt op 1,0 m diepte, is de hydrostatische druk:

hydro = tvl g h = 1 000 kg m3 2 9,81 N kg 1,0 m = 9,8 kPa en de totale druk:

ptot = patm + phydro = 101,3 kPa + 9,8 kPa = 111,1 kPa

Als op een vloeistof een drukkracht wordt uitgeoefend, ontstaat er een druk. Net zoals de luchtdruk wordt die druk onverminderd doorgegeven over de hele vloeistof. Dat principe staat bekend als de wet van Pascal. De wet van Pascal is geldig voor vloeistoffen, maar ook voor gassen. Dat kun je verklaren met het deeltjesmodel.

• In een vloeistof zitten de moleculen dicht bij elkaar. Als je op een hoeveelheid vloeistof een druk uitoefent, zal het volume van de vloeistof niet veranderen. De druk die wordt uitgeoefend op een vloeistof, plant zich in alle richtingen ongewijzigd voort, doordat elke molecule een kracht uitoefent op haar buur Er ontstaat een extra drukkracht op de wanden

• In een gas zitten de moleculen ver van elkaar. Als je op een hoeveelheid gas een druk uitoefent, zal het volume van het gas sterk veranderen. De druk die wordt uitgeoefend op een gas, zorgt voor een verhoging van de massadichtheid. Daardoor botsen de deeltjes meer tegen de wanden en ontstaat er een verhoogde gasdruk. Er ontstaat een extra drukkracht op de wanden.

Grafiek

De grootte van de druk op de vloeistof of het gas bepaalt het waargenomen effect:

• Als er openingen zijn in het vat, spuit de vloeistof of het gas er in alle richtingen even hard uit.

• Het vat kan vervormen of barsten.

VOORBEELD COMMUNICATIE BIJ DIEREN

Geluid is een drukgolf.

De veranderingen in druk verspreiden zich in alle richtingen evenveel.

• Als mensen praten, veroorzaakt de trilling van de stembanden een druk op de lucht. Die drukverandering zorgt voor een verhoging van de massadichtheid van de lucht en plant zich voort naar de gesprekspartner.

• Een dolfijn communiceert door geluid te produceren onder water. Door drukveranderingen die zich in alle richtingen voortplanten in het water, komt het geluid terecht bij zijn soortgenoten en/of natuurlijke vijanden.

De wet van Pascal vind je ook terug in heel wat (technologische) toepassingen.

In de volgende paragraaf bespreken we er drie.

Een druk die wordt uitgeoefend op een vloeistof of een gas, plant zich in alle richtingen onverminderd voort. Dat is de wet van Pascal Daardoor is de totale druk in een vloeistof die zich in de atmosfeer bevindt: ptot = patm +

` Maak oefening 7 t/m 9 op p. 214-215.

2.2 Technologische toepassingen

A UITSTROOMSNELHEID

OPDRACHT 22

Bestudeer de uitstroomsnelheid.

1 Bouw met twee identieke petflesjes de opstelling op de afbeelding na.

a Snijd de bodem van de flesjes.

b Bevestig een rietje of een dun glazen buisje door een gaatje in de dop.

c Gebruik rietjes met een duidelijk verschillende lengte.

2 Neem met twee leerlingen elk een flesje.

a Sluit met een vinger het rietje af en vul het flesje met een bekertje water.

b Zet het bekertje onder het rietje.

3 Wat zal er gebeuren als beide leerlingen tegelijk het rietje openen?

Duid je hypothese aan en test uit.

Hypothese Waarneming

Beide flesjes zijn even snel leeg.

Het flesje met het korte rietje is het snelst leeg.

Het flesje met het lange rietje is het snelst leeg.

4 Verklaar je waarneming.

Beide flesjes zijn even snel leeg.

Het flesje met het korte rietje is het snelst leeg.

Het flesje met het lange rietje is het snelst leeg.

©VANIN

5 Wat gebeurt er als je het flesje laat vallen nadat je je vinger hebt weggehaald?

Test uit en verklaar.

Om vloeistoffen in beweging te brengen, is er een drukverschil nodig. Aangezien de hydrostatische druk afhankelijk is van de hoogte, zorgt een hoogteverschil voor een drukverschil.

• De luchtdruk boven de vloeistof wordt onverminderd doorgegeven, zodat in punt 1:

h

• In punt 2 heerst enkel de luchtdruk, zodat in punt 2:

p2 = patm

• Het drukverschil is de hydrostatische druk:

Dp = p1 – p2

= patm + tvl ∙ g ∙ h – patm

= tvl ∙ g ∙ h

= phydro

Zolang er vloeistof in het vat zit (h > 0), is er een drukverschil en zal het water stromen. Hoe groter het hoogteverschil, hoe groter het drukverschil en hoe groter de uitstroomsnelheid.

Een watertoren staat op de hoogste plaats in de omgeving, om een zo groot mogelijke uitstroomsnelheid te hebben aan de waterkraan.

• Water wordt omhooggepompt naar de watertoren.

• Water stroomt spontaan uit een kraantje.

B VERBONDEN VATEN

Als er tussen twee vaten die met elkaar verbonden zijn, een drukverschil is, ontstaat er een stroming Als de druk langs beide kanten gelijk is (∆p = 0), is de vloeistof in rust.

Voor een open verbinding tussen twee vaten met dezelfde vloeistof is de hoogte van de vloeistof bij die evenwichtssituatie gelijk. Dat is de wet van de verbonden vaten of de wet van de communicerende vaten.

De vloeistof is in evenwicht, dus er is geen stroming onderaan de buis. Er is dus geen drukverschil tussen de punten 1 en 2 op eenzelfde hoogte in de buis. In beide benen werken (volgens de wet van Pascal) de atmosferische druk en de hydrostatische druk.

©VANIN

Als verschillende buizen verbonden zijn en gevuld worden met dezelfde vloeistof, liggen de vloeistofoppervlakken in hetzelfde horizontale vlak Dat geldt ook als de doorsnede en de vorm van de buizen niet gelijk zijn. De druk op elk horizontaal vloeistofoppervlak is dan in elke buis gelijk.

VOORBEELD ZEENIVEAU

De grootste verbonden vaten zijn de zeëen en oceanen. Onafhankelijk van rotsen en doorgangen in grotten onder water, is het oppervlak overal horizontaal (als je de golven buiten beschouwing laat). Vandaar dat je kunt spreken over het zeeniveau. Dat niveau is overal hetzelfde horizontale vlak.

OPDRACHT 23

Los het vraagstuk op.

Je giet in een U-vormige buis water en een onbekende vloeistof. De vloeistoffen zijn in evenwicht bij de hoogtes weergegeven op de afbeelding.

1 Rangschik de druk in de verschillende punten van klein naar groot.

2 Bereken de massadichtheid van de onbekende vloeistof.

Werk dat uit op een apart cursusblad.

Gegeven: twater = 1 000 kg m3 ; hwater = 6,00 cm; honbekend = 7,60 cm

Gevraagd: tonbekend = ?

3 Controleer je antwoord.

C HYDRAULISCHE PERS

OPDRACHT 24

Bestudeer het remsysteem van een auto.

Het remsysteem van een auto bestaat uit een dunne, met olie gevulde buis die afgesloten is door een zuiger verbonden met het rempedaal en door twee zuigers die een kracht uitoefenen op de wielen.

1 Bestudeer de afbeelding.

VERBONDEN VAT

2 Welk verband is er tussen de druk in punt 1 en punt 2? Verklaar.

Je duwt met een kracht F het rempedaal in. 1 2

3 Teken de krachten op de zuigers (met oppervlakte A) in punt 1 en punt 2.

4 Vul het verband tussen de gevraagde grootheden aan. de totale oppervlakte van de zuigers in punt 1 en punt 2 A2 = ∙ A 1 de totale krachtgrootte in punt 1 en punt 2 F

de uitgeoefende kracht en de kracht op de vier wielen F

Om een kracht te vergroten, gebruikt men vaak een hydraulisch systeem. Een hydraulisch systeem bestaat uit:

• een buis die gevuld is met een vloeistof. Meestal gebruikt men olie, omdat olie niet makkelijk bevriest en roest voorkomt bij de gebruikte metalen;

• twee zuigers met een verschillend oppervlak die de buis afsluiten.

We bekijken de werking bij een U-vormige buis.

Op de linkse zuiger (A1) wordt een kracht F 1 uitgeoefend. Daardoor ontstaat er een druk p1 op de vloeistof. Die druk plaatst zich onverminderd door naar de rechtse zuiger (wet van Pascal), waardoor er een kracht F2 uitgeoefend wordt op de rechtse zuiger (A2).

Het verband tussen beide krachten kun je afleiden uit de definitie van druk: p2 = p1 (wet van Pascal)

dus F2 A2 = F1 A1

Daaruit volgt: F2 = F 1 · A2 A1

Om de kracht F2 zo groot mogelijk te maken, moet A2 A1 > 1, dus A2 > A1.

Hoe groter de verhouding A2 A1 , hoe meer de kracht vergroot wordt.

Met een hydraulisch systeem wordt een kleine kracht omgezet in een grote kracht. Dat noem je het mechanisch voordeel van het hydraulisch systeem.

VOORBEELD HYDRAULISCHE PERS

De hydraulische pers wordt bijvoorbeeld gebruikt bij kranen en bulldozers om de arm te bewegen, om zware voorwerpen omhoog te krikken (bv. een wagen in een garage) en in remsystemen.

De wet van Pascal heeft veel technologische toepassingen.

Dit zijn drie veelvoorkomende principes die we gebruiken:

1 De uitstroomsnelheid wordt bepaald door het hoogteverschil van de vloeistof (bv. in een watertoren).

2 Als verbonden vaten in evenwicht zijn, is het vloeistofniveau in beide vaten even hoog (bv. in een sluis).

3 Met een hydraulisch systeem kun je de uitgeoefende kracht vergroten (bv. in een remsysteem).

` Maak oefening 10 t/m 15 op p. 215-217.

©VANIN

OPDRACHT 25

Kies de juiste zuigers om een auto op te tillen.

Welke combinatie van zuigers gebruik je? Duid aan.

Je duwt op een zuiger die even groot is als de zuiger waarop de auto staat.

Je duwt op een kleine zuiger. De auto staat op een grote zuiger.

Je duwt op een grote zuiger. De auto staat op een kleine zuiger.

3 Wat is de archimedeskracht?

3.1 Wet van Archimedes

OPDRACHT 26

Bestudeer het gewicht onder water.

Tijdens een zwempartijtje til je een vriend op. Je buigt door je knieën, zodat hij/zij makkelijk op je schouders kan, en dan sta je recht.

1 Waar ervaar je het gewicht van je vriend?

2 Wat gebeurt er met die kracht als je rechtop gaat staan?

De kracht blijft hetzelfde.

De kracht neemt toe.

De kracht neemt af.

3 Hoe komt dat volgens jou?

©VANIN

OPDRACHT 27 ONDERZOEK

Onderzoek de kracht op een ondergedompeld voorwerp.

1 Gebruik het labo bij het onlinelesmateriaal.

2 Vergelijk je verklaring in opdracht 26 met je besluit.

TIP

Wegens de distributiviteit kun je de gemeenschappelijke factoren afzonderen.

a ∙ b – a ∙ c = a ∙ (b – c)

Als een voorwerp ondergedompeld is in een vloeistof, ondervindt het een opwaartse kracht die even groot is als het gewicht van de verplaatste vloeistof. Archimedes beschreef als eerste die opwaartse kracht. Daarom staat dat fenomeen bekend als de wet van Archimedes en wordt de opwaartse kracht de archimedeskracht genoemd.

Dankzij die opwaartse kracht vallen dieren niet naar de bodem en kunnen ze onder water zwemmen op elke hoogte. De archimedeskracht neemt toe met het volume van het dier.

Je kunt de wet van Archimedes aantonen met experimenten of met behulp van de hydrostatische druk.

Een cilinder met grondoppervlak A bevindt zich rechtop in een vat dat gevuld is met een vloeistof met massadichtheid tvl.

• Er werkt een kracht F 1 op de bovenkant met als grootte:

A

• Er werkt een kracht F2 op de onderkant met als grootte:

A

De archimedeskracht is de resulterende kracht ten gevolge van de hydrostatische druk: FA = F1 + F2. (In de horizontale richting heffen de krachten elkaar op, omdat daar geen hoogteverschil is.)

Aangezien h2 > h1, is F2 > F 1 en is FA een kracht die verticaal omhoog gericht is, met als grootte:

FA = F2 – F 1 = (patm + tvl ∙ g ∙ h2) ∙ A – (

©VANIN

A

h1)

A = tvl ∙ g ∙ ∆h ∙ A (volume van de cilinder: V = ∆h ∙ A)

V (1)

Door de cilinder is er een hoeveelheid vloeistof V verplaatst.

De grootte van het gewicht Fg, vl van die verplaatste hoeveelheid vloeistof is: Fg, vl = mvl

g (2)

Uitdrukking (1) is gelijk aan uitdrukking (2): de grootte van de archimedeskracht is gelijk aan het gewicht van de verplaatste vloeistof.

VOORBEELD VISSEN

Onderwaterdieren ondervinden een opwaartse kracht door het water. Dankzij de opwaartse kracht vallen dieren niet naar de bodem en kunnen ze onder water zwemmen op elke hoogte. De archimedeskracht neemt toe met het volume van het dier.

OPDRACHT 28

Bestudeer een boot en een luchtballon.

1 Vul de tabel aan.

2 Vervolledig de afbeeldingen.

Hoe zie je dat er een opwaartse kracht werkt?

Welke stof oefent de opwaartse kracht uit?

a Arceer het ondergedompelde volume vloeistof of gas.

b Teken het zwaartepunt van het ondergedompelde volume.

c Teken en benoem de archimedeskracht.

De opwaartse archimedeskracht werkt op elk voorwerp dat zich in een vloeistof of gas bevindt. De vorm en de massa van het voorwerp spelen geen rol. Als het voorwerp zich niet helemaal in het gas of de vloeistof bevindt, wordt de grootte bepaald door het ondergedompelde deel (Vonder).

Het aangrijpingspunt vind je door in gedachten het zwaartepunt te bepalen van de vloeistof die of het gas dat het ondergedompelde deel vult.

De vier kenmerken van de archimedeskracht FA zijn:

• aangrijpingspunt: het zwaartepunt van het ondergedompelde deel,

• richting: verticaal,

• zin: naar boven,

• grootte: FA = tvl ∙ g ∙ Vonder (vloeistof) of FA = tgas ∙ g ∙ Vonder (gas).

©VANIN

Als een voorwerp ondergedompeld is in een vloeistof of een gas, ondervindt het een opwaartse kracht (de archimedeskracht FA) die even groot is als het gewicht van de verplaatste vloeistof of het verplaatste gas:

FA = tvl ∙ g ∙ Vonder (vloeistof) of FA = tgas ∙ g ∙ Vonder (gas)

Dat is de wet van Archimedes

` Maak oefening 16 t/m 18 op p. 218-219.

3.2 Zinken, zweven en drijven

OPDRACHT 29

Bestudeer de krachten op zwembadspeelgoed.

1 Vul de tabel aan voor beide situaties.

Een bal wordt onder water geduwd en losgelaten. Een duikstokje wordt onder water geduwd en losgelaten.

©VANIN

Wat gebeurt er op het moment dat je loslaat?

De bewegingstoestand verandert wel / niet. De bewegingstoestand verandert wel / niet. Geef de kenmerken van de resulterende kracht.

• richting:

• zin:

• grootte: F res 0

• richting:

• zin:

• grootte: F res 0 Waar komt het voorwerp tot rust?

De bal drijft / zweeft / zinkt. Het duikstokje drijft / zweeft / zinkt.

2 Welke krachten werken op de bal en het duikstokje als je ze loslaat?

3 Teken en benoem voor beide situaties de krachten op het moment dat je loslaat.

Op elk voorwerp met een massadichtheid tvw en een volume V dat volledig ondergedompeld is in een vloeistof met een massadichtheid tvl, werken twee krachten:

• de zwaartekracht F z, met als grootte: F z = m vw ∙ g = tvw ∙ V ∙ g

• de archimedeskracht FA, met als grootte: FA = tvl ∙ Vonder ∙ g

De resulterende kracht is F res = FA + F z. De grootte en de zin van de resulterende kracht als je het voorwerp loslaat, bepalen het gedrag van het voorwerp in de vloeistof. Het voorwerp zal bewegen totdat het een evenwicht bereikt: het zweeft, zinkt of drijft

Loslaten in de vloeistof

Evenwicht

Zweven 1

Berekeningen

Bij het loslaten:

FA = F z

tvl ∙ V ∙ g = tvw ∙ V ∙ g tvl = tvw

Er is evenwicht (F res = 0).

Het blokje is in rust Het zweeft in de vloeistof, omdat tvl = tvw

©VANIN

Bij het loslaten: FA < F z tvl ∙ V ∙ g < tvw ∙ V ∙ g tvl < tvw

Er is geen evenwicht (F res ≠ 0).

Het blokje beweegt naar beneden.

Het zinkt in de vloeistof, omdat tvl < tvw .

Op de bodem is er evenwicht, omdat de normaalkracht F n het blokje ondersteunt.

Bij het loslaten:

FA > F z tvl ∙ V ∙ g > tvw ∙ V ∙ g tvl > tvw

Er is geen evenwicht (F res ≠ 0).

Het blokje beweegt naar boven.

Het drijft in de vloeistof, omdat tvl > tvw .

Bij het drijven is er evenwicht, omdat de archimedeskracht afneemt tot F A, aangezien het ondergedompelde deel kleiner wordt:

F ’ A = F z tvl ∙ g ∙ Vonder > tvw ∙ g ∙ V

Vonder = tvw tvl ∙ V

Drijven

zwemblaas

VOORBEELD DRIJFVERMOGEN

Zowel in de natuur als in technologische toepassingen zijn er aanpassingen om een voorwerp de gewenste positie te laten aannemen in een vloeistof. Een voorwerp bestaat meestal uit verschillende stoffen. De gemiddelde massadichtheid bepaalt het drijfvermogen.

• De gemiddelde massadichtheid is laag: het voorwerp drijft.

Een eend bestaat vooral uit water, bot en lucht. De gemiddelde massadichtheid van een eend is kleiner dan die van water. Eenden drijven. Ongeveer 70 % van een eend zit boven water. Als eenden duiken voor een prooi, komen ze spontaan terug naar het oppervlak.

Dat principe wordt toegepast bij een schip. Het schip bestaat uit metaal en een zware lading, maar bij een juiste vorm ook uit heel veel lucht. Als de gemiddelde massadichtheid van het schip kleiner is dan de massadichtheid van het water, drijft het schip. Het ondergedompelde deel wordt bepaald door de verhouding tvw

• De gemiddelde massadichtheid wordt aangepast: het voorwerp stijgt of daalt.

Bij vissen zorgt de zwemblaas ervoor dat de vis omhoog of omlaag kan bewegen. De zwemblaas is een zakje dat kan opzwellen of krimpen door lucht toe te voegen of af te voeren. Als de blaas krimpt, stijgt de massadichtheid en kan de vis makkelijk naar beneden bewegen. Als de blaas vult met lucht, daalt de massadichtheid en kan de vis makkelijk naar boven bewegen.

©VANIN

Dat principe wordt toegepast bij een duikboot. Een duikboot heeft een dubbele buitenwand. Dat noem je de ballasttank. Door daar de juiste hoeveelheid lucht en water in te laten, kun je de duikboot naar boven of naar onderen laten bewegen.

Voor een voorwerp met een massadichtheid tvw dat volledig is ondergedompeld in een vloeistof met een massadichtheid tvl, geldt:

• Het voorwerp zinkt als tvw > tvl.

• Het voorwerp zweeft als tvw = tvl

• Het voorwerp drijft als tvw < tvl,.

` Maak oefening 19 t/m 21 op p. 220-221.

OPDRACHT 30

Bestudeer de werking van een boot en een duikboot.

warm water koud water warm zeewater koud zeewater

drijven zweven zinken

1 Teken en benoem de zwaartekracht en de archimedeskracht in het massapunt op elke figuur.

2 In welk water drijft het schip het hoogst? Verklaar.

©VANIN

3 Als een duikboot wil zweven, moet de verhouding lucht/water in de balasttanks goed gekozen worden. Waarop moet er gelet worden bij die keuze?

OPDRACHT 31

Los het vraagstuk op.

Een duikstokje en een strandbal worden ondergeduwd in het zwembad en losgelaten.

Het duikstokje heeft een volume van 60,0 cm³ en een massa van 200 g.

De bal heeft een volume van 45,0 dm³ en is gevuld met lucht (tlucht = 1,293 kg m3 ).

1 Werk het vraagstuk uit op een cursusblad.

a Bereken de resulterende kracht wanneer je de voorwerpen loslaat.

b Bereken het ondergedompelde deel van de bal wanneer hij drijft.

2 Controleer je antwoord via de QR-code.

ARCHIMEDES

VRAAGSTUK

Druk in en op een vloeistof

Kernbegrippen

Notities hydrostatische druk

• In een vloeistof ontstaat de hydrostatische druk door van de bovenliggende

phydro = met tvl de en h de

• De hydrostatische druk werkt in elke / verticale richting en is afhankelijk /onafhankelijk van de hoeveelheid vloeistof.

wet van Pascal

wet van Archimedes

• Een druk die wordt uitgeoefend op een vloeistof of een gas, plant zich onverminderd voort. Dat is de wet van Pascal.

Daardoor is de totale druk in een vloeistof die zich in de atmosfeer bevindt:

ptot =

• Dit zijn drie veelvoorkomende technologische toepassingen:

1 De uitstroomsnelheid wordt bepaald door het van de vloeistof (bv. in een watertoren).

2 Als verbonden vaten in evenwicht zijn, is het vloeistofniveau in beide vaten (bv. in een sluis).

3 Met een hydraulisch systeem kun je de uitgeoefende vergroten (bv. in een remsysteem).

• Als een voorwerp ondergedompeld is een vloeistof of een gas, ondervindt het een (de archimedeskracht FA) die even groot is als :

FA = tvl ∙ g ∙ Vonder (vloeistof) of FA = tgas ∙ g ∙ Vonder (gas)

Dat is de wet van Archimedes.

• Voor een voorwerp met een massadichtheid tvw dat volledig is ondergedompeld in een vloeistof met een massadichtheid tvl, geldt:

– Het voorwerp zinkt als

– Het voorwerp zweeft als .

– Het voorwerp drijft als .

Verbind het fenomeen met het voorbeeld.

Fenomeen

Voorbeeld

wet van Pascal • • Een zwembad kun je niet laten leeglopen via een stop: je krijgt de stop niet los.

hydrostatische druk • • Een blok hout van 500 kg drijft. Een gouden ring van 5 g zinkt.

wet van Archimedes • • Als je achteraan op een tube tandpasta knijpt, komt de tandpasta er vooraan uit.

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

GRAFIEKEN LEZEN

FORMULES OMVORMEN

VOORVOEGSELS EN MACHTEN

EENHEDEN OMZETTEN

BEREKENINGEN AFRONDEN

1 Een fles olijfolie is tot op een hoogte van 25,0 cm gevuld. De hydrostatische druk op de bodem is 2,30 kPa.

a Bereken de massadichtheid van de olijfolie in g cm3

Gegeven:

Gevraagd:

Oplossing:

b Vergelijk je antwoord met de massadichtheid van water. Kan dat kloppen?

2 Op welke diepte in een meer is de hydrostatische druk even groot als de normdruk? Duid aan.

3 Rangschik de volgende situaties volgens toenemende druk op de bodem.

4

Tijdens het duiken zwemt een duiker horizontaal onder een rots door. Welke uitspraak is correct? Duid aan.

De druk op de duiker blijft gelijk.

De druk op de duiker hangt af van de massadichtheid van de rots.

De druk op de duiker hangt af van de afmetingen van de rots.

De druk op de duiker hangt af van de massadichtheid en de afmetingen van de rots.

©VANIN

5 Stappen in een zwembad is moeilijker dan in de lucht. Hoe komt dat? Duid aan.

De kracht door de hydrostatische druk is groter dan de kracht door de atmosfeerdruk.

De kracht door de hydrostatische druk is kleiner dan de kracht door de atmosfeerdruk.

Water oefent een grotere weerstandskracht uit dan lucht.

Water oefent een kleinere weerstandskracht uit dan lucht.

6 Een stuwmeer (l = 900 m, b = 650 m) heeft een diepte van 80 m en is afgesloten door een dam (p = 1 000 kg m3 ).

a Bereken de hydrostatische druk op halve en op volledige diepte.

Gegeven: Gevraagd:

Oplossing:

b Teken de kracht die wordt uitgeoefend op de halve en de volledige diepte van de stuwdam.

c Verklaar de vorm van de dam.

d Hoe moet de dam aangepast worden bij een uitbreiding van het meer tot een lengte van 1,5 km?

Afb. 39

7 Een walvis zwemt in zee (t = 1 030 kg m3 ) en ondervindt een druk van 7,6 bar.

a Bereken de zwemdiepte en de kracht op zijn staart, die een oppervlakte van 1,7 m² heeft.

Gegeven: Gevraagd:

Oplossing:

b Hoe komt het dat de walvis niet samengedrukt wordt?

8 Om aan te tonen dat de druk zich in alle richtingen onverminderd voortplant, plaatste Pascal een dunne lange buis (rbuis = 0,30 cm) verticaal op een wijnvat (rwijnvat = 21 cm) dat volledig gevuld was met water. Hij ontdekte dat het vat barstte zodra de dunne buis tot een hoogte van 12,0 m gevuld werd met water. Bereken …

a de massa en het gewicht van het water in de buis, b de nettokracht die het water uitoefent op het deksel.

Gegeven: Gevraagd:

Oplossing:

9 Op de grafiek staat de druk als functie van de diepte weergegeven voor drie verschillende vloeistoffen die in drie gelijke bekers gegoten worden.

Rangschik de gevraagde grootheden van klein naar groot.

a de omgevingsdruk:

b de totale druk op de bodem:

c de hydrostatische druk op de bodem:

d de massadichtheid:

10 Het maximale waterniveau in een watertoren is 48,0 m hoger dan de badkamerkraan.

De minimale kraandruk is 3,80 ∙ 105 Pa. Bereken …

a de druk aan de kraan als de toren volledig vol is,

b de minimale vulhoogte.

Gegeven:

Gevraagd:

Oplossing:

11 Om dieren water te geven, gebruiken mensen vaak een drinkflesje zoals op de afbeelding.

a Duid het juiste antwoord aan en verklaar.

De fles is bovenaan zeker / misschien / zeker niet open.

b De druk in A is 900 hPa.

Welke uitspraak is correct? Duid aan.

pB = 900 hPa

pB < 900 hPa

pB > 900 hPa

©VANIN

Je kunt niets zeggen over de druk in B, want je kent de luchtdruk op dat moment niet.

12 Verklaar de onderstaande fenomenen.

a Je kunt de deur van een gezonken auto pas openen wanneer de auto volgelopen is met water.

b De dokter meet je bloeddruk met je arm ter hoogte van je hart.

c Als geurafsluiter gebruikt men een sifon.

d De tandpasta komt uit de tube als je achteraan duwt.

13 Twee glazen buizen zijn met elkaar verbonden door een gummislang. Eén buis zit vast aan een statief. De buizen zijn voor de helft gevuld met water. Welk van de figuren geeft de juiste stand van de waterniveaus weer wanneer de vrije buis opgetild wordt?

14

Bestudeer de afbeelding van een hevel.

a Bouw de hevel na.

b Hoe groot is het drukverschil tussen punt 1 en 2?

• Vul de juist hoogte in.

∆p = t ∙ g ∙

• Verklaar.

c Geef een toepassing van een hevel.

15 Bestudeer de afbeelding van drie ballonnen.

Welke uitspraak is correct? Duid aan.

De archimedeskracht is het grootst voor de ballon gevuld met lucht.

De archimedeskracht is het grootst voor de ballon gevuld met water.

De archimedeskracht is het grootst voor de ballon gevuld met helium.

©VANIN

De archimedeskracht is voor de drie ballonnen gelijk

Er werkt geen archimedeskracht op de ballonnen.

TIP

Werk zo lang mogelijk in formules, om het rekenwerk te beperken. Misschien lukt het je wel zonder rekentoestel!

16 Om de rekken aan te vullen in de winkel, gebruikt men een transpallet met een maximale last van 1 000 kg. Die hydraulische pers heeft een zuiger met een diameter van 4,0 cm en een zuiger met een diameter van 8,0 cm.

a Op welke zuiger oefent de man de kracht uit?

©VANIN

b Hoeveel kracht moet hij uitoefenen om de maximale last op te tillen?

Gegeven: Gevraagd:

Oplossing:

17 Een duikfles heeft een massa van 21,0 kg en een volume van 18,0 liter. Teken en bereken de krachten op de fles als de fles in lucht en in water losgelaten wordt.

Gegeven:

Gevraagd:

Oplossing:

Afb. 48

Afb.

18 Ga na of de kroon van goud is.

a Bekijk de legende van Archimedes en de kroon van de koning.

b Je kunt de echtheid van de kroon ook nagaan met een dynamometer.

Als je de kroon aan een dynamometer hangt, lees je 336,0 N af.

Als je de kroon onderdompelt in water, lees je 316,0 N af.

• Welk volume heeft de kroon?

• Is de kroon uit goud (tgoud = 19,3 g cm2 ) gemaakt?

Gegeven:

©VANIN

Gevraagd:

Oplossing:

VIDEO KROON ARCHIMEDES

19 Verklaar de volgende fenomenen.

a Een luchtballon kan stijgen en dalen.

b In een waterpas zit een gekromd buisje met een luchtbel in een vloeistof. De luchtbel in een waterpas staat niet in het midden op een schuin oppervlak.

©VANIN

c Een ijsberg bevindt zich voor 94 % onder water.

d Smeltend zee-ijs leidt niet tot een stijging van het zeeniveau. Welk ijs zorgt daar dan wel voor?

20 Een glas is gevuld met water en olie (tolie= 0,9 g cm3 ).

Een ijsblokje (volume van 3,0 cm³ en massa van 2,9 gram) wordt in het glas gelegd.

a Hoe gedraagt het ijsblokje zich in water?

b Hoe gedraagt het ijsblokje zich in olie?

c Toon aan met berekeningen.

d Teken het ijsblokje in de verschillende situaties.

ijsblokje in glas gevuld met water

ijsblokje in glas gevuld met olie

ijsblokje in glas gevuld met olie en water

21 Aan een houten latje worden twee identieke voorwerpen even ver van het draaipunt bevestigd.

Het geheel is in evenwicht (afbeelding 53).

Vervolgens wordt het ene blokje ondergedompeld in alcohol en het andere in water (afbeelding 54).

Welke beker is gevuld met alcohol? Verklaar.

` Verder oefenen? Ga naar .

Afb. 53

Afb. 54

1 Begripskennis

• Ik kan de druk in een vloeistof omschrijven

• Ik kan de druk in een vloeistof en de bijbehorende kracht berekenen.

• Ik kan de wet van Pascal omschrijven

• Ik kan de totale druk in een vloeistof berekenen.

• Ik kan de wet van Pascal toepassen.

• Ik kan de wet van Archimedes omschrijven

• Ik kan de wet van Archimedes bewijzen.

• Ik kan de wet van Archimedes toepassen

• Ik kan met een krachtenschema zinken, zweven en drijven verklaren

• Ik kan de voorwaarden voor zinken, zweven en drijven afleiden.

• Ik kan de voorwaarden voor zinken, zweven en drijven toepassen

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren

• Ik kan verbanden tussen grootheden onderzoeken

• Ik kan de gegevens van een trendlijn interpreteren.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan nauwkeurig krachten tekenen en optellen.

• Ik kan nauwkeurig berekeningen uitvoeren.

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

BEKIJK KENNISCLIP

A F

Druk veroorzaakt krachten in een vloeistof of een gas.

• Stroming van een gas of een vloeistof door een kracht:

F = D p ∙ A

• Opwaartse kracht (archimedeskracht  F A ) op een voorwerp dat ondergedompeld is:

g ∙ V onder (vloeistof) of

F A = t vl

g ∙ V onder (gas)

F A = t gas

Dat is de wet van Archimedes

Druk plant zich voort in een vloeistof of een gas. Een druk die wordt uitgeoefend op een vloeistof of een gas, plant zich in alle richtingen onverminderd voort.

• In een gas: verhoging van de massadichtheid en drukkracht op de wanden

• In een vloeistof: drukkracht op de naburige deeltjes en de wanden

Druk De grootheid druk is de maat voor de indrukking.

Grootheid met symbool SI-eenheid met symbool

druk p = F A pascal Pa

Als een kracht  F uitgeoefend wordt op een oppervlak met grootte A , wordt het oppervlak ingedrukt.

• Bij een klein contactoppervlak is het effect groot. Er ontstaat een grote druk.

• Bij een groot contactoppervlak is het effect klein. Er ontstaat een kleine druk.

Druk in een gas

• Ontstaat door de botsingen van gasdeeltjes tegen de wanden.

• Bij T  = 0 K (kelvinschaal) bewegen de deeltjes niet.

De gasdruk is nul.

D at is het absolute nulpunt.

• Atmosferische druk:

–Normdruk (= gemiddel de atmosfeerdruk op zeeniveau):

p 0 = 1,013 bar = 1,013 ∙ 10 5 Pa = 1 013 hPa

–Neemt af met de hoogt e.

Druk in een vloeistof

• Een voorwerp zinkt als

• Een voorwerp zweeft als vl

• Een voorwerp drijft als t < t vl .

©VANIN

Dat is de wet van Pascal . De totale druk in een vloeistof die zich in de atmosfeer bevindt: p tot = p atm + p hydro

• Ontstaat door het gewicht van de bovenliggende vloeistoflagen.

p hydro = t vl ∙ g ∙ h met t vl de massadichtheid van de vloeistof en h de diepte onder het vloeistofoppervlak

• Werkt in alle richtingen en is onafhankelijk van de hoeveelheid vloeistof.

Een kleine stap voor de mens ...

1 Als Buzz Aldrin zijn astronautenpak draagt, heeft hij een massa van 110 kg. Zijn schoenen hebben een oppervlakte van 380 cm². Bereken de druk op het maanoppervlak.

Gegeven:

Gevraagd:

Oplossing: Controle: Is de druk op het aardoppervlak groter of kleiner? Verklaar.

2 Hoe ontstaat de zuigkracht van een stofzuiger?

3 De onderzoekers nemen stalen van het maanstof. Kunnen ze daarvoor een stofzuiger gebruiken?

a Duid aan en verklaar.

Ja.

Ja, als de stofzuiger krachtiger is dan op aarde.

Ja, als de stofzuiger minder krachtig is dan op aarde.

Nee.

b Vergelijk je antwoord met je hypothese op p. 180.

Vervorming beschrijf je met de grootheid druk.

De druk hangt af van de kracht en van het contactoppervlak.

De deeltjes in gassen en vloeistoffen veroorzaken een druk. Als er een drukverschil is, ontstaat er stroming. Door een onderdruk ontstaat zuigkracht.

LICHT

` HOOFDSTUK 1: Hoe ontstaan kleur en schaduw?

1 Hoe plant licht zich voort?

Hoe ontstaan kleuren?

2 Hoe ontstaat schaduw?

` HOOFDSTUK 2: Welke eigenschappen hebben spiegelbeelden?

1 Hoe weerkaatst licht?

2 Welke eigenschappen heeft een spiegelbeeld bij een vlakke spiegel?

3 Welke eigenschappen heeft een spiegelbeeld bij een gekromde spiegel?

` HOOFDSTUK 3: Welke eigenschappen hebben beelden gevormd door doorzichtige stoffen?

1 Wat gebeurt er met licht dat doorgelaten wordt?

2 Welk beeld ontstaat bij breking aan een vlak scheidingsoppervlak?

3 Welke eigenschappen heeft een beeld gevormd door een lens?

Sterren kijken

Bestudeer de video van een heldere sterrenhemel.

1 Wat gebeurt er met de sterren?

2 Lees de drie uitspraken. Wie heeft gelijk volgens jou?

Sterren fonkelen omdat ze bewegen.

Sterren fonkelen omdat ze branden zoals een haardvuur of een kaarsje.

Een ster is een bolvormig hemellichaam dat door zijn hoge temperatuur licht geeft. De dichtste ster bij de aarde is de zon, op honderdvijftig miljoen kilometer. Door haar nabijheid kan ze de aarde verlichten. Alle andere sterren bevinden zich veel verder. De op een na dichtstbijzijnde ster bevindt zich op veertigduizend miljard kilometer. Het licht is vier jaar onderweg om de aarde te bereiken. We zien de sterren ’s nachts als stipjes aan de hemel.

Door het kunstmatige omgevingslicht is op veel plaatsen maar een klein deel van de sterren zichtbaar. Door hun grote afstand van ons kunnen we sterren niet met het blote oog bestuderen. Astronomen (of sterrenkundigen) gebruiken telescopen om sterren en alle andere fenomenen buiten de atmosfeer van de aarde te bestuderen.

STERREN STEEDS MINDER GOED TE ZIEN DOOR LICHTVERVUILING

©VANIN

` Hoe komt het dat we sterren zien en dat ze fonkelen?

Sterren fonkelen omdat de atmosfeer altijd in beweging is.

Ruim tachtig procent van de wereldbevolking kan ’s nachts nauwelijks sterren zien door lichtvervuiling. Dertig procent van de wereldbevolking kan zelfs helemaal geen sterren onderscheiden. De oorzaak is kunstmatige verlichting op de aarde, zo blijkt uit onderzoek.

Naar: www.hln.be

` Hoe bemoeilijkt het fonkelen het onderzoek naar sterren en welke oplossingen hebben astronomen daarvoor gevonden?

We zoeken het uit!

WEETJE

Lichtbronnen en donkere lichamen

OPDRACHT 1

Wanneer kun je voorwerpen zien?

1 Bestudeer de video van een lichtshow.

a Bestudeer de schermopnames tijdens en na de act Duid het kenmerk aan.

Tijdens de lichtshow Na de lichtshow

1 2

Je kunt enkele / alle voorwerpen zien. Je kunt enkele / alle voorwerpen zien.

b Beschrijf hoe de wielen door de lucht bewegen.

c Verklaar de kledingkeuze van de artiesten.

2 Wanneer kun je een voorwerp zien? Duid aan.

Enkel als het voorwerp licht produceert dat in je oog terechtkomt.

Enkel als het voorwerp licht weerkaatst dat in je oog terechtkomt.

Als het voorwerp licht produceert of weerkaatst dat in je oog terechtkomt.

OPDRACHT 2

Wat zijn lichtbronnen en donkere lichamen?

1 Noteer deze voorwerpen op de juiste plaats in het schema op de volgende pagina. aarde – beeldscherm – fluorescerende kledij – kattenogen – laser – lichtsticks –maan – Mars – mens – vuur – vuurvliegjes – wit blad papier – zon

2 Wat is het verschil tussen een lichtbron en een donker lichaam?

VIDEO LICHTSHOW

natuurlijke lichtbron, voorbeelden:

lichtbron

kunstmatige lichtbron, voorbeelden: voorwerp

OPDRACHT 3

Wat is een middenstof?

donker lichaam, voorbeelden:

1 Bestudeer de afbeelding van een visbokaal. Door welke gebieden is het licht gegaan, zodat jij de vissen kunt zien?

2 Een gebied met deeltjes waardoor licht beweegt, noem je een middenstof.

Geef twee andere voorbeelden van middenstoffen.

OPDRACHT 4 DOORDENKER

Heeft licht altijd een middenstof nodig om zich voort te planten?

Illustreer met een voorbeeld uit het dagelijks leven.

©VANIN

Voorwerpen zijn zichtbaar als er licht in het oog terechtkomt:

• Een lichtbron zendt zelf licht uit. Je kunt het licht rechtstreeks zien.

• Een donker lichaam zendt geen licht uit. Je kunt het zien door omgevingslicht dat erop weerkaatst.

Het licht beweegt door middenstoffen (zoals lucht, water en glas) en door het luchtledige (vacuüm).

Afb. 2 Aarde vanop de maan

Afb. 4 Zon

Afb. 3 Mars

Afb. 5

Hoe ontstaan kleur en schaduw?

LEERDOELEN

Je kunt al:

M het verschil tussen donkere lichamen en lichtbronnen beschrijven.

Je leert nu:

M omschrijven hoe licht zich voortplant;

M lichtstralen en lichtbundels schematisch voorstellen;

M het gedrag van licht ter hoogte van een donker lichaam beschrijven en schematisch voorstellen;

M het ontstaan van schaduw verklaren en schematisch voorstellen.

OPDRACHT 5

Verken schaduwbeelden.

1 Bestudeer de afbeeldingen.

6

2 Hoe ontstaan de schaduwbeelden?

Lichtbronnen produceren licht. Donkere lichamen zijn zichtbaar door het licht dat erop invalt.

In dit hoofdstuk zoek je verder uit wat er gebeurt met het licht dat invalt op voorwerpen. Je onderzoekt hoe kleuren en schaduwbeelden ontstaan. En misschien word je zo wel de volgende lichtartiest!

7

©VANIN

Formuleer een hypothese. Gebruik de termen ‘lichtbronnen’ en ‘donkere lichamen’.

a Afbeelding 6:

b Afbeelding 7:

3 We gaan op onderzoek om je hypotheses te testen!

1 Hoe plant licht zich voort?

1.1 Lichtstralen en lichtbundels

OPDRACHT 6

Bekijk de video van het wereldrecord ‘lasershow’ (met 320 lasers) op Pukkelpop.

1 Bepaal de kenmerken van licht.

Duid aan in de linkerkolom.

2 Hoe neem je die kenmerken waar in de lasershow?

Vul aan in de rechterkolom.

Kenmerk van licht

Licht plant zich rechtlijnig voort.

Licht plant zich niet rechtlijnig voort.

Er zijn (stof)deeltjes nodig om lichtstralen zichtbaar te maken.

Er zijn geen (stof)deeltjes nodig om lichtstralen zichtbaar te maken.

Een laserstraal kun je het best voorstellen door:

WERELDRECORD LASERSHOW

Waarneming in de show

De lichtbundel die onstaat door de bewegende laserstralen, kun je het best voorstellen door:

3 Geef het verschil tussen de vorm van een laserstraal en de lichtbundel die ontstaat door de bewegende laserstralen.

Het licht dat geproduceerd wordt door een lichtbron, beweegt zich voort door een middenstof. Als de samenstelling van die middenstof overal hetzelfde is, spreek je van een homogene middenstof

In een doorzichtige, homogene middenstof plant licht zich rechtlijnig voort. De lichtstraal is onzichtbaar. Door de weerkaatsing van een lichtstraal op deeltjes zie je het rechte pad van het licht.

De lichtsnelheid in een homogene middenstof is constant en afhankelijk van de middenstof. Licht heeft de hoogst mogelijke snelheid in een vacuüm:

vvacuüm = 299 792 458 m s of afgerond vvacuüm = 3,00 108 m s .

In de middenstof lucht is de lichtsnelheid vergelijkbaar.

In andere middenstoffen is de lichtsnelheid een stuk lager.

Als licht invalt op een glas water, heeft het een andere snelheid in elke middenstof. In het water zijn er meer deeltjes dan in de lucht, waardoor je het licht beter ziet.

Een lichtstraal stel je voor als een rechte met een pijlpunt in het midden

De pijl geeft de zin van de lichtstraal aan.

Een lichtstraal komt in werkelijkheid nooit alleen voor. Een lichtbron zendt altijd meerdere lichtstralen uit, die samen een lichtbundel vormen.

Er zijn drie soorten lichtbundels:

©VANIN

Verwar de voorstelling van een lichtstraal niet met een rechte (geen pijlpunt) of met een vector (pijlpunt op het uiteinde).

Wil je meer weten over lasers?

Ga dan naar de ontdekplaat bij het onlinelesmateriaal.

Divergerende lichtbundel Evenwijdige lichtbundel Convergerende lichtbundel

De lichtstralen gaan uiteen. De lichtstralen zijn evenwijdig. De lichtstralen komen samen in één punt.

VOORBEELD LICHTBUNDELS

Alle natuurlijke en de meeste kunstmatige lichtbronnen produceren een divergerende lichtbundel.

Een laserbundel is een evenwijdige lichtbundel. Omdat een laserbundel evenwijdig en heel smal is, noem je dat ook een laserstraal. Een laserstraal bezit heel veel energie. Enerzijds is dat gevaarlijk. Het veroorzaakt bijvoorbeeld oogschade als je rechtstreeks naar laserlicht kijkt. Anderzijds hebben lasers dankzij hun hoge energie ook veel technologische toepassingen.

TIP

TIP

Licht plant zich in een homogene, doorzichtige middenstof rechtlijnig voort. Je tekent de lichtstraal als een rechte lijn met een pijl die de zin aangeeft. De lichtsnelheid is afhankelijk van de middenstof Verschillende lichtstralen samen vormen een lichtbundel:

• Een divergerende bundel bestaat uit uiteenlopende lichtstralen die uit één punt vertrekken.

• Een evenwijdige bundel bestaat uit evenwijdige lichtstralen.

• Een convergerende bundel bestaat uit lichtstralen die samenkomen in één punt.

` Maak oefening 1, 2 en 3 op p. 238.

©VANIN

OPDRACHT 7

Bestudeer de afbeeldingen en hun beschrijving.

Er is één lichtstraal getekend. Teken twee andere lichtstralen om de vorm van de bundel duidelijk te maken.

De spots worden met lenzen bijgeregeld, zodat de divergerende lichtbundels de juiste breedte hebben om de artiest te belichten.

1 2 3

Een divergerende lichtbundel verandert bij weerkaatsing op een parapluvormig scherm in een evenwijdige lichtbundel Het fotomodel wordt gelijkmatig belicht tijdens de fotoshoot.

Zonlicht dat invalt op een glas, wordt een convergerende lichtbundel die convergeert in één punt. Na dat punt is de bundel divergerend.

1.2 Licht op donkere lichamen

OPDRACHT 8

Bestudeer hoe licht zich gedraagt op verschillende oppervlakken.

1 Vul de kenmerken van het gedrag van het invallende licht aan met: al het – een deel van het – geen

2 Hoe neem je dat waar op de afbeelding? Vul aan in de tabel.

1 Een spiegel:

• weerkaatst licht;

• absorbeert licht;

• laat licht door.

Waarneming op de foto:

©VANIN

2 Een raam:

• weerkaatst licht;

• absorbeert licht;

• laat licht door.

Waarneming op de foto:

3 Een houten vloer:

• weerkaatst licht;

• absorbeert licht;

• laat licht door.

Waarneming op de foto:

Bij de doorgang naar andere stoffen of bij de reflectie kan een witte lichtbundel een kleur krijgen. Hoe dat precies zit, leer je op diddt. TIP

Als licht invalt op een donker lichaam, treden er drie fenomenen op:

1 Het donkere lichaam weerkaatst het licht: het licht beweegt na terugkaatsing rechtlijnig, met een andere zin

2 Het donkere lichaam absorbeert het licht: het licht beweegt niet verder. De lichtenergie wordt opgenomen door het donkere lichaam.

3 Het donkere lichaam laat het licht door: het licht beweegt na de overgang rechtlijnig.

absorberen weerkaatsen doorlaten weerkaatsenabsorberendoorlaten

9

Donkere lichamen zijn zichtbaar doordat ze het licht weerkaatsen. De stof waaruit het donkere lichaam gemaakt is en onder welke hoek het licht invalt, bepalen de verhouding van het teruggekaatste, geabsorbeerde en doorgelaten licht

invallende laserstraal weerkaatste laserstraal absorptie absorptie

invallende laserstraal weerkaatste laserstraal doorgelaten laserstraal

Ondoorschijnende

Doorzichtige of doorschijnende stof

• Een ondoorschijnende stof laat geen licht door. Het licht weerkaatst en wordt geabsorbeerd. Bij spiegels wordt al het licht weerkaatst.

• Doorzichtige en doorschijnende stoffen laten (een deel van het) licht door. In welke richting dat gebeurt, hangt af van de combinatie van middenstoffen. Het licht wordt ook weerkaatst. Bij doorschijnende stoffen is er ook absorptie.

• Als een lichtbundel invalt op een ondoorschijnende stof, wordt die gedeeltelijk geabsorbeerd en gedeeltelijk teruggekaatst

• Bij een doorzichtige of doorschijnende stof wordt het licht ook gedeeltelijk doorgelaten.

` Maak oefening 4, 5 en 6 op p. 239.

Afb.

Afb. 10

stof

Afb. 11

2 Hoe ontstaat schaduw?

OPDRACHT 9

Bekijk de video van een schaduwact.

1 Omschrijf het begrip ‘schaduw’.

Gebruik de termen ‘lichtbron’ en ‘donker lichaam’ in je antwoord.

2 Wat denk jij? Markeer.

• Schaduw is altijd / soms / nooit scherp.

• Schaduw is altijd / soms / nooit even groot als het voorwerp.

• Schaduw ontstaat bij doorschijnende / doorzichtige / ondoorschijnende voorwerpen.

• Schaduw is altijd / soms / nooit zwart.

OPDRACHT 10 ONDERZOEK

Onderzoek schaduwvorming aan de hand van het labo bij het onlinelesmateriaal.

Vergelijk je hypothese uit opdracht 9 met je besluit.

©VANIN

Als licht invalt op een ondoorschijnend voorwerp, wordt er geen licht doorgelaten. Aangezien licht zich rechtlijnig voortplant, ontstaat er achter het voorwerp een donkere ruimte. Dat gebied, waar er geen of minder licht terechtkomt, noem je de schaduw. De scherpte en de kleur van de schaduw hangen af van de gebruikte lichtbron.

Bij één puntvormige lichtbron of een lichtbron die veel kleiner is dan het voorwerp, vertrekken de lichtstralen uit één punt. De divergerende lichtbundel komt terecht op en naast het ondoorschijnende voorwerp. Ter hoogte van het voorwerp worden geen lichtstralen doorgelaten, vanaf de rand (punt A en B op afbeelding 12) wel. Er ontstaat een scherpe, zwarte schaduw op de plaats waar er geen licht terechtkomt. Dat noem je de kernschaduw

©VANIN

Op een scherm zie je de vorm van het voorwerp verschijnen als een zwarte vlek. De grootte van de schaduw hangt af van de onderlinge posities van de lichtbron, het voorwerp en het scherm. Hoe feller het licht schijnt, hoe groter het contrast tussen licht en schaduw. Op afbeelding 13 zie je de scherpe zwarte schaduwen van een ridderspel.

Bij een niet-puntvormige lichtbron vertrekken de lichtstralen vanuit verschillende punten. De divergerende lichtbundels vanuit die punten komen terecht op en naast het ondoorschijnende voorwerp. Ter hoogte van het voorwerp worden geen lichtstralen doorgelaten, vanaf de rand (punt A en B op afbeelding 14) wel.

Doordat er lichtstralen met een verschillende richting invallen op het voorwerp, ontstaat er op een scherm een onscherpe schaduw:

• Centraal achter het voorwerp is er een gebied waar geen licht terechtkomt. Dat is de (zwarte) kernschaduw.

• Aan de randen van het voorwerp is er een gebied waar een gedeelte van het licht terechtkomt. Dat is de bijschaduw. De kleur van de bijschaduw is grijs of de kleur van de lichtbron.

Op afbeelding 15 zie je de onscherpe schaduw van een danseres. De zwarte kernschaduw is aan de randen omgeven door een bijschaduw.

Als licht invalt op een donker lichaam, wordt er licht geabsorbeerd

In het gebied achter het voorwerp ontstaat er een schaduw

Er zijn twee soorten schaduw:

1 Kernschaduw: het gebied waar er geen licht terechtkomt.

De kernschaduw is zwart.

2 Bijschaduw: het gebied waar een deel van het licht terechtkomt.

De bijschaduw is grijs of gekleurd.

De soort schaduw wordt bepaald door het type lichtbron

De grootte van de schaduw hangt af van de onderlinge posities van de lichtbron, het voorwerp en het scherm.

` Maak oefening 7 en 8 op p. 240-241.

1 Bestudeer opnieuw de afbeeldingen uit het begin van dit hoofdstuk.

2 Verklaar de beeldvorming.

a Afbeelding links:

• Welk type lichtbron wordt er gebruikt? Hoe zie je dat?

©VANIN

• Waar bevindt de lichtbron zich? Hoe zie je dat?

b Afbeelding rechts (uitbreiding):

• Welke lichtbronnen zijn gebruikt?

• Hoe ontstaan de andere kleuren? Verklaar.

• Welk gebied is de kernschaduw? Verklaar.

3 Vergelijk je hypothese op p. 246 met je besluit.

4 Maak zelf een verrassende foto of video waarin je schaduwbeelden gebruikt. Verklaar met een stralendiagram.

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

1 Welke uitspraak is correct? Duid aan.

Een lichtbundel plant zich rechtlijnig voort.

Een lichtstraal is divergerend, convergerend of evenwijdig.

Een lichtbron produceert nooit een convergerende lichtbundel.

Een laser produceert één lichtstraal.

2 In de bouwsector worden lasers veel gebruikt.

a Verklaar hun toepassing om …

• rechte lijnen te bepalen:

©VANIN

• afstanden te bepalen:

b Geef twee voordelen van een laser ten opzichte van een gewone lamp.

3 Bestudeer de video.

a Boots zelf de situatie na met een schoendoos en een kaars.

b Teken het beeld van de vlam.

BEELD BIJ BREKING BEELD BIJ LENZEN

SPIEGELBEELD

VIDEO CAMERA OBSCURA

4 Bestudeer de onderstaande voorwerpen.

a Benoem de voorwerpen met ‘doorzichtig’, ‘doorschijnend’ of ‘ondoorschijnend’.

b Vervolledig de stralengang op de afbeeldingen.

1 2

3

©VANIN

5 Geef een voorbeeld uit je woning van …

a een doorschijnend voorwerp:

b een doorzichtig voorwerp:

c een ondoorschijnend voorwerp:

6 Verklaar de onderstaande fenomenen.

a Op grote ramen worden vogelstickers gekleefd.

b In ondervragingsruimtes hangt een speciale spiegel.

7 Bestudeer de schaduw bij een doorschijnend voorwerp. Een doorschijnend voorwerp wordt belicht met een puntvormige lichtbron.

a Welke uitspraak is correct ? Duid aan.

Er ontstaat geen schaduw.

Er ontstaat een kernschaduw.

Er ontstaat een bijschaduw.

Er ontstaan een kernschaduw en een bijschaduw.

b Verduidelijk je keuze met een stralendiagram voor een rood doorschijnend voorwerp.

Benoem het licht en het schaduwgebied.

©VANIN

puntvormige lichtbron

Afb. 19

doorzichtig rood voorwerp

scherm

Afb. 20

8 Als de zon, de aarde en de maan op één lijn staan, ontstaat er een maans- of zonsverduistering.

a Bestudeer de onderstaande situaties.

b Benoem de situaties met ‘maansverduistering’ of ‘zonsverduistering’.

c Teken de schaduwvorming.

d Benoem de kernschaduw en de bijschaduw.

` Verder oefenen? Ga naar

©VANIN

maan

aarde

baan van de aarde

maan

baan van de maan

aarde

baan van de aarde

baan van de maan

1 Begripskennis

• Ik kan het verschil tussen donkere lichamen en lichtbronnen omschrijven aan de hand van voorbeelden.

• Ik kan een lichtstraal voorstellen

• Ik kan de rechtlijnige voortplanting van licht toepassen in oefeningen.

• Ik kan de drie types lichtbundels omschrijven en voorstellen.

• Ik kan de weerkaatsing, de absorptie en het doorlaten van licht op een donker lichaam omschrijven.

• Ik kan voorwerpen indelen in ‘doorzichtig’, ‘doorschijnend’ en ‘ondoorschijnend’.

• Ik kan de begrippen ‘kernschaduw’ en ‘bijschaduw’ omschrijven

• Ik kan de kernschaduw en de bijschaduw tekenen.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek opzetten volgens een gegeven stappenplan.

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan lichtstralen nauwkeurig tekenen.

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Welke eigenschappen hebben spiegelbeelden?

LEERDOELEN

Je kunt al:

M lichtstralen en lichtbundels tekenen;

M de weerkaatsing van licht op een oppervlak omschrijven.

Je leert nu:

M verschillende types spiegel kennen;

M het gedrag van licht ter hoogte van een spiegel beschrijven en schematisch voorstellen;

M spiegelbeelden construeren;

M de aard van een spiegelbeeld beschrijven.

OPDRACHT 11

Verken optische illusies.

1 Bestudeer de afbeeldingen.

Elk voorwerp weerkaatst (een deel van) het omgevingslicht. Als een voorwerp het licht (bijna) volledig weerkaatst, kun je er spiegelbeelden van andere voorwerpen in zien. We gaan op zoek naar de eigenschappen van die spiegelbeelden.

Soms brengen spiegelbeelden je in verwarring. Het zijn optische illusies. Wat zie jij, een hond of een beer?

©VANIN

2 Hoe denk je dat de optische illusie ontstaat? Formuleer een hypothese. a Afbeelding 22: b Afbeelding 23:

3 We gaan op onderzoek om je hypotheses te testen!

Afb. 22

Afb. 23

1 Hoe weerkaatst licht?

1.1 Spiegelwetten

OPDRACHT 12

Bestudeer het artikel.

©VANIN

De bewoners van het Italiaanse dorpje Viganella hebben tijdens de winter 83 dagen geen direct zonlicht. Daarom bedachten ze een oplossing voor die donkere winterdagen: ze bouwden een gigantische computergestuurde spiegel op een bergtop, om zo de zonnestralen naar het dorpje te reflecteren.

1 Uit welk materiaal zou je de spiegel maken? Verklaar.

2 Waarom is de spiegel computergestuurd?

3 Op de volgende afbeeldingen staat de voorstelling van de zon op een winterdag.

a Toon aan dat het dorp in de schaduw ligt, door de schaduw te tekenen op situatie A.

b Welke positie van de spiegel is volgens jou geschikt om de zon in het dorp te laten schijnen?

OPDRACHT 12 (VERVOLG)

c Ondersteun je hypothese door voor de drie situaties de verwachte stralengang op de spiegel te tekenen.

OPDRACHT 13 ONDERZOEK

Onderzoek de stralengang bij spiegels aan de hand van het labo bij het onlinelesmateriaal.

Kijk na het labo opnieuw naar de stralengang die je tekende bij opdracht 12.

a Vervolledig elke situatie met een normaal, de invalshoek en de terugkaatsingshoek.

b Vergelijk je hypothese met je besluit.

Een spiegel is een voorwerp met een heel glad oppervlak, dat al het licht weerkaatst. Omdat je metalen heel glad kunt maken, zijn de meeste spiegels gemaakt uit metaal, met glas als beschermingsmateriaal.

normaal n

invallende straal i

invalshoek î terugkaatsingshoek t teruggekaatste straal t

B

©VANIN

invalspunt I

24

Als een lichtstraal invalt op een oppervlak, kaatst het oppervlak die lichtstraal terug. Op afbeelding 24 is dat schematisch weergegeven.

1 De lichtstraal die invalt op het oppervlak, is de invallende straal i.

2 Het punt waar de invallende straal het oppervlak raakt, is het invalspunt I

3 De rechte door het invalspunt, loodrecht op het oppervlak, is de normaal n

4 De hoek tussen de invallende straal en de normaal is de invalshoek î.

5 De lichtstraal die de spiegel verlaat, is de teruggekaatste straal t .

6 De hoek tussen de teruggekaatste straal en de normaal is de terugkaatsingshoek t .

Bij de terugkaatsing van de lichtstraal gelden drie spiegelwetten:

 De invallende straal, de teruggekaatste straal en de normaal liggen in één vlak, loodrecht op de spiegel.

‚ De terugkaatsingshoek en de invalshoek zijn even groot: t = î

ƒ De stralengang is omkeerbaar. Als je de lichtstraal uit positie B laat vertrekken, komt ze terecht op positie A.

Om de normaal te tekenen op een gekromd of oneffen oppervlak, teken je eerst een rechte die raakt aan de kromme. n n

1.2 Lichtbundels na weerkaatsing

Als een lichtbundel invalt op een oppervlak, gelden de drie spiegelwetten voor elke lichtstraal. De oriëntatie van de lichtbundel ten opzichte van het oppervlak bepaalt de invalshoek en de normaal voor het invalspunt van elke lichtstraal. De teruggekaatste stralen vormen de lichtbundel na de weerkaatsing. In tabel 1 zie je de weerkaatsing van een evenwijdige lichtbundel op verschillende types oppervlakken. 1

Op een effen, vlak oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats dezelfde invalshoek Alle normalen hebben dezelfde oriëntatie.

 De teruggekaatste bundel op een vlakke spiegel is een evenwijdige bundel.

 Je noemt dat gerichte weerkaatsing.

Op een oneffen oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats een verschillende invalshoek De normalen hebben een verschillende oriëntatie.

 De teruggekaatste bundel op een oneffen oppervlak is willekeurig. Er is geen teruggekaatste lichtbundel zichtbaar.

 Je noemt dat diffuse weerkaatsing.

Op een effen, hol oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats een verschillende invalshoek Alle normalen gaan door het middelpunt van de cirkel.

 De teruggekaatste bundel op een holle spiegel is een convergerende bundel. De stralen komen samen in het brandpunt F vóór de holle spiegel

Op een effen, bol oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats een verschillende invalshoek Alle normalen gaan door het middelpunt van de cirkel.

©VANIN

 De teruggekaatste bundel op een holle spiegel is een divergerende bundel. De verlengden van de stralen komen samen in het brandpunt F achter de bolle spiegel

Tabel 1

Door het verschil in terugkaatsing van de lichtbundels in de verschillende situaties verschillen de spiegelbeelden

OPDRACHT 14

Bestudeer de optische illusies.

Duid de kenmerken van de beeldvorming aan.

• Het beeld is scherp / onscherp door gerichte / diffuse weerkaatsing.

• Het beeld is niet / wel vervormd omdat de spiegel niet / wel gekromd is.

1 2 3

©VANIN

• Het beeld is scherp / onscherp door gerichte / diffuse weerkaatsing.

• Het beeld is niet / wel vervormd omdat de spiegel niet / wel gekromd is.

• Het beeld is scherp / onscherp door gerichte / diffuse weerkaatsing.

• Het beeld is niet / wel vervormd omdat de spiegel niet / wel gekromd is.

De weerkaatsing van licht op een oppervlak kun je beschrijven met drie spiegelwetten:

1 De invallende straal, de teruggekaatste straal en de normaal liggen in één vlak

2 De terugkaatsingshoek en de invalshoek zijn even groot: t = î.

3 De stralengang is omkeerbaar

Als het oppervlak effen is, dan is er gerichte weerkaatsing. Een evenwijdige lichtbundel die invalt op een effen oppervlak, weerkaatst als een geordende lichtbundel

Op een oneffen oppervlak is er diffuse weerkaatsing. Een evenwijdige lichtbundel die invalt op een oneffen oppervlak, weerkaatst als chaotisch gerichte lichtstralen.

` Maak oefening 1 t/m 6 op p. 254-256.

2 Welke eigenschappen heeft een spiegelbeeld bij een vlakke spiegel?

OPDRACHT 15

Laat een kaarsje onder water branden.

1 Bouw de opstelling na: kleef een theelichtje in een aquarium met water.

2 Ga op zoek naar de plaats waar een brandend theelichtje in het aquarium lijkt te branden.

3 Duid de positie van het brandende theelichtje aan.

4 Bestudeer je waarneming. Duid aan.

a De voorkant van het aquarium is een / geen vlakke spiegel.

b Het kaarsje voor het aquarium is een voorwerp / een spiegelbeeld.

c Het kaarsje dat je ziet branden in het aquarium, is een voorwerp / een spiegelbeeld

d Ten opzichte van de spiegel staat het voorwerp even ver als / minder ver dan / verder dan het spiegelbeeld.

e Het spiegelbeeld is even groot als / kleiner dan / groter dan het voorwerp.

f Het spiegelbeeld staat rechtop / omgekeerd.

OPDRACHT 16

Construeer het spiegelbeeld van een kaarsje.

1 Bouw de opstelling na.

2 Zoek het spiegelbeeld.

a Kijk vanuit een aangeduid oogpunt naar de spiegel.

b Zet een kruisje op de plaats waar je het spiegelbeeld ziet.

c Herhaal voor het andere oogpunt.

d Zet een tweede kaarsje op de positie van het spiegelbeeld.

e Houd een blad papier ter hoogte van het spiegelbeeld.

Zie je het kaarsje branden op het papier?

f Verwijder de spiegel.

3 Construeer het gevolgde pad van het licht.

a Teken de lichtstraal van het kaarsje naar de spiegel.

b Teken de lichtstraal van de spiegel naar het oog.

4 Bestudeer de getekende stralen. Duid aan.

• De weerkaatsing van het licht op de spiegel verloopt wel / niet volgens de spiegelwetten.

• Het spiegelbeeld (B) bevindt zich op het snijpunt van de teruggekaatste stralen / het verlengde van de teruggekaatste stralen

5 Vervolledig de afbeelding met het beeldpunt.

spiegel

KENNISCLIP SPIEGELWETTEN

OPDRACHT 17

Als een voorwerp (V) zich voor een spiegel bevindt, ontstaat er een spiegelbeeld (B), doordat het invallende licht van het voorwerp weerkaatst op de spiegel.

• Als het voorwerp een lichtbron is (bv. een theelichtje), dan komt het geproduceerde licht vanuit de lichtbron terecht op de spiegel.

• Als het voorwerp een donker lichaam is (bv. jezelf) dan komt het weerkaatste licht vanuit het donkere lichaam terecht op de spiegel.

Voor elk punt van het voorwerp kun je met de spiegelwetten het beeldpunt tekenen:

• Je tekent (minstens) twee invallende lichtstralen vanuit het voorwerpspunt V.

• Je tekent de teruggekaatste stralen.

• Je verlengt de teruggekaatste stralen met een stippellijn.

• Het snijpunt van de verlengde teruggekaatste stralen is het beeldpunt B.

Bestudeer de afbeeldingen en hun omschrijvingen.

Vervolledig het stralendiagram met de zin van de lichtstralen, de invalshoek î en de terugkaatsingshoek t

Spiegelbeeld bij een rechtopstaande spiegel Spiegelbeeld bij een horizontale spiegel

Constructie van het spiegelbeeld (B) van de hiel (V) in een rechtopstaande spiegel

Liesbet kan dat spiegelbeeld zien, omdat er een teruggekaatste lichtstraal in haar oog terechtkomt (groene lichtstraal).

Constructie van het spiegelbeeld (B) van de jas (V) in een liggende spiegel

Sam kan dat spiegelbeeld niet zien, omdat er geen enkele teruggekaatste lichtstraal in haar oog terechtkomt.

©VANIN

Een spiegelbeeld heeft vier eigenschappen. Je kunt ze achterhalen door jezelf de juiste vragen te stellen.

1 Stand: Hoe staat het spiegelbeeld in vergelijking met het voorwerp (bij een rechtopstaande spiegel)?

Het spiegelbeeld bij een vlakke spiegel staat altijd rechtop Ook op foto 2 noem je het beeld ‘rechtop’. Als je de foto draait, zodat het wateroppervlak (= spiegel) verticaal staat, staat het spiegelbeeld rechtop: als je je blad draait, staat zowel de boom als zijn spiegelbeeld bovenaan.

2 Grootte: Hoe groot is de verhouding tussen de grootte van het beeld (hB ) en de grootte van het voorwerp (hV )?

Het spiegelbeeld bij een vlakke spiegel is even groot als het voorwerp. De vergrotingsfactor is 1 (m = hB hV = 1).

Op foto 1 lijkt het spiegelbeeld kleiner. Dat is te wijten aan het perspectief van waaruit de foto genomen werd.

3 Aard: Wordt het beeld gevormd door lichtstralen of door verlengden van lichtstralen?

Het spiegelbeeld bij een vlakke spiegel wordt gevormd door de verlengden van teruggekaatste lichtstralen. Het beeld is virtueel

In de wiskunde gebruik je bij spiegelingen de symmetriewet. Die is hetzelfde als de positieeigenschap bij vlakke spiegels. Je kunt die dus gebruiken om een constructie te maken.

OPDRACHT 18 DOORDENKER

Dat betekent dat je het niet kunt weergeven op een scherm. Onze hersenen interpreteren dat de lichtstralen recht naar ons toe zijn gekomen, waardoor we het beeld achter de spiegel zien verschijnen.

4 Positie: Waar ligt het beeld ten opzichte van de spiegel?

Het spiegelbeeld bij een vlakke spiegel ligt altijd even ver van de spiegel als het voorwerp. Elk punt van het voorwerp ligt symmetrisch ten opzichte van de spiegel. Dat noem je de symmetriewet bij een vlakke spiegel.

Op foto 1 lijkt de afstand niet even groot. Dat is te wijten aan het perspectief.

©VANIN

Bij een vlakke spiegel ontstaat een beeldpunt als het snijpunt van de verlengden van de teruggekaatste stralen. Het beeld heeft vier eigenschappen:

1 stand: Het spiegelbeeld bij een vlakke spiegel staat altijd rechtop 2 grootte: Het spiegelbeeld bij een vlakke spiegel is even groot als het voorwerp.

3 aard: Het beeld is virtueel. Dat betekent dat je het niet kunt weergeven op een scherm. Het beeld bevindt zich achter de spiegel. 4 positie: Het beeld en het voorwerp liggen symmetrisch ten opzichte van de spiegel. Dat noem je de vierde spiegelwet. Die symmetriewet helpt je om makkelijk het beeld te construeren.

` Maak ooefening 7 t/m 10 op p. 256-258.

Gebruik je kennis over spiegels om spiegelbeelden te programmeren.

Gebruik het stappenplan bij het onlinelesmateriaal.

Sla je programma's op in je onderzoeksmap.

a Programmeer met GeoGebra een applet om de beeldvorming te construeren.

b Programmeer met Java een spiegelbeeld van een foto.

TIP

3

Welke eigenschappen

heeft een spiegelbeeld bij een gekromde spiegel?

TIP

Ontdek in de ontdekplaat welke technologische toepassingen spiegels hebben.

OPDRACHT 19

Sferische spiegels zijn gekromde spiegels die een deel zijn van een bol. Als een voorwerp (V) zich voor een sferische spiegel bevindt, ontstaat er een spiegelbeeld (B), doordat het invallende licht van het voorwerp weerkaatst op de spiegel.

©VANIN

Voor elk punt van het voorwerp kun je met de spiegelwetten het beeldpunt bepalen.

Bij een holle spiegel worden de eigenschappen van het spiegelbeeld bepaald door het brandpunt van de spiegel en de positie van het voorwerp. Bij een bolle spiegel is het beeld altijd rechtopstaand, verkleind en virtueel

Bij gekromde spiegels bepalen de kromming en de positie van het voorwerp de eigenschappen van het beeld.

Bestudeer de drie spiegelbeelden.

1 Vul de tabel aan.

2 Boots de situaties van foto 1 en 2 na in de applet.

Welk type spiegel wordt gebruikt?

Welke grootte en stand heeft het beeld?

1 Bestudeer opnieuw de afbeeldingen uit het begin van dit hoofdstuk.

2 Verklaar de beeldvorming.

a Afbeelding links:

• Hoeveel spiegels zijn er gebruikt?

• Teken de randen van de spiegels.

• Hoe moet je de spiegels plaatsen om het patroon van de vloer te laten doorlopen? Verklaar. ten opzichte van het grondvlak: ten opzichte van de strepen:

b Afbeelding rechts:

• Hoe weerkaatst een lichtstraal die evenwijdig met de hoofdas invalt?

• Hoe weerkaatst een lichtstraal die door het brandpunt gaat? Welke spiegelwet gebruik je?

©VANIN

• Vervolledig de stralengang op de schematische voorstelling van de mirascoop. Het varken zit in het brandpunt van de bovenste spiegel.

3 Vergelijk je hypothese op p. 262 met je besluit.

4 Maak zelf een optische illusie met spiegels. Gebruik daarvoor een apart blad.

a Maak een foto of opstelling.

b Verklaar met een stralendiagram.

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

1 Bestudeer de afbeeldingen en hun beschrijving.

Vervolledig de afbeeldingen met:

• het invalspunt I,

• de teruggekaatste straal t,

• de invalshoek î,

• de terugkaatsingshoek t

De lichtstraal weerkaatst op een vlakke spiegel

De lichtstraal weerkaatst op een gekromde spiegel

©VANIN

De lichtstraal weerkaatst op een oneffen oppervlak

2 Een fietsreflector bestaat uit een reeks spiegeltjes die een hoek van 90° maken.

a Teken de teruggekaatste lichtstralen voor de weergegeven evenwijdige lichtstralen.

b Geef twee redenen waarom er geen vlakke spiegel gebruikt wordt.

BEELD BIJ BREKING BEELD BIJ LENZEN

SPIEGELBEELD

3

Lees het artikel.

Welke kromming heeft de glazen wand? Duid aan.

De wand is vlak.

De wand is hol.

De wand is bol.

Je kunt geen uitspraak doen over de kromming.

4

NIEUWE LONDENSE TOREN DOET AUTO’S ‘SMELTEN’ DOOR ZONLICHT

Londen heeft er een nieuwe toren bij, en dat zullen de inwoners van de Britse hoofdstad geweten hebben. De glazen constructie reflecteert het zonlicht en een klein stukje straat kan plots van de warmte genieten. Maar voor de eigenaar van een Jaguar was dat minder aangenaam nieuws, aangezien delen van zijn auto vervormd raakten. Bron: www.hln.be

In een zonnespiegelpark wordt de zonnewarmte gebruikt als milieuvriendelijk alternatief voor de opwarming door de verbranding van olie of gas.

a Bestudeer de lichtbundel die de zon produceert. Benoem het type bundel dicht bij en ver weg van de zon.

b Verklaar de werking van zonnespiegels door drie lichtstralen van een evenwijdige lichtbundel te tekenen die invallen op de drie types spiegelopstellingen.

lichtbundel lichtbundel 1 2 3

c Verklaar waarom de spiegels aangestuurd worden door een motor.

Afb. 30

5 Een persoon (P) staat voor een vlakke, een bolle en een holle spiegel. Om zo veel mogelijk te zien, kijkt hij naar de twee uiterste punten van de spiegel.

a Teken de lichtstralen die in zijn oog terechtkomen.

b Arceer het gebied dat hij kan zien door in de spiegel te kijken (= zijn gezichtsveld).

6 In het verkeer worden op kruispunten sferische spiegels gebruikt.

a Welke type spiegel zijn sferische spiegels?

b Geef het voordeel van zulke spiegels.

c Geef het nadeel van zulke spiegels.

7 Teken met vier lichtstralen het spiegelbeeld van de pijl.

a Waarom is een pijl geschikt om de eigenschappen van een spiegelbeeld te onderzoeken?

b Hoe kun je sneller het beeld tekenen?

8 Een vlaggenstok staat aan de rand van een vijver.

a Teken het spiegelbeeld van de vlaggenstok.

b Kan Mo op de andere oever het spiegelbeeld zien?

©VANIN

Bewijs door een lichtstraal te tekenen.

c Wat gebeurt er met het spiegelbeeld als het eendje begint te zwemmen? Verklaar.

9 Hoe groot moet een spiegel zijn om jezelf volledig te kunnen zien?

a Wat denk je? Duid aan.

even groot als jezelf

groter dan jezelf

een beetje kleiner dan jezelf

de helft zo groot als jezelf

Dat hangt af van de afstand tot de spiegel.

b Test uit.

c Verklaar je waarneming door de lichtstralen te tekenen waardoor je jezelf helemaal kunt zien.

d Is je voorspelling correct?

Afb. 33

Afb. 34

beeld

10 Verklaar de onderstaande fenomenen.

a De achterwand van een winkelrek is vaak een spiegel.

b Het opschrift op ziekenwagens staat vooraan op twee manieren geschreven.

` Verder oefenen? Ga naar

©VANIN

1 Begripskennis

• Ik kan de invallende straal, de invalshoek, de normaal, de teruggekaatste straal en de terugkaatsingshoek omschrijven en aanduiden op een afbeelding.

• Ik kan de spiegelwetten toepassen om de teruggekaatste straal te tekenen

• Ik kan gerichte en diffuse weerkaatsing omschrijven.

• Ik kan de stralengang van een evenwijdige lichtbundel op een vlakke en een gekromde spiegel omschrijven.

• Ik kan omschrijven waarom spiegelbeelden bij gekromde spiegels vervormd zijn.

• Ik kan de spiegelwetten toepassen om het beeld bij een vlakke spiegel te tekenen.

• Ik kan de kenmerken van een spiegelbeeld afleiden uit een stralendiagram.

• Ik kan de kenmerken van een spiegelbeeld bij een gekromde spiegel afleiden uit een beeldconstructie van een applet.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan invallende en teruggekaatste lichtstralen nauwkeurig tekenen.

• Ik kan het spiegelbeeld bij een vlakke spiegel nauwkeurig tekenen

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Welke eigenschappen hebben beelden gevormd door doorzichtige stoffen?

LEERDOELEN

Je kunt al:

M lichtstralen en lichtbundels tekenen;

M homogene, doorzichtige middenstoffen omschrijven.

Je leert nu:

M het gedrag van licht dat doorgelaten wordt, beschrijven en schematisch voorstellen;

M beelden bij de overgang naar een andere middenstof construeren;

M beelden bij lenzen construeren en hun eigenschappen beschrijven.

©VANIN

In je leefomgeving zie je veel doorzichtige voorwerpen: ramen, een glas water, een bril, het water in een zwembad … Misschien heb je al verrassende effecten opgemerkt. Een zwembad is dieper dan het lijkt, door een aquarium zie je gekke gezichten … Of vraag je je af wat een vergrootglas tot een vergrootglas maakt?

In dit hoofdstuk onderzoek je hoe licht zich gedraagt in doorzichtige stoffen met verschillende vormen en maak je kennis met (abstracte) kunstfoto’s.

OPDRACHT 20

Verken beelden gevormd door doorzichtige stoffen.

1 Bestudeer de afbeeldingen.

2 Hoe denk je dat de abstracte kunstfoto’s ontstaan? Formuleer een hypothese.

a Afbeelding 37:

b Afbeelding 38:

3 We gaan op onderzoek om je hypotheses te testen!

1 Wat gebeurt er met licht dat doorgelaten wordt?

1.1 Brekingswetten

OPDRACHT 21

Bestudeer uitspraken over het ontstaan van brand.

1 Lees de drie uitspraken. Wie heeft gelijk volgens jou?

2 Hoe kun je onderzoeken wie gelijk heeft?

Elk stuk glas kan brand veroorzaken. Enkel een gekromd stuk glas kan brand veroorzaken.

Dit kan niet door glas veroorzaakt zijn. Het moet een sigarettenpeuk geweest zijn.

OPDRACHT 22 ONDERZOEK

Onderzoek de stralengang bij de overgang naar een andere doorzichtige middenstof aan de hand van het labo bij het onlinelesmateriaal.

Kijk opnieuw naar de hypothese over glas die je in opdracht 21 opstelde. Vergelijk je hypothese met je besluit.

©VANIN

Als een lichtstraal overgaat van één homogene middenstof naar een andere homogene middenstof, verandert de lichtstraal van richting. Er is breking (of refractie) aan het scheidingsoppervlak, omdat de middenstoffen een verschillende optische dichtheid hebben.

Hoe groter de optische dichtheid, hoe lager de lichtsnelheid. In een vacuüm heeft het licht een snelheid vvacuüm = 299 792 458 m s = 3,00 · 108 m s In elke andere middenstof is de snelheid lager. Je kunt doorzichtige middenstoffen rangschikken volgens hun optische dichtheid, van optisch ijl (hogere lichtsnelheid) naar optisch dicht (lagere lichtsnelheid).

Afb. 39

optisch ijl hoge lichtsnelheid optisch dicht lage lichtsnelheid vvacuüm = 3,00 · 108 m s vdiamant = 1,24 · 108 m s

Op afbeelding 41 en 42 is schematisch de breking weergegeven voor de overgang van een optisch ijle middenstof naar een optisch dichtere middenstof en omgekeerd.

i invallende straal

stof 2: optisch dicht stof 1: optisch ijl s I I i invallende straal

stof 1: optisch ijl stof 2: optisch dicht

©VANIN

Afb. 41

r gebroken straal r gebroken straal n s n

Afb. 42

Overgang van een optisch ijle naar

Overgang van een optische dichte naar een optisch dichte middenstof een optisch ijle middenstof

1 Het oppervlak dat de grens vormt tussen twee doorzichtige middenstoffen, is het scheidingsoppervlak s .

2 De lichtstraal die invalt (vanuit de eerste middenstof) op het scheidingsoppervlak, is de invallende straal i

3 Het punt waar de invallende straal het oppervlak raakt, is het invalspunt I

4 De rechte door het invalspunt, loodrecht op het oppervlak, is de normaal n.

5 De hoek tussen de invallende straal en de normaal is de invalshoek î

6 De lichtstraal die doordringt in de tweede middenstof, is de gebroken straal r .

7 De hoek tussen de gebroken straal en de normaal is de brekingshoek r

Afb. 40

Bij de meest optisch dichte middenstof ligt de straal het dichtst bij de normaal. TIP

OPDRACHT 23

Bij de breking van de lichtstraal gelden drie brekingswetten:

➀ De invallende straal, de gebroken straal en de normaal liggen in één vlak. Dat vlak staat loodrecht op het scheidingsoppervlak.

➁ Er is een verband tussen de brekingshoek en de invalshoek:

a Een loodrecht invallende lichtstraal breekt niet: r = î = 0°

b Bij de overgang van een optisch ijle naar een optisch dichtere middenstof is er breking van een schuin invallende lichtstraal naar de normaal toe: r < î.

c Bij de overgang van een optisch dichte naar een optisch ijlere middenstof is er breking van een schuin invallende lichtstraal van de normaal weg: r > î.

Er is een wiskundig verband tussen de invalshoek en de brekingshoek. Als je nieuwsgierig bent, vind je meer informatie via de QR-code.

Zelf kun je de precieze hoeken bepalen met de applet.

➂ De stralengang is omkeerbaar. Als je op afbeelding 41 en 42 de lichtstraal uit positie B laat vertrekken, komt ze terecht op positie A.

De mate van breking is afhankelijk van het verschil in optische dichtheid en verschilt voor elke golflengte. Bij sommige invalshoeken en vormen van doorzichtige voorwerpen splitst een witte lichtstraal door breking op in de verschillende ROGGBIV-kleuren

Bestudeer de afbeeldingen van zonlicht dat invalt op voorwerpen.

Vul de tabel aan.

1

2

Door welke middenstoffen verplaatst het licht zich tussen punt A en punt B?

©VANIN

Hoe zie je dat het licht breekt?

WET VAN SNELLIUS

1.2

Lichtbundels na breking

Als een lichtbundel invalt vanuit een middenstof op een scheidingsoppervlak met een andere middenstof, gelden de drie brekingswetten voor elke lichtstraal. De oriëntatie van de lichtbundel ten opzichte van het oppervlak bepaalt de invalshoek en de normaal voor het invalspunt van elke lichtstraal. De gebroken stralen vormen de lichtbundel na de doorgang door het doorzichtige voorwerp. In tabel 2 zie je de breking van een evenwijdige lichtbundel op verschillende types van doorzichtige voorwerpen.

©VANIN

planparallelle plaat

1

doorzichtig voorwerp dat begrensd wordt door twee evenwijdige platte vlakken

bolle lens 2

doorzichtig voorwerp dat wordt begrensd door minstens één gekromd oppervlak en dat dikker is in het midden dan aan de rand

holle lens

doorzichtig voorwerp dat wordt begrensd door minstens één gekromd oppervlak en dat dunner is in het midden dan aan de rand

Op een effen, vlak oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats dezelfde invalshoek

Alle normalen hebben dezelfde oriëntatie.

 De bundel blijft na breking door een planparallelle plaat een evenwijdige bundel, die verschoven is ten opzichte van de invallende bundel.

Op een bol oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats een verschillende invalshoek.

Alle normalen gaan door het middelpunt van de cirkel

 De gebroken bundel op een bolle lens is een convergerende bundel. De stralen komen samen in het brandpunt F achter de bolle lens.

Op een hol oppervlak heeft het licht van een evenwijdige lichtbundel op elke plaats een verschillende invalshoek

Alle normalen gaan door het middelpunt van de cirkel

 De gebroken bundel op een holle lens is een divergerende bundel. De verlengden van de lichtstralen komen samen in het brandpunt F vóór de holle lens.

OPDRACHT 24

Bestudeer de afbeeldingen en hun omschrijving.

Noteer in de tabel het type doorzichtig voorwerp dat gebruikt wordt in beide situaties.

1 2

©VANIN

Door een evenwijdige verschuiving ten gevolge van breking lijkt de vrouw onthoofd in het water.

Het gekromde oppervlak van waterdruppels maakt een kunstfoto van M&M’s door de verkleining die ontstaat.

De breking van licht ter hoogte van het scheidingsoppervlak tussen twee homogene middenstoffen kun je beschrijven met drie brekingswetten:

➀ De invallende straal, de gebroken straal en de normaal liggen in één vlak.

➁ Er is een verband tussen de brekingshoek en de invalshoek:

• loodrecht invallende straal: geen breking: r = î = 0°

• optisch ijl naar optisch dicht: breking naar de normaal toe: r < î

• optisch dicht naar optisch ijl: breking van de normaal weg: r > î ➂ De stralengang is omkeerbaar.

Een evenwijdige lichtbundel die invalt op een doorzichtig voorwerp, breekt als een geordende lichtbundel:

• Bij een planparallelle plaat blijft een evenwijdige lichtbundel evenwijdig, maar verschoven na breking.

• Bij een bolle lens wordt een evenwijdige lichtbundel een convergerende lichtbundel na breking.

• Bij een holle lens wordt een evenwijdige lichtbundel een divergerende lichtbundel na breking.

` Maak oefening 1 t/m 4 op p. 276-277.

2 Welk beeld ontstaat bij breking aan een vlak

scheidingsoppervlak?

OPDRACHT 25

Maak het onzichtbare zichtbaar!

1 Bouw de opstelling na.

a Plak een munt vast in een ondoorschijnend bakje (bv. een ontbijtkommetje).

b Zet het bakje voor je neer.

c Verschuif het bakje totdat je het muntje net niet meer kunt zien.

2 Wat denk je dat er gebeurt als je water in het bakje giet?

©VANIN

3 Bestudeer je waarneming. Duid aan.

a De werkelijke positie van het muntje verandert wel / niet

b Het beeld van het muntje is op dezelfde plaats gebleven / verhoogd / verlaagd.

c Als je het muntje probeert te grijpen vanaf de positie waar je kijkt, lukt dat wel / niet

d Het muntje is zichtbaar als er lichtstralen vanuit het muntje in het oog terechtkomen /  het oog in het muntje terechtkomen.

OPDRACHT 26

Construeer het beeld van een muntje dat ondergedompeld is in water.

1 Bouw de opstelling na.

2 Richt de laserstraal (in de statiefklem), zodat ze terechtkomt op de rand van het muntje.

3 Verwijder het aquarium.

4 Teken in stippellijnen de lichtstraal op afbeelding 44.

laser in statiefklem statief aquarium met water

muntje op de bodem

Afb. 43

Afb. 44

5 Construeer het beeld van het muntje als je ter hoogte van de statiefklem naar het muntje kijkt.

a Teken (aan de hand van het experiment) de lichtstraal van de munt naar je oog. Welke brekingswet pas je toe?

b Teken de lichtstraal die in je oog terecht lijkt te komen.

c Teken de positie waar je het muntje ziet.

d Vervolledig afbeelding 45 met de normaal, de invalshoek en de brekingshoek. aquarium met water

muntje op de bodem

45

Als een voorwerp zich in een andere doorzichtige middenstof bevindt, ontstaat er een beeld, doordat het licht breekt ter hoogte van het scheidingsoppervlak. De lichtstralen die vertrekken vanuit het voorwerp, zijn de gereflecteerde lichtstralen van de omgevingsverlichting.

Voor elk punt van het voorwerp kun je met de brekingswetten het beeldpunt tekenen:

• Je tekent een lichtstraal vanuit het voorwerpspunt V naar het scheidingsoppervlak.

• Je tekent de gebroken straal.

• Je verlengt in stippellijnen de gebroken straal tot precies boven het voorwerp. Dat is het beeldpunt B.

Het beeld dat je ziet bij breking aan een vlak scheidingsoppervlak, wordt gevormd door het verlengde van de gebroken lichtstraal. Het beeld is virtueel. Dat betekent dat je het niet kunt weergeven op een scherm. Onze ogen interpreteren lichtstralen altijd recht, waardoor je het beeld verschoven ziet ten opzichte van het scheidingsoppervlak.

©VANIN

Als een voorwerp zich in een andere doorzichtige middenstof bevindt, ontstaat er een virtueel beeld dat verschoven is ten opzichte van het scheidingsoppervlak.

` Maak oefening 5 t/m 7 op p. 278-279.

OPDRACHT 27

Bestudeer de afbeeldingen en hun omschrijving.

Vervolledig het stralendiagram met de zin van de lichtstralen, de invalshoek en de brekingshoek.

©VANIN

De lichtstraal breekt van de normaal weg bij de overgang van water naar lucht. Het beeld B van de vis V komt dichter bij het scheidingsoppervlak voor een meeuw in de lucht.

De lichtstraal breekt naar de normaal toe bij de overgang van water naar lucht. Het beeld B van de meeuw V gaat verder van het scheidingsoppervlak voor de vis in het water.

OPDRACHT 28 DOORDENKER

Maak een applet om de beeldvorming van een punt na breking te construeren.

1 Gebruik het stappenplan bij het onlinelesmateriaal om in GeoGebra een applet te maken die de optische verschuiving van een punt bepaalt.

2 Sla de applet op in je onderzoeksmap.

KENNISCLIP BREKING

3 Welke eigenschappen heeft een beeld gevormd door een lens?

3.1 Beeldvorming

OPDRACHT 29

Bestudeer de werking van een vergrootglas.

1 Wat denk jij? Duid aan.

• Een vergrootglas geeft altijd / soms / nooit een vergroot beeld.

• Een vergrootglas geeft altijd / soms / nooit een rechtopstaand beeld.

• Een vergrootglas geeft altijd / soms / nooit een virtueel beeld.

2 Test het uit. Komt de hypothese overeen met je waarneming?

3 Ga op zoek naar een verklaring.

a Bestudeer het vergrootglas. Wat is dat?

b Ga in de applet op zoek naar beelden die overeenkomen met je waarnemingen. Gebruik veel stralen.

c Wat bepaalt de eigenschappen van het beeld?

d Hoe moet je het vergrootglas gebruiken om een rechtopstaand en vergroot beeld te bekomen?

©VANIN

Een lens is een doorzichtig voorwerp dat wordt begrensd door minstens één gekromd oppervlak. Dunne lenzen stel je symbolisch voor door een rechte met een pijlpunt die de kromming aangeeft.

Je duidt de kenmerken van de les erop aan:

• het brandpunt (F): het convergentiepunt van een evenwijdige lichtbundel,

• de brandpuntafstand ( f ),

• de hoofdas: een rechte door het midden van en loodrecht op de lens,

• het optisch middelpunt (O): het snijpunt van de hoofdas met de lens.

Een bolle lens is dikker in het midden en dunner aan de rand. De schematische voorstelling van een bolle lens is een rechte met pijlpunten volgens de kromming op beide uiteinden. Het brandpunt F is reëel.

©VANIN

Een holle lens is dikker aan de rand en dunner in het midden. De schematische voorstelling van een holle lens is een rechte met omgekeerde pijlpunten volgens de kromming op beide uiteinden. Het brandpunt F is virtueel.

Als een voorwerp (V) zich voor een lens bevindt, ontstaat er een beeld (B), doordat het invallende licht van het voorwerp gebroken wordt door de lens.

Voor elk punt van het voorwerp kun je met de brekingswetten het beeldpunt tekenen. Voor de meeste lichtstralen is dat veel werk: je moet het oppervlak en de normaal tekenen in elk punt voor de breking bij het binnen- en buitengaan van de lichtstraal in de lens.

Door kenmerkende lichtstralen te gebruiken die een eenvoudige breking hebben, kun je het beeld eenvoudig tekenen. Voor een dunne lens zijn dit de kenmerkende stralen:

➀ Een lichtstraal die evenwijdig met de hoofdas invalt, breekt door het brandpunt.

➁ Een lichtstraal die door het brandpunt invalt, breekt evenwijdig met de hoofdas. Dat volgt rechtstreeks uit ➀ en uit de omkeerbaarheid van de stralengang (derde brekingswet).

➂ Een lichtstraal die door het optisch middelpunt O invalt, breekt niet.

Om het beeld van een pijl op de hoofdas te tekenen, teken je de kenmerkende stralen vanuit de pijlpunt van het voorwerp V. Het snijpunt is het beeldpunt B. De voet van de pijl ligt op de hoofdas. Op afbeelding 47 zie je de beeldconstructie met de drie kenmerkende stralen bij een bolle lens.

KENNISCLIP LENZEN

OPEN APPLET

Een beeld gevormd door een lens heeft vier eigenschappen: positie, stand, grootte en aard.

Bij dunne lenzen hangen de eigenschappen en de beeldafstand (b = |OB|) af van de brandpuntsafstand (f = |OF|) en de positie ten opzichte van de lens (v = |OV|).

Je vindt die eigenschappen door de beeldconstructies te maken of door de applet te gebruiken.

OPDRACHT 30 ONDERZOEK

Onderzoek de beeldvorming bij lenzen aan de hand van het labo bij het onlinelesmateriaal.

OPDRACHT 31

Construeer de beelden bij een bolle lens voor verschillende voorwerpsafstanden.

Bij dunne lenzen hangen de eigenschappen en de beeldafstand (b  = |OB|) af van de brandpuntafstand (f = |OF|) en de positie ten opzichte van de lens (v  = |OV|).

1 Construeer het beeld met behulp van de kenmerkende stralen.

Eigenschappen

©VANIN

• virtueel / reëel

• rechtop / omgekeerd

• even groot / vergroot / verkleind

Vergroting

hB hV = =

b v = =

Eigenschappen

2 3 4 5

voorwerp

Vergroting

• virtueel / reëel

• rechtop / omgekeerd

• even groot / vergroot / verkleind hB hV = = b v = =

voorwerp

• virtueel / reëel

• rechtop / omgekeerd

• even groot / vergroot / verkleind hB hV = = b v = =

voorwerp

• virtueel / reëel

• rechtop / omgekeerd

• even groot / vergroot / verkleind hB hV = = b v = =

• virtueel / reëel

• rechtop / omgekeerd

• even groot / vergroot / verkleind hB hV = = b v = =

2 Vul de eigenschappen van het beeld aan.

3 Bestudeer de vergroting.

a Bereken de verhouding van …

• de hoogtes van het beeld en het voorwerp ( hB hV ),

• de beeldafstand en de voorwerpsafstand ( b v ).

b Wat stel je vast?

TIP

Ontdek in de ontdekplaat welke technologische toepassingen lenzen hebben.

Bij een lens ontstaan beelden door de gebroken lichtstralen. De eigenschappen van de beelden verschillen voor een bolle en een holle lens:

• Bij een bolle lens variëren de eigenschappen van het beeld als de voorwerpsafstand varieert.

• Bij een holle lens is het beeld altijd rechtop, verkleind en virtueel.

Je kunt het beeld construeren met de kenmerkende stralen.

` Maak oefening 8 en 9 op p. 279-280.

OPDRACHT 32

Bestudeer de beelden gevormd door een lens.

1 Vul de tabel aan.

2 Boots de situaties na in de applet.

1

©VANIN

2

Welk type lens wordt gebruikt? holle lens (voor bijzienden)

3

Welke grootte en stand heeft het beeld?

TIP

Je kunt het gelijkvormigheidskenmerk HH gebruiken.

3.2 Vergroting

In de meeste situatie is het beeld gevormd door een lens vergroot of verkleind. De vergroting m is de verhouding van de beeldgrootte hB tot de voorwerpsgrootte hV:

m = hB hV

Uit de gelijkvormigheid van de driehoeken DVV'O en DBB'O volgt dat de vergroting m ook de verhouding is van de beeldafstand b tot de voorwerpsafstand v:

m = hB hV = b v

©VANIN

De vergroting van een beeld kun je berekenen als m = hB hV = b v .

` Maak oefening 10 t/m 12 op p. 280-281.

OPDRACHT 33

Lost het vraagstuk op.

Je houdt een potlood van 10 cm op 50 cm voor een dunne bolle lens.

Er wordt een beeld gevormd op 33 cm achter de lens.

1 Werk het vraagstuk uit op een cursusblad.

a Teken de beeldvorming op schaal 1 : 10.

b Geef de eigenschappen van het beeld.

c Bereken de grootte van het beeld.

2 Controleer je antwoord.

VRAAGSTUK VERGROTING

OPLOSSINGSSTRATEGIE

• Lees het vraagstuk aandachtig.

• Maak een beeldconstructie.

Teken de lens symbolisch.

Teken de hoofdas met het optisch middelpunt.

Duid de gegevens aan op de afbeelding en bij de gegevens.

Teken het voorwerp (eventueel als een pijl).

Teken de beeldvorming met de kenmerkende stralen.

• Bestudeer het beeld om de eigenschappen te bepalen.

• Gebruik de formule voor vergroting om de gevraagde lengte te berekenen.

Afb. 48

1 Bestudeer opnieuw de afbeeldingen uit het begin van dit hoofdstuk.

2 Verklaar de beeldvorming.

a Afbeelding links:

• Welk type doorzichtig voorwerp wordt gebruikt?

• Hoe komt het dat de lijnen lijken te veranderen van zwart naar wit op sommige plaatsen?

b Afbeelding rechts:

• Welk type doorzichtig voorwerp wordt gebruikt?

• In welke richting is het glas gekromd?

• Welke stand en vergroting heeft het beeld?

• Boots de beeldvorming na in de applet.

3 Vergelijk je hypothese op p. 273 met je besluit.

4 Maak zelf een abstracte kunstfoto met een doorzichtig voorwerp.

a Maak een foto van de onderdelen en van de opstelling.

b Verklaar het ontstaan van de speciale effecten.

5 Druk je kunstfoto uit hoofdstuk 1, 2 of 3 af en hang hem op in de klas.

Zit je vast bij een oefening?

Misschien helpen deze QR-codes je weer op weg!

1 Wanneer ontstaat breking? Duid aan.

in alle middenstoffen voor elke invallende straal

bij de overgang tussen twee homogene middenstoffen voor elke invallende straal

bij de overgang tussen twee homogene middenstoffen voor elke schuin invallende straal

bij de overgang tussen twee homogene middenstoffen met een andere optische dichtheid voor elke invallende straal

bij de overgang tussen twee homogene middenstoffen met een andere optische dichtheid voor een schuin invallende straal

2 Bestudeer de afbeeldingen.

a Vervolledig de afbeeldingen met de normaal, de invalshoek en de brekingshoek.

b Duid de kenmerken van breking aan onder de afbeeldingen.

1 2 3

geen breking

breking naar de normaal toe

breking van de normaal weg

geen breking

breking naar de normaal toe

breking van de normaal weg

geen breking

breking naar de normaal toe

breking van de normaal weg

c Rangschik de drie middenstoffen volgens toenemende optische dichtheid.

©VANIN

BEELD BIJ BREKING

BEELD BIJ LENZEN

SPIEGELBEELD

3 Welk type doorzichtig voorwerp zit in de doos?

a Duid aan.

planparallelle plaat

holle lens

bolle lens

b Teken het voorwerp en vervolledig de stralengang.

©VANIN

4

Bestudeer de afbeelding van een koplamp.

a Hoe komt het dat de lichtbundel zichtbaar is?

b Om de lichtbundel minder divergerend te maken, plaatst men een gekarteld glas voor de koplamp.

Teken:

• de lichtbundel die je waarneemt op de afbeelding;

• de lichtbundel voor en na het glas.

gekarteld stuk glas

puntvormige lichtbron

c Welk type doorzichtig voorwerp is het gekartelde glas? Duid aan.

planparallelle plaat

holle lens

bolle lens

Afb. 49

Afb. 50

Afb. 51

5 Bestudeer de afbeelding.

luchtlagen werkelijke stand

a Teken de normaal bij elke overgang naar een volgende laag in de atmosfeer.

b Verklaar de getekende stralengang.

c Teken de positie waar je de zon ziet.

d Wordt de dag langer of korter door die atmosferische breking? Verklaar.

6 Bestudeer de afbeelding.

a Wat is er bijzonder?

b Waar heb je zelf al een vergelijkbare waarneming gedaan? aardoppervlak

7 Plaats een potlood of een lat in water, zodat het voorwerp half ondergedompeld is, zoals op de afbeelding.

a Wat zie je?

b Verklaar met een stralendiagram.

8 In de natuur zie je de opsplitsing van het witte zonlicht in de ROGGBIV-kleuren bij een regenboog.

a Welke situatie geeft de positie van de waarnemer, de zon en de regenboog correct weer?

b Hoe ontstaan de kleuren?

©VANIN

c Vervolledig de afbeelding van wit licht (RGB) dat invalt op een waterdruppel, met de groene en blauwe lichtstraal.

9 Een puntbron L bevindt zich voor een bolle lens en zendt een lichtstraal uit. Welke richting (1, 2, 3 of 4) volgt de lichtstraal nadat ze de lens doorlopen heeft?

©VANIN

10 Een brandende kaars van 20 cm hoog bevindt zich op 50 cm voor een bolle lens met een brandpuntafstand van 30 cm.

a Teken (op schaal) het beeld van de kaars.

b Geef de kenmerken van het beeld.

c Bereken de vergroting op twee manieren.

Bron: Vlaamse Fysica Olympiade

11 Met behulp van een bolle lens projecteer je een scherp beeld op een scherm. Je bedekt de helft van de lens.

a Wat zal er gebeuren volgens jou? Duid aan.

Het beeld zal helemaal verdwijnen.

Je kunt nog een deel van het beeld zien.

Je kunt het volledige beeld zien, maar minder duidelijk.

Het beeld zal onveranderd blijven.

b Test uit.

c Verklaar.

12 Van een insect dat zich op 37,5 cm van een bolle lens bevindt, wordt op 30,0 cm van de lens een reëel beeld gevormd dat 1,2 cm groot is.

a Bereken de vergroting en de grootte van het van het insect.

Gegeven:

Gevraagd:

Oplossing:

Controle: Wordt het insect vergroot of verkleind?

b Kun je het insect vergroten met de lens? Leg uit en ga na met de applet.

` Verder oefenen? Ga naar

©VANIN

1 Begripskennis

• Ik kan optisch ijle en optisch dichte middenstoffen omschrijven

• Ik kan het gedrag van licht bij de overgang van een optische ijle naar een optisch dichte middenstof (of omgekeerd) omschrijven

• Ik kan de invallende straal, de invalshoek, de normaal, de gebroken straal en de brekingshoek omschrijven en aanduiden op een afbeelding.

• Ik kan de brekingswetten toepassen om de gebroken straal te tekenen

• Ik kan de stralengang van een evenwijdige lichtbundel op een planparallelle plaat en lenzen omschrijven

• Ik kan de brekingswetten toepassen om het beeld bij een overgang naar een andere middenstof te tekenen.

• Ik kan de drie kenmerkende stralen bij een lens omschrijven en tekenen

• Ik kan het beeld bij een bolle lens tekenen met behulp van drie kenmerkende stralen.

• Ik kan de kenmerken van een beeld afleiden uit een stralendiagram.

• Ik kan de vergroting berekenen.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan lichtstralen nauwkeurig tekenen

• Ik kan het beeld bij de overgang naar een andere middenstof nauwkeurig tekenen.

• Ik kan het beeld bij bolle lenzen nauwkeurig tekenen

` Je kunt deze checklist ook op invullen bij je Portfolio.

©VANIN

JA NOG OEFENEN

Lichtbundels

• Rechtlijnige voortplanting van licht in homogene middenstoffen: lichtstralen

• Snelheid bepaald door samenstelling van de middenstof

• Divergerend, evenwijdig of convergerend

• De lichtkleur wordt bepaald door de hoeveelheid rood, groen en blauw licht ( additieve kleurmenging). Wit licht bevat alle kleuren evenveel.

Doorgelaten lichtbundel: overgang naar een andere middenstof

• Doorzichtige stof: al het licht gaat erdoor.

• Doorschijnende stof: een deel van het licht gaat erdoor.

• Er is breking : brekingswetten. Overgang optisch ijl  dicht: naar de normaal toe Overgang optisch dicht  ijl: van de normaal weg

©VANIN

Teruggekaatste lichtbundel

• Maakt donkere lichamen zichtbaar.

• Effen oppervlak: gerichte weerkaatsing

• Oneffen oppervlak: diffuse weerkaatsing

• Spiegelwetten gelden: Stralen en normaal liggen in één vlak.

t = î

De stralengang is omkeerbaar.

weerkaatsenabsorberendoorlaten

Geabsorbeerde lichtbundel

• Achter het voorwerp ontstaat schaduw .

— Kernschaduw: plaats zonder licht Bijschaduw: plaats met een deel van het licht

Lenzen De aard van het beeld hangt af van het type lens en de positie van het voorwerp.

Vergroting: m = h B

1 T eken het voorwerp als een rechtopstaande pijl op de hoofdas.

2 T eken een kenmerkende lichtstraal  ➀ en haar breking vanuit de pijlpunt.

3 Herha al voor een tweede kenmerkende lichtstraal ➁ .

4 Z oek het snijpunt van de twee kenmerkende stralen of hun verlengde v óó r de lens. (Gebruik stippellijnen om aan te geven dat het geen echte lichtstralen zijn.)

5 Het snijpunt is het beel dpunt van de pijlpunt.

Tip: Controleer door de derde kenmerkende straal te tekenen.

©VANIN

BEELDVORMING

Breking virtueel, verschoven

V r i glas

1 T eken een invallende lichtstraal ( i ) vanuit het voorwerpspunt V naar het scheidingsoppervlak.

2 T eken de normaal in het invalspunt.

3 Teken de gebroken straal ( r ) zodat a r < î : overgang van optisch ijl naar optisch dicht b r > î : overgang van optisch dicht naar optisch ijl Gebruik de applet als je de hoek precies wilt kennen.

4 V erleng de gebroken straal. Gebruik stippellijnen om aan te geven dat het geen echte lichtstralen zijn.

5 V erschuif het voorwerpspunt V volgens de richting van de normaal, totdat je de stippellijn snijdt. Dat is het beeldpunt B.

oog

Spiegelbeeld virtueel, rechtop, even groot en symmetrisch ten opzichte van spiegel voorwerp beeld spiegel

( n )

( n )

1 T eken een invallende lichtstraal ( a ) vanuit het voorwerp naar de spiegel.

2 T eken de normaal in het invalspunt.

3 T eken de teruggekaatste straal ( a’ ) zodat t = î .

4 Herha al voor een tweede lichtstraal ( b en b’ ).

5 V erleng beide stralen achter de spiegel. Gebruik stippellijnen om aan te geven dat het geen echte lichtstralen zijn.

6 Het snijpunt is het beel dpunt.

Tip: De meest eenvoudige lichtstraal is degene die loodrecht invalt op de spiegel ( c ).

OPEN APPLET

Sterren kijken

1 Sterren fonkelen aan de hemel. a Verklaar.

b Fonkelen de volgende sterren? Verklaar.

• sterren die je kunt waarnemen vanop Mars:

• sterren die je kunt waarnemen vanop de maan:

• de zon:

2 Astronomen bestuderen sterren met een telescoop.

a Bestudeer de werking van een telescoop met de applet.

• Verwijder het omhulsel (tube), zodat de stralengang zichtbaar is.

• Verschuif het oculair totdat je het beeldpunt ziet.

• Verschuif de ster een klein beetje omhoog en omlaag. Wat merk je?

b Welke eigenschappen heeft het beeld bij dit type telescoop?

c Waarom is de stand (rechtop of omgekeerd) van het beeld niet belangrijk?

©VANIN

d Verklaar waarom het fonkelen van sterren een nadeel is voor astronomen (die met telescopen met een vergroting van 100 werken).

WEETJE

Om het probleem van fonkelende sterren op te lossen, werd in 1990 de eerste ruimtetelescoop (Hubble) gelanceerd. Hubble bevindt zich buiten de dampkring en wordt dus niet gehinderd door breking ten gevolge van de atmosfeer. De beelden zijn een stuk helderder en scherper.

Op de website van NASA vind je alle informatie over de werking, maar ook video’s en beelden terug. Ter gelegenheid van de dertigste verjaardag van Hubble (2020) werd een overzichtsvideo gemaakt.

Kleine veranderingen in de atmosfeer veranderen het pad van het licht op een ongecontroleerde manier: de sterren fonkelen! Om toch scherpe beelden te maken, voeren astronomen hun metingen uit met telescopen net buiten de atmosfeer.

Notities ©VANIN

©VANIN

©VANIN