Coup de boost
1
T H ÉMATIQUES
DUSAIWOIR
JOYCE
VAN
H ÉMATIQUES 1
Coup de boost ÉditionsVANIN
Composition de Coup de boost mathématiques
Pour l’élève Livre-cahier
Pour l’enseignant Corrigé
Manuel numérique disponible sur Udiddit
Coup de boost mathématiques 1 Exercices d’entraînement
Auteure : Joyce Dusaiwoir
Couverture : Nor production
Mise en page : Nor Production
Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent.
La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.
L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si, malgré cela, quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.
ÉditionsVANIN
© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2024
Tous droits réservés.
En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.
1re édition, 2024
ISBN 978-94-647-0558-4
D/2024/0078/68
Art. 606256/01
175 LES DÉTERMINANTS TABLE DES MATIÈRES Domaine 1 – Nombres et opérations 1 – Familles de nombres • 1.1. Les ensembles 7 • 1.2. Les nombres 9 • 1.3. Le dénombrement 11 2 – Diviseurs et multiples • 2.1. Le vocabulaire 13 • 2.2. Les caractères de divisibilité 14 • 2.3. La justification dans la divisibilité 16 • 2.4. Les nombres premiers inférieurs à 100 18 • 2.5. Les diviseurs et les nombres particuliers 19 • 2.6. La factorisation première 21 • 2.7. Le Plus Grand Commun Diviseur (PGCD) de deux nombres 23 • 2.8. Les multiples 24 • 2.9. Le Plus Petit Commun Multiple (PPCM) de deux nombres ............................... 26 3 – Opérations avec les naturels • 3.1. Le vocabulaire des opérations ............................................................................................................... 27 • 3.2. La compensation dans l’addition 29 • 3.3. Les propriétés de l’addition 30 • 3.4. La compensation dans la soustraction 32 • 3.5. La multiplication et ses tables 33 • 3.6. Les propriétés de la multiplication 34 • 3.7. Les puissances 36 • 3.8. La division 37 • 3.9. Les priorités des opérations 38 • 3.10. La distributivité simple 40 4 – Opérations avec les entiers • 4.1. La valeur absolue et l’opposé 41 • 4.2. La somme de deux nombres entiers 42 • 4.3. Les propriétés de l’addition 43 • 4.4. La différence de deux nombres entiers 44 • 4.5. La règle des signes successifs 45 • 4.6. L’opposé d’une somme et l’opposé d’une différence 46 • 4.7. La multiplication de deux nombres entiers 47 • 4.8. Les propriétés de la multiplication 48 • 4.9. Les priorités des opérations ................................................................................................................... 49 5 – Opérations avec les rationnels • 5.1. La somme et la différence de rationnels .................................................................................... 51 • 5.2. Le produit de rationnels 53 • 5.3. La somme, la différence et le produit de rationnels 54 ÉditionsVANIN
6
Domaine 2 – Figures et solides
3
TABLE DES MATIÈRES 176
– Calculs littéraux • 6.1. Les expressions littérales 55 • 6.2. La somme et la différence dans le calcul littéral 56 • 6.3. Le produit dans le calcul littéral 58 • 6.4. La distributivité simple 59 • 6.5. La mise en évidence 60 • 6.6. Le calcul de valeurs numériques 62 • 6.7. Le dénombrement 65
– Équations • 7.1. Le vocabulaire 69 • 7.2. Les équations du type « x + a = b » 72 • 7.3. Les équations du type « a . x = b » .................................................................................................. 74 • 7.4. Les équations du type « a . x + b = c » 76
7
1 – Éléments de géométrie de base • 1.1. Les éléments de base 81 • 1.2. Les distances et les mesures 83 • 1.3. Les angles 85 • 1.4. La médiatrice d’un segment 87 • 1.5. La bissectrice d’un angle 89
– Figures planes • 2.1. Les polygones 91 • 2.2. Les triangles 93 • 2.3. Les droites remarquables du triangle 97 • 2.4. Les quadrilatères 99
2
– Solides • 3.1. Le vocabulaire ...................................................................................................................................................... 105 • 3.2. Les solides et les perspectives 108 • 3.3. Les solides et leurs vues 110 • 3.4. Les solides et leurs développements ......................................................................................... 111 • 3.5. Les positions relatives dans les solides 113
– Transformations du plan • 4.1. L’identification des transformations du plan 117 • 4.2. La symétrie orthogonale 119 • 4.3. La symétrie centrale 121 • 4.4. La translation 123 • 4.5. Les frises 125 ÉditionsVANIN
4
Domaine 3 –
1
6
Domaine 4 – Traitement des données
1
TABLE DES MATIÈRES 177
Grandeurs
– Unités de mesure • 1.1. Les unités de longueur 129 • 1.2. Les unités de capacité 130 • 1.3. Les unités de masse ...................................................................................................................................... 131 • 1.4. Les unités d’aire 133 • 1.5. Les unités de volume 134 • 1.6. Les unités de temps ...................................................................................................................................... 135 2 – Fractions • 2.1. La fraction sous différentes formes ............................................................................................. 137 • 2.2. La comparaison de deux fractions 140 • 2.3. L’encadrement d’un nombre rationnel 141 • 2.4. La simplification de fractions 142 • 2.5. La réduction de fractions au même dénominateur 143 3 – Proportions • 3.1. Les grandeurs directement proportionnelles 145 • 3.2. Les pourcentages 146 4 – Périmètres, aires et volumes • 4.1. Le périmètre 149 • 4.2. L’aire 151 • 4.3. Le volume 153
– Repérage • 5.1. La droite graduée et les nombres entiers 155 • 5.2. La droite graduée et les nombres rationnels (décimaux) 156 • 5.3. La droite graduée et les nombres rationnels (fractions) 157 • 5.4. Le repère cartésien 158
5
– Problèmes • 6.1. Les problèmes de diviseurs et de multiples 161 • 6.2. Les problèmes avec les nombres .................................................................................................... 162 • 6.3. Les problèmes de périmètre, d’aire et de volume 163 • 6.4. Les problèmes avec les équations 164
– Traitement des données • 1.1. Les graphiques de toutes sortes 169 • 2.2. La représentation de données numériques 170 • 3.3. L’analyse de graphiques et de diagrammes 172 ÉditionsVANIN
ÉditionsVANIN
Coup de boost Mathématiques est là pour t’aider à améliorer ta compréhension de la matière grâce à des synthèses théoriques et à un entraînement via de nombreux exercices systématiques.
Les notions à maîtriser sont présentées sous forme de fiches regroupées en 4 domaines :
1 Nombres et opérations
2 Figures et solides
3 Grandeurs
4 Traitement des données
Une synthèse théorique, illustrée d’exemples, t’explique de manière simple et visuelle les différentes notions à comprendre et à maîtriser.
ÉditionsVANIN
Chaque fiche est divisée en points matières clairement identifiés afin de te permettre de cibler les notions qui posent vraiment problème.
Des exercices diversifiés sont proposés en nombre afin que tu puisses suffisamment t’entraîner.
Des astuces et points d’attention sont disséminés dans l’ouvrage pour faciliter l’application de la théorie.
Des jeux et des activités récréatives te sont régulièrement proposés. De quoi s’entraîner tout en s’amusant !
Grâce à Coup de boost, les notions mathématiques n’auront plus de secret pour toi. Bon entraînement !
3 LES DÉTERMINANTS INTRODUCTION
ÉditionsVANIN
3 OPÉRATIONS AVEC LES NATURELS
3.1 Le vocabulaire des opérations
L’addition
Symbole de l’addition
1er terme
2e terme
20 + 4 = 24 Somme
1er terme
2e terme
La multiplication
1er facteur
2e facteur
La division
Dividende
Diviseur
La soustraction
Symbole de la soustraction
20 – 4 = 20 Différence
Symbole de la multiplication
20 4 = 80 Produit
Symbole de la division
20 : 4 = 5
Quotient
Numérateur
Dénominateur
La division
Symbole de la division
20 = 5 4
Quotient
1. Rédige une phrase complète pour déterminer le nombre en gras.
10 – 4 = 6 6 est la différence .
ÉditionsVANIN
10 . 4 = 40 4 est un facteur ou le 2e facteur.
a) 6 . 4 = 24
b) 5 – 4 = 1
c) 23 + 25 = 48
d) 12 + 45 = 57
e) 30 : 5 = 6
f) 7 . 9 = 63
g) 90 : 18 = 5
27 LES DÉTERMINANTS
2. Modifie les opérations en suivant les indications données.
La somme 12 + 64 en retranchant 50 au 2e terme. " 12 + 14
Le produit 12 . 64 en divisant les deux facteurs par 4. " 3 16
a) Retranche 11 au second terme de l’opération 57 - 26. ¦
b) Divise par 2 le diviseur de l’opération 360 : 12. ¦
c) Ajoute 3 aux deux termes de l’opération 54 + 38. ¦
d) Retranche 5 au premier facteur de l’opération 21 . 4. ¦
e) Ajoute 2 au dividende de l’opération 70 : 36. ¦
f) Divise par 3 le premier terme de l’opération 21 + 54. ¦
Complète ces mots croisés. (Essaie de le faire sans regarder la théorie. )
ÉditionsVANIN
Horizontalement
1. Le double de 3 est une … .
2. Le nombre qui est divisé est le … .
3. La … est l’opération dont le résultat est la différence.
4. Dans l’expression « 30 : 6 = 5 », 5 est le … .
5. « 3 – 2 » est la … entre 3 et 2.
6. Le … est l’élément sous la barre de la fraction.
7. Div 4 = {1 ; 2 ; 4} est l’ensemble des … de 4.
Verticalement
1. L’opération dont la somme est le résultat est l’… .
2. Dans l’expression « 4 + 5 = 9 », 4 est un … .
3. Le résultat d’une multiplication est le … .
4. « 6 + 1 » est la … de 6 et de 1.
5. Dans le triple de 2, 2 est un … .
6. Le … est l’élément au-dessus de la barre de fraction.
7. L’opération qui utilise les symboles « : » ou « » est la … .
OPÉRATIONS AVEC LES NATURELS 28
2 3 6 7 1 1 2 4 3 4 5 5 6 7
Garam – Complète les opérations dans la grille.
x – – + : x
3 3+2=
3.2 La compensation dans l’addition
Dans une addition, on peut effectuer une compensation croisée, ce qui signifie qu’on peut ajouter un nombre à un terme et soustraire ce même nombre au second terme sans changer le résultat.
232 + 398 = 230 + 400 = 630
232 + 378 = 210 + 400 = 610
Astuce
1. En t’aidant de la synthèse, utilise les flèches de la compensation, puis résous chaque addition.
289 + 361 =
567 + 273 =
Cette technique te permet d’effectuer plus rapidement les calculs !
526 + 294 =
2. Utilise la compensation (sans les flèches) et résous chaque addition.
232 + 398 = (232 – 2) + (398 + 2) = 230 + 400 = 630
ÉditionsVANIN
232 + 378 = (232 – 22) + (378 + 22) = 210 + 400 = 610
a) 776 + 344 =
b) 245 + 596 =
c) 653 + 487 =
d) 472 + 389 =
e) 299 + 158 =
f) 364 + 257 =
g) 553 + 269 =
OPÉRATIONS AVEC LES NATURELS 29
–5=3
+1= :3=
5–=2
=
= = = = =
–6= 4x2= +2=6
- 2 + 2 + 22 - 22
3.3 Les propriétés de l’addition
– L’addition est une opération commutative, ce qui signifie que, dans une somme de nombres naturels, l’ordre des termes n’influence pas le résultat.
1 + 2 + 3 = 2 + 3 + 1 = 3 + 1 + 2 = 6
– L’addition est une opération associative, ce qui signifie que, dans une somme de plus de deux nombres naturels, la manière de les grouper n’influence pas le résultat.
1 + 2 + 3 = (1 + 2) + 3 = 3 + 3 = 6
1 + 2 + 3 = 1 + (2 + 3) = 1 + 5 = 6
– L’addition est une opération qui admet 0 comme élément neutre, ce qui signifie qu’ajouter zéro à un nombre naturel donne une somme égale à ce nombre.
1 + 0 = 1 ou 0 + 23 = 23
1. Cite la propriété illustrée dans les calculs suivants.
4 + 5 + 6 = 4 + (5 + 6) ¦ L’addition est une opération associative.
a) 15 + 0 = 15 "
b) 3 + (5 + 2) = (3 + 5) + 2 "
c) (2 + 3) + 4 = (3 + 2) + 4 "
d) 78 + 0 = 0 + 78 "
e) 7 + 8 + 9 = 7 + (8 + 9) "
f) 69 + 0 = 69 "
2. Calcule en utilisant les propriétés de l’addition.
31 + 113 + 69 + 87 = 31 + 69 + 113 + 87 = (31 + 69) + (113 + 87) = 100 + 200 = 300
a) 42 + 116 + 34 + 58 =
ÉditionsVANIN
b) 115 + 0 + 85 =
c) 121 + 435 + 165 + 279 =
d) 31 + 456 + 29 + 444 =
OPÉRATIONS AVEC LES NATURELS 30
3. Complète les pointillés avec la propriété qui permet de passer d’une étape à la suivante (dans le cas où aucune des propriétés n’est utilisée, complète par « / »).
a)5 + 3 + 7 – 3 Ð
= 5 + 7 + 3 – 3 Ð
= 5 + 7 + (3 – 3) Ð
= 5 + 7 + 0 Ð
= 5 + 7 Ð
= 12
b)2 + 3 + 4 + 6 + 7 Ð
= 2 + 3 + (4 + 6) + 7 Ð
= 2 + 3 + 10 + 7 Ð
= 2 + 10 + 3 + 7 Ð
= 2 + 10 + (3 + 7) Ð
= 2 + 10 + 10 Ð
= 22
ÉditionsVANIN
Calcudoku – Complète la grille par des chiffres (de 1 à 3 pour la grille de 9 cases, de 1 à 4 pour la grille de 16 cases) pour obtenir la somme dans la forme en gras. Attention, tu ne peux pas avoir le même chiffre dans une même ligne ni dans une même colonne.
OPÉRATIONS AVEC LES NATURELS 31
3 6 4 5 6 614 5 9
3.4 La compensation dans la soustraction
Dans une soustraction, on peut effectuer une compensation parallèle, ce qui signifie qu’on peut ajouter/soustraire un nombre à un terme et ajouter/soustraire ce même nombre au second terme sans changer le résultat.
+ 2 + 2
2
532 – 398 = 534 – 400 = 134 481 – 122 = 479 – 120 = 359
- 2 +
1. En t’aidant de la synthèse, utilise les flèches de la compensation, puis résous chaque soustraction.
481 – 309 = 526 – 294 =
567 – 293 =
2. Utilise la compensation (sans les flèches) et résous chaque soustraction.
532 – 398 = (532 + 2) – (398 + 2) = 534 – 400 = 134
532 – 308 = (532 – 8) – (308 – 8) = 524 – 300 = 224
a) 776 – 394 =
b) 545 – 206 =
c) 953 – 487 =
d) 772 – 319 =
e) 491 – 108 =
f) 864 – 297 =
g) 553 – 214 =
ÉditionsVANIN
OPÉRATIONS AVEC LES NATURELS 32
h) 743 – 289 = -
7 + 7
3.5 La multiplication et ses tables
4, il suffit de multiplier par 2 et de multiplier encore par 2.
5, il suffit de multiplier par 10 et de diviser par 2.
9, il suffit de multiplier par 10 et de retirer 1x le nombre.
11, il suffit de multiplier par 10 et d’ajouter 1x le nombre.
25, il suffit de multiplier par 100 et de diviser par 4.
50, il suffit de multiplier par 100 et de diviser par 2
Pour 5, 25 et 50, tu peux permuter les opérations.
1. Calcule chaque produit en notant ton raisonnement.
47 . 4 = 47 . 2 . 2 = 94 . 2 = 188
a) 58 . 5 =
b) 69 . 9 =
c) 71 . 11 =
d) 23 . 25 =
e) 18 . 50 =
f) 82 . 4 =
g) 94 . 9 =
h) 45 . 50 =
2. Dans chaque série, entoure les nombres qui appartiennent aux tables proposées.
Pyramide de nombres – Complète chaque brique de la pyramide par le produit des deux briques sur lesquelles elle repose.
OPÉRATIONS AVEC LES NATURELS 33
Table de 4 " 2 8 12 34 56 Table de 9 " 18 3 63 81 37 Table de 3 " 9 3 21 43 61 Table de 8 " 28 4 53 18 54 Table de 7 " 7 1 14 42 58 Table de 6 " 12 6 54 78 42 25 23 270 6 5 3 2 POUR MULTIPLIER PAR
ÉditionsVANIN
3.6 Les propriétés de la multiplication
– La multiplication est une opération commutative : dans un produit de nombres naturels, l’ordre des facteurs n’influence pas le résultat.
1 . 2 . 3 = 2 . 3 . 1 = 3 . 1 . 2 = 6
– La multiplication est une opération associative : dans un produit de plus de deux nombres naturels, la manière de les grouper n’influence pas le résultat.
1 . 2 . 3 = (1 . 2) . 3 = 2 . 3 = 6
1 . 2 . 3 = 1 . (2 . 3) = 1 . 6 = 6
– La multiplication est une opération qui admet 1 comme élément neutre : multiplier un nombre naturel par 1 donne un produit égal à ce nombre.
1 . 23 = 23
– La multiplication est une opération qui admet 0 comme élément absorbant : multiplier un nombre naturel par 0 donne un produit égal à 0.
0 . 23 = 0
1. Cite la propriété illustrée dans les calculs suivants.
4 . 5 . 6 = 4 . (5 . 6)
La multiplication est une opération associative.
a) 15 . 0 = 0
b) 3 . (5 . 2) = (3 . 5) . 2
c) (2 . 3) . 4 = (3 . 2) . 4
d) 78 . 1 = 78
e) 7 . 8 . 9 = 7 . (8 . 9)
ÉditionsVANIN
f) 69 . 1 = 1 . 69
g) 1 . 96 = 96
h) 2 . 3 . 4 = 3 . 2 . 4
i) 0 . 74 = 0
OPÉRATIONS AVEC LES NATURELS 34
2. Calcule en utilisant les propriétés de la multiplication.
8 . 4 . 3 . 25 = 8 . 3 . 4 . 25 = (8 . 3) . (4 . 25) = 24 . 100 = 2 400
Astuce
Dans une multiplication, on va associer les facteurs dont le produit est égal à 10, 100, 1 000, etc.
2 . 5 = 10 ; 4 . 25 = 100 ; 8 . 125 = 1 000.
a) 2 . 22 . 50 . 3 =
b) 115 . 0 . 85 =
c) 8 . 36 . 125 . 2 =
d) 44 . 25 . 1 . 4 =
ÉditionsVANIN
3. Complète les pointillés par la propriété qui permet de passer d’une étape à la suivante (dans le cas où aucune des propriétés n’est utilisée, complète par « / »).
a)7 . 2 . 4 . 5 . 25 Ð
= 7 . 2 . 5 . 4 . 25 Ð
= 7 . (2 . 5) . (4 . 25) Ð
= 7 . 10 . 100 Ð
= 7 . 1 . 10 000 Ð
= 7 . 10 000 Ð
= 70 000
b)4 . 1 . 5 . 25 . 0 Ð
= 4 . 5 . 25 . 0 Ð
= 4 . 25 . 5 . 0 Ð
= (4 . 25) . (5 . 0) Ð
= 100 . 0 Ð
= 0
OPÉRATIONS AVEC LES NATURELS 35
3.7 Les puissances
Lorsque les facteurs d’un produit sont égaux, on convient d’écrire ce produit sous une forme abrégée : la puissance.
3 . 3 . 3 . 3 = 34 3 . 3 . 3 = 33
Base
3 4
2 . 2 . 2 . 2 = 24
Exposant Puissance
2² se lit « le carré de 2 », « la 2e puissance de 2 » ou « 2 exposant 2 ».
23 se lit « le cube de 2 », « la 3e puissance de 2 » ou « 2 exposant 3 ».
24 se lit « la 4e puissance de 2 » ou « 2 exposant 4 ».
Puissances par ticulières : 30 = 1 ; 31 = 3 ; 0³ = 0 ; 1³ = 1
1. Calcule les puissances en les décomposant.
27 = 2 . 2 . 2 . 2 . 2 . 2 . 2 = 128
104 = 5³ =
34 = 19 = 26 = 4³ =
2. Calcule mentalement les puissances.
2² = 6² = 13² = 3³ = 24 = 15² =
11² = 2³ = 6³ = 7² = 17² = 12 =
1³ = 12² = 04 = 10² = 32 = 5² =
4² = 14 = 8² = 14² = 07 = 16² =
20² = 28 = 18² = 9² = 19² = 25 =
Associe les bons éléments entre eux pour former la phrase ci-dessous.
① 19 = ? ② 3³ = ? 0 = A 1 = B2 = C29 = D16 = E 5 = F
③ 4² = ? ④ 5² = ? 6 =G7 = H27 = I49 = J10 = K11 = L
⑤ 7² = ? ⑥ 25 = ? 8 = M25 = N32 = O15 = P18 = Q17 = R
⑦ 91 = ? ⑧ 24 = ? 24 = S 56 = T U = 9 36 = V 3 = W 81 = X
AVEC LES NATURELS 36
OPÉRATIONS
①②③④⑤⑥⑦⑧ !
ÉditionsVANIN
3.8 La division
4, il suffit de diviser par 2 et de diviser encore par 2.
5, il suffit de diviser par 10 et de multiplier par 2.
8, il suffit de diviser par 2, puis par 2 et encore par 2.
POUR DIVISER PAR
25, il suffit de multiplier par 4 et de diviser par 100.
50, il suffit de multiplier par 2 et de diviser par 100.
Pour 5, 25 et 50, tu peux permuter les opérations. Pour le reste, on décompose le dividende.
1. Calcule chaque quotient en notant ton raisonnement.
108 : 4 = 108 : 2 : 2 = 54
a) 855 : 5 =
b) 1 250 : 50 =
c) 92 : 4 =
d) 1 440 : 8 =
e) 370 : 5 =
f) 8 200 : 25 =
2. Calcule chaque quotient en décomposant les dividendes.
1 491 : 3 =
1 491 : 3 =
a) 1 884 : 6 =
ÉditionsVANIN
b) 10 736 : 8 =
c) 17 973 : 9 =
OPÉRATIONS AVEC LES NATURELS 37
(1 200 + 270 + 21) : 3 = 1 200 : 3 + 270 : 3 + 21 : 3 = 400 + 90 + 7 = 497
500 – 9) : 3 = 1 500 : 3 – 9 : 3 = 500 – 3 =
(1
497
3.9 Les priorités des opérations
– On effectue en priorité :
① les calculs dans les parenthèses ;
② les puissances ;
③ les multiplications et les divisions ; ④ les additions et les soustractions.
Pour les multiplications/divisions et les additions/soustractions, il faut les résoudre dans l’ordre de lecture (de gauche à droite), car ce sont des opérations réciproques (même stade de priorité).
– L’opération prioritaire est l’opération à effectuer en premier.
– L’opération principale est l’opération à effectuer en dernier.
1. Coche les bonnes égalités. Pour celles qui ne sont pas cochées, ajoute des parenthèses pour corriger les égalités.
□ 6 + 4 . 2 = 14
□ 6 + 4 . 2 = 20
□ 24 : 4 . 2 = 3
□ 24 : 4 . 2 = 12
□ 2 + 3 . 4 + 5 = 45
□ 2 . 3 + 4 . 5 = 70
□ 2 . 3 + 4 . 5 = 46
□ 2 . 3 + 4 . 5 = 26
□ 2 . 3 + 4 . 5 = 50
2. Traduis chaque phrase par une expression mathématique.
La somme de 2 et du produit de 3 par 4. " 2 + 3 . 4
Astuces
Pour décoder (français " math), il faut savoir que la phrase commence toujours par l’opération principale. N’oublie pas l’utilisation des parenthèses quand c’est nécessaire.
a) La somme de 4 et de 2.
ÉditionsVANIN
b) La différence entre 4 et 2.
c) Le carré de 5.
g) La somme du produit de 2 par 3 et de 4.
d) Le produit de 4 par 2.
e) Le quotient de 4 par 2.
f) Le cube de 6.
h) La différence entre 24 et le quotient de 8 par 2.
i) Le quotient de la différence entre 24 et 8 par 2.
j) La différence entre le quotient de 24 par 8 et 2.
k) Le quotient de 24 par la différence entre 8 et 2.
OPÉRATIONS AVEC LES NATURELS 38
3. Traduis chaque expression mathématique par une phrase.
2 + 3 . 4 " La somme de 2 et du produit de 3 par 4.
Astuces
Pour coder (math " français), la traduction commence toujours par l’opération principale.
Repère donc l’(les) opération(s) prioritaire(s).
a) 5 – 1
b) 6 : 2
c) 3²
g) 4 . 5 – 3
h) 4 . (5 + 3)
i) 4 + 5 . 3
j) 4 – 5 . 3
k) 9 – 1³
d) 7 + 2
e) 3 . 8
f ) 2³
4. Calcule en respectant les priorités des opérations.
45 – (3 + 2)² = 45 – 5² = 45 – 25 = 20
Astuce
Dans chaque étape de calculs, repère l’opération prioritaire en l’entourant, en la soulignant ou en la mettant en couleurs.
a) 3 . (4 + 8) =
b) (2 + 5)² =
c) 2 + 5² =
ÉditionsVANIN
d) 36 : 3 . 4 =
i) 4 . 6 + (4 – 2) =
j) 8 . 3 – 5 . 2 =
k) (3 – 3) . 2 + 5 =
l) 5 + 3² . 2 =
m) (5 + 3)² . 2 =
n) (5 + 3) . 2² =
o) 5² + 24 : 4 . 2 =
p) (6 + 2)² : 8 – 4 =
e) 10² – 5 =
f ) (10 – 5)² =
g) (7 – 4) . 2 =
h) 36 . 3 : 4 =
OPÉRATIONS AVEC LES NATURELS 39
3.10 La distributivité simple
Pour multiplier une somme/différence par un nombre, il faut multiplier chaque terme de la somme/différence par ce nombre.
8 . 21 = 8 . (20 + 1) = 8 . 20 + 8 . 1 = 160 + 8 = 168
8 . 21 = (10 – 2) . 21 = 10 . 21 – 2 . 21 = 210 – 42 = 168
1. Applique la distributivité simple.
5 . (2 + 12) = 5 . 2 + 5 . 12 = 10 + 60 = 70 ou
5 . (2 – 12) = 5 . 2 – 5 . 12 = 10 – 60 = -50
a) 3 . (5 + 11) =
b) 8 . (20 – 1) =
c) (7 + 13) . 4 =
d) 7 . (20 – 5) =
e) (15 + 26) . 2 =
f) 9 . (12 – 2) =
2. Calcule en transformant un des deux facteurs en une somme ou une différence.
9 . 22 = (10 – 1) . 22 = 10 . 22 – 1 . 22 = 220 – 22 = 198 ou
9 . 22 = 9 . (20 + 2) = 9 . 20 + 9 . 2 = 180 + 18 = 198
a) 22 . 6 =
b) 101 . 18 =
c) 29 . 7 =
d) 12 . 98 =
e) 31 . 22 =
ÉditionsVANIN
f) 13 . 99 =
g) 102 . 45 =
h) 34 . 97 =
OPÉRATIONS AVEC LES NATURELS 40
– Un polyèdre est un solide limité par des faces planes (polygones).
– Un prisme droit est un solide dont les bases sont des polygones superposables et parallèles et dont les faces latérales sont des rectangles.
– Une pyramide est un polyèdre limité par un polygone (la base) et des triangles (les faces latérales) qui ont un sommet commun.
Les arêtes qui relient les bases sont parallèles et de même longueur ; cette longueur est appelée hauteur du prisme. Les arêtes non visibles sont en pointillés.
1. À l’aide de la synthèse, classe les objets suivants dans le tableau.
ÉditionsVANIN
105 LES DÉTERMINANTS
3 SOLIDES
3.1 Le vocabulaire
123 4 567 8 Polyèdre Non-polyèdre 1 2 3 4 5 6 7 8
2. Relis la synthèse et coche le(s) nom(s) correct(s) de chaque solide.
cône
cylindre
sphère
tétraèdre
cube
hexaèdre
ÉditionsVANIN
tétraèdre
pyramide à base carrée
cône
cône
cylindre
sphère
pyramide à base carrée
prisme droit à base carrée
prisme droit à base triangulaire
cône
cylindre
sphère
cube
parallélépipède rectangle
brique
prisme droit à base hexagonale
prisme droit à base carrée
prisme droit à base pentagonale
SOLIDES 106
– Un sommet d’un solide est un point.
– Une arête d’un solide est un segment de droite.
– Une arête cachée d’un solide est représentée en pointillés.
– Une face d’un solide est un polygone qui se note par ses sommets.
3. Dans chaque polyèdre, colorie une base en vert, une face latérale en bleu, un sommet en jaune et une hauteur en rouge. (Attention de ne pas superposer les couleurs !)
Base visible
Faces latérales visibles
Hauteur
4. Complète le tableau du dénombrement dans le prisme droit.
Nombre de côtés de la base
Nombre de sommets Nombre d’arêtes
Nombre de faces Prisme droit dont la base a n côtés
ÉditionsVANIN
SOLIDES 107
n n . 2 = 2nn . 3 =
+ 2 3 6 9 5
3nn
3.2 Les solides et les perspectives
P Les arêtes horizontales sont parallèles.
P Les arêtes verticales sont parallèles.
P Les arêtes obliques sont parallèles.
P La longueur est conservée pour les arêtes de la face avant et de la face arrière.
P La perpendicularité des arêtes est conser vée dans la face avant et dans la face arrière.
P Les arêtes horizontales sont parallèles.
P Les arêtes verticales sont parallèles.
P La longueur est conservée pour les arêtes de la face avant.
P La perpendicularité des arêtes est conser vée dans la face avant et dans la face arrière.
P Les arêtes verticales sont parallèles.
P Seule la longueur est conser vée pour l’arête avant de la face avant.
Perspective cavalière
Perspective avec un point de fuite
1. À l’aide de la synthèse, détermine la perspective.
ÉditionsVANIN
Perspective avec deux points de fuite
SOLIDES 108
1
4 5 6
2 3
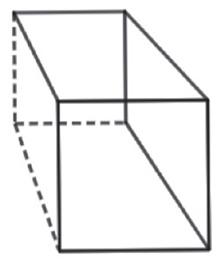
2. Trace les arêtes cachées en pointillés.
3. Achève les cubes et les parallélépipèdes rectangles dont certaines arêtes sont tracées.
4. Achève les cubes et les parallélépipèdes rectangles dont certaines arêtes sont tracées.
a) Construis un cube de 3 cm d’arête dont l’angle de fuite est de 30° et le rapport de la fuyante est de 2/3.
Astuce
Pour construire un cube ou un parallélépipède rectangle en perspective cavalière, il faut : ① tracer la face avant d’un carré ou d’un rectangle ; ② construire l’angle de fuite ; ③ tracer les 4 fuyantes en utilisant le rapport donné ; ④ relier pour faire apparaître la face arrière.
ÉditionsVANIN
b) Construis un cube de 2 cm d’arête dont l’angle de fuite est de 45° et le rapport de la fuyante est de 1/2.
SOLIDES 109
3.3 Les solides et leurs vues
Les vues coordonnées représentent les objets en se positionnant à trois endroits différents :
– vue de face ;
– vue de côté ;
– vue du dessus.
En t’aidant de la synthèse, détermine la vue pour chaque groupe de solides.
Vue du dessus
Groupe 1
ÉditionsVANIN
Vue
Groupe 2
Groupe 3
SOLIDES 110
du bas
Vue de droite
3.4 Les solides et leurs développements
Le développement d’un solide (patron) est une figure plane qui permet de construire ce solide après l’avoir pliée.
1. Relie chaque solide à son développement.
ÉditionsVANIN
SOLIDES 111
Solide Développement • • • • • • • • • • • • • • • •
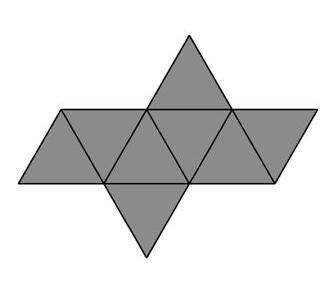
2. Barre les mauvais développements du cube.
3. Colorie la face bleue dans chaque développement du cube.
4. Reproduis le tracé sur chaque développement du cube en respectant les traits pleins et les pointillés.
5. Replace les lettres sur chaque développement du cube.
SOLIDES 112
A B C G H E D F A B C G H E D F A E H D B E F H G C C B E A ADH G CB E F D A C B H G D D AB C A B C
ÉditionsVANIN
3.5 Les positions relatives dans les solides
Y a-t-il un point ou une face d’intersection ?
Oui Non
L’angle formé par les deux arêtes ou les deux faces est-il de 90° ?
Les arêtes ou les faces sont-elles parallèles ? Oui Non Oui Non
Les deux arêtes ou les deux faces sont perpendiculaires. �
Les deux arêtes ou les deux faces sont sécantes. //
1. Complète les phrases.
Les sommets du cube sont A,
Les arêtes du cube sont [AB],
Les faces du cube sont ABCD,
Les deux arêtes ou les deux faces sont parallèles.
Les deux arêtes ou les deux faces sont gauches. g
SOLIDES 113
//
A B C G H E D F
ÉditionsVANIN
2. À partir du prisme droit ci-dessous, complète les pointillés par « parallèle », « perpendiculaire », « sécante » ou « gauche ».
AC est à MN.
LKJI est à LMNK.
AB est à EH.
BF est à FG.
3. Réponds par oui ou non aux questions relatives au prisme droit donné.
ÉditionsVANIN
a) Les faces CDJI et AFLG sont-elles parallèles ?
b) Les faces BCIH et HJKLG sont-elles sécantes ?
c) Les faces ABHG et FAGL sont-elles sécantes ?
d) Les faces AFEDCB et FEKL sont-elles perpendiculaires ?
e) Les arêtes [AB] et [ED] sont-elles perpendiculaires ?
f) Les arêtes [BH] et [CI] sont-elles sécantes ?
g) Les arêtes [CD] et [AG] sont-elles gauches ?
h) Les arêtes [HI] et [BH] sont-elles perpendiculaires ?
SOLIDES 114
A M N B L K G F I J H E C D A B I FE D G H C L K J
4. Complète les pointillés par le symbole //, //, � ou g.
a)
EF HG
EH DC
AD FG
BC FB
BC EF
ÉditionsVANIN
b)
EHGF ADCB
EHGF HGCD
DCBA FGCB
EHDA FGCB
EHDA EFBA
HG FGCB
AD EHGF
BC EFBA
HD ADCB
EF HGCD
SOLIDES 115
IJKLMN PQRSTO IJQP JKRQ LSTM IJQP IJKLMN KRSL JQ IJKLM IN PQRSTO IN QRSTOP ML KRSL IJ JK KR KL JQ ML IP MT ML LS QR IJ MN NO JK QR IJ MN IJ RS A B C G H E D F Q R J S T I N M P O K L
Jeu de cubes – Détermine le nombre de cubes qui composent la figure.
ÉditionsVANIN
SOLIDES 116