Racine Math - Livre-cahier 4e année - Trigonométrie/Géométrie

RACINE MATH GÉOMÉTRIE TRIGONOMÉTRIE

ÉditionsVANIN

LIVRE-CAHIER

TRIGONOMÉTRIE ÉditionsVANIN

RACINE MATH

GÉOMÉTRIE

Anne-Laure Andrieu

Justine Bellistrì

Marie-Noëlle Herkens

Anne-France Mauclet

Pauline Pirenne

Pierre Scourneau

RACINE MATH 4 – Livre-cahier : Géométrie – Trigonométrie

Composition de Racine Math 4

Pour l’élève

– 2 livres-cahiers

– des exercices numériques via Pour l’enseignant(e)

– un guide pédagogique

– un accès professeur via au manuel numérique, aux compléments et aux exercices numériques

Auteur(e)s : Anne-Laure Andrieu, Justine Bellistrì, Marie-Noëlle Herkens, Anne-France Mauclet, Pauline Pirenne, Pierre Scourneau

Couverture : Nord Compo

Mise en page : Nord Compo

Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent.

La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages.

En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes.

Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due.

C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.

L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si, malgré cela, quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.

ÉditionsVANIN

© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2024

Tous droits réservés.

En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.

1re édition : 2024

ISBN 978-94-647-0668-0

D/2024/0078/183

Art. 606698/01

INTRODUCTION

Bienvenue dans Racine Math 4.

Pour utiliser au mieux le potentiel de ce livre-cahier, voici quelques informations sur sa structure et sur les compléments numériques qui l’accompagnent.

Les différentes UAA (Unités d’Acquis d’Apprentissage) sont réparties dans deux livres-cahiers : – Analyse et statistique ; – Géométrie et trigonométrie.

Prérequis

Certaines UAA sont introduites par une partie « Prérequis » afin de rappeler les notions nécessaires à la découverte de la matière.

Introduction historique

Introduction historique

Afin de donner du sens à l’apprentissage, chaque UAA commence par une mise en contexte historique de la matière et par des exemples de son application dans le quotidien.

Toujours dans l’idée d’ancrer les concepts mathématiques dans la réalité, un défi t’est proposé à la fin de cette introduction. Avec tout ce que tu auras appris dans le chapitre, tu seras en mesure de le résoudre.

Découverte

La matière de chaque UAA est divisée en plusieurs parties cohérentes et structurées afin de garantir un apprentissage progressif et clair. Tu es ainsi invité(e) à découvrir la nouvelle matière de chaque partie via des activités, à la fin desquelles la rubrique πG résume ce qui a été découvert.

Théorie

La partie « Théorie » reprend les notions essentielles à la compréhension de la matière. Celles-ci sont classées dans différentes rubriques :

Exercices

Les exercices permettent d’appliquer la théorie vue.

Des exercices dits de « dépassement » sont parfois proposés et sont reconnaissables à ce logo :

1.

trigonométrique et angles orientés

Synthèse – Exercices récapitulatifs

Chaque chapitre se conclut avec une synthèse claire et précise. Celle-ci est suivie d’exercices récapitulatifs qui te permettent de retravailler de façon transversale toutes les notions vues.

GeoGebra

La visualisation de certaines notions et concepts mathématiques est rendue possible grâce à l’utilisation de l’application GeoGebra. Soit via des manipulations, soit via des vidéos, tu es invité(e) à découvrir une notion ou comprendre la construction d’un schéma. Les GeoGebra sont proposés via des codes QR mais sont également disponibles sur la plateforme numérique iDiddit.

iDiddit

La plateforme numérique de Van In – iDiddit – met à ta disposition du matériel complémentaire à utiliser en parallèle du livre-cahier Racine Math 4. Si tu souhaites t’entraîner, tu retrouveras ainsi sur iDiddit des exercices interactifs complémentaires accompagnés d’un rappel de la théorie.

Les modalités de connexion à la plateforme te sont expliquées dans le livre-cahier « Analyse –Statistique ».

ÉditionsVANIN

ÉditionsVANIN

GÉOMÉTRIE DANS L’ESPACE

Objectifs

Connaître

• Repérer les positions relatives de deux droites, de deux plans, d’une droite et d’un plan.

ÉditionsVANIN

Appliquer

• Représenter dans un plan un objet de l’espace.

• Construire un point de percée.

• Construire une section plane.

Transférer

• Justifier la construction d’un point de percée, d’une section plane.

• Vérifier la coplanarité de points, de droites.

• Construire l’ombre d’un objet.

• Interpréter une représentation plane d’un objet de l’espace.

Introduction historique

L’art de représenter des objets ou des espaces en trois dimensions sur une surface à deux dimensions s’appelle l’art de la perspective.

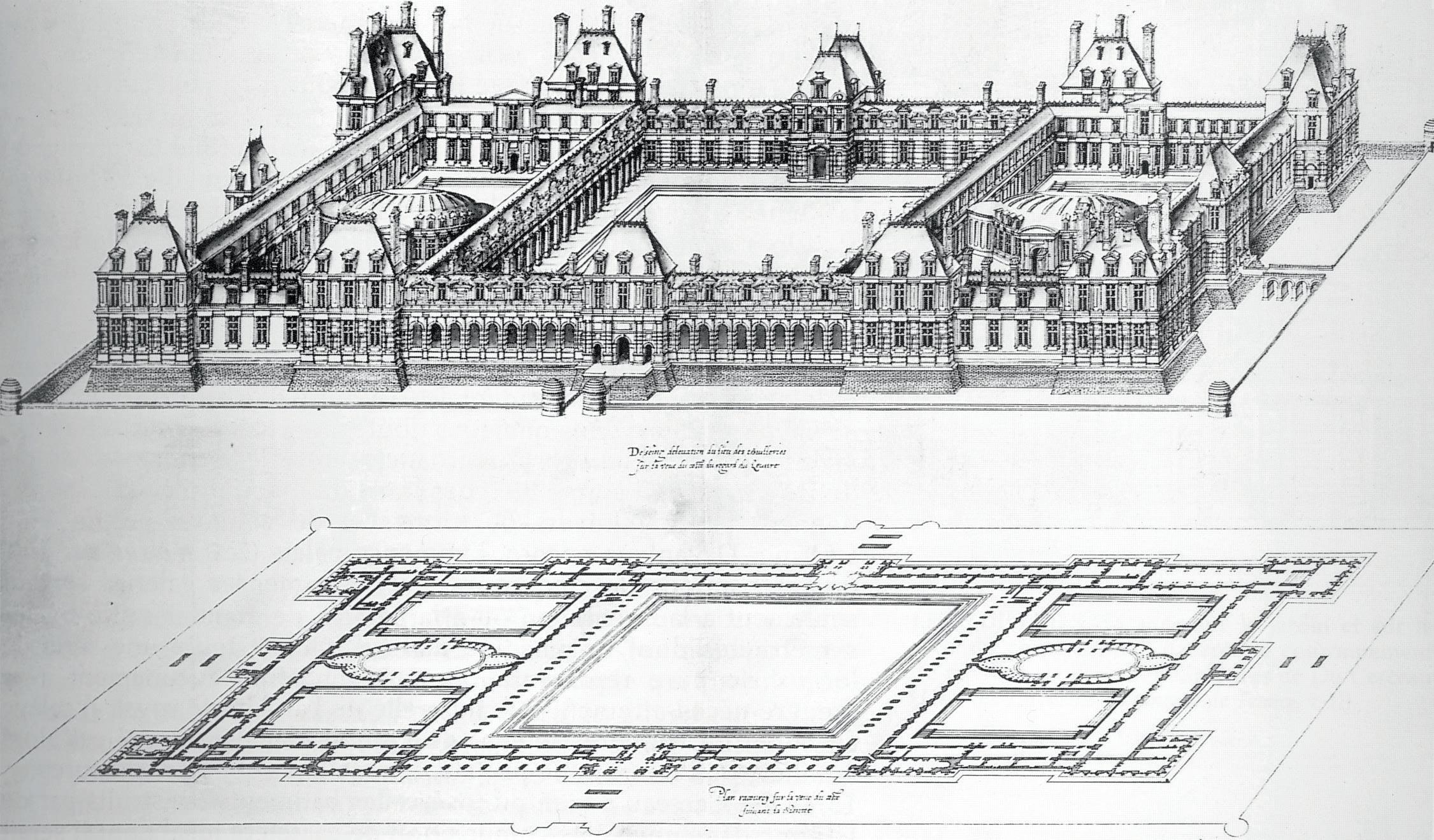
Avant la Renaissance, dans le domaine artistique, on ne se souciait pas de représenter la réalité de l’espace, et la perspective utilisée était la perspective cavalière

Au XVe siècle, les artistes et les architectes de la Renaissance se penchent sur une méthode de représentation plus réaliste : la perspective centrale (ou perspective avec point(s) de fuite).

Aujourd’hui, lorsqu’il s’agit de réaménager l’intérieur de notre maison, nous faisons appel à des entreprises spécialisées qui, la plupart du temps, commencent par proposer une visualisation du projet en trois dimensions.

ÉditionsVANIN

De plus, on ne se contente plus de représenter les objets sur une surface à deux dimensions. Les nouvelles technologies utilisent très fréquemment les impressions en 3D. Elles permettent par exemple de créer des pièces qui seront utilisées dans le domaine de la santé : des prothèses à des prix raisonnables, des implants dentaires ou autres (des côtes par exemple). La recherche s’axe même aujourd’hui sur des cœurs artificiels.

Mais comment en arrive-t-on à représenter sur une feuille de papier ou un écran (c’est-à-dire en deux dimensions) un objet ou un espace qui, lui, est en trois dimensions ? C’est un des enjeux de la géométrie dans l’espace.

L’objectif de ce chapitre sera de représenter des objets de l’espace tels que des solides et d’en étudier les propriétés.

Défi

Pour son anniversaire, Sofiane s’est rendu sur le site des pyramides de Gizeh et a pu les observer depuis une montgolfière. Il a pris une superbe photo des monuments et aimerait les reproduire en dessin avec leur ombre, mais il ne sait pas comment s’y prendre.

À la fin du chapitre, tu seras capable d’aider Sofiane à compléter son dessin.

Détail de la carte de la chartreuse de Sélignac, Raquelli, 1784

Vedutta di citta ideale, Francesco di Giorgio Martini, 1477

1. Représentation d’un objet dans l’espace

DÉCOUVERTE

Activité Les différents types de représentations

On peut représenter un objet de l’espace sur une surface à deux dimensions de différentes manières. Une maison, par exemple, peut avoir différentes représentations.

Forme développée Perspective cavalièrePerspective centrale

Vues coordonnées

1. Parmi ces quatre types de représentations, deux sont plus intéressantes pour visualiser rapidement l’objet en trois dimensions. Lesquelles ?

ÉditionsVANIN

2. Sur les représentations sélectionnées, prolonge les arêtes latérales. Quelle différence notes-tu ? πG

Pour représenter des objets en trois dimensions sur une surface à deux dimensions, nous utilisons les perspectives centrale et cavalière.

3. Voici un même cube représenté en perspective cavalière et en perspective centrale.

Représentation d’un cube en perspective cavalière

Représentation d’un cube en perspective centrale

Coche en fonction des caractéristiques correspondant à la perspective utilisée.

Perspective cavalière Perspective centrale

Deux droites sécantes dans la réalité sont représentées par deux droites sécantes.

Deux droites parallèles dans la réalité sont représentées par deux droites parallèles.

Deux droites perpendiculaires dans la réalité sont représentées par deux droites perpendiculaires.

Deux segments de même longueur dans la réalité sont représentés avec la même longueur.

πG

 Oui  Non  Oui  Non

 Oui  Non  Oui  Non

 Oui  Non  Oui  Non

 Oui  Non  Oui  Non

La perspective qui conserve le plus de propriétés de géométrie plane (comme le parallélisme des droites) est la perspective cavalière. C’est celle que nous utiliserons dans la suite du chapitre.

THÉORIE

Définition

ÉditionsVANIN

Représentation en perspective cavalière

Lorsqu’un objet est représenté en perspective cavalière :

– les éléments présents sur un plan frontal (défini plus loin) sont représentés sans déformation ;

– les perpendiculaires aux plans frontaux sont parallèles entre elles selon une direction préalablement choisie.

Exemple

Voici un cube et une pyramide à base rectangle représentés en perspective cavalière.

Remarque

Par convention, les lignes vues par l’observateur sont représentées en traits pleins et les lignes cachées en traits pointillés.

Vocabulaire

– Plan frontal : tout plan vu de face. Tout élément situé dans un plan frontal est représenté dans sa forme réelle : les angles ont leurs valeurs réelles et les longueurs sont représentées à l’échelle.

– Fuyante : toute droite perpendiculaire aux plans frontaux.

– Angle de fuite : l’angle α que forment toutes les lignes de fuite avec l’horizon du plan frontal.

– Coefficient de fuite : le nombre k par lequel les dimensions réelles des segments des fuyantes sont multipliées pour obtenir leurs dimensions sur le dessin.

On parle de représentation en perspective cavalière (α; k).

Pour le cube représenté ci-dessous, voici :

ÉditionsVANIN

Les plans frontaux

Les fuyantes

Exemple

Ci-dessous sont représentés un cube d’arête 3 cm en perspective cavalière (30°; 0,5) et un cube d’arête

Remarque

Un cube peut être représenté en perspective cavalière selon différents points de vue.

EXERCICES

1. Pour chaque représentation, détermine le type de perspective utilisé.

ÉditionsVANIN

2. Complète les dessins suivants afin qu’ils représentent des prismes droits en perspective cavalière.

3. Considérons le parallélépipède rectangle ABCDEFGH représenté ci-dessous en perspective cavalière de coefficient de fuite 0,8.

ÉditionsVANIN

(a) Donne la longueur de [AB] dans la réalité.

(b) Donne la longueur de [DH] dans la réalité.

(c) Donne la longueur de [FG] dans la réalité.

(d) L’angle de fuite a une amplitude de

(e) Dans la réalité, l’angle ADH  mesure

4. Sur le quadrillage ci-dessous où les points A et M sont placés,

(a) représente en perspective cavalière (20°; 0,6) un parallélépipède rectangle ABCDEFGH tel que :

• |AB| = 5 cm, |AD| = 3 cm et |AE| = 4 cm ;

• la face ABCD étant la face frontale avant.

(b) représente en perspective cavalière (30°; 0,5) une pyramide à base carrée SMNOP sachant que :

• chaque côté de la base MNOP mesure 3 cm ;

• |SO| = 4 cm ;

• SO est perpendiculaire au plan MNOP

ÉditionsVANIN

5. Le développement d’un prisme droit est donné à gauche. Représente ce prisme en perspective cavalière (30°; 0,75) à droite sachant que la face frontale avant est déjà représentée en bleu.

6. Construis un parallélépipède rectangle à l’aide de GeoGebra 3D dont la longueur vaut 5 unités, la largeur en vaut 3 et la hauteur en vaut 2.

7. Construis un cube en perspective cavalière (30°; 0,75) à l’aide de GeoGebra 2D.

2. Caractérisation d’une droite et d’un plan

DÉCOUVERTE 1

Activité Construction d’un cube

La vidéo suivante te montre comment construire un cube en trois dimensions, de manière à visualiser plus facilement les différents concepts présentés dans la suite du chapitre.

THÉORIE

La caractérisation des objets dans l’espace se base sur plusieurs axiomes. Tu as peut-être déjà rencontré ce terme, voici sa définition.

Définitions

Axiome et axiome d’incidence

Un axiome est une propriété admise sans démonstration.

Les axiomes représentent le fondement d’une théorie mathématique.

ÉditionsVANIN

Les axiomes d’incidence de la géométrie dans l’espace sont des axiomes qui fournissent des relations entre les points, les droites et les plans de l’espace.

Remarque

Conventions d’écriture

• Les points seront notés par des lettres majuscules.

• Les droites seront notées par des lettres minuscules (ou deux lettres majuscules).

• Les plans seront notés par des lettres grecques minuscules (ou trois lettres majuscules).

Vidéo

Propriétés

Axiomes d’incidences

• Deux points distincts de l’espace déterminent une et une seule droite.

Exemple : les points D et G déterminent la droite DG.

• Trois points distincts non alignés de l’espace déterminent un et un seul plan.

Exemple : les points D, C et G déterminent le plan DCG, qui peut aussi être noté DHG, HGC ou CDH.

• Si un plan contient deux points distincts, il contient la droite que les points déterminent.

Exemple : la droite DG est entièrement contenue dans le plan DCG. On notera DG ⊂ DCG.

ÉditionsVANIN

Propriété

Axiome d’Euclide

Si d est une droite et A un point ne lui appartenant pas, alors il existe une et une seule droite d′ parallèle à d, passant par le point A.

DÉCOUVERTE 2

Activité Caractérisation d’un plan

Le deuxième axiome d’incidence a fourni une manière de caractériser un plan : à l’aide de trois points non alignés.

Voici trois points X, Y et Z et le plan α qu’ils caractérisent représentés ci-dessous.

ÉditionsVANIN

1. Garde un point fixe.

(a) Quel objet mathématique pourrais-tu construire à l’aide des deux points restants ?

(b) Trace ta réponse sur le schéma ci-dessus.

2. On peut également tracer deux droites en exploitant ces trois points.

(a) Quelles positions pourraient avoir ces droites pour toujours caractériser le plan ?

(b) Représente chaque possibilité sur les schémas ci-dessous.

Z Y X

Z Y X

πG

ÉditionsVANIN

Tu viens de découvrir qu’un plan peut être entièrement défini de quatre manières différentes.

THÉORIE

Propriété

Un plan est entièrement déterminé par :

• trois points distincts non alignés ;

• une droite et un point ne lui appartenant pas ;

• deux droites parallèles distinctes ;

• deux droites sécantes.

Exemple

Le plan XYZ peut être défini par :

ÉditionsVANIN

les points X, Y et Z

la droite YZ et la droite qui lui est parallèle passant par X

les droites sécantes YZ et XZ.

EXERCICES

1. Soient les prismes droits à base hexagonale représentés ci-dessous.

(a) Les objets suivants permettent-ils de définir un plan ? Justifie.

I. Les points E, D et J  Oui –  Non

Justification :

II. La droite LK et le point R.  Oui –  Non

Justification :

III. Les droites DJ et PJ  Oui –  Non

Justification :

IV. Les droites AG et HN.  Oui –  Non

Justification :

(b) Définis d’une autre manière le plan ABC

2. Considérons les parallélépipèdes rectangles représentés ci-dessous. Pour chaque droite et plan définis ci-dessous, donne tous les points nommés sur le schéma qui lui appartiennent.

(a) La droite AB :

(b) La droite UW : �

(c) La droite VH :

(d) Le plan QRO :

(e) Le plan ALI :

(f) Le plan GLU :

3. Positions relatives des droites et des plans

DÉCOUVERTE

Activité Les différentes positions relatives de droites et de plans

À partir du cube représenté ci-dessous et en utilisant le cube construit dans l’activité page 17, découvre quelles sont les différentes positions relatives de deux droites, de deux plans et d’une droite par rapport à un plan.

1. Afin d’identifier les positions relatives de deux plans, coche la position des plans suivants l’un par rapport à l’autre.

(a) Les plans CDH et BCE sont :  parallèles confondus  parallèles distincts  sécants

(c) Les plans EFH et GEH sont :  parallèles confondus  parallèles distincts  sécants

(b) Les plans DAE et BCF sont :  parallèles confondus

 parallèles distincts  sécants

2. Afin d’identifier les positions relatives de deux droites, coche la position des droites suivantes l’une par rapport à l’autre.

ÉditionsVANIN

(a) Les droites AE et HE :  sont parallèles distinctes

 sont sécantes

 ne sont pas dans un même plan

(c) Les droites HG et BF :

 sont parallèles distinctes

 sont sécantes

 ne sont pas dans un même plan

(b) Les droites BC et HE :

 sont parallèles distinctes

 sont sécantes

 ne sont pas dans un même plan

Tu viens de découvrir que deux droites représentées en trois dimensions peuvent ne pas être incluses dans un même plan, on dit alors qu’elles sont non coplanaires.

Deux droites non coplanaires sont appelées des droites gauches.

3. Afin d’identifier les positions relatives d’une droite et d’un plan, coche la partie de phrase manquante afin que l’affirmation soit vraie.

(a) La droite DG est … ABC.  sécante au plan

 parallèle distincte au plan

 incluse dans le plan

(c) La droite EG est … FGH.

 sécante au plan

 parallèle distincte au plan

 incluse dans le plan

THÉORIE

Propriété πG

Positions relatives de deux plans

Plans sécants

(b) La droite CF est … ADE.  sécante au plan

 parallèle distincte au plan

 incluse dans le plan

L’intersection est une droite

Plans parallèles

Plans parallèles distinctsPlans parallèles confondus

Propriété

Positions relatives d’une droite et d’un plan

Droite parallèle au plan

Droite sécante au plan

Droite parallèle distincte au planDroite incluse dans le plan α

La droite perce le plan au point P

Propriété

d ∩ α = ∅ L’intersection est vide d ∩ α = d L’intersection est la droite elle-même

Positions relatives de deux droites

Droites coplanaires

Droites parallèles

Droites sécantes

ÉditionsVANIN

L’intersection est un point

Droites parallèles distinctes

Droites parallèles confondues

d ∩ d′ = ∅

L’intersection est vide

d ∩ d′ = d = d′

L’intersection est la droite elle-même

Droites non coplanaires

Droites gauches

d ∩ d′ = ∅

L’intersection est vide

EXERCICES

1. Dans le prisme droit à base triangulaire MNOPQR, donne :

(a) deux droites parallèles :

(b) deux plans parallèles :

(c) deux droites gauches :

(d) une droite et un plan sécants :

(e) deux droites sécantes :

(f) deux plans sécants :

2. Sachant que sur chaque cube, les points S, T, O et P appartiennent à une des arêtes, détermine si les droites ST et OP sont sécantes ou gauches. Tu peux t’aider de ton cube construit à l’activité de la page 17.

3. Soient les cubes ABCDJINK, DCFEKNML et HADGOJKP représentés ci-dessous.

(a) Détermine les positions relatives des droites et plans suivants. Précise quelle est l’intersection lorsque les objets sont sécants.

• Les droites AB et KN :

• Les droites IM et CN :

• Les droites HA et BA :

• Les droites HO et CB :

• Les plans IJK et OPK :

• Les plans DEC et GKN :

• Les plans HOP et DJL :

• La droite LE et le plan AJK :

• La droite OK et le plan BIN :

(b) Détermine l’intersection des droites et plans suivants.

• MO ∩ EK =

• AJD ∩ KLE =

• DF ∩ BO =

• BIL ∩ AD =

• JKN ∩ LM =

• IL ∩ CFM =

• CN ∩ JA =

• EFM ∩ HAD =

• HD ∩ ICN =

• GDK ∩ BIC =

• JN ∩ LN =

• HOF ∩ ELP =

4. Points de percée

Imagine une flèche qui traverse une cible. Le plan formé par la cible est percé par une droite formée par la pointe de la flèche. Le point d’intersection entre la cible et la pointe de la flèche est appelé point de percée

Définition

Point de percée

Le point de percée P d’une droite d dans un plan α est le point d’intersection de d et de α. On notera d ∩ α = {P}.

DÉCOUVERTE 1

Activité Points de percée obtenus par constructions immédiates

1. Considérons les points X ∈ AE et Y ∈ EF. Construis, si possible, le point de percée de la droite XY dans les plans α suivants :

(a) si α = BCG. Explique ton raisonnement.

(b) si α = ABC. Explique ton raisonnement.

(c) si α = DCH. Explique ton raisonnement.

Le point de percée d’une droite dans un plan n’existe que si la droite n’est pas parallèle au plan.

2. Dans l’animation GeoGebra suivante, considérons :

• le plan α = DCG ;

• la droite d = XY telle que X ∈ AB et Y ∈ BC ;

• un plan β qui contient la droite XY et le point Z ;

• la droite d′, l’intersection des plans α et β ;

• le point P, l’intersection des droites d et d′ .

(a) Fais varier la position du plan β, que nous nommerons plan auxiliaire, en bougeant le point Z Est-ce que le point P change de position ?

(b) Le point P étant le point de percée de d dans α, que peux-tu en conclure ? Dépend-il du plan auxiliaire β ?

THÉORIE

Méthodo

Construction d’un point de percée par constructions immédiates

Pour déterminer le point de percée P d’une droite d dans un plan α où d ∦ α :

1. on détermine un plan auxiliaire β, non parallèle à α, contenant la droite d ;

2. on détermine la droite d′, l’intersection des plans α et β (α ∩ β = d′) ;

3. d ∩ α = d ∩ d′ = {P}.

Remarque

ÉditionsVANIN

Le point de percée P se trouve bien à l’intersection de d et d′ car, comme d et d′ sont incluses toutes deux dans le plan β, ces deux droites sont bien sécantes. De plus, d′ étant également incluse dans le plan α, le point d’intersection de d et d′ appartient bien à α.

Vidéo

GeoGebra

EXERCICE

Dans chaque solide, construis le point de percée de la droite d dans le plan α Justifie ta construction.

(a) d = IJ et α = ADC sachant que I ∈ HE et J ∈ AE

(b) d = MN et α = ABD sachant que M ∈ BC et N ∈ AC

(c) d = QR et α = DGH sachant que Q ∈ BC et R ∈ BF.

DÉCOUVERTE 2

Activité Constructions de points de percée exploitant le théorème du toit

Dans l’animation GeoGebra suivante, considérons :

• la droite d = XY telle que X ∈ ABF et Y ∈ BCF ;

• un plan β qui contient la droite XY et le point Z.

1. Fais varier la position du plan β en bougeant le point Z. Comment est le plan β par rapport à la droite BF ?

2. Quelle est la particularité de la droite BF par rapport aux plans ABF et BCF ?

3. Comment pourrions-nous définir un plan auxiliaire β qui contient la droite XY ?

πG

Tu viens de découvrir le théorème du toit.

ÉditionsVANIN

4. En appliquant ce que tu viens de découvrir aux points précédents pour trouver un plan auxiliaire, construis le point de percée de la droite d = XY dans le plan α = EFG sachant que X ∈ ABF et Y ∈ BCF. Justifie ta construction.

THÉORIE

Théorème

Théorème du toit

Soient α1 et α2 deux plans sécants suivant une droite d et soient d1 et d2 deux droites incluses respectivement dans les plans α1 et α2.

• Si d1 et d2 sont parallèles, alors elles sont parallèles à d.

• Si d1 et d2 sont sécantes, alors leur point d’intersection appartient à d.

Méthodo

Construction d’un plan à l’aide du théorème du toit

Pour construire un plan passant par deux points A et B appartenant respectivement à deux plans sécants α et β :

1. on identifie la droite d, intersection des plans α et β ;

2. on trace deux droites d1 et d2 passant respectivement par A et par B qui sont soit parallèles à d, soit sécantes à d en un même point.

Un plan passant par A et B est alors le plan formé par les droites d1 et d2.

ÉditionsVANIN

Méthodo

Construction d’un point de percée à l’aide du théorème du toit

Pour déterminer le point de percée P d’une droite d dans un plan α où d ∦ α dans cette situation :

1. on construit un plan auxiliaire β, non parallèle à α, contenant la droite d grâce au théorème du toit ;

2. on détermine la droite d′, l’intersection des plans α et β (α ∩ β = d′) ;

3. d ∩ α = d ∩ d′ = {P}.

Vidéo

EXERCICE

Dans chaque solide, construis le point de percée de la droite d dans le plan α Justifie ta construction.

(a) d = WV et α = CGH sachant que W ∈ BFG et V ∈ EFG

(b) d = LS et α = ABD sachant que L ∈ ABC et S ∈ ACD.

(c) d = YZ et α = ABC sachant que Y ∈ ADS et Z ∈ BCS

DÉCOUVERTE 3

Activité Constructions de points de percée exploitant le parallélisme des faces

Dans l’animation GeoGebra suivante, considérons :

• la droite d = XY telle que X ∈ ADH et Y ∈ BCG ;

• un plan β qui contient la droite XY et le point Z.

1. Quelle est la position relative des plans ADH et BCG ?

2. Fais varier la position du plan β en bougeant le point Z. Quelle est la position relative de la droite d’intersection de β et ADH et de la droite d’intersection de β et BCG ?

ÉditionsVANIN

πG

Tu viens de découvrir que si un plan intersecte deux plans parallèles, alors les droites d’intersection entre les plans ainsi formées sont parallèles.

GeoGebra

3. En appliquant ce que tu viens de découvrir aux points précédents pour trouver un plan auxiliaire, construis le point de percée de la droite d = XY dans le plan α = EFG sachant que X ∈ ADH et Y ∈ BCG. Justifie ta construction.

THÉORIE

Plan sécant à deux plans parallèles

Si deux plans sont parallèles, alors tout plan sécant à l’un est sécant à l’autre et leurs intersections sont deux droites parallèles.

Démonstration

Soient deux plans α1 et α2 parallèles et soit β un plan qui est sécant à α1 et à α2.

1er cas : si α1 et α2 sont parallèles confondus

Il est évident que l’intersection entre α1 et β et l’intersection entre α2 et β forment deux droites confondues qui sont donc parallèles entre elles.

2e cas : si α1 et α2 sont parallèles distincts

Nommons d1 la droite d’intersection de α1 et β, et d2 la droite d’intersection de α2 et β

Montrons que ces deux droites ne peuvent être ni gauches ni sécantes :

• elles ne peuvent pas être gauches puisqu’elles sont contenues dans le plan β ;

• elles ne peuvent pas être sécantes puisqu’alors leur point d’intersection appartiendrait à d1 et donc à α1, mais également à d2 et donc à α2. Leur point d’intersection devrait donc appartenir à α1 et à α2, ce qui est impossible car ceux-ci sont parallèles distincts.

Comme elles ne sont ni gauches ni sécantes, d1 et d2 sont bien parallèles.

On a donc bien montré dans les deux cas que les droites sont parallèles.

Méthodo

Construction d’un point de percée en exploitant le parallélisme

Pour déterminer le point de percée P d’une droite d dans un plan α où d ∦ α dans cette situation :

1. on construit un plan auxiliaire β, non parallèle à α, contenant la droite d grâce à la construction de deux droites parallèles ;

2. on détermine la droite d′, l’intersection des plans α et β (α ∩ β = d′) ;

3. d ∩ α = d ∩ d′ = {P}.

EXERCICE

Dans chaque solide, construis le point de percée de la droite d dans le plan α Justifie ta construction.

(a) d = TK et α = EFG sachant que T ∈ DHG et K ∈ AEF

ÉditionsVANIN

Vidéo

(b) d = DE et α = ACC′ sachant que D ∈ ABC et E ∈ A′B′C′

(c) d = TJ et α = AFB sachant que T ∈ BCG et J ∈ ADE

′

5. Sections planes

En observant les différentes images ci-dessous, on remarque que dans chaque cas, un solide est traversé par un plan.

Définition

Une section plane est l’intersection entre un solide et un plan.

DÉCOUVERTE

ÉditionsVANIN

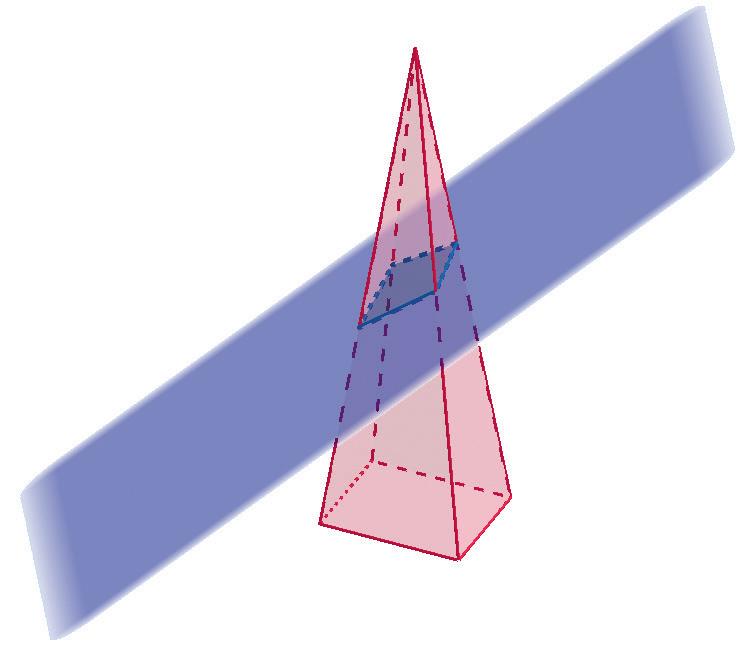
Activité Les propriétés utiles aux constructions de sections planes

L’animation GeoGebra suivante représente un cube et trois points I, J et K qui peuvent être déplacés. En déplaçant les points I, J et K, différentes sections du cube par le plan IJK apparaissent.

Quelles sont les différentes figures qui peuvent être obtenues ? GeoGebra

Remarque

Nous exploiterons à nouveau plusieurs propriétés vues pour les points de percée :

• si deux points appartiennent à un plan, la droite contenant ces deux points est entièrement contenue dans ce plan ;

• un plan sécant à deux plans parallèles les coupe suivant deux droites parallèles ;

• deux droites sécantes dans des plans sécants se coupent sur la droite d’intersection des deux plans.

THÉORIE

Méthodo

Construction d’une section plane

Pour déterminer la section d’un solide par un plan, nous devons trouver les intersections du plan et des faces du solide. Cela revient à déterminer des intersections du plan et des arêtes du solide.

Remarque

Pour faciliter la lecture des justifications, nous entourerons dans le tableau les points qui appartiennent à une des arêtes du solide considéré.

Exemples

• Construction de la section plane du tétraèdre ABCD par le plan FGH, sachant que F ∈ AD, G ∈ ABC et H ∈ AB.

• Construction de la section plane du cube ABCDEFGH par le plan IJK sachant que I ∈ HG, J ∈ CG et K ∈ AE.

Plan formant une face

Points lui appartenant

Segment obtenu

ABCBFGFEHEADABF DCG

J, W IK, V K, W I, J, V

[JW] [KV][KW][JV]

1. IJ ⊂ DCG, HD ⊂ DCG ⇒ IJ ∩ HD = {V}.

2. Comme DCG || ABF, je trace la droite d parallèle à la droite IJ passant par K.

3. d ⊂ ABF, BF ⊂ ABF ⇒ d ∩ BF = {W}. A

4. La section plane est le quadrilatère VJWK.

• Construction de la section plane du parallélépipède rectangle ABCDEFGH par le plan MNO sachant que M ∈ AD, N ∈ HG et O ∈ EF

Plan formant une face ABCBFGFEHEADABF DCG Points lui appartenant

1. Construis les sections des solides par les plans α. Justifie tes constructions.

(a) α = LMN sachant que L ∈ CD, M ∈ AD et N ∈ DB

(b) α = XYZ sachant que X ∈ HI, Y ∈ BC et Z ∈ JK.

ÉditionsVANIN

(c) α = SOU sachant que S ∈ AK, O ∈ AB et U ∈ MN

(d) α = RST sachant que R ∈ HG, S ∈ DH et T ∈ BF

(e) α = EFG sachant que E ∈ AD, F ∈ BC et G ∈

(f) α = IJK sachant que I ∈ AB, J ∈ EH et K ∈ FG

2. Construis les sections des solides par les plans α

(a) α = IJK sachant que I ∈ AB, J ∈ AD et K ∈ HDC.

(b) α = EFG sachant que E ∈ ABC, F ∈ AB et G ∈ CD.

(c) α = PQR sachant que P ∈ BF, Q ∈ GH et R ∈ DH

ÉditionsVANIN

(d) α = TOM sachant que T ∈ AB, O ∈ BC et M ∈ DC ′D ′

3. Explique pourquoi les polygones bleutés ci-dessous ne sont pas des sections planes du solide dans lequel ils sont représentés.

4. Les points placés sur les arêtes des solides suivants sont-ils coplanaires ? Justifie.

ÉditionsVANIN

5. Construis la section du tétraèdre ABCS par le plan défini par le point Q ∈ ABC et la droite d ⊂ BCS

6. Soit le triangle ABC une section plane du parallélépipède rectangle IJKLMNOP

ÉditionsVANIN

(a) Détermine l’intersection des plans

ABC et MNO. Indique ton raisonnement.

(b) Détermine l’intersection des plans

ABC et LKP. Indique ton raisonnement.

6. Ombres au soleil

DÉCOUVERTE 1

Activité Visualiser l’ombre du soleil à travers une fenêtre

Observons à travers une fenêtre par temps ensoleillé l’ombre formée sur le sol.

On assimilera les rayons du soleil à des droites parallèles vu la distance Terre-Soleil.

Rayonsdusoleil

Quelles sont les caractéristiques de cette construction ?

• L’ombre d’un segment est .

• Des segments parallèles ont pour ombre

Conséquence :

ÉditionsVANIN

L’ombre d’un parallélogramme est

On parle dans ce cas de projection parallèle.

DÉCOUVERTE 2

Activité Ombre d’un cube

On donne :

• le cube représenté ci-dessous

• le poteau [IJ] et son ombre au sol

L’objectif est de représenter l’ombre du cube au sol sur le schéma ci-dessus.

Pour cela :

1. Trace l’ombre au sol de chaque arête verticale du cube en utilisant les propriétés de parallélisme comme illustré ci-dessous pour le segment [BE] grâce à l’ombre de [IJ] qui est [IJ ′].

2. Complète les informations manquantes :

ÉditionsVANIN

• l’ombre de [BE ] est

• l’ombre de [DG] est

• l’ombre de [CF] est

On remarque que l’ombre de [AH] ne sera pas exploitée, car elle se trouve dans le cube.

3. Trace l’ombre du cube en construisant les segments appropriés.

πG

Pour tracer l’ombre d’une figure, on effectue une projection parallèlement à la direction du rayon lumineux sur le plan de projection.

THÉORIE

Définition

Projection parallèle

Soient un plan α et une droite d non parallèle à α.

À tout point M de l’espace, on fait correspondre le point M′ , intersection du plan α et de la droite parallèle à d passant par M.

Cette transformation est appelée projection sur le plan α parallèlement à la droite d

Le plan α est le plan de projection et la direction de d est la direction de la projection.

Méthodo

Construction d’une ombre

Pour représenter l’ombre d’une figure, nous utiliserons les propriétés de parallélisme ou les projections parallèles.

EXERCICES

1. Sachant que l’ombre du segment [AB] est déjà tracée, construis l’ombre du cube.

ÉditionsVANIN

2. Voici l’ombre d’un tétraèdre, représente l’ombre du piquet formé par le segment [AB].

SYNTHÈSE

Perspective cavalière

La perspective utilisée dans ce chapitre est la perspective cavalière Lorsqu’un objet est représenté en perspective cavalière :

• les éléments présents sur un plan frontal sont représentés sans déformation ;

• les perpendiculaires aux plans frontaux sont parallèles entre elles selon une direction préalablement choisie. Si un objet est représenté en perspective cavalière (α ; k), α représente l’angle de fuite et k le coefficient de fuite.

Axiomes

Axiomes d’incidence :

• Deux points distincts de l’espace déterminent une et une seule droite.

• Trois points distincts non alignés de l’espace déterminent un et un seul plan.

• Si un plan contient deux points distincts, il contient la droite que les points déterminent.

Axiome d’Euclide :

Si d est une droite et A un point ne lui appartenant pas, alors il existe une et une seule droite d′ parallèle à d passant par le point A

Caractérisation d’un plan

Un plan est entièrement déterminé par :

• trois points distincts non alignés

Exemple

Les points A, B et C déterminent le plan α. α

• une droite et un point ne lui appartenant pas Exemple

La droite d et le point A déterminent le plan α.

• deux droites parallèles distinctes

Exemple

Les droites d et d’ déterminent le plan α.

α d d′

• deux droites sécantes

Exemple

Les droites d et d’ déterminent le plan α. α d d′

Positions relatives de droites et de plans

Deux plans sont

sécants

L’intersection est une droite.

ÉditionsVANIN

confondus

L’intersection est le plan lui-même. α

parallèles

distincts

L’intersection est vide. α β α

La droite perce le plan.

L’intersection est un point.

α d P

α ∩ d = {P}

α ∩ d = d sécants

Une droite et un plan sont parallèles

La droite est incluse dans le plan.

L’intersection est la droite elle-même.

La droite n’est pas incluse dans le plan.

α d

L’intersection est vide.

non coplanaires

α d

α ∩ d = ∅

L’intersection est vide.

L’intersection est un point. gauches

Deux droites sont coplanaires parallèles

L’intersection est la droite elle-même. sécantes P

confondues d = d’ d ∩ d’ = d = d’

distinctes d

L’intersection est vide.

Propriétés utiles aux constructions de points de percée ou de sections planes

Théorème du toit

Soient α1 et α2 deux plans sécants suivant une droite d et soient d1 et d2 deux droites incluses respectivement dans les plans α1 et α2.

• Si d1 et d2 sont parallèles, alors elles sont parallèles à d.

• Si d1 et d2 sont sécantes, alors leur point d’intersection appartient à d.

Propriété : plan sécant à deux plans parallèles

Si deux plans sont parallèles, alors tout plan sécant à l’un est sécant à l’autre et leurs intersections sont deux droites parallèles.

Points de percée

Le point de percée P d’une droite d dans un plan α est le point d’intersection de d et de α. On notera d ∩ α = {P}.

Méthode de construction d’un point de percée

Pour déterminer le point de percée P d’une droite d dans le plan α :

1. on détermine un plan auxiliaire β, non parallèle à α, contenant la droite d (possiblement en exploitant le théorème du toit ou à l’aide de droites parallèles) ;

2. on détermine la droite d′, l’intersection des plans α et β (α ∩ β = d′) ;

3. d ∩ α = d ∩ d′ = {P}.

Illustrations :

Section plane

Une section plane est l’intersection entre un solide et un plan.

Méthode de construction d’une section plane

Les constructions de sections planes nécessitent de déterminer l’intersection entre le plan considéré et les arêtes du solide considéré. Cela peut demander la construction de droites parallèles ou d’un point de percée.

Illustrations :

ÉditionsVANIN

EXERCICES RÉCAPITULATIFS

1. Représente un cube en perspective cavalière (25°; 0,65) sachant que ses arêtes mesurent 5 cm.

2. Considérons les prismes droits représentés ci-dessous.

Repère les positions relatives des droites et plans suivants.

(a) EJ et GH

(b) OK et IJ

(c) CJ et KQ

(d) MON et QRL

(e) JIS et ABL

(f) CEM et FQG

(g) EO et FHR

(h) HP et ABD

(i) MT et AGT

3. Dans chaque solide, construis le point de percée de la droite d dans le plan α. Justifie ta construction sur une feuille à part.

(a) d = HT et α = ACD sachant que H ∈ BD et T ∈ BC

ÉditionsVANIN

(b) d = YO et α = AEF sachant que Y ∈ CH et O ∈ EH

(c) d = FG et α = CDE sachant que F ∈ BCE et G ∈ ABC

(d) d = WV et α = CFG sachant que W ∈ ABC et V ∈ FGH

(e) d = FM et α = EHC sachant que M ∈ DI

(f) d = MI et α = CGB sachant que M ∈ EFG et I

(g) d = SV et α = BGF sachant que S ∈ AD et V ∈ EF

(h) d = WY et α = BEF sachant que W ∈ EFG et Y ∈ DCG

4. Construis la section de chaque solide par le plan α indiqué. Justifie ta construction sur une feuille à part.

(a) α = OHM sachant que O ∈ AB et M ∈ AD.

(b) α = IJK sachant que I ∈ AB, J ∈ AD et K ∈ AC.

(c) α = PQR sachant que P ∈ AF, Q ∈ BD et R ∈ AB.

(d) α = AXE sachant que A ∈ GH, X ∈ GK et E ∈ FJM.

(e) α = SAM sachant que S ∈ OD, A ∈ OR et M ∈ DU.

(f) α = GSM sachant que G ∈ AB, S ∈ DE et M ∈ EF.

(g) α = LEO sachant que L ∈ WX, E ∈ XZ et O ∈ WYZ

(h) α = TUY sachant que T ∈ CD, U ∈ EFG et Y ∈ BC

5. Explique pourquoi les sections suivantes ne sont pas des sections planes du cube dans lequel elles sont représentées.

6. Montre que le point M appartient au plan ONS sachant que les points M, O, N et S appartiennent chacun à une arête du cube. Justifie ton raisonnement.

ÉditionsVANIN

7. Vérifie si les droites LU et NA sont coplanaires.

DÉFI

8. Te rappelles-tu au début de ce chapitre ? Pour son anniversaire, Sofiane s’est rendu sur le site des pyramides de Gizeh et a pu les observer depuis une montgolfière. Il a pris une superbe photo des monuments et aimerait les reproduire en dessin avec leur ombre, mais il ne sait pas comment s’y prendre. Son papa, bon dessinateur, a déjà reproduit l’ombre de la plus petite pyramide, celle de Mykérinos. À toi de construire l’ombre de la pyramide de Khéphren et celle de la pyramide de Khéops, la plus grande.

ÉditionsVANIN