Carrément Math

Livre-cahier A

4

Julien Deknock

Livre-cahier A

4 Julien Deknock

Composition de Carrément math 4

Pour l’élève : 2 livres-cahiers A et B

Pour l’enseignant : Deux livres de l’enseignant (comprenant le corrigé des livres-cahiers)

Des annexes, des exercices supplémentaires et des évaluations disponibles sur Wazzou

Les manuels numériques (A et B) téléchargeables sur Wazzou

Carrément math 4 – Livre-cahier A

Auteur : Julien Deknock

Illustrations : Achile (Thibaud Lissonnet)

Conception graphique : Octopus Creative Communication

Mise en page : NORDCOMPO

Couverture : Kiv’Là !

L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur. L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée. Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.

Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.

1re édition : 2023

ISBN 978-94-641-7798-5

D/2023/0078/149

Art. 602846/01

Chapitre 1 Les gratte-ciels à travers le monde .................... 5 1. Les nombres jusqu’à 1 000 5 2. Les solides et leurs empreintes 9 3. Les grandeurs de base 11 4. Les nombres jusqu’à 1 000 (suite) 15 5. Les solides et leurs empreintes (suite) 19 6. Lire et interpréter des données 21 7. La table de/par 7 23 Chapitre 2 La journée de Gillian ............................................... 25 1. L’heure de 5 minutes en 5 minutes 26 2. La commutativité 29 3. Le développement du parallélépipède rectangle 31 4. Arrondir et estimer 33 5. Le développement du cube 35 6. L’addtion en calcul écrit 39 7. Calculs de durées 41 8. Le tableau à double entrée 43 Chapitre 3 Un spor t... un terrain ............................................... 45 1. Les longueurs 47 2. L’addition en calcul mental 49 3. La soustraction en calcul mental 51 4. La soustraction en calcul écrit 53 5. Mesurer et tracer des segments en cm et en mm 55 6. Les visions de l’espace 57 7. Comprendre un problème 59 Chapitre 4 À la montagne .......................................................... 63 1. Lire, classer et dénombrer 64 2. La table de/par 8 69 3. Droite et segment de droite 71 4. Fractions de formes et de segments 73 5. L’euro 77 6. Rendre la monnaie 79

Table des matières

Chapitre 5 La ferme de grand-père ........................................ 81 1. Notion de périmètre ...................................................................................... 83 2. Les capacités ................................................................................................ 87 3. Lire et écrire des nombres jusqu’à 100 000 .................................................. 91 4. Multiplier par 2, 4 et 8 ................................................................................... 93 5. Les droites sécantes, perpendiculaires et parallèles .................................... 97 6. Représenter et reconnaitre des fractions ...................................................... 99 Chapitre 6 Les cookies d’Haly ................................................ 101 1. Les masses : kg, g et mg ............................................................................ 101 2. Les fractions équivalentes .......................................................................... 107 3. Les angles dans et en dehors des polygones ............................................. 113 4. Lecture de diagrammes ............................................................................... 117 Chapitre 7 Mathémartiste ....................................................... 119 1. Le carré, le losange, le rectangle et le parallélogramme 119 2. Tracer des droites perpendiculaires 123 3. La table de/par 9 127 4. Glisser, retourner et pivoter 129 5. Multiplication à 1 chiffre en calcul écrit 133 6. Addition par décomposition 137 7. Soustraction par décomposition 139 8. Périmètre du carré et du rectangle 141 Chapitre 8 Le système solaire ................................................ 147 1. Je joue avec les nombres 147 2. Tables de/par 7, 8 et 9 149 3. Multiplier et diviser par 10, 100 et 1 000 151 4. Multiplier par 5, 50 et 500 154 5. Construction de droites parallèles 157 6. Construire des parallélogrammes sur papier quadrillé 161 7. Le calendrier 165 8. L’arbre dichotomique 169 4 N-O Nombres et opérations SF Solides et figures G Grandeurs TD Traitement de données Exercice supplémentaire (facultatif)

Chapitre

Les gratte-ciels à travers le monde

1. Les nombres jusqu’à 1 000

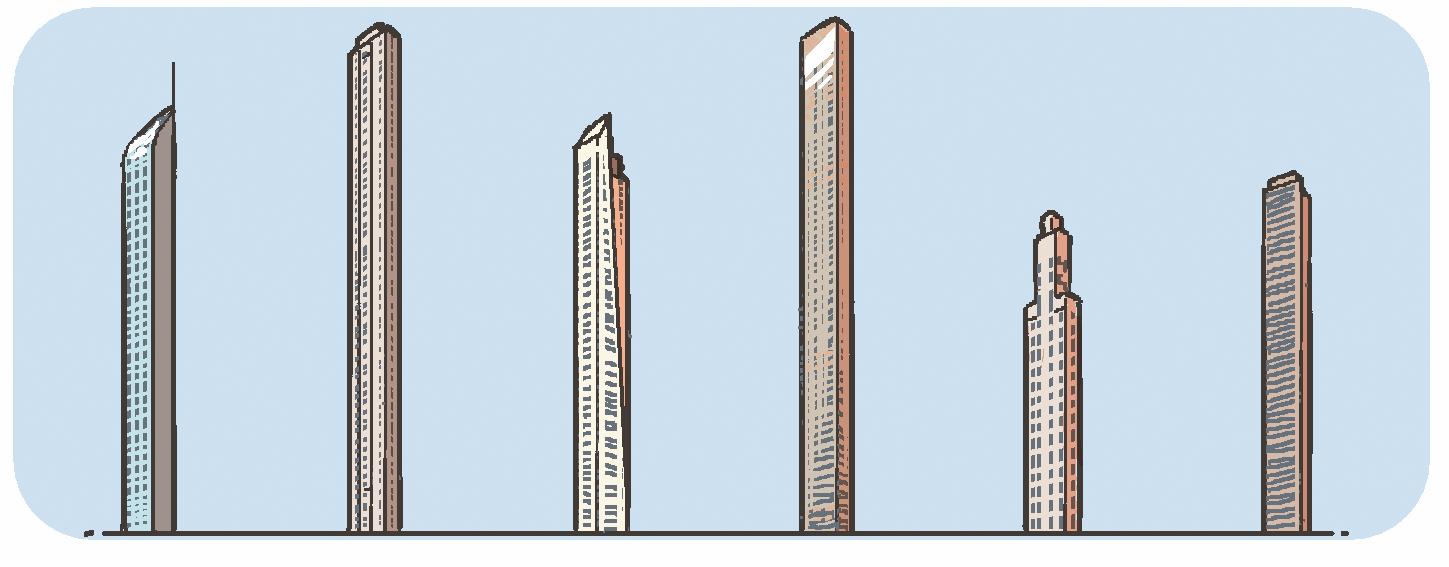
Voici différents gratte-ciels à travers le monde. Avec ton (ta) voisin(e), essaie de les replacer au bon endroit sur la carte.

Un peu d’aide ? Demande un atlas à ton enseignant(e).

1 NUM 1 5

N-O1

1. Burj Khalifa –Dubaï : 829 mètres The Shard –Londres : 306 mètres Federation Towers –Vostok Tower, Moscou : 373 mètres Shanghai Tower –Shanghai : 632 mètres Makkah Clock Royal Tower –La Mecque : 601 mètres One World Trade Center –New York : 541 mètres

1 2 3 4 5 6 7 8

Commerzbank Tower –Francfort : 259 mètres Willis Tower –Chicago : 441 mètres

Retrouve le nom des continents sur lesquels sont construites ces tours.

Classe ces 8 gratte-ciels en fonction de leur hauteur (du plus petit au plus grand).

Anecdotes

En 2013 a commencé la construction d’une nouvelle tour aux proportions énormes, puisqu’elle doit à terme atteindre une hauteur de 1 km. Il s’agit de la Jeddah Tower située en Arabie Saoudite . Elle a actuellement atteint un quart de sa hauteur et devrait être inaugurée en 2025.

Regarde attentivement l’Europe sur la 1re page… Elle est bizarre, non !?

Même si, géographiquement, le Groenland fait partie du continent nord-américain, il est en fait rattaché à la culture européenne, colonisé par les Norvégiens et ensuite rattaché au Danemark.

6 N-O2

<<<<<<<

601 m – 829 m – 441 m – 306 m – 259 m – 541 m – 632 m – 373 m

3. One World Trade Center Willis Tower Burj Khalifa Shanghai Tower Makkah Clock Royal Tower The Shard Federation Towers –Vostok Tower Commerzbank Tower

7 N-O3 Place le signe correct (< ou >). 478 678 224 976 328 382 571 517 465 456 343 334 5. Écris la hauteur de ces tours en lettres. 541 m cinq-cent-quarante-et-un mètres 259 m mètres 816 m mètres 481 m mètres 6. Ordonne ces nombres (attention aux signes). 447 – 118 – 535 – 753 – 906 – 375 <<<<< 337 – 608 – 806 – 733 – 542 – 245 >>>>> 335 – 535 – 353 – 253 – 533 – 355 <<<<< 4.

6.

Place approximativement la hauteur de ces gratte-ciels sur cette droite des nombres.

Burj Khalifa : 829 m

The Shard : 306 m

Shanghai Tower : 632 m

One World Trade Center : 541 m

Commerzbank Tower : 259 m

Willis Tower : 441 m

Avec une autre couleur, place ces autres tours sur la droite des nombres.

Pingan International Finance Center (9), Shenzhen (Chine) : 561 m

Torre Foster (10), Madrid (Espagne) : 250 m

Place ces deux tours au bon endroit sur la carte des continents (p. 5). Aide-toi d’un atlas.

Écris le nombre qui précède et le nombre qui suit.

829 306 373 632 601 541 259 441 N-O4 1000 100 0 900 800 700 600 500 400 300 200 830

2. Les solides et leurs empreintes

Voici les trous creusés par les ouvriers pour construire des bâtiments. Relie chaque trou au(x) bâtiment(s) à construire qui lui correspond.

9 SF1

L’architecte a envoyé les plans de certaines tours dans le mauvais sens. Recherche les trous correspondants.

Je dépose mes idées

Après ces deux exercices, que constates-tu ? Réfléchis avec ton (ta) voisin(e).

10 SF2

3. Les grandeurs de base

Les ascenseurs ont été installés dans un building. Quelles données mesurables ou quantifiables pourrais-tu relier à ces ascenseurs ?

Classe tes idées dans ce tableau. Indique dans la case verte le nom de la grandeur liée à chaque illustration. N’hésite pas à réfléchir avec ton (ta) voisin(e).

Mes idées Nos idées

12 5 m 5 L 5 kg 2 m 2 L 2 g 100 g 100 m 100 L 12 € 12 L 12 m 375 m 375 g 375 L 12 L 12 m 12 g

5 000 L5 000 g5 000 cm2 G2

Colorie la bonne case. 3.

15 000 g15 000 m15 000 L

13 G3

dans une même couleur les éléments qui se rattachent à la même grandeur.

la bonne case. 26 g 26 cm 26 L 10 m 10 g 10 L 140 L 140 cm 140 g 3 t 3 km 3 L 4,70 € 47 mm 47 g La masse d’un enfant Le contenu d’une bouteille de lait La longueur d’un poisson La valeur d’un manteau La surface de la cuisine 32 kg 1 L 17 m2 63 € 6 cm

Colorie

4. Colorie

Plus grand ou plus petit ? Colorie la bonne réponse.

J’explique avec mes mots

Les longueurs Les capacités Le cout Les masses L’aire

14 G4

1 m > < 1 L > < 1 g > < 1 m > < 1 g > < 1 m2 > < 5.

2. 4. Les nombres jusqu’à 1 000 (suite)

15 N-O5 Recompose ces nombres selon l’exemple.

Fais l’inverse.

10 10 10 10 10 100 100 100 100 1 1 = 452 447 100 100 100 100 100 100 100 100 1 1 1 1 1 1 = 10 10 10 10 100 100 100 100 100 100 1 1 1 1 1 1 1 = 10 10 10 10 10 10 10 10 100 100 100 1 1 1 1 1 1 1 1 1 = 10 10 10 10 10 10 100 1 1 1 1 1 1 1 1 1 = 10 100 100 100 100 1 1 1 1 1 1 = 10 10 10 10 10 10 1 1 1 1 = = 10 10 10 10 1 000 1 1 1 1 1 1 1 = 100 100 100 100 1 1 1 1 1 1 1 1 1 917 868 736 408 16 580 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 1 1 1 1 1 1 1 1 1 Lorsque je n’ai pas d’information concernant le rang, j’écris

16 N-O6 Situe précisément ces nombres sur les droites des nombres proposées. 118 96 485 515 4. 92 104106 450455 Situe approximativement ces nombres sur les droites des nombres. 469 813 224 284 354 409 512 1026 17 3. 150200300400500600 700800850 0 1000 240 300 400 480 162 176 243 270 252249 148 170

17 N-O7 Retrouve cette fois le nombre du départ. 441 5 7 1389 18 7 9 64 181 11 6. Complète le nom des colonnes de l’abaque suivant. Place ces nombres dans l’abaque. 829 Que représente le 8 ?  306 Que représente le 6 ?  632 Que représente le 3 ?  541 Que représente le 5 ?  259 Que représente le 9 ?  5. Synthèse 6 1 4

Je dépose mes idées

Regarde

18 Complète les droites suivantes. 7. 200300 020 400420 200225 025 600650 050 0125

attention les couples de comptage.

remarques-tu ? N-O8

avec

Que

5. Les solides et leurs empreintes (suite)

Retrouve les empreintes des différents solides. Coche les bonnes réponses dans le tableau.

Repasse en couleur sur les arêtes de ces différents solides.

Repasse en couleur sur les arêtes des solides de l’exercice 1.

Mets en évidence les sommets.

Mets les sommets de l’exercice 1 en évidence.

SF3

1. 2.

Complète ce tableau.

Face(s)

Arête(s)

Sommet(s)

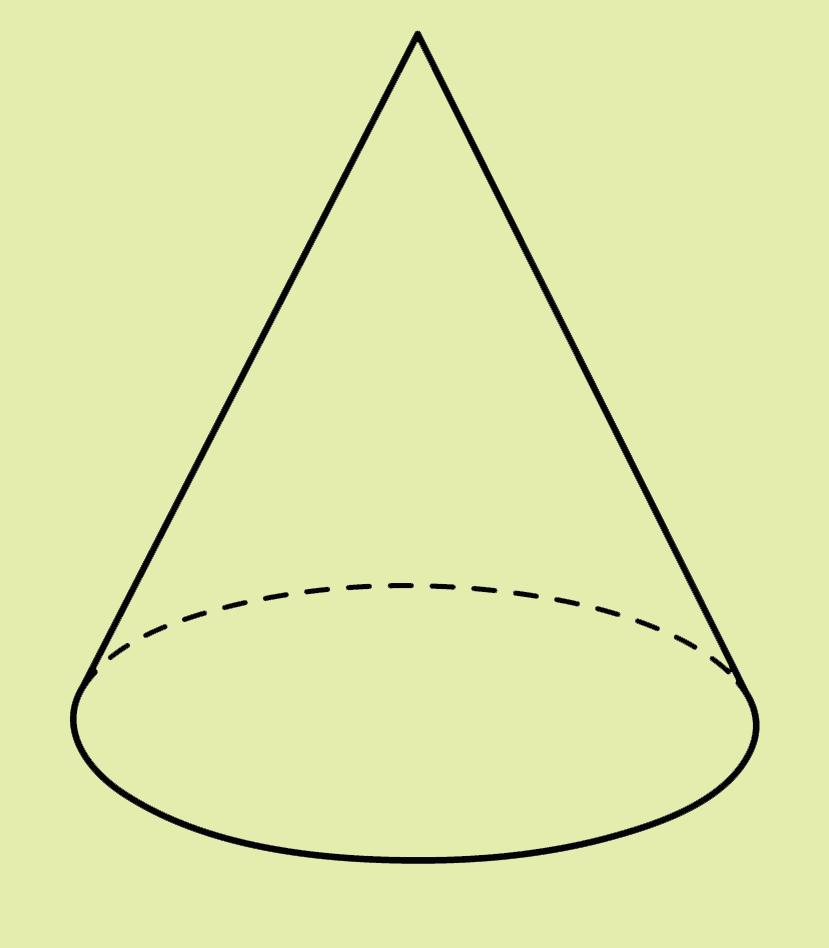
J’explique avec mes mots

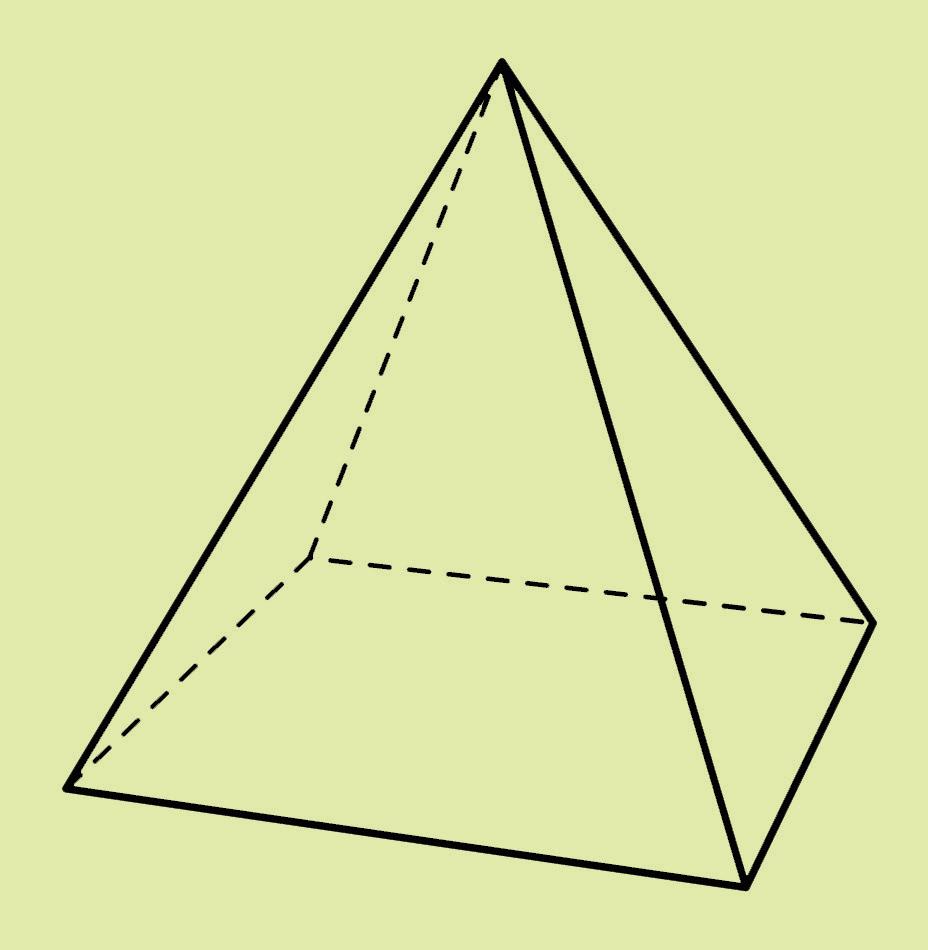
1. Pourquoi le cylindre ne possède pas d’arête ?

2. Pourquoi la sphère n’a pas de sommet ?

Synthèse

Je possède exclusivement des faces planes.

4. SF4

OUI NON

6. Lire et interpréter des données

Lola a regardé sur Internet les grandes tours de Belgique et elle les a représentées dans ce graphique. Observe et réponds aux questions.

La tour Paradis, Liège

La tour des Finances, Bruxelles-Ville Arteveldetoren, Gand La tour du Midi, Saint-Gilles Boerentoren, Anvers Europacentrum, Ostende

Quel est le plus haut gratte-ciel ? Donne son nom.

Quel(s) est (sont) celui (ceux) qui mesure(nt) moins de 100 m ?

À ton avis, comment s’appelle la tour qui mesure 136 m ?

Classe ces gratte-ciels du plus grand au plus petit. > > > > >

Quelles sont les tours comprises entre 125 et 150 mètres ? Donne leur nom.

Et celles entre 100 et 125 mètres ? Donne leur nom.

Sois le plus précis possible :

Arteveldetoren mesure entre et m.

La Tour des Finances mesure entre et m.

Quelle est la différence de hauteur entre « la tour du Midi (150 m) » et « l’Europacentrum (104 m) » ?

Quelle est la plus haute tour de la Région flamande ?

21 TD1

25 m 0 50 m 75 m 100 m 125 m 150 m ➀➁➂➃➄➅

Jules a commencé à réaliser un graphique sur la hauteur des grands arbres en s’aidant du tableau suivant, mais il n’a pas eu le temps de le terminer. Peux-tu l’aider ?

83 mètres115 mètres100 mètres25 mètres41 mètres

Donne un titre à ce tableau.

Quel est l’arbre le plus grand ?

Quelle différence de taille y a-t-il entre le General Sherman et l’Hyperion ?

Quel(s) est (sont) l’(les) arbre(s) qui dépasse(nt) les 100 mètres ?

Comment s’appelle l’arbre qui mesure 25 mètres ?

Dessine les arbres manquants dans le graphique.

General Sherman, Californie Hyperion, parc national de Redwood en Californie Eucalyptus, vallée de Styx en Tasmanie Cyprès d’Abarqu, Asie Arbre de Tule, Mexique

100 0

Général Sherman HyperionEucalyptus Cyprès d’Abarqu Arbre de Tule

2. TD2

7. La table de/par 7

La gestionnaire du CMotel a décidé de placer dix lieux récréatifs : un tous les 7 étages.

Voici les plans de cette tour. Indique sur les pointillés ce qui se trouve à l’étage correspondant à l’explication.

Complète le calcul comme dans le premier exemple.

• Loisirs :

– Piscine : avant-dernier lieu récréatif 9 × 7 = 63

– Arcade : à la moitié de la tour × 7 =

–

Panorama : au dernier étage × 7 =

– Bienêtre : au 7e lieu récréatif × 7 =

• Commerces :

– Centre commercial : au premier lieu récréatif × 7 =

– Artisans : installés entre le grill et le buffet × 7 =

– Souvenirs : au rez-de-chaussée × 7 =

• Restaurants (chiffres pairs restants, dans l’ordre) :

– Buffet × 7 =

– Pizzéria × 7 =

– Grill × 7 =

– Salade-bar × 7 =

23 N-O9

Imite l’exemplepourmontrerquelamultiplicationestuneadditionréitérée

35=5×7=7+7+7+7+756== 28=4×7=49== 21=3×7=42==

10×78×72×77×73×76×74×75×7 1449705628352142

Utilise descouleurs! 721402014732116123253426756 833411286497780573568727 71766773563469318947313388 8014362437701076397800750 2. 3.

= × N-O10 Exerce-toi! 5. :7 42 70 56 63 21 7 × 5 3 4 6 9 8 7

Relie chaquemultiplicationetsonproduit.

Retrouve lesmultiplicationscachées.

Chapitre 2

La journée de Gillian

NUM 1 25

1. L’heure de 5 minutes en 5 minutes

Tous à l’heure !

Retrouve et lis les différentes heures présentes dans la BD.

2.

1. Quelle heure est-il ? À l’aide de ton (ta) voisin(e), indique l’heure donnée par ces horloges.

Ajoute 30 minutes à chaque heure et inscris l’heure qu’il est à présent.

26 G6

h h h h h h

1 4 2 5 3 6

1 h 5 h 6 h

L’horloge de la maison n’est plus à l’heure. Aide la maman de Gillian à placer la grande aiguille correctement.

J’observe

Observe la petite aiguille, que remarques-tu ?

14 h 45 22 h 35 19 h 10 16 h 20 17 h 55 G7

Dessine la petite aiguille. 3. Dessine la petite aiguille.

4 h 15 18 h 55 11 h 40 23 h 05 14 h 30 4 h 05 8 h 45 6 h 25 9 h 10 12 h 35

9 h 10 9 h 30 9 h 50 4 h 10 4 h 30 4 h 50

Dessine l’heure sur ces différentes horloges.

Matin ou soir ? Transforme l’heure de ces horloges.

Quelle heure est-ce ? Recherche avec ton (ta) voisin(e). Aide-toi de ton horloge.

Je synthétise

28 G8

8 h 4517 h 3014 h 1010 h 0515 h 55     

3 h moins 15  14 h moins 20  6 h moins 10  8 h moins 5  7. 5 h 15 8 h 05 12 h 35 4 h 55 7 h 20 9 h 404 h 15 7 h 5511 h 105 h 30

les heures avant-midi les heures après-midi la petite aiguille la grande aiguille la grande aiguille la petite aiguille les heures avant midi les heures après midi

1. 2. La commutativité

Calcule le résultat de ces 2 opérations.

J’exprime mes idées

Quel calcul était le plus facile ?

D’après toi, pourquoi est-il plus facile ?

2.

Que pourrais-tu faire pour simplifier « le calcul plus compliqué » ?

Explique et réalise ensuite les changements dans le calcul.

Je synthétise

Complète cette phrase.

La commutativité consiste à

29 N-O11

14 cartes + 7 cartes

12 cartes

+ 6 cartes

+ 8 cartes + 6 cartes

14 7 6 12 8 6

Coche les calculs dans lesquels la commutativité est réalisable.

Sans donner de réponse, réorganise ces calculs.

478 + 56 + 122 + 14 =

37 + 366 + 113 + 32 =

481 + 55 + 19 + 145 =

232 + 254 + 68 + 146 =

142 + 337 + 218 =

Donne les réponses des calculs bien organisés.

78 + 441 + 112 + 19 = ...................................................................................................................................

123 + 37 + 24 + 376 =

123 + 69 + 20 + 366 =

159 + 41 + 25 + 235 =

447 + 153 + 56 + 24 =

Résous ces problèmes.

Organise correctement les calculs.

Gillian joue aux cartes durant la récréation. Au début, il possédait 37 cartes. Durant la première partie, il en a gagné 8 et, pendant la 2e, 13. Combien de cartes possède-t-il maintenant ?

Calcul Vérification

Phrase-réponse :

Lola collectionne les timbres. Elle en possède déjà 84. Son papa, revenant d’un voyage d’affaires, lui en a ramenés 12 alors que sa tante lui en a offerts 8 pour son anniversaire. Sa grand-mère décide de lui donner 26 timbres datant de la seconde guerre mondiale. Combien de timbres Lola possède-t-elle maintenant ?

Calcul Vérification

Phrase-réponse :

o 14 + 48 + 27 o 47 + 63 + 244 + 189 o 144 + 362 + 26 + 38 o 115 + 23 + 35 o 71 + 552 + 48 + 29 o 108 + 65 + 89 + 326

N-O12

3. Le développement du parallélépipède rectangle

Trace le contour de toutes les faces d’une boite que tu as choisie ou d’un solide de la classe sur du papier épais et ensuite découpe les différentes faces dessinées.

Assemble-les avec du papier collant pour reconstruire le solide.

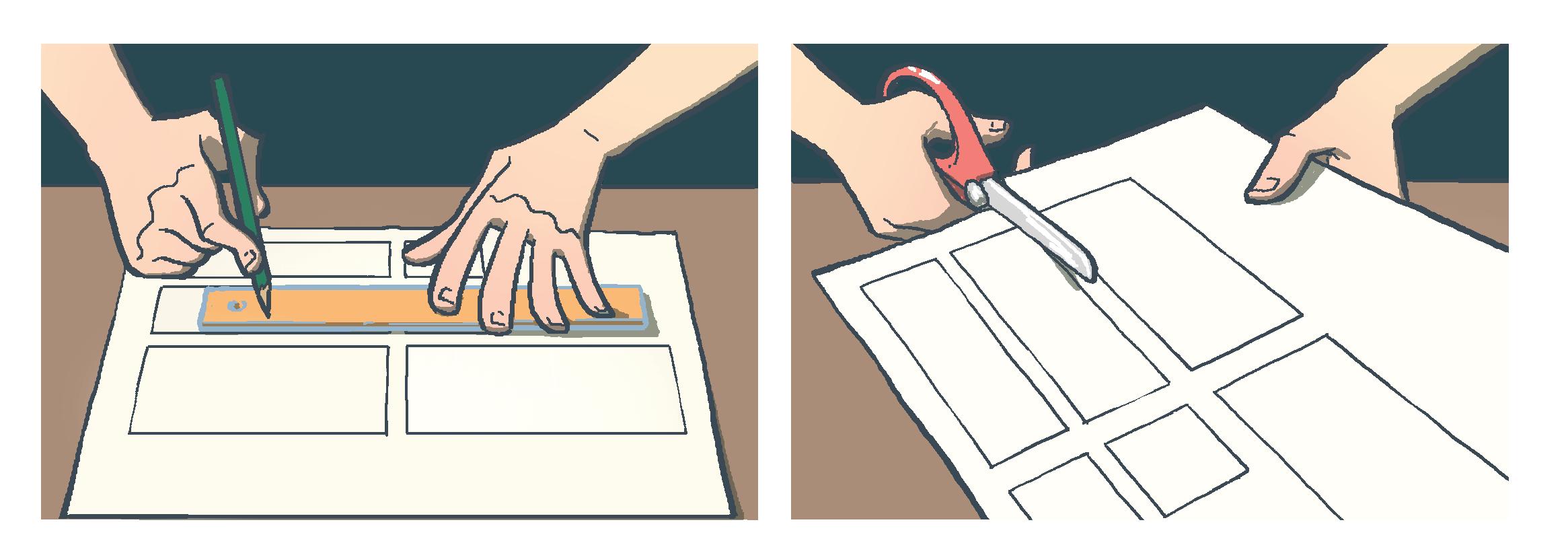
Après avoir constitué ton solide, découpe certaines arêtes, mais pas toutes. Toutes les faces doivent tenir en un seul et unique morceau.

Colle ton développement sur cette feuille.

Compare ton développement avec ton (ta) voisin(e).

5. 1. 2.

SF5

3. 4.

Je dépose mes idées

Que remarques-tu lorsque tu compares ton développement avec celui de tes voisins ?

5.

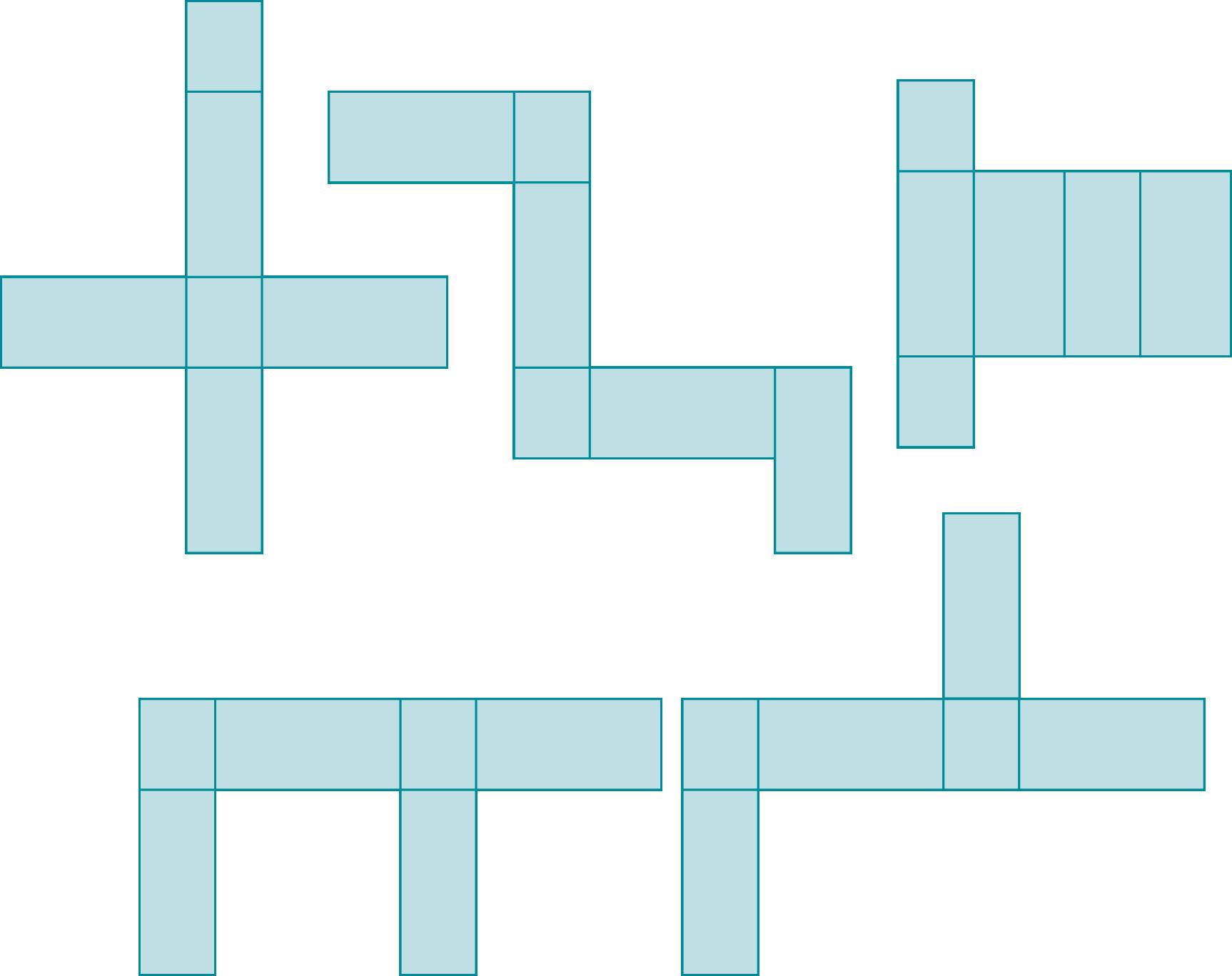
Entoure le(s) patron(s) qui représente(nt) le solide proposé.

SF6

1. 4. Arrondir et estimer

Avec ton (ta) voisin(e), essaie de trouver une méthode avec laquelle tu pourrais compter rapidement le prix approximatif des objets de la chambre de Gillian.

Zone de recherche

N-O13

Je dépose mes idées

Après une mise en commun, écris la règle établie par la classe.

Le signe présent dans l’exercice suivant ressemble à un signe « égal » mais il est composé d’une vague et signifie « vaut environ ».

34 Arrondis ces nombres selon la règle établie en classe. 441  107  386  284  632  851  556  ……........... 97  ……........... 474  ……...........

Colorie le bon arrondi du nombre situé dans la case colorée. 150184200 550577 600 200222250 800804850 5098100 350360400 100124150 450462500 2. Estime le résultat du calcul. ( ) ( ) 471 + 293~ ( ) ( ) 424 + 62~ ( ) ( ) 588 – 123~ ( ) ( ) 115 + 236~ ( ) ( ) 778 – 242~ ( ) ( ) 555 – 389~ ( ) ( ) 416 + 704~ ( ) ( ) 856 – 389~ ( ) ( ) 648 – 78~

34 N-O14

1.

5. Le développement du cube

Réalise toi-même ton propre cube.

Dessine sur un papier épais des carrés de 5 cm de côté. Combien dois-tu en dessiner pour réaliser un cube ? .......

Découpe tes carrés et assemble-les avec du papier collant pour former un cube.

Découpe les arêtes de ton cube en faisant attention à laisser les faces en un seul morceau.

Colle ton développement sur une feuille blanche.

Compare ton développement avec celui de ton (ta) voisin(e).

a) Qu’ont-ils en commun ?

b) Qu’ont-ils de différent ?

Je réfléchis

À ton avis, combien existe-t-il de développements d’un même cube ?

Colorie le(s) patron(s) qui représente(nt) le solide proposé. 2.

35 SF7

Le papa de Gillian lui demande d’aplatir les cartons. Retrouve le développement qui correspond au solide et relie

Dessine ce qui manque aux développements des différents solides.

• • • • • •

SF8

37 SF9

2 cm 4 cm 3cm

Voici un parallélépipède rectangle. Trace son développement sur ce quadrillage.

38 SF10

Trace

3 cm 1 cm 5cm

Voici un autre parallélépipède rectangle.

son développement sur ce quadrillage.

6. L’addition en calcul écrit

Voici le ticket des achats au magasin de chaussures. , avec ton/ta voisin(e), l’erreur réalisée par le caissier dans la somme

1 x équipement de sport Fizouri 119 €

1 x crosse de hockey Dianis 85 € 194 €

Je dépose mes idées

ces calculs en dessinant les étapes que tu réalises.

D U +184 9

C D U 41 7 +186 CDU C D U 282 + 7 69

CDU

N-O15

40 Estime et, ensuite, résous ces calculs écrits. 148 + 56 = 404 + 158 = 274 + 113 = CDU CDU CDU 148 404 2 7 4 + 56+158+113 323 + 248 = 188 + 356 = 836 + 88 = CDU CDU CDU 323 188 836 +248+356+ 88

408 + 136 = 744 + 186 = 555 + 78 = CDU CDU CDU 408 7 44 555 +136+186+ 7 8

ces calculs. CDU CDU CDU CDU 18 48 5 1 7 + 5 + 50 + 416 + 2 84 40 83 4 7 2 4. N-O16

Complète

7. Calculs de durées

Le papa de Gillian le conduit à son activité sportive vers 17 h 05 et attend jusqu’à 17 h 50. Combien de temps attend-il ?

Résous

a) Gillian part de la maison à 8 h 05 et revient vers 8 h 35. Calcule la durée de sa journée.

b) Gillian, sa sœur et son papa partent vers 9 h 25 pour aller à la brocante. Ils reviennent après 30 minutes. À quelle heure sont-ils revenus de la brocante ?

c) Haly s’occupe du chien du voisin pendant 45 minutes et celui-ci vient le rechercher vers 19 h 50. À quelle heure le voisin a-t-il déposé le chien ?

d) Maman envoie Haly chez le boucher et Gillian à la pharmacie. Haly part à 16 h 20 et son frère, 5 minutes plus tard. Gillian revient à 16 h 35 et Haly, à 16 h 40. Écris une phrase qui compare les deux durées.

Complète les horloges et, ensuite, calcule les durées.

Départ Arrivée

8 h 10 8 h 35

De 8 h 10 à 8 h 35, il y a ……………………

Départ Arrivée 14 h 35

De 14 h 35 à 14 h 55, il y a ……………………

Départ Arrivée

De 6 h 05 à 6 h 30, il y a ……………………

Départ Arrivée

De 20 h 05 à 20 h 50, il y a ……………………

14 h 55

6 h 05 6 h 30

20 h 05 20 h 50

3. G10

1.

8. Le tableau à double entrée

Les soirées et les weekends dans la famille de Gillian sont bien remplis et organisés à la seconde près. Observe le tableau et réponds aux questions.

Guy Brigitte Gillian Haly Boma

Lundi Cours de yoga de 19 h à 20 h

Rugby : de 18 h 15 à 20 h 15

Mardi Faire les coursesFaire les courses Cours de hockey

Mercredi

Conduire Gillian à son entrainement de sport (de 18 h 45 à 20 h 15)

Préparer à manger

Jeudi Rentrer du travail vers 21 h Sortie avec ses amies

Rugby : de 18 h 45 à 20 h 15

Réaliser un exposé sur le système cardiovasculaire

S’occuper du chien du voisin (Hulk)

Jeu de bridge chez la voisine

Regarder son feuilleton favori : Les cancres

S’occuper de ses petitsenfants

Vendredi Inviter toute la famille au bowling BowlingBowlingBowling S’occuper du chien du voisin (Hulk)

Samedi Conduire Gillian à son match et Haly au sien Faire la grasse matinée Aller à son match (9 h 45)

Dimanche Aller à la brocante avec ses enfants (de 6 h 20 à 12 h 10)

Aller à son match (14 h 50) Se promener dans le parc

Nettoyer la maison Aller à la brocante Aller à la brocante Jouer aux échecs dans son club

a) Quel est le jour où la famille va au bowling ?

b) Combien d’entrainements de sport Gillian a-t-il ?

c) Qui va au yoga le lundi ?

d) Quel est le jour d’entrainement d’Haly ? Colorie.

Lundi Dimanche Mercredi Vendredi Mardi Jeudi Samedi

TD3

e) Qui regarde son émission favorite le mardi ? Quel est le nom de l’émission ?

f) Vrai ou faux. Justifie si c’est faux.

1) Papa est au bowling le jeudi soir.

2) Boma se promène dans le parc le samedi.

3) La famille de Gillian compte 6 membres.

4) Toute la famille part en brocante le dimanche.

g) Quel jour la grand-mère est-elle seule avec les 2 enfants ?

h) Quels sont les jours où Boma est absente de la maison ? Colorie. Lundi Dimanche Mercredi Vendredi Mardi Jeudi Samedi

i) Combien de fois le chien Hulk est-il avec la famille de Gillian ? Entoure la bonne réponse.

j) Cite 3 activités sportives réalisées par les membres de la famille de Gillian.

k) Combien de temps y a-t-il entre le début du match de Gillian et celui de Haly ?

l) Combien de temps, le papa et les 2 enfants restent-ils à la brocante ?

m) Combien de temps dure l’entrainement de Gillian le mercredi ?

2 3 4 5

TD4 VRAI / FAUX VRAI / FAUX VRAI / FAUX VRAI / FAUX