Livre-cahier A Sébastien Bleus
Sébastien Bleus
ÉditionsVANIN
Livre-cahier A
Carrément MATH
Composition de Carrément math 6
Pour l’élève : 2 livres-cahiers A et B
Pour l’enseignant :
Deux livres de l’enseignant(e) (comprenant le corrigé des livres-cahiers)
Leurs versions numériques disponibles sur Wazzou
Les annexes, des exercices supplémentaires et des évaluations disponibles sur Wazzou
Les manuels numériques (A et B) téléchargeables sur Wazzou
Carrément math 6 – Livre-cahier A
Auteur :
Sébastien Bleus
Illustrations : M-A IZU (Marie-Anne Gueguen) et K'Naye
Conception graphique : Octopus Creative Communication
Mise en page : NORDCOMPO
Couverture : Kiv'là
L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.
L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.
Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.
Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.
1re édition : 2025
© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2025
ISBN 978-94-641-7802-9
D/2025/0078/34
Art. 602850/01
Chapitre
Les vacances de Manon et Raphaël
1. Bataille navale
Lis cette BD. 1.
As-tu déjà joué à la bataille navale ? Réponds aux questions.
Si tu as déjà joué, explique les règles du jeu à la classe.
Après avoir observé le plateau de jeu de Raphaël, quelle case aurait-il dû choisir pour remporter la partie ?
Avec ton (ta) voisin(e), effectue une bataille navale.
Dessine 5 bateaux de manière verticale ou horizontale :
–2 bateaux de 3 cases ;
–2 bateaux de 2 cases ;
–1 bateau de 1 case.
Attention, les bateaux ne peuvent pas se toucher ! Place tes bateaux dans la grille de gauche et note ceux de ton (ta) voisin(e) dans la grille de droite.
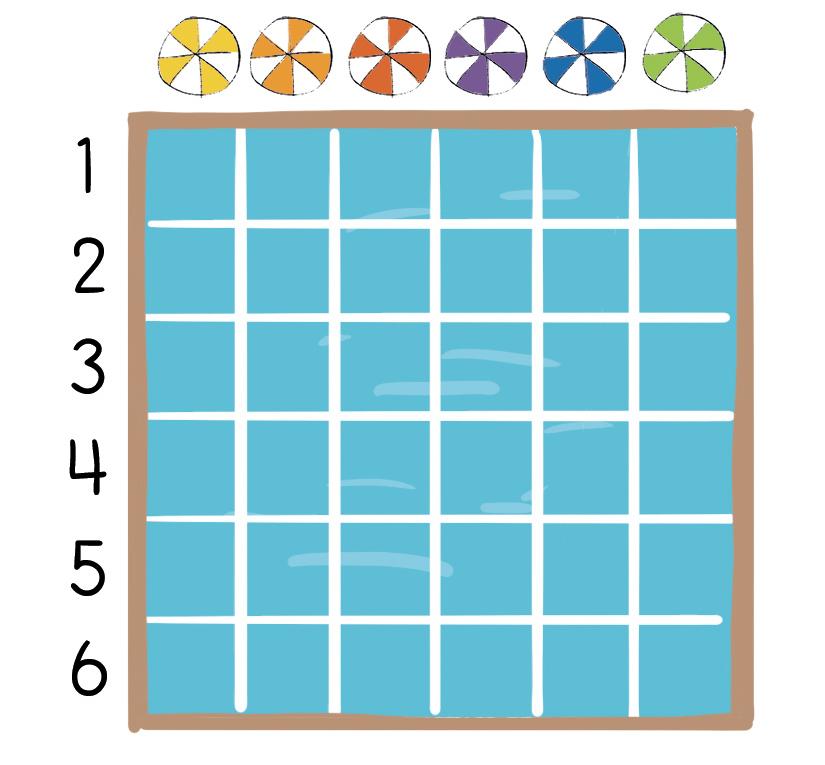
En observant le plateau de jeu, note à côté de chaque bateau sa position.
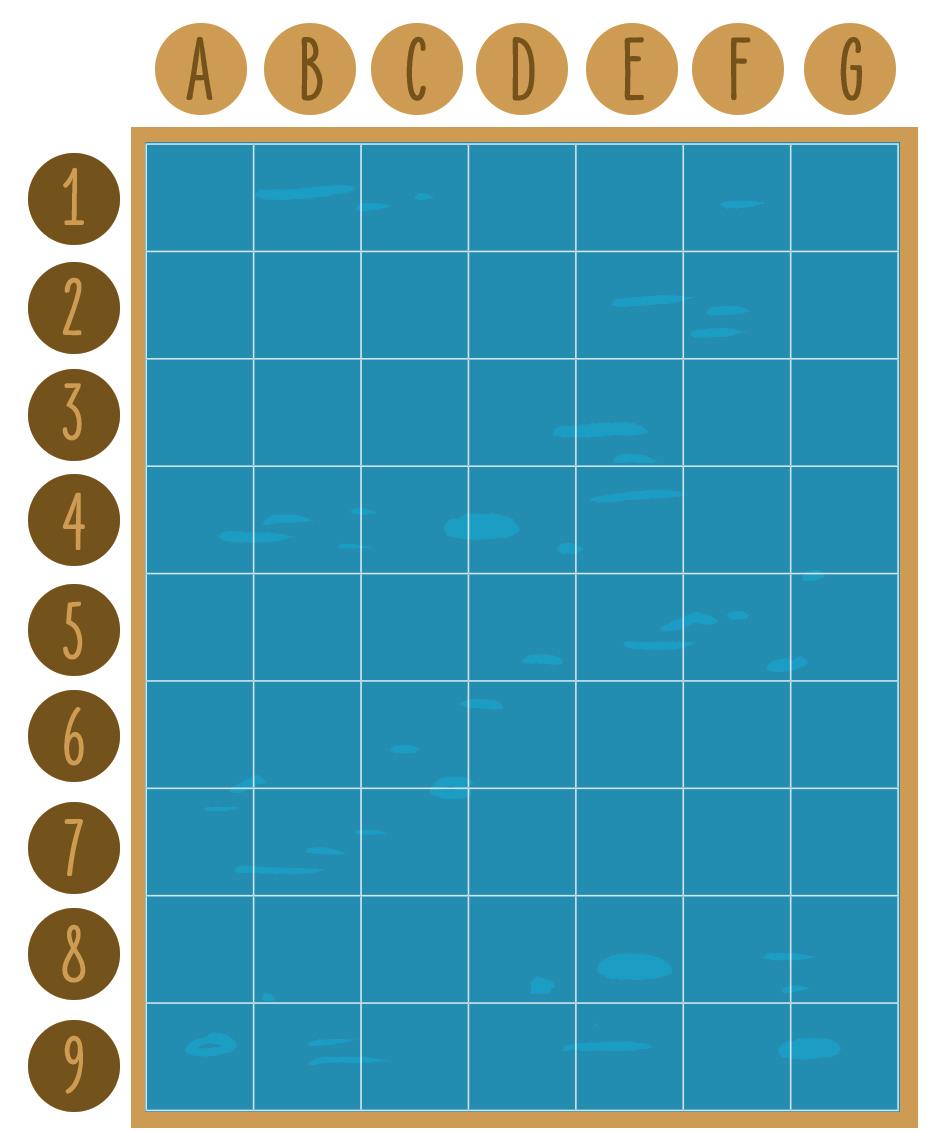
En t’aidant du quadrillage ci-dessous, donne les coordonnées des objets.
Dans le quadrillage ci-dessus, dessine ces éléments.
−Une casquette en (B,7)
−Un tube de crème solaire en (D,6)
−Un avion en (E,9)
−Un palmier en (I,3)
Observe ce quadrillage.
Quelle différence observes-tu par rapport aux quadrillages rencontrés précédemment ?
Repérer une case
Dans un quadrillage, on peut avoir besoin de repérer
Repérer un croisement
Dans un quadrillage, on peut avoir besoin de repérer
La case bleue a pour coordonnées ( , ).
On donne d’abord la lettre de la colonne, puis le nombre de la rangée.
Le croisement bleu a pour coordonnées ( , ).
On donne d’abord la lettre de la ligne verticale, puis le nombre de la ligne horizontale.
2. On mesure !
Colorie d’une même couleur ce qui doit être associé.
millilitre
compteur d’une voiture
gramme
degré
ÉditionsVANIN
balance de cuisine vitesse
cout
contenu d’un petit jus euro masse
capacité
longueur
caisse enregistreuse
kilomètre/heure
température centimètre
thermomètre
Retrouve la grandeur adéquate et colorie la bonne case.
kmkm/hglkgheures€
Le prix pour acheter du pain
La quantité d’eau dans une baignoire
La distance entre Namur et Portiragnes
La masse d’une grosse pomme
La vitesse maximale d’une petite voiture
Le temps de notre trajet en avion
La masse de ton (ta) voisin(e) de classe
La somme de ton compte en banque
La durée d’une journée à l’école
La capacité d’une piscine
Avec ton (ta) voisin(e), reconstruis ci-dessous tes différents abaques (longueurs, capacités et masses). dm l kg
Pour chaque unité de mesure proposée, trouve un instrument et une situation de la vie réelle. Justifie tes choix avec ton (ta) voisin(e) lorsque vous avez terminé.
Unité de mesure
secondes
Complète
Exemple : 1 m × 100 = 1 hm
1 km : = 1 m
1 cl × = 1 dal × 100 = 1 kg
Transforme.
masse d’un sac de pommes
1 g × = 1 hg 1 l : = 1 ml 1 kg × 1 000 = 1
200 ml = l23 cm = m
40 g = mg5,3 dm = mm
2 500 m = km8 000 kg = T
3,75 kg = g32,5 dag = kg
5 hl = l5 000 mg = hg
28 cl = ml23 dam = cm
0,3 m = mm34 cm = m
5,3 l = ml 6 T = kg
Résous ces problèmes.
a) Lorsqu’ils sont allés au marché, Manon et Raphaël ont acheté quelques ingrédients pour préparer un apéritif. Voici ce qu’ils ont acheté : 250 g de fromage, 1/5 kg d’olives, 5 400 mg de chips, 45 dag de saucisson. Quelle quantité totale de nourriture ont-ils achetée ?
b) Pour ce même apéritif, ils ont décidé de proposer à leurs amis un petit cocktail fruité. Voici les jus qu’ils ont achetés : 1,5 l de jus d’orange, 100 cl de jus de cerise, 0,2 dal de jus de mangue et 500 ml de jus de citron. Auront-ils assez pour eux et leurs 8 amis, sachant qu’ils prendront au moins 2 verres de 25 cl chacun ? Justifie ta réponse.
c) Léa et Nathan jouent chacun sur leur tablette lorsqu’un message d’alerte apparait : les batteries sont presque vides !
Ils doivent attendre que les tablettes se rechargent pour pouvoir continuer à jouer
La batterie de Léa est à 15 % et met 2 minutes pour recharger 1 %.
Celle de Nathan est à 20 % et met 1 minute 30 secondes pour recharger 1 %.
Ils ne pourront reprendre leur jeu que lorsque les batteries auront atteint 80 %.
Combien de temps Léa devra-t-elle attendre avant d’atteindre 80 % de charge ?
Combien de temps Nathan devra-t-il attendre avant d’atteindre 80 % de charge ?
Lequel pourra recommencer à jouer en premier et avec combien de minutes d’avance sur l’autre ?
3. Des millièmes aux milliards
Durant leurs vacances à Portiragnes, Manon et Raphaël se rendent à la municipalité locale afin d’obtenir quelques informations sur la ville où ils séjournent. Voici ce qu’ils ont reçu : Paris
PORTIRAGNES
Nice
Relie chaque nombre à son écriture en lettres.
Blason
ÉditionsVANIN
zéro
Pays France Région Occitanie DépartementHérault Arrondissement Béziers
Administration Démographie
Gentilité Portiragnais Population 3 247 hab. (2021 ) municipale Densité 161 hab./km²
Géographie
Coordonnées 43° 18’ 19” nord 3° 20’ 11” est Altitude 0 m – 41 m – 15 m (min. – max. – moy.)
Superficie 20,16 km² ou 20 160 000 m²
trois-mille-deux-cent-quarante-sept
quarante-et-un
quinze
vingt et seize centièmes
cinquante-et-un vingt-millions-cent-soixante-mille
Toulouse
Portiragnes
2. 3. 4. 5. 6.
Complète les noms des colonnes et, ensuite, place ces nombres correctement dans l’abaque.
1 238,91
1 239 129 021 384 348,382 67 601 129,003
Pour savoir comment compléter ton abaque, discutes-en avec ton (ta) voisin(e).
Classe des Classe des Classe des Classe des unités Classe des
Relie chaque nombre à son écriture.
210 199
5 280 199
1 000 192 199
203 300 000
Dictée de nombres
deux-cent-trois-millions-trois-cent-mille
deux-cent-dix-mille-cent-nonante-neuf
cinq-millions-deux-cent-quatre-vingtmille-cent-nonante-neuf
un-milliard-cent-nonante-deux-mille-centnonante-neuf
ÉditionsVANIN
Entoure le chiffre des UM en bleu, des D en rouge et des m en vert.
Retrouve le nombre.
3UM 2CM 1UM 4C 7D 8U =
9UM 6DM 8CM 7UM 4C 9U 4c =
4CM 5DM 7UM 3C 2D 6U 3d =
7DM 5UM 3CM 4UM 6C 2D 9U 1d =
3DM 5CM 2DM 7C 8 U 9D 5m =
Effectue cette fois le contraire et décompose les nombres en « classes ».
2 298 002 =
4 000 000 256 =
87 823 000,2 =
67 000,723 =
37,238 =
Que représente le 3 dans chaque nombre ci-dessous ? Complète
2 348 092
3 029 201 984
472 128 302 920 123,129
1 000 000,23
Zone de travail
78 120,306
Complète par classe.
236 126 123 = millions + mille + unités
2 183 931 012 = milliards + millions + mille + unités
128 031, 382 = mille + unités + millièmes
93 128 001, 981 = millions + mille + unité + millièmes
Décompose comme dans l’exemple.
239 234 = 200 000 + 30 000 + 9 000 + 200 + 30 + 4
12 120 =
13 100 409 =
310,32 =
239 006, 007 =
610 021, 209 =
<, > ou = .
2 039 923 3UM 2DM 4C 9d 9C
8 291,327 1DM 5d
720 192 102 7UM 2DM 3CM 8DM 192,428 1CM 9DM 2UM 4d 2c 8m
12. 13. 14. Zone de travail
<, > ou = .
7DM 8CM 5C 3D 6UM
1UM 3DM 8CM 1d
989 928,923
9 283 283,29 9m 6U 8,009
9CM 6DM 7UM 6CM 4DM 1 021 122 002
Classe ces nombres dans l’ordre croissant.
Classe ces nombres dans l’ordre décroissant.
Dans les nombres ci-dessus, entoure le chiffre des U en bleu, des UM en vert et des d en rouge.
1.
4. Les proportionnalités
Observe cette recette de cuisine.
Cookies maison
Dessert Temps de préparation : 15 min
Difficulté de la recette : ❀❀❀ Temps de cuisson : 10 min
Ingrédients (pour 4 personnes)
– 80 g de beur�e
– 1 œuf
– 80 g de sucre
– 1 sachet de sucre vanillé
– 160 g de farine
– 100 g de chocolat noir
– 1 cuillère à café de sel
– 1 cuillère à café de levure chimique
Préparation de la recette
Préparer le four à 180° (thermostat 6).
ÉditionsVANIN
Faire ramollir le beurre à température ambiante. Dans un saladier, mettre 80 g de beurre, incorporer le sucre, l’œuf entier, la vanille et mélanger le tout.
Ajouter petit à petit la farine mélangée à la levure, le sel et le chocolat coupé en petits morceaux.
Beurrer une plaque allant au four et former les cookies sur la plaque. Pour former les cookies, utiliser 2 cuillères à soupe et faire des petits tas espacés les uns des autres ; ils grandiront à la cuisson.
Recopie la liste des ingrédients nécessaires afin de pouvoir la réaliser en classe. Sois attentif(-ive) au nombre de personnes.
Oralement, explique ta réponse.
Nous organisons une fancyfair à l’école. Nous avons décidé de cuisiner des cookies pour 200 personnes afin de gagner de l’argent pour notre voyage de fin d’année. Dresse ci-dessous la liste des ingrédients nécessaires.
Réponds par vrai ou faux en fonction de la recette des cookies.
– Avec 1 kg de farine, j’aurai assez pour 80 personnes.
– Pour réaliser cette recette, j’ai besoin de 200 g de chocolat blanc pour 8 personnes.
– Avec 1 kg de chocolat noir, je peux en faire pour 20 personnes.
Complète ces étiquettes.
le kg
dépose mes idées
Voici deux graphes fléchés représentant chacun une situation. Indique si la situation montre une relation de proportionnalité directe. Justifie ta réponse.
Situation A
Dans un verger, un agriculteur récolte des pommes. Le graphe fléché montre la relation entre le nombre de pommes récoltées et le temps passé à travailler dans le verger.
Récolte de pommes
Kg de pommes récoltées
Situation B
Nombres d’heures passées dans le verger (en h)
– 2 heures → 10 kg de pommes – 4 heures → 20 kg de pommes – 6 heures → 30 kg de pommes
Une machine emballe des oranges en sacs. Le graphe fléché montre la relation entre le nombre de sacs emballés et le nombre d’oranges utilisées.
Emballage d’oranges
Nombre d’oranges
Nombre de sacs
– 1 sac → 8 oranges – 2 sacs → 14 oranges – 3 sacs → 23 oranges
Voici deux situations. Indique si la situation montre une relation de proportionnalité directe. Justifie ta réponse.
Situation A
Un sportif mesure la relation entre le nombre de répétitions d’exercices et l’énergie dépensée.
– 5 répétitions → 90 kcal
– 10 répétitions → 185 kcal – 15 répétitions → 290 kcal
Situation B
Un second sportif effectue des répétitions d’exercices et la dépense d’énergie est mesurée.
– 5 répétitions → 150 kcal
– 10 répétitions → 300 kcal
– 15 répétitions → 400 kcal
Lesquels de ces tableaux représentent une proportionnalité directe ? Justifie ta réponse en vérifiant les rapports entre les grandeurs.
1. Consommation d’eau (en litres) en fonction du nombre de jours
Nombre de jours Consommation d’eau (en litres)
2. Distance parcourue (en km) en fonction du nombre d’heures
d’heures
3. Quantité de pommes achetées (en kg) en fonction du prix payé (en €)
Pour chaque situation, identifie s’il s’agit d’une relation de proportionnalité directe. Colorie la bonne réponse.
Situation 1 : Paniers de légumes
– Analyse : Chaque panier coute 22 € et le prix total est proportionnel au nombre de paniers vendus. Pour chaque panier supplémentaire, le prix augmente de 22 €, ce qui est un rapport constant.
Situation 2 : Randonneurs
– Analyse : Au fil de la marche, le rythme diminue, ce qui rend les écarts de distance irréguliers (4 km, puis + 3 km, puis + 2 km, puis + 1 km).
Proportionnalité directe
Pas de proportionnalité directe
Proportionnalité directe
Pas de proportionnalité directe
5. Un peu d’entrainement : l’addition écrite
Estime avant d’opérer.
8 239 128 + 140 751 =
Estimation :
2 200 281 + 101 + 24 239 114 =
Estimation :
672 001,24 + 265 + 12 101,008 =
Estimation : 191 912 + 450 312 =
Estimation :
1 923 + 243 038 + 82 362 =
Estimation : 10,79 + 2 099,003 + 183 939 =
Estimation :
6. Un peu d’entrainement : la soustraction écrite
Estime avant d’opérer.
189 384 – 145 262 =
Estimation :
2 289 344 – 23 839 =
Estimation :
22 102 994 – 1 382 389 =
Estimation :
5 628 930 – 2 378 – 24 699 =
Estimation :
Estimation :
56 782 – 378,26 =
241 092 – 2 378,3 – 387,78 =
Estimation :