WISKUNDE KERN
methodeconcept / redactie
Boom voortgezet onderwijs
auteurs
Benjamin del Canho
Maartje Elsinga
Jacqueline Kooiman
Gijs Langenkamp
Florine Meijer
Chantal Neijenhuis
Willem Schaap
Renee Springer

methodeconcept / redactie
Boom voortgezet onderwijs
auteurs
Benjamin del Canho
Maartje Elsinga
Jacqueline Kooiman
Gijs Langenkamp
Florine Meijer
Chantal Neijenhuis
Willem Schaap
Renee Springer
1 Getallen
academie
Hoe zijn getallen ontstaan? 8
1.1 Positieve en negatieve getallen 12
1.2 Met negatieve getallen
vermenigvuldigen en delen 16
1.3 Breuken 20
1.4 Met breuken vermenigvuldigen en delen 24
1.5 Machtsverheffen 28
Toetsvoorbereiding 32
2 Vlakke figuren
academie
Van vlakvulling naar kunstwerk 36
2.1 Lijnen 40
2.2 Hoeken 44
2.3 Vlakke figuren 48
2.4 Tekenen en spiegelen 52
2.5 Symmetrie 56
Toetsvoorbereiding 60
3 Verbanden
academie
Waar ben ik op aarde? 64
3.1 Het assenstelsel 68
3.2 Verbanden 72
3.3 Formules en grafieken 76
3.4 Lineaire en kwadratische verbanden 80
3.5 Variabelen 84
Toetsvoorbereiding 88
4 Informatie verwerken
academie
Hoe win je de Amerikaanse verkiezingen ? 92
4.1 Data 96
4.2 Verhoudingen 100
4.3 Procenten 104
4.4 Diagrammen 108
4.5 Grafieken 112
Toetsvoorbereiding 116
5 Meetkundig rekenen
academie
Het metrieke stelsel 120
5.1 Lengte, tijd en snelheid 124
5.2 Omtrek en oppervlakte 128
5.3 Oppervlakte driehoek 132
5.4 Omtrek en oppervlakte cirkel 136
5.5 Inhoud 140
Toetsvoorbereiding 144
6 Vergelijkingen
academie
Hoe steil moet een trap zijn? 148
6.1 Lineaire formules 152
6.2 Vergelijkingen 156
6.3 Lijnen 160
6.4 Vergelijkingen oplossen 164
6.5 Vergelijkingen toepassen 168
Toetsvoorbereiding 172
7 Meetkundig redeneren
academie
Euclides en wiskundige bewijzen 176
7.1 Driehoeken 180
7.2 Vierhoeken 184
7.3 Hoeken berekenen 188
7.4 F- en Z-hoeken 192
7.5 Oppervlaktes berekenen 196
Toetsvoorbereiding 200
8 Algebra
academie
Wat is algebra ? 204
8.1 Rekenen met variabelen 208
8.2 Haakjes wegwerken 212
8.3 Ontbinden in factoren 216
8.4 Merkwaardige producten 220
8.5 Breuken met variabelen 224
Toetsvoorbereiding 228
Wiskundig redeneren
W1 Patroon zoeken 232
W2 Systematisch tellen 234
W3 Logisch redeneren 236
Register van begrippen 238
cm 7 cm
In dit hoofdstuk maak je kennis met verschillende soorten meetkundige figuren en leer je hoe je ze kunt tekenen en spiegelen. Ook maak je kennis met de kunst van Escher en van Mondriaan, leer je hoe de oude Grieken meetkundige figuren construeerden en wat palindroomgetallen zijn.
ACADEMIE
Van vlakvulling naar kunstwerk 36
2.1 Lijnen 40
2.2 Hoeken 44
2.3 Vlakke figuren 48
2.4 Tekenen en spiegelen 52
2.5 Symmetrie 56
Toetsvoorbereiding 60
DOEL > Je leert wat vlakvullingen zijn en je maakt kennis met de kunst van Escher.
Vlakvullingen Een aaneenschakeling van figuren die een vlak geheel opvult, zonder gaten of overlappingen, heet een vlakvulling. De meest eenvoudige vlakvulling bestaat uit vierkanten. Zo’n vlakvulling wordt vaak gebruikt in tegelpaden en vloeren. Ook met alleen rechthoeken of driehoeken kun je een vlakvulling maken, maar met alleen cirkels lukt dat niet. Een vlakvulling kan ook bestaan uit een patroon van twee of meer verschillende figuren, zoals vierkanten en driehoeken. De figuren kunnen daarin gedraaid of gespiegeld voorkomen.
M. C. Escher In het werk van de bekende Nederlandse kunstenaar en graficus M.C. Escher (1898–1972) spelen vlakvullingen een belangrijke rol. Op de bladzijde hiernaast zie je een vlakvulling met hagedissen. De figuren zijn zo gedraaid dat ze precies in elkaar passen. Eschers fascinatie voor geometrische patronen werd mede gewekt door de islamitische kunst die hij aantrof in het Alhambra, een middeleeuws fort in ZuidSpanje.
Patronen en oneindigheid Bij de meeste vlakvullingen is er sprake van een vast patroon dat zich herhaalt. Dit patroon kan bestaan uit een enkele figuur, maar ook uit een combinatie van verschillende figuren. In de vlakvulling van vierkanten in de afbeelding linksonder bestaat het patroon uit één vierkant, terwijl in de vlakvulling van vierkanten en driehoeken in de afbeelding rechtsonder het patroon bestaat uit vier vierkanten en acht driehoeken samen. In de vlakvullingen van Escher is het patroon soms moeilijk te vinden. Je kunt daarvoor het best kijken naar plekken waar drie of vier figuren samenkomen. In een vlakvulling loopt het patroon naar alle kanten oneindig ver door, maar op papier kun je natuurlijk maar een klein stukje afbeelden. Escher was hierdoor gefascineerd en heeft lang gezocht naar manieren om de suggestie van oneindigheid in zijn kunst te verwerken.
Drie vlakvullingen. De gekleurde lijnen markeren de vaste patronen.


OPDRACHTEN
v Tekstvragen
1 Maak een vlakvulling met de onderstaande driehoek. T 1
2 Leg uit waarom je geen vlakvulling met alleen cirkels kunt maken. T 1
3 a Maak een vlakvulling met de onderstaande twee figuren. T 1
b Geef in je vlakvulling het patroon aan. T 1
v Verdiepingsvragen
5 Door een vierkant of rechthoek als basis te nemen kun je zelf vlakvullingen zoals die van Escher maken. Dit doe je als volgt:
v Teken een vierkant of rechthoek.
v Haal aan de linkerkant iets van de figuur af of teken er iets bij en doe het tegenovergestelde aan de rechterkant.
v Doe iets soortgelijks bij de onder en bovenkant.
De resulterende figuur vormt een vlakvulling:
4 a Maak een vlakvulling met de pijlpunt. T 1
b Geef in je vlakvulling het patroon aan. T 1
a Escher heeft dit principe toegepast voor de tekening Vogel (Nr. 128) (zie afbeelding op de rechterbladzijde). Leg uit hoe. T 2
b Wat je van de linker of rechterkant af haalt, kun je aan de onder of bovenkant erbij tekenen en andersom. Dit resulteert in vlakvullingen waarin de figuren ten opzichte van elkaar gedraaid zijn. Escher heeft dit principe toegepast voor de tekening Hagedis (Nr. 104) (zie afbeelding op de rechterbladzijde). Leg uit hoe. T 2
c Ontwerp zelf een soortgelijke vlakvulling. I

m.c. escher , Vogel (Nr. 128), 1967
v Onderzoeksopdracht
6 Onderzoek met behulp van internet op welke manieren Escher heeft geprobeerd om de oneindigheid van vlakvullingen te laten zien in zijn werken Kleiner en kleiner, Cirkellimiet III en Draaikolken. In hoeverre vind jij dat Escher daar in deze drie werken in geslaagd is? Verwerk de uitkomsten van je onderzoek in een verslag, poster, presentatie of video. I

m.c. escher , Hagedis (Nr. 104), 1959
v Heb je het leerdoel bereikt?
R Ik weet wat een vlakvulling is.
T 1 Ik kan zelf vlakvullingen tekenen met eenvoudige figuren.
T 2 Ik kan zelf vlakvullingen tekenen met complexe figuren.
I Ik kan uitleggen hoe Escher vlakvullingen ontwierp en kan zelf een soortgelijke vlakvulling ontwerpen.
BEGRIPPEN
vlakvulling patroon
2.1
DOEL > Je leert wat lijnen zijn, wat evenwijdig is en wat loodrecht is en hoe je de afstand tussen een punt en een lijn bepaalt.
Lijnen Hiernaast zie je lijn l, halve lijn m met beginpunt K en lijnstuk AB
v Een lijn is recht en heeft geen begin en geen eindpunt.
Omdat een lijn oneindig doorloopt, kun je altijd maar een gedeelte van de lijn tekenen.
v Een halve lijn is een deel van een lijn met een beginpunt.
v Een lijnstuk is een deel van een lijn tussen twee punten.
Lijnen geef je aan met een kleine letter, punten met een hoofdletter.
Snijden, evenwijdig en loodrecht
v Twee lijnen l en m die door hetzelfde punt S gaan, snijden elkaar.
S heet het snijpunt
v Twee lijnen p en q die elkaar niet snijden, zijn evenwijdig
Je noteert dit als p ∕∕ q. In een figuur geef je dit aan met pijltjes op de twee lijnen.
v De snijdende lijnen r en s staan loodrecht op elkaar. Je noteert dit als ⊥. In een figuur geef je dit aan met het teken ⅂ bij het snijpunt.
l m q
S S
Afstand De afstand van een punt P tot een lijn l is de lengte van het kortst mogelijke lijnstuk tussen P en l. Dit lijnstuk staat loodrecht op de lijn en heet de loodlijn van P op l.
Tekenen en meten Met een geodriehoek kun je lijnen en lijnstukken tekenen en lengtes en afstanden meten. Hieronder zie je hoe je met een geodriehoek evenwijdige en loodrechte lijnen tekent. Om een lijn evenwijdig aan lijn q te tekenen, leg je een van de evenwijdige lijnen van je geodriehoek op q. Om een lijn loodrecht op lijn s te tekenen, leg je de loodlijn van je geodriehoek op s
snijdende lijnen l en m evenwijdige lijnen, p ∕∕ q loodrechte lijnen, r ⊥ s l P p s q r loodlijn
tekenen van lijn p, evenwijdig aan lijn q
tekenen van lijn r, loodrecht op lijn s
OPDRACHTEN — OEFENEN
v Lijnen
7 Werkblad 2.7
a Teken lijnstuk AC T 1
b Teken de lijn die door A en B gaat. T 1
c Teken de halve lijn die in B begint en door C gaat. T 1
v Snijden, evenwijdig en loodrecht
8 a Welke lijnen zijn evenwijdig in de onderstaande figuur? T 1
b Welke lijnen staan loodrecht op elkaar? T 1
v Afstand
10 Werkblad 2.10
a Meet de afstand in millimeters nauwkeurig van punt P tot lijn l T 1
b Meet de afstand in millimeters nauwkeurig van punt P tot lijn m T 1
v Tekenen en meten
11 Werkblad 2.11
a Teken de lijn door punt P die evenwijdig is aan lijn m. T 1
b Teken de loodlijn vanaf punt Q op lijn m. T 1
12 Werkblad 2.12
a Lijnstuk CD is 4 cm lang en is evenwijdig aan lijnstuk AB . Teken lijnstuk CD . T 2
b Lijn n staat loodrecht op AB en gaat door het midden van AB . Teken lijn n T 2
9 a Hoe geef je in een figuur aan dat twee lijnen loodrecht op elkaar staan? R
b Gegeven is dat twee lijnen p en q allebei loodrecht op lijn t staan. Hoeveel snijpunten hebben de lijnen p en q met elkaar? Leg je antwoord uit. I
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
v Ontdekken
13 Werkblad 2.13
Teken alle punten die 4 cm van onderstaande lijn af liggen. T 2
14 a Bepaal de afstand van punt P tot lijn m T 1
b Waarom kun je nu meteen zeggen wat de afstand van punt Q tot lijn m is? T 2
c Hoe kun je de afstand tussen twee evenwijdige lijnen bepalen? I Q P m l
R1 Langs een snelweg staan hectometerpaaltjes. Als op een paaltje 102,5 staat, dan is de afstand van het beginpunt van de weg tot het paaltje 102,5 kilometer. Een auto passeert het paaltje waarop 102,5 staat en even later een paaltje met 97,7.
I Hoeveel kilometer is de afstand tussen beide paaltjes?
II Hoeveel meter is dat?
15 Als twee lijnen elkaar snijden, dan doen ze dat in één punt. Drie of meer lijnen kunnen meer snijpunten hebben.
a Hoe vaak kunnen drie lijnen elkaar maximaal snijden? En vier lijnen? Maak van beide situaties een voorbeeldtekening. T 2
b Neem de tabel over en vul hem in. Welke regelmaat zie je? T 2
aantal lijnen 2 3 4 5 maximum aantal snijpunten
c Hoe vaak kunnen elf lijnen elkaar maximaal snijden? I
v Onderzoeken
16 Lees de tekst De kunst van Piet Mondriaan op de rechterbladzijde. Ontwerp zelf een tekening in de stijl van Piet Mondriaan. Geef in je tekening aan welke lijnen evenwijdig aan elkaar zijn en welke loodrecht op elkaar staan. T 2
lijn evenwijdig halve lijn loodrecht lijnstuk afstand van punt tot lijn snijden loodlijn snijpunt geodriehoek

De kunst van Piet Mondriaan
Piet Mondriaan (1872–1944) was een bekende Nederlandse schilder uit de vorige eeuw. Mondriaan was een invloedrijk lid van de Nederlandse kunststroming De Stijl, waarin strakke lijnen, primaire kleuren en versimpeling van vormen centraal stonden. Ook was Mondriaan een van de eerste schilders die volledig abstracte schilderijen maakten. Hij werkte alleen met horizontale en verticale lijnen en de primaire kleuren rood, blauw en geel, aangevuld met grijs, wit en zwart. Op deze manier wilde hij elke associatie met de wereld om ons heen vermijden en de universele basisvormen achter de zichtbare werkelijkheid in zijn kunstwerken vangen.
piet mondriaan , Compositie met groot rood vlak, geel, zwart, grijs en blauw (1921)
v Heb je het leerdoel bereikt?
R Ik weet wat lijnen, halve lijnen en lijnstukken zijn. Ook weet ik wat de begrippen loodrecht en evenwijdig betekenen.
T 1 Ik kan loodrechte en evenwijdige lijnen tekenen. Ook kan ik de afstand tussen een punt en een lijn bepalen.
T 2 Ik kan meerdere lijnen tekenen die loodrecht op elkaar staan of evenwijdig aan elkaar zijn.
I Ik kan met behulp van de begrippen loodrecht en evenwijdig beredeneren hoeveel snijpunten lijnen hebben.
DOEL > Je leert wat hoeken zijn en hoe je ze kunt meten en tekenen.
Hoeken Een hoek heeft twee benen en een hoekpunt
Hiernaast zie je hoek A. In een figuur geef je een hoek met een boogje aan. Je kunt hoek A ook noteren als ∠ A
De grootte van een hoek meet je in graden. De hoek tussen twee lijnen die loodrecht op elkaar staan, is 90 graden groot.
Je noteert 90 graden als 90°. Een hoek kan scherp, recht, stomp, gestrekt, overstrekt of vol zijn :
benen hoekpunt
scherpe hoek rechte hoek stompe hoek gestrekte hoek overstrekte hoek volle hoek kleiner dan 90° 90° groter dan 90° en 180° groter dan 180° en 360° kleiner dan 180° kleiner dan 360°
Hoeken meten Met een geodriehoek kun je meten hoe groot een hoek is. Dat doe je als volgt:
1 Leg de geodriehoek met de lange kant langs een been en de 0 precies op het hoekpunt.
2 Lees bij het andere been af hoe groot de hoek is. Hoek A is stomp, dus ∠ A = 125°.
Hoeken tekenen Met een geodriehoek kun je hoeken tekenen. Hieronder zie je hoe je ∠ B = 27° tekent.
1
Teken één been van de hoek. Zet de letter bij het hoekpunt.
2
Leg de geodriehoek met de 0 precies op het hoekpunt en de lange kant van de geodriehoek langs het getekende been. Zet een stip bij het juiste aantal graden.
De hoek is scherp, dus kies je deze kant.
3
Teken een lijn door het hoekpunt en de stip. Teken een boogje en zet het aantal graden erbij.
OPDRACHTEN
v Hoeken
17 a Geef aan of de volgende hoeken scherp, stomp of recht zijn. T 1
b Hoeveel graden is een rechte hoek? R
c Hoeveel graden kan een overstrekte hoek zijn? R
d Hoeveel graden kan een scherpe hoek zijn? R
18 Leg steeds uit of de volgende hoeken scherp, recht, stomp, gestrekt, overstrekt en/of vol kunnen zijn. I
a de helft van een gestrekte hoek
b de helft van een stompe hoek
c het dubbele van een gestrekte hoek
d het dubbele van een scherpe hoek
v Hoeken meten
19 Werkblad 2.19
Meet de volgende hoeken. T 1
20 Zie de bovenstaande afbeelding.
Op een boot kun je met een kompas de richting bepalen waarin je moet varen. Deze richting heet de koers. Een koers meet je als de hoek ten opzichte van het noorden. Je meet altijd met de klok mee. Zo is de koers die hoort bij het oosten 90°. T 2
a Hoeveel graden is de koers NO ?
b Hoeveel graden is de koers NNW ?
c Welke richting hoort bij een koers van 270°?
v Hoeken tekenen
21 Teken de volgende hoeken.
a ∠ A = 1° T 1
b ∠ B = 45° T 1
c ∠ C = 144° T 1
d ∠ D = 212° T 2
22 Teken een hoek van 90° en verdeel deze in drie even grote hoeken. T 2
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
v Ontdekken
23 Werkblad 2.23
Meet alle hoeken in onderstaande ster. T 2
24 De wijzers van een klok maken een hoek met elkaar.
a Hoeveel graden is de hoek om 15.00 uur? T 1
b En om 19.30 uur? T 2
c De grote wijzer wijst naar de 12. De hoek tussen de wijzers is 150°. Hoe laat kan het zijn? T 2
25 De aarde draait in 24 uur om haar as. T 2
a Hoeveel graden draait de aarde in een uur?
b Hoeveel minuten duurt het voordat de aarde 1 graad is gedraaid?
v Onderzoeken
26 Werkblad 2.26
Lees de tekst Zonshoogte op de rechterbladzijde. Hieronder zie je op twee momenten in het jaar de lengte van de schaduw van een paaltje als de zon op het hoogste punt aan de hemel staat.
a Bepaal in beide gevallen de zonshoogte. T 1
b Een van de tekeningen is in de zomer gemaakt, de andere tekening in de winter. Leg uit welke tekening bij de zomer en welke bij de winter hoort. T 1
paaltje
REKENEN 60° ?
R2 In de vierhoek zijn de hoeken samen 360°. Hoe groot is de hoek met het vraagteken?
27 Zonnepanelen werken optimaal als de zon er loodrecht op staat. In Nederland staan de zonnepanelen ten opzichte van de zon gemiddeld het best als ze een hoek van 35° met de grond maken en naar het zuiden zijn gericht.
a Wat wordt hierboven bedoeld met ten opzichte van de zon gemiddeld het best staan? T 2
b Maak een schets van deze situatie, waarbij de zonnestralen loodrecht op de zonnepanelen vallen. T 2
c Op platte daken staan zonnepanelen vaak in rijen achter elkaar. Voor een goede opbrengst mogen de panelen niet in elkaars schaduw staan als de zonnestralen er loodrecht op vallen. Hieronder zie je een begin van zo’n rij zonnepanelen. Onderzoek waar de volgende rij panelen het best kan staan. I 35°
BEGRIPPEN
hoek stompe hoek benen gestrekte hoek hoekpunt overstrekte hoek graad volle hoek scherpe hoek zonshoogte rechte hoek
zonshoogte
Zonshoogte
De zonshoogte is de hoek die de zon ten opzichte van de aarde maakt. Elke dag komt de zon in het oosten op. Aan het begin van de middag staat ze op het hoogste punt aan de hemel en in de avond gaat ze weer in het westen onder. In Nederland is de maximale zonshoogte in de zomer 61° en in de winter 14°. Met behulp van de schaduw van een paaltje kun je de zonshoogte bepalen.
zonshoogte
schaduw
paaltje
v Heb je het leerdoel bereikt?
R Ik weet wat hoeken zijn en welke soorten er zijn.
T 1 Ik kan hoeken tekenen en meten.
T 2 Ik kan hoeken gebruiken in realistische situaties.
I Ik kan redeneren over hoeken.
DOEL > Je leert wat driehoeken, vierhoeken, rechthoeken, vierkanten en cirkels zijn.
Driehoeken Een meetkundig figuur in een plat vlak heet een vlakke figuur. Een driehoek is een vlakke figuur met drie hoekpunten die verbonden zijn door lijnstukken. Deze lijnstukken heten de zijden van de driehoek. Hiernaast zie je driehoek ABC met hoekpunten A, B en C. Je kunt driehoek ABC noteren als ∆ ABC. Een driehoek heeft altijd twee scherpe hoeken. De derde hoek kan scherp, recht of stomp zijn: 2.3
scherphoekige driehoek rechthoekige driehoek stomphoekige driehoek drie scherpe hoeken één rechte hoek één stompe hoek
Vierhoeken, rechthoeken en vierkanten
v Een vierhoek is een vlakke figuur met vier hoekpunten en vier zijden. De lijnstukken tussen twee tegenover elkaar liggende hoekpunten heten diagonalen.
v Een rechthoek is een vierhoek waarvan de zijden loodrecht op elkaar staan. De tegenover elkaar liggende zijden van een rechthoek zijn even lang. De diagonalen van een rechthoek snijden elkaar middendoor. v Een vierkant is een rechthoek waarvan alle zijden even lang zijn. De diagonalen van een vierkant staan loodrecht op elkaar.
In een figuur geef je aan dat zijden even lang zijn door er dezelfde tekentjes op te plaatsen.
Cirkel Een cirkel is een figuur waarvan alle punten dezelfde afstand hebben tot een punt M. Dat punt heet het middelpunt van de cirkel. De grootte van een cirkel geef je aan met de straal of met de diameter De straal is de afstand van het middelpunt tot een punt op de cirkel. De diameter is twee keer deze afstand. Cirkels teken je met een passer
v Driehoeken
28 Welke van de volgende driehoeken zijn stomphoekig? T 1
29 Werkblad 2.29
In de figuur is een begin gemaakt met het tekenen van ∆ ABC. Hoek A is recht.
Maak de driehoek af. T 1
v Vierhoeken, rechthoeken en vierkanten
31 a Teken een vierkant met zijden van 4 cm. Teken ook de diagonalen. T 1
b Teken een rechthoek waarvan de kortste zijde 3 cm en de langste zijde 7 cm is. T 1
32 Geef aan of de volgende uitspraken juist of onjuist zijn. R
A Een vierhoek heeft twee diagonalen.
B De diagonalen van een rechthoek snijden elkaar middendoor en staan loodrecht op elkaar.
v Cirkel
33 a Teken een cirkel met een straal van 3 cm. T 1
b Teken ook een vierkant met zijden van 6 cm en de cirkel die door de hoekpunten van het vierkant gaat. T 2
c Meet de diameter van de cirkel die je in opdracht b hebt getekend. Geef je antwoord in millimeters nauwkeurig. T 1
34 Werkblad 2.34
a Teken alle punten die op 4 cm afstand van B liggen. T 1
b Teken alle punten die op 3 cm afstand van A en op 2 cm afstand van C liggen. T 2
c Teken alle punten die op 1 cm afstand van een van de zijden van ∆ ABC liggen. I
30 a Leg uit waarom een driehoek geen twee rechte hoeken kan hebben.
Tip: probeer zo’n driehoek te tekenen. T 2
b Leg uit waarom een driehoek geen twee stompe hoeken kan hebben. I
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
v Ontdekken
35 Werkblad 2.35
Hieronder zie je een kaart van de provincie
Overijssel. Geef op het werkblad aan welke plaatsen op minder dan 40 km afstand van Zwolle én op minder dan 20 km afstand van Almelo liggen. T 2
36 Werkblad 2.36
Hieronder zie je een zeshoek.
a Hoeveel scherpe hoeken heeft deze zeshoek? T 2
b Meet de grootste hoek in deze zeshoek. T 2
c De lijnstukken tussen twee niet naast elkaar liggende hoekpunten heten diagonalen. Teken alle diagonalen. Wat valt je op? T 2
37 Werkblad 2.37
Het onderstaande lijnstuk AC is een diagonaal van vierkant ABCD . Teken dit vierkant. T 2
v Onderzoeken
38 Lees de tekst Regelmatige veelhoeken op de rechterbladzijde.
a Neem de onderstaande tabel over en vul hem in. T 1
b Welke regelmaat zie je in de tabel? T 2
c Hoeveel zijden en hoeveel diagonalen heeft een regelmatige vijfentwintighoek? I
regelmatige veelhoek 3 4 5 6 7
aantal zijden
aantal diagonalen
39 Stel je een groep mensen voor waarbij iedereen elkaar één keer de hand schudt. Hoeveel keer is er dan handen geschud?
Dit is een bekend probleem uit de wiskunde dat het handenschudprobleem heet. Je kunt dit probleem oplossen met behulp van regelmatige veelhoeken. Elk hoekpunt stelt daarbij een persoon voor. I
a Leg uit wat de zijden en de diagonalen voorstellen.
b Hoeveel keer is er handen geschud in een groep van 5 mensen?
c En hoeveel keer in een groep van 25 mensen?
regelmatige driehoek
regelmatige vierhoek
regelmatige vijfhoek

regelmatige zeshoek
regelmatige zevenhoek
Regelmatige veelhoeken
Een regelmatige veelhoek is een vlakke figuur waarvan de zijden allemaal dezelfde lengte hebben en alle hoeken even groot zijn. In de natuur komen regelmatige veelhoeken op diverse plekken voor. Zo bestaan honingraten uit regelmatige zeshoeken. Dit geldt ook voor sommige basaltformaties, zoals de Giant’s Causeway (Pad der Reuzen) in NoordIerland.
v Heb je het leerdoel bereikt?
R Ik weet wat driehoeken, vierhoeken, rechthoeken, vierkanten en cirkels zijn.
T 1 Ik kan herkennen met wat voor soort driehoek ik te maken heb en ik kan cirkels tekenen met behulp van een passer.
T 2 Ik kan een tekening van een vlakke figuur afmaken als een deel gegeven is.
I Ik kan uitleggen wat regelmatige veelhoeken te maken hebben met het handenschudprobleem.
REKENEN BEGRIPPEN
R3 Van noord naar zuid is Nederland ongeveer 300 km lang en van oost naar west ongeveer 200 km breed.
Hoe groot zou de kaart van opdracht 35 zijn als heel Nederland erop afgebeeld zou staan?
vlakke figuur rechthoek driehoek vierkant zijde cirkel scherphoekige driehoek middelpunt rechthoekige driehoek straal stomphoekige driehoek diameter vierhoek passer diagonaal regelmatige veelhoek
DOEL > Je leert hoe je figuren kunt tekenen en spiegelen.
Tekenen Om een drie of vierhoek te kunnen tekenen, moet je voldoende informatie hebben over de grootte van de zijden en de hoeken. Soms heb je alleen een geodriehoek nodig, in andere gevallen ook een passer.
Voorbeeld
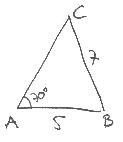
Teken ∆ ABC met AB = 5 cm, BC = 7 cm en ∠ A = 70°. Je maakt eerst een schets met alle gegevens (1). Dit hoeft niet heel precies en doe je zonder geodriehoek en passer. In de schets zie je dat je van hoek A het meest weet. Je begint daarom met het tekenen van deze hoek (2) en lijnstuk AB (3). Punt C ligt op 7 cm afstand van punt B en dus op een cirkel met een straal van 7 cm en middelpunt B Met je passer teken je het deel van deze cirkel dat het opstaande been van hoek A snijdt. Het snijpunt is punt C. Je kunt nu lijnstuk BC tekenen (4). Om te laten zien hoe je de driehoek hebt geconstrueerd, gum je constructielijnen niet uit, maar laat je ze staan.
Spiegelen Een driehoek ABC kun je spiegelen in een punt (1) of in een lijn (2). Je spiegelt hoekpunten A, B en C door op even grote afstand aan de andere kant van het punt of de lijn de punten A', B' en C ' te tekenen. ∆ ABC heet het origineel en ∆ A'B'C' het spiegelbeeld .
OPDRACHTEN — OEFENEN
v Tekenen
40 a Teken ∆ ABC met AB = 6 cm, BC = 8 cm en ∠ A = 35°. T 1
b Teken ∆ KLM met KL = 6 cm, ∠ K = 40° en ∠ L = 105°. T 1
41 a Teken een driehoek waarvan alle zijden 5 cm zijn. T 1
b Leg uit welke stappen je moet zetten om een driehoek met gelijke zijden te tekenen. T 1
42 Teken vierhoek PQRS met PQ = PS = 4 cm, QR = 5 cm, RS = 7 cm en ∠ Q = 112°. T 2
43 Teken ∆ ABC met AB = 5 cm, BC = 4 cm en ∠ A = 50°, waarbij ∆ ABC scherphoekig is. T 2
44 Kun je een driehoek tekenen waarvan alle drie de hoeken wel en de zijden niet bekend zijn? I
v Spiegelen
45 Leg uit wat het verschil is tussen spiegelen in een punt en spiegelen in een lijn. R
46 Werkblad 2.46
Spiegel onderstaande driehoek ABC in punt P T 1
47 Werkblad 2.47 Spiegel onderstaande driehoek PQR in lijn l. T 2
50 Werkblad 2.50 Spiegel de cirkel in lijn n T 2 2.4
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
v Ontdekken
48 Teken ∆ PQR met PQ = 5 cm en ∠ P = 90° en waarvan de langste zijde 8 cm is. T 2
49 Leg uit waarom er geen driehoek met zijden van 5 cm, 3 cm en 10 cm bestaat. I
v Onderzoeken
51 Lees de tekst Euclides en meetkundige constructies op de rechterbladzijde.
In deze opdracht ga je een regelmatige zeshoek construeren. T 2
v Teken een cirkel met een straal van 4 cm.
v Zet boven aan de cirkel een punt. Teken een nieuwe cirkel met dit punt als middelpunt en een straal van 4 cm.
v De cirkels snijden elkaar. Zet de passerpunt op zo’n snijpunt en teken weer een cirkel met een straal van 4 cm. Herhaal dit tot je helemaal rond bent.
REKENEN
52 Construeer de volgende afbeelding. I M n
R4 Bereken.
I
V
v De snijpunten zijn de hoekpunten van een regelmatige zeshoek. Teken de regelmatige zeshoek.

Euclides en meetkundige constructies
Euclides was een zeer beroemde Griekse wiskundige die rond 300 v.Chr. werkzaam was in de bibliotheek van Alexandrië. Zijn bekendste werk, Elementen, is een van de invloedrijkste boeken in de wiskunde. Het was tot aan het begin van de 20 ste eeuw de belangrijkste lesmethode wiskunde in het onderwijs, vooral in de meetkunde.
Euclides was van mening dat elke uitspraak bewezen moest worden. Hij vertrouwde daarbij niet op metingen van afstanden en hoeken. Meetkundige figuren mochten daarom alleen met een passer en een liniaal zonder markeringen getekend worden. Een figuur tekenen zonder dat je hoeken of afstanden kunt meten, heet construeren.
Euclides construeert met een passer een figuur. Detail van een fresco door Rafaël, De school van Athene (ongeveer 1510).
v Heb je het leerdoel bereikt?
R Ik weet wat spiegelen in een punt en een lijn is.
T 1 Ik kan figuren tekenen als er enkele hoeken en / of zijden bekend zijn. Ik kan ook figuren spiegelen.
T 2 Ik kan figuren tekenen en spiegelen in complexere situaties.
I Ik kan beredeneren wanneer een driehoek wel en wanneer die niet getekend kan worden en ik kan meetkundige figuren construeren.
BEGRIPPEN
spiegelen origineel spiegelbeeld construeren
2.5
DOEL > Je leert wat lijn-, punt- en draaisymmetrie zijn.
Lijnsymmetrie Als je een lijn in een figuur kunt tekenen zodat de twee helften elkaars spiegelbeeld zijn, dan heet de figuur lijn of spiegelsymmetrisch. De figuur verandert dan niet als je elk punt van de figuur in deze lijn spiegelt. Zo’n lijn heet een symmetrieas van de figuur. Als je een lijnsymmetrische figuur dubbelvouwt over een symmetrieas, dan passen de twee helften precies op elkaar. Een figuur kan meerdere symmetrieassen hebben.
Voorbeelden
Draaisymmetrie De figuur hiernaast blijft gelijk als je die een vijfde slag draait. Een dergelijke figuur, die bij draaien over minder dan een volle slag (360°) gelijk blijft, heet draaisymmetrisch. Het punt waar je de figuur omheen draait, heet het draaipunt. De kleinste hoek waarover je de figuur kunt draaien en waarbij de figuur gelijk blijft, heet de kleinste draaihoek. De figuur hiernaast heeft een kleinste draaihoek van 360° : 5 = 72°.
symmetrieas
1 symmetrieas 2 symmetrieassen 4 symmetrieassen P
Puntsymmetrie De figuur hiernaast blijft gelijk als je alle punten van de figuur in punt P spiegelt. Zo’n figuur heet puntsymmetrisch. Het punt waarin je de figuur spiegelt, heet het centrum van de figuur. Spiegelen in het centrum komt op hetzelfde neer als de figuur 180° draaien om het centrum. Een puntsymmetrische figuur is dus ook draaisymmetrisch over een hoek van 180°.
Voorbeelden
v draaisymmetrisch, kleinste draaihoek = 120° v draaisymmetrisch, kleinste draaihoek = 180° v puntsymmetrisch
v draaisymmetrisch, kleinste draaihoek = 60° v puntsymmetrisch v lijnsymmetrisch, 6 symmetrieassen
v Lijnsymmetrie
53 Werkblad 2.53
Je ziet vijf figuren.Welke figuren zijn lijnsymmetrisch? Teken alle symmetrieassen in deze figuren. T 1
54 Je ziet verschillende figuren. Welke figuren zijn lijnsymmetrisch? Geef voor deze figuren ook het aantal symmetrieassen. T 1
v Draaisymmetrie
56 Een mandala is een spiritueel symbool dat in het boeddhisme en het hindoeïsme door monniken gebruikt werd om te mediteren. Tegenwoordig kun je mandala’s ook in kleurboeken tegenkomen. De volgende mandala’s zijn draaisymmetrisch. Geef de kleinste draaihoek van beide mandala’s. T 1
55 Werkblad 2.55
Je ziet een deel van een lijnsymmetrische figuur met symmetrieas l. Het deel dat je ziet, bestaat uit een lijnstuk en een halve cirkel. Teken de complete figuur. T 2
57 Werkblad 2.57
Je ziet een deel van een draaisymmetrische figuur met als kleinste draaihoek 90°. Het punt dat getekend is, is het draaipunt. Teken de complete figuur. T 2
v Puntsymmetrie
58 Werkblad 2.58
Je ziet een deel van een puntsymmetrische figuur met centrum P. Teken de complete figuur. T 2
OPDRACHTEN
v Ontdekken
59 a Noem drie landen met een lijnsymmetrische vlag. Teken deze vlaggen in je schrift en geef daarin de symmetrieassen aan. T 1
b Noem drie landen met een puntsymmetrische vlag. Teken deze vlaggen in je schrift. T 1
60 Een regelmatige veelhoek is een vlakke figuur waarvan de zijden allemaal dezelfde lengte hebben en alle hoeken even groot zijn. Hieronder zie je een regelmatige zevenhoek.
a Hoeveel symmetrieassen heeft een regelmatige zevenhoek? T 2
Tip: schets een zevenhoek en teken daarin de symmetrieassen.
b Hoeveel symmetrieassen heeft een regelmatige achthoek? T 2
Tip: schets een achthoek en teken daarin de symmetrieassen.
c Hoeveel symmetrieassen heeft een regelmatige honderdhoek? En een regelmatige honderdeneenhoek? I
61 a Leg uit waarom een figuur pas draaisymmetrisch heet als de kleinste draaihoek kleiner is dan 360°. I
b Leg uit of een figuur een kleinste draaihoek van 50° kan hebben. I
c Leg uit of een figuur draaisymmetrisch kan zijn over een hoek van 50°. I
d Wat kun je zeggen over de kleinste draaihoek van een cirkel? I
v Onderzoeken
62 Lees de tekst Het 196-probleem op de rechterbladzijde.
a Waarom begint het rekenrecept met getallen die uit ten minste twee cijfers bestaan? I
b Hoeveel palindroomgetallen zijn er met drie cijfers? T 2
c Hoeveel palindroomgetallen zijn er met vier cijfers? En met vijf cijfers? Wat valt op? I
d Welk palindroomgetal krijg je als je begint met het getal 496 en het rekenrecept volgt? T 2
REKENEN
R5 In een regelmatige veelhoek zijn alle hoeken even groot.
I In een regelmatige achthoek is elke hoek 135°. Hoe groot zijn alle hoeken samen?
II In een regelmatige negenhoek zijn alle hoeken samen 1260°. Hoe groot is elke hoek?
Het 196-probleem
Een palindroom is een woord dat achterstevoren gelezen hetzelfde blijft, bijvoorbeeld kok, lepel en legovogel. Deze woorden zijn symmetrisch ten opzichte van hun midden. Er bestaan ook palindroomgetallen, bijvoorbeeld 55, 212, 57675 en 98733789. Als je deze getallen achterstevoren leest, krijg je steeds hetzelfde getal. Deze getallen zijn ook symmetrisch ten opzichte van hun midden.
Als een getal geen palindroomgetal is, kun je er met het volgende rekenrecept meestal een palindroomgetal van maken :
Noteer een positief geheel getal van ten minste twee cijfers. Schrijf daaronder de cijfers achterstevoren op en tel het nieuwe getal bij het oorspronkelijke getal op. Controleer of de uitkomst een palindroomgetal is. Is dit niet het geval, herhaal dit dan met het getal dat je als uitkomst hebt gekregen. Ga net zolang door tot je een palindroomgetal hebt.
Als je dit met het getal 245 doet, krijg je het palindroomgetal 787:
245 542 787
BEGRIPPEN
symmetrie kleinste draaihoek lijnsymmetrie puntsymmetrie spiegelsymmetrie centrum symmetrieas palindroom draaisymmetrie palindroomgetal draaipunt
Bij het getal 149 heb je twee stappen nodig: 149 941 1090 0901 1991
Bij het getal 89 moet je maar liefst 24 stappen doorrekenen voordat je bij het palindroomgetal 8 813 200 023 188 komt.
De vraag is of elk getal op deze manier een palindroomgetal oplevert. Voor het getal 196 zijn al meer dan een biljoen stappen doorgerekend, maar er is nog geen palindroomgetal uitgekomen.
Men denkt dat dit nooit zal gebeuren, maar zeker is dat niet. Er zijn meer van zulke getallen, maar 196 is het kleinste getal waarbij nog nooit een palindroomgetal is gevonden. Het vraagstuk of je altijd op een palindroomgetal uitkomt, wordt om deze reden ook wel het 196probleem genoemd.
v Heb je het leerdoel bereikt?
R Ik weet wat punt, lijn en draaisymmetrie zijn.
T 1 Ik kan de symmetrieassen van een lijnsymmetrische figuur tekenen en bepalen wat de kleinste draaihoek is van een draaisymmetrische figuur.
T 2 Ik kan incomplete figuren zo afmaken dat ze symmetrisch zijn.
I Ik kan uitleggen wat het 196probleem met symmetrie te maken heeft.
Kijk aan het eind van elke paragraaf of je de begrippen kent en het leerdoel hebt bereikt. Zo niet, lees dan de uitleg nog eens goed door of bekijk de uitlegvideo's. Maak daarna de volgende opdrachten.
v Academie
63 a Maak een vlakvulling met de onderstaande figuur. T 1
b In combinatie met een vierkant kun je met deze figuur twee verschillende vlakvullingen maken. Maak ze allebei. T 2
64 Kun je met elke driehoek een vlakvulling maken? Leg je antwoord uit. I
v § 2.1
65 Werkblad 2.65
a Lijn k gaat door punt A en is evenwijdig aan lijn l. Teken lijn k. T 1
b Lijnstuk AB snijdt lijn l in punt S. Lijn m gaat door S en staat loodrecht op lijnstuk AB. Teken lijn m. T 1
c Meet de afstand van punt B tot lijn l. Geef de afstand in millimeters nauwkeurig. T 1
66 Gegeven twee lijnen l en m
Wat betekent l ∕∕ m ? R
v § 2.2
67 Teken de volgende hoeken. T 1
a ∠ A = 42°
b ∠ B = 118°
68 a Hoeveel graden kan een gestrekte hoek zijn? R
b Hoeveel graden kan een stompe hoek zijn? R
v § 2.3
69 Werkblad 2.69
a Teken de cirkel met middelpunt A en een straal van 3 cm. T 1
b Wat is de grootst mogelijke afstand tussen twee punten die op deze cirkel liggen? Teken twee van zulke punten op de cirkel. T 2
c Teken alle punten die 3 cm van A en 5 cm van B af liggen. Laat zien hoe je de punten gevonden hebt. T 2
v § 2.4
70 Teken ∆ KLM met KL = 3 cm, KM = 6 cm en ∠ L een rechte hoek. T 2
71 Werkblad 2.71
∆ ABC wordt gespiegeld in een punt P Punt B' is het spiegelbeeld van B. Bepaal waar punt P ligt en maak het spiegelbeeld af. T 2
v Hoofdstuk 2
74 Werkblad 2.74
a Meet alle hoeken in de onderstaande figuur. T 1
b Geef aan of de hoeken scherp, recht of stomp zijn. T 1
c Teken de diagonalen van de vierhoek. T 1
d Wat voor soort driehoek is ∆ PRS ? T 1
e Leg uit of je een vierkant kunt tekenen met de hoekpunten P, Q en S en waarvan het vierde hoekpunt op lijnstuk PR ligt. I
v § 2.5
72 a Welke verkeersborden zijn lijnsymmetrisch? Geef bij deze borden ook het aantal symmetrieassen. T 1 b Welke borden zijn puntsymmetrisch? T 1
73 Hoeveel symmetrieassen heeft een cirkel? I
75 Leg uit of de volgende beweringen juist of onjuist zijn. I
A Evenwijdige lijnen kunnen niet loodrecht op elkaar staan.
B Een scherphoekige driehoek kan een stompe hoek hebben.
C Als de diagonalen van een vierhoek loodrecht op elkaar staan, is de vierhoek een vierkant.
D Het aantal diagonalen van een vijfhoek is altijd 5.
E Een figuur die draaisymmetrisch is met een kleinste draaihoek van 80° kan ook puntsymmetrisch zijn.
76 Welke regelmatige veelhoek heeft een kleinste draaihoek van 36° ? T 2