methodeconcept / redactie
Boom voortgezet onderwijs
auteurs
Corné van Berchum
Barbara van der Dussen
Tom Eitjes
Paul Gritter
Piet Hanemaaijer
Henk Hollander
Ilona van Houwelingen-Verkaik
Marieke Spijkstra
Francisca Stinnissen
Hilde van der Togt
Arjen Zomerman
1 Meetkunde
wiskundeweetje
Van tegelvloer naar kunstwerk 8
1.1 Punten, lijnstukken en lijnen 10
1.2 Snijden en evenwijdig 14
1.3 Loodrecht 18
1.4 Rechthoek, vierkant en driehoeken 22
1.5 Cirkel 26
praktische wiskunde
Architectuur 30
Toetsvoorbereiding 32
2 Getallen
wiskundeweetje
Romeinse cijfers 38
2.1 Grote getallen 40
2.2 Decimale getallen 44
2.3 Afronden 48
2.4 Handig vermenigvuldigen en delen 52
2.5 De rekenmachine 56
praktische wiskunde
Kassa 60
Toetsvoorbereiding 62
3 Grafieken
wiskundeweetje
Waar ben ik op aarde? 68
3.1 Assenstelsel en coördinaten 70
3.2 Punten tekenen in een assenstelsel 74
3.3 Grafieken 78
3.4 Grafieken aflezen 82
3.5 Grafieken tekenen 86
praktische wiskunde
Weergrafieken 90
Toetsvoorbereiding 92
wiskundeweetje
Kompas 98
4.1 Hoeken 100
4.2 Hoeken meten 104
4.3 Hoeken tekenen 108
4.4 Kijklijnen en kijkhoeken 112
4.5 Driehoeken 116
praktische wiskunde
Gezichtsveld en blikveld 120
Toetsvoorbereiding 122
5 Negatieve getallen
wiskundeweetje
Normaal Amsterdams Peil 128
5.1 Positieve en negatieve getallen 130
5.2 Rekenen op de getallenlijn 134
5.3 Optellen en aftrekken met negatieve getallen 138
5.4 Vermenigvuldigen en delen met negatieve getallen 142
5.5 Rekenvolgorde 146
praktische wiskunde Bankrekening 150
Toetsvoorbereiding 152
6 Vlakke figuren
wiskundeweetje
Meten is weten 158
6.1 Eigenschappen van vlakke figuren 160
6.2 Lijnsymmetrie 164
6.3 Lengte-eenheden 168
6.4 Omtrek van vlakke figuren 172
6.5 De omtrek van een cirkel 176
praktische wiskunde
Tangram 180
Toetsvoorbereiding 182
rechthoek KLMN
driehoek ABC
doel → Je maakt kennis met horizontale en verticale lijnen en met vlakvullingen.
Vlakvullingen
Hoeken
De tegels van een tegelvloer vormen samen een patroon.
In een patroon herhalen de vormen zich steeds. De tegels liggen zó tegen elkaar aan, dat er geen gaten tussen de tegels zitten: het hele vlak is gevuld. Zo’n patroon heet een vlakvulling.
Opdrachten — Vlakvullingen
Je ziet een tegelvloer getekend op een rooster. t1
a Maak de tegelvloer verder af volgens het patroon.
b Kleur de tegelvloer in.
horizontale lijn
verticale lijn
De vlakvulling hierboven noemen we een rooster. Het rooster bestaat uit horizontale en verticale lijnen.
Een horizontale lijn loopt van links naar rechts.
Een verticale lijn loopt van boven naar beneden.
Hieronder zie je een andere vlakvulling:
Voor de betegeling van een muur zijn twee soorten tegels gebruikt. Je ziet een deel van de muur getekend.
a Teken er een even groot stuk muur onder in hetzelfde patroon. t2
b Kleur de muur in. t1
3
Piet Mondriaan (1872-1944) was een Nederlandse schilder.
Hij maakte gebruik van vlakvullingen.
Op veel van zijn schilderijen werkte hij met horizontale en verticale lijnen. Hij gebruikte daarbij de kleuren rood, blauw, geel, grijs, wit en zwart.
Piet Mondriaan, ‘Compositie met groot rood vlak, geel, zwart, grijs en blauw’ (1921)
Hiernaast zie je een vlakvulling in de stijl van Mondriaan. Teken het na op het rooster hieronder. Gebruik een liniaal. t1
Maak nu zelf een vlakvulling op de manier van Mondriaan. Gebruik horizontale en verticale lijnen en kies dezelfde kleuren als Mondriaan. i
Woorden patroon horizontaal vlakvulling verticaal rooster Doel bereikt?
Kruis aan:
◻ Ik weet wat horizontale en verticale lijnen zijn. Ik weet wat r een vlakvulling is.
◻ Ik kan een eenvoudige vlakvulling op een rooster natekenen. t1
◻ Ik kan een vlakvulling met twee tegelsoorten afmaken. t2
◻ Ik kan zelf een vlakvulling maken met horizontale en i verticale lijnen.
doel → Je leert wat punten, lijnstukken en lijnen zijn en hoe je ze meet en tekent met de geodriehoek.
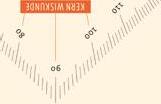
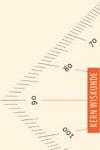
De geodriehoek
ɲ Liniaal
ɲ De lange zijde van je geodriehoek is een liniaal. Met de liniaal kun je rechte lijnen tekenen en lengtes meten.
ɲ Lengte meten
ɲ Leg de liniaal van de geodriehoek langs de lijn met de 0 op het beginpunt.
ɲ Lees bij het eindpunt de afstand af.
Voorbeeld
Op de tekening staan twee punten. Je meet de afstand tussen de twee punten zo:
ɲ Leg de geodriehoek met de 0 op het ene punt en lees bij het andere punt de afstand af.
Opdrachten — De geodriehoek
Vul in. r a Waarmee teken je een rechte lijn?
b Met je geodriehoek je lengtes. Je ziet hier vijf genummerde punten. a Teken rechte lijnen van 1 naar 3, van 1 naar 4, van 2 naar 4, van 2 naar 5 en van 3 naar 5. t1
AB = 7 cm A
b Wat voor figuur heb je getekend? Kleur deze in. t2
Je ziet hier de nummers 1 tot en met 6. t1
a De afstand tussen 1 en 2 is cm.
b De afstand tussen 3 en 4 is cm.
c De afstand tussen 5 en 6 is cm.
d Tussen welke twee punten is de afstand het grootst?
Je ziet hieronder een kaart met de Waddeneilanden.
a Vul in. Op de kaart is de afstand tussen de haven van Vlieland en de haven van Terschelling cm. t2
b Tussen welke twee eilanden die naast elkaar liggen is de afstand het grootst? t2
c Hoe groot is de afstand tussen de haven van Harlingen en de haven van Terschelling? i
Schiermonnikoog Ameland Terschelling
Holwerd Nes West-Terschelling Oost-Vlieland
Vlieland Texel
Harlingen
Schiermonnikoog
a Teken een lijn van de kat naar de boom. Teken ook een lijn van de hond naar de kat en van de hond naar de boom. t1
b Hoeveel centimeter is de langste lijn? t2
c Wie is het eerst bij de boom? i
Kijk naar de tekening. Drie personen staan op het strand. t2
a Wie is het dichtst bij de zee?
b Wie is het dichtst bij de visser?
Punt, lijnstuk en lijn
ɲ Punt
ɲ Een punt geeft een plaats aan.
ɲ Gebruik een hoofdletter om de punt een naam te geven.
Je ziet hier punt P. P punt P
ɲ Lijnstuk
ɲ De kortste weg tussen twee punten A en B is een lijnstuk.
ɲ Een lijnstuk heeft een beginpunt en een eindpunt.
ɲ Gebruik de letters van twee punten om het lijnstuk een naam te geven. Je ziet hier lijnstuk AB.
lijnstuk AB A B
ɲ Lijn
ɲ Een lijn is recht en heeft geen beginpunt of eindpunt.
ɲ Gebruik een kleine letter om de lijn een naam te geven.
Je ziet hier lijn l. l lijn I
Opdrachten — Punt, lijnstuk en lijn
a Wat is een lijnstuk? r
b Wat is het verschil tussen een lijn en een lijnstuk? t2
Meet de lijnstukken AB, CD en EF. t1
a AB = cm
b CD = cm c EF = cm
Bekijk de punten A, B, C en D.
a Teken de lijnstukken AB, BC, CD en AD. t1
b Meet de lijnstukken. Vul in:
De lijnstukken zijn cm. t1
c Teken lijnstuk AC. t1
d Omcirkel: lijnstuk AC is korter dan / even lang als / langer dan andere lijnstukken. t2
Hierboven zie je de kaart van Nederland.
a Teken de kortste afstand van Den Haag (D) naar
Zwolle (Z). t1
b Een helikopter vliegt van Den Haag naar Leeuwarden (L) via Haarlem (H). Op de terugweg vliegt de helikopter via Zwolle. Omcirkel het juiste antwoord:
De heenweg is korter / langer dan de terugweg. I
15
Je ziet een aantal lijnen en lijnstukken. Zet een kruisje bij de lijnen en een rondje bij de lijnstukken. r
Breinbreker
a Hoeveel rechte lijnen kun je door één punt tekenen?
b Een lijn gaat door twee punten. Hoeveel verschillende lijnen kun je door deze punten tekenen?
Woorden
geodriehoek lijnstuk liniaal lijn
punt Doel bereikt?
Kruis aan:
◻ Ik weet wat punten, lijnstukken en lijnen zijn. Ik weet hoe r je met een geodriehoek lijnen kunt tekenen en afstanden tussen twee punten kunt meten.
◻ Ik kan met de geodriehoek lijnen tekenen en t1 de lengte van lijnstukken meten.
◻ Ik kan bepalen wat het kortste lijnstuk is door lijnen t2 met elkaar te vergelijken.
◻ Ik kan mijn kennis over punten, lijnstukken en i lijnen toepassen op een plattegrond of een landkaart.
doel → Je leert wat ‘snijden’ en ‘evenwijdig zijn’ betekent. 1.2 S m l k
Snijdende lijnen
Snijden
ɲ Twee lijnen die door hetzelfde punt gaan, snijden elkaar.
ɲ Het punt waar lijnen elkaar snijden, heet het snijpunt.
ɲ Het punt S heet het snijpunt van l m l
Opdrachten — Snijdende lijnen
Je ziet lijn k. t1
a Teken een lijn m die lijn k snijdt.
b Zet het snijpunt erbij en noem dit S.
a Teken een lijn p en lijn q, die elkaar snijden. t1
b Zet het snijpunt erbij en noem dit T. t1
c Teken lijn r door T. t2
Bekijk de tekening.
a Teken een lijn s door A en C en een lijn t door B en C. t1
b Vul in. AC = cm en BC = cm. t1
c Teken een punt D op lijn l. t1
d Vul in. CD = cm. t1
e Vergelijk jouw tekening met die van een klasgenoot. Bespreek samen wie de kortste afstand heeft getekend. i
Welke foto hoort er niet bij? Leg je antwoord uit. i
Kijk naar de tekening rechtsboven. De lamp (L) veroorzaakt een schaduw onder de tafel.
a Teken een lijn vanuit punt L door punt S naar de grond. t1
b Teken een lijn vanuit punt L door punt T naar de grond. t1
c Zet punten M en N waar de lijnen de grond snijden. t1
d De lengte van de schaduw is cm. t2
Evenwijdige lijnen
Evenwijdig
ɲ Twee lijnen die elkaar niet snijden, zijn evenwijdig.
ɲ Gebruik het teken
voor evenwijdige lijnen: p ⁄ ⁄ q. Je zegt: ‘Lijn p is evenwijdig aan lijn q.’
ɲ Zet hetzelfde aantal pijltjes op evenwijdige lijnen in een figuur.
Geodriehoek
ɲ Op een geodriehoek staan ook evenwijdige lijnen.
ɲ Zo controleer je of lijnen evenwijdig zijn:
ɲ Leg de liniaal van je geodriehoek langs een lijn.
ɲ Ligt een evenwijdige lijn van je geodriehoek op de andere lijn? Dan zijn de lijnen evenwijdig.
l m evenwijdige lijnen
ɲ Zo teken je evenwijdige lijnen:
ɲ Leg een evenwijdige lijn van je geodriehoek op een lijn.
Bijvoorbeeld lijn l.
ɲ Teken langs de liniaal van je geodriehoek lijn m.
ɲ Zet pijltjes op de lijnen.
Opdrachten — Evenwijdige lijnen
a Met welk teken geef je in een figuur aan dat twee lijnen evenwijdig zijn? r
b Hoeveel evenwijdige lijnen staan er op je geodriehoek? t1
c Schrijf op: lijn l is evenwijdig aan lijn m. Gebruik tekens. t1
a Controleer met je geodriehoek of de lijnen k en m evenwijdig zijn. t1
b Teken op de lijnen een pijltje als ze evenwijdig zijn. t1 k m
a Teken een lijn die evenwijdig is aan lijn l. t1
b Noem de lijn m. t1
c Geef met een teken aan dat l
m. t1 l
Je ziet lijn m en de punten D en E.
a Teken een lijn evenwijdig aan lijn m door punt D.
Noem de lijn k. t2
b Teken een lijn evenwijdig aan lijn m door punt E.
Noem de lijn l. t2
D E
c Is k
l? Leg je antwoord uit. i
a Denk je dat lijn a en b evenwijdig zijn? t2
b Controleer met je geodriehoek of de lijnen a en b evenwijdig zijn. t1
Breinbreker
Twee lijnen die elkaar snijden hebben één snijpunt. Drie of meer lijnen kunnen meer snijpunten hebben.
a Teken twee snijdende lijnen.
b Teken een derde lijn die beide lijnen snijdt.
c Hoeveel snijpunten kun je met vier lijnen hebben?
Probeer het eerst op een kladblaadje.
Woorden
snijden snijpunt evenwijdig
Doel bereikt?
Kruis aan:
◻ Ik weet wat snijdende lijnen zijn en wat een snijpunt is. Ik r weet wat evenwijdig is en hoe ik dat aangeef in een figuur.
◻ Ik kan snijdende en evenwijdige lijnen tekenen. Ik kan met t1 de geodriehoek controleren of lijnen evenwijdig zijn.
◻ Ik kan een lijn door een punt tekenen evenwijdig aan t2 een andere lijn.
◻ Ik kan uitleggen wat het verschil is tussen snijdende i en evenwijdige lijnen.
doel → Je leert hoe je controleert of lijnen loodrecht staan en hoe je loodrechte lijnen tekent.
Loodrecht
ɲ Op een geodriehoek staat één lijn loodrecht op de liniaal.
Opdrachten — Loodrecht
Met welk teken geef je in een figuur aan dat twee lijnen loodrecht op elkaar staan? r
loodrechte
ɲ Je gebruikt het teken ⊥ voor loodrechte lijnen: p ⊥ q.
Je zegt: ‘Lijn p staat loodrecht op lijn q.’
ɲ In een figuur teken je een ⅂ bij het snijpunt van de lijnen die loodrecht op elkaar staan.
ɲ Zo controleer je of lijnen loodrecht op elkaar staan:
ɲ Leg de loodrechte lijn van je geodriehoek op een lijn.
ɲ Schuif de geodriehoek naar de andere lijn. Ligt de liniaal van je geodriehoek precies langs de andere lijn? Dan staan de lijnen loodrecht op elkaar.
m l m
l ⊥ m
a Controleer met je geodriehoek of lijn m loodrecht op lijn n staat. t1
b Teken in de figuur als lijn m loodrecht op lijn n staat. t1 n m
In de tekening staan lijn a en lijn b loodrecht op elkaar. Vul de tekening aan met de ontbrekende gegevens en tekens. t1
Bekijk de figuur hieronder. t1
a Sommige lijnen snijden elkaar loodrecht. Teken een bij de snijpunten van die lijnen.
b Welke lijnen zijn evenwijdig? Zet een > op die lijnen.
c Teken door punt P een lijn t, die evenwijdig is aan lijn l.
Bekijk het ontwerp voor een houten hek.
a Staan de hoekpalen en de horizontale planken loodrecht op elkaar? t1
b Teken in het hek twee planken die evenwijdig zijn aan de bovenste en de onderste plank. t2
Je ziet hieronder een figuur gemaakt met rechte lijnstukken. t2 Omcirkel zoveel mogelijk snijpunten waar lijnen loodrecht zijn.
Loodrechte lijnen tekenen
ɲ Een lijn loodrecht op een andere lijn teken je met je geodriehoek.
Voorbeeld
Teken een loodrechte lijn op lijn l.
ɲ Leg de loodrechte lijn van je geodriehoek op lijn l.
ɲ Teken langs de liniaal van je geodriehoek lijn m.
ɲ Nu geldt l ⊥
Opdrachten — Loodrechte lijnen tekenen
a Teken een lijn. Noem de lijn k. t1
b Teken lijn n loodrecht op k. t1
c Laat in de figuur zien dat k ⊥ n. t1
ɲ Zet het teken bij het snijpunt van de lijnen.
a Teken een lijn loodrecht op lijn l. De lijn loopt door punt P.
Noem de lijn r. t1
b Teken nog een lijn loodrecht op lijn l. De lijn loopt door punt Q.
Noem de lijn s. t1
c Wat weet je van de lijnen r en s? Omcirkel het juiste teken: lijn r en s zijn ⊥ / // i
d Geef dit aan met tekens in de figuur. t1
Je ziet hieronder een deel van de plattegrond van Amsterdam.
a Omcirkel het juiste antwoord: t2
De Vespuccistraat staat wel / niet loodrecht op Trambaan 13.
De Jan Maijenstraat loopt wel / niet evenwijdig aan Trambaan 13.
b Door de antwoorden bij opdracht a weet je dat de Vespuccistraat loodrecht op de Jan Maijenstraat staat.
Leg uit waarom. i
c Er komen straten loodrecht uit op Trambaan 13. t2
Breinbreker
De grote en de kleine wijzer van een klok staan loodrecht op elkaar. De kleine wijzer staat op de drie. Hoe laat is het?
Shackletonstraat S105
Mercatorstraat
Torresstraat
James Cookstraat Vespuccistraat
Vancouverstraat
John Franklinstraat
JanMaijenstraatTrambaan13
Marco Polostraat Admiralengracht
Woord
loodrecht
Doel bereikt?
Kruis aan:
◻ Ik weet wat loodrecht is en hoe ik dat aangeef in een figuur. r
◻ Ik kan met de geodriehoek controleren of lijnen loodrecht t1 op elkaar staan. Ik kan loodrechte lijnen tekenen.
◻ Ik kan een tekening maken met loodrechte lijnen. t2
◻ Ik kan uitleggen dat een lijn die loodrecht staat op de ene lijn, i ook loodrecht staat op een andere lijn die evenwijdig is aan die ene lijn.
doel → Je leert wat rechthoeken, vierkanten en driehoeken zijn.
Hoeken
Rechthoek en vierkant
ɲ Rechthoeken, vierkanten en driehoeken noem je vlakke figuren.
ɲ Rechthoek
Een rechthoek heeft vier hoekpunten.
De zijden van een rechthoek staan loodrecht op elkaar.
Hieronder zie je rechthoek KLMN met hoekpunten K, L, M en N.
Lijnstukken KL, LM, MN en KN zijn de zijden van de rechthoek.
Opdrachten — Rechthoek en vierkant
Waar of niet waar?
Zet een kruisje in de juiste kolom. r waar niet waar
Een vierkant heeft vier hoekpunten.
Een rechthoek heeft vier even lange zijden.
De zijden van een rechthoek staan loodrecht op elkaar.
ɲ Vierkant
Een vierkant heeft vier hoekpunten. De zijden van een vierkant staan loodrecht op elkaar en zijn allemaal even lang. De zijden van vierkant PQRS zijn 3 cm lang.
rechthoek KLMN vierkant PQRS P S Q R 3 cm 3 cm 3 cm 3 cm
Hieronder zie je een rechthoek. t1
a Noteer de letters van de hoekpunten. , , en .
b De rechthoek heet .
c Noteer de zijden van de rechthoek.
d Meet de zijden van deze rechthoek.
PQ = cm en QR = cm lang.
a Teken hieronder een rechthoek van 5 cm bij 3 cm. t2
b Zet bij de hoekpunten de letters K, L, M en N. t1
c Noteer de vier zijden van de rechthoek. t1
d Teken lijnstukken KM en LN in de rechthoek. t2
e De lengte van KM is cm. t1
Hiernaast zie je een vierkant.
a Noteer de hoekpunten van het vierkant. t1 , , en .
b Noteer de zijden van het vierkant. t1 , , en .
c Welke twee eigenschappen moet je controleren om zeker te zijn dat dit een vierkant is? t2
a Teken een loodrechte lijn vanuit punt D door lijnstuk AB. Noem het snijpunt S. t2
b Teken ook een loodrechte lijn vanuit punt C door lijnstuk AB. Noem het snijpunt T. t2
c Maak de lijnstukken ST, TC, CD en DS rood. t2
d De lijnstukken uit opdracht c zijn , , en cm lang. t2
e Figuur STCD is een . i
Bekijk de figuur hieronder.
a Meet de zijden van de gele rechthoek. cm en cm. t1
b Is de blauwe figuur een vierkant? Leg uit. i
Driehoeken
Hoeken
ɲ Driehoek
Een driehoek is een vlakke figuur met drie hoekpunten.
Je schrijft driehoek ABC als Δ ABC.
De driehoek heeft zijden AB, BC en AC.
B C driehoek ABC
ɲ Rechthoekige driehoek
In driehoek ABC staan AB en BC loodrecht op elkaar.
Deze driehoek noem je een rechthoekige driehoek.
B C rechthoekige driehoek ABC
Opdrachten — Driehoeken
Leg dat uit met een tekening. i 41 42
Welke driehoek is een rechthoekige driehoek? Omcirkel deze. t1
a Teken lijnstuk AC van 3 cm lang loodrecht op AB. t1
b Verbind de punten B en C met een lijnstuk. t1
c Welke soort figuur heb je nu getekend? t1
d Maak van deze figuur een rechthoek.
Je ziet hieronder een glas-in-loodraam.
a Hoe heten de witte vlakke figuren? t1
b Welke kleur(en) hebben de driehoeken? t1
c Welke vlakke figuur krijg je als je een blauwe en een gele figuur samenvoegt? i
Breinbreker
Bekijk de afbeelding hiernaast. Hoeveel vierkanten zie je?
Hieronder staan twee beweringen. Bespreek met een klasgenoot welke bewering waar is of welke beweringen waar zijn. Leg uit waarom. i
A Met twee even grote rechthoekige driehoeken kun je een rechthoek maken.
B Een vierkant kan bestaan uit vier rechthoekige driehoeken.
Woorden
vlakke figuur vierkant rechthoek driehoek hoekpunt rechthoekige driehoek zijde Doel bereikt?
Kruis aan :
◻ Ik weet wat rechthoeken, vierkanten en r driehoeken zijn.
◻ Ik kan rechthoeken, vierkanten en driehoeken t1 herkennen.
◻ Ik kan rechthoeken, vierkanten en driehoeken t2 tekenen.
◻ Ik begrijp hoe je met bepaalde vlakke figuren andere i vlakke figuren kunt maken.
doel → Je leert wat een cirkel is en hoe je een cirkel tekent met een passer.
Een cirkel tekenen
Een cirkel teken je met een passer. Dat doe je zo:
ɲ Bepaal de afstand tussen de benen van de passer. (hier: 4 cm)
ɲ Prik de scherpe punt in het midden van de cirkel. Het midden van de cirkel noem je het middelpunt (M).
ɲ Draai het been met de potloodpunt rond tot je een cirkel hebt.
Opdrachten — Een cirkel tekenen
Vul het juiste woord in. r
De scherpe punt van de passer staat in het van de cirkel.
a Teken een cirkel. t1
Zet de benen van je passer 3 cm uit elkaar.
benen van de passer
b Zet een M op de plek waar je de scherpe punt hebt gezet. t1
c De afstand van de rand van de cirkel tot punt M is cm. t1
a Meet 3 cm tussen de benen van je passer.
Teken met je passer een cirkel.
Noem het middelpunt M. t1
b Meet 2 cm tussen de benen met je passer.
Teken een cirkel met hetzelfde middelpunt M. t1
c Kleur het gebied tussen de twee cirkels. t1
d Bepaal de dikte van de gekleurde band. i
a Schrijf vier ronde voorwerpen op. t2 autoband
b Vergelijk je antwoorden met die van een klasgenoot.
Noteer de voorwerpen die jij niet had. t2
49
Teken de figuur hieronder na.
Zet de passerpunt steeds op een zwart punt.
De afstand tussen de benen blijft steeds gelijk.
Kleur de figuur. t2
De cirkel
Alle punten op een cirkel hebben dezelfde afstand tot het middelpunt, punt M.
ɲ M is het middelpunt van de cirkel.
ɲ Lijnstuk AB (door het middelpunt) is de diameter.
ɲ Lijnstuk CM is de straal.
ɲ De straal is de afstand van punt M tot een punt op de cirkel.
Als je een cirkel tekent, is de straal de afstand tussen de benen van een passer.
De diameter van een cirkel is twee keer zo groot als de straal van een cirkel.
ɲ Als je de diameter van een cirkel weet, kun je de straal berekenen: straal = diameter : 2
ɲ Als je de straal van een cirkel weet, kun je de diameter berekenen: diameter = 2 × straal
Voorbeelden
De cirkel hierboven heeft diameter AB = 4 cm.
De straal = diameter : 2 = 4 : 2 = 2 cm
Een cirkel heeft een straal van 5 cm.
De diameter = 2 × straal
= 2 × 5 = 10 cm
Opdrachten — De cirkel
Kruis het juiste vakje aan. r waar niet waar
Als je een cirkel tekent, is de afstand tussen de benen van de passer hetzelfde als de straal.
De straal is twee keer zo groot als de diameter.
Je berekent de diameter met diameter = 2 × straal.
Hier zie je een cirkel. Vul in. t1
a Lijnstuk geeft de diameter aan.
b Lijnstukken , en geven de straal aan.
c De straal van de cirkel is cm.
d De diameter van de cirkel is cm.
a Teken een cirkel met straal 1 cm. Zet M bij het middelpunt. t1
b Teken een cirkel met diameter 4 cm. Gebruik hetzelfde middelpunt. t2
Hier zie je een cirkel. Vul in. t1
a Het middelpunt van de cirkel is punt .
b Welke punten liggen op de cirkel?
c Meet de straal. De straal van de cirkel is cm.
d Meet de diameter.
De diameter van de cirkel is cm.
a Een cirkel heeft een straal van 5 cm.
Hoeveel centimeter is de diameter? cm t1
b Een cirkel heeft een diameter van 24 cm.
Wat is de straal? cm t1
Teken een cirkel die beide evenwijdige lijnen raakt. i
Wat is de straal? cm
Wat is de diameter? cm
Breinbreker
Het logo hieronder zie je weleens op een bankpasje staan. Het bestaat uit twee even grote cirkels.
Bereken de diameter van de cirkels.
5 cm 23 cm
Woorden cirkel diameter passer straal middelpunt Doel bereikt?
Kruis aan:
◻ Ik weet wat een cirkel is en ik weet wat de straal en r de diameter van een cirkel zijn.
◻ Ik kan een cirkel met een gegeven straal tekenen en t1 de straal en de diameter van een cirkel meten en berekenen.
◻ Ik kan een cirkel met gegeven diameter tekenen. t2
◻ Ik kan een cirkel tekenen waarbij ikzelf de diameter en i de straal moet bepalen.
doel → Je leert evenwijdige lijnen, loodrechte lijnen en vlakke figuren herkennen in gevels.
Havenhuis Antwerpen
Een architect ontwerpt gebouwen. Met verschillende lijnen en vormen in het ontwerp van de gevel zorgt de architect voor een bijzondere uitstraling van het gebouw. De gevel is het gedeelte van het gebouw dat aan de buitenkant te zien is.
Wat doet een architect? r
Bekijk de gevels van de gebouwen op de linker bladzijde. t1
a Welke vlakke figuur herken je in het glazen gebouw van het Havenhuis in Antwerpen?
Op de afbeelding is een gedeelte van de gevel van een parkeergarage te zien. Teken de gevel na. t2
b Welke vlakke figuur herken je in de ramen van het Stadskantoor in Den Haag?
Bekijk de afbeelding. t1
a Omcirkel het juiste antwoord. De lijnen b en d staan wel / niet loodrecht op elkaar.
b Welke lijnen lopen evenwijdig aan elkaar?
Ontwerp zelf een gevel van een kantoor. Gebruik verschillende lijnen voor de gevel en verschillende vormen voor de ramen. Werk op een kladblaadje. i
Doel bereikt?
Kruis aan:
◻ Ik weet dat een architect verschillende vlakke figuren en r lijnen gebruikt in een gevel.
◻ Ik kan vlakke figuren, evenwijdige lijnen en t1 loodrechte lijnen herkennen in gevels.
◻ Ik kan een gevelontwerp met evenwijdige en t2 loodrechte lijnen natekenen.
◻ Ik kan zelf met behulp van lijnen en vlakke figuren i een gevel ontwerpen. 59
ɲ Wiskundeweetje
Bekijk de vlakvulling hieronder. t1
a Welke drie vormen herken je in de vlakvulling?
Je ziet hier punten genummerd van 1 tot en met 9.
a Teken rechte lijnstukken van 1 – 2 – 3 – 4 – 5 – 1. t1
b Teken ook rechte lijnstukken van 6 – 7 – 8 – 9. t1
c De figuur is een . t2
d De figuur is cm hoog. t1
e Maak de tekening op je eigen manier af. t2
ɲ 1.1
b Er zijn verticale lijnen.
Meet de lijnstukken AB,
Vul in. r
a Als twee lijnen elkaar niet snijden, zijn de lijnen
b Het punt waardoor twee lijnen gaan, noem je het
Vul in. r
Als s ⊥ t, dan staan de lijnen s en t op elkaar.
Bekijk de figuur hieronder.
a Welke lijnen staan loodrecht op elkaar? t1
Bekijk de lijnen hieronder.
a Welke lijnen zijn evenwijdig aan elkaar? t1
b Zet de juiste tekens op de evenwijdig lijnen. t1
c Welke lijnen snijdt lijn a? t1
d Teken een lijn die evenwijdig is aan lijn a en lijn c snijdt.
Noem de lijn f. t2
e Teken het snijpunt S van de getekende lijn f en lijn c. t2
b Zet een loodrecht teken bij de snijpunten van die lijnen. t1
c Teken een lijn g loodrecht op lijn d. t1
d Leg uit waarom lijn g evenwijdig is aan lijn c. i
Wat is het verschil tussen een rechthoek en een vierkant? t1
Teken een cirkel met een diameter van 7 cm. t2
a Teken vierkant ABCD met zijden van 4 cm. t1
b Teken een lijnstuk waarmee je het vierkant in twee gelijke rechthoeken verdeelt. i
Een cirkel heeft een diameter van 12 cm.
Bereken de straal. t1
Een cirkel heeft een straal van 3,5 cm.
Bereken de diameter. t1
ɲ Praktische wiskunde - Architectuur
Bekijk het gebouw.
a Het dak loopt wel / niet evenwijdig aan de vloer. t1
b Trek met rood de evenwijdige lijnstukken over. t1
c Teken zelf een evenwijdige lijn precies tussen de evenwijdige lijnen in. t2
75
Hieronder zie je verschillende lijnen.
a Hebben lijn a en lijn b een snijpunt? t1
b Wat is het snijpunt van lijn c en lijn e? t1
c Welke lijnen zijn evenwijdig aan elkaar? t1
d Welke lijnstukken zijn even lang? i
ɲ Hoofdstuk 1
Teken de Nederlandse vlag in een rechthoek.
De vlag bestaat uit drie even grote horizontale banen. t2
76
Je ziet hier een Japanse en een Zweedse vlag. t2
a Welke vlakke figuren herken je in de Japanse vlag?
b Welke vlakke figuur herken je in de Zweedse vlag?
Japan Zweden