KAPITTELPRØVE 5 − NIVÅ 1
90 MINUTTER
1 Hva er riktig?
A Koordinatene til B er (2,−1).
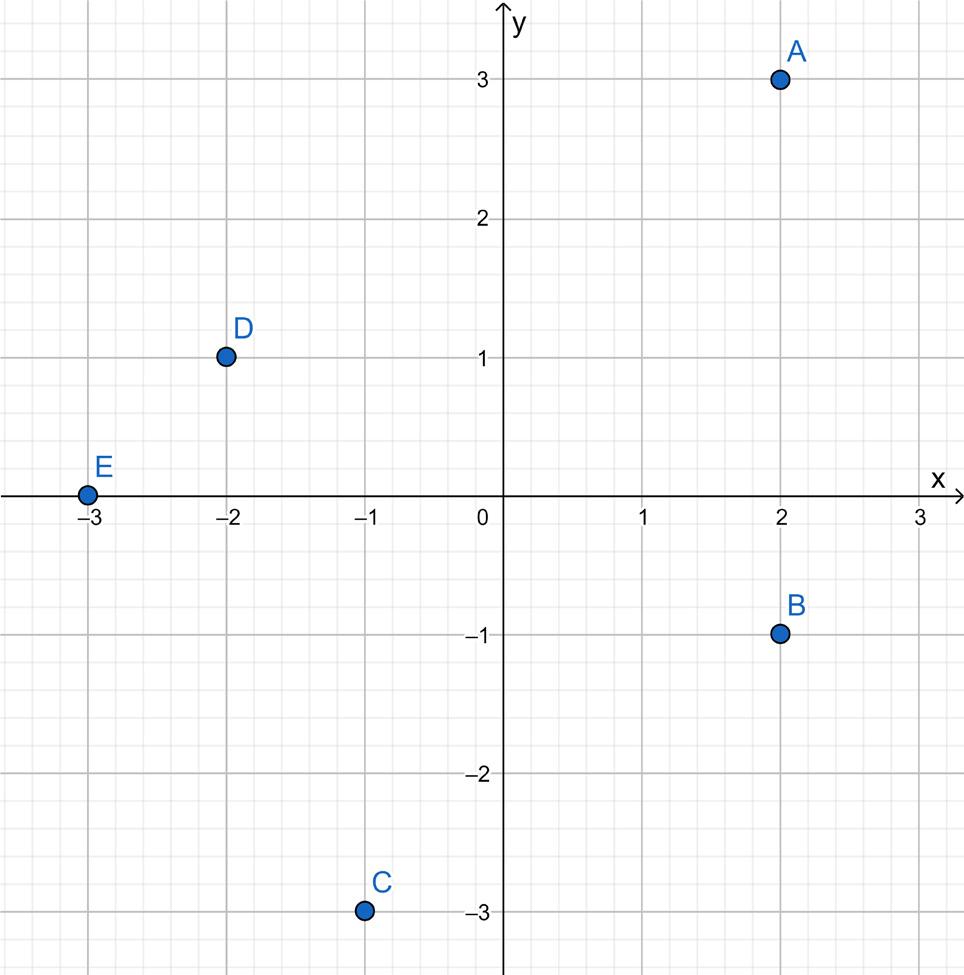
B Koordinatene til E er (−3,0).
C Koordinatene til C er (−3,−1).
D Det er bare punkt A som har positive koordinater.
2 Hva er koordinatene til A, B, C, D, E, F, G i koordinatsystemet?

1 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
3
Funksjonsuttrykk y = x.
A Lag en verditabell til funksjonsuttrykket. B Tegn funksjonen i rutenettet.
X −3 3 Y
4
Funksjonsuttrykket er y = 2x.
A Fyll ut verditabellen. X 2x y −3 2 · (−3) −6 −2 −1 0 1 2

2 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
B Tegn grafen i koordinatsystemet.
5 Når du tar drosje, betaler du en startpris + pris per kilometer. Startpris er 50 kroner + 10 kroner per kilometer. Funksjonsuttrykket er y = 50 + 10x.


A Hvor mye må du betale hvis du kjører 10 km?
B Hvor mye må du betale hvis du kjører 12 km?
3 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
6 Skriv begrepene i riktig boks.
koordinater,
4 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
x +
−3 −3 +
−2 −2 +
−1 −1 +
x-akse, y-akse, verditabell, koordinatsystem,
punkt, funksjonsuttrykk, graf 0 12 34 5 -1 -2 -1 -2 -3 -4 1 2 3 4 6 1 1 y = x+1 (3,2) x
1 y
1 −2
1 −1
1 0 0 0 + 1 1
7 Hva er funksjonsuttrykket til funksjonen?
8 Hva er funksjonsuttrykket til funksjonen?


5 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
9 Hva er riktig?
Funksjon 1 Funksjon 2 Funksjon 3 y = 2x y = 2x + 1 y = 4x
A Alle tre funksjoner blir en rett linje.
B To av funksjonene går gjennom samme punkt på x-aksen.
C Funksjon 1 har stigningstall 0.
D Funksjon 3 har stigningstall 4.
E Alle funksjonene vil gå gjennom 0 på x-aksen.
10 Melk koster 13 kroner per liter. Kari kjøper 5 liter melk.
Hvor mye betaler Kari til sammen?
A Lag et funksjonsuttrykk til teksten.
B Hva er stigningstallet?
C Lag en verditabell til funksjonsuttrykket.
D Tegn funksjonen.
11 Anna kjøper moreller som koster 23 kroner per kilo. Hun kjøper 4 kg.
Hvor mye betaler Anna til sammen?
A Lag et funksjonsuttrykk til teksten.
B Lag en verditabell til funksjonsuttrykket.
6 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 1
KAPITTELPRØVE 5 − NIVÅ 2
90 MINUTTER
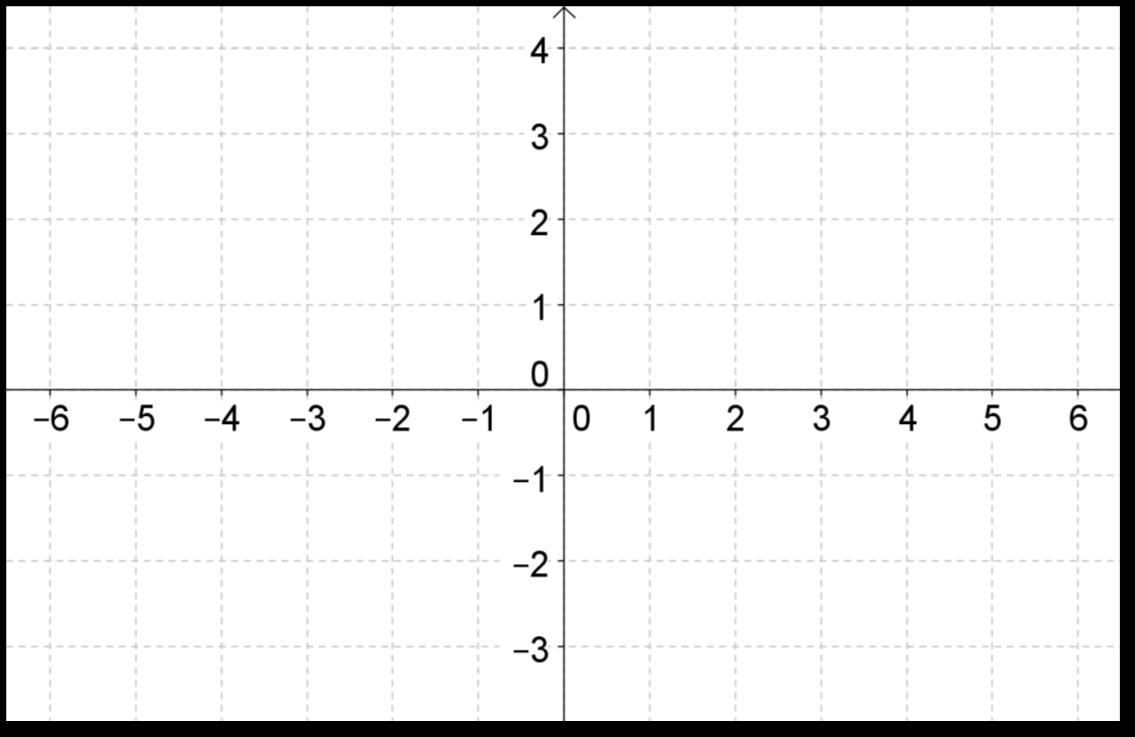
1 Merk av punktene (−3,−3), (3,−1), (1,4), (0,0) i koordinatsystemet.

2 Grafen er en rett linje.
Hva er riktig?
A Stigningstallet er 0.
B Stigningstallet er 2.
C Konstantleddet er −4.
D Konstantleddet er 2.
E Funksjonsuttrykket er 2x − 4.
F Funksjonsuttrykket er −4x + 2.
1 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2
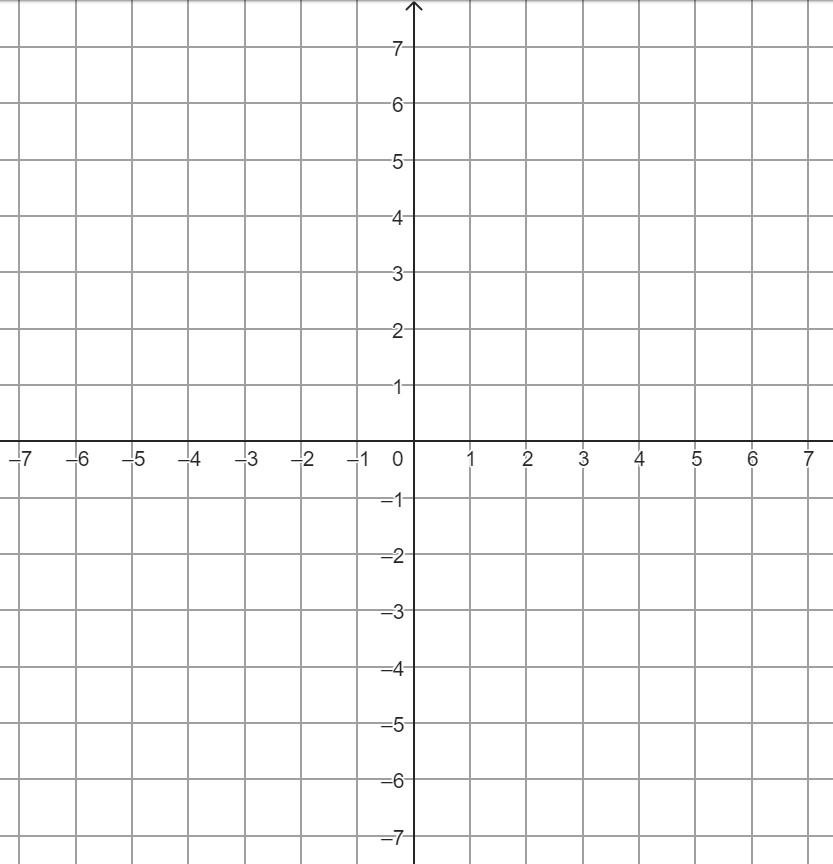
A Tegn funksjonen til funksjonsuttrykket y = 2x + 3.
B Hva er stigningstallet?
C Hva er konstantleddet?
D Hva er variabelen?
2 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2 3
4 Skriv inn begrepene i riktig boks.
x-akse, y-akse, verditabell, koordinatsystem, koordinater, punkt, funksjonsuttrykk, graf, konstant, variabel, stigningstall
3 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2
x x + 1 y −3 −3 + 1 −2 −2 −2 + 1 −1 −1 −1 + 1 0 0 0 + 1 1
-1 -2 -1 -2 -3 -4
0 0 12 34 5
1 2 3 4 6 1 1 y = x+1 (3,2)

4 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2
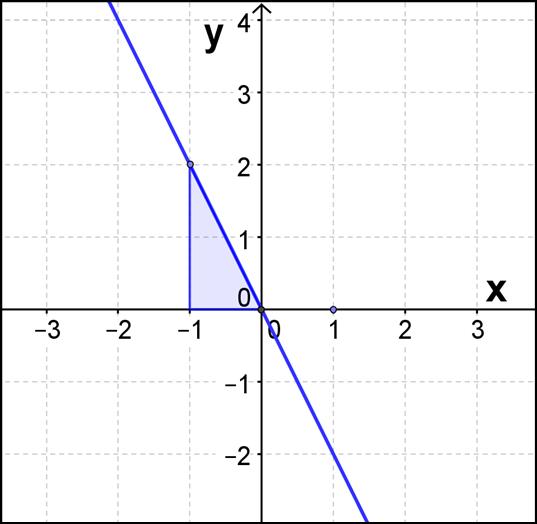
A
er stigningstallet til funksjonen? B
7 Du må betale 18,90 kr for en liten boks fløte (x). Verditabell: x funksjonsuttrykk y 1 18,90 kr 2 37,80 kr A Skriv et funksjonsuttrykk som viser hva du må betale (y) for x antall fløtebokser. B Hva er stigningstallet? KREMFLØTE
5 A Hva er stigningstallet til funksjonen? B Hva er funksjonsuttrykket til funksjonen? 6
Hva
Hva er funksjonsuttrykket til funksjonen?
8 Bruk opplysningene på tegningen. Hva er riktig?
25 kr
20 kr
15 kr
10 kr
5 kr
0 kr
5 kg 10 kg 15 kg 0 kg
A Funksjonsuttrykket er y = 6x.
B Funksjonsuttrykket er y = 5x.
C 5 kg epler koster 25 kroner.
D 1 kg eple koster 3 kroner.

E 2,5 kg koster 15 kroner.
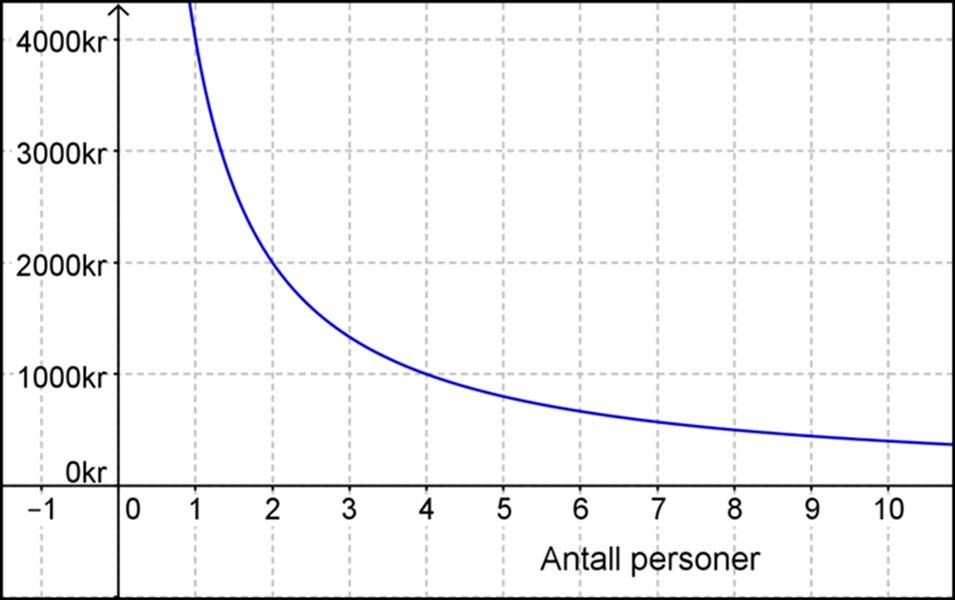
9 Noen venner leier en hytte sammen.
De må betale 4 000 kroner for å leie hytta i en uke. Hva er riktig?
A En person betaler 3 000 kroner.
B En person betaler 4 000 kroner.
C Fire personer betaler 500 kroner hver.
D Det er tre venner som leier hytta. De må betale 3 000 kroner hver.
E Fire venner leier hytta. De betaler 1 000 kroner hver.
F Grafen er en lineær funksjon.
G Grafen er en rett linje.
5 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2
10 Hva er riktig?
A En proporsjonal funksjon går alltid gjennom origo.
B Funksjonen er en proporsjonal funksjon.
C Stigningstallet til funksjonen er 2.
D Stigningstallet til funksjonen er −2.
E Funksjonen er en proporsjonal funksjon med et negativt stigningstall.
F Funksjonen har ikke en konstant.
11 Skriv funksjonsuttrykkene i riktige bokser.
A y = 2x − 1
B y = 4x
C y = −2x +2

D y = x
Funksjonsuttrykket har ingen konstant.
Funksjonsuttrykket har stigningstallet 4.
Funksjonen går gjennom origo.
Funksjonsuttrykket har et negativt stigningstall.
Funksjonsuttrykket har en konstant.
6 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 2
KAPITTELPRØVE 5 − NIVÅ 3
90 MINUTTER
1 Skriv inn begrepene i riktig boks. x-akse, y-akse, verditabell, koordinatsystem, koordinater, punkt, funksjonsuttrykk, graf, konstant, variabel, stigningstall
1 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
x +
y −3 −3 +
−2 −2 −2 +
−1 −1
x
1
1
1
−1 + 1 0 0 0 + 1 1 0 0 12 34 5 -1 -2 -1 -2 -3 -4 1 2 3 4 6 1 1 y = x+1 (3,2)
2
A Hva er stigningstallet til funksjonen?
B Hva er funksjonsuttrykket til funksjonen?
3

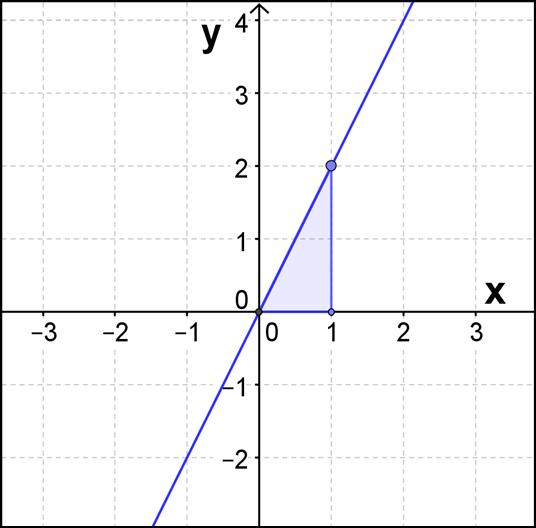
A Hva er stigningstallet til funksjonen?
B Hva er funksjonsuttrykket til funksjonen?
4 Du må betale 18,90 kr for en liten boks fløte.
A Skriv et funksjonsuttrykk (y) som viser hva du må betale for x antall fløtebokser.
B Hva er stigningstallet?
2 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
5 Knut sykler til jobben med en gjennomsnittsfart på 15 km/h. Formel: Vei (y)= fart · tid (x) A Skriv inn i verditabellen. x 15 km · x y 0,5 1 1,5 2 B Tegn inn i koordinatsystemet.
30 km
20 km
10 km
0 km
40 km 0,5 1 1,5 0 -0,5 2 2,5 3 3,5 4
x Tid timer
6 Bruk opplysningene på tegningen. Hva er riktig?
20 kr
15 kr
10 kr
y 0 kr
25 kr 5 kg 10 kg 15 kg 0 kg
A Funksjonsuttrykket er y = 6x. B Funksjonsuttrykket er y = 5x. C 5 kg epler koster 25 kroner. D 1 kg eple koster 3 kroner. E 2,5 kg koster 15 kroner.
5 kr

3 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
7 Noen venner leier en hytte sammen.
De må betale 4 000 kroner for å leie hytta i en uke.
Hva er riktig?
8
A En person betaler 3 000 kroner.
B En person betaler 4 000 kroner.
C Fire personer betaler 500 kroner hver.
D Det er tre venner som leier hytta. De må betale 3 000 kroner hver.
E Fire venner leier hytta. De betaler 1 000 kroner hver.
F Grafen er en proporsjonal funksjon.
H Funksjonsuttrykket til grafen er y = 3 000/x.

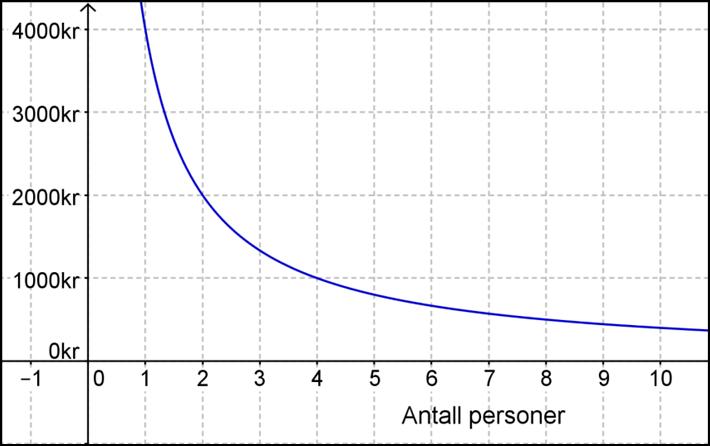
I Funksjonsuttrykket er y = 4 000/x.
J Grafen er en omvendt proporsjonal funksjon.
K Grafen er en hyperbel.
Hva er riktig?
A En proporsjonal funksjon går alltid gjennom origo.
B Funksjonen er en proporsjonal funksjon.
C Stigningstallet til funksjonen er 2.
D Stigningstallet til funksjonen er −2.
E Funksjonen er en proporsjonal funksjon med et negativt stigningstall.
F Funksjonen har ikke en konstant.
4 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
9 Skriv funksjonsuttrykkene inn i riktige bokser.
A y = 2x − 1 B y = 4x C y = −2x +2 D y = x

Funksjonsuttrykket har ingen konstant.
Funksjonsuttrykket har stigningstallet 4.
Funksjonen går gjennom origo.
Funksjonsuttrykket har et negativt stigningstall.
Funksjonsuttrykket har en konstant.
10 Katrine kjøper moreller som koster 15 kroner per hekto (hg).
Hun har 150 kroner.
Hvor mange kilo kan hun kjøpe?
A Lag et funksjonsuttrykk som viser teksten.
B Lag en verditabell.
C Tegn grafen i koordinatsystemet.
D Les av på grafen hvor mange hekto moreller hun kan kjøpe for pengene.
5 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
11 Fatima og Mohammed har invitert 25 venner til en stor fest.
De har kjøpt mat for 3 500 kroner, og gjestene skal hjelpe med å betale.
A Lag et funksjonsuttrykk som viser hvor mye hver gjest må betale.
B Hvor mye må hver gjest betale?

12 Åse kjøper 4 poser potetgull (x) og 2 flasker brus (y) og betaler 158 kroner.






Lars kjøper 2 poser potetgull (x) og 4 flasker brus (y) og betaler 154 kroner.
Hvor mye koster 1 pose potetgull (x) og 1 flaske brus (y)?

A Lag et likningssett av de to likningene.
B Bruk koordinatsystemet og løs oppgaven.
6 GRIP 3 MATEMATIKK KAPITTEL 5 · FUNKSJONER KAPITTELPRØVE 5 − NIVÅ 3
POTETGULL BRUS

























