La óptica del ojo humano: una revisión

OPTOMETRÍA

Dr. en Ciencias Sergio Vázquez y Montiel, Dr. en Ciencias Alexis Vázquez Villa Universidad Interserrana del Estado de Puebla-Ahuacatlán

Resumen

Se presenta una breve reseña histórica y una descripción de las principales características de las propiedades ópticas del ojo: el ojo es un instrumento óptico simple pero bastante optimizado. También se presenta una breve perspectiva histórica de cómo adquirimos conocimiento de los componentes ópticos del ojo, la córnea y el cristalino, describiendo las aberraciones monocromáticas en el eje de cada componente y el procedimiento paso a paso de construir modelos ópticos del ojo más y más precisos, hasta la comprensión actual de la óptica del ojo. En la última década, el uso de la tecnología de detección de frente de onda nos permite completar nuestra comprensión de la óptica del ojo como un sistema aplanático.

Introducción

El ojo humano es un ejemplo de un instrumento óptico relativamente simple que proporciona una funcionalidad excepcional. Pero aun con la simplicidad de la óptica ocular, hubo un largo proceso para alcanzar la comprensión casi completa que tenemos hoy. La óptica del ojo se asemeja a un diseño aplanático 1 con una corrección parcial de la aberración esférica y la coma. Esto se debe a un equilibrio natural entre las aberraciones de la córnea y el cristalino en el ojo joven, 2 que se pierde progresivamente durante el envejecimiento normal. 3 Aunque el interés en el ojo es intrínseco a la naturaleza humana, fue alrededor de la época de Galileo, siglo XVII, cuando comenzó la exploración científica del ojo. A partir de entonces, se avanzó continuamente, en parte debido a la evolución de los instrumentos ópticos, como el telescopio y microscopio, desarrollados paradójicamente para evitar las limitaciones de resolución del ojo. Sólo el campo de visión del ojo es superior al telescopio de Galileo. Sin embargo, el ojo humano se ve afectado por aberraciones cromáticas y esféricas, además de la coma y otras aberraciones de orden superior.

Antes de la época de Galileo, los fabricantes italianos de vidrio en Florencia 4,5 ya usaban y vendían gafas para la corrección de la presbicia y la miopía, basándose en pruebas empíricas, hasta que Kepler describió correctamente cómo las lentes esféricas compensan los errores de refracción como la miopía e hipermetropía. Sin embargo, llevó mucho tiempo caracterizar y corregir el astigmatismo. A principios del siglo XIX, Thomas Young describió correctamente el astigmatismo de su ojo izquierdo, 6 y tardó casi 30 años en encontrar la corrección astigmática adecuada. Fue Airy, en 1827, quien sugirió el uso de superficies de forma cilíndrica para compensar los errores de refracción a lo largo de ciertos meridianos, un diseño de gafas que todavía es muy común en la actualidad. 5

La primera observación de la aberración esférica en el ojo humano fue hecha por Thomas Young en su famosa publicación de 1801 “Sobre el mecanismo del ojo” 6,7 y más tarde por Helmholtz en su “Tratado sobre óptica fisiológica” en 1855. El efecto cromático en el ojo fue mencionado inicialmente por Newton 8 y luego por Young. 9 Sin embargo, la corrección de la aberración cromática mediante el uso de lentes sólo se intentó a mediados del siglo XX, 10 y recientemente se propusieron algunas variaciones del corrector que proporciona un rendimiento gran angular. 11

Breve historia de los principales avances en óptica del ojo

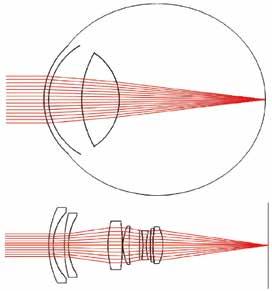
En el ojo sólo se usan dos lentes para enfocar la luz en la retina. Si se compara con un sistema óptico artificial diseñado para el mismo propósito, este número puede parecer

demasiado pequeño, ver la figura 1. El número de elementos montados en el sistema óptico artificial se debe a una mayor corrección de las aberraciones. No se pudo dilucidar si este tipo de estrategia de optimización también se presentó en el ojo humano hasta que se diera una caracterización de cada componente por separado, y eso tomó 400 años.

Figura 1. Ejemplo esquemático de un modelo de ojo humano comparado con un objetivo de cámara fotográfica.

Los contemporáneos de Galileo, Kepler, Scheiner y Descartes, contribuyeron a la comprensión inicial del ojo como un instrumento óptico, al darse cuenta de que la imagen de la retina estaba invertida y proporcionar la primera descripción de los componentes ópticos. Más tarde, Huygens construyó un modelo de ojo físico compuesto por dos hemisferios llenos de agua y un diafragma. Pero, fue sólo a principios del siglo XIX cuando Thomas Young produjo la primera descripción de óptica geométrica de la córnea y la lente. Los radios de curvatura de las superficies corneales y de la lente, así como la profundidad de la cámara anterior y los valores del índice de refracción, se estimaron sorprendentemente bien para esos tiempos. Más tarde, Moser (1844) y Listing (1851) construyeron ojos esquemáticos utilizando superficies esféricas para describir la córnea y el cristalino. El modelo de ojo de Listing fue mejorado por Helmholtz modificando las posiciones de las superficies de las lentes. Esos ojos esquemáticos eran tres modelos de superficie, uno para la córnea y dos para el cristalino. Tscherning midió por primera vez el radio de curvatura de la superficie corneal posterior, y describió el primer modelo de ojo esquemático de cuatro superficies en 1900. Al mejorar las técnicas para medir las curvaturas y distancias axiales del ojo, se propusieron varios modelos de ojos en el siglo pasado, y algunos de ellos se hicieron muy populares, como el modelo Gullstrand, 12 y los modelos de Le Grand 13 y Emsley. 14 El uso de estos modelos esféricos se limita a la óptica geométrica paraxial y se utilizaron para estimar los planos y puntos cardinales del ojo, para diseñar nuevos anteojos y, después de la primera cirugía moderna de cataratas en 1949, se implantó por primera vez un lente intraocular (LIO) en un ojo. 15

Sin embargo, estos modelos simples no podrían usarse para comprender completamente las aberraciones de cada componente. Debido a que las superficies utilizadas eran esferas con simetría de revolución, el trazado de rayos a través de los ojos esquemáticos mostraría de inmediato que los valores predichos no estaban de acuerdo con las mediciones. La precisión de los modelos se restringió a la óptica paraxial. Después de casi 350 años, las aberraciones reales de la córnea y el cristalino eran en gran medida desconocidas.

El primer intento de localizar dónde se origina el astigmatismo en el ojo fue realizado por Young en 1801. 6 Su curiosidad científica lo llevó a preguntarse si su propio astigmatismo se originó en la córnea o en el cristalino. Supuso que cuando se sumergiera en agua (con un índice de refracción similar al de la córnea), cancelaría la contribución corneal, y dado que el astigmatismo persistía, concluyo que era inducido por el cristalino.

Las fuentes de las aberraciones en el ojo no se estudiaron hasta la década de 1970, las primeras versiones de topógrafos corneales basadas en las deformaciones observadas en la imagen reflejada de una serie de anillos concéntricos en la córnea comenzaron a usarse como herramientas oftálmicas. Esto permitió la reconstrucción de la primera forma de la superficie corneal y, por lo tanto, el cálculo de las aberraciones corneales. En 1973, El Hage y Berny, 16 utilizando uno de estos instrumentos,

OPTOMETRÍA

OPTOMETRÍA

estimaron la aberración esférica de la córnea, obteniendo valores positivos, es decir, los rayos periféricos cruzan el eje óptico frente a los rayos paraxiales. Debido a que no había acceso directo al cristalino in vivo, midieron la aberración esférica del ojo total usando una prueba de Foucault. Cuando compararon ambos conjuntos de datos, se dieron cuenta de que la aberración esférica de la córnea era mucho mayor que la aberración esférica del ojo completo. Infirieron que la aberración esférica del cristalino debería tener valores negativos, proporcionando un equilibrio de la aberración esférica positiva de la córnea. Un experimento realizado más tarde por Millodot y Sivak, 17 usando lentes llenas de agua para cancelar la contribución corneal, obtuvo más variabilidad en el signo de la aberración esférica del cristalino. En 1993, Tomlinson et al. 18 confirmaron los resultados de El Hage y Berny.

Algunos de los avances en los instrumentos para evaluar objetivamente la calidad óptica del ojo nos permitieron revisar este tema en la década de 1990. Al usar la técnica de doble paso, 19,20 se propuso que no sólo la aberración esférica, sino también otras aberraciones de orden superior podrían equilibrarse entre la córnea y el cristalino. La introducción del sensor de frente de onda Hartmann-Shack para medir las aberraciones del ojo 21,22 permitió el diseño de experimentos adicionales, incluida la revisión de las mediciones de las aberraciones del ojo sumergido en agua. 23,24

Además, el uso de sensores de frente de onda Hartmann-Shack mejorados permitió realizar análisis en tiempo real de las aberraciones 28 y construir sistemas de óptica adaptativa para el ojo humano. 25,27

Los avances en la comprensión de los componentes ópticos condujeron a un mayor grado de complejidad en la elaboración de los modelos oculares esquemáticos. Intentando mejorar la predicción de las mediciones de aberración esférica, varios autores incorporaron superficies cónicas para describir la córnea y el cristalino. 29,31 Los valores de asfericidad corneal se tomaron de las mediciones de topografía corneal, pero los valores de asfericidad de la superficie del cristalino fueron difíciles de medir y, en muchos casos, se usaron como variables para ajustar el modelo a ciertos valores o se midieron a partir de cristalinos ex vivo. Hoy en día, los valores exactos de asfericidad de las superficies del cristalino aún son tema de discusión, con sólo datos disponibles de imágenes Scheimpflug ópticamente corregidas 32 que muestran grandes errores de desviación estándar en la repetibilidad. Los avances adicionales en los ojos esquemáticos agregaron un índice de gradiente refractivo al cristalino. 33,35 Sin embargo, las mediciones de este parámetro también son difíciles y escasas. Por lo general, se incorpora a los modelos ópticos a través de la optimización para adaptarse a una variable más fácil de medir, como los errores de refracción periféricos. Los nuevos modelos también se beneficiaron de los avances en la comprensión de las propiedades cromáticas del ojo, ya sea la aberración cromática longitudinal o la aberración cromática lateral. Otro aspecto modelado tradicionalmente es la acomodación, desde los modelos puramente paraxiales hasta modelos de ojo más sofisticados que incluyen los cambios de grosor, asfericidad e índice de refracción en función de la acomodación. 31,36

En general, los últimos modelos de ojos esquemáticos proporcionan resultados cercanos a la población promedio. Sin embargo, debido a la variabilidad individual en las aberraciones, podrían no ser precisas individualmente.

Comprensión actual de la óptica del ojo: diseño aplanático

La magnitud de las aberraciones de orden superior del ojo sólo representa aproximadamente alrededor del 10% de las aberraciones totales del ojo normal. 37 Aunque generalmente se presenta una gran variabilidad entre los sujetos, el efecto de estas aberraciones es crucial para degradar la calidad de la imagen retiniana del ojo humano. En términos de estadísticas en una población relativamente grande, 37,39 sólo la aberración esférica tiene un valor medio ligeramente positivo diferente de cero. Sin embargo, de interés no es sólo la magnitud global de las aberraciones en el ojo, sino también la contribución a esas aberraciones de los componentes oculares.

A este respecto, dos términos de aberración muestran un nivel significativo de compensación entre la córnea y el cristalino: aberración esférica y coma horizontal. En estos dos casos,

la córnea tiene valores más altos que el ojo completo. Para comprender el mecanismo subyacente de esta compensación, debemos saber más sobre las fuentes de estas aberraciones. El cristalino puede inducir una aberración esférica negativa principalmente debido a tres factores: curvatura, asfericidad e índice de refracción de gradiente. Las simulaciones con un modelo de lente con solo superficies esféricas muestran que la curvatura sola no puede ser responsable de inducir una aberración esférica negativa. Por lo tanto, la contribución de la lente debe determinarse por asfericidad o índice de gradiente. Hasta qué punto la contribución del cristalino es de uno u otro factor, o una combinación de ambos, aún no se determina experimentalmente.

La mejora de las técnicas de imagen in vivo de la profundidad de la cámara anterior podría permitirnos obtener datos más precisos de los perfiles de la superficie del cristalino que, en combinación con otros parámetros ópticos, podrían usarse para inferir el índice de gradiente y su contribución real a la aberración esférica negativa. La comprensión de la compensación de la coma requirió más experimentos. Inicialmente se planteó la hipótesis de que una ubicación particular del cristalino, con respecto a la córnea o el índice de refracción de gradiente del cristalino, podría inducir este efecto. 23 Sin embargo, nuevos experimentos indicaron que la desalineación angular entre la línea de visión y el eje pupilar estaba relacionada linealmente con la generación de coma tanto en la córnea como en el cristalino. 24,40 Esta desalineación angular se llama ángulo kappa, o lambda, del ojo, y la magnitud promedio en los ojos normales es de alrededor de 5 grados. 13 Esos ojos con un kappa de ángulo pequeño casi no mostraron compensación de coma, mientras que aquellos con un kappa de ángulo grande tenían valores grandes de coma corneal y lenticular, pero con signos opuestos.

Mediante el uso de un método basado en la grabación de imágenes de Purkinje, fue posible medir el ángulo kappa junto con la inclinación y la descentración de la lente. 41 La descentración del cristalino con respecto al centro de la pupila es no mayor que 0.3 mm. Los valores del ángulo kappa tiene magnitudes de alrededor de 5°.

Los modelos de ojos personalizados con trazado de rayos individual que introducen la topografía real completa de la córnea y una lente cristalina con los valores ajustados correspondientes de aberración esférica para cada sujeto mostraron que los valores reales de la descentración de la lente tenían un efecto muy pequeño en la compensación del coma. Sin embargo, descuidar los valores de ángulo kappa en cualquiera de los modelos de ojos personalizados tuvo un impacto muy significativo en los valores de coma. Esto sugirió que el coma estaba “de alguna manera” estrechamente relacionado con los valores del ángulo kappa.

El origen del ángulo kappa proviene de la no coincidencia sistemática de la posición de la fóvea y el punto donde el eje óptico intercepta la retina. El ángulo kappa es más pequeño en los miopes que en los hipermétropes. 13 Esto es fácil de entender basado en un modelo simple en el que las diferencias en esos ojos son la longitud axial, con una ubicación de la fóvea relativamente similar.

El siguiente paso para entender la compensación de aberraciones fue darse cuenta de que los signos opuestos en coma para la córnea y el cristalino se originan a partir de los diferentes factores de forma de cada componente. 1,2 Un modelo simplificado que utiliza la teoría de la aberración de Seidel para lentes sumergidas en medios de índice de refracción no simétricos 42 muestra que el coma depende de la forma de los componentes, la dependencia angular lineal, la posición del plano del objeto y los índices de refracción. Estos resultados fueron corroborados con cálculos exactos de trazado de rayos.

Un ejemplo de esta situación se muestra en la Fig. 2: los tres modelos de ojos tienen la misma córnea y potencia óptica para el cristalino. Sin embargo, las formas de las lentes son diferentes. El caso superior es la lente realista con la forma real, pero los otros dos casos, mientras que las lentes mantienen la misma potencia, tienen valores opuestos de factores de forma que no son fisiológicamente realistas. Para cada modelo, la luz entrante subtiende 5° con respecto al eje óptico, simulando un ángulo promedio de 5° kappa. En la columna derecha, se muestran las PSF (sin los términos simétricos de rotación) de cada caso.

OPTOMETRÍA

La situación que produce la menor cantidad de coma corresponde precisamente al modelo fisiológicamente preciso, mientras que el resto de las formas de las lentes, aunque ópticamente posibles, producen valores más altos de coma fuera del eje.

Figura 2. Ejemplos de modelos oculares y sus funciones asociadas PSF.

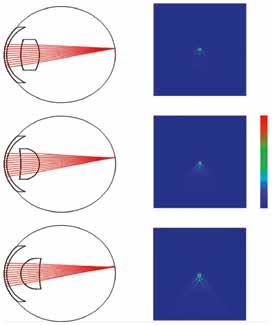
Estos resultados respaldan la idea de que la óptica del ojo es un diseño aplanático, una configuración donde la aberración esférica y el coma se corrigen aproximadamente. Debido a que la compensación no es perfecta, como puede existir en un sistema artificial, el ojo aún se ve afectado por esas aberraciones.

Del diseño del ojo a las correcciones oftálmicas: avances actuales y futuros

El hecho descrito en la sección anterior, que las aberraciones de la lente corneal y cristalina están parcialmente equilibradas, ha generado investigaciones sobre las situaciones hipotéticas en las que este ajuste fino podría verse interrumpido. Ciertamente, alguna modificación de la córnea o del cristalino puede ocurrir en situaciones de cirugía oftálmica, como la cirugía refractiva o de cataratas. Los procedimientos estándar de cirugía refractiva pueden alterar la compensación de la aberración, especialmente en correcciones de hipermetropía, 43 lo que lleva a la idea de que pueden requerirse mejores perfiles de ablación, lo que induce menos aberración.

Las cataratas son opacificaciones del cristalino que generalmente ocurren con la edad. La solución actual común es reemplazar la lente opaca por una LIO artificial. Los primeros trabajos experimentales sobre la calidad óptica in vivo de los ojos implantados con LIO mostraron una aparente paradoja. 44,45 La calidad de la imagen retiniana parecía ser similar a la de los pacientes normales de la misma edad. Las LIO se fabrican con altos estándares de calidad óptica, mejores que las lentes humanas más antiguas aisladas. Sin embargo, cuando se implanta en el ojo, la calidad óptica resultante no mejora significativamente. La compensación de las aberraciones en el ojo normal proporcionó una explicación a esta paradoja y, lo que es más interesante, una posible solución. La mejor LIO no está limitada por difracción, sino una lente con aberraciones opuestas a la de la córnea, que imita la situación en la lente cristalina joven. En realidad, esto abrió una nueva era para el diseño óptico de las LIO. Algunos diseños con óptica asférica se habían propuesto antes, pero fue dentro del contexto de la compensación de la aberración, con una mejor comprensión de la óptica del ojo, cuando esta tecnología estaba lista para ingresar al campo de la oftalmología.

Conclusiones

La mejor comprensión actual de la óptica del ojo seguramente contribuirá a nuevas aplicaciones. Prácticamente cada idea futura para la corrección visual deberá considerar cuidadosamente las propiedades ópticas del ojo.

La combinación de nuevos materiales y tecnologías quirúrgicas con la óptica, tiene el potencial de mejoras en cada enfoque. Las aplicaciones de óptica adaptativa 25,26 para la simulación visual y las pruebas y las imágenes de retina de alta resolución, todavía en su mayoría restringidas a los laboratorios de investigación, pronto pueden convertirse en procedimientos clínicos de rutina.

Completar la comprensión de las propiedades ópticas de la lente, y los cambios relacionados con el envejecimiento y la acomodación, siguen siendo temas abiertos desafiantes. Por supuesto, esta revisión no cubre todos los

problemas de la óptica del ojo, ya que se restringió a situaciones monocromáticas y sobre el eje. Sin embargo, las aberraciones periféricas tienen potencial en relación con los experimentos de progresión y control de la miopía, y las aberraciones cromáticas son otros aspectos interesantes que aún son objeto de una extensa investigación.

En el estudio del ojo humano, hay una convergencia de óptica física y fotónica junto con materiales, instrumentación y cirugía. Idealmente, una combinación de todas estas disciplinas permitirá proporcionar a los pacientes una mejor evaluación y corrección en el futuro.

Bibliografía

1.- P. Artal and J. Tabernero, “The eye’s aplanatic answer,” Nat.

Photon. 2, 586–589 (2008). 2.- J. Tabernero, A. Benito, E. Alcón, and P. Artal, “Mechanism of compensation of aberrations in the human eye,” J. Opt. Soc.

Am. A 24, 3274–3283 (2007). 3.- P. Artal, E. Berrio, A. Guirao, and P. Piers, “Contribution of the cornea and internal surfaces to the change of ocular aberrations with age,” J. Opt. Soc. Am. A 19, 137–143 (2002). 4.- N. J. Wade and S. Finger, “The eye as an optical instrument: from camera obscura to Helmholtz’s perspective,” Perception 30, 1157–1177 (2001). 5.- N. J. Wade, “Image, eye, and retina,” J. Opt. Soc. Am. A 24, 1229–1249 (2007). 6.- T. Young, “On the mechanism of the eye,” Philos. Trans. R. Soc.

London 91, 23–88 (1801). 7.- M. Koomen, R. Tousey, and R. Scolnik, “The spherical aberration of the eye,” J. Opt. Soc. Am. 39, 370–376 (1949). 8.- I. Newton, Opticks (1730), 4th ed., Book 1, Part ∂2, Prop. VIII. (reprinted by Bell, 1931). 9.- T. Young, “An account of some cases of the productions of colors, not hitherto described,” Philos. Trans. R. Soc. London 92, 387–397 (1802). 10.- A. C. S. Van Heel, “Correcting the spherical and chromatic aberrations of the eye,” J. Opt. Soc. Am. 36, 237–239 (1946). 11.- Y. Benny, S. Manzanera, P. M. Prieto, E.N. Ribak, and P. Artal,

“Wide-angle chromatic aberration corrector for the human eye,” J. Opt. Soc. Am. A 24, 1538–1544 (2007). 12.- J. P. C. Southall, Helmholtz’s Treatise on Physiological Optics (Optical Society of America, 1924), Vol. 1. 13.- Y. Le Grand and S. G. El Hage, Physiological Optics (Springer, 1980). 14.- H. H. Emsley, Visual Optics (Butterworth, 1952). 15.- N. H. L. Ridley, “Intraocular acrylic lenses after cataract extraction,” Lancet 259, 118–129 (1952). 16.- S. G. El Hage and F. Berny, “Contribution of the crystalline lens to the spherical aberration of the eye,” J. Opt. Soc. Am. 63, 205–211 (1973). 17.- M. Millodot and J. Sivak, “Contribution of the cornea and lens to the spherical aberration of the eye,” Vision Res. 19, 685–687 (1979). 18.- A. Tomlinson, R. P. Hememger, and R. Garriott, “Method for estimating the spherical aberration of the human crystalline lens in vivo,” Invest. Ophthalmol. Visual Sci. 34, 621–629 (1993). 19.- J. Santamaría, P. Artal, and J. Bescós, “Determination of the point-spread function of the human eye using a hybrid optical–digital method,” J. Opt. Soc. Am. A 4, 1109–1114 (1987). 20.- I. Iglesias, E. Berrio, and P. Artal, “Estimates of the ocular wave aberration from pairs of double-pass retinal images,” J. Opt.

Soc. Am. A 15, 2466–2476 (1998). 21.- J. Liang, B. Grimm, S. Goelz, and J. F. Bille, “Objective measurement of the WA’s aberration of the human eye with the use of

a Hartmann–Shack sensor,” J. Opt. Soc. Am. A 11, 1949–1957 (1994). 22.- P. M. Prieto, F. Vargas-Martín, S. Goelz, and P. Artal, “Analysis of the performance of the Hartmann–Shack sensor in the human eye,” J. Opt. Soc. Am. A 17, 1388–1398 (2000). 23.- P. Artal, P. A. Guirao, E. Berrio, and D. R.Williams, “Compensation of corneal aberrations by the internal optics in the human eye,” J. Vision 1, 1–8 (2001). 24.- P. Artal, A. Benito, and J. Tabernero, “The human eye is an example of robust optical design,” J. Vision 6, 1–7 (2006). 25.- J. Liang, D. R.Williams, and D. T. Miller, “Supernormal vision and high-resolution retinal imaging through adaptive optics,”

J. Opt. Soc. Am. A 14, 2884–2892 (1997). 26.- E. J. Fernández, I. Iglesias, and P. Artal, “Closed-loop adaptive optics in the human eye,” Opt. Lett. 26, 746–748 (2001). 27.- H. Hofer, L. Chen, G. Y. Yoon, B. Singer, Y. Yamauchi, and D. R.

Williams, “Improvement in retinal image quality with dynamic correction of the eye’s aberrations,” Opt. Express 8, 631–643 (2001). 28.- H. Hofer, P. Artal, B. Singer, J. L. Aragón, and D. R. Williams,

“Dynamics of the eye’s wave aberration,” J. Opt. Soc. Am. A 18, 497–506 (2001). 29.- W. Lotmar, “Theoretical eye model with aspherics,” J. Opt. Soc.

Am. 61, 1522–1529 (1971). 30.- A. C. Kooijman, “Light distribution on the retina of a wide angle theoretical eye,” J. Opt. Soc. Am. 73, 1544–1550 (1983). 31.- R. Navarro, J. Santamaría, and J. Bescós, “Accommodationdependent model of the human eye with aspherics,” J. Opt.

Soc. Am. A 2, 1273–1281 (1985). 32.- M. Dubbelman, G. L. van der Heijde, and H. A. Weeber,

“Change in shape of the aging human crystalline lens with accommodation,” Vision Res. 45, 117–132 (2005). 33.- H. L. Liou and N. A. Brennan, “Anatomically accurate, finite model eye for optical modelling,” J. Opt. Soc. Am. A 14, 1684–1695 (1997). 34.- D. Siedlecki, H. Kasprzak, and B. Pierscionek, “Schematic eye with a gradient index lens and aspheric surfaces,” Opt. Lett. 29, 1197–1199 (2004). 35.- A. Goncharov and C. Dainty, “Wide-field schematic eye models with gradient index lens,” J. Opt. Soc. Am. A 24, 2157–2174 (2007). 36.- S. Norrby, “The Dubbelman eye model analysed by ray tracing through aspheric surfaces,” Ophthalmic Physiol. Opt. 25, 153–161 (2005). 37.- J. F. Castejón-Mochón, N. López-Gil, A. Benito, and P. Artal,

“Ocular wave-front aberration statistics in a normal young population,” Vision Res. 42, 1611–1617 (2002). 38.- J. Porter, A. Guirao, I. G. Cox, and D. R. Williams, “Monochromatic aberrations of the human eye in a large population,” J.

Opt. Soc. Am. A 18, 1793–1803 (2001). 39.- L. N. Thibos, X. Hong, A. Bradley, and X. Cheng, “Statistical variation of aberration structure and image quality in a normal population of healthy eyes,” J. Opt. Soc. Am. A 19, 2329–2348 (2002). 40.- J. E. Kelly, T. Mihashi, and H. C. Howland, “Compensation of corneal horizontal/vertical astigmatism, lateral coma, and spherical aberration by internal optics of the eye,” J. Vision 4, 262–271 (2004). 41.- J. Tabernero, A. Benito, V. Nourrit, and P. Artal, “Instrument for measuring the misalignments of ocular surfaces,” Opt.

Express 14, 10945–10956 (2006). 42.- L. N. Hazra and C. A. Delisle, “Primary aberrations of a thin lens with different object and image space media,” J. Opt. Soc. Am.

A 15, 945–953 (1998). 43.- A. Benito, M. Redondo, and P. Artal, “Laser in situ keratomileusis disrupts the aberration compensation mechanismof the human eye,” Am. J. Ophthalmol. 147, 424–431 (2009). 44.- R. Navarro, M. Ferro, P. Artal, and I. Miranda, “Modulation transfer functions of eyes implanted with intraocular lenses,”

Appl. Opt. 32, 6359–6367 (1993). 45.- P. Artal, S. Marcos, R. Navarro, I. Miranda, and M. Ferro,

“Through focus image quality of eyes implanted with monofocal and multifocal intraocular lenses,” Opt. Eng. 34, 772–779 (1995).

OPTOMETRÍA