Nou Biaix, 50

Revista de la FEEMCAT i de la SCM

bia x uno i

ba nouiix

número 50

Consell de redacció:

Noemí Ruiz / Carlos Giménez (coords.)

Montserrat Alsina

Joan Carles Ferrer

Joan Miralles

Manuel Udina

© dels ar ticles, els seus autors

Coediten:

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com

,

sumari

Fotografia de la coberta: Pluja geomètrica

Lucia Hueto i Anna Mar tínez

Escola Rellinars al Periodicitat: semestr Nombre dexemplars: 1.700 ’

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Editorial 1 6 19 33 43 53 90

Edicions

de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430 comercial.edicions@ub.edu www.edicions.ub.edu

Puig Adam i la formació continuada del professorat de matemàtiques

Josefa Dólera-Almaida

Dolores Carrillo -Gallego

Encarna Sánchez-Jiménez

L’educació (matemàtica) és una arma de construcció massiva

Anton Aubanell i Joan Jareño

Cap a on va l’ensenyament de les matemàtiques?

Jordi Deulofeu Piquet

Els menuts també fem

Cyntia Riquelme Carvallo i Tana Serra Santasusana

Regressió i correlació lineal. Teoria i pràc tica

Francesc Carreras i Antoni Magaña

Mates al Carrer, matemàtiques per a tothom mates articles

Luis Cros Lombar te

Comtotsitotessabeu,elretornalanormalitatenalgunesàreesdesprésdelapandèmiadela covid-19 estàsentméslentdelqueseriadesitjable.Aquestéselcasdelarevista NouBiaix,per aixòvolemcomençardisculpant-nosambelsautorsilesautoresquefatempsqueesperen veurepublicatelseutreballiambelslectorsileslectoresquepotservancomençarapensar quelarevistadesapareixeria.Amés,durantel 2023s’haproduïtunrelleuenl’ediciódelarevistais’hainiciatunprocésderevisiódelsprocessosinternsperaconseguirserméseficients enlasevapublicació.Pertant,el NouBiaix ésunarevistavivaidesitgempoder-vos-enoferir moltsnúmerosmés.

Dinsd’aquestprocésdecanvi,usinformemque MariannaBoschhadeixatl’edicióperafrontarnousreptesprofessionals.Volemagrair-lilabonafeinafetailadedicaciódurantaquests anysalcapdavantdelarevistaidesitjar-limoltsèxitscomapresidentadel’ÀreaCientífica deCiènciesdel’educaciódinsdelaDivisiódeCoordinació,AvaluacióiSeguimentCientífici Tècnicdel’AgènciaEstatald’Investigaciód’Espanya.

Enaquestnúmero50 s’hanrecopilattresarticlesqueconvidenareflexionarsobrelaprofessiódedocentdematemàtiques:elseuorigen, elsconsensosielsreptesactualsifuturs. Totaixò,ambunamiradaconstructiva,suggerimentssobrelanecessitatdetenirunacultura compartida,ilafermaapostaquecaloptarperfomentareltreballcol¨laboratiudelacomunitat.Elsarticlesaportenmecanismesperseguirconstruintuncosdocentiunainfraestructura socialpreparadaperafrontarelsgransreptesquetenimielsquetindrem,acausadelmón canviantenquèvivim.

Enlalíniadelespropostesanteriors,elsarticlessegüentsmostrenactivitatsorientadesa l’educacióprimària(dinsdelnouprojecte«Femmatemàtiques»decinquèisisè)quemostren comespot,ambmaterialmanipulatiu,desenvoluparunaactivitatricamatemàticament. Ialnivelluniversitari,quepermetdesenvoluparestratègiesderesolucióqueinvolucrendiferentsconceptesoeinesmatemàtiquesicomaquestess’apliquenperresoldreproblemes reals.L’últimapropostas’emmarcaforadelcontextescolar(provapilotde«Matesalcarrer»a Mataró)ambl’objectiudecontribuiramodificarlavisióculturaldelesmatemàtiquesiaporta

lesindicacionsnecessàriesperreproduir-hoenaltresciutatsdeCatalunyaireprendreaixíun projecteglobaldeterritori.

Elprimerarticleambquèobrimaquestnounúmerodelarevista NouBiaix,«PuigAdamila formaciócontínuadelprofessoratdematemàtiques»,recullelsprincipalsfets,organismes (comelCentred’OrientacióDidàcticaolaComissióInternacionalperal’EstudiilaMillora del’EnsenyamentMatemàtic)imoviments,alsanyscinquantaiseixantadelsegle XX,que esvanocupard’establiriconcretarunmarcgeneraleuropeu,enrelacióambl’ensenyament delesmatemàtiquespreuniversitàries,delque araéselcicleactuald’educaciósecundaria. Unamostrad’aixòéseldecàlegdeladidàcticadelamatemàticapublicatel 1955,jaqueles líniesquemarcacontinuenregintlaculturaeducativaactual.L’articlemostraenquinsentitel catedràticcatalàPedroPuigAdamvavisualitzarlaimportànciadelaformaciódelprofessorat d’educaciósecundàriailesaccionsquevaimpulsar,quevanimplicarunamilloradelcos docent.Unavisióhistòrica,queelsdocentsmésjovespotserdesconeixen,quepermetubicar l’origendelsfonamentsdeleslíniesdeformaciódelprofessoratdematemàtiquesactuals.

Elsegonarticle,titulat«Educació(matemàtica)ésunaarmadeconstrucciómassiva»,parteix dereflexionssobreelpaperdel’ensenyamentdelesmatemàtiquesimostralesmúltiples vessantsd’aquestesdesd’unavisióglobal,considerantlesdiferentsetapeseducativesiel seupaperenlasocietat.Aportaideesiconsideracionsenrelacióambelsdiferentsagents quehiestaninvolucrats:desdel’esferaméspolítica,passantperlaformaciódelprofessorat, lainvestigacióeneducaciómatemàtica,lesassociacionsdeprofessionals,eltreballenxarxa, lesentitatsdedivulgació,etc.,finsalaresponsabilitatindividualdecadadocent.Amés, amagaunmisteriquedescobrireusiarribeualfinaldelalectura.

EltercerarticleésescritperJordiDeulofeu,coordinadordesdel 2013finsal 2023del’actual màsterinteruniversitarienFormaciódelProfessoratdeSecundàriadeMatemàtiquesiuna delespersonesreferentsenladifusiódelarecercaeneducaciómatemàtica.«Capaonva l’ensenyamentdelesmatemàtiques?»completaleslíniesmarcadesenelstextosanteriors ambpropostesactuals.Eltooptimistadel’autor,totilesdificultatsielsproblemesqueidentifica,éscontagiósideixaclarqueencarahihacamíperexplorartotsplegats.Finalment,ens sumemaanimaratothomaparticiparenelproperCongrésCatalàd’EducacióMatemàtica: C2 EM 2025.

Elquartarticle,titulat«Elsmenutstambéfem mates»iescritperCynthiaRiquelmeiTanaSerra,defensalanecessitatdecultivarelraonamentmatemàticdesdel’etapad’educacióinfantil,apartirdepresentaralsalumnessituacionsriquesqueestimulinelseupensamentespontaniiajudinelsmestresadisposard’einesadequadesperconduirelcreixementd’aquestraonamentmatemàticdelsinfants.Enaquestalínia,presentenunexempledel’activitatdelCercledeMestresdel’AssociaciódeBarcelonaperl’Estudiil’AprenentagedelesMatemàtiques (ABEAM);concretament,unrepteperalsmésmenutsanomenatLesTorresdelaReina, quedebensegurinspiraràelsmestresd’aquestaetapaaincorporaraquestnouenfocament alessevesaules.

Elcinquèarticle,escritperFrancescCarrerasiAntoniMagaña,presentademaneraforça rigorosapossiblesescenarisbasatsendadesrealsd’àmbitsmoltdiversos,comaraelsjocs,

l’economia,elsesportsielmónacadèmic,quepodenresultarpropersalsestudiantsienels qualsesjustifical’anàlisid’aquestesdadesapartirdelmodelderegressióicorrelaciólineal.

Sensdubteaquestmaterialpermetaldocentadaptaraquestaanàlisiaqualsevoljocdedades numèriquesposantl’èmfasienlainferènciadeconclusionsestadístiques,moltmésenllàde lameradescripciódelesdadesqueacostumaaser,malauradament,elmàximprofitque s’obtéasecundàriad’aquesttipusd’informació.L’aplicabilitatadiferentstreballsderecercadebatxillerat,perexemple,semblaòbviaperpermetrelegitimarelcairematemàticde nombrosespropostesSTEM.

Enelsisèarticle,LuisCrosensdescriulareeixidainiciativa«Matesalcarrer»,resultatdel’activitat delcorresponentgrupdetreballdelaFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya(FEEMCAT)iqueesvaplasmarenl’ediciócelebradaalscarrersde Mataról’octubredel 2022,quetindràcontinuïtatenlesedicionsdeBalagueriLleida.

Iniciativescomaquestatenenunvalorincalculableperquèdonensentitambcreativitata l’objectiucompartitpertotsnosaltresdenormalitzar,donarvisibilitatinaturalitzarlapresènciadelesmatemàtiquesenl’entorndelsnostresalumnesidelessevesfamílies.

articles articles

PuigAdamilaformació continuadadelprofessorat dematemàtiques

JosefaDólera-Almaida j.doleraalmaida@um.es

DoloresCarrillo-Gallego carrillo@um.es

EncarnaSánchez-Jiménez esanchez@um.es

DepartamentdeDidàcticadelesCiències MatemàtiquesiSocials.Facultatd’Educació UniversitatdeMúrcia

Resum Abstract

Ambl’aprovaciódelaLleid’ordenacióde l’ensenyamentmitjàde 1953esvanduraterme aEspanyadiferentsactivitatsdeformació permanentadreçadesalprofessoratd’educació secundària.El 1955PerePuigAdam,catedràtic d’institutdematemàtiques,vasernomenatpel CentrodeOrientaciónDidáctica(COD)per investigarsobrelareformailamillorade l’ensenyamentdelesmatemàtiquesal batxillerat.Apartird’aquellmomentva promourenombrosesactivitatsformativespera aquestcol¨lectiu.L’objectiud’aquesttreballés identificarquinesaccionsvadesenvoluparPuig Adam,enl’àmbitdelaformaciócontinuadadel professoratd’educaciósecundària,aladècada delscinquantaaEspanya.Perferaquesttreball s’hanconsultatdiversespublicacions professionals.Ocupaunllocdestacatlarevista EnseñanzaMedia,jaques’hivanpublicar nombrosescròniquessobreactivitats deformaciódestinadesalprofessoratde matemàtiques.Elsresultatsmostrenqueles ideesmetodològiquesqueesvanexposaren aquestesreunionsestavenlligadesalmodel pedagògicdePuigAdamilessevespropostes d’ensenyamentméscaracterístiques,entreles qualsdestacavaelmètodeheurístic.

AfterenactingtheSecondaryEducationLawin 1953,variousinitiativesaimedatproviding continuingprofessionaldevelopmentfor secondaryeducationteacherswereimplemented inSpain.In1955,PerePuigAdam,professoratthe InstituteofMathematics,wasappointedbythe CentrodeOrientaciónDidáctica (COD)tolead researchonthereformandimprovementof mathematicsteachinginuppersecondary education.PuigAdamstartedtoactivelypromote numeroustrainingactivitiesforthosestudents. Thisstudymainlyaimstoidentifythespecific activitiesPuigAdamdevelopedinthefieldof continuingprofessionaldevelopmentfor secondaryeducationteachersduringthe1950sin Spain.Severalprofessionalpublicationswere consultedtoconductthisresearch.Thejournal EnseñanzaMedia wasparticularlyimportant,as itpublishedalargenumberofarticlesonteacher traininginitiativesaimedatmathematics teachers.Theresultsshowthatthe methodologicalideasputforwardinthe publicationswereinlinewithPuigAdam’s teachingmodelandhismostcharacteristic teachingproposals,amongstwhichtheheuristic methodstoodout.

1.Introducció

Laformacióiperfeccionamentdelprofessoratd’educaciósecundàrianovaserunaspecte prioritariperalgoverndelrègimfranquistaentre 1936i 1953(Lorenzo, 1996, 2003).Aquesta tendènciavacomençaracanviarapartirdelaLleid’ordenaciódel’ensenyamentmitjàde 1953(Ministerid’EducacióNacional, 1953),que,enl’article42,deia:

ElMinisteriodeEducaciónNacionalcuidaráelnivelcientíficoypedagógicodelProfesoradodeEnseñanzaMedia,estimulandolamejoradelosmétodos,promoviendo,con lascolaboracionesdebidas,cursosdeformaciónydeperfeccionamientoprofesional,y vigilandolaspruebasdesuficiencia,selecciónypreparación(p. 1124).

LaLleipreteniaimpulsarlarenovacióielperfeccionamentdelsmètodeseducatiusenl’educació secundària,aixícomassegurarl’adequadapreparaciócientíficaipedagògicadelprofessorat debatxillerat.Peraaixòeranecessariqueesdesenvolupessininstitucions,experiènciesi publicacionsques’encarreguessindepromoureaquestsaspectesformatius(Lorenzo, 1996, 2003).Perdonarcomplimentaaquestadisposició, l’executiuvacrear,entrealtresòrgans,el CentrodeOrientaciónDidáctica(COD)ilaEscueladeFormacióndelProfesoradodeEnseñanzaMediapersenglesordresministerialsel 1954iel 1955,respectivament1 (Utande, 1964). Tambéesvanfernombrosesactivitatsconcretesquevancontribuirengranmaneraala modernitzaciódel’ensenyamentmitjà.Entrelesprincipalsactivitatsdeformaciópermanent queesvanduratermeaEspanyaapartirdelareformade 1953estrobenlessegüents (Lorente, 2011):

aq Reunionsd’estudidecatedràtics,agrupatsenseminarisdidàctics,amblaparticipaciód’inspectorsespecialistes.Aquestesreunions,organitzadespelCODentre 1956i 1957,pretenienrenovarelsmètodesd’ensenyamentatravésdel’intercanvid’experiènciesdocentsenl’àmbitnacional.

bq Reunionsd’estudi,convocadesambl’objectiudefomentarlacoordinacióencadadistricteuniversitarientreelprofessoratoficiald’institutsieldelscol¨legisreligiosos.

cq Cursetsd’actualitzaciócientíficaididàctica,dirigitsprioritàriamentalprofessoratdematèriesexperimentals.

d q Viatgesoexcursionsd’estudi,queespecialistes(inspectorsicatedràtics)endeterminadesmatèriesfanalllargdelageografiaespanyola.

eq Cursetsdepràctiquesperaprofessorsnooficials endeterminadesmatèries(matemàtiques,físicaiquímica,ciènciesnaturalsigeografiaihistòria).

ElCODvatenirunpaperrellevantenlaformaciócontinuadadelprofessoratd’educaciósecundària,jaqueunadelessevesfuncionsprincipalseradivulgarexperiènciesd’aulaitreballsderecercaentreelcosdocent,aixícomorganitzaripatrocinarreunionsdeprofessors perpropiciaruncontacteestretentreelsdiferentscentreseducatius(institutsicentresde l’Esglésiaidel’ensenyamentprivat).Larevista EnseñanzaMedia (1956-1971),dirigidaper l’inspectorDacioRodríguezLesmes,vacol¨laboraractivamentenlatascadivulgadoradel CODiesvaferressòdemoltesdelesactivitatsdeformaciódirigidesaaquestcol lectiu (Salcedo, 1956).

1.LaEscueladeFormacióndelProfesoradodeEnseñanzaMediavasercreadacomadependènciadel Centred’OrientacióDidàcticaiel 1962 vaassumirleslaborscorresponentsalaformaciópràcticadelprofessorat amblaintenciód’ampliaricentralitzarl’experiènciainiciadaanysabanspelCOD, 1954-1968(Lorenzo, 2003).

2.LaComissióInternacionalperal’EstudiielMilloramentde l’EnsenyamentMatemàticilasevainfluènciaenlarenovació del’ensenyamentdelesmatemàtiquesaEspanya

El 1950 esvacrearlaComissióInternacionalperal’EstudiielMilloramentdel’Ensenyament Matemàtic(enanglès,InternationalCommi ssionfortheStudyandImprovementofMathematicsTeaching,CIEAEM)ambl’objectiud’abordarelsproblemesdel’ensenyamentdeles matemàtiques,sobretotenl’educacióprimàriaisecundària.Vaserimpulsatpelprofessor CalebGattegno,professordedidàcticamatemàticadel’Institutd’EducaciódelaUniversitatdeLondres.LaComissiópreteniaaprofitarlesperspectivesqueespodienaportardes del’epistemologia,lapsicologiaolapedagogiapermillorarl’ensenyamentdelesmatemàtiques.Entreelsseusmembreshihaviafiguresrellevantsdelpanoramainternacionalde diferentscampsdisciplinaris:epistemòlegs ipsicòlegs,comJeanPiagetiEwartW.Beth;matemàtics,comGustaveChoquet,JeanDieudonnéiAndréLichnerowicz;ipedagogs,com CalebGattegno,EmmaCastelnuovoiWillyServais(Hodgson etal., 2013).

LaComissióconsideravaqueperassolirunareformaprofundaieficaçdelsprogrames,els mètodesilesfórmulesusadesenl’ensenyamentesnecessitava:

[...]deunlado,elconocimientoprofundodelasestructurasmatemáticasy,deotro,elconocimientonomenosesencialdelosprocesosevolutivosdelainteligenciayafectividad delniño,nosóloparacomprendermejorlagénesisdelosconceptosyjuiciosmatemáticosensumente,sinotambiénparatenerencuentalosfactoresdeatraccióneinterés quepuedenestimularlayfavorecerla(Puig, 1955a,p. 96).

EntrelesdiferentsfuncionsdelaCIEAEMocupavenunllocdestacatlacoordinaciódeles recerquesquedesenvolupavaendiferentspaïsosil’impulsdetreballsconjunts.Perdura termeaquestesfuncions,laComissióvaoptarperorganitzarreunionsinternacionalsamb l’objectiud’habilitarunespaipropiciperal’intercanvid’opinionsipuntsdevista.Tambéva promourelaformaciódegrupsdetreball(nacionalsiinternacionals)ivaapostarperpublicar lessevesrecerquesenobresconjuntes,amblafinalitatdedivulgar-lesentreelprofessorat. Quantal’ensenyamentdelesmatemàtiques,enlasegonadècadadelscinquantaesvan editarlesobres Laenseñanzadelasmatemáticas (Piaget,J. etal., 1971)i Elmaterialparala enseñanzadelasmatemáticas (Gattegno,C. etal., 1967).

PerePuigAdam(Barcelona, 12 demaigde 1900 Madrid, 12 degenerde 1960),catedràtic dematemàtiquesdel’InstitutodeEnseñanzaMediaSanIsidro(Madrid),esvaincorporara laCIEAEMel 1955iapartird’aleshoresvaparticiparactivamentenlesactivitatsorganitzadesperlaComissió.Atalld’exemple,s’al¨ludeixalpaperdestacatquePuigAdamvatenir enl’organitzaciódelaXIReunióndelaCIEAEM(Madrid, 1957),esdevenimentqueesvafer juntamentamblaIExposiciónInternacionaldeMaterialDidácticoMatemático.Aquestes activitatsvandespertarungran«interésentreelprofesorado,yaqueeraelprimerCertamen internacionalquelahistoriadelacienciaregistrasobreelmaterialdidácticomatemático» (Puig, 1958b,p.7).Ambl’objectiudeferarribaralprofessoratd’aquestadisciplinainformació detalladadelqueallís’esdevingué,elMinisteriodeEducaciónNacionalvapublicarelllibre Elmaterialdidácticomatemáticoactual (Puig, 1958),dedicatalaReunión Exposición(figura 1).Larevistaprofessional EnseñanzaMedia vasubratllarqueaquestapublicacióera«un valuosoelementodeorientaciónytrabajoparalosprofesoresdenuestraEnseñanzaMedia» (EnseñanzaMedia, 1959,p. 210).

Figura1.Cobertadelllibre Elmaterialdidácticomatemáticoactual.

TambéésremarcablelaparticipaciódePuigAdamcomamembredelgrupdetreballqueva elaborarles«Recomendaciones»peral’ensenyamentdelesmatemàtiquesenlaXIXConferènciaInternacionald’InstruccióPública(Ginebra, 1956),organitzadaperlaOrganitzacióde lesNacionsUnidesperal’Educació,laCiènciailaCultura(enanglès,UnitedNationsEducational,ScientificandCulturalOrganization,UNESCO)iperl’OficinaInternacionald’Educació (OIE),ladirecciódelaqualeraocupadaperPiagetenaquellmoment(González, 2008;Lozano, 1956;Puig, 1955a).

Elmovimentinternacionalderenovaciódelamatemàticaques’estavadesenvolupantenla dècadadelscinquantaialquals’hafetreferènciaenparàgrafsanteriors,pràcticamentva coincidireneltempsambl’aprovaciódelaLleid’ordenaciódel’ensenyamentmitjà(1953). Probablement,algunesdelesaccionsquel’executiuvaidearperimpulsarlarenovacióde l’ensenyamentdelesmatemàtiques,aEspanya,vanestarinfluenciadesperlesrecerquessobrel’ensenyamentdelesmatemàtiquesquelaCIEAEMestavafent.Unamostrad’aixòpodria serelnomenament,el 1955,dePuigAdampelCODperinvestigarsobrelareformailamillora del’ensenyamentmatemàticenl’àmbitnacional.Apartird’aquestmomentPuigAdames vapreocupard’incrementarlesrelacionsinternacionalsambdiversospaïsoseuropeusper tractarqüestionssignificativesdel’ensenyamentmitjàivaorganitzarreunionsdirigidesa catedràticsdematemàtiquesdetotEspanya,en lesqualss’informava,entrealtresaspectes, delsnousmètodesimaterialsques’estavenutilitzantforadel’àmbitnacional.PuigAdam consideravaquelaformaciódelcosdocentnofinalitzavaambl’obtenciódeltítol;creiaque, enaquestatasca,mainos’acabad’aprendreperquè«cuandosesabeleerenellibroabierto deunaclase,nuncaseterminaelprocesodeacumulacióndeexperienciasymejorayadaptaciónconsecuentedeprocedimientos»(Puig, 1958a,p. 10).Peraixòesvainvolucrariva participardemaneraactivaenlesactivitatsdeformaciópermanentdelprofessoratdegrau mitjàivaarribaradirigir-nealgunes.

Al’horadevalorarlesmesuresposadesenmarxapelrègim,caldestacarquemoltsdels modelspedagògicssobreelsqualsesbasavaaquesta«renovació»s’inspiravenenelspostulatsdel’escolanova,perlaqualcosa«nofuerontanNuevosyavanzados»(Lorente, 2011, p.682.)Ésmés,algunsautors,comMainer(2009)iViñao(2014),considerenquenovaarribar

aproduir-seunarupturatotalambelsmodelspedagògicsinstauratsabansdelaGuerraCivil iques’apreciaunacertacontinuïtatentreelsmodelsdeformaciódelprofessoratabansi desprésdelconflictearmat.

L’objectiud’aquesttreballésidentificarquinesaccionsvaduratermePuigAdam,enl’àmbit delaformaciócontinuadadelprofessoratd’educaciósecundària,perpromourelarenovació del’ensenyamentdelesmatemàtiquesenelbatxilleratdurantladècadadelscinquantaa Espanya.

Peralarealitzaciód’aquesttreballs’hanconsultatdiversespublicacionsprofessionals,com ara,entred’altres: RevistadeEducación, RevistadeSegundaEnseñanza, GacetaMatemática, BoletíndelaInstitucióndeFormacióndelProfesoradodeEnseñanzaLaboral i ButlletídelaSecció deMatemàtiquesdelaSocietatCatalanadeCiènciesFísiques,QuímiquesiMatemàtiques.S’ha prestatunaatencióespecialalarevista EnseñanzaMedia,jaques’hivanpublicarcròniques demoltesdelesactivitatsdeformaciópermanentdirigidesalprofessoratdematemàtiques queesvanferenladècadadelscinquanta.Ésmés,elmateixPerePuigAdamvareconèixer alapublicaciólasevatascaenladivulgaciódelesexperiènciesdesenvolupadesentornde ladisciplinadelesmatemàtiquesivaagrair-lil’interèsmostrat,malgratquenoeraunarevistaespecialitzadaenaquestamatèria.Fetque,vaassenyalarcontrariat,contrastavaamb l’escassaatencióquealgunespublicacionsexpertesenladisciplinahavienprestataaquestes activitats(Puig, 1958b).

Aquestestudiformapartd’unarecercamésàmpliasobrelesaportacionsdelprofessorPere PuigAdamal’educaciómatemàticaespanyola.Elsresultatsobtingutshandonatllocaalguns treballs:DóleraiSánchez(2019, 2023);Dólera etal. (2023a, 2023b);DóleraiCarrillo(2023a, 2023b).

3.Activitatsformativesperalprofessoratd’educació secundàriadematemàtiques

Lesactivitatsdeformacióprofessionalalesqualss’al¨ludeixenelsapartatssegüentsvan començarel 1956,desprésqueelCODencarreguésaPuigAdamdepromoureunarecerca sobrelespossibilitatsdemilloradel’ensenyamentdelesmatemàtiquesalbatxillerat.Entre 1956i 1960 anyenquèvamorirPuigAdam esvanfer,aescalanacional,tresreunions d’estudidecatedràticsaMadrid(1956-1957)itresreunionsd’estudiperalprofessoratd’un mateixdistricteuniversitari;aquestesúltimesesvancelebraraGranada(1956),València(1958)i Huelva(1960).Peralprofessoratnooficialqueimpartialadisciplinadematemàtiques,Puig Adamvadirigiruncursetdepràctiquesal’InstitutodeEnseñanzaMediaSanIsidrodeMadrid (1958).EnelsapartatssegüentsesfareferènciaalesactivitatsformativesenlesqualsPuig Adamvaparticipardemaneraactivaiesprestauninterèsespecialalesaportacionsqueva ferelprofessorenaquestesreunions.

3.1.Reunions d‘estudi per a catedràtics

Enl’àmbitnacional,laIReunióndeEstudiodeCatedráticosdeMatemáticas(Redacción, 1956) vatenirllocentreelsdies 20 i 24demarçde 1956aMadrid.Undelsacordsaconseguits

vaseradoptarcomanormagenerald’actuaciódidàcticael«Decálogodeladidácticadela matemáticamedia»,quevaserpublicatperPuigAdamenlarevista GacetaMatemática el 1955iqueestabliaelsegüent(Puig, 1955b):

I.Noadoptarunadidácticarígidasinoamoldarlaencadacasoalalumno.

II.NoolvidarelorigenconcretodelaMatemáticanilosprocesoshistóricosdesuevolución.

III.PresentarlaMatemáticacomounaunidad enrelaciónconlavidanaturalysocial.

IV.Graduarcuidadosamentelosplanosdeabstracción.

V.Enseñarguiandolaactividadcreadoraydescubridoradelalumno.

VI.Estimulardichaactividaddespertandointerésdirectoyfuncionalhaciaelobjetodel conocimiento.

VII.Promoverentodoloposiblelaautocorrección.

VIII.Conseguirciertamaestríaenlassolucionesantesdeautomatizarlas.

IX.Cuidarquelaexpresióndelalumnoseatraduccióndesupensamiento.

X.Procuraratodoalumnoéxitosqueevitensudesaliento.

Amés,PuigAdam,juntamentamblarestad’assistents,vandecidirafegiralesorientacions anteriorslaconsideraciósegüent:

Ejercerunaconstanteobservaciónsobrelasreaccionesdelosalumnos,adoptandouna posturaobjetivayexperimentalennuestrafuncióndidáctica,ytratandoalalumno,de acuerdoconlapsicología,conafectoenlugardecoacción,paraobtenerdeélelmáximo rendimiento(Redacción, 1956,p.48).

LaIIReunióndeEstudiodeCatedráticosdeMatemáticas(Redacción, 1957a)esvaferentre el 22 iel 28d’octubrede 1956.Elprogramadelareuniócontenia,entrealtres,elstemes següents:finsdel’ensenyament,mètodesd’ensenyamentheurísticimodelsdinàmics(Redacción, 1960,p. 134).Quantalprimerd’aquestsaspectes,esvaacordar:

[...]nuestraenseñanzapersigue,debeperseguirsiempre,noedelapreparacióndelalumno paraelexamen,sinolaformaciónedescobridelmismo.Noadiestraralalumnoparaque seaprendamuchasedescobedescobrirenunmomentodadooenuncieedescoperatoriassinpenetrarsusignificado,sinocapacitarleparasentir,dotarledeledescdehacer Matemática;hacerlever,operaryedesco.Enunapalabra:hacerleedescobrir(Redacción, 1957a,p. 10).

Elsprofessorsreunitsreconeixienqueeraurgentrevisarelsmètodesd’ensenyament.Sostenienqueelsmètodesactiushaviendedesplaçarlaclasseconferència,encaramoltarrelada enl’ensenyamentespanyold’aquellaèpocaienlaqualeldocentsoliaactuarcomunmer transmissord’informació.Vancoincidiraafirmar:

[...]dentrodelaenseñanzaactiva,elmodoeurístico[sic]vieneasersuprincipalmanifestación,talvezsupalancamáspotente;lamaneramássencilladecrearenelalumnolos centrosdeinterés,deestimularsufacultadcreadora,dedespertarsusdotesdeobservación(Redacción, 1957a,p. 12).

PuigAdamesvainteressarpelmètodeheurísticdesdelsseusiniciscomacatedràtic.Hodiu enelseuprimertreballsobreeducaciómatemàtica(Puig, 1926),quevapublicarelmateix anyquevaaprovarl’oposicióacatedràticd’institut,ihovacontinuarportantalapràctica

duranttotalasevatrajectòriaprofessional.Ensónunamostraelsnombrosostreballsqueva publicarsobremetodologiaheurística,enels qualsoferiaalprofessoratexemplesdetallats delliçonsheurístiquesquehaviaimplementat ambelsseusalumnes.Entreaqueststreballs estrobalasevaobraméscaracterística, Didácticamatemáticaeurística (Puig, 1956),queva seravaladaipublicadaperl’InstitutodeFormacióndelProfesoradodeEnseñanzaLaboral.

PuigAdamconsideravaqueaquestamanifestaciódel’ensenyamentactiuestavadestinadaa ocuparunpaperrellevantenlamillorairenovaciódeladidàcticamatemàticainovadubtar aaprofitarl’oportunitatdefamiliaritzarelsquivanassistiraaquestareunióambelmètode heurístic.Ambaquestaintenció,vadesenvolupardavantelpúblicalguneslliçonsheurístiques.Perexemple,vafer-neunasobregeometriadel’espaiambdotzealumnesdesegon cursdebatxillerat,enlaqual,atravésdematerialsquotidians,comaracarpetesiagullesde tricotar,vatreballarambelsestudiantselparal lelismedeplans,elparal lelismederectesi lesposicionsrelativesentrerectaipla(figura 2).

Font:Redacción(1957a,p.13).

Desprésdecadalliçó,PuigAdaminiciavaambelprofessoratassistentunaanimadaxerrada sobreelqueallís’haviaesdevingut.Ambaixòtractavadepromoureunareflexiócríticadel professoratsobredeterminatsaspectes:elscontingutstreballats,elrendimentdel’alumnat, l’interèsquedespertavaenelsnensl’activitatproposadaielmaterialemprat,entrealtres. Finalment,esvavalorarlapossibilitatd’implantarelmètodeheurísticalesaulesespanyoles iesvaconclourequeundelsseusprincipalsinconvenientseral’excessiunombred’alumnes perprofessorqueengeneralhihaviaal’aula.

PuigAdamtambévaremarcarelsbeneficisdel’úsdelsmodelsdinàmicsenl’ensenyament delesmatemàtiques.Atalld’exemple,vapresentaralprofessoratassistentalgunsdelsmaterialsqueellmateixhaviaelaborat,entreelsqualshihaviaelde«l’arrelquadrada»(figura 3),quelivapermetretreballarambelsseusalumnesdesegoncursdebatxilleratl’estructura operatòriadel’arrelquadradaambmaterialsquotidians(botons,tiresicartons).Estractava deconstruirambbotons,unavegadas’haviarepresentatelnombredelqualesvoliaobtenirl’arrelquadrada,elmajorquadratpossible(descomponent,sieranecessari,lesunitats d’ordresuperiorenaltresd’ordreimmediatamentinferior).D’aquestamanera,l’arrelquadradaescorresponiaambelcostatdelquadratielsbotonssobrantsrepresentavenlarestade l’operació(Puig, 1932).

Figura2.Momentd’unaclasseheurísticasobregeometriadel’espai.

Figura3.Materialperdesenvoluparlalliçóheurísticasobrelaregladel’arrelquadrada.

Font:PuigAdam(1958b,p.110).

LaIIIReunióndeEstudiodeCatedráticosdeMatemáticas(Redacción, 1957b)vatenirlloc entreel 10 iel 16dedesembrede 1956is’hivareflexionarcol¨lectivamentsobrelesorientacionsmetodològiquesquehavienderegirels quatreprimerscursosdebatxillerat.Fruit d’aquestareflexió,esvaconsiderarqueelsdos primerscursosdebatxillerathaviendetenir unmarcatcaràcterintuïtiuipràctic,ihavienderecórreral’úsdeprocedimentspreferiblementempírics,com,perexemple,elplegat,elpapertransparentoelsfilsperal’estudide lageometria.Elscursosterceriquart,encanvi,vanserdefinitscomunciclequeconstituïa unaetapadetransicióentreelsmètodesoprocedimentsempíricsielmètoderacional,on elsconeixementsmatemàticsespresentavenconstituintunaestructuralògicaperfectament entrellaçada.Esvaincidir,igualment,enlaconveniènciadepresentarlamatemàticaapartir d’exemplesconcrets,extretsigualmentdelavidarealdel’alumne,queserviaaixícoma exempled’aplicaciópràctica.Tambéesvaposarl’accentenlautilitzacióoconstruccióde modelsgeomètricssenzillsperpartdel’alumnat,jaqueesvaconsiderarquefinsitotlamera observaciópermetiaalsalumnesidentificarnombrosespropietatsmatemàtiques.

Arrandelesreflexionsmetodològiquesanteriors,PuigAdamvadestacarl’eficaçajudaque elsmodelsdinàmicsprestavenal’ensenyamentheurísticdelesmatemàtiquesivaressaltar l’interèsquedespertavenentre elsestudiants.Igualqueenla reunióanterior,vapresentar davantelsseuscompanysalgunsdelsúltimsmaterialsquehaviaideat,entreelsqualsva ocuparunllocdestacatelseumodeldegeoespai,peral’estudidelageometriaespacial (figura4),delqualvaconstruirdiversesversions.

Figura4.Representacióambelgeoespaid’unmodeldeformabledeparal lelepípede. Font:PuigAdam(1957,p.25).

ElgeoespaidePuigAdamestavainspiratenelgeoplàdelprofessorGattegnoiconsistiaen unacaixalescaresdelaqualestavenconstruïdesambllistonsestrets.Aixòpermetiaqueles configuracionsqueesrepresentavendinsdelacaixapoguessinservistesperl’estudiantdes dequalsevolperspectiva.PuigAdamdestacavaquelaversatilitatd’aquestmateriallihavia permèstreballarambelsseusalumnesnombrososcontingutsdelageometriaespacial,com, perexemple,laconstrucciódefiguresespacialsambcordills.Amés,elsllistonspodienser substituïtspertelesmetàl¨liques(figura5),jaqueaquestamodificaciónocomprometiala visibilitatdelmodel(Puig, 1957).

Figura5.Detalld’ungeoespaiambtelametàl licadissenyatperPuigAdam.

Font:PuigAdam(1958b,p.114).

3.2.Curset sobre didàctica de les matemàtiques per a professors no oficials

DesdelaIReunióndeEstudiodeCatedráticosdeMatemáticas(Redacción, 1956),elprofessoratoficialvacomprendrequelamilloradel’ensenyamentmatemàticespanyolrequeriala implicaciódetotalacomunitateducativa(tantdel’ensenyamentoficialcomdelnooficial). Peraixò,consideravennecessariquedesdelCODs’emprenguésuna«campanyarenovadora delaDidáctica»dirigidaexpressamentalprofessoratdecentresd’ensenyamentnooficial. SesuggeriaqueelCODhaviadeproporcionaraaquestscentresorientacióibibliografia específicasobreelsnousmètodesd’ensenyament,i,encasquefosnecessari,haviad’afavorir elcontactedirecteentreaquestscentresipersonesqualificadesquepoguessinoferir-losuna orientaciómésindividualitzada(inspectorsdeldistricte,catedràticsdelalocalitat,llicenciats especialitzats,etc.).Esconsideravaconvenientqueesfomentessinactivitatspersuscitarinterèsperlarenovaciódeladidàcticamatemàtica,comaraconferències,reunionsd’estudi, exposicionsdematerialsomodelsdidàctics,exemplificacionsdelliçonsd’aula,projeccions didàctiques,etc.

Davantaquestademanda,el 1958PuigAdamvadirigiruncurssobredidàcticadelesmatemàtiquesalbatxilleratadreçatalprofessoratdel’ensenyamentprivat(EnseñanzaMedia, 1958).Ambaquestaactivitat,queva serorganitzadapelCODentreel 14defebreril’1 de marçal’InstitutoSanIsidro,espreteniaaportarorientacionsdidàctiquesimetodològiques alprofessoratqueimpartiamatemàtiquesencentresprivatsiquenohaviarebutformació específicasobreladisciplinaqueensenyava.

PuigAdamvaferdavantelscursetistesdiverseslliçonsheurístiquesenlesqualsvancol laborar grupsreduïtsd’alumnesquepertanyienadiferentscursosdel’InstitutoSanIsidro.Perposar-

nealgunexemple,al ludiremaunalliçósobresimetriesenelplaquevaduratermeamb alumnesdeprimercursdebatxilleratienlaqualvaemprarcomamaterialdidàcticcartons ambfiguresgeomètriquesretallades;obéaunaaltralliçósobrevolumsdeprismesipiràmidesquevaferambalumnesdesegonitercercursdebatxilleratienlaqualvautilitzar elgeoespaiqueportaelseunomperrepresentar,mitjançantgomes,ladescomposiciódel prismaentrespiràmidesequivalents.Aixòvapermetrealsalumnes,segonselprofessor, deduirl’obtenciódelvolumdelapiràmideapartirdeladelprisma,reglaque,finsaaquell moment,eradesconegudaperells.

4.Reflexionsfinals

LesactivitatsdeformacióqueelCODvaorganitzarperalprofessoratdeladisciplinade matemàtiquesentre 1955i 1960 tenienunobjectiucomú:posarencontacteelprofessorat dematemàtiquesd’ensenyamentmitjà(Redacción, 1956).SegonsPuigAdam(1958a,p. 11), quevacol laborardemaneraactivaenaquestatasca,la«baseindispensable»delaformació continuadadelprofessoratresidiaen«unaintensavidaderelaciónentreelcuerpoenseñante».Queeldesenvolupamentdelliçonsmodeldavantelsassistentsfosunaactivitatrecurrent enlesreunionsielscursosquePuigAdamorganitzava,escorresponiaamblaconcepcióque elcatedràticteniasobrecomhaviadefer-selaformaciódidàcticadelprofessoratd’educació secundàriadematemàtiques,que,segonsell(1958a,p. 9),s’assemblavaa«laadquisiciónde unarte,yqueelartista,sinonaceyacreador,sólopuedeirhaciéndoseafuerzadecontagio».

PuigAdamcreiaqueperalamilloradel’ensenyamentdelesmatemàtiqueserenfonamentalslaimplicacióilaformacióadequadadelprofessorat.SeguiaaixílespropostesdelaInstituciónLibredeEnseñanza(ILE),comvaexpressarGinerdelosRíoseneldiscursd’inauguració delcurs 1880-1881:«dadmeelmaestroyosabandonolaorganización,ellocal,losmedios materiales;cuantosfactores,ensuma,contribuyenaauxiliarsumisión.Élsedaráartepara suplirlainsuficienciaolosviciosdecadaunodeellos».Aquestesideesvansertambérecollideseneldecretdecreaciódel’Institut-Escola,ambelqualPuigAdamvatenirrelació atravésdelSeminarioMatemáticodelaJuntadeAmpliacióndeEstudios(JAE).PuigAdam consideravaquel’organitzaciódereunionsdeseminariperiòdiquesentreelprofessoratera unaeinaeficaçdecanvi:

[...]elprofesoraislado,enambientealejadodelosgrandescentrosdecultura,pierde contactoconelmundocientíficoengestación,dejadepercibirsuslatidos,comonose alimentedetantoentantosucomunicaciónconélpormediodeenvíoderevistas,organizacióndecursillosdeampliacióndeconocimientos,intercambios,reuniones.Esta formaciónposcátedraescomplementonecesariodelaanterior[formacióninicial],yyo diríaquecasitanimportantecomoella(Puig, 1958a,p. 11).

Lesideesmetodològiquesqueesvanexposarenaquestesreunionsconstitueixenlabasede lesdeunormesdidàctiquesperal’ensenyamentdelesmatemàtiquesenelbatxilleratque PuigAdamvaelaborarel 1955.Laimportànciad’aquest«Decálogodeladidácticamatemáticamedia»(Puig, 1955b)resideixenelfetque,desprésdelasevapublicació,vaseradoptat pelsprofessorsd’educaciósecundàriaespanyolsenl’exercicidelasevatascadocentiesva presentarenlaXIXConferènciaInternacionald’InstruccióPública(Ginebra, 1956),i,segons Ausejo(2013),moltesdelesconclusionsd’aquestaconferènciacoincidienamblesexpressadesperPuigAdamenelseudecàleg.Enl’actualitat,aquestesnormesoorientacionsmeto-

dològiques«constituyenunareferenciaobligadaparatodosloseducadoresmatemáticosen elactualsiglo XXI»jaque«trasciendeneneltiempo,enelcontextodelastransformaciones quetienenlugarenlaenseñanzadelasciencias»i,pertant,sónunreferentperalesnoves generacionsdeprofessorsdematemàtiques(Arteaga,delSoliMedina, 2021,p.348).

L’evoluciódel’enfocamentdonatalsensenyaments(desdel’intuïtiuipràctic,ambintroducciógradualdelraonament,finsaarribaralsmètodesracionals)il’úsdematerialscoma models(fomentantelsrelacionatsamblavidadiària)vansertemesd’interèsenlesactivitats deformacióprofessionalqueesvanduraterme.AquestesideescontinuenlesquePuig AdamhaviaportatalapràcticaabansdelaGuerraCiviliqueestrobenenelstreballsque vapublicarsobreensenyamentdelesmatemàtiquesdesde 1926finsa 1939 (Puig, 1926, 1927, 1979).Sónpropostesconcordantsamblapràcticadel’Instituto-EscueladeMadridi l’Institut-EscoladeBarcelona.PuigAdamcompartiamoltesdelesideessobrel’ensenyament delesmatemàtiquesdeJosepEstalella,quivadirigirl’Institut-Escoladesde 1932 finsala sevamort,el 1938.Totsdosprofessorsconsideravenqueles«activitatsd’experimentació» exercienunpaperfonamentalenl’educaciómatemàticadel’alumne(GrupCúbic, 2019,p. 94),enelsentitquetotconeixementhaviadeserobtingutmitjançantunaaccióqueho provoqués.JosepEstalellavaconferiralainstituciócatalanaunestilpropiquevasermolt benvolgutperPuigAdam.Mostrad’aixòéselfetque,quanel 1937vahaverd’abandonar l’InstitutoSanIsidrodeMadrid acausadelaproximitatdelfrontdebatalla ,vasol licitar elseutrasllatcomaprofessoral’Institut-Escola.Desprésdeladefunciód’Estalella,enplena GuerraCivil,PuigAdamvasernomenatdirectordelcentreivacontinuarenaquestllocfins al’estiude 1939,tractantdesalvarl’obrad’Estalellaenuninstitutquejahaviacanviatelseu nompeldeVerdaguer.

LesaportacionsméspersonalsdePerePuig Adamenaquestesreunionsestanlligadesa lessevespropostesd’ensenyamentmatemàticméscaracterístiques:elmètodeheurístici elsmodelsdinàmics.PuigAdam,comamembre delaCIEAEM,estavaalcorrentdelsavençosques’estavenduentatermeendiferentspaïsossobreaquestsaspectesivapropiciar lasevadifusióenlamajorpartdelestrobadesqueorganitzavaelCODperalprofessorat. Ambl’execució,davantelsassistents,d’aquesteslliçonsheurístiques enlesqualsutilitzavageneralmentmodelsdinàmics PuigAdampreteniaproporcionarinstrumentsdecanvi metodològicalcosdocent.Amés,lareflexiócol lectivaqueesdesenvolupavadesprésde cadaintervenció,iqueellmateixfomentava,buscavaquecadaprofessorconstruíselsseus nousconeixementssobrel’ensenyamentdelesmatemàtiquesdemaneraactiva,atravésdel diàlegambelsaltres,comfeiaellenlessevesclassesambelsseusalumnes(Puig, 1956). AquestaésunaconductaqueestàenlíniaambelsobjectiusdelaILE:actuacióatravésdel professoratambaccionsperaunamillorformaciódelprofessorat.

Lesconclusionsquevansorgird’aquestesreunionsvandonarllocapropostesiideesinteressantsquevanpoderorientarlaDirecciónGeneraldeEnseñanzaMedia,fetquevaser corroboratperlarevista EnseñanzaMedia quanvaafirmarqueelsestudisilesconclusions queesvanaconseguirenaquestesreunionsvantenirelseureflexenelscuestionariosde matemáticasqueesvanpublicarel 1957(Redacción, 1960,p. 134).

5.Bibliografia

[1]Arteaga,E.;Sol,J.L.del;Medina,J.F.(2021).«DecálogodedidácticadelamatemáticadePuigAdam:unlegadoparalaformacióndeprofesoresdematemàtica». Revista UniversidadySociedad, 13(2),347-356.

[2]Ausejo,E.(2013).«Laintroduccióndela«matemáticamoderna»enlaenseñanzanouniversitariaenEspaña(1953-1971)». LaGacetadelaRealSociedadMatemáticaEspañola, 16(4),727-747.

[3]Gattegno,C.;Servais,W.;Castelnuovo,E.;Nicolet,J.L.;Fletcher,T.J.;Motard,L.;Campedelli,L.;Biguenet,A.;Peskett,J.W.;PuigAdam,P.(1967). Elmaterialparalaenseñanzadelas Matemáticas.Madrid:Aguilar.

[4]Piaget,J.;Beth,E.W.;Dieudonne,J.;Lichnerowicz,A.;Choquet,G.;Gattegno,C.(1971). La enseñanzadelasMatemáticas. Madrid:Aguilar.

[5]Dólera-Almaida,J.;Carrillo-Gallego,D.(2023a).«DynamicandMultipurposeTeachingModels attheFirstInternationalExhibitionofMathematicsTeachingMaterial». Education Sciences, 13(3), 265.https://doi.org/10.3390/educsci13030265.

[6]Dólera-Almaida,J.;Carrillo-Gallego,D.(2023b).«Títulos,índicesyprólogosdeloslibros intuitivosdeReyPastoryPuigAdam». HISTEMAT:RevistadeHistóriadaEducaçãoMatemática, 9, 1-18.

[7]Dólera-Almaida,J.;Sánchez-Jiménez,E.(2019).«Laresolucióndelaecuacióndeprimer gradoenlostextosdeReyPastoryPuigAdam». HISTEMAT:RevistadeHistóriadaEducação Matemática,5(3), 18-42.

[8]Dólera-Almaida,J.;Sánchez-Jiménez,E.(2023).«PedroPuigAdamyelmétodoheurístico enlaenseñanzadelasmatemáticasenEspaña». ElFuturodelPasado [acceptat].

[9]Dólera-Almaida,J.;Carrillo-Gallego,D.;Sánchez-Jiménez,E.(2023a).«PuigAdamyelInstitutoEscueladeMadrid». HME:HistoriayMemoriadelaEducación [acceptat].

[10]Dólera-Almaida,J.;Carrillo-Gallego,D.;Sánchez-Jiménez,E.(2023b).«PoliedrosenlaEducaciónSecundariaenEspaña(1955-1960):construccióndemodelosmatemáticos». Cabás, 29,77-92.https://doi.org/10.35072/CABAS.2023.84.72 005.

[11]EnseñanzaMedia(1956).«RenovacióndelosmétodosdidácticosenEspaña:matemáticas». EnseñanzaMedia, 2,47-49.

[12]EnseñanzaMedia(1957a).«Lasreunionesdeestudiodelprofesoradodeenseñanzamedia:matemáticas».3,8-21.

[13]EnseñanzaMedia(1957b).«Lasreunionesdeestudiodelprofesoradodeenseñanzamedia:IImatemáticas».6,5-15.

[14]EnseñanzaMedia(1958).«Referenciadedoscursosdedidácticadelasmatemáticas,celebradosenMadridyenValencia». 18 19, 29-39.

[15]EnseñanzaMedia(1959).«Anunciosobreellibro Elmaterialdidácticomatemáticoactual 37, 210.

[16]EnseñanzaMedia(1960).«Balancedecuatroañosdelabor».A:PuigAdam,P.(ed.). La matemáticaysuenseñanzaactual.Madrid:MinisteriodeEducaciónNacional, 132-136.

[17]GonzálezAstudillo,M.T.(2008).«LasideassobrelaeducaciónmatemáticadePedroPuig Adam¿precursorasdelamatemáticamoderna?» Quadrante, XVII(1), 93-108.

[18]GrupCúbic(2019).«Unamiradamatemàticaal’obradeJosepEstalellaiGraellsencommemoraciódelcentenaridelapublicaciódelseullibre«Ciènciacreativa». Noubiaix:RevistadelaFEEMCATilaSCM,44,88-94.

[19]Hodgson,B.R.;Rogers,L.F.;Lerman,S.;Lim-Teo,S.K.(2013).«InternationalOrganizations inMathematicsEducation».A:Clements,M.A.(Ken);Bishop,A.J.;Keitel,C.;Kilpatrick,

J.;Leung,F.(eds.). ThirdInternationalHandbookofMathematicsEducation.NovaYork: Springer, 901-947.

[20]Lorente,A.(2011).«ElpapeldelaInspeccióndeEducaciónenlaextensióndelaenseñanzamediayenlamejoradelosInstitutosantesdelaLGEde 1970».A:G.Vicente (ed.). HistoriadelaEnseñanzaMediaenAragón .Saragossa:PublicacionesdelaInstitución «FernandoelCatólico»(CSIC),673-692

[21]Lorenzo,J.A.(1996).«EvoluciónyproblemáticadelaeducaciónsecundariacontemporáneaenEspaña». RevistaComplutensedeEducación,7(2),51-79.

[22]Lorenzo,J.A.(2003). FormacióndelprofesoradodeenseñanzasecundariaenEspaña:pensamientoeinstituciones(1936-1970). Madrid:EditorialComplutense.

[23]Lozano,J.M.(1956).«LaXIXConferenciaInternacionaldeInstrucciónPúblicadeGinebra». RevistadeEducación,51, 16-19.

[24]Mainer,J.(2009). Laforjadeuncampoprofessional:Pedagogíaydidácticadelasciencias socialesenEspaña(1900-1970).Madrid:ConsejoSuperiordeInvestigacionesCientíficas.

[25]MinisteriodeEducaciónNacional(1953).«Leyde 26defebrerode 1953sobreOrdenación delaEnseñanzaMedia». BoletínOficialdelEstado,58,de 27defebrerde 1953, 1119-1130.

[26]PuigAdam,P.(1926).«Dospalabrasacercadelapedagogíamatemáticaenlasegunda enseñanza». RevistadeSegundaEnseñanza, 27,399-401.

[27]PuigAdam,P.(1927).«Klein,elInstitutoylaUniversidad». RevistadeSegundaEnseñanza, 32, 223-227.

[28]PuigAdam,P.(1932).«Demostraciónintuitivadelaregladelaraízcuadrada». Matemática Elemental, 20, 17-20

[29]PuigAdam,P.(1955a).«LaComisiónInternacionalparaelestudioymejoramientodela enseñanzamatemática.ProyectodeunainteresantereuniónenMadrid,abrilde 1957». RevistadeEducación,38, 96.

[30]PuigAdam,P.(1955b).«Decálogodeladidácticamatemáticamedia». GacetaMatemática, 5-6, 130-135.

[31]PuigAdam,P.(1956). Didácticamatemáticaeurística.Madrid:InstitutodeFormacióndel ProfesoradodeEnseñanzaLaboral.

[32]PuigAdam,P.(1957).«Unnuevomaterialparalaenseñanzaeurísticadelageometríadel espacio». EnseñanzaMedia,3, 22-26.

[33]PuigAdam,P.(1958a).«Sobrelaformacióndelprofesoradodematemáticasdegrado medio». BoletíndelaInstitucióndeFormación delProfesoradodeEnseñanzaLaboral, 1958, 3-12.

[34]PuigAdam,P.(1958b). Elmaterialdidácticomatemáticoactual.Madrid:Publicacionesde laRevistaEnseñanzaMedia/MinisteriodeEducaciónNacional.

[35]PuigAdam,P.(1979).«Elquèpodriaésserl’ensenyamentdelaMatemàticaal’InstitutEscola». ButlletídelaSecciódeMatemàtiquesdelaSocietatCatalanadeCiènciesFísiques, QuímiquesiMatemàtiques, 1, 19-30.

[36]Salcedo,M.M.(1956).«ElCentrodeOrientaciónDidáctica:loqueesyloquesepropone». EnseñanzaMedia, 1,5-7.

[37]Utande,M.(1964). Leydeordenacióndelaenseñanzamediade26defebrerode1953anotadaycomentada.Vols. I i II.Madrid:DirecciónGeneraldeEnseñanzaMedia.

[38]Viñao,A.(2014).«Laeducaciónenelfranquismo(1936-1975)». EducaremRevista,51, 1935.

L’educació(matemàtica) ésunaarmadeconstrucció massiva1

AntonAubanell

MMACA,GrupCúbicdelaUB

JoanJareño

ProfessorjubilatCRAMAT

Resum Abstract

Desdefamoltdetemps,elnostre professoratdematemàtiquesdetotesles etapeseducativesnouniversitàriesestà compromèsenunprocésdemillora: canviantenfocamentsgenerals,ajustantels continguts,enriquintmetodologies, atenentperfilsd’alumnesdiversos...Són unaprovad’aquestesforçlesnombroses activitatsdeformaciócontinuadaide milloraprofessional(enmodalitatsdiverses i,enmoltscasos,ambunagranparticipació) queesportenaterme,impulsadestantdes del’Administraciócomdesdeles associacionsquetenimaCatalunyaenel campdel’educaciómatemàticaique encapçalalaFEEMCAT(Federaciód’Entitats peral’EnsenyamentdelesMatemàtiques aCatalunya).Entreaquestesactivitats destaquenelscongressoscatalans d’EducacióMatemàtica,C2 EM,del 2016 (Barcelona)idel 2020 (Reus-Tarragona).En redactaraquestespàginess’hantinguten comptelesconclusionsdelprimer,els reptesformulatsenelsegonileslínies d’impulstreballadesentreelsdos.

Foralongtime,mathematicsteachersinall non-universityeducationalstageshavebeen engagedinaprocessofimprovement: changinggeneralapproaches,adapting content,enhancingmethodologies, addressingdifferentstudentprofiles,etc. Proofofthisendeavourisfoundinthe numerousactivitiesandeventsdedicatedto continuingprofessionaldevelopmentand improvement(invariousmodalities,and oftenwithgreatparticipation)promotedboth bythegovernmentandbyassociationsin Cataloniaspecialisedinmathematics education,headedbytheFederaciód’Entitats peral’EnsenyamentdelesMatemàtiquesa Catalunya(FEEMCAT,FederationofEntities fortheTeachingofMathematicsin Catalonia).Amongstthoseevents,two editionsoftheCatalanCongresseson MathematicalEducation,C2 EM,heldin2016 (Barcelona)and2020(Reus-Tarragona), standout.Inthispaper,theconclusionsofthe former,thechallengesoutlinedinthelatter, andtheinitiativesdevelopedbybothare considered.

1.Elpresentescritestàbasatenlaconferènciaambelmateixtítol(adaptaciómatemàticad’unaconeguda frasesovintatribuïdaaMarjaneSatrapi)queelsautorsvanimpartirenelCESIRE-CREAMATeldia 23defebrerde 2023 enocasiódelapresentaciódelsnodesd’impulsmatemàtic(NIM).Laconferènciaespotvisionarahttps://ja.cat/hmCII.

1.Perquèensenyemmatemàtiques?Laguineuil’àliga

Amésdelcreixementpersonal,undelsobjectiusgeneralsdel’educacióésferdepontentre l’individuilaculturadelasocietatalaqualpertany.Inos’esperaquenoméss’atenguinels aspectestransmissiusd’aquestacultura(fer-nosreceptors-coneixedors).L’objectiuvamés enllà.Espreténqueelconeixementques’obtinguisiguireflexiui,alavegada,actiu,transformador:quepossibilitieldesenvolupamentd’unacapacitatcríticail’assolimentd’unes capacitatsquepermetinferaportacionsenriquidoresperal’evolucióielprogrésdelapròpia cultura.

Senseentrarendefinicionsprecises,podementendrelaculturacomunconjuntcompartit desabers,deformesdeferipensar,idevalors. Sovintelterme«cultura»técognoms:cultura general,culturacientífica,culturaartística...Finsitotdevegades,cognomsmoltespecífics: culturadesostenibilitat,culturadegènere...Lamentablement,noéstanfreqüentsentira parlarde culturamatemàtica.Malgratqueelterme«enculturaciómatemàtica»vaaparèixer ambunacertaforçaalsanysnorantadelseglepassat,perexemple,ambAlanBishop,2 encara s’had’estendreméslaideaquepartdelanostrafeinacomadocentsésfacilitarl’entrada del’alumnatalmóndelaculturamatemàtica.Siassumimaquestobjectiucultural,assumim també,enconseqüència,eldedecidirquinssabers,quinesformesdepensariquinsvalors volemconrearenelnostrealumnat.Noéselllocdeferunallistaexhaustiva,peròpodem destacar-nealguns.

Entreelsvalorsrelacionatsamblamatemàticapodemesmentar,perexemple,l’estimapel repte,laconstànciaenlaresoluciód’unproblema,l’actitudd’interrogaciócontínua,elrigor, laconsciènciadelpesdel’argumentaciólògica(delracionalisme),elreconeixementdela importànciadelaquantificacióilamesura,elconreudelamiradamatemàtica,l’apreciació delasevabellesa...Bishop.3 (1988)afirmavaque«unaeducaciómatemàticanoéseducaciósinocontribueixgensaldesenvolupamentdevalors».I,anantmésenllà,esdemanavasi «potseraquestaésunadiferènciacrucialentreformaciómatemàticaieducaciómatemàtica».

Sobreelssabersmatemàtics,hemdeferalgunes reflexionsprèvies.Enprimerlloc,usualment parlemdesabersdedostipus:conceptesiprocediments.Enl’antigamatemàticagrega,una matemàticafundacional,segonslamaneraqueentenemlesmatemàtiquesencaraavuidia, diferenciavenentre mathema,referidaalaciènciaielconeixement,i logística,decaràcter operatiu.Enspodempreguntarsobrel’equilibridelapresènciadetotesduesalesnostres aules.Seguramentveuremquela logísticaencaraocupaunaquantitatexcessivadeltemps escolar.ElmatemàticJohnAllenPaulos.4 declaravaenunaentrevista:«Notécapsentiteducaraningúpercompetirambunacalculadoradecincdòlarsque,amés,sempreguanyarà». Enlanostradefensadel’educacióenlaculturamatemàticahemd’ampliarelssabersmés clàssicsqueacostumenaaparèixeralscurrículumsollibresdetext.Calconsiderartambé

2.Bishop,AlanJ.(1999). Enculturaciónmatemática:Laeducaciónmatemáticadesdeunaperspectivacultural. Barcelona:Paidós.

3.Bishop,AlanJ.(1988).«Mathematicseducationinitsculturalcontext».EducationalStudiesinMathematics,19/2, 179-191

4.Entrevistaaldiari ElPaís (17/5/2000):https://ja.cat/sUN9I.

altressabers,comelsrelatiusalahistòria,lapresènciadelamatemàticaenl’entorn,laseva utilitat,lessevescaracterístiquesinternes(quinpapertenenlesdefinicions,elsaxiomes,les conjectures,lesdemostracions,elsteoremes...).Despréstornaremaparlarsobreaquesta doblevisiódelamatemàtica.

Eltercerconjuntdecomponentsd’unaculturaquehemdestacatéseldelesformesdepensaridefer.Caleducarenelpensamentmatemàtic.Perexemple,enlesestratègiesderesoluciódeproblemes,enl’aplicaciódelraonamentlògic(inductiuideductiu),enlacercade patrons(demanar-nos:quèésigual?,quèésdiferent?, quèesmanté?,quèvaria?,com?),en l’aprenentatgedelamodelitzaciódesituacions...

Uncopplantejatel què culturalquecalincorporarenl’educaciómatemàtica,tocadecidirel com.Semblaclarqueelcomhadetenirunfortcomponentconstructiuperpartdelmateix alumnat,quehadepartirdelasevaacciómatemàtica.Tambétenimclarquelalíniadidàctica pertractaral’aula,tantelssaberscomelpensamentmatemàtic,passaperl’atencióalsprocessos:resoluciódeproblemes,raonamentiprova,comunicació,representacióiestabliment deconnexions.Aquestsprocessosensajudarantantaincorporarelssaberscomaformaren elpensamentmatemàtic.

Novoldríemconcloureaquestapartatsensedestacarunaspectedelamatemàticai,enconseqüènciadel’educació matemàtica,queenssemblacabdal.MogensNiss,matemàticiespecialistaeneducaciódanès,afirmavaque«Lesmatemàtiquesal’escolaesconverteixennotan solsencapacitattecnològicaalesfàbriques,sinótambéenqualitatdelesdemocràcies».5 En poquesparauless’apuntenelsdostipusd’aportacióque,fonamentalment,l’educaciómatemàticafaalaformaciódelsciutadans:donar einespotentsqueelsseranútilsperentendre iinteractuarambelmónqueelsenvoltaiposaralseuabastunformidablecosdeconeixements,sòlidicoherent,queeducaelraonamentiposademanifestlanecessitatdela fonamentacióracionaldelesidees.Estractadedosaspectesdelamatemàticaqueensconvidenacomparar-laambdosanimals:laguineuil’àliga.

‚ Laguineuconeixbéelseuentorn,sapontrobaraiguaimenjar,saponferuncau.La matemàticaésguineuquanmostraelseuaspectemésinstrumental:lasevaaplicació, lasevacapacitatperconstruirmodels...

‚ L’àligas’elevacapalceltalvegadapelsimplegustdecontemplarpaisatgesamplíssims,talvegadaperaugmentarlasevapotènciaiprecisióquanesllançasobreuna presa.Lamatemàticaésàligaquan,amblespotentsalesdelalògica,s’elevacapalcel del’abstraccióidesenvolupaideesquepotserserand’enormepotènciaperresoldre unproblemaconcret.

L’educaciómatemàticahauriadebuscaroportunitatsperanarprojectantaquestesduescaresquesónindissociablesiqueLluísA.Santaló.6 posavademanifestambparaulesmolt belles:«Lessevesaplicacionssónessencialsperamoure’nsenlavidailessevesconcepcions alimentenallòméspurdel’esperit».

Desd’aquestaperspectivasónbenvingutselsprojectesSTEAM(del’anglès science,technology,engineering,artsimathematics).Peròhauríemd’evitarunacertainvisibilitatounreduccionismemeramentinstrumentalomecanicistadelamatemàtica,delaqualhauríemdetenir curaquetambéesvisualitzessinlabellesaintrínseca,l’estructuraglobalilaconnexiódeles sevesidees,elsaspectesabstractesilesbasesdelseuvaluósipotentllenguatgeformal.No hauríemd’oblidarl’àligaquepotaportaralespervolarlluny.

2.Elsprocessos

Noentrarem,perqüestionsd’espai,enl’explicaciódelsprocessos.Peròensagradariaposarnomésunexempled’unproblemapermostrarlessevespossibilitatsperactivarsabersi pensament.

Elproblemaéselsegüent:7 «AMoçambic,perdelimitarelterrenyrectangularquehad’ocupar unacabana,s’utilitzenquatrecordesdelamateixalongitudlligadesperundelsseusextrems».

6.Santaló,LluísA.(1975). L’educaciómatemàticaavui.Barcelona:Teide.

7.«DelimitantelterrenyperferlescasesaMoçambic». BlogdelCalaix +ie:https://ja.cat/3NNLE.

Pertenirunproblemanonoméshemdetenirunasituació,sinó,comamínim,unapregunta. Miremalgunesdelesqueenspodemfer:

‚ Comhemd’utilitzarlescordesperobtenirunrectangle?

‚ Comsónelsperímetresilesàreesdelsdiferentsrectanglesquepodemobtenir?Iguals? Diferents?Siésaixí,comvarien?Màxims?Mínims?

‚ Isiaugmentemleslongitudsdelescordes?Comcreixenelsperímetresilesàreesdels rectanglesencomparacióambelcasanterior?

‚ Isiutilitzemcordesdemidesdiferents?Quinspolígonsobtindrem?

Elssabersimplicatsapareixeranonosegonslespreguntesinvestigades,ielsprocessosassociatsdependranmoltdelagestiódel’aula.Alataulasegüentenrecollimalguns.

[P:resoluciódeproblemes; R:raonamentiprova; Cn:connexions; Re:representació; Co:comunicació]

Problema

‚ Longitud,angles,mesura

‚ Característiquesdelrectangle

Sabers

‚ Perímetresiàreesdelrectangle

‚ Funcionsdediferentstipus(lineals,quadràtiques,trigonomètriques...)

‚ Classificaciódequadrilàters

‚ Estratègiesderesoluciócomparticularitzar,generalitzar...

‚ Úsderelacionsgeomètriquesid’einestrigonomètriques

Processos P

‚ Comprovacióderesultatsivaloraciódelasevaplausibilitat

‚ Formulaciódenovespreguntes

R ‚ Elaboracióicomprovaciódeconjectures ‚ Justificaciódelesdescobertes

Cn ‚ Relacionsentreperímetresiàrees,diagonals,angles...

‚ Ambdissenyiconstrucció(etnomatemàtica)

Processos Re

Co

3.7,4accions

‚ Experimentacióambmaterialsi/oGeoGebra, role-play

‚ Esquemes

‚ Taules

‚ Gràfiquesdefuncions

‚ Utilitzacióprecisadelllenguatgematemàticperdescriurelesideesgeomètriquesqueesposenenjoc.

‚ Explicaciódeprocedimentsiconclusions(oralment,perescrit,ambmurals...)percompartirienriquirconeixementsideixarconstànciadela feinafeta.

Totaacciónecessitaunactorquelaportiaterme.Enaquestespropostesdiferenciaremprincipalmenttresresponsablesperfer-lesrealitat:l’Administracióeducativa(AE),lesuniversitats (UN)ielsmateixosdocents(DO).Calaclarir,però,quemaientenemquehagindeseractors independents:ésimprescindibleunacol laboraciói,finsitot,complicitatentretotstres.

1.Emmarcar.Cal un marc administratiu que afavoreixi millores en l‘educació matemàtica (AE)

Unadelesresponsabilitatsclaresdel’Administracióeducativaésl’elaboraciódelcurrículum obligatori.Peròcalqueaquestestiguid’acord ambelstempsenquèvivimiestiguiactualitzat enleslíniesconfirmadesperlarecercaeducativailespropostesdelacomunitatmatemàtica. Hadeseruncurrículumdialogatambinterlocutorssolvents.ACatalunyajas’haactuaten aquestalínia,finsalpuntqueelcurrículumcatalàhaestatundelsinspiradorsdeldelaLlei orgànica3/2020,de 29 dedesembre,perlaqualesmodificalaLleiorgànica 2/2006,de3 demaig,d’educació(LOMLOE).Tambééscert queaquestscurrículums,perraonspurament polítiques,noestantenintprouestabilitat.Entreel 2007iel 2022 hemvisttrescurrículums diferents.Encaraquepodemseguirunalíniaevolutivadel’unal’altre,calreconèixertambé queuncurrículumnonomésespublica,sinóques’had’estendre,entendreimantenirun tempssuficient.Itothad’anaracompanyatdeplansformatiusextensius.

Unaaltrafuncióadministrativaésl’assignació d’untempsescolarespecíficisuficientales matemàtiques.Nielcurrículummésperfectetésentitsinoseliassignenuntempsiuns mitjansquepermetindesenvolupar-lo.Eltemps,eneducació,ésunbélimitat:lesbones didàctiquesrequereixentemps.Ilamancadetempspotcomprometreelsmillorspropòsits curriculars.Elmarchorariactualpermetunesmodificacionshoràriesquehanarribatareduir almínim,enalgunscentres,eltempsespecíficdel’àrea,senseestarsempreproucompensat percomestractenlesmatemàtiquesenl’espaidelstreballsdecaràcterinterdisciplinari.

Peraltrabanda,sabem,basant-nosenlesevidènciesdelarecercaeducativa,queéscabdalqueelscentrestinguinunalíniametodològicacomuna,compartida.Iqueaquestalíniaesmantinguientrelesdiferentsetapeseducatives.Peròaixònocaudelcel:caldonar tempsalscentrespertreballarconjuntamentaquesteslínies.Unaajudaimportantalacreaciód’aquestalíniametodològicacomunaéselreconeixement,al’educacióprimària,depersonesreferentsdecentrequetinguin,entrelessevesresponsabilitats,lacoordinaciódelsdiferentsnivells.Al’educaciósecundàriahihaespecialistesidepartamentsquedonenelmarc

peraaquestapossiblecoordinació.Peròalscentresdeprimàriaaquestafiguradel’especialista ésactualmentinexistent.

Enlamateixalíniaanteriorésimportantquel’Administraciótambépromoguiidonisuporta l’existènciadexarxesterritorialsqueimpulsinlamilloradel’educaciómatemàtica.Enaquest sentit,actualments’estanfentalgunspetitspassos,comelsNIM(nodesd’impulsmatemàtic)organitzatspelCREAMAT,CentredeRecursosperEnsenyariAprendreMatemàtiques,i elscentresderecursospedagògics(CRP).8

2.Formar.Cal cuidar la formació permanent i la formació inicial (DO-AE-UN)

L’oficid’ensenyar i,enconcret,ensenyarmatemàtiques éscomplex.Necessàriament,requereixunaactitud,unasensibilitat,unavoluntatque,endefinitiva,éselqueensfaentrar cadadiaal’aulaambunail lusiórenovada.Peròaixònoéssuficient.

Caldisposard’unconeixementmatemàticsòlid:notansolsdelscontingutsquecaltractar aclasse,sinódecontingutsmésavançatsqueofereixinunaperspectivamésàmpliadela matèria,incloent-hiaspectesdeculturamatemàticacom,perexemple,elshistòrics.Nodisposard’aquestabasepotprovocarqueeldocentsesentiincòmodedavantdelaclasse,que notinguiprouclarcapaonvolavançaricom;quenopuguitreuretotelprofitdocentdeles situacionsimprevistesquesorgeixenaclasse,delacontingència.

Caltenirunbonconeixementdidàcticqueajudiainteractuarpositivamentambelsalumnes, aentendreelsseusprocessosd’aprenentatgeiadisposard’unaàmpliabasederecursosde tipusdiversosperal’ensenyamentdelamatemàtica:materials,tecnològics,comunicatius, dedinàmicadegrups...Nodisposard’aquestbagatgecomprometlapossibilitatdefercanvis metodològicsprofunds,efectiusiduradors.

Aquestsconeixementss’hand’adquirir,sòlidament,enlaformacióinicialdemestresiprofessorsi,inexcusablement,s’hand’anaractualitzantalllargdetotalavidaprofessional.

Enlaformacióinicialcridal’atencióelcontrastentrel’èmfasiqueesposaenlaformació delsmestresd’educacióinfantiliprimàriaielqueesposaenlaformaciódelprofessorat d’educaciósecundària:

Enlaformacióinicialdemestresestreballenmoltelsaspectespedagògics,perònoesdedicaprouatencióalconeixementmatemàticatravésdel’experiènciadirectade«fermatemàtiques».Enaquestsentit,seriaimportantrecuperarl’especialitatdematemàtiquesenles facultatsd’Educació.

Siensreferimal’educaciósecundària,hemdereconèixerquetenimfacultatsambmencions, doblesgraus,itinerarisespecíficsdematemàtiquesialtresdisciplines,perònon’hihacap dematemàtiquesieducació.Hihajovesquedesitgenferdel’educaciómatemàticalasevaprofessióielnostresistemaelsnecessita.Enspodempermetrequelasevadisposiciói

8.NIM(WebCreamat):https://ja.cat/v5yUV.

aptitudilanecessitatsocialnoestrobin?Actualmentlaformacióinicialdelprofessoratde secundàriapassaperunmàsterquetéuncertmargedemillora(quantaladurada,elmodel il’extensiódelespràctiques).Tantdebo,algundia,enlesnostresuniversitats,hihagiun grauespecíficd’educaciómatemàticaperformarprofessoratdesecundària,ambunasòlida preparaciómatemàticaididàctica.Itantdebohihagiunprocedimentd’incorporacióala professiódocentcadavegadaambmésacompanyamentisuport.

Toteslesprofessions,iespecialmentlesqueactuenencampsd’evolucióràpida,comhoés l’educació,requereixenunprocéscontinuatdeformacióqueésgarantiadequalitatimotor d’innovació.Desdel’Administracióeducativacalpromoureiacompanyarelsprocessosde milloraatravésdemodelsdeformaciópermanentpropersal’aula,territorialitzats,enllaçats enxarxa...Enparticular,elscanvissubstancialsenelcurrículumhauriend’anaracompanyats d’unaformacióespecífica,prescriptivaigeneralitzada.

3.Escoltar per aprendre‘n.Fent xarxa guanyem qualitat,bon fer,ofici (DO-AE-UN)

Cadadocenthadecercarelsseusreferentsperanartrobant,dinsdelalíniageneraldel centre,elseupropiestil:referentsviscutscomaalumne,companysdefeinadocent,adoptats apartirdelectures,formacions...

Perònoestemsols.Hemd’assumirunaculturadecompartirpercréixerprofessionalmenti contribuiralcreixementdelsaltres.Caldonarvaloralfetdecrearxarxaialfibratassociacionista.Aquestfibrat,enl’àmbitdelesmatemàtiques,ésmoltricinotéparangóambeld’altres àmbitseducatius.

Enunaltrecamp,l’Administraciótambéhad’escoltar.Ipotfer-hotenintlaFEEMCAT,per exempleientrealtres,comundelsinterlocutorsméspotents.Peraconseguir-hotambéhauriadeserobjectiudelaFEEMCAT,amésdelseupropicreixementpelquefaasocisiaccions, adreçar-seal’Administracióambtotalaforçapossibleidesdel’autoritatquedonenlaquantitatdepersonesassociades,l’abastterritorialiladiversitat,larepercussióiqualitatdelseu treball.Tambéésimportantquel’Administraciódonisuportaaquestesaccions(delaFEEM-

CATod’altresgrups,associacionsoinstitucions),tantalesqueajudinaescoltar-seentre docents(jornades,congressos...),comalesdedinamitzaciódel’alumnat(ProvesCangur, FemMatemàtiques,Estalmat,Anemx ` Matemàtiques,MMACAiunllargetcètera).

Iencaraensagradariaafegirunaltreaspecteenaquestpunt.Calqueelsresultatsdelarecercaeducativaarribinalscentres.Elspontsqueconnectenrecercaipràcticasónencaraforça escassosifebles.Aixòseriaunamilloraperalsdoscamps,perquèunpontésbidireccional iaixíesretroalimentarien.Launiversitattéunpaperimportantenaquestterreny.L’escola volcontribuiraconstruirunasocietatdelconeixement,peròavegadestédificultatsal’hora d’usarelconeixementperalasevapròpiamillora.

4.Enriquir.Processos i millora d‘activitats (DO)

Ésimportantensenyarmatemàtiquesatravésd’activitatsriques,desituacionsd’aprenentatge rellevantsimatemàticamentsignificatives.Hihacriterisqueenspodenajudaraenriquir activitatsiquehauríemdetenirsemprepresents:

1.Intentarquelesactivitatsqueportemaclassesiguindeterrabaix(fàcilsd’accedir-hi, noexcloents),desostrealt(permetenavançarmolt,nolimiten)id’espaisamples(per permetreelprogrésdesdediferentsestilsd’aprenentatge).Hauremdeconjugarmési ressignificarelsverbs abaixar, apujar i eixamplar.

2.Donaralsprocessoslaimportànciaquetenenenl’accésalssabersialpensamentmatemàtic.Orientenmetodològicamentsónpalanquesd’enriquimentd’activitats:

‚ Laresoluciódeproblemeshad’estaralcentredel’educaciómatemàtica.Noestracta tansolsd’ensenyarperresoldreproblemesid’ensenyarsobrelaresoluciódeproblemes,sinóquecalensenyaratravésdelaresoluciódeproblemesrics,matemàticamentrellevants,bencontextualitzats...El sbonsproblemes,bentreballats,sóngrans constructorsdeconeixementmatemàtic!

‚ Elraonamenthauriad’estarsemprepresentenl’educaciómatemàticatransmetent implícitamentoexplícitamentelfetqueéselquedonasolidesaalcosdelesmatemàtiques.Els«...perquè?»iels«isi...?»sónexcel lentsinvitacionsaraonar.

‚ Lesconnexionssónundelsaspectesmésseductorsdelamatemàticaendossentits:

Lesconnexionsinternestrenquenlesfronteresentreelsblocstemàticsclàssics perquèmostrenlacoherènciainterna,launitatdelconeixementmatemàtic.Cada connexióésunaoportunitatdidàctica,especialmentsiésambelementsgeomètricsqueofereixenpossibilitatsdevisualització.

Lesconnexionsexternesensajudenaveurelamatemàticaquehihaenelqueens envolta,atravésdelasevapresènciaodelasevaaplicació.Sónoportunitatsper apropar-nosalsmodelsmatemàtics,perdiscutirsobrel’exactitudil’aproximació... perquèjanosiguinecessàrialapregunta«...iaixòperaquèserveix?».

‚ Lacomunicacióilarepresentacióensconvidenadonarimportànciaal’expressióde lesideesambparaules,ambsímbols,ambgràfics,ambtaules,ambesquemes...No tansolspercompartirideesmatemàtiquesambaltrespersones(compartintconstruïmconeixement),sinótambépermillorarlamateixacomprensiód’aquestesidees (ordenantconceptesidescobrintrelacions).

5.Escollir.Cal triar i gestionar bé les activitats (DO-AE)

Enunpuntanteriorhemparlatdelanecessitatd’escoltaribuscarelsnostresreferents.En aquestapartathiafegimladeconèixeriexplorarelsbancsd’activitats.Actualmenttenim lasort,gràciesalesnovestecnologiesdelainformació,depoderaccedirfàcilmentauna granquantitatdeproposteseducatives.Nomésperesmentaralgunesfonts,tenimwebscom lesdeNRICH,CREAMAT,BancdeRecursosdelFemMatemàtiques,ARC,PuntMat...Peròcal tenircriterisd’elecció:personalsigenerals.Perexemple,lariquesadel’activitat.EneldocumentdelaComissiód’ImpulsdelesConclusionsdelC2 EMsobre«activitatsdereferència» (2018)esplantejalallistadecriterissegüent,queenspotserorientadorasobrecomhadeser l’activitat:accessibleperal’alumnat,significativa,matemàticamentrellevant,activadoradel pensamentmatemàtic,extensiva,replicable,objectedemúltiplesenfocamentsirepresentacions,ifomentadoradelacol laboracióiladiscussióenunmarcdereflexió.

Enaquestepígraftambévoldríemdestacarque,enlesnostrestries,hemd’evitardonaruna visióreduccionistadelesmatemàtiques.Perexemple,sihemd’exercitaralgunapràctica,no callimitar-seatasquespuramentreproductives,orientadesal’automatització,sinóquepodemtrobarvariantsque,amés,convidinaferalgunamenadereflexióodescobertaparal lela,el queesconeixcoma«pràctiquesproductives».Perexemple,noéselmateixproposaruna llistaderestesquedemanarquantesrestesdiferentsespodenferapartirdequatrenúmeros concrets,operacióquepotportaralaformulaciódetotunconjuntdepreguntesnoves(quin éselresultatmésgran,quinéselméspetit,quantsresultatsdiferentshiha...).Aquestavisió reduccionistapotaparèixer«perillosament»enunaltreterreny:enmoltstreballsdecaràcterinterdisciplinari.Sinos’aprenenmatemàtiquesnovesinomésenslimitemafercàlculs reproductius,mésomenyscomplexos,ogràficsestadísticsdelsmésusuals,nomésestem potenciantunavisióempobridadelainstrumentalitatdelesmatemàtiques.

Peròquanparlemd’escollir,noensreferimnomésalatriad’activitats.Hihatotunconjunt dedecisionsperprendrereferidesacomfaremlesactivitatsal’aula:quinsmaterialsutilitzarem?,quèfaremindividualment?,quèfaremengrup?,comhofarem?...Amésd’aquests aspectes,éstambébopreveurecomseranlesnostrespreguntesiintervencions,comintentaremguiareldesenvolupamentdel’activitatcapalsobjectiusqueenshemmarcat.També sabemquesorgirancontingènciesiquehauremdepararatencióenlesquepuguinserinteressants.Finsitotcaldràrecollir-lesperincorporar-lesalnostrellistatdepossiblesintervencionsfuturessirepetiml’activitat.Defet,estractad’anarconstruintdemicaenmicael nostrepropibancderecursos,derecollirelquesiguieducativamentinteressantiproperala

nostramaneradefer.

Ensacabemdedonarmoltafeinacomadocents.Quinacompanyamentenspotdonarl’Administració?Lacreacióidifusiódebancsderecursos,facilitarl’accésaactivitatsdiversificadamentmodelitzadores,lacreaciódexarxespercompartirmaterialsentreiguals...Tambéen té,defeina!

6.Cal experimentar (DO)

Estemconvençutsquel’educaciómatemàticahadetenirunfortcomponentd’experimentació (ambmaterialsmanipulables,amb role-plays,ambjocs,ambaplicacionsdegeometriadinàmicacomelGeoGebra,ambfullsdecàlcul,ambentornsdeprogramaciócomSnap!o Scratch,finsitotambpaperillapis...).HenriPoincaréafirmava:«Noméshihadosmètodesper aensenyarfraccions:tallar,encaraquesiguimentalment,unpastís,ofer-hoambunapoma. Ambqualsevolaltremètoded’ensenyamentelsescolarsprefereixensumarnumeradorsamb numeradorsidenominadorsambdenominadors».9 L’experièncianos’oposaal’abstracció, sinóquepotserundelscaminsmésdirectesperarribar-hi.ElfísicifilòsofaustríacErnstMach deiaque«lamaneraméseficaçdepertorbarelprocésd’abstraccióconsisteixaabraçar-lo abansd’hora».10 Lesactivitatsd’experimentacióaclassedematemàtiquesnosónsimples anècdotes,nitrivialitzen;alcontrari,permetentreballarcontingutsavançatsconjecturant, explorant,descobrint,conceptualitzant(posantparaulesalsprocessosrealitzatsoalesidees descobertes)i,sical,demostrantiformalitzant.

Lesexperiènciespodenrespondreadiversesintencionsdidàctiques.Perexemple,sónútils per:

9.CitatperArnold,VladimirI.(1998).«Modelsmatemàticsdursimodelsmatemàticstous». Butlletídela SocietatCatalanadeMatemàtiques, 13/1,7-26.

10.CitatperSigmund,Karl(2023). ElsueñodelcírculodeViena. Barcelona:ShackletonBooks.

(si escau)

‚ Motivar:lacordadedotzenusosques’empravaal’anticEgipteperconstruirangles rectes.

‚ Simular:lamàquinadeGaltonpersimularladistribucióbinomialilacampanadeGauss.

‚ Construir:feruntriangleisòscelesplegantpaperotraçarcòniquesambfilsiregles.

‚ Demostrar:justificarlaparitatdelsresultatsdelessumesdeparellsisenarsambcubetsencaixables.

‚ Mostrar:observarlacoincidènciadelasumadelsanglesdetrianglesretallantelsanglesdediferentstrianglesfetsenpaperiposant-losadjacents.

‚ Plantejariresoldreproblemes:establirpatronsenelnombredecubetsencaixables queformenunasuccessiódefigurespolicúbiquesconstruïdesambundeterminatcriteri.

‚ Visualitzar:lesmediatriusendiagramesdeVoronoiaproximatsmitjançantLacasitosi aigua.

‚ Aplicar:utilitzarelteoremadeThalesperentendrelareduccióqueesprodueixen dibuixarelcontornd’unacarasobreunmirall.

Laimportànciadel’experimentacióenl’ensenyamentdelesmatemàtiquesesrecolliaen elrepte5delC2 EM 2020:«Potenciaremlacreaciódelaboratorisdematemàtiquesalsnostrescentresconsiderant-losunelementimportantenlacreaciód’ambientspropicispera l’experimentació».

7.Respectar.Tothom pot fer matemàtiques (DO)

Aquestterme,«respectar»,referital’alumnat,vamoltmésenllàdelrespectealapersona, alasevaformadeserialessevescreences.Tambévamésenllàdelrespectealseuritme d’aprenentatge,queésevidentquenoéselmateixperatotselsalumnes.Unadelesmostresmésimportantsderespecteenversellsésla confiançaenlessevespossibilitats.Sovint, senseadonar-nos-en,somelsmateixosdocentselsqueposemelslímitsdelquepodenfer idelqueno.Subestimemlessevescapacitats. Unexempleflagrantésquesovint,quanun grupd’alumnestédificultats,se’nssuggereix(normalmentdesd’algunestamentextern)un enfocamentadreçatalreforçexclusiudelesmecàniques,prescindintdelacomprensió.Ens diuenquel’importantéselsaberfer,noelsaber.Ésaixòunexemplederespectealsalumnes? Éscabdalajudar-losaanaragafantconfiançaiconsciènciadelespròpiescapacitatsmatemàtiques.Tothompot,enungrauounaltre,fermatemàtica.Latriailagestiódelesactivitats (acció5)téunagranimportànciaenl’assolimentd’aquestaautoconfiança.Peròentreels aspectesdegestión’hihaunque,perlasevaimportància,mereixunaatencióespecial:el tractamentdel’error...idel’èxit!

a)Gestionarconstructivamentl’error

Enunasituaciód’aprenentatge,l’errorhadeserunmaterialdeconstrucció,caltreure-liel caràcterdevaluadorquesolacompanyar-lo.Adaptantunaidead’OskarCymerman,podríem dir:«Esperemelserrors,acollimelserrors,respectemelserrors,analitzemelserrors,corregim elserrorsiaprenguemdelserrors».11 Sinomésensdediquemaencadenarconstatacions

11.Adaptatd’unpòsterd’OskarCymerman:https://ja.cat/PFZeL.

negativesd’errors,hihauràalumnesqueentraranenunaespiraldedesconfiançarespectede lessevespossibilitatsmatemàtiquesiacabarandientlamassaconegudafrase«jonoserveixo peralesmatemàtiques».Comasocietat,noenshopodempermetre.Suggerimposaratenció enelsmots:potserhauríemd’emprarambméscuralaparaula«error»idedonarmésjocala paraula«errada».N’hihaprouambconsultareldiccionaridel’Institutd’EstudisCatalansper veurequeladiferènciaésevident:

Error

1 1 Acciód’allunyar-sedelver,deljust.[...]

1 2 Concepte,opinió,doctrina,quenoestàconformealaveritat.[...]

2 1 Diferènciaentreunvalorestimatd’unaquantitatod’unaexpressiómatemàticaiel seuvalorexacte.

Errada

Acciód’erraroequivocar-se;l’efecte.[...]

b)Serproveïdorsd’èxits

Resnoésmésmotivadorquel’èxit,perpetitquesigui.Eneldesèpuntdelseudecàleg (1955),12 PerePuigAdamescrivia:«X.Procuraraqualsevolalumneèxitsqueevitinelseudesànim».Mésdeseixanta-cincanysdesprés,endiversesocasionshemsentitadiraCharlieGilderdale(UniversitatdeCambridge)que«enunaclassedematemàtiqueshihamoltscaminsper aquèelsalumnestinguinoportunitatsd’èxit».Estemconvençutsquemestresiprofessors hemdeserproveïdorsd’èxitsperalsnostresalumnes,ambreptesprogressiusbenajustats, perquèrequereixencertesforç,peròquesiguin assolibles.Éselmillorcamíperanaraportant confiançasobrelespossibilitatsdecadascúenl’àmbitdelesmatemàtiquesiperaconseguir unamajorimplicacióenelseuaprenentatge.

7,4.Sumar (DO-AE)

Potsersorprèntrobarundecimalencapçalantelnúmerod’aquestaacció.Ésunapetitallicènciaqueenspermetemperindicarquel’acciónoestànomésenmansdelsnostresactors principalsfinsara:docents,Administracióiuniversitat.Aranecessitemques’hiafegeixinaltresestamentsdelquepodríemanomenarlasocietatgeneralique,ambànimdeconcretar, podemparticularitzarenlesfamílies,elsmitjansdecomunicacióilacomunitatmatemàtica (mésenllàdel’educativa).Calcanviarnonoméslaimatgesocialqueestédelesmatemàtiques,sinólaimatgetradicionaldelqueéselseuensenyament-aprenentatge:el què iel com.Enaquestalínia,tambédesdelscentrestenimungrauderesponsabilitatenelcanvi sobreaquestapercepcióencarcarada.Podemajudaravisibilitzarquelesmatemàtiquessón moltmésque«mecanismesmisteriososnomésaptesperaunaselectapartdelapoblació», fentdivulgacióambpetitesexposicions,presentacionsovídeosdeltreballdel’alumnat.Les revistesoblogsdelscentrespodensertambéunbonvehicledepopularització.Peraltra banda,espotexplicaralesfamílieselprojecteeducatiumatemàticdelcentreperal’àmbitde lesmatemàtiques.Potseraixípodremesborrarelrecordpersonalqueparesimarespuguin tenirdelsmodelsd’ensenyamentméstradicionalsd’aquestaàrea.

Quantal’Administració,hihaundeurependentclar:crearunespaiwebd’informacióisuport alesfamílies,basatenelsenfocamentsilesmaneresdeferactualseneducaciómatemàtica.

4.Cloenda

Enaquesttancamentdel’articleensagradaria recordarlesparaulesdel’enyoratperiodista

JoanBarril(1952-2014):13

[...] éscuriosalanormalitatambquès’admetqueelsnensdetoteslesedatsmanifestinelbloqueigmentalalesmatemàtiques [...]. Jotambéerad’aquests.Il’edat m’haportatacreurequeelsnúmerossónmenystraïdorsquelesparaules.M’alimento d’aquestesperòsónellselsqueemtranquil litzen.Lesmatemàtiquesenspermetenla comprensiód’allòqueelssentitsnisospiten.Lesmatemàtiquessónelverdaderidioma universalquesaltacontinentsiqueunificaelsaberdesegles[...]. Lesmatemàtiquessón l’einaqueenspermetveureelquenitansolsintuïm.Esmereixenunplusdeprestigi. Lavergonyaieldolordel’analfabetvanmésenllàdelalectura.

Ensengresquem14 acontinuarambforçaelcamídemilloradelanostraeducaciómatemàtica?Tothom,desdelasevaescola,desdelasevaaula,desdelasevaresponsabilitat,desdela sevafamília,potaportar-hielseuesforçilasevail lusió.Hihaunafrase,atribuïdaaEduardo Galeano,amblaqualenspodemidentificar:«Muchagentepequeña,enlugarespequeños, haciendocosaspequeñas,puedecambiarelmundo».

13.Barril,Joan,«Lagraneina». LaVanguardia (17/9/2004).

14.Encaraquenosempreésborevelarelspetitsjocsamagatsenuntext,ensagradariaexplicaraquest. Mentrepreparàvemlaxerradaenquèesbasal’article,LauraMoreraensvaferobservarquee2˜7,4,elnostrenombre d’accions.Laconferènciaacabavaambunapetitaanimacióonlesdueslletresequeencapçalavenlesparaules«Ens engresquem?»estransformavenenlaigualtatesmentada.

Capaonval’ensenyament delesmatemàtiques?

JordiDeulofeuPiquet

ProfessorhonoraridelaUniversitatAutònomadeBarcelona

jordi.deulofeu@uab.cat

Resum Abstract

Aquestarticle,desd’unamiradapositivadel futurdel’educaciómatemàtica,reflexiona sobrel’estatdelespropostesactuals centradesenl’aprenentatgecompetenciali lessituacionsd’aprenentatgesignificatives al’aula.Laformaciódelprofessoratde matemàtiquesésclaupermillorarel sistemaeducatiu.Totiques’hanfet progressos,hihaunmargepermillorarel modelactual,perexemple,ambmés presènciadepràctiquesal’aulaenelMàster deFormaciódelprofessoratoambla formaciócontinuada.Partdelsreptes rellevantselstrobemrecollitsen https://ja.cat/ReptesC2EM.Calque dissenyarunaagendaperpodertreballar plegatsielCongrésCatalàd’Educació Matemàtica(C2EM)ésunbonespaiper fer-ho.

Adoptingapositiveviewpointonthefutureof mathematicaleducation,thisarticlereflects onthestateofcurrentproposalsfocusedon competency-basedlearningandmeaningful learningsituationsintheclassroom.The trainingofmathematicsteachersiskeyto improvingtheeducationalsystem.Although progresshasbeenmade,thereisroomfor improvementinthecurrentmodel.For instance,moreclassroompracticeinthe master’sdegreeinTeacherTraining,and continuingprofessionaldevelopmentare recommended.Outlinesofsomeofthe importantchallengescanbefoundat https://ja.cat/ReptesC2EM.Itisnecessaryto designanagendaaroundwhichwecanwork together,andtheCatalanCongresson MathematicalEducation(C2EM)istheideal placetodoso.

1.Introducció

Vullcomençaragraintl’oportunitatqueelseditorsdel NouBiaix m’hanofertdeparticiparen aquestnúmerotanespecialdelarevista.Arribaralnúmero50 ésunafitaimportantiunbon momentperreflexionarsobretotselstemesrelacionatsambl’ensenyamentil’aprenentatge delesmatemàtiques,aixícomsobretotselsaltresaspectesdelsqualss’ocupaladidàcticade lesmatemàtiques.Aixídoncs,aprofitantal mateixtempsquequanescricaquestarticlefa moltpocquem’hejubilat unaltrebonmotiuperreflexionarsobreelquehanestatels anyspassatsiintentarferpetitesprojeccionssobreelsquevindranenunfuturnollunyà ,

intentaréserfidelal’encàrrecdel’equipeditorialiexposaréunconjuntdereflexionssobre comveiglasituaciódel’ensenyamentdelesmatemàtiquesenaquestsmomentsiquinscrec quesónalgunsdelsreptesmésrellevantsdecaraaunfuturacurtimitjàtermini.

Senseavançarencaraleslíniesdelesmevesreflexions,síquevulldirqueintentaréentot momentnocaureeneltòpicsovintmoltarrelatsegonselqualenelstempspassatslescoses anavenmillorquearaielfuturenspresentaràsituacionsencarapitjorsdelesactuals.Alcontrari,sensenegarcanvis,dificultatsientrebancs,m’agradariaquedelesmevesparauleses desprenguésunavisiópositivad’unfuturamboportunitatsimportants,sempre,aixòsí,que lescosesesfacindemaneraraonableidefugintgremialismesquemoltesvegadesportena confrontacionsestèrils.

L’ensenyamentdelsinfantsidelsjoves i,enparticular,l’aprenentatgedelesmatemàtiques éstanimportant,tantperaellscomperatot elpaís,querequereixquetotselsqueenshi dediquemconfrontemlesnostresideesambunobjectiucomú:millorarlaformaciódetots elsnoisilesnoiespertalquequansiguinadultspuguinesdevenirciutadansdepledret. Aquestaés,enúltimainstància,lafinalitatdelesreflexionsquevenenacontinuació.

Hihatantstemesinteressantsqueafectenl’aprenentatgedelesmatemàtiquesi,mésen general,l’educaciómatemàtica,lamajoriad’ellsmoltrelacionats,queesfadifíciltrobarun filquepermetiexposar-losdemaneraordenada.Enlaprimerapartd’aquestarticleemreferiréal’evoluciódelcurrículumenelsdarrersanys,comafilconductorperidentificarel principalsreptesdel’educaciómatemàticaavuiienelfuturimmediat.M’estendréparlant delessituacionsd’aprenentatgeicaracteritzarélesactivitatscompetencialmentriques,un puntqueemsemblaclauperavançarcapaunvertaderaprenentatgecompetencial(Nissi Højgaard, 2011, 2019).Seguiréparlantdelprofessorat,enparticulardelasevaformació,tant lainicialcomlapermanent aspectequeconsiderocrucialperaunamillorageneral ,iproposarémodelsdeformacióqueemsemblenadequatsperabordarlesproblemàtiquesmés importants,entrelesqualsdestacolagestiódel’aula.Perconcloure,emreferiréalcongrés catalàd’educaciómatemàticaquesecelebraràaLleidael 2025i,enconcret,al’agendaque enformadereptesesvapresentaralesconclusionsdelC2 EM 2021 deTarragona-Reus.

2.Lesmatemàtiquesescolars,avui

Parlardelesmatemàtiquesescolarsésdifícilperquèhihamoltsnivells,moltscentresimoltes realitats,demaneraquegeneralitzarpotseragosaratperquèlesdiferènciesentreelsuns ielsaltressónnotables.Unprimerreferent,encaraqueteòricperòfàcilmentobjectivable, elconstitueixenlestendènciesilíniesmestresdelscurrículumspublicatsperlesadministracionseducatives.D’entrada,unamiradaal’evoluciódelscurrículumsdematemàtiques delsdarrersvintanys,ienparticularalsdecasanostra,ensmostrauncamícadavegada mésclarcapaunplantejamentcompetencialdel’aprenentatgedelesdiferentsdisciplines, enparticulardelesmatemàtiques,enquèelscontinguts(anomenatssabersenelsdarrers documentsdelnostrepaís),totiseguirsentrellevants,estanalserveidelescompetències. Elquel’alumnathad’aprendrenosónconceptesitècniques,sinólasevautilitzacióencontextosdiversosperresoldreproblemes,raonar,modelitzarorepresentaricomunicar.També s’observal’inicid’unatendènciaaconsideraràreesmésgeneralsquelesdisciplines,comara

l’àreaSTEM,1 iarelacionarlescompetènciesespecífiquesdelesmatèriesambunescompetènciesmésgeneralspròpiesdelesàrees.

Respecteaaquestatemàtica,voldriaferunaprimeraconsideracióenrelacióambunafrase quesovinthesentitiqueveadirunacosaaixícom«araelscontingutsnosónimportants». Calrepetirquedifícilmentespotferuntreballdedesenvolupamentdelsprocessosdeles matemàtiques,comararesoldreproblemes,raonarocomunicar,senseunconeixementdels conceptesmatemàticsclau.Laqüestióquealmeuentendrehauriadecentrareldebatés: coms’introdueixenaquestsconceptesclaui,enparticular,comesconsiderenlesdificultats cognitivesinherentsal’aprenentatgedelsconceptesicomesfauntreballquepermetique elsalumneselsreconstrueixinsemprequesiguipossibleise’lsapropiïnpertaldepoderlosaplicarrealmentasituacionsnoves(Arcavi, 1999).Perquè,sicreiemque«ensenyant»les ideesclauatravésd’exposicionsdelprofessorat,coms’hafetsempre,aconseguiremque l’alumnatelsaprenguiisobretotelssàpigaaplicar,seràdifícilavançarenl’aprenentatgetant conceptualcomcompetencialdelesmatemàtiques.

Sorgeix,doncs,unaideaanomenadasituaciód’aprenentatgeque,totinosernova,esplantejademaneraexplícitaeneldarrercurrículumique,almeuentendre,estrobaenelfocus delaproblemàticaactuali,previsiblement,delfuturacurt ipotsermitjà termini.Sense entraradefinirambprecisióquès’enténpersituaciód’aprenentatge,síqueenvulldestacar duescaracterístiques:elcontextonesformulalasituacióielreptequehauriadeprovocar enl’aprenent,ésadir,l’interèsperabordar-laitreballar-hi.Ditd’unaaltramanera,elnivell designificaciódelasituació,tantperaqui aprèncomperaallòquevolemqueaprengui. Altrecondiciómésestricteenladefinició(totiserinteressantsiqueésimportanttenir-les encomptesemprequesiguipossible),comara queelcontextdelasituaciósiguisocialment rellevant,noemsemblaquehagindeformarpartdelaideaclau,queésaconseguirun aprenentatgesignificatiu.

Unexemplepotseraclariràelqueintentodir:uncontextdejoc(d’estratègiaod’atzar),encara quesiguiunjocabstracte,potgenerarunabonasituacióperal’aprenentatgematemàtic al’aula?Lamevarespostaésafirmativasienelseuplantejamentespropiciaeldesenvolupamentdecompetències:enaquestcas,lapresadedecisions,laresoluciódeproblemes, l’argumentaciósobrelavalidesad’allòrealitzati/olacomunicaciódelsresultatsobtinguts (NavarroiDeulofeu, 2016).Tambésis’afavoreixunambiental’aulaonconstantmentesformulenpreguntes(elfamós«isi»tanimportantenl’aprenentatgedelesmatemàtiques)ion,a més,sorgeixendemaneranaturalconceptesmatemàticscurriculars(numèrics,geomètrics, probabilísticsofuncionals).Ésadir,siaclassehihaunclimad’experimentació,interrogació, discussióiargumentació,allòqueendiem unambientderesoluciódeproblemes.

Siesdonatotaixòiesparteixdel’experimentació enaquestcas,delapràcticadeljoc ambsentit ,i,amés,s’aconsegueixquel’alumnatvulguinonoméspracticareljoc,sinó plantejar-seiintentarrespondrelespreguntesqueformulemsobreell,enunambientonla col laboraciócontrarestaadequadamentelsaspectescompetitiuspropisdelsjocs,enstrobarem,almeuentendre,davantd’unasituaciód’aprenentatgereal.Si,encanvi,elcontext

1.STEM,del’anglès science,technology,engineeringandmathematics,delaqualexisteixlaformacatalana corresponent,CTEM,deciència,tecnologia,enginyeriaimatemàtiques.

ilamateixasituaciósónforçatsiesformulencomuna«excusa»pertreballardeterminats procediments,inogenerenrepte,totilasevapossiblerellevància,noestaremdavantd’una «bona»situaciód’aprenentatge.Nocaldir,pertancarl’exemple,quemoltesdelesmatemàtiquesquehihadarreredelsjocssóndegranrellevànciaiconstitueixenmodelsques’utilitzen peranalitzarsituacionssocialmentimportantsenelmarcdelateoriadejocs.

Aixídoncs,sil’objectiuprincipaldel’aprenentatgedelesmatemàtiquesésdesenvolupar processosiassolirnivellsdecompetència,unamanerad’apropar-sealacreaciódesituacionsd’aprenentatgeéspensarenactivitatscompetencialmentriqueso,millorencara,en l’enriquimentd’activitatsjaconegudesperfer-lescompetencialmentinteressants.Unavisióàmpliad’aquestenriquimentlapodeutrobarenl’article«Aprenderapensarmatemáticamenteenambientesderesolucióndeproblemas»(DeulofeuiVila, 2021),ondestacàvemelsquatrepilarsquecaltenirencompte: lapropostabase l’enunciatquepresentem al’alumnat , laplanificació elconjuntdedecisionsprèviesdelprofessorat , l’alumnat amblessevescreences,ideesprèvies,capacitatsiemocions i lagestiódel’aula totel queelprofessoratfaràal’aulaquanesduguiatermel’activitat.

Aixímateixipensantenlesactivitatsd’aprenentatgedequalsevolnivelldel’escolaritatobligatòria,dèiemqueunaactivitatricahadetenirlescaracterístiquessegüents:quesiguiaccessiblepertothom(terrabaixisostrealt)isignificativaperalresolutoriperalesmatemàtiques quevolemqueaprengui,queadmetimúltiplesenfocamentsitambédiferentsrepresentacions,quesiguimatemàticamentrellevant,queactivielpensamentmatemàtic,quefomenti lacol¨laboracióiladiscussióenunmarcdereflexiói,finalment,quesiguiextensible.Detallemunamicamésaquestessetcaracterístiques:

‚ Accessible: inclouunenunciatdelatascacomprensible,proporcionaoportunitatsd’èxit inicialperalamajoria,possibilitadiversosnivellsd’abordatgeideresolucióipermet treballararitmesdiferents(terrabaixisostrealt).

‚ Significativa: incitaalacuriositat(jasiguipelcontext,jasiguiperlaformulacióde latascaoperlesdinàmiquesgeneradespeldocentalvoltantdel’activitat)imanté l’interèspelrepte,jaque,totiserabordable,elquehemdeferperarribaralaresolució noésevidentd’entradaperal’alumnat.

‚ Varietatd’enfocaments: ésunatascaambunacertaobertura,notancadaentotsels sentitsiqueadmetrepresentacions,caminsd’abordatgei/oresolucionsdiverses.Les situacionstancadesiestandarditzades queesresolenaplicantunprocedimentúnic noesdevenensituacionsriques,amenys queeldocentfaciunagestióquepermeti obrir-lesigenerardiscussióalvoltantdelasevaresolució.

‚ Matemàticamentrellevant: implicaconceptesclau,portaaconstruircontinguts,promoul’aplicaciódecontingutsacontextosnous,necessitaferúsderaonamentsmatemàtics(inductiusi/odeductius),ilasevaresoluciórequereixl’úsdeconnexionsintramatemàtiquesoentrelesmatemàtiquesielmón.

‚ Activaelpensamentmatemàtic:potenciaelcicleformatperl’experimentació,l’estudi decasosparticulars,larealitzaciódeconjectures,laverificaciódelesconjecturesi,si escau,lageneralització,potencialacreativitatmatemàtica(flexibilitat,intuïció,originalitat,organització...)ipromoulaplanificacióilapresadedecisionsambsentitcrític.

‚ Fomentalacol laboració,lareflexióiladiscussió: provocalaconversamatemàtica al’aulailaconfrontaciód’ideesentreiguals,promoul’explicacióilajustificaciódel procés,aixícoml’anàlisiilarecercad’altresresolucions.

‚ Extensible: tantpermetampliarlamateixaactivitat(possibilitatdeformularnoves preguntes,d’estendrelatasca,degeneralitzar,millorarioptimitzarelprocés),com crearactivitatssimilarsapartird’aquesta.

Pertotelques’haexposat,entencqueuntema demàximarellevànciaenaquestsmomentsi enelfuturimmediatésuntreballintensiextens alvoltantdelacreaciódesituacionsd’aprenentatgeid’activitatscompetencialmentriquesentotselsnivellseducatius.Aquesttreball nos’hadelimitaraferpropostesperportaral’aula,sinóques’had’acompanyard’exemples realssobrelagestiód’aquestesactivitats,enquès’analitziiesdiscuteixielquepassaalesaules,pertaldepoderferpropostesdemilloratantdelesactivitatscomdelasevagestió(Calvo etal., 2016).Aquestdarreraspecteésclau:unaactivitatelplantejamentdelaqualpotserno ésgairerellevant,potesdevenir-hosise’nfaunagestióquepermeticrearunambientde resoluciódeproblemesal’aula(Abrantes, 1996;DeulofeuidelaFuente, 2022).Caltambé quefemunesforçpercrearinstànciesqueafavoreixincompartiraquesttreballentretotsi arribaraunnombremésimportantdedocentsquenopaselques’haaconseguitfinsara.

3.Laformaciódelprofessoratdematemàtiques

Enqualsevolprocésd’ensenyament-aprenentatgeelpaperdelprofessorat,entèsessencialmentcomunmediadorentrel’alumnatiallò quevolemqueaquestaprengui,ésmoltrellevanti,pertant,lasevaformació,tantlainicialcomlacontinuada,ésunelementclau,jaque unbonsistemadeformacióentotselsnivellsés,almeuentendre,unindicadorrellevantde laqualitatd’unsistemaeducatiu.Aixídoncs,consideroquetreballarpermillorarlaformació hadeserunatascaprioritària.

Enl’àmbitdelaformacióinicialdesecundàriaesvaferunpasimportantquanel 2009 es vainstaurarelmàsterdeFormaciódelProfessoratensubstituciódelvellipocútilcertificat d’aptitudpedagògica(CAP).Alnostrepaís,elcurs 2013-2014esvainiciarunmàsterdesistema,interuniversitari,del’especialitatdematemàtiques,coordinatperlaUniversitatAutònomadeBarcelona(UAB)iamblaparticipaciódecincuniversitats:UAB,UniversitatdeBarcelona,UniversitatObertadeCatalunya,UniversitatPolitècnicadeCatalunyaiUniversitatPompeuFabra.Elsinicisforencomplexospertald’encaixarlesdiferènciesentrelesdinàmiques delesdiferentsuniversitatsparticipants,peròapocapocensvamanarconeixentivamanar compartintobjectius,demaneraqueavui,enlasevaonzenaedició,elmàsterestàconsolidat.

Tanmateix,consideroqueunaformacióinicialprofessionalitzadoracomlaquetenim,totiels avençosquesignificarespecteaetapesanteriors,ésinsuficientperpoder-seconsiderard’alta qualitat.Personalment,socpartidarid’unmodelcomelquetenenmoltspaïsosd’Europa, ambungraudetresanysdeladisciplinaiunmàsterdedoscursosambunamajorpresència delpràcticum,autènticeixdelmàsterdes delpuntdevistatemporal,demaneraqueel segoncursdelmàsterpodriacentrar-seenunespràctiquesacompanyades,ambactivitats dellargadurada,tantd’observaciócomd’intervenció,iuntreballdefidemàster(TFM)de reflexióianàlisisobrelaintervenciódutaaterme.Tampocnos’hadedescartarelmodel simultani:ungrauespecíficquecombinielconeixementdeladisciplinaambl’aprenentatge

delaprofessiódedocent.Enqualsevolcas,atèseldesequilibridelsdarrersanysentreoferta idemandaqueensestàportantaunasituaciópreocupantdefaltadeprofessorat,calpensar enlesdiferentspossibilitatssense,almeuentendre,descartar-necap.

Nosembla,però,quelescoseshagind’anar,enunfuturimmediat,pelcamíqueheassenyalat.Mésaviatunasuposada«millora»semblaquevaassociadaalavariabledelapresencialitatdelaformació,cosaqueemsemblapreocupant,especialmentpelquefaalaformació inicial.Enelsdarrersanyss’hancomençataimplementarformacionsnopresencialsqueal meuentendrenosónlesmésadequadesperaldesenvolupamentdemoltesdelescompetènciesprofessionalsdelsdocents.Novulldir,però,quenopuguihaver-hiaspectesquees puguintreballardemaneraefectivaenunmarcvirtuali,pertant,quepuguinfuncionarbé. D’altrabanda,caltambétreballaràmpliamentl’úsdelsmitjanstecnològicspertaldegarantir lacompetènciadigitaldelprofessorat.

Tanmateix,elcomponenthumàisocialdelestasquesd’ensenyariaprendre,juntament amblaimportànciadelainteracciópresencialentreensenyantsiaprenents,emsemblen fonamentalsiinsubstituïbles,perlaqualcosacrecqueésnecessàriaunapresencialitatque vagiforçamésenllàdelpràcticum.Endefinitiva,noconsideroquelamillorsolucióalamanca deprofessoratdematemàtiquessiguioferirunnombreelevatdeplacesenmàstersambtota laformacióvirtualllevatdelpràcticum.

Laproblemàticadelprofessoratd’infantiliprimàriaésdiferenti,pertant,lespossibleslínies demilloratambé.Sesapquetenimunaformaciódegrauprofessionalitzadoraestablerta desdefatempsque,tanmateix,nogaranteixelsconeixementsdeladisciplinanecessaris peraunbonensenyamentdelesmatemàtiques,possiblementperquènoesgaranteixenels mínimsindispensablesenelmomentd’accediralgrau.S’hanfetesforçosimportantsenla introducciódeprovesperal’accésalsgrausdemestreenlesuniversitatspúbliquesdelpaísi calcontinuar-losimillorar-losmalgratlesreticènciesd’alguns,méscentradeseninteressos corporatiusqueenobjeccionsdefons.

D’altrabanda,sisomrealistesiacceptemque acurtterminidifícilmentaconseguiremmillorardemaneraclaraigeneralaquestasituacióenl’àmbitdelgrau,potserseriaadequat crearunsestudisdemàsteradreçatsalsgraduatsenmagisteriquepermetinaprofundiren l’ensenyamentdelesmatemàtiques,tantainfantilcomaprimària,pertald’esdevenir,enel futur,referentsdel’aprenentatgematemàtic enelsseuscentres.Avui,ques’estableixenperfilsdetotamena,aquest,queespotenllaçaramb laformaciócontinuada,potserensajudaria amillorarlasituacióalesescoles.

Peracabaraquestpunt,vullferunaconsideraciósobrelaformaciópermanentocontinuada. Duranttotselsanysquehetreballatenelmàsterdesecundàriaheconsideratqueundels objectiusfonamentalseraconvèncerelsestudiantsdeprofessorquelaformaciócontinuada eraunrequisitprioritariperesdevenirunbondocent.Lanostraésunaprofessióvivaien evoluciópermanentqueexigeixunamilloraiunaposadaaldiaconstant,i,pertant,crecque aquestanecessitatésindiscutible.

Arabé,hihamoltstipusdeformacionsinteressantspossibles,algunesdelesqualsjas’estan fent,peròcrecqueenelsproperstempscaldràdonarunarellevànciaespecialalesque s’ocupindelagestiódel’auladematemàtiques,treballinapartirdelapràcticarealdela

classe,experimentin,observinifacinpropostesdemillorad’aquestagestió.Unaformació quepretenguisertransformadorahadepartirde larealitatdel’aula,delesproblemàtiques idificultatsdelprofessorat,nopotestardeslligadadelasevarealitati,sobretot,hadetenir comaobjectiuprincipallamilloradel’acciódocentdelconjuntdeparticipants.

Unexempled’aquesttipusdeformacióésl’estudideclasses (dematemàtiques),traduccióde lessonstudy,queésunmodeldedesenvolupamentprofessionaldelsdocentsbasatenuna formació-acciócol¨laborativaqueconsisteixenlarealitzaciód’uncicleques’iniciaambeldissenyil’experimentaciód’unaactivitatd’aula,segueixambunaobservacióreald’aquestaila sevaanàlisicrítica,ifinalitzaambunapropostademillora.Totiqueestractad’unaformació entreiguals,sovinthiintervéunexpertqueactuacomaassessor.

L’estudideclassesésunmodeldeformacióqueesvainiciaralJapófamoltsanys,téuna llargatradicióenaquellpaísidespréss’haestèsaaltresllocsdelsmón,perexempleals EstatsUnits.Lesdiferènciesculturalsentreelsdiferentspaïsosi,enparticular,lavaloració detotelqueéscol lectiuperdavantdelqueésindividual,méspròpiadelescivilitzacions orientalsquedelesoccidentals,fanquel’aplicaciódelmodeloriginaljaponèsnoespugui ferdemaneramimètica,peròcrecquel’essènciad’aquesttipusdeformació,centradaen l’actuaciódelprofessoratal’aulailasevamillora,síques’hadepoderaplicaracasanostrai esticconvençutqueunapràcticasostingudad’unaformaciócomaquestapottenirresultats moltprofitososperalnostresistemaeducatiui,sobretot,peralamilloradel’ensenyament delesmatemàtiques.

Totiqueespodenferestudisdeclassesdiversos,depenentdelescondicionsdepartida, algunescaracterístiquesimprescindiblesd’unaformaciócomaquestasón:

‚ Formacióentreigualsamblacol laboraciód’unassessorqueproporcionaajudesals participantsenelsdiferentsmomentsdelcicle.

‚ Participacióactivadetotselsassistents,cadascundesenvolupantelseuroldemanera profunda,ambimplicacióicorresponsabilitatdetothom.

‚ Focalitzacióenlagestiódel’auladel’experimentadordirigidaapromoureunaprenentatgecompetencialdelesmatemàtiquesifixant-sedemaneraespecialencom aprenenelsestudiantsicomparticipenenelseuaprenentatge.

‚ Anàlisicríticaiconstructiva,apartirdelesdadesdel’observaciódelaclasse,ambla finalitatd’aportarpropostesdemillora,perònodejutjar.

Larecercafetaenl’estudideclassesésgran.UnabonaintroduccióaaquestmodeldeformacióéseltextdeMurata«Conceptualoverviewoflessonstudy»(2011),queésuncapítoldel llibre Lessonstudyresearchandpracticeinmathematicseducation (Hart,AlstoniMurata, 2011), dedicatal’estudideclasses.Tambésóninteressantsmoltsdelsexemplesqueapareixenen elllibre Elestudiodeclasesjaponés (Isoda,ArcaviiMena, 2007).

D’altrabanda,tambééspossibleidesitjable quemodelsdeformaciócoml’esmentatsecentrinencomesfademanerareall’avaluaciódelsaprenentatgesal’aula.Crecquequedamolt camíencaraperaconseguirquelamajoriadelsdocentsfacinunaavaluaciórealmentcompetencialiencaramésperquèconsiderinquelarellevànciadel’avaluaciónorauenelsjudicis,

sinóenlasevacontribuciódirectaalamilloradel’aprenentatge(DeulofeuiVillalonga, 2018). Peraixòésnecessariproposaridesenvoluparactivitatsd’avaluació,tantformativacomformadora,centradesaaprendremésimillorionesposielfocusenunaretroalimentacióque impliquiunarevisióconstantdelqueesvaaprenent.

M’atreveixoaapuntarquelaimportànciadelaretroalimentació,comunelementclaunonomésdel’avaluació,sinódel’aprenentatgeengeneral,encaranoéstingudaprouencompte. Calferunareflexióprofundasobre certespràctiquesencarahabituals com,perexemple, determinadesformesdecorrecciód’exercicisal’aula ,enelsentitd’analitzarquinaéslaseva vàluarealentermesd’aprenentatgeperatotl’alumnatd’unaclasse,jaquesovintaquestes pràctiquestenenunefectepositiuenunnombremoltreduïtd’alumnes.Introduiractivitats d’avaluacióenquès’impliquintotselsalumnes,tantenlarealitzaciócomenlavaloració, comaralespràctiquesdecoavaluacióid’autoavaluació,itambéfacilitareines,perexemple lesbasesd’orientacióqueactuencomabastideseneldesenvolupamentdeprocessoscomplexoscomlaresoluciódeproblemes,sónavençosqueenshand’ajudaraaconseguirque l’avaluació,tantlaformativacomlaformadora,acabiesdevenintundelsinstrumentsmés valuosospermillorarl’aprenentatge.Enaquestsentit,elmarcproposatperNeusSanmartí desdefaanys,lligataldesenvolupamentd’uncurrículumpercompetènciescomelnostre (Sanmartí, 2020),esdevéunaguiaexcel¨lent,peròenl’àmbitdel’educaciómatemàticaacasa nostrafaltenencaraméstreballsconcretsenaquestsentit,comeldeTorregrossa,Deulofeu iAlbarracín(2021),queserveixindeguiaalprofessoratiliproporcionin,almateixtemps, activitatsiinstrumentsd’avaluacióperportaral’aula.

Sibélarealitzaciódeformacionssimilarsalaqueacabodedescriurepotserdegranajuda is’hadepotenciar,crecrealmentqueelproblemaclauésl’extensiód’aquestaid’altresformacionsalagranmajoriadelprofessorat.Finsquenoaconseguimquetotselsimplicatsen l’ensenyamententenguinquecalferformaciócontinuada,iquelagranmajoriahiparticipin demaneraactiva,seràdifícilmillorarl’educaciómatemàticadelnostrepaís.Iperquèmillori cal,d’unabanda,posarelsmitjansnecessarisi,del’altra,quetotselsdocentsentenguem quecalimplicar-seenlaformaciócontinuada.

4.ElCongrésCatalàd’EducacióMatemàtica,C2

EM2025,unaoportunitat

Quanescricaquestarticlefaltenpocmésdevintmesosperquèlacomunitatd’ensenyants dematemàtiquesdeCatalunyaensretrobemaLleida,elsdies7,8i 9 dejuliolde 2025.Com sabeu,elCongrésd’EducacióMatemàticadel’any 2000,celebrataMataró,novatenircontinuïtat,finsqueel 2016esvacelebraraBarcelonaelCongrésCatalàd’EducacióMatemàtica (C2 EM),quetotsanomenen situem iqueorganitzalaFederaciód’Entitatsperal’Ensenyament delesMatemàtiquesaCatalunya(FEEMCAT).Aquestavegadasíquehihahagutcontinuïtat, ambelC2 EM 2021 deTarragona - Reus(lapandèmiavafer-loendarrerirunanyipassar-loa unformatenlínia)iarajahemcomençataprepararelC2 EM 2025,quecelebraremaLleida.

UnainiciativaqueemsemblainteressantdelC2 EMésqueenlesconclusionsfinalsespreténdissenyarunaagendaqueesdevinguiunaguiapertreballardurantelspropersquatre anys,elperíodeentrecongressos.Concretament,aldarrercongrés(2021)esvanconsensuar dotzereptesdirigitsamestresiprofessorat,que,passatsdosanys,segueixentenint,almeu entendre,unavalidesatotal.

Elsreptes,quepodeutrobarahttps://ja.cat/ReptesC2EM,espodenagruparenquatregrans àmbitsirepresenten,crecm,unabonaagendaperal’acció:

‚ Característiquesdelaformacióiniciali permanentdelprofessorat(reptes1i2). Hemde treballarperaunamillorformaciódelprofessoratdetotselsnivellseducatius,tant inicialcompermanent,lligadaalarealitatdel’alumnatd’avui,basadaenlaimportànciadel’ensenyamentcentratenprocessos,focalitzadaeneldesenvolupamentdeles competènciesprofessionalsdelsdocents ifonamentadaenunesbasesmatemàtiques ididàctiquessòlides.

‚ Necessitatdedinamitzareltreballcol laboratiu,enfortintequipsicreantxarxes(reptes3, 10,11i12).Siestemd’acordquelainteraccióésfonamentalperal’aprenentatgeiaixí tractemdefer-hoambl’alumnat,caltambéestimularlainteraccióentreelsdocents atotselsnivells.Peraixòpotenciaremlacreaciód’equipsdocentsenelscentreside xarxesintercentres,amblafinalitatdemillorarlanostratascacompartintmaterials, recursosiexperiències.

‚ Rellevànciadelesactivitatsd’aprenentatgeperal’aulailasevagestió(reptes4,5i6). Toti quenos’esmentademaneraexplícitalaimportànciadecrearsituacionsd’aprenentatge amblesideesclauassociadesdecontextirepte,síquehihareferènciesaavançarper talquelesactivitatsd’aulasiguincompetencialmentriques,enelsentitexposatanteriormentenaquestarticle,ialaimportànciadetenirbonsambientsperexperimentar iunabonagestióquefomentilainteracció.

‚ Elpapersocialdelesmatemàtiquesmésenllàdel’escola(reptes7,8i9). Quanquiaprèn trobasentitenelquefa,sesentcapaçdefer-hoigaudeixfent-ho,l’aprenentatgeés millorimésgratificant.Peròsilesexpectativesd’aprenentatgesónbaixesilesmatemàtiquesques’aprenenestantancadesal’aulaisenserelacióambelqueesfaalmón, llavorstindremunproblemaqueultrapassalatascadelsdocents.Cal,doncs,promoure laparticipaciódetothomalvoltantdelesmatemàtiques.

Comespotveure,tenimunnombreconsiderabledereptesrellevantsiplenamentactuals quedissenyenunaagendaalvoltantdelaqualpodremtreballarplegatsalllargdelsdosproperscursos.Tambéseràimportantfermésaportacionsperafrontarnovesproblemàtiques queelstempsactualsensvaginplantejant.

Bensegurquetothomtrobaràelseullocd’acordambelsseusinteressosilessevespossibilitats.Enaquestsentit,lesdiferentsassociacionsqueconformenlaFEEMCAT iespero quetambétoteslesaltresentitatsimplicadesenl’educaciómatemàtica s’aniranfentressò d’aquestaagendaitreballaranenaquestalíniapertalquetotsplegatsarribembenpreparats alCongrésdel 2025.Usconvidoatotesiatotsaparticiparenaquestgranrepteiatrobar-nos aLleidapercompartireltreballfetduranteltempsqueensseparadelCongrés.

5.Referències

[1]Abrantes,P.(1996).«ElpapeldelaResolucióndeProblemasenuncontextodeinnovacióncurricular». UNO:RevistadeDidácticadelasMatemáticas,8,7-18.

[2]Arcavi,A.(1999).«Yenmatemáticas,losqueinstruimos¿quéconstruimos?». Números, 38,39-56.

[3]Calvo,C.;Deulofeu,J.;Jareño,J.;Morera,L.(2016). Aprenderaenseñarmatemáticasenla educaciónsecundaria.Madrid:Síntesis.

[4]Deulofeu,J.;Vila,A.(2021).«Aprenderapensarmatemáticamenteenambientesderesolucióndeproblemes» A:GrupodeinvestigaciónenEducaciónMatemáticaUniversidad deAlicante(ed.). Ideasparalaeducaciónmatemática:PerspectivasdesdeelTrabajodeMaríaLuzCallejodelaVega.Múrcia:Compobell,41-68.

[5]Deulofeu,J.;DelaFuente,A.(2022).«Desarrollarlascompetenciasderesolucióndeproblemasymodelizaciónparaaprendermatemáticas».A: Aportacionesaldesarrollodelcurrículumdesdelainvestigacióneneducaciónmatemática .Granada:SEIEM/Editorialdela UniversidaddeGranada,373-398.

[6]Deulofeu,J.;Villalonga,J.(2018).«Resolucióndeproblemasyregulacióndelaprendizaje». EducatioSigloXXI,36(3), 153-175.

[7]Isoda,M.;Arcavi,A.;Mena,A.(2007). Elestudiodeclasesjaponés. Xile:UniversidadCatólica deValparaíso.

[8]Murata,A.(2011).«Introduction:ConceptualOverviewofLessonStudy».A:Hart,L.;Alston,A.;Murata,A.(eds.). LessonStudyResearchandPracticeinMathematicsEducation. Dordrecht:Springer.https://doi.org/10.1007/978-90-481-9941-9 1.

[9]Navarro,A.;Deulofeu,J.(2016).«Aprendiendoaresolverproblemasenuncontextode juegosdeestrategia». Suma,82, 9-17.

[10]Niss,M.;Højgaard,T.(eds.)(2011). CompetenciesandMathematicalLearning:IdeasandInspirationfortheDevelopmentofMathematicsTeachingandLearningin Denmark.Roskilde UniversityPress.Traduccióal’anglèsdel’originaldanès(2002).

[11]Niss,M.;Højgaard,T.(2019).«Mathematicalcompetenciesrevisited». EducationalStudies inMathematics, 102, 9-28.https://doi.org/10.1007/s10649-019-09903-9.

[12]Sanmartí,N.(2020). Avaluarésaprendre:L’avaluaciópermillorarelsaprenentatgesdel’alumnatenelmarcdelcurrículumpercompetències. Barcelona:GeneralitatdeCatalunya,Departamentd’Educació,GabinetTècnic.

[13]Torregrosa,A.;Deulofeu,J.;Albarracín,Ll.(2021).«Orientaciónycoevaluación:Dosaspectosclaveparalaevolucióndelprocesoderesolucióndeproblemes». Bolema,35,89-111. DOI: 10.1590/1980-4415V35N69A05.

Elsmenutstambé fem mates

CyntiaRiquelmeCarvallo Col legiPadreDamianSagradosCorazones(Barcelona) criquelm@xtec.cat

TanaSerraSantasusana1 EscolaVilaOlímpica(Barcelona) tserra@xtec.cat

Resum Abstract

Enaquestarticlepresentemeltreballde creaciódeproblemescompetencialspera infantsdesdelsquatrefinsalsdotzeanys quefaelgrupFemMatemàtiquesdela Federaciód’Entitatsperal’Ensenyamentde lesMatemàtiquesaCatalunya(FEEMCAT)i delCercledeMestresdel’Associacióde Barcelonaperal’Estudiil’Aprenentatgede lesMatemàtiques(ABEAM)perquè esdevinguinunafontderecursosperals docents.Exposemelnostreconvenciment quelafeinacomamestresésfercréixerel pensamentmatemàticquetotinfantté, fomentantquel’infantpuguiexpressarla sevamaneradeferiavançarenel raonamentilarepresentaciódeles matemàtiques.Exposemelprimerrepteo problemaperalsméspetitsimostresde resoluciód’alumnesd’edatsdiferents.

Thispaperpresentstheworkcarriedoutbythe Femmatemàtiques (Let’sdomath)groupofthe Federaciód’Entitatsperal’Ensenyamentde lesMatemàtiquesaCatalunya (FEEMCAT, FederationofEntitiesfortheTeachingof MathematicsinCatalonia)andthe Cerclede Mestres (Circleofteachers)ofthe Associacióde Barcelonaperal’Estudiil’Aprenentatgedeles Matemàtiques (ABEAM,BarcelonaAssociation fortheStudyandLearningofMathematics). Theydevelopedcompetency-basedproblemsfor childrenagedbetweenfourandtwelvewiththe aimofturningthemintoaresourceforteachers. Webelievethattheroleofteachersistonurture themathematicalthinkingpresentinall children,encouragingthemtoexpresstheirway ofdoingthings,andadvanceinmathematical reasoningandrepresentation.Wepresentthe firstchallengeorproblemyounglearnersare facedwith,aswellasexamplesofsolutionsfrom studentsofdifferentages.

Jafamésdevint-i-cincanysquesecelebraaCatalunyaelconcursFemMatemàtiques (https://fm.feemcat.org/).Durantlamajoriadetempshaestatadreçatalsnoisinoiesdesisè deprimàriaideprimerisegondel’educaciósecundàriaobligatòria(ESO).Desde 2022 s’hi vaincorporarcinquèdeprimària,iel 2024,s’haincorporatterceriquartd’ESO.Desdelcomençaments’hatreballatperestimularelsalumnesafermatemàtiques.S’hanproposattasques

1.MembresdelgrupFemMatemàtiquesdelaFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya(FEEMCAT)idelCercledeMestresdel’AssociaciódeBarcelonaperal’Estudiil’Aprenentatgede lesMatemàtiques(ABEAM).

que,especialmentenlaprimerafase,enquèesfomentaeltreballenpetitsgrups,estimulin laresoluciódeproblemesiexpressinelprocésderesoluciópermitjàdelraonament,laprova,lacomunicació,larepresentacióilesconnexions,aixícomeldescobrimentderegularitats, queésl’objectiufinaldelesmatemàtiques. ElcurspassatesvaplantejarampliarelFem Matemàtiquesalsalumnesdecinquèdeprimària,pertald’anarestenentaquestamanerade fermatemàtiques.

1.I,ara,FemMatemàtiquesperalsmésmenuts?

Sí,aquestéselnostrerepte:elFemmatemàtiquesatoteslesedatsdel’educacióinfantili primàriapertalquetotselsnensinenestinguinl’oportunitatdedesenvoluparelpensament matemàtic.Enaquestaocasió,adiferènciadecinquèisisè,noestractapasd’unconcurs, sinód’oferirtasques,activitatsisituacionsd’aprenentatgequefomentin Fermatemàtiques a lesaules,enunformatqueanomenem ElsReptesdelCercle.

I,sí,elsmésmenutstambépodenfer mates demaneraintuïtivaiinformal.Sirecollimelferde lescriaturesd’educacióinfantildavantdelseuentorn,podemconclourequeentotmoment esplantegenproblemesperquèse’lsposendavantsituacionsnovesperalesqualsnotenen capsolucióprevista:comobrirlaporta,sinoarriboalpany?Potseresposaràdepuntetes, saltarà,demanaràalgúquel’obri,aniràabuscarunacadirais’enfilarà...Tindràiniciatives, provarà,hihauràintentsinfructuososid’altresambèxit,imésendavantaplicaràlasolució trobadaalamateixasituacióoaunadesemblant.Sianalitzemelprocésemprat,ensadonaremquesegueixgairebéfilperrandaelque desitjaríemmoltsmestresquefessintotsels infantsdavantdelsreptesmatemàtics.Estracta,doncs,derecolliraquestferdinsdelcontext relacionatamblesmatemàtiques.

2.Fercréixerelpensamentmatemàtic

Estemconvençudesquetoteslescriatures,quanarribenal’escola,tenendintreseu,alaseva manera,pensamentmatemàtic,ilanostratascacomamestresésfer-locréixer.Vegem-ne unexemple.Elsinfantsd’educacióinfantil(I4)comentenalamestra:

Enaquellaclassehihamoltsnúmeros fanreferènciaalpanelldel’1 al 100 queveuena l’auladelserveid’acollidadel’escola.

Lamestravaabuscarelpanellise’lmirenentretots.

Quèhiveieu? preguntalamestra.

Adaltnoméshihaunnúmero,abaixn’hihados comentaunanena.

Alfinalhihatresnúmeros diuunaltre.

Aquítotstenenun 1 unnenassenyalalacolumna ontoteslesunitatssónun 1.

Laconversasobreelpanells’esténialgunsinfantsmanifesteninterèsperferunpanell.La mestraelreculli...

Bé,noestractaenaquestarticlededescriureaquestasituaciód’aprenentatge,sinómésaviat demostrarlespossibilitatsquetenenelsnensilesnenesderesoldreproblemes,peròtambé deplantejar-se’n.Quanunsvailetsd’educacióinfantil(I4)diuenquevolenferunpanell,això ésplantejar-seunproblema.

Apartirdel’observaciócomuniquenregularitatsiraonen:

Enaquestahiha 1 ienaquesta, 2 assenyalenl’altracolumna.

Perferelseupanell,provensensecessarfinsquetrobenformesperdibuixarquadrícules.

Unanenafaunpanellquetésiscolumnesialeshoreselsnombresnoliquedendisposats comalsaltresnensinenes,iaixògeneraunadiscussióentreells.Lamestraelsdemanacom potserqueelsnombresd’unpanellil’altrenoestiguinposatsdelamateixamanera.Algú conclouqueeld’aquellanenanotétantes piles esrefereixalescolumnes .S’haestablert unaconnexió.

Sientenemlesmatemàtiquescomelsaberqueestableixrelacionsiregularitatsallàon,aparentment,totésdiferent;

Sientenemlesmatemàtiquescomunprocés,comunamaneradeferidedescobrirper comprendremillorl’entorn,queimplica:plantejar-seiidentificarproblemes,provar,raonar, comunicar,representar,connectar,generalitzar;

Sientenemquetotselsnensinenes,alasevamanera,podenprogressarenelpensament matemàtic(competènciamatemàtica);

Sientenemqueemprarelllenguatgematemàticésfruitd’unprocésambsentitperacadascú,estaremd’acordquel’escolapotfercréixerelpensamentmatemàticdetotselsinfants.

3.Avançarenlarepresentaciódelesmatemàtiquesquefem

Peralsnensinenesd’educacióinfantiliprimàrial’escolaesdevélacasaon,nodeforma única,peròsíprincipalment,aprenenausarelllenguatgeverbalescrit(lecturaiescriptura), elllenguatgematemàtic,elllenguatgemusical...

Comprendreelllenguatgematemàticésunatascacomplexaperatotsperquèésunllenguatgeabstracteisintètic.Comtotllenguatge,téimplícitaunasimbologia.I,sí,elllenguatge matemàtichad’esdevenirsimbòlicperatoteslescriatures.Tots,d’unamaneraod’unaaltra, lihandepoderatorgarel«seu»significat.

Quanelsinfantss’impliquenenlaresoluciódeproblemes,volenexplicaralasevamanera comtrobenlesrespostes.Iésenaquestcom,enaquestprocés,quemostrenles«seves» formesparticularsipersonalsdedescriurequèhanfet,quèhanpensat,quèhanimaginat...: representenlessevesmatemàtiques.

Lesrepresentacionsdelsinfantsacostumenaseguirunaevolucióquevadelesmésconcretesalesméssimbòliques,demaneraquesovintlamostradel’experimentacióambmaterials apareixenprimerlloc;acontinuació,odeformasimultània,esfapresentlarepresentació verbal,moltesvegadesdinsdelaconversamatemàtica;desprésapareixeneldibuix,elsesquemesodiagrames,iésalfinalquanfanúsdelllenguatgematemàtic,quansóncapaços d’escriureillegirfrasesmatemàtiques,equacions.

Elsreptesqueesproposenperalsmésmenutscerquenqueespuguimanifestarunadiversitatderepresentacionsacadaaula.Iaraenspodríempreguntar:quinéselpaperdelamestra? Justamenteldefomentarquecadainfantpuguiexpressaralasevamaneraquèhafet.

4.ElprimerreptedelCercleperalsmésmenuts:LesTorresdelaReina

ElCercledeMestresdel’ABEAMésungrupdetreballdedidàcticadelesmatemàtiques d’infantiliprimàriaqueformapartd’aquestaassociaciódedocentsperal’ensenyamenti l’aprenentatgedelesmatemàtiquesdelescomarquesdeBarcelonaiqueparticipaenla creaciódeproblemesalconcursFemMatemàtiquesperacinquèisisèdeprimària.

Apartirdetoteslesideesanteriorsidelacreençaquedesdemoltpetitselsnenspoden feractivitatsqueimpliquinpensamentmatemàtic,uspresentemunadelesfeinesqueens havíemmarcatcomaobjectiuprioritari:ElsReptesdelCercle.ConsisteixaproposarproblemescompetencialscomelsdelaprimerafasedelconcursFemMatemàtiquesal’alumnatde l’etapad’educacióinfantilidelsciclesinicialimitjàd’educacióprimària.

Elprimerésunreptededicatalsinfantsd’educacióinfantilfinsasegonotercerdeprimària: lahistòriad’unareinaquevolconstruiruncastellambmoltestorres.Unahistòriaperquèels vostresnensineness’impliquiniajudinlareinaenelseudilema.

http://abeam.feemcat.org/web/cercle_mestres/les-torres-de-la-reina/.Font:MathPickle.

L’activitatespresentaendiversosapartats,queexposemacontinuació.

Enunciat

Hihaviaunavegadaunareinaquevoliaconstruiruncastellambtorres.Lesfadeslivandir quesivoliaquefosmàgic,toteslestorreshaviendetenirdiferentsalçades.

Lareinanomésteniadeublocsdepedra.Elshabitantsdelpoblevanpresentardiferents propostes...

Aquestcastellseriamàgic?...

Iaquest?...

Aralareinaensdemanaajudaanosaltres:podeutrobarunasolució?

QRperenllaçenunciatidibuixos.

Percomençar

Entretotsllegimelconte.TeniulapresentacióenPowerPoint,quepermetanarseguintla històriaiqueelsinfantshipuguinparticipar.

Unavegadallançatelrepte,podentreballarengrupspetitsiambcaixesgransperquèper separatpuguinpresentarlessevespropostes.

Sisónmésgrans,podenutilitzarcubsencaixableso multilink. Unavegadacadagruppresentalasevaproposta,esdiscuteixsicompleixonolescondicions.

Recursosperaldocent

‚ Ideescentrals:comptantpodemsaberquantsn’hiha.Pensamentadditiu:aplicarflexiblementlasumailarestaasituacionsconcretes.Equivalència.

‚ Etiquetes:descomposicióadditiva.Treballexhaustiuisistemàtic.

‚ Sentits:numèricialgebraic.

‚ Dimensions:resoluciódeproblemes.Raonamentiprova.

‚ Nivell :desdeP4finsalcicleinicialdeprimària.

‚ Perquèhemseleccionataquestproblema?

Aquestéselprimerdelsreptesquehemescollitperalsméspetits.Ésunproblemaqueté múltiplessolucionsiquepermetserresoltmitjançantl’experimentacióambmaterialifent diferentsproves.Darreredecadaprovaquefanelsalumnes,convéreflexionarambellssobre silasolucióésvàlidaonoiperquè.Hemd’aconseguirqueparlinentreellsiquejustifiquinla decisiópresaisiéscorrectaono.Totaixòprovocaràuntreballdelsprocessosderaonament iprova:

Silasolucióquehandonatnofunciona,quèhauremdeferperquèsíquefuncioni?

Itambéuntreballexhaustiupercercartoteslessolucionsquehiha:

Quantessolucionspossiblespodemdonar?

I,dintredelespossibilitatsdelsalumnes,podemintentarquesiguinmésomenyssistemàtics enlacercadetoteslespossiblessolucions:

Comsabeuquesóntoteslespossibles?

Compodemferpernodeixar-nos-encap?

Elproblemasecentraenelsentitnumèriciladescomposiciódel 10:relacionarlesdiferents descomposicionsdedos,tresoquatresumandsireconèixerque,totinoseridèntiques, tenenelmateixvalorsiesvinculadeformaclaraamblaidead’equivalència.Enelcasdels méspetits,podemcomençarperladescomposiciódel5odel6.

Abandaquehihamésd’unasolució,ladificultatrauenelfetquenonomésfemdescomposicionsendosnombres,sinóques’admetladescomposicióentresiquatrenombres(aspecte quemoltesvegadesnotreballemal’aula).

L’activitatgeneralapossibilitatd’expressardiferentsrepresentacions,desdelesfetesamb material(capses,policubs,gomets),passantperlespictòriques,mésgràfiques,finsalesque emprinllenguatgematemàtic:nombresisímbolsdelesoperacions.

Preguntesclau

Unavegadahanpresentatidiscutitalgunesdelespropostes,japodemcomençaraferun treballmésexhaustiu:

Hemtrobatalgunessolucions,però...

Compodeuassegurarquesóndiferents?

Enpodeutrobarmés?

Quèpodeuferpertrobar-nemés?

Podeutrobar-lestotes?

Quinaprovapodeuferperestarsegursquenon’hihamés?

Possibleextensió

Éselmateixlasolució 1, 2,3,4,quelasolució4,3, 2, 1?

Siconsideremquenoéselmateix,quantessolucionspossibleshihaurà?

Quèpassariasi,enllocdetenirdeublocs,entinguéssimnou?

Isientinguéssimonze?

Recursos

Materialperpoderexperimentar:capsesper alsméspetits,cubsencaixables,gomets...

Treballengrupspetits,engrupsgransiindividual.

Conversamatemàticaentorndelespropostesperacordar-nelessimilitudsilesdiferències.

Gestiódel’aulaperpartdelamestra:estimulari animaral’experimentació,alarepresentació delprocés,alraonamentdelesconnexions...

Mostresdelsnensinenes

Educacióinfantil4

Horepresentenamblescaixes:

Tradueixenlarepresentacióambcubsencaixables:

Mostrendiferentsdisposicionsambgometsdeformaindividual.Und’ellsexploraunadescomposicióquenos’hafetengrupgran.

Segondeprimària

Cerquendescomposicionsendos,tresiquatrenombres:

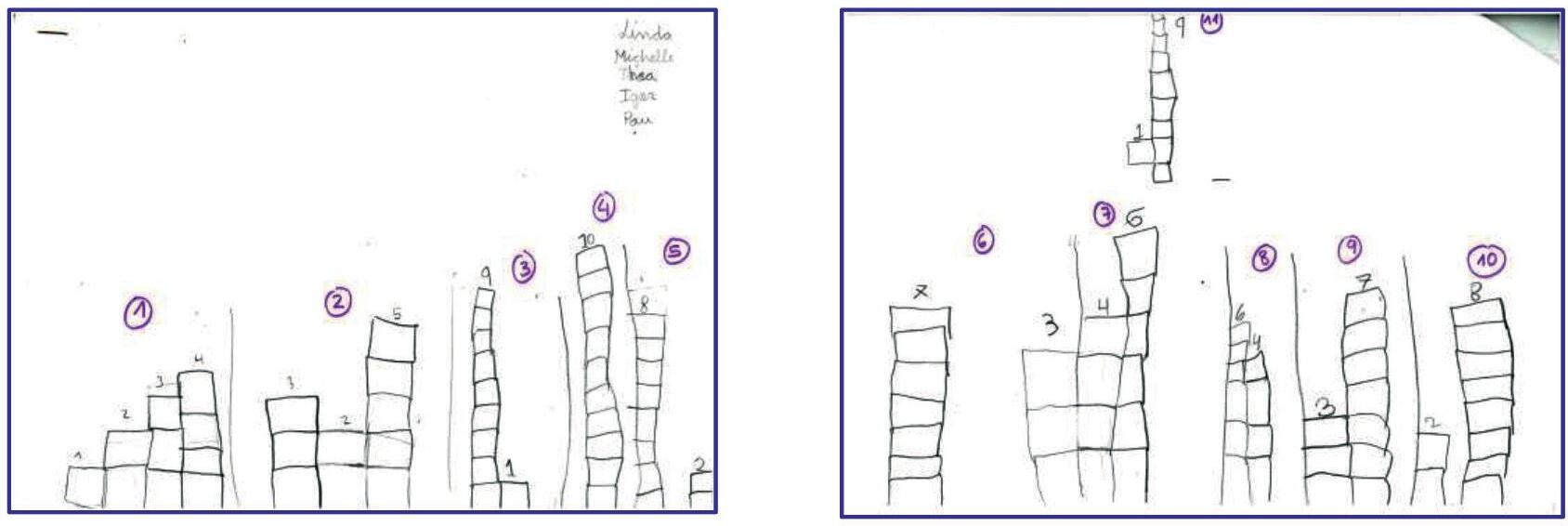
Indaguendescomposicionsenlesqualsnocanvienelsnombres,sinóladisposició:

5.Conclusions

Estemobertsalaparticipació!

EsperemquetantelFemMatemàtiquesdecinquè isisècomElsReptesdelCercle(quetrobareuahttps://abeam.feemcat.org/web/category/reptes-del-cercle/)esdevinguinbonsrecursosdeproblemescompetencialspertalqueelsfeualesvostresaules.

Estaremmoltsatisfetsqueensenvieulesrespostes,representacionsievidènciesdelesdescobertesdelsvostresalumnes.D’aquestamanerapodremfer-neunrecull,analitzarlesrespostesicompartir-les.

Desdelacreençaquetotselsinfantspodenfermatemàtiques.

Referènciesbibliogràfiques

[1]AssociaciódeBarcelonaperal’Estudiil’AprenentatgedelesMatemàtiques(ABEAM):Les TorresdelaReina.http://abeam.feemcat.org/web/cercle_mestres/les-torres-de-la-reina/.

[2]Federaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya(FEEMCAT): concurs«Femmatemàtiques».https://fm.feemcat.org/.

[3]GeneralitatdeCatalunya(gener 2023): Aramatemàtiques.Saber-nemésperensenyar-les millor.Dimensions. https://ateneu.xtec.cat/wikiform/wikiexport/cursos/curriculum/inf_pri /aramat/m3/index.

[4]Hamilton,G.(2010).«BuildingSkyscrapersofDifferentHeights». MathPickle.https://math pickle.com/project/4112/.

[5]NationalCouncilofTeachersofMathematics(2003). Principiosyestándaresparalaeducaciónmatemática.Sevilla:SociedadAndaluzadeEducaciónMatemáticaThales.

Teoriaipràctica

FrancescCarrerasiAntoniMagaña

DepartamentdeMatemàtiques, UniversitatPolitècnicadeCatalunya Autorperalacorrespondència. Adreçaelectrònica:antonio.magana@upc.edu.

Resum Abstract

Elprincipidelsmínimsquadratspermet construirlesduesrectesderegressiód’una distribucióbidimensional.Elcoeficientde correlacióentrelesduesvariables coincideixambl’arrelquadradadel productedelspendentsdelesduesrectes. Lageneralitzacióamésvariablessegueixun patrósimilar.Desprésd’unarevisió comentadad’aquestmaterialteòric, l’apliquemal’estudidediversessituacions concretesiinterpretemelsresultats obtinguts.

Theprincipleofleastsquaresmakesitpossible toconstructthetworegressionlinesofa two dimensionaldistribution.The correlationcoefficientbetweenthetwo variablescoincideswiththesquarerootofthe productoftheslopesofthetwolines. Generalizationtomorevariablesfollowsa similarpattern.Afteracommentedreviewof thistheoreticalmaterial,weapplyittothe studyofseveralconcretesituationsand interprettheresultsobtained.

Paraulesclau: distribucionsbiitridimensionals,correlacióiregressiólineal,errorquadràtic, sudoku,targetesdecrèdit,vendalliure,competiciófutbolística,qualificacionsacadèmiques, temperaturadexafogor.

Keywords: two andthree dimensionaldistributions,correlationandlinearregression,quadraticerror,sudoku,creditcards,freesale,footballcompetition,academicgrades,temperature humidityindex.

Codi(s)MSC2010:primari62 Estadística;secundaris62J05(RegressióLineal)i62P99 (Aplicacions).

MSC2010 Code(s):primary62 Statistics;secondary62J05(LinearRegression)and62P99 (Applications).

1.Introducció

Lesmatemàtiquesconstitueixenuncampcientíficmoltsingular.Perunabanda,sónuna ciènciaindependent,enelsentitqueéspossibledefinirconceptes,establirpropietatsiplantejariresoldreproblemes,totexpressatentermesestrictamentmatemàtics.Aquesta internalitat atrauisatisfàmoltsinvestigadors,quecentrenenellaelsseusesforçosiarribena resultatsadmirables.

Peraltrabanda,hihamatemàticsqueadmetenunvessantd’externalitat,segonselqualles matemàtiquessónd’utilitatperestudiarproblemesplantejatsforadelseuàmbitestricte, modelitzar los,iaplicar hilapotènciadeductivaielrigortípicamentmatemàticsperobtenirresultatsinterpretablesiprofitososenl’àmbitquehainspiratelproblema.Tambémolts investigadorsesdediquenaaquestsprocessosperquè,encertamanera,laconnexióamb larealitatexternaalesmatemàtiqueselsdónaunplusdesatisfacció.Perdescomptat,hiha matemàticsquetreballenenambdósvessants.

Enaquestarticlehemadoptatunaposturarelativamentmixtaiensproposemanalitzaramb einesmatemàtiquessituacionsbenconegudesquesemblenallunyadesdelesmatemàtiques.Hemseleccionatdiversessituacionsextretesdeldiaadiaileshemanalitzatambeines estadístiquesperobtenirconclusionssobrecadaunad’elles.Entrelessituacionsqueestudiemestroben,perexemple,ladificultatenlaresoluciód’unsudokudepenentdelnombre dedadesinicialsoelcomportamentdelsequipsenelcampionatdelligadelaPrimeraDivisió espanyoladefutbolmasculí.L’estudid’aquestscasoséslanostraaportacióal’externalitat quehemcomentatabans.Tanmateix,tambéheminclòsunasecciótècnicaprèviaonesjustifiqueniescomentenambdetenimentelsconceptesilespropietatsques’utilitzendesprés. Aixòpertanyal’àmbitdelainternalitat.

Enparticular,comamatemàticsenssemblaadmirableel principidelsmínimsquadrats.Suposemquevolemquantificarladispersiód’unconjuntdedades, tx1 ,x2 ,...,xn u,respecteauna mesuradecentralització x queresumeixelconjunt.Ésadir,volemcalcularladistànciaentre elconjuntdedadesiaquestamesura x .Unamanerapodriaserconsiderarlamitjanadels valorsabsolutsdelesdiferènciesentre x icadascunadeles xi ,ésadir,prendrela desviació mitjana:

Tanmateix,elvalorabsolutésunafunciónoderivableenelspuntsons’anul la.Aixòvaconduiraprendrelamitjanadelsquadratsdelesdesviacionsi,perconservarlamagnitudenquè s’expressenlesdades,aplicarfinalmentl’arrelquadrada:

cAquestaésl’anomenada desviaciótípica σx (respectea x )delconjuntdedades.

Defet,lamateixaideade mitjanaaritmètica jaésunaaplicaciódelprincipidelsmínimsquadrats:lamitjanaaritmètica x d’unconjuntdedades,definidacom

iutilitzadaambtantafreqüènciaenqualsevolcontext,ésl’únicamesuradecentralització queminimitzalasumadelsquadratsdelesdesviacionsrespecteaella.Aquestapropietat espotdemostrarfàcilmentambeinesdecàlculinfinitesimalo,alternativament,d’àlgebra lineal.Finsitotla mitjanageomètrica x g ,queesdefineixcom

esbasaenelfonsenelmateixprincipi,jaque,aplicantlogaritmes,

Elprincipidelsmínimsquadratséstambéelfonamentdelarectaderegressiód’unadistribucióbidimensionali,mésengeneral,permetdefiniricalcularlessolucionsaproximadesde qualsevolsistemad’equacionslineals.Enshase mblatoportúmostrar,enlasecciótècnica, comesconstrueixlarectaderegressió,tantdesdelpuntdevistadelcàlculinfinitesimalcom desdeldel’àlgebralineal.

Desprésd’aquestprefaci,passemadescriurel’organitzaciódel’article.Enlasecció 2 presentem,comamotivació,undelsexemplesqueestudiaremdesprés.Lasecció3,divididaen diversessubseccions,éslaparttècnica,onrecollim:unsumaridelsconceptesipropietats queaplicarem;uncomplementdedicatalarectaderegressiód’unadistribucióbidimensional;unaltreambelscomentarisaddicionals quehemcregutadients,iunaúltimasubsecció on,mésbreument,descrivimleseinesperestudiardistribucionstridimensionals.

Lesseccionssegüentsestandedicades,cadauna,aunexempleconcret:elssudokus(secció4),l’úsdelestargetesdecrèditenuncomerç(secció5),elpaperdelavendalliureenuna farmàcia,onhihaunaremuneracióoficialprovinentdelCatSalut(secció6),elcomportament delsequipsdefutbolenlalligadePrimeraDivisióespanyola(secció7),lesqualificacions acadèmiquesentresassignaturesestretamentrelacionades(secció8)ielconceptedetemperaturadexafogor(secció 9).Enelsexemples4 7ienlaprimerapartdel8,tractemamb distribucionsbidimensionals,mentrequeenlasegonapartdel8ienlesquatrepartsdel 9 estudiemdistribucionstridimensionals.Lasecció 10 presentalesconclusionsdeltreball. Finalment,donemunabibliografiacomentadasobreelstemestractatsenl’article.

Entotselsexempleseltractamentéssimilar.Calculemelsprincipalsparàmetresdelesdistribucionsrellevants:coeficientdecorrelació,rectaderegressió(pladeregressió,enelcasos tridimensionalsfinals),centredegravetatierror(s)quadràtic(s).Enelscasosbidimensionals afegimeldiagramadedispersió.Entotselsexemplescomentemelsresultatsi,siescau,les particularitatsespecífiquesdecadasituació.

Ensagradariaqueaquestarticleanimésalgunslectorsaaplicarlesmatemàtiquesaqualsevol nivell,desdelméselemental,comeldelnostretreball,finsalmoltsuperiordelaintel ligència artificial,l’anàlisidedadesmassives(bigdata)ol’aprenentatgeautomàtic(machinelearning), «lesjoiesdelacorona»actualsdel’opcióquehemanomenatexternalitat.

2.Unexempleil¨¨ lustratiu:sudokus

Tothomsapquèésunsudokuiquinproblemaplanteja.Ésuntrencaclosquesmatemàtic. Estractad’ompliramblesxifresdel’1 al 9 unaquadrículade 9 ˆ 9 cel lesdivididaen 9 subquadrículesde3 ˆ 3.Noespotrepetircapnúmeroencapfila,encapcolumnaniencap subquadrícula.Encadasudokuconcret,certescel lesjaportend’entradaelnúmeroposat (sónles dades).

Hihaduesintuïcionsquesón voxpopuli entreelsaficionatsalssudokus:(a)ambmenysde 17dadeslasoluciónoseràmaiúnica;(b)amb 17dadesoméssemprehihaunasolució única.L’any 2014,juntamentambdoscol legues,elmatemàticGaryMcGuire,delaUniversitatdeDublín,vademostrarcomputacionalmentquecapsudokuamb exactament 16dades tésolucióúnica,perònoqueamb 17dadesomésesgaranteixiquelasolucióésúnica. Defet,nosaltreshemtrobatunsudokuamb53dades(!)quetétressolucionsomés,cosa quedesmuntadeformaradicallaintuïció(b).McGuiretambévaconstatarquelamajoria desudokustenenunes 25dades.Unexempledesudokuamb 24dadesespotveurealafigura 1,oncuriosament(noésfreqüent)notemquehihasimetriahorizontalitambévertical, ipertanttambésimetriacentral,enlaposiciódelesdades.

Semblalògicpensarque,commenysdadestinguiunsudoku,mésdifícilseràresoldre’l. Aixònoéscappropietatgeneral.Sovinthihavaloracionsdeladificultatdelssudokusamb asteriscos,perògeneralmentlesfanlespersonesqueelsproposeni,pertant,podenser subjectives.

Figura1.Unsudoku.

Alasecció4tornaremaaquestexempleiensplantejaremsihiharelacióentreelnombrede dadesd’unsudokuielseugraudedificultatexpressatnumèricament(i,perforça,subjectiu).

3.Fonamentsteòrics

Enaquestaseccióexposemelsconceptesiresultatsdel’estadísticadescriptivaqueseran d’utilitatenelnostreestudid’exemplesco ncrets.Hiafegimduessubseccionsontractem ambmésdetenimentalgunspuntsiproveïmcomentarisidemostracionsdedeterminats resultats.Posemmésèmfasienelqueesrefereixadistribucionsbidimensionalsianalitzem mésbreumentelquefareferènciaadistribucionstridimensionals,comunamostradela generalitzaciónaturaldelcasanterioramésdimensions.

3.1.Distribucions bidimensionals

3.1.1.Recta de regressió i correlació lineal

Tenimdues sèriesdedades amb n termes: #» x “px1 ,x2 ,...,xn q i #» y “py1 ,y2 ,...,yn q.Consideradesconjuntament,formenuna distribucióbidimensional.Devegadesinteressasabersihiha relacióentrelesdadesdelaprimerasèrieilesdelasegonai,mésconcretament,siaquestarelacióésaproximadamentlineal.Encasquelarespostasiguiafirmativa,tésentitconstruir l’anomenada rectaderegressió,quedonaexplícitamentlarelacióentrelesvariables x i y . Aquestarectapermet,entrealtrescoses,ferprediccions:donatunvalorde x diferentdeles dadesdelaprimerasèrie,laimatgede x enlarectaderegressióensproporcionaelpossible valorde y quelicorrespondria.

L’únicarestriccióqueimposaremd’entrada ésqueelspuntsnoestrobintotsenunamateixa vertical,ésadir,quenotinguem x1 “ x2 “¨¨¨“ xn ,perquèenaquestcasnoexistiriarecta deregressióde y sobre x .Sesapqueles mitjanesaritmètiques són:1 x “ ř xi n i y “ ř yi n .

Iqueles desviacionstípiques σx i σy quedendefinidesperles variàncies respectives:

Tambésesapque

2 x “ x2 x 2 i,analògament, σ 2 y “ y2 y 2 , on x2 i y2 sónlesrespectivesmitjanesaritmètiquesdelsquadrats.Així,lavariànciaés«la mitjanadelsquadratsmenyselquadratdelamitjana».Lademostracióés,perexemplepera les x :

1 ř significaràsempre řn i“1 .Enqualsevolaltrecas,elslímitsdelsumatoriestaranespecificats.

Finsaquí,elsparàmetress’apliquenacadasèrieperseparat.Apartird’ara,elsparàmetres descriuranladistribucióbidimensionalidependrandelesduessèriesalhora.

La covariància delesduessèriesés cov px,y q“ řpxi x qpyi y q.Ésfàcilveureque

cov px,y q“ #» x. #» y n x y,

ésadir,elproducteescalardelsvectorsmenys n vegadeselproductedelesmitjanes.

El coeficientdecorrelaciór px,y q deladistribucióbidimensionalés r px,y q“ cov px,y q nσx σy “ řpxi x qpyi y q ařpxi x q2 řpyi y q2 .

Sempretenim r px,y qPr´1,1s,ilasegonaexpressióéslaméscòmodapercalcular-lo tabularment.Peramésdetallssobrecorrelacióicovariància,vegeumésavalllasecció3.1.3.

La rectaderegressiódeysobrex ésdelaforma

y y “ mpx x q,

on px,y q ésel centredegravetat deladistribucióiel pendentm és m “ cov px,y q nσ 2

pxi x q2 ,

on xy “ ř xi yi n éslamitjanadelsproductesdelesduessèries.Laquartaexpressióésla méscòmodasiestemfentelscàlculstabularment.Solserinteressantiil lustratiudibuixar el diagramadedispersió delesdadessobreunseixosrectangulars x y juntamentambla gràficadelarectaderegressió.Peramésdetallssobreelfonamentdelarectaderegressió, vegeulasecció3.1.2.

L’errorquadràtic d’aquestarectaderegressióés “ bÿpyi y ˚ i q2 , on y ˚ i “ y ` mpxi x q peracada pxi ,yi q.

L’errorpercapita 0 “ {n semblamésinteressantaefectescomparatius,jaquereparteix l’errortotalentreles n dades pxi ,yi q.Vabépercomparardistribucionsbidimensionalsambdiferentnombrededades n.Quanvolemcompararduesdistribucionsonelsrangsdevariació de y sónmoltdiferents,untercererrorsemblaadequat:consisteixadividirl’errorpercapita perlamitjanaaritmètica y ,queprenemcomarepresentativadetotselsvalorsde y encada cas,iobtenim,doncs,l’error(percapita)normalitzat ˚ 0 “ 0 {y .

3.1.2.La recta de regressió de y sobre x

Hihadosmètodesprincipalsperfonamentariobtenirlarectaderegressió:unésl’analític, basatenelcàlculinfinitesimal,il’altreésl’algebraic,basatenl’àlgebralineal.Totsdosestan inspiratspel principidelsmínimsquadrats:larectaderegressióminimitzalasumadelsquadratsdelesdesviacionsrespectealasèriedeles y o,equivalentment,l’errorquadràticdefinit uneslíniesmésamunt.

A.Mètodeanalític. Larectaderegressióésdelaforma

Idealment,totselspuntsdeladistribucióhauriendesatisferaquestaequació,ésadir,

Tanmateix,usualmentaquestsistemade n equacionsambduesincògnites a0,a1 notésolució perquèels n puntsnoestanalineats.Consideremlasumadelsquadratsdelserrorscomesosentreelsvalorsreals yi ,donatsperladistribució,ielsquedonarialarectaderegressió, y ˚ i “ a0 ` a1 xi .Tindremun«errortotal» E ,donatper

Aquesterrortotal E ,quedepènde a0 i a1 ,ésunafunciócontínua,diferenciableinonegativa,inotécapmàximabsolutperquè,quan a0 , a1 ototsdostendeixencapa 8, E tendeix tambécapa 8.Encanvi,comprovaremquetéunúnicmínimabsolut,quepodremlocalitzar comamínimlocal.Primerimposemquelesduesderivadesparcialsde E s’anul¨lin(condició necessàriadepuntcríticoextremlocal):

$ ’ ’ ’ ’ & ’ ’ ’ ’ % B E B a0 “ 2 řpa0 ` a

ésadir, $ ’ & ’ % ř yi “ na0 ` a1 ř xi , ř xi yi “ a0 ř xi ` a1 ř x 2 i . (1)

Aquestésunsistemadeduesequacionslinealsamblesincògnites a0 i a1 .Arafemlesderivadesparcialssegones:

Aquestesquatrederivadesparcialssegones,disposadestalcomestan, defineixenlamatriu hessiana HpE q delafunció E .Aquestamatriuéstambélamatriudelscoeficientsdelsiste-

ma(1)donatperl’anul laciódelesprimeresderivadesparcials,iobservemqueésconstant (independentde a0 i a1 ).Calculemaraelseudeterminant(persimplicitat,prescindimdels coeficients 2 detoteslesderivadessegones,cosaquenoafectaràelraonament):

det HpE q“ n ÿ x 2 i ´ÿ xi ¯2

Perveurequesempreéspositiu,comprovaremprimerque det HpE q“ ÿ 1ďiăjďn pxi xj q2 . (2)

Lademostracióésperinducciósobre n ě 2.(a)Pera n “ 2 tenim det HpE q“ 2px 2 1 ` x 2 2 q´px1 ` x2 q2 “px1 x2 q2 .

(b)Suposem n ě 3iquelafórmula(2)valpera 2,...,n 1.Aleshores,

det HpE q“ n řn 1 x 2 i `řn 1 xi ˘

Perhipòtesid’inducció,coneixemlasumadelsdosprimerstermes(entreclaudàtors);per tant, det HpE q“ ÿ 1ďiăjďn

on R recullelsdostermesrestants.Aratenim

Finalment,

Comquenototselspuntsdeladistribucióestrobenenunaúnicavertical,almenyshihaurà unparell i,j talsque xi ‰ xj ,idet HpE q seràpositiu.Pertant,hihaurànomésunpuntcrític.

Aplicant,perexemple,laregladeCrameralsistema(1),trobemelscoeficientsil’equacióde larectaderegressió,queés y “ n ř xi yi ř xi ř yi n ř x 2 i ´př xi q2 x `

Enelcas n “ 2,l’equacióanterioresredueixa

queéssimplementlarectaquepassapelsdospunts p

Aracomprovemqueenelpuntcrítichihaunmínimabsolutde E .Laformaquadràticadefinidaperlamatriu HpE q ésdefinidapositivasegonselcriterideSylvester,jaqueelseuprimer coeficientielseudeterminantsónpositius.AixòimplicaquelafórmuladeTaylordegrau 2 delafunció E enelpuntcrític p “pa0 ,a1 q és,peraqualsevolpunt px,y q delpla, E “ f p

jaque HpE q ésdefinidapositiva(elresidudelafórmulaés 0 perquè E ésunafunciópolinòmica desegongraude a0 ,a1 ).Aixòdemostraqueenelpuntcrític p “pa0 ,a1 q hiha(l’únic)mínim absolutde E

Tornantalcasgeneral,ésimmediatcomprovaramblaprimeradelesequacionsde(1)quela rectaderegressiópassapelcentredegravetatdeladistribució,jaque ř yi n “ a0 ` a1 ř xi n .

B.Mètodealgebraic. Tornemasuposarquelarectaquebusquemésdelaforma y “ a1 x ` a0

Novament,totselspuntsdeladistribucióhauriendesatisferaquestaequació.Aixòensdonariaunsistemade n equacionslinealsambduesincògnites: a1 i a0 .Escritenformabreu seria a1 xi ` a0 “ yi per i “ 1,2,...,n.

Enformamatricialelsistemas’escriu

o,mésexplícitament,

x1 1 x2 1 ... 1 xn 1

Engeneral,elsistemaseràincompatiblellevatqueels n puntsestiguinalineats.Entermes vectorials,busquemdinsdel’espai Rn unvector u1 delpla H generatper c1 “px1 ,x2 ,...,xn q i c2 “p1,1,...,1q talque u1 “ u,iés,doncs, u1 “ a1 px1 ,x2 ,...,xn q` a0 p1,1,...,1q“py1 ,y2 ,...,yn q“ u.

Queelsistemasiguiincompatiblesignificaque u “py1 ,y2 ,...,yn qR H,ipertantlarelació precedentésimpossible.L’alternativaproposadapel principidelsmínimsquadrats consisteix abuscarelvector u1 P Hméspròxim a u,ipertant u1 hadeserla projeccióortogonal de u sobre H perquèéslaque minimitza ||u u1 || entretotselsvectors u1 P H.Lacondicióque hadecomplir u1 P H perserlaprojeccióortogonalde u sobre H ésque u u1 K H,quees tradueixen u u1 K c1 i u u1 K c2

Aixòequivalaimposar u c1 “ u1 c1 i u c2 “ u1 c2 , quepodemexpressarmatricialmentcom

C t CX “ C t D, o,introduint A “ C t C i B “ C t D (A resultaquadrada 2 ˆ 2 isimètrica), AX “ B, sistemacompatiblei,amés,determinat(solucióúnica),jaqueexplícitamentqueda A “ ˆ ř x 2 i ř xi ř xi n ˙ i B “ ˆ ř xi yi ř yi ˙ , demaneraque det A “ det HpE q“ ÿ 1ďiăjďn pxi xj q2 ‰ 0

ilasolucióúnicadelsistema AX “ B éslamateixaquedonaelmètodeanalític.Amés, “||u u1 ||“ ?E,

queéselques’anomena errorquadràtic delarectaderegressióobtinguda.

Noésdifícilveurequeelpendent m delarectaderegressiódefinitenlasecció3.1.1 coincideixambelpendent a1 calculatenaquestasecció.Enefecte,dividintper n2 numeradori denominadorde a1 tenim,recordantque σ 2 x “ x2 x 2 , a1 “

segonslaterceraexpressióde m donadaenlasecció3.1.1.

3.1.3. Covariància cov(x,y) i coeficient de correlació r(x,y)

Percomençar,convénotarquelacovariànciaéssimètrica,ésadir, cov py,x q“ cov px,y q.Siles dadesestantotesenunamateixaverticalobéenunamateixahoritzontal,ésfàcilveureque cov py,x q“ 0 “ cov px,y q.

Aracaljustificarlesduesexpressionsd’aquestparàmetrequeapareixenalafórmuladelcoeficientdecorrelació r px,y q alasecció3.1.1.Peraaixò,noméscalcomprovarlaigualtatdels numeradors,jaqueelsdenominadorssón,òbviament,idèntics.I,enefecte, cov px,y q“ #» x. #» y n x y “ ÿ xi yi n x y “ n xy n x y “ npxy x y q, mentreque

ÿpxi x qpyi y q“ ÿ xi yi y ÿ xi x ÿ yi ` nx y “ npxy x y q

Passemaraalcoeficientdecorrelació.Tambépersimetriatenim r py,x q“ r px,y q i,enelsdoscasosextrems,l’horitzontalielvertical, r px,y q“ 0.

Esdefineixla variaciótotal de y com nσ 2 y “ ÿpyi y q2 .

Aracomprovaremque

Comencemperlaidentitat yi y “pyi y ˚ i q`py ˚ i y q.

Elevantalquadratelsdostermesisumantperatot i obtenim

aplicantlesequacions(1)alscoeficientsde a

Aixídoncs,lavariaciótotalquedadivididaendostermes:

Elprimertermedelsegonmembreésla variaciónoexplicada,mentrequeelsegontermeés la variacióexplicada perquèsegueixunpatródereferència,cosaquenofaelprimer.

El coeficientdecorrelaciór px,y q esdefineixcoml’arrelquadradadelquociententrelavariació explicadailavariaciótotal,ambsignepositiuonegatiusegonselsignedelpendent m dela rectaderegressió.Simbòlicament:

r px,y q“˘ d řpy ˚ i y q2 řpyi y q2 .

Aquestaésunadefinicióraonadade r px,y q.Hauremdecomprovarqueaquestaexpressióés equivalentalade r px,y q queapareixalasecció3.1 1.Abans,observemque r px,y qPr´1,1s i que,comacasosparticularsextrems:(a)silavariacióexplicadaésnul¨la, r px,y q“ 0;(b)sila variaciónoexplicadaésnul la, r px,y q“˘1.

Femlacomprovacióanunciada.Del’equaciódelarectaderegressiótenim y ˚ i y “ a1 pxi x q.

Pertant,

r 2 px,y q“ řpy ˚ i y q2 řpyi y q2 “ a2 1 řpxi x q2 řpyi y q2 .

Arabé,segonslaquartaexpressiódelpendent m enlasecció3.1.1,

Substituintal’equacióprèviaisimplificantunfactor řpxi x q2 resulta r 2 px,y q“ “ řpxi x qpyi y q‰2 řpxi x q2 řpyi y q2 i,endefinitiva,

px,y q“

Elsigne ˘ javaincorporatalnumeradord’aquestaexpressió.

Consideremfinalmentla covariànciapercapita

xy “

pxi x qpyi y q n .

Aleshoresenresultaunaexpressiósimplificadadelcoeficientdecorrelació:

Tambéelpendent m delarectaderegressióde y sobre x admetexpressionsméssimples:

Sielspuntsdeladistribuciónoestantampocenunamateixahoritzontal,pensemenlarecta deregressióde x sobre y ,queésanàloga mutatismutandis alade y sobre x quehemestat considerantexclusivamentfinsara,iescrivim

Ésobvique

i,pertant, mm1 “ r px,y q2 ,

expressióqueespodriaadoptarcomadefiniciódelcoeficientdecorrelació.Enparticular, silesduesrectesderegressiócoincideixen, m “ m1 ,hihaunacorrelaciólinealperfectai, pertant, r px,y q“ 1.Encanvi,si r px,y q“ 0,lesrectesderegressiósónperpendiculars.Espot interpretarque,engeneral,elcoeficientdecorrelacióveaserunamesuradel’angle α que formenlesduesrectes,encaraquelarelaciónoéssenzilla(lineal):

3.2.Distribucions tridimensionals

Percompletaraquestresumteòricconsideraremelcasd’unadistribucióambtresvariables. Tenim,doncs,tres sèriesdedades amb n termescadauna: #» X “pX1 ,X2 ,...,Xn q, #» Y “pY1 ,Y2 ,...,Yn q i #» Z “pZ1 ,Z2 ,...,Zn q.Consideradesconjuntament,formenuna distribuciótridimensional.L’única restriccióqueimposaremd’entradaésqueelspunts pXi ,Yi ,Zi q noestrobintotsenunamateixa vertical(paral lelaal’eix Z ),perquèenaquestcasnotindriasentitestablirunarelacióde Z comafuncióde X i Y .

Les mitjanesaritmètiques X , Y i Z esdefineixencomenelcasbidimensional.2 Elpunt pX,Y,Z q seràel centredegravetat deladistribució.Reservaremlescorresponentslletresminúscules x , y i z perales variablesnormalitzades,quesónlesdesviacionsdelesvariablesoriginals respectealessevesmitjanesaritmètiques:

x “ X X,y “ Y Y i z “ Z Z.

Tambéesdefineixencomenelcasbidimensionalles desviacionstípiques σX , σY i σZ ,determinadesperlesrespectives variàncies.Isegueixtenintvalidesaquecadavariànciaés«la mitjanadelsquadratsmenyselquadratdelamitjana».Vallapenaremarcartrespuntsde fàcilcomprovació:(a)lamitjanaaritmèticadelesvariablesnormalitzadesésnul¨la,ésadir, ř xi “ ř yi “ ř zi “ 0;(b)lessevesdesviacionstípiquescoincideixenamblesdelesvariablesoriginals, σx “ σX , σy “ σY i σz “ σZ ;(c)elcoeficientdecorrelaciódeduesqualssevol d’aquestesvariablescoincideixambeldelessevesvariablesnormalitzades,perexemple, r pX,Y q“ r px,y q.Totaixò,quetambéeravàlidenelcasbidimensional,seràd’utilitataquíper alleugerirlanotacióenalgunsmoments.

Ensocuparemarad’estudiartresconceptesprincipals:(a)elde pladeregressiólineal dela distribuciótridimensional,quedescriu,siexisteix,ladependènciaaproximadamentlineal d’unadelesvariables(escolliremla Z )enfunciódelesaltresdues(X i Y )iesbasaenel principi delsmínimsquadrats;(b)l’errorquadràtic quedonaaquestplad’equació Z “ f pX,Y q quanfem

serviraquestafuncióperestimarvalorsde Z apartirdevalorsde X i Y ;i(c)el coeficientde correlació(global) quemesuralaqualitatdeladependènciadonadaperlafunciólineal f

El pladeregressiólineal seràdelaforma

Z “ aX ` bY ` c. (3)

Lesconstants a,b,c sónels coeficientsderegressióparcial.Lasituacióideal(dependèncialineal perfecta)esdonariasi Zi “ aXi ` bYi ` c pera i “ 1,2,...,n.

Introduintlesvariablesnormalitzades x,y,z ,l’equació(3)passaaser z “ ax ` by.

Seguintunprocéssimilaraldelcasbidimensional,partimde zi “ axi ` byi . (4)

Multiplicantaral’equació(4)separadament,primerper xi idesprésper yi ,isumantencada castermeaterme,obtenim $ ’ & ’ % ř zi xi “ a ř x 2 i ` b ř xi yi , ř zi yi “ a ř xi yi ` b ř y 2 i , (5)

queéselsistemad’equacionslinealsquedeterminaelscoeficients a,b. 3 Escritmatricialment és: ˆ ř x 2 i ř xi yi ř xi yi ř y 2 i ˙ˆ a b ˙ “ ˆ ř zi xi ř zi yi ˙ .

Aplicant,perexemple,laregladeCramer,lasoluciódelsistemadona a “ ř zi xi ř y 2 i ř zi yi ř xi yi ř x 2 i ř y 2 i ´př xi yi q2 i b “ ř zi xi ř x 2 i ř zi xi ř xi yi ř x 2 i ř y 2 i ´př xi yi q2

3.Elsistemaequivalentamblesvariablesoriginalsés

ř Zi “ a ř Xi ` b ř Yi ` cn, ř Zi Xi “ a ř X 2 i ` b ř Xi Yi ` c ř Xi ,

ř Zi Yi “ a ř Xi Yi ` b ř Y 2 i ` c ř Yi . Eltractamentteòricd’aquestsistemaésforçaméscomplicatqueeldelsistema(5).

Aleshores,l’equaciódelpladeregressiódeZsobreXiY és

Z “ apX X q` bpY Y q.

Nota. Tanmateix,ésconvenientindicarque,enunexemplenumèric,ésmillorprepararuna taulanumèricaamblesdadesoriginalsielscàlculsaddicionalsnecessarisiresoldreelsistema detallatenlanota4,perobtenirl’equaciódelplaamblaforma

D’aquestamanerareduïmelspetitserrorsque indefectiblementimpliquenlesaproximacions.Tambéarrosseguemerrorssiintroduïmelsanomenats coeficientsdecorrelacióbinària, quesónelscoeficientsdecorrelaciódelestresdistribucionsbidimensionalssubjacentsala tridimensionalqueestemconsiderant:

Desprésdetenirencomptelesrelacions

i,anàlogament,

isimplificaralgunstermes,éscertquelesequacions(5)queden

o,enformamatricial,

AplicantlaregladeCramerobtenimlesexpressionsde a,b i,coma equaciódelpladeregressió dezsobrexiy , 4

4.Ésfàcilveureque,eliminantperexemplela y ,aquestaequacióesredueixa z

queésl’equaciódelarectaderegressióbidimensionalde z sobre x

Noobstantl’aspecteagradableisimètricd’aquestaequació,elscoeficientsdecorrelacióbinàriaquehiapareixenarrosseguenerrorsd’aproximaciópelseupropicàlcul,ipertornara lesvariablesoriginalsdelproblemacal,amés,introduirlesmitjanesaritmètiques.Peraixòen lanotademésamunts’hainclòselcomentarisobreelsexemplesnumèrics.

L’errorquadràtic de Z sobre X i Y esdefineixper

Tanmateix,ésméshabitualconsiderarl’errortípicdel’estima,queveaserun errorpercapita i ésdonatper

El coeficientdecorrelaciómúltipleRZ pX,Y q deladistribuciótridimensionalesdefineixcom

Aquestcoeficientdecorrelaciómúltiplesemprevariaentre 0 i 1.Comméss’acostaa 1,millor éslarelaciólinealentrelesvariables.Comméss’acostaa 0,larelaciólinealéspitjor.Siel coeficientés 1,larelaciólinealésperfecta.Siés 0,nohiharelaciólinealperòn’hipothaver d’unaltretipus.(Hihaexpressionsalternativesd’aquestsdosnousparàmetresentermesdels coeficientsdecorrelacióbinàriaque,perlesraonsjaexplicades,nofaremservir.)

4.Exemple:sudokus

Ensplantegemdonarrespostaalaqüestiósegüent:hiharelacióentreelnombrededades d’unsudokuielseugraudedificultatexpressatnumèricament?

Undenosaltresvatenirocasióderesoldreels 108sudokusd’unquadernpublicatperEdigramael 2021,onelsgrausdedificultatanunciatseren:***(16problemes),****(46problemes) o*****(46problemes).Elsvacompletaren,aproximadament,unmes.Und’ellseral’exemple delafigura 1 (secció 2)itotstenienelmateixtipusdesimetriahoritzontalivertical.

Desprésderesoldrecadasudoku,vavalorar-neladificultat,segonsaquestesopcions: F (fàcil), R (regular), D (difícil)i D˚ (moltdifícil).Sónels grausdedificultat,ensentitcreixent.Evidentment,aquestavaloraciótambééssubjectiva.De fet,esvaobservarque,sovint,ladificultat tambédepènunamicadela«lucidesa»dequiintentaresoldreelsudokuenelmomentde trobarlasolució,iaixòtambééslògic.Noésestranyqued’unproblemaqueesdeixaencallat alanit,se’ntrobilasoluciól’endemàalmatísenseexcessivesdificultats.

Noensaturaremaexplicarladiferènciaentre‘difícil’i‘moltdifícil’,peròéscertqueésnotable. Pertant,al’horadequantificarels quatregraus,l’assignacióhaestat: F “ 1, R “ 2, D “ 3i D˚ “ 5.Aquítambéhihasubjectivitat,ésclar.

Vegemenlataula 1 lagraelladefreqüències.Lavariable x descriulesdadesdecadasudoku, desde 21 finsa31,mentrequelavariable y descriuelgraudedificultat.Dinsdecadacel lahi halafreqüènciadecadaparell(dades,grau).Finsaquíarribaladescripciódelapartempírica, ésadir,elsresultatsdel’experiment.

Taula1.Freqüènciesdecadaparell(dades,graudedificultat).

Perexemple,dels 25sudokusamb x “ 27dades,n’hiha 20 quesónfàcils(F “ 1)i5de regulars(R “ 2).

Passemaraalapartanalítica.Estractadecomprovarsi‘menysdades,mésdifícil’ésuna hipòtesiplausibleiquinaéslarectaderegressiólinealde y sobre x ,ésadir,siespotpreveure ambcertaaproximacióelgraudedificultatd’unsudokuapartirdelessevesdades.Amb aquestobjectiuhemestudiatladistribucióbidimensional x,y .

Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór “ r px,y q entreduesvariables,quesempreestàal’interval r´1,1s,donaaquí r “´0,29.Significaquehihapocacorrelacióentre y i x ,ielsigne negatiuindicaque,molt grossomodo,commésdades,menysdificultat.

‚ La rectaderegressiódeysobrex dona y “ 5,20 0,14x .Espotveurerepresentada eneldiagramadelafigura 2.Comestàprevist,passapelcentredegravetat px,y q = (26,53, 1,49).

‚ L’errorquadràtic d’aquestarectaés “ 8,383.Mésinteressantsemblal’errorquadràtic percapita 0 ,quereparteixequitativamentl’errortotalentretotselssudokusestudiats idona 0 “ 0,078demitjanaperacadaun.

y :graudedificultat

D∗ = 5

4

D = 3

R = 2

F = 1

0

rectaderegressi´o: y = 5,20 0, 14x

coeficientdecorrelaci´o: 0, 295 (x , y)

20 2122 23 24252627 28293031

x :dades

Figura2.Diagramadedispersiódelssudokusestudiats.

Lafigura 2 ensdonael diagramadedispersió del’experiment.Caladvertirqueelgruixdecada cercleésaproximadamentproporcionalalafreqüènciadelaparella(dades,grau)corresponent.Espotobservarquelarectaderegressiódecreixitravessaelnuclideladistribució.A lasecciósegüentcompararemaquestsresultatsambelsques’obtenenenuncastotalment diferent.

5.Exemple:vendaambtargetesdecrèdit

El 2008esvainaugurarunafarmàciaenunbarrimodestdelaterceraciutatcatalana.El «farmacèuticconsort»,amicnostre,varebrediversosencàrrecsiensenvaparlarrecentment: und’ellserarevisarcadadiaelstiquetsdelspagamentsambtargetafetspelsclients,per comprovarsielbancabonaval’importnetcorresponentdesprésdequedar selacomissió del 0,3%sobrel’importbrut.Desdel’inicidelapandèmiafeiaaquestafeinanoadiarisinó uncoppersetmana,cosaquesuposavacomptarcadavegada6feixosdetargetes(dedilluns adissabte,llevatdelsfestius).

Desprésde 14anys,segonsvaexplicar,deuhaverrevisatmilersdetiquets,peròmainoels haviacomptat.L’any 2021 esvadecidirafer ho:disposa,doncs,peracadamesdel 2021,del nombredecompresfetesambtargetail’importtotalnet.Total:4.400 targetes.Lasensació aproximadaquetéésque«comméstargeteshiha,méspujal’importtotal»,encaraque aquestanoésunareglarígida.Compodríemcomprovaramblessevesdadesquingraude validesatélasevasensacióintuïtiva?

Tenimduessèriesde dades,cadaunaamb 12 components: elnombredetargetesdecadames i l’importtotalnetmensual. Sónvaloracionsobjectives.Tanmateix,l’experimentquedacondicionatpermoltsfactors:l’emplaçamentdelafarmàcia,eltipusdeclientelaqueté,l’elecció quefacadacliententrepagarenefectiuoambtargeta,l’efectedelapandèmia,etc.Inomés tenimlesdadesd’unany,mespermes.Pertant,elsresultatsdifícilmentserienextrapolables, nonomésaaltresfarmàciessinófinsitotaaltresanysd’aquesta.

Lataula 2 ensdonalesdadesdeladistribucióbidimensionalqueestudiarem.

Taula2.Nombremensualdetargetesdecrèditiimportsnetscorresponents.

mes gener febrer març abril maig juny targetes(x

mes juliol agost setembre octubre novembre desembre targetes(

Elnombredetargetes(x )ésunaquantitatdetresxifres,mentrequel’importeneuros(y )ve donatambquatrexifresidosdecimals.Aquestadiferènciafaqueeldiagramadedispersió hagideteniral’eixdeles y unaescaladiferentqueal’eixdeles x .

Passemaraalapartanalítica.Volemcomprovarsi«comméstargetes,mésimportnettotal» eraunahipòtesiplausibleiquinaeralarectaderegressiólinealde y sobre x ,ésadir,sies podiapreveureambcertaaproximaciól’importmensualapartirdelnombredetargetes.

Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór entreduesvariables,quesempreestàal’interval r´1,1s, donaaquí r “ 0,85.Significaquehihaunacorrelaciópositivanotableentre y i x ,cosa que grossomodo confirmalaintuïciódelnostreamic.

‚ La rectaderegressiódeysobrex dóna y “ 12,5x ` 500.Espotveurerepresentadaenel diagramadedispersiódelafigura3.

‚ L’errorquadràtic d’aquestarectaés “ 1,346,20 il’errorquadràticpercapita dona 0 “ 112,18demitjanaperacadames.Aquestésunerrornotableaprimeravista,ésadir, entermesabsoluts,peròcaltenirencompteelrangdelsvalorsde y .

Lafigura3donael diagramadedispersió del’experiment.Espotobservarquelarectade regressiócreixis’acostaforçaalamajoriadels 12 punts px,y q.Elnúmeroqueacompanya cadapuntenaquestafigurarepresentaelmescorresponent.

coeficientdecorrelaci´o: r = 0,85 rectaderegressi´o: y = 12, 5x + 500

Figura3.Diagramadedispersiódelesvendesambtargeta.

Comparemelsresultatsd’aquestestudidelestargetesambelsdelssudokus.Enelcasdels sudokus,lacorrelació r “´0,29 ésbaixaentermesabsoluts,ésadir,obviantelsigne,il’error percapitatambéés«petit»;encanvi,peralestargetes,lacorrelació r “ 0,85ésforçaalta il’errorpercapitatambéés«moltgran».Tanmateix,larectaderegressióperalestargetes semblamésajustadaalesdadesqueladelssudokus.Elmotiud’aquestacontradiccióaparent ésqueelrangdeles y és r1,5s peralssudokusiaproximadament r3,983 , 6,612s perales

targetes.Introduïmunsegonfactordenormalització,l’errorpercapitanormalitzat ˚ 0 “ 0 {y , definitalfinaldelasecció3.1 1.Lataula3comparatotselsvalorsrellevants.

Taula3.Comparacióambl’exempledelssudokus.

errorquadràtic errorpercapita mitjanadeles y errornormalitzat

Araesveuclarque,adequantencadacasl’errorpercapitaalrangdeles y (o,equivalentment, al’entorndelamitjanaaritmèticadeles y ),l’errorpercapitanormalitzatdelestargetesés bastantmenorqueeldelssudokus,comsuggereixenlesgràfiquesdelesrectesderegressió respectives.Sembla,doncs,queaquestúltimparàmetrereflecteixmillorelsdiagramesde dispersió.Ladiferènciaencaraseriamésgranprenentcomaparàmetre {y :donaria5,6226 peralssudokusi 0,2649 peralestargetes.

6.Exemple:vendalliure

Undelsparàmetresimportantsperalavaloraciód’unafarmàcia(perexemple,al’horad’una compravenda)éslaproporcióquepresentadevendalliure(desd’ara,VLL)eneltotald’ingressos. ElspreusdelaVLLnoestanregulats(d’aquíve elqualificatiu):cadafarmàciaelsdecideix ipotmodificar losentotmoment,encaraquehihaunacertauniformitat,sobretotentre farmàciespròximes.

Elssupermercatstenenproductesquetambéesvenenalesfarmàcies(parafarmàcia,per exemple)ipodenoferir losapreusinferiorsperquècomprenmésal’engròs.Finsalpunt quealgunesfarmàcies,desprésd’indagarenelssupermercatspròxims,acabenvenental mateixpreuoambpèrduesalgunsd’aquestsproductespernodeixarescaparclients.

Hihatresemplaçamentstípicsperaunafarmàcia:apropd’uncentred’atencióprimària (CAP),cèntricaoenunabarriada.LesfarmàciespròximesaunCAPdespatxenmoltesreceptes,coméslògic;lescèntriquestenenunaaltaVLL,finsitotsuperioralesreceptesdel SistemaCatalàdeSalut(desd’ara,SCS);finalment,lesfarmàciesdebarriadanodestaquen perlaVLL.

Elnostreobjectiuésl’estudidelarelacióentrel’importtotalquepagaelSCSieldelaVLL. Enscenyiremalesdadesmensualsdel 2021 delamateixafarmàciadel’exemple5.

Tenim,doncs,duessèriesde dades,cadaunaamb 12 componentsmensuals: l’abonament delSCS i l’importdelaVLL. Lataula4ensdonalesdadesdeladistribucióbidimensionalque estudiarem.

Taula4.DadesdelSCSidelaVLL.

mes gener febrer març abril maig juny

y )

mes juliol agost setembre octubre novembre desembre

EncaraqueelsimportsdelSCStenencincxifresenteresidosdecimals,mentrequelamajoria delsdelaVLLsóndequatrexifresenteresielsrangsdelesvariablessóndiferents,enel diagramadedispersiól’escaladel’eixdeles y seràlamateixaqueal’eixdeles x .Comala figura3,l’artificipernodesaprofitarespaihaconsistitasituarl’origendelseixosenelpunt (34,7).

Passemaraalapartanalítica.Volemveuresihihaunabonarelacióentrelesduessèriesde dadesiquinaéslarectaderegressióde y sobre x .

Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór entreduesvariables,quesempreestàal’interval r´1,1s, donaaquí r “ 0,5396.Pertant,laVLLestànomésrelativamentrelacionadaambels pagamentsdelSCS.

‚ El centredegravetat deladistribucióéselpunt px,y q“(39.914,34, 9.167,68).

‚ L’equaciódela rectaderegressiódeysobrex és y “ 0,2186x ` 442,6184.

‚ L’errorquadràtic d’aquestarectaés “ 3,326,34,l’errorquadràticpercapita dona 0 “ 277,19 demitjanaperacadamesil’errornormalitzat és ˚ 0 “ 0,0302.Aquestúltimestà comprèsentreeldelestargetes(0,0221)ieldelssudokus(0,0527).

Lafigura4donael diagramadedispersió del’experiment.Larectaderegressiócreixlentamentiesdistanciadelameitatdels 12 punts px,y q.Tambéhihamarcadaambtraçdiscontinu lapoligonalquevaunintsuccessivament,seguintl’ordredeles x creixents,elspuntsdela distribució(elnúmeroalcostatdecadapuntindicaelmesdel’any).Pensemquelasingular posiciódelpunt 12 s’explicaperquèaldesembrelagentincrementalacompradeproductes devendalliurecomaregalstípicsdel’època.Encanvi,labaixaproporciódevendalliuredels mesosd’agostinovembreésdeguda,respectivament,alesvacancesd’estiuial blackfriday, quenoespracticaalesfarmàcies.

7.Exemple:futboldelaPrimeraDivisióespanyola

LaPrimeraDivisiódelCampionatdeLligad’Espanyalaformen 20 equips.Durantlaprimera volta,cadajornadaesjuguen,doncs, 10 partits,cadaunalcampd’undelsdoscontrincants. Alasegonavoltafanelmateixperòalcampdel’altre.Pertant,entotalhiha38jornades, 19 alaprimeravoltai 19 mésalasegona.Quanunequipguanyaaunaltre,elprimerrep3 puntsielsegon 0.Siempaten,reben 1 puntcadaun.

ElsquatreprimersclassificatsjugaranlaChampionsLeaguelatemporadasegüent;elcinquèielsisèjugaranl’EuropaLeague.Al’altreextrem,elstresdarrersclassificatsbaixenala SegonaDivisiólatemporadasegüent;elssubstituiranelstresprimersclassificatsd’aquesta divisió(elsdosprimersdirectament,mentrequeeltercersurtd’eliminatòriesentreelsquatre següents,elsqueocupenlesposicions tercera,quarta,cinquenaisisena).

Coméslògic,elsresultatsdecadaequipalasegonavoltasolenserdiferentsdelsdelaprimeravolta.L’objectiud’aquestestudiésanalitzarelscomportamentsalaprimerailasegona volta.Prendremlesdadesdelatemporada 2020 2021 iensfixaremnomésenelsequips mésfortsd’unabandaienelsmésdèbilsdel’altra.Elsprimersestaninteressatsaquedaren els«llocseuropeus»;elssegons,afugirdelstresllocsmésbaixosdelaclassificaciófinal.

Demillorapitjor,enacabarlaprimeravoltaelsequipsmésfortsvanserelssegüents:AtléticodeMadrid,RealMadrid,Barcelona,Sevilla,Villarreal,RealSociedad,GranadaiBetis.El Villarrealteniagarantitl’accésalaChampionsLeagueperquèhaviaguanyatl’EuropaLeague latemporadaanterior 2019 2020 (normaeuropea).Tambédemillorapitjor,ameitatde temporadaelsequipsmésdèbilsvanserelssegüents:Getafe,AthleticdeBilbao,Valencia, Eibar,Valladolid,Alavés,Elche,OsasunaiHuesca.Entotsdoscasos,alfinaldelacompetició hivahaveralgunscanvisd’ordre.

Figura4.DiagramadedispersiódelaVLLvs.elSCS.

Ladobletaula5ensdonalapuntuaciódecadaequipenacabarlaprimeravolta(jornada 19)ialfinaldelatemporada(jornada38).Aixòensdonaràlesdades x,y deladistribució bidimensionalqueestudiarem,primerperalsequipsfortsidesprésperalsdèbils.Perraons d’espai,hemabreujatelsnomsd’algunsequips.

Taula5.Puntuacionsamigcampionat(jornada19)ialfinal(jornada38).

equip AMadrid RMadrid Barça Sevilla Villa RSoc Grana Betis J 19 (x ) 48 40

y )

equip

J 19 (x )

Geta AthB Valen Eibar Valla Alav Elche Osasu Huesca

Ambaquestesdadesjaesveuendiferènciesdecomportamentnotablesentreelsequips.A lameitatdelcampionat,elscincprimerstenienplaçaperalaChampionsLeague,ielsisèiel setè,peral’EuropaLeague,perònohihaviaresdefinitiu.Quedavenmoltspuntsperdisputar. ElBetis,perexemple,podiaaspiraraanaral’EuropaLeague.

Alabandabaixa,tambétotpodiacanviar.DemomentestavenenriscElche,OsasunaiHuesca,peròtambéperillavenAlavés,Valladolid,Eibar,Valencia...Degutalesdiferènciesentreel rangdevariacióde x ielde y entotsdoscasos,l’escalaperala y seràdiferentdeladela x en elsdiagramescorresponentsinclososmésavall.

coeficientdecorrelaci´o:0, 85584

AMadrid

RMadrid

Barcelona

Sevilla

(x, y)

RSociedad

Granada Betis

Villarreal

rectaderegressi´o: y = 1,71818x + 9,41818

errorpercapitanormalitzat: ε∗ 0 = 0, 01249

Figura5.Diagramadedispersiódelsequipsambaspiracionseuropees.

Passemaraalapartanalítica.Hemestudiatenelsdoscasosladistribucióbidimensional x,y . Enprimerllocconsideremelgrupdelsequipsforts.Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór entreduesvariables,quesempreestàal’interval r´1,1s, donaaquí r “ 0,85584.Significaquehihamoltacorrelacióentre y i x .Ésadir,els resultatsdelasegonavoltaestan,engeneral,enconsonànciaambelsdelaprimera.

‚ El centredegravetat deladistribucióéselpunt px,y q“(34,75,69,13).

‚ La rectaderegressiódeysobrex dóna y “ 1,71818x ` 9,41818.Espotveurerepresentadaenelprimerdiagramadedispersió(figura5).

‚ L’errorquadràtic d’aquestarectaés “ 6,90909,l’errorquadràticpercapita dona 0 “ 0,86364demitjanaperacadaequipil’errornormalitzat és ˚ 0 “ 0,01249.Aquestúltim ésforçabaixencomparacióambexemplesprevis.

Passemalgrupd’equipsdèbils.Lafigura6donaelseudiagramadedispersió.

coeficientdecorrelaci´o:0, 97929

rectaderegressi´o: y = 1,95288x + 1,97502

Huesca

x:puntsparcialsJ19 y:puntsfinalsJ38

errorpercapitanormalitzat: ε∗ 0 = 0, 06148 (x, y) Getafe

Figura6.Diagramadedispersiódelsequipsenriscdedescens.

Elsresultatsaquísónelssegüents:

‚ El coeficientdecorrelaciór entrelesduesvariablesdonaaquí r “ 0,97929.Significaque encarahihaméscorrelacióentre y i x ,ésadir,engeneral,entreelsresultatsdelesdues voltes.

‚ El centredegravetat deladistribucióéselpunt px,y q“(18,33,37,78).

‚ La rectaderegressiódeysobrex dona y “ 1,95288x ` 1,97502.Espotveurerepresentadaenelsegondiagramadedispersió(figura6).

AthBilbao

Valencia

Eibar

Valladolid

Alav´es

Elche

Osasuna

‚ L’errorquadràtic d’aquestarectaés “ 20,90301,l’errorquadràticpercapita dona 0 “ 2,32256demitjanaperacadaequipil’errornormalitzat surt ˚ 0 “ 0,06148.Aquest últimtambéésbaixencomparacióambalgunsexemplesprevis(nopastots).

Comparemaraelsdosgrupsd’equips.El coeficientdecorrelació,curiosament,ésmésaltper alsequipsdèbils.Aixòpotserdegutque,engeneral,elsequipsfortstenenmotivacionsi plantillessuperiorsper«mantenirisuperarelritme»durantlasegonavolta,mentrequeals dèbilselspassamésaviatelcontrari.Totiaixí,elsdos centresdegravetat comparteixenla propietatquelasegonacomponent(mitjanadepuntuacionsfinals)éseldobledelaprimera (mitjanadelaprimeravolta).

Enrelacióambla rectaderegressió,cincequipsfortsestanpersobre,iaixòsignificaques’han esforçatmésalasegonavolta,mentrequeelsaltrestreshanperdutpistonada.Analitzats individualment,l’AtléticodeMadridnohafetgaireelsdeuresihaacabatcampiómoltjustet. RealMadrid,BarcelonaiSevillahanperseveratihanmantingutelseuordreparticular.Els quatres’hanclassificatperalaChampionsLeague.LaRealSociedadielBetistambéhan apretatis’hanclassificatperal’EuropaLeague,superantelVillarreal,ques’harelaxatperquè tenialaChampionsgarantidapernormadelaUEFA.ElGranadaéselquemenysesforçhafet ihaquedatdesbancatpelBetis.

Entreelsdèbils,siss’hanesforçatielsaltrestresno.AquestssónelGetafe,ques’havist superatperl’AthleticielValencia,isobretotelValladolidil’Eibar,quecauenaSegonaDivisió juntamentambl’Huesca,quehafetunesforçgranperòìnsuficientperquèveniademolt avall.Delsaltressis,abandadelsjacomentats,l’AlavéshaigualatelGetafe,mentrequeElche iOsasunahansortitdelpou.

Finalment,els errorsquadràtic i percapita delsequipsdèbilssóneltripledelscorresponents alsforts,mentrequel’errornormalitzat éssisvegadessuperior.Aixòindicaquemésdela meitatdelsequipsdèbilss’handesviatmoltdelarectaderegressió,mentrequeentreels fortsnoméselGranadahaquedatclaramentllunydelarecta.

Comacomentarifinal,destacalaregularitatil’estabilitatalapartaltadelataula(equips forts)ilamancad’aquestespropietatsalapartbaixa(equipsdèbils),ambelcanvi(dramàtic) delsdosequipsquealfinalacompanyenl’HuescaaSegonaDivisió.Hihatretscomuns,com araqueenelsdoscentresdegravetatlasegonacoordenadadoblalaprimera:aixòésbo peralsfortsidolentperalsdèbils,quehaurienhagutdemillorardurantlasegonavolta. Elcoeficientdecorrelacióésaltenambdóscasos,peròtésignificatpositiuperalsfortsi negatiuperalsdèbils.Elstreserrorsquadràticstambémostrenqueelsequipsfortshanestat mésconsistents,mentrequeelsdèbilss’allunyenmoltmés,alabaixa,d’uncomportament regular.

8.Exemple:qualificacionsacadèmiques

Al’EscolaSuperiord’EnginyeriesIndustrial,AeroespacialiAudiovisual,ubicadaenelCampus deTerrassadelaUPC,hihadosgrausd’Aeronàutica:elgrauenEnginyeriaenTècniques Aeroespacials(GRETA)ielgrauenEnginyeriaenVehiclesAeroespacials(GREVA).Tanten l’uncomenl’altrehihatresassignaturesdematemàtiquesenelsdosquadrimestresinicials:

ÀlgebraiCàlculIdurantelprimer(tardor)iCàlculIIdurantelsegon(primavera).Nohiha establertsprerequisitsentreelles.

L’objected’aquestestudiéslapossiblerelacióentrelesnotesfinalsdelestresassignatures. EnscentraremenelGREVAi,mésconcretament,enlesnotesobtingudespelsestudiants durantelsquadrimestresdelatardorde 2016idelaprimaverade 2017.Elsdosprofessors quevanimpartiraquestestresassignaturesteniencriterisdequalificaciósemblants.

Alesactesfinalsconsten62 estudiantsmatriculatstantd’ÀlgebracomdeCàlculI,quatredels qualsnoesvanpresentaraÀlgebraperòsíaCàlculI,mentrequedosd’aquestsquatreiun tercernosurtenal’actadeCàlculII,que,pertant,tenia59 matriculats.D’entrada,assignarem un 0 enunaassignaturaacadaestudiantnomatriculatonopresentat(d’araendavant,NP, genèricament).Siconvé,modificaremaquestcriteridurantl’estudi.

Enlaprimerapartdel’estudimiraremderelacionarlesassignaturesperparellesi.pertant, hihauràtresparts:Àlgebravs.CàlculI,Àlgebravs.CàlculII,iCàlculIvs.CàlculII.Enprincipi, alavistadelstrestemarisnoespotdirquel’ÀlgebraielCàlculItinguingairespuntsde contacte,peròsíqueelCàlculIIfaúsdetècniquesestudiadesal’Àlgebraisobretot,comés lògic,aCàlculI.Elsresultatsobtingutspelsestudiantsenspodendonarunaideadelaseva capacitat(grupal)d’assimilaciódecadamatèria.Enunasegonapartanalitzaremlapossible relació conjunta deCàlculIIambÀlgebraiCàlculI.

Passemaraalapartanalítica.Hemestudiatenelstresprimerscasosdistribucionsbidimensionals.

8.1.Àlgebra i Càlcul I

Enaquestcasestudiaremladistribucióbidimensional x,y ,on x representalesnotesd’Àlgebra i y lesdeCàlculI.D’entrada,comjahaquedatdit,seguiremelcriterid’assignarun 0 alsNP, queafectaràquatreestudiantsquenoesvanpresentaraÀlgebra.Encanvi,els62 matriculats esvanpresentartotsaCàlculI.Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór Pr´1,1s entrelesduesvariablesdonaaquí r “ 0,0020.Significaquenohihapràcticamentcapcorrelacióentre y i x .

‚ El centredegravetat deladistribucióéselpunt px,y q“(6,6387,5,7081).Semblaque l’ÀlgebraresultaunamicamésfàcilqueelCàlculI.

‚ La rectaderegressiódeysobrex dona y “ 0,0013x ` 5,6992.Espotveurerepresentada perunalíniafinaeneldiagramadedispersió(figura7);elcentredegravetatéselsituat mésal’esquerradelsdospuntsdestacatsperuncerclemésgran.Ésgairebéhoritzontal imoltpocrepresentativadeladistribució,comauguravaelvalorde r .

‚ L’errorquadràtic d’aquestarectaés “ 12,5948,l’errorquadràticpercapita dona 0 “ 0,2031 demitjanaperacadaestudiantil’errornormalitzat és ˚ 0 “ 0,0356.Aquestúltim ésrelativamentbaixencomparacióambaltresexemplesprevisonhemtractattemes diversos.

rectaderegressi´oambNP: y = 0,0013x + 5,6992

rectaderegressi´osenseNP: y = 0,5776x + 1, 6338

coeficientdecorrelaci´oambNP:0,0020

coeficientdecorrelaci´osenseNP:0,6434

errorpercapitanormalitzat ambNP: ε∗ 0 = 0, 0356

errorpercapitanormalitzat senseNP: ε∗ 0 = 0, 0251

x :notad’ ` Algebra

Figura7.Diagramadedispersiód’ÀlgebraiCàlculI.

Tanmateix,fixem nosenelsquatreNPd’Àlgebra.Elspuntsqueelsrepresenteneneldiagramaestanal’eix y .Perveurequinainfluènciatéhaver losassignatun 0,hemrepetitl’estudi eliminant losdeladistribucióbidimensional.Llavors,elnombrededadess’hareduïta58i elsresultatssónelssegüents:

‚ El coeficientdecorrelació passaaser r “ 0,6434,quejaindicaunacorrelacióméspositivaentre y i x .

‚ El centredegravetat deladistribucióésaraelpunt px,y q“(7,0966,5,7328),que,lògicament,s’hamogutcapaladretailleum entcapamuntperquèelsquatreexclosos tenienunanotamitjanade5,35deCàlculI.Lanotamitjanad’Àlgebraarribaaraal notable,mentrequeladeCàlculIpujamenysdetrescentèsimes.

‚ La rectaderegressiódeysobrex dona y “ 0,5776x ` 1,6338.Araésclaramentcreixent iforçaadequadaal’aspectedeldiagramadepunts.Espotveurerepresentadatambé enlafigura7ielseucentredegravetatésmoltpròximalainterseccióamblarecta anterior.

‚ L’errorquadràtic d’aquestarectaés “ 8,9367,l’errorquadràticpercapita dona 0 “ 0,1441 demitjanaperacadaestudiantil’errornormalitzat és ˚ 0 “ 0,0251.Totstressón menorsqueelsdel’anàlisianterior,il’últimésrelativamentbaixencomparacióamb altresexercicisprevisquehemdutatermesobretemesdiversos.

Laconclusiósemblaclara:assignar 0 alsNPdesvirtuafortamentladescripciónumèricadela distribucióbidimensionaldelspuntsrestants.Encomptesdedonarunaltrevalornumèricals NP,seràmésencertatexcloure’lsenelscasossegüents.

8.2.Àlgebra i Càlcul II

Enaquestcasestudiaremladistribucióbidimensional x,y ,on x representalesnotesd’Àlgebra i y lesdeCàlculII.Vistal’experiènciadelcas8.1,suprimiremelssisestudiantsquenoesvan presentaraÀlgebra,aCàlculIIoacapdelesdues.Quedaran,doncs,56estudiantspresentats alesduesassignatures.Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór Pr´1,1s entrelesduesvariablesdonaaquí r “ 0,6182.Novamentindicaindicaunacorrelaciólleugeramentpositivaentre y i x .

‚ El centredegravetat deladistribucióéselpunt px,y q“(7,196429,5,683929).Lamitjana deCàlculIIésunpèlmenorquela deCàlculItrobadaenelcas8.1.

‚ La rectaderegressiódeysobrex dona y “ 0,5679x ` 1,5971.Éssimilaraladelcas8.1 i espotveurerepresentadaeneldiagramadedispersió(figura8),igualqueelcentrede gravetat,indicatperuncerclemésgran.

‚ L’errorquadràtic d’aquestarectaés “ 8,8961,l’errorquadràticpercapita dona 0 “ 0,1435demitjanaperacadaestudiantil’errornormalitzat és ˚ 0 “ 0,0252.Totstressón moltsemblantsalsdelcas8.1,peròl’últimésrelativamentbaixencomparacióamb altresexercicisprevisquehemdutatermesobretemesdiversos. x :notad’ ` Algebra y :notadeC`alculII

rectaderegressi´o: y = 0,5679x + 1,5971

coeficientdecorrelaci´o:0,6182

errorpercapitanormalitzat ε∗ 0 = 0, 0252

Figura8.Diagramadedispersiód’ÀlgebraiCàlculII.

ComparemaquestsresultatsambelsdelcasanteriorsenseNP.Lesrelacionsentreassignaturessóndetipusdiferent:ÀlgebraiCàlculIsón paral leles,ésadir,s’imparteixensimultàniament,mentrequeÀlgebraiCàlculIIson seqüencials eneltemps,ambelqueaixòimplica.

Tanmateix,elsparàmetressónmoltsemblantsenelsdoscasos.Així,perexemple,elcoeficientdecorrelacióésmoltsimilar.Lamitjanaaritmèticadel’Àlgebrahapujatenelsegon casperquès’hanexclòsdosestudiantsmés,mentrequelesdelsdosCàlculssónidèntiques. Elpendentdelarectaderegressiótambéés gairebéelmateix,ielmateixpassaambels treserrors.Síqueéscertqueladistribuciódelspuntsenaquestcassemblaméscompactao acumuladaal’entorndelarectaderegressióqueenelprimercas.

Abansdeprocediral’estudicaspercasnoesperàvemtrobartantasimil¨litud.

8.3.Càlcul I i Càlcul II

Finalment,estudiaremladistribucióbidimensional x,y ,on x representalesnotesdeCàlculI i y lesdeCàlculII.SeguiremsuprimintelsestudiantsquenoesvanpresentaraCàlculII (tots62 esvanpresentaraCàlculI).Quedaran,doncs,59 estudiantspresentatsalesdues assignatures. x :notadeC`alculI y :notadeC`alculII 0 12 3 4567

10 rectaderegressi´o: y = 0,5319x + 2,6451

coeficientdecorrelaci´o:0, 5814

errorpercapitanormalitzat

ε∗ 0 = 0, 0268

Figura9.DiagramadedispersiódeCàlculIiCàlculII.

Novament,larelacióentrelesduesassignaturesés seqüencial,peròaprioricalesperarquela segonaestiguirelacionadamésestretamentambCàlculIquenopasambÀlgebra,simplementpelscontingutsdelsprogramesrespectius.Elsresultatssónelssegüents:

‚ El coeficientdecorrelaciór Pr´1,1s entrelesduesvariablesdonaaquí r “ 0,5814.Indicaunacorrelaciópositivadèbilentre y i x

‚ El centredegravetat deladistribucióéselpunt px,y q“(5,832203,5,747458).

‚ La rectaderegressiódeysobrex dona y “ 0,5319x ` 2,6451.Espotveurerepresentada eneldiagramadedispersió(figura 9),igualqueelcentredegravetat,marcatambun cerclededoblegruix.

‚ L’errorquadràtic d’aquestarectaés “ 9,0928,l’errorquadràticpercapita dona 0 “ 0,1541 demitjanaperacadaestudiantil’errornormalitzat és ˚ 0 “ 0,0268.

Comparemelsresultatsd’aquestcasambelsdelscasos8.1 (senseNP)i8.2.Lataula6recull elsparàmetres.

Taula6.Comparativad’assignatures.

cas correlació rectade centrede error error regressió gravetat quadràtic normalitzat r m px,y q ˚ 0

1 Avs.C1 0,6434 0,5776 (7,10,5,73) 8,9367 0,0251

2 Avs.C2 0,6182 0,5679 (7,20,5,68) 8,8961 0,0252

3C1 vs.C2 0,5814 0,5319 (5,83,5,75) 9,0928 0,0268

Contràriamentalqueespodriaesperarsegonselstemarisdelestresassignatures,lacorrelaciódonavalorspròximsperò,curiosament,decreixentsseguintl’ordredelscasos.Larectade regressiósempreéscreixent,peròcadavegadaambmenyspendent,ielmésbaixéseldeC1 vsC2.Lescoordenadesdelcentredegravetatpresentenpetitesdiferències,possiblement degudesalsdiferentsconjuntsdeNPexclososencadacas.

Entotcas,lamitjanadel’Àlgebra,quesuperael7,ésmoltsuperioralesdelsdosCàlculs,que esmantenenmésapropdel6quedel5.EnelsdiagramesesnotamésdispersióentreAiC1, imenysentreAiC2 ientreC1 iC2,quedonendiagramesmés«compactes»alvoltantdela rectaderegressió.Finalment,l’errorquadràticaquíéscomparableperquèlesdadesdeles sèriesestantotesal’interval r0,10s ilesquantitatsdedadessónhomologables:58,56i59, respectivament.Aquesterrorésunamicamésaltcomparantelscàlculsimésbaixcomparant AiC1 oAiC2.L’errornormalitzattambéaugmenta,gairebéduescentèsimes,encomparar elsdoscàlculs.

8.4.Càlcul II vs Àlgebra i Càlcul I

Aquíensproposemanalitzarlacorrelacióglobalo conjunta deCàlculII(variable Z )respecte alesaltresduesassignatures(variables X i Y ,respectivament).Caldràferúsdetècniquesuna micaméscomplicadesquegeneralitzenlesdelcasbidimensional,estudiatrepetidamenten lesseccionsprèvies.

Lamostraconstadels56estudiantsqueesvanpresentaralestresassignatures.Recordem queCàlculIIésseqüencialrespecteaÀlgebraiCàlculI.Elscàlculsestanfetsoptimitzantles aproximacionsielsresultatssónelssegüents:

‚ El coeficientdecorrelació(global) de Z respectea X i Y dona RZ pX,Y q“ 0,7508.Aquest coeficientsempreestàal’interval r0,1s

‚ El centredegravetat deladistribucióéselpunt pX,Y,Z q“(7,1964,5,7964,5,6839).

‚ El pladeregressiódeZsobreXiY dona:

Z 5,6839 “ 0,3753pX 7,1964q` 0,4206pY 5,7964q

o,enunaformaequivalent, Z “ 0,3753X ` 0,4206Y ` 0,5451.

‚ Elfetquelasumadelsvalors Z ˚ quedonalarectaderegressiócoincideixiamblasuma delsvalors Z delesdadesenssemblameramentanecdòtic.

‚ Evidentment,aquestplapassapelcentredegravetat.

‚ L’errorquadràticpercapita d’aquestplaés 0 Z pX,Y q“ 1,0798.

Comparantambelsresultatsdelsestudisbidimensionalsresumitsenlataula6alfinalde lasecció8.3,observemqueelcoeficientdecorrelacióglobalésnotablementmillorqueels trescoeficientsdecorrelacióbinària.Aquest ésunresultatesperat,jaquel’ajustamentmilloraenconsiderarduesvariablesindependentsencomptesd’unadesola.Lavariaciódels coeficientsderivadelfetque X i Y estanrelacionadesentreelles.Finalment,C1 téuncoeficientmésgranqueA,cosaquetambésemblaraonablevistoselsprogramesdelestres assignatures.Tambéobservemque X “ 10 i Y “ 10 donen Z “ 8,5041.

Figura10.PladeregressiódeCàlculIIrespecteaÀlgebraiCàlculI.

Lescoordenadesdelcentredegravetat G sónmoltsemblantsalesdelscentresdegravetat binaris;defet,cadascunad’ellesestàcompresaentrelesdelsdosbinariscorresponentsiles diferènciespodenserdegudesalespetitesvariacionsenelnombred’estudiantsdecada estudi.Segonsl’equaciódelpladeregressió, Z creixquanunadelesvariables X,Y creixil’altra romanconstantototesduescreixen.

Enaquestcastridimensional,nosemblaadequatdonarlarepresentaciógràficadels56punts, peròpodemvisualitzar,alafigura 10,elpladeregressióenunadobleimatgeinclusiva. Finalment,l’errorpercapitanoéscomparableambelsbidimensionalsperquènoesdefineix comells;tanmateix,prenent ?56 0 Z pX,Y q =7,4833,obtenimunparàmetrehomologableque resultaforçamenorquetotselscorresponentserrorsquadràticsbidimensionals.Resumint, l’estuditridimensionalsemblaunboncomplementdelstresestudisbidimensionals.

9.Exemple:temperaturadexafogor

La temperaturadexafogor ésunconceptequepreténmesurarquantitativamentla«sensaciótèrmica»queexperimentaelcoshumàacausadelacombinaciódelatemperatura ambiental(temperaturadel’aire)ilahumitatrelativa.Laprimeranotíciasobreaquestaidea lavapopularitzar,almenysaCatalunya,AlfredRodríguezPicóaTV3,onvaexercircoma meteoròlegdesdel 1984finsal 2002.

Enl’actualitat,elsquedescriueneltempssolenparlardela(temperaturade) xafogor quan mereixuncomentariperquèésforçaméselevadaquelatemperaturaambiental.Defet,el concepte,degutaR.G.Steadman,vanéixercapal 1979.NoméscalanaralaViquipèdia,per exemple,perobtenirunainformaciómésdetallada.Enparticular,homhitrobaunafórmula (quehaestatrelativamentcriticada)querelacionalatemperaturadexafogorentermesdela temperaturaambientalilapressiódelvapord’aiguadel’atmosfera.

L’objectedelnostreestudinofareferènciaaaquestafórmula.Unatauladedadespublicada el 2017awww.marenostrum.org/meteorologia/xafogordonava 291 valorssimultanisdela temperaturaambiental,lahumitatrelativailatemperaturadexafogor -suposemquecalculadaamblafórmulaesmentadamésamunt -,amblaparticularitatdedividirlagraellaen cincblocsdediferentstonalitats(vegeulafigura 11).5

Hemvolgutcompararlacorrelaciódelaxafogorrespectealesaltresduesvariablesencada undelsblocs,numeratsdel’1 al4dedaltabaix,jaquehemreduïtelsdosúltimsaunde solperquèconsideremelcinquèunamicamarginal.Ésadir,analitzaremcadabloccom unadistribuciótridimensionalonlesvariablessón: X =temperaturaambiental, Y =humitat relativai Z =temperaturadexafogor.Obtindremelsparàmetresbàsicsdecadadistribuciói elsconfrontarem.ElwebdeMareNostrumassignalesinterpretacionssegüentsalscolors: 1 =perillextrem; 2 =perill;3=precaució;4=límitdeconfort;5=conforttèrmic.

5.Aras’hipottrobarunataulaactualitzadal’1 degenerde 2023queésidènticaalapresentadaaquí.

Figura11.Dadesempíriquessobretemperatura,humitatixafogor.Taulaextretade www.marenostrum.org/meteorologia/xafogor. Elsresultatsdelsparàmetress’hanarrodonitaunnombresuficientdedecimals.Elshem reunitenlataula7perpodercomparar loscòmodament.

Taula7.Comparativadexafogorperblocs. xafogor bloc 1 bloc 2 bloc3 blocs4i5 significat perillextrem perill precaució confort dades

Elscomentarissónelssegüents:

‚ Enelsquatreblocselscoeficients a,b sónpositius.Aixòvoldirque,segonselplade regressió,qualsevolincrementdelatemperaturaambienti/odelahumitatrelativa provocaunaugmentdelaxafogor,iésmoltmésacusadalainfluènciadelatemperaturaambientaljaque a ąą b.Tanmateix,aquestdobleefectedecreixalllargdels quatreblocs,demaneraqueésenelblocmarginalonésmenysrellevant.

‚ Elcoeficient c faunafunciódecorrecció.Envalorabsolutdecreix,iarribaadesaparèixerenelquartbloc.

‚ L’errorpercapitaésbaixsegonselrangdelaxafogor(r22,58s)inovariagairellevatdel segonbloc,onésmoltmésaltqueenelsaltrestres(aproximadamententreun42 %i un54%superior).

‚ Elcoeficientdecorrelaciótambéésforçaaltentotselscasos,sobretotenelsegoniel tercerbloc.Aixòfapensarqueelprimerblocielquartnosóntanrepresentatiusdela distribucióglobal.

‚ Elscentresdegravetatapareixen,encadabloc,entrelesdadesdelbloc,coméslògic,decreixenenlescoordenades X i Z itenenuncomportamentmésirregularala coordenada Y .

‚ Ésprobablequeelpladeregressiótotal,ésa dir,considerantconjuntamenttotesles dadesdeladistribució,siguiunamixturadelsquatreplansperblocs.Nohemconsideratnecessaricalcular lo.

10.Conclusions

Unavegadaanalitzatstotselsexemples,semblainteressantremarcarlavarietatd’àmbitsals qualsfanreferènciaicompararelsprincipalsresultatsobtinguts.Hihaunexempledejocindividual(sudoku),dosdesignificateconòmic(referitsaunamateixafarmàcia),undededicat alalligadePrimeraDivisióenduesfases(equipsfortsiequipsdèbils),unaltresobrequalificacionsacadèmiquesdividitenquatreparts,i unúltimsobreunconceptemeteorològic,la temperaturadexafogor,tambédesdoblatenquatreblocs.

Elsprimersquedendefinitsperdistribucionsbidimensionals,mentrequeelsdosúltims l’estudi detresassignaturessimultàniamentielsquatrecasosdexafogor corresponenadistribucionstridimensionals.Totssónexemplesdecasosconcretsi,pertant,ambresultatsen principinoextrapolables,peròsemblaclarquelametodologiaempradaentotselscasosés perfectamentaplicableaqualsevolaltrecasambdadesnumèriquesdiferentsi,sobretot,a situacionsqueespuguinmodelarentermesanàlegs.

Esposaenrelleu,doncs,unareflexiósobrecoml’úsd’unaeinad’implementaciósenzilla permetunaprimeraanàlisiquepotsermoltrellevantperdescriuresituacionseconòmiques, empresarials,educatives,etc.;endefinitiva,delasocietatactual.

Lataula8permetcopsarambuncopd’ulllainformacióprincipalobtingudaencadaexemple:elnombrededades;elcoeficientdecorrelació,queesmesurademaneradiferentenel casbidimensional(r )ieneltridimensional(R),coms’indicaenlataula(vegeulesseccions

3.1.1 i3.1.3);elpendentdelarectaderegressióenelcasbidimensional -ideaquenos’estén alcastridimensionalperquèpassematenirunpladeregressió -;i,finalment,elsdiversos tipusd’error -tresenelcasbidimensional,nomésdosenl’altre. 6 Elparàmetre ˚0 enels casostridimensionalsesdefineix,peranalogiaambelcasbidimensional,dividint 0 per Z , perpodercomparartotselserrorsnormalitzats.Elresultatésquetotsaquestserrors,llevat d’un,sóninferiorsa 0,1.Il’únicaexcepciónoarribaa 0,2

Taula8.Comparativadetotselsexemplesestudiats.

Ésdestacablelavarietatdelnombrededades.Tambéladelcoeficientdecorrelació,que donaunvalornegatiuiunaltrepròxima 0 alcostatdevalorsmoltpròximsa 1.Quelcom similarespotdirdelpendentdelarectaderegressió.Pelquefaalserrors,l’errorquadràtic delsdosexemplesdecaireeconòmicéselevatperquèsónelevadeslesquantitatsquedefineixenlasèrie y deladistribució.Peraixòhemintroduïtl’errorpercapita,quepermetfer comparacionsindependentmentdelnombrededades.Iencaramésl’errornormalitzat,que apareixal’últimacolumnaidonaunresultatquepermetcomparartotselsexemples.

Agraïments

VolemagrairlarevisiódutaatermeperMariannaBosch,queambelsseuscomentarisencertatsenshaajudatamilloraraquesttreball.Itambélarevisiólingüísticadutaatermeperdos correctorsanònimsquehanmilloratforçalapresentació.

6.L’asteriscdelsisètemaindicaquel’estudiestàfetassignantlaqualificació 0 atotselsnopresentats, criteriqueesdescartaenelstrescasossegüents.Comespotveure,lacorrelaciócreixmoltenprescindird’aquest criteri.

Bibliografiacomentada

Lesreferènciesquedonemsónunamica suigeneris.Aquestarticlenoésdelsque,devegades mésaviatmarginalment,connectenambmoltstreballsprevis,propisod’altresautors,com éshabitualenelsdedicatsala«internalitat».Esbasaennocionsd’estadísticaforçaconegudesiestudiasituacionsnoconsideradessovintenlaliteraturacientífica.

[1]EspecialSudokusnº 235(2021).Madrid:EdicionesPléyades.Peralesmateixesseccions.

[2]Jarne,G.;Pérez Grosso,I.;Minguillón,E.(1997). Matemáticasparalaeconomía.Madrid: MacGraw Hill.Perajudaracaptarelrerefonsdelnostreenfocament.

[3]Legendre,A.M.(1786).«MémoiresurlamanièrededistinguerlesMaximadesMinima dansleCalculdesVariations». MémoiresinHistoiredel’AcadémieRoyaledesSciences, pàg.7.Peralasecció3.TotiquesemblaqueGaussvaserelprimeradescobrirel mètodedelsmínimsquadrats,Legendrevaserelprimerquevapublicar lo.

[4]Legendre,A.M.(1819).«Méthodedesmoindrescarréspourtrouverlemilieuleplus probableentrelesrésultatsdedifférentesobservations». Mémoiresprésentéspardivers Savantsàlal’AcadémiedesSciencesdel’InstitutdeFrance,pàgs. 149 154.Novapresentaciódavantd’unauditoridiferent.

[5]McGuire,G.;Tugemann,B.;Civario,G.(2014).«ThereisNo 16 Cluesudoku:Solvingthe sudokuminimumnumberofcluesproblemviahittingssetenumeration». Experimental Mathematics 23(2),pàgs. 190 217.Peralesseccions 2 i4.

[6]Peña,D.;Romo,J.(1997). IntroducciónalaEstadísticaparalasCienciasSociales.Madrid: McGraw Hill.Peralcontingutdelasecció3.

[7]Spiegel,M.R.(1969). Estadística.Madrid:McGraw Hill.Unclàssicenelqueenshem basatalasecció3.

[8]Steadman,R.G.(1979).«TheassessmentofSultriness.PartI:Atemperature humidity indexbasedonhumanphysiologyandclothingscience». JournalofAppliedMeteorology 18(7),pàgs.861 873.Peralasecció 9.

[9]Steadman,R.G.(1979).«TheassessmentofSultriness.PartII:Effectofwind,extraradiationandbarometricpressureonapparenttemperature». JournalofAppliedMeteorology 18(7),pàgs.874 885.Peralasecció 9.Continuaciódel’articleanterior.

[10]Viquipèdia,onespodentrobarmoltstutorialssobreelstemesconcretsd’estadística empratsaquí.Peralasecció3.

[11]www.rfef.es.WebdelaRealFederaciónEspañoladeFútbol,onespodentrobarels resultatsilesclassificacionsdelaLligadePrimeraDivisió 2020 2021.Peralasecció7.

[12]mwww.marenostrum.org/meteorologia/xafogor(2017).Webonvaaparèixerlataula delafigura 11.Actualitzadaambdata 1 degenerde 2023.Peralasecció 9.

MatesalCarrer, matemàtiquesperatothom

LuisCrosLombarte

Professordesecundàriaal’EscolaPiadeSarriàde

CoordinadordelgrupSET,grupdejocsdeAssociació

Barcelonaperal’estudiil’aprenentatge delesMatemàtiques(ABEAM)

Resum Abstract

Moltesvegadessentimadir«profe de mates?...»,«...buf,quinpal»,«...amise’m donenmoltmalamentles mates,josocde lletres»,«...jolesodio,emfeienpatirmolta l’escola»,«profe,aixòperaquèserveix?»iun llargseguitdefrasessensesentitquemostren quelesmatemàtiquessónunapedraala sabatademoltagent.Quèpodemferper capgiraraquestsentiment?Enaquestarticle explicaremunapropostaqueportemals carrersdelnostreterritoriambl’objectiu d’aconseguirmostrarlesmatemàtiquesdes delseuvessantméslúdic,entretingut,divertit iproper,senseperdreelseurigorperajudara canviarelsprejudicissocialsfortamentarrelats enlanostrasocietatactualencontradeles matemàtiques.

1.Amorirebuig

Nowadaysitisnotunusualtohearsometough statementssuchasthese:«amathsteacher?...», «suchabore,man!»,aswellas«sorry,teacher,I willneverbegoodatmaths,Iamabookworm, anyway»,oreven,«dude,Idefinitelyhatemaths, theyweresuchanightmare,backatschool», and,ofcourse,«teacher,whatismathsfor, anyway?».Suchaninfamousdiscourseconfirms thatMathematicsisperceivedbymanyasbeing atruethornintheside.Theaimofthispaperisto proposeanewwaytolookatMathematics.We intendtodemonstratethatitcanbesuchan interestingfieldofinterestforeveryone.Also, theycandefinitelybequiteafunplayground.Let ushopethatthiswilleffectivelycontributeto gettingridoftheseprejudicesagainst Mathematicswhichseemtohavebeensodeeply rootedinoursocietyforsomanyyears.

Larelacióamblesmatemàtiquesésd’amoroderebuig,nohihatermemitjà.Aquestrebuig estàassociatamalesexperiènciesenèpoquesescolars.JahoescriviaClaudiAlsinaenel pròlegdelseullibre Elclubdelahipotenusa:

Undelssecretsmillorguardatsdelaculturaactualéselcaràcterprofundamentdivertitdelesmatemàtiques.Peraaconseguirqueaquestsecretnosurtialallumpública s’hanarticulattotamenad’estratègiesescolarsisocials.Abasedepissarresinintel¨ligibles, explicacionsexòtiques,suspensosabundantsillibresrigorososs’haaconseguitquela poblacióengeneral,llunydedescobrirelsecret,arribiacreuretotelcontrari.Finsalpunt quenoméslapresènciadelaparaula«matemàtica»provocajareaccionscontundents.

Desdefatemps,unreduït onotant grupd’amantsdelesmatemàtiquesenshemdecidit acanviaraquestatendènciaiaconseguirque aquestestigmaesredueixi.Noesperemque tothomestimilesmatemàtiques,però síqueelstinguiunamicad’estima.

Elqueesrecullenaquestarticleésunaaccióque hemfet,ianiremrepetintpelnostreterritori,permostrarelcaràcterdivertitientretingutdelesmatemàtiques,sobretotalespersones totalmentallunyadesd’elles.

2.D’onsorgeixaquestainiciativa?

Ambl’èxitdelainiciativadelDiaEscolardelesMatemàtiques,activitattotalmentarrelada alsnostrescentreseducatius,l’any 2020 se’nvacelebrarlavintenaedició.Veientquealvoltantdelesmatemàtiqueshihaunsentimentde repulsaacceptatperlasocietaticoneixent l’enormequantitatd’activitatsdivulgatives queesfanatotEspanya,laFederaciónEspañola deSociedadesdeProfesoresdeMatemáticas(FESPM)volimpulsarunaactivitatdedivulgació matemàticasemblantalDiaEscolardelesMatemàtiquesperòdirigidaatotalasocietat. L’objectiuprincipald’aquestaactivitatésmostrarlacaraamabledelesmatemàtiques,laque ensvaenamorariensfaseguir-neenamoratsencaraavuidia,perpoderanareliminantel prejudiciqueestéenverslesmatemàtiques.

Elmesdefebrerde 2019 laFESPMvaconvocarungrupdeprofessionalsdediferentssocietatsd’arreud’Espanyaquefemactivitatsalcarrerofiresdeciènciesidematemàtiquesper compartirlesnostresexperiènciesisaberquinshauriendeserelsrequisitsd’unbonMatesal Carrer.

DesprésdeduesjornadesdecompartirexperiènciesvamconclourequefaremMatesalCarrerquanapropemlesmatemàtiquesatothomforadelcontextescolardesd’unpuntde vistalúdic,divulgatiu,oferintactivitatsadaptadesadiferentsnivells.Estractademostrar lesmatemàtiquesgaudintambelles,ambentusiasme.Espodenoferirideesmatemàtiques complexesd’unaformanaturalial’abastdetothom.

Comdiuelseunom,ésunaactivitatqueesportaràatermealcarrer,enunllocperonpugui passejarlagent,comunaplaçaounpasseig,perpodertrobar-nosamblagentquenoaniria abuscarlesmatemàtiques,sinóqueselestrobaràis’emportaràunasorpresapositiva.

MatesalCarrerésunapropostaquedesenvoluparan,independentmentacadaterritori,personesdemaneravoluntàriasotaelparaiguad’unasocietatmatemàticadelmateixterritori, amblacol¨laboraciód’entitats,ambl’únicincentiudeferdivulgació.Entenentelcaràcter particulardecadaterritori,l’organitzaciódecadaMatesalCarrerconcretaràlesactivitats queespodenfer,totselsplantejamentssónvàlids.Unabonaideaéscrearmaterialsamb unaltcontingutdivulgatiu,presentatsentaulesaccessiblesdemaneraqueelsvisitantsels puguintocarihipuguinjugar.Espottenirencomptelapossibilitatqueelsvisitantsespuguinemportaracasaalgunacosafetaperellsmateixos.Lesactivitatsquefuncionenprou béambaquestformatsón:poliedrescreatsamb llaminaduresoambescuradentsiplastilina, enigmes,solitarisijocsd’estratègia,puzlestopològics,tangrams,jocsnumèrics,papiroflèxia (aquestestaulesaccessibless’hanfetservirenactivitatsmultitudinàriesalcarreraMadrid, Cornellà,laCorunya...).Al’horadedissenyarl’activitatcaltenirencomptel’espai,elnombre

devoluntarisieltempsdequèesdisposarà,peradequar-hielnombredetaules.Unaquantitatmoltgrandetaulesangoixaelvisitant,quevolveure-hototinotétemps.Siesdisposa d’espaiivoluntaris,éspreferiblerepetirlesmateixesactivitatsendiferentstaules.Afiqueels voluntarisdelestaulesnoesvegindesbordatsperlaquantitatdegentquepuguiestarala sevataula,ésimportanttenircartellsexplicatiusamblesinstruccionsdelesactivitatsclares, totique,semprequeespugui,éspreferiblequeelsvoluntarisacompanyinelsvisitantsa l’horadeferlesactivitats.Elscartellshandeportarellogotipdelasocietatquefadeparaigua. Tambécaldissenyartaulesaccessibles,perexemple,perinvidents.

Siestélapossibilitat,ésmoltbonaideaintroduiralguntipusd’espectaclequeespuguifer endiferentsmomentsdelajornada:espectaclesdemàgia,monòlegs,lecturaderelatsopoemes,passeigsmatemàtics...Perquèaquestapropostapuguidur-seatermecaldràdisposar d’unbonequipdeso.

PelquefaaladatadelMatesalCarrer,s’hadeferencapdesetmana.Ésmésfàcilperorganitzar-ho ambvoluntarisiperarribaratotelpúblic.D’altrabanda,ésmillorenhoraridematí,sipot serapartirdelesdeu,perquèabansnohihagent.Iallargar-lototeldiaimplicadisposar demoltsvoluntarisperfertorns.Comes faambelDiaEscolardelesMatemàtiques 12 de maig ,caldriafer-loelmateixdiaoelmateixcapdesetmanaperdonar-himésnotorietat aescalaglobal.Elcursacadèmic 2018-2019 esvaproposarcomadatael7d’abriloeldia mésaproppossible.Peralscursosvinentscaldràconcretarunadataentretoteslessocietats d’Espanyaperquènocoincideixiambaltresesdeveniments.

ComanexeentretotselsMatemáticasenlaCalle,toteslessocietatshandeferunamateixaactivitat:construirunmosaicdemaneracol laborativaentretotselsvisitants.Elcurs acadèmic 2018-2019 labasedelmosaicvaserl’osNazari.CadacurslaFESPMfaarribarals presidentsdelessocietatsdecadaterritorilaplantillaperduratermeelmosaicielpenjaràa lasevaweb.

Caldeixarclaralesinstitucions,quanespresentil’activitatperdemanarl’ocupaciódel’espai públic,queaixònoésunaactivitatd’ociitempslliure;ésculturasotaelguiatgedeprofessionalsdel’ensenyament,ambmaterialsdissenyatsperal’esdevenimentambunafinalitat didàcticaiatractiva,portadaatermeperuns«monitors»deluxe:totselsvoluntarisestan directamentrelacionatsambl’ensenyamentil’aprenentatgedelesmatemàtiques.

3.Quèproposemalnostreterritori?

LapropostaqueesvarecolliralajornadaorganitzadaperlaFESPMesvacompartiralnostre territoridurantlajornadadel’ABEAMdel’any 2019 ialC2 EMdel 2020.EntrelesduescomunicacionsvamformarungrupdetreballperposarenmarxaelprojectedeferunMatemáticas enlaCalleaCatalunya,sotaelparaiguadelaFederaciód’Entitatsperal’Ensenyamentdeles MatemàtiquesaCatalunya(FEEMCAT).

Desprésd’unesquantesreunionsidellargsdebatsvamacabarconcloentqueelnostreMatemáticasenlaCalleesdiràMatesalCarreritindràlescaracterístiquessegüents:

1.Esfaràelsmesosdesetembreooctubre,quepermetenferactivitatsalcarrersense patirlesinclemènciesmeteorològiques. Ésunmomentdelcursacadèmicenquètenim lesbateriesd’energiacompletamentcarregadesinohihagairesactivitatsmatemàtiquesalnostreterritori.

2.Seràunaactivitatitinerant.L’objectiud’aquestadecisióésferpartíciplagentdediferentspartsdelterritorianyrereany.

3.Esconvidaràelscentreseducatius,associacionsientitatsdelalocalitataparticiparde maneraactivaenl’organitzacióilarealitzaciódelajornada.

4.L’idealseriaqueunadelesactivitatsquees facidurantelMatesalCarrersiguiunpasseigmatemàticperlalocalitat.L’objectiud’aquestpasseigéspodermostrardiferents llocsdelalocalitatambullsmatemàtics.PerdeixarempremtaallloconesfacielMates alCarrer,lapassejadaquedaràregistradaalprojecteMathCityMapperquèespugui seguirfentunavegadahagiacabatlajornada.

5.Elpuntd’inicidelpasseigmatemàticseràellloconestrobielgruixdelesactivitatsde lajornada:taulesdivulgatives,jocsgegants,exposicions...

QuanvandissenyarlesactivitatsdelprimerMatesalCarrervamdecidirqueeramillorque elsparticipantsestiguessinalazonaifinalmentvanferelpasseigdinsdelaplaçaonesfeia elMatesalCarrer.Totiqueespotferpertotalalocalitat,recomanemqueesfacialmateix lloconesfaelgruixd’activitats.

SiobservemdesdeladistàncialesreflexionsfinalsqueesvanelaborarenelC2 EM 2020,podremveurequeambaquestaactivitatesdonarespostaadosdelsreptesquevamproposar peraaquestquadrienni:

Repte7:«Treballarempercanviarpreconceptessocialsarrelats,com«lesmatemàtiquessóndifícils»o«aixòperaquèserveix?»,peraltrescom«tothomserveix perlesmatemàtiques»o«lesmatemàtiquesensajudenainterpretarelmón».

Repte8:«Promouremactivitatsparticipativesonelsilesdocents,elsilesalumnesilessevesfamíliespuguingaudirplegatsd’experiènciesmatemàtiquespositives(fires,activitatsdecarrer,visites,concursos,jocs,tertúlies,etc.)».

Lapandèmiadecovid-19 del 2020 ilessevesrestriccionsposteriorsvanfrenarlanostrail lusió deportaratermeelnostreMatesalCarrer.Elsetembrede 2022 vamrebrelanotíciaque esdonavenperfinalitzadeslesrestriccionsper duratermeactivitatsmassivesal’airelliurei vamdecidirfer-loaquellmateixmesd’octubreaMataró,unaapostaarriscadaperòqueva sortirmoltbé.

4.ElnostreMatesalCarrer

Lapandèmiadecovid-19 vaaturarelsnostresdesitjosdeportaratermeelnostreMatesal Carrerl’any 2020.Vamestartreballantenlíniaperconsolidarungruporganitzador,divulgar elprojecteitenirlafeinafetaenelmomentqueespoguésfer.Totaixòensvapermetre organitzarlaprimeraedicióaMataróelmesd’octubrede 2022

Perdur-loatermevamconstituirungruporganitzadorformatpelsmembresdelgrupde treballquehemanatdesenvolupantlapropostaiperagentslocals,fonamentalsperferla propostadelamillormanerapossible,jaqueconeixenlesmillorsubicacions,elscontactes ilesdatesidònies.EnricCastells,LluísMoraiToniGomàvanserclauperaconseguirquela jornadaesdevinguésunèxittotal.

Mitjançantlesassociacionsdematemàtiquesdelterritoriesvaferunacridaalsseussocis perpresentarlesactivitatsdelajornada.Vamrebrelespropostesil’oferimentpercol laborar deSílviaMargelí,JuanDiego,RobertEscribano,JoanMiralles,JoanFolguera,JoanCarles Berroca,PolSan,MónicaCasasiTereLongueira.

Lajornadavaaplegarcatorzepropostestemàtiques:

1.Mosaic

2.Calculadora

3.CúpulesLeonardo

4.Màgianumèrica

5.Reptesmatemàtics

6.Nonaga

7.Speedcups

8.Microrobots

9.Bombollesdesabó

10.Primilògic-Kaprekar

11.Papiroflèxia

12.Estimacions

13.MaquetemMataró

14.Divermazo

1.Mosaic:portatalapràcticaperTutiComalatiJoanCarlesBerrocal,enaquestaproposta elsvisitantsagafavenlarajolatípicadeMataró,lapintavenil’enganxavenenunmuralper formarlesparaules«MATARÓMATEMÀTICA».

Totiquenoesvapodercompletarl’objectiu,valorempositivamentl’activitatperquètothom, gransipetits,esvaengrescaris’hovapassarmoltbé.

2.Calculadora:portadaalapràcticaperTutiComalatiJoanCarlesBerrocal,enaquestapropostatothomquepassavas’animavaaresoldreunsenigmesperendevinarnombresfent operacionsamblacalculadora.

Creiemqueanavadirigitaunpúblicmésgrande deuanys,eramassacomplicatperalspetits; perlaqualcosacreiemqueestariabébuscaralgunsenigmesperaells.

3.CúpulesLeonardodelMuseudeMatemàtiquesdeCatalunya(MMACA):portadesalapràcticaperJuanDiegoGarcia,alllargdelmatíesvaanaratenentelpúblicinteressatiesvan construirdiferentscúpulessenseparar.L’activitatvaagradarmolt.

4.Màgianumèrica:portadaalapràcticaperPuraFornalsiRobertEscribano,esvanpresentar diferentsjocsdemàgianumèricaise’nvaexplicarelperquè.Lataulavaestarplenaconstantmentperquès’hivaaproparmoltagent,tantjovescomadults.Peralspetitsesvafertambé unaserpdepapiroflèxia.

5.Reptesmatemàtics:portatsalapràcticaperJoanMirallesiJoanFolguera,esvanpresentardiferentsreptesdesobretaulaquevantenirmoltbonaacollida,sobretotlespecesper aconseguirfiguressimètriques.

Elsreptesdesobretaulaperalspetitsvancostarunamicamés,elscaliauncopdemà.Elque esvaposaraterraperfer«construccionsestables»(gossosdecolorsfetsambcubs)vaanar moltbéperalsméspetits.

6.Nonaga:portatalapràcticaperJuditRodríguez,TereLongueiraiPolSan,vaserunjocmolt dinàmic.Novaparard’entrargentajugarienalgunsmomentsfinsitothihaviagentesperant,totihaver-hidosjocsigualsdecostat.Lamajoriadelsparticipantserennensd’entre deuiquinzeanys,peròmoltsrepetieniavegadesdemanavenferequipambalgúperpoder jugarinohaver-sed’esperar.Amés,algunespersonesvandemanavaelnomdeljocion podiencomprar-lo.

7.SpeedCups:portatalapràcticaperMartaFarrés,quivadisposartresjocsdecubsgegants. Hivaparticiparmoltagentapartirdelaprimerahoradelajornada.Esvaferuntotaldevuitantapartidesdedeuminuts.Alguninfantva jugarmésd’unavegadaienalgunespartides elsparesjugavenielsnensmiraven.Vaserunajornadamoltdivertida.Comapropostade milloraespodriapensaraversionarlesnormesperadiferentsedats.

8.MicroRobots:portatalapràcticaperMonicaCasas,ésunjocdetaulaenversiógegantde 3m ˆ 3m.Vahaver-higentgairebétotal’estona.Elsnensjugavenambmoltentusiasme, peròelsméspetitsnoméspodienllançarelsdaus,noésunjocperapetits.

9.Bombollesdesabó:portadesalapràcticaperSílviaMargelíiEnricCastellà,esvanfera travésdeduesactivitats:

Volumsambaiguaacolorida:esvanferdiferentsexperimentsqueespodentrobara http://ja.cat/volums.

Propietatsambbombollesdesabó:basada enlaxerradad’AntonAubanell.Hihaun reculldelqueesvaferahttps://ja.cat/BKjXv.

10.Primilògic-Kaprekar:portatalapràcticaperCarlesMasjuanambelsmaterialsquevam fetserviracangur.org/festa-matmat.Larespostadelpúblicvasermoltbona.Potseraquesta activitateramés«depensar»queenaltrestaulesi,pertant,anavaadreçadaaparticipants mésgrans,cosaquevafrenarunamicalaparticipació.

11.Papiroflèxia:portadaalapràcticaperEstefaníaHernández,qui,ambeltítol«Quinesmatemàtiquesamagaunocelletdepaper?»,vapresentarlesdiferentsmaneresdeferunocellde paper.Totiaixò,l’objectiuprincipalnoeraelplegatensi,nilainterpretaciódelsdiagrames peraconseguirfer-lo,sinótoteslessorpresesmatemàtiquesques’amaguendurantidesprés delprocésdeplegat.Estreballenlaresoluciódeproblemes,elfetdefer-sepreguntes,el raonament,contingutsdeproporció,àrees,perímetres...

12.Estimacions:portadaalapràcticaperBernatAncochea,enaquestaactivitatesdemanava estimariconfirmardiferentsmesures.Exemples:midesdelaplaça,alçàriad’unedifici,angle queformaunaparet,capacitatdelscilindresquedelimitenunapartdelaplaça,nombre dequadratsquehihaalafinestradeferro...S’entregavaunfullambtoteslespropostes d’estimació,queespodentrobarahttps://ja.cat/zmnDl.

13.MaquetemMataró:portadaalapràcticaperRoserGarcíaiBertaMas,enaquestaactivitat grupdetreballdeprofessorsd’institutsdelaciutatvaproposartreballardesdelesescoles deMatarólesmatemàtiquesvinculadesal’exposiciódelamaquetadelaciutat,creadaper alumnesmajoritàriamentdesegond’ESO,quefatresanysqueesduuaterme.Enlajornada esvanpresentaralgunesactivitatsjafetessobrequèveiemalplànolquenoveiem insitu i alrevés;perexemple,sobresiéselmateixcórrervintmetrespelpasseigMarítimqueperla Riera,esmostravasobreunplànolunafletxadelamateixamidasobreunllocisobrel’altre, aixípodíemcomentareltemadelatopografiadelaciutat;tambévamvisualitzarrotondes quetenenunaltrecarrerfetdemaneraconcèntricaipreguntàvemcomhodevienconstruir, visualitzàvemrotondesno«rodones»ihiposàvemnomsibuscàvemcarrerscompletament paral¨lelsentreells...

Tambévamproposarunaactivitatdecreaciód’hiperboloides,quevaserunèxitivaferque acabéssimelmaterialunahoraabansdefinalitzarlajornada.

14.Divermazo:portatalapràcticaperLuisCros,ésunjocdetaula,peròalajornadaesvaemprarpermostrarlahistòriadelesmatemàtiques.Apartirdelsconeixementsdelsassistents sobrepersonatgesil¨lustresd’aquestaciènciaesfaunrecorregutpercuriositatsmatemàtiquesperpoderparlard’onsurtenelsconeixementsqueutilitzemiaprenemavuiendia. Entreelstemesquevamtractarhihalaimportànciadelesdoneseneldesenvolupamentde lesmatemàtiques.

Alataulavahaver-higenttotal’estona,detoteslesfrangesd’edat.Peralsnensméspetits ésunataulapocatractiva,peròexposadaambcurapotarribaraagradar-losiatransmetre’ls unamicadeconeixementsperaquantrobinalgunsdelspersonatgesal’aula.

Lajornadavaserunèxitrotund,jaquevanparticipar-hialvoltantdedues-centespersones. Peranimarajugar-hiesdonavaalagentunatargetaabansdepassarperlesdiferentstaules iquanpassavenpercadaactivitatse’lsposavaungomet.Siaconseguiendeugomets,que voliadirquehavienparticipatendeuactivitats,podienlliurarlatargetaiparticiparenel sorteigd’unescúpulesdeLeonardodesobretaula.

Tambévaserunèxitperlaubicació,alaplaçadel’Ajuntament,unllocdepasperarribar alagentquenotérelacióambl’educacióniamblesmatemàtiques.Aquestéselprincipal objectiudelMatesalCarrer:portarlesmatemàtiquesatothom.

ComapropostesdemilloraentomemlaqueensvaferarribarIsabelCabot,capdelDepartamentdeMatemàtiquesdel’escolaSalesiansMataró:proposaralsalumnesmésgrans(a partirdetercerd’ESO)delesescolesdelalocalitat,presentaralgunataula.Aixòelsimplicaen lajornadaielsconvidaaapropar-sealsseuscompanys,amicsifamiliars.Apartird’aquesta experiènciavasorgirlaideaquel’alumnatdetercerd’ESOpreparésunafirad’aquestescaracterístiquesalasevaescoladirigidaalciclesuperiordeprimàriaiaprimerisegond’ESO.

Perpartsevatambévamrebreunesparaulesquevamescoltardemoltagentelmateixdiaen acabarlajornada:«Lesactivitatsilafiraensvaagradarmoltienssemblaunaideafantàstica. Moltesgràciespertotalafeinadail’organització».

ElgruporganitzadorvolemdonarlesgràciesalComitèLocal,l’EscoladeMúsica,laBiblioteca Municipal,l’Ajuntament,atotselsvoluntarisialaFEEMCAT:senseelseusuportilaseva col laboraciólajornadanohauriasigutpossible.

5.Iaraquè?

QuantinguisaquestarevistaalesmansestarempreparantlaterceraediciódelMatesal Carrer,ladeBalaguerel 2024.Etconvidemaportarunataulad’activitatiaformarpartde l’equipd’organitzacióodelcomitèlocaldepreparaciód’aquestaedicióodelesproperes. Tambétenimpactadalaquartaedició,quefaremaLleidalaprimaverade 2025.

Paral¨lelamentaaquestaviaquehemcomençataCatalunya,s’hareobertlapropostadela FESPMd’aconseguirferunMatemáticasenlaCalledesdetoteslesfederacionselmateixdia. Tambéel 28d’octubrevamparticiparenunseminarinacionalperveurequèespotfer.Us mantindreminformatsdetotmitjançantlesvostresassociacionsilesjornadesqueanemfent alnostreterritori.

Esperemqueaquestarticleserveixiperdonaraconèixerelprojecteiconvidarellectora divulgar-loiasumar-s’hi.Elsorganitzadorsdel«Matesalcarrer»som:CarmeAymerich,Bernat Ancochea,TutiComalat,LuisCros,MartaFarrés,RoserGarcía,PuraFornals,CarlesMasjuan, JuditRodríguez,GlòriaSáncheziRamónTejedor.

6.Referències

[1]Alsina,C.(2008). Elclubdelahipotenusa. Barcelona:Planeta. [2] MathCityMap. 2019.https://mathcitymap.eu/es/. [3] Reptesc2em2020-2024. 2021.https://c2em.feemcat.org/reptes-c2em-2020-2024/.

Normes per a la presentació de contribucions

1. La revista NouBiaix acceptaper alasevapublicació contribucions originalsrelacionadesamb experiències didàctiques, activitats d’ensenyamen ti aprenentatge,escrits d’opinió,dedivulgaci ói d’investigació en el camp de la matemàtica ielseu ensenyamentenqualsevol nivell educatiu

2. Les contribucions rebudesseran avaluadesprèviamentper dosespecialistes reconeguts. La decisiópresa pelConsell de redacciósobre l’acceptació de la publicació serà notificada directamentals autors ambuna indicaci ódeladataaproximadadepublicaci ói el possiblerequeriment d’introduir modificacionseneltext.

3. Pera la presentaci ódetreballs originals, elsautorstrametran al’adreçanoubiaix@gmail.com un arxiu, en Word oenLaTeX.Els gràfics, elsdiagrames iles figureshaurandeser originals(no fotocopiats). Els arxius gràficsespresentaran en format epso tif.

4. La contribució hauràd’incorpora reltítol,elnom de l’autoro autors,lasevaadreçapostalprofessional completai la seva adreça electròn ica. S’adjuntaràunresum no més llarg de 300 paraules en català ianglès. Al finaldel document s’inclourà obligatòriamen tlabibliografiaper ordrealfabètic de cognoms,d’acordamb la normativaAPA, com en elsexemplessegüents:

Articles

Albertí, M. (2002).Les matemàtiques desd’una perspectivacultural: Etnomatemàtiques Biaix, 20, 6-25.

Llibres

Godino,J., Font,V.(2003) Razonamiento algebraico paramaestros.Granada :Universidad de Granada. Capítols de llibres

Edo, M.,Revelles, S. (2004).Situaciones matemática spotencialmentesignificativas. Dins M. Antóni B. Moll (ed.), Educación Infantil. Orientacionesy Recursos (0-6 años) (p. 410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales, M.,Font, V.,Planas, N. (2004).Estudio microetnográfico en tornoa un conocimiento matemático situado. Dins A. Franzé ialtres(ed.), ActasdelaI ReuniónCientíficaInternacional sobreEtnografía y Educación (CD-ROM).València: Germanía,Polis Paideia.

Pàginesweb

Geogebra pera Infantil iPrimària. https://www.geogebra.org/m/tkdC27m f

5. Els contingutsde NouBiaix estansubjectes llevatque s’indiquiel contrarieneltext, en lesfotografies oenaltresil.lustracions— auna llicència de Reconeixement-No comercial-Sense obra derivada 3.0deCreativeCommons,eltext complet de la qual es pot consultar ahttp://creativecommons.org/ licenses/by-nc-nd/3.0/es/deed.ca. Així,doncs,s’autoritza el públic en generala reproduir, distribuir i comunicar l’obra,sempreque es reconegui l’autoriai l’entita tque la publica, inose’nfaciunús comercial ni se’n difongui capobraderivada.

6. Elsarticlesespublicara nen llengua catalana.Només es traduiranalcatalàles contribucions acceptadesd’autorsnoresidents alsPaïsosCatalans.

7. Elsautorsesresponsabilitzarandel complimen tdeles normes establertesper al’autoritzaciódela reproducciódematerialprocedent d’altres fontsbibliogràfiques

8. Elsarticlestindran unaextensiómàximade 8000 paraules,inclosesles notesa peudepàgina, però s’accepten articles méscurts,d’entre 2000 i 4000 paraules

9. Femnotar queenaquesta publicació s’utilitza preferentmen telpuntper separardecimals, en lloc de la comarecomanadaper l’IEC, pertal de facilitarla comprensi ódeles expressionsmatemàtiques.