Nou Biaix, 51

Revista de la FEEMCAT i de la SCM

bia x uno i

número 51

Consell de redacció:

Noemí Ruiz / Carlos Giménez (coords.)

Montserrat Alsina

Joan Carles Ferrer

Joan Miralles

Manuel Udina

© dels articles, els seus autors

Coediten:

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P- IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM ) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com

,

sumari

Nombre dexemplars: 1.700 ’

Fotografia de la coberta:

Il·lusió de salt finit

Oriol Bote Vila

Vedruna Vall (Terrassa) al Periodicitat: semestr

ISSN : 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Edicions

de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona Tel.: 934 035 430 comercial.edicions@ub.edu www.edicions.ub.edu

Editorial 1 4 19 32 41 52 66

Del tot al no -res: divulgant el pensament borrós a partir d’una exposició al Museu de Matemàtiques

QueraltViladevall

Ángel Alsina

Joan Carles Ferrer Comalat

Algemat: àlgebra amb materials

AnnaVilaró Utrillo

Connexió entre el 2D i el 3D... amb GeoGebra!

Bernat Ancochea Millet

Guillem Bonet Carb ó

Viatge interplanetari: aprendre matemàtiques amb l’univers com a escenar i

Roser Matas Nadal

Xavier Sánchez Carrasco

Marc Faüchs Xifra

La pastisseria, la guerra de les galàxies i les matemàtiques

Jordi Arnau i Ballestar

Les construccions geomètriques euclidianes. La papiroflèxia i les matemàtiques cartesianes articles

Josep Pla Carrera

Delssisarticlesbasatsenexperiènciespersonalsquerecopilemenaquestnúmero51 del NouBiaix,n’hihatresquecorresponenadocentsdesecundàriaquedebutenenelmónde lespublicacions,iquepresentenpropostes que,prèviament,hantreballatambl’alumnat respectiu.

Volemagrairl’esforçqueelshacomportataquestrepteianimematothomacompartirexperiènciesquepuguinserinspiradores,iqueproposinunareflexiórigorosasobrelesmatemàtiques.Tambévolemdemanardisculpesalsautorsdelprimerarticlepelretardenlaprevisió inicialdepublicació,degutal’endarrerimentquevaafectarelnúmero50.

Elprimerarticle,«Deltotalno-res»,deQueraltViladevall,ÀngelAlsinaiJoanCarlesFerrer, mostraquealgunsconceptes quecalintroduiraedatsprimerenquessónlabaseperdesenvoluparnocionsmatemàtiquescomplexesenunfuturnogairellunyà:laclusterització,la ideaderegressiólogística,lalògicade«noAnoimplicaelcontrari»,etc.L’exposiciód’exemples escomplementaambunaclarajustificaciómatemàtica.Finalment,amésdel’agradablelecturaqueconvidaalareflexió,calposarenvalorelsmagníficsdibuixosd’unadelesautores perlaforçacomunicativaquedesprenen.

Enelsegonarticle,titulat«Algemat:àlgebraambmaterials»iescritperAnnaVilaró,creadora delmaterial,lectorsilectoresdescobriranl’origend’aquestprojectetanpersonalilesseves característiquesprincipals(peces,tauler...).L’articleplantejaunesquantesidees,peròheude saberquesitafanegeualapàginawebwww.annahelpme.comtindreuadisposicióunmón mésextens.Esperemqueelconeixementd’Algemat,unmaterialambautoriacatalana,pugui serunabonaajudaal’horadetreballarlestècniquesalgebraiquesque,jaensecundària, comportenunesforçd’abstraccióquedevegadeselsestudiantstrobendifícildefer.

Eltercerarticle,titulat«Connexióentreel 2Diel3D...ambGeoGebra!»,haestatescritper BernatAncocheaiGuillemBonet,benconegutspelsseguidorsdelprogramaridegeometria dinàmicaGeoGebra.Atravésdelasevaexperiènciamostrenunapropostaquepermetcompletaractivitatsquesesolendesenvoluparaprimàriaisecundàriasobrelaconstrucció3D defiguresambcartolina.Arabé,elmètoded’indagacióquefadefilconductordel’article,la

maneracomesvandesenvolupantlespreguntes,elfetdemirarlescosesdeldretidelrevés, tambépotinspirarelslectorsenunametodologiapercrearpropostespròpies.Finalment, coméscaracterísticdelacomunitatGeoGebra,elcodiéslliureial’abastdetothom.

Elquartarticle,escritperRoserMatas,XavierSáncheziMarcFaüchs,ensdescriuambtot detalleldissenyilaimplementacióal’aulad’unasituaciód’aprenentatgedel’àmbitSTEAM ambelsseusalumnesdeprimerd’ESOd’uncentred’altacomplexitat.Aquestaactivitatés plenamentreplicable:qualsevolequipdeprofessorsmotivatlapotplantejarsivolpromoure unússignificatiudelesmatemàtiquesenunentornSTEAM,potenciantlacol¨laboraciótant dedocentsdediferentsàmbitscomdelsalumnesmateixos,unobjectiuquenosempreés fàcilassolir.

Enelcinquèarticle,JordiArnauensmostracomespotabordareltemadelamodelització matemàticaambtotelrigornecessariipartintd’objectesbenconegutspelsalumnes,com arael«dònut»ilamíticaEstrelladelamortdelasagade Laguerradelesgalàxies.Propostes comaquestahandeservir,sensdubte,peraquèeltreballdelamodelitzaciómatemàtica, inclosademaneraexplícitaenelnoucurrículumdelesmatemàtiquesdebatxillerat,comenci aservistacomunobjectiual’abastdequalsevoldocentialhoracomunafontdemotivació peralsalumnesenplantejar-losreptesbasatsenl’anàlisid’objectesqueelssónmoltpropers.

Finalment,l’últimarticle,titulat«Lesconstruccionsgeomètriqueseuclidianesilapapiroflèxia:unafusiómatemàtica»,ésuntextcaptivadorescritperJosepPlaCarreraqueexplorala connexióentrelesmatemàtiquesclàssiquesil’artdelapapiroflèxia.L’autorensintrodueix ales«construccionsgeomètriqueseuclidianes»iles«matemàtiquescartesianes»,ihidetalla lestècniquesqueesbasenenelregleielcompàs,icomhanestablertelpuntdepartidaper trobarlasoluciódemoltsdelsproblemesgeomètricsclàssics.

Ellectordescobriràqueaquesteseinesfonamentals,queesremuntenal’escoladePlatói els«Elements»d’Euclides,són,encaraara,bàsicsenlaresoluciódeproblemesgeomètrics actuals.Amés,l’obraposademanifestquelapapiroflèxia,aparentmentsimple,amagaestructuresmatemàtiquessorprenents.Aquesttextésunainvitacióaexplorarlabellesadela matemàticaiafer-laaccessibleiinteressanttantaexpertscomapersonesqueexpressen curiositatenaquestsentit.

Voldríemquegaudíssiudetotselsarticlesiesperemqueusfacinaprendre,opotserreaprendre,aspectesrelacionatsambaquestmóndelesmatemàtiques,presentarreuitan extens.

articles articles

Deltotalno-res:divulgantel pensamentborrósapartir d’unaexposicióalMuseude Matemàtiques

QueraltViladevall

EstudiantdeldoctoratenEducaciódelaUdG iprofessoradeMultimèdiaalaUOC qviladevall@uoc.edu

ÁngelAlsina

FormadordemestresicatedràticdeDidàctica delesMatemàtiquesalaUniversitatdeGirona angel.alsina@udg.edu

JoanCarlesFerrerComalat

ProfessordeMatemàtiquesdelaUdGi màsterenDidàcticadelesMatemàtiques joancarles.ferrer@udg.edu

Resum Abstract

Aquestarticlepresentaelsresultatsde l’aprenentatgenoformalgeneratsenuna exposicióalMuseudeMatemàtiquesde Catalunya(MMACA)alvoltantdels principalsquantificadorsielpensament borrós.S’infereixquelesexposicionsde contingutmatemàticfomentenaquest tipusd’aprenentatgematemàtic,ipertant, se’ndesprènlaimportànciadepoder comptarambespaisquepromoguin activitatsd’aquestamena,comarael MuseudeMatemàtiques.

Thispaperpresentsthenon-formallearning generatedbyanexhibitionattheMuseumof MathematicsofCatalonia.Thetopicwasthe relationshipbetweenquantifiersandfuzzy thinking.Itisinferredthatexhibitionsof mathematicalcontentencouragethistype ofmathematicallearning,andthereforethat itisimportanttohaveplacesthatpromote thistypeofactivity,suchastheMuseumof Mathematics.

1.Introducció

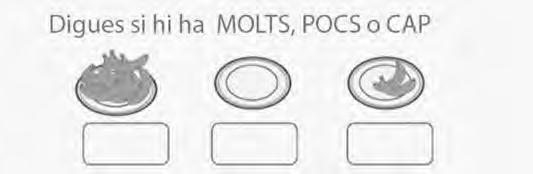
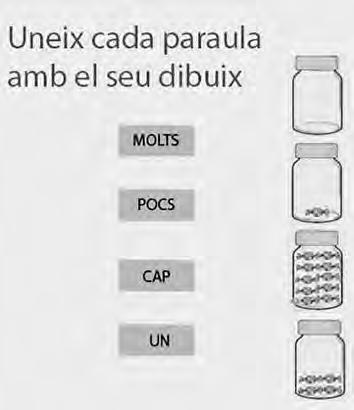
Elpoc,moltores(ocap)sónquantificadorsques’utilitzenperdesignarquantitatsindefinides relacionadesamblanumeració,elsqualspodenserintroduïtsal’escoladesd’edatsprimerenques(Canals, 1992).Peraquestmotiu,nose’nshadeferestranytrobartasquesapartir derecursosgràfics(fitxesclàssiques)comlesdelesfigures 1, 2 i3,quepermetentreballarel significatd’aquestsquantificadorsal’aula.

Figura1.Tascad’encerclarlasolució.

Figura2.Tascad’introduirtextencaselles.

Figura3.Tascad’unirambfletxes.

Tanmateix,enelsquadernsillibresdetextdematemàtiquesd’infantiloprimàriadifícilment esproposentasquessimilarspertreballarels poc, bastant o gens relacionatsamblaideade graduaciód’unaqualitat,totiqueCanals(1992)exposaqueapartirdelscincanyselsmenors tenenlacapacitatbendesenvolupadad’ordenarelementsd’unconjuntsegonslaparcialitat delapropietatqueeldefineix.Addicionalment,caltenirpresenttambéqueelscurrículums oficialsactualsd’infantiliprimària(MEFP, 2022a;MEFP, 2022b)dediquenescassaatencióa lagraduacióiescontinuencentrantadesenvoluparelpensamentsegonslalògicabinària ilateoriadeconjuntsclàssica.Enunfuturproper,gràciesenbonamesuraal’impulsdel movimentsocialdesexenobinari(Wilchins, 2007;Wilchins etal., 2020),aquestatendència podriacanviar,ihopodriaferseguintlapropostad’acceptarnovesideesgenèriques(Vendrell, 2009),delamàdelateoriadelsconjuntsborrosos(Zadeh, 1965),queacceptaqueels elementsd’unconjunthipodenpertànyerparcialment.

Considerantaquestsantecedents,lafinalitatdel’articleéspresentarianalitzarunaexposició temporalalMuseudeMatemàtiquesdeCatalunya(MMACA)quepreténdivulgarelsconjunts borrososcomunconeixementrellevantquedemicaenmicas’had’anarintroduintenel currículumdematemàtiquessiesvoltrencarlavisióbinàriadelarealitat.Així,enlaprimera partesfonamententeòricamentelsconjuntsborrosos;enlasegonaespresentenlesobres del’exposiciótemporal Deltotalno-res;i,finalment,enlatercera,s’exposenelsresultats esperatsielsnoesperatsapartird’aquestaexposició.

2.Elsconjuntsborrosos

Formalment,elsconjuntsborrososesrepresentenmatemàticamentambunaexpressióque identificacadaelementdel’universambelgraudepertinençaalconjunt.

Quans’acceptalaparcialitat depertinença,elsnombres μA pxi q podenservalorsrealsentre 0 i 1.Elbarreten A identificaelsvalors μA pxi q comapossiblesnombresentre 0 i 1,totsdos inclosos.

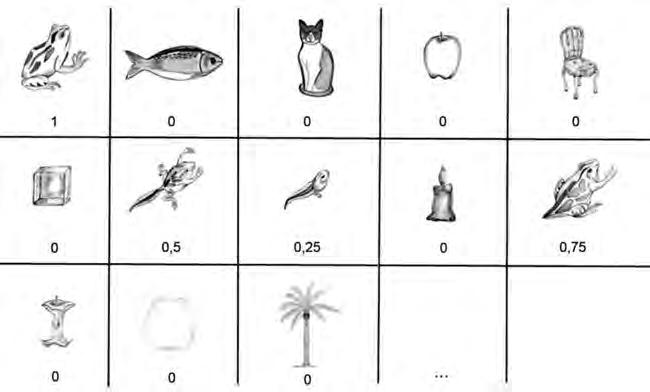
Enlafigura4esrepresentavisualmentunconjuntborrós.Apartird’unaselecciód’imatges delconjuntunivers,els xi delconjunt,esfixaperacadascund’aquestselementsungrau deveritatdelpredicat«sergranota»iquerepresentariaelsnombres μA pxi q definitsanteriorment.

Amésdel’estudidecomtrobarunpossiblegraudeveritatperacadaelement,hihamoltíssimsaltrestemesd’estudirelacionatsambaquestateoria,comperexemplelesmúltiples alternativesquese’nspresentenquanestractadedefinirelcomplementari,launióilaintersecciódeconjuntsborrosos.LesméshabitualssolenserlesdefinidesperZadeh(1965):

Tenintencompteaquestsantecedents,jas’hainiciatundebatenàmbitseducatiussobrela introducciódelsconjuntsborrososilasevateoriaassociadaenelcurrículumformal(Blanco etal., 2016;TrillasiGarcía-Honrado, 2019;Viladevall etal., 2023a).

Lanostraaportacióenaquestdebat,fruitdelesinvestigacionsenelmarcd’unatesidoctoral encurs,éslad’introduiralesprimeresetapeseducativeseltemadelgraudepertinençaconjuntamentambelsadverbisdequantitat,ésadir, elsquantificadors.Aquestaideapermetria, perexemple,nohaverdetreballarambnombresentre 0 i 1 oentrecapescalahomomòrficatipus 0 a 100.Lapropostaéscoherentambelfetqueenlainvestigacióambteoriade conjuntsborrososéspermèsqueenexperimentsdedeterminaciódegrauss’utilitzintermeslingüísticsperestablirelsvalorsnumèricsdelsgraus(KaufmanniAluja, 1988;Alsina,C.i Trillas, 1991).

Sobreaquestapossibletransformaciócurricular,demomentelquejaespotafirmarésque,a mesuraqueelnencreix,elseuraonamentlògictraspassaelbinarismeicomençaapercebre queéselgris,inoelblancoelnegre,elquepotsermésajustatquanestractadedescriure moltesdelessituacionsquel’envolten.Tambésabemque,ambunsanysmés,elmenor arribaatenirprouconeixementsperaplicardelamaneracorrectatotdetermesdegraduació qualitativaamultituddesituacionsquotidianes.Aleshores,enspreguntem:dequinamanera elsnensadquireixenaquestaprenentatge?

Baroody(1987)explicaqueelsinfantscomencenaconstruiraquestconeixementenunentorninformal,noescolar,apartirdelesinteraccionsambelmedifísicisocial,onespresenten escenariscomelsjocs,elscontesolesexposicions,elsqualsgenerenaprenentatgesd’una maneranaturaliespontània.AutorscomAlsina,À(2015),Alsina,À. etal. (2023),Geist(2014) oClementsiSarama(2015),entred’altres,hanexplicitataquestsconeixementsemergents denaturalesaintuïtivaiinformal.

L’experiènciaquepresentemmostrauncasparticulard’aprenentatgenoformalofertenun contextd’exposicióalMuseudeMatemàtiquesdeCatalunya.

Figura4.Elconjuntborrós Sergranota.

3.L’exposiciótemporal Deltotalno-res

L’exposiciótemporal Deltotalno-res esvaoriginarapartirdelapropostadelaUnitatde MatemàtiquesdelaUniversitatdeGirona.Aquestaexposicióvaseranunciadaenelweb delaSetmanadelaCiència 2021 iseguialaideadepopularitzarelpensamentborrós,tal coms’haviafetenlesexposicions FuzzyArt,exhibidaenelMuseudelaCiènciaCosmoCaixa (Viladevall, 2018)i L’increïbleenginydelsanimals (Viladevall, 2020),quehaestatexposadaen diversesbibliotequespúbliquesmunicipals.

AlsjardinsdelaqueactualmentéslaseuprincipaldelMMACA(Imatge 1)esvanmostrardeu obresdecreaciópròpiaperpartdelaprimeraautoradel’article(QueraltViladevall),lesquals tenienperobjectiumostrardeusituacionsquotidianesonespassavadeltotalno-res.

Elcartelldel’exposicióqueacompanyavalesobres(figura5)presentavaunaampliacióde l’obra Glaçons,fetaamblafinalitatqueelvisitantpoguéscopsarquelesobresespodien ampliarambmoltsméselementsintermedis.

Figura5.Cartelldel’exposició.

Imatge1.Obresdel’exposició.

Lainauguraciódel’exposicióesvaacompanyarambuntallerdecreaciód’unzoòtrop.Més d’uncentenardepersoneshivanparticipar.Enunatiradepaper,caliadibuixarelsdiversosestadisd’unullobrint-seitancant-se,decorarl’exteriordelzoòtropienganxar-neles parts,queacabavenformantaquestajoguina òpticainventadaperWilliamGeorgeHorner (imatge 2).

Latiradelzoòtrop(figura6)eraunprimerexemplequepermetiareflexionarsobreelconceptedegraduació,jaqueconteniaunaseqüènciad’unullobrint-seitancant-se,ipermetia tambétreballarcomexpressarambparaulesl’evoluciódelprocés:ullnoobert,ullunamica obert,ullmésobertquel’anterior,ullgairebéobertdeltotoullcompletamentobert.

Figura6.Seqüènciad’unullobrint-seitancant-se.

Enl’àmbitcientífic,cadascunadelesobresteniarelacióambelpensamentborrós,elqual permetdeixardepensarentermesdeveritatofalsedatabsolutesiclassificarlessituacions enunaescalaqualitativadegrausentrelesduespossibilitats.

Imatge2.Eltaller.

Enlavidarealtrobemmultituddesituacionsquesónmoltdifícilsoimpossiblesdeclassificar enunconjunt,comperexempledistribuirunconjuntdefruitesengrupsdemaduresono madures;classificartotselsmomentsdelapostadesolendiaonit;o,finsitot,classificarels instantsd’existènciad’unésserconsiderant-loviuomort.

Iésque,enunscontextosdeterminats,espotacceptarquelescosespodenseralmateix tempsenuncertgrauinoserenunaltregrau.L’exposiciópreteniaserunpetitreculld’aquestes situacionsambl’objectiusubjacentdeferreflexionarelvisitantsobreelsproblemesque ocasionavoler-hoclassificartotbinàriament.

Acontinuació,espresentendetalladamentcadascunadelesdeusituacionsilesobresactuals dissenyadesespecíficamentperil¨lustrar-les.Ambelles,ésfàcilintroduirenunpúblicadult lesideespresentsalssupòsitsdelateoriadeconjuntsborrosos,comaralanoexistènciade laparadoxasorites(situacions3.3.i3.4)olasubjectivitatdeladeterminaciódelsvalorsdel graudepertinençaalconjunt.

Prèviament,caldirqueavuidiaienalgunsàmbitsesconsideraqueunaexposició,mésque explicar,hadedespertarpreguntesenelvisitant(Wagensberg, 2000).Aquestaideaésla queensvaguiarapresentaralvisitantlesduesprimeresobresabansd’entrarenexplicacions decaràctermatemàtic.

Esperàvemqueelvisitant,ambaquestesdosprimersexemplesdesituacionsrealsmoltconegudesperatothom,hitornéstardod’horaperpreguntar-sequinarelaciótenienambla restadel’exposició.

3.1.Primera situació.Capgròs

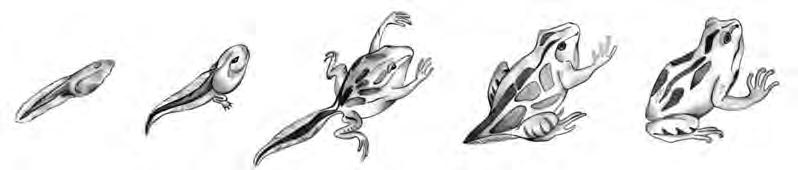
Enlafigura7espodenobservardiferentsestatsdelametamorfosidecapgròsagranota:les cincsituacionspresents,d’esquerraadreta,espodenetiquetarcomacapgròs,capgròsamb duespotes,capgròsambcosdegranotaogranotaambcuallarga,granotaambcuacurtai granota.

3.2.Segona situació.Glaçons

Figura8.Obra Glaçons,deQueraltViladevall.

Figura7.Obra Capgròs,deQueraltViladevall.

L’obra Glaçons (figura8)mostraeldesglaçd’unscubsdegelperfectes.Jaenlasegonaimatge,s’observaquelescaresilesaresteshanperdutunamicalaforma,iamesuraquel’aigua delsglaçonspassadesòlidaalíquidaladeformacióvaamésimés.

Elpasdesòlidalíquidésunasegonasituacióicònicaconegudapergransipetitsdesde sempre.Nohisolemreflexionar,peròenlessituacionsintermèdieshihaunapartsòlidaiuna partlíquidaalavegada.Pertant,tenimunsegonbonexempledecontextrealenelqualés acceptableafirmarambpensamentborrósquelescosespodenserinoserenuncertgrau.

3.3.Tercera

Aquestaobrateniaperobjectiupresentarformalmentelqueesconeixcomaparadoxasoritesoparadoxadelmunt.

Lapreguntaqueaquestaparadoxaplantejaéslasegüent:enquinmomentunmuntde sorradeixadeserunmuntquanentraiemgranets?(figura 9)Sitenimunmuntdesorraien traiemungranet,seguiremtenintunmunt.Aixòsemblainqüestionable.Pertant,unmunt desorramenysungranetéstambéunmuntdesorra.Elproblemasorgeixenpensarque aixòéscontradictoriambelfetquesianemtraientungranetdarrerel’altretardod’horaens quedaremambnomésunodosgranets,iningúconsiderariaqueunodosgranetsformen unmuntdesorra.

Enpensamentbinari,onlessituacionsnomésespodenclassificarcomaveritatomentida, s’esperaquesiespassadeveritatamentidademaneraseguida,enalgunmoments’ha depassardementidaaveritat.Aleshores,tésentitintentartrobarlarespostaaquinésel momentexacteenquèesdeixadetenirunmunt.

Laparadoxasoritesapareixenmoltessituacionsonhihaunadisminuciógraduald’unobjecte.Perexemple,siensanemmenjantunapomaapocapoc,enquinmomentdeixemde poderconsiderarqueésunapoma?

situació.Del munt al no munt

Figura9.Obra Delmuntalnomunt,deQueraltViladevall.

3.4.Quarta situació.De la poma a la no poma

Figura10.Obra Delapomaalanopoma,deQueraltViladevall.

ElmatemàticBartKoskovaserelprimeracomentar,enelseullibre Pensamentborrós (Kosko, 1995),queenaquestpensament,elqualacceptaqueelgraudepertinençad’unobjectea unconjuntpotserunvalorentreel 0 %iel 100 %,noesprodueixaquestaparadoxaatèsque simplements’acceptaqueacadamossegadatenimmenyspoma,peròquesempreespot veurecomapomaenungrauoenunaltre.

L’obradelafigura 10 corresponaunavisualitzaciód’aquestaidea:enlaprimeraimatgetenim pomaal 100 %;enlasegona,aproximadamental 95%;enlatercera,al60 %;enlaquarta, al35%;enlapenúltima,al8%;enladarreraal’1 %;isiensmengéssimtambélesllavorsi lacuatindríempomaal 0 %.Koskodedueixqueenacceptarelgraudepertinençaentreun 100 %finsaun 0 %semprepodemdirquetenimpoma,encaraquesiguienmoltpocgrau oenungrauigualazero.Aleshores,sisempretenimpoma,notésentitqueenspreguntem quandeixemdetenir-ne.

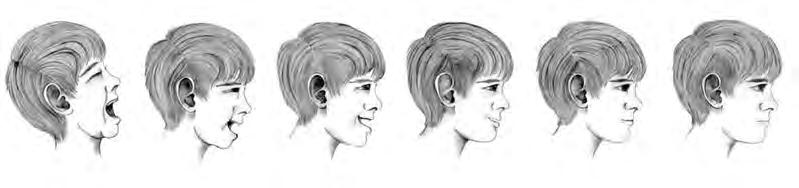
L’obradelafigura 11 preténmostrarquehihamultituddesituacionsqueespodengraduar entreel 100 %iel 0 %;enaquestcas,hemtriatl’alegria.Amés,preteniaobrirlareflexióque noestaralegrenoimplicahaverd’estarenfadat.

Elproblemadeconfondrelanegaciódelesafirmacionsamblesafirmacionscontradictòries (Linares etal., 2018)produeixerrors,comperexempleal’horadeconstruircorrectamentles escalesdeLikert,quesónunesescalesdequalificaciópergraduarelgraud’acordodesacord ambalguntemaoalgunacaracterística(Viladevall etal., 2023b).

Caltenirpresentque,atravésdelsgestosdelacaraidelcos,transmetemunagranquantitat d’informacióquemostralesemocionsquesentim.Defet,enl’ésserhumàpodemidentificar setemocionsbàsiquesqueestransmetenatravésdel’expressiófacial:l’alegria,latristesa,la por,l’enuig,elfàstic,elmenyspreuilasorpresa,sentimentsmoltsubjectiusipersonals.

Elriureéslamanifestacióexternahumanadel’emociód’alegria.Escomponbàsicamentd’una expressiófacialacompanyadad’unsodiscontinu.Sinohihaso,esparladesomriure.Lasevaexpressiómàximaesconeixcomagranriallada.

Somriure,riureogranrialladaexpressen,doncs,diferentsgrausd’intensitatdelmateixestat emocional.Elsomriuresuposaelgrauméslleu,ésd’àmbitméslocal,isolmanifestarmés sovintemocionsdesatisfaccióibonsdesitjos.Elriure,adiferènciadelsomriure,tévolum sonor,éspúblicinotori,ipotimplicartotelcos.Defet,encatalàienmoltsaltresidiomes,la

3.5.Cinquena situació.Alegria

Figura11.Obra Alegria,deQueraltViladevall.

paraulasomriurevedeson- iriure,onson- ésunprefixqueprovédelaformallatina sub-, quesignifica«persota»,iquemostralagraduaciódel’emoció.

3.6.Sisena situació.Plenitud

L’obraqueesmostraenlafigura 12,abandaquesegueixpresentantexemplesquotidians onespassadeltotalresgradualment,preteniaplantejarelques’anomenavaguetatdeles paraulesique,acausad’aquestavaguetat,potesdevenircomplicatdecidirenquinmoment assignemel 100 %oel 0 %aunasituaciói,pertant,caladmetreunacertaarbitrarietaten aquestaassignació.

Quandemanemqueensomplinungotd’aigua, normalmentnoesperemqueensl’omplin comalaprimeradelesimatges.Defet,jaconsideremelgotpleenunasituaciócomlaque mostralasegonaimatge.

Delamateixamanera,enlapenúltimaodarreraimatgeespodriaconsiderarqueelgotés buit,malgratqueencarahiquediunculd’aigua.

3.7.Setena

Enaquestaobra(figura 13),ambunapossiblegraduaciódel 100 %al 0 %,esreflexionatambé sobrel’úsdelesparaules.

Quandiemqueunapersonaésvella,notenimunaedatexactaalcap,perònohihadubte queunapersonad’aspectecomladelaprimeraimatgeespotconsiderarvella.Siestema propdels50 consideraremquelasegonadelesimatgesrepresentaunapersonaproperaala vellesaperòqueencaraconservajoventut.Ara bé,desdelpuntdevistad’unapersonajove de 15anys,totselsquepassende40 o50 jasónvells.

Així,aquestaobramostraquepersonesdiferentspodentenirpercentatgesd’acceptaciódiferentsi,pertant,presentalaideaquel’assignaciódelagraduaciópotserunaassignació subjectivarelacionadaambelmónrealqueensenvolta.

Figura12.Obra Plenitud,deQueraltViladevall.

situació.Vellesa

Figura13.Obra Vellesa,deQueraltViladevall.

3.8.Vuitena situació.Vent fort

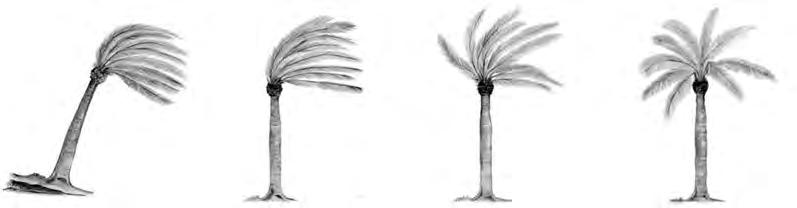
L’obraqueesmostraenlafigura 14serveixperintroduirlaclassificaciódesituacionssegons l’expressió«faunventfort».Científicament,segonsl’escaladelaforçadelvent,esconsidera ventfortelquebufaamésde39 km/h,velocitatenlaqualjatenimproblemespermantenir unparaiguaobert.

Araimaginemqueelventbufaa38,999999 km/hora.Qualsevolpersonadiriaqueelventés fort,peròlaclassificacióenpensamentbinaridiriaqueno,quelasituaciós’hadeclassificar dientquenofaunventfortencaraquesiguiincapaçdediferenciar,ambelssentits,aquesta situaciódelade39 km/h.

L’establimentdevalorsexactesdeclassificacióprovocasovintsituacionsabsurdescomaquesta.

3.9.Novena situació.Nivell de duresa

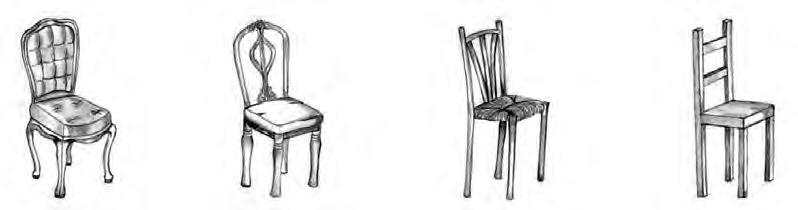
Figura15.Obra Nivelldeduresa,deQueraltViladevall.

L’obraestàinspiradaenundelscontesambquèelsinfantsaprenenpensamentnobivalent: LaRínxolsd’Or.Aquestanarraciócontéunagranquantitatd’exemplesdelfetquenototes lescaracterístiquesdelmónrealespodenclassificarenunestéonoesté(Viladevall etal., 2023a).Així,laRínxolsd’ortrobaunplatdesopamassacalenta,unplatdesopagenscalenta iunplatdesopaenelseupuntideal;unacadiramassatova,unademassaduraiunaamb elseientd’unaduresajusta(figura 15);unllitmoltalt,unllitpocaltiunllital’alçadaque consideraideal...

Elconteensportaalareflexiódecom,demanerainformal,ésadir,foradel’escola,apoca pocanemaprenentquelavidatémoltstonsdegrisiquelescosesnosónsempreblanques onegres.

Figura14.Obra VentFort,deQueraltViladevall.

3.10.Desena situació.Forma circular

Figura16.Obra Formacircular,deQueraltViladevall.

Aquestaobra(figura 16)tancaval’exposicióiestavainspiradaenelstreballsdeNataliaR. Shenger-Krestovnikova,unaestudiantdedoctorat d’IvanPàvlovquevadescobrirunfetsorprenentrelacionatamblaclassificacióbinària.

IvanPàvlovvaserprofessordeFisiologiaenl’AcadèmiaMèdicaImperialidirectordelDepartamentdeFisiologiadel’InstitutdeMedicina ExperimentaldeSantPetersburg,ivaformular elqueesvaanomenar«condicionamentclàssic»,queesbasaenl’estudisobrecoméspossibleprovocarunesrespostesdeterminadesapartird’unsestímulsprèviamentneutres.Atall d’exemple,ésmoltconegutl’experimentconsistentafersonarunmetrònom(popularment escreuqueesvautilitzarunacampana)justabansdedonaralimentaungos.Esvaarribara observarque,quanelgosteniagana,començavaasalivarenelmateixinstantquesentiael sodelmetrònom.

L’alumnadePàvlov,Shenger-Krestovnikova,tambétreballavaambcans,condicionant-los ambcerclesiel¨lipses.Quanelgosveiauncerclesabiaquelidonarienmenjar,peròsila figuraescorresponiaambunael lipse,l’animalnorebiaaliment.D’acordambelsprocessos normalsdediscriminació,elgosvaaprendreasalivarquanveiaelcercleianosalivarquan veial’el lipse.

Desprésd’aquestcondicionament,Shenger-Krestovnikovavaseguirl’experimentpresentant al’animalel lipsesbastantcirculars,demaneraqueeradifícildeterminarquanhihauriamenjariquanno.Enund’aquestsexperiments,enelmomentquel’el¨lipsevaadoptarunaforma moltcircular,algunsdelsgossosvanmostrarsobtadamentuncomportamentforçaestrany: udolaven,gemegaven,presentavenconductesdestructives...Lasituaciód’extremaincertesa vasermassaestressantenalguncas.Pàvlovvaanomenaraquestfenomen«neurosiexperimental»ivaplantejarlahipòtesiquelesneurosishumanesespodriendesenvolupard’una manerasemblant.Eldubtepatològicd’unsubjectesobrel’estatdenetejadelessevesmans ésuntípicexempledeneurosihumana(Laín, 1984).Elpensamentborróspotajudaraevitar l’apariciód’aquestesneurosis(Linares etal., 2020)i,pertant,espotjustificarlainclusiódel seuestudienelcurrículum.

4.Resultatsesperats,noesperatsiconclusions

Ambl’exposiciós’esperavaoferirlapossibilitatdecomprendrediversospuntsdelateoriade conjuntsborrosos(Zadeh, 1965).

Enprimerlloc,s’esperavaqueelvisitantadultpoguésarribaracomprendrequelateoria deconjuntsborrososacceptaqueelselementsd’unconjuntpodenpertànyerenungrau

determinatalconjuntsegonssiescompleixparcialmentelpredicatquedeterminaelconjunt percomprensió.Ésadir,s’esperavaqueelvisitantcomprenguésquel’oració««S»és«P»» espotcomplirenungraudeveritatentre 1 (elsubjecte«S»compleixsensecapdubtela propietat«P»)i 0 (sielsubjecte«S»nocompleixperreslapropietat«P»).

Ensegonlloc,s’esperavaqueelvisitantadultpoguéscomprendreque lateoriadeconjunts borrosospermetmodelardemaneracontinuadatransformacionsdel’entorn.L’obradela metamorfosidecapgròsagranotaoladeldesglaçd’unscubsdegelamblasevaampliació alcartelld’inicidel’exposiciótenienaquestaintenció.

Entercerlloc,s’esperavaqueelvisitantadultespoguésadonarqueenlateoriadeconjunts borrososnohihacapnecessitatd’haverde decidirenuncasdubtósentredosconjuntscomplementaris.Aixòhoesperàvemaconseguirambladelmuntdesorramostrantque notenimproblemesatrobarunelementqueestiguialmig.Elquetinguiassignatunvalor 0,5compleixaquestacondició.

Enquartlloc,s’esperavaqueelvisitantadultpoguéscomprendrequeunelementpotpertànyeradosconjuntsoposatssenseproblemes,alcontraridelquepassaenlateoriade conjuntsclàssica.Enelcasd’unael¨lipsemoltproperaauncercle,podempensarqueésun cercleambgraumoltpropera 1 ialavegadanohoési,pertant,potsertambéel lipse.

I,endarrerlloc,s’esperavaqueelvisitantadultpoguésveurequeenlateoriadeconjuntsborrosossemprehihallocperalasubjectivitatpersonal.Desdelaperspectivad’uninfant,una personad’1,70 md’alçadapotseralta,peròunjugadordebàsquetd’1,95mlapotconsiderar baixa.L’obra Vellesa teniaaquestpropòsit.

Lespreguntesilesreflexionsalvoltantdelesobresqueensanavenarribantdelpúblicadult assistentensvanconfirmarquel’objectiuesperatdelapartd’aprenentatgenoformalpodia serassolit.

Comamilloraperafuturesexposicions,comentarqueenllocd’afegirtextexplicatiuasotade lesobresesvaposaruncodiQRqueadreçavaaunàudio.Pensemquehauriaestatmoltmés eficientinclouretambéuntextasotadecadaobra,jaquenotothomteniaganesopossibilitatsd’escoltarelsàudios.Untextambdiversesmidesdelletra,lamésgrancomaexplicació moltpersobreperdespertarcuriositatiunademéspetitaambl’explicaciódetalladaseria elquevafaltarpermillorarl’experiènciadelsvisitantsalvoltantdelapartd’aprenentatge esperat.

Ambl’exposició,elquenos’haviaprevisteraveureexplícitamentdesenesdecasosdetransmissiómatemàticanoformalrelacionatsambparaulesqueexpressengraduaciód’unaqualitat.Sincerament,noenshavíemimaginatquelesobresportarienadesenesidesenesde paresaexplicarlesdiferentspartsalsseusfillsambquantificadorscom«poc»,«unamica», «molt»,«bastant»...Lagranquantitatdecasosobservatsensvaferadonarque,apartirdels pares,l’aprenentatgenoformaldelsadverbisdequantitatperdesignargraduacionsdepropietatsésactualmentunafontprincipald’aprenentatge.

Calcomentarque,enaquestsentit,potservaserunencertnoafegirelstextosquedèiem,ja queelsparesesvansentircompletamentlliurespe rexplicarelquevolienalsseusfills.Potser

lesexplicacionshauriengeneratunaltredebatalvoltantdel’aprenentatgeesperatinoens hauríemadonatmaid’aquestsegonaprenentatgenoformal.

Lesconclusionsqueespodenextreured’aquestaexperiènciaésquelesexposicionsdecontingutmatemàticpodenfomentarl’aprenentatgenoformalmatemàticmoltmésenllàdel queenspensem.Comquel’aprenentatgenoformalmatemàticésessencialperdominarles matemàtiquesformalsques’aprenenal’escola(Alsina, 2015),podeminferirqueunMuseu deMatemàtiquesésunregalperatotselsnensquehipodenanar.

Enaquestsentit,ésunprivilegiteniraCatalunyaunMuseudelesMatemàtiques,iencoratgemaseguirtreballantpertalquelessevesexposicionsiactivitatsarribinatantespersones comsiguipossible.

Referències

[1]Alsina,À.(2015). Matemáticasintuitivaseinformales de0a3años.Elementosparaempezar bien.Narcea.

[2]Alsina,À.,Borràs,L.,Doblado,R.iGrauvilardell,L.(2023).«Evaluacióndelasmatemáticas emergentesde 0 a3años». Edma0-6:EducaciónMatemáticaenlaInfancia,12(1),53-80.

[3]Alsina,C.iTrillas,E.(1991).«Fuzzysetsandmathematicseducation». FortheLearningof Mathematics,11(3), 16-19.

[4]Baroody,A.J.(1987). Children’sMathematicalThinking.Adevelopmentalframeworkfor preschool,primary,andspecialeducationteachers.TeachersCollegePress.

[5]Blanco-Fernández,Á.,Díaz-Díaz,P.,García-Honrado,I.,Ramos-Guajardo,A.B.iRodríguezMuñiz,L.J.(2016).«AproposalforassessingimpreciseconceptsinSpanishprimaryand secondaryschools». InternationalJournalofUncertainty,FuzzinessandKnowledge-Based Systems,24, 71-91.

[6]Canals,M.A.(1992). Perunadidàcticadelamatemàticaal’escola:1.Parvulari.Eumo.

[7]Clements,H.D.iSarama,J.(2015). ElAprendizajeylaEnseñanzadelasMatemáticasa TempranaEdad.LearningToolsLLC.

[8]Geist,E.(2014). Childrenarebornmathematicians:supportingmathematicaldevelopment, birthtoage8.Pearson.

[9]Kaufmann,A.iGil-Aluja,J.(1988). Modelosparalainvestigacióndeefectosolvidados. Milladoiro.

[10]Kosko,B.(1995). Pensamientoborroso:Lanuevacienciadelalógicaborrosa.Crítica.

[11]LaínEntralgo,P.(1984). Antropologíamédicaparaclínicos.Salvat.

[12]Linares-Mustarós,S.,Viladevall,Q.,Llacay-Pintat,T.iFerrer-Comalat,J.C.(2018).«Una introducciónalasideasfundamentalesdelalógicaborrosaatravésdelarte». Cuadernos delCIMBAGE,1(20), 133-156.

[13]Linares-Mustarós,S.,Viladevall,Q.iFerrer-Comalat,J.C.(2020).«Laclasificaciónenla teoríadeconjuntosborrosos».AEdunovatic(ed.), ConferenceProceedings:5thVirtualInternationalConferenceonEducation,InnovationandICT (p.653-654).REDINE(ReddeInvestigacióneInnovaciónEducativa).

[14]MinisteriodeEducaciónyFormaciónProfesional[MEFP](2022a).RealDecreto 95/2022, de 1 defebrero,porelqueseestablecenlaordenaciónylasenseñanzasmínimasdela EducaciónInfantil.BOE.

[15]MinisteriodeEducaciónyFormaciónProfesional[MEFP](2022b).RealDecreto 157/2022, de 1 demarzo,porelqueseestablecenlaordenaciónylasenseñanzasmínimasdela EducaciónPrimaria.BOE.

[16]Trillas,E.iGarcía-Honrado,I.(2019).«Latransversalidaddela‘lógica’borrosa,?‘unaoportunidadpedagógica?». CuadernosdelCIMBAGE,2(21), 201-217.

[17]VendrellFerré,J.(2009).«?‘Corregirelcuerpoocambiarelsistema?Latransexualidad anteelordendegénero». Sociológica(México), 24(69),61-78.

[18]Viladevall,Q.,Linares-MustarósiS.Ferrer-Comalat,J.C.(2015).«FuzzySets».AJ.C.FerrerComalat,S.Linares-MustarósiCorominasColl,D.(eds.), NewTechniquesforDecisionMakingunderUncertainty. ServeidepublicacionsdelaUniversitatdeGirona.

[19]Viladevall,Q.,Linares-Mustarós,S.iFerrer-Comalat,J.C.(2020). L’increïbleenginydelsanimals.Catàlegdelamostraexpositiva. ServeidePublicacionsdelaUniversitatdeGirona.

[20]Viladevall,Q.,Ferrer-Comalat,J.C.iAlsina,Á.(2023a).«Elcuentoinfantilcomoherramientaparaintroducirlosconjuntosborrososenlasprimerasedades». RevistaInfancia, EducaciónyAprendizaje,9(1),53-68.

[21]Viladevall,Q.,Linares-Mustarós,S.,Huertas,M.A.iFerrer-Comalat,J.C.(2023b).«UnderstandingtheAxiomsandAssumptionsofLogicalMathematicalSystemsthroughRaster Images:ApplicationtotheConstructionofaLikertScale». Axioms,12(12), 1064.

[22] Wagensberg,J.(2000).«Principiosfundamentalesdelamuseologíacientíficamoderna». Alambique,26, 15-19.

[23]Wilchins,R.(2007). BurntheBinary! RiverdaleAvenueBooksLLC.

[24]Wilchins,R.,Nestle,J.,Howell,C.,Rivera,S.,Wright,S.iReiss,G.( 2020). GenderQueer-Voices fromBeyondtheSexualBinary. RiverdaleAvenueBooksLLC.

[25]Zadeh,L.A.(1965).«Fuzzysets». Informationandcontrol, 8(3),338-353.

Algemat:àlgebra ambmaterials

AnnaVilaróUtrillo Professoradematemàtiquesdesecundària anna@annahelpme.com

Resum Abstract

Sovint,trobarunbonmaterialmanipulatiu dematemàtiquesquesiguiestructuratés dificultós.Iencaraésméscomplicat treballarcontingutscorresponentsal’ESO. Enaquestarticles’explical’experiència d’unaprofessoraque,comaresultatdela sevainvestigacióipràcticaal’aula,ha dissenyatunnoumaterialmanipulatiu.

S’aportenreflexionssobrediferents materialspertreballarl’àlgebrailaseva idoneïtatpercomplirelsobjectius establerts.Iméstard,s’exposaelmaterial d’autocreació:ALGEMAT(Àlgebraamb material)explicantambexemplescom permettreballardiferentsoperacions matemàtiques.

Findinggoodmathematicsmanipulative materialthatisstructuredisoftendifficult. Andevenmoresoifyouwanttoworkon contentforcompulsorysecondary education.Thisarticleexplainsthe experienceofateacherwho,asaresultofher researchandpracticeintheclassroom,has designednewmanipulativematerial. Reflectionsareprovidedondifferent materialsforworkingonalgebraandtheir suitabilitytoachievetheestablished objectives.Later,theself-creationmaterialis presented:ALGEMAT(algebrawithmaterial), explainingwithexampleshowitcanbeused tolearndifferentmathematicaloperations.

Abansdecomençaraexplicarquèésl’Algemat,ésimportantsabercomvasorgir.Som-hi!

1.Introducció

EmdicAnnaVilaróUtrillo,famésde 20 anysquesocprofessoradematemàtiquesasecundàriaisemprehetingutinterèsapodertreballarambmaterialsmanipulatius.

Comjasabeu,elsmaterialsmanipulatiussónunrecursqueensajudaaferelpasdelqueés concretalqueésabstracteial’assolimentdelescompetències,comtambéfacilital’atenció aladiversitat...Aquestaideaesvacomençaragestarfatemps,perexempleenaquesttext deThomasR.Post(1981):

Elusodelosmanipulativos,untipoparticularderecursos,sepresentaenelmarcodelas investigacionesrealizadasdesdelasprimerasdécadasdelsiglo XX enrelaciónconlaformaciónyevolucióndeconceptosenlosniños(Piaget, 1971;Dewey, 1938;Bruner, 1960; Dienes, 1969).Estasinvestigacionessugierenqueenalgunosmomentoslosconceptos delosniñosevolucionanatravésdelainteraccióndirectaconelambienteyqueprecisamentelosmanipulativossonvehículosquepermitenqueestosuceda.Laimportanciade estetipodeestudiosseasociaalreconocimientodelaposibilidaddequeseproporcione unconjuntodeevidencia«persuasiva»paralosdocentesdematemáticasenrelacióncon elusodematerialesmanipulativosenlaclasedematemáticas.

Mésrecentment,Goñi etal .(2011)fanreferènciaalfetqueenl’actualitatlamajoriad’informació ensarribaenduesdimensionsatravésdediaris,revistes,fotografies,ordinadors,tauletes..., iperaixòmateixésimprescindibletenirrecursosperfereltrajectefinsalaterceradimensió. Ésenaquestcamíonlamanipulaciód’objectesadquireixunaimportànciacabdal:noésel mateixveurerepresentacionsquetocar-les.

L’àlgebrarequereixunnivell d’abstraccióelevat,ienaquestsentitvaigestarbuscantun materialqueajudéselmeualumnatapassardelaconcrecióal’abstracciód’unamaneranatural.Queellsmateixospoguessintreureconclusionsatravésdel’observaciódelquehavien manipulat.

L’objectiueratreballarl’àlgebrafentconnexionsamblageometria,nombresenters,aritmètica,etc.,atravésd’uncontextgeomètricenl’espai.Ipelquefaacontingutsd’àlgebra,poder treballarsumes,restes,multiplicacionsidivisionsambpolinomis,factoritzacions,equacions de 1r, 2ni3rgrau,etc.

Aquestplantejamentéscoherentamblavisió d’algunsautorsqueindiquenque«passarde l’aritmèticaal’àlgebrasaltant-selageometriaespotconsiderarunerrordidàcticihistòric,

AnnaVilaróUtrillo.

quetéexplicacióenelcontextdelsegle XVII quanlaforçadelnoullenguatgesimbòlicva desplaçarelraonamentgeomètricvisual»(KatziBarton, 2007).

2.Exploraciódepropostespertreballarl’àlgebra

VaigcomençarutilitzantAlgebraTiles.Estractad’unespecesrectangularsiquadradesque espodenfabricaral’aulaambgomaevaipermetenferoperacionsambpolinomisfinsagrau 2.Podemdirqueposaenjocaspectesdelageometria 2D,jaquetenenencomptel’amplada il’alçada.

Figura1.AlgebraTiles.Lasegonafilacorresponalapartdeldarreredelespecesiensindiquenelsnegatius. (Font:https://www.smartick.es/blog/matematicas/algebra/)

Asotadecadapeça,hiconstalapartnegativai,pertant,nonecessitacaptaulerperindicarho.Noobstant,requereixquel’alumnattinguiunconeixementprofunddelsnombresenters. Pressuposaquel’alumnatdominalaregladelssignes.

Icomjas’hacomentat,noméstreballafinsamonomisdegrau 2.

Continuantamblarecerca,vaigdescobrirl’Algeblocksil’AlgebraLabGear.Dosmaterials utilitzatsmajoritàriamentagranpartd’AmèricaiAustràliaiqueerenmoltpocconegutsa Europa.Aquestsmaterialsestanformatsperunsprismesquepermetentreballarambmo-

Figura2.Pecesd’Algeblocks.(Font:DaSilva,2018,p.88.)

nomisdegrau3pelfetquetenenencomptel’alçada,l’ampladailafondària.Podemdirque permetenabordaraspectesgeomètricsde3D.

Pelquefaal’Algeblocks,lespecesnecessitenuntaulerpertald’identificarsisónpositiveso negatives.Itambénecessitadostaulersmés:unperalesequacionsiunaltreambeixos.

Caldirquequanemvaigdisposaraadquirirl’Algeblocks,emvaserimpossiblecomprar-loa causadelpreu,queeramoltelevat.

Alseutorn,l’AlgebraLabGearconstad’unespecessimilarsal’Algeblocks,perònoutilitza taulers.Col localespecesenunescairedeplàsticiperidentificarlesnegativeslessituaa sobredelespositives.

Aquestelvaigpoderadquirir,peròquanelvaigteniralesmanseldissenyemvadesil¨lusionar. Ésdeplàsticilespecessónmoltpetites,nodiferencialesvariablespercolorsieltreball ambelsnombresnegatiusnoésgaireintuïtiu.Enaquestsentit,semblavamésfuncional l’Algeblocks,peròtambééspocpràctichaverdetreballarambtrestaulersdiferents.

Totiquenohearribataferservircapdelsdosmaterialsesmentats,hansigutimprescindibles perconèixerientendrelapotencialitatd’aquestamenaderecursos.Tambéhihanombrosos estudisqueelsavaluenenl’aulaiaixòemdonavaunacertaseguretatpelquefaalsbons resultatsquepodenassolir(BlancoiSolares, 2017;DaSilva etal., 2017,etc.).

Aquestaexperiènciaambmaterialsprevisvasercrucialperdecidiridissenyarelmeumaterial fent-hilesadaptacionsqueemvansemblaradequades.Vaserelmomentd’anar-me’nal fuster(aixòvaseral 2020)ifer-lielprimerencàrrecdelquevoliaquefosl’Algemat.

3.ALGEMAT

L’Algematconstad’unacaixadefustaambdos taulersambunseixos,deutipusdeprismes diferentsiduespecesambelsímboligual,iestàpreparatperquèhipuguintreballarquatre alumnes.

Figura3.Pecesdel’AlgebraLabGear(Font:DidadxInc.).

Figura4.Pecesdel’Algemat(Font:elaboraciópròpia).

L’interèsdemoltsprofessorspertreballarl’àlgebraambmaterialsmanipulatiushadonatlloc anombrososrecursos.EntreelsmésestesoshihaelsblocsdeDienesielsregletsdeM. AntòniaCanals.Lataula 1 reculllesdiferènciesqueensproposenl’Algemat,l’Algeblocksi l’AlgebraLabGearrespectedelsque tenenméspenetracióaCatalunya.

Taula1.Comparativadematerialsmanipulatius.

BlocsdeDienes (1963)

Regletsde M.AntòniaCanals (anyssetanta)

Algemat(2020)

Algeblocks(1996)

AlgebraLabGear (1994)

Totiqueconstitueixenelmaterialbasedelsaltresquemencionem,només hipodemtreballarambunasolavariable.I,amés,lespecesquelarepresentencontenenunnombreexacted’unitats.Ésperaixòqueaquestmaterial estàmésindicatpertreballarelsnombresnaturals,elsdecimalspositius, etc.

Espotarribaratreballarl’àlgebraambelsreglets,peròpotcrearconfusió,ja quecadaregletcorresponaunnombreexacted’unitatsilaideadevariable esperd.Tampoccontépecesquerelacioninduesvariables.Pertant,estan mésindicatspertreballarl’aritmètica.

Ambaquestsmaterialspodemtreballarambduesvariablesilespecesno tenenassignatunnombreexacted’unitats.D’altrabanda,mantenenlaidea devariableitambéincorporenlespecesquerelacionenduesvariables: xy , x 2 y i y 2 x

Araquejahemvistcomvasorgirl’Algematiquè és,faremunapinzelladadecomesfaservir!

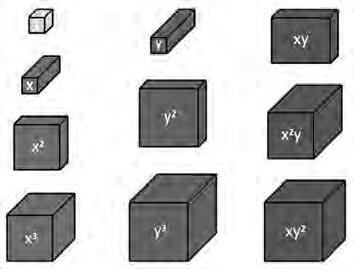
Figura5.Pecesdel’Algematamblasevadenominació.

Unaspecteimportantquecaldestacarésqueaquestespecesnotenensigne.Dependràd’on lessituemaltauler,dinselseixos(amaneradedistància,perexempleenlafigura6aladreta) oalsquadrantsdeltauler(amanerad’unió,en lafigura6al’esquerra),queseranpositiveso negatives.

Figura6.Representacionsde 2x.

Enlafigura6espotveurerepresentadal’expressió 2x deduesmaneresdiferents:lade l’esquerraés 2x “ 2 x ;pertant,agafem 2 peces x i,enaquestcas,comqueestanubicadesa lazonadeltaulernegatiu,tenimquelasevaequivalènciaéslaimatgedeladreta.

Perfer-homésentenedorivisualitzarlesconnexionsentrearitmèticaiàlgebra,faremoperacionsnomésambunitatsilesmateixesoperacionsambexpressionsalgebraiques.

Podemobservarquelaformageomètricaqueadoptenlesunesilesaltressónlesmateixes.

3.1.Operació suma

Figura7.Exempleoperativadesuma.

Podemferaquestaoperaciódinsunquadrantpositiudeltauler(comauniódeconjunts)oa dinsd’uneixpositiuenquèformaunalínia(sumadedistàncies).

Figura8.Exempled’operativadesumaambnombresdediferentsigne.

Dinsdeltaulernohipodenconviurelesmateixespecesenpositiuiennegatiualhora,jaque s’anul lenentreelles(formenzeros).Llavorslestrauremdeltauler(leshemratllatenlafigura8pertaldefer-hovisual).

Uncophemtretlespecesques’anul len,elresultatdel’operacióseràeldelespecesqueens hanquedat.

Passemaraaveurecoms’operaambexpressionsalgebraiques.

Figura9.Exempled’operativadesumaalgebraica.

Totiqueseguimelmateixprocedimentqueabans,calrecordarquenomésespodensumar irestarmonomissemblants.Ambl’Algematésforçaevident,jaquelespeceshandetenirla mateixaformailamateixamida.

3.2.Operació resta

Quannoméstreballemambunitatsconsideremlarestacomasumadenombresoposats. 3 1 “ 2

Posemlespecesaltaulercomsihihaguéssimescrit p`3q`p´1q“ 2.

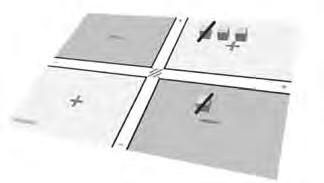
Figura10.Exempled’operativaderesta.

Pelquefaalesexpressionsalgebraiques,hemderecordarqueundelstressignificatsqueté elsímbolmenyséseldel’oposat.Pertant,totelquetinguemdarreredelsignemenys,els faremelseuoposat,canviant-loselsigne.Ésperaixòqueal’horadedistribuirlespecesal taulerjahofemambelsignecanviat.

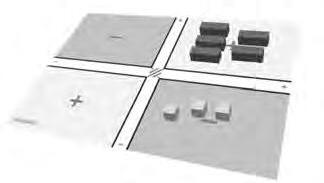
Figura11.Exempled’operativaderestaalgebraica.

Posemlespecesaltaulerfent: p3x 1q`p´2 ` 2x q:ésclarquetenim3x ` 2x “ 5x (peces rectangularsblavesdelafigura 11)i p´1q`p´2q“´3(pecesquadradesgroguesdela figura 11).

3.3.Operació multiplicació

Hemcomentatabansquesifemlessumesdinselseixosesformenlínies.Doncsara,ambles multiplicacionsdedosfactors,formaremquadratsorectangles.Hauremdeposarelsfactors enelseixosielresultatelformaràl’àreadelrectanglequehemconstruït.Estemtreballanten 2D!

Figura12.Exempled’operativademultiplicació.

Permultiplicarduesexpressionsalgebraiques,hauremdeposar-neunaenl’eixvertical(representaciódelvalor 2 enlafigura 12)il’altraenl’eixhoritzontal(representaciódelvalor3 enlafigura 12).D’aquestamaneraindiquemelvalordelscostatsquetindràelrectangleque hemdeconstruir.L’àreadelrectangleseràelresultatd’aquestamultiplicació.

Caltenirpresentunadelesnormesdelmètode:elrectangles’had’omplircomplintlacondicióquelespeceshand’encaixar.Quanunapeçaésalcostatd’unaaltra,elscostatshandeser iguals.Funcionacomuntrencaclosques.Vegemaralamaneracorrectadecol locarlespeces ambl’Algemat:

Figura13.Exemplesdecol¨locaciócorrectadepeces.

Maneraincorrectadecol locarlespecesambl’Algemat:

Figura14.Exemplesdecol locacióincorrectadepeces.

Pertant,perdescobrirelproductededuesexpressionsalgebraiques,perexemple px ` 3q¨ px ` 1q“ x 2 ` 4x ` 3,col¨locaremenelseixosl’enunciatcomindicalafigura 15iseleccionaremlespecesadequades(figura 16):aixíesconstrueixfísicamentl’expressióalgebraica desenvolupada.

Figura15.Enunciatdelamultiplicacióalgebraica.

Figura16.L’àreadelrectangleés elresultatdelamultiplicació.

Vegemaraunaltreexempleenquèlesexpressionsalgebraiquescontenenfactorsoposats: p´x ` 2q¨p3x 3q“´3x 2 ` 9x 6.Situem p´x ` 2q enl’eixverticalienl’horitzontalfem p3x 3q comespotobservarenlafigura 17.Enaquestcaselrectanglequehemdeconstruir ensocupaelsquatrequadrantsdeltauler.

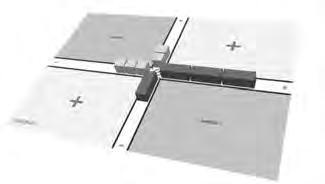
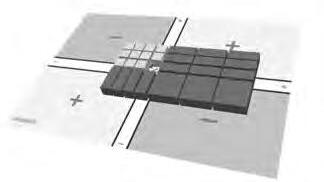
Figura18.Resultatdelamultiplicació.

Quanfemmultiplicacionsambpolinomis,hemdetenirencomptesicalferanul¨lacionsde peces(enelsexemplesexposatsnon’hiha)illavorsferelrecomptedelespecesdetotsels quadrants.

Isimultipliquem3factors?Trobaremprismesocubs.Estemtreballantambvolumsipertant, en3D!

Figura19.Enunciatdelamultiplicacióde3factors.

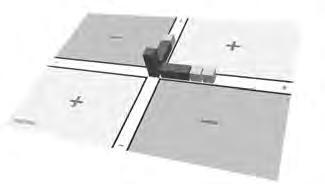
Figura20.Enunciatdelamultiplicacióalgebraica.

Figura17.Enunciatdelamultiplicació.

Enaquestcaselresultatdelamultiplicacióagafaelvolumd’unprisma(figura 21).

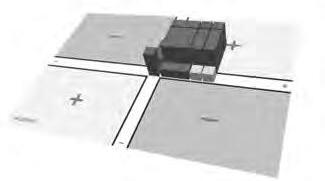
Figura21.Resultatdelamultiplicació.

3.4.Operació divisió

Quandividim,eldividendseràl’àread’unrectanglequehemdeconstruir,amblacondicióqueuncostatmesurielqueindicaeldivisor.Larespostalatrobemenl’altrecostatdel rectangle(eixhoritzontal,figura 22).

Figura22.Resultatdeladivisió. px 2 ` 3x ` 2q : px ` 1q“ x ` 2.

Sisituemeldivisorenl’eixvertical(comespotobservarenlafigura 23),aleshorescalformar unrectangleambeldividendtenintencompte queuncostathadesereldivisor.Elresultat deladivisióeltrobemenl’eixqueensquedavaperomplir(figura 24).

Figura23.Enunciatdeladivisió.

Figura24.Resultatdeladivisió.

3.5.Idees metodològiques per utilitzar Algemat a l’aula

Personalment,faigservirl’Algematal’inicidetotselscontingutsquehabitualmentesprogramenasegonitercerdel’ESO,iparal lelamentambladescobertadecomesfasegonsla tradició.Permetquel’alumnatvisualitzil’àlgebradinsuncontextgeomètricperquèdesprés puguintreurelessevesconclusions.Uncophohanentèsambelmaterial,lapreguntaés: comhofariessensel’Algemat?

Sihanentèsbéelsconceptessóncapaçosd’explicar-hodelamaneracomelprofessoratho fahabitualment.Tambéhihaprofessoratquel’utilitzaaquartd’ESOcomaconsolidacióde contingutsofinsitotaprimerdebatxilleratpertreballarunsaspectesconcrets.

Treballarambmaterialobligal’alumnatafocalitzarl’atenció,iaixíespodenevitaralgunesde lesconfusionsméshabituals.Dosexemples:

Ladinàmicademanipulaciódelespecesésbeneficiosaperquè:

‚ Ajudaafixar-semésenlalecturadel’enunciat(siésunasuma,unamultiplicació,etc.).

‚ Permetunacomprensiómésprofundadelesoperacionsbàsiques,jaqueesveuendes d’unaaltraperspectiva,vinculadaalaformageomètrica.

‚ Preveuenelsresultats(elsvisualitzen)ia mesuraqueavancennonecessitenmoureles peces.Ésllavorsquantreuenconclusions.

Tambéhitrobemalguneslimitacions,enaquestsmaterials,perexemple:

‚ Nopermetentreballarambnombresdecimalsnifraccionaris.Sempreestreballaambnombresentersperquènopodempartirlespeces.

‚ Noméss’hipottreballarambquantitatslimitades(segonslaquantitatdepecesdequè disposem).

‚ Nopermettreballarambmonomisdegrausuperiora3(volums).

Finalment,arribemalaconclusióquelesoperacionsques’hanaprèsaferambaritmètica tambéespodenferambàlgebraique,totes,mirant-lesdesdelpuntdevistageomètric, adquireixenunesformesconcretes.

ElmaterialAlgemattambépermet,abandadelesoperacionsquehemvist,ferequacions de 1r, 2ni3rgrau,itreballarconceptescomara:identitatsnotables,factorització,monomis semblants,valornumèricd’unpolinomi,etc.

Desprésd’acabardedissenyarl’Algematid’haver-loutilitzatambelsmeusalumnes,vaig pensarquepotseraltresprofessorshipodrienestarinteressats.Arabé,donaraconèixerel materialperellmateixésinsuficientsielqueespreténésimplementaruncanvienelsistema educatiu.Calunacompanyamentalprofessorati remarcarlaimportànciadelasevaformació contínua.Ésperaixòqueemvaigembrancarenelnaixementd’AnnaHelpMe,unprojecte quevolajudarelsprofessorsenl’obtencióderecursosmanipulatiusienl’anàlisidelsmaterials.Demaneraquefaigassessoramentadocents,imparteixocursosiescricllibresdivulgatius(Vilaró 2023a, 2023b).Sivoleusaber-nemés,podeuveureunavintenadevídeosque hoexpliquenawww.annahelpme.comodirectamentalcanaldelYoutubed’AnnaHelpMe.

Sihoheutrobatinteressant,usanimoacompartirl’Algematambaquellsprofessorsaqui encantariatrobarunmaterialmanipulatiuqueelspermetéstreballarlesmatemàtiquesa secundària!

4.Agraïments

Moltesgràciesalslectorsileslectoressiheuarribatfinsaquí!Vulladreçarunagraïment especialalaNoemíRuizMunzónperhaver-meajudataescriurel’article.

Bibliografia

[1]Blanco,Rocío;Solares,Cristina(2017).«Bloquesmultibase,Algeblocksyotrosrecursos paratocarlasMatemáticasenPrimariaySecundaria». VIIICIBEMLibroderesúmenes.FederaciónEspañoladeSociedadesdeProfesoresdeMatemáticasFESPM.

[2]Bruner,J.(1960).«TheProcessofEducation».Cambridge,MA:ThePresidentandFellows ofHarvardCollege.

[3]Dewey,J.(1938).«Thephilosophyofthearts». JohnDewey:TheLaterWorks, 13(357-368).

[4]Dienes,Z.P.(1969). AnElementaryMathematicsProgram.https://archive.org/details/ERIC _ED031397.

[5]Goñi,J.M.,Llenares,S.,López-Goñi,I.,Penalva,M.C.,Planas,N.,VallsJ.,Vanegas,Y.M., CorbalánF.iGiménez,J.(2011). DidácticadelasMatemáticas (vol. 12).Graó.

[6]Katz,V.J.Barton,Bill(2007).«Stagesinthehistoryofalgebrawithimplicationsforteaching. EducationalStudiesinMathematics,66, 185 201.

[7]Piaget,J. 1971. GeneticEpistemology,Editedby:Duckworth,E.NovaYork:Norton.

[8]Post,T.R.(1981).«Theroleofmanipulativematerialsinthelearningofmathematical concepts».A Selectedissuesinmathematicseducation (p. 109-131).Berkeley,CA:NationalSocietyfortheStudyofEducationandNationalCouncilofTeachersofMathematics, McCutchanPublishingCorporation.

[9]Silva,L.E.da(2018).«EnsinointradisciplinardeMatemáticaatravésdaresoluçãodeproblemas:ocasodoAlgeblocks».[PostgrauenEducaçãoMatemática,UniversidadeEstadualPaulista].http://hdl.handle.net/11449/154125.

[10] Silva,L.E.da;Camargo,A.S.M.de;Oliveira,P.C.(2021).«Propuestasdidácticaspara laeducaciónbásicaqueimplicanelusodelmaterialmanipulativoAlgeblocks». Revista ChilenadeEducaciónMatemática,vol. 13,núm. 2,p.68-77.

[11]VilaróUtrillo,Anna.«Algemat-Guiadidàctica».(2023a)ISBN: 978-84-09-52109-8.

[12]VilaróUtrillo,Anna.«Algemat-Quadern».(2023b)ISBN: 978-84-09-51902-6.

Connexióentreel2Diel 3D...ambGeoGebra!

BernatAncocheaMillet|GuillemBonetCarbó ACG(AssociacióCatalanadeGeoGebra) bancoche@xtec.cat|gbonet2@xtec.cat

Resum Abstract

Elprocésd’abstracciód’observarun desplegamentplaivisualitzarlafigura corresponenten3Dnoéssenzill,peròes pottreballarambdiferentsexercicis.En aquestarticlen’esmentaremunsquants. Parlaremd’activitatsquepodenajudara l’horadetreballarlavisióespaciali d’establirlaconnexióentreunpoliedreen l’espaiilasevadescomposicióenelpla. Tambéensproposemmodelitzar,idesprés construir,algunsd’aquests desenvolupamentsperconnectar-losamb lasevafiguraoriginalpassantdel 2Dal3Di viceversa.

Theabstractionprocessoflookingataflat displayandvisualisingthecorresponding figurein3Disnotsimple,butcanbeworked onwithdifferentexercises.Inthisarticle,we discusssomeofthem.Wetalkaboutother activitiesthatcanhelpwithspatialvision andestablishingtheconnectionbetweena polyhedroninspaceanditsdecomposition ontheflatplane.Wealsopropose modellingandthenbuildingsomeofthese developmentstoconnectthemwiththeir originalfiguregoingfrom2Dto3Dandvice versa.

1.Introduccióialgunsreferents

El 27defebrerde 2024esvacelebrarlaXVIJornadadel’AssociacióCatalanadeGeoGebra (ACG).Enaquestajornadavampoderseguirexperiènciesd’aulamoltinteressantsenquèel programadegeometriadinàmicahitéunpaperimportant.EnaquestsentitJeanBaptiste Étiennehaestatfontd’inspiracióperaquestarticle.Enlasevaexposició,elprofessorÉtienne, quetreballaalLycéeFrançaisdeMúrcia,va connectard’unamanerabrillantelGeoGebra amblamanipulaciódirectafentservirpaperitisoresatravésd’unproblemaclàssicdelcurrículumfrancès.Enelseutreballdescriul’estudideladissecciód’uncubatravésd’unplaoblic ambl’objectiud’exercirlavisióespacialiconnectarelsconceptesreferentsalageometria delplaambelsdel’espai.

LaideaproposadaperÉtienne(2024a)ésprousimple:escollirtrespuntssobreelcubiseccionarelcubfentservirelplaquepassaperaquestspunts.Peròcomespotferaixò?Proposa utilitzaruncubdigital,creatambGeoGebra,itallar-loambelpla.Uncopfet,caldissenyar elsdesplegamentsplansdecadascunadelesduesseccionsimuntar-losambGeoGebra,és adir,ferqueelprogramadegeometriadinàmicaconverteixieldesplegamentenundels cossos3Denquèhemdividitelcubinicial.Alhora,esdemanalacomprovacióambpaperi tisores,ésadir,esdemanaquel’alumneimprimeixielsdosdesplegamentsquehafetamb GeoGebraalfulldecartolinaiquemuntilesduespeces,construintd’aquestamaneraelcub inicial.Totplegatunaexperiènciamoltbonica.

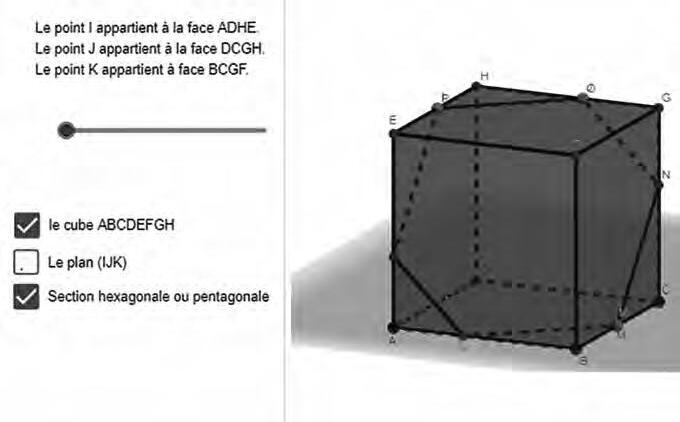
Imatge1.Seccióhexagonald’uncubtallatper unpla.ConstrucciódeJ.B.Étienne(2024b).

Aquestesideesensvanferreflexionarsobrelanostramaneradetreballarlageometriaen l’espai.Debensegurque,remenantentrelesdiferentsexperiènciesquehemportatal’aula, trobaríemactivitatsdemanipulacióinteressantscomaralad’esbrinarquantscossosplatònicshiha,lescaracterístiquesméssignificativesdelspoliedresarquimedians,laconstrucció deprismesipiràmidesilarelacióquehihaentreelsvolums,ladescobertadelafórmula d’Euler...Totplegatunconjuntd’experiènciesproumemorablesperseremmarcades.Desprésdelareflexióvamcomençaradissenyar-neunadenova:lacreaciódeldesplegament plad’unpoliedre.

2.Desplegamentplad’unpoliedre

Tothom,enl’adolescència,hamuntatpoliedresatravésdelseudesplegamentpla,convertint unesquemadeduesdimensionsenunafiguraenl’espai,totplegatunprocésmàgic.Uncop n’hemconstruïtunsquantsesprodueixuncanvidemiradaenlapersonaquemanipulaels cossos;nomésveienteldesenvolupamentplaiabansdecomençar-loaretallar,escomençaa imaginarquinseràelcosqueenresultarà.Aquestprocés,queesdevédemanerainconscient, enssemblafascinant.

Peròelcamípertreballariadquirirelsentitespacialésllarginos’integranomésmuntant unsquantsdesenvolupamentsplans.Caltreballardiferentsaspectesdelspoliedresenelpla ienl’espaiperanarestablintlesbasesdelaconnexióquepretenemcrear.

Comencemelnostrecamíambunaactivitatintroductòriadelquevindràdesprés.Ensproposemferunacercaexhaustivaitrobartotselspentòminospossibles.Ésprobablequeja haguemtreballataquestaactivitatanteriorment,enaquestcaspodríempassarlallistadels pentòminosdirectament.Perferlacercapotsermoltútill’úsdematerials,comaraelspolígonsqueencaixen.Aquestamenadematerials tambéensseràútilperampliarl’activitati preguntar-nosquinsdelspentòminostrobatspodenconvertir-seenuncubsensetapai,en aquestcas,lapreguntasegüentqueensvealpensamentseriaondeldesplegamenthauríem deposarlatapa.Aquestaactivitat,totiqueja ésmoltconeguda,ensserveixpercomençara introduirelsdesplegaments.

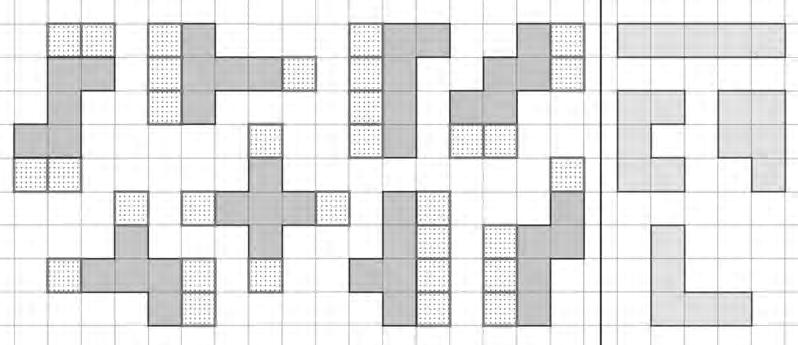
Imatge2.Pentòminosconvertiblesacapsaambpropostadetapa.

Lapropostapotserampliadaestudiantelspoliamants(figuresplanescreadesusantunnombredeterminatdetrianglesequilàters).Enaquestsegoncas,eldelspoliamants,costacopiar l’activitatquehemrealitzatambelspoliòminos,vistoscomadesplegamentsdecubs,jaque ambtrianglesequilàtersnoméspodemcreardospoliedresregularsamb«pocs»triangles:el tetraedre,amb4,il’octaedre,amb8.

L’estudidelprimercas,buscantquantstriamantshiha,ésmassasenzill,mentrequeeldel segonamblacercadelnombred’heptamantsésmassacomplex.Elquesíquepodemferés desferelcamíipartirjadelpoliedre.

Aquíenspreguntemsobreeldesplegamentpla d’unoctaedre(moltadequatpertreballar ambmaterials);uncoptrobat,eliminemundelstrianglesdelavoraienspreguntemonmés elpodríemposarperaconseguirtancarl’octaedre.Perexemple,enlaimatgesegüent,on posaríeuelvuitètriangleperobtenireldesplegamentd’unoctaedre?Quantesopcionshiha encadacas?

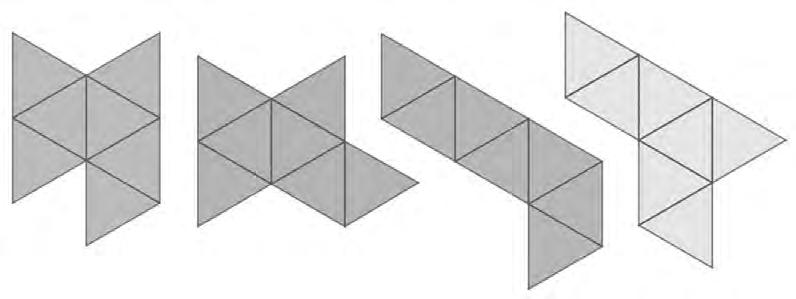
Imatge3.Quatreheptamants.Desplegamentd’unoctaedresensetapa.

Jahemcomentatqueal’horad’esbrinarquinspentòminosespodenconvertirencapses sensetapaésimportantl’úsdematerialmanipulable.L’úsdematerialsiviureelprocésde muntatgeenspermetgravarmentalmentunaseqüènciadefotogramesqueacabaconnectantcadadesplegamentamblasevafigurafinal:elcubo,enaquestdarrercas,l’octaedre.

Unsegonpasperenfortiraquestaconnexiópotserl’úsdematerialscreatsdigitalment,per exempleambGeoGebra.Elprogramapermetferlavisualitzaciódelplegamentdelcub(i d’altrespoliedres)enlafinestra3Dfentservirl’eina«Desplegament».Quancreemaquest desplegamentse’nsgeneraunpuntlliscantqueenspermetmuntaridesmuntarelcubde maneraautomàtica.

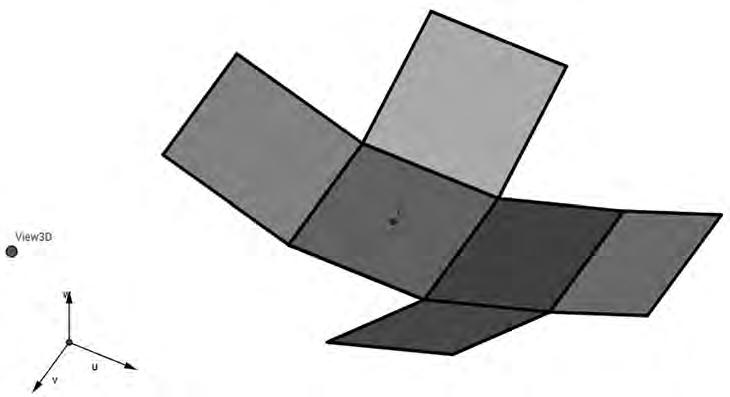
Imatge4.Desenvolupamentdelcub.ConstrucciódeD.Mentrard(2017).

Arabé,elGeoGebranomésensofereixundesplegamentdelcub.Quèpassaambelsaltres? EnsproposemqueelsalumnesmuntinelseupropicubambGeoGebrautilitzantqualsevol delsaltresdesplegamentstrobats.Uncopcreateldesplegamentescollitalafinestra 2Dfent servirels6quadratsquerepresentaranles6caresdelcub,aquestdesplegamentesvisualitza alafinestra3Ddemaneraautomàtica.Ara,lafeinaseràgirarcadascunadelescaresper

construirelcub.Aquítreballaremelgird’unacaraalvoltantd’uneix,ambl’eina«Rotacióal voltantd’uneix»delafinestra3D).

Unadarreraactivitatqueensagradaal’horadeconnectareldesplegamentplad’unpoliedre amblasevafigura3Désladecomprovarlafórmulad’Euler...Sihofemdirectamentsembla quenofunciona,quèpassa?Efectivament,hihavèrtexsiarestesqueesrepeteixen.Com podemtreballariconsolidaraquestaidea?Laprimeraopcióésanalitzardiferentsdescomposicionsd’unmateixpoliedre:semprequedadesaparellat,elmateixnombred’arestes idevèrtexs?Quinarelaciótenenambelpoliedre?

Imatge5.Activitatautocorrectivaperconnectarvèrtexsd’unoctaedre.

Unaaltrapropostaésladeconnectararestesivèrtexsqueescorresponguin.Comveiemen laimatge5,hemcreatunaaplicacióautocorrectivadeGeoGebraquepermetal’usuarifer propostesdequinsvèrtexsesrepeteixenionestansituatseneldesplegament.Uncopfet,el programamateixcorregeixelprocésipermetvisualitzaralafinestra3Dlacomprovacióde lacorreccióplegantdigitalmentlafigura.

3.Visualitzar,analitzar,modelitzariconstruir...ambGeoGebra

Enlesactivitatsanteriorshemcomençatafamiliaritzar-nosambelscossos«senzills»connectantelseudesenvolupamentamblavisióespacialdelcos.Elnostreobjectiuaraésavançar enlainvestigacióestudiantaquellscossos«menyssenzills»queesderivendelsquejahem estudiat.

AmbaquestobjectiupodemutilitzaralgunesaplicacionscreadesambGeoGebrapermodificarmínimamentlafiguraen3Didetectarquinscanviss’hanproduïtenelseudesenvolupamentpla.

Així,perexemple,podemanalitzarcomvaria eldesenvolupamentplad’unortoedreamesuraqueenmodifiqueml’alçada,oeldesenvolupamentplad’unapiràmidesienmovemla «punta»,fixant-nosespecialmentenquinescaracteríst iquesdeldesenvolupamentcanvieni quinesno.

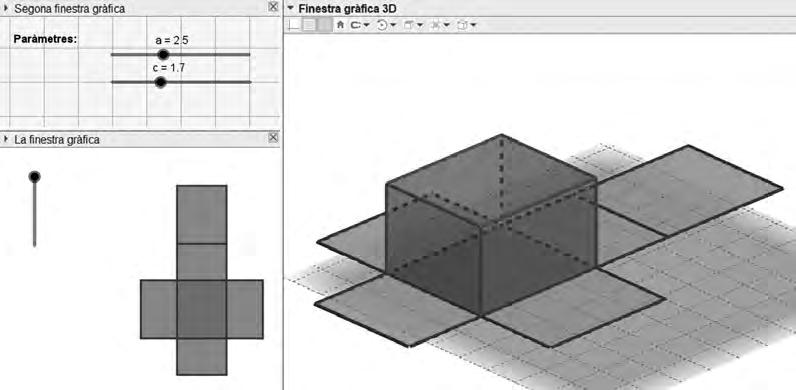
Imatge6.Desenvolupamentdel’ortoedre.

Enelcasdelapiràmiderectangulartambépodemanalitzareltraçdelspuntsassociatsal vèrtexeneldesplegament.Així,simovemelvèrtexendireccióvertical,enquinadirecció esdesplaçaranelsvèrtexsdelasevadescomposicióplana?Comesmodificaràlafigura?Isi elmovemenunadireccióhoritzontalenalçadaiparal¨lelaauncostat?Isihofemenuna direccióhoritzontalenalçadaperònoparal lelaacapcostat?

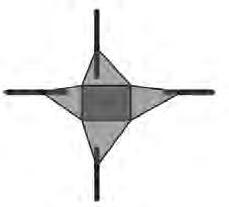
Imatge7.Estudidelaposiciódelsvèrtexsd’unapiràmiderectangular.

Alaimatge7esmostrapartd’aquestestudi,primermoventelvèrtexdemaneraperpendicularalabase.Alesduesdeladreta,elvèrtexesmousobreunalínia,ienelcascentralla líniaésparal lelaaundelscostatsdelabase,aldarrerno.

Podemcomplicartambél’anàlisiambpropostesdecanviméscomplexes,comaraladetruncarlespuntesolesarestesdelcubiveurequèpassallavorsambelseudesenvolupamentpla. L’ampliaciód’aquestaactivitatenscondueixaunestudimoltinteressantsobrelavariaciódel nombredecares,arestesivèrtexs,osobrelaformadelescares.

Peracabaraquestsecció,unpetitrepte...Usproposemvisualitzarquinesfiguresdonaran elssegüentsdesenvolupamentsplans(algunsdesplegamentsadmetenduessolucionsdiferents).Calretallartambéperlalíniadepunts.

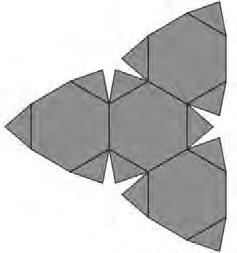
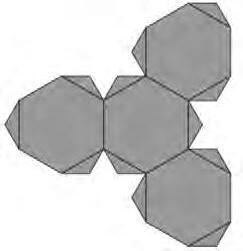
Imatge8.Exemplesdetresdesenvolupamentssemblants.

Comaobservaciód’aquestpetitexercici,elshexàgonssóntotsregularsilesalçadesdels trianglesisòscelesdelasegonaiterceraimatgesmesuren,respectivament,?i?delesalçades delstrianglesequilàtersdelaprimera.

UncopenshemfamiliaritzatprouambelsdesenvolupamentsplansdediferentsfigurespodemanarmésenllàiutilitzarelGeoGebraperdissenyaricrearunafiguraen3D.Volem muntaruncos«senzill»apartirdelseudesenvolupamentplad’unamanerasemblantacom hohemfetambelcubenl’apartatanterior.Perfer-hoésimprescindiblequeelsalumnes estiguinfamiliaritzatsambleseinesdelprograma.

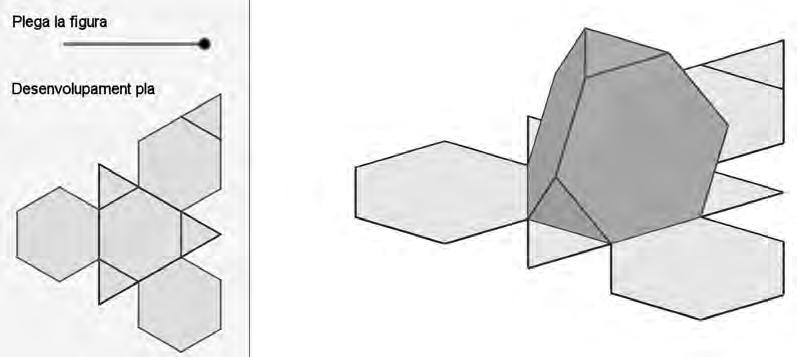
Imatge9.Tetraedretruncatcreatapartirdelseudesenvolupamentpla.

Ambaquestaactivitatcontinuemenlalíniadetreballarlavisualitzaciódecossosen3Di,en aquestaocasió,ensfixemespecialmentenelsanglesenl’espai,jaquehauremdegirarcares delafigurasegonsaquestsangles.

Latascarequereixunacertahabilitatitreballarambgirs,laqualcosapotpresentardificultatdeboncomençament.Peraixòésaconsellablemuntarprimereldesplegamentimprès enpaperiestudiar-neelsdiferentsgirs,lescombinacionsdemovimentsielsanglesquehi intervenen,idesprés,crearl’aplicació.Elsresultatsques’assoleixenacostumenasergrans obresd’art.

4.Ferpossiblel’impossible

Enaquestaúltimaseccióproposemcreareldesenvolupamentplad’unafiguraentresdimensionsaparentmentcomplicadaentrealgunesdeproposadesdigitalmentambGeoGebra. L’activitatrequereixl’úsdetotelques’hatreballatanteriormentiensserveixpertancarel cercle.

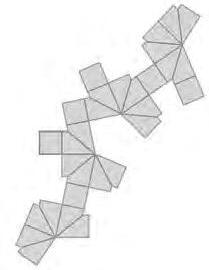
Imatge10.Cossosdemostraambelsdesenvolupamentsplansrespectius.

Totiquelapropostaéssimple,elreptequehihaaldarrereésimportant:dissenyareldesenvolupamentplad’unafigura«complicada»emprantalgunesdeleseinesdelafinestra 2DdelGeoGebra.Elnostreobjectiuenaquestaocasióésdoble:d’unabanda,treballarla visualitzaciód’uncos3Dobservantlarelació entrecares,arestesivèrtexs,idecidintquina ésladistribucióòptimaperendreçareldesplegament.Del’altra,creareldesplegamenten lafinestragràficadeGeoGebra iaquícaldràconsiderarlaformadelescares,lesdistàncies ielsangles.Alhora,ensobriràlapossibilitatdeferservireinesbàsiquesdelsmovimentsdel pla(translacions,simetriesigirs)peranarconstruinteldesplegamentdissenyat.

Uncopfetalapropostadedesplegament,laimprimiremencartolinailamuntaremper compararelresultatfinalamblafiguradigitalitzadadel’inici.D’aquestamanerahipodrem detectarpossibleserrorsicomprovarl’adequaciódelresultatfinalambelcosesperat.

Agraïments

Novolemacabarsenseposarenrelleul’esforçtitànicd’algunsalumnesal’horaderealitzar aquestesactivitatsque,uncopacabades,veientelresultatfinal,aconsegueixenprovocar-los unsomriuredesatisfacció.

Imatge11.DesplegamentsproposatsperM.MotoyamaaX.Foto:RikoOkaniwa.

TambévolemferunreconeixementdelstreballsdegransdissenyadorsdematerialsdeGeoGebra,comaraelsdeJ.B.ÉtienneilainestimableobradeMahoMotoyama,queensté fascinatsamblessevespropostesdedesplegamentsdefiguresaparentmentimpossibles.

Referènciesbibliogràfiques

[1]Ancochea,B.iBonet,G.(2024).«Desarrollosplanosdefigurasincreíbles».https://www.geo gebra.org/m/a4ceuatv.(Consultat 27/8/2024)

[2]Ancochea,B.iSorigué,I.(2017).«Cubos».https://www.geogebra.org/m/VBjNpksu/.(Consultat 12/8/2024)

[3]Étienne,J.B.(2023).«Solidesdel’espace».https://www.geogebra.org/m/bxvsjmsq/.(Consultat 12/8/2024)

[4]Étienne,J.B.(2024a).«Desarrollosdelossólidosobtenidos(secciónhexagonalregular)». https://www.geogebra.org/material/show/id/yx8at5y8/.(Consultat 12/8/2024)

[5]Étienne,J.B.(2024b).«GeoGebra,papelytijeras».https://www.geogebra.org/m/h5srzccw. (Consultat 12/8/2024)

[6]Mentrard,D.(2017).«Les 11 patronsducube».http://dmentrard.free.fr/GEOGEBRA/Maths/ HTML/Patroncubet.html.(Consultat 12/8/2024)

Viatgeinterplanetari: aprendrematemàtiquesamb l’universcomaescenari

RoserMatasNadal Docentdematemàtiques rmatas2@xtec.cat

XavierSánchezCarrasco Docentdebiologiaigeologia xsanche6@xtec.cat

MarcFaüchsXifra Docentdefísicaiquímica mfauchs@xtec.cat

Resum Abstract

Aquestarticlepresentaelprojecte«Viatge interplanetari»,unaexperiènciaeducativa quehapermèsal’alumnatdeprimer d’ESOdel’institutAntoniPousiArgila viurel’emociódel’aprenentatgedesd’una perspectivapràcticaicreativa.Atravésde laconstrucciódemaquetesaescaladel sistemasolarid’unabaseaMart,els estudiantshanfetunviatgequeelshadut atreballard’unamaneratangiblei significativaconceptesmatemàticscom l’escalailaproporció.Elprojectenonomés hamotivatelsalumnesaendinsar-seenel móndelesciènciesilesmatemàtiques, sinóquetambéhafomentatla col¨laboració,elpensamentcrítici laresoluciódeproblemes.Amés,ha demostratquelacoordinacióentre docentsdediferentsdisciplinespot transformarelprocésd’ensenyamenti convertir-loenunaaventuraapassionant ienriquidoratantperaalumnescompera professors.

ThisarticlepresentstheInterplanetary Journeyproject,aneducationalexperience thatallowed1st-yearsecondarystudentsat AntoniPousiArgilaHighSchoolto experiencethethrilloflearningthrougha practicalandcreativeapproach.Bybuilding scalemodelsofthesolarsystemanda Martianbase,studentsembarkedona journeythatmademathematicalconcepts likescaleandproportiontangibleand meaningful.Theprojectinspiredstudentsto delveintotheworldsofscienceand mathematicsandencouragedteamwork, criticalthinking,andproblem-solving.It highlightedhowinterdisciplinaryteacher collaborationcantransformteachinginto anexcitingandenrichingadventurefor studentsandeducators.

1.Introducció

Aquestarticleexplicaeldissenyilaimplementacióal’auladel projectedeciències«Viatgeinterplanetari»,fentèmfasiencom estreballenlesmatemàtiques.ÉsunprojecteSTEAM,acrònimanglèsqueenglobalesdisciplineseducativessegüents:Science, Technology,Engineering,ArtandMathematics(Ciència,Tecnologia,Enginyeria,ArtiMatemàtiques),adreçataalumnatdeprimerd’ESO, del’institutAntoniPousiArgiladeManlleu.

Estractad’uncentred’altacomplexitatambunaltpercentatged’alumnesambnecessitats educativesespecials,procedènciessocioeconòmiquesdesfavoridesiuncontextmulticultural.Aquestsfactorsfanquesiguiessencialadoptarmetodologieseducativesquenotan solsatenguinladiversitatsinóquetambémotiviniinvolucrintotselsalumnesenelprocés d’aprenentatge.

Eltreballperprojectespermetalsestudiantsaplicarelsseusconeixementsensituacionsreals isignificatives,demaneraqueesfomentaunacomprensiómésprofundadelsconceptesi unamésgranimplicacióenelpropiaprenentatge.Aquestenfocamentpromoueldesenvolupamentdecompetènciestransversalscomlacol laboració,lacomunicació,elpensament críticilacreativitat.

Peral’equipdedocentsqueparticipenenaquestprojecte,fermatemàtiquessignificamolt mésqueensenyararesoldreoperacionsiequacions.Implicaajudarelsestudiantsadesenvoluparunacomprensióprofundaifuncionaldelsconceptesmatemàtics,aplicant-losa situacionsrealsiinterdisciplinàries.Fermatemàtiquesenaquestcontextvoldirfomentar elpensamentcríticilaresoluciódeproblemes,ipertantelfetdepromourelescapacitats analítiquesideraonamentlògic.Tambésuposacol¨laborard’unamanerainterdisciplinària, integrantlesmatemàtiquesambciència,tecnologia,enginyeriaiarts.

2.Desenvolupament

Enelprojecte Viatgeinterplanetari estreballenelselementsdel’univers,il’estudisecentra enelsistemasolar.Lesactivitatsdematemàtiquesestandissenyadespertreballarlesunitats delongitudd’unamaneraproperaipràctica.Enunprimermoment,elsalumnesmesuren objectesquotidiansdinsiforadel’aula,fancanvisd’unitats,ifinalmentapliquenconceptes d’escalaifactorsdeconversió.

L’alumnattédosencàrrecsprincipals:

A.Determinarlesdistànciesdelsplanetesdel sistemasolarilessevesdimensions,plasmant aquestainformacióenunamaquetaaescala.

B.ConstruirunabaseaMartperalatripulaciód’HypatiaMars,1 ambl’objectiuquelahumanitats’hipuguiestablird’aquíaunsanys.

Aquestesactivitatstenenencomúdiversoselementsicriterisqueenguieneldisseny:

A. Contextualitzaciópràctica:Ambduestasquesesbasenenaplicacionspràctiquesdels conceptesmatemàtics.Elsalumnestreballenambmesuresrealsiprojectesconcrets,que fanqueperaellsl’aprenentatgesiguiméssignificatiuirellevant.

B. Interdisciplinarietat:Lesactivitatsintegrendiversosàmbitsdelconeixement.Elprojecte combinamatemàtiquesambciències,tecnologiaienginyeria,demaneraqueelsestudiantspodenveurecomesrelacionenis’apliquenconjuntamentlesdiferentsdisciplines.

C. Creativitatiinnovació:EnlaconstrucciódelamaquetailabaseaMart,esfomentala creativitatilainnovació,jaqueelsalumneshandepensarforadelsesquemesconvencionalsiexplorarnovesidees.

D. Autonomiairesponsabilitat:Lesactivitatsimpulsenl’autonomiadelsestudiants,jaque handeprendredecisionssobrecomabordarlestasquesigestionarelsrecursos.Això fomentaunsentimentderesponsabilitaticonfiançaenlessevespròpiescapacitats.

L’activitatdelamaquetadedistànciesalSols’inspiraenmaterialsirecursosdelprograma NetworkforAstronomySchoolEducation2 (NASE),entitatquepromocionaidonaeinesper treballarl’astronomiaaprimàriaiasecundària,iconcretamenteneltallerPlanetesiexoplanetes,elsautorsdelqualsónRosaM.Roser,HansDeegiRicardoMoreno(AvilésiDeeg, 2004).

Laideadeferunamaquetasurtdelprojecte«SeguimentdelamissióHypatia».Enaquest programa,lesdonescientífiquesllancenel reptedeconstruirunamaquetad’unamissióa Mart,oferintuncontextinspiradorirealistaperal’aprenentatgeinterdisciplinari.

2.1. Com ens organitzem?

Elprojecteesdesenvolupadurantquatrehoressetmanals,distribuïdesendosdiesambsessionsdedueshorescadadia.Undelsdies,lesdueshoresesfandemaneraconsecutiva, mentrequel’altre,lessessionsestanseparadesperl’esbarjo.Hihauntotaldequatregrups classe,ambcincprofessorsimplicatsenelprojecte,dosprofessorsdeciències,undetecnologia,undematemàtiques,undevisualiplàsticaielprofessord’orientació.Lesclassesesfan simultàniamentatotselsgrups(85alumnesentotal).

Acadagrupclassel’alumnatesreparteixendiferentsequipsdetresoquatrealumnes,cadascundelsqualss’inventaunnomrelacionatambelprojectequeelsidentifiqui.Cadaalumne/a téelseupropidiarideviatge,onreculllesreflexionssobreelquevaaprenent,anotales respostesalespreguntesqueelprofessoratfaperiòdicament,ielaborapetitsresumsiesquemes.Escombinenactivitatsindividualsidegrup,iesfomentatanteltreballcol laboratiu coml’aprenentatgepersonalitzat.

2.2. Activitats

Elprojecte Viatgeinterplanetari inclouunseguitd’activitatsseqüencialsdissenyadesper aprofundirenelconeixementdelsistemasolar idesenvoluparhabilitatscientífiquesimatemàtiquesentreelsalumnes.Lesactivitatssónlessegüents:

2.https://www.naseprogram.org/.

A. Construcciódelamaquetadelsistemasolaraescala:Elsalumnesconstrueixenuna maquetadelsistemasolaraescalatotconsiderantlagrandàriadelsplanetesiladistànciaquehihaentreells.Aquestexerciciproporcionaunacomprensiófonamentaldels conceptesd’escalaiproporció,aspectescrucialsperaprojectesposteriors.

B. Estudidelescaracterístiquesdelsplanetes:Cadagrupd’alumnesaprofundeixenles característiquesd’unplanetaespecífic.Després,hand’explicaraquestescaracterístiques alarestadelaclasse,iaixíesfomental’aprenentatgecol¨laboratiuil’habilitatdecomunicaciócientífica.

C. Investigaciósobrelavidaenaltresplanetes:Elsalumnesinvestiguenquinsplanetes podriensustentarvidabasant-seenlessevescaracterístiques.Aquestprocésimplicaaplicarcriteriscientíficsperavaluarl’habitabilitatplanetàriaidesenvoluparaixíelpensament críticileshabilitatsd’investigació.

D. EnfocamentenMart:UncopidentificatMartcomelplanetaambméspossibilitatsd’acollir vida,elsalumnesinvestiguenlescondicionsadversesquehitrobarien,comaralamanca d’aigualíquida,lestemperaturesextremesil’atmosferafina.Hand’explorarmaneresde superaraquestsreptes,ipertantfomentarlainnovacióilaresoluciódeproblemes.

E. ConstrucciódelamaquetadelabaseaMart:Finalment,espresentaelreptequeplantejalatripulaciód’HypatiaMars,crearunamaquetadecoms’imaginenunabasetripulada aMart,perquèlahumanitats’hipuguiestablird’aquíaunsanys.Aquestexercicicombina totselsconceptesapresos:aplicaelsconeixementsd’escalaiproporció,delescondicions ambientalsdelplanetailessolucionstecnològiquesperalasupervivènciahumana.

Aquestesactivitatsesdissenyennonomésperensenyarcontingutscientíficsimatemàtics, sinótambéperdesenvoluparcompetènciesclaucomlacol laboració,lacomunicació,elpensamentcríticilacreativitat.

2.3. Com treballem les matemàtiques?

Abansdecomençaratreballaramblesescalesesfanunseguitd’activitatspreparatòries (figures 1 i 2),paral¨lelesalprojecte,amblesqualsl’alumnatrepassalesunitatsdelongitud, prenmesuresambregleocintamètricaipracticaelscanvisd’unitats,aixíestreballaelsentit numèricidelamesura.

L’activitatdelafigura 1 ésméssenzillailafanprenentmidesamblacintaoelregle.

Lespartsretallablesdelesduesactivitatsnoestandisponiblesal’inici,leshiproporcionem alfinalpertalquecomprovinsielquehanescritéscorrecte.

L’activitatdelafigura 2 contéelementsquerequereixennombresgrans,distànciaentreplanetes,opetits,dimensionsdelacèl¨lula.

Figura1.Activitat1pertreballarlesunitatsdelongitud.

Figura2.Activitat2pertreballarlesunitatsdelongitud.

Lamotivaciódelaproblemàticasorgidaenlesfitxesanteriorsdonapeuaexplicarelsfactorsdeconversióiesfal’activitatdelafigura3(enblauhihalesrespostescomaguiaper aldocent).Enaquestaactivitatestreballenelsfactorsdeconversióutilitzantmesuresque l’alumnatconeixdelavidaquotidiana.Elsestudiantsreflexionensobrequinaéslaunitatde longitudmésadequadaperacadasituació,iaixídesenvolupenunacomprensiópràctica iaplicadadelsconceptesdeconversiód’unitats.Delssabersdelcurrículum,estreballael sentitdelamesura.

Figura3.Activitatpertreballarelsfactorsdeconversió.

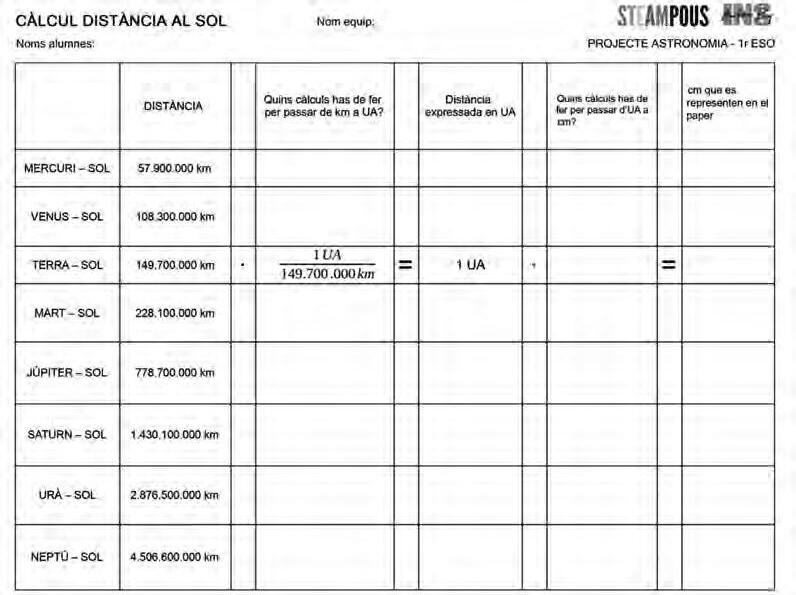
Figura4.Activitatpercalcularlesdistànciesencentímetres.

Enaquestaactivitatestreballaelconcepte demarged’errorenrelacióambelsdecimals. Elsalumnesaprenenquel’errorprocedeixdelaprecisiódel’instrumentdemesura,comla cintamètrica,quenoméspermetprendremidesfinsauncertgraudedetall(perexemple, finsalmil¨límetreocentímetremésproper).Aixògeneraunadiscussióal’aulasobrequants decimalsincloureenelresultaticomaquestnombreésdeterminatperl’aparellqueesfa servir.

Elsestudiantsreflexionensobrel’impacted’aquestmarged’errorquanconverteixenunitats (perexemple,decentímetresaquilòmetres),onpetitesvariacionsenelsdecimalspoden modificarelresultatsignificativament.S’estableixque,totiquehipodenhavermúltiplesrespostesvàlides,l’errors’hadeconsiderarijustificar,entenentquelaprecisiódelsdecimalsés condicionadaperl’instrument,nonoméspelcàlcul.Finalment,eldocentvalidalesrespostes tenintencompteaquestsfactors.

PeralaconstrucciódelamaquetahandecalcularaescalaladistànciaalSoldecadaplaneta, iperguiarl’alumnatenaquestscàlculsse’lsdemanaquefacin

l’activitatdelafigura4,oncalculenladistànciaencentímetresalSoldecadaplanetaaplicant l’escalaindicada.PrimerpassenelskmaUAiseguidaments’indicaque 1 UAserà 15cmal paper.

Seguidamentcomencenaconstruirlamaquetaaescalasobrepaper kraft,d’unscincmetres delongitud,detotselsplanetesdelsistemasolar,marcantelspuntsonescol¨locaràcada planeta.

Figura5.Activitatpercalcularelradiieldiàmetreencentímetresdecadaplaneta.

L’activitatdelafigura5esfaperguiarelsestudiantsal’horadecalculardequantscentímetresseràelradi,odiàmetre,decadaplaneta,apartirdelsradisexpressatsenquilòmetres, aplicantl’escalaindicadapelprofessorat.

Finalmentconstrueixen,utilitzantelcompàsilestisores,elsplanetesen 2D,peranar-los col¨locantsobreelpaper kraft.

Ambaquestamaquetal’alumnatvisualitzaipren consciènciadelesdistànciesentreplanetes ielseusradis.

Elprofessoratvaoptarperutilitzarduesescalesdiferentsperalarepresentaciódelsistemasolaralamaqueta,unaperalesdistànciesentreelsplanetesiunaaltraperalsradis planetaris.Aquestadecisióesvaprendreperquè,sis’utilitzéslamateixaescalaperalsdos elements,lesproporcionsserienimpracticables.Elsplanetesserienmassapetitsperservisiblessenseunalupa,obélamaquetahauriadeserd’unesdimensionsdesmesuradesper inclouretantlesdistànciescomelsradisdemaneraproporcional.Així,l’úsd’escalesdiferents permetqueelsalumnesvisualitzintantlesenormesdistànciesentreelsplanetescomles sevesdimensions,senseperdrelacomprensiódelesproporcionsreals.

Ambaquestaactivitatfinals’hatreballatlacompetènciamatemàticaCE1, 3 jaques’elabora unarepresentaciómatemàticaeficaç,ambrecursosmanipulablesquecondueixinalacom-

3.Competènciaespecíficamatemàtica 1:Interpretar,modelitzariresoldresituacionsdelavidaquotidiana pròpiesdelesmatemàtiquesid’altresàmbitsdelconeixementaplicantdiferentsestratègiesiformesderaonament perexplorarprocedimentsiobtenirsolucions.

prensiódesituacionsdelavidaquotidiana,coméselcasd’establirladistànciaentreels planetesdelsistemasolarilesmidesqueelscorresponen.

Caldestacarqueelsistemaplanetariésunarepresentacióen3D,peròquanesfal’estudi,les longitudsdelsradisespodenvisualitzaren 2D.Lesmesuresambreglespermetentreballar enunadimensió.Lariquesad’aquestenfocamentésqueambduesmagnitudsd’unasola dimensióespotmodelitzarunarealitattridimensional.Amés,eldiàmetre,quegeneralment ésconsideratunamesurasecundària,esconverteixenlamesuraprincipalenllocdelradi.

Pertancarl’activitatescol loquentoteslesmaquetesdecostat,iescomentenelspuntsfortsi detallsamillorar.L’alumnatmateixésquifalesreflexionsiprenconsciènciasialgunplaneta quedadesplaçatdelsplanetesdelscompanys,coms’observaenlafotodelafigura7.

Figura6.Fotografiesdelprocés.

Figura7.Fotografiadelesdiferentsmaquetes.

Peracabarl’activitat,l’alumnatrevisalesmaquetesiseleccionalaqueconsiderenmésben elaboradadecadaclasse.Aquestadecisióesprendemaneraconsensuada,tenintencompte laprecisiódelscàlculs,lacol locaciócorrectadelsplanetesilacuraenlapresentacióvisual. Lamaquetaescollidaespenjaalaparetdecadaclassecomareconeixementdeltreballben fet,itambéperquèserveixicomareferènciaperafutursprojectesidiscussionsal’aula.

3.Conclusions

Elprojecte Viatgeinterplanetari hademostratserunaexperiènciaeducativaenriquidorai motivadoraperal’alumnat.Atravésdelaconstrucciódemaquetesaescaladelsistemasolar id’unabaseaMart,elsestudiantshanadquiritunacomprensióprofundadelsconceptes d’escala,proporcióifactorsdeconversió,aixícomdelescaracterístiquesilescondicionsdels diferentsplanetes.

Aquestprojectehafomentatelpensamentcríticilaresoluciódeproblemes,ihaimpulsat elsalumnesaaplicarelsseusconeixementsteòricsasituacionspràctiques.Laintegració interdisciplinàriadeSTEAMhaproporcionatuncontextrealistaiaplicatperal’aprenentatge totfacilitantlacomprensiódelainterconnexióentreaquestesdisciplines.

Pelquefaalesmatemàtiques,quesovintsuposenunrepteperamoltsalumnes,elprojecte haofertoportunitatsdetreballaraquestsconceptesd’unamanerapràcticaiaplicada.Toti així,algunsalumneshantrobatdificultatsambelsconceptesd’escalaiproporció,itambé ambelsfactorsdeconversió.Aquestesdificultatshanposatdemanifestlanecessitatde proporcionarméssuportindividualitzatirecursosdidàcticsperajudar-losasuperaraquests entrebancsiconsolidarelsseusconeixementsmatemàtics.

Totiqueeltreballcol laboratiuhaestatclauperalprojecte,s’hantrobatdiversosentrebancs. Algunsalumneshantingutdificultatspertreballarengrup,generanttensionsiconflictes,i d’altresnohanparticipatprouactivament.Aixòhaevidenciatlanecessitatdereforçarleshabilitatsdetreballenequip,degestionarelsconflictesid’assegurarunaparticipacióequitativa detotselsmembresdelgrup.

4.Valoraciófinal

Elprojecte Viatgeinterplanetari haestatunaexperiènciamoltpositivatantperal’alumnat comperalprofessorat.Lacol laboracióentredocentsdediferentsdisciplineshaenriquitel procésd’aprenentatgeambunavisióglobalipràcticadeltreball.Cadaprofessorhaaportat lasevaexperiènciaenelseuàmbit,iaixòhapermèsdonarunarespostaméscompletai personalitzadaalesnecessitatsdelsalumnes.

Totiquelacoordinacióentreprofessorsilagestiódeltempshansuposatunrepte,elsbeneficisdeltreballenequiphansuperatlesdificultats.Aquestaexperiènciahademostratque elsprojectesinterdisciplinarisnonoméspotencienl’aprenentatgedelsalumnes,sinóquetambépromouenelcreixementprofessionaldels docents.Animemelprofessorataendinsar-se enprojectesinterdisciplinariscomaquest,jaqueofereixenuncontextd’aprenentatgemotivadoripràcticperal’alumnat,alhoraquepermetencrearunaxarxadesuportentreels professorsquefacilitalasevatascaeducativailafamésgratificant.

Bibliografia

[1]Avilés,J.A.B.iDeeg,H.J.(2004).«EscueladeInviernosobrePlanetasExtrasolares.IACnoticias». RevistadelInstitutodeAstrofísicadeCanarias,(1),4-7.https://www.iac.es/system/fi les/documents/2019-02/Winter_School_2004.pdf

Lapastisseria,laguerra delesgalàxiesiles matemàtiques

JordiArnauiBallestar

Catedràticjubilatd’EnsenyamentSecundari enl’especialitatdematemàtiques jarnau12@xtec.cat

Resum Abstract

Totiquemoltesvegadesnoens n’adonem,estemenvoltatsde matemàtiques.Enpodemdetectarenels estrismecànicsielectrònicsqueutilitzem habitualment;enlesformesgeomètriques quetenenalgunsproductesd’alimentació queconsumim;enelsefectesespecialsde lespel¨lícules;etc.Enaquestarticleel nostreobjectiuésmostrarles matemàtiquespresentsendosobjectes queenssónplenamentfamiliars:el productedepastisseriaconegutcoma berlinailafamosaEstrelladelaMortdela sagadepel¨lículesde Laguerradeles galàxies.Concretament,enscentrarema calcular-neelsvolumsutilitzant coneixementsmatemàticsal’abastdels alumnesdesegondebatxilleratcientífic. Alfinaldecadaapartatsuggerimactivitats complementàriesquepermeten interconnectardiversespartsdeles matemàtiquesiaixípodertenirunavisió globald’aquestaciènciainoveure-la noméscomunconjuntdetècniques individualssensecapmenaderelació.

Eventhoughweareoftennotawareofit, mathematicsisallaroundus.Itcanbefound inmanymechanicalandelectronicdevices thatweusedaily,inthegeometricalshapeof somefoodproducts,incinematicspecial effects,andsoon.Inthispaper,ouraimisto showsomeofthemathematicsthatcanbe foundinacoupleoffamiliaritems,namely thepastryproductknownasadoughnut, andthefamousDeathStarfromtheStar Warssaga.Wewillfocusoncalculatingtheir volumeusingamathematicalfoundations wellknownbypost-compulsorysecondary schoolstudents(scientificbranch).Attheend ofeachsection,somecomplementary activitiesaresuggestedasawayof interconnectingelementsofthe mathematicstogiveanoverallviewofthis science,ratherthanjustpresentinga collectionofunrelatedtechnicalskills.

1.Introducció

Lamancadetempsilanecessitatd’abastartotuntemarifaquesovintestreballinomésla partmecànicadelesmatemàtiquesiquese’ndeixidebandal’aplicaciópràctica,ésadir, laresoluciódeproblemesdelavidarealcomunaaplicaciódelsconeixementsmatemàtics adquirits,elques’anomenamodelització.Aquestamancançafaqueelsalumnesperdinde vistal’estretarelacióquelesmatemàtiquestenenamblarealitatqueelsenvoltaidonalloc, moltesvegades,alapregunta«iperaquèserveixenlesmatemàtiques?».

Ferqueelsalumnesentenguinlasevautilitatilapuguinexperimentardeprimeramà,per exemplesentcapaçosd’utilitzarlesmatemàti quespermodelitzarsituacionsquotidianes,pot ajudaraferquedeixindeserconsideradesunamatèriaàrida,difícilisensesentitiquese’n comenciaveurelabellesa.

Elcurrículumdematemàtiquesdesegondebatxilleratcientíficitecnològicinclouelcàlcul deprimitivesilessevesaplicacionsenelcàlculd’àreesivolumsderevolucióalvoltantde l’eixd’abscisses.Aquestarticleproposadosexercicisquepodenserunpetitexempledemodelitzaciómatemàticaenelcontextdelcàlculdeprimitivesiendiversesaplicacions,uns exercicisquepodenserunabonacloendad’aquesttemajaques’utilitzentotsicadaundels contingutsdesenvolupats.

2.Modelitzanteldònut

Unadelesfiguresmésconegudesdinsdelageometriaéseltor,unasuperfíciederevolució generadaperuncerclequegiraalvoltantd’uneixqueliéscoplanari.

Enl’àmbitdelapastisseriatenimelseuequivalentenlaberlina,elpastissetanomenatpopularmentdònut.

Quin és el volum d’un dònut?

Respondremaaquestapreguntacalculantrealmentquinéselvolumd’untoriaplicantla fórmulaobtingudaalcasdeldònut.

Elstreselementsquecaltenirencomptesón:

1.L’eixderotació,quecomhemdithadeseruneixcoplanariambelcerclequegiraalseu voltantpergenerareltor.

2.Elradi r delacircumferènciacentral,quecorresponalforatdelmig(figura 1).

3.Elradi R delacircumferènciaquegiraalvoltantdel’eixderotacióqueéscoplanariamb ella(figura 2).

Escollimcomaeixderotaciól’eixOXicomacentredelacircumferènciaderadi R elpunt quetépercoordenades p0,R ` r q.D’aquestamanerapodemcalcularelvolumdeltorsifem giraralvoltantdel’eixOXlacircumferènciaderadi R,centradaenelpunt C “p0,R ` r q ia l’interval r´R,Rs. 1

1.Espodenescolliraltressistemesdereferència.Deixemallectorlapossibilitatd’exploraraltresopcions.

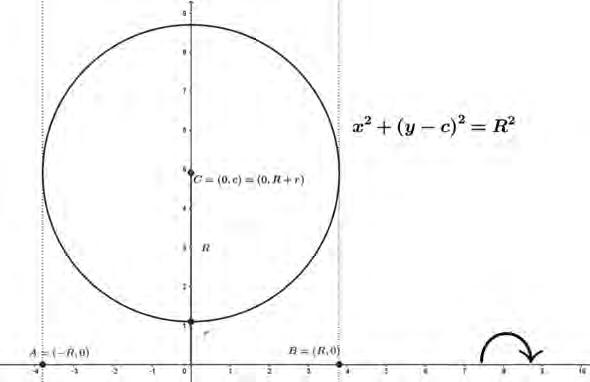
Sidiem c “ R ` r ,aquestacircumferènciatéperequació x 2 `py cq2 “ R2 .

Siaïllemlavariable y del’expressióanterior: y “ c ˘ ?R2 x 2

Figura1

Figura2

Figura3

D’onobtenimlesduesfuncionsquedeterminenelspuntsd’aquestacircumferència:

y “ c ` ?R2 x 2 peralspuntsdelameitatsuperior

y “ c ?R2 x 2 peralspuntsdelameitatinferior

Elvolumbuscatelpodemcalcularrestantelvolumderevoluciógeneratperlapartsuperior delacircumferència(figura4)ielvolumderevoluciógeneratperlapartinferiord’aquesta (figura5),totsdosal’interval r´R,Rs.

Partsuperior:

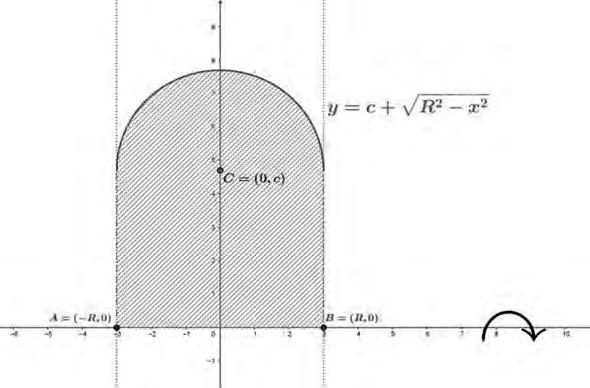
Partinferior:

Sisolapemgràficamentlesduesaccionsanteriors(figura6)ésclarqueelresultatd’aquesta restaseràelvolumderevoluciógeneratperlacircumferènciaderadi R icentreenelpunt p0,R ` r q engiraralvoltantdel’eixOXal’interval r´R,Rs.

Figura4

Figura5

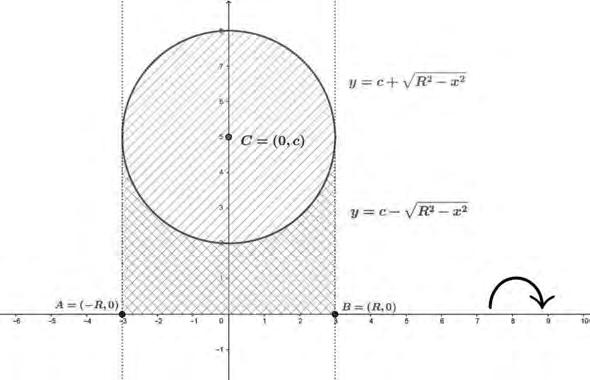
Així,lafórmuladelvolumbuscat seràdonadapelcàlculsegüent:

Isitenimencomptelasimetriadelproblema,ésequivalenta:

Agrupantlesduesintegralsenunatenim:

Aquestaúltimaintegrallaresoldremfentelcanvitrigonomètric:

Essentelsnousextremsd’integració:

Figura6

Amblaqualcosa:

Aixídoncs,tenintencompteque c “ R ` r ,elvolumdeldònutmodelitzatpeltorés:

3.Suggerimentsireflexionsfinals

Primerdetot,espotpreguntaralsalumnessiundònutésrealmentuntor,d’aquestamanera se’lspotsferentendreladiferènciaquehihaentremodelmatemàticirealitat.

Laprincipaldificultatquepodentenirelsestudiantsperresoldreaquestproblemaéscom començaraplantejar-lodemaneraquelasevaresoluciósiguialméssenzillapossible,ésa dir,comescollirunseixosdecoordenadesonpodersituar,delamillormanerapossible,l’eix derotacióilacircumferènciaapartirdelaqual,iperrotacióalvoltantd’aquesteix,esgenera eltor.

Altresdificultatspodenserlaresoluciód’algunesdelesintegralsqueespresentenenel procésdelcàlculdelvolum,jaquepressuposenunsconeixementssobrecanvisdevariable ideresoluciód’integralstrigonomètriquesmoltespecífics.Calferespecialatencióacomel canvidevariablemodificaelsextremsd’integració.

Comaaplicaciópràcticadelmodelmatemàticdesenvolupat,espodenrepartirunsquants dònutsentreelsestudiantspertalqueprenguinlesmesuresnecessàries(aconsellablemesurarelsdosdiàmetresperdesprésobtenirelsradis)percalcularelseuvolumi,apartir d’aquestesdades,ferunpetitestudiestadístic.Aquestestudielpodemorganitzarendues parts:

1.Comprovarsihihacorrelaciólinealentreelsdosradis R i r .

2.Difícilmenthihauràdosvolumsiguals(espotreflexionarambelsalumnesperquèpassaràaixò)peròésbencertque,perraonsdecontroldequalitat,elproductehadetenir unaformaiunvolumsemblantentoteslesunitatsi,enmitjana,aquestvolumhauriade serproperaunvalorteòricqueéslamitjanapoblacional.Potserinteressantcalcular,a partirdelamostra,unintervaldeconfiançaperaaquestamitjanapoblacional.Comque estractademesures,podemsuposarquelesdadesprovenentotesd’unapoblacióquesegueixunalleiNormal.

Recordemqueunintervaldeconfiançad’unparàmetrepoblacionalésunintervalnumèricconstruïtapartird’unamostra,elqualcontéelvalorreald’aquestparàmetreambuna probabilitatqueanomenemnivelldeconfiança.

Perferaquestestudicaltreballarambproductesquesiguindelmateixtipusidelamateixamarcacomercial.Ambl’experiènciademesuresfetespelsalumnesal’aula,unapossible mostradelesdadesobtingudesés:

Onelsradisdelescircumferènciessónexpressatsencentímetresielsvolumsencentímetres cúbics.

Ambaquestesdadess’obté:

X V “ 82,78 sV “ 0,97

ambuncoeficientdecorrelacióentre r i R de ρrR “ 0,6287.

Elnúvoldepunts,amblarectaderegressiócorresponent,és:

r=0,5802R-0,2377

Valors de r

1,31,351,41,451,51,55

Valors de R

Figura7

Espotraonarambelsalumnesperquèlacorrelaciónoésmésaltamostrantlespossibles fontsd’error:mesurespresesambpocaprecisióocura,nodeixendeserproductesindustrials obtingutsapartird’unmotlleambtoteslesimprecisionsqueaixòcomporta;lescircumferènciesnosóncircumferènciesperfectes...

Quantal’intervaldeconfiançaperalamitjanapoblacionaldelsvolums,elpodemcalcular ambunnivelldeconfiançadel 95%,ésadir, 1 α “ 0,95.Comquelamostraéspetita(10 dades)hauremd’utilitzarladistribuciót-Studentamb n 1 “ 9 grausdellibertat:

Sisubstituïmelsdiversosvalorss’obtéquel’intervaldeconfiançaperalamitjanadelsvolums delsdònuts,ambunnivelldeconfiançadel 95%,és:

Peracabar,iapartird’aquestsresultats,podríemestudiarquineshauriendeserlesdimensionsdelsembolcallsd’aquestsproductesdepastisseriapertaldegarantirquesempreels podremempaquetar.

4.Maytheforcebewithyou

Totselsfansde Laguerradelesgalàxies sabenquel’Estrelladelamortésunaarmadedestrucciómassiva,ladestrucciódelaqualésl’objectiuprimordialdelesforcesrebelsenalguns capítolsdelasaga.

Laformaquetéaquestaarmaéslad’unaesferadelaquals’haeliminatunpetitcasquet esfèricpertanyentaunaaltraesferaderadimoltméspetit,formantaixíunorificiqueésper onl’Estrelladelamortdisparaelseuraigdestructor(figura8).

Quin és el volum de l’Estrella de la mort?

Enaquestcaselselementsquecaltenirencomptesón:

1.Elradi R del’esferagran.

2.Elradi r del’esferapetitadelaqualestreuelcasquetesfèric.

3.Quelesduesesfereshandesersecants.

Persimplificarelproblema,podemsuposarquel’esferaderadi R espotgenerarfentgirar alvoltatdel’eixOXunacircumferènciadelmateixradiicentradaal’origendecoordenades O “p0, 0q,iquel’esferaderadi r espotgenerarfentgiraralvoltantdel’eixOXunacircumferènciadelmateixradiicentradaenelpunt C “pa, 0q on a ésladistànciaentreelscentresde lesduescircumferències.

Elvalordelparàmetre a nopotserqualsevol,jaquecomquelesduesesfereshandeser secantss’hadecomplir:

Figura8

Lesequacionsdelesrespectivescircumferènciessón:

C1 : x 2 ` y 2 “ R2

C2 : px aq2 ` y 2 “ r 2

Gràficament:

Elvolum V queestembuscants’obtésirestemdelvolum V1 ,corresponental’esferaderadi R, elvolum V2 generatengirarlaintersecciódelesduescircumferènciesalvoltantdel’eixOX.

Laprimerapartd’aquestainterseccióésdeterminadaperunarcdelacircumferència C2 : px aq2 ` y 2 “ r 2 ilasegonapartperunarcdelacircumferència C1 : x 2 ` y 2 “ R2 .

Figura9

Figura10

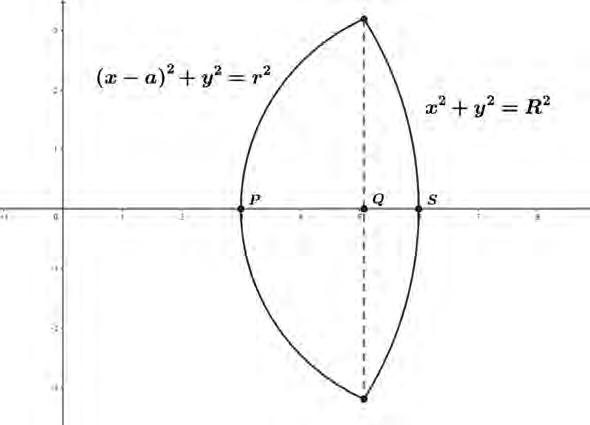
Pertantcaldràcalcularelvolum V2 enduesparts,laprimeraessentelvolumobtingutper larotaciódelapartpositivadelprimerarcentrelesabscissesdelspunts P i Q,ilasegonael volumobtingutperlarotaciódelapartpositivadelsegonarcentrelesabscissesdelspunts Q i S.Aquestespartspositivessón,respectivament,lesfuncions:

Necessitemcalcularlesabscissesdelstrespunts P,Q i S.

L’abscissadelpunt P “ C2 X OX

L’abscissacorresponentalpunt P és xP “ a r .

L’abscissadelpunt

L’abscissadelpunt S és xS “ R.

Aixídoncselvolumdel’Estrelladelamortserà:

;amblaqualcosa,sidesenvolupem l’expressióanterior,obtenim:

Pertant:

Recordemque

Aixídoncs:

Ésadir,elvolumdel’Estrelladelamortserà:

5.Suggerimentsireflexionsfinals

Comenelproblemadeldònut,laprimeradelesdificultatsambquèestrobaranelsalumnes enintentarresoldreaquestproblemaéselseuplantejamentinicial,ésadir,composicionar lesduescircumferènciesenunseixosdecoordenadesdemaneraqueelsparàmetres R,r,a siguinfàcilmentcontrolables.

Ladificultatprincipal,però,lapodentrobarenlaquantitatilacomplexitatdelscàlculs(llargs ifeixucs)uncoplesintegralsjas’hanresolt.Peracabarelproblemanon’hihaprouamb aplicarBarrow,calunamicadecàlculalgebraicpertrobarlafórmulasimplificadadelvolum. Siesconsideraqueésunatascacomplicadaperalsestudiants,se’lspotdonarlaresposta finalideixareldesenvolupamentdelscàlculscomunaactivitatforadel’aula;obéespot plantejarqueobtinguinlasolucióambdiferentstipusdeprogramari,generantaixí outputs diferentsquepermetenrealitzarigualmentun treballdemanipulacióalgebraicaperarribar alaconclusióquetoteslesexpressionssónequivalents.

Perutilitzaraquestmodelespotdemanarals alumnesqueproposindiversosvalorsperals paràmetres R,r i a amb R r ă a ă R ` r ,observinquinaspectetél’Estrelladelamort ambaquestsvalorsiencalculinelvolumcorresponent.Tambéespotobservarquintipus d’Estrelladelamorts’obtésielvalorde a ésdevalorspropersalsextrems R r i R ` r .

Concretament,si a “ R ` r obé a “ R r podemcomprovarquenohihauriaEstrelladela mort:lesduescircumferènciesserientangentsexteriorsenelprimercas(figura 11)itangents interiorsenelsegon(figura 12).

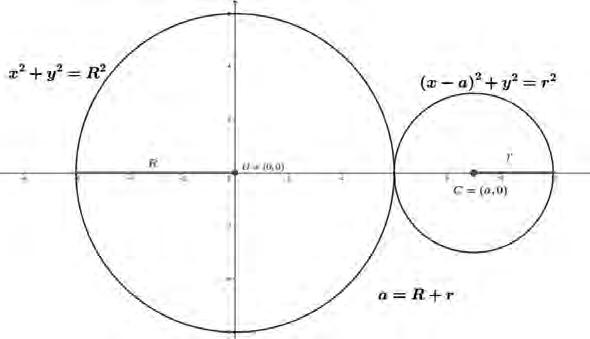
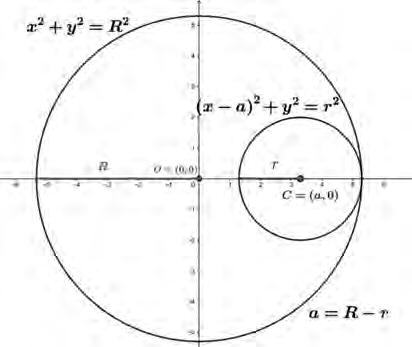
Comaaplicaciócomplementària,potsermoltinteressantferunapetitaimmersióenlageometriarelacionantelsdiversosvalorsquepodenadoptarelsparàmetres R,r i a amblaposició relativadeduescircumferències.

Jahemvistquèpassaenelscasos R r ă a ă R ` r :lescircumferènciessónsecants; a “ R r :lescircumferènciessóntangentsinteriors;i a “ R ` r :lescircumferènciessóntangents exteriors.

Faltasaberquanlescircumferènciessóninteriors(figura 13),quanlescircumferènciessón exteriors(figura 14)iquanlescircumferènciessónconcèntriques(figura15).Enconcret,cal estudiarlessituacionssegüents:

a ă R r,a ą R ` r i a “ 0

Figura11

Figura12

Figura13

Figura14

Figura15

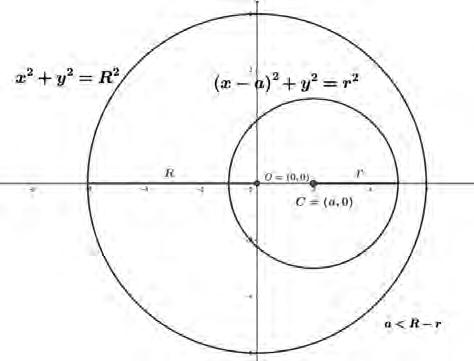
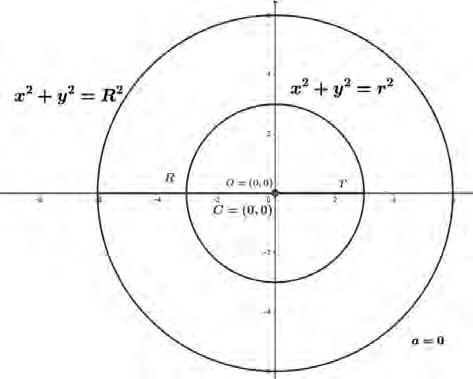
Éspossiblevisualitzartoteslespossiblesposicionsrelativesdeduescircumferènciesutilitzant, perexemple,elprogramaGeoGebra.

Lesactivitatsplantejadesenl’articlepermetenmostrarlesmatemàtiquescomuntotino comunconjuntdepartssensecapmenaderelacióentreelles,comnormalmentlesentenen elsestudiants.Ésmoltenriquidorveurequeenelprocésd’anàlisid’unproblema,ilaseva resolucióposterior,apareixendiferentsàreesdelesmatemàtiquesinterconnectades,queen aquestcasconcretsón:anàlisi,àlgebraigeometria;totesimprescindiblesdeprincipiafinal delproblemaestudiat.

Lesconstruccions geomètriqueseuclidianes. Lapapiroflèxiailes matemàtiquescartesianes1

JosepPlaCarrera Matemàticihistoriador

Resum Abstract

ElmeurenebotXandreemvademanarsili podiaexplicarquinaéslamatemàticaque hihaenlapapiroflèxia.Livaigrespondre ambaquestespàgines,quepublicael Nou Biaix enduesparts:«Lesconstruccions geomètriqueseuclidianes»i«La papiroflèxiailesmatemàtiques cartesianes».

Mynephew-grandsonaskedmetoexplainto himthemathematicsbehindorigami.I answeredhimwiththesepagesthat Nou Biaix hasdecidedtopublishintwoparts: «Euclidiangeometricconstructions»and «OrigamiandCartesianmathematics».

1.Lageometriaeuclidianadelregleielcompàs

1.1.El regle i el compàs

Comencempelcomençament.Perquèelregleielcompàs?

1.1.1.L’escola de Plató

Elsegle IV aC,Plató(427aC-347aC)2 potserforamillordirl’Escolaplatònica vafixarqueles úniqueseines queespodenacceptarenla construcciógeomètrica sónel regle [R]iel compàs

1.ComençataBarcelonael 29 d’octubrede 2023.

2.Sibéelseunomera«filld’Aristó»Αριστοκλ΄ησ,se’lconeixcomaΠλ΄ατων.Peraunabiografiadelsautors esmentats,vegeu[MT MacTutor:1994-2023].

[C] ésadir,els ginys quepodenconcórrerenlaconstrucciósónles rectes iles circumferències. 3

1.1.1a.Això,quèsignifica Significaqueels únicspunts ques’admetensónelsques’obtenen tallant duesrectes, unarectaiunacircumferència o duescircumferències.

Ésadir,encadaconstrucció s’obtéunpuntnou queesdevéunpuntacceptatenaquesta construccióienlesposteriors.

Deretruc,hosónlesrectesquepassenperdosd’aquestspuntsilescircumferènciesambel centreenundelspuntsiquepassenperl’altre.

Enlafigura 1,hiha,defet,duesmenesdefigures:

aq Enlesduesprimerescasellessuperiorsdel’esquerraveiemdospuntsi,enlescorresponentsdesota,larecta itambéelsegment ilacircumferènciaqueaquestsdospunts determinen.

bq Enlestressuperiorsdeladreta,hihaduesrectes,unarectaiunacircumferència,idues circumferències.Lesdesotamarquenelspuntsqueaquestsobjectesdeterminen,en tallar-se.

1.1.1b.Comprocedim? Percomençar,necessitemalmenysdospunts.S’acceptal’existència d’unsegmentunitat,ésadir,dospuntsqueensónelsextrems: 0 1 .Apartird’ells,esgeneren mésiméspunts: O,I,P1 ,P2 ,...,Pn ,...

Exemple1 VolemconstruirunquadratdecostatOI.

Perfer-ho, aq Hemde construir dospunts P3 i P4 demaneraqueelssegmentsd’extrems I i P3 , O i P4 ,i P3 i P4 siguinelscostatsdelquadrat.

bq Cal demostrar queelquehemconstruïtéselquevolíem.Ésadir,queelpolígon l OIP3 P4 devèrtexs O,I,P3 i P4 ésefectivamentunquadrat.

3.[Boyer:1949],nota52,p. 27.[Pla:2016],p. 256.

Figura1.Construccionsbàsiquesambregleicompàs.

Recordemladefiniciódequadrat:

Definiciódequadrat. Unquadratésunafiguralimitadaperquatresegmentsrectilinisigualsi perpendicularsdosados.4 5

Veiemelspassos aq, b)i cq quecalfer.Larestadepassossónanàlegs.

.

Pas0) Tenimelspunts O i I.

Pas a) Tiremlarecta L quepassaper O i I.[R]

Elsegment OI,d’extrems O i I,éselcostatambelqualvolemconstruirelquadrat.

Pas b) Ambcentreen I,femlacircumferència O1 quepassaper O.[C]

Aquestacircumferènciatalla L pelpunt P1 ,ques’hageneratdemaneracorrecta.Pertant, hipodemtreballar.

Pas c) Constadetressubpassos:

Subpàs c1 ) Ambcentreen O,tiremlacircumferència O2 quepassaperper P1 .[C]

Subpàs c2 ) I,ambcentreen P1 ,la O3 quepassaper O.[C]

Subpàs c1 i c2 ) Lescircumferències O2 i O3 estallenpelpunt P2 , 6 construïtcorrectament. Pertant,hipodemtreballar.7

Subpàs c3 ) Tiremlarecta L1 quepassapelspunts P2 i I.[R]

Aquestarectatalla O1 pelpunt P3 ,queéscorrecteique,pertant,podemutilitzar.

Nota1 Hemfetla perpendicular aunsegmentdonatperundelsseusextrems.

Ideterminaeldarrercostat,d’extrems P3 i I,delquadratbuscat.

4.[Pla:2018],DI 22,p.80.

5.Aquestsímbolindicaelfinald’unadefinició.

6.Sobrel’existènciad’aquestpunt,vegeulesnotes 269 i387de[Pla:2018],p.88i 113.

7.Fixeu-vosque,enrealitat,perdeterminarelpunt P2 noméscalelcompàs.

8.[Pla:2018],EI 46,p. 147-148.

8

Figura2.Construcciódequadratdecostat OI

Exercici1.Feuelspassosquefaltenpertald’aconseguirelsquatrecostatsdelquadrat.[Indicació.Elcostatquesurtdelpunt O és mutatismutandis comelqueacabemdefer:ésla perpendiculara OI pelpunt O.Elquartcostatésmoltméssimpled’obteniruncoptenimel punt P4 .Noméscall’úsdelregle.]

1.2.Elsd’Euclides Elements

Elsegle III aC,Euclides(Ε΄υκλε΄ιδησ)9 325aC-265aC)vaescriureels Elements (Στοιχεια),una delesobresmatemàtiquescabdalsdetotselstemps.

1.2.1.L’axiomàtica euclidiana

Eneltractateuclidiàesfixàl’axiomàtica delageometriagregad’acordamblesindicacions platòniquesilametodologiadelraonamentdeductiufixadaperAristòtil(Αριστοτ΄ελησ)(384 aC-322 aC).

L’autorhiestableix,abreujant,les definicions delsobjectesgeomètrics,les nocionscomunes oprincipisvàlidsenciènciaifilosofia ,iels postulats allòquehemd’admetre,sense demostració,comavertaderengeometria.

Ensíntesi,elspostulatsd’Euclideselspodemreduiraaqueststres:

Postulatdelarecta. Donatsdospunts,existeixsempreunarecta,inomésuna,que passapertotsdos. Ésadir,dospuntsdeterminenunarectaúnica

Postulatdelacircumferència. Donatsdospunts,existeixsempreunacircumferència,inomésuna,queentéuncomacentreiquepassaperl’altre. Ésadir,dos puntsdeterminenunacircumferènciaúnica.

Postulatdelesparal¨¨leleseuclidià. Donadaunarectaiunpuntexterioraella, sempren’hihaunaaltraquepassapelpuntdonatiésparal lelaaladonada ésa dir,quenolatalla.

Lageometriaqueaplicaaque stspostulatss’anomena geometriaeuclidiana.Éslaque aprenemal’escolailaquetreballaremaquí.

Lanegaciódelpostulatdelesparal¨lelescomportaduespossibilitats:

Postulatel¨ lípticdelesparal¨ leles. Pelpunt no éspossibletirarcaprectaparal lela aladonada.Lageometriaqueaplicaaquestpostulats’anomena geometriael¨líptica.

Postulathiperbòlicdelesparal leles Pelpuntéspossibletirar mésd’una recta paral¨lelaaladonada[ifinsitotinfinites].

Lageometriaqueaplicaa questpostulats’anomena geometriahiperbòlica.

Ilageometriaquenofaservircapd’aqueststrespostulatss’anomena neutral

9.[MT MacTutor:1994-2023].Vegeulanota 2 (pàgina66).Nohotornaremarecordar.

1.2.2.Els

problemes i els teoremes

UnaaltraqüestióimportantqueEuclidesrecullals Elements ésladistincióentrelesproposicions:els problemes iels teoremes

Un problema ésunaproposicióquedemana construir l’objectegeomètric.

Exempledeproblema. Construirunquadratd’uncostatdonat.

Enunproblema,comjahemindicatabans,calferduescoses:

aq Deprimer, construir l’objecte.

bq Després, demostrar quehemconstruïtelqueesdemanava.

AixíéscomprocedeixEuclidesenels Elements.Deles465proposicions, 98sónproblemes,i laresta,teoremes.10

Un teorema ésunaproposicióenlaqualesdemana demostrar unapropietatpartintdela definiciódel’objecte,lesnocionscomunesielspostulats.

Exempledeteorema. Lasumadelsanglesexternsd’untrianglearbitrariésigualaquatreangles rectes.11

1.2.2a.Unaqüestióepistemològica Enelcasdelsteoremes nocal quel’objectequetéla propietats’hagiconstruït.Ésunobjecte ideal.

L’exempledeteoremavalperal’heptàgonil’enneàgonregulars(polígonsregularsde7i 9 costats),quenoespodenferambregleicompàs.

Enelcasdelsproblemes,encanvi, cal construirl’objecte.Ésunobjecte real,ésadir, existeix.

Euclidesestableixl’existènciadelspolígonsregularsdetres,quatre,cinciquinzecostats diu coms’handeconstruiridemostraqueelshaconstruït.

I,comqueveuqueéspossibledimidiarunangle(2.1b,pàgina89),tambésónconstruïbles totselsques’obtenendoblantelnombredecostatsd’unjaconstruït.Ésadir,elsdesis,vuit, deu,dotze,setze,vint,etccostats.

1.2.2b.IntervéGauss Enspodemferlapreguntasegüent: Pregunta. N’hihamés,depolígonsregularsconstruïblesambregleicompàs?

10.Hihaunatraducciócatalanadels Elements d’Euclides,a[Pla:2018]i[Pla:2020].Enlínia,encatalà,a https://web.archive.org/web/20130901142522/http://euclides.org/menu/elements_cat/indexeuclides.htm#Llibre %20I.Lainformaciósobreelsteoremesielsproblemeslatrobareua[Pla:2018],§1.3,taules 1 2 i 1.3,p. 12-13.

11.Esbasaenelteoremaeuclidià:«Lasumadelsanglesinteriorsd’untriangleésigualadosanglesrectes». [Pla:2018],p. 12-13.Enlesgeometriesnoeuclidianes,lasumadelsanglesésméspetita(hiperbòlica)omésgran (el¨líptica)quedosanglesrectes.

Passarienmoltsseglesabansqueunjovededivuitanys,Gauss,establíselseuteorema:

Elpolígonregulardedissetcostatsésconstruïbleambregleicompàs.

Ienlasevaobra Disquisitionesarithmeticae (1801)demostra quetots elspolígonsregulars sónconstruïblesambregleicompàs.12

1.3.Variacions del regle i el compàs

Uncophemacceptatqueleseinesgeomètriquesacceptablessónelregleielcompàs,ens podemplantejaralgunespreguntes:

Pregunta. Podemferlesmateixesconstruccionsgeomètriques:

1.ambuncompàsambmemòriaqueambunsensememòria,ielregle?

2.ambuncompàsrovellatqueambundenorovellat,ielregle?

3.nomésambuncompàs?

4.nomésambunregle?

1.3.1.El regle i el compàs sense memòria

Definicionsdecompàsambisensememòria Uncompàs témemòria si,quanaixequemun delsdosextremsdelpaper,noestanca:recordaladarreradistànciaentreelsdospunts.En canvi,notémemòriasi,quanundelsdosextremsdeixadetocarelpaper,escol lapsacomsi tinguésunamolla.

Teorema. Ambdóscompassossónequivalents.

Ésadir,ambl’ajutdelregle,tantl’uncoml’altrepermetenferlesmateixesconstruccions.13

Aixòésconseqüènciadelaproposició 2 delllibreprimerdels Elements.

Proposició2. Éspossibletransportarunsegmentdonatambunextremenunpunttambédonat.

Aquestaproposiciós’estableiximmediatamentbasant-seenlaprimera.14

Proposició1. Éspossibleconstruiruntriangleequilàterdecostatdonat.

12. Disquisionesarithmeticae.[Gauss:1801].Ésuntextcomplex,lacomprensiódelqualdepènd’unsbons coneixementsprevis.Lasecció I,querecullmoltsdelsresultatsd’aritmèticaprecedents,ésmoltclaraientenedora, ilasevalecturamoltaconsellable.DisposemdelatraducciócatalanadeG.Pascual.Enaquesttext,CarlFreidrich Gauss(1777-1855)estableixqueelnombre N decostatsd’unpolígonconstruïbleambreglaicompàsésdelaforma N:“ 2m F1 Fr ,on m ě 0 iels Fk sónprimers,diferents,idelaforma Fk :“ 22k ` 1,amb k ě 0.Aquestsnombres, queesconeixenambelnomde nombresdeFermat,elsvaintroduirPierredeFermat(1607-1665)l’any 1640.Va conjecturarquetotsellserenprimers,peròl’any 1740 LeonhardEuler(1707-1783)vademostrarque F5 éscompost. Actualment,nosabemsipera m ą 5,n’hialgunquesiguiprimer.Laconjecturaaraésque,pera m ě 5,totsels Fm sóncompostos.

13.Ésevidentqueelcompàsambmemòriaté,enprincipi,méspossibilitatsquel’altre.

14.Capdelesduesdepèndelpostulatdelesparal¨leles.Sónproposicionsneutrals.

Euclidesfalesduesconstruccions ladelaproposició 1 iladela 2 ambuncompàssense memòria.15

1.3.1a.Transportd’unsegmentaunpunt D’entrada,fixem-nosenelproblemaqueproposalaproposició 2.

Problema. VolemtransportarunsegmentdonatABambunextremenunpuntCtambédonat (figura3).

Figura3.Eltransportd’unsegmentambuncompàsambmemòria.

1.3.1a1 .Ambelcompàsambmemòria Sitenimuncompàsambmemòriaivolemportar elsegment AB alpunt C (figura3),notenimcapproblema.

Construcció

‚ Punxemunapuntaenelpunt A delcompàsil’obrimfinsquel’altracaudamuntde B.

‚ Sil’aixequem,esmantéobertenaquestaposicióperquètémemòria.

‚ Elportemalpunt C .Ésadir,punxemenelpunt C il’altrapuntamarcaunpunt E [entota unacircumferènciadepossibilitats].

‚ Elsegment CE seràigualal AB [jaqueCtémemòria].

Ladificultatespresentaquanvolemresoldreaquestaqüestióambuncompàsquenoté memòria.

1.3.1a2 .Ambelcompàssensememòria Laconstruccióésunpelméscomplicada.Vegemneelspassos.16

Construcció

Pas1. Unimunextremdelsegmentdonat AB perexempleel B ambelpunt C alqual volemportar AB (figura4).[R]

Pas2.Construïmeltriangleequilàterdecostat BC , BGC .[Comveurem,hopodemfer,per laproposició 1,ambuncompàssensememòria.]

15.Comqueelcompàsd’Euclidesnotémemòria,necessitaestablirlaproposició 2

16.[Pla:2018],p.89-90

Elements d’Euclides.

Pas3. Tiremlarectaquepassaper G iperl’extrem B delsegment AB quehemtriat.[R]

Pas4. Ambcentreen B,femlacircumferència,d’arc Ň AD,quepassapelpunt A.[C]

Talla BD pelpunt D [unpuntvàlid].

Pas5. Ambcentreen G,tiremlacircumferènciaquepassapelpunt D,d’arc Ň DE .[C]

Pas6. Tiremlarectaquepassaper G ieldonat C .[R]

Tallalacircumferènciaper E [unpuntvàlid].

Elsegment CE queésiguala AB téunextremenelpunt C .Ésadir,éselsegment buscat.

Comsabemqueelsegment CE ésigualal AB?

Caldemostrar-hobasant-seenlanaturalesadelsobjectes,iaixòéselqueestableixenles definicionsilesproposicionsjaestablertes.

Definiciódecircumferència. Ésunacorbatancadaelspuntsdelaqualequidistenambunpunt donatques’anomena centre.Elssegmentsqueuneixenelsseuspuntsambelcentres’anomenen radis.Ésadir,totselsradissóniguals.

17

Definiciódetriangleequilàter. Untriangleequilàterésunafiguralimitadapertrescostats iguals.

Demostració

18

Pas1i2. Elssegments AB i BD,i GD i GE sóndosradisdelescircumferènciesd’arcs Ň AD i Ň DE . Pertant,sóniguals.[Definicióde ˝]

Pas3. Tenimque GD “ GB ` BD i GE “ GC ` CE i GB “ GC [Definicióde equilàter].

17.[Pla:2018],DI 20,p.80

18.[Pla:2018],DI 15i 16,p.79

Figura4.LaproposicióIIdels

Pas4. Sid’igualstraiemiguals,elquerestaésigualalqueresta.19

Pas5. Pertant,elssegments CE i BD sóniguals.

Pas6. Peròduescosesigualsaunatercerasónigualsentresi.20

Tenim,doncs,que AB “ BD i CE “ BD,i,pertant, CE “ AB

ProposicióI.Haquedatpendentveureque,ambuncompàsdesmemoriat, podemferun triangleequilàterdecostatdonatAB (figura5).

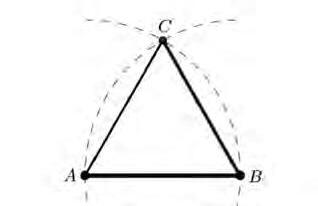
Construcció

Pas1i2. Ambcentresen A ien B iradis AB i BA,tiremsenglescircumferències.[C]

Estallenpelpunt C . 21

Pas3. Unim C amb A iamb B.[R]

Eltriangle ACB ésequilàter.

Comsabemqueésequilàter?Larespostaésfàcil.

Demostració

Perladefiniciódecircumferència, AC “ AB i BC “ BA,amb AB “ BA [éselmateixsegment]i Nc 1 [nota 20].

Ésadir, AC “ BC “ AB.Eltriangleés,doncs,equilàter.

Corol¨ lari. ÉspossibledimidiarelsegmentAB.

Construcció

Larecta CD (figura5)dimidiaelsegment AB.

19.ÉsunprincipideraonamentacceptatperEuclides:Nc3.[Pla:2018],p.85. 20.Pas6delademostracióanterior.[Pla:2018],Nc 1,p.85. 21.Nota6(pàgina68).

Figura5.LaproposicióI.

Exercici2.Demostreu-ho.22

Quèpassaria,però,sielcompàsestiguésrovellatinomésadmetésunaoberturafix.Ésadir,i sinomésadmetiaunradi?

1.3.2.El regle i el compàs rovellat

Elsegle X,elmatemàticiastrònomiraníMuhàmmadAbu-l-Wafà,conegutcomAbu-l-Wafà, 940´„998)vaescriureunobraforçaextensaenlaqualvaincloureuncapítol Sobrelesparts delageometriaquepodemferambuncompàsrovellat 23 enquèdonavarespostaafirmativaa lapregunta:

Pregunta. Éspossibleferlesmateixesconstruccionsambuncompàsrovellatiunregle?

Curiosament,aquestproblemafoutractat iestudiattambéperaltresmatemàtics.24 Alsegle XIX,elmatemàticsuísJakobSteiner(1796-1863)vapublicarunllibretdegeometria, Les construccionsgeomètriquesquepodemferambunregleiunsolcercle, 25 donantrespostaaun suggerimentdelmatemàticfrancèsJean-VictorPoncelet 1788-1867).

Elproblemad’Abu-l-Wafàespotcomplicarunamicamés.Enllocdedisposard’uncompàsrovellatquepermetfercircumferènciesd’unradifixambcentresdiversos,podemferel mateixdisposantd’unaúnicacircumferència,col¨locadaenuncentrefixiinamovibleperò conegut?26

1.3.2a.Tresconstruccionspossibles27

1.3.2a1 .Laperpendicularaunsegmentperunextremseu

Problema1. Volemtirarunaperpendicularper unextremd’unsegmentdonatAB.

Analitzemdoscasos:

1)Quanelcompàsnotémemòriai,deretruc,quanenté.

2)Quanelcompàsestàrovellat(figures7i8).

22.Comhemvist,enlesconstruccionsambelcompàs sensememòria,encadaactuació,uncopfixatel centreielpuntpelqualpassalacircumferènciaelcompàsno s’aixeca.Arabé,enactuacionsdiferentselcompàspot adoptaramplades radis diferents,quesóndeterminadespelcentreielpuntdonats.

23. Kit¯abf¯ım¯ayah . t¯ajilayhal-ş¯ani’minal-a’m¯alal-handasiyya.Vegeu,enlínia,https://shs.hal.science/ halshs-00645624,quepermetdescarregareldocumentenpdf.

24.Enlíniaahttps://shs.hal.science/halshs-00645624,quepermetdescarregareldocumentenpdf.

25. DiegeometrischenConstructionenausgeführtmittelsdergeradenLinieundeinesfestenKreises.Enlíniaa https://books.google.es/books?id=kdI3AAAAMAAJ.

26.[Martin:1998],capítol6,p. 97-105.Obé,enlínia:https://en.wikipedia.org/wiki/Poncelet%E2%80%93 Steiner_theorem.

27.[Berggren:1986],p. 92-96.Mostracincconstruccions.

Exercici3.Proveuquetotelqueespotferambuncompàssensememòriaespotferamb unquesíqueenté.

Cas1.Elcompàsnotémemòriaoenté,ésadir,éslliure.Comhemindicatalanota 2 (pàgina66),aixòhohemfetambuncompàssensememòria.Pelquefaalcompàslliure, vegeul’exercici3.

Cas2.Elcompàsestàrovellat.Nomésadmetunaobertura(figures6i7).

Construcció

Figura6.Compàsrovellat. Figura7.Úsdelcompàsrovellat.

Pas1. Tiremunacircumferènciaquedeterminaunpunt C delsegment AB [odelaseva prolongació].[Compàsrovellatambcentreen A]

Pas2. Tiremunacircumferènciaquepassaper A.[Compàsrovellatambcentreen C ]

Estallenpelpunt D.

Pas3. Tiremunacircumferènciaquepassaper A.[Compàsrovellatambcentreen D]

Pas4. Tiremlarectaquepassaper C i D.[Regle]

Tallemlacircumferènciadelpas3pelpunt G.

Pas5. Unim G i A.[Regle]

Elsegment GA ésperpendicularal AB pelpunt A,comvolíem(figura7). ♣

Exercici4. aq Proveuque,entotsdoscasos,hemaconseguitelquevolíem,ésadir,elsegmentperpendicular GA.[Indicació. Elsdosanglesqueelsegment GA determinaenlarecta AB sóniguals,segonsladefiniciód’Euclides].28

bq Valtambélademostració,sielpunt C cauenlaprolongaciódelsegment AB?

cq Ambaquestaconstrucció,podemdeterminarelpuntmitjà M de AB. 28.[Pla:2018],DI 11,p.77.

1.3.2a2 .Podemdimidiarunsegment29

Consideremunsegment AB.

Problema. Ensproposemdimidiar-lofentserviruncompàsrovellat comeldelafigura8(pàgina77).

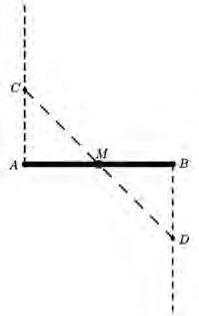
Figura8.Dimidiemunsegmentambuncompàsrovellat.

Construcció

Pas1. Pelspunts A i B,aixequemlesperpendiculars(figura 9).[1.3.2a1 ]

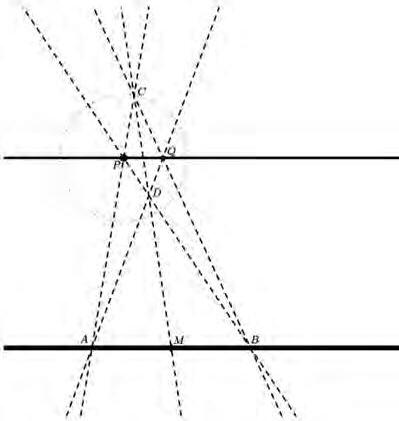
Figura9.Rectaparal lelaperunpuntexternambcompàsrovellat.

Pas2. Ambcentreenelspunts A i B,tiremlescircumferències(Noleshemdibuixat).[C rovellat]

29.Enelcorol¨laridelapàgina74,hemvistquehopodemferambuncompàslliure.

Tallemlesperpendicularspelspunts A i B per C i D,respectivament.

Pas3. Unimelspunts C i D.[Regle]

Tallemelsegment AB pelpunt M.

Aquestéselpuntbuscat.

Exercici5.Proveu-nelaveracitat.

1.3.2a3 .Laparal¨ ¨ lelaaunarectaperunpuntexterioraella.

Acabemaquestparàgraf construintlarectaparal¨lelaaunarectaquepassaperdospuntsAiB perunpuntexteriorPaella.

Hofaremnomésambuncompàsrovellat.30

Tenimunarectaquepassapelpunt A i B iunpunt P exterioraella.

Volemtirarunarectaparal lelaalarecta AB pelpunt P (figura 10).

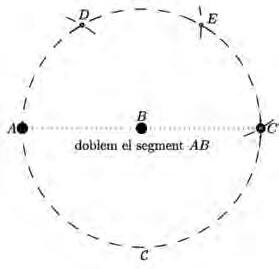
Construcció

Pas1. Unimelspuntsdelarecta AB ambelpunt P.[R]

Pas2. Triemunpunt C delarecta AP [Crovellatambcentreen P]

Pas3i4. Tiremlesrectes BC ilaquepassapelpunt C ielpuntmitjà M de AB. [Riexercici4c]

Aquestasegonatallalarecta BP pelpunt D

Pas5. Tiremlarecta AD.[R] Tallala BC pelpunt Q.

30.[Pla:2018],EI31,p. 128.

Figura10.Doblarunsegment.

Pas6. Tiremlarecta PQ.[R] Éslarectaparal¨lelabuscada.

Exercici6.Proveuquelarecta PQ ésparal¨lelaala AB.[Indicació.Apliqueuladefinicióderecta paral lela.31 ]

Nota2.SegonselgeòmetraFrancescoSeveri(1879-1961),n’hihaprouambunarcdecircumferènciadecentreconegutielregle.

1.4.El compàs sol [sense memòria]

Elsegle XVII,elmatemàticdanèsGeorgMohr(1640-1697)vaescriure Euclidesdanicus (Amsterdam, 1672),untextenquèdemostravaquetoteslesconstruccionsdels Elements d’Euclides queespodenferambregleicompàs,tambéespodenfernomésambcompàs.Malauradament,aquestpetitopusclevapassardesapercebutfinsalsegle XIX quanfouredescobert pelmatemàticitaliàLorenzoMascheroni(1750-1800)queelvapublicarenl’obra Geometria delCompasso (Pavia, 1797).Peraquestaraó,elresultatesconeixcomel teoremadeMohrMascheroni.

Enaquestaconstrucciótotselspunts,queenlesaltresconstruccionss’obtenientallantdues rectesounarectaiunacircumferència,s’hand’obtenirtallantduescircumferències,perquè, ennodisposarderegle,nopodemtirarrectes.32

Pertaldecopsar,comenelscasosanteriors,comfuncionaaquestatècnicapresentemalgunesconstruccions.

D’entrada,calqueparemesmentquearaunsegmentquedadeterminatpelsseusextrems. Elsegmentnohiésperquènotenimregle.33

1.4.1.La duplicació d’un segment donat

Problema DonatselspuntsAiB defet,elsegmentAB ,volemdeterminarunsegmentAC exactamentigualaldobledeAB.34

Tenimdospunts A i B.

Utilitzantnoméselcompàs,volemdeterminarunpunt C demaneraque(el A i C siguiel doblede(l) A i B.

31.[Pla:2018],DI 11,p.78.

32.Enpodemveureunaintroducciósenzillaa[Courant i Robbins:1941],p. 154-158,icompletaa [Martin:1998],p.53-68.

33.Nosaltres,però,dibuixaremunlíniamoltsubtildepuntsque,defet,nohiés,perquèajudaala imaginacióbasadaenelcostum.Elspuntsdonatselsrepresentemamb ‚ grossos;elspuntsqueensdisposema construiramb ˝,petits,ielquevolemtrobarperquèdeterminaelsegmentquebusquemambun ˝ mésgran.

34.Ambcompàssol,nomésconeixemelsextrems A i B delsegment,quedesignarem AB,irecordemque elsaltrespuntsdelsegment,sinos’hanconstruïtambcompàssol,nohisón.

Exercici7 aq Vegeulafigura 10 iproveuque[elsegment] A i C faeldobleque[el] A i B [Indicació.Ésfàcil.Calferelsvèrtexsdemighexàgonregularinscritenelcercledecentre B quepassaper A [oal’inrevés]iconsiderar C .]

bq Proveuque,sipodemferelsegment AC “ 2 AB “ AB ` AB,tambépodemferel AD “ AB ` nq ¨¨¨` AB,on n ésunnombrenatural.

1.4.2.El punt simètric d’un punt respecte d’un segment donat

Problema. Donatsunsegmentd’extremsAiBiunpunt arbitrariP,volemdeterminarelpuntQ, simètricdelpuntPrespectedelarectaAB.35

Construcció

Pas1i2. Ambcentres A i B,tiremlescircumferènciesquepassenper P.[C]

Estallenen Q,elsimètricde P respectede AB.

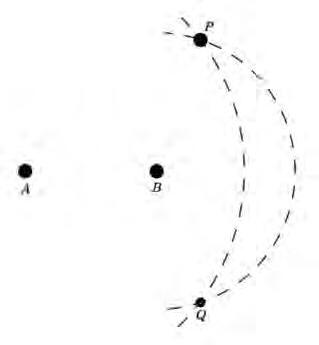
Figura11.Simètricd’unpunt P respected’unarecta AB.

Exercici8.Proveu-ho.

1.4.3.El punt mitjà d’un segment

Problema. VolemdeterminarelpuntmitjàMdelsegmentd’extremsAiB.

aq Sidisposemderegleicompàs,ésunproblemaqueesresolimmediatament.

bq Sinodisposemderegle,lescosesescompliquen,perquènopodemtirarelssegmentsd’extrems A i B,i C i D

35.Lafigura5(pàgina74)suggereixlamaneradefer-ho.Peranar-nos-hiacostumant,encertesocasions nodibuixaremelssegmentsrectilinisjaquenotenimregle.

Construcció

Pas1i2.Consideremlescircumferènciesde centres A i B quepassenper B iper A.

Estallenpelspunts C i D.

Pas3i4.Tiremelssegments AB i CD [R].

Estallenpelpunt M,queéselpuntque busquem.

Construcció

Pas1.Determinemunpunt C quefacique elsegmentd’extrems A i C siguieldobledel d’extrems A i B.[§1.4.1]

Pas2i3.Ambcentres A i C ,tiremlescircumferènciesquepassenper B i A,respectivament. [C]

Estallenpelspunts D i E

Pas4.Ambcentres D i E ,tiremlescircumferènciesquepassenper A.[C]

Estallenpelspunts A i M.

Elpunt M éselpuntbuscat.

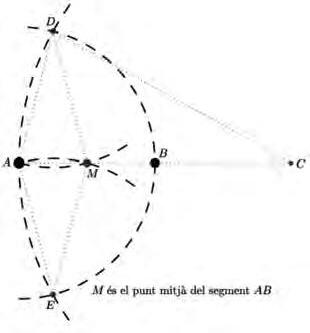
Exercici9.Proveulavalidesadelesduesconstruccions.[Indicació.Ladel’esquerraésfàcil. Peraladeladreta,apliqueulasemblançadelstrianglesisòsceles ADC i AMC ,iobtindreu que 1 2 “ AD AC “ AM AD i,deretruc, AM “ 1 2 AD.]

1.4.4.El punt mitjà d’un arc de circumferència donat

Problema. Donatunarcdecircumferència Ň ABd’extremsAiBicentreO,volemdimidiar-lo,ésa dir,volemtrobarunpuntmitjàMdel’arc Ň AB.

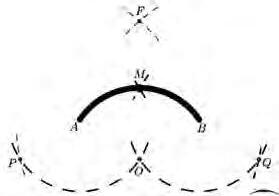
Construcció

Passos1i2. Ambcentres A i B,tiremlescircumferènciesquepassenper O.[C]

Estallenenelpunt O.

Passos3i4. Tiremlescircumferènciesdecentres A i B quepassenper B i A.[C]

Estallenamblesanteriorsper P i Q

Passos5i6. I,ambcentres P i Q,lesquepassenper Q i P.[C]

Estallenpelpunt F ,òbviament.

Pas7. Elpuntmitjà M delsegment FO éselsegmentbuscat.[§1.4.2] ♣36

Exercici9.Proveu-ho.

1.4.5.La suma i la resta de dos segments amb un vèrtex comú

Problema. DonatselssegmentsAOiOB,volemaconseguirelspuntsCiDdemaneraqueAC “ AO ` OBiAD “ AO OB[figura14aq].37

Figura13.Lasumailarestadedossegments.

Construcció

Pas1. Ambcentreen O,tiremlacircumferènciaderadi OB.[Compàs]

Pas2. Consideremelsimètric B1 de B respectedelarecta AO.[§1.4.2,pàgina80]

Pas3. Elspuntsmitjans C i D delsarcs Ŋ BCB1 i Ő BDB1 [§1.4.4,pàgina81]sónelspuntsbuscats. ♣

Exercici10.Proveuque:

aq Elpunt B1 estrobadamuntlacircumferènciadecentre O iquepassaper B.

bq Efectivament, AC “ AO ` OB,i AD “ AO OB.

36.Aquestesquatreoperacions,quepodensemblarmoltsimples,sónd’ungranutilitat.

37.Éselemental,jaque,ambelregle,podemdibuixarlarecta AO.Ambcentreen O iradi OA femla circumferènciaquetalla AO pelspunts C i D queestanevidentmentalineats.

1.4.6.El trasllat d’un segment a un punt

Unfetmoltimportantésqueelcompàssensememòriatémemòriaperquèpodemtraslladar unsegmentdonat AB aunpuntdonat C .

Construcció

Pas1. Femeltriangleequilàterdecostat AC ,ésadir,elpunt D.[Csensememòria]

Pas2. Consideremelpuntmitjà M delsegment AC .[§1.4.3,pàgina80]

Pas3. Ielpuntsimètric E de A respectede DM [§1.4.2,pàgina80]

Elsegment CE télalongitudde AB iunextremenelpunt C ,donats. ♣

Veiemaraunresultatquedepèndelfetqueelcompàstémemòria.

1.4.7.La quarta proporcional de tres segments

Problema. VolemdeterminarlaquartaproporcionaldeAB,CDiEF.

Construcció

Pas1. Perunpuntarbitrari O,tiremlescircumferènciesderadis CD i AB [figura 15].[Camb memòria]

Pas2. Perunpunt P delagran[deradi CD],tiremunacircumferènciaderadi EF .[Camb memòria]

Estallenpelpunt Q.

Pas3. Siguin M i N elspuntsquedeterminenlesdiferències OM i ON delsdosradis.[§1.4.5, pàgina82]

Elsegment MN éslaquartaproporcionaldelssegmentsdonats.38 ♣39

38.Quinaelegància!

39.Enaquestcas, CD AB “ PQ MN .Anàlogament,esfarienelsaltrescasospossibles.

Figura14.Traslladem AB alpunt C.

Figura15.Laquartaproporcional.

Exercici11.Proveulavalidesadelaconstruccióperobtenirallòquevolem.

1.4.8.La mitjana proporcional de dos segments

Unaltreproblemageomètricéselsegüent:

Problema. Volemdividirunsegmentdonatenduespartsdemaneraqueelrectangledecostats lespartssiguiequivalentalad’unquadratdonat.40

Donatselquadrat l PQ iunsegment ED,volemtrobarunpunt A de ED quedeterminiun rectangledecostats EA i AD equivalentenàreaa l PQ.

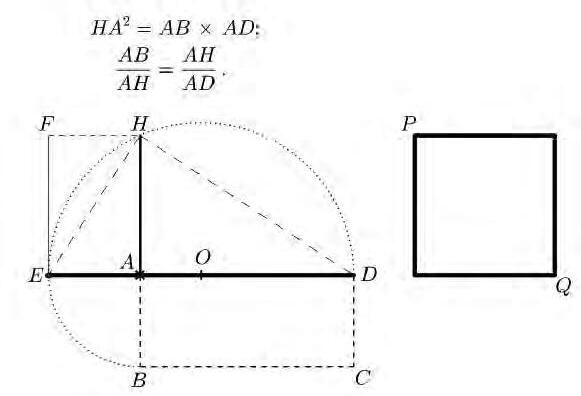
Figura16.Lamitjanaproporcional.

Construcció

Pas1. Dimidiemelsegmentdonat ED pelpunt O [§1.4.3,pàgina80].

40.Calqueelcostatdelquadratsiguiméspetitquelameitatdelsegmentdonat.

Pas2. Perell,tiremmitjacircumferènciaderadi OE [C].

Passos3i4. Pelpunt E ,tiremlaperpendicular EF a ED delongitudigualalcostatdelquadrat [§1.3.2a1 ,pàgina75iC].

Passos5i6. Pelpunt F ,tiremlaperpendiculara EF iconsideremelpunt H pelqualtallala semicircumferènciadelpas 2, 41 i,pelpunt H,alsegment ED,iconsideremelpunt A pel qualtalla ED.

Elpunt A éselpuntbuscat.42 ♣43

1.4.9.Amb un compàs sol podem fer el mateix que amb el regle i el compàs

Arapodemresoldrelaqüestióprimordial:

aq Compodemdeterminarelspuntspelsqualsestallenunarectaiunacircumferència?

bq Compodemdeterminarelpuntpelqualestallenduesrectes?

1.4.9a.Elspuntsdetalld’unarectaiunacircumferència

Problema. DonadaunacircumferènciadecentreOiradiriunarectaquepassapelspuntsAiB, volemtrobarelspuntsdetallPiQ.

Construcció Ésrealmentfàcil[figura 17a].

Pas1. Sigui M elpuntsimètricde O respectede AB.[§1.4.2,pàgina80]44

Pas2. Ambcentreenelpunt M iradi r ,tiremunacircumferència.[Cambmemòria]

Estallenpelspunts P i Q,quesónelspuntsquebuscàvem.

Figura17.Elspuntsdetalld’unacircumferènciadecentredonatiunarecta,ideduesrectes.

41.Tenimundiorisma.Calqueelcostatdelquadratsiguiméspetitoigualquelameitatdelsegment ED donat.

42.Quinaelegància!

43.Defet,hemdeterminatlamitjana HA delssegments EA i AD,ésadir,elrectangledecostats EA i ED equivalalquadratdonat.

44.Hemrefeteldibuixqueeldetermina.Podríem,doncs,haversuprimitl’ítem 1.4.2 (pàgina80).

Exercici12.Proveulavalidesadelaconstruccióperobtenirallòquevolem.

1.4.9b.Elpuntdetalldeduesrectes

Problema. DonadesduesrectesquepassenpelspuntsAiB,iCiD,volemtrobarelpuntPpel qualestallen.

Aquestproblema,forçamésdelicat,ésadequatperaplicarelmètodedel’anàlisiplatònica.

Suposem-loresolt,isigui P elpuntqueelresol.

Quèsen’extreud’això[figura 17b]?

Anàlisi

D’entrada,observemquelesrectesquepassenper C i P,iper D i P,hofanpelssimètrics D1 i C 1 de D i C ,respectedelarectad’extrems A i B. 45

Ara,talcomhihaescritalapartdedaltdelafigura[figura 17b],hemdedeterminarun segment CP quesiguilaquartaproporcionaldelssegments CC 1 ,DD1 i CC 1 ` DD1 .

Pertant,

Construcció

Pas1. Consideremelspunts C 1 i D1 simètricsdels C i D respectedelarectaquepassapels punts A i B.[1.4.2,pàgina80]

Pas2. Determinemelsegmentqueequivalalasumadelssegments CC 1 i DD1 .[§1.4.5,pàgina82]

Pas3. Determinemelsegment CH queequivalalaquartaproporcionalde CC 1 ,DD1 ielsegmentsumaobtingutalpas 2.[§1.4.7,pàgina83]

Pas4. Femlescircumferènciesdecentres C i C 1 iradi CH.[Cambmemòria]

Estallenpelpunt P quebusquem.

Exercici13.Proveulavalidesadelaconstruccióperobtenirallòquevolem.

1.4.10.El centre d’una circumferència donada com a simple figura

Enalgunesocasions,hemsuposatqueutilitzàvemunacircumferènciadelaqualenconeixíemelcentre O. 46

45.Malgratquenotenimregle,hemdibuixatlesrectesperajudaralaimaginació.

46.Siconeixemelcentre,elradinocalconèixer-lo,siconeixemelcentre.Noméscalagafarunpuntarbitrari P delacircumferència.Aleshores,elsegmentd’extrems O i P éselradi.

Araenspreguntemsiéspossibleevitaraquestalimitació.

Problema Volemdeterminarelcentredelafigurad’unacircumferènciadonada.

Construcció

Ésrealmentfàcil[figura 18].

Consideremdospuntsarbitraris A i B de C .

Figura18.Elcentred’unacircumferència.

Pas1. Per B,perexemple,tiremlaperpendicularalsegmentd’extrems A i B.[Nota 1,pàgina 68]

Tallalacircumferència C pelpunt D.[§1.4.6a,pàgina83]

Pas2. Cerquemelpuntmitjà O delsegmentd’extrems A i D.[§1.4.3b,pàgina80] ♣

Nota3. Enlafiguradeladretaienl’exercici 9 delapàgina82,hemvistquelasemblança delstriangles ADC i AMC permetestablir AD AC “ AM AD i,deretop, AD2 “ AC ˆ AM.

Aixòensportaaestablirunconceptegeomètricnou:la inversiód’unpuntrespected’una circumferència,que,deretop,permettambédeterminarelcentred’unacircumferència.47

1.5.El regle sol

Uncopesbrinadalapotènciadelacircumferènciasola,semblanaturalqueelsgeòmetreses preguntessinquinaésladelreglesol.Larespostaés:

Nomésambunreglenopodemfertotallòqueespotferambregleicompàs. Defet,noéspossibleconstruirlamitjanaproporcionaldedossegments.

AquestaqüestióselavaplantejarSteiner,motivatpelresultatdeMascheroni.Vaser,precisament,quanintentavaresoldreaquestaqüestióqueesvaadonarque,sidisposavad’una

47.Nosaltresometemaquestanovaaportació.Tanmateix,ellectorinteressatpotconsultarqüestions relacionadesamblainversióa[Courant i Robbins:1941],p. 154-155.

circumferència defet,n’hihaprouambunarcdecircumferència , 48 podiaferelmateix queambelregleielcompàs.49 Envaproporcionarunasoluciógeomètrica.50

Martin,encanvi,proporcionaunapresentacióbasadaenl’úsdelsnombres,unobjecteque nohaviaaparegutfinsaraidelqualenparlaremmésendavanta§4(pàgina 92).51

Entotelquehemfetnosaltresfinsaquí,noméshemnecessitatlageometria,seguintlamentalitatdels Elements d’Euclides.Noenshanfetfaltaelsnombresperares.

2.Elstresproblemesclàssics

Arabé,elsgrecsesvanplantejar, pergeneralització,tresproblemesgeomètricsqueesconeixencomels tresproblemesclàssics.

2.1.Preàmbul.La duplicació del quadrat i la dimidiació de l’angle

2.1a.Problema. Ambregleicompàs,podemdoblarunquadrat.

Ésadir,donatunsegment AB,ambregleicompàsenpodemferunaltre AC elquadratdel qualequivalaldobledeldecostat AB (figura 18a).

Construcció

Pas1. Femelquadratdecostat AB, l ABCD [RiC,§1.3.2a1 ,pàgina75

Pas2. Unimelsvèrtexs A i C . [R]

Exercici18.Elquadrat l ACEF ,decostat AC ,éseldobledel l ABCD decostat CD.[Indicació. Perdescomposiciótangram.]

48.Nota,pàgina79. 49.PodemveureunasíntesideltreballdeSteinerenlasecció VIII delcapítol4de[Courant i Robbins:1941], p. 209-210

50.[Courant i Robbins:1941],p. 209-210,recorreala geometriaprojectiva

51.[Martin:1998],capítol IV,p.69-82

Figura19.Duplicarelquadratidimidiarl’angle.

2.1b Problema Ambregleicompàs,podemdimidiarunangle.

Ésadir,donatl’angle z MON,podemdeterminatelpunt C quefaquelarectaquel’uneixamb O determinidosanglesiguals z MOC i y CON (figura 18b).

Construcció

Pas1. Ambcentreenelvèrtex O del’angleiradiarbitrari,tiremunarcdecircumferència.[C]

Tallaelscostatsdel’anglepelspunts A i B.

Pas2i3. Ambcentreenelspuntsdetall A i B,tiremelsarcsdecircumferènciaquepassen perl’altrepunt.[C]

Estallenpelpunt C .

Pas4. Tiremlarectaqueuneixelspunts O i C .[R]

Aquestarecta bisectriu dimidial’angle z MON;ésadir, z MOC “ y CON .

2.2.Els polígons regulars construïbles amb regle i compàs

Noésunproblemaclàssicgrecijan’hemparlata§1 2 2a i 1 2 2b (pàgina70).

2.3.La quadratura del cercle

Enels Elements d’Euclidess’estableixquetotafigurapoligonalés quadrable.Ésadir,espot ferunquadratdelamateixasuperfíciequelafigurapoligonal.

Totesbasaentresfets:

aq Dostrianglesquetenenlesbasesilesaltures iguals,encaraquetinguinunaformadiferent,tenenlamateixasuperfície.

bq Tottriangleequivalensuperfícieaunrectangleconstruïbleapartird’ellambRiC.

cq Totrectangleésquadrable,ielquadratespotconstruirambRiC.

Ésnatural,doncs,queelsgeòmetresgrecsespreguntessin: Hihafigureslimitadesperarcsde circumferència,construïblesambregleicompàsiquadrables?Ielcercle,hoés? Hipòcrates deQuios(470 aC-410 aC)vaproporcionartres lúnules quecomplienlesduescondicions.52

Aquestproblemaque, geomètricament,sembla anàleg alsaltresésdenaturalesa algebraica absolutamentdiferent i,pertant,nol’analitzarem.53

52.[Pla:2010],capítol3,§2,p. 93-105.[Pla:2016],§3.4.5i§3.4.7,p. 234-236,i 238-248. 53.Sihovoleufer,vegeu[Pla:2016],§3.4.5i§3.4.7ítem4,p. 234-236i 244-249.Ésd’uninterèsnotableel textd’Aristòtil,§A.6.13.2c1 ,[Pla:2016],p.434-435.

2.4.Generalitzem

Ésnatural ipropidelamatemàtica plantejar-seelsproblemesquesorgeixenper generalització.

Enconcret,

Problema. Ambregleicompàs,éspossible:

aq duplicarelcub?

bq trisecarl’angle?

Ésadir,

aq Donatuncubdevèrtexsdiametralmentoposats A i H (figura 20a),volemdeterminarel devèrtexsdiametralmentoposats B i S devolumdoblealdeldonat.

bq Donatunangle y BAC (figura 20b),volemdeterminarelspunts D o E demaneraquelarecta quepassapelspunts A,i D o E determinielsangles y BAD o y BAE igualsaunaterceraparto aduestercerespartdeldonat.54

Elsgeòmetresgrecsvantrobarmoltesmaneresderesoldreaquestproblema obéinventantcorbesqueensertalladesentresi,oambuncercle,aconseguienelpuntdesitjat,obé creantginysgeomètricsquehofessin ,perònovantrobarlamaneradefer-hoambreglei compàs.55

Lapreguntanaturalés:

aq Noerenprouhàbils?

bq Noespotfer?

Estavenconvençutsque no erapossiblefer-ho.56

Peròlademostraciómatemàticaprecisatrigariamoltssegles.Caliaques’haguéscanviatde paradigmaiquelageometrias’haguésalgebraitzatgràciesalesaportacionsdelsmatemàtics àrabsidelsdelRenaixementitalià.

54.Sipodemtrobarun trisector tambépodemtrobarl’altre,jaquesabemdimidiarangles.

55.[Pla:2026]comasíntesidelaqüestió.

56.[Pla:2026],§4.1 2f,p.89

Figura20.Duplicarelcubitrisecarl’angle.

Ensíntesi,esnecessitaval’aportacióquel’insignefilòsofRenéDescartes( 1596-1650)vafer enla Geométrie, 57 undelstresapèndixsde Lediscoursdelaméthode (1637).

Dos-centsanysméstard(1837),amb 23anys,Pierre-LaurentWantzel(1814-1848)responiala preguntaenunarticledesetpàginesenquèestablia:

Elsnombresrealsconstruïblesambregleicompàssónsolucionsd’unpolinomiirreductibleenunavariablexiambelscoeficientsracionalsdegrauambunapotència de2.58

3.IapareixenDescartesilaseva Geometria

Unasíntesibreudel’epistemologiaalgebraicadela geometriacartesiana, 59 basadaenl’àlgebraheretadadelsàrabsidesenvolupadapelsmatemàticsitaliansdelRenaixementi,enl’àlgebrasincopadailiteral,éslasegüent:

3.1.Les operacions numèriques que provenen de l’ús del regle i el compàs de segments amb nom

LaideadeDescartesésmoltsimple.

3.1.1.Els segments tenen nom

Consisteixa donarnom alssegmentsrectilinis,ésadir,aatribuir-loselvalordelasevalongitud,uncopfixatun segmentunitat,tantsiaquestalongitudés racionaloirracional, coneguda odesconeguda. 60

Així,doncs,tenimunsegmentde«nom» 1 ialeshoresassignemacadasegmentunnombre a,b,c...,x,y,z 61

3.1.2.Les operacions algebraiques de les construccions amb regle i compàs

Laqüestióés:compodemtraduiral’àlgebradels«noms» delsnombres allòqueobtenim quan,engeometria,femconstruccionsambregleicompàs?

57.Elcapítolprimerde Lagéométrie deRenéDescartesésuntextexcel lentimoltentenedor,iconstitueix unbontextpercomençarallegiroriginalsmatemàtics.Ensíntesi,contéelqueesdiua§3.1.2 i,atèsquedipsosem de `, , ,˜ i ? ,espodenresoldrelesequacionsdeprimergrauisegongrau X ` a “ 0 i Y 2 ` bY ` c “ 0,amb regleicompàs,jaque X “´a i Y “ b˘?b2 4a c 2 .Amés,eltextproporcionacomcalfer-hogeomètricament[Pla i Viader:1999],capítol 1,p. ‚.Peraunadescripciódelstrencamentsepistemològicsdelesaportacionsgeomètriques delfilòsoffrancèsenrelacióambelpensamentgrec,[Pla:1987].

58. [Wantzel:1837],§III,p.368.

59.Recordemque,devegades,Descartessignavaambelnomllatinitzat Cartesius. 60.Els nombresracionals erenelsúnicsqueacceptavenelsmatemàticsgrecsiconstituïenlabasedelaseva aritmètica.Els irracionals,ennoserexpressablescomapartsalíquotesde 1,noerenacceptats.Peraungeòmetra grec,ladiagonald’unquadratdecostat 1,sibéésconstruïbleambregleicompàs,téunalongitudque no és commensurable.Pertant,nolipodemassignarcapnombre.Podemveurelesdefinicions 1, 2 i3delllibre VII,dels Elements d’Euclides.[Pla:2020],p.87-88.

61.Descartesproposalesprimereslletres a,b,c,... peralsvalorsquesuposemdonatsilesdarreres x,y,z peralsvalorsdesconegutsquebusquem.

3.1.2a.Lasumailaresta. Ésclarquedonatsdossegments a i b,podemconstruirunsegmentdenom a ` b iunaltredenom a b (§1.4.5a,pàgina82).

3.1.2b.Lamultiplicacióiladivisió. Donatselsnoms 1,a i b,podemdeterminarelnomdels segmentsquartaproporcionald’ells.Sibusquem x i y demaneraque x 1 “ a b i y a “ b 1 ,tenim que x “ a b ique y “ a b.

3.1.2c.L’arrelquadrada. Donats 1 i a,s’obtégeomètricamentbuscantlamitjanaproporcionaldelssegmentsdelongitud 1 i a.Enefecte,si z designaaquestamitjana, z 2 “ a i,deretop, z “ ?a.

4.Cloenda

Sibé,comdèiem,l’einaalgebraicaenspermetdemostrarrigorosamentlaimpossibilitatde resoldreelsdosproblemesclàssicsambRiC,hihaunmètodegeomètric,la papiroflèxia o origami,quepermetresoldre’ls.Comhemindicatenlaintroducció,dedicaremunsegonarticleaveure,apocapoccomhemfetenaquestespàgines,elspassosqueportenaaquestes solucions.62

Bibliografia

[1][Berggren:1986]JohnLennartBerggren(1986). EpisodesinthemathematicsofMedieval Islam.NovaYork:Springer-Verlag.

[2][Boyer:1949]CarlB.(1949). Theconceptsofthecalculus,acriticalandhistoricaldiscussion ofthederivativeandtheintegral.Hafner.[Reeditatl’any 1959 ambeltítol Thehistoryofthe calculusanditsconceptualdevelopment.NovaYork:Dover.Enlíniaahttps://download.tux family.org/openmathdep/history/History_of_the_Calculus-Boyer.pdf].

[3][Courant i Robbins:1941]RichardCourantiHerbertRobbins(1941). Whatismathematics?.NovaYork:OxfordUniversityPress.[TraducciócastellanadeL.Bravo, ¿Quéesla matemática? Madrid:Aguilar(1955).Enlíniaahttps://www.cimat.mx/gil/docencia/ 2017/ mate_elem/[Courant,Robbins]What_Is_Mathematics( 2nd_edition_1996)v2.pdf].

[4][Dörrie:1932]HeinrichDörrie(1933). TriumphderMathematik.Breslau:FerdinandHirt. [TraduccióanglesadeD.Antin, 100GreatProblemsofElementaryMathematics.Theirhistoryandsolution.NovaYork:Dover, 1958].

[5][Gauss:1801]CarlFriedrichGauss(1801). Disquisitionesarithmeticæ.Leipzig:Gerh. Fliescher.[TraduccióipròlegdeG.PascualiXufré, Disquisicionsaritmètiques Barcelona, SocietatCatalanadeMatemàtiques(1996)].

[6][Martin:1998]GeorgeE.Martin Geometricconstructions.NovaYork:Springer-Verlag.

[7][MT MacTutor:1994-2023]Al’adreçahttps://mathshistory.st-andrews.ac.uk/Biographies/ s’indexenalfabèticamentlesbiografiesdelsmatemàticsaplegadesa«MacTutorHistory ofMathematics»,uníndexcreatl’any 1994imantingutaldiaperEdmundRobertsoni JohnO’Connordela SchoolofMathematicsandStatistics,igestionatperlaUniversitat. Normalment,elprimerítemdeles References decadapersonatgeenllaçaamblabiogra-

fiacorresponentdel DictionaryofScientificBiography (NewYork 1970-1990),editatper CharlesC.Gillispie.Enaquestcas,lesbiografiessónobrad’especialistesdiversos.

[8][Pla:2016]JosepPlaCarrera(2016). Històriadelamatemàticagrega:GrèciaI(deTalesi PitàgoresaPlatóiAristòtil.Barcelona:Institutd’EstudisCatalans.

[9][Pla:2018] (2018). Històriadelamatemàticagrega:GrèciaIIaels Elements d’Euclides: llibres I, II, III, IIII, V i VI).Barcelona:Institutd’EstudisCatalans.

[10][Pla:2020] (2020) Històriadelamatemàticagrega:GrèciaIIaels Elements d’Euclides: llibres VII, VIII, IX, X, XI i XII).Barcelona:Institutd’EstudisCatalans.

[11][Pla:2026] (2026) Històriadelamatemàticagrega:GrèciaIIIb.Altresobresd’Apol¨loni, ConóiDositeu,NicomedesiEratòstenes,Dionísodor,Dioclesi Elsmirallsustoris.Barcelona: Institutd’EstudisCatalans(pendentdepublicació).

[12][Pla i Viader:1999]JosepPlaCarreraiPelegríViaderCanals(1999). RenéDescartes.La geometria.Barcelona:Institutd’EstudisCatalans.

[13][Wantzel:1837]Pierre-LaurentWantzel«Recherchessurlesmoyensdereconnaîtresiun ProblèmedeGéométriepeutserésoudreaveclarègleetlecompas». JournaldeMathématiquesPuresetAppliquées, 1 (2), 1837,p.366–372.[Enlíniaahttp:/visualiseur.bnf.fr/ ConsulterElementNum?O=NUMM-16381&Deb=374&Fin=380&E=PDF].

Normes per a la presentació de contribucions

1. La revista NouBiaix acceptaper alasevapublicació contribucionsoriginalsrelacionadesamb experiències didàctiques, activitats d’ensenyamen ti aprenentatge,escritsd’opinió,dedivulgaci ói d’investigació enel camp dela matemàtica ielseuensenyamentenqualsevol nivell educatiu

2. Les contribucionsrebudesseran avaluadesprèviamentper dosespecialistesreconeguts. La decisiópresa pelConsell deredacciósobrel’acceptació dela publicació serànotificadadirectamentals autors ambuna indicaci ódeladataaproximadadepublicaci ói el possiblerequeriment d’introduir modificacionseneltext.

3. Pera lapresentaci ódetreballsoriginals, elsautorstrametran al’adreçanoubiaix@gmail.com un arxiu, en Word oenLaTeX.Els gràfics, elsdiagrames iles figureshaurandeser originals(no fotocopiats). Els arxius gràficsespresentaran en format epso tif.

4. La contribució hauràd’incorpora reltítol,elnom de l’autoro autors,lasevaadreçapostalprofessional completai la sevaadreça electròn ica.S’adjuntaràunresum només llarg de 300 paraules en català ianglès. Al finaldel document s’inclouràobligatòriamen tlabibliografiaper ordrealfabètic de cognoms,d’acordamb la normativaAPA, com enelsexemplessegüents:

Articles

Albertí, M. (2002).Les matemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques Biaix, 20,6-25.

Llibres

Godino,J., Font,V.(2003) Razonamiento algebraicoparamaestros.Granada :Universidad de Granada. Capítols dellibres

Edo,M.,Revelles, S. (2004).Situacionesmatemática spotencialmentesignificativas. Dins M. Antóni B. Moll (ed.), Educación Infantil.Orientacionesy Recursos (0-6 años) (p.410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales, M.,Font, V.,Planas, N. (2004).Estudiomicroetnográfico en tornoa un conocimiento matemático situado. Dins A.Franzé ialtres(ed.), ActasdelaI ReuniónCientíficaInternacional sobreEtnografía y Educación (CD-ROM).València: Germanía,Polis Paideia.

Pàginesweb

Geogebra pera Infantil iPrimària. https://www.geogebra.org/m/tkdC27m f

5. Els contingutsde NouBiaix estansubjectes llevatque s’indiquiel contrarieneltext, en lesfotografies oenaltresil lustracions— auna llicència de Reconeixement-No comercial-Sense obra derivada 3.0deCreativeCommons,eltext completdela qual es pot consultar ahttp://creativecommons.org/ licenses/by-nc-nd/3.0/es/deed.ca. Així,doncs,s’autoritza el públic en generala reproduir,distribuir i comunicarl’obra,sempreque es reconegui l’autoriai l’entita tquela publica, inose’nfaciunús comercial ni se’n difongui capobraderivada.

6. Elsarticlesespublicara nen llenguacatalana.Només es traduiranalcatalàles contribucions acceptadesd’autorsnoresidents alsPaïsosCatalans.

7. Elsautorsesresponsabilitzarandel complimen tdeles normes establertesper al’autoritzaciódela reproducciódematerialprocedent d’altres fontsbibliogràfiques .

8. Elsarticlestindran unaextensiómàximade 8000 paraules,inclosesles notesa peudepàgina,però s’acceptenarticles méscurts,d’entre 2000 i 4000 paraules

9. Femnotar queenaquesta publicació s’utilitza preferentmen telpuntper separardecimals, en lloc dela comarecomanadaper l’IEC, pertal defacilitarla comprensi ódeles expressionsmatemàtiques.