Alla scoperta del mondo 3. Matematica

A L L A SCOP E RTA DEL M O NDO

LEGGERE È INCONTRARE

L’edizione di questo sussidiario per la terza classe è espressione del consapevole lavoro di un gruppo di insegnanti che in questi anni ha condiviso la proposta didattica e ricercato o composto testi ed esercitazioni per una conoscenza elementare essenziale ed efficace.

Percorso di lettura e relativa proposta operativa

Manuela Callaioli, Barbara Righetti, Sara Fasoli, Giulia Zonca, Marta Frizzi, Mirella Amadori, Paola Brambilla (selezione delle letture)

· Micaela De Francesco, Lorena Cirnigliaro, Giulia Brizio (esercizi di grammatica) · Francesco Grava (proposta musicale)

· Denise Marchiori (lavori artistici dei bambini)

Percorsi disciplinari e relativi esercizi

Elena Lucca, Carlotta Piatti, Letizia Furli, Martina Archesso, Silvia Musso, Simona De Paolis, Giuliana Limonta (aritmetica)

· Armida Panceri (geometria) · Emanuela Casali, Matteo Dolci, Francesca Simonazzi (storia) · Marta Sangiorgio, Annabella Maffi, Ornella Rotundo, Silvia Locatelli, Alessandra Campagnari (geografia) · Angela Luoni, Carla Agostini, Viviana Mezzacapo, Paola Brambilla (scienze)

Consulenti

Raffaela Paggi (grammatica) · Raffaella Manara (matematica) · Maria Elisa Bergamaschini, Maria Cristina Speciani (scienze)

L’ESPANSIONE DIGITALE DEL TUO LIBRO

Sul sito www.itacascuola.it sono disponibili materiali integrativi per docenti e alunni. Inquadra il QR Code per:

accedere alla pagina del tuo libro

registrarti e accedere ai materiali digitali del tuo libro

Alla scoperta del mondo 3. Classe 3 www.itacaedizioni.it/scoperta-mondo-3

Prima edizione: luglio 2018 Nuova edizione: giugno 2024

© 2018 Itaca srl, Castel Bolognese

Tutti i diritti riservati

ISBN 978-88-526-0773-8

Progetto grafico: Isabel Tozzi

Coordinamento editoriale: Daniela Dal Pane

Coordinamento redazionale: Cristina Zoli

Impaginazione e cura editoriale: Isabel Tozzi

Illustrazioni: Valeria Valenza, Daniela Blandino

Stampato in Italia da Lito Terrazzi, Prato (PO)

Col nostro lavoro cerchiamo di rispettare l’ambiente in tutte le fasi di realizzazione, dalla produzione alla distribuzione. Stampiamo esclusivamente in Italia con fornitori di fiducia, riducendo così le distanze di trasporto.

scoprire le proposte di lettura

Avvertenza

L’itinerario di storia proposto nel nostro percorso per la scuola primaria prevede la presentazione delle civiltà fluviali in terza classe, perché siamo convinti che questa scansione sia la più adeguata al cammino di conoscenza dei bambini, con un maggior equilibrio di contenuti nel triennio e la possibilità di approfondire maggiormente le civiltà da cui origina la nostra tradizione occidentale. Al contempo, tale scelta ci sembra più rispettosa della categoria storica propria in quanto indugia meno sulle epoche per le quali il livello interpretativo è molto elevato e lascia più spazio ai dati storicamente documentati.

Grazie alla collaborazione con Seleggo, la versione digitale ottimizzata di questo libro per studenti dislessici può essere ottenuta in download gratuito registrandosi al sito www.seleggo.org ® I LIONS IT ALIANI PER LA DISLESSIA

Per esigenze didattiche alcuni brani sono stati ridotti e/o adattati.

L’Editore è a disposizione degli aventi diritto con i quali non è stato possibile comunicare, nonché per eventuali involontarie omissioni o inesattezze nella citazione delle fonti. La realizzazione di un libro comporta aspetti complessi, che richiedono particolare cura in ogni sua parte e nei controlli finali. Ciononostante è molto difficile evitare completamente refusi o imprecisioni.

L’Editore ringrazia chi vorrà inviare segnalazioni alla redazione, scrivendo al seguente indirizzo e-mail: itaca@itacalibri.it.

I nostri testi sono disponibili in formato accessibile e possono essere richiesti a: Biblioteca per i Ciechi Regina Marghera di Monza (http://www.bibliotecaciechi.it) o Biblioteca digitale dell’Associazione Italiana Dislessia (www.aiditalia.org/cosafacciamo-servizi).

Le fotocopie per uso personale del lettore possono essere effettuate nei limiti del 15% di ciascun volume dietro pagamento alla SIAE del compenso previsto dall’art. 68, commi 4 e 5, della legge 22 aprile 1941 n. 633.

Referenze fotografiche

Archivio Itaca · PxHere · The Metropolitan Museum of Art, New York: The Berggruen Klee Collection, 1987, 138; Shutterstock.com: Lomonovskyi 5, 50, 102, 115, Lexi Claus 15, Jo_Ana 18, Elen Koss 107, Elena Khmelniuk 119, Gringoann.art 119, grafikwork 120, photka 122, 124, Pretty Vectors 125, Granate Art 125, hakan2534 125, NiRain 125, Robert Kneschke 129, GagliardiPhotography 130, hshii 130, Saran_ Poroong 132, AndreyProektant 132, Roman Gorielov 134, krung99 134, hxdbzxy 134, KhanunHaHa 135, Sergiy Bykhunenko 136, Romrodphoto 140, moxumbic 140, africa924 140, ultramansk 140, Jesse Davis 142, gomolach 143, 145, Fahng_S 149.

A L L A SCOP E RTA DEL M O NDO

ARITMETICA

AGIRE CON I NUMERI

OPERARE, CALCOLARE E MISURARE PER COMPRENDERE E RISOLVERE NUOVI PROBLEMI

IL PROBLEMA: tappa 1

INCONTRIAMO UN PROBLEMA E OPERIAMO PER RISOLVERLO

PER COMINCIARE A RAGIONARE

Leggi, pensa, immagina, prova, aiutati con disegni e calcoli, poi rispondi

In quanti modi si possono disporre 12 ragazzi formando squadre con lo stesso numero di giocatori?

Puoi rappresentarlo in qualche modo?

1. Nel portafoglio la mamma ha delle banconote da 5 euro, delle monete da 2 euro, da 1 euro e da 50 centesimi.

In quanti modi riesce a pagare 8,50 euro di frutta combinando solo delle monete, oppure delle monete e delle banconote?

2. Ieri eravamo in 6 a giocare a carte e ciascuno ne aveva 2.

Oggi siamo in 4 a giocare, usando tutte le carte di ieri.

Sai dire quante carte toccheranno a ciascuno? Puoi far vedere come hai fatto?

Osserva e comprendi bene, leggi la domanda poi risolvi e rispondi

1. Quanti frutti ci sono?

Come hai trovato la risposta?

2. Quanti posti ci sono a tavola?

Quanti posti occupati (blu)?

Quanti posti liberi (bianchi)?

Come hai trovato la risposta alla terza domanda?

3. Quanto costano le 4 ciambelline?

Quanto costa 1 ciambellina?

Leggi e comprendi bene, poi risolvi e rispondi

1. In III A ci sono 28 bambini, in III B ce ne sono 26 e in III C 25. Quanti bambini ci sono in tutto nelle tre terze?

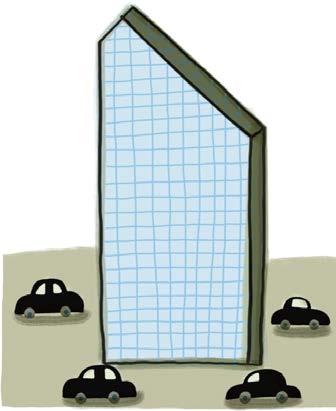
2. Il nuovo grattacielo di Milano ha 78 piani. Se il grattacielo più alto ne ha 120, quanti piani in più ha quest'ultimo rispetto al nuovo?

3. Gigi il meccanico ha una grande officina. In questo momento sta aggiustando 8 automobili. Quante ruote in tutto?

4. La maestra Carolina ha comprato per sua figlia 3 magliette e 4 paia di pantaloni, tutti di colori diversi. Aiuta Carolina a capire quanti e quali abbinamenti potrà fare con i vestiti acquistati.

5. Il papà compra per i suoi figli 3 libri che costano 12 euro l’uno e un gioco il cui prezzo è 19 euro. Quanti soldi spende il papà?

Leggi, pensa, immagina e risolvi

1. Cinque bambini confrontano le loro altezze. Si accorgono che:

z Matteo è più basso di Alice; z Pietro è più alto di Caterina; z Luca è più basso di Matteo; z Caterina è più alta di Alice.

Scrivi i nomi dei cinque bambini dal più basso al più alto.

2. Camilla ha già sistemato molti cubetti in questa scatola trasparente. Le restano ancora 50 cubetti. Camilla avrà abbastanza cubetti per riempire la scatola? Spiega perché.

Sai dire quanti cubetti ha già messo Camilla nella scatola? Spiega la tua risposta.

3. Francesco possiede una scatola che contiene dei cubi verdi e dei cubi arancioni. Costruisce parecchie torri rispettando il seguente modello:

z prima torre: 1 cubo verde;

z seconda torre: 5 cubi, 1 verde e 4 arancioni; z terza torre: 14 cubi, 10 verdi e 4 arancioni.

Francesco continua a costruire delle torri cambiando colore a ogni piano.

Quanti cubi di ogni colore utilizzerà Francesco per costruire, secondo questo modello, la sesta torre?

Spiega come hai trovato la tua risposta.

4. Lucia vuole colorare una pavimentazione come questa, rispettando le condizioni seguenti:

z ogni parte deve essere di un solo colore; z il blu tocca tutti i colori;

z il rosso e il giallo sono negli angoli a sinistra; z il rosso, il viola e il nero non toccano il verde; z l’arancione tocca il nero.

Colora la pavimentazione di Lucia rispettando tutte le condizioni. Spiega come hai fatto per trovarle.

CIFRE E NUMERI

il grattacielo ha 39 piani ed è alto 140 metri.

Ho pagato la tuta da ginnastica 47 euro e 50 centesimi.

Alla mattina mi sveglio alle 7 e mezza e devo essere a scuola per le 8 e 20.

I numeri sono intorno a noi

Li usiamo per indicare, contare, misurare… Ricorda che le CIFRE sono:

0 1 2 3 4 5 6 7 8 9

Usiamo le cifre per scrivere tutti i NUMERI :

Un numero può essere MINORE , UGUALE o MAGGIORE di un altro.

I numeri sono infiniti

C’è sempre un numero oltre quello che puoi pensare e un altro che lo precede.

Inserisci il precedente e il successivo dei numeri indicati:

successivo precedente

ESERCIZI ENTRO IL 100

La linea dei numeri

1. Due ranocchi fanno i salti lungo questa linea numerata:

Il primo ranocchio fa salti

lunghi 3: Il secondo ranocchio fa salti

lunghi 2:

Chi farà meno salti per arrivare a 18?

Perché?

2. Completa la linea numerata.

Quanto vale ogni salto? □ 5 □ 7 □ 11 □ 15 □ 19

Conta e traduci in cifra

1. Quante perle?

2. Quante perle?

Numeri del 100

1a. Scrivi i numeri che mancano adoperando due colori, come negli esempi.

2. Osserva le frecce che partono dalla casella 45. Scrivi nelle caselle i risultati che ottieni eseguendo i comandi delle frecce.

La freccia  dice

La freccia  dice

La freccia  dice

La freccia  dice

3. L’indirizzo incompleto

Anna ha organizzato a casa sua una festa e vuole invitare gli amici.

Ad ognuno ha spedito l’invito precisando la via dove abita, ma si è dimenticata di scrivere il numero della sua abitazione. Come faranno i suoi amici a trovarlo?

1° indizio: puoi scoprire il numero della via contando per 4 da 4 a 40.

2° indizio: è minore di 28.

3° indizio: non è un numero della tabellina del 3.

4° indizio: non bastano due mani per indicarlo.

5° indizio: la cifra delle decine è maggiore di quella delle unità.

Il numero della casa dove abita Anna è:

Chissà quanti amici riusciranno ad andare alla sua festa!

Mettiamo i numeri in ordine

1. Completa con il numero precedente e il successivo entro il 100.

2. Unisci i puntini. Cosa apparirà?

3. Scrivi il precedente di ogni numero.

4. Scrivi il successivo di ogni numero.

5. Completa la tabella.

6. Trascrivi i numeri in ordine crescente (dal più piccolo al più grande).

67 15 23 4 89 86 27 55 45 12

7. Trascrivi i numeri in ordine decrescente (dal più grande al più piccolo).

13 56 29 94 74 31 33 92 52 25

8. Osserva il segno e scrivi un numero adatto.

9. Inserisci i segni > oppure < tra i numeri.

10. Completa i confronti inserendo due numeri adatti a tua scelta.

ESERCIZI OLTRE IL 100

Mettiamo i numeri in ordine

1. Completa la tabella da 301 a 400 scrivendo i numeri mancanti nelle caselle libere.

2. Componi il numero più grande che esista con tre cifre diverse tra loro.

3. Scrivi tutti i numeri possibili contenenti queste 3 cifre: 2, 8, 7.

4. Unisci i puntini contando per 10 da 10 a 200. Cosa apparirà?

5. Completa con il numero precedente e il successivo oltre il 100.

–1

6. Scrivi il precedente di ogni numero.

7. Scrivi il successivo di ogni numero.

8. Completa con i numeri precedente e successivo, come nell'esempio.

8 9

9. Completa la tabella.

10. Trascrivi i numeri in ordine crescente (dal più piccolo al più grande).

11. Trascrivi i numeri in ordine decrescente (dal più grande al più piccolo).

12. Osserva il segno e scrivi un numero adatto.

327 < 580 = 632 > >

= 963 414 > 971 > <

13. Inserisci il segno > oppure < tra i numeri.

14. Completa i confronti inserendo due numeri adatti.

< e

> e

15. Indica se le affermazioni sono vere o false.

F

500 + 30 + 7 > 534 X

900 + 2 = 902

600 + 15 = 605

730 > 600 + 100 + 30

960 = 300 + 300 + 300 + 60

5 h = 50 da

80 da + 5 da = 850

700 > 7 h 0 da 0 u

293 < 30 da

ESERCIZI OLTRE IL 1˙000

1. Numera da 950 a 1˙150 usando il comando +10 . 950, 960,

2. Completa.

900 + = 1˙000

500 + = 1˙000

+ = 1˙000

+ = 1˙000

3. Numera da 9˙300 a 9˙900 usando il comando +100

9˙300, 9˙400,

+ = 1˙000

+ = 1˙000

4. Completa utilizzando il segno corretto: < >.

624 1˙248

1˙003

5. Completa utilizzando il segno adatto: < >.

1˙000 + 500 + 20 + 3 1˙000 + 500 + 20 + 9

1˙000 + 700 + 80 + 7 1˙000 + 7˙000 + 20 + 8

1˙000 + 300 + 20 + 4 1˙000 + 200 + 30 + 7

1˙000 + 200 + 9 1˙000 + 40 + 3

6. Metti il puntino e poi scrivi in lettere.

Esempio 4581 4 ˙ 581 quattromilacinquecentottantuno

5825 4154 8105 3950 4562

7. Riscrivi questi numeri in cifre.

Duecentoventimila

Seimilaottocentoventiquattro

Ottomilaventiquattro

Quattromilatrecentoquarantatré

Cinquemilaseicentouno

Tremiladuecentosette

8. Scrivi questi numeri in lettere.

1˙000

3˙715

8˙900

2˙002

9˙826

9. Metti i puntini e leggi a voce alta il numero.

10. Trascrivi i numeri in ordine crescente.

11. Trascrivi i numeri in ordine decrescente.

SISTEMA DECIMALE E VALORE POSIZIONALE

Il nostro sistema di numerazione si chiama

DECIMALE perché usa le dieci cifre e POSIZIONALE perché il valore delle cifre dipende dalla loro posizione.

Parole e simboli del sistema decimale k h da u

Ricordati

Usa il puntino o lo spazio per separare i periodi all’interno del numero, serve per leggere e riconoscere il numero.

3˙827

Osserva il significato e il valore dello zero in base alle sue diverse posizioni all’interno del numero. All’interno 4 0 5 Alla fine 4 5 0 Davanti 0 4 5

Contatore

Abaco

Multibase

Migliaia Centinaia Decine Unità

PERIODO DELLE MIGLIAIA

PERIODO DELLE UNITÀ SEMPLICI

hk dak uk h da u centinaia di migliaia decine di migliaia unità di migliaia centinaia semplici decine semplici unità semplici

5 7 3

Cinquecento settanta tré 5 2 1 9

Cinquemila e duecento dician nove

6 1 7 8 2

Sessant unomila e settecento ottanta due

Le equivalenze : la stessa quantità espressa in modi diversi

2 h 20 da 200 u

ESERCIZI

Alcuni strumenti ci aiutano: l’abaco e il multibase

1. Scrivi i numeri rappresentati in cifre e lettere.

h da u

h da u

da u

h da u

h da u

h

2. Collega con l’abaco giusto e scrivi i numeri rappresentati in cifre e lettere.

h da u

h da u

h da u

Scrivi i numeri in cifre poi rappresentali sull’abaco.

trecentocinquantaquattro

h da u

h da u

h da u h da u

ottocentoquattro centoventisette seicentotrentasei

4. Rappresenta i numeri cerchiando il materiale multibase corrispondente.

5. Riconosci, a seconda della posizione, il valore della cifra 7.

6. Indovina indovinello.

Il cinema vicino a casa mia contiene un certo numero di spettatori.

Il numero delle poltrone è un numero maggiore di 425 e minore di 440. La cifra delle centinaia è uguale a quella delle unità.

Il cinema vicino a casa mia contiene spettatori.

7. Riconosci, a seconda della posizione, il valore della cifra 3.

8. Cerchia in azzurro le unità, in rosso le decine, in verde le centinaia. 102 124

567 421 765 100 999 876

9. Componi e scrivi il risultato in cifre e lettere.

Esempio

200 + 80 + 2 = 282 = duecentoottantadue

100 + 50 + 3 = =

100 + 30 + 8 = =

400 + 7 = =

40 + 1 = =

10 + 5 = =

500 + 20 + 4 = =

300 + 20 + 1 = =

700 + 60 + 7 = =

10. Scrivi i numeri dati con scritture diverse, come nell’esempio. Esempio

Ecco le migliaia

1. Rispondi.

Se al numero 999 viene aggiunta una unità, quale numero si ottiene?

Quante unità occorrono per avere 1 migliaio?

Quante decine? Quante centinaia?

2. Numera per 1 da 991 a 1˙021 e poi da 1˙025 a 995.

3.

il numero e scrivilo in cifre nella tabella. k h da u mille sedici trecentootto cento diciassette cinquecentoquaranta cinquecentoquattro cinquantaquattro trecentoventi

4. Cerchia i numeri in cui la cifra 4 ha valore di centinaia. 2˙3 4 5

4 3 2 2˙ 0 0 4 4˙ 4 9 9 4 3 4 3 6˙ 4 5 0 7˙ 8 4 2

Leggi

5. Componi i seguenti numeri, poi scrivili in parola, seguendo l’esempio.

Esempio 1 h 5 k 9 u 3 da = 5˙139 cinquemilacentotrentanove

8 da 2 h 6 u 1 k =

2 u 6 da 4 k 7 h =

2 k 4 h 3 da 0 u =

4 da 1 h 1 u 6 k =

0 h 7 da 8 k 4 u =

0 k 8 h 6 da 8 u =

2 u 0 da 3 k 9 h =

7 h 5 u 9 k 9 da =

5 da 7 u 3 h 7 k =

2 da 1 k 6 h 7 u =

6. Cerchia in azzurro le unità, in rosso le decine, in verde le centinaia, in arancione le migliaia.

891 1˙980 1˙809 1˙089 918

1˙908 809 3˙639 7˙309 7˙676

7. Scrivi un numero con le seguenti cifre: 5, 6, 3, 0. 3 ha valore di migliaia.

8. Usa queste cifre per scrivere tutti i numeri possibili, seguendo la seguente regola: la cifra 9 deve avere sempre valore di decina.

3, 9, 0, 4

9. Componi.

Esempio 7 u, 3 h, 3 da = 7 + 300 + 30 = 337

3 h, 6 u, 5 da =

3 u, 2 k, 8 da, 6h =

7 da, 5 k =

4 u, 7 h, 5 k =

4 u, 3 h, 7 da =

2 da, 5 h =

10. Scomponi.

2 u, 2 h =

6 h, 6 u =

1 k, 9 da, 3 h =

2 k, 4 h, 6 da =

2 h, 8 da, 6 u =

4 h, 2 da, 6 u =

Esempio 1˙254 = 1000 + 200 + 50 + 4 = 1 k + 2 h + 5 da + 4 u

3˙800 = 684 = 40 =

2˙020=

11. Quanto manca al migliaio?

8 h + da

6 h + da

12. Completa le equivalenze.

5 h = u

10 da = u

3 h = u

10 h = u

15 k = u

20 u = da 1 h = u

5 k = u

4˙000 u= k

600 u = h

13. Completa le equivalenze.

30 h = u

6 k = da

50 da = h

300 da = k

13 k = u

80 da = h

50 u = da

700 u = da

30 da = h 7 k = h

50 da = h 18 da = u 13 k = h

2˙000 da = k

70 k = h

300 u = da

680 u = da

1˙000 u = h

600 u = h 15 h = da 23 h = u 5 k = u 6 k = da 8 k = h 12 k = h

14. Completa le equivalenze a tappe.

2˙000 u = 200 da = 20 h = 2 k

3 k = h = da = u

50 h = da = u = k

300 da = u = k = h

6˙000 u = h = da = k

30 u = h = da = u

10 h = k

300 da = k

18 h = da

10 k = da

20 h = u

METTITI ALLA PROVA

1. Quali numeri sono rappresentati sull’abaco?

h da u k h da u k

h da u k h da u k

2. Con 2, 5, 7 puoi comporre sei numeri diversi. Scrivili in cifre e in lettere.

CIFRE

h da u

LETTERE

3. Osserva, indica le quantità di unità, decine e centinaia e poi rispondi.

unità (u) decine (da) centinaio (h)

Quante unità servono per formare una decina?

Quante unità servono per formare un centinaio?

Quante decine servono per formare un centinaio?

4. Completa con i termini mancanti, poi osserva gli operatori e rispondi.

1 (da)

1 migliaio (k) × 100 1 (u) × 10 × 1000 1 (h)

Quante unità servono per formare un migliaio?

Quante unità servono per formare un centinaio?

Quante unità servono per formare una decina?

5. Completa in modo da ottenere come risultato 1 h. Osserva l’esempio.

1 h = 3 da e 7 da

1 h = 5 da e da

1 h = 9 da e da

1 h = 2 da e da

1 h = 8 da e da

1 h = 4 da e da

1 h = 1 da e da

1 h = 6 da e da

1 h = 7 da e da

IL PROBLEMA: tappa 2

PARTIAMO DAL TESTO DEL PROBLEMA

PARTIAMO DAL TESTO DEL PROBLEMA

Roberto, il papà di Marco, porta il figlio al cinema. Acquista un biglietto adulti a 8 euro e uno ridotto a 6 euro. Quanto spende il papà?

Il testo del problema descrive una situazione e pone una domanda

Per dare risposta occorre: z riconoscere nel testo o nella figura i dati utili ; z eseguire azioni, rappresentazioni, operazioni con i numeri per trovare una risoluzione ; z verificare il risultato ottenuto.

Attento ai dati

Ogni ora le campane suonano quattro volte. Quante volte il loro scampanio si ripete nell’arco di una giornata ?

Il dato è nascosto

Perché?

Ogni mattina io e i miei 2 fratelli andiamo a scuola insieme. Partiamo da casa alle 7 e 50 e arriviamo in classe alle 8 e 10: quanto tempo impieghiamo a percorrere il tragitto?

Il dato è inutile

Perché?

Attento alle operazioni

Per comprendere l’operazione da svolgere, immagina l’azione suggerita del testo e fai attenzione alle parole.

La scorsa settimana ho partecipato ad una sfida a carte tra compagni. Giocavamo in coppia: io ho ottenuto 28 punti, il mio compagno 36. Abbiamo unito i nostri punteggi: a quanto siamo arrivati?

Qual è l’azione?

Oggi è sabato e aiuto la mamma a stendere il bucato. Per ogni calzino occorre una molletta, per ciascuna maglietta ne occorrono due. Devo stendere 8 calzini e 3 magliette, di quante mollette ho bisogno?

Quali parole esprimono un dato importante?

3. I nonni di Luca vogliono regalare al nipote una cartella nuova e un astuccio. Sono indecisi tra una cartella blu da 78 euro e una rossa da 63 euro, un astuccio arancione da 14 euro e uno verde da 24 euro. Trova tutte le possibilità degli acquisti dei nonni e calcola quanto potrebbero spendere per ciascuna. Rappresenta anche con un disegno.

Segui gli indizi, ognuno è importante!

1. Apparecchiare . Sulla tavola della festa ci sono cucchiai, forchette e coltelli. Le forchette sono 3 in più dei cucchiai. I coltelli sono 2 in più delle forchette. Tra le posate, quali sono le più numerose? Perché? Quante di più?

2. Album di figurine . Luca ha ricevuto in regalo una scatola di figurine. L'ha subito aperta e attaccato sul suo album di calciatori le figurine mancanti.

Scopri quante figurine ha attaccato in tutto seguendo gli indizi (ogni indizio ti permette di scartare qualche possibilità fino ad arrivare a un unico numero).

z È un numero compreso tra 37 e 52.

z È maggiore di 4 decine.

z La cifra delle unità è maggiore di quella delle decine.

z Non è pari.

z È il minore.

3. Scambi di figurine

Gli amici vogliono fare scambi di figurine. Vuoi sapere quante figurine doppie ha trovato Tommaso nella scatola di figurine? Segui gli indizi e lo saprai!

È un numero che trovi contando per due da 10 a 40.

La cifra delle decine è minore di quella delle unità.

La cifra delle unità non è 4.

La somma delle sue cifre è minore di una decina.

La cifra delle decine è il doppio di 1.

Luca ha trovato figurine doppie da scambiare con gli amici!

5. Torneo di biglie. Alla festa si svolge un torneo di biglie. Alla prima partita giocano 5 bambini, ciascuno con 3 biglie. I primi 3 a terminare il percorso giocano la seconda partita, con tutte le biglie che sono state usate nella prima partita. Scopri quante biglie toccano a ciascun giocatore della seconda partita. Tutti e 3 hanno lo stesso numero di biglie? Risolvi e spiega come hai fatto.

6. Adesso che sei un esperto investigatore, prova a inventare tu un problema con indizi insieme a un tuo compagno.

Problemi con l’occhio sul calendario

1. O ggi è mercoledì e vado a calcio. Tra 5 giorni ho la mia prima lezione di flauto. In che giorno della settimana avrò la lezione di flauto?

2. Ieri era il 28 marzo. Quanti giorni mancano al compleanno della mamma che è l’8 aprile?

3. Io sono nata il 20 novembre. Paolo è nato un mese e 4 giorni dopo di me. In che giorno è nato Paolo?

4. In vacanza quest’estate andiamo in Liguria. Partiamo il 30 luglio e ci fermiamo 13 giorni. In che giorno ritorneremo a casa?

5. I nonni hanno trascorso in montagna 2 settimane e 6 giorni. Quanti giorni in tutto i nonni hanno trascorso in montagna?

Problemi con l’orologio

1. Sono le ore 12 e 10. Tra 26 ore c'è la mia gara. A che ore sarà la gara?

2. Oggi è domenica, tra 48 ore andrò da Giulia. Che giorno andrò da Giulia?

3. L'orologio a cucù di casa mia suona ogni mezz’ora. Quante volte suona in un giorno?

4. Calcola quante ore trascorri a scuola in una settimana. Se una mattina esco da casa con 13 minuti di ritardo rispetto al solito, a che ora arrivo a scuola?

PROBLEMI A TAPPE

Per arrivare alla soluzione, devi percorrere varie tappe. Le risposte che dai in una tappa possono diventare dati importanti per la tappa successiva!

Problemi con disegni: osserva le immagini, ragiona e calcola

1. Quanto costano tutti i palloncini? 2. Qual è il prezzo totale?

3. Quanto costa il cornetto?

4. Quanto costa la spremuta?

5. Quanto costano tre vasetti di yogurt?

6. Prima tappa . Un bambino della III A festeggia il compleanno a scuola con i suoi 26 compagni. Porta 6 fragole per ogni compagno.

Quante fragole ha portato in tutto?

Seconda tappa . Nel cestino preparato dalla mamma ci sono anche 32 cioccolatini da distribuire tra le 8 maestre presenti a scuola. Quanti cioccolatini riceverà ogni maestra?

7. Prima tappa . Oggi la maestra ha portato a scuola 3 scatole di libri per creare una biblioteca in classe. Dentro a ogni scatola ci sono 15 libri di fiabe e 20 libri di storia. Quanti libri ci sono in ogni scatola?

In tutto quante sono i libri per la biblioteca?

Seconda tappa . La maestra fa scegliere 2 libri a ciascuno dei suoi 24 alunni Anche lei ne sceglie 2. Quanti libri vengono scelti?

Terza tappa . All'inaugurazione della biblioteca vengono invitati anche i 17 alunni della IV A. Visto che loro non hanno una biblioteca, la maestra propone a ognuno di sceglierne 3.

Quanti libri restano nella biblioteca della classe III?

8. Prima tappa . La mamma ha acquistato un mazzo di fiori composto da 12 gerbere e 6 gigli.

Quanti fiori ci sono in tutto?

Seconda tappa . La mamma prende tutti i fiori e li distribuisce in 3 vasi. Quanti fiori metterà in ogni vaso?

PROBLEMI CON I DATI NASCOSTI

A volte dal testo del problema puoi dedurre alcuni dati per conoscenza personale, senza che siano scritti in cifra.

Scrivi per ogni problema il dato nascosto, segui l’esempio:

Alessia ha iniziato un nuovo libro della biblioteca. Durante il fine settimana ha letto 15 pagine al giorno. Quante pagine ha letto in tutto?

DATO NASCOSTO: 2 = il numero dei giorni del fine settimana è 2.

1. Durante la sua malattia Pietro doveva prendere 2 cucchiai di sciroppo al giorno per due settimane. Quanti cucchiai ha preso in tutto?

DATO NASCOSTO:

2. La maestra ha corretto i quaderni di italiano e i quaderni di matematica di ogni alunno della tua classe. Quanti quaderni ha corretto in tutto?

DATO NASCOSTO:

3. Il signor Arcimboldo ha raccolto 4 zucchine, una decina di pomodori e mezza dozzina di peperoni. Quanti ortaggi ha raccolto in tutto?

DATO NASCOSTO:

4. Marta ha 12 anni. Luca ne ha 10 di meno. Pietro ne ha il doppio di Luca. Quanti anni ha Pietro?

DATO NASCOSTO:

PROBLEMI CON DATI MANCANTI

Leggi con attenzione, sottolinea la domanda in rosso . Colora i dati di verde . Scopri le parole che non danno informazioni sufficientemente precise e colorale in giallo . Inserisci tu il dato mancante.

1. La fioraia Maria ha confezionato un bellissimo mazzo di fiori misti da mettere al centro del tavolo della sua cliente. Maria ha inserito nel mazzo 12 rose rosse, alcune rose bianche, 6 margherite, 6 tulipani e 3 girasoli. Quanti fiori ci sono in tutto nel mazzo preparato da Maria?

DATO MANCANTE:

2. È il momento della torta! I genitori di Caterina portano una torta al cioccolato e una torta di frutta. Le candeline sono divise su entrambe le torte. Caterina riesce a spegnerle tutte. Quante candeline ha spento?

DATO MANCANTE:

PROBLEMI CON

DATI INUTILI

Leggi, scrivi quale dato non ti servirà per trovare la risposta.

1a. Un ortolano ha piantato 6 file di 10 piante di pomodori ciascuna e 4 zucche. Quante piante di pomodori sono state sistemate in tutto?

DATO INUTILE:

2a. Alla gara di scacchi partecipano 4 scuole: 5 alunni arrivano dalla scuola di via Roma, 7 alunni da via Torino, 3 alunni da via Firenze e 9 alunni da via Ravenna. In tutto gli insegnanti sono 7. Quanti bambini gareggiano?

DATO INUTILE:

3. Martina ha in mano 7 palloncini, di cui 4 sono rosa. Ne volano via 2. Quanti palloncini le rimangono?

DATO INUTILE:

Inventa tu un problema a partire dai dati

1. 20: numero fiori rossi.

35: numero fiori gialli.

5: numero vasi.

2. 4: numero confezioni di succo.

6: numero bottiglie in ogni confezione.

3. 23 euro: costo di due libri.

5 euro: costo di due quaderni

12 euro: costo di un astuccio.

4. 145 centimetri: altezza di Luca.

187 centimetri: altezza di Giacomo.

Inventa tu un problema a partire dalla domanda

1. Quanti pancake sono avanzati?

2. Quante figurine in totale ha attaccato sull’album?

3. Quante ciliegie ha ricevuto ciascun bambino?

Scrivi una domanda adatta

1. Anna ha raccolto 47 conchiglie al mare. Tornata a scuola ne regala ai compagni 18.

2. Michela prepara 18 muffin al cioccolato per i suoi 6 ospiti.

3. Tommaso aiuta il papà nella serra. Semina 8 semi di pomodoro in ognuno dei 12 vasi.

METTITI ALLA PROVA

1. Questa mattina davanti alla stazione c’erano 13 biciclette. Durante la giornata ne sono arrivate altre 24. Alla sera 18 vanno via. Quante bici rimangono?

2. Per pagare un regalo per la mamma che costa 18 euro e 80 centesimi quali banconote e monete prenderesti?

Prova in altro modo:

3. I piatti della bilancia sono in equilibrio.

Quale peso indichiamo sull'etichetta bianca?

4. Per fare una bottiglia di vino occorrono

5 grappoli d'uva. Se i viticoltori vogliono riempire 24 bottiglie, quanti grappoli occorreranno?

Durante la vendemmia hanno raccolto 15 grappoli il primo giorno, 24 grappoli il secondo giorno e 32 grappoli l'ultimo giorno. Saranno sufficienti per riempire 24 bottiglie?

ADDIZIONE

ieri ho letto il mio libro fino a pagina 45, oggi sono andata avanti di 34 pagine. A che pagina sono arrivata?

Per risolvere questa situazione usiamo l’addizione

Con l’addizione operiamo alcune azioni: z aggiungere; z unire, mettere insieme; z andare avanti.

Trovane altre scoprendole nella tua esperienza quotidiana.

L’addizione può avere più di due addendi

18 + 20 + 31 = 69

Quando abbiamo più addendi possiamo:

I termini dell’addizione 45 + ADDENDO 34 = ADDENDO

SOMMA O TOTALE cambiare l’ordine degli addendi sommare prima alcuni addendi smontare un numero

La PROVA dell’addizione è un’addizione con gli addendi in diverso ordine.

Completa la tabella.

ADDENDO

Osserviamo i colori della tabella

arancione verde

Nella prima riga orizzontale e nella prima colonna verticale vediamo che se a un numero qualsiasi aggiungi zero, il numero non cambia.

5 + 0 = 5

La tabella dell’addizione si può completare sia a partire dagli addendi della riga orizzontale, sia partendo da quelli della colonna verticale.

2 + 7 = 9 e 7 + 2= 9

Vediamo allora che se scambi gli addendi, il risultato non cambia .

CALCOLA A MENTE

1. Che numero ottieni? + 1

STRATEGIE DI CALCOLO

2. Che numeri diventano?

Scomponi e componi i numeri per usare i numeri amici del 10 nelle unità, nelle decine e nelle centinaia.

Se devi aggiungere 9 o un numero che finisce per 9, a un qualsiasi numero, prima aggiungi 10, 20, 30… poi togli 1.

Se devi aggiungere 11 o un numero che finisce per 1 a un qualsiasi numero, prima aggiungi 10, 20, 30… poi aggiungi 1.

3. Calcola unendo i due addendi amici del 10, come nell’esempio.

5 + 8 + 2 =

5 + 10 = 15

5 + 8 + 5 = +

4. Calcola unendo i due addendi amici del 100, come nell’esempio.

5. Completa le addizioni. Fai tappa alla decina.

6. Esegui le addizioni. Rispetta l’ordine indicato dalle frecce.

7. Cerchia i numeri che è più conveniente associare, poi calcola.

17 + 4 + 3 =

15 + 5 + 6 = 13 + 48 + 2 =

8. Scomponi gli addendi, poi associali nel modo opportuno e calcola.

35 + 14 =

9. Somma i due numeri evidenziati e calcola.

23 + 7 + 8 =

10. Esegui gli esercizi usando la strategia di calcolo più adatta.

65 + 9 = (65 + ) - = 39 + 19 = ( + ) - =

11. Esegui gli esercizi usando la strategia di calcolo più adatta.

46 + 11 = (46 + 10) + =

88 + 21 = ( + ) + = 105 + 31 = ( + ) + = 119 + 41 = ( + ) + =

12. Cambia l’ordine degli addendi e calcola i risultati delle addizioni.

2 + 4 = 4 + =

+ 40 = 40 + =

13. Scrivi il numero che manca per ottenere come risultato 100. = 100 50 + 60 + 20 + 90 + 40 + 70 + 30 + 80 + 100 + 10 + 0 +

14. Cerca e circonda i numeri amici del 100 nascosti, poi calcola.

150 + 51 =

160 + 40 =

180 + 20 =

190 + 11 =

150 + 60 =

160 + 41 =

180 + 21 =

190 + 15 =

150 + 70 =

16. Arriva a mille.

600 + = 1˙000 980 + = 1˙000 50 + = 1˙000

+ 60 =

+ 75 =

+ 30 =

+ 35 =

160 + 45 = 180 + 30 =

15. Scrivi il numero che manca per ottenere come risultato 1˙000.

+ 61 =

+ 80 =

+ 31 =

+ 70 =

+ 110 =

17. Cerca e circonda i numeri amici del 1˙000 nascosti, poi calcola.

100 + 100 + 100 + 100 + 100 + 100 =

500 + 100 + 100 + 100 + 100 + 100 =

500 + 500 +500 =

500 + 500 + 200 =

500 + 500 + 800=

500 + 510 =

+

+

+

=

19. Scopri gli addendi mancanti, poi completa.

18. Completa la tabella.

20. Trova il numero che manca.

700 = 200 +

1˙000 = 500 +

900 = 820 +

800 = 775 +

600 = 300 +

500 = 50+

100 = 35 +

700 = 250 +

1˙000 = 200 +

900 = 50 +

800 = 150 +

600 = 30 +

500 = 5 +

100 = 20 +

300 = 15 +

21. Trova il risultato attraverso un calcolo a mente rapido.

13 + 5 + 9 + 12 =

22 + 16 + 7 =

19 + 5 + 6 + 8 =

120 + 50 + 36 =

40 + 60 + 35 =

24 + 18 + 26 =

22. Calcolo rapido.

60 + 30 =

420 + 20 =

539 + 10 =

647 + 30 =

438 + 40 =

300 + 100 = 200 + 300 =

23. Calcola con i numeri alti.

1˙030 + 1˙070 =

+ 31 =

+ 80 =

+ 400 = 300 + 500 =

+ 3˙370 =

+ 1˙300 =

+ 100 =

+ 50 =

+ 550 =

+ 800 =

ADDIZIONI IN COLONNA

ADDIZIONI IN COLONNA

Quando si devono sommare molti addendi o gli addendi sono numeri con molte cifre si possono eseguire i calcoli in colonna.

74 + 213 + 402 = h da u

7 4 +

2 1 3 +

4 0 2 =

6 8 9

AL Circo VENERDì C'ERANO

74 SPETTATORi, SABATO 213 E DOMENiCA 402.

QuANTi SPETTATORi iN TuTTO?

Scriviamo gli addendi uno sotto all’altro, mettendo le unità sotto alle unità, le decine sotto alle decine e le centinaia sotto alle centinaia.

Partendo dalle unità, sommiamo le cifre delle unità, poi quelle delle decine e così via.

ADDIZIONI IN COLONNA CON IL RIPORTO

364 + 218 =

Operiamo sull’abaco

Operiamo in colonna

h da u 1da h da u 3 6 4 + 2 1 8 = 5 8 2 1 1

Sommo le unità

4 + 8 = 12u

Cambio 10 u con 1 da e la RIPORTO nelle decine, poi sommo le decine e infine le centinaia.

Sommo prima le unità

4 + 8 = 12 1 da e 2 u

Scrivo il 2 nella colonna delle u

RIPORTO 1 da nella colonna delle da ; poi sommo le decine e infine le centinaia.

Il RIPORTO può essere nelle u , nelle da , nelle h …

CALCOLA IN COLONNA

1. Inserisci i numeri, poi esegui le addizioni senza cambi.

123 + 321= 43 + 622 = 904 + 54 =

da u

da u

2. Inserisci i numeri, poi esegui le addizioni con il cambio delle unità in decine.

124 + 58 = 306 + 139 =

+ 247 =

3. Inserisci i numeri, poi esegui le addizioni con il cambio delle decine in centinaia.

275 + 172 =

+ 170 =

+ 283 =

4. Inserisci i numeri, poi esegui le addizioni con due cambi.

24 + 389 =

+ 176 =

+ 245 =

5. Sul quaderno esegui le addizioni in colonna senza cambi con la prova, poi riporta i risultati sul libro.

876 + 121 =

+ 507 = 104 + 320 = 156 + 413 =

212 =

+ 87 =

6. Sul quaderno esegui le addizioni in colonna con il cambio delle unità in decine. 328 + 164 =

+ 215 =

+

+

=

+

+

=

=

Sul quaderno esegui le addizioni in colonna col cambio delle decine in centinaia.

+ 572 =

+ 143 =

+ 85 =

+ 91 =

+ 241 =

+ 770 =

7. Sul quaderno esegui le addizioni in colonna con due cambi.

149 + 764 =

+ 345 =

+ 241 = 784 + 118 =

+ 279 =

+ 99 =

8. Sul quaderno esegui le addizioni in colonna con tre addendi.

+ 109 + 241 =

+ 58 +332 =

+ 163 + 77 = 315 + 190 + 163 =

9. Sul quaderno esegui le addizioni in colonna oltre il mille. 1.736 + 58 + 347 = 66 + 2.198 + 319 =

+ 243 + 111 =

+ 224 + 31 =

+ 1.336 = 3.356 + 1.764 =

+ 29 + 257 =

+ 721 =

10. Sul quaderno esegui le addizioni in colonna con numeri sempre più alti.

+ 3.429 =

+ 54.012 =

+ 321 + 3.209 =

+ 12.344 =

+ 19 =

+ 23.426 =

PROBLEMI

L’addizione è l’operazione che mette insieme due o più quantità o aggiunge una quantità a un’altra.

Ci sono alcune parole che sono utili perché aiutano a riconoscere l’addizione:

insieme in tutto in totale ancora in più altri

Sottolinea queste parole nei problemi, scrivi l’operazione e la risposta

1. Sofia prepara il materiale per dipingere, ma ha trovato solo 14 pennelli. Andrea ne trova altri 14. Quanti pennelli hanno ora in tutto?

Calcolo:

Risposta:

2. Lucia risolve 3 problemi di matematica e Matilde ne completa altri 4. Quanti ne hanno risolti mettendoli insieme?

Calcolo:

Risposta:

3. Per la festa di compleanno Carlotta ha preparato 12 succhi di frutta, 6 bottiglie di acqua e 10 aranciate Quante bevande avrà Carlotta?

Calcolo:

Risposta:

4. Edoardo compra in cartoleria un quaderno a 2 euro, una penna a 3 euro e una scatola di pastelli a 11 euro. Trova quanto spende complessivamente.

Calcolo:

Risposta:

Leggi con attenzione, sottolinea le parole utili, i dati e cosa devi cercare

1. A una gita organizzata dalla scuola partecipano 20 alunni di III A e 16 alunni di III B. Quanti sono in tutto gli alunni che partecipano alla gita?

2. Luca ha messo su un vassoio 34 pasticcini. La mamma ne aggiunge altri 16. Quanti pasticcini ci sono in tutto sul vassoio?

3. In un mese Martina ha risparmiato 18 euro. Suo cugino Giacomo ha risparmiato 12 euro in più di lei. Quanto ha risparmiato Giacomo?

Risolvi sul quaderno

1a. Oggi al bar del parco sono seduti 67 bambini a mangiare il gelato e 14 sono ancora in coda alla cassa. Quanti bambini in tutto sono al bar del parco?

2a. Pietro trova in mare 9 conchiglie, il secondo giorno ne trova il doppio e il terzo giorno 4 decine. Quante conchiglie trova complessivamente Pietro in tre giorni?

3a. Carlo sta trasportando con il suo camion una scatola con 450 uova, una con 385 uova e una con 245 uova. Quante uova sta trasportando Carlo?

4. Giovanni ha 60 figurine, Paolo ne possiede la metà e Franco 2 decine di figurine. Chi possiede più figurine? Chi ne ha meno? Vogliono sapere quante sono tutte insieme. Aiutali a rispondere.

5. Alcuni uomini del Paleolitico sono radunati attorno a 5 focolari: attorno al primo ci sono 8 uomini, attorno al secondo ci sono 5 uomini, attorno al terzo ci sono 10 uomini, attorno al quarto ci sono 3 uomini e attorno all’ultimo ci sono 12 uomini. Quanti uomini del Paleolitico si stanno scaldando attorno al fuoco?

Dopo un po’ si aggiungono 17 donne e 11 bambini che erano rimasti nelle caverne, ora il clan è al completo. Quante persone si contano in tutto il clan?

6. Per la sua festa di compleanno, Sofia prepara 17 panini con il prosciutto, 18 con il tonno, 20 con il salame. Quanti panini ha preparato in tutto? Arriva anche la sua amica Gemma con una dozzina di panini con la marmellata. Adesso quanti sono i panini pronti?

1. Completa.

METTITI ALLA PROVA

2. Calcola a mente.

30 + 50 = 48 + 22 = 88 + 100 =

+ 31 =

+ 1 + 50 =

+ 300 =

3. Calcola in colonna.

415 + 68 = 524 + 90 + 145 =

+ 48 =

+ 250 =

+ 8 =

4. Sull'autobus ci sono 25 passeggeri. Alla fermata successiva ne salgono 13 in più e nessuno scende.Quanti sono ora i passeggeri?

Calcolo:

Risposta:

5. Risolvi.

Ad una partita di basket assistono 135 spettatori tifosi della squadra locale e 89 sostenitori della squadra ospite. Quanti spettatori in tutto?

Gli spettatori sono distribuiti sui quattro lati dello stadio. Osserva, calcola e indica fra questi gruppi di numeri quello utile per arrivare al totale.

SOTTRAZIONE

Ho una scatola con 70 pezzi per le costruzioni. Ne ho già usati 43. Quanti me ne restano?

Per risolvere queste situazioni usiamo la sottrazione

Con la sottrazione operiamo alcune azioni: z togliere; z riconoscere la differenza; z tornare indietro.

Trovane altre scoprendole nella tua esperienza quotidiana.

il nonno ha 70 anni, il papà ne ha 43.

Quanti anni hanno di differenza?

Osserviamo

La sottrazione è l’operazione inversa dell’addizione (e viceversa): permette dal risultato di tornare al numero di partenza.

La PROVA della sottrazione è l’addizione.

I termini della sottrazione 70 – MINUENDO 43 = SOTTRAENDO 27 RESTO O DIFFERENZA 27 + 43 =

Completa la tabella.

SOTTRAENDO

Osserviamo i colori della tabella

0 giallo

Tutti i numeri sulla diagonale sono zero perché quando minuendo e sottraendo sono uguali il risultato è zero.

5 – 5 = 0

verde grigio

Nella prima colonna i numeri sono uguali al minuendo perché se il sottraendo è zero, il resto è uguale al minuendo.

7 – 0 = 7

La tabella della sottrazione non è completa perché la sottrazione si può fare solo se il sottraendo è minore del minuendo.

8 – 4 = 4 4 – 8 = non si può fare con i numeri che fin qui conosciamo.

CALCOLO A MENTE E IN RIGA

1. Scrivi i numeri da 98 a 75 togliendo 1.

2. Scrivi i numeri da 313 a 296 togliendo 1.

3. Scrivi i numeri da 1˙023 a 1˙001 togliendo 1.

4. Completa.

5. Scopri la regola e continua la numerazione.

50 , 35 , 20 ,

335 , 325 , 315 , ,

45 , 40 , 35 , , , , , , ,

285 , 265, 245, , , , , , ,

come nell’esempio.

6. Osserva i numeri negli schemi e completa con gli operatori

7. Osserva gli operatori e completa con i i numeri mancanti come nell’esempio.

8. Numera togliendo ogni volta una decina.

9. Numera togliendo ogni volta un centinaio.

368 543 1.920

10. Quanto manca?

Da 35 a 40 manca

Da 50 a 100 manca

Da 43 a 50 manca

Da 25 a 49 manca

Da 25 a 45 manca

Da 48 a 100 manca

Da 70 a 98 manca

Da 130 a 200 manca

Da 15 a 30 manca

Da 35 a 70 manca

Da 38 a 40 manca

Da 250 a 350 manca

Da 60 a 100 manca

Da 110 a 140 manca

Da 120 a 200 manca

STRATEGIE DI CALCOLO

Scomponi e componi i numeri per fare tappa alla decina o alle centinaia usando i numeri amici del 10

Se devi sottrarre 9 o un numero che finisce per 9, a un qualsiasi numero, prima togli 10, 20, 30… poi aggiungi 1.

Se devi sottrarre 11 o un numero che finisce per 1, a un qualsiasi numero, prima sottrai 10, 20, 30… poi sottrai 1.

Se devi sottrarre numeri vicini tra loro , cerchi subito il complementare, cioè il numero che manca al sottraendo per arrivare al minuendo.

Calcola

1. Calcola in riga seguendo l’esempio.

Esempio 35 – 8 = (35 – 5) – 3 = 27

46 – 9 =

– 8 =

– 6 =

2. Calcola in riga seguendo l’esempio.

Esempio 64 – 26 = (64 – 20) – 6 = 38

46 – 17 = 26 – 19 = 83 – 35 = 75 – 28 =

– 39 =

– 28 =

– 16 =

– 32 =

3. Togli 9.

Esempio 21 – 9 = 21 – 10 + 1 = 12

– 9 =

– 9 =

4. Togli 11.

–

Esempio 15 – 11 = 15 – 10 – 1 = 4

5. Trova una strategia.

6. Quanto resta? 10 – 3 =

– 4 =

– 6 =

–

7. Completa i numeri in tabella.

–

8. Completa la tavola da 200 a 299. Aiutati con l’esempio delle frecce parlanti.

10. Trasforma e calcola. 80 u – 1 da = 80 –

9 da – 10 u = – = u 10 da – 3 da = – = u

u – 7 u = – = u

11. Arriva a mille. 1˙300 – =

9. Completa usando le frecce parlanti.

12. Calcola a mente, scegli la strategia più comoda e sicura per te.

36 – 19 =

40 – 23 =

72 – 54 =

24 – 18 = 100 – 85 =

– 26 = 32 – 17 =

– 29 =

– 35 =

– 83 =

– 15 =

– 36 =

– 28 =

– 19 =

– 27 =

13. I numeri sono più alti, ma la strategia non cambia!

2˙100 – 1˙040 =

– 35 =

– 28 =

–

– 19 =

– 19 =

500 – 9 = 3˙000 – 30 = 6˙400 – 2˙170 = 5˙000 – 1˙350 = 1˙840 – 677 =

14. A spasso nel tempo! Calcola i diversi periodi.

1 decennio (D) = 10 anni

1 secolo (S) = 100 anni

1 millennio (M) = 1.000 anni

2 D – 8 anni = anni

4 S – 3 D = anni

9 D – 12 anni = anni

6 S – 2 S = anni

8 D – 10 anni = anni

9 S – 4 S = anni

1 S – 4 anni = anni

5 S – 500 anni = anni

5 S – 50 anni = anni

SOTTRAZIONI IN COLONNA

SOTTRAZIONI IN COLONNA

Quando in una sottrazione il minuendo e il sottraendo sono composti da molte cifre si possono eseguire i calcoli in colonna.

457 – 136 =

h da u

4 5 7 –

1 3 6 = 3 2 1

nel carretto dei gelati ci sono 457 gelati.

nel pomeriggio se ne vendono 136. QuANTi gelati sono rimasti?

Scriviamo minuendo e sottraendo uno sotto all’altro, mettendo le unità sotto alle unità, le decine sotto alle decine e le centinaia sotto alle centinaia. Partendo dalle unità, sottraiamo le cifre delle unità, 7 – 6 = 1, poi quelle delle decine e così via.

SOTTRAZIONI IN COLONNA CON IL PRESTITO

652 – 236 = Operiamo sull’abaco

Calcoliamo in colonna

Sottraggo partendo dalle unità: 2 – 6 non si può fare; dalle 5 da prendo in PRESTITO 1 da e la cambio con 10 u : adesso ho 12 u: 12 – 6 = 6u. Tolgo con un segno le unità del sottraendo. Sono rimaste 4 da : 4 – 3 = 1 da (tolgo le da del sottraendo) e infine tolgo con un segno anche le h.

Sottraggo partendo dalle unità 2 – 6 non si può fare; dalle 5 da prendo in PRESTITO 1 da , che unita alle 2 u, fa 12 u. 12 – 6 = 6 u. Sottraggo le decine: ho 4 da al minuendo, perchè ne ho prestata una 4 – 3 = 1 da.

Proseguo sottraendo anche le h.

Anche le centinaia o le migliaia possono fare un PRESTITO !

CALCOLO IN COLONNA

Esegui le sottrazioni in colonna con la prova sul quaderno, riporta i risultati.

1. Sottrazioni in colonna senza prestito.

987 – 626 =

409 – 103 = 847 – 521 = 778 – 342 = 560 – 350 =

2. Sottrazioni in colonna con il prestito dalle decine.

247 – 128 = 683 – 425 =

790 – 353 = 137 – 128 = 538 – 219 =

3. Sottrazioni in colonna con il prestito dalle centinaia.

429 – 241 =

508 – 321 =

924 – 352 = 618 – 58 =

225 – 132 =

4. Sottrazioni in colonna con due prestiti.

452 – 185 =

350 – 154 =

500 – 205 =

603 – 374 =

876 – 678 =

5. Sottrazioni in colonna oltre il mille.

1˙030 – 874 = 2˙107 – 1˙308 = 5˙138 – 2˙324 = 3˙450 – 1˙225 = 2˙323 – 1˙144 =

6. Numeri sempre più alti: attento a incolonnare!

10˙413 – 6˙147 = 9˙374 – 3˙186 = 11˙101 – 6˙319 = 15˙840 – 3˙615 = 24˙300 – 12˙420 =

PROBLEMI

La sottrazione è l’operazione che toglie un numero da un altro o trova la differenza tra due numeri e quanto manca per raggiungere un numero.

Le parole utili a riconoscere una sottrazione possono essere queste:

in più di più di meno già in meno solo ancora

manca

avanza confronta resta

Sottolinea queste parole nei problemi, scrivi l’operazione e la risposta

1. Allo spettacolo teatrale organizzato dall’insegnante di inglese, sono stati invitati 196 alunni. Ne sono già arrivati 79. Quanti ragazzi devono ancora arrivare?

Calcolo: Risposta:

2. La maestra aveva comprato un pacco da 500 fogli di carta per fotocopie. Ha usato 300 fogli. Quanti fogli può ancora usare?

Calcolo: Risposta:

3. Sulla metropolitana c’erano 264 passeggeri. Alla prima fermata ne sono scesi 122. Quanti passeggeri sono rimasti sulla metro?

Calcolo: Risposta: Risolvi

1a. Un palazzo ha 7 piani; 3 sono illuminati. Quanti piani non sono illuminati?

Calcolo: Risposta:

2a. Gino ha 12 matite, Luca ne ha 8. Quante ne ha in più Gino?

Calcolo: Risposta:

3. Nel vaso ci sono 15 fiori, 9 sono tulipani. Quanti fiori non sono tulipani?

Calcolo: Risposta:

4. In un vaso ci sono 14 fiori, in un altro ce ne sono 22. Qual è la differenza?

Calcolo: Risposta:

5. Sara ha costruito una torre con 30 mattoncini colorati. Sua sorella Marta ha fatto una torre usando solo 17 mattoncini. Quanti mattoncini ha in più la torre di Sara?

Calcolo: Risposta:

6. Marco ha 15 anni, suo nonno ha 72 anni. Quanti anni di differenza ci sono tra nonno e nipote?

Calcolo: Risposta:

7. Edo e Riccardo giocano a basket. Edo oggi ha totalizzato 23 punti, Riccardo 34. Quanti punti in meno ha totalizzato Edo?

Calcolo: Risposta:

8. Nel salvadanaio di Federico ci sono 87 euro, in quello di sua sorella Emma ci sono 120 euro. Quanti euro ha in più Sara?

Calcolo: Risposta:

9. Cenerentola ha fatto i biscotti per i suoi amici topolini. La teglia conteneva 54 biscotti. I topolini ne hanno rosicchiati 21. Qual è la differenza fra i biscotti interi e quelli rosicchiati?

Calcolo: Risposta:

10. Mattia e Leonardo contano i loro soldatini. Mattia ne possiede 22, cioè 10 più di Leonardo. Quanti sono i soldatini di Leonardo?

Calcolo: Risposta:

11. La mamma ha acquistato una bella pianta fiorita a 15 euro da sistemare sul terrazzo. Ha pagato con una banconota da 50 euro. Quanto ha ricevuto di resto?

Calcolo: Risposta:

12. Per Natale a Ginevra hanno regalato un libro con 439 pagine. Dopo una settimana, a Ginevra mancano da leggere 197 pagine. Quante ne ha già lette?

Calcolo: Risposta:

13. Le maestre hanno raccolto i soldi per la recita scolastica. In tutto hanno bisogno di 257 euro, ma hanno raccolto solo 239 euro. Quanti soldi mancano?

Calcolo: Risposta:

14. Nella scatola del materiale della maestra ci sono 76 oggetti tra elastici e gessetti. Se gli elastici sono 48, quanti sono i gessetti?

Calcolo: Risposta:

15. In un vagone del treno ci sono 142 posti a sedere. Salgono 87 passeggeri. Quanti posti rimangono liberi?

Calcolo: Risposta:

16. Ad una festa sono stati riempiti 120 bicchieri di aranciata, dopo un'ora ne sono stati vuotati 78. Quanti bicchieri sono ancora pieni?

Calcolo: Risposta:

1. Torna al numero.

METTITI ALLA PROVA

2. Calcola a mente

3. Calcola in colonna.

Nello scaffale del supermercato a inizio giornata ci sono 350 mele. A fine giornata ne rimangono 162. Quante mele sono state vendute?

Quante mele devono essere aggiunte per averne 500 a disposizione il giorno dopo?

4. Risolvi.

MOLTIPLICAZIONE

devo realizzare gli inviti della mia festa di compleanno, attaccando uno sticker su un cartoncino. in cartoleria ci sono 8 diversi colori di cartoncino e 6 tipi di stickers. non mi resta che scegliere quale abbinamento sticker-colore preferisco. quanti sono tutti quelli possibili?

Per rispondere alla domanda, è utile organizzare una tabella che può visualizzare insieme tutti gli abbinamenti tra gli 8 colori e i 6 stickers: ogni casella rappresenta un abbinamento, il numero delle caselle della tabella dà il numero dei possibili abbinamenti.

Per contarle tutte, possiamo osservare che per ognuno degli 8 colori, ci sono 6 diverse caselle.

Contando “per 6” otto volte, facciamo l’operazione che le conta tutte: è la moltiplicazione.

6 × 8 = 48

La rappresentazione ci ricorda che moltiplicare è collegato a diverse azioni : z abbinare tra loro oggetti di due insiemi; z ripetere un’addizione; z schierare , cioè disporre ordinatamente, come nella quadrettatura, in righe e colonne

I termini della moltiplicazione

6 × FATTORE

8 = FATTORE

48 PRODOTTO

I fattori della moltiplicazione possono cambiare ordine

8 × 2 = 16

2 × 8 = 16

Questa proprietà può servire per fare la prova di una moltiplicazione.

Fai un sondaggio in classe per scoprire quale abbinamento piace di più.

Poi disegna e colora l'abbinamento che ha vinto e quello che hai votato tu.

Usando le tabelline, completa tu la TAVOLA PITAGORICA .

FATTORE

Osserviamo insieme

z Nella riga e nella colonna dello zero perciò possiamo dire che 0 × = × 0 =

z Nella riga e nella colonna dell’ uno perciò possiamo dire che 1 × = × 1 =

z Le caselle colorate sulla diagonale della tavola pitagorica sono speciali: infatti hanno i fattori

z Le caselle colorate in verde contengono lo stesso numero : infatti × = × = Come sono rispetto alla diagonale? Colora almeno altre 4 coppie di caselle che hanno la stessa relazione. Possiamo dire che: cambiando l’ordine dei fattori il prodotto non cambia.

z Nella riga e nella colonna del dieci si può vedere che 10 × = × 10 = perciò possiamo dire che

Un altro modo di vedere: il DECANOMIO

Osserviamo insieme

z Il numero dei quadretti di ogni rettangolino corrisponde al risultato della moltiplicazione

z Quando si hanno fattori uguali si ottengono rettangoli speciali: sono dei quadrati

z Cosa osservi nei rettangoli colorati in verde?

PARETE DI TABELLINE

1. Osserva le tabelline e completa

2. Ripassa bene le tabelline, poi completa la tabella.

3. Osserva e rispondi.

z Quante volte hai ottenuto il prodotto 21? Con quali coppie di fattori?

z Quante volte hai ottenuto il prodotto 12? Con quali coppie di fattori?

z Quante volte hai ottenuto il prodotto 16? Con quali fattori?

z Quante volte hai ottenuto 48? Con quali fattori?

z Ci sono numeri che compaiono una sola volta nella tavola?

z Ci sono numeri minori di 20 che non vedi nella tavola pitagorica?

4. Riconosci la moltiplicazione e risolvi.

Quante foglioline in tutto?

Quante figurine in tutto?

Quanti tentacoli in tutto?

Quante perline in tutto?

5. Nelle cartelle che seguono colora i multipli dei numeri indicati.

Segna con una X in quali cartelline sono state realizzate le quaterne (4 numeri colorati nella stessa riga).

A. B. C. D. E. F.

Completa e segna quanto tempo ci hai messo. Controlla se stai migliorando.

1. Esercitazione 1.

TEMPO: 5 × 4 =

2. Esercitazione 2.

TEMPO: 2 × 6 =

3. Esercitazione 3.

TEMPO: × 9 = 72 5 × = 15 × 6 = 42 × 8 = 56

4. Esercitazione 4. TEMPO:

5. E sercitazione 5.

TEMPO:

Completa

1. Nella tabella della moltiplicazione cerca il prodotto indicato di volta in volta e completa o scrivi le moltiplicazioni come negli schemi.

2. Scopro i fattori.

3. Scrivi i fattori mancanti e completa.

4. Completa la tabella.

Moltiplicare × 10, × 100, × 1.000

1. Moltiplica × 10: le unità diventano decine, ogni cifra cambia valore e si sposta a sinistra di un posto

5 ×

×

=

=

2. Moltiplica × 100: le unità diventano centinaia, ogni cifra cambia valore e si sposta a sinistra di due posti

2 × 100 = 4 × 100 =

×

=

=

×

×

×

=

=

3. Moltiplica × 1.000: le unità diventano migliaia, ogni cifra cambia valore e si sposta a sinistra di tre posti .

5 × 1.000 =

8 × 1.000 = 7 × 1.000 = 4 × 1.000 =

LA MOLTIPLICAZIONE E L’ADDIZIONE SI AIUTANO

12 × 3 = ( 10 + 2 ) × 3 = smontiamo il fattore 12 in due addendi 10 e 2

(10 × 3) + (2 × 3) = moltiplichiamo ciascun addendo per tre

30 + 6 = scriviamo i due prodotti

36 poi li sommiamo

1. Osserva, smonta i fattori e calcola. Segui l'esempio.

78 × 6 = (70 × 6) + (8 × 6) = 420 + 48 = 468

53 × 3 = ( × ) + ( × ) = +

45 × 5 = ( × ) + ( × ) =

123 × 4 = ( × ) + ( × ) + ( × ) =

2. Osserva, smonta i fattori e calcola.

425 × 2 = ( × ) + ( × ) + ( × ) =

37 × 9 = ( × ) + ( × )

708 × 6 = ( × ) + ( × ) + ( × ) =

IN COLONNA

Con una cifra al secondo fattore

21 × 4 =

Usiamo il multibase

21 = 2 da + 1 u

( 2 da + 1 u ) × 4 =

( 2 da × 4 ) + ( 1 u × 4 ) =

In colonna

×

=

Inizio sempre dalle unità:

z moltiplico le unità del 1° fattore per il 2° fattore; z poi moltiplico le decine del 1° fattore, per il 2° fattore.

8 da + 4 u = 84

Quando il secondo fattore ha due o più cifre

32 × 13 =

Osserva. Posso scomporre il 2° fattore e procedere così:

32 × 1 3 =

32 × ( 10 + 3 ) =

(32 × 10 ) + ( 3 2 × 3 ) =

+ (30 × 3 ) + (2 × 3) =

+ 90 + 6 = 416 In colonna

×

prodotto 32 × 1 da 2° prodotto

Sommo i due prodotti

z moltiplico il 1° fattore per le u del 2° z poi moltiplico il 1° fattore per le da del 2° ( lascio libero lo spazio nella colonna delle u, perchè moltiplico × 10 )

Con una cifra al secondo fattore e con riporto

214 × 3 =

Usiamo il multibase

214 = 2 h + 1 da + 4 u

( 2 h + 1 da + 4 u ) × 3 =

( 2 h × 3 ) + ( 1 da × 3 ) + ( 4 u × 3 ) =

In colonna

h da u 2 1 4 × 3 = 6 4 2

Inizio sempre dalle unità: z moltiplico le u del 1° fattore per il 2° fattore: 4 × 3 = 1 2 ; scrivo 2 nella colonna delle u e riporto 1 da nella colonna delle da ; 1

z poi moltiplico le da del 1° fattore, per il 2° fattore: 1 × 3 = 3 da, più 1da del riporto = 4 da ; z moltiplico le h : 2 h × 3 = 6 h

6 h + 4 da + 2 u = 642

ESERCIZI

1. Calcola attraverso passaggi scritti come nell’esempio.

Esempio 42 × 3 = (40 × 3) + (2 × 3) = 120 + 6 = 126

17 × 4 =

26 × 4 =

36 × 5 =

37 × 5 =

19 × 4 =

2. Esegui sul quaderno le moltiplicazioni in colonna, riporta i prodotti sul libro e scrivi la prova in riga.

Esempio 45 × 3 = 135 prova 3 × 135

67 × 7 = prova 7 ×

23 × 8 = prova ×

56 × 9 = prova ×

128 × 5 = prova ×

356 × 7 = prova ×

481 × 3 = prova ×

302 × 6 = prova ×

2.140 × 4 = prova ×

3.012 × 3 = prova ×

1.120 × 2 = prova ×

3. Moltiplicazioni con il moltiplicatore a due cifre. Sul quaderno esegui in colonna con la prova e riporta i prodotti sul libro.

33 × 13 =

15 × 12 =

14 × 25 = 13 × 15 = 19 × 12 = 22 × 18 =

24 × 16 = 14 × 34 =

34 × 15 = 17 × 23 = 25 × 21 = 42 × 23 =

4. Esegui le moltiplicazioni in colonna.

21 × 3 =

42 × 2 =

12 × 4 =

5. Completa le moltiplicazioni in colonna.

PROBLEMI

La moltiplicazione è l’operazione che combina e schiera tra loro due numeri o ripete più volte lo stesso numero.

Le parole utili a riconoscere la moltiplicazione sono:

in ogni a testa complessivo per ciasscuno in tutto

Leggi con attenzione, sottolinea le parole utili, i dati e che cosa devi cercare.

1. Ho 4 pacchetti di figurine. Ogni pacchetto ne contiene 5. Quante figurine ho in tutto?

Calcolo:

Risposta:

2. Ho nel portafoglio 4 banconote da 10 euro. Quanto ho in totale?

Calcolo:

Risposta:

3. Giovanni porta a scuola 7 sacchetti di caramelle con 8 caramelle ciascuno. Quante caramelle ci sono in tutto?

Calcolo:

Risposta:

4. Lucia distribuisce 3 libri a ciascuna delle sue 4 amiche. Quanti libri hanno in tutto?

Calcolo:

Risposta:

5. In spiaggia ci sono 3 file con 8 ombrelloni ciascuna. Quanti ombrelloni ci sono in spiaggia?

Calcolo:

Risposta:

6. A scuola sono appena arrivati 13 scatoloni contenenti ciascuno 7 palloni nuovi. Quanti palloni sono stati acquistati?

Calcolo:

Risposta:

7. Al compleanno di Luca mancano 5 settimane. Quanti giorni mancano?

Calcolo:

Risposta:

Problemi con una o due domande

1. Sara distribuisce 4 carte alle 4 giocatrici del tavolo.

Quante carte sono state distribuite?

Il mazzo contiene 40 carte. Quante ne rimangono?

2. La maestra ha fotocopiato 3 fogli per ciascuno dei suoi 26 alunni.

Quante fotocopie ha distribuito?

Per compito ne distribuisce altre 2 a testa.

Quante fotocopie sono state usate in totale quel giorno?

3. Quante dita si contano in tutto nelle mani di mezza decina di bambini?

Quante decine di dita?

4. Claudia ha comprato le palline per addobbare l’albero di Natale. Ha 2 confezioni con 9 palline rosse ciascuna e 4 confezioni con 12 palline d’oro. Quante sono in più le palline d’oro rispetto a quelle rosse?

Quante palline in totale metterà sull’albero?

5. La nonna ha confezionato 2 cappelli (uno verde e uno blu) e 3 pon-pon (uno giallo, uno rosso e uno blu). È indecisa sugli abbinamenti di colori: sai aiutarla a trovare tutte le combinazioni? Quante ne può fare?

6. Non mi ricordo quante sono le carte che uso per il gioco di memoria. So però che le ho schierate per righe e colonne componendo un rettangolo. Ogni riga ha 7 carte e le colonne sono 6. Sai aiutarmi a capire quante sono?

7. Per festeggiare il mio compleanno vorrei portare a scuola dei cioccolatini e darne 3 a ciascuno dei miei 24 compagni. Di quanti cioccolatini ho bisogno?

METTITI ALLA PROVA

1. Calcola velocemente.

3 × 8 = 40 × 3 = 4 × 9 = 60 × 6 = 7 × 6 = 70 × 8 = 9 × 8 = 50 × 9 =

2. Unisci ogni gruppo di monete o di biglietti al valore corrispondente.

3. Rispondi e disegna.

1. Quante figurine ha Leonardo se le ha disposte su 8 colonne e 12 righe?

2. Quanti cioccolatini servono al pasticciere per preparare

100 scatole con 12 cioccolatini per scatola?

4. Calcola in colonna.

La nonna ha preparato la sua buona marmellata di pesche, riempiendo 42 vasetti uguali tra loro. Per conservarli, li sistema in cantina sui 6 ripiani dello scaffale, che contengono ciascuno lo stesso numero di barattoli.

Quanti vasetti stanno su ogni ripiano dello scaffale?

Dobbiamo ripartire i 42 vasetti in 6 gruppi con ugual numero di vasetti, ogni gruppo riempirà un ripiano. Distribuiamo i vasetti uno per volta su ciascuno dei 6 ripiani, finché li abbiamo esauriti: su ogni ripiano stanno esattamente 7 vasetti.

Tra i numeri del problema abbiamo fatto una divisione : 42 : 6 = 7

L’operazione del dividere è collegata a diverse azioni: z raggruppare oggetti in gruppi con lo stesso numero di elementi; z distribuire un certo numero di oggetti in parti uguali; z cercare i fattori che moltiplicati tra loro danno un numero assegnato.

I termini della divisione

Osserviamo

La divisione è l’operazione inversa della moltiplicazione (e viceversa): permette dal risultato di tornare al numero di partenza. La prova della divisione è la moltiplicazione.

Usando la tavola pitagorica, completa la TABELLA DELLA DIVISIONE DIVISORE

Osserviamo insieme

z La colonna dello zero è tutta barrata: NON si può mai dividere un numero per zero .

z Nelle caselle della diagonale compare sempre il numero : infatti, un numero diviso per sé stesso dà come risultato 1

z Le caselle della seconda colonna ci portano a dire che dividendo un numero per 1 si ottiene

z Questa tabella NON è , anzi, è riempita solo .

Possiamo dire che: nella divisione NON si possono scambiare tra loro dividendo e divisore.

ESERCIZI

1. Completa seguendo l’esempio.

Esempio 35 : 5 = 7 perché 7 × 5 = 35

27 : 3 = perché × =

18 : 3 = perché × =

24 : 6 = perché × =

36 : 4 = perché × =

27 : 9 = perché × =

32 : 8 = perché × =

56 : 8 = perché × =

12 : 6 = perché × =

12 : 4 = perché × = 81 : 9 = perché × =

2. Calcola il termine mancante.

: = 10

: = 6

3. Calcola il quoto.

: 7 = perché × =

: 9 = perché × =

: 8 = perché × =

: 6 = perché × =

: 3 = perché × =

: 4 = perché × =

: 8 = perché × =

: 2 = perché × =

: 7 = perché × =

: 8 = perché × =

4. Completa le tabelle.

5. Completa la tabella, non scrivere nelle caselle blu.

6. Completa le tabelle, scrivi i divisori mancanti.

La metà

1. Colora la metà – un mezzo (½) – degli oggetti.

2. Osserva l’esempio e completa le operazioni scrivendo i risultati.

Esempio 2 : 2 = 1

20 : 2 =

200 : 2 = 2˙000 : 2 =

3. Completa queste frasi.

8 è la metà di

10 è la metà di

: 2 =

: 2 =

: 2 =

12 è la metà di 11 è la metà di 7 è la metà di 13 è la metà di

4. Calcola e scrivi sul tuo quaderno il doppio di: 20, 60, 100, 25, 33, 30, 70, 200, 42.

5. Calcola e scrivi sul tuo quaderno il triplo di: 50, 100, 25, 15, 23, 220, 18, 60, 35.

6. Calcola e scrivi sul tuo quaderno la metà di: 12, 10, 20, 30, 50, 24, 60, 100, 120, 180, 90.

7. Completa le tabelle.

: 2 =

: 2 =

: 2 =

DIVISIONI CON IL RESTO

Non sempre due numeri sono divisibili uno per l’altro; nell’operare una divisione può esserci un RESTO Nella prova , se la divisione ha il resto, occorre sommare il resto al prodotto.

Divisioni con il resto

1. Rappresenta le seguenti divisioni con il resto. Disegna oggetti semplici come nell’esempio.

20 : 6 = resto

2. Esegui con la prova.

18 : 5 = resto 23 : 7 = resto

Esempio 28 : 3 = 9 con resto 1

50 : 6 =

32 : 7 =

60 : 9 =

45 : 2 =

38 : 3 =

46 : 4 =

53 : 5 =

PROVA: 9 × 3 = 27 27 + 1 = 28

DIVISIONI IN COLONNA

RAPPRESENTIAMO CON IL MULTIBASE QUESTA DIVISIONE

75 : 3 =

75 =

Dividiamo le decine in 3 gruppi

7 da : 3 = 2 da resta 1 da

La cambio con 10 u che unisco

alle 5 u = 15 u

Dividiamo le unità

15 : 3 = 5 u

2 da + 5 u = 25

IN COLONNA

Dividiamo partendo dalla cifra di maggior valore.

7 5 : 3 = 2 5

1 5 0

7 da : 3 = 2 da con il resto di 1 da scrivo 1 da sotto alle da e “abbasso” le 5 u

1 5 : 3 = 5 u , resto 0; scrivo il 5 al risultato

Dividere un numero, il dividendo , per un altro, il divisore , è come calcolare quante volte il divisore è contenuto (diciamo “sta”) nel dividendo.

Osserva e calcola

z 6 9 : 3 = 2 3

Divido cercando quante volte il divisore (3) ci sta nel dividendo ( 6 9 ).

Inizio dalla cifra di maggior valore del dividendo (a sinistra).

6 9 : 3 = 2 …

6 9 : 3 = 2 3

6 - 9Il 3 nel 6 ci sta 2 volte (scrivo 2 al quoto);

torno “indietro” per calcolare il resto: 2 × 3 = 6 , al 6 0 resto; abbasso le 9 u , il 3 nel 9 ci sta 3 volte ( 3 al quoto);

torno “indietro” per calcolare il resto: 3 × 3 = 9 , al 9 0 resto.

z 6 4 5 : 3 = 1 1 3

Divido cercando quante volte il divisore (3) ci sta nel dividendo ( 6 4 5 ).

Inizio dalla cifra di maggior valore del dividendo (a sinistra).

6 4 5 : 3 = 2 …

6 4 5 : 3 = 2 1 5 - 4 1 5Il 3 nel 6 ci sta 2 volte” (scrivo 2 al quoto);

torno “indietro” per calcolare il resto: 2 × 3 = 6 , al 6 0 resto; abbasso le 4 da , il 3 nel 4 ci sta 1 volta ( 1 al quoto);

torno “indietro” per calcolare il resto: 1 × 3 = 3 , al 4 1 resto; abbasso le 5 u ; il 3 nel 1 5 ci sta 5 volte ( 5 al quoto);

torno “indietro” per calcolare il resto: 5 × 3 = 1 5 , al 1 5 0 resto.

Risolvi sul quaderno le divisioni in colonna con la prova, riporta il quoto sul libro

1. Divisioni senza resto.

69 : 3 =

: 4 =

: 5 =

: 2 =

2. Divisioni con il resto.

:

: 3 =

: 3 =

Problemi veloci

1a. Ho 12 matite e le divido in 4 scatole. Quante matite ci sono in ogni scatola?

2a. Ho 26 perline. Quanti anelli da 10 perline ciascuno riesco a fare?

3. In palestra la maestra dice agli scolari di prendere 2 birilli a testa. I birilli sono 18 e non ne rimane nessuno. Quanti alunni sono presenti?

4. Una mosca ha 6 zampe. Se vedo 24 zampe, quante mosche ci sono?

5. In un parcheggio ci sono 32 auto disposte 4 per fila. Quante file formano?

PROBLEMI

La divisione è l’operazione che distribuisce e raggruppa in parti uguali.

Le parole importanti della divisione possono essere:

in ogni a testa a ciasscuno in parti uguali

suddivide ordina distribuisce

lo stesso numero schiera contiene

Leggi con attenzione, sottolinea le parole importanti, quanto viene richiesto e i dati

1. In un vaso ci sono 24 biscotti. Alice, Carlo e Leo se li dividono in parti uguali. Quanti biscotti a testa?

Calcolo:

Risposta:

2. La maestra dà 35 libri in parti uguali a ciascuno dei 7 alunni incaricati di distribuirli alla classe. Quanti libri riceve ciascun alunno?

Calcolo:

Risposta:

3. La maestra prepara 72 mattoncini per giocare alle costruzioni. Divide gli alunni in 8 gruppi, quanti mattoncini avrà ogni gruppo?

Calcolo:

Risposta:

4. Hai 18 sedie da distribuire a 3 tavoli. Disponili in modo che ogni tavolo abbia lo stesso numero di sedie.

Calcolo:

Risposta:

Risolvi

1. Un fiorista compra 69 rose rosse e le sistema in 3 vasi. Quante rose ci saranno in ogni vaso?

2. 40 violette e 24 margherite vengono distribuite in 8 mazzi di fiori. Quante margherite e quante violette vanno in ciascun mazzo di fiori?

3. Il bagnino chiude tutte le sere gli ombrelloni del suo bagno. Gli ombrelloni sono disposti in ordine: sono 5 file da 12 ombrelloni ciascuna. Gliene mancano da chiudere ancora la metà. Quanti ombrelloni sono già stati chiusi?

4. Elisa ha un album di figurine e su ogni pagina ci stanno 9 figurine. Se ha 108 figurine, quante pagine ha già riempito?

5. Nel teatro della scuola ci sono 180 poltroncine. Ogni fila contiene 15 poltroncine. Quante file ci sono? Prima che iniziasse lo spettacolo sono state occupate 3 file. Quanti posti liberi ci sono ancora?

6. Per il gioco di memoria Omar ha distribuito le 72 carte su otto colonne. Quante righe ha fatto?

Puoi disporle in altro modo?

7. Simone deve consegnare per il torneo 217 medaglie da distribuire a 7 squadre.

Quante medaglie toccheranno ad ogni squadra?

8. Per preparare una festa al ristorante occorre disporre 186 persone su 6 grandi tavoli.

Trova quante persone si siederanno ad ogni tavolo.

9. Al centro estivo vengono distribuiti 240 braccialetti alle 6 squadre. Quanti braccialetti per ogni squadra?

In ogni squadra ci sono 10 bambini, quanti braccialetti a testa?

CAPISCO

z Leggo e comprendo il testo; z raccolgo i dati ; z individuo e capisco la richiesta ; z Riconosco quali dati sono utili e quali no

RAPPRESENTO

z con immagini o simboli i dati utili e le azioni.

CALCOLO

z con i numeri , scrivo le operazioni che mi permettono di arrivare alla soluzione.

VERIFICO E RISPONDO

z Rileggo la domanda ; z controllo se il mio operato risponde al quesito; z formulo una risposta attraverso una frase completa , che riprenda la domanda.

Roberto, il papà di Marco, porta il figlio al cinema, allo spettacolo delle ore 18 Acquista un biglietto adulti da 8 euro e uno ridotto a 6 euro Quanto spende il papà?

N.B. “ ore 18 ”: dato non utile

z 6 € z 8 €

8 + 6 =

Quanto spende il papà?

8 + 6 = 14 euro Risponde?

Sì, vado avanti. No, torno indietro e riparto.

Il papà spende euro…

PROBLEMI CON LE QUATTRO OPERAZIONI

1. In una vasca per i piccoli ci sono 35 palline gialle, 20 rosse e 23 blu. Con quante palline possono giocare i bambini? Se vogliamo fare un gioco solo con due colori quante palline posso prendere?

2. Edo ha 8 anni, Marco ha 3 anni meno di Giuseppe, Luca 2 meno di Marco. Calcola l’età di Luca.

3. La maestra ha comprato 14 panetti di pasta modellabile bianca e 26 di pasta colore marrone per fare delle statuine. Quanti panetti in tutto? Alla fine, sono avanzati 6 panetti. Quanti ne sono stati usati?

4. Gabriele ieri ha vinto 38 figurine. Oggi ne ha perse 18. Complessivamente Gabriele ha vinto o perso? Quante figurine ha?

5. Marco ha 57 figurine ne regala 17 a Giovanni che ne aveva 31. Chi ha più figurine ora?

6. Nel portalistini ci sono 44 buste, 18 sono vuote. Quante sono state utilizzate?

7. Hai 2 euro da spendere in dolciumi. Davanti alla vetrina delle caramelle osservi e fai i tuoi conti. Ogni caramella alla menta costa 15 centesimi, ogni caramella alla liquirizia costa 30 centesimi e quella al miele costa 10 centesimi. Un cioccolatino costa 50 centesimi.Vuoi assaggiarli tutti. Quali acquisti potresti fare per spendere tutti i soldi? Trova qualche possibilità.

8. Luca ha trascorso 5 giorni a Roma. L’albergo gli è costato 80 euro al giorno. Ha speso anche 153 euro per acquistare regali per parenti e amici. Quanto ha speso per l’albergo? Calcola quanto gli è costata la vacanza.

9. Su una rupe di Capo di Ponte sono state contate 200 incisioni camune. Durante le ultime piogge, sono cresciute alcune piccole piante che ne hanno coperte molte. Ora se ne vedono 84, trova quante sono state coperte.

10. Alla festa della scuola partecipano gli alunni della primaria e della secondaria. In tutto sono presenti 480 alunni, di cui 250 della primaria. Quelli della secondaria sono di più o di meno?

11. Cinque famiglie hanno preparato insieme la passata di pomodori. Alla fine della giornata hanno preparato 10 cassette con 21 bottiglie per cassetta. Quante bottiglie spetteranno ad ogni famiglia?

12. A causa di un semaforo guasto, su una strada si è formata una lunga coda di mezzi. In tutto i veicoli sono 168. Se le auto sono 94, le moto sono 36, quanti sono i camion?

13. Sandra sale le scale e conta i gradini delle rampe. Conta 8 volte 9 gradini. Di quanti gradini è salita Sandra?

Scende 2 rampe. Quanti gradini le mancano per arrivare al piano terra?

14. A settembre ogni alunno porta 4 quaderni a righe e 5 a quadretti. In classe ci sono 24 alunni. Quanti quaderni per ogni alunno?

Quanti quaderni a quadretti in tutto? Quanti quaderni a righe in tutto? In totale quanti sono i quaderni?

15. In palestra la maestra ha 10 ceste con dentro 4 palloni ciascuna. Vuole dare lo stesso numero di palloni alle 6 squadre che giocano. Quanti palloni avrà ogni squadra? Ne avanza qualcuno?

16. Tecla ha 34 dadi colorati per giocare. Matteo ne ha 56 e Michele ne ha 25. Invitano a giocare anche Sofia e Dario. Prima di iniziare si dividono equamente i dadi. Tutti riescono a riceverne lo stesso numero? Quanti a testa?

17. Per la festa di Marta la mamma ha preparato 6 torte e le ha tagliate in 10 fette ciascuna. Calcola il totale delle fette. Alla fine della festa sono avanzate 12 fette. Quante fette sono state mangiate?

18. La nonna distribuisce 45 euro in parti uguali ai 5 nipoti. Camilla ha nel suo borsellino 4 euro e 50 centesimi. Trova quanto possiede ora Camilla.

19. Per organizzare un gioco 53 bambini hanno a disposizione 3 nastri di colore diverso. Quante possibilità ha ogni bambino? Complessivamente quante possibilità hanno?

20. La maestra ha consegnato un cartoncino a ciascuno dei suoi 28 alunni. Ognuno dovrà ritagliare 3 triangoli e 2 rettangoli per una costruzione geometrica.

Quanto saranno in totale le figure ritagliate?

21. Scrivi il testo di un problema con addizione e moltiplicazione.

22. Scrivi il testo di un problema che si possa risolvere con questa operazione: 124 : 4 =

UN NATALE MATEMATICO

1. Per preparare il presepe i bambini hanno 56 statuine. Arriva la zia e porta altre 16 statuine. Quante statuine ci saranno nel presepe?

2. Alla Vigilia i bambini preparano i biscotti di Natale. Hanno a disposizione 5 formine e 6 colori per la glassa. Quante combinazioni formina-glassa possono ottenere?

Se nella teglia ci stanno 28 biscotti, riescono a realizzare tutte le combinazioni?

3. La mamma e Stella preparano i cappelletti per il pranzo di Natale. Calcolano 9 cappelletti a testa . Se gli invitati sono 7, quanti cappelletti dovranno fare?

4. La nonna cucina un dolce natalizio. Risolvi il messaggio segreto per sapere come si chiama. Scrivi sotto alle operazioni la lettera corrispondente al risultato e scoprirai il suo nome. A = 21 B = 27 C = 90 D =

5. La nonna prepara la tavola per il pranzo di Natale con la famiglia. Toglie dalla credenza 12 piatti piani, 12 piatti fondi e 12 piattini. Se nella credenza c’erano 72 piatti, quanti non vengono utilizzati?

6. Per decorare la tavola prepara 3 centritavola. In ognuno mette 4 rose, 2 stelle Natale, 3 camelie e 1 vischio. Quanti fiori in tutto le serviranno?

7. La mattina di Natale sotto l'albero ci sono 15 regali. Ogni bambino ha lo stesso numero di regali. Se i bambini sono 5, quanti regali avranno a testa?

Il mio bicchiere è capace di contenere tutta la bibita contenuta nella lattina: è molto grande!

MISURA

Nella fila della classe, Nicolò è il più alto.

La cartella di oggi è molto più pesante di quella di ieri!

La mia fotocopia è troppo estesa: non c’è spazio sulla pagina del quaderno!

Tutte queste vignette parlano della grandezza di qualcosa che osserviamo e che ci circonda.

Ci sono più grandezze: vediamone alcune di diverso tipo. La LUNGHEZZA delle linee, l’ ESTENSIONE delle superfici, l’ AMPIEZZA degli angoli sono grandezze geometriche. Il PESO e la CAPACITÀ sono grandezze fisiche.

La misura delle grandezze

Le grandezze dello stesso tipo possono essere confrontate tra loro.

Per mettere in ordine in base alla grandezza si deve operare un confronto .

Da questo confronto si ottiene un numero

Per misurare grandezze dello stesso tipo serve una misura campione , è l’unità di misura

Misurare significa vedere quante volte l’unità di misura è contenuta in ciò che si vuol misurare.

Unità campione (o unità di misura)

Per misurare riportiamo l’unità campione.

1 2 3 4 5 6

Ogni grandezza ha bisogno di essere misurata con un’unità di misura adeguata dello stesso tipo.

La superficie con una superficie.

Il peso con un peso.

La lunghezza con una lunghezza. La capacità con una capacità.

Se vogliamo fare delle misurazioni valide per tutti, è necessario scegliere unità di misura comuni.

Le unità di misura delle grandezze che abbiamo nominato, riconosciute da quasi tutto il mondo, si chiamano UNITÀ DI MISURA CONVENZIONALI

Sono:

z CHILOGRAMMO (Kg) per il peso;

z METRO QUADRATO (mq o m²) per l’estensione della superficie;

z METRO (m) per la lunghezza;

z LITRO (l) per la capacità.

A seconda delle dimensioni di ciò che misuro, è utile scegliere un’unità di misura della dimensione adatta: più è piccolo l’oggetto, più sarà comoda un’unità di misura piccola.

MISURE ANTICHE, SEMPRE UTILI

Gli uomini, già dall’antichità, hanno avuto bisogno di misurare, ad esempio un terreno o una costruzione, e hanno usato lo strumento che tutti portiamo sempre con noi: il corpo.

Le parti del corpo sono così diventate unità di misura.

Cubiti, spanne, palmi

Come misuravano gli antichi Egizi?

L’unità di misura di questa grande civiltà di architetti era il cubito, cioè la lunghezza del braccio a partire dal gomito fino alla punta del dito medio, il più lungo.

Grazie al cubito costruirono le loro grandiose piramidi.

Cosa puoi misurare con questa unità?

La lunghezza della cattedra, la lunghezza e la larghezza della tua aula o del corridoio.

Sarà per te più difficile utilizzarla per scoprire la lunghezza o la larghezza dell’astuccio, del libro che stai leggendo o del diario, perché troppo piccoli.

Gli Egizi, per misurare tutto ciò che era più corto del cubito, ricorrevano alle spanne: la lunghezza che intercorre tra la punta del pollice e quella del mignolo, quando la mano è ben aperta.

I bambini usano questo tipo di misura durante il gioco delle biglie di vetro, mentre gli adulti quando voglio esprimere una misura approssimativa: «Quel ragazzo è alta circa una spanna più di te».

E per le misure più corte di una spanna?

Gli Egizi usavano il palmo, ossia la larghezza di una mano con le dita unite, senza contare il pollice.

Piede, passo, doppio passo, miglio

Le unità di misura che usavano i Greci e i Romani erano il piede e il doppio passo.

Il doppio passo, come dice la parola, è lungo come due passi, quindi è la distanza tra il punto in cui si posa uno dei due piedi e quello in cui si appoggia nuovamente lo stesso piede mentre si cammina.

Per misurare lunghe distanze, i Romani utilizzavano il miglio,

unità di misura composta da mille doppi passi. Lungo le strade da loro costruite, infatti, vi erano le pietre miliari, lontane un miglio una dall’altra.

Come strumento per effettuare delle

misurazioni, in realtà, non usavano parti del proprio corpo, ma misure fisse, già definite, che chiamavano piedi perché lunghi più o meno come la lunghezza del piede di un adulto.

Utilizzavano i propri piedi solo per fare misurazioni approssimative; per quelle in cui era necessaria precisione sceglievano misure uguali per tutti, convenzionali.

COME SI FA A MISURARE?

Troviamo noi una misura

Mercoledì ci siamo divisi in sei gruppi. La maestra ha chiesto ad ogni gruppo di misurare qualcosa.

Due gruppi dovevano trovare la lunghezza della lavagna, altri due gruppi dovevano scoprire quale libro pesasse di più fra due indicati, e gli ultimi due quanta acqua potesse contenere l’annaffiatoio della classe.

Poi abbiamo raccontato la soluzione a cui siamo arrivati e abbiamo condiviso i nostri tentativi con tutta la classe.

Abbiamo capito che per misurare occorre usare una misura campione adeguata e che è necessario confrontare e contare quante volte la grandezza campione è contenuta.

Per la lunghezza della lavagna abbiamo usato sia la spanna della mano che i piedi.

Per il peso dei libri, dopo vari tentativi, abbiamo preso le biglie.

Per la quantità d’acqua abbiamo usato un bicchiere colmo colmo.

Una misura vale l’altra?

Venerdì siamo scesi in cortile e abbiamo fatto una veloce caccia al tesoro.

Una squadra ha nascosto il tesoro e indicato all’altra squadra il numero di piedi da contare (fissato un punto di partenza e la direzione); purtroppo il tesoro non è stato trovato: era molto più lontano.

Sapete perché?

Il piede di William che ha nascosto il tesoro era molto più lungo di quello di Elisa, la “cercatrice” dell’altra squadra.

Abbiamo concordato che il piede dovesse essere lo stesso.

La maestra ci ha spiegato che per risolvere questo problema sono state stabilite delle unità di misura “convenzionali” , valide per tutti.

Per la lunghezza è il metro

Per il peso è il chilogrammo

Per la capacità è il litro

Quale unità di misura useresti?

Oggi la maestra ci ha dato questa tabella e ci ha chiesto di rispondere:

La lunghezza del corridoio:

L’altezza di una matita

Il peso della cartella

Il contenuto di un bottiglione

Il peso di un panino

Il contenuto di un tubetto di tempera

L’altezza di un compagno

La distanza da casa a scuola

Compilando la tabella ci siamo accorti che alcuni oggetti erano troppo grandi o troppo piccoli per essere misurati con le unità di misura che abbiamo conosciuto.

Abbiamo deciso che servivano delle altre grandezze , maggiori o minori , adatte agli oggetti da misurare

“Come il centimetro” ha detto Ginevra.

La maestra ha confermato e ci ha presentato i multipli e i sottomultipli delle unità di misura.

Il sistema di misura funziona come il nostro sistema di numerazione decimale.

ESERCIZI

1. Prendi 7 matite colorate dal tuo astuccio e disponile in ordine crescente dalla più lunga alla più corta. Poi rappresentale con dei segmenti sul tuo quaderno rispettando le dimensioni.

2. Ridisegna in ordine decrescente, dal più lungo al più corto, i seguenti segmenti sul tuo quaderno rispettandone la lunghezza.

3. Elenca sul quaderno, in ordine crescente, dal più leggero al più pesante, questi oggetti presi dal tuo materiale scolastico: colla, forbici, matita grafite, gomma, righello.

4. Stima a occhio la lunghezza di ciascuna figura sulla pagina, poi esprimi la lunghezza in centimetri e millimetri. Infine controlla con il righello se la tua misura a occhio è corretta.

cm: mm:

cm:

cm: mm:

5. Procurati un’unità campione (una fettuccia, un nastrino, un pezzo di carta). Misura con questo campione la lunghezza di una sedia, del forno e del frigorifero. Riporta sul quaderno le tue misurazioni. In classe confronta i tuoi risultati con quelli dei compagni.

6. Confronta i regoli e completa le frasi.

Il regolo ciclamino è lungo come regoli rossi.

Il regolo marrone è lungo come regoli ciclamino.

Il regolo marrone è lungo come regoli rossi.

7. Utilizza i regoli per misurare la lunghezza del lato lungo del banco e registra le tue misurazioni. Confrontale poi con quelle dei compagni.

Il lato lungo del banco è lungo come regoli rossi.

Il l ato lungo del banco è lungo come regoli ciclamino.

Il l ato lungo del banco è lungo come regoli marroni.

Il l ato lungo del banco è lungo come regoli verdi.

Quale regolo è stato più adatto e preciso per la misurazione?

Hai misurato precisamente tutta la lunghezza del lato lungo?

Come puoi essere più preciso? Confrontati coi tuoi compagni.

8. Misura la lunghezza di una parete dell’aula utilizzando le parti del tuo corpo e registra le tue misurazioni.

Lato dell’aula = piedi

Lato dell’aula = palmi

Lato dell’aula = spanne

Lato dell’aula = cubiti

Confronta i risultati con quelli dei tuoi compagni costruendo una tabella. Cosa noti? Annota le tue osservazioni sul quaderno.

9. Rispondi:

Una quercia è alta:

A. 1 m

B. 50 m

C. 15 m

Un tavolo è largo:

A. 18 m

B. 1 m

C. 40 m

Un'auto è lunga:

A. 1 m

B. 5 m

C. 20 m

Uno stagno è profondo:

A. 2 m

B. 15 m

C. 75 m

Una giraffa è alta:

A. 5 m

B. 2 m

C. 10 m

Una porta è alta:

A. 2 m

B. 5 m

C. 35 m

10. Prendi 7 matite colorate dal tuo astuccio e disponile in ordine crescente dalla più lunga alla più corta. Poi rappresentale con dei segmenti sul tuo quaderno rispettando le dimensioni.

11. Ridisegna in ordine decrescente, dal più lungo al più corto, i seguenti segmenti sul tuo quaderno rispettandone la lunghezza.

12. Elenca sul quaderno, in ordine crescente, dal più leggero al più pesante, questi oggetti presi dal tuo materiale scolastico: colla, forbici, matita grafite, gomma, righello.

13. Stima a occhio la lunghezza di ciascuna figura sulla pagina, poi esprimi la lunghezza in centimetri e millimetri. Infine controlla con il righello se la tua misura a occhio è corretta.

GEOMETRIA

OSSERVARE LO SPAZIO E LE FIGURE

RICONOSCERE FIGURE SOLIDE E PIANE, LINEE E ANGOLI, CONFRONTARE E MISURARE PER DESCRIVERE FORME E RELAZIONI

LO SPAZIO E LE FIGURE

In geometria i modelli geometrici di oggetti reali si chiamano figure solide

Riconosciamo alcuni solidi geometrici collegando ogni figura al proprio nome.

cubo

I SOLIDI

IL PARALLELEPIPEDO

Osserviamo: è alto, è lungo ed è largo.

Le sue misure si chiamano altezza, larghezza, lunghezza.

Sono le dimensioni del solido.

Nel parallelepipedo riconosciamo:

6 facce rettangolari

12 spigoli 8 vertici

altezza lunghezza

1. Scrivi il nome di 3 oggetti che hanno la forma di parallelepipedo.

larghezza

2. Disegna 1 faccia del parallelepipedo.

IL CUBO

Il dado dei nostri giochi è un CUBO .

altezza lunghezza larghezza

6 facce quadrate 12 spigoli 8 vertici

Ricopriamo il cubo con la carta e vediamo il suo sviluppo.

1. Sul quaderno disegna una faccia del cubo e colorala.

2. Quale costruzione ha il maggior numero di cubetti?

FACCE, SPIGOLI, VERTICI

1. Completa la tabella aggiungendo a tua scelta l’ultimo solido.

MODELLO

Prisma

IL PUNTO DI VISTA

Possiamo guardare un oggetto o una costruzione da più punti di vista

faccia sinistra

Osserva con attenzione questo palazzo disegnato da diversi punti di vista

faccia destra dall’alto

Osserva questa piccola costruzione con cubetti

davanti

dietro

2. Disegna ora altre due facce della costruzione: dall’alto di lato

3. Da quanti pezzi è fatta questa costruzione? Disegna la faccia che hai di fronte e la sua impronta sul piano.

4. Fai una piccola costruzione con quattro o più scatole di forme diverse e disegnala osservandola da due punti di vista.

LE FIGURE PIANE

Le facce dei solidi sono figure piane. Impariamo a riconoscerle facendo la loro impronta sul foglio o proiettando la loro ombra.

Coloriamo di blu la superficie e ripassiamo col rosso il contorno di queste figure.

1. Disegna tu alcune figure piane.

I poligoni

Quando una parte di piano è delimitata da una linea spezzata chiusa si chiama poligono

1. Sappiamo denominare alcuni poligoni conosciuti.

2. Inventa una greca (sequenza di figure) utilizzando diversi poligoni.

LE LINEE

Osserviamo un disegno. Seguiamo con il dito una linea e poi tracciamola.

Osserviamo un paesaggio. Seguiamo con il dito una linea e poi tracciamola.

Un quadro di Paul Klee. Seguiamo con il dito una linea e poi tracciamola.

Osserviamo il cielo mentre passano gli aerei.

1. Su un foglio azzurro tracciamo le linee che lascia l’aereo.

2. Con le matite colorate proviamo a fare un disegno su un foglio tracciando linee diverse.

TANTE LINEE

Ripassa con il rosso le linee chiuse, con il blu le linee aperte. Poi cerchia con il verde le linee semplici, in nero le linee intrecciate.

LINEE PIANE semplici intrecciate aperte chiuse aperte chiuse

spezzate o poligonali curve

miste

LE RETTE

Proviamo a piegare un foglio, quel segno che lascia la nostra piegatura ci può fare immaginare cosa sia una retta. Anche il taglio delle forbici sul foglio può darci questa immagine.

Le rette possono incontrarsi.

Rette incidenti

Rette perpendicolari

Oppure possono non incontrarsi mai.

Rette parallele

LE SEMIRETTE E I SEGMENTI

I segmenti hanno una dimensione sola: la lunghezza .

semiretta

segmento

semiretta

1. Disegna con tre colori tre segmenti di diversa lunghezza.

Qual è il più lungo?

Come hai fatto a confrontarli?

2. Osserva la figura. Ci sono due segmenti della stessa lunghezza?

Come fai a confrontarli?

IL PERIMETRO

Osserva l’esempio a colori. Ora riporta la lunghezza dei lati della figura in nero, in modo tale che uno vicino all’altro formino un unico segmento: la somma dei lati. Hai disegnato la lunghezza del PERIMETRO della figura.

LE LINEE

NEI POLIGONI

Con materiale facilmente reperibile proviamo a costruire poligoni con diverso numero di lati. Possiamo utilizzare alcune asticciole con fermacampioni, il geopiano, dei listelli di cartone.

Riconosciamo tra questi poligoni le figure note: triangoli, quadrati, rettangoli, rombi, esagoni.

Colora di rosso i quadrati, di arancione i rettangoli, di verde i triangoli, di giallo i pentagoni e di blu gli esagoni.

GLI ANGOLI

Seguiamo un percorso e cambiamo direzione.

Prendiamo un foglio non rettangolare Facciamo due piegature. Le piegature del foglio evidenziano 4 angoli. Osserviamo le lancette dell’orologio. Possiamo riconoscervi due angoli. 1 2 3

L’ANGOLO RETTO

Guardando intorno a noi riconosciamo un angolo speciale: l’ angolo retto . Seguendo le indicazioni delle linee verdi e rosse nell’esempio, costruiamo con le piegature un angolo retto che sarà il nostro angolo campione.

Con la piegatura di un foglio colorato a fisarmonica possiamo costruire un angolo e vedere la sua apertura che varia, cioè l’ampiezza dell’angolo

Angolo retto

1. Riconosci angoli retti negli oggetti attorno a te.

Angolo retto

Angolo acuto

Angolo ottuso

Angolo piatto

Angolo giro

2. Su ciascun quadrante di orologio disegna le lancette in posizione tale che la loro apertura mostri ogni volta un angolo diverso, come indicato.

L’apertura delle due semirette che formano l’angolo si chiama ampiezza .

3. Disegna un angolo su un foglio bianco e uno su un foglio colorato, ritagliali e confrontali.

Qual è l’angolo più ampio?

Angolo retto

Angolo acuto

Angolo ottuso

Lato

Lato

Vertice Ampiezza dell'angolo

L’ampiezza di un angolo è misurata in gradi: l’angolo retto misura 90 gradi.

4. Prendi il tuo angolo campione e colora l’ampiezza degli angoli. Riconoscili e completa scrivendo che tipo di angoli sono.

5. Quanti angoli retti sono necessari per formare un angolo piatto?

6. Quanti angoli retti sono necessari per formare un angolo giro?

Angolo Angolo Angolo

Angolo Angolo

7. Disegna tu un angolo retto, uno acuto e uno ottuso.

8. Colora l’ampiezza degli angoli; in verde gli acuti, in rosso gli ottusi, in arancione quelli retti.

IL TANGRAM

Disegna sulla carta centimetrata questo simpatico gioco cinese, poi ritaglia seguendo le linee.

Le forme ottenute permettono diverse possibilità di gioco, prova a costruire tu diverse combinazioni e osserva le caratteristiche geometriche delle figure che lo compongono.

1. Riconosci le figure che lo compongono.

2. Costruisci figure equiestese.

Sovrapponi e confronta le diverse figure fra loro, osserva l’ampiezza dei loro angoli e scrivi le tue osservazioni.

LA SIMMETRIA

Il piccolo principe che assisteva alla formazione di un bocciolo enorme, sentiva che ne sarebbe uscita un’apparizione miracolosa, ma il fiore non smetteva più di prepararsi ad essere bello, al riparo della sua camera verde.

Sceglieva con cura i suoi colori, si vestiva lentamente, aggiustava i suoi petali ad uno ad uno.

Non voleva uscire sgualcito come un papavero.

Non voleva apparire che nel pieno splendore della sua bellezza.

[…] E poi, ecco che un mattino, proprio all’ora del levar del sole, si era mostrato.

E lui, che aveva lavorato con tanta precisione, disse sbadigliando:

“Ah! mi sveglio ora. Ti chiedo scusa… sono ancora tutto spettinato…”

Il piccolo principe allora non potè frenare la sua ammirazione:

“Come sei bello!”.

Antoine de Saint-Exupéry

1. Traccia la retta che divide ogni disegno in due parti simmetriche.

2. Disegna e colora la parte mancante, completa in modo da rispettare la simmetria.

3. Disegna la figura simmetrica.

4. Completa la facciata del castello rispettando la simmetria.

5. Traccia la retta che divide i portali in modo simmetrico.

6. Traccia la retta che divide queste figure in due parti simmetriche.

7. Con i sette pezzi del tangram puoi fare questa costruzione, disegna la figura ad essa simmetrica rispetto alla retta.

TRIANGOLI E QUADRILATERI

Andiamo a scoprire le figure a due dimensioni: LUNGHEZZA e LARGHEZZA.

I TRIANGOLI

I poligoni che hanno tre lati si chiamano triangoli

1. Costruisci con il materiale (geopiano, listelli) poligoni di tre lati.

2. In ogni riquadro segna tre punti poi uniscili tra loro con dei segmenti.

I QUADRILATERI

I poligoni che hanno quattro lati si chiamano

1a. Costruisci con il materiale (geopiano, listelli) poligoni di quattro lati.

2a. Disegna alcuni quadrilateri.

ESERCIZI

1. Disegna sul tuo quaderno le seguenti linee e scrivi il loro nome:

2. Disegna in rosso due rette parallele, in blu due rette perpendicolari, in verde tre rette incidenti. linea spezzata chiusa linea retta verticale linea curva aperta linea mista

3. Disegna un percorso con quattro cambi di direzione.

4. Disegna sul tuo quaderno i seguenti angoli: retto, ottuso, acuto, piatto e giro. Associa i nomi corretti alle parti che li costituiscono.

5. Colora solo i poligoni.

6. Filippo ha ricevuto un gioco formato da una tavola quadrettata e da tavolette di tre forme differenti. Il gioco consiste nel ricoprire interamente la tavola con meno tavolette possibili senza lasciare caselle vuote e senza che due tavolette si sovrappongano.

Fai una pavimentazione della tavola con meno tavolette possibili e disegna la tua soluzione.

Quante tavolette di ciascuna forma hai utilizzato?

Forma A:

7. Michela ha numerosi triangoli di cartoncino arancione, tutti uguali, cioè della stessa forma e della stessa grandezza.

Tenta di ricoprire interamente ciascuna delle figure disegnate qui a fianco, utilizzando ogni volta quattro dei suoi triangoli uguali.

È già riuscita a ricoprire la casa e il quadrato che sono colorati e sui quali si vedono bene i quattro triangoli.

Michela potrà ricoprire ciascuna delle altre figure usando sempre quattro triangoli uguali? Per ogni figura: z se è possibile, disegna in modo preciso i quattro triangoli; z se è impossibile, spiega perché.

Forma B:

Forma C:

Tavola quadrettata

Forma A Forma B Forma C

8. Con gli otto pezzi del suo puzzle, Paolo ha formato un poligono di sei lati, poi un rettangolo. Queste due figure sono colorate in verde qui sotto.

Con gli stessi otto pezzi di Paolo, cerca di riempire esattamente le sei forme ancora in bianco. Per ogni figura: z se è possibile, disegna precisamente gli otto pezzi all’interno della forma, senza che si sovrappongano; z se non è possibile, spiega perché.

9. Colora l’estensione o superficie. Poi ripassa il perimetro.

1. Osserva e rispondi.

METTITI ALLA PROVA

Segna gli angoli retti di queste figure e spiega come li hai riconosciuti.

Come puoi verificare che la tua risposta è corretta?

2. Scrivi i nomi dei solidi di questa costruzione.

3. Immagina di vedere la stessa costruzione dall’alto e disegna.

4. Disegna un quadrato che abbia il perimetro di 24 quadretti lineari:

5. Unisci con matita e righello i punti medi dei lati del quadrato. Quale figura hai ottenuto?

INDICE

MATEMATICA

IL

GEOMETRIA

ALLA SCOPERTA DEL MONDO

LIBRI DI TESTO PER LA SCUOLA PRIMARIA

ALLA SCOPERTA DEL MONDO 1

Classe 1

Fieri di saper leggere, scrivere, contare

Tre volumi indivisibili:

• Lettura · Percorsi disciplinari

• Prerequisiti · Italiano · Matematica

• Quaderno del corsivo

• Sillabario + Segnalibri didattici

ALLA SCOPERTA DEL MONDO 2

Classe 2

Il ritmo delle stagioni

Due volumi indivisibili:

• Lettura · Grammatica

• Matematica · Discipline

SCOPRI DI PIÙ SU ITACASCUOLA.IT

ALLA SCOPERTA DEL MONDO 3

Classe 3

Leggere è incontrare

Tre volumi indivisibili:

• Lettura · Grammatica

• Matematica

• Discipline

• Segnalibri didattici

ALLA SCOPERTA DEL MONDO 4

Classe 4

Occhi aperti

Sussidiario dei linguaggi

• Lettura · Grammatica

ALLA SCOPERTA DEL MONDO 5

Classe 5

La lettura, che avventura!

Sussidiario dei linguaggi

• Lettura · Grammatica

e sul Canale ITACASCUOLA su Itacaeventi!

ALLA SCOPERTA DEL MONDO 4

Classe 4

Sussidiario delle discipline

Due volumi indivisibili:

• Matematica

• Scienze · Geografia · Storia

ALLA SCOPERTA DEL MONDO 5

Classe 5

Sussidiario delle discipline

Due volumi indivisibili:

• Matematica

• Scienze · Geografia · Storia

• Lettura · Grammatica

• Discipline

• Matematica

• Segnalibri didattici

Alda Merini