https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html








































































































































1.
2)
3)
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


4. 1) CA, CD, CM, CN –
2)
5. 1) На рисунку зображені промені – NM, NP, NK, NF.
2) Серед променів, зображених на рисунку, єпара
6.

7.

D.
променів – NM і NK.
прямої – MN, MF, NF, FN, FM, NM.
Пряму можна ще назвати: BD, DB, BC, DC.
8. 1) Так, прямі m і CB перетинаються.
2) Прямій m належать точки A i L.
3) Прямій ВС належать точки С, В і Q.
4) Ані прямій m, ані прямій ВС не належать точки К і D.
9.


1) DP, DF, DE, EP, EF, PF.
2) Всього утворилося шість прямих.
3) Прямі розбивають площину на 16 частин.



Точки
Точки
12. (800 + 600) · 2 = 2800 (м) = 2,8 (км) – периметр парку; 1) 2,8 : 14 = 0,2 (год) = 60 · 0,2 = 15 (хв.) – витрачає на пробіжку Вадим; 2) 2800 : 50 = 56 (м/хв) – швидкість батьків Вадима.
Відповідь: 1) 15 хв, 2) 56 м/хв.
13. 1) відрізки з кінцем у точці М: АМ, BM, NM; 2) відрізки з кінцем у точці N: BN, AN, MN; 3) відрізки з кінцем у точці А: MA, BA, NA; 4) відрізки з кінцем у точці В: AB, MB, NB.

14.

62 – 50 = 12 мм Відрізок AB < CD на 12 мм.
собою. Отже, найменша кількість точок: 2023 + 2024 + 2025 – 3 = 6069.
Відрізок. Вимірювання відрізків. Відстань між двома точками
16. На рисунку зображені відрізки: АВ, АК, ВК, ВМ. АК = 38 мм, МВ = 12 мм. 17. На рисунку зображені відрізки: РС, PD, CD, PT. PC = 9 мм, PD = 31 мм, PT = 27 мм. 18. CD = 40 мм

19. АВ = 7 см 2 мм, MN = 6 см 3 мм. AB > MN, оскільки з двох відрізків більшим вважають той, довжина якого більша.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
20. KL = 5 см 9 мм, FP = 6 см 8 мм. FP > KL, оскільки

21. Оскільки довжина відрізка дорівнює сумі
будь-якою його внутрішньою точною, маємо:
1) АВ = АС + СВ = 5 см + 2 см = 7 см.
частин,
2) АВ = АС + ВС. Звідси ВС = АВ – АС = 12 дм – 9 дм = 3 дм.
22. 1) PQ = PK + KQ = 3 дм + 7 дм = 10 дм.
2) PQ = PK + KQ. Звідси PK = PQ – KQ = 8 см – 6 см = 2 см.
23. 1) Точки К, L і M лежать на одній прямій, оскільки KM = KL + LM, KM = 8 см + 3 см = 11 см. Точка L лежить між точками К і M.
2) Точки К, L і М не лежать на одній прямій,
Точка
Точка
27.
= 150
АС = АВ + ВС, BD = CD + BC. Оскільки АВ = CD, маємо BD = AB + BC, тому AC = BD.
28. Згідно з основною властивістю
маємо: АС = АВ + ВС, BD = CD + BC. Оскільки АС = BD, маємо AB + BC = CD + BC. Звідси AB = CD.
29. Згідно з основною властивістю вимірювання відрізків маємо:
AB = AC + CB, звідси CB = AB – AC = 40 см – 25 см = 15 см;
AB = AD + BD, звідси AD = AB – BD = 40 см – 32 см = 8 см;
AB = AD + CD + CB, звідси CD = AB – AD – CB = 40 см – 15 см – 8 см = 17 см. Відповідь: 17 см.
30. 1) CN = MN – MC = 50 см – 40 см = 10 (см) 2) CD = ND – CN = 16 см – 10 см = 6 (см)
Відповідь: 6 см.

31.
D, тоді CD = CM + MD = 5,2 см + 4,9 см = 10,1 см.

+ АС = 120 мм + 40 мм = 160 мм.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
см – 4,9 см = 0,3 см.

Відповідь: 10,1 см; 0,3 см.
32.Задача має два розв’язки.
І випадок.
AN = AM + MN = 7,2 см + 2,5 см = 9,7 см.
ІІ
випадок.

AN = AM – MN = 7,2 см – 2,5 см = 4,7 см.
33. 1) AC втричі менший від BC:
Нехай AC = x, тоді BC = 3x.
Відрізок AB складається з AC і BC:
AC + BC = AB
x + 3x = 14 дм
4x = 14 дм
x = 3,5 дм – АС.
BC = 3 ⋅ 3,5 дм = 10,5 дм
2) AC більший за BC на 1,8 дм:
Нехай AC = y + 1,8, тоді BC = y.
Відрізок AB складається з AC і BC:
AC + BC = AB
(y + 1,8) + y = 14 дм
2y + 1,8 = 14 дм
2y = 14 дм – 1,8 дм
2y = 12,2 дм
y = 6,1 дм – ВС. AC = 6,1 дм + 1,8 дм = 7,9 дм
3) AC : BC = 3 : 2:
Нехай AC = 3z, а BC = 2z.
Відрізок AB складається з AC і BC:
AC + BC = AB
3z + 2z = 14 дм
5z = 14 дм
z = 2,8 дм – АВ.
AC = 3 ⋅ 2,8 дм = 8,4 дм
BC = 2 ⋅ 2,8 дм = 5,6 дм Тепер

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
10,5 дм 8,4 дм 7,9 дм 6,1 дм 5,6 дм 3,5 дм
Перша столиця України - Харків.
34. 1) CM більший за DM на 0,6 см:
Нехай DM = x, тоді CM = x + 0,6.
Відрізок CD складається з CM і DM:
CM + DM = CD
(x + 0,6) + x = 8,4 см
2x + 0,6 = 8,4 см
2x = 8,4 см – 0,6 см
2x = 7,8 см
x = 3,9 см – DM.
CM = 3,9 см + 0,6 см = 4,5 см
2) CM : DM = 1 : 3:
Нехай CM = y, а DM = 3y.
Відрізок CD складається з CM і DM:
CM + DM = CD
y + 3y = 8,4 см
4y = 8,4 см
y = 2,1 см – СМ.
DM = 3 ⋅ 2,1 см = 6,3 см
Тепер
Прізвище українського
35. 1) Площа
S = πr²
де r - радіус круга,
π - математична константа.
Для r = 200 м:
S = π ⋅ (200 м)²
S = 3,14 ⋅ 40000 м²
S = 125600 м²
2) Довжина мотузка,
круга:
C = 2πr
де r - радіус круга.
Для r = 200 м:
C = 2π ⋅ 200 м
C = 2 ⋅ 3,14 ⋅ 200 м
C = 1256 м
Відповідь: 125600 м²; 1256 м. 36. 1) 52° - гострий кут (менше 90°)

2) 180° - розгорнутий
4)
5)
6)







= 93°12;
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
2) ∠АВС = 130°, ∠DBC = 70°.
3) ∠ABD = ∠ABC - ∠DBC = 130° - 70° = 60°.
45. ∠АМК = 45°, ∠PLF = 90°, ∠BNC = 100°.





BD –
кута АВС. ∠АBD = 25°, ∠DBC = 25°.

50. 1) 7°13´ + 12°49´ = (7° + 12°) + (13´ + 49´) = 19° + 62´ = 19°+ 1°12´ = 20°12´ 2) 52°17´ - 45°27´ = 51°77´ - 45°27´ = 6°50´
51. 1) 4° = 4 ⋅ 60´ = 240´ 2°15´ = 2 ⋅ 60´ + 15´= 120´+ 15´ = 135´

2) 5´ = 5 ⋅ 60´´= 300´´
2° = 2 ⋅ 60´ ⋅ 60´´ = 7200´´
1°3´ = 60 ⋅ 60´´ + 3 ⋅ 60´´ = 3780´´
52.

+
53.

- ∠АРС = 108° - 68° = 40°.
54.

55. 1) 180°; 2) 90°; 3) 30°; 4) 120°.
56. 1) 90°; 2) 180°; 3) 150°; 4) 60°.

57. ∠АОС = 2 3
=

-
= 2 3 ∙ 60° = 40°
= 60° - 40° = 20°
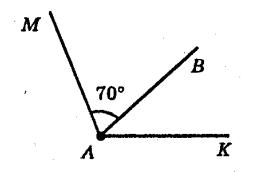
Згідно з умовою задачі ∠ВАК = 60% ∠МАВ. Отже, ∠ВАК = 70° ⋅ 0,6 = 42°.
∠МАК = ∠МАВ + ∠ВАК = 70° + 42° = 112°.
Відповідь:112°.
59.

Нехай АОС – заданий кут. ОМ – продовження сторони ОА за вершину О.
ОК – бісектриса кута АОС. ∠АОМ – розгорнутий, ∠АОМ = 180°.
∠КОМ = 142°, ∠АОМ = ∠АОК + ∠КОМ.
Отже, ∠АОК = 180° - 142° = 38°.
Оскільки ОК – бісектриса кута АОС,
Тоді ∠АОС = ∠АОК + ∠КОС =
Відповідь:76°. 60.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

1. Нехай ∠PQB = х, тоді ∠MQP = 4х. Градусна
кутів, на які він розбивається променем, що
∠MQB = ∠MQP + ∠PQB. Складемо рівняння:
4х + х = 120°
5х = 120°
х = 24°
Отже, ∠PQB = 24°, ∠MQP = 24° ⋅ 4 = 96°.
2. Якщо ∠PQB : ∠MQP = 3 : 2, то
∠PQB = 3х, ∠MQP = 2х, тоді
3х + 2х = 120;
5х = 120°
х = 24°
Отже, ∠PQB = 3 ⋅ 24° = 72°, ∠MQP = 2 ⋅ 24° = 48°.
3. Якщо ∠PQB на 20° > ∠MQP, то
∠MQP = х, ∠PQB = х + 20°
За властивістю кутів:
х + х + 20 = 120
2х = 100
х = 50
Отже, ∠MQP = 50°, ∠PQB = 50° + 20° = 70°.
Відповідь:КРАВЧУК.≈
62.

1. Нехай ∠САN = х, тоді ∠МАС = х + 14. Оскільки ∠MAN = ∠МАС + ∠СAN (згідно з основною властивістю вимірювання кутів), то маємо:
х + х + 14 = 84
2х = 84 – 14
2х = 70
х = 35
Отже, ∠САN = 35°, ∠МАС = 35° + 14° = 49°.
2. Якщо ∠МАС у 3р. < ∠САN, то
∠МАС = х; ∠САN = 3х
За властивістю кутів:
х + 3х = 84
4х = 84

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
х = 21
Отже, ∠МАС = 21°; ∠САN = 21 · 3 = 63°
Відповідь:ВАРШАВА.
63.

Оскільки ∠АОВ = ∠АОК + ∠КОВ, то ∠КОВ = ∠АОВ - ∠АОК = 180° - 140° = 40°.
Оскільки ∠BOL = ∠LOK + ∠KOB, то ∠LOK = ∠BOL - ∠KOB = 100° - 40° = 60°.
Відповідь:60°.
64.

Оскільки ∠COD = ∠COM + ∠MOD, то ∠СОМ = ∠COD - ∠MOD = 90° - 80° = 10°
∠CON = ∠COM + ∠MON
∠MON = ∠CON - ∠COM = 70° - 10° = 60°.
Відповідь:60°.
65. 28 м 50 см = 28,5 м
1) S = 28,5 ⋅ 16 = 456 (м2) – площа теплиці.
2) 456 ⋅ 30 = 13680 (кг) – кількість огірків.
3) 13680 ⋅ 18 = 246240 (грн) – виторг.
Відповідь:родина збере 13680 кг огірків; виторг від продажу огірків становитиме 246240 грн.
66.

Відповідь:Кравчук.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html







https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

KL = 6 см 8 мм; КР = 43 мм = 4 см 3 мм.
KL = KP + PL (за основною властивістю
Звідси PL = KL – KP = 6 см 8 мм – 4 см 3 мм = 2 см 5 мм.
Відповідь:2 см 5 мм.
74. MN = MA + AN; MN = MB + BN
75. 1) Відрізок АВ можна поділити


2) Можна зробити висновок, що відрізок можна
76.

Якщо АВ = 20 см, то АС =
AD = 1 2 �������� = 1 2 ∙ 10 = 5 (см)
АВ = AD + DB, звідси DB = AB – AD = 20 – 5 = 15 (см)
2) Якщо ВС = 12 дм, то АВ = 12 ⋅ 2 = 24 (дм)
АС = ВС = 12 дм
AD = 1 2 �������� = 1 2 ∙ 12 =6 (дм)
DB = AB – AD = 24 – 6 = 18 (дм)
77.

CN = CD – DN = 15 – 11 = 4 (см)
NM = CM – CN = 12 – 4 = 8 (см)
Відповідь:8 см.
78.


���� 2 .


на n + 1 частини.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
80. ∠АОВ = 40°; ∠АОС = 60°; ∠ВОС = 20°; ∠BOD = 140°; ∠COD = 120°; ∠AOD = 180°.
81. Ні, учень неправий, бо величина
обидва кути по 70°.
82. ∠КАС, ∠ВАМ, ∠ВАС, ∠МАК, ∠КАМ, ∠САК.
83.

∠АОВ – гострий,

84. 1)
Отже, за 1 хвилину стрілка
на 90°, за 7 хв – на 42°, за 23 хв – на 138°. 2) За 12 годин годинна стрілка


АОВ, отже, ∠АОВ = 2∠КОВ = 2 ⋅ 74° = 148°
86. 1) ∠АОЕ = ∠АОВ + ∠ВОС + ∠COD + ∠DOE (згідно з
вимірювання кутів).
Оскільки ∠АОВ = ∠ВОС, ∠COD = ∠DOE, то ∠АОЕ = 2(∠ВОС + ∠COD) = 2∠BOD ∠BOD = ∠AOE : 2 = 140° : 2 = 70°.
2) ∠BOD = ∠AOB + ∠DOE, оскільки ∠BOD = ∠BOC + ∠COD і ∠AOB = ∠BOC, ∠COD = ∠DOE. Отже, ∠АОЕ = 2∠BOD = 2 ⋅ 73° = 146°

Відповідь:1) 70°; 2) 146°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Введемо коефіцієнт пропорційності х, тоді ∠АОМ = 3х, ∠МОВ =4х.
∠АОВ = ∠АОМ + ∠МОВ. Складемо рівняння:
3х + 4х = 168
7х = 168
х = 24
Отже, ∠АОМ = 3 ⋅ 24° = 72°, ∠МОВ = 4 ⋅ 24° = 96°.
Відповідь:72° і 96°.
РОЗДІЛ 2. ВЗАЄМНЕ РОЗМІЩЕННЯ
88. На
89. 1) Ні, два суміжні кути не можуть дорівнювати 42° і 148°, оскільки 42° + 148° = 190°, а сума суміжних кутів дорівнює 180°.
2) Так, оскільки 90° + 90° = 180°.
3) Так, суміжні кути можуть дорівнювати 166° і 14°, оскільки 166° + 14° = 180°.
4) Ні, суміжні кути не можуть дорівнювати 23° і 156°, оскільки 23° + 156° = 179°, а сума суміжних кутів дорівнює 180°.
90. 1) Так, оскільки 13° + 167° = 180°.
2) Ні, оскільки 5° + 165° = 170°, а сума суміжних кутів дорівнює 180°.
3) Ні, оскільки 11° + 179° = 190°, 190° не дорівнює 180°.
4) Так, оскільки 91° + 89° = 180°.
91. 1) Позначемо невідомий кут х. Оскільки сума суміжних кутів
15° + х = 180°
х = 180° - 15°
х = 165°
2) Позначимо
+ х = 180°
х = 180° - 113°
х = 67°
Відповідь:

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
∠KON = ∠KOM - ∠NOM = 180° - 50° = 130°
Відповідь: 130°

94.
кутів дорівнює 180°.
∠АРС + ∠АРВ = 180°
∠АРС + 115° = 180°
∠АРС = 180° - 115° = 65°
Відповідь: 65°.

95.
72°, ∠COD = 15°.
∠BOD = ∠BOC + ∠COD = 72° + 15° = 87°
∠AOB суміжний
∠BOD + ∠AOB = 180°
∠AOB = 180° - ∠BOD = 180° - 87° = 93°
Відповідь: 93°.

МК – бісектриса кута М, ∠KML = 36°, ∠LMK = ∠KMN, оскільки
на два різних кути.
∠LMK = ∠KMN = 36°
∠LMN = ∠LMK + ∠KMN (згідно
кутів), ∠LMN = 36° + 36° = 72°. ∠BML суміжний з кутом LMN. Оскільки сума градусних мір
кутів дорівнює 180°, то ∠BML + ∠LMN = 180°, звідси:
∠BML = 180° - ∠LMN = 180° - 72° = 108°.
Відповідь: 108°.

97. Спільна сторона LM вертикальна.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

99. Оскільки суміжні кути рівні, то
х + х = 180° (оскільки сума суміжних
з цих суміжних кутів – прямий.
100. Нехай кожен
180° - х, оскільки сума суміжних кутів
кутами, рівні.
101. 1) Нехай ∠АОВ = х, тоді ∠СОА = х + 18°, маємо:
х + х + 18° = 180°
2х = 162°
х = 81° - ∠АОВ
∠СОА = 81° + 18° = 99°
2) Нехай ∠АОВ = х, тоді ВОС = 3 7 х, маємо:
х+ 3 7 х= 180°
10 7 х= 180°
х= 180 ∶ 10 7
х = 126° - ∠АОВ
ВОС = 3 7 ∙ 126° = 54°
Відповідь: 1) 81° і 99°; 2) 126° і 54°.
102. 1) Нехай ∠АОВ = х, тоді ∠СОА = 3х, маємо:
х + 3х = 180°
4х = 180°
х = 45° - ∠АОВ.
∠СОА = 3 ⋅ 45° = 135°
2) х + 0,25х = 180
1,25х = 180
х = 180 : 1,25
х = 144°
180° - 144° = 36°
Відповідь: 1) 45° і 135°; 2) 144° і 36°.
103. ∠РМК = 140° може бути
= 2х, ∠LNS = 5х, тоді за теоремою
+ РМК = 180°
2х + 140 = 180
2х = 40
х = 20°
М = 2 ⋅ 20 = 40° N = 5
20 = 100°
40° і 100°.

∠А = 180° - 80° = 100°
4х = 100°
х = 25°
∠В = 3 ⋅ 25° = 75°
Відповідь: 100° і 75°.
105. Нехай
Відповідь: 90°.

106. Оскільки ∠АОВ : ∠KQM = 1 : 2, то нехай ∠АОВ = х, ∠KQM = 2х,
- х, ∠MQL = 180° - 2х. За умовою ∠BOC : ∠MQL = 7 : 5, тому:
180°−х
180°−2х = 7 5
5(180° - х) = 7(180° - 2х)
900° - 5х = 1260° - 14х 9х = 360°
х = 40° - ∠АОВ.
∠KMQ = 2 ⋅ 40° = 80°.
Відповідь: 40° і 80°.
=
107. Нехай ∠АОВ = х, ∠KQM = х + 20°, тоді: ∠ВОС = 180° - х, ∠MQL = 180° - (х + 20°).
Оскільки ∠АОВ < ∠KQM, то ∠ВОС > ∠MQL. За умовою ∠MQL: ∠BOC = 5 : 6, тому:
160°−х
180°−х = 5 6
960° - 6х = 900° - 5х
х = 60° - ∠АОВ.
∠KMQ = 60° + 20° = 80°.
Відповідь: 60° і 80°.
108. Нехай один із суміжних кутів
Припустимо для визначеності, що х > 180° - х. Треба розглянути
1 випадок:
х = 2(х – (180° - х))
х = 2(2х - 180°)
х = 4х – 360°
3х = 360°
х = 120°
Суміжний
2 випадок:
ним кут - 60°.
180° - х = 2(х - 180° - х))
180° - х = 2(2х - 180°)
180° - х = 4х - 360°
5х = 540°
х = 108°
Суміжний з
кут - 180° - 108° = 72°. Відповідь: 120° і 60° або 108° і 72°.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

110. Відстань між точками А і С може дорівнювати
0,9 (см).
Відповідь: 1) ні; 2) так; 3) ні; 4) ні; 5) так; 6) ні.
111. S кільця = S великого круга – S меншого круга
���� кільця =�������� 2 −�������� 2 =����(���� 2 −���� 2 )
S кільця = 3,14 ⋅ (15² - 10²) = 3,14 ⋅ (225 – 100) = 3,14 ⋅ 125 = 392,5 (м²)
Відповідь: 392,5 м².
112. 1) КУТ; 2) ПРЯМА; 3) ЕВКЛІД; 4) ГЕОМЕТРІЯ.
§6. Вертикальні кути. Кут між двома прямими, що перетинаються
113. ∠АМР і ∠TMF; ∠AMF і ∠РМТ.
114. Ні, немає.
115. 1) За властивістю вертикальних кутів – вертакальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°.
2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°.
116. 1) За властивістю вертикальні кути рівні. Отже, кут, вертикальний до кута 42°, дорівнює 42°.
2) За властивістю вертикальні кути рівні. Отже, кут, вертикальний до кута 139°, дорівнює 139°.
117. На мал. 65 пари
118.

– суміжні. Тоді за
суміжних кутів ∠KPL + ∠LPM = 180°, звідси ∠KPL = 180° -
LPM; ∠KPL = 180° - 40° = 140°. ∠KPL і ∠NPM –
властивістю вертикальні кути рівні, отже, ∠NPM = 140°.
Відповідь: 40°; 140°; 140°.
119. ∠AML та ∠РМВ – вертикальні кути. ∠РМВ = ∠AML = 120°.
∠AML та ∠LMB – суміжні, отже, їх сума дорівнює 180°. ∠AML + ∠LMB = 180°, звідси
∠LMB = 180° - ∠AML; ∠LMB = 180° - 120° = 60°.
∠AMP та ∠LMB – вертикальні. ∠АМР = ∠LMB = 60°.
Відповідь: 60°; 120°; 60°.
120. Ні,
180° - 130° = 50°.
121. За

62°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
122. CD і

Відповідь: 55°.
123. ∠MON та ∠KOL – вертикальні, ∠МОК та ∠NOL – вертикальні. За властивістю вертикальні кути рівні, отже, ∠КОL = ∠MON = 110°.
∠МОК та ∠MON – суміжні, отже, ∠МОК +
MON = 180°, звідси ∠МОК = 180° - ∠MON = 180° - 110° = 70°.
∠NOL = ∠MOK = 70°.

Відповідь: 70°; 70°; 110°.
124. Оскільки OD доповняльний промінь
∠АОВ та ∠DOP, ∠DOA та ∠РОВ – вертикальні. За властивістю
Отже, ∠DOP = ∠AOB = 30°. ∠DOA та
DOA + ∠AOB = 180°, ∠DOA + 30° = 180°, ∠DOA = 150°. ∠POB = ∠DOA = 150°.

Відповідь: 30°; 150°; 150°.
125. 1) Оскільки
х + х = 180°
2х = 180°
х = 90°
Відповідь: всі кути по 90°.
2) При
суміжних. Сума двох будь-яких суміжних

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Нехай ∠1 = х, тоді ∠2 = х + 18°, тоді:
х + х + 18° = 180°
2х = 162°
х = 81°
х + 81° = 81° + 18° = 99°
Кут між прямими
2) ∠1 + ∠2 + ∠3 = 293°; отже, ∠3 = 293° - 180° = 113°.
Тоді ∠2 = 180° - 113° = 67° - кут між прямими.
3) х + 4 5 х = 180
1,8х = 180
х = 180 : 1,8
х = 100°
180° - 100° = 80°
Відповідь: 1) 81°; 2) 67°; 3) 100°.
128. 1) Два кути, які утворилися
Оскільки вертикальні кути рівні, то кути, про які
Нехай ∠1 = х, тоді ∠2 = 2х, тоді:
х + 2х = 180°
3х = 180°
х = 60° - кут між прямими.
2) х + 0,2х = 180
1,2х = 180
х = 180 : 1,2
х = 150°
180° - 150° = 30°
Відповідь: 1) 60°; 2) 30°.
129. ∠АМК = ∠СМР (як вертикальні)
81°.
у задачі, - суміжні.
∠СМР = 180° - (∠ВМС + ∠LMP) = 180° - (20° + 60°) = 100°, отже ∠АМК = 100°
Відповідь: 100°.
130. ∠АМВ = ∠LMP (як вертикальні)
∠LMP = 180° - (∠KML + ∠CMP) = 180° - (25° + 105°) = 50°, отже ∠АМВ = 50°.
Відповідь: 50°.
131. ∠4 = ∠1 (як вертикальні)
∠1 + ∠2 + ∠3 = ∠4 + ∠2 + ∠3 = 180°

Відповідь: 180°.
132. Нехай ∠

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

133.
2 см кожний. Отже, відстань
Відповідь: 18 см.
134. 1) Ні; 2) так; 3) ні; 4) ні; 5) так; 6) ні.
135. S вікна = 2 ⋅ 1,8 = 3,6 (м²)
3S вікон = 3,6 ⋅ 3 = 10,8 (м²)
S підлоги = довжина ⋅ ширину 35% від 14 = 14 ⋅ 0,35 = 4,9 (м)
S підлоги = 14 ⋅ 4,9 = 68,6 (м²)
����з
вікон
���� підлоги = 10,8 68,6 ≈0,16 < 0,2
Відповідь: норми дотримано.
136. ВА ⊥ ВС, BA ⊥ AD, CD ⊥ BC, CD ⊥AD

1) Маємо
Всього 1 + 4 + 9 = 14 квадратів. 2)

1. Як прямій а, так і прямій


9 ⋅ 2 = 18 (см)
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

дорівнює 80°. Отже, правильна відповідь – В) 80°.
7. Оскільки ВС= АВ + АС, 7 см = 4 см + 3 см, 7 см = 7 см, то точка А
між точками В і С.

Отже, правильна відповідь – А)
8. ∠СОК = ∠КОВ = 35° (оскількм ОК – бісектриса кута СОВ), ∠АОВ – розгорнутий,
= 180°, ∠АОВ = ∠АОК + ∠КОВ, 180° = ∠АОК + 35°, ∠АОК = 180° - 35° = 145°.
Отже, правильна відповідь – В) 145°.
9. Нехай один із суміжних кутів х, тоді другий 2х. Оскільки сума суміжних
180°, маємо:
х + 2х = 180°
3х = 180°
х = 60°
2х = 120°
Отже, правильна відповідь – Г) 120°.
10. Приавльна відповідь – В) 10.

11. ∠AON = ∠MON - ∠MOA = 180° - 120° = 60°
∠MOB = ∠MON - ∠NOB = 180° - 110° = 70°
∠BOA = ∠MON - ∠AON - ∠MOB = 180° - 60° - 70° = 50°

Отже, правильна відповідь – А) 50°.
- 180° - х, з другим - 180° - 2х, тоді:
180° - х – (180° - 2х) = 70°
180° - х - 180° + 2х = 70°
х = 70°
2х = 140°

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Отже, правильна відповідь – Г) 140°.
13. AM — 30 см (Г)
MN — 20 см (А)
NB — 24 см (Б) ЗАВДАННЯ
1. В ∈ а, D ∈ а, М ∉ а, С ∉ а.
2. 1) ∠А = 92° - тупий
2) ∠В = 180° - розгорнутий
3) ∠С = 90° - прямий
4) ∠D = 31° - гострий
3. ∠BAD і ∠KAN, ∠BAK i ∠DAN – вертикальні.
4. MN = CM + CN, звідски CM = MN – CN = 7,2 см – 3,4 см = 3,8 см.

Відповідь: 3,8 см.
5. ∠АОВ = 70°, ОС – бісектриса кута АОВ

6. ∠АОС і ∠СОВ – суміжні. ∠АОС + СОВ = 180°, ∠
∠СОВ –

між прямими АВ і CD.
Відповідь: 48°.
7. AN = AB – BN = 30 – 16 = 14 (см)
MB = AB – AM = 30 – 20 = 10 (см)
MN = AB – (AN + MB) = 30 – (14 + 10) = 30 – 24 = 6 (см)

Відповідь: 6 см.
180°, маємо:
х + х + 12° = 180°
2х = 168°
х = 84°


= 180° - 132° = 48°.
- 84° + 12° = 96° Відповідь: 84°, 96°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

АВ = АК + КВ = 9,3 + 3,7 = 13 (см)
розв’язок

АВ = АК – КВ = 9,3 – 3,7 = 5,6 (см) Додаткові вправи
10. ∠АОВ = 48°, ОС – бісектриса кута АОВ. ∠АОС = ∠СОВ = 48° : 2 = 24° (оскільки ОС –бісектриса кута АОВ). OD – доповняльний промінь до сторони ОА кута АОС. ∠AOD = 48°. ∠AOD = ∠AOC + ∠COD, звідси ∠COD = ∠AOD - ∠AOC = 180° - 24° = 156°.

Відповідь: 156°.
другим - 180° - 3х. Градусні міри цих кутів відносяться, як 7 : 3, тоді:
180°−х
180°−3х = 7 3 3(180° - х) = 7(180° - 3х)
540 – 3х = 1260 – 21х
18х = 720°
х = 40°
Отже, один з кутів дорівнює
Відповідь: 40°, 120°.




https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
142.
2)
3)
4)
143.

144.




https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
— це пряма, яка
перетинає іншу пряму під прямим кутом. Відрізок, який є частиною цієї прямої, також буде перпендикулярним до даної прямої, але це вже похідне поняття.
150. 1. 1) ∠CON = ∠COB - ∠NOB = 90° - 25° = 65°
2) ∠MOD = ∠CON = 65° (як вертикальні)
2. 1) ∠MOD = ∠MOB - ∠DOB = 150° - 90° = 60°
2) ∠CON = ∠MOD = 60° (як вертикальні)
Відповідь:1) 65°; 2) 60°.
151. 1. 1) ∠FOL = ∠NOF - ∠NOL = 140° - 90° = 50°
2) ∠KOP = ∠FOL = 50° (як вертикальні)
2. 1) ∠MOF = ∠PON = 37° (як вертикальні)
2) ∠KOF = ∠KOM + ∠MOF = 90° + 37° = 127°
Відповідь: 1) 50°; 2) 127°.
152. Промінь СВ – спільна сторона кутів АВС та
+ ∠СВМ = 90° + 90° = 180°.

Знайдемо суму цих кутів.
суміжні.
не спільні сторони суміжних кутів – доповняльні
на одній прямій. 153. Позначимо кожен з двох суміжних кутів, що утворилися х.
суміжних кутів х + х = 180°, 2х = 180°, х = 90°. Отже, кут, під яким перетинаються прямі, прямий. Тоді прямі – перпендикулярні.

154. 1) ∠BON = 180° - (∠AOE + ∠EON) = 180° - (20° + 110°) = 50°
2) ∠CON = ∠COB + ∠BON = 90° + 50° = 140°
Відповідь: 140°.
155. 1) ∠BON = ∠CON - ∠COB = 135° - 90° = 45°
2) ∠EOD = 180° - (∠AOE + ∠BON) = 180° - (25° + 45°) = 110°
Відповідь: 110°.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
156. 1) Позначимо ∠AOB = ∠COD = x; ∠BOC = ∠DOE = y. Оскільки ∠АОВ + ∠BOC + ∠COD + ∠DOE = 180°, то 2х + 2у = 180°; 2(х + у) = 180°; х + у = 90°.
2) ∠АОС = ∠АОВ + ∠ВОС = х + у = 90°, тому ОС ⊥АЕ.
3) ∠BOD = ∠BOC + ∠COD = х + у = 90°, тому ВО ⊥ OD. Задачу

157. Нехай ∠АОВ – заданий кут, ОК – бісектриса кута АОВ. РО ⊥ ОК, отже, ∠РОК


159. 1) MK = MN + NK = 3,2 + 4,1 = 7,3 (см) 2) MN = MK – NK = 7,8 – 2,5 = 5,3 (см)

160. Нехай один із суміжних кутів х, тоді другий х + 36°. Оскільки сума суміжних
дорівнює 180°, маємо: х + х + 36° = 180°; 2х = 144°; х = 72°.
Отже, один із кутів дорівнює 72°, другий - 180° - 72° = 108°.
Відповідь: 72°; 108°.
161. Знайдемо S1 рулону шпалер: 50 см = 0,5 м S1 рулону = 0,5 ⋅ 10 = 5 (м²)
Обчислимо S стін: S стін розміром 4,5 х 2,5: 4,5 ⋅ 2,5 = 11,25 (м²)
Таких стін у кімнаті дві: 2S = 11,25 ⋅ 2 = 22,5 (м²)
S стіни розміром 3 х 2,5: 3 ⋅ 2,5 = 7,5 (м²)
Таких стін дві: 2S = 7,5 ⋅ 2 = 15 (м²)
Загальна площа стін 22,5 + 15 = 37,5 (м²)
S стін – S
і вікон
S = 37,5 – 3,5 = 34 (м²) –

1) Знайдемо кількість рулонів: 34 : 5 = 6,8
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
2)
7 : 4 = 1,75
Отже, необхідно придбати 2 коробки клею
3) Обчислимо вартість шпалер:
7 ⋅ 240 = 1680 (грн)
Вартість клею: 85 ⋅ 2 = 170 грн
Загальна вартість покупки: 1680 + 170 = 1850 грн
Відповідь: 1) 7 рулонів; 2) 2 коробки клею; 3) 1850 грн.
162. АВ ∥ СD; BC ∥ AD

163. Сума двох суміжних сторін прямокутника дорівнює 32 : 2 = 16 (см). Позначимо
164.
165.
166. m ∥ a; b ∥ n.
167.









https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

175.

176.
с.

178. 1)

2) АВ = 2,6 см; АС = 2,1 см; ВС = 1,7 см АС + ВС = 2,1 + 1,7 = 3,8 (см)
3) АВ <
+ ВС 179. Нехай ∠AOD = х, тоді ∠BOD = 0,25х. ∠AOD і ∠BOD – суміжні, ∠AOD +
BOD = 180°, x + 0,25х = 180°; 1,25х = 180°; х = 144°. Отже, ∠AOD = 144°, ∠BOD = 36°. Оскільки
= 36° -

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

180. Примітка: 50 см = 0,5 м.
S плитки = 0,5 ⋅ 0,5 = 0,25 (м²)
S майданчика = 3,5 ⋅ 6,5 = 22,75 (м²)
22,75 : 0,25 = 91 (шт.) – кількість плиток.
91 ⋅ 52 = 4732 (грн) – вартість плитки.
Вартість додаткових матеріалів: 35% від 4732
4732 ⋅ 0,35 = 1656,2 (грн)
4732 + 1656,2 = 6388 грн 20 коп – всього
Відповідь: 6388 грн 20 коп.
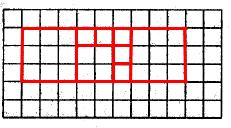
181. Площа вказаного квадрата є 2017² клітинок. Але число 2017² є непарним, тому
розрізати квадрат на дві частини, площа яких (у клітинках) однакова – неможливо. Тому






∠ANM і ∠BMN, ∠CNM i ∠DMN;
різносторонні кути: ∠ANM і ∠DMN; ∠CNM i ∠BMN;
кути: ∠ANK і ∠BMN; ∠KNC і ∠NMD; ∠ANM і ∠BML; ∠CNM і ∠DML.
185. Внутрішні односторонні кути: ∠PCM і ∠DMC; ∠FCM і ∠LMC;
∠PCB і ∠DMC; ∠BCF і ∠CML; ∠PCM і ∠DMK; ∠FCM і ∠LMK.









=
∠3 = 110° (як
∠5 = 120° (як
∠6 = 180° – 120° = 60° (як
∠7 = ∠6 = 60° (як
∠1).
).
∠8).
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

190.

191.

192.
∠4 = ∠1 = 50° (як вертикальний
до ∠1).
∠2 = 180° – 50° = 130° (як суміжний кут до ∠1).
∠3 = ∠2 = 130° (як вертикальний кут до ∠2).
∠7 = ∠6 = 130° (як вертикальний кут до ∠6).
∠5 = 180° – 130° = 50° (як суміжний кут до ∠6).
∠5 = ∠8 = 50° (як вертикальний кут до ∠8). а ∥ b, оскільки ∠2 = ∠6 = 130° (відповідні кути). Відповідь: а ∥ b.
∠1 + ∠2 = 118° + 62° = 180°; тому а ∥ b. ∠2
∠1 + ∠3 = 118° + 63° = 181°; тому
193.
∠1 + ∠2 = 121° + 60° = 181°;
∠2 = ∠3, тому прямі b ∥ с.
∠1 + ∠3 = 121° + 60° = 181°; тому
194.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
195.

196.

197.

198.

199.



1) ∠ABC = 115°.
2) За допомогою транспортира будуємо кут ∠PCK = 115°.
3) AB ∥ PC, оскільки відповідні кути ∠ABC і ∠PCK рівні (згідно з ознакою паралельності прямих).
1) ∠MNP = 125°.
2) За допомогою транспортира будуємо кут ∠APB = 125°.
3) MN ∥ АР, оскільки
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
3) ∠3 = 180° – ∠4 (за властивістю суміжних кутів);
∠6 = 180° – ∠5 (аналогічно);
∠3 + ∠6 = 180° – ∠4 + 180° – ∠5 = 360° – (∠4 + ∠5) = 360° – 190° = 170°.
Відповідь: 1) 190°; 2) 170°; 3) 170°. 201.

За умовою ∠3 + ∠6 = 160°. 1) ∠2 = 180° – ∠3 (за властивістю суміжних кутів), ∠7 = 180° – ∠6 (аналогічно).
Тому ∠2 + ∠7 = 180° – ∠3 + 180° – ∠6 = = 360° – (∠3 + ∠6) = 360° – 160° = 200°. 2) ∠1 = ∠3 (як вертикальні), ∠8 = ∠6 (аналогічно). ∠1 + ∠8 = ∠3 + ∠6 = 160°.
3) ∠4 = 180° – ∠3 (за властивістю суміжних кутів), (аналогічно).
Тому ∠4 + ∠5 = 180° – ∠3 + 180° – ∠6 = 360° – (∠3 + ∠6) = 360° – 160° = 200°.
Відповідь: 1) 200°; 2) 160°; 3) 200°.
202.

203.
Розглянемо 2 випадки:
∠ABC і ∠BCD – внутрішні односторонні кути.
∠ABC + ∠BCD = 70° + 100° = 170°.
дорівнює 180° (наслідок 2).
Відповідь: ні.

204.

так.

1-й випадок. Прямі а і с паралельні, оскільки
прямою b, рівні.
2-й випадок. Прямі а і с перетинаються.
Відповідь: ні.
205.

1-й випадок. Прямі а і b паралельні.
2-й випадок. Прямі а і b перетинаються.
Відповідь: ні.
206. MF – бісектриса кута KMN, то ∠KMN = 2 ∙ ∠FMK; KF – бісектриса кута MKP, то ∠MKP = 2 ∙ ∠MKF.

За умовою ∠MKF + ∠FMK = 90°.
Маємо ∠MKP + ∠KMN = 2 ∙ ∠MKF + 2 ∙ ∠FMK = = 2(∠MKF + ∠FMK) = 2 ∙ 90° = 180°.
Кути MKP і KMN – внутрішні односторонні, утворені
MN і KP січною MK. Оскільки ∠MKP + ∠KMN = 180°, то MN ∥ KP. 207.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
208.

209.

210.
1) ∠АВС = 70°.
2) m ⊥ BA, n ⊥ BC.
3) Кут між прямими m i n дорівнює 70°.
∠АОB = ∠BOC = 130°.
∠АОC = ∠AOD + ∠DOC,
∠AOD + ∠АОB = 180° (як суміжні кути).
Звідси ∠AOD = 180° – ∠АОB = 180° – 130° = 50°.
∠DOC + ∠BOC = 180° (як суміжні кути).
∠DOC = 180° – ∠BOC = 180° – 130° = 50°.
∠АОC = ∠AOD + ∠DOC = 50° + 50° = 100°.
Відповідь: 100°.
Радіус Землі становить приблизно 6378 км.
Довжина окружності Землі на рівні екватора: C=2πR
де R — радіус Землі.
Визначимо ефективні радіуси для верхівки


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
212.
1) Кути 5 і 4 – рівні; кути 2 і 7 – рівні.
2) Кути 1 і 3 – рівні.
3) ∠1 + ∠4 = 180° 213.
1) Кути 1 і 8 – рівні; кути 6 і 3 – рівні.
2) Кути 2 і 4 – рівні.
3) ∠2 + ∠3 = 180°
214.
1) ∠1 = 110° (як відповідний даному куту).
2) ∠2 = 180° – 110° = 70° (оскільки кут 110° і ∠2 – внутрішні різносторонні кути).
3) ∠3 = ∠1 = 110° (як вертикальні)
215.
Відомо, що m ∥ n, тоді:
1) ∠1 = 60° (як відповідний даному куту).
2) ∠2 = 180° – 60° = 120° (оскільки кут 60° і ∠2 –
3) ∠3 = ∠1 = 60° (як вертикальні)
216.

217.


різносторонні кути).
Нехай ∠1 = 140° .
∠3 = ∠1 = 140° (як вертикальні кути).
∠5 = ∠1 = 140° (як відповідні кути).
∠7 = ∠1 = 140° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути). Звідси
∠2 = 180° – ∠1 = 180° – 140° = 40°.
∠4 = ∠2 = 40° (як вертикальні кути).
∠8 = ∠4 = 40° (як відповідні кути).
∠6 = ∠8 = 40° (як вертикальні кути).
Нехай ∠2 = 50°.
∠4 = ∠2 = 50° (як вертикальні кути).
∠4 = ∠8 = 50° (як відповідні кути).
∠6 = ∠8 = 50° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути). Звідси
∠1 = 180° – ∠2 = 180° – 50° = 130°.
∠3 = ∠1 = 130° (як вертикальні кути).
∠5 = ∠1 = 130° (як відповідні кути).
∠7 = ∠5 = 130° (як вертикальні кути).

220.




https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

1) Нехай ∠2 = х, тоді
∠1 = х + 16°. Маємо:
х + х + 16° = 180°
2х = 164°
х = 82°
Отже, ∠2 = 82°;
∠1 = 82° + 16° = 98°.
2) Нехай ∠2 = х, тоді
∠1 = 3х. Маємо:
х + 3х = 180°
4х = 180°
х = = 45°
Отже, ∠2 = 45°; ∠1 = 3 ∙ 45° = 135°.
Відповідь: 1) 82° і 96°; 2) 45° і 135°; 3) 75° і 105°.
227.

1) Нехай ∠1 = х, тоді
∠2 = 4х. Маємо:
х + 4х = 180°
5х = 180°
х = 36°
Отже, ∠1 = 36°;
∠2 = 4 ∙ 36° = 144°.
2) Нехай ∠1 = х, тоді
∠2 = х + 8°. Маємо:
х + х + 8° = 180°
2х = 172°
х= 86°
Отже, ∠1 = 86°;
∠1 = 86° + 8° = 94°.
Відповідь: 1) 36° і 144°; 2) 86° і 94°; 3) 100° і 80°.
228.


3) Нехай ∠2 = 5х, тоді
∠1 = 7х. Маємо:
5х + 7х = 180°
12х = 180°
х = 15°
Отже, ∠2 = 5 ∙ 15° = 75°; ∠1 = 7 ∙ 15° = 105°.
3) Нехай ∠2 = 5х, тоді
∠1 = 4х. Маємо:
5х + 4х = 180°
9х = 180°
х = 20°
Отже, ∠2 = 5 ∙ 20° = 100°; ∠1 = 4 ∙ 20° = 80°.
∠1 = ∠3 = 120° (як вертикальні кути).
∠4 = ∠1 = 120° (як відповідні кути). Отже, a ∥ b
∠2 і ∠6 — відповідні, ∠2 = ∠6 = 110°.
∠5 і ∠2 — суміжні.
x + ∠2 = 180°
x + 110° = 180°
x = 180° – 110°
x = 70°
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


Відповідь: 1) 70°; 2) 65°; 3) 129°. 229.
∠1 і ∠2 суміжні кути. ∠1 + ∠2 = 180°, ∠2 = 180° –
∠1, ∠2 = 180° – 55° = 125°.
∠2 = ∠3 = 125° (як відповідні кути).
Отже, a ∥ b згідно з ознакою паралельності прямих. ∠4 і ∠5 — внутрішні різносторонні кути при паралельних прямих a і b і січній d.
∠4 = ∠5 = 65°.

∠1 + ∠2 = 48° + 132° = 180°. Оскільки ці кути внутрішні односторонні і їхня сума
180°, то
a і b паралельні (наслідок 2).
Розглянемо паралельні прямі a і b і січну d.
∠3 і ∠4 — внутрішні односторонні кути при паралельних прямих a і b і січній d.
∠3 + ∠4 = 180°
∠4 = 180° – ∠3
∠4 = 180° – 51°
∠4 = 129°.



∠3 = ∠4 = 80° (як вертикальні кути).
∠1 = ∠3 (як відповідні кути).
Отже, a ∥ b згідно з ознакою паралельності
прямих.
Розглянемо a ∥ b і січну d.
∠2 = ∠5 як відповідні кути.
Отже, x = 50°.
∠4 + ∠5 = 130° + 50° = 180°. Оскільки ці кути внутрішні односторонні та їхня сума дорівнює 180°, то згідно з наслідком 2 прямі a і b
паралельні. Розглянемо a ∥ b і січну d.
∠1 = ∠2 = 70° (як вертикальні кути).
∠2 і ∠3 — внутрішні односторонні кути, отже,
∠2 + ∠3 = 180°.
∠3 =
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

7 + ∠6 + ∠2 = 120°
3 = ∠2 = 40° (як
7 = 40
кути). ∠1 + ∠2 = 180° (як суміжні кути).
Звідси ∠1 = 180° – 40° = 140°.
∠4 = ∠1 = 140° (як вертикальні кути).
∠5 = ∠1 = 140° (як відповідні кути).
∠8 = ∠5 = 140° (як вертикальні кути).
Відповідь: чотири кути по 40°, чотири кути по 140°. 232.

Оскільки сума чотирьох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 128°, то це дві пари відповідних гострих кутів.
∠1 + ∠5 + ∠3 + ∠7 = 128°. Оскільки ці кути рівні, то кожен з них дорівнює 32°. ∠1 = ∠5 = ∠3 = ∠7 = 32°.
∠1 + ∠2 = 180° (як суміжні кути).
∠2 = 180° – ∠1 = 180° – 32° = 148°.
∠4 = ∠2 = 148° (як вертикальні кути).
∠6 = ∠2 = 148° (як відповідні кути).
∠8 = ∠6 = 148° (як вертикальні кути).
Відповідь: чотири кути по 32°, чотири кути по 148°.
233.

Відповідь: 130°.
234.

Через т. М проведемо пряму паралельні CD. KM ∥ CD, KM ∥ AB. Тоді ∠CMA = ∠CMK + ∠AMK.
Розглянемо AB ∥ KM і січну AM.
∠AMK = ∠MAB = 50° (як внутрішні різносторонні кути).
Розглянемо CD ∥ KM і січну CM.
∠CMK = ∠DCM = 80° (як внутрішні різносторонні кути).
Отже, ∠CMA = 80° + 50° = 130°

Відповідь: 100°.
KF
MN. KF ∥ MN, KF ∥ PL.
Тоді ∠MKP = ∠MKF + ∠PKF.
Розглянемо MN ∥ KF і січну MK. ∠MKF + ∠KMN = 180° (як внутрішні односторонні кути). ∠MKF = 180° – ∠KMN = 180° – 120° = 60°.
Розглянемо PL ∥ KF і січну KP. ∠PKF + ∠KPL = 180° (як внутрішні односторонні кути). ∠PKF = 180° – ∠KPL = 180° – 140° = 40°.
Отже, ∠MKP = 60° + 40° = 100° .
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
235.

236.

237.

238.

AB = 16 см.
1) BC = x см, AC = x + 2, x + x + 2 = 16; 2x = 14; x = 7.
Отже, BC = 7, AC = 7 + 2 = 9.
Оскільки a ∥ b, то ∠KBA = ∠BAL (як внутрішні різносторонні). Оскільки BC і AD —
то ∠CBA = ∠DAB (як половини рівних кутів).
цих
Розглянемо прямі BC і AD та січну AB. ∠CBA і ∠DAB — внутрішні різносторонні рівні, отже, BC ∥ DA. Отже, бісектриси двох внутрішніх різносторонніх кутів при паралельних прямих і січній паралельні.
Оскільки a ∥ b, то ∠MAK = ∠ABL (як відповідні кути).
Оскільки AC і BD — бісектриси цих кутів, то ∠ABD = ∠MAC (як половини рівних кутів). Розглянемо прямі AC і BD і січну MN: ∠MAC і ∠ABD — відповідні кути і рівні. Отже, AC ∥ BD.
Отже, бісектриси двох відповідних
2) BC = x см, AC = 3x см, x + 3x = 16; 4x = 16; x = 4.
Отже, BC = 4 см, AC = 3 · 4 = 12 см.
4 см 6 см 7 см 9 см 10 см 12 см
Відповідь: Франко.
239.
1) 20 · 20 = 400 (м2) –
2) 400 : 40 = 10 (г) – потрібно

3) 10 · 90 = 900 (грн) Відповідь: потрібно 900
3) Нехай AC = 5x, BC = 3x. 5x + 3x = 16; 8x = 16; x = 2.
Отже, BC = 3 · 2 = 6 см, AC = 5 · 2 = 10 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

241.
20 – (8 + 7) = 20 – 15 = 5 см.
АВ = 3 см
АС = 4 см СВ = 5 см Р = 3 + 4 + 5 = 12 см
Відповідь: довжина третьої сторони 5 см. 242. Розв’язання подано на малюнку.





https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Відповідь: А.
6.
180° – 35° = 145°.
Відповідь: В. 145°.
7.

Відповідь: В. 110°.
61° + 119° = 180°,
1) ∠CON = ∠MOD (як вертикальні); ∠CON = 20°. 2) ∠AON = ∠CON + ∠COA = 20° + 90° = 110°.
8. ∠1 + ∠4 = (180° – ∠2 ) + (180° – ∠3) = 360° – (∠2 + ∠3) = = 360° – 175° = 185°.

Відповідь: Б 185°.
9.

Відповідь: А. 80°.
∠2 = ∠3 = 70° (як вертикальні кути). ∠1 = ∠2 = 70° (як відповідні кути). Отже, a ∥ b згідно з ознакою паралельності прямих. Розглянемо a ∥ b і січну d. Кути 100° і x — внутрішні односторонні кути, отже, їхня сума дорівнює 180°. Тоді 100° + x = 180°; x = 80°.
10. 1) Позначимо ∠AOC = ∠BOD = х; ∠COK = ∠DOK = у.

Відповідь: В 90°.

Тоді 2x + 2y = 180° 2(х + у) = 180° х + у = 90° 2) ∠AOK = х + у = 90°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Відповідь: Б. 110°.
12.

Відповідь: Г. розгорнутий 13.





Через т. P проведемо пряму PK ∥ BA. Тоді
∠BPD = ∠BPK + ∠DPK.
Розглянемо BA ∥ PK і січну BP. ∠PBA + ∠BPK = 180° (як внутрішні односторонні кути).
∠BPK = 180° - ∠PBA = 180° - 100° = 80°.
Розглянемо PK ∥ DC і січну PD. ∠DPK + ∠CDP = 180° (як внутрішні односторонні кути).
∠DPK = 180° - ∠CDP = 180° - 150° = 30°.
Отже, ∠BPD = 80° + 30° = 110°
Оскільки OK бісектриса ∠AOC, цей кут розділяється на дві рівні частини: ∠AOK та ∠KOC. ∠AOC = ∠AOK + ∠KOC = 2∠KOC
Оскільки OL — бісектриса ∠COB, цей кут розділяється на дві рівні частини: ∠COL та ∠LOB.
∠COB = ∠COL + ∠LOB = 2∠COL За умовою, OK перпендикулярний до OL, тобто кут
між ними, ∠KOL, дорівнює 90°.
Оскільки ∠AOC складається з кутів AOK і KOC, а ∠COB складається з кутів COL і LOB, то: ∠AOB = ∠AOC + ∠COB = 2∠KOC + 2∠COL = = 2(∠KOC + ∠COL) = 2∠KOL = 2 ⋅ 90° = 180°.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


1) 1 і 2 - внутрішні різносторонні кути; 2) 1 і 3 - внутрішні односторонні кути; 3) 1 і 4 - відповідні кути. 4.



1) ∠KOM = ∠KOA + ∠AOM= 70° + 19° = 89°;
прямі KL і MN – не перпендикулярні.
2) ∠KON= ∠KOB – ∠NOB = 111° – 21° = 90°;
прямі KL і MN – перпендикулярні.

Нехай ∠1 = 78°, тоді ∠3 = ∠1 = 78° (як вертикальні кути), ∠5 = ∠1 = 78° (як відповідні кути), ∠7 = ∠5 = 78° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути),
∠2 = 180° – ∠1 = 180° – 78° = 102°.
∠4 = ∠2 = 102° (як вертикальні кути).
∠6 = ∠2 = 102° (як відповідні кути).
∠8 = ∠6 = 102° (як вертикальні кути).
78°, чотири

52°.
102°.
Оскільки AB ⊥ CD, то ∠AOC = 90°.
∠AOK = ∠AOC – ∠KOC, ∠KOC = ∠DOL = 38° (як вертикальні кути).
Отже, ∠AOK = 90° – 38° = 52°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Відповідь: 50°.
9.

Відповідь: 110°.
10.

36° і 144°. 11.
1 і ∠2
січній d. ∠1 + ∠2 = 40° + 140° = 180°. Згідно з наслідком 2
прямі a і b паралельні.
Розглянемо a ∥ b і січну c.
∠5 = ∠3 = 130° (як внутрішні різносторонні кути).
∠5 + ∠4 = 180° (як суміжні кути).
∠4 = 180° – ∠5 = 180° – 130° = 50°.
Проведемо пряму PR ∥ DC, тоді ∠BKD = ∠BKP + ∠DKP.
Розглянемо BA ∥ PR і січну BK. ∠BKP = ∠KBA = 40° (як
внутрішні різносторонні кути).
Розглянемо KR ∥ DC і січну KD. ∠DKP = ∠KDC = 70° (як
внутрішні різносторонні кути).
Отже, ∠BKD = 40° + 70° = 110°.
властивістю
x + 4x = 180°; 5x = 180°; x = 36°.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



245.

246.

1) Так, можна. Треба побудувати доповняльний промінь до будь-якої сторони даного кута. Наприклад, дано ∠DAE. Побудуємо промінь AB доповняльний до променя AD. Отримали ∠EAB суміжний з ∠DAE.
2) Можна побудувати два кути. Один побудували в п.1).
Проведемо доповняльний промінь AC до променя AE. Отримаємо ∠DAC, суміжний з ∠DAE.
Сума суміжних кутів дорівнює 180°.
Кут, суміжний з ∠ABC: 180° - ∠ABC.
Кут, суміжний з ∠MNL: 180° - ∠MNP.
Якщо ∠ABC < ∠MNP, то 180° - ∠ABC > 180° - ∠MNP.
Отже, більший суміжний кут буде у ∠ABC.

54°, 126°. 247.

30°; 150°.
248.

із суміжних кутів дорівнює
суміжних кутів 3x + 7x = 180°; 10x = 180°; x = 18°. Отже,
= 180°; 1,2x = 180°; x = 150°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Відповідь: 80°; 100°.
0,8
0,8x. x + 0,8x = 180° —
1,8x = 180°; x = 100°. Отже, один
100°, другий 100° × 0,8 = 80°.
249. ∠ABC заданий кут. KB бісектриса. ∠ABK = ∠KBC. ∠ABL — суміжний з ∠ABC. Нехай ∠ABL


3)
254.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
255.

Відповідь: 120°.
256.

Відповідь: 36°, 36°, 144°, 144°.
що
або ∠4.
Нехай ∠1 = x, ∠3 = ∠1 = x, тоді ∠2 = 2x.
∠1 + ∠2 = 180° — як сума суміжних кутів. x + 2x = 180°; 3x = 180°; x = 60°.
Отже, ∠1 = 60° , ∠2 = 2 × 60° = 120° .
1) Нехай ∠1 = x, ∠3 = ∠1 = x (як вертикальні кути). ∠2 + ∠4 = 4(∠1 + ∠3) = 2 × 4x = 8x. Сума всіх утворених кутів дорівнює 360°. 2x + 8x = 360°; 10x = 360°; x = 36°.
Отже, ∠1 = ∠3 = 36° , ∠2 = ∠4 = 180° - 36° = 144° .
2) Нехай ∠1 = x, ∠3 = ∠1 = x (як вертикальні кути).
∠1 + ∠3 = x + x = 2x.
∠2 + ∠4 = 4(∠1 + ∠3) = 2x + 160° . Сума всіх утворених
360°. 2x + 2x + 160° = 360°; 4x = 200°; x = 50°.
Отже, ∠2 = 180° - 50° = 130°.
Відповідь: 50°, 50°, 130°, 130°.
257. Нехай ∠4 = x, тоді ∠2

40°.
258.

259.


+ x = 8x; ∠1 +
∠1 = ∠3 = 3.5x. ∠4 + ∠
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

АВ ⊥ КР
261.
CD ⊥ AB; CK ⊥ AB; DK ⊥ AB.
262.
1) Оскільки AB ⊥ BC, то ∠AOC = 90°, ∠BOC = 90°.
∠AOK = ∠AOC − ∠KOC, ∠AOK = 90° − ∠KOC.
∠LOB = ∠BOC − ∠COL = 90° − ∠COL.
Оскільки ∠KOC = ∠COL, то ∠AOK = ∠LOB.
∠AOL = ∠AOC + ∠COL = 90° + ∠COL.
∠KOB = ∠COB + ∠KOC = 90° + ∠KOC.
Оскільки ∠KOC = ∠COL, то ∠AOL = ∠KOB.
2) ∠KOB = 90° + ∠KOC, ∠AOK = 90° − ∠KOC.
Отже, ∠AOK < ∠KOB.
263.

1) Так, ∠AOC = ∠COB = 45° 2) Так, ∠AOB = ∠COB = (360° – 90°) : 2 = 135°.
264.

265.

90° = 15

BL
ABC. ∠ABC = 2∠LBC, BM
CBD: ∠CBD = 2∠CBM.
∠LBC + ∠CBM = 90°. Знайдемо ∠ABD = ∠ABC + ∠CBD = 2∠LBC + 2∠CBM = 2(∠LBC + ∠CBM) = 2 × 90° = 180°.
кут ABD

AB
267.

268.

1)





https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html








274.

275. ∠
∠4 = ∠3 = 130° (як вертикальні кути).
276. Згідно
Оскільки
277.

= 0,8x.
x + 0,8x = 180°; 1,8x = 180°; x = 100°. Отже, ∠6 = 100°, ∠3 = 0,8 × 100° = 80°.
100°, 80°, 80°. 279.


CDB —
∠ABD = 72°, тоді
CBD = 180° - ∠ABD, ∠CDB = 180° - 72° = 108°; BO —
ABO = 1 2 ∠ABD = 1 2 ⋅ 72° = 36°; ∠CDO = 1 2 ∠CDB = 1 2 ⋅ 108° = 54°.
CDB,
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
AB.
BOM = ∠ABO = 36°;
DOM = ∠CDO = 54°. ∠BOD —
∠BOD = ∠BOM + ∠DOM; ∠BOD = 36° + 54° = 90°.
Відповідь: 90°.
280.

Проведемо пряму MP ∥ DC і пряму NF ∥ BA. ∠MNB = ∠MNF + ∠FNB.
Розглянемо DC ∥ MP і січну CM: ∠CMP = ∠DCM = 50° — як внутрішні різносторонні кути. ∠PMN = ∠CMN - ∠CMP = 80° - 50° = 30°.
Розглянемо MP ∥ NF і січну MN: ∠MNF = ∠PMN = 30° — як внутрішні різносторонні кути.
Розглянемо NF ∥ AB і січну NB: ∠FNB + ∠ABN = 180° — як внутрішні односторонні
кути.
∠FNB = 180° - 140° = 40°. Отже, ∠MNB = 30° + 40° = 70°.
Відповідь: 70°. РОЗДІЛ 3.
281.

282.

283.
§ 11. Трикутник і його елементи
P△MKL = MK + KL + LM = 2 + 3 + 4 = 9 (см).
Вершини трикутника: P, K, L. Сторони трикутника: PK, KL, LP. Кути трикутника: ∠KPL, ∠PKL, ∠KLP.

284.


Сторони трикутника: AM, MN, NA. Кути трикутника: ∠MAN, ∠AMN, ∠MNA.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
285.
25 мм = 2,5 см; 0,4 дм = 4 см.
P = 2,5 + 3,2 + 4 = 9,7 (см).
Відповідь: 9,7 см.
286.
29 мм = 2,9 см; 0,3 дм = 3 см.
P = 4,3 + 2,9 + 3 = 10,2 (см).
Відповідь: 10,2 см.
287.

288.

289.
AB = 2,8 см; BC = 1,5 см; AC = 3 см.
P = 2,8 + 1,5 + 3 = 7,3 см.
Відповідь: 7,3 см.
PL = 5,3 см; PK = 3,2 см; KL = 2,9 см.
P = 5,3 + 3,2 + 2,9 = 11,4 см.
Відповідь: 11,4 см.
Нехай довжина найменшої сторони трикутника дорівнює x см, тоді довжина
— 3x см, а третьої — (x + 7) см. Оскільки периметр трикутника
см,
рівняння: x + 3x + (x + 7) = 32; 5x + 7 = 32; 5x = 25; x = 5 (см).
Отже, довжина однієї сторони 5 см, другої — 5 ×
5 см, 15 см, 12 см.
290.
Нехай
третьої — 1,5x дм. Оскільки периметр
x + (x − 2) + 1,5x = 40; 3,5x − 2 = 40; 3,5x = 42; x = 12 (дм). Отже, довжина однієї сторони
— 12 × 1,5 = 18 дм. Відповідь: 12 дм, 10 дм, 18 дм. 291.


A
AB = 3 см,
— AC = 7 см. З'єднаємо точки B і C. Отримаємо △ABC.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
292.

293.
Нехай одна із сторін трикутника дорівнює 3x, друга — 4x, третя — 6x.
Оскільки P = 52 см, маємо рівняння: 3x + 4x + 6x = 52; 13x = 52; x = 4.
Отже, одна із сторін трикутника дорівнює 3 × 4 = 12 см, друга — 4 × 4 = 16 см,
третя — 6 × 4 = 24 см.
Відповідь: 12 см, 16 см, 24 см.
294.
Нехай одна із сторін трикутника дорівнює 2x, друга — 3x, третя — 4x. Оскільки P△ = 72,
маємо рівняння:
2x + 3x + 4x = 72; 9x = 72; x = 8.
Отже, одна із сторін трикутника дорівнює 2 × 8 = 16 (см), друга — 3 × 8 = 24 (см), третя
— 4 × 8 = 32 (см).
Відповідь: 16 см, 24 см, 32 см.
295.

296.

297.
△MNK, △MKN, △NKM, △NMK, △KNM, △KMN.
AB + BC = 11 см, BC + AC = 14 см, AC + AB = 13 см.
AB + BC + BC + AC + AC + AB = 11 + 14 + 13;
2(AB + BC + AC) = 38;
AB + BC + AC = 38 : 2 = 19 (см).
Відповідь: 19 см.

298.


∠ABC = 78°, BD бісектриса кута ABC.
∠ABD = ∠DBC = 39°. BE — допоміжний промінь до сторони
BC кута ABC.
∠EBA суміжний до ∠ABC, ∠EBA = 180° - 78° = 102°.
∠EBD = ∠EBA + ∠ABD = 102° + 39° = 141°.
Відповідь: 141°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
299.
1) 3 га 18 млн м3 = 54 (млн м3)
2) 2 км2 ⋅ 18 млн м3 = 200 га ⋅ 18 млн м3 = 3600 (млн м3)
300. У

§ 12. Рівність геометричних фігур
301.

1) AB = 2,5 см, CD = 2,8 см.
Отже, AB ≠ CD.

2) ∠M = 55°, ∠K = 55°.
Отже, ∠M = ∠K.
302.

1) MN = 3 см, PK = 3 см.
Отже, MN = PK.

2) ∠A = 60°, ∠B = 50°.
Отже, ∠A ≠ ∠B.
303.
1) Так, оскільки 1,7 см = 17 мм, то АК = MF.
2) Ні, оскільки градусні міри кутів різні.
304.

305.

1) ∠A = ∠M; 2) ∠B = ∠P; 3) ∠C = ∠L.

1) MP = DC; 2) PT = CK; 3) MT = DK.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

307.

308.
1) △AKM = △LPT; 2) △MAK = △TLP.
1) △ABC = △PFK; 2) △CAB = △KPF.

309.

310. 1)
Оскільки △ABC = △KLP, то їхні відповідні сторони рівні.
KL = AB = 6 см, BC = LP = 8 см, KP = AC = 10 см.
Оскільки △PMT = △DCF, то їхні
кути рівні. ∠D = ∠P = 41°, ∠M = ∠C = 92°, ∠F = ∠T = 47°.
△ABC = △CBA, тоді AB = CB, BC = BA, AC = CA.
Отже, у △ABC рівні сторони AB і BC.
312.
Оскільки △MNK = △MKN, то ∠M = ∠M, ∠N = ∠K, ∠K = ∠N.
Отже, у трикутника MNK ∠N = ∠K.
313.
Оскільки △ABC = △BCA, то AB = BC, BC = CA, AC = BA.
Отже, AB = BC = CA. △ABC — рівносторонній.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
P△ABC = 3 × AB = 3 × 7 = 21 (см).
Відповідь: 21 см.
314.
Оскільки △PKL = △KLP, то PK = KL, KL = LP, LP = KP. Отже, PK = KL = LP.
P△PKL = 27 см, P△DKL = 3PK, 27 = 3PK, PK = 9 см.
Відповідь: 9 см.
315.
Вісім точок, що
між крайніми точками дорівнює 112 см, то відстань між двома сусідніми точками
дорівнює 112 : 7 = 16 см.
Відповідь: 16 см.
316.

Відповідь: 30°, 60°, 90°.
317.
DOB
∠COD = 2x, ∠COA = 3x. ∠DOB + ∠COD + ∠COA = 180°, x + 2x + 3x = 180°; 6x = 180°, x = 30°. Отже, ∠DOB = 30°, ∠COD = 2 × 30° = 60°, ∠COA = 3 × 30° = 90°.
1. 1) V = 20 ⋅ 0,5 ⋅ 2,5 = 25 (м3) – об’єм кладки
2) 25 ⋅ 400 = 10000 (шт) – кількість цеглин
3) 25 20% = 25 0,2 = 5 (м3) –
2. 1) 10000 ⋅ 4,2 = 42000 (грн) –
розчину
2) 5 ⋅ 1520 = 7600 (грн) – вартість розчину
3) 42000 + 7600 = 49600 (грн) –
318.



321.
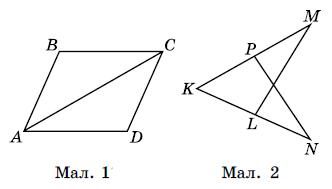

323. За умовою AB = BC. Оскільки BK ⊥ AC, то ∠ABK = ∠CBK = 90°, KB — спільна сторона. Отже, ΔABK = ΔCBK за двома сторонами і кутом між ними.

324. Оскільки PL ⊥ MN, то ∠PKM = ∠LKN = 90°. За умовою MK = KN, ∠M = ∠N. Отже, ΔMKP = ΔNKL за стороною і прилеглими


325.

326.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
За умовою KB = KC, ∠ABK = ∠DCK. ∠AKB = ∠DKC – як вертикальні кути. Отже, ΔABK = ΔDCK за стороною і

За умовою AB = CD, ∠ABC = ∠BCD. CB спільна сторона.
Отже, ΔABC = ΔDCB за двома сторонами і
ними.
327. Оскільки ОС

328.

кута AOB, то ∠AOC = ∠NOC. За умовою ∠OCM = ∠OCN, OC спільна сторона. Отже, ΔOMC = ΔONC за стороною
кутами.
За умовою ВО бісектриса кута ABC, BK бісектриса ∠АВС.
Отже, ∠МВО = ∠NВО. За умовою MN ⊥ BK, отже, ∠MOB = ∠NOB = 90°, ВО спільна сторона. ΔBMO = ΔBNO за стороною і двома прилеглими кутами. У рівних трикутників відповідні сторони рівні.
Отже, MO = NO. 329.


Розглянемо ΔBOC і ΔDOA: OC = OA, OB = OD, ∠BOC = ∠DOA, як вертикальні кути. Отже, ΔBOC = ΔDOA за двома сторонами і кутом
ними. Отже, BC = AD, оскільки у рівних трикутників
сторони рівні.
ΔBOA і ΔDOC: AO = OC, OB = OD, ∠BOA = ∠DOC

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
331.

332.
За умовою ∠LMK = ∠PKM і ∠LKM = ∠PMK. MK спільна сторона. Отже, ΔMKL = ΔKMP за стороною і прилеглими кутами.

333.

334.

335.

336.



Оскільки за умовою ΔABC = ΔA1B1C1, то у них відповідні сторони і кути рівні. Отже, AC1 = AC, ∠C1 = ∠C. Тоді ΔALC = ΔA1L1C1 за стороною і двома прилеглими кутами.
Оскільки за умовою ΔABC = ΔA1B1C1, то у них відповідні сторони і
Отже, AB = A1B1, ∠BAM = ∠B1A1M1.
Отже, ΔABM = ΔA1B1M1 за двома сторонами
трикутника, то трикутники рівні.
На мал. в ΔABC AB = 2 см, ∠CAB = 30°, ∠CBA = 60°, а в ΔACD: AB = 2 см, ∠BAD = 60°, ∠ADB = 30°. Проте ΔABC ≠ ΔABD.
ΔABK = ΔCBL, то
рівні. Отже, ∠A = ∠C, AB = CB, AK = CL. AL = AK + KL, CK = CL + KL, отже, KL спільний
для AL і CK, AL = CK.
ΔABL = ΔCBK за
ΔAKC = ΔALC, то
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

трикутників
сторони рівні. Отже, AM = AN. Розглянемо ΔAMP і ΔANP. AP спільна сторона. ΔAMP = ΔANP за двома сторонами і
між ними (∠MAP = ∠NAP, AM = AN). У рівних трикутників відповідні кути рівні, отже, ∠MPA = ∠NPA.
Оскільки ці кути суміжні і рівні, то маємо ∠MPA + ∠NPA = 180°; ∠MPA = ∠NPA = 90°.
Тож MN ⊥ AB.
339.
1) 13 см + 4 дм = 1,3 дм + 4 дм = 5,3 дм друга сторона трикутника
2) 4 дм : 2 = 2 дм третя сторона трикутника.
3) PΔ = 4 + 5,3 + 2 = 11,3 (дм).
Відповідь: 11,3 дм.
340. Якщо ці три кути

341.
тоді і решта кутів по 90°. Звідси a ⊥ c, b ⊥ c. Якщо ці три кути 1, 2, 3, тоді
90°. Отже, і інші кути по 90°. Звідси a ⊥ c, b ⊥ c.
1) 3,5 ⋅ 6 = 21 (м2) – площа підлоги
2) 0,07 0,4 = 0,028 (м2) – площа дощечки
3) 21 : 0,028 = 750 (шт)
Відповідь: потрібно 750 дощечок. 342.
РΔ = 6 + 6 + 8 = 20 (см).
Відповідь: 20 см. 343.
Можна скласти прямокутник 101 × 50.
Кожна сторона прямокутника буде складатися
1 × 1 і 1 × 100; 1 × 2 і 1 × 99; ...; 1 × 50 і 1 × 51.

shkola.in.ua

shkola.in.ua

345.






347.
TP
T
348. Оскільки у
PΔABC = 3 × AB = 3 × 12 = 36 (см).
Відповідь: 36 см.
349.
Оскільки
BC = P : 3 = 18 : 3 = 6 (см).
Відповідь: 6 см.

351.
8 + 4 = 12 (см).
бічні сторони AB і BC дорівнюють 7 см кожна, тоді основа AC = 7 - 2 = 5 (см). P = 7 + 7 + 5 = 19 (см).
Тоді периметр PΔ = 8 + 12 + 12 = 32 (см).
Відповідь: 32 см.
352.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

354.

355.
Нехай в ΔABC: AC основа, AB = BC = 7 см. PΔABC = 20 см.
Отже, маємо
P = AB + BC + AC. 20 = 7 + 7 + AC, AC = 20 - 14 = 6 (см).
Відповідь: 6 см.

Нехай в ΔAMN: AM = AN = 7 дм (як бічні сторони). PΔAMN = 18 дм.
Отже, AM + AN + MN = 18; 7 + 7 + MN = 18; MN = 18 - 14 = 4 (дм).
Відповідь: 4 дм.
356.


357.
Нехай в ΔACD: CD = 12 дм, PΔACD = 30 дм.
ΔACD = AC + AD + CD, 30 = AC + AD + 12, 30 = 2AC + 12 (оскільки AC = AD), 2AC = 18, AC = 9 (дм).
Відповідь: 9 дм.

Нехай в ΔABC: AB = BC, AC = 5 см, PΔABC = 17 см.
ΔABC = AB + BC + AC, 17 = AB + BC + 5, 17 = 2AB + 5 (оскільки AB = BC), 2AB = 12, AB = 6 (см).
Відповідь: 6 см.


За умовою ΔABC рівнобедрений, отже, AC = CB і ∠CAB = ∠CBA (за властивістю кутів рівнобедреного трикутника).
∠KAC і ∠CAB — суміжні, ∠KAC + ∠CAB = 180°, ∠KAC = 180° - ∠CAB.
∠ суміжні, ∠MBC + ∠CBA = 180°, ∠MBC = 180° - ∠CBA.
Оскільки ∠CAB = ∠CBA, то і ∠KAC = ∠MBC.
358. За умовою ΔKLM рівнобедрений


359.
рівнобедреного трикутника ∠MKL = ∠MLK. ∠MLK = ∠PLN — як вертикальні
Оскільки ∠MLK = ∠MKL, то ∠PLN = ∠MKL.
360.



AB = BC, PΔABC = 14 см. AB + BC = 14 - 6 = 8 (см), AB = BC = 8 : 2 = 4 (см). AC = PΔABC - (AB + BC) = 14 - 8 = 6 (см).
4 см, 4 см, 6 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


Нехай ΔABC рівнобедрений, AB = BC, P = 44 см.
Позначимо основу AC = x, тоді AB = x + 4, BC = x + 4.
Складемо рівняння: (x + 4) + (x + 4) + x = 44; 3x + 8 = 44; 3x = 36; x = 12.
Отже, AC = 12 см, AB = BC = 12 + 4 = 16 (см).
Відповідь: 12 см, 16 см, 16 см. 362.


Нехай ΔABC рівнобедрений, AB = BC, P = 35 дм.
Позначимо основу AC = x, тоді AB = BC = 2x.
Складемо рівняння: x + 2x + 2x = 35; 5x = 35; x = 7.
Отже, AC = 7 дм, AB = BC = 7 × 2 = 14 (дм).
Відповідь: 7 дм, 14 дм, 14 дм. 363.

364.


Оскільки ΔABC рівнобедрений (AB = BC) з основою AC, то ∠BAC = ∠BCA (за властивістю кутів рівнобедреного трикутника).
Розглянемо ΔCKA і ΔALC: AC — спільна, KA = LC (за умовою),
∠KAC = ∠LCA.
Отже, ΔCKA = ΔALC (за двома сторонами і кутом між ними).
Отже, AL = KC (як відповідні сторони).
Нехай ΔABC рівнобедрений, AB = BC, ∠KCA = ∠LAC.
Розглянемо ΔAOC.
Оскільки ∠KCA = ∠LAC, то за теоремою 2 ΔAOC — рівнобедрений.
Звідси OA = OC.
Розглянемо ΔKOA і ΔLOC. ∠KAO = ∠BAC - ∠LAC, ∠LCO = ∠BCA -
∠KCA.
Оскільки ∠BAC = ∠BCA і ∠KCA = ∠LAC, то ∠KAO = ∠LCO.
∠KOA = ∠LOC як вертикальні.
Отже, ΔKOA = ΔLOC за стороною і прилеглими кутами. Звідси AK = CL. 365.


Розглянемо ΔLCM і ΔMAK. CM = AK (за умовою),
LC = LB + BC, MA = MC + AC,
отже, LC = MA, оскільки MC = CB за умовою, BC = AC — як сторони рівностороннього ΔABC.
∠LCM = ∠MAK — як кути, суміжні з рівними кутами. ΔLCM = ΔMAK за двома сторонами і кутом між ними.
Звідси LM = KM.
Аналогічно з рівності ∠MAK та ∠KBL отримаємо KM = KL. Маємо LM = KM = KL. Отже, ΔKLM рівносторонній. 366.
shkola.in.ua


За умовою AB = BC = AC, AP = BK = LC, тоді PB = AB - AP, KC = BC – BK, AL = AC - LC, PB = KC = AL. Оскільки ΔABC —
367.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
368.

Оскільки ΔAOB і ΔCOD рівні, то рівні їхні відповідні
і сторони, тобто ВО = OD, ∠ABO = ∠CDO.
shkola.in.ua shkola.in.ua
Розглянемо ΔKBO і ΔLDO. ∠KOB = ∠LOD — як вертикальні кути. ΔKBO = ΔLDO за стороною і прилеглими кутами.
Отже, KO = OL, KB = DL.

Нехай довжина відрізка AK = x см, тоді BK = (48 - x) см.
За умовою 5AK = 7BK, отже маємо рівняння:
5x = 7(48 - x); 5x = 336 - 7x; 12x = 336; x = 28.
Отже, AK = 28 см, BK = 48 - 28 = 20 (см).
Відповідь: 28 см, 20 см.
370.
1) 100 12 10 = 12000 (м3) – повітря
2) 200 ⋅ 12000 = 2 400 000 (м3) – повітря очистять 200 каштанів за рік.
Відповідь: 2 400 000 м3 повітря.
371.
1) Конус, сукно; 2) сектор, корсет.
15. Медіана,
трикутника. Властивість бісектриси рівнобедреного трикутника
372.









1) AT висота трикутника ABC.
2) AN — медіана трикутника ABC.
3) AP — бісектриса трикутника ABC. shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua
AK
= ∠CKA = 90°.
375. Оскільки AK


shkola.in.ua
то ∠BAK = ∠CAK = 40° Отже, ∠BAC = ∠BAK + ∠CAK = 40° + 40° = 80°.
376. Оскільки AK


shkola.in.ua
377. AL, BN, CK – медіани ΔABC.


shkola.in.ua
то BK = KC = �������� 2 = 12 2 = 6 (см).
378. PL, CP, AM – бісектриси ΔABC.
shkola.in.ua


379. AK, CL, BM – висоти ΔABC.


shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
380. AE, BF, CD – висоти ΔABC.
shkola.in.ua


381.
shkola.in.ua


Оскільки висота рівнобедреного трикутника,
медіаною і бісектрисою, то: ∠CAK = ∠BAK, ∠ACK = ∠ABK, ∠AKC ∠AKB, AC = AB, CK = KB.
382. Оскільки бісектриса рівнобедреного трикутника,

383.


основи, є медіаною
∠EDP = ∠EFP,
DEP = ∠FEP, ∠EPD = ∠EPF, ED = EF, DP = PF.
shkola.in.ua shkola.in.ua
shkola.in.ua

384.






386.


387.


388.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Нехай в ΔABC BD бісектриса і висота.
∠ABD = ∠CBD, ∠BDA = ∠BDC, BD спільна сторона ΔABD і ΔCBD.
Отже, ΔABD = ΔCBD за стороною і прилеглими кутами. Оскільки у рівних трикутників відповідні сторони рівні, то AB = CB. Отже, ΔABC рівнобедрений.
Нехай в ΔABC BD медіана і висота.
∠BDA = ∠BDC = 90°, AD = DC, BD спільна сторона ΔABD і ΔCBD.
Отже, ΔABD = ΔCBD за двома сторонами і кутом між ними.
Оскільки у рівних трикутників відповідні сторони рівні, то AB = CB. Отже, ΔABC рівнобедрений.

shkola.in.ua

389.

ΔABC = ΔA1B1C1, отже, A1C1 = AC, ∠B1C1A1 = ∠BCA (як відповідні сторони і кути рівних трикутників).
AD бісектриса ΔABC, ∠BAD = ∠DAC. A1D1 бісектриса ΔA1B1C1, ∠B1A1D1 = ∠D1A1C1. Отже, ∠DAC = ∠D1A1C1.
ΔADC = ΔA1D1C1 за стороною і
прилеглими кутами.


390.
Нехай в ΔABC AB = BC, BF = FC = 1 2BC, BD = DA = 1 2AB, отже, AD = FC.
ΔADC = ΔCFA (оскільки AC спільна, ∠DAC = ∠FCA як кути при основі рівнобедреного трикутника, AD = FC як половини рівних сторін AB і BC). З рівності трикутників маємо: DC = FA.


391.

Нехай в ΔABC AB = BC, ∠BAC = ∠BCA, AF і CD бісектриси, тобто ∠FAC = ∠FAB = 1 2 ∠BAC, ∠DCA = ∠DCB = 1 2 ∠BCA, отже, ∠FAC = ∠DCA, ΔADC = ΔCFA (оскільки AC спільна, ∠FAC = ∠DCA, ∠DAC = ∠FCA).
З рівності трикутників маємо: AF = CD.


Нехай в ΔABC AB = BC, BD ⊥ AC, BD = 10 см, PΔABC = 40 см. PΔABC = AB + AD + BD, AB + AD = P - BD = 40 - 10 = 30 (см).
AB = BC - за умовою, AD = DC - оскільки BD є медіаною.
AB + AD = BC + DC, тоді PΔABC = AB + AD + BC + DC = 30 + 30 = 60 (см).
Відповідь: 60 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


393.
shkola.in.ua
Нехай в ΔABC CB = CA, BK = KA, PΔABC = 16 см, PΔACK = 12 см. PΔACK = CA + AK + KC, PΔABC = CA + AB + BC = CA + AK + KB + BC = 2(CA + KA) = 16 (см). CA + AK = 8 см, KC = PΔACK - (CA + AK) = 12 - 8 = 4 (см).
Відповідь: 4 см.


Нехай в ΔABC CN – медіана і бісектриса. Продовжимо медіану CN так, щоб NK = CN. Проведемо відрізки КА і КВ. Розглянемо ΔCNB і ΔKNA. CN = KN (за побудовою), NB = NA (за умовою). ∠ANK = ∠BNC (як вертикальні), отже, ΔCNB = ΔKNA за двома сторонами і кутом між ними. У рівних трикутників рівні відповідні кути і сторони, тож ∠NCB = ∠NKA, CB = KA.
Аналогічно з рівності трикутників CAN і KBN отримаємо ∠CAN = ∠BKN, AC = BK.
Розглянемо ΔCAN і ΔKBС. Вони рівнобедрені. AK = CA, CB = BK.
Отже, отримали AC = CB = AK = KB. У ΔABC дві сторони рівні, він рівнобедрений. 394. Нехай задані


395.
shkola.in.ua
a
b, то ∠1 = ∠3 = ∠5 = ∠7, ∠2 = ∠4 = ∠6 = ∠8 і ∠3 + ∠6 = 180°.
Нехай ∠3 = 30°, ∠6 = 140°. ∠3 + ∠6 = 170° ≠ 180°.
Отже, сума внутрішніх односторонніх кутів
180°. Кути ∠6 і ∠7 теж не можуть
відповідно 140° і 30°, бо вони суміжні.


396.


Нехай ΔABC рівносторонній, PΔABC = 12 см. ΔACD
рівнобедрений.
AD = CD, PΔACD = 18 см. AB = BC = AC (як сторони рівностороннього трикутника).
AC = P : 3 = 12 : 3 = 4 (см).
P = AC + AD + CD, AD + CD = P - AC = 18 - 4 = 14 (см).
Отже, AD = CD = 7 см.
Відповідь: 7 см.
Нехай ΔABC рівнобедрений, AB = BC, P = 69 см.
Позначимо довжину AB = x см, тоді AC = 0,3x см.
Складемо рівняння: x + x + 0,3x = 69; 2,3x = 69; x = 30.
Отже, AB = BC = 30 см, AC = 30 × 0,3 = 9 (см).
Відповідь: 30 см, 30 см, 9 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
1) 2 ∙ (9,4 + 6,5) = 31,8 (м) – периметр
2) 31,8 ∙ 3,2 = 101,76 (м2) –
3) 101,76 ∙ 0,09 = 9,1584 (м2) –
стін
4) 101,76 – 9,1584 = 92,6016 (м2) – площа
5) 2 ∙ 9,4 ∙ 6,5 + 92,6016 = 214,8016 (м2) –
6) 25 ∙ 214,8016 = 5370,04 ≈ 5370 грн.
Відповідь: за
398.
125 л = 125 дм³. Олесь
110 (дм3) = 110 л.
Відповідь:
399.
shkola.in.ua

400.


401.






403.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


404.
PK = ML, PM = KL за умовою, KM спільна сторона ΔРМК і ΔLKM.
Отже, ΔРМК і ΔLKM за трьома сторонами. У рівних трикутників відповідні кути рівні, отже, ∠РКМ = ∠LMK.


405.
З'єднуємо точку В і точку С. Отримаємо два трикутники: ΔABK і ΔCBK.
AB = BC, AK = KC за умовою, BK спільна сторона ΔABK і ΔCBK. Отже, ці трикутники рівні за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠ABK = ∠CBK. Отже, BK бісектриса кута ABC.


406.
shkola.in.ua
З'єднуємо т. М і т. L. Отримаємо два трикутники: ΔMPL і ΔMKL. MP = MK, PL = LK за умовою, ML спільна сторона ΔMPL і ΔMKL. ΔMPL = ΔMKL за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠PML = ∠KML. Отже, ML бісектриса кута PMK.


407.
AB = CD, AC = BD за умовою, DA спільна сторона ΔCDA і ΔBAD. ΔCDA = ΔBAD за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠BDA = ∠CAD. Ці кути є кутами ΔDAO, тоді за ознакою рівнобедреного трикутника ΔDAC рівнобедрений.

AO = OB, CO = OD за умовою. DOB = ∠COA як вертикальні кути Отже, ΔDOB = ΔCOA за

408.

shkola.in.ua
рівних трикутників
рівні, тому DB = CA. DA = DO + OA, CB = CO


409.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

410.

Ні, оскільки може бути AB = 6 см і MN = MP = 6 см; BC = AC = 8 см і NP = 8 см. Тому ΔABC може бути не рівний трикутнику MNP.

411.
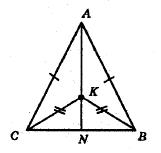
ΔACK = ΔABK за третьою ознакою рівності трикутників (оскільки AB = AC, BK = KC за умовою, AK спільна сторона). ∠CAK = ∠BAK, оскільки у рівних трикутників відповідні кути рівні. Отже, AN бісектриса трикутника ABC. У рівнобедреному трикутнику бісектриса, проведена до основи, є висотою, тобто AN ⊥ CB. Оскільки K ∈ AN, то AK ⊥ CB.


412.
shkola.in.ua

ΔDPN = ΔDPM за третьою ознакою рівності трикутників. Звідси виходить, що ∠MDP = ∠NDP, отже DK – бісектриса ΔDMN. Оскільки у рівнобедреного трикутника бісектриса, що проведена до основи є також висотою і медіаною, то MK = KN.

Треба кут 10° відкласти послідовно 9 разів (10 ⋅ 9 = 90°).
413.

414.

shkola.in.ua

Оскільки 4∠BAK = 5∠KAC, то = ∠BAK ∠KAC = 5 4 . Позначимо ∠BAK = 5х, тоді ∠KAC = 4х. Складемо рівняння: 5х + 4х = 126°; 9x = 126°; х = 14°.
Тримаємо: ∠BAK = 5 ∙ 14° = 70°; ∠KAC = 4 ∙ 14° = 56°. Відповідь: ∠ВАК = 70°; ∠КАС = 56°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
415.

shkola.in.ua

416.

Cума кутів ΔABC: 60° + 45° + 75° = 180°; Cума кутів ΔKLM: 45° + 45° + 90° = 180°.


shkola.in.ua shkola.in.ua
1. P = 4 + 7+ 10 = 21 (см).
Відповідь: Б) 21 см.
2.
Відповідь: Б) ∠T.
3.
САМОСТІЙНА
№ 3 (§§ 11–16)
Відповідь: Б) ∆ABC = ∆A1B1C1 (за другою ознакою).
4. (17 – 5 ) : 2 = 6 (см).
Відповідь: Г) 6 см.
5.



∠KOL = ∠MON (як вертикальні), тому ∆KOL = ∆MON (за першою ознакою).
Відповідь: В) ∆KOL = ∆MON.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Відповідь: В) CL.
7.




9.


10.
Нехай AB = х см, тоді AC = 2х см і BC = (х + 2) см. За умовою х + 2х + х + 2 = 22; 4х = 22 – 2; 4х = 20; х = 5 (см).
Тому BC = 5 + 2 = 7 (см); AC = 2 ∙ 5 = 10 (см).
Відповідь: Г) 10 см.
Оскільки ∆KLM = ∆MLK, то KL = ML і ∠K = ∠M.
Відповідь: А) 17 см.
Оскільки у ∆ABC AB = BC, то BK є не тільки висотою, а й медіаною і бісектрисою. Отже, хибним є твердження, що ∠ABC = ∠BKA, оскільки кут ABC гострий, а кут BKA прямий.
Відповідь: A) ∠ABC = ∠BKA.
Оскільки ∆ABC = ∆BCA, то ∠A = ∠B і ∠B = ∠C, тобто ∠A = ∠B = ∠C.
Тому ∆ABC рівносторонній і BC = CA = AB = 5 см.
Відповідь: Г) BC = 5 см; CA = 5 см.
11.



Оскільки CK бісектриса рівнобедреного трикутник, що проведена до основи, то CK є також і медіаною. Отже, AK = KB.
За умовою AC = CB.
P∆ABC = AC + AB + CB = 2АС + 2AK = 2(AC + AK). Тому AC + AK = 36 2 = 18 (см).
P∆AСК = AC + AK + CK. Тому CK = 30 – 18 = 12 (см).
Відповідь: Г) 12 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



shkola.in.ua

BM = MC, тому ∠MBC = ∠MCB. Оскільки AB = AC; BM = MC (за умовою) і AM – спільна сторона трикутників ABM і ACM. Тому ∆ABM= ∆ACM (за третьою ознакою).
Маємо ∠BAM = ∠САМ; ∠BMA = ∠CMA і ∠MBA = ∠MCA. Твердження ∠MBA > ∠MCA хибне. Відповідь: Б) ∠MBA > ∠MCA.
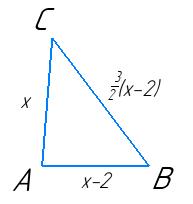
1) Нехай х – АС; АВ – х – 2; ВС –3 2(х – 2).
х + х – 2 + 3 2(х – 2) = 37;
2х – 2 + 1,5х – 3 = 37;
3,5х – 5 = 37; 3,5х = 42; х = 12 (см) – АС.
2) 12 – 2 = 10 (см) – АВ. 3) 37 – (12 + 10) = 37 – 22 = 15 (см) – ВС.
1. АВ – А. 10 см; 2. ВС – В. 15 см; 3. СА – Б. 12 см.



Вершини: М; N і K; Сторони: MN; NK і MK; Кути трикутника: ∠M; ∠N; ∠K.










shkola.in.ua

6.

1) 12 + 3 = 15 (см) бічна сторона трикутника;
2) P = 2 ∙ 15 + 12 = 42 (см).
Відповідь: 42 см.
7.
shkola.in.ua


1) AC = BD; DC = AD; CD спільна сторона трикутників ACD і BDC. Тому ∆ACD = ∆BDC (за третьою ознакою). 2) Звідси отримаємо, що ∠BCD = ∠ADC, що й треба
shkola.in.ua


Нехай AB = х см, тоді BC = 2х см і AC = (х + 3) см.
Складемо рівняння:
x + 2x + x + 3 = 23;
4х = 23 – 3;
4х = 20; х = 5.
Отже, AB = 5 см; BC = 2 ∙ 5 = 10 (см); AC = 5 + 3 = 8 (см).
Відповідь: 5 см; 10 см; 8 см. 9.


10.

shkola.in.ua


1) MP = 8 дм; P∆МКР = KM + KP + PM;
P∆МКР = 24 (дм), тому KM + KP= 24 – 8 = 16 (дм).
2) Оскільки ∆KML рівнобедрений з основою KL, тo KM = ML.
3) MP – медіана ∆KML, тому KP = PL.
4) P∆KML = KM + ML + KL = 2KM + 2KP = 2(KM + KP) = 2 ∙ 16 = 32 (дм).
Відповідь: 32 дм.
1) Оскільки ∆ANB = ∆AMB, то AN = AM і ∠NAB = ∠MAB.
2) AC спільна сторона трикутників ANC і AMC. ∆ANC = ∆AMC (за першою ознакою).
3) Звідси отримаємо, що NC = MC, що й треба було довести.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

За умовою 3х – х = 10; 2х = 10; х = 5 (см).
P∆MКL = 3 ∙ 5 = 15 (см).

Оскільки ∆MKL = ∆KLM, то ∠M = ∠K і ∠K = ∠L. Тому ∠M = ∠K = ∠L.
Тобто трикутник MKL
рівносторонній.
Позначимо MK = KL = ML = х (см).
Тоді P∆MКL = 3х.
Відповідь: 15 см. § 17. Сума кутів трикутника
417.
Сума кутів будь-якого трикутника
∠P + ∠L + ∠K = 180°
418.
1) Ні, бо 30° + 60° + 70° = 160°, а сума кутів трикутника дорівнює 180°.
2) Так, оскільки 70° + 40° + 70° = 180°.
419.
1) Ні, оскільки 50° + 70° + 80° = 200° ≠ 180°.
2) Так, оскільки 30° + 60° + 90° = 180°.
420.
Нехай ∠A невідомий кут трикутника.
1) ∠A = 180° - (43° + 54°) = 180° - 97° = 83°.
2) ∠A = 180° - (9° + 93°) = 180° - 102° = 78°.
3) ∠A = 180° - (83° + 89°) = 180° - 172° = 8°. 421.
Нехай ∠3 невідомий кут трикутника.
1) ∠3 = 180° - (15° + 38°) = 180° - 53° = 127°.
2) ∠3 = 180° - (28° + 105°) = 180° - 133° = 47°.
3) ∠3 = 180° - (7° + 91°) = 180° - 98° = 82°.
422.
1) якщо один з кутів трикутника
∠3 = 180° - 126° = 54°. 424.
∠A + ∠B + ∠C = 180°,
∠C = 180° - (∠A + ∠B) = 180° - 58° = 122°. 425.
Нехай ∠1 = 62°. ∠1 + ∠2 + ∠3 = 180°.
Звідси ∠2 + ∠3 = 180° - ∠1 = 180° - 62° = 118°.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

427.



428.
shkola.in.ua

429.
Нехай в ΔABC AB = BC.
За властивістю кутів рівнобедреного трикутника ∠BAC = ∠BCA. AB = AC, тоді ∠ABC = ∠ACB. Отже, маємо ∠BAC = ∠BCA = ∠ABC. Оскільки сума кутів трикутника дорівнює 180°, то ∠BAC = ∠BCA = ∠ABC = 180° : 3 = 60°.
Відповідь: 60°.
Нехай ΔABC рівнобедрений, AC = AB, ∠ACB = ∠ABC = 70°. Оскільки сума кутів трикутника дорівнює 180°, маємо: ∠CAB = 180° - (∠ACB + ∠ABC) = 180° - (70° + 70°) = 180° - 140° = 40°.
Відповідь: 40°.
Нехай ΔABC рівнобедрений, AC = AB, ∠ACB = ∠ABC = 45°.

∠CAB = 180° - (∠ACB + ∠ABC) = 180° - (45° + 45°) = 180° - 90° = 90°.
Відповідь: 90°.
shkola.in.ua

430.

Нехай ΔABC рівнобедрений, AC = AB, ∠CAB = 80°.
∠ACB = ∠ABC
∠CAB + ∠ACB + ∠ABC = 180°,
∠ACB + ∠ABC = 180° - 80° = 100°.
Отже, ∠ACB = ∠ABC = 100° : 2 = 50°.
Відповідь: 50°.
shkola.in.ua


431.

shkola.in.ua
Нехай ΔABC рівнобедрений, AC = AB, ∠CAB = 50°.
∠ACB = ∠ABC
∠CAB + ∠ACB + ∠ABC = 180°, ∠ACB + ∠ABC = 180° - 50° = 130°.
Отже, ∠ACB = ∠ABC = 130° : 2 = 65°.
Відповідь: 65°.


Мал. 1 ∠ABC = 70° (як
70°).
∠CAB = 180° - (∠ACB + ∠ABC) = 180°(80° + 70°) = 180° - 150° = 30°.
Мал. 2. ∠BCA = 180° - 135° = 45° (як суміжний кут
135°).
∠ABC = 180° - (∠BAC + ∠BCA) = 180°(75° + 45°) = 180° - 120° = 60°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

433.
shkola.in.ua

Мал. 1. ∠LMN = 50° (як вертикальний
кутом, рівним 50°).
∠LNM = 180° - (∠MLN + ∠LMN) = 180° - (70° + 50°) = 60°.
Мал. 2. ∠NML = 180° - 140° = 40° (як суміжний
кут з кутом, рівним 140°).
∠MNL = 180° - (∠MLN + ∠NML) = 180° - (50° + 40°) = 180° - 90° = 90°.
shkola.in.ua

У ΔABC ∠A = 50°, ∠B = 70°.

434.
shkola.in.ua
∠C = 180° - (∠A + ∠B) = 180° - (50° + 70°) = 180° - 120° = 60°.
Оскільки CP бісектриса
Відповідь: 30°.
C, то ∠ACP = ∠PCB = 60° : 2 = 30°.

У ΔABC ∠B = 65°, ∠ACP = 40°. Оскільки CP бісектриса кута C,

435.

то ∠ACB = 2∠ACP = 2 × 40° = 80°.
Отже, ∠A = 180° - (∠ABC + ∠ACP) = 180° - (65° + 80°) = 180° - 145° = 35°.
Відповідь: 35°.

436.

У трикутнику MNL ∠M + ∠N = 120°, ∠M + ∠L = 140°.
∠M + ∠N + ∠L = 180° як сума кутів трикутника.
∠L = 180° - (∠M + ∠N) = 180° - 120° = 60°,
∠M = 140° - ∠L = 140° - 60° = 80°,
∠N = 120° - ∠M = 120° - 80° = 40°.
Відповідь: 60°, 80°, 40°.
У ΔABC ∠A + ∠B = 100°, ∠A + ∠C = 130°.
∠A + ∠B + ∠C = 180° як сума кутів трикутника.
∠C = 180° - (∠A + ∠B) = 180° - 100° = 80°,
∠A = 130° - ∠C = 130° - 80° = 50°,
∠B = 100° - ∠A = 100° - 50° = 50°.
Відповідь: 80°, 50°, 50°. 437.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
438.
180°, що суперечить теоремі
є кут, не більший за 60°.
439.
Введемо коефіцієнт пропорційності х, тоді ∠A = 3x, ∠B = 4x, ∠C = 5x.
∠A + ∠B + ∠C = 180° (за теоремою про суму кутів трикутника).
Складемо рівняння: 3x + 4x + 5x = 180°; 12x = 180°; x = 15°.
Отже, ∠A = 3 × 15° = 45°, ∠B = 4 × 15° = 60°, ∠C = 5 × 15° = 75°.
Відповідь: 45°, 60°, 75°.
440.
Введемо коефіцієнт пропорційності х, тоді кути трикутника дорівнюють 2х, 3х, 5х.
Складемо рівняння: 2х + 3х + 5х = 180° (за теоремою про суму кутів трикутника).
10х = 180°; х = 18°.
Отже, кути трикутника дорівнюють: 2 × 18° = 36°, 3 × 18° = 54°, 5 × 18° = 90°.
Відповідь: 36°, 54°, 90°. 441.
shkola.in.ua


Нехай ΔKLM рівнобедрений, ∠L = x, тоді ∠K = ∠M = x + 15°.
Складемо рівняння: x + (x + 15°) + (x + 15°) = 180° (за теоремою
суму кутів трикутника). 3x + 30° = 180°; 3x = 150°; x = 50°.
Отже, ∠L = 50°, ∠K = ∠M = 50° + 15° = 65°.
Відповідь: 50°, 65°, 65°. 442.
shkola.in.ua

Нехай ΔKLM рівнобедрений, ∠K = ∠M = x, тоді ∠L = x + 24°. Складемо рівняння: x + x + (x + 24°) = 180° (за теоремою про суму кутів трикутника). 3x + 24° = 180°; 3x = 156°; x = 52°. Отже, ∠K = ∠M = 52°, ∠L = 52° + 24° = 76°. Відповідь: 52°, 52°, 76°. 443.

Припустимо, що кути в основі

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


shkola.in.ua

shkola.in.ua


Відповідь:
446.
shkola.in.ua


1) Нехай ∠C = х, тоді ∠В = х + 14°. Маємо рівняння:
80° + х + х + 14° = 180°;
2х = 180° – 94°;
2х = 86°;
х = 86° : 2;
х = 43°.
Отже, ∠С = 43°; ∠В = 43° + 14° = 57°.
2) Нехай ∠B = х, тоді ∠C = 3х. Маємо рівняння:
80° + х + 3х = 180°;
х + 3х = 180° – 80°;
4х = 100°;
х = 25°;
Отже, ∠B = 25°; ∠C = 3 × 25° = 75°.
3) ∠В ∠С = 2 3. Введемо
∠В = 2х, ∠С = 3х:
80° + 2х + 3х = 180°;
2х + 3х = 180° – 80°;
5х = 100°; х = 20°;
20° ∙ 2 = 40° – ∠В; 20° ∙ 3 = 60° – ∠С
75° 57° 60° 57° 25° 43°
За теоремою про суму кутів трикутника маємо: x + 2x + 36° = 180°; 3x = 144°; x = 48.
Отже, один з кутів дорівнює 48°, другий – 48° × 2 = 96°. Відповідь: 48°, 96°. 447.

shkola.in.ua


Розглянемо ΔAOB і ΔDOC.
∠AOB = ∠DOC (як вертикальні кути).
∠A = 180° - (∠B + ∠AOB),
∠D = 180° - (∠C + ∠DOC).
Оскільки ∠B = ∠C і ∠AOB = ∠DOC, то ∠A = ∠D.
ΔAOB = ΔDOC
448.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

449.

BC = B1C1, ∠A = ∠A1, ∠B = ∠B1.
У ΔABC: ∠C = 180° - (∠A + ∠B).
У ΔA1B1C1: ∠C1 = 180° - (∠A1 + ∠B1).
Оскільки ∠A = ∠A1 і ∠B = ∠B1, то ∠C = ∠C1.
Отже, ΔABC = ΔA1B1C1 за другою ознакою рівності трикутників (BC = B1C1, ∠B = ∠B1 - за умовою, ∠C = ∠C1 - за розв'язанням).


Нехай у ΔABC ∠A = 46°, ∠C = 64°, AP бісектриса ∠A, СК бісектриса ∠C. Розглянемо ΔAOC.
Оскільки AP бісектриса ∠A, то ∠OAC = 46° 2 = 23°.
Оскільки СК бісектриса ∠C, то ∠OCA = 64° 2 = 32°.
Отже, за теоремою про суму кутів трикутника маємо: ∠AOC + ∠OAC + ∠OCA = 180°.
Звідси ∠AOC = 180° - (∠OAC + ∠OCA) = 180° - (23° + 32°) = 180° - 55° = 125°.
Оскільки кут між прямими не перевищує 90°, то кутом
бісектриси кутів A і C, буде кут, суміжний з кутом AOC.
Отже, цей кут дорівнює 180° - 125° = 55°.
Відповідь: 55°.
450.
shkola.in.ua


Нехай у ΔABC ∠A = 70°, ∠B = 80°. BM ⊥ AC, AK ⊥ BC.
У ΔABM: ∠A = 70°, ∠BMA = 90° (оскільки BM висота).
∠A + ∠ABM + ∠BMA = 180° (за теоремою про суму кутів трикутника). Звідси ∠ABM = 180° - (∠A + ∠BMA) = 180° - (40° + 90°) = 180° - 160° = 20°.
З ΔABK: ∠B = 80°, ∠AKB = 90° (оскільки AK ⊥ BC).
За теоремою про суму кутів трикутника маємо: ∠BAK + ∠B + ∠AKB = 180°.
Звідси ∠BAK = 180° - (∠B + ∠AKB) = 180° - (80° + 90°) = 180° - 170° = 10°.
Розглянемо ΔAOB. ∠BAK + ∠ABM + ∠BOA = 180°.
Звідси ∠BOA = 180° - (∠BAK + ∠ABM) = 180° - (10° + 20°) = 180° - 30° = 150°.
Оскільки кут між прямими не перевищує
30°.
451. 1)

AOM = 180° - 150° = 30°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
452.
1) I
Відповідь: 28°, 76°, 76°.
II випадок. Нехай кут 28°
кут в основі дорівнює 28°, оскільки кути в основі рівнобедреного трикутника рівні.
Отже, кут у вершині рівнобедреного трикутника дорівнює 180° - (28° +
= 124°.
Відповідь: 28°, 28°, 124°.
2) Один з кутів рівнобедреного трикутника дорівнює 106°.
Це може бути тільки кут у вершині трикутника. Тоді сума кутів в основі дорівнює 180° - 106° = 74°, а кожен з кутів дорівнює 74° : 2 = 37° (оскільки кути в основі
рівнобедреного трикутника рівні між собою).
Відповідь: 106°, 37°, 37°. 453.
shkola.in.ua

ABC = 1 2 ∠EBA. Отже, ∠BAC + ∠ABC = 1 2 ∠DAB + 1 2
Нехай a∥b, c січна. ∠DAB і ∠EBA внутрішні односторонні кути, AC бісектриса кута DAB, BC бісектриса кута ABE. ∠DAB + ∠EBA = 180° (за властивістю внутрішніх односторонніх кутів). Оскільки АС бісектриса ∠DAB, то ∠BAC = 1 2 ∠DAB. Оскільки
DAB +
EBA) = 1 2 × 180° = 90°. З ΔABC: ∠BAC + ∠ABC + ∠BCA = 180° (за
∠BCA = 180° - (∠BAC + ∠ABC) = 180° - 90° = 90°.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
+ 15°) + (x + 15°) = 180°; 3x + 30° = 180°; 3x = 150°; x = 50°.
Відповідь: 50°, 65°, 65°. II випадок.
x + 15°. За теоремою
+ x + x + 15° = 180°; 3x = 165°; x = 55°. Отже, кожен
дорівнює 55° + 15° = 70°.
Відповідь: 55°, 55°, 70°. 456.


Нехай ΔKLM рівнобедрений. ∠K = ∠M = 72°, KP бісектриса
∠K, KP = 5 см.
Оскільки KP — бісектриса, ∠LKP = ∠PKM = 72° : 2 = 36°.
Розглянемо ΔKPM.
трикутника).
Звідси ∠KPM = 180° - (∠PKM + ∠LMK) = 180° - (36° + 72°) = 180° - 108° = 72°.
Отже,
KM = KP = 5 см.
457.

458.









https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


ΔABC = ΔABD, оскільки AB = AC = CB, AB = AD = DB. У рівних трикутників
рівні, тобто ∠CAB = ∠DAB = 60° (як кути рівностороннього трикутника). ΔCAD рівнобедрений. AO бісектриса, проведена з
висотою, тобто AO ⊥ CD, O ∈ AB, отже, AB ⊥ CD. 461.
1. 1) 20 ∙ 6 = 120 (м2) – площа клумби; 2) 120 ∙ 60 = 7200 (шт.) – цибулин
.
2. 1) 28 ∙ 0,85 = 23,8 (грн) – ціна упаковки зі знижкою; 2) 7200 : 3 = 2400 (шт.) – стільки потрібно упаковок цибулин;
3) 2400 ∙ 23,8 = 57120 (грн) – потрібно заплатити за тюльпани.
Відповідь: 1) 23,8 грн; 2) 57120 грн. 462.








466.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

468.










shkola.in.ua
474.

475.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Нехай ΔABC
вершині В.


KBC = ∠BAC + ∠BCA (згідно з теоремою 1).
Отже, ∠BAC + ∠BCA = 100° ,
BAC = ∠BCA = 50° (оскільки кути при основі рівнобедреного трикутника рівні).
Відповідь: 50°.
Нехай ΔMNK рівнобедрений. ∠M = ∠K = 55° . ∠DNK зовнішній

476.
N. За властивістю зовнішнього кута маємо:
∠DNK = ∠M + ∠K = 55° + 55° = 110° .
Відповідь: 110°.

Нехай ∠CAP = 105° (зовнішній кут

477.
shkola.in.ua
вершині A), ∠C = 45° . ∠CAP = ∠B + ∠C за властивістю зовнішнього кута трикутника. Звідси ∠B = ∠CAP - ∠C = 105° - 45° = 60° .
Відповідь: 60°.


478.



Нехай ∠BCD зовнішній кут при вершині C, ∠A = 18° , ∠BCD = 120°
∠BCD = ∠A + ∠B (за властивістю зовнішнього кута трикутника).
Звідси ∠B = ∠BCD - ∠A = 120° - 18° = 102° Відповідь: 102°.
Нехай ΔABC даний трикутник, ∠A = 45° , ∠C = 70° .
∠PBC = ∠A + ∠C = 45° + 70° = 115° (за властивістю зовнішнього кута трикутника).
∠BCM = 180° - ∠C = 180° - 70° = 110° (як кут суміжний з кутом C).
∠NAP = 180° - ∠A = 180° - 45° = 135° (як кут суміжний з
A).
Відповідь: 115°, 110°, 135°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


Нехай ΔKLM даний трикутник, ∠NKL = 110° , ∠LMP = 140° .
∠NKL + ∠LKM = 180° (як суміжні кути).
Звідси ∠LKM = 180° - 110° = 70° .
∠LMP + ∠LMK = 180° (як суміжні кути).
Звідси ∠LMK = 180° - 140° = 40° .
∠L + ∠LKM + ∠LMK = 180° (як сума кутів трикутника).
Звідси ∠L = 180° - (70° + 40°) = 180° - 110° = 70° .
Відповідь: 70°, 70°, 40°. 480.


481.


shkola.in.ua

shkola.in.ua


1) Нехай ΔABC даний трикутник, ∠BAD = 140° .
Нехай ∠B = x, тоді ∠C = x + 30°.
За властивістю зовнішнього кута трикутника:
∠BAD = ∠B + ∠C.
Складемо рівняння:
x + x + 30° = 140°;
2x = 110°;
x = 55°
Отже, ∠B = 55° , ∠C = 55° + 30° = 85° .
Відповідь: 55°, 85°.
2) Нехай ΔABC даний трикутник, ∠BAD = 140° , ∠B = x, тоді ∠C = 4x. За властивістю зовнішнього
кута трикутника маємо: ∠BAD = ∠B + ∠C.
Складемо рівняння:
x + 4x = 140°;
5x = 140°;
x = 28° .
Отже, ∠B = 28° , ∠C = 28° × 4 = 112° .
Відповідь: 28°, 112°.
ПРАПОР
1) Нехай ΔABC даний трикутник, ∠BCD = 120° , ∠B = x, тоді ∠A = x + 20°. За властивістю
зовнішнього кута трикутника маємо:
∠BCD = ∠A + ∠B.
Складемо рівняння: x + x + 20° = 120°; 2x = 100°; x = 50° .
Отже, ∠B = 50° , ∠A = 50° + 20° = 70° .
Відповідь: 50°, 70°.
2) Нехай ΔABC даний трикутник, ∠A = x, ∠B = 3x. За властивістю зовнішнього кута трикутника маємо:
∠BCD = ∠A + ∠B.
Складемо рівняння: x + 3x = 120°; 4x = 120°; x = 30° .
Отже, ∠A = 30° , ∠B = 3 × 30° = 90° .
Відповідь: 30°, 90°.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html




I випадок. Нехай ΔABC
(AB = BC), ∠A = ∠C. За властивістю
трикутника:
∠DBC = ∠A + ∠C = 118° ,
∠A = ∠C = 118° : 2 = 59° .
∠ABC = 180° - ∠DBC = 180° - 118° = 62° .
Відповідь: 62°, 59°, 59°.
II випадок. Нехай ΔABC даний рівнобедрений трикутник (BA = BC). ∠DAB і ∠BAC суміжні, їх сума дорівнює 180°.
∠BAC = 180° - 118° = 62°.
Оскільки ∠BAC = ∠BCA (як кути при основі рівнобедреного
трикутника), то ∠BCA = 62° .
∠A + ∠B + ∠C = 180° , ∠B = 180° - (∠A + ∠C) = 180° - 124° = 56° .
Відповідь: 62°, 62°, 56°. 483.


вершині.
Нехай ΔABC даний рівнобедрений трикутник (AB = BC).
∠A = ∠C (як кути
∠BDC = ∠A + ∠C за властивістю зовнішнього
42° = ∠A + ∠C, звідси ∠A = ∠C = 42° : 2 = 21° ∠B = 180° - 42° = 138° . Відповідь: 21°, 21°, 138°. II випадок. Зовнішній кут при основі. Цей випадок неможливий,
у трикутнику можливий тільки один тупий кут. 484.



Нехай ΔKNL даний трикутник.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


: ∠NLK = ∠K + ∠M = 7x + 9x = 16x.
∠PKL = ∠L + ∠M = 8x + 9x = 17x.
∠OMK = ∠K + ∠L = 7x + 8x = 15x. Отже, відношення
кутів 17 : 16 : 15.
Відповідь: 17 : 16 : 15. 487.


Нехай ΔPLK даний трикутник. ∠PKL і ∠LKR суміжні. KM бісектриса кута LKP. ∠PKM = ∠LKM. KN бісектриса ∠LKR, ∠LKN = ∠NKR. ∠PKL + ∠LKR = 180° , ∠PKM + ∠LKM + ∠LKN + ∠NKR = 180° , 2∠LKM + 2∠LKN = 180° , 2(∠LKM + ∠LKN) = 180° , ∠LKM + ∠LKN = 90° . Отже, KM ⊥ KN. 488.


Нехай ОК промінь, що проходить між сторонами ∠AOB, ∠AOK = x, ∠KOB = 90° - x. ∠KOB - ∠AOK = (90° - x) - x = 90° - 2x.
∠AOK + ∠KOB = 90° , 1 3(∠AOK + ∠KOB) = 30° .
Отже, 90° - 2x = 30°, 2x = 60°, x = 30°.
∠AOK = 30° , ∠KOB = 90° - 30° = 60° .
Відповідь: 30°, 60°. 489.


Нехай AB = 22,8 см, AC = x см, CD = 2x см, DB = (2x + 1,8) см.
Маємо рівняння: x + 2x + 2x + 1,8 = 22,8; 5x = 21; x = 4,2.
Отже, AC = 4,2 см, CD = 8,4 см, DB = 10,2 см.
Відповідь: 4,2 см, 8,4 см, 10,2 см. 490.
1. 1) 2 ∙ (32 + 18) = 100 (м) – периметр прямокутної ділянки; 2) 32 ∙ 18 = 576 (м2) – площа ділянок; 3) S□ = a2; a2 = 576 = 24 ∙ 24 ⇒ a = 24 (м) – сторона квадратної ділянки; 4) 24 ∙ 4 = 96 (м) – периметр квадратної ділянки. 100 м > 97 м; 96 м < 97 м.
Відповідь: садівник
2. 1) 100 + 96 = 196 (м) – всього потрібно паркану;
2) 196 – 97 = 99 (м) – потрібно докупити.
Відповідь: 99 м. 491.



АВ = 6 см, ВС = 3 см.
АВ : ВС = 6 : 3 = 2 (рази) Відповідь: сторона ВС у 2
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html





1) Прямокутний; MK – гіпотенуза, NK та MN – катети;
сторона MK.


1) PF гіпотенуза, PL і LF катети.
2) PF довша за PL, PF довша за LF, оскільки PF гіпотенуза.






На мал. 1 трикутники
катетами.
Оскільки AC = ML, CB = LP, то ΔACB = ΔMLP.
На мал. 2 трикутники рівні за катетом і прилеглим
Оскільки NF = DK, ∠N = ∠D, то ΔNFE = ΔDKO.
На мал. 1 трикутники
Оскільки CM = BA, ∠C = ∠B, то ΔCMK = ΔBAP. На мал. 2 трикутники рівні
. Оскільки EF = LN, DF = QN, то ΔEDF = ΔLQN.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

499.
shkola.in.ua

shkola.in.ua

500.
shkola.in.ua

shkola.in.ua

501.
shkola.in.ua

1) Нехай ∠B = 18°, тоді
∠C = 90° - ∠B = 90° - 18° = 72°.
2) Якщо ∠L = 87°, тоді
∠M = 90° - 87° = 3°.
Відповідь: 1) 72°; 2) 3°.
1) Нехай ∠M = 75°, тоді ∠L = 90° - ∠M = 90° - 75° = 15°
2) Нехай ∠R = 23°, тоді ∠P = 90° - ∠R = 90° - 23° = 67°.
Відповідь: 1) 15°; 2) 67°.
Нехай ΔABC прямокутний і рівнобедрений (∠B = 90° , BA = BC).
∠A = ∠C як кути в основі рівнобедреного
прямокутного трикутника дорівнює 90° і вони рівні, то ∠A = ∠C = 90° : 2 = 45° . Відповідь: 90°, 45°, 45°.


Нехай ΔABC рівнобедрений, AB = BC,
трикутника дорівнює 180°, маємо: ∠A + ∠B + ∠C = 180° , ∠B = 180° - (∠A + ∠C) = 180°90° = 90° . Отже, ΔABC прямокутний.
502. 1) Згідно з властивістю 3, катет


Отже, BC = 1 2 AB = 1 2 × 14 = 7 (см).
2) AB = 2BC = 2 × 5 = 10 (дм).
Відповідь: 1) 7 см; 2) 10 дм. 503.

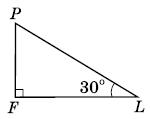

1) PF = 1 2 PL = 1 2 × 12 = 6 (дм); 2) PL = 2PF = 2 × 4 = 8 (см).
Відповідь: 1) 6 дм; 2) 8 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

505.


506.
Нехай ΔABC даний трикутник, ∠ABK = 36° , ∠KBC = 64° .
∠ABC = ∠ABK + ∠KBC = 36° + 64° = 100°.
З
прямокутного ΔABK маємо:
∠BAK = 90° - ∠ABK = 90° - 36° = 54° .
З
прямокутного ΔCBK маємо:
∠BCK = 90° - ∠KBC = 90° - 64° = 26° .
Відповідь: 100°, 54°, 26°.
Нехай ΔKLM рівнобедрений, LK = LM. Оскільки LN медіана рівнобедреного трикутника, то LN бісектриса і висота ΔKLM. ∠KLM
= 2∠KLN = 2 × 31° = 62° .
Оскільки сума кутів трикутника дорівнює 180°, то
∠K + ∠M + ∠L = 180° ,
∠K + ∠M = 180° - ∠L = 180° - 62° = 118°.
∠K = ∠M як кути в основі рівнобедреного трикутника.
∠K = ∠M = 118° : 2 = 59° .
Відповідь: 62°, 59°, 59°.

shkola.in.ua
507.

508.
кутом.
shkola.in.ua
катет. Отже, ΔMPK = ΔMLK за
shkola.in.ua


shkola.in.ua



1) Нехай в прямокутному ΔABC ∠B = x°, тоді ∠A = x° + 28°. Оскільки
то маємо рівняння: x + x + 28° = 90°; 2x = 90° - 28° = 62°; x = 62° : 2 = 31°.
Отже, ∠B = 31°, ∠A = 31° + 28° = 59°.
Відповідь: 31°, 59°.
2) Нехай в прямокутному ΔABC ∠A = x° , ∠B = 5x° . Оскільки сума
то маємо: x + 5x = 90°; 6x = 90°; x = 15°.
Отже, ∠A = 15° , ∠B = 15° × 5 = 75°
Відповідь: 15°, 75°.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


то маємо: 2x + 3x = 90°; 5x = 90°; x = 18°.
Отже, ∠A = 2 × 18° = 36° , ∠B = 3 × 18° = 54° .
Відповідь: 36°, 54°.
Відповідь: українська поетеса Ліна Василівна Костенко.
509.


shkola.in.ua





1) Нехай в прямокутному ΔABC ∠A = x° , ∠B = 4x° . Оскільки в прямокутному трикутнику сума гострих
90° , то маємо: x + 4x = 90°; 5x = 90°; x = 18°.
Отже, ∠A = 18° , ∠B = 18° × 4 = 72° .
Відповідь: 18°, 72°.
2) Нехай в прямокутному
∠A = x, тоді ∠B = x + 16°
Оскільки в прямокутному трикутнику сума
90° , то маємо:
x + x + 16° = 90°; 2x = 74°; x = 37° .
Отже, ∠A = 37°, ∠B = 37° + 16° = 53° .
Відповідь: 37°, 53°.
3) Нехай в прямокутному ΔABC ∠B = 5x, ∠A = 4x.
Оскільки сума гострих
трикутника дорівнює 90° , то маємо:
5x + 4x = 90°; 9x = 90°; x = 10°
Отже, ∠B = 5 × 10° = 50° , ∠A = 4 × 10° = 40° .
Відповідь: 50°, 40°.
Нехай в прямокутному ΔKNM (∠M = 90°) MP бісектриса, ∠KMP = ∠NMP = 90° : 2 = 45° , ∠K = 26° . 3 ΔKMP: ∠KPM = 180° - (∠K + ∠KMP) = 180° - (26° + 45°) = 109° .
∠MPK = 180° - ∠KPM = 180° - 109° = 71° .
дорівнює 71°. Відповідь: 71°.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
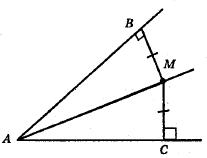
shkola.in.ua
513.

Нехай т. М розміщена всередині кута BAC, MB ⊥ AB, MC ⊥
AC, BM = CM. Доведемо, що точка М належить бісектрисі
A, тобто ∠BAM = ∠CAM.
ΔABM = ΔACM за гіпотенузою і катетом (AM спільна гіпотенуза, BM = CM), тоді ∠BAM = ∠CAM.

514.



Нехай в прямокутному ΔABC (∠B = 90°) BD ⊥ AC, ∠DBC = 32° .
З ΔBDC: ∠C = 90° - ∠DBC = 90° - 32° = 58° (оскільки сума гострих кутів прямокутного трикутника дорівнює 90°).
∠A + ∠C = 90° , ∠A = 90° - ∠C = 90° - 58° = 32° .
Відповідь: 58°, 32°.
Нехай ΔABC прямокутний (∠C = 90°).
CM і BN бісектриси, ∠BCM = ∠ACM = 90° : 2 = 45° ,
∠CBN = ∠ABN, ∠COB = 115°
З ΔCOB за теоремою
∠OBC + ∠COB + ∠BCO = 180° .
Звідси ∠OBC = 180° - 115° - 45° = 20°
Тоді ∠B = 2∠OBC = 2 × 20° = 40° .
З ΔABC: ∠A = 90° - ∠B = 90° - 40° = 50°.
Відповідь: 40°, 50°. 515.
:




shkola.in.ua


Нехай ΔABC рівнобедрений, AB = BC, ΔA1B1C1 рівнобедрений, A1B1 = B1C1, BK ⊥ AC, B1K1 ⊥ A1C1.
ΔABK = ΔA1B1K1 (за гіпотенузою AB = A1B1 і катетом BK = B1K1).
З рівності трикутників маємо ∠A = ∠A1, AK = A1K1.
Оскільки висота рівнобедреного трикутника є медіаною, то AK = KC, A1K1 = K1C1.
Враховуючи, що AK = A1K1, маємо AC = A1C1.
Отже, ΔABC = ΔA1B1C1 за двома сторонами і кутом між ними (AB = A1B1 за умовою, ∠A = ∠A1, AC = A1C1 за доведенням).
Нехай ΔABC прямокутний (∠C = 90°), ∠B = 60°, AB + CB = 30 см, СК медіана. ∠A = 90° - 60° = 30° (оскільки сума
90°). Нехай BC = x, тоді AB = 2x (оскільки катет прямокутного трикутника, що лежить проти кута 30°,
гіпотенузи). Складемо рівняння: x + 2x = 30; 3x = 30; x = 10, тоді 2x = 2 × 10 = 20. Отже, AB = 20 см. Оскільки СК медіана, проведена до гіпотенузи, то CK = 1 2 AB = 1 2 × 20 = 10 (см).
Відповідь: 20 см, 10 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


518.
Нехай ΔKMN прямокутний, ∠N = 90° , ∠M = 60°, MP = 4 см.
З ΔKMN: ∠K = 90° - ∠M = 30° . Оскільки MP бісектриса, то ∠KMP = ∠PMN = 60° : 2 = 30° . Отже, ΔPKM рівнобедрений, оскільки ∠K = ∠KMP, звідси PK = MP = 4 (см).
З ΔPMN: ∠PMN = 30° . Отже, PN = 1 2 MP = 1 2 × 4 = 2 (см).
KN = PK + PN = 4 + 2 = 6 (см).
Відповідь: 6 см.


519.


520.
Нехай у прямокутному трикутнику ABC (∠C = 90°), ∠PAB і
∠ABK - зовнішні кути при вершинах гострих кутів.
Нехай ∠PAB = x° , тоді ∠ABK = x° + 20°
∠CAB + ∠PAB = 180° (як суміжні кути), звідси
∠CAB = 180° - ∠PAB = 180° - x°
∠ABC + ∠ABK = 180° (як суміжні кути), звідси
∠ABC = 180° - ∠ABK = 180° - (x° + 20°) = 160° - x° Оскільки сума
90°, маємо рівняння: 180° - х + 160° - х = 90°; 2x = 250°; x = 125° .
Отже, ∠CAB = 180° - 125° = 55° , ∠ABC = 160 - 125° = 35° .
Відповідь: 55°, 35°.
Нехай у прямокутному ΔKLM (∠M = 90°) ∠NKL і ∠KLP
зовнішні кути, ∠NKL = 2x° , ∠KLP = 3x° .
∠MKL = 180° - 2x°, ∠KLM = 180° - 3x° (за властивістю суміжних кутів).
∠MKL + ∠KLM = 90°;
Отже, 180° - 2x + 180° - 3x = 90°; 5x = 270°; x = 54° .
Отже, ∠MKL = 180° - 2 × 54° = 180° - 108° = 72° ,
∠KLM = 180° - 3 × 54° = 180° - 162° = 18°
Відповідь: 72°, 18°.


Нехай CM - медіана, PΔACM = PΔCMB. Оскільки PΔACM = AC + CM + AM,
PΔCMB = BC + CM + MB і ці
рівні, то AC + CM + AM = BC + CM + MB.
Звідси AC + AM = BC + MB. Враховуючи, що AM = MB, матимемо AC = BC.
Отже, у трикутника ABC хоча
521. Нехай в ΔABC ∠A = x° , ∠B = x° + 20°, ∠C = 3x°



теоремою про
трикутника
: x + x + 20° + 3x = 180°; 5x = 160°; x = 32° . Отже, ∠A = 32° , ∠B = 32° + 20° = 52° , ∠C = 3 × 32° = 96° . Відповідь: 32°, 52°, 96°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


Нехай у ∆ABC AB = BC = x см, тоді AC = (x + 3) см. За умовою задачі маємо: x + 3 + 4 = x + x; x + 7 = 2x; x = 7.
Отже, AB = BC = 7 см, AC = 7 + 3 = 10 (см).
PΔABC = AB + BC + AC = 7 + 7 + 10 = 24 (см).
Відповідь: 24 см. 523.
1) 3,5 × 5,5 = 19,25 ≈ 20 (м2) – площа кімнати.
2) 130 × 20 = 2600 (грн) – потрібно заплатити за лінолеум.
Відповідь: 2600 грн. 524.



shkola.in.ua shkola.in.ua

АВ = 89 мм; ВС = 48 мм; АС = 66 мм.
(АВ + ВС) = 89 + 48 = 137 мм > АС = 66 мм; (AB + AC) = 89 + 66 = 155 мм > ВС = 48 мм; (AC + BC) = 66 + 48 = 114 мм > АВ = 89 мм.
Висновок: сума довжин двох сторін трикутника
525. § 20. Нерівність трикутника 526.
1) Трикутник зі сторонами 1 см, 2 см і 4 см не
4 см > 1 см + 2 см. 2) Трикутник зі сторонами 7 дм, 6 дм, 5 дм існує, бо
+

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
528.
Нехай невідома сторона трикутника дорівнює а см.
Тоді 8,4 - 2,8 < a < 8,4 + 2,8, тобто 5,6 < a < 11,2.
Оскільки а найбільше ціле число, що задовольняє умові 5,6 < a < 11,2, то a = 11 см.
Відповідь: 11 см.
529.
Нехай невідома сторона трикутника дорівнює а см.
Тоді 4,3 - 2,7 < a < 4,3 + 2,7, тобто 1,6 < a < 7.
Оскільки а - найменше ціле число, що задовольняє умові 1,6 < a < 7, то a = 2 см.
Відповідь: 2 см.
530.
1) Нехай сторони трикутника дорівнюють 2m, 3m і 4m.
Сторони трикутника можуть бути пропорційні числам 2, 3, 4, оскільки 4m < 3m + 2m, тобто виконується нерівність трикутника.
2) Нехай сторони трикутника дорівнюють 7m, 8m, 15m.
Сторони трикутника не можуть бути пропорційні числам 7, 8 і 15, оскільки 15m = 7m + 8m, тобто не виконується нерівність трикутника.
3) Нехай сторони трикутника дорівнюють 5m, 3m, 7m.
Сторони трикутника можуть бути пропорційні числам 5, 3 і 7, оскільки 7m < 5m + 3m, тобто виконується нерівність трикутника.
531.
1) Сторони трикутника не можуть бути пропорційні
трикутника.
2)
3)
трикутника 11m > 8m + 2m, де 8m, 2m, 11m
сторін трикутника. 532.
3 см, а основа дорівнює PΔ - (3 + 3) = 12 - 6 = 6 (см).
зі сторонами 3 см, 3 см
оскільки 6 см = 3 см + 3 см. Відповідь: ні, не може. 533.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Якщо a = 2, то PΔ = 2,5 + 1,2 + 2 = 5,7 (см). Якщо a = 3, то PΔ = 2,5 + 1,2 + 3 = 6,7 (см).
Відповідь: 5,7 см або 6,7 см. 535.
1) Якщо одна із сторін трикутника
30 см - 14 см = 16 см
2)
3) Одна із сторін трикутника не може
дорівнює 30 см - 16 см = 14 см і не виконується нерівність трикутника, бо 16 см > 14 см
(одна сторона більша суми двох інших).
536.
1) Одна із сторін трикутника не може дорівнювати 21 дм, бо сума двох інших сторін
дорівнює 40 дм - 21 дм = 19 дм і не виконується нерівність трикутника, бо 21 дм > 19 дм (одна сторона більша від суми двох інших).
2) Одна із сторін трикутника не може
40 дм - 20 дм = 20
3) Одна із сторін трикутника може дорівнювати 19 дм, бо
40 дм - 19 дм = 21
нерівність трикутника 19 дм < 21 дм (за умови, що ця сторона не менша
інших сторін). 537.
Припустимо, що такий трикутник існує. Тоді х см довжина однієї сторони, (х - 2) см
довжина другої сторони, (х + 4) см довжина третьої сторони. Складемо рівняння: x + (x - 2) + (x + 4) = 20; 3x + 2 = 20; 3x = 18; x = 6.
Отже, сторони трикутника дорівнюють: 6 см, 4 см, 10 см. Але трикутника з такими
сторонами не існує, бо не виконується нерівність трикутника 10 см = 6 см + 4 см.
Відповідь: ні. 538.
Припустимо, що такий трикутник існує. Нехай х см довжина однієї сторони, (х + 6) см довжина другої сторони, (х - 1) см
рівняння: x + (x + 6) + (x - 1) = 23; 3x + 5 = 23; 3x = 18; x = 6. Але трикутника зі сторонами 6 см, 12



shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

541.


shkola.in.ua
Нехай ∆ABC і ∆A1B1C1 - прямокутні.
AB = A1B1, BH ⊥ AC, B1H1 ⊥ A1C1, BH = B1H1.
∆ABH = ∆A1B1H1 (за катетом і гіпотенузою: AB = A1B1, BH = B1H1), тоді ∠A = ∠A1.
∆ABC = ∆A1B1C1 (за катетом і гострим кутом: AB = A1B1, ∠A = ∠A1).

542.

shkola.in.ua

543.

1) 360° : 32 = 11,25° = 11°15´ - становить 1 румб; 2) 11°15´ × 4 = 44°60´ = 45°
Відповідь: 4 румби становлять 45°.
1) AB = 50 мм; AB = 2OA = 2OB. 2) ∠AMB = 90°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
самостійна робота 4 (§§17-20) № 1 - 13
1.
Сума кутів трикутника дорівнює 180°, отже, кути 50°, 60°, 70° можуть бути кутами трикутника. Правильна відповідь В).
2.
shkola.in.ua

Проти більшого кута трикутника лежить
сторона. Правильна відповідь А). 3.

дорівнює 90° - 40° = 50°. Правильна відповідь В).
4.
5.

трикутника, оскільки 8 см > 2,7 см + 4,2 см.
Правильна відповідь Г).
7.
Оскільки другий кут прямокутного трикутника дорівнює 60°, то
проти кута 30° і дорівнює 8 см : 2 = 4 см.
Правильна відповідь Б).
8.



AOC,
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


Нехай в ∆ABC AB = BC, AK бісектриса, ∠KAC = 1 2 ∠BAC.
Нехай ∠KAC = x, тоді ∠A = 2x, ∠C = ∠A = 2x (як
основі рівнобедреного трикутника). Оскільки AK = AC, то ∆KAC рівнобедрений з основою KC. ∠K = ∠C (як кути при основі рівнобедреного трикутника), ∠K = 2x.
За властивістю суми
трикутника
x + 2x + 2x = 180°; 5x = 180°; x = 36°. Отже, ∠A = ∠C = 36° × 2 = 72° .
зовнішні кути трикутника дорівнюють 3x, 5x і 7x.
Оскільки сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°, маємо: 3x + 5x + 7x = 360°, 15x = 360°; x = 24°.
Отже, зовнішні кути дорівнюють 72°, 120°, 168°.
Тоді найменший з внутрішніх кутів трикутника дорівнює: 180° - 168° = 12°.
Правильна відповідь А).
12.


Нехай ∆АСВ прямокутний, ∠C = 90° , ∠B = 60°, CM медіана. ∠CAB = 30°, CB менший катет, CB = x см. AB = 2x (за властивістю катета, що лежить напроти кута 30°), CM = 1 2 AB = x (за властивістю медіани
Отже, CM + CB = 10 см, x + x = 10, 2x = 10. Отже, AB = 10 см. Правильна відповідь В). 13.





1. Оскільки CM – висота, то ∠CMB = 90°. Згідно теореми про суму кутів трикутника:
∠MCB = 180° – (∠CMB + ∠MBC) = 180° – (90° + 40°) = 50°.
2. Оскільки бісектриса CM ділить ∠С навпіл, то ∠MCB = 45°.
трикутника: ∠CMB = 180° – (∠MCB + ∠MBC) = 180° – (45° + 40°) = 85°.
3. ∠РBС = 1 2 ∠B = 1 2 × 40° = 20°. ∠MCB = 1 2 ∠С = 1 2 × 90° = 45°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html









https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


1) Нехай ∠A = x, тоді ∠B = 2x; ∠C = x − 16°.
2) Маємо x + 2x + x − 16° = 180°. 4x = 196°; x = 196° : 4; x = 49°.
3) Отже, ∠A = 49°; ∠B = 2 · 49° = 98°; ∠C = 49° 16° = 33°.
Відповідь: 49°; 98°; 33°.

shkola.in.ua

1) Нехай ∠KCB = 112° зовнішній кут
трикутника.
2) Оскільки ∠B : ∠A = 3 : 5, то можна
позначити ∠B = 3x; ∠A = 5x.
3) Маємо за властивістю
трикутника: 3x + 5x = 112°; 8x = 112°; x = 14°.
4) Отже, ∠B = 3 · 14° = 42°; ∠C = 5 · 14° = 70°.
Відповідь: 42°; 70°.

shkola.in.ua



1) ∠CBM = ∠MBD = 60° 2 = 30°
2) У △CBM за властивістю катета, що
лежить проти кута 30°, маємо BM = 2 · CM = 2 · 8 = 16 (см).
3) В △CBM: ∠B = 90° 60° = 30°
4) Трикутник BMD рівнобедрений, оскільки ∠MBD = ∠D = 30° , тому MD = MB = 16 (см).
5) CD = CM + MD = 8 + 16 = 24 (см).
Відповідь: 24 см.
1) Нехай ∠KAB, ∠ABM, ∠NCA зовнішні
кути трикутника. ∠KAB : ∠ABM : ∠NCA = 4 : 5 : 6.
Позначимо ∠KAB = 4x; ∠ABM = 5x; ∠NCA = 6x.
2) Маємо 4x + 5x + 6x = 360°. 15x = 360°; x = 360° : 15; x = 24°.
3) Тоді ∠CAB = 180° 4 · 24° = 84°; ∠ABC = 180° 5 · 24° = 60°; ∠BCA = 180° 6 · 24° = 36° .
4) ∠CAB : ∠ABC : ∠BCA = 84° : 60° : 36° = 7 : 5 : 3.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

544.

shkola.in.ua
1) Нехай AB = x см, тоді AC = (x − 3) см, BC = (x + 5) см.
2) Тоді x + x − 3 + x + 5 = 23; 3x − 5 = 23; 3x = 21; x = 7 (см).
3) Отже, AB = 7 см, тоді AC = 7 − 3 = 4 (см), BC = 7 + 5 = 12 (см).
4) Оскільки 7 + 4 < 12, то трикутника не існує.
Відповідь: Не існує.
Вправи для повторення розділу 3
shkola.in.ua

545.
Вершини: K, L, P. Сторони: KL, LP, PK. Кути: ∠K, ∠L, ∠P.

Нехай 18 + 6 = 24 (см) друга сторона трикутника, 24 : 2 = 12 (см) третя сторона. PΔ = 18 + 24 + 12 = 54 (см).
Відповідь: 54 см. 546.

547.

Відкладемо відрізок ML = 5 см. Від т. М відкладемо кут M = 40°, від т. L відкладемо кут L = 80°. На перетині сторін кутів позначимо т. Р. Отримаємо ∆MLP.
Нехай одна із сторін трикутника дорівнює х см, тоді друга 2х см, третя 0,8 × 2х = 1,6х. Отже, маємо рівняння: х + 2х + 1,6х = 46; 4,6х = 46; x = 10.
Отже, одна сторона трикутника дорівнює 10 см, друга 2 × 10 см = 20 см,
третя 1,6 × 10 = 16 см.
Відповідь: 10 см, 20 см, 16 см. 548.
AB + AC + AC + CB = 12 + 15, AB + CB + 2AC = 27.
Оскільки AB + BC = 13 см, маємо: 13 + 2AC = 27; 2AC = 27 - 13 = 14, AC = 7 (см).
AB = 12 - AC = 12 - 7 = 5 (см), CB = 15 - 7 = 8 (см).
Відповідь: 7 см, 5 см, 8 см. 549.
1) Сторони рівного трикутника дорівнюють 3 см, 7 см і 8 см.
2)
рівного трикутника

40°, 60°, 80°.
550.
Так, бо вони рівні. 551.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Ні, оскільки у рівних трикутників відповідні сторони рівні. 552.

shkola.in.ua
∆ABC = ∆ACB, AB = 7 см, BC = 4 см.
AC = AB = 7 см.
PΔABC = 7 + 4 + 7 = 18 (см).
Відповідь: 18 см. 553.

shkola.in.ua



Мал. 1. AB спільна сторона трикутників ACB і ADB. Вони рівні за першою ознакою рівності трикутників (AC = AD, AB спільна, ∠CAB = ∠DAB).
Мал. 2. MN спільна сторона трикутників MKN і NPM. ∆MKN = ∆NPM за другою ознакою рівності трикутників (MN спільна сторона, ∠KMN = ∠MNP, ∠PMN = ∠KMN).
AOD = ∠COB як вертикальні кути. ∆AOD = ∆COB AO = CO, DO = OB за умовою, ∠AOD = ∠COB за доведенням).
shkola.in.ua
555. MN спільна сторона трикутників MKN і MPN. ∆MKN = ∆MPN за другою ознакою рівності трикутників (MN спільна сторона, ∠PMN = ∠KMN, ∠KNM = ∠PNM).
shkola.in.ua


556. ∠BAK = ∠CDK як суміжні кути рівних кутів. ∆BAK = ∆CDK за першою ознакою рівності трикутників (BA = CD, AK = KD, ∠BAK = ∠CDK).


рівні,
BK = KC.
557. AX = AC, тому що ∆CAB = ∆XAB за



= ∠CAB, ∠XBA = ∠CBA), а
558.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

559.


shkola.in.ua

∠BCD = ∠DFE як суміжні кути рівних кутів.
DC – спільний відрізок сторін AC і FD. AC = AD + DC, FD = CF + DC, AC = FD.
Отже, ∆ABC = ∆DEF за першою ознакою (BC = EF, AC = FD, ∠BCD = ∠DFC).
1) ∆ABE = ∆ADC за другою ознакою (AB = AC за умовою, ∠A спільний, ∠ABE = ∠ADC = 90°, оскільки DC ⊥ AE, BE ⊥ AD). Із рівності трикутників маємо: AD = AE. Тоді BD = AD - AB, CE = AE – AC. Оскільки AB = AC за умовою, AD = AE за доведенням, то BD = CE.
2) ∆BOD = ∆COE за стороною і двома прилеглими кутами (BD = CE за доведеним в п. 1), ∠OBD = ∠OCE = 90°, ∠BDO = ∠CEO як кути рівних трикутників ACD і ABE. З рівності трикутників маємо BO = CO. ∆ABO = ∆ACO (за двома сторонами і кутом між ними: AB = AC - за умовою, BO = CO за доведенням, ∠ABO = ∠ACO). Із рівності цих трикутників маємо ∠BAO = ∠CAO, отже, AO бісектриса кута A.
560.
561.

1) PK = AP = 5 см, оскільки бічні
рівні.
2) ∠K = ∠A = 70°, оскільки кути при основі рівнобедреного трикутника рівні.

562.




AC = 5 см, AB = BC = 4 см. PΔABC = AB + BC + AC = 4 см + 4 см + 5 см = 13 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
563.
shkola.in.ua



ΔKLM – рівнобедрений, KL = LM, тоді ∠K = ∠M.
ΔK1L1M1 - рівнобедрений K1L1 = L1M1, тоді ∠K1 = ∠M1.
Оскільки ∠K = ∠K1, то ∠M = ∠M1.
Отже, ΔKLM = ΔK1L1M1 за другою ознакою рівності трикутників. 564.
Нехай у рівнобедреного ΔMNL MN = NL, ML = 3x см, тоді MN = NL = 4x.
За умовою задачі маємо 3x + 4x + 4x = 88; 11x = 88; x = 8.
Отже, ML = 3 × 8 = 24 (см), MN = NL = 4 × 8 = 32 (см).
Відповідь: 24 см, 32 см, 32 см.


566.
ΔABC - рівнобедрений, AC = CB, тоді ∠CAB = ∠CBA.
ΔABD - рівнобедрений, AD = DB, тоді ∠DAB = ∠DBA.
∠CAD = ∠CAB + ∠DAB, ∠CBD = ∠CBA + ∠DBA, ∠CAD = ∠CBD.
ΔACD = ΔBCD за першою ознакою трикутників
(AC = CB, AD = DB - за умовою, ∠CAD = ∠CBD).
1) Відрізок, що сполучає вершину із серединою протилежної сторони, називається
медіаною трикутника.
2) Перпендикуляр, проведений з його вершини до прямої, що є протилежною стороною, називається висотою трикутника.
3) Відрізок бісектриси кута трикутника, що сполучає вершину трикутника з точкою протилежної сторони називається бісектрисою трикутника. 567.

Нехай в рівнобедреному ∆MNK (MN = NK), NP
бісектриса (∠MNP = ∠PNK), NP = 5 см. Оскільки бісектриса рівнобедреного трикутника, проведена до основи, є його висотою і медіаною, то висота і медіана дорівнюють 5 см кожна.
Відповідь: 5 см, 5 см. 568.




∠NMK = ∠NKL - як кути при основі рівнобедреного трикутника.
∠MNK = ∠LNK - оскільки NK є бісектрисою, проведеною до основи.
∠NKM = ∠NKL = 90°, оскільки NK є висотою.
NM = NL - як сторони рівнобедреного трикутника.
MK = KL - оскільки NK - медіана рівнобедреного трикутника.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
shkola.in.ua


Нехай ΔABC = ΔA1B1C1, AM - медіана ΔABC (CM = MB), A1M1 - медіана ΔA1B1C1 (C1M1 = M1B1).
Розглянемо ΔABM і ΔA1B1M1: AB = A1B1 - як відповідні сторони рівних трикутників, ∠B = ∠B1як відповідні кути рівних трикутників. MB = M1B1 - як половини рівних сторін. Отже, ΔABM = ΔA1B1M1 за першою ознакою рівності трикутників. 570.

Оскільки ΔABC - рівнобедрений, то AB = BC. Оскільки BD – висота, то BD є бісектрисою, отже, ∠ABD = ∠CBD. ΔABO = ΔCBO за першою ознакою рівності трикутників (AB = BC, BO – спільна, ∠ABO = ∠CBO). Із рівності цих трикутників випливає, що AO = CO.
571.
shkola.in.ua


Оскільки ∠ABD = ∠ADB, то ΔABD - рівнобедрений згідно з ознакою рівнобедреного трикутника, тоді AB = AD.
Оскільки ∠DBC = ∠CDB, то ΔBCD - рівнобедрений згідно з ознакою рівнобедреного трикутника, тоді CB = CD.
ΔABC = ΔADC за двома сторонами і кутом між ними (AB = AD, BC = DC - за доведенням, ∠B = ∠D - як сума рівних кутів).
Із рівності цих трикутників маємо ∠BCA = ∠DCA.
Оскільки пряма AC містить бісектрису кута C рівнобедреного трикутника BCD, то пряма AC містить висоту ΔBCD. Отже, AC⊥BD. 572.


ΔAMK = ΔBMK (за першою ознакою рівності трикутників: AM = BMза умовою, MK - спільна сторона, ∠BMK = ∠AMK = 90° - за умовою).
Отже, BK = AK.
PΔABC = AB + BC + AC = AB + BK + KC + AC = AB + AK + KC + AC = a + PΔAMK = a + b.
shkola.in.ua
AC = PΔABC = (AB + BC) = a + b − (2a) = a − b.
Відповідь: a − b; a + b.



ΔABC = ΔCDA за
shkola.in.ua
трикутників,
575.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

Нехай у трикутників △ABC і △A1B1C1: AB = A1B1, AC = A1C1, BM = B1M1, де BM і B1M1 - медіани. Доведемо, що △ABC = △A1B1C1.
ΔABM = ΔA1B1M1 - за трьома сторонами, оскільки AB = A1B1 - за умовою, BM = B1M1 - за умовою, AM = A1M1 - як половини рівних сторін. Із рівності трикутників маємо ∠A = ∠A1. Тоді △ABC = △A1B1C1 - за першою ознакою рівності трикутників, оскільки AB = A1B1 - за умовою, AC = A1C1 - за умовою, ∠A = ∠A1 - за доведенням. 576.
1) ∠C = 180° - (∠A + ∠B) = 180° - (65° + 29°) = 86°
2) ∠C = 180° - (∠A + ∠B) = 180° - (37° + 116°) = 27° Відповідь: 1) 86°; 2) 27°. 577.
shkola.in.ua

1) Оскільки ∠KCB = 32° і СК - бісектриса, то ∠ACB = 2∠KCB = 2 × 32° = 64°. ∠B = ∠ACB = 64°, оскільки кути
рівні. Тоді ∠A = 180° - ∠ACB - ∠B = 180° - 64° - 64° = 52°.
2) ∠ACB = ∠B - оскільки ΔABC - рівнобедрений. ∠ACB = ∠B = 180° 56° 2 = 62°.
Оскільки СК - бісектриса, то ∠ACK = ∠KCB = 1 2 ∠ACB = 1 2 × 62° = 31°.
Відповідь: 1) 52°; 2) 31°. 578.
∠C = 180° - ∠A - ∠B = 180° - 76° - 28° = 76°. Отже, у трикутника ABC
рівні ∠A = ∠C = 76°, тобто ΔABC - рівнобедрений, AB = BC. 579.
shkola.in.ua

580.
сума
581.
shkola.in.ua



180°, то маємо: ∠A + ∠ABK + ∠KBC + ∠C = 180°, 60° + x + 40° + 45° = 180°, x + 145° = 180°, x = 180° - 145° = 35°.
180° - 60° = 120°.
2x + 3x = 120°; 5x = 120°; x = 24°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
З ΔAOH: ∠AOH = 180° - ∠OAH - ∠OHA = 180° - 30° - 90° = 60°.
Відповідь: 60°. 582.
shkola.in.ua


Нехай в ΔABC: BL бісектриса, BK висота, BK ⊥ AC, ∠KBL = 16°, ∠BCA = 50°. З ΔBKL: ∠BLK = 180° - ∠BKL - ∠KBL = 180°90° - 16° = 74°. ∠BLC + ∠BLK = 180° як суміжні кути, звідси ∠BLC = 180° - ∠BLK = 180° - 74° = 106°.
З ΔBLC: LBC = 180° - ∠BLC - ∠C = 180° - 106° - 50° = 24°.
Оскільки BL - бісектриса, то ∠ABC = 2 × 24° = 48°.
З ΔABC: ∠A = 180° - ∠ABC - ∠C = 180° - 48° - 50° = 82°.
Відповідь: 48°, 82°. 583.
1) Нехай x° - шуканий кут, тоді сума
5x.
x + 5x = 180°; 6x = 180°; x = 30°. Отже, шуканий кут дорівнює 30°.
2) Нехай x° - шуканий кут, тоді маємо рівняння: x + 40° = 180° - x; 2x = 140°; x = 70°. Отже, шуканий кут дорівнює 70°. 584.
shkola.in.ua



1) Нехай △ABC - рівнобедрений, AC = CB, ∠A = ∠B, AK –бісектриса, ∠AKB = 60°. Нехай ∠KAB = x, тоді ∠CBA = 2x.
∠KAB + ∠CBA + ∠AKB = 180° (за властивістю суми кутів трикутника).
x + 60° + 2x = 180°; 3x = 120°; x = 40°. Отже, ∠KAB = 40°, ∠KBA = 2 × 40° = 80°.
2) Нехай ΔABC - рівнобедрений, AC = AB, ∠A = ∠B.

AK - бісектриса, ∠CAK = ∠KAB, ∠AKC = 111°.
∠AKC + ∠AKB = 180° - як суміжні кути. ∠AKB = 180° - ∠AKC = 180° - 111° = 69°.
Нехай ∠KAB = x, тоді ∠B = 2x.
З ΔAKB: ∠KAB + ∠AKB + ∠KBA = 180°, x + 69° + 2x = 180°; 3x = 111°; x = 37°.
Отже, B = 37° × 2 = 74°, тоді ∠C = 180° - 2 × 74° = 180° - 148° = 32°.
Відповідь: 1) 80°; 2) 32°. 585. 1, ∠2, ∠3 –
shkola.in.ua

586.

shkola.in.ua

MNK


A = ∠BCA = 30°.
AB = BC, ∠A = ∠BCA.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
Звідси ∠B = 180° - ∠A - ∠BCA = 180° - 30° - 30° = 180° - 60° = 120°.
Відповідь: 120°, 30°, 30°. 587.
1) Зовнішній кут трикутника, не суміжний з кутом 80°, може дорівнювати 102°, оскільки 102° > 80°.
2) Зовнішній кут трикутника, не суміжний
80°, не може дорівнювати 80°, оскільки
3)
588.

shkola.in.ua
108°. 589.
shkola.in.ua


590.
shkola.in.ua

рівнобедреного трикутника, ΔABC – рівнобедрений.
Нехай ∠CBD = 140°, ∠A = 2x, ∠C = 3x.
маємо рівняння: 2x + 3x = 140°; 5x = 140°; x = 28°. Отже, ∠A = 2 × 28° = 56°, ∠C = 3 × 28° = 84°, ∠B = 180° - ∠A - ∠C = 180° - 56° - 84° = 40°. Відповідь: 56°, 84°, 40°. 591. Оскільки

shkola.in.ua

трикутника дорівнює 180°, то зовнішній
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
за 120°. 593.

shkola.in.ua
Нехай ∠CBF = ∠CAD = ∠C.
∠CBF = 180° - ∠CBA, ∠CAD = 180° - ∠CAB, тоді ∠C = ∠CBF - ∠CAD = 180° - ∠CBA - 180° + ∠CAB = ∠CAB - ∠CBA.
Звідси ∠CAB = ∠C + ∠CBA. ∠C + ∠CAB + ∠CBA = 180° (за теоремою про суму кутів трикутника). Оскільки ∠C + ∠CBA = ∠CAB, маємо ∠CAB + ∠CAB = 180°, 2∠CAB = 180°, ∠CAB = 90°. Отже, ΔABC – прямокутний. 594.

shkola.in.ua

595.
shkola.in.ua
1) Не слідує. На мал. ΔABC ≠ ΔDBC, проте BC ΔABC = BC ΔBCD.
2) Слідує.
3) Не слідує ΔABC ≠ ΔA1B1C1, проте ∠A = ∠A1 = 30°, ∠C = ∠C1 = 60°.
shkola.in.ua

1) ∠M = 90° - ∠K = 90° - 60° = 30°, оскільки сума гострих кутів прямокутного трикутника дорівнює 90°.
2) PK = �������� 2 = 24 2 = 12 (см), оскільки катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.
3) MK = 2PK = 30 × 2 = 60 (мм) - згідно з властивістю з прямокутних трикутників.
Відповідь: 1) 30°; 2) 12 см; 3) 60 мм. 596.

shkola.in.ua
Розглянемо ΔABC і ΔAPC: ∠B = ∠P, ∠BCA = ∠PCA, оскільки CAбісектриса кута C, AC - спільна сторона. Отже, ΔABC = ΔAPC за гіпотенузою і гострим кутом. 597.
shkola.in.ua


Нехай ΔKLM - прямокутний, ∠K = 3x°, ∠L = 7x°. Оскільки сума
трикутника дорівнює 90°, маємо: 3x + 7x = 90°; 10x = 90°; x = 9°. Отже, ∠K = 3 × 9° = 27°, ∠L = 7 × 9° = 63°.
Відповідь: 27°, 63°.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

Нехай у прямокутному ΔABC (∠B = 90°), BF ⊥ AC,
∠ABD = ∠DBC = 90° : 2 = 45°, ∠DBF = 15°. ∠FBC = ∠DBC∠DBF = 45° - 15° = 30°.
З прямокутного трикутника BCF: ∠BCF = 90° - ∠FBC = 90°30° = 60°.
З прямокутного ΔABC: ∠A = 90° - ∠C = 90° - 60° = 30°, оскільки сума гострих кутів трикутника дорівнює 90°.
Відповідь: 60°, 30°. 599.

shkola.in.ua
600.

601.
shkola.in.ua
Нехай ΔABC - прямокутний, AC = BC, CD ⊥ AB, CD = 5 см. Оскільки ΔABC - рівнобедрений, то CD - є медіаною.
Отже, AB = 2CD = 2 × 5 = 10 (см) за властивістю медіани
прямокутного трикутника. Відповідь: 10 см.
Нехай в прямокутному ΔABC (∠C = 90°), ∠A = α, ∠B = β, α + β = 90°.
∠MAB = ∠���� 2 = ���� 2 , ∠MBA = ∠���� 2 = ���� 2 , тоді ∠AMB = 180° - ∠MAB - ∠MBA = = 180°���� 2���� 2 = 180°1 2(α + β) = 180°1 2 × 90° = 180° - 45° = 135°.
∠LMB - суміжний з кутом AMB. ∠LMB = 180° - 135° = 45°.
Відповідь: 45°.

602.
shkola.in.ua
Нехай в ΔABC (∠A = 90°), ∠B = 30°, BA = 24 см, CD - бісектриса кута C; ∠BCD = ∠DCA. З ΔABC маємо: ∠C = 90° - ∠B = 90° - 30° = 60°.
∠BCD = ∠DCA = 60° : 2 = 30°. ΔBCD - рівнобедрений, оскільки ∠B = ∠BCD, отже, CD = BD. З ΔDCA: DA = 1 2CD (оскільки ∠DCA = 30°).
Отже, маємо: BA = BD + DA = CD + 1 2 CD = 24, 11 2CD = 24, CD = 24 : 11 2 = 24 : 3 2 = 48 3 = 16 (см).
Відповідь: 16 см.

Нехай ΔABC - рівнобедрений, AB = BC, AD ⊥ BC, ∠ABC = 120°, AD = a см.
З ΔABC: ∠A = ∠C = (180° - 120°) : 2 = 60° : 2 = 30°.
З прямокутного ΔADC: AC = 2AD = 2 × a = 2a (см)
Відповідь: 2a см. 603.

shkola.in.ua


Нехай в прямокутному ΔABC CD - медіана, CD = 10 см, ∠ACD : ∠DCB = 1 : 2, отже, ∠ACD = 90° : 3 = 30°, ∠DCB = (90° : 3) × 2 = 60°.
Оскільки медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи, то AB = 2CD = 2 × 10 = 20 см, CD = DB, CD = AD. Отже, ΔCDB – рівнобедрений, оскільки ∠DCB = ∠DBC = 60°. Оскільки сума кутів трикутника дорівнює 180°, то ∠CDB = 180° - (∠DCB + ∠DBC) = 180° - 120° = 60°. Отже, ΔCDB – рівносторонній, CB = CD = DB = 10 см. Відповідь: 20 см, 10 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua
Нехай у
ABC (∠C = 90°), CH - висота, CL - бісектриса, CM - медіана, ∠HCL = β. Доведемо, що ∠LCM = β. Оскільки CL - бісектриса, то ∠ACL = ∠LCB = 90° : 2 = 45°, тоді ∠ACH = ∠ACL - ∠HCL = 45° - β.
З прямокутного ΔACH: ∠A = 90° - ∠ACH = 90° - (45° - β) = 45° + β.
З прямокутного ΔABC: ∠B = 90° - ∠A = 90° - (45° + β) = 45° - β.
ΔCMB - рівнобедрений, оскільки CM = MB (за властивістю медіани, проведеної
гіпотенузи), тоді ∠MCB = ∠B = 45° - β.
Отже, ∠LCM = ∠LCB - ∠MCB = 45° - (45° - β) = 45° - 45° + β = β.
Отже, бісектриса прямого кута
вершини прямого кута, навпіл. 605.
Нехай третя сторона
1)
2)
3)
< a < 13.
5)
проведеними з
13. 606.
третя сторона трикутника дорівнює а см. Тоді 8,7 - 5,2 < a < 8,7 + 5,2; 3,5 < a < 13,9. Оскільки а - ціле число, то найменше ціле число, яке задовольняє умові, а = 4, найбільше – 13. Відповідь: 4 см, 13 см. 607.

608. 1)

shkola.in.ua
10 (см).
21 см.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
3m см, друга - 7m см.
Сторона 3m см не може бути стороною рівнобедреного трикутника, оскільки 7m > 3m + 3m. Отже, сторони трикутника дорівнюють 7m, 7m, 3m,
тоді 7m + 7m + 3m = 51, 17m = 51, m = 3.
Отже, сторони трикутника дорівнюють 7 × 3 = 21 (см), 3 × 3 = 9 (см).
Відповідь: 21 см, 21 см, 9 см.
610. (Усно.) Точка O – центр кола. Які з відрізків

shkola.in.ua
кола?
1) FK; QC; PL; 2) PL; 3) OP; OL; ОТ.
611. Знайдіть на малюнку хорду,

612.
shkola.in.ua
1) 4 см; d = 2r = 2 ∙ 4 = 8 (см); 2) 3,7 дм. d = 2r = 2 ∙ 3,7 = 7,4 (дм).
613.
1) 7 мм; d = 2r = 2 ∙ 7 = 14 (мм); 2) 4,8 см. d = 2r = 2 ∙ 4,8 = 9,6 (см).
614. Знайдіть
1) 8 дм;
r = ���� 2 = 8 2 = 4 (дм); 2) 2,6 см. r = ���� 2 = 2,6 2 = 1,3 (см);
615. Обчисліть радіус
1) 18 см;

r = ���� 2 = 18 2 = 9 (см); 2) 3,8 дм. r = ���� 2 = 3,8 2 = 1,9 (дм);
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
616.

shkola.in.ua
617.

shkola.in.ua
618.

shkola.in.ua
619.
shkola.in.ua

620.
1) 2 см; 2) 5 см; 3) 7 см; 4) 9,8 см; 5) 10,2 см; 6) 1 дм? Оскільки
кола є найбільшою хордою, отже, хорда цього
1) Може; 2) може; 3) може; 4) може; 5) не може; 6) не може.
621. Радіус
1) 1 дм; 2) 4 дм; 3) 6,7 дм; 4) 7,95 дм; 5) 8,3 дм; 6) 1 м?
1) Може; 2) може; 3) може; 4) може; 5) не може; 6) не може. 622.

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua
624. На
O,
= ∆POK. ΔMON = ΔROK за
∠A = 52°; 2) кута B, якщо ∠O = 94°.

shkola.in.ua
ΔOAB – рівнобедрений, оскільки OA = OB – як радіуси
тоді ∠A = ∠B.
1) Якщо ∠A = 52°, то ∠B = 52°, ∠O = 180° – ∠A – ∠B = 180° – 52° – 52° = 76°.
2) Якщо ∠O = 94°, то
∠B = (180° – ∠O) : 2 = (180° – 94°) : 2 = 43°.
Відповідь: 1) 76°; 2) 43°.
625. На малюнку точка O центр кола. Знайдіть градусну міру:
1) кута O, якщо ∠B = 48°; 2) кута A, якщо ∠O = 102°.

shkola.in.ua
ΔAOB – рівнобедрений, оскільки OA = OB – як радіуси кола, тоді
∠A = ∠B.
1) Якщо ∠B = 48°, то ∠A = 48°, ∠O = 180° – ∠A – ∠B = 180° – 48° – 48° = 84°.
2) Якщо ∠O = 102°, то
∠A = (180° – ∠O) : 2 = (180° – 102°) : 2 = 39°.
Відповідь: 1) 84°; 2) 39°.
626. На малюнку точка O центр кола, ∠COA = 32°. Знайдіть ∠CBA.

shkola.in.ua

ΔCOB – рівнобедрений, оскільки OC = OB – як радіуси кола, тоді
∠C = ∠B.
∠COB + ∠COA = 180° – як суміжні кути.
Звідси ∠COB = 180° – ∠COA = 180° – 32° = 148°.
Отже, ∠CBA = (180° – ∠COB) : 2 = (180° – 148°) : 2 = 16°.
Відповідь: 16°.

shkola.in.ua
∠C = ∠B.
∠COB = 180° – (∠C + ∠B) = 180° – 18° – 18° = 144°.
∠COB + ∠COA = 180° – як суміжні кути.
Звідси ∠COA = 180° – ∠COB = 180° – 144° = 36°.
Відповідь: 36°.
shkola.in.ua

629.

shkola.in.ua
630.

shkola.in.ua
631. Доведіть, що
shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
1)
M = 90°. ∠MAB = 90° – 60° = 30°.
AB = 2MB = 2 ∙ 5 см = 10 см.
Відповідь: 10 см.
точки
∠M = 90°.
∠A = 90° – ∠B = 90° – 60° = 30°.
MB = 1 2 AB = 1 2 ∙ 18 = 9 см.
Відповідь: 9 см.
Нехай AB і CD – хорди. OM ⊥ AB, ON ⊥ CD і OM = ON. Доведемо, що AB = CD. Оскільки OM ⊥ AB; ON ⊥ CD, то AM = MB, DN = CD, тобто, щоб довести, що AB = CD, досить довести, що AM = CN. ΔAOM = ΔCON (за гіпотенузою і катетом: OM = ON – за умовою, OA = OC – як радіуси кола), тоді AM = CN.
Отже, AB = 2AM = 2CN = CD. 632. Доведіть, що
shkola.in.ua


центра.
Нехай AB = CD, OM ⊥ AB, ON ⊥ CD. Доведемо, що OM = ON.
Оскільки OM ⊥ AB, то AM = MB, оскільки ON ⊥ CD, то CN = ND. ΔOMA = ΔONC (за
AM = CN – як

shkola.in.ua
OA = OC
OM = ON.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua
Нехай ∠CFB = ∠DFB, ∠CFD = 90°.
Оскільки ∠CFB = ∠DFB, то ∠CFA = ∠DFA –
до рівних кутів.
Оскільки ∠CFD = 90°, то ∠CFA = ∠DFA = 90° : 2 = 45°, тоді ∠CFB = ∠DFB = 180° – 45° = 135°.
Відповідь: 135°. 636. Доведіть

shkola.in.ua

2) 810
3) 711 : 70 ≈ 10,16 = 11

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
639. (Усно.)

640. (Усно.) Скільки
1) на колі; 1) Одну; 2) поза колом; 2) дві; 3) всередині кола? 3) жодної.
641. Накресліть коло, радіус
shkola.in.ua















645. На
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
KP
1) ∠OMN, якщо ∠NMP = 40°; 2) ∠KMN, якщо ∠OMN = 48°.
shkola.in.ua

1) Оскільки KP дотична до кола, то ∠OMP – ∠OMK = 90°. Тому ∠OMN = 90° – ∠NMP = 90° – 40° = 50°.
2) ∠KMN = 90° + ∠OMN = 90° + 48° = 138°.
Відповідь. 1) 50°; 2) 138°.
646. На малюнку KP дотична до кола, точка O центр кола. Знайдіть: 1) ∠NMP, якщо ∠OMN = 53°; 2) ∠OMN, якщо ∠KMN = 130°.
shkola.in.ua

1) Оскільки KP дотична до кола, то ∠OMP = ∠OMK 90°. Тому ∠NMP = 90° – ∠OMN = 90° – 53° = 37°.
2) ∠OMN = ∠KMN – 90° = 130° – 90° = 40°.
Відповідь. 1) 37°; 2) 40°.
647. З точки A до кола із центром
shkola.in.ua

648. З точки P

PM і PN. Доведіть, що промінь PQ бісектриса кута MPN.
shkola.in.ua


ΔQMP і ΔQNP – прямокутні, оскільки QM ⊥ MP, QN ⊥ NP.
ΔQMP = ΔQNP за двома катетами (QM = QN – як радіуси кола, PM = PN – як відрізки дотичних, проведених з однієї точки до кола). З рівності трикутників маємо ∠MPQ = ∠NPQ. Отже, PQ – бісектриса кута MPN. 649. Пряма MK дотична

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
= 53°.

shkola.in.ua
shkola.in.ua

652. Прямі MN і MK
Оскільки MK - дотична до кола, то OM ⊥ MK, ∠OMK = 90°. ΔOMN – рівнобедрений, оскільки OM = ON – як радіуси кола.
OMN
106°.
і МN – дотичні. OK ⊥ MK, ON ⊥ MN.
прямокутного ΔOKM: оскільки OM = 2OK,
∠KMN = ∠KMO + ∠OMN = 30° + 30° = 60° .
Відповідь: 60°.
∠OMN = 30°, MN = 7 см.
shkola.in.ua

ΔONM = ΔOKM
MN = MK – як
(ON = OK –
кола). Отже, ∠NMO = ∠KMO = 30°. ΔKMN – рівнобедрений, оскільки MN = MK, ∠MNK = ∠MKN = (180° – 60°) : 2 = 120° : 2 = 60° .
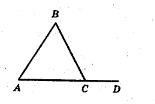
shkola.in.ua

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html






https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
∠IBK = 35°, ∠MCI = 25°.

661. У △ABC
∠CBK = 2∠IBK (оскільки BI – бісектриса кута A),
∠CBK = 2 ∙ 35° = 70°.
∠ACB = 2∠MCI (оскільки CI – бісектриса кута C),
∠ABC = 2 ∙ 25° = 50°.
∠B = 180° – ∠A – ∠C = 180° – 70° – 50° = 60°.
Відповідь: 60°.
I.
CAB = 70°, ∠CBA = 60°. Знайдіть ∠MCI.

shkola.in.ua
662. На

shkola.in.ua
∠C = 180° – ∠CAB – ∠CBA = 180° – 70° – 60° = 50°, CI – бісектриса кута C.
Отже, ∠MCI = ∠C : 2 = 50° : 2 = 25°.
Відповідь: 25°.
ΔCMI = ΔCLI (CM = CL, MI = IL).
ΔAMI = ΔAKI (AM = AK, MI = IK).
ΔKIB = ΔLIB (KB = LB, KI = LI). 663.
shkola.in.ua



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua


shkola.in.ua
668. У △ABC вписано коло, яке дотикається

shkola.in.ua
сторін AB, AC і BC у точках P, F і M відповідно. Знайдіть AP, PB, BM, MC, CF і FA, якщо AB = 8 см, BC = 6 см, AC = 12 см. Складемо систему рівнянь: � x z = 2 z + x = 12 x + z = 12 ⇒ � x z = 2 x + z = 12 2x = 14, x = 7. Отже, AP = FA = 7 см, PB = 8 – 7 = 1 см, BM = PB = 1 см, MC = 6 – 1 = 5 см, FC = MC = 5 см. Відповідь: AP = 7 см, PB = 1 см, BM = 1 см, MC = 5 см, CF = 5 см, FA = 7 см. 669.
shkola.in.ua

BK = 4 см, CL = 6 см, AM = 8 см.
BL = BK = 4 см, CM = CL = 6 см, AK = AM = 8 см.
AB = AK + BK = 8 см + 4 см = 12 см, BC = BL + CL = 4 см + 6 см = 10 см, AC = AM + CM = 8 см + 6 см = 14 см. Відповідь: 12 см, 10 см, 14 см.

shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

ΔABC
рівнобедрений (AB = BC), AK = 3 см, KB = 4 см.
AM = AK = 3 см, CM = LC = 3 см, BL = KB = 4 см. Отже, PΔABC = AK + KB + BL + LC + CM + AM = 3 см + 4 см + 4 см + 3 см + 3 см + 3 см = 20 см.
Відповідь: 20 см.
671. Коло, вписане в рівнобедрений трикутник,
см і 7 см, починаючи від
трикутника.

shkola.in.ua
Нехай ΔABC – рівнобедрений (AB = BC), KB = 5 см, AK = 7 см.
BL = KB = 5 см, AM = AK = 7 см, CM = CL = 7 см.
PΔABC = AK + KB + BL + CL + CM + AM = = 7 см + 5 см + 5 см + 7 см + 7 см + 7 см = 38 см.
Відповідь: 38 см. 672. Доведіть,
shkola.in.ua

shkola.in.ua

Отже, CK = AM.
кута. Нехай ΔABC – прямокутний (∠B = 90°), BK ⊥ AC, BM –бісектриса, ∠ABM = ∠CBM. Оскільки сума
прямокутного трикутника
90°, маємо: ∠BCA = 90° 5 ∙ 2 = 18° ∙ 2 = 36°, ∠BAC = 90° – 36° = 54°.
Оскільки BM – бісектриса, то ∠ABM = ∠CBM = 90° : 2 = 45°.
З прямокутного ΔBKC маємо: ∠CBK = 90° – ∠BCK = 90° – 36° = 54°.
Тоді ∠KBM = ∠CBK – ∠CBM = 54° – 45° = 9°.
Відповідь: 9°.
674. Яка швидкість поїзда (у км/год), якщо
360 обертів
(Прийміть π = 3.)
1) C = π ∙ d = 3 ∙ 1,2 = 3,6 (м) – довжина


shkola.in.ua
shkola.in.ua


shkola.in.ua
678.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


679. 1)
shkola.in.ua
1) MN = 5,4
MN.
2) PM = PN.

shkola.in.ua

shkola.in.ua
1) AB = 4,6см.
2) CA = CB.
ΔCKO = ΔAKO (за
катет).
ΔAMO = ΔBMO (за
AK = KC,
AM = MB, OM –спільний катет).
ΔCLO = ΔBLO (за
CL = LB,
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua



shkola.in.ua


shkola.in.ua


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


687.



shkola.in.ua
перпендикуляр співпадає
∠OAD = 1 2 ∠BAD = 60° : 2 = 30°. ΔAOD - прямокутний, тоді AO = 2OD.
радіус кола, вписаного в нього. 689. LM діаметр кола, хорди KL і
KLM.


690. I точка
shkola.in.ua

прямим кутом, то ∠LKM = 90°. ΔLKM - прямокутний, KL = KM
∠L = ∠M = 90° : 2 = 45°. Відповідь: 90°, 45°, 45°.

= ΔANB
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
9 га = 90000 м2 .
1) 90000 : 150 = 600 (м) – довжина
2) 2 ∙ (150 + 600) = 2 ∙ 750 = 1500 (м) – довжина огорожі.
Відповідь: 1500 м.
692.


shkola.in.ua
693. Точка O центр
1) ∠COB, якщо ∠CAO = 50°; 2) ∠CAO, якщо ∠COB = 110°.

shkola.in.ua
694. Точка O
1) ∠АОС = 180° – (50° + 50°) = 80°;
∠COB = 180° – 80° = 100°.
2) ∠АОС = 180° – 110° = 70°;
∠CAO = (180° – 70°) : 2 = 55°.
1) ∠NMB, якщо ∠MON = 140°; 2) ∠MON, якщо ∠BMN = 65°.

shkola.in.ua
1) ∠OMN = (180° – 140°) : 2 = 20°;
∠NMB = 90° – 20° = 70°.
2) ∠OMN = 90° – 65° = 25°.
∠MON = 180° – (25° + 25°) = 180° – 50° = 130°. 695.

Нехай AB = 32 см, EF = 20 см. AE + FB = 32 см – 20 см = 12 см, тоді EC + DF = AE + FB = 12 см. Отже, CD = EF – (EC + DF) = 20 см – 12 см = 8 см. Відповідь: 8 см.

696. (Усно.)
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

697.
1) 70°;
2) 190°.
698.
1) 20°; 2) 100°.

1) 70° : 2 = 35°;
2) 190° : 2 = 95°.
1) 20° ∙ 2 = 40°;
2) 100°
2 = 200°.


shkola.in.ua


shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
ANB = 70°. Кути AMB і ANB

702.

shkola.in.ua
CPD = 126°.

shkola.in.ua

703.
LOK = 128°.
Відповідно, ◡AMB = 70° ⋅ 2 = 140°.
◡ANB + ◡AMB = 360° ⇒
◡ANB = 360° – ◡AMB = 360° – 140° = 220°.
Відповідно, ∠ANB = ◡ANB : 2 = 220° : 2 = 110°.
shkola.in.ua
∠CPD = 1 2 ◡CKD. ◡CKD = 2∠CPD = 2 ∙ 126° = 252°.
◡CPD = 360° – ◡CKD = 360° – 252° = 108°.
∠COD = ◡CPD = 108°.
Відповідь: 108°.
LAK,

∠LOK = ◡LAK = 128°.
∠LAK = 1 2 ◡LPK = 1 2(360° – ∠LOK) = 1 2(360° – 128°) = 116°.
116°.

+ 2х = 360;
3х = 360; х = 120.
120° : 2 = 60°; 240° : 2 = 120°.

60°, 120°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


shkola.in.ua

= 55°. Доведіть, що хорди AB і CD взаємно перпендикулярні.



shkola.in.ua

а значить, вони рівні: ∠ВСD = ∠ВАD = 55°. У △ВСМ ∠
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

має три розв’язки.

shkola.in.ua


shkola.in.ua


shkola.in.ua

вдвічі менший:
∠АСВ = 1 2 ∙ 80° = 40°.
∠ВАС = ∠АСВ = 40° як кути при основі.
∠АВС = 180° – (∠АСВ + ∠ВАС) = = 180° – (40° + 40°) = 100°.
Відповідь: 40°, 40°, 100°.
II випадок. ∠АОВ = ◡АСВ = 80° (∠АОВ центральний), ◡АКВ = 360° – ◡АСВ = = 360° – 80° = 280°.
∠АСВ вписаний.
∠АСВ = 1 2 ◡АKВ = 280° : 2 = 140°.
∠CAB = ∠CBA = (180° – ∠АСВ) : 2 = = (180° – 140°) : 2 = 20°.
Відповідь: 140°, 20°, 20°.
III випадок. ∠АОВ = ◡AРВ = 80°,
∠АСВ = 1 2 ◡АРВ = 1 2 ∙ 80° = 40°.
∠САВ = ∠СВА = (180° – ∠АСВ) : 2 = = (180° – 40°) : 2 = 140° : 2 = 70°.
Відповідь: 40°, 70°, 70°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

три розв’язки.

shkola.in.ua



shkola.in.ua

shkola.in.ua


І випадок.
∠МОК = ◡МРС = 100°.
∠МNК = 1 2 ◡МРК = 1 2 ∙ 100° = 50°.
∠NMК = ∠NKM = (180° – ∠МNК) : 2 = = (180° – 50°) : 2 = 130° : 2 = 65°.
Відповідь: 50°, 65°, 65°.
II випадок ∠МОК = ◡МNK = 100.
◡МРK = 360° – ◡МNK = 360° – 100° = 260°.
◡МNK = 1 2 ◡МРК = 1 2 ∙ 260° = 130°.
∠NМК = ∠NКМ = (180° – 130°) : 2 = 50° : 2 = 25°.
Відповідь: 130°, 25°, 25°.
III випадок. ∠МОК = ◡МРК = 100°.
∠МNК = 1 2 ◡МРК = 1 2 ∙ 100° = 50°.
∠КМN = ∠МNК = 50° як кути при основі.
∠МКN = 180° – (∠КМN + ∠МNК) = = 180° – (50° + 50°) = 180° – 100° = 80°.
Відповідь: 50°, 50°, 80°.

= x; ◡AB = 2x; ◡BC = 6x. Складемо рівняння:
х + 2х + 6х = 360;
9х = 360;
х = 40° – ◡АС.
shkola.in.ua
2 ∙ 40° = 80° – ◡AB.
6 ∙ 40° = 240° – ◡ВС.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
∠ВАС = 240° : 2 = 120°;
∠
АВС = 40 : 2 = 20°;
∠АСВ = 80 : 2 = 40°.
Відповідь: 120°, 20°, 40°. 713.

714.

shkola.in.ua



shkola.in.ua shkola.in.ua

2)
кута 30°, маємо AO = BO 2 . Тому BO = 2 ∙ AO = 2 ∙ 5 = 10 (см). Відповідь. 10 см.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua



shkola.in.ua


shkola.in.ua


shkola.in.ua
shkola.in.ua
shkola.in.ua


shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
722.

shkola.in.ua
723.

shkola.in.ua
724. Радіуси
OK = 7 см. O1K = 5 см.
AB = 2 см.
OO1 = OK – O1K = 7 см – 5см = 2см.
shkola.in.ua

725.
кола мають:
1) зовнішній дотик;
OM = 3 см, O1M = 8 см.
OO1 = O1M + OM = 8 см + 3 см = 11 см.
shkola.in.ua

OM = 7 см, O1M = 5 см, OO1 = OM + O1M = 7 см + 5 см = 12 см.

shkola.in.ua
2) внутрішній дотик. OM = 8 см, O1M = 3 с, OO1 = OM – O1M = 8 см – 3 см = 5 см. 726.

shkola.in.ua

shkola.in.ua

як 2 : 5. OO1 = 12 дм, O1M : OM = 2 : 5. Нехай O1M = 2x, OM = 5x, тоді OO1 = 5x – 2x = 3x; 3x = 12; x = 12 : 3 = 4.
Отже, O1M = 2 ∙ 4 = 8 (дм), OM = 5 ∙ 4 = 20 (дм).
Відповідь: 20 дм, 8 дм.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

як 2 : 3.
Нехай OM = 2x, O1M = 3x.
OO1 = OM + O1M = 2x + 3x = 5x.
За умовою OO1 = 15см.
Отже, 5x = 15; x = 3.
OM = 2 ∙ 3 = 6 (см), O1M = 3 ∙ 3 = 9 (см).
Відповідь: 6 см, 9 см.
728. Відстань між центрами двох кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють: 1) 9 см і 3 см; 2) 5 см і 2 см; 3) 13 см і 1 см; 4) 9 см і 7 см.
Позначимо відстань між центрами кіл O1O2, радіуси кіл r1 і r2.
1) Оскільки 9 см + 3 см = 12 см, тобто O1O2 = r1 + r2, то кола дотикаються (зовнішній дотик кіл).
2) Оскільки 5 + 2 < 12, тобто O1O2 > r1 + r2, то кола не перетинаються.
3) Оскільки 13 см – 1 см = 12 см, тобто O1O2 = r1 – r2, то кола дотикаються (внутрішній дотик).
4) 9 см – 7 см < 12 см < 9 см + 7 см, тобто r1
729. Відстань між центрами двох кіл дорівнює 14 см. Визначте взаємне
1) 7 см і 5 см; 2) 16 см і 2 см; 3) 10 см і 5 см; 4) 7 см і 7 см.
r1 і r2.
1) 7 см + 5 см < 14 см, тобто O1O2 > r1 + r2. Отже, кола не перетинаються.
2) 16 см – 2 см = 14 см, тобто O1O2 = r1 - r2.
3) 10 см – 5 см < 14 см < 10 см + 5 см, тобто r1 – r2 < O1O2 < r1 + r2.
Отже, кола перетинаються.
4) 7 см + 7 см = 14 см, тобто O1O2 = r1 + r2. Отже, кола мають зовнішній дотик.
730. Два кола перетинаються в точках A і B. Точки O1 і O2 центри цих кіл. Доведіть, що O1O2 ⊥ AB.


ΔAO1O2 = ΔBO1A2 (за трьома сторонами (O1A = O1B – як радіуси, O2A = O2B – як радіуси, O1O2 – спільна сторона). З рівності трикутників маємо: ∠AO1O2 = ∠BO1O2 ΔAO1B – рівнобедрений, оскільки O1A = O1B, O1M –бісектриса, отже, O1M – висота, тобто O1M ⊥ AB, а звідси O1O2 ⊥ AB (так як O1O2 містить O1M).
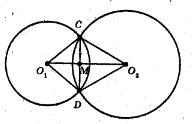
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



shkola.in.ua
Нехай O1O2 = 5 см, O2O3 = 7 см, O1O2 = 8 см.
Нехай O1A = r1, O2A = r2, O2B = r3, тоді
O1O2 + O2O3 + O1O3 = r1 + r2 + r2 + r3 + r3 + r1 = = 2(r1 + r2 + r3).
Тоді r1 + r2 + r3 = O₁O₂+O₂O₃+O₁O₃ 2 = 5+7+8 2 = 10 (см).
r1 = (r1 + r2 + r3) – O2O3 = 10 – 7 = 3 (см); r2 = (r1 + r2 + r3) – O1O3 = 10 – 8 = 2 (см); r3 = (r1 + r2 + r3) – O1O2 = 10 – 5 = 5 (см).
Відповідь: 3 см, 2 см, 5 см.

shkola.in.ua


shkola.in.ua
∠B + ∠A = 90°, звідси ∠A = 90° – ∠B = 90° – 60° = 30°. CB = 1 2 AB = 20 2 = 10 (см) (за
10 см.
що AB + CD = AD + BC.

shkola.in.ua
K, L, M, N
AK = AL, BL = BM, CM = CN, DN = DK.
AK + BM + CM + DK = AL + BL + CN + DN; (AK + DK) + (BM + CM) = (AL + BL) + (CN + DN); AD + BC = AB + CD.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


shkola.in.ua
2(a + b) = 12; a + b = 6; (1)
2(a + c) = 13; a + c = 6,5; (2)
2(b + d) = 16; b + d = 8. (3)
Отримаємо: c – b = 0,5.
c + d = 0,5 + 8 = 8,5. Отже, периметр
2 ∙ 8,5 = 17 (см). Відповідь: 17 см.



shkola.in.ua shkola.in.ua











https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua


1)
2)


shkola.in.ua

shkola.in.ua
3) Проведемо пряму KP. KP шукана пряма.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua
1)
2)
6) AP а, отже, і AK


754.

755.
shkola.in.ua


756.
shkola.in.ua

1)
3)

1)
3) DB = 1 4 BA.


shkola.in.ua
AB
CB
AD = 3 4 AB.
CD
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
757. Побудуйте ∆ABC, якщо AB = 4 см, BC = 6 см, CA = 7 см.

shkola.in.ua

План побудови.
1) AC = 7 см.
2) Дуга з центром у точці A із радіусом AB = 4 см.
3) Дуга з центром у точці C і з радіусом BC = 6 см.
4) Дуги з п. 2) і п. 3) перетинаються у точці В.
5) ∆ABC шуканий.
758. Накресліть довільний ∆ABC і побудуйте ∆ABD такий, що дорівнює трикутнику ABC. План побудови. 1) Дуга з центром у точці А і з радіусом АС.

shkola.in.ua

2) Дуга з центром у точці В і з радіусом BC. 3) Дуги з п. 1) і п. 2) перетинаються у точці D. 4)



shkola.in.ua

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



1) AB довільний
2) Дуга з центром у точці А і
3) Дуга з центром у точці В і
AB.
4) Дуги з п. 2) і п. 3) перетинаються у точці С.
5) ∆ABC рівносторонній і шуканий.
1) KL = а.
2) Дуга з центром у точці K i з радіусом b.
3) Дуга з центром у точці L і

shkola.in.ua
b.
4) Дуги з п. 2) і п. 3) перетинаються у точці М. 5) Рівнобедрений трикутник KLM шуканий.
762. Побудуйте ∆DEF, якщо DE = 6 см, ∠D = 40°, ∠E = 80°. План побудови. 1) DE = 6 см.

shkola.in.ua


shkola.in.ua

2) ∠ADE = 40°.
3) ∠DEB = 80°.
4) Промені DA i EB перетинаються у точці F. 5) ∆DEF шуканий.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
763. Побудуйте ∆NPT, якщо NP = 4 см, ∠N = 50°, ∠P = 100°. План побудови.

764.

shkola.in.ua
1) NP = 4 см.
2) ∠ANP = 50°.
3) ∠BPN = 100°.
4) Промені NA і PB перетинаються у точці Т.
5) ∆NPT – шуканий.
shkola.in.ua


shkola.in.ua



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
A і C.
3) ΔABC шуканий.


shkola.in.ua

766. Побудуйте ∆ABC, якщо AB = 3 см, AC = 5 см, ∠A = 105°.

shkola.in.ua
1) Будуємо кут ∠A = 105°.
2) На сторонах кута відкладаємо відрізки AB = 3 см, AC = 5 см.
3) ΔABC шуканий.
767. Побудуйте ∆KLM, якщо KL = 6 см, KM = 4 см, ∠K = 80°.

768.

shkola.in.ua

shkola.in.ua
1) Будуємо кут ∠K = 80°.
2) На сторонах кута відкладаємо відрізки KL = 6 см, KM = 4 см.
3) ΔKLM шуканий.
1) Будуємо AB = 4 см.
2) Будуємо ∠BAC = 70°.
3) Будуємо ∠BAC = 70°.
4) ΔABC шуканий.

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


771. Побудуйте рівнобедрений
shkola.in.ua shkola.in.ua


772.

AB і AC.
1) Знайдемо
2)

AB
1)
трикутник ABD за катетом BD = 6 2 = 3 (см) і AD = 4 см.
2) На промені BD від точки D відкладаємо DC = 3 см.
3) ΔABC шуканий. Оскільки AD
і медіана трикутника ABC, то трикутник ABC рівнобедрений.



Знайдемо кути при основі △АВС.
За теоремою про суму кутів трикутника:
∠A = ∠B = (180° − 80°) : 2 = 50°
Щоб отримати кут 50° для побудови, проведемо в умові PC⊥CD → ∠PCD = 90°.
Побудуємо бісектрису ∠MCD:
∠KCM = 40°; ∠MCP = 10°
∠KCP = 40° + 10° = 50°
Будуємо △АВС за основою AB і
Сторони кутів A і B перетинаються в т. C.
△АВС шуканий.
774. Побудуйте рівнобедрений трикутник,
100°.

shkola.in.ua shkola.in.ua shkola.in.ua
задано основу рівнобедреного трикутника AB = 6 см і ∠C = 100°.


трикутника.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua



shkola.in.ua


1)
2)
CA.
3) CM бісектриса прямого
бісектрисі CM.
5) Промінь AK перетинає пряму
точці В.
6) ∆ABC шуканий.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



shkola.in.ua

2) На продовженні променя AK відкладаємо
3)


shkola.in.ua

3)
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua




shkola.in.ua

6)
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua

1) На
AB.
2) ∠MAB = ∠A.
3) AL - бісектриса
4) На AL
5) Промінь BK

shkola.in.ua


shkola.in.ua


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

кути 30° і 60°.
1) Накреслити коло;
2) від довільної т. А відкласти радіус; AB = OA; ∠BOA = ∠OBA = ∠BAO = 60°;
3) поділити відрізок AB навпіл: BL = LA; OL медіана, бісектриса і висота; ∠BOL = ∠LOA = 30°. 784.
15°.

shkola.in.ua

1) Накреслити коло; 2) від т. А відкласти OA = AB; ∠BOA = 60°;
3) поділити відрізок AB навпіл: BL = LA; OL медіана, бісектриса і висота; ∠LOA = 30°;
4) поділити кут LOA навпіл: ON бісектриса; ∠NOM = ∠NOL = 15°.
785. Побудуйте без транспортира ∆ABC, у якого:
1) AB = 5 см, ∠A = 60°, ∠B = 45°; 2) AB = BC = 4 см, ∠B = 150°.



1) 1) Накреслити AB = 5 см; 2) із т. А і т. В радіусом циркуля 5 см опишемо дуги і отримаємо т. М; 3) провести промінь AM; ∠MAB = 60°; 4) продовжити відрізок AB і
т.
NB = BK;
5) з точок N і K провести рівні дуги; з'єднати т. L з т. B; LB ⊥ AB; 6) побудувати бісектрису ∠LBN; ∠NBF = ∠FBL = 45°;
7) продовжити відрізок BF до перетину з AM; т. C вершина ΔАСВ.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


2) Якщо AB = BC, то трикутник рівнобедрений.
∠A = ∠C = (180° – 150°) : 2 = 15°.
1) Побудувати рівносторонній трикутник APB;
2) поділити AP і PB навпіл: AM = MP, PN = NB; ∠NAB = ∠MBA = 30°;
3) відкласти AK = AB і BM = AB, з'єднати т. A і т. М, т. B і т. K; 4) поділити KB і AF навпіл: AE = EM, KL = LB; ∠LAB = ∠EBA = 15°; ∠ACB = 150°. ACB шуканий трикутник.
786. Побудуйте без транспортира ∆KMP, у якого:
1) KM = 4 см, ∠K = 30°, ∠M = 45°;
2) KM = MP = 5 см, ∠M = 120°.
1) 1) Накреслити KM = 4 см;
2) побудувати рівносторонній ΔKMF;
3) поділити бісектрису KN (вона також медіана і висота) ⇒ ∠NKM = 30°;
4) продовжити відрізок KM і відкласти від т. М рівні відрізки: CM = MD;
5) з точок C і D провести рівні дуги; з'єднати т. L і т. М; LM ⊥ KM;
6) побудувати бісектрису ∠LMC; ∠CME =



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
FP = KF.


shkola.in.ua
787. Побудуйте рівносторонній трикутник за його медіаною. Нехай задано CK медіану рівностороннього трикутника ABC.


shkola.in.ua



shkola.in.ua

1) Побудувати рівносторонній трикутник ABC, AC вдвічі більша за дану медіану; 2) поділити навпіл AB і BC; 3) позначити точку F – точку перетину медіан і бісектрис.
3) з т. F опустити перпендикуляр на AC і продовжити цей
FK = KN;
4) з'єднати т. N і т. C. FNC шуканий трикутник, KC його медіана.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

1) Нехай у ∆ABC: ∠A = 15°; ∠B : ∠C = 7 : 8.
Позначимо ∠B = 7х; ∠C = 8х.
2) Маємо 15° + 7х + 8х = 180°; 15х = 165°; х = 11°.
Отже, ∠B = 7 ∙ 11° = 77°; ∠C = 8 ∙ 11° = 88°.
3) Найменший із зовнішніх кутів
кутом трикутника. ∠KCA = 180° – 88° = 92°.
Відповідь. 92°.
790. Доведіть, що
кутів, однакової довжини.

shkola.in.ua shkola.in.ua
1) Нехай ∆ABC = ∆A1B1C1; CK і C1K1 бісектриси.

2) Оскільки ∆ABC = ∆A1B1C1, то BC = B1C1; ∠B = ∠B1. 3) Оскільки ∠ACB = ∠A1C1B1 та CK і C

рівних кутів). 4) ∆KCB = ∆K1C1B1 (за другою ознакою). Тому CK = C1K1, що й треба
30°,

shkola.in.ua


∠C = 90°; ∠A = 30°; AB = 60 см; CK –
1) У ∆ABC
2) ∠B = 90° – ∠A = 60°.
3) У ∆CKB: ∠KCB = 180° – (60° + 90°) = 30°. 4)
5) AK = AB – BK = 60 – 15 = 45 (см).
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
792. 1)
S = π ∙ r2 = 3,14 ∙ 15 = 47,1 (м2)
47,1 ∙ 40 = 1884 (л)
2)
35 ∙ 1884 = 65940 (грн). 793.
∠ABC = 120°;





1) ∠ABK = x°; ∠KBC = (x + 20)°; x + x + 20 = 120; 2x = 100; x = 50; x + 20 = 70;
2) ∠KBC = x°;
∠ABK = 3x°; x + 3x = 120; 4x = 120; x = 30; 3x = 90;
3) ∠ABK = 3x°; ∠KBC = 5x°; 3x + 5x = 120; 8x = 120; x = 15; 3x = 45; 5x = 75. Відповідь: КРАВЧУК.
2.


Б) 4 см.

shkola.in.ua shkola.in.ua
16 см; Г. 8 см


shkola.in.ua
shkola.in.ua




shkola.in.ua



shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


7 см
OO1 = 14 см, O1A = x, OA = x + 4.
Тоді x + x + 4 = 14; 2x = 10; x = 5.
Отже, O1A = 5 см, OA = 5 + 4 = 9 (см).
Відповідь: Б). 9. Хорди MN і KL перетинаються в точці A. ∠MKL = 30°, ∠KLN = 70°. Знайдіть градусну міру кута KAM. А. 30°; Б. 70°; В. 80°; Г. 100°


Вписаний кут MKL спирається на хорду ML. Також, на цю хорду, спирається вписаний кут MNL. Отже, ці
кути рівні: ∠MKL = ∠MNL = 30°.
Розглянемо трикутник ANL. В ньому нам відомі градусні міри двох кутів, а сума кутів трикутника рівна 180°. Тому:
∠NAL = 180° - ∠MNL - ∠KLN = 180° - 30° - 70° = 80°.
∠MAL = ∠КАМ як вертикальні кути.
Отже, ∠КАМ = ∠NAL = 80°.
Відповідь: В) 80°.
дорівнює 10 см. А. 10 см; Б. 15 см; В. 20 см; Г. 25 см




Нехай OB = OA = 10 см, ∠MBA = 60°.
З ΔBKM: ∠K = 90°,
∠OMB = 90° – 60° = 30°.
З ΔOMB: ∠B = 90°.
Згідно властивості
навпроти кута 30° маємо:
OM = 2OB = 2 ∙ 10 см = 20 см. Відповідь: В) 20 см.

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


shkola.in.ua
shkola.in.ua
1 – В; 2 – А; 3 – Г.
2.

52 мм.

shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua
shkola.in.ua


shkola.in.ua



shkola.in.ua

shkola.in.ua


shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua


shkola.in.ua
1) Будуємо пряму, позначаємо точку А і
2) Визначаємо кути
3) Будуємо ∠KAB = 65°.
4) Будуємо ∠LBA = 65°.
основі: ∠A = ∠B = 180° – 50° 2 = 65°.
5) Промені AK і BL перетинаються у точці С.
6) ∆ABC шуканий.
AK = AL = 5 см, LB = MB = KC = MC = 2 см.
PΔABC = AB + BC + CA = AL + LB + MB + MC + KC + KA = = 5 + 2 + 2 + 2 + 2 + 5 = 18 (см).
Відповідь: 18 см.
10. З точки A, що
точки дотику, ∠BAC = 60°. Знайдіть радіус
кола дорівнює 8 см.
shkola.in.ua


Нехай AB і AC
(В і
точки дотику), ∠BAC = 60°, OA = 8 см.
ΔABO = ΔACO (за катетом і гіпотенузою: OC = OB – як радіуси кола, OA – спільна
З рівності трикутників: ∠BAO = ∠CAO = 1 2 ∠BAC = 1 2 ∙ 60° = 30°. З прямокутного ΔABO (∠BAO = 30°) маємо: OB = 1 2 OA = 1 2 ∙ 8 = 4 (см). Відповідь: 4 см. 11. Не

shkola.in.ua
3) ∠DAB = 120°.

і C
794.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

795.



shkola.in.ua

797.

AKB, якщо ∠KOB = 130°.

shkola.in.ua

∠AOK = зовнішній кут до кута KOB.
∠AOK = 180° – 130° = 50°.
ΔAOK – рівнобедрений, оскільки OA = OK – як радіуси, тоді ∠OAK = ∠AKO = (180° – 50°) : 2 = 130° : 2 = 65°.
ΔKOB – рівнобедрений, оскільки OK = OB – як радіуси, тоді ∠OKB = ∠OBK = (180° – 130°) : 2 = 25°.
ΔAKB – прямокутний, оскільки
90°. Отже, ∠AKB = 90°. Отже, ∠A = 65°, ∠K

shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

радіусу.


801. AB

Нехай AB = BC = OC = OA, тоді ΔAOB і ΔBOC – рівносторонні.
∠A = ∠AOB = ∠ABO = 60°, ∠C = ∠OBC = ∠OCB = 60°.
∠ABC = ∠ABO + ∠OBC = 60° + 60° = 120°.
Відповідь: 120°.
90°.
∠KAB = x°, тоді ∠KBA = 4x°. x + 4x = 90°; 5x = 90°; x = 18.
Отже, ∠A = 18°, ∠B = 18° ∙ 4 = 72°.
Відповідь: 18°, 72°, 90°.
трикутника MON.


Нехай ОК = АК, MN ⊥ OA.
З ΔOMK: ∠OMK = 30°, оскільки OK = 1 2 OM.
ΔMON – рівнобедрений, оскільки OM = ON – як радіуси, тоді ∠ONM = ∠OMN = 30°, ∠MON = 180° – ∠ONM – ∠OMN = 180° – 30° – 30° = 120°.
Отже, в ΔMON ∠MON = 120°, ∠OMN = 30°, ∠MNO = 30°. Відповідь: 30°, 30°, 120°. 803.


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

805. Нехай OK
і кола, якщо: 1) OK = 12 см, r = 14 см; 2) r = 7 см, OK = 70 мм; 3) OK = 2 дм, r = 18 см; 4) r = 32 мм, OK = 0,3 дм?

shkola.in.ua
806.


shkola.in.ua


1) Пряма p перетинає коло, оскільки OK < r, 12 см < 14 см.
2) Пряма p дотикається до кола, оскільки OK = r, 7 см = 70 мм.
3) Пряма p
2 дм > 18 см.
оскільки OK > r,
4) Пряма p перетинає коло, оскільки OK < r, 0,3 дм < 32 мм.
shkola.in.ua

shkola.in.ua

AM = AN – за умовою).
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua

812.
Нехай BD і CK медіани, O центр кола, вписаного в ΔABC. Оскільки O точка
то BD і CK бісектриси, медіани і висоти, а бісектриси, медіани
shkola.in.ua



Нехай ΔABC рівнобедрений (AB = CB), E, F, D – точки
дотику.
За умовою EA : EB = 2 : 3. Нехай EA = 2x, EB = 3x.
Враховуючи рівність
точки до кола, маємо:
PΔABC = AB + BC + CA = (2x + 3x) + (3x + 2x) + (2x + 2x) = 14x.
За умовою P = 70 см, отже, 14x = 70 см, x = 5 см.
Тоді AB = BC = 2x + 3x = 5x = 5 ∙ 5 = 25 (см), AC = 2x + 2x = 4x = 4 ∙ 5 = 20 (см).
Відповідь: 25 см, 25 см, 20 см. 813. Накресліть

shkola.in.ua shkola.in.ua shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

AC.
815. Доведіть, що центр кола, описаного навколо рівностороннього трикутника, збігається із
shkola.in.ua


817.
shkola.in.ua

shkola.in.ua


shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua

shkola.in.ua


shkola.in.ua

∠АВС = 30° вписаний, ◡АС = 2∠АВС = 60°. ∠АОС центральний, ∠АОС = ◡АС = 60°. △АОС рівносторонній (АО = ОС, ∠АОС = 60°,
ОАС = ∠ОСА = 60°). Отже,
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


823.
shkola.in.ua
2) перетинаються.

shkola.in.ua

824.
shkola.in.ua
3 см, 8 см і 3 см.
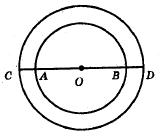
shkola.in.ua
1) AB = 4 см. Кола не перетинаються.
2) AB = 4 см. Кола перетинаються.
CA = 3 см, AB = 8 см, BD = 3 см.
AO = AB : 2 = 8 см : 2 = 4 см.
CO = CA + AO = 3 см + 4 см = 7 см. Відповідь: 4 см, 7 см. 825.

shkola.in.ua

якщо AB = 12 см. Нехай OB = 10x, OA = 7x.
AB = OB – OA = 10x – 7x = 3x.
За умовою 3x = 12 см, x = 4 см.
Тоді OB = 10 ∙ 4 = 40 (см),
OA = 7 ∙ 4 = 28 (см).
Відповідь: 40 см, 28 см.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

827.

кіл, якщо вони відносяться як 5 : 3. Розгляньте

shkola.in.ua

shkola.in.ua
828.
I випадок. Кола
зовнішній дотик.
Нехай O1K = 5x, OK = 3x,
тоді 5x + 3x = 16;
8x = 16; x = 2.
Отже, O1K = 5 ∙ 2 = 10 (см), OK = 3 ∙ 2 = 6 (см).
Відповідь: 10 см, 6 см.
II випадок. Кола мають внутрішній дотик.
Нехай OK = 5x, O1K = 3x.
Тоді O1O = OK – O1K = 5x – 3x = 2x; 2x = 16; x = 8.
Отже, OK = 5 ∙ 8 = 40 (см), O1K = 3 ∙ 8 = 24 (см).
Відповідь: 40 см, 24 см.

shkola.in.ua

shkola.in.ua shkola.in.ua



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

832.
shkola.in.ua

1)
shkola.in.ua



shkola.in.ua

shkola.in.ua

shkola.in.ua
точок K, L, M, N, F, E;
3) з'єднати т. A з т. P, т. B з т. D, т. C з т. Q і продовжити ці
∠A тупий.
1) Довільним радіусом провести дуги з т. A; 2) довільним радіусом провести
з т. B і т. C; з'єднати т. A і т. D; ∠BAD = ∠DAC; 3) радіусом AB = AC провести дугу з т. A, що перетинає AD; 4) довільним радіусом провести
з точок B і F, F і C; 5) з'єднати т. A з т. M, т. A з т. N; ∠BAM = ∠MAD = ∠DAN = ∠NAC = 1 4 ∠BAC ⇒ ∠BAM = 1 4 ∠BAC, ∠MAC = 3 4 ∠BAC.
1) На сторонах кута A позначимо точки B і C; з'єднаємо їх; 2) побудуємо ΔOMN =
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



shkola.in.ua
AB = AC, ∠A = 90° ⇒ ∠B = ∠C = 45°; AK ⊥ BC; BK = AK = KC.
1) Накреслити BC; 2) поділити BC навпіл і провести через т. K
перпендикуляр; 3) відкласти KA = KB = KC; 4) з'єднати т. A з т. B і т. C. ΔABC є шуканим.
кутом.





shkola.in.ua
1) Накреслити катет AB; 2) на сторонах ∠B провести
та позначити точки M і N; 3) по трьом сторонам
побудувати ΔBFK = ΔBMN; BF = BN, BK = BM, FK = MN; продовжити промінь BK; 4) від точки A
відрізки AE = AL; з точок E і L
радіусом провести дуги; 5) з'єднати т. D з т. A і продовжити промінь AD; точка
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

839.


AB < AC; ∠C = α.
1) Накреслити відрізок AC;
2) Побудувати ∠C = α;
3) з т. A провести дугу радіусом AB. Точки B1 і В2 вершина трикутників AB1C і AB2C, які є шуканими.

1) Знайдемо кути B i C
NT. Тоді ∠LNT= ∠B = ∠C.


shkola.in.ua

LNM



shkola.in.ua

2) NP – бісектриса кута ∠LNT. Тоді ∠PNL = ∠KBC.
3) ∠KBC = 180° – (∠C + ∠KBC). Для побудови кута BKC
∠C і ∠KBC; ∠DEF = ∠C; ∠DEG = ∠KBC. Тоді ∠GEH = ∠BKC.
4) Будуємо ∠KBC за стороною і
5) ∠KBQ = ∠CBK.
6) CK і BQ перетинаються
7) ∆ABC – шуканий.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua


shkola.in.ua
shkola.in.ua


shkola.in.ua
shkola.in.ua


3)
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

Нехай ΔABC рівнобедрений, AB = BC = 9 см, PΔABC = 24 см, тоді AC = PΔABC – (AB + BC) = 24 – (9 + 9) = 24 – 18 = 6 (см).
Відповідь: 6 см.
6. Дано: DC = MN, ∠CDN = ∠DNM . Довести: ΔCDN = ΔMND.

shkola.in.ua
shkola.in.ua
ΔCDN = ΔMND за першою ознакою рівності трикутників, оскільки DC = MN за умовою, ∠CDN = ∠DNM за умовою, DN спільна сторона.
7. Один з кутів трикутника дорівнює 68°, а другий на 14° більший
невідомі кути трикутника.

shkola.in.ua
Нехай ΔABC даний трикутник, ∠B = 68°.
Нехай ∠A = x°, тоді ∠C = x° + 14°.
∠A + ∠B + ∠C = 180°, x + 68° + x + 14° = 180°; 2x = 98°; x = 49°.
Отже, ∠A = 49°, ∠C = 49° + 14° = 63°.
Відповідь: 49°, 63°.
8. Побудуйте ΔABC, якщо AB = 6 см, AC = 3 см, ∠A = 50°. 1) Будуємо кут А. 2) На одному з променів відкладаємо АВ, на іншому АС.





3) З’єднуємо точки В і С. ΔABC –шуканий.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
29 : 25.



AB.
1) BK = 3AK; 2) BK ≥ 3AK.

2. ∠AOB = 120°.

Нехай у прямокутному трикутнику ABC (∠C = 90°) ∠A = x°, тоді ∠B = 90° x°.
За властивістю суміжних кутів ∠PAB = 180° – x°, ∠RBA = 180° – (90° – x°) = 90° + x°.
За умовою задачі маємо: 180° x 29 = 90°+x 25 , звідси 4500 – 25x = 2610 + 29x; 54x = 1890; x = 35.
Отже, ∠A = 35°, ∠B = 90° – 35° = 55°.
Відповідь: 35°, 55°. Задачі підвищеної
KOB = 10°.


3. Скільки

1) т. K; 2) відрізок AK.
Нехай ∠AOK = x.
Тоді ∠KOB = 120 – x.
3x – 2(120 – x) = 10;
3x – 240 + 2x = 10;
5x – 240 = 10; 5x = 250; x = 50.
∠AOK = 50°; ∠KOB = 70°.










shkola.in.ua

shkola.in.ua

5. Точки A, B і C належать прямій a, причому

що AC < 1,9AB. Порівняйте довжини відрізків BC і AB. Нехай AB = x. Тоді AC < 1,9x.

BC = AC – AB;
BC < 1,9x – x;
BC < 0,9x;
BC < 0,9AB.
6. На малюнку: ∠AOC − ∠BOD. OL і OP
кути: 1) AOL і COP; 2) LOP і AOC.
shkola.in.ua


∠AOD і ∠COB.
1) ∠COB = ∠AOB – ∠AOC; ∠AOD = ∠AOB – ∠BOD ⇒ ∠COB = ∠AOD.
OL, OP бісектриси ⇒ ∠AOL = ∠COP. 2) ∠LOP = ∠AOB – ∠AOL – ∠POB = ∠AOB – 2∠AOL. ∠AOC = ∠AOB – ∠COB = ∠AOB – 2∠COP ⇒ ∠LOP = ∠AOC.





shkola.in.ua



shkola.in.ua



1) 1 3 x + 5 6(180 – x) = 90; 2x + 900 – 5x = 540; 3x = 360; x = 120; α = 120°; 2) 1 3 x + 5 6x = 90; 2x + 5x = 540; 7x = 540; x = 771 7; α = 771° 7 .

shkola.in.ua


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


14.
перпендикулярні прямі?
27° ∙ 10 = 270°; 360° – 270° = 90°.
Відповідь: так.
15. Знайдіть градусну
16.


Нехай α = x. 2,6x = x + 180 – x + 180 – x; 2,6x = –x + 360; 3,6x = 360; x = 100.
Відповідь: 100°; 100°; 80°; 80°.
a + b + c a = 10, a + b + c b = 13, a + b + c – c = 9; �b + c = 10, a + c = 13, a + b = 9; 2a + 2b + 2c = 32; a + b + c = 16. P = 16 см.
17. Точки M і N середини сторін AB і AC трикутника ABC, AB = AC,

⊥
⊥ AC. Доведіть, що ∠NLK = ∠MKL. AM = 1 2 AB = 1 2AC = AN; ∠A спільний; ∠AMK = ∠ANL = 90° ⇒ ΔAMK = ΔANL ⇒ MK = NL. ΔMLK і ΔNLK: MK = LN; ∠LMK = ∠LNK = 90°; LK спільна сторона ⇒ ΔMLK = ΔNLK ⇒ ∠NLK = ∠MKL.

18.



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
ΔABC = ΔCDA, AB = CD = 40 см, BO = DO = 10


Нехай AC = x.
Тоді AB + BO + OC + AC = 40 + 10 + x + 30 + x = 100; 2x + 80 = 100; x = 10.
AC = 10;
AO = 40 – OC.
PΔAOC = 10 + 40 + 40 = 90 (см).
20. ΔABC рівнобедрений з основою AB. Медіани AA₁ і BB₁ продовжено
B₁

відрізки A₁K і B₁L відповідно так, що A₁K = AA₁ і B₁L = BB₁. Доведіть, що ∠ALC =


ΔAB1B = ΔAA1B: AB спільна; AB1 = BA1; ∠A = ∠B ⇒ ΔAB1B = ΔAA1B ⇒ AA1 = BB1, BL = AK.
ΔABL = ΔABK: AB спільна; BL = AK; ∠A1AB = ∠B1BA ⇒ ΔABL = ΔABK; AL = BK.
∠LAB = ∠KBA, ∠LAC = ∠KBC ⇒ ΔALC = ΔBKC.
21. Доведіть, що з точки перетину
кутом.



∠A + ∠C < 180° ⇒ ∠OAC + ∠OCA < 90° ⇒
∠AOC > 90°. 22. Дві сторони





1) Нехай AB = A1B1; BC = B1C1 і BM = B1M1, де BM і B1M1 медіани трикутників ABC і A1B1C1. 2)
3)
AM
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
4) ∆ABD = ∆A1B1D1 (за третьою
5) ∆ABM = ∆A1B1M1 (за першою ознакою), тому AM = A1M1, а
6) Отже, ∆ABC = ∆A1B1С1 (за трьома сторонами), що й треба було
24. Визначте вид
Трикутник гострокутний.
2) кожний з кутів менший від
Трикутник гострокутний 25. У трикутнику ABC кут C прямий. Сторону AB трикутника




shkola.in.ua

1) Позначимо ∠CAD = ∠DAB = х.


2) CP серединний перпендикуляр і висота ∆ABC. Тому АР висота ∆ADO.
3) Оскільки висота ∆ADO є також і медіаною, то AD = AO, а тому AP також і бісектриса
∆ADO. Маємо ∠OAP = х.
4) OA = OC (як радіуси), тому
∠OCA = ∠OAC = 3х.
5) Але в ∆ACP: ∠C = 90° – 2х.
Маємо 3х = 90° – 2х; 5х = 90°; х = 18°.
6) Отже, ∠CAB = ∠CBA = 2 ∙ 18° = 36°; ∠ACB = 180° – 2 ∙ 36° = 108°.
Відповідь: 36°; 36°; 108°.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
AC і BD

що AB > AC. Доведіть, що BD > CD.
ΔABC: AB > AC ⇒ ∠BCA > ∠ABC.

∠CBD < ∠ABC, ∠BCD > ∠BCA ⇒ BD > CD.
28. У трикутнику ABC AB > AC, AM медіана. Доведіть, що ∠CAM > ∠MAB.


shkola.in.ua

1) Продовжимо медіану AM за точку M на довжину AM, отримаємо точку D.
2) ∠CMD = ∠AMB (як вертикальні). Тому ∆CMD = ∆BMA (за першою ознакою). Тому ∠CDM = ∠MAB i CD = AB.
3) Оскільки AB > АС, то й CD > АС.
4) У ∆CAD: CD > АС, а тому ∠CAD > ∠CDA. Тому ∠CAM > ∠MAB, що й треба було довести.
29. Усередині рівностороннього трикутника ABC узято довільну точку K. Доведіть, що AK < BK + KC.

shkola.in.ua

1) ∠KAC < 60°; ∠KCA < 60°, тому ∠AKC > 60° і у ∆AКC кут AKC є найбільший. А отже, AC > AK.
2) У ∆BKC за нерівністю трикутника: BK + KC > BC. 3) Оскільки AC = BC і AC > AK і BK + KC > BC, то AK < BK + KC, що й треба було довести.

shkola.in.ua


1) Позначимо ∠B = х, тоді ∠A = 2х.
Тоді х + 2х = 90°; 3x = 90°; x = 30°.
2) Отже, ∠B = 30°, а тому AC = �������� 2
3) Позначимо AC = у (см), тоді AB = 2у см. За умовою у + 2у = а;
3у = а; у = ���� 3 (см).
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
гіпотенузи, то R = 2���� 2 = у = ���� 3 (см).
Відповідь: ���� 3 см.
31. У трикутнику ABC ∠C = 90°, ∠B = 40°. На сторонах AB і BC позначено точки K і L
так, що ∠LAK = 5°, ∠LCK = 10°. Знайдіть ∠LKC.








1) ∠BAC = 90° – ∠B = 50°.
2) ∠LAC = 50° – 5° = 45°.
3) ∠KCA = 90° – 10° = 80°.
4) У ∆CKA – ∠CKA = 180° – (80° + 50°) = 50°, тому ∆CKA рівнобедрений і CK = CA.
5) ∠CLA = 90° – 45° = 45°; тому ∆CLA –рівнобедрений і CL = CA.
6) CK =CA і CL = CA, тому CK = CL; тобто ∆CLK рівнобедрений і ∠LKC = ∠CLK = 180° – 110° 2 = 85°.
Відповідь: 85°.
= CA₁. Знайдіть ∠C.
1) За умовою AA1 ⊥ BC; BB1 ⊥ AC; AA1 = BB1 і AB1 = CA1.
2) ∆ABB1 = ∆CAA1 (за двома катетами), тому AB = CA, ∠ABB1 = ∠CAA1 і ∠C = ∠BAB1.
3) Оскільки ∠C = ∠BAB1, то ∆ABC рівнобедрений
AB = BC.
4) AB = CA і AB = BC, тому AB = CA = BC; ∆ABC рівносторонній; ∠C = 60°.
Відповідь: 60°.
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


1) Нехай ∆ABC рівнобедрений; ∠ACB = 120°; AC = CB = а (см); точка O центр
∆ABC.
2) OC серединний перпендикуляр до AB, а тому CD висота ∆ABC.
3) ∆ABC рівнобедрений з основою AB, тому CD є також і бісектрисою; ∠OCB = 120 2 = 60°.
4) OC = OB (як радіуси), тому ∆OCB рівнобедрений і ∠OBC = ∠OCB = 60°.
5) ∠СОВ = 180° – 2 ∙ 60° = 60°.
6) ∆COB рівносторонній; OC = CB = а см. Відповідь: а см.
35. AM і AN дотичні до кола, AM = m см. Пряма BC дотикається
периметр трикутника ABC. За властивістю відрізків

shkola.in.ua

з однієї точки, маємо AN = AM = m cм, BM = BK і CK = CN.
Нехай P см периметр трикутника ABC.
Тоді P = AB + BC + CA = AB + BK + KC + CA = AB + BM + CN + CA = (AB + BM) + (АС + CN) = AM + AN = m + m = 2m (см).
Відповідь. 2m см. 36.

shkola.in.ua
1) Нехай периметр ∆ОО1О2 = 20 см і R см радіус великого

2) Нехай K i L – точки
3) P∆OO1O2 = OO1 + OO2 + O1O2 = (OK – KO1) + (OL –L) + O1O2 = R – r + R – r + 2r = 2R.
4) Маємо 2R = 20; R = 10 (см).
Відповідь: 10 см.




shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
5) AK = AC – KC = b – r; BL = BC – CL = а – r.
6) Маємо AM = AK = b – r ; BM = BL = а – r.
7) AB = AM + MB;
c = b – r + a – r;
2r = a + b
shkola.in.ua








∆O2M2P – рівнобедрений.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html




1)

2)
3)





https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


44. Побудуйте точку, яка


shkola.in.ua

1) Побудуємо відрізок BK⊥а; BO = OK.
2) Пряма AK перетинає пряму а у точці С.
3) CO висота і медіана ∆BKC; тому ∆BKC рівнобедрений. Отже, CO бісектриса кута ACB; тобто пряма а містить бісектрису трикутника ABC.
1) Шукана точка точка перетину серединного перпендикуляра


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html











https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua






shkola.in.ua





shkola.in.ua

точок, рівновіддалених від кінців цього відрізка. Отже, пряма, що містить висоту (і водночас медіану, бісектрису) до
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua



shkola.in.ua


1) n ⊥ m; n і m перетинаються в
точці O; 2) Від точки K відкладаємо на прямій n два відрізки довжиною а см: OM = ON = а см;
3) Через точки M і N проводимо прямі b і с, кожна з яких перпендикулярна до n. Прямі b і с
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua



shkola.in.ua





https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html



shkola.in.ua

shkola.in.ua




shkola.in.ua

1) Накресліть
паралельні прямі (a i b).
2) Знайдіть середину
(побудувати пряму n⊥а і n⊥b, М – середина відрізка AB).
3) Проведіть пряму,

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua




shkola.in.ua


shkola.in.ua


https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua
shkola.in.ua

shkola.in.ua
shkola.in.ua


shkola.in.ua

shkola.in.ua





https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua

shkola.in.ua

shkola.in.ua



shkola.in.ua



https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html
1)
2)
4) ∆AB1C і ∆AB2C шукані.







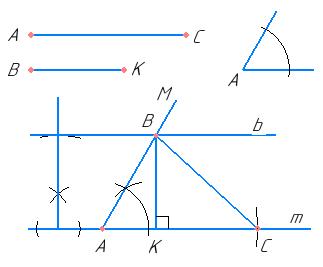
shkola.in.ua
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html

shkola.in.ua








цієї сторони. Нехай АС сторона трикутника, BL –висота, проведена до АС, r – радіус




описаного кола.
1) Будуємо рівнобедрений ∆OAC за стороною АС та радіусом r;
2) Будуємо коло радіусом r з центром у
точці О;
3) Будуємо серединний перпендикуляр відрізка АС;
4) З точки перетину відрізка АС

5) будуємо пряму m, що проходить
К;
6) пряма
7) будуємо BL⊥АС; 8) ∆ABC шуканий трикутник.


shkola.in.ua

https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua



1) Нехай AB основа рівнобедреного трикутника. Тоді P∆АВС – AB = 18 (см).
2) Але P∆АВС – AB = AC + CB. Оскільки AC = CB, то AC = CB = 18 2 = 9 (см).
Відповідь: так, 9 см.
1) Нехай ∠ABL = 120° зовнішній кут ∆ABC, у якого ∠C = 90°.
2) ∠ABC = 180° – 120° = 60°.
3) ∠A = 90° – 60° = 30°.
4) 3а властивістю

shkola.in.ua


∠O1AO2 = 60°; ∠AO1B = 120°.
1)
радіус кола із центром у точці O1 дорівнює r.
2) Тоді O1O2 = r, і коло, центром якого є точка O2 також має радіус r.
3) В ∆O1AO2: O1O2 = O1A = O2A = r. Тому AO1O2 рівносторонній, і ∠O1AO2 = 60°.
4) ∠AO1O2 = ∠O2O1B = 60°.
Тому ∠AO1B =120°.
https://shkola.in.ua/2218-hdz-heometriia-7-klas-ister-2015.html


shkola.in.ua

shkola.in.ua

1) За умовою ad = 6; ab = 16; cd = 15; bc = x (див. схему).
2) Оскільки ad = 6 і bс = х, то abcd = 6х.
3) Оскільки ab = 16 і cd = 15, то abcd = 16 ∙ 15; abcd = 240.
4) Тому 6х = 240; х = 40.
Відповідь. 40.
