https://shkola.in.ua/2406-hdz-heometriia-8-klas-merzliak-2016.html







QY ⊥ XW
сторін, протилежних вершин. Запишіть які-небудь три позначення цього чотирикутника.

Сусідні сторони: MK і KE, KE і EF, EF і FM, FM і MK.

Протилежні сторони: MK і EF, KE і MF. Протилежні вершини: M і E, K і F.
Позначення чотирикутника: MKEF, KEFM, EFMK.






https://shkola.in.ua/2406-hdz-heometriia-8-klas-merzliak-2016.html


Позначення чотирикутника: MKCA, KCAM, CAMK.
1) M, K, C, A;
2) MK, KC, CA, AM;
3) M і K, K і C, C і A, A і M;
4) M і C, K і A;
5) MK і KC, KC і CA, CA і AM, AM і MK;
6) MK і AC, MA і KC;
7) MC і KA. 6.

є чотирикутники MKEF, STOP, QLNR.



https://shkola.in.ua/2406-hdz-heometriia-8-klas-merzliak-2016.html



+
5x − 20° = 360°;
5x = 380°;
D = 76° 40° = 36°
Відповідь: 76°, 152°, 96°, 36° .

A : ∠B : ∠C : ∠D = 10 : 21 : 2 : 3.


shkola.in.ua

x + (x 2) + (x + 6) + 3x = 64;
6x + 4 = 64;
6x = 60;
x = 10.
— 10 + 6 = 16 (см), четверта — 3 ⋅ 10 = 30 (см
Відповідь: 10 см; 8 см; 16 см; 30 см.


https://shkola.in.ua/2406-hdz-heometriia-8-klas-merzliak-2016.html


що сторони CD і AD теж рівні. Нехай у чотирикутнику ABCD:
AB = BC, ∠ABD = ∠CBD, BD — діагональ.
Розглянемо трикутники ABD і CBD. У них:
1) AB = BC за умовою;
2) ∠ABD = ∠CBD за умовою;
3) BD — спільна сторона.
Отже, △ABD = △CBD за двома сторонами і кутом між ними (за I ознакою рівності трикутників).
Тому AD = BC = 6 см як відповідні елементи рівних трикутників.
Відповідь: 6 см. 17. Діагоналі чотирикутника


у чотирикутнику ABCD: AO = OC, BO = OD, BC = 6 см.
Розглянемо трикутники AOD і COD. У них:
1) AO = OC за умовою; 2) BO = OD за умовою;
3) ∠AOD = ∠COB як вертикальні.
Отже, △AOD = △COB за двома сторонами і кутом
ними (за I ознакою рівності трикутників).
Тому AD = BC = 6 см як відповідні елементи рівних трикутників.
Відповідь: 6 см.
18. У чотирикутнику MNKP відомо, що MN = NK, MP = PK, ∠M = 100°. Знайдіть кут K. Нехай у чотирикутнику MNKP: MN = NK, MP = PK, ∠M = 100° Добудовуємо діагональ PN.


Розглянемо трикутники NMP і NKP. У них:
1) MN = NK за умовою; 2) MP = PK за умовою;
3) PN — спільна сторона.
Отже, △NMP = △NMP за трьома сторонами
Тому ∠K = ∠M = 100° як відповідні елементи рівних трикутників.
Відповідь: 100° .
https://shkola.in.ua/2406-hdz-heometriia-8-klas-merzliak-2016.html
ABCD.
shkola.in.ua
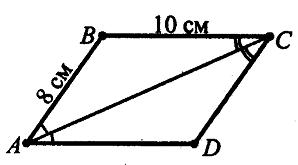
AB = 8 см, BC = 10 см.
Нехай у чотирикутнику ABCD:
∠BAC = ∠CAD, ∠BCA = ∠ACD, AB = 8 см, BC = 10 см. Розглянемо трикутники ABC і ADC. У них:
1) ∠BAC = ∠CAD за умовою; 2) ∠BCA = ∠ACD за умовою;
3) AC — спільна сторона.
Отже, △ABC = △ADC за стороною і двома прилеглими до
неї кутами (за I ознакою рівності трикутників).
Тому AB = CD = 8 см, BC = AD = 10 см як відповідні
елементи рівних трикутників.
Тоді PABCD = AB + BC + CD + AD = 8 + 10 + 8 + 10 = 36 (см).
Відповідь: 36 см.
20. У трикутнику ABC відомо, що ∠A = 44°, ∠B = 56°. Бісектриси кутів AK і BM

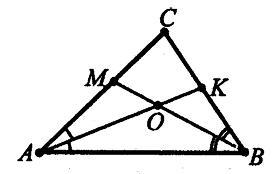
AK — бісектриса
CAB, то
MAO = ∠OAB = 44° : 2 = 22°.
Аналогічно ∠KBO = ∠OBA = 56° : 2 = 28°.
Розглянемо трикутник AOB. У ньому ∠OAB + ∠AOB + ∠OBA = 180°;
∠AOB = 180° (∠OAB + ∠OBA);
∠AOB =180° (22° + 28°) = 180° − 50° = 130°.
∠AOB і ∠MOK — вертикальні, тому ∠AOB = ∠MOK = 130°.
Розглянемо трикутник AKC.
У ньому ∠CAK + ∠AKC + ∠KAC = 180°;
∠AKC = 180° − (∠CAK + ∠KCA);
∠AKC = 180° − (22° + 80°) = 180° − 102° = 78°.
Розглянемо чотирикутник MOKC.
За теоремою про суму кутів чотирикутника
∠OMC + ∠MCK + ∠CKO + ∠KOM = 360°;
∠OMC = 360° (∠MCK + ∠CKO + ∠KOM);
∠OMC = 360° (80° + 78° + 130°) = 360° 288° = 72°.
Відповідь: 72° , 80° , 78° , 130° .
2) розглянемо чотирикутник AOBC. За
∠AOB + ∠OBC + ∠BCA = 360°;
∠AOB = 360° (∠CAO + ∠OBC + ∠BCA);
∠AOB = 360° (22° + 28° + 80°) = 360° 130° = 230°;
Відповідь: 22°, 230°, 28°, 80° .

