
mat e mat i k l ær e rv ej le d ning/web
helle nicola je n se n · be n t lindh ardt marie t egl h us møller aline a
1a
KonteXt+ 1a, Lærervejledning/web
© Alinea 2014
Forfattere: Helle Nicola Jensen, Bent Lindhardt, Marie Teglhus Møller
Ekstern redaktør: Bent Lindhardt
Redaktion: Susanne Schulian
Design: Susanne Gamsgaard og Jesper Frederiksen
Omslagsdesign: Jytte West og Jesper Frederiksen
Illustrationer: Jesper Frederiksen
Trykt hos: ScandinavianBook
1. udgave, 10. oplag 2022
ISBN: 9788723508058
ISBN overnummer: 9788723523792
Svanemærket tryksag 5041 0826
Scandinavian Print Group
Kopiering fra denne bog må kun finde sted på institutioner, der har indgået aftale med Copydan Tekst & Node.
Alinea støtter børn og unge
Alinea er en del af Egmont, der som Danmarks største mediekoncern har bragt historier til live i mere end 100 år. Egmont er en dansk fond, som hvert år uddeler 150 millioner kroner til børn og unge, der har det svært.
alinea.dk
Indhold
4Elementer i KonteXt+
6Fra KonteXt til KonteXt+
8Om www.kontextplus.dk
10Læringshjulet
12Anbefalinger til undervisningen
15Om forenklede Fælles Mål
17Om Familien Tal
19Tal og tælling
41Figurer og retning
59Tal i system
83 Plus
Elementer i KonteXt+


KonteXt i 1. klasse består af:




•1a og 1b Elevbøger/web
•1a og 1b Lærervejledninger/web
•1a og 1b Tavlebøger
•Skrivehæfte
•www.kontextplus.dk
Elevbog/web
Elevbøgerne er engangsbøger på 72 sider. Det er elevernes fællesbog, som indeholder kernestoffet til matematikundervisningen i 1. klasse.
Elevbog A og B består hver af fire selvstændige faglige hovedemner. Hvert af disse faglige hovedemner er selvstændige matematiske forløb struktureret efter læringshjulet – se senere.
Elevbog a Elevbog b
Tal og tælling Tal
Figurer og retningMønstre og tegning
Tal i system Minus
Plus Måling
Ved køb af elevbog får eleverne adgang til forskellige materialer på www.kontextplus.dk, se næste opslag.
Tavlebog
Elevbogen udgives også som tavlebog, der er et selvstændigt materiale. Det er en pdf-udgave af bogen til brug på IWB.
Skrivehæftet er et engangshæfte på 32 sider, som skal hjælpe eleverne til at udvikle en letlæselig talskrivning. Hvert opslag er fremstillet som en undervisningssekvens med motoriske øvelser samt øvelser i talskrivning.
Skrivehæfte
har primært fokus på give eleverne erfaringer og oplevelser, så færdigheder, eleverne skal tilegne sig. indeholder fire faglige stofområder. Hvert stofområde har Tal på de yngste årgange), som trækker faglige pointer frem en problemløsende som færdighedsopgaver, der uddybes Geogebra, tilknyttede test (EVA-ark). ekstraark den tilhørende kopimappe Her findes også arbejdsark til QR kode nederst på siderne – som er små korte forklaringer til www.matematik.dk/kontext er udbygget med flere ideer, mere elevbogen, får eleverne adgang til arbejdsark, applets, GeoGebra-filer, og Elevbog/web B www.matematik.dk/kontext 1a matematik elevbog helle nicola je matematik elevbog 1a alinea LENE LUNDGAARD DINESEN SKRIV TAL ALINEA 4 elementer i kontext+
Lærervejledning/web



Lærervejledningerne falder i to dele: De praktiske, faglige og pædagogiske problemstillinger, som ligger bag systemet, og en side til side-vejledning, som grundigt kommenterer hvert af de fire faglige hovedemner. Side til side-vejledningen består af •Et opslag, som gennemgår det faglige grundlag for kapitlet, herunder en klar reference til de forenklede Fælles Mål.
•En grundig gennemgang af hvert af de fire værksteder.
•Familien Tal-historier til oplæsning med tilhørende klassespørgsmål.
•Forslag til klassesamtale og intro-aktiviteter, som kan spore eleverne ind på det faglige stofområde.
•Gennemgang af elevbogens opgaver og de tilhørende arbejdsark fra webdelen.
•Mange gode ideer og supplerende aktiviteter (findes på www.kontextplus.dk).
•Ved køb af lærervejledning/web får læreren adgang til de forskellige materialer på www.kontextplus.dk – se næste opslag.
KonteXtplus.dk


Der er et tilhørende website, der følger bogens kapitler. Under hvert er indholdet bygget op som i bogen.
Websitet indeholder forældrefilm, værkstedsfilm, oplæsning af Familien Tal historierne, værksteds- og arbejdsark, GeoGebrafiler, regnearksfiler, aktiviteter og spil. Særligt til læreren er der en materialeliste over de anvendte konkrete materialer, facitliste, EVA ark, vejledning til EVA arkene samt en samlet pakke til hvert kapitel af filer til henholdsvis, arbejdsark, GeoGebrafiler og alle Aktiviteter og spil samlet i en fil. Da websitet er dynamisk, er det en god ide at orientere sig på websitet.
Øverst til højre i menulinjen finder man forslag til årsplaner og læringsmål med tegn på læring.

elementer i kontext+ 5
1a
matematik lærervejledning/web us møller
Fra KonteXt til KonteXt+

KonteXt+ følger op på KonteXt og forstærker principperne for god matematikundervisning. Grundlaget er stadig tankerne bag RME – Realistic Mathematic Education – som er udviklet og videreudviklet af Freudenthal-instituttet i Holland gennem mange år. Principperne er sat ind i en dansk ramme med respekt for de traditioner, der er for matematikundervisning i Danmark.
Fra hverdagen ind i matematikkens verden
Systemets navn er ikke tilfældigt. KonteXt+ tager udgangspunkt i, at matematik er lettest at forstå, når den opleves i en sammenhæng, som eleverne kender eller nemt kan indleve sig i. Hver af de faglige pointer, der præsenteres, tager derfor udgangspunkt i historier, som kunne have foregået i elevernes omverden. I 1. klasse bruger vi bl.a. værkstederne og historierne om Familien Tal til at give eleverne indsigt og erfaringer i de matematiske emner.
Målstyret undervisning
Der er styr på de faglige mål i KonteXt+. Hvert hovedemne og hvert delforløb har tydelige og klare faglige målsætninger, idet der er særlige faglige pointer, man inviteres til at fordybe sig i. Dette gør det lettere at orientere undervisning mod læringsmål.
Det er vigtigt, at eleverne forstår de faglige pointer
Man kan nogle gange foranledige sig til at tro, at elever har forstået noget, når de kan gengive viden og udføre visse færdigheder. Det lærte kan dog hvile på et meget skrøbeligt fundament, som ikke fungerer, når situationen ændrer sig. I KonteXt+ gøres der meget ud af at komme ind til den centrale matematik, så eleverne får lejlighed til at skabe mentale billeder af, hvordan tingene hænger sammen. Der gives derfor god tid til faglig fordybelse, men også til gentagelsen inden for hvert kapitel. Der er en varieret mængde opgaver, som kommer godt rundt i emnet.
Den sproglige dimension indgår som et centralt element. Vi opfatter sproget, som limen i forståelse og lægger derfor vægt på, at eleverne får talt med hinanden, og at elev og lærer får talt sammen. Ideer og opgaver til dette er øget i KonteXt+.
En opgave er ikke bare en opgave
Vi har valgt opgaver, hvori der indgår små udfordringer, så eleverne skal bruge omtanke i deres arbejde og ikke kun udføre rutinearbejde. Opgaverne følges ofte op på arbejdsarkene – på både lettere og vanskeligere niveau. Opgaverne varierer, så der er et passende udvalg af både lukkede og mere åbne opgaver.
6 elementer i kontext+
Ikke kun én måde, men mange måder
Der lægges vægt på, at eleverne oplever mange repræsentationsformer af de matematiske begreber, fx at eleverne oplever addition repræsenteret på tallinje, på regnepind, på den tomme tallinje, som bundtning ud fra 10-talssystemet osv. Eleverne får lejlighed til at arbejde med matematikken ud fra både konkrete materialer, skitser, diverse modeller samt digitale hjælpemidler.

Målstyret undervisning og evaluering er to sider af samme sag
En målstyret undervisning må følges op af evalueringsformer, som kan konstatere graden af målopfyldelse. Vi har derfor opprioriteret denne del i KonteXt+. Der er for hvert af de fire faglige hovedområder et særligt EVA-ark til vurdering af elevernes matematiske viden, færdigheder og forståelse. Derudover er der anbefalede observationer i undervisningen til at afgøre tegn på målopfyldelse.
om www.kontextplus.dk 7
Om www.kontextplus.dk
På www.kontextplus.dk findes forskellige materialer til brug i undervisningen. Der er en elevadgang, der følger en elevbog, og en læreradgang, der følger en lærervejledning. Læreren har adgang til det samme som eleverne, samt EVA-ark, aktivitetssider, serviceark, facitliste m.m. Webdelen er dynamisk og vil løbende blive suppleret med nye elementer. Eksempelvis findes følgende i webdelen, der følger bogens fire hovedemner:
Arbejdsark
Den tidligere kopimappe til elevbøgerne er erstattet af pdf-filer på www.kontextplus.dk. Der er arbejdsark til elevbogens to værksteder og til de to supplerende værksteder. Desuden er der et stort antal ark med supplerende opgaver og aktiviteter til elevbogen. Arbejdsarkene er placeret under de hovedemner, hvortil de skal anvendes.
Aktiviteter og spil
På www.kontextplus.dk har vi samlet alle supplerende aktiviteter og spil for 1.-3. kl. Undervejs i de enkelte kapitler giver vi forslag til, hvilke aktiviteter og spil der kan
indgå i det faglige arbejde. De supplerende aktiviteter er kun tilgængelige for læreren.
Serviceark
På www.kontextplus.dk findes også de forskellige typer af serviceark, som man får brug for i 1. klasse. Det er ark som isometrisk papir, udklipsark, spilleplader, talkort mm.









EVA-ark
Hvert kapitel afsluttes med en evaluering. Hertil findes en række ark, som kan bruges i forbindelse med denne evaluering, kaldet EVA-ark. Hvordan disse anvendes er beskrevet generelt i indledningen. Den konkrete anvendelse af EVAarkene kan man finde oplæg til på www.kontextplus.dk. EVA-arkene er kun tilgængelige for læreren.

8 om www.kontextplus.dk
alinea serviceark 5 Prikpapir 1 cm Prikpapir 1 cm 159 Kontext Kopimappe 3B_til tryk 11/03/07 10:23 Side 195 Kontext 3B Kopimappe ISBN 978-87-7988-421-2 Alinea navn 2Find lige mange. Lige mange arbejdsark 16 ja nej ja nej ja nej ja nej ja nej ja nej 1Er der lige mange? navn alinea Figurer på kryds og tværs arbejdsark 35 1Find brikkerne slags firkanter samme farve Spilleregler: Der må ikke være den samme slags firkant vandret, lodret eller på tværs. Den spiller, som ikke kan lægge en firkant, har navn Figurspillet arbejdsark 57 Farver Spilleregler: Farv på skift et felt på spillepladen. Det gælder om at farve fire felter samme farve, så de hænger sammen på denne måde: Vinderen er den, der først får farvet fire felter som vist sin farve. Spil også med, at man skal farve sådanne figurer for at vinde: navn alinea Sådan kan man også tælle · 1 arbejdsark 91
ark eva Figurer og retning 1 3 4 2 Klasse: Tegn selv gurer med mange rkanter. Tegn en gur magen til. Tegn en gur magen til. 5 7 8 6 Tegn en gur med kanter. Bestem selv, hvor mange kanter guren skal have.
Samtalebillede

Ved hvert af de 11 delforløb i hver elevbog er der en QR-kode nederst på siden. Den viser hen til en forældrevideo, som på få minutter sætter forældrene ind i idéen bag opgaverne, og som indeholder hints til måder at hjælpe på, vanskeligheder og løsninger.
GeoGebrafiler


Der er ekstra fotos at finde, som kan anvendes til brug i klassesamtalen ved indledningen af hvert af de fire faglige hovedemner. Disse kan fx anvendes ved brug af IWB.
Værkstedsfilm
Eleverne kan gå direkte ind på www.kontextplus.dk og arbejde med små enkle opgaver, som leger funktioner i GeoGebra ind i undervisningen, og som understøtter det faglige indhold i elevbogens opgaver.
Facitlister
Der er til hver bog 16 værksteder, hvor de otte vises i elevbogen. Disse otte værksteder vises i otte videofilm á 2-3 minutters varighed, som viser elever, der arbejder med værkstederne.

Forældrevideoer
På www.kontextplus.dk findes desuden facitlister til elevbøgerne. Disse er kun tilgængelige for læreren.
fra kontext til kontext+ 9
Læringshjulet
kapitel. Derudover er der anvisninger på de læringsmål, som knytter sig til hvert af af de fire hovedemner.
Hver af elevbøgerne er opdelt i fire faglige emner fx tal og tælling, figurer og retning, plus osv. Hvert af disse hovedemner er struktureret ud fra ovenstående læringshjul, som gennemløber en række progressive faser:
Fase 1: Førtanken, læringsmål og værksteder: Klassesamtalen, målsættelse og forhåndserfaringer gennem værkstedsarbejde
Fase 2: Matematik i en kontekst: Kontekstforståelse gennem oplæste og diskuterede historier om Familien Tal og opgaver, som er knyttet til

Fase 3: Opgaveløsning: matematik fordybelse og træning

Fase 4: Tænk tilbage – Evaluering



Fase 1: Førtanken, læringsmål og værksteder
I fase 1 får eleverne lejlighed til at skabe personlige praktiske og eksperimentelle erfaringer med matematikken. Gennem spil, undersøgelser, målinger, brug af konkrete materialer osv. får eleverne en forforståelse for det matematiske emne. Værkstederne skal således betragtes som en ”forfilm” til det kommende arbejde – ikke med forventning om, at eleverne her opnår de endelige færdigheder i stoffet, men de skal have ”snuset” til det. Dette arbejde tænkes udført i grupper á to-fire elever. Undervejs gennem det faglige hovedemne vil man som lærer kunne referere tilbage til disse praksiserfaringer.
I KonteXt+ er der kun præsenteret to værksteder i elevbogen. Hvis man vil supplere og bruge mere tid på dette arbejde, er der yderligere to værksteder på www.kontextplus.dk med tilhørende arbejdsark.
Tegningen fra elevbogen samt oplæg til værkstedet findes som arbejdsark til opsætning i klassen.
Til hvert værksted er der tilknyttet to elevevalueringer.
•En glad og sur smiley, hvor eleverne tager stilling til, om de kunne lide eller ikke lide værkstedet. De giver således udtryk for deres holdning til aktiviteten typisk med bemærkninger som ”det var sjovt/kedeligt” el.lign.


•En fjer og et lod, som skal symbolisere henholdsvis en svær eller nem aktivitetet. Her får eleverne lejlighed til at tage stilling til grad af udfordring i aktiviteten. Eleverne vil typisk bruge bemærkninger som ”det var svært/let” el.lign.
Det anbefales, at hvert hovedemne indledes med en klassesamtale evt. med klasseaktiviteter. Med klassesamtaler tænkes på elevinvolvering gennem spørgsmål og aktiviteter, som kan skabe en orientering for eleverne mod de centrale faglige pointer, emnet vil omhandle. Der er oplæg til klassesamtale og aktiviteter i indledningen til hvert
10 læringshjulet
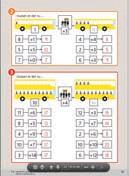
Tænk tilbage og evaluering Opgaveløsning Matematik i en kontekst Førtanken, læringsmål og værksteder Tal i system under 20 kr.? Hvad koster 20 kr. eller mere? Lav din egen menu. skriv, hvor mange 10ʼere og 1ʼere der er. 1 Leg med menukort 2 Gæt og tæl mange Du skal bruge Saks Lim Arbejdsark Du skal bruge Tælleglas Arbejdsark A B KG KG 67 68 69 70 71 72 73
Fase 2: Matematik i en kontekst
træning og forståelse for matematikken med udgangspunkt i overskrifter som ”Hvor skal tallet stå?” og ”Hvor mange kanter?”. Den første delopgave i hver opgave er altid besvaret, så eleven har lettere ved at afkode, hvad idéen i opgaven er. Opgaverne har ofte en tanke i sig, som udfordrer eleven, så man ikke blot udfører rutinearbejde. Bemærk, at der er QR-koder nederst i tekstfeltet, som henviser til forældrevideoer, som på få minutter kan give et overblik over opgaver og mulige vanskeligheder. De kan også ses på www.kontextplus.dk.
Der afsluttes med en grubler til de elever, som søger flere udfordringer.
Til hvert hovedemne er der 2-4 delforløb, som gennemløber fase 2 og 3 med hvert sit faglige emne. Delforløbet indledes med en illustration og et fagligt spørgsmål, som præsenteres gennem den oplæste historie om Familien Tal. Omfanget af oplæsning svarer til ca. fem minutter. Spørgsmål til den efterfølgende dialog med eleverne findes i lærervejledningen. Familien Tal består af far og mor og så ni børn – cifrene fra 1 til 9. Cifferet 0 støder senere til. Hver af disse ”cifferbørn” har deres egne egenskaber som Trætte Tre og Nysgerrige Ni osv. Her i lærervejledningen præsenteres familien, og på www.kontextplus.dk er der tegninger af alle familiemedlemmerne. Der knytter sig opgaver til, som udspringer af historie og kontekst.








Fase 3: Opgaveløsning – fordybelse og træning
På den sidste side i nederste hjørne henvises til supplerende arbejdsark, der hentes på www.kontextplus.dk til ekstraopgaver. Dette kan foregå som individuelt arbejde eller evt. som makkerarbejde.



Fase 4: Tænk tilbage og evaluering
Siderne efter historien om Familien Tal og de tilhørende opgaver er et delforløb af opgaver, som giver eleverne
Hovedemnet afsluttes med en evalueringsprocedure, som består af tre elementer:







•Den sidste side i hvert af de fire hovedemner, som i KonteXt+ er omdøbt til ”Tænk tilbage”, idet der er tale om opgaver, eleverne har løst tidligere.
•Særlige EVA-ark downloades fra www.kontextplus.dk. Et EVA-ark består af forside og en bagside. Forsiden indeholder spørgsmål og opgaver, som læses op af læreren. Bagsiden består af opgaver, som eleverne skal løse individuelt. På www.kontextplus.dk er der grundige beskrivelser af, hvad der kan læses ud af mulige fejl hos eleverne.
• Observationsark med udvalgte 3-4 tegn på læring til at vurdere graden af målopfyldelse hos de enkelte elever.
læringshjulet 11
1 101 2 40 111213141516171819 10 1023456789 20 Tæl pengene på tegningen tiere og enere. Skriv det skemaet og som Tæl pengene. Skriv tiere og enere skemaet, Hvor mange tiere og enere? kr. Hvor mange penge alt? 101 35 101 101 kr. kr. kr. 1 101 2 3 4 313233343536373839 30 222123242526272829 40 111213141516171819 10 1023456789 20 Tæl pengene pungene. Skriv, hvor mange tiere og enere der er. Skriv, Tegn beløbet. Skriv, hvor mange tiere og enere der er, og skriv hvor Tegn mønter. Tæl pengene på tegningen tiere og enere. Skriv det skemaet og som Tæl pengene. Skriv tiere og enere skemaet, Tæl pengene fra pungene på tegningen. Hvor mange tiere og enere? 101 kr. kr. Hvor mange penge alt? 101 35 101 101 kr. kr. kr. Hvor mange penge alt? 101 13 101 101 12 101 101 101 101 101 101 30 kr. kr. 12 kr. kr. kr. 34 kr. kr. kr. kr. 5 42 111213141516171819 10 1023456789 20 Brug det gamle tællesystem. Se lærervejledningen for historien. Skriv tallene. Tegn kugler, så det passer med tallene. Tegn kuglerne. 1 10 16 19 24 30 38 Sådan kan man også tælle. 6 101 101 101 101 1619 3038 1 2 7 grubler Under 10 kr. Fra 10 til 30 kr. Over 30 kr. kr. kr. kr. kr. kr. kr. 10 kr. kr. kr. kr. kr. kr. kr. kr. kr. 30 17 25 Hvor mange? Tegn mønter Tegn ting Tegn kuber Giv en pris. 111213141516171819 10 1023456789 20 1. Skriv tal rækkefølge på tallinjerne. Tæl mønter, ting og kuber og skriv, hvor mange tiere og enere der er. Skriv, hvor mange tiere og enere der er. Tænk tilbage 7. Skriv, hvad hver ting kan koste, så det passer med informationerne Grubler: Tæl tingene. Brug tællearket på arbejdsark 106. Skriv de tal der mangler. Tæl med tælleark. 105 104 103 102 101 100 101 kr. 101 37 kr. 101 101 101 101 21 30 Tegn nogle ting, tæl dem, og skriv hvor mange der er. Du bestemmer selv, hvad du vil tegne, 17 EVA-ARK 1 Tal og tælling 2 4
Anbefalinger til undervisningen
At arbejde med værksteder
Værkstederne anvendes som introduktion til de forskellige emner for, at eleverne kan få en indføring i disse på en meningsfuld måde gennem en social erfaringsdannelse. Dette sker i form af aktiviteter, der lægger op til hands on-opgaver, der indeholder undersøgende og eksperimenterende elementer. Ved at arbejde undersøgende og eksperimenterende tilgodeses flere vigtige aspekter ved læring, som ikke kan tilgodeses ved en undervisning, der traditionelt bygger på ”papir og blyant”. Praktisk matematik eller hands on-matematik kan give grundlag for en erfaringsdannelse om det, eleverne observerer og eksperimenterer.
Værkstederne giver eleverne mulighed for:
•At opleve, at matematik ikke kun er et teoretisk fag, men at faget også kan bestå af spil og lege, der kan relateres til deres hverdagserfaringer.
•At arbejde med matematikken på en anden måde end den traditionelle rutineprægede klasseundervisning.
•At udvikle individuelle og forskellige repræsentationer hos de enkelte elever for de matematiske begreber, der skal dannes.
•At kunne danne alternative repræsentationer og at kunne skifte mellem dem er en af de væsentligste kompetencer ved udviklingen af matematisk viden og kunnen.
Værkstedernes indhold er valgt således, at eleverne får mulighed for at arbejde dynamisk med begreberne, der i tillæg giver eleverne muligheder for at samtale i og om matematik. Lærerens observationer kan i denne arbejdsproces give ham et anderledes indblik i de forståelser, opfattelser og holdninger, den enkelte elev har i relation til matematik.
Organisationen af værkstederne
Hvert værksted i KonteXt+ er berammet til ca. 45 minutter. Der kan arbejdes med værkstederne på forskellig vis: •Man kan vælge at lade hele klassen arbejde i det samme værksted. Det vil betyde, at alle elever skal have den samme instruktion, den samme forklaring. Det kan være lettere i begyndelsen at overskue værkstedsarbejdet på denne måde. I nogle værksteder skal der anvendes konkrete materialer, så hvis man lader alle
elever arbejde i det samme værksted på en gang, skal der være flere materialer til rådighed.
•Man kan vælge at sætte flere værksteder i gang på samme tid. Det skaber et utroligt fagligt liv, og eleverne er tit både optagede af det, de selv laver, samt af det, der foregår i de andre grupper. Det kan kræve mere forberedelse i begyndelsen, men mindre i længden for læreren. Da meget skal ”sættes i gang” på samme tid, kræver det en arbejdsfacon, hvor eleverne accepterer, at læreren ikke kan være ”alle vegne på samme tid” – man lærer således eleverne en form for hjælp til selvhjælp. Der er desuden værksteder, der kræver mere støtte fra læreren end andre. Man kan derfor med fordel vælge at arbejde i fx to værksteder, hvor det ene værksted er mere selvkørende, hvilket frigiver tid til støtte i det andet værksted.
Ved hvert værksted i elevbogen er der som tidligere nævnt i nederste højre hjørne et felt med en glad og sur smiley, samt en vægt og en fjer, hvor eleverne tager stilling til, om de kunne lide at arbejde i værkstedet, og om hvor svært det var. Elevernes krydser kan man tage udgangspunkt i, når man taler med klassen om, hvordan værkstedsarbejdet er forløbet. Hvis en elev konsekvent sætter kryds over det sure ansigt, kan det også indikere, at her er der noget at tale om. Man skal dog være opmærksom på, at elevernes motiver kan være meget forskellige. Det kan selvfølgelig betyde, at eleverne ikke bryder sig om matematik, hvilket der kan være mange årsager til. Men det kan også betyde at tælleglasset med skruer i lugtede af rødbeder, og det var ulækkert!
Matematik og it
Vi har i KonteXt+ primært fokuseret på to centrale digitale værktøjer: regneark og dynamiske geometriprogrammer. I 1. klasse har vi valgt at introducere det dynamiske geometriprogram GeoGebra. Det er gjort at flere grunde:
•Det kan hentes gratis på internettet, så eleverne har mulighed for at bruge det på egne computere.
•GeoGebra er det mest udbredte dynamiske geometriprogram.
•Der er adgang til e-læringsmoduler på www.emu.dk.
•Der er adgang til onlinehjælp, og der er meget inspiration at hente på bl.a. YouTube.
•Det er under konstant udvikling.
12 anbefalinger til undervisningen
• Det er muligt at koble dynamisk geometri med regneark. •Programmet er intuitivt at bruge og kræver ikke megen instruktion.
•GeoGebra kan downloades til andre platforme end pc, fx iPad.
GeoGebra kan findes på www.geogebra.org. Her kan man vælge at hente programmet ned på sin pc, eller om man vil arbejde i programmet på hjemmesiden.
Der vil være adgang til GeoGebra-filerne knyttet til KonteXt+ på www.kontextplus.dk.
I 1. klasse er der primært valgt en legende og undervisningstøttende tilgang til brugen af programmet, så eleven får ”snuset” til det. Der vil indgå brug af enkle og overskuelige funktioner. Vi vil gradvist øge elevens anvendelse af programmet til at eksperimentere og konstruere med former og figurer.
Brug af lommeregner eller lignende digitale
værktøjer
Lommeregneren opfattes på lige fod med alle andre hjælpemidler. Det vil gøre det muligt at håndtere svære regnesituationer på dette klassetrin, som eleverne endnu ikke kan klare med blyant og papir eller i hovedet. I sådanne situationer vil elevernes mulighed for at anvende en lommeregner ofte være mere motiverende og lærerig end en henvendelse til læreren med udsagnet: “Det kan jeg ikke finde ud af”.
Endvidere kan lommeregneren anvendes til træning og forståelse af simpel addition, subtraktion, multiplikation og division på begyndertrinnet. Lad eleverne bruge lommeregneren til dette formål fra starten af. Man kan desuden opfordre dem til at stille opgaver til hinanden og at kontrollere svarene ved hjælp af lommeregneren.
Det bør derfor være et meget tidligt mål at lære eleverne at anvende lommeregneren. Dette hjælpemiddel kan styrke både elevernes talopfattelse, og anvendt som ovennævnt vil den også fremme elevernes “hovedregning”. Så i stedet for at vente med at bruge lommeregneren til eleverne kan det elementære og så tillade lommeregneren, vil det for langt de fleste elever være mere lærerigt og motiverende at gå den anden vej. Altså lære det ele-
mentære ved brug af lommeregneren og dermed senere overflødiggøre den ved de simple beregninger.
I kompetencemålene for 1.-3. klasse er netop beskrevet under hjælpemiddelkompetencen, at eleven kan anvende enkle hjælpemidler til tegning, beregning og undersøgelse.
Når man præsenterer lommeregneren som arbejdsredskab for første gang, skal man overveje, hvordan man gør det. Mange elever vil have lyst til og brug for at undersøge, lege og opfinde opgaver, før den indgår som hjælpemiddel og arbejdsredskab. Overvej også, hvilken slags lommeregner der indkøbes til eleverne. Der findes lommeregnere, hvor eleverne kan se, hvad de udregner, hvilket kan være en støtte for nogen.
Gruppesammensætning
Når man lader eleverne arbejde sammen om forskellige opgaver, skal man selvfølgelig overveje, hvilke elever der skal arbejde sammen. Skal alle arbejde med én, de er på niveau med, eller skal de arbejde med én, der er på et andet fagligt niveau?
Vi kan anbefale, at man laver makkerpar i klassen. Makkerparrene er lavet af læreren og bruges, når eleverne skal arbejde sammen to og to om forskellige opgaver, og også her skal man naturligvis overveje, hvordan parrene skal sammensættes. Faste makkerpar har bl.a. den fordel, at eleverne ikke skal bruge tid og energi på at finde en, der vil samarbejde. Læreren kan danne nye makkerpar, når hun fornemmer, at det er tid til luftforandring.
Der findes flere metoder til samarbejsturkturer fx inden for Cooperativ learning, som kan indgå i arbejdet, hvor man finder det passende.
Hvad gør man ved elever, som skal have ekstra udfordringer?
Når eleverne arbejder i klassen – det kan være både med værksteder og i elevbogen – vil man ofte opleve, at der kan være nogle, der er hurtigt færdige med arbejdet. Til disse elever er der til sidst i hvert delforløb Grubleren, som stadig er opgaver inden for emnet men med større faglig udfordring. Det skal dog pointeres, at det ikke nødvendigvis skal forbeholdes ”de hurtigste” at løse grub-
anbefalinger til undervisningen 13
leropgaverne. Opgaverne er ofte formuleret, så der kan være flere dybder og muligheder i måder at svare på.
Herudover henvises der til supplerende arbejdsark på www.kontextplus.dk. Vi har også i denne lærervejledning beskrevet spil, lege eller andre aktiviteter, man kan inddrage i undervisningen. Alle aktiviteter og spil er at finde samlet for 1.-3. kl. på www.kontextplus.dk.
Derudover vil vi opfordre til, at man arbejder med at lade eleverne udarbejde opgaver til hinanden.
Når en elev har udarbejdet en opgave, skrives den under og sættes i mappen med klassens opgaver. Andre elever kan vælge at løse en sådan elevopgave. Hvis eleverne ikke kan finde ud af opgaven, henvender han sig til den, der har lavet opgaven for at få hjælp. Denne elev skal så forklare opgaven. Når opgaven er løst, kontrollerer ophavsmanden resultatet. Man kan evt. aftale, at man altid udarbejder en opgave, før man løser en. Således løber man aldrig tør for opgaver.
Konkrete materialer og spil til 1. klasse
Vi anvender følgende konkrete materialer:
•Kuber (Bemærk, at der både er 1 cm- og 2 cm-kuber)
•Terninger, almindelige og tisidede
•Spillekort
•Lommeregnere
•Stopur
•Sandur
•Skolepenge som erstatning for kopierede mønter på serviceark
•Mosaikbrikker som erstatning for mønsterbrikkerne på servicearkene
•Blade og aviser til at klippe i
•Farveblyanter, sakse og limstifter
•Perler, snor og pinde (til enkelte værksteder)
Desuden anvender vi talkort til mange aktiviteter og spil. Talkort findes i forskellige udgaver – se servicearkene på www.kontextplus.dk. Vi anbefaler, at man evt. sammen med eleverne laver talkort, så der er et sæt til hver eller hver anden elev, så man nemt kan tage dem frem og bruge dem i undervisningen. Start med at lave tallene 0-20 og udvid så derefter løbende samlingen fx med tallene op til 50 og sidenhen med tallene op til 100.
På www.kontextplus.dk har vi beskrevet en mængde aktiviteter, hvor talkort inddrages.
Vi anbefaler desuden, at man inddrager spil i sin undervisning. Det at spille rummer utrolig mange kvaliteter, som matematikundervisningen kan drage fordel af. Mange elever er automatisk motiveret, når spilleelementet inddrages. Der arbejdes ligeledes med kommunikation og problemløsning. Der er en social gevinst ved det at spille, men også vanskeligheder knyttet til at vinde og tabe. Der skal muligvis ske en tilvending fra elevernes side til, at man nogle gange kan tabe, uden man taber ansigt. I denne sammenhæng kan det være godt, at spillene ikke tager for lang tid, så det ikke drejer sig om at finde én vinder og én taber, men at man vinder nogle gange og taber nogle gange.
Den bedste måde at lære et spil på er ved selv at spille spillet, helst sammen med en, der kender reglerne i forvejen. Næstbedst er det at se andre spille. Derfor vil vi gerne anbefale, at man fx lærer en mindre gruppe elever at spille spillet. Disse ”eksperter” kan så senere blive fordelt i andre grupper, hvor de så skal lære en ny gruppe spillet. Vi har selv rigtig gode erfaringer med denne arbejdsmetode. Der er også en sproglig sidegevinst med metoden, særligt for den elev der skal lære andre spillet. Her skal man selvfølgelig være opmærksom på, at man giver opgaven til de elever, der magter den.
Vi har på www.kontextplus.dk samlet en del spil, lege og andre aktiviteter, som med fordel kan anvendes i undervisningen. Undervejs i side til side-vejledningen refererer vi til spilleaktiviteter der, hvor vi tænker, de naturligt vil ligge i god forlængelse af emnet. Denne ”spillebank” kan også anvendes, hvis der er et fagligt emne, man gerne vil finde et spil til.
14 anbefalinger til undervisningen
Om Fælles Mål
Den anbefalede planlægningsmodel for undervisningen fremstår som en to-dimensionel matrix med de matematiske emner som den ene dimension og de matematiske kompetencer som den anden dimension.
Hver af nedenstående kasser er inddelt efter det område, de beskriver, og det færdighedsmål og vidensmål, som knytter sig til.
Område
Færdighedsmål Vidensmål
I 1. fase ser det ud som følger:
Problembehandling
Tal og algebra
Geometri og måling Statistik og sandsynlighed
Matrixmodellen af Fælles Mål i matematik
Modellen beskriver, at læringsmålene i matematik generelt har to sider – en kompenteceside og en emneside. Det vil sige, at der i et undervisningsforløb indgår udvalgte emnelæringsmål og kompetencelæringsmål. Det skal bemærkes, at det er ”generelt i et forløb” dvs. det ikke altid og hele tiden er tænkt, at kompetencer og stof smelter sammen – der vil være situationer, hvor stoffet tager overhånd og kompetencerne er begrænset, fx når man øver sig på tabeller, løser rutineopgaver osv., og der vil være situationer, hvor kompetencerne tager overhånd, og stoffet er meget nedtonet, fx ved strategispil som skak, ”mensalignende” opgaver osv. Vi vil løbende forholde os til disse muligheder, når vi bekriver de enkelte delforløb.
I indskolingsforløbet (1.-3. klasse) er der tre faser, som skal beskrive progressionen for hver overskrift, fx inden for tal, regnestrategier og algebra. De tre faser skal ikke opfattes som klassetrin, men er som tidligere skrevet en beskrivelse af progressionen. Vi finder det dog naturligt, at man kan se elementer af alle læringsmål i 1. klasse.
Problembehandlingskompetencen
Eleven kan bidrage til løsning af enkle matematiske problemer
Eleven har viden om kendetegn ved undersøgende arbejde
Modelleringskompetencen
Eleven kan undersøge enkle hverdagssituationer ved brug af matematik
Eleven har viden om sammenhænge mellem matematik og enkle hverdagssituationer
Ræsonnement- og tankegangskompetencen
Eleven kan stille og besvare matematiske spørgsmål
Eleven har viden om kendetegn ved matematiske spørgsmål og svar
Repræsentation- og symbolkompetencen
Eleven kan anvende konkrete, visuelle og enkle symbolske repræsentationer
Eleven har viden om konkrete, visuelle og enkle symbolske repræsentationer, herunder interaktive repræsentationer
Kommunikationskompetencen
Eleven kan deltage i mundtlig og visuel kommunikation med og om matematik
Eleven har viden om enkle mundtlige og visuelle kommunikationsformer, herunder med anvendelse af digitale værktøjer
om forenklede fælles mål 15
Modellering Ræsonnement
tankegang Repræsentation og symbolbehandling Kommunikation Hjælpemidler
og
Hjælpemiddelkompetencen
Eleven kan anvende enkle hjælpemidler til tegning, beregning og undersøgelse
Eleven har viden om konkrete materialer og redskaber
Tal
Eleven kan anvende naturlige tal til at beskrive antal og rækkefølge
Eleven kan anvende flercifrede naturlige tal til at beskrive antal og rækkefølge
Eleven har viden om enkle naturlige tal
Eleven har viden om naturlige tals opbygning i titalssystemet
Regnestrategier
Eleven kan foretage enkle beregninger med naturlige tal
Eleven har viden om strategier til enkle beregninger med naturlige tal
Algebra
Eleven kan opdage systemer i figur- og talmønstre
Eleven har viden om enkle figur- og talmønstre
Geometriske egenskaber og sammenhænge
Eleven kan kategorisere figurer
Eleven har viden om egenskaber ved figurer
Geometrisk tegning
Eleven kan beskrive egne tegninger af omverdenen med geometrisk sprog
Eleven har viden om geometriske begreber
Placeringer og flytninger
Eleven kan beskrive, hvordan objekter er placeret i forhold til hinanden
Eleven har viden om forholdsord, der kan beskrive placeringer
Måling
Eleven kan beskrive længde, tid og vægt
Eleven har viden om længde, tid og vægt
om forenklede fælles mål
Statistik
Eleven kan anvende tabeller og enkle diagrammer til at præsentere resultater af optællinger
Eleven har viden om tabeller og enkle diagrammer
Sandsynlighed
Eleven kan udtrykke intuitive chancestørrelser i hverdagssituationer og enkle spil
Eleven har viden om chancebegrebet
Om kapitlernes læringsmål
I hvert af de faglige kapitler beskrives de læringsmål, som er udledt af læringsmålene fra Fælles Mål. De er beskrevet henvendt til dig som lærer, men vi anbefaler en oversættelse til eleverne gennem eksempler og ordkort.
De matematiske kompetencer er ikke udspecificeret, men indgår løbende som en del af de aktiviteter og opgaver eleverne arbejder med.
Se en samlet oversigt over læringsmålene knyttet til Fælles Mål på www.kontextplus.dk
16
Om Familien Tal






På side 1 i elevbog 1A er Familien Tal tegnet. På arbejdsark 1-5 findes der tegninger af Familien Tal, så eleverne kan farvelægge figurerne. De kan kopieres i stor størrelse til farvelægning og klasseplakater, som man ønsker.
Elegante Et er meget optaget af sig selv og sit udseende. Det betyder, at alt hvad hun deltager i, har hun svært ved at gennemføre, fordi hun pludselig skal tjekke, om håret sidder, som det skal. Hun er også hjælpsom og omsorgsfuld.
Fjollede Fire fjoller altid rundt, svinger med arme og ben, synger og danser. De andre kan nogen gange godt blive lidt irriterede på hende, fordi hun sjældent hører efter og derfor skal ha’ alt gentaget. Men de kan også godt lide hende, fordi hun er fuld af godt humør og sjov at være sammen med.
Tænksomme To er den eftertænksomme. Hun undrer sig tit over, hvordan verdenen hænger sammen. Det er tit
Tænksomme To, der spørger: ”Hvordan kan det egentlig være, at …?” Hun har ofte selv en forklaring på matematikken og får ofte gode ideer.
Friske Fem er familiens spejder, der ved hvordan et bål tændes, en knude knyttes og en bivuak bygges. Hun kan lide nye oplevelser af enhver art.
Trætte Tre er sød og rar, men også sløv og træt og vil tit helst sove.
Sjove Seks er sjov på en lidt anden måde end Fjollede Fire. Han fortæller vittigheder; viser sjove tricks og kan mange gode historier, som ofte bliver lidt bedre og sjovere end de i første omgang er fortalt.
om familien tal 17
Seje Syv er selvfølgelig sej. Han kører på skateboard og er med på moden. Han elsker alt, hvad der går stærkt, i Tivoli er han i sit es. Han er modig. Og så er han en god kammerat.

Mor Tal er en mor, der beskytter sine børn, bager boller til dem og er sød og god. Men hun er også en bestemt dame, hvis der bliver kaos i tingene. Hun er den, der bestemmer, og når hun har sagt, hvordan tingene skal være, så bliver det sådan.
Far Tal er altid sød, og han gør gerne mange ting med sine talbørn. Han spiller spil med dem, læser højt, tager på mange forskellige ture, både cykelture, fisketure osv. Far Tal er også god til at bygge ting selv, og han arbejder ofte højlydt i værkstedet eller i haveskuret, eller han lægger fliser eller ordner køkkenhave.
Opfindsomme Otte er familiens Ole Opfinder. Han har tit en løsning på spørgsmål af forskellig art. Opfindsomme Otte elsker at finde på nye ting og er meget betænksom. Han tænker meget over tingene og overvejer nøje de beslutninger, han tager, og de svar han giver. Nogen gange går tingene ikke som planlagt.
Man kan i de første lektioner tale med eleverne om de forskellige ”talpersoner” på tegningen. Begynd med at lade eleverne fortælle, hvad de ser på tegningen. Spørg dem om nogle af figurerne virker genkendelige. Læs evt. op af ovennævnte beskrivelser. En samtale om Elegante Et kan tage udgangspunkt i følgende spørgsmål:
•Der er en figur, der hedder Elegante Et.
Hvem tror I, det er?
•Hvorfor tror I, det er hende/ham, der er Elegante Et?
•Hvordan ser Elegante Et ud?
Hvilken form har Elegante Et?
•Hvorfor hedder Et Elegante Et?
•Hvad vil det sige at være elegant?
Nysgerrige Ni er interesseret i alt, hvad der foregår omkring hende. Hun har det med at blive revet ud af det, hun er i gang med, fordi der pludselig lige er noget andet, hun skal undersøge. Hun er videbegærlig; alt nyt er spændende.
•Hvordan tror I, Elegante Et opfører sig?
•Hvad tror I, at Elegante Et kan lide at lave?



•Hvad er Elegante Ets livret? Yndlingsfag i skolen? Yndlingsfarve?
•Osv.
Bed allerede tidligt eleverne om at begrunde deres svar. Hvis eleverne tror, at Elegante Ets livret er salat, så skal de også fortælle, hvorfor de tror, det er sådan. Gennemgå gerne talfamilien med eleverne med udgangspunkt i ovenstående spørgsmål. Vær opmærksom på, at nogle af familiemedlemmerne har navne, som kan virke fremmede for eleverne. Hvad vil det fx sige at være nærig?
Nærige Nul er talbørnenes fætter. Han kommer til senere i bogen, hvor 0 introduceres. Nærige Nul kan godt have et strengt ydre, men inderst inde er han en dreng, der som alle andre godt kan lide sjov og ballade.
18 om familien tal
Tal og tælling
Tal og tælling
Læringsmål
Eleven kan anvende naturlige tal til at beskrive antal og rækkefølge
Eleven har viden om enkle naturlige tal
Børn anvender tal i mange sammenhænge, også inden de begynder i 1. klasse, og de har allerede haft et års undervisning i børnehaveklassen. Det er derfor vigtigt at kende til, hvor langt eleverne er i deres kendskab til tallene. Mange vil ofte have tilegnet sig en del færdigheder i at tælle sig til antal, men måske ikke altid indset, hvad det er, de siger, eller hvad det er, de gør. Da det er yderst centralt for en meget væsentlig del af matematikken at have en stærkt funderet talforståelse, har vi valgt at være tilbageholdende med at springe for hurtigt frem i den første elevbog. Vi har i stedet forsøgt gennem mange repræsentationsformer at konsolidere og generalisere deres viden, så alle er med fra starten.
Vi ved fra forskningen, at børn fødes med en startudrustning, som gør dem i stand til at se antal på op til 4 uden at tælle. Fænomenet omtales som ”subitizing”. Derudover er de i stand til, før de får sprog, at skønne mængder. Hvis der ligger 14 ting i en bunke og 28 ting i en anden, kan børn helt ned til 6 måneder ”se”, at der er flere i den bunke med de 28 genstande. Flere neuropsykologer, som arbejder med talblindhed, angiver svagheder i disse medfødte evner som en mulig rod til talblindes vanskeligheder. Skulle man støde på elever med sådanne problemer, vil man ofte komme til at presse dem for hårdt med store senere traumer til følge. Her skal vises påpasselighed.
Den indledende talforståelse er knyttet til tre færdigheder:
•At kunne tælle op til 20 og indse, at det sidstnævnte tal er det samlede antal
•At kunne identificere tallene og tallenes fremtrædelsesformer som mængdetal, ordenstal og symboltal
•At kunne gennemføre en-til-en-korrespondance
Tælling
Det at kunne tælle gennemløber ofte følgende faser hos mange børn:
Fase 1:
Eleverne har opfanget enkeltord, som de siger i en forkert rækkefølge ”2, 3, 4, 10, 6”. Tallene forbindes ikke til et antal, men opfattes som en remse.
Fase 2:
Eleverne kan tælle på remse, men forbinder ikke noget numerisk indhold til remsen. Tælling er en ordleg.
Fase 3:
Der er knyttet en genstand til de enkelte talord. De tegner for eksempel et tårn eller tænker i pæle, som sidder ved siden af hinanden. Den tredje pæl er således en bestemt pæl. Hvis den fjernes, er nummer tre væk. De har svært ved at tælle. Vi taler om at pegetælle.
Fase 4:
Eleverne indser, at det sidste tal i en tælling svarer til mængdeantallet. Dette er knyttet til spørgsmålet: ”Hvor mange …?”
Tællefærdighederne skal række til, at man vil kunne nævne et tilfældigt tal mellem 1 og 20, som eleverne skal kunne fortsætte tællingen med. Bemærk, at baglænstælling kan være ganske vanskeligt. I en undersøgelse, vi har foretaget på omkring 40 børn i begyndelsen af 1. klasse, var op mod en fjerdedel endnu ikke er klar, så det bør ikke problematiseres.
Lad evt. øvelser indgå, hvor eleverne tæller noget, som de ikke kan pege på, noget man er nødt til at erindre eller sanse sig til fx et antal skridt eller klap. Her er der ikke mulighed for at pege på tingene, idet de ikke er synlige.
Talidentifikation
Tallenes form og navn er også nødvendig viden. Der vil stadig være elever, som spejlvender 3- og 6-taller. Gør det ikke til et problem – de fleste erfaringer taler for at vente og se tiden an. I langt de fleste tilfælde rettes synet, så disse elever med tiden får retvendt tallene. Man skal ikke undlade at vise den ”rigtige” skrivevej, men anerkende, at der går lidt tid for at se det.
20 side til side-vejledning·tal og tælling
Eleverne skal kunne udpege et tal mellem 1 og 20, hvis de nævnes. De skal kunne ordne en tilfældig række af tal. De skal kunne sige tallene, når de udpeges.
Tal er ikke bare tal. Som hovedregel kan tal kategoriseres som symboltal, mængdetal og ordenstal.
Symboltal er talnavne, som ikke har en værdi, men som bliver brugt for at identificere et eller andet fremfor at bruge ord. Det er en opfattelse af tal som billeder, som et mærke i stedet for et navn, så man kan adskille ting eller personer fra hinanden: “De kalder Jørgen for nr. 17.”
“Jeg er med i gruppe 4.” “Mit telefonnummer er 46 35 38 24.” “På min bluse står der nr. 1.” Disse tal er således ikke tænkt som størrelser eller værdier. Det giver ikke mening at vurdere størrelsen på et telefonnummer, som er 1 større end 46 35 38 24.
Mængdetal eller kardinaltal er en angivelse af en mængde, fx ”der er 5 æbler”. Mængdetallene er det tal, man får, når man har talt færdigt fx ved at bruge fingrene. Forstadierne til at erklære en mængde for at svare til størrelsen 3 er en stillingtagen til, hvad det er for objekter, man tæller. Vær opmærksom på, at eleverne, som endnu ikke har set konsistensen af, hvad det er, man tæller, kan knytte ligegyldige egenskaber til tællingen. Det kan bl.a. ses, når eleverne bruger streger, når de tæller. Tæller man dyr, kan elefantens streg hos nogle være større end stregen for mus. Det virker urimeligt for barnet, at den samme streg tæller lige meget uafhængig af, om det er et lille eller et stort dyr.
Ordenstal er tal i relation til det foregående tal, altså tallene i rækkefølge: ”den tredje i rækken er en pige”. Ordenstallene er tallene lagt i rækkefølge eller talt i rækkefølge. Ordenstallene fremstår ofte sammen med tallinjen. Nyere undersøgelser antyder, at det kan være en mere kompliceret sag at få eleverne til at indse, at afstanden mellem tallene på tallinjen er 1. Vi har derfor bevidst udskudt tilgangen til forståelse af tallene via tallinjen til senere i bogen. Derudover ved vi, at det skaber forvirring, at det første tal på tallinjen ikke er 1, men 0, så det tager vi til den tid. Ordenstallene repræsenteres i første omgang ved talkort, som eleverne sorterer på mange måder.
En-til-en korrespondance
En anden forudsætning for at kunne operere med tal er evnen til at kunne sammenligne elementerne i to mængder for at kunne indse, at der er flere i den ene mængde frem for den anden mængde, eller at kunne konstatere at de to mængder er lige store. Eleverne skal være i stand til at parre et element fra den ene mængde med et element fra den anden mængde, som man parrer strømper to og to. Her skal eleverne vide, at et element er et element –forstået som ved dette eksempel. Til trods for stjernernes størrelse tæller de alle tre med værdien 1. Parrer man stjernerne med smileys, kan man se, at der bliver noget i overskud.
Indledende klassesamtale
Dette indledende foto skal ledsages af en klassesamtale, hvor eleverne spores ind på, hvad de skal arbejde med i den kommende tid i faget matematik. Samtalen kan tage udgangspunkt i spørgsmål af denne type:
•Hvad kan I se på fotoet?
•Hvor mange sten?
•Hvor mange muslingeskaller?
Når man drøfter, hvor mange sten der er, er der sandsynligvis ikke den store uenighed. Uenigheden kan opstå, når der skal tælles muslingeskaller, idet der er forskellige typer af skaller på fotoet. Et problem af samme type opstår i Familien Tal, da der i familien ikke er enighed om, hvilke typer af køretøjer der skal tælles med en dag i trafikken.
Efter samtalen om det konkrete foto med strandskallerne kan man bede eleverne om at reflektere over det at tælle:
•Hvad tæller I?
•Hvornår tæller I?
•Hvorfor tæller I?
•Hvorfor er det godt at kunne tælle?
Samtalen og fotoet skal gerne spore eleverne ind på, at de nu skal i gang med at arbejde med tal og tælling. Bemærk at der er supplerende fotos på hjemmesiden.
side til side-vejledning·tal og tælling 21



















































