I
Silvano Abati
Anna D'Ambrosio
Argomenti di IPOVISIONE
prismi in ottica, ortottica ed oftalmologia
Fabiano Gruppo Editoriale
Silvano Abati
Anna D'Ambrosio
6 Argomenti di IPOVISIONE
I prismi in ottica, ortottica ed oftalmologia
Prismi a P.R.I.S.M.A.
dal X Congresso P.R.I.S.M.A.
Professionisti Riabilitazione Ipovisione e Studio Malattie Associate (Associazione di Promozione Sociale) a.p.s.
Contributors
Davide Cacciatore, Antonia delli Calici, Anna Dickmann, Matteo Fusi, Giovanni Giacomelli, Roberto Iazzolino, Giuseppe Migliori, Roberta Rizzo, Giovanni Sato, Roberto Volpe
Revisione a cura di: Emanuela Tedeschi
Fabiano Gruppo Editoriale
© Copyright FGE srl
ISBN 978-88-31256-66-7
Marzo 2024
FGE srl
Sede Legale e Operativa: Reg. Rivelle, 7/F – 14050 Moasca (AT)
Redazione: Strada 4 Milano Fiori, Palazzo Q7 – 20089 Rozzano (MI) Tel. 0141 1706694 – Fax 0141 856013 – info@fgeditore.it – www.fgeditore.it
Gli Autori e l’Editore declinano ogni responsabilità per eventuali errori contenuti nel testo. Tutti i diritti sono riservati. È vietata ogni riproduzione totale o parziale.
Come il prisma devia la luce e il campo s’apre, s’apre dal chiuso velo
che serbando ignoto pare.
Così è simile al “lampo che le tue vesti” mostrano, finalmente ora
nel visibile ritorno.
Giovanni Sato
Introduzione
Per la verità i prismi hanno rappresentato per me un capitolo della oftalmologia abbastanza ostico durante il corso di specializzazione e credo che lo sia stato e lo sia ancora per molti studenti di oftalmologia, ortottica e ottica. Ricordo ancora che la domanda sui prismi da parte della Prof.ssa Boschi all’esame del primo anno era da tutti una delle più temute nonostante le belle lezioni che ci faceva ogni anno.
L’essermi dedicato per qualche anno alla oftalmologia pediatrica, sia dal punto di vista assistenziale che scientifico, e l’aver poi indirizzato la mia vita professionale alla ipovisione ed alla riabilitazione visiva mi ha costretto a fare i conti con le correzioni prismatiche, ad impararne l’utilizzo con i vantaggi e gli svantaggi.
Infine, l’aver insegnato per tanti anni nella scuola di specializzazione in Oftalmologia e nei corsi di laurea di Ortottica e Ottica-Optometria mi ha convinto che i prismi sono poco conosciuti e, spesso, sottoutilizzati sia nelle attività diagnostiche che nella compensazione di diverse patologie oculistiche.
Grazie a P.R.IS.M.A. un’intera sessione del Congresso 2023 è stata dedicata a questo argomento e nell’ambito del Consiglio Direttivo è stato deciso di procedere alla pubblicazione delle relazioni arricchite da ulteriori interventi a coprire tutto l’ambito dell’utilizzo dei prismi.
Ben venga, dunque, questo testo che, tramite l’esperienza di validi professionisti, ci apre la visuale su questo complesso e variegato capitolo della oftalmologia.
Dr Giovanni Giacomelli
CAPITOLO 1
Ottica dei prismi
Silvano Abati
CARATTERISTICHE DI UN PRISMA
Geometricamente è il solido generato da due facce piane e non parallele ABS’S e A’B’S’S (diottri piani), di indice di rifrazione n2 immerso in un mezzo di indice di rifrazione n1 (n2 > n1), figura 1.1.
Nella figura 1.1 abbiamo rappresentato un prisma dove sono evidenziate le facce interessate al cammino della radiazione: ABS’S faccia di incidenza, A’B’S’S faccia di emergenza (facce attive del prisma), queste individuano lo spigolo SS’ del prisma e l’angolo diedro a detto angolo rifrangente o angolo di rifrangenza. La superficie AA’B’B viene detta base del prisma.
Sezionando il prisma con un piano ortogonale allo spigolo otteniamo una sezione principale che ha la forma di un triangolo, figura 1.2.
Su questo piano la retta bisettrice dell’angolo di rifrangenza viene indicata come asse del prisma (o direzione del prisma); vedremo che tale direzione sarà necessaria quando dovremo prescrive un prisma come mezzo compensativo, figura 1.3.
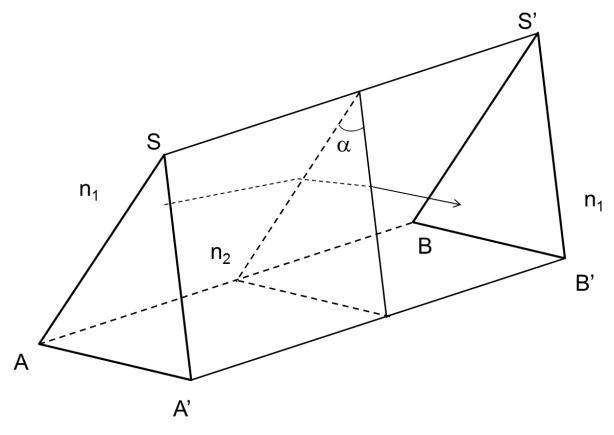
Figura 1.1. Rappresentazione di un prisma di indice di rifrazione n2 immerso in un mezzo di indice di rifrazione n1
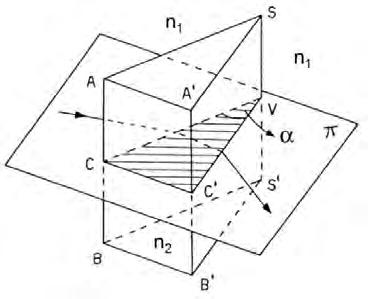
Figura 1.2. Intersezione di un prisma con un piano perpendicolare allo spigolo. Nella figura il prisma di indice di rifrazione n2 è immerso in un mezzo di indice di rifrazione n1
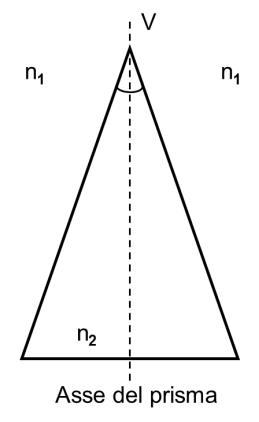
Figura 1.3. Nella figura un prisma immerso nello stesso indice di rifrazione con evidenziato l’asse del prisma.
Figura 1.4. Deviazione della radiazione monocromatica nell’attraversare un prisma di indice di rifrazione n2 > n1. Per le leggi della rifrazione si evidenzia il cambiamento di direzione della radiazione nei punti I e I’ e la deviazione totale d verso la base del prisma.
CAMMINO DELLA RADIAZIONE ATTRAVERSO UN PRISMA
Analizziamo adesso il cammino della radiazione di un raggio monocromatico che giace nel piano che ha definito la sezione principale, nell’attraversare il prisma, nella condizione citata in precedenza di n2 > n1. Si dimostra, applicando le leggi della rifrazione nei punti I e I’, che il raggio incidente subisce due deviazioni sulle due superfici per emergere dal prisma con una deviazione totale d verso la base del prisma, figura 1.4.
Si dimostra che la deviazione d è data dalla relazione: d = a (n2 – n1) / n1
Tale relazione è valida sotto specifiche ipotesi: che si lavori angoli di rifrangenza piccoli (prismi sottili a ≤ 15°) ed angoli di incidenza i < 30° (condizioni che si verificano normalmente in ottica oftalmica e che illustreremo nella dimostrazione di questa relazione per chi volesse documentarsi).
Se il prisma è immerso in aria n1 = 1, indicando con n l’indice di rifrazione n2 del prisma la relazione precedente si semplifica in: d = a (n – 1)
Tale relazione mette in evidenza che la deviazione d aumenta all’aumentare di a e all’aumentare d’ellindice di rifrazione n.
Per avere un ordine di grandezza di tale devizione consideriamo i valori degli indice di rifrazione delle lenti oftalmiche che variano tra 1,5 (materiali organi-
ci) a 1,9 (vetro minerale alle terre rare), abbiamo; per n = 1.5 una deviazione d=a 0,5; all’aumetare dell’indice avremo per n = 1,9 d=a 0,9
Si può altresì dimostrare che la deviazione d del prisma varia anche in funzione dell’angolo di incidenza i passando da un minimo dmin a un massimo dmax, variazioni comunque che non assumono importanza in ottica oftalmica.
DIMOSTRAZIONE
Nel riquadro viene riportata la dimostrazione di tale relazione e le condizioni per cui si verifica.
Tale condizione può riassumersi con la seguente regola: un raggio emerge da un prisma se a è inferiore o uguale a due volte l’angolo limite (2 il) del mezzo di indice di rifrazione n2 rispetto al mezzo di indice di rifrazione n1
Nel caso che a = 2 il si verifica che esiste un solo raggio incidente in grado, dopo due rifrazioni, di emergere dal prisma e precisamente se incide con un angolo i = 90° e emergerà dal prisma con un angolo r’ = 90°.
DISPERSIONE DI UN PRISMA
Quanto detto fino ad ora vale per una determinata lunghezza d’onda in quanto n2-1 (n2-1 = n2 / n1 ) varia al variare della lunghezza d’onda l
Se si estende il comportamento del prisma a radiazioni policromatiche, sempre nelle ipotesi di n2 > n1), il fenomeno della dispersione darebbe luogo ad una rappresentazione del tipo di figura 1.5.
La dispersione di un prisma viene misurata dalla relazione: Dispersione = dF – dC cioè dalla differenza della deviazione che il prisma introduce per la radiazione lF = 486,1 nm e lC = 656,3 nm.
FORMAZIONE DELL’IMMAGINE DI UN OGGETTO VISTO ATTRAVERSO UN PRISMA
Nella figura 1.4 abbiamo messo in evidenza il cammino di una radiazione che parte dal punto raggiante A, dobbiamo comunque ricordare che dal punto A partono infiniti raggi e che di ognuno di essi dobbiamo analizzarne il comportamento. La conclusione è rappresentata in figura 1.6. Essendo per le approssimazioni citate, la deviazione d dipendente solo da a e da n, essa risulterà uguale per tutti i raggi considerati.
Considerando quindi due, tre o più raggi uscenti da A e costituenti un cono, questi, emergendo dal prisma, vengono deviati di un angolo d formando un ulteriore cono avente il vertice, sul prolungamento dei raggi emergenti e cioè in A’. In base alle conclusioni raggiunte nei paragrafi precedenti, l’osservatore che riceve un cono di raggi emergenti dal prisma vede un punto luminoso A’ dove chiaramente non si trova il punto raggiante: dunque A’ è l’immagine di A data dal prisma. Come risulta dalla figura 1.6 per l’osservatore l’immagine A’ appare spostata, rispetto all’oggetto A, verso lo spigolo del prisma.
Da ciò la conclusione che un prisma introduce una deviazione della radiazione verso la propria base e per un osservatore che vi guardi attraverso, una equivalente rotazione dell’immagine di un oggetto verso lo spigolo del prisma stesso.
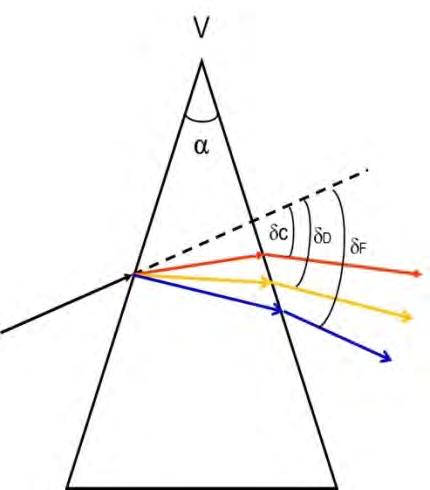
Figura 1.5. Dispersione di un prisma per radiazioni policromatiche
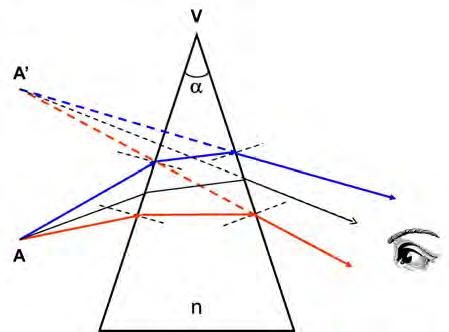
Figura 1.6. Immagine A’ di una sorgente puntiforme A. Si potrebbe dimostrare che tracciando una retta per A e A’ questa risulterebbe pressoché parallela alla bisettrice dell’angolo a
Tale comportamento si ha tutte le volte che il prisma è immerso in un mezzo ottico che ha un indice di rifrazione assoluto minore di quello del prisma.
UNITÀ DI MISURA DELLA DEVIAZIONE INTRODOTTA DA UN PRISMA
Volendo utilizzare i prismi come effetto compensativo precisiamo che le deviazioni introdotte da un prisma d possono essere espresse con varie unità di misura le principali sono:
• Deviazione in gradi (o deviazione di Landolt) di chiara interpretazione (D°)
• Deviazione in diottrie prismatiche (dtpr o D). Per diottria prismatica si intende lo spostamento di un centimetro dell’immagine da un oggetto posto ad un metro di distanza dal prisma stesso, per un osservatore che guardi l’oggetto attraverso il prisma, figura 1.7.
• Deviazione di Donnet o deviazione in centiradianti. Esprime l’angolo in frazione centesimale di radiante anziché in gradi. I risultati sono pressoché uguali a quelli in diottrie prismatiche.
Data l’abitudine di misurare gli angoli in gradi e, in ottica oftalmica, parlando di prismi in diottrie prismatiche, si dimostra che per passare da gradi a diottrie
Figura 1.7. Rappresentazione di una diottria prismatica; la figura per comodità non è in scala.
prismatiche basta moltiplicare per il valore 1,745.
La deviazione d = 1° corrisponde a d= 1,745 D
Se, ad esempio, a ha il valore di 10° ed n = 1,573 avremo per d° il valore di 5,73° e per d(D) il valore 10D [ d° = 10 (1,573 -1) = 5,73° corrisponde a d(D) = 5,73 . 1,745 = 9,9999D ]
Nella costruzione di una lente prismatica, utilizzando indici adeguati in relazione al valore diottrico della lente, sarà l’azienda che determinerà il valore di a per far si che d = a (n – 1) risulti del valore prismatico desiderato.
EFFETTO PRISMATICO EFFETTIVO O CORRETTIVO
Abbiamo visto come un prisma immerso in aria (stesse considerazioni valgono se il prisma è immerso in un mezzo ottico avente indice minore del prisma) ruoti la radiazione verso la propria base e quindi sposti l’immagine di un oggetto osservato, attraverso esso, verso il vertice.
DIMOSTRAZIONE
La deviazione dalla radiazione che attraversa il prisma viene chiamata più propriamente effetto nominale del prisma e generalmente indicato con d n e calcolato con la relazione vista: d n = a (n – 1)
La rotazione che l’occhio deve compiere, dietro il prisma, per ripristinare la fissazione, ossia per osservare l’immagine A’, sarà diversa da quella subita dalla radiazione, causa la posizione del prisma rispetto al punto su cui avviene la rotazione oculare, come evidente nella figura 1.8.
Tale angolo viene detto effetto prismatico effettivo o effetto correttivo del prisma ed è indicato con d e
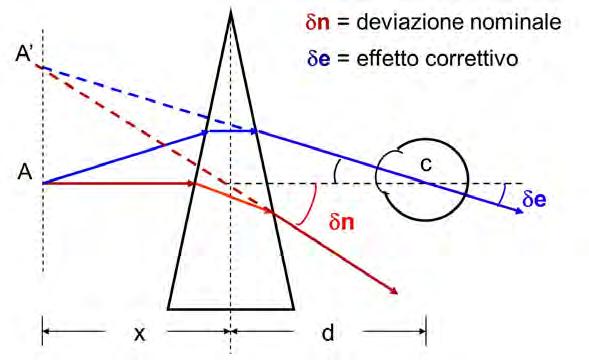
Figura 1.8. Schematizzazione delle differenze tra valore nominale e valore effettivo (correttivo) di un prisma
Si dimostra che tra effetto prismatico effettivo e l’effetto nominale del prisma sussiste la relazione:
d e = d n / [ 1 + (d / x)]
dove:
x = distanza dell’oggetto osservato dall’asse del prisma, espressa in cm; d = distanza del centro di rotazione oculare, sempre dall’asse del prisma espressa in cm.
Se ad esempio si considera una distanza del punto di osservazione x = 25 cm, per d = 25 mm (somma della metà lunghezza media dell’occhio con la distanza apice corneale-prisma di 13 mm), abbiamo come effetto correttivo, per un prisma di valore nominale di 8 D, un valore pari a circa 7,27 D; valore che risulta inferiore di circa il 10% rispetto al valore nominale.
È interessante notare che tale variazione non dipende dal potere del prisma, ma soltanto dal rapporto tra le distanze d e x.
Nel caso che si osservi un oggetto posto a distanza infinita abbiamo (x = ∞) avremo che: d e = d n cioè l’effetto nominale e correttivo coincidono per distanze molto maggiore della distanza centro di rotazione oculare-prisma.
[ Nella relazione: d e = d n / [1 + (d / x) ] sostituendo a x il valore infinito abbiamo che d / x diventa zero e pertanto d e = d n ]
RICETTAZIONE DI UN PRISMA
Abbiamo visto che un prisma è un mezzo ottico che imprime, alla radiazione che lo attraversa, una rotazione o deviazione verso la propria base e come, questa deviazione possa essere calcolata; conoscere la sola deviazione non è comunque sufficiente a fornire una informazione completa sul comportamento del prisma posto davanti all’occhio di un utilizzatore.
Il comportamento di un prisma con asse verticale sarà ben diverso da quello che avrebbe se avesse l’asse orizzontale oppure obliquo; dovremo pertanto indicare la direzione del prisma e la posizione della base lungo tale direzione (ad esempio base alta o bassa, oppure tempiale o nasale).
La ricetta di una prescrizione prismatica dovrà pertanto fornire:
– Potere del prisma, espresso nell’unità di misura scelta, ovvero il valore della deviazione prodotta.
– Direzione del prisma.
– Posizione della base del prisma lungo la direzione indicata.
La deviazione prismatica è pertanto una grandezza vettoriale, dal momento che è caratterizzata dalla conoscenza di tre parametri: modulo, direzione, verso.
I valori che individuano il prisma dovranno ulteriormente essere accompagnati dall’indicazione se questo dovrà essere posizionato sull’occhio destro o sinistro e in quale sistema si lavora; esistono infatti due modi distinti di localizzare i riferimenti sui rispettivi occhi a seconda che si parli del:
Sistema TABO (S.T.) o del Sistema Internazionale (S.I.), figura 1.9.
Nel sistema TABO gli zeri, per i due occhi, sono posizionati a destra (nasale per O.D. e tempiale per O.S.) e per andare da zero a 180° la rotazione avviene in senso antiorario; nel sistema Internazionale gli zeri sono nasali e le rotazioni per andare a 180° sono: per l’O.S. in senso orario e per l’O.D. in senso antiorario: per l’occhio sinistro si hanno quindi differenze tra i due sistemi.
Per l’occhio sinistro il passaggio di una prescrizione da un sistema all’altro si effettua: lasciando inalterato il valore del potere del prisma e la posizione della base, mentre la direzione, nel nuovo sistema, si otterrà facendo la differenza tra 180° ed il valore della direzione nel sistema di partenza:
Se l’angolo in un sistema è a, nell’altro sistema sarà (180 – a)
Nella figura 1.10 si mette in evidenza alcune posizioni che possono assumere i prismi su un occhio.
Per la ricettazione dei prismi, in particolare a livello costruttivo, risulta utile fornire i dati nel sistema 360° protractor.
In questo sistema l’effetto compensativo di un prisma è individuato, anche se in forma meno diretta, mediante due soli parametri, considerando di lavorare nel sistema TABO:
– valore del potere prismatico
– posizione della base utilizzando tutto l’angolo giro, quindi tutti i quattro quadranti del goniometro; in tale sistema la posizione della base cade esattamente laddove termina l’angolo indicato nella ricetta.
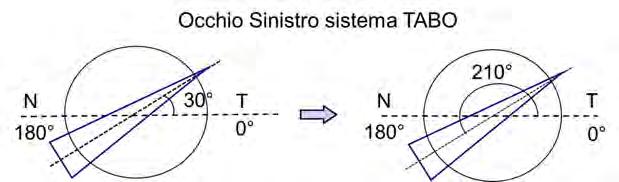
La ricetta prismatica per OSST: 4 D a 30° BN
Sarà espressa nel sistema 360° protractor come: 4 D a 210°, figura 1.11.
Si tenga presente che se la prescrizione per OS fosse data nel Sistema Internazionale si dovrà, per individuare la base nel sistema protractor, prendere come riferimento sempre lo zero a destra cioè il sistema TABO.
Figura 1.9. Sistema TABO e Sistema Internazionale. Si evidenzia che le differenze tra i due sistemi sono solo per l’occhio sinistro
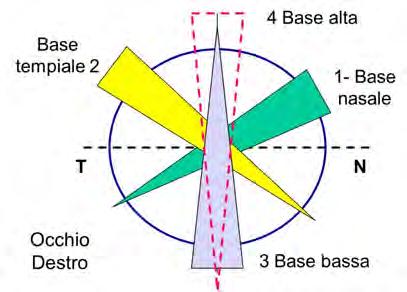
Figura 1.10. Nella figura per OD si mettono in evidenza il posizionamento di prismi
PRISMI CURVI E LORO COMPORTAMENTO
Un prisma oftalmico può essere ottenuto anche con due superfici di stessa curvatura che non presentino lo stesso asse, figura 1.12.
Se applichiamo la formula delle lenti spesse P = P1 + P2 – (e/n) . P1 P2 dove: – P1 e P2 sono i poteri delle due facce del prisma – e lo spessore
– n l’indice di rifrazione del prisma
Risulta evidente che P1 e P2 sono uguali ma di segno opposto quindi il termine P1 + P2 è zero, ciò non è comunque sufficiente per dire che il potere del prisma sia zero a causa del fattore (e/n) P1 P2 che non risulta trascurabile e varierà dal vertice alla base, causa la variazione dello spessore.
Le distorsioni introdotte di questi prismi variano in funzione della curvature usate e dipendono anche dalla distanza del prisma dall’occhio.
Senza entrare in approfondimenti, che richiederebbero altri concetti, possiamo dire che la variazione delle due curvature (sfera base) per ridurre l’ingrandimento asimmetrico, dovuto alla variazione di spessore del prisma, è circa 9.00 dt* (*Studi condotti fin da 1950 da K.N. Ogle) ed è generalmente tale valore che è consigliabile utilizzare per la realizzazione di tali prismi.
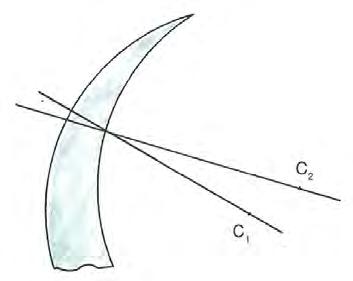
1.12. Rappresentazione di un prisma curvo
INGRANDIMENTO DI UN PRISMA CURVO
Ricordiamo che il rapporto tra le dimensioni dell’immagine retinica dell’occhio corretto e quello dello stesso occhio non corretto, o Ingrandimento totale in-
Figura
Figura 1.11. Passaggio dal sistema TABO al sistema 360° protractor
dotto dal sistema occhio lente, dipende dal prodotto di due fattori: Ingrandimento di Potenza (Pp) e Ingrandimento di forma(If):
I = I p • If
Dati rispettivamente da: Ip = 1 / (1 – d • P) e If = 1 / (1 – P1 • e / n)
dove:
d = distanza vertice posteriore lente (prisma curvo) punto nodale oggetto oculare;
P = potenza frontale posteriore del mezzo compensativo (quella misurata con il frontifocometro);
e = spessore del mezzo compensativo;
n = indice di rifazione;
P1 = potenza della superficie anteriore.
Esempio: consideriamo un prisma curvo con sfera base 9.00 dt, indice di rifrazione n = 1,5; spessore centrale 10 mm, abbiamo per l’Ingrandimento totale I, essendo per quanto detto l’ingrandimento di potenza 1, il valore:
I = I p • If = 1 • 1 / (1 – P1 • e / n) = 1 / (1 – 9 . 0.01/1,5) = 1,064
Corrispondente ad un ingrandimento del 6,4%
La problematica di tale ingrandimento è la sua variabilità in relazione alla variazione di spessore: minore al vertice, maggiore alla base e questo può essere a volte disturbante nell’uso di questi prismi.
PRISMI DI FRESNEL
Fin dalla prima metà del secolo scorso l’ingegnere Augustin Fresnel comprese che il potere diottrico di un prisma dipendeva soprattutto dalla differenza di spessore tra base e apice o tra centro e bordo. Questo principio viene oggi utilizzato per realizzare membrane di cloruro di polivinile (duroplastica di indice 1.525, di spessore di circa 1mm) che vengono fatte aderire per capillarità alla superficie interna delle lenti oftalmiche, sia minerali che organiche (prismi pres-on). I prismi pres-son vengono apprezzati soprattutto in sede di diagnosi di prescrizione, allorché si debba valutare i benefici e la tollerabilità di una lente prismatica oppure per modulare le modalità di un trattamento ortottico, figura 1.13. L’inconveniente, per altro trascurabile, è la riduzione di visus (circa 1/10) rispetto ai prismi convenzionali dovuti alle diffusioni che si presentano sulla discontinuità degli scalini che determinano una riduzione del contrasto. Relativamente all’ingrandimento prismatico questo risulta minore per i prismi di Fresnel rispetto ai prismi convenzionali data la riduzione dello spessore.
EFFETTI PRISMATICI DA DECENTRAMENTO DI LENTI SFERICHE
Un effetto prismatico, voluto o come errore dovuto ad un errato montaggio, può ottenersi decentrando una lente sferica e/o astigmatica sia essa positiva
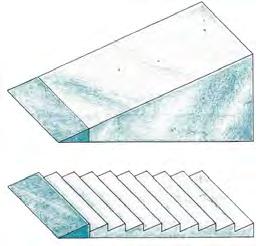
Figura 1.13. Prismi di Fresnel
Figura 1.14. Lenti sferiche come insieme di prismi: a) positive, b) negatine. In figura per comodità grafica si è considerato lenti biconvesse
che negativa. Le lenti sferiche possono infatti essere viste come costituite da tanti piccoli prismi tronchi giustapposti apice-base di potere progressivamente crescente man mano che ci allontaniamo dall’asse ottico della lente. Nel caso di lenti positive i prismi centrali si uniscono con la base parallela all’asse ottico, nelle lenti negative per il vertice, figura 1.14.
Dalla figura si evidenzia che solo la radiazione che incide lungo l’asse della lente non subisce deviazione.
Si evidenzia come utilizzando zone di lente fuori dal centro ottico, le immagini risultano condizionate da effetti prismatici tanto maggiori quanto maggiore è il potere diottrico della lente e tanto maggiore è la distanza dall’asse ottico. L’effetto prismatico d introdotto dal decentramento viene ottenuto dalla relazione del Prentice: d(D) = (h . P) / 10
Se h è in cm la relazione assume l’espressione d(D) = h . P dove:
– h è la distanza, in mm, del punto considerato dal cento ottico della lene, – P potere diottrico della lenti in valore assoluto. Se la lente è astigmatica dovremo calcolare il potere lungo la direzione del decentramento. Il potere del prisma viene ricavato da tale relazione, la determinazione delle direzione e la posizione della base rispetto all’occhio si ottengono: – per la direzione si unisce il punto con il centro ottico della lente, – per la base avremo: se lungo la direzione del decentramento la lente è positiva la base corrisponde alla posizione del centro ottico della lente, nelle lenti negative la base si colloca nella direzione opposta, figura 1.15. Da quanto detto ne deriva che decentrando una lente positiva la base del prisma si posizionerà nella direzione del decentramento; il valore del prisma
Figura 1.15. Posizione della base in lenti positive e negative
dipenderà dal decentramento e dal valore diottrico della lente lungo questa direzione. Per lenti negative la posizione della base del prisma sarà nella direzione opposta al decentramento e il valore seguirà quanto precedentemente detto.
Come per i prismi oftalmici, anche per gli effetti prismatici indotti dal decentramento di una lente è importante evidenziare le differenze esistenti fra potere prismatico nominale (valore ottenuto con la relazione di Prentice ottenuto per decentramento), e quello effettivo (il valore quando la lente la è approntata sull’occhiale).
Mentre per i prismi le differenze erano presenti solo nella visione prossima, nelle lenti, poiché l’effetto correttivo di quest’ultime varia con la distanza a cui sono poste dall’apice corneale, si avranno modificazioni anche per la visione all’infinito.
Considerazioni numeriche
Nella visione per lontano si ha:
– Con lenti negative de è sempre minore di dn
– Con lenti positive de è sempre maggiore di dn
Ci dobbiamo chiedere se queste differenze sono trascurabili o no?
La risposta è scontata: per bassi poteri sono trascurabili, per elevati poteri non lo sono.
Esempi:
P = + 5.00 dt. h = 5 mm d = 25 mm dn = (h • P) / 10 = (5 • 5.00) / 10 = 2,5 D de = dn / (1 – d • P) ed essendo (1 - d • P) = 0,875
avremo de = 2,5 / 0,875 = 2,86 D
P= +15.00 dt. h = 5 mm d = 25 mm dn = 7,5 D de = 12 D
Per ottenere un de di 7,5 D si dovrebbe decentrare la lente non di 5 mm ma di circa 3 mm
La relazione che esprime tale effetto, sia per lenti positive che negative, è la seguente:
de (D) = dn / (1 – d • P)
dove:
– de effetto prismatico effettivo, – dn effetto prismatico nominale, – d distanza centro di rotazione oculare lente, – P potere della lente
Nella visione per vicino le cose sono ancora più complicate e la relazione per la valutazione dell’effetto prismatico effettivo rispetto a quello nominale ottenuto in una lente per decentramento sia essa positiva che negativa, è regolato dalla relazione:
de (D) = dn / (1 – d • P + d / x)
dove:
– x distanza dal punto di fissazione alla lente in metri – d distanza centro di rotazione oculare lente in metri, – P potere della lente
Per lenti negative si ha, qualunque sia la distanza x, de < dn
Per lenti positive:
– Oggetto sul fuoco lente de = dn
– Oggetto tra fuoco e lente de < dn
– Oggetto oltre il fuoco de > dn
Considerazioni numeriche
P = + 10.00 dt. h = 10 mm d = 25 mm dn = (h · P) / 10 = (10 . 10) / 10 = 10 D
Tenendo presente che la lente di 10 dt ha una focale di 10 cm., avremo rispettivamente:
Per x = 10 cm de = 10 D
Per x = 20 cm de = 11,4 D
Per x = 5 cm de = 8 D
EFFETTI PRISMATICI DA DECENTRAMENTO DI LENTI ASTIGMATICHE
Per una lente puramente cilindrica si può ottenere un effetto prismatico per decentramento ma questo seguirà regole diverse di una lente sferica, non avendo la lente cilindrica lo stesso potere sui vari meridiani, avremo:
• Se il decentramento avviene sul meridiano di potere l’effetto prismatico si calcola con la formula del Prentice, la direzione sarà quella del meridiano di potere e la posizione della base in relazione al potere della lente su tale meridiano.
• Se il decentramento avviene lungo la direzione dell’asse (meridiano di potere zero) non avremo effetto prismatico.
• Se il decentramento viene effettuato su un meridiano obliquo rispetto ai meridiani principali della lente piano cilindrica la valutazione dell’effetto prismatico può essere fatto con diversi modi di risoluzione. Un metodo relativamente semplice può effettuarsi scomponendo il decentramento lungo i meridiani principali mediante relazioni trigonometriche, calcolare l’effetto prismatico sui meridiani principali (sull’asse l’effetto prismatico sarà zero) e quindi rimarrà solo l’effetto prismatico sul meridiano di potere con quella direzione e verso legato al segno di quel meridiano.
Per lenti sferocilindriche (la realizzazione della lente viene effettuata con costruzione sferotorica, per cui il risultato può differire di valori trascurabili) si dovrà fare riferimento alle due potenze sui due meridiani principali.
Se il decentramento è su uno dei due meridiani si applica direttamente la relazione del Prentice. Se il decentramento è in direzione obliqua, si dovranno trovare le componenti del decentramento lungo i meridiani principali, calcolarne il contributo prismatico in funzione delle potenze e quindi risalire all’effetto prismatico risultante.
Un esempio chiarirà la procedure da seguire.
Sia data la seguente prescrizione:
OSSI sf +2.50 cil 1.50 ax 90° 2 dtp a 50° BT le potenze sui due meridiani sono rappresentate nella figura 1.16.
Per il calcolo del decentramento, non conoscendo il valore lungo il meridiano a 50°, dovremo scomporre l’effetto prismatico lungo i due meridiani principali, avremo:
d180°(D) = d(D)• cos 50° = 2 • 0,643 ≈ 1,29(D)
d90°(D) = d(D)• sen 50° = 2 • 0,766 ≈ 1,53(D)
Figura 1.16. Rappresentazione grafiche di: a. OSSI sf +2.50 cil +1.50 ax 90° 2 dtp a 50° BT; b. decentramento risultante
Dalla relazione del Prentice: d(D) = (h • P) /10 otteniamo h = [d(D) • 10] / P
quindi: h180° = (1,29 • 10) / 4.00 ≈ 3,22 mm h90° = (1,53 • 10) / 2.50 ≈ 6,12 mm
Il valore del decentramento per ottenere quell’effetto prismatico e la direzione da dare alla lente sarà quindi: h = √(h2180° + h290° ) = √(3,222 + 6,122) ≈ 6,92 mm a = arctg (h90° / h180°) = arctg (6,12 / 3,22) ≈ 62,25°
Il calcolo si complicherebbe ulteriormente se la sferocilindrica fosse ad asse obliquo.
EFFETTI INDOTTI NELL’USO DEI PRISMI
Nell’uso oftalmico i prismi, oltre ad essere generalmente pesanti e antiestetici, data la disparità di spessore, si avrà anche una alterazione della definizione dell’immagine retinica, infatti:
– generano immagini dai contorni iridescenti a causa della composizione spettrale della radiazione policromatica che li attraversa (vedi "dispersione di un prisma").
– spostano l’immagine verso l’apice e ne introducono una distorsione caratterizzata da:
• aumento dell’ingrandimento angolare dell’immagine verso l’apice, lungo la linea base-apice (ingrandimento prismatico),
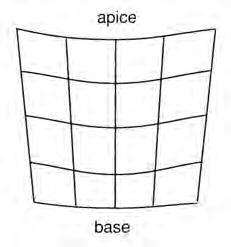
Figura 1.17. Distorsione introdotta da un prisma
• inclinazione delle linee parallele alla linea base-apice,
• curvatura delle linee immagini perpendicolari alla linea base-apice (metamorfopsia prismatica), figura 1.17.
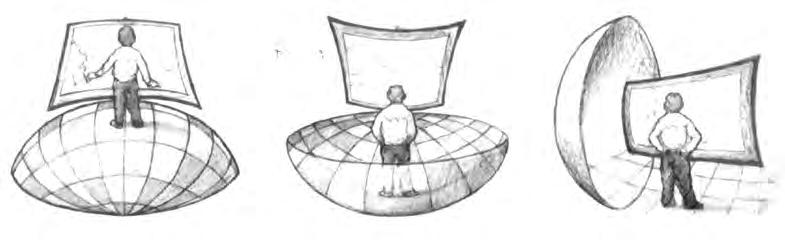
Figura 1.18. Deformazione dell’immagine introdotta da un prisma a base alta (a), a base bassa (b), a base laterale.
La distorsione introdotta da un prisma dipende dai seguenti
fattori, figura 1.18:
– distanza apice corneale-prisma
– potere del prisma
– spessore del prisma
– inclinazione del prisma rispetto all’occhio
Abbiamo inoltre che in corrispondenza dell’apice del prisma una porzione del campo
visivo della stessa ampiezza
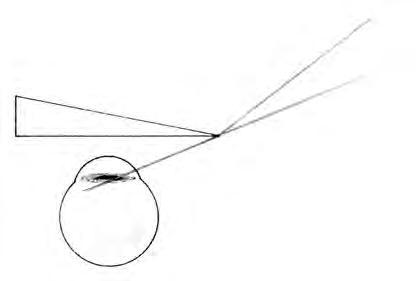
Figura 1.19. Scotoma marginale introdotto da un prisma
dell’angolo di deviazione del prisma viene funzionalmente eliminata (scotoma marginale, figura 1.19.)
Bibliografia
• Geometria della radiazione ottica, Abati S., Boccaccini G., Borchi E., Macii R., Fabiano Editore, 2002
• Occhiali in Ottica Oftalmica, Abati S., Montani G., Lovisolo C., Buratto L., CAMO Milano, 1993
• Geometria della radiazione ottica, Abati S., Borchi E., Macii R., IRSOO, Vinci (FI) 1993
• Clinical Visual Optics, Bennet A.G., Rabbe R.B., Butterworths, Londra 1989
• Fondamentals of Optics, Jenkins F.A., White H.E., Istituto Editoriale Universitario, Milano 1972