Journal of Automation, Mobile Robotics and Intelligent Systems, vol. 18, no. 1 (2024)

WWW.JAMRIS.ORG pISSN 1897-8649 (PRINT)/eISSN 2080-2145 (ONLINE)

Indexed in SCOPUS

VOLUME 18, N° 1, 2024

Journal of Automation, Mobile Robotics and Intelligent Systems

A peer-reviewed quarterly focusing on new achievements in the following fields:

• automation • systems and control • autonomous systems • multiagent systems • decision-making and decision support •

• robotics • mechatronics • data sciences • new computing paradigms •

Editor-in-Chief

Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Advisory Board

Dimitar Filev (Research & Advenced Engineering, Ford Motor Company, USA)

Kaoru Hirota (Tokyo Institute of Technology, Japan)

Witold Pedrycz (ECERF, University of Alberta, Canada)

Co-Editors

Roman Szewczyk (Łukasiewicz-PIAP, Warsaw University of Technology, Poland)

Oscar Castillo (Tijuana Institute of Technology, Mexico)

Marek Zaremba (University of Quebec, Canada)

Executive Editor

Katarzyna Rzeplinska-Rykała, e-mail: office@jamris.org (Łukasiewicz-PIAP, Poland)

Associate Editor

Piotr Skrzypczyński (Poznań University of Technology, Poland)

Statistical Editor

Małgorzata Kaliczyńska (Łukasiewicz-PIAP, Poland)

Typesetting SCIENDO, www.sciendo.com

Webmaster TOMP, www.tomp.pl

Editorial Office

ŁUKASIEWICZ Research Network

– Industrial Research Institute for Automation and Measurements PIAP

Al. Jerozolimskie 202, 02-486 Warsaw, Poland (www.jamris.org) tel. +48-22-8740109, e-mail: office@jamris.org

The reference version of the journal is e-version. Printed in 100 copies.

Articles are reviewed, excluding advertisements and descriptions of products.

Details are available at: https://www.jamris.org/index.php/JAMRIS/ LicenseToPublish

Editorial Board:

Chairman – Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Plamen Angelov (Lancaster University, UK)

Adam Borkowski (Polish Academy of Sciences, Poland)

Wolfgang Borutzky (Fachhochschule Bonn-Rhein-Sieg, Germany)

Bice Cavallo (University of Naples Federico II, Italy)

Chin Chen Chang (Feng Chia University, Taiwan)

Jorge Manuel Miranda Dias (University of Coimbra, Portugal)

Andries Engelbrecht ( University of Stellenbosch, Republic of South Africa)

Pablo Estévez (University of Chile)

Bogdan Gabrys (Bournemouth University, UK)

Fernando Gomide (University of Campinas, Brazil)

Aboul Ella Hassanien (Cairo University, Egypt)

Joachim Hertzberg (Osnabrück University, Germany)

Tadeusz Kaczorek (Białystok University of Technology, Poland)

Nikola Kasabov (Auckland University of Technology, New Zealand)

Marian P. Kaźmierkowski (Warsaw University of Technology, Poland)

Laszlo T. Kóczy (Szechenyi Istvan University, Gyor and Budapest University of Technology and Economics, Hungary)

Józef Korbicz (University of Zielona Góra, Poland)

Eckart Kramer (Fachhochschule Eberswalde, Germany)

Rudolf Kruse (Otto-von-Guericke-Universität, Germany)

Ching-Teng Lin (National Chiao-Tung University, Taiwan)

Piotr Kulczycki (AGH University of Science and Technology, Poland)

Andrew Kusiak (University of Iowa, USA)

Mark Last (Ben-Gurion University, Israel)

Anthony Maciejewski (Colorado State University, USA)

Krzysztof Malinowski (Warsaw University of Technology, Poland)

Andrzej Masłowski (Warsaw University of Technology, Poland)

Patricia Melin (Tijuana Institute of Technology, Mexico)

Fazel Naghdy (University of Wollongong, Australia)

Zbigniew Nahorski (Polish Academy of Sciences, Poland)

Nadia Nedjah (State University of Rio de Janeiro, Brazil)

Dmitry A. Novikov (Institute of Control Sciences, Russian Academy of Sciences, Russia)

Duc Truong Pham (Birmingham University, UK)

Lech Polkowski (University of Warmia and Mazury, Poland)

Alain Pruski (University of Metz, France)

Rita Ribeiro (UNINOVA, Instituto de Desenvolvimento de Novas Tecnologias, Portugal)

Imre Rudas (Óbuda University, Hungary)

Leszek Rutkowski (Czestochowa University of Technology, Poland)

Alessandro Saffiotti (Örebro University, Sweden)

Klaus Schilling (Julius-Maximilians-University Wuerzburg, Germany)

Vassil Sgurev (Bulgarian Academy of Sciences, Department of Intelligent Systems, Bulgaria)

Helena Szczerbicka (Leibniz Universität, Germany)

Ryszard Tadeusiewicz (AGH University of Science and Technology, Poland)

Stanisław Tarasiewicz (University of Laval, Canada)

Piotr Tatjewski (Warsaw University of Technology, Poland)

Rene Wamkeue (University of Quebec, Canada)

Janusz Zalewski (Florida Gulf Coast University, USA)

Teresa Zielińska (Warsaw University of Technology, Poland)

Publisher:

Copyright © 2023 by Łukasiewicz

Research Network - Industrial Research Institute for Automation and Measurements PIAP

1

Journal of Automation, Mobile Robotics and Intelligent Systems

VOLUME 18, N˚1, 2024

DOI: 10.14313/JAMRIS/1-2024

Contents

Aleksandra Urbanczyk, Krzysztof Kucaba, Mateusz

Wojtulewicz, Marek Kisiel‑Dorohinicki, Leszek

Rutkowski, Piotr Duda, Janusz Kacprzyk, Xin Yao, Siang Yew Chong, Aleksander Byrski

DOI: 10.14313/JAMRIS/1 2024/1 12

Maksym Grishyn, Kostiantyn Beglov

DOI: 10.14313/JAMRIS/1 2024/2

Low‐Cost Small‐Scale Autonomous Vehicle

Ismail Bogrekci, Pinar Demircioglu, Mustafa Yasir Goren

DOI: 10.14313/JAMRIS/1 2024/3

Application of Multilayer Neural Networks for Controlling a Line‐Following Robot in Robotic Competitions

Cesar Minaya, Ricardo Rosero, Marcelo Zambrano, Pablo Catota

DOI: 10.14313/JAMRIS/1 2024/4

Pearson Correlation and Ordered Weighted Average Operator in the World Stock Exchange Market

Martha Flores‑Sosa, Ernesto Leon‑Castro, Jose

M. Merigo

DOI: 110.14313/JAMRIS/1 2024/5

Using Reinforcement Learning to Select an Optimal Feature Set

Yassine Akhiat, Ahmed Zinedine, Mohamed Chahhou

DOI: 10.14313/JAMRIS/1 2024/6

67

Unlocking the Future of Secure Automatic Machines: Leveraging FaceReg with HRC & LBPH

Yamini Vijaywargiya, Mahak Mishra, Nitika Vats

Doohan

DOI: 10.14313/JAMRIS/1 2024/7

Submitted:8th February2023;accepted:17th July2023

AleksandraUrbanczyk,KrzysztofKucaba,MateuszWojtulewicz,MarekKisiel‑Dorohinicki,LeszekRutkowski, PiotrDuda,JanuszKacprzyk,XinYao,SiangYewChong,AleksanderByrski

DOI:10.14313/JAMRIS/1‐2024/1

Abstract:

Socio‐cognitivecomputingisaparadigmdevelopedfor thelastseveralyearsinourresearchgroup.Itconsists ofintroducingmechanismsinspiredbyinter‐individual learningandcognitionintometaheuristics.Differentver‐sionsoftheparadigmhavebeensuccessfullyapplied inhybridizingAntColonyOptimization(ACO),Particle SwarmOptimization(PSO),GeneticAlgorithms,Differ‐entialEvolution,andEvolutionaryMulti‐agentSystem (EMAS)metaheuristics.Inthispaper,wehavefollowed ourpreviousexperiencesinordertoproposeanovel mutationbasedonsocio‐cognitivemechanismandtestit basedonEvolutionStrategy(ES).Thenewlyconstructed versionswereappliedtopopularbenchmarksandcom‐paredwiththeirreferenceversions.

Keywords: metaheuristics,socio‐cognitivecomputing, globaloptimization

1.Introduction

Tacklingdif icultoptimizationproblemsrequires usingmetaheuristics[1],andveryoftenitisneeded tocreatenewones[2],i.e.bymodifyingorhybridizing theexistingalgorithms[3].

AlthoughSorensenhascriticizedthedevelopment ofnewmetaheuristics[4],wecontendthatusing metaphorsinourdailywork[5]notonlyfosterscre‐ativitybutalsomayresultinthediscoveryoftrulynew solutionsofconsideredissuesornovelmechanismsto solvethemautomatically.

Becauseclassicmetaheuriticsarefrequently inspiredbynature,theirfurthermodi ications frequentlycombinedifferentphenomenaobservedin therealworld.

Onedirectionofsuchmodi icationscomesfrom theveryin luentialSocial‐CognitiveTheoryintro‐ducedbyBandura[6].Accordingtothistheory, someofaperson’sknowledgecanbedirectlylinked toobservingothersduringtheirsocialinteractions, experiences,andexternalmediain luences.[7].Thus, despitelearningonlythroughherowntrialanderror, onecanreachhergoalssoonerthankstosuchobser‐vation[8].

Wehavealreadyintroduceddedicated mechanismsrootedinSocial‐CognitiveTheoryto selectedmetaheuristics(socio‐cognitiveACO[9]and

socio‐cognitivePSO[10]),obtaininggoodresults comparedtothereferencealgorithms.

Presently,wefocusonthegroupofevolutionary metaheuristics,andbymodifyingchosenalgorithms fromthisgroup,weaimtodevelopauniversalmech‐anismforvariationoperatorsthatwouldembodythe ideaofsocio‐cognitivelearningmechanisms.

Themaincontributionofthispaperisasocio‐cognitivelyinspiredmutationmechanism,thatmakes itpossibletoexchangetheinformationamongthe individualsinevolutionaryalgorithms.Theproof‐of‐conceptofthismechanismwasintroducedinthe researchpaperin2021[11]andwasredesigned andreimplementedbasedontheresultsachieved. Theef iciencyandef icacyofthenewversionof thealgorithmsaretestedusingwell‐knownhigh‐dimensional,multimodalbenchmarkfunctions.The proposedmethodisbasedoncopyingcertainparts ofthegenotypes(thuspassingtheknowledge)from thebetterones,andavoidingthepartsofsolutions oftheworstones.Inthispaper,weconsiderwell‐known (��+��) ES,butwebelievethatourmuta‐tionmechanismmaybeusedinabroaderrangeof algorithms.

Westartwiththereferencetostate‐of‐the‐art showingtheexistingmodi icationsofmetaheuristics, inparticularevolutionstrategies.Thenweshowthe novelmethodforintroducingsocio‐cognitivemecha‐nismsinto(��+��)evolutionstrategy.Weproviderele‐vantexperimentalresultsand,intheend,weconclude ourpapershowingthesummaryandthefuturework plans.

2.RelatedNon‐classicEvolutionary Algorithms

Thereareseveralmetaheuristicdiscoursesin whichthisworkcanbeanchored.Onthemostgeneral level(consideringthearchitectureoftheentirealgo‐rithm),itcanbetreatedasakindofhybridalgorithm [12]inthesamesensethatamemeticalgorithmisone [13]andmanyothersimilaralgorithms,developed intheresearchgroupoftheAuthors[14–16].The majorityofmemeticalgorithmsarebasedongenetic algorithm,andhaveintroducedsomelocalsearch orheuristiclearningmechanisms.Unlikethem,the describedalgorithmisbasedonanothermetaheuris‐ticoftheevolutionarycomputationgroup,namelythe evolutionstrategy[17,18].

Thesimilarityliesinthefactthatanovelmecha‐nism(i.e.,socio‐cognitivemutationoperator)isintro‐ducedinbetweenstandardstepsofthealgorithm.Our workshouldalsobeplacedinthecontextofvarious modi iedorhybridESs.Thepossiblemodi icationsof classicESsrangefromsimpletuningormanipulation ofcontrolparameterssuchasmutationstrengthor populationsize(step‐size)[19–21],throughcovari‐ancematrixadaptationevolutionstrategy(CMA‐ES) [22]toheterogeneoushybridsofES,whichareoften focusedonparticularapplication,e.g.vehiclerouting problem[23],optimizationofengineering,andcon‐structionproblems[24,25]andthenumberofwhich isapparentlynotveryhigh.

Takingintoaccountthelevelofthevariationoper‐atorsitself,ourpostulatedoperatorcanbecom‐paredtotheonepresentinthedifferentialevolution metaheuristic[26].ThecharacteristictraitofDEis themutationvariationoperator,whichoperateson parametervectorswithscaledpopulation‐deriveddif‐ferencevectors.Inthissense,itisnotjustarandomly performingoperator,asintraditionalEAsandESs,but itutilizestheinformationaboutcurrentpopulation, especiallyintheschemeshaving“best”inthenames, suchas ����/��������/1 and ����/������������−����−��������/1 thatusethebestsolutiontode inemutationdirec‐tions[27].Asimilaranalogyispresentbetweenclassic mutationandoursocio‐cognitivemutationoperator. Themechanicsofthenewoperatorcanberelatedto thewell‐knownTOPSIS(TechniqueforOrderofPref‐erencebySimilaritytoIdealSolution)method[28]. TOPSISisbasedontheideathatthechosenalterna‐tiveshouldbetheonewiththeshortestgeometric distancefromthepositiveidealsolutionandtheone withthegreatestgeometricdistancetothenegative idealsolution.

AsalreadymentionedintheIntroduction,we rootourworkinadiscourseofsocio‐cognitively inspiredalgorithms.The irstobjectiveofintroduc‐ingsociocognitivemechanismintoevolutionstrate‐giesservedasaproof‐of‐conceptthatturnedoutto bepromising[11],butpointedoutseveraldimen‐sionsformajorimprovements.The irstconclusion wasthatthesemechanismsthatoperatetowards bettersolutionsgivebetterresultsthanoperators basedonmovingawayfromtheworstindividuals.We decidedthatthecoreofourideawasasynergyof thesetwodirections,andthatthesecondpartmust betotallyredesignedinordertoworkasintended. Otherwise,itwouldbetoostraightforwardanalogy with����/��������/1andothersocio‐cognitivealgorithms describedin[29]and[30],sothenoveltywouldbe minimal.Thesecondlessonfromthepreviousattempt tomodifyESwasthatthealgorithmitselfshouldhave amoderatelevelofcomplexityinordertobeabasefor asuccessfulsocio‐cognitivemodi ication.Theexperi‐mentsperformedonthe(1+1)versionofES,aswell asthe (��,��) versionwerenotassuccessfulasthose basedonthe(��+��)versionofthealgorithm,which gavebetterresultsinallthebenchmarkstested,in contradictiontothe(��,��)versionthatwasbetteronly inoneofthem.Sowedecidedthatitwillbethebestto sticktothe(��+��)versionforourfurtherpurposes.

3.Socio‐cognitive (��+��) EvolutionStrategy

TheclassicalgorithmofEScanbedescribedas follows:

1) Initializeparentpopulation ���� ={��1,…,����}.Each oftheindividualscanbedescribedasfollows:��∋ ���� ={����,1,…,����,��,����,1,…,����,��},��,��∈ℕstandsfor anindividualcontainingagenotype ����,1,…,����,�� representingobjectiveparameters,andassociated ����,1,…,����,�� mutationstrategyparametersthatwill beadaptedinordertoguidethesearch.Thedimen‐sionalityoftheconsideredproblemis��. Later,we usethenotation ����,�� toreferto ����,��,whichis ��-th geneof ��-thgenotype.

2) Generate �� offspringindividualsformingtheoff‐springpopulation���� ={��1,…,����}inthefollowing procedure:

‐ Randomlyselect��parentsfrom���� (if��=��,then takeallofthem).

‐ Recombinethe��selectedparents(traditionallya pair)toformarecombinantindividual����,using anypossiblerecombinationmeans(traditionally averagingcrossoveroperatorwasused).

‐ Mutatethestrategyparameterset����,1,…,����,�� of therecombinant ���� (adaptinge.g.themutation diversitiesforthenextmutation).Traditionally, mutationisrealizedbyapplyingaperturbation basedon,forexampleuniformorGaussianran‐domdistributionoraddingorsubtractingacer‐tainvalueto(from)aselectedgene.

‐ Mutatetheobjectiveparameterset ����,1,…,����,�� oftherecombinant���� usingthemutatedstrategy parametersettocontrolthestatisticalproper‐tiesoftheobjectparametermutation.

3) Selectnewparentpopulation(usingdeterminis‐tictruncationselection)fromeithertheoffspring population ���� (thisisreferredtoascomma‐selection,usuallydenotedas“(��,��)‐selection”),or theoffspring���� andparent���� population(thisis referredtoasplus‐selection,usuallydenotedas “(��+��)‐selection”).

4) Goto2.untilterminationcriterionful illed. Wehavedecidedtointroducethesocio‐cognitive mechanismstothe (��+��) versionofES.Thisfol‐lowsfromtheapparentpotentialofsuchmechanisms developedearlierin[11].Wehavestudiedtheupdat‐ingpartoftheoperatorsappliedtherein,andintro‐ducedmodi icationsinordertoincreasetheiref icacy. Inparticular,wehaveaimedatincreasingthe exchangerateofinformationbetweentheindividuals incurrentpopulationwiththegoalofacceleratingthe learningrateofalgorithm.Inordertoachievethis,we splitasinglemutationstepintomultipleindependent sequentialmutations.The irstmutationisalwaysthe classicaloperatormeanttointroduceperturbationto thesolution’sgenome.Thefollowingoperatorormul‐tipleoperatorsaremeanttointroducefurthermodi i‐cationstothatsolutionthatareguidedbythecurrent stateofpopulation.

Inourexperimentswetestandevaluatethefol‐lowingsocialmutations:

1) FollowBest:

Outofthetop �� individuals ��1,…,���� incurrent populationrandomlyselectonethatwillbenow calledteacher ��.Withprobability ����,foreachof thecurrentlyoperatedonsolution’s �� genes ����, assignnewvalue���� ←���� +����(���� −����)where���� is thecorrespondinggeneof��and���� isfollowrate.

2) FollowBestDistinct:

Leteachindividual ���� beasequenceof �� genes ���� =(����,1,…,����,��).Outofthetop �� individ‐uals ��1,…,���� incurrentpopulationrandomly selectonethatwillbenowcalledteacher ��. Acrossthe��1,…,���� individualscalculatethestan‐darddeviationforeachofthegenepositions 1,…,�� resultingin ��1 ������,…,���� ������ where ���� ������ = ������(��1,��,…,����,��).Choose �� genepositionsper‐formingweightedrandomselectionacross1,…,�� using ��������������(��1 ������,…,���� ������) asvectorofproba‐bilities.Foreachof��chosengenepositionsofthe currentlyoperatedonsolution’s��genes���� assign newvalue ���� ←���� +����(���� −����) where ���� isthe correspondinggeneof��and���� isfollowrate.

3) RepelWorstGravity:

Outof �� worstindividualsinthecurrentpopu‐lationrandomlyselectoneindividual ������.While operatingonanindividual ������,withprobability ����,performthefollowingassignmentforevery gene ��: ����,�� ←����,�� +���� ⋅ ������(����) ��2 �� ,where ���� = (����,�� −����,��) iscalledadistanceingene ��, ������ isasignfunctionand���� isarepelrate.Thatway therepelmagnitudeisinverselyproportionalto thesquareddistanceforagivengene,andwitha directionawayfromthechosenworstindividual.

4) RepelWorstGravityMultistep:

Foreveryindividual ���� from �� worstindividu‐alsinthecurrentpopulationperformtheassign‐mentsdescribedabove.Thatwaytherepeleffect isstrongerandmoreversatile.

4.Experiments

Themainaimoftheexperimentsistoverifythe ef icacyofglobaloptimization(minimization)ofthe novelalgorithmsfortheselectedbenchmarkfunc‐tions(Ackley,DeJong,Rastrigin,andGriewank[31]) ofdimensions ��∈{100,500,1000}.Boththevalue obtainedinthelastiteration,andthetrajectoryofthe itnessfunctionsimprovementsareconsidered–in certainsituationsitisdesirabletohavearelatively fastconvergenceearlier,inothersituationsthefocus isplacedonthe inalresult.Theequationsusedforthe benchmarkfunctionsareasfollows:

‐ Ackley: ��(��)=−����−�� 1/��∑�� ��=1(��2 �� )

��1/��∑�� ��=1cos(������) +��+��;��=20;��=0.2;��= 2��;��∈[1∶��];−32.768≤��(��)≤32.768.��(��opt)= 0,��opt �� =0

‐ DeJong:��(��)= ∑�� ��=1 ��2 �� ,��∈[1,��];−5.12≤���� ≤ 5.12.��(��opt)=0,��opt �� =0

‐ Rastrigin:��(��)=10��+∑�� ��=1(��2 �� −10cos(2������)),��∈ [1,��];−5.12≤���� ≤5.12.��(��opt)=0,��opt �� =0.

‐ Griewank:��(��)= ∑�� ��=1 ��2 �� /4000−∏cos(����/√��)+ 1,��∈[1,��];−600≤���� ≤600,��(��opt)=0, ��opt �� =0

Figure1. PopulationtrajectoryforeachalgorithmonAckleyProblem1000.Eachverticalsliceatgivensteprepresents histogramofjoinedpopulationsoverallevaluationrunswithcolordepictinghistogramboxcount

Thefollowingalgorithmshavebeenbenchmarked:

‐ Original(��+��)ES,

‐ FollowBestES–withtheFollowBestmutation,

‐ FollowBestDistinctES–withtheFollowBestDis‐tinctmutation,

‐ RepelWorstGravityMultistepES–withtheRepel WorstGravityMultistepmutation,

‐ ComboDistinctGravityES–withtheFollowBest DistinctandRepelWorstGravitymutations,

‐ ComboDistinctGravityMultistepES–withtheFol‐lowBestDistinctandRepelWorstGravityMultistep mutations.

Figure2. TrajectoryofchangesofmeanfitnessfunctionvalueforGriewankproblemand (��+��) EvolutionaryStrategy, dependingonthenumberofiterations

Thestoppingcriteriawasreachingmaximum numberofiterationsofpopulationupdates(setas100 foralltheexperiments).Thenumberofindividuals inthepopulationwassetto ��= 200.Thefollowing settingshavebeenusedforthealgorithms:

‐ ��=20,��=140.

‐ ��good =0.1,��bad =0.1,��=0.01

‐ ��=1/��,where��isthenumberofdimensions,

‐ numberofthecurrentlybestorworstindividuals:5. Eachexperimenthasbeenrepeated12times,andthe meanvalueofthe itnessfunctionistakenasrefer‐ence.Thealgorithmshavebeenimplementedusing jMetalPy1 computingframework.Thesourcecodeis availableonrequest.Thecomputationshavebeen conductedonaPC‐classcomputer.

Figure3. TrajectoryofchangesofmeanfitnessfunctionvalueforAckleyproblemand (��+��) EvolutionaryStrategy, dependingonthenumberofiterations

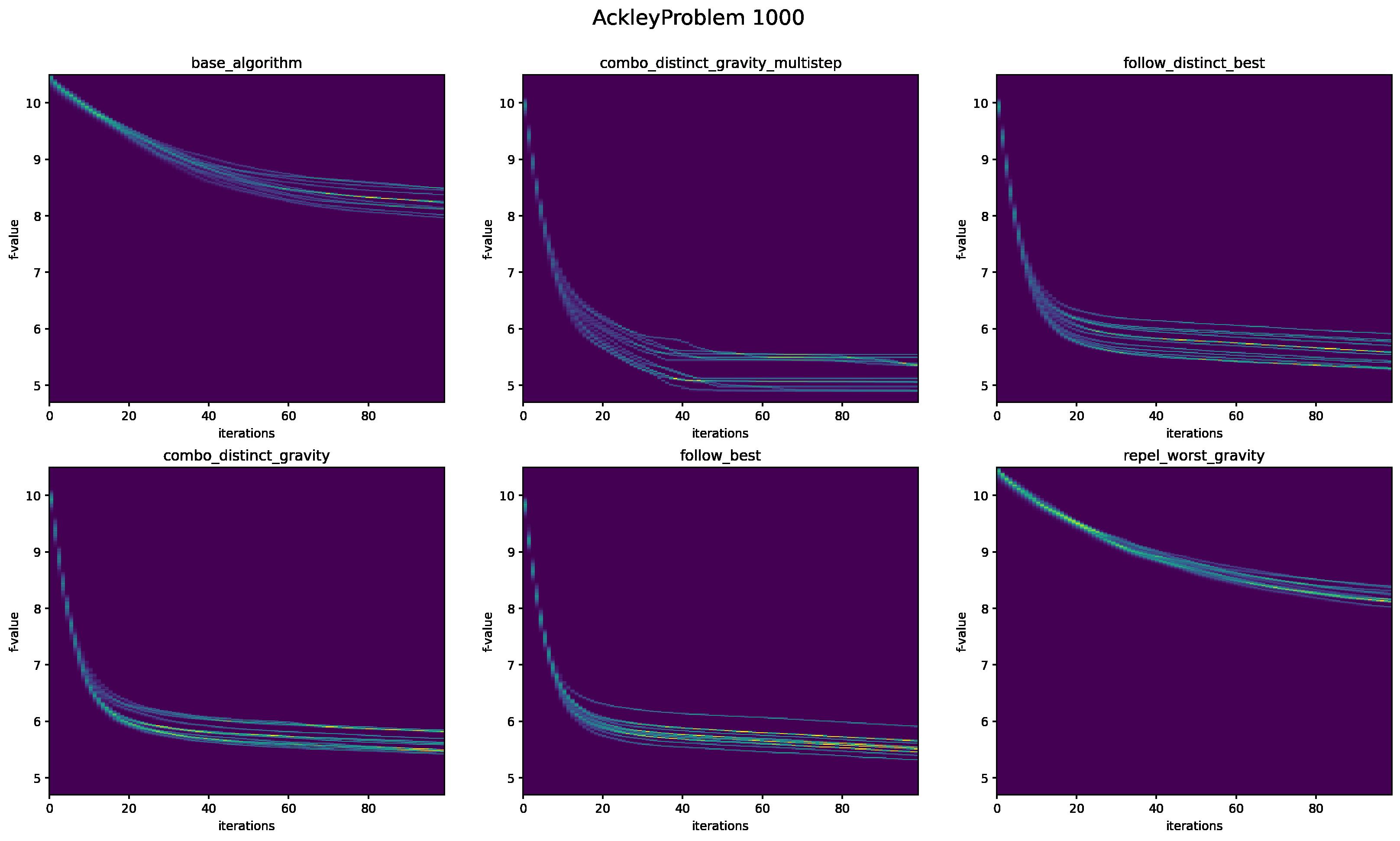
Westartwithobservationsofgeneralbehaviorand ontherepeatability(i.e.,consistencyofperformance inrepeatedruns)ofthealgorithmswhensolvingthe problemsforallthevariantsoftheproposedalgo‐rithms.Therefore,wehavepreparedhistogram‐like visualizationsofthecomputationruns.InFig. 1,the actualtrajectoriesofeachalgorithmscanbeseen. Moreover,eachverticalsliceshowsthecountofthe valuesobtainedateachiterationofthealgorithmfor allrepeatedexperiments.

Wecanclearlyseethatallthevariantsofthemod‐i ied (��+��) approachesarerepeatable.Moreover, theresultsobtainedforoneofbiggestproblemstack‐led,namelyAckleyin1000dimensionscanalsobe observedindetail.Beingconvincedoftherepeata‐bilityoftheexperimentswecanproceedwithsubse‐quentphasesofourstudies.

Nowwecanfocusonobservationsoftheaverages obtainedforallthebenchmarkproblemsaddressed withdifferentcon igurationsofthealgorithms.

Figure4. TrajectoryofchangesofmeanfitnessfunctionvalueforRastriginproblemand (��+��) EvolutionaryStrategy, dependingonthenumberofiterations

Itisclearfromobservationsoftheresultsthat ourmethods(includingthebasealgorithm)arevery effectiveinthecaseofGriewankandAckley(see Figs.2and3)problems.Notallourproposedmethods areeffectiveforDeJongandRastriginproblem(see Figs.5and4). Forexample,therepelworstgravity approachdoesnotalwaysleadtoimprovementsin

theperformanceoverthebasealgorithm.Thisis notsurprisingfollowingthemainimplicationofthe well‐known NoFreeLunchTheorem byWolpertand MacReady[2],inwhichoneoftheimportantsteps wouldbetooptimizetheparametersofthesearchfor eachindividualproblem.

Figure5. TrajectoryofchangesofmeanfitnessfunctionvalueforDeJongproblemand (��+��) EvolutionaryStrategy, dependingonthenumberofiterations

Ourmotivationforthisstudyistotesttheef i‐ciencyandef icacyofourproposedmechanismsin theirbaselinecon igurations.Assuch,wehavesought todeterminetheirgeneralcapabilitiestoimprovethe referenceESalgorithmoverthewholesetofselected benchmarkproblems.

Whenaparticularmechanismdidnotlead toimprovementbutleadtoloweraverageperformanceforaparticularbenchmarkproblem, resultsindicatethatthedifferenceisnotstatisticallysigni icant(e.g.,Table 2 forRepelWorst GravitycomparedwiththebaseorreferenceES algorithm)ontheGriewankProblemat ��=1000. Thissuggestsscopetooptimizetheparametercon‐igurationsofourproposedmechanismsthatwar‐rantfurther,futurestudies.Inadditiontoasystem‐aticparametersweeptoascertainoptimalparameter con igurationsforthemechanisms,otherapproaches wouldbetoapplysomededicatedalgorithmtuning methodsuchasiRace[32].Oneadditionalconclusion ofthisphaseisthatthebestofourmodi icationwas ComboDistGravityalongwithRepelBest.

Inadditiontoprovidingqualitativedescriptions ofthebehaviourofthealgorithmsissolvingthe benchmarkproblemsusinggraphs,wecorroborate

Table2. Dunntestp‐valuesofalgorithmpairsthat exceededthe0.01thresholdandareconsiderednot significantlydifferent

those indingswithquantitativeresults(e.g.,average withstandarddeviation)thatarepresentedinatabu‐larform.

Table1. Meanandstandarddeviationoffitnessvalueafter100iterationsof (��+��) ESanditshybridsfor100,500and 1000dim.problems

TheseresultsareprovidedinTable1.Theobserva‐tionscon irmthe indingsperceivedwhenanalyzing thegraphs,andtheinformationobtainedfromthe spreadofresultswhentheindividualalgorithmsare repeatedviastandarddeviationfurtherconvincesus abouttherepeatabilityofthosealgorithmsandsignif‐icanceofthe indings.

Wehavesystematicallyperformedvarioussta‐tisticaltestingonthequantitativeresultswehave obtained.First,wehaveappliedtheShapiro‐Wilktest withsigni icancethresholdof 0.05 tocheckwhether theobservedsamplehadanormaldistribution. The nullhypothesisthatthesampleobtainedforeach proposedalgorithmisrejected.Assuch,wepro‐ceedwiththeKruskal‐Wallistestinordertocheck whethertheircumulativedistributionfunctionsdif‐fered,and inallypairwisecomparisonsviaDunn’s testinordertocheckwhichonesweresigni icantly different.ExceptfortheresultslistedinTable 2,all otheralgorithmsachievedstatisticallysigni icantval‐ueswithp‐valuesbelow0.01(assumingthisvalueas signi icancelevel��)usingDunn’stest.

5.Conclusion

Inthispaper,weproposedandstudiednovel methodsforhybridizingsocio‐cognitiveinspirations inES.Theproposedalgorithmsarebasedontheprin‐cipleofintroducingcertainmechanismsofattracting thecurrentlymodi iedgenotypestothebestonesand repellingthemfromtheworstonesinthepopulation.

Ourexperimentsyieldedinterestingresults.It turnsoutthattheproposedmechanismswereappar‐entlysuccessfulfortwooffourtackledBenchmark problems(AckleyandGriewank)inallthedimensions tested.Weveri iedthisclaimthroughbothqualitative analysisviaplotsofthesearchperformancesofthe algorithmsandquantitativeanalysisviatheuseof systematicstatisticalanalysisonthesamplesofsearch performancesfromrepeatedrunsofthealgorithms. However,thesocio‐cognitivemutationwassuccessful forthetwootherproblems,namelyDeJongandRas‐trigin,onlyinthecaseof100dimensions.Itshould benotedthatwedidnotperformindividualtun‐ingoftheparameterssoastoobtainimprovements. Ourcurrentmotivationistoestablishthegenerality oftheproposedmechanismsastheyareinbaseline con iguration.

Nevertheless,weshowedthatdifferentvariants ofourmethodssucceeded–thereforefollowingthe well‐known NoFreeLunch theorembyWolpertand MacReady,inourfutureresearchwewouldliketo tuneourmethodstomeetparticularneedsofallthe tackledproblem.Moreover,wewillstudyifourmod‐i icationofthebasealgorithm(inthiscase,ES)will workaswellwhenappliedinothermetaheuristics,as themodi icationitselfcanbeperceivedasgeneralone, notparticularlyconnectedwithESthatisstudiedin thispaper. Notes 1https://github.com/jMetal/jMetalPy

AUTHORS

AleksandraUrbanczyk –AGHUniversity, Al.Mickiewicza30,30‐059Krakow,e‐mail: aurbanczyk@agh.edu.pl.

KrzysztofKucaba –AGHUniversity,Al.Mickiewicza 30,30‐059Krakow,e‐mail:kkcba98@gmail.com.

MateuszWojtulewicz –AGHUniversity, Al.Mickiewicza30,30‐059Krakow,e‐mail: mateusz.wojtulewicz@gmail.com.

MarekKisiel-Dorohinicki –AGHUniversity, Al.Mickiewicza30,30‐059Krakow,e‐mail: doroh@agh.edu.pl.

LeszekRutkowski –InstituteofSystemsScience Research,Warsaw,Poland;AGHUniversity, Al.Mickiewicza30,30‐059Krakow,e‐mail: rutkowski@agh.edu.pl.

PiotrDuda –CzestochowaUniversityofTechnology, Poland,e‐mail:piotr.duda@pcz.pl.

JanuszKacprzyk –InstituteofSystemsScience Research,Warsaw,Poland;AGHUniversity, Al.Mickiewicza30,30‐059Krakow,e‐mail: janusz.kacprzyk@ibspan.waw.pl.

XinYao –SouthernUniversityofScienceandTechnol‐ogy,Shenzhen,China,e‐mail:xiny@sustech.edu.cn. SiangYewChong –SouthernUniversityof ScienceandTechnology,Shenzhen,China,e‐mail: chongsy@sustech.edu.cn.

AleksanderByrski∗ –AGHUniversity,Al. Mickiewicza30,30‐059Krakow,Poland,e‐mail: olekb@agh.edu.pl,www:https://orcid.org/0000‐0001‐6317‐7012.

∗Correspondingauthor

ACKNOWLEDGEMENTS

Theresearchpresentedinthispaperreceivedsup‐portfromthePolishNationalScienceCentreproject no.2019/35/O/ST6/00570(AU),thefundsassigned byPolishMinistryofEducationandScienceto AGHUniversity(MKD,JK),bytheprogram“Excel‐lenceinitiativeresearchuniversity”fortheAGHUni‐versityinKrakow,theARTIQproject:UMO‐2021/ 01/2/ST6/00004and84ARTIQ/0004/2021(LR)and NCNProjectno.2020/39/I/ST7/02285(AB).

References

[1] Z.MichalewiczandD.B.Fogel, HowtoSolveIt: ModernHeuristics.SpringerScience&Business Media,2013.

[2] D.H.WolpertandW.G.Macready,“Nofreelunch theoremsforoptimization,” IEEETransactions onEvolutionaryComputation,vol.1,no.1,Apr. 1997,pp.67–82,doi:10.1109/4235.585893.

[3] E.‐G.Talbi, Metaheuristics:FromDesigntoImplementation.JohnWiley&Sons,2009.

[4] K.Sörensen,“Metaheuristics—themetaphor exposed,” InternationalTransactionsin OperationalResearch,vol.22,no.1,2015, pp.3–18,doi:10.1111/itor.12001.

[5] G.LakoffandM.Johnson, MetaphorsWeLiveBy Chicago,IL:UniversityofChicagoPress,2003. Accessed:Feb.16,2024.[Online].Available:http s://press.uchicago.edu/ucp/books/book/chic ago/M/bo3637992.html

[6] A.Bandura,“Self‐ef icacy:Towardaunifying theoryofbehavioralchange,” Psychological Review,vol.84,no.2,1977,pp.191–215,doi: 10.1037/0033‐295X.84.2.191.

[7] A.Bandura, Socialfoundationsofthoughtand action:Asocialcognitivetheory.inSocialfoun‐dationsofthoughtandaction:Asocialcognitive theory.EnglewoodCliffs,NJ,US:Prentice‐Hall, Inc,1986,pp.xiii,617.

[8] A.Bandura,D.Ross,andS.A.Ross,“Transmis‐sionofaggressionthroughimitationofaggres‐sivemodels,” TheJournalofAbnormalandSocial Psychology,vol.63,no.3,1961,pp.575–582,doi: 10.1037/h0045925.

[9] A.Byrski, etal.,“Socio‐cognitivelyinspiredant colonyoptimization,” JournalofComputational Science,vol.21,Jul.2017,pp.397–406,doi: 10.1016/j.jocs.2016.10.010.

[10] I.Bugajski, etal.,“EnhancingParticleSwarm OptimizationwithSocio‐cognitiveInspirations,” ProcediaComputerScience,vol.80,Jan.2016,pp. 804–813,doi:10.1016/j.procs.2016.05.370.

[11] A.Urbanczyk,B.Nowak,P.Orzechowski,J.H. Moore,M.Kisiel‐Dorohinicki,andA.Byrski, “Socio‐cognitiveEvolutionStrategies,”in ComputationalScience–ICCS2021,M.Paszynski,D. Kranzlmüller,V.V.Krzhizhanovskaya,J.J.Don‐garra,andP.M.A.Sloot,Eds.,inLectureNotes inComputerScience.Cham:SpringerInter‐nationalPublishing,2021,pp.329–342.doi: 10.1007/978‐3‐030‐77964‐1_26.

[12] E.‐G.Talbi,“ATaxonomyofHybridMetaheuris‐tics,” JournalofHeuristics,vol.8,no.5,Sep.2002, pp.541–564,doi:10.1023/A:1016540724870.

[13] Y.‐S.Ong,M.‐H.Lim,N.Zhu,andK.‐W.Wong, “Classi icationofadaptivememeticalgorithms: acomparativestudy,” IEEETransactionsonSystems,Man,andCybernetics,PartB(Cybernetics),vol.36,no.1,Feb.2006,pp.141–152,doi: 10.1109/TSMCB.2005.856143.

[14] RobertSchaefer,AleksanderByrski,Joanna Kolodziej,andMaciejSmolka.Anagent‐based modelofhierarchicgeneticsearch. Comput. Math.Appl.,64(12):3763–3776,2012.

[15] KamilPietak,AdamWos,AleksanderByrski,and MarekKisiel‐Dorohinicki.Functionalintegrityof multi‐agentcomputationalsystemsupportedby component‐basedimplementation.InVladimír Marík,ThomasI.Strasser,andAloisZoitl, editors, HolonicandMulti-AgentSystemsfor Manufacturing,4thInternationalConference onIndustrialApplicationsofHolonicandMultiAgentSystems,HoloMAS2009,Linz,Austria,

August31-September2,2009.Proceedings, volume5696of LectureNotesinComputer Science,pages82–91.Springer,2009.

[16] RobertSchaefer,AleksanderByrski,andMaciej Smolka.Stochasticmodelofevolutionaryand immunologicalmulti‐agentsystems:Parallel executionoflocalactions. Fundam.Informaticae, 95(2‐3):325–348,2009.

[17] I.Rechenberg, CyberneticSolutionPathofan ExperimentalProblembyIngoRechenberg.Royal AircraftEstablishment,1965.

[18] H.‐P.Schwefel, NumerischeOptimierungvon Computer-ModellenmittelsderEvolutions strategie:MiteinervergleichendenEinführung indieHill-Climbing-undZufallsstrategie.Basel: Birkhäuser,1977.doi:10.1007/978‐3‐0348‐5927‐1.

[19] D.V.Arnold,“Weightedmultirecombinationevo‐lutionstrategies,” TheoreticalComputerScience, vol.361,no.1,Aug.2006,pp.18–37,doi: 10.1016/j.tcs.2006.04.003.

[20] D.Brockhoff,A.Auger,N.Hansen,D.V.Arnold, andT.Hohm,“MirroredSamplingandSequen‐tialSelectionforEvolutionStrategies,”in ParallelProblemSolvingfromNature,PPSNXI, R.Schaefer,C.Cotta,J.Kołodziej,andG.Rudolph, Eds.,inLectureNotesinComputerScience. Berlin,Heidelberg:Springer,2010,pp.11–21. doi:10.1007/978‐3‐642‐15844‐5_2.

[21] T.‐Y.HuangandY.‐Y.Chen,“Modi iedevolution strategieswithadiversity‐basedparent‐inclusionscheme,”in Proceedingsofthe2000. IEEEInternationalConferenceonControl Applications.ConferenceProceedings(Cat. No.00CH37162),Sep.2000,pp.379–384.doi: 10.1109/CCA.2000.897454.

[22] N.HansenandA.Ostermeier,“Completely DerandomizedSelf‐AdaptationinEvolution Strategies,” EvolutionaryComputation,vol.9, no.2,Jun.2001,pp.159–195,doi:10.1162/1063 65601750190398.

[23] P.P.Repoussis,C.D.Tarantilis,O.Bräysy,and G.Ioannou,“Ahybridevolutionstrategyfor theopenvehicleroutingproblem,” Computers& OperationsResearch,vol.37,no.3,Mar.2010, pp.443–455,doi:10.1016/j.cor.2008.11.003.

[24] D.Koulocheris,H.Vrazopoulos,andV.Dertima‐nis,“Hybridevolutionstrategyforthedesignof weldedbeams,”in Proc.ofInt.CongressonEvolutionaryMethodsforDesign,Optimizationand ControlwithApplicationstoIndustrialProblems EUROGEN2003,2003.

[25] L.DosSantosCoelhoandP.Alotto, “Electromagneticdeviceoptimizationbyhybrid evolutionstrategyapproaches,” COMPEL–Theinternationaljournalforcomputation andmathematicsinelectricalandelectronic engineering,vol.26,no.2,Apr.2007,pp. 269–279,doi:10.1108/03321640710727638.

[26] R.StornandK.Price,“DifferentialEvolution–ASimpleandEf icientHeuristicforglobalOpti‐mizationoverContinuousSpaces,” Journalof GlobalOptimization,vol.11,no.4,Dec.1997, pp.341–359,doi:10.1023/A:1008202821328.

[27] KennethPrice,RainerM.Storn,andJouniA. Lampinen. DifferentialEvolution.inNatural ComputingSeries.Berlin/Heidelberg:Springer‐Verlag,2005.doi:10.1007/3‐540‐31306‐0.

[28] C.‐L.Hwang,Y.‐J.Lai,andT.‐Y.Liu,“Anew approachformultipleobjectivedecisionmak‐ing,” Computers&OperationsResearch,vol.20, no.8,Oct.1993,pp.889–899,doi:10.1016/ 0305‐0548(93)90109‐V.

[29] M.Nabywaniec,etal.,“Socio‐cognitiveOpti‐mizationofTime‐delayControlProblemsusing Agent‐basedMetaheuristics,”in 2022IEEE11th InternationalConferenceonIntelligentSystems (IS),Oct.2022,pp.1–7.doi:10.1109/IS57118. 2022.10019693.

[30] P.Kipinski,etal.,“Socio‐cognitiveOptimization ofTime‐delayControlProblemsusingEvolution‐aryMetaheuristics.”arXiv,Oct.23,2022.doi: 10.48550/arXiv.2210.12872.

[31] J.DieterichandB.Hartke,“EmpiricalReviewof StandardBenchmarkFunctionsUsingEvolution‐aryGlobalOptimization,” AppliedMathematics, vol.03,Jul.2012,doi:10.4236/am.2012.330215.

[32] M.López‐Ibáñez,J.Dubois‐Lacoste,L.Pérez Cáceres,M.Birattari,andT.Stützle,“Theirace package:Iteratedracingforautomaticalgo‐rithmcon iguration,” OperationsResearchPerspectives,vol.3,Jan.2016,pp.43–58,doi: 10.1016/j.orp.2016.09.002.

THECOALQUALITYCICSTHATINCREASESTHEWEARRESISTANCEOFHEAT

THECOALQUALITYCICSTHATINCREASESTHEWEARRESISTANCEOFHEAT

EXCHANGERTUBES EXCHANGERTUBES

Submitted:14th October2022;accepted:29th September2023 MaksymGrishyn,KostiantynBeglov

DOI:10.14313/JAMRIS/1‐2024/2

Abstract:

Thepaperdiscussesthethreatofdecommissioningtothe thermalpowerplant(TPP)heatexchangertubesbecause oferosionanddevelopsacomputer‐integratedcontrol system(CICS)fortheprocessofdistributionofsteam coalflowswithdifferentindicatorsofabrasivematerials content,whichisbasedonfuzzylogic.

TheproblemofrapiddecommissioningofTPPheat exchangers,particularlyabrasivedamagetofurnace screentubes,economizer,superheater,etc.Thismay indicateadiscrepancybetweentheexpectedfuelash contentandtheactualone,aswellasahighcontentof abrasiveimpuritiesinsteamcoal.

TheworkaimstodevelopaCICSofthewearresis‐tanceoftheheatexchangesurfaceofasteamboilerofa coal‐firedpowerplantbymeasuringandfuzzycontrolof thecontentofabrasiveimpuritiesinsteamcoal.

TheproblemsofdamagetotheequipmentoftheTPP boilerareinvestigated,andasystemforcontrollingthe wearresistanceofthesurfacebyautomaticfuzzycontrol ofthequalityofcoalisdeveloped.Theresultswere investigatedduringcoalpreparationandcombustionin thefurnaceofathermalpowerplanttoinvestigatethe effectivenessoftheproposedfuzzycontroller.Themodel resultsconfirmthefeasibilityofthefuzzycontrolmethod forthesystemwithdifferentcoalqualityparameters.

Keywords: Automaticcontrolsystem,Fuzzycontrol,Coal‐firedpowerplants,Variablequalityofcoal,Fuelenrich‐ment,Wearresistanceoftheheatexchanger

1.Introduction

Despitetheconstantincreaseintheuseofrenew‐ableenergysourcestocoverthedemandofmod‐ernenergysystems,accordingto[1,2],mostofthe world’selectricityisproducedbyclassicalthermal powerplants(TPP),inparticular,themainresource forelectricityproductioniscoal(about36.7%).Thus, theproblemsthatarisefromusingfuelarestillrel‐evanttoday.Inparticular,coalwithahighcontent ofabrasiveimpuritiesduringcombustioncreatesero‐sivewearoftheheatexchangesurfacetubescausedby themovementofsolidparticlesentrainedinthe lue gas,whichincreasestheriskofprematuredecommis‐sioningofthisparticularequipment.Further,inthis paper,itwillbereferredtoasabrasivewear.

Theproblemofqualityistheproblemof luctua‐tionsinthecompositionofcoalusedforcombustion, namely:highcontentofabrasivematerialintheash impurityofcoaloradiscrepancybetweenthespec‐i iedashcontent(declaredbythesupplier)andthe actualone.Thus,unscrupuloussupplierswhodeclare asmallashcontentcandeliverbadfueltoTPPs.

Currently,powerplantmanagementhasthe opportunitytosolvetheproblemoflow‐quality fuelinoneoftwoways:totrytoenrichlow‐quality fuel[3,4]ortomixitwithhigh‐qualityfuelinareserve warehouse.However,forthesuccessfulapplication ofthesesolutions,itisnecessarytounderstandhow usefulthefuelenrichmentwillbe,takingintoaccount thelossesduringenrichment,enrichmentcosts,and transportdelay,anditisalsonecessarytoknowthe exactcurrentcoalqualitytoeffectivelymanagethe fuelquality.

Sincemodernpowerplantsarenotequippedwith alaboratoryforadetailedinvestigationoftheabra‐sivecontentofashimpurities,thereisalsoaproblem withhowtocalculatedetailedcoalqualityindicators foraccurateassessmentofthewearresistanceofthe heatexchangesurfaceofthesteamboiler.Additional dif icultiesariseduetotheimpossibilityofpremature shutdownofthepowerplanttocheckthecondition oftheequipment.Itisalsoworthnotingthatitis dif iculttounambiguouslydividethequalityofcoal intocategoriestodistributethe lowsbetweenthe furnace,replenishmentofthereservestock,enrich‐mentequipment,andtheneedtoattractstocksfrom thereserveformixingandcombustioninthefurnace. Therefore,itisadvisabletocreateadvancedcontrol systemsforpowerplantsoperatingunderconditions ofchangingthequalityofsteamcoalbasedonfuzzy controlprinciples.

Thisworkdescribesthedevelopmentofapower plantautomationsystemtoenablethedetectionof inconsistenciesinthequalityofenergyfuelandto implementafuzzycontrollerforthedistribution offuel lowsdependingontheirquality.Section 2 presentsaliteraturereviewofcurrentresearchissues andsetsthemainobjectivesofthiswork.Thethird sectionisdevotedtothedevelopmentofafuzzy controlsystemforthewearresistanceoftheheat exchangesurfaceofasteamboilerofacoal‐ ired powerplantbycontrollingthequalityofsteamcoalat theexpenseoffuel lowdistribution,aswellasmod‐elingtheactionofthecontroldeviceatvariouscoal

qualityindicators,andthestudyoftheeffectiveness ofthefuzzycontrolsystem.

Theregulationwasbuiltonfuzzylogicbecause thedivisionofcoalqualityinto iveconditionalclasses wasproposed,butitisimpossibletodividetheclasses byabrasivenessindicators.Thefourthchapterispre‐sentedintheformofconclusionsandsuggesteddirec‐tionsforfurtherresearch.

Modernpowerplants,withtheirintricateoper‐ationaldynamics,oftengrapplewithuncertainties rangingfrom luctuatingfuelqualitytovariableenvi‐ronmentalconditions.Traditionalcontrolsystems, structuredaroundrigidmathematicalframeworks, sometimesfalterinthefaceofthesenonlinearitiesand ambiguities.Fuzzylogicstandsoutasasuperioralter‐native,adeptlymanagingsuchuncertaintiesthrough itsinherentdesignrootedinlinguisticvariablesand fuzzysettheory.Thisallowsformore lexible,intuitive decision‐makingthatmirrorshumanreasoningpat‐terns,makingitespeciallyvaluableintranslatingthe vastexperientialknowledgeofpowerplantoperators intoactionablecontrolalgorithms.Furthermore,its adaptivenatureensuresresilienceinchangingcon‐ditions,ensuringthatpowerplantsmaintainoptimal performanceevenamidstunforeseendisturbances.

2.RelatedWorks

Thecurrenttrendsofresearchinmodelingand managementscienceremainrelevanttomany ields ofendeavor[5].Despitespecialattentionbeingpaid tosuchareasassoftcomputing,uncertainty,biblio‐metrics,neuralnetworks,etc.,theenergy ieldisnot anexception.Nowadays,severalstudieshavebeen carriedoutonvarioustechnologiesforassessingthe harmfuleffectsoflow‐qualityfuelonthewearresis‐tanceoftheheatexchangesurface[6,7],predictingthe consequences,aswellasautomationofinstallations andtechnologicalcomplexestomaintainstableoper‐ationofthepowerplant.

Besides,[8]paysmuchattentiontothedescription andmodelingofplantsasawholeandtheirparts (heatexchangers,turbines,boilers,etc.),and[9]con‐siderssuchcontrolmethodsasPID‐law,fuzzylogic control,andothers.Thesematerialsexaminemeth‐odsofmaintainingthestabilityofpowersystemsby increasingthefuelsupply,butthetaskofsigni icantly reducingtheabrasivewearoftheheatexchangesur‐faceisnotsolved,whichcanleadtounpredictable consequencesintheformoftheprematureshutdown ofthepowerunitforunscheduledrepairs,whichwill beacriticalloadontheoverallpowersystem.

In[10],theissuesofashimpurityoffuel,its abrasiveeffectonTPPequipment,andassessmentof theef iciencyoffuelenrichmenttoreducetherisksof TPPcostsincaseofurgentrepairswereconsidered. TPPoperationispresentedintheformofamodel, whichwasexpressedinthesumoftotal inancialand othercostsassociatedwithmalfunctions:repairand replacementofequipment,additionalfuelpurchase, etc.Undertheconditionoffuelenrichment,thesavings inTPPcostsareexpressedduringthelifetimeofthe equipment,includingthecostsofenrichment[11,12].

Itwasconcludedthatitwouldbemore cost‐effectiveforTPPstopurchaseandsetup coalpreparationequipmentthantoshutdownthe powerunitforscheduledorunscheduledrepairs.

Itwouldbepossibletoabandonlow‐qualityfuel inadvanceandswitchtoreservefueltopreventthese risksfromapproaching,butthetaskissigni icantly complicatedbythefactthatitisimpossibletobe sureofthequalityoftheimportedsteamcoalorto measurethechangeinabrasivedamageoftheheat exchangersurfaceduringcombustiontoanalyzethe actualwearresistance[13,14].Eveniftherewassuch anopportunitytolearninreal‐timeaboutthedamage totheheatexchangesurfaceduringthecombustionof steamcoal,TPPsaretraditionallynotequippedwith alaboratorytostudythequalityofcoalcomposition. Additionaldif icultiesarealsoimposedbytheapprox‐imate(notexact)determinationofthepercentageof certaincomponentsinthecompositionofrawmateri‐als.Thus,tosuccessfullysolvethisproblem,itwasnec‐essarytocreateacomputer‐integratedcontrolsystem (CICS)fortheprocessofcoalfuel lowdistribution, regardlessofthecontentofabrasivematerialinthe ashimpurity,basedonfuzzylogic.

Muchattentionin[15,16]ispaidtocontrolbased onfuzzylogic,namely,acontrolmethodforregulat‐ingpowerandenthalpyintheboilerofa765MW coal‐ iredthermalpowerplantispresented,andfuzzy boilerpowercontrolbyasteamregulatingvalve.

Theapplicationoffuzzylogicincontrolsystems, especiallywithinthermalpowerplants,hasbeena topicofsigni icantinterestandstudyinrecentyears. Astheenergysectorfacesincreasedchallengesfrom varyingconditionsandtheneedforoptimizedper‐formance,fuzzycontrolsystemspresentanadaptable solution.

KondratenkoandKozlov’sexplorationintogener‐atingrulebasesforfuzzysystemsdelvesintotheuse ofModi iedAntColonyAlgorithms,demonstratingthe capabilityofsuchalgorithmstoenhancetheperfor‐manceandaccuracyofruleformulations[17].Fur‐thermore,a2022publicationbyKozlovetal.accen‐tuatestheimportanceoffuzzylogicinmanagingthe complexityofthepyrolysisprocess,especiallywhen dealingwithmunicipalsolidwasteofvaryingcompo‐sition[18].Thisunderscorestheadaptabilityoffuzzy systemsinhandlingheterogeneousinputs,asituation frequentlyencounteredinpowerplants.

Adifferentangletothestudyoffuzzylogicin powerfacilitieswaspresentedbySatyanarayanaetal. in2014,whoofferinsightsintoautomaticgeneration controlinpowerplants.Theirworkcomparatively evaluatestheperformanceofPID,PSS,andFuzzy‐PIDcontrollers,illuminatingtheuniquebene itsofthe Fuzzy‐PIDinachievingbetterstabilityandresponse times[19].

Theenvironmentallyconsciousfacetofpowergen‐erationishighlightedbyKozlovetal.,whoemphasize thedevelopmentandoptimizationof“GreenFuzzy Controllers”speci icallytailoredforreactorsinspe‐cializedpyrolysisplants[20].Theirapproachmarries theprinciplesofsustainablepowergenerationwith theadaptabilityoffuzzylogic.

[21]divesdeeperintotheparametricoptimiza‐tionoffuzzycontrolsystems.Byharnessinghybrid particleswarmalgorithmsequippedwithanelite strategy,theirresearchsetsanewbenchmarkin optimizingtheperformanceoffuzzycontrolsystems, openingnewdoorsforreal‐timeadaptivecontrolin powerplants.

Papers[22, 23]emphasizetheimportanceof fuzzycontrolsystemsinmanagingtemperatures, particularlyduringpyrolysisprocesses.Their researchunderscoreshowfuzzyPIDcontrolsystems canenhancethermalbehaviouranalysis,offering improvementsintemperatureregulationandoverall systemstability.

Themainpurposeofthepaperwastodevelop andstudyaCICSforthewearresistanceoftheheat exchangesurfaceofasteamboilerofacoal‐ ired powerplantbycontrollingthequalityofcoalbydis‐tributingthe lowofcoalsuppliedforcombustion.

Toachievethisgoal,thefollowingtaskswerefor‐mulated:

‐ todevelopamodelofthemeasuringchannelof abrasivematerialcontentinsteamcoalforaCICS;

‐ todevelopamathematicalmodelfordetecting inconsistencyoffuelqualityindicatorsduringits combustionintheTPPfurnace;

‐ todevelopacontroldevicebasedonfuzzylogicto controlthewearresistanceoftheheatexchangesur‐facebycontrollingthequalityofcoalbydistributing the lowofcoalsenttothefurnace;and

‐ tosimulatetheoperationoftheclosed‐loopcontrol systematdifferentindicatorsofcoalabrasiveness.

3.DevelopmentofaFuzzyCICSofWear ResistanceoftheHeatExchangeSurfaceof aSteamBoilerofaThermalPowerPlantby ControllingtheQualityofSteamCoal

BeforedevelopingtheCICS,itwasnecessaryto consider,andmodelthemeasuringchannelofsteam coalquality,andanalyzeandformmathematicalmod‐elsofthecontrolobject.

4.DevelopmentoftheModelofMeasuring ChannelofAbrasiveMaterialContentin SteamCoalfortheCICS

Usually,TPPsarenotequippedwithalaboratory totesteachbatchofcoal,butfromtimetotime,the qualityofpurchasedfuelmaydifferfromtheindicator inthedocuments,anditwasnecessarytodevelopa methodfordeterminingtheashcontentofthefuel.

Threemethodsofdeterminationwereformulated:

1) Basedonthepowerunitcapacityreductionata steadycoalconsumption,i.e.withanactivereduc‐tionofelectricitygeneration,itislikelythatthe carbonmassinthefuelismuchlowerthanspec‐i ied.

2) Basedonincreasedfuelconsumptionatconstant unitcapacity.Iftomaintaintheloadofthepower unit,itisnecessarytoincreasetheconsumptionof combustedfuel;italsoindicatesadecreaseinthe carboncontentofthecoalbatch.Inthismethod, fuelconsumptionisdeterminedusingautomatic conveyorscalesusedatTPPs.

3) Bydeterminingthemassofashintheashcollec‐torswhenusingelectrostaticprecipitatorsorsep‐aratorsinthepipesofTPPs,toanalyzewiththeir helpandknowledgeofthetechnicalcharacteristics oftheequipmentwhethermoreashisreceivedin theashcollectorthanispermissible.

Thesemethodswereconsideredinmoredetail.

The irstmethod:

LetEin(1)betheelectricitygenerationunderthe conditionofidealfuel.EnSiO2 istheelectricitygenera‐tion,includingthedeclarednSiO2 index,wherenSiO2 is thecontentofabrasivematerialincoal.

En������2 =��TPP ∗24∗Nturb ∗E(1−n������2), (1) where

Nturb –turbinepower;

��TPP –ef iciencyofthermalpowerplants;

Efact –actualelectricitygeneration.

IfEfact <EnSiO2,thentheactualabrasivenessofthe fuelexceedsthedeclaredone.

Thedisadvantageofthismethodisthatithas lowaccuracy.Atthesametime,evenanapproximate indicatoroftheactualabrasivenessofthematerialis unknown.

Inaddition,themainproblemwiththismethod isthatmostboilerunitshaveafuelsupplyregulator, whichdoesnotallowforthereductionofthepowerof turbines[9].

Accordingtothedisadvantagesofthemainprob‐lemofthe irstmethod, thesecondmethod isthat onecouldtrytodetermineiftheactualfuelcon‐sumptionincreasesfromthatwhichshouldbeatthe declaredabrasiveness.

Inthismethod,themaindrawbacksaresimilar tothe irstmethod.Thismethodofcalculatingabra‐sivenessisapproximate,anditwasverydif icultto understandtheactualashcontentandabrasivenessof thefuel.

Inthiscase,neithermethodwasveryeffective,but theyhadaplacetochecktheirdata.

Therefore, thethirdmethod wasadoptedasthe mainwaytocalculatetheashcontentofthematerial.

In[10],“ZaporizhzhiaTPP”inEnergodarcity (Ukraine)wasconsideredprototypeA.

Withoutlaboratoryanalysis,itisimpossibleto sayexactlywhatpartofthefueliscombustiblemin‐eralcontentandwhatpartisanabrasivematerial. Giventhatmostofthecombustiblemineralcontent simplyburns,andabrasivematerialaccumulateson the iltersandintheashdump,itwasassumedthat theactualashcontentduringcombustionwillbethe actualabrasiveness.Thatis,inthefuture,thesecon‐ceptswillbeidenti ied.

TheStateStatisticsServiceofUkraineregularly recordstheamountofgreenhousegasemissionsusing aformulaapprovedbytheMinistryofEnvironmental ProtectionandNaturalResourcesofUkraine.Thiswas usedtocalculateemissionsfromregularfuelcombus‐tion.Thus,from[26–28],thefollowingisformulated in(2):

EmCO2i=ACi∗LCVi∗EFi∗Ofi (2)

where:

EmCO2i –CO2 emissionsfromfuelcombustionof type(i),[tonsCO2]

ACi–activitydata:theamountoffuelcombustion oftype(i),[tonsorthousandm3 ].

LCVi–isthelowercalori icvalueoffueloftype(i) [TJ/torTJ/thousandm3].

EFi–istheCO2 emissionfactorforfueloftype(i) [tCO2/TJ].

OFi–istheoxidationfactorforfueloftype(i).

Themaincombustionproductsaccordingto[13, 26],whichneedtobepaidattentionto(listedasthe mainones)areCH4,N2O,andCO2

Thefollowingemissionvolumeswereobtainedfor TPPA:

CO2 –4,519,919.60m3; N2O–411.09m3; CH4 –373.10m3;

Total:4,520,703.79m3/h.

Inthecaseofsimultaneousoperationofatleast four ilters,itwasnecessaryto ind ilterswithacapac‐ityof1,309,880m3/h.

Thiswasdonetosavetimeonlaboratorytestsof unburnedfuelresidues.Further,themostpessimistic scenarioassumesthattheashcontentisanindicator oftheabrasivenessofsteamcoal.

Further,themethodofcalculatingtheactualash content(abrasiveness)ofthefuelwasconsidered.

Accordingto[24],“ZaporizhzhiaTPP”useselec‐trostaticprecipitatorsinitsproduction,whichisa moremodernandef icientwaytocollectash[25]. Usually,theef iciencyisabout97–98%,incontrastto outdatedwetashcollectors(Venturiscrubberswith remotedropletseparator)fromthe60sand70swith a iltrationef iciencyofabout50%.

Then,itbecamenecessarytoanalyzethediffer‐encebetweentheactualamountofashobtaineddur‐ingfuelcombustionandtheamountthatshouldhave beenobtainedaccordingtothedeclaredquality.

Thedif icultyofmeasuringtheconsumptionof mineralimpuritiespresentincoalfuelisthattheash residueformedaftercombustiondoesnotmoveina singlestreambutaccumulatesinsomecharacteristic places.Thisisfacilitatedbyashcollectors.

AccordingtotheashcollectingschemesofTPPs,in particularFigure2,itwassummarizedthatitispos‐sibletoestimatetheamountofashinashcollectors ofthreetypes:inthefurnace,intheeconomizerash collector,andthechimney ilterashcollector.

Filtersthatmeetthefollowingrequirementsare EGV2‐70‐12‐6‐6,EGV2‐70‐12‐6‐7,EGV2‐70‐12‐6‐8. Theconditionsof100%ashcapturewereconsidered tobuildthemodel.

Forfurtherconstructionofthetechnological model,theschematicdrawingofashandslagremoval fromtheprincipleof[8,14],Figure 3 isconsidered

Figure3. Schematicdrawingofashandslagremoval: 1–boilerfurnacechamber;2–ashcollector;3–bath withascraperconveyorforcontinuousashremoval;4–ashflushingapparatusoftheashcollector;5–slag crusher;6–flushingpump;7–ashchannel;8–sluice nozzle;9–receivinghopperofslurrywithmetal catcher;10–baghousepump;11–drainagepump;12–slurrypipelines;13–ashdump

Figure1. Schematicdrawingoftheelectrostatic precipitator

Figure2. Dynamicsofashaccumulationinthe combustionprocess.(1–coalbunker;2–coalmill;3–furnace;4–superheatertubes;5–filters;6–placesof ashaccumulationinashcollectors:furnace,economizer, andsmokefilters)

toinvestigateotherplacesofashaccumulationduring fuelcombustion.

Theabovedrawingshowsthattheashsettlesin theashdisposalchannelduringcombustion.Fromthe ilterandeconomizer,theashfallsdirectlyintotheash collectorandthen,usingaconveyor,intothebooker andfurtherintotheashdisposalarea.Withthehelp ofconveyorscales,itispossibletodeterminethemass ofmaterialthathasnotburned,buttherewasstilla problemwithashthatremainsdirectlyinthefurnace.

Accordingtothetechnologicalprocedureofash removal[14],the lyashfromtheashcollectorsmixes withashandslagthat lowsoutofthefurnacethrough theashchanneland,togetherwiththeprocess luid, createsashandslagslurry,whichgoestotheash disposalareathroughtheslurrypipeline.Itwouldbe possibletomeasuretheslurry lowrateintheslurry pipelineand,whendeductingthetechnical luid,to understandtheash low,itsrelationtothefuel low, andthedifferencebetweentheactualandthedeclared ashcontent.However,morerelevantistheamount ofashthatisvolatileandsettlesinashcollectors.It cancauseabrasivedamagetothepipesintheheat exchanger.Itwasproposedtoinstalla lowmeter intheashcollectorpipesthatdeliverashfromthe ashcollectorstomixwiththeslurry.Thishelpedto determinethecorrelationbetweentheash lowthat potentiallydamagesthepipesandtheactualashcon‐tentofthefuelasawhole.

Itwasproposedtousetheultrasonicslurry low meterDENCELL®UDF‐2tokeeprecordsofslurry low.Typically,theobjectswherethese lowmeters areimplementedareindustrialandproductionfacili‐ties,miningenterprises,miningandprocessingplants, mines,open‐pitmines,rawmaterialextractionenter‐prises,etc.

Tokeeprecordsofash lowfromashcollec‐torstomixingwiththemainslurry,itispro‐posedtousea lowmeter,SiemensSolids lowmeter SITRANS®WF300Series.

Thus,takingintoaccountthetransportdelayand thedensityofthetechnicalliquidintheslurry,it becamepossibletocalculatetheactualashcontent ofthefuelandhowitaffectsthewearresistanceof theheatingsurfacesofboilerequipment.Therefore, withthehelpofasmallamountofadditionalequip‐ment,theproblemofdeterminingtheabrasivenessof fuelintheabsenceofalaboratorywithfreeaccess wassolved.Thenextstepwastobuildamathemat‐icalmodelto indoutthediscrepancybetweenthe speci iedandactualindicatorsofthe lowofabrasive materialduringthecombustionofcoal.

5.DevelopmentofaMathematicalModelfor theDetectionoftheInconsistencyofFuel QualityIndicatorsDuringitsCombustionin theTPPFurnace

In[10],aparametricschemewasconstructedto understandtheTPPlinks,andtheselinkswerecom‐binedintheformofasystemofequations.Now,it

wasnecessaryto indthelinkswithexpressionsinash lows.

Theconnectionsbetweentheseparametersare describedbyasystemofequations(3):

⎧

Msl =Mfa1 +Mf_aa2 +MAda3

Mloss =Mfb1 +Mf_ab2 +MAdb3

Vres =Mfc1 +Mresc2 +Menc3

Top =Mfd1 +Mf_ad2 +MAdd3 +Mresd4 +Mend5

N=Mfe1 +Mrese2 +Mene3

, (3)

wherean,bn,cn,dm,en –constantcoef icients;n = 1,3;m=1,5

Mf –isthefuelconsumption,kg/h;

Men –istheenrichedfuelconsumption,kg/h;

Mres –isthereservefuelconsumption,kg/h;

Mf_a –isthe lyash lowfromashcollectors,kg/h;

MAd –istheashcontentoffuel,%;

Msl –isthe lowoftotalashandslagslurry,kg/h;

Top –istheoperatingtimebeforereplacingthe heatexchangerpipes,h;

Mloss –isthecarbonlossesduetothediscrep‐ancybetweenthedeclaredandactualashcon‐tent,whichislacking,whichmakesitnecessaryto enrichorusereserves,kg/h;

Vres –isthefuelstockinthereservewarehouse,t;

N–istheplantcapacity,MW.

Tocalculatethethreemaintasks:thevolumeof thefuelreserve,the lowofabrasive lyash,andthe operatingtimeoftheequipmentatthecurrentabra‐sivewearofpipesduringfuelcombustion,thissystem waswritteninanotherform.

Figure4. Parametricschemeoftheboilerunit

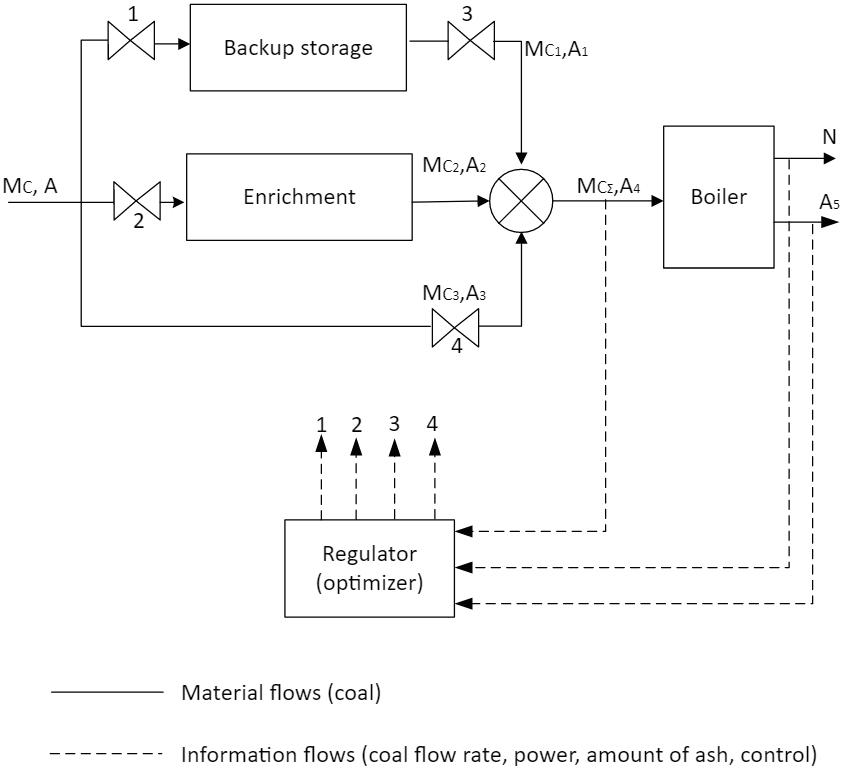
Thefollowingnotationsareusedinthe ig‐ure:Concentrator‐fuelenrichmentsystem,Grand Controller‐controlsystemconsistingoflocalregu‐lators,anddecision‐makingsystemforcoal low distribution.

Theparametricschemeandthesystemofequa‐tionswerepresentedinthefollowing(4):

Mf_a =Msl Ff_a(Mf,Ad)

Vres =V0 Fen(Mf,Ad,Men)

Top =T0 FT(Mf,Ad) (4)

Thefuelcombustionprocessintheinputfueland outputemissionstreamsisdescribed(5),withthe variableAdasafunctionoftime��:

dMAd d�� =(Mash+dMash)−(Msl+dMsl)

Mash Msl =0

dMAd d�� =dMash dMsl, (5)

whereMash –isthegeneralash lowconsumption.

Thus,theschemewasformulated,theregulator wasproposed,anditbecamepossibletocontrolthe lowofabrasivematerial.

6.DevelopmentofaControlDeviceBasedon FuzzyLogictoControltheWearResistance oftheHeatExchangeSurfacebyControl‐lingtheQualityofCoalbyDistributingCoal Flows

Thefollowingschemeofregulationofthemain lowsofTPPsisproposed.

Tosynthesizethecontroller,we irstconsid‐eredthesimulationmodeloftheCICSforregu‐latingthepowerunitpowersupplywithcoalfuel (Fig. 7),whichwasbuiltusing[8, 29].Thesimula‐tionwascarriedoutusingtheinteractivetoolMAT‐LAB®,Simulink®(LICENSING110721904–Math‐WorksTrial–22Oct2022).

Toregulatethepowerunitload,itissuf icientto useastandardPIDcontroller[30,31].

Inthiswork,attentionispaidtothedevelopment ofacontrolin luencetocomplywiththespeci ied abrasivenesscharacteristicsofcoalsuppliedforcom‐bustion.

In[6,7],theissuesofcalculatingtheratesofabra‐sivedamagetothepipepartoftheboilerunitduring fuelcombustionareconsidered.Thefollowingfor‐mula(6)isgiven:

T= (���� −��minw) (3,6⋅��sph ⋅GM), (6) whereTisthepossibleoperatingtimeoftheequip‐mentatthecurrentlevelofabrasiveness; ���� –pipelinewallthickness,mm; ��minw –standardmini‐mumpipelinewallthickness,mm;��sph –speci iclin‐earabrasivewearofthepipeline,mm/tofabrasivein thefuel lowofthecombustedmaterial;GM–mass lowrateofthematerial.

Thesheet(Fig.8)showsacomparisonoftheoper‐atingtimeatdifferentcoalabrasivenessvalues.The possibilityofdistributingthesuppliedcoal lowsin suchawayastoregulatetheabrasivenessofthemix‐turefeddirectlytothecombustionwasconsidered.

Takingintoaccounttheindicatorsoftheoperating time,theconditionalcoalclassesandthecontrolling in luenceonthecoalwereformulated,i.e.decisionson combustion,enrichment,refusalofcombustion,etc.

Giventhattheboundaryvaluesoftheclasseswere takenasconditional(fuzzy)sets,themostappropriate wasdecidedtousesystemsbasedonfuzzylogic.

Figure5. Parametricschemeoftheboilerunit expressedinashflows

Figure6. Theschemeofregulation

In[32–35],thecontrolofprocessesbasedon fuzzylogicwasinvestigated,fromwherethreemain advantagesofusingafuzzycontroldeviceovertra‐ditionalregulatorsofautomaticcontroltheorywere emphasized:

‐ thepossibilityofcombiningadaptivetypecon‐trollersbasedonclassicalPIDcontrollers;

‐ developmentofcomplexcontrollersforcontrol objectsthataredif iculttodescribebyanalytical means;and

‐ afastertransitionbetweencontrolprocesses.

Usingthematerialfrom[36–38],wewillbuilda fuzzycontroldevice.

Asinputinformation lowsforthefuzzycontroller, wetaketheashcontentofthefuel(furtherAds in thecontroller’srules),thefullnessofthereserve store,andthedistributionofthefuel lowinthe correspondingfractionsinthefollowingdirectionsis takenasthecontrolin luence:toreplenishthereserve storedirectlyforcombustion(burning),toenrichment (concentrator),andcompleterejectionofthecurrent coalandtheuseofthereserve(reserve_out).

TheconditionproblemofFigure8.1.corresponds tothecoalclassesfromFigure8andwillin luencethe choiceoffuelaction,whileFigure 8.2.willin luence thereplenishmentanduseofTPPreserve.

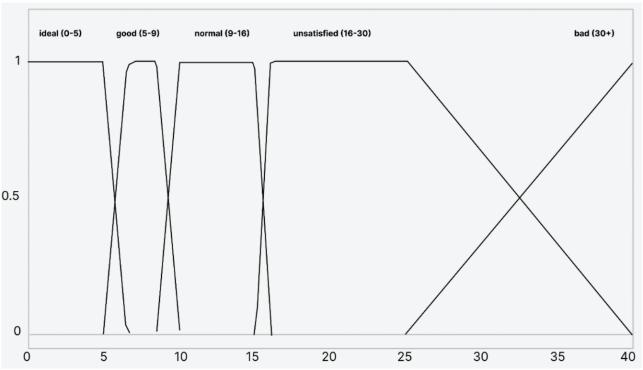
Therulesof lowdistributionwerespeci iedas follows(Fig.9): Where:St– lowofre illofthewarehouse;Br–lowforfuelcombustion;Cn– lowtotheconcentra‐tor;Re– lowofthereservefuelusage;ands/n/lmean small/normal/large lowlevel.

Thus,theschemeofthecontrolsystem(Grand Controller)Figure10:

RulesarepresentedinFigure11

Figure7. Simulationmodeloftheregulatorysystem

Figure8. Sheetofproposedcoalclasseswithrecommendationsforfuelclass

Figure8.1. VariablefuzzificationAd

7.ModellingtheInfluenceoftheControl DeviceatDifferentIndicatorsofCoal Abrasiveness

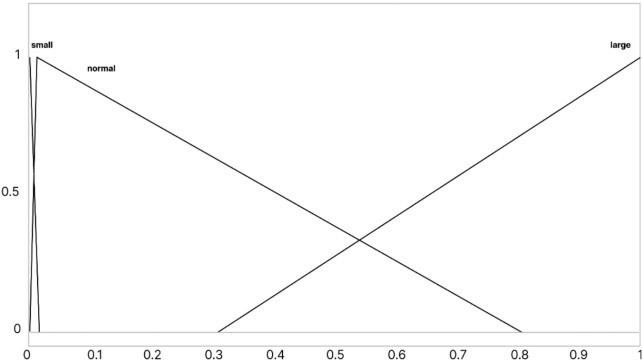
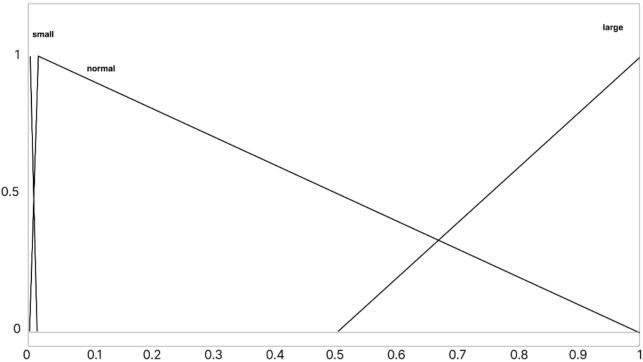
Theconstructedregulatorworksinsuchawaythat itdistributesinpercentagefractionsthedirectionsof steamcoal low.Itwasalsonecessarytocheckhow theregulatorworksatdifferentindicatorsofabrasive materialcontentinthefuel.

Modelingofthesystemshowedthat:

‐ Ifthecoalis“Perfect”,whenthereservestockis not illed,isalmostevenlydistributedbetweenthe furnaceandthereservestock,because,duetothe highcarboncontentandalmostzeroabrasivecon‐tent,thecombustionrequirementsarelowerthan forotherclassesofsteamcoal.

‐ Ifthecoalis“Good”,withanalmostfullandalmost emptystockpile,isdistributedbetweenthefurnace andthestockpileforreservereplenishmentinthe appropriateproportionsdependingontheneedfor areserve.

‐ Incaseofabrasivenessbetween“Normal”and “Unsatis ied”,thecoalisdividedbetweenthefur‐nace lowandtheenrichment lowandpartially mixedwiththereservecoal.

Atabrasivenessbetween“Unsatis ied”and“Bad” coalissentforbene iciationandmixedwiththe reserve.

Figure8.2. Variablefuzzificationstore

Figure9. Rulestableforafuzzycontroller

Figure9.1. Defuzzificationofcontrolinfluences

Figure9.2. Defuzzificationofcontrolinfluences

Figure10. Schemeofthecontrolunit(GrandController unit)Preparedbyauthors,usinginstructions from[30, 31, 38]

Figure11. CheckingtheresultsofrulesinFig. 9 inruleviewer

Figure12. Schemetotesttheresultsofcoalflowcontrol ataconstantabrasivenessof35%for100‐timeunits. Preparedbyauthors,usinginstructionsfrom[29, 38]

Figure13.1. Schematicforcheckingtheresultsofcoal flowcontrolwhentheabrasivenessindexissteadily increasingfor100‐timeunits.Preparedbyauthors, usinginstructionsfrom[29, 38]

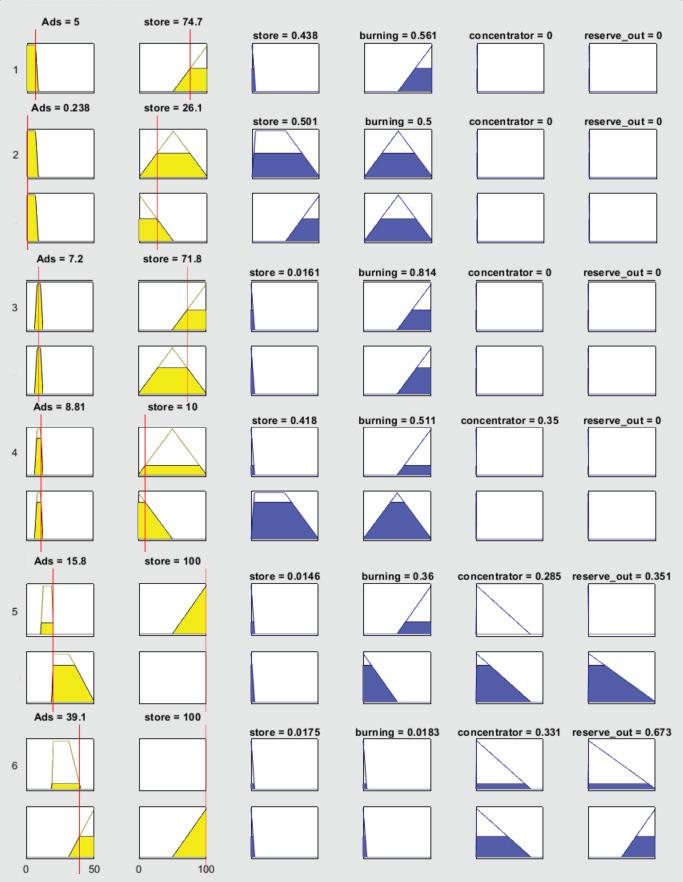
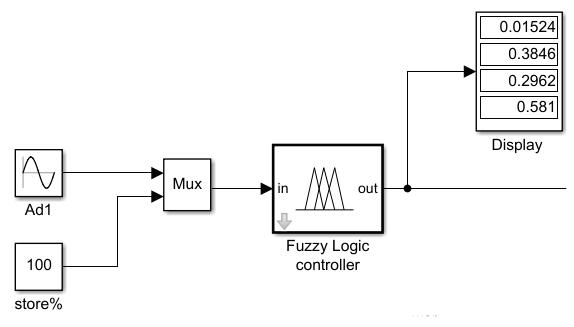
AtaconstantAd =35%,thegraphshowsthat mostofthecoalfuel lowtothecombustionfurnace willcomefromthereserve,whilethedeliveredcoal willbedistributedbetweenthefurnaceandthebene‐iciation.

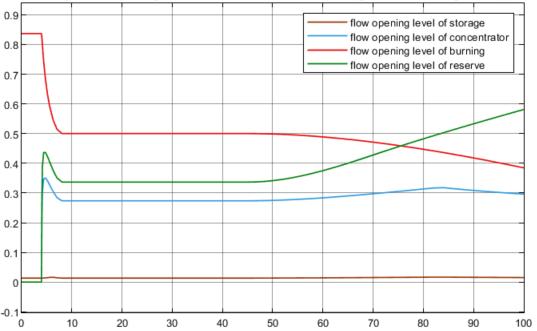
ThecasewhenAd isconstantlychangingiscon‐sidered.Itcontinuouslyincreasesfrom14%to35% during100‐timeunits.

TheresultsareshowninFigure13.2asfollows:

1) AttheinitialAd =14% (systemoperatingtime t0 =0 s),almosttheentirefuel lowissentto combustion.

2) Atthetimeofsystemoperationt1 =50s,theAd willchangeandwillbe24%.Therefore,thecon‐trollingin luencewillbethefollowingdistribution offuel lows–halfofthesteamcoalissentfor combustion,mixedwithreservefuel,andtherest issentforenrichment.

3) Attheendoftheexperiment(t2 =100)atAd = 35%,thelargestshareofthecombustedfuelwill bereserveenergycoal,whilethecoalfromthesup‐plierwillbepartiallyburnedandpartiallydirected toenrichment.

Withafuelashcontentof35%,withouta computer‐integratedcontrolsystem(CICS),TPP equipmentcanlastapproximately632days(less than2years)beforebreakingdown.However,with an ICS,iftheashcontentiskeptatthelevelofthe Normalclass,theequipmentcanlastfrom5to9 years.

Withasteadyincreaseinthecontentofabrasive materialinsteamcoal,theconsumption lowofthe reserveisincreased,andtheconsumption lowofthe suppliedashfuelisreduced.Thiswillhelpreducethe rateoferosionoftheheatexchangersurfacefromthe lowofabrasivematerialduringcombustion.Thus, itshouldbesummarizedthatwiththehelpofthe proposedregulator,thesettaskhasbeensolved.

8.Conclusion

Thispaperhasinvestigatedanddevelopedasys‐temforcontrollingthewearresistanceoftheheat exchangesurfaceofasteamboilerofacoal‐ ired powerplantbycontrollingthequalityofthecom‐bustedfuelbytheprocessofdistributingsteamcoal lowswithdifferentabrasivenesscontentusingfuzzy control.

Theproblemofmeasuringthecurrentquality ofcoalwasinvestigatedbycalculatingandcompar‐ingtheproposedequipmentandmodeledmeasuring channelofabrasivematerialcontentinsteamcoalfor aCICS.

Thenextstepwastodevelopamathematical modeltoidentifytheinconsistencyoffuelqualityindi‐catorsduringitscombustionintheTPPfurnace.The modelwasformulatedintheformofaparametric scheme,takingintoaccounttheregulator,asystemof equations,andtheprocessoffuelcombustioninthe lowsofinputfuelandoutputemissionswasrecorded intheformofadifferentialequation,wherethecoal abrasivenessindexwasvariable.

Subsequently,acontroldevicebasedonfuzzylogic wasdeveloped.Fortheintroductionofthefuzzycon‐troller,aconditionaldivisionofcoalqualityinto ive

Figure13.2. Chartofresultsfor 13.1

classeswasproposed,and,accordingly, ivecontrol in luenceswereproposed.Therulesforthedistribu‐tionofcoal lows,whichwillguidetheregulatorofthe CICS,wereformulatedandwrittendown,andcom‐putersimulationwascarriedouttocontrolthewear resistanceoftheheatexchangesurfacebycontrolling thequalityofcoalbydistributingthe lowsofcoalsent forcombustion.

Thedevelopedcontrolsystemhasbeenvalidated bysimulatingtheplantcontroltodeterminetheopti‐malcontrolactionfordifferentcoalqualities.Inaddi‐tion,thisCICSsuccessfullyreducestheharmfuleffects ontheequipment.

Theobtainedresultsofcomputersimulationcon‐irmthehighef iciencyoftheuseoffuelenrichment andthefuzzyCICS,whichallowsfortheobservation ofthecombustionoftherequiredamountofcoal tomaintaintheproperlevelofgridcapacitybutto reducetheharmfuleffectsofwearresistanceofthe heatexchangerofthecoal‐ iredpowerplant.

Furtherresearchshouldconsiderthelogistical problem,inparticular,themanagementoftransport delayofsteamcoalsupplyundertheconditionof differentfuelquality,aswellasproposeamethodfor controllingthesystemasawholeincombinationwith afuzzycontrolsystemofTPP.

AUTHORS

MaksymGrishyn∗ –DepartmentofSoftware andComputer‐IntegrationTechnologies,National University“OdesaPolytechnic”,65000Odesa,Ukraine, e‐mail:grishyn.m.v@opu.ua.

KostiantynBeglov –DepartmentofSoftware andComputer‐IntegrationTechnologies,National University“OdesaPolytechnic”,65000Odesa,Ukraine, e‐mail:beglov.kv@op.edu.ua.

∗Correspondingauthor

References

[1] IEA,“Worldgrosselectricityproductionby source,”2019;https://www.iea.org/data‐and‐statistics/charts/world‐gross‐electricity‐production‐by‐source‐2019

[2] IEA,“EnergyStatisticsDataBrowser,”2022;http s://www.iea.org/data‐and‐statistics/data‐tools/energy‐statistics‐data‐browser.

[3] M.R.Kadagala,S.Nikkam,andS.K.Tripathy, “AReviewOnFlotationOfCoalUsingMixed ReagentSystems,” MineralsEngineering, vol.173,2021,107217,ISSN0892‐6875, doi:10.1016/j.mineng.2021.107217.

[4] M.Polat,H.Polat,andS.Chander,“PhysicalAnd ChemicalInteractionsInCoalFlotation,” InternationalJournalofMineralProcessing,vol.72, no.1–4,2003,pp.199‐213,doi:10.1016/S0301‐7516(03)00099‐1.

[5] J.Ferrer‐Comalat,S.Linares‐Mustarós, J.M.Merigo,andJ.Kacprzyk,“Modelling

andSimulationinManagementSciences,” ProceedingsoftheInternationalConferenceon ModellingandSimulationinManagement Sciences(MS-18):Proceedingsofthe InternationalConferenceonModellingand SimulationinManagementSciences(MS-18), 2020,doi:10.1007/978‐3‐030‐15413‐4.

[6] S.N.PelykhandM.V.Maksimov,“TheMethodOf FuelRearrangementControlConsideringFuel ElementCladdingDamageAndBurnup”, ProblemsofAtomicScienceandTechnology,vol.87, no.5,2013,pp.84–90, https://vant.kipt.khar kov.ua/TABFRAME.html

[7] M.V.Maksimov,S.N.Pelykh,andR.L.Gontar, “PrinciplesOfControllingFuel‐Element CladdingLifetimeInVariableVVER‐1000 LoadingRegimes”, AtomicEnergy,vol.112,no.4, 2012,pp.241–249,doi:10.1007/s10512‐012‐9552‐3.

[8] W.Wang,J.Liu,Z.Gan,Y.Niu,andD.Zeng,“Flex‐ibleControlOfCombinedHeatAndPowerUnits BasedOnHeat‐PowerEstimationAndCoordi‐nation”, InternationalJournalofElectricalPower &EnergySystems,vol.123,2020,106261,ISSN 0142‐0615,doi:10.1016/j.ijepes.2020.106261.

[9] W.Tan,J.Liu,F.Fang,Y.Chen,“Tuningof PIDControllersForBoiler‐TurbineUnits”, ISA Transactions,vol.43,no.4,2004,pp.571–583,ISSN0019‐0578,doi:10.1016/S0019‐0578(07)60169‐4.

[10] M.V.GrishynandK.V.Beglov,“EvaluatingThe EffectivenessOfFuelEnrichmentToReduce TheRiskOfPowerPlantCosts,” Včenìzapiski Tavrìjs’kogonacìonal’nogounìversitetuìmenìV. Ì.Vernads’kogo.SerìâTehnìčnìnauki, vol.32, no.3,2021,pp.82–89,doi:10.32838/2663‐5941/2021.3/14.

[11] Z.Dong,R.Wang,M.Fan,andX.Fu,“Switch‐ingAndOptimizingControlForCoalFlota‐tionProcessBasedOnAHybridModel,” PLoS ONE,vol.12,no.10,2017,e0186553,doi: 10.1371/journal.pone.0186553.

[12] Q.Tian,H.Wang,andY.Pan,“Associations ofGangueMineralsinCoalFlotationTailing andTheirTransportationBehaviorsin theFlotationProcess,” ACSOmega, vol.7, no.31,2022,pp.27542–27549,doi: 10.1021/acsomega.2c02988.

[13] A.I.BrunetkinandM.V.Maksimov,“The MethodForDeterminationOfACombustible GaseCompositionDuringItsCombustion,” NaukovyiVisnykNatsionalnohoHirnychoho Universytetu,vol.5,2015,pp.83–90, http://nvngu.in.ua/index.php/uk/arkhiv‐zhurnalu/za‐vipuskami/1132‐2015/zmist‐5‐2015/tekhnologiji‐energozabezpechennya/3 162‐metod‐viznachennya‐skladu‐goryuchikh‐gaziv‐pri‐jikh‐spalyuvanni.

[14] Y.V.Shcheglov,N.V.Fedorova,andD.A.Shaforost, “TheAbrasivePropertiesofCoalPower PlantsAshandSlagMaterials,” SolidState Phenomena,vol.299,2020,pp.845–851,doi: 10.4028/www.scienti ic.net/SSP.299.845.

[15] I.Kocaarslan,E.Çam,andH.Tiryaki,“A FuzzyLogicControllerApplicationFor ThermalPowerPlants”,EnergyConversion andManagement,vol.47,2006,pp.442‐458. doi:10.1016/j.enconman.2005.05.010.

[16] A.Z.Cipriano,“FuzzyPredictiveControl forPowerPlants”, AdvancedFuzzyLogic TechnologiesinIndustrialApplications,Advances inIndustrialControl,2006,pp.279–297,doi: 10.1007/978‐1‐84628‐469‐4_19.

[17] Y.P.KondratenkoandA.V.Kozlov,“Generation ofRuleBasesofFuzzySystemsBasedon Modi iedAntColonyAlgorithms,” Journalof AutomationandInformationSciences,vol.51, no.3,2019,pp.4–25,doi:10.1615/JAutomatIn‐fScien.v51.i3.20.

[18] O.Kozlov,Y.Kondratenko,H.Lysiuk,V.Kryvda, andO.Maksymova,“FuzzyAutomaticCon‐trolofthePyrolysisProcessfortheMunicipal SolidWasteofVariableComposition,” Journal ofAutomation,MobileRoboticsandIntelligent Systems,vol.16,no.1,2022,pp.83–94,doi: 10.14313/JAMRIS/1‐2022/9.

[19] S.Satyanarayana,R.K.Sharma,MuktaandA.K. Sappa,”AutomaticGenerationControlInPower PlantUsingPID,PSSAndFuzzy‐PIDController,” 2014InternationalConferenceonSmartElectric Grid(ISEG),Guntur,India,2014,pp.1–8,doi: 10.1109/ISEG.2014.7005618.

[20] O.Kozlov,G.Kondratenko,Z.Gomolka,andY. Kondratenko,“SynthesisandOptimizationof GreenFuzzyControllersfortheReactorsof theSpecializedPyrolysisPlants,” GreenITEngineering:Social,BusinessandIndustrialApplications,StudiesinSystems,DecisionandControl, V.Kharchenko,Y.Kondratenko,andJ.Kacprzyk, eds.,Springer,Cham,2019,pp.373–396,doi: 10.1007/978‐3‐030‐00253‐4_16.

[21] Y.P.KondratenkoandA.V.Kozlov,“Parametric OptimizationOfFuzzyControlSystemsBased OnHybridParticleSwarmAlgorithmsWithElite Strategy,” JournalofAutomationandInformation Sciences, vol.51,no.12,2019,pp.25–45.

[22] Q.Buetal.“TheEffectOfFuzzyPIDTemperature ControlOnThermalBehaviorAnalysis AndKineticsStudyOfBiomassMicrowave Pyrolysis”, JournalofAnalyticalandApplied Pyrolysis,vol.158,2021,105176,doi: 10.1016/j.jaap.2021.105176

[23] X.Liu,S.Wang,andL.Xing,”FuzzySelf‐Tuning PIDTemperatureControlForBiomassPyroly‐sisFluidizedBedCombustor,” 20102ndIEEE

InternationalConferenceonInformationManagementandEngineering,2010,pp.384–387, doi:10.1109/ICIME.2010.5477837.

[24] M.Ovcharenko,“DTEKinvestuie117mlnhrn naekolohichnumodernizatsiiuPrydniprovs’koii TES,” uprom.info;https://uprom.info/news/en ergy/dtek‐investuye‐117‐mln‐grn‐na‐ekologic hnu‐modernizatsiyu‐pridniprovskoyi‐tes/(in Ukranian).

[25] G.L.Fisher,D.P.Y.Chang,andM.Brummer, “FlyAshCollectedfromElectrostatic Precipitators:Microcrystal‐linesStructures andtheMysteryoftheSpheres,” Science, vol.192,no.4239,1976,pp.553–555,doi: 10.1126/science.192.4239.553.

[26] GuaranteesOfCitizens’EnvironmentalRights, Document1264‐XI,Article10,LawOfUkraine OnEnvironmentalProtection;https://zakon.ra da.gov.ua/laws/main/1264‐12?lang=en#Text

[27] V.G.Vasilenko,“MethodicalRecommendations forEvaluationofGreenhouseGasEmissionsby TypeofActivityofFacilities,AnnextotheOrder oftheMinistryofEnvironmentalProtectionand NaturalResourcesofUkraineonApprovalof MethodicalRecommendationsforEvaluationof GreenhouseGasEmissionsbyTypeofActivityof Facilities№404,”2021,https://mepr.gov.ua/fi les/docs/nakazy/2021/404%D0%BD%D0%B4 1.pdf(inUkranian).

[28] D.V.Chugunkov,G.A.Seyfelmliukova,V.P. Kuzema,andA.E.Bogdanova,“Researchon structureofash‐slagpulpanditsin luence onpipelines’attritionofathermalpower plants’hydraulicashremovalsystem,” Journalof Physics:ConferenceSeries,vol.1370,no.1,2019, doi:10.1088/1742‐6596/1370/1/012015.

[29] L.A.Kumar,A.Kalaiarasi,andY.U.Maheswari, PowerElectronicswithMATLAB,CambridgeUni‐versityPress,2017.

[30] L.Wang,S.Chai,D.Yoo,L.Gan,andK.Ng,“PID andPredictiveControlofElectricalDrivesand PowerConvertersusingMATLAB/Simulink,” IEEEPress,2015.

[31] L.Wang,“PIDControlSystemDesignandAuto‐maticTuningusingMATLAB/Simulink:Design andImplementationusingMATLAB/Simulink,” IEEEPress,2020.

[32] M.Jamshidi,V.Kreinovich,andJ.Kacprzyk, AdvanceTrendsInSoftComputing,Springer, 2013.doi:10.1007/978‐3‐319‐03674‐8.

[33] J.Kacprzyk,MultistageFuzzyControl:APrescriptiveApproach,JohnWiley&SonsInc.,1997.

[34] E.SzmidtandJ.Kacprzyk,”Distancesbetween intuitionisticfuzzysets,” FuzzySetsandSystems,vol.114,no.3,2000,pp.505–518,doi: 10.1016/S0165‐0114(98)00244‐9.

[35] E.SzmidtandJ.Kacprzyk.“AConsensus‐ReachingProcessUnderIntuitionisticFuzzy

PreferenceRelations”,InternationalJournalof IntelligentSystem,vol.18,2003,pp.837–852, doi:10.1002/int.10119.

[36] W.Pedrycz,K.Li,andM.Reformat,“Evolution‐aryReductionOfFuzzyRule‐BasedModels,” FiftyYearsofFuzzyLogicanditsApplications, Springer,2015,pp.459–481,doi:10.1007/978‐3‐319‐19683‐1_23.

[37] J.Jantzen, FoundationsofFuzzyControl:APracticalApproach,2nded.,JohnWiley&SonsInc, 2013,doi:10.1002/9781118535608.

[38] S.N.Sivanandam,S.Sumathi,andS.N.Deepa, IntroductiontoFuzzyLogicusingMATLAB, SpringerInternationalPublishing,2007,doi: 10.1007/978‐3‐540‐35781‐0.

LOW‐COSTSMALL‐SCALEAUTONOMOUSVEHICLE LOW‐COSTSMALL‐SCALEAUTONOMOUSVEHICLE LOW‐COSTSMALL‐SCALEAUTONOMOUSVEHICLE

Submitted:11th July2023;accepted:10th October2023

IsmailBogrekci,PinarDemircioglu,MustafaYasirGoren

DOI:10.14313/JAMRIS/1‐2024/3

Abstract:

Alow‐costsmall‐scaleautonomousvehiclereferstoa self‐drivingvehiclethatisdesignedtobeaffordable andsuitableforsmallerapplicationsorspecificpur‐poses.Inthisstudy,thefireflyalgorithmwasutilizedto addressobstacleavoidancechallengesinthepresenceof dynamicorstaticallypositioneduncertainobstacles.The autonomousvehiclesuccessfullyreachedtheintended destination,demonstratingasatisfactorylevelofaccu‐racy.Regardlessofthestartingpoint,thevehiclearrived atthepredeterminedpositionwithinanareameasuring 5metersindiameter.Theachievementofsuchresults canbeattributedtothecost‐effectiveselectionofsen‐sors,utilizationofasimplealgorithm,andtheimple‐mentationofamoderatelypoweredprocessorandcircuit components.

Keywords: Autonomousdrive,Unmannedgroundvehi‐cle,Sensors,Fireflyalgorithm

1.Introduction

Thesigni icanceoflow‐costsmall‐scale autonomousvehiclesinvariousdomainsand applicationsisnoteworthy.Severalkeyreasons contributetotheirvalue:

Accessibility:Low‐costsmall‐scaleautonomous vehiclesincreasetheaccessibilityofautonomoustech‐nologytoawiderrangeofusers.Thiseliminates inan‐cialbarriersandenablesindividuals,researchers, hobbyists,andsmallbusinessestoexploreandexper‐imentwithautonomoussystems.

EducationandResearch:Small‐scaleautonomous vehiclesprovideapracticalandhands‐onplatform foreducationalinstitutions,researchers,andstudents toengageinlearningandconductingexperimentsin ieldssuchasrobotics,arti icialintelligence,control systems,andcomputervision.Theyfacilitatethestudy ofautonomousvehiclealgorithms,behavior,andsen‐sorintegrationwithincontrolledenvironments.

TestingandPrototyping:Small‐scaleautonomous vehiclesarewell‐suitedfortestingandprototyping newalgorithms,software,andhardwarecomponents. Theyenabledeveloperstovalidatetheirideas,per‐formsimulations,andgatherreal‐worlddataona smallerandmoremanageablescalebeforetransition‐ingtolargerandmoreexpensiveplatforms.

InnovationandEntrepreneurship:Low‐cost small‐scaleautonomousvehiclesfosterinnovation andentrepreneurshipbyempoweringindividuals andstartupstodevelopnewapplicationsandservices basedonautonomoustechnology.Theyserveas afoundationforbuildingproofs‐of‐conceptand minimum‐viableproductsinindustriessuchas deliveryservices,agriculture,surveillance,and environmentalmonitoring.

SkillDevelopment:Engagingwithlow‐costsmall‐scaleautonomousvehiclespresentsanopportunity forindividualstodevelopskillsinareassuchas programming,robotics,sensorintegration,andsystem integration.Thisfacilitatesthegrowthofatalent poolcomprisingautonomoussystemdevelopersand professionalswhocontributetotheadvancementof the ield.

SafetyandTestingGrounds:Small‐scale autonomousvehiclescanserveastestinggrounds forevaluatingandre iningautonomoussystemsand safetyprotocolsbeforereal‐worlddeployment.They providecontrolledenvironmentsforidentifyingand addressingpotentialrisksandchallengeswithout compromisingsafety.

TechnologicalAdvancement:Thedevelopmentand adoptionoflow‐costsmall‐scaleautonomousvehi‐clesdrivetechnologicaladvancementsinsensortech‐nology,arti icialintelligence,machinelearning,and computervision.Thisfostersinnovationandpushes theboundariesofautonomoussystems,resultingin improvedef iciency,reliability,andperformance.

Insummary,low‐costsmall‐scaleautonomous vehiclesplayacrucialroleindemocratizing autonomoustechnology,promotingeducationand research,facilitatinginnovationandentrepreneur‐ship,andadvancingthe ieldofautonomoussystems asawhole.Theyserveassteppingstonesforindi‐vidualsandorganizationstoexplore,experiment,and contributetothegrowingecosystemofautonomous vehiclesandrelatedapplications.

2.LiteratureReview

Rapidadvancesinautonomousvehicle(AV)tech‐nologyareexpectedtobringaboutatransforma‐tionintransportationhabits.Despitetheirlimited presenceontheroad,publicpreferences,acceptance, andadoptionintentionsrelatedtoAVshavebeen thesubjectofinvestigationbyagrowingbodyof research[1].Autonomousvehicleliteraturereviews provideinsightsontech,control,sensors,human

factors,security,andprivacy,informingresearch’s currentstateandfuturedirections.

Theacceptabilityofdifferentautonomousvehi‐clebehaviorsincon lictsdependsonvariousfac‐torslikesocietalnorms,legalconstraints,andethical frameworks.Understandingthesein luentialfactors iscrucialforcreatingeffectiveguidelinesandpoli‐cies.Futureresearchcanexplorespeci icaspectslike ethics,safetyalgorithms,real‐timedecision‐making, andhuman‐machineinterfacesinmoredepth[2].

Thelong‐termeffectsofautonomousvehicleson thebuiltenvironmenthavegainedsigni icantatten‐tionduetothepotentialtransformativeimpactof thistechnology.Developingconceptualframeworksto studythelong‐termeffectsofautonomousvehicles onthebuiltenvironmentrequiresaninterdisciplinary approach.Incorporatingelementsfromurbanplan‐ning,transportationengineering,environmentalsci‐ence,socialsciences,andpublicpolicycanprovidea comprehensiveunderstandingofthecomplexinterac‐tionsandpotentialconsequences[3].

Designinganddevelopingthesoftwarestackof anautonomousvehicleusingtheRobotOperating System(ROS)inconjunctionwithhardwaremod‐ulesresponsibleforcontrollingthecarrequirescare‐fulintegrationbetweensoftwareandhardwarecom‐ponents.Throughoutthedevelopmentprocess,itis essentialtoconsidersafety,reliability,andsystem redundancy.Implementmechanismstohandlesen‐sorfailures,communicationerrors,andemergency situations.Adheretosafetyguidelinesandregulatory requirementstoensuretheautonomousvehicleoper‐atessafelyandcomplieswithapplicablelaws.Addi‐tionally,considerleveragingexistingROSpackages, libraries,andtoolsthatprovidefunctionalitiesforsen‐sorintegration,actuatorcontrol,andplanningand controlalgorithms.TheROSecosystemoffersnumer‐ousresourcesthatcanacceleratedevelopmentand provideasolidfoundationforautonomousvehicle softwarestacks[4].

AsAVtechnologyevolves,thereisapossibility thattraf iclanesandon‐streetparkingspotscould bedownsizedorrecon iguredtoaccommodatethe ef iciencyandsafetyfeaturesofAVs.Thisdownsizing couldresultintheavailabilityofadditionalspareroad spaceinfutureurbanstreets.Itisessentialforurban planners,policymakers,andcommunitiestoproac‐tivelyconsiderthepotentialrepurposingofspareroad spaceasAVtechnologyadvances.Throughcareful planningandcollaboration,citiescanleveragethis opportunitytocreatemorelivable,sustainable,and people‐centricurbanenvironments[5].

Researchonpathplanningforautonomousvehi‐clesbasedontheFrenetsystemhasgainedsigni icant attentioninrecentyears,providingamathematical frameworkfordescribingthemotionofaparticle alongacurveinthree‐dimensionalspace.Itisparticu‐larlyusefulforpathplanninginautonomousvehicles asitallowsforef icienttrajectorygenerationandcon‐trol.Theroadbehaviorofacarwassimulatedusing a ive‐foldpolynomialalgorithmmodel,whichallows

forthegenerationofpathtrajectoriesthatmimicdif‐ferentdrivingbehaviors.

Byanalyzingtherateofchangeoflateralandverti‐calvelocity,aswellaslateralandverticalacceleration undervariousbehaviors,itbecamepossibletoesti‐matethepredictiontimeforthecar[6].

Autonomousvehiclesrelyonacombinationof sensorstoperceivetheirsurroundingsandmake informeddecisions.Inthisreview,alistofsensorslike LiDAR(LightDetectionandRanging),Radar(Radio DetectionandRanging),andCameras(RGB,monocu‐lar,stereo,ormulti‐camerasetups)commonlyusedin autonomousvehiclesareexplainedindetail[7].

Of linemappingforautonomousvehicleswith low‐costsensorsgaveafeasibleapproach,especially whenhigh‐precisionmappingdatawasnotastrict requirement[8].Whilelow‐costsensorsmaynotoffer thesamelevelofaccuracyashigh‐endsensors,they canstillprovidevaluabledataforbasicmappingpur‐poses.

Vision‐basednavigationandguidancesystems offernumerousbene itsinagriculturalapplications, includingincreasedef iciency,reducedlaborrequire‐ments,improvedaccuracy,andoptimizedresource utilization.Ongoingadvancementsincomputervision, machinelearning,androboticscontinuetoenhance thecapabilitiesandreliabilityofthesesystemsinthe agriculturalsector[9].

Map‐basedlocalizationmethodsusing3D‐LiDAR (LightDetectionandRanging)sensorshaveproven tobeeffectiveinprovidingaccurateandrobustlocal‐izationforautonomousvehicles.Byleveragingthe richspatialinformationcapturedby3D‐LiDARsen‐sors,thesemethodsenablevehiclestodetermine theirpositionwithinapre‐builtmap.Curb‐map‐based localizationleveragestheuniquecharacteristicsof curbsidefeatures,whicharerelativelystableanddis‐tinguishableinurbanenvironments.Byfocusingon curbsandassociatedfeatures,thisapproachcanpro‐videpreciseandreliablelocalization,eveninchalleng‐ingscenarioswithlimitedGPSavailabilityorcom‐plexroadlayouts.Itisimportanttonotethatcurb‐map‐basedlocalizationmaybeusedincombination withothersensorinputs,suchasGPS,IMU,orcamera data,toenhancetheoveralllocalizationaccuracyand robustness[10].

Nonetheless,thefull‐scaledeploymentof autonomousvehiclescontinuestofacesigni icant obstaclesconcerningsafetyconcerns.Theseconcerns stemfromarangeofissueswithinthevehicles themselvesandexternalfactorsintheiroperational environments.Addressingthesesafetychallengesis imperative.Sensordataplaysacriticalroleinthis endeavorbyprovidingvaluableinsightsintothe currentoperationalstatusofautonomousvehicle systemsandthein luenceofexternalenvironmental factors.Suchdatahelpsinmonitoringandmitigating risks,contributingtotheoverallsafetyandreliability ofautonomousvehicletechnology[11,12].

3.MaterialsandMethods

IntheMaterialsandMethodssection,thestudy examineseachstageandresultseparately,encom‐passingequipment,algorithms,andmethods.

Firstly,thebillofmaterialsisprovidedinFig‐ure1.Whenselectingcomponents,considerationsare giventofactorssuchascost,functionality,compati‐bility,andeaseofaccesstoresources,aimingforsuc‐cessfulimplementationintheexperimentalresearch. Thematerialsaredescribedwithgeneralinformation, includingvisualsofthecomponents,technicalspeci i‐cations,andbriefcommentsbasedontheconducted experimentsandstudies.

Furthermore,inthemethodsection,thedesign stagesofthevehicleareexplained,includingcalcu‐lationsandthesoftwarealgorithmforautonomous driving.

3.1.Materials

TheL298NMotorDriverUnitisconsideredan optimalmotordrivermodulefordrivingDCandStep‐perMotors.Itiscomposedofa78M055Vregulator andL298motordriver.WiththeL298NModule,up to4DCmotorsor2DCmotorswithdirectionand speedcontrolcanbeoperated.Intheexperimental study,twoofthemwereusedasdirectionalandspeed controllers,resultinginthecontroloftwowheelsby1 L298Nmotordriver.

TheU‐BloxGY‐NEO6MV2GPSunitisaGPSmodule thatintegratesaU‐BloxNEO‐6MGPSreceiverwithan externalantenna.

TheArduinoMega2560isamicrocontrollerboard basedontheATmega2560microcontroller,responsi‐bleformanagingallthecomponentsoftheentirecir‐cuitandthefunctionsexpectedfromtheautonomous drive.TheselectionoftheArduinoMega2560was drivenbytheeaseofaccessingcodesources,thecost ofthemicrocontrollerunit,anditscompatibilitywith othercircuitmembers.

TheHC‐SR04isanultrasonicdistancesensor commonlyutilizedinvariousapplications,includ‐ingrobotics,automation,andproximitysensing.The ultrasonicmeasuringmoduleHC‐SR04technicallyis abletomeasurearangeof20mmto4000mmdueto itstechnicaldatasheetprovidedbythemanufacturer, witharangeaccuracythatmayreachupto3mm. Themodulesconsistofultrasonicsoundreceivers, transmitters,andcontrollingcircuits.Theessential workingprincipleinvolvesusingtheIOtriggertosend ahigh‐levelsignalforapproximately10us.Thesensor emitsan8,40kHzultrasonicpulseanddetectsthe returnsignalpulse.ThedurationofthehighoutputIO time,whenthesignalreturns,correspondstothetime takenfromultrasonictransmissiontoreception.

TheHMC5883Lisamagnetometersensor designedtomeasuremagnetic ieldstrengthand direction.Itiscommonlyemployedinapplications suchasnavigation,robotics,andmagnetometer calibration.

The6VDCbrushedmotorwithareducerand wheelrepresentsastandardcon igurationutilizedin thisexperimentalstudy.

3.2.Methods

Firstly,whendeterminingthebasicdimensionsof thevehicle,carefulconsiderationwasgiventoeluci‐datehowthedecisionsweremade.Oneofthemain factorstakenintoaccountwasthemanufacturability oftheparts,whichledtotherealizationthat3Dprint‐ingwasthemostsuitableoptionforimplementingthe experimentalcar.Consequently,thissetaconstraint onthedesigntokeepthedimensionsascompactas possible.Additionally,thefunctionalityofthesensors andelectromechanicalpartsposedfurtherconsidera‐tionsthatnecessitatedlongerdimensions.Ultimately, consideringthesevariousconditions,thedimensions oftheautonomouscarweredetermined.

InFigure 2,itcanbeobservedthatthewheels havebeenpositionedata5‐degreecamberangle.The reasonfortheselectionofapositive5‐degreecamber angleistoensurethatthetireremainsconnectedtoits reducerwithouttheneedforfasteningorgluing.Fur‐thermore,whentheshockabsorbersarecompressed, thecamberanglechangestoanegativevalueifitwas initiallysetatzerodegrees.However,ifthecamber angleissettoapositivevalue,evenwhenloadedat fullcapacity,thecamberanglewillremainpositiveor zero,therebymaintainingvehicledynamicsanddrive stability.

Pathplanningalgorithmsplayacriticalrolein autonomousvehicles’abilitytonavigatesafely,ef i‐ciently,andadaptivelyindynamicenvironments.

Figure1. Billofmaterials(mainassembliesandparts)

Figure2. Basicdimensionsoftheautonomousvehicle (dimensionsinmm)

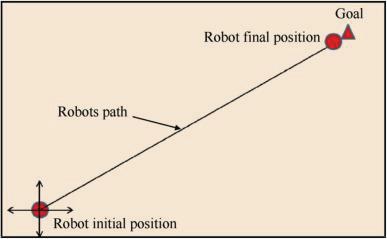
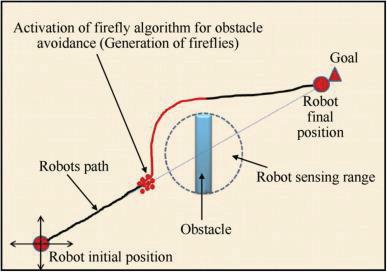
obstaclede initionisillustrated,whichisapplicableto objectswithaheightgreaterthan30mm,considering theirdynamiccapabilities.

Thesealgorithmsoptimizetrajectories,ensurecol‐lisionavoidance,handlecomplexmaneuvers,consider humaninteraction,andcontributetooverallef iciency andreliability.Thepathplanningalgorithmfunctions bydeterminingtheshortestlinebetweenthestarting pointanddestinationpoint,asillustratedinthe igure below.Sensors2,3,andfourservethesamepurpose asshowninFigure8,buttheplacementofthreesen‐sorsextendstherangeofobstacledetection.

BytheapplicationoftheFire lyAlgorithm(FA)to pathplanning,thesearchspaceofpossiblepathscan beexploredbytheautonomousvehicle.Thesepaths areevaluatedbasedontheir itnessvaluesanditer‐ativelyre inedto indoptimalornear‐optimalsolu‐tions,consideringthede inedobjectivefunction.

Itshouldbeemphasizedthattheperformanceand suitabilityoftheFire lyAlgorithmasanoptimization techniqueforpathplanningdependonthespeci ic problem,environment,andobjectives.Toassessand adapttheFire lyAlgorithmforoptimalresultsina givenapplicationscenario,comparisonswithother pathplanningalgorithmsandcarefulparametertun‐ingarenecessary.

Duringthecalculationofpositionsandbearing degrees,theshortestrouteisgeneratedtonavigate towardthedestination.Intheeventofanobstacle detectedbythesensorsatadistanceshorterthan 520mm,thevehiclewillsteerinanotherdirectionto bypasstheobstacle.Afterplacingsensorsat10degree anglebetweengroundandsensorsnormalaxis,ideal distancehadbeencalculatedas514.83mmtodetect 30mmobstacle.That514.83mmdistancehadbeen roundedto520mmbyself‐decisionduetomakethe calculationseasierandgainingadditionalsaferdis‐tance5.17mm.Atthispoint,theFire lyAlgorithm (FA)loopisinitiatedtonavigatearoundobstacles withintheshortestdistance.InFigure4,thevehicle’s

Theconditionforoneofthesensorsissetatasafe distanceof520mm(whichisanoptimizedvalue)to ensurethatobstaclesarenotapproached.Insitua‐tionswherethisconditionisnotmet,theAVbreaks itsheadingloopandinitiatestheFAalgorithmloop togenerate ire liesinthevicinityoftheobstacles,as demonstratedinFigure5.

Severalrandom ire liesareproducedandposi‐tionedneartheobstacles,andthebrighter ire lies areselectedfromthisgroup.Brighter ire liesreferto newstartingpointsthatprovidethemaximumsafe distancebetweentheobstacleandthe ire ly.TheAV maintainsthisgenerationandselectionprocessof thebrightest ire lyuntilitsuccessfullyavoidsobsta‐clesthatcanbedetectedbytheultrasonicsensor distances.

The lowchartoftheFire lyAlgorithmisexplained inFigure 6,andthepseudocodeoftheFire lyAlgo‐rithmisprovidedinFigure7

BeforetheapplicationoftheFire lyAlgorithm(FA) formulationtothesoftwareoftheautonomousvehicle (AV),theAV’sresponsetoencounteringanobstacle canbesummarizedinthefollowingsteps:

Initialization:TheAVandthetargetpositionare initialized.

CalculationofHeadingDegree:Theheading degreebetweentheAV’scurrentGPSpositionandthe targetpositioniscalculated.

ObstacleDetection:Duringtheheadingphase,if anobstacleisdetectedbytheAV,theheadingloopis interrupted,andtheFAloopisactivated.

Fire lyPopulationGeneration:Apopulationof ire‐liesisgeneratedbytheAVinthevicinityofthe detectedobstacle.

BrightestFire lySelection:TheAVemploysa it‐nessequationtoselectthebrightest ire lyfromthe generatedpopulation.

HeadingLoopActivation:TheAVactivatesthe headingloopagaintocalculateanewroutebetween thebrightest ire ly’spositionandthetargetposition.

Figure3. Shortestlinebetweeninitialandfinalposition ofautonomousvehicle(AV)

Figure4. Autonomousvehiclefaceswithanobstacle. (dimensionsinmm)

Figure5. Activationoffireflyalgorithm

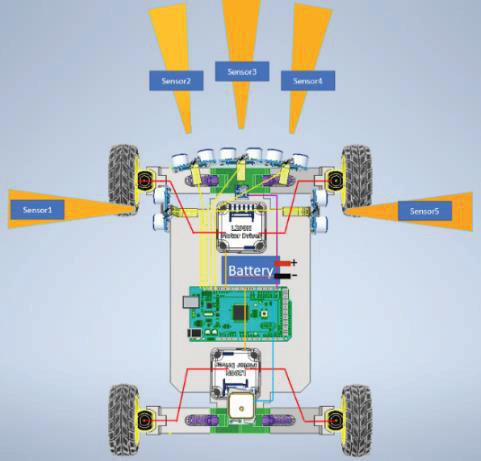
Byfollowingthesesteps,theAVdynamically adjustsitspathandnavigatestowardthetargetwhile effectivelyavoidingobstaclesencounteredalongthe way.

Dfo = (xO xfi)2 +(yO yfi)2 (1)

TheEuclideandistance,referredtoasDfo, betweenthepositionofa ire lyandanearbyobstacle isacrucialparameterinthealgorithm.Inthisstudy, theDfovaluesareobtainedthroughsensorreadings, speci icallyfrom ivesensors(seeFig. 8).These sensorreadingsserveasthecalculatedDfovalues,as representedinEquation(1).

Dfg = (xg xfi)2 +(yg yfi)2 (2)

DfgistheEuclideandistancebetween ire lyand targetpointshowninEq.(2).

���� =��1 1 min���� ∈����‖��fo‖ +��2 ⋅‖Dfg‖ (3)

Thecalculationofthe ire ly’spathoptimization, denotedas i,isperformedusingtheformulapro‐videdinEquation(3).Inthisequation,K1represents aparameterthatsigni iesthesafetylevelofthepath, whileK2denotesaparameterde iningthemaximum andminimumpathlengthsforrouting.Aftertheposi‐tionsandparametersarecomputedandsetbythe user,themicrocontrollerunit(MCU)initiatestheexe‐cutionofthealgorithmdescribedinEquation(3),sub‐sequentlydeterminingtheoptimal ire ly.

NavigationwithObstacle:TheAVproceedsto movetowardthetargetpositionwhileencountering anobstacle.IftheAVencountersanotherobstacle duringthisprocess,steps3to6arerepeatedtoensure obstacleavoidance.

Finally,asillustratedinFigure8,theautonomous vehicle(AV)calculatesanewroutebetweentheinitial point(selected ire lybytheMCU)andthe inalpoint (targetsetbytheuser).

Thelibraryincludesallthenecessaryfunction keysforuser‐de inedoperations.Additionally,amath libraryhasbeenincorporatedtoperformcalculations relatedtopositionsdetectedbysatellites.Aftercon‐iguringthepowerandsignalpinsoftheGPSmodule, avoidGPSloophasbeenimplemented,asdepictedin Figure9.

Figure6. Flowchartoffireflyalgorithm

Figure7. Pseudocodeoffireflyalgorithm

Figure8. CircuitdiagramofAV

Forthebearingdegreecalculationsofthemagne‐tometer,formulaswerewritteninthesoftwareedi‐torprogramofArduino.Magneticdeclinationisalso consideredwhilecalculatingthebearingdegreeofthe vehicle(Fig.10).

Thevehicleoperatesusingtwomainloops.The irstloopisresponsibleforcalculatingtheheading, bearingdegree,andpositionofthevehicle,allowingit tonavigatetowardadesireddestination.Asthevehi‐cleapproachesthedestination,theheadingdegree isrecalculatedbasedongeometricrulestoensure accuracy.

Thesecondloopisdedicatedtoobstacleavoid‐ance.Thevehiclereliesonsensorsasits“eyes”to detectobstacles.Ifthedistancebetweenthevehicle andanobstaclefallsbelowtheprede inedsafedis‐tanceof520mm,themicrocontrollerinterruptsthe mainloopandswitchestotheobstacleavoidanceloop. Inthismode,themicrocontrollerprovidesdirectives tosteerthevehicleandpreventcollisionsuntilasafe distanceismaintained.Onceallthesensorsdetectand con irmtheabsenceofobstaclesalongthevehicle’s path,themicrocontrollertransitionsbacktotheloop thatdirectsandguidesthevehicletowarditsdesig‐nateddestination.

Theexperimentwasdesignedtobeconductedin outdoorconditions,involvingobstacleswith ivedif‐ferentgeometricshapesconstructedfromcardboard. Thesespeci icshapeswerechosentoevaluatethe vehicle’sabilitytoavoidobstacles.The iguresbelow (Figure 11(a)–11(e))illustratethe ivedistinctgeo‐metricobjectsusedintheexperiment.

The ivedifferentshapeswereselectedbasedon theirlevelofdif icultyfordetectionbyultrasound sensors.Theseshapeswillbepositionedinvarious orientationsduringthetenmeasurementsofthevehi‐cle’sperformance.Thecrenel‐shapedobstacle,inpar‐ticular,waschosenduetoitscomplexstructure,pre‐sentingasigni icantchallengeforultrasoundsensors.

Thevehicle’sratedspeedhasbeenmeasuredas0.5 meterspersecond.Toevaluateitsspeedcapabilities, aspeedtestwasconductedonthestreet,coveringa distanceof2.5meterswithin5seconds.Byapplying theformulaspeed = distance ÷ time,aspeedof0.5 m/swascalculated.

Figure9. VoidGPSloop

Figure10. Bearingdegreecalculation

Figure11(a). Pyramidshapedobstacle

Figure11(b). Cubeshapedobstacle

Whileperformingthesmall‐scaleautonomous vehiclesoutdoortest,thetemperatureofthesunny daywas24degreesCelsius,thehumiditywas%52, andthewindspeedwas12km/h,1018hPa,anddur‐ingthetest,thevalueswerealmostexactlythesame duetotheshorttestdurations.Inadditiontothat, aircurrentsareimportantformeasurementaccuracy; however,aircurrentsmustbeatseriouslevels,such asinstormyweather,whichhasspeedsover60km/h. Duringtestday,thewindspeedwas12km/h,which isafairlevelofaircurrentthatwouldbeneglectedfor accuracy.

BasedontheinformationprovidedinFigure 12, theinitialpositionoftheautonomousvehicle(AV) wasdeterminedusingGPSreadingsas38.516534, 27.044097.ThetargetpositionfortheAVwasselected as38.516808,27.043947.Usingthebearingdegree calculationformula,themicrocontrollerunitoftheAV determinedthebearingdegreetobe 23.18degrees. Toobtaintheactualbearingdegree,360degreeswere addedtothenegativevalue,resultingina inalbear‐ingdegreeof336.81degrees.Additionally,thetravel distancewascalculatedtobe32.94meters.

Figure11(c). Cylindricalshapedobstacle

Figure11(d). Triangularprismshapedobstacle

Figure11(e). Crenel‐shapedobstacle

Figure12. Obstacleavoidanceoutdoortest

Figure13. Headingdegreeexperimentalsensorreadings

WhentheAVwaspositionedtothetargetloca‐tions,sensorreadingswerepresentedabovein Figure 13.Withthesesensorreadings,thepercent‐ageoferrorwouldbecalculated.Firstly,theaverage valueoftheeightexperimentalreadingswillbecalcu‐latedas:

336.45+336.22+336.30+336.37

+336.60+336.30+336.29

+336.37

8 =336.36 (4)

%Error= |ExperimentalValue TheoreticalValue| TheoreticalValue ×100 (5)

ThenfollowingEq.(5)wasusedtocalculateper‐centageoferrorformagnetometersensor:

%Error= |336.36−336.81| 336.81 ×100=%0.13Error (6)

Thenavigationprocessexhibitedaremarkablylow leveloferror,whichishighlyfavorable.Additionally, thecontinuousmeasurementofsensorswhilethe autonomousvehicleisprogressingtowardthetar‐getdestinationsigni icantlyminimizesanypotential errors,especiallyasthedistancetraveledbecomes shorter.

Anotherroutingtestwasconductedatadifferent location,asdepictedinFigure14(a).Theinitialposi‐tionwasdeterminedas38.447223,27.226783,and thetargetpositionwassetas38.447524,27.227266. Thecalculatedbearingdegreeforthisparticularroute was51.49degrees.

Duringtheroutebetweenthetwopositions, ive differentobstacleswithvaryinggeometricshapes wererandomlyplaced,asdepictedinFigure 14(b) Theautonomousvehicle(AV)operatedatarated speedof0.5m/s.Atotaloftenmeasurementswere conducted,recordingthetimetakenandthepathtrav‐eledbytheAVduringeachmeasurement.

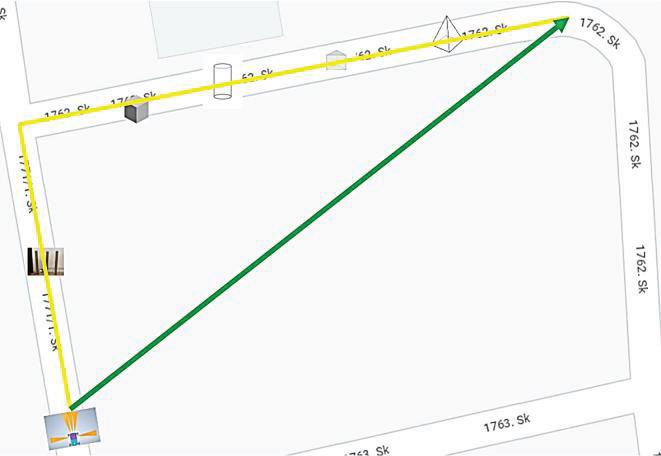
Thetimemeasurementswererecordedusinga stopwatchonamobilephone.Thisprocesswas repeatedtentimesforeachcase.Thepathstraveled bythevehicleweremanuallymarkedonasketch‐book.ThepointsweremeasuredusingGoogleMaps, asdepictedinFigure15(a).

Theidealpath,whichistheshortestlinebetween thetwopositions,wascalculatedtobe98.25meters. ThisidealpathisrepresentedbytheyellowlineinFig‐ure15(b).Ontheotherhand,theEuclideandistance betweenthetwopositionsis53.52meters.

Figure14(a). Experimentaldriveroute

Figure14(b). Experimentaldriveroutewithfive differentgeometricalshapedobstacles

Figure15(a). Traveledpointsanddistance

Figure15(b). IdealrouteandEuclideanDistance betweentwopositions

4.Results

Duringtheexperimentaldrive,asimpleroutewas chosentoconducttests.Theinitialpositionwasat coordinates38.447223,27.226783,andthetarget positionwasatcoordinates38.447524,27.227266. Thevehiclecalculatedthebearingdegreeas51.49 degrees.

Asthevehiclestartedtomove,itdeterminedthe shortestpath,representedbytheyellowhatchedline. However,duetothepresenceofsidewalks,thevehicle followedthepathindicatedbythebluecontinuous line.Thevehicledetectedthesidewalksasobstacles, soinsteadofdrivingoverthem,itchosetostayonthe road.Theexperimentaldrivewasrepeatedtentimes, asdepictedinFigure16.

Uponcompletingtheexperimentalmeasurements, the9thtrialdrewattentionduetoitstraveldistance of120meters,whichwas21.75meterslongerthan theidealpathlengthof98.25meters.Thisdisparity maybeattributedtoerrorsinobstacleavoidanceand GPS inalpositionestimation.Theremainingvalues appearedtobewithinanacceptablerange.Inorder tocalculatetheerror,itisnecessarytodeterminethe averagedistancetraveledbytheautonomousvehicle (AV).

113.4+108.1+106.7+105.5+110.8

ByusingEq.(6):

Theerrorvalueof12.3%needstobeevaluateddue toitseffectontraveltime.Itisevidentthatthis12.3% errorwillleadtoa12.3%increaseintraveltime.

Thevehicle’sarrivalwascompletedwithinacircle withadiameterof5meters,asdepictedbytheblue hatchedlinesinFigure14(a).Basedonobservations, anaccuracyof2.5metersinradiusisconsidered acceptable.

TheFire lyAlgorithm,knownforitseffective‐nessincomplexandcrowdedenvironments,has demonstrateditscapabilitytohandlebothlinearand nonlinearproblems.Itexhibitsahighconvergence speedwhilenotrequiringahigh‐performanceMCU (MicrocontrollerUnit)andhasshownfastresponses duringtheAV’smission.

TestsconductedwithoututilizingtheFire lyAlgo‐rithmresultedinconfusionduringseveraltrials.It appearedthattheAVencountereddif icultiesinsolv‐ingobstacleavoidanceproblems,leadingtoastateof confusion.

Ultimately,theadvantageofthisalgorithmlies initssimplestructure,whichdoesnotnecessitate acomplexandexpensivecontrollingunit.Thecost advantagesassociatedwithitfurtherenhanceits applicability.

5.Conclusion

Theprimaryobjectiveofthisstudywastodesign andmanufactureanautonomousvehicle(AV).Dur‐ingthedesignphase,carefulconsiderationwasgiven topotentialcomponentssuchascameras,ultrasonic sensors,andLiDARs,takingintoaccountfactorslike cost,compatibility,andalgorithms.Afterthorough researchandevaluation,itwasdeterminedthatultra‐sonicsensorswerecapableofdetectingobstacles effectivelyinoutdoorconditionswhilealsooffer‐ingacostadvantageandastraightforwardworking principle.

Thealgorithmwasintentionallydesignedtobe simpleinordertoavoidencounteringcomplexbugs duringsimulateddeliveryoperations.TheGPSposi‐tionerrorsremainedwithinamanageablerange,with adiameternotexceeding5meters,whichwasdeemed suf icientfortheintendedoperations.However,the magnetometerwasoccasionallyaffectedbyenviron‐mentalconditionsthatcouldnotbepreciselyidenti‐ied.Thisinterferencemayhavebeencausedbyfac‐torssuchascellphonesignalsorotherelectroniccom‐ponentswithinthevehicle.Despitetheseoccasional challenges,theAVsuccessfullyreachedthetargetafter deviatingmomentarily,whichcanbeconsideredneg‐ligiblesinceitwastheinitialtrialontheroadsduring theadaptationphase.

Theactualimplementationandfeasibilityofsuch low‐costsmall‐scaleautonomousvehicleswilldepend onvariousfactors,includingtechnologicaladvance‐ments,regulatoryframeworks,andmarketdemand.

Figure16. ExperimentaldriveofAV[13]

Inconclusion,thefollowingsuggestionsandrec‐ommendationscanbemade:

‐ Forapplicationsotherthanmailandpackagedeliv‐ery,advancedpositioningsensorsmayberequired toensureoptimalperformancebasedonspeci ic operationalneeds.

‐ Creatinglow‐costautonomousrobotscancollect dataonairquality,temperature,humidity,and otherparameters,helpingresearchersandenviron‐mentalagenciesgathervaluableinformation.

‐ Thenextstageofthestudywouldinvolveincor‐poratingmobileapp‐controlledpositionsandreal‐timevehicletrackingononlinemaps.Thiswould necessitatewirelesscommunicationandpresenta newandchallengingtaskincon iguringtheentire system.

AUTHORS

IsmailBogrekci –Dept.ofMechanicalEngineering, FacultyofEngineering,AydinAdnanMenderes University,Efeler,Aydin,Turkey,e‐mail: ibogrekci@adu.edu.tr.

PinarDemircioglu∗ –InstituteofMaterials Science,TUMSchoolofEngineeringandDesign, TechnicalUniversityofMunich(TUM),Garching, Munich,85748,Germany/Dept.ofMechanicalEng, FacultyofEng,AydinAdnanMenderesUniversity, Aydin,Turkey,e‐mail:pinar.demircioglu@tum.de; pinar.demircioglu@adu.edu.tr.

MustafaYasirGoren –SchneiderElectricInc., MechanicalDesignEngineer,Izmir,Turkey,e‐mail: m.yasirgoren@hotmail.com.

∗Correspondingauthor

References

[1] Q.Zhang,T.Zhang,andL.Ma,“HumanAccep‐tanceOfAutonomousVehicles:ResearchSta‐tusAndProspects,” InternationalJournalof IndustrialErgonomics,vol.95,2023,1–15.doi: 10.1016/j.ergon.2023.103458.

[2] G.Nativel‐Fontaine,V.Lespinet‐Najib,R.Cazes, C.Dupetit,C.DeGasquet,M.Chevrie,F.Aïoun, andL.Ojeda,“ExplorationOfTheAcceptabil‐ityOfDifferentBehaviorsOfAnAutonomous VehicleInSo‐CalledCon lictSituations,” Accident Analysis&Prevention,vol.186,2023,pp.1–11. doi:10.1016/j.aap.2023.107041.

[3] A.R.Pimenta,M.Kamruzzaman,andG.Cur‐rie,“Long‐TermEffectsOfAutonomousVehi‐clesOnTheBuiltEnvironment:ASystematic ScopingReviewTowardsConceptualFrame‐works,” TransportReviews,2023,pp.1–35.doi: 10.1080/01441647.2023.2189325.

[4] A.O.Prasad,P.Mishra,U.Jain,A.Pandey,A. Sinha,A.S.Yadav,R.Kumar,A.Sharma,G. Kumar,K.H.Salem,A.Sharma,andA.K.Dixit, “DesignAndDevelopmentOfSoftwareStackOf

AnAutonomousVehicleUsingRobotOperat‐ingSystem,” RoboticsandAutonomousSystems, vol.161,2023,pp.1–12.doi:10.1016/j.robot. 2022.104340.

[5] Y.Joo,S.Kim,B.Kim,G.H.Cho,andJ.Kim, “AutonomousVehiclesAndStreetDesign: ExploringTheRoleOfMediansInEnhancing PedestrianStreetCrossingSafetyUsingA VirtualRealityExperiment,” AccidentAnalysis &Prevention,vol.188,2023,pp.1–12.doi: 10.1016/j.aap.2023.107092.

[6] Y.WangandZ.Lin,“ResearchOnPathPlan‐ningForAutonomousVehicleBasedOnFrenet System”, JournalofEngineeringResearch,2023, pp.1–6.doi:10.1016/j.jer.2023.100080.

[7] H.A.Ignatious,H.Sayed,andM.Khan,“An OverviewOfSensorsInAutonomousVehicles,” ProcediaComputerScience,vol.198,2022, pp.736–741,doi:10.1016/j.procs.2021.12.315.

[8] Z.Wang,X.Zhao,andZ.Xu,“Of lineMapping ForAutonomousVehiclesWithLow‐CostSen‐sors,” Computers&ElectricalEngineering,vol.82, 2020,pp.1–11.doi:10.1016/j.compeleceng.20 20.106552.

[9] Y.Bai,B.Zhang,N.Xu,J.Zhou,J.Shi,and Z.Diao,“Vision‐BasedNavigationAndGuid‐anceForAgriculturalAutonomousVehiclesAnd Robots:AReview,” ComputersandElectronics inAgriculture,vol.205,2023,pp.1–20.doi: 10.1016/j.compag.2022.107584.

[10] L.Wang,Y.Zhang,andJ.Wang,“Map‐Based LocalizationMethodforAutonomousVehicles Using3D‐LIDAR”, IFAC-PapersOnLine,vol.50, no.1,2017,pp.276–281.doi:10.1016/j.ifacol .2017.08.046.

[11] S.Kitajima,H.Chouchane,J.Antona‐Makoshi, N.Uchida,andJ.Tajima,“ANationwideImpact AssessmentofAutomatedDrivingSystemson Traf icSafetyUsingMultiagentTraf icSimula‐tions”, IEEEOpenJournalofIntelligentTransportationSystems,vol.3,2022,pp.302–312.doi: 10.1109/Ojits.2022.3165769.

[12] H.T.Zheng,C.Y.Chen,S.Li,F.Zheng,S.E.Li, Q.Xu,andJ.Q.Wang,“Learning‐BasedSafeCon‐trolforRobotandAutonomousVehicleUsing Ef icientSafetyCerti icate,” IEEEOpenJournalof IntelligentTransportationSystems,vol.4,2023, pp.419–430.doi:10.1109/Ojits.2023.3280573.

[13] M.Y.Goren,“DesigningandManufacturingSmall ScaleAutonomousVehicle,”UnpublishedM.Sc. Thesis,2023‐M.Sc.‐043,AydinAdnanMenderes University,Turkey,2023.

Abstract:

APPLICATIONOFMULTILAYERNEURALNETWORKSFORCONTROLLINGA LINE‐FOLLOWINGROBOTINROBOTICCOMPETITIONS

APPLICATIONOFMULTILAYERNEURALNETWORKSFORCONTROLLINGA LINE‐FOLLOWINGROBOTINROBOTICCOMPETITIONS

APPLICATIONOFMULTILAYERNEURALNETWORKSFORCONTROLLINGA LINE‐FOLLOWINGROBOTINROBOTICCOMPETITIONS

Submitted:6th September2023;accepted:27th October2023

CesarMinaya,RicardoRosero,MarceloZambrano,PabloCatota

DOI:10.14313/JAMRIS/1‐2024/4

Thepaperpresentsanapproachforcontrollingaline‐followingrobotusingartificialintelligencealgorithms. Thisstudyaimstoevaluateandvalidatethedesign andimplementationofacompetitiveline‐followingrobot basedonmultilayerneuralnetworksforcontrollingthe torqueonthewheelsandregulatingthemovements. Theconfigurationoftheline‐followingrobotconsistsof achassiswithasetofinfraredsensorsthatcandetect thelineonthetrackandprovideinputdatatotheneural network.Theperformanceoftheline‐followingrobot onarunningtrackwithdifferentconfigurationsisthen evaluated.Theresultsshowthattheline‐followingrobot respondedmoreefficientlywithanartificialneuralnet‐workcontrolalgorithmthanwithaPIDcontrolorfuzzy controlalgorithm.Atthesametime,thereactionandcor‐rectiontimeoftherobottoerrorsonthetrackisearlier byabout0.1seconds.Inconclusion,thecapabilitiesofa neuralnetworkallowtheline‐followingrobottoadaptto environmentalconditionsandovercomeobstaclesonthe trackmoreeffectively.

Keywords: Robotics,Line‐followingrobot,Artificialneu‐ralnetworks

1.Introduction

Autonomousline‐followingrobotsinthelast decadeshavebeenofincreasinginterestfortheir involvementinvarious ieldsrangingfromindustry tohealthcare,education,logistics,transportation,and roboticcompetitions[1,2].Nowadays,robotdevelop‐mentfocusesonachievinghighprecision,speed,and stabilitylevels.Intelligentmobilerobotscombinecon‐trolengineering,electronics,computerscience,soft‐ware,andmechanics.

Anautonomousline‐followingrobotrecognizes andfollowsapathtracedbyablacklineona latwhite surface.Thecontrolsystemdetectsthelineandregu‐latestherobottokeepitonitspathwhileconstantly correctingfordeviations[3].Theserobotsareoften implementedinacademicsettings,suchasteaching techniquesinrobotics,controlsystems,orarti icial intelligence[4].Thearchitecturesharedbymostline‐followingrobotsincludesachassis,linedetectionsys‐tem,locomotionsystem,andcontrolunit.Varioussen‐sorscandetecttheseblacklinesdescribingthetraced routeforthis—theserangefromlow‐costdetection modulestoexpansivevisionsystems[5].

Numerousstudies[6–8]havehighlightedtheuse‐fulnessofinfraredsensorsforlinedetectionsystems. Thesearelocatedontheundersideoftherobotbase andemitabeamofinfraredlight,whichallowsusto detecttheamountofinfraredlightre lectedfromthe groundsurface.Themainreasonforchoosingthissen‐sorisitsrangeforlinedetectionfromaminimumof 100cmtoamaximumof500cm.Inaddition,theycon‐sumelowpowerandcanbeplacedinsmallspaces[9]. However,severalstudies[10–12]haveshownthatthe useofcamerascanbeanalternativeforlinedetec‐tionbycapturingimagesanddescribingtheground environmentwhilesendingthemtoanimagepro‐cessingsystemtodetecttheline.However,inthelast decades,authorshaveexperimentedwithnewtech‐niquessuchascolorsegmentation,edgedetection, ormoreadvancedmethodswithconvolutionalneural networkstoidentifyandseparatethebackgroundline andallowmoreaccuratetracking[13].

Therobotcontrolsystemallowsmonitoringand takingactiononthecollecteddataordetermining whatactiontherobotshouldtaketostayonthe line,suchasadjustingdirectionorspeed.In[14],the authorsdescribetheimplementationofa ieldpro‐grammablegatearrayknownasFPGAinthecontrol systemoftheline‐followingrobottodevelopthesen‐sordataprocessingandcontrolalgorithmef iciently. Inaddition,theFPGAcanbeeasilyreprogrammed andadjustedtosuitdifferentscenariosorspeci ic requirementsoftheline‐followingrobot.Mostofthese FPGAimplementationsaretask‐orientedfortheentire roboticsystemorareusedforparticularapplica‐tions[15].

Severalauthorshaveinvestigatedalgorithms appliedtothecontrolofaline‐followingrobot. Kaderetal.havetriedtoexplaintheapplicationof aPIDcontrolalgorithmtocorrectthecurrenterror betweentherobotpositionandthetracedlineby calculatingacontrolsignalthatrecti iestherobot trajectoryinrealtime[16].Ontheotherhand,Nikolov etal.highlighttheneedtoapplyahistogram iltering oftheMarkovprocesseffectivelytothevelocityand lengthmeasurements,thusmitigatingthecurrent positionerror[17].Inadifferentstudy,Wuetal. highlighttheimplementationofanewfuzzysliding modecontrollerandbacktrackingalgorithmfor trajectorytracking.

Thisbacktrackingcontroltechniqueeliminates posedeviationsoftherobotbasedonitsmathemat‐icalmodel[18].Recently,anintelligenttechniquefor robotspeedcontrolusingacombinationoffuzzylogic andsupervisedmachinelearninghasbeenproposed usingnumericalsimulations[19].However,thereis littleprogressinthediscussionofintelligentcontrol tools.Therefore,aninvestigationfocusedonusing arti icialintelligencealgorithmsforthecontroland performanceofaline‐followingrobotisrelevant.

Thisstudyaimstoevaluateandvalidatethedesign andimplementationofaline‐followingrobotbasedon neuralnetworkstocontrolthetorqueonthewheels andregulatethemovements.Theline‐followingrobot isanautonomousguidedvehicle(AVG)thatfollowsa trajectorydeterminedbyablackorwhiteline.Using asetofanalogre lectancesensorsincorporatedinthe competitionrobot,itcandetectthelineonthetrack, andbasedonthevaluesacquiredbythecontroller, theneuralnetworkincorporatedintheprogramming willinterpretthesesignalsandsetthebestspeed parameterstofollowthetrajectoryinastraightlineor thecurves,inordertoguaranteethebestperformance oftherobotonthetrack.

Thearticleisorganizedintosixsections:Section1 Introduction,Section2Line‐followingrobotarchitec‐ture,Section 3 Implementationoftheneuralcontrol network,Section 4 Tests,Section 5 Results,andSec‐tion6Conclusions.

2.Line‐followingRobotArchitecture

Inthissection,wedescribethearchitectureofthe line‐followingrobotthatconsistsofseveralessen‐tialcomponentswhichworktogethertoachieveits functionality.Figure 1 providesinformationonthe criticalelementsoftheline‐followingrobotstructure. Theseelementsaresystematicandcomplementeach other;inthis igure,itcanbeseenthatitconsistsof sevenblocksthatcanvaryaccordingtotheirapplica‐tion[20].

The irstelementfocusesontheenvironmentin whichitisimmersed.Then,thereisthesecondele‐mentthatincorporatesthephysicalcomponentsin chargeofcapturingthesignalsofthevariables.These signalsarethendirectedtothethirdelement,which consistsofacontrolboardinchargeofinterpreting themandissuingcorrespondingactions.

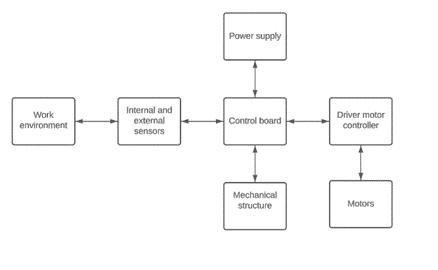
Itthenmovesontothefourthelement,repre‐sentingthepointofcontrolinteractioninsynchro‐nizationwiththemotorsinthe ifthelement.The sixthelementcoversthegeneralpowersupplyofthe robot.Finally,theseventhelementencompassesthe mechanicalstructurethatholdsalltheelectricaland mechanicalcomponentsoftherobot[21].

2.1.EmbeddedLine‐followingRobotPlatform

Thefollowingpartswereusedintheconstruction oftherobot:2wheels,2DCmotors,abasestructure,a controlboardconsistingofamicrocontroller,amotor controlcircuit,alinefollowermodule,aBluetooth connectionmodule,andapowersupplycircuit.The locomotionusedforitsconstructionisofdifferential type.Forthisreason,itisessentialtoconsiderparticu‐laritiessuchastherobot’schassis,thesensors’dimen‐sioningconcerningthechassis,andthedimensioning ofthemotor‐res[22].

Thechassisisthephysicalstructurethatsup‐portsalltheelementsoftherobot.Foritsdesign, theimplementationofaprintedcircuitboard(PCB) isconsidered,wheretheelectricalschematicthat showsallthecomponentsandtheirconnectionswith eachotherisintegrated.Theschematicincludesthe sensors,motorcontroller,microcontroller,communi‐cation,andpowersupply.Thestructure’sdesignis visualizedinFigure 2,wheretheprimaryconsider‐ationofthechassisdesignistheneedforastruc‐turethatensuresasolid,functionalbasethatcan accommodateallcomponents,ensuringsmoothand precisemovementsalongtheroute.Itisessentialto considertheweightofthechassistoavoidexcessive energyconsumptionand lexibilitytoimproverobot performanceondifferentsurfacesandmaintaintrac‐tion[23].

2.2.ControlUnit

Microcontrollersareveryimportantinconstruct‐ingtheline‐followingrobotbecausetheyhelpmoni‐tor,control,andtakeactionwiththedataobtained. Thesedevicesintegrateasinglechip’scentralprocess‐ingunit,memory,andperipherals.Themostcommon controllersareArduino,RaspberryPi,andPIC.Thanks tomicrocontrollers,robotscanperformvarioustasks, fromcontrollingbasicmovementstoexecutingmore complexfunctionsinchangingenvironments[24].

Figure1. Blockdiagramoftheoperationoftheline‐followingrobot

Figure2. Robotchassisconstruction–PCB

Inthisstudy,theArduinoMega2560microcon‐trollerformsthebasisofthelinefollowerrobot,which receivesthesignalsfromeachconnectedcomponent andconsequentlyprovidesthedesiredoutput.Itisthe brainoftheentiresystemandiscodedasrequired. Themicrocontrollerinterpretsthedatareceivedby thesensorsandgeneratescontrolcommandsthat drivetherobot’smotors.Thesecommandsallow adjustingthespeedanddirectionofthemovementto keeptherobotfollowingthelineprecisely;Figure 3 showstheconnectionoftheelementsconnectedto themicrocontroller[25].Figure3alsoshowsthecom‐ponentsoftherobot:QTR‐8Aanalogre lectancesen‐sor(A),theQTR‐1RCRe lectanceSensor(B),Arduino Mega2560(C),Battery(D),andWheels(E).

2.3.LaneDetectionSystem

Thelanedetectionsystemofaline‐followingrobot iscriticaltoitscorrectoperation.Thissystemisbased onopticalsensors,suchasphototransistorsorre lec‐tionsensors,whichcandetectthedifferencebetween re lectivitybetweenthelineandthebackground[26]. Inthisresearch,theQTR‐8Aanalogre lectancesensor wasimplementedforthetrackdetectionsystem.This electronicdevicehaseightinfraredsensors,i.e.apho‐totransistorLEDmounted9.5mmfromeachother, allowingamoreextendedrangewhendetectingthe tracedroute.Theselectedsensorbelongstothetype ofexteroceptivesensorthatdetectschangesinthe robot’sexternalenvironment.IthasanLEDthatemits radiationintheinfraredspectrum,whichhitsthe groundandcausesare lection,whichiscapturedby thephototransistor;theamountofre lectiondepends onthecoloroftheground[27].Todeterminetheline’s positionandgeneratecontrolcommands,astructure wasfabricated,asshowninFigure4.withtheanalog re lectancesensorQTR‐8A(A),whichallowstherobot tofollowthelinepreciselyandcontinuously.

2.4.LocomotionSystem

Thissectionmentionsthedimensioningofthe enginesandtheirelectroniccontrolsystem.The motorsareresponsibleforthecorrectdisplacement oftherobotonthetrack,soitisessentialtocarryout correctdimensioning,takingintoaccountthemotor torquethattherobotneedsforeachwheel.

Thebehaviorofthetorqueaboutthewheelsis directlyproportional,i.e.ahightorqueisneededwhen theradiusofthewheelsislarge,thusreducingtherev‐olutionsofthewheeland,therefore,thespeedofthe robot;ontheotherhand,ifthemotortorqueissmall andtheradiusofthewheelsissmall,therevolutions ofthewheelwouldbefaster.Consequently,thespeed oftherobotwouldincrease,whichinourcase,isideal forlookingforasmalltorque[28].Equation(1)can beusedtocalculatetherequiredmotortorque;the accelerationtobeachievedisamatterofjudgment.

��=��⋅(��+��⋅sin(��))⋅�� (1)

Where:

T:Torqueofthemotor.

M:totalMassoftherobot.

a:Acceleration.

��:Angleoftheplane.

g:Gravity.

r:Radiusofthewheels

Thedatawehavearethemassoftherobotandits components,whichisequalto170grams;thismass wasobtainedbyweighingtherobotonascale.In additiontothis,wearelookingtomanageanaccel‐erationaround2m/s2,andtheradiusofthewheels tobeimplemented1(cm).Finally,theangleofthe trackiszero.FromEquation(1),itisobtainedthat therequiredtorqueisequivalentto0.0042Nm.To controlthemotorsthatallowthemovementofthe linefollowerrobotinamoreprecise,moreef icient wayinthedirectionandspeedofthemotors.Finally, acontrollerwasselectedTB6612FNGbecauseofits dimensionsanditsapplicationsinsimilarstudies[29] werechosenforthiscasestudy.

3.NeuralNetworkforLine‐followingRobot

Thecontrolleroftheline‐followingrobotisafun‐damentalpartofitscorrectoperation;forthisreason, amultilayerneuralnetworkisusedtoimprovethe accuracyofdecision‐making.

Figure3. Microcontrollerandrobotplatform

Figure4. Lanedetectionsystembracketdesign

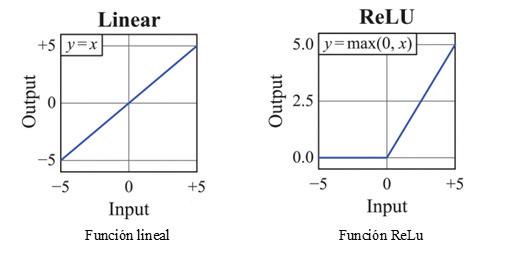
Theneuralnetworkpredictsthepositionofthe robotontherouteandprovidesacontrolsignal thatallowstherobottocontrolthemovementofthe motors[30].Thestructureoftheimplementedneural networkisvisualizedinFigure 5.Thisnetworkwas constructedusingmultiplehiddenlayers.Theinput layerconsistsofoneneuron,ahiddenlayerofsix neurons,andanoutputlayeroftwoneurons.Each layeroftheneuralnetworkreceivesavalueofthe lossfunctioninthecurrentstate,andtheconnection weightofeachneuronisadjustedaccordingly.

3.1.ImplementationoftheNeuralNetworkController

Thissectiondescribesinputdatacollectiontothe neuralnetworkandtheoutputdata.Figure6.shows howtheinputdata�� areobtainedusingthesensors ineachpositionwheretherobotcanbeonthelineso thattheneuralnetworkcanrespondcorrectlytoany situationandmakedecisionstomaintainthetrajec‐torythatdescribestheroute.Thedataobtainedfrom theQTR‐8Aanalogre lectancesensorsarefedtothe inputlayerofthemultilayerneuralnetwork.

Theoutputdata��correspondstothePWMvalue requiredinthemotors,whichdependsontheposition oftherobotonthelineandtendstochangeconstantly.

Someinputdataandoutputdataareshownin(2).

Theextractionofweightsandbiasesarefunda‐mentalcomponentsintheneuralnetwork.These valuesallowthebehaviortobeadjustedandrepresent morecomplexnon‐linearfunctions.

3.2.ActivationFunction

Theactivationfunctionmakesthenon‐linearrela‐tionshipbetweentheinputandtheoutputmore effective.Differentactivationfunctionscanbeused forthedifferentneuralnetworklayers[31];themost commonlyusedoptionsareshowninFigure 7.Rec‐ti iedLinearUnit(ReLU)neuronsareusedforthe hiddenlayers;inmachinelearning,ReLUandLinear arethemostpopularactivationfunctions,expressed inFigure7.Inourstudy,theReLUactivationfunction passestheinformationfromtheinputlayertothe hiddenlayer,withthepeculiaritythatthenegative valuesarecanceled,lettingthepositivevaluespass withoutmodifyingorcancelingthem.Thelinearacti‐vationfunctionisusedattheneuralnetwork’soutput; thishasthecharacteristicoflettingthevaluesithasat itsinputpassthroughwithoutmodifyingthem.

3.3.ModelEvaluation

Thelearningoftheneuralnetworkwasaccom‐plishedoff‐linebyscanningdataintheworkenviron‐mentbyKeraslibraryinPython.Thefulldatasetwas usedtotraintheproposedneuralnetwork,andthe performanceofthenetworkwasdeterminedforthat samedataset.Theevaluationoftheimplementedpre‐dictionmodelwasperformedbychangingthetraining parametersandepochsinordertoachievesatisfac‐toryresults.Thehyperparametersusedinthismodel canbevisualizedinTable1.Thelossfunctionisamea‐surethatevaluateshowwellthemodelmakespredic‐tionsbasedonthepredictedoutputsandtheactual outputs.Ourstudyusedthemeanabsoluteerrorloss functionandobtainedalowerrorbutwithmanyinter‐actionsorepochs.TheSDG(StochasticDownward Gradient)optimizerwasusedtoreducetheerrorand thenumberofinteractionsorepochs.

Figure5. Neuralnetworkarchitectureimplemented

Figure6. Positionoftherobotonthelane

Figure7. Activationfunctions

Table1. Hyperparametersofthepredictionmodel

Additionally,ameanabsoluteerrorregression metricwasused,whichdidnotminimizetheerrorbut servedtoevaluatethetrainingresults.Theoptimal networkstructureiscreatedbycomparingtheloss functionvaluesoverthegeneratedsamples.

4.Test

Oncetheassemblyoftherobothasbeencom‐pletedanditisworkingcorrectly,thesoftwareand hardwarepartoftherobotistested.Oncetheassem‐blyoftherobothasbeencompletedandthesoftware andhardwareareworkingcorrectly,thenecessary testsarecarriedouttoevaluateitsoperation,for whichthetrackusedintheSUCREBOT2022robotics competition,whichcanbeseeninFigure8,istakenas areference.

Thisitemalsoexplainsthemodi icationsand improvementsmadetosolveerrorswhenthelinefol‐lowerrobotwasontrack.Thisistheresultofdifferent participationinroboticscompetitions.

The irsttestscarriedoutontherobotwerethe useofaprintedcircuitboardofdrillingtechnology, withathicknessof1mm,whichincreasedtheweight oftherobot.Atthisstage,the inalprototypewasalso modi iedusingsurfacemounttechnologywithathick‐nessof0.8mm.Thefollowingtestswerecarriedout abouttheadherenceoftheline‐followingrobotonthe track.Therefore,thewidthofthewheelswaschanged from2cmand3.7cm,respectively.Finally,another essentialpointtoobservethecorrectoperationof therobotonthetrackwastoconsiderthedistance thesensorsshouldhaveconcerningthechassis,for

whichtestswerecarriedoutwithdifferentdistances ofthesensorsrangingfrom6.8cmto10.5cm.Figure9 showsthe inalprototypeoftheline‐followingrobot.

5.ResultsandDiscussions

5.1.ModelTraining

Duringtheneuralnetworktraining,thebestper‐formanceachievedwasatepoch2500withanabso‐lutemeansquareerrorof2.2355.Thetrainingperfor‐manceplotisshowninFigure10

Theoptimizedweightandbiasmatrixesobtained duringthetrainingprocessareshownin(3).

0,

w

w

��

−0,0842,701] (3c)

���� =[2,7562,757] (3d)

where ������ istheweightvectorfortheweightsfrom theinputtothehiddenlayer,������ istheweightvector fortheweightsfromthehiddenlayertotheoutput layer,���� isthebiasvectorfromtheinputtothehidden layer,and���� isthevectorfrominputbiastopaoutput layer.

InthegraphofFigure11,itisevidentthatthereal outputisclosetotheestimatedone,whichisenough toconsiderthatthemodelworks.Aftertrainingand testingtheneuralnetwork,theobtainedweightsand biasparametersareimplementedfortorqueand motioncontrolintheArduinoIDEinC++.

Figure8. Line‐followingrobotlanedimensions

Figure9. Finalprototypeoftheline‐followingrobot

Figure10. Trainingperformanceplot

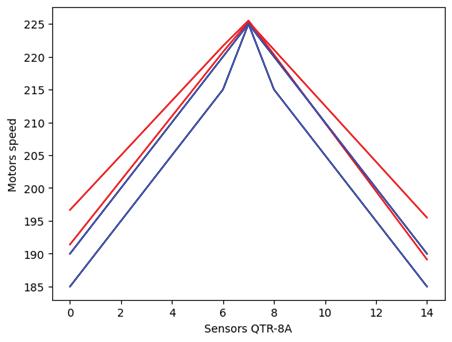
Table4. Timeresultswithdifferentopticalsensor distancesfromthechassis

5.2.RobotPrototypeSetup

Fourtestswereperformedduringeachcon igura‐tionoftheprototyperobot,andtheaveragemeasured valuewastaken.FromthedatainTable 2,theline‐followingrobotshowedhighspeedandmaneuverabil‐ityonthelanebyusingsurfacemounttechnologyin thechassisduetoitslowweight.

Table 3 showsthattheline‐followingrobothas excellenttrackstabilitywhenthetirewidthincreases. Thismakesitasuitableoptionwhenthereareirregu‐laritiesinthelane.

Thedifferencebetweenthedistancesofthesen‐sorsfromthechassisishighlightedinTable 4.By equippingthesensorsatadistanceof6.8cm,the line‐followingrobotshowedaccurateabilitiesinscan‐ningthetrackwhileavoidingsigni icantdeviationsor irregularities.

Table 5 showstheresultsobtainedbetweenthe twocontrollersbyperformingfourtracktestswiththe bestfunctioningprototypeinthemodi ications.

Table5. TimingresultswithPIDcontrollerandneural network

Thisstudyindicatesthattheline‐followingrobot hadamoreeffectiveresponsewithanarti icialneural networkcontrolalgorithmbecauseofitsabilityto learncomplexpatternsandadaptindifferentenviron‐mentscomparedtothePIDcontrolalgorithm,whichis simpleandeffectiveinpredictablesystems,butdoes notworkwellinnon‐linearsituations.Ontheother hand,thefuzzycontrolalgorithmtendstobecom‐plicatedbycon igurationandtuningandneedstobe morerobustinpredictableenvironments.Thesecond important indingwasthat,withtheimplementation ofthiscontrolalgorithm,thereactiontimeandcorrec‐tionoftherobottoerrorsonthetrackisfaster.

Thepresent indingsalsosupportthestudiesof Farkhetal.[22],whoconcludethatneuralnetworks arewellsuitedformobilerobotsbecausetheycan operatewithimpreciseinformation,i.e.differentenvi‐ronments.Whenprocessingsignalsfromsensors, theneuralnetwork‐basedcontrolalgorithmresponds fastertotakeaction.

Theresultsofthepresentstudyalsosuggeststhe useofarti icialneuralnetworkstoimproveperfor‐mance,bothinaccuracyandabilitytoadapttovar‐ioussituations.Thelearningcapabilityoftheneural networkenabledtherobottofacereal‐timechallenges andeffectivelyfollowcomplicatedroutes.

ResultsofKaderandotherauthorsintheir research[16]proposeaPIDcontrolalgorithmthat alsoallowsasmoothandstableresponseoftherobot asitfollowstheline,butwithalatercorrectiontime comparedtotheresultsobtainedwithaneuralnet‐work,consideringthatthistimeisindispensablein roboticcompetitions.

Oncarryingouttestsontheline‐followingrobot betweenthePIDcontrollerandtheneuralnetwork,it wasestablishedthatthetimestakenbytherobotto travelalongthetrackarealmostthesameforthetwo controllers;thevariationbetweenthetwoisinmil‐liseconds.However,thePIDcontrollerpresentsspe‐ci icerrorswhentherobottravelsalongthetrackin astraightline;atthatmoment,itshowsveryconstant

Figure11. Actualandestimatedoutput

Table2. Resultsofprototypeswithdifferentassembly elements

Table3. Timeresultswithdifferenttiredimensions

zigzaggingmovements.Inthesameway,inthecurves, therobotmakesabruptmovements,unliketheneural networksthatmakethemsmoother,whichcausesthe movementsonthetracktotakelesstime.

6.Conclusion

Aspartofthemechanicaldesign,itwasfound thatthechassisofthelinefollowerrobotplaysa vitalrolesincethisiswherealltheelectronicand mechanicalelementsarelocated.Thispartwascar‐riedoutconsideringthesmallestpossiblesizebecause inthedifferentroboticscompetitions,therearelim‐itationsregardingthisparameter,anditissought thattherobotcanpassthehomologationwithout anyproblem.Consideringthesizeanddesignofthe linefollowerrobotinthisstudy,theidealweightis 170grams,whichguaranteestherobot’sgoodperfor‐manceandstabilityonthetrack.Inaddition,itallowed forgreateragilityandresponsivenesswhenchanging directiononobstacles.

Theinfraredsensorsthatmakeuptheline‐followingrobot,bothlateralandfrontal,arefunda‐mental,astheywillberesponsibleforkeepingthe robotontrack.Forthisreason,thedistanceofthe sensorsconcerningtherobotchassiswilldependon theradiusofthecurvesonthedifferenttracks;in ourstudy,theidealdistanceis6.8cm,representing amorepreciseandfasterperformanceindetecting theroute.Ifanincorrectlocationofthesesensors, nomatterhowwellthemechanical,electronic,and programmingpartsareworking,therobotwillnotbe abletoful illitsfunctionproperly.

Theneuralnetworkwasimplementedasamulti‐layerperceptronmodelwithlinearregression,which provedthatitcouldworksuccessfullyonaline‐followingrobot,takingintoaccountthatitisnotnec‐essarytoaddmorethanonehiddenlayerintheneural network,dependingonthecomplexityoftheproblem andtheamountoftrainingdataavailable.Thehidden layerusedtheReLUactivationfunctiontointroduce non‐linearitiesintothenetworkandallowedthecap‐tureofcomplexrelationshipsbetweenthesensorsand theoutput.

AUTHORS

CesarMinaya∗ –DepartmentofElectronics,Instituto TecnológicoSuperiorRumiñahui,Sangolquí,171103, Ecuador,e‐mail:cesar.minaya@ister.edu.ec.

RicardoRosero –DepartmentofElectronics, InstitutoTecnológicoSuperiorRumiñahui,Sangolquí, 171103,Ecuador,e‐mail:ricardo.rosero@ister.edu.ec.

MarceloZambrano –Departmentof Electronics,InstitutoTecnológicoSuperior Rumiñahui,Sangolquí,171103,Ecuador,e‐mail: marcelo.zambrano@ister.edu.ec.

PabloCatota –DepartmentofElectronics,Instituto TecnológicoSuperiorRumiñahui,Sangolquí,171103, Ecuador,e‐mail:pablo.catota@ister.edu.ec.

∗Correspondingauthor

References

[1] O.Gumus,M.Topaloglu,andD.Ozcelik,“TheUse ofComputerControlledLineFollowerRobots inPublicTransport,” ProcediaComput.Sci., vol.102,no.August,2016,pp.202–208,doi: 10.1016/j.procs.2016.09.390.

[2] A.Latif,H.A.Widodo,R.Rahim,andK.Kunal, “ImplementationofLineFollowerRobot BasedMicrocontrolleratmega32a,” J.robot. Control,vol.1,no.3,2020,pp.70–74,doi: 10.18196/jrc.1316.

[3] M.Antony,M.Parameswaran,N.Mathew, V.S.Sajithkumar,J.Joseph,andC.M.Jacob, “DesignAndImplementationOfAutomatic GuidedVehicleForHospitalApplication,” Proc. 5thInt.Conf.Commun.Electron.Syst.ICCES 2020,no.Icces,2020,pp.1031–1036,doi: 10.1109/ICCES48766.2020.09137867.

[4] O.F.GómezandU.E.Gómez,“KinematicSimula‐tionOfALineFollowerRobotForTheCreation OfTheProgrammingVideogameRustyRoads InTheUnityFramework,” Inf.Tecnol.,vol.28, no.5,2017,pp.55–64,doi:10.4067/s0718‐07642017000500008.

[5] A.AharariandY.Ueda,“LowPassFilterApplied toColorSensorofLineFollowerRobot,” Procedia ComputerScience,vol.154,2018,pp.693–698, doi:10.1016/j.procs.2019.06.108.

[6] V.G.R.Caitite,D.M.G.DosSantos,I.C.Gregorio, W.B.DaSilva,andV.F.Mendes,“DiffusionOf RoboticsThroughLineFollowerRobots,” Proc.–15thLat.Am.robot.Symp.6thBrazilianrobot. Symp.9thWork.robot.Educ.LARS/SBR/WRE 2018,2018,pp.604–609,doi:10.1109/LARS/S BR/WRE.2018.00109.

[7] H.A.Calderón,C.Mejía,andL.Cobo,“Imple‐mentaciónDeUnRobotMóvilSeguidorDeLínea YDetectorDeObstáculosConComunicación Bluetooth,” ReviewOntare,vol.4,no.2,2017, pp.99–118,doi:10.21158/23823399.v4.n2.20 16.1639.

[8] S.Kokare,“UsingZigBee,” 2018FourthInt.Conf. Comput.Commun.ControlAutom.,2018,pp.1–5.

[9] J.Chaudhari,A.Desai,andS.Gavarskar,“Line followingRobotUsingArduinoForHospitals,” 20192ndInt.Conf.Intell.Commun.Comput.Tech. ICCT2019,2019,pp.330–332,doi:10.1109/IC CT46177.2019.8969022.

[10] W.K.BornandC.J.Lowrance,“Applicationof ConvolutionalNeuralNetworkImageClassi ica‐tionforaPath‐FollowingRobot,” 2018IEEEMIT Undergrad.Res.Technol.Conf.URTC2018,2018, pp.11–14,doi:10.1109/URTC45901.2018.924 4781.

[11] C.F.Hsu,C.T.Su,W.F.Kao,andB.K.Lee,“Vision‐BasedLine‐FollowingControlofaTwo‐Wheel Self‐BalancingRobot,” Proc.-Int.Conf.Mach. Learn.Cybern.,vol.1,2018,pp.319–324,doi: 10.1109/ICMLC.2018.8526952.

[12] J.Sarwade,S.Shetty,A.Bhavsar,M.Mergu,andA. Talekar,“LineFollowingRobotUsingImagePro‐cessing,” Proc.3rdInt.Conf.Comput.Methodol. Commun.ICCMC2019,no.Iccmc,2019,pp.1174–1179,doi:10.1109/ICCMC.2019.8819826.

[13] R.Javanmard,A.H.Zabbah,M.Karimi,andK. Jeddisaravi,“LineFollowingAutonomousDriv‐ingRobotUsingDeepLearning,” 6thIran.Conf. SignalProcess.Intell.Syst.ICSPIS2020,2020,doi: 10.1109/ICSPIS51611.2020.9349547.

[14] A.Moulay,F.Laou i,T.Benslimane,andO. Abdelkhalek,“FPGA‐BasedCar‐LikeRobotPath FollowerwithObstacleAvoidance,” Proc.2020 Int.Conf.Math.Inf.Technol.ICMIT2020,2020, pp.125–131,doi:10.1109/ICMIT47780.2020. 9047008.

[15] A.Ghorbel,N.BenAmor,andM.Jallouli,“Design OfAFlexibleRecon igurableMobileRobot LocalizationSystemUsingFPGATechnology,” SNAppliedScience,vol.2,no.7,2020,doi: 10.1007/s42452‐020‐2960‐4.

[16] M.A.Kader,M.Z.Islam,J.AlRa i,M.R.Islam, andF.S.Hossain,“LineFollowingAutonomous Of iceAssistantRobotwithPIDAlgorithm,” 2018Int.Conf.Innov.Sci.Eng.Technol.ICISET 2018,no.October,2018,pp.109–114,doi: 10.1109/ICISET.2018.8745606.

[17] D.Nikolov,G.Za irov,I.Stefanov,K.Nikov,andS. Stefanova,“AutonomousNavigationAndSpeed ControlForLineFollowingRobot,” 2018IEEE 27thInt.Sci.Conf.Electron.2018-Proc.,2018, pp.1–4,doi:10.1109/ET.2018.8549580.

[18] X.Wu,P.Jin,T.Zou,Z.Qi,H.Xiao,andP. Lou,“BacksteppingTrajectoryTracking BasedonFuzzySlidingModeControlfor DifferentialMobileRobots,” JournalofIntelligent Robotics,vol.96,no.1,2019,pp.109–121,doi: 10.1007/s10846‐019‐00980‐9.

[19] M.S.GharajehandH.B.Jond,“SpeedCon‐trolForLeader‐FollowerRobotFormationUsing FuzzySystemAndSupervisedMachineLearn‐ing,” Sensors,vol.21,no.10,2021,pp.1–14,doi: 10.3390/s21103433.

[20] S.Tayal,H.P.G.Rao,S.Bhardwaj,andH.Aggar‐wal,“LineFollowerRobot:DesignandHardware Application,” ICRITO2020-IEEE8thInt.Conf. Reliab.InfocomTechnol.Optim.(TrendsFutur. Dir.),2020,pp.10–13,doi:10.1109/ICRITO48 877.2020.9197968.

[21] I.P.Latini,W.E.Barioni,M.Teixeira,F.Neves‐Jr., andL.V.R.deArruda,“Comparisonbetween Line‐FollowersandFreeMovementRobotsin TasksExecutioninaSimulatedEnvironment,” in 2022LatinAmericanRoboticsSymposium (LARS),2022BrazilianSymposiumonRobotics (SBR),and2022WorkshoponRoboticsin Education(WRE),2022,pp.145–150.doi: 10.1109/LARS/SBR/WRE56824.2022.9995776.

[22] R.Farkh,K.AlJaloud,S.Alhuwaimel,M.T. Quasim,andM.Ksouri,“ADeepLearning ApproachForTheMobile‐RobotMotion ControlSystem,” IntelligentAutomation&Soft Computing,vol.29,no.2,2021,pp.423–435, doi:10.32604/iasc.2021.016219.

[23] A.RoyandM.M.Noel,“DesignOfAHigh‐SpeedLineFollowingRobotThatSmoothlyFol‐lowsTightCurves,” ComputerandElectrical Engineering,vol.56,2016,pp.732–747,doi: 0.1016/j.compeleceng.2015.06.014.

[24] B.G.Fernándezetal.,“Roboticsvs.Game‐Console‐BasedPlatformstoLearnComputer Architecture,” IEEEAccess,vol.8,2020, pp.95153–95169,doi:10.1109/ACCESS.2020. 2994196.

[25] M.H.Nushra,Q.A.Rahman,S.M.F.Mursalin,N.B. Asad,M.M.AsifSyeed,andM.M.Islam,“Smart CarParkingWithTheAssistanceOfLineFol‐lowingRobot,” 2019Int.Conf.Sustain.Technol. Ind.4.0,STI2019,vol.0,2019,pp.24–25,doi: 10.1109/STI47673.2019.9068046.

[26] J.W.Lok,W.M.W.Muda,andA.N.Woro,“Devel‐opmentOfWarehouseRobotWithAdvanced LineFollowingAndBackgroundColorSensors,” JournalofAdvancedManufacturingTechnology, vol.15,no.2,2021,pp.23–34.

[27] H.Murcia,J.D.Valenciano,andY.Tapiero,“Devel‐opmentofaLine‐FollowerRobotforRobotic CompetitionPurposes,” AppliedComputerSciencesinEngineering,2018,pp.464–474.

[28] L.ScrewandD.Loads,“MotorTorqueCalcula‐tion,” Wire,no.86,pp.1–5.

[29] B.Zeng,J.Zhang,L.Chen,andY.Wang,“Self‐balancingcarbasedonARDUINOUNOR3,” 2018IEEE3rdAdvancedInformationTechnology,ElectronicandAutomationControlConference(IAEAC),2018,pp.1939–1943.doi: 10.1109/IAEAC.2018.8577775.

[30] R.Chai,H.Niu,J.Carrasco,F.Arvin,H.Yin, andB.Lennox,“DesignandExperimental ValidationofDeepReinforcementLearning‐BasedFastTrajectoryPlanningandControlfor MobileRobotinUnknownEnvironment,” IEEE Trans.NeuralNetworksLearn.Syst.,2022,doi: 10.1109/TNNLS.2022.3209154.

[31] T.Guillod,P.Papamanolis,andJ.W.Kolar,“Arti i‐cialNeuralNetwork(ANN)BasedFastandAccu‐rateInductorModelingandDesign,” IEEEOpen J.PowerElectron.,vol.1,2020,pp.284–299,doi: 0.1109/OJPEL.2020.3012777.

Abstract:

PEARSONCORRELATIONANDORDEREDWEIGHTEDAVERAGEOPERATORINTHE WORLDSTOCKEXCHANGEMARKET

PEARSONCORRELATIONANDORDEREDWEIGHTEDAVERAGEOPERATORINTHE WORLDSTOCKEXCHANGEMARKET

PEARSONCORRELATIONANDORDEREDWEIGHTEDAVERAGEOPERATORINTHE WORLDSTOCKEXCHANGEMARKET

Submitted:26th May2023;accepted:22nd October2023

MarthaFlores‑Sosa,ErnestoLeon‑Castro,JoseM.Merigo

DOI:10.14313/JAMRIS/1‐2024/5

Thestockmarketisofgreatimportanceforthefinan‐cialdevelopmentofacountryduetothelargevol‐umeoftransactionstherein.Analyzingthecorrelation betweenindicesintheworldhelpsusfigureoutwhich variablesaremostimpactful.Thispaperproposesthe useoforderedweightedaverage(OWA)operatorsin combinationwiththePearsoncoefficienttocreatea measureofcorrelationthatcananalyzeawiderangeof possiblescenariosthatgofromminimumtomaximum. Thenewframeworkscanaddadditionalinformationto theprocessofcorrelation.Theworkpresentsanapplica‐tionintenofthelargeststockexchangesintheworld. Theresultssuggestabroadpositivecorrelationthatis reinforcedintimesofinstability.

Keywords: Stockmarket,OWAoperator,Pearsoncoeffi‐cient,Financialdevelopment

1.Introduction

Theworld inancialmarketisessentialinthe developmentofeconomicprocessessinceitcon‐tributestothetransferof inancial lowsbetween agents.Thestockmarketestablishesacloseconnec‐tionwiththeproductivesectortotheextentthateach countryhasdevelopedits inancialsystem[1,2].Inthe lastdecades,therehasbeenaconsiderableincrease inthenumberoftransactionsandtheirvaluesin stockmarkets.Therefore,manyofitsaspectshave beeninvestigatedtosearchforknowledgeandclarify thephenomenainthemarkets.Inthissense,issues suchasvariablesthataffectit[3,4],modeling[5,6], forecasting[7,8],andintegrations[9,10]havebeen studied.

Marketintegrationhasallowedmanyofthestock marketstomoveinsynchronywhenfortuitousevents occur,andsomeindicestendtoaffectotherstoagreat extent.Baruniketal.[11]showthatintimesofinsta‐bility,thecorrelationofthestockmarketwithother indicators,suchasgoldandoil,becomesstronger. JungandChang[12]foundthatstockstendtocluster byPearsoncorrelationandpartialcorrelation.Intend‐ingtoknowtherelationshipofworldstockmarkets overtime,Wangetal.[13]proposeanetwork‐based Pearsoncoef icienttoanalyzesomestockexchanges.

ThisworkproposesaPearsoncoef icientwith OWAaggregationoperatorstoanalyzeworldstock markets.TheOWAoperators[14]areaparameterized familyofaggregationoperators,whosemaincharac‐teristicisthereorderingoftheattributesthatallowan analysisofmultiplescenariosthatgofromminimum tomaximum.Oneofthemostpopularextensionsisthe inducedoperatorIOWA[15].Itusesamorecomplex reorderusinginducedvariables.Forthetreatment ofuncertaindata,operatorswithadditionalvectors havebeenproposed.ThePOWAoperator[16]consid‐ersprobability,andtheorderedweightedaveraging‐weightedaverage(OWAWA)[17]operatorusesan extraweighting.Notethatalltheseideascanbeuni‐iedinasingleoperatorcalledIPOWAWA[18].Since itsinception,theOWAoperatoranditsextensions havebeenusedsuccessfullyinstatisticalprocedures suchasregressionsissue[19, 20],standarddevia‐tion[21],variance,andcovariance[22,23].

ThispaperusestheIPOWA,IOWAWA,and IPOWAWAoperatorsintheformofvariancesand covariancestocalculatethePearsoncorrelation coef icient.ThenewmethodologyiscalledPC‐IPOWA, PC‐IOWAWAandPC‐IPOWAWA.Themainobjective istoobtainacorrelationcoef icientthat,inaddition toconsideringscenariosthatgofromminimumto maximum,canconsiderprobabilitiesandweights whenenvironmentsofuncertaintyexist.Inorder to indimportantinformationin inancialmarkets, weanalyzethecorrelationofsomeofthemost representativestockexchangesintheworld.

Thepaperisdevelopedasfollows:Section 2 presentsasummaryofthemethodologiesused.Sec‐tion 3 showsthenewproposedPearsoncoef icient andOWAoperators.InSection 4,ageneralizationof thenewstructureispresented.Section5developsthe applicationoftheOWAcorrelationcoef icientsinthe stockmarket.Finally,theconclusionsoftheworkare describedinSection6.

2.Preliminaries

Belowisabriefdescriptionoftheapproaches usedintheproposalofthiswork.TheOWAoperator, someofitsextensions,andthePearsoncoef icientare de ined.

2.1.OWAOperatorandExtensions

Theorderedweightedaveraging(OWA)opera‐tor[14]providesamethodtoaggregateseveralargu‐mentsthatdiebetweenthemaximumandmini‐mum.Themaincharacteristicisthereorderingofthe attributevectorthatgoesfromminimumtomaximum (AOWA)orfrommaximumtominimum(DOWA).The OWAoperatorisde inedasfollows:

De inition1. AnOWAoperatorwithdimensions n isamodel������∶���� →�� suchthatithasassociated weightsvector�� thus���� =∈[0,1]and∑�� ��=1 ���� =1, then:

������(��1,��2,…,����)= �� ��=1 ��������, (1) where���� isthe��thlargest����.TheOWAoperatorisa meanoperatorasitsatis iestheconditions:

‐ Monotonicity:if ���� ≥̂���� then ��(��1,…,����)≥ ��(̂��1,…,̂����)for��.

‐ Commutativity:Theinitialindexingofdearguments doesn’tmatter.

‐ Idempotent:if���� =��forall j,so��(����,…,����)=��. IfthereorderingoftheOWAargumentsisnotcon‐sidered,thenwecanuseinducedvariablesforit.The inducedweightedaverageoperator(IOWA)[15]uses argumentpairscalledOWApairs,withtheobjective ofinducinganorderingandaggregationofthesecond components.Itcanbede inedasfollows:

De inition2. AnIOWAoperatorisamapping ��������∶���� →�� ofdimensionnwithanassociated weightsvector ��=[��1,��2,…,] wnT,suchthat 0≤���� ≤1 and ���� +⋯+���� =1,withan inducedIOWApair ⟨����,����⟩,where ���� isthevariable thatinducedorderand���� istheargumentofthevari‐able,theformulaisasfollows:

IOWA(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)= �� ��=1 ��������, (2) where ���� isthevalue ���� intheIOWApairthathave the ��thmostextensive ����.TheIOWAoperatorsatis‐iestheconditions:Monotonicity,Commutativityand Idempotent.

Inpractice,probabilitycanbeofgreatimportance toknowthecharacteristicsofacurrentphenomenon. Merigó[16]proposestheprobabilisticOWA(POWA) operator,whichprovidesauni icationoftheprobabil‐itiesandtheOWAoperators.Itconsidersthedegreeof importanceofeachoneintheaggregationprocess.

Then: De inition3.APOWAoperatorisamapping POWA∶���� →�� associatedwithaweightvector �� whereitscomponentslieintheunitintervalandsum toone.Additionally,ithasanassociatedprobability vector �� with ∑�� ��=1 ���� =1 and ���� ∈[0,1],according tothefollowingequation:

��������(��1,��2,…,����)= �� ��=1 ��������, (3) where���� isthe jthlargestin��1,��2,…,����.Thereissuch arelationshipbetweenprobabilitiesandweightsas �� =������ +(1−��)���� with��∈[0,1].If��=0,the PAoperatorappears,andif��=1,theOWAoperator isobtained.

Insomecases,theimportantinformationin decision‐makingisgivenbyothertypesofweightings thatcancapturedifferentphenomena.TheOWAWA operatorwasproposedbyMerigó[17],anditusesthe OWAoperatorandweightedaverage(WA)inthesame formulation.Thede initionisasfollows:

De inition4. AnOWAWAoperatorofdimension n isamodel����������∶���� →��associatedwithaweight vector ��=[��1,��2,…,����]�� suchthat 0≤���� ≤ 1 and ∑�� ��=1 ���� =1.Additionally,ithasanassociated weightvector �� with ∑�� ��=1 ���� =1 and ���� ∈[0,1],so that:

����������(��1,��2,…,����)= �� ��=1 ��������, (4)

where ���� isthe jthlargest ����.Theweightvectoris composedas ���� =������ +(1−��)����.TheOWAWA operatorhassimilarpropertiestotheOWAoperator.

ThePOWAoperatorandOWAWAoperatorcanalso useadifferentreorderofarguments.TheIPOWAoper‐ator[24]andIOWAWAoperator[25]considerinduced variablesforthereorderprocess.Theformulasareas follows:

����������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)= �� ��=1 ��������, (5)

where ���� isthe ��thlargestvalueofthe ����.Thereisa weightvector��suchthat���� =∈[0,1];����+⋯+���� = 1,andaprobabilityvector �� with ∑�� ��=1 ���� =1;���� ∈ [0,1],thedegreeofimportanceis �� =������+(1−��)����.

������������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)= �� ��=1 ��������, (6) where���� isthevalue���� intheIOWAwiththe��thlargest ����.Theweightvectorconsiderstwovectors �� such that ���� =∈[0,1]; ���� +⋯+���� =1,and �� where ∑�� ��=1 ���� =1;���� ∈[0,1],thedegreeofimportanceis ���� =������ +(1−��)����

Itispossibletoputtogetheralltheideasseen aboveinoneformulation.TheIPOWAWAopera‐tor[18]uni iestheIOWA,theweightedaverage(WA)

andtheprobabilisticaggregation(PA)inoneformula‐tionthatcandealwithriskanduncertainty.Itcanbe de inedasfollows:

De inition5. AnIPOWAWAoperatorofdimension n isamapping ��������������∶���� →��,ifithastwo associatedweightingvectors W and V andprobability vector P,whereitscomponentslieintheunitinterval andsumtoone.

Additionally,aninducedIOWApair⟨����,����⟩iscon‐sidered,then:

��������������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩) =��1 �� ��=1 �������� +��2 �� ��=1 �������� +��3 �� ��=1 ��������, (7)

where���� isthevalue���� withthe��thlargest����,and��1, ��2 and��3 ∈[0,1],with��1 +��2 +��3 =1.Thespecial casesappear:if��1 =1,wegettheIOWAoperator.If ��2 =1,theWAisformed.If��3 =1,thePAisobtained. If��1 =��,wecreatetheprobabilisticweightedaverage (PWA).

2.2.VariancesandCovariancesOWA

TheOWAoperatorhasamultidisciplinaryappli‐cationusingtheideaofweightingandreorderingin othermethodologies.TheOWAoperatorswithvari‐ances(Var‐OWA)[26]adaptthearithmeticvariance toavectorofparameterizedweights,accordingtothe followingequation:

De inition6. AvarianceOWAofdimension n is amodel ������∶���� →�� withanassociatedweights vector �� thus 0≤���� ≤1 and ∑�� ��=1 ���� =1,thena variancecomponent���� =(���� −��)2 isassociatedwith aweightvalue���� inthefollowingway:

������−������(��1,…,����)= �� ��=1 ��������, (8)

where���� isthelargestofthe(���� −��)2 ,�� istheOWA operatormean.Meanwhile,thecovarianceisformu‐latedusingasimilarprocedure.Merigó[27]proposed thecovariancewithOWAoperators(Cov‐OWA).So:

De inition7. AcovarianceOWAisamodel ������∶���� →�� ofdimension ��,wherethereisa weightsvector��=[��1,��2,…,����]�� thus0≤���� ≤1 and���� +⋯+���� =1,thenthevariancecomponent ���� =(���� −��)(���� −��)isassociatedwithaweight���� Theformulaisasfollows:

������−������(��,��)= �� ��=1 ��������, (9)

where���� isthe��thlargestofthe(���� −��)(���� −��),���� istheargumentvariableofthesetofelements ��, ���� istheargumentvariableoftheset��.�� and�� arethe OWAmeansofXandY,respectively.

2.3.PearsonCoefficient

Acommonframeworkformeasuringthelinear relationshipbetweentwovariablesisthePearson Correlation(PC)coef icient[28,29].Itcanbeanindex simpleandeasytoapplywithinterestingresultsin decision‐making.Then:

De inition8. ItisaPCcoef icientifgivenasetof variables(����,����),sothe��=1,…,��∶���� ∈���� ,���� ∈ ����,wehaveamodel ����∶���� →��.Theformulaisas follows:

����= ������(��,��) ������(��)������(��) , (10) where ������(��,��) isthecovariance (���� ��)(���� ��) Variance X is(���� ��)2 .Variance Y is(���� ��)2.The�� and��arethearithmeticmeans.

3.ProbabilisticWeightedOWAonPearson Correlation

Therelationshipoftwovariablescanincludesev‐eralaspectsthatarenotcapturedbythearithmetic Pearsoncoef icient.Probabilitymeasuresthecer‐taintywithwhichaneventcanoccur.Inthissense,a Pearsoncoef icientwithprobabilisticOWAoperators (PC‐POWA)offersacorrelationcoef icientthatcon‐nectstheprobabilityinthecalculationofthePC.The PC‐POWAcanbede inedasfollows:

Proposition1. APC‐POWAofdimension n isa model ��������∶���� →�� withtwosetsofvariables ���� ∈����,���� ∈���� thathasanassociatedweighting vector��with���� ∈[0,1]and���� +⋯+���� =1.Then:

����−��������(��1,…,����)

= ������−��������(��,��)

������−��������(��)×������−��������(��)

= ∑�� ��=1 ����(���� −��)(���� −��),

[∑�� ��=1 ����(���� −��)2][∑�� ��=1 ����(���� −��)2] , (11)

where ���� isthecalculationofvariancesandcovari‐ances jthlargest.Thecomponents���� =(���� −��)2 and ���� =(���� −��)(���� −��)invarianceandcovariancehave anassociatedweight����.ThePC‐POWAhasthesame proprietiesthatOWAoperators,thisis:

‐ Monotonic.If���� ≥̂���� then,wehave:

��(����−��������(��1,��2,…,����))

≥��(����−��������(̂��1,̂��2 …,̂����)).

‐ Symmetry.If ��=��1,��2,…,����;��′ =��′ 1��′ 2,…,��′ ��, then:

��(����−��������(��1,��2,…,����))

=��(����−��������(��′ 1,��′ 2,…,��′ ��)).

‐ Idempotent.If���� =��,forall��=1,…,��,then:

��(����−��������(��1,��2,…,����)=��.

Example1. Consideravariable(X=2,4,6)anda variable(Y=5,8,3),aweightvector(W=0.3,0.3,0.4) andaprobabilityvector(P=0.4,0.4,0.2)anda��=0.6.

��=0.34,0.34,0.32

POWAmeans:

��=(6×0.34)+(4×0.34)+(2×0.32)=4.04

��=(8×0.34)+(5×0.34)+(3×0.32)=5.38

VariancesandcovariancesPOWA:

������−��������(��)

=(6−4.04)2 +(4−4.04)2 +(2−4.04)2

=(4.16×0.34)+(3.84×0.34)

+(0.001×0.32)=2.72

������−��������(��)

=(8−5.04)2 +(5−5.04)2 +(3−5.04)2

=(6.86×0.34)+(5.66×0.34)

+(0.14×0.32)=4.30

������−��������(��,��)

=[(6−4.04)(8−5.38)]

+[(4−4.04)(5−5.38)]

+[(2−4.04)(3−5.38)]=(5.13×0.34)

+(4.85×0.34)+(0.01×0.32)=3.40

����−��������(��1,…,����)

= 3.40

√2.72×4.30 =0.99

Pearson’scoef icientcanalsobecalculatedbyadding additionalweightvectorswhereimportantinforma‐tionaboutthecorrelationscanbeadded.ThePC‐OWAWAcananalyzethecorrelationsinmorecomplex scenarios.Itcanbede inedasfollows:

Proposition2. APC‐OWAWAisamapping ����������∶���� →�� ofdimension n withtwosetsof variables ����;���� thathasanassociatedweighting vector��withcomponentsthatlieintheunitinterval andsumtoone.Theformulationisasfollows:

����−����������(��1,…,����)

where ������−���������� and ������−���������� arecal‐culatedasequations()()byOWAWAoperators.The PC‐OWAWAsharestheproprietiesonOWAoperators: monotonic,symmetricandidempotent.

Itisimportanttonotethattheassignmentof weightsisanessentialpointintheOWAaggregation operators.So,manywaysofmeasuringthedegreeof overestimationandunderestimationhavebeenpro‐posed.Yager[30]proposesthedegreeoforness.This is,if ��1 =1,wehaveapure“or”operator.The formulationisobtainedasfollows:

��(��)= �� ��=1 �� ∗ �� ��−�� ��−1 , (13)

where�� ∗ �� isthe���� withthe��thlargest���� value.

Additionally,Yager[30]alsosharestheentropyof dispersion,whichcapturesthevariabilityandtheuse oftheinputsbytheweightsasfollows:

��(��)=− �� ��=1 ����ln(����). (14)

Thebalance[31]measuresthedegreeofselec‐tionbetweenfavoringthehighervaluedelementsor lower‐valuedelements,then:

������(��)= �� ��−1 ��+1−2�� ��−1 ���� (15)

Thedivergence[32]distinguishesbetweentwo OWAweightsvectors,so:

������(��)= �� ��=1

(16)

Thevectorweightmeasurementcanbeusedto calculatethecharacteristicsofthePC‐OWAWAandall theproposalsseenhere.Insomecases,therelation‐shipbetweentwovariablesmaybeaffectedbyvari‐ouselementsthatchangevaluesfromonemomentto another.

Theapproachesdiscussedabovecanalsobe extendedtouseinducedvariables.ThePC‐IPOWAcan connecttheprobabilitiesandthein luenceofother variablesonthestudyintoacoef icientofcorrelation. Themainadvantageisthatwecananalyzesituations inamuchmorecomplexwayasrealitycanpresenton someoccasions.Itcanbede inedasfollows: Proposition3. APC‐IPOWAofdimension n isa model����������∶���� →��withtwosetsofvariables���� ∈ ����,���� ∈���� thathasanassociatedweightingvector �� with ���� ∈[0,1] and ∑�� ��=1 ���� =1,additionally,an inducedIPOWApair ⟨����,����⟩ andaprobabilityvector Pisconsidered.Theformulationcanbede inedas follows:

where ���� isthecalculationofvariancesandcovari‐anceswiththe jthlargest��1.The�� and�� areIPOWA means.

Inthissense,theIOWAWAoperatorcanalsobe usedtocalculatethePearsoncoef icient.ThePC‐IOWAWAisacorrelationcoef icientthatcombines somecharacteristics:1)inducedcriteriaforreorder‐ingargumentsand2)anadditionalweightedvector thatisconsideredwhittheweightedvectorOWA.Itis developedasthefollowingde inition:

Proposition4. APC‐IOWAWAisamodel ������������∶���� →�� withtwosetsofvariables����;���� withtwoweightingvectorsWand V suchthatboth have 0≤���� ≤1 and ∑�� ��=1 ���� =1,additionally,an inducedIPOWApair⟨����,����⟩.Sothat: ����−������������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)

= ������−������������(��,��) ������−������������(��)×������−������������(��)

= ∑�� ��=1 ����(���� −��)(���� −��), [∑�� ��=1 ����(���� −��)2][∑�� ��=1 ����(���� −��)2] , (18)

where ���� arethecalculationofvariancesandcovari‐anceswiththe jthlargest��1.The��and��areIOWAWA means.

Example2. Considerthedatapreviouslyseen:the variable(X=2,4,6)andthevariable(Y=5,8,3),a weightvector(W=0.3,0.3,0.4)aweightedvector(V =0.2,0.3,0.5),anda��=0.6.Additionally,aninduced vector(U=10,15,12).

��=0.26,0.3,0.44

IOWAWAmeans:

��=(4×0.26)+(6×0.3)+(2×0.44)=3.72

��=(8×0.26)+(3×0.3)+(5×0.44)=5.18

VariancesandcovariancesIOWAWA:

������−������������(��)

=(4−3.72)2 +(6−3.72)2 +(2−3.72)2

=(5.19×0.26)+(2.95×0.3)

+(0.07×0.44)=2.26

������−������������(��)

=(8−5.18)2 +(3−5.18)2 +(5−5.18)2

=(4.75×0.26)+(0.03×0.3)

+(7.95×0.44)=4.74

������−������������(��,��)

=[(4−3.72)(8−5.18)]

+[(6−3.72)(3−5.18)]

+[(2−3.72)(5−5.18)]

=(−4.97×0.26)

+(0.30×0.3)

+(0.78×0.44)=−0.85

����−������������(��1,…,����)

= −0.85

√2.26×4.74 =−0.26

Onecanobservethattheresultscanvaryinquan‐tityandsignwhenweuseinducedoperatorscompar‐ingexercises1and2.

ThePearsoncoef icientcanalsoconsidervery complexscenarioswhereuncertaintyandriskare present.ThePC‐IPOWAWAisacorrelationcoef icient thatusesinducedcomponents,weightedmeansand probabilitytomeasuretherelationshipoftwovari‐ables.Withinthesecharacteristics,itcancollecta seriesoffactorsthataffectthevariablesandprefer‐encesorprobabilitiesofeachdata.ThePC‐IPOWAWA canbede inedasfollows:

Proposition5. APC‐IPOWAWAofdimensionnis amapping ��������������∶���� →�� ifithastwosetsof variables����;���� andthreeweightingvectorsW,Pand V suchthathavecomponentsrangingfromzerotoone andthesumisone,soaninducedIPOWApair⟨����,����⟩ isused.Then:

����−��������������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)

= Cov IPOWAWA(��,��)

var IPOWAWA(��)×������−��������������(��)

= ∑�� ��=1 ����(���� −��)(���� −��), [∑�� ��=1 ����(���� −��)2][∑�� ��=1 ����(���� −��)2] , (19)

where��and��areIPOWAWAmeans.Thecomponent withtheweight���� istheonethathasthelargest��1 Theweightvectorcanbecalculatedas ��1 =��1��1 + ��2��1 +��3��1,where��1 +��2 +��3 =1 Example3. Considerthedatausedinprevious examples:thevariable(X=2,4,6)andthevariable (Y=5,8,3),aweightvector(W=0.3,0.3,0.4),proba‐bilityvector(P=0.4,0.4,0.2)aweightedvector(V= 0.2,0.3,0.5),andaC=0.3,0.4,0.2.Theinducedvector is(U=10,15,12).

��=0.33,0.35,0.32

IPOWAWAmeans:

��=(4×0.33)+(6×0.35)+(2×0.32)=4.06

��=(8×0.33)+(3×0.35)+(5×0.32)=5.29

VariancesandcovariancesIPOWAWA:

������−��������������(��)

=(4−4.06)2 +(6−4.06)2 +(2−4.06)2

=(3.76×0.33)+(4.24×0.35)

+(0.003×0.32)=2.72

������−��������������(��)

=(8−5.29)2 +(3−5.29)2

+(5−5.29)

2 =(5.24×0.33)

+(0.08×0.35)+(7.34×0.32)=4.10 ������−��������������(��,��)

=[(4−4.06)(8−5.29)]

+[(6−4.06)(3−5.29)]

+[(2−4.06)(5−5.29)]

=(−4.44×0.33)+(0.59×0.35)

+(−0.16×0.32)=−1.30

����−��������������(��1,…,����)

= −1.30 √2.72×4.10 =−0.39

Inthiscase,vectorCindicatesthatthecombinationof probabilityandweightsbringsusclosertoarithmetic means.

4.GeneralizedtheInducedPearson Coefficient

Atechniquethatcanbeusedforcomplexanalysis andgeneratingadditionalscenariosisthegeneralized orquasi‐arithmeticmean.Wecangeneralizethenew proposalspreviouslyseeninthequasi‐PC‐IPOWA,the quasi‐PC‐IOWAWA,andthequasi‐PC‐IPOWAWA.They arede inedasfollows:

Proposition6. Aquasi‐PC‐IPOWAofdimension n isamodel����������∶���� →��withasetofvariables���� ∈ ���� andasecondset ���� ∈���� whichhaveanasso‐ciatedweightingvector �� with ���� ∈[0,1] and ∑�� ��=1 ���� =1 andanassociatedprobabilityvector �� with ∑�� ��=1 ���� =1 and ���� ∈[0,1].Additionally,an inducedIPOWApair⟨����,����⟩isconsidered.Then:

����������−����−����������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)

= ����������−������−����������(��,��)

����������−������−����������(��)

×����������−������−����������(��) (20)

Particularcase Quasi-PC-IPOWA

���� = 1 ��,��������������

wherethequasi‐varianceandcovarianceIPOWAare calculatedasfollows:

��������−����������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)

=��−1 �� ��=1

������(����), (21)

��������−����������(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩)

=��−1 �� ��=1 ������(����), (22)

���� and���� arethevarianceandcovariancewiththe jth elementwiththelargestvalueof����;���� istheinduced orderofvariables; ��(����) and ��(����) arecontinuous strictlymonotonicfunctions.

Proposition7. Aquasi‐PC‐IOWAWAisamapping ������������∶���� →��withasetofvariables���� ∈���� and aset���� ∈���� suchasanassociatedweightingvector �� andaprobabilityvectorP,whichcomponentsare rangingfromzerotooneandthesumisone.Addition‐ally,aninducedIPOWApair⟨����,����⟩isconsidered.So:

Quasi PC IOWAWA(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩) = ����������−������−������������(��,��) ����������−������−������������(��) ×����������−������−������������(��) (23)

wherethevariancesandcovariancearecalculatedin aquasi‐formas()().

Proposition8. Aquasi‐PC‐IPOWAWAisamapping ��������������∶���� →�� withasetofvariables ����;���� suchasanassociatedweightingvector �� with ���� ∈ [0,1] and ∑�� ��=1 ���� =1,aprobabilityvector �� with ∑�� ��=1 ���� =1 andweightedvector �� with ∑�� ��=1 ���� =1 and ���� ∈[0,1].Additionally,aninducedIPOWApair ⟨����,����⟩isconsidered.Theformulationisasfollows:

Quasi PC IOWAWA(⟨��1,��1⟩⟨��2,��2⟩,…,⟨����,����⟩) = ����������−������−������������(��,��) ����������−������−������������(��)

×����������−������−������������(��) (24)

Additionally,thefamiliesofthegeneralizedPC‐IPOWA,PC‐IOWAWA,andPC‐IPOWAWAoperatorcan beseeninTables1–3.

Quasi‐arithmeticPearsoncoef icientinducedprobabilisticorderedweighted(Quasi‐PC‐IPOWA)

��(��)=���� GeneralizedPC‐IPOWA

��(��)=�� PC‐IPOWA

��(��)=��2

Pearsoncoef icientinducedprobabilisticorderedweightedquadraticaverage(PC‐IPOWQA)

��(��)→����,��������→0 Pearsoncoef icientinducedprobabilisticorderedweightedgeometricaverage(PC‐IPOWGA)

��(��)=��−1

Pearsoncoef icientinducedprobabilisticorderedweightedharmonicaverage(PC‐IPOWHA)

��(��)=��3 Pearsoncoef icientinducedprobabilisticorderedweightedcubicaverage(PC‐IPOWCA)

��(��)→����,��������→∞ Maximum

��(��)→����,��������→−∞ Minimum

Table1. FamiliesofgeneralizedPC‐IPOWA

Table2. FamiliesofgeneralizedPC‐IOWAWA

Particularcase Quasi-PC-IOWAWA

���� = 1 ��,��������������

��(��)=����

Quasi‐arithmeticPearsoncoef icientinducedorderedweightedaveraging‐weighted(Quasi‐PC‐IOWAWA)

GeneralizedPC‐IOWAWA

��(��)=�� PC‐IOWAWA

��(��)=��2

Pearsoncoef icientinducedorderedweightedaveraging‐weightedquadraticaverage(PC‐IOWAWQA)

��(��)→����,��������→0 Pearsoncoef icientinducedorderedweightedaveraging‐weightedgeometricaverage(PC‐IOWAWGA)

��(��)=��−1

��(��)=��3

Pearsoncoef icientinducedorderedweightedaveraging‐weightedharmonicaverage(PC‐IOWAWHA)

Pearsoncoef icientinducedorderedweightedaveraging‐weightedcubicaverage(PC‐IOWAWCA)

��(��)→����,��������→∞ Maximum

��(��)→����,��������→−∞ Minimum

Table3. FamiliesofgeneralizedPC‐IPOWAWA

Particularcase Quasi-PC-IPOWAWA

���� = 1 ��,��������������

��(��)=����

Quasi‐arithmeticPearsoncoef icientinducedprobabilisticorderedweightedaveraging‐weighted (Quasi‐PC‐IPOWAWA)

GeneralizedPC‐IPOWAWA

��(��)=�� PC‐IPOWAWA

��(��)=��2

��(��)→����,��������→0

Pearsoncoef icientinducedprobabilisticorderedweightedaveraging‐weightedquadraticaverage (PC‐IPOWAWQA)

Pearsoncoef icientinducedprobabilisticorderedweightedaveraging‐weightedgeometricaverage (PC‐IPOWAWGA)

��(��)=��−1 Pearsoncoef icientinducedprobabilisticorderedweightedaveraging‐weightedharmonicaverage (PC‐IPOWAWHA)

��(��)=��3 Pearsoncoef icientinducedprobabilisticorderedweightedaveraging‐weightedcubicaverage(PC‐IPOWAWCA)

��(��)→����,��������→∞ Maximum

��(��)→����,��������→−∞ Minimum

Duetothesigni icantgrowthofmarketsworld‐wide,itiscommonforturmoilinsome inancial marketstoaffectothers.Theimpactsofstockmar‐ketinterdependencebecomeclearerininstability [33–35].

SinceMarkowitz[36]considerstheinterdepen‐denceofmarketsasatriggerforrisk,manystudies haveemergedtomeasuretheexistingrelationship. Inthissense,severalstudieshavebeenproposedas theinterrelationofmarketsinemergingeconomies [37,38],therelationshipwithotherprices[39,40],and witheconomicgrowth[41,42].

Theyear2020wasaperiodofinstabilitywherethe COVIDpandemichadarelevantimpactonworldstock markets[43,44].Giventhisscenario,itisinterestingto knowthecorrelationobservedbetweensomeofthe mostin luentialstockexchanges.

Therefore,thisresearchconsidersanapplication ofthemethodologyofPearsoncorrelationwithOWA operatorsintenofthemostextensivestockindexes intheworld.TheperiodstudiedisfromJanuaryto

Table4. Dataanalysis

5.PearsonCorrelationwithOWAOperatorsin StocksMarket

Table5. vectorweights

Table6. OWAmeans

Table7. VariancesOWA

Table8. CovariancesOWA

December2020.Theprocessforobtainingresultsis describedinthefollowingsteps:

Step1. Thedatastudiedarede inedintermsof indexandperiod.

Step2. OWAvectorsaredescribed.Vectorsof weights,probabilities,andinduced.

Step3. CalculationofOWAmeans.

Step4. Calculationofvariancesandcovariances withthedifferentOWAoperators.

Step5. Results.ThePearsoncorrelationwithOWA operatorsisde inedinthetenstockexchanges.

5.1.TheProcessinPearsonCorrelationwithOWAs

Inordertoanalyzethecorrelationbetweensome stockexchanges,thefollowinghasbeencarriedout:

Step1. Tenrepresentativeindexesofin luential stockexchangeshavebeenselected:NYSE,NASDAQ, HangSeng,Nikkei225(Nikkei),Euronext100 (Euronext),FTS100(FTS),BSESensex(BSE),S&P‐tsx,S&Pasx200(S&P‐asx).Thedataaremonthlyfor theyear2020.Table4showstheinformation.

Step2. OWAweightsvectors.Toestimatethe means,variancesandcovarianceswiththeproposed

Table9. Pearsoncoefficientwitharithmeticmeans

Table10. PC‐IPOWAresults

Table11. PC‐IOWAWAresults

Table12. PC‐IPOWAWAresults

Table13. PC‐IPOWAWAcorrelationsbyranges

0.9to1

NYSE‐Nikkei

NYSE‐Euronext

0.7-0.89

0.5-0-69 0.30-0.49

minor0.29andnegative

NYSE‐NASDAQ NYSE‐FTSE NASDAQ‐Hangseng NASDAQ‐FTSE

NYSE‐Shanghai NASDAQ‐Euronext NASDAQ‐S&P‐asx Shanghai‐FTSE

NYSE‐BSE NYSE‐Hangseng Shanghai‐Euronext Shanghai‐Hangseng

NYSE‐S&P‐tsx NNYSE‐S&P‐asx Hangseng‐Nikkei Shanghai‐S&P‐asx

NASDAQ‐Shanghai NASDAQ‐Nikkei Hangseng‐FTSE Nikkei‐FTS

Nikkei‐BSE NASDAQ‐BSE FTSE‐S&P‐tsx FTSE‐BSE

Euronext‐S&P‐tsx NASDAQ‐S&P‐tsx

Euronext‐S&Ptasx Shanghai‐Nikkei

BSE‐S&P‐tsx Shanghai‐BSE

S&Ptxs‐S&P‐asx Shanghai.S&P‐tsx

Hangseng‐Euronext

Hangseng‐BSE

Hangseng‐S&P‐tsx

Hangseng‐S&Ptasx

Nikkei‐Euronext

Nikkei‐S&P‐tsx

Nikkei‐S&P‐asx

Euronext‐FTSE

Euronext‐BSE

FTSE‐S&P‐asx

BSE‐S&P‐asx

OWAextensions,aseriesofadditionalvectorsare necessary.Theprobabilityvector(P)wasestablished withacriterionthatclosevaluesaremorelikelyto occur.TheOWAvector(W)isarandomselection.

Theweightedvector(WA)valuedmorethemonths whenCOVIDstarted.Forpracticalpurposes,the inducedvector(I)ineachcaseordersthedatabydate fromtheclosesttothefurthest.Table 5 showsthe information:

Step3.ThecalculationofthecorrelationwithOWA operatorsimpliesthatthemeansOWAareconsidered toreplacethearithmeticmeans.Table 6 showsthe meansOWAofeachoftheindices.

Step4. VariancesandcovariancesOWAcalculation. Previouslyseenmeansaresubstitutedforvariances andcovariances.Table7showsthevariancesforeach oftheindicatorsdependingontheOWAoperator used.

NotethattheIPOWAoperatoroverestimatesthe variances.TheIOWAWAoperatoristheonewiththe smallestvariances,whichindicatesthatthemonthsof thestartofthecoviddidnotin luencethevariation oftheindicesuntilmonthslater.Thecovariancesare describedinTable8.

Theideaabouttheestimationpreviouslyseen appliesthesameinthecovariancesandthechosen OWAoperator.

Step5. Usingthevariancesandcovariancesfor eachOWAoperatorinthePearsoncoef icientformula, theresultsareobtained.Inordertomakeacompari‐sonwitharithmeticcalculations,theresultsare irst presentedwithoutOWAoperators.Table9showsthe data.

TheindiceswiththemostcorrelationareNASDAQ‐Shanghai,Nikkei‐BSE,NYSE‐BSE,NYSE‐S&P‐tsx, BSE‐S&P‐tsx,Euronext‐S&P‐asxandS&P‐tsx‐S&P‐asx. Additionally,thereisanegativecorrelationbetween

NASDAQ‐FTSEandShanghai‐FTSE.Withtheseresults, wewentontoanalyzetheinformationwithOWA operators.Table10presentstheresultsofPC‐IPOWA.

Notethatwhenweuseprobabilitiesandsubesti‐matethemonthswithmorevariations,thecorrelation increasesslightlyforindiceswithacorrelationgreater than0.9.AninterestingissueisthattheNASDAQ‐FTSE correlationturnspositive.Intheuseoftheweighted vector,Table11showsthePC‐IOWAWAresults.

Whenacriterionthattakesthemonthsofthe onsetofCOVIDintoaccount,theresultisverysimilar tothearithmeticaverage.Onecanobserveonlya slightincreaseinthecorrelations.Thenweconnect thelasttwoproposalsandcalculatethePC‐IPOWAWA. Table12presentstheinformation.

NotethatwhenamorecomplexOWAoperatoris used,thenegativevaluesdisappear.However,thecor‐relationscontinuetoretainsimilarorslightlyhigher values.Inordertoknowtowhatextenteachofthe indicescorrelates,weplacethemindifferentranges. Table13showstheorder.

Onecanseethatthemostcommoncorrelationof theindicesisbetween0.7to0.89.Almost50%ofthe correlationsareinthisrange.OnlytheNASDAQ‐FTSE andShanghai‐FTSEcorrelatelessthan0.3.Withinthe correlationsgreaterthan0.9,theNYSEcorrelation withotherindicessuchasNikkei,Euronext,BSE,S&P‐tsxandhowthesearealsostronglyrelatedtoeach other.

6.Conclusion

Stockmarketsareessentialindevelopingcoun‐tries,giventhenumberofparticipants,themove‐ments,andthevariablesthatcausethemtobecomeof greatinterest.Withtheincreasingintegrationofmar‐kets,itisevidentthattheindicesofstockexchanges withsimilarcharacteristicstendtomovetogether.

Howimportantisthisrelationship,andwhatques‐tionsthatbecomeimportantfordecision‐makingin the inancialarea?

ThisworkproposesaPearsoncoef icientthat usesOWAaggregationoperatorsinitsformulation.In ordertoanalyzestockindicesandothercomplexdata, inducedaggregationoperators(IOWA),probabilistic (IPOWA),andweighted(IOWAWA)areused.Themain advantageistoobtainacorrelationcoef icientthatcan beoverestimatedorunderestimatedbythedecision‐makeraccordingtotheinformationavailable.Inthis sense,thePearsoncoef icientresultswithOWAoper‐atorscanbeanalyzedinawiderangeofscenarios.

Thenewmethodologyisappliedtotenindicesof majorstockexchangesintheworld.Themainresults showthattheseindicestendtohaveapositivecorrela‐tiontodifferentdegrees.Thecorrelationsincreasein timeswhenthevariancesarehigher.Inthe irstyearof COVID‐19,thecorrelationbetweenindicesincreased slightly.Evencorrelationsthatwereslightlynegative turnpositivewhenconsideringprobabilityandweight inthemonthsaftertheonsetofthepandemic.The highestcorrelationsarefoundbetweentheindices NYSE‐Nikkei‐Euronext,BSE,andS&P‐tsx.

AUTHORS

MarthaFlores-Sosa –UniversidadAutónomade Occidente,BlvdLolaBeltrans/n,80020,Sinaloa, Mexico,e‐mail:martha. lores@uadeo.mx.

ErnestoLeon-Castro∗ –FacultyofEconomicsand AdministrativeSciences,UniversidadCatólicadela SantísimaConcepción,Concepción,Chile,Instituto TecnologicodeSonora,UnidadNavojoa,Ramon CoronasinnumeroColoniaITSON,Sonora,Mexico, C.P.85860,e‐mail:eleon@ucsc.cl.

JoseM.Merigo –SchoolofInformation,Systems &Modelling,FacultyofEngineeringandInforma‐tionTechnology,UniversityofTechnologySydney, 81Broadway,Ultimo,2007,NSW,Australia,e‐mail: jose.merigo@uts.edu.au.

∗Correspondingauthor

ACKNOWLEDGEMENTS

ResearchsupportedbyRedSistemasInteligentesand ExpertosModelosComputacionalesIberoamericanos (SIEMCI),projectnumber522RT0130inPrograma IberoamericanodeCienciaandTecnologiaparael Desarrollo(CYTED).

References

[1] R.Barro,“Thestockmarketandinvestment,” The ReviewofFinancialStudies,vol.3,no.1,1990, pp.115–131.

[2] L.Wang,“Stockmarketvaluation,foreign investment,andcross‐countryarbitrage,” Global FinanceJournal,vol.40,2019,pp.74–84.

[3] N.NguyenandC.Trouong,“Theinformation contentofstockmarketsaroundtheworld:A culturalexplanation,” JournalofInternational

FinancialMarkets,InstitutionsandMoney, vol.26,2013,pp.1–29.

[4] I.Tsai,“Thesourceofglobalstockmarketrisk:A viewpointofeconomicpolicyuncertainty,” EconomicModelling,vol.60,2017,pp.122–131.

[5] D.GilesandY.Li,“Modellingvolatilityspillover effectsbetweendevelopedstockmarketsand Asianemergingstockmarkets,” International JournalofFinance&Economics,vol.20,no.2, 2014,pp.155–177.

[6] W.Mensi,S.Hammoudeh,S.ShahzadandM. Shahbaz,“Modelingsystemicriskanddepen‐dencestructurebetweenoilandstockmarkets usingavariationalmodedecomposition‐based copulamethod,” JournalofBanking&Finance, vol.75,2017,pp.258–279.

[7] R.Efendi,N.ArbaiyandM.Deris,“Anew procedureinstockmarketforecastingbased onfuzzyrandomauto‐regressiontimeseries model,” InformationSciences,vol.441,2018, pp.113–132.

[8] A.Bukhari,M.S.S.Raja,S.Islam,M.Shoaiband P.Kuman,“Fractionalneuro‐sequentialARFIMA‐LSTMfor inancialmarketforecasting,” IEEE Access,vol.8,2020,pp.71326–71338.

[9] G.Caporale,K.YouandL.Chen,“Globaland regionalstockmarketintegrationinAsia:A panelconvergenceapproach,” International ReviewofFinancialAnalysis,vol.65,2019,p. 101381.

[10] C.BotocandS.Anton,“Newempiricalevidence onCEE’sstockmarketsintegration,” TheWorld Economy,vol.43,no.10,2020,pp.2785–2802.

[11] J.Barunik,E.KocendaandL.Vacha,“Gold,oil, andstocks:Dynamiccorrelations,” International ReviewofEconomics&Finance,vol.42,2016, pp.186–201.

[12] S.JungandW.Chang,“Clusteringstocksusing partialcorrelationcoef icients,” PhysicaA:StatisticalMechanicsanditsApplications,vol.462, 2016,pp.410–420.

[13] G.Wang,C.XieandH.Stanley,“Correlation structureandevolutionofworldstockmarkets: EvidencefromPearsonandpartialcorrelation‐basednetworks,” ComputationalEconomicsvolume,vol.51,2018,pp.607–635.

[14] R.Yager,“Onorderedweightedaveragingaggre‐gationoperatorsinmulti‐criteriadecisionmak‐ing,” IEEETrans.Syst.ManCybern.B,vol.18, 1988,pp.183–190.

[15] R.YagerandD.Filev,“Inducedorderedweighted averagingoperators,” IEEEtransactionsonsystems,manandcybernetics,vol.29,no.2,1999, pp.141–150.

[16] J.Merigó,“ProbabilitiesintheOWAoperator,” ExpertSystemswithApplications,vol.39,2012, pp.11456–11467.

[17] J.Merigó,“Auni iedmodelbetweentheweighted averageandtheinducedOWAoperator.,” ExpertSystemswithApplications,vol.39,no.9, pp.11560–11572,2011.

[18] J.Merigó,C.Lobato‐CarralandA.Carrillero‐Castillo,“DecisionmakingintheEuropeanUnion underriskanduncertainty,” EuropeanJournal InternationalManagement,vol.6,no.5,2012, pp.590–609.

[19] R.YagerandG.Beliakov,“OWAOperatorsin RegressionProblems,” IEEETransactionson FuzzySystems,vol.18,no.1,pp.106–113,2010.

[20] M.Flores‐Sosa,E.Avilés‐Ochoa,J.Merigó,and R.Yager,“VolatilityGARCHmodelswiththe orderedweightedaverage(OWA)operators,” InformationSciences,vol.565,2021,pp.46–61.

[21] E.León‐Castro,L.Espinoza‐Audelo,J.Merigó, E.Herrera‐ViedmaandF.Herrera,“Measuring volatilitybasedonorderedweightedaverage operators:Agriculturalproductspricescaseof use,” FuzzySetsandSystems,2020.

[22] J.Merigó,M.GuillenandJ.Sarabia,“TheOrdered WeightedAverageintheVarianceandthe Covariance,” InternationalJournalofIntelligent Systems,vol.30,no.9,2015,pp.985–1005.

[23] J.Merigó,“Auni iedmodelbetweentheweighted averageandtheinducedOWAoperator,” Expert SystemswithApplications,vol.38,no.9,2011, pp.11560–11572.

[24] R.Yager,K.EngemannandD.Filev,“Onthe conceptofimmediateprobabilities,” InternationalJournalofIntelligentSystems,vol.10,1995, pp.373–397.

[25] J.Merigó,“Auni iedmodelbetweentheweighted averageandtheinducedOWAoperator,” ExpertSystemswithapplicacions,vol.38,2011, pp.11560–11572.

[26] R.Yager,“Ontheinclusionofvarianceindecision makingunderuncertainty,” InternationalJournalUncertainFuzzyKnowl-BasedSystems,vol.4, pp.401–419,1996.

[27] J.Merigó,“Auni iedmodelbetweentheweighted averageandtheinducedOWAoperator,” Expert SystemswithApplications,vol.38,pp.11560–11572,2011.

[28] K.Pearson,“Mathematicalcontributionstothe theoryofevolution‐III.Regression,heredity,and panmixia,” PhilosoplicalTransactionsoftheRoyal SocietyA,vol.18,1896,pp.253–318.

[29] J.Benesty,J.Chen,Y.Huang,andI.Cohen,“Pear‐sonCorrelationCoef icient,” NoiseReductionin SpeechProcessing,vol.2,2009,pp.1–4.

[30] R.Yager,“Onarderedweightedaveragingaggre‐gationoperatorsinmulti‐criteriadecisionmak‐ing,” IEEETransactionsSystems.ManCybernetics B,vol.18,1988,pp.183–190.

[31] R.Yager,“ConstrainedOWAaggregation,” Fuzzy SetsandSystems,vol.81,1996,pp.89–101.

[32] R.Yager,“HeavyOWAoperators,” FuzzyOptimizationandDecisionMaking,vol.1,2002, pp.379–297.

[33] D.BlesserandJ.Yang,“Thestructureofinterde‐pendenceininternationalstockmarkets,” JournalofInternationalMoneyandFinance,vol.22, no.2,2003,pp.261–267.

[34] X.Zhang,X.Zheng,andD.Zeng,“Thedynamic interdependenceofinternational inancialmar‐kets:Anempiricalstudyontwenty‐sevenstock markets,” PhysicaA:StatisticalMechanicsandits Applications,vol.472,2017,pp.32–42.

[35] J.Chevallier,“Marketintegrationand inancial linkagesamongstockmarketsinPaci icBasin countries,” JournalofEmpiricalFinance,vol.46, 2018,pp.77–92.

[36] H.Markowitz,“Portafolioselection,” TheJournal ofFinance,vol.7,1852,pp.77–91.

[37] S.Paramati,A.Zakari,M.Jalle,S.KaleandP. Begari,“Thedynamicimpactofbilateraltrade linkagesonstockmarketcorrelationsofAus‐traliaandChina,” AppliedEconomicsLetters, vol.25,no.3,2018,pp.141–145.

[38] R.Dias,J.VidigaldaSilva,andA.Dionisio,“Finan‐cialmarketsoftheLACregion:Doesthecri‐sisin luencethe inancialintegration?,” InternationalReviewofFinancialAnalysis,vol.63,2019, pp.160–173.

[39] P.Ferreira,E.Pereira,M.F.daSilva,andH.Pereira, “Detrendedcorrelationcoef icientsbetweenoil andstockmarkets:Theeffectofthe2008crisis,” PhysicaA:StatisticalMechanicsanditsApplications,vol.517,2019,pp.86–96.

[40] S.Singhal,S.Choudhary,andP.Biswal,“Return andvolatilitylinkagesamongInternational crudeoilprice,goldprice,exchangerateand stockmarkets:EvidencefromMexico,” Resources Policy,vol.60,2019,pp.255–261.

[41] H.HouandS.Cheng,“Thedynamiceffectsof banking,lifeinsurance,andstockmarketson economicgrowth,” JapanandtheWorldEconomy, vol.41,2017,pp.87–97.

[42] T.FufaandJ.Kim,“Stockmarkets,banks,and economicgrowth:Evidencefrommorehomoge‐neouspanels,” ResearchinInternationalBusiness andFinance.,vol.44,2018,pp.504–517.

[43] S.Baker,N.Bloom,S.Davis,K.Kost,M.Sammon, andT.Viratyosin,“TheUnprecedentedStock MarketReactiontoCOVID‐19,” TheReviewof AssetPricingStudies,vol.10,no.4,2020,pp.742–758.

[44] B.Ashraf,“Stockmarkets’reactiontoCOVID‐19:Casesorfatalities?,” ResearchinInternational BusinessandFinance,vol.54,2020,p.101249.

[45]

J.RodgersandW.Nicewander,“Thirteenwaysto lookatthecorrelationcoef icient,” TheAmerican Statistician,vol.42,no.1,1988,pp.59–66.

[46]

[47]

G.Kabir,S.Tesfamariam,J.Loeppky,andR.Sadiq, “IntegratingBayesianLinearRegressionwith OrderedWeightedAveraging:UncertaintyAnal‐ysisforPredictingWaterMainFailures,” Journal ofRiskandUncertaintyinEngineeringSystems, PartA:CivilEngineering,vol.1,no.3,2015.

USINGREINFORCEMENTLEARNINGTOSELECTANOPTIMALFEATURESET USINGREINFORCEMENTLEARNINGTOSELECTANOPTIMALFEATURESET

Submitted:23rd February2022;accepted:25th January2023

YassineAkhiat,AhmedZinedine,MohamedChahhou DOI:10.14313/JAMRIS/1‐2024/6

Abstract:

FeatureSelection(FS)isanessentialresearchtopicin theareaofmachinelearning.FS,whichistheprocess ofidentifyingtherelevantfeaturesandremovingthe irrelevantandredundantones,ismeanttodealwithhigh dimensionalityproblemstoselectthebestperforming featuresubset.Intheliterature,manyfeatureselection techniquesapproachthetaskasaresearchproblem, whereeachstateinthesearchspaceisapossiblefeature subset.Inthispaper,weintroduceanewfeatureselec‐tionmethodbasedonreinforcementlearning.First,deci‐siontreebranchesareusedtotraversethesearchspace. Second,atransitionsimilaritymeasureisproposedsoas toensureexploit‐exploretrade‐off.Finally,theinforma‐tivefeaturesarethemostinvolvedonesinconstructing thebestbranches.Theperformanceoftheproposed approachesisevaluatedonninestandardbenchmark datasets.TheresultsusingtheAUCscoreshowtheeffec‐tivenessoftheproposedsystem.

Keywords: Featureselection,Datamining,Decisiontree, Reinforcementlearning,Dimensionalityreduction

1.Introduction

Withtheadventofhigh‐dimensionaldata,typ‐icallymanyfeaturesareirrelevant,redundantand noisyforagivenlearningtaskastheyhaveharm‐fulconsequencesintermsofperformanceand/or computationalcost.Moreover,alargenumberoffea‐turesrequiresalargeamountofmemoryorstorage space.Applyingdataminingandmachinelearning algorithmsinhigh‐dimensionaldatausuallyleadsto thedowngradingoftheirperformanceduetoover‐ittingproblem[1,2].Giventheexistenceofalarge numberoffeatures,machinelearningmodelsbecome intricatelycomplicatedtointerpretastheircomplex‐ityincreasesleadingtotherestrictionofthegeneraliz‐ability.Therefore,reducingthedimensionalityofdata hasbecomeindispensableinrealworldscenariosto successfullybuildunderstandableandaccuratemod‐elsthatcanimprovedata‐miningperformanceand enhancemodelsinterpretability.Dataminingcantake advantageofdimensionalityreductiontoolswhich areintegralparameterscentraltodatapre‐processing toreducethehighnessofdatadimensionality[3].

Dimensionalityreductioncanbecategorizedintofea‐tureextractionandfeatureselection(see igure1) [4–6].Featureextractionaimsattransformingthe originalfeaturespacetoanewreducedone,where featureslosetheirmeaningduetothetransformation

[7–9,9,10].Incontrasttofeatureextraction,feature selectionistheprocessofidentifyingtherelevantfea‐turesandremovingtheirrelevantandredundantones withtheobjectiveofobtainingthebestperforming subsetoforiginalfeatureswithoutanytransformation [11–13].Thus,theconstructedlearningmodelsusing theselectedsubsetoffeaturesaremoreinterpretable andreadable.Thisgivespreferencetothereliable applicabilityoffeatureselectionasaneffectivealter‐nativeprioritizedoverfeatureextractioninmanyreal‐worlddatasets.Themajorreasonsforapplyingthe featureselectionarethefollowing:

‐ Makingmodelseasiertointerpret.

‐ Reducingresourcesrequirement(shortertraining time,smallstoragecapacityetc.).

‐ Avoidingthecurseofdimensionality.

‐ Avoidingtheover‐ ittingproblem,thus,abetter model.

‐ Improvingaccuracy:lessnoiseindatameans improvedmodelingaccuracy.

Ingeneral,featureselectionalgorithmsarecate‐gorizedinto:Supervised,Semi‐supervisedandUnsu‐pervisedfeatureselection[12,14–18].Inthispaper, weputmoreemphasisonsupervisedfeatureselec‐tion,whichisathreefoldapproach,Filter,Wrapper [19–23],andEmbedded[24–26](seeFig. 1).Filter Methodsrelyontherelationshipbetweenfeatures andclasslabel(suchasdistance,dependency,corre‐lationetc.)toassesstheimportanceoffeatures.This categoryisapre‐processingstep,whichisindepen‐dentfromtheinductionalgorithm.Filtersareknown bytheireaseofuseandlowcomputationalcost.On thecontrary,theWrapperapproachgeneratesmod‐elswithsubsetsoffeatures.Then,itusespredic‐tionperformanceasacriterionfunctionoraguiding‐compasstoorientthesearchforthebestfeaturesub‐set.Thisapproachtakesintoaccounttheinteractions betweenfeatures.Generally,Wrappersachievebetter performancethansomeFiltermethods.TheEmbed‐dedapproachperformsfeatureselectionbyimplica‐tionwhilesimultaneouslyconstructingmodels,which makesthemlesscostlyintermsofexecutiontimethan wrappersdo.

1.1.ResearchObjectives

Inthispaper,weintroduceanewfeedbacksystem basedonreinforcementlearningtosolvethefeature selectionproblem.Thesystemkeepsexploringthe statespacewhileitismovingthroughtheavailable spaceoffeaturestoselectthebestsubset.Inthissys‐tem,wehaveusedthedecisiontreebranches.There‐fore,eachsubsetisrepresentedbyabranch.The mainideaoftheproposedfeatureselectionalgorithm istoselecttheapplicablesubsetoffeatures,which aremostlyinvolvedinconstructingef icientbranches. Initspreliminaryoutset,thesystemendeavorsto buildthe irstbranchwithoutanypre‐installedknowl‐edge(exploringtheenvironment).Asiterationstran‐spireinlinearlysuccessivealternation,thesystem accumulatesexperiencesthatfurnishthegroundfor constructingbetterbranches(diverse,relevant,etc.) usingthepropoundedTransitionSimilarityMeasure (TSM).Outofthebestbranches,weselectthemost utilizedfeaturesincreatingthem(SeetheFig.2).The contributoryaspirationsandthequintessentialmain‐springsofthisstudyarefourfold.

1) Areinforcementlearning‐basedmethodisdevel‐opedtobeusedinselectingthebestsubsetof features.

2) Theproposedsystemtraversesthestatespaceto selecttheinformativesubsetusingamodi iedver‐sionofdecisiontreebranches.Sincethetransi‐tionbetweenstates(featuresubsets)iscontrolled usingDecisiontreebranches,theproposedsys‐temisstraightforwardlyaccessible.Asaresult,the spotlightedsolution,througheffectiveimplemen‐tationofthesuggestedfeatureselectionmethod, ourproposedsystemisrenderedcomprehensively interpretable.

3) Transitionsimilaritymeasure(TSM)isintended tomaintaintheprogressivesustainabilitythe system’senvironmentalexplorationbycreating newbranchesandsimultaneouslyexploitingwhat haslearnedtoavoidredundancyandmaximize diversity.

4) Theproposedsystemcanbeadaptedtoanyprob‐lem(itisnotdependentonaspeci icdataset) becauseourfeatureselectionproblemisconsid‐eredasreinforcementlearning.

Theremainderofthispaperisorganizedasfol‐lows:sectiontwopresentstherelatedworks.Section threeisdevotedtotheproblemandourintroduced contributions.Inthefourthsection,theresultsofthe proposedsystemareintroduced.Astothelastsection, itisputforwardtoconcludethiswork.

2.RelatedWorks

Extensiveresearchanddeeplythoroughbreak‐throughshavebeendisclosedinthedomainoffeature selectionasanever‐evolving ieldofstudy[3,13,19, 27].Inthissection,somewrapperalgorithmssimilar tothefundamentaloneencompassedbythispaperare brie lyreviewed.The irstalgorithmisubiquitousin FSstateoftheart,whichisforwardselection[28,29]. (1)itstartswithanemptysubset;(2)addstothe subsetthefeaturethatincreasesitsperformance;(3) repeatsStep2untilallfeatureshavebeenexaminedor untilnobetterperformanceispossible;(4)returns thesubsetoffeaturesthatyieldsmaximumperfor‐manceonthevalidationset[30].Thismethodisfast andeffective,butittendstoover‐ itthevalidationset. In[20],theauthorsproposedanewalgorithmenti‐tledensemblefeatureselection,whichsigni icantly reducesthisproblem.

Figure1. Featureselectioncategorization

FeatureSpace

Traversingthesearchspace bycreatingDTbranches

DecisionTreebranches (Algorithm1)

Thebestbranchesare identifiedaccordingtothe (Bestfeaturesubbsets) Rewardfunction

TransitionSimilarityMeasure (TMS) BestConstructed Branches Optimalsubset

First,foreachfeature,theytraindifferentmodels usingdifferentclassi icationalgorithms.Then,they storetheminalibraryofmodels.Second,theyuse aselectionwithreplacementtechnique[30]to ind theoptimalsubsetofmodelsthat,whenaveraged together,achievesexcellentperformance.Another wrappermethodbasedongraphrepresentationis proposedin[14],wherethenodedegreeisusedas acriteriontoselectthebestfeaturessubsetamong thewholefeaturesspace.Thisalgorithmconsistsof twophases:(1)Choosingfeaturestobeusedingraph construction.(2)Constructingagraphinwhicheach nodecorrespondstoeachfeature,andeachedgehas aweightcorrespondingtothepairwisescoreamong featuresconnectedbythatedge.Finally,thebestfea‐turesarethenodeswiththehighestdegree.In[31],a pairwisefeatureselection(FS‐P)hasbeenintroduced, featuresareevaluatedinpairsusingdecisiontree classi ier.First,itranksfeaturesindividually.Second, itinvolvesthemachinelearningalgorithm(Decision tree)toevaluatepairsoffeatures.In[32,33],awell‐knownwrapperapproachispresented,RecursiveFea‐tureEliminationusingRandomForest(RFE).RFEper‐formsfeatureselectionrecursively.Atthe irstitera‐tion,themodel(Randomforest)istrainedonwhole setofattributes.Afterrankingfeaturesaccordingto themodel’simportance,theleastimportantfeatures areeliminated.Asiterationtakesplace,theconsider‐ingsetoffeaturesbecomesmallerandsmalleruntil thedesirednumberoffeaturesisreached.

Featurespacecontainesall features(irrelevant,noisy, redundant,andrelevant)

TMSisusedtoensure theexploit/exploretrade-off ofreinforcementlearning

Theoptimalsubsetincludes themostinvolvedfeaturesin constructingthebestbranches

Randomforestsareamongthemostpopular machinelearningalgorithms[34].Thankstoits performance,robustness,andinterpretability,RFhas provedthefrequencyofitsbene icialapplicability. Theycanselectinformativevariables[11].RFper‐formsfeatureselectionusingmeandecreaseimpu‐rityandmeansdecreaseaccuracycriteria[35].Mean decreaseimpurityisusedtomeasurethedecrease intheweightedimpurityintreesbyeachfeature. Therefore,thefeaturesarerankedaccordingtothis measure.Meandecreaseaccuracyisameasureof thefeatureimpactonmodelaccuracy.Thevalues ofeachfeaturearepermuted irst.Then,wemea‐surehowthispermutationdecreasesmodelaccu‐racy.Theinformativefeaturesdecreasethemodel accuracysigni icantly,whileunimportantfeatures donot.

Asopposedtothetraditionalfeatureselection(FS) formalizationandtheinspirationgeneratedfromthe reinforcementlearningapproach,thefeatureselec‐tionproblemcanbeeffortlesslyhandledwiththeprof‐itablereliabilityofourproposedsystem.Thefeature spaceusingourapproachcanbeseenasaMarkov decisionprocess(MDP)[36,37],whereeachsubset offeaturesisrepresentedbyastate(decisiontree branch).Oursystemexploresthestatespacewhileit exploitsthegatheredexperiencessofarusingthepro‐posedtransitionsimilaritymeasure(TSM).In[38],the authorsproposedamethodbasedonreinforcement learning(RL)forselectingthebestsubset.First,they useanAOR(averageofrewards)criteriontoidentify theeffectivenessofagivenfeatureindifferentcon‐ditions.AORistheaverageofthedifferencebetween

Figure2. Flow‐chartoftheproposedfeedbackfeatureselectionsystem

twoconsecutivestatesinseveraliterations.Second, theyintroduceanoptimalgraphsearchtoreducethe complexityoftheproblem.

Thewayoursystemtraversesfromonestate toanotherishandledusingdecisiontreebranches torepresenteachstate,asmentionedbefore.Inits totality,thistechniqueissimilartothewayRFcre‐atesbranch.TheRFmethodcreatesmultipletrees. Foreachtree,onlyarandomsubsetofinputvari‐ablesisusedateachsplittingnode.Therefore,the inaltreesofRFareindependentofeachother,and theydonotlearnfromthepreviouslycreatedtrees. Ontheotherhand,oursystemcanlearnfromprior attempts.Ateachiteration,itexploresnewbranches andexploitstheassimilatedknowledgetocreate highly‐performativeandqualitativeonesinthesubse‐quentiteration.

3.FeedbackFeatureSelectionSystem

Thispaperforegroundstothebringsanewfea‐tureselectionsystembasedonreinforcementlearn‐ing;theproposedsystemprincipallycomprisesthree parts.First,decisiontreebranchesareusedtotra‐versethesearchspace(featuresspace)tocreatenew rules(branchesorfeaturesubsets)andselectthebest featuresubset.Second,atransitionsimilaritymeasure (TSM)isintroducedtoensurethatthesystemkeeps exploringthestatespacebycreatingnewbranches andexploitingwhatithaslearnedsofartocircum‐venttheproblematicimplicationsorthedrawbacksof redundancy.Finally,therelevantfeaturesarethemost involvedonesinconstructingthebranchesofhigh quality.Forfurtherillustrativeexplications,thesub‐sequentsectionwillaccessiblyresurfacethegeneral frameworkofreinforcementlearninganddelineate theknow‐howdimensionsinwhichoursystemcan synthesizethebene itsofthispowerfulapproach.

3.1.ReinforcementLearningProblem

RListhemostactiveandfast‐developingareain machinelearningandisoneofthreebasicmachine learningapproaches,alongsidesupervisedlearning andunsupervisedlearning.RLconsistsofthefol‐lowingconcepts:Agent,environment,actions,and reward.TheagenttakesactionAandinteractswith anenvironmenttomaximizethetotalrewardreceived R.Atiterationt,theagentobservesstateStfromthe environment.Inreturn,theagentgetsarewardRt. Theagenttakesaction ����.Inresponse,theenviron‐mentprovidesthenextstate ����+1 andreward;the processcontinuesuntiltheagentwillbeabletotake therightactionsthatmaximizethetotalreward.The agentmustbalancebetweenexploitingwhathasbeen learnedsofarandcontinuouslyexploringtheenvi‐ronmenttogathermoreinformationthatmayhelpin maximizingthetotalreward.

‐ Agent:Anagenttakesactions.Inourcase,theagent istheproposedfeatureselectionsystem.

‐ Actions istheensembleofallpossiblemovesthe agentcanmake,foroursystem,theactionsarethe nodesthatmaybeusedtocreateabranch.

‐ Environment isthefeaturespacethroughwhich thesystemmoves.Itreceivesthesystem’scurrent stateandactionasinput;then,itreturnsthereward andthenextstateofthesystem.

‐ State isthecurrentsituationwheretheagent inds itself.Inourcontext,thisisthecurrentnodeofthe branch.

Asthereinforcementconceptsaretransparently tackledandhighlighted,thefollowingstepsmay unfoldindepthwiththeconstitutivemainstayorthe technicalinfrastructureofourproposedalgorithm.

Thefeatureselectionsystem(agent)scrutinizes theenvironment,andthenstartswithasinglenode arbitrarilywithoutanypre‐stockpiledknowledge (explorationphase),whichbranchesintopossibleout‐comes.Eachofthoseoutcomesleadstothenextnodes (action).Toindicatehoweffectivethechosenaction is,adifferencebetweentwoconsecutivestatesispro‐duced.Sincethedepthisnotyetreached,thesystem keepsaddingonenodeatatimeinordertocreate abranch.Asiterationstakeplace,thesystemassem‐blesexperiencesandbecomesabletotakeactions thatmaximizetheoverallrewardR.Asayieldedoff‐spring,branchesofhighqualityarecreated.Atran‐sitionsimilaritymeasureisproposedtoestablisha balancedequipoisebetweenexploitingwhathasbeen learnedsofartochoosethenextactionthatmaximizes rewards,andcontinuouslyexploringthefeaturespace toachievelong‐termbene its.Thewayweconstruct thebranchisthesameasthedecisiontree(c4.5),the differenceiswhenweaddanodetothebranch,we retainonlythebestbranchwiththehighestthresh‐old.Thefollowingstepsgivemorepreciseinformation aboutcreatingabranch.

3.2.StepstoCreateaDTBranch

Westartwitharandomfeatureastherootofthe branch.Aslongasthebranchdidnotreachthedesired depthorminsampleleafyet,thesystemkeepsadding tothebranchonenodeatatime.Theaddednodeisthe oneweobtainedusingthefeatureanditsthreshold thatproducesthehighestAUCscore(AreaUnderthe CurveROC).Theideabehindusingdepthandmin simpleleafparametersasstoppingcriteriaistoavoid asmuchaspossibletheover‐ ittingproblem.Themost commonstoppingmethodisminsampleleaf,whichis theminimumnumberofsamplesassignedtoeachleaf node.Ifthenumberislessthanagivenvalue,thenno furthersplitcanbedone,andthenodeisconsidereda inalleafnode.Besides,thedepthofthebranchisvery usefulincontrollingover‐ ittingbecausethedeeper thebranchis,themoreinformationcapturedbythe dataandmorethesplitsithas,whichleadstopredict wellonthetrainingdata.However,itfailstogeneralize ontheunseendata.

3.3.RewardFunction

ArewardfunctionR[38]isusedtocalculatethe scoreateachlevelofthebranchbycomputingthe differencebetweenthescoreofthecurrentbranch anditsscoreafteranewnodeisadded(DS).TheDS indicateshowusefulthenewlyaddedfeatureis.

Algorithm1:CreateaDTbranch

1: Createtherootnodeandchoosethesplitfeature.Choosethe irstfeaturerandomly.

2: Computethebestthresholdofthechosenfeature.

3: Splitthedataonthisfeatureintosubsetsinordertode inethenode.

4: ComputetheAUCscoreonleftandonrightofthenode,then,wekeepthebranchwiththebestAUCscore.

5: Addthechildrennodetorootnode.

6: Choosethenextbestfeature.

7: RepeatfromSTEP2toSTEP5untilthedesireddepthorminsampleleafofthebranchisreached.

Thisfunctionisde inedasfollows: (�������������� −��������������������)×log (‖��������������������������‖) (1)

Where�������������� and�������������������� isthescoreofthe currentbranchandthescoreafteraddinganewnode, �������������������������� isthelengthofsamplesusedtosplitan internalnode.

3.4.TransitionSimilarityMeasure

Definition(Transition)

Atransitionistheprocessinwhichsomething changesfromonestatetoanother.Inoursystem,the transitionisthelinkbetweentwosuccessivenodesof thesamebranch.

TransitionSimilarityMeasure

Weproposedatransitionsimilaritymeasure (TSM)toensurethatoursystemkeepsexploringthe statespace,learningnewrules,andpreventingthe redundantbranches.Foreachbranch,westockall transitionswiththecorrespondingsamplesusedto spliteachinternalnode.Sincethealgorithmisiter‐ative,differentbranchesmaysharethesametransi‐tions,whichisnotaproblem.Inthecasewhenthe majorityofthesamples(higherthanagiventhresh‐old)areequallyusedbythosetransitionsofdifferent branches,thosetwotransitionsaredeemedsimilar, whichisahugeproblem.Allowingsimilartransitions tobeindifferentbranchescanleadtoconstructing redundantanduselessbranches.

Therefore,thesystemkeepslearningthesame rulesandbranches.Thismeansthatthesystemwill beexpensiveintermsofexecutiontime,whilethe systemshouldbelessresourcesconsuming(runtime andstoragerequirement),andthebranchesshouldbe stronganddiverse.

Thesimilaritybetweentwotransitionsiscom‐putedbythefollowingformula:

������= |��1∩��2| ‖��������������������������‖ (2)

Where‖��1∩��2‖isthenumberofsharedsamples betweentwotransitions.

3.5.TheProposedFSmethod

Sincetheproposedalgorithmisiterative,thenum‐berofiterationNisgivenastheinput.Thereward functionissettozeroatthebeginning.Oursystem startswithanemptysetF,andateachiteration,the systemcreatesanewbranchandaddsittoF.Ifthe nextsubset(branch)isalreadyexperiencedbythe system(seenbythesystem),thesystemusesthis gatheredexperiencesintheupcomingiterations.Oth‐erwise,thesystemkeepsexploringnewrules,new patterns,andnewbranches.

3.6.StartingExample

Toexplaintheproposedalgorithmfurther,wesug‐gestthefollowingexample.Wesupposethatwehave adatasetof10features.The igurebellow(Fig. 4) containsthewholespaceoffeatures.Thepurposeis

Figure3. Reinforcementlearningframework

toselectthebestsubsetoffeaturesusingtheproposed system.

1) Firstiteration 4(b):Thesystemtraversesthefea‐turesspaceandcreatesthe irstbranchwithout anypriorknowledge.Ateachlevelofthebranch, thesystemstorestheAUCscoreusingthereward functionR.Moreover,itstoreseachtransition(2← 3, 3←9, 9← 5, 5←6)anditscorresponding subsetofsamples.

2) Theseconditeration4(c):Aswecanseeinthesec‐onditeration,thetransition(3←9)appearedfor thesecondtime.HeretheTSM(transitionsimilar‐itymeasure)shouldbeinvolved.Iftwotransitions ofdifferentbranchesaresimilar(nodeswithgreen color),thesystemshouldnotallowthemtobein thenextbranches(thecurrentbranchincluded). Thesystemhastoexplorethestate’senvironment to indnewrulestopreventtheredundancyin creatingbranches.

3) TheNiteration4(d):AfterNiterations,thesystem iscapableofidentifyingthebestbranchesusing thegatheredexperiencesduringeachiteration. Thetoprankedbranchesconstructedusingthe systemaretheillustratedinthesub igure4(d).

Figure4. FBSproposedalgorithmmainsteps

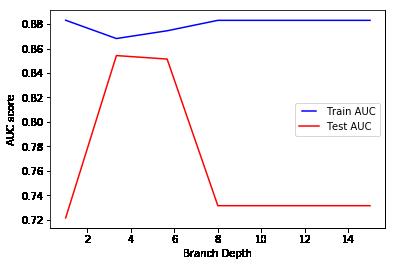
FromtheaboveFigure 4,itisclearthatthe topsubsetoffeaturesis[3, 5, 10],becausethose featuresareinvolvedthemostincreatingthebest branches.

4.ExperimentalResultsandDiscussion

Thisexperimentalsectionatteststotheef iciency oftheproposedfeedbackfeatureselectionsystem (FBS)inselectingthebestfeatures.Twobenchmarks havebeenconducted,andthenthepro itableservice‐abilityofoursystemisappraisedbycomparingit withtwofeatureselectionalgorithms.The irstone isthepopularwrapperalgorithmnamedRecursive FeatureEliminationRFE(RFE‐RF).Thesecondoneis thepairwisefeatureselectionalgorithm(FS‐P),which isrecentlyproposedandproveditseffectivenessin identifyingthebestfeatures[31].

4.1.BenchmarkingDatasets

Inthispaper,ninebinaryclassi icationdatasets havebeenemployedindifferentexperimentaldesign aimingtoevaluatetheperformanceoftheproposed featureselectionmethod.

Thedatasetsarechosentobedifferentintermsof classdistribution(balancedorimbalanced),linearity, datasetshift,numberofinstancesandvariables.The datasets,whicharepubliclyavailable,arecollected anddownloadedfromUCIrepositoryandkaggleplat‐form[39].Anoverviewofthemaincharacteristicsof eachdatasetisillustrativelytabulatedinTable1

4.2.ExperimentsSettings

Twoexperimentalendeavorsareundertakento estimatetheworkableprospectsandtheconsequen‐tialrami icationsofourproposedsystem.Initially,we

Table1. Characteristicsofthebenchmarkingdatasets.

Table2. Characteristicsofthebenchmarkingdatasets.

Figure5. Over‐fittingproblem

(a) Dataset:creditcard

(d) Dataset:Eye

(g) Dataset:Caravan

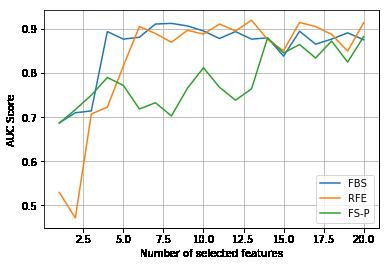
(b) Dataset:sonar

(e) Dataset:musk

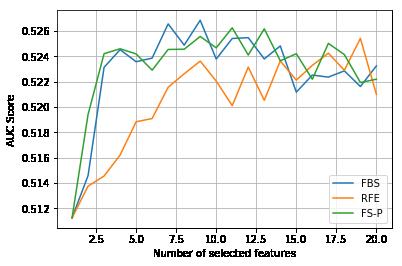
(h) Dataset:Numerai

willempiricallyembodytheapplicationsofthepro‐posedalgorithmsbasedonthedatasetsdisplayedin Table 1 intermsofAreaUndertheRocCurve(AUC) whereFBSiscomparedwiththepairwisemethod, namelyFS‐PandwithRFE.

Incorrelativeparallelismwiththepreviousstep, thesubsequentstagewilldemonstratetheeligible capabilityoftheFBSsysteminencirclingthepractical subsetasswiftlyaspossiblethroughtheexclusive employmentofthefewfeaturessupplementedbysec‐ondbenchmarking.

Alldatasetsaresegmentedintotwosubsets; onesubsetisemployedfortrainingandtestingthe branchesusingcross‐validationwith3‐foldswhilethe othersubsetisquarantinedandcastaside(holdout set)andtheperformanceofthe inalselectedfeature subsetisevaluatedonit.Forthesakeofafaircom‐parison,the inalselectedsubsetusingFBS,FS‐P,and RFEisevaluatedusingaRandomForestwithagrid searchstrategyforthehyper‐parameters.TheAUC scoreiscalculatedusingtheoutofbag(OOB)scoreof therandomforestclassi ier.Sincethebenchmarking datasetsusedinthispapertoevaluatetheproposed systemareunbalanced,theAUCmetricisconsidered thebestchoice.Moreover,theAUCmetricgenerally canbeviewedasabettermeasurethanaccuracy[40].

(c) Dataset:spambase

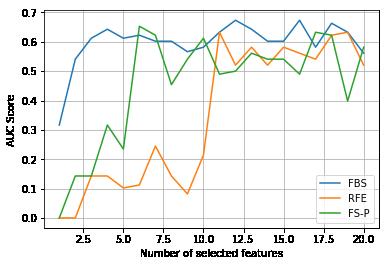
(f) Dataset:SPECT

(i) Dataset:Ionosphere

4.3.FeedbackSystemParameters

TheFeedbacksystemparametersincorporatea systematictrilogyofchangeableparameterswhich areinadynamicalterationinaccordancewitheach dataset.

‐ Sisthesimilarityvalue.

‐ Disconcernedwiththeindicationofthebranches’ depth.

‐ Nre lectsthenumberofiterations.

Toexemplifytheprobablechangeabilityofthese parameters.Datasetswithlargesize,theNandD valuesshouldbehighersincethebestbranches,in thiscase,shouldbedeeper.Thefollowingtablesup‐plementsapanoramicoverviewunderlyingthebest parametersusedforeachdataset.

Asclearlyarticulatedintheaforementionedsec‐tion,thechoiceofparametersisindispensable.The followinggraphdelineatesthein luenceofthedepth parameter(D)onthequalityoftheconstructed branchesusingthesonardataset.Thisgraphicplot displaysasummativesnapshotofthetrainandthetest AUCscoresafterthegraduallyexponentialvariationof Dparameterfrom1to15isful illed.

Therecordedoutcomesonthesonardatasetshow clearlythatthebranchespronetoover‐ itforlarge depthvaluesbecausethebranchesperfectlypredict

Figure6. Performanceofoursystemcomparedwiththeselectedfeaturesselectedbypairwisemethodonnine benchmarkdatasets

allofthetraindata(theblueline).However,theyfail togeneralizeonunseendata(theredline).Ascanbe visuallyobserved,thebestdepthforthesonardataset itselfequalsthree(D=3).

4.4.ConductedExperiments

TheproposedmethodiscomparedtotheRFEand FS‐PapproachsintermsofpredictionAUCscore.In thismanuscript,twoempiricallyconclusiveandthor‐oughgoingexperimentsareconducted.

1) FirstExperiments:Toevaluateourproposed approachFBS,wecomparetheobtainedperfor‐mance(intermsofAUCscore)byFBSwiththe wrappermethod(Recursivefeatureelimination withrandomforestRFE)andwiththepairwise algorithmFS‐P.

2) SecondExperiments:Thisexperimentiscon‐ductedtoshowtheabilityoftheproposedsystem FBSinachievingthemaximumperformanceusing justafewfeatures.Forafaircomparisonbetween FBS,FS‐P,andRFE,we ixthegeneratedsubsetsize forallalgorithmscomparedasfollows:subsetof size5(������5, ����−��5, ������5),asubsetofsize10

(������10,����−��10,������10)andsubsetof15(

4.5.ResultsandDiscussion

Afterselectingthefeaturesubset,thesameclas‐si ier(RF)isessentiallymandatorytocalculatethe AUCscore.TheRandomforestisutilizedtodetermine thetestperformanceforthetop‐rankedfeaturesof eachemployeddataset.Thecomparativejuxtaposi‐tionbetweenFBS,FS‐PandRFEisaccessiblyrepre‐sentedinFigure6(Firstexperiment).

Asstated,ourfeatureselectionalgorithmFBS exceedsandoutstripsFSPandRFEconsiderablyin almostalldatasets,suchasSPECT(Figure6(f)),credit card(Figure 6(a)),ionosphere(Figure 6(i)),musk (Figure 6(e)),caravan(Figure 6(g)),andsonar(Fig‐ure6(b)),exceptforspambasedataset(6(c)).

Forthenumeraidataset(Figure6(h)),ourmethod hasarestrictivelylimited,ifnotdowngradedperfor‐manceatthebeginningcomparedtoRFEandFS‐P.As ourmethoddoesnotselectjustthebest‐rankedfea‐tureasastartingpointtopreventselectingasubop‐timalsubsetbutalsoattempttomaximizetheoverall performanceoftheselectedsubsettakingintoaccount

Figure7. TheperformanceofFBS,RFEandFS‐Pusingfeaturesubsetsof5,10,and15features

theinteractionsbetweenfeatures.Aftertheselection ofthenumeraidataset’s ifthfeature(Figure 6(h)), theaforementionedbehavioralveracityisrendered observable,andFBSshowsitsdrasticallyimproved performanceoverFS‐PandRFE.

Table 2 showsthebestparametersusedinour feedbacksystem.Theinsightfulbottom‐lineconclu‐sionwecanexcerptfromthetableisthatthechoiceof thebestparameterstouseineachdatasetiscrucial, whichmeansthattheparametersshouldbecarefully chosentoconstructbrancheswithhighquality.

Thepurposeoftheproposedfeatureselection methodisnotonlytoimprovetheclassi ication performancebutalsotoyieldexcellentperformance usingaminimumnumberoffeatures(selectthe fewestpossiblenumberoffeatures).

Figure 7 showsthenumberofselectedfeatures withthehighestAUCscoreonninebenchmarksdata sets.Asitisillustratedthroughthisbenchmarking, FBSselectstheproperfeaturescomparedwithFS‐P andRFEalmostinalldatasets.Onepointtomention hereisthattheproposedfeedbacksystemcan ind thebestsubsetusingaminimumamountoffeatures, asshowninFigure 7.Thus,theminimumresources requirement,fastexecution,andbettergeneralization.

5.Conclusion

Inthispaper,wehaveproposedanewfeature selectionmethodbasedonthedecisiontreebranches concepttorepresentfeaturesubsets.Theproposed systemdealswiththeFSproblemasareinforcement learningproblem;thesystemtriesto indacompro‐misebetweenexploringthesearchspacebyexperi‐encingnewrules(creatingnewbranches)andexploit‐ingthegatheredexperiencessoastochoosetheright actions(relevantfeature).Theexploit/exploretrade‐offiscontrolledbytheproposedTSM.Theproposed systemcanconstructthebestbranches,hence,select‐ingthebestsubsetoffeatures.

Toassesstheeffectivenessoftheselectedfeatures usingourproposedmethod,wehaveconductedan extensivesetofexperimentsusingninebenchmark‐ingdatasets.Theresultscon irmthattheproposed feedbackfeatureselectionsystemisnotonlyeffective atselectingthebestperformingsubsetsoffeatures thatproducethebestperformancebutalsochoosethe fewestnumberoffeatures.

AUTHORS

YassineAkhiat∗ –DepartmentofInformatics,fac‐ultyofsciencesdharelmahraz,USMBA,FezMorocco, e‐mail:yassine.akhiat@usmba.ac.ma.

AhmedZinedine –DepartmentofInformatics,fac‐ultyofsciencesdharelmahraz,USMBA,FezMorocco, e‐mail:ahmed.zinedine@usmba.ac.ma.

MohamedChahhou –DepartmentofInformatics, facultyofsciences,UAE,TetouanMorocco,e‐mail: mchahhou@hotmail.com.

∗Correspondingauthor

References

[1] R.Roelofs,S.Fridovich‐Keil,J.Miller,V.Shankar, M.Hardt,B.Recht,andL.Schmidt,“Ameta‐analysisofover ittinginmachinelearning,”in Proceedingsofthe33rdInternationalConference onNeuralInformationProcessingSystems,2019, pp.9179–9189.

[2] X.Ying,“Anoverviewofover ittinganditssolu‐tions,”in JournalofPhysics:ConferenceSeries,vol. 1168,no.2.IOPPublishing,2019,p.022022.

[3] M.Li,H.Wang,L.Yang,Y.Liang,Z.Shang,and H.Wan,“Fasthybriddimensionalityreduction methodforclassi icationbasedonfeatureselec‐tionandgroupedfeatureextraction,” ExpertSystemswithApplications,vol.150,p.113277,2020.

[4] H.Liu,H.Motoda,andL.Yu,“Aselectivesampling approachtoactivefeatureselection,” Arti icial Intelligence,vol.159,no.1‐2,pp.49–74,2004.

[5] Y.Akhiat,Y.Asnaoui,M.Chahhou,andA.Zine‐dine,“Anewgraphfeatureselectionapproach,” in 20206thIEEECongressonInformationScience andTechnology(CiSt).IEEE,2021,pp.156–161.

[6] D.M.Atallah,M.Badawy,andA.El‐Sayed,“Intel‐ligentfeatureselectionwithmodi iedk‐nearest neighborforkidneytransplantationprediction,” SNAppliedSciences,vol.1,no.10,pp.1–17,2019.

[7] I.Guyon,S.Gunn,M.Nikravesh,andL.A.Zadeh, Featureextraction:foundationsandapplications Springer,2008,vol.207.

[8] I.GuyonandA.Elisseeff,“Anintroductiontofea‐tureextraction,”in Featureextraction.Springer, 2006,pp.1–25.

[9] A.Yassine,“Featureselectionmethodsforhigh dimensionaldata,”2021.

[10] Y.Manzali,Y.Akhiat,M.Chahhou,M.Elmohajir, andA.Zinedine,“Reducingthenumberoftrees inaforestusingnoisyfeatures,” EvolvingSystems,pp.1–18,2022.

[11] Y.Akhiat,Y.Manzali,M.Chahhou,andA.Zine‐dine,“Anewnoisyrandomforestbasedmethod forfeatureselection,” CYBERNETICSANDINFORMATIONTECHNOLOGIES,vol.21,no.2,2021.

[12] S.Abe,“Featureselectionandextraction,”in Supportvectormachinesforpatternclassi ication Springer,2010,pp.331–341.

[13] J.Cai,J.Luo,S.Wang,andS.Yang,“Featureselec‐tioninmachinelearning:Anewperspective,” Neurocomputing,vol.300,pp.70–79,2018.

[14] Y.Akhiat,M.Chahhou,andA.Zinedine,“Fea‐tureselectionbasedongraphrepresentation,”in 2018IEEE5thInternationalCongressonInformationScienceandTechnology(CiSt).IEEE,2018, pp.232–237.

[15] J.C.Ang,A.Mirzal,H.Haron,andH.N.A.Hamed, “Supervised,unsupervised,andsemi‐supervised featureselection:areviewongeneselection,” IEEE/ACMtransactionsoncomputationalbiology

andbioinformatics,vol.13,no.5,pp.971–989, 2015.

[16] L.A.BelancheandF.F.González,“Reviewand evaluationoffeatureselectionalgorithmsinsyn‐theticproblems,” arXivpreprintarXiv:1101.2320, 2011.

[17] G.ChandrashekarandF.Sahin,“Asurveyonfea‐tureselectionmethods,” Computers&Electrical Engineering,vol.40,no.1,pp.16–28,2014.

[18] B.NithyaandV.Ilango,“Evaluationofmachine learningbasedoptimizedfeatureselection approachesandclassi icationmethodsfor cervicalcancerprediction,” SNAppliedSciences, vol.1,no.6,pp.1–16,2019.

[19] A.Bommert,X.Sun,B.Bischl,J.Rahnenführer, andM.Lang,“Benchmarkfor iltermethodsfor featureselectioninhigh‐dimensionalclassi ica‐tiondata,” ComputationalStatistics&DataAnalysis,vol.143,p.106839,2020.

[20] Y.Akhiat,M.Chahhou,andA.Zinedine,“Ensem‐blefeatureselectionalgorithm,” International JournalofIntelligentSystemsandApplications, vol.11,no.1,p.24,2019.

[21] L.ČehovinandZ.Bosnić,“Empiricalevaluation offeatureselectionmethodsinclassi ication,” Intelligentdataanalysis,vol.14,no.3,pp.265–281,2010.

[22] Y.Asnaoui,Y.Akhiat,andA.Zinedine,“Fea‐tureselectionbasedonattributesclustering,”in 2021FifthInternationalConferenceOnIntelligent ComputinginDataSciences(ICDS).IEEE,2021, pp.1–5.

[23] Y.Bouchlaghem,Y.Akhiat,andS.Amjad,“Feature selection:Areviewandcomparativestudy,”in E3SWebofConferences,vol.351.EDPSciences, 2022,p.01046.

[24] A.Destrero,S.Mosci,C.D.Mol,A.Verri, andF.Odone,“Featureselectionforhigh‐dimensionaldata,” ComputationalManagement Science,vol.6,pp.25–40,2009.

[25] V.FontiandE.Belitser,“Featureselectionusing lasso,” VUAmsterdamResearchPaperinBusiness Analytics,vol.30,pp.1–25,2017.

[26] I.GuyonandA.Elisseeff,“Anintroductiontovari‐ableandfeatureselection,” Journalofmachine learningresearch,vol.3,no.Mar,pp.1157–1182, 2003.

[27] R.Zebari,A.Abdulazeez,D.Zeebaree,D.Zebari, andJ.Saeed,“Acomprehensivereviewofdimen‐sionalityreductiontechniquesforfeatureselec‐tionandfeatureextraction,” JournalofApplied ScienceandTechnologyTrends,vol.1,no.2,pp. 56–70,2020.

[28] J.MiaoandL.Niu,“Asurveyonfeatureselection,” ProcediaComputerScience,vol.91,pp.919–926, 2016.

[29] L.C.Molina,L.Belanche,andÀ.Nebot,“Feature selectionalgorithms:Asurveyandexperimental evaluation,”in 2002IEEEInternationalConferenceonDataMining,2002.Proceedings. IEEE, 2002,pp.306–313.

[30] R.Caruana,A.Niculescu‐Mizil,G.Crew,and A.Ksikes,“Ensembleselectionfromlibrariesof models,”in Proceedingsofthetwenty- irstinternationalconferenceonMachinelearning,2004, p.18.

[31] A.Yassine,C.Mohamed,andA.Zinedine,“Fea‐tureselectionbasedonpairwiseevalution,”in 2017IntelligentSystemsandComputerVision (ISCV).IEEE,2017,pp.1–6.

[32] B.Gregorutti,B.Michel,andP.Saint‐Pierre, “Correlationandvariableimportanceinrandom forests,” StatisticsandComputing,vol.27,no.3, pp.659–678,2017.

[33] J.Kacprzyk,J.W.Owsinski,andD.A.Viattchenin, “Anewheuristicpossibilisticclusteringalgo‐rithmforfeatureselection,” JournalofAutomationMobileRoboticsandIntelligentSystems, vol.8,2014.

[34] L.Breiman,“Randomforests,” Machinelearning, vol.45,no.1,pp.5–32,2001.

[35] H.Han,X.Guo,andH.Yu,“Variableselec‐tionusingmeandecreaseaccuracyandmean decreaseginibasedonrandomforest,”in 2016 7thieeeinternationalconferenceonsoftware engineeringandservicescience(icsess).IEEE, 2016,pp.219–224.

[36] R.SuttonandA.Barto,“Reinforcementlearn‐ing:Anintroduction.2017.ucl,” ComputerScienceDepartment,ReinforcementLearningLectures,2018.

[37] Y.FenjiroandH.Benbrahim,“Deepreinforce‐mentlearningoverviewofthestateoftheart.” JournalofAutomation,MobileRoboticsandIntelligentSystems,pp.20–39,2018.

[38] S.M.H.Fard,A.Hamzeh,andS.Hashemi,“Using reinforcementlearningto indanoptimalsetof features,” Computers&MathematicswithApplications,vol.66,no.10,pp.1892–1904,2013.

[39] M.Lichman,“Ucimachinelearningrepository [http://archive.ics.uci.edu/ml].irvine,ca:Uni‐versityofcalifornia,schoolofinformationand computerscience,” URL:http://archive.ics.uci. edu/ml,2013.

[40] F.F.Provost,“T.,andkohavi,r.thecaseagainst accuracyestimationforcomparingclassi iers,” in ProceedingsoftheFifteenthInternationalConferenceonMachineLearning,1998.

Abstract:

UNLOCKINGTHEFUTUREOFSECUREAUTOMATICMACHINES:LEVERAGING FACEREGWITHHRC&LBPH

UNLOCKINGTHEFUTUREOFSECUREAUTOMATICMACHINES:LEVERAGING FACEREGWITHHRC&LBPH

UNLOCKINGTHEFUTUREOFSECUREAUTOMATICMACHINES:LEVERAGING FACEREGWITHHRC&LBPH

Submitted:18th July2023;accepted:20th October2023

YaminiVijaywargiya,MahakMishra,NitikaVatsDoohan

DOI:10.14313/JAMRIS/1‐2024/7

WeproposeaComputerVisionandMachineLearning equippedmodelthatsecurestheATMfromfraudulent activitiesbyleveragingtheuseofHaarcascade(HRC) andLocalBinaryPatternHistogram(LBPH)classifierfor facedetectionandrecognitioncorrespondingly,whichin turndetectfraudbyutilizingfeatures,likePINandface recognition,helptoidentifyandauthenticatetheuserby checkingwiththetraineddatasetandtriggerreal‐time alertmailiftheuserturnsouttobeunauthorizedalso. Itdoesnotallowthemtologinintothemachine,which resolvestheATMsecurityissue.thissystemisevaluated onthedatasetofreal‐worldATMcamerafeeds,which showsanaccuracyof90%.Itcaneffectivelydetectmany frauds,includingidentitytheftandunauthorizedaccess whichmakesitevenmorereliable.

Keywords: ATM,Computervision,PIN,HRC,LBPHrecog‐nizer,Facedetection,Facerecognition,Frauddetection, SMTPmodule

1.Introduction

AnAutomatedTellerMachine(ATM)isanelec‐tronictelecommunicationdeviceinventedinearly 1970s,whichareoneoftheoldestandmostsecure machineryusedtodate,butfornearly30years,noth‐inghasbeendonetoimprovethissystem’ssecurity, andduetotheamelioration&globaldigitalization,it isevenmorevulnerabletotheftsandfrauds,which leadtoamassivelossofcapitaloftheusersandtheir banks.Thismachineenablescustomerstowithdraw cashfromtheirbankaccountswithouthavingdirect contactwiththebankstaffandhavebecomeapopu‐larmodeoftransactionfor inancialclients,including cashwithdrawals,deposits,andothertransactions. Banksarebecomingincreasinglyconcernedaboutthe securityofATMsduetotheincreaseincasesoffraud andmoneylossattheATMs.

Therapidameliorationoftechnologyandglobal digitalizationhaveledtonewandmoresecureATM models,asnewthreatsalsoemergedaybydaythat couldunderminetheirsecurity.Despitetheadvan‐tagesofautomation,ATMsystemsexpose inancial institutionstofraud.

ThecurrentATMmodelsuseacardandaPIN code,whichmaketheminclinedtosuchattacksas astolencard,staticPINs,cardfraud,andhackingof PINs.Fraudstersusenumeroustechniquestoextract sensitiveinformationfromATMusers,includingskim‐mingdevicesandfakekeypads.Theseincidentsnot onlyresultinsigni icant inanciallossesbutalsocause harmtothereputationofthebankingindustry.

OnewaytoincreasethesecurityofanAutomatic TellerMachineisbyprovidingPersonalIdenti ication Number(PIN),facedetection,andfacerecognition. FacedetectionalgorithmslikeHaarcascade(HRC) andforfacerecognitionLBPH(LocalBinaryPattern Histogram)canhelpidentifyindividualsattemptingto conductfraudulenttransactionsatATMs.

HRCarehighlyaccurate,fastspeed,andcandetect facesinreal‐timevideo/images,andontheother hand,LBPHusesmicro‐patterns,whichdescribethe looksandkeepexecutiontimeshort.

ByusingcamerasinstalledatATMstocapturethe facesofusers,theHaarcascadealgorithmcanquickly identifytheuserbymatchingthepinoftheregistered personwiththeirface,andiftheuserisunauthorized, itdoesnotallowthemtologintotheAutomaticTeller MachineandsendoutanalertemailtotheAuthorized useremailID.Thistechnologycanalertbankof icials ofsuspiciousactivity,allowingthemtotakeprompt actionandpreventfraud.

Figure1. ATMmachine

2.LiteratureSurvey

In2012,HosseinRezaBabaei,OfentseMolala‐pataandAbdulHayAkbarPandoretal.,[5]devel‐opedasystemusingBiometricsFacialRecognition methodtoincreasethesecurityoftheAutomatic tellerMachines.Inthisstudy,theybuiltthesystem usingRapidApplicationDevelopmentlifecycle,which makesitahighqualitysystem.

In2015,MohsinKarovaliyaa,SaifaliKarediab, SharadOzac,Dr.D.R.Kalbandedetal.,[8]Introduced anewconceptofrandomlygeneratingOTPthatfrees theuserfromrememberingthePINsduringtransac‐tionatAutomaticTellermachine(ATM),andfeatures likefacerecognitionareusedwithit,makingthesys‐temmoreconvenientandusable.Thisresearchstudy utilizesPCAbasedfacerecognitiontechnique.

In2018,T.S.VishnuPriya,G.VinithaSanchez, N.R.Raajanetal.,[7]cameupwithlocalbinarypattern algorithmforfacerecognition(FR)inordertoful il thedownsideofnotidentifyingtheidenticaltwinsin BiometricFRmethod.Inthisstudytheyexplainhow thelocalbinarypatternswereusedtoidentifytheface inidenticalsituationsbecausetheLBPmethodcan describeappropriatelythemicropatternspresentin theface.

AsS.Hazraetal.[11]proposed,anATMisanelec‐tronicdevicethatallowsbankingtransactionswithout staffinteraction.AuniqueIDcardwithaPINisneeded touseit.AproposedSmartATMserviceusesIoTand ComputerVision‐basedtechnologywith ingerprint, face,andOTPveri icationstoenhancesecurityand reducefraudrisk.

In2020,M.S.Minu,KshitijArun,AnmolTiwari, PriyanshRampuriaetal.[6]proposedanideaabout howhomesecuritycanbeimprovedbyleveraging MachineLearningalgorithmsforfacedetectionand recognitionusingHaarcascadeclassi ier.Inthis,they explainedcompletesystem lowonhowtheModules areworkingintheprojectandtellhowImageIden‐ti icationandRecognitionisbeingdone.TheKNN algorithmisusedtocomparethefeaturesfromthe imagedatabaseafterfeatureextractionfromthesam‐pleimage.

In2020,Dr.SSasipriya,Dr.P.MayilVelKumar,S. Shenbagadevietal.[9]proposethatthefacialrecog‐nitionsystemshouldreplaceATMcardswithanRFID tag.Thecapturedfaceimageofapersoniscompared withthedatabasestoredimageafterwhichtheoutput resultissenttocontrolunitthroughserialcommuni‐cation.Ifthepersonisunauthorized,analertmessage issenttotheauthorizeduser.ThisstudyutilizesHaar cascadeandLocalbinarypatternAlgorithm.

In2021,AnirudhaBShetty,Bhoomika,Deeksha, JeevanRebeiro,Ramyashree,etal.[13]comparedtwo facerecognitionalgorithms:HaarCascadeandLocal BinaryPatternfortheclassi icationoffacesinan image.TheyconcludedthataccuracyofHaarCascade Algorithmisgreater,butitsexecutiontimeisalso higherthanlocalbinarypattern.

In2022,J.Ferdinand,C.Wijaya,A.N.Ronal,I.S. Edbert,andD.Suhartonoetal.[4]proposedaface

Table1. Inputparameters

recognitionsystemusingFaceNetcombinedwiththe HaarCascadeClassi ier.Inthissystem,customers inserttheircard,anditwilldetectandstarttoidentify theirface.Ifitdoesnotmatch,thecardwillbeblocked. Thisproposedsystemachievesaccuracyof90.93%.

3.DatasetDescription

Inthisstudy,themodelregisterspeoplebytaking inputasName,Pin,andEmailID,andcapturesand storestheirfaceimagesfortrainingpurposesinaCSV File.

4.ProposedSystem CheckCamera

Thecheckcameramoduleisavitalcomponent ofanyfacialrecognitionsystemthatemployscam‐eratechnology.Itswholepurposeistoensurethat thecamerasarefunctioningproperlyandthatthe imagesitcapturesaresuitableforfacialrecognition,

Figure2. CSVfiledataset

Figure3. Modulesflow

whichneedsgoodqualityresolution.Thehigherthe cameraresolutions,thebetterthequalityofthe images,whichcanimprovetheaccuracyofthewhole system.Therefore,itisnecessarytoensurethatthe camerainstalledattheATMcancapturetheimage inthedesiredresolutionforoptimalperformanceof thesystem.Anothercrucialfactortocheckduringthis moduleisthecamera’spositioning.Ideally,thecamera shouldcapturetheentirefaceofthepersonstanding infrontoftheATMtoensurethatthefacialrecognition systemcanaccessallthenecessaryfacialfeaturesfor accurateidenti ication.

CaptureImage

ThismoduleutilizestheHaarcascademachine learningalgorithmfromtheOpenCVmodule,as explainedin[3].Thiscomponentcapturesimagesof individualsstandinginfrontofanATMandprocesses themtodetectthepresenceandlocationoftheirfaces usingtheHaarcascadealgorithm.Duringthisprocess, theuserispromptedtoprovidetheirname,emailID, andPINtoregisterasanewcustomer.Thesedetails arestoredinaCSV ile(Fig. 2).Aftersubmittingthe details,thecameraisactivated,displayingtheuser’s faceinarectangularframe(Fig. 4(i)).Thecamera capturesover100imagesofthepersonandstoresthe resizedimagesfortrainingpurposes.Alltheseimages werestoredinafolderwiththename,ID,andlabelin theJPGformat(Fig.4(ii)).

Training

Tocompletethetask,wefollowaseriesofsteps. Initially,weloadthecascade,whichwillactasa facedetector.Subsequently,weextractthefaces andtheircorrespondingIDsfromtheimages.then itproceedstotrainthefaceimagestogetherwith theirrespectiveIDsusingtheLBPH(LocalBinary PatternsHistogram)recognizerfunction(Figs. 4(i), 4(ii), 5).Thesefunctionswereimplementedthrough the‘cv2.face_LBPHFaceRecognizer.create()’method. Moreover,weemploythe‘Thread()’functionfrom thethreadingmoduletocreateaseparatethread speci icallyforthetrainingprocess.Finally,westore theobtainedembeddings,orfacialfeatures,fromthe traininginaYAML ileforfurtherstepofrecognizing (Fig.5).

Testing&Recognizing

Inthismodule,weanalyzeadatasetconsisting ofregisteredaswellasnon‐registeredfacestothe account.Todetectfacesaccurately,weutilizeahaar cascadeclassi ier.Subsequently,theLBPHrecognizer functionwasusedtoidentifyandauthenticatethe detectedfacesbyusingthetrainedembeddingsstored inaYAML ileearlier.therecognitionprocesscom‐prisesvariousscenarios.Asuccessfulmatchbetween aregisteredaccountandthedetectedfaceiscon‐sideredaTruePositiveoutcome,signifyingavalid veri ication.

Figure4(i). DemoofFaceDetectedwhichgetsresized

Figure4(ii). Trainingimages

Figure5. Flowchartforfacedetection&recognition

Conversely,ifaregisteredaccountfailstomatch thedetectedface,itfallsintothecategoryofFalse Negative,indicatinganinconsistency.

Also,whenthemodelrecognizesthefaceofan unregisteredaccount,that’sthecaseofFalsePositive, representinganincorrectidenti ication.Lastly,when themodelfailstorecognizeafacethatisnotlinkedto anyregisteredaccount,itfallsunderthecategoryof TrueNegative,accuratelyindicatingtheabsenceofa linkedaccount.

Uponcompletingrecognition,thesystemallows theusertoproceedwiththetransactionifauthorized. However,ifitdetectsfraud,thesystemsendsanalert emailusingthesmtplibmodule,fetchingentriesfrom theCSV ile(Fig.2)oftheauthorizedaccountholder andstoppingthelogintotheATMmachine(Fig.10).

Withthisinformation,thebankandaccount holdercantakenecessarymeasurestopreventthe transaction,thuspreventinglossofcapitalandmaking thesystemmoresecure.

5.SoftwareDesign

5.1.HaarCascadeClassifier(HRC)

TheHaarCascade,originallyproposedbyPaul ViolaandMichaelJonesetal.in2001[1],isawidely usedobjectdetectionalgorithmspeci icallydesigned foridentifyingfacesinimagesandvideos.

ItemploysHaarfeatures(Fig.6),whichconsistof whiteandblackpixelsrepresentingdifferentregions ofthefacebasedonbrightness(Fig.7).Todetectfaces, thealgorithmslidesawindowof ixedsizeacrossthe imageatvariousscales.

Ateachposition,itcomputes iverectangularfea‐turesbycomparingthesumofblackandwhiteregion pixels.Iftherearesigni icantvariationsinpixelinten‐sitiesorfeatures,thealgorithmidenti iestheregion asaface;otherwise,itisanon‐faceregion.Train‐ingtheHaarCascademodelinvolveslargenumberof positiveimagescontainingfacesandnegativeimages withoutfaces.Themodeliscomposedofmultiple stages,eachcomprisingasetofweakclassi iers. Theseclassi iersaretrainedusingAdaptiveBoosting, whichselectsthemosteffectivefeaturesfordistin‐guishingbetweenpositiveandnegativeobjects.Pre‐trainedHaarCascadeclassi iermodels,suchas“haar‐cascade_frontalface_default.xml”areavailableinXML formatontheOpenCVGitHubrepository.Byloading thesepre‐trainedclassi iers,real‐timefacedetection canbeperformedwithouttheneedforcustomtrain‐ingorparameteradjustment.

ToapplythisAlgorithm,weutilizedPythonand OpenCV[3]function“cv2.CascadeClassi ier(),”which loadscascadesasinput,andtodetectfaces“detect‐MultiScale()”functionwasused,whichparameters include.

Scalefactorparameterisutilizedtodecreasethe imagesize.Asmallerscalefactorcanresultinfaster detection,butsmallerfacesmaybemissed.However, amoresigni icantscalefactormayleadtoslower detectionbutcandetectsmallerfaces.So,ascalefactor of1.3isused.

Theminimumneighborsparameterspeci iesthe numberofneighborsaregionshouldhave.Increasing thisparameterwilldecreasefalsepositivesbutmay alsomisssomefaces.Therefore,avalueof5isused. minimumsizeparameter(30,30)speci iesthe minimumfacesizethatcanbedetected.Increasing thisparametercanboostthedetectionprocessspeed, butsmallerfacesmaybemissed.

The lagsparameterisusedtoenableordisable certainfeaturesofthedetector,suchasscalingthe imagewiththesameaspectratioasthedetector oroptimizingthedetectorforspeed,soweused “cv2.CASCADE_SCALE_IMAGE.”

5.2.LocalBinaryPatternHistogram(LBPH)

TheLocalBinaryPattern(LBP)isawell‐establishedvisualrepresentationwidelyemployed incomputervisionproposedin[10, 12]andis speci icallydesignedfortexturecategorization.It isavariationderivedfromtheTextureSpectrum modelproposedin1990andhasgainedsubstantial recognition.

Initiallyintroducedin1994,theLBPtechnique servesasarobustfeaturefortextureanalysis.It operatesbyapplyingtheLBPoperatortoexamine individualimagesascollectionsofmicro‐patterns. Thefrequencyofoccurrenceofthesemicro‐patterns throughouttheimageisthencapturedinahistogram ofLBPvalues.Toconstructthefeaturevector,theface imageisdividedintonon‐overlappingregions(R0, R1,…,Rm).

Figure6. Haarfeatures

Figure7. Haarfeaturescomputinginanimage

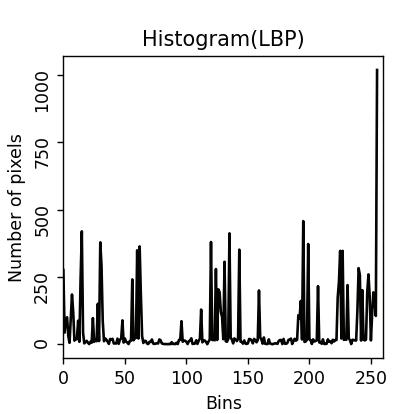
IntheoriginalLBPmethod,pixelsarelabeledby comparingtheircentralpixelvalue(threshold)with thevaluesoftheir 3×3 neighborhood(Fig. 8).This comparisonassignsdistinctnumericalvaluestocom‐monfeaturessuchasedges,lines,andpoints[2].Dur‐ingtherecognitionofatestface,thealgorithmcalcu‐latestheLBPofthetestface,dividesitintoregions, andcreatesahistogramforeachregion.Thesehis‐togramsarethenconcatenatedintoonehistogram (Fig.9)representingtheentireimage.Thenalgocom‐parestheEuclideandistancebetweenthehistogramof thetestfaceandthehistogramsofthetrainedfaces.If thedistancefallsbelowaprede inedtolerancevalue, itisconsideredamatch.Thisapproachenablesef i‐cientandrobustfacerecognitionbyusingthespatial informationcapturedbytheLBPoperatorandthe histogramrepresentation.

IntheOpenCVlibrary,thefunction “cv2.face_LBPHFaceRecognizer.create()”isemployed fortheLBPHalgorithm.Thisfunctionalsofacilitates readingtheYAML ilecontainingrelevantdata.The “predict()”methodisutilizedtopredictthelabeland con idencevalueofanewfaceinatestimage.

5.3.ThreadingModule

TheThreadingModuleinPythonisusedtocreate andmanagethreadsinaprogram.Itallowsmulti‐plethreadstorunconcurrentlywithinasinglepro‐cess,improvingtheperformanceandresponsiveness oftheprogram.Inthecontextofourproject,itis usedforimagetraining.Itcanalsobeusedtospeed

upthetrainingprocessbyallowingmultipleimages tobeprocessedsimultaneously.Thiscansigni icantly reducethetimerequiredfortraining.

Parametersinthemoduleusedinthesystem.

Target:IttakesanarrayofFacesandIDsfor training.

5.4.Smtplib

ThesmtplibmoduleinPythonprovidesawayto sendemailsusingSMTP(SimpleMailTransferPro‐tocol).ItallowsyoutoconnecttoanSMTPserver, authenticatewithausernameandpassword,and sendemailstooneormorerecipientsbyusingthis “server.sendmail(sender_email,receiver_email,mes‐sage)”functionofthemodule.

Withthis,youcansendtextorHTMLmessages, addattachments,andsetvariousemailheaders,such asthesubject,sender,andrecipient.Youcanalsouseit tohandleerrorsandexceptionsthatmayoccurduring theemail‐sendingprocess.

6.Result&Discussion

Wecanimplementthissysteminthe ieldbylever‐agingcloudserversofbanksthatstorethedataof theregisteredperson.Bydoingthis,theATMmachine doesnothavetostorethedataoftensofmillionsof customers,andinfact,itcanaccessthisinfoautomat‐icallybygeneratingtheAPIrequesttothoseservers, whichgivestheaccesstousedataoftheindividual foritsrecognitionsystemalsoverifywhetherthecus‐tomerislegitornotandthiswholeprocesswillbe completedwithin iveseconds.

Inthisstudy,theexecutionisperformedonareal‐timedatasetbyusingtheHaarcascadeforfacedetec‐tionandLBPHforfacerecognition.Asanoutcome,we foundoutthatthismethoddepictsadesirableresult forthevariousmeasuresandthusleadstothehigher ef iciencyofoursystem.

Figure8. TransformationofgrayimagetoLBPimages

Figure9. Concatenatedhistogramofeachregion

Figure10. Blockdiagramofsystem

FortheAccuracycalculation, Case1– TruePositive(TP):Theaccountisreg‐istered,andtheModelmatchesthefaceoftheperson correctly.

Case2– FalseNegative(FN):Theaccountisreg‐istered,butthefacedoesnotmatch.

Case3– FalsePositive(FP):Theaccountisnot linkedyetthemodelstillmatchestheface.

Case4– TrueNegative(TN):Theaccountisnot linked,andthemodelalsodoesnotrecognizetheface oftheperson.

Accuracy=(TP+TN)/(TP+TN+FP+FN) (1)

Were,TP:TruePositive,TN:TrueNegative, FP:FalsePositive,FN:FalseNegative

ByusingEquation(1),theAccuracyobtainedfrom oursystemis90%.

ForPrecision,

Precision=TP/(TP+FP) (2)

ByusingEquation(2),thePrecisionobtainedis 0.933.

ForRecall,

Recall=TP/(TP+FN) (3)

ByusingEquation(3),theRecallwasobtainedas 0.89.

ForF1Score,

F1=(2∗Precision∗Recall)/(Precision+Recall) (4)

ByusingEquation(4),theF1scorewasobtained as0.91.

7.Conclusion

Inthisstudy,weproposeamachinelearning modelthatcanaccuratelydetectandprovidesecurity towardsanywrongfulintentionsofAutomaticteller machineFraudandthemoneywithinit.Itcanidentify andissuereal‐timealerts/warningmessagesifaper‐son’sfacedoesnotmatchtheauthorizedpost’sactual faceandstate,asthiscouldraisesuspicion.

Basedonthesemessages,necessaryactionscanbe takenimmediatelytopreventsigni icantproblemsin thefuture.

Thus,withthehelpofalgorithmslikeHaarCas‐cadeandLBPH(LocalBinaryPatternHistogram),a modelisdevelopedthatcanissuewarningsandalerts toauthoritiesbeforeanyunauthorizedtransactions occur.Thismodelresultsinanaccuracyof90percent withlowerfalsepositiverates,whichmakesitmore secure&trustworthy.

Facialrecognitioniswidelyrecognizedasoneof themostsecurebiometricsystems,especiallygood forhigh‐levelsecuritypurposeslikepreventingany wrongfulintentionforthemoneyofanyaccount holderandprovidingsecurityforATMs.

AUTHORS

YaminiVijaywargiya∗ –Medi‐capsUniversity, Indore,MadhyaPradesh,India,e‐mail: yaminivijaywargiya2001@gmail.com.

MahakMishra –Medi‐capsUniversity,Indore,Mad‐hyaPradesh,India,e‐mail:missmahak.j@gmail.com.

NitikaVatsDoohan –Medi‐capsUniversity, Indore,MadhyaPradesh,India,e‐mail: nitika.doohan@gmail.com.

∗Correspondingauthor

References

[1] P.ViolaandM.Jones,“RapidObjectDetection UsingaBoostedCascadeofSimpleFeatures,” Proc.IEEEComp.Soc.Conf.USA,December2001, vol.1,p.1,doi:10.1109/CVPR.2001.990517.

[2] R.J.Rasras,etal.,“DevelopingDigitalSignalClus‐teringMethodUsingLocalBinaryPatternHis‐togram,” InternationalJournalofElectricaland ComputerEngineering(IJECE),vol.11,no.1, 2021,pp.872–878.doi:10.11591/ijece.v11i1.

[3] G.BradskiandA.Kaehler,“LearningOpenCV: ComputervisionwiththeOpenCVlibrary,” O’ReillyMed.Inc.USA,2008.

[4] J.Ferdinand,C.Wijaya,A.N.Ronal,I.S.Edbert, andD.Suhartono,“ATMSecuritySystemMod‐elingUsingFaceRecognitionwithFaceNetand HaarCascade,” 20226thInternationalConferenceonInformaticsandComputationalSciences (ICICoS),2022,pp.111–116,doi:10.1109/ICI‐CoS56336.2022.9930563.

[5] H.R.Babaei,O.Molalapata,andA.A.Pandor, “FaceRecognitionApplicationforAutomatic TellerMachines(ATM),” ICIKM,vol.45,2012, pp.211–216.doi:10.9756/BIJSESC.8273.

[6] M.S.Minu,etal,“FaceRecognitionSystemBased OnHaarCascadeClassi ier,” InternationalJournalofAdvancedScienceandTechnology,vol.29, no.5,2020,pp.3799–3805.

[7] T.V.Priya,G.VinithaSanchez,andN.R.Raajan, “FacialRecognitionSystemUsingLocalBinary Patterns(LBP),” InternationalJournalofPure andAppliedMathematics,vol.119,no.15,2018, pp.1895–1899.

[8] M.Karovaliya,S.Karedia,S.Oza,andD.R. Kalbande,“EnhancedSecurityforATMMachine withOTPandFacialRecognitionFeatures,” ProcediaComputerScience,vol.45,2015,pp.390‐396,ISSN:1877‐0509,doi:10.1016/j.procs.20 15.03.166.

[9] S.Sasipriya,D.P.Kumar,andS.Shenbagadevi, “FaceRecognitionBasedNewGenerationATM System,” EuropeanJournalofMolecular&Clinical Medicine,vol.7,no.4,2020,pp.2854–2865.

[10] T.Ahonen,A.Hadid,andM.Pietikainen,“Face DescriptionwithLocalBinaryPatterns:Appli‐cationtoFaceRecognition,” IEEETrans.Pattern AnalysisandMachineIntelligenceIEEEComp. Soc.,vol.28,2006,pp.2037–2041.

[11] S.Hazra,“SmartATMService,” 2019Devices forIntegratedCircuit(DevIC),Kalyani,India, 2019,pp.226–230,doi:10.1109/DEVIC.2019 .8783820.

[12] K.S.doPrado,“FaceRecognition:Understand‐ingLBPHAlgorithm,” Medium.Accessed:Feb.16, 2024.[Online].Available:https://towardsdatas cience.com/face‐recognition‐how‐lbph‐works‐90ec258c3d6b

[13] A.B.Shetty,Bhoomika,Deeksha,J.Rebeiro,and Ramyashree,“FacialRecognitionUsingHaarCas‐cadeAndLBPClassi iers,” GlobalTransitionsProceedings,vol.2,no.2,2021,pp.330–335,doi: 10.1016/j.gltp.2021.08.044.