Journal of Automation, Mobile Robotics and Intelligent Systems, vol. 18, no. 2 (2024)

WWW.JAMRIS.ORG pISSN 1897-8649 (PRINT)/eISSN 2080-2145 (ONLINE) VOLUME 18, N° 2, 2024

Indexed in SCOPUS

Journal of Automation, Mobile Robotics and Intelligent Systems

A peer-reviewed quarterly focusing on new achievements in the following fields: • automation • systems and control • autonomous systems • multiagent systems • decision-making and decision support • • robotics • mechatronics • data sciences • new computing paradigms •

Editor-in-Chief

Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Advisory Board

Dimitar Filev (Research & Advenced Engineering, Ford Motor Company, USA)

Kaoru Hirota (Tokyo Institute of Technology, Japan)

Witold Pedrycz (ECERF, University of Alberta, Canada)

Co-Editors

Roman Szewczyk (Łukasiewicz-PIAP, Warsaw University of Technology, Poland)

Oscar Castillo (Tijuana Institute of Technology, Mexico)

Marek Zaremba (University of Quebec, Canada)

Executive Editor

Katarzyna Rzeplinska-Rykała, e-mail: office@jamris.org (Łukasiewicz-PIAP, Poland)

Associate Editor

Piotr Skrzypczyński (Poznań University of Technology, Poland)

Statistical Editor

Małgorzata Kaliczyńska (Łukasiewicz-PIAP, Poland)

Typesetting

SCIENDO, www.sciendo.com

Webmaster TOMP, www.tomp.pl

Editorial Office

ŁUKASIEWICZ Research Network

– Industrial Research Institute for Automation and Measurements PIAP

Al. Jerozolimskie 202, 02-486 Warsaw, Poland (www.jamris.org) tel. +48-22-8740109, e-mail: office@jamris.org

The reference version of the journal is e-version. Printed in 100 copies.

Articles are reviewed, excluding advertisements and descriptions of products.

Papers published currently are available for non-commercial use under the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 (CC BY-NC-ND 4.0) license. Details are available at: https://www.jamris.org/index.php/JAMRIS/ LicenseToPublish

Editorial Board:

Chairman – Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Plamen Angelov (Lancaster University, UK)

Adam Borkowski (Polish Academy of Sciences, Poland)

Wolfgang Borutzky (Fachhochschule Bonn-Rhein-Sieg, Germany)

Bice Cavallo (University of Naples Federico II, Italy)

Chin Chen Chang (Feng Chia University, Taiwan)

Jorge Manuel Miranda Dias (University of Coimbra, Portugal)

Andries Engelbrecht ( University of Stellenbosch, Republic of South Africa)

Pablo Estévez (University of Chile)

Bogdan Gabrys (Bournemouth University, UK)

Fernando Gomide (University of Campinas, Brazil)

Aboul Ella Hassanien (Cairo University, Egypt)

Joachim Hertzberg (Osnabrück University, Germany)

Tadeusz Kaczorek (Białystok University of Technology, Poland)

Nikola Kasabov (Auckland University of Technology, New Zealand)

Marian P. Kaźmierkowski (Warsaw University of Technology, Poland)

Laszlo T. Kóczy (Szechenyi Istvan University, Gyor and Budapest University of Technology and Economics, Hungary)

Józef Korbicz (University of Zielona Góra, Poland)

Eckart Kramer (Fachhochschule Eberswalde, Germany)

Rudolf Kruse (Otto-von-Guericke-Universität, Germany)

Ching-Teng Lin (National Chiao-Tung University, Taiwan)

Piotr Kulczycki (AGH University of Science and Technology, Poland)

Andrew Kusiak (University of Iowa, USA)

Mark Last (Ben-Gurion University, Israel)

Anthony Maciejewski (Colorado State University, USA)

Krzysztof Malinowski (Warsaw University of Technology, Poland)

Andrzej Masłowski (Warsaw University of Technology, Poland)

Patricia Melin (Tijuana Institute of Technology, Mexico)

Fazel Naghdy (University of Wollongong, Australia)

Zbigniew Nahorski (Polish Academy of Sciences, Poland)

Nadia Nedjah (State University of Rio de Janeiro, Brazil)

Dmitry A. Novikov (Institute of Control Sciences, Russian Academy of Sciences, Russia)

Duc Truong Pham (Birmingham University, UK)

Lech Polkowski (University of Warmia and Mazury, Poland)

Alain Pruski (University of Metz, France)

Rita Ribeiro (UNINOVA, Instituto de Desenvolvimento de Novas Tecnologias, Portugal)

Imre Rudas (Óbuda University, Hungary)

Leszek Rutkowski (Czestochowa University of Technology, Poland)

Alessandro Saffiotti (Örebro University, Sweden)

Klaus Schilling (Julius-Maximilians-University Wuerzburg, Germany)

Vassil Sgurev (Bulgarian Academy of Sciences, Department of Intelligent Systems, Bulgaria)

Helena Szczerbicka (Leibniz Universität, Germany)

Ryszard Tadeusiewicz (AGH University of Science and Technology, Poland)

Stanisław Tarasiewicz (University of Laval, Canada)

Piotr Tatjewski (Warsaw University of Technology, Poland)

Rene Wamkeue (University of Quebec, Canada)

Janusz Zalewski (Florida Gulf Coast University, USA)

Teresa Zielińska (Warsaw University of Technology, Poland)

Publisher:

1

Journal of Automation, Mobile Robotics and Intelligent Systems

VOLUME 18, N˚2, 2024

DOI: 10.14313/JAMRIS/2-2024

Contents

Effective Nonlinear Predictive and CTC‐PID Control of Rigid Manipulators

Piotr Tatjewski

DOI: 10.14313/JAMRIS/2‐2024/8

17

SoC‐FPGA Based Concept of Hardware Aided Quantum Simulation

Jacek Długopolski, Jakub Czerski, Mateusz Knapik

DOI: 10.14313/JAMRIS/2‐2024/9

Improving Teaching Using Artificial Intelligence and Augmented Reality

Amal Zouhri, Mostafa EL MALLAHI

DOI: 10.14313/JAMRIS/2‐2024/13

Simultaneous Localization and Mapping of a Mobile Robot with Stereo Camera Using ORB Features

Younès Raoui, Mohammed Amraoui

DOI: 10.14313/JAMRIS/2‐2024/14

72

Research to Simulate the Ship’s Vibration Regeneration System Using a 6‐Degree Freedom

Gough‐Stewart Parallel Robot

Nguyen Duc Anh, Nguyen Quang Vinh 10.14313/JAMRIS/2‐2024/10 24

31

Comparative Analysis of CNN‐Based Smart Pre‐Trained Models for Object Detection on DOTA

Hina Hashmi, Rakesh Kumar Dwivedi, Anil Kumar

DOI: 10.14313/JAMRIS/2‐2024/11

46

A Numerical Analysis Based Internet of Things (IoT) and Big Data Analytics to Minimize Energy Consumption in Smart Buildings

Amal Zouhri, Abderahamane EZ‑ZAHOUT, Said Chakouk, Mostafa EL MALLAHI

DOI: 10.14313/JAMRIS/2‐2024/12

Design of Small‐Phase Time‐Variant Low‐Pass Digital Fractional Differentiators and Integrators

Mateusz Saków

DOI: 10.14313/JAMRIS/2‐2024/15

83

Diagnostics Based Patient Classification for Clinical Decision Support Systems

Gaurav Paliwal, Aaquil Bunglowala, Pravesh Kanthed

DOI: 10.14313/JAMRIS/2‐2024/16

DOI:10.14313/JAMRIS/2‐2024/8

Abstract:

MANIPULATORS

MANIPULATORS

Submitted:24th October2023;accepted:14th December2023

PiotrTatjewski

Effectivenonlinearcontrolofmanipulatorswithdynam‐icallycoupledarms,likethosewithdirectdrives,is thesubjectofthepaper.Model‐basedpredictivecon‐trol(MPC)algorithmswithnonlinearstate‐spacemod‐elsandmostrecentdisturbanceattenuationtechnique areproposed.Thistechniquemakescontrollerdesign andonlinecalculationssimpler,avoidingnecessityof dynamicmodelingofdisturbancesorresortingtoaddi‐tionaltechniqueslikeSMC.Thecoreofthepaperare computationallyeffectiveMPC‐NPL(NonlinearPrediction andLinearization)algorithms,wherecomputationsat everysamplearedividedintotwoparts:predictionof initialtrajectoriesusingnonlinearmodel,thenoptimiza‐tionusingsimplifiedlinearizedmodel.Foracompari‐son,aknownCTC‐PIDalgorithm,whichisalsomodel‐based,isconsidered.Itisappliedinstandardformand alsoproposedinmoreadvancedCTC‐PID2dofversion. Forallalgorithmsacomprehensivecomparativesimu‐lationstudyisperformed,foradirectdrivemanipulator underdisturbances.Additionalcontributionofthepaper isinvestigationofinfluenceofsamplingperiodandof computationaldelaytimeonperformanceofthealgo‐rithms,whichispracticallyimportantwhenusingmodel‐basedalgorithmswithfastsampling.

Keywords: manipulatorcontrol,nonlinearcontrol,model predictivecontrol,CTC‐PIDcontrol,fastsampling,delays

1.Introduction

Roboticmanipulatorshavebeenbroadlyutilized invariousautomatedindustrialapplications.Con‐trollersareneededforthemanipulators,whichassure adequatetrackingperformanceduringfast,safeand smoothmotions.Roboticmanipulatorsarecomplex, nonlinearmechatronicsystems.Thus,thecontrollers mustperformnonlinearandmultivariablemotion tasks.Therearemanysolutionstothisproblempre‐sentedforyearsintheliterature,startingfromclassi‐calmultiloopPIDcontrolstructures.Thissolutionis stillpopularinpractice,especiallyforsystemswith gearswhichcaneffectivelydampcouplingeffects betweenindividuallinks.Itisnottheaimofthispaper todeliverareviewofstructuresandalgorithmsof manipulatorcontrol,withfulllistofrelatedrefer‐ences.Weareluckythatareviewpaperhasbeenvery recentlypublishedonthesubject[1],theinterested readerisreferredthere.

Anearliercomprehensivereviewpapercanbe herealsorecommended[2].Textbooksonmanipu‐latorcontrol,includingstandardPD/PIDcontroland moreelaboratePIDstructureswithgravitycompensa‐tionandwithcomputedtorquecontrol(CTC),arealso worthmentioning[3,4].

Model‐basedpredictivecontrol(MPC)isnow anestablishedadvancedcontroltechnology,repre‐sentedbynumerousalgorithmsandsoftwarepack‐agesappliedsuccessfullyinindustrialpractice,espe‐ciallytoprocesscontrol,see,e.g.,[5–13].MPCalgo‐rithmshavebeensuccessfullyapplied irsttoindus‐trialmultivariablesystemswithstronginteractions, activeconstraints,dif icultdynamics,whereclassi‐calPIDcontrolcouldnotprovidesatisfactoryper‐formance.MPCisamodel‐basedtechnologyneeding morecomputingpower;thus,itwas irstappliedto processeswithslowdynamics.Applicationstofaster processeswerethendeveloped,ontheonehand,by applicationofmorepowerfulandfastercomputers, andontheotherhand,bydevelopmentofsubopti‐malbutsimplerandfasterversionsofalgorithms. Thelatterdevelopmenttookplacewhenconstructing MPCalgorithmswithnonlinearprocessmodels.Then simpler,easiercomputableprocessmodelversions orapproximationswereused,likelinearparameter‐varying(LPV),fuzzyorneuralnetworkmodels,and nonlinearmodelsofspecialstructurelikeWiener models,see,e.g.,[8,9,14–17].

Roboticmanipulatorsarenonlinearsystemsper‐formingfastmotions,thusoperatingwithshortsam‐plingperiods.Therefore,directapplicationsofMPC withnonlinearmodelandonlineoptimizationhave beendif icultandwerereportedintheliterature rarelyandonlyrecently,withspeci icdevelopments tomakeoptimizationmoreef icient,see[18,19].On theotherhand,thenatureofthemanipulatorcon‐trolproblem,amultivariableonewithpossiblestrong interactionsandactiveconstraintsseemsperfectly suitedforapplicationofMPC.Therefore,therewere trialsreportedinrecentyearstodevelopsimpler MPC‐basedmanipulatorcontrol.Themaindif iculty, onlinenonlinearoptimization,wasusuallyreplaced byaquadraticoneusinglinearapproximations,orby problemswithLMI(linearmatrixinequalities)con‐straints.OneapproachwastouseaLPVrepresenta‐tionofthenonlinearmodel,see,[20,21].Theother andmoreoftenmetapproachwastouseanonline linearization.

Wilsonet.al.[22]appliedDMCalgorithmwithstep responsemodelrecalculatedateverysamplinginstant bysimulationofthenonlinearmodel.Linearization ofthemodelatcurrentpointwasapplied,e.g.,in [9,21,23].Thelinearmodelwasthenusedbothto outputpredictionandquadraticoptimizationatevery sample(theMPC‐NSLmethod,see[9]).Toovercome dif icultiesduetononlinearity,theapproachwithMPC appliedtothesimpli iedlinearsystemafterfeedback linearizationbyCTC(computedtorquecontrol)has beenproposed,see[24–27].However,itseemsthat applicationofMPCtoextremelysimplelinearsystem afterCTClinearizationisnotagoodsolution.MPC itselfisapowerfultechniquecapabletocopewith nonlinearities,equippedalsowitheffectivemecha‐nismsofdisturbanceattenuation.Itspotentialcan‐notbewellutilizedwhenfeedbacklinearizationis appliedwithnotadequatelyaccuratemodel,asMPC cannotthenutilizestructuralpropertiesoftheoriginal manipulatormodel.

Theproblemtoattenuatedisturbances,boththese stemmingfrommodelinaccuracies(parameteruncer‐tainty,unmodeleddynamics)andthesefromexternal in luences,isavitaloneincontrolsystemdesign.To copewithit,acombinationofMPCwithPID[22]or withSMC(slidingmodecontrol)hasbeenproposed, see[24, 25, 27].However,thisledtounnecessarily overcomplicated,multiloopcontrolsystems.Therea‐sonforthatwasthatonlyrecentlyanef icienttech‐niqueofdisturbancemodelingandattenuationwas proposedforMPCwithstate‐spacemodels,with irst applicationstoprocesscontrolsystems.Itisespecially effectiveforcaseswithmeasuredstateasitremoves thentheneedtoapplydynamicobservers/ iltersof disturbances,see[28–31].Thetwolatterpaperscon‐siderbothcases,withmeasuredandunmeasured (observed, iltered)state,andasigni icantgeneral‐izationfrommeasuredtounmeasuredstate.Thecase withmeasuredstateisoftenmetinmanipulatorcon‐trol,withthestateconsistingofbothpositionsand velocities.

Theaimofthispaperistopresentanapplication ofstate‐of‐the‐artrealizationsofnonlinearMPCalgo‐rithmstomanipulatorcontrol,notresortingtoSMCor otheradditionaltechniquestoattenuatedisturbances ortofeedbacklinearizationbyCTC.InSection2, theappropriateMPCalgorithmswillbepresented. First,themostgeneralMPC‐NOalgorithm(MPCwith NonlinearOptimization)usinganonlinearmanipula‐tormodelwillbebrie lydescribed,furtherusedas abenchmark.Then,muchmoreeffectiveMPCalgo‐rithmswithnonlinearpredictionandlinearization (MPC‐NPL)willbepresented,whicharethecoreofthe paper.The irstoneiswithappropriatelyorganized constrainedquadraticprogramminginsteadofnon‐linearoptimization.Thenext,computationallymost effective,willbederivedasananalytical(explicit) versionofthepreviousone.Allthealgorithmswill beusingthedisturbanceattenuationtechniqueas proposedin[29,30].Organizationofthecalculations withintheMPC‐NPLalgorithmsleadingtoshortest executiontimeswillbealsodiscussed.

InSection3,resultsofacomprehensivecom‐parativesimulationstudyofapplicationsofallthe algorithmstocontroladirectdrivemanipulatorwill bereported,fordifferentreferencetrajectoriesand differentdisturbances.Theseincludeexternaldis‐turbingtorqueandsubstantialdifferencesbetween manipulatoranditsmodelinthefeedbackloop, bothinparametersandinunmodelleddynamics. Theresultswillbealsocomparedwiththoseforthe CTC‐PIDalgorithm,inknownstandardformandin enhancedCTC‐PID2dofstructure.Investigationsofthe in luenceofsamplingperiodandofadelaycausedby thetimeofcomputationsonalgorithmsperformance willbeanadditionalcontributionofthepaper.

Thepaperisasigni icantlyextendedandEnglish versionofthepaper[32]publishedrecentlyinPol‐ish.Exceptforminorimprovements,mainextensions involve, irstly,anewconceptofcomputationalstruc‐turesoftheMPC‐NPLalgorithmsleadingtoshortest executiontimes.Furthersigni icantextensionisthe designandinvestigationofeffectiveversionsofboth MPCandCTC‐PIDalgorithmsformanipulatorcon‐trolforpiecewiseconstantreferencetrajectories.This includesMPCwithadditionalinternalreferencetra‐jectoriesandCTCwithmultiloopPIDin2dofstructure. Allthedescribedextensionsarevalidatedbyapplica‐tiontocontrolofadirectdrivemanipulatormentioned above.Conclusionswillbethelastpartofthepaper.

2.ModelPredictiveControlAlgorithms

2.1.ModelsoftheManipulator

Weconsiderthefollowingwell‐knownnonlinear continuous‐timedynamicmodelofa��‐dofrigidbody robotmanipulator[1–4],

��(��)̈��+��(��,̇��)̇��+��(̇��)+��(��)=��, (1) where ��, ̇�� , ̈��∈�� �� arevectorsofjointpositions, velocitiesandaccelerations,respectively,��(��)isthe inertiamatrix,��(��,̇��)isthematrixofcentripetaland Coriolisforces,��(̇��)isthefunctionrepresentingfric‐tion, ��(��) isthegravityvector,and �� isthecontrol inputvector(motortorques).

De inethestatevector���� =[���� ̇�� �� ]∈��2��.Then, (1)canbewritteninstandardform

̇��= ̇�� −��(��)−1[��(��,̇��)̇��+��(̇��)+��(��)]+��(��)−1�� (2)

UsingtheEulerdiscretizationschemewithintegration step����,wegetthediscrete‐timemodel:

, (3) ��(��)=��(��). (4)

subjectto∶−predictionequationscalculating��(��+��|��)usingthemodel forgivenvalues��(��|��),...,��(��+��−1|��),��=1,...,��,

Asimpli ied,continuousanddifferentiablemodel withviscousfrictiononly, ��(̇��)=���� withdiago‐nalmatrix ����,willbeusedforMPCdesign,treating static(Coriolis)frictionasunmodelleddynamics.This modelwillbefurtherwritteninstandardshortform ��(��+1)=��(��(��),��(��)), (5) ��(��)= C��(��). (6)

2.2.MPC‐NOAlgorithm(withNonlinearOptimization)

Denoteby �� thenumberofsamplingperiods ���� de iningthepredictionhorizonandby���� thenumber ofsamplingperiodsde iningthecontrolhorizon.We de inethedynamicoptimizationproblemofMPC‐NO controlleraspresentedinEq.(7),where ��(��+��|��), ��(��+��|��),etc.,denotevaluesofthemanipulatorout‐putsandcontrolinputs,respectively,predictedforthe sample��+��atthecurrentsample��,see,e.g.,[9,30]. For ��=0,wehave ��(��+0−1|��)=��(��−1), whichisthemanipulatorcontrolinputcalculatedat theprevioussamplinginstant.For ��≥����,weset ��(��+��|��)=��(��+���� −1|��).Matrices Ψ, Λ are diagonalmatricesofpositiveweightingcoef icients and ||��||Ψ ≜ √����Ψ��.Thecontroltrajectory ��(��) is thedecisionvectorof(7), ��(��)��= ��(��|��)�� ��(��+1|��)�� ⋯��(��+����−1|��)�� (8)

Forformulationofoutputpredictionsoverthepre‐dictionhorizon��,theapplieddisturbanceattenuation techniqueiscrucial.In[28],”constantstatedistur‐bancemodel”waspresentedforMPCwithlinearstate‐spacemodels,withtheproofshowingitassuresoffset‐freecontrolforasymptoticallyconstantdisturbances (includingmodelingerrors).In[29, 30]generaliza‐tionstononlinearsystemsweregiven.Thisconstant statedisturbancemodelisasfollows,

��(��)=��(��)−��(��|��−1)=��(��)−��(��(��−1),��(��−1)). (9)

Thismeansthat ��(��) isthedifferencebetweenthe state��(��)measuredatcurrentsample��andthestate ��(��|��−1)predictedforthissampleatprevioussam‐ple ��−1.Itis”constant”asthesamevalue ��(��) is assumedoverwholepredictionhorizon,i.e., ��(��+1|��)=��(��+2|��)=⋯=��(��+��−1|��)=��(��). (10)

Havingde inedthedisturbancemodel,stateand thenoutputpredictionequationscanbeformulated, foranygivencontrolinputtrajectory(8):

��(��+1|��)=��(��(��),��(��|��))+��(��), ��(��+2|��)=��(��(��+1|��),��(��+1|��))+��(��), ⋮ ��(��+��|��)=��(��(��+��−1|��),��(��+��−1|��))+��(��), (11) where ��(��+��|��)=��(��+����−1|��), ��=����,...,��−1, ��(��+��|��)= C��(��+��|��),��=1,...,��. (12)

Withpredictionequations(11)‐(12),MPCoptimiza‐tionproblem(7)isfullyde inedandcanbesolved,at eachsamplinginstant.The irstelement��(��|��)ofthe obtainedoptimalcontroltrajectory��(��)isthensent tomanipulatoractuatorsasthecurrentcontrolsignal ��(��).Atthenextsamplinginstantnewmeasurements areavailableandthewholeMPCalgorithmisrepeated (recedinghorizontechnique).

SubsequentMPCoptimizationproblems(7)usu‐allydifferonlyslightlyatconsecutivesamples,with changesinafewparameters:newstatemeasurement ��(��)andlastcontrolvalues��(��−1).Insuchcases,the techniqueof”warmstart”maybeef icient,i.e.,using previousoptimalcontroltrajectory ��(��−1) asthe basisfornewinitialcontroltrajectory ��0(��).Dueto therecedinghorizon,thisconsistsinmodifyingthe ��(��−1)byomittingthe irstsubvector��(��−1|��−1)and repeatingthelastone.Thewarmstartshouldbeef i‐cientforlongercontrolhorizons����.Itisusuallynot thecaseofmanipulatorcontrol,whenfastsampling andreducedcomputationalloadarerequired.

TheMPC‐NOalgorithmwillbetreatedfurtherin thepaperasanoptimalpatterntobecomparedwith fasterbutsuboptimalMPCalgorithms.However,due todevelopmentofstillmorepowerfulandcheaper microcontrollersandimprovementsinnonlinearopti‐mizationprocedures,theareaofpossibleapplications ofalgorithmswithnonlinearoptimizationiswiden‐ing,see,e.g.,[18,33].

2.3.MPC‐NPLAlgorithms(withNonlinearPrediction andLinearization)

AstraightforwardwaytosimplifytheMPC‐NO algorithmistoconstructanadaptivealgorithmthat,at eachsamplinginstant,linearizesthenonlinearmodel andthenusesthestandardMPCalgorithmwiththe linearmodelforpredictionandoptimization.Itis knownasMPC‐NSLtechnique(NonlinearwithSucces‐siveLinearizations),see,e.g.,[6,9,21].However,this algorithmmaynotbesuccessful,especiallyforsys‐temswithstrongernonlinearities.Thecomputation‐allycomparableandmorewidelyapplicableapproach isthealgorithmthat,ateachsamplinginstant, irstly performspredictionoftheinitialoutputtrajectory usingthefullnonlinearmodel.Then,inthesecond phase,itperformslinearizationandappliesoptimiza‐tionusingtheincrementallinearmodel,toimprove theinitiallycomputedtrajectory.Suchalgorithmwill bedenotedbyMPC‐NPL(MPCwithNonlinearPredic‐tionandLinearization),see,e.g.,[9].

SubsequentstepsoftheMPC‐NPLalgorithm,at ��‐thsamplinginstant:

1) Themanipulatorstate ��(��) ismeasured(oresti‐mated),��(��)iscalculatedaccordingto(9).

2) Initialtrajectoryofcontrolinputs ��0(��) isdeter‐minedoverthepredictionhorizon,

��0(��)��=[��0(��|��)�� ��0(��+1|��)��⋯��0(��+��−1|��)�� ].

Using ��0(��),theinitialtrajectoryofstates ��0(��) (consistingof ��0(��+��|��),��=1,…,��)andthen theinitialtrajectoryofoutputs ��0(��) (consisting of��0(��+��|��),��=1,…,��)arecalculatedusingthe nonlinearmodel:

��0(��+��|��)=��(��0(��+��−1|��),��0(��+��−1|��))+ +��(��), (13)

��0(��+��|��)= C��0(��+��|��),��=1,…,��, (14)

where��0(��|��)=��(��)isthemeasuredstate.

3) Thestateequationislinearizedatcurrentpoint (��(��), ��0(��|��)).Matrix M(��) describinglinear relationbetweenincrementsofcontrol(overini‐tialcontroltrajectory)andcorrespondingincre‐mentsofoutputs(overinitialoutputtrajectory)is calculated,

△��(��)= M(��)⋅△��(��), (15) where △��(��)�� =

�� △��(��+1|��)��

��−1|��)�� , (16) △��(��)�� = △��(��+1|��)�� △��(��+2|��)�� ⋯

�� , (17) where △��(��|��)=��(��|��)−��(��−1),

etc

4) TheMPC‐NPLquadraticoptimizationproblem (23)withthelinearizedmodel(15)issolved,with thesolution△��(��+��|��),��=0,...,���� −1

5) The(sub)optimalcontroltrajectoryiscalculated: ��(��+��|��)=��0(��+��|��)+ �� ��=0 △��(��+��|��), ��=0,...,����−1, ��(��+��|��)=��(��+���� −1|��),��=����,...,��−1. (18)

6) Firstsubvectoroftheoptimalcontroltrajectory, ��(��|��),issenttotheactuatorsasthecurrentcon‐trolleroutput(manipulatorcontrolinput)��(��) Initialcontroltrajectory��0(��)canbeeitheracon‐stantone,consistingoflastmanipulatorcontrolinput ��(��−1),i.e.,��0(��+��|��)=��(��−1),��=0,...,��−1,or thetrajectoryaccordingto”warmstart”technique,i.e., ��0(��+��|��)=��(��+��|��−1),��=0,...,��−2,��0(��+��− 1|��)=̂��(��+��−2|��−1).The irstisrecommended forveryshortcontrolhorizon(���� ≤2)andsmall ����,acasetypicalforfastdynamics.Itisthecaseof manipulatorcontrol;thus,furtherpresentationwill bewiththistrajectory.Thelatteronemayincrease ef iciencyforlonger����,butneedsareformulationof ��(��) in(23).Thiswillbeomitted,duetothegiven reasonandtoshortenthelengthofthepaper. Atpoint3,anincrementallinearstate‐spacemodel isobtainedafterlinearization

��(��+1)= A(��)��(��)+ B(��)��(��), (19)

Themanipulatormodel(3)islinearwithrespectto ��(��),hencelinearizationisnotneededtoget B(��), B(��)=������(��(��))−1.Toget A(��),partialderiva‐tivesmustbecalculatedforthelast��stateequations in(3)only,asshowninEq.(20),where �� ����(��)[⋅] denotesmatrixofpartialderivativesofthefunction insquarebrackets(theJacobimatrix).Afterlineariza‐tion,matrices A(��), B(��)and C areusedtocalculate thedynamicmatrix M(��),whichhasthestructure

1(��) 0 0

⎢ ⎢

(��)=

⎢ ⎢ ⎢ ⎣

2(��) M1(��)⋯ 0 M3(��) M2(��)⋯ 0

⋮ ⋱ ⋮

����(��) M����−1(��)⋯ M1(��) M����+1(��) M����(��)⋯ M2(��)

⋮ ⋮ ⋮ M��(��) M��−1(��)⋯ M��−����+1(��)

, (21) where M��(��)= C [I+A(��)+A(��)2+⋯+A(��)��−1] B(��), (22) with M1(��)= CB(��).Thestructure(21)‐(22)is standardforMPCalgorithmswithlinearstate‐space models,see,e.g.,[9,34].

Atpoint4.,thequadraticprogramming(QP)prob‐lemshowninEq.(23)issolved.Itisastandardform oftheMPCoptimizationproblemwithalinearmodel, with(16)asthevectorofdecisionvariables,see, e.g.,[9].

Thefundamentaldifferencebetween(23)anda QPproblemforMPCwithalinearmodelonlyisthat nowtheinitialtrajectoryoftheoutputs,��0(��+��|��), ��=1,…,��,iscalculatedusingthenonlinearmodel, notthelinearone,andthedynamicmatrix M(��) is subjecttoadaptation.

2.4.Analytical(Explicit)MPC‐NPLAlgorithm

Toreducefurtheronlinecomputations,ananalyt‐ical(explicit)versionoftheMPC‐NPLalgorithmhas beendeveloped.Theideaisto ind, irst,thepoint minimizingthequadraticfunction ��(��) of(23)only, neglectingtemporarilyinequalityconstraints.Next, thecalculated(unconstrained)valuesaretrimmedto limitsofinequalityconstraints.Thisaddsadditional suboptimality,butsigni icantlyreducesthecompu‐tationalload.Moreover,applicationexampleshave shownthatsuchfasteralgorithmcanbealmostas effectiveastheonewithconstrainedQPoptimization forcaseswithlimitedactivityofinequalityconstraints (forinactiveconstraintsresultsareequivalent).

Thefunction ��(��) in(23)isstrictlyconvex,thus itsminimumcanbeeasilycalculatedsolvinglinear equationsofnecessaryoptimalityconditions:

[M(��)��ΨM(��)+Λ]Δ��(��)= M(��)��Ψ[��������(��)−��0(��)], (24) whereΨ=diag{Ψ,…,Ψ},Λ=diag{Λ,…,Λ}areblock‐diagonalmatrices,consistingof��blocksΨandof���� blocksΛ,respectively,and

Thesolution ��(��) of(24)yieldstheunconstrained (sub)optimaltrajectoryofcontrolincrements(over theinitialtrajectory)onthecontrolhorizon:

�� = △��(��|��)�� △��(��+1|��)�� ⋯

△��(��+����−1|��)�� (27)

The irstsubvector △��(��)=△��(��|��) isnowtrimmed tolowerandupperlimitsofrateofchangeconstraints, −△�������� and △��������,respectively,withtheresult △��(��).Next, ��(��)=��(��−1)+ △��(��) istrimmed tolowerandupperlimitsofamplitudeconstraints, �������� and��������,withtheresultingcontrolsignal��(��) satisfyingallconstraints.Thisisshownschematically inFigure1,whichpresentsthestructureofthealgo‐rithm.ItwillbecalledMPC‐NPL analyticalalgorithm (MPC‐NPLa).Itis”analytical”becausethesolution Δ��(��)of(24)canbeexpressedbyanalyticalformula Δ��(��)=[M(��)��ΨM(��)+Λ]−1M(��)��Ψ ⋅[��������(��)−��0(��)]. (28)

However,solvingsetoflinearequations(24)needs signi icantlylesscomputationsthanapplicationofthe inversematrixformula(28).Therefore,itisrecom‐mendedwhen M(��) isrecalculatedateachsampling instant.However,ifitisrecalculatedlessoften,then using(28)maybereasonable.

Thealgorithmdescribedintheprevioussection willbedenotedMPC‐NPLn(numerical),todistin‐guisheditfromMPC‐NPLa.

2.5.EfficientComputationalStructuresforMPC‐NPL MaincomputationalloadwhenperformingMPC‐NPLalgorithmsisdueto:

1. Calculationofthenonlinearmodel(13)��timesto gettheinitialoutputtrajectory��0(��)

2. Linearizationofthenonlinearmodel,involving �� calculationsofthismodelwhenapplyingnumeri‐calapproximationofpartialderivatives.Thencal‐culationofthedynamicmatrix M(��)ofdimension (��⋅��)×(����⋅��),accordingto(21).

3. SolvingtheMPCoptimizationproblem.Ifnumeri‐calalgorithmisapplied,thenQPprocedureisused andthecomputationalloaddependsmainlyonthe numberofoptimizationvariableswhichis ����⋅��. Whenapplyinganalyticalalgorithm,thesetof���� �� linearequations(24)issolvedorsubstitution (28)iscalculated,withcomputationalloaddueto computation(andpossiblyinversion)ofquadratic matrix M(��)��ΨM(��)+Λofdimension����⋅��. Lookingattheaboveanalysis,itcanbeseen thatthecomputationalloaddependsonmanipulator dimensionality��,whatcouldbeexpected.Itdepends alsoonthelengthofpredictionandcontrolhorizons, �� and ����,respectively,whicharedesignparameters ofMPCalgorithms.Todecreasethetimeofcomputa‐tionsasmuchaspossible,thehorizonsshouldbeas shortaspossible–butpreservingadequatecontrol performance.Thisconcerns irstofallcontrolhorizon ����,asitdirectlyin luencesdimensionalityoftheMPC optimizationproblem.Luckily, ���� canbeveryshort –intheexamplemanipulatorconsideredinthenext section, ���� =2 occurredtobeaverygoodchoice, even���� =1couldhavebeenconsidered.Thelength ofpredictionhorizon �� mustbesuf icientlylong,to assureappropriatecontrolperformanceandrobust‐ness,see,e.g.,[9,34]–butnolongerthannecessary (theoretically,itisnotlimitedfromabove).Itshould bealsonotedthatlengthof �� dependsonphysical dynamicsofthecontrolledprocess(themanipulator), thusthefastersamplingoftheMPCcontroller,the longer��mustbedesigned.

Havingselectedthehorizons,organizationofcal‐culationsiscrucialtodecreasethetime.First,the matrix(21)canbecalculatedef iciently,despiteits complexity.IthasToeplitzblock‐structure;thus,only its irstblock‐columnconsistingofmatrices M��(��) mustbecalculated.Duetostructureofeq.(22),this calculationscanbeeffectivelyorganizedinarecursive way:

P1 = B(��), M1(��)= CP1, P�� = B(��)+ A(��)P��−1, M��(��)= CP��,��=2,…,�� (29)

thusconsistingof��−1multiplicationsandadditions ofminorsizematrices,asmultiplicationby C means reductionofeach P�� toits irst �� rows.Certainly, computationalloaddependsalsooncomplexityofthe

linearization, calculation ofk M() solution of QP 0 MPC-NPLcontroller prediction of Y (k)

xk, uk()(1) uk()

ParallelcomputationalstructureofMPC‐NPL

manipulatoritself,onitsnumberofdegreesoffree‐dom ��,whichisalsothenumberofnonlinearequa‐tionsinthemodelusedtocalculatetheinitialtrajec‐toryinpoint1andlinearizedmodelinpoint2above. Thus,dimensionofthematrix M(��)(21),dependent on A(��), B(��) and C ofthelinearizedmodel,also dependson��

Itshouldbenotedthatcalculationsenlistedin points1and2abovecanbeperformedindependently, theonlycommonelementaretheinitialdata.Thus, applyingtwo‐processorparallelcomputationstruc‐tureshouldleadtoreductionofcomputationtime. SuchstructureisdepictedinFigure2

ExpierienceinapplicationofMPC‐NPLalgorithms showsthatlinearizationmaybeupdatedlessfre‐quently,notateverysamplinginstant,butrepeated every ���������� samplesonly, ���������� >1.Inparticular, thisworkswellforweakernonlinearitiesorwhen fastsamplingisapplied,whichisstandardinmanip‐ulatorcontrol.Then,controlstructurecanbealso designedwithlinearizationandcomputationof M(��) performedbyadistinctsupervisoryprocessor(com‐puter),whereasbasicprocessorcalculatestheini‐tialoutputtrajectoryandperformstheoptimization, withintheshortsamplingperiod����. Linearizationisthesamebothinthenumerical andanalyticalNPLalgorithms.Butthereisadiffer‐enceinoptimizationproblems.Inthenumericalalgo‐rithm,thesupervisoryprocessorcalculatesandtrans‐mitsmatrix M(��)tothebasicprocessor,neededtofor‐mulatetheQPproblem.Inthetheanalyticalalgorithm, morecalculationscanbeshiftedtothesupervisory processor.Asthesamematrix M(��) isusedduring subsequent���������� samplingperiods,itisbettertouse explicitformula(28)thantosolvelinearequations (24).

Figure1. StructureoftheMPC‐NPLanalyticalalgorithm

Figure2.

u k k+1 k–1 k+2 k+3 uk() uk(-1) xk() cT u xk+(2)

Figure3. Timedependencesindigitalcontrolsystem withunitarycomputationalcontroldelay ����

Moreover,whatthebasicprocessorreallyneedsis the irst��rowsofthematrix

K(��)= M(��)��ΨM(��)+Λ −1 M(��)��Ψ, (30) calculatedbythesupervisoryprocessor.Denoteby K1(��) irst �� rowsof K(��),thenoptimizationtask performedbythebasicprocessorreducestosubsti‐tution

△��(��)= K1(��)[��������(��)−��0(��)], (31) followedbytrimming △��(��) totheconstraints,as describedintheprevioussection.Thisisthefastest realizationoftheMPC‐NPLalgorithm.

Despiteeffortstominimizethetimeofcomputa‐tionsasmuchaspossible,thistimemaybecompa‐rableoralmostequaltothelengthofthesampling period����,forfastsampling.Thus,itintroducescom‐putationalcontroldelay���� tothefeedbackloop.The mostpracticalcaseitthatof ���� =����,whichwill befurtherconsidered.Possibilitytousethemodel augmentedbythisdelayisanadvantageoftheMPC algorithms.Forthecontroldelay ���� =����,this resultsinaugmentingthemanipulatorstateto ���� = [���� �� ����]∈��3��,andthestateequations(3)to

��(��+1)=

��(��)+���� ̇��(��) ̇��(��)−�� �� ��(��(��))−1[��(��(��))̇��(��)+ ��(��)

+��(̇��(��))+��(��(��))−��(��)] (32)

Itshouldbepointedoutthatthementionedcom‐putationaldelay ���� isanadditionalunitarydelay, whichaddstothestandardunitarydelayofdigital control–resultinginthe irstreactionofthestateon thecontrolsignal ��(��) aftertwosamplingperiods. ThisisschematicallyshowninFigure 3,where ��(��) denotescontrolsignalcalculatedusinginformation (measurements)obtainedattimeinstant��.

3.Controlofadirectdrivemanipulator

3.1.ModelsforManipulatorSimulationandController Design

Theplanartwo‐linkexperimentaldirectdrive manipulator(EDDM)willbeconsidered,itis describedindetailin[35].Itsschematicdiagram isshowninFigure 4.Vectorsofjointangles

Figure4. Schematicdiagramoftheexperimentaldirect drivemanipulator

andcontroltorquesare ��(��)=[��1(��)��2(��)]�� , ��(��)=[��1(��)��2(��)]��,respectively.Matricesand functionofitsmodel(1)are:

(33)

Physicaldatagivenin[35]leadtothefollowingvalues ofmodelparameters:

1 =2.352������2 , ��2 =0.102������

=8.05���� for 1<0,

��2 =1.734����, togetherwithlimitsoncontroltorques:

1������=200����, ��2������=15����.

Weusedthediscrete‐timeversion(3)‐(4)ofthe modelforsimulationofthemanipulatoritselfwithin thefeedbackcontrolloop,withveryshortintegration step���� =0.0001��.Itsdiscrete‐timedynamicsmimics thenperfectlythecontinuous‐timeone.Fordesignof MPCcontrollers,asimpli iedcontinuousanddifferen‐tiablemodelwasused,withCoulombfrictionomitted (treatedasunmodeleddynamics),i.e.��(̇��)=����̇�� .The controllersamplingperiod���� (���� ≫����)wasused.

Table1. ValuesofISEforMPCalgorithmswithcubicreferencetrajectories,forfew ���� anddifferentdisturbances

Thefollowingscenarioofsimulationswasapplied:

• Simulationhorizon:length2.5s.Referencetrajecto‐rieswithtwochangesofjointspositions(angular, inradians), irstchangestartingat0.15s,secondat 1.5s.Thechangesareimplemented:

1) alongcubictrajectories,witheachcubictrajec‐torydurationtime0.5s.

2) assteps,i.e.,referencetrajectoriesarepiecewise constant.

• Disturbances:

– external(Z1):atorque 4���� addedattheinput tothesecondlinkatmiddlepoint1.25softhe simulationhorizon;adisturbancetypicalfortest‐ingcontrollerperformance,includingmanipula‐torcontrollers,see,e.g.,[3];or

– parametricuncertainty(P1):changeodmanipu‐latordynamicsbyaddingamassof1kgatthe endofthesecondarm.Thisleadstochangeof manipulatorparameterstothevalues:

��1 =2.596������2 , ��2 =0.144������2 , ��3 =0.154������2 , ��4 =42.88����, ��5 =3.351����. Theseparametersde inethemanipulatorasthe processinthefeedbacklooponly,controllersare designedusingthepreviouslygivennominalval‐uesofparameters.

• Controlperformancede inedbyISE(integrated squarederrors)criterion:

InthedesignprocessofMPCcontrollers,weight‐ingparametersintheperformancefunctionhasbeen foundtobeappropriatewithvalues[��1��2]=[1010], [��1 ��2]=[0.00010.001],assuringstableandrobust performance.Noticethatdifferencesinvaluesofthe weights �� and �� correspondtodifferencesinranges ofthecorrespondingvariables(scaling).Sampling period ���� =0.005swasbasicallyassumed,butper‐formancewithanothervalueswasalsoinvestigated. Differentpredictionhorizonsweretested, ��=18has beenchosenfor ���� =0.005sasatradeoffbetween computationalloadandperformance/robustness.

3.2.ResultswithMPC‐NOandMPC‐NPLControllers

Acomprehensivecomparisonofcontrolperfor‐mancewithallMPCalgorithmspresentedinthispaper isgiveninTable 1,forthecasewithcubicreference trajectories.ItisintermsofvaluesofISEindex(37), whichmakesthecomparisoneasier.Simulationswere performedinMatlabenvironment,usingfornonlin‐earoptimization”fmincon”andforQP”quadprog” procedures.Formodellinearization,”SymbolicMath” toolboxwastried.But,duetoextremelycomplexfor‐mulaeobtained,numericalapproximationofpartial derivativeswasapplied,withresultspracticallyequiv‐alent,verysmalldifferencesdidnotin luencedcontrol systembehaviour.Threecaseswereconsidered:with unmodeleddynamicsdenotedby”Cf”(Coulombfric‐tion)only,withCfandexternaldisturbingtorque(Zu) orparameteruncertainty(P1)added.

where �������� isthenumberofsamplingperiods ���� alongthesimulationhorizon. Itshouldbepointedoutthattheassumeddistur‐banceandparameterinaccuracyarequitesigni icant. Thedisturbingtorqueisabout27%ofmaximalsec‐ondactuatortorque(15����),changesinparameters ��1,…,��5 arealsoquitelarge.Additionally,nonlinear unmodelleddynamicsispresent(Coulombfriction).

Veryshortcontrolhorizons����=1and����=2assure thesmallestdimensionalityofnonlinearoptimiza‐tionproblems, ���� ×��= 2and4,respectively,thus theshortestonlinecomputation(optimization)time. Thechoice ����=2resultsinbettercontrolperfor‐mance,butperformancewith ����=1maybeaccept‐ablewhencomputationtimeiscritical.ISEvaluewith ����=3isonlyslightlybetterthanfor ����=2,butwith increasedcomputationalload.Foreachofthedis‐turbancecases,resultsforallthreealgorithms,NO, NPLnandNPLa,arepracticallyidentical.Thetrajecto‐riesarevisuallyundistinguishable,thereforearepre‐sentedfortheMPC‐NPLnalgorithmonly,inFigures5 and6,forexternaldisturbanceandparameteruncer‐tainty,respectively.Noticethatexternaldisturbance andparameteruncertaintyarewellattenuated,with minordifferencesforthesamecontrolhorizons.

Figure5. TrajectoriesforMPC‐NPLnwith ����=2andexternaldisturbance(Zu)

Figure6. TrajectoriesforMPC‐NPLnwith ����=2andparametricdisturbance(P1)

Forpiecewiseconstantreferencetrajectories,a directapplicationofeventheMPCalgorithms(aspre‐sentedhitherto)leadsusuallytoexcessivesaturation ofcontrolsignalsandtoovershoots.Butitispos‐sibletoavoidthis,byaddinginternalMPCmecha‐nismtransformingpiecewiseconstantreferencetra‐jectories ��������(��) intointernalreferencetrajectories ����������(��)ofexponentialtype,see,e.g.,[17],[27].This involvesreplacingthe irstsumintheperformance function��(��)in(7)withthesum

and 0≤�������� <1isascalingparameter.For�������� =0, ����������(��+��|��)=��������(��),butthelarger�������� >0the slowertheconvergenceof����������(��+��|��)to��������(��), overthepredictionhorizon.Thistechniqueenables toachievesmooth,overshoot‐freetrajectoriesofthe manipulatorarms.

Figures7and8showmanipulatortrajectoriesfor MPC‐NPLnalgorithmwithandwithoutinternalrefer‐encetrajectorytechnique,respectively,withexternal disturbance.Theadvantageofusingthistechnique canbeclearlyseen.ComparisonofFigures 5 and 7 leadstoconclusionthattheapproachdescribednow isapossiblealternativetosmoothcubictransitions betweenpositions,butinthecubiccasethetrajecto‐riesofcontrolinputsaremoresmooth,withoutsatu‐ration.

=

Figure7. TrajectoriesforMPC‐NPLnwith ����=2, �������� =0.95 anddisturbanceZu;piecewiseconstantreference trajectories

Figure8. TrajectoriesforMPC‐NPLnwith ����=2, �������� =0 anddisturbanceZu;piecewiseconstantreferencetrajectories

MorecomprehensiveresultsareshowninTable2, intermsofISEvalues.Trajectoriescorrespondingto theseresultsaresimilartothoseshowninFigure 7

Thesituationiswithsigni icantconstraintactivity (saturationofcontrolinputs),thereforeapplicationof analyticalalgorithmleadstoinferiorresults.

Thepresentedresultsclearlyindicate,forboth smoothcubicandabruptstepchangesbetweenref‐erencepositions,thatmuchsimplerMPC‐NPLalgo‐rithmscanbeusedpracticallywithoutlossofcontrol quality,insteadofmorecomputationallyinvolvedand lesscomputationallyrobustMPC‐NOone(asnonlin‐earoptimizationislessrobustthanaquadraticone). Thelossofperformancecanbeonlyawaitedwith mostsimpleMPC‐NPLanalyticalversion,incaseswith signi icantactivityofconstraints.

3.3.CTC‐PIDandCTC‐PID2dofControl,Comparisons withMPC

Toevaluateperformance,applicabilityofMPC algorithmstocontrolofroboticmanipulatorsfairly,a comparisonwithexistingtechniqueshouldbedone. Themostcommonlyusedinindustryistheclassical decentralizedPIDcontrol,e.g.,[1,4,36],particularly whenjointmotorsarewithgears,reducingcross‐couplingeffectsbetweenjoints.However,implemen‐tationandtuningofPIDcontrollersmustbemade withcare,toovercomepossibleovershoots.

CTC‐PIDcontrol,withexternalstepdisturbanceat1.25s

Table2. ISEforMPCalgorithmswith ��������=0.95,fortwo valuesof ���� anddifferentdisturbances,forpiecewise constantreferencetrajectories; 1) overshoot4%forsecondstep,eliminatedwith ��=22, 2) overshoot18%forsecondstep,with ��=22reducedto10%

disturb.

Possiblesolutionsare,e.g.,partitionedPDcontrol orPIDwithreferencetrajectorypre iltering,see,e.g., [4].Insomeinstances,double‐loopP‐PIcontrolof positionandvelocitycanbeutilized.However,for manipulatorswithstrongerinteractions,likethose withdirectdrivemotors,themodel‐basedalgorithms areratherrecommended.Thewellknownsolutionis herethecomputedtorquecontrol(CTC),whichlin‐earizesanddecouplesthemanipulator,withPD/PID controllerswithaccelerationfeedforwardontopof thelinearizedmanipulator,see,e.g.,[1,4,36].Com‐parisonofMPCwiththiscontrolstructureseemstobe fair,asbotharenonlinearandmodel‐based.

RecalltheCTC‐PIDcontrolleralgorithm,see,e.g., [1,4,36]:

where �������� istheoutputofamultiloopPIDcon‐troller.Inserting(40)intothemanipulatordynam‐ics(1)resultsinclosedloopdynamicsconsistingof �� thirdorderdynamicalsystemswithPIDgains ������, ������ and������ asparameters,��=1,...,��.Assumingpole placementndesign,polesofcharacteristicequations yieldsformulaeforPIDgains.

Table3. ValuesofISEforCTC‐PIDandMPC‐NPL algorithms,fordifferentdisturbances,withcubic referencetrajectoriesbetweenpositions

CTC-PID MPC-NPLn (��1=18,��2=20) (��=18,����=2) disturb. ISE disturb. ISE none 0.0015⋅10−3 Cf 0.0321

Apopularchoicetogetovershoot‐freeresponse istoassumeonetriplerealpole,see[4, 37],then tuningallgainsofeverySISOPIDcontrollerisbyone parameter, ������ =3��2 �� , ������ =3����, ������ =��3 �� ,where −���� (���� >0)istheassumedpolevalue.Thisvalueis usuallychosenaccordingtorequiredsettlingtime����, foratriplepole��≈8/����,see[37].Assuming���� =0.5 sforbotharms(timeequaltotheperiodofposition changealongcubictrajectories),weget��1 =��2 =16. However,fortrackingsmoothtrajectorieslikecubic onesfurther ine‐tuningisreasonable,bytrialand errormethod.Afterthatwehave inallychosen��1 = 18,��2 =20

Selectedsimulationresultsarepresentedin Table3andinFigure9.Forperfectmodeling(without disturbances),CTC‐PIDissuperior.Butunder disturbances,MPC‐NPLprovidesbetterperformance: signi icantlybetterISEvalues,smallercontrolerrors and,moreover,moresmoothcontroltrajectories, ascanbeseencomparingFigures 9 and 5.Despite thefactthatCoulombfrictionispresentinCTC feedbackmodel(40),see(35),whereasitistreated asumodeleddynamicsinMPCalgorithms.

Figure9.

Figure10. CTC‐PID2dof(CTCPID‐F)control, ����=0.15s,withexternalstepdisturbanceatat1.25s

=T c mod., L=0kg

Figure11. TrajectoriesforMPC‐NPLnwith ����=0.005sandcontroldelay ���� =����,externaldisturbanceZu

Table4. ValuesofISEandovershoot �� forCTC‐PID2dof andMPC‐NPLalgorithms,fordifferentdisturbances, withpiecewiseconstantreferencetrajectories

CTC-PID2dof MPC-NPLn (��1=��2=16,����=0.15) (��=18,����=2) disturb. ISE �� disturb. ISE ��

Itisgenerallynotrecommendedtomakeabrupt stepchangesofconstantreferencepositions,when leavingtoshapemanipulatortransitiontrajectoriesto dynamicsofthefeedbackcontrolloopwithstandard

PIDcontrollersonly,asthisusuallyleadstoexces‐sivesaturationofcontrolsignalsandlargeovershoots. However,augmentingPIDcontrollersbydynamic pre ilteringofpiecewiseconstantreferencesignals improvesthesituation.SuchPIDstructurewithaset‐pointpre ilterisusuallycalledaPID2dofcontroller. Weappliedsuchstructuretoourmanipulator,with irstorderinertialpre ilterswithtimeconstant���� = 0.15s,foreacharm.ForPIDsettings,weapplied��1 = ��2 =16,resultingfromassumedsettlingtime����=0.5 sforbotharms,see[37],toperfectlycoincidewith timeofcubicpositionchange.Addingpre iltersto CTC‐PIDalgorithmscanbetreatedasatechniquecor‐respondingtoaddinginternalreferencetrajectoriesto MPCalgorithmsandshould,therefore,leadtoafair comparisonofbothalgorithms.Selectedresultsare presentedinTable4andFigure10

Table5. ValuesofISEforMPC‐NPLandCTC‐PIDalgorithmsforvarioussamplingintervals ����,withoutandwith computationalcontroldelay ���� =����,forcubictransitiontrajectoriesbetweenreferencepositions

Figure12. TrajectoriesforMPC‐NPLnwith

TheresultsindicatethattheMPCalgorithm providesbetterperformance,especiallyunder disturbances.Despitepre iltering,theCTC‐PID2dof (CTC‐PID‐F)algorithmsuffersthenovershootsand slightlylongersettlingtime(overshootswould bemuchlargerwithoutpre iltering).Whenthese def iciencesareacceptable,thisalgorithmcouldbea designalternative.

3.4.ImpactofSamplingPeriodandComputationTime Delay

Model‐basedalgorithmsneedtoperformmore computationsthansimplerPIDalgorithms.Thiscan resultintangibledelayinimplementationofcontrol signalsduetocomputationtime.

Therefore,weinvestigatedimpactofbothsam‐plingperiodlengthandcontroldelayonperformance ofalgorithmsconsideredinthepaper,inparticular MPC‐NPLandCTC‐PID.Mostpracticallyimportantis thedelayequaltoonesamplingperiod.Itmeansthat, usingnewmeasurementsobtainedatthebeginningof thesamplingperiod,calculationsofthenewcontroller outputmustbe inishedwithinthisperiod,tosendthis outputtotheactuatorsattheendofthisperiod(or beginningofthenextone).

Thein luenceofsuchadditionalunitarycomputa‐tionaltimedelay���� =���� oncontrolperformancewas investigated.Selectedresultsofcomparisonsaresum‐marizedinTable 5,forbothcasesofconsidereddis‐turbances.Thecaseswithoutcontroldelaysarealso given,foreasycomparisons.Controlwiththreesam‐plingperiodswasinvestigated:����=0.01s,����=0.005s and����=0.0025s.InMPCalgorithms,appropriaterela‐tionofthepredictionhorizon��totheprocessdynam‐icsmustbepreserved,physically.

Thatiswhylongerpredictionhorizons��,givenin numbersofsamplingperiods,correspondtoshorter valuesof����.Valuesof�� equalto12,18and26were chosenfordecreasingvaluesof ����,respectively.But ����=2couldbeusedinallcasesaseffectivecontrol horizon.

LookingattheresultsforMPC,itcanbeseenthat decreasing���� improvesISEvalues.Decreasebyfactor 2,from0.01sto0.005s,decreasesISEevenmore, thesameoccurredforthedecreasefrom0.005sto 0.0025s.Consideringresultswithoutandwithcontrol delay,wecanseethatthesmaller ���� thesmallerdif‐ferencebetweenthecorrespondingvalues.Forlargest value����=0.01,deteriorationofISEafterintroduction ofcontroldelayismostvisible.Thatisthereason why ����=0.005shasbeenchosenasthebasicsam‐plingperiodinthepaper.WithdecreaseofISE,con‐trolerrorsshoulddecreasesimilarly,exemplarycon‐irmationisgivenbycomparingFigures 11 and 12, showingmanipulatortrajectorieswithcontroldelay for����=0.005sand0.0025s.

AnalysingresultsobtainedwithCTC‐PIDcontrol wecanseethatincreaseof ���� from0.005sto0.01s increasesISEvaluessigni icantly,butwithdecreaseof ���� to0.0025simprovementismarginal.Ontheother hand,withMPCthisimprovementwassigni icant.The reasonisthatforfastsamplingPIDtuningisasfor continuous‐timecontrol.Therefore,thefastersam‐plingthebetterdiscrete‐timePIDcontrollermimics continuous‐timePIDoneandthesmallerdifferences whendecreasingthesamplingperiod.Forobvious reasons,thesmaller���� thelessthenegativeimpactof computationaldelay.

4.Conclusion

Applicationofeffectiveandmostup‐to‐datenon‐linearMPCalgorithmswithstate‐spacemodelsto manipulatorcontrolwaspresented,incomparison withstandardandenhancedrealizationsofCTC‐PIDalgorithms.MPCalgorithmswerepresentedwith mosteffective,recentlyproposeddisturbanceatten‐uationtechnique[30],whichavoidsnecessityof dynamicmodelingofdisturbances,bothexternalor internal,ortoresorttoalternativeadditionaltech‐niquestoattenuatedisturbances,likeSMC,asmetin severalpapersonMPCcontrolofmanipulators.

Thecoreofthepaperiscomputationallyeffective MPC‐NPLalgorithm(NonlinearPredictionwithLin‐earization),presentedintwoversions:the irstwith constrainedQPoptimizationandthesecond,compu‐tationallysimpler,withunconstrainedoptimization andaposteriorimatchingtheunconstrainedresult withinequalityconstraints.Detaileddiscussionon organizationofcalculationsleadingtoshortestexecu‐tiontimewasprovidedforMPC‐NPLalgorithms.For allalgorithmsacomprehensivecomparativesimula‐tionstudywaspresentedinthepaper,withexper‐imentaldirectdrivemanipulator,undersigni icant externalandparametricdisturbances.Resultswere comparedwiththoseobtainedwithknownCTC‐PID algorithm,whichisalsomodel‐basedandusingthe

nonlinearmanipulatormodel.Thecomparisonswere performedfortwoshapesofreferencetrajectories: smoothcubicorpiecewiseconstant.Forthesecond case,MPCwithadditionalinternalreferencetrajecto‐riesandCTC‐PID2dofalgorithmhavebeenproposed andshowntoleadtopracticallyusefulresults,which seemstobeanoveltyinmanipulatorcontrollitera‐ture.Forallconsideredcases,theMPC‐NPLalgorithms havebeenshowntoperformbetterorsigni icantly betterthanCTC‐PIDalgorithms.However,whencer‐taindeteriorationinaccuracyandsmallovershoots (whichcanoccurafterstepchangesofreferencetra‐jectories)areacceptable,CTC‐PIDorCTC‐PID2dof algorithmscouldbeadesignalternative.

Additionalcontributionofthepaperisinvestiga‐tionofthein luenceofsamplingperiodlengthand computationaldelayonperformanceofMPCandCTC‐PIDalgorithms.Thisisimportantfordesignofmodel‐basedcontrolalgorithmswithfastsampling,asthey requiremorecomputations.

Itisbelievedthattheresultspresentedin thepapershouldbeinterestingforbothapplied researchersandindustrialpractitionersinthe ieldof manipulatorcontrol.

AUTHOR

PiotrTatjewski∗ –WarsawUniversityofTechnol‐ogy,Nowowiejska15/19,Warsaw,Poland,e‐mail: piotr.tatjewski@pw.edu.pl.

∗Correspondingauthor

References

[1] M.W.Spong.Anhistoricalperspectiveonthecon‐trolofroboticmanipulators. AnnualReviewsof Control,Robotics,andAutonomousSystems,5:1–31,2022.

[2] M.F.Khan,R.Islam,andJ.Iqbal.Controlstrate‐giesforroboticmanipulators.In Proceedings ofthe2012InternationalConferenceofRobotics andArti icialIntelligence,Rawalpindi,Pakistan, 2012.

[3] F.L.Lewis,D.M.Dawson,andC.T.Abdallah. Robot ManipulatorControlTheoryandPractice.CRC Press,BocaRaton,2003.

[4] R.Kelly,V.Santibanez,andA.Loría. Control ofRobotManipulatorsinJointSpace.Springer, London,2005.

[5] E.F.CamachoandC.Bordons. ModelPredictive Control.SpringerVerlag,London,1999.

[6] J.M.Maciejowski. PredictiveControl.Prentice Hall,Harlow,England,2002.

[7] T.L.Blevins,G.K.McMillan,W.K.Wojsznis,and M.W.Brown. AdvancedControlUnleashed.The ISASociety,ResearchTrianglePark,NC,2003.

[8] S.J.QinandT.A.Badgwell.Asurveyofindustrial modelpredictivecontroltechnology. Control EngineeringPractice,11:733–764,2003.

[9] P.Tatjewski. AdvancedControlofIndustrialProcesses.SpringerVerlag,London,2007.

[10] L.Wang. ModelPredictiveControlSystemDesign andImplementationusingMATLAB.Springer Verlag,London,2009.

[11] K.J.HolkarandL.M.Waghmare.Anoverviewof modelpredictivecontrol. InternationalJournal ofControlandAutomation,3(4):47–63,2010.

[12] T.L.Blevins,W.K.Wojsznis,andM.Nixon. AdvancedControlFoundation.TheISASociety, ResearchTrianglePark,NC,2013.

[13] J.B.Rawlings,D.Q.Mayne,andM.M.Diehl. Model PredictiveControl:Theory,Computation,and Design2ndEdition.NobHillPublishing,Santa Barbara,California,2017.

[14] I.L.Huang,H.H.Lou,J.P.Gong,andT.F.Edgar. Fuzzymodelpredictivecontrol. IEEETransactionsonFuzzySystems,8(6):665–678,2000.

[15] M.Ławryńczuk. ComputationallyEf icientModel PredictiveControlAlgorithms:ANeuralNetwork Approach.StudiesinSystems,DecisionandControl,Vol.3.SpringerVerlag,Heidelberg,2014.

[16] M.M.Morato,J.E.Normey‐Rico,andO.Sename. Modelpredictivecontroldesignforlinear parametervaryingsystems:Asurvey. Annual ReviewsinControl,49:64–80,2020.

[17] M.ŁawryńczukandP.Tatjewski.Offset‐freestate‐spacenonlinearpredictivecontrolfor Wienersystems. InformationSciences,511:127–151,2020.

[18] T.Rybus,K.Seweryn,andJ.Z.Sasiadek.Appli‐cationofpredictivecontrolformanipulator mountedonasatellite. ArchivesofControlSciences,28(1):105–118,2018.

[19] S.Kleff,A.Meduri,R.Budhiraja,N.Mansard,and L.Righetti.High‐frequencynonlinearmodelpre‐dictivecontrolofamanipulator.In Proceedings oftheIEEEInternationalConferenceonRobotics andAutomation,Xi’an,China,2021.

[20] P.BumroongsriandS.Kheawhom.Interpolation‐basedoff‐lineMPCforLPVsystems.In Proceedingsofthe10thIFACInternationalSymposiumon DynamicsandControlofProcessSystems,Mum‐bai,India,2013.

[21] P.S.G.Cisneros,A.Sridharan,andH.Werner. Constrainedpredictivecontrolofarobotic manipulatorusingquasi‐LPVrepresentations. IFACPapersOnlineConferencePaperArchive, 51(26):118–123,2018.

[22] J.Wilson,M.Charest,andR.Dubay.Non‐linear modelpredictivecontrolschemeswithappli‐cationona2linkverticalrobotmanipulator. RoboticsandComputer-IntegratedManufacturing,41:23–30,2016.

[23] A.Benniran.Predictiveoptimizingreference governorforconstrained2dof’srobotwith abruptset‐pointtrajectories. JournalofApplied Science,SabrathaUniversity,1:39–49,2018.

[24] A.Ferrara,G.P.Incremona,andL.Magni.A robustMPC/ISMhierarchicalmulti‐loopcontrol schemeforrobotmanipulators.In Proceedings ofthe52ndConferenceonDecisionandControl, Florence,Italy,2013.

[25] G.P.Incremona,A.Ferrara,andL.Magni.MPCfor robotmanipulatorswithintegralslidingmodes generation. IEEE/ASMETransactionsonMechatronics,22(3):1299–1307,2017.

[26] S.Bouzoualegh,E.Guechi,andY.Zennir.Model predictivecontrolofathreedegreesoffreedom manipulatorrobot.In Proceedingsofthe3rd InternationalConferenceonAdvancedSystems andEmergentTechnologies,pages84–89,Ham‐mamet,Tunisia,2019.

[27] D.Nicolis,F.Allevi,andP.Rocco.Operational spacemodelpredictiveslidingmodecontrolfor redundantmanipulators. IEEETransactionson Robotics,36(4):1348–1355,2020.

[28] P.Tatjewski.Disturbancemodelingandstate estimationforoffset‐freepredictivecontrolwith state‐spacedprocessmodels. InternationalJournalofAppliedMathematicsandComputerScience,24(2):313–323,2014.

[29] P.Tatjewski.Offset‐freenonlinearpredic‐tivecontrolwithmeasuredstateandunknown asymptoticallyconstantdisturbances.InK.Mali‐nowski,J.Józefczyk,andJ.Światek,editors, Aktualneproblemyautomatykiirobotyki,pages 288–299.AcademicPublisherEXIT,Warszawa, Poland,2014.

[30] P.Tatjewski.Offset‐freenonlinearModelPre‐dictiveControlwithstate‐spaceprocessmod‐els. ArchivesofControlSciences,27(4):595–615, 2017.

[31] P.TatjewskiandM.Ławryńczuk.Algorithmswith stateestimationinlinearandnonlinearmodel predictivecontrol. ComputersandChemicalEngineering,143:1–19,2000.

[32] P.Tatjewski.Nieliniowesterowaniepredyk‐cyjneramionmanipulatorów(Nonlinearpredic‐tivecontrolofmanipulatorarms). Pomiary AutomatykaRobotyka,27(2):47–58,2023.

[33] L.GarciaandE.Rosero. Non‐linear model‐basedpredictivecontrolfortrajectory trackingandcontroleffortminimizationin asmartphone‐basedquadrotor. Journalof Automation,MobileRoboticsandIntelligent Systems,16(4):13–18,2022.

[34] P.Tatjewski. Sterowaniezaawansowane procesówprzemysłowych(AdvancedControlof IndustrialProcesses),Second,revisededition (e‐book,inPolish).AcademicPublishingHouse EXIT,Warszawa,2016.

[35] F.ReyesandR.Kelly.Experimentalevaluation ofidenti icationschemesonadirectdriverobot. Robotica,15:563–571,1997.

[36] M.Spong,S.Hutchinson,andM.Vidyasagar. RobotModelingandControl.J.WileyandSons, 2005.

[37] A.BożekandL.Trybus.TuningPIDandPI‐PIservocontrollersbymultiplepoleplacement. BulletinofthePolishAcademyofSciencesTechnicalSciences,70(1):1–12,2022.

SOC‐FPGABASEDCONCEPTOFHARDWAREAIDEDQUANTUMSIMULATION

Submitted:24th February2023;accepted:13th July2023

JacekDługopolski,JakubCzerski,MateuszKnapik

DOI:10.14313/JAMRIS/2‐2024/9

Abstract:

Contemporaryindustryandscienceexpectations towardstechnologicalsolutionssetthebarhigh. Currentapproachestoincreasingthecomputing powerofstandardsystemsarereachingthelimitsof physicsknowntohumankind.Fast,programmable systemswithrelativelylowpowerconsumptionarea differentconceptforperformingcomplexcalculations. Highlyparallelprocessingopensupanumberof possibilitiesinthecontextofacceleratingcalculations. ApplicationofSoC(SystemOnChip)withFPGA(Field‐ProgrammableGateArray)enablesthedelegatingof apartofcomputationstothegatesmatrix,thereby expeditingprocessingbyusingparallelizationof hardwareoperations.Thispaperpresentsthegeneral conceptofusingSoCFPGAsystemstosupporttheCPU (CentralProcessingUnit)inmanymoderntasks.While sometasksmightbereallyhardtoimplementonan FPGAinareasonabletime,theSoCFPGAplatform allowsforeasylow‐levelinterconnections,andwith suchvirtualizedaccesstothehardwarecomputing resources,itisseenasmakingFPGAs,orhardwarein general,moreaccessibletoengineersaccustomedto high‐levelsolutions.Theconceptpresentedinthearticle takesintoaccountthelimitedresourcesofcheaper educationalplatforms,which,however,stillprovide aninterestingandalternativehybridsolutiontothe problemofparallelizationandaccelerationofdata processing.Thisallowsencounteredlimitationstobe overcomeandtheflexibilityknownfromhigh‐level solutionsandhighperformanceachievedwithlow‐level programmingtobemaintainedwithouttheneedfora highfinancialbackground.

Keywords: FPGA,SoC,quantumcircuit,parallelcomput‐ing,webservice,acceleratingcalculations

1.Introduction

Nowadays,practicallyeverysectorofhumanactiv‐itybene itsfromtechnologicalsolutions.Accelerat‐ingandoptimizingexistingprocessesandautomat‐ingnewoneswillimprovequalityandusercomfort. Growingdemandforcomputingpowerhascausedthe creationofnewintegratedcircuitswithcomputing coresthatareclockedatevenhigherfrequencies.It carrieswithitanincreaseintheenergyrequiredand, consequently,ariseofemittedheatthathastobe dissipated.

Forthisreason,engineershasintroducedsystems composedofmanycomputationalunits,enablingpar‐alleloperations.Anotherperspectiveoptionisthe FPGAchip–amatrixofindependentlycon igurable logicgates,whichprovidesnaturallymassiveparal‐lelismthatincreasesthecomputingpowerwhilecon‐sumingmuchlessenergy.

Programmablegatearraysconsistofalargenum‐berofadvancedlogicalunits,veryfastRAM(Random AccessMemory)blocksandspecializedDSP(Digital SignalProcessing)modules,alleffectivelysurrounded byinternalhardwareconnectionbuses.Therearealso programmableinput/outputblocksatlogicalarrays andboundariesforcommunicationwithotherexter‐nalcomputingunits.Currently,FPGAsystemsare commonlyusednotonlyfordigitalsignalprocessing butforregularcomputingtasksaswell.They ind applicationswhenhighlyfastdatacomputingandpro‐cessparallelizationarerequired,e.g.insatellitesoft‐ware,militaryradars,GPSandcellularphonesystems, andalsoinimageprocessing,emulationofphysical phenomenaandinsolutionsthatrequirehigh‐speed communicationnetworks.Commercialorganizations, aswellasresearchinstitutions,commonlyturnto FPGAinmanyapplications.

Standardcomputingsystemshaveusuallysepa‐ratedCPUs,GPUs(GraphicsProcessingUnits),periph‐erals,devicescontrollers,etc.Inthecaseofmobile processorsdedicatedtothesmartphoneandtablet market,allunitsdescribedabovetendtobeintegrated andimplementedonasinglechipcalledSoC(System onChip).SoCsystemshavemanybene itsintheera oftheIoT(InternetofThings).SoCFPGAschips,in additiontotheProgrammableLogicArrayavailable inside,alsocontainaready,built‐inCPUprocessorand dedicatedveryfastcommunicationchannelsbetween thetwomentionedparts.Theyprovidethefollow‐ingadvantages:miniaturization,integration, lexibil‐ity,computingacceleration,energysavingsandlow TCO(TotalCostofOwnership).Ahardwaredescrip‐tionlanguageisusedtocon iguretheFPGA.Sys‐temVerilogandVHDLarecurrentlythemostpopu‐larsolutionsonthemarket.Bytheuseofsynthesis tools,aninternalcommunicationlinkslistisgener‐ated.Finally,thecreatedcon igurationismappedto agivenchip.Whenthecon igurationisbeingmapped, aproblemoflackofresourcesmayoccur;hence,itis importanttooptimizelogicfunctionsduringtheFPGA applicationdevelopmentprocess.

Theproblemoflimitedresourcesmayconcern, inparticular,cheaperplatforms,e.g.educationalplat‐formssuchastheonedescribedlaterinthisarticle. Themainconceptelaboratedinthispaperisadirect answertothisresourcelimitation.Themaincontribu‐tionsofthepaperareasfollows:

‐ Generalideaofhardwaresupportforcalculations inwebservices,whichtakesintoaccounttheCPU of load,parallelizationandasynchronousdatapro‐cessingwithlimitedresources.

‐ Apracticalexampleoftheimplementedabovecon‐ceptistheuseofhardwareaccelerationintheform ofanFPGAcoprocessorontheexampleofanedu‐cationalwebservicedesignedtoperformquantum calculations,whichincludes:

‐ ProgrammingFPGAlogicforasynchronousoper‐ation;

‐ Con igurationofcommunicationbetweenFPGA andCPUprocessor,andaproposalonhowto constraintherepresentationoftransferreddata, importantinthecaseofcheapandresource‐limitedsystemsand

‐ UsingcreatedFPGA‐basedcoprocessorservices directlyfromtheinternalmainprocessor. Thepaperisorganizedasfollows:Section 2 pro‐videsanoverviewofrelatedworks;Section3de ines thegeneralideaofhardwaresupportforcalculations withanemphasisonSoCFPGA;Section 4 describes communicationstandardsandhardwaredetails;Sec‐tion5presentsapracticalexample–web‐basedquan‐tumtoolkitsimilartoIBMQuantumComposer[2] withFPGA‐basedquantumgatesoperations;Section6 summarizesthepaper.

2.RelatedWorks

Heterogeneousprogrammablesystem‐on‐chip (SOC)FPGAdevices,whichcombinebothgeneral‐purposeprocessorsandrecon igurablefabricsand provideacompellingplatformformanysystems applicationsusingIoTtechnology[11].Theauthors payattentionheretothehardwareabstraction. Accordingtothem,FPGAshouldbebettervirtualized inordertobecomeavailableforengineersthatare accustomedtosoftwareAPIabstractionsandfast productdelivery.

ASICs(ApplicationSpeci icIntegratedCircuits) areveryexpensive,andtherefore,cheapersolutions areusuallyimplementedforprototypingpurposes. ThetimeofdevelopmentofanASICplatformisalso longandrequiresexpertknowledge.Forexample,the authorsof[7]arguethat”FPGAsarelessdenseand slowerthanASICs,buttheir lexibilityoftenmorethan makesupforthesedrawbacks”,inparticular,asfar aspriceandavailabilityisconcerned.TheSoCFPGA canprovideaproperabstractionlayer.Thankstothis, suchsystemsaremuchcheapertoimplementcom‐paredtoASICsbutstillgivemorebene itsoverpurely CPU‐basedsystems.

Itisworthmentioningthatinthetimesofcloud solutionsmanyleadingcompaniesintroducehard‐wareintheirportfolioasIaaS(InfrastructureasaSer‐vice)inordertoreducetheircosts.Anexampleofsuch aCloud‐ScaleAccelerationArchitecture,usingFPGA technologyasamainacceleratorinthedatacentre, ispresentedin[6].ManydatacentresdeployFPGA intheirinfrastructureswithtwomainapproaches: FPGAtightlycoupledtotheCentralProcessingUnit (CPU)orFPGAasastandalonecomponent[13].This trendshowsthatFPGAsarewillinglyusedbycompa‐niesprovidingcomputingsolutions.In[8],theauthors proposeageneralframeworkforhardware‐based webapplicationsthattakeadvantageofcloud‐based FPGAstomakethisapproachmoreaccessibletousers. Theiraimistomakeiteasiertoaccessthebene its ofFPGAwithoutanyextraeffort.Veryoften,hard‐wareaccelerationisusedinAI(Arti icialIntelligence) systems,especiallyindataprocessingrelatedtothe machinelearningalgorithms,asshownin[12].

Undoubtedly,itmustbesaidandadmittedthatthe bestsimulationeffectsofquantumsystems,similar torealphysicalphenomena,canbeobtainedusing onlyprogrammableFPGAlogic.Itsmassiveparal‐lelismandnaturalreal‐timecapabilityisirreplace‐able.Theauthorof[10],usingatensornetwork formalism,showsoneofthemethodsofsuchan approach.However,withsmall‐capacityFPGAs,their programmablelogicdepletesveryquickly,greatlylim‐itingtheexpandabilityofthesimulator.Thenthetech‐niquesofhybriduseofSoCFPGAchipsdescribedin thisarticlecancomeinveryhandy.Thankstothem, thesimulationsystemcanbedividedbetweenthe FPGAlogicandthebuilt‐inprocessor,leavingonlythe keyfragmentsofparallelcalculationsforthesimula‐tionontheFPGAside.

3.GeneralIdeaofHardwareSupportfor Calculations

Furtherincreasingthecomputingpowerisstill possiblebyproducingmulti‐coremicroprocessorsor bybuildingcomputersbasedonmanyindependent computingunits.Certainly,thispotentiallyenables theuseofparallelalgorithmsinapplicationsrequir‐ingfastcalculations.Creatingusefulsystemsfor suchcomputationalarchitecturesisnoteasy,either becauseoftheneedtoprovidefastexternalcommuni‐cationchannelsbetweenprocessorsorbecauseofthe limitedabilitytoscalehardwaredesignedforthese systems.Anincreasingnumberofcoresorproces‐sorsinsuchsystemsisverydif icult.FPGAtechnology canhelphere.Inasingleprogrammableintegrated circuit,onecancon igureawholegroupofindepen‐dentprocessorsandthenimplementanyalgorithm ofmassivelyparalleldataprocessingforthem.Itis mucheasiertocreatesomeparallelapplicationsif anadd‐onHPS(HardProcessorSystem)isintegrated withtheFPGAmatrixinonechip,theso‐calledSoC FPGAchip.Allfastand lexibleconnectionsbetween FPGAhardwareblocksandHPSarethenoptimally implementedinsidethesameintegratedcircuit.

Beingonthesamesilicon,communication betweenCPUandFPGAconsumeslesspowerin comparisontoseparatechips.Theintegration ofinternalconnections(bridges)betweenthe processorandtheFPGAleadstosubstantiallyhigher communicationbandwidthandlowerlatency[7]. ThegeneralconceptofCPU(HPS)supportthrough theuseofparallelprocessingunitsinSoCFPGAs systemscomparedtoCPU‐onlysystemsispresented inFigure1andFigure2

Parallelexecutioncomparedtothesequentialone resultsinreducedruntime.Delegatingsomecalcula‐tionstoseparatemoduleresultsinadditionallyreleas‐ingtheprocessor’sresources,which,atthesametime, isabletoperformothertaskswhenprogrammed effectively.TheFPGAmatrixisahardwarecompo‐nentthatperfectly itsthisconcept.Aproperlypro‐grammedmatrixiscapableofparallelingthecommis‐sionedcalculationsandthusreturnstheresultsfaster. Asuf icientlylargeFPGAmatrixcanbebrokendown intofunctionalfragments,eachcapableofperform‐ingdifferenttasks.Thisapproachenablestheuseof hardwareaccelerationinadistributedsystem,where computationsupportisessentialformanyproblems. Anexampleofsuchasolutionisasystemconsisting ofmanywebservicesusingsupportincalculations. Thesewebservicesdelegatetheirworktoappropriate fragmentsoftheFPGAmatrixandthenreadresults fromthem.Therepresentationofthedatasentto thematrixshouldbecarefullyconsidered,depend‐ingontheselectedFPGAprogrammingmethod.This isespeciallyimportantwhenthesystemhaslimited resources.ProcessorsandFPGAsintegratedtogether canformaninterestingbasisformanyembeddedsys‐tems.Thisintegrationofbroadprocessorfunctional‐ityandtheFPGAabilitytoperformmassivelyparallel operationsinreal‐time,andalltheseinasinglechip, makessuchanembeddedsystemamuchmoreversa‐tileandef icientcomputingplatform.

4.CommunicationStandardsandHardware

Details

Therearemanycommunicationstandardsavail‐abletotransferdatabetweentheCPUandFPGA.In general,theCPUandFPGAcanbeconnectedviaPCIe (PCIExpress),RIFT,CAPIorXillybus.Also,MultiGiga‐bitTransceiversorevenEthernetispossible[14].

Theabundanceofcommunicationstandardsintro‐duces lexibility,butatthesametime,requiresthe implementationofanappropriatephysicallayerfor theselectedstandard.Inordertoimprovecommu‐nication,SoCFPGAsupportsindustry‐standardAXI (AdvancedeXtensibleInterface)bus[9].Comparedto previouslymentionedsolutions,i.e.PCIeorEthernet, thisstandardrequiresfewerresourcesandprovides stillbetterperformance[14].Thiscanbeviewedas thevirtualisationofhardwareresources.

Theideaofhybriddataprocessingsystembased onFPGAandCPUcombinedinonechip,presented above,canbeimplementedontheIntelCycloneVSoC FPGAchipusedbytheauthorsofthisarticletotestthe concept.ThereadyAtlas‐SoChardwaredevelopment platform[5]wasused.Thesystemhasabuilt‐inpro‐cessorcalledHPS(HardProcessorSystem)basedon ARMCortex‐A9architecture,operatingatafrequency of925MHz,andaprogrammableFPGAmatrixwith40 thousandlogicalelements.Thehardwaredesignplat‐formhasmanybuilt‐incomponents,makingitideal forprojectprototyping.

TheHPShasthreebridgesthatusememory‐mappedinterfacestoFPGAsbasedontheArm AdvancedMicrocontrollerBusArchitecture(AMBA) andAdvancedeXtensibleInterface(AXI)[1].Inother words,themoduleresponsibleforthecontrolof theFPGAsystemcontainsnecessaryinformation aboutthemappingofphysicalportstotheirvirtual addressesbywhichithasdirectaccesstoFPGA.The HPS‐FPGAbridgesschemaispresentedinFigure3.

LightweightAXIhasapermanent32‐bitconnec‐tiontoFPGAandallowsworkinginamain‐agent mode,wherethemainisinHPSandallowsaccessto memory‐mappedFPGAportsworkinginagentmode. DespitethefactthatAXIsupports32,64and128 bits,andalsoworksfaster,accordingtoIntel’sdocu‐mentation,thisbridgeisusedforburstinformation transfer,thereforeitisnotrecommendedtouseitto accessperipheralregistersintheFPGAstructure.The LWH2FBridgeandtheF2SInterfacewereusedinthe describedherepracticalexample.

Figure1. CPUonly system Figure2. SoCFPGAsystem

Figure3. HPS–FPGAbridges[1]

5.PracticalExampleofUsingtheConcept

Inordertodemonstratetheapplicabilityofthe conceptpresentedhere,theveryrapidlydeveloping ieldofquantumcomputinghasbeenselected.Quan‐tumcomputingischaracterizedbyamassivelyparal‐lelwayofprocessinginformation.Simulatingthistype ofcomputationonaclassiccomputerismoredif icult themorequbitsyouwanttosimulate.Therefore,the paralleldataprocessingpotentialofFPGAscangreatly facilitatethistypeofsimulation.

Quantumcomputingisa ieldthatcombinescom‐puterscienceandquantummechanics.Itdealswith usingthepropertiesofquantumsystemstopro‐cessinformationthatisclassicallyunattainable.The basicinformationcarrierinquantumcomputingisthe qubit,whichisthequantumequivalentoftheclassical bitusedincomputerscience.Aqubitisdescribedby anarbitrarylinearcombinationofbasestates,inthis case:’0’and’1’.Therefore,aqubitisaquantumsuper‐positionof’0’and’1’.Duringthecalculations,aqubit valuemaycovertheentirespectrumofsuchsuper‐positions,accordingtothelawofprobability.Oper‐ationsonqubitsarerepresentedbyquantumgates thatconceptuallycorrespondtologicgatescommonly usedinalmosteveryclassicalhardware.Thisrefers tothemostpopularquantummodelofhowinforma‐tionisprocessed.Quantumgatesarebasicoperations performedontheavailablequbitstoimplementa quantumalgorithm,whichcanbeindirectlycompared tobitoperationsperformedbyclassicallogicgates. Diracnotation,alsocalledbra‐ketnotation,isused tosimplydenotequantumstatesandtodistinguish themmoreeasilyfromclassicalstates.Thenotation usesanglebracketsandaverticalbartoconstruct appropriatesymbols.Thismakesiteasiertodescribe theprocessesofquantummechanics,inparticular operationsperformedbyquantumgates.

Aketisoftheform |Ψ⟩ andmathematicallyit denotesavectorΨinacomplexvectorspace.Physi‐cally,itrepresentsastateofsomequbit.UsingDirac notation,thequantumstatescorrespondingtoclas‐sical’0’andclassical’1’canbeexpressedas |0⟩ and |1⟩.Mathematicallytheyrepresentthefollowingvec‐tors(1):

|0⟩= 1 0 |1⟩= 0 1 (1)

Anyqubit,whichisanarbitrarylinearcombination ofbasestates:|0⟩and|1⟩,isdescribedasasuperposi‐tion(2):

|Ψ⟩=��|0⟩+��|1⟩ (2) where�� and�� arecomplexnumberssuchthat��2 + ��2 =1.Quantumgates,ontheotherhand,canberep‐resentedbymatrices.Anexampleofasimplequantum gateisaPauli‐Xgate(X),whichhasthepropertyof changingthestate|0⟩tothestate|1⟩andviceversa.By applyingaquantumgateonaqubit,theappropriate operationisperformed.Inthefollowingcases,gateX negatesthequantumstate(3):

��|0⟩=|1⟩ ��|1⟩=|0⟩ (3)

Pauli‐Xgateexpressedinmatrixrepresentationis shownbelow(4):

01 10 (4)

Quantumgatesareusedtobuildquantumsystems thatprocessqubitsinsuperpositionstates.Thestate ofamulti‐qubitsystemisexpressedbyatensorprod‐uctwhileapplyingaquantumgatetoaqubitimplies amatrixmultiplicationbyavector.The inalstepin theprocessingofaquantumalgorithmisalwaysthe measurementofspeci icqubits,andeachmeasure‐mentofaqubitcausesitswavefunctiontocollapse andbringitsstatedowntooneofthebasestates. Systemscomposedofmultipleparallelquantumgates, whensimulatedonaclassicalcomputer,arecalcu‐latedsequentially,gatebygate,operationbyopera‐tion.Conversely,aquantummachinecalculatesthe stateofsuchacircuitinaninstant.Contrarytoaclassic processor,aproperlycon iguredFPGAinmanycases cansigni icantlyfacilitatetheef icientemulationof thisquantumbehaviour.Anexemplarysystemcreated onthebasisoftheproposedconceptisasimpleweb serviceimplementedontheSoCFPGAplatformand intendedforlearningtheworkingprinciplesofbasic quantumgates.Ausercancreateasimplequantum circuitthroughawebbrowser,andthenobservethe statesofallqubitsatmanypointsinthecircuitinreal time.Adedicatedmodeallowspartofthecalculations tobeperformedontheFPGA.

Themaincomponentsofthesystemare:client application,serverandquantumsimulationmodule onHPSandthecoprocessorresponsibleforhardware emulationofquantumoperationsonFPGA.Thissys‐temarchitectureispresentedinFigure 4.Theclient sendsrequeststotheserverandwaitsfortheresults inresponses.TheServercommunicateswiththeFPGA throughtheSimulationModuletosendpartofthe mostintensivecomputationstoit.Then,thework isparallelizedandcomputedasynchronouslyinside FPGAprogrammablelogiccircuits.

TheSimulationModulemanagesthiscommunica‐tionusingtheBridgebetweentheHPSprocessorand theFPGAlogicmatrix.Additionally,ausercommuni‐cateswiththeSystemviatheInternetusingtheREST APIstandard.

Figure4. Systemarchitecture

1.Client

Theclientapplicationisawebsitecreatedwiththe Reactframework[3]thatconnectstotheservervia theRESTprotocol.Itstaskistoenablethegraphical creationofquantumcircuitsandcommunicationwith theserver.Figure5demonstratestheinterfacewitha customquantumcircuitelaborated.

Theusercancomposecircuitsbydraggingquan‐tumgates:ID,Pauli‐X,Pauli‐Y,Pauli‐Z,Hadamard,S, S*,T,T*andCNOT.Theinterfaceadditionallyprovides descriptionsandmatrixrepresentationsofallavail‐ablegates.

Theproposedsystemiscapableofviewingthe resultsofthecalculationsperformedaftereachopera‐tionbyaspeci icquantumgate.Theseresultsarenota measurementofthesystem,butarawrepresentation oftheresultsofgateoperationsonthestateofthe qubits.Thisapproachhasbeenadoptedtofacilitate theunderstandinganddebuggingofthecreatedquan‐tumcircuits.Inthepresentedexample,whichisonlya simpleproofoftheconceptdescribedinthearticle,a typicalquantummeasurementoperationhasnotbeen implementedbutcouldbeaddedifneeded.Theimple‐mentationofthequbitsmeasurementoperationcould usearandomnumbergeneratorasanapproxima‐tionofthequantumprobability,fromwhoseresults andalsobasedonthecurrentquantumstateofthe measuredqubits,the inalclassicalstateofthequbits wouldbedetermined.

Thequantumcircuitwizardpresentedhereis exemplary,sothenumberofavailablequantumgates hasbeenlimitedtothemostbasicones.However, extendingthesystemwithfurthergatesalsowould notbeademandingtask,astheimplementation methodinterpretsthegatetypesinagenericway, basedontheirmatrixrepresentations.Addingmore gateswouldonlyinvolvede iningtheappropriate matricesandpreparingthemforhandlingbythe Client.

2.Server

TheservermoduleisaJavawithSpringframework [4]application.Itexecutesincomingrequestsfromthe client.Afterreceivingquantumgatescircuitinforma‐tionintherequest,thedataisappropriatelyconverted andsenttotheSimulationModulelocatedinthesame HPSpartofthechip.Then,afterreceivingtheresults, theserversendsthembacktotheclient.TheServeris responsibleforstartingandcontrollingtheoperation

oftheSimulationModule.FromtheServerlevel,pass‐inginputdatatothesystemispossiblethroughtheuse oftheSimulationModuleprogramarguments,while readingtheoutputdataishandledthroughstandard output.

3.SimulationModule

Thesimulationmoduleorganisescalculationsof processestakingplaceinthesimulatedquantumcir‐cuit.Aftertheappropriatetransformationofthequan‐tumgatematrix,itorderscalculationstotheCopro‐cessor,i.e.logicalcircuitlocatedintheFPGApartof thechip.Theresultsarecomputedcolumnbycolumn inthecircuit.Afterreceivingtheresultsofthesecalcu‐lations,theSimulationModulereconnectsthemwith therestofthedataandsendsthesimulationeffectsto theServer.

4.Bridge

TheBridgeenablesthecommunicationbetween theSimulationModuleandtheFPGAcoprocessor. ItusesalightweightinterfacebasedontheAXI (AdvancedeXtensibleInterface)standard.Thedata issentback(read)fromFPGAusingtheF2Sinter‐faceandmemorymapping.Thedataisimmediately transferredtotheFPGAviaAXIandrecordedinthe appropriatelocalregisters.

5.Coprocessor

Thesimulationprocessofquantumcomputations takesplacepartiallyonaprogrammableFPGAmatrix, whiletheSimulationModulelocatedontheHPSis responsibleforthecontroloftheentireprocess.The simulationinsidetheFPGAisbasedonperforming basicarithmeticoperationsovercomplexnumbers, inparticular:addition,subtractionandmultiplica‐tion.Thispartofthesimulatorisdevelopedinthe VHDLhardwaredescriptionlanguage.Notethatthe approachtotheproblemandhardwareimplemen‐tationofthelogiconFPGAisverysimple.Thepri‐marypurposeofthisexampleistoshowtheideaof hardware‐aidedsimulationusingtheSoC‐FPGAplat‐form.

Inquantumcomputing,allnumbersarerepre‐sentedinthe ieldofcomplexnumbers.Oursolution isbasedonsimpleobservationandminimizesthe numberofrequiredresourcestorepresentcomplex numbersandallowstokeep loatingpointprecision. Mostofthebasicquantumgatesavailableinthesys‐temconsistof0sand1s.Hadamardgate,forinstance, hasanadditionalvalue: 1 √2.However,itcanbestill brokendownintoabsolutevaluesandamatrixthat consistsofonly0sand1s(5).

Figure5. Clientapplication’sinterface

Allvaluessuchas 1 √2,inthatcase,canbestored directlyonHPS;whereas,matricescanbesentto FPGA.Torepresentvaluesfromtheset‐1,0,1weneed only2bitsandwedonotneedtoimplement loating‐pointrepresentationonFPGA.Inthe irststep,we needtobuildaninitialqubitstate.Next,wecalculate the inalstaterow‐wiseanditeratecolumnbycolumn. Asasimpleexample,let’sconsiderthecircuitfrom Figure5

|��1��2⟩=��������((��⊗����)|00⟩) (6) whereIDandCNOTgatesarede inedasfollows:

(7)

designedintheReactframework,throughaJava Spring‐basedapplication,withalow‐levelFPGA‐basedparallelcoprocessor.Animportantadvantageof thedemonstratedsystemarchitectureandcomputing conceptistheeaseofintegrationofhigh‐leveltech‐nologiesandsolutionscommonlyusedcommercially withtheirownhardwareaccelerator,whichhasnow becomepossiblethankstotheuseoftheSoCFPGA platform.

6.Conclusion

Intheaboveequationfromanexample(6),allthe elementsapartfromtheHadamardgateconsistof0s and1s.Toensurethatallmatricesconsistofonly0s and1s,temporaryHadamardgateH’isintroduced(7).

Next,theequationcanbetransformedtothe inal form(10)thatconsistsofvectorsandmatriceswith only0sand1s(11). |��1��2⟩= 1 √2��������((��′ ⊗����)|00⟩) (10)

Thehardware‐aidedparallelcomputingconcept basedontheSoC‐FPGAcouldhavemanymoreappli‐cationsthanjustthequantumsimulationshownhere. Thedemonstratedarchitectureofahardwareplat‐formequippedwithaprogrammableFPGAmatrixis aversatiletechnicalsolutionthathasagoodchanceof evengreaterexpansioninthefuture,especiallyinthe ieldofprocessordevelopmentandcloudinfrastruc‐ture.The lexibilityofFPGAprogrammingfacilitates theprototypingofawiderangeofnewtechnological solutions.Theimplementationofanextensivesys‐temwithmanymodulesonasmallplatformisabig technicalchallenge.Asolutionliketheoneshownin thisresearch,availabletoeveryone,showsthatwith creativity,manylimitationscanbeomittedandthe entiresystemcanbene itfromincreasedcomputing powerwhilestillkeepinglowerenergyconsumption. ThisisacrucialaspectforR&Dprojectsattheinitial stepofadvancementwhenthecostsofprototyping shouldbeadjustedtotheriskoftheproject.De initely, morecomplexalgorithmssuchasWaveletorFourier transformationsforfastsignalsanalysisorotherscan bene itfromthehybridimplementationsonSoC‐FPGA platforms.

AUTHORS

Fromequation(11)allmatricesaresenttoFPGA. Requiredmatrixmultiplicationsandtransformations canbeperformedsimultaneouslythankstotheuse ofFPGA.The inalresultistheFPGAoutput(vector) multipliedbytheabsolutevalue 1 √2 storedonHPS (12).

Theconceptofrestoringappropriatevaluesonthe HPSisthebasisoftheimplementationofthehardware coprocessor.Themaindisadvantageoftheelaborated solutionistheadditionalloadontheprocessorthat mustrecreatetheresult.Nevertheless,inorderto transfer loatingpointnumbers,theprocessorwould havetoconvertandthenrecreatetheappropriate formaswell.

Byconnectingtwodifferentplatforms:FPGAand HPS,itwaspossibletocombineahigh‐levelGUI

JacekDługopolski∗ –FacultyofComputerScience, AGHUniversityofKrakow,al.A.Mickiewicza30,30‐059Kraków,Poland,e‐mail:dlugopol@agh.edu.pl. JakubCzerski –EuropeanOrganizationforNuclear ResearchCERN,Espl.desParticules1,1211Meyrin, Switzerland,e‐mail:jakub.marek.czerski@cern.ch. MateuszKnapik –CyberOwlLtd,No1Colmore Square,Birmingham,UnitedKingdom,B46AA,e‐mail: mateusz.knapik@cyberowl.io.

∗Correspondingauthor

ACKNOWLEDGEMENTS

Theresearchpresentedinthispaperwaspartially supportedbythefundsassignedtoAGHUniversity ofScienceandTechnologybythePolishMinistryof ScienceandHigherEducation.

References

[1] “An796:Cyclone®vandarria®vsocdevice designguidelines”.

[2] “Ibmquantumcomposer”. https://quantum‐computing.ibm.com/composer/files/new Accessed:27/6/2022.

[3] “Reactlibrary”,https://reactjs.org.

[4] “Springframework”,https://spring.io.

[5] “Atlas‐sockit‐usermanual”,2015.

[6] A.M.Caul ield,E.S.Chung,A.Putnam, H.Angepat,J.Fowers,M.Haselman,S.Heil, M.Humphrey,P.Kaur,J.‐Y.Kim,D.Lo, T.Massengill,K.Ovtcharov,M.Papamichael, L.Woods,S.Lanka,D.Chiou,andD.Burger,“A cloud‐scaleaccelerationarchitecture”.In: 2016 49thAnnualIEEE/ACMInternationalSymposium onMicroarchitecture(MICRO),2016,1–13.doi: 10.1109/MICRO.2016.7783710.

[7] M.C.Herbordt,Y.Gu,T.VanCourt,J.Model, B.Sukhwani,andM.Chiu,“Computingmodels forfpga‐basedaccelerators”, ComputinginScienceEngineering,vol.10,no.6,2008,35–45.doi: 10.1109/MCSE.2008.143.

[8] S.Hoover,“Hardwareacceleratedwebapplica‐tionsusingcloudfpgas”,2018.

[9] Z.Jiang,N.Audsley,D.Shill,K.Yang,N.Fisher, andZ.Dong,“Briefindustrypaper:Axi‐interconnectrt:Towardsareal‐timeaxi‐interconnectforsystem‐on‐chips”.In: 2021IEEE 27thReal-TimeandEmbeddedTechnologyand ApplicationsSymposium(RTAS),2021,437–440. doi:10.1109/RTAS52030.2021.00046.

[10] M.Levental,“Tensornetworksforsimulating quantumcircuitsonfpgas”,2021.

[11] X.Li,C.Fei,andD.Maskell,“Fpgaoverlays: Hardware‐basedcomputingforthemasses”, 2018.doi:10.15224/978‐1‐63248‐144‐3‐12.

[12] S.Mittal,“Asurveyoffpga‐basedaccelera‐torsforconvolutionalneuralnetworks”, Neural ComputingandApplications,vol.32,2020.doi: 10.1007/s00521‐018‐3761‐1.

[13] R.Skhiri,V.Fresse,J.Jamont,B.Suffran,and J.Malek,“Fromfpgatosupportcloudtocloud offpga:Stateoftheart”, InternationalJournal ofRecon igurableComputing,vol.2019,2019,1–17.doi:10.1155/2019/8085461.

[14] A.Wicaksana,“Portableinfrastructureforhet‐erogeneousrecon igurabledevicesinacloud‐fpgaenvironment”,2018.

RESEARCHTOSIMULATETHESHIP’SVIBRATIONREGENERATIONSYSTEMUSINGA

RESEARCHTOSIMULATETHESHIP’SVIBRATIONREGENERATIONSYSTEMUSINGA

6‐DEGREEFREEDOMGOUGH‐STEWARTPARALLELROBOT 6‐DEGREEFREEDOMGOUGH‐STEWARTPARALLELROBOT

6‐DEGREEFREEDOMGOUGH‐STEWARTPARALLELROBOT

Submitted:7th November2023;accepted:19th December2023

NguyenDucAnh,NguyenQuangVinh

DOI:10.14313/JAMRIS/2‐2024/10

Abstract:

Thisarticlepresentsresearchresultsonbuildingamodel toreproduceshipvibrationsbasedonaparallelrobot with6degreesoffreedomontheGough‐Stewartplat‐form.Vibrationdataattheship’scenterofgravity,cal‐culatedbysimulationsoftware,willbeinputtedintothe model.TheregenerativecontrolsystemusesasimplePID controllertocontrolinputtrajectorytracking.Simulation resultsonMatlab/Simulinksoftwarehavedemonstrated thereproductionofshipvibrationswithintheallowable error.

Keywords: robot,shipvibrationreconstruction,vibration simulation

1.Introduction

Thevibrationofshipsundertheimpactofocean wavesisoneofthemostcomplextypesofoscillations. Thestudyofshipvibrationsplaysanimportantrole inshipdesign,installation,stablecontrolofshipboard systemsshipdrivingsimulation[5,11,12].Because theship’svibrationiscomplex,makingactualmea‐surementscostsbothmoneyandtime,itisdif icult tocoveralltypesofshipsanddifferenttypesofwave levels.Therefore,thestudyofreproducingshipvibra‐tionsonsimulationmodelsorsemi‐naturalmodelsis ofgreatsigni icanceinsteeringsimulationproblems, especiallyinresearchproblemsofstablecontrolsys‐temsequipmentplacedonboard.TheGough‐Stewart 6‐degree‐of‐freedomparallelrobotconsistsofawork‐ingstage(movingbase)linkedtoa ixedbasethrough sixlegsbyballorpropellerjoints.Therobothas6 legsthataredrivenbyelectricmotorsorhydraulic cylinders.Therobot’sstructureallowsmovementin6 degreesoffreedomfortheworkstagebychangingthe lengthofeachleg.Parallelrobotscancreatevibrations similartotheactualvibrationsofmovingvehiclessuch asships,cars,andairplanes.Therefore,parallelrobots with6degreesoffreedomoftheGough–Stewartplat‐formareoftenusedin lightsimulationsystemsand ship‐drivingsimulationsystems[11].Incurrentprac‐tice,theproblemsofcalculatingandreproducingship vibrationsaremainlycalculatedbasedon2D[13],or 3Dmodels[5,11].Theyaremostlyusedinconstruc‐tionprojectstosimulatethemotionofshipsandserve thetrainingprocessofshipdrivers[11].

Theoscillationsreproducedindrivingsimulation systemsareusuallyoscillationsgivenintheformof harmonicfunctions.Simulationsoftwareallowsuse tochangetheamplitudeandperiodofoscillations. Becausetheoscillationsofoceanwavesareverycom‐plex,modelingintheformofharmonicoscillations isnotappropriate,theyshouldbemodeledbasedon theenergyspectrumanddirectionofwavepropaga‐tion.Fromthewavevibrationdataindigitalform,the ship’svibrationdataindigitalformcanalsocanbe calculatedasinputtoregeneratetheship’svibration. Thisisthemaincontentthatthisarticlepresentswith theapplicationofthe6‐degree‐of‐freedomGough‐Stewartparallelrobotmodeltoreproducevibrations. Thenextpartsofthearticleincludeoceanwavemod‐elsandshipmotionmodels.Thentheconstructionof ashipvibrationreconstructionsystem,thecontentof simulationresearch,andtheevaluationofresultsare provided.

1.1.VibrationofaShiponSeaWaves

Oceanwavesareformedbytheimpactofwind, astronomicalgravity,and loatingvehiclessuchas ships.Theyareoftendescribedbywaveheight,length, andperiod[2].Theverticaldifferencebetweenthe elevationoftheadjacentcrestandtroughdetermines waveheight.InThisarticleintroducesoceanwaves formedduetothepresenceofwind.Oceanwaves canbeunderstoodasasuperpositionofmultiplehar‐monicwaves,eachofwhichhasitsamplitude,fre‐quency,andphase,ascanbeseeninFigure1[4].There aretwomainmodelstodescribeoceanwaves[2]: one‐dimensionalwaves(long‐crestedsea)inFigure2 andmulti‐dimensionalwaves(Short‐crestedsea)in Figure 3.Accordingtowindspeed,oceanwavesare dividedinto10levelsfrom0to9,corresponding tothewave’soscillationamplitude[2].Manymathe‐maticalmodelsdescribetheoscillationsofdifferent oceanwavessuchaswavemodelsbasedonwave theories,wavemodelsbasedonenergyspectrum, andwavepropagationdirection.Thevibrationequa‐tionsofoceanwavesarebasedonwavetheories suchasAirylinearwavetheory,Stokeswavetheory, andCnoidalwavetheorypresentedinthedocuments model[3,10].Oneaccuratewavemodelisbasedonthe energyspectrumanddirectionofwavepropagation.

Figure1. Superpositionofwavesandwavespectrum

Commontypesofwaveenergyspectrainclude theNeumannenergyspectrum,Bretschneiderenergy spectrum,Pierson‐Moskowitzenergyspectrum,JON‐SWAPenergyspectrum,andTorsethaugenenergy spectrum.Intheframeworkofthisarticle,aone‐dimensionalwaveoscillationmodelisusedtostudy shiposcillationandreproducethatoscillation.The oceanwavemodelequation,[8]ispresentedinequa‐tion(1)below:

Figure2. Shipmodelsandcoordinatesystems

where: ��11 = ��(��)��(��); ��12 =��(��)��(��)��(��)−��(��)��(��); ��13 =��(��)��(��)+��(��)��(��)��(��); ��21 =��(��)��(��); ��22 =��(��)��(��)+��(��)��(��)��(��); A23 =��(��)��(��)��(��)−��(��)��(��); ��31 =−��(��); ��32 =��(��)��(��); ��33 =��(��)��(��); ��

where: ����‐wavenumber; ����‐wavelengthofthe ����ℎ wavecomponent;��‐oscillationfrequency;����‐Random phaseofthe����ℎ wavecomponent;Δ��‐constantdevi‐ationbetweenwavefrequencies;��‐wavedirection angle;��(��)‐energyspectrumofthewave.Inthisarti‐cle,theBretschneiderenergyspectrumisusedwith thefollowingformula[2]:

= 1.25

where:����:istheaveragewaveheight(theaverageof one‐thirdoftheheightofthehighestwaves).

1.2.ShipMotionModel

Considerashipwithmassm,withdimensions oflength,widthandheightdenotedL,B,Hrespec‐tively.The ixedG0(OXYZ)coordinatesystemis attachedtotheearth.CoordinatesystemG1(ONVW) isattachedtotheship;thecoordinateoriginis atthecenterofgravity;theOXaxisisalongthe ship’shullandpointstowardsthebowoftheship; andtheOZaxisisperpendiculartotheship’sdeck surface(Figure 2).Statevariableswhenstudying shipmotioninclude:[��,��,��,����,����,����,��,��,��,��,��,��]�� where: [��,��,��]��‐Thepositionoftheship’scenterof gravityisdescribedinacoordinatesystemattached totheearth;[����,����,����]��‐Thevelocityoftheship’s centerofgravityisdescribedinacoordinatesystem attachedtotheship;[��,��,��]��‐Euleranglesdescribe therotationofthecoordinatesystemaxesattachedto theshipwiththecoordinatesystemaxesattachedto theearth;[��,��,��]��‐Rotationalvelocityina ixedcoor‐dinatesystemattachedtotheship.Therelationship andidenti icationofstatevariablesaredeterminedas follows:

where R isthenumberofrotations,determined accordingtotheexpressionbelow:

= cos; ��

=������Thevelocityoftheship’scenterofgravityis determinedasfollows[2]:

where: ����:dampingconstantofvelocity;��‐densityof water;m:massoftheship;

ThetransfermatrixTisde inedasfollows:

Therotationalaccelerationina ixedcoordinatesys‐temattachedtotheshipisdeterminedasfollows[2]:

where: ����,����,����‐Torsionalmemoryfrictioncoef i‐cient[��.��/��];

,����,����‐Momentofinertiaoftheship accordingtothepillars����,����,���� ofthecoordinate systemattachedtotheship;

���� ‐Totalexternal forcemomentactingontheship’shull.Inthisarticle, forsimplicityweassumetheshipisintheanchored position,thepropellerdoesnotmove,ignoringthe massaddedtotheship,theforceofthewind,and theforcesactingontheshipincludethethrustofthe water(forcehydrostaticforce),gravity,Coriolisforce andcentripetalinertialforce.Therefore,thetrain’s equationofmotionin[2]canbewritteninasimple formasfollows:

Figure3. Blockdiagramofshipvibrationregeneration system

where:��=[ ̇��̇��̇�� �� �� �� ]��‐velocityvector ofcoordinatesystemG1relativetocoordinatesys‐temG0; M����‐massmatrixandinertiatensorofthe ship; I��1istheship’sinertialtensorwithrespectto theG1coordinatesystem; D��‐linearviscousfriction dampingmatrix; C����‐matrixwithcomponentsdue totheCoriolisinertiaforce[14]andtheship’sradial inertiaforce.Thewavemodelandshipmotionmodel presentedinthissectionhavebeenusedinthewave simulationandshipsimulationtoolkitoftheLINK‐SICcenteratLinkopingUniversity[7].Thesimulation processandresultsusingthistoolarepresentedin section4ofthisarticle.

2.BuidingaShipVibrationReproduction System

2.1.BlockDiagramofShipVibrationReconstruction System

Figureshowstheblockdiagramoftheship vibrationsignalreconstructionsystem.Thissystem includestwomaincomponents:theship’soscillating actuatorandthecontroller.Theshipvibrationregen‐erationsystemhasthefollowingworkingprinciple: Whenthesystem’sinputhasshipvibrationsignals,the system’scontrollerwillrelyontheinputsignaland feedbacksignaltocreatethesignals.Theactuatorcon‐trolsignaloscillatesaccordingtotheinputsignals.In thispaper,weuseshipvibrationsignalsfromthesim‐ulationtoolkitoftheLINK‐SICcenterwiththeinput informationbeingpositionandEulerangles;Theactu‐atorusesa6‐degree‐of‐freedomparallelrobotmodel (theGough–Stewartplatform)[1];Thecontrolleruses aPIDcontroller.Solvingkinematicproblemsofpar‐allelrobotsandcalculatinganddesigningcontrollers arepresentedindetailbelow.

2.2.ParallelRobotInverseKinematicsModel

Therobot’skinematicdiagramisshowninFigure 4.The ixedbaseandworkingstagesoftherobotare respectivelydenoted��1,��1 thecenterofjointsonbase ��1andcenterofjointsonlink��1aredenotedas��1��,��1�� respectively (��=1..6).The ixedcoordinatesystem ����0��0��0 ismountedatthecenterofthebase��1,the 00��0 axispointsup,the ��0 axispassesthroughthe midpointofthelineconnectingthetwojoints��11 and ��16.Thecoordinatesystem ��1��1��1��1 isattachedto thecenteratpoint��1,withthe��1��1 axispointingup, andthe ��1��1 axispassingthroughthemidpointof thelineconnecting ��11 and ��16.TheStewart‐Gough typeparallelrobothasjointslocatedona ixedbase orworkinglinkB1arrangedinsymmetricalpairsand locatedonthesamecircle.

Figure4. Parallelrobotkinematicdiagram

Theanglebetween ��0��11 and ��0��13 is 1200,the anglebetween��0��11 and��0��13 is1200.Lettheradius ofthecirclecreatedbythejointsonsurfaceB1and theradiusofthecirclecreatedbythejointsonsurface P1be��1�� and��1�� respectively.Theangle��11��0��12 is ��1��.Theangle��11��0��12 is��1��.Theanglebetweenaxis ��0��0 andvector��1�� is��1��,theanglebetweenaxis��1��1 andvector��1�� is��1��.Thedistancesfromthecenterof thebaseB1andthejointP1totheirrespectivejoint centersare��1�� and��1�� respectively.Thelengthsofthe legsare��1��,��=1,..,6respectively.

(10)

Thecenterpositionofthejointsinthecorresponding coordinatesystemsattachedtothebaseandworking linkisdeterminedasfollows:

Thegeneralizedcoordinatesoftherobotinjointspace includethelengthvariablesofthe6legs:

Thevectordeterminesthepositionanddirectionof theworkingstage:

Therotationmatrixfromthe��1 coordinatesystemto the ��0 coordinatesystemcorrespondingtotheroll, pitch,yawangles��,��,��is:

31=−S(��1);C12=C(��1)S(��1)S(��1)−C(��1)S(��1);

22=C(��1)C(��1)+S(��1)S(��1)S(��1); C32=C(��1).S(��1);C13=S(��1)S(��1)+C(��1)C(��1)S(��1); C23=C(��1)S(��1)S(��1)−C(��1)S(��1); C33=C(��1)C(��1);�� Δ =cos;�� Δ =������

Thelengthvectorofarobotlegiscalculatedas follows:

(15)

Figure5. Controldiagramoftheshipvibration regenerationsystem

Projectthevectorequationstothe��0 coordinatesys‐tem:

Figure6. Sequenceofsimulationstep

(a)Wavescomefromthe bowoftheship

(b)Wavescomefromthe bowoftheship

Figure7. Simulationresultsoflevel6wavesandships onwavesin02directions

Noteabovethat��1���� is0.Thelengthofonelegofthe robotiscalculatedasfollows:

Basedonequations(17),(18),theleglengthswillbe calculatedaccordingtothevariablesintheworking space.

3.ControllerDesign

Thebasicgoalofthecontrollerfortheshipvibra‐tionregenerationsystemisthatbasedonthedesired trajectoryoftheworkingstage ��1 includingposition anddirection,itwillbecalculatedintothecorrespond‐ingdesiredtrajectoryatthelegusinginversekinemat‐ics.Finally,acontrollerforeachlegisusedtocontrol thelegstofollowthatdesiredtrajectory.Inthisway, wegetthe luctuationsoftheworkingstagefollowing the luctuations.

M(X)X + h(X, X)= J��F (19)

Usingtheparallelrobotdynamicsmodelin[6]and expressedinexpression(19).Inwhich: M(X) isthe inertiamatrix; h(X, X)isamatrixconsistingofnonlin‐earcomponentsincludingCoriolisforce[9,10],cen‐tripetalforceandgravityforce; ��= {��1,��2,...,��6}�� forcevectorsofcorrespondinglegs;�� istheJacobian matrix.Tokeepitsimple,inthispaper,wedesigna simplePIDcontrollerwiththeinputbeingtheposition errorandtheerrorvelocity,andtheoutputbeing theforcevectoronthepins.Thecontroldiagramof thesystemispresentedinFigure 5 Thissectionwill presentsimulationcontent,includingoceanwaveand shipvibrationsimulations.

Signalssimulatingshipvibrationswillbeinput intothevibrationreconstructionsystem.The sequenceofstepswillbeillustratedinFigure6below.

3.1.SimulateOceanWaves

Inthisoceanwavesimulation,inordernotto losegeneralityaswellassimulationvolume,thisarti‐cleconducts02simulationsoflevel6wavesofone‐dimensionalwavetypewithwavemodel(1)andspec‐trum(2)accordingto2directionsrelativetotheship: wavesenteringtheship’sbow 1800 andwavesper‐pendiculartotheship’sside 900.Wavesimulation softwareofLINK‐SICcenter[7].Thewavesimulation resultsarepresentedinFigure7

3.2.SimulatingShipVibrations

Afterreceivingthewavesimulationresults,the ship’svibrationsaresimulated.Theshipparame‐tersusedareasfollows:Vessellength(L)=137m; Amountofwateroccupied(��)=25.105N;Shipwidth (B)=15m;Shipheight(H)=16m;Heightofship’scen‐terofgravity(����)=2,5��.Usingtheshipsimulation programofLINK‐SIC[7]withthesimulationcondition thattheshipisanchored,thesimulationresultsinFig‐ure8aretheoscillationsoftheship’scenterofgravity correspondingtothewavedirections.Fromtheship vibrationsimulationresultsinFigure 8,wecansee thefollowingpoints:1)TheXandYparametersof theship’scenterofgravitychangesmallandfollowa linearform,truetoreactwhenthereisimpactwave;2) Z‐parameter luctuationsaresigni icantwithampli‐tudesupto4m(wavelevel6haswaveamplitudesup to6m);3)Euleranglesreactwithamplitudeslessthan 10degrees.Fromthesecomments,whenappliedto theshipvibrationreconstructionsystem,weneedto processthissignalbecausetheZ‐axistravelparame‐tersoftheparallelrobotaredif iculttoguaranteeupto 6mandtheparametersintermsofXandYcoordinates canbeequaltozero.

(a)Wavescomefromthebowoftheship

(b)Wavescomefromthebowoftheship

Figure8. Simulationresultsofshipvibrationsonlevel6 wavescomingfromtheship’sbow

Therefore,theinputtotheshiposcillatorsystem focusesonparametersalongtheZ‐axisandEuler angles.

3.3.SimulatetheOscillationRegenerationSystem

TheGough‐Stewart6‐degree‐of‐freedomparal‐lelrobotmodelinthisarticleusestheparameters oftheeMotion‐1500/2700‐6DOF‐650‐MK1parallel robotfromBoschRexroth.Thebasicparametersofthe eMotion‐1500parallelrobotareasfollows:Fixedbase (���� (��)=1,28; ℎ�� (��)=0.172; ���� =120; ����=8,6);Work stage(���� (��)=0.931;ℎ�� (��)=0.152;���� =120;����=20,6); Themassoftherobotmovingpartdoesnotinclude theload:1755kg;Maximumload:1500kg;Weightof 1foot:140kg;Journeyofoneleg:0,62morHeightof workingplaneatlowestposition:1,25m.

MatlabMultibodytool[13].Theinputtothemodel isthe luctuationattheship’scenterofgravityposi‐tion.Theseoscillationshavebeenprocessedtomatch themovementsoftheeMotion‐1500robot.Thisinput signalhasbeenprocessedwithrefindexinFigures13 to16below.PIDcontrollerparametersforoscillation regenerationsystem ���� =5.104,���� =2.104,���� = 4.103 .

Figure9. Simulationdiagramofthevibration regenerationsystemonMatlab/Simulink

Figure10. Graphreproducingthefluctuationcenter positionandtheerroroftheship’swhenthewavego straightintheship’sbow

Thesimulationmodeloftheship’svibrationregen‐erationsystemusingtheeMotion‐1500parallelrobot withPIDcontrolleronMatlabsoftwareispresentedin Figure9

FromthesimulationmodelinFigure9,,theoscil‐lationregenerationsystemissimulatedwiththefol‐lowingcases: Case1:Vibrationoftheshipwithalevel6unidirec‐tionalwavecomingfromtheship’sbowFigure7a.

(a)

(b)

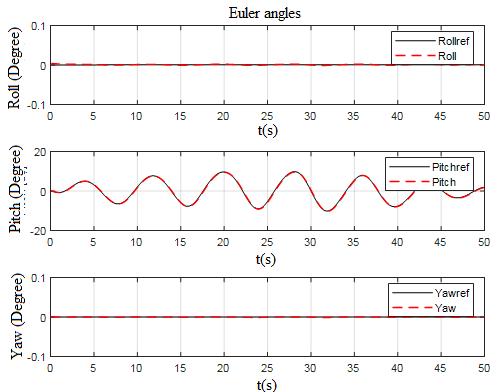
Figure11. GraphreproducingfluctuationsEulerangles anderrorsofshipwhenwavesgostraightintheship’s bow

TheinputsignaloftheShipVibrationRegeneration SysteminFigure 7 ahasbeenprocessedintoXand Ychannelsignalsintosmalloscillations,whiletheZ channelisregulatedforthemaximummotioncapabil‐ityoftheeMotion‐1500parallelwaverobotworking stage.Simulationresultsofposition,Eulerangleand correspondingerrorofthiscasearepresentedinFig‐ure10andFigure11.

Case2:Vibrationoftheshipwithlevel6unidirec‐tionalwavescomingfromthesideoftheship(Figure7 b).TheinputsignaloftheShipVibrationRegeneration SysteminFigure 7 b)issimilarlyprocessedastheX andYchannelsignalsintosmalloscillations,whilethe Zchannelisregulatedforthemaximummovement abilityoftherobotworkstageeMotion‐1500wave. Thesimulationresultsofthiscasearepresentedin Figure12andFigure13

Evaluation:Fromtheabovetwosimulationcases,it canbeobservedthattheshipvibrationregeneration systemdesignedabovehascreatedvibrationsthat followtheinputvibrationswithsmallerrorsinboth positionanddirection.Theerrorissmallforposition, theerrorislessthan5cm,whiletheerrorislessthan 1degreeforwaveswiththelargestwaveheightof4‐6 m,withaperiodofabout20‐25.Thisisalargewave levelandisoftenthecriticalthresholdforcontroland stabilizationsystemsinstalledonships.

Figure12. Graphreproducingcenterposition fluctuationanderrortheship’swhenwavesgostraight intheship’sside

Figure13. Graphreproducingthefluctuationsofthe ship’scenterEuleranglesandtheerrorswhenwaves entertheship’sbow

(a)

(b)

(a)

(b)

(a)

(b)

4.Conclusion

Thearticlehaspresentedresearchonaone‐dimensional(long‐crested)oceanwavemodel,a modelofshipmotionandit’soscillationsonagiven wavebackgroundwithtwocasesofwavestraveling fromtheship’sbow(180degrees)andwaveshitting thesideoftheship(90degrees)whentheshipstands atanchor,thesestudiesusedtheLINK‐SICprogram suite.Thestudyofwaveandvibrationmodelsplays animportantroleinbuildingasimulationmodelof theVibrationRegenerationSystemwitha6‐degree‐of‐freedomGough‐Stewartparallelrobot.Thevibra‐tionreconstructionsystemmodeloftheship’scenter ofgravityisobtainedonMatlab/Simulinksoftware throughtheMatlabMultibodytoolwhichprocesses theinputsignaltosuitthesystemandsimulatethe system.Thesimulationresultsensuretheaccuracyof reproducingshipvibrations.Fromtheseresults,the articlehassolvedtheproblemofreproducingship centerlineoscillationsasabasisforcreatingoscilla‐tionsatanypositionoftheship,servingresearchon otherproblems(e.g.installingweaponstabilization systems,electro‐opticalsights,etc.).Theresultsofthis researchserveasabasisforperformingvibration reconstructiononarealrobotsysteminstep1,step2 (Figure6)willbeperformedbyactualmeasurements, whilestep3willbedemonstratedonarealistic6‐degree‐of‐freedomGough‐Stewartparallelrobotsys‐tem.

AUTHORS

NguyenDucAnh –UniversityofFirePrevention andFighting,174KhuatDuyTien,HaNoi, VietNam,e‐mail:anhpchp@gmail.com,www: daihocpccc.edu.vn.

NguyenQuangVinh∗ –AcademyofMilitarySci‐enceandTechnology,HoangSam,HaNoi,Viet Nam,e‐mail:vinhquang2808@gmail.com,www:vin‐hquang2808.wordpress.com.

∗Correspondingauthor

References

[1] Nguyen,C.,Antrazi,S.,Zhou,Z.andCampbellJr, C.Analysisandimplementationofa6DOFStew‐artPlatform‐basedroboticwrist. Computersand ElectricalEngineering.17,191–203(1991).doi: 10.1016/0045‐7906(91)90035‐X.

[2] Fossen,T.Handbookofmarinecrafthydrody‐namicsandmotioncontrol.(JohnWileyand Sons,2011).

[3] Vinh,N.andVanPhuc,P.ControloftheMotion OrientationofAutonomousUnderwaterVehi‐cle. ProcediaComputerScience.150pp.69‐77 (2019).doi:10.1016/j.procs.2019.02.015.

[4] Faltinsen,O.Sealoadsonshipsandoffshore structures.(Cambridgeuniversitypress,1993). ISBN‐10:0521458706.

[5] Ghadimi,P.,Dashtimanesh,A.,Faghfoor Maghrebi,Y.andOthersInitiatinga mathematicalmodelforpredictionof6‐DOFmotionofplaningcraftsinregular waves. InternationalJournalOfEngineering Mathematics.2013pp.1–16(2013).doi: 10.1155/2013/853793.

[6] Taghirad,H.Parallelrobots:Mechanicsandcon‐trol.(CRCpress,2017.ISBN‐10 : 1138077380, ISBN‐13:978‐1138077386.

[7] Wu,H.,Wu,Y.,Zhang,Y.andZhang,Y. Intelligentencryptionmethodforwireless sensingsignalofunderwatervehicles. InternationalJournalOfVehicleInformation AndCommunicationSystems.7,366–380(2022. doi:10.1504/IJVICS.2022.129034.

[8] Debnath,L.Nonlinearwaterwaves.Academic Press:SanDiego.(1994).ISBN0‐12‐208437‐3. xviii,544pp.

[9] VInh,N.,DucThanh,N.,MinhDac,H.andDang Khoa,T.Identifyaerodynamicderivativesofthe airplaneattitudechannelusingaspikingneu‐ralnetwork. InternationalJournalOfAviation, Aeronautics,AndAerospace.7,3(2020.doi: 10.15394/ijaaa.2020.1490.

[10] Kornev,N.Shipdynamicsinwaves.(University Rostock,Germany2012)

[11] Shenhua,Y.,Xinghua,W.andGuoquan,C.Design andimplementonintelligentshiphandlingsim‐ulator. 2010InternationalConferenceOnDigital ManufacturingandAutomation.1pp.473–477 (2010).doi:10.1109/ICDMA.2010.216.

[12] Xiufeng,Z.,Yicheng,J.,Yong,Y.,Hongxiang,R. andXiuwen,L.Shipmotionmodelingandsim‐ulationinShipHandlingSimulator. 2012InternationalConferenceOnAudio,LanguageAnd ImageProcessing.pp.1051–1056(2012).doi: 10.1109/ICALIP.2012.6376771.

[13] Yan,J.,Jia,F.,Qian,C.&Fang,Y.AMATLAB Multi‐BodySimulationPlatformTowardMulti‐pleFlappingWingVehicles. 202342ndChinese ControlConference(CCC).pp.4574‐4579(2023). doi:10.23919/CCC58697.2023.10239965.

[14] Karapetkov,S.,Uzunov,H.,Dechkova,S.& Uzunov,V.Impactofinertialforcesoncar occupantsinavehicle‐ ixedbarrierfront crash. Symmetry.15,1998(2023).doi: 10.3390/sym15111998.

Submitted:24th April2023;accepted:20th September2023

HinaHashmi,RakeshKumarDwivedi,AnilKumar

DOI:10.14313/JAMRIS/2‐2024/11

Abstract:

Inthispaper,weproposedacomparativeresearch projectontheclassificationofvariousobjectsinsatellite imagesusingsomepre‐trainedmodelsofCNN(VGG‐19,ResNet‐50,Inception‐V3,EfficientNet‐B7)andR‐CNN. Inthisresearchwork,wehaveusedtheDOTAdataset, whichcombinesdatafrom14classes.Wehaveimple‐mentedabove‐mentionedpre‐trainedmodelsofCNN andR‐CNNtoachieveoptimalresultsforaccuracyas wellasproductivityindetectionofvariousobjectssuch asships,tenniscourts,swimmingpools,vehicles,and harborsfromremotelyaccessedimages.Inthisstudy,a convolutionalneuralnetwork(CNN)isusedasthebase model.Forcomplexcomputationsandforspeedingup results,transferlearningisused.Withthehelpofexper‐imentalanalysis,wehavediscoveredthatR‐CNNand Inception‐V3performedbestoutofthefivepre‐trained models.

Keywords: remotesensingimages,CNN,R‐CNN,transfer learning,objectdetection

1.Introduction

Arti icialIntelligence(AI)canbeconsideredasthe futurefortheworldbyseeingtheongoingprogress ofAIinvarious ields.Manyindustriesarecurrently growingdependentonAIbasedapplications.Astime passes,advancementsandimprovisationsarecontin‐uouslyprogressinginthe ieldofAIalongwithIT[1]. IntherecentpastitwasnotthoughtthatAIwould playthismajorroleinourday‐to‐daylives,asitwas consideredsomethingoutofthe ieldofscience,only usedfortheimplementationofrobots,andthatkind ofthing.ButAIhasprovenitselfarequiredelementof manydisciplines,frombasicrequirementslikefacial recognitiontocomplexcalculationslikeautomation, andsoon.Thedigitalindustriesgainedcontrolof variousbasicchallengesthroughthedigitaltransfor‐mationofAItechnologies.TheworkabilitiesofAIsys‐temshaveforcedAItositatthecoreofvariousdevel‐opmentalindustries[2].TheintegrationofAIfeatures withmanyotherapplicationshasreducedtheover‐burdenofdevelopersinmaintainingandimproving productivity,ef iciency,andquality.Fromthe ieldsof manufacturingandresearchtosmarthealthcareand inancesystems,AIhasbroughtmanythingsontoa singleplatforminashortperiodoftime.

AIhasmadepossiblethedevelopmentofITsys‐temsatabroadlevel.

AIandmachinelearning(ML)arethe ieldsthat correspondtoeachotherasanintegralpartofcom‐puterscience.Mostcommonly,AIandMLareusedas synonyms,buttheyaredifferentfromeachother,asAI canbedescribedasthesimulationofhumanthrough machinefordevelopingmanycapabilitiessuchas thinkinganddecisionmaking.MLisapartofAI,the foundationoftheprocessoftrainingthecomputers withthehelpofdatasetstoaccomplishAItasks.ML isusedtobuildsmartsystemsbyimplementingvar‐iouslearningalgorithms.WiththehelpoftheseML algorithms,thecomputerscanperformvarioustasks suchasobjectdetection,recognition,localization,and classi ication[3]inimagesaswellastheapplications suchasfrauddetectioninlivevideosaswell[4].These automatedsystemsaredevelopedbyMLalgorithms tolearnfromtrainingimagesandthemodelissmart enoughtokeepitselfupdatedwhileproducingoutputs withoutanyhumaninteraction.

1.1.NewParadigmsofAI‐basedComputing–theML toDL

Therehasbeenanoutperformanceofexpecta‐tionsintermsoftheperformanceofdeeplearning (DL)models,andtheresultsachievedarestateof theart.DeeplearningtechniquesareasubsetofML butimprovetheprocessoftrainingandlearning.DL achievespowerfulresultsbylearningfromreal‐world datainanestedandhierarchicalform.Thebiggestand advantageofDLoverMListhatDLlearnshigh‐level featuresfromtrainingdataintheformofimagesand videosasanincrementalprocess.DLoverMLsolves anyprobleminanend‐to‐endapproachwhereasML followstheapproachofbreakingdownaproblemin severalpartstosolvetheproblemasawhole.For example,formultiple‐objectsdetection,DLtechnolo‐gieslikeYOLOtaketheinputintheformofimageand videoandproducetheoutputintheformofobject locationwithnameofobjectwhereasinMLalgo‐rithmslikeSVM,otheralgorithmslikebounding‐box objectdetectionisrequiredinitiallyforidenti ication ofallpossibleobjects.DLoutshinesthis,asthereis nolimitationandworriesaboutfeatureengineeringin variousapplicationssuchasimageclassi ication[5], anomalydetection,videosurveillance,instanceseg‐mentation[6],andobjectdetection.

OneofthemostdemandingapproachesofDLis objectdetection,whichisoneofthemostpopular areastoday.However,objectdetectionhasevolved fromabout20yearsago.Before2014,objectdetec‐tionwasperformedbyseveraltraditionalapproaches: Viola‐JonesDetector(2001),HOGDetector(2006), DPM(2008).Roughlyfrom2014,DLtechniquescame intoexistence,withone‐andtwo‐stageobjectdetec‐tionalgorithms.Varioustwo‐stageobjectdetectors, suchasSPPNetandRCNN(2014),FastR‐CNNand FasterR‐CNN(2015),MaskRCNN(2017),GRCNN (2021),FPN(2017),andone‐stagedetectorssuchas SSD(2016),YOLO(2016),RetinaNet(2017),YOLOv3 (2018),YOLOv4(2020),YOLOR(2021)areperform‐ingbyachievingstate‐of‐the‐artresultsinthe ieldof objectdetection.

1.2.FacetsofAdvancedDL

DeepRepresentationLearningordeeplearning (DL)hasimprovedanddramaticallyachievedsuccess performingvariouslearningtasksinpastfewyears. Traditionalneuralnetworkormultilayerperception isaformofneuralnetworkthatrepresentstheframe‐workofconnectedlayers.Itisusedinvariousclassi i‐cationandregressiontasks.Arti icialNeuralNetwork (ANN)generallyinvolvesmultilayerperceptrons,Con‐volutionalNeuralNetworks(CNN),RecurrentNeural Network(RNN),andmore.Deeplearningtechniques areservinginvariousdimensions:objectdetection, classi ication,objectrecognition,speechrecognition, naturallanguageprocessing,bio‐informatics,visual imagerecognition,drugdiscovery,visualartprocess‐ing,andsoon.Deeplearningfollowsmultiplelayersto extractthehighestanddeepestfeaturesofdata.Each layerproducesmoreabstractandsigni icantfeatures. Fromrawdataintheformofimagesandvideos,fea‐turelevelsateachsuccessivelevelareextracted.

1.3.ConvolutionalNeuralNetwork

Inthenearpast,CNNattractedresearchers,andit hasachievedremarkablefameandsuccessbecauseof itsworkingnature.Ituseskernelmethodsalongwith weight‐sharingprocesses.CNNhassetitsbenchmarks invariousdomains,mostspeci icallyincomputer vision.CNNisanadvancedformoftraditionalneural networks,processingcomplexdataatinitialstagesof computationandpre‐processing.CNNisanadvanced formofdeeplearningthatacceptsimagesorvideos asinput,assignsweightstovariousobjectspresentin videoorimages,andablydetectsanddifferentiates variousobjectsfromeachother.Abovevariousother deep‐learning‐basedneuralnetworkmodels,CNNis achievingexcellentresultsinmultipledomains.

Convolutionalneuralnetworkshaveseverallay‐ers,includingtheinputlayer,theconvolutionallayer, thepoolinglayer,andthefullyconnectedlayer.In ordertoobtainattributesfromtheinputimage,the convolutionallayerapplies ilters.Inordertoreduce computation,thepoolinglayerdown‐samplesthe imagebeforethefullyconnectedlayermakesthe inal prediction.Withthehelpofgradientdescentand back‐propagation,thenetworklearnsthebest ilters.

Eachsuccessiveconvolutionlayerisfollowedby apoolinglayerusingnonlinearfunctionstoreduce thesizeoftheinputlayer.Inaddition,theyfacilitate thereductionoftheamountofcomputationandpara‐metricinformationinthenetwork.Casteluccioetal., 2015,indicatethatitalsohelpscontrolover‐ itting.A [2x2] ilterisusedinFigure1torepresentthepooling operation.Poolingoperationsincludethefollowing:

‐ Layersofconvolutionconsistoflearnable ilters(or kernels)thathavethesamewidth,height,anddepth astheinputvolume(3ifit’sanimageinputlayer).

‐ Asanexample,let’stakea34x34x3imageandrun convolution.Itispossibletocreate iltersaslargeas axax3,whereacanbeanythingfrom3,5,or7,but smallerthanthesizeoftheimage.

‐ Forwardpass iltersarecalculatedinstepsbysliding each ilteracrosstheinputvolumeasadotproduct ofkernelweightsandpatches.

‐ Thestrideofeach ilterisdeterminedbythenumber ofstepsandtheheightofeach ilteristheheightof theinputvolume.

‐ Theoutputvolumeoftheoutputvolumewillconsist ofadepthequaltothenumberof ilters.Asweslide our ilters,theoutputvolumewillhavea2‐Doutput. All ilterswillbelearnedbythenetwork. Itisalsoknownascovnetswhenitisacomplete architecturebasedonConvolutionNeuralNetworks. Everylayerofacovnetisadifferentiablefunction thattransformsonevolumeintoanother.Let’stakean imageof32x32x3dimensionsandrunanetworkon it.

InputLayers:Thesearelayerswhereweprovide inputtoourmodels.Imagesorsequencesofimages arecommonlyusedasinputsinCNN.Rawinputfor thislayeris32x32pixels,32x32pixels,and3x3pixels.

ConvolutionalLayers:Aninputdatasetispro‐cessedwiththislayer,whichextractsthefeaturefrom it.Imageinputisprocessedusingasetoflearnable ilterscalledkernels.A ilter/kernelistypicallya2x2, 3x3,or5x5matrix.Thisfunctioncalculatesadot productbetweenkernelweightsandcorresponding inputimagepatchesbasedoninputimagedata.This layerproducesfeaturemapsasitsoutput.We’llgeta 32x32x12outputvolumeifweuse12 iltersforthis layer.

Figure1. WorkflowDiagramofCNN

ActivationLayers:Anactivationlayeraddsnon‐linearitytoanetworkbyaddinganactivationfunc‐tiontoitsoutput.Aconvolutionlayer’soutputwill beactivatedelement‐by‐element.InadditiontoRELU: max(0,x),Tanh,andLeakyRELU,somecommonacti‐vationfunctionsareRELU:max(0,x),andLeakyRELU. Therefore,theoutputvolumewillhavedimensions 32x32x12duetothevolumeremainingunchanged.

Covnetpoolinglayer:Thislayerisperiodically insertedintothecovnetsandisusedtoreducethe volumeofthecomputation,whichinturnreduces memoryusage.Thislayeralsopreventsover itting.A maximumpoolinglayerandanaveragepoolinglayer aretwocommontypesofpoolinglayers.Withamax‐imumpooland2x2 ilters,wewillhavea16x16x12 volume.

Flattening:Afterconvolutionandpooling,thefea‐turemapsare lattenedintoone‐dimensionalvectors, whichcanbeusedforcategorizationorregression.

FullyConnectedLayers:Thislayercalculatesthe inalclassi icationorregressiontaskbasedonthe inputfromthepreviouslayer.

OutputLayer:Aseachclass’soutputisconverted intoitsprobabilityscorebythelogisticfunction,the outputisthenfedintoasigmoidorsoftmaxfunction forclassi icationpurposes.

1.4.TheAdvancementUsingTransferLearning

Inthecurrentscenario,deeplearninghasachieved theremarkablestrengthsintrainingdeepneuralnet‐workstoachieveaccuracyinpredictionsanddecision making.Thenetworkiscapableenoughtogettrained throughlabels,sentences,images,andpredictionsas well.Transferlearningistheadvancedattractionand charminthe ieldofAIasitallowsreusinganexist‐inglabeleddatanetworktrainedonsomespeci ic taskordomain.Thispre‐trainedmodelcanbeused forsomeotherproblemofinteresthavingthesame nature.Thepre‐trainedmodelisusedastheinitial stepforadifferentmodelbeingdevelopedforsome othertaskthatinvolvescomputer‐visionorArti icial Intelligence.Neuralnetworksbasicallyperformthe edgesdetectionatthe irstlayerandformittothe middlelayer;lateronitperformstheproblem‐speci ic featuresatthe inallayers.Whenwedevelopamodel usingsmartandadvancedtransferlearningtechnol‐ogy,thetaskinvolvedininitialandmiddlelayersgets

reduced,onlywehavetoperformtheretrainingpro‐cessatthelatterlayers.

AsFigure 3 isshowingthepre‐trainedmodels areusedastheinitialstepinbuildingorcustomiz‐inganyexistingmodel.Inthetransferlearning,the customizedmodelusespre‐trainedmodeltotrainits neuralnetworksonanewdataset[9].Bythegrowing advancementsoftransferlearningitisofferinganum‐berofbene itstotheresearchersthatmajorlyinclude reducingtrainingtime,improvingperformance,etc. Itinvolvestheuseofvariouspre‐trainedmodelsas astartingpointthatistrainedonaproblem;this reducesthedevelopmenteffortsandtime.Itis lexible approachalsoitallowscustommodelbuilding.Anum‐beroftopratedmodelsareprovidedbyKerastrained onImageNettoperformimageprocessingtaskslike VGG,ResNet,andInceptionv3[10].

1.5.Contributions

Thisresearchprimarilycontributesthefollowing:

1.5.1. Demonstratinghowdeeplearningtechniques canbeusedforobjectdetectionusingtransferlearn‐ingtechniques

1.5.2. Identifyandcompareaccuracyandprecision ofdifferentCNN‐basedpre‐trainedmodels.

1.5.3. Forachievingstate‐of‐the‐artperformance, thesemodelsareevaluatedontheDOTAdataset.

1.6.OrganizationofPaper

Section 1 containsthefundamentalaspectsof NewParadigmsofAI‐basedComputingalongwith facetsofdeeplearningandtheadvancementsoftrans‐ferlearningintoday’sAIworld.Section 2 givesa briefdiscussionofobjectdetectioninsatelliteimages. Section 3 highlightsthesurveyaboutvariousexist‐ingtoolsandtechniquesforobjectdetectioninsatel‐liteimagesusingdeeplearningapproaches.Sec‐tion4givesin‐depthstudyofhighlevelandarchitec‐turalviewoftransferlearningparadigms.Section 5 de inesthecomparativeanalysisofvariousCNNbased pre‐trainedmodelsforobjectdetection.Section 6 is dedicatedtothedetailsofdatasetusedfortheexperi‐mentation.

Figure2. Maxpooling

Figure3. Workflowoftransferlearning

transfer precision performance, New facets transfer brief images. various detection in approaches. and paradigms. various detection. used towards training, Section 8 the

classes like buildings, trees, grassland, shorelines, aircrafts, overpass, oiltank, playgrounds, etc (Figure 4isshowing).Mostcommonly,extractionof various deep internal features from remote imagery is done throughconvolutionalneuralnetwork(CNN).

Figure4. Demonstrationofclass‐basedObject Detectioninremotesensingimages

Fig 4. Demonstration of class-based Object Detection in remote sensing images

3. Various Tools &Techniques

Section7movestowardsmodelimplementations inwhichmodeltraining,processingandresultsare discussed.Section8showsthesummaryandfuture directionfortheresearch.

2.ObjectDetectioninRemoteSensedImagery

In1983,Chittinenietal.[12]proposedaframework for line and edge detection in multi-dimensional images. They have represented edges as the direct jump to functions and the weighted sum to expand grey-tone surface in multi-dimensional images. In their work, the noise isassumed as Gaussian. Computational efficiency is achieved by recursive relations. The experiments are performed on Landsatsatellitedata.

Duringtheyears1993and1994,Ionescuetal.[25] focusedtheirresearchondeterminingthefeaturesof SARimages,sincetheseimageshaveahigherlevelof complexityduetonoiseandqualityissuesassociated withthem.FeatureextractionfromSARimagesof large‐scaleobjects,suchasrivers,lakes,andhighways, wasaccomplishedinthispaperusinganautomated algorithm.Todetecthomogenousareas,thewater‐shedalgorithmwasemployed.Intheaboveareas, possibleobjectsaredetectedbasedonsimilarities betweenneighboringregionsanddifferencesfrom backgroundareas.Fortheexperiments,imagesofthe OttawaareaareusedthroughSARimagery.

During the years 1993 and 1994, Ionescu et al. [25] focusedtheirresearchondeterminingthefeaturesof

SincethisistheageofArti icialIntelligence,com‐putervisiontechnologyisusedandappliedtointer‐pretandanalyzetheimagestoextractimportantand usefulinformationfromit.Amongallthosecomputer visionimageprocessingtechniques,objectdetection playsavitalroletodetectvariousobjectsavailability inanimageorvideo.Withtheimprovedversions ofobjectdetection,objectidenti icationandlocaliza‐tioncanalsobedoneontheimages.Wheneveritis requiredtocountortrackthepreciselocationsofthe objectsinanimageorvideo,objectdetectionalso helpsinlabelingtheobjectsinanimage.

Objectdetectioninsatelliteimagesisachallenging issueasthesetypesofimageshavedifferentkindof resolutionsanddimensionsascomparedtonormal images.Stillalotofresearchhasbeendoneinthe ieldofsatelliteandaerialimagerytogetdesired informationforEarthobservation,changedetection, agriculturalareas,etc.Overrecentyearsthespatio‐temporalearthobservationdataisincreasingdras‐tically.Thisdataisusefultoextractimportantand hiddeninformationtomonitor,controloranalyze land‐surfacedynamicsinahugerange.Someappli‐cationareasofsatelliteimageprocessinginvolvedis‐tortionofsettlements,urbangrowth,vegetationcover areas,wateravailabilityetc[11].Mostcommonlythis kindofstudyinvolvesvariousclasseslikebuildings, trees,grassland,shorelines,aircrafts,overpass,oil‐tank,playgrounds,etc(Figure 4 isshowing).Most commonly,extractionofvariousdeepinternalfea‐turesfromremoteimageryisdonethroughconvolu‐tionalneuralnetwork(CNN).

3.VariousTools&Techniques

In1983,Chittinenietal.[12]proposedaframe‐workforlineandedgedetectioninmulti‐dimensional images.Theyhaverepresentededgesasthedirect jumptofunctionsandtheweightedsumtoexpand grey‐tonesurfaceinmulti‐dimensionalimages.In theirwork,thenoiseisassumedasGaussian.Compu‐tationalef iciencyisachievedbyrecursiverelations. TheexperimentsareperformedonLandsatsatellite data.

ThedetectionofforestcoverchangesfromLand‐satTMdatawas irstdescribedbyCoppinetal. [ext6]in1994.Thesensorcalibrationoffsetsare minimizedbyusingmultipleyearsofimagery.The waterre lectancevalueisobtainedwithacorrelation mechanismbetweenbi‐temporalbandpairstypically rangingfrom0.9884to0.9998combinedwithdark objectsubtraction.Weappliedtwodifferentchange detectionalgorithmstobi‐temporalvegetationindex pairsforintervalsoftwo,four,andsixyears.Radio‐metricallyde inedchangeclassesareinvestigated. Thisstudydemonstrateshowre lectiveTMdatacan beusedtostratifyforestcoverchangeinaforest coverchangeassessmentphasebeforemoredetailed analysis.

TheIndianRemoteSensing(IRS)satelliteimagery wasusedbyMandaletal.[15]todetectman‐made objectslikeroads,bridges,airports,andindustrial areasin1996.Fortheinitialclassi ication,theimage pixelsareclassi iedintosixtypesoflandcoverusinga multi‐valuedrecognitionsystem.Someheuristicrules aboutspatialknowledgeandtheirinter‐relationships areappliedonclusteredimagestoidentifycertain targets.Byusingmultipleclassi ications,thedetection processbecamemoreeffective.

In1996,Rongetal.[13]presentedamodelfortar‐getdetectionfornotonlyman‐madethings,butalso fornaturalbackgrounds.Theyhaveusedakindofself‐organizingmodelforbackgroundlearning,andthen appliedsomereinforcementlearningonthatmodel throughcontextualinformation.Experimentalresults showthattheyhaveachievedoptimalresultsintheir work.

In1999,Ngetal.[14]triedtodetecthumanfaces. Withthismodel,facescanbedetectedinmultiple viewsandposescanbeestimatedatanear‐framerate. TheirworkextendsSVMstomodelthe2Dappearance ofhumanfacesthatundergononlinearchangesovera viewsphere.

Aspartoftheirdevelopmentofasystemforimage analysis,Garnessonetal.[15]proposedtheMulti ExpertSystemforSceneInterpretationandEvaluation (MESSIE)basedongeometry,context,andradiom‐etry.Thesystembasicallyoperatesongeometrical modelling.Astudyisundertakentoascertainthe classofanobjectbyexaminingitsgeneralstructure. Thedevelopedmodelidenti iesobjectsofinterestini‐tially.Additionally,byexaminingthecharacteristics

Aircraft Oil tank Overpass Playground

ofgatheredsalientobjects,onecanconcludefurther searchfornewobjectsinthescene.Astudyidenti ies roadsandbuildingsusingsuburbanimages.

Anautomatedmethodfordetectingandclassify‐inghiddentargetsinhyper‐spectralimageswaspro‐posedbyRenetal.[16]in1998,whichiscapable ofidentifyingtargetswithoutpreviousknowledge.A benchmarkisachievedinthreephases.First,wewill chooseaband.Second,wewillapplyabandrationing approach,and, inally,wewilluseATDCA(Automatic TargetDetectionandClassi icationAlgorithm).By analyzingimagescenesfromtheHyper‐spectralDigi‐talImageryCollectionExperiment(HYDICE),weeval‐uatetheeffectivenessoftheCADCM.Theseresults demonstratethatthismodeliscapableofdetecting targetshiddenbynaturalbackgroundshades,man‐madeobjects,orshadeeffects.

Shufeltetal.[17]examinedtheperformanceeval‐uationoffourmonocularbuildingextractionmethods byusingimagespaceandobjectspacematriceson 83imagesof18buildingsin1999.Inthisanalysis, theyexaminehowimageobliquityeffectssystemper‐formance,aswellasobjectcomplexity.Additionally, theyanalyzedtheimpactofedgefragmentationonthe system.Toextractbuildings,weusedphotogrammet‐ricprimitiverepresentationsandstrictobjectspace modeling.

AccordingtoShanksetal.[18],theydevelopeda systemthatdetectscloudinessandaerosolpollution onremotesensingsignalstominimizetheirdeleteri‐ouseffects.Theyhavereviewedexistingcloudimpacts reductiontechniquesinthispaper.

Fromairbornelightandrange(LIDAR)imagery, Haithcoatetal.developedanautomatedmethodfor extractingthefootprintofbuildingsandreconstruct‐ingtheir3Dshapein2001[19].Theobjectshigher thanthegroundsurfaceare irstextractedfromadig‐italsurfacemodel(DSM).Thesize,height,andshape ofabuildingdistinguishitfromotherobjects.Inorder toimprovethequalityoftheextractedbuildingfoot‐prints,anorthogonalalgorithmisapplied.Ridgelines andslopesareusedtoidentifyroofs.Inthe inalstep ofaccuracyassessment,theresultsarecomparedwith manuallydigitizedbuildingreferencedata.

Buildingfeaturescanbeextractedfromimagesin threestepsbyChenetal.[20]in2002.Anarti icialneu‐ralnetwork–supervisedalgorithmisusedtocatego‐rizeroofsusingRGBcolorbandsandimagetextures. Ahybridapproachofedgeandregionsegmentation isthenappliedtoextractusefulspatialinformation aboutobjects.Theresultsarethenre inedusingthe spatialinformation.TestsareconductedonAUSIM‐AGE/spltradedigitalimagery.

ThemodeldevelopedbySecordetal.[21]used LIDARaerialimagesandrangedatatoapproachtrees. Inthispaper,theyproposedatwo‐stepprocessfor detectingtrees,includingsegmentationandclassi‐ication.Here,weightedfeaturesareusedtoseg‐mentusingtheregion‐growingalgorithm.Weights aredeterminedusingtherandomwalklearning method.Thisapproachallowsforcontroloftherate ofmisclassi icationthroughweightedsupportvector machines.Experimentsdemonstrateitseffectiveness.

Chaudhurietal.[22]usedmultispectralimagery in2008todiscoverbridgesoverwaterbodies.Mul‐tispectralimagesareclassi iedintoeighttypesof landcoverusingthemulti‐seedsupervisedclassi‐icationtechnique.Tri‐levelimagesarecreatedby identifyingwater,concrete,andbackgroundinforma‐tionfromclassi ication.Furthermore,thestudyuses aknowledge‐basedapproachtorevealthespatial arrangementofthebridgeanditssurroundings.A recursivescanningmethodisusedtoextracttheriver features.Bridgepixelsareidenti iedusingneighbor‐hoodoperators.Aspatialresolutionof23.52misused fortestingontheIRS‐1C/1‐Dsatellite.

UsingTerraSAR‐XScanSARimages(19‐mresolu‐tion)asadatasourcein2010,Paesetal.[14]proposed conceptsforshipdetection.TSXimagesarecompared withtheK‐distributionbymeansoftheKolmogorov‐Smirnovtesttodeterminethegoodnessof it.This isdoneinadevelop‐and‐verifytargetdetectionalgo‐rithm.

Usinganeighborhoodmodelbasedonloosespa‐tialcontingency,Grantetal.[23]presentedamethod fordetectingamorphousobjectsin2012thatuses amaximumprobabilitytotellwhetherapixelsur‐roundedbytheobjectofinterestcontainsitaswell. Theevaluationisdoneonhypothesisimagery.

Usingpanchromaticsatelliteimagery,Elbakary etal.[24]developedamethodfordetectingshadows in2014.Thismethodusesageometricactivecon‐tourmodel.Ontheimage,shadowsanddarkareas aresegmentedafterdetection.Todistinguishthereal shadowsfromothershadows,theyproposedselecting thebestthresholdandboundarycomplexitymetric. Performanceisalsovalidatedthroughexperiments.

In2016,theautomaticcontent‐basedanalysis[25] presentedbySevoetal.allowsforarbitraryobjectsto bedetectedinaerialimages.Thispaperimplementsa two‐stagetrainingmodelandthenveri iesitagainst remoteimageryusingconvolutionalneuralnetworks. UCMerced’sdatasetisusedtotestthemodel’saccu‐racy,whichis98.6%.

AfeaturefusionmethodwasproposedbyYu etal.[27]in2019thatutilizedmultiplelayersof remotelysensedimagestoextractsomeofthe ine‐grainedfeatures,sincetheimageshaveanumber ofsimilaritiesanddifferencesbetweenclasses,along withmultidirectionalobjects.Initially,ResNet50is appliedtoextractthefeaturesfrommultiplelayers, andthenchannelattentionisappliedtoenhancethem. Fusionisperformedusingmultilayerbilinearpooling andfeatureconnections.Thetrainingmodelisbuilt usingPyTorch,adeeplearningframework.

ThepaperbyYuetal.in2020[26]outlinedan approachtodetectvehiclesfromremoteimagingthat reliesonconvolutionalcapsulenetworks.Inthebegin‐ning,animageissegmentedintosuperpixels,and patchesaregeneratedwithoutredundantinforma‐tion.Finally,repetitivedetectioniseliminatedusing non‐maximumsuppression.

Table1. Classificationbasedontoolsusedbyvariousresearchers

Algorithm/ModelMethodology

MSCNN(Yaoetal.2021)

DCL‐basedobjectdetectionmethod Xiwen(Yaoetal.,2021)

SE‐MGMM(Xueetal.2021)

ConvolutionalcapsuleNetwork(Yu etal.,2020)

PTAN(Apatch‐basedthree‐stage aggregationnetwork)(BingSui1,etal. 2020)

Compatibilitylossclusteringmethod (CLCM)YongsaiHanetal.,2020

ObjectrelationshipreasoningCNN (ORRCNN)(Lietal.,2020)

AASM(Feminetal.,2020)

DataSet

VHRsatelliteimagesforgeospatial applications.Challengingdatasetfor theNWPUVHR‐10.Theimagesrange from0.5mto2.0minresolution.

NWPU‐VHR‐10.v2dataset

Syntheticapertureradarimages

OpenaccessRemoteimagery

1.DOTA

2.NWPUVHR‐10

1.DOTA

2.UCAS‐AOD

3.NWPUVHR‐10

4.RSOD‐Dataset

AerialImage.dataset(AID)[16],UC MercedLand‐Usedata set&WHU‐RS19dataset

HRSC2016dataset

Findings

Filtersshouldbereplacedwith smallerones

Aconvolutionbasedondepth followedbyaconvolutionbasedon points

Kernelswithsmallsizesareused

Skipconnectionsareusedtoidentify mappings

Optimizesaccuracyaswellas loating‐pointoperationswith multi‐objectiveneuralarchitecture search.

Finegrainedfeaturesfrommultiple layers

Accuracyformultibanddata

Openaccesssatelliteimages AbilityandEf iciencyareconsidered R‐CNNalgorithmwithdialed convolution(Weietal.,2020)

Activecontourexcludingedgesmodels (Raietal.,2020)

DeeplearningalgorithmsonNVIDIA DGX‐1supercomputer(Larionovetal., 2020)

SelectiveSearchandEdgeBoxes(Farooq etal.,2017)

AnenhanceddeepCNNbased(Deng etal.,2017)

Two‐stagetrainingmodelusing convolutionalneuralnetwork(Sevo etal.,2016)

Neighborhoodmodel(Grantetal.,2012)

SyntheticApertureRadar(SAR) images

Pre‐traineddatasetof SpaceNet ine‐tunedonplanet database.

NWPUVHR‐10

VHR‐10dataset

UCMercedDataset

hypothesisimageryandDIRSIG

Accuracywithrespecttoitsfeature extraction

Workingabilityondensedataset

TimeComplexity&Ef iciencyare performed

Resultinginhighrecallrates

Substantialnumberofdensely packedobjects

Arbitraryobjectsaredetected

Amorphouslyshapedobjects Kolmogorov‐Smirnov(Paesetal.,2010)

Amodeltodetectbridgesoverwater bodies(Chaudhurietal.,2008)

TerraSAR‐X(TSX)ScanSARimages (19‐mresolutoin)

IRS‐1C/1‐Dsatelliteimagesof23.5 23.5m.

Experimentalresultsindicatethattheproposed methodachievesitsbenchmarksbetterthanthetradi‐tionalmethodsintermsofcompleteness,correctness, andquality.

Inthisstudy,theauthorseekstovisualizethe interpretationsofdeepconvolutionalneuralnetworks foraerialimagesandtocomprehendhowtheseinter‐pretationsvaryacrossdatasetsorunderdifferent networkweightconditions.Theirvisualization ind‐ingsshedlightontherobustnessandgeneralizabil‐ityofwell‐knownnetworkslikeVGG19,ResNet50, andDenseNet121.AIDandUCMdatasetsareusedto showhowcommonclassi icationmethodslikeconvo‐lutionalnetworkshaveevolvedtoincludeobjectand texturedetectors[28].

Multispectralimageryareprocessed

TanandLe[7]createdthe inalfamilyofCNNs forimagerecognitioncoveredinthisstudy,theEf i‐cientNets,usingthesamesearchspaceinlate2019. ThebaselinemodelEf icientNet‐B0performedsimi‐larlytoMnasNetbecausethesearchspaceremained unchangedandtheoptimizationtechniquewassame asMnasNet.Thescalingstrategy,however,iswhat makesEf icientNetsuccessful.TanandLe[7]pre‐sentedcompoundscaling,balancingscalinginthenet‐work’sdepth,width,andresolution.Incomparisonto AlexNetsevenyearsearlier,asaresultEf icientNet‐B7 achieved97.1%acc@5at66Mparameters.

Figure5. (a)Notutilizingknowledgefromother domains.(b)Transferlearningutilizespriorknowledge fromanotherdomain

3.1.ClassificationBasedonToolsUsed

Table 1 showsthecomparisonofmodelsdevel‐opedbymanyresearchersforvariousparameters onthedifferentdatasets.Theprimeobjectiveofthis classi icationistocategorizevariousdeeplearning algorithmsforvariousparameterslikeaccuracy,time complexity,changedetection,speed,andhighrecall rate.

4.Pre‐TrainedModelingBasedonCNN

4.1.HighLevelViewofTransferLearningParadigm

Learningfromonedomainortasktoanotheris easyforusashumans.Wedonothavetostartover whenweencounteranewtask.Then,wecanlearn andadaptfasterandmoreaccuratelytothenewtask fromourpreviousexperiences[29].Wehavewit‐nessedastoundingleapsintheapplicationofarti i‐cialintelligenceinrecentyears,thankstoadvancesin supervisedandunsupervisedmachinelearning.Our technologyhasreachedapointwherewecandevelop automaticvehicles,robotswitharti icialintelligence, anddiseasedetectionsystemsthatarehuman‐levelor superhuman.

Machinelearningmodelsarenotcapableofgen‐eralizingbeyondthecircumstancesencounteredto increasetheirperformance[30].Theywereinspired bythehumancapacitytotransferknowledge,which hasledthemtofocusduringtraining[31],which hamperstheirabilitytoontransferlearningto resolvetheseissues.Whencomparedtothetradi‐tionalmachinelearningparadigm,wherelearning occursinisolation,notutilizingknowledgefromother domains(Figure 5(a)),andtransferlearningutilizes priorknowledgefromanotherdomain(source)to learnaboutanewdomain(target)(Figure5(b)).

4.2.ArchitecturalViewofTransferLearningParadigm

Asapowerfuldeeplearningtechniqueincom‐putervision,TransferLearning(TL)isapowerfultool forconstructinghigh‐performancemodels.Knowl‐edgecanbere‐usedacrossdifferentareasusingTL— theknowledge‐reusabilityconcept.Youdon’tneedto reinventthewheelwitheachnewsituationormodel. Youcanleveragepreviousexperience.Byapplying previousknowledgetonewtasks,youcanperform themmoreef iciently.Anexampleoftransferlearning iswhenamodeldevelopedforonetaskisusedasthe basisofamodeldevelopedforanother.

Thisisapopularmethodofdevelopingneural networksasthestartingpointforcomputervision andnaturallanguageprocessingtasksduetothe enormouscomputerresourcesandtimerequiredfor developingneuralnetworksontheseproblems,as wellasthehugeleapsinperformancetheyprovide whendealingwithrelatedproblems.Insimplerterms, transferlearningentailsre‐trainingamodelforasec‐ondbutrelatedtaskafterithasbeentrainedtoper‐formthe irsttask.TheFigure 7 illustratestransfer learningovertraditionallearning.

Lookingatthediagramabove(Fig. 6),wesee thatbothmodelsfordifferenttasksaretrainedfrom scratchinthetraditionalapproachthatiswithout transferlearning.Atransferlearningapproach,how‐ever,usesourdatasettotrainapre‐trainedmodelthat canperformadifferenttask.Whenyoupayattention, youcanseethatthedatasetinred(thesecondone)is smallerthanthe irst.Transferlearningconsistsofthe followingsteps:

1) Determinetheweightsofthenetwork.

2) Trainonyournewimagesafterunfreezingthe “head”layersthatarefullyconnected.

3) Trainingwiththeweightsfromtheprevioustrain‐ingandunfreezingthelatestconvolutionallayers. Ifwedonotdo#2,wewilltriggerlargegradient updates.

5.ComparisonofPre‐trainedCNNModelsfor ObjectDetection

AsdiscussedinSection4,intransferlearning,we canuseanalready‐trainedmodelfornewtasksby usingalargedataset.Duetothefactthatthedatasets havebeenvetted,wecanbesurethatthequalityofthe datasetsishigh.Thisreducesthecostoftrainingdeep‐learningmodels.Insatelliteobjectdetection;across researchandindustry,somedatasetsarehighlypop‐ular.Following(Table 2)aresomeoftheprominent ones:

Table2showsvariousdatasetsforsatelliteimages likeDOTA,GoogleEarth,andothers.Thecategories ofobjectsindatasetsarealsomentioned.DOTAhas 14categoriesforvariousobjectslikeharbor,storage tank,ship,baseballdiamond,groundtrack ield,etc. Numberofinstancesandnumberofimagesshowsthe countforvariousobjectclassesandthenumberof picturesinthedataset,respectively.

Figure6. Transferlearningvstraditionallearning

Table2. DatasetsforSatelliteImagery[32]

Maincategories

14categories: Harbor,storagetank, ship,baseball diamond,ground track ield,soccerball ield,tenniscourt, Airplane,large vehicle,roundabout, helicopter,swimming pool,bridge, basketballcourt

Twocategories: Vehicle,Airplane

Tencategories:,ship, baseballdiamond, storagetank,tennis court,groundtrack ield,basketball court,harbor,bridge, airplane,andvehicle

Earth

2017)

Earth

Google Earthand Vaihingen

Fourcategories: storagetank, airplane,overpass playground, Google Earthand Tianditu

Onecategory:oilwell

etal.,2015)

NWPUVHR‐10 (Chengetal., 2014,2016b; ChengandHan, 2016a)

2015;Longetal., 2017)

Google Earth Oilwelldataset (Wangetal.,2021) Zhangetal.(2021)

Inthispaper,wehavecovered ivepre‐trained modelsofCNN(VGG‐19,ResNet50,Inception‐V3,and Ef icientNet‐B7)andR‐CNNforobjectdetectionfrom satellitedata.Thesemodelsareprominentintheir ieldsandarewidelyusedintheindustryaswell.By thesuccessfulexecutionofthesemodelsonDOTAwe havemadeacomparativeanalysisfor indingthebest modelwithoptimalresultsintermsofaccuracyand precision.Hereisthein‐depthdiscussionabouteach.

5.1.VGG‐19

Aconvolutionalneuralnetworkwithadepthof19 layersiscalledtheVGG.Intheirarticle“VeryDeep ConvolutionalNetworksforLarge‐ScaleImageRecog‐nition,”K.SimonyanandA.ZissermanfromtheUni‐versityofOxfordputforththeCNNmodelknownas VGG‐19.Inthetop ivetests,CNNperformsat92.7% accuracyontheImageNetdataset,whichconsistsof over14millionimagesdividedinto1000classes[33]. InILSVRC‐2014,thismodelwasamongthewell‐knownones.Bysequentiallysubstitutingseveral33 kernel‐sized iltersforAlexNet’sbigkernel‐sized il‐ters(11and5,respectively,inthe irstandsecond convolutionallayers),itimprovesuponAlexNet.Up to1000itemscanbecategorizedbythisnetwork duetoitspre‐training.Thenetworkwastrainedwith 224x224‐pixelcoloredpictures,whichindicatesthat thematrixhadtheshape(224,224,3).Hereissome quickinformationonitssizeandcapabilities.

AccordingtoFigure 7,thenetworkreceivedan RGBimagewitha ixedsizeof(224*224),indicating thatthematrixhadtheshapeof(224,224,3).One preprocessingstepwasappliedtoeachpixel,which calculatedtheaverageRGBvalue[34].Usingkernels withasizeof(3x3)andastridesizeof1pixel,they wereabletocovertheentireimage.Spatialpadding wasappliedtotheimagetomaintainitsspatialreso‐lution.A2x2pixelwindowwasusedformaxpooling withstride2.Toenhanceclassi icationaccuracyand computationtime,aRecti iedLinearUnit(ReLu)was addedafterward.Theperformanceofthismodelwas signi icantlybetterthanpreviousmodelsthatused tanhorsigmoidfunctions.Athirdlayerwasimple‐mentedusingasoftmaxfunctionthatuseda1000‐way ILSVRCaspartoftheclassi ication,whilethe irsttwo layershadasizeof4096.

Figure7. ArchitectureofVGG‐19

5.2.ResNet50

Aconvolutionalneuralnetworkwith50layersin depthiscalledResNet50.Youmay indthemodel performanceresultsonMicrosoft’sarticletitledDeep ResidualLearningforImageRecognition,whichwas developedandtrainedin2015.Totrainthismodel, hundredsofthousandsofphotosweretakenfrom theImageNetdatabase.Thenetwork,likeVGG‐19,can categorizeupto1000objectsbasedon224x224pixel coloredimages[35].

Ascanbeobserved,thereare4comparablelayers utilizingmerelydifferent iltersizesafterbeginning withasingleconvolutionallayerandMaxPooling.All oftheselevelsusethe3*3convolutionprocess.Addi‐tionally,weareomittingorskippingthelayerbetween everytwoconvolutions.Identityshortcutconnections arewhatisreferredtoasresidualblocksandare whathavemissedconnections.Simplyput,theResNet authorsdemonstratethatapplyingaresidualmapping issigni icantlysimplerthanapplyingtheactualmap‐pingandthatthisshouldbedoneforalllayers.It’salso noteworthytonotethattheResNetcreatorsclaimthat performanceshouldn’tdegradeasweaddmorelayers tothemodel[36].Contrarytowhatweobservedin Inception,thisisnearlyidenticaltoVGG‐19inthat itjustinvolvesstackingResNetlayersontopofone anotherwhilealteringtheunderlyingmapping.

5.3.Inception‐V3

Szegedy irstdescribedtheInceptionmicro‐architectureintheirwork“Goingdeeperwith convolution”in2014.AscanbeseeninFigure9,the InceptionModulemerelyappliesconvolutionstothe inputusingvarious iltersizes,appliesMaxPooling, andthenconcatenatestheoutcomeforthefollowing Inceptionmodule[37].Comparedtoitspredecessors, Inceptionv3features42layersandalowererrorrate.

5.4.EfficientNet‐B7

Ef icientNetB7isastate‐of‐the‐artconvolutional neuralnetworkthatwastrainedandreleasedto thepublicbyGooglewiththepaper“Ef icientNet: RethinkingModelScalingforConvolutionalNeural Networks”in2019.

Figure11. Comparativeperformancesofpopular modelsincl.EfficientNetfamily

TheEf icientNetimplementationsrangefromB0 toB7,andeventhesimplestimplementation,Ef i‐cientNetB0,isoutstanding.InitsTop‐1accuracyper‐formance,itachieved77.1%with5.3millionparame‐ters[38].

Mobileinvertedbottleneckconvolutionisoften knownasMBConv(andisrelatedtoMobileNetv2). Thefollowingscalingcoef icientsareincludedintheir compoundscalingformulaaswell.

‐ Depth=1.20

‐ Width=1.10

‐ Resolution=1.15

AnewfamilyofEf icientNets,Ef icientNetB0 toEf icientNetB7,isconstructedusingthisalgo‐rithm[39].Theperformanceofthisfamilyincom‐parisontootherwell‐likedmodelsisdepictedinthe straightforwardgraphthatfollows(Fig.11).

Figure8. ArchitectureofResNet‐12,abasicmodel

Figure9. Inception‐V3architecture

Figure10. EfficientNet‐B7architecture

Figure12. R‐CNN:RegionswithCNNfeatures

Figure13. Numericaldataofobjectsused

5.5.R‐CNN

Oneoftheearliestinvestigationsintodeep learning–basedobjectdetectionisR‐CNN.VGGNetand ResNetmethodswereusedtotrainthenetwork,and itwasduringthisprocessthatthenumberofclasses +backgroundfortheclassi ierlayerwascalculated. Therangeof0to1isusedtocalculatethesimilarity ratio.Thesimilarityratioofthesearchobjectto theimageisrepresentedbythisnumber.Regardless ofthenumberofclasses,theR‐CNNtestprocedure offers2000differentareas[40].Fouroftheclosest placesfromamongthese2000differentregionsare suggestedforeachclass,asseeninFigure12.

6.Dataset

Inthispaper,theDOTA(Xiaetal.,2018)dataset issuedfortheexperimentationpurpose.14kindsof objectswereidenti iedinthedataset.Fortraining,888 photosofvarioussizeswereused.Highqualitypho‐tographsinthesizerangeof432x559to5193x6054 arereferredtoastrainingimages.Thereare888pho‐toswith49053objectsdividedinto14classes.The testinvolved277photos.Thesepicturesareavailable insizesrangingfrom448x511to6313x6400.The imagesconsistofbothnighttimeblack‐and‐whiteand coloredphotographs.TheDOTAdataset’sobjectcoor‐dinatesarereorganizedintorectangulardimensions. Thevaryingsizesofthehighresolutionsamplesinthe datasetarethoughttobeacrucialfactorindetermin‐inghowwelldeeplearningmodelsperformgenerally. Therefore,itwasintendedtodemonstratethenumer‐ousaspectsinwhichthecrisiswillmanifestitself. Thereare13,772itemsinallthroughoutthephotos utilizedforthetest.Figure13depictsthetrainingand testingclassroomstogetherwiththeamountofitems ineachone.

7.ModelImplementation:Training,Process‐ing,andResults

ThedeeplearningmodelingtoolPytorchwasused toimplementallofthecalculation’scode.Asthe computingsystem,wehaveusedaworkstationwith anRTX2070SUPERgraphicscard,anAMDRyzen7 3700XCPU,and32‐GBofRAM.

Figure14. Testresultsofimplementeddeeplearning models

888photosthatweredividedinto14classesare usedfortrainingpurposes.Becauseoftheextensive trainingtime,thenumberofepochswaslimitedtoa minimum.

DeeplearningmodelsVGG‐19,Ef icientNet‐B7, ResNet,InceptionV3,andR‐CNNweretrained.

Thetestingphasewasinitiatedfollowingthe completionofeachalgorithm’strainingoperations. AccordingtoIoU>0.5,precisionandrecallvalueswere computed.Asaresult,theratesofeachalgorithm’s detectionofobjectsfrom14classesweremade.Fig‐ure14displayssomegraphicsshowingtheprecision andrecalllevelsattainedforthis.

Thegraphsshowprecisionandrecallvaluesfor studiedmodelsandobjectclasses.Therecallvalue startsat0andgrowstowards1,whilethegraphic precisionvaluestartsat1andmovestowards0in determinationswithahighperformancerate.This conditionmakesitclearthatthegraphicswiththe highestperformanceratesachievegoodresults.

7.1.Results&Discussions

Figure15displaystheexperimentationresultsby studiedCNNmodels.Theresultsofeachmodelare displayedseparately.Itisclearthatimageswithhigh spatialresolutiongivebetterresultsincomparison tolowspatialresolutionimages.These indingslead totheoutcomesof14objectsbeingdetected;5deep algorithmicvaluesforeachobjectareshowninbold inthetableoflearningmodelsTable3

InceptionV3

Continued

Resultsofobjectdetectionofvariousdeep learningmodels

Table3liststheobjectdetectionperformance ind‐ingsfor5deeplearningtechniquesover14classes. Thelastrowofthetablealsoincludestheaverage performanceratesforeachmodel.

Accordingtotheresults,theInceptionV3andR‐CNNmodelshadthehighestaverageperformance rates(18.78and41.78respectively).R‐CNNoutper‐formedothermodelsindetectingseveralclasses withstate‐of‐the‐artresults.VGG‐19hadthelowest averageperformance,scoring19.5,32.64,and15.42, 38.07,respectively.Thetenniscourthasthehighest availabilityrateofanyobject,at52,34,anditwas acquiredusingResNet‐50.Roundaboutandbridge hadthelowest indingrate,at9.09.Inallmodels,it wasdiscoveredataverylowrate.Thelimitedquantity oftrainingandtestingsamplesisbelievedtobeoneof thecausesofthelowavailabilityrateofroundabout andbridgelessons.However,itisbelievedthatthe modelsareunabletode ineobjectsthatfallunderthe roundaboutandbridgeobjectclassinawaythatis accurate.Thesetwoclassesareregardedaslacking sometraining.Thesamplesinthedatasetareclose tothegroundsurfaceandaresimplerforthemodel toidentifyintermsofshapeafterexaminationofthe tenniscourtpicturesamples,theobjectclasswith thehighestavailabilityrate.Modelswithfewerlayers tendtoperformbetterthanmodelswithmorelayers, accordingtoresearch.Thisisinterpretedasevidence thatwhendetectingmanyobjects,deeplearningmod‐elsshouldn’tfavorthosewithahighnumberoflay‐ers.Thetwomostsuccessfulresultsinobjectclasses areshowninTable 4 inlightoftheresultsfromthe models.

Featurecomparisonresultsofexperimentedpre‐trainedmodelsareshowninTable4.Theaccuracyof thesemodelsintop‐1andtop‐5predictionsisalso determinedwhentheywereusedforclassi ication andacomparisonoftheseaccuraciesisshowninthe tablebelow(Table5).

Figure15.

Figure15.

Table3. Resultsofobjectdetectionofvariousdeeplearningmodels

Table4. Class‐wiseobjectclassesdetectionresult

Models ObjectClassesDetected

TopTwoObjectClasses

VGG‐19 BaseballDiamond,Harbor BaseballDiamond,Harbor ResNet StorageTank,TennisCourt TennisCourt,StorageTank InceptionV3 LargeVehicle,GroundTrackField,Plane,SmallVehicle,Soccer BallField,TennisCourt TennisCourt,LargeVehicle, R‐CNN SwimmingPool,LargeVehicle,BaseballDiamond,Harbor,Plane, SmallVehicle,Ship,SoccerBallField, LargeVehicle,Plane Ef icientNet‐B7 GroundTrackField,Ship,StorageTank,SwimmingPool SwimmingPool,Ship

Table5. Featurecomparisonresultofstudiedtransfer learningmodels Module

Table6. ComparisonofModelswithrespectto classificationaccuracy

Inthispaper,severalobjectdetectiontechniques likeCNN(VGG‐19,ResNet‐50,Inception‐V3,and Ef icientNet‐B7)andR‐CNNetc.arediscussedand compared.Fromthediscussions,itwasfoundthatR‐CNNisimprovedmorethanotherCNN‐basedpre‐trainedmodelsintermsofaccuracyandprecision whileworkingwiththeDOTAdataset.ButInceptionv3 alsoacquiresnexttotoppositionindetectingmultiple classesfromsatelliteimagesafterR‐CNN.

Theresultsmakeitclearthatassoonasthe numberofclassesformultipleobjectdetectionrises, performanceratefalls.Itisalsonotedthatobject detectionbecomesmorechallengingasthesizeofthe imagesproducedbyhigh‐resolutionremotesensing rises.Ithasbeenshownthatallalgorithmsstruggleto detectobjectsinphotographsthataretakenabovethe groundandcoversubstantiallybiggerareas.Thenum‐berofdetectedobjectsandtheirperformancehas beenfoundtogrowasthe ieldofviewnarrows. Accordingtotheclassi ications,randomselectionwas usedtochoosethephotosinthedatasetthatwouldbe usedfortrainingandtesting.

Asperthefuturedirection,itcanbestatedthat forresearchtobedoneinthisdomain,pickingthe appropriatesamplesiscrucialfortestingstructures. Abetterevaluationoftheoutcomeswilldependon thenumberofsamplestobeutilizedinthetraining exceedingaparticularthreshold.Byeliminatingthese issueswhiledoingtrainingandtestingwillproduce betterresults.Researcherswhoareinterestedinthis areashouldtakeextracaretoconsidertheseissues. WemightadvisethatmultispectralLIDARdatabe usedtotestthesemodels.

AUTHORS

HinaHashmi∗ –CollegeofComputingSciences &InformationTechnology,TeerthankerMahaveer University,Moradabad,244001,India,e‐mail: hinahashmi170@gmail.com.

RakeshKumarDwivedi –CollegeofComputing Sciences&InformationTechnology,Teerthanker MahaveerUniversity,Moradabad,244001,India, e‐mail:dwivedi.rakesh02@gmail.com.

AnilKumar –IndianInstituteofRemoteSensing (IIRS),IndianSpaceResearchOrganisation (ISRO),Dehradun,248001,India,e‐mail: aniliirsisro@gmail.com.

∗Correspondingauthor

ACKNOWLEDGEMENTS

Firstandforemost,weextendourheartfeltappreci‐ationtoouradvisors,fortheirinvaluableguidance, expertise,andcontinuoussupportthroughoutthis researchproject.Theirinsightsandconstructivefeed‐backhavebeeninstrumentalinshapingthiswork. Wearealsothankfultoourcolleaguesandfellow researcherswhoprovidedvaluableinputandsugges‐tionsduringthecourseofourstudy.Theircollabora‐tionanddiscussionsgreatlyenrichedourunderstand‐ingofthesubjectmatter.Weextendourgratitudeto thecreatorsoftheDOTAdatasetandtheauthorsofthe pre‐trainedmodelsweutilizedinourresearch.Their effortsindatacollectionandmodeldevelopmenthave madethisworkpossible.

Additionally,weappreciatethesupportand encouragementfromourfriendsandfamily throughoutthisjourney.Lastbutnotleast,wewould liketoexpressourappreciationtothereviewersand editorsfortheirvaluablefeedbackandsuggestions, whichhelpedenhancethequalityofthispaper.

Thisresearchwouldnothavebeenpossible withoutthecollectiveeffortsandsupportofallthese individualsandorganizations.Thankyouforyour contributionstoourwork.

References

[1] M.Sharp,R.Ak,andT.Hedberg.“Asurveyof theadvancinguseanddevelopmentofmachine learninginsmartmanufacturing.” Journalof ManufacturingSystems,48,2018,170–179.doi: 10.1016/j.jmsy.2018.02.004.

[2] A.D.Preez,G.A.Oosthuizen.“Machine learningincuttingprocessesasenablerfor smartsustainablemanufacturing.” Procedia Manufacturing,33,2019,810–817.doi: 10.1016/j.promfg.2019.04.102.

[3] H.Hashmi,R.K.Dwivedi,A.Kumar,“Identi i‐cationofObjectsusingAI&MLApproaches: State‐of‐the‐Art,”202110thInternationalCon‐ferenceonSystemModeling&Advancementin ResearchTrends(SMART),2021,pp.1–5,doi: 10.1109/SMART52563.2021.9676273.

[5] K.He,X.Zhang,S.Ren,J.Sun,“Deepresidual learningforimagerecognition,”in: CVPR,2016.

[6] R.Girshick,J.Donahue,T.Darrell,J.Malik,“Rich featurehierarchiesforaccurateobjectdetection andsemanticsegmentation,”in: CVPR,2014.

[7] M.Tan,Q.V.Le,“Ef icientNet:RethinkingModel ScalingforConvolutionalNeuralNetworks.” Proc.Mach.Learn.Res. 97,2019,6105–6114.

[8] Pan,S.J.,andYang,Q.“ASurveyonTransfer Learning.” IEEETransactionsonKnowledgeand DataEngineering,vol.22,no.10,2010,1345–1359.doi:10.1109/tkde.2009.191.

[9] X.Sunetal.,“Multi‐typeMicrobialRelation ExtractionbyTransferLearning,”2021IEEE InternationalConferenceonBioinformatics andBiomedicine(BIBM),Houston,TX,USA, 2021,pp.266–269,doi:10.1109/BIBM52615. 2021.9669738.

[10] X.Wang,S.LiuandC.Zhou,“Classi ication ofKneeOsteoarthritisBasedonTransfer LearningModelandMagneticResonance Images,”2022InternationalConferenceon MachineLearning,Control,andRobotics (MLCR),Suzhou,China,2022,pp.67–71,doi: 10.1109/MLCR57210.2022.00021.

[11] Z.Xia,J.Liu,X.Chen,X.Li,andP.Chen,“Airplane ObjectDetectioninSatelliteImagesBasedon AttentionMechanismandMulti‐scaleFeature Fusion,”20224thInternationalConference onRoboticsandComputerVision(ICRCV), Wuhan,China,2022,pp.142–147,doi: 10.1109/ICRCV55858.2022.9953228.

[12] C.B.Chittineni,“EdgeandLineDetectionin MultidimensionalNoisyImageryData,”in IEEE TransactionsonGeoscienceandRemoteSensing, vol.GE‐21,no.2,pp.163–174,April1983,doi: 10.1109/TGRS.1983.350485.

[13] S.RongandB.Bhanu,“Modelingclutter andcontextfortargetdetectionininfrared images,”ProceedingsCVPRIEEEComputer SocietyConferenceonComputerVisionand PatternRecognition,1996,pp.106–113,doi: 10.1109/CVPR.1996.517061.

[14] J.NgandShaogangGong,“Multi‐viewfacedetec‐tionandposeestimationusingacompositesup‐portvectormachineacrosstheviewsphere,” ProceedingsInternationalWorkshoponRecog‐nition,Analysis,andTrackingofFacesandGes‐turesinReal‐TimeSystems.InConjunctionwith ICCV’99(Cat.No.PR00378),1999,pp.14–21, doi:10.1109/RATFG.1999.799218.

[15] P.Garnesson,G.Giraudon,andP.Montesinos, “Animageanalysis,applicationforaerial imageryinterpretation,”[1990]Proceedings. 10thInternationalConferenceonPattern Recognition,AtlanticCity,NJ,USA,1990,pp.

[4] H.Kumar,S.A.Hashmi,KhanandS.Kazim Naqvi,“SSE:ASmartFrameworkforLive VideoStreamingbasedAlertingSystem,”2021 10thInternationalConferenceonSystem Modeling&AdvancementinResearchTrends (SMART),2021,pp.193–197,doi:10.1109/ SMART52563.2021.9675306.

210–212,vol.1,doi:10.1109/ICPR.1990.11 8094.

[16] HsuanRenandChein‐IChang,“Acomputer‐aideddetectionandclassi icationmethodfor concealedtargetsinhyperspectralimagery,” IGARSS’98.SensingandManagingtheEnviron‐ment.1998IEEEInternationalGeoscienceand RemoteSensing.SymposiumProceedings.(Cat. No.98CH36174),1998,pp.1016–1018,vol.2, doi:10.1109/IGARSS.1998.699658.

[17] J.A.Shufelt,“Performanceevaluationandanaly‐sisofmonocularbuildingextractionfromaerial imagery,”in IEEETransactionsonPatternAnalysisandMachineIntelligence,vol.21,no.4,pp. 311–326,April1999,doi:10.1109/34.761262.

[18] J.G.ShanksandB.V.Shetler,“Confronting clouds:detection,remediationandsimulation approachesforhyperspectralremotesensing systems,”Proceedings29thAppliedImagery PatternRecognitionWorkshop,2000,pp.25–31, doi:10.1109/AIPRW.2000.953599.

[19] T.L.Haithcoat,W.Song,andJ.D.Hipple,“Build‐ingfootprintextractionand3‐Dreconstruction fromLIDARdata,”IEEE/ISPRSJointWorkshop onRemoteSensingandDataFusionoverUrban Areas(Cat.No.01EX482),2001,pp.74–78,doi: 10.1109/DFUA.2001.985730.

[20] KepingChenandR.Blong,“Extractingbuilding featuresfromhighresolutionaerialimagery fornaturalhazardsriskassessment,”IEEE InternationalGeoscienceandRemoteSensing Symposium,2002,pp.2039–2041,vol.4,doi: 10.1109/IGARSS.2002.1026437.

[21] J.SecordandA.Zakhor,“TreeDetectioninUrban RegionsUsingAerialLidarandImageData,” in IEEEGeoscienceandRemoteSensingLetters, vol.4,no.2,April2007,pp.196–200,doi: 10.1109/LGRS.2006.888107.

[22] D.ChaudhuriandA.Samal,“AnAutomaticBridge DetectionTechniqueforMultispectralImages,” in IEEETransactionsonGeoscienceandRemote Sensing,vol.46,no.9,Sept.2008,pp.2720–2727, doi:10.1109/TGRS.2008.923631.

[23] C.S.Grant,T.K.Moon,J.H.Gunther,M.R.Stites andG.P.Williams,“DetectionofAmorphously ShapedObjectsUsingSpatialInformationDetec‐tionEnhancement(SIDE),”in IEEEJournalof SelectedTopicsinAppliedEarthObservationsand RemoteSensing,vol.5,no.2,April2012,pp.478–487,doi:10.1109/JSTARS.2012.2186284.

[24] M.I.ElbakaryandK.M.Iftekharuddin,“Shadow DetectionofMan‐MadeBuildingsinHigh‐ResolutionPanchromaticSatelliteImages,”in IEEETransactionsonGeoscienceandRemote Sensing,vol.52,no.9,Sept.2014,pp.5374–5386, doi:10.1109/TGRS.2013.2288500.

[25] SevoandA.Avramović,“ConvolutionalNeural NetworkBasedAutomaticObjectDetectionon

AerialImages,”in IEEEGeoscienceandRemote SensingLetters,vol.13,no.5,May2016,pp.740–744,doi:10.1109/LGRS.2016.2542358.

[26] D.Yu,H.Guo,Q.Xu,J.Lu,C.Zhao,and Y.Lin,“HierarchicalAttentionandBilinear FusionforRemoteSensingImageSceneClas‐si ication,”in IEEEJournalofSelectedTopicsinAppliedEarthObservationsandRemote Sensing,vol.13,2020,pp.6372–6383,doi: 10.1109/JSTARS.2020.3030257.

[27] Y.Yu,T.Gu,H.Guan,D.LiandS.Jin,“Vehicle DetectionfromHigh‐ResolutionRemoteSens‐ingImageryUsingConvolutionalCapsuleNet‐works,”in IEEEGeoscienceandRemoteSensing Letters,vol.16,no.12,Dec.2019,pp.1894–1898, doi:10.1109/LGRS.2019.2912582.

[28] B.VasuandA.Savakis,“ResilienceandPlasticity ofDeepNetworkInterpretationsforAerial Imagery,”in IEEEAccess,vol.8,2020,pp. 127491–127506,doi:10.1109/ACCESS.2020. 3008323.

[29] X.Sunetal.,“Multi‐typeMicrobialRelation ExtractionbyTransferLearning,”2021IEEE InternationalConferenceonBioinformatics andBiomedicine(BIBM),Houston,TX,USA, 2021,pp.266–269,doi:10.1109/BIBM52615. 2021.9669738.

[30] B.Huang,X.Chen,Y.Sun,andW.He,“Multi‐agentcooperativestrategylearningmethod basedontransferLearning,”202213th AsianControlConference(ASCC),Jeju, Korea,Republicof,2022,pp.1095–1100, doi:10.23919/ASCC56756.2022.9828357.

[31] ZouandQ.Zhang,“eyeSay:MakeEyes SpeakforALSPatientswithDeepTransfer Learning‐EmpoweredWearable,”202143rd AnnualInternationalConferenceoftheIEEE EngineeringinMedicine&BiologySociety (EMBC),Mexico,2021,pp.377–381,doi: 10.1109/EMBC46164.2021.9629874.

[32] M.ThoreauandF.Wilson,“SaRNet:ADataset forDeepLearningAssistedSearchandRescue withSatelliteImagery,”202112thInternational SymposiumonImageandSignalProcessingand Analysis(ISPA),Zagreb,Croatia,2021,pp.204–208,doi:10.1109/ISPA52656.2021.9552103.

[33] N.Dey,Y.D.Zhang,V.Rajinikanth,R.Puga‐lenthi,andN.S.M.Raja,“CustomizedVGG19 architectureforpneumoniadetectioninchestX‐rays.” PatternRecognitionLetters, vol.143,2021, 67–74.

[34] A.Bagaskara,M.Suryanegara,“Evaluationof VGG‐16andVGG‐19DeepLearningArchitecture forClassifyingDementiaPeople.”In20214th InternationalConferenceofComputerandInfor‐maticsEngineering(IC2IE)(pp.1–4).IEEE.

[35] S.Mascarenhas,M.Agarwal,“Acomparison betweenVGG16,VGG19andResNet50archi‐tectureframeworksforImageClassi ication.”

In2021InternationalConferenceonDisruptive TechnologiesforMulti‐DisciplinaryResearch andApplications(CENTCON)(vol.1,pp.96–99). IEEE.

[36] B.Koonce,B.Koonce,B.“ResNet50.Convolu‐tionalNeuralNetworkswithSwiftforTensor‐low:ImageRecognitionandDatasetCategoriza‐tion,”2021,pp.63–72.

[37] M.G.D.Dionson,P.B.ElJireh,“Inception‐V3 architectureindermatoglyphics‐basedtemper‐amentclassi ication.” PhilippineSocialScience Journal,vol.3,no.2,2020,pp.173–174.

[38] L.P.Kothala,L.P.,andGuntur,S.R.(2022, December).SegmentationofIntracranialHem‐orrhagethroughanEf icientNetB7‐basedUNET model.In2022InternationalConferenceon SmartGenerationComputing,Communication andNetworking(SMARTGENCON)(pp.1–5). IEEE.

[39] M.K.Islam,C.Kaushal,M.A.Amin,“Smart Home‐HealthcareForSkinLesionsClassi ication WithIotBasedDataCollectionDevice.”Kushtia, Bangladesh:IslamicUniversity,2021.

[40] Y.W.Chao,S.Vijayanarasimhan,B.Seybold,D.A. Ross,J.Deng,R.Sukthankar,R.(2018).“Rethink‐ingthefasterr‐cnnarchitecturefortemporal actionlocalization.”In ProceedingsoftheIEEE conferenceoncomputervisionandpatternrecognition.2018.pp.1130–1139.

[41] P.Bharati,A.Pramanik,“Deeplearning techniques—R‐CNNtomaskR‐CNN:a survey.” ComputationalIntelligenceinPattern Recognition:ProceedingsofCIPR,2020,pp. 657–668.

Submitted:3rd April2023;accepted:16th September2023

AmalZouhri,AbderahamaneEZ‑ZAHOUT,SaidChakouk,MostafaELMALLAHI

DOI:10.14313/JAMRIS/2‐2024/12

Abstract:

Thenewwaveofperformanttechnologydevicesgener‐atesmassiveamountsofdata.Thesedevicesareused incities,homes,buildings,companies,andmore.One ofthereasonsfordigitalizingtheirtasksisthatover thepastfewyears,therehasbeenaninterestinreduc‐ingcarbonemissionsandincreasingenergyefficiency tocreateafriendlyecosystemandprotectnature.One ofwhichgrantedtheexplosionofdata.Afterdeploying thesenewdevices,asignificantincreaseintheuseofthe otherfaceofenergytoimplementthecomponentsofthe newdeviceswasnoticed.Aboveall,theinterconnection oftheseintelligentdevicesisthecentralconceptofthe InternetofThings(IoT).Thisdomainhaswidenedthepos‐sibilitiesfortheinterconnectionofbuildingmanagement systems(alsonamedSmartGrids)anddevicesforbetter energymanagement.Furthermore,itspotentialisreal‐izedonlyafterorganizingandanalyzingalargeamount ofdata.Real‐timemanagementandmaintenanceofbig dataarecriticaltoimprovingenergymanagementin buildings.Thebenefitsofbigdataanalyticsgobeyond savingsonelectricitybills.Itcanprovidecomfortfor buildingusersandextendthelifeofbuildingequipment, enhancingthevalueofcommercialbuildings.Intelli‐gentinterconnectionofabuilding’stechnicalinstallations (lighting,heating,hotwater,photovoltaicinstallations, etc.)notonlyallowsforconnectedmanagementofthis equipmentbutalsomeetshighenergyefficiencycriteria thatindicateanincreaseincomfortandenergysavings. Withbuildingautomation,thetechnicalinstallationsofa buildinginteractoptimally.Inthisarticle,wewillsimulate anintelligentbuildingbasedontheCiscopackettracer software.Tobettermanagetheenergyconsumptionof ourproject,wewillfocusontheprocessingofdatain real‐time,especiallysincewewillhaveamassiveamount ofdatageneratedbythesensors,whichmakestheuseof bigdatamandatory.

Keywords: virtualsmartgrid,modernelectricitynet‐works,intelligentlymanage,generationconsumption, stability,electricitysupplyanddemand,packettracer

1.Introduction

Inthepast,abuildingneededonlyfourwalls, aroof,andsometimesa loortofunction.Build‐ingprojectshavebecomemuchmorecomplexas moresophisticatedtechnologieshavebeencreated, includingwirelessnetworks,networkedcomputers, electricity,andtelephones.Modernstructuresare equippedwithsophisticatedsystemsthatprovide comfortandinformation,makingthemalmostlike livingorganisms[1].

TheadventoftheInternetofThings(IoT)and bigdatahasbroughtaboutasigni icanttransforma‐tioninthe ieldofsmartbuildings.Smartbuildings aredesignedtobemoreenergy‐ef icient,sustainable, andresponsivetotheneedsoftheiroccupants[2–5]. ByintegratingIoTtechnologiesandharnessingbig data[6],thesebuildingscanoptimizeenergycon‐sumption,improveoccupantcomfort,andenhance overalloperationalef iciency[7, 8].Onekeyaspect ofasmartbuildingisthecollectionandanalysisof vastamountsofdatageneratedbyvarioussensors anddevicesinstalledwithintheinfrastructure.These sensorscontinuouslymonitordifferentparameters, suchastemperature,humidity,occupancy,lighting, andenergyusage,amongothers[9–13].Thedatacol‐lectedisthenprocessedandanalyzedusingsophisti‐catedalgorithmsandarti icialintelligencetechniques togainvaluableinsightsintobuildingperformance andoccupantbehavior[14].

Energyconsumptionisamajorconcerninmod‐ernsociety,andsmartbuildingsaimtotacklethis challengebyemployingIoT‐basedsensornetworks forreal‐timedatacollection.Thedatacollectedfrom thesesensorsallowsbuildingmanagerstooptimize heating,ventilation,andairconditioning(HVAC)sys‐tems,lighting,andotherenergy‐consumingcompo‐nents,leadingtoreducedenergywastageandcost savings[15–17].Moreover,theintegrationofsmart buildingtechnologiesenablesbetterpredictionand controlofenergydemand,whichisparticularlycrucial intoday’senergy‐constrainedworld.Advancedenergy storagesolutions,suchassmartphasechangemate‐rial(PCM)walls,canhelpstoreexcessenergyand releaseitduringpeakdemandperiods,makingbuild‐ingsmoreenergy‐independentandresilient[18]. Additionally,smartbuildingspromoteoccupantwell‐beingbymonitoringindoorenvironmentalquality (IEQ)factors,suchasairquality,temperature,and humidity[15–19].

IoT‐basedairqualitysensorscandetectcommon insulationproblemsandensurehealthyindoorenvi‐ronmentsbytimelydetectingandaddressingissues relatedtoventilationandaircirculation.Thecombi‐nationofIoTandbigdatatechnologieshasopened upnewpossibilitiesforenhancingenergyconsump‐tioninsmartbuildings.Throughtheintegrationof intelligentsystems,data‐drivendecision‐making,and optimizedresourceutilization,smartbuildingsare revolutionizingthewayweconstruct,manage,and inhabitourbuiltenvironments,leadingustowarda moresustainableandenergy‐ef icientfuture.

Theincreasinginterestinintelligentbuildingsand theemergenceofnewtechnologiesinthisareahas resultedinanumberofstudiesthataimedatimple‐mentingdifferenttypesofapplications.Theseinclude energyoptimization,simplifyingbuildingmanage‐ment,improvingresidentcomfort,reactivealarm management,personalprotection,assetprotection, intrusionmanagement,andsoon.Recentresearch hassuggesteddescribingbuildingswithconsistent metadatamodeling.Thesepracticesarebasedonsen‐soryontologies,subsystems,andrelationships,ensur‐inginteroperabilityandportabilityofapplications.At present,wecannottalkaboutsmartbuildingswithout mentioningtwoinseparablecomponents,namelythe InternetofThings(IoT),whichismadeofallthecon‐nectedsensors,andthestorageenvironmentforthe datageneratedbythesesensors.Ithasbecomethekey technologicalelementinsmartbuildings.Anymodern constructiondesignedtobesmartneedstoincorpo‐rateconnectedobjects.Inaddition,itisimpossibleto makesuchbuildingssmartanddynamicwithoutana‐lyzingthedatageneratedbythismassofconnected objects.Oneofthemostrecentadvancesinthis ield istheintelligentbuilding,whichisahighlyenergy‐ef icientarchitecturecapableofcontrollingthestor‐age,distribution,andsupplyofenergy.Itaimsto achieverationalconsumptionbyusingthetechnolo‐giesofconnectedobjects(IoT)andmassdatapro‐cessing.Thisnotioncallsforaconceptcalled“Smart Grids,”whicharecurrentlyusedinelectricitydistri‐butionnetworkstomanageenergyinthebestpos‐sibleway.Thisinvolvestakingintoaccountallthe actionsofstakeholders(consumers,users,andpro‐ducers)inordertomodifytheproductionanddistri‐butionofenergyaccordingto luctuationsindemand, particularlyconsumptionpeaks.Thismethodreduces wasteandimprovesenergysupply.Theinhabitants ofabuildingcanbeassuredofabalancedproduc‐tionanddistributionofenergybyapplyingthisidea tothatspeci icstructure.Themainpurposeofthis workistoexamineexistingdocumentationonsmart buildings,focusingonIoTandbigdata,whichare thetwomajortechnologycomponentsinourcontext. Thispaperisstructuredasfollows:itintroducesthe conceptofintelligentbuildingsandrelatedtechnolo‐gies.Then,itfocusesonthe ieldoftheInternetof Things,itsarchitecture,anditsapplications.Anoper‐ationtestfollowsthissectionandexaminesanalytical approachesappliedbasedonabigdataecosystem, andafterthat,aconclusionforthispaperisthe inal step.Therestofthepaperconsistsoftherelatedwork

inSection2;Section3providesanoverviewofSmart Grids;Section4discussesbigdatapredictiveanalytics forSmartGridstability;theresultsanddiscussionin Section 5,and inally,Section 6 forconclusionand perspective.

2.RelatedWork

Concerningtheanalysisofbuildingstounderstand energyuse,theinitialsolutionsweremainlyaimedat usingnondeterministicmodelsbasedonsimulations. Avarietyofsimulationtoolsareavailablewithdif‐ferentcapacities.Parketal.estimatedthatresearch intotheapplicationofbigdatatosmartcityconstruc‐tioninvolvesbuildingatechnicalframeworkforthe developmentofsmartcitiesfromthepointofview ofexploring,managing,analyzing,andapplyingdata paths.Talarisetal.haveanalyzedandfoundthatwhile searchanglesarevaried,thesesearchesarebasedon webAPIinformationintegration,metadata,seman‐ticaggregation,andknowledgegraphicstechnology remainingattheconceptuallevel,andhowtomake gooduseofbigdatatechnologyneedsfurtherclar‐i ication.Simonetal.discussthatifalargersystem isrequiredtoextractdatafromtheenergyef iciency managementplatformatalaterstage,thisisoften notfeasible.Evenwherepossible,itisnecessaryto customizethedevelopmentofinterfacesandcorre‐spondingtransmissionprotocols,whichislongand expensive.Atpresent,thedevelopmentandconstruc‐tionofsmartbuildingsathomeandabroadareinthe developmentandexplorationstage.Jiangetal.believe thattheenergyef iciencyofbuildingsistheuseof intelligenttechnologiesformeasuringtheenergycon‐sumptionofbuildingsandanalyzingtheenergyef i‐ciencyofequipment,adoptionofsystemsintegration methodsinordertobuildplatformsformeasuring andmanagingenergyconsumption,andbyaglobal managementoftheenergyef iciencyofbuildingsin thesupplyofhotwater,lighting,appliancesandother aspectsinordertoobtainbetterenergysavingeffects. Chrysietal.(2020)presentpracticalapproachesto enhanceenergyef iciencyandenvironmentalsustain‐abilitythroughtheadoptionofsmartbuildingtech‐nologiesandIoT‐basedenergymanagementstrate‐gies;thisisachievedbyanonlinearmodellinking powerdemandtotherequiredtemperaturepro ile.A geneticalgorithmbasedonsuchamodelisthenused tooptimizeenergyallocation,matchtheuserthermal constraints,andallowthemixed‐integerdeterministic optimizationalgorithmtodeterminetheremaining energymanagementactions.Consequently,amore integralvisionisneededtoprovideaccuratemodels ofenergyusedinbuildings[21–32].

3.TheoreticalStudy

3.1.SmartGrids

A“SmartGrid”referstoanelectricalenergydistri‐butionsystemthatautonomouslyadjuststoproduc‐tionanddemand.TheSmartGridintegratesandmod‐i iesproductionandconsumptionmodelstoachieve

optimalsafetyandenergyef iciency.Thisisfacili‐tatedbyanetworkofsensors,real‐timedatatrans‐mission,analysistools,bigdata,andotheradvanced techniques.

3.2.CharacteristicsofSmartGrids

SmartGridscanbede inedbyfourkeycharacteris‐tics: lexibility,reliability,accessibility,andeconomy.

Flexibility:SmartGridsenableprecisemanage‐mentofthebalancebetweenenergyproductionand consumption.

Reliability:SmartGridsenhancetheef iciencyand securityoftheentireenergydistributionnetwork.

Accessibility:SmartGridsfacilitateseamlessinte‐grationofrenewableenergysourcesintothesystem.

Economy:SmartGridsleadtoenergyandcostsav‐ingsduetoimprovedmanagementofenergyproduc‐tionandconsumption.

3.3.InternetofThings(IoT)

TheIoTreferstoadistributednetworkconnecting physicalobjectscapableofcommunicatingwitheach other,otherdevices,orcomputers.Theseobjectscan detectoractupontheirenvironment.Thedatatrans‐mittedbythesedevicescanbecollectedandanalyzed torevealinsightsandsuggestactionsthatsavemoney, increaseproductivity,orimprovethequalityofgoods andservices.

3.4.ConnectedObjects

InthecontextoftheInternetofThings,a“con‐nectedobject”denotesanyelectronicdevicecapable ofcommunicationandinformationexchangeviaaPC, tablet,oranyotherdeviceequippedwithwirelessor Bluetoothconnectivity.

3.5.CharacteristicsofConnectedObjects

Connectedobjectspossessthefollowingdistinc‐tiveattributes:

Identi ication:Eachobjecthasauniqueidenti ica‐tioncode,suchasabarcode,IPaddress,orRFIDtag.

EnvironmentalAwareness:Theseobjectsare equippedwithdetection,analysis,treatment,and alertingcapabilities,makingthemsensitiveto theirsurroundings.Theycanmeasureparameters liketemperature,humidity,gaslevels,andenergy consumption.

Interactivity:Theconnectionbetweenanobject andthenetworkcanbepermanentortemporary, dependingontheobject’sspeci icneedsandfunction.

VirtualRepresentation:Eachconnectedobjecthas auniquesignatureandphysicalmanifestation,repre‐sentedvirtuallyintheIoTsystem.

3.6.TheConstituentPartsofIoT

FiveessentialcomponentsconstitutetheIoTsys‐tem:

Sensor:Measuresexternalparametersintheenvi‐ronment.

EmbeddedSoftware:Allowstheconnectedobject tostore,retrieve,process,andevaluatedatabefore transmission.

TransmissionChip:Facilitatesdatatransmission afterprocessing.

CustomerInterface:Renderstransmittedinforma‐tionunderstandableandusefultotheuser.

Battery:Providespowertotheconnectedobjects, enablingtheirfunctionality.

4.HomeAutomationandItsObjectives

4.1.HomeAutomation

Itisthesettingupofnetworkslinkingthedifferent equipmentofthehouse(suchastheWiiFisystem, thehomeautomation,andthekitchenandbathroom appliances).

Itincludesawiderangeofservices,allowingthe integrationofcontemporarytechnologiesinthehome. Asaresult,wemaydistinguishbetweentwoareas ofapplicationhomeautomation:

‐ Thmanagementofenergy low(water,gas,and electricity),whichincludesthecontrolofheating, lighting,ventilation,andhouseholdappliances

‐ Thecontrolofinformation lowcomingfromthe computer,radio,andphone

4.2.ObjectivesofHomeAutomation

Homeautomationcontributessigni icantlytothe realizationofaperfectlifetothehumanbeing,with fourmainobjectives(comfort,security,energysaving andhealth).

Comfort

‐ Opendoorsandwindowswithoutforceusingthe cellphone.

‐ Turnonandoffthelightremotely.

‐ Airconditioningofthehouse(hotinwinterandcold insummer).

‐ Therefrigeratordeclaresitsneedforfoodthrougha messageonmobile.

‐ Createlifescenariosandautomateyourhome.

Security

‐ Protectthehouseagainsttheft.

‐ Avoidaccidentsofburnedgas, ireandelectrocu‐tion.

‐ Centralizethehouse(alldoorsandwindowsclose).

‐ Monitorthehouseremotelythroughcamerasand alarms.

‐ The ixedtelephoneautomaticallycallthe ire departmentincaseofemergency.

EnergySaving

‐ Controlthelightingofthehouse.

‐ Setthemachinesforacertainperiodoftimelike washingmachine.

‐ Turnoffenergy‐consumingobjectsifyouarenot goingtousethem,forexample,ifyouaresleeping andleavetheTVon.

‐ Controlthethermalexchangeswiththeoutside. Optimizationofdomestichotwaterproduction

Health

‐ Homeautomationhelpstheelderlyanddisabledto handlethingsinthehouses.

‐ Sensorsandmeasurementsofthehealthofpatients, suchasbloodpressure,bodytemperature,and bloodsugarlevels.

‐ Makethemedicalvisitremotelythroughspecial equipmentplacedinthehome.

5.PracticalStudy

Wewillpresentthesimulationpartperformedby theCiscoPacketTracersoftware

5.1.PacketTracer

PacketTracerisaCiscosoftwarethatallows thebuildingofavirtualphysicalnetwork.Theuser buildstheirnetworkusingequipmentsuchasrouters, switches,orcomputers,andrecentversionsofPT integrateIoTequipment(smartdevices,sensors,actu‐ators,microcontrollers,smartwindows,smartfans, smartlights,alarmsirens,etc.).Thisequipmentis linkedviaconnections(variouscables,optical iber, etc.).Oncealltheequipmentisconnected,itispossible foreachofthemtocon iguretheIPaddressesandthe availableservices.

5.2.EquipmentUsedfortheSimulation

Weusedavarietyofequipmentinoursimulation, includingconnectedobjects,programmableobjects, testobjects,andintermediateequipment.

1) ConnectedObjects:Thefollowing igureillustrates thedifferentequipmentused:

Figure1representedtheconnectedobjectsused inthesimulation.

2) ProgrammableObjectsandTestObjects:Forthe testwewilluseobjectslike ire,andforthemove‐ment,weusethemovementofthemouseand programmablecardsliketheMCU.

3) IntermediateEquipment:Therouter,theswitch, HomeGetway,themodem,thecloud,theserversto controloursystem,andanantennaforthecellular networkaresomeoftheintermediatedeviceswe used.

5.3.ConfigurationOutsidetheBuilding

1) RouterCon iguration:ThetwoIoTandDNS servers,aswellastheCloud,thecentralof ice serverandtheSwitch,areallconnectedtothe routerthroughitsthreeGigabitEthernetports.We willcon igureitontheCLI.

2) Con igurationoftheServers:Wehavetwoservers tocon igureIoTserverandDNSserver,forboth wewillspecifyanIPaddressplustheaddressof GetwayandDNS.

3) The3G/4GCellularNetwork:Wehavechosenacel‐lularnetwork(3G/4G),whichallowsustoconnect totheserverviaaSmartphoneatgreatdistances, inordertohavethepossibilitytoremotelycontrol alltheequipmentconnectedtotheIoTserver.

5.4.ConfigurationInsidetheHouse

1) HomeGetway:Itsroleistolinkallconnected objectseitherwiredorwirelessandgivethemIP addresses.Wehavesecuredthesystemagainst hackersbyWPA2‐PSKauthenticationwithapass‐word,thistypeisthemosteffectiveandtakesa longtimeforthehackertoaccessthenetwork.

2) ConnectedObjects:Wehaveconnectedtheobjects withtheHomeGetwayinawirelesswaywhere wehavemadeamodi icationinthenetworkcard (changetoWiFitype)andclickedontheSmart Devicebuttonsothattheyhavethepossibilityof accessingthenetwork.programmingpart:Weare goingtousethemicrocontroller“BoardsMCU.” Thisequipmentisprogrammabletocontroland commandataskinthedesiredway,wherewehave chosentheScriptlanguageinFigure2

Figure1. ArchitectureIoTconnectedobjectsusedinthesimulation

Serverinterfacetocontroltheobjects

detected,thedoorsopen,thealarmgoesoff,giving peopletimetoescapethebuilding.

Thecreationoftheconditionsrequiresthatthe objectsworkatthesametimeoroneaccordingtothe other.Therewillbeamasterobjectandslaveobjects. Whenthemasterobjectturnson,theslaveobjectsalso turnon,andthesamegoesforturningoff.

IntelligentbuildingplanninginFigure3simulates justoneapartmentinthebuilding,anditsprototype iscomposedofabedroom,alivingroom,akitchen,a bathroom,andacorridor.

Wehaveplacedourobjectsintheapartmentina homogeneouswayinordertocoveralltheapartment, andwehaveplacedtheHomeAwaysothatitiscon‐vergenttoalltheobjectsandsothattherewillnotbe cutsofconnectionoraweakeningof low,thenwewill controlsometasks,namely:

‐ Thesecuritysystem:byusingthesurveillancecam‐eraequippedwithamotiondetectorandasiren. Thus,whenthedetectordetectsamovement,the webcamrecordseverythingthathappensandthe alarmsounds.

‐ The iredetectionsystem:Wealsotestedthe ire detectionsystem,andfoundthatassoonasa ireis

‐ Thebuildingtemperaturecontrolsystem:Inthis system,weplacedathermostatthatmeasuresthe temperatureofthebuildingafteritturnsontheair conditionerorthefurnaceaccordingtothemea‐suredtemperature.

‐ Controlofdoorsandwindows:Oneofthefunctions ofanintelligentbuildingistheremotecontrolof doorsandwindows.Astheseareconnectedtothe homenetwork,wecanopenandclosethemusing oursmartphones.

‐ Lightingcontrol:Wecanalsocontrolthelightinthe smartbuildingeitherautomaticallywiththemotion sensorsorwiththesmartphoneusingtheIoTmon‐itorapplicationFigure4,wecanaccessthenetwork andtheIoTserverthroughoursmartphone,PCand tablet.

Figure2. ProgrammingtheMCUboard

Figure4.

Figure3. Intelligentbuildingplanning

6.EnergyEfficiencyintheFieldofIntelligent Buildings

Whenthebuilding’sequipmentisintelligentlyand effectivelyinterconnected,wecaneasilymanageand controltheenergyconsumptionthrougharemote controlthatenablesthepilotingoftheseconnected devicesthroughacellphone.Bydoingso,wecan instantlydetectanyunusualvaluethatwillbehigher thantheaverageconsumptionbyenergyclassand identifymorequicklytheerrors, laws,andirregular‐itiesinthefunctioning.

Whenwetalkaboutthereductionofenergycon‐sumption,wearenecessarilytalkingaboutbuildings sincetheyofferahighpotentialforenergysavings andrepresentmorethan40%ofthetotalenergycon‐sumption.

Dailyliferequiresalotofenergy(Fig.5),cooling insummer,lightingatnight,hotwater,etc.Ourenergy supplyrelieslargelyonfossilfuels,thecombustionof whichgeneratesCO2 emissions.

Buildingsareresponsibleforthelargestshare ofCO2 emissionsindevelopedcitiesandcanbe classi iedaccordingtoenergyclassesrangingfrom classA(0to50kWh/m2 peryear(mostef icient housing))toclassG(451kWh/m2 andmore(very energyintensive)).Weconsideralowenergybuilding (BBC)whentheconventionalconsumptionofprimary energyofthebuildingforheating,cooling,ventilation, hotwaterproduction,andlightingislessthanorequal to50%oftheconventionalconsumptionreference (50kWh/m2/year).ConsumptionisexpressedinkWh ofenergyandbroughtbacktothesquaremeterof surface.

Themainobjectiveistoreducetheneeds:“pas‐sive”energyef iciency,andtosuperviseandman‐agethetechnicalequipmentofthebuilding:“active” energyef iciency.

Thisgivesenergygainsbyactingondifferent humanandmaterialparameters,amongthebestprac‐ticestouseistheuseofef icientproducts,toreduce energyconsumption,itisessentialtochooseequip‐mentwiththebestpossibleenergyef iciency,thatisto saythebestratiobetweenenergyconsumedandthe serviceprovided.

Ontheotherhand,theintegrationofrenewable energies,theuseoftheseenergiesinanapproachof energyimprovementallowstoobtainapartofthe energynecessarytothebuilding(electricity,heating, sanitaryhotwater)inarenewablewayandthusto decreaseoreveneliminatetheexternalenergycon‐tribution.ThusThemetering/measurementofcon‐sumption:Theenergymanagementofabuildingcon‐sists irstofallincounting/measuringtheconsump‐tions.

Fortheelectricalandgaspart,aclassicinstallation includesageneralmeterwhichprovidestheglobal consumptionsfortheirinvoicingbytheenergydis‐tributor.Anoptimizedinstallationincludesinaddi‐tiontothegeneralmeter,permanentsub‐meters. Theirmainroleistoestablishthedistributionof energyconsumptionbyitem(heating,domestichot water,ventilation...).

Thecountingormeasurementofconsumption allowstherealizationoftheenergybalance,the awarenessbytheuserormanagerofconsumption andisusedfortheestimationoftheenergysaving potential.Italsoguaranteesafollow‐upintimeofthe energyperformance.

‐ multiplythepowerofyourappliances(inKW)by thetimeofuse(inhours);

‐ thenmultiplyitbythepriceperkilowatt‐hour.

Theresultwillallowyoutoknowwhichappliances consumeexcessiveamountsofenergy.

7.RelationshipofBigDatawithIntelligent Buildings

Facedwiththeevolutionofscience,technologies areevolvingatthesametime,amongthemtheIoT, whichallowsobjectstobeconnectedtotheInternet. Thisseesthe lowofimmeasurabledatagenerated throughtheobjectsconnected,whichmakesitimpor‐tanttobeabletolinktheseinnovationstobigdata.

TheIoTandbigdatacoexisttoallowforsignif‐icanttechnologicaladvances,asthevolumeofdata exchangedincreasesandthenumberofobjectscon‐nectedtotheInternetmultiplies.

Thebigdatacollectedbytheconnecteddevices canbeusedinreal‐timeoperations,suchasmoni‐toringenergyconsumptionandreactingaccordingto thesituation,eitherbychanging,repairing,ormaking anotherproposal.

Thesystemcanbeincorporatedwithfunctionsto controltheenergyconsumedbythedevicesaccording totheuser’swishes.Iftheelectricityconsumption exceedsathresholdvaluesetbytheuser,theappli‐cationisnoti ied.

SmartIoTdevicescancollectenergyusagedata fromeachunitandstoreitinadatabasebasedthatcan

Figure5. Worldenergyconsumption

beanalyzedandreportedonforenergyconservation andanalysis.

Buildingscannotbemadeintelligentordynamic without irstexaminingthedataproducedbythisvast networkofinterconnectedthings.The irststepinthe analysisprocessissettingupaproperecosystemto store,clean,andpreparethedata.However,forsmart buildings,storingandretrievingvastamountsofdata inrealtimeisdif icult.

Ingeneral,therearethreetiersthatmakeupan intelligentsysteminanintelligentbuilding:Atthe inputdatainfrastructurelevel,allthedatasources producedbythelinkedbuildingobjectsarerep‐resented,includingenergyusage,humiditylevels, indoorandoutdoortemperatures,etc.Thesystem infrastructurelevel,whichenablesthegathering,pro‐cessing,combining,andstorageofdatainaNoSQL database,servesasthebrainoftheintelligentsys‐tem.Asaresult,itpermitstheuseofthisdatafor reportingpurposesonly,orforknowledgeextraction bydataminingalgorithmsormachinelearningby arti icialintelligencealgorithms.Thesystem’scatalog ofservicesthatareavailabletobuildingmanagers, inhabitants,energysuppliers,etc.isrepresentedby theservicelevel.

ThreelayersmakeuptheIoTarchitecture: Thelayerofperceptionisinchargeofsensingand datagathering.

Datatransitishandledbythenetworklayer,which alsoenablesthefusionofdifferentdevicesandcom‐municationinfrastructure.

Thetoplayerwhereusersinteractisknownasthe applicationlayer.

Severalapplicationswillresultfromtheuseof IoTinsmartbuildings,including:Accesstobuilding facilitiesthatis lexibleandrealtime;Energymanage‐mentisthemacroviewofenergyusageinrelationto buildingenergyef iciency;Locationofresourcesand occupantsincreasingindoorcomfort.

Figure6representsthechoiceofbigdatatechnol‐ogybasedontheenormousamountofdatagenerated everysecondinthiscontextofintelligentbuildings andapproachedcriticallevels.Forprocessingmassive amountsofdata,numeroussolutionshavebeenput forth.AlthoughSparkandHadoop,thetwomostpop‐ularproductsonthemarket,arebothlargescaledata

Figure7. Overallenergyconsumptionpermonth frameworks,theirapplicationsaresomewhatdiffer‐ent.Iftheoperatingandreportingrequirementsare largelystaticandwecanwaitforthebatchprocessing to inish,theMapReducemethodofoperationmight beenough.Ontheotherhand,wewillprobablyneed touseSparkifweneedtoanalyzestreamingdata,such asanalyzingsensordatainasmartbuilding,orifthe applicationscallforaseriesofactions.

Sparkistheidealsolutioninthissituation.The processofexaminingvariousformsofdatatodraw patternsandinformationusingvariousdatamining techniquesisknownasknowledgeextractionfrom data.Theanalysisofthismassiveamountofdatacon‐tributestotherealizationoftheworldwidegoalof smartbuildings,whichistosimplifybuildingman‐agement,cutenergyuse,secureresourcesandpeople, andprovideamoreconvenientlivingenvironment.

8.ApplicationandEvaluation

Inordertoexamineenergyconsumption,weuti‐lizedadatasetnamed“HomeC”whichcomprisesof variousobjectsandroomsthathavebeenmodeled afterreal‐lifecounterparts.

ThroughouranalysisofFigure 7,wediscovered theenergyconsumptionofeachindividualroomand object.Weobservedthatsomeroomshadhighercon‐sumptionlevelsthanothers,andourgoalwasto reducethisconsumption.Toachievethis,weanalyzed theobjectspresentintheseroomstoidentifypotential candidatesforremovalorreplacement.

Figure6. Generalarchitectureofsmartbuildings

8.1.DatasetDescription

OurdatasetisthusintheformofaCSV ileinclud‐ingweatherdataaswellashouseholdappliancemea‐surementsfromasmartmeterfor365daysinaperiod of1minute.Thetypeofvariablesisimportantfordata visualization:

used[kW]:Totalenergyused,gen[kW]:Total energyproducedusingsolarorotherenergysources, Houseoverall[kW]:Representstheoverallenergy consumptionofthebuilding,fortheothervariables, itistheenergyusedbyaparticularappliance(dish‐washer,oven,refrigerator,well,microwave).

8.2.DataExploration

AfterreadingthedatafromSpark,wewillper‐formdatapreprocessing.Thisinvolvesrenamingthe columnstoremovespacesandtheunit[kW],delet‐ingthevalues,groupingsomecolumns(suchasthe consumptionofthekitchenswehaveinthebuilding), andchangingtheformatofthetimeinsecondstoY‐m‐dH‐M‐S.Thus,theinformationwillbeavailablefrom 2021‐01‐015:00:00to2021‐12‐1703:29:00;Then, wewillreorganizethecolumns.ThedatainFigure8 representtheinformationaboutthedatathatwill appearlikethis:

Wecandifferentiateenergydataandweatherdata todeterminethemonthinwhichwewillconsumethe mostenergy.Wecanseethetotalenergyconsumption foreverymonth.Todeterminethemonthinwhichwe willconsumethemostenergy,wecanseethetotal energyconsumptionforallthemonths.

Afurnaceconsumeselectricitytopowerthefan thatcirculatesheatedairthroughoutabuilding,as wellastoignitethegasoroilusedtogenerateheat. Figure 9 representsconsumptionfordevices.The electricityconsumedbyafurnacedependsonseveral factors,includingthesizeoftheunit,theef iciency rating,andthelengthoftimeitisinuse.Inourdata, thefurnaceconsumesmorethan63%ofelectrical energy.

WeutilizedtheK‐meanstechnique,whichdivides thedataintoapredeterminednumberofclusters,to identifytheclasses.Asaresult,therearetwoclassesof roomsenergy:“Homeof ice,”“Winecellar,”“Kitchen,” “Barn,”and“Livingroom.”

Figure8. Informationaboutthedata

Figure9. Consumptionfordevices

Thereisalsoaclassofdevicesenergythat comprises:“Dishwasher,”“Furnace,”“Fridge,”“Garage Door,”“Well,”and“Microwave.”

Let’sconsidertheclassofroomsinordertobetter understandhowwecanmanagetheenergyconsump‐tionoftheconnectedmachinesintheintelligentbuild‐ing.Wewillmonitortheconsumptionofeachmember oftheclasssothatifoneofthemexceedstheaver‐ageof0.22054800000000002kW,wemustdecideto removeit.Thisismadepossiblebycommunication betweendevices.Here,wehaveanalyzedthecaseof onedayonly,butwecangeneralizeitlaterforallthe days.

Figure10showsthatthekitchenusesasigni icant amountmoreenergythanaverage.

9.Conclusion

Themodernizationofcitieshaschangedtheritual ofenergyconsumptionandnewtechnologyusage. Thismodernization,nowcalledSmartGrid,hastened theevolutionofinterconnectionbetweendevices. Thisinterconnectionofsmartdevices(whicharethe sourceofdatasensorslikesatellitesandcameras andorganizationliketheservicesgrantedtoclients) requiresimportantanalysiscapabilities.Thisisdone withthehelpofbigdatatoolstoensurereal‐time analysisandprovideenvironmentalcontext.Thisway, theconsumerhastheabilitytoremotelycontroltheir energyusage,andpriceratescanbeupdatedifthe levelapproachesacertainlimit.Asaresult,theyare allowedtomakethechoiceoftheeffectivetimetouse anydevice.Thisarticlehaspointedoutmanyfeatures ofhomeautomationandaddeditsobjectives,followed bytheutilityofavirtualnetworksoftware(i.e.,packet traceranditsnecessaryequipment).Finally,thisarti‐cleexpoundedontheroleofbigdataintheoperation, management,andmanipulationofthegenerateddata.

AUTHORS

AmalZouhri∗ –SidiMohammedBenAbdellah University,FacultyofSciencesDharElMahraz, LISACLaboratory,Fez,Morocco,e‐mail: amal.zouhri@usmba.ac.ma.

AbderahamaneEZ-ZAHOUT –FacultyofSciences–MohammedVUniversityAdjunctProfessorat SSE“SchoolofScienceandEngineering”Al AkhawaynUniversity–IfraneMorocco,e‐mail: a.ezzahout@um5r.ac.ma.

SaidChakouk –ResearcherProfessoratFacultyof LettersandHumanSociety,MohammedVUniversity inRabat,e‐mail:s.chakouk@um5r.ac.ma.

MostafaELMALLAHI –SidiMohammedbenAbdellah University,HighNormalSchool,Fez,Morocco,e‐mail: mostafa.elmallahi@usmba.ac.ma.

∗Correspondingauthor

References

[1] C.K.Metallidou,K.E.Psannis,E.A.Egyptiadou, “EnergyEf iciencyinSmartBuildings:

IoTApproaches,Journals&Magazines,” IEEEAccess,vol.8,March11,2020.doi: 10.1109/ACCESS.2020.2984461.

[2] L.P.C.Zangheri,D.Paci,M.N.E.Labanca,S.T. Ribeiro,S.Panev,P.Zancanella,andJ.‐S.Broc, “AssessmentofSecondLong‐TermRenovation StrategiesUndertheEnergyEf iciencyDirec‐tive,”Luxembourg,U.K.:PublicationsOf iceof theEuropeanUnion,2019.Available:https://ec .europa.eu/jrc/en/publication/assessmentse cond‐long‐term‐renovation‐strategies‐under‐energy‐efficiency‐directive

[3] A.P.Plageras,K.E.Psannis,C.Stergiou,H. Wang,andB.B.Gupta,“Ef icientIoT‐basedsen‐sorbigdatacollection–processingandanal‐ysisinsmartbuildings,”FutureGener.Com‐put.Syst.,vol.82,pp.349–357,May2018.doi: 10.1016/j.future.2017.09.082.

[4] R.Wegmueller,G.Magnin,J.Robadey,andE.‐L. Niederhauser,“Controlledactivethermalstor‐ageinsmartPCMwallsforenergyindepen‐dentbuildingapplications,”inProc.5thInt.Conf. Renew.Energy,Gener.Appl.(ICREGA),AlAin, UnitedArabEmirates,Feb.2018,pp.154–157, doi:10.1109/ICREGA.2018.8337575.

[5] N.Khan,N.Pathak,andN.Roy,“Detecting commoninsulationproblemsinbuiltenviron‐mentsusingthermalimages,”inProc.IEEE Int.Conf.SmartComput.(SMARTCOMP),Wash‐ington,DC,USA,Jun.2019,pp.454–458,doi: 10.1109/SMARTCOMP.2019.00087.

[6] M.Sophocleous,P.Savva,M.F.Petrou,J.K. Atkinson,andJ.Georgiou,“Adurable,screen‐printedsensorforinsituandreal‐timemoni‐toringofconcrete’selectricalresistivitysuitable forsmartbuildings/citiesandIoT,”IEEESensors Lett.,vol.2,no.4,pp.1–4,Dec.2018,doi:10. 1109/LSENS.2018.2871517.

[7] A.Kumar,A.Kumar,andA.Singh,“Energyef i‐cientandlowcostairqualitysensorforsmart buildings,”inProc.3rdInt.Conf.Comput.Intell. Commun.Technol.(CICT),Feb.2017,pp.1–4, doi:10.1109/CIACT.2017.7977310.

[8] N.Haidar,N.Tamani,F.Nienaber,M.T. Wesseling,A.Bouju,andY.Ghamri‐Doudane, “Datacollectionperiodandsensorselection methodforsmartbuildingoccupancy prediction,”inProc.IEEE89thVeh.Technol. Conf.(VTC‐Spring),Apr.2019,pp.1–6,doi:10. 1109/VTCSpring.2019.8746447.

[9] S.Antonov,“Smartsolutionfor iresafetyina largegarage,”inProc.Int.Conf.CreativeBus. SmartSustain.Growth(CREBUS),Sandanski, Bulgaria,Mar.2019,pp.1–4,doi:10.1109/CRE‐BUS.2019.8840089.

[10] G.Cavalera,R.C.Rosito,V.Lacasa,M. Mongiello,F.Nocera,L.Patrono,andI.Sergi, “AninnovativesmartsystembasedonIoT technologiesfor ireanddangersituations,”

inProc.4thInt.Conf.SmartSustain.Technol. (SpliTech),Split,Croatia,Jun.2019,pp.1–6,doi: 10.23919/SpliTech.2019.8783059.

[11] P.G.Jeyasheeli,andJ.V.J.Selva,“AnIOT designforsmartlightingingreenbuildings basedonenvironmentalfactors,”inProc.4th Int.Conf.Adv.Comput.Commun.Syst.(ICACCS), Coimbatore,India,Jan.2017,pp.1–5,doi: 10.1109/ICACCS.2017.8014559.

[12] A.Pandharipande,M.Zhao,andE.Frimout,“Con‐nectedindoorlightingbasedapplicationsina buildingIoTecosystem,”IEEEInternetThings Mag.,vol.2,no.1,Mar.2019,pp.22–26,doi: 10.1109/IOTM.2019.1900016.

[13] A.Zakharov,A.Romazanov,A.Shirokikh,and I.Zakharova,“Intellectualdataanalysissys‐temofbuildingtemperaturemodemonitoring,” inProc.Int.RussianAutom.Conf.(RusAuto‐Con),Sochi,Russia,Sep.2019,pp.1–6,doi: 10.1109/RUSAUTOCON.2019.8867611.

[14] N.M.Elsayed,R.A.Swief,S.O.Abdellatif,and T.S.Abdel‐Salam,“Photovoltaicapplicationsfor lightingloadenergysaving:Casestudies,educa‐tionalbuilding,”inProc.Int.Conf.Innov.Trends Comput.Eng.(ITCE),Aswan,Egypt,Feb.2019, pp.564–569,doi:10.1109/ITCE.2019.8646485.

[15] P.D.Leo,F.Spertino,S.Fichera,G.Malgaroli, andA.Ratclif,“Improvementofself‐suf iciency foraninnovativenearlyzeroenergybuilding byphotovoltaicgenerators,”inProc.IEEEMilan PowerTech,Milan,Italy,Jun.2019,pp.1–6,doi: 10.1109/PTC.2019.8810434.

[16] K.R.Babu,andC.Vyjayanthi,“Implementa‐tionofnetzeroenergybuilding(NZEB)pro‐totypewithrenewableenergyintegration,”in Proc.IEEERegion10Symp.(TENSYMP),Kochi, India,Jul.2017,pp.1–5,doi:10.1109/TENCON‐Spring.2017.8069994.

[17] I.Ilhan,M.Karakose,andM.Yavas,“Designand simulationofintelligentcentralheatingsystem forsmartbuildingsinsmartcity,”inProc.7thInt. IstanbulSmartGridsCitiesCongr.Fair(ICSG), stanbul,Turkey,Apr.2019,pp.233–237,doi: 10.1109/SGCF.2019.8782356.

[18] T.SonnekalbandS.Lucia,“Smarthotwater controlwithlearnedhumanbehaviorformin‐imalenergyconsumption,”inProc.IEEE5th WorldForumInternetThings(WF‐IoT),Limer‐ick,RepublicofIreland,Apr.2019,pp.572–577, doi:10.1109/WF‐IoT.2019.8767171.

[19] D.Alulema,M.Zapata,andM.A.Zapata,“An IoT‐basedremotemonitoringsystemforelec‐tricalpowerconsumptionviaWeb‐application,” inProc.Int.Conf.Inf.Syst.Comput.Sci.(INCIS‐COS),Quito,Ecuador,Nov.2018,pp.193–197, doi:10.1109/INCISCOS.2018.00035.

[20] A.M.Ali,S.A.A.Shukor,N.A.Rahim,Z.M.Razlan, Z.A.Z.Jamal,andK.Kohlhof,“IoT‐basedsmart

airconditioningcontrolforthermalcomfort,”in Proc.IEEEInt.Conf.Autom.ControlIntell.Syst. (I2CACIS),Selangor,Malaysia,Jun.2019,pp. 289–294,doi:10.1109/I2CACIS.2019.8825079.

[21] G.AlsuhliandA.Khattab,“Afog‐basedIoT platformforsmartbuildings,”inProc.Int. Conf.Innov.TrendsComput.Eng.(ITCE), Aswan,Egypt,Feb.2019,pp.174–179,doi: 10.1109/ITCE.2019.8646480.

[22] X.Zhang,M.Pipattanasomporn,T.Chen,andS. Rahman,“AnIoT‐basedthermalmodellearning frameworkforsmartbuildings,”IEEEInternet ThingsJ.,vol.7,no.1,Jan.2020,pp.518–527,doi: 10.1109/JIOT.2019.2951106.

[23] J.Aguilar,A.Garces‐Jimenez,N.Gallego‐Salvador, J.A.G.DeMesa,J.M.Gomez‐Pulido,andA.J. Garcia‐Tejedor,“Autonomicmanagementarchi‐tectureformulti‐HVACsystemsinsmartbuild‐ings,”IEEEAccess,vol.7,2019,pp.123402–123415,doi:10.1109/ACCESS.2019.2937639.

[24] S.Rastegarpour,M.Ghaemi,andL.Ferrarini,“A predictivecontrolstrategyforenergymanage‐mentinbuildingswithradiant loorsandther‐malstorage,”inProc.SICEInt.Symp.Control Syst.(SICEISCS),Tokyo,Japan,Mar.2018,pp. 67–73,doi:10.23919/SICEISCS.2018.8330158.

[25] A.Gillespie,T.F.Xulu,S.I.NoubissieTientcheu, andS.D.Chowdhury,“Buildingdesigncon‐siderationsforanenergyef icientHVACsys‐tem,”inProc.IEEEPES/IASPowerAfrica,Cape Town,SouthAfrica,Jun.2018,pp.1–6,doi: 10.1109/PowerAfrica.2018.8520995.

[26] B.Seng,C.Magniont,S.Spagnol,andS. Lorente,“Evaluationofhempconcretethermal properties,”inProc.Int.IEEEConf.Ubiquitous Intell.Comput.,Adv.TrustedComput., ScalableComput.Commun.,Cloudbigdata Comput.,InternetPeople,SmartWorldCongr. (UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld), Toulouse,France,Jul.2016,pp.984–989, doi:10.1109/UIC‐ATC‐ScalComCBDCom‐IoP‐SmartWorld.2016.0154.

[27] ElMallahi,I.,Rif i,J.,Tairi,H.,Ez‐Zahout, A.,andMahraz,M.A..(2023).ADistributed BigDataAnalyticsModelsforTraf icAccidents Classi icationandRecognitionbasedSparkMlLib Cores.JournalofAutomation,MobileRobotics andIntelligentSystems,16(4),62‐71.doi: 10.14313/JAMRIS/4‐2022/34.

[28] RahmanSha ique,FurqanRustam,SheriffMur‐tala,AncaDeliaJurcut,GyuSangChoi,“Advanc‐ingAutonomousVehicleSafety:MachineLearn‐ingtoPredictSensor‐RelatedAccidentSeverity”, IEEEAccess,vol.12,pp.25933–25948,2024.

[29] NassimSohaee,ShahramBohluli,“Nonlinear AnalysisoftheEffectsofSocioeconomic,Demo‐graphic,andTechnologicalFactorsontheNum‐berofFatalTraf icAccidents”,Safety,vol.10, no.1,pp.11,2024

[30] I.E.Mallahi,A.Dlia,J.Rif i,M.A.Mahrazand H.Tairi,“PredictionofTraf icAccidentsusing RandomForestModel,”2022InternationalCon‐ferenceonIntelligentSystemsandComputer Vision(ISCV),Fez,Morocco,2022,pp.1–7,doi: 10.1109/ISCV54655.2022.9806099.

[31] Nasry,A.,Ezzahout,A.,andOmary,F.. (2023).PeopleTrackinginVideoSurveillance SystemsBasedonArti icialIntelligence. JournalofAutomation,MobileRobotics andIntelligentSystems,17(1),59–68.doi: 10.14313/JAMRIS/1‐2023/8.

[32] Ndayikengurukiye,A.,Ez‐zahout,A.,Aboubakr ,A.,Charkaoui,Y.,andFouzia,O.(2022). ResourceOptimisationinCloudComputing: ComparativeStudyofAlgorithmsApplied toRecommendationsinaBigDataAnalysis Architecture.JournalofAutomation,Mobile RoboticsandIntelligentSystems,15(4),65–75. doi:10.14313/JAMRIS/4‐2021/28.

Submitted:1st April2023;accepted:1st August2023

AmalZouhri,MostafaELMALLAHI

DOI:10.14313/JAMRIS/2‐2024/13

Abstract:

Withtherapidadvancementsintechnology,theedu‐cationallandscapeiswitnessingsignificanttransforma‐tionsinpedagogyandclassroomdynamics.Twopromi‐nenttechnologies,ArtificialIntelligence(AI)andAug‐mentedReality(AR),aregainingprominenceinthefield ofeducation,promisingtorevolutionizethewayteaching andlearningtakeplace.Thisarticleexploresthepotential benefits,challenges,andpracticalapplicationsofinte‐gratingAIandARintotheteachingprocesstoenhance studentengagementandlearningoutcomes.

TheintegrationofAIineducationbringsforthper‐sonalizedlearningexperiences.AI‐poweredalgorithms analyzevastamountsofstudentdata,includinglearning patterns,strengths,andweaknesses,tocreatetailored learningpaths.Thisindividualizedapproachhelpseduca‐torsidentifystudents’uniqueneedsandprovidetargeted support,ensuringthatnostudentisleftbehind.More‐over,AI‐basedchatbotsandvirtualteachingassistants areincreasinglybeingusedtoaddressstudentqueries promptly,providingreal‐timesupportandfosteringa moreinteractivelearningenvironment.

AR,ontheotherhand,enablestheoverlayofvirtual objectsandinformationinthereal‐worldenvironment.. Studentscanexplorecomplexconceptsthroughvisualiza‐tions,simulations,andinteractivedemonstrations,facili‐tatingadeeperunderstandingofabstracttopics.ARalso fosterscollaborationandteamworkamongstudents, promotingactivelearningandpeer‐to‐peerknowledge sharing.

CombiningAIandARtechnologiesoffersapowerful synergyintheeducationalrealm.AIcananalyzeAR‐generateddataandadaptinstructionalstrategiesinreal time,respondingtoindividualstudents’progress.This synergynotonlyenhanceslearningoutcomesbutalso empowersteacherswithdata‐driveninsights,enabling themtomakeinformeddecisionsabouttheirteaching methodologies.

However,successfullyimplementingAIandARinedu‐cationcomeswithitschallenges.Issuesrelatedtodata privacy,ethicalconsiderations,andtheneedforeffective teachertraininginutilizingthesetechnologiesrequire carefulattention.Additionally,thedigitaldividecanexac‐erbateeducationalinequalities,asnotallstudentshave equalaccesstotechnologyoutsidetheclassroom.

Collaborationbetweeneducators,researchers,and technologydevelopersiscrucialtoovercomethesechal‐lenges.Thedevelopmentofuser‐friendly,accessible,and ethicallysoundAIandARtoolscanensureinclusivityand

maximizethepotentialbenefitsofthesetechnologiesin education.Theaimistoinvestigatewhethertheuseof ARtechnologycanenhancestudents’understandingand masteryofphysicsconceptsthroughvisualizationsand simulations.Spatialintelligenceplaysacrucialroleinvar‐ioussubjects,includingphysics,asitenablesstudentsto creatementalmodelsandrepresentationsofobjectsand expressions.Whilespatialintelligenceisnotaninnate skill,itcanbedevelopedthroughinteractionswithreal andvirtualobjects.ARasacutting‐edgetechnology,has thepotentialtoillustratephysicalapplicationsandsig‐nificantlyaidstudentsinvisualizingandcomprehending complexphysicsconcepts.

Keywords: educationaltransformation,improvingteach‐ing,artificialintelligence,augmentedreality,education technology

1.Introduction

Inrecentyears,therehasbeengrowinginter‐estinexploringtheintegrationofARtechnologyin physicseducationtoenhancestudents’academicper‐formanceandspatialskills.ARprovidesaunique opportunitytobridgethegapbetweentheoretical conceptsandreal‐worldapplications,offeringinter‐activeandimmersivelearningexperiences.Thisintro‐ductionprovidesanoverviewofthepotentialimpact ofintegratingARintophysicseducationandhighlights relevantresearchstudiessupportingthisapproach. ARhasgainedsigni icantattentioninthe ieldof education,offeringopportunitiestoenhancelearn‐ingexperiencesandaddressthechallengesassociated withtraditionalinstructionalmethods.Researchers suchasKlopferetal.[1]haveproposedthedevel‐opmentofanARplatformforenvironmentalsimu‐lations,highlightingthepotentialofARtechnology increatingimmersivelearningenvironments.Wu[2] hasexploredtheopportunitiesandchallengesofinte‐gratingARineducation,sheddinglightonthetrans‐formativepotentialofthistechnology.Akçayırand Akçayır[3]haveprovidedempiricalevidenceonthe advantagesandchallengesassociatedwithARforedu‐cation,emphasizingitsimpactonstudentlearning outcomes.Inthedomainofphysicseducation,Kucuk andSener[4]conductedameta‐analysisexamining theeffectsofARapplicationsonlearningphysics.

Their indingsshedlightonthepositivein lu‐enceofARinenhancingconceptualunderstanding andengagement.MustafaserkanandAbdüsselam Hasan[5]suggestedthatARcanenhancephysicsstu‐dents’comprehensionofcomplexconcepts,exempli‐iedbytheeffectofamagnetic ieldonacurrent‐carryingwire.Moreover,Wang,Lei,andSun[6]inves‐tigatedtheeffectsofARonstudentengagement, achievement,andimmersioninscienceeducation. TheirstudydemonstratedthepotentialofARtocre‐ateinteractiveandimmersivelearningexperiences thatfosterdeeperstudentengagementandimproved academicperformance.Inspeci icphysicscontexts, IulianRaduandXiaomengHuang[7]developedAR simulationsformotiongraphs,showcasingtheeffec‐tivenessofARinenhancingphysicslearningexperi‐ences.ZahariasandMichael[8]exploredtheeffects ofARonstudentachievementandself‐ef icacyina STEMeducationcourse,demonstratingpositiveout‐comesassociatedwithARintegration.Furthermore, Sirakaya[9]conductedanempiricalstudyhighlight‐ingthepotentialofARasatooltoimprovestudents’ spatialability,acriticalskillinphysicseducation.Julio Cabero‐Almenara[10]focusedonenhancingphysics educationthroughAR,emphasizingthebene itsofAR technologyinvisualizingandunderstandingphysics concepts.Thesestudiescollectivelyemphasizethe potentialimpactofintegratingARinphysicseduca‐tion,rangingfromenhancingconceptualunderstand‐ingandengagementtoimprovingspatialabilitiesand overallacademicperformance.ByleveragingARtech‐nology,educatorscancreatedynamicandinteractive learningenvironmentsthatbridgethegapbetween theoryandpractice,fosteringdeepercomprehension andengagementamongphysicsstudents.

Inthedomainofphysicseducation,YupengLin andZhonggenYu[11]conductedameta‐analysis examiningtheeffectsofARapplicationsonlearning physics.Their indingsindicatedthatARcanenhance conceptualunderstandingandengagementamong physicsstudents.ÖzerenandTop[12]investigated theeffectsofARonstudentengagement,achieve‐ment,andimmersioninscienceeducation.Their studydemonstratedthatARcancreateinteractiveand

immersivelearningexperiencesthatfosterdeeper studentengagementandimprovedacademicperfor‐mance[15–20].

VidakMovreŠapićandMešić[13]developedAR simulationsformotiongraphs,showcasingtheeffec‐tivenessofARinenhancingphysicslearningexperi‐ences.IsmailandFestiana[14]focusedonenhanc‐ingphysicseducationthroughAR,emphasizingthe bene itsofusingthistechnologyinvisualizingand understandingphysicsconcepts.Thesestudiescol‐lectivelyhighlightthepotentialimpactofintegrating ARinphysicseducation,rangingfromenhancingcon‐ceptualunderstandingandengagementtoimproving academicperformanceandvisualizationofphysics concepts.ByleveragingARtechnology,educatorscan createdynamicandinteractivelearningenvironments thatbridgethegapbetweentheoryandpractice,fos‐teringdeepercomprehensionandengagementamong physicsstudents.Therestofthispaperisorganized asfollowsaftertheintroduction:Section2represents theproposedmethod,suchasARforphysicalLearn‐ingandDataprocessing,andthediscussioninSec‐tion 3 providesevidenceoftheeffectivenessofinte‐gratingGeogebraAR.

2.ProposedMethod

2.1.ARforPhysicalLearning

TheuseofARforphysicallearninghasbeenshown tobeapromisingapproachforenhancingstudent learningandmotivation.However,moreresearchis neededtofullyunderstandAR’simpactonstudent learningandtodeterminethemosteffectivemethods forusingARinphysicseducation.

TheARversionofphysicallearningandteach‐ingoffersaninnovativeapproachbyallowingstu‐dentstogenerate3Dobjectsandphysicalfunctions inareal‐worldenvironment.Theuserinterfaceof theGeogebraARapplicationisstraightforwardand intuitiveasFigure1,providingstudentswithasimple waytoenteralgebraicexpressionsandseeimmedi‐ategraphicrepresentationsoffunctions.Thisvisual andinteractiveapproachtophysicallearninghasthe

Propositionsystem

Table1. Summaryandinterpretationofthequestionnairedatathroughdescriptiveanalysis

potentialtoimprovestudents’understandingofphys‐icalconceptsthroughmanipulativelearning.

2.2.DataProcessing

Thestudyutilizedthreedifferentdatacollection methodstogatherinformation.The irstwasapre‐test PurdueSpatialVisualization.

Theseconddatacollectionmethodwasapre‐test/post‐testwrittenassessmenttodetectprior knowledge.Thethirdmethodwasaquestionnaire toassessthemotivationlevelsoftheexperimental group.Thesethreeinstrumentswereusedtoevaluate thelearningstandardsofthefunctionsblockwithin thecurriculumofthesubjectAcademicPhysics.Fig‐ure2showsthepropositionsystemcomponentwith inputdeviceforthissystemisthecameraofthesmart‐phone,whichisusedtoscanaQRcodeonatextbook. ThisQRcodelikelycontainsinformationthatisused bytheGeogebraapplicationtoidentifythetextbook andretrieveanyrelevantvirtualcontent.Oncethevir‐tualandrealcontenthavebeenprocessed,thesystem displaystheaugmentedcontentonthesmartphone screen,whichactsasthedisplaydevice.

Table 1 presentstheresultsoftheLikertscale questionnaire,whichprovidesinsightsintostudents’ motivation,feasibility,andperceptionoftheirexperi‐encewithARtechnology.Amongthetotalnumberof studentssurveyed,60%expressedtheiragreementin usingARresourcesforcontentlearninganddevelop‐ingskills.Itisworthnotingthatasigni icantmajority ofstudentsreportedhighlevelsofmotivationand interestinworkingwithAR,indicatingitspotentialto engagestudentsinthelearningprocess.Additionally, alargemajorityofstudentsaf irmedtheeaseofuse oftheGeogebraARapplication,indicatingthatitwas accessibleanduser‐friendlyforthem.

These indingssuggestthatintegratingARtech‐nologyinphysicseducationcanpositivelyin luence students’motivation,interest,andperceivedusability, potentiallyenhancingtheiroveralllearningexperi‐enceandengagementwiththesubjectmatter.

3.Discussion

Thestudypresentedinthediscussionprovides evidenceoftheeffectivenessofintegratingGeoge‐braARintoclassroommethodologytoteachphysi‐calfunctions.Theresultsshowthattheexperimental group,whichwasexposedtothetechnology,outper‐formedthecontrolgroupintermsofunderstanding theconceptoffunction,identifyingcharacteristicsof functions,completingactivitiesinashortertime,and achievinghigherscoresinthe inalwrittentest.The studyalsofoundthatGeogebraARisintuitiveand simpletouse,makingiteasyforstudentstolearnand useeffectively.TheintegrationofGeogebraARinto teachingmethodologycanchangetheroleofteachers, astheybecomemoreofaguidetostudentsrather thanjustatransmitterofknowledge.Thisencourages criticalandcreativethinking,autonomy,andfreedom forstudents.Theuseoftechnologyshouldalways becontextualizedwithinapedagogicalframeworkto ensureitseffectivenessandavoidpotentialnegative impactsonlearning.Thestudypresentsacompelling casefortheuseofGeogebraARinteachingphysical functions,anditprovidesimportantinsightsintothe potentialbene itsandchallengesofintegratingedu‐cationaltechnologyintoclassroommethodology.Itis recommendedthatteachersexploretheuseofGeoge‐braARandothersimilartechnologiestoenhancestu‐dentlearningandengagement.

Figure2.

4.Conclusion

Inconclusion,thisstudyinvestigatedtheimpactof integratingARtechnology.The indingssuggestthat theuseofARtechnologyhasthepotentialtoenhance students’understandingandmasteryofphysicscon‐ceptsbyprovidingvisualizationsandsimulations. Spatialintelligence,acriticalskillinphysicsandother subjects,allowsstudentstocreatementalmodelsand representationsofobjectsandexpressions.Whilespa‐tialintelligenceisnotinnate,itcanbedeveloped throughinteractionswithrealandvirtualobjects.AR, asaninnovativetechnology,offerstheabilitytoillus‐tratephysicalapplicationsandsigni icantlysupports studentsinvisualizingandcomprehendingcomplex physicsconcepts.

TheoutcomesoftheLikertscalequestionnaire shedlightonstudents’motivation,feasibility,andper‐ceptionregardingtheirexperiencewithARtechnol‐ogy.Amongthetotalnumberofstudents,amajor‐ity(60%)agreedtouseARresourcesforcontent learningandskilldevelopment.Importantly,nearly allstudentsreportedworkingwithhighmotivation andinterest,whilealargemajorityexpressedthat theGeogebraARapplicationwaseasytouse.These indingshighlightthepositivereceptionofARtech‐nologyamongstudentsanditspotentialtoengage andenhancetheirlearningexperiences.Insummary, theintegrationofARtechnologyinphysicseduca‐tionholdspromiseforimprovingstudents’academic performanceandspatialskills.ByleveragingAR’s visualizationsandsimulations,educatorscancreate immersiveandinteractivelearningenvironmentsthat fosterstudents’understandingandengagementwith physicsconcepts.Furtherresearchandexplorationof AR’simpactonphysicseducationarewarrantedto continueadvancingitseffectivenessasapedagogical tool.

AUTHORS

AmalZouhri∗ –SidiMohammedBenAbdellah University,FacultyofSciencesDharElMahraz, LISACLaboratory,Fez,Morocco,e‐mail: amal.zouhri@usmba.ac.ma.

MostafaELMALLAHI –SidiMohammedBenAbdellah University,HighNormalSchool(ENS),Fez,Morocco, e‐mail:mostafa.elmallahi@usmba.ac.ma.

∗Correspondingauthor

References

[1] E.Klopfer,K.Squire,“Environmental Detectives—thedevelopmentofanaugmented realityplatformforenvironmentalsimulations,” EducationTechResearchDev,vol.56,2008,pp. 203–228.doi:10.1007/s11423‐007‐9037‐6.

[2] H.K.Wu,S.W.Y.Lee,H.Y.Chang,J.C.Liang, “Currentstatus,opportunitiesandchallenges ofaugmentedrealityineducation,”Comput‐ers&Education,vol.62,2013,pp.41–49.doi: 10.1016/j.compedu.2012.10.024.

[3] M.Akçayır,G.Akçayır,“Advantagesandchal‐lengesassociatedwithaugmentedrealityfor education:Asystematicreviewoftheliterature,” EducationalResearchReview,vol.20,2017, pp.1–11.doi:10.1016/j.edurev.2016.11.002.

[4] S.Kucuk,N.Sener,“Ameta‐analysisontheeffects ofaugmentedrealityapplicationsinlearning physics,”Computers&Education,vol.125,2018, pp.390–399.doi:10.1002/cae.22628.

[5] M.Karal,“Theeffectofusingaugmentedreality andsensingtechnologytoteachmagnetismin highschoolphysics,” TechnologyPedagogyand Education,vol.29,no.1,2020,pp.1–18.doi: 10.1080/1475939X.2020.1766550.

[6] J.Wang,Z.Lei,C.Sun,“Theeffectsofaugmented realityonstudentengagement,achievement, andimmersioninscienceeducation,”Journalof EducationalTechnology&Society,vol.21,no.3, 2018,pp.222–234.doi:10.30935/cet.444119.

[7] I.Radu,X.Huang,G.Kestin,B.Schneider, “Enhancingphysicslearningthrough augmented,Howaugmentedrealityin luences studentlearningandinquirystyles:Astudyof 1‐1physicsremoteARtutoring,”Computers& Education:XReality,vol.2,2023,p.100011.doi: 10.1016/j.cexr.2023.100011.

[8] P.Zaharias,D,Michael,“EffectsofAugmented RealityonStudentAchievementandSelf‐Ef icacyinVocationalEducationandTraining,” JournalofScienceEducationandTechnology, vol.27,no.6,pp.551‐564.doi:10.13152/ IJRVET.5.1.1.

[9] M.Sirakaya,E.K.Cakmak,“Augmentedreality asatooltoimprovestudents’spatialability: Anempiricalstudy,”InternationalJournalFor ResearchInVocationalEducationAndTraining, vol.5,2018,pp.1–18.doi:10.13152/IJRVET. 5.1.1.

[10] J.Cabero‐Almenara,“EducationalUsesofAug‐mentedReality(AR):ExperiencesinEducational Science,”Sustainability,vol.11,no.18,p.4990. doi:10.3390/su11184990.

[11] Y.Lin,Z.Yu,“Ameta‐analysisoftheeffectsof augmentedrealitytechnologiesininteractive learningenvironments,”ComputerApplication AndEngineeringEducation,02April2023.doi: 10.1002/cae.22628.

[12] S.Özeren,E.Top,“Theeffectsofaugmented realityapplicationsontheacademicachieve‐mentandmotivationofsecondaryschoolstu‐dents,”MalaysianOnlineJournalofEducational Technology,vol.11,no.1,2023,pp.25‐40.doi: 10.52380/mojet.2023.11.1.425.

[13] A.Vidak,I.MovreŠapić,V.Mešić,“ARin teachingaboutphysics: irst indingsfroma systematicreview,”JournalofPhysics:Con‐ferenceSeries,vol.2415.doi10.1088/1742‐6596/2415/1/012008.

[14] A.Ismail,I.Festiana,T.I.Hartini,Y.Yusal, A.Malik,“Enhancingstudents’conceptual understandingofelectricityusinglearning media‐basedaugmentedreality,”Journalof PhysicsConferenceSeries,vol.1157,no.3.doi: 10.1088/1742‐6596/1157/3/032049.

[15] ElMallahi,I.,Rif i,J.,Tairi,H.,Ez‐Zahout, A.,&Mahraz,M.A.(2023).ADistributed BigDataAnalyticsModelsforTraf icAccidents Classi icationandRecognitionbasedSparkMlLib Cores.JournalofAutomation,MobileRobotics andIntelligentSystems,16(4),62–71.doi: 10.14313/JAMRIS/4‐2022/34.

[16] RahmanSha ique,FurqanRustam,SheriffMur‐tala,AncaDeliaJurcut,GyuSangChoi,“Advanc‐ingAutonomousVehicleSafety:MachineLearn‐ingtoPredictSensor‐RelatedAccidentSeverity”, IEEEAccess,vol.12,pp.25933–25948,2024.

[17] NassimSohaee,ShahramBohluli,“Nonlinear AnalysisoftheEffectsofSocioeconomic,Demo‐graphic,andTechnologicalFactorsontheNum‐berofFatalTraf icAccidents”,Safety,vol.10,no. 1,pp.11,2024

[18] I.E.Mallahi,A.Dlia,J.Rif i,M.A.Mahrazand H.Tairi,“PredictionofTraf icAccidentsusing RandomForestModel,”2022InternationalCon‐ferenceonIntelligentSystemsandComputer Vision(ISCV),Fez,Morocco,2022,pp.1–7,doi: 10.1109/ISCV54655.2022.9806099.

[19] Nasry,A.,Ezzahout,A.,andOmary,F.(2023). PeopleTrackinginVideoSurveillanceSystems BasedonArti icialIntelligence.Journalof Automation,MobileRoboticsandIntelligent Systems,17(1),59–68.doi:10.14313/JAMRIS/ 1‐2023/8.

[20] Ndayikengurukiye,A.,Ez‐zahout,A.,Aboubakr, A.,Charkaoui,Y.,&Fouzia,O.(2022).Resource OptimisationinCloudComputing:Comparative StudyofAlgorithmsAppliedtoRecommenda‐tionsinaBigDataAnalysisArchitecture.Jour‐nalofAutomation,MobileRoboticsandIntel‐ligentSystems,15(4),65–75.doi:10.14313/ JAMRIS/4‐2021/28.

Submitted:2nd November2022;accepted:18th January2023

YounèsRaoui,MohammedAmraoui

DOI:10.14313/JAMRIS/2‐2024/14

Abstract:

SimultaneousLocalizationandMapping(SLAM)is appliedtorobotsforaccuratenavigation.Thestereo camerasaresuitableforvisualSLAMastheycangive thedepthofthevisuallandmarksandmoreprecise estimationsoftherobot’spose.Inthispaper,wepresent asurveyofSLAMmethods,eitherBayesianorbio‐inspired.ThenwepresentanewmethodofSLAM,which wecallstereoExtendedKalmanFilter,improvingthe matchingbycomputingtheinnovationmatricesfromthe leftandtherightimages.Thelandmarksarecomputed fromOrientedFASTandRotatedBRIEF(ORB)features fordetectingsalientpointsandtheirdescriptors.The covariancematricesofthestateandtherobot’smap arereducedduringtherobot’smotion.Experimentsare doneontherawimagesoftheKittidataset.

Keywords: Simultaneouslocalizationandmapping, stereocameras,extendedKalmanfilter,mobilerobots, navigation

1.Introduction

SimultaneousLocalizationandMapping(SLAM)is anessentialtaskforrobotnavigation.Itallowsthe robottoreachitsgoalwithouterrorsbecauseitis suitableforplanninganoptimalpathandavoiding obstacles.Therobotusesseveralsensorstoconstruct maps,suchascameras,LIDARarrays,orIMUs.As mapsarecomputedwhentherobotmoves,local‐izationisvitalformapping.Severalnewmapping methodshaverecentlyappearedtoallowtherobot tobeautonomousinindoorenvironments,allowing robotstodotaskssuchascleaninghouses.Also,out‐doorenvironmentsmustbemappedfortaskssuchas autonomousdriving.

TherobotSLAMincludesseveraltechniques, whichcanbedividedintoBayesianandbio‐inspired methodsusingneuralnetworksanddeeplearning. TheBayesianapproachconstructsmapsbytaking datafromsensorsandbuildingrepresentationsof theenvironmentusinglandmarks,pointclouds,or graphs.Thebio‐inspiredtechniquesareinspiredby neuroscience,especiallytheplacecellsandthegrid cellstobuildrepresentations.Anotherdistinction betweenSLAMmapsisthattheycanbemetrical ortopological.Themetricalmapsarebasedonthe extractionandtrackingoflandmarkscomputedusing theSLAMmethods.

Thetopologicalmapsconstructgraphsrepresent‐ingplacesandthenlinkthoseplaceswithedges.The edgesintopologicalmapsaresuitableforplanningas theyshowthecostofnavigationfromoneplaceto anotherbyavoidingobstacles.Moreattentionisgiven toeachtechniqueinthefollowingparagraphs.

TheBayesianmappingmethodsaredividedinto thosethatuselandmarksandthosethatuseobjects. Bothoptimizetherobot’sposeandthemapregarding themotioncommandsandtheobservations.Mapping withlandmarksisgenerallybasedoncreatingsparse representationsoftheenvironmentwiththevisionor laserscans.Mappingwithobjectsusesdeeplearning techniquestodetecttheobjects;thesedeeplearn‐ingdetectionsrequireincreasedGPUperformances butaremoreaccurate.Thedataassociationinsuch scenariosisaccomplishedusingsemanticlabelsto associatethe3Dobjectsinthemapwiththenew measures.Moreover,topologicalmapswithobjects usedeeplearningmethodsforobjectdetectionand scenesegmentation.Theyusetheconceptofplace,a nodeinagraphrepresenting,forinstance,anof ice andakitchen,andtherelationbetweentheplaces’ edges.Eachplacecouldbeaclassobtainedwithscene segmentationwithConvolutionalNeuralNetworksor asetofobjects.

Incontrast,bio‐inspiredmethodsrelyuponthe domainofnavigationofthemammalbrains.Gridcells andtheplacecellsinthemammalianentorhinalcortex andthehippocampusareresponsibleforlocalization andmapping.Thesecellsprovidemachineryforthe indexingofposesandplacesthroughpathintegra‐tionandperceptions.Themammalcanconstructa topologicalmapthatallowsittonavigateaccurately toitsgoal.Bio‐inspiredmethodsaimtoreplicatethis processinroboticSLAMapplications.

Thispaperaims irsttomakeashortsurveyof SLAMmethodsandthentopresentanewmethod ofSLAMwithstereocamerasusingORBfeatures. ThenewmethodextendstheMonocularSLAMbut usestheORBfeaturessuitableforSLAMduetotheir robustnesswhenviewpointsandscalechange.This newmethodimprovestheactivesearchalgorithms usedinMonocularSLAMbyconsideringtherightand leftimagesmeasurementstoincreasethenumberof matchings.

Figure1. Thecreationoftwoplacesusingobjects detectedwithConvolutionalNeuralNetworksby consideringeachobjectasavertexinagraphandtwo placesareconnectedwithanedge

Thepaperisorganizedasfollows:First,wepresent asurveyofvisualSLAMmethods;second,ourmethod‐ology,whichconsistsoffusinginformationfromthe stereocameratoincreasethenumberofcorrect matchingsin ilteringtheobservations,third,we adresstheexperimentsandresults; inally,wepresent theconclusion.

2.ASurveyofSLAMTechniques

VisualSLAMusinglandmarks

Thepaper[18]presentsamethodoflocalization andmappingwithRadioFrequencyIdenti iers,which usestheBlackwellizedlocalizationtechniquebased onparticle ilters.Itextendsthemetricalmapping withatopologicalmapfortrolleynavigationina supermarket.Thepaper[4]presentsasurveyofthe SLAMmethodsduringthelastdecade.Theseminal workofvisualSLAMis[6],whichusedExtended KalmanFilter(EKF)withamonocularcamera.The work[15]presentsamethodofvisualSLAMthatini‐tializesthelandmarkusingtheirinversedepth.This measurementchangeswhenthecameramoves,and thusitscovarianceisreduced.Whenanewlandmark iscreated,thenumberofdetectedlandmarksislow, anditsinversedepthisalsoinitialized.TheORBSLAM 2and3usesbundleadjustmentinsteadofEKFto updatethecurrentposeandalltheposesfromthe startposition[16],[5].Itdescribesthescenewiththe visualbagofwordsDBow2library[10],whichare usedforplacerecognitionaswell.

2.1.BrainInspiredSLAM

Theworkin[2]issigni icantasitbuildsasystemof localizationandmappingusingthegridandplacecells knowledge.Itusesacontinuousattractornetworkto implementaneural ieldtomodeltherobot’spath integration.

Figure2. 2mapscreatedwiththeGrowingWhen RequiredNetworkbyclusteringtheplacesby computingdistancesbetweenthecurrentoneandthe othersbasedontheactivityoftheneurons

ItbuildsaHebbianneuralnetworktomodelthe placerecognitionoftherobot.Amapisbuilttoshow intheworldframetheactivityoftheposecellnet‐work.Thismapissemi‐topological,anditconnects thenodeswithedgesrepresentingthedirectionofthe motionoftherobot’shead.ApathplanningDijkstra algorithmisimplementedaswellintheRatSLAM.An extensionofRatSLAMcalledNeuroSLAMisdeveloped todealwith3dimensionsexperiencemaps,including theXYZworldframecoordinates.Inthiswork,the depthisalsocodedintheposecellnetwork[28].In [19],anewbrain‐inspiredSLAMsystemthatextends theNeuroSLAMandexploitsthesemanticsofscenesis developed.Ittrainsacontinuousattractornetworkby stimulatingitwithvisualobjects.Then,itconstructs 2D/3Dexperiencemapsandrelaxthem.

2.2.SLAMwithObjects

[26]builtaSLAMsystemwithdynamicobjects atdifferentsemanticlevels.Theyproposedamissed detectioncompensationalgorithmbasedonthespeed invarianceinadjacentframes.[27]proposedareal‐timeandrobustvisualSLAMsystembasedonORB‐SLAM2foradynamicenvironment.Theyincorpo‐rateddeeplearningobjectdetectionforpreprocess‐ingdatareliedondynamictargetsorstaticobjects. Theyreducedthetrackingerrorsandenhancedthe accuracyofthecomputationoftheposeandthemap. [7]workedwithsemanticandgeometricuncertainty inherentinobjectdetectionmethods,modeledthe non‐lineardataassociationwithobjects,anddevel‐opedamax‐mixturetypemodelthataccountsformul‐tipledataassociationhypothesesforobjectdetection

withMobileNetSingle‐ShotmultiboxDetection(SSD). [8]solvedthesemanticSLAMproblemusingnon‐parametricbeliefpropagation.[22]formulatedlidar inertialodometryatopafactorgraphbymarginalizing oldlidarscanstoaglobalmap.

2.3.PlaceRecognition

Thesurveyin[14][13]presentedseveralmeth‐odsforVisualPlaceRecognition(VPR)andhowitis shapedbytherecentadvancesindeeplearning.Then thesurveyshowshowmetric‐learnedtechniquesare usedtodevelopsuchsystemsinthepresenceofocclu‐sionsanddistortionsintheimages.Theyconcluded thatthefuturetrendsinimageclassi ication,object detection,andmethodsrelatedtolearningobjects suchasbuildingswouldaffectlong‐termplacerecog‐nition.Inrecentresearch,deeplearningmethods havebecomeusefulinVPR,suchasin[24]where theyboostedtheperformanceoflearnedfeatures withgeometrictransformationsbasedonreasonable domainassumptionsaboutnavigationonaground plane.Besides,detectingloopclosureswiththeVPR approachisveryimportantasitallowscorrectionof therobot’strajectoryonatopologicalmap.InORB‐SLAM2and3[5,16],theydetectcandidatesofloops byextractingandcomparingavisualbagofwords ORBfeaturesfromthecurrentkeyframeandthosenot directlyconnectedtothiskeyframeandwhicharecon‐nectedintheCovisibilitygraph.[25]developedanew deeplearningtechniquetodetectloopclosuresusing hierarchicalretrievalofframesfromvideostreams collectedbyamobilerobot.

In[17],aself‐supervisedapproachusingdeep learningisproposedtoallowrobotlearningfrom examplesofloopsthatusedGPS‐aidednavigation.The robotlearnedadistancemetricforvisualdescriptors usingConvolutionalNeuralNetworksforplacerecog‐nition.Theyusedacorsetmethodtodetectloopsfor retrievingframes[25].Thereareseveralmethodsto detectplacesandcreatemaps.Anotherapplicationof VPRsystemsisusingobjectsinsteadofvisualfeatures. In[9],objectsaredetectedfromKinect3Ddatausedto buildatopologicalgraphofobjects(seeFig.1).Then fromthisgraph,atopologicalmapiscreatedwhere placesaredetectedbasedonthedistancebetween objects.Apair‐wisematchingscorebetweenthecur‐rentandpreviousplacesiscomputedtodecideifa placeisfamiliartodetecttheloop.Thispair‐wise matchingscoredependsontheenvironment.Image‐qualityhigh‐resolution3Dpointcloudscanalsobe usedtoidentifyplacesbydescribingsceneswith DBoWfeaturesandthenapplyingPerspective‐n‐Point (PnP)todetectplaces[23].Finally,placescanalso bedetectedusingsemanticsegmentationtocreate su lemapsfromregisteredframesbyusingCondi‐tionalRandomFieldsorsemanticlabelingtocorrelate objectstoscenesextractedwithconvolutionalneural networks[1].

2.4.BrainBasedNavigation

Thenavigationusingbio‐inspiredmodelscanbe doneformappingorlocalization.Oneoftheseminal worksinmodelingtheassociativelearninginplace cellsandgridcellsisin[20].

Figure3. Overviewofourmethod

Anassociativeneuralnetworkmodelstheposi‐tioningofamammalwithplacecellsforplacerecogni‐tionorgridcellsforlocalizationatdifferentscalesin thespace.

Anothermodelforexplainingconnections betweenplacecellsandgridcellsisdevelopedin[12]. Thisonehasinputsandoutputsfromplacecell activities.Bylearningweightsofconnectionstothe hiddenlayerrepresentingthegridcells,triangular patternsaregenerated.Inhibitoryconnectionsare usedbetweentheneuronsofthehiddenlayers,which makesthemodelrecurrentaswell.

Thenavigationisnotonlyreliedontheplaceand gridcellsbutalsotoobjectvectorcellsusedbythe braintomemorizetheplacesthatvisitedananimal bytakingaslandmarkstheobjectsregardlesstotheir type[11].Ithasbeenshownthattheobjectvectorcells spikewhentheanimalisnearanobject.Eachobject reliesononeorseveralneurons.Theneurons’ iring ielddependsonthedistanceandthevectorbetween theanimalandthedetectedobject.Thosecellscreate amemoryoftheanimalabletoknowwhenaplaceis familiar.

TheGrowingWhenRequirednetworksarealso usedin[29]tomodeltheplacecellsactivities.This auto‐associativenetworkcancreatemapsoftherobot forplanninginatopologicalgraphwherenodesare theplaces,andtheedgesarethepathbetweenplaces (Fig.2).Thecostofeachpathdependsontheexistence ofanobstacle.Thus,adirectandforwardmodelofthe robotmotionisdevelopedwithdynamicneural ields, whichtakeasstimulithecameradataandpredicts theactionsthattherobotshouldtake[29].Theslow‐nessofthevariationoftheactivitiesoftheplacecells andheaddirectioncellsismodeledwithSlowFeature Analysis.

Themodelingoftheactivityofgridcellsincomplex environmentshasbeenperformedwithdeeprein‐forcementlearningnetworksin[3].Patternssimilarto theexperimentsareobtainedbytrainingadeepneu‐ralnetworkthatlearnsfromtheplacecells’activities andheaddirectioncells.Therefore,thearti icialagent canlocalizeitselfinanunfamiliarenvironmentusing themodel.

3.PresentationoftheStereoSLAMwithFusion ofInnovationJacobians

3.1.OverviewandContribution

Wepresentinthispaperanewmethodofvisual SimultaneousLocalizationandMapping(Fig.3)using stereocameraswhichprovidesthedepthofthe3d camerapoints.TheproblemofSLAMistackledwith the ilteringapproachusingExtendedKalmanFilter toestimatetheposeoftherobotandthemaps.We startbyinitializingoursystemwithasetoflandmarks computedwithtriangulationofORBfeaturepoints (Fig. 4).Thestateofthecamera(Eq. 1)isupdated withtheperceptionofthoselandmarks.Astherobot acquiresstereoimages,ithasasanobservationofthe rightandtheleftimages.

Whenusingonlytherightortheleftimages,we noticedsomestepswheretherobotcouldnotupdate theposewithEKFcausedbythelackofcorrectmatch‐ingsorbecausethejacobianoftheinnovationisvery high.Whenitisthecase,theactivesearchregioninthe newframecannotbeprocessedbecauseitdependson theeigenvaluesofthecovarianceoftheinnovation. Therefore,wecomputetheinnovationmatricesfor therightandleftimagesanddomatchingagainstthe ORBfeaturepointsusingtemplatematchings.Then wefusethetwomeasuresbydiscardingtheredundant features.Thestepscharacterizingoursystemareas following(seealgorithm):

Result: AlgorithmofStereoEKFSLAM matched_landmarks={}

X=null for i ≤ len(way_points) do if map={} then initialize_map() initialize_state() end else if len(matched_landmarks ≤ 50 then initialize_new_landmarks() end

[����,Σ��]=prediction(slam,robot_model) compute_covariance_of_new_landmarks() for j ≤ len(all_landmarks) do if landmark[j]isobservable then ℎ������=inverse_stenope_model (landmark[j],right)

ℎ������=inverse_stenope_model (landmark[j],left)

������=observationJacobian(ℎ������) ������=observationJacobian(ℎ������) end end

����=compute_innovation_matrix_right()

����=compute_innovation_matrix_left()

���� =matching(����,����)

[����,Σ��]=update(����,Σ��,̂����,ℎ��) end end

1) ExtractionofORBfeatures: WechooseORBfea‐turesforthesceneunderstandingastheyare invarianttorotationandmulti‐scale.Thuswhen weusethem,therobotcouldupdatethelandmarks ofthemappoints(landmarks).Theyareextracted witharateof0.03secondperimage,whichisper‐formantcomparingtoSURF0.04secondorSIFT 0.13second.TheORBdescriptorusesarotated versionofBRIEFaccordingtotheorientationofthe keypoints[21].

2) Initializationthemap: Themapisinitializedwith 50landmarkscomputedbytriangulatingORBfea‐turesintherightandleftimages.Theinitialposes ofthelandmarksarecomputedatthereference frame.Theinitialposeofthecameraistakenatthe referencepositionalso.

Figure4. MatchingofORBfeaturesbetweentwoleftandrightimagesbytaking20matchingsusingthecorrespondance ofkeypointsinsidetheredrectangleplane

3) Extractionofframesandkeyframes: Weextract aframecomposedoftherobot’sposeateachstep, including3dcoordinatesandthequaternion,and theangularandlinearvelocities.Italsoincludes theORBfeaturepointsandtheirBRIEFdescrip‐tors.WecreateaKeyframeiftherobotpassesfour frames.

4) Computationoftheinnovation: Weprojectthe 3Dmappointsintherightandtheleftcameras,and wecomputethetwoinnovationmatrices.Thenwe domatchingsintheleftandtherightimagesusing thetwoinnovationmatriceswhichareofsize(2,2).

5) FilteringwithEKF: The ilteringisdoneforeach keyframebyapplyingtheExtendedKalmanFilter (EKF).Theupdateisdonebyprojectingtheland‐marksofthemapintherightandleftimageplanes. Thematchingpointsareusedfortheupdate.

3.2.StateVectoroftheStereoCamera

Let’shavethestateofthecamera ixedontherobot givenwiththefollowingvector(Eqs.1,2):

(1)

Where������ isthe3dposeofthecameraintheabsolute frame,���� istheorientationquaternion,���� isthelinear velocity,and���� istheangularvelocity.

Thecovarianceoftheposeofthecameraisa13*13 matrixrepresentedby:

Thedepthdiscomputedusingthetriangulation ofmatchingfeaturepointsbyconsideringtheepipo‐larconstaint.Intheworldframe,thelandmark(map point)isgivenwiththefollowingequation:

Where������ and������ aretherotationandthetranslation matricesfromtherobottotheworldframegivenwith thevisualodometrymoduleoftherobot.

Themotionmodelofthecamera

Weobtainthelinearandangularvelocitiesfrom visualodometryusingviso2_rosnodeintheRobotic andOperationSystem(ROS).Wemodi iedthemotion modelin[6]asthevelocityisnotconstant(Eq. 5). Westartbyinitializingthe irstposeofthecamera; then,wecomputethenew3dposebymultiplyingthe previousposebytherotationmatrix������ andadding theproductofthevelocityandthetimeslotbetween twosuccessiveframes.

���� has3components����,���� and����.dtisthetimediffer‐encefromthet‐1tot

Weconverttherotationquaternionofthecamera toEulerangles,��,��,and��

Weupdatethoseanglesusingtheangularvelocity vector��(Eqs.6,7,8):

3.3.TheRepresentationoftheVisualFeature

WerepresenteachvisualfeatureasaCartesian vectorintheworld[���� =����,����,����]where���� iscom‐putedbythetriangulationofORBfeaturesfromthe leftandtherightimageplanesusingthebaselineof thestereocamera.Westartbyinitializingthemapby severalfeaturesobtainedbyastereocamera.Weuse ORBfeaturesassalientfeaturestodescribethe irst frame.Toobtainthefeaturesinthecameraframe,we applythetriangulationEquation(3):

Wherebisthebaselineexpressedinmeter,��0 and ��0 arethecoordinatesoftheopticalcenter,fisthe focaldistanceexpressedinpixels,and ���� and ���� are thecoordinatesofthematchedfeatureintheright image.

Where��=[����,����,����]istheangularvelocityof thecamera.

Thenweexpress����,����,���� intermsofthequater‐nion.

Thenextcamerastateisexpressedwiththevector ofdimension(13,1)(Eq.9):

(9)

Observationsofthelandmarks

Thecameracapturestheimage,andtherobot observesthenearestlandmarksonthemap.Bymatch‐ingmappointstoimagepoints,therobotcancorrect itspose.Thenitshouldprojectthemusingtheinverse pinholemodeltothenewkeyframe.

Letushavetheposeofthelandmark ���� inthe worldframe.Theposeofthisfeatureinthecamera frameisgivenwithitsobservation:

Where ������ istheinverseoftherotationmatrix givenbytransformingthequaternionoftherobot statetoarotationmatrix,and ���� istheposeofthe cameraintheworldframe.

Togetcoordinatesofthepredictedfeature,we multiplyitbytheintrinsicparametersoftherightand theleftcameras:

Fortheleftcamera,theobservationisgivenwith (Eq.11).

Where

�� and

�� arethestandard cameracalibrationparameters.

Thesameequationisfortherightcameraexpects thatweuseitsspeci icintrinsicparameters.

3.4.ActiveSearch

Weprojectthelandmarksintheleftandtheright imagestomakedataassociationsbetweentheland‐marksandthedetectedORBfeaturesassociatedwith them.Weprojectontheleftandtherightimageplanes tocomputetheleftandrightinnovationsmatrices. Thenwelookforthebestmatchingsusingthetem‐platematchingalgorithmforthetwoimages.Wecon‐siderthetwoplanesbecausewhenweuseonlytheleft ortherightimage,itappearsthatinsomeplaces,we donothavealotofassociationsornooneatall.Thus, theupdateisnotaccurate.Withourmethod,ateach step,wehavegoodassociation.

Estimationofthecamerapose

TheExtendedKalmanFilterappliedtovisual SLAMwithstereocamerasissimilartooneofthe monocularcamerasin[6]and[15]insuchawaythatit usestheactivesearchtomatchthepredictedfeatures andthemeasuredones.Indeed,Todeterminethearea inwhichweapplytemplatematching,weshouldcom‐putetheJacobianmatrix���� givenwith(Eq.12):

Inordertocomputetheerroronthefeature,we shouldcomputethecovarianceofeachinitializedfea‐ture(Eq.13):Inthecontextofstereocamera,thecom‐putationof ������ ��ℎ isdonewiththefollowingequation becausewehave3componentsoftheimagepoint:

(12) here���� istheposeofthecamera,������ isthedistorted featurepointintheimage,and���� isthefeatureinthe worldframe.Also,Risthenoiseoftheobservationof pixels.

Also,������ isthecovarianceoftherobotposeofsize (13*13). �������� isthecovariancebetweenthecamera poseandthefeaturea13*6matrix,and �������� isthe transposeof ��������,andP�������� isthecovarianceofthe featuresa3*3matrix.

Where (����,����) and (����,����) aretheimagecoordi‐natesintheleftimageanditscorrespondinginthe rightimage,andbisthebaseline,andfisthefocal length.

ThejacobianS(12)iscomputedforthetwoplanes andthematchingisperformedusingtheleftandright jacobians.Indeed,somepointshavethejacobianvery high,sotheuncertaintyellipsearoundthemeasured ORBfeaturepointisnotsuitable.Thatiswhywe shouldusealotofmatchings.

Estimationofthecameraposeanditscovariancewith EKFSLAM

WeusetheExtendedKalmanFiltertocomputethe newestimatedposeofarobot,forthatwecompute theKalmangainusingtheequation(Eq.14):

Where:

Histhejacobianofthemeasurescomputedusing themodelofobservationofthestereocamera.We computeHfortherightandtheleftcamerasbymea‐suringeachlandmark.Itisobservableifitispro‐jectedontheimageplane.Thejacobiansarecomputed bydifferentiatingthehfunction(seeEq. 10)bythe poseofthecameraanditsquaternion.Wecompute theupdatedposeofthecamerausingtheequation (Eq.15):

Where ���� isthepredictedrobotstatewiththe motionmodel,���� isthemeasuredmatchedmappoints. Moreoverwecomputetheupdatedcovarianceusing thisformula(Eq.16):

Where����+1 isthepredictedcovarianceofthecam‐eraandIisanidentitymatrixofsize(13+numbreof features)*(13+numbreoffeatures).

4.ResultsandDiscussion

Experiments

Wehaveimplementedoursystemusingthe PythonlanguageonROSmelodicdistribution.We usedtheKittidataset(2011_09_26_drive_0017)for thetests.Theodometrydataisobtainedwiththe visualodometrynode(viso_2ros),whichwerunin of linetoobtainthelinearandangularvelocities.

Table1. Theintrinsicparametersofthestereocamera (leftandrightplanes)havethesamevalues

�� 7.21��−4 m

Table2. Noiseofvelocities

Noiseoflinearvelocity 6m/s

Noiseofangularvelocity 1rad/s

Figure5. Thetrajectoryobtainedwithvisualodometry withtheviso2rospackageofROS

ThetrackingmethodisimplementedinaPython threadtoallowparallelprogrammingsuchasin[16]. WeusedthecalibrationdataavailableintheKitti dataset(table(1).

Oursystemallowsustoupdatethecamerapose andthelandmarkswiththeEKF.Thechoiceofthe noisesontheimagepixelsandtherobotposesisas follows:5pîxelsforcomputingcovarianceofthepixel measurements ����,6m/sforthelinearvelocity,and 1rad/sfortheangularvelocity.

4.1.TheTrajectoryoftheCameraUsingVisualOdome‐try

Weusedviso_2rospackagetocomputethetrajec‐toryofthekitticarusingthemono_odometernode. Weobtainthefollowingtrajectory(Fig.5): Weaddsomenoisetothistrajectorytoapply thepredictionstepoftheExtendedKalmanFiltering (Fig.2).theredlinerepresentsthetruetrajectoryof therobotwhichisusedtoevalueatethealgorithmof positioncomputation.Usingthepredictionequations, weobtainthefollowing igurewhereweremarkthat thecovarianceofthepositionincreases,whichisnor‐malastherobotdoesnotcorrectitspositionregarding thegroundtruth.

Figure6. Predictedpositionsandcovariancesofthe camera

Figure7. Theestimationoftheposeoftherobotin2D. Theellipsesofthecovariancearereducedinsidethe trajectoryoftherobotduetotheapplicationofEKF

Figure8. Theprojectionofthelandmarksofthemapon therightandtheleftimagesinthetime ��1.Thered ellipsesrepresentthecovariancesofthenear landmarksobservedinthenewkeyframe.

4.2.UpdateofthePoseofRobot

Weupdatethestateoftherobot(Fig. 7)by il‐teringnoiseaccumulatedonthelinearandangular velocities,whichdependsonthelocationofthecam‐eraanditsquaternion.Thefollowing igureshows theestimationoftherobotposeswithcovariances reducedcomparingtothepredictedcase(Fig.6).The covarianceoftheerrorontheestimationoftherobot poseisreducedaftertherobotismoving.

Figure9. Theprojectionofthelandmarksofthemapon therightandtheleftimagesinthetime ��2.Thered ellipsesrepresentthecovariancesofthenear landmarksobservedinthenewkeyframe.

Figure10. Detectedlandmarksusingtheprojectionon thecameramodelintheplaneXY

Figure11. Thetrackingofthelandmark48withthe ellipsesofthecovarianceintheplaneXZ(Zisthedepth)

4.3.UpdateandManagementofMap

Toupdatethemap,weusethecorrectionstepof theEKFbutafterdoinganactivesearchofthecorrect matchestoreobservethemappointsandreducetheir uncertainty.Thematchingthresholdofthetemplate matchingissetto0.8.Thepatchofthetemplatematch‐ingissetto20pixels.Weconsidertheundistorted ORBfeaturepointsinourimplementation.

The igures(Figs. 8, 9)showthetrackingofthe ORBfeatureswithEKF.

Moreover,thecomputedlandmarksattimetshow theirXYposeswithuncertainty(Fig.10).Thislatestis reducedwhenthecameramovesbecauseoftheappli‐cationoftheKalmangain.Wealsoshowtheevolution ofthelandmarkofnumber48(Fig.11).Inthis igure, werepresenttheXZcoordinatesintheimageplaneto viewthedepthofthefeatures.Thislatestshouldbe lowerthanathresholdtoacceptit.Thisthresholdis setinourexperimentto40∗����������������

4.4.Discussion

WeremarkintheFigure7thattheellipseofcovari‐ancesisreducedbecauseoftheapplicationofthe updateoftheextendedKalman ilter.Whenwecom‐paretotheFigure 6,theellipsesaresmaller.When

weincreasethenumberofextractedORBfeatures,the resultisbetter,butthecomputationtimeishigher becauseofthecomplexityofthetemplatematching. Also,ifthenumberofobservablelandmarksislower thanathresholdateachkeyframe,weshouldadd newfeaturestothemap.Wesetthethresholdto50 featuresforourexperiment.otherwizewekeeponly 50observationsfromthecamerawhicharetakenran‐domly.

5.Conclusion

Inthispaper,wepresentedanewmethodofstereo SLAMusingtheORBfeaturepoints.Weimprovedthe jacobianmatrixoftheimageobservationoftheupdate oftheEKFtoincludematchingfromtheleftandthe rightimagesusingtwojacobiansofthevariationof themeasuresoftheORBfeatures.Thisoptimizethe ilteringwithEKF.Weprovedthatourmethodreduces theerror’scovarianceassociatedwiththestateofthe robotandthemap.Wementionedthatstereocameras withORBfeaturesareconvenientforvisualSLAM aswecouldgetthedepthbytriangulationwithout inversedepthparametrization.Fromperspective,we couldusevisualobjectsinsteadoflandmarkstoget theobservationsanduseaneuralnetworklearning algorithmforcreatingthemetricalmapsuchasGrow‐ingWhenRequiredNetworks.Wecouldalsodevelop aSLAMbasedontheposesoflandmarksusingacom‐petitiveneuralnetwork.

AUTHORS

YounèsRaoui –PhysicsDepartment,LaboratoryCon‐ceptionandSystems,FacultyofSciences,Mohammed VUniversityinRabat,4,AvenueIbnBattouta,BP1014, Rabat,Morocco,e‐mail:y.raoui@um5r.ac.ma. MohammedAmraoui –ComputerSciencesDepart‐ment,IntelligentProcessingandSecuritySystems Team,FacultyofSciences,MohammedVUniversity inRabat,4,AvenueIbnBattouta,BP1014,Rabat, Morocco,e‐mail:m.amraoui@um5r.ac.ma.

References

[1] Ambrus,R.,Claici,S.,Wendt,A.:Automatic roomsegmentationfromunstructured3‐ddata ofindoorenvironments.IEEERoboticsand AutomationLetters2,749–756(2017)

[2] Ball,D.,Heath,S.,Wiles,J.,Wyeth,G.,Corke,P., Milford,M.:Openratslam:anopensourcebrain‐basedslamsystem.AutonomousRobots34,1–28(042013).doi:10.1007/s10514‐012‐9317‐9

[3] Banino,A.,Barry,C.,Uria,B.,Blundell,C.,Lil‐licrap,T.,Mirowski,P.,Pritzel,A.,Chadwick, M.J.,Degris,T.,Modayil,J.,Wayne,G.,Soyer,H., Viola,F.,Zhang,B.,Goroshin,R.,Rabinowitz,N.C., Pascanu,R.,Beattie,C.,Petersen,S.,Sadik,A., Gaffney,S.,King,H.,Kavukcuoglu,K.,Hassabis, D.,Hadsell,R.,Kumaran,D.:Vector‐basednaviga‐tionusinggrid‐likerepresentationsinarti icial agents.Nature557,429–433(2018)

[4] Cadena,C.,Carlone,L.,Carrillo,H.,Latif,Y., Scaramuzza,D.,Neira,J.,Reid,I.D.,Leonard,J.J.: Simultaneouslocalizationandmapping:Present, future,andtherobust‐perceptionage.CoRR abs/1606.05830(2016),http://arxiv.org/abs/ 1606.05830

[5] Campos,C.,Elvira,R.,Rodríguez,J.J.G.,Mon‐tiel,J.M.M.,Tardós,J.D.:Orb‐slam3:Anaccurate open‐sourcelibraryforvisual,visual‐inertial andmulti‐mapslam(2020)

[6] Davison,A.,Reid,I.,Molton,N.,Stasse,O.: Monoslam:Real‐timesinglecameraslam.IEEE TransactionsonPatternAnalysisandMachine Intelligence29,1052–1067(2007)

[7] Doherty,K.,Baxter,D.,Schneeweiss,E.,Leonard, J.:Probabilisticdataassociationviamixture modelsforrobustsemanticslam.2020IEEE InternationalConferenceonRoboticsand Automation(ICRA)pp.1098–1104(2020)

[8] Doherty,K.,Fourie,D.,Leonard,J.:Multimodal semanticslamwithprobabilisticdataassocia‐tion.2019InternationalConferenceonRobotics andAutomation(ICRA)pp.2419–2425(2019)

[9] Finman,R.,Paull,L.,Leonard,J.:Towardobject‐basedplacerecognitionindensergb‐dmaps. 2015IEEEInternationalConferenceonRobotics andAutomation(ICRA)(2015)

[10] Gálvez‐López,D.,Tardós,J.D.:Bagsofbinary wordsforfastplacerecognitioninimage sequences.IEEETransactionsonRobotics28, 1188–1197(2012)

[11] Høydal,Ã.,Skytøen,E.,Andersson,S.,Moser, M.B.,Moser,E.:Object‐vectorcodinginthe medialentorhinalcortex.Nature568,1–8(04 2019).doi:10.1038/s41586‐019‐1077‐7

[12] Kiggundu,A.,Weber,C.,Wermter,S.:Acompress‐ingauto‐encoderasadevelopmentalmodelof gridcells(022017)

[13] Lowry,S.M.,Sünderhauf,N.,Newman,P., Leonard,J.J.,Cox,D.D.,Corke,P.I.,Milford, M.J.:Visualplacerecognition:Asurvey.IEEE Trans.Robotics32(1),1–19(2016).doi: 10.1109/TRO.2015.2496823.

[14] Masone,C.,Caputo,B.:Asurveyondeepvisual placerecognition.IEEEAccess9,19516–19547 (2021).doi:10.1109/ACCESS.2021.3054937,

[15] Montiel,J.,Civera,J.,Davison,A.:Uni iedinverse depthparametrizationformonocularslam.In: Robotics:ScienceandSystems(2006)

[16] Mur‐Artal,R.,Tardós,J.D.:Orb‐slam2:Anopen‐sourceslamsystemformonocular,stereo,and rgb‐dcameras.IEEETransactionsonRobotics 33,1255–1262(2017)

[17] Pillai,S.,Leonard,J.J.:Self‐supervisedvisual placerecognitionlearninginmobilerobots. CoRRabs/1905.04453(2019), http://arxiv.or g/abs/1905.04453

[18] Raoui,Y.,Göller,M.,Devy,M.,Kerscher,T., Zöllner,J.M.,Dillmann,R.,Coustou,A.:R id‐basedtopologicalandmetricalself‐localization inastructuredenvironment.2009Interna‐tionalConferenceonAdvancedRoboticspp.1–6 (2009)

[19] Raoui,Y.,Weber,C.,Wermter,S.:Neoslam:Neu‐ralobjectslamforloopclosureandnaviga‐tion.In:Arti icialNeuralNetworksandMachine Learning‐ICANN2022‐31thInternationalCon‐ferenceonArti icialNeuralNetworks,Bristol, England,September6‐9,2022,Proceedings,Part II(2022)

[20] Rolls,E.,Stringer,S.,Elliot,T.:Entorhinalcortex gridcellscanmaptohippocampalplacecellsby competitivelearning.Network:Computationin NeuralSystems17,447–465(2006)

[21] Rublee,E.,Rabaud,V.,Konolige,K.,Bradski, G.:Orb:Anef icientalternativetosiftor surf.In:2011InternationalConferenceon ComputerVision.pp.2564–2571(2011).doi: 10.1109/ICCV.2011.6126544

[22] Shan,T.,Englot,B.,Meyers,D.,Wang,W.,Ratti, C.,Rus,D.:Lio‐sam:Tightly‐coupledlidarinertial odometryviasmoothingandmapping(2020)

[23] Shan,T.,Englot,B.J.,Duarte,F.,Ratti,C.,Rus,D.: Robustplacerecognitionusinganimaginglidar. CoRRabs/2103.02111(2021),https://arxiv.or g/abs/2103.02111

[24] Tourani,S.,Desai,D.,Parihar,U.S.,Garg,S.,Sar‐vadevabhatla,R.K.,Krishna,K.M.:Earlybird: Loopclosuresfromopposingviewpointsfor perceptually‐aliasedindoorenvironments.CoRR abs/2010.01421(2020),https://arxiv.org/abs/ 2010.01421

[25] Volkov,M.,Rosman,G.,Feldman,D.,III,J.W.F., Rus,D.:Coresetsforvisualsummarization withapplicationstoloopclosure.In:IEEE InternationalConferenceonRoboticsand Automation,ICRA2015,Seattle,WA,USA,26‐30 May,2015.pp.3638–3645.IEEE(2015).doi: 10.1109/ICRA.2015.7139704.

[26] Xiao,L.,Wang,J.,Qiu,X.,Rong,Z.,Zou,X.: Dynamic‐slam:Semanticmonocularvisuallocal‐izationandmappingbasedondeeplearningin dynamicenvironment.RoboticsAuton.Syst.117, 1–16(2019)

[27] Yongbao,A.,Ting,R.,Xiao‐qiang,Y.,Jia‐lin,H., Lei,F.,Jianbin,L.,Ming,L.:Visualslamin dynamicenvironmentsbasedonobjectdetec‐tion.DefenceTechnology(2020)

[28] Yu,F.,Shang,J.,Hu,Y.,Milford,M.:Neuroslam: abrain‐inspiredslamsystemfor3denviron‐ments.BiologicalCybernetics113(5‐6),515–545(December2019).doi:10.1007/s00422‐019‐00806‐9,https://eprints.qut.edu.au/198 104/

[29] Zhou,X.,Weber,C.,Wermter,S.:Robot localizationandorientationdetectionbased onplacecellsandhead‐directioncells.In: Lintas,A.,Rovetta,S.,Verschure,P.F.M.J., Villa,A.E.P.(eds.)Arti icialNeuralNetworks andMachineLearning‐ICANN2017‐26th InternationalConferenceonArti icialNeural Networks,Alghero,Italy,September11‐14, 2017,Proceedings,PartI.LectureNotesin ComputerScience,vol.10613,pp.137–145. Springer(2017).doi:10.1007/978‐3‐319‐68600‐4_17.

DESIGNOFSMALL‐PHASETIME‐VARIANTLOW‐PASSDIGITALFRACTIONAL

DOI:10.14313/JAMRIS/2‐2024/15

Abstract:

DIFFERENTIATORSANDINTEGRATORS

DIFFERENTIATORSANDINTEGRATORS

Submitted:3rd October2023;accepted:8th February2024

MateuszSaków

Thedesignmethodandthetime‐variantfiniteimpulse response(FIR)architectureforreal‐timeestimationof fractionalandintegerdifferentialsandintegralsarepre‐sentedinthispaper.TheproposedFIRarchitectureis dividedintotwoparts.Small‐phasefiltering,integerdif‐ferentiation,andfractionaldifferentialandintegration onthelocaldataareperformedbythefirstpart,which istime‐invariant.Thesecondpart,whichistime‐variant, handlesfractionalandglobaldifferentiationandintegra‐tion.Theseparationofthetwopartsisnecessarybecause real‐timematrixinversionoranextensiveanalyticalsolu‐tion,whichcanbecomputationallyintensiveforhigh‐orderFIRarchitectures,wouldberequiredbyasingle time‐variantFIRarchitecture.However,matrixinversion isusedinthedesignmethodtoachievenegligibledelay inthefiltered,differentiated,andintegratedsignals. Theoptimumoutputobtainedbythemethodofleast squaresresultsinthenegligibledelay.Theexperimental resultsshowthatfractionalandintegerdifferentiation andintegrationcanbeperformedbytheproposedsolu‐tion,althoughthefractionaldifferentiationandintegra‐tionprocessissensitivetothenoiseandlimitedres‐olutionofthemeasurements.Insystemsthatrequire closed‐loopcontrol,disturbanceobservation,andreal‐timeidentificationofmodelparameters,thissolutioncan beimplemented.

Keywords: fractionaldifferentiation,fractionalintegra‐tion,FIRfilter,digitalfiltersynthesis

1.Introduction

Thefractional‐ordercalculushasawidespread potentialforapplication.Currently,thiscomplex mathematicaloperatorbene itsthemodellingofbio‐logical,chemical,control,electrical,andeven inancial systems[1–23].However,thepracticalimplementa‐tionofthefractional‐ordercalculusisextremelydif i‐cultduetothelackofrealcomponentsthatcanrealize thismathematicaloperation[5,24–28].Inthecase oftheintegerdifferentiationandintegration,passive electricalcomponentssuchascapacitorsandcoilscan carryouttheseoperationsontheanaloguesignal[29]. Moreover,thedigitalrepresentationofthereal‐time integer‐ordercalculusisalsotrivialandaddressedby existingsolutionsandscienti icpapers[4,5,30–33].

However,therearenorobustpassivecomponents capableofrealizingthegeneralizedarbitraryorderof thefractionalcalculus,whichallowsformoreaccurate andreal‐timecontrol,modelling,andsimulationofthe realsystems[4,5].

Theliterature[4,5],presentsthreecommonmath‐ematicalde initionsofthearbitrary‐orderderiva‐tiveandintegralproposedbyRiemann–Liouville, Grünwald–Letnikov,andCaputo[1–5].Thesemath‐ematicalde initionscanbeimplementedbyusing thetime‐domain[4,5,34–36],andfrequency‐domain designmethods[4,5].Oneofthefrequency‐domain designmethodsisOustaloup’sapproximation,which isbasedonarecursivedistributionofzerosand polesintoafrequencyinterval[37].Thismethod wasre inedtoachieveabetter itinthefrequency responsein[38].Anotherdesignmethodisbased onCharef’sapproximation,whichhastwoversions. The irstversionapproximatesafunctionofsin‐gularitiesofpolesandzeroswithinalimitedfre‐quencybandwidthwithrespecttoade inedapprox‐imationerror[39],whilethesecondversionextends theCharefmethodbyincludingadditionalarbitrary poles[39].ThenextdesignmethodisCarlson’s approximationmethod[40],whichisbasedonthe Newtoniterativeroot‐ indingalgorithm.Moreover, therearenoniterativedesignmethods,suchasMat‐suda’sapproximation,whereasetoflogarithmically spacedfrequenciesisusedtoapproximatetheideal fractional‐orderfunction[41];andthecontinuedfrac‐tionexpansionapproximation,whichisalsousedfor evaluationofthefractional‐orderfunctionsbecauseit convergesfasterthanpowerseriesexpansions[42]. Matsuda’sapproximationmethodwasalsore inedin [43,44],byapplyingtheSanathanan–Koernerleast‐squaresmethod[45].Afurtherre inementofMat‐suda’smethodisthemodi iedstabilityboundary locus ittingapproximation[27,46],whichisbased onanadditionalclosed‐loopsystemcomposedbya proportional‐integralcontroller.

Morefrequency‐domainapproximationmethods canbefoundintheliterature,suchastheFourier seriesandinverseFouriertransformmethod[34], vector ittingmethod[47],Abdelbaki’smethod[48], Maione’sapproximation[49],andThiele’sapproxima‐tion[50].Inallthesecases,however,theidealtransfer functionofafractionaldifferentiatororintegratoris approximatedbyaninteger‐orderrationaltransition functionthroughthepole‐zeropairs.

Therefore,theinteger‐orderrationaltransition functioncanbesynthesizedwithpassiveanalogue componentsorimplementedintoadigitalreal‐time system.Nevertheless,theapproximationcanbevalid onlyforalimitednumberoffractionalordersandthe differencebetweentheresponsesoftheidealtransfer functionanditsapproximationisunknown[4,5].Fur‐thermore,allthefrequency‐domaindesignmethods provideonlyapproximationinalimitedfrequency bandwidth,thus,theygivelessimportancetotheparts ofthefrequencyresponseinthebordersandoutside ofthisbandwidth.Hence,inthelow‐pass ilterdesign case,thisresultsinpoorapproximationinthepass‐bandfrequencyandpoorattenuationforthestopband frequency,and/orampli icationinthestopbandfre‐quencyspectrum[4,5].

Thefrequency‐domaindesignmethodscanbe adaptedtodigitalarchitectures,suchasthein i‐niteimpulseresponse(IIR)andthe initeimpulse response(FIR) ilters[5, 51].Toadaptcontinuous transferfunctionstotheirdiscreteequivalents,two typesofdiscretizationmethodscanbeused[52–58],thedirect[53, 54]andtheindirectdiscretiza‐tion[59,60].Moreover,therearemethodsthatwere introducedtodesignboththeintegerdifferentiators andintegrators[61–69].Inthecaseofinteger‐order designmethods,thetransferfunctionofadigitalinte‐grator(basedontherectangularrule)canbeinverted andstabilizedtoobtaintheIIRdifferentiator[61].A similardesignapproachwaspresentedin[62, 63], wheretheintegratorisobtainedbycombiningboth therectangularandtrapezoidaltechniques.Inthis case,thedifferentiatorisalsoobtainedbyinvert‐ingandstabilizingtheintegratortransferfunction. Analternativedesignmethodwaspresentedin[64], wherethedigitalintegratorisdesignedwithrespect totheSimpsonintegrationrule,andthedifferentiator isobtainedagainbyinvertingtheintegratortrans‐ferfunction.Anotherdesignmethodisbasedonthe closed‐formNewton‐Cotesintegrationformula[68], wherethethird‐orderdigitaltrapezoidalintegrator isobtainedandinvertedtoformthedifferentiator. Anothersolutionwasproposedin[70],wherethe adaptationofthemethodofleastsquareswasused todesigntheintegerFIRdifferentiator.Furthermore, alternativemethodsaretheAdomiandecomposition method[71],theChebyshevcollocationmethod[72, 73],andthepredictor–correctorapproachbasedon theAdams–Bashforth–Moultonmethod[74–76].Nev‐ertheless,thesethreemethodsarenotrobustenough tobeimplementedinareal‐timesystem,andare thereforelimitedtonumericalsimulationsonly[4,5].

Thedirectandindirectdiscretizationmethods leadtoadiscretetransferfunction,whichhasthe samedrawbacksasthetransferfunctiondesigned withrespecttothefrequency‐domaindesignmeth‐ods.Hence,onlytheFIRandIIRintegerdifferentiators andintegratorscanestimatetheiroutputwithrespect totheclose‐to‐idealmagnituderesponse.However, onlyonesolutionallowsdesigningtheintegerFIR differentiatorthatischaracterizedbyanegligible

phaseshiftinthepassbandfrequencyandsigni icant attenuationinthestopbandfrequencyspectrum[70]. Othersolutions[61–69]arecharacterizedbylinearor nonlinearphaseresponses,whichleadtoatimedelay inthedifferentiatedandintegratedsignalsorimpre‐ciseresponsewithrespectto(periodic)signalswith varyingfrequency.This,inturn,limitstheirapplica‐tionsinclosed‐loopcontrolandreal‐timeestimation andrecoveryofthestatevariablesin,e.g.,disturbance observerdesign[77–85].

Inthispaper,thetime‐variantFIRarchitectureand itsdesignmethodforreal‐timelocalandglobalfrac‐tionalandintegerdifferentiationandintegrationare presented.TheproposedFIRarchitectureisdivided intotwoparts.Smalldelay(small‐phaseshift) ilter‐ing,integerdifferentiation,andpotentiallylocalfrac‐tionaldifferentiationandintegrationareperformed bythe irstpart,whichistime‐invariant.Thispart isbasedonthepreviouslyintroducedFIR ilterand integerdifferentiatorarchitecturespresentedin[70], andisalsoextendedtothefractional‐ordercalculus inthispaper.Fractional(global)differentiationand integrationareperformedbythesecondpart,which istime‐variant.Theseparationofthetwopartsisnec‐essarybecausereal‐timematrixinversionorexten‐siveanalyticalsolutions,whichcanbecomputation‐allydemandingforhigh‐orderFIRarchitectures,are requiredbythetime‐variantFIRarchitecture.More‐over,matrixinversionisusedinthedesignmethodto ensuresmalldelayintroducedintothe iltered,differ‐entiated,andintegratedsignalsbybothpartsofthe FIRarchitectures.Theoptimumoutputobtainedby themethodofleastsquaresresultsinthenegligible phaseshiftintroducedbytheFIRarchitecture.

Thispaperisorganizedasfollows:Section 2 describestheproblemsregardingtheimplementation ofthefractionaldifferentiatorsandintegrators;Sec‐tion 3 introducesthetime‐variantFIRarchitecture anditsdesignmethod;Section4discussestheexper‐imentalresults;andSection5concludesthepaper.

2.ProblemStatement

Thefractionalderivative(integral)[1–5,51]ofthe powerfunction��(��)=���� isgivenby:

(1) wheretheintegerorder �� oftheintegerderivative (integral)isgeneralizedtoanarbitraryorder �� by replacing��!and(��−��)!withgammafunctionsΓ(��+1) andΓ(��−��+1),respectively.If��−��+1>0,the gammafunctionΓ(��−��+1)[1–5,51]canbecomputed asfollows:

(2)

Furthermore,if��−��+1≤0,thegammafunction Γ(−��)canbecomputedbyusingthere lectionprop‐ertyofthegammafunctionasfollows:

Γ(−��)= −��csc(����) Γ(��+1) (3)

Basedon(1)withrespectto(2)and(3),thefrac‐tionalderivative(integral)ofagivenfunction ��(��) transformedintoapolynomialof �� byusingTaylor seriesexpansionisgivenby:

����(��)=

(4)

where���� isthe����ℎ coef icientofthegivenpolynomial. Theprobleminthiscaseisthatthetransferfunctionof theFIRarchitecture( ilter,differentiator,orintegra‐tor)describedby:

(5)

where �� isthe ��‐transformand �� istheorderof theFIRarchitecture,mustcalculatethecombineddif‐ferentiatedandintegratedoutput.Unfortunately,the FIRarchitecturedoesnotstoreandusedataout‐sidethelimiteddataset(localsamplesofthemod‐i iedsignal)usedtocalculatetheoutputofthatFIR architecture.Therefore,theFIRarchitecturedoesnot includetimebase,anditcannotestimateboththe globalintegerintegralsandthefractionalorderdiffer‐entials/integrals.

3.Time‐variantFIRArchitectureandItsDesign

Theproposedtime‐variantFIRarchitecture, designedaccordingtotheproposeddesignmethod, consistsoftwoseparateparts.Bothpartsareshown inFigure1.

The irstandsecondpartsoftheFIRarchitecture aredesignedseparately.The irstpartperforms il‐tering,integerandlocalfractionaldifferentiationand integration.Whenthe irstpartisdesignedasalow‐passFIR ilter,thesecondpartcanactasbothan integer‐andfractional‐orderdifferentiatorandinte‐grator.

BothFIRarchitecturesconsistofdelaylinesbuilt fromunitarydelays��−1,whichcreate���� consecutive delayedsignalsfromtheinputsignal ��[��].The irst architectureconsistsofgains ����(����) andthesum blocks Σ.ThesecondFIRarchitectureusesamulti‐plexer(MUX)toobtain���� signalsfromthedelayline. Thesesignalsaremultipliedbymatrices ����(��) and ����(��)toobtaintheresultingoutput��[��].

The irstpartisdesignedaccordingtothealgo‐rithmpresentedin[70],whichwasdevelopedto designsmall‐phaseFIR iltersandinteger‐orderdif‐ferentiators.However,inthiswork,twomodi ications tothetimesamplevectoroftheFIRarchitecture ���� areintroduced.Thetimesamplevectorisdescribed asfollows:

�� =[1−��,1+Δ��−��,…,1+(����

(6) where���� ∈ℕistheorderofthe irstFIRarchitecture and��standsfortransposeoperator.

The irstmodi icationintroducesthesampling periodΔ��in(6).Thismodi icationeliminatestheneed forthegainscalingfactor(−1/Δ��)����,where���� isthe orderoffractionalderivative/integral.Thescalingfac‐torwasrequiredin[70]toadjustthegainoftheFIR differentiatorwithrespecttothesamplingrate.In(6), thescalingfactoriseliminatedbecauseitbecomesa complexnumberforfractionaldifferentialsandinte‐grals.

Thesecondmodi icationallowsdesigningatime delay �� introducedbythe irstFIRarchitecture.The purposeofdesigningthetimedelayistoincrease theattenuationofthestopbandfrequency.TheFIR ilterandintegerdifferentiatordesignedwithrespect to[70]minimizesthephaseshiftandattenuationof thestopbandfrequencybyestimatingtheoutputof theFIRarchitecture,whichisoptimalwithrespectto themethodofleastsquares.Theintroductionofthe timedelayallowstheoutputoftheFIRarchitectureto becalculatedwithrespecttothesamplessurrounding the ilteredsampleofthesignalinsteadof ilteringthat samplebasedononlythepastsamples[70].

Thetimesamplevector(6)isusedtocreatethe followingmatrix:

(7) where���� ∈ℕcorrespondstotheorderofatheoretical polynomial ittedbytheFIRarchitecture.Theweights ofthisFIRarchitecturearecalculatedasfollows:

(8)

where

Γ(1)

���� =

Γ(1−����), Γ(2)

Γ(2−����),…,

Γ(����)

Γ(���� −����),

Γ(���� +1)

Γ(���� −���� +1) , (9)

where���� isthevectorofweightstransformingtheleft‐sidedMoore–Penrosegeneralizedinversesolutionin (8)totheFIRarchitectureweights ����(����).The ���� vectorisgeneralizedtoanarbitraryorderofthe it‐tedpolynomial����,andfractional‐orderofthederiva‐tive/integral���� inthegammafunctionΓ(����,����).

The irstFIRarchitecturecanbeusedto ilter, differentiate,andintegratethesignal ��[��].However, theoutput��[��]willcorrespondonlytothelocal(frac‐tional)differentialsandintegralsatthepointwith respecttothetimesamplevector(6).Tosolvethis problem,theadditionaltime‐variantFIRarchitecture wasintroduced.

InthesecondFIRarchitecture,alltheparameters aretime‐dependent.Therefore,thetimesamplevec‐tor����(��)ofthesecondFIRarchitectureincludestime‐base��,andisdescribedasfollows:

����(��)=[��,��−Δ��,��−2Δ��,…,��−(���� −2)Δ��, ��−(���� −1)Δ��]�� , (10)

where ���� ∈ℕ correspondstotheorderofatheo‐reticalpolynomial, ittedagainbythetime‐variantFIR architecture.In(10)thereisnoneedtointroducethe delaybecause ilteringislefttothe irstFIRarchitec‐ture.Basedon(10),thetime‐dependentmatrix����(��) isdescribedasfollows:

����(��)=[��0 ��(��),��1 ��(��),…,������−1 �� (��),������ �� (��)], (11)

where���� ∈ℕcorrespondstotheorderofthe itted polynomialinthesecondFIRarchitecture.Then,(11) isusedtoobtaintheweightsofthesecondFIRarchi‐tectureasfollows:

����(��)=����(��)((���� ��(��)����(��))−1 ����(��)), (12)

where

��

�� , Γ(���� +1) Γ(���� −���� +1) ������−���� , (13) where ����(��) isagainthetime‐dependentvectorof weightstransformingtheleft‐sidedMoore–Penrose generalizedinversesolutionin(12)totheFIRdif‐ferentiatorandintegratorweights ����(��).The ����(��) vectorisalsogeneralizedtoanarbitraryorder itted polynomial����,andfractional‐orderofthederivative andintegral���� inthegammafunctionΓ(����,����).Fur‐thermore,(8)includesthetimebasewhichisde ined asthepowerfunctions��(����−����) .

TheentireFIRarchitecture(Fig. 1)wasdivided intotwopartsbecauseasingletime‐variantFIRarchi‐tecturedesignedaccordingto(10)–(13)requiresreal‐timematrixinversionorananalyticalsolutionof(12). Inthiscase,matrixinversionof(12)canbecom‐putationallyintensive,especially,forhigh‐orderFIR architectures.

Therefore,theentireFIRarchitecturestructure wasdividedintothetime‐invariantandtime‐variant parts,whereinthecaseofthetime‐variantpart,the orderofFIRstructurecanbeaslowaspossible(���� > ����) and(���� >����),becausethe ilteringprocess islefttothe irstpart.Furthermore, ����(��) consists ofonly ��2 �� parameters,thus,thedifferentiationand integrationordercanbeupdatedinreal‐timewithout theneedtorecalculatetheparametersoftheentire FIRarchitecture.

Therearetwomainlimitationsoftheproposed solution.The irstlimitationcomesfromtheabil‐itytoapproximateinputsignal ��[��] bythetime‐variantFIRarchitecture.Iftheorderofthepolyno‐mial ���� islowerthanthetheoreticalorderofthe polynomialapproximatinginputsignal��[��],theerror betweenoutput ��[��] andtheoreticalintegerinte‐gralandfractional‐derivativesandfractional‐integrals approximating ��[��] willincreaseasthedifference increasesbetweenordersofpolynomials.Moreover, analyticalsolutionof(12)leadstomathematical expressionssuchas��(����)+Δ��(����).Inthiscase,if��≫ Δ��,numericalerrorswillappearafternumericalaccu‐racyisreachedduringcalculationof��(����)+Δ��(����) Furthermore,differentiatororintegratordesigned accordingtoproposedmethodwillestimateitsoutput withrespecttozeroinitialconditions.Nevertheless, despitetheselimitations,therearesystemsoriented onclosed‐loopcontrol,disturbanceobservationsand real‐timeidenti icationofmodelparameters,where proposedsolutioncanbeimplemented.

4.ExperimentalEvaluation

��)

Intheexperiments,therewerethreesignalsfrom threedifferentsystemsconsidered.The irstsys‐temwasthelinearactuatorDSZY1‐24‐05‐A‐050‐IP65 anditsvoltageinputsignal.Thesecondsystemwas theincrementallinearencoderL18‐F10‐0120‐05‐0‐CP03/Wwiththedisplacementfeedback.Thethird systemwastheKUKAiiwaR820manipulatorwiththe angularpositionfeedbackfromitsencoders.

The irstsignalwastheanaloguesignalmea‐suredinvolts,whichwascharacterizedbythenoise describedbythenormaldistribution��(0,0.001).The secondsignalwasthedisplacementsignalmeasured inmm,wheretheminimumincrementalmotionis1.0 ��m(accuracygradeat1.0m:3.0��m).Thethirdsignal correspondedtotheangularpositionofajointofthe manipulatormeasuredindegrees,wherethemini‐mumincrementalmotionwas3.0–4.0 ��deg.Unfor‐tunately,demonstrationsofthe iltering,fractional‐orderdifferentiationandintegrationbasedontheran‐domsignals(obtainedfromthedescribedsystems)

wouldbedif icultduetotheunknownfractionaldif‐ferentialsandintegralsofthesesignals.Therefore,the samesignals(functions ��(��))wereusedasthebase fortheexperimentalevaluation,wherethequalityof eachsignalwasdescribedbynoiseandtheobservable minimumincrementalmotioncharacterizingeachof thediscussedsystems.

Moreover,thereweretwotypesoftestsconducted. Inthe irsttest,theabilityto ilter,differentiateand integratebasedonlyonthelocaldatawasinvesti‐gated.Then,inthesecondgroupofthetests,the abilityof iltering,integer‐andfractional‐orderdif‐ferentiation,andintegrationwithrespecttothetime base(globally),wasevaluated.Frequencyresponses werenotconsideredbecausethelocal(fractional)FIR differentiator/integratorfrequencyresponsesdonot correspondtotheirequivalenttheoreticalresponses. Furthermore,thetime‐variantFIRarchitectureelim‐inatesthepossibilityofitsanalysisinthefrequency domain.

Inthe irsttest,function ��(��)=��2 wasused. Thisfunctionwasaffectedbythenoisedescribedby thedistribution ��(0,0.1).Inthiscase,thenoisewas signi icantly(onehundredtimes)higherthaninthe irstsystem.Thesamplingfrequencyofthetestsig‐nalwas16384Hz,whileparametersofthe irstFIR architecturewere ��=0, ���� =16384,and ���� =2 Hence,theFIRarchitectureestimateditsoutputbased onsamplesupto1sfromthepast.Theresultsare presentedinFigure2

Inthe irstgroupoftests(Fig. 2), ivedifferent iltering(Fig. 2a),integer‐(Fig. 2b)andfractional‐order(Fig.2c)differentiation,andfractional‐(Fig.2d) andinteger‐order(Fig. 2e)integrationexamplesare presented.Inallthecases,theoutputoftheFIRarchi‐tectureisincloserange(basedonvisualinspection) toitscorrespondingtheoreticalfunction(itslocaldif‐ferentialandintegral).However,thefunction��(��)was not ittedtothedata��(��)+��(0,0.1).Therefore,there isanoticeabledifferencebetweentheoutputsofthe FIRarchitectures,andthefunction ��(��) andthecor‐respondingtheoreticaldifferentials/integrals.Inthis case,therecoveryoftheoriginalsignal��(��)isamore demandingprocessthanalocal itofthisfunction withrespecttotheleastsquares‐basedregression. However,theoutputfromtheFIR ilter(Fig.2a)was 0.060%differentfromtheoutputfromtheoriginal signalf(t).Inthecaseoftheinteger(��=1,Fig.2b) andthefractional(��=1/2,Fig. 2c)differentiation, thedifferencesbetweentheresponsesfromtheFIR architectureandthecorrespondingtheoreticaldiffer‐ential ������(��) ������ were0.001%and0.011%,respectively. Inthecaseofthefractional(��=−1/2,Fig.2d)and theinteger(��=−1,Fig.2e)integral,thedifferences betweentheresponsesfromtheFIRarchitectureand thecorrespondingintegralvalueswere0.147%and 0.273%,respectively.

Figure2. ComparisonofdifferentFIRarchitecture outputsduringlocaldifferentiationandintegration:(a) referencesignalwithandwithoutnoisecomparedto theFIRfilteroutput;(b)idealintegerdifferentialfor ��=1 comparedtotheFIRdifferentiatoroutput ���� =1; (c)idealfractionaldifferentialfor ��=1/2 comparedto theFIRdifferentiatoroutput ���� =1/2;(d)ideal fractionalintegralfor ��=−1/2 comparedtotheFIR integratoroutput ���� =−1/2;(e)idealintegerintegral for ��=−1 comparedtotheFIRintegratoroutput ���� =−1

The irstFIRarchitecturedesignedwithrespect to(6)–(9)canprovideonlyaccurateresponsesbased onthesignalsamplesstoredinthedelaylineofthat FIRarchitecture.Theseresponsesareonlytruelocally. Therefore,theproposedFIRarchitecturecanwork asa ilteroranintegerdifferentiator.Nevertheless, localfractional‐differentiatorsandinteger/fractional‐integratorscanalso indawideareaofapplica‐tion.Aperfectexampleisthefractionalproportional‐derivative‐integralcontroller,wheretheresponsesof eachofthecontroller’scomponentscanbeestimated locally.

Moreover,theproposedFIRarchitectureintro‐ducesanegligibletimedelayintotheclosed‐loopsys‐tem.Thus,thesmall‐phase‐shift ilteringhasaposi‐tiveimpactontheresponsedynamicsandstabilityof closed‐loopcontrolsystems.Unfortunately,onlythe FIR ilterandintegerdifferentiatorcanbeusedfor otherpurposessuchasthereal‐timeidenti ication anddisturbanceobserverdesign.

Inthesecondgroupoftests,thefunction��(��)was dividedintothreeparts.Inthe irstpart, ��(��)=��2 , ��∈(0,30].Inthesecondpart,��(��)=−40��+2100,��∈ (30,60].Inthethirdpart,��(��)=0.2(��−75)3+374.9, ��∈(60,90].

Thesefunctionswerechosentocreatesimilarcon‐ditionsfortheFIRarchitecturessuchas(angular) velocitycorrespondingtotherateofthe(angle)posi‐tionchangeofthesecondandthirdsystem,andthe voltagesignalfromtheanaloguecontrolleroutputin the irstsystem.Theonlyexceptionsarethediscon‐tinuoustransitionsbetweenthesefunctions.The irst consideredsystemisthelinearactuatorwithnoise describedbythenormaldistribution��(0,0.001),that affecteditsvoltageinputsignal.Theresultsarepre‐sentedinFigure3.

TheFIRarchitectureparametersusedtoobtainthe resultspresentedinFigure3,were��=0,���� =40, and ���� =1 forthe irsttime‐invariantarchitecture, and���� =4and���� =3forthesecondtime‐variant FIRarchitecture.Moreover,thesamplingfrequencyof theFIRarchitecturewasreducedto8Hz.Thesam‐plingfrequencyoftheinputsignalremainedthesame (16384Hz).Again, ivedifferentoutputexamplesare discussed.The ilteringresultsarepresentedinFig‐ure 3a,theintegerandfractionaldifferentiationin Figure3candFigure3d,andthefractionalandinteger integrationinFigure3eandFigure3f,respectively.

Basedontheresults(Fig. 3),theoutputofthe FIRarchitectureswasincloserangetothetheoretical functions,andsowereitsglobal(fractional)differen‐tialsandintegrals.Asinthe irsttest,no ittingwas donetothedata��(��)+��(0,0.001).Inthecasesofinte‐ger(��=1,Fig.3b)andfractional(��=1/2,Fig.3c) differentiation,theaverageabsolutedifferencewith respecttothemaximumabsolutevalueofthetheoret‐icalsignalwas3.78%and144%,respectively.Unfor‐tunately,theseaveragevalueswerestronglyaffected bytheerrorsappearingduringthetransitionstates betweenthefunctions.Therefore,themedianwas usedtocompareintegerandfractionaldifferentiation results.Inthiscase,themedian‐baseddifferencewas reducedto0.19%and1.04%,respectively.Inthecase ofintegration,theaveragedifferenceswerecompa‐rabletothoseoffractionaldifferentiation(178.36% and188.46%forthefractionalandintegerintegra‐tion,respectively),whilethemediandifferenceswere reducedto1.19%and1.10%forthefractionaland integerintegration.

Figure3. ComparisonofdifferentFIRarchitecture outputsduringglobaldifferentiationandintegration–analoguesignalexample:(a)referencesignalwithand withoutnoisecomparedtotheFIRfilteroutput;(b) magnified(a)within ��∈[74.5,75.5];(c)idealinteger differentialfor ��=1 comparedtotheFIRdifferentiator output ���� =1;(d)idealfractionaldifferentialfor ��=1/2 comparedtotheFIRdifferentiatoroutput ���� =1/2;(e)idealfractionalintegralfor ��=−1/2 comparedtotheFIRintegratoroutput ���� =−1/2;(f) idealintegerintegralfor ��=−1 comparedtotheFIR integratoroutput ���� =−1

Comparableresultsandproblemswereobserved whenthefractionaldifferentiationandintegration wereappliedtothesignalobtainedfromthedigital encoderofthethirdsystem.Theresultsarepresented inFigure4

TheFIRarchitectureparametersusedtoobtainthe resultspresentedinFigure4,were��=0,���� =1000, and ���� =2 forthe irsttime‐invariantarchitecture, and���� =4,and���� =3forthesecondtime‐variant FIRarchitecture.ThesamplingfrequencyoftheFIR architecturewasreducedto4096Hz.Thesampling frequencyoftheinputsignalremainedalsothesame

Figure4. ComparisonofdifferentFIRarchitecture outputsduringglobaldifferentiationandintegration–digitalencodersignalexample:(a)referencesignalwith andwithoutnoisecomparedtotheFIRfilteroutput;(b) idealintegerdifferentialfor ��=1 comparedtotheFIR differentiatoroutput ���� =1;(c)idealfractional differentialfor ��=1/2 comparedtotheFIR differentiatoroutput ���� =1/2;(d)idealfractional integralfor ��=−1/2 comparedtotheFIRintegrator output ���� =−1/2;and(e)idealintegerintegralfor ��=−1 comparedtotheFIRintegratoroutput ���� =−1. (16384Hz).Again,inthecaseofthesignalfromthe digitalencoderofthethirdsystem, ilteringresultsare presentedinFigure 4a,integerandfractionaldiffer‐entiationinFigure 4candFigure 4d,andfractional andintegerintegrationinFigure 4eandFigure 4f, respectively.

BasedontheresultspresentedinFigure 4,the outputoftheFIRarchitectureswasalsocompara‐bletothetheoreticalfunctionscorrespondingtothe global(fractionalandinteger)differentialsandinte‐grals.Theinteger (��=1,Figure 4b)andfractional (��=1/2,Figure 4c)differentiationresultswere characterizedbyanaveragedifferenceof2.09%and 435.00%,respectively.Again,thisaverageindicator

wasstronglyaffectedbytheerrorsappearingduring thetransitionstatesbetweenthefunctions.Hence,the median‐baseddifferencewasreducedto0.000016% and0.010%fortheintegerandfractionaldifferen‐tiation,respectively.Theaveragedifferencescorre‐spondingtothefractionalandintegerintegration were526.87%and554.31%,whiletheequivalent mediandifferenceswerereducedto0.04%and0.02%, respectively.

Thesametestswereconductedwithrespecttothe secondsystem,wheretheobservableminimumincre‐mentalmotionwasatthelevelofasinglemicrometer. Inthiscase,however,theFIRarchitecturesrequired adrasticreductionofthesamplingfrequency,which wasreducedto4Hz.TheremainingFIRarchitecture parameterswere ��=0, ���� =40,and ���� =2 for the irsttime‐invariantarchitecture,and���� =4,and ���� =3forthesecondtime‐variantFIRarchitecture. Therestoftheparametersandconditionsremained thesameasinthetwoprecedingexperiments.

Inthecaseoftheinteger(��=1)andfrac‐tional(��=1/2)differentiation,theaveragedif‐ferencewas4.84%and145.92%,whilethemedian differencewas0.37%and0.12%,respectively.The averagedifferencescorrespondingtothefractional andintegerintegrationwere183.81%and197.19%, whilethecorrespondingmediandifferenceswere 0.06%and0.04%,respectively.

Unfortunately,fractionaldifferentiationcombines differentiationandintegration.Therefore,thispro‐cessisextremelysensitivetonoisebecausethecor‐respondingerrorincreasesineachcomputationcycle intheFIRarchitecture.Nevertheless,byreducingthe samplingfrequencyofthe irstFIRarchitecturemore attenuationwasachievedforthestopbandfrequency ofthisarchitecture.Thus,itprovidedabetter iltered datasetforthesecondtime‐variantFIRarchitecture.

Thetimedelayintroducedtothemethodof designoftheproposedFIRarchitecturesigni icantly increasedtheattenuationofthestopbandfrequency ofthe irstFIR ilter.However,thisdelayalsointro‐ducedaphaseshifttothe ilteredsignal.Inresult,it drasticallyincreasedtheerroroftheestimatedoutput. Hence,thereductionofthesamplingfrequencyturned outtobeabettersolutiontoincreaseattenuationof theproposedFIRarchitecturethanintroductionofa delaytothatarchitecture.Nevertheless,fractionaldif‐ferentiationandintegrationrequireanextremelevel ofattenuationforthestopbandfrequencywhichwas achallengefortheproposedsolution.Inthiscase, theparametersofeachofthediscussedFIRarchitec‐turesweresetaccordingtovisualinspectionoftheir responses.Therearethereforetwochallengesforthis solution,whichareincreasingtheattenuationofthe stopbandfrequencyandoptimizingtheFIRarchitec‐tureparameters.

Moreover,adaptationoftheproposeddesign methodintoanIIRdigitalarchitecturecouldsolvethe problemsofthenumericalerrorsandtherequired timebase.However,itisnotatrivialtaskduetothe adaptationofthemethodofleastsquaresintothe

designmethodoftheproposedFIRarchitectureand thestabilityproblemsofanIIRdigitalsystem.

5.Conclusion

Inthispaper,thedesignmethod,andthetime‐variantFIRarchitectureforreal‐timeestimationof localandglobalfractionalandintegerdifferentiators andintegratorswerepresented.TheproposedFIR architecturewasdividedintotwoparts.Inthe irst part,theFIRarchitecturewastime‐invariant,whilein thesecondpart,theparametersofthearchitecture wereestimatedwithrespecttothetimebase.The separationintotwoindependentpartswasnecessary becauseasingletime‐variantFIRarchitecturewould requirereal‐timematrixinversionorextensiveana‐lyticalsolutions.Thematrixinversioninthedesign methodwascriticaltoensuresmalldelay(phaseshift) causedbyeachoftheFIRarchitectures.Thesmall delayresultedfromtheoptimumoutputobtained withrespecttothemethodofleastsquares.Unfortu‐nately,therearelimitationsoftheproposedsolution. The irstlimitationisthelimitedabilitytoapproxi‐matetheinputsignalbythetime‐variantFIRarchi‐tecture,whilethesecondlimitationisstrictlyrelated tothenumericalerrors.Moreover,sincefractionaldif‐ferentiationcombinesdifferentiationandintegration, thisprocessisextremelysensitivetothenoiseand thelimitedresolutionofthemeasurements.However, byreducingthesamplingfrequencyofthe irstFIR architectureorincreasingitsorder,moreattenuation canbeachievedforthestopbandfrequencyofthepro‐posedFIRarchitecture.Furthermore,despitethese limitations,therearesystemsorientedonclosed‐loop control,disturbanceobservationsandreal‐timeiden‐ti icationofmodelparameters,wheretheproposed solutioncanbeimplemented.

AUTHOR

MateuszSaków∗ –ResearchInstituteofSignals,Sen‐sorsandSystems,SchoolofEngineering&Physical Sciences,Heriot‐WattUniversity,Edinburgh,UKEH14 4AS,Scotland,UK,e‐mail:sakow.mat@gmail.com.

∗Correspondingauthor

References

[1] K.OldhamandJ.Spanier, Thefractionalcalculustheoryandapplicationsofdifferentiationand integrationtoarbitraryorder.Elsevier,1974.

[2] H.Sun,Y.Zhang,D.Baleanu,W.Chen,andY. Chen,“Anewcollectionofrealworldapplica‐tionsoffractionalcalculusinscienceandengi‐neering,” CommunicationsinNonlinearScience andNumericalSimulation,vol.64,pp.213–231, 2018.

[3] I.Petráš, Fractional-ordernonlinearsystems: modeling,analysisandsimulation.SpringerSci‐ence&BusinessMedia,2011.

[4] J.D.Colín‐Cervantesetal.,“Rationalapproxima‐tionsofarbitraryorder:Asurvey,” Fractaland Fractional,vol.5,no.4,p.267,2021.

[5] B.T.Krishna,“Studiesonfractionalorderdif‐ferentiatorsandintegrators:Asurvey,” Signal processing,vol.91,no.3,pp.386–426,2011.

[6] L.Debnath,“Recentapplicationsoffractionalcal‐culustoscienceandengineering,” International JournalofMathematicsandMathematicalSciences,vol.2003,no.54,pp.3413–3442,2003.

[7] S.Manabe,“Thenon‐integerintegralandits applicationtocontrolsystems,” MitsubishiDenki laboratoryreports,vol.2,no.2,1961.

[8] M.AxtellandM.E.Bise,“Fractionalcalculus applicationincontrolsystems,”in IEEEconferenceonaerospaceandelectronics,1990:IEEE, pp.563–566.

[9] W.JifengandL.Yuankai,“Frequencydomain analysisandapplicationsforfractional‐order controlsystems,”in Journalofphysics:Conference series,2005,vol.13,no.1:IOPPublishing,p.268.

[10] A.Charef,“Analoguerealisationoffractional‐orderintegrator,differentiatorandfractional PI��D�� controller,” IEEProceedings-ControlTheoryandApplications,vol.153,no.6,pp.714–720, 2006.

[11] N.Ferreira,F.Duarte,M.Lima,M.Marcos,and J.Machado,“Applicationoffractionalcalculusin thedynamicalanalysisandcontrolofmechanical manipulators,” Fractionalcalculusandapplied analysis,vol.11,no.1,pp.91–113,2008.

[12] J.TenreiroMachadoandA.Galhano,“Anew methodforapproximatingfractionalderivatives: applicationinnon‐linearcontrol,” ENOC-2008, pp.1–5,2008.

[13] J.Mocak,I.Janiga,M.Rievaj,andD.Bustin,“The useoffractionaldifferentiationorintegration forsignalimprovement,” MeasurementScience Review,vol.7,no.5,pp.39–42,2007.

[14] G.Li,Y.Li,H.Chen,andW.Deng,“Fractional‐ordercontrollerforcourse‐keepingof underactuatedsurfacevesselsbasedon frequencydomainspeci icationandimproved particleswarmoptimizationalgorithm,” Applied Sciences,vol.12,no.6,p.3139,2022.

[15] M.Shitikova,“Fractionaloperatorviscoelastic modelsindynamicproblemsofmechanicsof solids:Areview,” Mechanicsofsolids,pp.1–33, 2022.

[16] F.Özköse,M.Yavuz,M.T.Şenel,andR.Habbireeh, “FractionalordermodellingofomicronSARS‐CoV‐2variantcontainingheartattackeffect usingrealdatafromtheUnitedKingdom,” Chaos, Solitons&Fractals,vol.157,p.111954,2022.

[17] X.Zhang,G.Yang,S.Liu,andA.J.Moshayedi, “Fractional‐ordercircuitdesignwithhybridcon‐trolledmemristorsandFPGAimplementation,”

AEU-InternationalJournalofElectronicsand Communications,vol.153,p.154268,2022.

[18] P.Bertsias,S.Kapoulea,C.Psychalinos,andA.S. Elwakil,“Acollectionofinterdisciplinaryappli‐cationsoffractional‐ordercircuits,”in Fractional OrderSystems:Elsevier,2022,pp.35–69.

[19] M.Joshi,S.Bhosale,andV.A.Vyawahare,“Asur‐veyoffractionalcalculusapplicationsinarti icial neuralnetworks,” Arti icialIntelligenceReview, pp.1–54,2023.

[20] E.Yumuk,M.Güzelkaya,andİ.Eksin,“Arobust fractional‐ordercontrollerdesignwithgainand phasemarginspeci icationsbasedondelayed Bode’sidealtransferfunction,” Journalofthe FranklinInstitute,vol.359,no.11,pp.5341–5353,2022.

[21] G.Gembalczyk,P.Gierlak,andS.Duda,“Model‐ingandcontrolofanunderactuatedsystemfor dynamicbodyweightsupport,” AppliedSciences, vol.11,no.3,p.905,2021.

[22] G.Gembalczyk,P.Domogała,andK.Leśniowski, “ModelingofUnderactuatedBallandBeam System—AComparativeStudy,”in Actuators, 2023,vol.12,no.2:MDPI,p.59.

[23] Y.Wang,G.Wang,G.Yao,andL.Shen,“Research ontheCharacteristicsofOperatingNon‐UniformityofaHigh‐PressureCommon‐Rail DieselEngineBasedonCrankshaftSegment Signals,” IEEEAccess,vol.9,pp.64906–64917, 2021.

[24] M.SugiandK.Saito,“Non‐integerexponents inelectroniccircuits:F‐matrixrepresentation ofthepower‐lawconductivity,” IEICETRANSACTIONSonFundamentalsofElectronics,CommunicationsandComputerSciences,vol.75,no.6,pp. 720–725,1992.

[25] I.Podlubny,I.Petráš,B.M.Vinagre,P.O’Leary, andL’.Dorčák,“Analoguerealizationsof fractional‐ordercontrollers,” Nonlinear dynamics,vol.29,pp.281–296,2002.

[26] B.KrishnaandK.Reddy,“Analysisoffractional orderlowpassandhighpass ilters,” Journalof ElectricalEngineering,vol.8,no.1,pp.4–4,2008.

[27] M.Koseoglu,F.N.Deniz,B.B.Alagoz,andH. Alisoy,“Aneffectiveanalogcircuitdesignof approximatefractional‐orderderivativemodels ofM‐SBL ittingmethod,” EngineeringScience andTechnology,anInternationalJournal,vol.33, p.101069,2022.

[28] Z.M.Shah,M.Y.Kathjoo,F.A.Khanday,K.Biswas, andC.Psychalinos,“Asurveyofsingleandmulti‐componentFractional‐OrderElements(FOEs) andtheirapplications,” MicroelectronicsJournal, vol.84,pp.9–25,2019.

[29] M.E.VanValkenburg,“Introductiontomodern networksynthesis,”,1960.

[30] M.SakówandK.Marchelek,“Designandoptimi‐sationofregression‐typesmallphaseshiftFIR

iltersandFIR‐baseddifferentiatorswithopti‐mallocalresponseinLS‐sense,” MechanicalSystemsandSignalProcessing,vol.152,p.107408, 2021.

[31] R.Karthick,A.Senthilselvi,P.Meenalochini,and S.SenthilPandi,“Designandanalysisoflinear phase initeimpulseresponse ilterusingwater strideroptimizationalgorithminFPGA,” Circuits, Systems,andSignalProcessing,vol.41,no.9,pp. 5254–5282,2022.

[32] F.Arellano‐Espitia,M.Delgado‐Prieto,A.‐D. Gonzalez‐Abreu,J.J.Saucedo‐Dorantes,andR.A. Osornio‐Rios,“Deep‐Compact‐Clusteringbased anomalydetectionappliedtoelectromechanical industrialsystems,” Sensors,vol.21,no.17,p. 5830,2021.

[33] Y.Zhouetal.,“Transientmeasurementofmecha‐tronicmulti‐parametersandkineticsperfor‐mancesforlinearpiezoelectricmotors,” Measurement,vol.203,p.112032,2022.

[34] D.P.Atherton,N.Tan,andA.Yüce,“Methodsfor computingthetimeresponseoffractional‐order systems,” IETControlTheory&Applications,vol. 9,no.6,pp.817–830,2015.

[35] C.Hwang,J.‐F.Leu,andS.‐Y.Tsay,“Anoteon time‐domainsimulationoffeedbackfractional‐ordersystems,” IEEETransactionsonAutomatic Control,vol.47,no.4,pp.625–631,2002.

[36] R.S.Barbosa,J.T.Machado,andI.M.Ferreira, “TuningofPIDcontrollersbasedonBode’sideal transferfunction,” Nonlineardynamics,vol.38, pp.305–321,2004.

[37] A.Oustaloup,F.Levron,B.Mathieu,andF. M.Nanot,“Frequency‐bandcomplexnoninteger differentiator:characterizationandsynthesis,” IEEETransactionsonCircuitsandSystemsI:FundamentalTheoryandApplications,vol.47,no.1, pp.25–39,2000.

[38] D.Xue,C.Zhao,andY.Chen,“Amodi iedapprox‐imationmethodoffractionalordersystem,”in 2006internationalconferenceonmechatronics andautomation,2006:IEEE,pp.1043–1048.

[39] A.Charef,H.Sun,Y.Tsao,andB.Onaral,“Fractal systemasrepresentedbysingularityfunction,” IEEETransactionsonAutomaticControl,vol.37, no.9,pp.1465–1470,1992.

[40] G.CarlsonandC.Halijak,“Approximationoffrac‐tionalcapacitors(1/s)^(1/n)byaregularNew‐tonprocess,” IEEETransactionsonCircuitTheory,vol.11,no.2,pp.210–213,1964.

[41] F.MatsudaK,“H(in inity)optimizedwave‐absorbingcontrol‐Analyticalandexperimental results,” JournalofGuidance,Control,and Dynamics,vol.16,no.6,p.1146–1153,1993.

[42] A.N.Khovanskii,Theapplicationofcontinued fractionsandtheirgeneralizationstoproblems inapproximationtheory.NoordhoffGroningen, 1963.

[43] K.Bingi,R.Ibrahim,M.N.Karsiti,S.M.Hassam, andV.R.Harindran,“Frequencyresponsebased curve ittingapproximationoffractional‐order PIDcontrollers,” InternationalJournalofApplied MathematicsandComputerScience,vol.29,no.2, pp.311–326,2019.

[44] K.Bingi,R.Ibrahim,M.N.Karsiti,S.M.Hassan, andV.R.Harindran, Fractional-ordersystemsand PIDcontrollers.Springer,2020.

[45] C.SanathananandJ.Koerner,“Transferfunction synthesisasaratiooftwocomplexpolynomials,” IEEEtransactionsonautomaticcontrol,vol.8,no. 1,pp.56–58,1963.

[46] F.N.Deniz,B.B.Alagoz,N.Tan,andM.Koseoglu, “Revisitingfourapproximationmethodsfor fractionalordertransferfunctionimplementa‐tions:Stabilitypreservation,timeandfrequency responsematchinganalyses,” AnnualReviewsin Control,vol.49,pp.239–257,2020.

[47] B.GustavsenandA.Semlyen,“Rationalapproxi‐mationoffrequencydomainresponsesbyvector itting,” IEEETransactionsonpowerdelivery,vol. 14,no.3,pp.1052–1061,1999.

[48] A.Djouambi,A.Charef,andA.Besançon, “Optimalapproximation,simulationandanalog realizationofthefundamentalfractionalorder transferfunction,” InternationalJournalof AppliedMathematicsandComputerScience,vol. 17,no.4,pp.455–462,2007.

[49] G.Maione,“Continuedfractionsapproximation oftheimpulseresponseoffractional‐order dynamicsystems,” IETControlTheory&Applications,vol.2,no.7,pp.564–572,2008.

[50] G.Maione,“Closed‐formrationalapproxima‐tionsoffractional,analoganddigitaldifferentia‐tors/integrators,” IEEEjournalonemergingand selectedtopicsincircuitsandsystems,vol.3,no. 3,pp.322–329,2013.

[51] C.‐C.Tseng,“DesignoffractionalorderdigitalFIR differentiators,” IEEESignalprocessingletters, vol.8,no.3,pp.77–79,2001.

[52] L’.Dorèák,J.Terpák,I.Petráš,andF.Dorèáková, “Electronicrealizationofthefractional‐order systems,” ActaMontanisticaSlovaca,vol.12,no. 3,pp.231–237,2007.

[53] Y.ChenandB.M.Vinagre,“AnewIIR‐typedigital fractionalorderdifferentiator,” Signalprocessing, vol.83,no.11,pp.2359–2365,2003.

[54] B.M.Vinagre,Y.Q.Chen,andI.Petráš,“Two directTustindiscretizationmethodsfor fractional‐orderdifferentiator/integrator,” Journalofthefranklininstitute,vol.340,no.5, pp.349–362,2003.

[55] M.Aoun,R.Malti,F.Levron,andA.Oustaloup, “Numericalsimulationsoffractionalsystems: anoverviewofexistingmethodsandimprove‐ments,” NonlinearDynamics,vol.38,pp.117–131,2004.

[56] G.Maione,“Adigital,nonintegerorder,differ‐entiatorusinglaguerreorthogonalsequences,” InternationalJournalofIntelligentControland Systems,vol.11,no.2,pp.77–81,2006.

[57] A.Djouambi,A.Charef,andA.V.Besançon, “Approximationandsynthesisofnoninteger ordersystems,” IFACProceedingsVolumes,vol. 39,no.11,pp.265–268,2006.

[58] J.T.Machado,“Analysisanddesignoffractional‐orderdigitalcontrolsystems,” SystemsAnalysis ModellingSimulation,vol.27,no.2‐3,pp.107–122,1997.

[59] B.KrishnaandK.Reddy,“Designoffrac‐tionalorderdigitaldifferentiatorsandintegra‐torsusingindirectdiscretization,” FractionalCalculusandappliedanalysis,vol.11,no.2,pp.143p‐151p,2008.

[60] B.KrishnaandK.Reddy,“Designofdigitaldiffer‐entiatorsandintegratorsoforder,” WorldJournal ofModellingandSimulation,vol.4,no.3,pp.182–187,2008.

[61] M.A.Al‐Alaoui,“Novelapproachtodesigning digitaldifferentiators,” ElectronicsLetters,vol. 28,no.15,pp.1376–1378,1992.

[62] M.A.Al‐Alaoui,“Noveldigitalintegratoranddif‐ferentiator,” Electronicsletters,vol.29,no.4,pp. 376–378,1993.

[63] J.LeBihan,“Novelclassofdigitalintegratorsand differentiators,” ElectronicsLetters,vol.29,no. 11,pp.971–973,1993.

[64] M.A.Al‐Alaoui,“NovelIIRdifferentiatorfromthe Simpsonintegrationrule,” IEEETransactionson CircuitsandSystemsI:FundamentalTheoryand Applications,vol.41,no.2,pp.186–187,1994.

[65] M.A.Al‐Alaoui,“Fillingthegapbetweenthe bilinearandthebackward‐differencetrans‐forms:aninteractivedesignapproach,” InternationalJournalofElectricalEngineeringEducation,vol.34,no.4,pp.331–337,1997.

[66] M.A.Al‐Alaoui,“Novelstablehigherorders‐to‐ztransforms,” IEEETransactionsonCircuitsand SystemsI:FundamentalTheoryandApplications, vol.48,no.11,pp.1326–1329,2001.

[67] A.‐A.M.Al,“Al‐Alaouioperatorandthe ��‐approximationfordiscretizationanalogsys‐tems,” Factauniversitatis-series:Electronicsand Energetics,vol.19,no.1,pp.143–146,2006.

[68] N.Q.Ngo,“Anewapproachforthedesignof widebanddigitalintegratoranddifferentiator,” IEEETransactionsonCircuitsandSystemsII: ExpressBriefs,vol.53,no.9,pp.936–940,2006.

[69] M.A.Al‐Alaoui,“Novelapproachtoanalog‐to‐digitaltransforms,” IEEETransactionsonCircuits andSystemsI:RegularPapers,vol.54,no.2,pp. 338–350,2007.

[70] M.SakowandK.Marchelek,“Designandoptimi‐sationofregression‐typesmallphaseshiftFIR

iltersandFIR‐baseddifferentiatorswithopti‐mallocalresponseinLS‐sense,” MechanicalSystemsandSignalProcessing,vol.152,p.107408, 2021.

[71] D.CafagnaandG.Grassi,“Fractional‐orderChua’scircuit:time‐domainanalysis, bifurcation,chaoticbehaviorandtestforchaos,” InternationalJournalofBifurcationandChaos, vol.18,no.03,pp.615–639,2008.

[72] A.DabiriandE.A.Butcher,“Numericalsolu‐tionofmulti‐orderfractionaldifferentialequa‐tionswithmultipledelaysviaspectralcolloca‐tionmethods,” AppliedMathematicalModelling, vol.56,pp.424–448,2018.

[73] A.DabiriandE.A.Butcher,“Stablefractional Chebyshevdifferentiationmatrixforthenumer‐icalsolutionofmulti‐orderfractionaldifferential equations,” NonlinearDynamics,vol.90,pp.185–201,2017.

[74] K.Diethelm,N.J.Ford,andA.D.Freed,“A predictor‐correctorapproachforthenumeri‐calsolutionoffractionaldifferentialequations,” NonlinearDynamics,vol.29,pp.3–22,2002.

[75] W.Deng,“Numericalalgorithmforthetimefrac‐tionalFokker–Planckequation,” JournalofComputationalPhysics,vol.227,no.2,pp.1510–1522,2007.

[76] C.Li,J.Xiong,W.Li,Y.Tong,andY.Zeng, “Robustsynchronizationforaclassoffractional‐orderdynamicalsystemvialinearstatevari‐able,” IndianJournalofPhysics,vol.87,pp.673–678,2013.

[77] M.SakówandK.Marchelek,“Model‐freeand time‐constantpredictionforclosed‐loopsys‐temswithtimedelay,” ControlEngineeringPractice,vol.81,pp.1–8,2018.

[78] M.Saków,“Novelrobustdisturbanceobserver,” ISAtransactions,vol.104,pp.255–277,2020.

[79] Y.Cui,H.Sun,andL.Hou,“Decentralizedevent‐triggeredadaptiveneuralnetworkcontrolfor nonstrict‐feedbacknonlinearinterconnected systemswithexternaldisturbancesagainst intermittentDoSattacks,” Neurocomputing,vol. 517,pp.133–147,2023.

[80] D.T.Tena,“Designofdisturbanceobservers basedontheirimplementabilityinindustrial controlsystems,”UniversitatJaumeI,2022.

[81] D.Tena,I.Peñarrocha‐Alós,andR.Sanchis, “Performance,robustnessandnoiseampli ica‐tiontrade‐offsinDisturbanceObserverControl design,” EuropeanJournalofControl,vol.65,p. 100630,2022.

[82] N.Fink,G.Zenan,P.Szemes,andP.Korondi, “ComparisonofDirectandInverseModel‐based DisturbanceObserverforaServoDriveSystem,” ActaPolytechnicaHungarica,vol.20,no.4,2023.

[83] V.L.KorupuandM.Muthukumarasamy,“Acom‐parativestudyofvariousSmithpredictorcon ig‐urationsforindustrialdelayprocesses,” ChemicalProductandProcessModeling,vol.17,no.6, pp.701–732,2021.

[84] S.Chen,W.Xue,andY.Huang,“Analyticaldesign ofactivedisturbancerejectioncontrolfornon‐linearuncertainsystemswithdelay,” Control EngineeringPractice,vol.84,pp.323–336,2019.

[85] S.Guo,Y.Liu,Y.Zheng,andT.Ersal,“A DelayCompensationFrameworkforConnected Testbeds,” IEEETransactionsonSystems,Man, andCybernetics:Systems,vol.52,no.7,pp.4163–4176,2021.

SYSTEMS

Submitted:28th December2022;accepted:13th June2023

GauravPaliwal,AaquilBunglowala,PraveshKanthed DOI:10.14313/JAMRIS/2‐2024/16

Abstract:

ThewidespreadadoptionofElectronicHealthcare Recordshasresultedinanabundanceofhealthcare data.Thisdataholdssignificantpotentialforimproving healthcareservicesbyprovidingvaluableclinical insightsandenhancingclinicaldecision‐making.This paperpresentsapatientclassificationmethodology thatutilizesamulticlassandmultilabeldiagnostic approachtopredictthepatient’sclinicalclass.The proposedmodeleffectivelyhandlescomorbiditieswhile maintainingahighlevelofaccuracy.Theimplementation leveragestheMIMICIIIdatabaseasadatasourceto createaphenotypingdatasetandtrainthemodels. Variousmachinelearningmodelsareemployedinthis study.Notably,thenaturallanguageprocessing‐based One‐Vs‐Restclassifierachievesthebestclassification results,maintainingaccuracyandF1scoresevenwith alargenumberofclasses.Thepatientdiagnostic classpredictionmodel,basedontheInternational ClassificationofDiseases9,showcasedinthispaper, hasbroadapplicationsindiagnosticsupport,treatment prediction,clinicalassistance,recommendersystems, clinicaldecisionsupportsystems,andclinicalknowledge discoveryengines.

Keywords: multiclasspatientclassification,multi‐label patientclassification,electronichealthcarerecords, MIMICIII,naturallanguageprocessing,deeplearning

1.Introduction

ElectronicHealthRecords(EHR)containawealth ofdataaboutpatients,includingpersonaldetails, medicalhistory,labreports,diagnostics,andclini‐calnotesfromhospitalstays[1].Extractingaccurate contextualinformationandknowledgefromEHRsis crucialduetothegroupingandlinkageofdatawith previoushealthcareevents[35].EHRdatacomprises bothstructuredandunstructuredtypes.Structured datatypicallyincludespersonaldetailsanddiagnos‐tic/clinicalcodes,whileunstructureddataencom‐passestreatmentcourses,cliniciannotes,andlab reports.

ClinicalcodesinEHRsrepresentproceduresand diagnosesassociatedwithapatient’sstayandare usedforreporting,management,andbillingpurposes. Theyserveaspracticalsourcesofinformationinmon‐itoringandresearchapplications,followingstandards suchasICPC[5]andICD[2–4].

ThetransitionfromICD‐9toICD‐10hassignif‐icantlyincreasedthecomplexityofcodingsystems, makingitchallengingforcaregiversorclinicalcoders toassigncodes.Existingapplicationshavefocused mainlyoncodesystembrowsabilitybutofferlim‐itedassistanceincoding[6].Computer‐assistedcod‐ingsystemssupportcaregiversbysuggestingcodes, providingrelevantinformation,and,insomecases, automaticallyassigningcodeswithouthumaninter‐vention[6].

Manyclinicalcodingsystemsoperateincontrolled settings,receivinginformationfromlimitedsources andpredictingarestrictedsetofcodes[7].Whilesome oftheseapproachesperformwell,theyaredif icult toadapttodifferentenvironmentsorscaleforlarger datasets.Recentresearchhasexploredtheuseofreal‐worlddatabases,suchasMIMICIII,toovercomethese limitations[8].

Retrievinginformationfromstructureddataisrel‐ativelyeasiercomparedtounstructureddata.How‐ever,extractingknowledgefromstructureddataalone mayyieldlimitedinsightsandresultininaccuracies andfalsepredictions.Unstructureddata,suchasclini‐calnotesandlabreportsinEHRs,havethepotentialto providemoreaccurateknowledgeifeffectivelylever‐aged.Manuallylabelingavastvolumeofunstructured datafromvarioussourcesistime‐consumingand impractical.Automatedinformationretrievalusing NaturalLanguageProcessing(NLP)offersamoreef i‐cientandscalablealternativetomanualmethods[36].

Identifyinggroupsofindividualswithsharedchar‐acteristicscangreatlybene itthehealthcareindustry. These indingscanbeutilizedinvarioussecondary analyses,includingcomputationalphenotypingfor patientcohortidenti ication,clinicaldecisionsupport, evidence‐basedtreatment,andresearch.Thispaper presentstheimplementationofmulticlasspatient classi icationusingdifferentmachineanddeeplearn‐ingmodelsonstructureddata.Themodelsutilize librariessuchassklearn,Keras,andTensorFlowAPIs, withMIMICIIIservingasthedatasource.Thesystem automaticallyassignscodestopatientsbasedonclini‐caldiagnoses.Thepaperalsoaddressesunstructured databyperformingmulti‐labelclassi icationusing NLPmodels,speci icallyemployingaone‐vs‐restclas‐si ier.

Thepaperisorganizedintosixsections.Sec‐tions 1 and 2 provideanintroductionandliterature review,respectively.Section 3 describesthedesign methodologyemployed,whileSection 4 focuseson implementationdetails.Resultsandconclusionsare presentedinSections5and6,respectively.

2.LiteratureReview

Machinelearninganddeeplearninghavegained signi icantattentioninrecentyears,leadingtoexten‐siveresearchinthis ield.However,mostofthework inautomatedclinicalcodegenerationhasbeencon‐ductedonlimiteddummydata[9, 10, 39, 62].To addressthis,recenttechniqueshavebeendeveloped forlayeredpredictionandclassi icationofreal‐world datasets,leveragingthesparsityofoutputcodes[9, 10, 39].TheMIMICdatabaseiscommonlyusedas abenchmarkbyresearcherstoevaluatenewtech‐nologies[8].Forinstance,Perotteetalutilizedthe MIMICIIdatabasetopredicthigher‐leveldiagnostic codes,whichwasfurtherextendedtopredictcom‐pletecodes[9].Otherresearchershavefocusedon predictingICD10PCScodesfromclinicaldischarge summaries[10].

Whilethesemethodologiesdependonaccessi‐bleandcomprehensiveclinicaldischargereports, manyclinicalsummariesstilllackimportantinfor‐mation,anddifferentserviceprovidersandhospitals mayhavevaryingstylesofmaintainingdetails.To compensateformissinginformation,techniqueshave beenproposedforpredictingandidentifyingpatient cohortsbasedonhigh‐throughputphenotyping[3,11, 12,40].

Auni ieddataviewhasbeenachievedbymap‐pingstructuredandunstructureddatatostandard‐izedUMLS[12, 13, 37, 38].Althoughthisapproach ispowerfulfordataconversion,itintroducesdepen‐denciesontheusedontologies,requiringsubstantial effortstomaplocalontologiesinclinicalnotesor terms[14,41].Unstructureddatasourcescanalsobe convertedormappedusingabag‐of‐wordsrepresen‐tation,eitherthroughearlyorlatedataintegration fromthesourceitself[15].Thedensityofinformation featuresfromdifferentsourcescancreatestrongeror weakerstructuredrepresentations.Directlyfeeding datafromthesourcetothemeta‐classi ieroftenyields betterresults,butthismayresultindatalossduetoa singledatapoint[60].

Arecentstudyintroducedadeepneuralnetwork withstackedauto‐encoders,knownas“deeppatient,” tocreatevectorrepresentationsofpatients[16].The structuredandunstructureddatasourceswerepre‐processedusingsubjectmodelingfordatageneral‐ization[17].Thisdatarepresentationmethodcanbe appliedtodiversemedicalapplications,focusingonly onthemostinterestingfeatures[42,61].

Forlimiteddata,algorithmicperformancecan beimprovedusingfeatureselectionalgorithms[18, 19, 43].Inclassi icationtasks,variousapproaches areavailabletoimprove itnessbyrankingfeatures

towardsaclass.Onesuchmethodaimsto indanom‐inalsetoffeaturesbyreducingredundanciesamong them[20].Thisapproachselectsfeaturesstrongly correlatedwithoptimizingtheclassi icationtask. However,relyingsolelyonstronglycorrelatedfea‐turesmaynotcontributetoaccuratepredictions[21].

Whilefeature‐basedredundancycalculation methodscanaddresstheseissues,theymaynotyield signi icantresultswhenappliedtoalargenumber ofclassesorfeatures[22].Anotherfeatureselection technique,theMarkovblanketmodel,offersgood resultsforfeatureselection.Thismethodutilizesa Bayesiannetworkandprovidesef icientsolutions.

Noteworthypatientclassi icationtechniques foundduringthesurveyincludediseasephenotypes inEHRsusingmachinelearning[28],analgorithm torecognizepatientswithAutismSpectrum Disorder[29],andlearningfromheterogeneous temporaldata[30].

Additionally,“Interpretablepatientclassi ication usingintegratedpatientsimilaritynetworks”presents anovelapproachtoclassi icationusingclinicalpre‐dictorsbasedongenomicdata[31].PierreCourtio etal.demonstratedtheuseofpatientclassi icationfor predictingoutcomesin“Deeplearning‐basedclassi i‐cationofmesotheliomaimprovespredictionofpatient outcome”[32].

3.Methodology

Inthisstudy,theMIMIC‐IIIdatabasewasuti‐lizedastheprimarysourceofdata.TheMIMIC‐III,shortforMedicalInformationMartforIntensive CareIII,isapubliclyavailableclinicaldatabase[25]. Itcontainscomprehensiveinformationaboutcancer patientswhowerehospitalizedinthecriticalcareunit attheBethIsraelDeaconessMedicalCenterbetween 2001and2012.TheMIMIC‐IIIdatabaseencompasses healthcarerecordsofapproximately40,000patients, includingtheirbasicdemographicinformation,diag‐nostics,vitalsigns,clinicalprocedures,laboratorytest results,caregivernotes,medications,andmortality data.ThisextensivedatasetinMIMIC‐IIIsupportsvar‐ioustypesofstudies,rangingfromthedevelopmentof decisionsupportsystemstoelectronictooladvance‐mentsinhealthcare.

Forthisparticularstudy,weutilizedtheMIMIC‐III databaseasanelectronichealthcarerecordtoclassify cancerpatientsbasedontheprovideddiagnostics. Thisclassi icationcanbefurtheremployedtoassist doctorsinpredictingthemostappropriatecourseof actionforeachpatient.

TheMIMIC‐IIIdatabasecomprises40tableswith 534columnsandnearly720millionrecords.These tablesandrecordsareinterconnectedusingidenti‐ierssuchassubjectIDandadmissionID.Itisworth notingthatalldatawithinthedatabasehavebeenfully de‐identi iedtoensurethepreservationofpatientpri‐vacyandcon identiality.

DuetotheenormoussizeofthedataintheMIMIC‐IIIdatabase,interpretingandunderstandingthedata posedasigni icantchallenge.Thedatabasecontained datadistributedacrossvarioustables,asillustrated inFigure 1.Tofacilitatedataanalysis,theMIMIC‐III databasewasinitiallyimportedintoPostgreSQL.An interfacetothedatabasewasdevelopedtogainacom‐prehensiveunderstandingoftheMIMIC‐IIIschema. Figures2and3depicttheinterfacedesignedtointer‐actwiththeMIMIC‐IIIdatabase.

Foravisualdemonstrationofthegraphicaluser interface(GUI),avideoshowcasingitsfunctionalityis availableonYouTubeviathefollowinglink:https:// www.youtube.com/watch?v=9eNtfb3oR‐E&lc=UgyH ko8pYeyGp9H‐DHp4AaABAg.Additionally,thefront‐enddesigncodefortheinterfacecanbedownloaded fromGitHubusingthefollowinglink:https://github.c om/gvpaliwal/Mimic‐III

Foranalysisandprediction,thedataprimarily selectedfromtheMIMICIIIdatasetwasobtainedfrom ivemaintables:admissions,drgcodes,diagnoses_icd, d_icd_diagnoses,andnoteevents.Thesetablespro‐videdessentialinformationforthestudy,including patientadmissionsdetails,diseasediagnosticsinICD9 codes,andclinicalnotes.

Toaddresstheissueofdataimbalance,various datapreprocessingandselectiontechniqueswere employed.The irstfourtables,namelyadmissions, drgcodes,diagnoses_icd,andd_icd_diagnoses,pro‐videdstructureddatathatcouldbepreprocessedand utilized.Thesetablescontainedpatientdetails,dis‐easediagnosticsintheformofICD9codes,andthe diagnosiscodeassociatedwiththediseaseforwhich thepatientwasadmittedorbilled.Byconsideringthe diagnosiscodeastheclasslabelforthepatient,the datasetenabledtheapplicationofbothsupervised andunsupervisedmachinelearningtechniques.

Ontheotherhand,thenoteeventstablecontained unstructuredtextdataintheformofclinicalnotes. Thistextdatawassuitableforapplyingnaturallan‐guageprocessing(NLP)models.Themainfocusofthe studywastoassignsingleormultipleclasslabelstoa patientbasedonthediagnosticsandclinicalnotes.

Thestudyaimedtodevelopacomprehensive approachtopatientclassi icationandpredictionby combiningthestructuredandunstructureddatafrom thesetables.

4.ImplementationDetails

MachineLearninginhealthcarehasdemonstrated itspowerinsortingandclassifyinghealthdata,as wellasacceleratingdoctors’clinicaldecision‐making processbyprovidingpredictionsthatcansavelives andsimplifytasks.ForthetaskofPatientClassi ica‐tion/CohortIdenti ication,ourprimaryfocuswason utilizingML/DLmodelsthathaveshownpromising accuracywhenappliedtohealthcaredataforsimilar tasks.

Inthissection,wewillpresentimplementa‐tionsofmulticlasspatientclassi icationusingvari‐ousmachineanddeeplearningmodelsspeci ically designedforstructureddata.Thesemodelsaimto assigncodestopatientsbasedontheirclinicaldiagno‐sisautomatically.Furthermore,wewilldelveintothe realmofunstructureddataandemployNaturalLan‐guageProcessing(NLP)modelstoperformmulti‐label classi ication.Thisapproachenablesustoextract meaningfulinformationfromclinicalnotesandmake predictionsbasedontheunstructureddata.

Bycombiningthestrengthsofbothstructuredand unstructureddataanalysis,weaimtodevelopacom‐prehensiveframeworkforpatientclassi icationand predictioninhealthcaresettings.

Figure1. MIMICIIIschemadetails

4.1.DataPreprocessing

IntheinitialdatasetextractedfromtheMIMICIII database,therewere651,047recordscorresponding to58,976admissionsand46,520uniquepatientstays. Thedatasetincludedatotalof6,985uniqueICD‐9 diagnosticcodes.Tosimplifytheanalysis,thesediag‐nosticcodeswereaggregatedinto891ICD‐9diagnos‐ticblockchaptercodesbasedonthedescriptionspro‐videdinthedatabase.Thesediagnosticblockchapter codeswerethenusedtopredicttheclassorassign labelstothepatients.

Asapreprocessingstep,weremovedthe diagnosticblockchaptercodesrelatedto externalinjuries,poisoning,oranysupplementary classi ications,asthesecausesareevent‐drivenand notsuitableforanalytics.Afterthisremoval,wewere leftwithatotalof625ICD‐9diagnosticblockchapter codes.

Duetothelargenumberofclasses,accurately determiningtheclassusinganypredictivemodel becamechallenging.Additionally,thedataremained skewedandunbalancedduetothevaryingfrequen‐ciesofdifferentdiseases.Toaddressthisissue,we selectedspeci icdatasetsfromhospitalstaysbasedon theoccurrencefrequenciesoftheICD‐9blockchapter

Figure2. MIMICIIIdatabasefrontend

Figure3. MIMICIIIdatabasefrontend

codes.Thisapproachallowedustocreatebalanced datasetsfortrainingandevaluationpurposes.

Table1summarizestheoccurrencefrequenciesof differentICD‐9diagnosticcodes,whichin luencedthe selectionofdatasetsforanalysis.

Afterapplyingthedesignatedthresholdstoselect hospitalstayswithdifferentfrequentchaptercodes, weobtainedgroupsofhospitalstayswithvarying frequencies.Themostfrequentchaptercodehadan occurrencefrequencyof21,329.Wethenlinkedthe HCFAdrugcodesfromthedrgcodestabletothe selectedhospitalstays,whichrepresentedthedrugs forwhichthepatientsweretreatedandbilled.

ThenoteeventstableintheMIMICIIIdatabase containedawealthofunstructuredtextinformation, includingvariousclinicalnotessuchasdemographic details,servicesprovided,allergies,chiefcomplaint, medicalhistory,socialhistory,physicalexam ind‐ings,pathologyandscanreports,medicationdetails, dischargeinformation,andfollow‐upinstructions.To cleanthedata,weremovedstopwordsandspe‐cialcharactersandconvertedthetexttolowercase, preparingitforfurtheranalysis.

Afterthedatapreprocessingsteps,weendedup withfourdatasetgroups,eachcontainingrecordswith speci icICD‐9chapterfrequencies.Thesegroupswere suitableforvariouspredictiveanalyticstasks.The nextstepwastosplitthedataintotrainandtestsets andapplydifferentlearningmodelsforanalysisand predictionpurposes.

4.2.ModelImplementationonStructuredData

4.2.1.K‐nearestNeighbor

Thek‐nearestneighbors(KNN)algorithmisa supervisedclassi icationmethodthatutilisesproxim‐itytomakepredictionsaboutagivendatapoint.It canbeappliedforbothclassi icationandregression tasks.Inourstudy,weemployedtheKNNalgorithmas aclassi icationmodeltopredictandidentifypatients withsimilarcharacteristicsbasedontheirdiagnostic information[44–46].

ToimplementtheKNNalgorithm,weutilized theKNeighborsClassi ierandRadiusNeighborsClassi‐ierwithaspeci iednumberofneighborssetto25 forKNeighborsClassi ierandthedefaultradiusfor RadiusNeighborsClassi ier.Thedistanceweightfunc‐tionwasusedinthepredictionprocess.Thealgorithm parameterwassetto“auto”,allowingthemodelto automaticallyselectthemostsuitablealgorithmfor computingthenearestneighborsbasedonthepro‐videdvalues.Weexperimentedwithdifferentdistance metricsforcomputationbutultimatelyfoundthatthe defaultmetric,Minkowski,yieldedthebestresults,so weutiliseditinourimplementation.

4.2.2.NaiveBayesClassifier

TheNaiveBayes(NB)algorithmisaclassi ication methodthatassumesindependencebetweenfeatures andutilizesprobabilitytheorytomakepredictions.It hasbeenwidelyusedinvariousmedicalapplications andhasshowngoodperformance[59].Althoughthe independenceassumptionsmaynotalwaysholdtrue

inreality,NaiveBayescanstillprovideeffectiveresults inmanymedicalscenarios[47,50].

Inourstudy,wetrainedtheNaiveBayesalgorithm inasupervisedlearningsetting.Weimplemented threedifferentvariantsoftheNBclassi ier:Gaus‐sianNB,CategoricalNB,andMultinomialNB.Theprior probabilitiesinthemodelweresettonone,andthe variancesmoothingwassettothedefaultvalue.Prior tofeedingthedataintotheNaiveBayesclassi ier, weappliedmin‐maxscalingtonormalizethedata. Theadditivesmoothingparameter,alsoknownasthe alphavalue,wassetto1inourimplementation.

4.2.3.DecisionTreeClassifier

Thedecisiontreealgorithmisasupervisedlearn‐ingapproachthatcanbeusedforbothregression andclassi icationtasks.Itemploysagreedysearch strategyto indthebestsplitpointsinatree‐likestruc‐ture.Thedecisiontreealgorithmfollowsadivideand conquermethodology,recursivelysplittingthedata untilmostorallrecordsareclassi iedunderdifferent labels[49].

Inourstudy,weutilisedthedecisiontreealgo‐rithmalongwithcross‐validationtoevaluatehow wellthemodel itsthedata.Additionally,weexplored therandomforestmethod,whichimprovesaccuracy bycombiningmultipledecisiontrees.Randomforest classi iersareparticularlyeffectivewhentheindivid‐ualtreesareuncorrelated[48].Decisiontreesare highlyinterpretable,makingthempopularinhealth‐careanalytics(ch8dt).Theycanhandlecomplexdata patternsandserveasthefoundationforensemble models[51,52].

Weimplementedseveraldecisiontreemodels usingscikit‐learn,includingDecisionTreeClassi ier, AdaBoostClassi ier,RandomForestClassi ier,Bag‐gingClassi ier,andGradientBoostingClassi ier.The numberoftreesorestimatorsintherandomforest wassetto100.Duetocomputationallimitations,we setthemaximumdepthofthetreesto15.Thequality ofasplitwasmeasuredusingtheGinicriterion,and theremainingparameterswerekeptasdefaultorset to“auto”.

4.2.4.SupportVectorMachines

SupportVectorMachines(SVMs)areareliable classi icationmethodthatcanincreaseamodel’spre‐dictiveaccuracywithoutover ittingthetrainingset. Theyareparticularlyeffectivewhendealingwith datasetsthathavemanypredictors.Inthecontextof electronichealthrecord(EHR)data,SVM‐basedmeth‐odshavebeenutilisedintheliteraturetoaddress classi icationtasksandhavebeenshowntoprovide quick,accurate,andreliableresults,especiallywhen dealingwithimbalancedclasses[53,54].

Inourstudy,weimplementedthesupportvec‐torclassi ierusingdifferentkernels,includinglinear, polynomial,andradialbasisfunction(rbf)kernels. Theregularizationparameter(C)wassetto1,which controlsthetrade‐offbetweenachievingalowtrain‐ingerrorandallowingforalargermargin.

Table1. ICD‐9Diagnosticcodesoccurrencefrequency

Forthepolynomialkernel,thedegreeoftheker‐nelfunctionwaslimitedto5.Otherparameterssuch asthekernelcoef icient,kernelfunctionindependent term,shrinkingheuristic,probabilityestimates,and tolerancevaluesweresettotheirdefaultor“auto”val‐ues.Thesesettingswerechosentoprovideabalanced andeffectiveclassi icationmodel.

4.2.5.DeepNeuralNetwork

Arti icialNeuralNetworks(ANNs)areasubset ofmachinelearningtechniquesthatcanbepowerful toolsinhealthcarediagnosisandanalytics,leading toimprovedhealthcaredeliveryandreducedcosts [55,56].Inourstudy,weemployedamulticlassneural networkclassi iertocategoriseandgroupdataeffec‐tively.

Implementingmulticlassneuralnetworkscanbe challengingduetothenonlinearnatureofclasslabels. Toaddressthis,werepresentedthelabelsasbinary vectorsoflengthK,wherea1atthekthposition correspondstoalabelofk.Anactivationfunction wasappliedattheoutputtolearntheoutputvector. Thisapproachallowedustogeneratevalidprobability distributionsbysummingoverallthevaluesofkto normalizethelikelihood[26].

Weusedatraditionaltrainingmethodologyto trainthemodelbutwithanobjectivegradientspeci i‐callydesignedformultinomiallogisticregression[33, 34].Weexperimentedwithvariouscombinationsof parametersto ine‐tunethemodelforbetterresults.

Thetuneddeeplearningneuralnetworkarchitec‐tureutilisedabaselinesequentialmodelwithdense layers.ThemodelemployedtheRecti iedLinearUnit (relu)activationfunctionforhiddenlayersandthe softmaxactivationfunctionfortheoutputlayer.Cate‐goricalcross‐entropywasusedasthelossfunctionto mitigatetraininglosses,withtheAdamoptimiserfor modeloptimisation.Theevaluationmetricusedwas accuracy.Themodelwastrainedusing10‐foldcross‐validationwith200epochs.

Toassesstheperformanceoftheclassi iermodel, wecalculatedthebaselineaccuracy,whichservesasa benchmarkforcomparison.

4.2.6.NLP‐basedModels

NaturalLanguageProcessing(NLP)isa ieldof studythatenablescomputerstounderstandandinter‐prethumanlanguage,bothspokenandwritten.

Bycombiningmachinelearning,statistics,deep learningmodels,andrule‐basedcomputationallin‐guisticsmodelling,NLPallowscomputerstoprocess andanalyselargevolumesofnarrativeinformation, suchasclinicalnotesinhealthcaresystems.Thisis particularlyimportantbecauseclinicalnotesareoften storedinnon‐standardizedandunstructuredformats, makingitchallengingtoextractmeaningfulinsights fromthem.

Inourimplementation,weutilisedNLPtechniques tocaptureandanalyseunstructuredinformationfrom clinicalnotes.WeemployedtheMultiLabelBinarizer fromthesklearnlibrarytotransformtheclinicalnotes intotargetvariables.Thesetargetvariableswerethen usedtocalculatethetermfrequency‐inversedocu‐mentfrequency(tf‐idf)vectorvalues,whichrepresent theimportanceofwordsintheclinicalnotes.Weseta maximumof10,000featuresforthetf‐idfrepresenta‐tion.

Forclassi ication,weusedtheOneVsRestClassi‐ier,whichallowsustohandlemulti‐labelclassi ica‐tiontasks.Thisclassi iertrainsmultiplebinaryclassi‐iers,eachtreatingonelabelasthepositiveclassand therestasthenegativeclass.Weevaluatedthemodel’s performanceusingtheF1score,whichisameasureof themodel’saccuracyinclassifyingmultiplelabels.

ByemployingNLPtechniques,weaimedtotrans‐formtheunstructuredinformationinclinicalnotes intoaformatthatcanbeunderstoodandutilisedby adecisionsupportsystem,enablingmoreeffective healthcareanalyticsanddecision‐making.

5.ResultsandDiscussion

ThemachinelearningandNLPimplementations aredoneon4frequency‐basedselecteddatasets. TheNaiveBayesclassi iers’performancewasweakest amongtheimplementedmodelsonthegivendata set.Thedeeplearninganddecisiontreesmodelsper‐formedreasonablywellwithfewerclassesbutfailed tomaintainaccuracywhenthenumberofclasseswas increased.Table 2 showsthedetailedperformance measureresultsfordifferentmodels.

TheNLP‐basedmodelprovidedthebestscoresin diagnosticlabelprediction.Theinformationlosswhile trainingthemodelwascalculatedas0.005.Thetrue positiverateforthemodelwascalculatedtobearound 99%.Figures4and5canbereferredtoforthecom‐parativeanalysisofaccuraciesandF1scoresofdiffer‐entmodels,respectively.Figure6showsaprediction screenshotofanNLP‐basedmulti‐labelclassi ier.

1 K‐Nearest neighbor KNeighbors Classi ier

Neighbors Classi ier

96.44,F1 score:0.93

Accuracy: 73.21,F1 score:0.62

Accuracy: 23.66,F1 score:0.42

Accuracy: 10.01,F1 score:0.21

97.31,F1 score:0.94

54903 Accuracy: 78.56,F1 score:0.68

Accuracy: 26.41,F1 score:0.41

56202 Accuracy: 18.66,F1 score:0.22

Accuracy: 26.48,F1 score:0.51

Accuracy: 11.25,F1 score:0.23

F1score:0.18

Accuracy: 78.22,F1 score:0.69

Accuracy: 43.55,F1 score:0.44

18.64,F1 score:0.26

16.11,F1 score:0.22

Accuracy: 79.21,F1 score:0.72

44.00,F1 score:0.43

17.88,F1 score:0.25

16.01,F1 score:0.22

Table2. Continued

Sr.N. Learning Model Implemented Variant

DecisionTree Classi ier

AdaBoost Classi ier

3

DecisionTree classi ier

RandomForest Classi ier

Bagging Classi ier

Gradient Boosting Classi ier

Accuracy: 25.48,F1 score:0.51

Accuracy: 13.45,F1 score:0.13

Accuracy: 9.60%,F1 score:0.12

78.22,F1 score:0.80

Accuracy: 23.44,F1 score:0.48

Accuracy: 12.56,F1 score:0.21

Accuracy: 10.23,F1 score:0.20

98.64,F1 score:0.96

Accuracy: 86.55,F1 score:0.91

Accuracy: 73.23,F1 score:0.86

Accuracy: 25.60,F1 score:0.59

Accuracy: 96.75,F1 score:0.97

Accuracy: 86.49,F1 score:0.89

Accuracy: 72.59,F1 score:0.72

Accuracy: 24.23,F1 score:0.62

96.87,F1 score:0.97

Accuracy: 87.54,F1 score:0.90

Accuracy: 70.27,F1 score:0.73

Accuracy: 22.45,F1 score:0.64

64.23,F1 score:0.51

16.21,F1 score:0.23

Accuracy: 11.12,F1 score:0.21

F1score:0.19

45.21,F1 score:0.41

12.87,F1 score:0.15

63.68,F1 score:0.50

Accuracy: 17.11,F1 score:0.24

Accuracy: 11.21,F1 score:0.21

F1score:0.19

98.86,F1 score:0.96

Accuracy: 83.45,F1 score:0.92

Accuracy: 74.03,F1 score:0.84

Accuracy: 63.54,F1 score:0.76 6 NLPbased Logistic Regression OneVsRest Classi ier

Toanalyzetherelationbetweenaccuracyand records,alessformalapproachwasusedtomeasure thestrengthoftherelationshipbetweenthem.Spear‐man’srankcorrelationcoef icienttestingisappliedto

Accuracy: 98.68,F1score: 0.98,TP:100

Accuracy: 87.23,F1score: 0.96,TP:99.6

Accuracy: 86.42,F1score: 0.92,TP:99.4

Accuracy: 82.86,F1score: 0.89,TP:98.8

testthehypothesisofassociation.Thepairsofobser‐vationshavebeenrandomlyselectedandranksare assignedwithinthesample.

Differentmachinelearningmodelaccuracies

Figure5. DifferentmachinelearningmodelF1scores

Figure6. NLPbasedmulti‐labelclassification

Figure4.

Table3. tstatisticsanalysisdetailsforspearman’srank correlationhypothesistesting

CorrelationCoef icient(rs) 0.983884884

Samplesize(n) 10

degreeoffreedom(df)=(n 2) 8

tstatistic 15.56375323 levelofSigni icance(��) 0.05

Thistestmakesnoassumptionsabouttheproba‐bilityrelationbetweentwovariables. ����: thereisno relationshipbetweenaccuracyandrecords. ��1: there isarelationshipbetweenaccuracyandrecords. The detailsoftheanalysisareshowninTable3

Aspertheresultsobtainedfromspearman’srank correlationhypothesistestingthepvalueislessthan thealphavalue.Hence,H0isrejectedi.e.thereisarela‐tionshipfoundbetweenaccuracyandrecords.Using thetestresult,wecanconcludethatthereexistsa relationshipbetweenaccuracyandrecordsprediction onthegivendataconsideringthenumberofclassesto beconstant.

6.ConclusionandFutureDirection

Thepresentedpatientclassi icationmodelholds greatpotentialforthehealthcaresystem.Thesuperior performanceoftheNLP‐basedmulti‐labelprediction modelssuggeststheireffectivenessinaccuratelypre‐dictingapatient’sclassbasedontheprovideddiag‐nostics.Withalargernumberofrecordsavailablefor trainingthemodel,itisexpectedthattheprediction accuraciesofthesemodelswillimproveevenfurther.

Thismodel’sapplicationsarewide‐rangingand cangreatlybene itvariousaspectsofthehealthcare system.Somepotentialapplicationsincludediag‐nosticsupport,lineoftreatmentprediction,clini‐calassistance,recommendersystems,clinicaldeci‐sionsupportsystems,andclinicalknowledgediscov‐eryengines.Thesepredictionscanprovidevaluable insightsandassisthealthcareprofessionalsinmaking informeddecisions,therebyimprovingthequalityand ef iciencyofpatientcare.

MoreadvancedNLP‐basedmethodscan beexploredandimplementedtoenhancethe predictions’performance.Theseadvancementsmay includeincorporatingtechniquessuchastransfer learning,contextualembeddings,orattention mechanisms,whichhaveshownpromisingresultsin naturallanguageprocessingtasks.

Thestatisticaltestappliedtoassessthemodel accuracyclearlyindicatesthatasthenumberof recordsincreases,theaccuracyofthemodelis expectedtoimprove.Thissuggeststhatcollectingand incorporatingmorepatientdataintothetrainingpro‐cesswilllikelyyieldmoreaccuratepredictions.

Itisworthnotingthatthedatausedfortraining themodel,particularlywhendealingwithalarger numberofdiagnosticchaptercodes,maybeskewed duetounevenfrequencyofdiseaseoccurrences.How‐ever,theNLP‐basedmodelsdemonstratedtheability tomaintainaccuracyandF1scores,indicatingtheir robustnessinhandlingsuchimbalances.

Inthefuture,incorporatingadditionaldetails availableintheMIMICIIIdatabasecanfurther enhancethepredictionaccuracies.Theseadditional detailsmayincludepatientdemographics,medical history,laboratoryresults,medications,andotherrel‐evantfactorsthatcanprovideamorecomprehensive understandingofthepatients’conditionsandfacili‐tatemoreaccuratepredictions.

Overall,thepresentedpatientclassi icationmodel, particularlytheNLP‐basedapproaches,showsgreat potentialforimprovingdecisionsupportandpoint‐of‐careservicedeliveryinhealthcaresystems.Fur‐theradvancementsandincorporationofricherpatient datacanleadtoevenmoreaccurateandvaluablepre‐dictions.

AUTHORS

GauravPaliwal∗ –SVKM’s,NarseeMonjeeInsti‐tuteofManagementStudies,Indore,India,e‐mail: gaurav.paliwal@nmims.edu.

AaquilBunglowala –SriAurobindoInstituteofTech‐nology,Indore,India,e‐mail:aaquilbun@gmail.com. PraveshKanthed –ChoithramInterventional Spine&PainCentre,Indore,India,e‐mail: praveshkanthed@gmail.com.

∗Correspondingauthor

References

[1] C.‐J.Hsiao,E.Hing,“Useandcharacteristicsof electronichealthrecordsystemsamongof ice‐basedphysicianpractices,” NCHSDataBrief,vol. 111,2012,pp.1–8.

[2] G.S.Alotaibi,C.Wu,A.Senthilselvan,M.S. McMurtry,“ThevalidityofICDcodescoupled withimagingprocedurecodesforidentifying acutevenousthromboembolismusing administrativedata,” Vasc.Med.,vol.20,no. 4,2015,pp.364–368.doi:10.1177/1358863X1 5573839.

[3] W.Q.Wei,P.L.Teixeira,H.Mo,R.M.Cronin, J.L.Warner,J.C.Denny,“Combiningbilling codes,clinicanotes,andmedicationsfrom electronichealthrecordsprovidessuperior phenotypingperformance,” J.Am.Med.Inform. Assoc.,vol.23,no.e1,2016,pp.20–27.doi: 10.1093/jamia/ocv130.

[4] WorldHealthOrganization,“InternationalClas‐si icationofDiseases(icd),”2012.

[5] H.Lamberts,I.Okkes,etal,“Icpc‐2,” International Classi icationofPrimaryCare,1998.

[6] S.Pakhomov,J.D.Buntrock,C.G.Chute, “Automatingtheassignmentofdiagnosis codestopatientencountersusingexample‐basedandmachinelearningtechniques,” J.Am. Med.Inform.Assoc.,vol.13,no.5,2006,pp. 516–525,doi:10.1197/jamia.M2077.

[7] M.H.Stan ill,M.Williams,S.H.Fenton,R.A. Jenders,W.R.Hersh,“Asystematicliterature reviewofautomatedclinicalcodingand classi icationsystems,” J.Am.Med.Inform. Assoc.,vol.17,no.6,2010,pp.646–651,doi: 10.1136/jamia.2009.001024.

[8] A.E.W.Johnson,T.J.Pollard,L.Shen,L.‐W.H. Lehman,M.Feng,M.Ghassemi,B.Moody,P. Szolovits,L.A.Celi,R.G.Mark,MIMIC‐III,“Afreely accessiblecriticalcaredatabase,” Sci.Data,vol.3, 2016,p.160035,doi:10.1038/sdata.2016.35.

[9] A.Perotte,R.Pivovarov,K.Natarajan,N. Weiskopf,F.Wood,N.Elhadad,“Diagnosiscode assignment:modelsandevaluationmetrics,” J. Am.Med.Inform.Assoc.,vol.21,no.2,2014,pp. 231–237,doi:10.1136/amiajnl‐2013‐002159.

[10] M.Subotin,A.R.Davis,“ASystemforPredict‐ingICD‐10‐PCSCodesfromElectronicHealth Records,” WorkshoponBioNLP(BioNLP),2014, pp.59–67.

[11] S.Abhyankar,D.Demner‐Fushman,F.Callaghan, “Combiningstructuredandunstructureddatato identifyacohortofICUpatientswhoreceived dialysis,” J.Am.Med.Inform.Assoc.,vol.21,no.5, 2014,pp.801–807.

[12] J.Pathak,K.R.Bailey,C.E.Beebe,S.Bethard, D.S.Carrell,P.J.Chen,etal,“Normalizationand standardizationofelectronichealthrecordsfor high‐throughputphenotyping:TheSHARPncon‐sortium,” J.Am.Med.Inform.Assoc.,vol.20,no. e2,2013,pp.e341–e348,doi:10.1136/amiajnl‐2013‐001939.

[13] O.Bodenreider,“TheUni iedMedicalLanguage System(UMLS):Integratingbiomedicaltermi‐nology,” Nucl.AcidsRes.,vol.32,suppl.1,2004, pp.D267–D270,doi:10.1093/nar/gkh061.

[14] RIZIV, Rijksinstituutvoorziekte-eninvalidite itsuitkeringennomenclature,http://www.riziv. fgov.be/NL/nomenclatuur/Paginas/default.as px>

[15] E.Scheurwegs,K.Luyckx,L.Luyten,W.Daele‐mans,T.VandenBulcke,“Dataintegrationof structuredandunstructuredsourcesforassign‐ingclinicalcodestopatientstays,” J.Am.Med. Inform.Assoc.,vol.23,no.e1,2016,pp.11–19, doi:10.1093/jamia/ocv115.

[16] R.Miotto,L.Li,B.A.Kidd,J.T.Dudley,“Deep patient:Anunsupervisedrepresentationtopre‐dictthefutureofpatientsfromtheelectronic healthrecords,” Sci.Rep.,vol.6,no.April,2016, p.26094,doi:10.1038/srep26094.

[17] R.Cohen,M.Elhadad,N.Elhadad,“Redundancy inelectronichealthrecordcorpora:Analysis, impactontextminingperformanceandmitiga‐tionstrategies,” BMCBioinform.,vol.14,no.1, 2013,p.10,doi:10.1186/1471‐2105‐14‐10.

[18] S.M.Vieira,L.F.Mendon a,G.J.Farinha,J.M.C. Sousa,“Modi iedbinary{PSO}forfeatureselec‐tionusing{SVM}appliedtomortalityprediction ofsepticpatients,” Appl.SoftComput.,vol.13,no. 8,2013,pp.3494–3504.

[19] T.Botsis,M.D.Nguyen,E.J.Woo,M.Markatou, R.Ball,“TextminingfortheVaccineAdverse EventReportingSystem:Medicaltextclassi ica‐tionusinginformativefeatureselection,” J.Am. Med.Inform.Assoc.,vol.18,no.5,2011,pp.631–638.

[20] I.Guyon,A.Elisseeff,“Anintroductionto variableandfeatureselection,” J.Mach. Learn.Res.,vol.3,2003,pp.1157–1182,doi: 10.1016/j.aca.2011.07.027.arXiv:1111.6189v1.

[21] R.Kohavi,G.H.John,“Wrappersforfeature subsetselection,” Artif.Intell.,vol.97,no.1–2,1997,pp.273–324,doi:10.1016/S0004‐3702(97)00043‐X.

[22] H.C.Peng,F.Long,C.Ding,“Featureselection basedonmutualinformation:criteriaof max‐dependency,max‐relevance,andmin‐redundancy,” IEEETrans.PatternAnal.Mach. Intell.,vol.27,no.8,2005,pp.1226–1238.

[23] S.Fu,M.C.Desmarais,“Markovblanketbased featureselection:areviewofpastdecade,” ProceedingsoftheWorldCongressonEngineering 2010,vol.I,2010,pp.321–328.

[24] I.Tsamardinos,L.E.Brown,C.F.Aliferis,“The max‐minhill‐climbingBayesiannetworkstruc‐turelearningalgorithm,” Mach.Learn.,vol.65, no.1,2006,pp.31–78,doi:10.1007/s10994‐006‐6889‐7.

[25] A.E.W.Johnson,T.J.Pollard,L.Shen,L.Lehman, M.Feng,M.Ghassemi,etal,“MIMIC‐III,A freelyaccessiblecriticalcaredatabase,” Scienti ic Data,2016,doi:10.1038/sdata.2016.35.Avail‐ablefrom: http://www.nature.com/articles/ sdata201635

[26] B.Dolhansky, Arti icialNeuralNetworks:Linear MulticlassClassi ication(Part3)September27, 2013inmlprimers,neuralnetworks,http://ww w.briandolhansky.com/blog/2013/9/23/artifi cial‐neural‐nets‐linear‐multiclass‐part‐3

[27] E.Scheurwegs,B.Cule,K.Luyckx,L.Luyten,W. Daelemans,“Selectingrelevantfeaturesfromthe electronichealthrecordforclinicalcodepredic‐tion,” JournalofBiomedicalInformatics,vol.74, 2017,pp.92–103.

[28] S.M.Zhou,F.Fernandez‐Gutierrez,J.Kennedy, R.Cooksey,M.Atkinson,S.Denaxas,C.Sudlow, “De iningdiseasephenotypesinprimarycare electronichealthrecordsbyamachinelearning

approach:acasestudyinidentifyingrheuma‐toidarthritis,” PloSone,vol.11,no.5,2016,p. e0154515.

[29] T.Lingren,P.Chen,J.Bochenek,F.Doshi‐Velez, P.Manning‐Courtney,J.Bickel,etal,“Elec‐tronichealthrecordbasedalgorithmtoidentify patientswithautismspectrumdisorder,” PloS one,vol.11,no.7,2016,p.e0159621.

[30] J.Zhao,P.Papapetrou,L.Asker,H.Boström, “Learningfromheterogeneoustemporaldatain electronichealthrecords,” JournalofBiomedical Informatics,vol.65,pp.105–119.

[31] S.Pai,S.Hui,R.Isserlin,M.A.Shah,H.Kaka, G.D.Bader,“netDx:interpretablepatientclassi‐icationusingintegratedpatientsimilaritynet‐works,” MolecularSystemsBiology,vol.15,no.3, 2016,p.e8497.

[32] P.Courtiol,C.Maussion,M.Moarii,E.Pronier,S. Pilcer,M.Sefta,T.Clozel,“Deeplearning‐based classi icationofmesotheliomaimprovespredic‐tionofpatientoutcome,” NatureMedicine,vol. 25,no.10,2019,pp.1519–1525.

[33] B.Dolhansky,2013, Arti icialneuralnetworks: Mathematicsofbackpropagation(part4),https: //www.briandolhansky.com/blog/2013/9/2 7/artificial‐neural‐networks‐backpropagation‐part‐4

[34] B.Dolhansky,J.A.Bilmes,“Deepsubmodular functions:De initionsandlearning.Advancesin NeuralInformationProcessingSystems,”vol.29, 2016,pp.3404–3412.

[35] G.Paliwal,A.Bunglowala,P.Kanthed,“Anarchi‐tecturaldesignstudyofelectronichealthcare recordsystemswithassociatedcontextparame‐tersonMIMICIII,” HealthandTechnology,2022, pp.1–15.

[36] H.Sharma,C.Mao,Y.Zhang,H.Vatani,L.Yao, Y.Zhong,Y.Luo,“Developingaportablenatu‐rallanguageprocessingbasedphenotypingsys‐tem,” BMCMedicalInformaticsandDecisionMaking,vol.19,no.3,pp.79–87.

[37] A.P.Reimer,A.Milinovich,“UsingUMLSforelec‐tronichealthdatastandardizationanddatabase design,” JournaloftheAmericanMedicalInformaticsAssociation,vol.27,no.10,2020,pp. 1520–1528.

[38] H.Zhang,T.Lyu,P.Yin,S.Bost,X.He,Y.Guo,J. Bian,“Ascopingreviewofsemanticintegration ofhealthdataandinformation,” International JournalofMedicalInformatics,2022,p.104834.

[39] D.Yuvaraj,A.M.U.Ahamed,M.Sivaram,“Astudy ontheroleofnaturallanguageprocessinginthe healthcaresector,” MaterialsToday:Proceedings, 2021.

[40] H.Sharma,C.Mao,Y.Zhang,H.Vatani,L.Yao, Y.Zhong,etal,“Developingaportablenatural languageprocessingbasedphenotypingsystem,”

BMCMedicalInformaticsandDecisionMaking, vol.19,no.3,2019,pp.79–87.

[41] S.Moosavinasab,E.Sezgin,H.Sun,J.Hoffman,Y. Huang,S.Lin,“DeepSuggest:Usingneuralnet‐workstosuggestrelatedkeywordsforacompre‐hensivesearchofclinicalnotes,” ACIopen,vol.5, no.01,2021,pp.e1–e12.

[42] B.Wang,Y.Sun,Y.Chu,D.Zhao,Z.Yang,J.Wang, “Re iningelectronicmedicalrecordsrepresenta‐tioninmanifoldsubspace,” BMCbioinformatics, vol.23,no.1,pp.1–17.

[43] E.O.Omuya,G.O.Okeyo,M.W.Kimwele,“Feature selectionforclassi icationusingprincipalcom‐ponentanalysisandinformationgain,” Expert SystemswithApplications,vol.174,2021,p. 114765.

[44] U.A.Bhatti,L.Yuan,Z.Yu,S.A.Nawaz,A. Mehmood,M.A.Bhatti,etal,“PredictiveData ModelingUsingsp‐kNNforRiskFactorEvalua‐tioninUrbanDemographicalHealthcareData,” JournalofMedicalImagingandHealthInformatics,vol.11,no.1,2021,pp.7–14.

[45] N.Wang,Y.Huang,H.Liu,Z.Zhang,L.Wei, X.Fei,H.Chen,“Studyonthesemi‐supervised learning‐basedpatientsimilarityfromheteroge‐neouselectronicmedicalrecords,” BMCmedical informaticsanddecisionmaking,vol.21,no.2, 2021,pp.1–13.

[46] C.Comito,D.Falcone,A.Forestiero,Diagnosis predictionbasedonsimilarityofpatientsphys‐iologicalparameters.In Proceedingsofthe2021 IEEE/ACMInternationalConferenceonAdvances inSocialNetworksAnalysisandMining,pp.487–494.

[47] W.M.Shaban,A.Rabie,A.I.Saleh,M.A.Abo‐Elsoud,“AccuratedetectionofCOVID‐19 patientsbasedondistancebiasedNa ve Bayes(DBNB)classi icationstrategy,” Pattern Recognition,vol. 119,2021,p.108110.

[48] V.Jackins,S.Vimal,M.Kaliappan,M.Y.Lee, “AI‐basedsmartpredictionofclinicaldisease usingrandomforestclassi ierandNaiveBayes,” TheJournalofSupercomputing, 77(5),2021,pp. 5198–5219.

[49] J.M.Bae,“Theclinicaldecisionanalysisusing decisiontree,” Epidemiologyandhealth,vol. 36, 2021.

[50] S.H.Rukmawan,F.R.Aszhari,Z.Rustam,J.Pande‐laki,“Cerebralinfarctionclassi icationusingthe k‐nearestneighborandnaivebayesclassi ier,” JournalofPhysics:ConferenceSeries,Vol.1752, No.1,2021,p.012045.

[51] L.I.Qi,“Patientclassi icationwithensemble treebasedmodellingfordecisionsupportin acuteclinicalcaresettings,”Doctoraldisserta‐tion,RMITUniversity.

[52] A.Singh,A.Dhillon,N.Kumar,M.Hossain, G.Muhammad,M.Kumar,“eDiaPredict:An

Ensemble‐basedframeworkfordiabetespredic‐tion,” ACMTransactionsonMultimidiaComputing CommunicationsandApplications,vol.17,no.2s, 2021,pp.1–26.

[53] T.Razzaghi,O.Roderick,I.Safro,N.Marko,“Mul‐tilevelweightedsupportvectormachineforclas‐si icationonhealthcaredatawithmissingval‐ues,” PloSone,vol.11,no.5,2021,p.e0155119.

[54] D.M.Abdullah,A.M.Abdulazeez,“MachineLearn‐ingApplicationsbasedonSVMClassi icationA Review,” QubahanAcademicJournal,vol.1,no.2, 2021,pp.81–90.

[55] N.Shahid,T.Rappon,W.Berta,“Applicationsof arti icialneuralnetworksinhealthcareorga‐nizationaldecision‐making:Ascopingreview,” PloSone,vol.14,no.2,2019,p.e0212356.

[56] W.Liu,Z.Wang,N.Zeng,F.E.Alsaadi,X.Liu,“A PSO‐baseddeeplearningapproachtoclassifying patientsfromemergencydepartments,” InternationalJournalofMachineLearningandCybernetics,vol.12,no.7,2021,pp.1939‐1948.

[57] B.S.Panchbhai,V.M.Pathak,“ASystematic ReviewofNaturalLanguageProcessingin Healthcare,” JournalofAlgebraicStatistics,vol. 13,no.1,2022,pp.682–707.

[58] B.Zhou,G.Yang,Z.Shi,S.Ma,“Naturallanguage processingforsmarthealthcare,” IEEEReviewsin BiomedicalEngineering,2022.

[59] K.M.Al‐Aidaroos,A.A.Bakar,Z.Othman, “Medicaldataclassi icationwithNaiveBayes approach,” InformationTechnologyJournal,vol. 11,no.9,p.1166.

[60] I.Korobiichuk,A.Ladanyuk,R.Boiko,S. Hrybkov,“FeaturesofControlProcessesin Organizational‐Technical (Technological) SystemsofContinuousType,” Journalof Automation,MobileRoboticsandIntelligent Systems,vol.14,no.4,pp.11–17.doi: 10.14313/JAMRIS/4‐2020/39.

[61] S.Yous i,M.Rhanoui,M.Mikram,“Compara‐tiveStudyofCNNandLSTMforOpinionMin‐inginLongText,” JournalofAutomation,Mobile RoboticsandIntelligentSystems,vol.14,no.3,pp. 50–55.doi:10.14313/JAMRIS/3‐2020/34.

[62] A.Ndayikengurukiye,A.Ez‐zahout,A.Aboubakr, Y.Charkaoui,O.Fouzia,“ResourceOptimisation inCloudComputing:ComparativeStudyofAlgo‐rithmsAppliedtoRecommendationsinaBig DataAnalysisArchitecture,” JournalofAutomation,MobileRoboticsandIntelligentSystems,vol. 15,no.4,pp.65–75.doi:10.14313/JAMRIS/4‐2021/28.