Physical Metallurgy & Materials Design Laboratory, Department of Mechanical Engineering & Material Science

Calphad modeling and prediction of magnetic phase diagram for the Fe-Cr-Ni system

Peiyun Feng, Liangyan Hao, Wei Xiong

Physical Metallurgy & Materials Design Laboratory, Department of Mechanical Engineering & Material Science

Peiyun Feng Peiyun Feng was born and raised in Chengdu, China. She transferred to Pittsburgh for undergraduate study and her passion for computational material science motivates her to become a researcher in material science and mechanical engineering.

Dr. Wei Xiong is the director of the Physical Metallurgy and Materials Design Laboratory at the University of Pittsburgh. Using the computational methods with high-throughput experiments, his lab works in materials design and advanced manufacturing, which covers a wide range of inorganic Wei Xiong, Ph.D. materials, and focuses on studying process-structure-property-performance relationships.

Significance Statement

Fe-Cr-Ni alloys are one of the most studied ternary alloy systems. In this work, the lack of experimental data for the Fe-Cr-Ni ternary thermodynamics at low temperatures was solved by theoretical modeling. The compositional dependency of both magnetic transition temperature and magnetic moment was studied, which contributes to superalloy development.

Category: Computational Research

Keywords: Magnetic phase diagram, Fe-Cr-Ni, Fe-Cr,

Fe-Ni

Abstract

The compositional dependency of both magnetic transition temperature and magnetic moment of binary Cr-Fe, Fe-Ni, and Cr-Ni alloys, and ternary Fe-Cr-Ni alloys was investigated using magnetic modeling. Previous work on these systems were mainly based on the Inden–Hillert–Jarl magnetic model and Weiss Factor introduced by Hertzman and Sundman. In this work, a revised model proposed by Xiong was applied to study the compositional dependency of both magnetic transition temperature and magnetic moment, which reduced artificial parts of calculations. The reliability of the revised model was proved by the fact that calculated Curie temperature, Néel temperature, and magnetic moment of three binary systems all agree well with experimental data. The predicted variation trend of ternary magnetic properties was also supported by available experimental and theoretical calculation results. The low-temperature properties prediction can be benefited by the showing the improvement of description of the magnetic phase diagrams. The improved simulation of thermodynamic properties is critical to steel and superalloy development.

1. Introduction

The Fe-Cr-Ni alloy is one of the frequently used and studied materials. Many industrial austenitic, ferritic, and martensitic steels are formed based on this alloy system [1]. Their distinct magnetic and mechanical properties make them the promising candidate for structural and functional materials. For example, 304 stainless steel with a significant content of Fe, Cr, Ni is frequently applied in light water and fast breeder reactors [2]. However, there have been limited experimental data for the Fe-Cr-Ni ternary thermodynamics at low temperatures due to slow kinetics, which makes the equilibria to be hard to reach [1]. To solve this problem, theoretical modeling such as ab initio calculations [3] is usually applied. In this work, the compositional dependency of both magnetic transition temperature and magnetic moment was studied to understand the magnetic ordering contribution to the alloy thermodynamics of the Fe-Cr-Ni ternary alloys, which is critical to steel and superalloy development.

The Inden-Hillert-Jarl (IHJ) magnetic model was proposed in the Calphad annual conference in 1978 [4]. This model was designed only for the ferromagnetic (FM) state. To evaluate the antiferromagnetic (AFM) state, Hertzman and Sundman improved the model by introducing the so-called Weiss Factor (-1 for body-centered cubic and -3 for face-centered cubic) [5]. This model applied a single Redlich-Kister [6] polynomial to fit both the Curie temperature and Néel temperature. This has the advantage that both FM and AFM were fitted, and the critical magnetic transition point could be found where this fitted curve passed zero. But large discrepancy between the fitted curve and experimental information occurs when using this model to demonstrate features of both FM and AFM states simultaneously. Artificial parts of fitting curves will result from this model, thus leading to inaccurate

prediction. Xiong et al. [7] improved the IHJ model by using two Redlich-Kister polynomials to fit the Curie and Néel temperatures separately and this model was adopted in this work. Besides, the effective magnetic moment that presents the real magnetism distribution to reproduce the heat capacity suggested by Xiong et al. [7] was used. Local magnetic moment of atoms can be used to calculate the effective magnetic moment, otherwise, the fitting of heat capacity due to magnetism can generate a reasonable value of the effective magnetic moment.

2. Thermodynamic Modeling

Experimental magnetic transition temperature and local magnetic moment available in literature [9-46] were collected for ternary Fe-Cr-Ni and binary Cr-Fe, Fe-Ni, and Cr-Ni alloys. The Redlich-Kister series expansions (Eqs. (1)-(2)) were applied to fit the magnetic properties of binary systems.

(1)

(2)

where xA and xB are compositions for element A and B, respectively. T(A) (T(B)) and β(A) (β(B)) are magnetic transition temperature and magnetic moment of pure element A (B). a and b are the constant in the Redliche-Kister polynomial term used to fit experimental data. In this work, those parameters are fitted by Thermo-Calc. It is noteworthy that all magnetic properties for pure Fe, Cr and Ni were from values published in the SGTE database [7].

Based on Xiong’s revised model [8], the endpoints of each fitted polynomial were set to be the pure element parameters, which are also called unary parameters. If the element is antiferromagnetic, the Curie temperature is negative, and the Néel temperature is positive, vice versa. Ternary parameters of Fe-Cr-Ni alloys were fitted in the same way by inputting both unary parameters of pure Fe, Cr, and Ni and binary parameters of Cr-Fe, Fe-Ni, and Cr-Ni alloys. All these parameters were used for describing the compositional dependency of magnetic properties. The local magnetic moment of atoms was used to calculate the effective magnetic moment through Eq. (3):

(3)

where β* is the effective magnetic moment, xi is the composition of element i and βi is the local magnetic moment of element i.

3. Results and Discussion

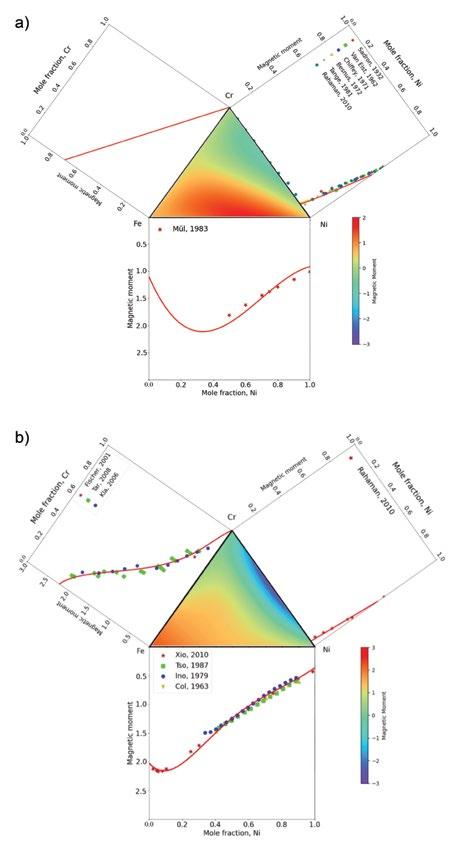
Figure 1: Magnetic moment (μB) at 298 K for the Fe-Cr-Ni alloys (a) of fcc phase and (b) of bcc phase. Symbols denote the experimental data [9-23]. Red solid lines represent the effective magnetic moment calculated in this work using Xiong’s revised model.

Figure 2: Magnetic transition temperature for the Fe-Cr-Ni alloys (a) of fcc phase and (b) of bcc phase. Symbols denote the experimental data [24-46]. Red solid and dashed lines (no experimental data for certain systems) represent the Curie temperature calculated in this work using Xiong’s revised model, while blue solid lines represent the Néel temperature calculated in this work.

Figs. 1 and 2 shows the magnetic property curves of binary Cr-Fe, Fe-Ni, and Cr-Ni alloys in this work. The Curie and Néel temperatures were described by two separate Redlich-Kister polynomials. If both fitted Curie and Neel temperatures curves are below zero at specific composition, that indicates that the real magnetic transition temperature is zero and this phase is non-magnetic. As shown in Fig. 2, there is no cross point of Curie and Néel temperature curves above 0 K, which means that FM and ATM states would not co-exist above 0 K. Consequently, there will not be artificial part of fitted Néel temperature curves by using this improved model. Comparing with experimental data points, the fitted curves in both Figs. 1 and 2 demonstrate that the binaries could be described satisfactorily by this improved model. As a result, the prediction of magnetic properties of binary systems requires high accuracy. For some systems Néel temperature parameters were not fitted because some phases in certain systems do not exhibit AFM state. For example, bcc Fe-Ni binary system only shows FM state over its whole composition range.

Thermodynamics in low-temperature range is of vital importance to the magnetism of alloys and thus have significant needs in various applications. The reliability of the descriptions of unaries and binaries would directly influence the reliability of ternary prediction. By extrapolation of resulted binary properties and fitting of ternary experimental data, the compositional dependency of the magnetic transition temperature and magnetic moment for ternary Fe-Cr-Ni alloys were shown by heatmaps in the middle triangle of Figs. 1 and 2. Normalized by the color bar, the variation of colors in the heatmaps demonstrates the general trend of Curie temperature, Néel temperature and magnetic moment variation. Figure 1(a) shows that the effective magnetic moment decreases rapidly with increasing Cr content in the fcc phase. This is because Cr does not exhibit large magnetic moment in fcc phase (magnetic moment is 0 for pure Cr in fcc phase). Figure 1(b) shows that similar trend occurs in bcc phase of Fe-Cr-Ni alloys. The magnetic moment reaches maximum at the Fe rich side and decreases as Fe content decreases. For magnetic transition temperature shown in the heatmaps in Fig. 2, a boundary could be seen where Curie temperature drops to below zero (from red to purple). This possibly demonstrates the composition range where FM transforms to ATM. In conclusion, these figures demonstrate reasonable descriptions of magnetic phase diagrams of Fe-Cr-Ni alloys.

4. Summary

In this work, a revised magnetic model [9] was applied to calculate the magnetic properties of ternary Cr-Fe, FeNi, Cr-Ni, and Fe-Cr-Ni alloys. The calculated Curie temperature, Néel temperature, and magnetic moment of three binary systems all agree well with experimental data, which proves the reliability of the new magnetic model adopted in this work. Meanwhile, the extrapolation from the binary systems to the Fe-Cr-Ni system can satisfactorily predict the same variation trend of magnetic properties suggested by available experimental and theoretical calculation results. This work can hopefully stress the importance of magnetic models for the further development of the CALPHAD method and draw more attention to the improvement of description of magnetic phase diagrams.

5. Acknowledgements

Swanson School of Engineering at University of Pittsburgh. W.X. acknowledges funding from the National Science Foundation under award DMR - 1808082, and from the University of Pittsburgh, through the Central Research Development Fund (CRDF).

6. References

[1]Wróbel J S, Nguyen-Manh D, Lavrentiev M Y, et al. Phase stability of ternary fcc and bcc Fe-Cr-Ni alloys, J. Physical Review B. 91 (2015) 1098-0121. [2]Toyama T, Nozawa Y, Van Renterghem W, et al. Grain boundary segregation in neutron-irradiated 304 stainless steel studied by atom probe tomography, J. Journal of nuclear materials. 425 (2012) 71-75. [3]Kro ̈mann et al. Phys. Stat. Sol. B 251, 54, 2014. [4]Hillert M, Jarl M. A model for alloying in ferromagnetic metals. Calphad. 2 (1978) 227-238. [5]Hertzman S, Sundman B. A thermodynamic analysis of the Fe-Cr system, J. Calphad. 6 (1982) 67-80. [6]Redlich O, Kister A T. Algebraic representation of thermodynamic properties and the classification of solutions, J. Industrial & Engineering Chemistry. 40 (1948) 345-348. [7]Dinsdale A T. SGTE data for pure elements, J. Calphad. 15 (1991) 317-425. [8]Xiong W, Chen Q, Korzhavyi P A, et al. An improved magnetic model for thermodynamic modeling, J. Calphad. 39 (2012) 11-20. [9]Liangyan Hao, Andrei Ruban, Wei Xiong. CALPHAD Modeling Based on Lattice Stability from Zero Kevin and Improved Magnetic Model: A Case Study on the Cr-Ni System. CALPHAD, to be published. [10] Sadron C. Ferromagnetic moments of elements and the periodic system, J. Ann. Phys. 17 (1932) 371-452. [11] Van Elst H C, Lubach B, Van den Berg G J. The magnetization of some nickel alloys in magnetic fields up to 15 kOe between 0° K and 300° K, J. Physica. 28 (1962) 1297-1317. [12] B. Chiffey and T. Hicks. The spontaneous moment of nickel-chromium alloys. Physics Letters A. 34 (1971) 267–268. [13]Besnus M J, Gottehrer Y, Munschy G. Magnetic properties of Ni Cr alloys, J. Physica Status Solidi. 49 (1972) 597-607. [14]Tange H, Yonei T, Goto M. Forced Volume Magnetostriction of Ni-Cr Alloys, J. Journal of the Physical Society of Japan. 50 (1981) 454-460. [15] Kankainen A, Elomaa V V, Eronen T, et al. Mass measurements in the vicinity of the doubly magic waiting point Ni 56, J. Physical Review C. 82 (2010). [16]Müller J B, Hesse J. A model for magnetic abnormalies of FeNi Invar alloys, J. Zeitschrift für Physik B Condensed Matter. 54 (1983) 35-42. [17] Xiong W, Zhang H, Vitos L, et al. Magnetic phase diagram of the Fe–Ni system, J. Acta materialia. 59 (2011) 521-530.

[18]Tsoukalas et al. Zeitschrift für Metallkunde. 78 (1987) 498-501. [19]Inoue J, Yamada H, Shimizu M. Calculation of the Magnetic Properties for fcc Fe–Ni Alloys, J. Journal of the Physical Society of Japan. 46 (1979) 1496-1503. [20] Collins M F, Forsyth J B. The magnetic moment distribution in some transition metal alloys, J. Philosophical Magazine, 8 (1963) 401-410. [21]Fischer S F, Kaul S N, Kronmüller H. Critical magnetic properties of disordered polycrystalline Cr 75 Fe 25 and Cr 70 Fe 30 alloys, J. Physical Review B, 65 (2002). [22]Tarafder K, Ghosh S, Sanyal B, et al. Electronic and magnetic properties of disordered Fe–Cr alloys using different electronic structure methods, J. Journal of Physics: Condensed Matter. 20 (2008). [23] Klaver T P C, Drautz R, Finnis M W. Magnetism and thermodynamics of defect-free Fe-Cr alloys, J. Physical Review B. 74 (2006). [24]Peschard M. Contribution a l’etude des ferronickels, D. Univ. de Strasbourg. (1925) [25]Gossels G. Versuche über die Stabilität der Hysteresis Fe-Ni‐Legierungen, J. Zeitschrift für anorganische und allgemeine Chemie. 182 (1929) 19-27. [26] Morita H, Fujimori H, Hashimoto S, et al. Study on the Fe-Ni phase diagram by multilayer samples, J. Journal of magnetism and magnetic materials. 126 (1993) 173-175. [27]Fukamichi K. Magnetically Insensitive Ternary Invar Alloys of Cr, Fe and 4d Transition Metals, J. Transactions of the Japan Institute of Metals. 18 (1977) 81-86. [28]Yamamoto H. A study on the nature of aging of FeCr alloys by means of the Mössbauer effect, J. Japanese Journal of Applied Physics. 3 (1964) 745. [29]Adcock, J. Iron Steel Inst. 124 (1931) 99. [30]Rajan N S, Waterstrat R M, Beck P A. Temperature‐Dependence of the Electrical Resistivity of bcc Cr–Fe Alloys, J. Journal of Applied Physics. 31 (1960) 731-732. [31]P. Oberhoffer and H. Eisen. Stahl und Risen. 47 (1927) 2021-2031. [32]R. Vilar and G. Cizeron, Mem. Etud. Sci. Rev. Met. 79 (1982) 687. [33]Tsunoda Y, Mori M, Kunitomi N, et al. Strain wave in pure chromium, J. Solid State Communications. 14 (1974) 287-289. [34] Mitchell M A, Goff J F. Electrical Resistivity and the Depression of the Néel Temperature in Cr-Mo and CrFe, J. Physical Review B. 5 (1972) 1163. [35]Swartzendruber L J, Itkin V P, Alcock C B. The Fe-Ni (iron-nickel) system, J. Journal of phase equilibria. 12 (1991) 288-312. [36]A. A. Jansson, Thermodynamic Evaluation of the Cu–Fe–Ni System, Report No. TRITA-MAC 0340, The Royal Institute of Technology. (1987) 1–10. [37]Simpson M A, Smith T F. Thermodynamic studies and magnetic ordering of Ni-Cr alloys close to the critical composition, J. Australian Journal of Physics. 35 (1982) 307-320.

[38]Chaudhary V, Ramanujan R V. Magnetocaloric properties of Fe-Ni-Cr nanoparticles for active cooling, J. Scientific reports. 6 (2016) 1-9. [39]Iorga A, Codescu M M, ŞABAN R, et al. Low Curie Temperature in Fe-Cr-Ni-Mn Alloys, J. UPB Sci. Bull., Series B. 73 (2011) 8. [40]Almasan C, Datta T, Edge R D, et al. Low-temperature phase and magnetic interactions in FCC Fe-Cr-Ni alloys, J. Journal of magnetism and magnetic materials. 80 (1989) 329-338. [41]Rhys-Jones T N, Grabke H J, Kudielka H. The effects of various amounts of alloyed cerium and cerium oxide on the high temperature oxidation of Fe-10Cr and Fe-20Cr alloys, J. Corrosion Science. 27 (1987) 49-73. [42] Lavrentiev M Y, Wróbel J S, Nguyen-Manh D, et al. Magnetic cluster expansion model for random and ordered magnetic face-centered cubic Fe-Ni-Cr alloys, J. Journal of Applied Physics. 120 (2016). [43] Wróbel J S, Nguyen-Manh D, Lavrentiev M Y, et al. Phase stability of ternary fcc and bcc Fe-Cr-Ni alloys, J. Physical Review B. 91 (2015). [44] Ōhara S, Kōmura S, Takeda T. Magnetic Properties of Pseudo-Iron Fe1-x (Cr0. 5Ni0. 5) x Ternary Alloys, J. Journal of the Physical Society of Japan. 34 (1973)14721476. [45]Rode V, Deryabin A, Damashke G. Ferro-antiferromagnetic transition in the alloy system Fe 65 (Ni 1-x Cr x) 35 at low temperatures, J. IEEE Transactions on Magnetics. 12 (1976) 404-406. [46]Warnes L A A, King H W. The low temperature magnetic properties of austenitic Fe-Cr-Ni alloys: 2. The prediction of Néel temperatures and maximum susceptibilities, J. Cryogenics. 16 (1976) 659-667.