HORS-SÉRIE POUR LA SCIENCE #126 - FÉVRIER 2025

HORS-SÉRIE

« La combinaison du collectif et de l’individuel observée chez les fourmis, les abeilles et les termites devrait être une inspiration pour les sociétés humaines »

Bruno Corbara Université Clermont-Auvergne

Insectes sociaux

LES ARCHITECTES DU MONDE

Les abeilles mellifères, un fléau ?

Les secrets de l’intelligence collective La vie intérieure d’un insecte Les termites façonnent les paysages

La science expliquée par ceux qui la font

MAGAZINE / HORS-SÉRIE / DIGITAL / 25+ ANS D’ARCHIVES

Choisissez votre formule d’abonnement pourlascience.fr/abonnements

Édition française de Scientific American

02.25/03.25

HORS-SÉRIE

Dans un pays de tous les temps…

par Loïc Mangin

Rédacteur en chef adjoint à Pour la Science

En 1804, Napoléon Ier choisit pour son empire et pour lui-même un emblème : au premier, l’aigle, au second, l’abeille. L’insecte a pour lui de représenter « une république qui a un chef », ou bien l’association de « l’aiguillon et du miel ». Mais l’interprétation la plus pertinente (et apocryphe…) est peut-être ailleurs : l’empereur comme l’hyménoptère s’y entendent pour bouleverser le monde ! C’est sans doute aussi pour cette raison que les Barberini, une puissante famille italienne du XVIIe siècle – qui compta un pape, nombre de cardinaux –, et avant eux les Mérovingiens, ont choisi l’abeille pour symbole. Tous auraient eu raison, car, domestique ou non, elle est la clé de voûte de nombreux écosystèmes, naturels et agricoles. Elle rejoint en cela tous les autres insectes sociaux, termites et fourmis, qui, grâce à leur intelligence collective et les e ets de groupe (qui peut compter plusieurs millions de membres), ont une influence notable sur la planète. Leurs colonies façonnent les paysages avec une ampleur insoupçonnée, que révèle ce numéro. En un mot, le monde ne serait pas ce qu’il est sans insectes sociaux. Dans la série animée qui porte son nom, Maya l’abeille n’a qu’une envie : découvrir le monde avec ses amis Willy et Flip. En fait, elle veut contempler son œuvre…

Ont contribué à ce numéro

Aurore Avarguès-Weber. est directrice de recherche du CNRS au Centre de recherches sur la cognition animale, à l’université de Toulouse. Elle a reçu la médaille de bronze du CNRS en 2019

Bruno Corbara est enseignant-chercheur à l’université Clermont-Auvergne, membre du laboratoire Microorganismes génome environnement, et directeur de la publication de la revue Espèces

Emmanuelle Porcher est écologue et biologiste de l’évolution au Muséum national d’histoire naturelle, ainsi que professeuse au Collège de France (chaire annuelle « Biodiversité et écosystèmes »).

Guy Théraulaz est directeur de recherche au Centre de recherches sur la cognition animale, au Centre de biologie intégrative de Toulouse.

www.pourlascience.fr

01 Les architectes du monde INSECTES SOCIAUX

p. 6 Repères

Des schémas, des chi res, des définitions… : toutes les clés pour entrer sereinement dans ce numéro.

p. 10 Grand témoin

Bruno Corbara

L’importance des insectes sociaux sur l’environnement est sans doute sous-estimée

Un incroyable talent

p. 18 L’intuition géométrique des abeilles

Alain Satabin

Point d’alvéoles sans géométrie !

p. 26 It’s a trap !

Sean Bailly

Les mauvais souvenirs aident les fourmis à s’orienter.

p. 30 Dans la tête d’un insecte

Mariana Lenharo

La conscience chez les insectes est « une possibilité réaliste ».

p. 34 Pour le plaisir !

Grace Van Deelen

Les bourdons jouent à faire rouler des boules. De quoi s’interroger…

p. 36 Pas folle, l’abeille !

Aurore Avarguès-Weber

Les capacités cognitives des abeilles sont stupéfiantes.

02 03

Aux sources du collectif

p. 46 Une intelligence façon puzzle

G. Théraulaz, J. Gautrais, S. Blanco, R. Fournier et J.-L. Deneubourg

L’art de résoudre collectivement de multiples problèmes.

p. 56 Le secret de la socialité

Jordana Cepelewicz

L’origine des castes est à chercher du côté de l’insuline.

p. 62 Des termitières écoconçues

Guy Théraulaz

Pourquoi les nids de termites inspirent les architectes.

p. 66 Voyage au centre de la termitière

PORTFOLIO

Des faiseurs de planète

p. 76 Le paradoxe des abeilles mellifères

Alison McAfee

Les abeilles domestiques nuisent à l’environnement.

p. 84 La fable de la fourmi et du lion

Sean Bailly

Il était une fois une fourmi… qui mit les lions au régime.

p. 88 Paysagistes en sous-sol

Lisa Margonelli

Les termites façonnent la végétation à grande échelle.

p. 96 Le bzzz et l’éclair

ENTRETIEN avec Giles Harrison et Ellard Hunting

p. 100 Sauvons les pollinisateurs !

Emmanuelle Porcher, Clélia

Sirami et Thibault Gandara

La protection de ces auxiliaires de l’agriculture est indispensable.

p. 1 09 Rendez-vous

110 En image

112 Rebondissements

116 Infographie

118 Les incontournables

Faire société

Les insectes sociaux sont apparus il y a plusieurs millions d’années et ont conquis le monde en développant une extraordinaire variété de morphologies et de comportements.

Ce qui n’empêche pas certains d’entre eux d’être menacés…

Hexapodes

Protoures

Diploures

Insectes

Neoptères

Dictyoptères

Polynéoptères

Lumétaboles Acercaria

Holométaboles

UNE PHYLOGÉNIE COMPLEXE

Déterminer les liens de parenté entre les di érentes espèces, genres, tribus… d’insectes est une tâche ardue sur laquelle planchent de nombreux experts. Les arbres obtenus sont souvent remaniés, en désaccord les uns avec les autres, et il est di cile d’en faire la synthèse. Néanmoins, cet arbre simplifié (les pointillés sont des raccourcis) retrace les grandes étapes de l’histoire évolutive des insectes sociaux et met en évidence l’éloignement entre, d’une part, la branche des termites et, d’autre part, celle des hyménoptères chez qui la socialité (en rouge) est apparue plusieurs fois.

E. Søvik et al., Function and evolution of microRNAs in eusocial Hymenoptera, Front. Genet., 2015.

Mantodea (mantes)

Blatodea (termites)

Coléoptères

Lépidoptères (papillons)

Diptères (mouches)

Hyménoptères

Symphita

Apocrita (abeilles, fourmis, guêpes)

Parasitoïdes

L’e et pare-brise, c’est-à-dire la baisse drastique de la quantité d’insectes s’écrasant sur les vitres des véhicules quand ils roulent, illustre le déclin des populations d’insectes.

Aculeata

Chrysidoidea

Apini

Euglossini

Bombini

Meliponini

Autres tribus

Allodapini

Autres tribus

Lasioglossum spp.

Autres espèces

Halictus

Autres genres

Augochlorini

Autres tribus

Autres sous-familles

Formicidae

Autres sous-familles

Polistinae

Vespinae

Autres sous-familles

Stenogastrinae

Autres sous-familles

UN DÉCLIN INEXORABLE

Depuis plus de vingt ans, les études s’accumulent et convergent : l’ensemble des populations d’insectes, et pas seulement les pollinisateurs (voir Sauvons les pollinisateurs !, par E. Porcher et al., page 100), s’e ondrent. La diminution serait de 70 à 80 % dans les paysages européens mixtes agro-industriels et se constate à tous les niveaux : abondance (le nombre d’individus), diversité (le nombre d’espèces) et biomasse (le poids). Les principales causes sont la destruction de l’habitat du fait de l’agriculture intensive et de l’urbanisation, l’utilisation de pesticides, les espèces invasives, le réchau ement climatique, la pollution, l’éclairage artificiel…

FOURMIS, ABEILLES, TERMITES…

DES FOURMIS FORMIDABLES

On compte 16 600 espèces *, toutes sociales.

Selon une étude de 2022, au moins 20 millions de milliards de fourmis existent sur Terre.

La biomasse totale des fourmis sur Terre (mesurée en matière sèche) est estimée à 12 millions de tonnes, soit 20 % de celles des humains.

Une supercolonie de fourmis d’Argentine, Linepithema humile, s’étend sur 6 000 kilomètres, du nord de l’Italie jusqu’à la Galice, en passant par le sud de la France, Gibraltar et le Portugal.

La fourmi des bois Formica yessensis a construit une supercolonie de 45 000 nids à Hokkaido, au Japon, abritant plus de 1 million de reines et 306 millions d’ouvrières.

En Europe, la plus grande colonie connue est en Suisse, dans le Jura : 200 millions de Formica paralugubris ont bâti un réseau de 1 200 fourmilières s’étendant sur 70 hectares.

Chez les fourmis pot-de-miel, qui rassemblent plusieurs espèces, certaines ouvrières, dites « fourmis gourdes » accumulent du miellat de pucerons dans leur abdomen et le tiennent à la disposition des autres membres de la colonie.

Environ 1 % des espèces de fourmis sont sans reine.

Certaines fourmis, comme Polyergus rufescens, ont des esclaves. Elles enlèvent les larves, les cocons et les nymphes d’autres espèces et mettront à leur service les ouvrières qui en naîtront.

La marabunta est un déplacement massif de fourmis légionnaires. À raison de 200 mètres par jour, la colonie se déplace sans que rien ne l’arrête, pas même les cours d’eau.

À partir de ses expérimentations, l’entomologiste américain Justin Schmidt a établi une échelle de douleur (1 à 4) liée aux piqûres d’hyménoptères. En bas figurent de petites abeilles de la famille des Halictidae Apis mellifera et les frelons sont à 2. Le degré 3 correspond à la fourmi rouge moissonneuse Pogonomyrmex barbatus Et au sommet (au-delà de 4)

figurent les fourmis Paraponera, dont Paraponera clavata. Son surnom de bullet ant lui vient de sa piqûre aussi douloureuse qu’une balle de fusil.

DES ABEILLES PAS

Au moins 20 000 espèces d’abeilles (2 000 en Europe et 1 000 en France métropolitaine).

10 % sont sociales.

L’abeille Anthidium manicatum, de la famille des Megachilidae, est dite « cotonnière », car elle a l’habitude de gratter des feuilles velues pour confectionner des boules de poils dont elle ornera son nid.

Anthidium manicatum.

L’osmie cornue Osmia cornuta, une des espèces qui fréquentent le plus les hôtels à insectes, est un pollinisateur particulièrement apprécié dans les vergers et les potagers, au point de faire l’objet d’un élevage, l’osmiculture.

En visitant les fleurs, certaines abeilles charpentières (elles creusent leur nid dans du bois mort), ou xylocopes, percent les tubes floraux à leur base pour voler le nectar sans emporter de pollen.

Certaines abeilles, notamment le genre Coelioxys, se comportent à la façon des coucous : les femelles pondent dans les nids d’autres espèces qui prendront soin des larves parasites, au détriment des leurs propres.

Coelioxys inermis Myrmecocystus

* Pour les fourmis comme pour les autres insectes sociaux, et même plus généralement tous les insectes, le nombre d’espèces est probablement sous-estimé.

TROIS MOTS POUR UNE INCROYABLE DIVERSITÉ

COMME LES AUTRES

Depuis les années 1970, et avec une accélération depuis les années 1990, on constate une mortalité anormale et récurrente des colonies d’abeilles domestiques Apis mellifera, en France, dans le reste de l’Europe, et, à partir de l’hiver 2006-2007, aux États-Unis. Les causes de ce « syndrome d’e ondrement des colonies d’abeilles » sont multiples, variables selon les pays, et di ciles à démêler : parasites, virus, champignons, bactéries, dégradation des habitats, réchau ement climatique, pesticides…

Le frelon asiatique, ou frelon à pattes jaunes Vespa velutina, a été importé en 2004. Plus précisément, Quentin Rome, du Muséum national d’histoire naturelle, à Paris, a retracé son parcours. Une reine fécondée, le « patient zéro », a voyagé depuis Shanghai, dans une poterie transportée en conteneur, et s’est envolée d’une ferme horticole du Lot-et-Garonne. Depuis, l’indésirable fait des ravages dans les colonies d’abeilles.

TERMITES HIER ET AUJOURD’HUI

2 600 espèces, toutes sociales. La biomasse des termites équivaut à 100 millions de tonnes.

En juin 2024, une équipe de l’université de Stellenbosch, en Afrique du Sud, a annoncé la découverte de termitières, toujours habitées (par l’espèce Microhodotermes viator), âgées de 34 000 ans ! Au début des travaux, les Néandertaliens existaient encore…

En 2018, Stephen Martin, de l’université de Salford, à Manchester, et ses collègues ont rapporté la découverte dans la région du Nordeste, au Brésil, d’un vaste réseau de termitières interconnectées par des tunnels dont les premiers travaux auraient commencé il y a quatre mille ans. Il s'étend sur une surface d’environ 230 000 kilomètres carrés (quand le territoire de l’Hexagone couvre 550 000 kilomètres carrés).

La surface couverte par les termitières (du vert au rouge, la probabilité de présence augmente de 0 à 1). À droite, la silhouette de la GrandeBretagne, pour comparaison.

Les termitières les plus élevées, dites « cathédrales », sont celles de colonies champignonnistes qui vivent en Afrique de l’Est : leurs nids font jusqu’à 8 mètres de hauteur !

Les termites dites « boussoles » Amitermes meridionalis perçoivent le champ magnétique terrestre et utilisent ces informations pour, lors de la construction, orienter leurs nids selon un axe est-ouest. Le sommet de la termitière est également rétréci de façon à former une crête. Pour quelles raisons ? O rir le moins de surface possible au soleil à la mi-journée et éviter la surchau e !

Les termites sont les animaux qui produisent le plus de méthane (par rapport à leur masse), et l’on estime qu’on leur doit 3 % de l’ensemble du méthane produit par le vivant. Leur contribution doit être prise en compte dans les modèles climatiques, particulièrement ceux qui portent sur les zones tropicales.

Vespa velutina

Nids d’Amitermes meridionalis

Un incroyable talent

Depuis peu, les insectes, et notamment les abeilles, ont rejoint le club de plus en plus ouvert des espèces dotées d’une conscience. Quoi d’étonnant à cela, tant les prouesses de ces animaux ne cessent de surprendre les chercheurs qui les étudient, et c’est particulièrement vrai des insectes sociaux. Quelques exemples ? Les bourdons s’amusent. Les fourmis déjouent les pièges. Mieux, les abeilles, avec 100 000 fois moins de neurones qu’un humain, savent compter, classer des objets par catégories et elles réussissent à certains tests mieux que les primates ! On saisit pourquoi Kepler leur a attribué « une âme ».

Les alvéoles des abeilles semblent la solution optimale pour économiser la cire tout en maximisant le volume. Le prouver est une autre a aire…

L’intuition géométrique des abeilles

Alain Satabin

Si elle ne craint pas le vide, la nature a horreur de l’effort inutile ! De fait, dans nombre de phénomènes, l’économie prévaut : le rayon lumineux choisit le chemin le plus court ; les corps pesants se stabilisent là où leur énergie est minimale ; une goutte de liquide en apesanteur adopte une forme sphérique parfaite, minimisant ainsi sa surface Et parmi les formes géométriques naturelles, qu’en est-il de la structure du nid d’abeilles ? N’est-elle pas assez surprenante pour laisser croire qu’elle est due au hasard ? L’idée d’une forme minimale, grâce à laquelle l’abeille utiliserait le moins de cire possible pour construire des alvéoles de volume donné , a , depuis l’Antiquité , suscité nombre d’études, suppositions et démonstrations.

La présence de cellules de part et d’autre d’un plan semble assez naturelle , car le fond des alvéoles en servant doublement est « rentabilisé ». En revanche, le reste de la structure est plus délicat à appréhender et son étude a été menée sur trois fronts : le problème de la « vue de face hexagonale », celui du fond et celui d’un nid en deux dimensions.

LA CONJECTURE DU NID D’ABEILLES

Le premier problème a trait au pavage du plan Malgré quelques différences minimes observées dans une vraie ruche, nous voyons que les alvéoles sont des tubes de section constante, de profondeur fixe, de volume donné et aux parois d’épaisseur invariable. Le problème d’économie de cire est alors celui de la recherche d’un pavage du plan par des formes d’aire donnée, de sorte que la

― En bref

> Dès l’Antiquité, on perçut que les rayons des ruches optimisent le volume disponible par rapport à la cire utilisée.

> Cela se traduit en 3 problèmes de géométrie, relatifs à la forme hexagonale des alvéoles, à leur fond et à leur agencementles et leur agencement.

> À ce jour, un seul a été totalement démontré.

longueur des courbes (les parois des alvéoles) le délimitant soit la plus petite possible. Ce problème est resté longtemps connu sous le nom de « conjecture du nid d’abeilles » : il s’agissait de démontrer que le pavage en hexagones réguliers offre la meilleure solution. Cette preuve n’a été fournie qu’en 1999, par Thomas Hales, de l’université du Michigan, qui l’année précédente avait démontré la conjecture de Kepler sur la meilleure façon d’empiler des sphères. Le fond des alvéoles, objet du deuxième problème, n’est pas plat, mais constitué de trois losanges terminant le prisme hexagonal « en pointe ». Est-ce la configuration qui minimise la quantité de cire pour un volume égal ? Nous verrons que l’étude, en trois dimensions cette fois, des faces de contact avec les cellules opposées a fait couler beaucoup d’encre et que la minimalité de la forme adoptée par les abeilles est remise en cause. Enfin, le dernier problème ramène à l’étude de la vue « en coupe » d’un rayon : il s’agit là de paver une bande de plan en minimisant la longueur totale des parois Là encore, des questions restent en suspens. Revenons à la première question. Le pavage hexagonal régulier d’un nid d’abeilles est remarqué dès l’Antiquité : Aristote le mentionne dans son Histoire des animaux et Pline l’Ancien dans son Histoire naturelle. Ce dernier rapproche même la forme observée et les six pattes des abeilles ! La première étude mathématique de ce pavage date du IVe siècle Dans ses Collections mathématiques, Pappus d’Alexandrie affirme que les abeilles adoptent la forme hexagonale par souci d’économie de cire et leur attribue une

Au IVe siècle, dans ses « Collections

mathématiques », Pappus d’Alexandrie

affirme que les abeilles adoptent

la forme hexagonale par souci d’économie de cire et leur attribue

une « intuition géométrique »

« intuition géométrique » . Treize siècles plus tard, Érasme Bartholin réfute cette interprétation et pense plutôt que les ouvrières fabriquent des cellules cylindriques, mais que les forces de pression s’exerçant sur les parois , dues à la construction simultanée d’alvéoles contiguës, déforment les cercles pour les transformer en hexagones Cette idée sera reprise, en 1753, par Buffon dans son Traité d’histoire naturelle.

Dans son étude, Pappus formule des hypothèses restrictives: le plan est pavé avec des polygones réguliers, tous identiques, d’aire donnée et assemblés par leurs côtés Pour un tel recouvrement sans trous, seuls trois candidats subsistent: le triangle équilatéral, le carré et l’hexagone régulier.

Pour chacune de ces formes, dont on fixe arbitrairement l’aire égale à 1, quelle est celle dont le périmètre est minimal ? Un triangle équilatéral d’aire 1 a un côté de longueur 2/4√3 et donc un périmètre de 6/4√3, soit environ 4,56. Un carré d’aire 1 a un côté de longueur 1, et donc un périmètre de 4. Enfin, un hexagone régulier d’aire 1 a pour côté 4√12/3 et donc pour périmètre 2 × 4√12, soit environ 3,72. Ce dernier est donc élu solution du problème de Pappus.

Dans un pavage, chaque côté sert deux fois (sauf ceux du bord du recouvrement). Le rendement d’un pavage est alors mesuré en calculant le rapport de la somme des longueurs des côtés par la somme des aires des pavés Si k régions, chacune d’aire 1, sont délimitées par des frontières de longueur totale L(k), le rapport L(k)/k mesure la rentabilité du pavage. Lorsque le pavage est étendu au plan tout entier, le nombre de cellules

L’intuition géométrique des abeilles

et la longueur des frontières deviennent infinis. On contourne cette difficulté en calculant le rapport précédent pour un pavage situé dans un disque (incluant un nombre fini de régions), puis en étudiant son comportement lorsque le rayon du disque tend vers l’infini. Pour un pavage hexagonal du plan, ce rapport tend vers 4√12 soit la moitié du périmètre trouvé plus haut, car chaque frontière sert exactement deux fois.

PASSER PAR LA SPHÈRE

L’avancée significative suivante aura lieu plus de 1 500 ans après ! En 1943, le mathématicien hongrois László Tóth résout le premier problème à partir d’hypothèses moins restrictives que celles de Pappus, notamment de ne pas avoir toutes les mêmes formes, ni même qu’elles soient des polygones réguliers. Sur une sphère de rayon 1, il analyse son découpage en n régions convexes de même aire, où n est un entier supérieur ou égal à 4. La convexité reste importante (une surface est convexe quand le plus court chemin reliant deux de ses points reste à l’intérieur de la surface).

Cette convexité oblige la frontière entre deux régions à suivre une géodésique (un grand cercle) de la sphère puisque le moindre « renflement » de ce bord priverait la zone adjacente de sa convexité. On en déduit que les cellules de l’étude de Tóth sont des polygones sphériques, c’est-à-dire qu’ils résultent de la projection sur la sphère d’un polyèdre convexe de même centre. L’intérêt d’une sphère plutôt qu’un plan apparaît ici, car on peut utiliser l’égalité d’Euler :

pour un polyèdre convexe à F faces, S sommets et A arêtes, on a F + S – A = 2.

À l’aide, entre autres, de cette égalité et du fait qu’un polygone convexe d’aire donnée a un périmètre minimal lorsqu’il est régulier, Tóth démontre que la longueur totale des frontières (sur la sphère) est supérieure à une expression M n, dépendant de n, qui est homogène à une longueur.

Pour de grandes valeurs de n, M n devient équivalente à 4√12 × √n × S, où S est l’aire de la sphère. Le raisonnement est mené sur une sphère de rayon 1, mais le résultat subsiste sur une sphère quelconque. Quand on découpe la sphère, le résultat se circonscrit à une zone sphérique d’aire

A, encadrant p cellules de même aire : pour de grandes valeurs de p, la longueur totale de bordures L(p) est, au mieux, égale à 4√12 × √p × A .

Avec une sphère de rayon très grand ainsi pavée par des cellules d’aire 1, l’aire A du domaine étudié est égale à p, soit le nombre de régions qu’il contient, et la longueur du réseau de segments sphériques correspondant est donc au minimum équivalente à 4√12 × p. Quand on identifie une petite portion de sphère de très grand rayon à un domaine plat, nous retrouvons le problème des abeilles Lorsque p tend vers l’infini, le meilleur rapport L(p)/p est 4√12, qui est, nous l’avons vu précédemment, celui d’un assemblage d’hexagones réguliers. Les abeilles sont, à ce stade, déjà confortées dans leur choix de structure hexagonale, mais l’hypothèse de la convexité est encore de trop pour une généralisation complète du problème. Elle est pourtant nécessaire dans la démonstration de

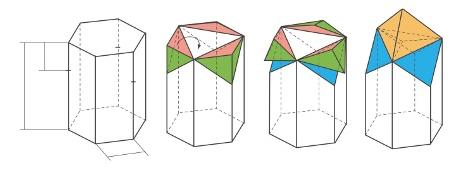
Un prisme hexagonal est-il le plus économique en cire ?

Partons d’un prisme hexagonal (à gauche) dont le côté de la base est égal à 1 et la hauteur à 3. Puis, plaçons à une distance x de la base supérieure (ABCDEF) les points B’, D’ et F’homologues des points B, D et F, puis faisons pivoter de 180° les trois tétraèdres ABCB’, CDED’ et EFAF’ autour des segments respectifs AC, CE et EA (à droite). Le prisme est devenu une alvéole d’abeille. Par construction, le volume reste inchangé, c’est-à-dire égal à 9√3/2. La somme des aires est exprimée par une fonction F(x) dont l’étude révèle qu’elle atteint un minimum pour x égal à √2/4, soit environ 0,354 ; l’aire vaut alors environ 20,121.

Tóth : son raisonnement ne résiste pas à l’abrogation de ce prédicat Il ajoute dans un ouvrage de 1964, où il revient sur ce sujet par un autre biais, que « la démonstration du résultat dans le cas général semble induire des difficultés considérables ».

UNE CONVEXITÉ EMBARRASSANTE

En 1994, dans un document consacré à l’étude des bulles de savon en deux dimensions, Frank Morgan, du Williams College, à Williamstown, aux États-Unis, établit un résultat important en affaiblissant les hypothèses de Tóth. Un nombre entier n étant fixé, le mathématicien considère l’ensemble des réseaux de courbes continues « suffisamment lisses » délimitant n régions bornées dont les aires ont, elles aussi, été fixées à l’avance. L’ensemble des longueurs de ces graphes possède une borne inférieure, celle qui correspond à un

graphe limite En d’autres termes, une certaine suite de graphes, répondant chacun aux hypothèses de départ, converge vers un graphe dont la longueur est cette borne inférieure.

Ensuite, le mathématicien montre que ce graphe limite est doté des mêmes qualités que les graphes de la suite dont il est né Ce dernier point est important, car il n’est pas rare, en mathématiques, qu’une suite d’objets tous munis d’une même propriété la perdent après passage à la limite Ainsi, dans le plan, il existe bien un réseau de courbes de longueur minimale encadrant un nombre fixé de régions bornées d’aires données. De plus, Frank Morgan prouve que ce graphe minimal est constitué d’un assemblage d’arcs de cercles et de segments de droites se rejoignant aux sommets par groupes de trois, selon des angles de… 120°, l’indice d’un pavage hexagonal.

Dans le cas d’un pavage infini du plan par des cellules d’aire unité (égale à 1), on mesure le rapport longueur/aire pour la partie située dans un disque. Au début de l’année 1999, Frank Morgan montre qu’il est équivalent, d’une part, de tronçonner ainsi un pavage infini, puis d’estimer la meilleure limite de ce rapport lorsque le diamètre du disque tend vers l’infini et, d’autre part, de considérer, pour chaque entier n, le meilleur pavage à n régions (issu de son étude de 1994) et de calculer la limite du rapport longueur/aire associé quand n tend vers l’infini

De plus, il prouve qu’il existe un réseau de courbes correspondant à cette borne inférieure de tous les rapports limite Ainsi prolonge-t-il son résultat de 1994 à un pavage infini et, même

si la conjecture du nid d’abeilles n’est pas encore tombée à ce stade, l’existence d’une solution ne fait plus de doute.

Le pavage du plan en hexagones réguliers fournit un rapport limite de 4√12. Aussi, la preuve que ce nombre est justement la borne inférieure citée précédemment mettrait un point final à la conjecture. C’est chose faite en juin 1999, lorsque

Thomas Hales prouve que le meilleur rapport limite possible, pour un réseau de courbes planes délimitant une infinité de régions bornées et d’aire unité, est toujours supérieur à 4√12. La conjecture du nid d’abeilles devenait un théorème : le plus court réseau de frontières délimitant des régions planes d’aires égales est bien le pavage en hexagones réguliers adopté par les abeilles… depuis des millions d’années.

UN PROBLÈME DE FOND

Examinons le deuxième problème posé par les abeilles. L’astronome Kepler détermine les paramètres des trois losanges formant le fond d’une cellule, mais ses travaux passeront inaperçus L’étude de ce problème resurgit au début du XVIIIe siècle lorsque l’astronome Maraldi mesure le plus précisément possible les angles des losanges de raccordement (109° 28’et 70° 32’) et attribue aux abeilles l’adoption de cette forme par sa simplicité de fabrication et son aspect esthétique Les cellules étant des prismes hexagonaux terminés par trois losanges, Réaumur cherche quelle forme de ce type possède, pour un volume donné, une surface minimale Il confie le problème au

« À la fin les abeilles en sauraient trop, et l’excès de leur gloire en est la ruine » F

mathématicien suisse Samuel Koenig, qui publie dans les Mémoires de l’Académie une solution obtenue par le calcul différentiel. Il trouve, à 2 minutes d’arc près, les angles mesurés par Maraldi : les abeilles ont résolu un problème d’optimisation en utilisant les méthodes de Newton et Leibniz ! Cette interprétation est toutefois récusée par Fontenelle, secrétaire perpétuel de l’Académie, pour qui « à la fin les abeilles en sauraient trop, et l’excès de leur gloire en est la ruine ».

MARALDI ENCORE ET TOUJOURS

Une partie de la communauté scientifique reste troublée par le fait que les abeilles adoptent une forme si proche de la solution optimale sans opter carrément pour celle qui minimise la quantité de cire. D’autres mesures sont faites… mais rien n’y fait, les alvéoles persistent à respecter les angles de Maraldi ! En 1743, le mathématicien écossais Colin Maclaurin reprend le problème, révèle une erreur dans les calculs de Koenig et trouve, à la minute d’arc près, les angles de Maraldi. On découvrira la cause de l’erreur : les tables de logarithme utilisées par Koenig étaient fausses !

En postulant que les alvéoles sont élaborées à partir d’un prisme droit hexagonal , les

dimensions de ce dernier dépendent de la morphologie des abeilles et doivent répondre à certaines contraintes.

L’observation montre que la profondeur d’une cellule est environ trois fois le côté de l’hexagone régulier Aussi, nous détaillerons la construction de l’alvéole sur la base d’un prisme hexagonal de côté 1 et de hauteur 3. La face d’entrée à une aire de 3√3/2 et avec un fond d’alvéole plat, son volume vaudrait 9√ 3 /2 et sa surface 18 + 3√3/2, soit 20,598.

Existe-t-il une forme de même aire d’entrée (un hexagone régulier de côté 1) et de même volume total, dont l’aire des parois est plus petite encore ? Oui, la forme observée par Kepler et Maraldi, puis étudiée par Koenig et Maclaurin (voir la figure page 22) : son aire vaut 20,121, soit moins que celle à fond plat ; les losanges fermant la cellule ont pour diagonales √3 et √3/2. Le calcul des angles confirme les mesures de Maraldi

En 1964, Tóth, décidément passionné par les ruches, élabore une structure répondant aux mêmes contraintes, mais plus économique. L’aire des parois de la nouvelle forme est égale à environ  20,112, soit légèrement inférieure à celle de la forme de Maraldi, adoptée par les abeilles. Comme Tóth le fait remarquer, ce gain ne représente que

LE PROBLÈME DU NID D’ABEILLES EN DEUX DIMENSIONS

Il consiste à trouver les pavages d’une bande par des polygones convexes superposables les plus économiques en cire. Plusieurs cas de figure sont possibles (en haut, de a à g). Quand chaque alvéole a un point sur le bord opposé à celui de son ouverture, le pavage est dit « réduit » (g). Pour résoudre ce problème (en bas), Michael Bleicher et László Tóth tracent deux droites (h) D’1 et D’2 qui, parallèles aux bords (D1 et D2) de la bande, sont en contact avec au moins un point des régions ouvertes sur l’autre côté. Le pavage est alors constitué de parallélogrammes et de triangles (i, en rouge) dont le périmètre est minimal quand les premiers sont des rectangles et les seconds des triangles isocèles (en vert). La solution des abeilles (j, où x = 0,289) est l’un des pavages minimaux. a b c d e f g h i

0,34 % de l’aire de l’alvéole Il reste toutefois conscient que cette étude porte sur des parois d’épaisseur nulle, ce qui n’a pas de réalité, et envisage que les abeilles adoptent peut-être bien une surface minimale si l’épaisseur de cire formant les parois de leurs cellules est prise en compte Cette remarque était étonnamment visionnaire.

En 1994, Denis Weaire et Robert Phelan, du Trinity College, à Dublin, ont étudié des films de savon En injectant une solution savonneuse entre deux lames de verre, ils obtiennent précisément la forme de Tóth, qui serait donc apparemment une forme minimale. Toutefois, ils remarquent qu’en épaississant les parois des alvéoles, la structure des fonds bascule brutalement sur celle que les abeilles ont adoptée. Ainsi ces dernières utiliseraient bien la forme optimale.

UN NID EN DEUX DIMENSIONS

En 1965, Michael Bleicher et László Tóth se penchent sur le troisième problème, celui du nid d’abeilles en deux dimensions On cherche le pavage de plus petit périmètre d’une bande de plan ; ce pavage, constitué de cellules polygonales convexes superposables, est tel que chaque cellule possède un seul côté sur un bord de la bande (l’ouverture), et que, lorsque deux cellules sont superposées, les ouvertures se correspondent Les contraintes du problème ont deux conséquences. D’abord, deux cellules dont les ouvertures, ou bases, sont sur le même bord se déduisent l’une de l’autre par une translation ou par une symétrie par rapport à une droite perpendiculaire au bord. Ensuite, deux cellules dont les bases ne sont pas sur le même bord se déduisent l’une de l’autre

L’intuition géométrique des abeilles

par une symétrie selon l’axe médian des deux bords, éventuellement suivie d’une translation ou d’une symétrie ponctuelle dont le centre est situé sur cet axe médian. Les auteurs ont également recours à la notion de pavage réduit, quand chaque alvéole possède aussi un point sur le bord opposé de sa base Une fois ces contraintes posées, les mathématiciens montrent (voir l’encadré page ci-contre) que la solution des abeilles est l’une des plus économiques. Si beaucoup des énigmes mathématiques soulevées par l’architecture des nids d’abeilles sont résolues, plusieurs questions restent en suspens. Certes, le premier problème est entièrement élucidé dans son énoncé le plus général. Il en va différemment du deuxième problème : la forme polyédrale de Tóth est plus économique que celle de Maraldi pour fermer les alvéoles, mais n’y en a-t-il pas une autre encore moins gourmande en surface ? Qu’en est-il quand on n’impose pas aux cellules d’être construites à partir de prismes droits hexagonaux réguliers ? Il reste donc à résoudre le problème en ne fixant que les contraintes d’aire d’entrée et de volume de l’alvéole.

Le troisième problème traite justement de cela, mais en deux dimensions La démonstration que nous avons détaillée fixe des contraintes assez fortes : que se passe-t-il dans un cadre plus général ? Et enfin, qu’en est-il si l’épaisseur des parois est prise en compte dans le problème spatial ? Pas de doute, la surprenante architecture d’un nid d’abeilles garde encore quelques mystères…

Doit-on se ranger à l’avis de Kepler, selon qui « les abeilles sont douées d’une âme et, de ce fait, capables de faire de la géométrie » ?

L’auteur

> Alain Satabin ancien professeur de mathématiques au lycée Gaspard-Monge de CharlevilleMézières, est président de l’association Oméga-Ardenne astronomie pour la promotion de la vulgarisation scientifique.

> T. Hales, The honeycomb conjecture, Discrete and Computational Geometry, 2001.

> F. Morgan, The hexagonal honeycomb conjecture, Trans. AMS, 1999.

> D. Weaire et R. Phelan, Optimal design of honeycombs, Nature, 1994. À lire

Aux sources du collectif

Ensemble, tout devient possible. Telle pourrait être la devise des fourmis, abeilles et termites, tant ensemble, par milliers, ces insectes sont capables d’exploits. On comprend mieux désormais comment ils peuvent construire des nids parfois gigantesques sans plan établi et pourtant parfaitement adaptés : plonger en leur cœur donne le tournis. Ils sont si performants qu’ils inspirent d'autres architectes, humains cette fois, pour concevoir leurs bâtiments. Cette intelligence collective, fruit d’innombrables interactions, est mise en œuvre dans de nombreux contextes : construire un nid, donc, mais aussi franchir un obstacle, se débarrasser des cadavres…

Chez les insectes sociaux, les activités des individus sont coordonnées grâce à des réseaux complexes d’interactions. C’est le meilleur moyen de résoudre collectivement de multiples problèmes.

Une intelligence façon puzzle

G. Théraulaz, J. Gautrais, S. Blanco, R. Fournier et J.-L. Deneubourg

Les fourmis ont des comportements collectifs complexes et coopératifs. Ici, elles s’assemblent pour constituer un pont vivant leur permettant d’atteindre une cible hors de portée.

> Les insectes sociaux (fourmis, termites, abeilles…) sont capables de comportements collectifs intelligents.

En bref

> Ils ne résultent pas des capacités des individus pris isolément, mais de leurs interactions.

Les fourmilières, les termitières et les nids d’abeilles sont des chefs-d’œuvre d’architecture si complexes et si fonctionnels qu’on a du mal à croire qu’ils n’ont pas été pensés dans leur intégralité avant d’être construits, comme l’est n’importe quel bâtiment humain. Et pourtant, tel est bien le cas : il n’y a pas de « grand organisateur » ! De même, certains problèmes, tel le choix d’une source de nourriture ou d’un site de nidification, trouvent une solution sans qu’une quelconque entité ait une vue d’ensemble de la situation. La division du travail au sein d’une colonie témoigne également d’un bel ordonnancement qui semble régir les activités de chacun des membres. Mais à y regarder de plus près, l’ordre s’évanouit…

DES FOURMIS CONTRADICTOIRES

En effet, l’observation détaillée d’une fourmilière révèle des comportements individuels aléatoires, conflictuels et a priori peu compatibles avec de telles performances collectives Ainsi, au sein d’une colonie, il n’est pas rare qu’une fourmi détruise le travail qu’une autre a accompli peu avant. Comment des comportements individuels apparemment désordonnés et des interactions multiples entre individus peuvent-ils aller de pair avec un comportement collectif cohérent ?

Longtemps, savants et naturalistes se sont interrogés sur cette question de l’émergence de l’ordre à partir du désordre Et ce n’est qu’avec de nouveaux outils conceptuels développés en éthologie et en physique statistique que les mécanismes de coordination chez les insectes sociaux ont pu être révélés.

> Fondées sur des principes simples, ces interactions entraînent l’émergence de comportements complexes et autoorganisés.

> Des simulations mathématiques aident à comprendre les mécanismes en jeu dans cette intelligence collective.

Parmi ces mécanismes, les processus d’autoorganisation ont fait l’objet d’une attention particulière, car on les retrouve dans de nombreux comportements collectifs Ces phénomènes au cours desquels les éléments d’un système s’organisent « spontanément » sont bien connus en physique et en chimie sous le nom de « structures dissipatives », découvertes par Ilya Prigogine L’un des exemples les plus connus est celui des cellules de convection, ou cellules de Bénard, du nom d’Henri Bénard, qui, en 1900, les a mises en

Des fourmis qui ont accès à des cadavres uniformément répartis sur le pourtour d’une arène (a) transportent d’abord les cadavres et forment des tas disposés régulièrement sur le pourtour (b). Puis certains tas sont privilégiés, et, pour finir, les tas les plus gros attirent toujours plus de cadavres, dans un processus autocatalytique d’amplification (c et d). De plus, les tas sont régulièrement espacés.

La densité de cadavres influe sur le comportement des fourmis. Quand elle est faible, les fourmis forment des tas isolés qui fluctuent et disparaissent (a). Lorsqu’elle est élevée, les tas perdurent (b). Enfin, avec des cadavres dispersés sur toute la surface de l’arène et une densité encore plus importante, les fourmis bâtissent des « chambres » (c).

évidence en chauffant la face inférieure d’une couche de liquide visqueux Dès que la différence de température entre les deux faces du fluide dépasse une valeur critique, des rouleaux de convection apparaissent et s’organisent parallèlement les uns par rapport aux autres, formant d’étonnantes figures géométriques Les méthodes d’études de telles structures spatiotemporelles dans des systèmes physiques ou chimiques aident désormais à mieux comprendre l’émergence de la complexité dans les sociétés d’insectes

LES NÉCROPOLES DE FOURMIS

Illustrons nos propos en détaillant un comportement collectif que l’on constate chez de nombreuses espèces de fourmis : l’agrégation des cadavres. Il s’agit de l’un des multiples exemples de comportements collectifs connus chez les insectes sociaux qui reposent sur un mécanisme d’autoorganisation CChez les fourmis, d'autres phénomènes du même type interviennent également dans la recherche alimentaire et dans

certains aspects de la division du travail et de la construction du nid Chez les abeilles, ils jouent un rôle dans le choix des sources de nectar et de pollen ou d’un nouveau site de nidification. Enfin, chez les termites, ils interviennent dans la construction du nid

Les fourmis rassemblent les cadavres afin de réduire les risques d’infections dans la colonie. Toute fourmi morte libère des substances chimiques, dont l’acide oléique, qui incite les ouvrières à s’en emparer et à les rejeter à l’extérieur du nid. Les dépouilles sont agrégées et forment des tas que l’on nomme, par abus de langage, des « cimetières ». Ce comportement ne serait qu’une simple anecdote si une observation, faite dans notre laboratoire, n’avait relancé l’intérêt pour son étude

Lorsque des corps de fourmis sont dispersés sur le pourtour d’une arène à laquelle ont accès les ouvrières d’une colonie, ces dernières constituent en quelques heures plusieurs petits tas Puis, au cours du temps, les fourmis détruisent certains de ces tas et déplacent les cadavres sur d’autres tas jusqu’à ce que , au terme du

processus, seul subsiste un petit nombre d'entre eux, régulièrement espacés Ainsi, un motif spatial régulier à grande échelle émerge des activités individuelles. Il s’agit d’un comportement collectif complexe où une structure cohérente naît des interactions d’un grand nombre d’individus La compréhension de ce phénomène nécessite de considérer, d’une part, deux niveaux d’observation – individuel et collectif – et, d’autre part, l’étude de sa dynamique sur des échelles de temps compatibles avec le déroulement des différents processus. Pour expliquer et pour prévoir le comportement collectif, on détermine d’abord des lois statistiques du comportement d’un animal dans chacune des situations rencontrées Ces lois relient la nature et l’intensité des signaux environnementaux perçus par un individu et la probabilité qu’un comportement particulier apparaisse chez cet individu.

À partir de ces lois, on élabore ensuite un modèle de comportement individuel avec lequel on étudie le rôle des interactions des individus dans l’émergence du comportement collectif. Revenons à nos morts Dans l’expérience réalisée, le nombre de cadavres est constant au cours du temps ; quant à la cinétique de croissance des tas, elle est de type logistique. Une courbe de croissance dite « logistique » décrit l’évolution d’un phénomène où une phase de croissance exponentielle est suivie d’une phase où la croissance est

auto-inhibée : plus la taille du tas est importante, plus sa vitesse de croissance augmente, mais le processus autocatalytique s’interrompt quand toutes les dépouilles isolées ont disparu. Ensuite, la taille du tas varie autour d’une valeur moyenne. Comment ce mécanisme de croissance profite-t-il seulement à certains tas ?

LES LOIS DES POMPES FUNÈBRES

Pour répondre, on examine les comportements individuels de transport des cadavres, c’est-à-dire que l’on segmente les différentes situations rencontrées par une fourmi au cours de ses pérégrinations dans l’arène Que fait une fourmi lorsqu’elle rencontre des corps isolés ou des amas ? Sa propension à ramasser les cadavres est-elle constante ou dépend-elle des conditions rencontrées ? Pour chacune de ces situations, on détermine une probabilité d’exécuter une action en observant le comportement moyen des fourmis, puis l’on construit des lois de comportement statistiques qui reflètent le comportement moyen d’un grand nombre de fourmis confrontées à une même situation

Une fourmi transportant un cadavre le dépose (même quand aucun tas n’est présent à l’endroit du dépôt) au bout d’une longueur qui suit une loi de décroissance exponentielle Cette loi indique que ce comportement est un

Les fourmis Oecophylla construisent un nid grâce à la coopération de tous les individus de la colonie. Elles rapprochent les bords de deux feuilles qu’elles attachent ensuite avec la soie sécrétée par les larves.

De la masse d’une colonie de fourmis émerge un comportement donné grâce à des boucles de rétroaction.

Décisions collectives !

Chez les insectes sociaux, les processus d’autoorganisation conduisent à l’émergence de structures collectives à partir des interactions individuelles, sans que ces structures soient codées explicitement chez les individus. Ces phénomènes sont caractérisés par des boucles de rétroaction positive et négative, des bifurcations et, dans certains cas, plusieurs états stables sont possibles. Les comportements des insectes sociaux sont souvent associés à des boucles de rétroaction positives. Grâce à ces boucles, les fluctuations (des écarts à la moyenne) sont amplifiées et donnent naissance à une structure. Elles jouent un rôle fondamental dans la genèse de structures. Les boucles de rétroaction négative les stabilisent en contrebalançant les effets des boucles de rétroaction positive. Les bifurcations traduisent le changement brutal du comportement d’un système autoorganisé lorsque certains paramètres du système varient.

Par exemple, ces bifurcations s’observent dans le recrutement alimentaire de masse chez les fourmis quand une colonie est confrontée à l’exploitation de deux sources de nourriture identiques. Pour assurer le

recrutement de récolteuses, les fourmis déposent des phéromones sur la piste lorsqu’elles se déplacent de la source de nourriture vers le nid. Quand la taille de la colonie est petite, les deux sources de nourriture sont exploitées de façon identique. En revanche, quand la taille de la colonie et le nombre de récolteuses augmentent, une bifurcation se produit : l’une des sources est plus exploitée que l’autre. Ce phénomène résulte des fluctuations de concentration de phéromones sur chacune des deux pistes : à mesure que de plus en plus de fourmis choisissent la piste où la concentration est la plus élevée, cette concentration ne cesse d’augmenter.

Ce processus est autocatalytique, car les fourmis qui rentrent au nid renforcent toujours davantage la piste la plus marquée. Au final, les fourmis récolteuses n’empruntent plus qu’une seule des deux branches. Ce phénomène explique des prises de décisions collectives qui émergent à l’échelle d’une colonie.

Enfin, quand plusieurs états stables coexistent, le système converge vers l’un ou l’autre de ces états selon son histoire.

La complexité des nids des termites Apicotermes découle d’un décalage spatial et temporel dans la croissance des éléments qui les composent

phénomène sans mémoire apparente (on parle de « comportement markovien ») : la probabilité qu’une fourmi dépose le cadavre transporté ne dépend pas de son histoire antérieure, c’est-àdire du temps déjà passé à le transporter. Durant chaque intervalle de temps, le nombre de fourmis qui déposent leur charge est proportionnel au nombre de fourmis occupées à ce transport

De surcroît , plus un tas est important , moins une fourmi est portée à y prélever un cadavre, mais plus elle a tendance à en ajouter. En revanche, les corps isolés sont rapidement emportés L’activation des dépôts et l’inhibition des prises lorsque la taille des tas augmente sont les deux mécanismes responsables de leur croissance autocatalytique

La fourmi estime - t- elle la taille de l’amas près duquel elle se trouve ? Non, car le rayon de perception des fourmis Messor utilisées dans cette expérience est d’environ 5 millimètres , alors que les tas sont en moyenne 10 fois plus gros Or, avec un comportement de type markovien, dont le seul paramètre est le nombre de cadavres perçus par la fourmi dans un rayon de perception très petit par rapport à la taille du tas, on peut reconstruire le comportement statistique de prises et de dépôts observé lorsque la taille du tas varie. Pour une fourmi, la différence essentielle entre un tas de petite taille et un de grande taille tient à la durée moyenne qu’elle passe dans des zones de forte densité de cadavres associées à une forte probabilité de dépôt. En d’autres termes, plus un tas est grand, plus la fourmi passe du temps à le parcourir et plus elle

a de chances d’y déposer un cadavre. Ainsi, il n’est pas nécessaire que la fourmi connaisse la taille d’un tas pour se délester de son poids

Outre ces lois de prise et de dépôt, on identifie les caractéristiques du déplacement des fourmis qui permet aux cadavres de « diffuser » dans l’espace L’analyse des trajectoires des fourmis rend possible le calcul de leur vitesse moyenne de déplacement, et de la probabilité de changer de direction au cours du temps. Dans une arène, les fourmis se déplacent le plus souvent en suivant les bords internes : ce tropisme naturel est nommé « thigmotactisme »

CHANGEMENT D’ÉCHELLE

Ainsi, le déplacement des fourmis est fortement contraint par le milieu et tout changement de direction se traduit soit par un éloignement du bord de l’enceinte, soit par un demi-tour. La distribution des distances parcourues par une fourmi avant qu’elle ne fasse demi-tour suit aussi une loi de décroissance exponentielle similaire à celle que l’on relève pour le dépôt spontané des cadavres. Nous disposons désormais des lois de comportement individuel pour les prises, les dépôts et les déplacements Comment entraînent-elles une organisation spatiale régulière à une échelle qui dépasse largement celle des fourmis ?

Dans un premier temps, on peut vérifier, et nous l’avons fait, que ces lois sont suffisantes pour reproduire les structures étudiées au moyen d’une simulation informatique où des fourmis virtuelles reproduisent les comportements individuels des

Les termites du genre Apicotermes ont développé l’art de la construction des nids à un niveau inégalé dans le règne animal. Ces insectes vivent exclusivement en Afrique, dans la forêt et la savane, et construisent leurs nids sous terre entre 20 et 60 centimètres de profondeur. De forme ovoïde et pouvant atteindre une hauteur de quelques dizaines de centimètres, les nids sont couverts de petits orifices comme des gargouilles disposées en lignes très régulièrement espacées et qui parcourent toute la circonférence externe de la paroi (voir la figure a)

L’ORIGINE DE LA COMPLEXITÉ

L’intérieur est constitué d’une succession de vastes chambres superposées reliées par des rampes linéaires et hélicoïdales (b et c)

Les ouvriers termites construisent ces nids spectaculaires au moyen de boulettes de terre. Les insectes sécrètent également une phéromone de construction dont ils imprègnent les boulettes et qui guide leur comportement bâtisseur. La dynamique collective qui résulte des interactions entre ces insectes et les structures qu’ils construisent produit une boucle de rétroaction complexe : l’architecture

du nid dicte à chaque instant les espaces accessibles aux termites ; la densité des individus dans les di érentes zones du nid détermine à son tour la concentration de phéromone de construction qui y est présente ; et enfin cette dernière sert de gabarit pour le remodelage de l’architecture du nid par les termites. Les simulations numériques d’un modèle mathématique intégrant l’ensemble de ces processus reproduisent fidèlement la structure des nids d’Apicotermes avec des planchers régulièrement espacés qui sont reliés en certains endroits par des rampes linéaires et hélicoïdales (f) L’analyse du modèle montre également que ces rampes proviennent de la création de défauts topologiques ou de dislocations. Au cours du remodelage du nid par les termites, il arrive que des planchers contigus ne soient plus alignés. Ce désalignement crée alors soit des dislocations dites « coin » au niveau desquelles apparaissent des rampes linéaires reliant les étages adjacents, soit des dislocations « vis » (un désalignement des planchers autour d’un plan de glissement) qui fournissent l’axe de rotation autour duquel apparaissent des rampes hélicoïdales (d et e). Ainsi la complexité des nids des Apicotermes découle d’un décalage spatial et temporel dans la croissance des di érents éléments qui les composent.

fourmis réelles. L’étape suivante consiste à identifier les contributions des différents mécanismes intervenant dans la formation des structures collectives

Cependant, les propriétés collectives observées se déduisent difficilement de la connaissance des lois statistiques du comportement individuel Par exemple, ces lois ne nous aident pas à prédire directement l’évolution du nombre et de l’organisation spatiale des tas. Cette difficulté est liée en grande partie au comportement non linéaire des lois macroscopiques qui résultent des interactions impliquées dans l’agrégation des cadavres Par conséquent, on doit expliciter ces lois, et un modèle mathématique, à l’échelle macroscopique (par opposition à l’échelle individuelle), améliore notre compréhension du système en autorisant une analyse des situations complexes où de multiples variables sont couplées et sur lesquelles l’intuition est inopérante.

À partir des lois statistiques de comportement des individus, on peut obtenir les lois régissant les grandeurs examinées à l’échelle collective, telles la densité de cadavres ou celle de fourmis vivantes en chaque point de l’espace. On dispose alors d’un modèle mathématique déterministe de l’évolution de ces champs de densité. Grâce aux techniques d’analyse des systèmes non linéaires, on peut caractériser le rôle des différents paramètres du comportement individuel et de l’environnement sur l’ensemble des propriétés qui émergent au niveau collectif.

Le principal intérêt d’un modèle mathématique est de déterminer les effets qualitatifs et quantitatifs

de chaque paramètre sur la dynamique et les caractéristiques spatiales et temporelles des structures collectives Un modèle fournit également des explications contre-intuitives et des prédictions surprenantes. L’analyse du modèle montre qu’il existe une densité critique de cadavres en deçà de laquelle les fourmis ne peuvent former d’agrégats

LE JARDIN AUX SENTIERS QUI BIFURQUENT

Cette prédiction est vérifiée expérimentalement lorsque la densité de cadavres est petite : aussitôt apparu , un petit tas est rapidement détruit. La densité initiale joue ici le rôle d’un paramètre dit « de bifurcation » qui influe sur le comportement qualitatif du système : certains changements de la valeur de ce paramètre entraînent l’apparition de nouvelles solutions. L’augmentation de la densité fait passer d’une répartition homogène des cadavres à une

La description de phénomènes collectifs en biologie et en physique par une même famille de modèles atteste des principes génériques d’organisation

autre solution spatiale caractérisée par un certain nombre de tas régulièrement distribués Pour des densités supérieures , de nouvelles solutions, notablement différentes des tas obtenus à faible densité, sont possibles. Ainsi, avec une très haute densité de cadavres, les fourmis élaborent plusieurs « chambres » séparées par des « murs ». Ces propriétés résultent des interactions non linéaires des différents processus qui gouvernent l’agrégation des corps . Elles sont en quelque sorte « contenues » de façon latente dans les lois du comportement individuel , et seule l’analyse du modèle macroscopique les révèle. Grâce à ces propriétés qui se manifestent au niveau collectif, une colonie produit des structures spatiales di ff érentes lorsque les conditions environnementales sont modifiées sans que les fourmis changent leur comportement. Une autre propriété est la régularité des structures produites, propriété qui avait initialement retenu notre attention. Le modèle en dévoile la cause : les fourmis qui assurent la diffusion des cadavres dans tout l’espace sont des vecteurs de communication entre les agrégats Cette diffusion rend les échanges entre deux tas d’autant plus importants qu’ils sont proches l’un de l’autre. Les prises incitant les prises et les dépôts les dépôts, dès qu’une petite fluctuation de taille apparaît sur un tas, elle est amplifiée et conduit à la disparition de l’autre. Au-delà d’une certaine distance entre deux amas, l’intensité des échanges devient suffisamment faible pour qu’ils puissent coexister

L’INTELLIGENCE ÉPARPILLÉE, DISPERSÉE, VENTILÉE…

Par ailleurs, l’analyse du modèle montre qu’un changement des valeurs de certains paramètres du comportement des fourmis se traduit par des différences qualitatives importantes des structures collectives Ainsi, la distance moyenne parcourue par une fourmi avant de faire demi-tour, lorsqu’elle longe la paroi interne de l’arène, influe notablement sur la dynamique d’agrégation et le nombre de tas produits Quand cette distance est grande, les fourmis diffusent beaucoup plus rapidement : tous les tas de l’arène échangent des cadavres et seul un très petit nombre de gros tas subsiste. En revanche, lorsque la distance parcourue avant de changer de

direction est courte, l’échange de cadavres entre deux tas voisins devient négligeable, car la diffusion est trop faible, et les tas sont plus nombreux.

Le modèle mathématique déterministe que nous avons élaboré appartient à la classe générale des modèles non linéaires de transitions de phase employés en physique pour expliquer des phénomènes tels que la croissance de gouttes de liquide dans un nuage de vapeur.

La description de certains phénomènes collectifs en biologie et en physique par une même famille de modèles atteste l’existence de principes génériques d’organisation à l’œuvre dans ces systèmes. On peut notamment élucider de multiples phénomènes collectifs chez les insectes sociaux, et, plus généralement, dans les sociétés animales. On comprend alors comment l’intelligence peut être éparpillée, dispersée, ventilée…

Les auteurs

> Guy Théraulaz est directeur de recherche au Centre de recherches sur la cognition animale, à Toulouse.

> Jacques Gautrais est chargé de recherche au Centre de recherches sur la cognition animale, à Toulouse.

> Stéphane Blanco est maître de conférences au Laboratoire d’énergétique, à Toulouse.

> Richard Fournier est professeur au Laboratoire d’énergétique, à Toulouse.

> Jean-Louis Deneubourg est professeur émérite à l’université libre de Bruxelles et maître de recherche au FNRS.

À lire

> A. Heyde et al., Self-organized biotectonics of termite nests, PNAS, 2021.

> A. Khuong et al., Stigmergic construction and topochemical information shape ant nest architecture, PNAS, 2016.

> G. Théraulaz et al., Spatial patterns in ant colonies, PNAS, 2002.

Des faiseurs de planète

À quoi ressemblerait la Terre sans les insectes sociaux ? Assurément pas à celle que nous connaissons.

Pris individuellement, ils sont certes petits, mais ensemble ils transforment les écosystèmes dans des proportions insoupçonnées. Dans les savanes, ils créent des hot spots de biodiversité végétale dont les herbivores profitent, ou bien modifient les chaînes alimentaires et mettent les lions au régime. Ils seraient même capables de modifier le climat ! Mais là où leur influence se fait le plus ressentir, c’est dans l’agriculture : 80 % des espèces cultivées dépendent d’insectes pollinisateurs. Nos paysages seraient vraiment di érents sans eux.

On associe souvent aux abeilles domestiques une image de bienfaits pour la nature. Il n’en est rien. Elles sont certes essentielles pour l’agriculture, mais c’est au prix de dommages sur l’environnement.

Le paradoxe des abeilles mellifères

Alison McAfee

Pour beaucoup de gens , les abeilles mellifères Apis mellifera symbolisent la prospérité, la durabilité et le respect de l’environnement Mais , en ma qualité de spécialiste de ces insectes, je dois avouer que seul le premier élément de cette liste me paraît défendable . En effet , bien qu’elles soient particulièrement importantes pour l’agriculture en ce qu’elles pollinisent nombre de cultures vivrières , les abeilles mellifères ont l’inconvénient de déstabiliser les écosystèmes naturels en entrant en compétition avec les espèces indigènes , dont certaines sont en danger d’extinction

SE TROMPER D’ABEILLE

L’essor de l’apiculture de loisir, qui est aujourd’hui une activité à la mode pour nombre de particuliers, a été la conséquence de fortes campagnes de sensibilisation visant à « sauver les abeilles » Ainsi, aux États-Unis, on compte des centaines de milliers d’apiculteurs amateurs, tandis qu’en France, ils étaient quelque 70 000. Mais Apis mellifera en tant qu’espèce est celle qui a le moins besoin d’être sauvée parmi les abeilles Les médias leur accordent une attention disproportionnée par rapport aux pollinisateurs indigènes , et des messages confus ont conduit de nombreux citoyens à croire qu’ils œuvraient pour l’environnement en revêtant le voile de l’apiculteur Malheureusement, ils font probablement plus de mal que de bien. « L’apiculture est faite pour les êtres humains ; ce n’est pas une pratique de conservation pour la

― En bref

> Avec l’idée d’aider à la préservation de l’environnement, beaucoup de particuliers se sont lancés dans l’apiculture récréative.

> Avec les professionnels, ils contribuent à augmenter considérablement les populations d’abeilles domestiques.

> Cependant, ces insectes entrent en concurrence déloyale avec les espèces sauvages et indigènes qui, pourtant, pollinisent la majorité des plantes cultivées.

> Les e orts de protection et les fonds alloués doivent donc être redirigés.

biodiversité », explique Sheila Colla, de l’université York, à Toronto, au Canada. « Les gens pensent à tort qu’élever des abeilles mellifères, ou simplement les aider, serait aussi une aide pour les cousines indigènes, qui sont, elles, vraiment menacées d’extinction. »

La biologiste a récemment publié une analyse de près d’un millier de commentaires soumis par des citoyens en réponse au projet de plan d’action pour la santé des pollinisateurs de l’Ontario, une proposition qui prévoyait une réglementation plus stricte des pesticides néonicotinoïdes (des substances reconnues pour leur neurotoxicité sur les abeilles, entre autres, et soupçonnées d’être impliquées dans le syndrome d’effondrement de leurs colonies). Malgré l’intérêt marqué du public pour les abeilles et la pollinisation, ainsi que le soutien important apporté à une réglementation plus stricte des pesticides , Sheila Colla et ses collègues ont constaté que les citoyens avaient une compréhension étonnamment faible de la diversité des pollinisateurs et de leur rôle dans la pollinisation. « L’accent mis sur les néonicotinoïdes, les risques qui y sont associés et les abeilles domestiques a détourné une grande partie des ressources consacrées à la protection des pollinisateurs sauvages contre les menaces les plus importantes qui pèsent sur eux », déplore la spécialiste. Elle est à juste titre frustrée par le détournement de l’attention vers la sauvegarde des abeilles domestiques alors que, du point de vue des défenseurs de l’environnement, ce sont les espèces indigènes qui ont le plus besoin d’être soutenues.

1,3 million

C’est le nombre

de colonies d’Apis

mellifera en France

Et si les entreprises apicoles, donc centrées sur l’abeille domestique, appuient souvent, en parallèle, des initiatives en faveur des abeilles indigènes (alors que pourtant, elles tirent bénéfice de leur déclin), comme le développement d’habitats qui leur sont favorables, les contributions financières sont dérisoires par rapport à ce qui devrait être alloué pour vraiment soutenir cette cause.

Pour une raison inconnue, peut-être parce qu’elles sont petites, les abeilles mellifères ne sont généralement pas considérées comme l’animal d’élevage intensif qu’elles sont L’Amérique du Nord compte des millions de colonies d’Apis mellifera (en France, elles seraient 1,3  million). À raison d’environ 30 000 abeilles par colonie (la taille d’une unité de pollinisation), cela représente des milliards d’abeilles mellifères, beaucoup plus que le nombre d’habitants. Les fortes densités de colonies d’abeilles mellifères, butineuses extrêmement généralistes, en monopolisant les ressources florales, augmentent la concurrence entre les pollinisateurs indigènes pour le butinage, ce qui accroît encore la pression sur ces espèces déjà en déclin

DE L’ABEILLE AUX CANARIES

Cependant , déterminer l’influence des abeilles mellifères sur les écosystèmes naturels impose de procéder à des tests empiriques Il est possible, par exemple, que les différences dans les habitudes de butinage (heures de la journée, espèces privilégiées , saisonnalité… ) avec les abeilles indigènes n’entraînent qu’une faible concurrence effective Mais comment déterminer l’effet de leur introduction sur la communauté pollinisatrice indigène alors qu’elles sont déjà si omniprésentes ?

Heureusement, ce n’est pas le cas des îles Canaries. Et Alfredo Valido et Pedro Jordano, du Conseil espagnol de la recherche, y ont vu une chance. Dans les hautes terres du parc national

Un xylocope

Les abeilles sauvages

En France, 15 % seulement de la pollinisation des plantes à fleurs cultivées est e ectuée par les abeilles domestiques, le reste (85 %) l’étant par des insectes sauvages. Parmi eux, on compte une multitude d’abeilles, le plus souvent solitaires, et se distinguant d’Apis mellifera en ce qu’elles ne produisent pas de miel. Ces abeilles sauvages sont plus pacifiques que leurs cousines domestiques, et la plupart n’ont pas de dard. Environ 20 000 espèces ont été décrites à travers le monde, dont un millier en France. Certaines espèces ne dépendent que d’un seul type

de fleur : par exemple, l’anthocope du pavot a besoin du coquelicot pour tapisser son nid dans le sol. À l’inverse, les tomates ne peuvent être pollinisées e cacement que par les bourdons, qui sont les seuls à pouvoir faire vibrer ces fleurs pour qu’elles libèrent leur pollen. Pourtant, selon l’Union internationale pour la conservation de la nature (UICN), 46 % des espèces de bourdons d’Europe sont en déclin et 80 % sont menacées. En France, on rencontre six familles aux caractéristiques sociales similaires, mais se distinguant par leur source de nectar : les Andrenidae

(Andrena, Panurgus…) sont les plus répandues, sont spécifiques des astéracées (laitues, artichauts…) ; les Apidae (Apis, Xylocopa…) parmi lesquelles figurent l’abeille domestique Apis mellifera et les bourdons (le genre Bombus) ; Colletidae (Colletes et Hylaeus…) ; Halictidae (Halictus, Sphecodes…) pollinisatrices notamment du maïs et du tournesol ; Megachilidae (Megachile, Osmia…) essentielles pour les carottes, la luzerne… ; Melittidae (Dasypoda, Melitta…). C’est dire si les abeilles sauvages sont nécessaires à notre alimentation ! Loïc Mangin

de Teide, des milliers de colonies d’abeilles mellifères sont introduites de façon saisonnière pour la production de miel et retirées dès que les fleurs cessent de produire du nectar Des conditions idéales pour mener des expérimentations , dont les résultats , publiés en  2019, mettent à mal l’image des abeilles mellifères… De fait, leur introduction a réduit la connectivité des réseaux plantes-pollinisateurs. L’imbrication et la modularité, deux indicateurs de la résilience des écosystèmes, ont également diminué.

Alors que certaines espèces de plantes ont bénéficié d’une meilleure fructification , les fruits prélevés à proximité des ruchers ne contenaient que des graines avortées. « L’impact des ruches est si important que l’on peut détecter des perturbations entre les plantes et les pollinisateurs dès le lendemain de l’installation de ces dispositifs, constate Alfredo Valido. En introduisant des dizaines ou des centaines de ruches, la densité relative des abeilles mellifères augmente de façon exponentielle par rapport aux pollinisateurs sauvages », poursuit-il. Cela entraîne une réduction drastique des ressources florales (pollen et nectar) à l’intérieur de la zone de butinage Et son collègue conclut : « L’apiculture aurait des e ff ets plus néfastes qu’on ne l’imaginait sur la biodiversité. »

Selon les chercheurs, ce qu’ils ont montré pour les îles Canaries vaut pour d’autres écosystèmes où les abeilles mellifères sont introduites, même si l’impact spécifique de l’apiculture peut varier. En effet , Apis mellifera ne parvient pas toujours à s’imposer au sommet d’un réseau

local de pollinisateurs et leur suprématie sur les abeilles indigènes dépend de nombreux facteurs. Par exemple, Nicholas Balfour et ses collègues de l’université du Sussex , en Angleterre , ont constaté que les bourdons indigènes restaient de meilleurs compétiteurs sur les fleurs tubulaires de lavande, en partie grâce à leur proboscis (langue) plus long Ailleurs encore, les abeilles domestiques ne semblent pas avoir autant d’influence que dans les îles Canaries. Ainsi, après leur introduction dans le nord de la Patagonie , les bourdons et les abeilles mellifères non indigènes ont supplanté les espèces indigènes en tant que visiteurs floraux les plus fréquents , mais cela n’a eu aucun effet sur les taux de visite réels des abeilles indigènes

PERTURBATEURS D’ÉCOSYSTÈMES

Bien que chaque écosystème ait ses propres particularités sur le plan des pollinisateurs et des plantes à fleurs présentes, les études pratiquées dans des contextes moins particuliers tendent à confirmer les résultats obtenus dans les îles Canaries De fait, des travaux menés en Amérique du Nord ont confirmé que les abeilles mellifères perturbaient bien le système autochtone de pollinisation. Autre constat : les abeilles mellifères sont aussi très efficaces pour polliniser certaines espèces de « mauvaises herbes », ce qui modifie et déstabilise l’ensemble des communautés végétales. Nombre de ces adventices sont également

Les apiculteurs adorent secrètement les plantes invasives : leur prolifération est

si lucrative…

envahissantes , notamment le genêt à balais Cytisus scoparius , la ronce d’Arménie Rubus armeniacus , la renouée du Japon Reynoutria japonica… Or les apiculteurs adorent secrètement les plantes invasives. Leur prolifération fournit un flux de nectar lucratif et prévisible.

Même avec cet apport de nourriture , les abeilles mellifères, et a fortiori les espèces indigènes , n’en ont parfois pas assez . Dans les basses terres de Vancouver, au Canada , j’ai entretenu à des fins de recherches un ensemble de 15 à 20  ruches Bien qu’elles fussent installées dans une zone à forte densité végétale, je n’ai jamais eu autant de difficulté à garder mes abeilles en vie.

LE SPECTRE DU VARROA

Les ruches étaient infestées de maladies. J’ai même euthanasié une colonie présentant des symptômes de loque américaine, une pathologie très infectieuse due à la bactérie Paenibacillus larvae. Bien qu’en début de saison elles aient été totalement exemptes de Varroa destructor, cet acarien parasite dévastateur, les ruches ont dû être traitées à l’acaricide à la fin de l’été De plus, les colonies n’ont pas produit de miel Dans certains endroits, la densité des colonies est devenue trop élevée, facilitant la propagation des maladies et exacerbant les problèmes de mauvaise alimentation S’il est si difficile de garder en bonne santé des abeilles domestiques, comment ne pas imaginer que les pollinisateurs sauvages souffrent durement ?

Pourtant, nous ne devons pas les négliger. Je voyais dans les abeilles mellifères une espèce passerelle et croyais que l’intérêt porté à leur santé et à leur prospérité serait aussi bénéfique aux espèces indigènes. Cela a pu être le cas en de rares occasions, mais il est de plus en plus évident que l’engouement pour les abeilles mellifères est délétère pour les abeilles indigènes Et désormais, je regarde l’apiculture d’un autre œil.

L’autrice

> Alison McAfee est chercheuse à l’université de ColombieBritannique, au Canada.

Cet article est une traduction de « The problem with honey bees », paru sur le site Scientificamerican.com le 4 novembre 2020.

À lire

> L. Foster et al., Mechanisms of pathogen and pesticide resistance in honey bees, Physiology, 2024.

> A. Nicholls et al., Understanding public and stakeholder attitudes in pollinator conservation policy development, Environmental Science & Policy, 2020.

> A. Valido et al., Honeybees disrupt the structure and functionality of plant-pollinator networks, Scientific Reports, 2019.

RENDEZ- VOUS

P. 112

REBONDISSEMENTS

DES ACTUALITÉS SUR LES THÈMES DES HORS-SÉRIES PRÉCÉDENTS

P. 118

LES INCONTOURNABLES

DES LIVRES, DES EXPOSITIONS, DES PODCASTS… À NE PAS MANQUER

P. 110

EN IMAGE UNE IMAGE QUI A RÉCEMMENT FAIT L’ACTUALITÉ

P. 116

INFOGRAPHIE

UN BON SCHÉMA VAUT MIEUX QU’UN LONG DISCOURS

Une comète superstar

Le 9 janvier 2023 pour l’un et le 22 février de la même année pour l’autre, l’observatoire de la Montagne Pourpre (Tsuchinshan en mandarin), près de la ville de Nankin, en Chine, et l’Asteroid Terrestrial-impact Last Alert System (Atlas), un système de surveillance astronomique robotisé géré par l’institut d’astronomie de l’université de Hawaii, ont repéré indépendamment une nouvelle comète baptisée C/2023 A3 (TsuchinshanAtlas), venue du fond du nuage d’Oort. Elle a atteint son périhélie (le point de la trajectoire le plus proche du Soleil) le 27 septembre 2024. C’est donc à cette période que, chaleur oblige, l’objet céleste s’est paré d’une queue de gaz et de poussières le rendant possiblement visible depuis la Terre à l’œil nu, en fonction de son éclat apparent. Ce fut bien le cas, grâce notamment à plusieurs circonstances favorables : par exemple, début octobre, la queue bénéficiait d’un rétroéclairage solaire, et sa magnitude fut maximale le 9 de ce mois-là. Ce fut l’occasion pour beaucoup d’astronomes, amateurs ou non, de rivaliser en clichés spectaculaires, tel celui-ci, sélectionné par la Nasa. L’image a été prise à la fin mai 2024, lorsque la comète (en haut, page ci-contre) est passée presque devant deux galaxies lointaines (ci-contre et ci-dessous).

Loïc Mangin

REBONDISSEMENTS

HORS-SÉRIE N° 125 : DERNIÈRES NOUVELLES DE L’INFINI

Un trou noir « granivore » très gourmand

« James-Webb » a repéré, avec « Chandra », un trou noir supermassif qui est 40 fois trop brillant par rapport à la théorie. Mais on peut l’expliquer…

Le télescope spatial James-Webb (JWST) est l’œil le plus perçant jamais construit pour scruter l’espace : en portant son regard « infiniment » loin, il nous apporte nombre d’informations cruciales sur la jeunesse de l’Univers, avec des images à chaque fois spectaculaires, le Hors-Série n° 125 : « Dernières nouvelles de l’infini » en apportait des preuves éclatantes ! Depuis juin 2022, date de la mise en service de l’engin, les découvertes se succèdent. L’une des dernières en date concerne la formation des trous noirs supermassifs nichés au cœur de la plupart des galaxies, notamment la nôtre, la Voie lactée. Observés de plus en plus loin dans l’Univers, ils se seraient donc formés très tôt : mais comment ont-ils pu accumuler autant de matière en si peu de temps ? C’est une énigme. Un élément de réponse est apporté par les résultats récents des équipes du JWST, à la Nasa, qui se sont associées à celles de l’observatoire Chandra, un autre télescope spatial, conçu pour étudier le rayonnement X émis par di érents objets célestes. Dans le catalogue « Cosmos Legacy Survey » de milliers d’objets recensés par ce dernier satellite, les astronomes ont débusqué un objet étonnant : le trou noir LID-568, situé dans une galaxie naine, observée telle qu’elle

était 1,5 milliard d’années seulement après le Big Bang. Il s’agit d’un trou noir supermassif, mais de faible masse, 7,2 millions de masses solaires tout de même, qui a la particularité d’aspirer la matière à une vitesse phénoménale, supérieure à plus de 40 fois la limite théorique. Cette « barrière » théorique – la limite d’Eddington, du nom de l’astrophysicien britannique Arthur Eddington, qui l’a établie pour la première fois en 1921 – a été définie au départ pour des étoiles : elle consiste en une valeur maximale que peut prendre leur luminosité, car au-delà la pression de radiation prendrait le pas sur la gravité, et les constituants de l’objet seraient éjectés. Appliqué à un trou noir, cela signifie qu’en théorie il ne peut pas dépasser un certain niveau

Une galaxie naine et un trou noir particulièrement glouton (vue d’artiste).

d’accrétion de matière.

Comment dès lors expliquer la voracité apparente de LID-568 ?

Selon les auteurs de l’étude il faut y voir une confirmation du scénario de formation des trous noirs supermassifs à partir de « graines », traces de l’e ondrement soit des premières étoiles soit de nuages de gaz. Et le trop fort rayonnement observé résulterait de l’ingestion par LID-568 d’une telle graine. L’émission est vraisemblablement transitoire, mais elle est une première preuve observationnelle de l’hypothèse des graines.

Loïc Mangin

H. Suh et al., A super-Eddingtonaccreting black hole ~1.5 Gyr a ter the Big Bang observed with JWST, Nature Astronomy, 2024.

REBONDISSEMENTS

HORS-SÉRIE N° 124 : SCIENCE ET SPORT

Pour gagner au disc golf !

Des physiciens ont déterminé la position idéale du pouce au lancer de disque de ce sport méconnu.

Il n’est peut-être pas encore une discipline olympique, mais il est en plein essor, et la science s’y intéresse, aussi aurait-il mérité sa place dans le Hors-Série n° 124 : « Science et sport ». Il s’agit du disc golf, qui associe frisbee et golf. L’objectif est de lancer des disques vers une cible, un « trou » qui consiste en un panier surmonté d’une couronne en chaînes métalliques, distantes de 60 à 250 mètres du point de lancer initial. Comme au golf, on peut le pratiquer sur un parcours de 18 cibles (parfois 27) et l’on dispose de plusieurs types de disques : des drivers pour les longues distances jusqu’aux putters pour finir le « trou » en passant par les « approches », ou mid-ranges, chacun se distinguant par son poids et son épaisseur.

La France compte 97 parcours,

contre plus de 7 000 aux États-Unis, qui dominent largement le paysage de ce sport. Et en toute logique, c’est dans ce pays, plus précisément au Berry College, à Mount Berry, en Géorgie, que des chercheurs se sont penchés sur la physique du disc golf. Avec la participation de membres de la Professional Disc Golf Association, Zachary Lindsey et ses collègues se sont intéressés à la meilleure façon de tenir un disque, ici un mid-range de 21,6 centimètres de diamètre, en se concentrant sur la position du pouce, le seul doigt situé au-dessus de l’engin volant. Ils ont mesuré la vitesse angulaire et la vitesse de déplacement de ce dernier, à l’aide de détecteurs embarqués, selon que le pouce est plus ou moins éloigné du bord. Résultat ?

Le meilleur compromis est obtenu avec un pouce à 3 centimètres du bord. Il ne vous reste plus qu’à aller briller dans l’un des 22 clubs de disc golf a liés à la Fédération nationale du sport en milieu rural (FNSMR) et reconnus par la Commission nationale de disc golf.

L. M.

HORS-SÉRIE N° 123 : DANS L’INTIMITÉ DES GÉANTS

Le cri du Parasaurolophus le soir au fond des bois

Le Hors-Série n° 123 : « Dans l’intimité des géants » s’en faisait largement l’écho, le champ des possibles dans l’étude des dinosaures s’élargit, et on a de plus en plus accès à la vie quotidienne des reptiles du Mésozoïque. Ainsi en est-il de leurs vocalises. Lors du 187e Congrès de la société américaine d’acoustique, qui s’est tenu du 18 au 22 novembre 2024, Hongjun Lin, de l’université de New York, a présenté les propriétés d’une reconstitution (virtuelle et physique) de la crête d’un Parasaurolophus. Cet animal à bec de canard, de la famille des hadrosaures, qui vivait il y a 70 millions à 80 millions d’années, a en e et le crâne prolongé vers l’arrière par une longue protubérance creuse. Le physicien a bel et bien confirmé que l’organe fonctionne comme une caisse de résonance, ce qui confirme une hypothèse en concurrence avec celle d’un rôle de thermorégulation.

L. M.

Acousticalsociety.org

N. Koch et al., The e ects of thumb position on backhand disc golf throws of a midrange disc, AIP Advances, 2024.

La meilleure façon de tenir un disque au disc golf.

HORS-SÉRIE

HORS-SÉRIE POUR LA SCIENCE

Rédacteur en chef adjoint : Loïc Mangin

MENSUEL POUR LA SCIENCE

Rédacteur en chef : François Lassagne

Rédactrice en chef adjointe : Marie-Neige Cordonnier

Rédacteurs : François Savatier et Sean Bailly

Développement numérique : Philippe Ribeau-Gésippe

Conception graphique : Céline Lapert et Ingrid Leroy

Direction artistique : Céline Lapert

Maquette : Pauline Bilbault, Raphaël Queruel, Ingrid Leroy et Ingrid Lhande

Réviseuses : Anne-Rozenn Jouble, Isabelle Bouchery, Maud Bruguière et Marie-Louise Desfray

A contribué à ce numéro : Philippe Grangier

Directeur marketing et développement : Frédéric-Alexandre Talec

Chef de produit marketing et partenariats : Ferdinand Moncaut ferdinand.moncaut@pourlascience.fr

Assistant administratif : Thomas Petrose

Direction des ressources humaines : Olivia Le Prévost Fabrication : Marianne Sigogne et Stéphanie Ho

Directeur de la publication et gérant : Nicolas Bréon

WWW.POURLASCIENCE.FR

170 bis bd du Montparnasse 75014 Paris

Tél. : 01 55 42 84 00

PUBLICITÉ FRANCE

stephanie.jullien@pourlascience.fr

ABONNEMENTS

Abonnement en ligne : https://www.pourlascience.fr/abonnements/ Courriel : serviceclients@groupepourlascience.fr

Tél. : 01 86 70 01 76 Du lundi au vendredi de 9 h à 13 h Adresse postale : Service Abonnement – Groupe Pour la Science 20, rue Rouget-de-Lisle 92130 Issy-les-Moulineaux

Tarif d'abonnement Formule Intégrale 1 an (12 numéros du magazine + 4 numéros Hors-Série + accès au site) : 99 euros Europe / Reste du monde : consulter https://www.pourlascience.fr/abonnements/

DIFFUSION

Contact réservé aux dépositaires et di useurs de presse – TBS SERVICES

Tél : 01 40 94 22 23

SCIENTIFIC AMERICAN

Interim Editor-in-Chief : Jeanna Bryner President : Kimberly Lau

2024. Scientific American, une division de Springer Nature America, Inc. Soumis aux lois et traités nationaux et internationaux sur la propriété intellectuelle. Tous droits réservés. Utilisé sous licence. Aucune partie de ce numéro ne peut être reproduite par un procédé mécanique, photographique ou électronique, ou sous la forme d’un enregistrement audio, ni stockée dans un système d’extraction, transmise ou copiée d’une autre manière pour un usage public ou privé sans l’autorisation écrite de l’éditeur. La marque et le nom commercial « Scientific American » sont la propriété de Scientific American, Inc. Licence accordée à « Pour la Science SARL ».

© Pour la Science SARL, 170 bis bd du Montparnasse, 75014 Paris. En application de la loi du 11 mars 1957, il est interdit de reproduire intégralement ou partiellement la présente revue sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20 rue des Grands-Augustins, 75006 Paris).

Origine du papier : Finlande • Taux de fibres recyclées : 0 % • « Eutrophisation » ou « Impact sur l’eau » : Ptot 0,003 kg/t

Imprimé en France – Maury imprimeur S.A. Malesherbes – N° d’imprimeur : 281 721 – N° d’édition : M0770726-01 – Dépôt légal : février 2025. Commission paritaire n° 0927K82079 – Distribution : MLP – ISSN 1 246-7685 – Directeur de la publication et gérant : Nicolas Bréon.

La Science dans votre boîte mail

Inscrivez-vous à notre newsletter hebdomadaire

La base de données qui rassemble toutes les femmes scientifques de renommée internationale

AcademiaNet offre un service unique aux instituts de recherche, aux journalistes et aux organisateurs de conférences qui recherchent des femmes d’exception dont l’expérience et les capacités de management complètent les compétences et la culture scientifque.

AcademiaNet, base de données regroupant toutes les femmes scientifques d’exception, offre:

• Le profl de plus des 2.300 femmes scientifques les plus qualifées dans chaque discipline – et distinguées par des organisations de scientifques ou des associations d’industriels renommées

• Des moteurs de recherche adaptés à des requêtes par discipline ou par domaine d’expertise

• Des reportages réguliers sur le thème »Women in Science«

Partenaires