POUR LA SCIENCE - AVRIL 2024

Mathématiques LE DESSOUS DES CARTES DU RULPIDON

Médecine UN MICROBIOTE CONTRE LA SCLÉROSE EN PLAQUES

Physique LE SKYRMION, BULLE MAGNÉTIQUE SOUS CONTRÔLE

Quelles perspectives pour la fin du siècle ?

04/24

MENSUEL POUR LA SCIENCE

Rédacteur en chef : François Lassagne

Rédacteurs en chef adjoints : Loïc Mangin, Marie-Neige Cordonnier

Rédacteurs : François Savatier, Sean Bailly

HORS-SÉRIE POUR LA SCIENCE

Rédacteur en chef adjoint : Loïc Mangin

Développement numérique : Philippe Ribeau-Gésippe

Directeur marketing et développement : Frédéric-Alexandre Talec

Chef de produit marketing : Ferdinand Moncaut

Directrice artistique : Céline Lapert

Maquette : Pauline Bilbault, Raphaël Queruel, Ingrid Leroy, Ingrid Lhande

Réviseuses : Anne-Rozenn Jouble, Maud Bruguière, Isabelle Bouchery et Camille Fontaine

Assistante administrative : Finoana Andriamialisoa

Directrice des ressources humaines : Olivia Le Prévost

Fabrication : Marianne Sigogne et Stéphanie Ho

Directeur de la publication et gérant : Nicolas Bréon

Ont également participé à ce numéro :

Patrice Bouchet, Quentin Chesnais, Nicolas Claidière, Guillaume Le Hir, Clémentine Laurens, Florian Moreau, Miria Ricchetti, Pierre Sepulchre, Bernard Zalc

PUBLICITÉ France

stephanie.jullien@pourlascience.fr

ABONNEMENTS

www.boutique.groupepourlascience.fr

Courriel : serviceclients@groupepourlascience.fr

Tél. : 01 86 70 01 76

Du lundi au vendredi de 8 h 30 à 12 h 30 et de 13 h 30 à 16 h 30

Adresse postale :

Service abonnement groupe Pour la Science 20 rue Rouget-de-Lisle

92130 Issy-les-Moulineaux.

Tarifs d’abonnement 1 an (12 numéros)

France métropolitaine : 59 euros – Europe : 71 euros

Reste du monde : 85,25 euros

DIFFUSION

Contact kiosques : À Juste Titres ; Alicia Abadie

Tél. 04 88 15 12 47

Information/modification de service/réassort : www.direct-editeurs.fr

DISTRIBUTION

MLP

ISSN 0 153-4092

Commission paritaire n° 0927K82079

Dépôt légal : 5636 – Avril 2024

N° d’édition : M0770558-01

www.pourlascience.fr

170 bis boulevard du Montparnasse – 75 014 Paris

Tél. 01 55 42 84 00

SCIENTIFIC AMERICAN

Editor in chief : Laura Helmuth

President : Kimberly Lau

2024, Scientific American, une division de Springer Nature America, Inc Soumis aux lois et traités nationaux et internationaux sur la propriété intellectuelle Tous droits réservés Utilisé sous licence Aucune partie de ce numéro ne peut être reproduite par un procédé mécanique, photographique ou électronique, ou sous la forme d’un enregistrement audio, ni stockée dans un système d’extraction, transmise ou copiée d’une autre manière pour un usage public ou privé sans l’autorisation écrite de l’éditeur La marque et le nom commercial «Scientific American» sont la propriété de Scientific American, Inc Licence accordée à «Pour la Science SARL» © Pour la Science SARL, 170 bis bd du Montparnasse, 75014 Paris En application de la loi du 11 mars 1957, il est interdit de reproduire intégralement ou partiellement la présente revue sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20 rue des Grands-Augustins, 75006 Paris).

Origine du papier : Autriche

Taux de fibres recyclées : 30 %

« Eutrophisation » ou « Impact sur l’eau » : Ptot 0,007 kg/tonne

Imprimé en France

Maury Imprimeur SA Malesherbes

N° d’imprimeur : 276 814

François Lassagne Rédacteur en chef

ALERTE BLANCHE

Les glaciers fondent. Le réchauffement climatique est à l’œuvre. Ne le sait-on pas déjà ? Ne le sait-on que trop bien ? Il est devenu difficile d’échapper aux gros titres des journaux, qui alertent régulièrement sur tel épisode caniculaire, telle sécheresse qui se prolonge – début mars, en Espagne, la Catalogne enregistrait son quarantième mois de pluviométrie en dessous des normales saisonnières. Et pourtant nous y revenons, encore : oui, les glaciers fondent, dans toutes les régions du monde.

Le bilan des vingt années passées, établi pour les glaciers continentaux, hors inlandsis du Groenland et de l’Antarctique, est édifiant. Et les projections pour la fin du siècle le sont davantage : en 2100, la moitié des glaciers de la planète auront disparu. Pourquoi insister sur ce constat de transformation profonde et rapide de l’environnement, provoqué par le changement climatique ? Parce qu’il aura des conséquences importantes pour des centaines de millions de personnes. Et parce que la science, patiemment, précisément, nous aide à comprendre de quoi sera fait notre futur. Les familiers de la montagne ont déjà un pied dans cet avenir plus chaud : le retrait des glaciers se voit, à l’œil nu, d’année en année.

Faut-il faire le deuil des géants blancs ? Pour certains d’entre eux, oui. Surtout, au-delà du deuil de certaines provinces du royaume des glaces, c’est celui d’un futur qui se contenterait de répéter le passé qui se profile. Une Terre à la température moyenne s’élevant de 2 °C ou plus est une autre Terre. La perspective de passer de l’une à l’autre suscite des réactions que la psychologie du deuil aide à comprendre.

Le deuil s’accompagne souvent du déni, de la colère, de la dépression. Voilà qui peut faire écho au climatoscepticisme et au mirage des solutions technologiques, aux réactions véhémentes contre « l’écoterrorisme », ou encore à l’écoanxiété. Le chemin du deuil se prolonge usuellement, in fine, par l’acceptation. L’acceptation, ici, d’un avenir différent… Il est plus que temps de s’engager dans cette phase, si l’on veut se donner la chance d’aller le plus lentement possible vers cet avenir et y entrer sans heurts. C’est le message que nous envoient les glaciers, aujourd’hui, depuis leurs avant-postes dans le futur climatique. Il n’est pas trop tard pour l’écouter. n

OMMAIRE s

N° 558 / Avril 2024

ACTUALITÉS GRANDS FORMATS

P. 6

ÉCHOS DES LABOS

• Fumer perturbe notre immunité, pour longtemps

• Un impact à l’origine de la Terre boule de neige ?

• L’extinction du Cambrien n’en était pas une

• Des « organoïdes » cérébraux améliorés

• Dans quel sens pivote l’arroseur de Feynman ?

• La théorie des cordes aurignaciennes

P. 18

LES LIVRES DU MOIS P. 20

DISPUTES ENVIRONNEMENTALES

Nouveaux OGM et vieilles recettes

Catherine Aubertin

P. 22

LES SCIENCES À LA LOUPE

Le prix des preuves

P. 44

MATHÉMATIQUES LE DESSOUS DES CARTES DU RULPIDON

Sylvie Benzoni-Gavage et Rémi Coulon

P. 58

PHYSIQUE LE SKYRMION : UNE BULLE MAGNÉTIQUE SOUS CONTRÔLE

CAHIER PARTENAIRE

PAGES I À III (APRÈS LA P. 67)

Stockage géologique de déchets radioactifs

Parrainé par

LETTRE D’INFORMATION

NE MANQUEZ PAS

LA PARUTION DE VOTRE MAGAZINE GRÂCE À LA NEWSLETTER

• Notre sélection d’articles

• Des offres préférentielles

• Nos autres magazines en kiosque

Inscrivez-vous www.pourlascience.fr fr

Yves Gingras

En couverture : © composition : Pour la Science ; Warming stripes: © Ed Hawkins / Wikimedia commons (CC BY-SA 4.0 Deed)

Les portraits des contributeurs sont de Seb Jarnot Ce numéro comporte un courrier de réabonnement posé sur le magazine sur une sélection d’abonnés.

L’étude des surfaces mathématiques trouées constitue un défi de taille. Pour appréhender le rulpidon, figure emblématique à trois trous, on s’interroge sur la possibilité de le « cartographier » en respectant certaines contraintes

Charles-Élie Fillion et Hélène Béa

Dans certains matériaux, des ensembles d’atomes sont susceptibles de former des « skyrmions » Ces structures magnétiques ont le potentiel de devenir un support de mémoire pour l’électronique

P. 52

IMMUNOLOGIE

UN « BON » MICROBIOTE CONTRE LA SCLÉROSE EN PLAQUES ?

Anne-Katrin Pröbstel et Lena Siewert

Dans la sclérose en plaques, le système immunitaire se retourne contre son propre organisme et détruit des neurones Mais un acteur inattendu pourrait bloquer cette attaque : le système digestif et sa flore intestinale.

P. 66

PHYSIQUE

QUAND LES SKYRMIONS PASSENT EN 3D

Sean Bailly

Les skyrmions sont des structures magnétiques aux propriétés étonnantes Leur géométrie, restreinte à deux dimensions, a lancé les physiciens sur les traces de leurs alter ego en trois dimensions, les hopfions.

P. 72

HISTOIRE DES SCIENCES

L’ASTRONOME QUI RÉFORMA LA SCIENCE

Stephen Case

Au début du xixe siècle, le savant John Herschel contribua à libérer la science du règne aristocratique en Grande-Bretagne et à la moderniser dans le monde entier

P. 24

GLACIOLOGIE

GLACIERS EN SURSIS

P. 25

« D’ICI À 2100, LA MOITIÉ DES GLACIERS AURONT DISPARU »

Entretien avec Romain Hugonnet et Étienne Berthier

Partout dans le monde, la fonte des glaciers continentaux s’intensifie En cartes, les perspectives pour la fin du siècle

P. 31

« NOUS DEVONS COMPRENDRE CE QUI BRISE LES PLATEFORMES GLACIAIRES »

Entretien avec Richard Alley

RENDEZ-VOUS

P. 80

LOGIQUE & CALCUL DES PREMIERS AUX PSEUDO-PREMIERS

Jean-Paul Delahaye

Les nombres premiers suscitent des travaux foisonnants Leur quête par des tests probabilistes a ouvert un riche terrain de jeu

P. 86

ART & SCIENCE

Prendre le bouleau du bon côté Loïc Mangin

P. 88

IDÉES DE PHYSIQUE

Tirer la nappe sous les couverts

Jean-Michel Courty et Édouard Kierlik

P. 92

CHRONIQUES DE L’ÉVOLUTION

Le plus ancien eucaryote pluricellulaire Hervé Le Guyader

Si les plateformes glaciaires géantes de l’Antarctique se détachaient, le niveau des mers s’élèverait de plusieurs mètres

P. 36

MINÉS PAR LE FOND

Giovanni Baccolo et Cristian Ferrari

Les glaciers alpins reculent désormais nettement chaque année, fragilisés par des mécanismes de fonte inédits

P. 96

SCIENCE & GASTRONOMIE Des soufflés de bonne tenue Hervé This

P. 98 À PICORER

LES EXOPLANÈTES GLACÉES GROSSISSENT EN S’ÉVAPORANT

Sur les milliers d’exoplanètes observées, celles ayant un rayon compris entre 1,6 et 2,2 fois celui de la Terre sont quasi absentes. Une explication se dessine.

Àce jour, plus de 5 000 exoplanètes ont été découvertes. Et certaines brillent par leur absence : les exoplanètes ayant un rayon d’environ deux fois celui de la Terre sont bien moins courantes. De part et d’autre de cet intervalle, les super-Terres, plus petites que deux fois notre monde, et les mini-Neptunes, plus grandes, abondent. Comment donc expliquer ce « rift subneptunien » ? Grâce à de nouvelles simulations numériques, Remo Burn, astrophysicien à l’institut Max-Planck, à Heidelberg, en Allemagne, et ses collègues ont montré qu’il pouvait être éclairci par la migration de planètes recouvertes d’un océan glacé. Les planètes se forment par accrétion dans le disque de gaz et de poussières qui entoure une jeune étoile. Plus elles naissent proches de cette protoétoile, plus elles sont rocheuses et sèches. La faute au rayonnement de l’astre , qui fait s’évaporer l’eau du corps des planètes

Le rayonnement a aussi une influence sur leur atmosphère : au cours du temps, le gaz est arraché à l’attraction de la planète et dispersé dans l’espace Ainsi, puisqu’elles perdent de l’atmosphère, ces planètes « rétrécissent », au point que leur rayon atteint difficilement deux fois celui de la Terre Ce sont les super-Terres, l’une des classes d’exoplanètes les plus communes. Un autre type d’exoplanètes souvent rencontré dans les observations sont les miniNeptunes Comme ces mondes n’existent pas dans le Système solaire , les spécialistes connaissent très mal leur structure et leur évolution, mais ils pensent qu’ils sont recouverts d’une atmosphère d’hydrogène et d’hélium, plus de deux fois plus épaisse que celle de la Terre Et entre les super-Terres et les miniNeptunes ? Rien. Ou très peu.

Pour Remo Burn, la solution est à trouver dans deux paramètres longtemps omis dans les simulations numériques : l’eau et la migration des planètes. D’abord, si l’accrétion des planètes s’effectue au-delà de la ligne des glaces, c’est-àdire assez loin de l’étoile pour que l’eau subsiste, alors elles sont fortement hydratées « L’eau sur Terre ne représente que 0,1 % de sa masse. Ici, on parle de planètes dont la moitié de la masse pourrait être constituée d’eau glacée », compare

le chercheur Ensuite, de nombreux indices tendent à montrer que les planètes ne restent pas là où elles ont été formées Par conséquent, si ces planètes gelées migrent vers leur étoile, alors la glace fond jusqu’à créer une épaisse atmosphère de vapeur d’eau Elles deviennent ainsi plus grosses que des super-Terres, pour atteindre des tailles comparables aux grandes mini-Neptunes. « Ces planètes ne seraient donc pas seulement recouvertes d’hydrogène et d’hélium comme on le pensait, mais aussi d’une forte portion d’eau », complète Remo Burn Ainsi , d’après les simulations des chercheurs, les planètes glacées qui migrent vers leur étoile voient leur eau se transformer en vapeur et elles augmentent en taille Elles s’accumulent vers 2,4 rayons terrestres. À l’inverse, les planètes nées près de leur étoile perdent progressivement leur atmosphère et diminuent en taille Elles s’accumulent vers 1,4 rayon terrestre. Ces deux effets conjoints creuseraient le rift subneptunien n

Évrard-Ouicem Eljaouhari

Vue d’artiste d’une exoplanète dont la glace d’eau se vaporise à mesure que la planète migre vers la partie centrale du système stellaire. ©

EN BREF

Pourquoi la myrtille est bleue

Si on vous demande de citer un fruit bleu, la myrtille vient spontanément à l’esprit. Pourtant, elle ne contient pas de pigment bleu. Rox Middleton, de l’université de Bristol, au Royaume-Uni, et ses collègues se sont intéressés à la cire qui recouvre la surface de ces baies. Ce matériau transparent est composé de structures nanométriques cristallines toutes de même forme, mais c’est leur distribution désordonnée qui interagit avec la lumière et di use préférentiellement dans le bleu et l’ultraviolet. Les chercheurs ont ensuite montré comment extraire la cire et la recristalliser de façon contrôlée pour créer des surfaces bleues. Science

QUAND UN VIRUS DONNE DES AILES

Les cicadelles brunes sont d’importants vecteurs de virus des plantes. L’espèce Laodelphax striatellus, en particulier, fait partie des insectes les plus nuisibles pour les cultures de riz, car elle véhicule le virus de la rayure du riz (RSV). Or, récemment, l’équipe de Feng Cui, de l’Académie chinoise des sciences, à Pékin, a montré que le virus influait sur la longueur des ailes de l’insecte. Dans une expérience contrôlée, les chercheurs ont observé que le taux de mâles à ailes longues était deux fois plus important chez les spécimens porteurs du virus (79 %) que chez les spécimens sains (37 %), tandis que toutes les femelles présentaient des ailes courtes.

L’équipe a ensuite déterminé le mécanisme en jeu : dans les testicules de l’insecte, le virus active l’expression d’un gène (dont le rôle était jusque-là inconnu). Cela engendre une cascade de réactions moléculaires qui interviennent dès les premiers stades du développement larvaire des cicadelles brunes et se traduisent, in fine,

Exposition jusqu’au 20 mai 2024

Place du Trocadéro

Paris 16e

Réservation conseillée

Le virus de la rayure du riz déclenche une cascade de réactions moléculaires chez son hôte qui conduisent ce dernier à arborer des ailes plus longues (en haut) que chez un insecte non porteur du virus (en bas)

par des ailes plus longues Avec cet avantage morphologique, ces insectes voleraient plus longtemps, et donc plus loin, ce qui favoriserait la dispersion du virus de la rayure du riz sur une zone plus large n

W. R.-P.

À l’occasion de l’exposition, découvrez le programme culturel du Musée de l’Homme

En mars et avril , profitez d’une exceptionnelle expérience musicale ! Deux instrumentistes guident la visite de Préhistomania , interprétant des œuvres contemporaines directement inspirées des relevés d’art préhistorique.

Les mercredis après-midi , les chercheurs du Muséum présentent aux visiteurs « leur » Galerie de l’Homme dans un tête-à-tête privilégié : primatologues, démographes, anthropologues et préhistoriens partagent en direct leurs savoirs, leurs expériences et leurs découvertes.

Retrouvez tout le programme et réservez vos visites et ateliers en famille sur museedelhomme.fr

MNHN 2023 © Institut Frobenius, Francfort-sur-le-Main MNHN Service collections

J. Yu et al., PNAS, 2024.

« Notre lien aux autres vivants est si intime qu’il nous altère »

Interpellé par les idées reçues et trompeuses qui pullulent sur l’évolution biologique ou culturelle et sur nos liens aux autres espèces vivantes, le biologiste Marc-André Selosse en explique les tenants et aboutissants. Stupeur et biologie : c’est fascinant !

Pourquoi avez-vous écrit ce livre ?

Dans mes conférences, je devine ou j’entends souvent, en échangeant avec le public, des conceptions du vivant biaisées ou erronées, de mon point de vue de biologiste J’ai voulu renverser les idées reçues sur la nature et les réécrire en y inscrivant l’humain, qui se croit trop affranchi du reste du vivant Je revisite notre posture dans les écosystèmes et l’évolution Celle-ci nous amène à éviter certaines pratiques de consommation ou de gestion des milieux, mais elle offre aussi des perspectives insoupçonnées d’action : basé sur des histoires naturelles, ce livre apporte de bonnes nouvelles pour la santé, l’alimentation, le lien entre les sexes…

Dans l’évolution, y a-t-il plus de gagnants que de perdants dans la lutte pour la survie ?

On voit les gagnants, adaptés et capables de se reproduire : la nature semble « bien faite ». Pourtant, non seulement personne ne l’a « faite », mais il y a des perdants dans la sélection naturelle Elle produit un charnier invisible d’individus ou d’espèces qui se sont moins reproduits et n’ont pas laissé de descendants. C’est plutôt mal

fait pour eux… Cela joue pour les humains : sous les tropiques, une carnation noire évite des cancers de la peau grâce à la mélanine qui protège des UV ; aux latitudes élevées, la peau claire laisse passer les UV, moins abondants, mais vitaux pour fabriquer la vitamine D Sous les tropiques, les individus à peaux claires ont disparu sans descendance, tandis que ceux à peaux sombres étaient éliminés aux hautes latitudes…

Les cultures sélectionnent-elles des traits biologiques ?

Oui ! Une spécificité de l’homme est son évolution culturelle, qui ressemble d’ailleurs fort à l’évolution biologique par ses mécanismes et son caractère perpétuel. Elle interagit avec l’évolution biologique : par exemple, partout où l’on élève des vaches pour les traire, la digestion du lactose a été sélectionnée à l’âge adulte ; dans les populations qui cultivent des céréales, les gènes de l’amylase salivaire, une enzyme attaquant l’amidon des graines, sont plus actifs Nous sommes à la confluence de deux évolutions, culturelle et biologique – sans toujours le comprendre ni vouloir les maîtriser

Sommes-nous encore liés aux autres espèces vivantes ?

Nous sommes soumis à une règle des écosystèmes : les espèces ont des liens de dépendance. Pensez à celles que vous mangez (méditez cela devant votre frigo, avant d’en faire votre propre chair au repas suivant) ou à celles qui vous habillent (devant votre armoire… peut-être en bois !). Imaginez tous les organismes qui ont été nécessaires à ces espèces-là et qui donc vous servent indirectement… L’autonomie est un mythe et notre lien aux autres vivants est si fort et intime qu’il peut nous altérer. Prenons l’exemple du cadmium, un métal toxique qui contamine les engrais phosphatés fournis aux plantes : par leur biais, il passe dans nos assiettes et surcontamine la moitié des Français, exposée à un surcroît de problèmes rénaux et osseux ou de cancers !

Biologiquement, a-t-on toujours besoin d’un plus petit que soi ?

Oui, c’est notre dépendance interne au vivant : nous sommes habités d’un microbiote fait de bactéries et de levures aussi nombreuses que nos cellules humaines. Il nous maintient en bonne santé, et aujourd’hui sa baisse de diversité est une des causes

Marc-André Selosse, professeur de biologie au Muséum national d’histoire naturelle, est responsable de l’équipe Interactions et évolution végétale et fongique de l’Institut de systématique, évolution, biodiversité, un laboratoire commun CNRS/MNHN/ Sorbonne Université/EPHE/ Université des Antilles.

Nature et préjugés, Acte Sud, 2024 448 pages, 25 euros

de l’explosion moderne des maladies du métabolisme (obésité, diabète), du système immunitaire (asthme, allergie…) et du système nerveux (Parkinson, autisme…). Notre mode de vie occidental, excessivement hygiénique, affecte la biodiversité du microbiote et ses fonctions Mon livre, au rebours, explore des gestes salvateurs, comme manger des végétaux riches en fibres nourrissant le microbiote ou éviter les savons et les aliments riches en conservateurs ou en émulsifiants… Cette dépendance-là, nous pouvons la gérer au quotidien !

Sommes-nous les seuls animaux qui produisent des déchets ?

Non, pas du tout ! L’air que nous respirons est un déchet de plantes, les forêts sont pleines de feuilles mortes… Mais ces déchets, produits depuis longtemps, ont sélectionné des espèces qui les consomment. Les nouvelles molécules de l’industrie chimique (plus de 5 000 par an !) et nos plastiques (aux deux tiers non recyclés), eux, sont trop récents pour être dégradés Ils engendrent des perturbateurs endocriniens et des cancérigènes, toxiques pour les écosystèmes et pour nous…

Côté déchets positifs, nous devons retrouver le rôle d’engrais de nos poubelles de table et… de notre urine : fertiliser, c’est aussi notre lien au vivant ! Les Français urinent chaque année le tiers des besoins en azote et en phosphore de leur agriculture, mais ils le dispersent dans des stations d’épuration Retrouvons le sens biologique de nos déchets !

D’un point de vue biologique, avons-nous une conception dangereuse de l’égalité homme-femme ? Oui, mon ouvrage aborde cette facette du biologique en nous : la différence entre les sexes, que nous gérons plutôt mal Un exemple d’égalité dangereuse, c’est la notice unisexe des médicaments : comme ceux-ci sont testés sur des hommes, les surdosages et les effets indésirables sont deux fois plus fréquents pour les femmes ! Nous méconnaissons ce qui a dessiné les sexes et leur comportement chez l’humain, et nous allons jusqu’à nier parfois cet héritage biologique. Par exemple, les hommes harcèlent souvent les femmes, mais les mâles des dauphins ou des moineaux ne font pas autrement avec leurs femelles : lutter contre ces dérives intolérables chez nous passe par la compréhension de leurs racines, non seulement culturelles, mais surtout biologiques. C’est à ce prix qu’on construira une équité entre hommes et femmes.

Qui est Arnaud Rafaelian, qui a illustré votre livre avec un humour aussi décapant que désopilant ? D’abord un ami ! Mais aussi un dessinateur qui aide à prendre du recul face au texte en souriant ou… en raillant Il appuie le propos tout en l’allégeant…

ET AUSSI

METAVERTIGO

Emmanuel Grimaud

La Découverte, 2024 320 pages, 22 euros

La croyance en la réincarnation est toujours prégnante dans la civilisation indienne. Un anthropologue a suivi les séances d’une psychothérapeute qui emploie la transe hypnotique pour diriger des transformations psychiques par « régression » dans une « vie antérieure ». Il nous invite par ces séances de « cinéma mental » dans une fascinante exploration du psychisme et, par là, de la civilisation de l’Inde. À quand celle de l’onirisme européen par un anthropologue indien ?

LA TYRANNIE DE LA REPRODUCTION

René Frydman

Odile Jacob, 2024

208 pages, 21,90 euros

L’un de ceux qui ont le plus aidé les personnes en mal d’enfants lance une alerte quant à l’avènement d’un « marché de la reproduction ». Par-delà la FIV, dont il est l’un des pères, il explique la GPA, la gre e d’utérus, la spermatogenèse artificielle, le clonage, la possible mise au point d’utérus artificiels… et discute de ces possibles « aberrations biologiques ». Nous prenons conscience alors qu’en voulant apporter une aide, notre société est passée à la « production de grossesses » et à ses risques.

LES RYTHMES DU VIVANT

Helen Pilcher

Delachaux & Niestlé, 2024 208 pages, 24,90 euros

Propos recueillis par François

Savatier

La nature est régie par des cycles. Ainsi, il y a certains rythmes dans la façon dont les espèces se remplacent, dans les extinctions de masse, mais aussi dans les migrations animales, dans le fonctionnement des écosystèmes, la croissance de leurs agents, dans leurs horloges biologiques, leur reproduction, etc. Ce livre plaisant, aux nombreux schémas et illustrations particulièrement intelligentes et e caces, en fait prendre conscience.

Glaciers en sursis N

En 2022, pour la première fois, la chaleur de l’été a provoqué l'amincissement des glaciers au sommet du massif du Mont-Blanc. Partout dans le monde, la fonte des glaciers continentaux s’intensifie. En jeu : l’élévation du niveau des mers, et la déstabilisation des ressources en eau douce.

otre planète abrite de l’ordre de 300 000 glaciers continentaux On les classe usuellement en deux grandes catégories : les glaciers, à proprement parler, et les calottes polaires Ces dernières se limitent à l’Antarctique et au Groenland, et se distinguent par leur taille (respectivement 13 millions et 2 millions de kilomètres carrés environ). Le plus grand glacier, ensuite, ne s’étend « que » sur 20 000  à 30 000 kilomètres carrés À titre de comparaison, la surface du glacier d’Aletsch, le plus grand des Alpes européennes, occupe un peu moins de 100 kilomètres carrés. Ces monstres de glace présentent des morphologies très variées : glaciers de chaînes de montagnes sculptant de typiques vallées « en U », mini-calottes créant leur propre topographie sur le continent , comme celle de l’Eyjafjallajökull, en Islande ; champs de glace, comme en Alaska, où des pointes rocheuses émaillent une couche de glace épousant la topographie…

Si la masse des glaciers est modeste, au regard des calottes polaires, ils fondent si vite qu’ils contribuent fortement à la hausse du niveau de la mer. Entre 2000 et 2019, les glaciers d’Europe centrale ont ainsi perdu le tiers de leur masse, d’après l’atlas mondial établi en 2021 par

L’ESSENTIEL

> Entre 2000 et 2019, les glaciers continentaux, à l’échelle mondiale, ont perdu 4,5 % de leur masse. Cette perte a atteint 33 % en Europe centrale.

> L’exploitation des données d’instruments embarqués sur certains satellites révèle d’importantes variations régionales, et une tendance globale : le réchau ement a ecte l’ensemble des massifs glaciaires.

> De récentes projections prévoient que d’ici à 2100, selon le niveau de réchau ement envisagé, les glaciers continentaux auront perdu 26 à 41 % en masse, a ectant des centaines de millions de personnes, dépendant de ces ressources en eau ou vivant dans des zones inondables en raison de la hausse du niveau des mers.

une équipe constituée autour de Romain Hugonnet, glaciologue alors au Laboratoire d’études en géophysiques et océanographie spatiales (Legos), à Toulouse, aujourd’hui à l’université de Washington À l’échelle globale, les glaciers ont perdu, sur cette période, 267 gigatonnes de glace par an C’est comme s’il fondait, chaque année, une couche de glace de 50 centimètres d’épaisseur recouvrant toute la France métropolitaine Et à l’avenir ? À l’échelle globale, encore, les glaciers devraient perdre entre 26 et 41 % de leur masse d’ici à 2100, par rapport à 2015, selon l’augmentation de la température moyenne mondiale, entre 1,5 °C et 4 °C Cela correspond à une hausse de 90 à 154 millimètres du niveau marin, et à la disparition de 49 à 83 % des glaciers de la planète, selon les projections publiées par une équipe menée par David Rounce, de l’université de Fairbanks, en Alaska, en janvier 2023.

La contribution de la fonte des glaciers à la hausse du niveau de la mer peut sembler modeste. Elle ne doit pas masquer un autre enjeu essentiel de cette disparition annoncée : le rôle de château d’eau joué par les glaciers. Dans les Andes ou dans l’Himalaya, en particulier, ceux-ci sont situés à la tête de bassins-versants de grands fleuves, qui viennent alimenter des régions fortement peuplées, où l’irrigation

François Lassagne

Dans l’ouest canadien, au sein de la chaîne Saint-Élie, les glaciers Stairway (à gauche) et Kaskawulsh (à droite) se rejoignent. Dans cette région du monde, les glaciers ont perdu 9,1 % de leur masse ces vingt dernières années.

joue un rôle clé Or les glaciers stockent l’eau sous forme solide pendant les saisons humides et froides, et la restituent pendant les saisons sèches. La perte des glaciers menace ces grands équilibres… Y compris en Europe En moyenne annuelle , dans les Alpes , les glaciers n’influencent pratiquement pas le débit du Rhône ou du Rhin Cependant , lors d’événements extrêmes ponctuels – canicules, grandes sécheresses –, comme les canicules de  2003 ou de 2022, ils sont susceptibles de jouer un rôle important, soutenant les débits des fleuves En 2003, il a été estimé que la fonte des glaciers, en août, correspondait à environ 40 % du débit du Rhône près de son embouchure . Qu’est-ce qui influe sur le devenir des glaciers ? Certaines régions, parmi celles qui accueillent ces châteaux d’eau englacés, sont-elles particulièrement impactées par le réchauffement climatique ? Comment les calottes polaires, et leurs immenses glaciers avançant sur l’eau, se comporteront-elles à l’avenir ? Les glaciologues, exploitant données satellites et mesures de terrain, s’emploient à répondre à ces questions… brûlantes. n

ROMAIN HUGONNET glaciologue à l’université de Washington, spécialiste de l’analyse des données géospatiales

ÉTIENNE BERTHIER glaciologue au Laboratoire d’études en géophysiques et océanographie spatiales (Legos, Toulouse), spécialiste de la réponse des glaciers au changement climatique

D’ici à 2100, la moitié des glaciers auront disparu

Pourquoi est-il indispensable de disposer d’un atlas précis de la dynamique des glaciers dans le monde ?

Étienne Berthier : Jusqu’au quatrième rapport du Giec, les estimations de perte de masse des glaciers venaient uniquement de l’extrapolation des mesures de terrain Ce qui limitait le champ couvert à une cinquantaine de glaciers environ – aujourd’hui, de l’ordre d’une centaine – à travers le monde ; des glaciers mal répartis, et surtout limités aux massifs accessibles (dans les Alpes, en Amérique du Nord…), même si des équipes émergent dans les pays comme l’Inde ou la Chine, notamment, ce qui augure d’une couverture un peu plus représentative En 2013, un article de recherche versé au cinquième rapport du Giec, appuyé sur des méthodes de mesure par satellite, a mis en lumière le fait que les glaciers suivis sur le terrain n’étaient pas vraiment représentatifs , région par région Il devenait clair que chaque glacier ayant son comportement propre, on ne pouvait pas se limiter à quelques glaciers témoins Il fallait établir une cartographie exhaustive Romain Hugonnet : C’est ce qu’on s’est attaché à faire, il y a une dizaine d’années, cet effort aboutissant à l’article issu de ma thèse, en 2021, présentant un atlas global de l’évolution de la masse des glaciers de 2000 à 2019 (voir page 28) On a commencé par valider la méthodologie, dans le massif du Mont-Blanc. Puis on l’a appliquée à des grandes régions à fort enjeu, qui nous intéressaient tout particulièrement : les hautes montagnes d’Asie, très peuplées ; les Andes, pour lesquelles on se posait pas mal de questions… avant de passer à l’échelle globale.

Qu’est-ce qui a rendu possible l’établissement d’atlas globaux ? R. H. : Il faut partir de l’idée qu’on produit, à partir des données acquises par satellites, des modèles numériques de terrain.

Non pas des modèles physiques, avec des équations de mécanismes physiques, mais plutôt des modèles topographiques , qui estiment l’altitude de la surface terrestre.

Le principal ingrédient de nos modèles, ce sont les archives de l’instrument Aster, embarqué à bord du satellite Terra, de la Nasa, qui est en orbite depuis 1999, acquiert des images régulièrement et dont l’archive est devenue libre de droit autour de 2015. La mise à disposition d’outils open source a rendu possible d’automatiser considérablement les procédures de traitement de ces archives ; c’est indispensable, car pour arriver à notre atlas global, il faut traiter de l’ordre de 500 000 couples stéréographiques Cela passe par une mise en cohérence : dès qu’on a une image (un couple stéréographique), on déduit une topographie du glacier. Pour chaque point à la surface d’un glacier quelque part dans le monde, nous avons abouti à une quarantaine de ces topographies entre  2000 et  2019, dont il a fallu corriger les biais éventuels, les décalages… Les données étaient là depuis longtemps, mais il a fallu développer les « briques » technologiques à même de les exploiter de manière massive et complète.

Si on voulait poursuivre le même exercice, et mettre à jour l’atlas, aurait-on les données satellites nécessaires ?

R. H. : Aster devrait rester en orbite jusqu’en 2025. On prévoit, avec Étienne, une mise à jour en 2026. Cela n’a pas de sens de le faire tous les ans, parce que les données ne sont pas acquises si régulièrement La résolution temporelle de notre estimation est plutôt de quatre ou cinq ans Aster observe un glacier, en moyenne , deux fois par an Mais c’est très variable La requête de l’archive elle-même est chronophage Nous allons attendre que ce soit vraiment pertinent, pour ajouter une période de cinq ans aux quatre périodes de cinq ans étudiées, couvrant les vingt dernières années. Après la fin de l’exploitation d’Aster s’ouvre une grande incertitude pour nous : il n’y aura pas de continuité des données, car aucun autre satellite de mêmes capacités d’observation n’est prévu par les agences spatiales En revanche , on dispose aujourd’hui d’instruments spatiaux à très haute résolution, notamment à bord des satellites Pléiades, du Cnes, très utilisés pour des études très détaillées La résolution, de l’ordre d’une cinquantaine de centimètres , produit des topographies extrêmement précises. Pour l’étude d’un processus particulier, pour suivre quelques glaciers, c’est très intéressant.

E. B. : C’est ainsi que nous avons étudié l’impact de la canicule de 2022 sur les glaciers du massif du Mont-Blanc Grâce à ces instruments, nous avons vu que l’amincissement a

été exceptionnel et s’est propagé jusqu’au sommet des glaciers Pour qualifier de tels événements extrêmes , c’est très bien . Mais cela ne permet pas une couverture globale et régulière. Ces satellites acquièrent des images à la demande , ils ne construisent pas d’archives complètes.

Qu’est-ce qu’apportera une mise à jour de l’atlas ?

EN CHIFFRES

49 % la proportion de glaciers en moins dans le monde d’ici à 2100 (réchau ement de 1,5 °C)

33 m par jour la vitesse d’écoulement du glacier Jakobshavn, dans la calotte groenlandaise

4,5 % perte mondiale de masse des glaciers, entre 2000 et 2019

1 kg de CO2 émis provoquent la fonte de 15 kg de glace

R. H. : Le fait qu’on ait constaté d’importantes variations spatiales et temporelles, en soi, justifie de vouloir continuer à étudier les glaciers à l’échelle globale Par exemple, la perte de masse des glaciers islandais a ralenti après 2010. On se demande combien de temps ça va durer et quand la perte de masse est susceptible d’accélérer à nouveau. À l’inverse, en Nouvelle - Zélande , nous avons observé une véritable dégringolade : des glaciers presque stables entre 2000 et 2004, puis des bilans de masse complètement négatifs ces 10 dernières années… Dans quelle mesure cette plongée estelle susceptible de se poursuivre ? Ces résultats surprenants appellent d’autres observations Quels sont les résultats qui vous ont surpris en constituant votre atlas ?

E. B. : L’étude du massif du Mont- Blanc nous a complètement sidérés. Jusqu’à présent, nous observions des amincissements des langues glaciaires, dans les parties basses, de l’ordre de 5 mètres, parfois jusqu’à 15 mètres par an , alors que les parties hautes étaient

Il y a environ 300 000 glaciers dans le monde, et ils fondent tous

vite £

plutôt stables, pratiquement sans amincissement Avec la canicule de 2022, il est apparu que les parties hautes aussi étaient directement attaquées, sur 2 à 3 mètres, au sommet du mont Blanc, au dôme du Goûter, au-dessus de 4 000 mètres Depuis les premières mesures de Joseph Vallot, en 1905, jusqu’en 2010 environ, il n’y avait presque pas de variations On savait que ces glaces très froides se réchauffaient Mais désormais on voit que se produisent aussi des tassements très forts du manteau neigeux , de la fonte sûrement , du regel, qui produisent une réduction de l’épaisseur Il convient de comprendre dans quelle mesure c’est localisé dans certaines régions, ou si c’est quelque chose qui se produit partout, et quelles vont être les rétroactions possibles liées au fait que ces parties hautes commencent à s’amenuiser

Avez-vous observé d’autres comportements inattendus ?

E. B. : Nous avons observé , in situ , des effondrements de glaciers : des fractions entières de se séparent du reste, et tombent dans les vallées. Typiquement, en 2016, sur le plateau du Tibet, ce phénomène a affecté deux glaciers, chacun de 5 à 6 kilomètres carrés. Ils ont perdu 40 % de leur volume en l’espace de quelques secondes. Cela a produit des avalanches monstrueuses, atteignant des volumes de 70 à 80  millions de mètres cubes. Ça s’est produit dans d’autres régions Il est difficile, pour l’heure , de l’attribuer au changement

climatique Seul un suivi régulier donnera des éléments tangibles pour comprendre ce qui provoque ces effondrements

Comment passe-t-on de votre atlas global, récapitulant vingt ans d’évolution des glaciers, aux projections du devenir des glaciers à la fin du siècle, selon les différents scénarios de réchauffement identifiés dans les rapports du Giec ?

R. H. : Il est possible de faire des projections sans cet atlas. Mais il permet de les contraindre fortement, grâce aux observations L’idée est de construire un modèle physique, s’appuyant sur des équations, pour représenter le bilan de masse des glaciers Ce modèle va pouvoir convertir les données des réanalyses climatiques (passé) et des projections climatiques (futur), donc essentiellement des données de température et de précipitations en dynamique de changement de masse des glaciers.

Vitesse par an

Dans les zones apparaissant en rouge sur cette carte de vitesse d’écoulement du glacier du Mont-Cook, en NouvelleZélande, la glace, en surface, parcourt plus de 500 mètres par an.

Sont notamment modélisés les liens entre fonte et température, et entre précipitations et accumulation Les précipitations étant souvent assez mal contraintes et résolues, c’est en s’appuyant sur les données de notre atlas que l’on va pouvoir obtenir un modèle plus réaliste, et ainsi de meilleures projections Avec un plus : notre atlas donne la possibilité de faire des calibrations glacier par glacier, ce qui est intéressant , car ils répondent différemment au réchauffement Si par exemple on prend deux glaciers côte à côte dans le massif du Mont-Blanc, la perte de masse peut varier d’un facteur 1 à 3, voire 4, selon la taille, la distribution en altitude Prenons le glacier des Bossons, qui part presque du sommet du mont Blanc. Il est très pentu, avec une très grande zone d’accumulation Son amincissement sur les dix dernières années est trois à quatre fois moindre que celui de la mer de Glace ou du glacier d’Argentière, qui ont de grandes langues glaciaires à basse altitude

DE LA VITESSE D’ÉCOULEMENT AU VOLUME DES GLACIERS

Pour déterminer la vitesse à laquelle la glace s’écoule, on utilise des méthodes de corrélation appliquées à des séries d’images satellites des glaciers. Ces méthodes permettent de quantifier directement le déplacement des motifs en surface, comme les crevasses. En combinant ces observations avec des données sur la pente d’un glacier, et par des hypothèses sur la déformation de la glace et les conditions à la base du glacier, on peut estimer l’épaisseur et donc le volume des glaciers. Connaître précisément le volume et la distribution des épaisseurs des glaciers est essentiel pour a ner les estimations de leur évolution future et évaluer le potentiel d’élévation du niveau des mers ainsi que les changements de la ressource en eau glaciaire.

ROMAIN MILLAN, ANTOINE RABATEL Institut des géosciences de l’environnement, Grenoble

L’ESSENTIEL

> Pour comprendre les surfaces trouées au-delà de leur seule topologie, une approche consiste à dessiner des cartes sur ces objets.

> Cartographier des surfaces mathématiques « trouées » amène à convoquer des outils mathématiques variés : topologie mais aussi théorie

des graphes, théorie des groupes…

> Sur le rulpidon, neuf couleurs sont su santes pour colorier n’importe quelle carte. Mais inutile d’espérer y dessiner une carte symétrique à neuf régions : c’est impossible.

LES AUTEURS

SYLVIE BENZONIGAVAGE professeuse à l’université Claude-Bernard Lyon 1

RÉMI COULON directeur de recherche, CNRS, université de Bourgogne

Le dessous des cartes du rulpidon

L’étude des surfaces mathématiques trouées constitue un défi de taille. Pour appréhender le rulpidon, figure emblématique à trois trous, on s’interroge sur la possibilité de le « cartographier » en respectant certaines contraintes.

Le rulpidon (voir ci-contre) est un drôle d’objet. Il est l’emblème d’un tout nouveau musée des mathématiques : la maison Poincaré, attachée à l’institut Henri-Poincaré, Sorbonne Université et CNRS, qui a ouvert ses portes en septembre à Paris – une sculpture monumentale de cet objet, signée Ulysse Lacoste, trône d’ailleurs dans le jardin du musée Cette forme géométrique trouée, qu’on voit ronde ou carrée en fonction de l’angle depuis lequel on la contemple, n’est pas facile à appréhender – par exemple, en dépit des apparences, elle n’a que trois trous, et non quatre (voir la rubrique « Art et science » dans Pour la Science n° 553 et S Benzoni-Gavage, Le rulpidon sous toutes les coutures, Dunod, 2024). Pour tenter de l’appréhender, une bonne approche consiste à sortir ses crayons de couleur pour essayer de dessiner des cartes sur sa surface Ce faisant, c’est tout un voyage mathématique qui se profile, qui amènera à emprunter des chemins aussi riches qu’inattendus. Et qui permettront, en définitive, de mieux saisir la richesse et l’intérêt de cette forme trouée

Tout le monde a déjà travaillé sur un fond de carte en géographie. Sur une carte représentant des pays ou des régions délimitées par des frontières, l’une des premières tâches peut consister à colorier chaque région de sorte que deux régions frontalières quelconques soient de couleurs différentes, pour bien les distinguer Une question naturelle, d’un point de vue mathématique, est de savoir combien de couleurs sont nécessaires pour colorier de cette manière n’importe quelle carte. La réponse est apportée par le théorème des quatre couleurs, dont l’origine remonte au xix e siècle mais dont la preuve formelle date seulement de quelques dizaines d’années : pour colorier une carte plane, ou un globe terrestre, il suffit d’au plus quatre couleurs.

Le théorème dit que quatre couleurs suffisent toujours : il ne dit pas qu’elles sont nécessaires pour colorier une carte donnée Il existe en effet des cartes plus simples, qui nécessitent moins de couleurs C’est le cas d’un damier, seulement bicolore. Il a ceci de particulier que toutes les régions (les carrés du damier) se rencontrent en des « points quadruples » (c’est-à-dire des

Pour aborder les problèmes de coloriage de cartes sur des surfaces trouées (à droite, le rulpidon), on fait appel à des résultats sur les graphes complets, comme celui à neuf sommets représenté ici, qui ne peut être dessiné que sur une surface comportant au moins trois trous. Pour cette raison, on doit répéter des sommets quand on le dessine à plat, si l’on veut éviter que des arêtes s’intersectent.

et les routes, les arêtes Colorier un graphe revient à attribuer une couleur à chaque sommet de sorte que deux sommets quelconques reliés par (au moins) une arête soient de couleurs différentes De manière générale , le coloriage de graphes est un sujet de recherche actif en informatique théorique, qui a également de multiples applications pratiques, des emplois du temps aux plans de table en passant par le sudoku.

COLORIAGE DE GRAPHES

En représentant chaque région d’une carte par un sommet d’un graphe, et en reliant deux sommets de ce graphe si et seulement si les régions correspondantes sont frontalières sur la carte, on ramène un problème de coloriage de carte à un problème de coloriage de graphe.

points où quatre carrés se rejoignent). Pour une carte qui ne contient que des points « triples » (où trois régions se rejoignent), on peut penser à un maillage en nid d’abeilles, constitué d’hexagones, que l’on peut colorier avec trois couleurs (mais pas deux). En s’évadant du plan, on peut aussi colorier de trois couleurs seulement les faces d’un cube

Dans l’univers infini des cartes, certaines nécessitent pourtant vraiment quatre couleurs Ainsi, quatre régions toutes frontalières les unes des autres, dessinées dans le plan ou sur la sphère, nécessitent d’emblée quatre couleurs On appelle « carte complète » une telle carte, constituée de régions toutes frontalières les unes des autres

Peut-on trouver une carte complète à plus de quatre régions ? Dans le plan ou sur la sphère, non ! Car si nous avions n régions, toutes frontalières des n – 1  autres, nous aurions besoin de n couleurs différentes pour les colorier Avec n > 4, cela mettrait en défaut le théorème des quatre couleurs – qui assure que quatre couleurs sont toujours suffisantes. Il en va autrement si l’on cherche à dessiner des cartes sur des surfaces plus compliquées, par exemple des surfaces trouées, comme une bouée, un bretzel… ou un rulpidon. Il s’avère en effet qu’il existe une infinité de théorèmes de coloriage sur les surfaces à trous, le nombre de couleurs nécessaires croissant avec le nombre de trous.

Avant d’en arriver au coloriage de telles surfaces trouées, nous devons faire le lien entre les cartes et un autre objet mathématique important : les graphes. Un graphe se définit grosso modo comme un ensemble de points, appelés « sommets », reliés par des arêtes. Il peut par exemple représenter un réseau de routes entre des villes, ces dernières étant les sommets

Les questions de coloriage de cartes et de graphes sont étroitement liées. En e ff et , la forme des régions n’a aucune importance pour trouver comment colorier une carte : ce qui compte, c’est de savoir quelles régions sont frontalières En choisissant un point par région et en reliant deux à deux les points correspondant à des régions frontalières, on obtient un réseau de routes imaginaires : c’est un graphe, mathématiquement parlant (voir la figure cicontre). Colorier la carte revient alors à colorier le graphe On peut dessiner puis colorier des graphes dans le plan, sur la sphère… ou sur des surfaces trouées

La surface trouée la plus simple est la bouée, dont le nom mathématique est le « tore » On peut la dessiner comme un objet en 3D, ou bien l’ouvrir mentalement à plat La figure plane ainsi obtenue est comme l’écran dans lequel se baladait Pac -Man : en sortant d’un côté on rentre par l’autre au même niveau !

La représentation à plat du tore est commode pour dessiner des graphes. Le graphe sur la page ci-contre est à cinq couleurs Tous ses

On peut dessiner des graphes dans le plan, sur la sphère, ou sur des surfaces trouées £

sommets sont connectés deux à deux : on dit que c’est un graphe complet à cinq sommets

Le coloriage d’un graphe complet à n sommets nécessite (exactement) n couleurs Comment est-il donc possible d’avoir un graphe complet à cinq sommets, alors que le théorème des quatre couleurs semble assurer que cinq couleurs ne sont jamais nécessaires pour colorier une carte (et donc un graphe) ? Justement

parce que le tore n’est ni le plan, ni la sphère : c’est une surface trouée. Bien sûr, on peut dessiner dans le plan cinq sommets et les relier deux à deux par des arêtes. Mais on observera toujours au moins deux arêtes qui se croisent, signe que le graphe n’est pas planaire : un graphe planaire se reconnaît au fait que dessiné sur le plan, ses arêtes ne s’intersectent pas

Pour dessiner un graphe non planaire et y voir clair, sans que les arêtes s’intersectent, on peut répéter des sommets et des arêtes, comme c’est le cas dans la figure ci-contre. On peut en fait dessiner des graphes plus compliqués , par exemple celui qui est représenté sur la page 48. Sur cette figure il faut imaginer que l’on recolle chaque paire d’arêtes répétées, en l’occurrence les arêtes 3-4, 3-5, 3-7, 4-5 et 4-7. Même si ce n’est pas évident à première vue, ce graphe est tracé sur le tore, et correspond au coloriage également représenté sur la page 48.

On constate de plus que chacun de ses sept sommets est connecté aux six autres : c’est un graphe complet Un graphe complet à sept sommets est le maximum qu’on puisse faire sur le tore.

Sur une surface donnée, l’existence d’un graphe complet à n sommets équivaut à l’existence d’une carte complète à n régions Dans le plan ou sur la sphère, le nombre n maximal pour lequel il existe un graphe complet à n sommets est donc de quatre, à nouveau en raison du théorème des quatre couleurs Qu’en est-il sur les surfaces à trous ? On a vu que ce nombre maximal est au moins égal à sept sur le tore Comment passe-t-on de quatre dans le plan à sept sur le tore ? Cela dépend en fait d’une donnée caractéristique de la surface : son genre

GRAPHES ET NOMBRE CHROMATIQUE

Le genre d’une surface est le terme mathématique décrivant son « nombre de trous ». C’est une notion de topologie La sphère n’a pas de trou : on dit qu’elle est de genre 0. Le tore est le modèle de surface à un trou, de genre 1, donc.

En recollant deux tores comme pour faire une bouée à deux places, on obtient une surface de genre 2. Plus généralement, en recollant g tores, on obtient une surface de genre g. C’est ainsi que l’on obtient toutes les surfaces « sans bord » (contrairement à un disque, dont le bord est un cercle, ou encore à une paille, qui a un bord en deux morceaux : un cercle à chacune de ses extrémités), « compactes » (qui tiennent dans une boîte finie) et « orientables » (avec deux faces, contrairement au ruban de Möbius, qui n’en a qu’une).

Certaines surfaces trouées, sans bord, compactes et orientables, ne ressemblent pas à des

tores recollés On peut pourtant déterminer leur genre en imaginant qu’on les déforme comme de la pâte à modeler, sans rien déchirer ni recoller, pour se ramener à cette forme de collage de tores Par exemple le rulpidon peut se déformer en un triple tore : il est de genre 3. Une manière de s’en convaincre est d’imaginer qu’on met la tête dans le rulpidon. Si c’était un bol, on ne verrait aucune sortie. Dans le rulpidon, en tournant la tête de part et d’autre, on en voit trois : l’une à gauche, une deuxième droit devant, et la dernière à droite Il y a donc exactement trois trous Pour aborder notre question sur l’existence d’un graphe complet à n sommets ( ou d’une carte complète à n régions) sur une surface donnée, définissons une autre notion mathématique qui nous sera utile : le nombre chromatique d’une surface. Il est défini comme le plus petit nombre de couleurs permettant de colorier n’importe quel graphe tracé sur cette surface On ne s’intéresse qu’à des tracés de graphes sans intersections d’arêtes – sinon le nombre chromatique ne serait pas bien défini.

Gerhard Ringel a démontré en 1954 que le nombre chromatique d’une surface orientable est aussi le nombre n maximal pour lequel il existe un graphe complet à n sommets tracé sur cette surface Ce résultat était en fait connu pour les surfaces de genre g ≤ 6 depuis les travaux de Lothar Heffter en 1891.

Le nombre chromatique d’une surface est donné en fonction de son genre par la « formule de Heawood » Cette formule est vraie pour tout genre , mais sa démonstration pour le genre 0 (Appel et Haken, 1978), qui donne le théorème des quatre couleurs, est ultérieure à la démonstration pour un genre non nul (Ringel et Youngs, 1968). Et encore, la première est assistée par ordinateur alors que la démonstration pour g ≥ 1 repose sur des arguments que l’on peut entièrement expliciter à la main. Pour les surfaces de genre 0, le nombre chromatique donné par la formule de Heawood est 4. Pour le genre 1, il est bien de 7, comme évoqué précédemment Pour le genre 3 (cas du rulpidon), il est de 9.

SYMÉTRIES

La surface trouée la plus simple est le tore, de genre 1. On peut le dessiner comme un objet en 3D, ou « l’ouvrir » à plat. La figure plane est comme l’écran dans lequel se baladait Pac-Man : en sortant d’un côté, on rentre par l’autre, au même niveau. Cette représentation est commode pour dessiner des graphes, comme le graphe complet à cinq sommets représenté ici.

Revenons à nos surfaces trouées ellesmêmes. Il y a diverses manières de représenter une surface de genre donné On a vu , par exemple, que l’on peut représenter le tore en 3D ou bien ouvert à plat Ce sont deux représentations équivalentes du point de vue topologique, mais pas du point de vue géométrique, car les distances ne sont pas respectées en passant d’une représentation à l’autre – pour ouvrir à plat une bouée, il faut que le matériau

soit élastique et qu’on l’étire à certains endroits On constate aussi que le triple tore et le rulpidon ne se ressemblent guère En particulier, ils n’ont pas les mêmes symétries. Par « symétrie d’une surface », on entend ici une transformation isométrique (c’est-à-dire qui respecte les distances) de notre espace à trois dimensions, qui laisse la surface invariante.

L’art de dessiner des cartes, ou des graphes, sur des surfaces trouées est difficile. Il l’est d’autant plus si l’on cherche à respecter certaines symétries. Bien sûr on peut penser aux cartes symétriques que constituent certains pavages, comme ceux de l’Alhambra, à Grenade. Mais ces pavages , au même titre que les damiers ou les nids d’abeille , sont loin de la quête qui nous intéresse ici : celle de cartes symétriques complètes

La carte complète sur la figure ci-contre est tracée sur le tore avec les symétries de l’heptagone. Si cela semble presque naturel, il n’est pas évident, à partir de la figure du graphe à plat, de se convaincre qu’il peut être tracé sur le tore avec ces symétries ! Ce que l’on peut vérifier directement sur un tel graphe à plat, en revanche, c’est le genre de la surface sur laquelle on peut le tracer. Cette vérification repose sur une égalité appelée « formule d’Euler », qui indique que pour un polyèdre à s sommets, f faces et a arêtes, tracé sur une surface de genre g , on a : s +  f – a = 2 – 2g. Sur notre exemple, on constate qu’il y a f = 14 triangles, s = 7 sommets, et a = 21  arêtes (attention à ne pas oublier que celles du bord de la figure sont répétées deux à deux), de sorte que s + f – a = 0 : ceci est la signature d’un polyèdre tracé sur une surface de genre 1 (le tore, donc).

La question qui nous intéresse est de tracer des graphes complets ( ou des cartes complètes) le plus symétriques possible, ou du moins d’une manière qui respecte les symétries de l’objet géométrique choisi pour représenter la surface Pour un triple tore, on voudrait respecter les symétries du triangle. Pour un rulpidon, on voudrait au minimum respecter les symétries du carré.

TABLEAUX D’ADJACENCE

On se doute que le problème est différent d’un cas à l’autre, même si le graphe est le même du point de vue topologique Mais encore faut-il, au préalable, connaître un tel graphe ! La suite explique comment en obtenir

L’article de Heffter en 1891, dans lequel il étudie le nombre chromatique pour les surfaces de genre g ≤ 6, comporte très peu de dessins En revanche, il contient des « tableaux d’adjacence » fournissant de quoi tracer à plat

Ce graphe complet à sept sommets ne peut être dessiné que sur une surface de genre supérieur ou égal à 1 : dans une représentation à plat, on répète les sommets pour éviter que les arêtes ne s’intersectent.

(sans croisements mais avec répétitions de sommets et d’arêtes) des graphes complets jusqu’à douze sommets

Étant donné un graphe dont les sommets sont numérotés de manière unique, un tableau d’adjacence est un tableau de nombres qui décrit tous les voisins de chaque sommet Chaque ligne commence par le numéro du sommet dont on observe les voisins, puis donne la liste des numéros des voisins dans l’ordre où on les rencontre, en tournant autour du sommet dans un sens fixé à l’avance et identique pour tous – c’est là où le fait que l’on se concentre sur les surfaces orientables est important On peut commencer n’importe où autour du sommet, pourvu qu’on en fasse le tour complet À titre d’exemple, le tableau d’adjacence du graphe complet à sept sommets est présenté ci-contre (en bas).

On constate sur le tableau qu’il est bien complet , puisque chacun des sept numéros est présent une fois (et une seule) sur chaque ligne : chaque sommet est relié par une arête (et une seule) à chacun des six autres.

Cette carte complète tracée sur le tore correspond au graphe ci-dessus. Elle respecte les symétries de l’heptagone. Dans le tableau d’adjacence (ci-dessous) du graphe complet précédent, chaque ligne correspond à un sommet et donne la liste de ses voisins. À partir de ce seul tableau, on peut retrouver le graphe.

Plus le nombre de sommets augmente, plus il est difficile de trouver un tableau d’adjacence correspondant à un graphe complet La combinatoire (c’est-àdire le nombre de configurations possibles pour les voisins d’un sommet) augmente très vite avec le nombre total de sommets Il y a en effet (n – 2) ! permutations circulaires de (n – 1) voisins, donc si l’on essayait au hasard les configurations de voisins de n sommets il faudrait tester jusqu’à n (n – 2) ! tableaux Ce fut un tour de force de Heffter, par des arguments arithmétiques, de résoudre le problème jusqu’à n = 12.

S’il est facile, bien qu’un peu fastidieux, de déduire un tableau d’adjacence à partir d’un graphe tel que celui ci - contre , l’opération inverse est plus délicate Avec « seulement » sept sommets, le dessin est assez facile, car on peut juxtaposer des hexagones entourant les sommets tout en respectant les règles d’adjacence, puisque les hexagones pavent le plan. Un tel dessin est d’ailleurs l’un des rares que l’on trouve dans l’article de Heffter Mais si l’on essaie de procéder de la même manière pour tracer un graphe à plus de sept sommets, le dessin devient rapidement inextricable, car on ne peut pas juxtaposer des polygones à sept côtés ou plus sans que les angles entre les arêtes autour de chaque sommet soient trop écrasés.

Pour s’affranchir de cette difficulté, une méthode consiste à repérer dans le tableau tous les triplets de sommets reliés deux à deux, formant un triangle dans le graphe On peut alors

dessiner et juxtaposer ces triangles sans problème. On repère aussi, pour les dessiner avec les triangles, les polygones du graphe éventuellement associés à des points multiples (quadruples ou plus) dans la carte En l’occurrence, ce ou ces polygones sont explicitement mentionnés par He ff ter en complément de ses tableaux d’adjacence Des cartes complètes correspondant aux graphes de He ff ter sont dessinées sur le triple tore et sur le rulpidon dans le livre de Sylvie Benzoni-Gavage précité. Toutefois, la méthode adoptée ne permet pas d’obtenir des symétries sur le rulpidon – elle est au contraire extrêmement tortueuse On en voit ci-dessus quatre projections.

Une autre approche est celle de l’informaticien à l’université de Californie à Berkeley Carlo Séquin, qui conçoit ses propres graphes complets et cartes complètes dans une quête de symétrie formulée ainsi : « Trouver la carte complète le plus symétrique possible sur une surface de genre minimal » Il a en particulier trouvé sur le triple tore une belle carte complète à neuf régions, très symétrique Parmi ses symétries, on trouve la rotation d’angle 120° autour d’un axe perpendiculaire au plan de symétrie horizontal et passant par le centre du triple tore, ainsi que la rotation d’angle 180° autour d’un axe horizontal passant par le centre d’un trou et au milieu des deux autres. Ces symétries n’ont pas d’équivalent sur le rulpidon, aussi la carte transposée sur ce dernier n’est-elle pas très symétrique, même si elle l’est d’une certaine manière plus que la précédente (voir le patron de rulpidon colorié page 50)

UNE CARTE SYMÉTRIQUE SUR LE RULPIDON ?

La formule de Heawood assure qu’en tant que surface de genre 3, le rulpidon admet des cartes complètes avec neuf régions Peut-on, cependant, produire une telle carte qui respecte les symétries de la forme, ou au moins certaines d’entre elles ?

Des surfaces de genre plus petit admettent des cartes complètes bien symétriques. Sur la sphère , par exemple , on peut tracer un tétraèdre et donc aussi une carte complète à quatre régions ayant naturellement les symétries du tétraèdre. On a aussi vu une carte

Ces quatre projections de la carte complète à neuf régions que l’on peut dessiner sur le rulpidon, construite à partir du tableau d’adjacence de Lothar Heffter, ont été obtenues grâce à la méthode de Sylvie Benzoni-Gavage. Le résultat n’est pas symétrique.

complète à sept régions sur le tore qui a les symétries de l’heptagone. Dans le cas du rulpidon, la situation se complique Rappelons que par « symétrie » on entend ici une transformation de l’espace qui laisse globalement le rulpidon invariant, qui ne le déforme pas : on parle plus précisément d’« isométries » Parmi elles, on trouve : – les symétries du carré (si on regarde le rulpidon par le dessus) – par exemple la rotation ρ d’angle 90° autour de l’axe vertical ; – la réflexion σ par rapport au plan horizontal. On notera que deux isométries peuvent être composées : si on applique une isométrie γ1 puis une isométrie γ2 laissant toutes les deux le rulpidon invariant, la composition γ2 ○ γ1 laissera aussi le rulpidon invariant L’une de ces symétries joue un rôle très particulier : l’isométrie qui laisse tous les points à leur place On l’appelle l’« identité ». Si on compose l’identité avec n’importe quelle autre symétrie γ, le résultat sera toujours γ. Par ailleurs il existe toujours une isométrie qui « défait » ce que γ a fait Cet inverse, noté γ – 1 , est tel que γ – 1 ○ γ est en fait l’identité Mathématiquement on dit que l’ensemble de toutes ces symétries , que l’on notera Γ, forme un « groupe »

À force d’observations et de raisonnement, on se convainc que Γ contient exactement seize isométries Certaines d’entre elles ne sautent pas tout de suite aux yeux – par exemple, la composition ρ ○ σ

Revenons donc aux cartes, et plus particulièrement aux cartes complètes symétriques Par carte symétrique sur le rulpidon, on entend une carte que n’importe quelle symétrie du rulpidon envoie sur elle-même (avant coloriage). Considérons une carte complète à neuf régions sur le rulpidon , et tâchons de comprendre quelles sont ses propriétés On va voir que 9 et 16 (le nombre de ses symétries) sont deux nombres qui ne font pas bon ménage Ils imposent en fait des contraintes très fortes.

Chaque symétrie du rulpidon doit nécessairement envoyer une région de cette carte sur une autre région (éventuellement la même). Dit autrement, elle « permute » les régions de la carte Dans un premier temps, nous allons donc complètement oublier quelles pourraient

être les formes de ces régions, comment elles s’enroulent sur le rulpidon, etc., pour ne retenir que le fait suivant : on veut faire en sorte que ses seize symétries permutent les éléments d’une collection de neuf objets (les neuf régions de la carte). Cette approche va permettre d’exploiter des notions de théorie des groupes Celle-ci offre un cadre abstrait permettant d’étudier des problèmes d’origines très variées (géométrie, combinatoire, algèbre, etc.).

THÉORIE DES GROUPES

Pour aborder ce problème, on peut classer les régions par « orbites » : deux régions r et r’ sont dans une même orbite, notée o, s’il existe une symétrie qui envoie r sur r’. Le « stabilisateur » d’une région r est l’ensemble des symétries dans Γ qui laissent cette région à sa place. La théorie des groupes permet de montrer les deux faits importants suivants : – le nombre de symétries dans le stabilisateur d’une région r divise le nombre de symétries dans Γ ; – le nombre ne dépend en fait que de l’orbite o de r Autrement dit, si r et r’ sont deux régions dans une même orbite, alors leurs stabilisateurs ont le même nombre d’éléments On notera ce nombre co. Rappelons-nous que Γ contient seize symétries. Ainsi les valeurs possibles pour co sont 1,

Patron de rulpidon sur lequel est dessinée la carte complète à neuf régions de l’informaticien Carlo Séquin. On n’y retrouve pas les symétries qui seraient présentes si cette même carte était dessinée sur le triple tore.

2, 4, 8, et 16 (les diviseurs de 16). La « formule des classes » – une formule importante en théorie des groupes – a pour conséquence la relation suivante :

∣R∣ =∑ ∣Г ∣ c0 o∈O

où | R |  est le nombre d’objets permutés par Γ (ici, les régions de la carte), O l’ensemble des orbites et |Γ| le nombre d’éléments dans Γ (ici, le nombre de symétries de la surface). Dans notre cas précis, on a donc :

9 =∑16

c0 o∈O

Puisque 9 est impair, l’une des valeurs du rapport 16/co doit être impaire Or on a vu que les valeurs possibles de co sont 1, 2, 4, 8, et 16. La seule pour laquelle 16/co est impair est co = 16 : il existe donc nécessairement une orbite o telle que co = 16. Par définition, cela signifie que n’importe quelle région r dans cette orbite est fixée par les seize éléments de Γ Ceci signifie donc que cette orbite ne contient qu’une seule région r, car, par définition, toute région dans cette orbite est l’image de r par un élément de Γ… et que les éléments de Γ laissent tous r invariante

Comme annoncé, nous n’avons pas utilisé ici le fait que nous travaillions avec des régions du rulpidon. On a en fait montré cet énoncé général : si un groupe à seize éléments permute une collection de neuf objets, alors l’un d’eux est nécessairement fixé par tous les éléments du groupe

GRAPHES ET CARTES SYMÉTRIQUES

Pour tenter de dessiner une carte complète à neuf régions à la surface du rulpidon, le raisonnement que nous avons déroulé plus haut invite à tenter d’abord d’y tracer un graphe complet à neuf sommets Car si nous pouvions tracer un tel graphe en respectant les symétries du rulpidon, alors nous serions en mesure de créer une carte complète symétrique. Mais il s’avère que c’est impossible

Supposons en effet qu’il existe un graphe complet à neuf sommets et symétrique sur le rulpidon . En particulier, les symétries du groupe Γ doivent permuter ces neuf sommets Au vu de la discussion précédente , l’un des sommets doit être fixé par toutes les symétries de Γ. Or il n’existe pas de point à la surface du rulpidon fixé par toutes ses symétries Pour s’en convaincre il suffit de regarder la rotation de 180° autour de l’axe qui traverse le rulpidon horizontalement à travers l’un de ses

BIBLIOGRAPHIE

trous Les seuls points fixes de cette rotation sont justement le long cet axe, qui n’intersecte pas le rulpidon : il n’y a donc aucun point du rulpidon fixé par cette symétrie. Ce raisonnement par l’absurde démontre donc qu’il n’existe pas de graphe complet symétrique à neuf sommets sur le rulpidon

Est- ce à dire qu’il n’existe pas de carte complète symétrique à la surface du rulpidon ? La conclusion n’est pas aussi rapide. En effet, regardons une configuration simplifiée à l’extrême : essayons de dessiner une carte symétrique complète… avec une seule région Une telle carte est associée à un graphe réduit à un unique sommet et sans arête Si un tel graphe pouvait être dessiné sur le rulpidon en respectant toutes ses symétries, son unique sommet devrait être fixé par toutes les symétries, ce qui n’est pas possible comme on vient de le faire remarquer Cependant, il existe bien une carte symétrique à une seule région : il suffit de prendre pour cette dernière tout le rulpidon ! Exclure l’existence d’un graphe complet symétrique ne permet donc pas d’exclure l’existence d’une carte complète symétrique. Il faut pour cela un autre argument

Les cartes qui nous intéressent vérifient une contrainte supplémentaire : les régions ne comportent pas de « trous », elles ressemblent à des disques déformés C’est en particulier le cas de la région supposément laissée invariante par toutes les symétries du rulpidon, en supposant qu’une carte symétrique complète à neuf régions existe Or un théorème de topologie des années 1940 dû à Paul Althaus Smith stipule que si un groupe Γ à seize éléments préserve une figure ayant la forme d’un disque, il doit nécessairement fixer un point sur ce disque Pour le problème qui nous intéresse, ce résultat implique que non seulement il existe une région de la carte laissée invariante par toutes les symétries dans Γ, mais qu’un point de cette région doit lui aussi être fixé Ce qui n’est pas possible comme on l’a vu. Ainsi il n’existe pas de carte complète à neuf régions qui respecte toutes les symétries du rulpidon.

Puisqu’une carte complète totalement symétrique ne peut exister, il est naturel de se demander quelles symétries peuvent être « sauvées » : existe-t-il une carte complète qui respecte une partie seulement des symétries du rulpidon ? En réalité, des arguments similaires à ceux qui précèdent montrent qu’il est impossible de dessiner sur le rulpidon un graphe complet à neuf sommets qui respecte la moindre de ses symétries (à part, bien sûr, l’identité).

P.

Du côté des cartes, la situation n’est guère meilleure. Autant dire qu’il faut abandonner l’idée de dessiner des cartes complètes à neuf régions qui soient symétriques Place, donc, à la créativité des artistes pour dessiner des cartes dont l’asymétrie n’a d’égale que la beauté ! n

S. Benzoni-Gavage, Le Rulpidon sous toutes ses coutures, Dunod, 2024.

C. Séquin, Easy-tounderstand visualization models of complete maps, Proceedings of Bridges 2023 : Mathematics, Art, Music, Architecture, Culture, 2023.

G. Ringel, Farbensatz für orientierbare Flächen vom Geschlechte p > 0, Journal für die reine und angewandte Mathematik, 1954.

A. Smith, Fixed-point theorems for periodic transformations, American Journal of Mathematics, 1941.

Quand les skyrmions passent en 3D

Les skyrmions sont des structures magnétiques aux propriétés étonnantes. Leur géométrie, restreinte à deux dimensions, a lancé les physiciens sur les traces de leurs alter ego en trois dimensions, les hopfions.

Dans les disques durs, l’information est conservée en exploitant la direction du moment magnétique des atomes « spin » Des configurations plus complexes reposant sur un groupe de spins, offrent des possibilités plus intéressantes, avec des densi tés de stockage plus élevées. Les skyrmions sont une piste attractive, notamment parce que leur structure topologique les rend très stables (voir l’article page 58) L’organisation des spins qui composent un skyrmion est bidimensionnelle, voire quasi tridimensionnelle dans la mesure où les skyrmions peuvent s’empiler en formant une colonne, mais cette dimension ne contient pas d’information pertinente. L’idée des skyrmions peut être généralisée à une structure véritablement tridimensionnelle, on parle d’« hopfions » (en hommage au mathématicien Heinz Hopf). Alors que les premiers skyrmions ont été observés en 2009, les hopfions manquaient à l’appel. Or, en 2023, Filipp Rybakov, de l’université d’Uppsala, et ses collègues en ont mis en évidence, par l’expérience n

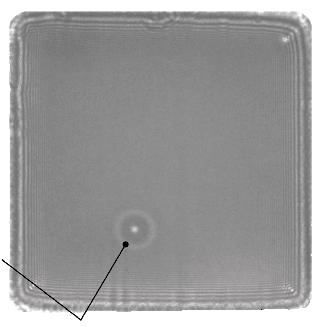
DU SKYRMION À L’HOPFION

Les chercheurs ont travaillé avec un matériau magnétique composé de fer et de germanium dans lequel ils parviennent à produire des colonnes de skyrmions. En manipulant avec minutie un champ magnétique externe, ils ont réussi à créer un hopfion autour de la colonne d’un skyrmion (ci-dessus). Avec un microscope électronique sensible à l’aimantation du matériau (ci-contre), ils voient un point (la colonne du skyrmion vue du dessus) entouré d’un anneau, l’hopfion.

Sean Bailly

UN TORE DE SPINS

L’hopfion prend la forme d’un tore dans lequel les spins ont un comportement collectif et pivotent progressivement. À l’instar de la structure topologique du skyrmion,

CC BY 4.0 Deed (en bas)

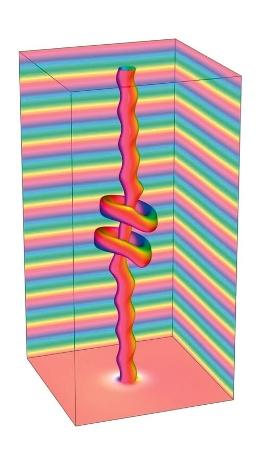
UN ZOO DE CONFIGURATIONS

En changeant les paramètres de l’expérience, les chercheurs ont observé de nombreuses configurations différentes : avec un hopfion s’enroulant une ou plusieurs fois autour de la colonne du skyrmion ; ou s’enroulant autour de plusieurs colonnes, comme ci-dessus avec un total de onze colonnes.

F. Zheng et al., Hopfion rings in a cubic chiral magnet, Nature, 2023.

Stockage géologique de

déchets radioactifs

Comment s’assurer de la tenue à très long terme des bétons ?

[CONTEXTE]

De nombreux pays ont opté pour le stockage des déchets radioactifs les plus nocifs dans des couches géologiques profondes.

La France a opté pour un enfouissement à 500 mètres dans une couche d’argile de 130 mètres d’épaisseur. Elle est censée assurer l’isolement de la radioactivité pendant plusieurs centaines de milliers d’années.

La création d’une telle installation près de Bure, en Meuse - HauteMarne, est en cours d’instruction. Baptisée Cigéo, elle accueillerait les premiers déchets dans plusieurs décennies.

Une fois les déchets stockés, il est nécessaire de sceller définitivement les puits à l’aide de « bouchons » d’argile gonflante. Pour qu’ils soient efficaces, leur gonflement doit être contraint par des structures en béton. Mais comment s’assurer que la dégradation du béton ne compromette pas ce confinement mécanique sur une durée d’isolement de plusieurs centaines de milliers d’années ?

Nous sommes dans l’Aveyron, à Tournemire, à 250 mètres sous terre, dans un ancien tunnel ferroviaire. L’eau, provenant d’un aquifère calcaire, suinte des parois. Dans un recoin, elle coule à travers un bac au fond duquel sont plongés une centaine de petits cylindres de 3 centimètres de diamètre sur 1 centimètre de hauteur. Ces échantillons apparemment insignifiants sont des pâtes de ciment et des bétons. En 2010, c’est grâce à eux que les chercheurs et chercheuses de l’IRSN ont révélé un phénomène peu étudié par la communauté scientifique : la précipitation de phases appelées «magnésiennes» dans les bétons dits «bas pH». « Nous testions deux formulations de ces bétons envisagées pour Cigéo en plus du béton Portland, classiquement utilisé dans le génie civil, raconte Alexandre Dauzères, responsable du Laboratoire d’étude et de recherche sur les transferts et les interactions dans les sous-sols (LETIS) à l’IRSN. En caractérisant les échantillons afin d’estimer leur évolution chimique et mécanique, nous avons découvert ces précipités magnésiens. » Problème : dans certaines conditions, ils produisent un endommagement des échantillons en quelques mois seulement.

Le laboratoire souterrain où ont été menées ces expérimentations est installé dans un ancien tunnel ferroviaire acquis par l’IRSN en 1992. Long de 1 885 mètres, il dispose de six galeries creusées dans une formation argileuse similaire à celle où l’Andra (Agence nationale pour la gestion des déchets radioactifs) prévoit de construire Cigéo. « Depuis trente ans, nous y scrutons l’évolution de l’argile exposée à des environnements de stockage sur les plans minéralogiques, chimiques, mécaniques, ainsi que le transfert de l’eau et des éléments en solution, poursuit le chercheur. Ces études sont très complexes du fait de la multitude de mécanismes impliqués et des interactions à caractériser puis à modéliser sur des millénaires entre des matériaux pour lesquels les connaissances sur ces durées sont limitées. » Les recherches actuelles portent, d’une part, sur la dégradation chimique, mécanique, hydrique et thermique des composants et, d’autre part, sur les outils de surveillance utilisés durant les cent cinquante ans d’exploitation de Cigéo, le temps prévu pour construire le stockage et y déposer les déchets.

Image MEB d’un mortier hydraulique romain, premier béton bas pH de l’histoire.

La sûreté des systèmes de fermeture

Le projet Cigéo concerne les déchets radioactifs les plus nocifs, les résidus du traitement et du recyclage du combustible nucléaire pour l’essentiel, soit 3 % de nos déchets nucléaires. Actuellement, ils sont entreposés dans des installations de surface à La Hague, Cadarache ou Marcoule. L’intérêt de la roche argileuse est qu’elle est très peu perméable : l’eau, piégée dans sa microstructure au cours des temps géologiques, s’y déplace de quelques centimètres par million d’années. Le risque de voir la radioactivité migrer jusqu’à la surface ou atteindre les aquifères, principalement lié à la diffusion des radionucléides contenus dans l’eau, est faible. Cigéo comporte un réseau de puits, descenderies et galeries tapissés de béton armé. Ces infrastructures doivent être opérationnelles tout au long de la phase d’exploitation, le stockage devant rester réversible. Si ces bétons ne résistent guère plus de cent ans, leurs fissures seraient réparables tant que les ouvrages restent accessibles. Après la fermeture du stockage, les infrastructures, remplies de déblais issus des creusements, seraient immergées d’eau en quelques millénaires, les ouvrages se dégradant alors sans affecter la sûreté. Il est toutefois capital d’assurer la performance des systèmes de fermeture du stockage à l’issue de l’exploitation.

À ce jour, l’Andra prévoit des scellements constitués d’un bouchon de 35 mètres de long sur 10 mètres de diamètre dans une argile particulièrement gonflante qui peut gagner dix fois son volume en se réhydratant. Elle aurait alors les mêmes propriétés que la roche. Baptisée « bentonite », cette argile est couramment utilisée pour

l’étanchéité d’édifices, la construction de digues ou le comblement de carrières. Son gonflement s’opérerait avec le retour de l’eau dans les puits et descenderie, provenant de l’aquifère calcaire présent au-dessus du stockage. Cette déformation serait contenue de part et d’autre par un ouvrage en béton (un « massif d’appui ») d’une dizaine de mètres de long conçu pour résister pendant plusieurs centaines de milliers d’années à la contrainte mécanique engendrée.

Des bétons bas pH

Une des options considérée à ce stade de développement de Cigéo pour ces scellements est une nouvelle formulation cimentaire, développée spécifiquement. Car couler de tels gros blocs de béton peut poser problème quant à leur de tenue à long terme en raison d’une montée en température trop importante à cœur. Rappelons que le béton est fabriqué à partir de ciment, une poudre minérale sèche à base de calcaire et d’argile qui durcit quand on la mélange avec de l’eau : cela produit un liant appelé C-S-H (silicate de calcium hydraté). Cette hydratation entraîne une réaction exothermique liée à la quantité de ciment. Pour la limiter, des bétons contenant moins de ciment ont été développés depuis les années 2000 par les différents organismes en charge du stockage géologique des déchets radioactifs.

Dans ces nouvelles formulations, nommées « bétons bas pH », près des deux tiers du ciment est remplacé par des matériaux pouzzolaniques, à haute teneur en silice, de type cendres volantes ou fumée de silice. Ceux-ci font baisser le pH de l’eau qui subsiste dans les micropores du béton. Dans le cas du béton Portland, cette eau est très alcaline (pH 13 à 13,5) en raison de la potasse caustique (KOH)

LE PROJET DE STOCKAGE CIGÉO

LE PROJET DE STOCKAGE CIGÉO

ZONE DESCENDERIE

ZONE PUITS

Structure du site et ses infrastructures

Le projet Cigéo comporte des puits pour la circulation du personnel et du matériel, une double descenderie, long tunnel incliné de 5 kilomètres pour acheminer les colis de déchets, et des galeries menant aux alvéoles pour stocker ces colis.

COMMENT RÉAGIT LE BÉTON BAS PH EXPOSÉ À L’EAU ARGILEUSE

Revêtement déposé

Remblai Massif d’appui en béton bas pH

Revêtement

Enrichissement en calcium

Croute de calcite

Noyau gonflant mis en place au toit de l’unité silto-carbonatée (USC)

Enrichissement en magnésium

Zone saine

et de la soude (NaOH) provenant du ciment. Le pH se limite à 11,5 dans le cas des bétons bas pH.

La surprise de l’attaque magnésienne

« Depuis 2008, nous testons en laboratoire la tenue des bétons bas pH lorsqu’ils sont exposés à l’eau argileuse, précise Alexandre Dauzères. Cette eau, dont le pH est neutre, est multi-ionique : elle contient des carbonates, du magnésium, des sulfates... Cela produit trois grands types de perturbations chimiques : la lixiviation, qui conduit à la dissolution de certains minéraux du béton, la carbonatation (liée à la présence de CO2) qui crée des microfissurations, et l’attaque magnésienne, qui provoque la formation de silicates de magnésium hydratés (ou M-S-H) à l’interface avec l’argile. » Depuis la découverte du phénomène, trois thèses ont été menées à l’IRSN sur ce précipité magnésien. Ses impacts méritent en effet d’être étudiés avec soin. Car les M-S-H formés remplacent totalement ou partiellement la matrice cimentaire à base de C-S-H. « Or ils ont des propriétés moins cohésives, poursuit-il. Cela explique le vieillissement prématuré que nous avons observé, avec des fissures importantes apparues en seulement quatre mois. »

Les résultats obtenus par l’IRSN ont permis de mettre à jour les bases de données thermodynamiques internationales qui recensent les précipités et les réactions chimiques, sur lesquelles reposent les modélisations de tenue à long terme du béton. Grâce à ces dernières, on peut vérifier le comportement du béton aux échelles micro et macroscopique dans n’importe quel environnement aqueux.

« Notre code de calcul est fondé sur ces bases de données, enrichies de nos propres résultats, sur des lois thermodynamiques et sur un modèle de transport réactif, souligne le chercheur. Aujourd’hui, grâce à la prise en compte de l’attaque magnésienne, nos modélisations sont en parfait accord avec les résultats de nos expérimentations à l’échéance de cinq à six ans. » Et pour s’assurer que les prévisions de vieillissement du béton sont valides et permettent de simuler l’évolution à long terme, le code de calcul sera testé sur des analogues archéologiques de béton pouzzolaniques dans le cadre d’une nouvelle thèse. Les modélisations auront lieu, d’une part, sur des échantillons prélevés sur des piles d’un pont romain construit il y a deux mille ans, aujourd’hui immergées dans la baie de Naples (Italie), et, d’autre part, sur un béton similaire reconstitué par une équipe d’archéologues et plongé depuis vingt ans dans la mer au large de Brindisi, ce qui fournit une donnée à moyen terme. Et pour avoir en outre des références à très court terme, l’IRSN fabrique ces mêmes bétons et les fera tremper dans de l’eau de mer pour pouvoir les comparer aux échantillons précédents, sachant que les principes de chimie thermodynamique sont les mêmes qu’en eau douce.

« Si nos résultats sont en bonne adéquation sur un béton immergé quelques mois, vingt ans ou deux millénaires, nous pourrons avoir confiance dans notre base de données et dans nos modèles, conclut Alexandre Dauzères. D’autant plus que l’environnement de Cigéo, moins salin, est chimiquement moins complexe à modéliser. »

Schéma d’un scellement de descenderie dans Cigéo d’après l’Andra (dossier de DAC - 2023)

Illustration des mécanismes de dégradation dans un béton bas pH

Comme l’attestent les analyses des restes de piles de pont à Pouzzoles, près de Naples (Italie), les Romains avaient inventé et utilisaient déjà des formulations de bétons très proches des bétons bas pH quant à leur composition.

☐ N° 557 (mars. 24)

— ⨯ 9,50 €

— ⨯ 9,50 €

☐ N° 556 (fev. 24)

— ⨯ 9,50 €

— ⨯

☐ N° 555 (janv. 24)

— ⨯

—

— ⨯

1 / JE COCHE LES RÉFÉRENCES ET JE RENSEIGNE LES QUANTITÉS CI-DESSUS ET JE REPORTE LE TOTAL CI-DESSOUS

Total à régler : – , €

2 / J’INDIQUE MES COORDONNÉES

☐ M. ☐ M me

Nom :

Prénom :

Adresse :

Code postal : Ville :

Téléphone :

Courriel :

J’accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON

—

— ⨯

— ⨯

3 / JE RETOURNE LE COUPON ET MON RÈGLEMENT

PAG24VPC

J’émets un chèque à l’ordre de Pour la Science du montant total de la commande. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante :

Abonn’escient – TBS Group Service abonnement Groupe Pour la Science 20 rue Rouget de Lisle - 92130 Issy les Moulineaux

COMMANDEZ PLUS SIMPLEMENT !

En vous rendant sur notre site internet vous pourrez :

●  Retrouver toute notre collection

●  Vérifier la disponibilité des anciens numéros

●  Acheter les numéros en version numérique (4,49 €)

●  E ectuer un paiement en ligne

Pour cela, scannez le QR code ci-contre ou rendez-vous sur boutique.groupepourlascience.fr

Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr

En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante :https://rebrand.ly/CGV-PLS. O re valable jusqu’au 21/12/2022 en France Métropolitaine uniquement. Les prix a chés incluent les frais de port et les frais logistiques. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour La Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous

9,50 €

☐ N° 554 (déc. 23)

⨯ 9,50 €

☐ N° 553 (nov. 23)

⨯ 9,50 €

☐ N° 552 (oct. 23)

9,50 €

☐ N° 546 (avril 23)

9,50 €

☐ N° 547 (mai 23)

9,50 €

☐ N° 549 (juillet 23)

9,50 €

☐ N° 548 (juin 23)

☐ N° 550 (août 23)

9,50 €

☐ N° 551 (sept 23)

L’AUTEUR

LOÏC MANGIN

rédacteur en chef adjoint à Pour la Science

PRENDRE LE BOULEAU DU BON CÔTÉ

Fruits de nombreuses collaborations avec les scientifiques, les œuvres de Karine Bonneval invitent à renouer les liens avec le végétal, et notamment avec le bouleau, cet injustement mal-aimé.

Le printemps pointe le bout de son nez, et avec lui, certes le soleil, la chaleur, le réveil de la nature… mais aussi certains désagréments , car c’est aussi la saison des allergies ! Et parmi les plantes les plus redoutées figure en bonne place, avec les graminées, l’armoise… le bouleau. Toutes sont des espèces anémophiles, c’est-à-dire dont la fécondation est assurée par le vent, et non par exemple par des insectes : aussi pour être transportés les grains de pollen sont-ils minuscules et donc particulièrement aptes à envahir les muqueuses nasales et y déclencher des réactions inflammatoires. Les phénomènes d’allergie allant s’amplifiant , il n’est pas étonnant que le bouleau n’ait pas bonne presse et soit le plus souvent associé aux éternuements, au nez qui coule, aux yeux

qui démangent… Et c’est bien dommage… L’artiste Karine Bonneval s’est lancée dans la réhabilitation de cette essence, et bien plus encore.

En effet, ses œuvres, dont de nombreuses font l’objet d’une grande exposition carte blanche conçue avec l’association Siana au Domaine de Chamarande, dans l’Essonne, sont pour la plupart nées d’une réflexion sur ce que l’humain a de commun avec les plantes. Sculptures et installations invitent à se mettre à la place de ces dernières, à bouger, respirer avec elles et même à les écouter. Pour la plupart, elles ont été conçues en collaboration étroite avec des scientifiques.

Ainsi, Écouter la terre, qui consiste en douze pièces de céramique (élaborées avec Charlotte Poulsen) fichées dans du

terreau, donne à entendre les sons liés à l’activité de la faune du sol. Ils ont été enregistrés grâce à un capteur fabriqué pour l’occasion avec Fanny Rybak, bioacousticienne à l’université Paris-Saclay. Autre exemple, Dendromité, respirer avec l’arbre est un film, réalisé avec Claire Damesin, écophysiologue de l’arbre à l’université Paris-Saclay, qui révèle par le biais d’une caméra infrarouge à objectif refroidi les émissions ténues de CO2 des troncs.

Quant au bouleau, il est au cœur de plusieurs œuvres conçues avec Nicolas Visez, aérobiologiste au Laboratoire avancé de spectroscopie pour les interactions, la réactivité et l’environnement (Lasire), de l’université de Lille. Ainsi, Berkanan (voir la photographie ci-dessus) est constitué d’une fontaine à sève de bouleau (un fluide paré de nombreuses

vertus médicinales), en céramique à nouveau, dont les vasques reprennent la forme des écailles des chatons de l’arbre, ces inflorescences d’où s’échappent les grains de pollen par millions au printemps. L’ensemble est disposé au milieu de plusieurs troncs blancs du végétal dans lesquels on doit voir autant d’individus. Et c’est l’un des apports de Karine Bonneval aux travaux du Lasire après deux ans d’échanges avec les scientifiques qui y travaillent. Dans quelle mesure l’emplacement d’un bouleau, pris isolément, et les conditions qui y règnent, notamment de pollution, influent-ils sur la quantité de pollen et son pouvoir allergisant ? C’est l’objet d’une thèse en cours au laboratoire lillois, où plusieurs arbres sont suivis de près en ville, sur un ancien terril, sur le campus…

Murmures du bouleau, une sculpture en vannerie associée à un tapis, est ornée de larmes de savon au pollen de bouleau et de « portraits » de ces grains produits au Lasire. Il s’agit de chromatographies sur papier d’extraits de pollen : les divers composés migrent différemment dans le support et sont de la sorte séparés. En les confectionnant, les équipes du Lasire ont détecté un composé intriguant, du fer. Ce métal, qui sort rapidement du grain quand l’humidité est importante (c’est le cas dans les muqueuses), jouerait-il un rôle dans les réactions inflammatoires liées aux allergies ? Des travaux sont en cours pour répondre.

L’objectif de ces collaborations est, selon l’artiste, de « refaire famille avec le bouleau » et ne plus voir en lui qu’une source de contrariétés. De fait, chez les

Celtes, pour qui Berkanan était la rune associée au bouleau, cet arbre, le premier du calendrier, était symbole de naissance et de renouveau. Puisse - t- il, selon les vœux de Karine Bonneval, être celui d’une nouvelle attention, facilitée par la science ici portée aux plantes, et plus généralement aux vivants qui nous entourent. n

« Se planter – Récolter le soleil et cultiver la pluie », au Domaine de Chamarande, dans l’Essonne, jusqu’au 28 avril 2024. chamarande.essonne.fr

L’auteur a publié : Pollock, Turner, Van Gogh, Vermeer et la science… (Belin, 2018)

Berkanan (2022) est une fontaine en grès émaillé, cordes, sève et tronc de bouleau, conçue en collaboration avec la céramiste Charlotte Poulsen.

JEAN-MICHEL COURTY ET ÉDOUARD KIERLIK professeurs de physique à Sorbonne Université, à Paris

TIRER LA NAPPE SOUS LES COUVERTS

Comment retirer une nappe d’une table dressée sans casser de vaisselle ? Trucs et astuces pour un tour spectaculaire plus facile qu’il n’y paraît.

L’une des applications de la physique, et non des moindres, est de briller dans les dîners en ville… surtout si l’on s’en prend à la table de ce même dîner ! En effet, l’un des plus spectaculaires « tours de physique » consiste à retirer une nappe d’une table dressée en y laissant assiettes, verres, couverts… quasiment à la même place Difficile ? Non, cette prouesse est bien plus facile à réaliser qu’il n’y paraît. Découvrons les lois de la physique qui rendent possible ce tour et les astuces qui garantissent de le réussir sans risque pour le service en cristal et la porcelaine.

Cette expérience et ses variantes sont couramment utilisées pour illustrer la notion d’inertie C’est effectivement l’inertie de tous les objets présents sur la table qui explique qu’ils restent en place lorsqu’on tire la nappe d’un geste rapide

Elle se manifeste ici de façon nette parce que la force de frottement qu’exerce la nappe en mouvement sur la base des objets n’augmente pas avec sa vitesse.

FROTTEMENTS ET VITESSE

C’est l’une des propriétés du frottement entre solides : lors d’un glissement de l’un sur l’autre, la force de frottement entre les deux est presque constante. De plus, la valeur de cette dernière ne dépend pas de la taille de l’aire de contact entre les solides Elle est proportionnelle à la force qui presse un solide contre l’autre et qui, ici, n’est rien d’autre que le poids des objets disposés sur la nappe. Le coefficient de proportionnalité, ou plutôt le coefficient de frottement dynamique , vaut typiquement 0,3 entre une assiette et une nappe. Les amateurs de physique

Attention, un tour spectaculaire, et néanmoins facile, mais pour lequel un peu d’entraînement peut s’avérer nécessaire…

le vérifieront facilement en scotchant un smartphone sur une assiette, en faisant glisser cette dernière sur la nappe et en mesurant sa décélération avec une application spécifique, comme « phyphox » Durant toute la phase de ralentissement, la décélération mesurée est constante et vaut typiquement 3 mètres par seconde carrée (3 m s-2), soit 0,3 fois l’accélération de la pesanteur.

C’est cette même accélération constante que subira l’assiette – et en fait tous les objets qui l’accompagnent sur la table –quand on tirera la nappe, quelle que soit la vitesse de cette dernière Des mesures (toujours avec smartphone) faites par les auteurs montrent qu’on tire environ 50 centimètres de nappe en un dixième de seconde Cela signifie d’abord que la vitesse de tirage est typiquement de 5 mètres par

seconde Ensuite, un objet près du bord verra l’intégralité du bout de nappe défiler sous lui : il sera donc accéléré à 3 m s-2 pendant 0,1 seconde.

Pour un physicien, c’est l’analogue d’une petite chute libre : il en déduira que la vitesse acquise par l’objet sera de 30 centimètres par seconde et qu’il se sera avancé de 1,5 centimètre Attention, une fois la nappe passée , l’objet se retrouve avec une certaine vitesse sur la table nue où il décélère.

Comme le coefficient de frottement entre les objets et la table est du même ordre que celui que l’on compte entre les objets et la nappe, il s’arrête sur une distance de 1,5 centimètre : cela fait un déplacement total de 3 centimètres. C’est un maximum Les objets plus éloignés du bord ont moins de surface de

UN TOUR DE FORCES

Lorsqu’on tire une nappe d’une table dressée, quelles sont les forces en présence ? Le poids des di érents objets (en rouge), les forces de frottement (en jaune) et enfin la réaction de la table (en bleu). Précisons que plus la nappe va vite, plus les objets bougeront lentement, car plus la durée d’action de la force de frottement sera brève.

Nappe

Vitesse

nappe qui glisse sous eux et bougent donc proportionnellement moins.

UNE VOITURE DE COURSE

Si l’on souhaite tirer plus de nappe, disons 3 mètres, il faut gagner en vitesse. En effet, si on tire toujours à 5 mètres par seconde, 6 fois plus de temps est nécessaire et le déplacement d’un objet sera multiplié par 36, correspondant donc à plus de 1 mètre dans l’exemple précédent ! Pour envisager des expériences plus « grand format » comme on peut le voir sur certaines vidéos, où une nappe est tirée sous une grande tablée de 16  convives, mieux vaut utiliser à la place des mains… une voiture de course C’est ce qui a été réalisé dans l’émission « Street Science » en tirant à une vitesse de 160 kilomètres par heure la nappe accrochée par un câble à un tel

bolide Une astuce a toutefois été indispensable pour assurer la réussite. Après une première tentative infructueuse, avec verres et assiettes chamboulés, les expérimentateurs ont placé des feuilles de plastique entre les objets et la nappe. Ainsi, en réduisant encore drastiquement le coefficient de frottement, rien n’a bougé à la seconde tentative Sans aller dans de telles extrémités, quelques considérations pratiques vous aideront à réussir avec une plus petite tablée D’abord le choix de la nappe est primordial ! Elle doit être lisse et glissante,

Les auteurs ont notamment publié : En avant la physique !, une sélection de leurs chroniques (Belin, 2017).

Table

donc sans broderies Pas la peine d’avoir une nappe en soie, la grande majorité des textiles synthétiques suffiront Point important, aucun ourlet n’est permis : celui-ci entraînerait les objets au passage En pratique, le plus simple est de couper une nappe en deux par le milieu (que ne ferait-on pas pour épater ses amis !).

Quant aux objets à déposer sur la nappe, aucune contrainte tant que l’objet n’est pas susceptible de l’accrocher ! Cela interdit pour les fourchettes, le dressage à la française, c’est-à-dire pointes vers le bas, et impose, hélas, la tradition anglaise, avec les pointes perfidement orientées vers le haut Pour plus d’effet , nous conseillons des verres à pied , ça n’augmente pas le risque et c’est bien plus impressionnant. Les remplir d’un peu de boisson colorée, comme du vin, ajoute encore au spectacle.

Ensuite, il importe de bien se positionner par rapport à la table. Deux choix sont possibles : de face ou de profil La seconde option autorise dans la limite des contraintes exposées précédemment, de plus grandes nappes, car le corps ne gêne pas Le mouvement est en revanche plus délicat à maîtriser et nécessite beaucoup d’entraînement

La position de face est quant à elle plus simple Dans cette position, avec un peu de concentration, il est tout à fait possible de réussir la manipulation du premier coup sans aucun entraînement. Positionnez-vous de sorte que si vous inclinez un peu le buste vers l’avant, bras tendus, vous touchiez juste le bord de la table avec le bout des doigts (80  centimètres environ). La longueur de nappe à pouvoir passer sous les objets est alors la distance entre le corps et la table moins une trentaine de centimètres

BIEN SAISIR LA NAPPE

La façon de se saisir de la nappe est très importante Il est essentiel qu’aucun pli n’apparaisse sur la nappe lorsqu’on la tire Un réflexe commun consiste à saisir la nappe avec les mains écartées puis à les rapprocher l’une de l’autre Le résultat est la formation d’une poche durant le mouvement qui entraîne tout ce qui se trouve sur la table. L’écartement idéal des mains correspond à la largeur des épaules De plus une fois la nappe tenue, elle doit rester bien tendue dans le sens perpendiculaire au mouvement à venir en tirant avec ses mains vers les côtés Cette tension sera maintenue jusqu’à la fin de l’expérience. En ce qui concerne la longueur, prenez le bord de la nappe et froncez-le dans les

À VOS MARQUES, PRÊT, TIREZ !

De face, à environ 80 centimètres de la table, inclinez un peu le buste vers l’avant en gardant les bras tendus. Tenez également la nappe tendue sans créer de pli ou de poches, et, quand vous tirez, veillez à garder constant l’écart entre vos bras jusqu’à la fin. Et hop, le tour est joué !

mains de sorte qu’il reste une trentaine de centimètres de nappe entre la table et les mains Rapprochez ensuite les mains vers la table. Ces 30 centimètres de jeu vous permettront d’accélérer les mains avant que la nappe ne commence à glisser. Lorsque ce sera le cas , sa vitesse sera presque maximale et vous minimiserez la durée du glissement sous les objets

Dernière recommandation : tirer horizontalement Le plus sûr et le plus simple est de penser au point d’arrivée final des mains : la partie du corps qui est au niveau de la table, en général la ceinture Vient ensuite le moment crucial où il vous faut tirer le plus rapidement possible, sans hésiter. En ajoutant un mouvement de rabat des poignets durant ce mouvement, vous obtiendrez une vitesse de nappe encore plus grande À vous de jouer

Avec beaucoup d’entraînement, peutêtre arriverez-vous même à remettre la nappe sous les couverts comme le fait Mat Ricardo dans « Tablecloth 2.0 », voire à transférer la nappe d’une table à une autre, dans « Tablecloth 3.0 » Tenté ? Prenez alors comme lui la précaution de placer l’intégralité des objets situés sur la table sur des plateaux avec un rebord courbé vers le haut : la nappe glissera mieux

Précision importante : les auteurs déclinent toute responsabilité concernant une éventuelle casse de vaisselle n

M. Françon, Expériences de physique, Revue d’optique théorique et instrumentale, 1963.

Plusieurs vidéos

Le principe d’inertie : youtu.be/z2HxzZkCFIA

Passer une nappe d’une table à l’autre : youtu.be/o94Pm-Cty3M

Tirer une nappe avec une voiture de course : youtu.be/IB7oTNuPg_M

BIBLIOGRAPHIE

HORS-SÉRIE

☐ N° 122 (fev 24)

— ⨯ 12,40 € = , €

☐ N° 116 (août 22)

— ⨯ 12,40 €

☐ N° 121 (nov 23)

— ⨯ 12,40 € = , € ☐ N° 120 (août 23)

— ⨯ 12,40 €

— ⨯ 12,40 €

☐ N° 114 (fév. 22)

— ⨯ 10,40 €

☐ N° 119 (mai 23)

— ⨯ 12,40 €

☐ N° 113 (nov 21) — ⨯ 10,40 €

☐ N° 118 (janv. 23)

— ⨯ 12,40 € = , €

☐

— ⨯ 10,40 €

OUI, je commande des numéros de Pour la Science Hors-série

1 / JE COCHE LES RÉFÉRENCES ET JE RENSEIGNE LES QUANTITÉS CI-DESSUS ET JE REPORTE LE TOTAL CI-DESSOUS

Total à régler : – , €

2 / J’INDIQUE MES COORDONNÉES

☐ M. ☐ M me

Nom :

Prénom :

Adresse :

Code postal : Ville :

Téléphone :

Courriel :

J’accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON

☐ N° 117 (nov. 22)

— ⨯ 12,40 € = , €

☐

— ⨯ 10,40 € = , €

3 / JE RETOURNE LE COUPON ET MON RÈGLEMENT

PAG24VPC

J’émets un chèque à l’ordre de Pour la Science du montant total de la commande. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante :

Abonn’escient – TBS Group Service abonnement Groupe Pour la Science 20 rue Rouget de Lisle - 92130 Issy les Moulineaux

COMMANDEZ PLUS SIMPLEMENT !

En vous rendant sur notre site internet vous pourrez :

●  Retrouver toute notre collection

●  Vérifier la disponibilité des anciens numéros

●  Acheter les numéros en version numérique (5,99 €)

●  E ectuer un paiement en ligne

Pour cela, scannez le QR code ci-contre ou rendez-vous sur boutique.groupepourlascience.fr

Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr

En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante :https://rebrand.ly/CGV-PLS. O re valable jusqu’au 21/12/2022 en France Métropolitaine uniquement. Les prix a chés incluent les frais de port et les frais logistiques. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour La Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous

N° 110 (fév. 21)

N° 112 (août 21)

☐ N° 115 (mai 22)

L’AUTEUR

HERVÉ LE GUYADER

professeur émérite de biologie évolutive à Sorbonne Université, à Paris

LE PLUS ANCIEN EUCARYOTE PLURICELLULAIRE

Les premiers organismes comportant plusieurs cellules dotées d’un noyau sont apparus bien plus tôt qu’on ne le pensait. Il s’agissait très probablement d’algues vertes.

La découverte de fossiles très anciens constitue parfois une avancée biologique capitale. C’est ainsi que, tout récemment, en explorant des gisements chinois dont la qualité paraît de plus en plus surprenante à mesure qu’on les étudie, une équipe de l’Académie des sciences du pays a complètement modifié l’idée que l’on avait de la chronologie d’apparition des premiers eucaryotes pluricellulaires – les organismes comportant plusieurs cellules pourvues d’un noyau, dont font partie les animaux et les plantes

Les premières cellules apparues sur Terre étaient procaryotes, c’est-à-dire dépourvues de noyau. Divers fossiles

unicellulaires témoignent de leur existence dès l’Archéen (période géologique entre 4 et 2,5 milliards d’années), plus précisément il y a environ 3,8 milliards d’années. Quelque 300 millions d’années plus tard, soit assez vite à l’échelle des temps géologiques, des filaments pluricellulaires se sont organisés, comme en témoignent les stromatolithes, des concrétions calcaires que produit aujourd’hui encore le métabolisme de cyanobactéries, des bactéries photosynthétiques structurées en filaments.

Les stromatolithes se fossilisent très bien et les plus anciens connus remontent en effet à environ 3,5 milliards d’années. Détecter des traces de cyanobactéries dans ces derniers n’a cependant pas été une mince affaire. Les observations de William Schopf, de l’université de Californie à Los Angeles ont été essentielles. En 1993, il étudia avec soin des stromatolithes dans un gisement de

Urospora wormskioldii est une algue verte filamenteuse, printanière et éphémère, qui pousse sur des rochers plats dans les zones de balancement des marées des côtes de l’océan Pacifique nord.

env. 5 mm

Les filaments comptent souvent plus de vingt cellules, toutes dotées d’un noyau, comme chez tous les eucaryotes.

:

Urospora wormskioldii

Longueur : jusqu’à 30 cm

Largeur : 0,2 à 2 mm

La cellule terminale est hémisphérique, traduisant une zone de croissance.

EN CHIFFRES

278 1,635 MILLIARD

C’est le nombre de microfossiles de Qingshania magnifica que l’équipe chinoise a étudiés. Leur longueur atteignait parfois 860 µm. Celle des cellules variait entre 15 et 190 µm, et leur diamètre, entre 20 et 194 µm. Certaines contenaient une endospore de 15 à 21 µm de diamètre.

Les schistes de Chuanlinggou, dans le nord de la Chine, constituent une roche vieille de 1,635 milliard d’années, où les fossiles sont particulièrement bien conservés.

l’ouest de l’Australie vieux de 3,465 milliards d’années. Il y détecta au microscope des « microbes filamenteux » qu’il interpréta logiquement comme des cyanobactéries.

Ces bactéries, qui réalisent une photosynthèse avec dégagement d’oxygène, étaient donc présentes bien avant la première Grande Oxygénation, cette période entre 2,4 et 2 milliards d’années durant laquelle l’atmosphère terrestre s’est considérablement enrichie en oxygène. Puis, tout au long de l’Archéen, et ensuite du Paléoprotérozoïque (entre 2,5 et 1,6 milliards d’années), de nombreuses autres colonies bactériennes – donc procaryotes – se sont développées.

Comme U. wormskioldii, le fossile de Qingshania magnifica, trouvé dans le nord de la Chine, est constitué d’une série de cellules cylindriques de taille variable.

140

C’est le nombre de genres d’organismes pluricellulaires filamenteux connus. Onze d’entre eux sont bactériens, un est archéen. Ceux qui restent sont eucaryotes.

Des eucaryotes, en revanche, point de trace avant la fin du Paléoprotérozoïque. Les plus anciens vestiges unicellulaires connus sont vieux d’environ 1,65 milliard d’années, ce qui suggère que près de milliards d’années se sont écoulées entre leur apparition et celle des filaments de bactéries. Surtout, jusqu’à présent, vu les fossiles connus, on pensait que les premiers filaments pluricellulaires eucaryotes s’étaient formés très tardivement. Mais était-ce une réalité biologique ou la conséquence d’un manque de fossiles ? La découverte de l’équipe chinoise vient justement de balayer la première option.

LE CAP DU MILLIARD D’ANNÉES

Auparavant, plusieurs équipes avaient trouvé des populations relativement abondantes d’anciens eucaryotes pluricellulaires, mais ces dernières remontaient toutes à environ 1 milliard d’années… et s’apparentaient chacune à une branche différente des eucaryotes actuels : une algue rouge, Bangiomorpha pubescens, découverte en 2000 dans l’île Somerset, dans l’archipel arctique canadien, et datée tout récemment de 1,050 milliard d’années ; une algue verte, Proterocladus antiquus , décrite en 2020 dans un gisement du nord de la Chine, dans une péninsule proche de la Corée du Nord, vieille de 0,950 milliard d’années ; un hypothétique champignon,

Ourasphaira giraldae, trouvé en 2019 dans le nord du Canada, en face de l’île Victoria, remontant à 0,890 milliard d’années ; et enfin, découvert en 2021 dans un ancien récif fossilisé du nord-ouest du Canada, près de l’Alaska, le plus ancien animal fossilisé connu – une éponge datant elle aussi de 0,890 milliard d’années.

On s’interrogeait donc : avait-il fallu plus de 600 millions d’années aux eucaryotes pour développer un organisme pluricellulaire, soit deux fois plus de temps que les procaryotes ou, tout simplement, les fossiles intéressants n’avaient-ils pas encore été trouvés ? C’est alors que l’équipe de Maoyan Zhu, de l’Académie chinoise des sciences, en collaboration avec Andrew Knoll, le spécialiste reconnu de la paléontologie précambrienne de l’université Harvard, aux États-Unis, a décrit des eucaryotes multicellulaires vieux de plus de 1,6 milliard d’années. Dans la formation Chuanlinggou, dans le nord de la Chine, elle a trouvé des échantillons mieux préservés du fossile Qingshania magnifica, découvert en 1989 dans ce même gisement. À l’époque, à cause de la mauvaise qualité des photographies publiées et de la difficulté d’accès à la publication, l’étude du fossile avait reçu peu d’attention. Maoyan Zhu et ses collègues l’ont donc recommencée en examinant les nouveaux échantillons par des techniques modernes de spectroscopie.

UNE ALGUE ANCESTRALE

En macérant les schistes à l’acide, ils ont libéré des filaments droits ou courbés d’un maximum de vingt cellules. Certains filaments sont particuliers. Leurs cellules contiennent une structure ovoïde présentant toujours la même taille, la même forme, la même transparence, la même localisation. Bref, ce n’est pas un artefact, mais bel et bien un objet biologique que les chercheurs interprètent comme une endospore comparable à celles que l’on trouve chez de nombreuses algues filamenteuses et qui interviennent dans leur reproduction.

Mais ne serait-ce pas une cyanobactérie ? Bien que la taille et la forme ne prêchent pas pour une telle identité, les chercheurs ont voulu le vérifier. Pour cela, ils ont comparé le spectre Raman de Q. magnifica avec ceux de cyanobactéries actuelles et fossiles. Les différences sont très nettes, et tout laisse penser qu’il s’agit d’une algue filamenteuse eucaryote ressemblant à certaines algues vertes actuelles comme l’ulvophycée Urospora wormskioldii

DES FOSSILES À L’ARBRE DES EUCARYOTES

En comparant les gènes des eucaryotes actuels, il est possible de reconstituer un arbre de parenté de ce groupe avec une estimation des dates d’apparition des embranchements, depuis Leca (Last eukaryotic common ancestor), leur ancêtre commun le plus récent – ou le groupe de cellules qui, ensemble, présentaient toutes ses caractéristiques –, jusqu’à aujourd’hui. On y voit que la découverte de Qingshania magnifica, le plus ancien eucaryote pluricellulaire connu, vieux de 1 635 millions d’années (Ma), comble un grand vide, puisque les autres fossiles connus d’eucaryotes pluricellulaires (les points colorés) sont bien plus récents.

000

Paléoprotérozoïque

Leca

Les plus anciens eucaryotes unicellulaires connus (∿1 650 Ma)

538,8 750

000 Ma

Néoprotérozoïque Mésoprotérozoïque

Pha.

SAR

Haptophytes

Algues vertes

Algues rouges

Amibozoaires

Champignons

Holozoaires

Qingshania magnifica (∿1 635 Ma)

En d’autres termes, la pluricellularité est survenue très vite après l’apparition des eucaryotes unicellulaires : en 15 millions d’années d’après les fossiles connus. La nouvelle séquence temporelle sur Terre s’écrit comme suit : 4,54 milliards d’années, formation de la Terre ; 4,28 milliards d’années, premières traces de vie ; 3,8 milliards d’années, premières cellules procaryotes ; 3,465 milliards d’années, premières bactéries filamenteuses ; 1,650 milliard d’années, premiers unicellulaires eucaryotes ; 1,635 milliard d’années, premiers eucaryotes filamenteux ; 0,890 milliard d’années, premier animal fossilisé. Puis, depuis l’explosion cambrienne d’il y a 540 millions d’années, tout s’accélère.

Sans doute trouvera-t-on des fossiles plus anciens qui viendront encore bouleverser cette chronologie, mais en attendant on peut supposer que les eucaryotes sont devenus pluricellulaires bien plus vite que les procaryotes. Ce qui soulève une nouvelle question : pourquoi une telle différence ? Serait-ce parce que la pluricellularité existait déjà chez les procaryotes et a facilité celle des eucaryotes, par transfert de gènes ou autre ? Ou parce que les eucaryotes se sont vite dotés d’une matrice extracellulaire plus complexe, ce qui a favorisé les interactions cellule-cellule ? Vivement le prochain fossile ancien. n

Hervé Le Guyader a notamment publié : Ma galerie de l’évolution (Le Pommier, 2021).

BIBLIOGRAPHIE

L. Miao et al., 1.63-billion-year-old multicellular eukaryotes from the Chuanlinggou Formation in North China, Sci. Adv., 2024.

A. H. Knoll et al., Life : The first two billion years, Phil. Trans. R. Soc. B, 2016.

J. W. Schopf, Microfossils of the Early Archean Apex Chert : New evidence of the antiquity of life, Science, 1993.

OFFRE D’ABONNEMENT 1 AN

ABONNEZ-VOUS À

Le magazine papier 12 numéros par an

Le magazine en version numérique 12 numéros par an

Le hors-série papier 4 numéros par an

Le hors-série en version numérique 4 numéros par an

Accès à pourlascience.fr Actus, dossiers, archives depuis 1996

VOTRE TARIF D’ABONNEMENT

3 FORMULES AU CHOIX

FORMULE PAPIER

FORMULE PAPIER + HORS - SÉRIE

59 €

Au lieu de 84,00 €

30 % de réduction *

79 €

Au lieu de 123,60 €

36 % de réduction *

FORMULE INTÉGRALE

99 €

Au lieu de 183,60 €

46 % de réduction *

PAG24STD

Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr

OUI , je

m’abonne pour 1 an à

Je choisis ma formule (merci de cocher) 1

FORMULE PAPIER

• 12 n° du magazine papier

FORMULE PAPIER + HORS SÉRIE

• 12 n° du magazine papier

• 4 n° des hors-séries papier

FORMULE INTÉGRALE

• 12 n° du magazine (papier et numérique)

• 4 n° des hors-séries (papier et numérique)

59 €

Au lieu de 84,00 €

79 €

Au lieu de 123,60 €

99 €

Au lieu de 183,60 €

• Accès illimité aux contenus en ligne

J’indique mes coordonnées 2

☐ M. ☐ M me

Nom :

Adresse :

Code postal : Ville :

Téléphone :

Prénom :

Courriel : (indispensable pour la formule intégrale)

J'accepte de recevoir les o res de Pour la Science

Je retourne le bulletin d'abonnement et mon règlement 3

☐ OUI ☐ NON

J’émets un chèque à l’ordre de Pour la Science du montant de l’abonnement. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante : Abonn’escient – TBS Group Service abonnement Groupe Pour la Science 20 rue Rouget de Lisle - 92130 Issy les Moulineaux

COMMANDEZ PLUS SIMPLEMENT !

Pour découvrir toutes nos o res d’abonnement et e ectuer un paiement en ligne, scannez le QR code ci-contre avec votre téléphone ou rendez-vous sur pourlascience.fr/abonnements/

* Réduction par rapport au prix de vente en kiosque et l’accès aux archives numériques. Durée d’abonnement : 1 an. Délai de livraison : dans le mois suivant l’enregistrement de votre règlement. O re valable jusqu’au 31/03/2024 en France métropolitaine uniquement. Pour un abonnement à l’étranger, merci de consulter notre site boutique.groupepourlascience.fr. Photos non contractuelles. Vous pouvez acheter séparément les numéros de Pour la Science pour 7 € et les hors-séries pour 9,90 € En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante : https://rebrand.ly/CGV-PLS. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour la Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous invitons à prendre connaissance de notre charte de protection des données personnelles à l’adresse suivante : https://rebrand.ly/charte-donnees-pls. Conformément à la réglementation applicable (et notamment au règlement 2016/679/UE dit « RGPD ») vous disposez des droits d’accès, de rectification, d’opposition, d’e acement, à la portabilité et à la limitation de vos données personnelles. Pour exercer ces droits (ou nous poser toute question concernant le traitement de vos données personnelles), vous pouvez nous contacter par courriel à l’adresse protection-donnees@pourlascience.fr.

L’AUTEUR

HERVÉ THIS physicochimiste, directeur du Centre international de gastronomie moléculaire AgroParisTech-Inrae, à Palaiseau

PDES SOUFFLÉS DE BONNE TENUE

Quelles proportions d’ingrédients perme ent à des soufflés de gonfler et de rester ainsi ?

our faire gonfler les soufflés, il y a ces trois lois que j’ai découvertes il y a des années, à savoir bien battre les blancs d’œufs en neige ferme, faire une croûte dans la partie supérieure avant la cuisson et, surtout, chauffer par le fond : si les soufflés gonflent, c’est surtout parce que l’eau de la préparation, évaporée de la partie inférieure des ramequins, produit un grand volume de vapeur, qui pousse les couches vers le haut. Quand les blancs sont fermes ou quand une croûte est présente, les bulles de vapeur sont mieux retenues, ce qui contribue ainsi à un gonflement plus prononcé. En théorie, une préparation de 100 grammes de soufflé pourrait engendrer plus de 15 litres de soufflé final.

Le gonflement étant obtenu, quelle est la juste proportion des ingrédients utilisés, qui fait tenir un soufflé ? Pour un soufflé au fromage, par exemple, la préparation de base est une sauce épaisse, faite essentiellement de farine, de lait, de beurre, et de fromage. On y ajoute des jaunes d’œufs, tandis que les blancs d’œufs sont battus en neige à part. Quelle est l’influence relative des blancs et des jaunes ? Des soufflés avec beaucoup de blanc d’œuf tiendraientils mieux ou moins bien que des soufflés avec beaucoup de jaune ?

Nous avons étudié expérimentalement ces questions lors du dernier séminaire de gastronomie moléculaire, en divisant une même base de soufflé en trois parties égales et en comparant des soufflés faits entièrement avec des blancs, ou entièrement avec des jaunes, ou avec des œufs entiers, les jaunes étant dans la sauce tandis que les blancs étaient battus en neige. Les résultats ont été nets : pour les soufflés avec beaucoup de blanc, le développement est bien supérieur, mais la consistance est

Privilégier les blancs d’œufs produit un gonflement très marqué, mais ce sont les protéines des jaunes qui assurent la bonne tenue du soufflé.

très fragile : les énormes soufflés que l’on récupère à la sortie du four redescendent rapidement. Pour les soufflés avec beaucoup de jaune d’œuf, le gonflement est moindre, mais les soufflés, bien mieux pris, se tiennent bien mieux aussi. Le résultat est intermédiaire pour les soufflés avec jaunes et blancs d’œufs.

Pourquoi ces différences ? Il y a d’abord le fait que le jaune et le blanc ont des proportions d’eau et de protéines différentes. Un blanc d’œuf, c’est environ 35 grammes d’eau et 5 g de protéines. Ces protéines peuvent coaguler, faisant tenir le soufflé, mais seulement quand la température est assez élevée. Or dans l’intérieur d’un soufflé, la température peut rester à 60 degrés quand le cœur reste un peu moelleux. Pour les jaunes, il y a seulement 10 grammes d’eau, d’où le moindre gonflement, mais il su ffi t de considérer un œuf dur pour comprendre que la coagulation est plus forte : non seulement, le jaune contient 5 grammes de protéines mais ces protéines-là réagissent di ff éremment des protéines du blanc. Oui, réagissent : leurs protéines contiennent des résidus de cystéine, qui portent des groupes « thiols » (un atome de soufre lié à un atome d’hydrogène). Leur dénaturation, causée par l’échauffement, permet l’établissement de liaisons particulières nommées « ponts disulfures », qui lient les protéines : c’est la coagulation.

Finalement, comment faire nos soufflés ? On pensera aux blancs pour avoir du gonflement et de la légèreté, mais on pensera aux jaunes si l’on préfère un peu de tenue. Et, de toute façon, on appliquera les trois lois rappelées en début d’article. n

SOUFFLÉ AU GRAND MARNIER

Dans une casserole, cuire 35 g de farine avec autant de beurre jusqu’à légère coloration blonde (« roux »).

Dans une autre casserole, chau er 250 g de lait avec une gousse de vanille fendue en deux et grattée. Retirer la gousse.

Verser ce lait vanillé chaud sur le roux et cuire jusqu’à épaississement.

À part, fouetter 4 jaunes d’œufs et 50 g de sucre jusqu’à ce que le mélange blanchisse (« ruban »).

Ajouter les jaunes blanchis et une cuillerée de Grand Marnier à la préparation précédente.

À part, battre les 4 blancs d’œufs en neige ferme. Leur ajouter 75 g de sucre, et poursuivre le battage.

Ajouter les blancs en neige sucrés à la première préparation.

Beurrer les ramequins et saupoudrer du sucre glace sur le beurre.

Verser la préparation dans les ramequins, et cuire au four à 220 °C (partie basse, chau age par le fond, si possible) pendant quinze minutes.

Saupoudrer de sucre glace.

PICORER À

p. 24

p. 92

1,6 MILLIARD

Retrouvez tous nos articles sur www.pourlascience.fr

Durant la canicule de 2022, les langues glaciaires de ce massif se sont amincies jusqu’au sommet, au dôme du Goûter, au-dessus de 4 000 mètres. Jusqu’alors, les parties hautes étaient plutôt stables et les amincissements concernaient les parties basses.

£

p. 7

p. 44

7 MONT- BLANC

Les plus anciens vestiges connus d’eucaryotes, les organismes dont les cellules sont dotées d’un noyau, comme les animaux, les plantes et les champignons, sont vieux d’environ 1,6 milliard d’années. Les eucaryotes sont donc probablement apparus plus de 2 milliards d’années après les premières cellules formées sur Terre, dépourvues de noyau, dont des fossiles témoignent de l’existence il y a environ 3,8 milliards d’années.

Faisons davantage confiance au vivant pour s’adapter et acceptons que la productivité forestière diminue £

JONATHAN LENOIR écologue au CNRS

p. 88

Pour colorier n’importe quelle carte sur un tore, il faut sept couleurs. Cela semble en contradiction avec le théorème des quatre couleurs qui stipule qu’il faut quatre couleurs pour colorier n’importe quelle carte du plan… mais le tore contient un trou et cela change tout !

p. 14

160 KILOMÈTRES PAR HEURE

C’est la vitesse à laquelle la nappe d’une grande table dressée pour seize convives a été tirée sans que les objets ne bougent. Pour mener à bien cette expérience, les animateurs de l’émission américaine « Street Science » ont placé des feuilles de plastique entre les objets et la nappe afin de réduire les frottements et accroché celle-ci par un long câble… à une voiture de course.

RÉTROTRANSPOSON

Les rétrotransposons sont des séquences d’ADN, parfois d’origine virale, qui s’insèrent dans le génome de leur hôte lors d’une infection et se démarquent par leur capacité à s’y déplacer et à s’y multiplier. Chez l’humain, ils constituent environ 40 % de son génome !

p. 66

Dans certains matériaux, en influant sur les caractéristiques magnétiques d’ensembles d’atomes, il est possible de former des sortes de « bulles magnétiques » qui se déplacent très vite : des « skyrmions ». Ces objets ont une structure bidimensionnelle, mais en 2023, des physiciens ont créé pour la première fois leur pendant en trois dimensions : des « hopfions ».

Cet encart d’information est mis à disposition gratuitement au titre de l’article L. 541-10-18 du code de l’environnement. Cet encart est élaboré par CITEO.

TRIONS SYSTÉMATIQUEMENT

LUNDI 8 AVRIL

JOURNÉE PROFESSIONNELLE À DESTINATION DES PROFESSIONNEL·LES DE LA MÉDIATION CULTURELLE, SCIENTIFIQUE ET DES RECHERCHES PARTICIPATIVES

CAEN | NORMANDIE Soutenu par Soutenu par

TOUTE LA SEMAINE

JOURNÉES ET SOIRÉES

RENCONTRES

ATELIERS CONFÉRENCES GRATUIT SUR INSCRIPTION