Pour La Science #559 • Mai 2024.

OÙ SE CACHE

L’AVANTAGE QUANTIQUE ? Neurosciences

QUAND LE SOMMEIL SE FAIT THÉRAPIE Mathématiques

L’INFINIE FINESSE DES FRACTALES CARRÉES

DES CITÉS PERDUES EN AMAZONIE

Il y a 3 000 ans, une civilisation avancée bâtissait des villes-jardins

Abonnez-vous

formule intégrale à partir de 8,20 € / mois sans engagement

• Tout pourlascience.fr

• Le téléchargement Pdf

• Les archives depuis 1996

• La revue (12 numéros / an)

• Le Hors-Série (4 numéros / an)

Pour s’abonner et découvrir toutes nos o res, flashez ici.

MENSUEL POUR LA SCIENCE

Rédacteur en chef : François Lassagne

Rédacteurs en chef adjoints : Loïc Mangin, Marie-Neige Cordonnier

Rédacteurs : François Savatier, Sean Bailly

HORS-SÉRIE POUR LA SCIENCE

Rédacteur en chef adjoint : Loïc Mangin

Développement numérique : Philippe Ribeau-Gésippe

Directeur marketing et développement : Frédéric-Alexandre Talec

Chef de produit marketing : Ferdinand Moncaut

Directrice artistique : Céline Lapert

Maquette : Pauline Bilbault, Raphaël Queruel, Ingrid Leroy, Ingrid Lhande

Réviseuses : Anne-Rozenn Jouble, Maud Bruguière et Isabelle Bouchery

Assistante administrative : Finoana Andriamialisoa

Directrice des ressources humaines : Olivia Le Prévost

Fabrication : Marianne Sigogne et Stéphanie Ho

Directeur de la publication et gérant : Nicolas Bréon

Ont également participé à ce numéro : Isabelle Bellin, Nicolas Claidière, Valérie Daux, Clémentine Laurens, François Parcy, Magali Proffit, Philippe Rossi, William Rowe-Pirra, Mary Sears, Patrizia Tavella, Antoine Tilloy

PUBLICITÉ France

stephanie.jullien@pourlascience.fr

ABONNEMENTS

https://www.pourlascience.fr/abonnements/

Courriel : serviceclients@groupepourlascience.fr

Tél. : 01 86 70 01 76

Du lundi au vendredi de 8 h 30 à 12 h 30 et de 13 h 30 à 16 h 30

Adresse postale : Service abonnement groupe Pour la Science

20 rue Rouget-de-Lisle

92130 Issy-les-Moulineaux

Tarifs d’abonnement 1 an (12 numéros)

France métropolitaine : 69 euros – Europe : 82,20 euros

Reste du monde : 91,20 euros

DIFFUSION

Contact kiosques : À Juste Titres ; Alicia Abadie

Tél. 04 88 15 12 47

Information/modification de service/réassort : www.direct-editeurs.fr

DISTRIBUTION

MLP

ISSN 0 153-4092

Commission paritaire n° 0927K82079

Dépôt légal : 5636 – Mai 2024

N° d’édition : M0770559-01

www.pourlascience.fr

170 bis boulevard du Montparnasse – 75 014 Paris

Tél. 01 55 42 84 00 SCIENTIFIC

interdit de reproduire intégralement ou partiellement la présente revue sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20 rue des Grands-Augustins, 75006 Paris).

Origine du papier : Autriche

Taux de fibres recyclées : 30 %

« Eutrophisation » ou « Impact sur l’eau » : Ptot 0,007 kg/tonne

Imprimé en France

Maury Imprimeur SA Malesherbes

N° d’imprimeur : 277 412

DITO É

François Lassagne Rédacteur en chef

LA QUÊTE D’EL VERDE

Ils espéraient découvrir l’Eldorado, des villes oubliées sous le couvert de la forêt, regorgeant d’or. Las, les contrées de l’Amazonie ne recelaient rien de tel. Parmi les premiers Européens à s’y aventurer, le conquistador Francisco de Orellana, en 1541, avait pourtant rapporté la présence de cités s’étalant sur plus de 10 kilomètres de longueur. Avait-il rêvé ? Sans doute son témoignage contribua-t-il au fantasme de l’Eldorado. Mais on sait aujourd’hui qu’il y eut bien des villes dans les vallées amazoniennes des Andes. Des villes non pas couvertes d’or, mais intimement mêlées au vert de la forêt environnante. Non pas El Dorado, mais El Verde !

Si la civilisation qui les bâtit fut rapidement décimée par les maladies que les Européens amenèrent avec eux, elle eut néanmoins le temps de laisser des traces. Et quelles traces ! L’archéologue américaniste Stéphen Rostain en a entrepris la quête à hauteur d’homme, d’abord, lors de nombreuses expéditions. Il a ensuite littéralement pris de la hauteur, les cherchant depuis le ciel, mobilisant la technique du lidar, dont les ondes pénètrent la canopée. Dans la vallée de l’Upano, en Équateur, des infrastructures, inscrites sur plus de 600 kilomètres carrés (six fois la surface de Paris), se sont alors révélées. Un urbanisme agraire, apparu il y a 3 000 ans, sommeillait sous le couvert végétal. Stéphen Rostain fait dans ce numéro le récit de cette incroyable découverte, qui éclaire l’histoire du continent sud-américain d’un nouveau jour. « Les Andes n’ont plus l’apanage des vastes centres cérémoniels ou d’urbanisation autochtone, comme le Machu Picchu ou Pachacamac chez les Incas », insiste le chercheur.

Les cités-jardins qu’inventa la civilisation de l’Upano passèrent par une emprise humaine considérable sur la forêt native. Il fallait terrasser, élever des tertres, creuser des routes. Elle n’en tissa pas moins des liens serrés entre le monde végétal, devenu ressource agricole, et infrastructures urbaines. Une inspiration pour notre monde contemporain, à l’heure où la déforestation se poursuit à un rythme préoccupant, en dépit de l’engagement pris, lors de la COP26, d’y mettre fin d’ici à 2030. Selon le rapport publié début avril par le World Resources Institute, les régions tropicales ont perdu 3,7 millions d’hectares de forêt primaire en 2023. À défaut de ressusciter « El Verde », l’urbanisme de demain parviendra-t-il à laisser au monde végétal une place indispensable, pour atténuer et prévenir les effets du réchauffement climatique ? n

NE MANQUEZ PAS LA PARUTION DE VOTRE MAGAZINE GRÂCE À LA NEWSLETTER LETTRE D’INFORMATION

• Notre sélection d’articles

• Des offres préférentielles

• Nos autres magazines en kiosque

Inscrivez-vous www.pourlascience.fr

P. 6

ÉCHOS DES LABOS

• La fonte des glaces perturbe la mesure du temps

• La santé des Français s’est améliorée entre 1990 et 2019

• Les plantes grandissent surtout l’après-midi

• Une pâte à modeler néandertalienne

• Vers un diagnostic précoce de la maladie de Charcot

• Bételgeuse tourne-t-elle trop vite ?

P. 16

LES LIVRES DU MOIS

P. 18

DISPUTES

ENVIRONNEMENTALES

La meilleure façon de marcher

Catherine Aubertin

P. 20

LES SCIENCES À LA LOUPE

De quoi les scientifiques sont-ils responsables ?

Yves Gingras

P. 32

NEUROSCIENCES

GUÉRIR

PAR LE SOMMEIL

Ingrid Wickelgren

Stimuler le cerveau endormi pourrait soulager les personnes souffrant de pertes de mémoire, d’accidents vasculaires cérébraux ou de troubles de la santé mentale.

P. 40

PALÉOCLIMATOLOGIE

« NOUS N’AVONS PAS ENCORE

DÉCLENCHÉ UN RÉCHAUFFEMENT

EXCESSIF »

Michael E Mann

Les leçons tirées du passé lointain de notre planète, durant laquelle elle s’est couverte de glace ou a dépassé les températures actuelles, aident à prendre la mesure du changement climatique que nous vivons, et de l’urgence à le contenir

En couverture : © Antoine Dorison

Les portraits des contributeurs sont de Seb Jarnot

Ce numéro comporte un courrier de réabonnement posé sur le magazine sur une sélection d’abonnés.

P. 52

ÉTHOLOGIE

L’OUTIL, PORTE D’ENTRÉE VERS LES INTELLIGENCES

Michael Haslam et Abigail Desmond

L’utilisation d’outils n’est pas l’apanage des humains Il est temps de repenser ce qu’elle révèle de l’intelligence des animaux et de leur évolution.

P. 58

NEUROANATOMIE

NOTRE « PETIT CERVEAU », MAÎTRE DES ÉMOTIONS ET DU MOUVEMENT

Douglas Fields

Le cervelet ne gère pas seulement nos mouvements, il les associe à nos émotions et régule nos interactions sociales.

P. 44

INFORMATIQUE

OÙ SE CACHE L’AVANTAGE QUANTIQUE ?

Charlie Wood

Dans quelles situations un ordinateur quantique est-il vraiment plus puissant qu’un ordinateur classique ? C’est une question étonnamment subtile à laquelle les physiciens sont toujours confrontés, des décennies après l’avènement de l’ère quantique

P. 64

BIOLOGIE

MISER SUR LES DÉFENSES NATURELLES DES PLANTES

Sylvain Raffaele

Difficile d’imaginer l’incroyable bataille que se livrent plantes et pathogènes, chacun pour sa survie…

P. 22 ARCHÉOLOGIE

DES CITÉS PERDUES EN AMAZONIE

Stéphen Rostain

Il y a 3 000 ans, au piémont des Andes, en Équateur, une civilisation agraire avancée s’est développée dans la forêt amazonienne.

P. 72

HISTOIRE DES SCIENCES

JULES MARCOU, TRAPPEUR GÉOLOGUE

Daniel Raichvarg

Cet enfant du Jura troqua ses livres contre les caravanes du Far West. N’en déplut à ses confrères théoriciens.

RENDEZ-VOUS

P. 80

LOGIQUE & CALCUL

L’INFINIE FINESSE DES FRACTALES CARRÉES

Jean-Paul Delahaye

Les fractales carrées présentent une variété de topologies qu’on réussit seulement maintenant à comprendre et à classer

P. 86

ART & SCIENCE

Auprès de mon arbre… Loïc Mangin

P. 88

IDÉES DE PHYSIQUE

La détente souffle le chaud

Jean-Michel Courty et Édouard Kierlik

P. 92

CHRONIQUES DE L’ÉVOLUTION

Le double effet du génome de la myxine Hervé Le Guyader

P. 96

SCIENCE & GASTRONOMIE

Quand le bleu voit rouge

Hervé This

P. 98

À PICORER

L’ESSENTIEL

> Dans les années 1990, d’importantes agglomérations de plateformes sont repérées et étudiées pour la première fois dans la vallée de la rivière Upano, en Équateur.

> Des fouilles « horizontales » révèlent la chronologie à deux périodes de la culture « upano »

et les premières explorations aériennes suggèrent que le site est très étendu.

> Une vaste campagne lidar révèle ensuite sa structure d’ensemble et son immensité : plus de 600 kilomètres carrés, soit six fois la surface de Paris, sont urbanisés !

L’AUTEUR

STÉPHEN ROSTAIN

archéologue au laboratoire Archéologie des Amériques (CNRS, université Panthéon-Sorbonne)

Des cités perdues en Amazonie

Il y a 3 000 ans, au piémont des Andes, en Équateur, une civilisation agraire avancée s’est développée dans la forêt amazonienne.

Nous sommes en 1541. Une barque de fortune navigue au gré du courant de l’Amazone. Parti de Quito en quête de cannelle et d’or, le conquistador Francisco de Orellana et une soixantaine de soudards sont les premiers Espagnols à descendre le majestueux fleuve tropical Au fil de l’eau, ils longent des villes autochtones qui les surprennent : « Nous parvînmes à [ ] un village qui devait avoir plus de deux lieues de long [soit près de 10 kilomètres], d’où partaient de nombreux chemins vers l’intérieur des terres », écrivit le prêtre participant au voyage Un témoignage qu’ultérieurement personne ne prit au sérieux en Espagne : le doute qu’il suscitait se confirma après que les expéditions ultérieures ne rapportèrent ni autochtones ni villes le long du fleuve Aujourd’hui nous savons pourquoi : le choc épidémiologique dû à l’arrivée des bactéries et des virus amenés par les Européens avait déjà dépeuplé les berges de l’Amazone Dès lors, l’existence de cités perdues en Amazonie fut rejetée dans le domaine des légendes, faisant la part belle à d’imaginaires villes oubliées pleines d’or. Ce fantasme de l’Eldorado – mot espagnol signifiant « le doré » – a perduré jusqu’à nos jours.

Si l’Eldorado est bien du folklore pour nigauds, on sait désormais qu’avant l’arrivée des Européens , de grandes villes ont existé dans la forêt pluviale Depuis les années 2000,

nous avons accumulé les découvertes archéologiques de grandes agglomérations des alentours de l’an mille dans le Haut Xingu , au Brésil, et dans les Llanos de Mojos, en Bolivie De plus, des terrassements anciens étendus apparaissent peu à peu dans différentes parties de l’Amazonie . Les Andes n’ont donc plus l’apanage des vastes centres cérémoniels ou d’urbanisation autochtone, comme le Machu Picchu ou Pachacamac chez les Incas Mais , jusqu’à présent, rien n’avait surpassé les récentes révélations de l’investissement urbain de la vallée amazonienne de l’Upano au cours des premiers millénaires avant et après le début de notre ère : là, des communautés agricoles ont développé une civilisation, qui, à partir d’il y a presque 3 000 ans, s’est épanouie pendant plus d’un millénaire jusque vers 600 de notre ère, avant que l’occupation de la vallée ne s’interrompe pour 200 ans, pour reprendre entre 800 et 1200 de notre ère

Pourquoi cette interruption ? La raison en reste indéterminée , mais comment ne pas penser que le Sangay avait fait des siennes ?

Localisée juste au nord de la vallée de l’Upano, cette énorme montagne est un strato - volcan strombolien vieux de 500 000 ans , culminant à 5 260 mètres d’altitude (voir page 27, en haut). Or le Sangay est en éruption continue depuis… 1934. Cette activité soutenue, mais relativement modérée, est typique des volcans stromboliens Cependant, il est envisageable

La technique du lidar révèle la configuration des sites archéologiques de la vallée de la rivière Upano.

que l’énorme volcan connaisse parfois des épisodes destructeurs, tels que des éruptions pliniennes ou encore des émissions massives de cendres mêlées de gaz, se prolongeant au point de rendre la région peu habitable

Un tel épisode a - t- il eu lieu pendant la seconde partie du Ier millénaire de notre ère ?

L’histoire éruptive du Sangay étant malheureusement peu connue à ce stade, tant il est dangereux de se trouver sur ses flancs, nous ne savons pas Plusieurs détails accréditent cependant l’idée que la cohabitation des populations humaines avec le cracheur de feu est parfois difficile. Ainsi, les chutes de cendres entraînées par un épisode éruptif de 2021 ont a ff ecté pas moins de cinq des vingt- quatre provinces équatoriennes Et puis , le nom Sangay provient d’une racine quechua signifiant « terrifiant » , indice , peut- être , que la cohabitation des humains avec l’imposante montagne puisse être parfois délicate. Au point de s’interrompre ?

UNE VALLÉE OUBLIÉE REDÉCOUVERTE

La seule chose que nous pouvons dire est que ce volcan est dangereux depuis longtemps, puisque dans le folklore local, le Sangay est comparé à « un phare au-dessus de la mer », c’est-à-dire au-dessus de la forêt qu’il domine, et dans laquelle il permet de s’orienter de loin, car on perçoit toujours de nuit la lumière émise par ses flammes. Pareille tradition suggère que les habitants de la région ont toujours connu le volcan actif, ce qui accroît la probabilité que le Sangay, comme le Vésuve, un autre volcan strombolien , a pu parfois devenir plinien Une chose au moins est certaine : en faisant régulièrement pleuvoir des cendres dans son entourage , le Sangay l’a rendu extrêmement fertile, ce qui explique la prospérité des dizaines de milliers d’anciens cultivateurs de la vallée de l’Upano

S’étendant le long du piémont oriental des Andes, au sud de l’Équateur, et enfermée entre deux cordillères, les Andes à l’ouest et le Cutucú à l’est, cette vallée constitue une zone frontière entre deux écosystèmes ( voir la carte page ci - contre ) Le paysage dominant est

La rivière Upano naît sur les flancs sud du volcan Sangay puis s’enfonce profondément dans la forêt amazonienne, où elle forme de nombreuses tresses.

typique de la haute forêt humide amazonienne, mais déjà apparaissent des traits montagnards andins C’est là, entre montagne et forêt, où tremblements de terre et éruptions volcaniques émaillent la chronique, que se trouvent les vestiges d’un ancien système urbain, viaire et agraire, d’une ampleur remarquable.

Équateur

Comment furent-ils révélés ? L’histoire de l’archéologie du bassin de l’Upano commença véritablement à la fin des années 1970 lorsque le missionnaire salésien Giovanni Bottasso (1936-2019), en poste dans le bourg colon naissant de Macas, dans la vallée, reçut son confrère équatorien joséphite Pedro Porras (1910-1990). Connaissant sa passion pour l’archéologie, il l’emmena dans un endroit oublié où il avait découvert un site fait d’une dizaine de gros monticules artificiels rectangulaires en terre, disposés géométriquement en bordure du ravin de l’Upano. Stupéfait par cette trouvaille, Pedro Porras s’attribua la paternité du lieu et y organisa peu après des fouilles archéologiques, aboutissant à une classification céramique et à une première chronologie. Quand, en 1995, je suis arrivé en Équateur, j’ai décidé d’organiser de nouvelles fouilles archéologiques sur ce site a priori prometteur, en coopération avec les archéologues du pays. Je n’avais nulle conscience de l’immensité de ce que j’allais découvrir. J’ai vite compris , cependant , que l’envergure inhabituelle de l’implantation et le grand nombre des tertres exigeraient qu’une méthode de fouille adaptée soit appliquée . J’optai pour l’approche par décapage de grandes aires, une méthodologie dite « de fouille horizontale » Si cette technique fut pensée à l’origine par le grand préhistorien André Leroi-Gourhan (1911-1986), ce fut toutefois l’archéologue tchèque Bohumil Soudský (1922-1976) qui la valida dans les années 1950 en fouillant le site néolithique de Bylany, en Bohême centrale Là ne subsistaient en effet que des empreintes de fosses , de trous de poteaux et autres tranchées de fondation dans le sol, qui en outre se trouvaient sous des épaisseurs de terre Bohumil Soudský fit décaper précautionneusement le sol à la pelle mécanique, ce qui lui permit de dresser une carte de l’habitat, d’y situer les activités, voire d’en retracer l’histoire

En Amazonie équatorienne, la technique n’avait jamais été appliquée sur un site archéologique, de sorte que sa mise en œuvre sur les monticules artificiels de la vallée de l’Upano dans le cadre des fouilles que j’organisai de 1996 à 2001 constitua une innovation notable Nous raclâmes avec des pelles chaque couche d’occupation sur une ample surface tout en laissant en place les vestiges et traces, étudiés en détail ultérieurement Pour comparaison, on ne réalisait jusque - là que des sondages stratigraphiques

sur 1 mètre carré, qui fournissaient des informations limitées. Le décapage à grande échelle de plateformes de l’Upano a permis l’étude systématique de l’ensemble des traces de même époque Si cette méthodologie a tout d’abord laissé perplexes certains habitués locaux aux fouilles par petit sondage, les résultats obtenus finirent par convaincre Parmi ceux-ci, on peut souligner les modes de construction des tertres, les sols d’habitat et la culture matérielle révélés, les plantes cultivées et consommées, la définition des différents peuples qui se succédèrent avec plus de cinquante datations obtenues et, in fine, la possibilité de reconstituer une histoire culturelle complexe.

VERS UNE PREMIÈRE VISION D’ENSEMBLE

Je pus ainsi établir que l’occupation de la vallée avait commencé il y a près de 3 000 ans, et que , pendant plus d’un millénaire , elle a produit un urbanisme original d’ampleur inédite en Amérique du Sud, composé de grands monticules et plateformes rectangulaires, de basses places carrées , de rues et de routes droites creusées de plus de 10  mètres de largeur reliant les complexes de tertres, le tout intégrant des champs drainés dans un tissu urbain entouré de terrasses cultivées (voir la figure page  26) À l’époque où , en Gaule , les cultures celtiques commençaient à s’établir, et tandis qu’en Mésoamérique, les Mayas et les Olmèques prospéraient déjà, les premiers terrassiers-constructeurs de la région furent les membres d’une culture que l’on appelle

5 km

Rivière

Densité de tertres par km2

Route principale

Route secondaire

Continuité possible

Traversée possible de l’Upano

L’immense site archéologique laissé par la civilisation upano dans le Haut Upano est placé ci-dessus dans son contexte géographique. Les taches rouges correspondent aux plus grandes concentrations de tertres, en d’autres termes aux principales agglomérations.

Sangay

Site Upano

« upano », d’après le nom de la rivière Au cours des siècles, ils investirent l’ensemble de la vallée en multipliant les implantations de plateformes connectées par des routes. Puis, après la longue interruption sans habitant , peutêtre explicable par des éruptions du Sangay ou des changements climatiques, des monticules furent réoccupés entre 800 et 1200 de notre ère par des groupes huapulas, culture définie grâce aux décapages, à l’époque où en France régnaient les Capétiens

Ces résultats des travaux de terrain nous avaient persuadés que le phénomène archéologique local était d’ampleur, mais à quel point ?

Pour répondre à cette question , il était nécessaire de changer de perspective À la fin des années 1980, j’avais développé en Guyane une méthodologie de repérages archéologiques aériens dans les marécages côtiers, technique jusqu’alors largement ignorée par les archéologues travaillant dans le milieu amazonien. J’avais ainsi arpenté des kilomètres de littoral en ULM, découvrant et photographiant grâce à ces survols des milliers de buttes de 1 à 5  mètres de diamètre disposées en damier, en réalité des champs surélevés précolombiens

Toutes ces prospections aériennes ont révélé l’ampleur insoupçonnée des terrassements réalisés par les communautés guyanaises avant le contact avec les Européens

Par la suite, j’avais mis en œuvre cette archéologie aérienne dans d’autres régions

Ce relevé lidar du site de Copueno, dans la vallée de l’Upano, révèle des groupements de plateformes organisées autour d’un tertre central. Des routes les relient, entre lesquelles se trouvent des champs quadrillés de drains.

d’Amazonie, notamment en Équateur Difficile cependant d’appliquer la même approche dans la vallée de l’Upano, à cause du couvert forestier qui occulte la plupart des constructions. Certes, les vols en avion ou en hélicoptère nous permirent de repérer plusieurs complexes de plateformes artificielles dans des espaces déforestés, mais il était hélas impossible d’obtenir une vision globale des installations précolombiennes dispersées dans le paysage. Je suspectais cependant déjà une occupation ancienne de très grande ampleur.

PRENDRE DE LA HAUTEUR

Ce n’est qu’après la popularisation d’une technique puissante apte à révéler les structures camouflées, le lidar (pour Laser imaging detection and ranging) que cette envergure put apparaître Cette technique, en effet, dévoile le modelé exact du sol sous la canopée À la différence du radar et de ses ondes radio, le lidar emploie des ondes électromagnétiques proches de la lumière visible, presque toujours issues d’un laser Les allers - retours rapides d’un faisceau assez puissant pour passer entre le couvert végétal et atteindre le sol permettent, en mesurant depuis un avion les temps de vol de millions d’impulsions successives, de pratiquer une télémétrie à grande échelle. Une fois débarrassé informatiquement du bruit induit par la végétation, la topographie apparaît à l’écran On obtient de cette manière un rendu

En haut, le « Terrifiant » – le volcan Sangay –est encore en train de faire des siennes. Ce puissant volcan strombolien, sans doute parfois plinien, est si élevé qu’il semble posé sur les nuages. Au centre, le complexe de plateformes est constitué de trois tertres qui en entourent un quatrième, central. Un chemin, datant sans doute des périodes upano et huapula, longe cet ancien habitat upano. En bas, cette route reliant les agglomérations upanos, creusée dans le sol afin de la maintenir horizontale, est dirigée du nord au sud.

très précis des constructions humaines de pierre ou de terre

Au début des années 2010, je rencontrai un groupe de techniciens russes venus en Équateur pour y essayer la technologie lidar sur des sites archéologiques Je leur conseillai évidemment la vallée de l’Upano et les aidai à monter un projet C’est ainsi qu’en 2015, l’Institut équatorien du patrimoine culturel accepta de financer une couverture d’imagerie lidar de 600 kilomètres carrés dans le bassin de l’Upano. J’obtins plus tard de l’institut les données de base consistant en une multitude de points lumineux enregistrés par le faisceau laser Pour interpréter ces données brutes, il fallut s’adjoindre la collaboration d’un spécialiste, en la personne de l’archéologue télédétecteur Antoine Dorison, formé sur les sites mexicains durant son doctorat Pendant deux ans, Antoine analysa les images que nous confrontions aux informations de terrain que j’avais récoltées durant mes missions sur place C’est ce travail qui mit au jour un incroyable paysage culturel

DES VILLES DANS LA FORÊT Là où on ne distinguait auparavant que quelques tertres artificiels et chemins creusés, surgirent sur l’imagerie numérique une myriade de structures anthropiques réalisées par les Upanos. Les premières choses que l’on repère sur le terrain ou sur les vues lidar sont les tertres artificiels de terre. La télédétection a permis d’en dénombrer pour le moment plus de 6 400. Ce sont en majorité des plateformes rectangulaires allant de 10 à 100 mètres de longueur, de 3 à 20 mètres de largeur et de 2 à 8 mètres de hauteur Leur disposition suit un patron assez standardisé qui consiste à délimiter une place basse carrée par des tertres périphériques, avec éventuellement une plateforme centrale (voir ci-contre, au milieu) Les complexes les plus courants mesurent 40 mètres de côté. Mes fouilles archéologiques ont précédemment démontré qu’une maison fut autrefois construite à leur sommet, pour s’isoler de la très forte humidité du sol et d’autres raisons sans doute

L’ESSENTIEL

> Certains calculs menés par un ordinateur quantique sont simulables avec un ordinateur classique, d’autres sont hors de portée. Il est cependant di cile de savoir quels problèmes peuvent être résolus exclusivement par des moyens quantiques.

> Pour le déterminer, les spécialistes ont exhibé trois critères très di érents : l’intrication, la magie (une opération qui change la phase d’un qubit) et la magie fermionique (une opération qui intervertit deux qubits).

L'AUTEUR

Où se cache l’avantage quantique ?

Dans quelles situations un ordinateur quantique est-il vraiment plus puissant qu’un ordinateur classique ? C’est une question étonnamment subtile à laquelle les physiciens sont toujours confrontés, des décennies après l’avènement de l’ère quantique.

Il y a plus de quarante ans, le physicien Richard Feynman a souligné que la construction de systèmes reposant sur des principes quantiques permettrait d’accéder à des capacités de calcul supérieures à celles des ordinateurs « classiques » Ce discours, prononcé en 1981, est souvent considéré comme un événement fondateur de l’informatique quantique Feynman a terminé sa présentation sur une boutade désormais célèbre : « La nature n’est pas classique, bon sang, et si vous voulez faire une simulation de la nature, vous feriez mieux de la faire avec la mécanique quantique. »

Cette vision s’est concrétisée en  1994 quand le mathématicien Peter Shor a proposé la première utilisation potentiellement révolutionnaire des ordinateurs quantiques. Une importante partie de la sécurité du monde numérique repose sur l’hypothèse que la factorisation de grands nombres est une tâche difficile qui prend du temps. Or Peter Shor a montré comment manipuler les qubits – la version quantique des bits d’information qui

peuvent être une combinaison de l’état « 0 » et de l’état « 1 » – pour y parvenir en un clin d’œil , du moins par rapport aux méthodes classiques connues

Les chercheurs sont tout à fait convaincus (même s’ils n’en sont pas absolument certains ) que l’algorithme quantique de Shor surpasse tous les algorithmes classiques, car, malgré les enjeux considérables, personne n’a réussi à casser les méthodes de chiffrement modernes avec une machine classique Mais pour des tâches moins prestigieuses que la factorisation, il est difficile de dire avec certitude si les méthodes quantiques sont supérieures. La quête d’autres applications intéressantes est devenue une sorte de jeu de devinettes aléatoire « Ce n’est pas une approche très efficace » , souligne Crystal Noel, chercheuse à l’université Duke , aux États - Unis

Au cours des vingt dernières années, une confédération informelle de physiciens et de mathématiciens s’est efforcée d’identifier plus clairement la puissance du domaine quantique Leur objectif ? Trouver une façon d’évaluer le

Ce texte est une traduction de l’article The quest to quantify quantumness, publié par Quanta Magazine, le 19 octobre 2023.

L’ordinateur quantique Quantum System One d’IBM est le premier système commercialisé de ce type. Il comprend vingt qubits. Pour mener des calculs intéressants, il faudra beaucoup plus de qubits, et il restera à vérifier que ces calculs ne peuvent être menés sur une machine classique.

© Satoshi Kawase, pour IBM

CHARLIE WOOD journaliste scientifique, spécialisé en physique et astrophysique

« caractère quantique » d’un système Ils rêvent de définir une métrique qu’ils estimeraient pour chaque arrangement de qubits produit par un calcul quantique. Si la valeur est faible, il sera facile de simuler ce calcul sur un ordinateur de bureau. Si elle est élevée, les qubits représentent la réponse à un problème vraiment difficile et hors de portée de tout appareil classique.

En bref, les scientifiques recherchent l’ingrédient physique qui caractérise la puissance potentielle des dispositifs quantiques et qui identifie les situations où l’ordinateur quantique a réellement l’avantage sur l’ordinateur classique. « C’est là que commence le caractère quantique au sens le plus rigoureux du terme », insiste Bill Fefferman, de l’université de Chicago

Leur quête a été fructueuse , voire trop fructueuse Au lieu de trouver une seule métrique , les spécialistes en ont découvert trois , chacune représentant une façon distincte de séparer les domaines quantique et classique Les physiciens et les informaticiens se sont alors efforcés d’établir la topographie exacte de ce royaume quantique divisé en trois régions. Durant l’été 2023, trois groupes de recherche ont annoncé qu’ils avaient dressé la meilleure carte à ce jour de la moins connue des trois provinces, ajoutant des détails cruciaux à la compréhension de l’endroit où se termine le classique et où commence véritablement le domaine quantique.

Il est « tout à fait fondamental d’appréhender où se situe cet horizon », déclare Kamil Korzekwa, de l’université Jagellon, à Cracovie, en Pologne, l’un des chercheurs à l’origine de ces nouveaux travaux « Il est indispensable de comprendre ce qui est vraiment quantique dans un système quantique »

L’INTRICATION, LE CANDIDAT ÉVIDENT

Dans les années 1990, l’ingrédient physique qui rendait les ordinateurs quantiques puissants ne laissait aucun doute. Il devait s’agir de l’intrication, le lien quantique « étrange » entre des particules distantes qu’Erwin Schrödinger lui-même avait identifié comme « le trait caractéristique de la mécanique quantique ».

« L’intrication a été mentionnée très rapidement », note Richard Jozsa, mathématicien à l’université de Cambridge « Et tout le monde a supposé qu’il n’y avait rien à ajouter. »

Pendant un certain temps, il a semblé que la recherche de cette épice quantique cruciale avait pris fin avant même d’avoir commencé

L’intrication correspond à un phénomène par lequel deux particules forment un état indissociable dans lequel leurs propriétés sont fortement corrélées, au-delà de ce que peut expliquer la physique classique. Lorsque les particules ne sont pas intriquées , il est possible de les suivre individuellement Mais

lorsqu’elles le sont , la modification ou la manipulation d’une particule dans un système implique de tenir compte de ses liens d’intrication avec d’autres particules. Cette tâche croît de manière exponentielle à mesure que l’on ajoute des particules. Pour spécifier de façon complète l’état de n qubits intriqués, il faut de l’ordre de 2 n bits classiques ; pour calculer l’effet de la modification d’un qubit, il faut e ff ectuer environ 2n opérations classiques Pour un système avec 3 qubits, cela ne représente que 8 étapes. Mais pour 10 qubits, c’est 1 024 opérations, ainsi le temps de calcul de la solution (c’est-à-dire la difficulté du problème) augmente de manière exponentielle Dit autrement, seul un ordinateur quantique devrait réussir à résoudre un problème contenant de l’intrication

En  2002, Richard Jozsa a contribué à la mise au point d’un algorithme simple qui utilise un ordinateur classique pour simuler un « circuit » quantique , c’est- à - dire une série spécifique d’opérations e ff ectuées sur des qubits Si l’on donne au programme classique une configuration initiale de qubits, il prédit le résultat final après que les qubits ont traversé le circuit quantique. Avec son collègue Noah Linden , Richard Jozsa a prouvé que , tant que son algorithme simulait un circuit qui n’intriquait pas les qubits, il pouvait traiter un nombre de plus en plus grand de qubits sans que le temps d’exécution soit exponentiellement plus long.

L’intrication seule ne suffit pas pour saisir toute la richesse de l’océan quantique £

En d’autres termes, il a montré qu’un circuit quantique sans intrication était facile à simuler sur un ordinateur classique D’un point de vue informatique , le circuit n’était pas intrinsèquement quantique La collection de tous ces circuits sans intrication ( ou , de manière équivalente, tous les arrangements de qubits qui résulteraient de ces circuits sans intrication) formait une sorte d’île simulable classiquement dans une vaste mer quantique

Dans cette mer, on trouve aussi les états résultant de circuits véritablement quantiques, ceux pour lesquels une simulation classique prendrait des milliards d’années. Pour cette raison, les chercheurs en sont venus à considérer l’intrication non seulement comme une propriété quantique, mais aussi comme une ressource quantique : l’ingrédient nécessaire pour atteindre les profondeurs inexplorées, où résident de puissants algorithmes quantiques comme celui de Shor

Aujourd’hui, l’intrication reste la ressource quantique la plus étudiée « Si vous demandez à 99  physiciens sur 100 [ce qui fait la puissance des circuits quantiques ], la première chose qui leur vient à l’esprit est l’intrication », souligne Bill Fefferman En 2022, ce chercheur et ses collègues ont montré que pour une classe particulière de circuits quantiques , l’intrication détermine entièrement la di fficulté de simuler de façon classique ces circuits « Dès que l’on atteint un certain niveau d’intrication , indique le chercheur, on peut prouver la di ffi culté du circuit Aucun algorithme [classique] ne fonctionne. »

Mais la preuve de Bill Fefferman n’est valable que pour un seul type de circuit. Or, depuis une vingtaine d’années, les chercheurs savent que l’intrication seule ne suffit pas pour saisir toute la richesse de l’océan quantique « Malgré le rôle essentiel de l’intrication, avertissaient Richard Jozsa et Noah Linden dans leur article de 2002, il est néanmoins trompeur de considérer l’intrication comme la ressource unique pour la puissance de calcul quantique . » La quête du caractère quantique ne faisait que commencer

UN THÉORÈME SURPRENANT

Richard Jozsa savait que l’intrication n’est pas le dernier mot en matière de calcul quantique , car quatre ans avant ses travaux , le physicien Daniel Gottesman avait démontré le contraire Lors d’une conférence tenue en  1998, en Tasmanie , ce chercheur avait expliqué qu’un type particulier de circuit quantique pouvait être simulé par un ordinateur classique, peu importe la quantité d’intrication qu’on y injecte.

Dans la situation qu’il a décrite en partenariat avec le mathématicien Emanuel Knill , l’opération d’intrication ne coûte pratiquement rien. On peut intriquer autant de qubits que l’on veut et un ordinateur classique peut toujours suivre. « Le théorème de Gottesman-Knill a été l’une des grandes surprises des années 1990 pour les spécialistes de ce domaine », raconte Kamil Korzekwa

La possibilité de simuler classiquement l’intrication semblait un peu miraculeuse, mais il y avait un hic. L’algorithme de GottesmanKnill ne s’applique qu’aux circuits quantiques, qui s’en tiennent aux portes logiques quantiques

ALGORITHMES QUANTIQUES

Un algorithme consiste en une séquence finie d’instructions pour résoudre un problème spécifique. Les algorithmes classiques manipulent des bits et opèrent sur des ordinateurs classiques. Leurs pendants quantiques reposent sur des bits quantiques (ou qubits) et exploitent la superposition des qubits et leur intrication. Ils ne peuvent fonctionner que sur des ordinateurs quantiques, dont le développement est un domaine de recherche très actif.

En algorithmique, une notion importante est l’évolution du temps de calcul en fonction de n, le nombre de données en entrées. Un problème est considéré comme di cile quand le temps croît exponentiellement avec n, et facile si la croissance est polynomiale. Or, pour certains problèmes dont on ne connaît pas d’algorithmes classiques e caces, des versions quantiques rendent ces problèmes faciles à traiter. Mais cela ne signifie pas que pour tous les problèmes, un algorithme quantique sera toujours plus rapide.

QUELQUES ALGORITHMES QUANTIQUES OU FAMILLES D’ALGORITHMES NOTABLES

Algorithme de Deutsch-Jozsa

David Deutsch a proposé en 1985 l’un des premiers algorithmes quantiques, qu’il a amélioré avec Richard Jozsa en 1992. Cet algorithme appartient à la classe des algorithmes de recherche à « oracle ». L’objectif est de caractériser une fonction qui est cachée dans une boîte noire en lui soumettant di érentes entrées et en analysant la sortie. Dans le cas de Deutsch-Jozsa, on sait juste que la fonction retourne toujours la même valeur 0 ou 1 pour toutes les entrées, ou renvoie à parts égales 0 et 1. Dans le cas classique, s’il y a n bits d’entrée, il faut donc tester la moitié des configurations possibles plus une (soit 2n – 1 + 1) pour avoir la réponse. Dans le cas quantique, il su t d’une superposition de n qubits et la réponse est directement obtenue. Cet algorithme n’a, à ce jour, aucune utilité. Par ailleurs, des méthodes classiques, de type Monte-Carlo, qui évaluent aléatoirement un nombre limité de configurations, obtiennent de bons résultats.

Algorithme de Shor

Développé par Peter Shor en 1994, il est probablement l’algorithme quantique le plus connu, car il permet de factoriser un nombre de n bits en un temps polynomial (de l’ordre de (log n) 3). Parce qu’on ne connaît pas d’algorithme classique pour résoudre ce problème de factorisation, de nombreux systèmes de chi rement reposent sur ce dernier. Or, avec l’avènement des ordinateurs quantiques, ces méthodes deviendraient obsolètes. En 2001, IBM aurait mis en œuvre l'algorithme de Shor sur un système de 7 qubits et aurait permis de factoriser 15 en 3 fois 5... mais les conditions de ce calcul font débat.

Algorithme de Grover

Il s’agit d’un algorithme de recherche fondé sur un oracle et proposé en 1996 par Dov Grover. Il permet par exemple de retrouver e cacement un nom dans un annuaire à partir du numéro de téléphone. Si ses applications semblent nombreuses, il n'est pas sûr que cet algorithme soit mis en œuvre car le gain réel est très faible.

Algorithmes d’optimisation

Il existe une vaste famille d’algorithmes capables de résoudre des systèmes d’équations linéaires, des équations di érentielles ou qui visent à optimiser des réseaux de neurones. Leur gain reste à évaluer.

Simulateurs de systèmes quantiques

Comme le soulignait Richard Feynman, la meilleure façon de simuler un système quantique serait d’utiliser un ordinateur quantique. Dans un système à n particules, il faut prendre en compte 2n interactions possibles, ce qui est impossible pour un ordinateur classique pour un n grand. Certains algorithmes classiques parviennent dans certains cas à concurrencer les simulations quantiques, mais de nombreuses situations sont encore des problèmes ouverts.

dites « de Clifford » (les portes sont des petits circuits quantiques manipulant un petit nombre de qubits). Mais si l’on ajoute une seule « porte T », au rôle apparemment inoffensif, qui consiste juste à tourner un qubit d’une certaine manière (elle opère un changement de phase d’un angle π/4), le programme classique n’est plus capable de mener le calcul en un temps raisonnable

L’intrication est une ressource quantique essentielle mais pas toujours suffisante pour garantir qu’un ordinateur classique est tenu en échec La porte T semblait fabriquer une nouvelle sorte de ressource quantique –  quelque chose d’intrinsèquement quantique qui ne peut pas être simulé sur un ordinateur classique Très vite, Sergey Bravyi, qui travaillait alors à l’institut Landau de physique théorique en Russie, et Alexei Kitaev, à Caltech (l’institut de technologie de Californie), ont donné à ce caractère quantique produit par la rotation interdite de la porte T un nom accrocheur : la magie.

ET LA MAGIE OPÈRE...

En 2004, les deux physiciens ont montré comment rendre un calcul vraiment quantique. Ils ont, pour cela, élaboré deux approches : il suffit d’inclure une porte T dans le circuit luimême ; ou bien il faut initialiser le calcul avec un « état magique » de qubits qui a été préparé avec des portes T par un autre circuit et l’introduire dans un circuit de Clifford. Quoi qu’il en soit, la magie est essentielle pour obtenir le caractère quantique tant recherché.

En 2016, Sergey Bravyi et David Gosset, chercheur à l’université de Waterloo , au Canada , ont découvert une méthode pour mesurer la quantité de magie dans un ensemble de qubits Ils ont mis au point un algorithme classique pour simuler des circuits à faible degré de magie Pour chaque porte T supplémentaire , leur programme prend exponentiellement plus de temps pour le calcul (bien que la croissance ne soit pas aussi explosive que dans d’autres cas ). Ils ont finalement démontré l’efficacité de leur méthode en simulant classiquement un circuit contenant des centaines de portes de Clifford et près de cinquante portes T.

Aujourd’hui , de nombreux chercheurs exploitent les ordinateurs quantiques en mode Clifford (ou de manière approchée), précisément parce qu’ils peuvent utiliser un ordinateur classique pour vérifier si les systèmes fonctionnent correctement.

La magie s’imposait donc comme une nouvelle ressource quantique. Mais contrairement à l’intrication, qui a commencé comme un phénomène physique familier, les physiciens n’étaient pas sûrs que la magie avait beaucoup d’importance en dehors des ordinateurs

CIRCUITS QUANTIQUES

Pour représenter un algorithme quantique, indépendamment de la réalisation physique, on utilise des diagrammes nommés « circuits quantiques » dans lesquels le temps s’écoule de gauche à droite. Chaque qubit est associé à une ligne horizontale. Son état initial est placé à l’extrémité de la ligne puis traverse des portes logiques qui opèrent des transformations sur le qubit ou sur la combinaison de plusieurs qubits. Le résultat est l’ensemble des qubits qui sont obtenus à la fin du circuit.

Les portes quantiques sont les briques élémentaires qui constituent les circuits. Elles sont équivalentes aux portes logiques des circuits classiques, mais ont la particularité d’être toutes réversibles (ce qui implique notamment qu’elles ont autant de qubits en entrée qu’en sortie).

Opération (ou « porte ») sur un qubit

Qubit 1

Qubit 2

Qubit 3

Qubit 4

Qubit 5

Opération sur deux qubits connectant deux lignes horizontales

Temps

EXEMPLES DE PORTES

La porte de Pauli-X

On parle aussi de « porte bit-flip ». Elle agit sur un seul qubit et transforme un qubit 0 en 1, et inversement.

La porte de Hadamard

État initial État final Opération

Porte Pauli X

I 1>

I 0>

Elle agit aussi sur un unique qubit et transforme le qubit |0> et le qubit |1> en des superpositions d’états, avec la même probabilité de mesurer |0> et |1>. Cette porte opère à l’échelle d’un qubit la transformée de Fourier quantique.

La porte T

Cette porte ne modifie pas la probabilité de mesurer |0> ou |1>. Mais elle applique un changement de phase sur le qubit |1>, avec un déphasage φ = π/4. Cette porte introduit la composante

La porte swap

Cette porte intervertit deux qubits. Elle introduit ainsi la « magie fermionique » dans le circuit. Le circuit simule alors des particules (des fermions) qui interagissent, un problème di icile à résoudre avec un algorithme classique.

I 0>

I 0>

I 0>

« magique » dans le circuit quantique qui rend certains problèmes di iciles à simuler pour un ordinateur classique.

I 0>

I Q2>

quantiques Or des résultats récents suggèrent que c’est pourtant le cas.

En 2021, des chercheurs ont identifié certaines phases de la matière, qui sont dotées d’un caractère magique, de la même façon que de nombreuses phases de la matière présentent des modèles particuliers d’intrication « Nous avons besoin d’estimateurs de complexité informatique plus fins, comme la magie, pour classifier de façon la plus complète possible le vaste paysage des phases quantiques de la matière », commente Timothy Hsieh, physicien à l’institut Perimeter pour la physique théorique, au Canada, et qui a contribué à ces travaux Dans un autre domaine, Alioscia Hamma, de l’université de Naples, et ses collègues ont récemment étudié s’il était possible – en théorie – de reconstituer les pages d’un livre avalé par un trou noir en observant uniquement le rayonnement qu’il émet La réponse est oui, dit le chercheur, « à condition que le trou noir ne présente pas trop de magie »

Pour de nombreux physiciens, dont Alioscia Hamma, les ingrédients physiques nécessaires pour rendre un système extrêmement quantique semblent clairs Une combinaison d’intrication et de magie serait essentielle. Aucun des deux critères n’est suffisant à lui seul Si un état a un score de zéro pour l’une ou l’autre de ces métriques, vous pouvez le simuler sur votre ordinateur de bureau, avec un peu d’aide des approches de Richard Jozsa (si l’intrication est nulle) ou de Sergey Bravyi et David Gosset (si la magie est nulle).

Et pourtant, la quête quantique se poursuit, car les informaticiens savent que même la magie et l’intrication ne garantissent pas le caractère quantique d’un système

LA MAGIE FERMIONIQUE

La troisième métrique quantique a commencé à prendre forme il y a un peu plus de vingt ans Mais jusqu’à récemment, c’était la moins développée des trois. En 2001, l’informaticien Leslie Valiant a découvert un moyen de simuler une troisième famille de problèmes quantiques Alors que la technique de Richard Jozsa se concentrait sur les circuits sans intrication et que l’algorithme de Bravyi-Gosset pouvait résoudre les circuits sans trop de portes T, l’algorithme de Leslie Valiant était limité aux circuits dépourvus de « porte d’échange » , une opération qui prend deux qubits et échange leurs positions.

Tant que vous n’intervertissez pas les qubits, vous pouvez les intriquer et leur insuffler autant de magie que vous le souhaitez, vous vous retrouverez sur une nouvelle île accessible aux ordinateurs classiques Mais dès que vous commencez à mélanger les qubits, le problème dépasse les capacités de n’importe quelle machine classique

C’était « plutôt bizarre , déclare Richard Jozsa, comment le simple fait d’échanger deux qubits peut-il vous donner toute cette puissance ? » Quelques mois après la découverte de Leslie Valiant, deux physiciens théoriciens chez IBM, Barbara Terhal et David DiVincenzo, ont découvert la raison derrière cette ressource quantique. Ils ont montré que les circuits sans portes d’échange de Leslie Valiant, connus sous le nom de circuits matchgate ,

Avec les portes T, la magie s’impose comme une nouvelle ressource quantique £

simulaient secrètement une classe bien connue de problèmes physiques

De la même façon qu’un programme informatique peut simuler un système physique (la croissance d’une galaxie, des réactions nucléaires ,  etc .), un circuit quantique peut aussi simuler une situation physique . Dans le cas des circuits « matchgate », il s’agit de groupes de fermions, une famille de particules élémentaires , à l’instar des électrons Lorsque les portes d’échange ne sont pas utilisées , les fermions simulés n’interagissent pas, ou sont dits « libres » Ils n’entrent jamais en collision les uns avec les autres. Ce type de problèmes sont assez faciles à traiter pour les physiciens, parfois même avec un crayon et du papier Ainsi , les circuits matchgate , qui simulent le comportement de fermions libres sans interaction, sont faciles à résoudre avec des moyens classiques.

Mais lorsque des portes de permutation sont utilisées, les fermions simulés interagissent, s’entrechoquent et présentent des comportements complexes. Ces problèmes deviennent difficiles à simuler, voire impossibles

Cependant, après leur découverte initiale, les circuits matchgate ont été peu explorés Ils n’étaient a priori pas particulièrement intéressants Les choses ont changé au cours de l’été 2023. Trois groupes de chercheurs ont indépendamment mis à profit les travaux de Sergey Bravyi, David Gosset et leurs collègues pour s’attaquer au problème – un rapprochement fortuit qui, au moins dans un cas, a été découvert

lorsque des fermions ont été évoqués autour d’un café (comme c’est souvent le cas quand des physiciens se réunissent).

Les équipes ont coordonné la publication de leurs résultats en juillet 2023. En substance, les trois groupes ont modifié les outils mathématiques que les pionniers de la magie avaient mis au point pour explorer les circuits de type Clifford et les ont appliqués au domaine des circuits matchgate. Sergii Strelchuk et Joshua Cudby, de l’université de Cambridge, se sont attachés à mesurer mathématiquement la ressource quantique qui fait défaut aux circuits matchgate. Sur le plan conceptuel, cette ressource correspond à « l’interactivité », c’est-àdire à la capacité des fermions simulés à se détecter les uns les autres L’absence d’interactivité est classiquement facile à simuler, et l’augmentation de l’interactivité rend les simulations plus difficiles Mais dans quelle mesure un supplément d’interactivité rendil les simulations plus difficiles ? Peut- on contourner ce critère ? « Nous n’avions aucune intuition Nous avons dû partir de zéro » , raconte Sergii Strelchuk.

Les deux autres groupes ont mis au point un moyen de décomposer un état difficile à simuler en une énorme somme d’états plus faciles à simuler. Ils ont ainsi établi une sorte de dictionnaire permettant de transposer les algorithmes de simulation classiques du monde des circuits de type Clifford au monde de ceux de type matchgate. « En résumé, tout ce que nous avions pour les circuits [de type Clifford], nous pouvions maintenant les traduire » , déclare Beatriz Dias , physicienne à l’université technique de Munich, « de sorte que nous n’avons pas besoin de réinventer tous ces algorithmes »

Désormais, des algorithmes plus rapides peuvent simuler de manière classique des circuits comportant quelques portes d’échange. Comme pour l’intrication et la magie, le temps de calcul de ces algorithmes augmente exponentiellement avec l’ajout de chaque porte interdite. Mais ces algorithmes représentent une avancée significative

Oliver Reardon-Smith, qui a travaillé avec Kamil Korzekwa et Michał Oszmaniec, de l’Académie polonaise des sciences, à Varsovie, estime que leur programme est capable de simuler, près de 3 millions de fois plus vite que les méthodes précédentes, un circuit avec 10 coûteuses portes d’échange. Leur algorithme permet aux ordinateurs classiques de s’enfoncer un peu plus dans la mer quantique et réduire la zone dominée par les applications quantiques « Il y a une demande considérable à pouvoir simuler des ordinateurs quantiques avec des moyens classiques, insiste Oliver Reardon-Smith, nous voulons développer les outils pour le faire aussi vite que possible et à moindre coût »

LES INGRÉDIENTS DE L’AVANTAGE QUANTIQUE

TL’intrication

Ce phénomène quantique établit de fortes corrélations entre les propriétés de deux particules, de sorte qu’elles ne peuvent être décrites individuellement. Les physiciens ont montré ces dernières années que ce lien est une propriété non locale. Lorsqu’une paire de particules se trouve dans une superposition d’états, la mesure sur une particule fixe instantanément l’état de chacune des deux, même si elles sont très éloignées l’une de l’autre.

La magie

Dans un circuit quantique, les qubits subissent de nombreuses transformations, certaines étant faciles à simuler par des approches classiques. Les chercheurs ont eu la surprise de constater qu’une opération, a priori simple, consistant à accomplir un déphasage sur le qubit, réalisé par une porte T, rendait le système très di icile à reproduire par des moyens non quantiques.

Quant à l’appellation de la ressource « interactivité » produite par les portes d’échange, elle n’a pas encore de nom officiel Certains parlent simplement de « magie », et d’autres proposent des expressions telles que « trucs non fermioniques » Sergii Strelchuk préfère le terme de « magie fermionique »

Aujourd’hui, les chercheurs ont des moyens simples pour évaluer le caractère quantique d’un système Chacune des trois métriques (intrication, magie et magie fermionique) est associée à une méthode classique de simu–lation. Si une collection de qubits est peu

La réponse à la question de savoir ce qui rend quantique un système n’est plus aussi évidente qu’avant £

La magie fermionique

Un des objectifs des ordinateurs quantiques est de pouvoir simuler des systèmes régis par les lois de la mécanique quantique. Un algorithme quantique peut donc simuler un ensemble de particules fermioniques (c’est-à-dire dont le spin est égal à 1/2 comme l’électron). Les spécialistes ont constaté que si le circuit quantique associé ne procède pas à un échange (swap) entre deux qubits, cela est équivalent à des fermions qui n’interagissent pas entre eux. Si des qubits sont échangés, on introduit des interactions dans le système et celui-ci devient di icile à simuler avec un ordinateur classique.

mathématiques utilisés pour intégrer la complexité de l’univers quantique dans des cadres plus simples L’intrication apparaît comme une ressource lorsqu’on applique la mécanique quantique suivant le formalisme d’Erwin Schrödinger, qui repose sur son équation éponyme pour prédire comment la fonction d’onde d’une particule évolue dans le temps C’est la version de la mécanique quantique que l’on trouve dans les manuels, mais ce n’est pas la seule

Lorsque Daniel Gottesman a mis au point sa méthode de simulation des circuits de type Clifford, il l’a formulée à partir d’une version plus ancienne de la mécanique quantique , développée par Werner Heisenberg Dans le cadre mathématique de Heisenberg, l’état des particules ne change pas Ce sont les « opérateurs » – les objets mathématiques que vous pourriez utiliser pour prédire les chances d’une certaine observation – qui évoluent. Se limiter aux fermions libres implique de considérer la mécanique quantique à travers encore un autre prisme mathématique

intriquée, qu’elle a peu de magie ou qu’elle simule un groupe de fermions presque sans interactions , les chercheurs savent qu’ils peuvent reproduire ce système sur un ordinateur de bureau classique Tout circuit quantique dont le score est faible au regard de l’une de ces trois métriques quantiques se trouve non loin des rives d’une île classique, et ne sera certainement pas le prochain algorithme de Shor

D’AUTRES ÎLES À L’HORIZON

« En fin de compte, [l’étude des simulations classiques] nous aide à comprendre où se cache l’avantage quantique », conclut David Gosset Mais plus les chercheurs se familiarisent avec ces trois façons différentes de mesurer le caractère quantique d’un groupe de qubits, plus le rêve initial de trouver un paramètre unique qui englobe tous les aspects du caractère quantique semble vain Or l’intrication , la magie et la magie fermionique sont très différentes les unes des autres, de sorte que la perspective de les unifier dans le cadre d’une métrique quantique pour calculer le temps d’exécution le plus court possible semble lointaine.

« Je ne pense pas que cette question ait un sens, note Richard Jozsa. Il n’y a pas une seule chose qui, si on l’injecte en plus grande quantité, rend le système plus difficile à simuler. »

Les trois ressources quantiques semblent plutôt être des artefacts des langages

Chaque langage mathématique rend compte avec éloquence de certains aspects des états quantiques, mais au prix d’un brouillage d’une autre propriété quantique Ces propriétés maladroitement formulées deviennent alors la ressource quantique dans ce cadre mathématique – l’intrication, la magie et la magie fermionique Selon Richard Jozsa, pour surmonter cette limitation et identifier une caractéristique quantique unique, il faudrait étudier tous les langages mathématiques possibles pour exprimer la mécanique quantique et rechercher des caractéristiques universelles qu’ils partageraient tous

Ce n’est pas une proposition de recherche particulièrement précise, mais les scientifiques étudient déjà d’autres langages quantiques que les trois principaux , ainsi que les ressources quantiques correspondantes qui les accompagnent. Timothy Hsieh, par exemple, s’intéresse aux phases de la matière quantique qui produisent des probabilités négatives absurdes lorsqu’elles sont analysées de manière standard. Il a découvert que cette négativité peut définir certaines phases de la matière, tout comme la magie.

Il y a quelques dizaines d’années, la réponse à la question de savoir ce qui rend quantique un système semblait évidente Aujourd’hui, les chercheurs en savent davantage, mais elle n’est plus si tranchée Après vingt ans d’exploration des premières îles classiques, nombreux sont ceux qui pensent que leur voyage ne s’achèvera jamais. Même s’ils continuent d’affiner leur compréhension des endroits où l’avantage quantique n’existe pas , ils savent qu’ils ne seront peut-être jamais en mesure de dire précisément où il se trouve n

BIBLIOGRAPHIE

S. Oliviero et al., Unscrambling quantum information with Cli ord decoders, Physical Review Letters, 2024.

O. Reardon-Smith et al., Improved simulation of quantum circuits dominated by free fermionic operations, en ligne sur arXiv, 2023.

B. Dias et R. Koenig, Classical simulation of non-Gaussian fermionic circuits, en ligne sur arXiv, 2023.

J. Cudby et S. Strelchuk, Gaussian decomposition of magic states for matchgate computations, en ligne sur arXiv, 2023.

T. D. Ellison et al., Symmetry-protected sign problem and magic in quantum phases of matter, Quantum, 2021.

Miser sur les défenses naturelles des plantes

Difficile d’imaginer l’incroyable bataille que se livrent plantes et pathogènes, chacun pour sa survie. Pour assurer la nôtre, serons-nous capables de faire pencher la balance en faveur des plantes, qui nous nourrissent ?

Chaque année , 20 % de la production mondiale de blé est perdue en raison de maladies

De manière générale , depuis les années  1990, l’incidence des maladies des plantes n’a cessé d’augmenter. Les épidémiologistes notent également la multiplication de maladies dites « émergentes » , qui n’avaient encore jamais été détectées sur telle espèce végétale ou dans telle région du monde. Certaines ont eu par le passé des conséquences catastrophiques, et plusieurs menacent les équilibres économiques régionaux, d’autant plus que les plantes sont en contact avec toujours plus de microbes inconnus En cause : le changement climatique, le fractionnement des écosystèmes et l’intensification du commerce mondial, qui modifient les aires de répartition des plantes et déplacent les populations de ravageurs et d’agents pathogènes, parmi lesquels les champignons semblent constituer la principale menace

Qui des plantes ou de leurs pathogènes tirera le mieux son épingle du jeu ? Quelles pistes sont susceptibles de faire pencher la

L’ESSENTIEL

> Les plantes livrent une véritable bataille au long cours contre des microorganismes pathogènes. Partout, elles font face à de nouvelles épidémies dues à des champignons, des bactéries et des virus, accentuées par le changement climatique et la mondialisation.

> Les pathogènes innovent sans cesse pour produire des molécules plus agressives,

échapper ou détourner les mécanismes de défense des plantes. Le système immunitaire végétal s’adapte aussi et riposte, mettant l’agresseur en quarantaine et produisant rapidement des molécules de défense.

> Cette capacité évolutive des plantes est un vivier de solutions naturelles ou d’ingénierie génétique pour réduire l’utilisation de pesticides de synthèse.

L’AUTEUR

SYLVAIN RAFFAELE biologiste moléculaire au Laboratoire des interactions plantes-microbesenvironnement (Inrae)

Les agents pathogènes des plantes sont souvent inféodés à une ou quelques espèces végétales, que l’on retrouve dans le nom de la maladie qu’ils causent. C’est le cas de la rouille du blé, champignon originaire d’Amérique du Sud, qui a été signalé en Asie pour la première fois en 2016.

balance en faveur des plantes, en particulier de celles qui nous nourrissent ? Pour les identifier, il faut en premier lieu expliquer l’aptitude de certains microbes à affecter des plantes auparavant épargnées Nous avons tous le souvenir vif de l’émergence du Covid-19 dans nos vies fin 2019. Le virus responsable, un descendant d’une souche qui infectait des animaux, était initialement incapable d’attaquer l’homme Mais au gré de mutations génétiques aléatoires, qui engendrent de nouveaux variants , une lignée de virus a changé d’hôte et incorporé l’homme au répertoire de ses victimes

À L’ASSAUT !

De même, nombre d’agents pathogènes des plantes sont inféodés à une ou quelques espèces végétales, que l’on retrouve souvent dans le nom de la maladie qu’ils causent , comme la cloque du pêcher, le chancre du platane ou la rouille du blé. La liste des espèces chez qui un microbe est pathogène définit son spectre d’hôtes. Qu’est-ce qui le limite et comment change-t-il au fil de l’évolution, provoquant l’émergence de nouvelles maladies ?

Les agents pathogènes sont souvent spécialisés dans l’infection d’une espèce végétale, car déclencher une maladie nécessite des outils moléculaires particulièrement adaptés à la plante attaquée Pour survivre , les agents pathogènes sont souvent dépendants de leur hôte Ils doivent détourner le fonctionnement des cellules végétales à leur profit : pour cela, ils produisent des molécules appelées « effecteurs de pathogénicité ». Ceux-ci agissent soit hors de la cellule du pathogène, dans l’espace intercellulaire, soit directement dans la cellule végétale Leurs rôles sont majeurs et divers : détruire la plante (on parle alors de « toxine »), favoriser la libération de nutriments, créer un environnement favorable au microbe, inactiver les défenses des plantes, etc. Ce sont très souvent des protéines, qui interagissent avec une ou plusieurs molécules cibles de la plante.

En parallèle, le système immunitaire des plantes s’adapte pour reconnaître la structure ou les produits de l’activité des effecteurs de pathogénicité. De leur côté, ceux-ci cherchent à manipuler efficacement les cellules des plantes sans être repérés par le système immunitaire végétal À l’échelle évolutive , c’est une véritable course à l’armement qui est engagée entre les effecteurs de pathogénicité et le système immunitaire végétal. Et la pression est constante, car ces molécules se diversifient rapidement : chaque agent pathogène dispose d’un répertoire de plusieurs dizaines, voire centaines, d’effecteurs, dont la séquence varie très vite d’une génération à l’autre Pour cela, les gènes codant pour les effecteurs sont souvent situés sur des régions particulièrement instables du génome Ils sont tellement

variables qu’il était jusqu’à récemment impossible de suivre leurs liens de parenté. Ce qui nous limitait beaucoup pour recenser les e ff ecteurs , suivre leur évolution et prédire leur fonction

À partir de la fin des années 2000, la cristallographie et la résonance magnétique nucléaire ont cependant donné à voir les premières structures d’effecteurs protéiques, fournissant de précieux détails sur leur façon d’interagir avec d’autres protéines, et révélant des coïncidences inattendues. Les équipes de Sophien Kamoun, du laboratoire Sainsbury, et de Mark Banfield , du Centre de recherche

John-Innes, en Grande-Bretagne, de Thomas Kroj, à Inrae, et d’André Padilla, au Centre de biochimie structurale de Montpellier, ont ainsi découvert que des e ff ecteurs de séquences génétiques très différentes partageaient plus ou moins la même structure tridimensionnelle C’est par exemple le cas pour le mildiou du poivron et celui de la pomme de terre, ou pour la rouille du riz et la tache brune du blé. On entrevoyait alors le fait qu’il puisse exister des familles d’effecteurs, ce qui donnait une base commune à des pathogènes très éloignés

Toutefois la complexité de l’analyse, coûteuse et chronophage, ne permettait pas de l’appliquer à grande échelle.

Jusqu’à l’avènement d’outils d’intelligence artificielle avec lesquels il devenait possible de généraliser des comparaisons de génomes complets. Avec des logiciels comme AlphaFold, développé par Google DeepMind en 2021, il est

Une course aux armements se joue entre les végétaux et leurs pathogènes £

devenu possible de prédire en quelques minutes et de façon précise la structure des protéines. Dès lors, nos travaux et ceux de l’équipe de Ksenia Krasileva, de l’université de Berkeley, aux États-Unis, ont permis de classer la majorité des milliers d’effecteurs de champignons en quelques dizaines de familles structurales Certaines pourraient être très anciennes et remonter aux toutes premières cellules eucaryotes Des liens existent donc, peut- être , entre les variations au sein des

familles d’effecteurs et la biologie des organismes qui les produisent.

L’autre surprise a été de constater que des familles structurales d’effecteurs étaient présentes chez des microbes au style de vie très différent, pathogènes ou non. Cela laisse supposer que, malgré une structure similaire, leur activité aurait pu avoir fortement divergé au cours du temps, ou être dirigée contre d’autres microbes en compétition pour les ressources de la plante, plutôt que contre la plante ellemême. Nous avons également fait une découverte essentielle : pour maintenir une structure similaire malgré des séquences génétiques très différentes, certaines régions en surface des effecteurs adoptent des conformations instables, potentiellement plus réactives, permettant peut-être de varier les molécules avec lesquelles ils peuvent se lier. Il nous reste néanmoins beaucoup de choses à comprendre Comment l’activité des effecteurs évolue-t-elle au sein des familles structurales ? Comment le réchauffement climatique affectera-t-il l’évolution des populations de pathogènes et les effecteurs qu’ils utilisent ?

DÉMASQUER LES AGRESSEURS

Nous nous interrogeons aussi sur la réponse des plantes à ces agressions . Contrairement aux animaux , elles ne possèdent pas de cellules immunitaires circulantes À la place, toutes les cellules végétales ont la capacité de déclencher des défenses immunitaires innées, telles que la production de molécules antibiotiques et de signaux d’alerte pour les cellules voisines Ces défenses vont même jusqu’à l’autodestruction des

Pour se développer, les agents pathogènes détournent le fonctionnement des cellules végétales à leur profit (à gauche, l’ergot du seigle, Claviceps purpurea). Les plantes déploient plusieurs mécanismes de défense pour les neutraliser. Le séneçon produit par exemple des anthocyanes (à droite, la coloration violette) pour lutter contre la rouille (pustules).

cellules pour créer un environnement physicochimique défavorable à l’agresseur.

Au préalable, il faut que la cellule végétale ait détecté la présence de l’ennemi. Pour cela, chacune possède une batterie de récepteurs immunitaires qui entrent en action simultanément , certains à sa surface , d’autres en interne . Ces premiers agents de défense se lient avec des effecteurs de pathogénicité, les produits de leur activité ou d’autres motifs moléculaires caractéristiques des agents pathogènes. Ils ont, en outre, une autre mission : assurer la transmission du signal d’alerte vers le noyau de la cellule puis les cellules voisines pour que les défenses se mettent en place, et ceci de façon robuste au gré des évolutions des molécules qui les agressent

Une myriade de récepteurs immunitaires de surface est ancrée à la membrane plasmique qui entoure la cellule végétale Chacun, doté d’un module de reconnaissance situé à l’extérieur de la cellule, est capable de se lier à certaines molécules ou portions de molécules produites par les agents pathogènes Lorsqu’une liaison est ainsi établie, un module de transmission, situé cette fois à l’intérieur de la cellule, donne l’alerte en transférant des ions phosphate à des protéines avoisinantes Certains récepteurs de surface n’ont pas de module de transmission fonctionnel À la place, ils s’associent avec un corécepteur, dépourvu quant à lui de domaine de reconnaissance

Celui-ci joue le rôle de transmetteur universel : capable de reconnaître des agents pathogènes variés, il donne l’alerte en parallèle des multiples récepteurs Cette division du travail o ff re plus de flexibilité aux récepteurs pour

© Sylvain Raffaele

LES MALADIES DES PLANTES MENACENT L’ÉQUILIBRE DU MONDE

Les maladies des cultures vivrières ont fait payer un lourd tribut à l’humanité. En 1845, le mildiou détruit les récoltes de pomme de terre en Irlande. Aggravée par les insu sances du gouvernement britannique à gérer le problème, la famine qui s’ensuit provoque plus de 2 millions de morts et une émigration massive vers les ÉtatsUnis notamment. Pendant la Seconde Guerre mondiale, c’est une épidémie d’helminthosporiose (un champignon qui s’attaque aux céréales) qui fait chuter la production de riz de 25 % au Bengale. Les réserves du pays étant alors mobilisées pour nourrir les troupes britanniques, la pénurie alimentaire provoque 2 millions de victimes bengalaises. Plus récemment, entre 2008 et 2013, en Amérique centrale, la rouille du café, un autre champignon, provoque une extrême pauvreté et une famine chez les producteurs du Honduras, du Salvador et du Guatemala, entraînant là encore d’importants flux migratoires vers les États-Unis. On sait, depuis, que les épidémies de rouille du café sont concomitantes à des augmentations des températures minimales journalières. S’il n’est pas toujours facile d’identifier les causes de ces épidémies, pour certaines, le changement climatique ou la mondialisation sont clairement pointés. C’est le cas de la rouille du soja qui a touché la côte est des États-Unis en 2004, transmise par des souches de champignons pathogènes apportées d’Amérique du Sud par l’ouragan Ivan. Depuis 2013, une

campagne de communication dans les aéroports de l’Union européenne alerte sur les risques de propagation de la lèpre des oliviers, une maladie bactérienne probablement originaire d’Amérique centrale, dont l’impact est évalué à 10 milliards d’euros de pertes sur les cinquante prochaines années. En 2016, le champignon de la rouille

Mildiou

Rouille du soja

Rouille du café

Lèpre des oliviers

Helminthosporiose

Pyriculariose du blé

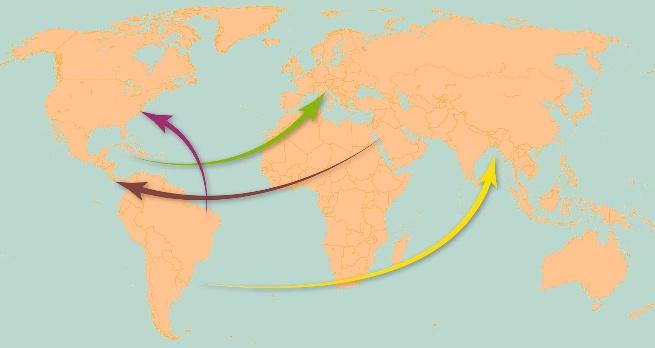
1845

du blé, originaire d’Amérique du Sud, a été signalé pour la première fois en Asie et a durement a ecté la production céréalière du Bangladesh. Ces phénomènes nous alertent sur les conséquences potentielles majeures que des maladies de plantes peuvent provoquer tant en matière de production alimentaire que d’équilibres socioéconomiques. 2004 Pertes > 240 millions de dollars

2008-2013

s’adapter aux variations des molécules produites par les pathogènes D’une espèce végétale à l’autre, des récepteurs ont évolué pour reconnaître des portions di ff érentes d’une même molécule d’agent pathogène en faisant appel au même corécepteur

Les récepteurs immunitaires à l’intérieur de la cellule ont eux aussi une structure modulaire . Leurs modules de reconnaissance agissent selon deux stratégies Certains établissent des liaisons directement avec l’effecteur de pathogénicité quand celui-ci a réussi à pénétrer dans la cellule végétale. D’autres sont sous forme de complexe protéique inactif contenant une protéine appât, et parfois une protéine de jonction La protéine appât mime la cible d’un effecteur, ce qui lui permet d’interagir avec ce dernier et d’activer le complexe récepteur. La conséquence la plus spectaculaire de cette activation est que la cellule végétale attaquée déclenche rapidement sa propre mort pour isoler l’intrus La cascade de réactions qui relie les récepteurs immunitaires et

2 millions de morts, émigration massive

2013

Pertes de 4-10 milliards d’euros

la mort de la cellule est longtemps restée une énigme La surprise fut de constater qu’il n’y a parfois aucun intermédiaire : le récepteur, une fois activé , est capable de détruire luimême sa cellule. Comment est-ce possible ? Grâce à la formation d’assemblages de protéines en anneaux appelés « résistosomes » En 2019, les équipes de Hong-Wei Wang, Jian-Min Zhou et Jijié Chai, de l’université de Pékin, furent les premières à les mettre en évidence grâce à l’imagerie par cryomicroscopie La liaison entre l’effecteur et la protéine appât active un module d’assemblage du récepteur, déclenchant l’association de plusieurs copies. Au centre du résistosome se trouvent des copies d’un troisième module qui peut avoir deux activités. Soit il permet au résistosome de se coller à la membrane plasmique de la cellule et d’ouvrir un canal perméable aux ions calcium, provoquant alors la mort rapide de la cellule . Cela place , en quelque sorte, l’agresseur en quarantaine Soit il synthétise de petites molécules , comme

1940

2 millions de morts

2016

Chute de 52 % de la production au Bangladesh

autant de signaux capables d’activer la formation de nouveaux complexes protéiques : d’autres résistosomes qui vont poursuivre la défense, mais aussi de nouvelles structures essentielles pour amplifier le message transmis par les récepteurs immunitaires de surface, créant ainsi un lien entre les différents systèmes de surveillance de la cellule végétale

Ce système simple et direct joue un rôle crucial dans la course évolutive avec les ennemis des plantes. Ainsi, en 2023, l’équipe de Sophien Kamoun a mis en évidence un mécanisme permettant à certains résistosomes de centraliser la réponse à de multiples effecteurs Plus généralement, les connaissances acquises ces cinq dernières années sur les récepteurs immunitaires des plantes nous ouvrent de nouvelles possibilités pour accroître, voire modifier, le spectre des molécules qu’ils reconnaissent, réduire le risque de détournement des ressources de la cellule végétale par des effecteurs de pathogénicité, et renforcer l’efficacité du système immunitaire végétal

ORGANISER L’EFFORT DE GUERRE

Les plantes ont développé d’autres moyens efficaces pour à la fois dissuader les insectes phytophages et réduire la multiplication des microbes. Des moyens qui donnent de la saveur à notre alimentation et étendent notre pharmacopée. Ainsi, le goût de la moutarde, celui du café ou encore du piment sont largement dus à des molécules dont la production est contrôlée par des gènes de défense Ces molécules sont principalement de deux natures : des protéines et des métabolites secondaires, c’està-dire des molécules issues de l’activité des protéines, non essentielles au fonctionnement de la cellule. La production de ces dernières fait appel à des réactions enzymatiques parfois complexes Ce n’est pas neutre en matière

énergétique pour la plante, de sorte que miser sur des défenses activées uniquement en cas d’agression semble être une stratégie écologique moins coûteuse. Néanmoins, la production de ces molécules de défense fait, elle aussi, l’objet d’une course évolutive entre plantes et agents pathogènes Ceux-ci utilisent par exemple des effecteurs pour supprimer la production de molécules de défense par les cellules végétales. Ils développent également des résistances, en produisant des protéines ou des enzymes capables d’éliminer les molécules de défense des plantes ou de les rendre moins efficaces Pour rester dans la course, les plantes innovent en produisant de nouvelles molécules

Sur cette vue en fluorescence, le mildiou de la pomme de terre (en rouge) attaque des cellules d’épiderme d’une feuille de tabac (noyau et cytoplasme visibles, en vert). Le pathogène émet des projections au contact des cellules végétales à partir desquelles il injecte des effecteurs.

Des éléments génétiques mobiles, naturellement abondants dans le génome des plantes, sont parfois les moteurs de ces innovations. Ils sont capables de créer des copies d’eux-mêmes ou de changer de position sur les chromosomes pour permettre aux plantes de produire de nouvelles molécules antimicrobiennes au gré des attaques Nous pensons même qu’ils pourraient largement contribuer à la diversification des défenses végétales Le mécanisme le mieux documenté de ce genre est celui grâce auquel certaines plantes de la famille de l’arabette des dames (Arabidopsis thaliana), une des espèces modèles préférées des biologistes, produisent un nouveau métabolite secondaire de défense appelé 4-OH-ICN

L’histoire remonte à un peu moins de 13  millions d’années, chez l’ancêtre de l’arabette des dames. Un élément génétique mobile s’est inséré en amont de l’un des nombreux gènes de cytochrome P450, permettant à celuici de s’exprimer lors de l’attaque d’un agent pathogène, lançant la production d’un cytochrome P 450 particulier Les cytochromes fonctionnent à la chaîne pour synthétiser des métabolites secondaires. Le nouvel élément de la chaîne de production, activé en cas d’attaque chez l’arabette, modifie la succession des réactions, ce qui provoque la synthèse de 4-OH-ICN que très peu de plantes savent produire. De nombreux cas d’insertion d’éléments génétiques mobiles ont été répertoriés dans le génome des plantes, mais sans que l’on sache très bien l’impact sur les métabolites produits et sur la défense contre les pathogènes

Parmi les molécules de défense des plantes, on trouve également des protéines appelées

« Pathogenesis Related » (PR), synthétisées en grande quantité lors d’une attaque par des gènes de défense dédiés. On les classe en 17 familles. Les protéines de la famille PR1 sont connues depuis les années 1990 pour leur effet antimicrobien bloquant la croissance des bactéries et des champignons par un mécanisme encore non élucidé Une de leurs capacités insoupçonnées a été découverte récemment : ces protéines

© Sylvain Raffaele

possèdent à leur extrémité onze acides aminés formant un peptide nommé « CAPE1 ». Celui-ci peut être libéré et agir de façon autonome comme un signal d’alerte transmis de cellule à cellule Certains champignons ont trouvé la parade : ils produisent des effecteurs qui bloquent la libération de CAPE

En analysant la diversité et la régulation du génome des plantes en parallèle de tests phy siologiques, on a découvert que le cas de CAPE1 n’était pas isolé petits peptides baptisés « kines », circulant entre les cellules végé tales , sont capables de moduler la réponse des plantes à l’environnement en se liant à des protéines réceptrices dédiées Là encore, certains agents pathogènes ont trouvé la parade : ils sécrètent des e qui miment les phytocytokines perturbant ainsi le système d’alerte de la plante verse , certaines plantes peuvent mimer des effecteurs de pathogénicité pour propa ger le signal de détresse… Avec l’avancée des recherches, nous réalisons sans cesse à quel point cette course moléculaire cache un vivier de solutions naturelles pour préserver un système immunitaire végétal efficace face au changement climatique, et à la menace de l’émergence de nouvelles souches pathogènes capables de contourner les défenses des plantes

AIDER LES PLANTES À SE DÉFENDRE

Jusque-là, les approches classiques de la protection des plantes ont eu tendance à utiliser des substituts chimiques pour pallier les faiblesses de leurs défenses naturelles. Cela était en grande partie dû à notre manque de connaissance du sujet Les progrès récents de la biologie moléculaire et évolutive nous permettent désormais d’explorer leur diversité ainsi que leur potentiel d’adaptation Quelles espèces végétales ou quelles variétés disposent naturellement de récepteurs immunitaires capables de reconnaître les maladies en recrudescence sur une culture donnée ou dans une région donnée ? Lesquelles possèdent les variants insensibles aux effecteurs des agents pathogènes actuels ? Quels variants naturels sont efficaces en condition de température élevée ou de sécheresse ?

Pour apporter des réponses à ces questions, nous exploitons les effecteurs de pathogénicité comme des « hameçons » moléculaires à gènes de résistance des plantes Nous testons leur activité sur un grand nombre de variétés de plantes et nous comparons le génome de celles qui déclenchent une réponse immunitaire avec celles qui en sont incapables Cela a déjà permis de révéler l’identité de plusieurs récepteurs immunitaires, à même, entre autres, de détecter les pathogènes du pied noir du tabac et de

BIBLIOGRAPHIE

M. C. Derbyshire et S. Ra aele, Surface frustration re-patterning underlies the structural landscape and evolvability of fungal orphan candidate e ectors, Nat. Commun., 2023.

M. P. Contreras et al., Sensor NLR immune proteins activate oligomerization of their NRC helpers in response to plant pathogens, EMBO J., 2023.

J. B. Ristaino et al., The persistent threat of emerging plant disease pandemics to global food security, PNAS, 2021.

J. Wang et al., Reconstitution and structure of a plant NLR resistosome conferring immunity, Science, 2019.

B. Barco et al., Expansion of a core regulon by transposable elements promotes Arabidopsis chemical diversity and pathogen defense, Nat. Commun., 2019.

la pourriture brune des cabosses du cacaoyer Il est aussi possible de sélectionner des variétés de plantes dépourvues de cibles auxquelles les effecteurs puissent se lier ou d’identifier les variants de cibles qui échappent à l’activité des effecteurs pour réduire par exemple la sensiou au Une autre stratégie consiste à scruter la compétition entre cette fois pour découvrir de nouvelles molécules naturelles permettant de réduire le développement des mêmes

Outre ces pistes basées sur une utilisation raisonnée de la diversité les recherches récentes en phytopathologie ont fait émerger de nouvelles solutions de synthèse comme des vaccins à ARN pour plantes ou des peptides en mesure de réduire la ecteurs de pathogénicité en cacité pour lutter contre la pourriture grise des fruits et légumes et la fusariose de l’orge Les peptides de synthèse, susceptibles d’activer spécifiquement certains régulateurs de l’immunité, ont donné de premiers résultats probants pour réduire l’alternariose et la moucheture de la tomate À la suite des premiers résultats en serre et en parcelles expérimentales, l’impact global de ces stratégies sur la microflore reste encore à évaluer.

Par ailleurs, de manière générale, l’édition du génome des plantes offre un panel de possibilités particulièrement remarquable Ainsi, en supprimant de façon très précise quelques bases dans le génome de céréales, il est possible de rendre celles-ci insensibles aux effecteurs de pathogénicité C’est ce qui a été fait depuis 2019 sur des parcelles expérimentales en Chine, avec le blé, le riz ou le maïs, devenues complètement résistantes à l’oïdium, à la pyriculariose ou au chancre bactérien, trois des principales maladies des céréales Une autre voie explorée consiste à manipuler génétiquement l’expression de régulateurs naturels de l’immunité des plantes pour préserver leur fonctionnement à température élevée . De quoi les aider à faire face au réchauffement climatique

En domestiquant les plantes depuis le néolithique, l’homme a influencé leur adaptation pour répondre à ses besoins alimentaires. C’est ce qui lui a permis de conquérir la planète et d’assurer la subsistance de milliards d’humains Cela s’est fait au prix de graves déséquilibres qui menacent les écosystèmes et désormais les systèmes agricoles euxmêmes. La biologie moléculaire évolutive des plantes ouvre de nouvelles pistes pour influencer cette adaptation et s’en inspirer pour faire face aux défis actuels et futurs sans utiliser d’intrants chimiques n

Cet assemblage de récepteurs immunitaires, appelé « résistosome », se forme lors de la reconnaissance de l’un des effecteurs de la rouille du blé.

P. 80 Logique & calcul

P. 86 Art & science

P. 88 Idées de physique

P. 92 Chroniques de l’évolution

P. 96 Science & gastronomie

P. 98 À picorer

L’INFINIE FINESSE DES FRACTALES CARRÉES

Les fractales carrées présentent une variété de topologies qu’on réussit seulement maintenant à comprendre et à classer.

L’AUTEUR

JEAN-PAUL DELAHAYE professeur émérite à l’université de Lille et chercheur au laboratoire Cristal (Centre de recherche en informatique, signal et automatique de Lille)

Le tapis de Sierpiński est l’une des plus élémentaires figures fractales Il a été présenté à l’Académie des sciences de Paris à la séance du 25 avril 1916 par Émile Picard, qui parlait pour le mathématicien polonais Wacław Sierpiński Une note de ce dernier a ensuite été publiée dans les comptes rendus de l’Académie , dans laquelle le savant définit ainsi ce qu’on appelle maintenant « le tapis de Sierpi ń ski » : « Soit Q un carré donné , par exemple le carré dont les sommets sont les points (0,0), (0,1), (1,0) et (1,1). Divisons le carré Q en neuf carrés plus petits et excluons l’intérieur de celui qui contient le centre du carré Q Sur chacun des huit carrés qui resteront opérons de même , et ainsi de suite ad infinitum » Nous noterons S0 le carré initial (que Sierpiński, lui, note Q), puis S1, S2,  etc., les étapes de la construction , conduisant à l’infini au tapis S (voir l’encadré 1).

Cette dernière propriété résulte de ce que l’aire de S0 est 1, puis qu’à chaque étape de la construction, cette aire est multipliée par 8/9. Donc l’aire de Sn (qui contient S) vaut (8/9)n , nombre qui tend vers 0 quand n tend vers l’infini.

Remerciements à Jean-François Colonna (CMAP de l’École polytechnique), qui a réalisé les illustrations de cet article.

Jean-Paul Delahaye a notamment publié : Au-delà du Bitcoin (Dunod, 2022).

La fractale S est autosimilaire : chacune des huit parties qui composent S est une version trois fois plus petite et parfaitement similaire à S. Il faut noter que toutes les fractales n’ont pas cette propriété : le célèbre ensemble de Mandelbrot, par exemple, n’est pas parfaitement autosimilaire

La fractale S est par ailleurs infiniment mince, ce qui signifie deux choses :

(a)  On ne peut placer à l’intérieur de S aucun disque de rayon non nul ;

(b)  L’aire de S est nulle, c’est-à-dire que S peut être enfermée dans des sous-ensembles du plan d’aires ε, avec ε > 0 aussi petit qu’on le veut

Bien qu’infiniment mince , le tapis de Sierpiński S est un sous-ensemble infini non dénombrable du plan : même si c’est étonnant, il contient exactement autant de points que le carré de départ S0 La démonstration est élémentaire : S est contenu dans le carré de départ, donc il contient un nombre de points inférieur ou égal à celui de S0 Par ailleurs, S contient au moins autant de points que le segment reliant le point de coordonnées (0,0) au point de coordonnées (1,0), car aucun point de ce segment n’est jamais retiré dans la construction Or on sait qu’un segment contient une infinité de points équivalente à celle d’un carré plein (c’est un résultat dû à Georg Cantor). Donc S contient au moins autant de points que le carré plein Autrement dit, le carré plein, l’ensemble S et le segment reliant les points de coordonnées (0,0) et (1,0) ont tous un nombre de points égal – qui vaut l’infini du continu

DIMENSION FRACTALE

La dimension fractale de S est log(8)/ log(3) ≈ 1,8927, ce qui signifie qu’il est « plus gros » qu’une ligne ou une courbe (de dimension 1) mais « moins gros » qu’une partie du plan de surface non nulle (donc de dimension 2). Il existe plusieurs façons de calculer cette dimension, mais toutes donnent le même

© Jean-François Colonna (toutes les illustrations)

résultat La notion de dimension fractale est assez naturelle : soit S0 un carré plein de côté 1, pour tout entier k > 1, il se divise en k2 carrés identiques de côté 1/k. Un segment de droite de longueur 1 se divise, lui, en k1 segments de droite de longueur 1/k. L’exposant qui apparaît dans le nombre d’objets qu’on obtient quand on divise un objet en objets similaires de taille k fois plus petite indique la dimension de l’objet : 2 pour le carré plein, 1 pour le segment de droite Dans le cas du tapis de Sierpiński, on a noté qu’il se divise en 8  objets de taille 3  fois plus petite, et donc aussi en 64 objets de taille 9  fois plus petite,  etc. Si on doit lui attribuer une dimension, ce serait donc l’exposant e tel que 3e = 8, 9e = 64, etc Cela donne log(3e) = log(8), donc e × log(3) = log(8) ; e = log(8) / log(3). On vérifie aussi que le même e donne 9e = 64,  etc Il est donc naturel d’attribuer la dimension log (8) / log (3) au tapis de Sierpi ń ski D’autres approches confirment cette valeur. Que cette dimension ne soit pas un nombre entier justifie qu’on parle de « fractale ».

Il existe des variantes de S en dimension 3 ou même plus, mais nous allons nous concentrer ici sur les variantes en dimension 2, qui constituent une collection d’objets fractals autosimilaires dont les propriétés topologiques ont été récemment l’objet de très fines études donnant naissance à un chapitre nouveau de la géométrie

LE TAPIS DE SIERPI Ń SKI DE 1916

fractale Ce sera pour nous l’occasion de voyager dans les structures de l’infiniment fin, dont nous pourrons saisir la délicatesse et l’étrangeté

Le schéma général de construction qui a stimulé les mathématiciens est une généralisation immédiate de la construction de Sierpiński. Elle produit une infinité de variantes de S, appelées les «fractales carrées» (fractal squares en anglais).

Dans ce que nous nommerons « le procédé général de Sierpiński », on se donne un entier k ≥ 2, et on divise le carré initial S0 en k2 petits carrés de même taille. On enlève certains de ces carrés , dont la liste E est fixée une fois pour toutes. On recommence la même opération sur les carrés restants, et on poursuit ad infinitum, comme l’écrivait Sierpiński Les encadrés donnent des exemples, dont les plus connus sont la fractale de Vicsek , le T majuscule fractal et le L majuscule fractal

Un petit carré obtenu après la division en k2 parties du carré de départ peut être repéré par le numéro de la ligne auquel il appartient – un nombre entier entre 0 et k – 1 – et le numéro de la colonne auquel il appartient –  encore un entier entre 0 et k – 1. Ces deux entiers constituent les coordonnées du carré considéré À chaque entier k ≥ 2 et à chaque sous-ensemble E de coordonnées correspond, par le procédé général de Sierpiński, un sous-ensemble du plan L(k,E), qu’on écrira simplement L quand

On part d’un carré plein construit autour des quatre points de coordonnées (0,0), (1,0), (1,1) et (0,1). Le tapis de Sierpiński S est le résultat obtenu quand on retire l’intérieur du carré central du carré initial découpé en neuf carrés de même taille, puis qu’on recommence le même procédé sur chacun des huit petits carrés restants, et ainsi de suite à l’infini. Plus précisément, si l’on note S0 le carré initial, puis S1, S2, etc., les sous-ensembles successifs de la construction, le tapis de Sierpiński est la limite de la suite (Sn), c’est-à-dire l’intersection de tous les Sn. Le tapis S est un ensemble infini non dénombrable : il peut être mis en bijection avec l’ensemble de nombres réels. Les points d’ordonnée 1/2 de S ont pour abscisses les points de l’ensemble triadique C de Cantor (représenté ci-contre), découvert en 1874 par le mathématicien irlandais Henry Smith et étudié par le mathématicien allemand Georg Cantor en 1883. On l’obtient en retirant le tiers central du segment réel [0,1] et en réitérant l’opération sur chacun des deux segments ainsi créés, et ainsi de suite indéfiniment. L’ensemble C est constitué des nombres réels entre 0 et 1 qui n’utilisent pas de 1 quand on les écrit en base 3 1

le contexte sera assez clair Sauf exception, ce L est une fractale. On notera Ln(k,E), ou Ln quand le contexte est clair, la n-ième étape de la construction. Les fractales carrées sont tous les L qu’on obtient par ce procédé

Le tapis de Sierpiński de 1916 est associé au choix k = 3 et E = {(1,1)}, car parmi les neuf carrés du découpage, on les garde tous sauf celui du centre, dont les coordonnées sont (1,1). La fractale de Vicsek s’obtient quant à elle de

LE PROCÉDÉ GÉNÉRAL DE SIERPIŃSKI

Plutôt que de partir d’un carré divisé en neuf, on part d’un carré divisé en k2 plus petits carrés tous identiques. On se fixe un ensemble E de petits carrés qu’on retire parmi eux, et on recommence l’opération sur chacun des carrés restants. Pour identifier les carrés à enlever, on les numérote comme sur le dessin ci-contre. La limite des ensembles obtenus après un retrait de carrés, deux retraits, etc., est ce qu’on appelle une « fractale carrée ». La donnée de k et d’un ensemble E de coordonnées désignant les carrés à enlever détermine une fractale carrée. Si on prend k = 2 et E = {(0,1),(1,0)}, les étapes de construction donnent simplement la diagonale du carré de départ. La fractale de Vicsek est quant à elle obtenue avec k = 3 et E = {(0,0),(2,0),(0,2),(2,2)}.

(1,1) (2,1)

(1,0) (2,0)

Le L majuscule fractal provient de k = 3 et E = {(1,1),(2,1),(1,2),(2,2)} Le T majuscule fractal provient de k = 3 et E = {(0,0),(2,0),(1,0),(1,2)}.

Le cas qui donne la diagonale

La fractale de Vicsek

Le L majuscule fractal

Le T majuscule fractal

deux façons différentes , qui fournissent le même motif tourné de 45° :

(a)  k = 3 et E = {(0,0),(2,0),(0,2),(2,2)}

(voir l’encadré 2) ;

(b)  k = 3 et E = {(1,0),(0,1),(2,1),(1,2)}

(voir l’encadré 4).

L’ensemble limite L sera souvent infiniment déchiqueté ou découpé, mais il y a quelques exceptions Si, par exemple, on prend k = 2, E = {(1,0),(0,1)} (on ne garde que les deux carrés de coordonnées (0,0) et (1,1) après avoir découpé S0 en 4), la construction conduit à un simple segment de droite diagonal joignant les points de coordonnées  (0,0) et (1,1) (voir l’encadré 2) Autre exemple ne conduisant pas à un ensemble déchiqueté : on n’enlève aucun carré, E = ∅ Dans ce cas, la construction en partant du carré S0 n’évolue pas et donne S0 lui-même à l’infini

La dimension fractale des objets obtenus s’obtient facilement en généralisant le cas du tapis de Sierpiński (k = 3, E = {(1,1)}). Pour une fractale carrée obtenue à partir de k et de E contenant m éléments, la dimension fractale de la forme L obtenue est log(k2 – m)/ log(k). Cette dimension est inférieure à 1 si on enlève beaucoup de carrés à chaque étape (précisément, si on en laisse moins de k), sinon elle est comprise entre 1 et 2.

PLUSIEURS TOPOLOGIES INFINIES

Une série de travaux mathématiques récents menés par des chercheurs et chercheuses en Chine, en Russie et en Autriche ont permis de mieux comprendre ces structures infiniment découpées résultant du procédé général de construction de Sierpiński

Le cas le plus simple, que nous appellerons le « cas classique », est celui où on n’obtient qu’une figure sans découpage infiniment fin, qui sera soit une droite, soit un rectangle Les autres cas, où L est infiniment déchiqueté ou découpé, se rangent dans deux catégories principales, chacune se séparant à nouveau en plusieurs souscatégories. Comprendre ces figures demande un petit effort, car bien sûr nous ne sommes pas habitués à penser ou imaginer des structures géométriques possédant des découpages infiniment fins. Il faut deviner ce qui se passe quand on descend dans leurs détails de plus en plus petits et nombreux. On ne voit qu’imparfaitement ces structures puisque, bien sûr, tout dessin qu’on tentera n’aura qu’une précision limitée. Cette exploration est une sorte de voyage mathématique dans les variantes de l’infiniment fin. Les deux grandes catégories infiniment découpées sont le « cas connexe » et le « cas non connexe », que nous appellerons le « cas éclaté » La distinction se fonde sur la possibilité ou non de passer continûment d’un point de L à tout autre point de L, sans quitter L On est dans le

cas connexe lorsque la fractale L obtenue est d’un seul tenant : on peut joindre deux points quelconques de L en traçant un chemin – une courbe continue – qui reste dans L. Un résultat simple et intéressant, démontré en 2010 par Ligia-Loreta Cristea et Bertran Steinsky, permet de reconnaître immédiatement cette situation : L est connexe si et seulement si chaque étape de la construction Ln est connexe (voir les encadrés 3 et 4). Plus précisément encore : soit L est connexe, soit il existe une étape n à partir de laquelle tous les Lp (pour p ≥ n) ne sont pas connexes, et alors L n’est pas connexe.

Dans le cas connexe, il peut y avoir ou non des « boucles internes » La situation « connexe avec existence de boucles » est celle du tapis de Sierpiński de 1916 : il existe des chemins continus internes à L formant des boucles qui ne se recoupent pas Autrement dit, partant d’un point de L, on peut suivre un chemin continu pour y revenir sans repasser deux fois par le même point. Dans cette classe des fractales connexes avec boucle interne, il y a aussi le « L majuscule fractal » (voir l’encadré 2), le « H majuscule fractal », le « S couché fractal » et la « croix trouée fractale » (voir l’encadré 3).

CONNEXES ET FRAGILES : LES DENDRITES

La seconde situation, dans le cas connexe, est celle où la fractale carrée ne présente pas la moindre boucle : il n’est jamais possible de partir d’un point et d’y revenir en suivant un chemin continu qui ne se recoupe pas. On parle alors de « dendrite » Ce vocabulaire est emprunté à la biologie : certaines cellules, dont les neurones, semblent posséder des excroissances qui présentent des fourches plusieurs fois de suite – mais, bien sûr, en biologie il n’y a qu’un nombre fini de telles séparations Les branches des arbres sont, elles aussi, des dendrites finies Pour nos fractales carrées, en revanche , quand des bifurcations se produisent, c’est une infinité de fois, et l’ensemble limite est donc une sorte d’arbre infini localisé dans un domaine borné (voir l’encadré 4)

Deux sortes de points composent une telle fractale carrée dendritique L : les « points extrêmes » et les « points séparateurs ». Un point extrême est une extrémité de branche infinie : quand on le retire à L, L reste connexe. C’est par exemple le cas des points de coordonnées (0,1), (1,1) et (1/2 , 0) du T majuscule fractal (voir l’encadré 2) Ce ne sont pas les seuls points extrêmes, et on peut même montrer que dans le cas du T majuscule fractal, il y en a une infinité non dénombrable –  c’est-àdire autant que de réels

Les points séparateurs des dendrites sont les autres points (par exemple le point de coordonnées (1/2 , 1) pour le T majuscule fractal).

Quand on retire un tel point, la fractale est « cassée » : elle cesse d’être connexe , car il devient impossible de joindre par un chemin continu certains couples de points.

Les sous-ensembles A du plan qui ne sont pas connexes se décomposent en sous-ensembles connexes aussi grands que possible, dont la réunion donne A, qu’on appelle les « composantes connexes de A » Dans le cas du T majuscule fractal, enlever un point séparateur donnera un sous-ensemble du plan comportant deux ou trois composantes connexes. Enlever le point de coordonnées (1/2 , 1) sépare par exemple cette

FRACTALES CARRÉES CONNEXES AVEC BOUCLES

Les fractales carrées se classent en catégories qu’il est intéressant de bien comprendre. Lorsque tous les points d’une fractale carrée peuvent être joints les uns aux autres par des courbes continues, on dit que la fractale est d’un seul tenant, ou connexe. Elle peut alors contenir ou non des courbes continues bouclées.

Le tapis de Sierpi ń ski de l’encadré  1 contient bien sûr de telles boucles, dont la plus grande est celle du périmètre du carré de départ. Le H majuscule fractal contient

lui aussi des boucles, de même que le S couché fractal et la croix trouée fractale. Cependant, toute courbe fermée dans le S couché fractal ou la croix trouée fractale a une longueur infinie : une telle courbe est en effet contrainte de faire des détours à toutes les échelles, ce qui allonge son trajet sans limite !

En revanche, il existe des boucles de longueur finie dans le H majuscule fractal ou le tapis de Sierpiński – en raison de l’existence, dans ces deux dernières fractales, de segments verticaux et horizontaux. 3

Le H majuscule fractal

Le S couché fractal

La croix trouée fractale

fractale en trois composantes connexes : la partie centrale qui descend jusqu’au point de coordonnées (1/2 , 0), une partie à droite composée d’un T fractal de taille 1/3 collé à un T fractal de taille 1/9, et une partie à gauche symétrique à celle de droite.

Même si ce n’est pas tout à fait évident, il existe pour le T majuscule fractal des points qui, lorsqu’on les retire, donnent seulement deux composantes connexes. C’est le cas, par exemple, des points de coordonnées (1/3 , 1) et (2/3 , 1), et plus généralement des points dont les coordonnées sont de la forme (k/3n , 1) avec n un entier strictement positif et k un entier compris entre 1 et 3n – 1. Plus précisément, les points d’ordonnée y = 1 qui séparent le T majuscule fractal en trois composantes sont tous ceux dont l’abscisse est de la forme x = (1 + 2k) / (2 × 3n), avec n un entier positif ou nul et (1 + 2k)  un entier impair compris entre 1 et 2 × 3n – 1. Tous les autres points (à l’exception des extrémités du segment) le séparent en deux

La fractale de Vicsek (voir les encadrés 2 et 4) possède des points séparateurs qui le coupent en quatre composantes connexes. Cette fractale est très connue des physiciens, qui l’utilisent pour concevoir des antennes, et

LES DENDRITES FRACTALES

Les fractales carrées connexes ne contenant pas de boucle se nomment des dendrites. Leur forme générale est celle d’un arbre dont chaque branche possède une infinité de bifurcations. Dans une telle fractale, deux points quelconques peuvent être joints par une courbe continue unique. C’est bien clair pour la fractale de Vicsek, dont on donne ci-dessous une seconde réalisation comme fractale carrée. Dans cette fractale, joindre deux points est toujours faisable par un chemin de longueur fini. Pour le taureau fractal et le Loch Ness fractal, en revanche, ce n’est plus possible : deux points peuvent toujours se joindre par une courbe continue, mais celle-ci aura nécessairement une longueur infinie.

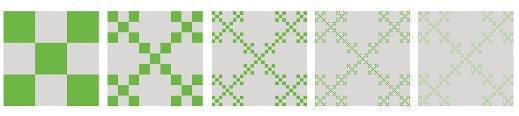
La fractale de Vicsek (bis)

Le taureau fractal

Le Loch Ness fractal

aujourd’hui encore on étudie les propriétés des dispositifs physiques construits en se basant sur sa forme La fractale de Vicsek contient aussi des points séparateurs qui donnent deux composantes connexes – par exemple, le point de coordonnées (1/2 , 2/3) – mais n’en contient pas qui donnent trois composantes connexes

Un résultat assez étonnant a été démontré en 2023 par Dmitry Drozdov et Andrei Tetenov : dans le cas d’une fractale carrée connexe, enlever un point peut maintenir la fractale d’un seul tenant ( point extrême ), peut la couper en deux, trois ou quatre composantes connexes, mais ne le coupera jamais en k composantes connexes pour k > 4.

Les fractales carrées dendrites se divisent en deux catégories bien nettes Il y a celles (comme la fractale de Vicsek) qui contiennent des segments et celles qui n’en contiennent pas – dont par exemple le Taureau fractal et le Loch Ness fractal (voir l’encadré 4). Dans le premier cas, joindre deux points extrêmes se fait en empruntant un chemin unique ne se recoupant pas qui est de longueur finie Dans le second cas, il existe une unique manière de joindre deux points extrêmes sans repasser pas le même point, mais la longueur du trajet sera toujours infinie La situation de ces fractales est un peu étrange et analogue à la frontière du célèbre flocon de Von Koch : deux points ne sont jamais très éloignés à vol d’oiseau l’un de l’autre et ils peuvent être joints l’un à l’autre par une courbe continue, pourtant si vous voyagez à vitesse finie, le trajet qui permet de joindre deux points distincts exigera toujours un temps infini. Une classification encore plus fine des fractales carrées dendritiques, en 7 sous-catégories, a été proposée en 2023 par Dmitry Drozdov et Andrei Tetenov, montrant que comprendre l’infiniment petit sera peut-être une tâche… sans fin

LE CAS ÉCLATÉ

Revenons à présent sur la situation où la fractale carrée L n’est pas connexe –  le « cas éclaté » ( voir l’encadré  5) . Quand un sousensemble A du plan n’est pas connexe , un grand nombre de situations sont possibles. Il peut y avoir un nombre fini des composantes connexes, une infinité dénombrable ou une infinité non dénombrable Pour une fractale carrée éclatée, seul le cas fini et le cas infini non dénombrable sont possibles Dans le cas infini, les composantes connexes peuvent être réduites à des points –  on dit alors que L est totalement discontinu – mais il peut aussi y avoir des segments de droite, ce qui se produit fréquemment Dans ce dernier cas, ce sont uniquement des segments de droites parallèles entre eux

Comme expliqué au début de l’article , chaque fractale carrée est définie à partir d’un entier k et d’un ensemble de coordonnées E :

LES FRACTALES CARRÉES ÉCLATÉES

5

Lorsqu’une fractale carrée n’est pas connexe, elle peut posséder un nombre fini de composantes connexes, ou au contraire en avoir un nombre infini. Selon les cas, les composantes connexes sont des segments de droite ou des points. Lorsque les composantes connexes sont réduites à des points, on dit que la fractale carrée est totalement discontinue.

ce sont des données finies On peut donc envisager des algorithmes qui, à partir de ces données, indiquent les propriétés topologiques de la fractale produite par le procédé général de Sierpiński C’est ce qui a été fait par Jian-Ci Xiao en 2020 : il a proposé un algorithme qui, après avoir associé un graphe aux données, en déduit si le nombre de composantes connexes de la fractale est fini et calcule alors ce nombre Ce type de résultats illustre l’idée qu’analyser et connaître les propriétés d’ensembles fractals infiniment fins est possible par des procédés finis Le fini donne parfois accès à l’infini, comme quand en arithmétique on démontre par un raisonnement fini qu’il existe une infinité de nombres premiers, et bien d’autres choses

Le cas de l’éclatement en un nombre infini de composantes connexes réduites chacune à un point est intéressant, car il permet d’imaginer une structure pour notre univers qui explique le paradoxe d’Olbers. Ce paradoxe résulte de l’idée que, même si la densité des étoiles dans l’espace est très faible , si elles sont réparties assez aléatoirement et uniformément alors dans toute direction une droite finit par rencontrer une étoile Si les photons ne perdent pas d’énergie en voyageant vers nous sans rencontrer d’obstacles, la luminosité de la surface d’une étoile est indépendante de sa distance Donc, dans l’hypothèse où toute direction d’observation intercepte la surface d’une étoile, le ciel nocturne devrait être aussi brillant que la surface d’une étoile

moyenne comme notre Soleil : il devrait être totalement lumineux et nous aveugler. Or ce n’est pas le cas : le ciel nocturne est presque entièrement noir !

Plusieurs solutions au paradoxe sont connues, mais l’une d’elles, proposée en 1907 par Edmund Edward Fournier d’Albe et ensuite rendue plus précise par Benoît Mandelbrot s’appuie sur les structures fractales totalement discontinues Elle consiste à imaginer qu’il y a bien des étoiles partout dans l’espace (qu’on suppose infini) mais qu’elles sont réparties comme les points d’une fractale totalement discontinue, analogue en trois dimensions à celle présentée en bas à droite dans l’encadré 5, en imaginant qu’on en prolonge la structure au-delà du carré de départ. Cela conduit à une répartition des étoiles qui a les propriétés suivantes :

(a) Il y a bien des étoiles partout ;

(b) La densité d’étoiles dans une sphère de rayon donné n’est jamais nulle ;

(c) Pourtant, plus le rayon de cette sphère est grand, plus la densité d’étoiles est faible ;

(d) Avec une telle structure le ciel n’est pas totalement lumineux.

L’imagination mathématique s’est affinée en concevant les fractales , qui par ailleurs posent une multitude de problèmes amusants et intrigants. Même avec les contraintes strictes du procédé de Sierpiński, on se trouve confronté à des situations non triviales, qui nous éclairent et même nous aident à comprendre l’infiniment fin n

BIBLIOGRAPHIE

D. Drozdov et A. Tetenov, On the classification of fractal square dendrites, arXiv preprint, 2023.

J. C. Xiao, Fractal squares with finitely many connected components, Nonlinearity, 2021.

K. S. Lau et al., Topological structure of fractal squares, Mathematical Proceedings of the Cambridge Philosophical Society, 2013.

L. L. Cristea et B. Steinsky, Connected generalised Sierpiński carpets, Topology and its Applications, 2010.

L. L. Cristea et B. Steinsky, Curves of infinite length in 4 × 4-labyrinth fractals, Geometriae dedicata, 2009.

W. Sierpiński, Sur une courbe dont tout point est un point de ramification, Comptes Rendus hebdomadaire des séances de l’Académie des sciences, 1915.

Fractale carrée avec trois composantes connexes

Fractale carrée totalement discontinue

Fractale carrée composée de segments obliques

Fractale carrée avec deux composantes connexes

L’AUTEUR

HERVÉ LE GUYADER professeur émérite de biologie évolutive à Sorbonne Université, à Paris

LE DOUBLE EFFET DU GÉNOME DE LA MYXINE

Le séquençage du génome de cet animal a non seulement résolu une énigme ancienne sur la diversification des premiers vertébrés, mais aussi mis au jour les circonstances qui ont favorisé le succès évolutif de ceux à mâchoires.

La myxine Eptatretus burgeri est un mets de choix en Corée et au Japon Mais ce n’est sans doute pas ce qui a motivé le séquençage récent du génome de ce nécrophage des fonds marins du Pacifique. L’opération était en effet particulièrement délicate, car, au cours des divisions cellulaires, l’ADN de cet animal subit un réarrangement par élimination de chromosomes. La seule solution consistait donc à se concentrer sur un tissu exempt de division cellulaire, une glande sexuelle (le testicule, en l’occurrence) – une approche qui nécessitait la résolution de di ffi cultés techniques importantes. Quel est donc, alors, l’intérêt de cette prouesse ? N’était-ce pas un travail bien ardu pour la satisfaction de quelques zoologistes ? Au contraire Ce génome a permis de résoudre une énigme sur laquelle butaient les biologistes depuis plusieurs décennies : éclaircir les événements majeurs advenus à la source des vertébrés

Dans l’histoire évolutive des espèces, la duplication de l’ensemble du génome est un événement clé souvent associé à des innovations sur les organismes et à des spéciations. Chez les plantes à fleurs, par exemple, les duplications de génomes ont largement enrichi les réseaux de régulation de gènes, à la source de réponses de plus en plus fines aux stress environnementaux. Chez les vertébrés, cependant, le problème est compliqué.

Dès 1970, Susumu Ohno, généticien au City of Hope National Medical Center, en Californie, a émis l’hypothèse que le génome des mammifères actuels serait le résultat d’au moins une double duplication du génome (une première duplication, puis une deuxième de l’ensemble). Mais le séquençage du génome humain, puis ceux d’autres mammifères comme la souris, n’apporta pas de réponse claire et le début des années 2000 fut le siège de débats conflictuels. Pour certains, Susumu Ohno avait raison, pour d’autres, il n’y avait eu qu’une seule duplication. D’autres encore semblaient démontrer qu’il n’y avait eu que des duplications limitées à quelques parties de chromosomes. En réalité, à l’époque, on ne disposait pas de génomes séquencés en

Les myxines sont des animaux marins sans mâchoires ni vertèbres, de tailles comprises entre 18 et 127 centimètres suivant les espèces.

Généralement enfouies dans la vase, les myxines n’en sortent que pour se nourrir des poissons morts ou malades qu’elles écorchent par succion et morsures.

Hervé Le Guyader a notamment publié : Ma galerie de l’évolution (Le Pommier, 2021).

EN CHIFFRES

16 513

C’est le nombre de gènes codant des protéines recensés chez la myxine Eptatretus burgeri, pour un génome comptant environ 3 milliards de nucléotides. À comparer aux quelque 20 000 gènes codants de l’humain et 3 milliards de nucléotides de son génome…

Leurs yeux dégénérés sont recouverts d’une peau.

Myxine de Stout (Eptatretus stoutii)

Taille : jusqu’à 60 cm de longueur

Leur bouche est entourée de barbillons couverts de récepteurs sensoriels. Elle comprend des plaques dentigères actionnées par un ensemble de cartilages et de muscles.

nombre suffisant pour vraiment résoudre le problème.

Il fallut attendre 2005 pour que Paramvir Dehal et Jeffrey Boore, du laboratoire national Lawrence-Berkeley, en Californie, apportent une contribution cruciale en utilisant, en plus des génomes complets humain et murin, ceux d’un poisson téléostéen, le fugu, et d’un chordé non vertébré – un tunicier, la cione – dont le génome avait été séquencé peu auparavant et qui servait d’espèce extérieure au groupe des vertébrés. Rappelons que les chordés rassemblent les animaux caractérisés par un axe rigide – la chorde –qui sert de soutien à l’organisme. Les vertébrés sont ceux qui organisent des

ENTRE 498,4 ET 485,2 MILLIONS D’ANNÉES

La deuxième duplication du génome des vertébrés s’est produite au Cambrien terminal, il y a entre 498,4 millions et 485,2 millions d’années, une période où ce groupe a connu une grande diversification.

106

Les angiospermes – les plantes à fleurs –portent les traces, dans leur génome, de 106 événements de duplication, dont 46 associés à une augmentation de leur taux de diversification.

vertèbres autour de la chorde. Les chordés non vertébrés sont donc essentiels pour connaître le génome de l’ancêtre des vertébrés.

L’HYPOTHÈSE 2R

En se penchant sur les groupes de gènes qui, au sein d’un même génome, présentent des homologies de séquence, les deux biologistes prouvèrent l’existence d’une double duplication du génome chez les vertébrés, hypothèse appelée 2R (R pour round, « tour »), et expliquèrent le pourquoi des débats. Pour parvenir à un tel résultat, il fallait croiser les données de génomique sur une phylogénie précise et, surtout, comparer les génomes de vertébrés avec celui d’un chordé proche.

Vu l’éloignement phylogénique du fugu et des deux mammifères, les deux tours de duplication ont eu lieu « à la base de l’arbre des vertébrés ». Certes, mais comment avoir plus de précision ? Même réponse : il faut plus de génomes, avec une phylogénie exacte des animaux étudiés. C’est ce qui s’est produit.

D’une part, grâce au séquençage du génome de sujets bien choisis, la phylogénie des chordés s’est précisée. En 2006, une équipe canadienne a placé les tuniciers au plus proche des vertébrés, où ils ont détrôné l’autre groupe de chordés non vertébrés, les céphalochordés, alors que l’anatomie plaidait pour le contraire. Et en 2008, le génome d’un céphalochordé, un amphioxus, a été séquencé, offrant des données précieuses.

D’autre part, les zones d’ombre dans la phylogénie des vertébrés se sont estompées. Ceux-ci rassemblent deux grands groupes, distingués par la présence ou l’absence de mâchoires. Les agnathes (lamproies et myxines) n’en ont pas. Tous les autres – les gnathostomes (poissons osseux et cartilagineux, tétrapodes) – en ont deux. Depuis longtemps, on savait que les gnathostomes forment un groupe monophylétique, c’est-à-dire avec un ancêtre commun exclusif. Mais pour les agnathes, ce n’était pas clair. Au XIX e siècle, les zoologistes les avaient rassemblés en un groupe a priori homogène, les « cyclostomes ». Mais dans les années 1980, une étude fine des caractères anatomiques les avait séparés, plaçant les lamproies plus près des gnathostomes que les myxines, ces dernières étant dépourvues de certains traits que les deux premiers groupes partageaient. Toutefois, en 2011, une étude minutieuse de leur développement a montré que ces caractères manquants existaient chez l’embryon, puis régressaient chez l’adulte. Le taxon des cyclostomes était ressuscité !

Les vertébrés se partagent donc en deux taxons, les cyclostomes et les gnathostomes. Et la question sur les duplications se précise : ont-elles eu lieu avant ou après leur séparation ? Diverses équipes ont tenté d’y répondre, mais les données, très partielles, produisaient des résultats contradictoires. Et pour cause : une portion de l’arbre était pauvre en génomes séquencés.

Les gnathostomes étaient surreprésentés, avec des poissons et des tétrapodes. Le groupe extérieur comprenait des tuniciers et des céphalochordés. Mais, chez les cyclostomes, il n’y avait que des lamproies. Or sans myxine, il était difficile de déceler si les caractères repérés étaient spécifiques aux cyclostomes ou seulement aux lamproies. C’est ainsi qu’une imposante équipe internationale rassemblée par Juan PascualAnaya, de l’université de Málaga, en Espagne, et Yong Zhang, de l’Académie chinoise des sciences, s’est attachée à séquencer le génome de la myxine côtière Eptatretus burgeri et à l’intégrer dans la base de données.

IL Y A DUPLICATION ET DUPLICATION

Résultat : ce qui avait échappé jusqu’alors aux biologistes apparaît clairement. Le génome des cyclostomes est lui-même le fruit d’une triplication

COMMENT LES VERTÉBRÉS SE SONT DIVERSIFIÉS

Dans l’arbre des chordés, le nœud clé est celui des vertébrés. Les nœuds précédents ont donné des animaux simples – des céphalochordés comme l’amphioxus et des tuniciers comme la cione. Les vertébrés se scindent en deux groupes d’importance inégale. Les cyclostomes (myxines, lamproies) ont gardé une structure et une écologie monotones tandis que les gnathostomes ont conquis tous les habitats avec des formes foisonnantes. Les génomes se sont multipliés en peu de temps : une première duplication pour tous (1R), une triplication pour les cyclostomes (CR) et une deuxième duplication pour les gnathostomes (2R), dont la qualité paraît être une cause de leur réussite.

Amphioxus chinois (Branchiostoma belcheri)

Cione (Ciona intestinalis)

Cyclostomes

Chordés

Vertébrés CR 1R 2R

Gnathostomes

Ostéichthyens

Myxine côtière (Eptatretus burgeri)

Lamproie marine (Petromyzon marinus)

Roussette nuageuse (Scyliorhinus torazame)

Fugu (Takifugu rubripes)

Cœlacanthe africain (Latimeria chalumnae)

Rat-taupe nu (Heterocephalus glaber)

600 500 400 300 200 100 0

Millions d’années

survenue chez un ancêtre de ce taxon. Ce qui brouillait évidemment les pistes pour comprendre les duplications de l’hypothèse 2R. Tout s’éclaircit. La première duplication s’est produite à la base de l’arbre, avant la séparation cyclostomesgnathostomes, puis la deuxième est spécifique des gnathostomes. De plus, l’étude de la diversité des gènes ainsi dupliqués fait apparaître un fait crucial : la première duplication est sans conteste un événement d’autopolyploïdie, c’est-à-dire de doublement d’un même génome, tandis que la deuxième est un événement d’allopolyploïdie, c’est-à-dire d’addition de deux génomes différents (mais bien sûr proches phylogénétiquement). Une conclusion que corrobore peu après une équipe indépendante avec le génome d’une autre myxine, Eptatretus atami

La différence est de taille, car une allopolyploïdie entraîne des déséquilibres génomiques, avec comme conséquences des réarrangements chromosomiques, des changements dans la structure de la chromatine, dans la méthylation de l’ADN, dans l’activation des éléments transposables, ce qui conduit à des innovations évolutives et des diversifications écologiques. Serait-ce le secret de la réussite évolutive des gnathostomes ? n

BIBLIOGRAPHIE

D. Yu et al., Hagfish genome elucidates vertebrate wholegenome duplication events and their evolutionary consequences, Nat. Ecol. Evol., 2024.

F. Marlétaz et al., The hagfish genome and the evolution of vertebrates, Nature, 2024.

S. Kuraku et al., Timing of genome duplications relative to the origin of the vertebrates : Did cyclostomes diverge before or after ?, Mol. Biol. Evol., 2009.

P. Dehal et J. L. Boore, Two rounds of whole genome duplication in the ancestral vertebrate, Plos Biol., 2005.

OFFRE D’ABONNEMENT 1 AN

papier 12 numéros par an

magazine en version numérique 12 numéros par an

hors-série papier 4 numéros par an Le hors-série en version numérique 4 numéros par an Accès à pourlascience.fr Actus, dossiers, archives depuis 1996

Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr

OUI , je m’abonne pour 1 an à

Je choisis ma formule (merci de cocher) 1

• 12 n° du magazine papier

• 4 n° des hors-séries papier

• 12 n° du magazine (papier et numérique)

• 4 n° des hors-séries (papier et numérique)

• Accès illimité aux contenus en ligne

J’indique mes coordonnées

☐ M. ☐ Mme

Nom : Prénom :

Adresse :

Code postal : Ville :

Téléphone :

Courriel : (indispensable pour la formule intégrale)

J'accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON

Je retourne le bulletin d'abonnement et mon règlement 3

J’émets un chèque à l’ordre de Pour la Science du montant de l’abonnement. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante : Abonn’escient – TBS Group Service abonnement Groupe Pour la Science 20 rue Rouget de Lisle - 92130 Issy

Pour découvrir toutes nos o res d’abonnement et e ectuer un paiement en ligne, scannez le QR code ci-contre avec votre téléphone ou rendez-vous sur pourlascience.fr/abonnements/

* Réduction par rapport au prix de vente en kiosque et l’accès aux archives numériques. Durée d’abonnement : 1 an. Délai de livraison : dans le mois suivant l’enregistrement de votre règlement. O re valable jusqu’au 31/03/2024 en France métropolitaine uniquement. Pour un abonnement à l’étranger, merci de consulter notre site boutique.groupepourlascience.fr. Photos non contractuelles. Vous pouvez acheter séparément les numéros de Pour la Science pour 7 € et les hors-séries pour 9,90 € En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante : https://rebrand.ly/CGV-PLS. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour la Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous invitons à prendre connaissance de notre charte de protection des données personnelles à l’adresse suivante : https://rebrand.ly/charte-donnees-pls. Conformément à la réglementation applicable (et notamment au règlement 2016/679/UE dit « RGPD ») vous disposez des droits d’accès, de rectification, d’opposition, d’e acement, à la portabilité et à la limitation de vos données personnelles. Pour exercer ces droits (ou nous poser toute question concernant le traitement de vos données personnelles), vous pouvez nous contacter par courriel à l’adresse protection-donnees@pourlascience.fr.

La simulation multiphysique favorise l’innovation

Pour innover, les ingénieurs ont besoin de prédire avec précision le comportement réel de leurs designs, dispositifs et procédés. Comment ? En prenant en compte simultanément les multiples phénomènes physiques en jeu.

scannez-moi pour en savoir plus

comsol.fr/feature/multiphysics-innovation