PROZESSTECHNIK

Optimierung von Sandwichverbunden

Sandwichverbunde mit Kavitäten im Kern

Bei Sandwichstrukturen können in der Kernschicht makroskopische Aussparungen vorgesehen werden, sodass lokal Kavitäten entstehen. Dies bringt neben einer Einsparung von Gewicht den Vorteil von zusätzlichem Bauraum mit sich, welcher z.B. durch den Einbau funktionaler Komponenten genutzt werden kann (Bild 1).

Markus Henne1, Luca Müller1

Während die mechanische Analyse von Sandwichstrukturen mit homogenen Kernen in der Fachliteratur umfassend dokumentiert ist und dem Stand der Technik entspricht, gibt es für Sandwichstrukturen mit lokalen, makroskopischen Kavitäten keine allgemeingültigen Formeln zur Dimensionierung. Da für die Auslegung derartiger Bauteile bisher aufwändige FE-Analysen durchgeführt werden mussten, besteht das Bedürfnis nach einer analytischen Wegleitung zur Grobdimensionierung. Die vorliegenden Ausführungen begrenzen sich dabei vorerst auf Sandwichbalken mit unterschiedlichen Belastungen (Bild 2).

Versagensarten

Mechanisch belastete Sandwichstrukturen können auf verschiedene Arten in ihrer Funktion versagen. Neben unzureichender Steifigkeit, dem Überschreiten der Festigkeiten in Deckschichten, Kern oder der Verbindung zwischen Kern und Deckschicht, spielen insbesondere Instabilitäten eine grosse Rolle. Sind die Deckschichten aufgrund der Kavitäten nur noch lokal vom Kern gestützt, besteht eine erhöhte Gefahr von lokalen Instabilitäten. Es kann zum Beulen der Deckschichten über den freistehenden Feldern oder zum Ausbeulen der schlanken Kernstege kommen.

Modellierung des mechanischen Verhaltens

Zur Charakterisierung des mechanischen Verhaltens von Sandwichbalken mit Kavi-

1 Prof. Dr. Markus Henne, Luca Müller, IWK, Fachbereich Mechanische Systeme Bild 1: Tragfläche einer Fixed Wing Drohne mit integrierter Elektronik.

Bild 2: Sandwichbalken mit rechteckigen Aussparungen.

täten werden neben theoretischen Betrachtungen umfangreiche Parameterstudien mit FE-Simulationen durchgeführt. Dabei wird der Einfluss der Materialeigenschaften und geometrischen Proportionen auf die Spannungsverläufe, Verformungen und Instabilitäten untersucht. Basierend auf den theoretischen Grundlagen und den Ergebnissen aus den numerischen Parameterstudien werden die bekannten analytischen Modelle durch semi-empirisch hergeleitete Formeln erweitert, um so den Einfluss von rechteckigen Kavitäten zu berücksichtigen. Es hat sich gezeigt, dass sich Sandwichbalken mit Kavitäten unter reiner Biegebeanspruchung ähnlich verhalten wie solche ohne Kavitäten. Das Biegemoment wird dabei in ein Kräftepaar umgewandelt, das in den Deckschichten zu Zug- bzw. Druckspannungen führt. Die Verformung kann durch Lösen der Biegedifferentialgleichung unter Berücksichtigung der entsprechenden Randbedingungen ermittelt werden. Ist der Sandwichbalken zusätzlich zur Biegung durch Querkräfte beansprucht, entstehen in den Deckschichten Sekundärspannungen, welche sich mit den Biegespannungen überlagern. Diese Sekundärspannungen wirken in der Deckschichtebene und äussern sich in einem ebenen Spannungszustand. Zur Berechnung der Sekundärspannungen werden die freistehenden Felder über den Kavitäten als isotrope Platten betrachtet. Gemäss Verformungs-Spannungs-Beziehungen aus der Plattentheorie rufen Krümmungen und Drillungen Spannungen in den Deckschichten hervor. Die Sekundärspannungen erreichen insbesondere im Randbereich der Kavitäten ihr Maximum (Bild 3). Das Verhalten lässt sich durch Betrachtung

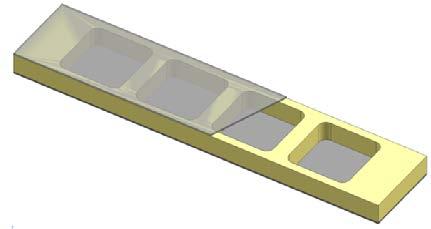
Bild 3: FE-Analyse eines Sandwichbalkens: Spannungen auf der Deckschicht in Balkenrichtung (oben), Beulen der druckbeanspruchten Deckschicht (unten).

der Verformung in diesem Bereich erklären: An den Übergängen zu den Kavitäten ändert sich die Schubsteifigkeit des Sandwichverbundes. Dadurch ergibt sich eine Änderung in der Durchsenkung, was im Randbereich der Kavität – abhängig von den vorliegenden Steifigkeitsverhältnissen von Kern- und Deckschichtmaterial – eine erhöhte Krümmung der dünnen Deckschichten zur Folge hat (Bild 4). Die Schubsteifigkeit des Kerns im Bereich der Kavitäten kann angenähert werden, indem die Schubsteifigkeit der Schaumstege über die ganze Breite «verschmiert» wird. Mit einer Mittelung der Schubsteifigkeit über die ganze Balkenlänge lässt sich durch Lösen der Differentialgleichung die Durchsenkung annähernd exakt berechnen. Im Kern führen die Querkräfte wie bei gewöhnlichen Balken zu Schubspannungen. Diese Schubspannungen werden an Querschnittsänderungen durch die Kavitäten lokal überhöht. Die kritische Spannung hinsichtlich Beulen der Deckschichten lässt sich mit der Formel zur Berechnung der Beulspannung bei eingespannten, druckbeanspruchten Flächen abschätzen. Die Formel wird derart erweitert, dass sie die weiche Bettung der Deckschichten auf dem Kern berücksichtigt. Ein Ausbeulen der Kernstege ist theoretisch möglich, wird aber nicht erwartet, weil die Schaumstrukturen in der Praxis nicht derart schlank gefertigt und verklebt werden können, dass Beulen zu erwarten ist, bevor die Festigkeit des Kerns überschritten wird.

Validierung anhand von 4-Punkt Biegeversuchen

Die Erkenntnisse aus den FE-Analysen und den hergeleiteten Formeln wurden an-

Bild 4: Durchsenkung am Übergang zu Kavität, links: starke Krümmung durch steifen Kern und weiche Deckschichten, rechts: schwache Krümmung durch weichen Kern und steife Deckschichten.

hand verschiedener Proben mit 4-PunktBiegeversuchen überprüft. Die Proben setzen sich aus einem Rohacell IG-F Kern mit vier quadratischen Taschen und Deckschichten aus AN AW 1050A zusammen. Die theoretisch berechnete Steifigkeit der Proben und das Versagen der Strukturen konnte für dünne Deckschichten validiert werden. Bei dickeren Deckschichten wird die Steifigkeit und maximal erreichbare Kraft unterschätzt, weil in der Modellbildung davon ausgegangen wird, dass die Querkräfte alleine vom Kern aufgenommen werden. Verifiziert werden konnte zudem, dass die Kavitäten im Kern die Biegesteifigkeit des Gesamtverbundes bei den betrachteten geometrischen Verhältnissen kaum beeinflussen. Das elastische Beulen der Deckschichten konnte anhand von Kameraaufnahmen verfolgt werden und führte zu lokalen grossen Deformationen, nicht jedoch zum Kollaps der Struktur (Bild 5).

Optimierung mit evolutionärem Algorithmus in Matlab

Die hergeleiteten Formeln für Verformung, Belastungen und lokale Instabilitäten flies-

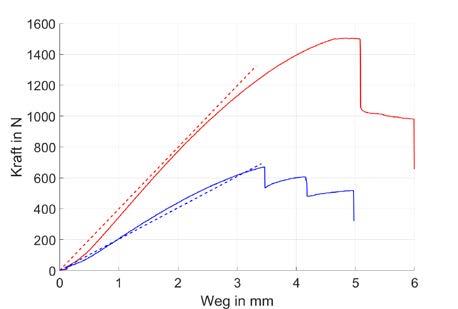
Bild 5: Kraft-Weg-Diagramm von zwei verschiedener Proben. Gestrichelt: analytisch; durchgezogen: 4-Punkt Biegeversuch. sen in die Nebenbedingungen einer Optimierung zur Evaluierung der optimalen Sandwichkonfiguration ein. Dazu wird ein Matlab-Skript entwickelt, welches für verschiedene Lastfälle die optimalen Materialien, Grösse der Kavität und Dicke der Deckschicht ermittelt. Die Optimierung kann hinsichtlich der Zielgrössen variieren. Es kann sich z.B. um eine Minimierung des Gewichts bei geforderter Mindest-Kavitätsgrösse handeln oder um eine Maximierung der Steifigkeit pro Gewicht. Das Skript nutzt einen bereits in Matlab implementierten evolutionären Algorithmus. Es handelt sich dabei um eine ableitungsfreie Methode, die durch den teilweise diskreten Suchraum benötigt wird. Diskret deshalb, weil die Materialeigenschaften wie Dichte, Steifigkeit und Festigkeit in einem Wert, dem Materialtyp zusammengefasst sind und untereinander nicht über Funktionsbeziehungen beschrieben werden können. Darüber hinaus ist die Funktionsweise des evolutionären Algorithmus leicht verständlich und die Anwendung in Matlab mit wenig Programmieraufwand möglich. Das Prinzip beruht darauf, dass Lösungskandidaten als Individuen in Generationen durch Rekombination und Mutation verändert werden. Angelehnt an die Evolution überleben nur Individuen, welche die Zielfunktion hinreichend und die Nebenbedingungen gänzlich erfüllen. Somit können sie ihre Merkmale an die nächste Generation weitergeben (survival of the fittest). Dieser Prozess wird wiederholt durchlaufen und das beste Individuum einer Generation nähert sich schrittweise dem globalen Optimum an. Das Skript ermöglicht eine Dimensionierung und gleichzeitige Optimierung von Sandwichbalken mit Kavitäten innerhalb weniger Sekunden Berechnungszeit in Matlab.

Kontakt IWK Institut für Werkstofftechnik und Kunststoffverarbeitung Luca Müller Eichwiesstrasse 18b CH-8645 Rapperswil-Jona +41 58 257 47 70 rj-iwk@ost.ch www.iwk.hsr.ch