








Marc van Zanten



Petra van den Brom-Snijders












met online leeromgeving eDition











Marc van Zanten



Petra van den Brom-Snijders












met online leeromgeving eDition





Reken-wiskundedidactiek






























C C C
Getal
a Welke breuk ligt precies in het midden tussen 1 3 en 1 5 ?
b Welke breuk ligt precies in het midden tussen 1 3 en 1 4 ?
Verhouding
Dit jaar gaan 3 op de 5 Nederlanders op vakantie, tegenover 4 op de 7 Belgen. Gaan er relatief gezien meer Nederlanders of meer Belgen op vakantie? En in absolute zin?
Bewerking
a Wat is het verschil tussen 2 : 3 en 2 3 ?
b Wat is het verschil tussen 6 : 2(1+2) en 6 2(1 + 2) ?
B
B quotiënt
Breuken kunnen drie betekenissen hebben: ze kunnen een getal aangeven, een verhouding, en een bewerking. De breuk als getal kan worden geplaatst op de getallenlijn, net zoals hele getallen en decimale getallen. De breuk als verhouding geeft een relatief gegeven aan, bijvoorbeeld ‘een kwart van de jonge basisschoolleraren is man.’ De breuk als bewerking ten slotte, is per definitie een deling.
Rationaal getal
Breuken zijn rationale getallen. Een definitie hiervan is: een rationaal getal is het quotiënt van twee hele getallen, waarvan de tweede niet 0 is. Ook gehele getallen, inclusief 0 en negatieve getallen zijn rationale getallen. De noemer is dan 1. Zo is bijvoorbeeld 10 te noteren als 10 1 , 0 als 0 1 en -5 als - 5 1 . Een quotiënt is de uitkomst van een deling. Het quotiënt van 2 en 3, oftewel de uitkomst van 2 : 3, is 2 3 . ‘Ratio’ betekent verhouding. Een breuk is dus een
verhoudingsgetal
verhoudingsgetal, het is de verhouding tussen twee hele getallen (de teller en de noemer).
Bdeel van een geheel deel van een hoeveelheid verdeling
Breuken hebben verschillende verschijningsvormen. Een breuk kan een deel van een totaal aangeven. Dat kan een deel van een geheel zijn, bijvoorbeeld 1 8 deel van een taart of 1 5 deel van een lot. Het kan ook een deel van een hoeveelheid zijn. Bijvoorbeeld 3 4 van het stadion met 12.000 plaatsen is gevuld voor een wedstrijd. Bij beide varianten geeft de breuk een verdeling aan, bijvoorbeeld de verdeling van een taart in acht stukken of de verdeling tussen het aantal bezette plaatsen en lege plaatsen in een stadion.


breuk als maat
Net als hele getallen en decimale getallen komen breuken voor als meetgetal. Voorbeelden zijn anderhalve meter, een half uur of, zoals in de afbeelding hieronder, 1 2 inch. De inch is een lengtemaat uit het imperiale systeem (zie het boek Meten, meetkunde en verbanden, hoofdstuk 2). Ook als maat kom je breuken tegen, bijvoorbeeld twee halfjes bruin brood of anderhalve vlaai.


verhouding
De breuk als verhouding komt vaak voor in nieuwsberichten, zoals ‘Een derde van de speeltuinen in Nederland heeft onveilige toestellen’, ‘Driekwart van de schoolleiders is aangemeld in het schoolleidersregister’, en in het bericht hieronder. Het verschil met de verschijningsvorm deel van een hoeveelheid is dat er bij de verschijningsvorm verhouding geen sprake is van een specifieke, bepaalde hoeveelheid (zoals bij deel van een hoeveelheid), maar dat de verhouding kan worden toegepast op verschillende hoeveelheden. Zelfs als je die niet precies weet, zoals ‘alle Nederlandse consumenten’.
‘Achteraf betalen’ verleidt één vijfde van consumenten vaker tot onnodige aankopen
De komst van ‘buy now pay later’ heeft het koopgedrag van consumenten flink veranderd. Ruim één vijfde (22%) van de Nederlandse consumenten doet sindsdien vaker onnodige aankopen. Wat opvalt is dat vooral de jongere generatie hier vatbaar voor is. Een ruime meerderheid (59%) is namelijk tussen de 18 en 34 jaar. Dit in tegenstelling tot de iets oudere generatie van 35 tot en met 54 jaar (31%).
Bron: https://www.baaz.nl/achteraf-betalen-verleidt-een-vijfde-van-consumenten-vaker-totonnodige-aankopen
De breuk als kans
CBreuken worden ook gebruikt om kansen aan te duiden. Bijvoorbeeld bij dit vraagstuk ‘de kans op een witte bonbon’.
Je hebt drie doosjes met bonbons. In het ene zitten twee witte bonbons, in het andere zitten twee pure bonbons en in het derde doosje zitten een pure en een witte bonbon. Je kiest willekeurig een van de drie doosjes en pakt daaruit ook weer willekeurig een van de twee bonbons. Die bonbon is wit. Wat is nu de kans dat de andere bonbon in het gekozen doosje ook wit is? 1 3 of 1 2 of 2 3 ?
Brekengetal operator
Ten slotte komen breuken weer net als hele en decimale getallen voor als rekengetal en als operator. Met een rekengetal wordt formeel gerekend, bijvoorbeeld 4 2 3 + 2 3 . Een voorbeeld van de breuk als operator, oftewel bewerker, is 1 4 × 20.
De verschillende verschijningsvormen zijn geen elkaar uitsluitende categorieen. Zo kan de uitkomst van een deling als 2 pizza’s delen met 3 kinderen een deel van een geheel betreffen, namelijk 2 3 pizza. De breuk als punt op de getallenlijn heeft ook een meetaspect: hoe ver is deze breuk verwijderd van nul? In de realiteit van alledag komen voornamelijk eenvoudige breuken voor, zoals in de voorbeelden hierboven. In andere gevallen worden meestal procenten gebruikt, zoals je ook kunt zien in het bericht over achteraf betalen hierboven.
CDe breuk als operator
Waarom is 1 99 × 99 gelijk aan 1?
Allemaal breuken
CIn de afbeelding hieronder zie je breuken in een krantenkop, in reclame, als beeld van de halve maan en als klankduur in de vorm van de muzieknoten.
Welke verschijningsvormen herken je hierin?

Deel van een geheel
Welk deel van de figuren is gekleurd?
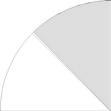
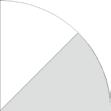
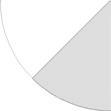
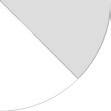


Eerlijke verdeling
Jarise verdeelt 5 koeken eerlijk onder 8 personen. Ieder krijgt meer dan een 1 2 koek. Hoeveel meer?
gelijkwaardige breuken equivalente breuken
Gelijkwaardige breuken hebben verschillende noemers maar dezelfde waarde. Bijvoorbeeld 3 6 , 5 10 en 500 1000 hebben allemaal dezelfde waarde van een 1 2 en kunnen dus allemaal worden vereenvoudigd tot een 1 2 . In plaats van gelijkwaardige breuken wordt ook wel van equivalente breuken gesproken.
Vereenvoudigen van breuken is het zo eenvoudig mogelijk opschrijven van een breuk. Dit kan door de teller en de noemer te delen door hetzelfde getal. Bij bijvoorbeeld 500 1000 kunnen teller en noemer beide worden gedeeld door 100. Dus 500 1000 = 5 10 . Maar 5 10 kan verder worden vereenvoudigd door de teller en de noemer te delen door 5. Dat levert een 1 2 op en die kan niet verder worden vereenvoudigd. Breuken vereenvoudigen kun je dus ook omschrijven als het bepalen van díe schrijfwijze van een breuk waarbij teller en noemer onderling ondeelbaar zijn.
grootste gemene deler (GGD)
Door teller en noemer beide te delen door de grootste gemene deler (GGD) krijg je in één stap een breuk die niet verder te vereenvoudigen is. De GGD is dus het grootste getal waardoor je de teller en noemer allebei kunt delen. Van 500 en 1000 is de GGD 500, dus teller en noemer beide delen door 500 levert in één stap op 500 1000 = 1 2 .
Gelijknamige breuken ongelijknamige breuken
Gelijknamige breuken zijn breuken met dezelfde noemer. Ongelijknamige breuken kunnen altijd gelijknamig worden gemaakt. Bijvoorbeeld 3 4 en 5 6 kunnen gelijknamig worden gemaakt door de tellers en de noemers van beide breuken te vermenigvuldigen met de noemer van de andere breuk.
Dus 3 4
Gelijknamig maken van breuken komt van pas bij het vergelijken, ordenen, optellen en aftrekken van breuken.
kleinste gemene veelvoud (KGV)
In het voorbeeld van 3 4 en 5 6 is echter ook een kleinere gezamenlijke noemer mogelijk dan 24. Met behulp van het kleinste gemene veelvoud (KGV) kunnen breuken gelijknamig worden gemaakt met een zo klein mogelijke noemer. In dit voorbeeld betekent dat het KGV van 4 en 6 is 12, dus de breuken kunnen onder de kleinste gemeenschappelijke noemer 12 worden gebracht: 9 12 en 10 12
GGD en KGV
Om de breuk 153 255 te vereenvoudigen, ga je op zoek naar de GGD van de teller en de noemer, dus van 153 en 255. Nu wist Euclides (330 v. Chr.) al dat het verschil van 153 en 255, dus 102, dezelfde gemeenschappelijke deler heeft. Nogmaals een paar keer het verschil bepalen (153 – 102 = 51 en 102 – 51 = 51) levert het getal 51 op. Dat is inderdaad de gezochte GGD, want 153 = 3 × 51 en 255 = 5 × 51.
In schema:
102 = 51 + 51 = 2 × 51
153 = 102 + 51 = 3 × 51
255 = 153 + 102 = 5 × 51
Om breuken als 2 153 en 2 255 op te tellen, moet je deze gelijknamig maken. De noemers vermenigvuldigen levert 39.015 op, maar het KGV van 153 en 255 is veel kleiner. We weten dat 153 = 3 × 51 en 255 = 5 × 51 en daarvan kunnen we het KGV afleiden. Dat is 3 × 5 × 51 = 765. Dus
Meer over de GGD en het KGV lees je in het boek Hele getallen, hoofdstuk 1.
GGD en KGV in groep 8
AVerschillende reken-wiskundemethodes bieden het bepalen van de GGD en het KGV aan in groep 8.
a Zoek uit of de methode van je praktijkschool dit onderwerp aanbiedt. Als het wordt aangeboden, hoe ziet dat er dan uit?
b Probeer met een groepje leerlingen van groep 8 enkele opgaven uit met de GGD en het KGV. Wat zijn de moeilijkheden die leerlingen hierbij ondervinden? Welke ondersteuning kun je bieden?
Deel van een hoeveelheid
C C C
Leroy zegt dat je voor het optellen van breuken eerst een gemeenschappelijk veelvoud moet bepalen. Pas die aanpak van Leroy toe op 1 42 + 8 105 door te denken aan het getal 210. Hoe komt Leroy aan 210?
Autobussen
Twee autobussen, A en B, vertrekken gelijktijdig van een busstation. Bus A is steeds na 1 1 2 uur terug op het busstation, bus B steeds na 1 1 4 uur. Over hoeveel uur treffen ze elkaar weer voor het eerst op het busstation?
Redeneren en rekenen
1 Bereken en schrijf de uitkomst zo eenvoudig mogelijk op.
a
2 Welke uitkomst is groter?
a 6 7 × 5 13 of 6 7 + 5 13
b 6 7 : 5 13 of 6 7 –5 13
c 6 7 × 13 5 of 6 7 : 13 5
3 Wat komt op de plaats van de puntjes?
a 1 6 + … = 1 5
b … –1 6 = 1 5
c 13 7 × … = 13
d 1 5 × … = 1 6
e : 24 25 = 3 5
In het dagelijks leven kom je veel breukentaal tegen: de helft, een halfje, een half uur, anderhalf uur, een kwart, een kwartier, driekwart, een derde, enzovoort. Kinderen spreken weleens van ‘de grootste helft’, wat wiskundig gezien niet klopt, maar ze geven hiermee het grootste deel aan (als iets in tweeën is verdeeld).
De formele rekentaal omvat de termen ‘teller’, ‘noemer’, ‘breukstreep’, ‘gelijkwaardig’, ‘gelijknamig’ en ‘vereenvoudigen’. De formele notatie van breuken gaat met een horizontale ( 1 5 ) of schuine (1⁄5) breukstreep tussen teller en noemer.
Elk heel getal groter dan 0 kan een noemer zijn. Dus naast gangbare breuken als halven, vijfden, tienden en honderdsten bestaan er ook breuken als drieduizendsten, miljoensten en quadriljardsten. Verschillende breuktypen kennen verschillende benamingen, zoals je in de tabel hieronder ziet.
Onechte breuk Niet vereenvoudigd gemengd getal
Samengestelde breuk
Uitspraak
C C
Breuk waarvan de teller en noemer zelf ook een breuk zijn
Welke breuken kunnen horen bij de volgende uitspraak: ‘drie-honderd-achttien-duizendste’?
Old school
Maak de onderstaande opgaven met samengestelde breuken voor aanstaande basisschoolleraren.
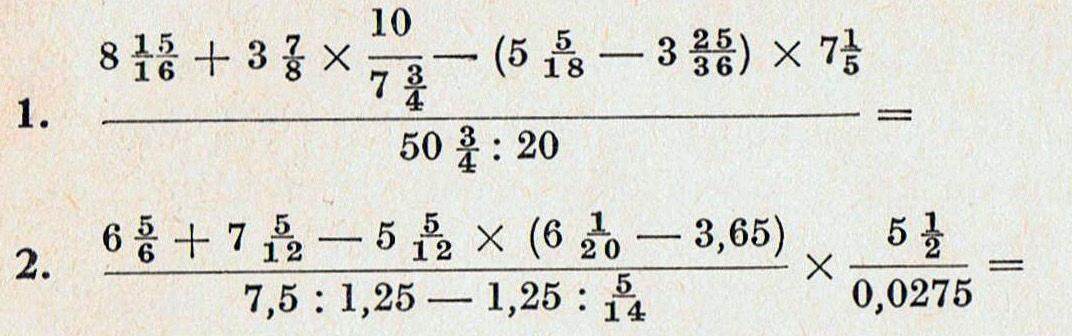
Bron: Wij rekenen (1956). Opgaven voor opleidingsscholen.
Dankzij verschillende bewaard gebleven papyrusrollen is het een en ander bekend over de rekenkunst in het Egypte van voor onze jaartelling. Een van de bekendste rollen is de Rhind-papyrus. Deze stamt uit ongeveer 1650 tot 1550 voor Christus. Op deze rol staan verschillende wiskundige problemen en de oplossingen daarvan. Daaruit blijkt dat de Egyptenaren toen al breuken kenden. Als een deling niet uitkwam op een heel getal, werkten ze verder met breuken. De Egyptenaren gebruikten voornamelijk stambreuken. Uitzondering daarop was de blijkbaar veelvoorkomende breuk 2 3 en volgens sommige bronnen ook 3 4
Een van de opgaven van de Rhind-papyrus is 19 gedeeld door 8. Deze opgave werd opgelost door 8 in te passen in 19. Daarbij werd gebruikgemaakt van verdubbelen en halveren. Dat ging als volgt (hieronder in onze eigen getalsymbolen genoteerd).
1 maal 8 (verdubbelen)
2 maal 16
1 2 maal 4 (halveren)
1 4 maal 2 (halveren)
1 8 maal 1 (halveren)
Daarmee is het getal 19 bereikt: 16 + 2 + 1. De uitkomst van 19 gedeeld door 8 is dus 2 1 4 1 8 (2 + 1 4 + 1 8 ).
Egyptische splitsing
CDe Egyptenaren gebruikten voornamelijk stambreuken. Elke gewone breuk is te schrijven als een som van stambreuken met verschillende noemers. Dat wordt wel een Egyptische splitsing genoemd. Bij 3 8 is dat 1 4 en 1 8 , zoals je hierboven al zag. En bij bijvoorbeeld 4 7 is dat 1 2 + 1 7
a Schrijf de Egyptische splitsing op van 5 6 .
b Schrijf de Egyptische splitsing op van 7 8
c Schrijf de Egyptische splitsing op van 7 15 .
d Wat is de algemene aanpak om Egyptische splitsingen te vinden?
BAIn gesprek met kinderen – Wat zijn breuken?
Wat verstaan kinderen onder breuken? Ga in gesprek met een groepje kinderen om erachter te komen wat breuken voor hen betekenen. Start het gesprek bijvoorbeeld met de vraag wat breuken zijn en of ze een breuk kunnen tekenen. Vervolgens kan je ze een eenvoudige breuk voorleggen, bijvoorbeeld 1 2 , en vragen wat die betekent. Wat betekenen 1 2 liter en 1 2 meter? Is 5 3 ook een breuk? En 4 2 4 ?
Kortom, ga met kinderen in gesprek over wat zij weten en begrijpen van breuken. Het gesprek kun je voeren met kinderen uit groep 5 en 6, maar ook met kinderen uit groep 7.
Wissel nadien je ervaringen uit met je medestudenten of praktijkcollega’s.
Wat voor verschillende en overeenkomende reacties kregen jullie? Welke verschillen waren er tussen groepjes leerlingen uit groep 5, 6 en 7?
Het formele breukenonderwijs start over het algemeen in groep 6. Daarvoor hebben de kinderen al allerlei informele ervaringen opgedaan met breuken. Al vanaf de kleutergroepen komen leerlingen begrippen tegen als de helft, een half (uur) en een kwart (kwartier). Bij meetactiviteiten komen kinderen breuken bijvoorbeeld al tegen als twee en een halve stap.
Breuken op de basisschool
Begripsvorming
Informele ervaringen met breuken
De helft, half uur, kwart, kwartier, tweeënhalve stap

Verschijningsvormen van breuken

Ontwikkelen van procedures
Vergelijken en ordenen

Gelijknamig maken
Bewerkingen uitvoeren ondersteund met modellen

Vlot leren rekenen
Flexibel toepassen In situaties
In verdere rekenen-wiskunde
Vanaf groep 1
Vanaf groep 6
kinderen met zwemdiploma A
kinderen met zwemdiploma A en B
kinderen zonder zwemdiploma
a b ± c d = ad bd ± bc bd = ad + bc bd Voortgezet onderwijs
Bvoorstelbare situaties
wiskundetaal
Bij de formele introductie van breuken wordt aangesloten bij de informele voorkennis van leerlingen en bij voorstelbare situaties. Aandacht voor de wiskundetaal is hierbij erg belangrijk. Verschillende manieren van noteren en uitspreken (‘een kwart’, ‘een vierde’ en 1 4 ) worden expliciet met elkaar verbonden. Zo wordt informeel taalgebruik van de leerlingen aangevuld met formeel taalgebruik.

Een voorstelbare situatie en wiskundetaal bij de introductie van breuken. Bron: Getal & Ruimte Junior
eerlijk verdelen
deel van een geheel
De introductie en het begin van het formele breukenonderwijs zijn erg belangrijk voor de begripsvorming. Om die te ondersteunen, maken methodes veel gebruik van de context eerlijk verdelen, wat voor kinderen een logische en betekenisvolle activiteit is. Door zelf dingen eerlijk te verdelen, ‘maken’ de leerlingen als het ware zelf breuken, zoals in de voorbeeldopgave hieronder. Het gaat in dit voorbeeld om de verschijningsvorm deel van een geheel (zie paragraaf 2.1.1).
deel van een hoeveelheid
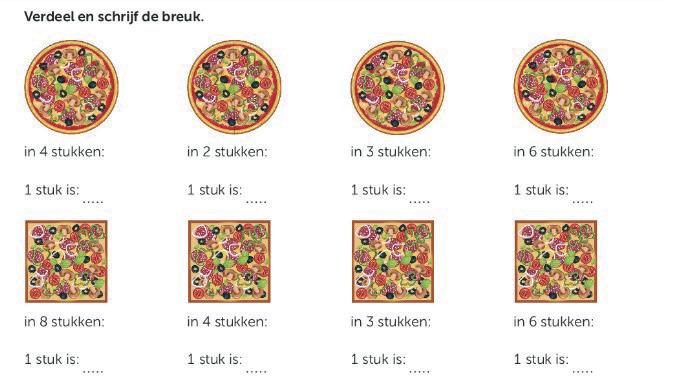
Bron: Alles Telt Q, groep 6
Bron: Alles Telt Q, groep 6 meten meetgetal
Een andere veelgebruikte situatie is die van meten met stroken, waarbij het dus gaat om de verschijningsvorm breuk als meetgetal. Leerlingen meten bijvoorbeeld hun tafel op, met stroken van papier. Als dat niet precies uitkomt, wordt de strook in gelijke delen gevouwen om preciezer te kunnen meten. Vervolgens worden stroken gebruikt om uitkomsten van metingen te noteren in breukentaal. Daarbij worden stroken gebruikt die in verschillende aantallen stukken zijn verdeeld. Er worden zowel dingen gemeten die langer zijn dan een of meerdere stroken, als zaken die korter zijn dan één strook.
Bron: De Wereld in Getallen, groep 6
In sommige methodes komt ook al vrij snel de verschijningsvorm deel van een hoeveelheid voor. Deze wordt in eerste instantie gekoppeld aan de verschijningsvorm deel van een geheel. Bijvoorbeeld in de volgende opgave, waarin het deel van een hoeveelheid is te herkennen in het deel van de totaalprijs in hele euro’s en het deel van een geheel in de stukken van de pizza’s.
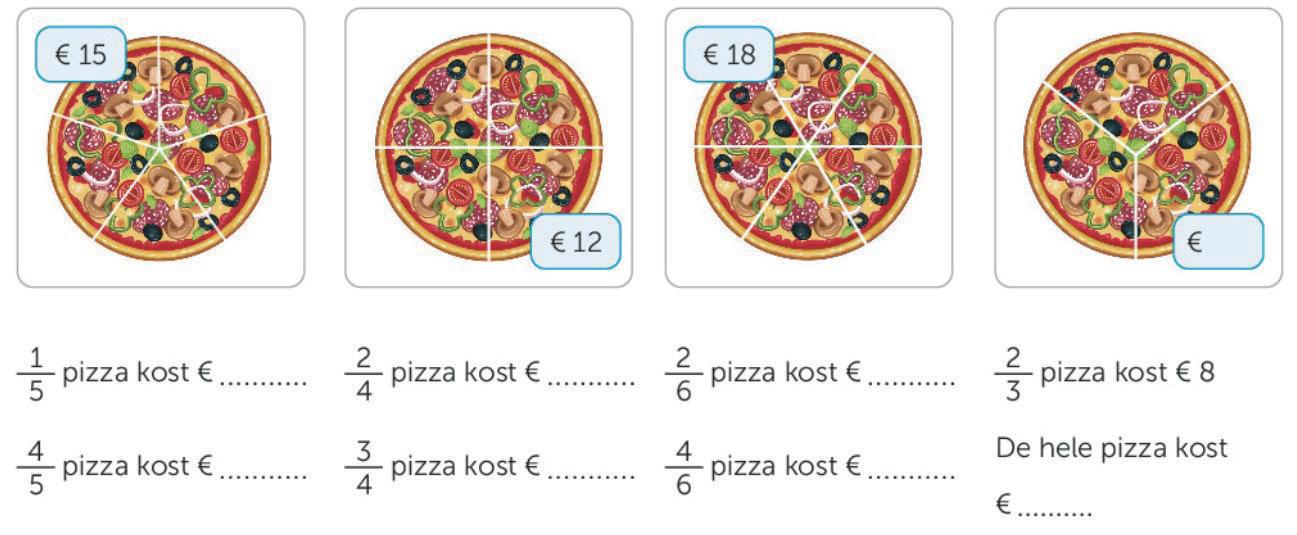
A BIntroductie breuken in de methode van je praktijkschool
a Ga in de methode van je praktijkschool op zoek naar de eerste lessen waarin breuken aan de orde komen. Vanuit welke situaties worden breuken aangeboden? Welke betekenissen (zie paragraaf 2.1) en verschijningsvormen (zie paragraaf 2.1.1) worden daarbij gebruikt? Welke niet?
b Als bepaalde betekenissen en verschijningsvormen niet voorkomen in de eerste breukenlessen in de door jou bekeken methode, zou je die dan wel aan de orde willen stellen? Waarom wel of waarom niet? Wissel je ideeën uit met je medestudenten of collega’s.
Breuken vormen een ambigu concept. Dat betekent dat ze meerdere betekenissen hebben (zie paragraaf 2.1). Voor kinderen zijn breuken het eerste wiskundig ambigue concept waarmee ze in aanraking komen en dat is meteen een van de moeilijkheden ervan. Omdat breuken de betekenis van zowel een getal als een verhouding kunnen hebben, kunnen ze absolute en relatieve gegevens representeren en dat is voor kinderen een lastig onderscheid (zie paragraaf 1.3).
whole number bias
Een tweede moeilijkheid is dat kennis die leerlingen over hele getallen hebben opgedaan, bij breuken opeens niet meer lijkt te kloppen. Zo kunnen kinderen denken dat vermenigvuldigen altijd groter maakt, maar bij vermenigvuldigingen met breuken is dat niet altijd het geval. Denk bijvoorbeeld aan 1 2 × 3 of 1 2 × 2 3 . Het onterecht gebruiken van kennis over hele getallen bij breuken staat bekend als de ‘whole number bias’. Dit veroorzaakt misconcepties als 1 5 is groter dan 1 4 , vanuit de kennis dat 5 groter is dan 4, of dat 1 3 ná 1 2 zou komen op de getallenlijn, net zoals 3 komt na 2. Aan de verschillen tussen hele getallen en breuken moet nadrukkelijk aandacht worden geschonken. Niet alleen bij de introductie van breuken, maar vaak ook nog later in het onderwijsleerproces.
B
Het gaat er bij breuken niet alleen om dat leerlingen de basisbewerkingen leren uitvoeren, maar ook dat zij inzicht krijgen. Onder breukbegrip vallen verschillende aspecten van het redeneren en rekenen met breuken, zoals:
• verschillende betekenissen en verschijningsvormen van breuken kunnen onderscheiden, bijvoorbeeld breuken als het resultaat van eerlijk delen, maar ook andere verschijningsvormen;
• weten dat een (echte) breuk een getal is kleiner dan 1, tussen 0 en 1;
• het relatieve karakter van breuken begrijpen: breuken verwijzen vaak naar een deel van iets (breuk als verhouding);
• inzicht hebben in de relaties tussen breuken, decimale getallen, verhou-
Acontext
dingen en procenten, en getalsrelaties kunnen beredeneren, bijvoorbeeld tussen 1 2 en 2 4 , maar ook tussen 1 2 en 0,5, 50% en 4 : 8;
• inzicht hebben in gelijkwaardigheid en gelijknamigheid;
• breuken kunnen vergelijken en (globaal) kunnen plaatsen op de getallenlijn.
Belangrijk bij vermenigvuldigen en delen met breuken (zie paragraaf 3.4.3) zijn met name de inzichten dat een breuk een deling is en dat vermenigvuldigen en delen elkaars inverse bewerking zijn.
Concrete situaties
Alle verschijningsvormen van breuken worden in methodes gebruikt om breukbegrip te bevorderen. In de vorm van contexten ondersteunt dit het denken en laat het zien waar breukenkennis van pas komt. Hieronder zie je een voorbeeld.
a Ga in de methode van je praktijkschool op zoek naar contexten met breuken die verwijzen naar concrete situaties. Zoek een voorbeeld bij elke verschijningsvorm van breuken (zie paragraaf 2.1.1). Soms zijn er meerdere verschijningsvormen te herkennen binnen één context.
b Waar worden de verschillende verschijningsvormen voor gebruikt? Zit daar overlap bij en zijn er ook verschillen?
c Wissel je bevindingen uit met je medestudenten of collega’s. Zo krijg je een verzameling van voorbeelden van breukencontexten die je in je eigen onderwijs kunt gebruikten.

Bron: Alles Telt Q, groep 6
Situatie bedenken
C A
a Bereken de uitkomst van 1,5 : 2 3
b Bedenk een reële situatie bij deze opgave.
Eerlijk verdelen
Eerlijk delen kan vaak op meerdere manieren. Denk maar aan een vouwblaadje dat je in vieren wilt delen: dat kan in gelijke vierkantjes maar ook in vier gelijke stroken.
Ga met leerlingen aan de slag met vouwblaadjes. De uitdaging is om verschillende manieren te vinden om de blaadjes eerlijk in meerdere gelijke delen te vouwen of te knippen. In vieren is een mooi begin, maar in drieën vormt een nieuwe uitdaging. Naast vierkante vouwblaadjes kun je gebruikmaken van stroken. Je praktijkschool heeft misschien ook ronde vouwblaad-
Ajes. Hoe pakken je leerlingen het aan als je ze vraagt om deze eerlijk in gelijke delen te verdelen? Kunnen de leerlingen de gevouwen delen ook benoemen als breuk?
Old school
In deze opgave uit een oude methode worden delingen op twee manieren genoteerd: met het deelteken en in de breuknotatie. Leg deze opgave voor aan een groepje leerlingen uit groep 6, 7 of 8. Hoe pakken zij de opgave aan? Zien ze de relatie tussen de linker en de rechter opgaven? Je kunt de opgave downloaden van Edition.

Bron: Dit is rekenen! (1960) Opgave voor klas 3 (groep 5)
Benoemde breuken
B
B
In de methodes staan breuken vaak in de volgende vorm: 2 3 reep of 1 2 meter. Achter de breuk wordt met een woord of afkorting aangegeven waarvan de breuk een deel is: liter, stok, pizza, kg, enzovoort. Het lijkt misschien niet zoveel uit te maken of een woord of letter is toegevoegd, maar dat doet het wel! Immers, het denken wordt ondersteund en het rekenen vergemakkelijkt door aan iets concreets te denken waarvoor de breuk staat. De benoeming vormt een brug tussen de concrete situatie en het formele rekenen, net zoals modellen dat doen.

Bron: Alles Telt Q, groep 6
3.3.2 Gebruik van modellen
Er zijn veel modellen te gebruiken bij breuken: het cirkelmodel, de strook of stok, de (dubbele) getallenlijn, het rechthoekmodel en de verhoudingstabel. Ze ondersteunen het denken en vormen een brug tussen concreet voorstelbare breuksituaties en het formele redeneren en rekenen met breuken. Sommige modellen zijn al bekend voor leerlingen, zoals de verhoudingstabel, die ook
Bal in lagere groepen kan worden gebruikt bij de tafels van vermenigvuldiging. Andere modellen zijn nieuw of worden alleen voor breuken gebruikt, zoals breekstokken. Elk model heeft zijn eigen gebruiksmogelijkheden en beperkingen.
Cirkelmodel
Het cirkelmodel maakt goed zichtbaar dat een breuk een deel van een geheel kan zijn. Het kan goed worden gebruikt om leerlingen te laten ervaren dat het bij breuken gaat om gelijke stukken en het aantal stukken zoals in de opgave hieronder.
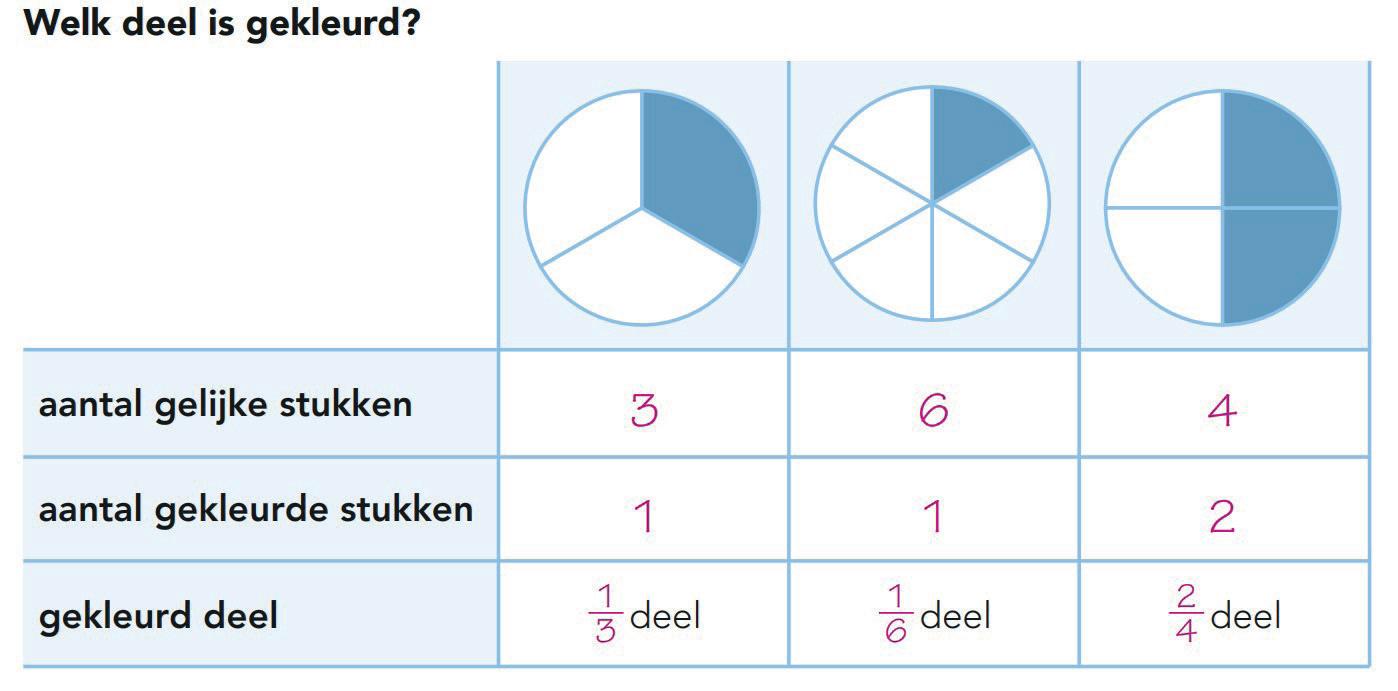
Bron: De Wereld in Getallen, groep 6
Ook kunnen eenvoudige breuken worden vergeleken, zoals je hieronder ziet. Het cirkelmodel kan voortvloeien uit contextsituaties waarin bijvoorbeeld pizza’s, taarten of kazen eerlijk worden verdeeld.
Aflezen 1 2 = 3 6 op het cirkelmodel.
Een nadeel van het cirkelmodel is dat het zelf tekenen, met precieze verdelingen, zeker voor kinderen niet makkelijk is. Het cirkelmodel is daarom vooral bruikbaar als kant-en-klaar getekend model in het leerlingenmateriaal, voor op het digibord of als concreet materiaal.

CMagnetische breukencirkels
Bron: Heutink
Het pizzarestaurant (1)
In een pizzarestaurant worden aan tafel 1, waar 6 kinderen zitten, 5 pizza’s verdeeld. Aan tafel 2 zitten 8 kinderen die 7 pizza’s eerlijk verdelen.
a Aan welke tafel krijgen de kinderen het meest?
b Hoe groot is het verschil tussen de porties aan tafel 1 en tafel 2?
Het pizzarestaurant (2)
BCIn een pizzarestaurant zitten 5 kinderen aan tafel 1 met 3 pizza’s. Aan tafel 2 zitten 3 kinderen met 2 pizza’s. Aan tafel 1 krijgt ieder kind 3 5 pizza, aan tafel 2 is er voor ieder kind 2 3 pizza. De kinderen besluiten de tafels aaneen te schuiven, want dat is veel gezelliger. Nu zitten ze dus met 8 kinderen aan 1 tafel en hebben ze in totaal 5 pizza’s te verdelen. Voor iedereen is er dus 5 8 pizza. De conclusie lijkt te zijn dat 3 5 + 2 3 samen 5 8 zou zijn. Maar dit klopt niet! Wat gaat er fout in deze redenering?
Rechthoekmodel
Het rechthoekmodel representeert zowel de verschijningsvorm deel van een geheel als deel van een hoeveelheid. Ook dit model kan voortvloeien uit eerlijk-verdeelsituaties. Het gaat dan om zaken die als een geheel te zien zijn en ook eenvoudig in stukjes gedeeld kunnen worden, zoals plakken chocolade. Belangrijk voordeel van het rechthoekmodel is dat het makkelijk zelf kan worden getekend en in stukjes verdeeld (zie paragraaf 3.4.1). Bij het cirkelmodel is dat voor kinderen soms lastiger, bijvoorbeeld bij derden of vijfden. Een nadeel kan zijn dat de stukjes zelf ook weer een rechthoek vormen en daardoor als een geheel op zich kunnen worden gezien. Maar dat kan worden ondervangen door ook de hele rechthoek zichtbaar te houden, zoals dat in de voorbeeldopgave hieronder gebeurt.

Bron: Getal & Ruimte Junior, groep 6
BCRepen verdelen
Twee repen chocolade worden eerlijk verdeeld over drie kinderen. Hoeveel krijgt ieder kind?
Tanja zegt 2 3
Joris zegt 2 6
Pieternel zegt 1 3 .
a Welke leerling geeft het correcte antwoord?
b Kun je de redeneringen van de andere twee leerlingen achterhalen?
Strookmodel
Het strookmodel is, evenals het cirkelmodel en het rechthoekmodel, te gebruiken om een deel van een geheel te visualiseren. Met de strook kunnen kinderen ook zelf handelend bezig gaan, bijvoorbeeld door een strook in vieren te vouwen waardoor vierden ontstaan. Daarnaast is de strook, zoals al in paragraaf 3.2 beschreven, in te zetten om mee te meten, aansluitend op de verschijningsvorm breuk als meetgetal. Een strook van een bepaalde lengte dient als maat, waarmee zaken worden opgemeten die niet precies een aantal hele stroken lang zijn, maar ook een bepaald deel van de strook beslaan. Zo ontstaan breuken bij het meten. Bij getekende stroken moet je wel duidelijk hele stroken onderscheiden van delen van stroken. Zo is het potlood in de volgende voorbeeldopgave 2 hele stroken en 1 3 deel van een strook lang.
 Bron: De Wereld in Getallen, groep 6
Bron: De Wereld in Getallen, groep 6
breekstok
Je kunt in methodes allerlei varianten van het strookmodel tegenkomen. Denk aan horizontaal en verticaal, leeg en met schaalverdeling, schematisch getekende stroken of stroken in een vorm die verwijst naar een achterliggende context, met en zonder getallen erbij genoteerd. Al deze varianten kun je zelf ook inzetten bij het geven van uitleg. Verwant aan de strook zijn de zogenoemde breekstokken. Dit materiaal bestaat uit kunststofstokken die zijn ingedeeld in een aantal gelijke, losse delen. De delen kunnen ‘knikken’ doordat ze aan de binnenkant met elkaar zijn verbonden door een elastiek. De modellenstrook en (breuken)stok liggen in elkaars verlengde. Beide modellen kunnen als materiaal worden ingezet, met beide kan worden gemeten en met beide kunnen breuken worden vergeleken.

Breekstokken
De 2-stok is een stok die verdeeld is in twee stukken. Die stukken worden op een gegeven moment benoemd als elk 1 2
Met breekstokken kunnen gelijkwaardige breuken worden bepaald. Eerst door af te lezen, maar al gauw door te redeneren. Bijvoorbeeld als volgt: één stuk van de 4-stok is even lang als twee stukken van de 8-stok, want één stuk van de 4-stok betekent de stok in vier stukken verdelen en daarvan één stuk nemen. En twee stukken van de 8-stok betekent de stok in achten verdelen en daarvan twee stukken nemen. Zo’n redenering kan zo nodig nog worden gecontroleerd door de stokken erbij te pakken.
Varianten van het strookmodel
AHierboven worden vier punten genoemd waarop het strookmodel kan variëren: horizontaal of verticaal, leeg of met schaalverdeling, schematisch getekend of in een vorm die verwijst naar een achterliggende context, met of zonder getallen erbij genoteerd. Ga in reken-wiskundemethodes op zoek naar voorbeelden van elke variant en waarvoor ze worden gebruikt. Wissel uit met je medestudenten of collega’s. Ontdekken jullie nog meer varianten?
ALeerlingenwerk
Jantine maakt de volgende opgave.
Hieronder staat 2 3 strook. Teken de hele strook.
Jantine deelt de strook in drieën en tekent de volgende strook.
Hoe zou jij Jantine helpen om tot een goede redenering te komen?
BGetallenlijn en dubbele getallenlijn
Op de getallenlijn kunnen breuken worden gepositioneerd en geordend, net zoals hele getallen (zie het boek Hele getallen) en decimale getallen (zie hoofdstuk 5). Op een getallenlijn worden breuken bijvoorbeeld als volgt geplaatst: om 2 5 te plaatsen op een getallenlijn tussen 0 en 1 verdeel je eerst het stuk tussen 0 en 1 in vijven en vervolgens neem je het tweede stukje (of streepje).
Bij een getallenlijn die al onderverdeeld is in vijf stukjes, lukt het veel kinderen al snel om 2 5 correct te plaatsen. Maar als de getallenlijn anders is onderverdeeld, bijvoorbeeld in 10 stukjes, dan blijkt dat voor sommige kinderen in eerste instantie lastiger. Sommigen plaatsen 2 5 dan op de plaats van 2 10 . Een verklaring hiervoor is dat kinderen de streepjes aftellen en zo verkeerd uitkomen. De leerlingen letten dan wel op de teller, maar letten bij het positioneren niet op de noemer.
lege getallenlijn
Voor het correct positioneren, moeten de kinderen leren om teller en noemer in samenhang te zien. Om dat te bereiken, kun je een lege getallenlijn gebruiken, waarbij de leerlingen eerst de getallenlijn zelf onderverdelen (waarvoor ze dus moeten letten op de noemer) en daarna de breuk plaatsen (waarvoor ze moeten letten op de teller). Na het aldus positioneren van bijvoorbeeld 2 5 kan worden gevraagd om op diezelfde getallenlijn nu ook bijvoorbeeld 3 10 te plaatsen. Daarvoor moeten de leerlingen dan de getallenlijn verder onderverdelen, waarbij zichtbaar wordt dat de al geplaatste 2 5 nu op de plek van het vierde streepje blijkt te staan.
BDe dubbele getallenlijn wordt verder gebruikt bij het bepalen en oefenen van gelijkwaardige breuken en relaties met decimale getallen. Soms gebeurt dat ook voor relaties met procenten, maar daarvoor is de strook geschikter. De strook representeert namelijk een geheel en dat komt overeen met 100%. De dubbele getallenlijn kan in elk getallengebied worden toegepast, net als de gewone getallenlijn. Dus ook bij breuken groter dan 1 oftewel gemengde getallen. De getallenlijn en dubbele getallenlijn worden verder gebruikt bij het visualiseren van de vier basisbewerkingen optellen, aftrekken, vermenigvuldigen en delen met breuken.
AVerhoudingstabel
Ook de verhoudingstabel kan het rekenen met breuken ondersteunen. Hieronder zie je een voorbeeld waarbij de breuk een verhouding weergeeft en de verhoudingstabel kan worden gebruikt om het absolute aantal kinderen dat op vakantie gaat te berekenen. De verhoudingstabel kan ook worden gebruikt om gelijkwaardige breuken te bepalen of om breuken te vereenvoudigen.

Bron: Pluspunt, groep 7
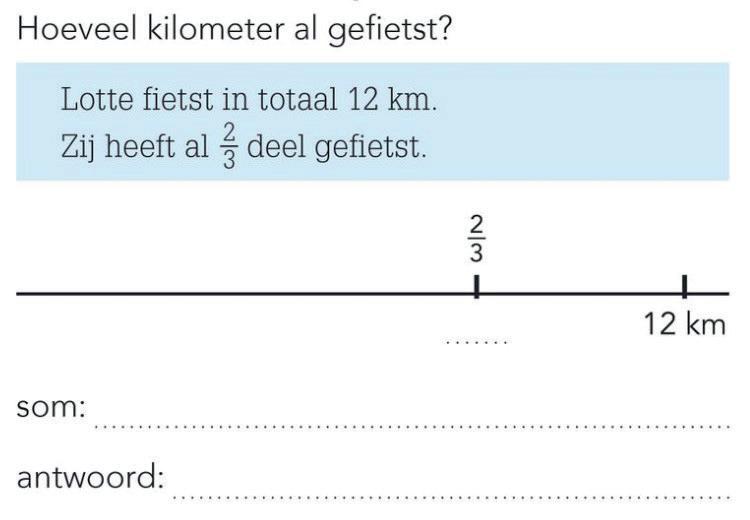
De fietsroute – Verschijningsvormen, contexten en modellen
Voor het soepel laten verlopen van het leerproces moeten contexten en modellen op elkaar aansluiten. Niet elke context en elke verschijningsvorm past zomaar bij elk model.
Bekijk de volgende opgave eens op context, verschijningsvorm en model. Je ziet dat de context het rijden van een fietsroute is, waarbij wordt gevraagd om de afgelegde route aan te geven. Het gaat dus om de verschijningsvorm deel van een geheel (de hele route). Het gebruikte model is de getallenlijn; die staat erbij getekend en past goed bij de context, want een fietspad kun je weergeven als een lijn. De getallenlijn is geschikt om breuken op te positioneren, dus in deze opgave sluiten verschijningsvorm, context en model goed op elkaar aan. Ga in een methode op zoek naar breukenopgaven met contexten waarbij ook een model staat getekend of waar in een model de context kan worden herkend. Welke combinaties van context en verschijningsvorm met welk model vind je? Probeer per verschijningsvorm aan te geven welke modellen hierbij voorkomen en welke niet.

ABron: Alles Telt Q, groep 7
Concrete materialen
Van oudsher worden op de basisschool allerlei materialen gebruikt om het begrip te bevorderen. De oude breukenappeltjes hieronder bijvoorbeeld, werden gebruikt om de verschijningsvorm deel van een geheel te illustreren. Welke breukmaterialen heeft je praktijkschool in huis? Welke modellen herken je in de materialen? Onderzoek in welke groepen deze materialen worden gebruikt en waarvoor. Hoe worden de materialen ingezet en hoe vaak? Zijn de leraren tevreden over de materialen of missen ze nog iets? Wat leer jij hiervan als aanstaand leraar basisonderwijs?

Oude breukenappeltjes
AEen experiment – Opgaven op verschillende handelingsniveaus? Zoek een opgave uit, bijvoorbeeld de formele opgave 3 : 1. Deze presenteer je op verschillende handelingsniveaus (zie paragraaf 10.3.1). Wanneer je deze opgave in een context plaatst, kun je bijvoorbeeld denken aan het volgende. Vader heeft 3 liter limonade aangemaakt. Hij verdeelt deze voor de picknick in flesjes van 1 3 liter. Hoeveel flesjes kan hij vullen?
Als je een model gebruikt, bijvoorbeeld het strookmodel, kun je denken aan het volgende.
Hoeveel halve stroken kun je knippen?
Ook zou je de getallenlijn als model kunnen gebruiken. Je krijgt dan bijvoorbeeld de opgave: Hoe vaak past 1 2 in 3?
AOnderzoek de reactie van leerlingen op deze opgaven, die van elkaar verschillen qua handelingsniveau, maar wiskundig gezien hetzelfde zijn. Je kunt ze eerst de formele opgave voorleggen, daarna het model en tot slot de contextsituatie. Maar je kunt daarin natuurlijk ook variëren. Je legt dan bijvoorbeeld bij het ene kind eerst de formele opgave voor, en bij het andere kind eerst de contextopgave, enzovoort. Je kunt de opgaven ook voorleggen aan kinderen met verschillende onderwijsbehoeften bij rekenen-wiskunde (zie hoofdstuk 11). Wat valt je op? Welke consequenties hebben de geconstateerde verschillen voor je onderwijs?
Old school
Het gebruik van schematische tekeningen als modellen in methodes is niet nieuw. Hieronder zie je twee voorbeelden uit een oude methode. Welke verschijningsvormen van breuken herken je? Welke modellen?


Bron: Functioneel rekenen (1958). Opgaven voor klas 4 (groep 6)
Rekenles met breuken
Zoek een les uit waarin wordt gerekend met breuken, bij voorkeur een les die je zelf gaat geven.
a Zoek in de methode welke modellen en betekenisverlenende contexten voorafgaand aan jouw les worden gebruikt, passend bij de leerinhouden van de les. Hoe komen deze terug in de les? Zijn ze inmiddels losgelaten of worden ze nog steeds gebruikt?
b Bereid de les op zo’n manier voor dat je gebruik kunt maken van de eerdere modellen en contexten in je uitleg of in de extra hulp aan je leerlingen.
c Noteer je bevindingen. Heb je de contexten en modellen kunnen gebruiken? Wat was het effect? Wat werkte goed en wat minder? Heb je een idee hoe dat kwam?
BDe benodigde voorkennis voor breuken omvat de basisbewerkingen. Voor het redeneren en rekenen met breuken, waaronder het bepalen van gelijknamige en gelijkwaardige breuken en het vereenvoudigen van breuken, moet het vermenigvuldigen en delen goed worden beheerst. Met name de tafels van vermenigvuldiging en de deeltafels moeten ten minste geautomatiseerd en liefst gememoriseerd zijn. Als dat nog niet het geval is, moet daarmee extra worden geoefend.
In het verlengde hiervan is het handig dat leerlingen al ervaring hebben met verhoudingsgewijs redeneren in een verhoudingstabel, bijvoorbeeld bij het leren van de tafels.
Informele voorkennis omvat zaken als ‘de helft’ en ‘een kwart’. Sommige reken-wiskundemethodes besteden hieraan voorafgaand aan de introductie van breuken nog nadrukkelijk aandacht, zoals je in de voorbeeldopgave hieronder ziet.

Alles Telt Q, groep 5
Bron:niveaus van abstractie
Doordat breuken een ambigu concept zijn (zie paragraaf 3.3), kun je aan het eind van de basisschool grote verschillen zien tussen leerlingen bij deze leerstof. Sommige leerlingen kunnen dan al formeel redeneren en rekenen met breuken, terwijl anderen daarmee nog veel moeite hebben. Daarom zie je in reken-wiskundemethodes veel modellen getekend bij breukenopgaven. Het handelen en redeneren kan op die manier op verschillende niveaus van abstractie plaatsvinden, zowel ondersteund door een context of model, als formeel (zie paragraaf 10.3.2).
Welke is groter?
BCwhole number bias
Welke breuk is groter? Schrijf op hoe je redeneert.
a 25 331 of 26 331
b 87 151 of 87 152
c 2 15 of 3 17
d 2 5 of 4 7
e 36 38 of 37 39
f 47 46 of 46 45
Bij breuken werkt vergelijken en ordenen anders dan bij hele getallen. Door de whole number bias kunnen kinderen, zeker aan het begin van het onderwijsleerproces, vergissingen maken bij de volgorde van breuken. Dat 1 2 groter is dan 1 3 enzovoort, wordt daarom veel geoefend. Methodes bieden door middel van modellen veel ondersteuning van het denken. Daarbij worden breuken vergeleken aan de hand van vragen naar wat meer of wat langer is. Vervolgens wordt ook gevraagd naar wat evenveel of even lang is. Gelijkwaardigheid komt daarmee binnen bereik, een belangrijk inzicht.

Verder wordt de getallenlijn veel gebruikt om breuken te ordenen en te positioneren in allerlei variaties van opgaven (zie ook paragraaf 3.3.2).
Bron: Pluspunt, groep 6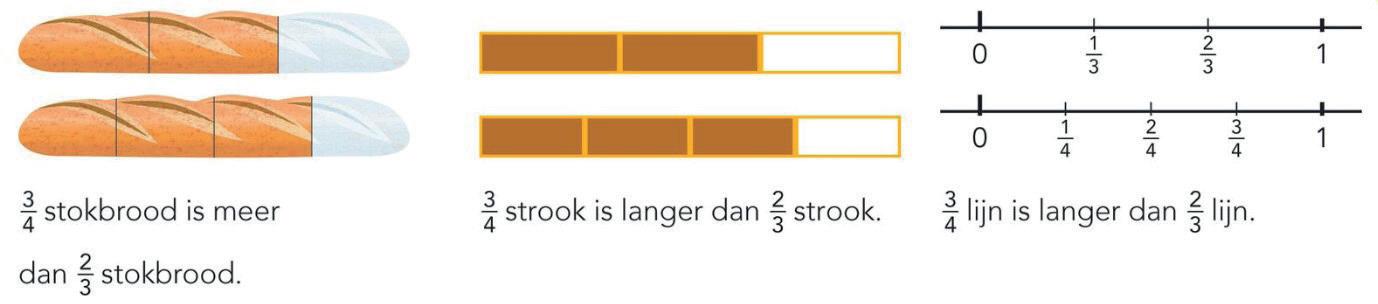
CBron: Getal & Ruimte Junior, groep 6
Breuken op de getallenlijn
a Gelijke stukken op de getallenlijn. Welke breuken horen op de plaatsen van de vraagtekens?
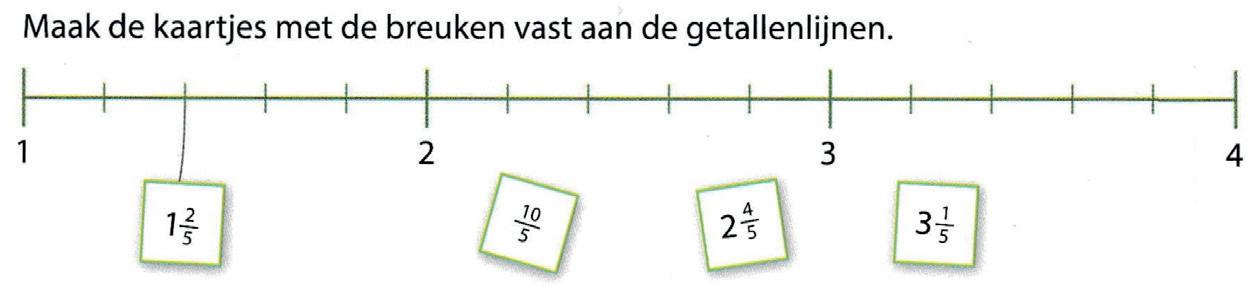
b Gelijke stukken op de getallenlijn. Welke breuken horen op de plaatsen van de vraagtekens?
BCVan klein naar groot
Zet deze breuken in volgorde van klein naar groot. Controleer je antwoorden met de rekenmachine. De uitdaging is om een redenering op te zetten in plaats van alle breuken gelijknamig te maken.
a 2 3 –3 7 –6 11
b 4 5 –8 9 –19 25
c 3 7 –3 11 –7 13
d 5 7 –9 14 –11 21
e 1 7 –2 13 –3 22
f 2 3 –4 9 –7 15
Vergelijken van breuken
Een aanleiding om breuken te vergelijken kan liggen in een vraag als: ‘Aan welke tafel krijg je meer, aan een tafel met drie pannenkoeken voor vier kinderen of aan een tafel met vier pannenkoeken voor vijf kinderen?’ Dit is een betekenisvolle vraag voor kinderen. Deze situatie laat zich makkelijk schematiseren met het cirkelmodel, passend bij de vorm van een ronde pizza.
groter gemeen veelvoud bemiddelende grootheid ondermaat
Drie pannenkoeken voor vier kinderen en vier pannenkoeken voor vijf kinderen geschematiseerd met het cirkelmodel.
Het rechthoekmodel biedt echter meer mogelijkheden voor het vergelijken van breuken dan het cirkelmodel. Kijk bijvoorbeeld naar de tekening van Yereth (groep 7) bij de volgende vraag. Koeno en Anita hebben een gelijke reep chocolade. Koeno eet 1 2 plak op, Anita eet 1 3 reep op. Hoe kan die reep eruitgezien hebben? Wie heeft er meer op?
Yereth verzint zelf hoe een reep eruitziet die zowel in tweeën als in drieën kan worden verdeeld: dat is een plak met 12 stukjes. Daarvan kan hij de helft en een derde kleuren. Hij ziet zo dat Koeno meer op heeft, en hoeveel meer: 2 van de 12 stukjes, oftewel 2 12 deel en dat is vereenvoudigd 1 6 deel.
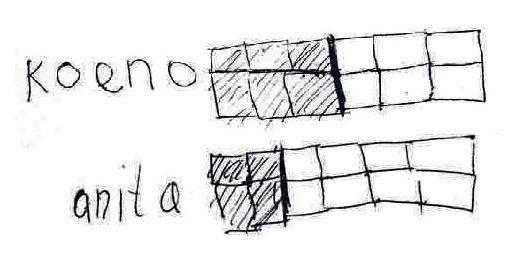
Een paar dingen vallen op bij deze aanpak. Allereerst is het voor kinderen veel makkelijker om een rechthoek dan een cirkel te tekenen met een verdeling. Dat komt doordat een rechthoek makkelijk kan worden uitgebreid of gecorrigeerd. Aan de tekening van Yereth kun je dat ook zien, deze is als het ware opgebouwd uit meerdere stukken. Ten tweede tekenen kinderen bij deze opgave niet altijd een reep met 6 stukjes, wat voor de hand lijkt te liggen. Ze tekenen vaak een reep met 12 stukjes en soms met 24 stukjes. Kinderen maken dus niet vanzelf gebruik van het kleinste gemene veelvoud (KGV) (in dit geval 6), maar in eerste instantie vaak van een groter gemeen veelvoud (in dit geval 12 of 24).
Dergelijke opgaven met het rechthoekmodel bereiden voor op optellen en aftrekken met breuken (zie paragraaf 3.2.4 ). Een plak met een bepaald aantal stukjes of blokjes heeft daarbij een rol als zogenoemde bemiddelende grootheid. De stukjes worden gebruikt als ondermaat: het aantal stukjes levert de noemer van de gelijknamige breuken op. Deze aanpak is te herkennen in het werk van Yereth.
In actuele reken-wiskundemethodes kom je allerlei varianten tegen waarin kinderen breuken vergelijken met behulp van het rechthoekmodel, al dan niet in de vorm van bijvoorbeeld verschillende plakken chocolade. Hieronder zie je een voorbeeld.

Bron: Pluspunt, groep 6
Bvereenvoudigen gelijknamig
Gelijkwaardigheid
Het gaat bij inzicht in gelijkwaardigheid zowel om het inzicht dat breuken op verschillende manieren kunnen worden genoteerd, als om het inzicht dat het bij delingen met dezelfde uitkomst om dezelfde verhouding gaat. Gelijkwaardige breuken kunnen voortkomen uit eerlijk verdelen: 3 stokbroden voor 4 kinderen is ieder 3 4 stokbrood, maar 6 stokbroden voor 8 kinderen is ook ieder 3 4 stokbrood. En zo zijn er meer verdelingen te vinden die passen bij het verdeelresultaat 3 4 .
Het kunnen bepalen van gelijkwaardige breuken is voorwaardelijk voor het leren vereenvoudigen en gelijknamig maken van breuken. Voor het kunnen bepalen van gelijkwaardige breuken, het vereenvoudigen van breuken en het gelijknamig maken van breuken is een goede beheersing van de tafels van vermenigvuldiging nodig.
3 4 6 8 9 12 12 16 …
Verschillende verhoudingen bij de breuk 3 4 in een verhoudingstabel
Het bepalen van gelijkwaardigheid gebeurt in methodes met behulp van de getallenlijn, het cirkelmodel, rechthoekmodel en strookmodel. Gelijkwaardige breuken worden daarvan afgelezen door te kijken wat even lang, evenveel of even groot is. Bij het voorbeeld hieronder gaat het om de verschijningsvorm deel van een geheel. Bij het kijken wat even lang is, kan het ook gaan om de verschijningsvorm breuk als meetgetal en bij evenveel om het deel van een hoeveelheid.
vereenvoudigen
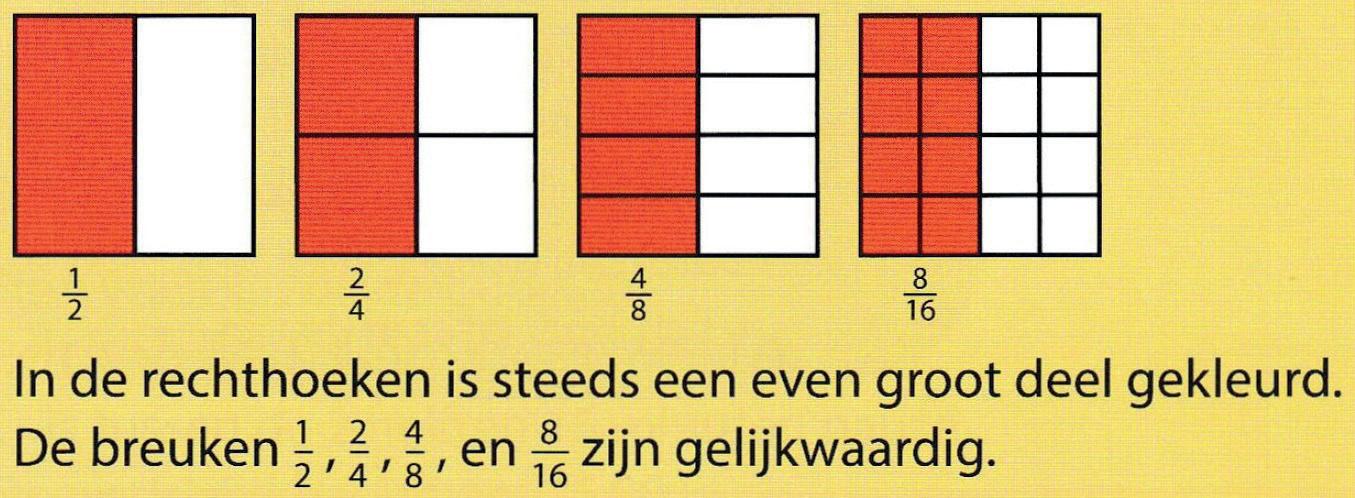
Bron: Getal & Ruimte Junior, groep 7
Een aandachtspunt bij het zo aflezen van gelijkwaardige breuken is dat sommige leerlingen daarin kunnen blijven steken en niet komen tot het beredeneren van gelijkwaardige breuken. Omdat het in principe mogelijk is om gelijkwaardige breuken te bepalen door alleen goed te kijken, is het niet noodzakelijk om echt te beredeneren welke breuken gelijkwaardig zijn, zonder dat je ze voor je ziet. Sommige onderzoekers vinden daarom dat enkel het aflezen van gelijkwaardige breuken van bijvoorbeeld stroken het breukbegrip niet stimuleert. Leerlingen moeten ook oefenen met het vinden van gelijkwaardige breuken zonder een ondersteunende tekening.
Je ziet dan ook allerlei varianten van opgaven in methodes waarbij aan leerlingen meer wordt gevraagd dan alleen het aflezen van gelijkwaardige breuken. Voorbeelden daarvan zijn het zelf tellen van de delen waarom het gaat of het zelf kleuren van gelijke delen, zoals je hieronder ziet. Daarmee zijn leerlingen concreet handelend bezig en worden ze gestimuleerd om zelf actief na te denken over het bepalen van de tellers en de noemers van gelijkwaardige breuken.

Bron: Alles Telt Q, groep 7
Ook in de opgave hieronder, die gaat om het vereenvoudigen ven breuken, moeten leerlingen meer doen dan alleen aflezen. Je kunt hierin breuken als verhoudingen herkennen, in de context van bewoners van een flatgebouw. De gegeven verdelingen 4 van de 16 en 8 van de 16 moeten als een zo ver mogelijk vereenvoudigde breuk worden genoteerd.
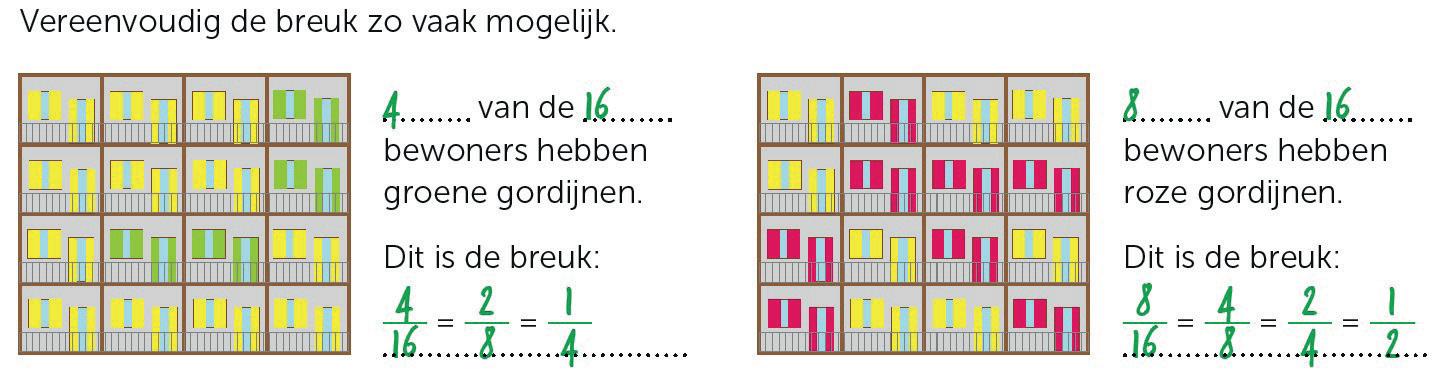
ABron: Alles telt Q, groep 7
Wiskundetaal: breuken vereenvoudigen
Sommige kinderen zeggen in plaats van breuken vereenvoudigen weleens ‘breuken kleiner maken’. Dit is niet correct. Een vereenvoudigde breuk is immers niet kleiner dan de oorspronkelijke breuk, maar juist gelijkwaardig oftewel even groot. Het informele (en foute) ‘kleiner maken’ moet zo snel mogelijk worden vervangen door het correcte ‘vereenvoudigen’.
Doe eens een onderzoekje onder de leerlingen van je praktijkgroep. Vraag ze wat ‘vereenvoudigen van een breuk’ betekent. Geven ze antwoorden als ‘zo eenvoudig mogelijk opschrijven’? Of geven ze antwoorden als ‘kleiner maken’? Ga in dat laatste geval met ze in gesprek. Vraag bijvoorbeeld of de breuk echt kleiner wordt of dat deze evenveel waard blijft.
Bproductief oefenen
Uiteindelijk moeten veelvoorkomende gelijkwaardige breuken snel paraat zijn, zodat deze kennis vlot kan worden gebruikt bij het vereenvoudigen van en rekenen met breuken. Deze kennis moet dus worden geoefend. Een aansprekende vorm hiervoor is het zogenoemde productief oefenen (zie paragraaf 10.3.2). Hieronder zie je daarvan een voorbeeld, waarbij leerlingen bij gegeven breuken zelf gelijkwaardige breuken bepalen.

Bron: Alles Telt Q, groep 7
AOld school ‘Huisgenoten’ is een aansprekende term voor gelijkwaardige breuken, die in vroegere methodes wel werd gebruikt. De term verwees naar breuken die thuishoren op hetzelfde punt op de getallenlijn. Deze breuken wonen als het ware in hetzelfde huis, gebouwd op een bepaald punt op de getallenlijn. Kinderen kunnen hiermee uit de voeten wanneer zij in staat zijn om gelijkwaardigheid te beredeneren. Dan kunnen ze onderzoeken hoeveel huisgenoten ze van bepaalde breuken kunnen vinden.
Gebruik ‘huisgenoten’ in groep 6, 7 of 8 eens als productieve oefenvorm (zie paragraaf 10.3.2). Welke informatie levert je dit op over de beheersing van gelijkwaardigheid van je leerlingen? Welke verschillen zie je tussen leerlingen?

Bron: Rekenrijk (2009), groep 7
Positioneren op de getallenlijn
Vereenvoudig de volgende breuken en plaats ze vervolgens op een getallenlijn.
33 48 –14 21 –12 28 –22 7 –14 3 –35 25 –50 15 –48 15
Breuken tussen breuken
Stanja zegt: ‘Als je van twee breuken de tellers optelt en de noemers optelt en de uitkomsten daarvan noteert als een nieuwe breuk, dan ligt die breuk tussen de oorspronkelijke breuken in.’
Laat zien dat deze redenering klopt.
Farey-rijtjes
Er zijn vier echte breuken met noemer 3, namelijk 0 3 , 1 3 , 2 3 en 3 3 en vijf met noemer 4, namelijk 0 4 , 1 4 , 2 4 , 3 4 en 4 4 . Als je al deze getallen op een getallenlijn plaatst, vallen sommige getallen samen. Voeg je nog alle echte breuken met noemer 1 en met noemer 2 toe, dan houd je uiteindelijk 7 getallen over: 0, 1 4 , 1 3 , 1 2 , 2 3 , 3 4 en 1. Dit heet een Farey-rijtje.
a Bepaal de grootte van de sprongen als je het Farey-rijtje afloopt.
b Voeg alle echte breuken met noemer 5 toe en bepaal opnieuw de grootte van de sprongen.
c Voeg alle echte breuken met noemer 6 toe en bepaal opnieuw de grootte van de sprongen.
d Als je het goed hebt gedaan zijn alle sprongen stambreuken.
De danswedstrijd
Op een feestje kondigt de dj aan dat er een prijs wordt uitgeloofd aan het paar dat de fraaiste Latin dans laat zien. Als de wedstrijd is begonnen, danst 3 5 deel van de aanwezige dames met 2 3 deel van de heren in de zaal.
a Zijn er meer dames dan heren op dit feest, of evenveel dames als heren, of meer heren dan dames?
b Teken de situatie met behulp van stroken.
c Het hoeveelste deel van de aanwezigen danst?
BNet als bij hele getallen wordt optellen en aftrekken met breuken voorafgegaan door tellen en terugtellen met sprongen. Alleen zijn de sprongen nu natuurlijk met breuken.

Bron: Alles Telt Q, groep 6
De betekenissen van de basisbewerkingen optellen en aftrekken met breuken zijn hetzelfde als bij hele getallen. Zo kan optellen de betekenis hebben van samennemen of toevoegen, en aftrekken eraf halen of het verschil bepalen. Een essentieel verschil in moeilijkheid bij het optellen en aftrekken van breuken is of het gaat om gelijknamige of ongelijknamige breuken. Begonnen wordt met eenvoudige opgaven als een breuk bij een heel getal optellen (3 + 1 4 = …) en een breuk aanvullen tot een hele ( 1 3 + … = 1). Dat laatste wordt eerst voorbereid door opgaven waarbij een deel van een geheel is getekend, dat moet worden aangevuld tot het geheel. Zoals bijvoorbeeld in de volgende opgave, waarin een deel van een touw is getekend en de leerling de tekening moet aanvullen tot het hele touw is getekend (hieronder zie je de tekeningen uit het antwoordenboekje).

Bron: Pluspunt, groep 6
gelijknamige breuken
Vervolgens komt het optellen en aftrekken van gelijknamige breuken aan de orde. Daarbij kunnen op formeel niveau al de eerste moeilijkheden optreden, namelijk dat tellers wel worden opgeteld of afgetrokken en noemers niet. Om hieraan tegemoet te komen, wordt eerst op concreet niveau gerekend. Zoals in de opgave hieronder, waarbij in de getekende taart het rechthoekmodel valt te herkennen.
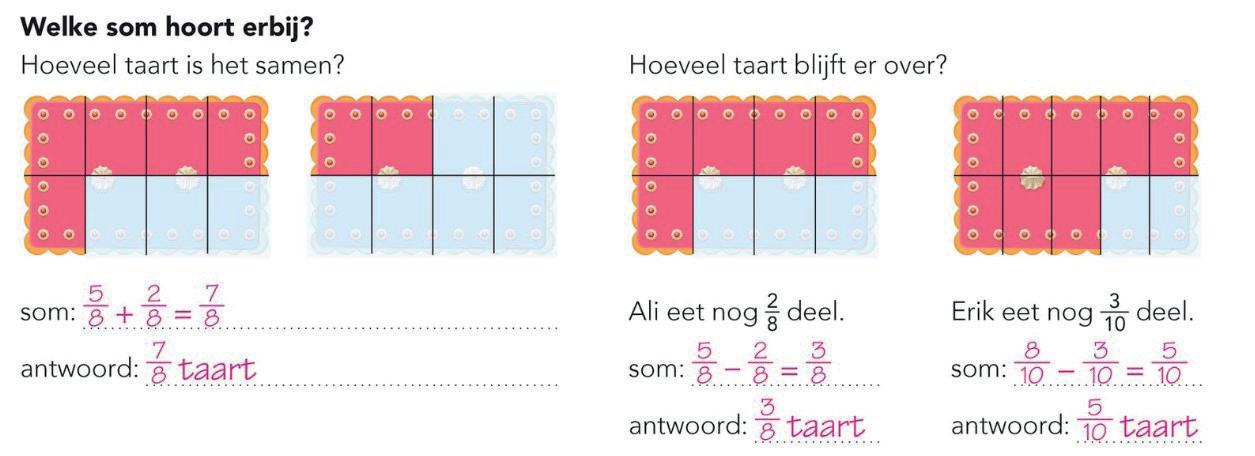
Bron: De Wereld in Getallen, groep 7
Ook ondersteuning van de getallenlijn kan hierbij helpen, zoals je in het volgende voorbeeld ziet.

Bron: Getal & Ruimte Junior, groep 7
Bongelijknamige breuken
ongelijknamige breuken
Gelijknamig maken
Om ongelijknamige breuken te kunnen optellen en aftrekken, is het nodig om breuken gelijknamig te kunnen maken of om gelijkwaardige breuken uit het hoofd te kennen. Als leerlingen bijvoorbeeld de gelijkwaardige relatie 1 2 = 3 6 kennen, en de relatie 1 3 = 2 6 , dan kunnen zij met die kennis 1 2 en 1 3 optellen ( 3 6 + 2 6 = 5 6 ) en aftrekken ( 3 6 − 2 6 = 1 6 ).
Optellen en aftrekken van ongelijknamige breuken is dus geen probleem als een leerling de betreffende gelijkwaardige breukrelaties paraat heeft. Maar dat is niet altijd het geval. Er zijn dan globaal gezien drie manieren om het gelijknamig maken aan te pakken en aan te leren.
bemiddelende grootheid ondermaat regelgeleid
Een eerste mogelijkheid is via een bemiddelende grootheid (zoals al beschreven in paragraaf 3.4.1). Plakken chocolade kun je in allerlei groottes kopen, met verschillende aantallen stukjes. Deze stukjes kunnen fungeren als ondermaat bij het samenvoegen van breuken (optellen) of bij het bepalen van het verschil daartussen (aftrekken). Hiervoor kun je allerlei contexten gebruiken zoals plakken chocolade of stukken taart, zoals in het voorbeeld hieronder. Je herkent bij deze opgave zowel de verschijningsvorm deel van een geheel (de taart), als deel van een hoeveelheid (het aantal stukken van de taart).

Bron: Pluspunt, groep 8
Een tweede, formele en meer regelgeleide mogelijkheid, is het met elkaar vermenigvuldigen van de noemers om te bepalen wat een mogelijke gemeenschappelijke noemer is. Bijvoorbeeld bij 2 3 en 3 4 . De noemers 3 en 4 vermenigvuldigen levert 12 op, dus van beide breuken kunnen twaalfden worden gemaakt ( 2 3 = 8 12 en 3 4 = 9 12 ). Een nadeel van deze manier is dat het soms onnodig veel rekenwerk oplevert (en daardoor meer kans op fouten). Bijvoorbeeld bij 3 4 en 5 12 : als je de noemers met elkaar vermenigvuldigt, levert dat (4 × 12 =) 48 op. Van beide breuken kunnen dus achtenveertigsten worden gemaakt: 3 4 = 36 48 en 5 12 = 20 48 . Maar in dit geval kan het vereenvoudigen sneller en makkelijker door van de vierden twaalfden te maken.

Bron: Alles Telt Q, groep 7
KGV
Een derde manier, waarbij het bezwaar van de vorige manier niet geldt, is gebruikmaken van het KGV om breuken gelijknamig te maken (zie paragraaf 2.1.2) . Bij bijvoorbeeld 3 4 en 5 6 moet het KGV van de noemers 4 en 6 worden gebruikt; dat is niet 24, maar 12. Deze manier is eveneens regelgeleid, maar kan ook worden aangeleerd aansluitend op het werken met een bemiddelende grootheid. Het gaat dan feitelijk om een verkorting: wat is het kleinst benodigde aantal stukjes van een bemiddelende grootheid? Wat is bijvoor-
Abeeld het kleinste aantal stukjes van een reep die je in vieren en in zessen kunt verdelen? Je komt het gebruikmaken van het KGV echter ook meer formeel, regelgeleid tegen, zoals in het voorbeeld hieronder.
Gelijknamig maken bij optellen en aftrekken?
Om ongelijknamige breuken op te tellen of af te trekken, moeten ze eerst gelijknamig worden gemaakt. Maar is dat wel altijd zo? Waarschijnlijk weet jij 1 2 + 1 4 direct, zonder te rekenen en dus ook zonder gelijknamig te maken. Welke opgaven weten kinderen direct en bij welke moeten ze eerst gelijknamig maken? Waar ligt de grens tussen die twee typen opgaven?
a Maak een klein testje met formele opgaven waarmee je dit gaat onderzoeken bij leerlingen uit groep 7 of 8. Gebruik opgaven die getalsmatig verschillen in moeilijkheid. Vergelijk bijvoorbeeld 1 2 + 1 4 met 5 7 –4 6 . Welke opgaven neem je op in je test en hoeveel? Waarin verschillen jouw opgaven qua moeilijkheid? Waarom denk je dat?
b Neem de test af bij een paar leerlingen met uiteenlopende onderwijsbehoeften bij rekenen-wiskunde (zie hoofdstuk 11). Vraag ze hardop te denken. Wat zijn je bevindingen? Klopte jouw inschatting van de moeilijkheidsgraad?
Makkelijke en moeilijke opgaven verzinnen
Aproductief oefenen
Met behulp van productief oefenen kan je een goed beeld krijgen van wat jouw leerlingen al wel of nog niet beheersen. Zeker als je vraagt om een ‘moeilijke’ of een ‘makkelijke’ opgave te verzinnen, zoals in dit voorbeeld voor groep 6.
Verzin zelf een antwoord op een breukopgave passend bij de leerstof van groep 6, 7 of 8. Vraag leerlingen uit de betreffende groep om daarbij een makkelijke en een moeilijke opgave te bedenken en vraag ze ook uit te leggen waarom ze dat vinden.
Zijn de reacties van de leerlingen vergelijkbaar of lopen ze juist uiteen? Wat leer je hiervan over de beheersing van de leerlingen?

Bron: Alles Telt Q, groep 6
CC A
Welke breuken horen op de plaats van de puntjes?
a 1 2 + 1 4 + 1 6 + 1 12 = ...
b 1 2 − 1 4 + 1 6 + ... = 1
c 1 3 + 2 5 + 5 6 − ... = 1
d 1 2 − 1 3 + 1 4 − 1 5 + ... = 1
Een lange optelling
a Beredeneer of de uitkomst van 1 2 +
+ 1 128 meer of minder is dan 1.
b Hoeveel meer of minder?
Leerlingenwerk
Reinier schrijft in zijn werkschrift: 1 4 + 2 4 = 3 8
Als de leraar bij Reinier informeert hoe hij aan dit antwoord is gekomen, zegt Reinier: ‘Kijk maar naar mijn tekening.’
B
betekenissen van bewerkingen
Hoe redeneert Reinier? Welke vervolgvraag zou jij stellen aan Reinier? Welke uitleg zou je geven? Wissel uit met je medestudenten of collega’s. Welke verschillende ideeën verzamel je zo?
Anders dan bij optellen en aftrekken met breuken, komen bij vermenigvuldigen en delen met breuken de betekenissen van de basisbewerkingen niet helemaal overeen met de betekenissen ervan bij hele getallen. De volgorde maakt uit. Een heel getal keer een breuk, bijvoorbeeld 4 × 1 3 , kun je opvatten als 1 3 + 1 3 + 1 3 + 1 3 . Dus als de al bekende betekenis van vermenigvuldigen, namelijk herhaald optellen. Maar bij het omgekeerde, een breuk keer een heel getal, zoals 1 3 × 4, krijgt de bewerking vermenigvuldigen een voor kinderen nieuwe betekenis: een deel nemen ergens van, in dit geval het 1 3 deel nemen van 4. Met gemengde getallen, bijvoorbeeld 2 1 2 × 1 3 , ligt het weer net anders. Je kunt hierbij bijvoorbeeld eerst tweemaal 1 3 nemen (herhaald optellen) en dan de helft nemen van 1 3 (een deel nemen van).
Bij delen kun je opdelen of inpassen onderscheiden: hoe vaak gaat het ene in het ander. Bij 6 : 3 4 is de vraag bijvoorbeeld: hoe vaak past 3 4 in 6? Dit is herhaald aftrekken. Verdelen, bijvoorbeeld hoeveel krijgt ieder, kan worden
Vermenigvuldigen
gebruikt bij het delen van breuken door een heel getal, bijvoorbeeld 4 5 : 4. In de tabel hieronder zie je een overzicht van deze betekenissen.
Betekenissen van vermenigvuldigen en delen met breuken
De breuk is het vermenigvuldigtal
4 × 1 3
Herhaald optellen
Delen
whole number bias deling inverse bewerking
De breuk is de deler
6 : 3 4
Herhaald aftrekken of opdelen
De breuk is de vermenigvuldiger
1 3 × 4
Een deel nemen van
De breuk is het deeltal
4 5 : 4
Verdelen
Als leraar moet je goed rekening houden met het gegeven dat een vermenigvuldiging met een echte breuk (een breuk kleiner dan 1) uitpakt als een deling. En omgekeerd, dat delen door een echte breuk een groter getal oplevert, oftewel uitpakt als vermenigvuldiging. Bijvoorbeeld: 4 × 1 3 is hetzelfde als 4 : 3. En de deling 2 : 1 5 is hetzelfde als 2 × 5. Als je met een echte breuk vermenigvuldigt, is de uitkomst kleiner dan het begingetal, en bij een deling door een echte breuk wordt de uitkomst juist groter. Dit is tegenovergesteld aan wat kinderen hebben geleerd bij hele getallen en druist dus in tegen hun voorkennis. De whole number bias kan hier dus problemen opleveren. En wat ook lastig kan zijn is dat niet alleen 4 × 1 3 hetzelfde is als 4 : 3, ook 1 3 × 4 is hetzelfde als 4 : 3. Bij delen is dat niet zo: 2 : 1 5 = 2 × 5, maar 1 5 : 2 is niet 5 × 2. Wanneer leerlingen alleen de rekenprocedures leren, zonder begrip, zijn dit lastige kwesties. Methodes blijven daarom lang de betekenis van vermenigvuldigen en delen met breuken ondersteunen met modellen en situaties, zoals in het voorbeeld hieronder.

Dat alleen is echter niet genoeg. Ook de volgende inzichten zijn belangrijk.
• Een breuk is een deling.
• Vermenigvuldigen en delen zijn elkaars inverse bewerking.
Daarvan wordt gebruikgemaakt in het volgende voorbeeld.
 Bron: Pluspunt, groep 7
Bron: Pluspunt, groep 6
Bron: Pluspunt, groep 7
Bron: Pluspunt, groep 6
commutatieve eigenschap
Je ziet in de voorbeelden hierboven dat een heel getal maal een breuk op een andere manier wordt ondersteund dan een breuk maal een heel getal. Er zijn onderzoekers die erop wijzen dat leerlingen deze vermenigvuldigingen kunnen gaan opvatten als verschillende typen opgaven, die niets met elkaar te maken zouden hebben. Daarom is ook inzicht in de commutatieve eigenschap van vermenigvuldigen (8 × 5 = 5 × 8) belangrijk. Dan weet je immers dat 4 × 1 3 hetzelfde is als 1 3 × 4 en is het niet vreemd meer dat zowel 4 × 1 3 als 1 3 × 4 hetzelfde zijn als 4 : 3.
Deel van een hoeveelheid
BCa 1 7 deel van 77 × 77 =
b 1 13 ×39 × 17 =
c 5 8 deel van 5 × 160 =
d 1 4 ×7 × 300 =
Deel van een geheel, hoeveelheid en meetgetal Wanneer je ergens een aantal van hebt dat je eerlijk verdeelt, zoals vijftien snoepjes die je eerlijk deelt met z’n drieën, herkennen kinderen hierin natuurlijk eerder de deelopgave 15 : 3 dan de breukopgave 1 3 deel nemen van 15. Voor het breukrekenen is de relatie tussen die twee opgaven belangrijk. Kinderen moeten leren dat ze een opgave als 1 3 × een geheel, een hoeveelheid of een meetgetal kunnen uitrekenen door te delen door 3. Het gaat hierbij om het eerdergenoemde inzicht dat een breuk een deling is. Voorafgaand aan formele opgaven als 1 5 × 20 komen eerst opgaven aan bod waarin het gaat om 1 5 deel nemen van 20. Het taalgebruik ‘deel nemen van’ laat horen dat hier kan worden gedeeld. In methodes kom je een variatie aan opgaven tegen waarin vermenigvuldigen met breuken wordt gekoppeld aan het deel nemen van iets. Hieronder zie je enkele voorbeelden.


Bron: Alles Telt Q en Pluspunt, groep 6

ADeel van 60-spel
Het deel van 60-spel speel je met twee of meer personen. Gebruik twee dobbelstenen met de cijfers 1 tot en met 6. Het doel is om als eerste 150 punten te halen.
Ieder gooit om de beurt met de dobbelstenen. Van de worp wordt een breuk gemaakt. Die breuk vermenigvuldig je met 60. De uitkomst bepaalt het aantal punten dat je krijgt, als volgt.
2 en 3 2 3 × 60 40
1 en 4 1 4 × 60 15 2 en 2 2 2 × 60 60
Bedenk varianten van dit spel om bewerkingen met breuken te oefenen. Een eenvoudige variant is bijvoorbeeld ‘deel van 120’, maar je kunt ook variëren met bewerkingen en dobbelstenen. Probeer altijd uit hoe een variant uitpakt voor je het met leerlingen speelt. Als je bijvoorbeeld twee tienkantige dobbelstenen gebruikt, moet je er rekening mee houden dat er dan ook zevenden kunnen worden gegooid. Wat zou een getal ‘deel van …’ kunnen zijn als je tienkantige dobbelstenen gebruikt? (Tip: denk aan het KGV.)
Nog een deel van 60
CHet bepalen van 3 5 deel van 60 kan door 60 te delen door 5 en het resultaat daarvan maal 3 te doen.
a Zou het ook kunnen door 60 te vermenigvuldigen met 3 en het resultaat daarvan door 5 te delen?
b Denk je dat deze twee manieren bij elk deel van elk getal altijd hetzelfde antwoord opleveren?
Breuk keer breuk
B wiskundetaal
Het lastigst voor kinderen bij vermenigvuldigen met breuken is het vermenigvuldigen van breuken met breuken, bijvoorbeeld 1 2 × 3 5 . Door de getallen te variëren, is hierin een opbouw in moeilijkheid aan te geven. Zo is 1 2 × 2 5 op te vatten als de helft van 2 5 (en dat is 1 5 ), terwijl je bij 1 2 × 3 5 eerst een gelijkwaardige breuk voor 3 5 moet zoeken die je makkelijker door twee kunt delen. Bijvoorbeeld 6 10 .
Hieronder zie je een opgave waarin het cirkelmodel en het rechthoekmodel worden gebruikt om te illustreren wat breuk keer breuk betekent. Hierbij is de wiskundetaal van groot belang om kinderen te laten doorgronden wat er bij deze opgave eigenlijk gebeurt: 1 3 × 1 4 is het derde deel nemen van een kwart en dus hetzelfde als 1 4 delen door 3. De partjes van het cirkelmodel en
de stukjes van het rechthoekmodel fungeren hier als ondermaat die de gemeenschappelijke noemer van de twee breuken aangeeft.

Bron: Getal & Ruimte Junior, groep 7
Repen verdelen
ATwee repen chocolade worden eerlijk verdeeld over drie kinderen. Hoeveel krijgt ieder kind?
Tanja zegt 2 3
Joris zegt 2 6 .
River zegt 1 3 .
a Welke leerling geeft het correcte antwoord?
b Kun je de redeneringen van de andere twee leerlingen achterhalen?
Herkansing
C C C
Van een groep studenten haalt 2 3 deel een toets in één keer. De studenten die de toets niet haalden, doen mee aan een herkansing. Van hen haalt 3 5 de toets alsnog. Er zijn na deze twee kansen nog 172 studenten die de toets niet gehaald hebben.
a Hoe groot is de groep studenten die de toets gedaan heeft?
b Welk deel van de totale groep studenten haalde de toets na twee pogingen niet?
Voldoende of goed
Twee derde van de 81 kandidaten had een voldoende voor de toets; het zesde deel van de voldoendes was een 8 of hoger.
a Hoeveel studenten hadden een voldoende?
b Hoeveel studenten hadden minstens een 8?
c Kun je vraag b beantwoorden zonder eerst vraag a uit te rekenen? Zo ja, hoe dan?
Casino
Iemand gaat naar een casino en verliest daar aan de roulettetafel 3 4 deel van het geld dat hij heeft meegenomen. Vervolgens verliest hij van het resterende geld 2 5 deel bij de fruitautomaten. Hij heeft nu nog € 300 over.
Hoeveel geld heeft die persoon verloren?
Bhandelingsniveau
Opdelen
Er worden allerlei situaties en modellen gebruikt voor vermenigvuldigen en delen met breuken. Hieronder staat een voorbeeld over delen, met de verschijningsvorm breuk als meetgetal. Hierbij hoort de situatie van het uitschenken, oftewel opdelen van iets. In dit voorbeeld: hoeveel bekers van 1 5 liter schenk je uit een kan van 1 liter? De achterliggende vraag hierbij is: hoe vaak zit het erin? Deze vraag kan ook worden gesteld bij de formele opgave 1 : 1 5 ; hoe vaak past 1 5 in 1? Delen wordt bij breuken dus in eerste instantie opgevat als opdelen, oftewel inpassen hoe vaak iets ergens in past. In de opgave hieronder mogen kinderen tekenen op de maatbeker of sprongen maken op de getallenlijn, maar ook het denken aan inpassen is een mogelijkheid. Op deze manier is differentiatie naar handelingsniveau mogelijk (zie paragraaf 10.3.1). De ene leerling zal tekenend tot de oplossing komen, een ander denkend aan de getallenlijn en weer een ander redenerend over inpassen.

Met het opdelen of inpassen van breuken als meetgetallen zijn alle deelopgaven met breuken in principe inzichtelijk te maken, zoals je in onderstaand schema kunt zien.
Bron: De Wereld in Getallen, groep 8ADelen als opdelen of inpassen
Breuken vouwen
Breuken vouwen komt in methodes veel voor aan het begin van de leerlijn, als stroken worden gevouwen, waarbij breuken ontstaan. Maar ook vermenigvuldigen en delen met breuken kan worden gevouwen. Vouw een A4’tje in de lengte in tweeën, dan zie je de helft. Vervolgens vouw je het papier in de breedte in drieën. Nu heb je 1 2 : 3 = 1 6 gevouwen! En ook 1 2 × 1 3 . Probeer dit eens uit met leerlingen en vraag ze vervolgens welke breukopgaven ze nog meer kunnen vouwen. Waarmee komen ze?
Bgelijkwaardigheid

Breuken vouwen. Het achterliggend model is het rechthoekmodel
Redeneren op formeel niveau bij delen met breuken
Op meer formeel niveau is inzicht in gelijkwaardigheid onmisbaar. Neem bijvoorbeeld de opgave 3 4 : 2. Eerst moet een gelijkwaardige breuk worden gezocht die gemakkelijk kan worden gedeeld door 2. Bij 3 4 wordt dat 6 8 .
Daarna kan de opgave worden uitgerekend: 6 8 : 2 = 3 8 . Hierbij wordt een beroep gedaan op de eerder verworven kennis en vaardigheden omtrent gelijkwaardige breuken. Met andere woorden, als het breukbegrip op dat gebied niet goed is ontwikkeld, hoef je met kinderen nog niet aan delen (of optellen en aftrekken) met breuken te beginnen! Bij vermenigvuldigen met breuken ligt dat anders, daarbij heb je geen gelijkwaardigheid nodig.
verhoudingsgewijs redeneren
Een andere manier waarbij formeel redeneren helpt bij het delen met breuken zie je hieronder. Deeltal en deler worden evenveel vergroot. De verhouding tussen beide getallen blijft dan gelijk, dus blijft het quotiënt, het antwoord, hetzelfde. Het gaat hier dus om verhoudingsgewijs redeneren.

Bron: Getal & Ruimte Junior, groep 7
COld school
Maak de volgende oude opgave. Hoe bouw jij elke opgave om? Vergelijk met een medestudent of collega. Hebben jullie dit hetzelfde gedaan of zijn er verschillen?

CBron: Nieuw rekenboek (1937). Opgave voor klas 6 (groep 8)
Delen door een breuk is …
Soms reiken leraren kinderen wel de formele rekenregel ‘delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde’ aan. Bij gebrek aan inzicht kan dat echter fouten opleveren als ‘ 1 3 : 1 5 = 3 × 1 5 ’. Als je de regel niet begrijpt, moet je immers niet alleen de regel onthouden, maar ook in welke situatie je de regel wel of niet kunt toepassen. Bovendien moet je weten hoe de regel precies werkt, want wát je moet omdraaien, staat er niet bij. Deze rekenregel veroorzaakt dan ook gemakkelijk fouten en onbegrip.
a Kun je de regel ‘delen door een breuk is vermenigvuldigen met het omgekeerde’ uitleggen? Het omgekeerde waarvan? Kan je deze regel inzichtelijk maken voor je medestudenten of collega’s?
b Hoe zit het als je de regel omkeert: ‘vermenigvuldigen met een breuk is delen door het omgekeerde’? Is deze regel ook waar? Waarom wel of waarom niet?
AGelijknamig maken bij vermenigvuldigen en delen?
Voor vermenigvuldigen en delen met breuken hoeft niet gelijknamig te worden gemaakt. Toch doen leerlingen dat soms wel. Hoe zou dat komen? Is dat erg? Is het handig?
a Maak hiervoor een testje met een paar formele opgaven die naar jouw inschatting uiteenlopen in moeilijkheidsgraad. Je hebt er niet veel nodig; drie vermenigvuldigopgaven en drie deelopgaven is genoeg.
b Observeer je leerlingen tijdens hun oplossingsproces en vraag hen hardop te denken. Hoe lossen jouw leerlingen de opgaven op? Met welke deelstappen? En gebruiken ze modellen? Zo ja, welke? Zijn er leerlingen bij die gelijknamig maken? Hoe verloopt dan het oplossingsproces?
c Je kunt aan je leerlingen ook de vraag voorleggen of ze wel of niet gelijknamig moeten maken en waarom dan wel of niet.
d Overdenk je bevindingen. Wat betekenen ze voor jouw onderwijs? Wat zijn zaken om rekening mee te houden bij breukenonderwijs?
CBloed geven
Sanquin Bloedvoorziening heeft op een dag 350 donoren, die elk een halve liter bloed geven.
a Hoeveel liter bloed is er die dag in totaal gegeven?
b Bloed bestaat voor 11 20 deel uit plasma. Hoeveel liter plasma is er die dag binnengekomen?
c Het bloed wordt in buisjes gedaan met een inhoud van een twintigste liter. Hoeveel buisjes worden er op die manier gevuld?
Een rondje door de klas
Het groepje van Birgit
De opgave is 2 1 3 × 3 1 2 =….
Birgit doet 2 × 3 + 2 × 1 2 + 1 3 × 3 + 1 3 × 1 2 .
Jan doet 2 × 3 + 1 3 × 1 2 .
Lea doet 2,33 × 3,5.
Freek doet 3 × 2 1 3 × 2 × 3 1 2 : 6.
Welke leerling(en) voert/voeren een wiskundig correcte procedure uit om deze opgave uit te rekenen?
Het groepje van Elena
De vraag is bedenk een situatie bij de opgave 2 1 3 × 3 1 2 .
Elena zegt: ‘Twee en een derde kilo kipkluifjes van 3,50 per kilo kopen.’
Sam zegt: ‘De oppervlakte van een kamertje van 2,3 meter bij 3,5 meter bepalen.’
Samira zegt: ‘Twee en een derde meter verder dan drie en een halve meter gesprongen.’
Rinske zegt: ‘Twee en een derde taart voor drie en een halve persoon.’
Welke leerling(en) geeft/geven een correct antwoord?
Het groepje van Achmed
De opgave is 2 1 3 : 3
Achmed zegt: 2
Brian zegt:
Cloë zegt:
Desly zegt: (12 + 2) : (18 + 3) = 14 : 21 = 2 : 3 = 2 3 .
Welke leerling(en) geeft/geven een correct antwoord?
Doordenkers
Kijk eerst goed en bereken dan.
a 17 8 × 5 17 + 3 8 =
b 13 7 × 5 26 + 9 14 =
c Een breuk met teller 66 wordt zover mogelijk vereenvoudigd tot 3 11 . Wat is de noemer van de oorspronkelijke breuk?
Cd Een breuk met noemer 66 wordt zover mogelijk vereenvoudigd tot 3 11 .
Wat is de teller van de oorspronkelijke breuk?
e Maak de opgaven hieronder.
Bron: Alles Telt Q, groep 7
Gemiddelde
a Het gemiddelde van 1 2 en 3 4 is …
b Het gemiddelde van 1 10 en 1 9 is …
c Het gemiddelde van 1 2 , 1 3 en 1 5 is …
d Het gemiddelde van 2 3 , 3 4 en 5 6 is …
CUitdaging
Kies een willekeurige breuk met oneven teller en noemer, bijvoorbeeld 17 23 . Tel bij deze breuk 1 op in de vorm van 23 23 . Je krijgt dan een breuk met een even teller. Halveer de breuk en ga daarmee door totdat de teller weer oneven is. Je vindt dan 5 23 . Dat is het tweede getal van je rij.
Met deze breuk ga je weer dezelfde procedure uitvoeren als eerst, dus 1 bijtellen en daarna zo vaak halveren tot de teller oneven is. Je vindt dan 7 23 . Als je zo blijft doorgaan, komt op zeker moment in de rij weer de breuk 17 23 , waarmee je begon, tevoorschijn.
Ba Verklaar waarom je altijd op je beginpunt uitkomt.
b Wat is de langste rij die je kunt maken als je met een willekeurige breuk begint?
Zoals beschreven in hoofdstuk 1, hangen breuken nauw samen met decimale getallen en verhoudingen. Hieronder staat een mooie voorbeeldopgave over de samenhang van breuken met decimale getallen. Samenhang met overige leerstof wordt daaronder gekarakteriseerd.

Bron: Alles Telt Q, groep 8
Basisbewerkingen
Voor het bepalen van gelijknamige en gelijkwaardige breuken (waaronder het vereenvoudigen van breuken) moet het vermenigvuldigen en delen goed worden beheerst, met name de tafels van vermenigvuldiging en de deeltafels (zie begin paragraaf 3.4). In groep 6, 7 en 8 moet die kennis worden onderhouden. Als de beheersing onvoldoende is, moet hierop extra worden ingezet, anders wordt het leerproces bij breuken te veel belemmerd.
Wiskundetaal
B
De betekenis van de breukstreep en het deelteken zijn hetzelfde. Dit inzicht is van belang voor vermenigvuldigen en delen met breuken (zie paragraaf 3.4.3) en vanwege de voorbereiding op algebra in het voortgezet onderwijs.
Meten
Een van de verschijningsvormen van breuken is de breuk als meetgetal. Hoewel die in de realiteit wel voorkomt, worden meetgetallen vaker als decimaal getal genoteerd. Toch heb je hier bij de begripsvorming rond breuken wel iets aan, vooral als je kinderen zelf dingen laat opmeten. Vanuit het meten van objecten met stroken (zie paragraaf 3.2) kunnen immers ook breuken ontstaan, net zoals bij het eerlijk verdelen. Als leerlingen dingen gaan opmeten met papieren stroken, blijkt al gauw dat niet alles precies een aantal stroken lang is. Door het vouwen en verdelen van een strook kan preciezer worden gemeten. Een leerlingentafel blijkt bijvoorbeeld 3 1 4 strook lang te zijn. Het vraagt wat voorbereiding om de kinderen zelf daadwerkelijk te laten meten met stroken, maar het levert wel het nodige inzicht op!
Babsolute relatieve
Verbanden
Bij verbanden worden gegevens niet alleen met hele getallen aangegeven, maar ook met breuken, zoals te zien is in de voorbeeldopgave hieronder. Hierbij wordt ook expliciet de relatie gelegd tussen absolute gegevens (de aantallen kinderen) en relatieve informatie (de delen kinderen).

Bron: Pluspunt, groep 6
ACKoffie of thee?
Op tafel staan twee koppen, precies even groot en even vol. De ene kop bevat thee en de andere koffie.
Een lepel vol koffie uit de koffiekop wordt in de kop met thee gegoten. De thee wordt geroerd totdat het perfect gemengd is. Daarna wordt een lepel (even groot en even vol als eerst) met het thee-met-koffiemengsel teruggegoten in de koffie. Zit er nu meer thee in de koffie, of meer koffie in de thee?
Samenhang in de methode
Om inzicht in breuken te bevorderen, is het van belang om breuken in samenhang met andere concepten aan te bieden, zoals in de voorbeeldopgave over het zwemdiploma.
a Ga in de methode van je praktijkschool op zoek naar opgaven waarin breuken in samenhang met andere wiskundige concepten worden aangeboden. Lukt het om een variatie aan voorbeelden te vinden bij verschillende concepten?
b Wissel je bevindingen uit met je medestudenten of collega’s. Zo krijg je een verzameling van voorbeelden van breuken in samenhang met andere concepten die je in je eigen onderwijs kunt gebruiken.
De lijst met alle begrippen uit dit hoofdstuk vind je op eDition.
















De driedelige serie Reken-wiskundedidactiek vormt een belangrijke bron voor aanstaande leraren basisonderwijs voor het vak rekenen-wiskunde.




De uitgangspunten van deze boeken zijn:
Opgezet vanuit de indeling van de Kennisbasis Wiskunde voor de pabo: hoe komen deze voor in de realiteit, om welke wiskunde(taal) gaat het en hoe kun je eraan werken in de basisschool.
Aandacht voor A-B-C in samenhang: Activiteiten in de praktijk, Bronnen met theoretische inzichten en het eigen niveau van geCijferdheid.
In elk deel is aandacht voor gelegenheid-tot-leren (opportunityto-learn) van rekenen-wiskunde: aandacht voor doelgericht werken, zicht op leerlijnen, en differentiatie die bijdraagt aan gelijke onderwijskansen.
Dekkend voor de Kennisbasis Wiskunde en de inhouden van de landelijke kennistoets Wiskunde voor de pabo.
Absoluut

Met breuken, decimale getallen, verhoudingen en procenten gaat er voor kinderen een nieuwe (wiskunde)wereld open. Deze concepten hebben veel met elkaar te maken, en zijn tegelijkertijd verschillend van elkaar. Procenten zijn een verschijningsvorm van verhoudingen en decimale getallen zijn een uitbreiding van ons getalsysteem. Breuken zijn een geval apart: een breuk kan een verhouding weergeven, is een getal en ook nog een bewerking. In dit boek lees je er alles over. Aan bod komt hoe je bassischoolleerlingen grip kunt laten krijgen op deze pittige leerstof en wat jij als leraar in je onderwijs kunt doen om hen daarbij te begeleiden. De nadruk ligt op de groepen 5 tot en met 8, maar er is ook oog voor informele ervaringen met breuken en verhoudingen in de eerdere groepen.
Bij de boeken is er een ondersteunende online leeromgeving, eDition, met aanvullend materiaal
9 789006 074666

