(吳祖諺)
處理物理問題需要學會建立物理通感,這 種感覺通常可在初期階段透過量綱分析去 訓練自己對物理學的洞察力與對結果的判 斷力。但很常時候對學生而言則往往會是 因為英文題目的描述過長而導致解題能力 下降,以一道關於簡諧運動的問題為例:
極小值的關係為何?這些都是關於簡諧運 動的基本觀念,必須掌握。在解該題型前 不妨先將題目試想成以下方式:
��(��)=��(1 �� +��2��)
這道題的意思是,對一個處於靜態平衡狀 態的系統施加一定程度的擾動而導致系統 稍微偏離原來的穩定平衡狀態(即當位能 達到極小值時),這種現象就叫簡諧運動。
今 有一 質 量為 的 質點 ,處於位能
��(��)=��(1 �� +��2��)

焦耳 的空間。當質
點受到一定程度的擾動而稍微偏離穩定平
衡點 ��0 = 1 �� 公尺 時開始做簡諧運動。
試估算該質點(簡諧振子)的運動週期,
為質點的空間坐標。
這是一道融合觀念與運算的題目。特別值 得注意的是,在閱讀題目方面,原文使用 的詞匯并不單刀直入,或許是刻意複雜化 題目的本質來測驗讀者對觀念的理解度, 同時也測驗讀者的英文閱讀能力。首先考 慮何謂擾動?何謂平衡點?平衡點與位能
意思是指,一度空間中的一個單位質量為 的質點在位能場 ��(��)=��(1 �� +��2��) 中 處於靜態平衡。其中 和 為正數。試計 算出該簡諧運動在其位能達到極小值時的 角頻率,並以其得出周期。這樣讀起來是 為了直觀化題目的意思,從重點下手去直 接計算題目中所問的核心問題。解法思路 可分為「能量守恆攝動法」與「基本力學 觀念法」兩種。吾人先從基本觀念法(即 牛頓 胡克)出發,深入了解題目的主要 力學觀念。
關於簡諧運動的一道基礎題型
Fig. 欠阻尼振盪視覺圖 首先了解質點在平衡點處不受力,因此有
�� = ���� =0

⇒ ���� ���� =0 從而獲得保守力場函數及系統的均衡點
��(��)= �� ��2 ����2 =0
⇒ �� ��2 =����2
⇒��2 = �� ����2
⇒�� =± 1 �� ≡��0
從這得知 ��0 =±1 �� 是穩定平衡點,即位
能位於該處的極小值,亦即在 ±1 �� 時質點 沒有動能,處於一個穩定平衡狀態,該處 又稱為均衡點。再根據簡諧運動的定義, 當質量為 的質點在一度空間中受到胡 克定律的支配而運動時(如彈簧 猶如 粒子在彈性力的作用下發生振動),該行 為就稱為簡諧運動。這裏的「簡」特別指 「線性恢復力」的意思。「線性」是個數 學概念,而在物理內有著「彈簧恢復力正 比於位移的一次方」的意義。因此考慮彈 力(可由級數展開推導之)
�� = ����
對一保守力場求導數則獲位能的二階導數
���� ���� = �� = ��2�� ����2
該目的是為了獲得靜態中的有效彈力常數 ⇒��(��)= 2�� ��3
在上述中已獲得穩定平衡點 ��0 = 1 �� ,將 其代入彈力常數的函數 則得 值 ��(1��)=2����3
之所以不考慮 ��( 1 ��) 是因為振盪頻率不
可為複數。將胡克定律與牛頓第二運動定 律結合,並對比彼此位移與加速度之間的
關係則可得 �� =√�� �� 從而得出 �� =√2����3 �� 。
最後根據彈簧振動的周期公式做引申得到 �� = 2�� �� =2��√ �� 2����3
以上吾人是從「力量」的觀點來分析問題 並得出周期。另外一種思路是透過「能量」 的觀點來思考周期的問題。首先考慮系統 的位能場函數,將其靠近位能極小值 ��0 的地方以泰勒展開式表現
由力學能守恆定理得知,當物體開始振動 時,動能與彈力位能相互交替變化,因此 在靜態平衡下位能轉換成動能,最終得到 以下彈力位能的近似值
最後由
與前例的結果有著異曲同工之處。該方法 與前方法相較之下略需要一點代數上的小 技巧來幫助簡化估算過程。當然也可以直 接利用能量守恆定理,對時間微分為零 (ⅆ�� ⅆ�� =0) 來得到振動頻率 ��。
最後額外要提的是如何透過量綱分析(即 因次法)來判斷物理題目的結果。考慮一 道由電阻率找電阻的題型(高醫106):
0ⅇ �� ��

在此題目剛好給的函數較為簡單,因此積 分起來很容易。倘若積分函數較為複雜, 則可通過因次法在無需積分的條件下觀察 出結果。首先考慮題目中的選項皆為代號, 且彼此之間有少許選項擁有 �� 或 ��,其 餘則無,此外選項沒有係數。然而已知 1 ⅇ 1 是積分後代入上下限的結果,本 身為純量,因此不具因次也不算係數。按 照這樣來判斷可確定能用因次法來處理。 首先列出公式,依照選項型式有 �� 跟 �� 和

�� ,不難判斷出是歐姆定律,�� = ���� �� ,因
此答案的因次也會是 ���� �� 的型式,很自然
地可排除掉������三個選項,再由 �� 的上下 限代入即可直接看出選項��是最終結果。
這樣思考可省去做積分的時間。
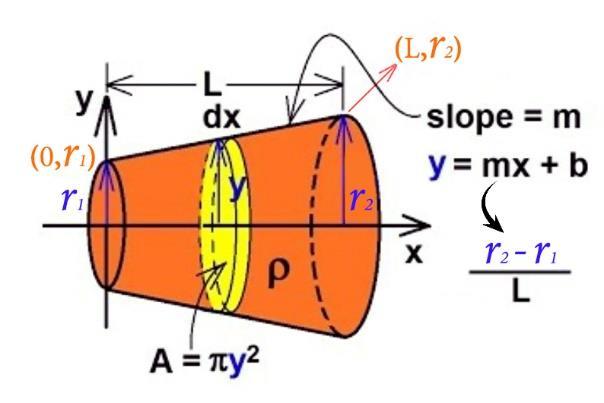
實際的計算可從一般的圓柱幾何推廣至截 錐幾何來獲得更完整的解。首先考慮電流 通過有長 �� 和不同兩面的截錐體

由歐姆定律出發
因此得到最終解
吾人可將截錐體進行以下數學分析:
此時的函數 ��(��) 可為任意線性函數,利
用該公式解亦可求得前例的問題,只不過 需積分。
利用線性函數的定義求出斜率
