Paul T Wu
Abstract: A fundamental grasp of Gauss's flux theorem in electrostatics is essential at the commencement of a freshman physics course. Nevertheless, its utilization in gauging gravitational field intensities receives comparatively lesser emphasis in mechanics. Conceptually, both Newton's law of gravitation and Coulomb's law of electrostatics adhere totheinversesquarelaw.AccordingtoNewtonianmechanics,thislawdictatesthataparticle tracesanellipticaltrajectorywheninmotion,aphenomenonmirroredinelectrostaticcharges. Furthermore, both gravitational and electrostatic forces exhibit potential energy, where their respective potentials satisfy Laplace's equation, ��2�� =0 . When gravitational and electrostatic forces are derived from their potentials, which scale as ��(��)∝�� 1 , the resulting force fields vary inversely with the square of the distance, ��(��)= ��(��)∝�� 2 . Newton's law and Coulomb's law share a fundamental structural identity, thereby leading Gauss's law to find application in both gravitational and electromagnetic domains alike. This paper delves into the application of Gauss's flux theorem for determining gravitational field strength.Itusesaphysicsproblemfromthe2023postgraduatemedicalschoolentranceexam at Tsinghua University in Taiwan, which was under appeal at the time, as a case study.
Keywords: Potential field, Laplace’s equation, Poisson’s equation, spherical harmonics, spherically symmetric, Green’s function, Green’s identities, Gauss’s theorem, field strength.
Consider the problem of measuring the intensity of the gravitational field sourced by a point mass, described as follows:
The mass density inside a planet is usually not uniform. However, the mass density of the concentric shells of a spherical planet is about the same when the planet is decomposed into concentric spherical layers. As a result, for a spherical planet �� of radius ��, the mass density can be treated as a function of its distance to the center of the planet
Assuming the gravitational field strength at the planet’s surface is ����≳�� ≝��0 Show that at �� = 1 2 ��, the magnitude of the gravitational field is less than half that experienced at planet X's surface, yet remains nonzero, that is,
A planet’s density usually increases as we go inwards from the crust to core. Suppose a planet called �� is an oblate spheroid of radius �� and that its density �� is modeled by
where �� is the radial distance from the center, ��0 is constant. The approximate volume of a spherical shell of radius �� and thickness ���� is given by
=4����2 ��(������������)
so the mass in this shell is given by
where ��(��) is the mass density as a function of the given coordinates ��∈ℝ3, which yields a more general equation in spherical coordinates
or in Cartesian coordinates,
Therefore, the total mass as a function of �� is given by the integral
For
Remark 1. The ratio of ���� and ��½�� is
shows
and
THEOREM 1 THE DIVERGENCE THEOREM
Let �� be a compact domain (an enclosed volume) in ℝ3 with piecewise-smooth boundary ����. If �� is a smooth vector field in ��; then the flux of �� across the boundary ���� of �� is
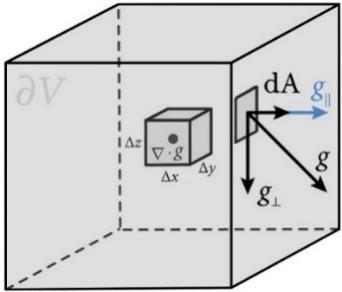
Proof. The steps to complete the theorem for general regions should be as follows; first prove it for rectangular regions, then use the Jacobian to prove it for regions smoothly parameterized by rectangular regions, and finally paste such regions together to form any region. Here we will prove only for the case of rectangular solids. Using sides parallel to the axes to divide �� into multiple small cuboids. Assuming the center of one of the cuboids is defined at ��(��,��,��) with sides of length ����, ����, and ���� Let ��=⟨����,����,����⟩ be a smooth vector field, that is,
Thus, the values of �� at the midpoint of the surface areas of two faces �������� perpendicular to the x-axis are ��+ 1 2 ���� ���� ���� and �� 1 2 ���� ���� ���� respectively. That being the case, the sum of the surface integrals upon the two faces perpendicular to the x-axis becomes
Similarly, the sum of the surface integrals upon the two faces perpendicular to the y-axis with area �������� becomes
The sum of the surface integrals upon two faces perpendicular to the z-axis with area �������� becomes
Accordingly, let the entire surface of the cuboid be �� ′ , we have
However, the volume of the cuboid is indeed ������������. Treating it as ���� yields
Consequently, we arrive at the fact that
Remark 2. Using Theorem 1, we can measure the flux of a vector field across the boundary of a domain based on the integral of the divergence of the field over the domain itself.
Remark 3. The following criteria must be met for Theorem 1 to be applicable to specific types of volumes ��:
1. �� must be bounded and contained by a body Ω≝{��∈ℝ3:‖��‖≤��} for some �� ∈ℝ+
2. �� has a complete, closed boundary surface �� =���� that cannot be entered or exited without crossing the boundary ��.
3. �� is oriented outward from ��.
4. Suitable geometries include: spheres, ellipsoids, cuboids, tetrahedra, etc.
THEOREM 2 THE GAUSS FLUX THEOREM FOR GRAVITY
Let ��(��) be a neighborhood of ��=(��,��,��) contained in V, that is, a spherical ball �� ≝ {��∈ℝ3 ∶‖��‖≤��} of radius ��, and �� ̂ the outward unit normal on ����. Let �� be a continuously differentiable vector field defined on an open set containing ��; then the flux of �� across the boundary ���� of �� is
Proof. Since �� is calculated from the integral of the point-mass contributions of the masses distributed in ℝ3 , proving this equality requires only showing the same for a mass concentrated at one point, origin for example. By Newton’s law, the gravitational force between two masses ��1
and ��2 at distance �� is equal to ��1��2�� ��2
The gravitational field strength is generated by a mass �� located at the origin, according to Newton’s law: ��(��,��,��)=���� 1 ��2 +��2 +��2
2 +��2 +��2 =
⟨��,��,��⟩ (√��2 +��2 +��2)3.
In this field, �� ��=0. Consider a small sphere ��0 of radius �� centered at the origin, and let �� be the solid lying between ��0 and ��. By the Gauss-Ostrogradski formula,
As a result, it is sufficient to prove Gauss’s law for sphere ��0. On this sphere the flow ��⋅�� ̂ has the form ��⋅�� ̂ =��(��)�� ̂ ⋅�� ̂ =��(��), which is constantly equal to ���� ��2 according to Newton's law of universal gravitation. Integrating it over the sphere gives
�� being the total mass ∭ ��(��)��3�� �� inside �� with ����, proving the theorem.
Remark 4. The vector �� ̂ is the outward unit normal on the boundary of ��, that is,
Definition 1. A vector that is perpendicular to the plane or a vector and has a magnitude 1 is referred to as a unit normal vector, that is,
Definition 2. Given two nonzero vectors �� and �� in ℝ��, the dot product is defined as,
THEOREM 3 THE DOT PRODUCT THEOREM
Given �� is the angle defined as the unique �� ∈[0,��] between two nonzero vectors �� and ��, the following definition for the dot product between �� and �� is equivalent to Definition 2
Proof. The Law of Cosines and the magnitudes property of the dot product, ��⋅��=‖��‖2 , allow us to relate

Fig 2. Vector method of deriving the cosine rule.
Using the properties of the dot product, we can rewrite the left side as
Substituting back into the Law of Cosines yields
Definition 3. If �� is a smooth vector field defined on a piecewise smooth oriented surface �� with unit normal vector �� ̂, then the flux of �� across �� is
Remark 5. We know ��⋅����=��⋅��̂���� is true by Definition 3, �� is the radius of spherical Gaussian surface ���� (the boundary of the spherical ball), and �� is the radius of planet ��. In accordance with Definition 1 and Theorem 2, Gauss’s formula yields the equality
where ‖��̂‖=1 and ������(��)= 1. Therefore,
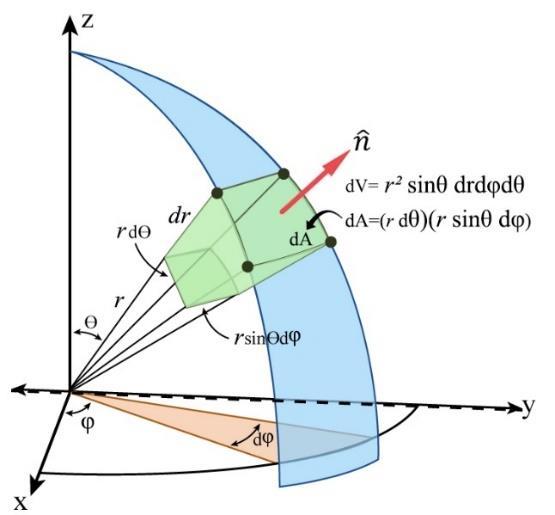
Fig 3. Geometry of spherical section
Using the aforementioned theorems, definitions and remarks, we can rewrite the formula as ��(4����2)= 4������
�������� being the total mass inside the spherical ball of radius �� with boundary ���� of ��. Mass outside the spherical ball makes no contribution. For the case of uniform density, this is equal to �� = 4 3 ����3�� and �� = 4 3��������. Furthermore, we know from Theorem 2,
Due to its conservative nature, the gravitational field must have an associated potential function. In this case, ��= ����. Together with �������� =∭ ��(��)��3�� �� we can rewrite the above equation as
Transforming the left hand integral by Theorem 1 gives
This is true for all volumes ��. By reversing the volume integrals, we obtain ��⋅( ����)= 4������(��).
It follows that the Newtonian gravitational potential ��(��), which is spherically symmetric about a given point in space ��∈ℝ3 , satisfies the gravitational Poisson equation
where �� =‖��‖ is simply the distance of the position from the origin This is an inhomogeneous linear partial differential equation of elliptic type with a source term that is a function of ��, i.e., ��(��)=4������. For the corresponding total mass contained within the closure ��∪���� (the closed volume bounded by ����), we have
which can be derived from Theorem 1
It is worth mentioning that the way in which different coordinate systems find solutions differs Each method has its advantages and limitations. In Cartesian coordinates, the gravitational Poisson equation in ℝ3 is described by
for which the equation is separable. Assuming the solution to the Poisson equation has the form
(��)
The main goal is to substitute this series expansion for ��(��,��,��) into the Poisson equation and solve 4����⋅��(��,��,��)=������ +��
+������ In spherical polar coordinates (radial distance ��, polar angle ��, and azimuthal angle ��), the equation in ℝ3 is then described by
for which the solution of the equation can be represented by spherical harmonics expansion,
where
(��) are the associated Legendre functions of order �� and degree �� which satisfy
the associated Legendre equation when �� and �� are integers, �� ≥0, �� ≤�� ≤�� These functions are of great importance in quantum mechanics as they are used to construct the spherical harmonics a set of special functions reappeared as solutions to the Schrödinger equation for the hydrogen atom in spherical polar coordinates. Poisson's equation can also be solved using other coordinate systems, but they are not the topic to be discussed here.
Remark 6. As a matter of convention, the scalar potential of a vector field �� is a function that satisfies ��=����. However, when the vector field �� represents a force so that the force pushes an object from a higher potential to a lower potential, then �� is a function that satisfies ��= ����
Remark 7. The Poisson equation ��2�� =4������ can be used to measure the gravitational potential when �� is known. When �� =0, the equation becomes homogenous without the source term, which reduces to the Laplace equation.
Under the spherical system, the fundamental solution to ��2�� =4������ can be obtained through the Green function, that is, treating Green’s functions as propagators to solve for ��(��) in which �� is the general coordinate of �� To do so, we shall first discuss Green’s identities as these are particularly used for converting integrals with gradients and divergences into integrals with normal derivatives In this case, we motivate the derivation of gravitational potential using the Green function, and examine scenarios in which it might be applicable to measuring gravitational potential.
PART I: THE DERIVATION OF GREEN’S FIRST AND SECOND IDENTITIES
Let us recall Theorem 1, which is the divergence theorem:
We set ��=���� with �� a ��2 scalar function on some region �� ⊂ℝ��, that is, a twice continuously differentiable function on ��, we then obtain
Similarly, but set ��=������ with �� and �� a ��1 scalar function and a ��2 scalar function respectively on some region �� ⊂ℝ��, we then have
̂����.
Using an extension of the product rule, that is, ��⋅(����)=(����)⋅��+����⋅��, we find the equation to be equivalent to
��(����
⋅��̂)����, �� or alternatively to be equivalent to
This is known as Green’s first identity By reversing the roles of �� and �� yields
Furthermore, subtracting the above equation from the previous equation we then obtain Green’s second identity, which is valid for any pair of function (��,��) expressed as follows:
Definition 4. A boundary condition is considered symmetric for the Laplace operator ��2 on �� if
for all pairs of functions (��,��) that satisfy the boundary condition.
Remark 8. In Green’s second identity, the term ����, which is equivalent to ���� ���� ̂, denotes the directional derivative of �� in the direction of the outward pointing surface normal �� ̂ of the surface element ����, that is,
Remark 9. Dirichlet, Neumann, and Robin boundary conditions are symmetric.
PART II: THE DERIVATION OF GREEN’S REPRESENTATION FORMULA
Now, continue from Green’s second identity, we let �� =��, where �� is the Green function taken to be a fundamental solution of the Laplacian
In ℝ3 , without boundary conditions, ��(��,����) has the form
We shall give a complete proof to this by introducing Fourier transform method later. However, Green’s third identity states that any twice continuously differentiable function (harmonic) �� on ��, i.e., a solution to the homogeneous Poisson equation ��2�� =0, can be expressed as an integral over the boundary ���� as
in which ���� ∈�� and �� is on ����. This is also known as Green’s representation formula, a direct application of Green’s second identity to the pair of functions being the radial solution ��(��) and ��(��)= 1 4��‖�� ����‖
used to construct solutions to the Poisson equation for Dirichlet boundary condition.
To prove the Green function possesses the above form, consider the system in the open bounded region �� with boundary ����: ��2��(��)=4������(��) in which �� is a given coordinate vector in ℝ3 such that ��=⟨������������������,������������������,����������⟩, 4������(��) is the source term of the system, and ��(��) is our solution. Since ��2 is a linear differential operator, i.e., ��2:����(Ω)→���� 2(Ω) for any open set Ω⊆ℝ�� , the solution to a general system of this type can be expressed as an integral over a distribution of source given by 4������(��):
��) �� [4������(����)]��3����
in which the Green function describes the response of the system at the point �� to a point source located at ����: ��2��(��;����)=��(�� ����), and the point source is given by the Dirac delta function ��(�� ����).
PART III: THE CONSTRUCTION OF GREEN’S FUNCTION
Rewrite the above equation by setting the source at the origin such that ���� =0, we have ��2��(��)=��(��).
As a matter of convenience, let us introduce a new variable ��=�� ���� in which ���� =0:
Now, compute for ��(��) with the aid of Fourier transforms:
where �� is a wave vector ��=⟨��
and ��=⟨��,��,��⟩ so that
These are the Fourier representation of ��(��) and ��(��) respectively. For the Laplacian of the scalar field ������⋅�� we have ��⋅��=⟨����,��
so that
In the Cartesian coordinate system, let ��(��,��,��)=��
�� , which is equivalent to that of the one in the general coordinate system
Therefore, we have
Since
we then have
By definition, the Laplacian of the Green function is the ��-function:
Matching the integrands on both sides, we have
Accordingly,
in which �� is arbitrary. For the integral above, we know the elementary volume under the spherical coordinate system is ���� =������������
The transformation
Thus, the function can be integrated over every point in ℝ3 by:
Substituting �� =����cos�� and
Plugging the result gives
This is the Dirichlet’s discontinuous integral, which can be tackled by the Laplace transform method or the calculus of residues. We prioritize the Laplace transform technique for now.
First notice that when �� >0
Due to convenience, let ���� =��, and the form ∫
follows.
Definition 5. Given a function ��(��) defined for all �� ≥0, the Laplace transform of �� is the function �� defined as follows:
for all values of �� for which the improper integral converges.
By Definition 5, we are aware that ��(��)=ℒ{1}=∫
. Notice that the integral ∫
0 ���� is equal to the integral ∫ ��
��
, and therefore we have
THEOREM 4 FUBINI’S THEOREM
Let ��, �� be complete measure spaces, �� be ��×�� measurable. If ∫ |��(��,��)|��(��,��)<∞��×�� then
Proof. In the language of vector calculus, the theorem says that if �� is bounded on the rectangle ℾ≝{(x,y)∶a≤x≤b,c≤y≤d}, then
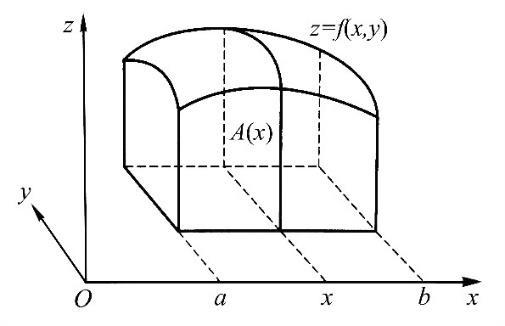
Fig 4 The Illustration of Fubini’s Theorem
The above statement describes a function of two variables ��(��,��) being integrable over a closed rectangle ℾ. If there exists an integral ℎ(��)=∫ ��(��,��)����
for every �� ∈[��,��], then the integral is integrable on the interval [��,��], which yields
We place the partition points in the interval [��,��]
and write ������ as ��
(�� =1,2, ,��) Clearly, to arrive at the conclusion of the theorem we only need to prove that
Here, ���� represents a random point within the interval [����,���� 1], with �� denoting the maximum value among all ������. Subsequently, position the partition points within the interval [��,��]:
and write ������ as ���� ���� 1 (�� =1,2, ,��). Consider each partition point through [��,��] and [��,��] as lines parallel to the coordinate axes, which divide ℾ into multiple small rectangles (this is a partition of ℾ), and mark ℾ���� as [����,���� 1]×[����,���� 1] where �� =1,2, ,��;�� =1,2, ,�� Now, writing
Since ���� ∈[���� 1,����], it yields
Multiplying these inequalities by ������ respectively and adding them up one by one yields
Note that the left and right sides of this inequality are the upper and lower Darboux sums of ��(��,��) upon the partitions made. Since ��(��,��) is integrable on ℾ, when all ������,������ tend to zero, both sides of this inequality tend to
By squeeze theorem for limits, we have
It can be deduced similarly that if ��(��,��) is integrable on ℾ=[��,��]×[��,��], and for all �� ∈ [��,��] the integral ∫ ��(��,��)������ �� exists, then the iterated integral ∫ ����∫ ��(��,��)������
�� �� also exists and the following equation holds:
It is important to note, however, that if the target function is positive, the matter of convergence can be bypassed, in which case we have Tonelli’s theorem In physics, Fubini’s theorem means that an n-dimensional object can be represented as a spectrum of layers of shapes made up of (�� 1) dimensions. Thus, a 3D volume can be represented by a set of layers made up of 2D planes
Corollary 2. If we are integrating over the rectangle ℾ=[��,��]�� ×[��,��]�� where ��(��,��) can be factored as ��(��)ℎ(��), then Fubini’s theorem will lead to:
Proof. By Theorem 4, let a function of single variable ��(��) be integrable on the closed interval [��,��], and ��(��) be integrable on the closed interval [��,��]. Then, the following holds:
In our problem, according to Theorem 4 we can find a function �� such that ��(��,��)=���� ���� so that |�� ���� sin��|≤��(��,��) for every nonnegative �� and ��. Furthermore, ∫ ��(��,��)∞ 0 ���� =1 for every �� >0; hence, Fubini’s theorem applies:
Since
When �� =0, we have
When �� <0, we have
However, we choose the value �� 2 since our �� is greater than zero. As a matter of course, we can also obtain the same result by Cauchy’s residue theorem
Definition 6. Suppose ��(��) is continuous on ℝ except at ��0 ∈(��,��), then the Cauchy principal value is defined by
provided the limit converges
Remark 10. In Definition 6, ‖�� ��
Certainly,
By definition 6, as we let �� go to infinity and �� go to zero, the integral over the resulting closed contour tends to the Cauchy principal value:
in which �� denotes the principal value of an analytic multivalued function. Therefore, we consider the function ℎ(��)=�� 1������and define the positive indented semicircle, that is, letting �� and �� be �� >�� >0, and consider the region �� bounded by ���� =[ ��, ��]∪���� ∪[��,��]∪���� where ���� is the upper semicircle of ‖��‖=��, and ���� is the upper semicircle of ‖��‖=��
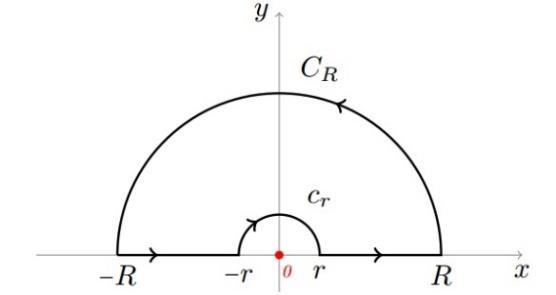
Fig 5 The indented semicircle of Dirichlet’s integral
LEMMA 1 JORDAN’S LEMMA OF ‖�� ��0‖→0
Suppose an arc of the semicircle of radius r centered at ��0 is ���� ≝‖�� ��0‖=��, ������(��)∈ [��,��] and ��(��) is continuous on ���� in which �� is sufficiently small. If
‖=��→0[��⋅��(��)]=�� is uniformly valid for �� ∈����, that is, regardless of ������(��)∈[��,��], then
Corollary 3. If ��(��) has a simple pole at ��0 then the following definition for the residue of ��(��) at ��0 is equivalent to the �� of Lemma 1:
Remark 11. Alternatively, Lemma 1 can also be stated as follows:
Suppose ��(��) is holomorphic near �� =��0. Fix ��0 ∈(0,2��). If ���� denotes a counter-clockwise oriented arc of angle ��0 on the circle of radius �� centered at ��0, then
Proof. By the substitution �� =��0 +�������� with the fact that ���� =������������ where ���� =arg(����), then
which clearly goes to zero when ‖�� ��0‖=�� →0.
Remark 12. If �� =�������� with �� >0 and �� ∈( ��,��], then ������(��)≝{������(��)+2����|�� ∈ℤ} in which the ������ is an angle, while the ������ is its measure. This implies that principal argument always lies between �� to �� In addition, multi-valued nature of ������(��) can be visualized by using Riemann surfaces [1]
LEMMA 2 JORDAN’S LEMMA OF ‖��‖→∞
Suppose ��(��) is continuous on the semicircle of radius �� in the upper half plane ���� ≝‖��‖=�� in which �� =��������,�� ∈[0,��] for �� to be sufficiently large and
is uniformly valid on ����, that is, regardless of ������(��)∈[0,��], then
where �� >0.
Proof. Since ������ ��→+∞��(��)=0 is valid uniformly, ∀�� >0 there exists ���� >0 so that when �� >���� there is an inequality for every �� ∈ℂ such that |��(��)|=������ 1, and therefore
By Jordan’s inequality
for
, we then obtain
proving the lemma.
Since ℎ(��) is continuous on ���� and analytic within �� enclosed by ����, by Cauchy’s integral theorem:
ℎ(��)����.
Therefore, it implies
By Lemma 1, due to the fact
we have
By Lemma 2, due to the fact that ������ ��→0
Consequently,
]=0 is uniformly valid on ����, we have
so that, by taking imagery parts, we obtain
However, we can also evaluate it directly by using properties of definite integrals,
and let �� = �� and
, by changing the signs of the limits of integration we obtain
Plugging the value into the Green function yields
By reversing the roles of �� and �� ����, we obtain the Green function
PART IV: THE SEEKING OF THE FUNDAMENTAL SOLUTION OF THE POTENTIAL FIELD
Substituting the result into the equation of the potential field ��(��) yields the general solution to Poisson’s equation in which
The expression represents the sum of all mass components contributing to the total potential on a given coordinate. The integral of a spherical symmetric mass over an external point can be calculated analytically for certain cases, resulting in a function of the distance to the center of the sphere described as follows:
Recall the gravitational field strength is the magnitude of the gravitational field. This shows that
which matches the outcome done by Gauss’s law In our case, the function of density ��(��) is well-defined so the gravitational field strength can be calculated as follows: (suppose �� is the radial displacement of the Gaussian sphere, that is, the distance of the observation point)
For ��≳��: (The field strength on the surface of planet ��: inversely proportional to ��)
Since the observation point is located outside planet ��, we have
For ��<��: (The field strength inside planet ��: proportional to ��)
Since the observation point is located inside planet �� and its coordinate is ��, then all spherical shells that have radius exceeding �� do not contribute to the gravitational field at the observation point. Correspondingly, we obtain
For ��≳½��: (The field strength on the surface of the inner solid sphere of radius ½�� enclosed by planet ��: inversely proportional to ��)
Since the observation point is located inside planet �� but outside the inner solid sphere and its coordinate is ��, then all spherical shells that have radius exceeding �� do not contribute to the gravitational field at the observation point. Correspondingly, we have
Given the fact that we have
by comparing 1 2��0 and ��½�� we obtain
Clearly, the field inside the planet decreases towards its center, whereas the field outside the planet behaves like a point source. The conclusion shows that
Q.E.D.
REFERENCES
1. Callahan, James J. (2010), Advanced Calculus: A Geometric View (NY: Springer-Verlag) pp. 452-453. (高等微積分: 幾何視角觀)
2. Gelca, Răzvan and Andreescu, Titu (2007), PUTNAM and BEYOND (NY: SpringerVerlag) pp. 578. (普特南數學競賽習題集)
3. Kaufman, Alexander A. (1992), Geophysical Field Theory and Method: Gravitational, Electric, and Magnetic Fields (CA: Academic Press) pp. 155-156. (地球物理的場論與方法: 重力場、電場和磁場)
4. Rudin, Walter (1976), Principles of mathematical analysis, McGrew Hill, 3rd ed. (數學分析 原理)
5. Zorich, Vladimir A. (2000), Mathematical Analysis II (Berlin: Springer-Verlag) pp. 278280. (數學分析 II)
EXTERNAL LINKS
1. Campuzano, Carlos Ponce J. (2019), Complex Analysis: A Visual and Interactive Introduction, principal argument [1] (complex-analysis.com/) 複分析: 視覺與互動式教學
2. Fufaev, Alexander (Фуфаев, Александр), Physics illustrations [2]. (en.universaldenker.org/physiker/alexander-fufaev) 物理視覺效果圖 散度定理
3. Hunt, Robert (2002), Mathematical Methods II (Natural Sciences Tripos, Part IB) Christ’s College Cambridge Lecture Notes for Chapter 2: Poisson’s Equation. (damtp.cam.ac.uk/user/reh10/lectures/) 劍橋大學基督學院 2002 年數學方法 II 講義: 泊松方程
4. Khan, Amir (2010), Potential Field Theory Lecture 2: Newtonian Potential and Applications, ETH Zurich Lecture Notes. (jupiter.ethz.ch/~akhan/amir/Teaching.html) 蘇黎 世聯邦工科學院位場論講義: 牛頓位及其應用
5. Morrow, James (2012), Honors Advanced Calculus, MATH335, Fubini’s Theorem [3], University of Washington. (sites.math.washington.edu/~morrow/335_12/fubini.pdf) 西雅圖 華盛頓大學榮譽高等微積分班 富比尼定理
6. National Tsing Hua University (2023), 2023 Entrance Examination (Physics) given by the post-baccalaureate program in medicine, question 46. (adms.site.nthu.edu.tw/p/406-1207246483,r6125.php?Lang=zh-tw) 清華大學學士後醫學院 2023 學年度理化試題第 46 題
