Abstract: A basic understanding of Gauss's flux theorem in electrostatics is imperative at the beginning of university physics. The theorem is, however, seldom used in determining theintensityofgravitationalfieldsinintroductorycalculus-basedphysics.Fromaconceptual standpoint, both Newton’s gravitational and Coulomb’s electrostatic forces obey the inverse square law. In Newtonian mechanics, the inverse square law of force states that a particle follows an elliptical path when moving. The same phenomenon occurs with charges in electrostatics Likewise, gravitational and electrostatic forces all possess potential energy whose corresponding potentials satisfy the Poisson equation without a source term, i.e., ��2�� =0. When the electrostatic and gravitational forces are equal to the derivative of their potential's negative value, the force field will be inversely proportional to distance r, that is, ��(��)∝�� 1 ⇒��(��)= ��(��)∝�� 2. Newton's law of universal gravitation and Coulomb's law of electrostatics are essentially the same. Therefore, Gauss's law is also applicable for gravitation.Inthispaper,wecanlearnabouthowGauss'sfluxtheoremisused indetermining the intensity of gravitational fields through a physics problem of the 2023 entrance examination presented by Tsinghua University’s post-baccalaureate program in medicine
Consider the problem of measuring the intensity of the gravitational field sourced by a point mass, described as follows:
The mass density inside a planet is usually not uniform. However, the mass density of the concentric shells of a spherical planet is about the same when the planet is decomposed into concentric spherical shells. As a result, for a spherical planet �� of radius ��, the mass density can be treated as a function of its distance to the center of the planet
��(��)=��0 (1 �� 2��)
Assuming the gravitational field strength at the planet’s surface is ����>�� ≝��0 Show that at �� = 1 2 ��, the gravitational field has a magnitude smaller than half that of planet ��'s surface but is not zero, that is,
A planet’s density usually increases as we go inwards from the crust to core. Suppose a planet called �� is an oblate spheroid of radius �� and that its density �� is modeled by
��(��)=��0 (1 �� 2��)
where �� is the distance from the center, ��0 is constant. The approximate volume of a spherical shell of radius �� and thickness ���� is given by
so the mass in this shell is given by
where ��(��) is the mass density as a function of the coordinates ��∈ℝ3, which yields a more general equation in spherical coordinates
or in Cartesian coordinates,
Therefore, the total mass as a function of �� is given by the integral
Theorem 1. Let �� be a compact domain in ℝ3 with piecewise-smooth boundary ����. If �� is a smooth vector field in ��; then the flux of �� across the boundary ���� of �� is
Proof. Using planes parallel to the coordinate planes to divide �� into multiple small cuboids. Assuming the center of one of the cuboids is defined at ��(��,��,��) with sides of length Δx, Δy, and Δz. Let
be a smooth vector field, that is,
Thus, the values of �� at the midpoint of two faces of area �������� perpendicular to the x-axis are ��+ 1 2 ���� ���� ���� and �� 1 2 ���� ���� ���� respectively. That being the case, the sum of the surface integrals upon the two faces perpendicular to the x-axis becomes
Similarly, the sum of the surface integrals upon the two faces perpendicular to the y-axis with area �������� becomes
The sum of the surface integrals upon two faces perpendicular to the z-axis with area �������� becomes
Accordingly, let the entire surface of the cuboid be �� ′ , we have
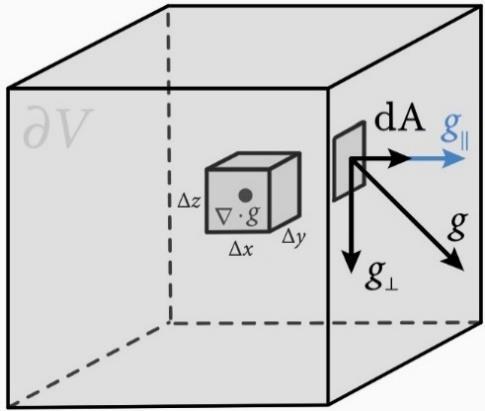Fig 1. Divergence theorem
However, the volume of the cuboid is indeed ������������. Treating it as ���� leads us to
Consequently, we arrive at the fact that
Remark 2. Using Theorem 1, we can measure the flux of a vector field across the boundary of a domain based on the integral of the divergence of the field over the domain itself.
Remark 3. The compact domain �� denotes the enclosed volume.
Remark 4. The following criteria must be met for Theorem 1 to be applicable to specific types of volumes ��:
1. �� must be bounded, contained by a “box” {��∈ℝ3
for some
2. �� has a complete, closed boundary surface �� =���� that cannot be entered or exited without crossing the boundary ��
3. �� is oriented outwards from ��.
4. Suitable geometries include: spheres, ellipsoids, cuboids, tetrahedra, etc.
Theorem 2. Let ��(��) be a neighborhood of ��=(��,��,��) contained in V, that is, a spherical ball ��
3:‖��‖≤��} of radius ��, and �� ̂ the outward unit normal on ����. Let �� be a continuously differentiable vector field defined on an open set containing ��; then the flux of �� across the boundary ���� of �� is
Proof. Since �� is calculated from the integral of the point-mass contributions of the masses distributed in ℝ3 , proving this equality requires only showing the same for a mass concentrated at one point, origin for example. By Newton’s law, the gravitational force between two masses ��1 and ��2 at distance �� is equal to ��1��2�� ��2 The gravitational field strength is generated by a mass �� located at the origin, according to Newton’s law:
In this field, �� ��=0. Consider a small sphere ��0 of radius �� centered at the origin, and let �� be the solid lying between ��0 and ��. By the Gauss-Ostrogradski formula,
As a result, it is sufficient to prove Gauss’s law for sphere ��0. On this sphere the flow �� �� ̂ is constantly equal to ���� ��2 . Integrating it over the sphere gives 4������, �� being the total mass
inside �� with ����, proving the theorem.
Remark 5. The vector �� ̂ is the outward unit normal on the boundary of ��, that is,
Definition 1. A vector that is perpendicular to the plane or a vector and has a magnitude 1 is referred to as a unit normal vector, that is,
Definition 2. Given two nonzero vectors �� and �� in ℝ��, the dot product is defined as,
Theorem 3. Given �� is the angle defined as the unique �� ∈[0,��] between two nonzero vectors �� and ��, the following definition for the dot product between �� and �� is equivalent to Definition 2:
Proof. By the Law of Cosines and the fact that ��⋅��=‖��‖
Using the properties of the dot product, we can rewrite the left side as
Substituting back into the Law of Cosines yields
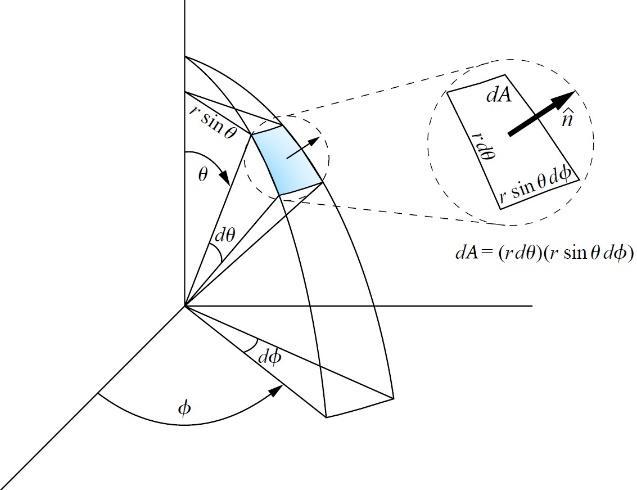
Definition 3. If �� is a smooth vector field defined on a piecewise smooth oriented surface �� with unit normal vector �� ̂, then the flux of �� across �� is
Remark 6. We know �� ����=�� ��̂���� is true by Definition 3, and �� is the radius of spherical Gaussian surface ���� (the boundary of the spherical ball), and �� is the radius of planet ��. In accordance with Definition 1 and Theorem 2, Gauss’s formula yields the equality
where ‖��̂‖=1 and ������(��)= 1. Therefore,
Using the aforementioned remarks, definitions and theorems, we can rewrite the formula as
�������� being the total mass inside the spherical of radius �� with boundary ���� of ��. Mass outside the spherical body makes no contribution. For the case of uniform density, this is equal to �� = 4 3 ����3�� and �� = 4 3��������. In addition, we know from Theorem 2,
Due to its conservative nature, the gravitational field must have an associated potential function ��. In this case, ��= ����. Together with �������� =∭
we can rewrite the equation of Theorem 2 as
Transforming the left hand integral by Theorem 1 gives
This is true for all volumes �� and implies
It follows that the gravitational potential �� satisfies the Poisson equation
Now given that ��(��)=��0 (1 �� 2��) we can measure the gravitational field strength as follows. For �� >��: (The field strength on the surface of planet ��: inversely proportional to ��)
For �� >½��: (The field strength on the surface of the inner solid sphere enclosed by planet ��: inversely proportional to
Given the fact that we have
REFERENCE
Callahan, James J. (2010), Advanced Calculus: A Geometric View (NY: Springer-Verlag) pp. 452-453. (卡拉漢，高等微積分：幾何視角觀)
Fufaev, Alexander (Фуфаев, Александр), Physics illustrations, en.universaldenker.org/physiker/alexander-fufaev (富法耶夫：物理視覺圖)
Gelca, Răzvan and Andreescu, Titu (2007), PUTNAM and BEYOND (NY: Springer-Verlag) pp. 578. (杰拉與安德萊斯庫：普特南數學競賽習題集)
Hunt, Robert (2002), Mathematical Methods II (Natural Sciences Tripos, Part IB) Christ’s College Cambridge Lecture Notes for Chapter 2: Poisson’s Equation. (劍橋大學基督學院 2002 年
數學方法 II 講義 泊松方程)
National Tsing Hua University (2023), 2023 Entrance Examination (Physics) given by the postbaccalaureate program in medicine, question 46. (清華大學學士後醫學院 2023 物理試題)
Zorich, Vladimir A. (2000), Mathematical Analysis II (Berlin: Springer-Verlag) pp. 278-280. (卓
里奇，數學分析 II)
https://issuu.com/ujalatsuyen