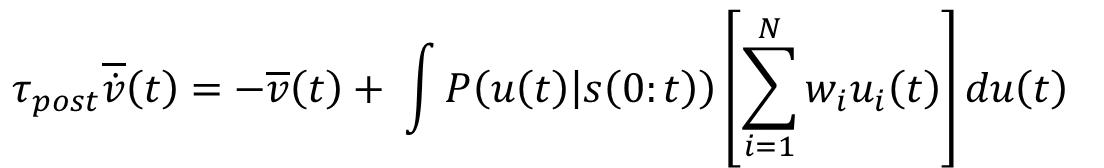
12 minute read
Biophysical Modeling of Nonlinear Dendritic Computations
Akshan Bansal
Advertisement
Nonlinear dendritic integration is crucial for the optimal processing of correlated inputs, may play a role in the location of dendritic clusters, and can be modeled biophysically. Linear integration is necessary for the processing of uncorrelated inputs where presynaptic neurons and postsynaptic dendrites are at a distance. The study make advancements in the field by expanding the study of dendritic computation to large scale networks using in vivo and in vitro statistics and produces high resolution results. Further studies need to involve optogenetic tools, and vary controls from spontaneous network activity to nonnaturalistic activity across single stimulus dimensions. Understanding of neural mechanisms related to processing can in the future be applied to neuromorphic hardware and machine learning for greater efficiency in processing.
The computational ability of the human brain has previously been attributed to multi-layer neuronal networks capable of performing mathematical calculations individuals neurons could not, where neurons acted as simple point-like switches which merely summed up incoming potentials and upon exceeding a threshold, fired action potentials, (London and Hausser, 2020). Models that did view single neuron systems as a computational entity through the use of logic gates were highly restricted due to simplistic input measures, the lack of consideration given to the different internal structures of a neuron, and the lack of tools available to record activity along the various components of a dendrites, (Li, 2019). The finding that voltage signals decreased in magnitude whilst propagating along the axon pointed neuroscientists towards the idea that signals are compartmentalized and may be processed independently within the neuron, (Koch, 1982). This countered the long established view in computational neuroscience that single artificial neurons could not perform a nonlinear operation known as a XOR function, (Minsky and Papert, 1969). Although, developments in the field have led to plausible biophysical mechanisms modelling not only the ability of single neurons to act as a two-layer neural network but also the ability of dendrites to perform XOR and a host of other operations, it is unknown how dendritic nonlinearities contribute to computations at the level of the neural circuit, (Poirazi, 2003). Patterned stimulation of cortical pyramidal cells from the neocortex and hippocampus using two-photon glutamate uncaging and electrophysiology was executed to obtain in-vitro postsynaptic activity patterns consistent with a biophysical model that accounts for spatio-temporal variation and is built upon naturalistic in-vivo statistics. This depicted that the optimal response of a dendritic nonlinearity is dictated by presynaptic population statistics, that these nonlinearities are essential for the efficient integration of signals in neural circuits with analog computation, and the necessity of NMDA receptor activation for optimal dendritic integration. The associated novel biophysical model not only adds to the list of computational operations a neuron and its dendritic tree can perform but also draws light to the matter of single neuron systems and subsystems and their influence at the level of the neocortical circuit. This shift in the way we think model involves the linear integration of information within a branch, its conversion through a sigmoidal nonlinearity, and the al nonlinearity model was found to be valid across supralinear
about the processing power of the human brain will influence the representation of neuronal structures and the organization of information in machine learning, hebbian plasticity, and memory, (Richards, 2019).
Major Results Section
Correlated information sources require nonlinear integration of presynaptic somatic membrane potentials due to the arisal of a bottleneck in circuit computations where the relationship between the presynaptic and postsynaptic neurons is dictated by analog variables as seen in cortical coding, (Cepelewicz, 2020; Clark and Hausser, 2006). By making this assumption about the arithmetic being performed by the postsynaptic cell, and reFigure 1.0: Linear versus optimal response https://doi.org/10.7554/eLife.10056.010
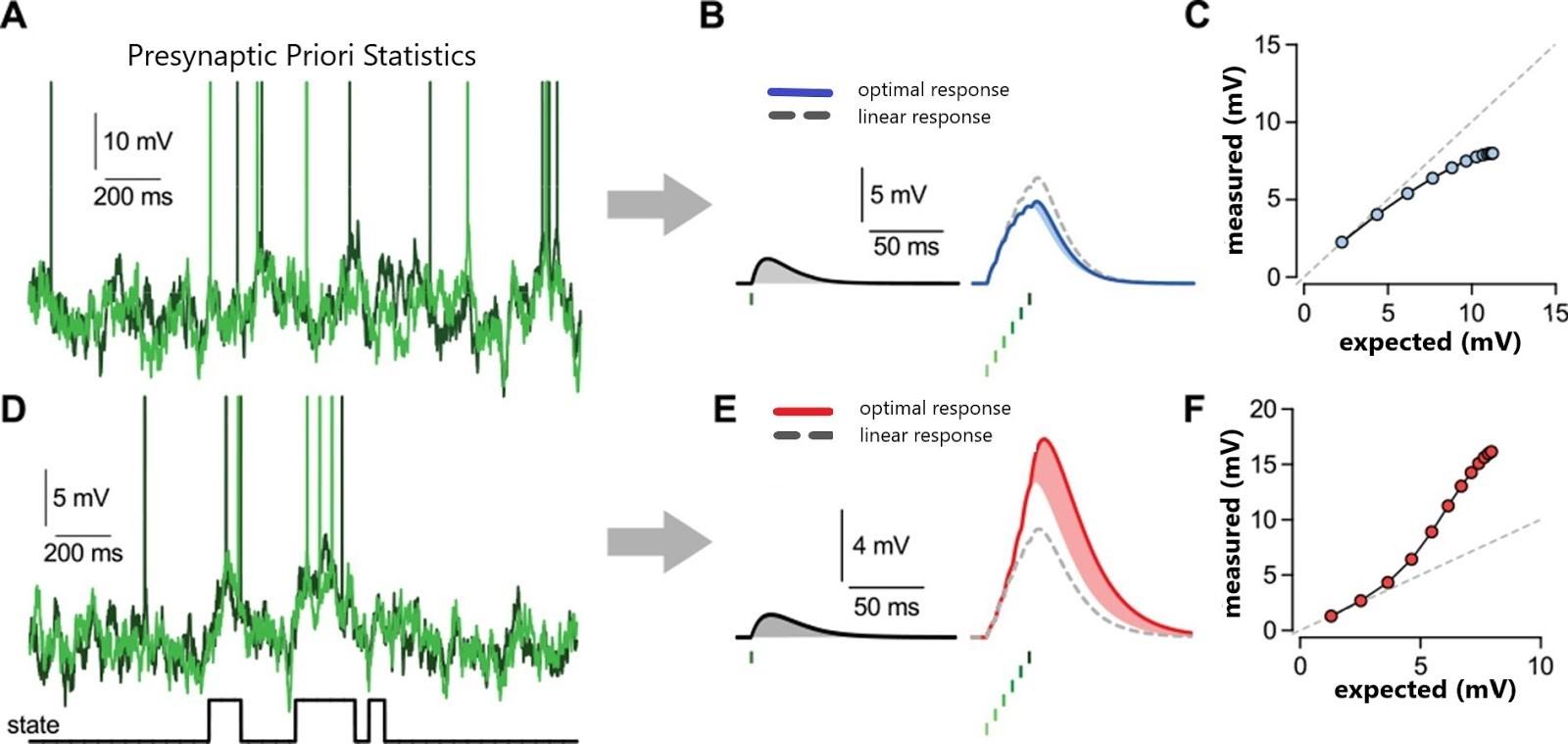
Statistical models derived presynaptic statistics in line with in vitro and in vivo multielectrode readings of neuronal cortical population after which comparison between the linear response and the optimal response dictated by the aforementioned equation revealed that linear integration was optimal for uncorrelated inputs (A-C), and nonlinear integration was optimal for correlated inputs (D-F).
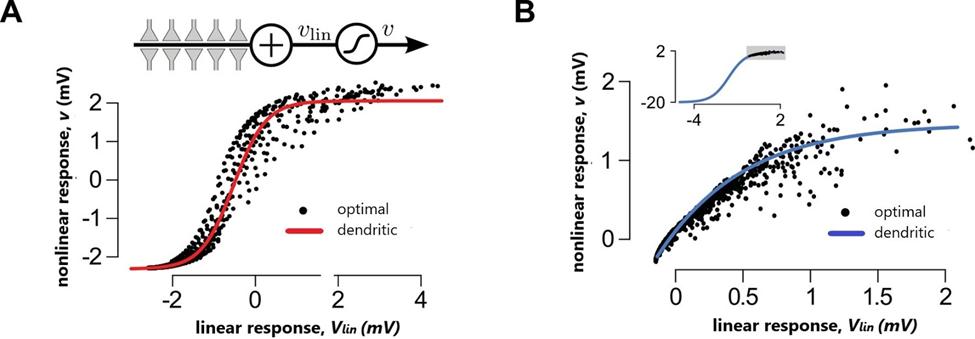
Figure 2.0: A simple model of nonlinear dendritic integration can approximate the optimal response https://doi.org/10.7554/eLife.10056.012
A simple, biophysically-motivated, canonical model of nonlinear dendritic integration was shown to closely approximate the optimal response when the majority of presynaptic neurons switch between a quiescent state and an active state. This ultimate formation of the local dendritic response. The sigmoidstricting presynaptic values by in vivo data from cortical popula
and sublinear integration.
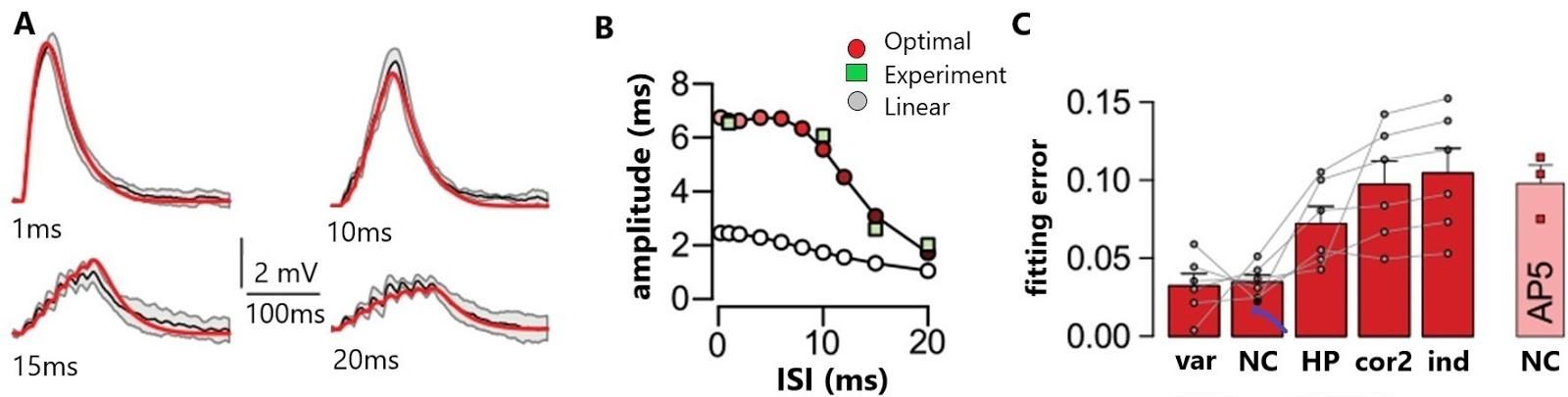
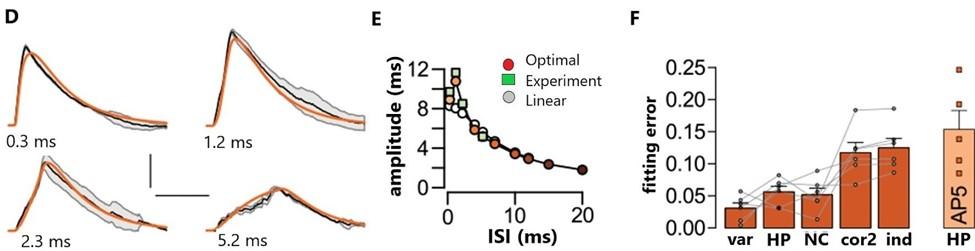
Figure 3.0: Nonlinear dendritic integration and presynaptic input statistics https://doi.org/10.7554/elife.10056.018
There’s an ideal fit between the optimal response and nonlinear integration in single cortical neurons, (Figure 3A, 3D). Response amplitudes (ms) were seen to depend on the interstimulus interval (ISI) and were well predicted by the optimal across supralinearity and sublinearity, (Tzilivaki, 2019). It has been shown that linear integration with a single global dendritic nonlinearity can fit the response of neurons to naturalistic input patterns, (Ujfalussy, 2016). In addition, nonlinearities are essential for the efficient computing of information due to resources saved during encoding, (Tzilivaki, 2019). The effect of (Pfister, 2010). The majority of the results are in line with and
response, (Figures 3B, 3E). Correlations of the second order (cor2) or independent presynaptic firing (ind) resulted in poor fits with the optimal response in comparison to populations in the neocortex (NC) and the hippocampus (HP) across a varying range of conditions, (Figure 3C, 3F). Presynaptic cortical function was found to determine the location of the dendritic nonlinearity as seen by the inability of the optimal response to be a good fit when hippocampal rather than neocortical activities were matched for presynaptic statistics in cortical pyramidal neurons. Furthermore, NMDA receptor activation proved to be inter-stimulus intervals on response amplitudes and synaptic efficacies along with the presence of fast evolving, analog potentials and computation in cortical structures was noted,
crucial for optimal dendritic integration. build upon previous works. These findings can alter machine learning and neuromorphic hardware platforms to represent single neuron systems as 2 stage networks to increase processing ability, and storage, (Stockel, 2019).
Conclusions/Discussion
The optimal response, the computation performed by a postsynaptic cell in relation to specific presynaptic statistics, was defined as:
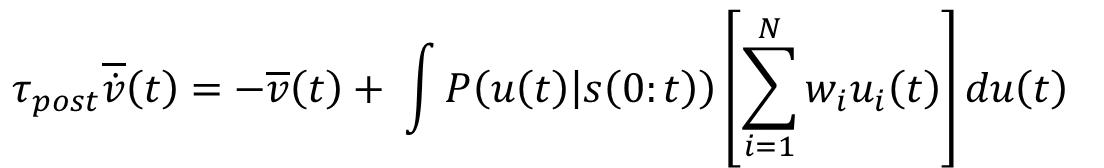
The function successfully modelled in vitro measurements of the nonlinear integration of correlated inputs in single cortical neurons based on a given set of in vivo input statistics. The observed dependence of response amplitudes on interstimulus intervals points to the conclusion that not only is there nonlinear dendritic computation but also that dendritic nonlinearities are efficiently tuned to presynaptic activity patterns. Furthermore, it was also revealed that synaptic clustering of nonlinear neural assemblies exhibits an optimal integration of correlated inputs. Novel interpretations come in the form of suggesting the essential role of NMDA receptors in dendritic nonlinearities, and the idea that short term neural plasticity plays a role in tuning the form of the optimal response to presynaptic statistics. In addition, the study pushes for further investigation of the relationship between the structure of correlations and morphological clustering. It was concluded that nonlinear dendrites are compulsory for the successful processing of varying spatio-temporal lishing a causal link between single system and network level
Figure 4.0: Clustered connectivity and optimal response https://doi.org/10.7554/eLife.10056.015
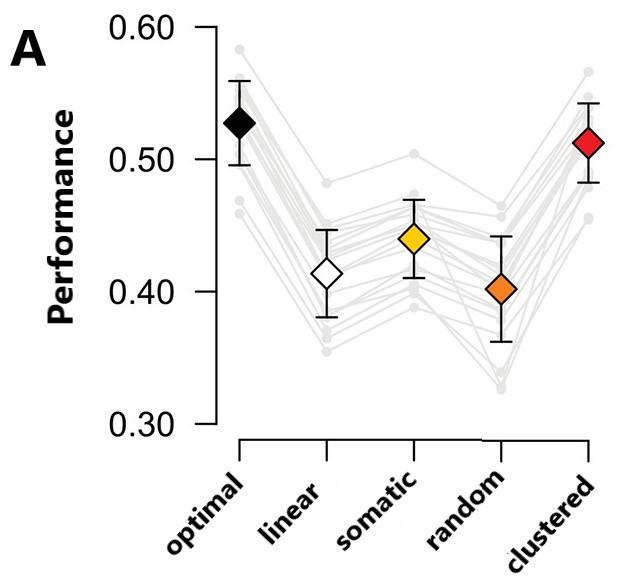
Figure 4.0 shows a comparison of a model with linear dendrites and a soma, a model in which only the soma is nonlinear, and two models with nonlinear dendrites with either random or clustered connectivity. Nonlinear dendrites with clustered connectivity between the presynaptic neuron and the dendritic branches proved to be at performance par with the optimal
The modeling of dendritic computational function by a simple method of nonlinear integration has previously been seen in FS basket cells in both the hippocampus and prefrontal cortex activity and that they hence play a vital role in higher level computation in neural circuits. These findings work towards estab
response. computations and naturalistic behaviors. This will aid in the better understanding of short term dendritic plasticity and processing ability in vertebrates and the application of neural structures to machine learning.
Critical Analysis
The authors have done an excellent job at extending controls for not only data sets extracted for in vivo neuronal population statistics from pre-existing works but also when examining the link between nonlinear clustered dendrites and optimal re-
-sponse. Relationships were studied whilst varying various presynaptic statistics such as ISI, number of neurons, and hippocampal and neocortical input values. For results displayed in Figure 3.0, It was made sure that in vitro stimuli activated dendrites in a range comparable to in vivo conditions and hence integration was observed from a physiologically relevant context. Crucially, application of Bayesian Information Criterion ensured that the significant match between predicted and actual dendritic nonlinearities was not due to an overfitting error and the presence of an additional parameter.
There exists a wealth of resources supporting the fundamentals used to build the framework of the study and the model of the inputs is dependent on the species and brain area in question
optimal response. Neuronal systems in the neocortex and hippocampal pyramidal cells display analog communication to perform basic arithmetic function economically and accurately, (Laughlin and Sejnowski, 2003). The study built upon this idea by suggesting that nonlinear integration would then be necessary for efficient processing of varying spatial-temporal patterns and that it could be modeled biophysically, (Poirazi and Mel, 2001; Grienberger et al., 2014). Although, the presence of nonlinear integration has previously been shown in the visual and somatosensory cortices, the authors expand the field by presenting proof in an unprecedented large scaled network model whilst not only varying input statistic spatially and temporally but also considering computations at the level of the distanced synapses. However, in the case that the null hypothesis is correct, it may be that neurons with overlapping receptive fields are creating excessive noise. An alternate theory would be that there exists only single neural systems initially, and then occurs rapid neural plasticity and reconfiguration to form local synaptic clusters upon encountering correlated activity. This theory concurs with evidence that supports the existence of probationary or silent phases in newly formed synapses, “Poirazi and Mel, 2001). Summarily, this suggests that synapse clusters and their location in relation to presynaptic correlated
dendrite, (Smith et al., 2013; Xu et al., 2012). as well as the history a person may have in encountering tested stimulus.
The authors should continue their pursuit of the accurate representation of neural assemblies by modifying in vitro stimulation parameters and structural details to match those in vivo as this will aid in the better understanding of short term dendritic plasticity and processing ability in vertebrates and the application of this neural structure to machine learning. Further experiments should test the ability of the model to predict the location and clustering of postsynaptic branches based on presynaptic correlations as there exists contradicting evidence based on varying controls like in vivo spontaneous network activity, and non-naturalistic activity across single stimulus dimensions, (Kirchner and Gjorgjieva, 2019).
Future Directions
Future repetitions of the experiment should modify in vitro stimulation parameters and structural details to match those in vivo through the use of voltage dyes which allow for the detection of subthreshold synaptic potentials in addition to spiking activity, (Rost et al., 2017). The use of dendrite targeted optogenetic tools such as fluorescent sensors and optogenetic actuators to visualize signaling events and manipulate cellular activity should be used so that the authors may compare naturalistic data rather than predicted values for the biophysical model. More importantly, these techniques can be used to further explore the disputed link between the presence and location of synaptic clusters and correlated inputs. I believe the results would be in line with the notion that correlated activity in presynaptic cells is tied to the nearby clustering of synapses whereas independent activity leads to linear processing in more
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16. Ujfalussy, B. B., Makara, J. K., Branco, T., & Lengyel, M. (2015). Dendritic nonlinearities are tuned for efficient spike-based computations in cortical circuits. eLife, 4, e10056. https://doi.org/10.7554/eLife.10056 Grienberger, C., Chen, X., & Konnerth, A. (2014). NMDA Receptor-Dependent Multidendrite Ca2 Required for Hippocampal Burst firing in Viv. Neuron, 81(6), 1274-1281. Doi:10.1016/j.neuron.2014.01.014 Smith, S., Smith, I., Branco, T. et al. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo . Nature 503, 115–120 (2013). https://doi.org/10.1038/nature12600 Xu, N., Harnett, M., Williams, S. et al. Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature 492, 247–251 (2012). https://doi.org/10.1038/nature11601 Poirazi, P., & Mel, B. W. (2001). Impact of Active Dendrites and Structural Plasticity on the Memory Capacity of Neural Tissue. Neuron, 29(3), 779-796. Doi:10.1016/s0896-6273(01)00252-5 Cepelewicz, J. (2020). Hidden Computational Power Found in the Arms of Neurons. Retrieved June 12, 2020, https:..www.quantamagazine.org/neural-dendrites-reveal-their-computational-power-20200114/ Poirazi, P., Brannon, T., & Mel, B. W. (2003). Pyramidal Neuron as Two-Layer Neural Network. Neuron, 37(6), 989-999. Doi: 10.1016/s0896-6273(03)00149-1 Rentinal ganglion cells: A functional interpretation of dendritic morphology. (1982). Philosophucal Transfactions of the Royal Society of London. B, Biological Sciences, 298(1090), 227-263. Doi:10.1098/rstb.1982.0084 Li, S., Liu, N., Zhang, X., Mclaughlin, D. W., Zhou, D., & Cai, D. (2019). Dendritic computation captured by an effective point neuron model. Proceedings of the National Academcy of Sciences, 116(30), 15244-15252. Doi:10.1073/pnas.1904463116 Richards, B.A., Lillicrap, T.P., Beaudoin, P. et al. A deep learning framework for neuroscience. Nat Neurosci 22, 1761–1770 (2019). https://doi.org/10.1038/s41593-019-0520-2 Clark, B., & Hausser, M. (2006). Neural Coding: Hybrid Analog and Digital Signaling in Axons. Current Biology, 16 (15). Doi:10.1016/j.cub.2006.07.007 Tzilivaki, A., Kastellakis, G. & Poirazi, P. Challenging the point neuron dogma: FS basket cells as 2-stage nonlinear integrators. Nat Commun 10, 3664 (2019). https://doi.org/10.1038/s41467-019-11537-7 Ujfalussy, B. B., Makara, J. K., Lengyel, M., & Branco, T. (2018). Global and Multiplexed Dendritic Computations under in viv like Condition. Neuron, 100(3). Doi:10.1016/j.neuron.2018.08.032 Pfister, & Lengyel, Mate. (2010). Synapes with short term plasticity are optimal estimators of presynaptic membrane potentials. Nature Neuroscience. 13.1271-5. 10.1038/nn.2640 Sotckel, A., & Eliasmith, C. (2019). Passive nonlinear dendritic interactions as a general computational resource in functional spiking neural networks. 1-28. Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neuronal networks. Science (New York, N.Y.), 301 (5641), 1870–1874. https://doi.org/10.1126/science.1089662










