WORD VERSION | 2023 EDITION
NOW / CHUYỂN GIAO QUA EMAIL


Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNh Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thu Nguyen Thanh Tu Group ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection 40-60 ĐỀ THI THỬ TỐT NGHIỆP THPTMÔN TOÁN - NĂM 2023 - SOẠN CHUẨN CẤU TRÚC MINH HỌA BGD NGÀY 1-3 (Đang cập
nhật) (ĐỀ SỐ 1-10)
ORDER
vectorstock com/28062405
TAILIEUCHUANTHAMKHAO@GMAIL COM
12 B. 24
12
Câu 6: Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng ( )P : 230 xz−+= . Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng ( )P ?
( )2;1;3 u =− . B. ( )2;0;3 v = .
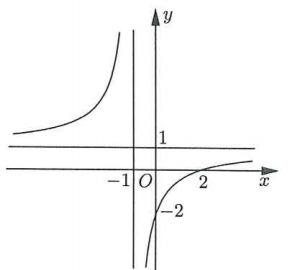
Câu 7: Cho hàm số axb y cxd + = + có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm
ố đã cho và trục tung là
Câu 8: Cho 22 11 ()d3; ()d2fxxgxx==−
. Khi đó
ng
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 1 PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 MÔN TOÁN ĐỀ SỐ: 01 – MÃ ĐỀ: 101 Câu 1: Điểm M trong hình vẽ bên biểu diễn phức nào sau đây? A. 1 2 zi =+ . B. 2 2 zi =− . C. 3 12 zi =+ . D. 4 12 zi =− . Câu 2: Trên khoảng ( ) 0, +∞ , đạo hàm của hàm số 3 log2023 = yx là A. 1 ln3 y x ′ = . B. 1 2023 ′ = y x . C. 1 y x ′ = . D. 1 2023ln3 ′ = y x . Câu 3: Trên khoảng ( ) 0, +∞ , đạo hàm của hàm số 7 3 yx = là A. 10 3 3 ' 10 yx = . B. 4 3 3 ' 7 yx = . C. 4 3 7 ' 3 yx = . D. 4 3 7 ' 3 yx = . Câu 4: Tập nghiệm của bất phương trình 2422xx+ < là A. ( );4−∞ B. ( )0;4 C. ( )0;16 D. ( ) 4; +∞ Câu 5: Cho cấp số nhân ( ) n u có số hạng đầu 1 3 u = và số hạng thứ hai 2 6 u =− . Giá trị của 4
b
C.
D.
u
ằng A.
24
A.
C.
D.
2;0;1
( )0;2;1 w =− .
( )
n =− .
A. (0;2) B. (2;0) C. (2;0) D. (0;2)
s
() 2 1 ()()d
A. 5 B. 5 C. 1 D. 1 1 2 O M y x
fxgxx + bằ
Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A. 1 1 x y x + = B. 1 2 x y x = C. 1 x y x = D. 1 2 x y x + =
Câu 10: Trong không gian Oxyz , cho mặt cầu () S có phương trình là 222 22430xyzxyz++−−−−= . Mặt cầu () S có tâm I và bán kính R là
A. () 2;2;4 I và 3 R = . B. () 2;2;4 I và 4 R = .
C. () 1;1;2 I và 3 R = D. () 1;1;2 I và 4 R =

Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng () :2z30Pxy−−−= và () :z20.Qx −−= Góc giữa hai mặt phẳng () P và () Q bằng
A. 30° B. 45° C. 60° D. 90°
Câu 12: Cho số phức ()5 1 zi =− . Tìm phần ảo của số phức wiz =
A. 4 B. 4 C. 4i D. 4i
Câu 13: Thể tích V khối lập phương cạnh 3a là
A. 3 81 Va = B. 3 9 Va = C. 3 Va = D. 3 27 Va =
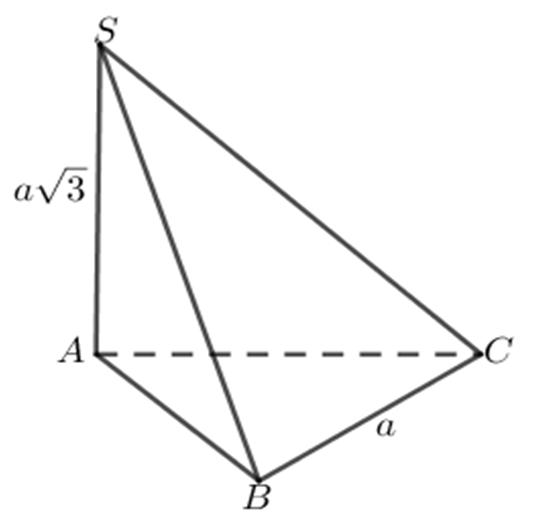
Câu 14: Cho hình chóp . SABC có đáy là tam giác đều cạnh 2a , cạnh bên SA vuông góc với đáy và 3 SAa = . Tính thể tích V của khối chóp SABC
A. 3 1 2 Va = . B. 3 3 4 Va = . C. 3 22Va = . D. 3Va = .
Câu 15: Trong không gian Oxyz , cho mặt cầu () S có tâm () 1;3;2 I và tiếp xúc mặt phẳng () Oyz .
Phương trình của () S là
A. ()()() 222 1322xyz −++++= . B. ()()() 222 1321xyz ++−+−= .
C. ()()() 222 1321xyz −++++= .
Câu 16: Phần ảo của số phức 27=− zi bằng:
D. ()()() 222 1322xyz ++−+−= .
A. 7 . B. 7i . C. 2. D. 7 .
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 2
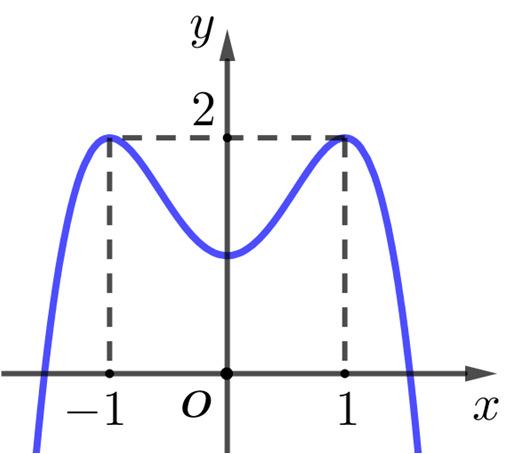
( )yfx = xác định và liên tục trên đoạn [ ]2;2 và có đồ thị là đường cong trong hình vẽ sau.
Điểm cực tiểu của đồ thị hàm số ( )yfx = là
A. 1 x = B. 2 x =− C. ( )1;2 M D. ( )2;4 M

Câu 20: Đường tiệm cận ngang của đồ thị hàm số 24 1 x y x = có phương trình là
A. 2 y = B. 2 x = C. 1 x = D. 4 y =
Câu 21: Bất phương trình 2 log3 x < có tập nghiệm là
A. ( ) 8; +∞ B. ( );8−∞ C. ( )0;8 D. ( );6−∞
Câu 22: Số cách chọn 2 học sinh từ 12 học sinh là
A. 2 12C B. 212 C. 2 12A D. 122
Câu 23: Trong các hàm số dưới đây, hàm số nào có họ tất cả các nguyên hàm là hàm số () , ln x a FxC a =+ ( 0,1, aaC >≠ là hằng số).
A. ( ) x fxa = B. () 1 fx x = C. ( ) ln.fxx = D. ( ) afxx =
Câu 24: Cho ()
x=10fxd . Khi đó ()
23x fxd
A 32 B. 36 . C. 42 . D. 46 .
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 3
ng kính đáy bằng 6 và độ dài đường sinh 6 l = . Diện tích xung quanh của hình nón đã cho bằng A. 6π B. 108π C. 36π D. 18π
không
Oxyz , điểm nào dưới đây thuộc đường thẳng 1 :5 23 xt dyt zt =− =+ =+ . A. ( )1;2;5 P B. ( )1;5;2 N C. ( )1;1;3 Q D. ( )1;1;3 M
ố
Câu 17: Cho hình nón có đườ
Câu 18: Trong
gian
Câu 19: Cho hàm s
5 2
5 2
+
bằng
Câu 25: Cho ()Fx là một nguyên hàm của hàm số () 6sin3 fxxx =+ và () 2 0 3 F = . Khẳng định nào sau
đây đúng?
A. () 2 cos3 31 3 x Fxx=++ . B. () 2 cos32 3 33 x Fxx=−+ .
C. () 2 cos3 31 3 x Fxx=+− . D. () 2 cos3 31 3 x Fxx=−+ .
Câu 26: Cho hàm số ()fx có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. () ;2−∞− B. () 2;2 C. () 1;3 D. () 2; +∞
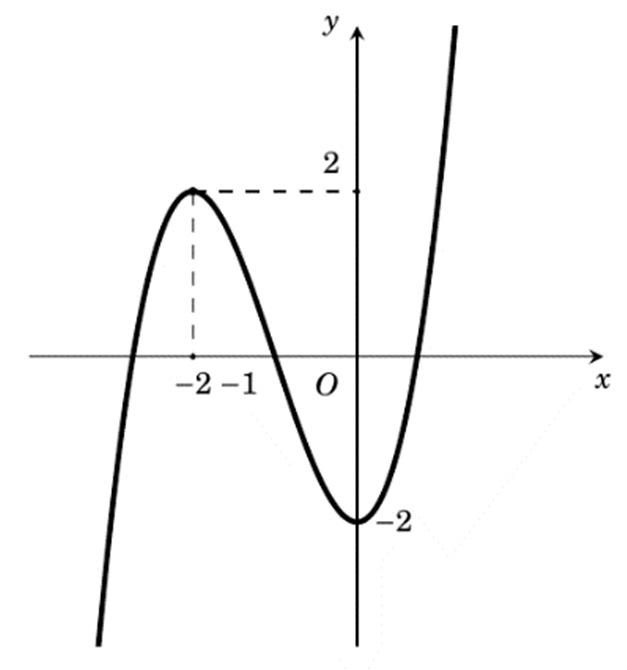
Câu 27: Cho hàm số () ==+++ 32 yfxaxbxcxd và có đồ thị là đường cong trong hình vẽ bên. Hàm số ()fx đạt cực đại tại điểm nào dưới đây?
A. =−2 x .


DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 4
B. =−1 x . C. = 1 x . D. = 2 x Câu
ực dương tùy ý,
2 3 log.ab bằng A.
B.
33 2loglog
+ C. 33 1 loglog 2 ab + D. 332loglogab
i hạn bởi đồ thị hàm số 2 3 yxx =− và trục hoành. Tính thể tích V của vật thể tròn xoay sinh ra khi cho () H quay quanh trục Ox . A. 81 10 V π = . B. 81 10 V = . C. 9 2 V = . D. 9 2 V π = . Câu 30: Cho hình lăng trụ tam giác đều . ABCABC′′′ có cạnh đáy bằng a và cạnh bên bằng 2 a . Góc giữa hai mặt phẳng () ABC ′ và () ABC bằng A. 30° . B. 60° . C. 45° . D. 90° .
28: Với , ab là các số th
()
33 log2logab +
()
ab
Câu 29: Cho hình phẳng () H giớ
Câu 31: Cho hàm số ( )yfx = xác định và liên tục trên khoảng ( ) ; −∞+∞ , có bảng biến thiên như hình
vẽ:
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình ( ) 20 fxm+= có đúng 3 nghiệm phân biệt?
A. 7 B. 11
C. 8 D. 13
Câu 32: Cho hàm số ()fx có đạo hàm trên ℝ là ( ) 2 '()1fxxx=− . Hàm số đã cho đồng biến trên khoảng
A. ( ) 1; +∞ B. ( ) ; −∞+∞ C. ( )0;1 D. ( );1−∞
Câu 33: Từ một hộp có 15 viên bi trong đó có 6 viên bi màu đỏ và 9 viên bi màu xanh. Lấy ngẫu nhiên
đồng thời 3 viên bi. Xác suất để 3 viên bi có cả hai màu
A. 8 35 B. 12 65 . C. 27 35 D. 4 91
Câu 34: Tích các nghiệm của phương trình 2 33 loglog(9)40 xx−−= bằng
A. 6 . B. 3 . C. 3 . D. 27 .
Câu 35: Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn ( ) 152 izi +−+= là một đường tròn tâm
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 5
I
A.
= . B. ( )2;3 I , 2 R = . C. ( )2;3 I , 2 R = . D. ( )2;3 I , 2 R = . Câu 36: Phương trình nào sau đây là phương trình đường thẳng đi qua hai điểm ( )2;1;3 A , ( )3;0;1 B ? A. 4 1 54 xt yt zt =+ =− =+ . B. 2 1 34 xt yt zt =+ =− =−− . C. 3 14 xt yt zt =− = =+ . D. 4 1 54 xt yt zt =+ =−− =+ . Câu 37: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( ) :240Pxy−−= và điểm ( )1;1;0 M Tìm tọa độ điểm M ′ là điểm đối xứng với M qua ( )P . A. ( )3;3;0 M ′ B. ( )2;1;3 M ′ C. ( )0;2;1 M ′ D. ( )2;3;1 M ′ Câu 38: Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh ,a SA và vuông góc với mặt phẳng đáy. Tính khoảng cách từ trọng tâm G của tam giác SAB đến mặt phẳng ( ) SAC . A. 3 2 a . B. 2 6 a . C. 3 6 a . D. 2 4 a . Câu 39: Số nghiệm nguyên của bất phương trình () ( ) ()() 2 22 2log2log2115 xxxx +−−≥+− là A. 5 B. 6 C. 7 D. 4 4 1 x y' y 3 2 + 0 +∞ ∞ ∞ +∞ 0+
và bán kính R lần lượt là
( )2;3 I , 2 R
Câu 40: Chohàmsố ( )fx liêntụctrên R .Gọi ( ) ( ) , FxGx làhainguyênhàm của ( )fx trên R thỏa
mãn ( ) ( ) 888FG+= và ( ) ( ) 002FG+=− .Khi đó () 0 2 4d fxx bằng
A. 5 4 B. 5 4 C. 5 D. 5
Câu 41: Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 432223yxmxmx =−++− có điểm
cựctiểumàkhôngcó điểmcực đại?
A. 2. B. 4. C. 5. D. 6.
Câu 42: Hai số phức z , w thay đổi nhưng luôn thỏa mãn đẳng thức () 2 2022.2022 12122 w z izizi + +−−=+− .Giátrị lớnnhấtcủa w là
A. 20212 4 . B. 10112 2 . C. 20232 4 . D. 2019 .
Câu 43: Cho hình hộp đứng ABCDABCD ′′′′ có đáy là hình thoi, góc 60 BAD =° đồng thời AAa ′ = Gọi G là trọng tâm tam giác BCD . Biết rằng khoảng cách từ G đến mặt phẳng ( )ABD
Câu 45: Trêntậpcácsố phức,xétphươngtrình 2 80 zmzm−++= ( m làthamsố thực).Cóbaonhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm 12 , zz phân biệt thỏa mãn ( ) ( ) 22 1122 8 zzmzmmz +=−− ?
A. 12 . B. 6 . C. 5 . D. 11.
Câu 46: Trongkhônggianhệ trụctọa độ Oxyz ,cho đườngthẳng 11 : 112 +− == xyz d , ( )1;1;1 I .Viết phươngtrìnhmặtphẳng ( )P chứa đườngthẳng d , đồngthờikhoảngcáchtừ I đếnmặtphẳng ( )P bằng 3.
A. ( ):20Pxyz−+−= , ( ):7520Pxyz+++=
B. ( ):20Pxyz−++= , ( ):7520Pxyz+++= .
C. ( ): 20 Pxyz−+−= , ( ):7520Pxyz++−= .
DẠYKÈMQUYNHƠNOFFICIAL
D. ( ):20Pxyz−++= , ( ):7520Pxyz++−=
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 6
′ bằng 21 21 a .Tínhthể tíchkhốihộp ABCDABCD ′′′′ theo a A. 2 6 a 3 B. 3 6 a 3 C. 2 2 a 3 D. 3 2 a 3 Câu 44: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) 22 .ln2,1;xfxxfxxfxx ′ −+=∀∈+∞
ở
đồ
ị (
2
. A. 3 2 S = B. 1 2 S = C. 5 3 S = . D. 2 S =
, ( ) ( ) 0,1;fxx>∀∈+∞ và () 2 1 e e f = . Tính diện tích S hình phẳng giới hạn b
i
th
)
,0,, yxfxyxexe ====
Câu 47: Cóbaonhiêucặpsố nguyên ( ) , xy thỏamãn
22 3 log33. 2 xy xxyyxy xyxy +
A. 1. B. 2. C. 4. D. 6.
Câu 48: Chohìnhnón đỉnh S ,tâmmặt đáy O vàcódiệntíchxungquanhbằng 2 20 aπ .Gọi A và B là hai điểmthuộc đườngtròn đáysaocho độ dàicung AB bằng 1 3 lầnchuvicủa đườngtròn đáy.
Biếtrằngbánkính đáybằng 4a ,khoảngcáchtừ O đếnmặtphẳng ( )SAB bằng
A. 213 13 a B. 13 13 a C. 1213 13 a D. 613 13 a
Câu 49: Trongkhônggian Oxyz ,chohai điểm ( )2;7;2 A và ( )1;3;1 B .Xéthai điểm M và N thay
đổithuộcmặtphẳng ( )Oxy saocho 3 MN = .Giátrị lớnnhấtcủa AMBN bằng
A. 43. B. 310 . C. 85. D. 65.
Câu 50: Cóbaonhiêugiátrị nguyêncủatham số ( )2022;2022 m ∈− để hàmsố ( ) 3 212xmx y ++− =
đồngbiếntrên ( )1;3 ?
A. 4034 B. 2022 C. 4030 D. 4032
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 7
()()
=−+−+ +++
---------- H
T ----------
Ế
DẠYKÈMQUYNHƠNOFFICIAL
3: Trênkhoảng ( ) 0, +∞ , đạohàmc
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 8 BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.A 5.B 6.D 7.A 8.D 9.A 10.C 11.A 12.A 13.D 14.D 15.B 16.A 17.D 18.B 19.C 20.A 21.C 22.A 23.A 24.B 25.D 26.B 27.B 28.A 29.A 30.A 31.A 32.A 33.C 34.C 35.C 36.D 37.A 38.B 39.B 40.B 41.A 42.B 43.D 44.A 45.C 46.B 47 48.D 49.D 50.C HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Điểm M tronghìnhvẽ bênbiểudiễnphứcnàosau đây? A. 1 2 zi =+ B. 2 2 zi =− C. 3 12 zi =+ D. 4 12 zi =− Lời giải ( )2;1 M là điểmbiểudiễncủasố phức 1 2 zi =+ . Câu 2: Trênkhoảng ( ) 0, +∞ , đạohàmcủahàmsố 3 log2023 = yx là A. 1 ln3 y x ′ = B. 1 2023 ′ = y x C. 1 y x ′ = D. 1 2023ln3 ′ = y x Lời giải Tacó ()
2023ln3ln3 ′ ′ == x y xx . Câu
ahàmsố 7 3 yx = là A. 10 3 3 ' 10 yx = . B. 4 3 3 ' 7 yx = . C. 4 3 7 ' 3 yx = . D. 4 3 7 ' 3 yx = . Lời giải Ta có: 7 3 yx = 4 3 7 ' 3 yx =
24
A. ( );4−∞ . B. ( )0;4 . C. ( )0;16 . D. ( ) 4; +∞ . Lời giải Ta có 24 22244 xx xxx + <⇔<+⇔< . Tập nghiệm của bất phương trình ( );4 S =−∞ . Câu 5: Cho cấp số nhân ( ) n u có số hạng đầu 1 3 u = và số hạng thứ hai 2 6 u =− . Giá trị của 4u bằng A. 12 . B. 24 . C. 12 . D. 24 . 1 2 O M y x
2023 1
ủ
Câu 4: Tập nghiệm của bất phương trình
22xx+ < là
639=+⇔−=+ =− uuddd
41 333(9)24uud=+=+−=−

DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 9
Ta
Lời giải
có: 21
i đây
ủ
A. (
2;1;3 u =−
B. ( )2;0;3 v = . C. ( )0;2;1 w =− . D. ( )2;0;1 n =− . Lờ
giải Ta có (
P
ận (
2;0;1
=− làm 1 vectơ pháp tuyến. Câu 7: Cho hàm số axb y cxd + = + có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là A. (0;2) B. (2;0) C. (2;0) D. (0;2) Lời giải Câu 8: Cho 22 11 ()d3; ()d2fxxgxx==− . Khi đó () 2 1 ()()d fxgxx + bằng A. 5 . B. 5 . C. 1 . D. 1 . Lời giải Ta có () 222 111 ()()d()d()d3(2)1 fxgxxfxxgxx+=+=+−= . Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Câu 6: Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng ( )P : 230 xz−+= . Vectơ nào dướ
là một vectơ pháp tuyến c
a mặt phẳng ( )P ?
)
.
i
)
: 230 xz−+= nh
)
n
Câu 10: Trong không gian Oxyz , cho mặt cầu () S có phương trình là 222 22430xyzxyz++−−−−=
. Mặt cầu () S có tâm I và bán kính R là
A. () 2;2;4 I và 3 R = B. () 2;2;4 I và 4 R =

C. () 1;1;2 I và 3 R = . D. () 1;1;2 I và 4 R = .
Lời giải
Mặt cầu () S có tâm () 1;1;2 I và bán kính () 222 11233 R =++−−=
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng () :2z30Pxy−−−= và
() :z20.Qx −−= Góc giữa hai mặt phẳng () P và () Q bằng
A. 30° B. 45° C. 60° D. 90° Lời giải Ta có () :2z30Pxy−−−= VTPT () 1 2;1;1 n =−−
:z20Qx −−= VTPT () 2 1;0;1 n =−
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 10 A. 1 1 x y x + = . B. 1 2 x y x = . C. 1 x y x = . D. 1 2 x y x + = . Lời giải Đồ
ố
ệm cận ngang và đường tiệm cận đứng lần lượt là 1
= và 1 x =
thị hàm s
đã cho có đường ti
y
, cắt trục Oy tại điểm () 0;1 nên hàm số đó là 1 1 x y x + =
Khi
()()() ()() () 12 222222 12 . 2.10.11.1 3 cos, 2 . 211.101 nn PQ nn +−+−− === +−+−++− .
củ
số
c
A.
C.
D.
ời
ải
()
đó ()() ()
Do đó ()() (),30PQ =° . Câu 12: Cho số phức ()5 1 zi =− . Tìm phần ảo
a
phứ
wiz = .
4 B. 4
4i
4i L
gi
= . Tính thể tích V của khối chóp SABC
Ta có tam giác đều cạnh 2a nên
Thể tích V của khối chóp .
A. ()()() 222 1322xyz −++++= . B. ()()() 222 1321xyz ++−+−= .
C. ()()() 222 1321xyz −++++= .
D. ()()() 222 1322xyz ++−+−= .
Lời giải
Mặt cầu tâm () ;; Iabc và bán kính bằng R có phương trình:
()()() 222 2 xaybzcR −+−+−= .
Vậy mặt cầu () S có tâm () 1;3;2 I và bán kính bằng () (),O1RdIyz== có phương trình:
()()() 222 1321xyz ++−+−=
Câu 16: Phần ảo của số phức 27=− zi bằng:
A. 7 . B. 7i . C. 2. D. 7 .
Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
Phần ảo của số phức 27=− zi là 7
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 11 Ta có ()()() 52 12144. wiziiiiii ==−=−−=−− Như vậy phần ảo của số phức w là 4 . Câu 13: Thể tích V khối lập phương cạnh 3a là A. 3 81 Va = B. 3 9 Va = C. 3 Va = D. 3 27 Va = Lời giải Thể tích V khối lập phương cạnh 3a là ()3 3 327 Vaa == . Câu 14: Cho hình chóp . SABC có đáy là tam giác đều cạnh 2a , cạnh bên SA vuông góc với đáy và 3 SAa
B. 3 3 4
=
C. 3
=
D. 3Va =
ờ
ả
A. 3 1 2 Va = .
Va
.
22Va
.
. L
i gi
i
2 2 43 3 4 ABC a Sa ∆ ==
SABC bằng 23 11 .3.3 33SABCABC VSASaaa ∆ === . Câu 15: Trong không gian Oxyz , cho mặt cầu () S có tâm () 1;3;2 I và tiếp xúc mặt phẳng () Oyz
ương trình
ủ
S là
Ph
c
a ()
A. ( )1;2;5 P B. ( )1;5;2 N C. ( )1;1;3 Q D. ( )1;1;3 M Lời giải
t dtt =− =+⇔= =+
Vậy điểm ( )1;5;2 N thuộc đường thẳng d
Câu 19: Cho hàm số ( )yfx = xác định và liên tục trên đoạn [ ]2;2 và có
DẠYKÈMQUYNHƠNOFFICIAL
hình vẽ sau. Điểm cực tiểu của đồ thị hàm số ( )yfx = là A. 1 x = . B. 2 x =− . C. ( )1;2 M . D. ( )2;4 M . Lời giải Dựa vào đồ thi hàm số ta thấy điểm cực tiểu của đồ thị hàm số ( )yfx = là ( )1;2 M . Câu 20: Đường tiệm cận ngang của đồ thị hàm số 24 1 x y x = có phương trình là A. 2 y = . B. 2 x = . C. 1 x = . D. 4 y = .

PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 12
đáy bằ
6 và độ dài đường sinh 6 l = . Diện tích xung quanh của hình nón đã cho bằng
π B. 108π C. 36π D. 18π Lời giải Diệ
đã
6
2
xq Srlπππ .
ể
ướ
ây
ộ
đườ
ẳng 1 :5 23 xt dyt zt =− =+ =+ .
Câu 17: Cho hình nón có đường kính
ng
A. 6
n tích xung quanh của hình nón
cho là:
..618
===
Câu 18: Trong không gian Oxyz , đi
m nào d
i đ
thu
c
ng th
Thế tọa độ điểm ( )1;5;2 N vào đường thẳng 11 :550 223t
đồ thị là đường cong trong
x x x x →+∞→+∞ == và
4 2 24 limlim2 1 1 1 xx x x x x
Câu 21: Bất phương trình 2 log3 x < có tập nghiệm là A. ( ) 8; +∞ . B. ( );8−∞ . C. ( )0;8 . D. ( );6−∞ .
Lời giải
Ta có 3 2 log30208 xxx <⇔<<⇔<<
Tập nghiệm của bất phương trình là ( )0;8 .
Câu 22: Số cách chọn 2 học sinh từ 12 học sinh là
A. 2 12C . B. 212 . C. 2 12A . D. 122 .
Lời giải
Số cách chọn 2 học sinh từ 12 học sinh là số các tổ hợp chập 2 của 12 phần tử
Vậy có
2 12C cách thoả đề
Câu 23: Trong các hàm số dưới đây, hàm số nào có họ tất cả các nguyên hàm là hàm số () , ln x a FxC a =+ ( 0,1, aaC >≠ là hằng số).
A. ( ) x fxa = B. () 1 . fx x = C. ( ) ln.fxx = D. ( ) afxx =
Lời giải
Ta có ()()dd, ln x x a FxfxxaxC a ===+ ( 0,1, aaC >≠ là hằngsố).
5
2 x=10fxd . Khi đó ()
2 23x fxd + bằng
A 32 B. 36 . C. 42 . D. 46 . Lời giải
Câu 25: Cho ( )Fx là một nguyên hàm của hàm số ( ) 6sin3 fxxx =+ và () 2 0 3 F = . Khẳng định nào sau
đây đúng?
A. () 2 cos3 31 3 x Fxx=++ . B. () 2 cos32 3 33 x Fxx=−+ .
DẠYKÈMQUYNHƠNOFFICIAL
C. () 2 cos3 31 3 x Fxx=+− . D. () 2 cos3 31 3 x Fxx=−+ .
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 13
Lời giải
Vì 4 2 24 limlim2 1 1 1 xx →−∞→−∞ ==
Do đó đường thẳng 2 y = là đường tiệm cận ngang của đồ thị hàm số đã cho.
5
Câu 24: Cho ()
Ta có ()() 555 222 23x = 2.x3x = 6 +3.10 =36 fxddfxd++
Lời giải
Họ nguyên hàm của ()fx là ()() 2 1 d6sin3d3cos3 3 fxxxxxxxC =+=−+
Vì () 2 0 3 F = nên 12 1 33 CC −+=⇔=
Vậy () 2 1 3cos31 3 Fxxx=−+ .
Câu 26: Cho hàm số ()fx có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. () ;2−∞− B. () 2;2 C. () 1;3


Lời giải
Hàm số đã cho đồng biến trên khoảng () 2;2 .
D. () 2; +∞
Câu 27: Cho hàm số () ==+++ 32 yfxaxbxcxd và có đồ thị là đường cong trong hình vẽ bên. Hàm số ()fx đạt cực đại tại điểm nào dưới đây?
Câu 28: Với , ab là các số thực dương tùy ý, ()
DẠYKÈMQUYNHƠNOFFICIAL
() 2 333 log.log2logabab =+
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 14
B. =−1 x . C. = 1 x . D. = 2
Lời giải T
đồ
ị
số đạt cực đại tại =−1. x
B.
. C. 33 1 loglog 2 ab
. D. 332loglog
Lời giải
A. =−2 x .
x
ừ
th
ta thấy hàm
2 3 log.ab bằng A. 33 log2logab + .
() 33 2loglogab +
+
ab⋅⋅ .
DẠYKÈMQUYNHƠNOFFICIAL
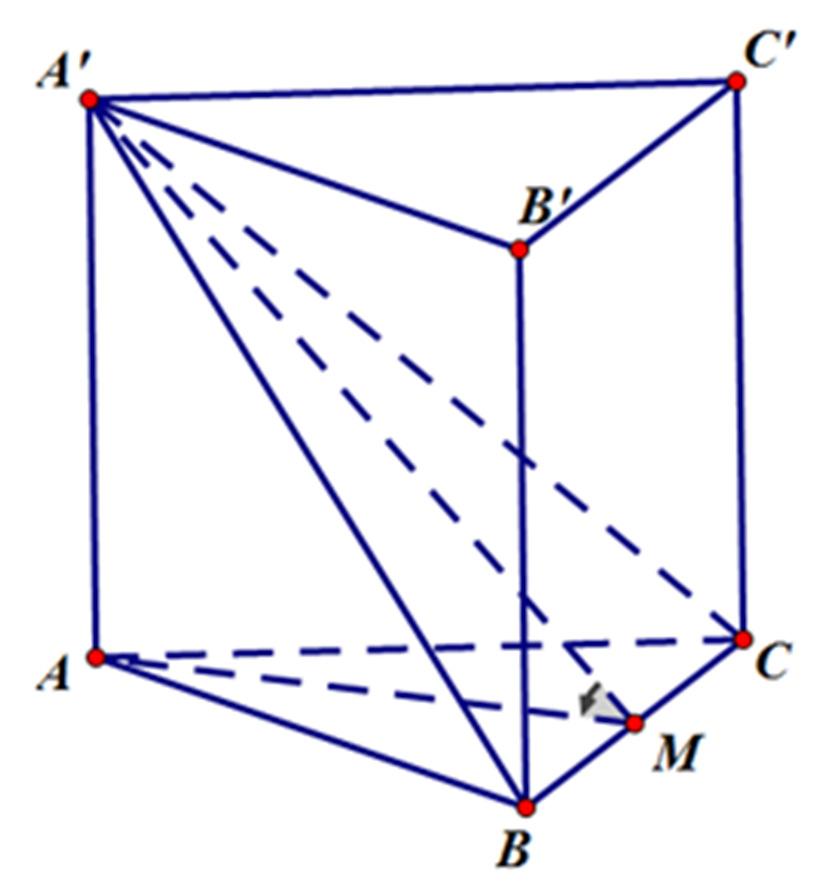
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 15 Câu 29: Cho hình phẳng () H giới hạn bởi đồ thị hàm số 2 3 yxx =− và trục hoành. Tính thể tích V của vật thể tròn xoay sinh ra khi cho () H quay quanh trục Ox A. 81 10 V π = . B. 81 10 V = . C. 9 2 V = . D. 9 2 V π = . Lời giải Phương trình hoành độ giao điểm: 2 0 30 3 x xx x = −=⇔ = . () 3 2 2 0 3 Vxxdx π =− () 3 234 0 96xxxdx π =−+ 3 5 34 0 3 3 25 x xx π =−+ 5 3433 3.3.3 25 π =−+ 81 10 π = . Câu 30: Cho hình lăng trụ tam giác đều . ABCABC′′′ có cạnh đáy bằng a và cạnh bên bằng 2 a . Góc giữa hai mặt phẳng () ABC ′ và () ABC bằng A. 30° . B. 60° . C. 45° . D. 90° . Lời giải Gọi M là trung điểm của cạnh BC . Tam giác ABC đều nên ta có: AMBC ⊥ ABCABC′′′ là lăng trụ đều nên () AAABCAABC ′′ ⊥ ⊥ Từ và ta suy ra () BCAAMBCAM ′′ ⊥ ⊥ Ta lại có ()() ABCABCBC ′ ∩= ()() () ();; ABCABCAMAMAMA ϕ ′′′ ===
a AA AM a ϕ ′ === .

Ta có: 3 2 tan 3 3 2
Suy ra 30 ϕ=°
Câu 31: Cho hàm số ()yfx = xác định và liên tục trên khoảng () ; −∞+∞ , có bảng biến thiên như hình
vẽ:
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình () 20 fxm+= có đúng 3 nghiệm phân biệt?
A. 7 . B. 11. C. 8 . D. 13 . Lời giải
Phương trình: ()()20 2 m fxmfx+=⇔=
Đồ
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 16
thị hàm số ()yfx = cắt đường thẳng 2 m y = tại ba điểm phân biệt khi và chỉ khi: 4284 2 m m −<<⇔>>− . Mà m + ∈ ℤ Suy ra: {} 1;2;3;4;5;6;7 m ∈ Câu 32: Cho hàm số ()fx có đạo hàm trên ℝ là () 2 '()1fxxx=− . Hàm số đã cho đồng biến trên khoảng A. () 1; +∞ B. () ; −∞+∞ C. () 0;1 D. () ;1−∞ Lời giải Ta có: () 2 0 '()010 1 x fxxx x = =⇔−=⇔ = . 4 1 x y' y 3 2 + 0 +∞ ∞ ∞ +∞ 0+
Câu 33: Từ một hộp có 15 viên bi trong đó có 6 viên bi màu đỏ và 9 viên bi màu xanh. Lấy ngẫu nhiên
đồng thời 3 viên bi. Xác suất để 3 viên bi có cả hai màu
A. 8 35 B. 12 65 .
27 35 .
4 91 .
i gi
i Số phần tử của không gian mẫu : ( ) 3 15 455 nCΩ==
Gọi A là biến cố “ Lấy ra 3 viên bi có đủ cả hai màu”
+ TH1: 1 viên đỏ và 2 viên xanh: 12 69.216CC =
+ TH2: 2 viên đỏ và 1 viên xanh: 21 69.135CC =
Suy ra: ( ) 216135351 nA =+=
Xác suất để lấy ra ba viên bi có đủ cả hai màu là: () ( ) () 35127 45535 nA PA n === Ω .
Câu 34: Tích các nghiệm của phương trình 2 33 loglog(9)40 xx−−= bằng A. 6 . B. 3 . C. 3 . D. 27 . Lời giải
Điều kiện: 0 x >
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 17
x −∞ 0 1 +∞ '()fx 0 0 + Vậ
+∞ .
Bảng xét dấu
y hàm số đồng biến trên khoảng ( ) 1;
C.
D.
Lờ
ả
2 2
3 2 33 3 27 log3 loglog60 1 log2 . 9 x x xx x x = = ⇔−−=⇔⇔ =− =
33333 loglog(9)40loglog9log40 xxxx −−=⇔−−−=
27.3 9 = Câu 35: Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn ( ) 152 izi +−+= là một đường tròn tâm I và bán kính R lần lượt là A. ( )2;3 I , 2 R = B. ( )2;3 I , 2 R = C. ( )2;3 I , 2 R = D. ( )2;3 I , 2 R = Lời giải ( ) 152 izi +−+= 5 2 1 i z i −+ ⇔+= + ( ) 232zi ⇔−−= 2 IM ⇔= , với ( ) Mz , ( )2;3 I .
Tích các nghiệm là: 1
i ∆ là đường thẳng đi qua , AB thì ∆ nhận ( )1;1;4 AB =− làm vectơ ch
loại đáp án B và C.
Phương trình chính tắc của ∆ là: 213 114 xyz −−+ == .
=+
=−−
ph
ng. Do đó
Câu 37: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( ) :240Pxy−−= và điểm ( )1;1;0 M
A. ( )3;3;0 M ′ B. ( )2;1;3 M ′ C. ( )0;2;1 M ′ D. ( )2;3;1 M ′ Lời giải
Gọi H là hình chiếu vuông góc của điểm ( )1;1;0 M trên mặt phẳng ( ) :240Pxy−−= . Khi đó
có tọa độ điểm ( )2;1;0 H
Do điểm M ′ là điểm đối xứng với M qua ( )P nên H là trung điểm của đoạn MM ′ . Vậy tọa
độ điểm M ′ là ( )3;3;0 M ′ .
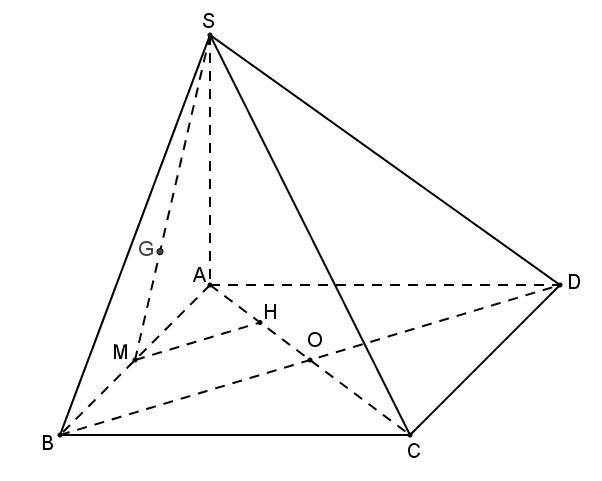
Câu 38: Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh ,a SA và vuông góc với mặt phẳng
đáy. Tính khoảng cách từ trọng tâm G của tam giác SAB đến mặt phẳng ( ) SAC .
A. 3 2 a B. 2 6 a C. 3 6 a D. 2 4 a Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 18 Vậy tập hợp tất cả các điểm biểu diễn số phức z là đường tròn tâm ( )2;3 I , bán kính 2 R = Câu 36: Phương trình nào sau đây là phương trình đường thẳng đi qua hai điểm ( )2;1;3 A , ( )3;0;1 B ? A. 4 1 54 xt yt zt =+ =− =+ . B. 2 1 34 xt yt zt =+ =− =−− . C. 3 14 xt yt zt =− = =+ . D. 4 1 54 xt yt zt =+ =−− =+ . Lờ
ải Gọ
i gi
ỉ
ươ
Ta thấy ( )4;1;5 M −∈∆ nên ∆ có phương trình tham số là: 4 1 54
xt yt zt =+
Tìm tọa độ điểm M ′ là điểm đối xứng với M qua ( )P .
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 19 . Gọi M là trung điểm của AB , và gọi AC cắt BD tại O . Ta có ( ) ( ) () () , 2 3 , dGSAC SG SM dMSAC == () () () () 2 ,, 3 dGSACdMSAC = . Gọi H là hình chiếu của M trên AC . Khi đó ( ) MHSAC ⊥ nên () () 112 , 244 a dMSACMHBOBD ==== Vậy () () 222 ,.346 aa dGSAC == . Câu 39: Số nghiệm nguyên của bất phương trình () ( ) ()() 2 22 2log2log2115 xxxx +−−≥+− là A. 5 B. 6 C. 7 D. 4 Lời giải Điều kiện: () () 2 2 2 2 2 2 2 2 2 20 2 2 210 1 2 2 log20 1 2 2 1 log210 21 1 211 1 x x x x x x x x x x x x x x x x x >− >− > +> > −> ≥ ⇔⇔⇔ <− +≥ =− <− ≥− −≥ +≥ ≥ −≥ ≤− . Ta có 1 x =− là một nghiệm của bất phương trình đã cho. Với 1 x ≥ , bất phương trình () ( ) ()() 2 22 2log2log2115 xxxx +−−≥+− () () () () ()() 2 2 22 222 22 22 log2log2145log2log212144 xxxxxxxxx ⇔+−−≥−−⇔+−−≥−−++ ( ) ( ) ( ) ( ) () 2222 2 2 log4444log2121* xxxxxx ⇔+++++≥−+− Đặt 2 2 44 21 uxx vx =++ =− , khi đó ( )* có dạng 22 logloguuvv +≥+ .
2
0 0 2320* x y xmxm
= ′ =⇔ −++=
n trên khoảng () 1; +∞ , do
ng trình ta được: 2 0 260. 3 x xx x = −=⇔ = Ta có xét dấu y ′ như sau: Ta thấy khi 2 m =− hàm số đã cho có một điểm cực tiểu và không có điểm cực đại. +) Trường hợp 2: Phương trình có không có nghiệm 0 x = , khi đó 2 m ≠−
ươ
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 20 Xéthàmsố 2(t)log ftt =+ có () 2 22 log 1 ()110 2log2.ln2.log t ft ttt ′ ′ =+=+> nênhàmsố đồng biế
đó
22
uuvvuv +≥+⇔≥ Khi
. Kết hợp với điều kiện ta có 115xvx=−≤≤ . Vì x ∈ ℤ nên {} 1;1;2;3;4;5 x ∈− . Câu 40:
ố
fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 888FG+= và ()() 002FG+=− . Khi đó () 0 2 4d fxx bằng A. 5 4 B. 5 4 C. 5 D. 5 Lời giải Ta có: ()() ()() ()() 88 00 GFC GxFxC GFC =+ =+ =+ ()() 2(8)8 (8)(0)5. 2(0)2 (0)(0)2 888 F FC FF FC F G G += ⇔⇔−= + += =− +=− Vậy: () () 8 0 0 2 115 ()(8)(0) 4 4. d 44fxftdtFF x ==−= Câu 41: Có bao nhiêu
ị nguyên
ủ
tham
ố m để hàm số () 432223yxmxmx =−++− có điểm cực tiểu mà không có điểm cực đại? A. 2. B. 4. C. 5. D. 6. Lời giải Ta có ()()
()()
DẠYKÈMQUYNHƠNOFFICIAL
bpt
loglog
đó 222442145015 xxxxxx ++≥−⇔−−≤⇔−≤≤
Cho hàm s
()
giá tr
c
a
s
322 46222232 yxmxmxxxmxm ′ =−++=−++
+) Trường hợp 1: Phương trình có nghiệm 0 x = , khi đó 2 m =− . Thay 2 m =− vào ph
Dễ thấy phương trình có 2 nghiệm phân biệt thì phương trình '0 y = có 3 nghiệm đơn phân
biệt, khi đó hàm số đã cho có cả điểm cực đại và điểm cực tiểu.
Khi phương trình vô nghiệm hoặc có nghiệm kép thì phương trình '0 y = có 1 nghiệm đơn
hoặc 1 nghiệm đơn và 1 nghiệm kép, lúc này hàm số đã cho có 1 điểm cực tiểu 0 x =
Như vậy, khi 2 m ≠− , hàm số đã cho có một điểm cực tiểu khi và chỉ khi phương trình vô
nghiệm hoặc có nghiệm kép, điều này xảy ra khi và chỉ khi phương trình có 0 ∆≤ .
∆≤⇔−+≤⇔−−≤⇔≤≤−+
44104410 0982098160. 99 mmmmm
() 22
Mà m ∈ ℤ , suy ra { }0;1 m∈
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 42: Hai số phức z , w thay đổi nhưng luôn thỏa mãn đẳng thức
2 2022.2022 12122 w z izizi + +−−=+− . Giá trị l
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 21
()
ớn nhất của w là A. 20212 4 B. 10112 2 C. 20232 4 D. 2019 Lời giải Ta có: zizi −=+ nên 2 2 2 21 zizzizi −−=−=+ Phương trình () 2 2022.2022 12122 w z izizi + +−−=+− () ( ) 2 20221 122 w z izii + ⇔++=+− () () ( ) 22 2022 22 w zi zizii + ⇔+−+++= ( )1 . Điều kiện: w0 ≠ suy ra 0 zi+≠ hay 0 zi+> Đặt tzi =+ , 0 t > ta có phương trình ( )1 ()() ( ) 22 2022 22 w zi tti + ⇔−++= ()() 2222 2022 22 w t tt −++= () 2 4 w2022 24 t t ⇔= + 2 2 1 10112 4 t t = + 2 2 110112 w10112. 2 4 2. t t ⇔≤= dấubằngxảyrakhi 2 2 4 t t = 2 2 zi ⇔+= 10112 w 2 i ⇔=− .
′ ∩= nên () () () () () () 1 ,,, 3 GO dGABDdAABDdAABD AO ′′′ == .
Dễ thấy ( )BDAAO ′ ⊥ ,trong ( )AAO ′ vẽ AHAO ′ ⊥ tại H .
Khi đó ()() () , AHBD AHABDdAABDAH AHAO ⊥ ′′ ⊥ =
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 22 Câu 43: Cho hình hộp đứng ABCDABCD ′′′′ có đáy là hình thoi, góc 60 BAD =° đồng thời AAa ′ = Gọi G làtrọng tâm tam giác BCD . Biết rằng khoảng cách từ G đến mặt phẳng ( )ABD ′ bằng 21 21 a .Tínhthể tíchkhốihộp . ABCDABCD ′′′′ theo a . A. 2 6 a 3 . B. 3 6 a 3 . C. 2 2 a 3 . D. 3 2 a 3 . Lời giải Gọi O làgiao điểmcủa AC và BD . Tacó ( ) AGABDO
′ ⊥
ọ
làcạnhhìnhthoi ABCD ,tacó 60
nên ABD∆ đều.
3 2 x AO = ,khi đó 222222 111741 33 xa AHAOAAaxa =+⇔=+ = ′ .
ể tíchkhốihộ
ABCDABCD ′′′′ là 2 33 ..2. 42 ABCDABCDABCD aa VAASa 3 ′′′′ ′ === Câu 44: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) 22 .ln2,1;xfxxfxxfxx ′ −+=∀∈+∞ , ( ) ( ) 0,1;fxx>∀∈+∞ và () 2 1 e e f = . Tính diện tích S hình phẳng giới hạn bởi đồ thị ( ) 2 ,0,, yxfxyxexe ==== . A. 3 2 S = B. 1 2 S = C. 5 3 S = . D. 2 S = Lời giải G O H D' C' B' A' D C B A
G
i x
BAD =°
Suyra
Th
p .
Tacó: ()()() ( ) () () 22 2 2
' 1 'ln2ln2 fx xfxxfxxfxxxx fxfx −+=⇔−+= , ( ) 1; x ∀∈+∞ .
( ) ( ) ( ) 2 .ln2,1;xgxxgxxx ′ ⇔+=∀∈+∞ với () () 1 gx fx =
() ( ) ln2 gx gxxx x ′ ⇔+= , ( ) 1; x ∀∈+∞ () ( ) lndd2d gx gxxxxxx x ′ += () ( ) ( ) 2 lndd gxgx gxxxxxC xx ⇔−+=+ ( ) 2 ln gxxxC⇔=+ , ( ) 1; x ∀∈+∞ .
Do () () 2 2 1 e0 e fgeeC =⇔=⇔= .
Suyra ( ) 2 ln gxxx = , ( ) 1; x ∀∈+∞
() () 2 0,1; ln x gxx x =>∀∈+∞ () () ln xx yxfx gxx === , ( ) 1; x ∀∈+∞
e ln13 ddln 22 e x Sxfxxxx x ====
.
Câu 45: Trên tập các số phức, xét phương trình 2 80 zmzm−++= ( m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm 12 , zz phân biệt thỏa mãn
( ) ( ) 22 1122 8 zzmzmmz +=−− ?
A. 12 . B. 6 . C. 5 . D. 11. Lời giải Tacó 2 432mm ∆=−− làbiệtthứccủaphươngtrình.
cphân biệt.Tacó 2 11 8 zmzm=−− suyra ( ) 2 2 1212 88zmzmzzmmm +=+−−=−− do đó ( ) ( ) 22 1122 8 zzmzmmz +=−− ( ) 22 1288 mmzmmz⇔−−=−− . Nếu 12.0zz = thì 808mm += =− khôngthỏamãn.Khi đó 2 12 80 mm zz −−> ⇔ = 2 12 80 mm zz −−> ⇔ =− 2 80 0 mm m −−> ⇔ = hệ vônghiệm.
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 23
Tacó () 22 2 ee 2 ee
TH1:Xét 2 8 04320 4 m mm m > ∆>⇔−−>⇔ <− khi đóphươngtrìnhcóhainghiệmthự
ng thẳng 11 : 112 +− == xyz d , ( )1;1;1 I . Viết
phươngtrìnhmặtphẳng ( )P chứa đườngthẳng d , đồngthờikhoảngcáchtừ I đếnmặtphẳng ( )P bằng 3.
A. ( ):20Pxyz−+−= , ( ):7520Pxyz+++=
B. ( ):20Pxyz−++= , ( ):7520Pxyz+++= .
C. ( ): 20 Pxyz−+−= , ( ):7520Pxyz++−= .
D. ( ):20Pxyz−++= , ( ):7520Pxyz++−=
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 24 TH2:Xét 048 m ∆<⇔−<< khi đóphươngtrìnhcóhainghiệmphứcphânbiệtvà 12zz = , tacó ( ) ( ) 22 1122 8 zzmzmmz +=−− ( ) 22 1288 mmzmmz⇔−−=−− 2 133 2 80 133 2 m mm m + ≥ ⇔−−≥⇔ ≤ .Kếthợp điềukiệnta được { }3;4;5;6;7 m ∈− Vậycótấtcả là 5 số nguyêncầntìm. Câu 46: Trong không gian hệ trục tọa độ Oxyz , cho đườ
Lời giải
ấy ( )-1;1;0 M , ( )0;0;-2 N thuộc đườngthẳng d . Phươngtrìnhmặtphẳng ( )P códạng ( ) 222 0,0axbyczdabc +++=++≠ Tacó: () () () () 222222 0 202 |||| d,3 33 MP abddab NPcddc abcdabcd IP abcabc ∈ −++==−+ ∈⇔−+=⇔= ++++++ = == ++++ 22 2 22 2 2 5270 3 22 cab cab dab dab aabb abab ababab =− =− ⇔=−⇔=− −−= +++−=++ ()() 2 570 cab dab abab =− ⇔=− +−= 2 57 2 ab cab dab ab cab dab =− =− =− ⇔ = =− =−
L
=− =−
=−
= =− =−
Với 57 2 ab cab dab
Câu 47: Có bao nhiêu cặp số nguyên ( ) , xy thỏa mãn ()() 22 3 log33. 2 xy xxyyxy xyxy + =−+−+ +++
A. 1. B. 2. C. 4. D. 6. Lời giải
Điều kiện 22 00. 2 xy xy xyxy + >⇔+> +++ ()() 22 3 log33 2 xy xxyyxy xyxy + =−+−+ +++
( ) ( ) 2222 33 2log2log233 xyxyxyxyxyxy ⇔+−+++=++−−
( ) ( ) 2222 33 2log22log2233 xyxyxyxyxyxy ⇔++−+++=+++−−
( ) ( ) ( ) 2222 3 3 2log33332log22 xyxyxyxyxyxy ⇔+++=+++++++
Xét hàm đặc trưng ( ) ( ) 3 2log,0;,ftttt=+∈+∞ ta có () () 2 10,0;. .ln3 ftt t ′ =+>∀∈+∞
Suy ra hàm ( ) ft đồng biến trên khoảng ( ) 0;+∞ .
Phương trình ( ) ( ) 2222 332233 fxyfxyxyxyxyxy ⇔+=+++⇔+++=+
( ) 223320xyxyy ⇔+−+−+=
322322 3610 33yyy −+ ⇔−++≥⇔≤≤ . Do y
DẠYKÈMQUYNHƠNOFFICIAL
2
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 25
Với 2 ab cab dab
. Chọn bộ số ( ) ( );;;1;1;1;2abcd =− ( ) P:20 xyz−++= .
Chọn bộ số ( ) ( );;;7;5;1;2abcd = ( ) P:7520 xyz +++= .
∈ ℤ nên
0;1;2 y ∈ + Với 0 y = , ta được 2 1 320 2 x xx x = −+=⇔ = . + Với 1 y = , ta được 2 0 20 2 x xx x = +=⇔ =− .
Điều kiện của y để phương trình có nghiệm là () ( ) 2 2 34320 yyy −−−+≥
{ }
Vậy có 6cặp số thỏa mãn đề bài.
Câu 48: Cho hình nón đỉnh S , tâm mặt đáy O và có diện tích xung quanh bằng 2 20 aπ . Gọi A và B là
hai điểm thuộc đường tròn đáy sao cho độ dài cung AB bằng 1 3 lần chu vi của đường tròn đáy.
Biết rằng bán kính đáy bằng 4a , khoảng cách từ O đến mặt phẳng ( )SAB bằng
A. 213 13 a . B. 13 13 a . C. 1213 13 a . D. 613 13 a .
Lời giải
Ta có 22 20.4.205 xq Srlaalala ππππ ==⇔=⇔=
()() 22 22 543 SOSAOAaaa =−=−= .
Gọi M là trung điểm của đoạn thẳng AB . Khi đó ( ) ABSOM ⊥ . Gọi H là hình chiếu vuông góc của O lên SM . Suy ra ( )OHSAB ⊥ hay ( ) ( ) , dOSABOH = .
Vì độ dài cung AB bằng 1 3 lần chu vi của đường tròn đáy nên góc 12060AOBMOB =° =°
Ta có cos.cos4.cos602 OM MOBOMOBMOBaa OB = ==°=
Suy ra
() () 22 2222 111111613 13 23 OHa OHOMOSOH aa =+⇔=+⇔= .
Câu 49: Trong không gian Oxyz , cho hai điểm ( )2;7;2 A và ( )1;3;1 B . Xét hai điểm M và N thay
đổi thuộc mặt phẳng ( )Oxy sao cho 3 MN = . Giá trị lớn nhất của AMBN bằng
A. 43 . B. 310 . C. 85 . D. 65 . Lời giải

DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 26
0
1 x
x = +=⇔ =−
+ Với 2 y = , ta được 2
0
xx
o (Oxy)
Gọi B′ là điểm đối xứng với B qua mặt phẳng ( )Oxy , suy ra ( ) 1;3;1, BBNBN ′′ −= và , AB′
ở cùng phía so với mặt phẳng ( )Oxy .
Lấy điểm K sao cho BKNM ′ = ( BNMK ′ là hình bình hành), khi đó 3 BKMN ′ == , BNMK ′ = .
Do // BKMN ′ nên BK ′ nằm trên mặt phẳng ( )α đi qua B′ và song song với mặt phẳng ( )Oxy
, suy ra ( )α có phương trình 1 z = .
Do 3 BK ′ = nên K thuộc đường tròn ( ) C nằm trên mặt phẳng ( )α có tâm là B′, bán kính 3 R = .
Gọi H là hình chiếu của A lên ( ) ( )2;7;1 H α và '5 HBR => , E là giao điểm của tia đối của tia BH ′ với ( ) C .
Ta có AMBNAMBNAMMKAK ′ −=−=−≤ 2222 AHHKAHHE=+≤+ .
Mà 1,538AHHEHBBE ′′ ==+=+= suy ra 22 1865 AMBN−≤+= .
Dấu ”=” xảy ra khi ,
KE MAKAMMKAK ≡ ∈−= ( ) 0 MAEOxyM⇔=∩=
Vậy giá trị lớn nhất của AMBN bằng 65
Câu 50: Có bao nhiêu giá trị nguyên của tham số ( )2022;2022 m ∈− để hàm số ( ) 3 212xmx y ++− =
đồng biến trên ( )1;3 ?
A. 4034 . B. 2022 . C. 4030 . D. 4032 . Lời giải
Xét hàm số ( ) ( ) 3 212fxxmx=++− ( ) 2 321fxxm ′ =++
Hàm số ( )yfx = đồng biến trên ( )1;3 khi và chỉ khi xảy ra 2 trường hợp sau:
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 27
) M B' E A N H K
M
(α
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 28 TH1: Hàm số ( )yfx = đồng biến trên ( )1;3 và ( ) 10 f ≥ ( ) ( ) () ( ) () 2 2 0 1;3 3210 1;3 10 20 213 213 1;3 0. 0 0 fxx xmx f m m mxx m m m ′ ≥∀∈ ++≥∀∈ ⇔⇔ ≥ ≥ +≥− +≥−∀∈ ⇔⇔⇔≥ ≥ ≥ TH2: Hàm số ( )yfx = nghịch biến trên ( )1;3 và ( ) 10 f ≤ ( ) ( ) () ( ) () 2 2 0 1;3 3210 1;3 10 20 2127 213 1;3 14. 0 0 fxx xmx f m m mxx m m m ′ ≤∀∈ ++≤∀∈ ⇔⇔ ≤ ≤ +≤− +≤−∀∈ ⇔⇔⇔≤− ≤ ≤ Kết hợp 2 trường hợp ta có 14 m ≤− hoặc 0 m ≥ . Mà ( )2022;2022 m ∈− nên có 4030 giá trị nguyên của m thỏa mãn. ---------- HẾT ----------
ủa 3u bằng
A. 16 . B. 32 . C. 32 . D. 16 .
Câu 6: Trong không gian Oxyz , cho mặt phẳng () :3–20Pxz += . Vectơ nào dưới đây là một vectơ pháp tuyến của () P ? A. 4 (1;0;1) n =−−

Câu 7: Cho hàm số 32 yaxbxcxd =+++ có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm
a đồ
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 1 PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 MÔN TOÁN ĐỀ SỐ: 02 – MÃ ĐỀ: 102 Câu 1: Cho số phức 32=− zi Điểm nào sau đây biểu diễn số phức z ? A. () 3;2 M . B. () 3;2 N . C. () 3;2 P . D. () 3;2 Q . Câu 2: Đạo hàm của hàm số 5log yx = là A. ln5 x y ′ = B. 1 y x ′ = C. 1 ln5 y x ′ = D. 1 5ln x Câu 3: Trên khoảng () 0; +∞ , đạo hàm của hàm số 34 yx = là : A. 3 1 3 yx ′ = . B. 4 3 yx ′ = . C. 3 4 3 yx ′ = . D. 1 3 yx ′ = . Câu 4: Tập nghiệ
ủ
ất phương trình 23 1 5 25 x+ > là: A. 5 ; 2 −+∞ . B. 5 ; 2 −∞− . C. () 0; +∞ . D. 1 ; 2 −+∞ . Câu 5: Cho cấp số nhân () n u biết 2 8 u =− ; 5 64 u = . Giá trị c
m c
a b
B. 1 (3;1;2) n =− C. 3
D. 2
n =−
(3;1;0) n =−
(3;0;1)
A. () 0;1 B. () 0;1 C. () 1;0 D. () 1;0
8: Biết () 3 2 x4fxd = và () 3 2 x1gxd = . Khi đó: ()() 3 2 xfxgxd bằng: A. 3 . B. 3 . C. 4 . D. 5 . Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường
đây?
củ
thị hàm số đã cho và trục tung là điểm nào trong các điểm sau
Câu
cong trong dưới
Câu 12: Cho số phức 2 (1)(12)=++ zii có ph
thể tích khối chóp SABC
Câu 15: Trong không gian Oxyz , phương trình mặt cầu có tâm (3;1;2) I và tiếp xúc với mặt phẳng () Oxy là
A. 222 (3)(1)(2)4 xyz −+−++= B. 222 (3)(1)(2)9 xyz −+−++=

C. 222 (3)(1)(2)1 xyz ++++−=
D. 222 (3)(1)(2)4 xyz ++++−=
Câu 16: Trong mặt phẳng tọa độ, biết điểm () 2;7 M là điể
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 2 A.
=−+ . B. 42 2 yxx =− . C. 32 3 yxx =− . D. 32 3
=−+ .
ặt cầu ()()()() 222 :12316Sxyz
t
B.
1;2;3
C.
1;2;3
D.
42 2 yxx
yxx
Câu 10: Trong không gian Oxyz , cho m
−+++−= . Tâm của () S có
ọa độ là A. () 1;2;3 .
()
.
()
.
() 1;2;3 .
()
() Oxy
đị
A.
B.
C.
α
D. o45 α = .
ầ
ả
là A. 2
B. 2 . C. 2 . D. 4 .
đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích của khối lăng trụ đã cho bằng A. 3 16a B. 3 4a C. 3 16 3 a D. 3 4 3 a Câu
có đáy ABC là tam giác đều cạnh a . Biết ()
Tính
A. 4 a B. 3 2 a C. 3 4 a D. 3 3 4 a
Câu 11: Trong không gian với hệ tọa độ Oxyz , gọi α là góc giữa hai mặt phẳng
:3210Pxyz−++= và mặt phẳng
. Khẳng
nh nào sau đây đúng?
o30 α = .
o60 α = .
o90
= .
n
o
i .
Câu 13: Cho khối lăng trụ có
14: Cho hình chóp SABC
SAABC ⊥ và 3 SAa =
m biểu diễn số phức z . Phần thực của z bằng A. 7 . B. 2 . C. 2 . D. 7 . Câu 17: Diện tích toàn phần ( tpS ) của một hình trụ có độ dài đường sinh 2 la = , bán kính ra = bằng A. 2 tp Sa π = B. 2 4 tp Sa π = C. 2 6 tp Sa π = D. 2 8 tp Sa π = Câu 18: GK2 - K12 - THPT Lương Thế Vinh - Hà Nội - Năm 2021 - 2022) Trong không gian Oxyz , đường thẳng 321 : 112 xyz d +−− == đi qua điểm nào dưới đây?
A. ( )3;2;1 P B. ( )1;1;2 Q C. ( )3;2;1
( )3;2;1 M
Câu 19: Cho hàm số ( )yfx = có đồ thị là đường cong như hình vẽ
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có điểm cực đại là ( )1;3 .
B. Đồ thị hàm số có điểm cực tiểu là ( )1;1
C. Đồ thị hàm số có điểm cực đại là ( )1;1
D. Đồ thị hàm số có điểm cực đại là ( )3;1 .
Câu 20: Đường tiệm cận đứng của đồ thị hàm số 53 1 x y x + = −+ có phương trình là
A. 1 x = . B. 5 x =− . C. 1 y = . D. 5 y =− .

Câu 21: Tập nghiệm của bất phương trình ( ) 2 log312 +< x là
A. 1 ;1 3
B. 11 ; 33
Câu 22: Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn? A. 16 . B. 2 . C. 64 .
3 .
Câu 23: Biết ( ) sin3 fxdxxC =+
. Mệnh đề nào sau đây là mệnh đề đúng?
A. ( ) 3cos3 fxx =− B. ( ) 3cos3 fxx = C. () cos3 3 x fx =−
=
() cos3 3 x fx = Câu 24: Nếu ()
ng A. 5 . B. 3 .
Câu 25: Họ nguyên hàm của hàm số () 2x 3 fxe x =+ A. ( )
d3ln x fxxexC =++
4 .
1.
DẠYKÈMQUYNHƠNOFFICIAL
Câu 26: Cho hàm số ( )fx có đồ thị như sau :
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 3
D.
N
C.
−∞
1 ;1 3
D. ( );1
D.
2
2 1
C.
D.
D.
1 d3fxx
thì ()
4d fxxx
bằ
2
B.
2
2 x e fxxxC
.
2
2 x
. D. (
2 d3ln x fxxexC
.
()
d3ln
=++
C. ()
d3ln
e fxxxC =++
)
=++
.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. () 0; +∞ .
() ;1−∞− .
() 2;2 .
() 1; −+∞ .
Câu 27: Cho hàm số ()fx có bảng biến thiên như hình vẽ sau :
Giá trị cực tiểu của hàm số đã cho bằng
A. 4
Câu 28: Với mọi , ab thỏa mãn
A. 2 9 ab = .

3
0
33 loglog5 ab+= , khẳng định nào sau đây đúng?
1
243 ab = . C. 2 243 ab+= . D. 3 15 ab+= .
Câu 29: Tính thể tích vật thể tròn xoay tạo ra khi quay phần hình phẳng giới hạn bởi đồ thị 2 yxx =− , trục Ox quanh trục .Ox
A. 5 6 . B. 30 π . C. 1 30 . D. 5 6 π .
Câu 30: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a cạnh bên bằng 5a . Góc giữa mặt bên và mặt phẳng đáy bằng
A. 60° B. 30° C. 70° D. 45°
DẠYKÈMQUYNHƠNOFFICIAL
Câu 31: Cho hàm số 42 ()21yfxxx ==−++ có đồ thị là đường cong như bên dưới. Số các giá trị nguyên dương của m để phương trình 42 91830 xxm−++= có 4 nghiệm phân biệt là A. 5 B. 7 C. 8 D. 4
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 4
C.
D.
B.
C.
D.
B.
2
2
B.
A. Đường tròn tâm ( )1;2 I , bán kính 2 R =
B. Đường tròn tâm ( )2;1 I , bán kính 2 R = .
C. Đường tròn tâm ( )2;1 I , bán kính 2 R = .
D. Đường tròn tâm ( )1;2 I , bán kính 2 R =
Câu 36: Trong không gian Oxyz , đường thẳng đi qua điểm ( )1;2;3 A và song song với đường th
ng 135 : 231 xyz d −+− == có phươ
( ) 3 2;3;5 M .
Câu 38: Cho hình chóp . SABC có đáy là tam giác đều cạnh 2a và SA vuông góc với mặt phẳng đáy, độ dài SA bằng a Khoảng cách từ A đến mặt phẳng ( )SBC bằng
25 5 a B. 5 5 a
21 7 a
Câu 39: Tính tổng tất cả các nghiệm nguyên của bất phương trình ( ) 22 22 log3log410 xxxx+−+−+≤ . A. 4 . B. 6 .
5 . D. 3 .
Câu 40: Cho hàm số ( )fx liên tục trên R . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên R thỏa
( ) ( ) 8818FG+= và ( ) ( ) 002FG+= . Khi đó ()
0 cos.8sind xfxx π bằng
8
8
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 5 Câu 32: Cho hàm số ( )yfx = liên tục trên ℝ và có ( ) ( )( ) 2 21 fxxxx ′ =+− . Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng sau? A. ( )2;3 . B. ( )1;1 . C. ( )0;2 . D. ( );1−∞ . Câu 33: Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Tính xác suất để tổng các số ghi trên thẻ chia hết cho 3 . A. 11 171 B. 1 12 C. 9 89 D. 409 1225 Câu 34: Tích các nghiệm của phương trình 2 22 loglog0 4 x x += bằng: A. 3. B. 1 3 . C. 1. D. 1 2 . Câu 35: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễ
là
n số phức z thỏa mãn điều kiện 22 zi−+=
ng trình tham số là A. 1 23 35 xt yt zt =+ =−− =+ . B. 12 23 3 xt yt zt =+ =−+ =− . C. 12 33 5 xt yt zt =+ =−+ =− . D. 2 32 13 xt yt zt =+ =− =−+ . Câu 37: Trong không gian Oxyz , cho điểm ( )3;2;5 M Điểm đối xứng của điểm M qua trục Oz là A. ( ) 1 3;2;5 M . B. ( ) 2 0;0;5 M . C.
ẳ
D. ( ) 4 0;0;5 M .
C.
D.
A.
3 2 a
C.
A.
C.
D.
mãn
2
1 B. 1
+= . B. 221 ab+=− . C. 4 ab+= . D. 22 ab+= .
Câu 43: Chohìnhlăngtrụ đứng ABCABC′′′ có đáylàtamgiácvuôngcân đỉnh A ,mặtbênlà BCCB′′ hìnhvuông,khoảngcáchgiữa AB′ và CC ′ bằng a .Thể tíchkhốilăngtrụ ABCABC′′′ là A. 3 2a . B.
Câu 44: Cho hàm số ( ) 32 2 fxxaxbxc =+++ với a , b , c là các số thực. Biết hàm số ( ) ( ) ( ) ( )gxfxfxfx ′′′ =++ cóhaigiátrị cựctrị là 4 và 4 .Diệntíchhìnhphẳnggiớihạnbởi các đường ( ) () 12 fx y gx = + và 1 y = bằng
A. 2ln3 B. ln3 C. ln18 D. ln2
Câu 45: Trêntậphợpcácsố phức,xétphươngtrình ( )( ) 116 zazaz −−+−= ( a làthamsố thực).Có baonhiêugiátrị của a để phươngtrình đócóhainghiệm 1z , 2z thỏamãn 22 12 42 zz+= ?
A. 1 B. 2 C. 3 D. 4
Câu 46: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 12 : 121 xyz d +− == . Gọi ( )P là mặt phẳng chứa đườngthẳng d vàtạo vớimặt phẳng ( ) :2220Qxyz−−−= một góccó số đonhỏ nhất. Điểm ( )1;2;3 A cách mặt phẳng ( )P một khoảng bằng:
A. 3 B. 53 3 C. 711 11 D. 43 3
Câu 47: Có bao nhiêu cặp số nguyên thoả mãn 02020 y << và 3 33369log x xyy+−=+ ?
A. 9 . B. 7 . C. 8 . D. 2019 .
Câu 48: Cho khối nón đỉnh S có đường cao bằng 2a ; SA , SB làhai đường sinh của nón. Khoảng cách từ tâm đườngtròn đáy đếnmặtphẳng ( )SAB bằng a vàdiệntíchtamgiác SAB bằng 2 2a .Tính bán kính đáy của hình nón?
A. 5 5 a . B. 25 5 a . C. 5 6 a . D. 53 6 a
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 6 Câu 41: Cho hàm số ( )fx có đạo hàm ( ) 2 2 ()(1)4 fxxxx ′ =−− .Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 ()212 gxfxxm =−+ có đúng 5 điểm cực trị? A. 18 . B. 17 . C. 16 . D. 19 . Câu 42: Cho số phức zabi =+ ( ) , ab ∈ ℝ thỏa mãn 2 2 z zi + + là một số thuần ảo. Khi số phức z có môđun nhỏ nhất, hãy tính ab + A. 0 ab
3
3
D. 3 2 2
2 3 a . C.
a .
a .
. Câu 49: Trong không gian với hệ trục tọa độ ,Oxyz cho mặt cầu ()()()() 222 :2114Sxyz−+−+−= và điểm ( )2;2;1 M .Một đường thẳng thay đổi qua M và cắt ( ) S tại hai điểm , AB . Khi biểuthức 4 TMAMB =+ đạt giá trị nhỏ nhất thì đoạn thẳng AB có giá trị bằng A. 43. B. 4. C. 53 . 2 D. 23 ( ) ; xy
DẠYKÈMQUYNHƠNOFFICIAL
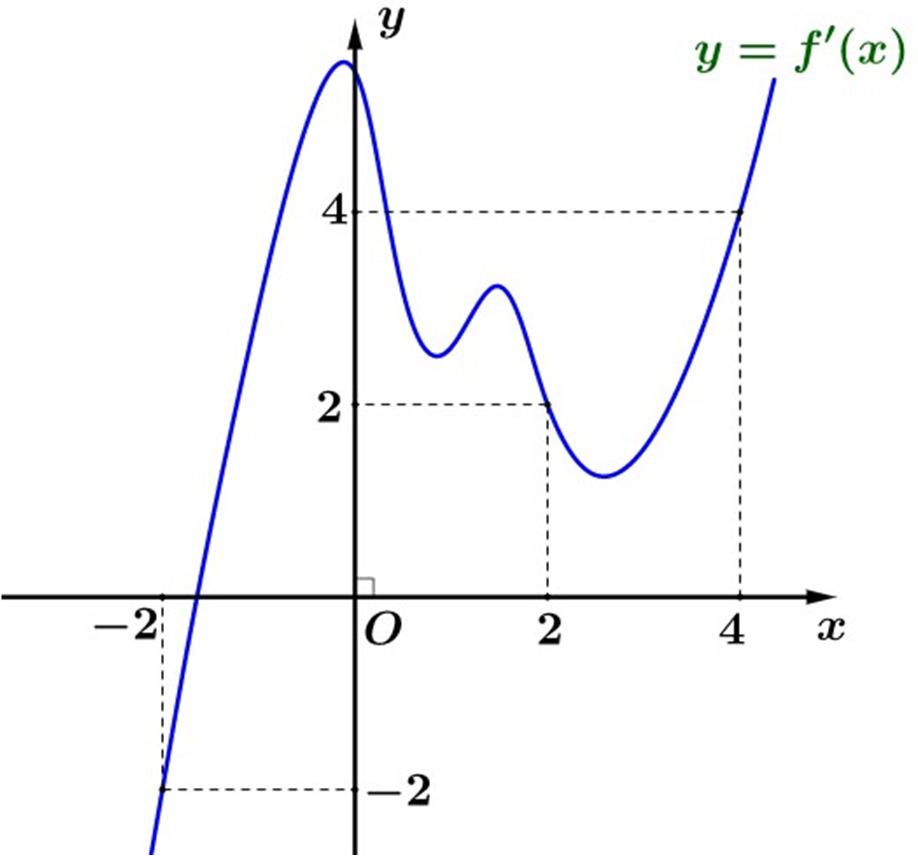
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 7 Câu 50: Chohàmsố ()yfx = liêntụctrên ℝ ,biết ()24. f = Biếthàmsố ()yfx ′ = có đồ thị như hình vẽ Hàm số ()() 2 242810gxfxxx =−−+− đồng biến trên khoảng nào dưới đây? A. ();1.−∞ B. ()1;3. C. ()3;4. D. ()4;. +∞ ---------- HẾT ----------
1: Cho số phức 32=− zi .
Đạo hàm của hàm số 5log yx = là
ln5 x y ′ = . B. 1 y x ′ = .
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 8 BẢNG ĐÁP ÁN 1.C 2.C 3.C 4.A 5.D 6.D 7.A 8 9 10.D 11.D 12.B 13 14.C 15.A 16.B 17 18.A 19.A 20.A 21.C 22.C 23.B 24.B 25.B 26.A 27.A 28.B 29.B 30 31.A 32.A 33.D 34.D 35.B 36.B 37.A 38.D 39.B 40.B 41.B 42.A 43.D 44.D 45.B 46.A. 47.B 48.D 49.B.C 50.C HƯỚNG DẪN GIẢI CHI TIẾT Câu
? A.
C.
3;2
D.
3;2 Q Lời giả
Ta
ể
Câu
A.
C.
D.
Lời giải Ta có 1 ln5 y
′ = Câu 3: Trên khoảng
0; +∞ , đạo hàm của hàm số 3 4 yx = là : A. 3 1 3 yx ′ = . B. 4 3 yx ′ = . C. 3 4 3 yx ′ = . D. 1 3 yx ′ = . Lời giải Trên khoảng ( ) 0; +∞ ta có 4 34 3 yxx == , do đó tacó: 41 3 3344 33 yxxx ′ ′ === . Câu 4: Tập nghiệm của bất phương trình 23 1 5 25 x+ > là: A. 5 ; 2 −+∞ B. 5 ; 2 −∞− C. ( ) 0; +∞ D. 1 ; 2 −+∞ Lời giải Ta có: 2323215 555232 252 xx xx ++−>⇔>⇔+>−⇔>− . Vậy tập nghiệm củabất phương trình đã cho là: 5 ; 2 S =−+∞
Điểm nào sau đây biểu diễn số phức z
( )3;2 M B. ( )3;2 N
( )
P
( )
i
có 32 32 =+ =− zi zi có điểm bi
u diễn là ( )3;2 P .
2:
1 ln5 y x ′ = .
1 5ln x .
x
( )
Câu
ải
Câu 7: Cho hàm số 32 yaxbxcxd =+++ có đồ thị là đường cong trong hình vẽ bên.Tọa độ giao điểm

của đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau
ừ đồ thị, ta dễ thấy đồ thị hàm số cắt trục tung tại điểm có tọa độ
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 9 Câu 5: Cho cấp số nhân () n u biết 2 8 u =− ; 5 64 u = . Giá trị của 3u bằng A. 16 . B. 32 . C. 32 . D. 16 . Lời giải
3
uuqq = =−
==
Tacó
52 .2
Vậy 32 .16uuq
6:
không gian Oxyz , cho mặt phẳng () :3–20Pxz += . Vectơ nào dưới đây là một vectơ pháp tuyến của () P ? A. 4 (1;0;1) n =−− B. 1 (3;1;2) n =− C. 3 (3;1;0) n =− D. 2 (3;0;1) n =− Lời gi
Trong
A.
0;1 B.
0;1 C.
D.
1;0 L
T
() 0;1 . Câu 8: Biết () 3 2 x4fxd = và () 3 2 x1gxd = . Khi đó: ()() 3 2 xfxgxd bằng: A. 3 . B. 3 . C. 4 . D. 5 . Lời giải Ta có ()()()() 333 222 413 fxgxdxfxdxgxdx−=−=−= Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây?
()
()
() 1;0
()
ời giải
. D. () 1;2;3 . Lời giải
()
Mặt cầu ()()()() 222 2 : SxaybzcR −+−+−= có tâm là () ;; Iabc
Suy ra, mặt cầu ()()()() 222 :12316Sxyz−+++−= có tâm là () 1;2;3 I .
Câu 11: Trong không gian với hệ tọa độ Oxyz , gọi α là góc giữa hai mặt phẳng () :3210Pxyz−++= và mặt phẳng () Oxy . Khẳng định nào sau đây đúng?
A. o30 α = B. o60 α = C. o90 α = D. o45 α = Lời giải

Mặt phẳng () P có một vectơ pháp tuyến là () 1;3;2 Pn =− .
Mặt phẳng () :0Oxyz = có một vectơ pháp tuyến là () 0;0;1 n = .
Tacó o |.|1 cos45
nn nn αα == =
|||| 2 P P
Câu 12: Cho số phức 2 (1)(12)=++ zii có phần ảo là
A. 2i . B. 2 . C. 2 . D. 4 .
Lời giải
Tacó 2 (1)(12)42 =++=−+ ziii
Vậy số phức z có phần ảo 2 b = .
Câu 13: Chokhốilăngtrụ có đáylàhìnhvuôngcạnh a vàchiềucaobằng 4a .Thể tíchcủakhốilăngtrụ
đã cho bằng
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 10 A. 42 2 yxx =−+ . B. 42 2 yxx =− . C. 32 3 yxx =− . D. 32 3 yxx =−+ . Lời giải Từ hình dạng của đồ thị ta loại phương án C và D. Nhận thấy lim() x fx →±∞ =−∞ suy ra hệ số của 4 x âm nên chọn phương án A.
mặt cầu ()()()() 222 :12316
tọ
A.
B.
1;2;3 . C.
Câu 10: Trong không gian Oxyz , cho
Sxyz−+++−= . Tâm của () S có
a độ là
() 1;2;3 .
()
1;2;3
23..44 day VShaaa === .
Câu 14: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a . Biết ()SAABC ⊥ và 3 SAa = .
Tính thể tích khối chóp SABC . A. 4 a B.
Tacó SA là đường cao hình chóp Tam giác ABC đều cạnh a
Vậy thể tích cần tìm là:
2313 ..3 344 SABC aa Va==
Câu 15: Trongkhônggian Oxyz ,phươngtrìnhmặtcầucótâm (3;1;2) I vàtiếpxúcvớimặtphẳng () Oxy là
A. 222 (3)(1)(2)4 xyz −+−++=

C. 222 (3)(1)(2)1 xyz ++++−=
B. 222 (3)(1)(2)9 xyz −+−++=
D. 222 (3)(1)(2)4 xyz ++++−=
Lời giải
Bán kính của mặt cầu là (;())22. IRdIOxyz===−=
Phương trình mặt cầu là 222 (3)(1)(2)4. xyz −+−++=
Câu 16: Trongmặtphẳngtọa độ
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 11
B. 3 4a C. 3 16 3 a D. 3 4 3 a Lời giải
A. 3 16a
3
C. 3 4 a D. 3 3 4
Lời giải
2 a
a
2 3 4 ABC a S∆ =
nên
,biết điểm () 2;7 M là điểmbiểudiễnsố phức z .Phầnthựccủa z bằng A. 7 B. 2 C. 2 D. 7 Lời giải Điểm () 2;7 M là điểm biểu diễn số phức 27 zzi =−+ . Vậy, phần thực của z bằng 2 .
17: Diện tích toàn phần ( tpS ) của một hình trụ có độ dài đường sinh 2 la = , bán kính ra = bằng A. 2 tp Sa π = . B. 2 4 tp Sa π = . C. 2 6 tp Sa π = . D. 2 8 tp Sa π = . Lời giải
Câu
Câu 18: Trong không gian Oxyz
Vậy ( )3;2;1 Pd −∈ .
Câu 19: Cho hàm số ( )yfx = có đồ thị là đường cong như hình vẽ
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có điểm cực đại là ( )1;3 .
B. Đồ thị hàm số có điểm cực tiểu là ( )1;1 .
C. Đồ thị hàm số có điểm cực đại là ( )1;1
D. Đồ thị hàm số có điểm cực đại là ( )3;1 .
Lời giải
Quan sát đồ thị ta thấy được điểm cực đại là ( )1;3 .
Câu 20: Đường tiệm cận đứng của đồ thị hàm số 53 1 x y x + = −+ có phương trình là
A. 1 x = .

DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 12
có
ệ
tích toàn
ầ
hình trụ: 222222426 tp Srlraaa πππππ =+=+=
Ta
di
n
ph
n
,
ng thẳ
321 : 112 xyz d +−− == đi qua điểm nào dưới đây?
đườ
ng
. B. (
1;1;2 Q . C. ( )3;2;1 N . D. ( )3;2;1 M . Lời giải Xét điểm ( )3;2;1 P ta có: 332211 000 112 −+−− ==⇔== .
A. ( )3;2;1 P
)
B. 5 x =− . C. 1 y = . D. 5 y =− . Lời giải Ta có 11 53 limlim 1 xx x y x ++→→ + ==−∞ −+ 1 x = là đường tiệm cận đứng của đồ thị hàm số 53 1 x y x + = −+ .
21: Tập nghiệm của bất phương trình ( ) 2 log312 +< x là A. 1 ;1 3 B. 11 ; 33 C. 1 ;1 3 D. ( );1−∞ Lời giải
Câu
ĐK: 1 3 >− x ( ) 2 log3123141 +<⇔+<⇔<
Kết hợp với điều kiện ta được nghiệm củabất phương trình là 1 1 3 −<< x
Vậy tập nghiệm củabất phương trình 1 ;1. 3
Câu 22: Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn?
A. 16 B. 2 C. 64 D. 3
Lời giải
Mua một cây bút mực có 8 cách
Mua một cây bút chì có 8 cách.
Công việc mua bút là hành động liên tiếp, theo quy tắc nhân ta có 8.864 = cách.
Câu 23: Biết ( ) sin3 fxdxxC =+ . Mệnh đề nào sau đây là mệnh đề đúng?
A. ( ) 3cos3 fxx =− B. ( ) 3cos3 fxx = C. () cos3 3 x fx =− D. () cos3 3 x fx = Lời giải
Áp dụng định nghĩa nguyên hàm.
Câu 24: Nếu ()
d3fxx = thì ()
4d fxxx
bằng
A. 5 B. 3 C. 4 D.
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 13
xxx
2 1
2 1
1 Lời giải Ta có: () 2 1 4d fxxx () 22 2 2 1 11 d4d32363fxxxxx =−=−=−=− . Câu 25: Họ nguyên hàm của hàm số () 2x 3 fxe x =+ A. ( ) 2 d3ln x fxxexC =++ . B. () 2 d3ln 2 x e fxxxC =++ . C. () 2 d3ln 2 x e fxxxC =++ . D. ( ) 2 d3ln x fxxexC =++ . Lời giải () 2 d3ln 2 x e fxxxC =++
Câu 26: Cho hàm số ()fx có đồ thị như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. () 0; +∞ B. () ;1−∞− C. () 2;2


Lời giải
D. () 1; −+∞
Nhìn vào đồ thị, hàm số đã cho đồng biến trên khoảng () ;2−∞− và () 0; +∞
Câu 27: Cho hàm số ()fx có bảng biến thiên như hình vẽ sau :
Giá trị cực tiểu của hàm số đã cho bằng
A. 4 B. 3 C. 0 D. 1
Lời giải
Dựa vào BBT, ta có giá trị cực tiểu của hàm số là CTy () 3 y = 4=− .
Câu 28: Với mọi , ab thỏa mãn 2 33 loglog5 ab+= , khẳng định nào sau đây đúng?
A. 2 9 ab = . B. 2 243 ab = . C. 2 243 ab+= . D. 3 15 ab+= .
Lời giải
Ta có: 22252 333 loglog5log(.)5.3.243 abababab +=⇔=⇔=⇔= .
Câu 29: Tính thể tích vật thể tròn xoay tạo ra khi quay phần hình phẳng giới hạn bởi đồ thị 2 yxx =− , trục Ox quanh trục Ox
A. 5 6 B. 30 π C. 1 30
Lời giải
D. 5 6 π
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 14
Câu 30: Cho hình chóp tứ giác
i
Gọi O là tâm hình vuông ABCD . Khi đó ()SOABCD ⊥
Gọi H là trung điểm cạnh CD . Ta có: OHCD ⊥ và 2 CD HDOHa === .
Do SCD∆ cân tại S nên SHCD ⊥ .
Vậy góc giữa mặt bên () SCD và mặt phẳng () ABCD là góc SHO .
Trong SHD∆ vuông tại H ta có 222252 SHSDHDaaa =−=−= .
Khi đó 1 cos60 22 OHa SHOSHO SHa === =° .
Câu 31: Cho hàm số 42 ()21yfxxx ==−++ có đồ thị là đường cong như bên dưới. Số các giá trị nguyên dương của m để phương trình 42 91830 xxm−++= có 4 nghiệm phân biệt là
A. 5


B. 7
C. 8
Lời giải Ta có
D. 4
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 15 Hoành độ giao điểm của đồ thị 2 yxx =− và trục hoành là 0 x = và 1 x = . Thể tích khối tròn xoay cần tìm là ()() 11 2 2432 00 2 30 Vxxdxxxxdx π ππ =−=−+=
.
có cạnh đáy bằng 2a cạnh bên bằng 5a . Góc giữa mặt bên
ẳ
đáy bằng
B.
° . C. 70°
D.
°
L
đều
SABCD
và mặt ph
ng
A. 60° .
30
.
45
.
ời giả
Số nghiệm của phương trình là là số giao điểm của đồ thị hai hàm số ( ) 12 9
= + = .

yfx m y
Dựa vào đồ thị hàm số ( )yfx = và đồ thị của hàm số 12 9 m y + = PT có 4 nghiệm phân
biệt 12 1236 9 m m + ⇔<<⇔−<< , mà m là số nguyên dương.
Suy ra { } 1; 2; 3; 4; 5 m ∈
Vậy có 5 giá trị nguyên dương của m thỏa mãn yêu cầu của bài toán.
Câu 32: Cho hàm số ( )yfx = liên tục trên ℝ và có ( ) ( )( ) 2 21 fxxxx ′ =+− . Hàm số đã cho nghịch
biến trên khoảng nào trong các khoảng sau?
A. ( )2;3 . B. ( )1;1 . C. ( )0;2 . D. ( );1−∞ .

Lời giải ()()()
BBT: Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng ( ) ( )1;2;3 +∞⊃
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 16 ( ) ( ) () 42 42 4242 91830 *921120 12 9211221 9 xxmxxm m xxmxx −++=⇔−−++= + ⇔−−=−−⇔−++=
2 0 2101 2 x fxxxxx x = ′ =+−=⇔= =−
Câu 33: Có 50 tấm thẻ đánh số từ 1 đến 50. Rút ngẫu nhiên 3 thẻ. Tính xác suất để tổng các số ghi trên thẻ chia hết cho 3 .
A. 11 171 . B. 1 12 . C. 9 89 . D. 409 1225 . Lời giải Số phần tử không gian mẫu: 3 50 19600 C Ω== .
Gọi A là tập các thẻđánh số a sao cho 150 a ≤≤ và a chia hết cho 3. { } 3;6;...;4816AA = =
Gọi B là tập các thẻ đánh số b sao cho 150 b ≤≤ và b chia 3 dư 1. { } 1;4;...;4917BB = =
Gọi C là tập các thẻ đánh số c sao cho 150 c ≤≤ và c chia 3 dư 2 { } 2;5;...;5017CC = =
Với D là biến cố: “Rút ngẫu nhiên 3 thẻ được đánh số từ 1 đến 50 sao cho tổng các số ghi trên thẻ chia hết cho 3 ”. Ta có 4 trường h
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 17
ợp xảy ra:
ng hợp 1: Rút 3 thẻ từ A : Có 3 16C Trường hợp 2: Rút 3 thẻ từ B : Có 3 17C . Trường hợp 3: Rút 3 thẻ từ C : Có 3 17C Trường hợp 4: Rút mỗi tập 1 thẻ: Có 16.17.174624 = . Suy ra 33 1716 2.46246544DCC=++= Vậy xác suất cần tìm 6544409 196001225 D P === Ω Câu 34: Tích các nghiệm của phương trình 2 22 loglog0 4 x x += bằng: A. 3 B. 1 3 C. 1 D. 1 2 Lời giải ĐKXĐ: 0 x > 2 22 2 2222222 2 2 log1 loglog0logloglog40loglog20 1 log2 4 4 x x x xxxxx x x = = += +−= +−= =− = Vậy tích các nghiệm của phương trình là: 11 2. 42 = . Câu 35: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện 22 zi−+= là A. Đường tròn tâm ( )1;2 I , bán kính 2 R = .
Trườ
B. Đường tròn tâm ( )2;1 I , bán kính 2 R =
C. Đường tròn tâm ( )2;1 I , bán kính 2 R =
D. Đường tròn tâm ( )1;2 I , bán kính 2 R = .
Lời giải
Gọi zxyi =+
() ()() ()() 2222 22212212214 zixyixyxy −+=⇔++−=⇔++−=⇔++−=
Vậy tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là đường tròn tâm ( )2;1 I , bán kính 2 R = .
Câu 36: Trong không gian Oxyz , đường thẳng đi qua điểm ( )1;2;3 A và song song v
xyz d −+−
A.
Đườ
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 18
==
ươ
ố là
ới đường thẳng 135 : 231
có ph
ng trình tham s
1
=+ =−− =+ . B. 12
3 xt yt zt =+ =−+ =− . C. 12 33 5 xt yt zt =+ =−+ =− . D. 2 32 13 xt yt zt =+ =− =−+ . Lời giải
23 35 xt yt zt
23
ng thẳng 135 : 231 xyz d −+− == có vectơ chỉ phương là ( )2;3;1 u =− Đường thẳng đi qua điểm ( )1;2;3 A và song song với đường thẳng d có vectơ chỉ phương là ( )2;3;1 u =− nên có phương trình tham số là 12 23 3 xt yt zt =+ =−+ =− Câu 37:
không gian Oxyz , cho điểm ( )3;2;5 M . Điểm đối xứng của điểm M qua trục Oz là A. ( ) 1 3;2;5 M . B. ( ) 2 0;0;5 M . C. ( ) 3 2;3;5 M . D. ( ) 4 0;0;5 M . Lời giải Điểm đối xứng của điểm ( )3;2;5 M qua trục Oz là ( ) 1 3;2;5 M . Câu 38: Cho hình chóp . SABC có đáy là tam giác đều cạnh 2a và SA vuông góc với mặt phẳng đáy, độ dài SA bằng a Khoảng cách từ A đến mặt phẳng ( )SBC bằng A. 25 5 a B. 5 5 a C. 21 7 a D. 3 2 a Lời giải
Trong
Gọi M là trung điểm BC , dựng AHSM ⊥ , khi đó ta hoàn toàn chứng minh được ( )AHSBC ⊥ . Thật vậy:
Vì () BCAM BCSAMBCAH BCSA ⊥ ⊥ ⊥ ⊥ .
Từ và suy ra ( )AHSBC ⊥ .
Ta có: 3 AMa = , ASa = , suy ra 22222 111113 32 a AH AHASAMaa =+=+⇔= .
Vậy () () 3 ,2 a dASBCAH==
Câu 39: Tính tổng tất cả các nghiệm nguyên của bất phương trình ( ) 22 22 log3log410 xxxx+−+−+≤ .
A. 4 . B. 6 . C. 5 .
3 . Lời giải
Điều kiện: 0 x > Ta có ( ) ( ) ( ) 2222 22 22 log3log410log33log44* xxxxxxxx +−+−+≤⇔+++≤+ .
Xét hàm số ( ) 2log fttt =+ trên ( ) 0; D =+∞ . Ta có () 1 10 ln2 fttD t ′ =+>∀∈ hàm số f đồng biến trên D .
Suy ra ( ) ( ) ( ) 22 *343413 fxfxxxx ⇔+≤⇔+≤⇔≤≤ .
Vậy tập hợp các nghiệm nguyên của bất phương trình là { }1;2;3 .
Câu 40: Cho hàm số ( )fx liên tục trên R . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên R thỏa
mãn ( ) ( ) 8818FG+= và ( ) ( ) 002FG+= . Khi đó () 2 0 cos.8sind xfxx π bằng
DẠYKÈMQUYNHƠNOFFICIAL
A. 1. B. 1. C. 8 . D. 8 . Lời giải
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 19
D.
DẠYKÈMQUYNHƠNOFFICIAL

PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 20 Ta có: ()() ()() ()() 88 00 GFC GxFxC GFC =+ =+ =+ ()() 2(8)18 (8)(0)8. 2(0)2 (0)()2 8818 0 F FC FF F FG G C += ⇔⇔−= += = = + + Vậy: () () 2 0 8 0 11 88()(8)(0)1. cos.8sind ft xdtF xF fx ==−= π Câu 41: Cho hàm số ()fx có đạo hàm () 2 2 ()(1)4 fxxxx ′ =−− .Có bao nhiêu giá trị nguyên dương của tham số m để hàm số () 2 ()212 gxfxxm =−+ có đúng 5 điểm cực trị? A. 18 . B. 17 . C. 16 . D. 19 . Lời giải Ta có: ()22 1 ()0(1)400 4 x fxxxxx x = ′ =⇔−−=⇔= = , trong đó 1 x = là nghiệm kép. () ()() () 2 2 ()212412212 gxfxxmgxxfxxm ′′ =−+ =−−+ Xét ()() () 2 4122 0120 xf xxxm g ′ =⇔ ′ −+= () () 2 2 2 2 22 3 3 2121() 2121 2121 2120 212421242 x x xxml xxm xxm xxm xxmxxm = = −+= −+= ⇔⇔ −=− −+= −+=−=− nên ta loại phương trình 2 2121 xxm−+= ) Xét hàm số 2 212 yxx =− có đồ thị, có đạo hàm '412yx=− Ta có bảng biến thiên Để ()gx có đúng 5 điểm cực trị thì mỗi phương trình ()() 1;2 đều có hai nghiệm phân biệt khác 3 . Do đó, mỗi đường thẳng 4 ym =− và ym =− phải cắt đồ thị tại 2 điểm phân biệt có hoành độ khác 3.
Nhận xét: đường thẳng 4 ym =− luôn nằm trên đường thẳng ym =−
Suy ra 18 m−<− 18 m ⇔< .
Vậy có 17 giá trị m nguyên dương.
Câu 42: Cho số phức zabi =+ ( ) , ab ∈ ℝ thỏa mãn 2 2 z zi + + là một số thuần ảo. Khi số phức z có môđun
nhỏ nhất, hãy tính ab + .
A. 0 ab+= . B. 221 ab+=− . C. 4 ab+= . D. 22 ab+= .
Ta có ,, zabiab=+∈ ℝ . Gọi ( ) ; Mab là điểm biểu diễn cho số phức z .
Có () 22 w 22 zabi ziabi +++ == +++ ( )
2222
aabbababi ab ++++−+++
2201 20 aabb ab +++=
Có ( ) 22 1220 abab ⇔+++=
Suy ra M thuộc đường tròn tâm ( )1;1 I , bán kính 2 R =
Vì đường tròn đi qua gốc tọa độ nên khi số phức z có môđun nhỏ nhất thì điểm ( ) ; Mab trùng gốc tọa độ. Vậy 0 ab+=
Câu 43: Cho hình lăng trụ đứng ABCABC′′′ có đáy là tam giác vuông cân đỉnh A , mặt bên là BCCB′′
hình vuông, khoảng cách giữa AB′ và CC ′ bằng a . Thể tích khối lăng trụ ABCABC′′′ là
Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
PHÁT TRIỂN ĐỀ THAM KHẢO THI TỐT NGHIỆP THPT NĂM 2023 Page 21
Lời giải
= ++ ( ) ( ) ( )( ) ()2 2
= ++
( ) ( ) ( ) ()2 2
( ) ()2 2 22 2 abiabi ab ++−+
2
w là số thuần ảo
⇔ ++≠
B. 3 2 3
D.
2 2
A. 3 2a
a C. 3 a
3
a
































