METHODECONCEPT / REDACTIE
Boom voortgezet onderwijs
AUTEURS
Benjamin del Canho
Jacqueline Kooiman
Gijs Langenkamp
Chantal Neijenhuis
Sibren Stienstra
Roosmarij Vanhommerig
Vera de Visser

METHODECONCEPT / REDACTIE
Boom voortgezet onderwijs
Benjamin del Canho
Jacqueline Kooiman
Gijs Langenkamp
Chantal Neijenhuis
Sibren Stienstra
Roosmarij Vanhommerig
Vera de Visser
© 2021 Boom voortgezet onderwijs, Groningen, The Netherlands
Behoudens de in of krachtens de Auteurswet van 1912 gestelde uitzonderingen mag niets uit deze uitgave worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elek tronisch, mechanisch door fotokopieën, opnamen of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever.
Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikelen 16h t /m 16m
Auteurswet 1912 jo. besluit van 27 november 2002, Stb 575, dient men de daarvoor wettelijk verschuldigde vergoeding te voldoen aan de Stichting Reprorecht te Hoofddorp (postbus 3060, 2130 kb , www.reprorecht.nl) of contact op te nemen met de uitgever voor het treffen van een rechtstreekse regeling in de zin van art. 16l, vijfde lid, Auteurswet 1912. Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16, Auteurswet 1912) kan men zich wenden tot de Stichting PRO (Stichting Publicatie- en Reproductierechten, postbus 3060, 2130 kb Hoofddorp, www.stichting- pro.nl).
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, recording or otherwise without prior written permission of the publisher.
isbn 978 94 9322 4315 www.boomvoortgezetonderwijs.nl

KERN Wiskunde is een RTTI-gecertificeerde methode en onderscheidt vier soorten vragen:
r Reproductievragen
t1 Trainingsgerichte toepassingsvragen
t2 Transfergerichte toepassingsvragen
i Inzichtvragen
Voor meer informatie over de RTTI-systematiek, zie www.docentplus.nl.
Boekontwerp & omslag René van der Vooren, Amsterdam
Opmaak & technische tekeningen PPMP, Wolvega
1 Getallen
wiskunde in de praktijk Hoe werkt geheimschrift? 8
1.1 Veelvouden en delers 10
1.2 Machten 16
1.3 Wortels 22
1.4 Wortels herleiden 28
1.5 Het decimale getallenstelsel 34
Toetsvoorbereiding 40
2 Ruimtemeetkunde
wiskunde in de praktijk Hoe maak je een voetbal? 44
2.1 Ruimtefiguren 46
2.2 Inhoud van ruimtefiguren 52
2.3 Punten, lijnen en doorsnedes 58
2.4 Aanzichten en kijklijnen 64
2.5 Uitslagen en oppervlakte 70
Toetsvoorbereiding 76
3 Lineaire verbanden
wiskunde in de praktijk Hoe kunnen vogels efficiënt vliegen? 80
3.1
Lineaire verbanden 82
3.2 Recht evenredige verbanden 88
3.3 Lineaire vergelijkingen 94
3.4 Lijnen 100
3.5
Lineaire ongelijkheden 106
Toetsvoorbereiding 112
4 Kansrekening
wiskunde in de praktijk Hoe krijg je antwoord op gevoelige vragen? 116
4.1
4.2
Tellen: roosterdiagram en boomdiagram 118
Tellen: wegendiagram en systematisch noteren 124
4.3 Kansen 130
4.4 Kansen berekenen 136
4.5 Met en zonder terugleggen 142
Toetsvoorbereiding 148
Bijlage 150
Register van begrippen 156
In dit hoofdstuk leer je verschillende eigenschappen van getallen kennen. Ook leer je wat machten met negatieve exponenten zijn en wat wortels zijn en hoe je ermee kunt rekenen. Je maakt nader kennis met het decimale getallenstelsel en je leert de namen van grote en kleine getallen. Tot slot kom je te weten hoe geheimschrift werkt, hoe een maandkalender in elkaar zit, wat bomen met fractals te maken hebben, wanneer wortels mooi uitkomen, waar het wortelteken vandaan komt en hoe je met Romeinse cijfers rekent.
WISKUNDE IN DE PRAKTIJK Hoe werkt geheimschrift? 8
1.1 Veelvouden en delers 10
1.2 Machten 16
1.3 Wortels 22
1.4 Wortels herleiden 28
1.5 Het decimale getallenstelsel 34
Toetsvoorbereiding 40
DOEL Je leert hoe je berichten kunt versleutelen en ontcijferen met behulp van het caesarcijfer.
Cryptografie Als je een bericht naar iemand wilt sturen en niet wilt dat iemand anders het kan lezen, kun je het bericht onleesbaar voor anderen maken door het in geheimschrift te zetten. Dit heet het versleutelen of coderen van het bericht. De ontvanger moet dan wel weten hoe het geheimschrift ontcijferd of gedecodeerd kan worden. Vaak heeft hij hiervoor een sleutel nodig, die aangeeft op welke manier de tekst is veranderd in geheimschrift. De tak van de wiskunde die zich bezighoudt met geheimschriften heet cryptografie.
Het caesarcijfer Geheimschriften bestaan al heel lang. Een van de oudste en bekendste versleutelingstechnieken is het caesarcijfer. Hierbij wordt elke letter van een bericht vervangen door een andere letter die een vast aantal plaatsen verderop in het alfabet staat. Als je alle letters bijvoorbeeld drie plaatsen in het alfabet verschuift, wordt elke A een D, elke B een E, enzovoort. Letters aan het eind van het alfabet verschuiven weer naar voren. Zo wordt elke X een A, elke Y een B en elke Z een C. In de illustratie hieronder zie je hoe dat werkt.
Het caesarcijfer is genoemd naar Julius Caesar (100 v.Chr.–44 v.Chr.), die met zijn veldheren had afgesproken dat in berichten elke letter drie plaatsen in het alfabet opgeschoven werd. Een bericht werd zo onleesbaar voor iemand die het onverhoopt zou onderscheppen. Het caesarcijfer is echter eenvoudig te ontcijferen, ook als je niet weet hoeveel plaatsen de letters verschoven zijn. Schrijf hiervoor (een deel van) de gecodeerde boodschap op en verschuif de letters eerst één plaats, dan twee plaatsen en ga net zolang door tot de tekst leesbaar is. Omdat het alfabet 26 letters heeft en er dus maar 25 verschuivingen mogelijk zijn, kun je met bovenstaande methode een tekst die versleuteld is met het caesarcijfer altijd wel ontcijferen. Daarom gebruikte Caesar voor belangrijke berichten ook wel ingewikkelder codeermethoden. Maar omdat de meeste mensen destijds nauwelijks konden lezen, was het caesarcijfer meestal voldoende veilig. Bovendien was deze manier van versleutelen nog niet bekend en wist men dus ook niet hoe je het gecodeerde bericht eenvoudig kon ontcijferen.
Caesarcijfer waarbij alle letters drie plaatsen naar rechts zijn opgeschoven in het alfabet. Om de versleutelde tekst zlvnxqgh te ontcijferen, moeten alle letters drie plaatsen naar links worden verschoven.
OPDRACHTEN
Tekstvragen
1 a Wat is het caesarcijfer? R
b Leg uit op hoeveel verschillende manieren je een bericht kunt versleutelen met het caesarcijfer. T1
2 a Versleutel het woord kern met het caesarcijfer waarbij alle letters vier plaatsen in het alfabet worden opgeschoven. T1
b Het volgende bericht is versleuteld met het caesarcijfer. Ga na wat de oorspronkelijke tekst is. T1 ydo dn uzzm bzczdh
c Versleutel zelf een bericht met het caesarcijfer en laat een klasgenoot het ontcijferen. T1
3 Kunnen onderstaande teksten versleutelingen zijn van dezelfde tekst, maar dan met een andere verschuiving? Leg je antwoorden uit. T2
a mors en zbef b kz en ma
Heb je het leerdoel bereikt?
R Ik weet wat het caesarcijfer is.
T1 Ik kan teksten versleutelen en ontcijferen met het caesarcijfer.
T2 Ik kan uitleggen hoe je met twee draaischrijven teksten met het caesarcijfer kunt versleutelen en ontcijferen.
I Ik kan zelf de eigenschappen van een geheimschrift onderzoeken en uitleggen hoe het werkt.
Verdiepingsvraag
4 Met behulp van twee draaischijven kun je gemakkelijk een bericht met het caesarcijfer versleutelen. Ook kun je een versleuteld bericht er weer makkelijk mee ontcijferen. Leg in eigen woorden uit hoe en waarom dit werkt. T2
Onderzoeksopdracht
5 Er zijn verschillende varianten op het caesarcijfer die lastiger te ontcijferen zijn. Maar ook met deze varianten kun je berichten tegenwoordig niet veilig meer versleutelen. Zoek op internet twee varianten op het caesarcijfer. Leg uit hoe deze werken en waarom het niet veilig is deze geheimschriften te gebruiken voor berichten. Verwerk je resultaten in een presentatie, nieuwsartikel, video, poster of quiz. I
B e GRIPP en geheimschrift decoderen versleutelen sleutel coderen cryptografie ontcijferen caesarcijfer
DOEL Je leert wat het kleinste gemeenschappelijke veelvoud en de grootste gemeenschappelijke deler zijn.
Kleinste gemeenschappelijke veelvoud Als je een getal met een geheel getal vermenigvuldigt, heet het resultaat een veelvoud van dat getal. Zo zijn −20, 0, 10 en 25 allemaal veelvouden van 5, maar −17 en 8 niet. Het kleinste gemeenschappelijke veelvoud van twee positieve gehele getallen is het kleinste positieve getal dat een veelvoud is van beide getallen. Zo is 18 het kleinste gemeenschappelijke veelvoud van 6 en 9. Je noteert dit als kgv(6, 9) = 18. Je kunt het kleinste gemeenschappelijke veelvoud van twee getallen vinden door van beide getallen de veelvouden op te schrijven en na te gaan wanneer deze voor het eerst overeenkomen.
Voorbeelden
1 Bepaal kgv(15, 25).
Veelvouden van 15 zijn: 15, 30, 45, 60, 75, 90, …
Veelvouden van 25 zijn: 25, 50, 75, 100, …
Het kleinste getal dat een veelvoud is van zowel 15 als 25 is 75.
Dus kgv(15, 25) = 75.
2 Bepaal kgv(60, 75).
Veelvouden van 60 zijn: 60, 120, 180, 240, 300, 360, …
Veelvouden van 75 zijn: 75, 150, 225, 300, 375, …
Het kleinste getal dat een veelvoud is van zowel 60 als 75 is 300.
Dus kgv(60, 75) = 300.
Breuken gelijknamig maken Als je twee breuken gelijknamig maakt, zorg je ervoor dat beide noemers gelijk worden. Je zoekt naar het kleinste getal dat een veelvoud is van beide noemers, dus naar het kleinste gemeenschappelijke veelvoud.
Voorbeeld
Maak 3 8 en 5 12 gelijknamig.
kgv(8, 12) = 24
3 8 = 3 3 8 3 = 9 24
5 12 = 5 2 12 2 = 10 24
De gehele getallen zijn: …, –4, –3, –2, –1, 0, 1, 2, 3, 4, …
Getallen groter dan 0 zijn positief.
OPDRACHTEN — OEFENEN
Kleinste gemeenschappelijke veelvoud
6 a Welke van de volgende getallen zijn veelvouden van 7? T1
20 / 35 / 91 / 107 / 140
b Welke van de volgende getallen zijn veelvouden van 1 4? T2
1 2 / 5 16 / 7 8 / 1 3 4 / 10
7 a Wat is het kleinste gemeenschappelijke veelvoud van twee positieve gehele getallen? R
b Geef de eerste tien veelvouden van 3. T1
c Geef de eerste tien veelvouden van 8. T1
d Bepaal kgv(3, 8). T1
8 Gegeven zijn de getallen 12 en 20. T1
a Geef alle positieve veelvouden onder de 100 van deze twee getallen.
b Bepaal kgv(12, 20).
9 Bepaal het kleinste gemeenschappelijke veelvoud van de volgende paren getallen. T1
a 3 en 16
b 9 en 20
c 15 en 40
10 Bepaal het kleinste gemeenschappelijke veelvoud van de volgende paren getallen. T1
a 9 en 24
b 12 en 14
c 35 en 245
Breuken gelijknamig maken
11 Maak de volgende breuken gelijknamig met behulp van het kleinste gemeenschappelijke veelvoud. T1
a 3 4 en 5 12
b 2 9 en 1 24
c 7 12 en 3 14
12 Bereken. Gebruik het kleinste gemeenschappelijke veelvoud om de breuken gelijknamig te maken. T1
a 7 8 + 1 12
b 5 12 + 11 18
c 4 25 + 7 30
Grootste gemeenschappelijke deler Als je een geheel getal a deelt door een geheel getal b en de uitkomst weer een geheel getal is, is a deelbaar door b. Het getal b heet dan een deler van a. Zo is 2 een deler van 8, want 8 : 2 = 4. Een geheel getal is even als 2 een deler is van dat getal, anders is het oneven. De grootste gemeenschappelijke deler van twee positieve gehele getallen is het grootste getal dat een deler is van beide getallen. Zo is 5 de grootste gemeenschappelijke deler van 10 en 35. Je noteert dit als ggd(10, 35) = 5. Je kunt de grootste gemeenschappelijke deler van twee getallen vinden door van beide getallen alle delers op te schrijven en dan na te gaan wat de grootste deler is die overeenkomt.
Voorbeelden
1 Bepaal ggd(18, 30).
De delers van 18 zijn: 1, 2, 3, 6, 9 en 18.
De delers van 30 zijn: 1, 2, 3, 5, 6, 10, 15 en 30.
Het grootste getal dat een deler is van zowel 18 als 30 is 6.
Dus ggd(18, 30) = 6.
2 Bepaal ggd(39, 130).
De delers van 39 zijn: 1, 3, 13 en 39.
De delers van 130 zijn: 1, 2, 5, 10, 13, 26, 65 en 130.
Het grootste getal dat een deler is van zowel 39 als 130 is 13.
Dus ggd(39, 130) = 13.
Breuken vereenvoudigen Als je een breuk vereenvoudigt, deel je de teller en de noemer door hetzelfde getal. Je zoekt naar het grootste getal dat een deler is van beide, dus naar de grootste gemeenschappelijke deler.
Voorbeeld
Vereenvoudig 30 36 ggd(30, 36) = 6
30 36 = 30 : 6 36 : 6 = 5 6
Als b een deler is van a, dan is –b dat ook. Meestal wordt alleen gekeken naar positieve delers. In dit hoofdstuk is dat ook zo.
OPDRACHTEN — OEFENEN
Grootste gemeenschappelijke deler
13 a Van welke van de volgende getallen is 3 een deler? T1
25 / 99 / –32 / –111
b Geef alle delers van 54. T1
c Welk positieve gehele getal onder de 16 heeft de meeste delers? T2
d Leg uit of 0 even of oneven is. T1
14 a Wat is de grootste gemeenschappelijke deler van twee positieve gehele getallen? R
b Geef alle delers van 24. T1
c Geef alle delers van 44. T1
d Bepaal ggd(24, 44). T1
15 Bepaal de grootste gemeenschappelijke deler van de volgende paren getallen. T1
a 12 en 28
b 15 en 36
c 8 en 45
16 Bepaal de grootste gemeenschappelijke deler van de volgende paren getallen. T1
a 15 en 35
b 30 en 42
c 100 en 325
17 Geef aan welke van de volgende beweringen onjuist zijn. Geef bij die beweringen een voorbeeld waarbij de bewering niet klopt. T2
A De som van twee oneven getallen is altijd even.
B Als je een even getal door 2 deelt, is de uitkomst altijd even.
C Als 2 en 3 delers van een getal zijn, is 6 dat ook.
D Als 2 en 4 delers van een getal zijn, is 8 dat ook.
Breuken vereenvoudigen
18 Vereenvoudig met behulp van de grootste gemeenschappelijke deler. T1
a 16 24 d 15 35
b 20 90 e 30 42
c 21 84 f 100 325
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
Ontdekken
19 Een volmaakt getal is een getal dat gelijk is aan de som van zijn echte delers (dat zijn alle delers behalve het getal zelf). Het kleinste volmaakte getal is 6.
a Laat zien dat 6 een volmaakt getal is. T1
b Het eerstvolgende volmaakte getal ligt tussen 20 en 30. Welk getal is dit? T2
20 a Geef de afmetingen van alle rechthoeken waarvan de oppervlakte 120 is en de lengte van de zijden gehele getallen zijn. T2
b Is het aantal delers van 120 even of oneven? Leg je antwoord uit. T2 c Noem drie getallen met een oneven aantal delers. I
21 Twee schaatsers schaatsen met een constante snelheid rondjes op een ijsbaan. De eerste schaatser doet 40 seconden over elk rondje, de tweede schaatser heeft steeds 6 seconden meer nodig. Op een gegeven moment passeren ze tegelijkertijd de startlijn. Na hoeveel tijd komen beide schaatsers voor het eerst opnieuw tegelijk over de startlijn? I
22 Een bakker wil haar klanten met kerst een doosje met kerstkransjes en bonbons geven. Zij heeft 1000 kerstkransjes en 400 bonbons en ze wil hiermee zoveel mogelijk doosjes vullen zonder kerstkransjes of bonbons over te houden. Elk doosje krijgt dezelfde inhoud. Hoeveel doosjes kan de bakker vullen en hoeveel kerstkransjes en bonbons zitten er in elk doosje? I
Onderzoeken
23 Lees de tekst Maandkalenders op de rechterbladzijde.
a Op wat voor dag viel 5 februari 2021? En 21 juli 2019? T1
b Op wat voor dag zal 1 januari 2029 vallen? T2
24 a In welk jaar na 2021 valt 1 januari voor het eerst weer op een vrijdag? T2
b In welk jaar na 2020 valt 1 januari voor het eerst weer op een woensdag? T2
c In welk jaar na 2023 valt 1 januari voor het eerst weer op een zondag? T2
25 a In welk jaar kun je voor het eerst weer de maandkalender van 2021 gebruiken als je niet let op het jaartal? T2
b In welk jaar kun je voor het eerst weer de maandkalender van 2020 gebruiken als je niet let op het jaartal? I
Let op: 2020 is een schrikkeljaar.
c Op wat voor dag zal 1 januari 2105 vallen? I
d Op wat voor dag viel 1 januari 1900? I
B e GRIPP en veelvoud kleinste gemeenschappelijke veelvoud deelbaar deler even oneven grootste gemeenschappelijke deler
Maandkalenders
Op een maandkalender kun je zien op welke dag een bepaalde datum valt. Zo kun je op de maandkalender hiernaast zien dat 1 januari 2020 op een woensdag viel.
Een maandkalender kun je een jaar later niet meer gebruiken, omdat de dagen dan zijn verschoven. Zo viel 1 januari 2021 niet op een woensdag, maar op een vrijdag. Dit komt doordat een week altijd zeven dagen heeft en het aantal dagen in een jaar geen veelvoud van 7 is. Een jaar heeft namelijk 365 = 52 × 7 + 1 dagen of, in het geval van een schrikkeljaar, 366 = 52 × 7 + 2 dagen. Omdat 2020 een schrikkeljaar was, is 1 januari 2021 twee dagen verschoven ten opzichte van 2020. In de maandkalender van 2022, 2023 en 2024 is 1 januari steeds één dag verschoven ten opzichte van het jaar ervoor. In de maandkalender van 2025 is 1 januari twee dagen verschoven ten opzichte van 2024, want dat is weer een schrikkeljaar. Je kunt bepalen of een jaar een schrikkeljaar is door na te gaan of het jaartal deelbaar is door 4. Zo is 2020 deelbaar door 4 en dus een schrikkeljaar. Deze regel geldt echter niet altijd. Als een jaartal deelbaar is door 100, dan is het geen schrikkeljaar, tenzij het jaartal deelbaar is door 400. Zo was het jaar 1900 geen schrikkeljaar, maar het jaar 2000 wel.
R e K enen
R1 Bereken. I 1 4 : 13 : 1 2 III 1 5 : 3 − 1 3 II 1 3 × (3 1 3 − 1 5) IV 5 × (1 6 + 1 5) : 1 3
januari
Heb je het leerdoel bereikt?
R Ik weet wat veelvouden en delers zijn en ken het verschil tussen even en oneven.
T1 Ik kan het kleinste gemeenschappelijke veelvoud en de grootste gemeenschappelijke deler van twee getallen vinden.
T2 Ik kan redeneren over eenvoudige eigenschappen van getallen.
I Ik kan het kleinste gemeenschappelijke veelvoud en de grootste gemeenschappelijke deler gebruiken in praktische situaties.
DOEL Je leert hoe je met machten kunt rekenen.
Machten Als je een getal een aantal malen met zichzelf vermenigvuldigt, kun je die berekening korter schrijven als macht, bijvoorbeeld 34. De exponent 4 geeft aan hoe vaak het grondtal 3 als factor wordt gebruikt: 34 = 3 3 3 3.
Let op het verschil tussen –24 en (–2) 4 :
–24 is gelijk aan het tegengestelde van 24 = 2 · 2 · 2 · 2 = 16, dus −24 = −16. Je kunt dit ook uitrekenen als –24 = –(24) = –(2 · 2 · 2 · 2) = –16.
(–2) 4 is gelijk aan –2 · –2 · –2 · –2 en dat is 16.
Voorbeelden
2 0,43 = 0,4 · 0,4 · 0,4 = 0,064
3
OPDRACHTEN — OEFENEN
Machten
26 Neem over en vul in. T1
a 23 = 2 =
b 54 = =
c ( 4)3 = − 4 =
d ( 6)4 = … … … … = …
27 Neem over en vul in. T1
a (1 2)3 = 1 2
4
c (3 5)2
d (2 3)4
28 Bepaal steeds het grondtal. T2
a 64 = 3 c 128 = 7
b 169 = 2 d 1 000 000 = 3
29 Bepaal steeds de exponent. T2
a 81 = 3 c 1 27 = (1 3)
b 256 = 4 d 1 512 = (1 2)
30 Bereken zonder rekenmachine. T1
a (–3)2 e –25
b –32 f (–2)5
c –33 g –26
d (–3)3 h (–2)6
31 Bereken zonder rekenmachine. Controleer vervolgens je antwoorden met behulp van je rekenmachine. T2 a 104 − 102 e 3 · (32 – 4) · 23 b (−7)3 − 32 f 9 · 25 − 64 23 c 50 − 44 g 62 + (−6)2 d 53 – 52 + 54 h 100 52 − (52 − 42)
Machten vermenigvuldigen Als je twee machten met hetzelfde grondtal met elkaar vermenigvuldigt, mag je de exponenten bij elkaar optellen. Zo is 32 34 gelijk aan 32 + 4 = 36. Door de machten uit te schrijven, zie je waarom dit zo is: 32 34 = 3 3 3 3 3 3 = 36
2 + 4 drieën
Voorbeelden:
1 33 32 = 33 + 2 = 35 = 243
2 5 54 = 51 + 4 = 55 = 3125
3 42 · 42 = 42 + 2 = 44 = 256
Machten delen Als je een macht door een macht met hetzelfde grondtal deelt, mag je de exponenten van elkaar aftrekken. Zo is 35 32 gelijk aan 35 2 = 33. Door de machten uit te schrijven, zie je waarom dit zo is: 5 – 2 drieën
35 32 = 3 3 3 3 3 3 · 3 = 33
Voorbeelden
1 37 33 = 37 3 = 34 = 81
2 74 73 = 74 3 = 71 = 7
3 24 2 = 24 21 = 24 − 1 = 23 = 8
OPDRACHTEN — OEFENEN
Machten vermenigvuldigen
32 Neem over en vul in. R Bij het met elkaar vermenigvuldigen van machten met hetzelfde grondtal, mag je de exponenten .
33 Neem over en vul in. T1 a 42 44 = (4 … ) (4 … … … ) = 4 b 33 32 = (3 …
34 Neem over en vul in. T1
b 76 · 72 = 7 = …
c 3 · 32 = 3 · 32 = 3 = …
d 53 · 5 = 5 = …
e 43 · 47 = 4 = f 102 · 105 = 10 =
35 Schrijf als één macht. T1
a 59 512
b 98 94
c 4 42
d 0,715 0,75
e 112 112
f 52 57
Machten delen
36 Neem over en vul in. R Als je een macht door een macht met deelt, mag je de van elkaar aftrekken.
37 Neem over en vul in. T1
38 Neem over en vul in. T1
39 Schrijf als één macht. T1
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
Ontdekken
40 a Hoeveel lagen papier heb je als je een vel papier drie keer dubbelvouwt? T2
b Laat zien dat je na tien keer vouwen ongeveer 1000 lagen papier hebt. T2
c Een vel papier met een dikte van 0,1 mm is zo vaak dubbelgevouwen dat het 1,28 cm dik is. Hoe vaak is het dubbelgevouwen? T2
d De gemiddelde afstand van de aarde tot de maan is ongeveer 385 000 km. Hoe vaak zou je een vel papier met een dikte van 0,1 mm moeten dubbelvouwen om deze afstand te overbruggen? I
41 Je kunt een term met één van de drie factoren
34 · 35 , 34 35 en (34)5 vermenigvuldigen.
Geef aan bij welke factoren de volgende berekeningen horen. Leg je antwoorden uit. T2
A vier keer met 3 vermenigvuldigen en daarna vijf keer door 3 delen
B vijf keer vier keer met 3 vermenigvuldigen
C vier keer met 3 vermenigvuldigen en daarna vijf keer met 3 vermenigvuldigen
42 2 24 = 2 2 2 2 2 = 1 23 = 1 8
Bereken op een soortgelijke manier: T2
a 34 35
b 72 77
c 104 108
Onderzoeken
43 Lees de tekst Boomfractals op de rechterbladzijde. De eerste keer dat je het voorschrift toepast, vertakt de stam van de boomfractal op de rechterbladzijde zich in zes kleinere takken. Stel dat je het voorschrift in totaal vier keer achter elkaar toepast. Bereken hoeveel takken de boom dan in totaal heeft. T2
44 Je gaat nu zelf een fractal van een boom tekenen. De stam van deze boom vertakt zich in drie takken die 3 4 keer zo lang zijn. Elke tak vertakt zich in drie takken die opnieuw 3 4 keer zo lang zijn. Hieronder zie je de eerste twee stappen. I
a Pas het voorschrift in totaal vier keer toe. b Hoe lang zijn de kleinste takken als je het voorschrift in totaal acht keer toepast? En als je dat in totaal twintig keer doet? Rond je antwoord af op drie decimalen.
c Bedenk twee manieren waarop je het voorschrift kunt aanpassen om een ander soort boomfractal te krijgen.
Boomfractals
Een fractal is een figuur waarbij een kleiner gedeelte er hetzelfde uitziet als het geheel. Zo’n figuur kun je tekenen met behulp van een voorschrift dat je op steeds kleinere schaal achter elkaar toepast.
Bij de fractal die je hiernaast ziet, is eerst de stam van de boom getekend. De stam vertakt zich in zes takken die half zo lang en minder dik zijn. Elke tak vertakt zich in zes takken die opnieuw half zo lang en minder dik zijn. Als je dit voorschrift verschillende malen achter elkaar toepast, ontstaat er een boom.
Door het voorschrift te wijzigen, kun je verschillende soorten ‘boomfractals’ maken.
R e K enen
R2 Een gemiddelde boom levert 300 kg papier op. Eén vel A4papier weegt 5 gram.
I Hoeveel vellen A4papier levert één gemiddelde boom?
II In een pak zitten 500 vellen A4papier. Hoeveel pakken papier kun je van één boom maken?
Heb je het leerdoel bereikt?
R Ik ken de regel voor het met elkaar vermenigvuldigen van machten met hetzelfde grondtal. Ook ken ik de regel voor het delen van een macht door een macht met hetzelfde grondtal.
T1 Ik kan machten met hetzelfde grondtal met elkaar vermenigvuldigen of door elkaar delen.
T2 Ik kan het grondtal of de exponent bepalen in berekeningen met machten.
I Ik kan beredeneren hoe vaak je een vel papier zou moeten dubbelvouwen om de afstand van de aarde tot de maan te overbruggen.
B e GRIPP en macht exponent grondtal fractal
DOEL Je leert wat wortels zijn.
Wortels Als je de lengte van een zijde van een vierkant met een oppervlakte van 25 wilt bepalen, zoek je een getal waarvan het kwadraat 25 is. Dit getal heet de wortel van 25 en noteer je als √25 Omdat 5 5 = 25 geldt √25 = 5. Het berekenen van de wortel van een getal heet worteltrekken. Zo is √36 = 6, want 6 6 = 36. Er is afgesproken dat een wortel altijd groter dan of gelijk aan 0 is. Daarom is –6 geen wortel van 36, ook al is −6 −6 = 36. De wortel van een negatief getal bestaat niet, want een kwadraat is altijd 0 of positief. √−25 bestaat dus niet. Maar pas op: √25 bestaat wel. √25 is het tegengestelde van √25 en dus gelijk aan −5.
Voorbeelden
1 √16 = 4, want 42 = 4 4 = 16
2 √0,01 = 0,1, want 0,12 = 0,1 · 0,1 = 0,01
3 (√7 )2 = √7 · √7 = 7
4 √ 9 16 = 3 4, want (3 4)2 = 3 4 · 3 4 = 9 16
5 √32 = 3, want √32 = √9 , en 3 · 3 = 9
6 √ 49 bestaat niet
7 √49 = − 7
8 √10 · √10 = 10
9 √0,25 = 0,5, want 0,52 = 0,5 · 0,5 = 0,25
10 √2,25 = 1,5 want 1,52 = 1,5 · 1,5 = 2,25
OPDRACHTEN — OEFENEN
45 Teken een getallenlijn van 0 tot 10. Geef met pijltjes aan waar de getallen √4 , √9 en √ 1 4 liggen. T1
46 Neem over en vul in. T1
a 52 =…, dus √… = 5
b 72 = …, dus √… = 7
c 42 = …, dus √… = 4
d 102 = …, dus √… = 10
47 Neem over en vul in. T1
a √64 = …, want … 2 = 64
b √9 = …, want … 2 = 9
c √1 = …, want … 2 = 1
d √144 = , want 2 = 144
e √1 4 = , want 2 = 1 4
f √0,16 = , want 2 = 0,16
48 Neem over en vul in. T1
a √4 = 2, want 2 =
b √121 = , want 2 =
c √ 1 16 = , want 2 =
d √ = 13, want 2 =
e √ = 20, want 2 =
f √ = 0,09, want 2 =
49 Bereken zonder rekenmachine. T1
a √49 d √0,04
b √225 e (√3,5 )2
c √ 4 9 f √5,52
50 Welke van de volgende uitdrukkingen is/zijn waar? Leg je antwoorden uit. T2
√ 16 = −4
√16 = −4
√11 · √11 = 11
√20 · √20 = 400
51 Je ziet hieronder drie vierkanten. T2
a Bereken de lengte van de zijden van de eerste twee vierkanten.
b Bereken de oppervlakte van vierkant III. 169 cm 121 cm2 64 cm2
cm
Volgorde van berekenen Je moet berekeningen in de juiste volgorde uitvoeren. De juiste rekenvolgorde is:
1 eerst uitrekenen wat tussen haakjes staat;
2 dan machtsverheffen en worteltrekken;
3 dan vermenigvuldigen en delen van links naar rechts;
4 dan optellen en aftrekken van links naar rechts.
Onder het wortelteken worden haakjes weggelaten. √16 − 7 betekent hetzelfde als √(16 − 7) en dit is gelijk aan √9 = 3
Ook wordt het vermenigvuldigingsteken voor wortels weggelaten:
2 √9 betekent hetzelfde als 2 √9 en dit is gelijk aan 2 3 = 6.
Voorbeelden
1 3 + 2 √16 − 7 − 7 = 3 + 2 √9 − 7 = 3 + 2 · 3 − 7 = 3 + 6 − 7 = 9 − 7 = 2
Wortels benaderen √25 en √1 4 komen op een geheel getal en een breuk uit: √25 = 5 en √1 4 = 1 2. Veel wortels komen niet zo mooi op een geheel getal of een breuk uit. Dat geldt bijvoorbeeld voor √10 , want er bestaat geen geheel getal of breuk waarvan het kwadraat 10 is. √10 is groter dan √9 en kleiner dan √16 , dus ligt √10 ergens tussen 3 en 4 in (zie de getallenlijn hiernaast). Je noteert dit als 3 < √10 < 4. Met je rekenmachine kun je een nauwkeurige benadering vinden: √10 = 3,1622… ≈ 3,16 √10 is dus ongeveer gelijk aan 3,16. Laat wortels die je niet als geheel getal of breuk kunt schrijven altijd in je antwoord staan, tenzij om een benadering wordt gevraagd. Zo heeft een vierkant met een oppervlakte van 10 cm2 zijden met een lengte van √10 cm. Afgerond op drie decimalen is dit 3,162 cm.
OPDRACHTEN — OEFENEN
Volgorde van berekenen
52 Neem over en vul in. T1
a √9 + 42 = √9 + = √ =
b 5 √121 − 12 = 5 − 12 =
c 3 + √6 + 5 2 = 3 + √ = 3 + =
d 6 √69 + 31 + 72 = 6 … + … = … + … = …
53 Bereken zonder rekenmachine. T1
a √2 + 7 d 6 + 3 √5 − 4
b 5 √25 + 11 e −10 √6 + 2 · 5
c 7 − √3 · 12 f √72 − 32
54 Bereken zonder rekenmachine. T2
a √32 + 42 c 11 16 + √25 16
b 52 − √5 · √5 d 2 √3 − 4 · 1 2
Wortels benaderen
55 Teken een getallenlijn van 0 tot 5. Geef met pijltjes aan waar de getallen √2 , √3 en √5 ongeveer liggen. Je mag je rekenmachine gebruiken. T1
56 Rond de volgende wortels af op twee decimalen. Gebruik je rekenmachine. T1
a √17 c √160
b √68 d √1200
57 Je kunt schatten hoe groot een wortel is zonder een rekenmachine te gebruiken. T1
a Neem de tabel over en vul hem in.
getal 0 1 2 3 4 5 6 kwadraat 7 8 9 10 11 12
b 12 ligt tussen de kwadraten 9 en 16. Tussen welke twee gehele getallen ligt √12 ?
c Tussen welke twee kwadraten ligt 34?
d Tussen welke twee gehele getallen ligt √34 ?
58 Geef aan tussen welke twee gehele getallen de volgende wortels liggen. Gebruik geen rekenmachine. T1 Tip: kijk naar de tabel van de vorige opdracht.
a < √61 <
b < √120 <
c < √88 <
d < √23 <
59 Geef aan tussen welke twee gehele getallen de volgende wortels liggen. Gebruik geen rekenmachine. T1
a √38 c √240
b √95 d √1000
OPDRACHTEN
Ontdekken
60 Bereken als dat kan. Leg anders uit waarom dit niet kan. Gebruik geen rekenmachine. T2
a √( 10)2 d √102
b √ 102 e (√10 )2
c (√ 10 )2 f ( √10 )2
61 Gebruik geen rekenmachine.
a Toon aan dat 2 < √5 < 2,5. T2
b Toon aan dat 2 1 5 < √5 < 2 1 4. T2
c Rond √21 af op een geheel getal. I
62 a Bereken met behulp van inlijsten de oppervlakte van het vierkant hieronder. T2
b Bereken de omtrek van het vierkant. Rond je antwoord af op drie decimalen. T2
Onderzoeken
63 Lees de tekst Wortels die mooi uitkomen op de rechterbladzijde. Leg zonder rekenmachine uit of je de volgende wortels kunt schrijven als een geheel getal of een breuk. T2
a √10 c √25 36
b √169 d √1 7
64 In deze opdracht ga je na of je √3 1 16 als een breuk kunt schrijven. T2
a Schrijf het getal onder het wortelteken als één breuk.
b Leg uit of je deze wortel als een breuk kunt schrijven.
65 Bereken zonder rekenmachine. T2
a √0,49
b √71 9
B e GRIPP en wortel worteltrekken rekenvolgorde
Wortels die mooi uitkomen
Als je √16 op je rekenmachine intoetst, krijg je als uitkomst 4. En als je √9 4 intoetst, krijg je als uitkomst 1,5, want √9 4 = √3 2 3 2 = 3 2 = 1,5
Dit zijn voorbeelden van wortels die je kunt schrijven als een geheel getal of een breuk. Hieronder zie je wat je als antwoord krijgt als je √2 intoetst.
√2
1,414213562
Maar als je 1,4142135622 berekent, krijg je niet precies 2. De uitkomst die op het scherm staat, klopt dus niet helemaal. Het getal is afgerond. √2 is een voorbeeld van een wortel die je niet kunt schrijven als een geheel getal of een breuk. Dit is vaak zo bij wortels. Wortels kun je alleen als een geheel getal of een breuk schrijven als het getal onder het wortelteken een kwadraat van een geheel getal is of een getal is dat je kunt schrijven als een breuk waarvan zowel de teller als de noemer een kwadraat van een geheel getal is. Zo zag je hierboven dat je √9 4 als een breuk kunt schrijven, omdat zowel de teller als de noemer van de breuk een kwadraat van een geheel getal is. √ 2 25 kun je niet als een breuk schrijven, want de teller is geen kwadraat van een geheel getal. Let er op dat de breuk wel zo ver mogelijk vereenvoudigd moet zijn. Zo kun je √18 8 wel als breuk schrijven (18 8 = 9 4), maar zijn 18 en 8 geen kwadraten.
Heb je het leerdoel bereikt?
R Ik weet wat wortels zijn en in welke volgorde ik een berekening moet uitvoeren.
T1 Ik kan de wortel van een getal berekenen of benaderen. Ook kan ik berekeningen met wortels in de juiste volgorde uitvoeren.
T2 Ik kan uitleggen wat een wortel met een vierkant te maken heeft en ik kan ingewikkelde berekeningen met wortels maken.
I Ik kan zonder rekenmachine wortels op gehelen nauwkeurig benaderen.
R e K enen
R3 100 gram rauwe wortels bevat ongeveer 5,2 gram koolhydraten en 0,2 gram vet. Eén portie is ongeveer 200 gram.
I Hoeveel gram koolhydraten bevat anderhalve portie rauwe wortels?
II Hoeveel gram vet bevat anderhalve portie rauwe wortels?
III In hoeveel kg wortels zit 100 gram vet?
DOEL Je leert hoe je met wortels kunt rekenen.
Wortels optellen en aftrekken Wortels kun je net als andere getallen bij elkaar optellen of van elkaar aftrekken. Zo is √2 + √2 gelijk aan 2 √2 = 2 √2 . En 7 √2 2 √2 = 5 √2 . Met je rekenmachine vind je 2 √2 ≈ 2,83 en 5 √2 ≈ 7,07. Je mag termen als √2 , 2 √2 en 3 √2 bij elkaar optellen en van elkaar aftrekken omdat onder het wortelteken hetzelfde getal staat. Dit zijn gelijksoortige wortelvormen 1, √2 en 4 √3 zijn niet gelijksoortig. Je kunt 1 en √2 daarom wel bij elkaar optellen, maar niet verder herleiden dan 1 + √2 . Net zo kun je √2 wel van 4 √3 aftrekken, maar niet verder herleiden dan 4 √3 √2 . Met je rekenmachine kun je uitrekenen hoe groot de resulterende getallen ongeveer zijn: 1 + √2 ≈ 2,41 en 4 √3 √2 ≈ 5,51.
Voorbeelden
1 3 √2 + 5 √2 =
Wortels vermenigvuldigen en delen Wortels kun je net als andere getallen met elkaar vermenigvuldigen. Je vermenigvuldigt dan de getallen die onder de worteltekens staan met elkaar. Zo is √3 · √7 =
45
3 · 7 = √21 . Delen werkt op dezelfde manier. Je deelt de getallen die onder de worteltekens staan door elkaar. Zo is
15
Voorbeelden 1
OPDRACHTEN — OEFENEN
Wortels optellen en aftrekken
66 Herleid zonder rekenmachine. T1 a 3 √2 + 5 √2 = √2 d 4 √2 − √2
b 5 √3 + 4 √3 = √3 e 7 √15 − 4 √
67 Herleid indien mogelijk. Gebruik geen rekenmachine. T1
Wortels vermenigvuldigen en delen
71 Neem over en vul in. T1
68 Herleid zonder rekenmachine. T1
72 Bereken zonder rekenmachine. T1
69 Herleid zonder rekenmachine. T1 a 5 √2 + 6 √3 − 12 √2
70 Bereken de omtrek van de volgende figuur. T2
73 Bereken zonder rekenmachine. T2
74 Bereken de oppervlakte van de figuur in opdracht 70. T2
WORTELS HERLEIDEN 1.4
Wortels vereenvoudigen Sommige wortels kun je vereenvoudigen. Doe dit altijd zo ver mogelijk. Als het getal onder het wortelteken een kwadraat als deler heeft, kun je de wortel van het kwadraat voor het wortelteken brengen. Je gebruikt daarvoor de regel voor het vermenigvuldigen van wortels.
Voorbeelden
1 √8 = √4 2 = √4 √2 = 2 √2
2 √32 = √16 2 = √16 √2 = 4 √2
3 √27 = √9 3 = √9 √3 = 3 √3
4 √75 = √25 3 = √25 √3 = 5 √3
OPDRACHTEN — OEFENEN
Wortels vereenvoudigen
75 a Door welk kwadraat kun je 45 delen? T1
b Vereenvoudig √45 zonder rekenmachine te gebruiken. T1
76 Neem over en vul in. T1
a √60 = √
77 Vereenvoudig de volgende wortels. Gebruik geen rekenmachine. T1
a √18 d √50
b √40 e √72
c √48 f √110
78 Laat met een berekening zien dat T2
a 2 √18 = 6 √2
b 3 √45 = 9 √5
c 5 √98 = 35 √2
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
Ontdekken
79 Herleid zonder rekenmachine. T2
a 4 √8 + 3 √2
b 2 √5 + 11 √125
80 a Een rechthoek heeft een lengte van 2 √7 en een oppervlakte van 14. Bereken de breedte van de rechthoek. T2
b Een driehoek heeft een basis van 15 en een hoogte van 4 √3 . Bereken de oppervlakte van de driehoek. T2
81 Hieronder zie je drie vierkanten. De oppervlakte van het grootste vierkant is twee keer zo groot als de oppervlakte van het middelste vierkant. De oppervlakte van het middelste vierkant is twee keer zo groot als de oppervlakte van het kleinste vierkant. De lengte van de zijden van het middelste vierkant is 10 cm. Bereken de omtrek in cm en de oppervlakte in cm2 van alle drie de vierkanten. Rond je antwoorden indien nodig af op één decimaal. I
Onderzoeken
82 Lees de tekst Het wortelteken op de rechterbladzijde. Leg in eigen woorden uit waar het woord wortel en het wortelteken vandaan komen. T2
83 Hieronder vind je een fragment uit Die Coß waarin Rudolff enkele optellingen bespreekt. Op de eerste regel staat ‘ √8 zu √18 facit √50 ’. Dit betekent hetzelfde als √8 + √18 = √50 . Maak de volgende opdrachten zonder rekenmachine. T2
a Vereenvoudig √8 , √18 en √50 .
b Toon aan dat √8 + √18 = √50 .
c Toon aan dat de volgende twee berekeningen ook kloppen.

10 cm
R e K enen
R4 Het leerlingenstatuut van een school bestaat uit acht hoofdstukken van elk vier bladzijden. Het leerlingenstatuut wordt dubbelzijdig geprint. Er zitten 1226 leerlingen op deze school.
I Hoeveel vellen papier zijn er nodig om aan alle twaalf leden van de leerlingenraad een leerlingenstatuut te kunnen geven?
II Hoeveel vellen papier zijn er nodig om aan alle leerlingen een leerlingenstatuut te geven?
Het idee van een wortel was al in de oudheid bekend, maar Arabische wiskundigen hebben in de middeleeuwen de wortel pas zijn naam gegeven.
Het kwadraat van een getal werd door hen ‘ma l’ genoemd, dat hoofdsom betekent. Het bijbehorende getal noemden zij ‘jid r’, dat wortel van een plant betekent. De Arabieren gaven hiermee aan dat volgens hen de hoofdsom als het ware afkomstig is uit zijn wortel. Zij gebruikten het woord wortel overigens niet alleen voor het omgekeerde van een kwadraat, maar ook voor de oplossingen van een vergelijking. Dit laatste is nog steeds het geval in Engelstalige landen, waar de oplossingen van een vergelijking ook wel ‘the roots of the equation’ worden genoemd. Het Engelse woord ‘root’ betekent wortel.
Ook Nederlandse wiskundigen gebruiken soms het woord wortel om een oplossing van een vergelijking mee aan te duiden. De Duitse wiskundige Christoff Rudolff (1499−1545) was de eerste die het wortelteken √ gebruikte. Hiernaast zie je een fragment uit zijn boek Die Coß (1525), waarin hij het wortelteken introduceert. Waarom hij voor dit teken heeft gekozen, is niet helemaal duidelijk. Het is mogelijk dat Rudolff het heeft afgeleid van de letter r, de beginletter van het Latijnse woord ‘radix’, dat wortel betekent. Maar er zijn ook aanwijzingen dat het afkomstig is van een punt met een staart eraan. Rudolff gebruikte nog niet het horizontale streepje dat een wortel tegenwoordig heeft (√i ). Deze toevoeging is afkomstig van de Franse filosoof en wiskundige René Descartes (1596−1650). Rudolff heeft niet alleen het wortelteken geïntroduceerd, maar gebruikte ook als eerste de definitie x 0 = 1

Fragment uit een herdruk van ‘Die Coß’ (1525) door christoff rudolff
Hier zie je de eerst bekende keer dat het wortelteken werd gebruikt.
Heb je het leerdoel bereikt?
R Ik weet wanneer je wortels bij elkaar mag optellen of van elkaar mag aftrekken.
T1 Ik kan wortels optellen, aftrekken, vermenigvuldigen, delen en vereenvoudigen.
T2 Ik kan de omtrek en de oppervlakte berekenen van vlakke figuren waarvan de afmetingen wortels zijn.
I Ik kan redeneren over de omtrek en oppervlaktes van vlakke figuren waarvan de afmetingen wortels zijn.
B e GRIPP en wortelvorm gelijksoortige wortelvormen
DOEL Je leert hoe het decimale getallenstelsel werkt en hoe je getallen in de wetenschappelijke notatie opschrijft.
Machten van 10 Als je de machten 103, 102 en 101 uitschrijft en op een rijtje zet, zie je dat ze steeds tien keer zo klein worden: 103 = 1000, 102 = 100 en 101 = 10. Deze regelmaat kun je voortzetten. Je krijgt dan 100 = 1, 10−1 = 0,1 en 10−2 = 0,01; enzovoort.
Leer de volgende machten van 10 uit je hoofd. Als je het getal als macht van 10 schrijft, zie je aan de exponent hoeveel nullen het getal heeft.
duizend = 103 = 1000 één duizendste = 1 103 = 10−3 = 0,001
miljoen = 106 = 1 000 000 één miljoenste = 1 106 = 10−6 = 0,000 001
miljard = 109 = 1 000 000 000 één miljardste = 1 109 = 10−9 = 0,000 000 001
biljoen = 1012 = 1 000 000 000 000 één biljoenste = 1 1012 = 10−12 = 0,000 000 000 001
Het decimale getallenstelsel Het decimale getallenstelsel bestaat uit de tien cijfers 0 tot en met 9. De plaats waar een cijfer in een decimaal getal staat, bepaalt de waarde van dat cijfer. Zo staat in het getal 7125,4 de 7 voor 7 duizendtallen, de 1 voor 1 honderdtal, de 2 voor 2 tientallen, de 5 voor 5 eenheden en de 4 voor 4 tienden. Van links naar rechts neemt de waarde van een cijfer dus steeds met een factor tien af. Je kunt decimale getallen daarom als een som van machten van 10 schrijven: 7125,4 = 7 103 + 1 102 + 2 101 + 5 100 + 4 10−1
Voorbeelden
1
2
=
OPDRACHTEN — OEFENEN
Machten van 10
84 Schrijf de volgende getallen als macht van 10. R
a 1 miljoen d 1 duizendste
b 1 miljard e 1 miljoenste
c 1 biljoen f 1 miljardste
85 Schrijf de volgende getallen uit in cijfers. R
a 1 miljoen c 1 duizendste
b 1 biljoen d 1 miljardste
86 Schrijf de volgende getallen uit in cijfers. T1
a 10 duizend c 1 honderdste
b 100 miljoen d 1 tienduizendste
87 Schrijf de volgende getallen uit in cijfers. T1
a 3 duizend c 2 miljoenste
b 5 miljard d 4 biljoenste
88 a Rond 5603 af op duizendtallen. T1
b Rond 105 158 695 af op miljoenen. T2
c Rond 6 329 651 000 af op miljarden. T2
d Rond 59 625 781 000 000 af op biljoenen. T2
89 Op 30 januari 2021 telden de Verenigde Staten naar schatting 332 129 757 inwoners. T2
a Waarom heeft het niet veel zin om dit aantal zo nauwkeurig weer te geven?
b Rond dit aantal af op miljoenen.
Het decimale getallenstelsel
90 Gegeven is het getal 6391,75. T1
a Hoeveel duizendtallen heeft dit getal?
b Wat is de betekenis van het cijfer 5 in dit getal?
91 Neem over en vul in. T1
6,56 =
105,80
92 Neem over en vul in. T1
a 524 = 5 · 10 + 2 · 10 + 4 · 10
b 1709 = 1 · 10 + 7 · 10 + 9 · 10
40 203
265 000
93 Schrijf de volgende getallen als som van machten van 10. T1
a 4205 c 15,25
b 61 726 d 3,562
94 Bereken. Gebruik geen rekenmachine. T1
HET DECIMALE GETALLENSTELSEL 1.5
Wetenschappelijke notatie Een groot getal als 12 500 000 000 is door de vele cijfers lastig om te lezen of mee te rekenen. Daarom wordt zo’n getal vaak geschreven als een vermenigvuldiging van een getal tussen 1 en 10 met een macht van 10. Je krijgt dan 1,25 × 1010 Dit heet de wetenschappelijke notatie
Heel kleine getallen worden ook vaak in de wetenschappelijke notatie geschreven. De exponent van de macht van 10 is dan negatief. Bijvoorbeeld 0,000 003 = 3 1 1 000 000 = 3 10−6
Voorbeelden
1 9800 = 9,8 1000 = 9,8 103
2 3 000 000 = 3 1 000 000 = 3 106
3 0,7 = 7 · 1 10 = 7 · 10−1
getal tussen 1 en 10 a · 10n
In plaats van de vermenigvuldigingspunt wordt ook vaak het ×symbool gebruikt.
4 0,000 065 = 6,5 · 1 100 000 = 6,5 · 10−5 5 7 104 = 7 10 000 = 70 000 6 1,18 102 = 1,18 100 = 118 7 9 · 10−3 = 9 · 1 1000 = 0,009 8 2,764 · 10−5 = 2,764 · 1 100 000 = 0,000 027 64
OPDRACHTEN — OEFENEN
Wetenschappelijke notatie
95 Noem twee voordelen van de wetenschappelijke notatie. R
96 Neem over en vul in. T1
a 2000 = 2 10
b 65 000 = 6,5 10
c 0,05 = 5 1 = 5 10
d 0,0022 = 2,2 1 = 2,2 10
97 Neem over en vul in. T1
a 169 = 1,69 · 10
b 82 015 = 8,2015 · 10
c 50 169 = 5,0169 · 10
d 0,152 = 1,52 · 10
e 0,000 67 = 6,7 · 10
f 0,000 428 7 = 4,287 · 10
98 Schrijf in de wetenschappelijke notatie. T1
a 305 c 0,000 123
b 673 000 d 0,000 005 5
99 Schrijf als decimaal getal. T1
a 3 105 f 6 10−4
b 3,021 102 g 7,9 10−3
c 5,6 105 h 5,912 10−8
d 1,91 103 i 1,2605 10−2
e 9,39 104 j 1,092 10−6
100 Schrijf de volgende getallen in de wetenschappelijke notatie. T2
a Begin 2021 waren er wereldwijd ongeveer 7 831 000 000 mensen.
b De diameter van een menselijke cel is ongeveer 0,000 015 meter.
c De Melkweg bevat ongeveer 200 miljard sterren.
101 Schrijf het antwoord in de wetenschappelijke notatie. Rond het getal dat voor de macht van 10 staat af op drie decimalen. T2
a 7700 · 2800
b 2230
c 3 · 0,6945
d 0,000 24 · 0,000 333
OPDRACHTEN — ONTDEKKEN & ONDERZOEKEN
Ontdekken
102 Geef aan welke bewering juist is.
Iemand van 31 jaar is ongeveer: T2
A 1 miljoen seconden oud
B 1 miljard seconden oud
C 1 biljoen seconden oud
103 Schrijf in de wetenschappelijke notatie. T2
Tip: gebruik je rekenmachine.
a 5 100 000
b 8 miljard gedeeld door 2 miljoen
c een miljoenste deel van 350
d 8 · 105 0,5 · 10−2
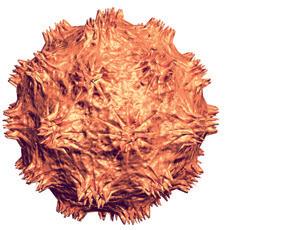
104 De griep wordt veroorzaakt door het influenzavirus. Virussen zijn zo klein dat ze alleen onder een speciale microscoop zichtbaar zijn. Onderstaande afbeelding van het influenzavirus is met behulp van zo’n microscoop gemaakt en dus sterk vergroot.
In werkelijkheid is de diameter van het influenzavirus ongeveer 80 miljoenste van een millimeter. Hoeveel keer is de afbeelding vergroot? Schrijf je antwoord in de wetenschappelijke notatie. I
Onderzoeken
105 Lees de tekst Romeinse cijfers op de rechterbladzijde. T1
a Schrijf de getallen 15 tot en met 20 in Romeinse cijfers.
b Welk getal is CCCLIX?
c Schrijf het huidige kalenderjaar als Romeins getal.
106 Voer de volgende berekeningen uit in Romeinse cijfers, dus zonder de getallen eerst om te zetten in decimale getallen. Controleer daarna je antwoord door de getallen wel om te zetten.
a LXXII + XXXIV T1
b DCXCIX + MCCCXXXVI T1
c CCCVII · III I
107 Op gebouwen zie je vaak Romeinse cijfers die het bouwjaar aangeven. Wat is het bouwjaar van onderstaand gebouw? T2

108 Voor welk getal onder de 1000 heb je de meeste Romeinse cijfers nodig? I
Romeinse cijfers
Meer dan 2000 jaar geleden hebben de Romeinen een getallenstelsel ontwikkeld waarbij je de waarde van een getal bepaalt door de waarden van de verschillende Romeinse cijfers bij elkaar op te tellen. In het Romeinse getal CXVII staat de C voor 100, de X voor 10, de V voor 5 en I voor 1. CXVII is dus gelijk aan 100 + 10 + 5 + 1 + 1 = 117.
Je schrijft Romeinse cijfers van hoog naar laag.
De cijfers I, X en C kun je voor een hoger cijfer schrijven om aan te geven dat je de waarde van het hogere cijfer ermee verlaagt. Zo is XC gelijk aan 100 – 10 = 90.
Romeinse cijfers speciale combinaties I 1 IV 4 V 5 IX 9 X 10 XL 40
L 50 XC 90
C 100 CD 400
D 500 CM 900 M 1000
Heb je het leerdoel bereikt?
R Ik weet wat het decimale getallenstelsel is en ik ken de voordelen van de wetenschappelijke notatie. Ook ken ik de naam van enkele machten van 10.
T1 Ik kan getallen als som van machten van 10 schrijven en ik kan decimale getallen omschrijven naar de wetenschappelijke notatie en omgekeerd.
T2 Ik kan rekenen met grote en kleine getallen.
I Ik kan de vergroting van een afbeelding van iets heel kleins berekenen.
Je kunt twee Romeinse getallen bij elkaar optellen door alle Romeinse cijfers achter elkaar te zetten, deze te sorteren van hoog naar laag en daarna waar mogelijk lagere Romeinse cijfers samen te voegen tot hogere.
Bij getallen met combinaties zoals IV, moet je deze eerst uitschrijven in lagere cijfers voordat je alle cijfers achter elkaar zet: IV IIII. In de uitkomst moet je waar mogelijk lagere cijfers weer samenvoegen tot hogere cijfers: IIII IV.
Voorbeeld
LXXI + LXXIV = | IV uitschrijven.
LXXI + LXXIIII = | Alle cijfers achter elkaar zetten.
LXXILXXIIII = | Sorteren van hoog naar laag. LLXXXXIIIII = | LL en IIIII samenvoegen.
CXXXXV = | XXXX omschrijven.
CXLV | Controle: 71 + 74 = 145.
B e GRIPP en decimaal getallenstelsel decimaal getal wetenschappelijke notatie Romeinse cijfers
R e K enen
R5 Een zwembad heeft een lengte van 25 m en een breedte van 10 m. Het water in het zwembad is 2,5 m diep.
I Hoeveel liter water bevat het zwembad?
II Hoeveel zwembaden met bovenstaande afmetingen kun je vullen met 10 miljard liter water?
Kijk aan het eind van elke paragraaf of je de begrippen kent en het leerdoel hebt bereikt. Zo niet, lees dan de uitleg nog eens goed door of bekijk de uitlegvideo’s. Maak daarna de volgende opdrachten.
Wiskunde in de praktijk
109 a Leg uit wat het caesarcijfer is. R
b Ontcijfer het volgende bericht, dat versleuteld is met het caesarcijfer. T1 tu juuhbydw yi wumehfud
§ 1.1
110 a Welk getal heeft de meeste delers: 17 of 33? T1
b Geef alle oneven delers van 30. T2
c Geef alle delers van 200 die een veelvoud van 25 zijn. T2
111 a Bepaal kgv(15, 36). T1
b Bepaal ggd(24, 80). T1
§ 1.2
112 Bereken zonder rekenmachine. T1
a 0,33 d (−2)7
b (3 7)2 e (1 6)3
c (–2)6 f 0,42
113 Bereken zonder rekenmachine. T2
a 35 – 2 (–4)2 c 100 –52 + 16 24
b 32 – 23 – (–1)8 d (1 2)2 –54 33
114 Schrijf als één macht.
a 24 212 T1 c 53 52 55 T2
b 550 515 T1 d 124 1218 12 T2
§ 1.3
115 Bereken zonder rekenmachine. T1
a √81 d ( √5 )2
b √0,01 e 3 √16 1
c √ 4 49 f 1 + √8 2 2
116 Bereken zonder rekenmachine. T2
a √132 122 6
b √102 √10 · √10
117 Hieronder zie je twee vierkanten. Het kleine vierkant is ontstaan door de middens van de zijden van het grote vierkant met elkaar te verbinden. De lengte van de zijden van het grote vierkant is 10 cm. Bereken de lengte in cm van de zijden van het kleine vierkant. Rond je antwoord af op twee decimalen. T2 ? 10 cm
§ 1.4
118 Herleid zonder rekenmachine. T1
a 3 √2 + 2 √5 + 8 10 √2 b 2 √5 + 1 4 √7 – 4 √5 + 1
119 Vereenvoudig zonder rekenmachine te gebruiken. T1
a √54 b √80
120 Bereken zonder rekenmachine.
a 6 √12 √ 1 3 T1 c 2 √21 √7 T1
b ( 3 √6 )2 T2 d √11 √( 5)2 T2
121 Bereken de omtrek en de oppervlakte van driehoek ABCD. T2
Hoofdstuk 1
125 Vul in: <, > of = T2
a 100 000 95 c √24 2 √5
b 1 63 (1 4)3 d 7,2 1011 8 biljoen
126 De snelheid van het licht (in vacuüm) is ongeveer 3 108 m/s. T2
a Hoeveel km/h is dit? Gebruik de wetenschappelijke notatie.
b Hoeveel seconden doet licht erover om 25 meter af te leggen? Gebruik de wetenschappelijke notatie. Rond het getal dat voor de macht van 10 staat af op een geheel getal.
122 Ga zonder rekenmachine na welk getal groter is. I
a 4 √8 of 7 √2
b 3 √5 of 5 √2
§ 1.5
123 Schrijf in de wetenschappelijke notatie. T1
a 2 000 000 c 0,000 48
b 34 000 d 0,000 000 219
124 Schrijf als decimaal getal. T1
a 6 104 c 2,7 10−3
b 4,93 108 d 1,12 10−7
c De gemiddelde afstand van de aarde tot de zon is ongeveer 150 miljoen km. Hoelang doet het licht van de zon erover om de aarde te bereiken? Rond je antwoord af op minuten nauwkeurig.
127 In een machine zitten twee tandwielen die in elkaar grijpen. Het kleine tandwiel heeft twaalf tanden en het grote twintig.
Hoe vaak moet je het grote tandwiel minimaal ronddraaien, zodat beide tandwielen een geheel aantal keren hebben rondgedraaid? I