Direzione Discipline • Matematica 4

IMPARIAMO METODO MATEMATICA

12 Che cosa ci insegna la MATEMATICA

NUMERI

14 I primi numeri

6 Parole per… CONOSCERE Numeri e Armonia

18 Il nostro sistema di numerazione

19 Esercizi

10 I grandi numeri

11 Esercizi

12 Dossier problemi

Le tappe del problema

14 Dalla testa ai piedi

16 L’addizione

17 Le proprietà dell’addizione

18 Esercizi

20 La sottrazione

21 La proprietà della sottrazione

22 Esercizi

24 Problem solving In partenza per…

26 La moltiplicazione

27 Le proprietà della moltiplicazione

29 Esercizi

30 La divisione

31 La proprietà della divisione

32 La divisione in colonna

34 Esercizi

36 Dossier problemi

I dati del problema

38 Le domande del problema

40 I multipli

41 I divisori

42 Dal più facile...

43 ... al più difficile

44 Dossier problemi Il procedimento risolutivo

46 Diversi procedimenti

47 Diversi modi per rappresentare il procedimento risolutivo

48 Problem solving A spasso per il mercato

50 La frazione

51 Esercizi

52 Le frazioni complementari

53 Le frazioni proprie e improprie

54 Confrontare le frazioni

56 Le frazioni equivalenti

57 Esercizi

58 La frazione di un numero

59 Esercizi

60 Dal più facile...

61 ... al più difficile

62 per imparare Le frazioni nell’arte

164 Problem solving Un giro in libreria

166 Le frazioni decimali

167 Esercizi

168 Le frazioni decimali e i numeri decimali

169 I centesimi e i millesimi

170 I numeri decimali

171 Esercizi

172 Confrontare i numeri decimali

173 Esercizi

174 Addizioni e sottrazioni con i decimali

175 Esercizi

176 Moltiplicazioni e divisioni per 10 • 100 • 1 000

177 Moltiplicazioni con i numeri decimali

178 Divisioni con i numeri decimali

179 Problem solving Pausa in viaggio

180 Dal più facile...

181 ... al più difficile

MISURE

182 Le prime misurazioni

184 Parole per… CONOSCERE Eureka!

186 Le misure di lunghezza

187 Le equivalenze

188 Le misure di capacità

189 Esercizi

190 Le misure di massa-peso

191 Peso lordo • Peso netto • Tara

192 Dal più facile...

193 ... al più difficile

113 Retta • Semiretta • Segmento

114 L’angolo

115 Vari tipi di angolo

116 Simmetria e traslazione

117 La rotazione

118 I poligoni

119 Classificare i poligoni

120 I triangoli

121 Esercizi

122 I quadrilateri

123 Esercizi

124 I parallelogrammi

125 Esercizi

126 I trapezi

127 Esercizi

128 per imparare Linee e forme geometriche nell’arte

130 Il perimetro

131 L’area

132 Isoperimetria ed equiestensione

133 Comporre e scomporre figure

134 Le misure di superficie

135 Esercizi

136 L’area del rettangolo e del quadrato

137 Esercizi

138 L’area del parallelogramma

139 L’area del rombo

140 Esercizi

141 Problem solving Il parco divertimenti

142 L’area del trapezio

143 Esercizi

144 L’area del triangolo

145 Problem solving

Tra i resti antichi

194 Problem solving Comprare online: ordini e consegne

196 Le misure di valore

197 Costo unitario e costo complessivo

198 Spesa • Guadagno • Ricavo

189 Esercizi

100 Educazione finanziaria Tu e il denaro

102 Le misure di tempo

103 Esercizi

104 Dal più facile...

105 ... al più difficile

GEOMETRIA

106 Le forme nella realtà

108 Parole per… CONOSCERE La coppa di Pitagora

110 Linee • Figure piane • Solidi

111 Esercizi

112 Le Linee

146 Dal più facile...

147 ... al più difficile

148 Educazione civica L’informazione consapevole

RELAZIONI, DATI e PREVISIONI

150 Le relazioni

151 Gli schemi

152 Le classificazioni e i diagrammi

154 La statistica

155 La moda e la media

156 I grafici

157 Esercizi

158 Certo • Possibile • Impossibile

159 Il calcolo delle probabilità

160 Dal più facile...

161 al più difficile

162 Compito di realtà

Indagine sulla raccolta differenziata

MATEMATICA

Che cosa ci insegna la MATEMATICA

Che cos’è la Matematica

La Matematica non è solo numeri. È una scienza che studia e rappresenta la realtà.

Per capire le quantità, lo spazio, la misura, le relazioni tra i fatti, la probabilità, abbiamo bisogno della Matematica.

La Matematica non è solo sui libri

Ti piace giocare con i videogiochi? Usi il computer per giocare o fare delle ricerche? Videogiochi e computer non esisterebbero senza la Matematica. La vita di ogni giorno è piena di “Matematica”, anche se non ce ne accorgiamo. È proprio questo il bello della Matematica: ci è utile e riusciamo a usarla anche senza conoscerla a fondo, perché il suo utilizzo ci risulta naturale.

Come si “fa” Matematica

• Cercando di immaginare le situazioni.

• Applicando le tecniche di calcolo.

• Trovando strategie di soluzione.

Come “parla” la Matematica

La Matematica ha un suo linguaggio particolare semplice ed efficace.

Con pochi segni riesce a rappresentare situazioni complesse. Pensa a un problema: segni che indicano numeri e operazioni che rappresentano una situazione. Di quante parole avresti bisogno per spiegarlo?

Non c’è una sola Matematica

Quante facce ha la Matematica?

Se, per esempio, entri in una pasticceria, ne incontri molte:

• l’aritmetica, cioè i numeri delle paste, delle torte, dei clienti…

• la geometria, cioè la forma delle torte, lo spazio occupato dal bancone…

• la misura, cioè il peso dei dolci, il loro costo…

• la statistica, cioè l’indagine sui dolci più venduti, le previsioni di vendita…

I PRIMI NUMERI

Anche i numeri hanno una storia?

Certo! La loro storia inizia nel lontano passato e possiamo vederla rappresentata su una linea del tempo e su una carta geostorica.

L’osso di Ishango

È un osso di babbuino trovato nell’Africa

Centrale. Risale a circa

Vi è incisa una serie di tacche suddivise in tre righe.

L’osso di Vestonice

In Repubblica Ceca è stato ritrovato l’osso di una zampa di lupo che risale a 32 000 anni fa. Vi sono incise una serie di tacche raggruppate per 5. Questo fa pensare che i nostri antenati utilizzassero le mani per contare.

I numeri babilonesi

I popoli mesopotamici incidevano le loro cifre sui gettoni e sulle tavolette di argilla con segni cuneiformi. Furono i Babilonesi a semplificare questi segni.

Un solo segno veniva ripetuto per indicare le quantità fino a 9. Un segno diverso indicava il 10, che si ripeteva proseguendo fino a 60, numero che veniva scritto come l’1, ma più grande.

Per i numeri maggiori si utilizzavano altri simboli: per esempio, il 600 era indicato come un 10 con sopra 60.

I numeri egizi

Gli Egizi utilizzavano disegni semplici per rappresentare i numeri. Ogni simbolo aveva un valore fisso e per indicare i numeri occorreva fare un’addizione: per esempio, un fiore di loto (1 000) e una corda (100) indicavano il numero 1100.

Da allora i numeri ne hanno percorsa di strada… una strada fatta di conoscenza e di scambio tra i popoli, per migliorare sempre di più il sapere e la vita di tutti e tutte.

Parole per... CONOSCERE di CRISTINA DELL’ACQUA

Benvenute e benvenuti nella biblioteca della mitica maestra Margherita! Guardate: è una biblioteca con il tetto trasparente! Margherita ha un superpotere: lei conosce tantissimi racconti, che ama narrare ai suoi alunni e alle sue alunne.

Durante tutto l’anno, la maestra Margherita condurrà la classe in un percorso in cui, grazie a storie del passato, si potrà avere uno sguardo nuovo sul presente.

Oggi ci racconterà che i numeri sono intorno a noi, più di quanto ci immaginiamo. E dove ci sono numeri c’è armonia, una parola che impareremo a conoscere.

numeri e armonia

Aritmetica, arte e armonia hanno in comune la radice ar-, che in tante parole greche dà l’idea di connettere tra di loro parti diverse che insieme formano qualcosa di bellissimo, in armonia! Non ci credete? Eppure, i Greci la pensavano così: il bello non è solo questione di gusto, ma di un insieme di armonia.

Una statua greca è bella se il piede è lungo un sesto dell’altezza, la testa un ottavo e il volto un decimo.

Regole numeriche: arte e aritmetica.

Un giorno studierete la sezione aurea, che è il simbolo dell’armonia tra le misure numeriche. Se non ne avete mai sentito parlare, sicuramente l’avete già vista, senza saperlo, nelle forme a spirale di alcune conchiglie, delle galassie, dei cicloni e dei petali di una rosa.

I numeri sono così, danno forma e bellezza a ciò che ci circonda.

LIFE

SKILLS

PAROLE per CONOSCERE

• Galileo Galilei, un famoso scienziato, diceva che il libro della natura è scritto usando il linguaggio matematico.

Per leggere la natura occorre conoscere la Matematica. Tu che cosa ne pensi? Parlane con l’insegnante e con la classe.

Quando volete fare una bella fotografia è importante scegliere il formato e l’inquadratura. Dare armonia alle vostre fotografie è questione di numeri. Anche gli schermi non sono tutti uguali. I più belli hanno un formato che rende l’immagine più simile alla percezione dei vostri occhi. L’armonia colpisce sempre!

Parole

IL NOSTRO SISTEMA DI NUMERAZIONE

Ti spiego

ARGOMENTO

I numeri e il valore delle cifre.

REGOLA

Le cifre sono i simboli che usiamo per scrivere i numeri. Sono 10. Con esse formiamo qualsiasi numero. La cifra 0 serve anche a indicare una posizione vuota nella composizione del numero.

Il nostro sistema di numerazione è:

• decimale, perché raggruppa in base 10: 10 u = 1 da 10 da = 1 h 10 h = 1 k

• posizionale, perché ogni cifra ha un valore differente in base al posto che occupa all’interno del numero:

546 6 vale 6 u, cioè 6

465 6 vale 6 da, cioè 60

654 6 vale 6 h, cioè 600

Capisco

• Utilizzando le cifre 5 • 2 • 8, scrivi tutti i numeri possibili.

• Scrivi in ordine crescente i numeri che hai trovato.

Esercizi

1 Rappresenta ciascuna quantità sull’abaco e scrivi il numero. 3 h 2 da 6 u

Direzione Invalsi

Io ho 12 biglie.

Alice

Io abito in via Roma, 12.

• Chi esprime una quantità? .................................

• Chi indica un ordine?

Leo

1 Scomponi i numeri. Segui l’esempio.

5 304 = 5 k (5 000) 3 h (300) 0 da (0) 4 u (4)

7 845 = ...... k (..................) ...... h (..................) ...... da (...............) ...... u (......)

4 338 = k ( ) h ( ) da ( ) u ( )

2 015 = k ( ) h ( ) da ( ) u ( )

3 665 = k ( ) h ( ) da ( ) u ( )

2 Componi i numeri. Segui l’esempio.

7 k • 3 h • 6 u = 7 000 + 300 + 6 = 7 306

3 k • 1 h • 4 da • 6 u = + + + =

4 k • 2 h • 1 da • 5 u = .................. + .................. + .................. + .................. = ..................

1 k • 6 da • 8 u = + + =

4 k • 9 h • 4 u = + + =

3 Metti in ordine le cifre da quella con maggior valore a quella con minor valore, poi scrivi il numero.

Segui l’esempio.

9 da 3 u 5 h 4 k = 4 k 5 h 9 da 3 u = 4 593

3 da 7 h 8 u 1 k = k h da u =

6 h 2 k 6 u 8 da = k h da u =

5 k 2 da 1 u 4 h = k h da u =

5 Che valore ha la cifra evidenziata? Indicalo. Segui l’esempio.

3 8 04

8 h 800

6 Trova nel numero la cifra indicata e colorala. Segui l’esempio.

4 Colora nello stesso modo i riquadri che hanno lo stesso valore.

7 Leggi i numeri scritti in lettere e scrivili in cifre.

Settemilatrecentosei .....................

Novemilaundici Quattromilasettecentouno ..................... Tremilaottocentotrenta

Ti spiego

ARGOMENTO

I GRANDI NUMERI

Scrivere e leggere numeri che indicano

grandi quantità.

REGOLA

Le classi possono essere delle:

• unità semplici;

• migliaia.

Ogni classe è composta da tre ordini: centinaia, decine, unità.

Tra una classe e l’altra si lascia un piccolo spazio.

classe delle migliaia classe delle unità semplici

centinaia decine unità centinaia decine unità hk dak uk h da u 100 000 10 000 1 000 100 10 1

Capisco

• Leggi il numero.

hk dak uk h da u

6 3 2 9 4 5

Seicentotrentaduemilanovecentoquarantacinque

• Leggi e scrivi il numero.

Cinquecentoquarantaduemilaottocentonovantasei

hk dak uk h da u

Pienone!

125 376 persone!

Intelligenza visiva

Centoventicinque MILA trecentoset tantasei

Direzione Invalsi

Ho pensato un numero. Ho aggiunto una decina di migliaia e ho ottenuto 145 910. Che numero avevo pensato?

• Alice aveva pensato al numero: 135910 155910 145900

1 Scrivi il numero rappresentato su ciascun abaco.

2 Leggi i numeri scritti in lettere e scrivili in cifre.

Duecentotrentamilacentododici ................................................

Trentaseimilanovecentonovantaquattro

3 Scrivi i numeri in lettere.

Settecentocinquantaduemilatrecentoventisei

Ottocentosessantatremiladuecentoventuno

140 250 mila 507 300 ................................................................................................................................................................................................................. 100 654

4 Confronta i numeri inserendo i simboli > (maggiore) o < (minore).

5 Trova e scrivi un numero compreso tra i due numeri indicati.

10 000 < <

6 Scrivi il numero precedente e il numero successivo.

7 A quanto corrisponde 1 uk? E 1 dak? E 1 hk? Rifletti, poi completa le tabelle.

Le tappe del problema

Problemi Nel linguaggio comune “avere un problema” indica una situazione spiacevole, da superare trovando una soluzione. Anche in Matematica è così, con la sola differenza che non sempre le situazioni problematiche sono spiacevoli, anzi molte volte è divertente cercare di risolverle.

Partenza

Quando devi risolvere un problema non devi farti prendere dalla fretta di raggiungere il risultato. Devi seguire un percorso a tappe.

Tappa 1

Leggi il problema con attenzione per capire bene il testo.

Andrea ha bisogno di un nuovo astuccio e di un quaderno.

In cartoleria gli astucci costano tutti 15 euro e ogni quaderno costa 2 euro. Ha a disposizione 20 euro.

Quanto spenderà in tutto? Quanto avrà di resto?

Tappa 2

Immagina la situazione e rappresentala con un semplice disegno.

Tappa 3

Leggi le domande per capire che cosa ti chiede il problema. Sottolinea le domande con colori diversi.

Tappa 4

Individua le informazioni, cioè i dati Evidenzia i dati. Scrivili.

Tappa 5

Individua il procedimento, cioè trova le operazioni. Scrivile e calcola.

Tappa 6

Rileggi le domande e scrivi le risposte.

Dalla testa ai piedi

1 Ricordi le tappe fondamentali per risolvere i problemi?

Mettile in pratica.

Tappa 1

Leggi con attenzione.

Emma ha messo in vendita a prezzo scontato 7 berretti rossi, 6 blu, 8 gialli. Emma ha venduto tutti i berretti a 12 euro l’uno.

Quanti berretti ha venduto?

Quanto ha incassato dalla vendita?

Tappa 3

Leggi le domande.

Sottolinea le domande. Scrivile qui e pensa a che cosa devi trovare.

• • Tappa 5

Trova le operazioni. Scrivile e calcola.

Tappa 2

Immagina la situazione.

Tappa 4

Individua i dati Evidenzia i dati e scrivili.

7 = berretti

6 = berretti

8 = berretti .................

12 euro = costo

Tappa 6

Scrivi le risposte

• Emma ha venduto .................................................................................

• Emma ha incassato

2 Leggi con attenzione il problema e indica con X la rappresentazione grafica giusta.

Poi risolvi sul quaderno.

Emma, all’ingrosso, ha acquistato 6 buste di magliette. In ogni busta ce ne sono 3.

Le magliette sono blu oppure rosse. Quelle blu sono 5.

Quante magliette ha acquistato? Quante sono le magliette rosse?

3 Leggi con attenzione il problema.

Carlo, nel negozio di Emma, ha comperato 2 paia di calze per ciascuno dei suoi 3 figli.

Ogni paio costa 4 euro.

Quante paia di calze ha comperato Carlo?

Quanto ha speso?

• Ecco come tre bambini hanno scritto i dati. Indica con X quelli scritti nel modo giusto.

2 = paia di calze in tutto

3 = numero dei figli

4 = costo di un paio di calze in euro

2 = paia di calze per figlio

3 = numero dei figli

4 = costo di un paio di calze in euro

2 = paia di calze per figlio

3 = numero dei figli

4 = costo totale in euro

• Ecco come tre bambini hanno risolto il problema. Indica con X il procedimento giusto.

Ti spiego

ARGOMENTO

L’operazione che unisce, aggiunge, aumenta quantità.

REGOLA

addendo 243 + addendo 502 = somma o totale 747

• L’addizione può sempre essere eseguita.

• Nell’addizione lo zero è l’elemento neutro perché non modifica la somma.

3 + 11 = 14

3 + 11 + 0 = 14

• Nelle addizioni in colonna devi rispettare il valore posizionale delle cifre. Poni attenzione ai cambi.

Esercizi

1 Esegui sul quaderno.

Senza cambio

L’ADDIZIONE

Capisco

• A che cosa serve l’addizione? Indica con X.

Lia ha 5 figurine. Teo ne ha 7. Quante figurine hanno insieme?

5 + 7 = 12

Unire.

Aggiungere. Aumentare.

Tea ha 4 magneti. Ne compera altri 2. Quanti magneti ha ora?

4 + 2 = 6

Unire.

Aggiungere.

Aumentare.

Alba ha 10 anni. Gaia ha 6 anni in più. Quanti anni ha Gaia?

10 + 6 = 16

Unire.

Aggiungere. Aumentare.

Con il cambio

85 + 113 + 701 =

23 451 + 16 348 =

30 705 + 125 093 =

a. 234 + 125 = 306 + 471 = 942 + 57 = 32 + 811 = b. 105 + 324 + 570 =

Direzione Invalsi

c. 548 + 247 = 589 + 312 =

605 + 197 =

286 + 814 = d. 333 + 241 + 118 =

505 + 273 + 136 =

88 099 + 10 122 =

68 547 + 422 343 =

• Formula la domanda del problema in modo che si risolva con un’addizione. Lucia aveva nel portafogli 50 euro. Ha comperato un giornale da 4 euro, un quaderno da 2 euro e, facendo colazione al bar, ha speso 4 euro.

ti guido • È necessario utilizzare tutti i dati?

Ti spiego

ARGOMENTO

LE PROPRIETÀ DELL’ADDIZIONE

Modi per facilitare i calcoli

nelle addizioni.

REGOLA

Proprietà commutativa dell’addizione

• Se cambi l’ordine degli addendi, il totale non cambia.

La proprietà commutativa si utilizza per fare la prova dell’addizione.

3 + 75 = 78

75 + 3 = 78

Proprietà associativa dell’addizione

• Se sostituisci due o più addendi con la loro somma, il totale non cambia.

99 + 1 + 20 = 120

100 + 20 = 120

Per facilitare il calcolo, si può scomporre un addendo in due numeri e poi applicare la proprietà associativa.

105 + 15 =

100 + 5 + 15 =

100 + 20 = 120

Intelligenza visiva

4 pizzette con le olive, 5 con i funghi.

5 pizzette con i funghi, 4 con le olive.

Capisco

• Esegui a mente e completa.

25 + 5 = 5 + 25 =

8 + 18 = 18 + 8 =

Hai cambiato l’ordine degli

La somma non è 15 + 5 + 50 = + 50 = 10 + 18 + 2 = 10 + =

Per facilitare il calcolo dell’addizione hai unito prima due

47 + 23 =

40 + + 23 =

40 + ........... = .................

Hai scomposto un addendo in ............... numeri e poi hai unito uno dei due numeri al

1 Esegui le addizioni sul quaderno. Fai la prova applicando la proprietà commutativa.

a. 235 + 146 = 674 + 189 =

564 + 237 =

b. 236 + 108 + 320 = 48 + 306 + 231 =

480 + 34 + 96 =

2 Evidenzia i due addendi che ti conviene associare per semplificare il calcolo.

Es. 7 + 98 + 2 = 100 + 7 = 107

10 + 92 + 8 = + =

25 + 15 + 4 = + =

100 + 100 + 3 = + =

1 + 9 + 5 000 =

+

=

c. 1 342 + 2 677 = 3 406 + 2 835 = 16 456 + 22 634 = d. 3 742 + 1 540 + 2 004 = 12 435 + 43 001 + 29 122 =

+ 223

+ 76 011 =

3 Applica la proprietà commutativa e quella associativa per semplificare il calcolo.

Es. 12 + 11 + 8 + 9 = 12 + 8 + 11 + 9 = 20 + 20 = 40

7 + 5 + 5 + 13 =

90 + 80 + 10 + 20 =

200 + 10 + 30 + 100 = 18 + 4 + 12 + 6 =

4 Indica con X i problemi che si risolvono con un’addizione. Poi risolvi sul quaderno.

Giada sta leggendo un libro di 144 pagine. Il libro del suo amico Peter ha 24 pagine in più. Quante pagine ha il libro di Peter?

Giada e Peter contano i loro libri: in tutto ne hanno 84. Ne regalano 15 alla biblioteca della scuola.

Quanti libri hanno in tutto ora?

Giada ha una libreria con tre scaffali. Dispone 24 libri sul primo scaffale, 18 sul secondo, 14 sul terzo. Quanti libri ci sono nella libreria di Giada?

Giada ha letto 167 pagine di un libro di avventura. Le mancano 36 pagine a finirlo. Quante pagine ha il libro?

Direzione Invalsi

• Stima il risultato. Indica con X. 302 + 495 = Circa… 700 800 3 900 + 1 143 = Circa… 4 000 5 000 13 005 + 454 = Circa… 13 500 17 000

• Ora esegui le operazioni e scrivi i risultati sui puntini. Quante stime erano corrette? su 3.

ti guido • Non ti viene chiesto il risultato esatto, ma una stima quindi… arrotonda gli addendi!

Calcolo mentale

• Per eseguire velocemente le addizioni a mente puoi utilizzare questi piccoli “trucchi”.

Scomponi il secondo addendo in modo da raggiungere la decina successiva al primo addendo. Poi aggiungi ciò che è rimasto.

28 + 18 = (28 + 2) + 16 = 30 + 16 = 46

Arrivo alla decina.

5 Utilizza la strategia che hai imparato per eseguire a mente queste addizioni. Fai “ tappa al 10”.

+ 15 = ....................

Calcolo mentale

+ 19 = ....................

Aggiungo 9, 99, 999

se devi aggiungere che cosa fai? esempio 9 aggiungi 10 e togli 1 72 + 9 = (72 + 10) – 1 = 81 99 aggiungi 100 e togli 1 325 + 99 = (325 + 100) – 1 = 424 999 aggiungi 1 000 e togli 1 1 876 + 999 = (1 876 + 1 000) – 1 = 2 875

6 Completa le tabelle.

Competenze

Addizionare vuol dire aggiungere.

• La somma può essere minore di ciascun addendo? Sì No

• Quando la somma è uguale a uno degli addendi?

7 Non c’è un solo modo per eseguire i calcoli a mente. Tra questi sistemi, tu quale sceglieresti?

LA SOTTRAZIONE

ARGOMENTO

L’operazione che calcola:

• il resto;

• la differenza tra due quantità;

• quanto manca a completare una quantità.

REGOLA

minuendo 345 –sottraendo 103 = resto o differenza 242

• Con i numeri naturali la sottrazione può essere eseguita solo se il sottraendo è minore o uguale al minuendo 147 – 148 = con i numeri naturali non è possibile

• Sottraendo 0 a un numero si ottiene il numero dato. 11 – 0 = 11

• Nelle sottrazioni in colonna devi rispettare il valore posizionale delle cifre. Poni attenzione ai cambi.

OPERAZIONI INVERSE

La sottrazione è l’operazione inversa dell’addizione. – 8 20 12 + 8

Perciò l’addizione può essere usata come prova della sottrazione.

Capisco

• A che cosa serve la sottrazione? Indica con X.

Sul tavolo del ristorante c’erano

7 bicchieri. 2 si sono rotti. Quanti bicchieri sono ancora interi?

7 – 2 = 5

Calcolare il resto.

Trovare la differenza.

Calcolare quanto manca.

Sul tavolo A ci sono 3 piatti, sul tavolo B ce ne sono 5.

Quanti piatti in più ci sono sul tavolo B? Quanti piatti in meno ci sono sul tavolo A?

5 – 3 = 2

Calcolare il resto.

Trovare la differenza.

Calcolare quanto manca.

A un tavolo ci sono sedute 8 persone. I tovaglioli sono 5.

Quanti tovaglioli bisogna aggiungere?

8 – 5 = 3

Calcolare il resto.

Trovare la differenza.

Calcolare quanto manca.

• Formula la domanda del problema in modo che si risolva con una sottrazione. Poi risolvi.

Stella è all’aeroporto. Ha con sé una valigia che pesa 25 kg (che metterà nella stiva) e un bagaglio a mano che pesa 7 kg. Può portare a bordo un bagaglio a mano del peso massimo di 5 kg.

Direzione Invalsi

LA PROPRIETÀ DELLA SOTTRAZIONE

spiego

ARGOMENTO

Un modo per facilitare i calcoli nelle sottrazioni.

REGOLA

Proprietà invariantiva della sottrazione

• Aggiungendo o togliendo a entrambi i termini della sottrazione lo stesso numero, il risultato non cambia.

35 – 15 = 20

40 – 20 = 20 + 5 + 5

35 – 15 = 20

30 – 10 = 20 – 5 – 5

Proprietà invariantiva e il calcolo rapido

• 1253 – 29 = 1224

Capisco

• Leggi e completa.

• Tiago ha 10 anni e Sara ha 6 anni. La differenza tra le loro età è di 4 anni.

• L’anno scorso avevano 9 e 5 anni: la differenza tra le loro età era diversa? Sì No

• Tra 10 anni avranno 20 e 16 anni: la differenza tra le loro età sarà diversa? Sì No

• Osserva e calcola.

– 8 =

Esercizi

1254 – 30 = 1224

• 1251 – 11 = 1240

+ 1 + 1 – 1 – 1

1250 – 10 = 1240

Per facilitare il calcolo mentale applica la proprietà invariantiva arrotondando il sottraendo.

1 Applica la proprietà invariantiva. Per facilitare il calcolo, arrotonda il sottraendo. 460 – 19 = + 1 + 1

– 20 =

2 Esegui a mente.

4 150 – 19 =

– 29 =

– 39 =

– 23 =

– 41 = 3 184

=

Calcolo mentale

• Per eseguire velocemente le sottrazioni a mente puoi

utilizzare questi piccoli “trucchi”.

Scomponi il sottraendo in modo da raggiungere la decina precedente al minuendo. Poi togli ciò che è rimasto.

45 – 9 = (45 – 5) – 4 = 40 – 4 = 36

1 Fai tappa alla decina precedente ed esegui.

Faccio tappa alla decina precedente.

49 – 13 = 33 – 12 = 23 – 7 = 47 – 14 = 58 – 11 = 41 – 8 = 35 – 14 = 76 – 16 =

Calcolo mentale

se devi togliere che cosa fai? esempio

Tolgo 9, 99, 999

9 togli ............. e aggiungi ............. 98 – 9 = (98 – 10) + 1 = 89 99 togli ............. e aggiungi ............. 205 – 99 = (205 – 100) + 1 = 106 999 togli e aggiungi 2 306 – 999 = (2 306 – 1 000) + 1 = 1

2 Esegui a mente.

150 – 9 = .................... 756 – 9 = 150 – 99 = .................... 756 – 99 = 1 500 – 999 = .................... 7 560 – 999 = 1 500 – 99 = .................... 7 560 – 9 =

3 Esegui le sottrazioni sul quaderno. Fai la prova applicando l’operazione inversa.

a. 389 – 258 = 984 – 562 = b. 782 – 491 = 805 – 472 = c. 17 654 – 11 368 = 31 520 – 10 817 = d. 46 500 – 13 608 = 70 000 – 54 600 =

Direzione Invalsi

• Con quale operazione risolvi il problema?

a. Giulio ha 20 €, 15 € in meno di quanto gli occorre per comprare il casco della bicicletta.

Quanto costa il casco? 20 + 15 = 35 20 – 15 = 5

b. Valeria ha nel portafogli 45 €, 12 € in più del casco della bicicletta che desidera.

Quanto costa il casco? 45 + 12 = 57 45 – 12 = 33

ti guido • Per non sbagliare, immagina la situazione. Le parole “meno” e “più” potrebbero ingannarti.

4 Quale operazione devi fare? + 12 ? 25 – 12

25 + 12 = 37 25 – 12 = 13

5 Scrivi i segni delle operazioni e i numeri che mancano.

Ho pensato un numero. Ho aggiunto 12 e ho ottenuto 25. Quale numero avevo pensato?

6

+ 11 = 22 + 5 = 9

+ 20 = 27

7 Completa le operazioni usando l’operazione inversa. Esegui i calcoli sul quaderno.

6 Completa le operazioni calcolando a mente. a. 880 + = 1 000 1 000 – 880 =

8 Completa le sottrazioni. In questo caso non puoi usare l’operazione inversa, ma devi calcolare la differenza tra il minuendo e il resto.

a. 175 – = 75 175 – 75 = b. 510 – = 10 – = 500 – = 300 500 – 300 = 140 – = 100 – =

9 Leggi e risolvi sul quaderno.

a. Alla prima fermata dello scuolabus scendono 18 bambini e bambine, alla seconda 27 e lo scuolabus si svuota. Quanti bambini e bambine hanno utilizzato lo scuolabus?

b. Con lo scuolabus sono arrivati a scuola 53 bambini e bambine. Alla prima fermata sono saliti 15 bambini e bambine. Quanti ne sono saliti nelle fermate successive?

• Quale problema si risolve con un’addizione?

• Quale con una sottrazione?

Problem solving

In partenza per…

La soluzione di un problema è un percorso a tappe. Allenati su questo percorso per essere in grado di raggiungere la meta.

1 Copri le immagini. Leggi con attenzione il problema e immagina tu la situazione. Poi guarda le immagini e indica con X quale rappresenta la situazione.

Nadir sta partendo per Londra in aereo per incontrare 3 amici.

Prepara il trolley, che vuoto pesa 3 kg. I vestiti pesano 6 kg. Nadir metterà in valigia 3 confezioni di formaggio italiano da 1 kg da regalare agli amici.

All’imbarco il trolley viene pesato per verificare che non superi il peso di 12 kg.

Nadir potrà imbarcare il suo bagaglio?

2 Leggi con attenzione il problema. Poni attenzione ai dati.

Indica Sì se il dato è espresso in modo corretto, No se non lo è.

All’aeroporto, prima di partire, Giada fa i conti delle spese che ha sostenuto fino a quel momento. Per il biglietto aereo ha pagato 135 €. Ha prenotato un’automobile per 7 giorni pagando 32 € al giorno. Il costo del soggiorno in albergo è di 415 €.

Quanto ha speso per noleggiare l’automobile?

Quanto ha già speso per la vacanza?

135 € = costo del biglietto aereo

7 = numero dei giorni di noleggio auto

32 € = costo totale del noleggio auto

415 € = costo giornaliero dell’albergo

Sì No

Sì No

Sì No

Sì No

3

Osserva le operazioni che risolvono il problema. Poi inserisci i dati nel testo.

Al bar dell’aeroporto Licia, Arturo e Fatima hanno consumato tranci di pizza che costano l’uno e per le bibite hanno pagato

Quanto hanno pagato le pizze? Quanto hanno pagato in tutto?

11 × 3 = 33

33 + 12 = 55

4 Leggi con attenzione. Poi indica con X a quali domande puoi rispondere.

Al duty-free il profumo Incanto è esposto a 116 €, ma viene venduto con 20 € di sconto. Le scatole di cioccolatini Dolcelatte costano 11 €.

Federico compera il profumo Incanto e 2 scatole di cioccolatini Dolcelatte.

Quanto costa il profumo?

Quanto spende Federico per i cioccolatini?

Quanto spende Federico in tutto?

Quanto riceve di resto Federico?

5 Leggi il problema. Poi indica con X il procedimento corretto per risolverlo.

All’aeroporto Amina, Sara, Leila e Giulia gestiscono insieme il bar dell’area delle partenze e quello dell’area degli arrivi.

L’incasso della giornata di ieri è stato di 4 800 € per un bar e di 5 220 € per l’altro.

Quanto hanno incassato in tutto?

Quanto spetterà a ciascuna proprietaria? 5 220 + 4 800 = 10 020

020 : 2 = 5 010

6 Riordina il testo numerando le varie parti del problema. Poi scrivi i dati, le operazioni e le risposte.

Quanti posti rimarranno liberi?

Il personale di bordo fa salire 32 persone in business class.

Dati

Quante persone ci saranno sull’aereo quando l’imbarco sarà completo?

L’aereo per Parigi può imbarcare 212 passeggeri.

Devono ancora salire 121 persone in classe economica.

Procedimento risolutivo

Risposte

Ti spiego

ARGOMENTO

LA MOLTIPLICAZIONE

L’operazione che ripete più volte la stessa quantità o calcola le combinazioni.

REGOLA

La moltiplicazione è un modo più breve per scrivere un’addizione con gli addendi tutti uguali. fattore fattore prodotti parziali prodotto totale h da u 1 5 × 1 2 = 3 0 + 1 5 0 = 1 8 0

• L’1 è l’elemento neutro della moltiplicazione.

12 × 1 = 12

1 × 37 = 37

• Lo 0 è l’elemento assorbente della moltiplicazione, perché “assorbe” l’altro fattore.

12 × 0 = 0

Esercizi

Capisco

• A che cosa serve la moltiplicazione? Indica con X.

Per Halloween, Enzo appende 4 fantasmini in cucina, 4 in sala, 4 in camera. Quanti ne appende?

4 + 4 + 4 = 12

4 × 3 = 12

Ripetere più volte lo stesso numero. Calcolare le combinazioni.

Alice prepara i cappelli da strega: 2 tipi diversi, di 3 colori diversi. Quanti diversi cappelli?

Con il fiocco

Senza fiocco

2 × 3 = 6

Ripetere più volte lo stesso numero. Calcolare le combinazioni.

1 Le tabelline sono fondamentali per eseguire le moltiplicazioni. Ripassale.

5 × 6 = 6 × 6 =

4 × 6 = .............

0 × 6 = 7 × 7 =

=

LE PROPRIETÀ DELLA MOLTIPLICAZIONE

Ti spiego

ARGOMENTO

Modi per facilitare i calcoli nelle moltiplicazioni.

REGOLA

Proprietà commutativa della moltiplicazione

• Se cambi l’ordine dei fattori, il prodotto non cambia. Usi la proprietà commutativa per fare la prova della moltiplicazione.

6 × 5 = 30

5 × 6 = 30

Proprietà associativa della moltiplicazione

• Se sostituisci due o più fattori con il loro prodotto, il prodotto finale non cambia.

15 × 2 × 10 = 300

30 × 10 = 300

Proprietà distributiva della moltiplicazione

• Se sostituisci un fattore con due numeri la cui somma è uguale al fattore stesso, moltiplichi il primo fattore per entrambi i numeri e sommi i risultati, il risultato non cambia.

7 × 14 = 98

7 × (10 + 4) = 7 × 10 + 7 × 4 = 70 + 28 = 98

Per facilitare il calcolo, si possono utilizzare anche più proprietà.

2 × 7 × 5 =

2 × 5 × 7 =

10 × 7 = 70 proprietà commutativa proprietà associativa

Capisco

• Leggi e completa.

Se non ricordi il risultato di 4 × 7, puoi pensare al risultato di 7 × 4?

4 × 7 = ................ 7 × 4 = ................

Hai applicato la proprietà

Se devi eseguire a mente una serie di moltiplicazioni, per esempio 2 × 2 × 3 × 2, puoi eseguirle tutte insieme?

2 × 2 × 3 × 2 = ................ × 3 × 2 = = × 2 =

Hai applicato la proprietà

Se tu hai comperato 14 bustine da 3 figurine e il tuo amico ha comperato prima 9 bustine e poi altre 5 bustine, chi ha una quantità maggiore di figurine?

14 × 3 =

9 × 3 + 5 × 3 = + =

Hai applicato la proprietà

Esercizi

1 Applica la proprietà distributiva, osservando i passaggi necessari.

12 × 15 =

Scomponi un fattore 12 × (10 + 5) = Moltiplica il primo fattore per i due numeri 12 × 10 + 12 × =

Somma i due prodotti + =

Ti spiego

REGOLA

Moltiplicatore a una cifra

Moltiplica il secondo fattore per le unità del primo fattore.

Attenzione al riporto! h

Moltiplicatore a due cifre

Moltiplica le unità del secondo fattore per il primo fattore. Ottieni il primo prodotto parziale.

Moltiplica il secondo fattore per le decine del primo fattore. Aggiungi il riporto.

Scrivi 0 (zero) al posto delle unità. Moltiplica le decine del secondo fattore per il primo fattore. Ottieni il secondo prodotto parziale.

Somma i due prodotti parziali.

Quando il secondo fattore è un numero con 3 cifre, procedi nello stesso modo.

Quando moltiplicherai la cifra delle centinaia, inserisci 2 zeri segnaposto al posto delle unità e delle decine.

Moltiplicazioni per 10 • 100 • 1000

Quando moltiplichi per 10 • 100 • 1000, ciascuna cifra aumenta il suo valore di 10 • 100 • 1000 volte. In pratica devi aggiungere 1 • 2 • 3 zeri.

94 × 10 = ...................

× 100 = ...................

× 1000 = ..................

1 Applica la proprietà commutativa ed esegui a mente.

3 × 4 = × =

7 × 8 = × = 9 × 8 = × = 5 × 9 = ................ × ................ = .......................

2 Evidenzia i due fattori che ti conviene associare e calcola. Segui l’esempio.

Es. 5 × 25 × 4 = 5 × 100 = 500 10 × 10 × 9 = × = 2 × 5 × 13 = × = 6 × 10 × 10 = ................ × ................

3 Applica la proprietà distributiva ed esegui a mente. Segui l’esempio.

15 × 5 = (10 × 5) + (5 × 5) = + =

× 4 =

4 Esegui in colonna.

5 Esegui le moltiplicazioni.

× 10 = ................

× 10 =

× 10 =

6 Risolvi.

• Lorin va in campeggio. Con sé porta 6 magliette e 3 pantaloni. Quante combinazioni di abbigliamento può avere?

• Nello shop del campeggio ci sono 10 espositori con 15 magneti ciascuno. Quanti magneti sono esposti?

• Stima il risultato. Indica con X.

99 × 7 = Circa… 600 700

183 × 8 = Circa… 800 1500

211 × 5 = Circa… 1000 2000

ti guido • Per sapere se le tue stime sono corrette devi eseguire le operazioni.

Direzione Invalsi

LA DIVISIONE

Ti spiego

ARGOMENTO

L’operazione che permette di ottenere gruppi uguali da una stessa quantità o distribuire in parti uguali.

REGOLA

dividendo resto divisore quoziente

3 7 4 1 9

• Con i numeri naturali puoi eseguire

la divisione solo se il dividendo è maggiore o uguale al divisore.

30 : 5 = 6 è possibile

5 : 30 = con i numeri naturali non è possibile

• Se dividi 0 per qualsiasi numero, ottieni sempre 0. 0 : 4 = 0

• È impossibile dividere un numero per 0.

7 : 0 = è impossibile perché nessun numero moltiplicato per 0 dà 7.

• Se dividi un numero per 1, ottieni il numero stesso. 25 : 1 = 25

OPERAZIONI INVERSE

La divisione è l’operazione inversa della moltiplicazione. : 5

45 9 × 5

Perciò la prova della divisione è la moltiplicazione.

Capisco

• A che cosa serve la divisione? Indica con X.

Omar dispone 15 rose in tre vasi. Quante rose in ogni vaso?

15 : 3 = 5 Raggruppare. Distribuire.

Omar ha disposto 12 piantine di viole in cassette. In ciascuna cassetta ha messo 4 piantine di viole. Quante cassette ha utilizzato?

12 : 4 = 3 Raggruppare. Distribuire.

Esercizi

1 Quale problema si risolve con una divisione? Indica con X.

Pino prepara le crostatine alle fragole. Su ognuna mette 6 fragole. Con 108 fragole, quante crostatine prepara? In una scatola regalo, Pino mette 8 cioccolatini. Quanti cioccolatini servono per 15 scatole?

LA PROPRIETÀ DELLA DIVISIONE

Intelligenza visiva

Capisco

• Leggi e completa.

Con 6 uova Dario prepara 2 frittate.

Andrea compera 20 scatolette di cibo per gatti. Le darà al suo gatto in 10 giorni: 2 scatolette al giorno.

Se Andrea acquisterà il doppio delle scatolette, il cibo basterà per un numero doppio di giorni.

Se ne acquisterà la metà, il cibo basterà per 5 giorni.

In tutti i casi, però, il gatto mangerà 2 scatolette al giorno.

Esercizi

Ti spiego

ARGOMENTO

Un modo per facilitare i calcoli nelle divisioni.

REGOLA

Proprietà invariantiva della divisione

Se raddoppia le uova… raddoppia anche le frittate.

• Moltiplicando o dividendo per uno stesso numero, diverso da 0, sia il dividendo sia il divisore, il risultato non cambia.

Questa proprietà è utile per semplificare i calcoli.

1 Applica la proprietà invariantiva ed esegui le divisioni a mente.

Ti spiego

REGOLA

LA DIVISIONE IN COLONNA

Con il divisore di una cifra

3 4 7 5

3 0 6 4

• Metto il cappellino sulle prime due cifre perché 3 è minore di 5.

• Quante volte il 5 sta nel 34? 6 volte. Scrivi 6 nel risultato.

• Trovo il resto: moltiplico 6 × 5 e scrivo il risultato sotto 34. Poi eseguo la sottrazione.

3 4 7 5

3 0 6 9

4 7

4 5 2

• Abbasso il 7 accanto al resto.

• Quante volte il 5 sta nel 47? 9 volte. Scrivo 9 nel risultato.

• Trovo il resto: moltiplico 9 × 5 e scrivo il risultato sotto 47.

Poi eseguo la sottrazione.

La divisione è finita. 347 : 5 = 69 resto 2

Con il divisore di due cifre

a)

8 4 2 1

8 4 4 0

b) 1 3 9 4 3

• Quante volte il 2 è contenuto nell’8? 4 volte. L’1 è contenuto nel 4 almeno 4 volte? Sì.

Scrivo 4 al quoziente.

• Trovo il resto: moltiplico 4 × 21, scrivo il risultato sotto il dividendo e trovo il resto.

84 : 21 = 4 resto 0

• Metto il cappellino su 139 perché 13 è minore di 43.

1 0 1

1 2 9 3

• Quante volte il 4 è contenuto nel 13? 3 volte con il resto di 1 (1 decina).

Questa decina andrà unita al 9. Il 3 è contenuto nel 19 almeno 3 volte? Sì.

Scrivo 3 al quoziente.

• Trovo il resto: moltiplico 3 × 43, scrivo il risultato (129) sotto il dividendo e trovo il resto.

139 : 43 = 3 resto 10

c) 1 6 3 5 7

1 1 4 2 4 9 1

• Quante volte il 5 è contenuto nel 16? 3 volte con il resto di 1. Il 7 è contenuto nel 13 almeno 3 volte? No.

• Allora provo una volta di meno. Il 5 nel 16 è contenuto 2 volte con il resto di 6. Il 7 è contenuto nel 63 almeno 2 volte? Sì. Scrivo 2 al quoziente.

• Trovo il resto: moltiplico 2 × 57, scrivo il risultato (114) sotto il dividendo e trovo il resto.

163 : 57 = 2 resto 49

d) Nei casi precedenti hai diviso subito tutto il dividendo, perché, “mettendo il cappellino”, prendevi in considerazione tutte le cifre. Ma non sempre è così!

1 3 9 8 3 1

1 2 4 4 5

Esercizi

1 5 8

1 5 5 3 1

• Quante volte il 3 è contenuto nel 13? 4 volte con il resto di 1.

L’1 è contenuto nel 19 almeno 4 volte? Sì. Scrivo 4 al quoziente.

• Trovo il resto: moltiplico 4 × 31, scrivo il risultato (124) sotto la parte del dividendo che ho diviso e trovo il resto (15).

Ma la divisione non è terminata!

Abbasso l’8 ed eseguo la divisione 158 : 31.

• Quante volte il 3 è contenuto nel 15? 5 volte con il resto di 0.

L’1 è contenuto nell’8 almeno 5 volte? Sì. Scrivo 5 al quoziente.

• Trovo il resto: moltiplico 5 × 31, scrivo il risultato (155) sotto il numero che ho diviso e trovo il resto (3).

1398 : 31 = 45 resto 3

1 Esegui le divisioni sul quaderno.

a. 96 : 32 = 48 : 24 = 84 : 42 = 156 : 52 = 288 : 72 = 189 : 63 =

b. 248 : 82 = 376 : 74 = 412 : 93 = 297 : 68 = 515 : 84 = 602 : 75 =

c. 168 : 52 = 139 : 22 = 160 : 31 = 259 : 61 = 348 : 43 = 216 : 43 =

d. 125 : 23 = 205 : 53 = 245 : 42 = 191 : 69 = 105 : 36 = 218 : 55 =

e. 1469 : 58 = 2812 : 66 = 4718 : 63 = 1889 : 46 = 2381 : 62 = 1543 : 71 =

1 Esegui le divisioni in colonna sul quaderno.

a. 252 : 3 =

175 : 5 =

378 : 9 =

b. 504 : 8 = 672 : 7 = 503 : 6 =

2 Esegui le divisioni in colonna sul quaderno.

1° step (resto 0)

c. 1 456 : 2 =

6 540 : 5 =

8 444: 4 =

d. 7 615 : 6 =

2 213 : 7 =

5 728 : 9 =

a. 88 : 22 = 69 : 23 = 80 : 40 = 1° step (con il resto)

2° step (“cappellino” su 3 cifre)

b. 68 : 32 = 49 : 23 = 99 : 31 =

4° step (provo una volta di meno)

c. 155 : 31 = 219 : 73 = 364 : 91 = 3° step (con resto anche all’interno)

d. 175 : 53 = 409 : 75 = 239 : 69 =

e. 94 : 33 = 88 : 25 = 61 : 35 = 82 : 27 = 4° step (provo una volta di meno)

f. 145 : 38 = 215 : 46 = 303 : 79 = 271 : 68 = 5° step (provo più volte di meno)

g. 215 : 39 = 106 : 28 = 181 : 37 = 235 : 48 =

6° step (più difficili!)

h. 999 : 32 = 659 : 23 = 1 299 : 41 = 1 452 : 56 =

Divisioni per 10 • 100 • 1000

Quando un numero viene diviso per 10 • 100 • 1000, ciascuna cifra diminuisce il suo valore di 10 • 100 • 1000 volte. In pratica devi togliere 1 • 2 • 3 zeri.

7000 : 10 = 700

7000 : 100 = 70

3 Esegui le divisioni.

: 1 000 = 5 000 : 100 =

5 000 : 10 =

:

:

: 1000 = 7

4 Quale operazione devi fare? × 6 ? 48 : 6

6 × 48 = 48 : 6 = 8

5 Scrivi i segni delle operazioni e i numeri che mancano.

Ho pensato un numero. L’ho moltiplicato per 6 e ho ottenuto 48. Quale numero avevo pensato?

6 Completa le operazioni usando l’operazione inversa. Esegui i calcoli sul quaderno.

a. 26 × .............. = 1 300 1 300 : 26 = ..............

9 × = 225 225 : = 12 × = 216 : = b. .............. : 16 = 21 21 × 16 = .............. : 100 = 41 41 × 100 = : 36 = 25 × =

7 Per calcolare la metà o il doppio di un numero “utilizzi” il numero 2. Colora la parola giusta.

Per ottenere la metà: moltiplico divido per due.

Per ottenere il doppio: moltiplico divido per due.

8 Colora il segno dell’operazione necessaria. Poi risolvi i problemi sul quaderno.

a. Con il suo videogioco Alì ha completato 15 percorsi, ciascuno dei quali gli ha assegnato 120 punti. Quanti punti ha totalizzato in tutto Alì? × :

9 Risolvi i problemi sul quaderno.

In un sito archeologico sono arrivati studenti e studentesse di archeologia. Lavoreranno in 12 gruppi da 12 persone ciascuno. In mensa siedono in tavoli da 16 posti. Quanti sono gli studenti e le studentesse?

Quanti tavoli occupano in mensa?

b. Emma, invece, ha totalizzato 1 200 punti in 8 gare, ciascuna con lo stesso punteggio. Quanti punti ha realizzato in ciascuna gara? × :

Direzione Invalsi

• Paolo moltiplica due numeri e ottiene un risultato uguale a uno dei fattori. Qual è l’altro fattore?

ti guido • Pensa a qual è l’elemento neutro della moltiplicazione.

I dati del problema

I dati utili o inutili

Per risolvere un problema è necessario:

• identificare i dati utili;

• eliminare i dati inutili, cioè le informazioni che non servono per risolvere il problema.

Intelligenza visiva

In uno scavo archeologico della Mesopotamia sono stati ritrovate 27 tavolette che riguardano i miti e 35 che trattano di astronomia. 12 tavolette dei miti sono da restaurare. Quante sono le tavolette dei miti intatte?

I dati impliciti

Talvolta i dati sono impliciti (nascosti), cioè non sono espressi chiaramente con i numeri, ma attraverso parole che indicano una quantità: dozzina, metà, doppio, mese, settimana…

Intelligenza visiva

• Sottolinea i dati nel testo.

• Che cosa devi trovare? ?

• Quali sono i dati utili?

• C’è un dato inutile? Se sì, quale?

L’archeologo Alberto ha trovato 8 vasi. La sua collega Angela ne ha trovati il doppio. Quanti vasi ha trovato Angela?

• C’è un dato nascosto?

Sottolinea in rosso, nel testo, la parola che lo nasconde.

• Completa i dati.

8 = vasi trovati da Il doppio di 8 = vasi trovati da

I

Un problema non può essere risolto se i dati a disposizione non sono sufficienti.

Al laboratorio di restauro sono arrivati reperti di 3 differenti scavi. Dal primo sono arrivati 50 reperti, dal secondo 80. Quanti reperti sono arrivati dai 3 scavi in tutto?

• Quale dato manca per rispondere alla domanda?

I dati contraddittori

Un problema non può essere risolto se i dati o la domanda sono tra di loro contraddittori

Per la fine degli scavi è stata organizzata una festa. Sono state cucinate 40 frittelle. Ciascuno dei 15 invitati ne mangia 3. Quante frittelle mangiano tutti gli invitati? Quante frittelle rimangono?

• Perché questo problema è “impossibile”?

Esercizi

1 Nello scavo archeologico sono state trovate 12 ruote di carro, 54 frecce e 87 tavolette di argilla. Sono state portate al museo 42 frecce. I custodi sorvegliano gli altri reperti.

Quante frecce devono essere ancora portate al museo?

• Quali sono i dati utili?

• Ci sono dati inutili? Se sì, quali? ...................................

• Ci sono dati mancanti? Se sì, quali?

• Ci sono dati nascosti? Se sì, quali? ............................

2 Nel laboratorio 5 teche contengono le tavolette di argilla da restaurare. Alberto e Angela insieme restaurano 3 tavolette al giorno.

Quante ne hanno restaurate dopo i giorni trascorsi al sito?

• Quali sono i dati utili?

• Ci sono dati inutili? Se sì, quali? ...................................

• Ci sono dati mancanti? Se sì, quali?

• Ci sono dati nascosti? Se sì, quali? ............................

Le domande del problema

In un problema sono le domande che ti indicano il processo risolutivo, cioè le operazioni necessarie per risolvere il problema.

Talvolta, se ci sono due domande, i dati forniti dal testo permettono di rispondere a entrambe le domande.

1 Risolvi il problema sul quaderno. Viola, la geologa, raccoglie campioni di roccia: 63 sul Picco Blu, 49 sul Picco dell’Aquila e 32 sul Picco del Camoscio. Quanti campioni di roccia ha raccolto Viola? Viola e il suo collega Stefano hanno scattato 136 fotografie. Viola ne ha scattate 85. Quante foto ha scattato Stefano?

2 Cerchia con due colori differenti i dati necessari per rispondere alla 1a e alla 2a domanda. Poi risolvi il problema sul quaderno.

Le rocce trovate in superficie vengono messe in parti uguali in 8 cassette. In ciascuna cassetta ci sono 12 rocce. Le 72 rocce trovate negli strati profondi vengono messe in scatole da 9.

Quante scatole occorrono per le rocce degli strati profondi?

Quante rocce di superficie vengono trasportate?

Devi per forza rispondere a una domanda prima dell’altra? Sì No

Il dato che trovi rispondendo alla prima domanda, ti serve per rispondere alla seconda? Sì No

Talvolta i dati forniti permettono di rispondere direttamente solo alla prima domanda. Per rispondere alla seconda occorre utilizzare il dato ottenuto.

Se le domande sono più di una, occorre capire:

• se per rispondere a una devi prima rispondere all’altra o se esse non sono collegate;

• quali dati servono per rispondere a una domanda e quali per rispondere all’altra.

3 Risolvi il problema sul quaderno.

Viola ha catalogato i differenti tipi di roccia. Ha riempito 15 contenitori, ciascuno dei quali contiene 36 sassi.

Quanti sassi ha raccolto Viola?

Alla mostra di geologia i sassi vengono esposti in teche. In ogni teca ci sono 9 sassi. Quante teche occorrono?

4 Leggi il testo del problema e rispondi.

Il gruppo di Viola ha trovato uno scheletro fossile di Tirannosauro Rex.

I reperti vengono sistemati in 4 container che saranno caricati sulla nave. In ogni container vengono messe 96 casse. Con un camion invece verranno spedite 89 casse con gli attrezzi di scavo.

Quante casse in tutto vengono spedite?

A volte non puoi rispondere subito alla domanda del problema perché ti manca un’informazione che devi trovare rispondendo a una domanda non scritta: la domanda nascosta.

La domanda ti chiede quante casse sono state spedite, sia con la nave sia con il camion.

Qual è il dato che non conosci?

Indica con X quale domanda ti devi porre per trovarlo.

Quante casse vengono caricate sulla nave?

Quante casse vengono spedite con il camion?

5 Scrivi la domanda nascosta, poi risolvi i problemi sul quaderno.

a. Nel sito lavorano in tutto 25 persone. Ognuna di esse ha consumato 4 <l di acqua potabile al giorno.

Domanda nascosta: ..................................................................................................................................................

La spedizione è durata 58 giorni. Quanta acqua hanno consumato durante tutta la spedizione?

b. Per delimitare la zona di scavo vengono utilizzati 346 paletti.

Sono state portate 25 scatole, ognuna delle quali contiene 20 paletti.

Domanda nascosta: ..................................................................................................................................................

Quanti paletti non sono stati utilizzati?

6 Risolvi il problema sul quaderno.

Viola e il suo gruppo devono esplorare una caverna lunga 940 m.

Il primo giorno ne esplorano 45 m, il secondo giorno ne hanno esplorati altri 174 m, dove hanno trovato stalattiti e stalagmiti. Il terzo giorno hanno proseguito per altri 240 m e hanno trovato un laghetto profondo 6 m. Quanti metri di caverna devono ancora esplorare?

Ti spiego

ARGOMENTO

I risultati delle moltiplicazioni.

REGOLA

I multipli di un numero si ottengono moltiplicando il numero stesso per qualsiasi altro numero naturale.

• Ogni numero ha infiniti multipli. Per esempio, i multipli di 5

sono 0, 5, 10, 15 … 500 … 5 405 …

• Un numero può essere multiplo di più numeri.

12 = 3 × 4

12 = 6 × 2

12 = 12 × 1

12 è multiplo di 1 • 2 • 3 • 4 •

6 • 12

Esercizi

I MULTIPLI

Capisco

• Osserva e completa.

• I numeri scritti in rosso sono i risultati delle moltiplicazioni del 2 per i primi numeri interi.

Sono tutti multipli del numero .................

• Scrivi in verde i risultati della tabellina del 3. Hai trovato i primi del 3.

• Completa la tabella della moltiplicazione.

1 Per ciascun numero, scrivi almeno altri 5 multipli.

2 0, 2, 4 5 0, 5, 10

3 0, 3, 6 6 0, 6, 12

4 0, 4, 8 8 0, 8, 16

2 Nella tabella che hai completato sopra colora, nei risultati, i seguenti numeri come indicato. Poi completa.

0 è multiplo di tutti i

0 6 10

6 è multiplo di 1, 2, , 6.

10 è multiplo di ........................................................................................................................

Ti spiego

ARGOMENTO

I risultati delle divisioni con resto zero.

REGOLA

I divisori di un numero sono i numeri che lo dividono esattamente.

• I divisori non sono infiniti. Puoi trovare tutti i divisori di un numero.

• 0 non è divisore di alcun numero.

• Tutti i numeri (tranne 1) hanno almeno due divisori: il numero 1 e se stessi.

• I numeri che hanno solo due divisori (1 e se stessi) sono chiamati numeri primi.

• Se un numero è divisore di un altro, questo è suo multiplo.

è divisore di 3 12

è multiplo di

I DIVISORI

Capisco

• Completa.

4 : 4 = ..........................

4 : 0 = impossibile

I divisori di 4 sono i numeri , ,

Esercizi

1 Completa la tabella scrivendo i risultati delle divisioni solo se il resto è 0. Otterrai alcuni divisori dei numeri che sono nella colonna verticale. Poi rispondi.

• Di quali numeri è divisore il numero 3? ............... e ...............

• Di quali numeri è divisore il numero 5? e

• Di quali numeri è divisore il numero 7? e

• C’è un divisore comune a tutti? Sì No

Quale? .....................................................................................................................................

• C’è un divisore comune a tutti i numeri pari? Sì No

Quale?

2 Per ciascun numero, scrivi i suoi divisori. Poi completa.

numeri primi.

1 In ciascuna coppia, colora il numero maggiore. 1 560 1 600

2 Indica con X la corrispondenza giusta.

3 Per ciascun numero, scrivi il precedente e il successivo.

4 Indica con X il numero corrispondente.

5 Indica con X quali proprietà ha ciascuna operazione.

commutativa associativa distributiva invariantiva addizione sottrazione moltiplicazione divisione

6 Esegui sul quaderno e riporta il risultato.

7 Cerchia in rosso i

8 Cerchia in blu i divisori di 32.

9 Risolvi sul quaderno.

Arianna festeggia i 18 anni con i suoi fratelli: Claudio che ha 17 anni e Lino che ne ha 19. Sulla torta mette tante candeline quanti sono gli anni di tutti e tre. Quante candeline metterà sulla torta?

10 Leggi i “nomi” dei numeri. Poi scrivili in cifre.

Settecentomilasette

Seicentomilasette Seicentomilasettantasette

Settecentomilaventisette Settecentomilasettecento Seicentomilasettanta

11 Scrivi i numeri dell’esercizio 10 in ordine dal minore al maggiore.

12 Scrivi il numero.

13 Completa scrivendo l’operatore mancante.

14 Esegui a mente utilizzando le proprietà e le strategie di calcolo.

+ 150 + 1 =

15 Esegui sul quaderno e riporta il risultato.

16 Inserisci i numeri nel diagramma.

Inserisci i numeri nel diagramma.

18 Risolvi sul quaderno.

Nel magazzino del museo di scienze naturali ci sono 1 434 minerali con venature gialle e 1 542 con venature verdi. Vengono riposti in parti uguali in 16 contenitori. Quanti minerali sono riposti in ciascun contenitore?

Il procedimento risolutivo

Per risolvere i problemi occorre comprendere quali operazioni sono necessarie. La serie di operazioni che devi eseguire è un algoritmo.

Il diagramma è la rappresentazione grafica dell’algoritmo, cioè della sequenza a catena delle operazioni. Con il diagramma puoi riuscire ad avere sempre presente tutto il procedimento necessario per risolvere i problemi.

Intelligenza visiva

Al museo sono stati realizzati alcuni diorami di ambienti naturali. Nel diorama della savana ci sono 3 leoni, 2 elefanti, 4 giraffe. Quanti animali in tutto?

Al museo sono stati realizzati diorami di ambienti naturali.

Nel diorama dei luoghi freddi ci sono alcune coppie di pinguini che stanno covando le uova. Ogni coppia ha un solo uovo e le uova sono 13. Quanti pinguini ci sono? Accanto ai pinguini ci sono 9 foche intente a mangiare alcuni pesci. I pesciolini sono 153. Quanti ne sono stati calcolati per ogni foca?

Diagramma che indica che i dati relativi alla prima domanda non vengono utilizzati per rispondere alla seconda.

Il costo della riproduzione di un tricheco è di 1350 euro. I trichechi da sistemare sono 7. Quanto spende il museo per i trichechi?

Poiché il lavoro è stato eseguito in un laboratorio all’estero, la spedizione è costata 2450 euro. Quanto ha speso il museo in tutto?

Diagramma che indica che i dati del problema permettono di rispondere alla prima domanda. Per rispondere alla seconda domanda occorre utilizzare il dato ottenuto.

Anche se ci sono domande nascoste, puoi visualizzare il procedimento con un diagramma.

Scrivi la domanda nascosta, poi completa il diagramma e risolvi il problema.

Nel diorama del bosco sono stati sistemati 8 scoiattoli, ognuno nella sua tana. Nelle tane sono state messe in parti uguali 96 noci. In ogni tana sono state poste anche 9 ghiande. Quanti frutti sono stati messi in ciascuna tana?

Domanda nascosta:

Esercizi

1 Risolvi i problemi sul quaderno, utilizzando i diagrammi.

2 domande non collegate. Nel diorama dalla foresta ci sono 8 pappagalli e 54 farfalle. Per fare le code dei pappagalli sono state utilizzate 96 penne. Ogni farfalla, come tutti gli insetti, ha 6 zampe. Quante penne per ciascun pappagallo? Quante zampe sono state necessarie per le farfalle?

2 domande collegate. Sono stati preparati 350 insetti per vari diorami. Ne sono stati utilizzati 290 e i rimanenti sono stati conservati in scatolette da 12 insetti. Quante scatolette sono state riempite?

Con la domanda nascosta. Le formiche sono rappresentate con 3 file da 38 formiche rosse ciascuna e 25 formiche nere non in fila. Quante formiche in tutto?

Diversi procedimenti

1 Leggi con attenzione. Questo problema può essere risolto con due procedimenti diversi. Completa i diagrammi che indicano i due procedimenti differenti.

In una galleria d’arte, per l’inaugurazione di una mostra di quadri si organizza un convegno. Gli invitati sono 120. Per ognuno di loro è stato preparato un opuscolo informativo del costo di 4 euro ciascuno. Viene offerto un rinfresco che costa 23 euro a invitato. Quanto spende la pinacoteca per questa iniziativa?

1 opuscolo Costo rinfresco per 1 invitato

A volte un problema può essere risolto seguendo procedimenti risolutivi differenti.

1 opuscolo

rinfresco per 1 invitato

2 Leggi questi problemi e collega ciascuno al suo procedimento risolutivo, scrivendo la lettera corrispondente. Poi risolvi i problemi completando gli schemi.

a. Nella prima sala della galleria ci sono quadri di fiori. 20 rappresentano fiori nel prato e 50 fiori nel vaso. Vengono venduti 25 quadri. Quanti quadri di fiori rimangono?

b. Nella seconda sala ci sono 70 quadri di ritratti. 25 sono ritratti di donne e gli altri di uomini. La direttrice toglie 20 ritratti di uomini. Quanti ritratti di uomini rimangono?

c. Nella sala dedicata ai paesaggi ci sono 20 quadri di paesaggi di mare e 25 di montagna. Ieri i quadri erano 70. Alcuni sono stati venduti. Quanti quadri sono stati venduti?

Costo

Costo

Invitati

Costo

Diversi modi per rappresentare il procedimento risolutivo

Puoi rappresentare il procedimento risolutivo in modi differenti, attraverso:

• una serie di operazioni;

• una catena di operazioni;

• un diagramma.

1 Leggi il problema e sottolinea i dati.

Per rifare le pareti della cucina Antonio ha acquistato 12 scatole da 48 piastrelle ciascuna. Il piastrellista utilizza 498 piastrelle. Quante piastrelle rimangono?

• Scrivi i dati e le domande.

12 = Domanda nascosta: 48 = Domanda esplicita: 498 =

• Rappresenta il procedimento con:

una serie di operazioni

– Trovo quante piastrelle ha acquistato Antonio …………………. – Trovo quante piastrelle rimangono

una catena di operazioni

(48 × ……..……) –……..…… = ……..…… piastrelle piastrelle piastrelle acquistate utilizzate rimaste

• Scrivi la risposta.

Competenze

un diagramma

Indica con X i due algoritmi risolutivi corretti. Per il pavimento Antonio ha acquistato 3 scatole di piastrelle blu e 4 scatole di piastrelle rosse. Ciascuna scatola costa 104 €. Quanto spende Antonio per le piastrelle del pavimento?

(3 + 4) × 104 = 104 × 3 + 104 × 5 = 3 × 104 + 5 =

Problem solving

A spasso per il mercato

Adesso mettiti alla prova fissando la tua attenzione su dati, domande e algoritmi.

1 Leggi con attenzione i problemi. Prima di risolverli sul quaderno, rispondi alle domande e completa.

a. Il pescivendolo Ceschin va al mercato ogni 2 settimane.

Oggi ha esposto una cassetta di sardine da 12 kg, una di orate da 17 kg, una di branzini da 15 kg. Alla fine della giornata gli sono rimasti 6 kg di pesce. Quanti chilogrammi di pesce ha venduto?

C’è un dato inutile? Sì No

C’è una domanda nascosta? Sì No

b. La signora Laudice vende calze. Sul banco ci sono due espositori: uno con 23 paia di calzettoni di lana, nell’altro ce ne sono il doppio, ma di cotone. Quante paia di calze ha esposto?

C’è un dato nascosto? Sì No

C’è una domanda nascosta? Sì No

c. La fioraia Rosetta compera al vivaio 10 piante di rose a 15 € l’una e 15 piantine di azalee a 13 € l’una. Quanto ha speso?

Ci sono domande nascoste? Sì No Quante?

Scrivile.

2 Indica con X quale testo del problema corrisponde alla soluzione proposta. Poi completa.

Gigi, che vende scarpe, ha in cassa 250 €.

Spende 10 € per acquistare i sacchetti e 18 € per ordinare il pranzo.

10 + 18 = 250 – =

Dati

Risposta

Quanto ha ora in cassa Gigi?

Gigi, che vende scarpe, aveva in cassa 250 €.

Poi ha venduto un paio di sandali da 10 € un paio di scarpe da 18 €.

Quanto ha ora in cassa Gigi?

3 Risolvi i problemi completando i diagrammi dell’algoritmo.

a. Amin ha portato al mercato 56 casse di pomodori dal peso di 12 kg l’una.

Alla fine della giornata di lavoro gli sono rimasti 6 kg di pomodori.

Quanti chilogrammi di pomodori ha venduto?

Problem solving

b. Ugo ha comperato 4 kg di uva al costo di 2 euro al chilogrammo e una confezione di castagne che costa 5 euro. Ha pagato con una banconota da 20 euro. Quanto riceve di resto?

4 Osserva la situazione e risolvi il problema sul quaderno.

Io ho venduto 15 magliette a 11 € l’una.

Io ho venduto 27 pantaloni a 13 € l’uno.

Io ho incassato 560 €. Più o meno di loro due insieme?

5 Risolvi i problemi sul quaderno.

a. Il signor Alì ha esposto 16 leggins che vende a 12 euro l’uno. Al termine della mattinata ne ha venduti la metà. Quanto ha incassato?

b. La signora Adele oggi ha venduto un piumone a 65 euro e alcuni completini per bambini. In tutto ha incassato 275 euro. Ogni completino ha il prezzo di 35 euro.

Quanti completini ha venduto?

c. Nella bancarella dei formaggi vengono vendute confezioni da 15 mozzarelline. Il signor Luigi vuole preparare un aperitivo per i suoi amici. Perciò compera 4 confezioni di mozzarelline con cui preparerà degli spiedini da 3 mozzarelline ciascuno. Quanti spiedini può preparare?

LA FRAZIONE

ARGOMENTO

Una o più parti di un intero diviso in parti uguali.

REGOLA

Frazionare significa dividere in parti di uguale grandezza. La frazione ti dice in quante parti uguali è stato diviso un intero e quante ne sono state considerate.

Il numeratore indica il numero delle parti considerate.

1

3

Ti spiego •

La linea di frazione indica che è stata eseguita una divisione in parti uguali.

Il denominatore indica in quante parti è stato diviso l’intero.

Ciascuna delle parti in cui è stato diviso l’intero è una unità frazionaria. L’unità frazionaria è una frazione con numeratore 1.

Esercizi

Intelligenza visiva

In quante parti è divisa la bandiera?

Le parti sono uguali?

Come chiameresti una sola parte?

Un terzo.

Un quarto.

In quante parti è divisa la torta?

Le parti sono uguali?

Come chiameresti una sola parte?

Un ottavo.

Un mezzo.

1 Osserva e completa.

In quante parti è stato diviso l’intero? ..............

Quante parti sono state colorate?

La frazione che rappresenta la parte colorata è 2 5 .

Si legge due

2 Osserva i disegni e rispondi: l’intero è stato frazionato? Sì No

No

No

3 Scrivi la frazione rappresentata.

4 Colora secondo le indicazioni. 3

Competenze

Questo foglio è stato diviso in parti.

• Le parti hanno la stessa forma? Sì No

• Le parti hanno la stessa grandezza? (conta i quadratini) Sì No

• Ogni parte è 1 4 dell’intero foglio? Sì No

Frazionare significa dividere un intero in parti di uguale grandezza.

La forma delle parti può anche essere

Ti spiego

ARGOMENTO

LE FRAZIONI COMPLEMENTARI

Le frazioni che completano l’intero.

REGOLA

La frazione complementare

è quella frazione che, aggiunta a un’altra, forma l’intero.

“Complementare” significa

“che completa”.

1 3 + 2 3 = 3 3 = 1

Intelligenza visiva

• A quale frazione corrisponde la parte rossa? ..............

• A quale frazione corrisponde la parte blu?

• Le parti rossa e blu insieme formano l’intero?

Capisco

• Colora in rosso la frazione indicata e in azzurro la parte rimanente. Scrivi la frazione che rappresenta la parte rimanente.

Le frazioni si possono sommare: 5 8 + 8 = 8 = 1

Esercizi

1 Colora in viola la frazione indicata, in giallo la frazione complementare e completa l’addizione. Segui l’esempio.

2 Per ciascuna frazione, colora quella complementare.

Competenze

= = 1

“appare” come una frazione, ma rappresenta un intero.

Si chiama frazione apparente.

LE FRAZIONI PROPRIE E IMPROPRIE

Intelligenza visiva

La parte evidenziata è più o meno di una crostata intera?

Ti spiego

ARGOMENTO

Le frazioni che rappresentano una parte minore o maggiore dell’intero.

REGOLA

Le frazioni proprie rappresentano una parte minore dell’intero. Il numeratore è minore del denominatore.

Le parti evidenziate sono più o meno di una crostata intera?

Capisco

Le frazioni improprie rappresentano una parte maggiore dell’intero. Il numeratore è maggiore del denominatore, ma non è suo multiplo. 2 3 4 3

• Colora la parte indicata dalla frazione. Poi completa scrivendo minore, uguale o maggiore.

La frazione rappresenta una parte dell’intero.

La frazione rappresenta una parte all’intero.

La frazione rappresenta una parte dell’intero.

Ti spiego

ARGOMENTO

CONFRONTARE LE FRAZIONI

Anche le frazioni, come i numeri, si possono confrontare.

REGOLA

Per confrontare due frazioni devi osservare sia il denominatore sia il numeratore. Se due frazioni hanno lo stesso denominatore, è maggiore quella con il numeratore maggiore. 3 5 > 2 5 2 5 < 3 5

Esercizi

• Confronta e rispondi.

Capisco Le due frazioni 3 5 e 2 5 sono state rappresentate nell’intero e su una linea. 3

• Le due frazioni hanno lo stesso denominatore? Sì No

• Quale delle due frazioni rappresenta una quantità maggiore?

1 Colora le frazioni rappresentate e confrontale. 7 11 5

2 Scrivi le frazioni rappresentate e confrontale.

3 La linea dei numeri, da 0 a 1, è stata divisa in 12 parti uguali. Scrivi al posto giusto le frazioni date, 4 poi ordinale dalla minore alla maggiore. 6 12 • 11 12 • 1 12 • 3 12

• Confronta e rispondi.

• Le due frazioni hanno lo stesso numeratore? Sì No

• La frazione che rappresenta la quantità maggiore è 2

Esercizi

1 Colora le frazioni rappresentate e confrontale.

Ti spiego REGOLA

Se due frazioni hanno lo stesso numeratore, è maggiore quella con il denominatore minore.

2 Scrivi le frazioni rappresentate e confrontale.

3 Luca, Tea, Livia, Samuel preparano le tessere per una decorazione. Colora tu la parte che ciascuno di loro ha colorato. Poi rispondi.

• Chi ha colorato la parte maggiore?

• La frazione che rappresenta la parte più grande ha il denominatore maggiore? Sì No

• Chi ha colorato la parte minore?

Ti spiego

ARGOMENTO

LE FRAZIONI EQUIVALENTI

Le frazioni che hanno lo stesso

valore.

REGOLA

Due o più frazioni sono equivalenti se sono scritte in modo differente ma indicano la stessa parte dell’intero. 1 2 = 2 4 = 4 8

Ti spiego

REGOLA

Per trasformare una frazione in un’altra equivalente, occorre moltiplicare o dividere sia il numeratore sia il denominatore per lo stesso numero.

Esercizi

1 Trasforma ciascuna frazione in un’altra equivalente.

• Colora le parti indicate dalle frazioni, poi rispondi.

• Le tre frazioni indicano la stessa quantità? Sì No

• Le tre frazioni sono scritte utilizzando gli stessi numeri? Sì No

• Le frazioni 1 2 , 2 4 , 4 8 hanno lo stesso valore, cioè sono equivalenti? Sì No

• Scrivi l’operatore necessario per trasformare una frazione in un’altra equivalente.

2 Colora le frazioni equivalenti a quella data.

1 Questi interi sono stati frazionati. Collega la frase alla rappresentazione, completa e poi colora.

2 parti su 6, cioè due sesti, cioè ......... .........

1 parte su 3, cioè un terzo, cioè

5 parti su 7, cioè , cioè

2 Dividi gli interi nelle parti indicate e colora la frazione.

3 Rappresenta ciascuna frazione sulla linea: dividila nelle parti indicate dal denominatore e colora le parti indicate dal numeratore. 2 3 5 7

4 Per ciascun intero o gruppo di interi, colora e scrivi:

una frazione propria una frazione impropria una frazione apparente

5 Scrivi l’operatore che trasforma ciascuna frazione in un’altra equivalente.

6 Confronta le frazioni e inserisci il segno < o > .

Ti spiego

ARGOMENTO

LA FRAZIONE DI UN NUMERO

Come frazionare un insieme di oggetti o una quantità.

REGOLA

Per calcolare la frazione di un numero:

• dividi la quantità per il denominatore: troverai l’unità frazionaria;

• poi moltiplica

l’unità frazionaria per il numeratore. 2 3

Capisco

Luigi ha 12 mele. Ne usa 2 3 per fare una torta.

Luigi divide le mele in parti uguali.

Ogni parte è una unità frazionaria.

Quante mele in una unità frazionaria? .............

Luigi prende 2 gruppi di mele (2 unità frazionarie).

Quante mele in 2 gruppi, cioè in 2 3 ?

Esercizi

1 Osserva e completa l’algoritmo, cioè la catena di operazioni per giungere al risultato.

1 Calcola la frazione del numero. Aiutati con i disegni.

2 Calcola a mente.

2

3 Scrivi le operazioni necessarie per calcolare la frazione del numero. Poi esegui le operazioni sul quaderno e riporta i risultati. 3 25 di 75 =

4 Risolvi i problemi sul quaderno.

a. In classe quarta ci sono 18 bambini e bambine. 2 9 di loro giocano a pallacanestro. Quanti giocano a pallacanestro?

b. Nel ristorante di Asia sono stati acquistati 15 kg di pesche. 1 5 di esse sono state scartate perché non erano buone.

Quanti chilogrammi di pesche sono stati scartati?

Quanti chilogrammi di pesche sono stati utilizzati?

c. Omar è in viaggio per lavoro. Deve percorrere 420 km.

Decide di fare una sosta dopo aver percorso 2 7 della strada. Dopo quanti chilometri si ferma? Quanti chilometri gli rimangono da percorrere dopo la tappa?

• Linda ha alcune fragole. Ne mangia 4 che corrispondono a 1 3 di tutte le fragole. Quante fragole ha?

ti guido • Per risolvere il problema, disegna 4 fragole che corrispondono a 1 3

Disegna le altre unità frazionarie che ti mancano. Conta le fragole.

Direzione Invalsi

1 Colora l’unità frazionaria e poi scrivila.

2 Colora la parte indicata dalla frazione.

3 Completa l’addizione scrivendo la frazione complementare.

4 Colora sulla linea la parte che rappresenta la frazione. Poi rispondi.

5 Trasforma ciascuna frazione in altre due a essa equivalenti.

7 Completa le frazioni affinché il confronto sia giusto.

Uguale denominatore

Uguale numeratore

9 Lisa ha 8 mattoncini delle costruzioni, di cui 1 4 sono verdi. Quali sono i mattoncini di Lisa?

Indica con X.

10 Completa la tabella. Poi scrivi le frazioni sulla linea dei numeri.

Andrea ha 15 piantine fiorite.

sono rosse, 2 5 sono gialle,

altre sono viola. Colora le piantine nel modo giusto.

Com’è andata?

per imparare

Che cos’hanno in comune queste opere d’arte?

L’altezza totale della testa

è 1 8 dell’altezza del corpo.

Sono stati gli artisti Greci i primi a scolpire statue di corpi umani come immagine della bellezza. Per rappresentare la bellezza, rispettavano delle proporzioni matematiche. Lisippo, uno scultore greco, fu uno degli artisti che utilizzò le frazioni per le sue sculture.

Sulla moneta dell’euro è rappresentato l’Uomo Vitruviano di Leonardo da Vinci. Questo disegno riprende le antiche regole di proporzione perfetta tra le parti del corpo. L’altezza del corpo è uguale alla dimensione delle braccia aperte a croce.

L’ombelico si trova al centro del corpo.

Questo è il particolare della testa dell’Uomo Vitruviano in cui sono evidenziate le proporzioni delle varie parti del volto.

Volto di un atleta greco.

La misura dai capelli alla base del mento è uguale a 1 10 dell’altezza del corpo.

Ora prova tu.

M A E T S

Un giro in libreria

Ora è il momento di utilizzare le frazioni in problemi che descrivono situazioni reali.

1 Nella libreria Libri Belli sono esposte 18 borse di stoffa di colore diverso.

2 9 sono rosse, 1 6 sono blu e le altre sono gialle.

Quante borse ci sono per ciascun colore?

• Per trovare quante sono le borse rosse, devi calcolare di 18.

Dividi in gruppi e ne colori in rosso.

Scrivi le operazioni: 2 9 di 18 =

• Per trovare quante sono le borse blu, devi calcolare ......... di 18.

Dividi in gruppi e ne colori in blu.

Scrivi le operazioni: 1 6 di 18 =

• Colora le altre borse in giallo e poi scrivi la risposta.

2 In un portamatite ci sono 48 matite con il marchio Libri Belli. I 3 8 sono rosse e le altre sono blu.

Quante sono le matite blu? Puoi risolvere il problema in due modi. Leggi e completa.

1o modo

• Trova 3 8 di tutte le matite, cioè il numero delle matite . Scrivi le operazioni:

• Trova il numero delle matite blu.

Scrivi l’operazione:

2o modo

• Qual è la frazione complementare che corrisponde alle matite blu?

• Calcola il valore della frazione complementare. Scrivi le operazioni:

Problem solving

3 Risolvi i problemi sul quaderno.

a. In questa settimana sono stati venduti 75 astucci. I 14 25 di essi sono astucci piccoli. Quanti astucci piccoli sono stati venduti?

b. Nell’espositore ci sono 96 magneti con frasi celebri tratte da libri. I 3 16 dei magneti hanno forma rotonda e gli altri sono di forma rettangolare. Quanti magneti sono di forma rettangolare?

4 Leggi che cosa dice il commesso Filippo e indica con X quale immagine rappresenta il lavoro che ha svolto.

Ho già sistemato 3 7 dei taccuini nell’espositore. Sono quelli colorati.

5 Risolvi i problemi sul quaderno.

a. Nella cesta delle occasioni ci sono 135 libri. I 2 15 sono libri per bambini che vengono venduti a 4 euro ciascuno. Quanto si incassa dalla vendita di tutti i libri per bambini?

b. Nel reparto delle guide turistiche sono esposte 27 guide della casa editrice Tour, 18 della casa editrice Viaggiare e 43 della casa editrice Pianeta. Oggi sono stati venduti i 5 11 di tutte le guide che erano esposte. Quante guide sono state vendute? Ogni guida è stata venduta a 23 €. Quanto si è ricavato dalla vendita delle guide?

c. A Libri Belli sono arrivate 14 casse da 36 libri ciascuna. Il commesso li sta sistemando sugli scaffali. Ne ha già esposti 5 21 . Quanti libri ha già esposto?

Direzione Invalsi

• Osserva e leggi il fumetto: quanti quaderni c’erano nella scatola?

Questi sono 1 5 dei quaderni che c’erano nella scatola.

5 9 20 25

ti guido • Devi risalire all’intero conoscendo il valore dell’unità frazionaria.

LE FRAZIONI DECIMALI

Ti spiego

ARGOMENTO

Le frazioni con denominatore 10, 100, 1000.

REGOLA

Le frazioni con denominatore 10, 100, 1000… si chiamano frazioni decimali: 1 10 • 1 100 • 1 1000 …

1 u = 10 d = 100 c = 1000 m

Questo è un intero, cioè una unità.

Questo è un decimo

Questo è un centesimo

Questo è un millesimo

Capisco

• Osserva, completa e rispondi.

Quanti decimi occorrono per formare un intero? 1 10

L’intero è stato frazionato in parti uguali: ciascuna parte rappresenta 1 (1 decimo • 1 d).

Quanti centesimi occorrono per formare un intero? 1 100

L’intero è stato frazionato in parti uguali: ciascuna

parte rappresenta 1 (1 centesimo • 1 c).

1 u = 10 d 1 u = 100 c

L’intero è stato frazionato in parti uguali: ciascuna

parte rappresenta 1 (1 millesimo • 1 m).

Quanti millesimi occorrono per formare un intero? 1 1000

1 u = 1 000 m

1 Completa la linea dei numeri scrivendo le frazioni che mancano.

2 Osserva e rispondi. Poi trasforma le frazioni in frazioni equivalenti.

• Quanti centesimi sono stati colorati? .................................................

•

• Quanti decimi sono stati colorati?

•

• Quanti millesimi sono stati colorati?

• A quanti centesimi corrispondono?

• A quanti decimi corrispondono?

3 Osserva la frazione che rappresenta la parte colorata e rispondi.

• Quanti decimi sono stati colorati?

• La frazione vale più o meno di 1?

•

2?

LE FRAZIONI DECIMALI E I NUMERI DECIMALI

Ti spiego

ARGOMENTO

Scrivere le frazioni decimali

sotto forma di numeri decimali.

REGOLA

I numeri decimali possono

rappresentare una parte più piccola dell’intero.

Le frazioni decimali possono essere trasformate in numeri

decimali.

1 10 (1 decimo • 1 d)

• Osserva e completa. Capisco

• 1 decimo è più o meno di 1 unità? .....................

• 1 decimo è più o meno di 0 unità?

• 1 10 (1 decimo) si scrive u d 0 , 1 ,

Completa.

u , d Si legge zero virgola uno.

0 , 1

Esercizi

1 Completa la tabella.

I CENTESIMI E I MILLESIMI

Ti spiego ARGOMENTO

Le parti più piccole del decimo.

REGOLA

Nei numeri decimali, oltre ai decimi, possono essere presenti i centesimi e i millesimi.

1 100 (1 centesimo • 1 c)

u , d c

0 , 0 1

Si legge zero virgola zero uno.

1 1000 (1 millesimo • 1 m)

u , d c m

0 , 0 0 1

Si legge zero virgola zero zero uno.

Esercizi

1 Scrivi la frazione e il numero decimale.

centesimi

centesimi

millesimi

Capisco

• Osserva e completa.

Questo è un decimo. 0 0,1 0,2

Questo è 1 100 • 1 centesimo (1 c)

• Dove devi inserire 1 100 sulla linea dei numeri?

Prima o dopo 0,1?

• 1 centesimo è più o meno di 1 unità?

• Più o meno di 1 decimo?

Questo è 1 1000 • 1 millesimo (1 m)

• 1 millesimo è più o meno di 1 unità?

• Più o meno di 1 decimo?

• Più o meno di 1 centesimo? ...................

centesimi

I NUMERI DECIMALI

Ti spiego

ARGOMENTO

I numeri con la virgola.

REGOLA

I numeri decimali sono formati da una parte intera e una parte decimale. La virgola separa le due parti.

u , d c m

0 , 1 8 7

Il numero si legge zero virgola centottantasette.

Dalla frazione al numero decimale

• Procedi così per trasformare una frazione decimale in un numero decimale. Capisco

• Scrivi il numeratore: 15

• Metti la virgola in modo che dopo di essa ci siano tante cifre quanti sono gli zeri del denominatore: 1,5 15 10 32 10

• Scrivi il numeratore: 9

• Metti la virgola: ,9

• Mancano le unità! Metti gli zeri segnaposto: 0,9 9 10 7 10

• Scrivi il numeratore:

• Metti la virgola:

• Scrivi il numeratore: ..............

• Metti la virgola:

• Metti gli zeri segnaposto:

Facile! 1 zero 1 cifra decimale, 2 zeri 2 cifre decimali…

Dal numero decimale alla frazione decimale

• Procedi così per trasformare un numero decimale in una frazione decimale.

1,25

• Scrivi al numeratore il numero senza virgola: 125

• Scrivi al denominatore 1 seguito da tanti zeri quante sono le cifre dopo la virgola: 125 100 0,33

• Scrivi il numero senza virgola:

• Scrivi 1 seguito dagli zeri: 100

Facile! 1 cifra decimale 1 zero, 2 cifre decimali 2 zeri…

1 Completa la tabella. Segui l’esempio.

frazione numero decimale in cifre in lettere abbreviazione u , d c m

2 Trasforma le frazioni in numeri decimali.

3 Trasforma i numeri decimali in frazioni decimali.

4

la frazione in lettere e colora il numero decimale corrispondente. Segui l’esempio.

Scrivi

Ti spiego

CONFRONTARE I NUMERI DECIMALI

ARGOMENTO

I numeri decimali possono essere confrontati.

REGOLA

Per confrontare due o più numeri decimali, si confrontano prima le parti intere, poi le parti decimali.

Capisco

• Procedi così per confrontare due numeri decimali.

5,4 è maggiore o minore di 3,896?

6,7 è maggiore o minore di 6,584?

Confronta la parte intera 5 > 3.

Perciò 5,4 > 3,896

Confronta la parte

La parte intera è ………........................................….. cominciando dai decimi. 7 > 5 perciò 6,7 > 6,584

4,65 è maggiore o minore di 4,68?

La parte intera e i decimi

Confronta i centesimi.

5 < 8

sono Perciò 4,65 < 4,68

Se anche i centesimi sono uguali, confronta i millesimi.

Esercizi

Facile! Se nella parte decimale il numero di cifre è diverso, aggiungi gli zero segnaposto per pareggiare le cifre e facilitare il confronto.

18,4 è maggiore o minore di 18,307?

18,400 > 18,307 perché

400 > 307

1 Confronta inserendo > o < .

a. Parte intera diversa.

b. Osserva i decimi.

c. Osserva i centesimi. 74,88 74,89 1,43 1,42 6,106 6,119 5,94 5,95

d. Metti gli zeri segnaposto.

1 Componi i numeri inserendo le cifre nella tabella.

1 u • 5 d • 7 c , 1 da • 5 u • 3 d ,

1 u • 5 d • 7 c • 8 m

• Scrivi in ordine dal maggiore al minore i numeri che hai inserito in tabella. • • da u d c m

2 Completa. Segui l’esempio.

Tredici virgola centodue 13,102

Cento virgola uno

Centodue virgola novantuno

• Hai scritto le cifre dei decimi, centesimi, millesimi, a destra o a sinistra della virgola?

Milletrecento virgola centosei ............................. da uk h u d c m 1 3 , 1 0 2 ,

3 Scomponi i numeri.

4 Componi i numeri, in alcuni dovrai inserire gli zeri segnaposto. Segui l’esempio. 4 u 3

5 Ordina dal minore al maggiore.

6 Tra i due numeri, inserisci un numero possibile.

7 In ciascun gruppo, i numeri sono stati scritti in ordine crescente, ma un numero è fuori posto. Cerchialo. Poi con una freccia inseriscilo al posto giusto.

ADDIZIONI E SOTTRAZIONI CON I DECIMALI

Ti spiego

REGOLA

Nelle addizioni e sottrazioni devi incolonnare i numeri rispettando il valore posizionale. Se i numeri sono decimali, fai attenzione alla posizione della virgola.

• Scrivi i numeri dell’addizione e sottrazione incolonnando bene.

• Nella parte decimale, dove c’è un “buco vuoto” inserisci gli zeri segnaposto.

• Esegui le operazioni. Ricordati di iniziare dalla cifra più a destra.

34,265 + 3,2 + 11,17 = 25,5 – 4,378 =

Capisco da u d c m , + , + , = , , da u d c m , –, = , ,

Esercizi

1 Aggiungi gli zeri segnaposto ed esegui le addizioni. Segui l’esempio.

103,55 + 7,3 + 2,419 = 35,4 + 18,94 + 1,502 = 109,345 + 2,44 + 15,5 =

137,25 – 24,186 = 394,108 – 172,3 = 915,81 – 103,708 = da h u d c m

1 0 3 , 5 5 0 + 7 , 3 0 0 + 2 , 4 1 9 = , , da h u d c m

2 Aggiungi gli zeri segnaposto ed esegui le sottrazioni. Segui l’esempio.

1 3 7 , 2 5 0 –2 4 , 1 8 6 = , , da h u d c m –= , da h u d c m –= , da h u d c m + + = , da h u d c m + + = ,

1 Esegui il comando dato dalle frecce.

2 Osserva bene gli esempi. Poi completa le tabelle. – 0,1 + 0,1

3 Esegui le addizioni sul quaderno.

a. 67,23 + 44,51 = 70,21 + 15,48 = 6,741 + 8,904 =

b. 38,23 + 9,55 + 6,72 = 15,23 + 25,78 + 95,24 = 85,764 + 0,322 + 11,834 =

4 Esegui le sottrazioni sul quaderno.

a. 15,3 – 8,7 = 22,8 – 10,4 = 78,2 – 65,5 = b. 7,45 – 4,38 = 14,81 – 8,75 = 4,58 – 2,75 =

5 Risolvi i problemi sul quaderno.

c. 11,5 + 4,576 + 85,63 = 4,876 + 23,2 + 6,77 = 95,1 + 0,008 + 0,54 =

c. 5,67 – 4,3 = 3,78 – 1,9 = 0,5 – 0,24 = d. 3,456 – 2,544 = 5,894 – 4,75 = 2,67 – 1,589 =

a. Sara e suo fratello Giacomo vorrebbero regalare alla nonna una pianta che costa 35,00 €, perciò contano i loro risparmi. Sara ha 18,50 €. Suo fratello ha 4,40 € in meno di Sara.

Quanti soldi ha Giacomo? Quanto hanno insieme i due fratelli? È sufficiente la somma per acquistare la pianta?

b. Milena dal cartolaio ha acquistato un diario che costa 12,40 €, un quaderno da 2,80 € e una confezione di matite dal costo di 7,70 €. Paga con una banconota da 50,00 €. Quanto riceverà di resto?

Direzione Invalsi

• Quale numero devi addizionare a 4,77 per arrivare a 5? 1,23 0,33 1,33 0,23

ti guido • Da quanti centesimi è composta una unità?

MOLTIPLICAZIONI E DIVISIONI

PER 10 • 100 • 1 000

Ti spiego

ARGOMENTO

Si sposta la virgola e cambia il valore delle cifre.

REGOLA

Nelle moltiplicazioni e divisioni per 10, 100, 1000 ciascuna cifra cambia posto e il suo valore diventa 10, 100, 1000 volte più grande o più piccolo.

Se il numero è decimale, la virgola si sposta:

• verso destra se moltiplichi; • verso sinistra se dividi.

• Osserva le moltiplicazioni e scrivi i risultati.

2,13 × 10 = 2,13 × 100 =

× 1 000 = Capisco

• Osserva le divisioni e scrivi i risultati. 143,5 : 10 =

• Osserva. 12 : 10 = 1,2 Se il numero ha solo la parte intera, devi immaginare la virgola dopo le unità. , × 10 × 10 × 10

: 100 =

• La virgola si è spostata a destra. a sinistra. Di quanti posti?

2,13 × 10 = 21,3

2,13 × 100 = 213

2,13_ × 1 000 = 2 130 143,5 : 10 = 14,35 143,5 : 100 = 1,435 143,5 : 1 000 = 0,1435

: 1 000 =

• La virgola si è spostata a destra. a sinistra. Di quanti posti? × 10 posto × 100 posti × 1 000 ............ posti : 10 posto : 100 posti : 1 000 posti

MOLTIPLICAZIONI CON I NUMERI DECIMALI

Ti spiego

REGOLA

Esegui le moltiplicazioni con i numeri decimali come quelle con i numeri interi.

Poi, per inserire la virgola nel prodotto, conta le cifre decimali complessive dei due fattori. Quando uno dei fattori è minore di 1, il prodotto è minore dell’altro fattore.

Capisco

3 3 × 1, 5 3 3 × 1, 5 = 1 6 5 3 3 0 4 9, 5

Prova tu

6, 4 × 2, 5

Quante cifre decimali in tutto nei fattori? 1

Quante cifre decimali nel prodotto?

0,2 × 4 = ...............

Quante cifre decimali in tutto nei fattori?

Quante cifre decimali nel prodotto? Scrivi la virgola.

0, 2 × 4 = 0, 8 Uno dei fattori è minore di 1?

Il risultato è maggiore o minore dell’altro fattore?

Esercizi

1 Il risultato non ha la virgola. Inseriscila tu al posto giusto.

a. 32 × 2,8 = 896 4,5 × 34 = 1530 9,2 × 88 = 8096

b. 3,2 × 2,3 = 736

4,2 × 6,8 = 2856

5,1 × 6,7 = 3417

c. 1,8 × 2,31 = 4158

6,33 × 22 = 13926

2,05 × 1,4 = 2870

d. 9,45 × 33,2 = 313740

167 × 5,42 = 90514 3,16 × 66,9 = 211404

2 Esegui le moltiplicazioni sul quaderno.

a. 26,1 × 22 = 2,45 × 7 =

b. 7,3 × 9,4 = 2,7 × 7,7 = c. 9,1 × 89 = 14,3 × 66 = d. 19,2 × 2,5 = 708 × 3,8 =

Direzione Invalsi

• Esegui queste moltiplicazioni.

8 × 0,5 = ............ 18 × 0,5 = ............ 12 × 0,5 = ............

• Moltiplicare per 0,5 equivale a dividere per:

2 5 10

ti guido • Osserva i risultati e trova che parte sono del primo fattore.

Ti spiego

REGOLA

DIVISIONI CON I NUMERI DECIMALI

Se il dividendo è un numero decimale, metti la virgola nel quoziente prima di iniziare a dividere la parte decimale.

Se il divisore è un numero decimale, trasformalo in numero intero applicando la proprietà invariantiva.

Quando il divisore è minore di 1, il quoziente è maggiore del dividendo.

Capisco

Dividendo decimale

Scrivi la virgola al quoziente quando la incontri per indicare che stai dividendo i decimi. Ricorda che anche il resto è decimale. 12,4 : 3 = 4,1 resto 1 decimo, cioè 0,1.

Divisore decimale

64 : 1,6 = 40

640 : 16 = 40 × 10 × 10

Quando il divisore è un numero decimale, devi trasformarlo in un numero intero applicando la proprietà invariantiva. 1 2, 4 3 0 4 4, 1 1

3 : 0,5 = 6 3 : 0,5 = 6 30 : 5 = 6 × 10 × 10

Il divisore è minore di 1? Il risultato è maggiore o minore del dividendo?

Prova tu

2 6, 7 4

Prova tu

3, 5 0, 7

Esercizi

1 Esegui le divisioni sul quaderno.

a. 345,5 : 5 = 23,59 : 9 = 89,52 : 8 = 134,1 : 6 = b. 56,7 : 2,1 = 49,6 : 3,4 = 87,36 : 1,3 = 25,76 : 2,3 = c. 456,6 : 12 = 65,78 : 23 = 96,338 : 22 = 74,52 : 54 = d. 16,2 : 0,6 = 11,2 : 0,8 = 44,38 : 0,7 = 30,05 : 0,5

Pausa in viaggio

I problemi con le frazioni sono sempre intorno a noi nella realtà quotidiana. Ci hai mai fatto caso?

1 Completa le domande intermedie per rispondere alla seconda domanda, poi risolvi il problema sul quaderno.

In una stazione di servizio ci sono in sosta 64 veicoli: moto e automobili.

I 3 16 sono moto. Quante sono le moto? Quante ruote in tutto potresti contare?

Naturalmente, le moto hanno tutte 2 ruote e le automobili 4.

• Quante sono le ?

• Quante sono le ruote delle ....................................................?

• Quante sono le ?

• Quante sono le ruote delle ....................................................?

2 Indica con X la domanda a cui non è possibile rispondere e completa. Poi risolvi il problema sul quaderno.

La signora Alice si è fermata a fare rifornimento di benzina. Ha speso 63,50 € per la benzina, 13,40 € per un litro di olio motore e 8,40 € per un litro di liquido per il tergicristallo. Ha pagato con una banconota da 100 euro.

1. Quanto ha speso in tutto?

2. Quanti litri di benzina ha messo nel serbatoio?

3. Quanto ha ricevuto di resto?

Non posso rispondere alla domanda numero perché

3 Risolvi il problema completando gli schemi.

Al bar ci sono 40 panini, di cui la metà sono vegetariani. I panini vegetariani costano 5,50 € l’uno, gli altri 6,30 € l’uno. Quanto si incassa dalla vendita di tutti i panini? ............

5,50 ............ 6,30 ............

4 Risolvi i problemi sul quaderno.

a. Nell’espositore della zona shopping vi sono 45 occhiali da sole. I 2 9 hanno le lenti a specchio.

Quanti non hanno le lenti a specchio?

b. Gli occhiali con le lenti a specchio vengono venduti a 29,70 €. Quelli non a specchio hanno un costo pari a 8 9 di quelli a specchio. Quanto costa un paio di occhiali non a specchio?

c. Il cioccolato viene venduto a 3,60 € a tavoletta ma chi compra più di 5 tavolette avrà uno sconto di 0,40 a tavoletta. Mirko ha comperato 6 tavolette. Quanto ha speso?

1 Colora solo le frazioni decimali. 3

2 Completa la tabella. frazioni in lettere numero decimale 3 10 tre 0,3 cinque decimi

3 Trasforma le frazioni in numeri decimali.

4 Trasforma i numeri decimali in frazioni decimali.

5 Componi i numeri. Se necessario, inserisci gli zeri segnaposto.

6 Scomponi i numeri.

7 Completa le tabelle.

8 Numera per 0,2 da 2 a 4. Segui l’esempio.

9 Numera per 0,3 da 0 a 3. Segui l’esempio.

+ 0,3

0,3

10 Scrivi un numero che renda vero il confronto.

11 Indica V (vero) o F (falso).

3 decimi = 0,3 V F 3 centesimi < 1 V F

12 Per ciascuna operazione, colora con lo stesso colore la casella del risultato.

13 Completa. 2,3 ×

14 Scrivi il numero mancante.

15 Esegui le operazioni sul quaderno.

Obiettivi • Conoscere i numeri decimali e saper operare con essi.

MISURE

Le prime misurazioni

La misurazione è nata quando i Sapiens, diventati stanziali, cominciarono a delimitare campi, costruire argini, palazzi, templi. Le prime unità di misura di lunghezza facevano riferimento alle parti del corpo umano. Ecco le misure utilizzate dagli Egizi. UNITÀ

1 dito 1,88 cm

1 palmo = 4 dita 7,5 cm

1 cubito regale = 7 palmi 52,5 cm

cubito spanna palmo dito

Il cubito regale corrispondeva alla misura dell’avambraccio del faraone: dal gomito al dito medio.

Il cubito era diviso in 7 palmi e ogni palmo corrispondeva a 4 dita.

Le superfici si misuravano in giornate. Una giornata corrispondeva alla quantità di terra che poteva essere arata in un giorno. In seguito venne utilizzata la pertica, un lungo bastone che serviva per misurare i confini del campo.

Per commerciare era necessario conoscere la quantità di grano, olio, vino… che veniva scambiata. Per misurare i cereali si utilizzavano dei contenitori.

La merce veniva misurata non in base al peso, ma in base al suo volume, cioè in base allo spazio che occupava.

Questo sistema di misurazione è ancora adottato in alcuni mercati in Africa, in Asia e nel Centro e Sud America.

Più avanti si utilizzarono le bilance a stadera Il contrappeso veniva spostato su un’asta che riportava in tacche il peso della merce sul piatto.

Per misurare il tempo, gli antichi Egizi utilizzavano gli obelischi che, proiettando la loro ombra sul terreno, segnavano il trascorrere delle ore.

Ma si servivano anche di clessidre ad acqua, per misurare tempi più brevi.

E oggi?

Questi diversi sistemi non hanno creato problemi finché gli scambi commerciali sono avvenuti in territori molto ristretti.

Quando gli scambi di merci hanno cominciato a coinvolgere Paesi differenti, questi sistemi non erano più validi.

È per questo motivo che nel 1961 un gruppo di studiosi e studiose ha istituito il Sistema Internazionale delle Unità di Misura (abbreviato SI).

Questo Sistema ha stabilito le regole condivise da molti Paesi del mondo, tra i quali l’Italia.

Le bilance a due bracci erano usate dagli Egizi.

Parole per... CONOSCERE

di CRISTINA DELL’ACQUA

E U R E K A !

Vi è mai capitato di fare una scoperta scientifica mentre fate un bagno nella vostra vasca?

Archimede, geniale matematico dell’antichità, ci è riuscito, e oggi la maestra Margherita ce lo racconta.

Archimede è un personaggio geniale e bizzarro. È nato a Siracusa, ma viaggia molto per studiare. È così che da Siracusa va ad Alessandria d’Egitto, capitale della ricerca scientifica dell’epoca. Lì ci sono la Biblioteca più grande del mondo antico e il Museo, che si chiama così perché è la casa delle Muse.

Archimede incontra giovani come lui che vengono da culture diverse e per capirsi parlano il greco antico, un po’ come noi oggi parliamo l’inglese.

Archimede vive immerso nei suoi pensieri e nel suo mondo fatto di numeri e figure geometriche, al punto che a volte si dimentica persino di mangiare e di lavarsi, ma non la volta in cui fa una grande scoperta proprio mentre fa il bagno nella sua vasca.

Il re di Siracusa, Gerone, per fare un dono agli dèi consegna un lingotto d’oro a un orafo perché gli faccia una corona.

L’orafo consegna al re una bellissima corona dello stesso peso dell’oro che aveva ricevuto. Ma Gerone dubita che la corona sia tutta d’oro. Come provare l’inganno?

Il re pensa che Archimede possa aiutarlo.

Il matematico ci pensa molto e un giorno, proprio mentre fa il bagno, ha un’intuizione: vede che, immergendosi nell’acqua, questa sale verso i bordi.

Allora si precipita fuori dalla vasca e, senza neanche rivestirsi, corre dal re gridando: Eureka!, che in greco significa: ho trovato!

Due oggetti dello stesso materiale, che hanno lo stesso peso e lo stesso volume, se immersi nell’acqua devono spostare la stessa quantità d’acqua.

Archimede si fa dare la corona, un lingotto d’oro dello stesso peso della corona e uno dello stesso peso della corona ma d’argento. Poi li immerge uno alla volta in una bacinella d’acqua.

Osservando la quantità di acqua che fuoriesce dalla bacinella dopo ogni immersione, scopre l’inganno. Ma nel frattempo... l’orafo è scappato!

LIFE SKILLS PAROLE per CONOSCERE

• La parola Museo deriva da Muse, le nove figlie di Zeus protettrici delle Arti e delle Scienze. Con la classe, cerca informazioni su Urania, la musa “matematica”.

Attraverso una serie di misurazioni, Archimede fa una scoperta importantissima. Le misurazioni accompagnano da migliaia di anni il progresso dell’essere umano!

di CRISTINA DELL’ACQUA

LE MISURE DI LUNGHEZZA

ARGOMENTO

I suoi sottomultipli sono 10, 100, 1000 volte minori dell’unità: decimetro, centimetro, millimetro. Ti spiego

Le unità di misura per la lunghezza, l’altezza, la profondità, lo spessore, la distanza tra due luoghi…

REGOLA

Il metro (m) è l’unità fondamentale delle misure di lunghezza.

I suoi multipli sono 10, 100, 1000 volte maggiori dell’unità: decametro, ettometro, chilometro.

Intelligenza visiva

Esercizi

1 Inserisci le misure in tabella.

Capisco

LE EQUIVALENZE

Ti spiego

Intelligenza visiva

Capisco

• Osserva il righello e rispondi.

• Quanti centimetri occorrono per formare 1 dm?

• Quanti millimetri occorrono per formare 1 cm?

• Quanti millimetri occorrono per formare 1 dm? ...................

• Esegui le equivalenze.

1 dm = cm Hai moltiplicato per 1 cm = mm Hai moltiplicato per

1 dm = mm Hai moltiplicato per

10 cm = dm Hai diviso per 10 mm = cm Hai diviso per 100 mm = dm Hai diviso per

ARGOMENTO

Esprimere la stessa lunghezza con marche diverse.

REGOLA

Eseguire una equivalenza significa esprimere la stessa misura utilizzando unità di misura diverse. Quando esegui una equivalenza, se passi:

• da una unità di misura maggiore a una minore, moltiplichi per 10, 100, 1000…

• da una unità di misura minore a una maggiore, dividi per 10, 100, 1000

La marca, cioè il simbolo dell’unità di misura, si riferisce sempre alla cifra dell’unità. Es.: 13,5 m 27 dm

Esercizi

1 In ciascuna misura, evidenzia la cifra che si riferisce alla marca.

2 Esegui le equivalenze.

a. 1 m = dm

3 dm = ............... cm

4 cm = ............... mm

5 km = hm

6 m = cm

operativo, pp. 204-205

b. 10 m = dam 40 cm = ............... dm

600 cm = ............... m

100 m = hm 4000 m = km

c. 12 m = dm

9 km = ............... m

50 dm = ............... m

350 cm = m 120 m = hm

Ti spiego

ARGOMENTO

LE MISURE DI CAPACITÀ

Le unità di misura per le quantità di liquidi.

REGOLA

Il litro (<l ) è l’unità fondamentale delle misure di capacità.

Capisco

Intelligenza visiva

Multipli Unità fondamentale Sottomultipli ettolitro

Esercizi

1 Evidenzia la cifra che corrisponde alla marca, poi scomponi ciascuna misura. Segui l’esempio.

3,48 <l = 3 ............ 4 ............ 8 ............ 7,45 da<l = 7 4 5 2,76 h<l = 2 7 6

2 Esegui le equivalenze.

• Quali contenitori, insieme, hanno la capacità di un litro?

ti guido • Esprimi tutte le capacità utilizzando la stessa unità di misura. Direzione Invalsi

1 In ciascuna misura, evidenzia la cifra che si riferisce alla marca.

4,6 c<l • 2,89 h<l • 1,83 da<l • 205 d<l • 0,9 <l • 873,4 d<l • 403 c<l • 135 <l

2 Inserisci le misure nella tabella, poi scrivi il valore di ciascuna cifra. Osserva l’esempio. km hm dam m dm cm mm

2,76 m 1,456 km

35,86 dam

3920 mm

677,1 cm 10,52 hm

3 Componi ciascuna misura. Segui l’esempio.

8 m 5 dm = 8,5 m

9 dm 8 cm = dm

7 km 9 hm = hm

2 cm 4 mm = mm 8 m 5 dm = 85 9 dm 8 cm = 7 km 9 hm = 2 cm 4 mm =

4 Esegui le equivalenze prima delle operazioni.

7 dm + 35 cm = dm Devi trasformare i cm in 300 m + 4 hm = hm Devi trasformare i 1,5 km – 900 m = m Devi trasformare i

5 Colora nello stesso modo le misure equivalenti.

3 <l 30 c<l 3 da<l

30 d<l 300 d<l 3 d<l

7 Esegui le equivalenze.

a. 45 km = hm

9 hm = ................... m

500 <l = da<l

2 m 7 dm 6 cm

6 Indica con X l’equivalenza corretta. 91,8 <l = 918 d<l 918 da<l 8 da<l = 0,8 h<l 0,8 <l

421 c<l = <l b. 23 m = dm 9 dm = ...................

Ti spiego

ARGOMENTO

LE MISURE DI MASSA-PESO

Le unità di misura per le quantità di materia.

REGOLA

Il chilogrammo (kg) è l’unità fondamentale delle misure di massa-peso. Esse misurano la quantità di materia da cui è formata ogni cosa (la massa).

I sottomultipli del grammo sono utilizzati per pesare oggetti molto leggeri, come i farmaci.

Sottomultipli

1 Evidenzia la cifra che corrisponde alla marca. Segui l’esempio.

Intelligenza visiva

Capisco

Ti spiego

PESO LORDO • PESO NETTO • TARA

ARGOMENTO

I pesi che tengono conto del contenuto e del contenitore.

REGOLA

Peso lordo: il peso del contenitore e del contenuto. peso netto tara peso lordo +

Peso netto: il peso del contenuto.

peso lordo tara peso netto –

Tara: il peso del contenitore.

peso lordo peso netto tara –

Capisco

• Osserva e completa.

Esercizi

Il peso netto è il peso solo della 500 g

La tara è il peso solo del ............................... 200 g

Il peso lordo è il peso totale della e del contenitore. ........... g

1 Scrivi i pesi al posto giusto nello schema e calcola il peso mancante.

• Un pacchetto di biscotti pesa 380 grammi. La confezione pesa 40 g. Quanto pesano i biscotti?

• Una lampada molto delicata pesa 3,5 hg. Viene confezionata in una scatola imbottita di cotone che pesa 4,8 hg. Quanto peserà la scatola quando conterrà la lampada?

1 Per ciascun elemento rappresentato, scrivi quella che, secondo te, è l’unità di misura giusta.

2 Per ciascun elemento rappresentato, scrivi quella che, secondo te, è l’unità di misura giusta.

3 Per ciascun elemento rappresentato, scrivi quella che, secondo te, è l’unità di misura giusta.

4 Completa.

1 m = .......... dm 1 m = cm 1 m = mm

5 Esegui le equivalenze prima delle operazioni.

6 Completa.

7 Completa le equivalenze scrivendo la marca.

400 m = 4 ....................

3 400 mm = 3,4

2,5 dam = 250

72 kg = 7 200 ....................

910 g = 9,1

230 cg = 23

700 c<l = 7 ....................

1,5 da<l = 15

820 <l = 8 200

8 In ciascun gruppo ci sono misure equivalenti. Trovale e sottolineale con lo stesso colore.

9 Completa la tabella. Poi rispondi.

10 In ciascun gruppo, colora la misura maggiore.

• La tara può essere maggiore del peso lordo? Sì No

• La tara può essere maggiore del peso netto? Sì No peso lordo peso netto tara

• Il peso lordo può essere minore del peso netto? Sì No

11 Osserva il disegno e risolvi il problema sul quaderno.

Luca è partito da casa sua due ore fa per recarsi a Torino. Quando è partito, il contachilometri dell’auto segnava 10 150, ora il contachilometri segna

10 340 chilometri. Quanti chilometri ha percorso fino ad ora?

Quanti chilometri avrà percorso quando giungerà a Torino?

Quale numero segnerà il contachilometri all’arrivo?

12 Esegui le equivalenze.

2,8 km = m

560 cm = dm 0,5 dag = hg 2,1 kg = g 0,11 h<l = <l 35 d<l = <l

Problem solving

Comprare online: ordini e consegne

Tutti i giorni molte persone ordinano prodotti online. Quanti problemi ci sono per consegnare a domicilio i prodotti!

1 Riordina il testo del problema, numerando. Poi risolvi sul quaderno.

Il meccanico le dice: “Dovrai fare il prossimo cambio a 33 000 chilometri”.

Tra quanti chilometri dovrà fare il cambio dell’olio?

Sara controlla il suo contachilometri: segna 22 548 km.

Sara, autista di un pullmino per le consegne a domicilio, fa il cambio dell’olio al suo automezzo.

2 Leggi con attenzione il problema.

Sugli scaffali del reparto sedie erano riposte 9 file da 12 sedie di legno e 12 file da 15 sedie di plastica. Ogni sedia di legno pesa 4,5 kg e ogni sedia di plastica pesa 2,8 kg. Sara ha caricato 68 sedie per la consegna. Quante sedie sono rimaste in magazzino?

Ora indica con X se devi rispondere alle domande nascoste elencate per risolvere il problema.

• Quante sono le sedie di legno? Sì No

• Quanto pesano le sedie di legno? Sì No

• Quante sono le sedie di plastica? Sì No

Infine risolvi il problema sul quaderno.

• Quanto pesano le sedie di plastica? Sì No

• Quante sono le sedie in tutto? Sì No

• Quanto pesano in tutto le sedie? Sì No

3 Rispondi alle domande, poi risolvi i problemi sul quaderno.

a. Sahid ha un ristorante e spesso fa ordini online. Ogni giorno nel suo locale si consumano circa 45 <l di acqua minerale. Questa mattina ha ordinato le bottiglie da 7,5 d<l necessarie per i prossimi 15 giorni. Quante bottiglie ha ordinato Sahid?

Qual è la domanda nascosta? Scrivila.

b. Sara deve consegnare 52 scatole piccole da 3,5 kg ciascuna e 28 scatole grandi da 6,3 kg ciascuna. Alle ore 14 ha consegnato 3 4 delle scatole. Quante scatole deve ancora consegnare?

Ci sono dati inutili? Se sì, scrivili.

4 Leggi con attenzione il problema, poi completa la rappresentazione e i calcoli per risolvere.

Sara ha delle consegne fisse da fare dal lunedì al venerdì. Il lunedì percorre 30 km. Nei giorni successivi percorre ogni giorno 3 000 metri più del giorno precedente. Quanti chilometri percorre durante tutta la settimana di lavoro?

lunedì martedì mercoledì giovedì venerdi

km + 3 km =

Totale della settimana

5 Risolvi il problema precedente con un algoritmo.

30 km viene ripetuto volte. 3 km viene ripetuto volte.

Perciò l’algoritmo per risolvere il problema è: 30 × ..................... + 3 × ..................... = ...............................

6 Risolvi i problemi sul quaderno.

a. Simone ha ordinato per il suo ufficio 8 computer nuovi. Ogni computer pesa 1,6 kg e il relativo imballaggio pesa 350 g. Quanti chilogrammi pesa l’intera consegna?

b. Nel magazzino sono giunte dalla Liguria 15 bottiglie di olio. Il peso netto di ogni bottiglia è di 700 g. La bottiglia vuota pesa 1,5 hg. Le bottiglie, per la consegna, devono essere messe in una scatola che può portare al massimo 14 kg. Le bottiglie potranno essere confezionate tutte in quella scatola oppure no?

LE MISURE DI VALORE

Ti spiego

ARGOMENTO

Le misure che indicano i costi dei prodotti.

REGOLA

Il denaro è l’unità di misura per il valore economico di merci e servizi.

In Italia e in altri Paesi europei la moneta in uso è l’euro. Il suo simbolo è € (glifo). In Italia si scrive generalmente dietro al numero.

Un euro è formato da 100 centesimi.

Quindi, quando scrivi il valore monetario con un numero decimale, devi scrivere sempre decimi e centesimi.

8,30 € 8,3 €

Sì No

Capisco

1 moneta da 1,00 € equivale a:

• 100 monete da 1

• 2 monete da 50

• 20 monete da 5 .............................

• 5 monete da 20

Esercizi

1 banconota da 5,00 € equivale a:

• 10 monete da 50

• 5 monete da 1

• 25 monete da 20

Intelligenza visiva

Monete

Banconote

1 banconota da 50 € equivale a:

• 5 banconote da 10

• 10 banconote da

• 25 monete da .............................

• 50 monete da 10 .............................

1 Scrivi il valore di ciascun gruppo di denaro.

• 50 monete da

COSTO UNITARIO E COSTO COMPLESSIVO

Ti spiego

ARGOMENTO

Il costo di un solo oggetto o di tanti

oggetti dello stesso tipo.

REGOLA × quantità : quantità costo unitario costo complessivo

Esercizi

Capisco

• Osserva e completa.

1,50 € COSTO UNITARIO cioè costo di solo elemento acquistato.

€ COSTO COMPLESSIVO cioè costo di gli elementi acquistati.

1 Completa la tabella. Se necessario, esegui le operazioni sul quaderno.

Quando si fa la spesa è importante capire se il costo si riferisce a un chilogrammo (un litro, un metro) di merce o a un ettogrammo (o ad altri sottomultipli o multipli della misura).

2 Risolvi il quesito.

• Una confezione di gomme costa 6,00 €. Una sola gomma costa 2,00 €. Quante gomme ci sono nella confezione?

3 Osserva il costo unitario e scrivi il costo complessivo. Se necessario, esegui le operazioni sul quaderno.

4 Osserva il costo di ciascuna confezione e scrivi il costo unitario della merce.

Ti spiego

ARGOMENTO

SPESA • GUADAGNO • RICAVO

Intelligenza visiva

• Osserva i disegni e cancella l’opzione errata.

A. Piero compra/vende la frutta dal grossista. È la sua spesa.

B. Piero vendendo la frutta ricava/spende del denaro. È il suo ricavo.

A volte il negoziante ha una perdita, se vende qualcosa a un prezzo minore di quanto l’ha pagata.

I costi visti dalla parte di chi vende. REGOLA spesa guadagno ricavo + ricavo guadagno spesa –ricavo spesa guadagno –spesa ricavo perdita

C. Piero a fine giornata conta quanti soldi ha in più di quelli spesi, cioè quanto ha guadagnato/speso È il suo guadagno.

• Completa scrivendo: spesa, guadagno, ricavo.

: il denaro che il negoziante incassa. : il denaro che il negoziante spende per acquistare la merce.

: la differenza tra il ricavo e la spesa, cioè quanto denaro il commerciante aggiunge alla sua spesa.

Capisco

1 Luisa ha questi soldi nel portafoglio.

• Luisa riesce a comprare i pantaloni? Sì No

2 Risolvi i quesiti. Nelle parentesi scrivi: spesa • guadagno • ricavo.

• Un negoziante ha venduto una borsa non più di moda a 45,50 € ( ). L’aveva pagata 50,00 € (............................). Quanto ha perso?

• Nel negozio di elettrodomestici un frullatore costa 48,00 € ( ). Il prezzo all’ingrosso è di 37,50 € (............................) l’uno. Quanto guadagna il negoziante su ciascun frullatore? Quanto guadagna se vende 12 frullatori?

4 All’autonoleggio “Viaggia sereno” il costo del noleggio di un’auto è di 21,00 € per ogni giorno feriale e di 25,00 € per ogni giorno del fine settimana (sabato e domenica). Quanto costa noleggiare un’auto per un’intera settimana? Quanto costa noleggiarla per 12 giorni partendo da lunedì?

5 Ivan compra un libro che costa 25,80 €. Paga con una banconota da 50,00 €. Quanto riceve di resto? Indica con X.

3 Ognuno di questi bambini ha dei soldi nel borsellino. Calcola quanti ne mancano a ciascuno per arrivare ad avere 10 euro. Completa la tabella.

nome euro posseduti euro che mancano

Alice 1,50 .....................

Davide 6,00

Lara 5,70

Pietro 0,50

Michele 9,20

Emma 2,50

• Osserva i disegni.

Direzione Invalsi 2,50 €

• Quanto costano un pallone e un camion?

ti guido • Il costo di una coppia di macchinine non cambia anche se sono di forma diversa.

TU E IL DENARO

Ho un desiderio

Le scarpe di Luca sono il top!

Le voglio anch’io!

di vengono dal lavoro .

Non ti servono scarpe nuove. E poi quelle scarpe costano davvero tanto!

Tu che cosa diresti al bambino? Indica con X.

Insisti, vedrai che te le compreranno!

Se proprio per te è importante, contribuisci in qualche modo alla spesa.

Ti servono proprio quelle scarpe?

Pensa: non ti sembra una spesa eccessiva?

Secondo te, perché succede che scarpe simili abbiano prezzi così diversi?

Che cosa devi imparare a controllare quando acquisti qualcosa? Indica con più X.

La qualità del materiale.

La marca.

Che cosa ne dice la pubblicità. Se è utilizzata da persone famose.

Ho ricevuto dei soldi

Per il tuo compleanno hai ricevuto in dono 50 euro. Che cosa fai? Indica con X.

Ne spenderai una parte e ne metterai una parte nel salvadanaio.

Li spenderai tutti subito.

Li metterai tutti nel salvadanaio.

Immagina di aver deciso di spendere tutti i tuoi 50 euro.

Scrivi 3 cose che compreresti e completa la tabella.

Che cosa comprerai È utile? È indispensabile? Non ti serve, ma ti piace molto?

Chi paga?

Chi paga questi danni?

Se lo sai, scrivilo.

Le panchine, gli autobus, le pensiline di attesa… sono beni pubblici. Il costo per ripararli o sostituirli viene sostenuto dal Comune o da altri enti pubblici con i soldi delle tasse pagate dai cittadini e dalle cittadine.

Anche i soldi per pagare i lavori pubblici provengono dalle tasse.

Sai quali sono i lavori pubblici? Sai che cosa sono le tasse?

Lavorate in gruppo. Scrivete le vostre risposte, poi discutetene insieme.

Ti spiego

ARGOMENTO

LE MISURE DI TEMPO

Capisco

• Scrivi: ore • minuti • secondi.

Le misure indicate dall’orologio o dal calendario.

REGOLA

Il tempo si misura in secondi, minuti, giorni, mesi, anni…

Le misure di tempo non seguono il sistema decimale.

• Il secondo (s) è l’unità fondamentale delle misure di tempo.

• I multipli del giorno sono: mese 28, 29, 30, 31 giorni anno 12 mesi 365 giorni

• I multipli dell’anno sono: millennio 1000 anni

secolo 100 anni decennio 10 anni lustro 5 anni

Esercizi

1 Completa lo schema scrivendo le unità di misura di tempo.

Segna le

Segna i

Segna i

2 Completa le equivalenze. 1

1 Completa le tabelle. Segui l’esempio.

2 Scrivi quale unità di misura usi per misurare quanto tempo è passato:

• dal tuo primo giorno di scuola

• dal primo giorno della classe quarta

• da quando è suonata la sveglia questa mattina ……………......…..

• da quando hai iniziato a leggere questo esercizio

3 Leggi gli orari di questo negozio e rispondi.

• Per quante ore è aperto il negozio il lunedì? ……………......…..

• Per quante ore è aperto il negozio il sabato?

• Per quante ore è aperto il negozio negli altri giorni della settimana, senza considerare la domenica?

• Per quante ore è aperto il negozio in una settimana?

• Sono le 16:30 di martedì: posso entrare? Sì No

4 Osserva questa parte di calendario e rispondi.

• In quali giorni sono segnati gli orari in cui il sole sorge e in cui tramonta?

• Quante ore e minuti di luce ci sono il giorno 18?

• Il giorno 18 il sole tramonta alcuni minuti prima rispetto al giorno 11: quanti?

5 Esegui le operazioni.

1 h + 1 h e 30 min = ………...... h e ………...... min

30 min + 30 min = h

20 min + 2 h e 10 min = h e min

1 h e 30 min + 1 h e 30 min = ………...... h

min + 20 min = h

1 Completa la tabella. Segui l’esempio.

guadagno o perdita? di quanto?

€

€

2 Osserva e rispondi.

3 A quanti centesimi corrisponde?

• Quanti soldi ha Linda nel borsellino?

• Quanto le manca per acquistare il giocattolo?

€ = centesimi 0,75 € = centesimi

4 Completa la tabella.

5 Completa.

1 minuto = secondi

10 minuti = secondi

4 ore = minuti

€ = centesimi 2,10 € = centesimi

3 ore = minuti

1 giorno = ore

2 giorni = ore 120 secondi = minuti 180 secondi = minuti

minuti = ora

minuti = ore

ore = giorni

ore = giorni

6 Rispondi.

• Ho 80 centesimi Quanto manca per arrivare a 1 euro? ..............................

• Ho 75 centesimi. Quanto manca per arrivare a 2 euro?

• Ho 1 euro e 20 centesimi. Quanto manca per arrivare a 3 euro?

7 Completa la tabella. 8 È pomeriggio. Luca è appena arrivato in stazione.

Prezzo per 1 hg

Prezzo per 1 kg

Il suo treno partirà tra 25 minuti. A che ora partirà il treno?

Alle 3:65 Alle 4:05 Alle 15:65 Alle 16:05

9 Lavora con un compagno o una compagna. Insieme rispondete alle domande.

• Giulio oggi ha guardato due episodi di “Oggy e i maledetti scarafaggi”. Quanto sono durati?

• Ilenia ha acceso il televisore alle 17:20 e lo ha spento alle 18:15.

Quanto tempo ha trascorso guardando la TV?

• Ilenia ha poi acceso di nuovo il televisore per vedere “Friendly Club”. Per quanto tempo è rimasto spento il suo televisore?

Direzione Invalsi

• Enrico è indeciso. Al supermercato lo stesso tè viene venduto in confezioni diverse. Qual è la confezione più conveniente? Indica con X. ti guido • La più conveniente è la confezione che costa meno o quella che ha un costo minore al litro?

Oggy e i maledetti scarafaggi 16:00 - 17:10 17:10 - 18:20

Com’è andata?

GEOMETRIA

LE FORME NELLA REALTÀ

La geometria non è nata come studio delle figure, ma è nata dall’esigenza di misurare. Infatti il nome “geometria” significa “misurazione della Terra”.

Con i Greci la geometria si sviluppò come studio delle forme.

La geometria nasce presso gli antichi Egizi. Il Nilo, quando straripava, modificava i confini dei campi. Il faraone inviava perciò i suoi funzionari per calcolare di quanto il terreno si fosse rimpicciolito o ingrandito, per stabilire una nuova tassa. Ecco perché la parola “geometria” indicava una misurazione.

La geometria iniziò ad accompagnare l’architettura: gli edifici importanti venivano realizzati sulla base di figure geometriche e di equilibrio tra le misure delle diverse parti.

Le antiche costruzioni non solo rispettavano le figure geometriche e le loro proporzioni, ma anche un altro importantissimo aspetto della geometria: la simmetria.

Noi, anche senza studiare la geometria, possiamo vederla intorno a noi.

Ma chi ha guidato i “cervelli matematici” a scoprire le forme geometriche? La natura!

Parole per... CONOSCERE

di CRISTINA DELL’ACQUA

LA COPPA di Pitagora

Viviamo immersi nella geometria.

Guardatevi intorno: la penna, lo zaino e le ruote delle automobili sono figure geometriche. Come lo è il bicchiere che usate per bere.

E c’è chi con un bicchiere, o meglio, una coppa, ha fatto una scoperta geniale. Ce lo racconta la maestra Margherita.

Pitagora è stato un grandissimo matematico, ma anche un filosofo, un grande amante della musica e poi un campione olimpico.

Insomma, un personaggio leggendario!

Quando era ancora nella pancia di sua mamma, si racconta che l’oracolo di Delfi abbia predetto ai suoi genitori che avrebbe fatto grandi cose per l’umanità. Pitagora era un personaggio talmente leggendario che a lui sono state attribuite scoperte che non aveva fatto ma che aveva solo divulgato. E c’è chi addirittura crede che Pitagora non sia mai esistito.

Più leggendario di così...!

Una delle invenzioni più particolari è quella della “coppa di Pitagora”, un bicchiere che insegna a bere con moderazione.

Si racconta che a Samo, in Grecia, dove il matematico era nato intorno al 570 a.C., gli era stato chiesto di inventare un modo per far bere meno vino a tavola.

LIFE

SKILLS

PAROLE per CONOSCERE

A vederla dall’esterno, la “coppa di Pitagora” è una coppa come tutte le altre, ma all’interno ha un segreto: al centro c’è una piccola colonna che assomiglia a una cannuccia a forma di U rovesciata, con due fori.

Una cannuccia che sfrutta una proprietà dei liquidi e punisce chi riempie troppo la coppa, svuotandola completamente.

• Il motto di Pitagora era: “Tutto è numero”. Secondo lui, l’Universo e ogni aspetto della vita poteva essere descritto con i numeri. Tu che cosa ne pensi? Parlane con la classe.

• Pitagora immaginava i numeri come un insieme di palline disposte in modo da formare delle figure geometriche. Con la classe, scopri che cosa sono i “numeri triangolari”.

Immaginate la faccia stupita di chi a tavola vedeva il suo bicchiere di vino svuotarsi quando se ne versava troppo! Una figura geometrica può aiutare a essere moderati, più di mille parole.

di CRISTINA DELL’ACQUA

Ti spiego

ARGOMENTO

LINEE • FIGURE PIANE • SOLIDI

La rappresentazione delle forme che sono nella realtà.

REGOLA

Le linee sono figure geometriche con una sola dimensione: la lunghezza. lunghezza

Le figure piane sono figure geometriche con due dimensioni: lunghezza, larghezza. lunghezza larghezza

I solidi sono figure geometriche con tre dimensioni: lunghezza, larghezza, altezza. lunghezza altezza larghezza

Intelligenza visiva

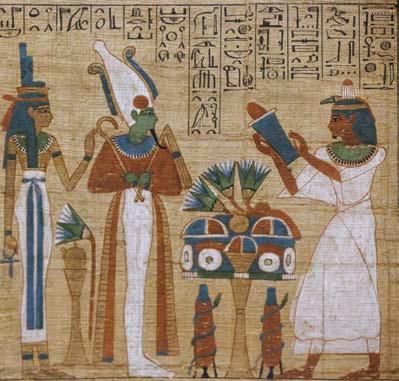
• Su un foglio disegna 3 linee, come mostrato qui a fianco.

• Le linee hanno una sola dimensione: la Capisco

• Disegna un altro segmento per chiudere la linea. Ritaglia la figura che hai ottenuto.

• Con la linea chiusa hai formato un ..........................................................., che è una figura e ha due dimensioni: la e la

• Arrotola il rettangolo.

• Hai ottenuto un , che è una figura e ha tre dimensioni: la , la e la

1 Scrivi: linea • figura piana • solido.

2 Indica con X per completare le frasi e scrivi i nomi giusti nei cartellini.

• Questo è: un solido. una figura piana. una linea.

• È un: quadrato. rettangolo. cubo.

• Le figure piane che lo chiudono sono: 4 6 8

3 Collega ciascun solido al gruppo di figure piane con cui si può costruire, riportando la lettera corrispondente. Poi completa le frasi.

piramide

parallelepipedo

cilindro

• Un parallelepipedo è formato da 6 , uguali a due a due.

• Una piramide a base quadrata è formata da ............. quadrato e ............. triangoli uguali.

• Un cilindro è formato da cerchi e un

LE LINEE

ARGOMENTO

Le figure geometriche con una sola dimensione.

REGOLA

Ciascuna linea ha tre caratteristiche, una per ciascuno dei tre gruppi.

Una linea può essere:

chiusa aperta

Ti spiego retta curva spezzata mista intrecciata semplice

Intelligenza visiva

• Scrivi “aperta” o “chiusa”. Capisco

• Scrivi “semplice” o “intrecciata”.

• Scrivi “retta”, “curva”, “spezzata” o “mista”.

1 Scrivi le tre caratteristiche di ciascuna linea.

Ti spiego

RETTA • SEMIRETTA • SEGMENTO

ARGOMENTO

Una linea speciale e le sue parti.

REGOLA

• La retta non ha né inizio né fine. Si indica con una lettera minuscola. a retta

La posizione delle rette

semiretta semiretta b c

• La semiretta ha un inizio (origine), ma non ha una fine. Si indica con una lettera minuscola. O

Due rette sul piano possono avere diverse posizioni.

segmento

• Il segmento ha un inizio e una fine. Si indica con due lettere maiuscole.

Le rette parallele mantengono sempre la stessa distanza e non si incontrano mai.

• Osserva e rispondi. Capisco

• Ha un inizio? Sì No

Le rette incidenti si incontrano e formano 4 angoli, uguali a due a due.

Le rette perpendicolari sono particolari rette incidenti: quando si incontrano formano 4 angoli tutti uguali tra loro.

• Ha una fine? Sì No O

pp. 214-215

• Ha un inizio? Sì No

• Ha una fine? Sì No A

• Ha un inizio? Sì No

• Ha una fine? Sì No

L’ANGOLO

Ti spiego ARGOMENTO

Una parte di piano.

REGOLA

lato ampiezza

L’angolo è la parte di piano compresa tra due semirette che hanno la stessa origine. Il punto di origine si chiama vertice; le semirette sono i lati dell’angolo.

Di ogni angolo si può misurare l’ampiezza utilizzando il goniometro.

L’unità di misura dell’ampiezza

è il grado, il cui simbolo è ° .

Per misurare l’ampiezza di un angolo, procedi così:

• fai coincidere il vertice dell’angolo con il centro del goniometro;

• fai coincidere uno dei lati con la linea che passa per lo zero;

• leggi sul goniometro il numero indicato dall’altro lato.

Capisco

• Prendi due matite e appoggiale sul banco come è illustrato nei 4 disegni. Poi rispondi.

• Quando hai disegnato un angolo? Indica con più X

Esercizi

1 Scrivi l’ampiezza degli angoli.

VARI TIPI DI ANGOLO

Ti spiego

REGOLA

Un angolo, in base alla sua ampiezza, può essere: acuto, ottuso, retto, nullo, piatto, giro.

Capisco

• Visualizza gli angoli utilizzando due bastoncini. Tieni sempre fermo un bastoncino e fai ruotare l’altro, come se fossero le lancette di un orologio.

I due lati sono sovrapposti. Nessuno dei due lati ha compiuto una rotazione.

Angolo nullo: misura 0°

Un lato ha compiuto mezzo giro. I due lati dell’angolo sono uno il proseguimento dell’altro.

Angolo piatto: misura 180°

I due lati sono sovrapposti, ma un lato ha compiuto una rotazione completa.

Angolo giro: misura 360°

Un lato ha compiuto un quarto di giro. I due lati sono perpendicolari. O

Angolo retto: misura 90°

Esercizi

Un lato ha compiuto una rotazione minore di un quarto di giro. L’angolo acuto è minore dell’angolo retto.

Angolo acuto: misura meno di 90°

1 Per ciascun angolo, scrivi se è retto, ottuso, acuto.

Un lato ha compiuto una rotazione maggiore di un quarto di giro. L’angolo ottuso è maggiore dell’angolo retto.

Angolo ottuso: misura più di 90°

Ti spiego

ARGOMENTO

SIMMETRIA E TRASLAZIONE

Gli spostamenti delle figure sul piano.

REGOLA

Le isometrie sono spostamenti di figure sul piano: la figura cambia posizione, ma non cambia né forma né dimensioni.

La simmetria, la traslazione, la rotazione sono isometrie.

La simmetria

Con la simmetria la figura si ribalta rispetto a un asse. L’asse di simmetria può essere interno o esterno.

asse di simmetria interno asse di simmetria esterno

La traslazione

Con la traslazione la figura viene spostata in linea retta.

A A' vettore di traslazione

Figura Figura traslata

Intelligenza visiva

• Ripassa le figure e indica con X. Capisco

La bandierina è stata: spostata (traslata). ribaltata, cioè è simmetrica.

La bandierina è stata: spostata (traslata). ribaltata, cioè è simmetrica.

Esercizi

1 Ripassa in rosso il vettore che segna la corretta traslazione.

LA ROTAZIONE

Ti spiego

REGOLA

La rotazione

La rotazione è lo spostamento di una figura che ruota intorno a un punto.

La rotazione ha:

• un centro di rotazione, il punto attorno al quale la figura ruota;

• un verso, che può essere orario o antiorario;

• un’ampiezza di rotazione, cioè la misura dell’angolo formato dalla figura che si è spostata.

• Ripassa le figure e indica con X. Capisco

Centro di rotazione

O ampiezza verso Figura ruotata

La bandierina è stata: spostata (traslata). ruotata.

ribaltata, cioè è simmetrica.

Esercizi

1 Disegna la figura ruotata. Segui le indicazioni. 2 Per ciascuna figura, segna il centro di rotazione e completa.

Ampiezza: 90°

Verso antiorario

Ampiezza: 270°

Verso antiorario

Ampiezza: Verso: Ampiezza: Verso:

Figura

Ti spiego

ARGOMENTO

Le figure piane con angoli e lati.

REGOLA

I poligoni sono figure piane, delimitate da una linea spezzata chiusa. Un poligono può essere:

• convesso, quando i prolungamenti dei suoi lati non lo attraversano:

I POLIGONI

Capisco

• Colora il quadratino per collegare alla definizione.

Non è un poligono perché non è una figura chiusa.

È una figura piana, ma non è un poligono perché è chiuso da una linea mista.

È un poligono perché è chiuso da una linea spezzata.

• Leggi con attenzione e scrivi i nomi.

• concavo, quando i prolungamenti di due o più lati lo attraversano:

Esercizi

1 Osserva i prolungamenti dei lati e scrivi concavo o convesso.

Poligono Poligono

• Il lato è ciascun segmento della linea che forma il contorno.

• Il vertice è il punto in cui due lati si incontrano.

• L’angolo è lo spazio compreso tra due lati consecutivi.

• L’altezza è il segmento che parte da un vertice e arriva perpendicolarmente sul lato opposto.

• La diagonale è il segmento che collega due vertici non consecutivi.

• L’asse di simmetria è la retta che divide il poligono in due parti simmetriche.

CLASSIFICARE I POLIGONI

Ti spiego REGOLA

I poligoni prendono il nome dal numero di lati e angoli che possiedono: triangolo, quadrilatero, pentagono… I poligoni possono essere classificati in base alle caratteristiche dei lati e degli angoli.

• Lati uguali: poligono equilatero.

• Angoli uguali: poligono equiangolo.

• Angoli e lati uguali: poligono regolare.

Capisco

• Colora il quadratino della figura che ha tutti i lati uguali.

Scrivi: equilatero • non equilatero.

• Colora il quadratino della figura che ha tutti gli angoli uguali.

Scrivi: equiangolo • non equiangolo.

• Angoli e lati diversi: poligono irregolare.

Esercizi

1 Completa. Poi scrivi il nome del poligono e se è equilatero, equiangolo, regolare, irregolare.

Numero lati

Numero angoli ............

Numero vertici È un È un poligono

Numero lati

Numero angoli ............

Numero vertici

È un È un poligono

I TRIANGOLI

Ti spiego ARGOMENTO

I poligoni con il minor numero di lati.

REGOLA

Il triangolo è un poligono con 3 lati, 3 angoli, 3 vertici.

• In base ai lati, un triangolo può essere equilatero, scaleno, isoscele.

• In base agli angoli, un triangolo può essere ottusangolo, rettangolo, acutangolo.

• In un triangolo le altezze sono tre perché tre sono i vertici. Talvolta l’altezza cade all’esterno del triangolo, sul prolungamento della base.

altezza

• La somma degli angoli interni di un triangolo è sempre di 180°, cioè un angolo piatto.

Capisco

• I differenti tipi di triangoli sono classificati in base ai lati e agli angoli. Osserva i lati e completa.

I lati sono tutti uguali?

Sì No

Questo è un triangolo

...................................................................

I lati di questo triangolo sono tutti

Questo è un triangolo

...................................................................

Questo triangolo ha lati uguali?

Sì No Quanti?

Questo è un triangolo

• Osserva gli angoli e completa.

L’angolo colorato è un angolo ..............................................

Questo è un triangolo ottusangolo

L’angolo colorato è un angolo ..............................................

Questo è un triangolo rettangolo

I tre angoli del triangolo sono tutti

Questo è un triangolo acutangolo.

1 In ciascun triangolo, traccia dal vertice B l’altezza relativa alla base e poi completa.

Nell’ultimo triangolo l’altezza coincide con

2 Completa la tabella con le caratteristiche di ciascun triangolo. Indica con due X. a b c d e f

triangolo equilatero scaleno isoscele acutangolo rettangolo ottusangolo

3 In ciascun triangolo, calcola la misura del terzo angolo.

Direzione Invalsi

• Quale di questi triangoli è impossibile? Indica con X e spiega perché non può esistere. Rettangolo equilatero. Rettangolo isoscele. Rettangolo scaleno.

È un triangolo impossibile perché

ti guido • Ricorda la misura degli angoli del triangolo equilatero, quale è la somma degli angoli interni e come è fatto un triangolo rettangolo.

I QUADRILATERI

Ti spiego

ARGOMENTO

I poligoni con quattro lati.

REGOLA

I quadrilateri sono poligoni con 4 lati, 4 angoli, 4 vertici, 2 diagonali. Sono classificati in base alle caratteristiche dei lati e degli angoli.

• I trapezi hanno una coppia di lati paralleli.

• I parallelogrammi hanno due coppie di lati paralleli e uguali.

• I rettangoli hanno tutti gli angoli retti e due coppie di lati paralleli e uguali.

• I rombi hanno tutti i lati uguali e due coppie di lati paralleli.

• I quadrati hanno tutti i lati uguali e tutti gli angoli retti.

Capisco

• Scrivi il nome di ciascun quadrilatero.

QUADRILATERI rettangoli parallelogrammi trapezi rombi quadrati

1 Leggi le caratteristiche. Indica con X il quadrilatero a cui si riferiscono e scrivine il nome.

• Una coppia di lati paralleli, non uguali.

• Due coppie di lati paralleli e uguali a due a due.

• Due coppie di lati paralleli e uguali a due a due; angoli tutti uguali.

• Due coppie di lati paralleli; lati tutti uguali; angoli uguali a due a due.

• Ha sia le caratteristiche dei rombi sia quelle dei rettangoli: due coppie di lati paralleli, tutti i lati uguali, tutti gli angoli uguali.

2 Completa le figure per ottenere la figura piana richiesta.

quadrato

Ti spiego

ARGOMENTO

I PARALLELOGRAMMI

Un particolare gruppo di quadrilateri.

REGOLA

I parallelogrammi sono quadrilateri con i lati paralleli e uguali a 2 a 2.

Sono parallelogrammi il romboide (o parallelogramma proprio), il rombo, il rettangolo, il quadrato.

Capisco

• Leggi, osserva e completa.

Il romboide (o parallelogramma proprio):

• ha i lati uguali e a due a due;

• ha gli angoli a due a due;

• ha ................ diagonali, diverse tra loro, che si tagliano a metà;

• non ha assi di simmetria.

Il rettangolo ha:

• i lati e a due a due;

• gli tutti uguali e tutti retti;

• due ....................................., ..................................... tra loro, che si tagliano a metà e non sono perpendicolari;

• due assi di simmetria.

Il rombo ha:

• i lati tutti e paralleli a due a due;

• gli angoli a due a due;

• due ....................................., diverse tra loro, che si tagliano a metà e sono perpendicolari;

• due assi di simmetria che sono le diagonali.

Il quadrato ha:

• i lati a due a due e tutti ;

• gli tutti uguali e tutti retti;

• due ....................................., ..................................... tra loro, che si tagliano a metà e sono perpendicolari;

• quattro assi di simmetria.

1 In ciascuna figura, traccia le due diagonali. Poi rispondi.

2 In ciascuna figura, traccia un’altezza. In una figura è già tracciata. Poi rispondi.

• Quali, tra questi poligoni, hanno le diagonali uguali? ............................................................................

• Quali hanno le diagonali perpendicolari?

• Tra questi poligoni, in quali l’altezza coincide con un lato? ................................................................

• In quali l’altezza non si trova lungo il contorno? h

3 Osserva i segmenti tratteggiati e indica con X quelli che NON sono assi di simmetria.

4 Completa.

• Un poligono equilatero ha tutti i uguali.

• Un poligono equiangolo ha tutti gli uguali.

• Un poligono regolare ha ........................ e ........................ uguali.

5 Scrivi nei cartellini la caratteristica giusta. Scegli tra: poligoni equilateri • poligoni regolari • poligoni equiangoli.

pp. 223-224

I TRAPEZI

Ti spiego

ARGOMENTO

Un quadrilatero che NON è un parallelogramma.

REGOLA

Il trapezio è un quadrilatero con una sola coppia di lati paralleli, che sono la base maggiore e la base minore. Gli altri due lati si chiamano lati obliqui.

Un trapezio può essere scaleno, isoscele, rettangolo.

Capisco

• Scrivi al posto giusto: lato obliquo • base maggiore • base minore.

• Leggi, osserva e completa.

Ci sono differenti tipi di trapezi in base ai lati e agli angoli.

altezza diagonale

I lati hanno misure diverse?

Sì No

Gli angoli hanno tutti

ampiezze diverse? Sì No

È un trapezio scaleno.

Esercizi

I lati obliqui hanno la stessa misura? Sì No

Gli angoli hanno ampiezze

uguali a due a due? Sì No

È un trapezio isoscele.

I lati hanno misure diverse?

Sì No

Quanti angoli retti ci sono?

È un trapezio rettangolo.

1 Colora il quadratino in rosso per i trapezi scaleni, in blu per i trapezi rettangoli, in verde per i trapezi isosceli.

1 Nel trapezio isoscele disegna le diagonali e l’asse di simmetria, poi colora nello stesso modo gli angoli uguali. Infine completa le sue caratteristiche.

• Il trapezio isoscele ha: diagonali di uguale lunghezza. asse di simmetria.

Due angoli sono acuti e tra loro.

Gli altri due angoli sono ...................................... e ......................................

2 Per ciascuna affermazione, indica V (vero) o F (falso).

• Il trapezio è un quadrilatero. V F

• Il trapezio è un parallelogramma. V F

• Il trapezio ha una coppia di lati paralleli e uguali. V F

3 In ciascun trapezio, segna in rosso l’altezza. Poi rispondi.

• I lati non paralleli del trapezio si chiamano lati obliqui. V F

• La base minore è sempre meno lunga di ciascun lato obliquo. V F

In quale trapezio l’altezza coincide con un lato?

4 In ciascun trapezio, colora: in rosso la base maggiore, in blu la base minore, in arancione i 2 lati obliqui. Poi traccia in verde l’altezza. Infine rispondi.

Quale, tra i segmenti che hai colorato o tracciato, non è sul contorno della figura?

Direzione Invalsi

• Osserva i quadrilateri e rispondi.

A B C D E

Quali sono trapezi?

Quali sono trapezi rettangoli?

Qual è il trapezio isoscele?

Qual è il rettangolo?

• Colora due figure per ottenere un altro trapezio.

ti guido • Osserva bene le figure e non farti confondere dalla loro posizione. Per l’ultima consegna, hai diverse possibilità.

per imparare

Linee e forme geometriche nell’arte

Per molto tempo nelle opere d’arte (statue, sculture, quadri, bassorilievi) veniva rappresentato ciò che era possibile vedere nella realtà. Per questo gli artisti riproducevano figure umane, paesaggi, elementi reali come fiori, animali, oggetti.

Molti artisti poi cominciarono a produrre opere d’arte che non rappresentavano oggetti reali, ma astraevano, cioè prendevano dalla natura gli enti geometrici: linee, figure piane e solidi.

Gli elementi geometrici venivano poi composti in opere artistiche molto originali.

Questo movimento artistico fu chiamato “astrattismo” perché non si rappresentavano oggetti reali.

Vasilij Kandinsky, pittore nato a Mosca nel 1866, può essere considerato uno dei fondatori della pittura astratta.

Secondo Kandinsky le linee, le forme e i colori possono

essere associati alle emozioni.

Una linea orizzontale ricorda l’immobilità, la linea obliqua indica il movimento, la linea curva la calma e quella spezzata il nervosismo.

Kandinsky dava molta importanza ai colori e li associava agli strumenti musicali e alla musica, un’altra arte fondata su precise regole matematiche.

Il giallo, colore potente, viene associato al suono della tromba; il rosso, colore caldo, al suono di una tuba, l’azzurro al flauto, il verde al violino, l’arancione a una campana. Il bianco, che è la somma di tutti i colori dell’iride, è paragonato al “non suono”, cioè alla pausa tra un suono e l’altro.

M A E T S

Tutto quello che hai imparato sull’arte astratta di Kandinsky potrebbe ispirarti un tuo capolavoro geometrico. Provaci!

Kandinsky nei suoi quadri utilizza molte forme geometriche.

Per lui il quadrato è la forma geometrica più stabile, perciò rappresenta la concretezza.

Nel triangolo, gli angoli acuti indicano dinamicità. Il cerchio invece è una forma tranquilla, che tende alla quiete.

Ti spiego

ARGOMENTO

La misura del contorno di una figura piana.

REGOLA

Il contorno di una figura piana è una linea chiusa. La sua misura è il perimetro (P). I perimetri si esprimono con le misure di lunghezza. Per calcolare il perimetro di un poligono si sommano le misure dei lati.

Esercizi

IL PERIMETRO

Capisco

• Misura con il righello e completa.

• Calcola il perimetro: + + + = = cm

1 Misura ciascun lato e calcola il perimetro. Poi controlla se coincide con la lunghezza del segmento A–A1 .

2 Misura i lati e calcola il perimetro (P).

• Calcola il perimetro: + + + = = cm

L’AREA

• Ricopri ciascuna figura con il campione indicato e scrivi l’area (A). Capisco Campione

Ti spiego

ARGOMENTO

La misura dello spazio occupato da una figura piana. REGOLA

Lo spazio occupato dalle superfici si può misurare. La misura della superficie si chiama area. Per l’area occorre utilizzare unità di misura adatte, cioè altre figure piane prese come campione.

Esercizi

1 Per ciascuna figura, scrivi l’area (A): utilizza come unità di misura il quadretto .

2 Determina l’area (A) utilizzando diverse unità di misura. A = A = A = A =

Ti spiego

ISOPERIMETRIA ED EQUIESTENSIONE

ARGOMENTO

Stesso perimetro o stessa area.

REGOLA

Le figure che hanno perimetro uguale sono isoperimetriche.

Le figure che hanno area uguale sono equiestese.

Capisco

• Determina il perimetro (P) o l’area (A) richiesti usando il campione indicato. Poi rispondi alle domande.

B P = P =

• Le figure A e B hanno la stessa forma? Sì No

• Le figure A e B hanno lo stesso perimetro?

Sì No

• Le figure A e B sono isoperimetriche? Sì No

• Le figure C e D hanno la stessa forma? Sì No

• Le figure C e D hanno lo stesso perimetro?

Sì No

Sono isoperimetriche? Sì No

• Le figure C e D hanno la stessa area? Sì No

Sono equiestese? Sì No

Esercizi

1 Queste figure sono formate da tanti triangoli equilateri. Per ciascuna, scrivi il perimetro e l’area, poi esegui quanto richiesto.

• Ripassa con lo stesso colore il contorno delle due figure isoperimetriche: b e

• Colora nello stesso modo la superficie delle figure equiestese:

COMPORRE E SCOMPORRE FIGURE

Ti spiego

REGOLA

Due o più figure piane composte dagli stessi poligoni sono equivalenti.

Intelligenza visiva

Capisco

• Osserva le figure A e B e scrivi i loro nomi.

• Le figure A e B sono state composte in modo da ottenere 3 poligoni diversi. Scrivi il nome dei poligoni ottenuti.

Esercizi

1 Segui le indicazioni per scomporre le figure e completa.

• Traccia l’altezza dal punto B.

Quali figure hai ottenuto?

• Traccia la diagonale AC.

• La loro area è uguale alla somma delle aree delle figure A e B? Sì No esagono

• Le tre figure ottenute hanno la stessa area? Sì No

Quali figure hai ottenuto?

Ti spiego

ARGOMENTO

LE MISURE DI SUPERFICIE

Le misure convenzionali per misurare le superfici.

REGOLA

L’unità di misura per le superfici è il metro quadrato (m2 ). Il numero 2 indica le due dimensioni del campione. Nelle misure quadrate, per passare da una unità di misura all’altra, occorre moltiplicare o dividere per 100.

Capisco

• Quanti centimetri quadrati sono contenuti in un decimetro quadrato?

1 dm2 = cm2

• Quanti mm2 sono contenuti in 1 cm2?

1 cm2 = mm2

• Quanti mm2 sono contenuti in 1 dm2? 1000 10000

decimetro quadrato

1 Quale misura è la più adatta per misurare queste superfici? Cerchiala.

• hm2 • dam2

3 Osserva ed esegui le equivalenze.

2 Per ciascuna superficie, cerchia la misura impossibile.

4 Completa.

80 dm2 + dm2 = 1 m2

5 Completa le tabelle.

Competenze

• Volete misurare l’area della superficie del banco. Avete a disposizione 20 quadrati da 1 dm2. Come dovete disporli per riuscire a ricoprire bene tutta la superficie? Da dove iniziate? Se i decimetri quadrati a vostra disposizione non fossero sufficienti, che cosa potete fare? Riuscite a trovare una soluzione che non comporti la costruzione di altri decimetri quadrati?

L’AREA DEL RETTANGOLO E DEL QUADRATO

Ti spiego

ARGOMENTO

Come calcolare la misura della superficie, cioè come calcolare l’area.

REGOLA

h

b

Area rettangolo (A) = base × altezza

A = b × h

Area quadrato (A) = lato × lato

A = <l × <l

Capisco

• Osserva e completa.

Questo rettangolo ha la base di 6 cm e l’altezza di 3 cm.

Colora i centimetri quadrati della base. Quanti sono? ....................

Colora con colori diversi le altre righe di centimetri quadrati.

Quante righe hai colorato in tutto?

Quanti centimetri quadrati hai colorato in tutto?

6 × .................... = ....................

Hai moltiplicato la misura della base per la misura dell’

Questo quadrato ha la base di 4 cm e l’altezza di 4 cm.

Colora i centimetri quadrati della base. Quanti sono?

Colora con colori diversi le altre righe di centimetri quadrati.

Quante righe hai colorato in tutto?

Quanti centimetri quadrati hai colorato in tutto?

× =

Hai moltiplicato la misura della base per la misura dell’

Base e altezza nel quadrato sono uguali

Perciò hai moltiplicato la misura del lato per il lato stesso.

1 Calcola l’area (A) di ciascun rettangolo ( 1 cm).

A = × = cm2

A = × = cm2

2 Calcola il perimetro (P) e l’area (A) di ciascun quadrato.

7 dm

5 dm

A = × = cm2

P = ............ × 4 = .............. dm

A = × = dm2

P = × = dm A = × = dm2

3 Calcola il perimetro (P) e l’area (A) di ciascun rettangolo.

5 m

3 m

P = + + + = m

A = × = m2

4 Risolvi i problemi sul quaderno.

2 m

4 dm P = × = dm A = × = dm2

P = = m A = × = m2 9 m

a. Andrea disegna un rettangolo che ha dimensioni 8 cm e 10 cm. Disegna poi un quadrato isoperimetrico al rettangolo. Quanto misura il lato del quadrato? Quanto misura la sua superficie?

b. Teresa disegna un rettangolo. La base misura 15 cm. L’altezza è pari ai 2 3 della base. Qual è l’area del rettangolo? Qual è il perimetro?

228-229, 231

Ti spiego

L’AREA DEL PARALLELOGRAMMA

ARGOMENTO

Come calcolare la misura della superficie trasformando la figura.

REGOLA

Puoi scomporre un parallelogramma in due figure e poi ricomporle formando un rettangolo equiesteso al parallelogramma. Perciò anche l’area del parallelogramma si calcola moltiplicando la misura della base per la misura dell’altezza. Area parallelogramma = base × altezza

A = b × h

• Osserva e completa.

Esercizi

1 In ciascun parallelogramma, traccia l’altezza e misurala. Poi calcola il perimetro (P) e l’area (A).

cm

cm

cm 2,2 cm P = + + + = cm A = × = cm2

P = + + + = cm

A = × = cm2

L’altezza ha diviso in 2 parti il parallelogramma proprio (o romboide).

Con le stesse 2 parti si può formare un Colorale.

Le figure A e B hanno la stessa area? Sì No

Capisco b h figura A figura B b h

2 Risolvi il problema sul quaderno. Rita ha ritagliato una bandierina a forma di parallelogramma con la base di 14 cm, l’altezza di 8 cm e il lato obliquo di 9 cm. Calcola l’area e il perimetro della bandierina.

Quaderno operativo, pp. 228-229, 231

L’AREA DEL ROMBO

Capisco

• Osserva e completa.

Le diagonali hanno diviso in 4 parti il rombo. Con le stesse parti si può formare un . Colorale.

La figura A e B hanno la stessa area?

La base del rettangolo è uguale alla

maggiore del rombo.

L’altezza del rettangolo è uguale alla metà della minore del rombo.

Ti spiego

ARGOMENTO

Come calcolare la misura della superficie trasformando la figura.

REGOLA

Puoi scomporre un rombo in 4 triangoli e poi ricomporlo formando un rettangolo equiesteso al rombo in cui:

• la base è uguale a una diagonale del rombo;

• l’altezza è uguale a metà dell’altra diagonale del rombo.

Perciò l’area del rombo si calcola moltiplicando la misura di una diagonale per la misura dell’altra diagonale. Poi si divide per 2. Area rombo = diagonale maggiore × diagonale minore : 2

A = D × d : 2

Esercizi

1 Calcola il perimetro (P) e l’area (A) di ciascun rombo.

2 Risolvi il problema sul quaderno.

Nel cortile di Elia c’è una aiuola a forma di rombo con la diagonale maggiore lunga 6 m e la diagonale minore lunga 3,6 m.

Il lato dell’aiuola è lungo 3,5 m. Calcola l’area e il perimetro dell’aiuola.

figura A

figura B

lato (base) altro lato altezza Perimetro Area

rettangolo 32

2 Disegna sul quaderno le figure indicate: rispetta le misure date. Poi calcola l’area.

Parallelogramma A base = 9 cm altezza = 4 cm

Parallelogramma B base = 6 cm altezza = 5 cm

Rombo A d = 3 cm D = 5 cm

Rombo B D = 6 cm d = 3 cm

3 Misura con il righello i lati obliqui dei parallelogrammi che hai disegnato. Sul quaderno calcola il perimetro delle quattro figure.

4 Risolvi i problemi sul quaderno.

a. In un aquilone a forma di rombo l’asta (diagonale) più lunga misura 90 cm e quella più corta è i 2 3 di quella più lunga.

Quanto misura l’asta (diagonale) più corta?

Quanti centimetri quadrati di tela servono per fare l’aquilone?

b. Una piccola coperta gialla rettangolare con la base di 110 cm e l’altezza di 90 cm ha al centro il disegno di un rombo arancione con la diagonale minore di 75 cm e la diagonale maggiore di 80 cm. Calcola l’area della parte gialla della coperta.

c. Un parallelogramma ha la base di 20 cm, l’altezza di 20 cm. Il lato misura obliquo di 21,5 cm. Un quadrato ha il lato di 20 cm. Calcola l’area e il perimetro di entrambe le figure. Quale ha il perimetro maggiore?

Che cosa hai notato confrontando le aree delle due figure?

Direzione Invalsi

• A quale frazione dell’area del parallelogramma corrisponde il rettangolo rosa? 1

ti guido • Ricorda che i parallelogrammi possono essere trasformati in rettangoli equiestesi.

Il parco divertimenti

Nel parco divertimenti i bambini e le bambine giocano, senza rendersi conto di essere immersi nella geometria.

1 Risolvi i problemi sul quaderno.

a. All’ingresso del parco c’è un cartello con la mappa. Il cartello è composto da un quadrato sormontato da un triangolo equilatero. Osservalo e calcola il perimetro del cartello.

b. Vicino all’ingresso del parco c’è una grossa vasca di sabbia dalla forma rettangolare. La base misura 5 m e l’altezza 3 m. Lungo il bordo verrà costruito un cordolo di pietra per contenere la sabbia. Il muratore ha chiesto un compenso di 9,50 € al metro. Quanto si spenderà per costruire il cordolo?

c. Al centro del parco vi è una pista di forma rettangolare utilizzata per gli skateboard. La base misura 32 m e l’altezza 26 m. Si deve cambiare la pavimentazione e ricostruire il cordolo protettivo. Quanto metri quadrati di pavimentazione si devono rifare? Quanto misura il cordolo di recinzione?

2 Leggi il problema e osserva le formule del perimetro del rombo e del quadrato. Poi numera le tappe del processo risolutivo (la prima è già segnata) e risolvi sul quaderno.

Nel parco ci sono 6 aiuole di forma quadrata e 4 a forma di rombo. Il lato di ciascuna aiuola è di 4,5 m. Per recintarle sono stati acquistati 200 m di rete metallica. I metri comperati sono sufficienti o no? Quanti metri di rete mancano o avanzano?

P quadrato = <l × 4

1 Trovare quante sono le aiuole.

Confrontare il perimetro delle aiuole con la lunghezza della rete.

Trovare il perimetro di tutte le aiuole.

P rombo = <l × 4

Trovare la differenza tra perimetro e lunghezza della rete.

Trovare il perimetro di un’aiuola.

L’AREA DEL TRAPEZIO

Ti spiego

ARGOMENTO

Come calcolare la misura della superficie raddoppiando la figura.

REGOLA

Se componi un parallelogramma raddoppiando il trapezio, questo parallelogramma avrà:

• la base formata dalla base maggiore più la base minore del trapezio;

• l’altezza uguale a quella del trapezio.

Perciò l’area del trapezio si calcola moltiplicando la somma delle basi per la misura dell’altezza e poi dividendo per 2.

Area trapezio = ( base maggiore + base minore) × altezza : 2 A = ( B + b) × h : 2

Capisco

• Osserva e completa.

X

Y

• La figura X è un

• La figura Y è un

• Per trasformare X in Y il trapezio è stato scomposto o raddoppiato?

Perciò l’area del parallelogramma Y è il doppio di quella del trapezio X.

La base del parallelogramma è formata dalla base maggiore e dalla base del trapezio.

Esercizi

1 Usa il righello e segna le misure. Poi calcola il perimetro (P) e l’area (A) dei trapezi.

1 Con queste figure componi un trapezio rettangolo e calcola l’area.

A = ( ) × : = cm2

2 Risolvi questi problemi. Segna le misure sulle figure ed esegui i calcoli sul quaderno.

Un trapezio scaleno ha un lato obliquo lungo 14 cm. L’altro lato è lungo 2 cm in meno. La base maggiore misura 18 cm. Il perimetro è di 55 cm. Quanto misura la base minore?

1) Trovo la misura

Operazione

2) Trovo la misura

Operazione ........................................................................................................

3) Trovo la misura

Operazione

La base maggiore di un trapezio rettangolo misura 12 cm, quella minore è la metà di quella maggiore.

L’altezza è di 8 cm. Calcola l’area.

3 Leggi il problema e completa.

Un trapezio isoscele ha il perimetro di 56 cm. La base maggiore misura 28 cm, la base minore 14 cm. Quanto misura un lato obliquo?

Numera in ordine che cosa devi trovare. Poi completa.

La misura di un lato obliquo. La misura dei lati obliqui. La misura delle basi.

1) Trovo la misura

2) Trovo la misura

3) Trovo la misura .......................................................................................

Operazione

Operazione

Operazione ......................................................................................................

Ti spiego

ARGOMENTO

L’AREA DEL TRIANGOLO

Come calcolare la misura della superficie raddoppiando la figura.

REGOLA

Puoi comporre un rettangolo raddoppiando il triangolo. L’area del rettangolo è il doppio di quella del triangolo.

Perciò l’area del triangolo si calcola moltiplicando la misura della base per la misura dell’altezza e poi dividendo per 2.

Area triangolo = base × altezza : 2

A = b × h : 2

• Osserva e completa. Capisco

• La figura A è un

• La figura B è un

• Per trasformare A in B il triangolo è stato scomposto o raddoppiato?

Perciò l’area del rettangolo B è il doppio di quella del triangolo A.

Esercizi

1 Per ciascun triangolo, disegna l’altezza. Poi misura i lati e l’altezza. Infine calcola il perimetro e l’area.

2 Sul quaderno, calcola perimetro (P) e area (A) di questi triangoli. Se necessario, esegui le equivalenze.

Tra i resti antichi

Viola e Jacopo abitano vicino a un sito archeologico. Un giorno decidono di visitarlo. Viola si chiede: – Come se la saranno cavata con la geometria gli abitanti di questo antico luogo?

1 Risolvi i problemi sul quaderno.

a. Nel sito archeologico, durante gli scavi, sono venuti alla luce i resti di una casa a base quadrata, con il lato di 4 m. Quanti metri quadrati avevano a disposizione gli abitanti di quella casa?

b. Vicino a una casa sono stati trovati i resti di un recinto di forma rettangolare destinato agli animali. La base è di 12 m e l’altezza 7,60 m. Si è scoperto che era esattamente diviso a metà: una parte per le pecore, una parte per le capre. Quanti metri quadrati erano destinati alle capre?

c. Nella zona a est sorgeva un piccolo tempio con il pavimento a forma di triangolo equilatero con la base di 15 m e l’altezza di 13 m. Quanto misurava la superficie del pavimento del tempio? Qual era il suo perimetro?

d. L’archeologo sta osservando le piastrelle a forma di rombo che ricoprivano una parte della parete del tempio. La diagonale maggiore è lunga 8 cm, quella minore 5 cm. Qual è l’area di ciascuna piastrella?

2 Risolvi il problema completando il diagramma dell’algoritmo.

La vasca di raccolta dell’acqua della città aveva questa forma e le dimensioni elencate dall’archeologo. Qual è l’area della vasca? Qual è il dato inutile?

B = 38 m

b = 22 m

h = 20 m

<l = 21,5 m

1 Quanti poligoni vedi?

2 Completa le figure per ottenere quanto richiesto.

triangoli quadrilateri ottagono ............ ottagono esagoni rettangoli triangolo un non poligono un triangolo un pentagono un esagono

3 Completa le tabelle scrivendo le formule che mancano.

poligono perimetro area quadrato

rettangolo b h (b + h) × 2

romboide <l b h (b + <l obliquo) × 2

poligono perimetro area rombo <l D d

triangolo

4 In ciascun quadrilatero, traccia tutti gli assi di simmetria possibili. Poi completa.

• La figura non ha assi di simmetria.

• La figura B ha ............... assi di simmetria.

• La figura C ha assi di simmetria.

A B C

5 Per ciascuna affermazione, indica V (vero) o F (falso).

• Un poligono può essere chiuso da una linea mista. V F

• Una figura piana può essere chiusa da una linea mista. V F

• Gli angoli del poligono sono la metà dei suoi lati. V F

6 Completa la tabella calcolando il perimetro e l’area delle figure. Se necessario, esegui le operazioni sul quaderno.

poligono perimetro area

2,5 cm 3 m 5 m

3,5 dm 2 dm

Obiettivi

2,5 dm

• Conoscere le caratteristiche dei poligoni; saperne calcolare perimetro e area.

• Tutti i poligoni hanno diagonali. V F

• Un poligono può avere al massimo 24 lati. V F

• Un poligono può avere 3 lati. V F

• Un poligono può avere solo 2 angoli. V F

Direzione

Invalsi

• Osserva questi triangoli: hanno tutti la stessa base e la stessa altezza. Rispondi.

• Le tre figure sono equiestese? Sì No

• Le tre figure sono isoperimetriche? Sì No

ti guido • Ricorda le formule per calcolare l’area e il perimetro del triangolo.

Com’è andata?

Cittadinanza digitale

L’INFORMAZIONE

CONSAPEVOLE

Ogni giorno i mass media, internet, le chat ci forniscono una quantità enorme di informazioni e dati. Ma da dove vengono tutte queste informazioni? Sai come utilizzarle?

Ricavare informazioni

I numeri permettono di rappresentare e interpretare la realtà in modo efficace e rapido. Le informazioni date attraverso i numeri riassumono situazioni anche molto complesse. Ci aiutano a comprendere meglio i problemi e le difficoltà del vivere insieme, guidandoci nelle scelte che dobbiamo fare per diventare cittadini e cittadine consapevoli.

Ogni persona nel mondo produce più di 3 kg di spazzatura al giorno!

Allarme acqua! In Italia ciascuno ne consuma 140 litri al giorno!

bere e cucina pulizia e giardino lavatrice wc bagno e doccia utilizzo rubinetto per igiene personale

Le immagini ti aiutano a comprendere meglio le informazioni, a capire come potresti ridurre i consumi e diventare un cittadino o una cittadina consapevole? Come?

La realtà e i dati

Per comprendere la realtà abbiamo bisogno di dati. Ma dobbiamo essere certi che i dati a nostra disposizione siano corretti! Occorre controllare bene la fonte, cioè chi fa circolare la notizia, poi dobbiamo sempre porci delle domande e valutare se ciò che leggiamo è vero, verosimile, impossibile.

• Di questi bambini, solo uno riporta un dato reale. Colora il semaforo corrispondente in verde.

Mi ha sorpreso questo dato: solo 500 bambini/e in Italia praticano uno sport.

Ho letto su Internet che 99 bambini/e su 100 della Scuola Primaria hanno uno smartphone.

Sul giornale ho letto che calcio e nuoto sono gli sport più praticati dai bambini e dalle bambine.

I computer, gli smartphone, Internet… sono molto importanti e ci possono essere di grande aiuto. Dobbiamo però usarli in modo consapevole perché potrebbero anche diventare molto pericolosi!

LE RELAZIONI

ARGOMENTO

I collegamenti che aiutano a comprendere la realtà.

REGOLA

Puoi esprimere le relazioni attraverso tabelle, con l’uso di frecce o con diagrammi. Ti spiego Intelligenza visiva

• Completa la tabella inserendo le X. Capisco

1 Osserva questi numeri, scopri la regola che li collega e scrivila sui puntini. Poi continua la serie.

GLI SCHEMI

Capisco

• Leggi quale problema si pone oggi il signor Impiccionis.

Sara, Ilaria e Carlo abitano in tre case vicine, ai numeri 1, 3, 5. Tutti e tre coltivano gerani sui balconi: uno li ha rossi, uno lilla, l’altro gialli. Sara abita vicino a Ilaria, ma non vicino a Carlo, e ha i gerani rossi. Carlo abita al n.1 e coltiva gerani lilla. Dove abita Ilaria?

• Sembra complicato risolvere il problema, ma diventa facile inserendo i dati in una tabella. Dove abita Sara, che non abita vicino a Carlo? Di quale colore sono i suoi fiori? E Ilaria?

Numero civico 1 3 5

Nome Carlo

Colore gerani lilla

Esercizi

Ti spiego

ARGOMENTO

Le rappresentazioni che aiutano a capire le relazioni.

REGOLA

Per risolvere i problemi si può ricorrere a disegni, tabelle, schematizzazioni che rendono più chiare le relazioni tra i dati.

1 Stella gioca con i bastoncini calamitati e a mano a mano aumenta la sua costruzione in questo modo. Scopri la regola completando la tabella.

bastoncini per i triangoli

per i collegamenti

2 Ivan con i fiammiferi costruisce queste casette. Osserva e rispondi.

• Quanti fiammiferi occorrono per costruire la prima casetta?

• E per costruire la seconda? ............... E per costruire la terza? ...............

• Con quale operazione puoi calcolare quanti fiammiferi servono per costruire 10 casette? ( 6 × 10 ) – 1 ( 5 × 10 ) + 6

LE CLASSIFICAZIONI E I DIAGRAMMI

ARGOMENTO

Riconoscere le caratteristiche comuni in un gruppo di elementi.

REGOLA

Per classificare devi definire il criterio di classificazione e il gruppo di elementi da classificare.

Per classificare puoi utilizzare differenti diagrammi: quelli di Eulero-Venn sono insiemi che racchiudono elementi che hanno una caratteristica comune. Rimangono fuori dall’insieme quelli che non la posseggono.

Capisco

• Scrivi le caratteristiche degli insiemi. Scegli tra le parole nei riquadri.

Intelligenza visiva

numeri naturali < di 20 e pari • numeri naturali • numeri naturali < di 20 numeri dispari • numeri pari

Nei sottoinsiemi ci sono gli elementi che hanno sia la caratteristica del sottoinsieme sia tutte quelle degli insiemi in cui sono contenuti.

A volte ci sono elementi comuni a due o più insiemi: in questo caso gli insiemi hanno una intersezione in cui sono inseriti gli elementi che hanno le caratteristiche dei due o più insiemi. numeri pari • numeri multipli di 5

numeri pari e multipli di 5

A volte due insiemi non hanno elementi in comune

Le classificazioni si possono rappresentare anche con il diagramma di Carroll (o tabella a doppia entrata) e il diagramma ad albero.

• Osserva e completa.

Capisco non poligoni

Esercizi

1 Inserisci gli elementi nei tre diagrammi, riportando le lettere che li contraddistinguono.

calze lunghe calze non lunghe calze a righe calze non a righe

calze lunghe e a righe calze lunghe calze a righe a righe non a righe a righe non a righe non lunghe calze lunghe

calze

FIGURE PIANE

Ti spiego

ARGOMENTO

La scienza che raccoglie e organizza le informazioni su vari argomenti.

REGOLA

Le indagini statistiche sono ricerche fatte per conoscere le preferenze di un gruppo di persone o per raccogliere informazioni su vari argomenti.

Il numero di preferenze espresse, in statistica, si chiama frequenza.

Esercizi

LA STATISTICA

Capisco

• Fai un’indagine statistica.

1. Stabilisci qual è il fatto che vuoi conoscere. La merenda preferita.

Il tipo di bicicletta che piace di più.

2. Scegli il campione, cioè le persone a cui ti rivolgi.

I bambini e le bambine della tua classe.

I bambini e le bambine delle classi 4.

3. Prepara le domande da porre. Per esempio: qual è la tua merenda preferita?

4. Raccogli e registra i dati in una tabella di frequenza.

5. Elabora i dati e mostrali attraverso un grafico.

1 Greta ha fatto un’indagine nella sua classe. Ogni persona ha espresso una sola preferenza. Osserva la tabella di frequenza e rispondi alle domande.

• Quante persone hanno partecipato all’indagine?

• Quale potrebbe essere stato l’oggetto dell’indagine?

• Quale meta ha avuto più preferenze?

• Quale meta ha avuto il minor numero di preferenze?

Intelligenza visiva

LA MODA E LA MEDIA

Capisco

Ti spiego

ARGOMENTO

I dati statistici più utilizzati.

REGOLA

La moda è il dato che appare con un maggior numero di preferenze.

La media si ottiene sommando tutti i dati e dividendo il risultato per il numero dei dati.

• Giulia, titolare di un negozio di abbigliamento, ha svolto un’indagine per conoscere i gusti dei suoi clienti e delle sue clienti e ha domandato loro: “Che colore preferisci?”

Osserva la tabella di frequenza e completa le frasi.

colore preferenze

7 7 7 7 7 7 7 7 7 7

7 7 7 7 7

7 7 7 7 7 7

7 7 7 7 7 7 7 7 7 7 7 7

• Il dato che appare con maggiore frequenza è il colore

• Perciò si può dire che la moda è il colore

• Giulia ha segnato le vendite di t-shirt nella scorsa settimana.

lunedì martedì mercoledì giovedì venerdì sabato 3 6 5 7 9 12

• Giulia vuole sapere qual è la media delle t-shirt vendute in un giorno.

Ha fatto queste operazioni: prima ha sommato tutti i dati.

3 + 6 + + + + =

Poi ha diviso il risultato per il numero dei giorni …...…… : 6 = …...……

La media delle magliette vendute è : è come se avesse venduto magliette ogni giorno.

Quaderno operativo, p. 236

I GRAFICI

Ti spiego

ARGOMENTO

Gli strumenti per rendere chiara e semplice la lettura dei dati raccolti in un’indagine.

REGOLA

• L’ideogramma rappresenta i dati attraverso dei simboli, disegni che ricordano l’argomento trattato.

• L’areogramma rappresenta i dati attraverso parti di un cerchio o di un quadrato.

• L’istogramma rappresenta i dati attraverso colonne verticali o barre orizzontali.

• I bambini della 4a A hanno svolto un’indagine per sapere qual è l’animale preferito.

Campione: classe 4a A Tabella di frequenza

Indagine: animale preferito.

Capisco animale cane cavallo gatto gufo leone frequenze 8 2 6 1 3

Ideogramma

• Leggi la tabella di frequenza e colora i simboli.

Legenda: 1 disegno = 2 preferenze

Areogramma

• Osserva l’areogramma e colora i quadratini. = cavallo = gatto = leone = cane = gufo

Istogramma

• Disegna le 5 colonne.

leone

1 Osserva i dati e rispondi.

Sono stati raccolti i dati riguardanti il numero di turisti giunti a Milano e a Firenze dall’11 al 15 ottobre.

• In quale città si è registrata la maggior presenza di turisti?

• Possiamo affermare che a Milano ci sono sempre stati meno turisti che a Firenze in questa settimana? ......................................................

2 Calcola la media delle presenze di turisti a Milano e a Firenze.

• Milano:

• Firenze:

3 Leggi e rispondi.

Luca passa molte ore davanti al televisore. Ha registrato in un istogramma il tempo passato a guardare la televisione in una settimana.

• Quante ore Luca passa in media davanti al televisore ogni giorno?

• In quali giorni ha guardato la televisione per un numero di ore superiore alla media? .................................

Direzione Invalsi

• Indica con X l’areogramma che rappresenta i dati della tabella di frequenza.

Pizze vendute nella settimana:

Margherita 50

Ortolana 30

Capricciosa 40

Funghi 20

ti guido • I dati non si riferiscono alla percentuale, ma alla quantità di pizze vendute.

La legenda ti guida a trovare il grafico con i settori della giusta grandezza.

CERTO • POSSIBILE • IMPOSSIBILE

Ti spiego

REGOLA

Il calcolo delle probabilità riconosce quali fatti sono certi (accadranno sicuramente), possibili (potranno accadere) o impossibili (non accadranno mai).

Intelligenza visiva

• Indica con X quale vincita è impossibile.

Capisco

• Scrivi: certo, possibile, impossibile.

• Se oggi è lunedì, domani sarà martedì. Questo è

• Se oggi è lunedì, domani non sarà sabato. Anche questo è

• Se oggi è lunedì, domani sarà giovedì. Questo è ................................................

• Il film che ho visto è molto bello. Questo è solo per chi lo afferma.

• Ho un biglietto della lotteria. Forse vincerò. Questo è

Esercizi

1 Immagina di lanciare un dado a sei facce. Per ogni evento scrivi se è certo, possibile, impossibile.

• Uscirà un numero pari. .........................................................

• Uscirà un numero dispari.

• Uscirà un numero maggiore di 6.

• Uscirà un numero minore di 7.

• Uscirà un numero da 1 a 6. .........................................................

• Uscirà il numero 0.

IL CALCOLO DELLE PROBABILITÀ

Ti spiego

ARGOMENTO

Le possibilità che un fatto avvenga.

REGOLA

Se un fatto è possibile, cioè potrebbe accadere, la matematica cerca di stabilire quanta probabilità c’è che il fatto accada. Si può esprimere la probabilità che un fatto accada attraverso una frazione. La probabilità dipende dal numero di casi favorevoli e dal numero di casi possibili.

Probabilità = casi favorevoli casi possibili

Esercizi

1 Osserva il disegno e completa.

Capisco

• Se tiri un dado, quale tra queste situazioni è la più probabile?

Esce il numero 1.

Esce un numero compreso tra 2 e 6.

Esce un numero pari.

• Tirando un dado qual è la probabilità che esca il numero 5?

C’è 1 possibilità (caso favorevole) su ............... casi possibili (i 6 numeri segnati sul dado) che esca il numero 5.

Perciò la probabilità è 1 su 6 6

• Nel sacchetto ci sono palline colorate.

• Le palline verdi sono , le rosse sono , le blu sono

• La probabilità di pescare una pallina blu è di 6 su 15, cioè

• La probabilità di pescare una pallina rossa è di 4 su 15, cioè

• La probabilità di pescare una pallina verde è di ........... su 15, cioè

2 In un sacchetto ci sono 8 cioccolatini al latte, 6 cioccolatini fondenti e 4 cioccolatini al caffè. Silvia ne prende uno senza guardare nel sacchetto. Calcola le differenti probabilità.

• Cioccolatino al latte casi favorevoli su casi possibili probabilità = .........

• Cioccolatino fondente casi favorevoli su casi possibili probabilità = .........

• Cioccolatino al caffè casi favorevoli su casi possibili probabilità =

1 Osserva i coccodrilli e disegna le frecce che indicano la relazione: è più lungo di

2 Completa la tabella scrivendo i numeri al posto giusto. Poi scrivi tu, se possibile, un altro numero in ciascuna sezione della tabella.

12 • 13 • 2 • 14 • 6 • 21

multipli di 6

non multipli di 6

Colora la casella in cui non hai inserito alcun numero e spiega perché non è stato possibile farlo. ................................................................................................................................ pari dispari

3 Osserva l’ideogramma e completa la tabella di frequenza.

Legenda: 1 simbolo = 10 confezioni

Ideogramma

Tabella di frequenza

Quantità venduta

pelati

biscotti

riso

pasta

4 Osserva la tabella di frequenza e disegna le colonne dell’istogramma.

Libri letti dai bambini di 4a D

Istogramma

5 Guido questa settimana ha registrato queste temperature. Osserva e rispondi.

• Qual è la media delle temperature minime?

( + + + + + + = ) : 7 =

• Qual è la media delle temperature massime?

( + + + + + + = ) : 7 =

6 Una società sportiva sta osservando i dati delle iscrizioni a mini-basket dello scorso anno. Nel grafico mancano le colonne relative ai bambini di 11 anni: 10 maschi e 11 femmine.

Disegnale. Poi rispondi.

Legenda: = maschi = femmine temperatura lunedì martedì mercoledì giovedì venerdì sabato domenica

• Quante sono le bambine di 10 anni?

• Quanti sono i maschi di 9 anni?

• Quanti bambini e bambine di 8 anni, in tutto, frequentano il corso?

8 9 10 11

7 Osserva e completa.

età

• Quale età costituisce la moda di questa indagine?

Vera sceglie a occhi chiusi, tra queste, una maglietta da indossare.

La probabilità che scelga una maglietta:

• a fiori è di su , perciò

• a tinta unita è di su , perciò

• a righe è di su , perciò .........

È più probabile che Vera scelga una maglia

a , ma non è certo.

Com’è andata?

Obiettivi

• Riconoscere e rappresentare relazioni e classificazioni. Interpretare e rappresentare i dati mediante i grafici.

INDAGINE SULLA RACCOLTA DIFFERENZIATA

Ormai la raccolta differenziata è diventata una buona abitudine.

Chiunque dovrebbe sapere dove si devono gettare la carta, la plastica, il vetro...

Più difficile è sapere come vadano smaltiti rifiuti un po’ particolari.

Fate un’inchiesta per scoprire quanto conoscete le norme del vostro Comune.

1. Chiedi a ciascun compagno e a ciascuna compagna se sanno dove vanno smaltiti questi rifiuti.

2. Prepara un istogramma come questo. farmaci scaduti pile piatti rotti giocattoli elettronici

3. Nel grafico, colora in verde un quadratino per ciascuna risposta affermativa e in rosso un quadratino per ciascuna risposta negativa.

4. Ora, insieme, osservate i risultati. Se le risposte negative sono molte... è necessario darsi da fare e informarsi!

5. Preparate un cartellone che spieghi dove vanno gettati questi particolari rifiuti.

• I farmaci si introducono negli appositi contenitori in farmacia.

• Le pile vengono raccolte in appositi contenitori situati in punti differenti: supermercati, isole ecologiche...

• I piatti rotti vanno gettati nel cassonetto della spazzatura indifferenziata.

• I giocattoli elettronici vanno portati nelle isole ecologiche.

Quaderno degli esercizi

164 Prova d’ingresso

Le operazioni

165 Prova d’ingresso

Scomposizioni e problemi

166 Il nostro sistema di numerazione

168 I grandi numeri

170 L’addizione e le sue proprietà

171 La sottrazione e la sua proprietà

172 Addizioni e sottrazioni

173 La moltiplicazione e le sue proprietà

174 La divisione e la sua proprietà

176 Moltiplicazioni e divisioni per 10 • 100 • 1 000

177 Calcolo veloce

178 Dossier problemi I dati e le domande

179 I multipli e i divisori

180 Dossier problemi Il procedimento risolutivo

181 Problemi graduati

182 Direzione Logica! !

183 R icordo quanto imparato

184 Le frazioni

185 Oltre l’unità frazionaria

186 Le frazioni complementari

187 Confronto di frazioni

188 Le frazioni equivalenti

189 Costruire le frazioni

190 La frazione di un numero

192 Problemi con le frazioni

193 Le frazioni decimali

194 Frazioni decimali e numeri decimali

195 I numeri decimali

196 I numeri decimali

197 Addizioni con i numeri decimali

198 Sottrazioni con i numeri decimali

200 Divisioni con i numeri decimali 201 Problemi con i numeri decimali 202 Direzione Logica! !

icordo quanto imparato

204 Le misure di lunghezza

206 Le misure di capacità 208 Le misure di massa-peso

210 Peso lordo • Peso netto • Tara 211 Le misure di valore

Direzione Logica! !

quanto imparato 214 Linee • Figure piane • Solidi

Con il righello e la squadra 216 Usare il goniometro 217 Classificare gli angoli

Le isometrie

I poligoni

Il triangolo

222 Disegnare i triangoli

223 I parallelogrammi

224 I parallelogrammi 225 I trapezi 226 Il perimetro e l’area

199 Moltiplicazioni con i numeri decimali TINKERING

Le misure di superficie 228 Aree dei quadrilateri 230 Area e perimetro del triangolo 231 Problemi di Geometria

Logica! !

• La

1 Esegui le operazioni in colonna.

+ 27 =

LE OPERAZIONI

2 Prova di tabelline. Hai 5 minuti di tempo per scrivere i risultati. Quando hai terminato, rispondi.

=

• Ricordavi bene tutte le tabelline? ..............

• Se hai avuto delle difficoltà, quali sono le tabelline che devi ripassare?

3 Esegui le divisioni in riga.

4 Esegui le operazioni in colonna.

SCOMPOSIZIONI E PROBLEMI

1 Componi i numeri. Segui l’esempio.

3 h 4 da 6 u = 300 + 40 + 6 = 346

5 h 6 u = + = 9 da 7 u = + =

2 h 1 da 3 u =

2 Completa le uguaglianze. Segui l’esempio.

30 da = 300 17 h = 15 da = 19 da = 19 h = 85 da = 18 da = 16 da =

3 Inserisci < , > , = .

4 Completa le tabelle.

5 Leggi con attenzione i problemi, colora il segno dell’operazione necessaria, poi risolvili sul quaderno.

a. Nella scuola di Tiziana le bambine sono 185 e i bambini sono 178. Quante femmine in più dei maschi ci sono?

b. Nel teatro Manzoni ci sono 15 file da 8 poltrone ciascuna. Quante persone possono prendere posto in quel teatro?

c. Il pizzaiolo Luca oggi ha preparato 90 pizze al salame, 105 pizze con la mozzarella e 48 pizze vegetariane. Quante pizze ha fatto?

d. La maestra Anna ha comperato una confezione da 104 matite. Nella scatola ci sono matite di 8 colori diversi e per ciascun colore ce n’è lo stesso numero. Quante matite rosse ci sono nella scatola?

IL NOSTRO SISTEMA DI NUMERAZIONE

Nella nostra numerazione, che è in base 10, ogni cifra ha un valore differente in base al posto che occupa.

1 Rappresenta il numero sull’abaco colorando le palline nel modo opportuno. Poi rispondi ed esegui.

• Da quante cifre è composto il numero 2 222?

• Da quali cifre è composto il numero 2 222? .............................................

• Scrivi il valore di ciascuna cifra che compone il numero 2 222.

h da u

2 Scrivi il numero rappresentato sull’abaco e rispondi.

• Quando sull’asta non ci sono palline, quale cifra scrivi?

• Lo zero indica l’assenza di quantità. Potevi non scriverlo?

3 Scrivi il numero.

3 k = 3 000

4 Scrivi il valore della cifra 8. Segui l’esempio.

5 Cerchia nel numero la cifra che ha il valore evidenziato.

6 Completa la tabella.

+ 1 h – 1 h + 1 da – 1 da

432 762 2981 3480 4710 3140

7 Inserisci > , < , = .

4 k 40 h

35 da 300 u

5000 u 5 k

7 h 80 da

600 da 6 k

73 h 900 u

2 k 20 h

8 Scomponi i numeri e scrivi il valore di ciascuna cifra. Segui l’esempio.

3 581 = 3 k (3 000) 5 h (500) 8 da (80) 1 u (1)

2 963 = 1 872 =

3 044 = 4 808 = 5 122 =

9 Inserisci ciascuna cifra nella tabella al posto giusto e componi i numeri.

k h da u numero

20 h 3 k

8 k 80 da

44 da 6 h

75 h 7500 u

23 da 2 h

50 da 5 h

400 u 4 k

6 da 4 k 3 u

7 k 4 da 1 h

5 u 3 k

1 da 9 h 4 k

10 Scrivi i seguenti numeri in ordine crescente. Poi rispondi. 198 • 918 • 891 • 189 • 981 • 819

• I numeri sono formati dallo stesso numero di cifre? Quante?

• Sono formati dalle stesse cifre?

Quali sono?

• Le cifre nei diversi numeri hanno lo stesso valore?

11 Utilizzando le stesse cifre del numero 340, scrivi:

• due numeri maggiori di 340:

• un numero minore di 340:

12 Utilizzando le stesse cifre del numero 4002, scrivi:

• due numeri maggiori di 4002:

• tre numeri minori di 4002:

I GRANDI NUMERI

1 Rappresenta i numeri sull’abaco.

2 In ciascuna coppia, colora il numero maggiore.

300 000 299 999

3 Leggi i numeri e scrivili in cifre.

• dodicimilatrecento

• duecentoseimilanovanta

• ventottomilatrecento

• cinquecentomila

• quarantatremilasettecentoquarantotto

• trecentoquattromiladuecentotrentasei

• centocinquantamiladuecentotrenta …..................…....…….

• centomilaquattro

4 Leggi i numeri. Quando trovi il segno 3 , leggi “mila”. Poi scrivili in lettere. Segui l’esempio.

22 3 150 ventiduemilacentocinquanta

3

3

5 Scrivi il valore della cifra. Segui l’esempio.

5 hk = 500 000

6 Scrivi il valore della cifra evidenziata. Segui l’esempio. 163 502 6 dak 60 000

201

423

7 Componi il numero, poi scrivilo. Segui l’esempio.

2 hk e 5 da = 200 000 + 50 = 200 050

4 dak e 8 h = + =

7 hk e 2 u = + =

8 Scrivi il numero precedente e quello 9 successivo.

9 Completa la tabella.

10 Cerchia nel numero la cifra indicata.

3 dak 332 833

5

11 Mario acquista una casa e la arreda. Trascrivi le spese effettuate in ordine crescente.

12 Scrivi i seguenti numeri in ordine decrescente.

L’ADDIZIONE E LE SUE PROPRIETÀ

Ricorda!

Proprietà commutativa

5 + 3 = 3 + 5

Proprietà associativa

10 + 90 + 4 + 6 = 100 + 10

1 Applica la proprietà commutativa ed esegui le addizioni. 1 + 120 + 9 = + + =

+ 45 + 900 = ............................

+ 900 + 17 =

+ 1000 + 80 =

2 Applica la proprietà associativa ed esegui le addizioni. Segui l’esempio.

100 + 23 + 7 = 100 + 30 = 130

98 + 2 + 500 = + = 999 + 1 + 300 = + =

+ 25 + 75 = + =

+ 5 + 95 = + =

+ 800 + 200 = + =

3 Scomponi, poi applica la proprietà associativa ed esegui le addizioni. Segui l’esempio.

93 + 107 = 93 + 7 + 100 = 100 + 100 = 200

88 + 1 012 =

010 + 90 = ...........................

92 + 18 =

+ 21 =

4 Completa. Riconosci quali proprietà sono state applicate e scrivile.

33 + 7 + 50 = 40 + 50 = Proprietà

23 + 250 = 250 + 23 = Proprietà

1 005 + 45 = 1000 + 5 + 45 = 1 000 + 50 = ........................... Scomposizione e proprietà ..........................................................

99 + 300 + 1 = 99 + 1 + 300 = 100 + 300 = Proprietà e

5 Esegui le addizioni sul quaderno. Poi applica la proprietà commutativa per eseguire la prova.

a. Con 1 cambio

456 + 1 623 =

89 + 2 408 =

1 509 + 1 940 =

7 653 + 1 284 =

2 715 + 4 275 =

3 009 + 549 =

b. Con 2 cambi

4 580 + 3 678 =

2 504 + 2 867 = 765 + 3 175 =

5 618 + 2 297 = 895 + 3 224 =

8 765 + 1 135 =

c. Con più di 2 cambi

2 764 + 3 448 =

5 199 + 2 801 =

3 909 + 2 291 = 5 243 + 2 857 =

1 509 + 3 698 =

4 515 + 3 596 =

d. Con più di 2 cambi

149 + 2 456 + 3 765 =

4 672 + 1 549 + 1 002 =

8 552 + 1 207 + 875 =

7 126 + 1 985 + 345 =

4 827 + 1 235 + 59 =

3 904 + 125 + 1 484 =

LA SOTTRAZIONE E LA SUA PROPRIETÀ

Ricorda! Proprietà invariantiva

144 – 98 = 46 975 – 103 = 872 +2 +2 – 3 – 3

146 – 100 = 46 972 – 100 = 872

1 Applica la proprietà invariantiva e scrivi il risultato.

– 18 =

52

2 Cancella la scelta sbagliata.

Addizioni e sottrazioni sono operazioni simili / inverse. Quindi per fare la prova della sottrazione occorre eseguire un’addizione / un’altra sottrazione.

3 Completa.

– = 14

4 Esegui le sottrazioni sul quaderno con la prova.

a. Con 1 cambio

475 – 284 =

892 – 579 = 906 – 554 = 721 – 518 =

2 567 – 1 747 =

7 653 – 7 082 =

3 452 – 1 281 = 3 563 – 1 751 =

b. Con 2 cambi

582 – 384 = 915 – 536 = 655 – 278 = 523 – 328 =

3 456 – 1 827 = 8 403 – 2 811 =

2 750 – 1 673 = 2 417 – 1 809 =

c. Con più di 2 cambi

2 500 – 1 787 =

5 703 – 1 926 =

9 230 – 5 472 =

3 024 – 1 247 =

7 003 – 4 357 =

6 213 – 2 554 =

3 000 – 1 264 =

5 301 – 3 519 =

ADDIZIONI E SOTTRAZIONI

1 Esegui a mente. Ricorda le strategie di calcolo.

a. 18 + 6 = ..............

25 + 7 =

28 + 8 =

25 – 9 =

35 – 7 =

42 – 8 =

27 + 9 = ..............

2 Scopri l’operatore e continua la numerazione.

3 Risolvi i problemi sul quaderno.

a. Una fabbrica di monopattini elettrici sta preparando il carico da inviare a un rivenditore. Sul camion sono stati caricati 137 monopattini neri, 378 rossi.

Restano da caricare 264 monopattini metallizzati. Quanti monopattini saranno consegnati?

b. La stessa fabbrica il mese scorso ha consegnato 1230 monopattini ai rivenditori di Milano. A quelli di Genova sono arrivati 354 monopattini. Quanti monopattini in più hanno ricevuto i rivenditori di Milano?

c. Il negozio “Caschi in Bici” espone questo cartello: “Tutti in bici con il casco. Offerta speciale! Caschi per adulti 22 euro. Caschi per bambine e bambini 16 euro”. Quanto costano in più i caschi per adulti?

d. Per promuovere la sicurezza, “Caschi in Bici” ha offerto alcuni gadget: 89 fasce fosforescenti da applicare al braccio e 98 lucette frontali. Quante lucette in più rispetto alle fasce sono state offerte? Quanti gadget sono stati messi a disposizione?

LA MOLTIPLICAZIONE E LE SUE PROPRIETÀ

Ricorda! Proprietà commutativa Proprietà associativa Proprietà distributiva 8 × 4 = 4 × 8 2 × 5 × 4 × 5 = 10 × 20 24 × 17 = (24 × 10) + (24 × 7)

1 Applica la proprietà commutativa ed esegui le moltiplicazioni.

7 × 20 = 20 × 7 =

4 × 100 = ............................ × ............................ = ............................

2 × 15 = × =

6 × 30 = × =

7 × 11 = × = 4 × 12 = ............................ × ............................ = ............................

2 Applica la proprietà associativa ed esegui le moltiplicazioni.

4 × 4 × 2 = 4 × 8 = 10 × 3 × 3 = ............................ × ............................ = ............................

× 2

3 Applica la proprietà distributiva ed esegui le moltiplicazioni.

35 × 13 = (35 × 10) + (35 × 3) = 350 + 105 =

17 × 12 = (17 × 10) + (17 × ) = + =

9 × 27 = (............... × ...............) + (............... × ...............)

×

4 Completa. Riconosci quali proprietà sono state applicate e scrivile.

3 × 5 × 2 × 10 = 3 × 10 × 5 × 2 = 30 × 10 =

25 × 5 × 4 × 2 = 25 × 4 × 5 × 2 = 100 × 10 =

Proprietà e

Proprietà e

15 × 12 = (15 × 10) + (15 × 2) = 150 + 30 = Proprietà

7 × 2 × 5 × 2 = 14 × 10 = .........................

4 × 5 × 2 × 5 = 20 × 10 =

6 × 22 = (6 × 20) + (6 × 2) = 120 + 12 =

Proprietà ...........................................................................................................

Proprietà

Proprietà

5 Esegui le moltiplicazioni sul quaderno. Poi applica la proprietà commutativa per eseguire la prova.

a. 25 × 7 =

48 × 9 = 89 × 7 = 33 × 6 = 92 × 5 = 73 × 8 =

b. 24 × 35 = 64 × 82 = 55 × 41 = 96 × 46 = 80 × 75 = 49 × 37 =

c. 205 × 22 = 142 × 35 = 108 × 38 = 49 × 221 = 37 × 251 = 88 × 204 =

× 105 =

× 127 =

× 212 =

× 123 =

× 207 =

d. 245 × 47 = 76 × 192 = 305 × 28 = 42 × 375 = 190 × 87 = 39 × 364 = e. 127 × 54 = 72 × 237 = 394 × 58 = 79 × 137 = 56 × 230 = 47 × 308 = f. 136 × 242 =

LA DIVISIONE E LA SUA PROPRIETÀ

Ricorda! Proprietà invariantiva

2 Applica la proprietà invariantiva e scrivi il risultato.

14 000 : 700 =

3 Per ciascuna affermazione, indica V (vero) o F (falso).

• Se il divisore è 1, il risultato è uguale al dividendo.

• Se il divisore è 1, il risultato è sempre 1.

• Se il divisore è 0, il risultato è uguale al dividendo.

• Se il divisore è 0, la divisione è impossibile.

• Se dividendo e divisore sono uguali, il risultato è 1.

• Se il dividendo è 0, il risultato è sempre 0.

4 Completa.

36 : = 9 42 : = 6 48 : = 8

:

5 Esegui le divisioni in colonna sul quaderno.

1 Indica con X.

• L’operazione inversa della divisione è: la sottrazione. la moltiplicazione.

F

F

F

6 Esegui le divisioni.

48 : 12 = 99 : 33 =

: 21 =

: 35 = 4 8 1 2

7 Esegui le divisioni in colonna sul quaderno.

1° step (resto 0)

step (con il resto)

: 46 =

: 21 =

: 11 = 48 : 24 = 64 : 32 =

4° step (provo una volta di meno)

: 32 =

: 44 = 49 : 11 =

:

2° step (“cappellino” su 3 cifre) 243 : 55 = 567: 62 = 854 : 93 = 407 : 65 = 200 : 32 = d.

3° step (con resto anche all’interno)

6° step (tutto insieme!) 99 : 33 = 75 : 25 =

95 : 35 = 80 : 24 = 63 : 38 = 99 : 39 = 88 : 12 = e.

: 38 =

: 52 =

: 84 =

: 47 =

: 63 = f. 4° step (provo una volta di meno)

8 Rispondi, poi completa gli schemi.

Qual è l’operazione inversa della divisione?

9 Collega ogni problema all’operazione che lo risolve.

Un contadino ha raccolto 800 kg di pomodori e li pone in cassette che possono contenere ciascuna 16 kg.

Quante cassette riempie?

800 × 16 = 800 : 16 =

5° step (provo più volte di meno)

: 49 =

: 27 =

: 36 =

: 48 =

: 24 = g.

748 : 29 = 1235 : 43 = 4563 : 54 = 2056 : 21 = 1200 : 28 = h.

All’ortomercato oggi sono state vendute 800 cassette di merce. Ogni cassetta contiene 16 kg di ortaggi. Quanti chilogrammi di ortaggi sono stati venduti?

MOLTIPLICAZIONI E DIVISIONI

PER 10 • 100 • 1000

1 Completa le tabelle.

2 Completa scrivendo 10, 100, 1 000.

3 Scrivi il numero che manca.

4 Completa scrivendo l’operatore e il numero.

5 Nel magazzino di un colorificio ci sono molte confezioni diverse di matite. Quante matite? Completa la tabella.

CALCOLO VELOCE

Le strategie di calcolo veloce sono molto utili per semplificare il lavoro.

1 Colora con lo stesso colore i due numeri che danno come risultato 1 000 se sommati insieme.

2 Calcola a mente e completa le tabelle.

Se devi moltiplicare velocemente un numero per 20, moltiplichi per 2 e poi moltiplichi per 10.

Se devi dividere velocemente un numero per 20, dividi per 10 e poi dividi per 2.

3 Calcola a mente. 35 × 20 = 140 × 20 =

: 20 =

: 20 = ................. 9 × 30 = 11 × 30 =

: 30 = 330 : 30 = ................. 4 × 300 = 21 × 300 =

Che cosa fai se devi moltiplicare o dividere per 200? Per 300? Per 3000?

: 300 = 2700 : 300 = ................. 14 × 2000 = 8 × 600 = 770 : 70 = 2000 : 400 = .................

Se devi moltiplicare velocemente un numero per 5, moltiplichi per 10 e poi dividi per 2.

Se devi dividere velocemente un numero per 5, moltiplichi per 2 e poi dividi per 10.

4 Calcola a mente.

14 × 5 = 44 × 5 =

× 5 =

I DATI E LE DOMANDE

1 Leggi i problemi ed esegui.

a. Mara ha comperato 650 g di pane. Ogni panino pesa 50 g e costa 35 centesimi. Quanti panini ha comperato Mara?

• Sottolinea in verde la domanda e in rosso i dati.

• Qual è il dato inutile? ......................................................................................................

b. Marina sta preparando alcuni muffin. Ne ha disposti 36 nella teglia del forno in file ordinate. Quante file ha fatto?

• Sottolinea in verde la domanda e in rosso i dati.

• Puoi risolvere il problema? .......................................................................................

• Quale dato ti manca?

c. Il parcheggio del supermercato è su 3 piani: sia al primo piano sia al secondo ci sono 120 posti. Il parcheggio del terzo piano è un po’ più piccolo e ha 84 posti.

Quanti sono i posti nel parcheggio del supermercato?

Ora i posti occupati sono 264. Quanti posti sono liberi?

• Sottolinea in verde le domande e in rosso i dati.

• Quale dato è inutile? ........................................................................................................

• Di quale informazione non espressa con i numeri naturali devi tenere conto per rispondere alla prima domanda?

2 Evidenzia in giallo i dati necessari per rispondere alla prima domanda, in azzurro quelli relativi alla seconda domanda.

Filippo vuole acquistare un’automobile che costa 17450 €. Aveva già risparmiato 9450 €. Questo mese ha accantonato ancora 845 €. Quanti soldi ha ora Filippo? Quanto gli manca per potere acquistare l’automobile?

3 Scrivi le domande nascoste, poi risolvi sul quaderno.

Allo stadio è in programma un concerto: il biglietto intero costa 24 € e quello ridotto 12 €. Sono stati venduti 142 biglietti interi e 48 biglietti ridotti.

Qual è stato l’incasso totale?

• Domande nascoste: ........................................................................................................................................

• Risposta:

I MULTIPLI E I DIVISORI

Moltiplicando un numero per qualsiasi altro numero ottieni un suo multiplo. 9 • 18 • 9000 Sono multipli di 9.

1 • 5 • 7 • 35 Sono divisori di 35, perché lo dividono esattamente, senza resto.

1 Inserisci i numeri nel diagramma di Venn. Poi rispondi indicando con X. 2 • 4 • 6 • 12 • 18 • 24

• Non hai trovato numeri che sono multipli solo di 6 e non di 2. Perché?

Quei numeri esistono, ma non erano stati indicati.

Tutti i multipli di 6 sono sempre anche multipli di 2. multipli sia di 2 sia di 6 multipli di 2 multipli di 6

2 Colora solo i multipli di 8. Poi rispondi.

• I multipli di un numero pari sono solo numeri pari? 4 7 8

3 Colora solo i multipli di 9. Poi rispondi.

4 Cerchia i divisori di ciascun numero.

• I multipli di un numero dispari sono solo numeri dispari?

• Sono solo numeri pari? ....................................

6 Ciascun gruppo di numeri nel riquadro ha un divisore comune: cerchialo. Segui l’esempio.

7 Completa scrivendo “è multiplo” oppure “è divisore”.

IL PROCEDIMENTO RISOLUTIVO

1 Collega l’algoritmo al testo adatto.

11 × 4 = 44

60 × 4 = 120

120 + 44 = 164

4 amici in pizzeria hanno ordinato 4 pizze e 4 bibite dello stesso costo. In tutto hanno pagato 60 €. Una pizza costa 11 euro.

Quanto costa ciascuna bibita?

11 × 4 = 44

60 – 44 = 16

16 : 4 = 4

4 amici hanno comperato 4 tute uguali e 4 zainetti uguali. Ciascuna tuta costa 60 € e ogni zainetto costa 11 €.

Quanto hanno speso in tutto?

2 Per questo problema si possono formulare due domande. Scrivile, poi risolvi i problemi utilizzando i diagrammi.

Guido chiede al negoziante il prezzo dei calzini: viene così a sapere che quelli corti costano 3,30 € al paio e quelli lunghi 4,50 €. Decide di comperare 6 paia di calzini lunghi.

1.

2.

diagramma 2 × diagramma 1 –

3 Leggi, osserva e risolvi.

Hazal deve comperare alcuni oggetti per la sua neonata Lorin. Ha a disposizione 150 €. Ha bisogno del biberon e dello scalda-biberon.

Hazal, oltre a ciò che le serve, compera altri tre oggetti. Che cosa può comperare?

Scrivi due soluzioni che hai trovato.

PROBLEMI GRADUATI

1 Risolvi i problemi sul quaderno.

Con 1 domanda e 1 operazione

a. Una strada provinciale lunga 124 km deve essere tutta asfaltata. Gli operai ne hanno già asfaltata la metà. Quanti chilometri di strada sono già stati asfaltati?

b. Nel negozio di dolci Luisa ha scelto 4 tipi di caramelle e per ciascun tipo ha acquistato 18 caramelle. Quante caramelle ha comperato?

Con 2 domande e 2 operazioni

c. Enzo compera 4 confezioni di merendine, ognuna delle quali ne contiene 8. Paga con una banconota da 20 euro e riceve di resto 12 euro.

Quante merendine ha comperato?

Quanto le ha pagate?

d. Nella scuola di Milena ci sono 164 bambine e 152 bambini. Quest’anno gli studenti della scuola sono 35 più dello scorso anno. Quanti, tra maschi e femmine, frequentano la scuola di Milena? Quanti, tra maschi e femmine, la frequentavano lo scorso anno?

e. Il cartolaio ha acquistato 156 pacchi da 8 quaderni ciascuno. I pacchi di quaderni a quadretti sono 62. Quanti quaderni ha acquistato il cartolaio? Quanti sono i quaderni a quadretti?

Con 1 domanda e 2 operazioni

f. La fruttivendola ha a disposizione 900 g di insalata rossa e 450 g di insalata soncino. Con le due insalate mescolate prepara sacchetti da 75 g ciascuno. Quanti sacchetti prepara?

g. Per il compleanno del nonno i suoi nipoti hanno preparato 45 tartine al salmone, 24 al tonno, 33 al formaggio e 18 al prosciutto. Le dispongono in parti uguali su 3 grandi vassoi. Quante tartine metteranno su ciascun vassoio?

h. In casa di Luigi solo lui e suo fratello bevono latte. Luigi consuma 150 c<l di latte al giorno, suo fratello ne consuma 125 c<l . Quanto latte consumano in una settimana?

Con 1 o 2 domande e più operazioni

i. Per il suo compleanno Federica porta in classe 3 buste che contengono 24 caramelle ciascuna e 3 buste con 12 lecca lecca ciascuna. Divide i dolci tra tutti i 18 bambini e bambine della classe.

Quanti dolci riceve ciascuno?

l. Paola compera un’automobile che ha il prezzo base di 19 500 euro cui vanno aggiunti 2 400 euro per gli optional che ha richiesto. Quanto pagherà l’automobile?

Paola versa subito 4 500 euro e paga la parte rimanente in 24 rate mensili.

A quanto ammonta ciascuna rata?

m. Al parco divertimenti sono arrivate 3 comitive: la prima è composta da 12 persone, la seconda da 10 e la terza da 15.

Si mettono in fila per salire sulle montagne russe, tranne 5 di loro che preferiscono rimanere a terra. Quante persone vogliono salire sulle montagne russe?

Se ciascun vagoncino può contenere 8 persone, quanti vagoncini serviranno?

1

Direzione Logica!

a. Usando una sola volta ciascuna di queste cifre, scrivi:

• il numero più grande possibile:

• il numero più piccolo possibile:

b. Usando due volte ciascuna di queste cifre, scrivi:

• il numero più grande possibile: .......................................

• il numero più piccolo possibile:

2 Scrivi l’operazione che risolve il problema.

In un parcheggio alle ore 8 c’erano 43 automobili. Ora ce ne sono 135. Nell’ultima ora sono uscite 28 automobili e non ne sono entrate altre. Quante automobili c’erano un’ora fa nel parcheggio?

• Formula un’altra domanda in modo che il problema si risolva con un’operazione diversa.

In un parcheggio alle ore 8 c’erano 43 automobili. Ora ce ne sono 135. Nell’ultima ora sono uscite 28 automobili e non ne sono entrate altre.

• Scrivi l’operazione che risolve il problema.

3 Nell’operazione, ciascuno dei tre simboli rappresenta una cifra diversa. L’ovale vale 8. Quanto vale il triangolo?

IL NOSTRO SISTEMA DI

NUMERAZIONE

decimale: raggruppa in base 10

10 u = 1 da

10 da = 1 h

10 h = 1 k

L’ : aumenta, unisce, aggiunge.

Proprietà: commutativa,

posizionale: ogni cifra ha un valore differente in base al posto che occupa

546 6 vale 6 465 6 vale 60

I numeri si raggruppano in , ciascuna composta da 3 ordini

Classe delle .......................................... Classe delle unità semplici

centinaia centinaia decine hk uk da

LE OPERAZIONI

La : ripete più volte la stessa quantità.

Proprietà: , ,

Multipli e divisori

La : toglie, fa capire quanto manca, trova la differenza. Proprietà:

La : distribuisce, raggruppa.

Proprietà:

I di un numero sono il prodotto di quel numero per qualsiasi altro numero intero.

I di un numero sono quelli che lo dividono esattamente senza resto.

LE FRAZIONI

La frazione è un numero particolare che indica una quantità o un intero diviso in parti uguali.

Per riconoscere il tipo di frazione devi osservare il denominatore e il numeratore.

1 Colora il quadratino solo delle figure che sono state frazionate.

2 Scrivi l’unità frazionaria di ciascun intero e colorala.

3 Dividi l’intero in base alle parti indicate dalla frazione e poi colora l’unità frazionaria.

4 Dividi il segmento in base alle parti indicate 5 dalla frazione e poi colora l’unità frazionaria.

OLTRE L’UNITÀ FRAZIONARIA

1 Scrivi la frazione corrispondente alla parte colorata, sia in cifre sia in lettere.

2 Colora la parte indicata dalla frazione.

3 Rappresenta la frazione: il denominatore ti indica le parti in cui devi dividere l’intero, il numeratore ti indica le parti che devi colorare.

LE FRAZIONI COMPLEMENTARI

1 Completa scrivendo le frazioni complementari. • Parte blu

Parte scura

Parte chiara . + = 1

Parte gialla .

• Parte azzurra . + = 1 • Parte arancio

2 Colora in giallo la parte indicata dalla frazione e in verde la frazione complementare. Poi scrivi la frazione complementare.

3 Colora sul segmento, in rosso, la frazione complementare. Poi completa.

4 Completa scrivendo la frazione complementare.

CONFRONTO DI FRAZIONI

1 Colora la parte indicata. Sugli altri interi colora 2 frazioni maggiori di quella data e scrivile.

2 Colora la parte indicata. Sugli altri interi colora 3 frazioni minori di quella data e scrivile.

3 Completa.

Se due frazioni hanno uguale denominatore, è minore quella con il numeratore

4 Completa le disuguaglianze scrivendo un numeratore possibile.

5 Completa.

Se due frazioni hanno uguale numeratore, è minore quella con il denominatore ..............................................................

6 Completa le disuguaglianze scrivendo un denominatore possibile.

7 Scrivi le frazioni in ordine:

LE FRAZIONI EQUIVALENTI

Due frazioni equivalenti indicano la stessa quantità anche se sono scritte in modo diverso.

1 Colora la parte indicata. Poi confronta le parti colorate e completa.

Le frazioni 3 4 e sono equivalenti. Le frazioni e sono equivalenti.

2 Nella seconda figura colora la parte equivalente a quella colorata nella prima, poi scrivi la frazione.

3 In ciascun intero, colora la frazione equivalente a quella data e scrivila.

4 Scrivi la frazione rappresentata. Poi completa.

Sono equivalenti a 1 4 le frazioni rappresentate sulle figure

5 Colora le frazioni equivalenti a quella data.

COSTRUIRE LE FRAZIONI

Procurati vari mattoncini per le costruzioni di diversi colori.

1 Costruisci questi interi con i tuoi mattoncini.

Come vedi, lo stesso intero può essere costruito con mattoncini che rappresentano frazioni di valore diverso.

2 Divertiti a costruire lo stesso intero utilizzando i mattoncini che hai usato prima, ma disposti in modo diverso. Guarda questo esempio. 1 2 + 1 4 + 1 8 + 2 16 = 1 intero

3 Componi questo intero, prima con mattoncini tutti uguali tra loro e poi con mattoncini diversi.

Adesso puoi giocare con tutte le figure che vuoi!

LA FRAZIONE DI UN NUMERO

1 Indica con X l’immagine che rappresenta la frazione 2 .

2 Scrivi l’unità frazionaria a cui corrisponde ciascun gruppo. Poi completa. 1 4 di 12 = ..............

3 In ciascun gruppo, colora gli elementi indicati dalla frazione. Poi completa.

4 Colora secondo le indicazioni. Poi completa e rispondi.

1 3 dei triangoli sono rossi, gli altri sono gialli.

• I triangoli rossi sono • I triangoli gialli sono

• 1 3 di 15 =

• Qual è la frazione complementare a 1 3 ?

• A quale frazione dell’intero corrispondono i triangoli gialli?

1 4 dei palloncini sono gialli, 3 5 sono blu e i rimanenti sono azzurri. 1 4 di 20 = ................................................................ 3 5 di 20 =

5 Si tiene una festa in giardino. Il barman per preparare 1 caraffa di limonata utilizza 4 5 di acqua minerale e 1 5 di succo di limone. Completa la tabella.

Limonata Acqua minerale

Succo di limone

5 caraffe 4 caraffe caraffa

10 caraffe caraffe caraffe 15 caraffe .............. caraffe .............. caraffe 6 Calcola la frazione del numero.

PROBLEMI CON LE FRAZIONI

1 Segui le indicazioni e risolvi il problema.

Stella ha a disposizione 1836 €. Ne spende i 3 4 per acquistare un computer. Quanto costa il computer?

• Devi trovare a quanti euro corrispondono i 3 4 di 1836 €.

• Trova il valore di 1 4 di 1836 1836 : 4 =

• Trova il valore di 3 4 di 1836 .................. × 3 = ..................

2 Quali operazioni risolvono il problema?

Indica con X il procedimento corretto. Poi completalo.

Nella fabbrica di biscotti Dolceforno sono state prodotte 2400 scatole di biscotti al cioccolato. Per un guasto della macchina impacchettatrice, 5 16 sono da scartare. Quante scatole di biscotti sono da scartare?

3 Risolvi sul quaderno.

a. Nel parcheggio di un rivenditore di auto ci sono 128 automobili. I 3 8 sono auto ibride.

Quante sono le auto ibride? Quanto sono le automobili non ibride?

b. Lucrezia trascorrerà un weekend in un rifugio in montagna. Il rifugio dista da casa sua 144 km. I 3 4 del percorso sono in autostrada. Quanto è lungo il percorso non in autostrada?

c. Gli iscritti alla mini-maratona di Poggi Ridenti sono 270. I 3 15 sono adulti e gli altri sono bambini e bambine. Quanti sono i bambini e le bambine?

d. Questa settimana, a Pompei, ci sono state 12000 presenze. 8 25 erano turisti di viaggi organizzati. Quanti turisti sono giunti a Pompei con viaggi organizzati in questa settimana?

4 Osserva la tabella e risolvi il problema sul quaderno.

Hotel Splendor

Prezzi per una notte

Camera singola 95 €

Camera doppia 150 €

Camera a 3 letti 160 €

Sconto di 1 3 per soggiorni di 7 giorni o più.

Osman e Jessica, con i loro tre figli, alloggiano all’Hotel Splendor.

• Quanto pagano per una notte?

• Quanto pagherebbero se si fermassero una settimana?

LE FRAZIONI DECIMALI

2 Scrivi 3 frazioni decimali. Le frazioni decimali hanno come denominatore 10, 100, 1 000.

1 Cerchia le frazioni decimali. 3

3 Colora la parte rappresentata dalla frazione, poi rispondi e indica con X.

• Hai colorato un intero?

• Quanti decimi hai colorato?

• Il numero rappresentato da questa frazione decimale vale: meno di 1. più di 1.

• Quanti interi hai colorato?

• Quanti altri decimi oltre l’intero hai colorato?

• Il numero rappresentato da questa frazione decimale vale: meno di 1. più di 1.

• Hai colorato un intero?

• Quanti centesimi hai colorato?

• Il numero rappresentato da questa frazione decimale vale: meno di 1. più di 1.

• Quanti interi hai colorato?

• Quanti altri centesimi oltre l’intero hai colorato?

• Il numero rappresentato da questa frazione decimale vale: meno di 1. più di 1.

FRAZIONI DECIMALI

E NUMERI DECIMALI

I numeri decimali sono i numeri con la virgola. Si possono trasformare in frazioni decimali e viceversa.

1 Scrivi la frazione in lettere. Segui l’esempio.

2 Colora il numero decimale corrispondente.

3 Completa la tabella. 5 Trasforma ciascun numero decimale in frazione decimale.

4 Trasforma ciascuna frazione decimale in numero decimale.

I NUMERI DECIMALI

I numeri decimali sono formati da una parte intera e una decimale Le due parti sono divise da una virgola.

1 Inserisci i numeri nella tabella.

Parte intera Parte decimale

1398,76

542,016

12748,5

672,381 ,

dak uk h da u d c m

2 Completa.

2 unità = ............... decimi

50 decimi = unità

6 unità = centesimi

900 centesimi = ............... unità

4 unità = millesimi

8 000 millesimi = unità

3 decimi = ............... centesimi

70 centesimi = decimi 1 centesimo = millesimi

3 Scrivi in cifre i seguenti numeri decimali. otto decimi = ……...........…… cinque centesimi = sette millesimi = nove decimi = tre e due decimi = ……...........…… quindici e due centesimi = nove e sette millesimi = centotrenta e due decimi =

4 Scrivi sotto forma di numero decimale. Segui l’esempio.

5 Scrivi il valore della cifra in colore. Segui l’esempio.

I NUMERI DECIMALI

1 Componi i numeri inserendo le cifre nelle tabelle.

scomposizione u d c m numero

4 u 5 m

7 d 6 c

8 m 3 u

5 c 4 d 2 u

4 u 3 d ,

2 Componi i numeri. Segui l’esempio.

2 u 3 d 5 c = 2 + 0,3 + 0,05 = 2,35

scomposizione u d c m numero

7 u 9 m 6 d 3 u 5 m 6 d 1 u 8 m 5 c ,

4 u 1 d 9 c = + + = 3 u 2 d 1 c = + + =

5 u 6 d 8

3 Cancella gli zeri NON necessari. Segui l’esempio.

4 Confronta i numeri decimali inserendo > , < , = . 8,34 8,4

5 In ciascuna serie di numeri, cerchia in blu il numero minore e in rosso il numero maggiore.

6 Scrivi i prezzi dei giocattoli in ordine crescente.

ADDIZIONI CON I NUMERI DECIMALI

Nelle addizioni con i numeri decimali bisogna fare molta attenzione al valore di ciascuna cifra e incolonnare in modo corretto.

1 Scrivi le sequenze tenendo conto del comando. + 0,1

+ 0,3

2 Completa le addizioni.

0,8 + = 1

0,6 + = 1

0,9 + ............... = 1

3 Indica con X l’addizione che NON è stata incolonnata nel modo corretto. Poi esegui le altre. Se necessario, aggiungi gli 0 segnaposto.

4 Completa le tabelle. +

5 Scrivi gli zeri necessari per pareggiare le cifre decimali. Poi esegui le addizioni sul quaderno. 3,2 …...... + 4,563 = 67,843 + 11,9 = 0,45 + 23,981 = 1,1 …...... + 2,75 …...... + 8,108 = 7,42 + 0,487 + 0,3 = 3,402 + 11,21 + 6,5 =

6 Esegui le operazioni sul quaderno. a. 12,34 + 38,22 = 78,19 + 20,07 = 51,04 + 66,78 = 9,36 + 16,05 = 0,428 + 12,7 = b. 5,67 + 3,288 = 16,7 + 9,827 = 0,093 + 1,27 = 18 + 46,16 = 2,877 + 28,5 =

SOTTRAZIONI CON I NUMERI DECIMALI

Come per le addizioni, anche per le sottrazioni con i numeri decimali è importante incolonnare nel modo corretto.

1 Scrivi le sequenze tenendo conto del comando. – 0,1 3

– 0,3

2 Completa le sottrazioni. 1,6 – = 1 1,9 – = 1 1,8 – ............... = 1

3 Segna con X la sottrazione che NON è stata incolonnata nel modo corretto. Poi esegui le altre. Se necessario, aggiungi gli 0 segnaposto. 2 5, 4 6 7 –1 3, 6 =

4 Completa le tabelle. – 0,3

5 Scrivi gli zeri necessari per pareggiare le cifre decimali. Poi esegui le sottrazioni sul quaderno. 2,5 – 1,48 = 6,57 – 3,2 …...... = 9 – 4,1 = 10 – 0,27 = 7,605 – 2,1 …...... = 50,81 – 46,328 =

6 Esegui le operazioni sul quaderno.

a. 24,45 – 12,53 = 71,93 – 29,46 = 11,08 – 9,17 = 36,1 – 27,48 = 43,32 – 17,55 = b. 20,14 – 7,1 = 9,8 – 4,56 = 12,3 – 8,27 = 17,05 – 14,66 = 24,3 – 12,84 =

MOLTIPLICAZIONI

CON I NUMERI DECIMALI

Se moltiplichi per 10, 100, 1000, la virgola si sposta verso destra

Per le moltiplicazioni in colonna conta quante sono in tutto le cifre decimali dei fattori. Il risultato deve avere lo stesso numero di cifre decimali.

1 Completa la tabella. 2 Scrivi il fattore mancante.

......................... × 10 = 85,3 × 10 = 4,5 × 100 = 578,9 × 100 = 1 456 × 1000 = 2 345 × 1000 = 4 682 × 10 × 100 × 1 000 3,546 5,607 2,703 6,21 0,78

3 Esegui in colonna. Poi evidenzia le cifre decimali dei fattori e dei prodotti e rispondi.

3, 5 × 8, 9 =

• Quante cifre decimali nel primo fattore?

• Quante cifre decimali nel secondo fattore?

• Quante cifre decimali nel prodotto finale?

4 Esegui a mente.

1, 7 4 × 6, 2 =

• Quante cifre decimali nel primo fattore?

• Quante cifre decimali nel secondo fattore?

• Quante cifre decimali nel prodotto finale?

0,5 × 3 = 0,2 × 6 = 0,9 × 5 = 0,7 × 2 = 1,2 × 8 = 2,5 × 4 = 4,2 × 3 = 5,2 × 2 =

5 In ciascuna moltiplicazione, colora le cifre decimali dei due fattori. Poi, nel risultato, inserisci la virgola al posto giusto.

4,55 × 2,7 = 12285

8,92 × 0,6 = 5352

7,2 × 4,11 = 29592 9,23 × 6,6 = 60918

6 Esegui le moltiplicazioni sul quaderno con la prova.

a. 25 × 8,3 = 43 × 1,9 = 33 × 2,6 =

b. 1,4 × 2,7 = 5,9 × 4,1 = 2,4 × 3,9 =

73 × 4,25 = 31025 8,26 × 48 = 39648

c. 1,25 × 2,1 = 3,04 × 1,6 = 8,25 × 2,5 =

10,9 × 2,15 = 23435 8,2 × 3,56 = 29192

d. 0,43 × 11,5 = 2,64 × 8,05 = 2,99 × 0,11 =

DIVISIONI CON I NUMERI DECIMALI

Se dividi per 10, 100, 1000, la virgola si sposta verso sinistra. Se il divisore è un numero decimale, devi trasformalo in un numero intero applicando la proprietà invariantiva.

1 Esegui le divisioni in riga.

87,4 : 10 =

76,82 : 10 = 5,7 : 10 = ........................ 32,4 : 10 =

2 Scrivi il dividendo.

:

:

3 Applica la proprietà invariantiva per trasformare il divisore in un numero intero. Poi esegui a mente.

4 Esegui a mente.

:

:

: 9 = 3,6 : 6 = 3,8 : 2 = 5,5 : 5 =

5 Esegui le divisioni sul quaderno con la prova. d. 34,35 : 6,8 = 72,05 : 5,2 = 8,974 : 7,1 =

a. 254,9 : 8 = 485,3 : 7 = 376,85 : 9 =

b. 80,66 : 0,4 = 7,894 : 0,3 = 16,44 : 0,9 =

c. 23,66 : 14 = 40,71 : 23 = 39,59 : 32 =

PROBLEMI CON I NUMERI DECIMALI

1 Risolvi i problemi sul quaderno.

a. Al cinema Stella sono presenti 85 adulti e 45 bambini. Il costo del biglietto per gli adulti è di 13 euro, quello per i bambini è la metà. Quanto costa il biglietto per un bambino? Quanto si è incassato dalla vendita di tutti i biglietti?

b. Tania vuole fare un regalo a sua madre. Compera un foulard che costa 25,50 €. Per la confezione spende 2,30 € e per il biglietto d’auguri 2,40 €. Tania aveva a disposizione 40 euro per questo regalo. Quanto le è avanzato?

c. Alla gara campestre di 15 km si sono iscritti 144 atleti e atlete. Gli iscritti alla seconda gara, la corsa a ostacoli, sono 7 12 di quanti partecipano alla gara campestre. Quanti atleti e atlete partecipano alla corsa a ostacoli? Quanti atleti e atlete sono presenti complessivamente alle due gare? Per ciascuna persona che partecipa a una gara si è speso 2,30 € per il pettorale. Qual è stata la spesa totale?

d. Nel ristorante di Gianna oggi sono state consumate 54 bottiglie di acqua frizzante e 48 di acqua naturale. Le bottiglie sono tutte da 0,75 <l . Quanti litri di acqua sono stati consumati?

e. Lucia ama molto lo yogurt e ogni giorno ne mangia 0,25 <l . Oggi ha comperato 5 confezioni da 0,5 <l . Per quanti giorni saranno sufficienti?

f. In edicola Mario ha comperato 8 bustine di figurine che costano 0,80 € l’una e l’album che costa 2,50 €. Quanto ha speso in tutto?

g. Nel bar “Buongiorno” sono stati serviti 50 caffè al costo di 1,40 € l’uno e 85 cappuccini al costo di 2,10 € l’uno. Quanto è stato l’incasso?

h. Emanuela ha comperato una maglietta che costa 12,80 €, una gonna a 27,50 € e un berretto a 8,60 €. Il negoziante le ha fatto uno sconto di 8,00 € sul prezzo totale. Quanto ha pagato Emanuela i suoi acquisti?

i. Linda con alcune amiche va dal gelataio. Compera 6 coni grandi, 2 coni medi e una granita. Osserva il cartello dei prezzi e calcola quanto spende.

Cono grande 3,50 €

Cono medio 2,80 €

Cono piccolo 2,30 €

Granita 3,60 €

l. Per preparare le lasagne Lorenzo usa 2 mozzarelle da 1,25 hg l’una e 3 pacchetti di formaggio grattugiato da 0,9 hg l’uno. Quanti grammi di latticini utilizza?

m. 4 amici sono andati in pizzeria. Questo è il conto che è stato portato. Federico decide di pagare il dolce per tutti, e la parte rimanente del conto viene divisa in 4 parti uguali.

Quanto paga ciascuno degli altri ragazzi? Quanto paga Federico?

Pizze 41,60 €

Dolci 16,30 €

Bevande 9,00 €

Totale 66,90 €

Direzione Logica!

1 Questa figura è 1 8 di una figura intera.

Quale tra queste potrebbe essere la figura intera? Trovala e frazionala in 8 parti.

2 Giulia ha preso 3 mele, che corrispondono a 1 5 delle mele che c’erano nel cestino.

Disegna le mele che sono rimaste nel cestino e rispondi.

3 Leggi i fumetti: tu che cosa risponderesti?

Quante mele c’erano nel cestino prima che Giulia ne prendesse alcune? .................... 1 5 corrisponde a 0,5 o a 0,2? 6 4 di pizza sono una pizza e mezza o 2 3 di pizza? È maggiore 1 3 del doppio di 15 o il doppio di 1 3 di 15?

Frazionare significa in parti

LE FRAZIONI

è una frazionaria.

La frazione è quella che aggiunta a un’altra forma l’intero.

Le frazioni proprie rappresentano una parte minore dell’intero. Le frazioni rappresentano una parte maggiore dell’intero

Per calcolare la frazione di un numero:

• si divide il numero per il

• poi si moltiplica il risultato per il

I NUMERI DECIMALI

Le frazioni decimali hanno come denominatore 10, 100, 1000.

Le frazioni decimali possono essere trasformate in numeri

I numeri decimali sono numeri formati da una parte intera e una parte

La parte decimale è più ................................................... dell’unità.

La divide la parte intera dalla parte parte decimale dak uk ........ ........ u , ........ ........ m

LE MISURE DI LUNGHEZZA

L’unità fondamentale delle misure di lunghezza è il metro Ricorda che la marca si riferisce alla cifra delle unità.

1 Inserisci le misure nella tabella.

10 dm • 0,9 dam • 1,4 dm • 350 cm • 100 cm • 76 cm • 8 dm • 1000 mm • 150 dm minori di 1 m uguali a 1 m maggiori di 1 m

2 Cerchia la cifra indicata dalla marca.

65,43 m • 0,74 km • 47,8 cm • 96,32 dam • 0,8 hm • 125 dm • 187 mm

3 Inserisci le misure in tabella, poi esprimile con altre unità di misura. Segui l’esempio.

dam = 8,765 km 98,304 dam m = hm

160,5 cm mm = m

2,49 km ................... hm = ............... dam 4678,2 m ................... hm = .................. dm

4 Somma le lunghezze dei tratti del percorso dei fiumi. Otterrai la loro lunghezza. 1000 m

• Po km • Tevere km • Arno .............................. km

5 Scomponi ciascuna misura. Segui l’esempio.

15,4 dam = 1 hm 5 dam 4 m

50,64 m = 1,754 km = ....................................................................................................... 58,7 cm = 0,19 hm =

6 Completa le tabelle di equivalenze.

7 Esegui le equivalenze.

cm =

8 Scrivi la marca.

7,45 km = 745 ………........… 2,5 m = 25

9 Risolvi i problemi sul quaderno.

a. Anna va e torna da scuola a piedi per 5 giorni alla settimana. La distanza tra la sua casa e la scuola è di 1,4 km. Quanti chilometri percorre Anna in una settimana per andare e tornare?

b. L’insegnante della 4a C ha comperato un grande rotolo di carta, lungo 30 m. Taglia 4 pezzi da 1,5 m per preparare dei cartelloni. Quanti metri di carta rimangono?

c. In partenza per le vacanze Pietro percorre 15 km in città per arrivare all’autostrada, 320 km in autostrada e 23,6 km su strade statali. Si ferma per fare una sosta dopo aver percorso 180 km. Quanti chilometri gli mancano, dopo la sosta, per giungere a destinazione?

d. Una corsa ciclistica prevede 4 tappe. La prima è lunga 85 km, la seconda 96,7 km, la terza 103,7 km e l’ultima, a cronometro, è lunga solo 950 m. Quanti chilometri devono percorrere in tutto i ciclisti? Qual è la differenza tra la tappa più lunga e quella più corta?

LE MISURE DI CAPACITÀ

L’unità fondamentale delle misure di capacità è il litro.

1 Inserisci le misure nella tabella.

minori di 1 <l uguali a 1 <l maggiori di 1 <l

2 Cerchia la cifra indicata dalla marca.

3 Inserisci le misure in tabella, poi esprimile con altre unità di misura. Segui l’esempio.

4 Unisci le misure in ordine crescente. Che cosa ti è apparso?

5 Scrivi la misura complementare.

6 Scomponi ciascuna misura.

453 <l = 276 m<l = 591 d<l = 825 c<l = 1,56 h<l = 34,2 da<l =

<l = 6,32 d<l =

7 Completa le tabelle di equivalenze.

8 Esegui le equivalenze.

9 Scrivi la marca.

c<l = 1,75

10 Risolvi i problemi sul quaderno.

a. Gianni compera 6 bottiglie di aranciata da 1,5 <l e una confezione da 6 brick di succhi di frutta da 0,33 c<l l’uno. Quanti litri di succhi di frutta ha comperato?

Quanti litri di bibite (aranciate e succhi) in tutto ha a disposizione?

b. Gaia va a fare il pieno di benzina. La colonnina del distributore segna che ha comperato 35,5 <l di benzina. Il serbatoio pieno contiene 5 da<l di benzina.

Quanta benzina c’era nel serbatoio prima che Gaia facesse il pieno?

c. Ivan deve bagnare i fiori sul balcone. Riempie per 3 volte una bottiglia da 1,5 <l e per 4 volte una caraffa da 2 <l . Quanti litri di acqua ha utilizzato?

d. Per preparare la panna cotta per 6 persone occorrono 3 d<l di panna. Quanta panna occorre per preparare la panna cotta per 12 persone?

LE MISURE DI MASSA-PESO

L’unità fondamentale delle misure di massa-peso è il chilogrammo

1 Inserisci le misure nella tabella.

1000 g • 600 g • 9,9 hg • 0,01 Mg • 10 dag • 0,001 Mg • 100 dag • 1200 g • 99 hg

minori di 1 kg uguali a 1 kg maggiori di 1 kg

2 Cerchia la cifra indicata dalla marca.

44,5 kg • 869 g • 31,5 cg • 154 dg • 3998 mg • 14 hg • 3,5 Mg

3 Inserisci le misure in tabella, poi esprimile con altre unità di misura. Segui l’esempio. Mg h di kg da di kg kg hg dag g dg cg mg 3,761 kg 3 7 6 1

hg

4 Osserva il peso di ciascuna confezione, poi completa le frasi.

Mirko compera 2 kg di biscotti, cioè confezioni.

Teresa compera 1,5 kg di cereali, cioè confezioni e 1,2 kg di burro che corrispondono a confezioni

Paola compera 9 hg di burro, cioè confezioni.

5 Scomponi ciascuna misura.

550 g = 130 mg = 934 dag = ........................................................................................................ 567 dg = 74,5 cg = 1,65 hg = 6,78 kg = ........................................................................................................... 89,3 hg =

6 Completa le tabelle di equivalenze.

7 Esegui le equivalenze.

1,34 Mg = kg 36,4 kg = hg 26 g = cg 6,703 hg = g 400 dg = g 2 578 kg = Mg 38 dag = hg 2,5 hg = kg

8 Scrivi la marca.

700 g = 7

15 hg = 1,5

2800 kg = 2,8

500 mg = 0,5

9 Risolvi i problemi sul quaderno.

12,4 kg = 124 3,1 hg = 310

10,2 cg = 102

800 mg = 0,8

a. Tania e Antonio stasera hanno ospiti: devono preparare la cena per 12 persone. Comperano 5 scatole di pesce congelato: ognuna contiene 480 g di prodotto.

Quanti grammi di pesce potrà mangiare ciascuna persona?

b. Una gelataia, per ognuno dei 5 gusti di frutta, ha preparato 5,2 kg di gelato. La sera pesa il gelato di frutta rimasto: 1,8 kg.

Quanti chilogrammi di gelato alla frutta ha venduto?

c. Il signor Fabio è in aeroporto. Ha con sé un bagaglio a mano da 5,2 kg e due valigie che pesano 12,5 kg e 8,5 kg. La compagnia aerea permette di imbarcare due valigie del peso complessivo massimo di 20 kg. Il bagaglio a mano può pesare fino a 8 kg.

Quanti chilogrammi dovrà spostare Fabio dalle valigie al bagaglio a mano?

d. Per preparare la macedonia, il cuoco usa 9,4 kg di banane, 1,8 kg di fragole, 7,8 kg di mele e 6 kg di pere. Quanto pesa tutta la frutta? Lo scarto (bucce, semi...) è pari a 1 4 del peso totale della frutta. Quanti grammi pesa lo scarto?

PESO LORDO • PESO NETTO • TARA

Il peso netto è il peso del contenuto. La tara è il peso del contenitore

Il peso lordo è il peso di contenuto e contenitore.

1 Osserva i disegni. Inserisci i pesi nello schema e calcola il peso mancante. Se necessario, esegui l’equivalenza.

peso netto tara

peso lordo

peso netto tara

peso lordo

peso netto tara

peso lordo

2 Completa scrivendo l’operatore.

• peso lordo peso netto = tara

• peso lordo tara = peso netto

• tara peso netto = peso lordo

• peso netto tara = peso lordo

4 Risolvi i problemi sul quaderno.

hg

Equivalenza

Operazione

Operazione

Equivalenza

Operazione

3 Completa la tabella. Se necessario, esegui le equivalenze sul quaderno.

peso netto

a. Una confezione di yogurt da 10 vasetti ha il peso lordo di 1,5 kg. La confezione (cartone e vasetti di plastica) pesa 2,5 hg. Qual è il peso netto di un vasetto di yogurt?

b. Sulla scatola di cereali che Felipe mangia a colazione c’è scritto: peso lordo 390 g. La scatola vuota pesa 40 g. Felipe consuma ogni giorno la stessa quantità di cereali. Una scatola è sufficiente per 5 giorni. Quanti grammi di cereali mangia al giorno?

LE MISURE DI VALORE

1 Quanto manca per acquistare l’oggetto?

2 Osserva ciascun problema rappresentato dalle immagini e trova la soluzione.

3 Completa la tabella. 4 Rispondi.

merce ricavo spesa guadagno perdita

• 12 palline costano 6,00 €. Qual è il loro costo unitario?

• Una gomma costa 2,50 €. Ne compro 3. Qual è il costo complessivo?

• Con 8,40 € quanti coni gelato da 2,10 € posso acquistare?

Direzione Logica!

1 Leggi ciò che dicono i personaggi. Compila l’orario di arrivo e rispondi alle domande.

Sono arrivato ultimo. Ho tagliato il traguardo alle 15:30.

Sono arrivata 5 minuti dopo Sergio e 10 prima di Nico.

Hurrà! Ho vinto! Sono arrivata mezz’ora prima dell’ultimo arrivato e 5 minuti prima della seconda!

Primo arrivato

Secondo arrivato

Terzo arrivato

Quarto arrivato

Quinto arrivato Nico 15:30

Ho finito la corsa 15 minuti prima di Nico.

Ho fatto un’ottima corsa, ma sono arrivata seconda!

La corsa è iniziata alle ore 13:40.

• Quanto tempo ha impiegato il primo arrivato?

• Quanto tempo ha impiegato Gemma?

nome orario d’arrivo

km

MISURE DI LUNGHEZZA

multipli unità fondamentale sottomultipli

dam dm

MISURE DI CAPACITÀ

multipli unità fondamentale sottomultipli

da<l d<l m<l

LE MISURE

MISURE DI MASSA-PESO

multipli unità fondamentale sottomultipli

h di kg da di kg dag g

sottomultipli del grammo dg cg

La marca indica sempre le

Eseguire un’equivalenza significa esprimere la stessa misura utilizzando unità di misura

Da una unità di misura maggiore a una minore: si moltiplica per 10, 100, 1000…

Da una unità di misura minore a una maggiore: si per 10, 100, 1000…

LINEE • FIGURE PIANE • SOLIDI

Linee, figure piane e solidi si differenziano per il numero di dimensioni

1 Per ciascuna figura, scrivi il nome delle dimensioni indicate.

2 Scrivi se la definizione si riferisce a una retta, a una semiretta, a un segmento e completa.

È una linea che non cambia mai direzione: è illimitata.

Si indica con una lettera

È una linea che non cambia mai direzione: ha un inizio e una fine.

Si indica con due lettere

È una linea che non cambia mai direzione: ha un inizio, ma non ha fine.

Si indica con una lettera .....................................................

3 Ripassa in blu le rette perpendicolari, in rosso quelle incidenti, in verde quelle parallele.

Come disegnare...

CON IL RIGHELLO E LA SQUADRA

RETTE PERPENDICOLARI

1 Traccia una linea usando il righello o la squadra.

2 Fai coincidere un lato della squadra con la linea che hai tracciato, come vedi nella figura.

3 Traccia una linea lungo l’altro lato della squadra. Le due linee sono perpendicolari.

RETTE PARALLELE

1 2 3 Procedi come hai fatto prima.

4 Poi, tenendo sempre un lato della squadra sulla linea, sposta la squadra di qualche centimetro.

5 Traccia un’altra linea lungo il lato della squadra. Questa linea e quella che hai tracciato in precedenza sono parallele.

Dal tinkering all’arte

• Su un foglio a quadretti disegna un quadrato con il lato di 24 quadretti.

• Calcola la metà di ciascun lato, metti un punto e uniscili: ottieni un altro quadrato.

• Metti un punto su ogni quadretto delle diagonali del quadrato interno.

• Metti un punto su ogni quadretto dei lati del quadrato esterno.

• Traccia le linee colorate, osservando il disegno a fianco per riprodurlo.

Quando avrai imparato bene la tecnica, prova a fare lo stesso disegno su un foglio bianco utilizzando la riga e la squadra per disegnare il quadrato iniziale.

TINKERING TINKERING

USARE IL GONIOMETRO

L’ampiezza di un angolo si misura in gradi Lo strumento che si utilizza è il goniometro.

• Usa il goniometro per disegnare angoli dell’ampiezza desiderata.

Devi disegnare un angolo di 130°.

1 Traccia un segmento: sarà un lato dell’angolo. Fai un punto su un estremo: sarà il vertice dell’angolo.

2 Appoggia il goniometro sul segmento in modo che esso passi per lo zero e il centro del goniometro coincida con l’estremo del segmento che hai segnato.

3 Cerca sul goniometro il punto che indica 130 e disegna un puntino.

4 Togli il goniometro e collega il puntino che hai fatto con l’estremo del segmento (il vertice che avevi già segnato).

Ecco disegnato l’angolo!

1 Usando la tecnica che hai imparato, disegna gli angoli indicati. angolo di 160° angolo di 45° angolo di 35° ampiezza

2 Leggi la misura sul goniometro e scrivi l’ampiezza di ogni angolo. Ricorda che dovrai leggere l’ampiezza sull’arco interno o su quello esterno. Guarda il lato che passa per lo zero: dovrai leggere l’ampiezza sull’arco su cui è segnato lo zero.

CLASSIFICARE GLI ANGOLI

1 Disegna l’altro lato in modo da ottenere l’angolo richiesto.

angolo acuto angolo retto angolo ottuso angolo piatto

2 In base all’ampiezza dell’angolo, stabilisci e scrivi se è acuto, ottuso, retto, piatto, giro, nullo.

32° angolo ..............................................

175° angolo

15° angolo

1° angolo

0° angolo ..............................................

3 Utilizza una squadra o l’angolo retto del quaderno come campione ed esegui quanto indicato. In ogni angolo si distinguono lati, ampiezza, vertice

a. Nelle tre figure individua i 9 angoli retti e colorali.

180° angolo ..............................................

92° angolo

90° angolo

360° angolo

100° angolo ..............................................

b. In questa figura, colora in verde gli angoli acuti (4).

c. Nelle figure, colora in rosa gli angoli ottusi (4), in verde quelli acuti (8), in rosso quelli retti (2).

LE ISOMETRIE

Simmetria, traslazione e rotazione sono spostamenti di figure sul piano.

1 Il disegnatore, nel riprodurre la figura simmetrica, ha compiuto 3 errori. Riesci a trovarli?

2 Per ciascuna figura, disegnane una simmetrica. Poi scrivi se l’asse di simmetria è orizzontale, verticale, obliquo.

3 Qui vedi raffigurate due figure simmetriche. Misura la distanza di ciascun punto dall’asse di simmetria (il lato di ogni quadretto è lungo 0,5 cm). Poi rispondi.

Distanza dall’asse di simmetria:

A cm A1 cm

B .............. cm B1 .............. cm

C cm C1 cm

D cm D1 cm

Che cosa noti? ...................................................................................................

4 Disegna le figure traslate secondo le indicazioni.

• Direzione: verticale

• Verso: alto

• Misura: 4 cm (8 quadretti)

• Direzione: orizzontale

• Verso: destra

• Misura: 3 cm (6 quadretti)

1

5 Osserva la rotazione e completa.

• Ampiezza:

• Verso:

• Direzione: orizzontale

• Verso: sinistra

• Misura: 3,5 cm (7 quadretti)

2

• Ampiezza:

• Verso:

6 Disegna la stessa figura, ruotandola ogni volta di 90° in senso orario.

3

I POLIGONI

Ogni poligono è chiuso da una linea spezzata e ha sempre almeno 3 lati

1 Colora solo i poligoni.

2 Scrivi i nomi degli elementi del poligono indicati.

3 Completa le definizioni.

Il lato di un poligono è ogni segmento che

L’altezza è il segmento che

La diagonale è il segmento che collega

4 In questo poligono traccia:

• in blu un’altezza;

• in rosso una diagonale;

• in viola un asse di simmetria.

5 Osserva i poligoni e scrivi a quale figura si riferisce ciascuna informazione.

Non ha assi di simmetria. Figura

È un poligono regolare. Figura

È un poligono equilatero, non regolare. Figura

Ha tutti gli angoli ottusi. Figura

Una sua altezza coincide con un lato. Figura

Ha un solo asse di simmetria. Figura

IL TRIANGOLO

I triangoli si denominano in base alle caratteristiche degli angoli e dei lati.

1 Quale tra questi elementi dei poligoni non puoi trovare mai in un triangolo? Indica con X. altezza diagonale asse di simmetria lato vertice angolo

2 Colora:

a. in giallo i triangoli equilateri, in azzurro i triangoli scaleni, in rosa i triangoli isosceli

b. in verde i triangoli acutangoli, in viola i triangoli ottusangoli, in blu i triangoli rettangoli

3 Disegna i triangoli indicati.

Un triangolo rettangolo isoscele

Un triangolo rettangolo scaleno

Un triangolo ottusangolo isoscele

Un triangolo acutangolo isoscele

4 Osserva e rispondi.

Questo è un triangolo equilatero.

• Come sono tra di loro i 3 angoli?

• Quanto misura ciascuno di essi?

Questo è un triangolo rettangolo isoscele.

• Come sono tra di loro i 2 angoli acuti?

• Quanto misura ciascuno di essi?

DISEGNARE I TRIANGOLI

Per disegnare un triangolo isoscele procedi nel seguente modo.

1 Traccia una linea orizzontale: sarà la base.

2 Traccia l’altezza relativa alla base: segna un punto a metà della base e fai partire da lì una linea perpendicolare.

3 Scegli un punto qualsiasi sull’altezza e collegalo con gli estremi della base.

Per disegnare un triangolo equilatero devi usare il compasso e procedere nel seguente modo.

1 Traccia la base.

2 Apri il compasso tanto quanto la base.

3 Punta il compasso prima su una estremità del lato e traccia un arco.

4 Poi fai lo stesso sull’altra estremità. Il punto di incontro degli archi sarà l’altro vertice.

5 Congiungi

un triangolo può avere i lati di qualsiasi lunghezza?

Fai questa esperienza e deduci.

1. Ritaglia 3 striscioline di carta o tre bastoncini di questa lunghezza:

Possono essere i lati di un triangolo? Prova a costruirlo. Non ci sei riuscito! Perché?

2. Ora taglia la striscia più lunga in modo che sia possibile costruire il triangolo e misurala. È lunga più o meno di 9 cm?

la regola dice che…

Ogni lato del triangolo deve essere più corto della somma degli altri due.

I PARALLELOGRAMMI

I parallelogrammi sono quadrilateri che hanno due coppie di lati paralleli e uguali.

1 Colora:

• in blu i quadrilateri NON parallelogrammi;

• in rosso i quadrilateri che sono parallelogrammi.

2 Ora rispondi indicando con X.

• Come puoi definire le figure che non hai colorato? Poligoni non quadrilateri. Non poligoni. Non si possono definire.

3 Classifica le figure in rosso nell’es. 1: scrivi in tabella al posto giusto le lettere che li identificano.

rettangolo quadrato rombo Parallelogramma proprio o romboide

4 Quale parallelogramma ha le caratteristiche elencate? Disegnalo e scrivi il suo nome.

1 4 lati uguali, due diagonali perpendicolari, ma non uguali.

2 4 lati uguali, due diagonali perpendicolari e uguali.

3 I lati uguali a due a due, due diagonali uguali.

4 I lati uguali a due a due, due diagonali non uguali.

I PARALLELOGRAMMI

1 Colora la casella in rosso per i rettangoli, in giallo per i quadrati. Poi rispondi.

2 Confronta le caratteristiche del quadrato (Q) e del rettangolo (R), indicando con X.

4 lati uguali a due a due

4 lati tutti uguali

4 angoli retti

2 diagonali uguali

2 diagonali uguali e perpendicolari

2 assi di simmetria

4 assi di simmetria

poligono equiangolo

• I quadrati sono rettangoli particolari?

• Per quale figura non hai colorato il quadratino?

Perché?

3 Colora la casella in rosso per i romboidi, in giallo per i rombi. Poi rispondi.

• Per quale figura non hai colorato il quadratino?

Perché?

poligono regolare

l’altezza coincide con il lato

4 Confronta le caratteristiche del romboide (R) e del rombo (RO), indicando con X.

4 lati uguali a due a due

4 lati tutti uguali

4 angoli uguali a due a due

2 diagonali

2 diagonali perpendicolari

2 assi di simmetria

nessun asse di simmetria

poligono irregolare

poligono equilatero

I TRAPEZI

Il trapezio è un quadrilatero con una coppia di lati paralleli

1 Colora:

• in arancione la base maggiore;

• in verde la base minore;

• in rosso i lati obliqui;

• in viola l’altezza;

• in giallo la diagonale;

• in marrone l’asse di simmetria. A D

2 Colora nello stesso modo il trapezio, il suo nome e la sua definizione.

Trapezio isoscele

Ha tutti i lati e tutti gli angoli diversi.

Trapezio scaleno

Ha due lati obliqui uguali. Gli angoli sono uguali a due a due.

Trapezio rettangolo

3 Collega i vertici per disegnare i lati obliqui e colora gli angoli uguali. Poi traccia in entrambe le figure due altezze e completa.

Ha due angoli retti.

figura A figura B

• La figura A è un trapezio ........................ perché ha ....................................................................................................................................................................

• La figura B è un trapezio perché ha

1 Completa.

IL PERIMETRO E L’AREA

Le figure piane sono chiuse da una linea e occupano uno spazio

La misura del contorno di una figura piana si chiama ..........................................................................................

Due figure sono isoperimetriche se

2 Misura i lati e calcola il perimetro.

Perimetro = AB + BC + CD + DE + EA

Perimetro = + + + + = cm

5 Accanto alle figure, disegnane due equiestese.

3 Completa le definizioni.

L’area è la misura .........................................................................................................................................

Due figure sono equiestese se hanno la stessa

4 Due figure sono equiestese. Quali? Colorale.

6 Usando le unità di misura convenzionali, per ciascuna figura calcola perimetro (P) e area (A).

LE MISURE DI SUPERFICIE

Ogni misura di superficie è 100 volte minore di quella che la precede e 100 volte maggiore di quella che la segue.

1 Inserisci le misure in tabella, poi scomponile.

Segui l’esempio.

m2 8 6 5

38,29 m2

159 dm2

2853 dm2

461 cm2 7415 cm2

8,65 m2 = 8 m2 6 da di dm2 5 dm2

38,29 m2 = 3 da di 8 2 da di 9

159 dm2 = 1 5 da di 9

2853 dm2 = 2 da di ................. 8 ................. 5 da di

461 cm2 = 4 6 da di 1

cm2 = 7 da di 4 1 da di 5

2 Inserisci le misure in tabella, poi esegui le equivalenze. Segui l’esempio.

3

5740 dm2 5 7 4 0

9563 dm2

13,74 dam2

85,29 dam2

1,57 hm2

5,62 km2

3 Colora nello stesso modo le misure equivalenti.

5740 dm2 = 57,40 m2

9563 dm2 = m2

13,74 dam2 = ............................. m2

85,29 dam2 = m2

1,57 hm2 = m2

5,62 km2 = m2

4 Indica il valore della cifra evidenziata. Segui l’esempio.

AREE DEI QUADRILATERI

1 Per ciascuna figura, misura i lati. Poi calcola perimetro (P) e area (A).

1 P = = cm A = = cm2

2 P = .............................................. = .............. cm A = = cm2 3 P = = cm A = = cm2 4 P = .............................................. = .............. cm A = = cm2

2 Misura i lati di tutte le figure, le diagonali dei rombi e l’altezza dei romboidi. Poi calcola perimetro (P) e area (A) di ciascuna figura. Se necessario, esegui le operazioni sul quaderno.

1

3 Completa le formule.

Rettangolo

P = (b + ) ×

A = b ×

4

Quadrato

= ×

= ×

Per ciascun trapezio, misura i lati e un’altezza. Poi calcola perimetro (P) e area (A).

Se necessario, esegui le operazioni sul quaderno.

5 Risolvi sul quaderno. Disegna le figure richieste e segna sui lati le misure.

Un quadrato e un rettangolo sono isoperimetrici. Il rettangolo ha la base di 10 cm e l’altezza di 6 cm. Quanto misura il perimetro di ciascun poligono? Qual è l’area del rettangolo?

Quanto misura il lato del quadrato? Qual è l’area del quadrato?

6 Risolvi sul quaderno. Disegna le figure (non in grandezza reale) e segna sui lati le misure.

a. Un rettangolo ha la base di 15 cm e l’altezza di 8 cm. Calcola il perimetro e l’area.

b. Un romboide ha la base di 12 cm e l’altezza di 8 cm. L’altro lato misura 1 dm.

Calcola il perimetro e l’area.

c. Un quadrato ha il perimetro di 36 cm. Quanti decimetri misura il lato? Calcola l’area.

d. Il perimetro di un rettangolo è di 60 cm. La base misura 20 cm. Quanto misura l’altezza?

e. Un trapezio rettangolo ha la base maggiore di 150 cm, la base minore di 90 cm, l’altezza di 80 cm, il lato obliquo di 100 cm. Calcola il perimetro e l’area del trapezio.

f. Un trapezio isoscele ha la base maggiore di 50 cm, la base minore di 30 cm, il lato obliquo di 22 cm e l’altezza di 20 cm. Calcola il perimetro e l’area del trapezio.

AREA E PERIMETRO DEL TRIANGOLO

1 Per ciascun triangolo, misura i lati e un’altezza. Poi calcola perimetro (P) e area (A). Se necessario, esegui le operazioni sul quaderno.

2 Osserva questi triangoli e rispondi.

I triangoli hanno tutti uguale base.

• Hanno anche uguale altezza?

• Hanno tutti la stessa area?

• Hanno tutti lo stesso perimetro?

• Qual è l’area di ciascun triangolo?

3 Risolvi sul quaderno. Disegna sempre i triangoli richiesti (non in grandezza reale) e segna sui lati le misure.

a. Un triangolo equilatero ha il perimetro lungo 66 cm. Quanto misura un lato?

b. Un triangolo equilatero ha il lato di 16 cm. Un triangolo isoscele ha la base di 14 cm e i lati di 17 cm. Quale dei due triangoli ha il perimetro più lungo?

c. Un triangolo isoscele ha la base lunga 10 cm e il perimetro di 40 cm. Quanto misura il lato obliquo? L’altezza è di 14 cm. Calcola l’area.

d. Un lato obliquo di un triangolo isoscele misura 6 cm. Il perimetro è di 19 cm. Quanto misura la base? L’altezza è di 5 cm. Calcola l’area.

PROBLEMI DI GEOMETRIA

1 Completa le figure e le formule per il calcolo dell’area.

Rettangolo

A = × h

A = × Romboide

Trapezio

A = (B + ) × :

2 Risolvi i problemi sul quaderno. Poi riporta il risultato.

a. Un giardino rettangolare ha la base doppia dell’altezza che misura 32 m.

Calcola in metri il perimetro e l’area del giardino in metri quadrati.

P = m

A = m2

b. Un rombo ha la diagonale maggiore di 3,6 m.

La diagonale minore è la metà della maggiore.

Calcola l’area in decimetri quadrati.

A = ........................ dm2

Quadrato

A = <l ×

A = D × : Rombo

Triangolo

A = × :

c. Un romboide ha la base lunga 1,2 dm, l’altezza di 0,8 dm e il lato obliquo di 9 cm.

Calcola in centimetri il perimetro e in centimetri quadrati l’area.

P = cm A = cm2

d. Un trapezio rettangolo ha la base maggiore di 24 cm. La base minore è la metà della base maggiore e l’altezza è 1 3 della base maggiore.

Calcola l’area in decimetri quadrati.

A = dm2

Direzione Logica!

1 Per trovare la risposta giusta puoi utilizzare il sistema che ritieni più opportuno.

Disegna le figure, fai i calcoli, immagina la situazione… L’unica cosa che non puoi fare è… tirare a indovinare!

Se in un rettangolo la base rimane uguale, ma l’altezza diventa la metà, allora l’area:

• diventa la metà

• diventa 1 4

• diventa 1 16

2 Osserva. Poi rispondi e completa.

Una figura che si trova dentro un’altra (diversa) ha sempre area minore?

Se il lato del quadrato diventa la metà, allora l’area del nuovo quadrato:

• diventa la metà

• diventa 1 4

• diventa 1 16

Una figura dentro un’altra (diversa) ha sempre perimetro minore?

Una figura meno estesa di un’altra può anche avere perimetro

3 Osserva, rispondi e completa.

Disegna accanto a un triangolo equilatero un altro uguale, ma rovesciato

Ottieni un parallelogramma particolare.

Quale?

Aggiungi a sinistra un terzo triangolo senza ruotarlo. Ottieni un ……….......................................……….

Hai ottenuto un Avresti potuto aggiungere il triangolino da qualsiasi parte della figura?

enti geometrici

Le linee hanno una sola dimensione:

Le .................................................... hanno due dimensioni: e

I hanno tre dimensioni: , e

L’.................................................... è la parte di piano delimitata da due semirette che hanno la stessa origine.

L’angolo può essere:

• nullo 0°

• 90°

• piatto 180°

• giro 360°

• ottuso > 90°

• < 90°

LE FIGURE GEOMETRICHE

quadrilateri

I quadrilateri sono figure con lati, angoli. Sono quadrilateri:

triangoli I triangoli sono figure con lati, angoli.

In base ai lati: equilatero isoscele

In base agli angoli:

ottusangolo acutangolo ....................................

LE CLASSIFICAZIONI

Le caratteristiche degli elementi ti guidano a classificarli attraverso i diagrammi.

1 Classifica gli elementi inserendo la lettera corrispondente nel diagramma di Venn. Se non conosci le caratteristiche di questi animali, cerca le informazioni o chiedi all’insegnante.

A balena

B trota

C cavallo

D pettirosso

E orca

F koala

G stella marina

H vongola

mammiferi vivono in acqua

2 Scrivi almeno un elemento, tra quelli dell’esercizio precedente, che abbia le caratteristiche indicate.

• È un mammifero, ma NON vive in acqua. ............................................................................................................................................................................

• Vive in acqua, ma NON è un mammifero.

• Non è un mammifero e NON vive in acqua.

• È un mammifero e vive in acqua.

3 Inserisci nel diagramma di Carroll almeno 4 elementi per ciascuna casella. numeri minori o uguali a 20 maggiori di 20 pari ............................................................... ............................................................... non pari

4 Inserisci gli elementi nella casella giusta, riportando la lettera che li contraddistingue.

poligoni

regolari non regolari quadrilateri non quadrilateri regolari non regolari

5 Scrivi le caratteristiche in base alle quali sono state classificate queste persone.

6 Nella classe di Arturo ci sono 18 bambini e bambine:

7 • 5 praticano solo nuoto;

8 • 4 giocano solo a basket;

9 • 3 praticano sia nuoto sia basket;

10 • gli altri e le altre non praticano alcuno sport.

Quale tra questi diagrammi di Venn rappresenta in modo corretto la situazione?

Indica con X.

7 Osserva questo diagramma. A quale dei testi si riferisce? Indica con X.

Nella classe di Serena 11 hanno animali domestici. 6 bambini hanno un cane, 2 bambini hanno un gatto, 3 bambini hanno altri animali.

Nella classe di Serena 11 bambini hanno animali domestici. 6 bambini hanno un cane, 2 bambini hanno un gatto, 3 bambini hanno sia un gatto sia un cane.

LA MODA • LA MEDIA

1 Le classi quarte cominciano a pensare a come si troveranno alla Scuola Secondaria. Perciò hanno svolto un’indagine per conoscere quanto tempo dedicano allo studio le ragazze e i ragazzi più grandi. Leggi e rispondi.

Indagine: tempo dedicato ogni giorno allo studio

Campione che ha partecipato all’indagine: due classi prime della Scuola Secondaria Gianni Rodari

• Secondo te, quale o quali domande possono aver posto?

• I dati sono stati raccolti in questa tabella:

tempo dedicato allo studio giornalmente meno di 30 minuti da 30 minuti a 1 ora da più di 1 ora a 2 ore più di 2 ore frequenze 8 15 16 6

Qual è la moda, cioè il dato che ha la maggiore frequenza? ……......................................................................................................

2 Leonardo frequenta il primo anno di liceo. Pone a confronto i voti delle verifiche del primo quadrimestre suoi, di alcuni amici e di alcune amiche.

VERIFICA DI… settembre ottobre novembre dicembre

• Qual è la moda, cioè il voto che è stato assegnato il maggior numero di volte?

• Per ciascun ragazzo/a, calcola qual è la media dei suoi voti.

Lorenzo (7 + 8 + 7 + 6 + 7) : 5 = .................................... : 5 = ....................................

Gaia = =

Clelia = =

Francesco ............................................................................ = .................................... = ....................................

• L’insegnante ha detto loro che la media dei voti ricevuti dalla classe è 7,5.

Quali, tra questi ragazzi e ragazze, hanno una media di voti superiore a quella della classe?

3 Risolvi il quesito e rispondi.

Un atleta si allena tutti i giorni. Dal lunedì al mercoledì si allena per 2 ore al giorno, giovedì e venerdì le ore diventano 3, ma il sabato e la domenica si allena per 1 ora soltanto. Quante ore, in media, si allena al giorno?

I GRAFICI

Per costruire un grafico occorre leggere con attenzione tutti i dati

1 In Comune è stato esposto un grafico che riporta la ripartizione dei materiali riciclabili ritirati in questo mese con la raccolta differenziata. Leggi le informazioni.

• Il materiale più raccolto è la plastica.

• La parte che corrisponde alla carta è uguale a quella del vetro e dei metalli insieme.

• È stato raccolto più vetro che metallo.

Ora colora i 4 settori come indicato.

• In verde: i metalli.

• In giallo: la carta.

• In azzurro: la plastica.

• In rosa: il vetro.

2 Al supermercato hanno registrato in un istogramma queste vendite settimanali:

Disegna la colonna mancante. Poi, sotto ciascuna colonna, scrivi quale ortaggio rappresenta.

ANCORA GRAFICI

1 In tabella sono riportati i risultati dell’indagine svolta da una classe riguardo la disciplina scolastica preferita.

Leggi i risultati e completa l’istogramma.

Disciplina Frequenze

italiano 4

matematica 4 inglese 1 arte 6 storia 5

2 Un gruppo di bambini e bambine ha riportato i dati dell’inchiesta in un ideogramma, ma ha commesso due errori. Individuali e correggili.

Legenda = 2 preferenze

3 Leggi e indica con X quale grafico corrisponde alla temperatura di Luca.

Materia Preferenze

italiano matematica inglese arte storia

Luca ieri, lunedì, aveva la febbre alta, ma oggi la temperatura è nella norma.

LA PROBABILITÀ

Le frazioni servono anche a esprimere la probabilità

1 In un vaso ci sono palline gialle, verdi, rosse.

Osserva, leggi ed esegui.

a. Colora le palline in modo che le frasi siano vere.

• Ci sono 4 possibilità su 12 di pescare una pallina rossa.

• Le possibilità di pescare una pallina gialla sono due in più di quelle di pescare una pallina rossa.

• Le altre palline sono verdi.

b. Indica con una frazione la probabilità relativa a ciascun tipo di pallina.

2 Un mazzo di carte è formato da 40 carte, di 4 semi diversi: picche, cuori, quadri, fiori.

Per ciascun seme, ci sono 10 carte come queste. Osserva, leggi ed esegui.

Pallina rossa = Pallina gialla = Pallina verde = 1 2 3 4 5 6 7 1 2 3 4 5 6 7

a. Rispondi.

• Quante possibilità ci sono di pescare una carta di cuori? su

• Quante possibilità ci sono di pescare una figura? su

• Quante possibilità ci sono di pescare un asso? su

• Quante possibilità ci sono di pescare un asso di picche? su

b. Completa scrivendo minore di, maggiore di, uguale a.

• La possibilità di pescare un re è quella di pescare un fante.

• La possibilità di pescare una carta di fiori è quella di pescare una figura di qualsiasi tipo.

• La possibilità di pescare una carta di quadri è .................................................. quella di pescare un sette.

c. Indica con X.

Estraendo una carta a caso, è più probabile prendere:

una carta di quadri. un quattro. una figura. un re.

Estraendo una carta a caso, è meno probabile prendere:

una carta di cuori. un fante. una figura. una carta da 1 a 5.

RELAZIONI, DATI E

PREVISIONI

Le indagini statistiche servono per raccogliere su vari argomenti.

• La è il dato che appare con maggior numero di preferenze

• La ................................................... si ottiene sommando i dati e dividendo il risultato per il numero dei dati.

Classificare significa riconoscere le caratteristiche in un gruppo di elementi. Le classificazioni possono essere rappresentate con differenti diagrammi.

Diagramma di ..................................

Diagramma di Diagramma ad .................................

I sono strumenti che servono per visualizzare i dati raccolti nelle indagini statistiche.

Materia Preferenze

L’ rappresenta i dati attraverso simboli

L’ rappresenta i dati attraverso barre verticali o orizzontali

L’ rappresenta i dati attraverso parti di un cerchio o di un quadrato.

Responsabile editoriale: Mafalda Brancaccio

Responsabile di progetto: Valentina Dell’Aprovitola

Redazione: Giulia De Giorgi

Responsabile di produzione: Francesco Capitano

Progetto grafico: Ilaria Raboni

Impaginazione: Bluedit - Torino

Supervisione grafica: Carmen Fragnelli

Illustrazioni: Bluedit - Torino

Copertina: Carmen Fragnelli, Elisabetta Giovannini

Ricerca iconografica: Giulia De Giorgi

Referenze iconografiche: Shutterstock, Archivio Spiga

Stampa: Tecnostampa – Pigini Group Printing Division Loreto – Trevi 25.83.102.0

È assolutamente vietata la riproduzione totale o parziale di questa pubblicazione, così come la trasmissione sotto qualsiasi forma o con qualunque mezzo, senza l’autorizzazione della Casa Editrice.

Produrre un testo scolastico comporta diversi e ripetuti controlli a ogni livello, soprattutto relativamente alla correttezza dei contenuti. Ciononostante, a pubblicazione avvenuta, è possibile che errori, refusi, imprecisioni permangano. Ce ne scusiamo fin da ora e vi saremo grati se vorrete segnalarceli al seguente indirizzo: redazione@elionline.com

Tutti i diritti riservati

© 2025 La Spiga, Gruppo Editoriale ELi info@gruppoeli.it

equilibri

#PROGETTOPARITÀ

EquiLibri • Progetto Parità è un percorso intrapreso dal Gruppo Editoriale ELi, in collaborazione con l’Università di Macerata, per promuovere una cultura delle pari opportunità rispettosa delle differenze di genere, della multiculturalità e dell’inclusione. Si tratta di un progetto complesso e in continuo divenire, per questo ringraziamo anticipatamente il corpo docente e coloro che vorranno contribuire con i loro suggerimenti al fine di rendere i nostri testi liberi da pregiudizi e sempre più adeguati alla realtà.

CLASSE

AMBITO SCIENTIFICO

Sussidiario Matematica con Quaderno operativo 4

Sussidiario Scienze e Tecnologia con Quaderno operativo 4

Verifiche Matematica-Scienzecienze e Tecnologia 4

ISBN per l’adozione: 978-88-468-4520-7

#altuofianco

CLASSE

AMBITO ANTROPOLOGICO

Sussidiario Storia con Quaderno operativo 4

Sussidiario Geografia con Quaderno operativo 4

Verifiche Storia-Geografia 4

Atlante multidisciplinare 4-5

ISBN per l’adozione: 978-88-468-4519-1

KIT DOCENTE comprensivo di guida alla programmazione , risorse didattiche , percorsi semplificati e tutto il necessario per il corso

LIBRO DIGITALE (scaricalo seguendo le istruzioni all’interno della copertina) con LIBRO LIQUIDO ACCESSIBILE: volumi sfogliabili , esercizi interattivi , VIDEO , cartografia digitale , audiolibri .

Ambiente di apprendimento interattivo per la verifica delle competenze disciplinari.

PACK UNICO

AMBITO ANTROPOLOGICO e AMBITO SCIENTIFICO

ISBN per l’adozione: 978-88-468-4538-2

Oltre l’insegnamento Educ Ability