
1 1


1 1
HELE GRUNNSKOLEN, FRA 1. TIL 10. KLASSE
Kapittel 1 3
© 2024 Kagge Forlag AS
Omslagsdesign: Anne Vines
Sats: Anne Vines
Illustrasjoner: Anne Vines
Papir: Amber Graphic 120 g
Boka er satt med 11/13 pkt Garamond Trykk og innbinding: PNB Print, Latvia
ISBN: 978-82-489-3654-1
Kagge Forlag AS Akersgata 45 0158 Oslo www.kagge.no
Materialet i denne utgivelsen er vernet etter åndsverkloven. Det er derfor ikke tillatt å kopiere, avfotografere eller på annen måte gjengi eller overføre hele eller deler av utgivelsens innhold uten at det er hjemlet i lov, eller følger av avtale med Kopinor.
Enhver bruk av hele eller deler av utgivelsen som innmating eller som treningskorpus i generative modeller som kan skape tekst, bilder, film, lyd eller annet innhold og uttrykk er ikke tillatt uten særskilt avtale med rettighetshaverne.
Bruk av utgivelsens materiale i strid med lov eller avtale kan føre til inndragning, erstatningsansvar og straff i form av bøter eller fengsel.
4 Kapittel 1
Kapittel 1: Det nye matematikkfaget ...............................................16
Det nye matematikkfaget sett med øynene til Kenneth, en vanlig fyr uten matematikk i utdanningen ..............................
Det nye matematikkfaget – har det egentlig endret seg så mye? En førsteamanuensis forklarer .....................................................
Kapittel 2: Hva lærer barna på 1. til 4. trinn? .................................
Hva sier læreplanen at barna skal lære i løpet av 1. skoleår og hvorfor? .................................................................................. 33
Foreldreperspektivet på matte i første klasse 37 Hvordan kan du hjelpe ditt barn med å lære dette? .......................... 38
2. trinn .............................................................................................41
Hva sier læreplanen at barna skal lære i løpet av 2. skoleår og hvorfor? ...................................................................................41
Foreldreperspektivet på matte i andre klasse ......................................45
Hvordan kan du hjelpe ditt barn med å lære dette? .......................... 47
3. trinn .............................................................................................53
Hva sier læreplanen at barna skal lære i løpet av 3. skoleår og hvorfor? ...................................................................................53
Foreldreperspektivet på matte i tredje klasse 65
Hvordan kan du hjelpe ditt barn med å lære dette? .......................... 66
4. trinn ............................................................................................ 71
Hva sier læreplanen at barna skal lære i løpet av 4. skoleår og hvorfor? .................................................................................. 71
Foreldreperspektivet på matte i fjerde klasse ......................................76
Hvordan kan du hjelpe ditt barn med å lære dette? .......................... 78
Kapittel 3: Hva lærer barna på 5. til 7. trinn? 80
5. trinn .............................................................................................81
Hva sier læreplanen at barna skal lære i løpet av 5. skoleår og hvorfor? ...................................................................................81
Foreldreperspektivet på matte i femte klasse ..................................... 87
Hvordan kan du hjelpe ditt barn med å lære dette? .......................... 89
6. trinn ............................................................................................ 98
Hva sier læreplanen at barna skal lære i løpet av 6. skoleår og hvorfor? .................................................................................. 98
Foreldreperspektivet på matte i sjette klasse ................................... 104
Hvordan kan du hjelpe ditt barn med å lære dette? 106
7. trinn ............................................................................................108
Hva sier læreplanen at barna skal lære i løpet av 7. skoleår og hvorfor? .................................................................................108
Foreldreperspektivet på matte i sjuende klasse .................................
Kapittel 4: Hva lærer barna på 8. til 10. trinn?
Hva sier læreplanen at barna skal lære i løpet av 8. skoleår og hvorfor? ................................................................................ 126
Foreldreperspektivet på matte i åttende klasse ................................. 131
Hvordan kan du hjelpe ditt barn med å lære dette? ......................... 133
9. trinn ........................................................................................... 135
Hva sier læreplanen at barna skal lære i løpet av 9. skoleår og hvorfor? ................................................................................. 135
Foreldreperspektivet på matte i niende klasse ..................................139
Hvordan kan du hjelpe ditt barn med å lære dette? ......................... 141
10. trinn .........................................................................................146
Hva sier læreplanen at barna skal lære i løpet av 10. skoleår og hvorfor? .................................................................................146
Foreldreperspektivet på matte i tiende klasse ................................... 154
Hvordan kan du hjelpe ditt barn med å lære dette? ......................... 157
Kapittel 5: Elever som strever og elever som presterer på høyt nivå i matematikk ..................................................................160
Elever som strever i matematikk 161
Elever som presterer på høyt nivå i matematikk ............................. 164
Kapittel 6: Teknologi i matematikkfaget 168 Pedagogisk programvare .................................................................. 169
verktøy ............................................................................... 170 Programmering ............................................................................... 175
Oppsummering og ressurser ..........................................................180
Forskjellen på undervisning og lekser ..............................................180
Hva slags spørsmål kan det være lurt å stille barna? 182
Vær en rollemodell og ikke en fasit! .................................................184
Ressurser for å bli en bedre leksehjelper ........................................... 187
Stikkordregister .............................................................................. 189
Kapittel 1 9
Nei, mamma! Det er ikke slik vi skal gjøre det!
Mange foreldre opplever at barna deres gir dem slike klare beskjeder når de forsøker å hjelpe med leksene. Når de så spør om barnet kan vise dem matteboka og hvordan det står at oppgaven skal løses der, så ser barnet forundret på dem. For de har ikke noen fast mattebok, men på skolen jobber de muntlig, med diverse oppgaveark og digitale ressurser.
Med et samfunn i endring har også behovene for hva slags kompetanse som er viktig å vektlegge i matematikk, endret seg.
Teknologien gjør at vi alltid har hjelpemidler for hånden for å gjøre beregninger, noe som krever at vi mennesker bør være noe mer enn en kalkulator. Hvis alt vi kan i matematikk er å regne ut svar, så er kalkulatorer stort sett både raskere og mer korrekte enn oss. Som en konsekvens er det viktig at vi er bedre til å behandle tall fleksibelt, se etter sammenhenger, gjøre overslag og vurdere svarene. Vi bør være kreative problemløsere som kan bruke matematikken og
teknologien til å løse utfordringer i samfunnet. Dette gjenspeiler også gjeldende læreplan som kom i 2020. Utfordringen er at samtidig som vi fikk en ny læreplan med en klar retningsendring i at vi i større grad skal verdsette prosessen og ikke bare finne rett svar, traff også en pandemi oss. I tillegg valgte mange skoler å investere i nettbrett med digitale ressurser framfor å kjøpe inn fysiske læreverk. Denne kombinasjonen gjorde at skole–hjem-samarbeidet ble utfordrende for mange foreldre, og dette gjelder ikke bare foreldre som selv synes at matematikk er vanskelig. Mange foreldre strever i dag med å forstå hva som er formålet med det barna deres gjør i matematikk, og de mangler en bok de kan følge med i, og vet ikke hvordan de kan skaffe seg informasjon.
Denne frustrasjonen blant foreldre brakte de to forfatterne av denne boka sammen. De to kjente hverandre fra Tekna (en fagforening for folk med mastergrad i tekniske- eller naturvitenskapelige fag), der Linda er medlem og Kenneth jobber. Kenneth, som selv er pappa, så hvordan denne frustrasjonen over leksehjelp i matematikk var en utfordring for mange foreldre, og foreslo at
Tekna burde lage et leksehjelpkurs. Det var her Linda ble koblet på som fagperson. Hun er utdannet allmennlærer, og har tatt videreutdanning innen matematikkdidaktikk, som er vitenskapen om læring og undervisning av matematikk. I dag jobber hun på Universitetet i Agder, og underviser lærerstudenter i matematikk samt forsker på det samme feltet. Hun forsto derfor at et slikt kurs var noe hun kunne både designe og gjennomføre. Slik ble det, og det første kurset ble holdt allerede i 2019. Etter det har kurset vært holdt i ti forskjellige byer i Norge, og tilbakemeldingene har vært svært positive. Kursdeltakerne har opplevd kurset som nyttig, og en del av dem har spurt om hvorfor ingen har forklart dem om slike matterelaterte utfordringer før. Ja, du hørte rett. Foreldre som selv har minimum en mastergrad innen realfag, føler et behov for å komme på kurs for å lære mer om hvordan de kan hjelpe barna sine med matteleksene.
Det hendte at kursdeltakere sendte e-post med spørsmål om det fantes noen bøker eller nettressurser der de kunne lese seg opp på tematikken i leksehjelpkurset, og Linda innså at det fantes ikke. Hun skjønte at for foreldre er det utfordrende å skulle sette seg inn i dette på egen hånd, og det gjelder både foreldre som har en del matematikkbakgrunn selv, og foreldre som opplever matte som utfordrende. Sakte, men sikkert, vokste derfor tanken om denne boka fram, men Linda visste at dette var noe hun ikke kunne skrive alene.
Denne boka er ikke veldig teknisk. Den skal være en invitasjon til leseren til å sette seg inn i de mer overordnede tankene om hva det er viktig å kunne i matematikk, hvorfor det er viktig, og gi konkrete råd og tips til hvordan du som foresatt kan støtte ditt barn med matteleksene. Vi håper dette er en bok du som leser kan kjenne deg igjen i.
Vi presenterer kort bakgrunnen vår, slik at du kan vite litt mer om hvor vi kommer fra, og hva som driver vårt engasjement.
Linda Gurvin Opheim
I dag jobber jeg som førsteamanuensis ved Universitetet i Agder, der jeg underviser og forsker på læring av matematikk. Som bakgrunn er jeg utdannet allmennlærer, og har jobbet flere år i grunnskolen. Nærheten til skolen, elever og praksisfeltet har alltid vært viktig for meg, og en stor del av jobben min er derfor å jobbe tett med skoler og lærere om å utvikle best mulig praksis rundt matematikkundervisningen. Jeg har i tillegg engasjert meg gjennom å holde kurs for foreldre i regi av fagforeningen Tekna om hvordan de kan hjelpe barna sine med matteleksene. Gjennom dette arbeidet har jeg i økende grad sett behovet til foresatte for hjelp til å forstå matematikkfaget i dagens skole.
Kenneth Stubhaug Karlsen
Jeg er utdannet samfunnsviter, har jobbet mye med kommunikasjon, og har egentlig holdt meg unna matematikk helt siden jeg hoppet av på videregående. Nå har jeg tre døtre hjemme, på to, fire og åtte, og jeg er i gang med å hjelpe den eldste med leksene, men jeg aner jo ikke hva jeg driver med. Så da Linda ringte meg og lurte på om jeg ville være med å skrive bok, svarte jeg så klart ja, fordi dette er boka jeg selv ønsker meg!
Mitt bidrag er å gi et foreldreperspektiv på det Linda skriver om matematikkfaget på de ulike trinnene samt å gi et lekmannsperspektiv på læreplanen og matematikkfaget generelt. Siden mine barn er relativt små ennå, har jeg også snakket med mange i skriveprosessen og hentet innspill fra flere som har litt eldre barn enn meg. Jeg håper at du som leser boka, kommer ut litt styrket i troen på egne ferdigheter, og ikke minst at du finner inspirasjon til å hjelpe dine egne barn med matteleksene.
Er det nødvendig å undervise matematikk annerledes?
Det er lett å stille seg selv dette spørsmålet, for hvorfor endre på noe som fungerte for deg selv? I årevis har barn sittet og øvd på å sette opp regnestykker, så hvorfor skal ikke dagens barn gjøre det samme? Da Linda for første gang møtte en person som hevdet at det var unødvendig at alle barna skulle lære seg standardalgoritmene for de fire regneartene (altså å sette opp pluss-, minus-, gange- og delestykker), trodde hun han tullet. Dette var i 2011, og for Linda virket det da utenkelig at ikke alle barn skulle lære noe så grunnleggende. I dag har hun et helt annet syn på dette, og du vil forstå hvorfor når du leser videre om hva det er barna bør kunne på de ulike trinnene.
Det at ting har fungert tidligere, er i tillegg bare en delvis sannhet. For det første er det mange som sitter igjen med svært negative følelser etter matematikkfaget på skolen, og regnestykkene vi lærte, krever enormt mye øving for at vi skal klare å bruke dem. Dette så vi et tydelig eksempel på i en episode i realityserien 71 grader nord – Norges tøffeste kjendis fra 2021. I dagens samfunn har alle tilgang på teknologiske hjelpemidler til enhver tid, men det finnes et unntak – i realityserier. Her blir deltakerne fratatt mobiltelefoner og må håndtere utfordringer uten dette hjelpemiddelet. I en av episodene av 71 grader nord skulle deltakerne bevege seg mellom poster og løse ulike utfordringer. En av oppgavene lagene møtte, var regnestykket: 1780 : 89
Deltakerne hadde blyant og papir tilgjengelig, men ingenting annet. Her står altså en gruppe voksne mennesker som alle har fullført videregående skole, og skal i fellesskap finne svaret på en matematikkoppgave med relativt små tall. Flere i gruppa begynner umiddelbart å stresse, og prøver å tenke tilbake til skolegangen og den metoden de lærte for å løse divisjonsstykker. De kommer med kommentarer som: «Husker jeg dette, da?» og «Hadde det bare vært ett tall ...» Det er tydelig at deltakerne forsøker å huske det de en gang lærte på skolen, men ingen av dem kommer på hvordan
det var. Den deltakeren som løser oppgaven, er Petter Schjerven, og han løser den ikke med divisjonsalgoritmen. Han forsøker i stedet å tenke motsatt, og han velger å regne med 90 i stedet for 89. Schjerven regner seg raskt fram til at 90 · 20 = 1800. Så hvis regnestykket hadde vært 1800 : 90, så hadde svaret vært 20. Nå er 1780 bare 20 mindre enn 1800, men dette passer bra siden vi skal dele på 89 og ikke 90, altså blir det riktig med en 20-er mindre. Det betyr at svaret på oppgaven må være 20. Så 1780 : 89 = 20. Han trengte ikke kalkulator eller papir, og han brukte ikke standardalgoritmen for deling som vi lærte på skolen. Dette er akkurat den kompetansen vi ønsker at dagens elever skal utvikle, det å være fleksible med tall og se muligheter i stedet for å lete etter regler. Og det er i tillegg et eksempel på at de standardalgoritmene vi lærte da vi gikk på skolen, ikke alltid er så anvendelige som vi kanskje tror.
Boka bruker den nye læreplanen i matematikk fra 2020 som bakgrunn for hvordan vi går igjennom regnemetoder, ettersom det finnes veldig mange forskjellige læreverk over hele landet. Vi vil med denne boka prøve å treffe alle, og derfor må læreplanen og det den forteller om kompetansemål og vurderinger for hvert trinn, ligge til grunn for det vi skriver om. Det er altså definert hva elevene skal kunne, men metodikk, didaktikk og bøker vil variere fra lærer til lærer og fra skole til skole. Det som også er viktig å huske på, er at denne nye læreplanen i matematikk først ble innført høsten 2020 for grunnskolens ni første trinn, og høsten 2021 for 10. trinn, så det er nok flere som fortsatt er i en overgang mellom måten det ble undervist på tidligere og måten det skal undervises på nå. Ikke minst fordi koronapandemien traff landet samtidig, noe som gjorde at både lærere og elever sto i en svært vanskelig situasjon i lang tid. Disse forskjellene i undervisning kommer vi nærmere inn på i kapittel 1. Noen av dere vil ha nytte av å lese boka fra perm til perm, men hvis du er ute etter noe rent konkret som gjelder for ditt barns klassetrinn – kan du slå rett opp i kapittel 2, 3 og 4, og finne det
Introduksjon
trinnet du er ute etter. Dette er hovedkapitlene i boka, og det er her mye av den konkrete matematikken forklares. I tillegg har vi laget et stikkordregister bakerst i boka, med henvisninger til hvilke sider begrepene forklares. På denne måten kan du bruke boka som et oppslagsverk dersom det er et tema du står fast på.
I det første kapittelet skriver vi litt om dette nye mattefaget og hvordan du som forelder kan spille en god og viktig rolle for ditt barn. Her kommer vi inn på spørsmål som om det virkelig var noe vits i å fornye faget så mye som det har blitt gjort. Her kan vi avsløre allerede nå at svaret på det spørsmålet er et høyt og rungende ja! For samfunnet har endret seg og er i så hurtig endring – at selv om mattefaget ikke har endret seg, er behovet for kompetanse annerledes nå enn før. Bare de teknologiske endringene de siste få årene gjør at vi trenger å tenke nytt og annerledes – også om mattefaget. Vi trenger ikke å konkurrere med teknologien og lære barna våre det som vi enkelt kan få hjelp til med teknologiske hjelpemidler som er kommet for å bli. I dette kapittelet skriver vi også om læreplanen og kjerneelementene.
I kapittel 2 går vi igjennom læreplanen fra 1. til 4. trinn. I kapittel 3 står 5. til 7. trinn for tur, og i kapittel 4 skriver vi om ungdomstrinnene fra 8. til 10. klasse. I disse kapitlene tar vi for oss viktige konsepter og strategier som det jobbes med på hvert trinn i skolen. Her konkretiseres den nye tankegangen i matematikkfaget med eksempeloppgaver og foreldreperspektivet. Kapittel 2, 3 og 4 er selve kjernen i boka , og du kan slå rett opp på ditt barns trinn og finne det du trenger for å hjelpe. Det kan selvfølgelig hende at du da må bla deg litt bakover for å se hvordan det de lærer nå, henger sammen med det de skal ha lært på tidligere trinn.
I kapittel 5 skriver vi om elever som strever og elever som presterer godt i matematikk, og i kapittel 6 tar vi for oss noen av de mest nyttige og anvendte teknologiske hjelpemidlene, før du til slutt finner en oppsummering som inkluderer ressurser som finnes på nett. I oppsummeringen finner du også noen nyttige tips til hvordan du kan være en god leksehjelper for ditt barn. Til sist i boka finner du et stikkordregister for hurtig oppslag, dersom du kommer over noe i leksene til barnet ditt som du trenger å finne kjapt.
Kapittel 1 15
16 Kapittel 1
Det nye matematikkfaget sett med øynene til Kenneth, en vanlig fyr uten matematikk i utdanningen
Nå snakkes det for alvor om en realfagskrise i Norge. Jeg mener at et steg i riktig retning til å løfte matematikk som et fag flere ønsker å gå videre med senere i skolelivet, er den nye læreplanen i matematikk som kom i 2020.
Slik som jeg husker matte fra min oppvekst var det ganske rigid, men nå ser det ut til å ha blitt en vridning mot det kreative, det oppdagende, det utforskende og det problemløsende. Bare se på hva lærerplanen sier om fagets relevans og sentrale verdier: «Matematikk skal forberede elevene på et samfunn og arbeidsliv i utvikling ved å gi dem kompetanse i utforsking og problemløsing», og videre:
«[n]år elevene får tid til å tenke, reflektere, resonnere matematisk, stille spørsmål og oppleve at faget er relevant, legger faget til rette for kreativitet og skapertrang. Matematikk skal bidra til at elevene utvikler evne til å jobbe selvstendig og samarbeide med andre gjennom utforsking og problemløsing, og kan bidra til at elevene blir mer bevisste på sin egen læring. Når elevene får mulighet til å løse problemer og mestre utfordringer på egen hånd, bidrar dette til å utvikle utholdenhet og selvstendighet.»
Det er nærmest poetisk å lese slike ambisjoner for et fag som for mange oppleves som strukturelt, firkantet og nærmest det motsatte av kreativt. Jeg mener dette er et strålende utgangspunkt for oss som foreldre og foresatte når det gjelder å bidra til at våre barn lykkes med å føle mestring i matematikkfaget. Jeg tror matematikkfaget sliter med at mange foreldre overfører sin frykt for matte til barna sine. Hvor mange ganger har du ikke hørt at «matte ikke er noe for meg», eller «i vår familie er vi ikke så gode i matte», eller du har kanskje til og med hørt foreldre unnskylde sine barn med at «jeg har aldri kunnet matte, så jeg skjønner godt at min sønn heller ikke får det til». Dette holder bare ikke – beklager til alle foreldre der ute. Og når dere nå har kjøpt denne boka, håper jeg at dersom dere har vært i denne situasjonen før – skal dere i alle fall aldri tilbake dit igjen!
Talenter krever bredde
Jeg mener at det nye matematikkfaget er en del av løsningen på den realfagskrisen Norge står i, og ikke minst at vi igjen kan gjøre det sterkere når vi måler ferdighetene i faget gjennom eksempelvis den internasjonale PISA-undersøkelsen. PISA står for Programme for International Student Assessment, og måler 15-åringers kompetanse i lesing, matematikk og naturfag. Norge har deltatt i undersøkelsen siden 2003, og i 2022 leverte vi tidenes dårligste resultat i matematikk. Målingene i PISA gir nok et ufullstendig bilde av hvordan det står til med våre barns matematikkferdigheter, men det er uansett et stort varsko. Vi trenger at flere velger studier som krever realfag i høyere utdanning. Det får vi ikke til dersom ferdighetene blant barna i grunnskolen ikke strekker til. Og bare så det er sagt: Jeg mener ikke at alle skal velge realfag på videregående, men jeg mener at alle skal ha muligheten. Da har vi ikke råd til å miste elever allerede på barneskolen. Her spiller vi som foreldre en viktig rolle som motivator, hjelper og støtte. Vi skal ikke være lærere, men vi skal tilrettelegge for at matematikk kan få en plass rundt middagsbordet på samme måte som resten av skolefagene og det andre som opptar oss som familie.
Det virker kanskje litt rart, men jeg liker å sammenligne matematikk med fotball. I fotball handler det ofte om de beste. Om talentutvikling og landslag og hvem som til enhver tid er best. Slik kan det også føles i matematikken. At du må være best for å få det til. Men hva er fotballen for alle de andre som ikke er best, og hva gjør fotball for dem, for de rundt dem, for familien, for barna og for talentene? Fotball er stort fordi det er tilgjengelig, det er plass til alle, og det er rom for å være både god og mindre god. De gode må tross alt ha noen å spille både mot og med fram til de blir så gode at de kan spille mot hverandre i eliten. Jeg mener noe av det samme gjelder for matematikk. Det er plass til mange, for ikke å si alle, og du trenger ikke være den raskeste, beste og med den kjappeste løsningen på utregninger i tredje klasse for å sette pris på matte og ikke minst bruke det til å skaffe deg en utdanning og til
nye matematikkfaget
sist et yrke. Jeg mener ikke at de beste ikke skal få den tilretteleggingen de trenger, men innenfor både fag og idrett har de beste noe inni seg som ikke så mange har. Derfor mener jeg at det ikke bør være et overordnet mål for fotball å utvikle talenter, men å holde flest mulig lengst mulig i fotball. Fordi for det første er det svært vanskelig å forutse hvem som blir best før de faktisk slår igjennom.
Og for det andre vil de som ikke ble helt best, være med på å fylle roller i fotballen til evig tid som trenere, lagledere, foreldre, 4. divisjonsspillere på det lokale laget, dommere og heiagjeng for neste generasjon. Slik er det også med matematikk. Vi trenger så klart de største talentene til å drive utvikling og flytte grenser for hva vi trodde var mulig. Men vi trenger også de vanlige folkene som fyller alle samfunnsroller vi har som krever at du behersker matematikk, men ikke nødvendigvis at du er Elon Musk eller Albert Einstein (uten sammenlikning for øvrig).
Jeg mener det nye mattefaget kan være med å åpne opp dørene til matematikkens verden for flere barn og unge (og deres foreldre).
Og jeg håper at denne boka vil bidra til at du som leser kan forsere utfordringer som du møter når du snakker med barna dine om matematikken de lærer på skolen – enten du er ubevandret i matematikk fra før, eller selv anser deg som flinke i matte.
Når barna dine begynner på skolen, kan du ved hjelp av læreplanen som ligger tilgjengelig hos Utdanningsdirektoratet, både sette deg inn i hva barna skal lære og se sammenhengen mellom målene for de ulike trinnene. Det er viktig å huske på at læreplanen er skrevet for å beskrive forholdet mellom faget, lærere og elever, og ikke for foreldre. Bakgrunnen for at vi i denne boka vil referere en del til læreplanen, er at det finnes veldig mange læreverk i Norge, og disse er konstruert forskjellig. Men felles for alle er at de skal bidra til å oppnå kompetansemålene i læreplanen. Læreplanen i matematikk finner du her: https://www.udir.no/lk20/mat01-05.
Det som er verdt å merke seg allerede i starten, er at læreplanen
i matematikk har definerte kompetansemål og vurderingskriterier etter hvert trinn, foruten 1. trinn. Her skiller matematikk seg ut. Andre større fag, som for eksempel norsk og engelsk, har kun kompetansemål og vurderingskriterier etter 2., 4., 7., og 10. trinn. Det vil si at det for oss foreldre føles litt lettere å skulle følge med på hva barna egentlig skal kunne fra år til år når det gjelder matematikk.
Det gir også gode muligheter til å identifisere de mulige hullene i kunnskapen, og fylle dem.
Jeg nevnte at jeg synes læreplanen har en god visjon og begynnelse. Dette kan du lese i avsnittet i læreplanen som heter «Fagets relevans og sentrale verdier». Leser du videre i læreplanen, kommer du til kjerneelementene. Og der det hele startet poetisk, møter du nå litt mer utfordrende ordbruk som kanskje ikke resonnerer like godt med den gjengse forelder. I matematikk er det seks kjerneelementer: utforsking og problemløsing, modellering og anvendelse, resonnering og argumentasjon, representasjon og kommunikasjon, abstraksjon og generalisering og til sist matematiske kunnskapsområder. Hvis du synes dette høres overveldende ut, er vi i samme båt. Men fortvil ikke, Linda forklarer dem alle ettertrykkelig litt senere i dette kapittelet, når hun forklarer mer om det nye mattefaget sett fra hennes perspektiv. Akkurat nå holder det å vite at kjerneelementene er det viktigste i faget. Altså det barna må lære for å mestre og bruke faget. Det jeg er mest glad for, og der hvor jeg mener at jeg kan bidra som pappa, og ikke minst noe jeg savnet da jeg selv gikk på skolen, er kjerneelementet som heter resonnering og argumentasjon. Det var jo når det ble for mange regler og utregningsledd ble droppet, at jeg selv falt av matematikken i min ungdom. Nå virker det som at nettopp «veien til målet» og det å skjønne mer av hvorfor vi gjør som vi gjør i matematikk, har fått mer plass i faget enn det hadde da jeg vokste opp. Det gjør meg glad!
Det nye matematikkfaget
Hvordan skal du så lese denne læreplanen, lurer du kanskje på?
Aller først, det beste med læreplanen er at du uavhengig av læreverk, kan sette deg inn i hva barna skal lære og se sammenhengen mellom målene for de ulike trinnene. Det første bildet under viser læreplanen slik du finner den.
Her har jeg valgt tredje trinn som eksempel. Alle trinnene er bygget opp likt. Du ser her at hvert trinn har kompetansemål som
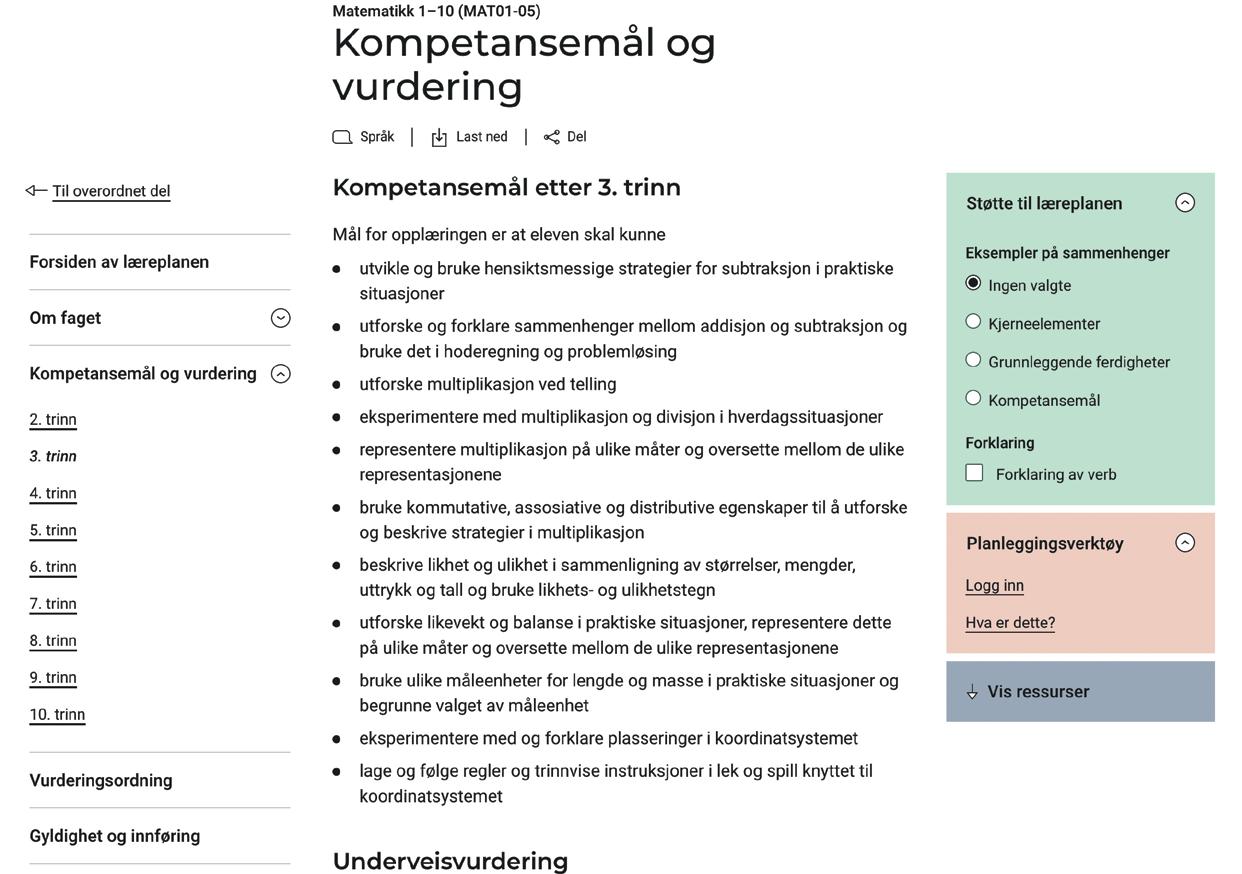

Faksimile er hentet fra læreplanen på udir.no.
elevene skal kunne etter gjennomført trinn, og en underveisvurdering. På venstre side kan du velge de ulike elementene i læreplanen som du vil lese om. I nedtrekksmenyen «Om faget» finner du blant annet «Fagets relevans og sentrale verdier» samt kjerneelementene som tidligere nevnt. På høyre side finner du «Støtte til læreplanen», som du kan bruke for å se sammenhengene mellom det de lærer på de ulike trinnene, og mellom kjerneelementene og de grunnleggende ferdighetene og kompetansemålene for hvert trinn. Jeg fortsetter med læreplanen på tredje trinn som eksempel. På bildet under kan du se at jeg ikke har valgt noe støtte til læreplanen i det høyre feltet.

Faksimile er hentet fra læreplanen på udir.no.
Det nye matematikkfaget
Mens i bildet under har jeg valgt å krysse av i feltet for kompetansemål. Da kan du velge å vise både hva det aktuelle kompetansemålet bygger på og hva det leder til, og du finner sammenhengen mellom hva de lærer nå, hva de skal ha lært før og hva det leder til at de skal lære senere.

Faksimile er hentet fra læreplanen på udir.no.
Her er det selvfølgelig ikke å forvente at foreldre og foresatte skal sette seg inn i hele læreplanen til alle fag i grunnskolen, men akkurat når det gjelder matematikk har det faktisk gitt meg et par aha-opplevelser å lese læreplanen. For meg som har lav selvtillit i matematikk, har det å lese i læreplanen bidratt til å ufarliggjøre
nye matematikkfaget
faget for meg. Det er ikke slik at du må lese og gjøre deg kjent med hele læreplanen, men det er greit å ha en oversikt over hvordan den er bygget opp, og vite at du kan sjekke den og finne kompetansemål og vurdering for hvert trinn. For deg som er flink i matte, kan læreplanen gi viktig innsikt i hvordan matematikk faktisk læres på skolen nå, hvis du er usikker på hvordan dine ferdigheter kan brukes i leksehjelpingen.
Som kanskje ikke alle vet, endres ikke læreplaner så veldig ofte. For å gi litt historisk kontekst kan jeg nevne at vi har hatt disse læreplanene i grunnskolen siden andre verdenskrig: Normalplanen fra 1939, Mønsterplanen fra 1974, Mønsterplanen fra 1987, Læreplanverket fra 1997, Kunnskapsløftet fra 2006 og Kunnskapsløftet fra 2020. Som dere kan se, endres læreplanene etter ti til femten år i nyere tid. En slik endring skaper gjerne store forandringer, og det første du tenker om den norske skolen, er nok ikke at den snur seg raskt. Derfor varer gjerne læreplaner lenge når det først er gjort en endring, og hvis vi ser historisk på det, kommer antagelig nåværende læreplan til å vare i alle fall i ti til femten år.
nye matematikkfaget
En førsteamanuensis forklarer
Da jeg først leste Kenneths beskrivelse av det nye matematikkfaget, hadde jeg i starten lyst til å korrigere ham og si at nei, det er ikke slik at alt dette er helt nytt. Men så reflekterte jeg litt videre, og innså at for mange vil det oppleves akkurat slik Kenneth erfarte det: som et helt annet fag enn da han selv gikk på skolen. Endringer skjer vanligvis sakte og med små justeringer, og dette gjelder også matematikkfaget. Mange forskere er frustrerte over at det er så vanskelig å få gjennomført endringer i skolen, men dette er en konsekvens av den sammensatte jobben lærere står i, som medfører at ting tar tid. Lærere trenger omfattende kunnskap, de skal i tillegg ha oversikt over den beste måten å undervise dette på, de skal være sosialarbeidere, omsorgspersoner og nærmest uendelig mye mer. Det
Det nye matematikkfaget
er ikke tilfeldig at lærere ofte gjør det godt i spørrekonkurranser og liknende, for de må kontinuerlig sette seg inn i ny kunnskap gjennom jobben sin. Det å gjøre ting på en ny måte, koster. Spesielt hvis du behersker og er god til den måten du har undervist på tidligere, krever det mot og ståpåvilje å likevel endre undervisningsmåte fordi du forstår at elevene kan være tjent med det.
Alle læreplanene i matematikk har vektlagt at elevene skal utvikle en kompetanse utover det å kun gjennomføre beregninger. Selv om vi går helt tilbake til Normalplanen av 1939, vektlegges det riktignok at elevene skal kunne hurtig, praktisk og sikkert løse lettere regneoppgaver, men det beskrives også at det skal gjøres på en forstandig måte. I tillegg skal elevene kunne gjøre rede for løsningen, og du kan finne beskrivelser av at læreren bør forsøke å knytte oppgavene opp mot elevenes hverdag, og i tillegg gis det eksempler på åpne oppgaver der elevene selv kan stille spørsmål. Det er altså ingen stor nyhet at vi regner matematisk kompetanse som noe mer enn å finne svaret på en oppgave. Det som derimot er en større utfordring, er å vite hvordan du skal kunne tilrettelegge for en slik undervisning samt mestre det.
Det er ingen tvil om at læreplanen i matematikk fra 2020 (LK20) er en krevende læreplan for lærere å undervise etter. Et stort skille mellom den forrige og denne læreplanen er at det nå er en del av forskriften at elevene skal utvikle kompetanse innenfor måter å jobbe matematisk på , og at dette skal gjennomsyre hele undervisningen i grunnskolen og videregående opplæring. Dette er de kjerneelementene som Kenneth allerede har nevnt. I tidligere læreplaner har det vært spesifisert at elevene for eksempel skal jobbe med problem løsing, men dette har av noen vært oppfattet som at de da setter av en uke eller to til å jobbe med problem løsing, og så går de tilbake til den vanlige regningen. I LK20 står det at alle kompetansemål skal ses i lys av teksten om faget, som inkluderer kjerneelementene. Dette er en litt tung setning, men det betyr i praksis at når du underviser i matematikk, så skal du alltid ha kjerneelementene: Utforsking og problemløsing, modellering og anvendelser, resonnering og argumentasjon, representasjon og kommunikasjon,
abstraksjon og generalisering i bakhodet i tillegg til de matematiske kunnskapsområdene, og du bør tenke over hvordan det å jobbe med for eksempel likninger, også kan være med på at elevene blir bedre i ett eller flere av kjerneelementene. I tillegg er det slik at du ikke kan vente med å undervise i noen av kjerneelementene. I LK20 står det helt klart at elevene for eksempel skal jobbe med kjerneelementet abstraksjon og generalisering, og dette gjelder for alle elever. En lærer som jobber på 2. trinn, kan ikke tenke at dette passer best på videregående, der elevene har forutsetninger for å kunne abstrahere og formulere bevis, nei, hen må finne en måte for å tilpasse og jobbe med denne kompetansen med 7–8-åringer. Dette er for mange en ny måte å jobbe på, og det krever mye å gjøre slike endringer i undervisningen. I tillegg til kjerneelementene har programmering kommet inn i læreplanen i matematikk som noe helt nytt. Det medfører at lærere som mest sannsynlig ikke har noe utdanning i programmering selv, skal undervise elever i hvordan de skal bruke programmering som et verktøy for å løse matematiske problemer. Vi skriver mer om dette i kapittelet om teknologi i matematikkfaget.
Matematikkfaget er som tidligere nevnt ikke helt nytt, men jeg kan forstå at det oppleves slik. Jeg har nå forklart litt om utviklingen og den krevende jobben lærerne står i, og at endringer tar tid. Den enkleste måten å oppdage endringer på, er å se noe på nytt som du ikke har sett på lenge. Bare tenk på ungene i familien som vokser til. Du som foresatt merker i liten grad mange av forandringene som skjer, mens en onkel som ikke har sett barnet ditt på et par år, kan kommentere hvor mye barnet har vokst eller forandret seg. Du legger ikke alltid merke til endringer på samme måte når du står midt oppi det, og slik er det med matematikklasserommet også. Kenneth som ikke har hatt noe forhold til matematikkfaget på mange år, ser derimot med en gang at det har skjedd massevis av endringer. Og det har det også! Sakte, men sikkert har vi kontinuerlig endret og forbedret måten vi underviser i matematikk på, og dagens skole er derfor svært annerledes enn for bare 20–30 år siden. En ny læreplan som setter tydelig krav til lærerne om at matematisk kompetanse er mer enn å finne et svar, er i tillegg med på
å eskalere endringene. Læreplanen gjenspeiles i hva som kreves av elevene på eksamen, noe som igjen gjør at lærere ikke kan bagatellisere for eksempel det at elevene skal være vant med å argumentere faglig for sine svar. De siste årene vil du derfor kunne se større endringer i typen matematikkoppgaver elevene får, hva de blir bedt om å gjøre, og hvordan undervisningen organiseres. Du vil også oppleve at det kan være store forskjeller fra skole til skole og lærer til lærer. Noen lærere har allerede undervist etter mange av disse prinsippene i årevis, mens andre lærere er helt i startgropa av å forsøke å finne ut av hvordan de kan undervise for å oppfylle læreplanen, og ikke minst lære seg å beherske dette. Vi bør derfor ha respekt og forståelse for at dette er krevende for lærere, og ikke forvente at de skal være spesialister på dette med en gang. Det viktigste er at de jobber for å utvikle seg og egen undervisning i henhold til læreplanen og barns matematikklæring. Og så håper vi at denne boka kan gi deg som foresatt et verktøy i å støtte ditt barns helhetlige matematikkompetanse på hjemmefronten. På den måten blir dere et godt team.
Jeg skal nå gå igjennom kjerneelementene og kort forklare hva som ligger i dem, og hva dette kan bety i praksis for ditt barn.
Dette kjerneelementet handler mye om at eleven ikke skal få ferdig presentert alle svar og framgangsmåter. Problemløsing kan defineres som et problem der du i utgangspunktet ikke kjenner til noen klar strategi for å finne svar. Dette betyr at regnestykket 3 · 12 kan være problemløsing for en 2.-klassing på 7 år, fordi hen ikke har lært noen strategi for å finne svaret på denne typen oppgaver. Innenfor dette kjerneelementet, er det derfor ønskelig at elever skal bygge opp en utholdenhet i å jobbe med vanskelige oppgaver, og systematisk prøve ut ulike strategier og løsningsmetoder. Under dette kjerneelementet nevnes også algoritmisk tenkning, som er koblet til programmering. Du kan lese mer om dette i kapittelet om teknologi i matematikkfaget, som starter på side 168.
Dette kjerneelementet er knyttet tettest på hverdagen til elevene, men er for mange det kjerneelementet som også er vanskeligst å forstå. Her handler det om å sette seg inn i reelle problemer fra virkeligheten, oversette dette til et matematisk språk, gjennomføre beregninger og deretter vurdere disse svarene opp mot virkeligheten igjen. Koblingen mellom den virkelige verden og matematikken er derfor essensielt i dette kjerneelementet. Dette kan tidvis være utfordrende når du er på skolen og matematikk er et skolefag, så her er det nyttig med støtte hjemmefra også. Som forelder står du tross alt i flere reelle situasjoner med barnet ditt.
Det som kan gjøre modellering vanskelig å forstå, er at flere av modelleringsfasene skiller seg fra det mange forbinder med matematikk tradisjonelt. Noe av det viktigste du gjør i modellering, er å ta valg og avgrense og forenkle virkeligheten til et matematisk språk, som gjør at du likevel kan si noe om virkeligheten. For at elevene skal få erfaring med dette, medfører det at de får oppgaver som kan virke svært åpne og vanskelige å forstå. For eksempel: Hvor mye vann bruker en gjennomsnittsperson i løpet av en måned? Hvordan kan du lage en best mulig parkeringsplass ut av en rektangulær tomt på 5000 kvadratmeter? Dette er eksempler på modelleringsoppgaver som mange vil oppfatte som at dette ikke er matematikk, fordi du ikke ender opp med avanserte beregninger. Da er det viktig å være klar over at kompetanse i modellering og anvendelser handler om å beherske alle stegene i en modelleringssyklus, og å kunne se hele syklusen i sammenheng. Dette forutsetter ikke nødvendigvis at det må være kompliserte utregninger underveis. Samtidig finnes det eksempler på modelleringsoppgaver som inneholder det også. Ta bare eksemplene fra koronapandemien vi har vært igjennom. Der ble det presentert relativt avanserte matematiske modeller av hvordan smitten kunne spre seg, effekten av vaksine og liknende. For å oppsummere forutsetter matematisk modellering at elevene skal ta valg og gjøre avgrensninger, samt hele tiden vurdere både modellene de utformer og svarene de får opp imot virkeligheten.
Her må jeg innrømme at jeg ble gledelig overrasket over at Kenneth var såpass positiv til dette kjerneelementet, på vegne av usikre matteforeldre. Ofte opplever jeg at mange tenker det er enklere å bare «gjøre matematikk», og at det krever mer å resonnere seg fram til hva som er et logisk svar og argumentere for dette i etterkant. Men kanskje er dette også et uttrykk for den hjelpeløse følelsen en del har hatt i egen skolegang, der de gjorde mange utregninger uten å skjønne hvorfor eller hva de egentlig gjorde. Da kan jeg forstå at det oppleves motiverende å få lov til å tenke selv og være i stand til å følge et resonnement. For det er nettopp dette elevene skal utvikle. De skal kunne formulere egne resonnementer for å forstå og løse problemer samt kunne følge andres logiske resonnementer. Argumentasjon handler om at elevene begrunner framgangsmåter, resonnementer og løsninger, og beviser at disse er gyldige. Dette er ganske ambisiøse mål, men samtidig har jeg langt mer troen på at elevene utvikler evnen til å argumentere for løsninger gjennom hele skoleløpet enn tidligere, der mange fikk bakoversveis da de skulle formulere bevis for første gang på videregående skole. I denne boka vil du merke hvordan vi forklarer både hva det er forventet at elevene skal kunne være i stand til å resonnere og argumentere over samt hvordan du som foresatt kan være med og støtte disse prosessene.
Tidligere var ofte matematikklasserommene de stille klasserommene. Jeg var en av dem som nøt nettopp dette. Jeg elsket å sitte i fred på plassen min og bare regne meg igjennom oppgave etter oppgave. Selv om vi ikke skal undervurdere det å øve på ferdigheter, slik jeg gjorde i klasserommet, skjer mye viktig læring i matematikk gjennom kommunikasjon. Det er i samtaler der noen er uenig med deg, eller tenker annerledes, at dere i fellesskap utvikler læring. Samtidig, hvis du skal kunne resonnere og argumentere, har du
også et behov for å kunne kommunisere dette på en god måte. Det å kunne bygge opp en solid, logisk argumentasjon og formidle dette overbevisende, er en svært viktig kompetanse i dagens samfunn.
Matematikkfaget gir oss en unik mulighet til nettopp å jobbe med dette, og der det faglige må ligge i bunnen for god kommunikasjon. Representasjoner i matematikk er viktige, fordi vi må bruke en form for representasjon for å framstille matematikk som er abstrakt i seg selv. For eksempel kan mengden tre framstilles som symbolet 3, som en tegning med tre rundinger, romertallet III og på mange flere måter. Tall er en vanlig representasjon, men det kan egentlig være hva som helst som representerer noe matematisk, for eksempel en graf eller en tallinje. Det å kunne bruke gode representasjoner samt veksle mellom ulike representasjoner, er også med på å utvikle kommunikasjonsevner. Grafiske illustrasjoner, tabeller, statistiske oversikter med mer, vi er alle kjent med hvordan slike representasjoner kan virke svært overbevisende i aviser samt hjelpe oss til å forstå sammenhenger. Det å beherske varierte representasjoner samt kunne oversette mellom disse, er derfor en viktig del av det å utvikle kompetanse i kommunikasjon.
Dette er antagelig et kjerneelement som de fleste forbinder med matematikk, men der en del mener at det først er egnet for eldre elever når de har det grunnleggende på plass. Det er likevel mulig å jobbe med dette med langt yngre elever. Når 9-åringer skal generalisere, handler det ikke om at de skal utforme et induksjonsbevis for å bevise formelen for trekanttall, men det kan handle om noe så enkelt som at når de lærer om oddetall og partall, blir de utfordret på om det er slik at alle tall er enten oddetall eller partall? Uansett alder og hva du jobber med i matematikken, har det stor verdi å løfte blikket og reflektere over om det du jobber med alltid gjelder, om det finnes unntak, og hva som er ytterpunktene. Ta for eksempel multiplikasjon og kommutativitet, som vi skriver om på 3. trinn. Elevene lærer at rekkefølgen i et multiplikasjonsstykke
er likegyldig. Du får altså det samme svaret om du skriver 5 · 7 eller 7 · 5. Samtidig som de lærer dette, kan det være viktig å jobbe med når kommutativitet, som det heter, gjelder. For dette fungerer glimrende i addisjon og multiplikasjon, men blir feil i subtraksjon og divisjon. Det å kontinuerlig jobbe med abstraksjon og generalisering, er derfor en svært viktig kompetanse innenfor alle nivåer av matematikk.
Dette kjerneelementet skiller seg fra de andre. Mens de fem første kjerneelementene handler om hvordan elevene skal jobbe med matematikk, handler dette kjerneelementet om det matematiske innholdet i det de skal jobbe med. Her vil du finne igjen de mer kjente kunnskapsområdene tall og tallforståelse, algebra, funksjoner, geometri, statistikk og sannsynlighet.
Matematikk og regning har ikke egentlig endret seg, men samfunnet har sterkere behov for en mer sammensatt matematisk kompetanse enn for bare 50 år siden. Derfor vektlegger også læreplanen tydeligere at elevene må lære seg hvordan de jobber med matematiske utfordringer, og ikke bare å finne svar. Kanskje er ikke dette nytt for deg, og kanskje er dette måten du selv har tenkt om matematikkfaget lenge. Eller kanskje opplever du dette som en annerledes måte å tenke på, og at mye av faget ikke likner på det du husker fra egen skolegang, som Kenneth. Uansett hvilke tanker du sitter igjen med nå, skal vi lose deg igjennom hva dette kan bety i praksis for de ulike alderstrinnene opp igjennom grunnskolen, og så satser vi på at dette blir stadig klarere gjennom boka.