Michael Clancy, Sudarshan Sekhar, Aaron Batista, Patrick Loughlin

Extensions and analysis of a virtual balancing task for studying sensory-motor control

Michael Clancy a , Sudarshan Sekhar, PhD a , Aaron Batista, PhD a , Patrick Loughlin, PhD a a Department of Bioengineering, University of Pittsburgh

Michael Clancy is an undergraduate student who has been studying Bioengineering at the University of Pittsburgh since 2016. His research interests include motor control and sensory feedback; and machine learning and neural networks.

Michael Clancy

Sudarshan Sekhar did his bachelor’s in electrical engineering from Anna University in Madras, India. He then did his masters & PhD at the University of Tuebingen, Germany, and is currently a postdoc at the University of Pittsburgh.

Sudarshan Sekhar, PhD

Aaron Batista is an Associate Professor in Bioengineering at the University of Pittsburgh. Prior to joining Pitt’s faculty he earned a PhD in Computation and Neural Systems at the California Institute of Technology, and pursued postdoctoral research at Stanford University. Dr. Batista’s research include the neurophysiology of skilled behavior.

Aaron Batista, PhD

Patrick Loughlin, PhD

Patrick Loughlin is a Professor and Associate Chair of Bioengineering at the University of Pittsburgh, which he joined in 1993 after earning a PhD in Electrical Engineering from the University of Washington. His research interests include sensory integration in motor control; control of human movement; sensory substitution, haptics, vibrotactile feedback; brain-computer interfaces; computational models; and signal processing. Dr. Loughlin is a Fellow of the American Institute for Medical and Biological Engineering (AIMBE), the Acoustical Society of America (ASA), and the Institute of Electrical and Electronics Engineers (IEEE).

Significance Statement

Understanding how the brain encodes sensory information about its surroundings and in turn generates neural signals that drive movement could enable us to restore sensory-motor function to paralyzed individuals, through the development of brain-computer interfaces. Virtual object manipulation provides a means by which to experimentally investigate native sensory-motor function in controlled conditions that are a balance between natural yet highly variable movements versus highly repeatable yet simple movements such as point-to-point reaching. Here we analyze and extend one such task, the Critical Stability Task (CST).

Category: Methods Keywords: motor control, sensory feedback, virtual object manipulation, neural networks, modeling

Abstract

Brain-computer interfaces (BCIs) aim to restore motor control to individuals with motor impairments by using recordings of brain activity to control the actions of a device, such as a prosthetic limb, robotic arm, or cursor on a computer monitor. To train a BCI to learn the mapping from neural activity to intended action, subjects are typically asked to perform highly stereotypical and repeatable tasks, such as repeatedly moving a cursor to a particular location on a screen while the activity of small groups of neurons is recorded. In contrast, most natural movements are more complex and varied, with motor and sensory actions working in concert in a feedback loop to control movement. However, acquiring and analyzing neural data while subjects perform natural movements in real environments is a very challenging undertaking. In the laboratory, virtual object manipulation provides a balance between natural yet highly variable movements versus simple yet highly repeatable movements. One such virtual task is the “Critical Stability Task” [1], which is a simulated balancing task akin to keeping a broom upright in the palm of one’s hand. Because the CST imposes a tight coupling between sensory feedback and motor action resulting in non-stereotypical movements, it provides a new experimental paradigm for the design and testing of BCIs. The two aims of this study were, first, to implement and test extensions to the CST, and second, to model and simulate the behavioral response of subjects performing CST. The extensions altered the underlying dynamics of the system, and as such they will enable future investigations into sensory integration and motor action to manipulate or control increasingly complex dynamical systems.

1. Introduction

Understanding how the brain decodes sensory information about its surroundings and in turn generates neural signals that drive movement could restore function to impaired individuals, through the development of brain-computer interfaces (BCIs) and advanced neuroprosthetics. To learn the mapping from neural activity to intended action, most BCIs are trained on highly reproducible and stereotypical tasks, such as repeatedly moving a cursor to a particular location on a screen while the activity of small groups of neurons is recorded. BCIs constructed in this way are very effective at allowing users to execute relatively simple but important actions such as moving a cursor on a screen to type or navigate a webpage.

In contrast, most natural movements are more complex and varied, with motor and sensory actions working in concert in a feedback loop to control movement. Consider, for example, the intricate sensory-motor coupling required to generate the precise movements necessary to ride a bicycle without falling, or to balance a broom in the palm of one’s hand. However, acquiring and analyzing neural data from natural movements in real environments is a very challenging undertaking. Virtual object manipulation provides a reasonable compromise between natural yet highly variable movements versus simple yet highly repeatable movements. One such virtual task is the “Critical Stability Task” (CST) [1], which is a simulated balancing task, akin to keeping a broom upright in the palm of one’s hand. Because the CST imposes a tight coupling between sensory feedback and motor action resulting in non-stereotypical movements, it provides a new experimental paradigm for the design and testing of BCIs, as well as the study of sensorimotor control in general.

The purpose of the present study is to extend and refine the CST to enable the investigation of more complex behaviors. To achieve this, two aims were pursued: (1) to implement modifications to the CST, and test human performance on the modified task, and (2) to model and simulate the behavioral response of Rhesus monkeys performing the CST as a first step towards system identification of their underlying sensory-motor control. The modifications of the CST that were implemented altered the dynamics of the system. Specifically, the current implementation of the CST is a so-called ``first-order’’ system, which in theory is the simplest unstable system to control, requiring only sensory information about the position of the object. Higherorder dynamics as implemented here place greater demands on sensorimotor control that in theory require the subject to utilize additional sensory information about the system state, such as its position, velocity and acceleration. As such, these extensions of the CST should allow future investigations into sensory integration and motor action to control increasingly complex systems.

2. Methods The Critical Stability Task (CST)

The CST is a virtual object manipulation task wherein subjects must make hand movements in order to keep a cursor on a screen from drifting left or right away from screen-center (Fig. 1).

Figure 1: An example from a standard CST trial, where the y axis indicates the time of the trial (stabilizing the cursor for 6 seconds is a success). The x-axis shows the horizontal onscreen cursor position over the duration of the trial. When the subject brings their hand to the center of the display monitor the trial starts, the cursor shown in gray then begins to drift horizontally off screen until corrective subject movements are made. The subject must aim to have their hand motions be equal and opposite to the cursor motions in order to stabilize the cursor. If the cursor drifts too far from the center, the trial ends and is counted as a failure.

As originally formulated, the CST is governed by a first-order differential equation [Jex 1966],

(1)

where the cursor velocity y'(t) depends on the cursor position, y(t), as well as the subject’s hand position, x(t), and the parameter λ>0 determines the task difficulty. In particular, the larger that λ is, the faster the cursor moves. In addition, because λ is nonnegative, the cursor will drift away from screen-center with increasing velocity in the absence of hand movements; specifically, when x(t) = 0, the cursor position (i.e., the solution to Eq. (1)) is given by y(t) = y 0 e λt , where y 0 is the initial cursor position. In order for the cursor not to move, i.e., such that its velocity is zero (y'(t) = 0 in Eq. (1)), the subject must make hand movements that are exactly equal and opposite to the cursor position: x(t) = –y(t). Hence, the CST is a feedback-driven task, in that sensory information about the cursor position is crucial for good performance (Fig. 2). Because of motor noise and sensorymotor delays, this ideal performance cannot be achieved in practice; hence, at some value of λ, the subject will eventually be unable to control the cursor, and it will rapidly drift off-screen, which we flag as a failure at the task. In this way, the parameter λ provides a quantitative measure of each subject’s sensory-motor control, with larger values being indicative of better performance.

Figure 2: A CST feedback control model. The blue pathway designates motor control based on sensory information (red) about the cursor. A future goal is to identify the unknown motor and sensory functions, H m and H s , by introducing motor and/or sensory perturbations (d m and d s ).

The CST has been used to study sensory integration in balance [7], impairment of executive function and motor control [6], as well as mental workload [5] and neurological health [3, 4]. The CST was recently adapted for animal experiments in sensory-motor control via the discrete-time algorithm [1],

y[n+1] = ay[n] + (a – 1)x[n]

(2)

where x[n] and y[n] are the hand and cursor position, respectively, at the current time nT s , y[n+1] is the cursor position to be rendered at the next update, and T s is the update interval. As with the differential equation formulation of the CST in Eq. (1), the parameter a = e λTs > 1 determines task difficulty, with larger values causing the cursor to move faster. Additionally, in the absence of hand movements (x[n] = 0), the cursor will diverge from screen center, with position given by y[n] = a n y 0 . As with the original formulation in Eq. (1), in order for the cursor not to move in this discrete-time version of the CST (i.e., such that y[n+1] = y[n]), the subject must make hand movements that are exactly equal and opposite to the current cursor position: x[n] = –y[n]. This ideal performance is not possible because of sensory-motor delays and noise, and hence subjects will lose control of the cursor at some value of the parameter a, called the “critical instability value” (CIV).

Aim 1: Extensions of the CST

As shown above, for ideal performance (i.e., a stationary cursor), only information about the position of the cursor is necessary in the “first-order” instantiation of the CST (Eq. (2)). In theory, increasing the “order” of the CST will necessitate additional sensory information about the cursor (e.g., position, velocity, acceleration) in order to succeed at the task.

For example, consider a second-order version of the CST given by

y[n+1] = 2ay[n] – a 2 y[n–1] + (a – 1)x[n] (3)

Here, in order for the cursor not to move (y[n+1] = y[n]), hand movements must be generated according to

x[n] = K 0 y[n] + K 1 y[n–1]

or equivalently, (4)

x[n] = K p y[n] + K v (y[n] –y[n–1])

where (5)

K0 = (1 –2a) ⁄ (a–1), K 1 = a 2 ⁄ (a–1), K p = (a–1), K v = –a 2 /(a–1)

(6)

Hence, in this second-order instantiation of the CST, hand movements depend on the current and prior cursor positions, which is analogous to requiring information about cursor position and velocity (Eq. (5), where the velocity is approximated by the discrete-time difference y[n] –y[n–1]). In the first aim of this study, we implemented higher-order versions of the CST, to allow future experiments to investigate the sensory requirements necessary to perform the task.

Aim 2: Simulation and Modeling

With reference to the feedback control model shown in Fig. 2, a desired future goal is to describe the monkey’s underlying sensory-motor control by computing the motor and sensory functions, H m and H s , respectively. As a step in that direction, the second aim of this study was to simulate the behavioral response of Rhesus monkeys performing the (first-order) CST.

Simulations of CST performance were generated by a neural network designed using the Deep Learning and Machine Learning toolboxes provided by Mathworks. A Long Short-Term Memory (LSTM) neural network was chosen because it has “memory”, that is, the current output from the network can effect the next output. The LSTM was trained on Rhesus monkey behavioral data (hand and cursor positions) obtained during CST trials (140 training trials). At each time increment, the network was trained to predict the subject’s hand position at the next time increment, given information about the current cursor and hand. The cost function was the root mean squared error (RMSE) between the actual and predicted hand position. Different LSTM network architectures and types of training data (i.e., position only v. position + velocity) were investigated. The best network contained one LSTM layer with ten neurons, a dropout rate of 45%, and used the current hand position along with the current cursor position and velocity in order to predict the next hand position.

After training, the optimized network was tested on held out data (37 trials) to assess its ability to predict the next hand position at each time increment. The network was also tested on its ability to perform the CST in place of a live subject; for these tests, the network was seeded with an initial hand position (i.e., hand position at the start of the trial) drawn from a distribution created from subject data. If the network was able to successfully perform the CST for first order, it could then be tasked with performing second order CST, as a first step towards quantifying the effect of increasing the system order.

3. Results

Example trials of a subject (MC) performing the first- and second-order CST are shown in Fig. 3; a successful trial and a failed trial are shown in each case. We observed experimentally that a second-order implementation of the CST (Eq. (3)) was more difficult for the human subject to control than the first-order implementation (Eq. (2)). Fig. 4(a) shows the success rate as a function of increasing the value of the parameter “a” in equation 3 (i.e., increasing task difficulty) for a human subject (MC) performing the first-order CST, while Fig. 4(b) shows the success rate for the second-order CST. In both cases, performance degrades as the task becomes more difficult; the value of the system’s parameter “a” at which the subject fails 50% of the time on average (i.e., the CIV) is marked by ‘x’ in each plot. The CIV achieved for the secondorder case is substantially lower than for the first-order case. Our derivations in Eqs. (3)-(6) provide theoretical insights into why higher-order versions of the CST are more challenging to control. In particular, unlike the first-order CST for which ideal performance (i.e., stationary cursor) requires hand movements that depend only on the cursor position and are independent of task difficulty (x[n] = – y[n]), ideal performance at higher-order versions of the CST changes with task difficulty (parameter “a”), and moreover requires additional sensory information about the cursor beyond just its position. In particular, a second-order version of CST requires information about cursor position and velocity (Eq. (5)), and the degree to which this information is utilized to generate a control action depends on task difficulty (i.e., the position and velocity gains in Eq. (5) are functions of the parameter “a”).

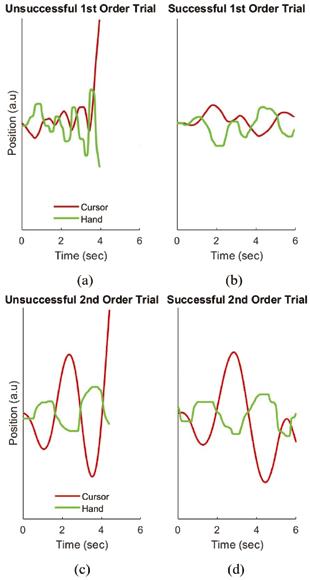
Figure 3: Example trials showing the horizontal cursor and hand position versus time for a subject performing the first-order CST ((a) unsuccessful trial, (b) successful trial) and the second-order CST ((c) unsuccessful trial, (d) successful trial). The vertical scale is the same in all plots.

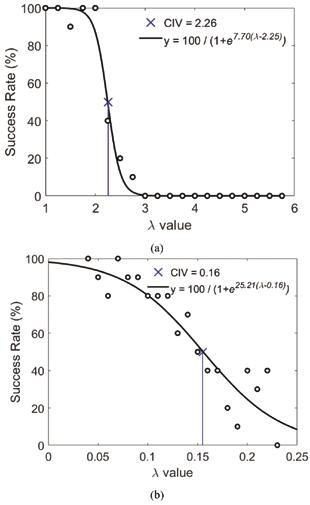
Figure 4 (above): Success rate of subject over a range of parameter values for the (a) first-order CST and (b) second order CST. The best fit line (black) to the data is a sigmoidal curve, displayed in the legend. The critical instability value (CIV) marked by a blue ‘x’ and displayed in the legend of each plot provides the value at which the subject can successfully complete the CST 50% of the time.

Figure 5 (right): (a) Cursor (red) and hand (green) position of a subject during one trial of the first-order CST, along with the predicted hand position (black dotted). (b) optimizing input parameters for the neural network, the red star indicates the network chosen to perform CST in place of a subject. The combination of cursor position and velocity and hand position had the lowest combination of RMSE and standard deviation among the 37 test trials. The abbreviations indicate the information the network was given at time t 1 to predict the hand position at time t 2 (C=cursor, H=hand, p=position, v=velocity, a=acceleration). (c) Three different trials of the neural network performing the CST.

Fig. 5(a) shows the cursor and hand position of a subject from one trial of the (first-order) CST, along with the hand position predicted by the neural network at each subsequent time increment, given the current cursor and hand information. The RMSE between the actual and predicted hand positions was 0.38 for this trial; the overall RMSE of the 37 test trials was 0.37 +/- .17. The bar graphs in Fig. 5(b) show the optimization of the combination of inputs to the network (cursor and hand position, CpHp, cursor position and velocity Cpv, etc.) Fig. 5(c) shows three different trials of the neural network performing the first-order CST.

4. Discussion and Conclusion

A benefit of the CST for studying sensory-motor control is that it challenges both the forward (motor) and the feedback (sensory) pathways of the control loop: successful task execution necessitates the use of sensory feedback about the cursor state in order to generate appropriate hand movements. By varying a single parameter, it can probe a subject’s skill and behavior over a range of task difficulty. Prior to this study, only a first-order version of the CST had been used (Eq. (1)), which in theory requires information about only the cursor position in order to succeed at the task.

Manipulating a system with higher-order dynamics requires additional sensory information about the state of the system, and places a greater demand on sensory-motor performance. As shown by Eqs. (3)-(6), unlike the first-order CST for which ideal performance (i.e., stationary cursor) requires hand movements that depend only on the cursor position and are independent of task difficulty (x[n] = – y[n]), ideal performance at higher-order versions of the CST changes with task difficulty (parameter “a”), and moreover requires additional sensory information about the cursor beyond just its position. In particular, a 2nd order version of CST requires information about cursor position and velocity (Eq. (5)). Consistent with the theoretical predictions stemming from Eqs. (3)-(6), we found empirically that our second-order implementation of the CST was indeed more difficult for a subject to control than was the first-order CST, as evidenced by the much smaller parameter values for which the subject was successful (Fig. 4).

Following derivations analogous to the 2 nd order case, one can readily show that information about cursor position, velocity and acceleration would be necessary for ideal performance at a 3 rd order CST, and 4 th order would require that information plus the change in acceleration (i.e., “jerk”). Hence, higher-order versions of the CST become increasingly more demanding on the sensory feedback necessary to succeed at the task, and the degree to which this sensory information is combined to generate a motor action changes with task difficulty. These results provide some guidance on the possible forms of the transfer functions H m and H s in Fig. 2. In particular, if a subject is able to control an N th -order CST, then the transfer functions must provide accurate estimates about the cursor states required for control (e.g., position, velocity, and acceleration for a 3 rd -order CST). The neural network simulations provided a first step toward modeling sensory-motor control during CST performance. Utilizing behavioral data from a rhesus monkey, we trained a neural net to perform the first-order CST. Interestingly, while in theory the firstorder CST requires sensory information only about the position of the cursor, best performance at the first-order CST by our neural network was achieved utilizing information about the cursor position and velocity, as well as the previous hand position; i.e., the neural network generated the next hand position as

x[n+1] = f{y[n],y[n-1],x[n]}

(7)

Intriguingly, the trained network was unable to perform the second-order CST; our human subject also found the second-order CST much more difficult to perform, requiring additional practice even after having become adept at the first-order CST. Future research will explore what sensory information subjects use to perform the CST, and if/how this changes with task difficulty and the order of the system.

5. Acknowledgements

Funding provided by the University of Pittsburgh Swanson School of Engineering, and NIH R01 HD090125.

6. References

[1] Quick KM, Mischel JL, Loughlin PJ, Batista AP. ``The critical stability task: quantifying sensory motor control during ongoing movement in nonhuman primates.’’ J Neurophysiol 120 5 164 2181 2018

[2] Jex H, McDonnell J, Phatak A. ``A “critical” tracking task for manual control research.’’ IEEE Trans Hum Factors Electron HFE 7: 138 145, 1966. doi : 10.1109/THFE.1966.232660.

[3] Potvin AR, Doerr JA, Estes JT, Tourtellotte WW. Portable clinical tracking-task instru- ment. Med & Bological Eng & Comput 15: 391–7, 1977.

[4] Kondraske GV, Potvin AR, Tourtellotte WW, Syndulko K. A computer-based system for automated quantitation of neurologic function. Biomed Eng IEEE Transactions on 00: 401–414, 1984. [5] Burke MW, Gilson RD, Jagacinski RJ. ``Multi-modal information processing for visual work- load relief,’’ Ergonomics 23: 961–975, 1980.

[6] Ramaekers JG, Kauert G, van Ruitenbeek P, Theunissen EL, Schneider E, Moeller MR. High-potency marijuana impairs executive function and inhibitory motor control. Neuropsychopharmacol 31: 2296–303, 2006.

[7] Kadkade PP, Benda BJ, Schmidt PB, Wall C. ``Vibrotactile display coding for a balance prosthesis.’’ IEEE Transactions on Neural Syst Rehabil Eng 11: 392–9, 2003.