u Demonstrating the antibiofouling property of the Clanger cicada wing with ANSYS Fluent simulations

Demonstrating the antibiofouling property of the Clanger cicada wing with ANSYS Fluent simulations

Brady C. Pilsbury, Paul W. Leu

The Laboratory for Advanced Materials at Pittsburgh, Department of Industrial Engineering

Brady C. Pilsbury Brady Pilsbury is originally from Warren, NJ. His interests in science, writing, and law drive him to become a patent agent.

Dr. Leu is an Associate Professor in the Department of Industrial Engineering and the Department of Mechanical Engineering and Materials Science. He received his BS in Mechanical Engineering at Rice University in 2002, his MS from Stanford University in 2004, and his PhD from Stanford Paul W. Leu, Ph.D. University in 2008. Dr. Leu’s lab research focuses on designing and understanding advanced materials by computational modeling and experimental research.

Significance Statement

Microdroplets released upon coughing, sneezing, or speaking are one source of spread for human viruses. Simulation results illustrate how the introduction of nanostructures inspired by the Clanger cicada wing to a surface can limit microdroplet adhesion and help reduce the spread of pathogens due to contact with surfaces.

Category: Computational Research

Keywords: Nanostructures, Antibiofouling,

ANSYS Fluent

Abstract

The Clanger cicada wing is known to have an antibiofouling effect related to the particular pattern of nanostructures on the wing surface. Understanding the mechanisms that create this effect allows for the development of effective antibiofouling nanostructured surfaces, which can help reduce the spread of pathogens. Water repellency is well established as one such mechanism, which this study seeks to validate with the use of water droplet simulations conducted in ANSYS Fluent. The 2D simulations show how the addition of Clanger cicada wing inspired nanostructures to a flat surface impacts surface hydrophobicity and water droplet contact angle hysteresis. A pre-existing empirical dynamic contact angel model was implemented to capture differences in contact angle hysteresis between the flat and nanostructured surface. The application of such a model to a nanostructured surface has not been previously attempted within ANSYS Fluent. The water droplet achieved a greater contact angle and lower contact angle hysteresis on the nanostructured surface when compared to the flat control, indicating that the drop entered the Cassie-Baxter state and would roll off the surface at low incline angles. These results support the repellence of microdroplets containing pathogens as one mechanism through which the Clanger cicada wing achieves a strong antibiofouling effect.

1. Introduction

The wings of insects like the Clanger cicada (Psaltoda claripennis) have been observed to have highly hydrophobic and antibiofouling properties due to the presence of nanopatterns on the surface of their wings [1]. The behavior of microdroplets on such nanopatterned surfaces has implications for public health, since viruses and other pathogens can be transferred through microdroplets. Surfaces designed to strongly repel and roll off microdroplets can help reduce the spread of pathogens.

The water repellency of a surface is often characterized by a water droplet contact angle measurement. This angle refers to the angle formed by the gas-liquid and solid-liquid interfaces at the points along the bottom edge of the droplet where all three phases meet. Convention dictates that a surface is hydrophilic when its contact angle is less than 90°, hydrophobic when the contact angle is greater than 90°, and superhydrophobic when the contact angle exceeds 150° [2]. Nanoscale surface roughness can allow a droplet to enter the Cassie-Baxter state, which is characterized by the droplet resting atop protrusions from the surface and bridging over lower elevation regions of the surface instead of penetrating them [2]. Water droplets in the Cassie-Baxter state tend to have a high contact angle, low contact angle hysteresis, and an associated low run off angle [2]. Contact angle hysteresis refers to the

variation in the contact angle of droplets as they move laterally across a surface [2]. Figure 1 shows a generic water droplet in the Cassie-Baxter state when atop a surface containing nanopillars and displays how the contact angle is typically measured.

Figure 1. Shows a generic water droplet suspended above a set of nanopillars in the Cassie-Baxter state with the characteristic high contact angle.

Surfaces on which water droplets reside in the Cassie-Baxter state are expected to make good antibiofouling surfaces. Microdroplets that cannot penetrate into the nanostructures will tend to roll off without leaving residual liquid behind, limiting the ability of any bacteria or viruses present in the droplets to proliferate on the surface. This project seeks to demonstrate the anti-biofouling nature of the Clanger cicada wing by simulating the impact of water droplets onto an array of nanopillars inspired by the cicada wing’s nanopattern. Results were obtained through 2D simulations using the Volume of Fluid (VOF) model in ANSYS Fluent.

Previous research has used the VOF model in ANSYS Fluent to study the impact of adjusting the ratios between height, width, and spacing of nanopillars on droplet wetting behavior [3]. Other researchers have developed and implemented dynamic contact angle models in ANSY Fluent that capture changes in a droplet’s contact angle as it moves across a flat surface [4]. This project builds off previous work by applying a dynamic contact angle model to compare the differences in contact angle hysteresis and general wetting behavior between a flat surface and a nanostructured surface inspired by the Clanger cicada wing. The simulations support the already well-established theory that water droplet repellency is a key mechanism by which the Clanger cicada wing achieves its antibiofouling effect and offer a succinct demonstration of how nanoscale modification of a surface can help yield an antibiofouling effect [1].

2. Methods

2.1 Experimental Set Up

All simulations were completed in 2D using the VOF model implemented in ANSYS Fluent. Each simulation considered a droplet of water 2 µm in diameter initialized as a sphere just above the surface with an initial downward velocity of 0.3 m/s. It is assumed that the general wetting behavior of the droplet scales to larger droplets, though the time-scale for droplet spreading and recoiling likely varies with droplet size. The water droplet had the following material properties: density ρ = 1000 kg/m3, viscosity m = 1 × 10-3 Pa·s, and surface tension s = 7. 20 × 10-2 N/m. Gravity was set to 9.8 m/s2 in the negative y-direction at the beginning of all simulations. 2.2 Simulated Surfaces

The simulations compared the behavior of a water droplet when impacting a flat surface and a nano patterned surface. The nano patterned surface consisted of an array of rectangular pillars 200 nm in height, 60 nm in width, and with 170 nm of space between the center of pillars. These dimensions correspond to the dimensions of the nanostructures found on the Clanger cicada wing, although the rectangular shape of the simulated pillars does not match the rounded cone shape of the pillars on the cicada wing [1]. The flat surface contained no protrusions.

2.3 Dynamic Contact Angle Model

A dynamic contact angle model was used during simulations and compared to a static contact angle model to verify it was functioning as intended.

The dynamic contact angle model is based on the tendency of a generic droplet moving across a surface to see an increase in contact angle on the advancing side of the droplet and a decrease in contact angle on the receding side, as seen in Figure 2.

Figure 2. Schematic of a water droplet rolling across a flat surface, with a greater contact angle on the advancing side of the droplet and lower contact angle on the receding side.

Usually, the effect of droplet motion on contact angle is constrained by a maximum advancing contact angle and a minimum receding contact angle, which form upper and lower bounds around the static contact angle [4]. The values of these angles will depend on the balance of interfacial tensions associated with the water-vapor and water-solid interfaces [2]. For a flat surface, the balance of these tensions is largely determined by the chemical composition of the surface. However, textured surfaces that disrupt the liquid-solid interface will also disrupt the balance of interfacial tensions, yielding equilibrium,

advancing, and receding contact angles that may differ from an otherwise chemically identical flat surface [2]. The range of angles set by the maximum advancing and minimum receding contact angle is often used to characterize the contact angle hysteresis. It is possible for a droplet to achieve a contact angle at any value between the maximum and minimum bounds as it transitions between states of motion. Capturing the dynamic behavior of contact angle within that range can be difficult to simulate, but the ANSYS Act extension developed by Yokoi et. al. captures it with the equations

where qd(Ucl ) = min (q e +(Ca/Ka ), qmda ) if Ucl ≥0 (1) qd(Ucl ) = min (q e +(Ca/Kr ), qmdr ) if Ucl ≤0 (2)

Ca=mU

CL/s

(3) and Ucl is the velocity of the contact line, qd is the dynamic contact angle, q e is the static equilibrium contact angle, qmda is the maximum advancing contact angle, qmdr is the minimum receding contact angle, K a is the advancing material related constant, and K r is the receding material related constant [4]. Ca is the Capillary number and a dimensionless parameter that captures the relative effect of viscous drag forces (numerator) and surface tension or capillary forces (denominator).

Yokoi’s model was designed as an empirical model that retroactively fits itself to experimental data. This limits the applicability of the model, but still allows for fair analysis of the general impact that nanostructures have on contact angle hysteresis. For the purposes of this simulation, the static contact angle was set at 90°, the maximum advancing angle at 114°, the minimum receding angle at 52°, K a at 9 x 10-9, and K r at 9 x 10-8 in order to best match the experimental results found by Yokoi et al. for a water droplet on a chemically treated silicon surface [4]. This limits the applicability of any values calculated during the simulation to specialized silicon wafers, but the general effect of the nanostructures is applicable to a broader range of chemical substrates.

The dynamic contact angle model was tested against a static contact angle model in which the static contact angle was set at 90°, equivalent to the static equilibrium contact angle in the dynamic model. 2.4 Simulated Conditions

Four test conditions were considered; Model I consisted of the droplet impacting a flat surface with the static contact angle model, Model II considered a flat surface with the dynamic contact angle model, Model III considered the pillared surface with the static contact angle, and Model IV considered the pillared surface with the dynamic contact angle model.

The models were compared based off of the apparent contact angle of the water droplet, which refers to the angle of the liquid-gas interface relative to the horizontal, as opposed to the liquid-solid interface, which, strictly speaking, would become vertical if the liquid partially wrapped around the rectangular nanopillars.

3. Results

It was expected that a greater contact angle and lower contact hysteresis would be observed on the pillared surfaces (Models III and IV for contact angle and lower contact hysteresis, respectively), relative to the flat surface (Models I & II). Since Models I and III used a static contact angle model, they were not expected to show any contact angle hysteresis and instead maintain the same contact angle over the course of the simulation. The approximated advancing, receding, and static apparent contact angles for each Model are shown in Table 1.

Model Advancing Contact Angle

I 90°

II 114°

III

IV 140°

147°

Receding Contact Angle

90°

80°

140°

135°

Static Contact Angle

90°

90°

140°

140°

Table 1 Shows the maximum advancing contact angle, minimum receding contact angle, and static contact angle observed under each model.

Under Model I, the droplet maintained an apparent contact angle of 90° throughout the simulation as it spread and recoiled on the surface, which can be seen in Figure 3.

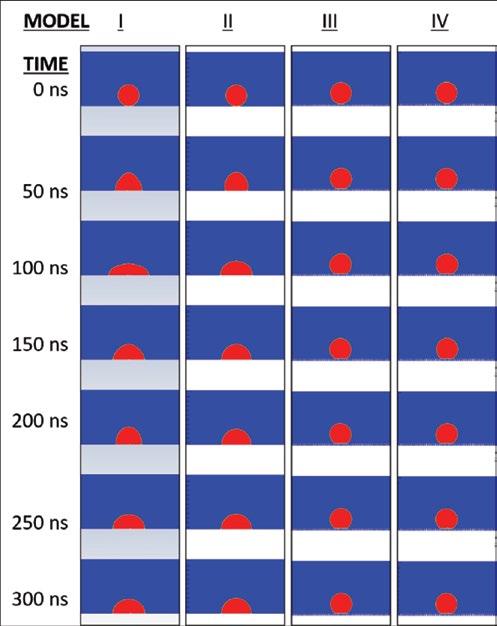
Figure 3. The shape of the droplet under each model is shown in snapshots taken every 50 ns for 300 ns under four model conditions: I – flat surface, static contact angle II – flat surface, dynamic contact angle III – nanopillar surface, static contact angle IV – nanopillar surface, dynamic contact angle

Model II allowed the droplet to achieve an advancing contact angle of 114° as the droplet spread out over the surface, which was occurring after 50 ns. The droplet later reached a receding contact angle of approximately 80° as the droplet recoiled, which was occurring after 100 ns. The dynamic contact angle approached the static equilibrium contact angle of 90° as the droplet came to rest for the rest of the simulation. Under Model III, the droplet achieved an apparent contact angle of 140° and the droplet did not spread across the surface nearly as much as it had on the flat surface. Model IV yielded an identical static contact angle to Model III and saw limited droplet spread over the surface. Model IV also yielded a smaller range of contact angle hysteresis compared to the flat surface in Model II. No new droplet behaviors occurred in any model after 300 ns.

4. Discussion

The droplets simulated on the nanopillars demonstrated behavior characteristic of the Cassie-Baxter state, achieving high contact angles and low contact angle hysteresis. Despite the static contact angle being set to 90° in both Model I and model 3, the apparent contact angle in Model III, when the droplet was on the array of nanopillars, was estimated to be much higher at 140°. Models II and IV implemented the same dynamic contact angle model, but the droplet in Model II had a contact angle that varied by up to 32°, while the droplet on the nanopillars in Model IV maintained a high apparent contact angle with only a 12° difference between its advancing and receding angles. These results can be attributed to the gaps between pillars in Models III and IV disrupting the liquid-solid interface, which limits the droplets overall adhesion to the surface. In turn, this allows cohesive forces to dominate such that a more consistent droplet shape is maintained. The higher apparent contact angle and lower apparent contact angle hysteresis observed on the pillars is in accordance with the typical behavior of droplets in the Cassie-Baxter state, and is strongly associated with a lower run-off angle, meaning that a droplet could slide off of the pillared surface more easily [2]. This feature lends the Clanger cicada wing its self-cleaning and antibiofouling properties.

5. Conclusions

As the risks of antibiotic resistant bacteria and global virus outbreaks have become increasingly pronounced in recent years, there is a heightened importance in understanding how the spread of pathogens can be mitigated. One mechanism to limit the spread of pathogens via surface contact is through the creation of strongly hydrophobic surfaces that strongly repel microdroplets that may contain bacteria or viruses. This antibiofouling effect can be achieved via the fabrication of nanostructures on surfaces that suspend microdroplets in the Cassie Baxter state. In this state, the liquid-solid interface of the droplet is disrupted, weakening the overall adhesion of the droplet to the surface. This weak adhesion is characterized by a high contact angle, low contact angle hysteresis, and a low runoff angle. Simulations conducted in ANSYS Fluent confirmed that the nanostructures of the Clanger cicada wing are capable of drastically increasing the hydrophobicity of a surface while reducing contact angle hysteresis. This mechanism accounts for the strong antibiofouling nature of the Clanger cicada wing and can be applied when fabricating surfaces to inhibit the ability of pathogens to proliferate on them.

6. Acknowledgments

This project was funded by Swanson School of Engineering and the Office of the Provost at the University of Pittsburgh and was conducted under the guidance of Paul W Leu.

7. References

[1] S. Podogin et al. Biophysical Model of Bacterial Cell Interactions with Nanopatterned Cicada Wing Surfaces. Biophysical Journal, 103 (2013) 835-840. https:// doi.org/10.1016/j.bpj.2012.12.046 [Accessed Nov 20,2020]. [2] E. Celia et al. Recent advances in designing superhydrophobic surfaces. Journal of Colloid and Interface Science. 402 (2013) 1-18. https://doi.org/10.1016/j. jcis.2013.03.041 [Accessed Nov 20, 2020]. [3] Z. Yang et al. Numerical Study on Size Effects in the Wettability of Textured Surfaces. IOP Conf. Ser.: Earth Environ. Sci, 252 (2019). http://doi.org/10.1088/17551315/252/2/022105 [Accessed Jan 7, 2021]. [4] K. Yokoi et al. Numerical studies of the influence of the dynamic contact angle on a droplet impacting on a dry surface, Physics of Fluids, 21 (2009). http://doi. org/10.1063/1.3158468 [Accessed: Nov 20,2020].