ZOOLOGIE Le phénoménal rat-taupe nu Logique PARCOURIR L’INFINI AVEC DES ROBOTS Évolution LE MONDE PERDU DES PREMIERS EUCARYOTES Paléoanthropologie L’ARRIVÉE DISPERSÉE D’HOMO SAPIENS SUR LE SOL EUROPÉEN L 13256551 HF: 7,00 €RD DOM : 8,50 € –BEL./LUX. 8,50 € –CH : 12,70 FS –CAN. 12,99 $CA –PORT. CONT. 8,50 € –MAR. 78 DH –TOM 1 100 XPF Édition française de Scientific American –Septembre 2023n° 551 POUR LA SCIENCE 09/23 L’enquête de Delphine del Marmol vétérinaire
LE MONDE (QUANTIQUE) EST-IL IMAGINAIRE ?
3€ * 99


Scanner ce QR Code avec votre téléphone pour commander votre numéro, ou rendez-vous sur boutique.groupepourlascience.fr












Une sélection d’articles rédigés par des chercheurs et des experts À découvrir dans la collection AnthropologieAPPARUE Migrations SE SONT IMPOSÉS EN EUROPE Agriculture DES CÉRÉALES NÉOLITHIQUE LA RÉVOLUTION * Les THEMAS sont maintenant compris dans les formules d’abonnements intégrale et numérique Une lecture adaptée aux écrans 3 Thema SAPIENS l'odyssée l'humanité SOMMAIRE P/04/NOTRE GRANDE FAMILLE BERNARD WOOD P/16/UNE ESPÈCE MOSAÏQUE SILVANA CONDEMI ANNA DEGIOANNI LA NAISSANCE DES CULTURES MODERNES FRANCESCO D’ERRICO P/12/L’ARBRE PHYLOGÉNÉTIQUE HUMAIN P/30/« HOMO SAPIENS » VIEILLIT D’AU MOINS 100 000 ANS FRANÇOIS SAVATIER LA PLUS INVASIVE DES ESPÈCES MAREAN LA CULTURE, MOTEUR DE L’ÉVOLUTION HUMAINE KEVIN LALAND L’HOMME S’EST-IL AUTODOMESTIQUÉ ? HERVÉ LE GUYADER LE JOUR OÙ L’HUMANITÉ A FAILLI DISPARAÎTRE MAREAN P/92/UNE ÉVOLUTION EN MARCHE HAWKS P/35 P/82 Thema-PLS-020-sapiens-sommaire.indd T0 37 p
Directrice des rédactions : Cécile Lestienne
MENSUEL POUR LA SCIENCE
Rédacteur en chef : François Lassagne
Rédacteurs en chef adjoints : Loïc Mangin, Marie-Neige Cordonnier
Rédacteurs : François Savatier, Sean Bailly
HORS-SÉRIE POUR LA SCIENCE
Rédacteur en chef adjoint : Loïc Mangin

Développement numérique : Philippe Ribeau-Gésippe
Community manager et partenariats : Aëla Keryhuel aela.keryhuel@pourlascience.fr
Directrice artistique : Céline Lapert
Maquette : Pauline Bilbault, Raphaël Queruel, Ingrid Leroy, Ingrid Lhande
Réviseuses : Anne-Rozenn Jouble, Maud Bruguière et Isabelle Bouchery
Assistant administratif : Bilal El Bohtori
Responsable marketing : Frédéric-Alexandre Talec
Direction du personnel : Olivia Le Prévost
Fabrication : Marianne Sigogne et Stéphanie Ho
Directeur de la publication et gérant : Nicolas Bréon
Ont également participé à ce numéro : Christian Bizouard, Silvana Condemi, Antoine Kouchner, Maïa Ponsonnet, Teva Vernoux
PUBLICITÉ France
stephanie.jullien@pourlascience.fr
ABONNEMENTS
www.boutique.groupepourlascience.fr
Courriel : serviceclients@groupepourlascience.fr
Tél. : 01 86 70 01 76
Du lundi au vendredi de 8 h 30 à 12 h 30 et de 13 h 30 à 16 h 30
Adresse postale :
Service abonnement groupe Pour la Science
20 rue Rouget-de-Lisle
92130 Issy-les-Moulineaux.
Tarifs d’abonnement 1 an (12 numéros)
France métropolitaine : 59 euros – Europe : 71 euros
Reste du monde : 85,25 euros
DIFFUSION
Contact kiosques : À Juste Titres ; Alicia Abadie
Tél. 04 88 15 12 47
Information/modification de service/réassort : www.direct-editeurs.fr
DISTRIBUTION
MLP
ISSN 0 153-4092
Commission paritaire n° 0927K82079
Dépôt légal : 5636 – Septembre 2023
N° d’édition : M0770551-01
www.pourlascience.fr
170 bis boulevard du Montparnasse – 75 014 Paris
Tél. 01 55 42 84 00
SCIENTIFIC AMERICAN
Editor in chief : Laura Helmuth
President : Kimberly Lau
2023. Scientific American, une division de Springer Nature America, Inc.
Soumis aux lois et traités nationaux et internationaux sur la propriété intellectuelle. Tous droits réservés. Utilisé sous licence. Aucune partie de ce numéro ne peut être reproduite par un procédé mécanique, photographique ou électronique, ou sous la forme d’un enregistrement audio, ni stockée dans un système d’extraction, transmise ou copiée d’une autre manière pour un usage public ou privé sans l’autorisation écrite de l’éditeur. La marque et le nom commercial «Scientific American» sont la propriété de Scientific American, Inc. Licence accordée à «Pour la Science SARL».
© Pour la Science SARL, 170 bis bd du Montparnasse, 75014 Paris.
En application de la loi du 11 mars 1957, il est interdit de reproduire intégralement ou partiellement la présente revue sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20 rue des Grands-Augustins, 75006 Paris).
Origine du papier : Autriche
Taux de fibres recyclées : 30 %

« Eutrophisation » ou « Impact sur l’eau » : Ptot 0,007 kg/tonne
IMAGINAIRE AU NATUREL
Les nombres imaginaires donnent des nombres négatifs quand ils sont élevés au carré. Troublante définition, quand on sait que le carré d’un nombre négatif aussi bien que positif est… positif : (– 2)2 et 22 valent toujours 4. Et cela est vrai, que l’on parle de nombres entiers naturels ou négatifs, de nombres rationnels (qui sont le résultat d’une fraction, comme 0,33 333…) ou encore de nombres irrationnels (comme ou π). Pour les nombres imaginaires… La règle est, donc, différente. Et ce à quoi ils renvoient se distingue aussi.
Il est évident en effet que les entiers naturels se rapportent à ce qui est dénombrable : le titre de cet édito comporte 3 mots. Les entiers relatifs se raccrochent tout aussi aisément à ce dont nous prenons la mesure : une température de 43 °C est excessivement chaude, de – 43 °C excessivement froide. Le lien entre les nombres rationnels et notre réalité se conçoit sans mal : un gâteau d’anniversaire sera coupé en parts représentant 1/8 de sa totalité. Les irrationnels eux-mêmes se ramènent aisément à notre expérience du réel. Tracez un cercle ; sa circonférence est égale à son diamètre multiplié par π.
Et les nombres imaginaires, alors ? Les mathématiciens du XVIe siècle les ont inventés pour résoudre des équations polynomiales. Fort commodes, ils gênaient cependant leurs inventeurs. C’est cette gêne qui conduisit René Descartes à les qualifier… d’imaginaires.
Imprimé en France
Maury Imprimeur SA Malesherbes
N° d’imprimeur : 272 208
Aujourd’hui, les nombres imaginaires semblent enfin avoir trouvé leur place : au sein même du réel. Les physiciens, comme les mathématiciens, les utilisent au quotidien. Mais il est à présent prouvé, à la fois par des travaux théoriques et par leur vérification expérimentale, que la mécanique quantique ne peut expliquer les résultats de certaines expériences si on exclut les nombres imaginaires de son formalisme. Voici les nombres imaginaires installés au cœur de la réalité physique, faisant basculer le réel dans ce qui semblait purement imaginaire aux mathématiciens.
Ces résultats sont susceptibles d’améliorer la compréhension fondamentale de la physique quantique et, par là, de guider le développement des machines et dispositifs de communication quantiques. Des technologies tout sauf imaginaires. n
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 3
DITO É
François Lassagne Rédacteur en chef
ACTUALITÉS GRANDS FORMATS
P. 6
ÉCHOS DES LABOS
• Même minimale, la cellule est capable d’évoluer
• Le défi éthique des neurotechnologies
• Quand les jours ne duraient que dix-neuf heures
• Les microtubules, des capteurs de force
• La chute rare d’un sommet
• Souci chez les quasars ?

• Une bactérie impliquée dans l’endométriose ?
• Un pulsar exotique
P. 16
LES LIVRES DU MOIS
P. 18 DISPUTES ENVIRONNEMENTALES Un Giec du plastique ?
Catherine Aubertin
P. 20
LES SCIENCES À LA LOUPE La course au classement
Yves Gingras
P. 34
BIOLOGIE ANIMALE

LES POUVOIRS
EXTRAORDINAIRES DU RAT-TAUPE NU
Delphine del Marmol
Ce petit rongeur d’aspect singulier présente des propriétés étonnantes qui en font un modèle prometteur pour la recherche sur le vieillissement et le cancer.
P. 42
ZOOLOGIE
QUI ES-TU
RAT-TAUPE NU ?

Marie-Neige Cordonnier
Outre sa remarquable résistance au vieillissement, l’animal arbore de nombreuses caractéristiques surprenantes…
P. 50
PALÉOANTHROPOLOGIE
fr
LETTRE D’INFORMATION

NE MANQUEZ PAS
LA PARUTION DE
GRÂCE À LA NEWSLETTER
• Notre sélection d’articles
• Des offres préférentielles
• Nos autres magazines en kiosque
© Eric Isselee/Shutterstock
Les portraits des contributeurs sont de Seb Jarnot
Ce numéro comporte un courrier de réabonnement posé sur le magazine sur une sélection d’abonnés.
SAPIENS EN EUROPE : TROIS VAGUES VENUES DU LEVANT ?

François Savatier
L'arrivée d'Homo sapiens en Europe : une invasion brutale, exterminatrice pour Néandertal, selon la vision communément admise Mais une autre réalité se profile : la migration aurait progressé en plusieurs vagues.
P. 61
ETHNOLINGUISTIQUE
DES VOIX SURGIES DU FOND DES ÂGES
Anvita Abbi
Une famille de langues en voie de disparition, dans les îles Andaman, suggère que les peuples anciens utilisaient leur corps comme modèle de la réalité.
4 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023
Inscrivez-vous www.pourlascience.fr
551 / Septembre 2023
Édition française Scientific American09/23 LE MONDE (QUANTIQUE) EST-IL IMAGINAIRE ? En couverture :
sakkmesterke/Shutterstock
N°
OMMAIRE s
©
VOTRE MAGAZINE
CAHIER PARTENAIRE PAGES I À III (APRÈS LA P. 46)
par Mieux estimer l’exposition aux radiations du personnel navigant
Parrainé
P. 70
HISTOIRE DES SCIENCES
LE FIN MOT DE PASCAL SUR LES INDIVISIBLES
João Cortese et Dominique Descotes
La richesse de l’écriture du philosophe, dont on fête cette année le quadricentenaire de la naissance, ne saurait se limiter aux Pensées
On découvre encore aujourd’hui l’étendue de sa finesse dans ses écrits mathématiques
P. 22
PHYSIQUE QUANTIQUE
LE MONDE EST-IL IMAGINAIRE ?
RENDEZ-VOUS
P. 78

LOGIQUE & CALCUL

PARCOURIR L’INFINI AVEC DES ROBOTS
Jean-Paul Delahaye

D’intéressants problèmes algorithmiques se posent quand on cherche à piloter des robots pour explorer une grille infinie
P. 84
ART & SCIENCE
Le feu et l’aiguille
Loïc Mangin
P. 88
IDÉES DE PHYSIQUE
Plus haut le jet d’eau
Jean-Michel Courty et Édouard Kierlik
Les nombres imaginaires sont une astuce mathématique étonnamment efficace pour mener des calculs. Mais ils seraient bien plus que cela. Sans eux, la théorie quantique standard est incapable de décrire certaines expériences !
P. 30
MATHÉMATHIQUES
« LA THÉORIE QUANTIQUE RENOUVELLE LA QUESTION DU RAPPORT ENTRE RÉEL PHYSIQUE ET MODÉLISATION
MATHÉMATIQUE »
Entretien avec Frédéric Patras
Les physiciens ont très tôt fait des nombres imaginaires, apparus dès la première moitié du XVIe siècle, de précieux outils mathématiques fondamentaux La mécanique quantique leur attribue désormais un rôle essentiel.
P. 92
CHRONIQUES DE L’ÉVOLUTION
Le monde perdu des premiers eucaryotes
Hervé Le Guyader
P. 96
SCIENCE & GASTRONOMIE
Salades bien relevées
Hervé This
P. 98 À PICORER
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 5
Marc-Olivier Renou, Antonio Acín, Miguel Navascués
MÊME MINIMALE, LA CELLULE EST CAPABLE D’ÉVOLUER
P. 6 Échos des labos
P. 16 Livres du mois
P. 18 Disputes environnementales
P. 20 Les sciences à la loupe
Dans cet ensemble de cellules minimales, vues au microscope électronique, chaque cellule contient moins de 500 gènes et dérive de la bactérie Mycoplasma genitalium
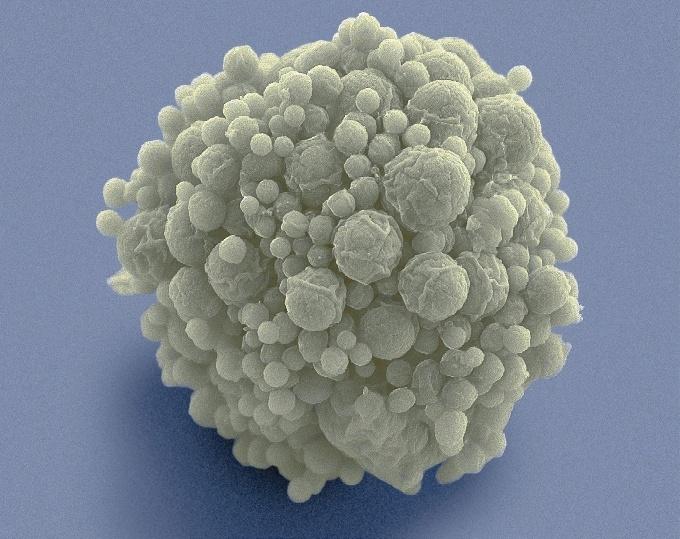
Un organisme dont chaque gène est indispensable à sa survie semble plus vulnérable à une mutation fatale. Pourtant, la nature trouve toujours le moyen de s’adapter !
Qui n’a pas des tournevis en double ou des clés Allen en plusieurs exemplaires dans sa boîte à outils ? C’est parfois pratique : si l’un d’eux se casse ou se perd, on peut quand même finir ses travaux… Cette idée s’applique-t-elle aussi aux gènes ? Par exemple, la plante herbacée originaire du Japon Paris japonica, avec son nombre record de 150 milliards de paires de bases, ne possède pas que des gènes indispensables ou essentiels, si bien qu’une mutation a peu de risque de mettre en péril la survie de l’organisme : des gènes redondants prennent le relais si un gène devient défaillant. Mais en est-il de même pour une cellule dite « minimale », c’est-à-dire
une cellule dont le génome contiendrait seulement les gènes nécessaires à son fonctionnement ? Une seule mutation risquerait de rendre l’un d’eux inopérant et de compromettre le maintien en vie
États-Unis, et son équipe ont voulu tester cette hypothèse.
L’aventure dans la réduction des génomes a commencé dans les années 1990. Le constat que certaines bactéries prospèrent, se multiplient et s’adaptent à des changements de conditions avec des génomes limités à quelques milliers de gènes a inspiré de nombreux généticiens Jusqu’où peut-on réduire le génome d’un organisme qui reste viable et capable de se répliquer ? Craig Venter, cofondateur de l’institut qui porte son nom, à La Jolla, en Californie, a relevé ce défi.
de la cellule. Dès lors, évoluer par mutations successives semble difficile, voire impossible pour un tel organisme. Jay Lennon, de l’université de l’Indiana, aux
En 2016, en partant du génome de Mycoplasma genitalium , une bactérie vivant dans le conduit urinaire humain et présentant seulement 525 gènes , l’équipe a construit JCVI-syn3.0, une cellule synthétique possédant 473 gènes. Chaque gène était ici nécessaire pour garantir la viabilité de l’organisme.
Cet organisme peut-il évoluer ou estil bloqué par sa configuration minimale ?
6 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023
ÉCHOS DES LABOS
BIOLOGIE CELLULAIRE
£
£
La cellule de synthèse JCVI-syn3.0 contient 473 gènes
© Tom Deerinck et Mark Ellisman, du Centre américain de recherche en imagerie et microscopie de l’université de Californie à San Diego
Jay Lennon et ses collègues ont travaillé à partir d’une variante de JCVI-syn3.0, notée JCVI-syn3B, qui inclut une vingtaine de gènes non indispensables mais en facilitent la manipulation . Ils ont d’abord comparé la valeur adaptative de cette souche artificielle avec la bactérie Mycoplasma genitalium d’origine : JCVIsyn3B part avec une capacité relative à se reproduire deux fois plus faible que la souche sauvage. Les chercheurs ont ensuite mené une évolution dirigée en laboratoire, c’est-àdire qu’ils ont laissé les deux souches, artificielle et sauvage, se répliquer sur près de 2 000 générations pendant 300 jours. Premier constat, le rythme de mutation par nucléotide et par génération est équivalent dans les deux cas

Le génome minimal n’a donc pas entravé cette dynamique naturelle de Mycoplasma genitalium. Seconde observation, la cellule de synthèse JCVI-syn3B s’est vite adaptée à son environnement et a exhibé une évolution efficace À la fin de l’expérience, la vitesse de croissance de JCVI-syn3B mutée avait rejoint celle de départ de Mycoplasma genitalium.
Ainsi, les cellules minimales sont tout aussi capables que les autres d’accumuler un grand nombre de mutations pour augmenter leur faculté de se développer. « Jay Lennon et ses collègues ont identifié qu’une partie des gènes mutés au cours de l’évolution dirigée sont impliqués dans la construction de la membrane et dans la division cellulaire, détaille AnneGaëlle Planson, de l’Inrae Ces modifications semblent donc être plus importantes pour la cellule minimale qu’une amélioration de l’acquisition de substrats déjà présents dans l’environnement »
La simplification du génome avec la perte de certains gènes est un phénomène courant dans la nature – on l’observe surtout quand un microorganisme coévolue avec un hôte dans une relation pathogène ou mutualiste Ces nouveaux résultats illustrent comment la réduction du génome n’est pas nécessairement un frein à l’évolution , et même comment, dans certains cas, elle ouvre davantage de pistes pour l’évolution de gènes essentiels , qui dans des conditions moins extrêmes changent beaucoup plus lentement n
Sean Bailly
NEUROSCIENCES
Le défi éthique des neurotechnologies
Le 13 juillet 2023 s’est tenue au siège de l’Unesco, à Paris, une conférence sur l’éthique des neurotechnologies. Hervé Chneiweiss, ancien président du comité international de bioéthique de l’Unesco, nous en décrit les enjeux.
En quoi consistent les neurotechnologies ?
Les neurotechnologies regroupent toutes les techniques qui enregistrent l’activité cérébrale, quelle que soit la forme de cet enregistrement (activité électrique, modification du flux sanguin, etc.), et toutes celles qui modifient l’activité cérébrale. Le potentiel médical, diagnostic et thérapeutique, est très important.
Le cerveau n’est pas un organe comme les autres. Il est à la base de notre identité, de nos états cognitifs, de ce que nous pensons, de nos émotions, etc.
Il se pose donc des questions sur l’atteinte à l’identité personnelle, à la liberté de pensée et d’agir ou à la vie privée (garder ses pensées pour soi).
On trouve par exemple dans le commerce des casques qui aideraient à mieux dormir, ou qui font du « neurofeedback », pour mieux se concentrer. Il n’y a aucune base scientifique pour valider l’e cacité de ces systèmes. Et dans certains cas, les conditions générales d’utilisation demandent que les droits sur les données soient cédés à l’entreprise qui fabrique le casque, et qu’elle puisse partager ces informations avec un tiers.
Faut-il distinguer ici l’usage médical de l’usage non médical ?
Tout à fait. En France, les dispositifs médicaux sont réglementés et soumis à la surveillance de l’ANSM (l’Agence nationale de sécurité du médicament et des produits de santé). Dans toute procédure de soin, il y a toujours une dimension éthique. Ce n’est donc pas nouveau.
En ce qui concerne les usages non médicaux, on entre dans un tout autre monde où les entreprises peuvent faire à peu près ce qu’elles veulent. C’est un peu le Far West. La recherche privée a déjà investi plus de 40 milliards d’euros et on prévoit que dans la prochaine décennie, c’est au moins la même somme qui sera injectée.
Il y a donc urgence à établir des garde-fous éthiques…
Les scientifiques n’ont pas attendu qu’Elon Musk investisse 1 milliard
de dollars dans Neuralink ou que la FDA (la Food and Drug Administration, l’administration américaine des denrées alimentaires et des médicaments) lui donne une autorisation pour mener des essais cliniques chez l’humain. Ils y réfléchissent depuis longtemps et sensibilisent les États. Le rapport de 2021 de l’Unesco était déjà l’aboutissement d’un long cycle de réflexion.
La série de conférences de cette année porte sur une question précise : « Les neurotechnologies remettent-elles en question les droits de l’homme ? » Il y a deux écoles. La première, menée par la fondation Neurorights, du neurobiologiste Rafael Yuste, de l’université Columbia, a rme que oui, il faut inventer de nouveaux droits de l’homme, parce que la vie privée cognitive n’est pas garantie par les traités actuels et la charte des Nations unies. Le Comité international de bioéthique de l’Unesco est d’avis que la vie privée cognitive est une forme de vie privée et la liberté de pensée est déjà garantie par les droits de l’homme. Néanmoins, ces traités et lois ont été écrits avant et hors du contexte du développement des neurotechnologies. Il y a donc un travail à mener pour réa rmer les « neurodroits » dans ces textes.
Au niveau des États, certains cadres ont-ils déjà été mis en place ?
Le Chili est le premier pays à avoir inscrit la liberté cognitive dans sa constitution. Les spécialistes sont très intéressés de voir comment certains cas concrets vont être confrontés à cette constitution. Quelques pays comme l’Espagne ou le Japon se penchent sérieusement sur le sujet. Dans ce contexte, les traités internationaux sont importants. Il faut que des organismes comme l’Unesco et l’OCDE (l’Organisation de coopération et de développement économiques) émettent des recommandations (on parle de soft law, en anglais) et que cela se traduise par des lois dans les États (hard law).
Rapport de l’Unesco sur l’éthique des neurotechnologies de 2021. bit.ly/PLS551_Unesco
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 7
HERVÉ CHNEIWEISS Neurologue à l’Inserm
Propos recueillis par Sean Bailly
R. Z. Moger-Reischer et al., Nature, 2023.
GÉOSCIENCES
QUAND LES JOURS NE DURAIENT QUE DIX- NEUF HEURES
La durée du jour s’est allongée au cours de l’histoire de la Terre. Mais il y a entre 2 et 1 milliard d’années, elle aurait stagné autour de dix-neuf heures.
Cela semble évident : sur Terre, la durée d’une journée est d’environ vingt-quatre heures. Mais il n’en a pas toujours été ainsi. La longueur du jour dépend de la vitesse de rotation terrestre : plus celle-ci est élevée, plus les journées sont courtes. En moyenne, la vitesse de rotation de la planète diminue avec le temps, en raison de la « friction » liée aux forces de marée qui s’exercent entre la Terre et la Lune. La durée du jour s’allonge donc depuis des milliards d’années. Mais cet accroissement est-il progressif ou par paliers successifs ? Les derniers travaux de Ross Mitchell, de l’Académie chinoise des sciences, et Uwe Kirscher, de l’université de Tübingen, en Allemagne, penchent en faveur de la seconde hypothèse.
Les chercheurs ont utilisé les données de 22 études cyclostratigraphiques , qui permettent d’étudier l’évolution des paramètres de la rotation terrestre ( les cycles de Milankovitch) dans les dépôts sédimentaires. Comme un paramètre de ces cycles dépend, entre autres, de la vitesse de rotation de notre planète, ils en ont déduit la durée du jour au cours de l’histoire de la Terre D’après leurs résultats, celle-ci s’est allongée de façon régulière jusqu’à il y a 2 milliards d’années, puis a stagné à une valeur d’environ dix-neuf heures au milieu du Protérozoïque, avant de reprendre son augmentation il y a 1 milliard d’années.
Pour expliquer cette stabilisation pendant 1 milliard d’années, Ross Mitchell et Uwe Kirscher invoquent l’accélération provoquée par les effets de marée exercés par le Soleil sur l’atmosphère terrestre En effet, alors que les marées océaniques lunaires (les marées au sens courant) ont tendance à faire diminuer la vitesse de rotation terrestre, les marées atmosphériques solaires, qui s’expliquent surtout par l’effet du réchauffement cyclique des masses d’air par le Soleil, ont tendance à l’accroître À l’heure actuelle, l’effet de la Lune est plus grand que celui du Soleil : la rotation de la Terre ralentit lentement mais sûrement.
Cependant, sur la période de 1 milliard d’années identifiée par les deux chercheurs, la rotation de la Terre étant plus rapide, la « friction » avec la Lune était plus faible De plus, à
Actuellement, la durée du jour est de vingt-quatre heures. Mais, par le passé, la planète tournait plus vite sur elle-même et les jours étaient plus courts.
la suite de la Grande Oxygénation, il y a environ 2,3 milliards d’années, de grandes quantités d’ozone se seraient accumulées dans la stratosphère Elles auraient amplifié l’effet des marées solaires. Ces dernières auraient alors compensé l’effet des marées lunaires, expliquant la stabilité observée.
La période concernée correspond à ce que les géologues appellent « le milliard ennuyeux », au cours duquel la vie a peu évolué, ce qui pourrait notamment concorder avec cette stagnation de la durée du jour À partir d’il y a 1 milliard d’années, quand la durée du jour a recommencé à augmenter (peut-être à la faveur de modifications atmosphériques), les journées plus longues ont permis une photosynthèse bactérienne plus soutenue, et donc une seconde accumulation de dioxygène dans l’atmosphère, nécessaire à l’émergence de la vie pluricellulaire. n
Nicolas Butor
8 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 ÉCHOS DES LABOS © Nasa/Noaa/Suomi NPP –VIIRS
R. N. Mitchell et U. Kirscher, Nature Geoscience, 2023.
La drosophile comptable
Comme l’abeille, la drosophile est capable d’évaluer des quantités d’objets. Mercedes Bengochea, de l’Institut du cerveau, à Paris, et ses collègues ont montré que cette mouche sait comparer des nombres et a une préférence pour les plus grandes valeurs. Les chercheurs ont ensuite identifié les neurones du lobe optique impliqués dans cette activité.
Or ces mêmes neurones interviennent aussi dans les comportements sociaux. Il est important de savoir compter ses amis et ses ennemis !
Cell Reports, 14 juillet 2023.
Prothèses dentaires uniques
Une équipe de l’Inrap a récemment fouillé l’ancien site de l’église Saint-Genès, à Clermont-Ferrand. Elle a notamment découvert le squelette d’une femme qui présentait des prothèses dentaires sur les deux incisives centrales de l’os maxillaire. Ces dents de substitution se composent d’un pivot métallique dans la dent et d’une couronne artificielle. Cas unique illustrant un procédé décrit par un chirurgien-dentiste, Pierre Fauchard, dans son Traité des dents, de 1746. Inrap, 1er août 2023.
La pollution néfaste pour l’œil
Le glaucome est la deuxième cause de cécité dans le monde.
En suivant une cohorte de 683 personnes pendant dix ans, Laure Gayraud, de l’Inserm, et ses collègues ont constaté un amincissement accéléré de la couche des fibres nerveuses de la rétine, caractéristique de cette maladie neurodégénérative, chez les individus les plus exposés à une pollution atmosphérique aux particules fines. Et ce même avec des niveaux d’exposition inférieurs aux seuils réglementaires de l’Union européenne. Environmental Research, 21 juin 2023.
BIOLOGIE VÉGÉTALE
DES FLEURS SOUS TERRE
Les chercheurs l’ont baptisé Pinanga subterranea, car ce palmier a la particularité de former ses fleurs et ses fruits parfois jusqu’à 10 centimètres de profondeur. Il a été découvert par hasard en 1997 par Paul Chai, ancien botaniste du service des forêts en Malaisie. On connaît 171 espèces de plantes à fleurs dont les fleurs ou les fruits poussent sous terre. On suppose que c’est pour se protéger de la chaleur ou encore des herbivores. Mais comment une plante à fleurs peut-elle être pollinisée et disséminer ses fruits lorsque ses organes sont exclusivement sous terre ?
Agusti Randi , botaniste à la fondation Natural Kapital de Pontianak, à Bornéo, et à l’université de Singapour, et une équipe des Jardins botaniques royaux de Kew, en GrandeBretagne , ont découvert qu’un cochon sauvage, le cochon barbu (Sus barbatus), creusait et mangeait les fruits rouges du palmier La dissémination des graines est assurée, mais la pollinisation reste mystérieuse « Même si la famille des palmiers est très étudiée , on en sait très peu sur les pollinisateurs de chacune des 2 500 espèces connues, et encore moins en ce qui concerne les 140 espèces de Pinanga » , précise Sidonie Bellot , botaniste aux Jardins botaniques royaux de Kew « Une
MATHÉMATIQUES ET UN 9e NOMBRE DE DEDEKIND 2

C’est au terme de plusieurs années de recherche et de 1 500 heures de calculs que Lennart Van Hirtum, de l’université de Paderborn, en Allemagne, Patrick De Causmaecker, de KU Leuven, en Belgique, et leurs collègues ont calculé ce « neuvième nombre de Dedekind ».
Introduit par Richard Dedekind en 1897, le n-ième nombre de Dedekind est tout simplement le décompte des fonctions booléennes monotones avec n termes en entrée. Une fonction booléenne prend en entrée une liste de « vrai » et de « faux » et restitue une sortie unique « vrai » ou « faux » Ces fonctions sont dites « monotones » si , lorsqu’une entrée change de faux à vrai, la sortie ne peut pas passer de vrai à faux
des hypothèses est l’autofécondation, avance Benedikt Kuhnhäuser, collègue de la chercheuse Elle est d’autant plus probable vu la proximité des fleurs mâles et femelles, mais reste à vérifier par des analyses anatomiques et génétiques. »
Cette espèce étonnante, nouvelle pour la science, est en fait bien connue des habitants locaux qui en consomment les fruits depuis des décennies quand ils arpentent les forêts. La recherche a parfois un temps de retard… n
 Isabelle Bellin
Isabelle Bellin
Ces nombres deviennent vite difficiles à calculer, ils croissent double-exponentiellement – à peu près à vitesse 22n Avec la puissance grandissante des supercalculateurs et les progrès en mathématiques, environ tous les trente ans un nouveau terme de la suite est trouvé. Le dernier en date avait été calculé en 1991. n
Charlotte Mauger
L. Van Hirtum et al., en ligne sur arXiv, 2023.
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 9
EN BREF
86 386 577 668 298 411 128 469 151 667 59 8 498 812 366.
Ce palmier Pinanga subterranea, à Bornéo, a la particularité de produire des fleurs et des fruits cachés dans le sol, sous la surface.
©
A. Randi et al., Palms, 2023 ; B. G. Kuhnhäuser et al., Plants, People, Planet, 2023.
Agusti Randi (en haut) ; © satoshi takahata/Shutterstock (en bas)
Le monde est-il imaginaire ?
Les nombres imaginaires sont une astuce mathématique étonnamment efficace pour mener des calculs. Mais ils seraient bien plus que cela. Sans eux, la théorie quantique standard est incapable de décrire certaines expériences !

22 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 PHYSIQUE
QUANTIQUE
L’ESSENTIEL
> Les nombres imaginaires et leur généralisation, les nombres complexes, ont pendant longtemps été considérés comme un outil pour simplifier les calculs.
> Toute la physique classique peut se formuler sans les nombres complexes, ainsi qu’une partie de la physique quantique. Certains scientifiques pensaient que cela pouvait s’étendre à tout
le formalisme de la théorie quantique standard.

> De récentes expériences ont mis à l’épreuve cette idée et montrent, au contraire, que ces nombres sont indispensables à la théorie quantique standard.
LES AUTEURS
MARC-OLIVIER
RENOU
physicien au centre Inria de Saclay et à l’École polytechnique
ANTONIO ACÍN directeur de recherche à l’Institut des sciences photoniques à Castelldefels, en Espagne


MIGUEL NAVASCUÉS directeur de recherche à l’Institut d’optique quantique et d’information quantique à Vienne, en Autriche

POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 23 © Andrea Ucini
Certaines questions étonnantes peuvent conduire à des réflexions profondes sur la nature des choses. Il y a trois ans , deux d’entre nous , Antonio Acín et Marc-Olivier Renou, discutaient dans un bureau à l’Institut des sciences photoniques, près de Barcelone. « Il y a un sujet dont je voulais parler avec toi, a commencé Antonio, c’est un problème que Miguel [ Navascués ] et moi essayons de résoudre depuis des années. La théorie quantique standard peut-elle fonctionner sans les nombres imaginaires ? »
Quand on multiplie par lui-même (on dit aussi « mettre au carré ») un nombre réel, qu’il soit positif ou négatif, le résultat est toujours positif Cette opération ne produit jamais un nombre négatif, et pourtant certains problèmes algébriques semblaient requérir l’impossible Les mathématiciens ont alors trouvé de façon spécifique des nombres qui , mis au carré , donnent un résultat négatif. Ces nombres, dits « imaginaires » , et leur généralisation , les nombres complexes, se sont imposés dans tous les domaines des mathématiques, car ils ont ouvert de nouveaux champs de recherche et facilitent la résolution de diverses questions difficiles. Les physiciens les ont aussi adoptés, car ils simplifient les calculs Mais très vite, les scientifiques se sont interrogés sur la nature des nombres complexes De la même façon que l’on considère que les nombres entiers ont une certaine réalité dans la mesure où ils sont utilisés pour énumérer des objets physiques , qu’en est-il des nombres complexes ? Sont-ils juste un outil pour alléger les opérations, ou sont- ils davantage ? Peut- on s’en passer ou sont-ils indispensables ?
LES NOMBRES COMPLEXES, INDISPENSABLES ?
Toute la physique classique peut se formuler sans les complexes. Ils ne seraient donc qu’une aide de calcul Mais du côté de la mécanique quantique, la situation n’est pas aussi claire La version la plus courante de la théorie repose sur les nombres complexes. Mais si nous nous limitons aux nombres réels, nous obtenons une nouvelle théorie physique : la théorie quantique réelle Au cours de la première décennie du XXIe siècle, plusieurs équipes ont montré que cette version « réelle » de la théorie quantique était capable de modéliser correctement les résultats d’une vaste classe d’expériences quantiques. Ces résultats ont conduit de nombreux scientifiques à penser que la théorie quantique réelle était en mesure de décrire n’importe quelle expérience quantique. Le choix de travailler avec des nombres complexes plutôt qu’avec des nombres réels ne reposerait donc pas sur une nécessité physique :
Champ magnétique oscillant (rouge)
Champ électrique oscillant (jaune)
La lumière est représentée par des champs électrique et magnétique complexes en rotation
La lumière est composée d’un champ électrique et d’un champ magnétique qui oscillent. La théorie de l’électromagnétisme fait appel à des nombres complexes pour décrire la lumière.
il s’agissait simplement d’une question de commodité mathématique
Pourtant, cette conjecture n’a pas été prouvée Pouvait-elle être fausse ? Après cette discussion dans le bureau d’Antonio Acín, nous avons lancé un projet de plusieurs mois pour réfuter la théorie quantique réelle. Nous avons fini par trouver une expérience quantique pour laquelle les modèles quantiques réels ne sont pas capables d’expliquer les résultats Notre découverte implique que les nombres imaginaires sont un ingrédient essentiel de la formulation standard de la théorie quantique : sans eux, la théorie perdrait une partie de son pouvoir prédictif. Qu’est-ce que cela signifie ? Cela suggère - t- il que les nombres imaginaires existent d’une manière ou d’une autre ? Cela dépend du sérieux avec lequel on prend l’idée que les éléments de la théorie quantique standard , ou de toute autre théorie physique , « existent » et qu’ils ne sont pas simplement des recettes mathématiques pour décrire des observations expérimentales et faire des prédictions.
RIVALITÉS MATHÉMATIQUES
L’histoire des nombres complexes a commencé au début du XVI e siècle , lorsque le mathématicien italien Antonio Maria del Fiore a provoqué en duel le professeur Niccolò Fontana « Tartaglia » (le bègue). À l’époque, en Italie, il était possible de défier un professeur de mathématiques dans un « duel mathématique », et si on l’emportait, on récupérait le poste de son adversaire En conséquence, les mathématiciens avaient tendance à garder leurs découvertes pour eux, ne déployant leurs théorèmes, corollaires et lemmes que pour gagner des batailles intellectuelles
Ce texte est une adaptation de l’article Imaginary universe, publié par Scientific American en avril 2023.
Sur son lit de mort, le mentor de Fiore, Scipione del Ferro, avait donné à son disciple une formule pour résoudre les équations de la forme x3 + ax = b, également connues sous le nom d’« équations cubiques » . Fort de la
24 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 PHYSIQUE QUANTIQUE LE MONDE EST-IL IMAGINAIRE ? Sauf mention contraire, les illustrations sont de Jen Christiansen
Propagation de la lumière
technique de son maître, Fiore présenta trente équations cubiques à Tartaglia et le mit au défi de trouver la valeur de x dans chaque cas
Or Tartaglia découvrit la formule peu de temps avant le concours Il résolut les problèmes et remporta le duel. Plus tard, il confia sa formule au médecin et scientifique Jérôme Cardan (Gerolamo Cardano en italien), qui lui promit de ne jamais la révéler à quiconque Malgré son serment, Cardan trouva une preuve de la formule et la publia sous son nom La formule compliquée contenait deux racines carrées (l’opération inverse de mettre au carré), de sorte qu’il était entendu que, si les nombres à l’intérieur des racines étaient négatifs, l’équation n’aurait pas de solution, car il n’existe pas de nombres réels qui, au carré, produisent un nombre négatif
Au milieu de ces intrigues, un autre savant, Rafael Bombelli, fit l’une des découvertes les plus célèbres de l’histoire des mathématiques. Il trouva des équations cubiques dont il connaissait des solutions et pour lesquelles la formule de del Ferro-Tartaglia-Cardan exigeait néanmoins le calcul de la racine carrée d’un nombre négatif dans une étape intermédiaire Bombelli comprit qu’il était possible de mener le calcul à son terme avec la formule en admettant qu’il existe un nouveau type de nombre dont le carré est égal à – 1. En supposant que les variables de la formule étaient de la forme a + √ –1 × b, où a et b sont des nombres « normaux » alors les termes multipliés par √ –1 finissent par s’annuler, et le résultat est la solution « normale » de l’équation.
Au cours des siècles suivants, les mathématiciens ont étudié les propriétés des nombres de la forme a + √–1 × b, appelés « complexes » Au XVIIe siècle, Descartes a introduit la notation i = √–1, le nombre « imaginaire », pour l’opposer aux nombres normaux, qu’il nommait « réels » Les mathématiciens utilisent encore cette terminologie aujourd’hui
Les nombres complexes se sont révélés être un outil fantastique , non seulement pour résoudre des équations, mais aussi pour simplifier les mathématiques de la physique classique, c’est-à-dire la physique développée jusqu’au XXe siècle L’électromagnétisme et la compréhension classique de la lumière en sont un exemple. Il est plus commode de décrire la lumière comme des champs électriques et magnétiques complexes en rotation que comme des champs réels oscillants, bien qu’il n’existe pas de champ électrique imaginaire (voir la figure page 24) De même, les équations qui reproduisent le comportement des circuits électroniques sont plus faciles à résoudre si l’on prétend que les courants électriques ont des valeurs complexes, et il en va de même pour les ondes gravitationnelles.
Avant le XXe siècle, toutes ces opérations avec des nombres complexes étaient surtout
considérées comme des astuces mathématiques. Dans tous les cas, les termes imaginaires finissent par disparaître et les grandeurs physiques et mesurables (températures, positions des particules, champs, etc.) sont des nombres réels, des vecteurs ou des fonctions réelles. La mécanique quantique, une théorie physique introduite au début du XXe siècle pour comprendre le monde microscopique, allait radicalement remettre en cause cette situation.
UNE PRÉSENCE QUI IRRITE
Dans la théorie quantique standard, l’état d’un système physique est représenté par un vecteur de nombres complexes, nommé « fonction d’onde » Dès le départ, ce recours aux nombres complexes est allé à l’encontre des convictions profondes selon lesquelles les théories physiques doivent être formulées en termes de grandeurs réelles Erwin Schrödinger, auteur de l’équation de Schrödinger, qui régit l’évolution de la fonction d’onde, a été l’un des premiers à exprimer le mécontentement général de la communauté des physiciens Dans une lettre adressée au physicien Hendrik Lorentz le 6 juin 1926, Schrödinger a écrit : « Ce qui est désagréable ici, et en fait directement contestable, c’est l’utilisation de nombres complexes Il est certain que Ψ [la fonction d’onde] est fondamentalement une fonction réelle » Au début, le malaise de Schrödinger semblait simple à résoudre Le physicien a reformulé la fonction d’onde en remplaçant un seul vecteur de nombres complexes par deux vecteurs réels. Schrödinger insistait sur le fait que cette version était la « vraie » théorie et que les nombres imaginaires n’étaient qu’une simple commodité Depuis, les physiciens ont trouvé
QUE SONT LES NOMBRES IMAGINAIRES ?
Un nombre « imaginaire », quand on le multiplie par lui-même, donne un résultat négatif. Les nombres complexes combinent un nombre imaginaire et un nombre réel. Les nombres réels incluent les nombres rationnels (qui s’écrivent comme le rapport de deux nombres entiers) et les nombres irrationnels (qui ne peuvent pas s’écrire de cette façon). Les entiers (positifs, négatifs, avec le zéro) sont un sous-ensemble des nombres rationnels. Les entiers naturels sont les nombres entiers positifs.
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 25
£
Les physiciens ont adopté les nombres complexes car ils simplifient les calculs £
Nombres complexes Nombres imaginaires Nombres réels Nombres irrationnels Nombres rationnels Entiers Entiers naturels
encore d’autres moyens de réécrire la mécanique quantique en se fondant uniquement sur les nombres réels Mais aucune de ces alternatives ne s’est jamais imposée. La théorie quantique standard, avec ses nombres complexes, dispose d’une règle pratique qui permet de représenter facilement la fonction d’onde d’un système quantique composé de nombreuses parties indépendantes, une caractéristique qui fait défaut à ces autres versions.
Que se passe-t-il alors si nous limitons les fonctions d’onde aux nombres réels et conservons la règle quantique habituelle pour composer des systèmes avec de nombreuses parties ?
À première vue, pas grand-chose Lorsque nous exigeons que les fonctions d’onde et les opérateurs aient des entrées réelles, nous obtenons ce que les physiciens appellent souvent la « théorie quantique réelle », qui est très similaire à la théorie quantique standard : si nous vivions dans un monde quantique réel, nous pourrions encore effectuer des calculs quantiques, nous envoyer des messages secrets en échangeant des particules quantiques et téléporter l’état physique d’un système subatomique sur des distances intercontinentales
Toutes ces applications sont fondées sur les caractéristiques contre-intuitives de la théorie quantique, telles que les superpositions, l’intrication et le principe d’incertitude, qui sont toujours présentes dans la théorie quantique réelle. Parce que cette formulation incluait ces caractéristiques quantiques incontournables, les physiciens ont longtemps supposé que l’utilisation de nombres complexes dans la théorie quantique était fondamentalement une question de commodité, et que la théorie quantique réelle était tout aussi valide que la théorie quantique standard En ce matin d’automne 2020, dans le bureau d’Antonio Acín, nous avons commencé à nous demander si cela était vrai
L’EFFICACITÉ DU TEST DE BELL
Pour réfuter la théorie quantique réelle, nous devions concevoir une expérience dont les prédictions seraient différentes dans les deux théories Pour cela, nous nous sommes appuyés sur un précédent historique.
Bien qu’il soit l’un des fondateurs de la théorie quantique, Albert Einstein n’a jamais cru que notre monde était aussi contre-intuitif que la théorie le suggérait. Il pensait que même si la théorie quantique faisait des prédictions exactes, elle devait cacher une théorie plus profonde dans laquelle ses particularités apparemment paradoxales seraient résolues et cette théorie serait « classique » (c’est-à-dire que l’état physique d’une particule élémentaire serait entièrement déterminé et ne serait pas fondé sur des probabilités).
Nous savons aujourd’hui que l’intuition d’Einstein était erronée, car toutes les théories
classiques de ce type ont été falsifiées En 1964, le physicien John Bell a montré que certains effets quantiques ne pouvaient être décrits par aucune théorie classique. Il a imaginé une catégorie d’expériences , aujourd’hui nommées « tests de Bell », qui implique deux protagonistes, Alice et Bob, travaillant dans des laboratoires distincts. Une personne située dans un troisième lieu envoie à chacun d’eux une particule qu’ils mesurent indépendamment. Bell a prouvé que dans toute théorie classique aux propriétés bien définies (le type de théorie qu’Einstein espérait voir s’imposer), les résultats de ces mesures obéissent à certaines conditions, connues sous le nom d’inégalités de Bell. Ensuite, John Bell a prouvé que ces conditions sont violées dans certaines configurations, où Alice et Bob mesurent un état quantique particulier dans lequel les particules sont dites « intriquées ». La propriété importante est que les inégalités de Bell sont valables pour toutes les théories classiques auxquelles on peut penser, aussi alambiquées soient-elles Par conséquent, des expériences dont les résultats violent cette inégalité suffisent à réfuter toutes ces théories
Divers tests de Bell réalisés en laboratoire depuis lors ont permis de mesurer exactement ce que prédit la théorie quantique. En 2015, des expériences de Bell effectuées à Delft, aux Pays-Bas, à Vienne, en Autriche, et à Boulder, au Colorado, ont réussi à le faire, tout en comblant les lacunes que les projets précédents avaient laissées ouvertes Ces résultats ne nous disent pas que notre monde est quantique ; ils prouvent plutôt que, contrairement à ce que pensait Einstein, il ne peut être régi par la physique classique
Pourrait - on concevoir une expérience similaire à celle de Bell qui exclurait la théorie quantique fondée sur les nombres réels ? Pour relever ce défi, nous avons d’abord dû imaginer une expérience standard de théorie quantique dont les résultats ne peuvent pas être décrits par les mathématiques de la théorie quantique réelle Cette expérience de pensée ( gedankenexperiment ) devait ensuite être
26 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 PHYSIQUE QUANTIQUE LE MONDE EST-IL IMAGINAIRE ?
Les physiciens ont longtemps pensé que la théorie quantique réelle était irréfutable £
THÉORIE COMPLEXE OU RÉELLE ?
Pour savoir si les nombres complexes sont indispensables à la théorie quantique, les physiciens ont imaginé une expérience qui a ensuite été réalisée en laboratoire. Dans cette expérience, deux sources émettent des photons (les particules de lumière) vers trois observateurs : Alice, Bob et Charlie. En reproduisant l’expérience un grand nombre de fois, les chercheurs obtiennent des statistiques sur les mesures. Par ailleurs, ils montrent que ces statistiques sont impossibles à décrire par la théorie quantique réelle.
Théorie quantique complexe
Photons intriqués
Source de photons 1
Source de photons 2
Théorie quantique réelle
Source arbitraire
Source arbitraire
Alice mesure la direction de la polarisation
Bob fait une mesure combinée
Charlie mesure la direction de la polarisation
Mesure arbitraire
Mesure arbitraire
Mesure arbitraire Particules intriquées
Statistiques cumulées des mesures
Opération répétée de nombreuses fois
Peu importe la description de l’expérience dans le cadre de la théorie quantique réelle, il est impossible d’obtenir les statistiques dérivées de la théorie complexe.
mise à l’épreuve en laboratoire pour voir si les mesures confirmaient les prédictions de la théorie standard Avec ce projet, nous espérions convaincre de façon définitive les plus sceptiques que le monde n’est pas décrit par la version réelle de la théorie quantique.
Notre première idée, la plus simple, était d’essayer d’améliorer l’expérience originale de Bell pour falsifier la théorie quantique réelle Malheureusement, deux études indépendantes publiées en 2008 et en 2009 – l’une par Károly Pál et Tamás Vértesi et l’autre par Matthew McKague, Michele Mosca et Nicolas Gisin –avaient montré que cela ne fonctionnerait pas. Ces chercheurs avaient mis en évidence que la théorie quantique réelle prédisait les mesures de n’importe quel test de Bell possible aussi bien que la théorie quantique standard. Ces résultats ont été un argument fort pour convaincre la plupart des scientifiques que la théorie quantique réelle était irréfutable Il fallait trouver autre chose…
Deux mois après notre conversation, notre petit projet avait rassemblé huit physiciens
théoriciens de Castelldefels, Genève et Vienne
En novembre 2020, nous avons trouvé une expérience dans la théorie quantique standard donnant des résultats qui ne peuvent pas être décrits par la théorie quantique réelle L’idée était d’abandonner le scénario standard de Bell, dans lequel une source unique distribue des particules à plusieurs parties distinctes , et d’envisager une configuration avec plusieurs sources indépendantes. Nous avions observé que, dans un tel scénario, connu des physiciens sous le nom de « réseau quantique », la méthode Pál-Vértesi-McKague-Mosca-Gisin n’est pas en mesure de décrire les résultats expérimentaux prédits par la théorie quantique standard avec les nombres complexes C’était un début prometteur, mais ce n’était pas suffisant : à l’instar de ce que Bell a accompli pour les théories classiques, nous devions exclure l’existence de toute forme de description quantique réelle, aussi subtile et alambiquée soit-elle, susceptible d’expliquer les résultats des expériences sur les réseaux quantiques.
DES SOURCES MULTIPLES
Dans un premier temps, nous avons envisagé des réseaux complexes impliquant six expérimentateurs et quatre sources Finalement, nous avons opté pour une expérience quantique plus simple avec trois expérimentateurs distincts appelés Alice, Bob et Charlie et deux sources de particules indépendantes La première source envoie deux particules de lumière (photons), l’une à Alice et l’autre à Bob ; la seconde envoie des photons à Bob et Charlie. Ensuite , Alice et Charlie choisissent une direction pour mesurer la polarisation de leurs particules, soit « horizontal » soit « vertical », tandis que Bob mesure ses deux particules En répétant cette opération à plusieurs reprises, nous pouvons établir un ensemble de données statistiques montrant la fréquence de corrélation des mesures d’Alice et de Charlie (voir l’encadré ci-contre).
Ensuite, pour s’assurer que les statistiques observées ne pouvaient être décrites par aucun système quantique réel , nous nous sommes appuyés sur un concept puissant connu sous le nom d’« autotest » Celui-ci permet à un scientifique de certifier à la fois un appareil de mesure et le système qu’il mesure Qu’est-ce que cela signifie ? Imaginez un appareil de mesure, par exemple une balance Pour garantir sa précision, il faut la tester avec un étalon de masse certifiée Mais comment certifier cette masse ? Vous devez utiliser une autre balance, qui doit elle-même être certifiée, et ainsi de suite. En physique classique, ce processus n’a pas de fin De façon surprenante, dans la théorie quantique, il est possible de certifier simultanément un système mesuré et un appareil de mesure, comme si la
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 27
balance et la masse à tester vérifiaient mutuellement leur étalonnage.
En gardant à l’esprit l’autotest, notre preuve d’impossibilité s’est déroulée comme suit. Nous avons conçu une expérience dans laquelle, pour n’importe quel résultat de Bob, les statistiques de mesure d’Alice et de Charlie ont autotesté leur état quantique partagé. En d’autres termes, les statistiques de l’une confirment la nature quantique de l’autre, et vice versa. Nous avons constaté que la seule description des dispositifs compatible avec la théorie quantique réelle devait être précisément la version Pál-VértesiMcKague-Mosca-Gisin, dont nous savions déjà qu’elle ne fonctionnait pas pour un réseau quantique Nous sommes donc parvenus à la contradiction que nous espérions : la théorie quantique réelle était falsifiable
DE L’EXPÉRIENCE DE PENSÉE AU LABORATOIRE
Cette prédiction théorique devait encore passer l’épreuve de l’expérience en conditions réelles Or un dispositif en laboratoire n’est jamais parfait et ne reproduit pas exactement l’expérience de pensée idéalisée Ces imperfections allaient-elles laisser une petite fenêtre pour sauver la théorie quantique réelle ? En fait non, nous avons montré que, malgré ces défauts, tant que les statistiques de mesure observées par Alice, Bob et Charlie étaient assez proches de celles de l’expérience de pensée , elles n’en restaient pas moins impossibles à restituer avec des systèmes quantiques réels. Cette situation était très similaire à celle du théorème de Bell : nous avons ainsi défini une « inégalité de Bell » pour la théorie quantique réelle et prouvé qu’elle pouvait être violée par la théorie quantique complexe, même en présence de bruit et d’imperfections Cette inégalité et la prise en compte des conditions réalistes d’une expérience de laboratoire rendaient notre approche testable en pratique . La bonne nouvelle est que , dans le cadre de notre démonstration, la précision expérimentale requise pour falsifier la théorie quantique réelle, bien qu’exigeante, était à la portée des technologies actuelles Lorsque nous avons annoncé nos résultats, nous espérions que ce n’était qu’une question de temps avant que quelqu’un, quelque part, relève le défi.
Cela s’est produit vite Deux mois seulement après avoir rendu notre découverte publique, un groupe d’expérimentateurs de Shanghai a rapporté avoir mis en œuvre notre expérience de pensée avec des qubits supraconducteurs, c’est-à-dire la version quantique des bits d’ordinateur À peu près au même moment, une équipe de Shenzhen nous a aussi contactés pour discuter de l’adaptation de notre expérience avec des systèmes optiques
BIBLIOGRAPHIE
Z. D. Li et al., Testing real quantum theory in an optical quantum network, Physical Review Letters, 2022.
M.-O. Renou et al., Quantum theory based on real numbers can be experimentally falsified, Nature, 2021.
M. Weilenmann et R. Colbeck, Self-testing of physical theories, or, is quantum theory optimal with respect to some information-processing task ?, Physical Review Letters, 2020.
R. Hanson et K. Shalm, Des tests sans faille de l’intrication quantique, Pour la Science, n° 504, octobre 2019.
Quelques mois plus tard , nous avons pris connaissance d’une autre version optique de l’expérience, également réalisée à Shanghai Dans chaque cas, les expérimentateurs ont observé des corrélations entre les mesures que la théorie quantique réelle ne pouvait pas expliquer. Bien qu’il reste encore quelques lacunes expérimentales à combler, ces trois expériences prises ensemble rendent l’hypothèse quantique réelle très difficile à soutenir
SONDER TOUJOURS PLUS LOIN
Nous savons maintenant que ni la théorie classique ni la théorie quantique réelle ne sont en mesure d’expliquer certains phénomènes du monde Dans la même logique, si de futures versions de la théorie quantique sont proposées comme alternatives à la théorie standard, une technique similaire sera peut-être une voie efficace pour tenter de les exclure Mais pourrions-nous aller plus loin et falsifier la théorie quantique standard elle-même ?
Si nous parvenions à le faire , à l’heure actuelle, nous n’aurions pas de théorie alternative pour décrire le monde microscopique Mais les physiciens ne sont pas certains que la théorie quantique standard est nécessairement juste Elle n’a pas été complètement testée dans certains régimes, par exemple avec des systèmes comprenant un très grand nombre de particules
À l’inverse, certains chercheurs tentent de prouver qu’aucune théorie autre que la théorie quantique ne fonctionne. Une de nos collègues, Mirjam Weilenmann, et Roger Colbeck, tous deux à l’institut d’optique quantique et d’information quantique, à Vienne, ont récemment soutenu qu’il serait possible d’écarter toutes les théories physiques alternatives par le biais d’expériences appropriées de type Bell Si cela était confirmé , ces expériences montreraient que la mécanique quantique est en effet la seule théorie physique compatible avec les observations expérimentales . Cette possibilité est vertigineuse : pouvonsnous vraiment espérer démontrer que la théorie quantique avec les nombres complexes est si spéciale ? n
28 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 PHYSIQUE QUANTIQUE LE MONDE EST-IL IMAGINAIRE ?
L’hypothèse quantique réelle devient très difficile à soutenir £
Partez à la découverte de votre cerveau



Les clés de la cognition et du bien-être livrées par les meilleurs spécialistes


Un grand dossier mensuel pour découvrir un sujet en profondeur

Des conseils validés par des psys et des neuroscientifiques





Les dernières avancées présentées par les chercheurs eux-mêmes
cerveauetpsycho.fr

Retrouvez toutes nos o res d’abonnements ou rendez-vous sur sur boutique.groupepourlascience.fr



















Qui es-tu rat-taupe nu ?
Un système sensoriel unique
Comme nombre de mammifères vivant dans des tunnels obscurs et étroits, le rat-taupe nu a une vue et une audition limitées, mais il présente aussi plusieurs particularités. Ses organes sensoriels les plus importants sont ses vibrisses… et ses dents La moitié de son cortex somatosensoriel – la région du cerveau qui traite les informations sensorielles – est consacrée à ces deux organes, dont 30 % à ses seules incisives

DES VIBRISSES HYPERSENSIBLES
Le rat-taupe nu n’a pas de fourrure, mais n’est pas nu pour autant : il présente des vibrisses sur le museau, mais aussi une centaine sur tout le corps, espacées en dix rangées. Ces poils sont innervés et mécanosensibles. À la moindre stimulation de l’un d’eux, l’animal oriente son museau vers la source en une fraction de seconde.

DES DENTS AGILES
Creuser des galeries, chercher de la nourriture, combattre ses congénères, manifester son agressivité par des grincements… Le rat-taupe nu utilise ses incisives pour de multiples tâches. Elles poussent hors de sa gueule, ce qui permet à ses lèvres de se fermer lorsqu’il gratte le sol. Les deux incisives inférieures se meuvent indépendamment, lui offrant une dextérité sans égale parmi les rongeurs pour manipuler des objets.
ZOOLOGIE
42 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023
© Neil Bromhall/Nature Picture Library (double page) © Dr. Matthew Pamenter (hypoxie) ; © Neil Bromhall/Shutterstock (les trois autres photos)
Outre sa remarquable résistance au vieillissement, l’animal arbore de nombreuses caractéristiques surprenantes.
Par Marie-Neige Cordonnier, rédactrice en chef adjointe à Pour la Science
UNE PEAU PEU INNERVÉE
L’innervation de la peau entre les vibrisses est plus éparse chez le rat-taupe nu que chez d’autres espèces. En revanche, elle est bien plus dense dans les follicules des vibrisses qui parsèment son corps.
UNE VISION SOUS-DÉVELOPPÉE
Doté de petits yeux qu’il ouvre rarement, le rat-taupe nu ne semble pas capable de voir. En revanche, il perçoit des changements de luminosité.
UNE OUÏE MÉDIOCRE
La sensibilité du système auditif du rat-taupe nu est faible, en particulier dans les hautes fréquences, comme chez nombre de rongeurs vivant sous terre. Ce n’est pas étonnant : les sons de haute fréquence se propagent moins loin dans le sous-sol que ceux de basse fréquence. L’évolution a préservé la sensibilité aux basses fréquences, vitale dans les galeries parcourues par l’animal.
UN GOÛT SÉLECTIF
Comme les autres mammifères, le rat-taupe nu est attiré par le sucre et rebuté par l’amer. Il n’aime pas non plus la nourriture acide, mais son seuil de tolérance est plus élevé que celui de la souris.
UN ODORAT CLASSIQUE… OU PRESQUE
La capacité du rat-taupe nu à déceler des odeurs semble similaire à celle d’un rat. Il distingue ainsi si un individu appartient à sa colonie ou non, ou dans quelle chambre de sa galerie il se trouve. Une différence, cependant : son organe voméronasal, spécialisé dans la détection des phéromones, est minuscule et ne croît plus après la naissance.
RÉGULATEUR DE TEMPÉRATURE
Les rats-taupes nus sont capables de baisser leur température corporelle lors d’une pénurie d’oxygène, comme le montrent ces deux photos prises avec une caméra thermique, l’une en conditions normales (21 % d’oxygène dans l’air, à gauche), l’autre en situation d’hypoxie (7 % d’oxygène, à droite).




POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 43
Un animal eusocial
Les rats-taupes nus vivent au sein de colonies comptant parfois jusqu’à 300 individus, dans un vaste réseau de galeries susceptible de s’étendre sur plusieurs kilomètres de large et plusieurs mètres de profondeur Contrairement à la plupart des mammifères, ils sont eusociaux : dans chaque colonie, la reproduction est réservée à certains d’entre eux (la reine et quelques mâles fertiles) et, même si l’on n’observe pas de castes bien définies, le travail des rongeurs non fertiles est organisé en plusieurs tâches, comme le forage et la défense des tunnels, la récolte de nourriture, les soins aux jeunes et le départ de la colonie En effet, on a repéré des individus de phénotype distinct quittant leur groupe natal pour explorer le monde en surface et, parfois, fonder une autre colonie
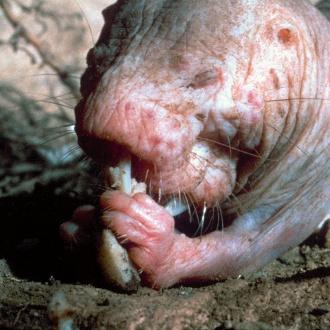
DES RACINES ET RIEN D’AUTRE
Dans la nature, les rats-taupes nus se nourrissent en général de racines, de tubercules et de bulbes qu’ils trouvent en creusant des galeries. La plus importante colonie trouvée, en 1980, vivait sous un champ de patates douces, à Lerata, au Kenya. Comme nombre de petits mammifères vivant dans un milieu aride, ils ne boivent pas et se suffisent de l’eau directement contenue dans leurs aliments et de celle qu’en extrait leur métabolisme.
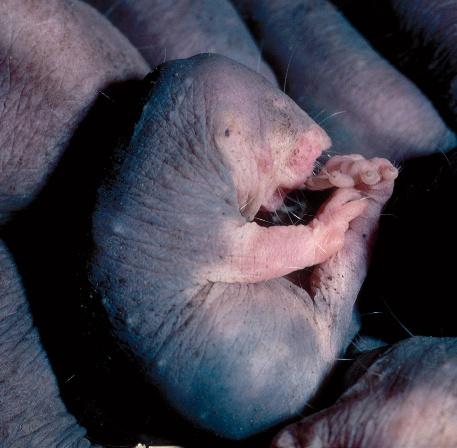


UN DIALECTE PAR COLONIE
Gazouillements, couinements, pépiements, grognements… Bien que leur ouïe soit peu performante, les rats-taupes nus possèdent un large panel de vocalises. Selon une hypothèse, les tunnels offriraient un « effet stéthoscope » qui amplifierait les sons et contrebalancerait les mauvaises capacités auditives des rongeurs. En 2021, Alison Barker, du centre Max-Delbrück pour la médecine moléculaire, à Berlin, et ses collègues ont montré que chaque colonie possède un dialecte et une sorte d’accent qui lui sont propres, et qui renforceraient la cohésion de groupe et les interactions sociales. Ce dialecte, qui relève de l’acquis, comme chez les humains, semble porté par la reine, car si une nouvelle la remplace, il change aussi.
UN SOMMEIL DE CONCERT
Les rats-taupes nus dorment blottis les uns contre les autres dans une pièce réservée à cet usage, ce qui maintient leur température interne durant le sommeil. Leur cycle d’éveil et de repos est indépendant de la lumière du jour, mais dans certaines circonstances il est possible de les entraîner à acquérir un rythme circadien d’activités en les exposant à la lumière.
44 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023
ZOOLOGIE QUI ES-TU, RAT-TAUPE NU ?
© Aydan Metev/Shutterstock (en haut et au centre) ; © Neil Bromhall/Nature Picture Library (en bas)
Portrait d’une reine
La femelle rat-taupe nu fertile – la reine – a le statut social le plus élevé de la colonie Son rôle principal est la reproduction, mais elle patrouille aussi, semblant surveiller le travail des autres individus Plusieurs comportements témoignent de sa position dominante : elle bouscule les membres de la colonie, dort par-dessus tout le monde dans le nid et marche sur les autres pour les dépasser dans les tunnels Enfin, elle maintient sa position en affrontant les éventuelles femelles non fertiles qui viendraient la défier…

QUI VA GARDER LES ENFANTS ?
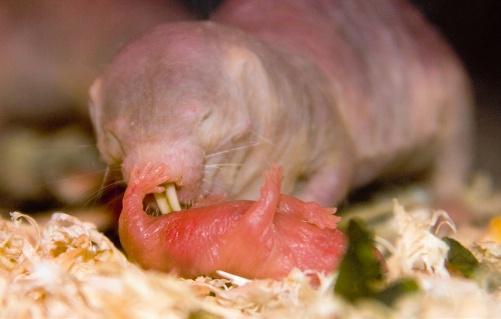
Ce n’est pas la reine qui s’occupe des petits, mais des membres non fertiles de la colonie, qu’ils soient mâles ou femelles. Ils déplacent les bébés, les tirent, les poussent, les réchauffent, les nettoient. Comme chez d’autres mammifères, la toilette provoque parfois la miction et la défécation, dont les excréments sont alors mangés par le toiletteur. Les petits eux-mêmes, grâce à des vocalisations spéciales, quémandent des fèces aux autres individus. Avec la reine, ce sont les seuls à se comporter ainsi.
UNIQUE, OU PRESQUE
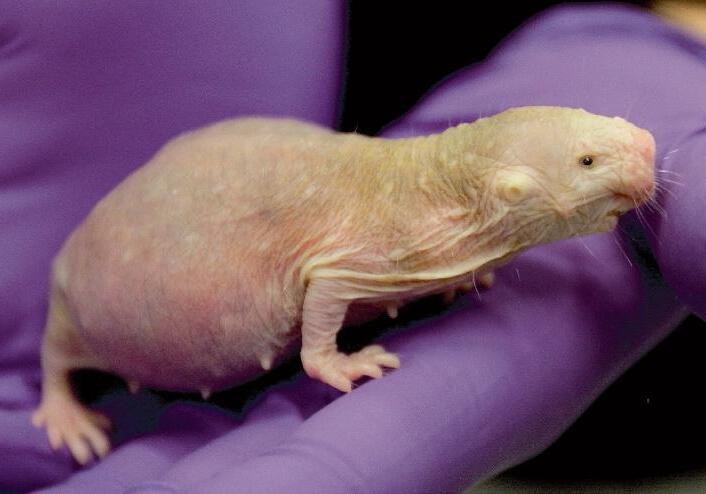
Plus grande que les autres individus (elle a une poussée de croissance quand elle prend ce rôle) et d’espérance de vie plus longue, la reine se distingue par sa colonne vertébrale arquée. En général, elle est unique et si une autre émerge dans la colonie, des combats s’engagent. Cependant, il arrive que des reines cohabitent, surtout si elles ont un lien de parenté (mère-fille ou sœurs).
FERTILE POUR LA VIE
Contrairement aux femelles des autres mammifères, dont le nombre d’ovocytes, fixé avant la naissance, diminue avec l’âge, la reine n’entre jamais en ménopause. On pensait que c’était dû au fait que les rats-taupes nus femelles présentaient un très grand nombre de précurseurs d’ovocytes au début de leur vie, mais Miguel Brieño-Enríquez et ses collègues, de l’université de Pittsburgh, aux États-Unis, ont récemment avancé une autre explication : les femelles produiraient de nouveaux ovocytes tout au long de leur vie. Mais seule l’accession au rôle de reine déclencherait leur maturation. Après une gestation d’environ soixante-dix jours, les reines donnent naissance à des portées de plus en plus nombreuses, constituées parfois d’une vingtaine de petits.
BIBLIOGRAPHIE
R. Bu enstein et al. (éd.), The Extraordinary Biology of the Naked Mole-Rat, Advances in Experimental Medicine and Biology, Springer, 2021.


POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 45
© Neil Bromhall/Shutterstock (médaillon en haut à droite)
; © Felix Petermann/MDC (reine sur fond noir)
; © Danny Ye/Shutterstock (médaillon à gauche)
; © Associated Press/Eric Gay (reine sur fond violet) © belizar/Shutterstock (en bas)
L’ESSENTIEL LES AUTEURS
> En 1658-1659, Blaise Pascal a proposé, sous le nom de plume d’Amos Dettonville, une méthode pour calculer des aires et des volumes.
> Comme nombre de ses contemporains, il s’est inspiré de la géométrie des indivisibles, inaugurée par l’Italien Bonaventura Cavalieri quelques années plus tôt.
> On a longtemps pensé qu’en exposant une méthode fondée sur des indivisibles, Pascal se contredisait, lui qui déclarait ailleurs que l’espace est divisible à l’infini.
> Mais l’analyse littéraire de son texte révèle moins un paradoxe que la subtilité des mathématiques présentées.
JOÃO CORTESE professeur de philosophie au Collège Paul-VI, au Brésil, et chercheur associé au laboratoire Sphere, du CNRS et de l’université Paris Cité


DOMINIQUE DESCOTES professeur émérite de littérature française à l’université ClermontAuvergne
Le fin mot de Pascal sur les indivisibles
La richesse de l’écriture du philosophe, dont on fête cette année le quadricentenaire de la naissance, ne saurait se limiter aux « Pensées ». On découvre encore aujourd’hui l’étendue de sa finesse dans ses écrits mathématiques.
En 1658, Blaise Pascal lança anonymement aux géomètres contemporains , sous la forme d’un concours, un défi : résoudre une série de problèmes relatifs à la cycloïde Cette courbe est celle que trace un point fixé au bord d’une roue lorsque celle-ci roule sans glisser le long d’une droite, si bien qu’il n’était pas rare, à l’époque, de la nommer tout simplement « roulette » Les problèmes que posait Pascal dans son concours visaient à la caractériser Il s’agissait de déterminer la quadrature de l’espace de la roulette (l’aire sous la cycloïde), ou encore la cubature (le volume) des solides engendrés par la rotation de cet espace autour de son axe vertical ou de sa base horizontale, ainsi que le centre de gravité de ces figures Malgré les réclamations du jésuite Antoine de Lalouvère et de
l’Anglais John Wallis, Pascal constata qu’aucun concurrent n’était parvenu à résoudre tous les problèmes proposés. En 1658-1659, il développa donc, dans un traité intitulé Lettres de A . Dettonville, une méthode très générale qui apportait des solutions non seulement dans le cas de la cycloïde , mais aussi dans celui d’autres courbes
Le nom de plume choisi pour ce traité – Amos Dettonville – prouve qu’il attachait une grande importance à cette œuvre mathématique : il s’agit d’une anagramme de deux autres pseudonymes retrouvés dans ses écrits religieux, Louis de Montalte et Salomon de Tultie
Il avait choisi le premier pour signer ses Provinciales , une série de lettres publiées en 1656-1657 visant à mettre à la portée des profanes des questions de théologie auxquelles ils n’avaient pas accès, et le second pour un
70 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 HISTOIRE DES SCIENCES
Blaise Pascal (ici sur une gravure du XIXe siècle réalisée par le peintre lyonnais Hippolyte Flandrin et le graveur alsacien Jean Bein) mettait autant de soin à écrire ses opuscules mathématiques qu’à consigner ses réflexions philosophiques et théologiques.

POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 71
© Wellcome Collection (Public Domain Mark 1.0)
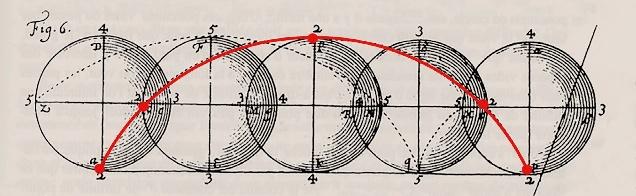
La cycloïde est la courbe que décrit un point fixe sur une circonférence lors d’une révolution complète de celle-ci, comme le parcours d’un trou sur le bord d’une roue lors d’un tour de celle-ci (en rouge). Pascal défia les savants de calculer l’aire sous la courbe et le volume des solides de révolution de la demi-cycloïde (par rapport à son axe vertical ou sa base horizontale), ainsi que le centre de gravité de ces figures.
ouvrage inachevé en faveur de la religion chrétienne, dont on retrouve des fragments parmi ses Pensées Or, jusqu’à présent, les Lettres de A Dettonville posaient un défi d’interprétation aux historiens : la méthode qu’y présente Pascal soulevait la question de savoir s’il faisait intervenir des indivisibles au sens propre, c’est-à-dire des éléments géométriques qui ne peuvent pas être divisés, alors que dans un autre opuscule mathématique intitulé De l’esprit géométrique ( de date incertaine , que l’on suppose vers 1655), le savant déclarait que l’espace est divisible à l’infini ! Pascal, dont l’écriture est si fine dans ses Pensées, s’était-il laissé prendre au piège d’un paradoxe dans ses écrits mathématiques, malgré toute l’importance qu’il leur accordait ? À l’heure où l’on fête le quadricentenaire de sa naissance, on aurait pu croire que la question resterait en suspens à jamais, mais des recherches récentes viennent d’apporter un éclairage nouveau sur les Lettres de A . Dettonville, le dernier ouvrage scientifique auquel il a travaillé, et de lever le paradoxe
UNE CYCLOÏDE DANS LE BERCEAU DE L’ACADÉMIE DES SCIENCES
Inconnue des Anciens, la cycloïde n’a gagné l’attention des savants que quelques décennies avant que Pascal lançât son concours Marin Mersenne, en particulier, s’y était intéressé dès 1628. Jusqu’à sa mort en 1648, cet ecclésiastique de l’ordre des Minimes avait joué un rôle central dans la diffusion des problèmes scientifiques en France et à l’étranger, et avait largement contribué à faire connaître les mystères entourant cette courbe qui ressemblait à une ellipse, mais n’en était pas une C’était lui qui l’avait appelée « roulette ». Pascal, qui dès l’adolescence fréquentait la toute jeune académie Mersenne avec son père et assistait aux débats animés de cette société savante parisienne , berceau de la future Académie des sciences, en avait très certainement entendu parler lors de ces séances. Il en avait aussi probablement discuté avec Gilles Personne de Roberval, un autre membre de l’académie avec
qui il était en contact et qui étudiait celle qu’il appelait « trochoïde » ( du grec trokhós , « roue »). Surtout , le défi de la cycloïde lui donnait l’occasion de développer et d’éprouver une méthode générale pour calculer des aires et des volumes.
En effet, en 1658, Pascal n’était plus du tout un novice en mathématiques. Sa passion pour cette discipline remontait même à sa jeunesse Si on laisse de côté le récit de sa sœur, selon lequel il aurait redécouvert des propositions d’Euclide à l’âge de 12 ans, le fait est qu’à 16 ans il avait déjà publié un Essai sur les coniques, suivant le modèle d’étude des coniques du géomètre Girard Desargues, un autre membre de l’académie de Mersenne Et plus tard , vers 1654, il s’était consacré à la construction de son célèbre triangle arithmétique, qui visait entre autres à calculer des sommes de suites de nombres de façon quasi automatique Par l’étude systématique de ce triangle, il cherchait à en développer plusieurs usages, notamment à l’aide de résultats auxquels il était arrivé lors d’un échange de lettres avec le mathématicien toulousain Pierre de Fermat, un des correspondants réguliers de Mersenne
LA DOUBLE MÉTHODE DES INDIVISIBLES DE CAVALIERI
En 1635, le mathématicien italien Bonaventura Cavalieri a proposé deux méthodes des indivisibles pour calculer l’aire ou, comme ici, le volume d’une figure géométrique. Dans la première, il décrit une telle figure comme étant composée de « toutes » (omnes, en latin) ses sections élémentaires, sans épaisseur (ses « indivisibles »). Ainsi, une pyramide, par exemple, est composée de « tous » ses triangles. La deuxième consistait à comparer les di érentes sections de deux figures géométriques comme celles représentées ici pour en déduire la comparaison entre les deux figures elles-mêmes. La question de l’« hétérogénéité » des indivisibles par rapport aux figures soulevée par cette méthode a suscité maintes interrogations : dans le cas présent, comment des triangles sans épaisseur pourraient-ils constituer une pyramide ?
Pour Cavalieri, il suffisait de comparer les différentes sections élémentaires composant deux figures géométriques, par exemple un cône et une pyramide, pour comparer les figures elles-mêmes.
72 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 HISTOIRE DES SCIENCES LE FIN MOT DE PASCAL SUR LES INDIVISIBLES Cycloïde : © Domaine public, d’après A. Tacquet (1612-1660), Dissertation physico-mathématique sur les roulements du cercle (traduction d’un texte paru en latin au XVII e siècle), Courrier du Centre International Blaise-Pascal, 1992 ; schéma : © Pour la Science
h h = =
C’est sous le pseudonyme d’Amos Dettonville, dans un ouvrage intitulé Lettres de A. Dettonville, paru en 1659, que Pascal publia la « solution de tous les problèmes touchant la roulette qu’il avait proposés publiquement au mois de juin 1658 ».

Une des questions qui intéressait particulièrement Pascal à l’époque du concours était un problème que les mathématiciens grecs se posaient déjà au IVe siècle avant notre ère, et probablement avant : calculer l’aire et le volume de diverses figures géométriques plus complexes que le carré ou le cube En effet, si aujourd’hui, on emploie le calcul intégral développé à la fin du XVIIe siècle par Gottfried Leibniz et Isaac Newton, du temps de Pascal, on essayait encore de résoudre ce problème Les mathématiciens grecs procédaient par dichotomie, une méthode rigoureuse, mais longue et laborieuse que les savants du XVIIe siècle tentaient de remplacer En particulier, sous l’impulsion de Bonaventura Cavalieri, on assistait au développement de techniques dites « méthodes des indivisibles ». Le jésuate italien avait inauguré cette géométrie des indivisibles dans son ouvrage Geometria indivisibilibus continuorum nova quadam ratione promota (« Géométrie, développée d’une nouvelle manière par les indivisibles des continus »), publié en 1635, puis d’autres savants l’avaient suivi en proposant des variantes, en particulier Evangelista Torricelli en Italie, Isaac Barrow en Angleterre et Gilles Personne de Roberval en France.
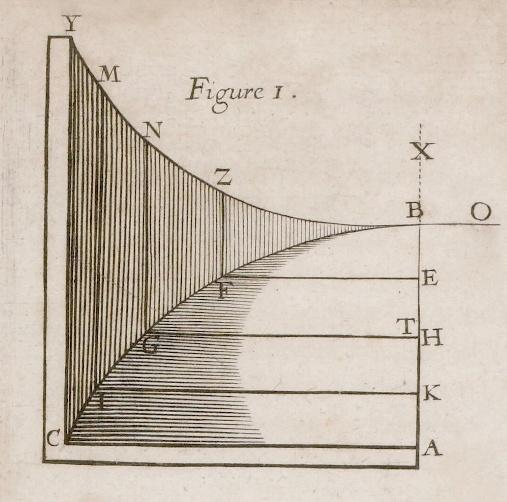
La figure 1 des Lettres de A. Dettonville montre un triligne ABC, c’est-à-dire une figure plane constituée d’une base (CA), d’un axe (AB) et d’une courbe (BC), divisé en « une multitude indéfinie de plans parallèles entre eux », dont on voit la trace dans le plan de la figure (CA, IK, GH, FE). Pour calculer l’aire de la figure, Pascal somme les aires des rectangles EF.EB, GH.HE, IK.KH, etc. ainsi construits.
En substance, pour Cavalieri, les corps géométriques étaient engendrés par des éléments, appelés « indivisibles », comportant une dimension de moins qu’eux. Ainsi, une surface était constituée de segments parallèles assemblés, et un volume de surfaces planes parallèles. Pour calculer l’aire et le volume de figures géométriques, il s’agissait donc de comparer les indivisibles qui les composaient avec ceux d’autres figures d’aire et de volume connus (voir l’encadré page ci-contre) Mais évaluer des figures géométriques par leurs indivisibles ne résolvait pas tout : en particulier, quel était le statut de ces éléments par rapport aux figures qu’ils composaient ? S’agissait-il de portions « hétérogènes » aux grandeurs (des lignes sans largeur composant une surface, des surfaces sans épaisseur composant un volume), comme
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 73 ©
0011 1
30
Clermont-Auvergne Métropole, Overnia, cotes Em
à Em 0011
(en haut) ; B. Pascal, Lettres de A. Dettonville © Bibliothèque nationale de France, département Réserve des livres rares, RES-V-859 (10)
Les le res de A. De onville posaient un défi aux historiens £
le suggérait Cavalieri, ou « homogènes » à elles (de petites surfaces composant une surface, un petit volume composant un volume) ? La décision sur cette question variait d’un auteur à l’autre, ainsi que la façon de traiter les problèmes à l’aide d’indivisibles. Aussi, chaque méthode des indivisibles comportait des particularités propres à son auteur, notamment dans ses fondements C’est dans ce paysage que Pascal a proposé la sienne, à l’occasion de son défi sur la roulette
QUELS SONT LES INDIVISIBLES DE PASCAL ?
Comme ses contemporains, le savant divise une figure géométrique en un assemblage de petits éléments, mais sa méthode se distingue par plusieurs aspects Il choisit de diviser une figure géométrique en « une multitude indéfinie de plans parallèles entre eux et également distants ». Dans la figure page 73, par exemple, il divise le « triligne » ABC (c’est-à-dire la figure plane constituée de la base CA , l’axe AB et la courbe BC) par des plans perpendiculaires à la figure, qui la rencontrent selon les droites CA , IK , GH, FE, de sorte que sur l’axe AB apparaissent de « petites portions » AK, KH, HE, EB. Ces petites portions seront la base de rectangles dont il faudra faire la somme pour retrouver la figure cherchée : dans cet exemple, pour retrouver le triligne ABC, il s’agit de sommer les rectangles EF EB, GH HE, IK KH, etc (Pascal écrit plutôt « etc. » que nos trois points pour indiquer une suite indéfinie de quantités).
On remarque que, comme d’autres (dont Roberval), Pascal a choisi l’homogénéité : les rectangles ont bien deux dimensions, de même que la grandeur en question (le triligne). En revanche, la somme obtenue ne constitue pas précisément le triligne, car les rectangles ne sont pas identiques aux portions de la grandeur cherchée. Mais cela n’est pas grave, écrit Pascal dans un « Avertissement », car – c’est la grande innovation – « la somme des portions substituées ne diffère de la somme des véritables que d’une quantité moindre qu’aucune donnée » Dans une procédure étonnante, il opère une quantification des différences pour arriver non pas à l’identité parfaite, mais à une sorte d’égalité sous la condition d’une erreur rendue moindre qu’aucune grandeur donnée, possible car faite à partir d’une division indéfinie de la grandeur
Entendue ainsi , la méthode est en ellemême assez rigoureuse Mais quels en sont les indivisibles ? Dans sa description, en effet, si Pascal se réfère au « langage des indivisibles » et à la « doctrine des indivisibles », il n’indique jamais ceux de sa méthode Doit - on en conclure qu’il s’agit de ses « petites portions » et des rectangles qu’elles composent , et constater alors que le savant est ici cohérent
Pour calculer l’aire de ce demi-disque, présenté dans les Lettres de A. Dettonville, Pascal propose explicitement de sommer une multitude indéfinie de rectangles ZM.ZZ, soit des grandeurs homogènes à l’aire de la figure, c’est-à-dire de même dimension.
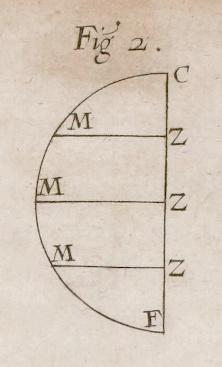
avec l’idée que l’espace est divisible à l’infini, mais en contradiction avec le sens propre du mot « indivisible » ? Et quel est le statut, pour lui , des di ff érences entre la grandeur et la somme des rectangles, elles aussi de l’ordre de l’indéfiniment petit, mais avec un rôle distinct dans les calculs ?
Pour répondre à ces questions, il est nécessaire de revenir au mode d’écriture de Pascal, même si on a ici affaire à un traité savant. Pour ce faire, il est crucial de considérer le style géométrique de Dettonville et de s’éloigner du style symbolique qui s’est imposé dans les commentaires des œuvres mathématiques pascaliennes depuis la traduction des propositions de Pascal en symboles par le mathématicien Maximilien Marie, au milieu du XIXe siècle Cette traduction est utile pour expliciter les étapes du raisonnement, mais, en raison de la transposition, elle dissimule les démarches du savant Or examiner comment Pascal présente ses résultats – en quel langage, sous quel aspect, avec quelles subtilités – est, dans le cas présent, tout aussi important que les résultats eux-mêmes
En effet, comme l’a montré l’un de nous ( Dominique Descotes ) en 2001 dans son ouvrage Blaise Pascal, littérature et géométrie, dans ses lettres, Dettonville ne donne pas d’un coup tous ses résultats : un rythme de présentation et de persuasion s’impose au lecteur, dans ce qui évoque même de la dramaturgie. Son écriture est donc tout aussi élaborée que celle de Pascal dans ses Pensées. Pensées où il écrit justement : « Tout auteur a un sens auquel tous les passages contraires s’accordent ou il n’a point de sens du tout » Difficile, dans ces conditions, de croire qu’il ait pu laisser une contradiction dans l’ensemble de son œuvre Le défi qui se pose ici est donc de nature interprétative, voire herméneutique au sein même de la géométrie La rigueur mathématique a-telle résisté à l’usage des mots fait par Pascal ? La seule façon de le savoir est de s’efforcer de comprendre ses mathématiques à la lumière de
À LIRE
J. F. N. B. Cortese, Infini et disproportion chez Pascal, Honoré Champion, 2023.
Pascal aborde-t-il l’infini de la même façon dans ses écrits mathématiques et ses réflexions philosophiques ? En explorant ces deux corpus, l’auteur met en relief des comparaisons entre des éléments qui paraissent pourtant incomparables à première vue, comme des distances infinies, des quantités hétérogènes et même l’infini et le fini. Mais cela n’enlève rien à la cohérence de l’œuvre pascalienne, dont l’unité demeure.

74 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 HISTOIRE DES SCIENCES LE FIN MOT DE PASCAL SUR LES INDIVISIBLES B. Pascal, Lettres de A. Dettonville © Bibliothèque nationale de France, département Réserve des livres rares, RES-V-859 (10)
LE STYLE GÉOMÉTRIQUE D’AMOS DETTONVILLE
Dans ses Lettres de A. Dettonville, Blaise Pascal utilise un style géométrique novateur à plus d’un titre pour décrire sa méthode de calcul des aires, volumes et centres de gravité de figures. En particulier, rapprochant géométrie et arithmétique, il introduit des « sommes triangulaires ». Celle des quantités A, B, C, D, commençant par A, par exemple, se définit ainsi :
grand pouvoir de synthèse en mettant en exergue la pondération des di érents éléments sommés : en supposant que les quantités additionnées sont pendues à une balance, la somme triangulaire aide à déterminer à quel endroit y placer un pivot pour qu’elle soit équilibrée. Bien que cela puisse être simplement vu comme une reformulation de la loi du levier d’Archimède, cette disposition donne à Pascal l’occasion de montrer d’un seul coup s’il y a de l’équilibre dans une balance ou pas. Il l’illustre avec la figure suivante :
Il semblerait que cela se résume à indiquer la somme de quantités multipliées par les nombres naturels, à savoir 1 × A + 2 × B + 3 × C + 4 × D. Néanmoins, la particularité de présenter une disposition géométrique de la somme permet à Pascal d’avoir un plus
Dans cette figure, les poids 3, 5 et 4 pendent du bras AB de la balance, et les poids 9 et 8 du bras AC. Y a-t-il équilibre ? Oui, car la somme triangulaire du bras AB est égale à celle du bras AC :
son principe d’interprétation – en d’autres termes d’explorer le style géométrique de Pascal à la recherche du sens selon lequel s’accordent même les passages qui sembleraient contradictoires
UN STYLE GÉOMÉTRIQUE TRÈS… ARITHMÉTIQUE
Or en menant cette exploration, on s’aperçoit que le style de Dettonville est particulièrement novateur En effet, contre toute attente, pour résoudre des problèmes relevant de la géométrie, il utilise des outils d’arithmétique et de statique (voir l’encadré ci-dessus) C’est d’ailleurs à propos de ces outils qu’apparaît la seule occurrence du mot « indivisible » dans les Lettre de A Dettonville, dans un sens purement relationnel entre deux grandeurs de dimensions différentes (voir l’encadré page 76). Mais si la référence directe à un « indivisible » fait exception dans l’ouvrage, que sont, finalement, les indivisibles de la méthode de Pascal dans le langage que parle Dettonville ?
Selon une interprétation que l’un de nous (João Cortese) a proposée récemment avec l’historien des mathématiques David Rabouin, du laboratoire Sphere, à l’université Paris Cité et au CNRS, nous pensons que les commentateurs de l’œuvre pascalienne sont passés un peu vite des « petites portions » de Dettonville aux « indivisibles » , comme si les deux choses étaient identiques Or rien ne l’oblige si l’on suit le texte pascalien en filigrane, puisque Pascal ne précise jamais les indivisibles de sa méthode
Si indivisible il y a, il doit être pris au sens relationnel de n’être qu’un « indivisible à l’égard de » quelque chose , à savoir une
Mais en quoi l’équilibre d’une balance est-il utile pour résoudre les problèmes de Dettonville ? Reprenons le triligne ABC page 73 et considérons son axe AB comme une balance. Les poids qui y pendent sont alors justement les rectangles construits à partir des « petites portions » que Pascal somme. Cela lui permet de trouver le point d’équilibre de la balance – ce qu’indique une des coordonnées du centre de gravité du triligne, objet d’un des problèmes du défi de la roulette.
L’indivisible de Pascal est une quantité négligeable par rapport à un autre ordre £
quantité négligeable par rapport à un autre ordre Or, dans l’exemple du triligne, autant les « petites portions » – les bases des rectangles –que les différences entre la figure et la somme des rectangles peuvent assumer ce rôle , puisque les unes comme les autres sont indéfiniment petites vis-à-vis de la grandeur géométrique considérée
D’autre part, quant aux sommes qui constituent les grandeurs, Pascal clarifie les choses un peu plus loin dans son texte en prenant pour exemple le calcul de l’aire d’un demi-disque (voir la figure page ci-contre) : par la « somme de lignes », il ne faut rien entendre d’autre que « la somme d’un nombre indéfini de rectangles faits de chaque ordonnée avec chacune des petites portions égales du diamètre, dont la somme est un plan, qui ne diffère de l’espace du demicercle que d’une quantité moindre qu’aucune donnée » Dans son exemple, il ne s’agit donc pas de faire la somme des ordonnées ZM, mais
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 75 B A C 4 5 3 9 8
9 8 8 25 4 5 3 4 5 4 25 A B C D B C D C D D
LES INDIVISIBLES SELON PASCAL
Dans toutes les Lettres de A. Dettonville, Pascal n’emploie qu’une unique fois le terme « indivisible » tout seul (hors des expressions telles que « doctrine des indivisibles » ou « langage des indivisibles ») ; voici dans quel contexte. Au cours de son raisonnement pour déterminer le centre de gravité d’une figure, il définit non seulement une somme triangulaire (voir l’encadré page 75), mais une « somme pyramidale ». Celle de trois quantités A, B, C est la somme de toutes les sommes triangulaires construites à partir de A, puis de B en supprimant A, puis de C en supprimant A et B :
A B C B C C B C C C
Ce qui équivaut à 1 × A + 3 × B + 6 × C, mais que Pascal présente en disposition géométrique.
Le savant montre alors que dans le triligne ABC page 73, la somme des quantités (les petites portions AK, KH, HE, etc.) multipliées chacune par le carré d’un nombre naturel est égale à deux fois leur somme pyramidale moins leur somme triangulaire, soit en notation moderne :
1 × AK + 4 × KH + 9 × HE + etc. = 2 × Somme pyr.(AK, KH, HE, etc.) –Somme triang.(AK, KH, HE, etc.).
Mais comme il y a une indéfinité de petites portions dans le triligne, il considère que cette égalité équivaut à la suivante, où la somme triangulaire a disparu :
1 × AK + 4 × KH + 9 × HE + etc. = 2 × Somme pyr. (AK, KH, HE, etc.).
Comment cela est-il possible ? C’est en le justifiant que Pascal utilise le terme « indivisible » : « cette somme triangulaire n’est qu’un indivisible à l’égard des sommes pyramidales, puisqu’il y a une dimension de moins, et que c’est la même chose qu’un point à l’égard d’une ligne, ou qu’une ligne à l’égard d’un plan, ou qu’un plan à l’égard d’un solide, ou enfin qu’un fini à l’égard de l’infini ; ce qui ne change point l’égalité ». Le sens du mot « indivisible » est ici bien figuré et marque la notion de négligeabilité d’une grandeur par rapport à une autre. Et si les mystérieux indivisibles de la méthode de Dettonville avaient la même signification ?
BIBLIOGRAPHIE
J. F. N. B. Cortese et D. Rabouin, « Sur les indivisibles chez Pascal » , dans A. Cousson (éd.), Passions géométriques. Mélanges en l’honneur de Dominique Descotes, Honoré Champion, 2019.
D. Descotes, Pascal, le calcul et la théologie, Les génies de la science, n° 16, 2003.
D. Descotes, Blaise Pascal : littérature et géométrie, Presses Universitaires Blaise Pascal, 2001.
C. Merker, Le Chant du cygne des indivisibles – Le calcul intégral dans la dernière œuvre scientifique de Pascal, Presses universitaires de Franche-Comté, 2001.
plutôt de celle des rectangles ZM ZZ On y retrouve donc un élément homogène à la grandeur cherchée, ce qui nous éloigne des apories qu’on pourrait reprocher aux méthodes des indivisibles, une somme finie de points ne constituant jamais une ligne. Que conclure de là ? Premièrement, qu’il n’y a pas de contradiction entre l’opuscule De l’esprit géométrique et les Lettres de A Dettonville, car les indivisibles sont traités dans chaque ouvrage par un biais différent En effet, dans De l’esprit géométrique, si Pascal critique les personnes qui ne peuvent pas concevoir l’espace divisible à l’infini, il n’exclut pas l’existence d’indivisibles vis - à - vis des grandeurs auxquelles ils se rapportent Dire qu’une somme (finie) de points ne peut constituer une ligne ne signifie pas que les points n’existent pas, mais seulement que le passage de l’un à l’autre ne saurait se faire par une somme finie Deuxièmement, que Pascal est resté rigoureux puisqu’il n’a jamais identifié explicitement les indivisibles dont il est question dans sa méthode Les « petites portions » sont des indéfiniment petits qui ne sont ni « indivisibles » au sens étymologique du mot ni ce qui détermine la rigueur de la méthode. S’il fallait désigner les indivisibles de celle-ci, ce seraient donc plutôt les différences entre la grandeur et la somme de portions homogènes, car ces différences sont celles qui subissent d’abord la quantification d’« être moindres qu’aucune grandeur donnée » et qui rendent possible la fondation de la méthode En fait , ce qui change de sens dans les « Avertissements » des Lettres de A Dettonville est moins l’usage du mot « indivisible » que la méthode des indivisibles elle - même , radicalement renouvelée par
Pascal
Une contribution clé de sa méthode est l’introduction d’une abstraction à partir du calcul : les différences entre la grandeur et la somme, par opposition aux « petites portions », qui, elles, se réfèrent à des éléments homogènes à la grandeur. Ces deux sortes d’éléments étant « moindres qu’aucune grandeur donnée », on pourrait ainsi croire que la méthode de Pascal opère avec un « néant qui existe », à la fois rien (si on considère les différences comme négligeables) et quelque chose (si on considère les éléments géométriques – tels les rectangles des petites portions – qui entrent dans les sommes).
VERS LE CALCUL INTÉGRAL MODERNE
Les indivisibles ont donné encore lieu à beaucoup de discussions, notamment à un débat sur la bonne conceptualisation des infinitésimaux, qui s’est poursuivi jusqu’au XIXe siècle et a atteint une nouvelle phase lorsque le mathématicien Augustin-Louis Cauchy a proposé de fonder le champ disciplinaire de l’« Analyse » non pas sur des infinitésimaux, mais sur des limites, avec une approche évoquant d’ailleurs celle de Pascal Quoi qu’il en soit, l’ouvrage de Pascal a joué un rôle fondamental dans la genèse du calcul moderne Les travaux de Leibniz, qui constituent la base d’une bonne partie du calcul intégral et différentiel enseigné encore aujourd’hui, ont comme source d’inspiration les ouvrages de Pascal, que le savant allemand a pu consulter lors de son séjour à Paris en 16721676. C’est finalement en opérant une mutation radicale de la méthode des indivisibles que Pascal a déclenché le chant du cygne des indivisibles, en arrivant aux limites de cette méthode mais en contribuant ainsi à ouvrir la voie vers le calcul intégral moderne n
76 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 HISTOIRE DES SCIENCES LE FIN MOT DE PASCAL SUR LES INDIVISIBLES
OUI, je commande des numéros de Pour la Science Hors-série








1 / JE COCHE LES RÉFÉRENCES ET JE RENSEIGNE LES
QUANTITÉS CI-DESSUS ET JE REPORTE LE TOTAL CI-DESSOUS
Total à régler : – , €

2 / J’INDIQUE MES COORDONNÉES
☐ M. ☐ M me
Nom :
Prénom :
Adresse :
Code postal : Ville :
Téléphone :
Courriel :
J’accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON
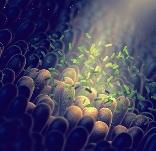


3 / JE RETOURNE LE COUPON ET MON RÈGLEMENT
J’émets un chèque à l’ordre de Pour la Science du montant total de la commande. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante :

Abonn’escient – TBS Group Service abonnement
COMMANDEZ PLUS SIMPLEMENT !
En vous rendant sur notre site internet vous pourrez :
● Retrouver toute notre collection
● Vérifier la disponibilité des anciens numéros
● Acheter les numéros en version numérique (5,99 €)
● E ectuer un paiement en ligne
Pour cela, scannez le QR code ci-contre ou rendez-vous sur boutique.groupepourlascience.fr

Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr
En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante :https://rebrand.ly/CGV-PLS. O re valable jusqu’au 21/12/2022 en France Métropolitaine uniquement. Les prix a chés incluent les frais de port et les frais logistiques. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour La Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous invitons à prendre connaissance de notre charte de protection des données personnelles à l’adresse suivante : https://rebrand.ly/charte-donnees-pls. Conformément à la réglementation applicable (et notamment au règlement 2016/679/UE dit « RGPD ») vous disposez des droits d’accès, de rectification, d’opposition, d’e acement, à la portabilité
et à la limitation de vos données personnelles. Pour exercer ces droits (ou nous poser toute question concernant le traitement de vos données personnelles), vous pouvez nous contacter par courriel à l’adresse protection-donnees@pourlascience.fr. COMPLÉTEZ VOTRE COLLECTION DÈS MAINTENANT ! Groupe Pour la Science – Siège social : 170 bis, boulevard du Montparnasse, CS20012, 75680 Paris Cedex 14 – Sarl au capital de 32 000 € – RCS Paris B 311 797 393 – Siret : 311 797 393 000 23 – APE 5814 Z 13252 148 F: 7,00 € La stratégie nationale polaire 2030 promet la France de retrouver son lustre aux pôles Yan Ropert-Coudert, écologueetdirecteurdel’institut polairefrançaisPaul-Émile-Victor Climat, biodiversité, niveau des mers… HORS-SÉRIE Notre avenir se joue aux PÔLES La bombe à retardement du pergélisol Aires marines protégées, une solution ? En Arctique, le réchauffement s’emballe Le glacier de l’apocalypse sous surveillance 7,90 Édition française de Scientific AmericanQUELS RÔLES POUR LES LONGÉVITÉ L’EXCEPTION HUMAINE MÉDECINE DES MICROBES CONTREGRAND TÉMOIN Éric Bapteste HORS-SÉRIE INTESTIN, POUMONS, BOUCHE, PEAU… Les vrais pouvoirs des sur notre santé
PAG23VPC
☐ N° 120 (août 23) ⨯ 12,40 € = , € ☐ N° 119 (mai 23) ⨯ 12,40 € = , € ☐ N° 118 (janv. 23) ⨯ 12,40 € = , € ☐ N° 117 (nov. 22) ⨯ 12,40 € = , € ☐ N° 116 (août 22) ⨯ 12,40 € = , € ☐ N° 115 (mai 22) ⨯ 12,40 € = , € ☐ N° 108 (sept 20) ⨯ 10,40 € = , € ☐ N° 109 (nov. 20) ⨯ 10,40 € = , € ☐ N° 112 (août 21) ⨯ 10,40 € = , € ☐ N° 110 (fév. 21) ⨯ 10,40 € = , € ☐ N° 113 (nov 21) ⨯ 10,40 € = , € ☐ N° 114 (fév. 22) ⨯ 10,40 € = , €
HORS-SÉRIE
Pour la Science 20 rue Rouget de Lisle - 92130 Issy les Moulineaux
Groupe
PLUS HAUT LE JET D’EAU
Quand on pince l’extrémité d’un tuyau d’arrosage, l’eau va souvent plus loin. Selon une idée reçue, c’est une histoire de débit, mais il n’en est rien !
Vous arrosez un jardin et, hélas, votre tuyau trop court et la faiblesse du jet vous empêchent d’atteindre le massif de fleurs tout au fond ! Qu’à cela ne tienne, vous pincez l’extrémité du tuyau, le jet devient plus puissant et sa portée augmente : vos fleurs seront bien arrosées Comment expliquer ce phénomène que chacun d’entre nous a pu expérimenter y compris en jouant avec le robinet de la cuisine ? L’affaire est plus subtile qu’elle n’en a l’air : la viscosité de l’eau y tient un rôle primordial et la longueur du tuyau peut jouer des tours dans certaines conditions. Et non, ce n’est pas une histoire de débit
ASSURER LA BONNE PRESSION
Si l’eau va plus loin quand on pince le tuyau, c’est qu’elle en sort plus vite. Pour expliquer cela, la première idée qui vient en effet à un physicien est de dire que le débit , c’est- à - dire le volume d’eau qui sort du tuyau par seconde, est constant.
Ce n’est qu’une façon d’exprimer la conservation de la matière : l’eau qui rentre à un bout du tuyau doit bien en sortir Comme ce débit est égal au produit de la section du tuyau par la vitesse de l’eau qui s’écoule à l’intérieur, à débit fixé, si on réduit la section, on augmente la vitesse et donc l’énergie cinétique du jet. Et quel que soit son devenir (le jet peut se fragmenter, par exemple), une vitesse plus élevée se traduit par une portée augmentée Mais alors, en réduisant toujours plus la section, la vitesse augmenterait donc jusqu’à l’infini ? Non , évidemment.

Où nous sommes-nous trompés ? En pratique, le réseau public de distribution d’eau est conçu pour délivrer l’eau à une pression à peu près constante : cela peut dépendre de votre éloignement au château d’eau ou de l’état et de la sinuosité des canalisations qui acheminent l’eau jusque chez vous, mais la pression au robinet est souvent de l’ordre de 2 ou 3 fois la pression atmosphérique
C’est un peu comme le réseau électrique : la tension est fixée (220 V), mais le courant – le débit de charges électriques –dépend du nombre d’appareils branchés Pour l’eau, le débit est fonction du nombre de robinets ouverts en même temps : qui n’en a pas fait l’amère expérience sous la douche quand elle ne coule plus parce que quelqu’un a ouvert un autre robinet… Il peut aussi dépendre de la longueur du tuyau utilisé, comme on le verra.
En tout cas, il est certain que si on ferme progressivement une canalisation ou que l’on pince un tuyau, on augmente la résistance à l’écoulement. Comme dans un circuit électrique, une résistance plus élevée signifie moins de courant, donc un débit moindre En revanche, cela ne nous dit rien sur la vitesse de l’écoulement. Pour connaître cette vitesse, on doit s’intéresser à la façon dont l’eau s’écoule après son arrivée au compteur Une pression de disons 2 bars au - dessus de la pression atmosphérique est la pression que l’on aurait en bas d’une citerne


88 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 IDÉES DE PHYSIQUE LES AUTEURS
©
JEAN-MICHEL COURTY ET ÉDOUARD KIERLIK professeurs de physique à Sorbonne Université, à Paris
Illustrations de Bruno Vacaro
En pinçant l’extrémité d’un tuyau d’arrosage, on augmente la puissance et la portée du jet d’eau… au détriment de certains.
DU CHÂTEAU AU TUYAU
D’un château d’eau (à gauche) jusqu’au bout du tuyau (à droite), l’eau s’écoule puis est éjectée à une vitesse (u et v) et à un débit qui dépendent de la hauteur h du réservoir, mais aussi de la longueur L du tuyau (ou de la tuyauterie de votre maison) et de la constriction de l’extrémité, par exemple lorsque le bout d’un tuyau d’arrosage est pincé. La pression au point E et au point de sortie H est égale à la pression atmosphérique ; la pression est maximale au point d’entrée en F, puis diminue le long du tuyau jusqu’au point G où elle subit une perte supplémentaire due à la constriction entre G et H.
remplie d’eau jusqu’à une hauteur de 20 mètres ( voir la figure ci - contre ). Imaginons qu’on fait un trou en bas de cette citerne À quelle vitesse l’eau jaillirait- elle ? Si la citerne est grande et le trou petit, cette vitesse est donnée par la formule de Torricelli, du nom du physicien et mathématicien italien qui l’a découverte en 1643 ; elle est égale à la racine carrée du double du produit de l’accélération de la pesanteur par la hauteur, soit ici 20 mètres par seconde
TURBULENT ET VISQUEUX
Maintenant branchons en bas de cette citerne un tuyau que, pour simplifier, on imagine parfaitement horizontal . Que devient la vitesse dans le tuyau ? En raison de la conservation du débit à l’intérieur du tuyau, de diamètre constant, cette vitesse est bien la même de la sortie de la citerne à l’extrémité où l’eau jaillit Si jamais on supposait que l’écoulement ne s’accompagnait d’aucune dissipation d’énergie, on obtiendrait exactement le
même résultat que la formule de Torricelli, qui ne dépendrait ni de la longueur du tuyau ni de son diamètre Pincer le tuyau n’aurait donc aucune autre conséquence que la réduction du débit
À ce stade du raisonnement, il nous faut faire intervenir la viscosité, dont la valeur quantifie les frottements au sein du liquide lorsqu’il s’écoule Hélas, dans les cas que nous envisageons, le régime de l’écoulement est dit « turbulent » , contrairement à ce qui se passe dans des
capillaires, des tuyaux de petit diamètre, où les couches de fluide glissent les unes sur les autres (l’écoulement est dans ce cas laminaire) : ici, les couches se mélangent en permanence, ce qui dissipe de l’énergie et la vitesse est quasiment la même sur toute la section du tuyau
Ces effets visqueux sont complexes et se prêtent mal aux calculs analytiques des physiciens. Il faut s’en remettre à des abaques (des tables numériques établies expérimentalement) comme le diagramme

POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 89
Tuyauterie Constriction L F E h u v G H
Château d’eau
de Moody, qui permet d’estimer la perte de charge, c’est-à-dire la diminution de la pression tout au long du tuyau : elle est proportionnelle à sa longueur, mais dépend aussi de sa rugosité et de la vitesse moyenne de l’eau à l’intérieur. Par ailleurs, cette vitesse moyenne est aussi fixée par la différence entre la pression nominale au compteur (les 2 bars) et la pression au début du tuyau (le point F de la figure page précédente) qui est justement égale à la perte de charge puisqu’on a la pression atmosphérique à l’autre bout ! C’est un serpent qui se mord la queue. Prenons un exemple : avec un tuyau parfaitement lisse de 17 mètres avec un diamètre de 2 centimètres, on peut estimer que la vitesse d’écoulement moyenne est de l’ordre de 5 mètres par seconde. Si le tuyau atteignait 90 mètres, on n’aurait plus que 2 mètres par seconde, c’est-àdire un débit divisé par 10 par rapport à celui mesuré au niveau du compteur. Ainsi , à cause de la viscosité , plus un tuyau est long, plus la vitesse et le débit diminuent (voir la figure ci-contre) L’effet est cependant atténué quand son diamètre augmente En pratique, la moindre rugosité, disons de l’ordre du millième du diamètre, va aussi affecter (à la baisse) vitesse et débit.
MOINS DE DÉBIT
POUR PLUS DE VITESSE
Maintenant , que se passe - t- il si on pince le tuyau au niveau de sa sortie ? Il y aura une perte de charge en plus qui va dépendre de la constriction (la diminution du diamètre de l’écoulement) et de la vitesse de l’eau à ce niveau , qui est justement la vitesse que l’on cherche Cette vitesse est reliée à la vitesse à l’intérieur du tuyau en raison de la conservation du débit de l’eau . Mais ce n’est pas pour cela qu’on peut reprendre les résultats précédents. Comme dans un circuit électrique, si vous rajoutez une résistance quelque part, vous modifiez les courants partout Cela explique pourquoi le problème est si difficile.
On peut cependant essayer d’anticiper les conséquences de cette constriction Plus de résistance, moins de débit ; moins de débit, vitesse nécessairement plus faible dans le long tuyau donc, tout le reste étant égal par ailleurs, moins de perte de charge à l’intérieur du tuyau, mais une perte de charge supplémentaire à l’endroit de la constriction Qu’est-ce qui va l’emporter ?
Pour une vitesse donnée et constante dans le long tuyau, la perte de charge dans
AH QU’IL EST LAID LE DÉBIT DE L’EAU
Comment varie la vitesse d’éjection de l’eau – ici le paramètre (v/vT)2, où v est la vitesse d’éjection au bout du tuyau et vT la vitesse de Torricelli, c’est-à-dire avec un écoulement sans dissipation d’énergie – d’un tuyau de longueur L et de diamètre D selon sa constriction (le diamètre de l’extrémité est noté d) ? Lorsque d = D (d/D = 1), c’est-à-dire qu’il n’y a pas de constriction, plus la longueur L est grande comparativement au diamètre D (le rapport L/D augmente, de haut en bas sur l’axe de droite), plus la vitesse d’éjection et le débit diminuent en raison de la viscosité de l’eau. Quand la constriction est plus importante (d/D diminue et se rapproche de 0, cas extrême où l’eau ne coule plus), la vitesse d’éjection augmente si le rapport L/D est su samment grand (de l’ordre de 100) : c’est ce qui se passe avec votre tuyau d’arrosage.
le tuyau croît avec la longueur tandis que celle dans la constriction n’en dépend pas, d’une part, et ces pertes dépendent toutes deux du carré de la vitesse, d’autre part. Réduire la vitesse dans le long tuyau, en réduisant le débit, aura donc nécessairement plus d’impact sur la première perte de charge (due à la longueur) plutôt que sur la seconde (due à la constriction) à partir d’une certaine longueur de tuyau
C’est ce que confirme une étude numérique récente qui a révélé une belle variété de comportements . Pour des tuyaux courts (un rapport de l’ordre de 10 entre longueur et diamètre ), la constriction réduit la vitesse d’éjection et l’eau va donc moins loin. Dès que le tuyau est assez long (un rapport longueur/diamètre au-delà supérieur à 100, ce qui est fréquent avec un tuyau de jardin), plus la constriction est importante , plus la vitesse d’éjection est élevée, mais plus le débit sera alors réduit. C’est ce que l’on observe le plus : on peut arroser loin, mais peu. Pour des tuyaux intermédiaires, on a un maximum de vitesse pour une certaine constriction. De quoi expérimenter chez soi, pas trop loin du compteur : vos fleurs vous remercieront ! n
Les auteurs ont notamment publié : En avant la physique !, une sélection de leurs chroniques (Belin, 2017).
M.-R. Alam, Why does water shoot higher if we partially block the garden hose outlet ?, American Journal of Physics, 2021.
R. Humbert, Water Nozzles, The Physics Teacher, 2005.
90 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 IDÉES DE PHYSIQUE
BIBLIOGRAPHIE
1000 500 200 100 50 30 10 0,1 - 1 L/D d/D = 1 d/D = 0 d/D (v/v T ) 2 0 0,2 1 0,6 0,2 0,8 0,4 0 0,6 0,4 0,8 1
COMPLÉTEZ VOTRE COLLECTION DÈS MAINTENANT !
OUI, je commande des numéros de Pour la Science





1 / JE COCHE LES RÉFÉRENCES ET JE RENSEIGNE LES
QUANTITÉS CI-DESSUS ET JE REPORTE LE TOTAL CI-DESSOUS
Total à régler : – , €



2 / J’INDIQUE MES COORDONNÉES
☐ M. ☐ M me
Nom :
Prénom :
Adresse :

Code postal : Ville :


Téléphone :
Courriel :
J’accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON



3 / JE RETOURNE LE COUPON ET MON RÈGLEMENT
J’émets un chèque à l’ordre de Pour la Science du montant total de la commande. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante :
Abonn’escient – TBS Group Service abonnement Groupe Pour la Science 20
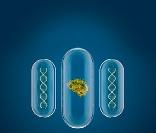
92130 Issy
COMMANDEZ PLUS SIMPLEMENT !
En vous rendant sur notre site internet vous pourrez :
● Retrouver toute notre collection
● Vérifier la disponibilité des anciens numéros

● Acheter les numéros en version numérique (4,49 €)

● E ectuer un paiement en ligne
Pour cela, scannez le QR code ci-contre ou rendez-vous sur boutique.groupepourlascience.fr


Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr
En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante :https://rebrand.ly/CGV-PLS. O re valable jusqu’au 21/12/2022 en France Métropolitaine uniquement. Les prix a chés incluent les frais de port et les frais logistiques. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour La Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous invitons à prendre connaissance de notre charte de protection des données personnelles à l’adresse suivante : https://rebrand.ly/charte-donnees-pls. Conformément à la réglementation applicable (et notamment au règlement 2016/679/UE dit « RGPD ») vous disposez des droits d’accès, de rectification, d’opposition, d’e acement, à la portabilité et à la limitation de vos données personnelles. Pour exercer ces droits (ou nous poser toute question concernant le traitement de vos données personnelles), vous pouvez nous contacter par courriel à l’adresse protection-donnees@pourlascience.fr.
Groupe Pour la Science – Siège social : 170 bis, boulevard du Montparnasse, CS20012, 75680 Paris Cedex 14 – Sarl au capital de 32 000 € – RCS Paris B 311 797 393 – Siret : 311 797 393 000 23 – APE 5814 Z NEUROSCIENCES Comment le cerveau trie l’information Anthropologie AUX ORIGINES DU CHIEN Écologie LE RÔLE CLÉ DU VIVANT LE CARBONE DANS LE SOL Histoire des sciences LE RETOUR SOUS-MARIN 13256 7,00Édition française Scientifi American Février 2023544 02/23 Mandy Bartsch Le défi énergétique des nouvelles MACHINES QUANTIQUES SEXE ET GENRE Pourquoi la biologie n’explique pas tout Biophysique LA BOUSSOLE QUANTIQUE DES OISEAUX Mathématiques LA SIMPLICITÉ, UN BIAIS DE L’ÉVOLUTION ? Physique QUAND LE CHAMPAGNE FRANCHIT LE MUR DU SON 13256 542 7,00 RD Édition française de Scientific American12/22 Thierry Hoquet Une solution au paradoxe de l’information ? DES TROUS DE VER AU CŒUR DES TROUS NOIRS MATHÉMATIQUES Les surprises des nombres friables Volcanologie LA PALMA, D’UNE ÉRUPTION Biologie QUAND ACCÉLÈRE L’ÉVOLUTION Physique ÉTRANGES NANOÉCHELLES 13256 7,00 € Édition française de Scientific American Septembre 2022539 POUR LA SCIENCE 09/22 Le regard de Jean-Paul Delahaye mathématicien ALZHEIMER Vers un traitement précoce de la maladie ?
PAG23VPC
☐ N° 550 (août 23) ⨯ 9,50 € = , € ☐ N° 549 (juillet 23) ⨯ 9,50 € = , € ☐ N° 548 (juin 23) ⨯ 9,50 € = , € ☐ N° 547 (mai 23) ⨯ 9,50 € = , € ☐ N° 546 (avril 23) ⨯ 9,50 € = , € ☐ N° 545 (mars 23) ⨯ 9,50 € = , € ☐ N° 539 (sept. 22) ⨯ 9,50 € = , € ☐ N° 540 (oct. 22) ⨯ 9,50 € = , € ☐ N° 542 (déc. 22) ⨯ 9,50 € = , € ☐ N° 541 (nov. 22) ⨯ 9,50 € = , € ☐ N° 543 (janv. 23) ⨯ 9,50 € = , € ☐ N° 544 (fév. 23) ⨯ 9,50 € = , €
Rouget de
Moulineaux
rue
Lisle -
les
Cette amibe, ici observée en lumière polarisée, porte une thèque, une coquille dure fabriquée à partir de particules minérales et d’autres organismes comme les diatomées.
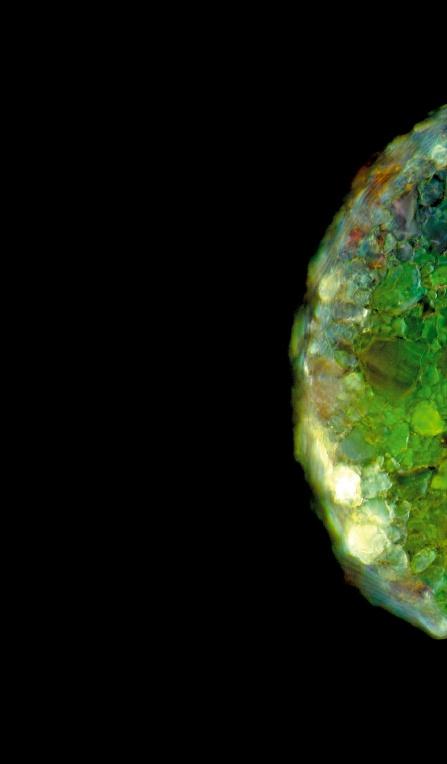
LE MONDE PERDU
DES PREMIERS EUCARYOTES
Qui eût cru que des molécules fossiles liées à la famille du cholestérol me raient au jour des écosystèmes insoupçonnés vieux de 1,5 milliard d’années ?
En 1912, Arthur Conan
Doyle met en scène le professeur George Challenger, un explorateur parti à la recherche d’un haut plateau isolé en Amérique du Sud. Il y trouvera Le Monde perdu , où voisinent de multiples organismes décrits par la paléontologie de l’époque – iguanodons , ptérodactyles , stégosaures… Ne nous y trompons pas, Conan Doyle savait son roman irréaliste et très éloigné des bases de la biologie évolutive Le monde perdu n’a de sens que dans un passé exploré par les paléontologues Mais peut- on , à partir de l’étude des organismes actuels, avancer des hypothèses sur l’existence d’éventuels organismes anciens , pas encore trouvés lors de fouilles ? C’est le pari qu’a fait récemment une équipe internationale sous la houlette de Jochen Brocks, de l’université de Canberra, en Australie. Dans un article fascinant , elle a ainsi révélé l’existence, au Mésoprotérozoïque,
il y a entre 1 et 1,8 milliard d’années, d’un « monde perdu » d’eucaryotes, les organismes dont les cellules possèdent un noyau individualisé
LA TENTATIVE D’ERNST HAECKEL
En 1866, le biologiste allemand Ernst Haeckel proposait un principe de « récapitulation », qu’il érigea alors en loi, selon lequel l’ontogénie – la succession des stades de développement d’un organisme au cours de son embryogenèse – récapitule la phylogénie – la succession des stades évolutifs acquis par les espèces ancestrales. Bien que présentant de nombreux contre-exemples, cette proposition, qui n’est certainement pas une loi, permet toujours de formuler des hypothèses sur des caractères ancestraux et l’existence de fossiles qui les arboreraient.
En 1994, le biochimiste allemand Konrad Bloch, lauréat du prix Nobel

Les amibes sont l’une des plus anciennes lignées d’eucaryotes actuels.
en 1964 pour avoir participé au déchiffrement de la voie de biosynthèse du cholestérol, suggéra de transposer ce principe en biochimie. La voie de biosynthèse des molécules de la famille du cholestérol – les stérols – comprend une trentaine de réactions catalysées par des enzymes. Tout d’abord, des condensations de petites molécules mènent au squalène, un terpène linéaire de trente atomes de carbone. Puis le squalène se cyclise en protostérols qui, après de multiples retouches enzymatiques, donnent des stérols. Vu la complexité de cette chaîne de biosynthèse, Konrad Bloch a
92 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 CHRONIQUES DE L’ÉVOLUTION L’AUTEUR
HERVÉ LE GUYADER professeur émérite de biologie évolutive à Sorbonne Université, à Paris
© Science Photo Library / Mis, Marek
Les amibes du genre Di ugia, le plus vaste parmi les amibes à thèque, vivent dans les marais et autres habitats d’eau douce, où elles se nourrissent principalement d’algues et de champignons.
EN CHIFFRES
C’est le nombre de dérivés de protostérols découverts dans la formation géologique de Barney Creek, dans le nord de l’Australie, datant de 1 640 millions d’années.
100 30 5
La voie de biosynthèse du cholestérol – une molécule constituée de 27 atomes de carbone et 4 cycles –compte plus de 30 réactions.
Amibe du genre Di ugia
Taille : entre 15 et 500 µm
Toutes les amibes utilisent des pseudopodes pour se déplacer en adhérant à un substrat.
émis l’hypothèse qu’elle s’est construite pas à pas au cours des temps géologiques. Des molécules de cette chaîne, qui sont, pour les cellules actuelles, des précurseurs des stérols, auraient alors été celles que les cellules utilisaient à une époque reculée.
Les stérols jouent un rôle clé chez les eucaryotes actuels. Chez les animaux, le cholestérol soutient et renforce la membrane des cellules. Dispersé dans la bicouche de phospholipides qui la constitue, il la rigidifie et lui confère la résistance mécanique nécessaire pour se courber. Il est donc indispensable pour que les
La Terre a connu cinq périodes glaciaires majeures : la glaciation huronienne, il y a entre 2,4 et 2,1 milliards d’années, la glaciation cryogénienne (720-630 millions d’années), les glaciations andine-saharienne (460-420 millions d’années) et du Karoo (360-260 millions d’années), et la dernière ère glaciaire, qui a culminé il y a 21 000 ans.
mouvements des cellules embryonnaires se déroulent sans déchirement de la membrane au cours du développement. Il sert aussi de protecteur thermique de la membrane. À haute température, la fluidité de celle-ci augmente, ce qui menace son organisation. Or le cholestérol diminue cette fluidité. À basse température, il joue le rôle d’antigel et maintient la fluidité de la membrane, l’empêchant de se solidifier. D’autre part, localement dans la paroi cellulaire, il se concentre en « radeaux » – des structures qui portent des protéines essentielles dans les échanges avec l’environnement cellulaire et qui ancrent le cytosquelette de microtubules et d’actine. Chez d’autres organismes pluricellulaires, des stérols différents – le stigmastérol pour les plantes, l’ergostérol pour les champignons – jouent un rôle tout aussi crucial.
Tous les eucaryotes pluricellulaires actuels en possédant, il a été admis que le plus récent ancêtre eucaryote commun, ou LECA (last eukaryotic common ancestor), en présentait aussi. Et que les produits de la dégradation des stérols au fil du temps – des stéranes – sont des biomarqueurs de cellules eucaryotes, que les géologues cherchent et dosent dans les sédiments. Or si les stéranes
POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 / 93
LE MYSTÈRE DES STÉRANES DISPARUS
Jusqu’à il y a 800 millions d’années, les enregistrements géologiques combinés de microfossiles d’eucaryotes et de stéranes – produits de dégradation des stérols – apparaissent cohérents : durant le Néoprotérozoïque, les eucaryotes modernes (en vert) augmentent, en particulier les algues
rouges (rhodophytes), puis connaissent une expansion massive dominée par les algues vertes (chlorophytes). Or, avant cette date, on trouve des microfossiles d’eucaryotes, mais plus de stéranes. Ces microfossiles correspondraient à un monde perdu d’eucaryotes (en orange) n’arborant pas de stérols, mais des précurseurs.
Milliards d’années
Alvéolates
Rhizariens
Haptophytes
Chlorophytes
Rhodophytes
Holozoaires
Mycètes
Amoebozoaires
associés aux animaux, plantes et champignons sont systématiquement trouvés jusqu’au début du Néoprotérozoïque, il y a 800 millions d’années, avant cette date fatidique on détecte toujours des microfossiles d’eucaryotes, mais plus de stéranes. L’hypothèse communément admise était que ces derniers étaient dégradés et difficilement détectables.
C’est là que Jochen Brocks et son équipe entrent en scène, en reprenant l’idée de Konrad Bloch. On ne trouve pas de stéranes, certes. Mais cherche-ton les bonnes molécules ? Peut-être que des cellules eucaryotes n’avaient alors pas encore construit la voie complète de biosynthèse des stérols et qu’elles utilisaient dans leurs membranes des molécules qui, actuellement, en sont des précurseurs. Ils sont donc allés à la recherche de protostérols. Auparavant, ils ont réalisé une maturation artificielle d’un mélange de précurseurs des stérols, afin d’identifier leurs produits de dégradation. Ce sont ces molécules qu’ils ont recherchées, d’abord sur des bitumes et des huiles datant du Mésozoïque (des dépôts pétrolifères, par exemple), puis dans des schistes australiens datant de 1 640 millions d’années. Réussite totale ! Les protostérols quasiment exclusifs trouvés indiquent la présence massive de cellules eucaryotes dépourvues de stérols
modernes dans leurs membranes. LECA existait peut-être déjà, mais avec une descendance en faible proportion, d’où l’absence de stérols dans les schistes.
IMPLACABLE CRYOGÉNIEN
Un nouveau scénario se dessine. Dans le Néoprotérozoïque s’insère un épisode surprenant où la Terre est devenue une boule de glace – d’où son nom : le « Cryogénien ». À cette époque, de multiples lignées eucaryotes peuplaient les océans. Mais, du point de vue membranaire, elles se partageaient sur un caractère essentiel. Les descendants de LECA possédaient des stérols modernes, tandis que les autres ne disposaient que des protostérols. Or le cholestérol et ses analogues chez les plantes protègent les membranes contre le froid. La sélection naturelle a alors agi de manière puissante. Les eucaryotes munis de stérols modernes ont survécu, les autres ont disparu, assurant la fin, sur une Terre boule de glace, d’un véritable monde perdu jusqu’à présent insoupçonné.
Ainsi, c’est la chimie qui a résolu le problème de la disjonction entre microfossiles et marqueurs biochimiques. Et la virtuosité technique étonnante de l’équipe de Jochen Brocks. Trouver des biomarqueurs dans des schistes de 1,5 milliard d’années, même Konrad Bloch n’y croyait pas ! n
Hervé Le Guyader a notamment publié : Ma galerie de l’évolution (Le Pommier, 2021).
BIBLIOGRAPHIE
J. J. Brocks et al., Lost world of complex life and the late rise of the eukaryotic crown, Nature, 2023.
J. J. Brocks et al., The rise of algae in Cryogenian oceans and the emergence of animals, Nature, 2017.
E. Dufourc, Sterols and membrane dynamics, J. Chem. Biol., 2008.
K. Bloch, « Evolutionary perfection of a small molecule », dans Blondes in Venetian Paintings, Yale Univ. Press, 1994.
94 / POUR LA SCIENCE N° 551 / SEPTEMBRE 2023 CHRONIQUES DE L’ÉVOLUTION
© Pour la Science, d’après J. J. Brocks et al., Lost world of complex life and the late rise of the eukaryotic crown, Nature, 2023
Phanérozoïque Néoprotérozoïque Mésoprotérozoïque Groupe souche hypothétique des eucaryotes Eucaryotes récents LECA Explosion cambrienne Paléo. 1,6 1,0 0,72 0,63 0,54 0 Plus ancien fossile connu Expansion Cryogénien
OFFRE D’ABONNEMENT 1 AN
ABONNEZ-VOUS À
Le magazine papier 12 numéros par an
Le magazine en version numérique 12 numéros par an
Le hors-série papier 4 numéros par an
Le hors-série en version numérique 4 numéros par an
Accès à pourlascience.fr
Actus, dossiers, archives depuis 1996
BULLETIN D’ABONNEMENT
Une question ? Contactez notre service clients à l'adresse : serviceclients@groupepourlascience.fr
☐ M. ☐ Mme
Nom : Prénom :
Adresse :
Je choisis ma formule (merci de cocher) 1
FORMULE PAPIER
• 12 n° du magazine papier
FORMULE PAPIER + HORS SÉRIE
• 12 n° du magazine papier
• 4 n° des hors-séries papier
FORMULE INTÉGRALE
• 12 n° du magazine (papier et numérique)
• 4 n° des hors-séries (papier et numérique)
• Accès illimité aux contenus en ligne
Code postal : Ville :
Téléphone :
Courriel : (indispensable pour la formule intégrale)
J'accepte de recevoir les o res de Pour la Science ☐ OUI ☐ NON
J’indique mes coordonnées 2 Je retourne le bulletin d'abonnement et mon règlement 3
J’émets un chèque à l’ordre de Pour la Science du montant de l’abonnement. J’adresse le bulletin et mon chèque par courrier postal à l’adresse suivante :

Abonn’escient – TBS Group
Service abonnement Groupe Pour la Science 20 rue Rouget de Lisle - 92130 Issy les Moulineaux





COMMANDEZ PLUS SIMPLEMENT !
Pour découvrir toutes nos o res d’abonnement et e ectuer un paiement en ligne, scannez le QR code ci-contre avec votre téléphone ou rendez-vous sur boutique.groupepourlascience.fr
* Réduction par rapport au prix de vente en kiosque et l’accès aux archives numériques. Durée d’abonnement : 1 an. Délai de livraison : dans le mois suivant l’enregistrement de votre règlement. O re valable jusqu’au 31/03/2024 en France métropolitaine uniquement. Pour un abonnement à l’étranger, merci de consulter notre site boutique.groupepourlascience.fr. Photos non contractuelles. Vous pouvez acheter séparément les numéros de Pour la Science pour 7 € et les hors-séries pour 9,90 € En souscrivant à cette o re, vous acceptez nos conditions générales de vente disponibles à l’adresse suivante : https://rebrand.ly/CGV-PLS. Les informations que nous collectons dans ce bulletin d’abonnement nous aident à personnaliser et à améliorer les services que nous vous proposons. Nous les utiliserons pour gérer votre accès à l’intégralité de nos services, traiter vos commandes et paiements, et vous faire part notamment par newsletters de nos o res commerciales moyennant le respect de vos choix en la matière. Le responsable du traitement est la société Pour la Science. Vos données personnelles ne seront pas conservées au-delà de la durée nécessaire à la finalité de leur traitement. Pour la Science ne commercialise ni ne loue vos données à caractère personnel à des tiers. Les données collectées sont exclusivement destinées à Pour la Science. Nous vous invitons à prendre connaissance de notre charte de protection des données personnelles à l’adresse suivante : https://rebrand.ly/charte-donnees-pls. Conformément à la réglementation applicable (et notamment au règlement 2016/679/UE dit « RGPD ») vous disposez des droits d’accès, de rectification, d’opposition, d’e acement, à la portabilité et à la limitation de vos données personnelles. Pour exercer ces droits (ou nous poser toute question concernant le traitement de vos données personnelles), vous pouvez nous contacter par courriel à l’adresse protection-donnees@pourlascience.fr.
FORMULE PAPIER FORMULE PAPIER + HORS - SÉRIE FORMULE INTÉGRALE
VOTRE TARIF D’ABONNEMENT 59 € Au lieu de 84,00 € 79 € Au lieu de 123,60 € 99 € Au lieu de 183,60 € 3 FORMULES AU CHOIX 30 % de réduction * 36 % de réduction * 46 % de réduction *
Groupe Pour la Science - Siège social : 170 bis, boulevard du Montparnasse, CS20012, 75680 Paris Cedex 14 - Sarl au capital de 32 000 € - RCS Paris B 311 797 393 - Siret : 311 797 393 000 23 - APE 58.14 Z 59 € Au lieu de 84,00
€ Au
99 € Au
€ 79
lieu de 123,60 €
lieu de 183,60 €
€
1-F-PAP-N-12N-59
1-F-INT-N-12N-99 € 1-F-HSPAP-N-12N-79 €
OUI , je
m’abonne pour 1 an à
PAG23STD
É TUDE DE CAS



Concevoir des dispositifs d’ablation par RF grâce à la multiphysique.

Pour modéliser correctement l’ablation de tissus par radiofréquence (RF), la simulation doit tenir compte du courant électrique, de la production de chaleur et de l’augmentation de la température dans le tissu humain. C’est là qu’intervient la simulation multiphysique.
en savoir plus comsol.blog/RF-tissue-ablation






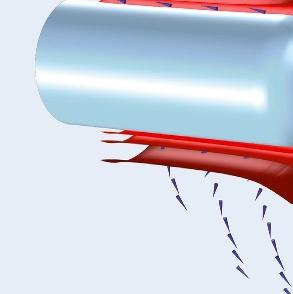

Le logiciel COMSOL Multiphysics® est utilisé pour la conception et la simulation des dispositifs et des procédés dans tous les domaines de l’ingénierie, de la fabrication et de la recherche.




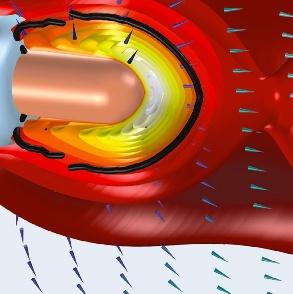
































 Isabelle Bellin
Isabelle Bellin