Saimm 202212 dec

The Southern African Institute of Mining and Metallurgy

OFFICE BEARERS AND COUNCIL FOR THE 2022/2023 SESSION

Honorary President

Nolitha Fakude

President, Minerals Council South Africa

Honorary Vice Presidents

Gwede Mantashe

Minister of Mineral Resources and Energy, South Africa

Ebrahim Patel

Minister of Trade, Industry and Competition, South Africa Blade Nzimande

Minister of Higher Education, Science and Technology, South Africa

President Z. Botha

President Elect W.C. Joughin

Senior Vice President E. Matinde

Junior Vice President G.R. Lane

Incoming Junior Vice President T.M. Mmola

Immediate Past President I.J. Geldenhuys

Honorary Treasurer W.C. Joughin

Ordinary Members on Council

W. Broodryk G. Njowa

Z. Fakhraei S.J. Ntsoelengoe

R.M.S. Falcon (by invitation) S.M. Rupprecht B. Genc M.H. Solomon

K.M. Letsoalo A.J.S. Spearing

S.B. Madolo A.T. van Zyl

F.T. Manyanga E.J. Walls M.C. Munroe

Co-opted to Members

K. Mosebi A.S. Nhleko

Past Presidents Serving on Council

N.A. Barcza C. Musingwini

R.D. Beck S. Ndlovu

J.R. Dixon J.L. Porter

V.G. Duke M.H. Rogers

R.T. Jones D.A.J. Ross-Watt

A.S. Macfarlane G.L. Smith

M.I. Mthenjane W.H. van Niekerk

G.R. Lane–TPC Mining Chairperson

Z. Botha–TPC Metallurgy Chairperson

M.A. Mello–YPC Chairperson

K.W. Banda–YPC Vice Chairperson

Branch Chairpersons

Botswana Being established

DRC Not active

Johannesburg N. Rampersad

Namibia Vacant

Northern Cape I. Tlhapi

North West I. Tshabalala

Pretoria Vacant

Western Cape A.B. Nesbitt

Zambia J.P.C. Mutambo (Interim Chairperson)

Zimbabwe A.T. Chinhava

Zululand C.W. Mienie

PAST PRESIDENTS

* W. Bettel (1894–1895)

* A.F. Crosse (1895–1896)

* W.R. Feldtmann (1896–1897)

* C. Butters (1897–1898)

* J. Loevy (1898–1899)

* J.R. Williams (1899–1903)

* S.H. Pearce (1903–1904)

* W.A. Caldecott (1904–1905)

* W. Cullen (1905–1906)

* E.H. Johnson (1906–1907)

* J. Yates (1907–1908)

* R.G. Bevington (1908–1909)

* A. McA. Johnston (1909–1910)

* J. Moir (1910–1911)

* C.B. Saner (1911–1912)

* W.R. Dowling (1912–1913)

* A. Richardson (1913–1914)

* G.H. Stanley (1914–1915)

* J.E. Thomas (1915–1916)

* J.A. Wilkinson (1916–1917)

* G. Hildick-Smith (1917–1918)

* H.S. Meyer (1918–1919)

* J. Gray (1919–1920)

* J. Chilton (1920–1921)

* F. Wartenweiler (1921–1922)

* G.A. Watermeyer (1922–1923)

* F.W. Watson (1923–1924)

* C.J. Gray (1924–1925)

* H.A. White (1925–1926)

* H.R. Adam (1926–1927)

* Sir Robert Kotze (1927–1928)

* J.A. Woodburn (1928–1929)

* H. Pirow (1929–1930)

* J. Henderson (1930–1931)

* A. King (1931–1932)

* V. Nimmo-Dewar (1932–1933)

* P.N. Lategan (1933–1934)

* E.C. Ranson (1934–1935)

* R.A. Flugge-De-Smidt (1935–1936)

* T.K. Prentice (1936–1937)

* R.S.G. Stokes (1937–1938)

* P.E. Hall (1938–1939)

* E.H.A. Joseph (1939–1940)

* J.H. Dobson (1940–1941)

* Theo Meyer (1941–1942)

* John V. Muller (1942–1943)

* C. Biccard Jeppe (1943–1944)

* P.J. Louis Bok (1944–1945)

* J.T. McIntyre (1945–1946)

* M. Falcon (1946–1947)

* A. Clemens (1947–1948)

* F.G. Hill (1948–1949)

* O.A.E. Jackson (1949–1950)

* W.E. Gooday (1950–1951)

* C.J. Irving (1951–1952)

* D.D. Stitt (1952–1953)

* M.C.G. Meyer (1953–1954)

* L.A. Bushell (1954–1955)

* H. Britten (1955–1956)

* Wm. Bleloch (1956–1957)

* H. Simon (1957–1958)

* M. Barcza (1958–1959)

* R.J. Adamson (1959–1960)

* W.S. Findlay (1960–1961)

* D.G. Maxwell (1961–1962)

* J. de V. Lambrechts (1962–1963)

* J.F. Reid (1963–1964)

* D.M. Jamieson (1964–1965)

* H.E. Cross (1965–1966)

* D. Gordon Jones (1966–1967)

* P. Lambooy (1967–1968)

* R.C.J. Goode (1968–1969)

* J.K.E. Douglas (1969–1970)

* V.C. Robinson (1970–1971)

* D.D. Howat (1971–1972)

* J.P. Hugo (1972–1973)

* P.W.J. van Rensburg (1973–1974)

* R.P. Plewman (1974–1975)

* R.E. Robinson (1975–1976)

* M.D.G. Salamon (1976–1977)

* P.A. Von Wielligh (1977–1978)

* M.G. Atmore (1978–1979)

* D.A. Viljoen (1979–1980)

* P.R. Jochens (1980–1981)

* G.Y. Nisbet (1981–1982)

A.N. Brown (1982–1983)

* R.P. King (1983–1984)

J.D. Austin (1984–1985)

* H.E. James (1985–1986)

H. Wagner (1986–1987)

* B.C. Alberts (1987–1988)

* C.E. Fivaz (1988–1989)

* O.K.H. Steffen (1989–1990)

* H.G. Mosenthal (1990–1991)

R.D. Beck (1991–1992)

* J.P. Hoffman (1992–1993)

* H. Scott-Russell (1993–1994)

J.A. Cruise (1994–1995)

D.A.J. Ross-Watt (1995–1996)

N.A. Barcza (1996–1997)

* R.P. Mohring (1997–1998) J.R. Dixon (1998–1999) M.H. Rogers (1999–2000)

L.A. Cramer (2000–2001)

* A.A.B. Douglas (2001–2002) S.J. Ramokgopa (2002-2003)

T.R. Stacey (2003–2004)

F.M.G. Egerton (2004–2005)

W.H. van Niekerk (2005–2006)

R.P.H. Willis (2006–2007)

R.G.B. Pickering (2007–2008)

A.M. Garbers-Craig (2008–2009)

J.C. Ngoma (2009–2010)

G.V.R. Landman (2010–2011)

J.N. van der Merwe (2011–2012)

G.L. Smith (2012–2013)

M. Dworzanowski (2013–2014)

J.L. Porter (2014–2015)

R.T. Jones (2015–2016)

C. Musingwini (2016–2017)

S. Ndlovu (2017–2018)

A.S. Macfarlane (2018–2019)

M.I. Mthenjane (2019–2020)

V.G. Duke (2020–2021)

I.J. Geldenhuys (2021–2022)

Editorial Board

S.O. Bada

R.D. Beck

P. den Hoed

I.M. Dikgwatlhe

R. Dimitrakopolous* M. Dworzanowski* L. Falcon B. Genc

R.T. Jones

W.C. Joughin

A.J. Kinghorn

D.E.P. Klenam

H.M. Lodewijks D.F. Malan

R. Mitra* H. Möller

C. Musingwini S. Ndlovu

P.N. Neingo M. Nicol*

S.S. Nyoni M. Phasha P. Pistorius P. Radcliffe N. Rampersad

Q.G. Reynolds I. Robinson

S.M. Rupprecht K.C. Sole A.J.S. Spearing* T.R. Stacey E. Topal* D. Tudor* F.D.L. Uahengo D. Vogt*

*International Advisory Board members

Editor /Chairman of the Editorial Board R.M.S. Falcon

Typeset and Published by

The Southern African Institute of Mining and Metallurgy PostNet Suite #212 Private Bag X31 Saxonwold, 2132 E-mail: journal@saimm.co.za

Printed by Camera Press, Johannesburg

Advertising Representative

Barbara Spence Avenue Advertising Telephone (011) 463-7940 E-mail: barbara@avenue.co.za ISSN 2225-6253 (print) ISSN 2411-9717 (online)

Directory of Open Access Journals

Contents

Journal Comment: In defence of a responsible mining industry by D. Vogt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv

President’s Corner: Play in the mineral industry’s world of permacrisis by Z. Botha v

NEWS OF INTEREST

PROFESSIONAL TECHNICAL AND SCIENTIFIC PAPERS

The

spillover effect of industrial action on the profitability of platinum

mining companies

by B. Ceki, M.L. Pududu, and K. Mohajane . . . . . . . . . . . . . . . . . . . . . . . . . . 681

This study aimed to determine the effects of industrial action on profitability of platinum mining companies in South Africa. Contrary to international literature suggesting that spillover effects of industrial action positively effect competing mining companies, this study shows the opposite. The results show that profits in the platinum sector decreased significantly during the strike period for both the affected and competing companies. The study contributes to the scarce literature on the spillover effect of industrial action on the profitability of mining companies in a developing economy.

Ventilation optimization through digital transformation by T. Chikande, H.R Phillips, and F.T. Cawood 687

This paper introduces a novel concept of ventilation optimization through digital transformation, targeting mainly room and pillar platinum mines. The authors designed and installed a ventilation on demand system to minimize the use of redundant air in underground operations. Fourth industrial revolution techniques were applied to the environmental monitoring and tracking systems, thereby optimizing air quantity demands. The mine managed to reduce its annual power consumption by 23%. The system was designed to harness the full benefits such as productivity enhancement, reduced power costs, and improved worker health.

THE INSTITUTE, AS A BODY, IS NOT RESPONSIBLE FOR THE STATEMENTS AND OPINIONS ADVANCED IN ANY OF ITS PUBLICATIONS.

Copyright© 2022 by The Southern African Institute of Mining and Metallurgy. All rights reserved. Multiple copying of the contents of this publication or parts thereof without permission is in breach of copyright, but permission is hereby given for the copying of titles and abstracts of papers and names of authors. Permission to copy illustrations and short extracts from the text of individual contributions is usually given upon written application to the Institute, provided that the source (and where appropriate, the copyright) is acknowledged. Apart from any fair dealing for the purposes of review or criticism under The Copyright Act no. 98, 1978, Section 12, of the Republic of South Africa, a single copy of an article may be supplied by a library for the purposes of research or private study. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means without the prior permission of the publishers. Multiple copying of the contents of the publication without permission is always illegal.

U.S. Copyright Law applicable to users In the U.S.A. The appearance of the statement of copyright at the bottom of the first page of an article appearing in this journal indicates that the copyright holder consents to the making of copies of the article for personal or internal use. This consent is given on condition that the copier pays the stated fee for each copy of a paper beyond that permitted by Section 107 or 108 of the U.S. Copyright Law. The fee is to be paid through the Copyright Clearance Center, Inc., Operations Center, P.O. Box 765, Schenectady, New York 12301, U.S.A. This consent does not extend to other kinds of copying, such as copying for general distribution, for advertising or promotional purposes, for creating new collective works, or for resale.

The Journal of the Southern African Institute of Mining and Metallurgy

SAIMM Webinar Abstract: Decarbonizing the mining sector by 2040 vi

Simulation of production processes and associated costs in mining using the Monte Carlo method by M. Mathey 697

The application of the Monte Carlo technique to production planning and everyday economic decision-making in mine production management is demonstrated. The logic is detailed using an example of underground production with continuous miners (CMs) and truck haulage. It is argued that the availability of equipment and personnel is the predominant variable influencing mine output and productivity. Some general interdependencies of availability, utilization, productivity, and costs of production processes are outlined. Finally, several possible options and their consequences for improving production are explored.

Studies on fluorination of Fe₃O₄ (magnetite) by NH₄HF₂ by L. Zhang, Y. Zhou, H. Wang, and C. Mo 705 Fluorination of magnetite (Fe3O4) by NH4HF2 was investigated using simultaneous thermogravimetry and differential thermal analysis and by observing the morphology and phase changes using scanning electron microscopy with energy dispersive X-ray spectroscopy and X-ray diffractometry. Results indicated that fluorination with the involvement of oxygen started at room temperature, dominated at 178.4OC, and completed at 200OC with the formation of only (NH4)3FeF6. At 550OC, the oxidation of FeF3 caused the formation of FeOF/Fe2O3.

Stochastic analysis of dig limit optimization using simulated annealing by J.R. van Duijvenbode and M.S. Shishvan 715 A stochastic analysis tool is presented that can be used with the results of heuristic dig-limit optimization to increase confidence in the results for dig-limit delineation in open-pit mining. First, an enhanced simulated annealing algorithm for dig-limit optimization is described, after which the algorithm is tested on ten different blasts at the Marigold mine, Nevada, USA, as a case study. The results were analysed with a destination-based ensemble probability map and an analysis of the final solution data distribution. The analysis tool provides block destination probabilities and box plots, and could assist in making well-informed design decisions in areas of uncertainty.

Flyrock in surface mining – Limitations of current predictive models and a better alterative through modelling the aerodynamics of flyrock trajectory by T. Szendrei and S. Tose ........................................................................... 725

Historical approaches to the problem of flyrock are inherently incapable of addressing root causes of flyrock and the projection velocity and give no information on the influence of rock size and shape on the flight distance, nor on the question of flyrock velocity. Flight trajectory calculations neglect the effects of air resistance on the trajectory. Trajectory models cannot propel sizeable rocks to distances much beyond 150 m. Trajectory calculation with air drag affords the most promising approach to the prediction of flyrock range. A unique feature of the proposed flight modelling is that it collapses all suspected causes of flyrock to the launch velocity. This indicates that the root causes of flyrock lie in the mechanisms of momentum transfer to broken rock and suggests new avenues of study.

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride: Effect of leaching conditions by M.R. Serwale, T. Coetsee, K.C. Sole, and S. Fazluddin ................................................. 733

Titanium sponge produced by lithiothermic reduction of titanium tetrachloride feedstock is contaminated by a range of lithium and chloride species. We examined the effects of particle size, temperature, and HCl concentration as input leaching variables on the removal of chlorides from the crude titanium sponge. Experimental results confirmed that effectiveness of leaching and removal of dissolved impurities from the sponge are dependent on leaching kinetics, which are influenced by temperature, particle size, and morphology. Leaching at 14°C in either 1 M or 0.032 M HCl yielded a titanium sponge product that met the ASTM standard specification for commercially pure Grade 1 titanium.

A

simulation

model to study truck-allocation options

by W. Zeng, E.Y. Baafi, and H. Fan ..................................................................... 741

A discrete event simulator, TSJSim, for evaluating the stochastic and dynamic operational variables in a truck-shovel system is presented. The simulation results indicate that the trends all demonstrated similar patterns as the fleet size varied. As the system fleet size increased, the system production tons first increased significantly and then remained relatively constant. The bunching time decreased when the truck-allocation strategies were applied. In a simulated truck-shovel network system with multiple traffic intersections, by assigning trucks at the intersections, both productivity and fleet utilization increased.

In defence of a responsible mining industry Journal Comment

In the aftermath of COP27, and with insurer Aon reporting 29 weather-related disasters, each causing more than $1.0 billion in damage, between January and September this year, it is becoming clearer that humanity has to do something. And every credible attempt to define that ‘something’ has included a need for more metals – copper for generating and transmitting electricity, lithium for batteries, steel for the structure of wind turbines, silicon for solar cells, even potentially uranium for nuclear power.

But at the same time, mining has become connected in people’s minds with dirty energy – mining equals coal. That’s leading to a dangerous narrative. In the UK, students at Exeter University, home of the Camborne School of Mines, have been bombarded by posters from the ‘Fossil Free Careers Campaign’, which also campaigns against the mining industry. They have called for a ban on promotion of mining careers on Exeter campus and have already succeeded at Birkbeck University of London.

While this might seem irrelevant in the UK with its small remaining mining industry, Australia is also struggling to attract young people from an environmentally conscious generation into mining. It is only a matter of time before the anti-mining mindset makes its way to South Africa.

Without ignoring our challenges, it is up to us to promote the industry unapologetically for what it is: the only way we’re going to source sufficient metals to meet our energy needs from renewable resources, and a vital contributor to the vision of a sustainable way of life. Let’s get out and talk at school careers days, local clubs and societies. and get the word out.

D. Vogt

President’s Corner

Play in the mineral industry’s world of permacrisis

Iam struggling to describe the year 2022. While reflecting on the subject, I realized that I didn’t want to tell anyone what happened during 2022, but how it felt. In my attempt to do this I came across the word ‘permacrisis’ (and it has been chosen as The Collins Dictionary’s word of the year).

Permacirsis has been described beautifully in the news as ‘the dizzying sense of lurching from one unprecedented event to another, as we wonder bleakly what new horrors might be around the corner’. From the energy crisis to soaring commodity prices, from struggling rail infrastructure to the climate crisis (and fossil fuels), to potential wars impacting inflation, it seems like crises might just be the word we are looking for.

However, crisis can also mean change. It could indicate the arrival of a positive shift, it could mean innovation! Progress is driven by crises. We just need enough agility to hold to the paradox that innovation cannot happen without failure; collaboration and growth cannot happen without conflict. We need crises to fuel innovation. Although 2022 had its fair share of disasters, this could open the door for creativity and innovation. We need relationships and collaboration to foster innovation.

The Harvard Study of Adult Development may be the longest study of adult life that’s ever been done. This study tracked the lives of 724 men over 75 years, year after year, asking about their work, their home lives, and their health. About 60 of the original 724 men were still alive during 2015. The clearest message from this 75-year study was: Good relationships keep us happier and healthier.

As we close the door on 2022 and walk into 2023, I’m wondering how can I promote innovation? How do I build meaningful relationships to foster collaboration and increase happiness?

Dr Stuart Brown, psychiatrist, clinical researcher, and founder of the National Institute for Play notes that play is the single most important factor in determining our success and happiness. It has a profound impact on how we parent, educate, innovate, and our productivity.

Dr Brown has conducted over 6000 interviews with people to obtain their ‘play histories’ and found that the ability to play is critical not only to being happy, but also to sustaining social relationships and being a creative, innovative person. He emphasizes that play has many social interaction benefits and is actually the foundation of all personal relationships (Play: How it Shapes the Brain, Opens the Imagination, and Invigorates the Soul, 2009).

It is very important to note that the opposite of play is NOT work, but really depression. Play sets the stage for socialization, nourishing the roots of trust, empathy, caring, and sharing. Adults who do not regularly activate their play nature may experience their lives as tinged with depression, and may lack the optimism, adaptability, and resiliency to perform well in their work and family lives.

So, as we say goodbye to 2022 and open the door to all the possibilities that 2023 holds, I want to ask, how will you measure your life and the impact you have on your environment? How will you build relationships and nourish trust and empathy? I want to encourage everyone to slow down, play more, give yourself freedom from time constraints, diminish your consciousness of self, focus on the power of relationships, and make the next year your most creative year yet!

Z. Botha President, SAIMM

SAIMM Webinar Abstract

Decarbonizing the mining sector by 2040

The mining industry is among the heaviest generators of greenhouse gases globally. While the goal of the Paris Accord is to achieve carbon neutrality for the planet by 2050, many mining companies, such as Anglo American and Sibanye-Stillwater, have committed to carbon neutrality by 2040.

Decarbonization is often simplistically interpreted as being about renewable energy and the use of fossil fuels, but its far more complex than that. From a mining perspective, decarbonization mines has very specific, and often ostensibly disparate, dimensions to consider. These range from deep-seated social anthropological factors such as social and industrial practices and behaviour to the highly technological solutions to decarbonize energy usage. From a technology perspective it is possible to decarbonize the mining sector by 2040, but there is inevitably a trade-off between economics and the pragmatic application of these interventions. At the other end of the decarbonization spectrum, many of the social interventions are beyond the control or influence of the mining companies, but there is much that can de done.

In South Africa, most of the larger companies have established programmes to implement renewable energy projects, many of which are driven by sheer economic considerations and the high cost of Eskom’s energy supply, while at the same time these projects will contribute substantially to the decarbonization of these mines. There are at present 29 mining companies undertaking 89 energy projects totalling 6 .5 G W capacity. These comprise 6.2 GW of solar, 0.2 GW. These comprise 6.2GW of solar, 0.2GW, 8MW Biomass energy and 84MW of battery storage. More recently, Anglo American announced a joint venture with Envusa Energy, who plan to roll out a further 5 GW of renewable energy, bringing the total commitment of the mining industry to the establishment of 12–15 GW of renewable energy utilities. This represents almost 40% of the nameplate Eskom generating capacity of 38 GW.

The total capex required is excess of between US$12,5–15.0 billion, or R225–270 billion. Much of this capital will be funded by offshore finance and constitutes substantial FDI. Complementing the renewable energy programmes, many mining companies, such as Anglo American and Exxaro, have coherent circular economy, zero waste to landfill projects and economic diversification strategies directed towards a Just Transition in the sector. Although these projects are established, they are effectively in their infancy and not enough to reach the 2040 targets. The mining sector is only just starting out on this journey and there is much more to do.

Mitigating the impacts of greenhouse gases through structured decarbonization and just transition strategies in the mining sector requires a trans-disciplinary systems-based approach. This must bridge the ostensibly disparate causalities and design integrated functional and economic value chains that serve to eliminate greenhouse gases through related carbon-neutral processes in the mining value chain. The SAIMM ESGS Committee’s decarbonization programme outlines the issues to be addressed and describes the architecture of mining decarbonization value chains. The objective of the webinar, held on 14 September 2022, was to create an awareness and understanding of the cardinal issues around decarbonization of mines in South Africa and to start a structured dialogue around these issues within our membership. If you would like a copy of the presentation please contact Nazli Mamdoo at nazli@saimm.co.za.

Professor Michael Solomon Chairman, SAIMM ESGS

The Journal of the Southern African Institute of Mining and Metallurgy

Affiliation:

1Department of Financial Accounting, University of South Africa, South Africa.

2Department of Financial Governance, University of South Africa, South Africa.

Correspondence to: B. Ceki Email: ntoyab@unisa.ac.za

Dates: Received: 31 May 2021 Revised: 29 Jul. 2022 Accepted: 30 Aug. 2022 Published: December 2022

How to cite: Ceki, B., Pududu, M.L., and Mohajane, K. 2022

The spillover effect of industrial action on the profitability of platinum mining companies.

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 681–686

DOI ID: http://dx.doi.org/10.17159/24119717/1647/2022

ORCID: B. Ceki https://orcid.org/0000-00029827-0732

M.L. Pududu https://orcid.org/0000-00025523-749X

K. Mohajane https://orcid.org/0000-00024367-9549

The spillover effect of industrial action on the profitability of platinum mining companies

by B. Ceki1, M.L. Pududu2, and K. Mohajane2

Synopsis

This study was aimed at determining the effects of industrial action on profitability in the South African platinum mining sector. We compared companies where employees engaged in industrial action (affected companies) to strike-free companies (competing companies). Industrial action refers to strikes by rockdrillers, as these strikes typically result in the shutdown of production at the mines affected. A t-statistics analysis of significant differences in revenue and earnings of affected and non-affected platinum companies was conducted using data from platinum mining companies listed on the Johannesburg Stock Exchange from 2011 to 2015. Contrary to international studies, which suggest that the spillover effects of industrial action positively affect competing companies, our findings show that profits in the platinum sector decrease significantly during strike periods for both affected and competing companies. The results indicate industrial action is a threat to the profitability of all companies, and that employee demands should be prioritized and negotiated before they result in industrial action. Improved dialogue between management, labour unions, and employees in the platinum mining industry is recommended.

The study contributes to the scanty literature on the effect of industrial action on the profitability of mining companies in a developing economy.

Keywords

industrial action, profitability, platinum mining, mining industry.

Introduction

The mining industry is a significant contributor to the South African economy. It employs more than 1.4 million, a number higher than all the other industries in South Africa (Mnwana, 2015; Moloi, 2015; Chambers of Mines of South Africa, 2014). The platinum sector is the major contributor to the GDP in the mining industry, followed by the gold mining sector (Mnwana, 2015). However, the mines have been plagued with crippling and costly labour strikes. The Lonmin plc platinum strike that lasted for six weeks in 2012 resulted in the death of 34 mineworkers (Thomas, 2018). A subsequent strike in 2014 led to a five-month shutdown in the operations of six large platinum miners (Bohlmann, van Heeden, and Dixon, 2015; Alexander, 2013). The cost of these strikes to the affected mining companies is estimated at approximately a 23 billion South African rand in lost revenue and R10.7 billion in employee earnings (Bohlmann, van Heeden, and Dixon, 2015).

There is little information in the literature on how strikes in the platinum mines affect the profitability of competing platinum companies that did not have strikes. Profitability in this study refers to revenue and earnings before interest, tax, depreciation, and amortization (EBITDA). The strikes considered here relate to industrial action by underground rock-drillers; these strikes usually lead to the production shut-down of the affected mines. Affected companies refers to companies that suffered strikes, while competing companies refers to companies that did not have strikes.

The motivation for the study is to shed light on the effect of strikes on the profitability of companies affected and the spillover effects on competing companies. Most platinum mining companies not affected by strikes did not disclose spillover effects of the strikes, nor did they disclose strikes as a high-risk factor in their financial statements, hence the need to investigate spillover effects (Moloi, 2015) and to ascertain whether strikes are a risk factor that should be disclosed in the financial statements. Similar studies on the spillover effect of strikes on competing companies in industries other than mining have been done internationally, and shown conflicting results; these are briefly discussed below.

McDonald and Bloch (1999) found that strikes in a manufacturing company in Australia had a significant positive effect on the profitability of competing companies that did not suffer strike action.

De Fusco and Fuess (1991) found that strikes in the Australian airline industry had a significantly negative effect the market value of the affected companies, and a significant positive effect on market value for competing companies. Kramer and Vasconcellos (1996) found no significant effect of strikes on the market value of competing companies in the US vehicle manufacturing industry. These studies were conducted in developed countries and on industries other than mining. South African studies on industrial action in the mining industry have examined the national economic effect of strikes in platinum mines, while others examined strike effects on financial statement disclosures (Bohlmann, van Heeden, and Dixon, 2015; Moloi, 2015). For example, Bohlmann, van Heeden, and Dixon (2015) found that the 2014 platinum mining strike in South Africa had a negative effect on the economy which will continue into the future. The Bohlmann, van Heeden, and Dixon (2015) study was an economywide study, and the results may differ when considering the effect of strikes on profitability at the company level. Therefore, the present study extends the existing literature by providing a developing country context and focusing on an industry not yet examined.

The strikes considered in previous studies were of short duration compared to those in the present study. For example, the 2014 platinum strike lasted for five months compared to an average of three days for strikes in international studies (Bohlmann, van Heeden, and Dixon, 2015; Dabscheck, 1991; Neumann and Reder, 1984). The length of a strike may have a spillover effect on the profitability of competing companies. Profitability in previous studies was measured using a profit cost margin (i.e. profit divided by total income) (McDonald and Bloch, 1999), while this study uses earnings before tax, interest, depreciation, and amortization (EBITDA) as a measure of profitability. EBITDA is a better measure of profitability because it excludes fixed costs such as depreciation and amortization (Bouwens, Kok, and Verriest, 2019). Revenue was used to examine if there is a significant difference between the revenues of the affected and competing mines.

Considering the previous studies discussed, it is of interest to examine the following research question: Is there a spillover effect on the profitability of competing mining companies due to strikes in affected mining companies in the platinum mining sector?

The findings will provide insight to managers, shareholders, and other stakeholders regarding whether strikes in mining companies affect the competing mining companies’ profitability.

Background: Industrial action in the South African mining sector

Mineworkers generally have a low level of education; they work long hours, often under adverse health and safety conditions and are easily exploited by mining executives attempting to maximize profit margins (Mnwana, 2015; Alexander, 2013). Mineworkers live under poor conditions as they cannot afford a reasonable standard of living with their low wages while supporting big families at home (Mnwana, 2015). Even skilled mineworkers such as engineers and artisans suffer stress related to remuneration and fringe benefits, and fatigue due to long working hours (Thasi and van der Walt, 2020; Pelders and Nelson, 2019).

Low wages have always been the root cause of the mining strikes. For example, the 2012 strike at Lonmin Platinum plc, which resulted in the deaths of 34 mineworkers, was a strike

over wage demands (Mnwana, 2015; Alexander, 2013). The mineworkers were demanding wages of R12 500 (which is $892 using an average exchange rate for 2016 of R14 to the US dollar), which would amount to at least three times the wages they were earning at the time (Antin, 2013). Another significant strike in the platinum sector took place in 2014, again due to unmet wage demands, and lasted for five months. The affected companies were Anglo American Platinum Ltd, Lonmin Platinum plc, and Impala Platinum Holdings (Bohlmann, van Heeden, and Dixon, 2015; Moloi, 2015; Alexander, 2013; Kaonga and Kgabi, 2011). The mineworkers were still demanding a basic wage of R12 500. The strike ended when management agreed to increase wages by R1 000 for the next three years and reach the R12 500 wage demand by 2017 (Sinwell, 2019).

Literature review

Most research on strikes focuses on the causes, duration, costs and benefits of strikes, and political dynamics (Onyembukwa, 2021; de Kadt, Kanu, and Sands 2020; Benya, 2015; Chinguno, 2015; Mnwana, 2015; Stewart, 2013; Alexander et al., 2012; Barchiesi, 1999). There is a small body of literature based on international studies that reports mixed results regarding the effect of strikes on profitability of both affected and competing companies (Kramer and Vasconcellos, 1996; de Fusco and Fuess, 1991). A recent South African study considered the effect of strike announcements on company value instead of the effect of strikes on profitability of affected and competing firms (Afik, Haim, and Lahav, 2019).

International studies

A study conducted on the US airline industry found that a strike negatively affects the share price of an affected company, while the profits of a competing company are positively affected (de Fusco and Fuess, 1991). However, the authors caution that the results could be different for manufacturing companies, which can build up inventory before the strike. This is impossible in the airline industry. Therefore, a follow-up study by Kramer and Vasconcellos (1996) examined the effect of strikes on share returns of competing companies in the vehicle manufacturing industry over time. They used event analysis to study the share returns of the strike-free companies in the same industry before, during, and after the strike. Kramer and Vasconcellos (1996) found that the strike-hit companies were negatively affected but insignificantly so, which may be due to stockpiling prior to the strike. The positive spillover to the competing companies was not statistically significant. Another study, in the Australian manufacturing industry, revealed that strikes result in increased profitability for competing companies (McDonald and Bloch, 1999).

Neumann (1980) studied the effect of strikes on company value as measured by the stock market and found that a strike initially had a negative effect, but a positive one after the strike ended. He also found that the effect on the value of the affected companies was negative but insignificant because the market anticipated the strike (Neumann, 1980). Becker and Olson (1986) also examined the effect of strikes on a firm’s share price by conducting an event analysis and found an insignificant negative effect of strikes on the share price of the affected company. Afik, Haim, and Lahav (2019) found that an announcement of an impemding strike had a negative effect on the value of Israeli companies. Therefore, the literature shows that strikes do not have a significant negative affect on the affected companies, but do positively affect the competing companies.

The spillover effect of industrial action on the profitability of platinum mining companies

The Journal of the Southern African Institute of Mining and Metallurgy

In summary, earlier international studies suggest that strikes have a negative effect on the affected company’s profitability and a positive effect on the competing companies’ profitability.

South African research on the effect of mining strikes on affected companies

Most studies on mining strikes in South Africa focus on the political and human resource dynamics (Onyebukwa 2021; de Kadt, Johnson-Kanu, and Sands 2020; Schultz, 2020; RodnyGumede and Swart 2020 Tinsley, 2019; Bavu, 2015; Benya, 2015; Chinguno, 2015; Mnwana, 2015; Alexander, 2013; Stewart, 2013). The few studies that examined the effect of strikes on profitability and share value only looked at affected mining companies. these are briefly discussed next.

Bhana (1997) examined the effect of strikes on the shareholder value of the affected companies. The study found that the value of shares decreases at the announcement of the strike and during the strike, and does not increase significantly at the end of the strike. Seedat (2013) found that share prices of affected gold mining companies steadily decreased before, during, and after the strike. The decrease began as soon as the strike was announced. At the economy level, Bohlmann, van Heeden, and Dixon (2015) predicted that the negative effect of the five-month platinum belt strike in 2014 on the South African economy would continue to be felt for the next 20 years.

The few studies done in South Africa suggest that the affected mining companies are negatively affected by strikes, but are silent on the spillover effect of strikes on competing companies. The current study is aimed at closing this gap in the literature. We also investigate the spillover effect of strikes in the mining industry in the context of a developing economy; a topic that does not appear to have been examined in the literature. As mentioned above, the international studies found a positive spillover effect of strikes on competing companies. Therefore, the hypotheses for the study are:

1 Competing platinum mining companies’ revenue is affected by strikes at the affected platinum mining companies.

2 Competing platinum mining companies’ EBITDA is affected by strikes at the affected platinum mining companies.

Theoretical framework

The theory of the offset factor is adopted in the study. This theory, which is also called Christenson’s theory, states that the effect of work stoppages due to industrial action on the production of the striking company should be offset by competing companies not striking (Paarsch, 1990; Christenson, 1953). Paarsch (1990) adds that the competing companies should increase output, resulting in more sales. Paarsch also found that when there is no excess production from competing companies and the strike is prolonged, the prices of the products increase. This theory is applied in the current paper because a similar concept is studied – whether industrial action that affects production affects the profitability of competing companies in the platinum mining sector. The principles of this theory support the hypotheses stated above.

Methodology

The quantitative method is employed for the study using secondary data from audited financial statements of platinum mining companies, which can be regarded as reliable. Robust t-statistics were used to examine the statistical significance

of the difference in the mean revenue and mean EBITDA for affected mining companies compared with competing companies (Papangkorn et al., 2021). T-statistics have been used in accountancy to determine if there is a significant difference between the mean of two groups (Dalci et al., 2013). Revenue and EBITDA figures of the companies were scaled by total assets to minimize the risk of outliers (Smith and Wright, 2004). T-statistics were used because the number of observations is less than 30 per sample for both affected and competing mining companies (15 and 20 companies respectively). The data has been standardized to follow a normal distribution in order to minimize the risk of outliers, in line with the method of Smith and Wright (2004).

The companies included in the study are platinum mining companies listed on the Johannesburg Stock Exchange (JSE) between 2011 and 2015. Financial information was extracted from audited financial statements available from the INET BFA expert database (formerly McGregor), consisting of all JSE-listed companies’ financial statements and operating information. Strikes took place in 2012 (25 days) and 2014 (106 days). Three mines had strikes in 2012, and five were strike-free. In 2014, four mines had strikes, and four mines did not. The standard formula used to compute the t-statistics (Cressie and Whitford, 1986) is: where

n₁ = Number of observations in affected mining companies sample

n₂ = Number of observations in competing mining companies sample

μ₁ = Population mean of observations in affected mining companies sample

μ₂ = Population mean of observations in competing mining companies sample

x₁ = Mean of observations in affected mining companies sample

x₂ = Mean of observations in competing mining companies sample

s² ₁ = Standard deviation of affected mining companies sample

s² ₂ = Standard deviation of competing mining companies sample

This is a standard formula used to compute the t-statistics for observations in the samples such as revenue, EBITDA, their mean values,- and standard deviations.

Results and discussion

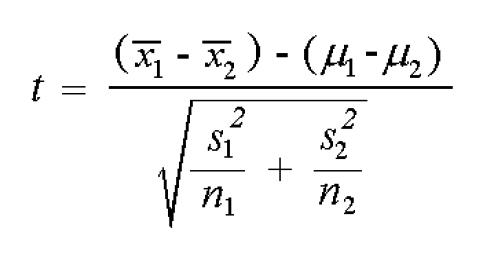
In Table I, N represents the number of observations for affected and competing companies. Three companies had strikes over the five years, resulting in 15 observations for affected companies in strike period 1. There are 20 observations for the four companies that were strike-free in strike period 2 over the 5-year period. The average mean, standard deviation, and standard error values are presented in scaled monetary values (rands). The confidence interval shows the lower and upper limits of scaled amounts expected for revenue and EBITDA.

Hypothesis 1: Revenue

Based on the t-statistic = 5.16 and p-value = 0.000 (see Table I), the results show that the mean revenue difference between affected and competing platinum companies is statistically

The spillover effect of industrial action on the profitability of platinum mining companies

Two-sample t-statistics for the platinum sector

N Mean Standard Standard 95% t-statistic P-value Decision deviation error mean confidence

Revenue Strike 15 0.465 0.147 0.038 (0.1678; 0.3866) 5.16 0.000*** There is an effect

No strike 20 0.187 0.169 0.038

EBITDA Strike 15 –0.006 0.183 0.047 –0.1206, 0.1946) 0.48 0.636 No effect

No strike 20 –0.043 0.274 0.061

No strike 20 0.342 0.162 0.036

*** test at 1% significant level, ** test at 5% significant level and * test at 10% significant level

significant at the 1% level. Therefore, the results suggest that the revenue reported by platinum mining companies that experienced strikes is significantly different from that reported by strike-free companies. This difference may be due to a significant decrease in the revenue of the affected companies (Anglo American Platinum, Lonmin Platinum, and Impala Platinum Holdings) due to the 106 strike days in 2014 (Bohlmann, van Heeden, and Dixon, 2015). Competing mining companies (Royal Bafokeng Platinum Ltd, Atlasta Resources Corp., Jubilee Platinum plc, and Northam Platinum Ltd) saw an increase in revenue, although it was not significant.

The results agree with prior studies, so hypothesis 1 is accepted. De Fusco and Fuess (1991), found a similar result in the US airline industry, where the share price of an affected company was negatively affected by the strike and there was a positive spillover effect on the profitability of the competing companies. McDonald and Bloch (1999) found a similar result. The results also echo the principles of the offset theory, which suggests that lack of supply of products from the affected company is offset by increasing sales from competing companies (Paarsch, 1990). However, in the case of the platinum sector, because the revenues of the competing companies are small compared with the affected companies, the overall difference in revenue is negative, as discussed next, and which supports the findings of Bohlmann, van Heeden, and Dixon (2015).

Hypothesis 2: EBITDA

Based on the t-statistic = 0.48 and p-value = 0.636 (see Table I, the results show that the EBITDA difference between platinum mining companies that experienced strikes and those that were strike-free is not statistically significant (5% level).

Therefore, using EBITDA as a measure, hypothesis 2 is rejected. There is no significant difference; instead, there was a decrease in EBITDA across the entire platinum sector. There was also a decrease in the profitability of competing platinum companies. This finding is in line with Kramer and Vasconcellos (1996), who found no significant effect of strikes in the US vehicle industry on the market value of competing companies. The reasons for the overall decrease in EBITDA across the platinum sector were not considered in this research and will be a topic for future investigation. However, it is possible that salaries were increased across the industry to meet employee demands and avoid further strikes, among other reasons.

The results discussed above illustrate the importance of using different variables when measuring the effect of strikes on profitability. Previous studies similar to this used only profit cost margin as a measure of profitability (McDonald and Bloch,

1999) and found a positive spillover effect on the profitability of competing companies. This study used two variables to measure the effect of strikes on profitability: revenue and EBITDA. As indicated above, when revenue is used as a variable in determining if there was a significant difference between affected and competing companies, the results showed a positive difference for competing companies. This contrasts with the results when EBITDA is used; there was no statistically significant difference between the affected and competing companies’ profitability, and the strikes negatively affected all companies in the sector.

In summary, based on the results above and in contrast with prior literature, the overall spillover effect of strikes on the profitability of platinum mines is negative. There was a positive spillover effect on revenues of competing companies, but the effect was not significant enough when costs are deducted from revenue, as seen from the negligible difference when EBITDA is used. Instead, all platinum mines experienced a decrease in profitability.

Conclusion

Whereas previous studies have shown that companies not affected by a specific strike in the same industry see a positive affect on profits, this study has shown the contrary. The spillover effect of strikes negatively affected the earnings before interest and tax of non-striking platinum mining companies. While the research shows the negative effect of strikes on the platinum mines’ profitability, it does not pronounce on whether strikes are good or bad, as sometimes they are the only instrument available for employees to show their dissatisfaction. However, the findings suggest that it is in the interest of all mines in the sector to attempt to settle employees’ demands before they result in a strike.

It is crucial to improve dialogue between management, labour unions, and employees to avoid costly strikes in the mining sector. We suggest that mining companies should also disclose strike risks in their financial statements, and how they will mitigate these risks, as this will create investor and stakeholder confidence, knowing that risk is adequately managed.

Further research to examine strikes and their effect on profitability in other mining sectors such as gold, iron ore, coal, and diamonds would be fruitful. Another useful research area would be to examine how increases in staff costs affect the profitability of the strike-hit mines to determine whether there is a positive effect on profitability when salary demands are met. It will also be of interest to assess if strikes benefit the employees and determine the bargaining power of labour unions.

The spillover effect of industrial action on the profitability of platinum mining companies

The Journal of the Southern African Institute of Mining and Metallurgy

References

Afik, Z., Haim, R., and Lahav, Y. 2019. Advance notice labour conflicts and firm value—An event study analysis on Israeli companies. Finance Research Letters, vol. 31. pp. 410−414. https://doi.org/10.1016/j.frl.2018.12.005

Alexander, P. 2013. Marikana, turning point in South African history. Review of African Political Economy, vol. 40, no. 138. pp. 605−619.

Alexander, P., Lekgowa, T., Mmpoe, B., Dinwell, L., and Xezwi, B. 2012. Marikana: A view from the mountain and a case to answer. Jacana Media, Auckland Park, Johannesburg.

Antin, D. 2013. The South African mining sector: An industry at a crossroads. Economic Report South Africa, December 2013. https://southafrica.hss.de/ fileadmin/user_upload/Projects_HSS/South_Africa/170911_Migration/Mining_ Report_Final_Dec_2013.pdf

Barchiesi, F. 1999. The public sector strikes in South Africa: A trial of strength. Monthly Review, vol. 51, no. 5. pp. 15.

Becker, B.E. and Olson, C.A . 1986. The effect of strikes on shareholder equity. ILR Review, vol. 39, no. 3. pp. 425−438.

Bavu, S.B. 2015. The prevalent and violent industrial action in the mining industry: The need to curb the prevalent and violent strike action in South Africa PhD thesis, University of KwaZulu-Natal.

Benya, A. 2015. The invisible hands: Women in Marikana. Review of African Political Economy, vol. 42, no. 146. pp. 545−560.

Bhana, N. 1997. The effect of industrial action on value of shares listed on the JSE. Investment Analysts Journal, vol. 44, no. 3. pp. 43–49.

Bohlmann, H.R., van Heeden, J.H., and Dixon, P.B. 2015. The effect of the 2014 platinum mining strike in South Africa: An economy-wide analysis. Economic Modelling, vol. 51. pp. 403–411. https://doi.org/10.1016/j.econmod.2015.08.010

Bouwens, J., de Kok, T., and Verriest, A. 2019. The prevalence and validity of EBITDA as a performance measure. Dans Comptabilité Contrôle Audit 2019/1 (Tome 25), pp. 55−105. Mis en ligne sur Cairn.info le 17/04/2019. https://doi. org/10.3917/cca.251.0055

Chamber of Mines. 2014. Annual Report. https://www.mineralscouncil.org.za/ industry-news/publications/annual-reports/send/15-archived/132-annualreport-2013-2014 [accessed 20 July 2016]

Chinguno, C. 2015. The unmaking and remarking of industrial relations: The case of Impala Platinum 2012 - 2013 platinum strike wave. Review of African Political Economy, vol. 42, no. 146. pp. 577−590.

Christenson, C.L. 1953. The theory of the offset factor: The effect of labor disputes upon coal production. American Economic Review, vol. 43, no. 4. pp. 514−547.

Cressie, N.A.C. and Whitford, H.J. 1986. How to use the two sample t-test. Biometrical Journal, vol 28, no 2, pp. 131−148.

Dabscheck, B. 1991. A decade of striking figures. Economic & Labour Relations Review, vol. 2, no. 1. pp. 172−196.

Dalci, I., Arasli, H., Tumer, M., and Baradarani, S. 2013. Factors that influence Iranian students’ decision to choose accounting major. Journal of Accounting in Emerging Economies, vol. 3, no. 2. pp. 145−163.

De Fusco, R.A. and Fuess, S.M. 1991. Effects of airline strikes on struck and nonstruck carriers. Industrial and Labor Relations Review, vol. 44, no. 2. pp. 324–333.

De Kadt, D., Johnson-Kanu, A., and Sands, M.L. 2020. Electoral accountability and state violence: The political legacy of the Marikana massacre. SocArXiv, 28 March 2020. doi:10.31235/osf.io/5uxzv Kaonga, B. and Kgabi, N.A. 2011. Investigation into presence of atmospheric particulate matter in Marikana, mining area in Rustenburg Town, South Africa. Environmental Monitoring and Assessment, vol. 178, no 1. pp. 213−220.

Kramer, J.K. and Vasconcellos, G.M. 1996. The economic effect of strikes on the shareholders of nonstruck competitors. Industrial and Labor Relations Review, vol. 49, no. 2. pp. 213−222.

McDonald, J.T. and Bloch, H. 1999. The spillover effects of industrial action on firm profitability. Review of Industrial Organization, vol. 15, no. 1. pp.183−200.

Mnwana, S. 2015. Mining and community struggles on the Platinum Belt: A case of Sefikile Village in the North West Province South Africa. The Extractive Industries and Society, vol. 2, no. 3. pp. 500−508.

Moloi, T. 2015. A critical examination of risks disclosed by mining companies pre and post Marikana event. Problems and Perspectives in Management, vol. 13, no. 4. pp. 14−22.

Neumann, G.R . 1980. The predictibility of strikes: Evidence from the stock market. Industrial and Labor Relations Review, vol. 33, no. 4. pp. 525−535.

Neumann, G.R. and Reder, M.W. 1984. Output and strike activity in U.S. manufacturing: How large are the losses? Industrial and Labor Relations Review, vol. 37, no. 2. pp. 197–211.

Onyebukwa, C.F. 2021. The dilemma of natural resources and upsurge of conflicts in Africa: A cursory look at the Marikana management approaches in South Africa. Political Economy of Resource, Human Security and Environmental Conflicts in Africa. Palgrave Macmillan, Singapore. pp. 277−296.

Papangkorn, S., Chatjuthamard, P., Jiraporn, P., and Chueykamhang, S. 2021. Female directors and firm performance: Evidence from the Great Recession. International Review of Finance, vol. 21, no. 2. pp. 598−610.

Pelders, J. and Nelson, G. 2019. Contributors to fatigue at a platinum smelter in South Africa. Journal of the Southern African Institute of Mining and Metallurgy, vol. 119, no. 3. pp. 313−319. http://dx.doi.org/10.17159/2411- 9717/2019/v119n3a11

Paarsch, H.J. 1990. Work stoppages and the theory of the offset factor. Journal of Labor Economics, vol. 8, no. 3. pp. 387–417.

Rodny-Gumede, Y. and Swart, M. 2020. Marikana Unresolved: Massacre, Culpability and Consequences. City Press, Cape Town.

Schultz, C. 2020. The Marikana massacre and the unstable geographies of capital: spatialising financialisation. Politikon, vol 47, no. 1. pp. 42−61.

Seedat, A. 2013. The effects of strikes in the South African gold mining industry on shareholder value. PhD thesis, University of the Witwatersrand).

Sinwell, L. 2019. Turning points on the periphery? The politics of South Africa’s platinum-belt strike wave in Rustenburg, Northwest and Northam, Limpopo, 2012–2014. Journal of Southern African Studies, vol. 45, no. 5. pp. 877−894.

Smith, R.E. and Wright, W.F. 2004. Determinants of customer loyalty and financial performance. Journal of Management Accounting Research, vol. 16, no. 2. pp. 183–205.

Stewart, P. 2013. Kings of the mine: Rock drill operators and the 2012 strike wave on South African mines. South African Review of Sociology, vol. 44, no. 3. pp. 42−63.

Thasi, M. and van de Walt, F. 2020. Work stress of employees affected by skills shortages in the South African mining industry. Journal of the Southern African Institute of Mining and Metallurgy, vol. 120, no. 3. pp. 243−250. http://dx.doi. org/10.17159/2411- 9717/666/2020

Thomas, K. 2018. 'Remember Marikana': Violence and visual activism in postapartheid South Africa. ASAP/Journal, vol. 3, no. 2. pp 401−422.

Tinsley, M. 2019. Constructing and contesting the post-apartheid state: Political discourse and the Marikana strike. Language, Discourse & Society, vol. 7, no. 2, pp.15−33. u

The spillover effect of industrial action on the profitability of platinum mining companies

Introduction to MultiplePoint Statistics

COURSE

DATE:

19-22 JUNE 2023

ONLINE VIA ZOOM

OBJECTIVES

The Multiple-Point Statistics (MPS) approach can be applied to model spatial or temporal variability when dense data sets are available to train the algorithm. The main strength of the approach is that goes beyond two point statistics and allows to model complex patterns and condition well the simulation with dense hard data sets. These methods can handle categorical variables such as rock types or lithofacies, and continuous variables such as petrophysical properties, remotely sensed data, or geophysical surveys. The course will focus on the Direct Sampling method which is one of the most flexible approach available today. During the course, participants will learn the fundamental aspects of the Direct Sampling algorithm and will have the opportunity to apply them in practice through a wide range of tutorials and hands on using Python scripting.

Lecturers:

PhD from École des Mines de Paris in 1996 (honours), Lecturer in hydrogeology at the Swiss Federal Institute of Technology Zurich (ETHZ) from1997 to 2001. Water supply engineer in Kankan,Guinea for the French ministry of Cooperation from 1992 to 1993. His research focuses on groundwater hydraulics in porous and fractured rocks, upscaling techniques, and innovative geostatistical methods for uncertainty quantification. He has been working on the regional modeling of saltwater intrusions in Cyprus and Tunisia. He has participated to numerous international projects such as the evaluation of the groundwater resources in the north-west of the Sahara (Mauritania) for the world bank. He was editor of Hydrogeology Journal, president of the geoENVia association and is currently a member of the leadership team of the Groundwater Committee of the International Association of Hydraulic Research (IAHR). He is the author of more than 100 scientific articles in international journals and covering a wide range of topics. His current research is focused on the development of multiple-point statistics methods as well as pseudo genetic approaches for heterogeneity modeling, uncertainty quantification and inverse groundwater modeling.

University

Julien Straubhaar, Prof. Dr., born in 1979, senior researcher in the stochastic hydrogeology group of the University of Neuchâtel. He holds a PhD in applied mathematics (University of Neuchâtel, 2007), with a focus on numerical methods for partial differential equations and in particular preconditioners for linear equations. His current research mainly deals with geostatistics and inverse methods. He is author of more than 20 scientific papers published in international journals and he has been a reviewer for several scientific journals. Over the last ten years, he has been heavily involved in the development of parallel multiple-point statistics algorithms, in particular Impala and Deesse softwares, which are available in professional products.

The spillover effect of industrial action on the profitability of platinum mining companies

The Journal of the Southern African Institute of Mining and Metallurgy

PHILIPPE RENARD UNIVERSITY OF NEUCHATEL, SWITZERLAND

JULIEN STRAUBHAAR UNIVERSITY OF NEUCHÂTEL

Prof. Philippe Renard and Prof. Julian Straubhaar

Philippe Renard, Prof. Dr. Eng., (born 1967), Professor of Hydrogeology at the

of Neuchatel, Switzerland (2006-present),

Affiliation:

1Zimbabwe Platinum Mines, Zimbabwe.

2Visiting Professor, University of the Witwatersrand, Johannesburg, South Africa (Posthumous).

3Former Director, Wits Mining Institute, University of the Witwatersrand, Johannesburg, South Africa.

Correspondence to: T. Chikande Email: chikandet@yahoo.com

Dates: Received: 15 Dec. 2021 Revised: 29 Sep. 2022 Accepted: 5 Oct. 2022 Published: December 2022

How to cite: Chikande, T., Phillips, H.R., and Cawood, F.T. 2022

Ventilation optimization through digital transformation.

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 687–696

DOI ID: http://dx.doi.org/10.17159/24119717/1950/2022

ORCID: T. Chikande https://orcid.org/0000-00017886-339X

Ventilation optimization through digital transformation

by T. Chikande1, H.R Phillips2, and F.T. Cawood3

Synopsis

Underground mines require electricity to operate both the main surface fans and auxiliary systems, with primary ventilation systems typically accounting for approximately 40–60% of the mine’s overall electricity consumption. The primary reason for this considerable expense is that most underground ventilation systems are designed for peak demand, regardless of the actual demand, which is commonly dictated by diesel equipment usage in trackless mining operations. Most platinum mines on the Great Dyke in Zimbabwe tend to operate their ventilation systems at this peak level, despite the mine’s air quantity being well in excess of the ‘true’ ventilation needs. This is due to a lack of appropriate ventilation controls. The authors designed and installed a ventilation-on-demand system at one of the bord and pillar platinum mines to minimize the use of redundant air in underground operations. Fourth industrial revolution techniques were applied to the environmental monitoring and tracking systems thereby optimizing air quantity demands. The mine managed to reduce its annual power consumption by 23% through the implementation of manual control and time-of-day scheduling levels of the ventilationon-demand concept. There was also a 6% productivity improvement, mainly attributable to an increased face time as a result of the significant reduction in the re-entry period following a blast. This paper introduces a novel concept of ventilation optimization through digital transformation targeting mainly room and pillar platinum mines. A system was designed, installed, and commissioned, though there is currently an ongoing optimization process to harness the full benefits such as productivity enhancement, reduced power costs, and improved worker health.

Keywords

mine ventilation, ventilation on demand, internet of things, power savings, ventilation optimization.

Introduction

In mechanized platinum mines, underground air is contaminated primarily by diesel vehicles and blasting operations. Research shows that mine ventilation systems consume enormous amounts (40–60 of the total) of electrical energy, hence the need to identify potential energy saving opportunities through the adoption of digital transformation (Acuna and Allen, 2017). Digital transformation is the process of using digital technologies to create new or modify existing business processes, culture, and customer experiences to meet changing business and market requirements. Mine ventilation systems have been given augmented attention in recent decades as a result of the ever-increasing cost of energy, increased degree of mechanization, and increasingly stringent health and safety regulations (Hardcastle and Kocsis, 2001). There is still room for improvement in optimizing the key performance indicators in mining, i.e., safety, productivity, and costs, by maintaining the required air quantity in working areas based on the nature of activities undertaken. For example, in a large mechanized operation, if the mine wishes to reduce air quantity through eliminating redundant air supply, the resultant power consumption or cost will be reduced due to the cubic relationship of fan speed and power (Bluhm and Smit 2014).The increased power demand from ventilation systems due to increased mechanization necessitates optimization of the amount of air delivered underground through the application of fourth industrial revolution techniques. The fourth industrial revolution is characterized by the convergence and complementarity of emerging technology domains, including nanotechnology, biotechnology, new materials, and advanced digital production. It is a fusion of advances in artificial intelligence (AI), robotics, the Internet of Things (IoT), 3D printing, genetic engineering, quantum computing, and other technologies. Ventilation on demand systems, coupled with advanced control processes to modulate the quantity of air supplied by main surface fans and auxiliary fans, can optimize underground ventilation systems.

The use of fourth industrial revolution concepts can enhance productivity and safety, reduce costs of ownership, and enable monitoring of all processes in real time (Cawood, 2019). The IoT,

Ventilation optimization through digital transformation

together with other digital revolution techniques, is investigated and implemented in the mining industry mainly for process optimization by identifying and eliminating bottlenecks along the mining value chain.

The IoT is a system of interrelated computing devices, mechanical and digital machines, objects, animals, or people that are provided with unique identifiers (UIDs) and the ability to transfer data over a network without requiring human-tohuman or human-to-computer interaction (Kumar, 2019).

Mining on the Great Dyke of Zimbabwe poses several challenges, including fluctuating mineral prices, safety concerns, productivity optimization, and low metal grades (Matthews, 2020).

Underground mining operations are a technically challenging and hazardous environment for workers through inadequate ventilation, exposure to dust, heat, and gas, as well as the threat of rockfalls or even a more widespread mine collapse.

Recent studies have shown that ventilation systems in highly mechanized platinum mines could be responsible for 40 to 60% of the mines’ energy consumption (de Souza, 2018). The full ventilation on demand concept has not been adopted or rolled out in any bord and pillar mining operation worldwide due to the nature of mining operations (Develo et al., 2016). Efficient air distribution in bord and pillar platinum mines can be achieved through the integration of IoT and empirical techniques extracted from real-time data. The ventilation system is capable of being adjusted in real time to meet the triggered ventilation demand based on the activities being undertaken. This paper describes various options to optimize and apply the concept to hard rock bord and pillar platinum mines operating on the Great Dyke.

A review of relevant literature

Although the concept of ventilation in underground mines may seem relatively simple, getting the right quantity and quality of air to where it is needed when it is needed in an expanding mining environment is an elaborate operation that requires an array of ventilation components. Typical ventilation systems consist of main surface fans, air regulators, and underground doors that distribute air through the mine. Air requirements in an area depend on the number of people and the machinery deployed there.

The fourth industrial revolution has been evolving for many years and has created an ever-increasing motivation for mining companies to embrace digital transformation to optimize mining key performance indicators (KPIs). The IoT, artificial intelligence, and data analytics are all components of the fourth industrial revolution and have impacted on the way companies operate (Cawood, 2019). Most mining companies are considering harnessing such emerging technologies and others have been proactively exploring fourth industrial revolution solutions over the last decade (Cawood, 2019). Substantial benefits and efficiencies are expected from the implementation of fourth industrial revolution techniques, and Cawood (2021) pointed out that such technologies have potentially lucrative benefits in the extraction of minerals. Extensive work has also been undertaken in other mining activities such as the exploration field, which has seen some development of sensing technologies in the modelling of geological deposits (Abrahamsson, et al., 2009).

Some fruitful gains from digital transformation include time-saving, lower energy costs, improved health and safety of employees, and better predictive maintenance which will subsequently improve machine availability (Kumar et al., 2019).

Creamer (2018) highlighted that the mining industry is the economic driver of much of Africa, hence the need to embrace digital transformation in all mining operations.

Creamer (2018) also pointed out that there is a gap that needs to be bridged in the mining sector regarding fourth industrial revolution technologies. In addition, there are currently dips in local performance indicators in the mining sector despite it being at the dawn of a technology revolution. It is imperative to adopt digital transformation throughout the whole mining value chain to improve processes aligned to value. Cawood (2019) highlighted that digital transformation in the mining industry should be anchored on automation, decision support, and analytics. Matthews (2020) pointed out that the drive towards the application of fourth industrial revolution techniques is mainly attributable to changing global demand, market volatility, and increased costs. Ventilation, being a critical facet of any underground mining operation, should therefore not be ignored because it accounts for a large percentage of power costs, as well as being vital for the health and safety of employees. Digital transformation in mine ventilation will provide great insight into safety, process optimization, and enhanced operational efficiencies. However, there is still little clarity on how fourth industrial revolution technology will unfold and what its overall bearing on ventilation systems will be (Acuna and Allen, 2017).

This paper focuses on ventilation optimization through digital transformation. An optimized ventilation system was developed and installed for trial purposes at one of the Zimbabwean platinum mines and is therefore used as a base case for illustrating the benefits of VOD (ventilation on demand) systems.

VOD architecture

VOD is the ability to direct air in an underground mine to the area that requires it, at the quantity needed for the local activities and ambient conditions at the time (Acuna and Allen, 2017). According to Tran-Valade and Allen (2013), there are five control strategies that are considered for VOD:

➤ User control, also referred as manual control (level 1)

➤ Time of day scheduling (level 2)

➤ Event based (level 3)

➤ Tagging (level 4)

➤ Environmental (level 5).

The five identified strategies can be used individually or in concert. This paper will focus more on manual control and time of day scheduling (levels 1 and 2 application) since the other levels have not yet been achieved and are still under investigation. Prevailing trends within the global mining industry, including operating at greater depth, are generally demanding significant air quantities, not only for ventilation but also for cooling purposes. The drive to minimize greenhouse gas emissions in countries heavily reliant on coal-fired power stations increases the importance of managing power consumption in the mining industry (Hardcastle and Kocsis, 2001).

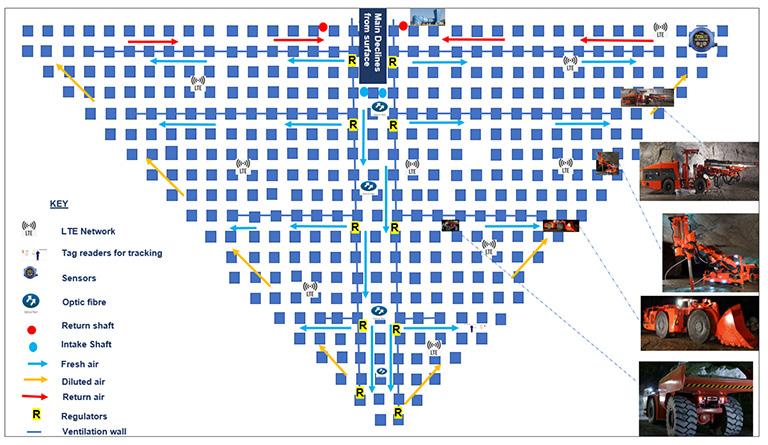
The current ventilation mechanism at most mines operating on the Great Dyke in Zimbabwe entails the use of a negative pressure system (exhaust ventilation application). Figure 1 shows a ventilation layout for a typical mechanized board and pillar operation. A VOD model was developed by the a-uthors and was applied to a mechanized mine that uses four 850 kW primary surface fans and twelve underground auxiliary fans. Each main surface fan has a rated motor capacity of 850 kW with a duty of 200 m³/s and a static pressure of 3.1 kPa. Foul air is exhausted out

The Journal of the Southern African Institute of Mining and Metallurgy

Ventilation optimization through digital transformation

of the mine through upcast shafts and the intake air is drawn into the mine via a series of declines and fresh air intakes raise-bored from surface. Ventilation walls are built along roadways which are mined at every tenth stope panel. Intake air is controlled into each section by means of regulators, which are normally placed in each roadway. The mines currently use brattices to regulate air flowing into all production sections. Such brattices were replaced with automatic doors during the VOD trial. The louvers are manually controlled depending on sectional demand, which depends on the number of people and the amount of operational equipment in any section. The designed and installed VOD system comprises a communication backbone (Long Term Evolution network or LTE) , tagging and tracking system, variable speed fan drives, and air quality stations. LTE is a standard for wireless broadband communication for mobile devices and data terminals.

Foul air is exhausted by means of a negative pressure system using main surface fans and fresh air enters the mine via a series of intake shafts and declines. Energy efficiency of mine ventilation systems, including automated ventilation control, is achieved by means of an algorithm for optimal ventilation control, controlled recirculation, and dynamic assignment of air quantity lower limits in real-time mode. The authors designed an optimized VOD system that links tagging and tracking systems and environmental monitoring stations with primary and auxiliary ventilation systems. The amount of air drawn into a section will be automatically determined by the number and types of diesel equipment in use, the heat load, number of people working in a particular section, and other exceptional airborne pollutants.

The VOD system designed and trialed by the authors consists of the key components shown in Figure 2.

In addition to reducing the fan power consumption, the VOD system was developed to ensure a healthy underground working environment through:

➤ Dilution of hazardous substances which affect the health and safety of employees

➤ Climate control through modulation of air quantity to create a conducive working environment

➤ Quicker evacuation of blasting gases, thereby improving productivity

➤ Better utilization of existing infrastructure, thereby resulting in better control of capital and operating expenditure by minimizing additional costs associated with redundant air

➤ Producing accurate and consistent ventilation survey measurements.

The VOD system utilizes airflow sensor feedback to perform an online optimization process on main ventilation fans and underground auxiliary fans. Some of the system components incorporated into the VOD structure include:

➤ Variable speed drives (VSDs) – All primary and auxiliary fans are equipped with variable speed drives so that fans can be allowed to run at different speeds based on the actual demand. The air quantity delivery is controlled through changes in the rotational speed of new fans.

➤

Automated ventilation doors – these are installed in all main roadways of each section and ventilation district. Each automatic door is equipped with sensors so that the quantity of air entering a section can be controlled and is primarily dependent on the deployment of operational equipment and personnel in that particular zone. Louvres will automatically adjust depending on air demand.

➤ Main surface fans – these form the basis of the system since the air quantity for each fan is controlled by using VSDs informed by environmental monitoring stations.

➤ Tagging and tracking system – selectively delivers appropriate air volumes to the production workings according to the various mining activities being undertaken. It is essential to know where, when, and for how long these air quantities are needed. In mechanized bord and pillar mines, this means knowing the location of production, development, and service vehicles, together with their characteristics. This is

Figure 1–Typical ventilation layout for a bord and pillar operation

Ventilation optimization through digital transformation

achieved using a vehicle identification and tracking system. All vehicles and cap lamps are equipped with electronic chip sensors for tracking capability and this subsequently determines the desired quantities of air to dilute heat and other pollutants. The tag readers are located at strategic points throughout the mine to give live readings throughout the shift.

➤ Monitoring system – an environmental monitoring system allows for an activity-based ventilation system to provide and maintain adequate working conditions within all production workings. Firstly, the required air quantity to all working faces must be maintained. For this reason, non-intrusive ultrasonic airflow sensors were installed along the main haulages and inside fan drifts. Secondly, the quality of air delivered to all working areas must also be monitored and for this reason, gas sensors, diesel particulate matter (DPM) sensors, and dust sensors were installed in all sections. To ensure the equipment operators are always exposed to safe underground environmental conditions, DPM sensors were installed on dump trucks and load haul dump machines (LHDs).

➤ Data management and communication systems – these include the process logic of ventilation control systems by which information is processed and outcomes determined (Kumar et al., 2019). The VOD system requires a communication backbone which runs from surface to underground operations. Fibre-optic cables and a Long-Term Evolution (LTE) network were installed covering both surface and underground operations. The software to integrate all system components is being configured and this will be maintained annually through a license key.

➤ Operator workplace – all data was integrated into one server so that reports and trends can be extracted using any connected device either on surface or underground. Data collected and analysed by the system sensors includes ventilation KPIs such as air quantity, air velocity,

airborne pollutant values, and fan pressure readings. Other information to be graphically displayed includes: ∙

Mine ventilation overview layout ∙

Det-ails regarding performance of main surface fans ∙ Ventilation layout for each section ∙

Rate of change alarms and advanced alarm statistics for mine ventilation ∙

Production statistics displays – current and historical trends ∙

Overall mine ventilation KPIs ∙

Total energy consumption, run-time, energy statistics per fan, and mode of operation ∙ Trends and logged data for all important data-sets. The VOD control philosophy ensures the capability of a system to alter environmental conditions in a ventilation district and comprises smart sensors and control servers. Automatic fire suppression systems are also installed in areas with a high fire load index. There are five levels of VOD. The mine is currently operating on level 2 and is in the process of trialling level 3, as described below.

User control or manual control

User control strategy is the first level that allows for manual control or setting of operational points for the different components of the ventilation system. These include the following:

➤ Main and secondary fans – Main fans can be connected to start directly online or be equipped with soft starters or variable frequency drives (VFDs) to save energy (TranValade and Allen, 2013). It is more common to have auxiliary fans connected to steel ducting, but soft starters should be considered for energy savings and safety when considering flexible ducting. All main surface fans (4 × 850 kW) were equipped with VFDs. This was considered as the first step towards automation and the mine reduced its energy consumption by 36% as described later.

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 2–VOD model developed by the authors

Ventilation optimization through digital transformation

➤ Regulators and doors – Regulators are used for controlling airflow by increasing the airway resistance, thereby decreasing the air quantity. The mine installed automated ventilation doors (non-airlock) to prevent the flow of air while still allowing travelling and transportation to take place. The doors are efficient, economical, and require minimum maintenance. Figure 3 shows typical automatic doors installed at the mine.

➤ Manual operational point settings – can be divided into two subcategories

(a) Fixed setting: For fans these settings correspond to on or off, or in a case where a VSD is available, to set the frequency of the fan drive to deliver just the air quantity required (Tran-Valade and Allen, 2013). For regulators and doors, the fixed settings correspond to a percentage of the opening from zero to 100%.

(b) Proportional integral derivative (PID) control loop: This is a feedback control loop to achieve a desired set-point based on a measured process variable (Tran-Valade and Allen, 2013). In this case, the setpoint is the opening of the regulator or door, and the measured process variable is the air quantity. This capability is not available at the manual or first level, but in the third level, as described below.

Time of day scheduling

The second control strategy achieved was Time of day scheduling’. This refers to the concept of triggering different set-points of the fans, regulators, and doors based on the time input to follow a certain schedule (Tran-Valade and Allen, 2013). Assuming that the sensor deployment in the mine is limited or nonexistent, as could be the case for this level, then the logical extension of level 1 (manual control) is to couple it with a timer to trigger sequences of changes in the set-point of the ventilation system such as fans, doors, and regulators in a semi-automated way (Tran-Valade and Allen, 2013). This application is a limited version of the main concept behind level 2, which from a broader point of view should be called the ‘action trigger’. If the action trigger concept is constrained to act based on a timer only, the result is effectively Time of day scheduling. If the action trigger could be coupled to other environmental variables or data as triggers, the opportunity for different applications and savings could be enhanced even further. However, this also requires a more extensive deployment of sensors underground. The mine programmed all main surface fans to run at different speed set-points depending on time of the day. This is described later in this paper.

Event-based

The third control strategy is the Event-based strategy. Tran-Valade and Allen (2013) indicated that it is the ‘automatic trigger of prescribed actions in reaction to configured events’. This control strategy can be summarized as the action trigge function based on alternative inputs other than the timer and the environmental variables. Just like the Time of day scheduling, this control strategy uses the same principle as the action trigger but based on any variable available that could be conveyed to the software making the decision. It could potentially be a combination of variables with a certain logic. The potential for applications of

this control strategy is significant, for example, optimizing blast fume clearance and mine fire response. Additionally, the Eventbased strategy can also be used to trigger cascade use of fans, for example to turn a booster fan on if an auxiliary fan is turned on, to secure the supply of fresh air across the main drift (Nie. and Wei, 2017).

Tagging and tracking

The fourth control strategy is Tagging and tracking. This represents a major step forward in both the capacity to understand where people and equipment are located, and in terms of infrastructure required to locate them (Tran-Valade and Allen, 2013). This control strategy requires the implementation of a tagging and tracking system, and integration of its associated communication system with the ventilation software. The airflow distribution of the mine can then be based on the location of personnel and equipment. It is also based on rules to calculate the air quantity that must be assigned to each parameter. The tagging control strategy is commonly associated with the concept of ventilation on demand as the air quantity can be allocated across the mine according to the location data of both personnel and equipment that is generated in real time, (Wang et al., 2014). The tagging and tracking system was recently commissioned but is not currently linked to the VOD system. That will be the next step towards the optimzation process of underground ventilation systems.

Environmental

The fifth control strategy is Environmental and considers the automatic control of ventilation systems based on real-time environmental data. This can be based on several sensor inputs such as gas, dust, DPM, temperature (heat stress) etc., assuming the sensors can work underground and provide real-time information. In this regard, the performance of dust and DPM online sensors is still work in progress, but with encouraging results in recent years (Wang et al., 2014). Environmental control will be used in two ways, (a) as a fail-safe in case of flammable or noxious gas exceeding safe limits or (b) as the ultimate control strategy. Coupled with any of the other control strategies, the environmental strategy acts as a fail-safe in case of an environmental variable exceeding the pre-set boundaries, for example high CO (carbon monoxide) or a temperature above the heat rejection of 27.5°C for unacclimatized workers. This could be referred to as the quantity and quality approach of the environmental control strategy. As a stand-alone strategy environmental control allows the ventilation system to distribute the airflow according to environmental variables such as gas or dust concentration (Wang et al., 2014). Figure 4 shows a typical gas sensor interface at the mine. The gas detection system has been commissioned but not configured and linked to the main ventilation system at this time.

Figure 3–Automatic ventilation doors

Ventilation optimization through digital transformation

The mine has already applied both level 1 and level 2 stages of a VOD strategy. Preliminary results over the past three months showed some significant power savings and an increased productivity because of the increased face time by utilizing a portion of the re-entry period. At the last optimization stage, changes in the modulation of air quantity will be initiated by one of the following.

1. Increased air quantity demands due to additional vehicles or personnel entering a ventilation district. For this reason, all vehicles and employees are being monitored by a tagging and tracking system.

2. Environmental conditions within a particular ventilation district. Such conditions are currently monitored using realtime air quality monitoring stations comprising gas, dust, air quantity, and temperature sensors. When any of the parameters is above the specific pollutant’s Occupational Exposure Limit (OEL), the system will automatically adjust to ensure that airborne pollutants are diluted and reduced to concentrations below the OEL.

3. Timing parameters – less air is required during nonproductive periods such as shift changeovers. Other timing parameters include blast clearance periods, maintenance, holiday periods, and other non-production activities such as safety talks and machine maintenance. Modulation of airflow will also be set to be time-based.

From a mine timetable for a typical day-shift, it can be noted that for some activities the air quantity can be reduced to 40% of the normal requirements through the use of VSDs. As a starting point, the flow was reduced to 50% during non-productive periods as illustrated in Figure 6. The primary fans were programmed to run at full speed during the first two hours of re-entry to allow for quicker blast clearance before being reduced to 50% for peak production time when all diesel machines were at the working faces. Since the mine has currently not reached its full production, VSDs are currently set at a maximum speed of 85% during peak production face times to supply the required total air flow of 700 m³/s. Figure 5 shows how air flow varies when (i) there is no control on main surface fans, (ii) when control is by means of radial vane controls (RWCs), and (iii) through time of day scheduling (VOD level 2 control).

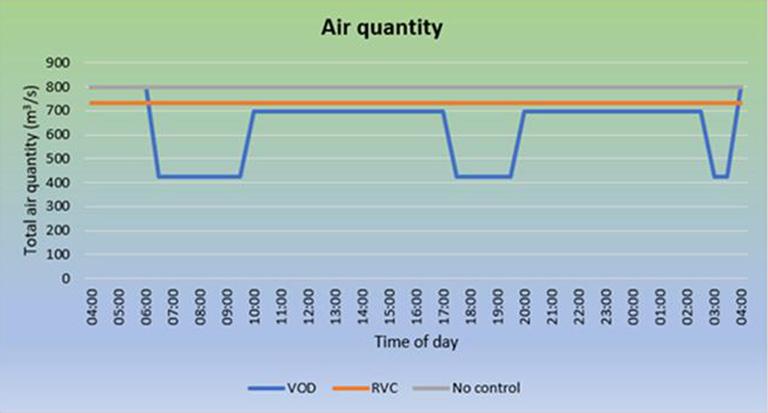
Power measurements were captured directly from the system and the results obtained demonstrated significant power savings. Each 850 kW fan equipped and controlled using RWCs consumes an instantaneous power of 671 kW at a RVC setting of 85% to give a flow of 175 m³/s

VFDs were commissioned to start the implementation of VOD. For the same air quantity, the instantaneous power reduced significantly from 671 kW to 426 kW. This reveals a power reduction of 36.5%, which translates to 2.1 MWh per year per fan (obtained from (671 – 426) × 24 × 365), thus a combined annual power cost saving of US$1.1 million (assuming four fans running and an average unit electricity cost of US$0.1292 per kWh).

The system was designed to monitor both air quantity and quality in real time. For time-of-day scheduling, the main surface fans were programmed to modulate air quantity as shown in Figure 5, and the total measured power varies as illustrated in Figure 6.

The overall energy gains by implementing VOD level 2 were derived from a zero base and Table II shows the assumptions used in deriving the predicted annual energy savings. The base case does not include VOD and represents the current set-up at all operations in the research area. It assumed 100% air quantity supply throughout the year without any airflow moulation and

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 5–Planned air flow modulation per day

Figure 4–Real-time gas monitoring at the mine

Ventilation optimization through digital transformation

Figure 6−Instantaneous energy consumption per day

96% utilization was factored in to cater for maintenance periods. It can be concluded that by rolling out a full VOD system at the mine where the trials are being undertaken, an annual power saving of approximately US$0.5 million can be achieved for primary fans with a combined power load of 3.4 MW (850 kW × 4) as shown in Table I.

In addition to power savings, there was a 6% productivity improvement due to increased face time. The system also created conducive working conditions, prompting the underground workforce to produce more efficiently. The minimum re-entry period for the mine was four hours, which conforms with the Zimbabwean legislation and regulations (Zimbabwe, 1989). Realtime monitoring was used to establish the actual time required to clear all blasting fumes, and this was later used as the ‘true’ re-entry period for the mine. After a blast gas concentrations such as carbon monoxide increase up to a peak value and then gradually decrease, depending on the type of explosives used and the ventilation adequacy. Figure 7 shows how carbon monoxide concentration varies with time in a 24-hour period which includes the blast window at the mine. Figure 8 shows the ventilation system’s response to changing CO levels. Real-time monitoring of gases reduces the risk of sending underground employees to poorly ventilated areas which haven’t been fully cleared of gases.

VOD systems allow mines to clear blasting fumes faster than the projected time by allowing fans to operate at full speed.

The mine where trials are taking place was simulated and the results revealed that the blasting fumes will clear in 2 hours. This finding was then substantiated by real-time gas readings taken after conducting a blast, as shown in Figure 7. A re-entry exemption from the normal four hours to two hours was applied for and approved by the Zimbabwe Ministry of Mines. The mine utilized the additional two hours gained by reducing re-entry time and converted it into face time as a productivity enhancement strategy. This, however, increased operating costs in the form of additional labour and incentivizing the current employees

Table I

VOD energy gains

Description

Base case VOD

Total power for main fans (kW) 3 400 3 400

Main fans utilization 96% 82%

Total auxiliary power (kW) 450 450

Auxiliary fans utilization 80% 30%

Total nominal power (kW) 3 715 3 238

Annual operational days 365 365 Daily hours 24 24

Annual power consumption (kWh) 32541648 28 367 508 Energy difference (kWh) 4 174 140 Unit cost (US$/kWh) 0.1292 Power savings (US$) 539 299

Figure 7–Actual carbon monoxide concentrations on 11 February 2021

Peak production gains

Description Data

Total annual production 2 Mt/a

Daily production target (t) 5523

Hourly production (15 hours per day face time)(t) 368

Increase in daily production due to VOD (t) 736

Increase in daily tonnage with efficiencies (due to VOD) (t) 552

Annual production gains from VOD (t) 201 600

6E* grade (g/t) 3.48

Platinum (Pt) grade (g/t) 1.582

Annual cost of mining additional tonnage (US$) 6 048 000

Milling costs of additional tonnage (US$) 3 024 000

Other additional costs (US$) 1 935 360

Total costs for addition tonnage (US$) 11 007 360

Revenue from additional ounces (US$) 12 902 400

Yearly profits (US$) 1 895 040

Assuming 15% of additional revenue (US$) 1 806 336

Platinum, pa-lladium, gold, rhodium, ruthenium , iridium

Table III

VOD cost breakdown

VOD component

Total cost (US$)

VSDs for main surface fans 654 668

VSDs for auxiliary fans 490 656

Tagging and tracking system 179 974

Airflow and gas monitoring stations 166 266

Dust and DPM monitoring systems 144 000

Pressure and temperature sensors 31 650

Automatic doors 230 384

Engineering services 132 432

Software fee 47 362

Additional communication backbone 532 000

Condition monitoring 114 532

through overtime payment. Table II shows the annual projected production gains at the trialled mine.

Production gains were made, having increased the speed of surface fans in the blasting window and instituted accurate monitoring of air quality The additional production time gained improved productivity, to an additional revenue of US 1.8 milllion as shown in Table II.

Financial evaluation

A feasibility study was conducted before carrying out the trial. The VOD system is linked from the underground operations to surface system servers, which will also in future be linked with the employee database. A financial evaluation of the designed system was based on actual quotations and invoices from suppliers of each of the system components. The benefits of this system include improved health and safety of underground workers, increased productivity, and reduced power costs. The cost components of the system are shown in Table III

From the achieved and predicted gains (both productivity and energy gains), it can be concluded that the payback period of the whole VOD system is about 1.5years. A 10-year financial analysis of the system is shown in Figure 9.

The mine has since achieved level 2 VOD. From full production going forward, starting in the year 2025, power cost gains will be averaging US$0.5 million per annum as compared to

Annual operating costs 113 136

Total cost for the system 2 837 060 Contingency (10%) 283 706 Total cost for the system with contingency 3 120 766

the ramping up period from 2021 to 2024, when there will be huge power savings. The average annual savings are projected to be 23% (US$2.533 million from 3.293 million) if the full VOD system is rolled out, as shown in the waterfall chart in Figure 10.

Conclusions

Ventilation remains an expensive necessity for underground mining. Current mining trends, including the increased degree of mechanization, would generally result in demands for more air and consequently increased power consumption. Power usage is not only a cost issue but is increasingly becoming an environmental issue when, worldwide, the mining industry is trying to reduce greenhouse gas emissions. In Southern Africa, with its primary reliance on coal-fired power stations and a constrained electricity supply, this is acutely relevant.

For Zimbabwean platinum mines, it is believed that by reviewing the way ventilation systems are designed and exploring future technologies that reduce energy demands, considerable savings in electricity usage can be achieved. Optimized ventilation

The Journal of the Southern African Institute of Mining and Metallurgy

quantity response

Ventilation optimization through digital transformation

Figure 9–Financial analysis

Figure 10–VOD control strategies annual power costs

systems in mechanized bord and pillar mines remain challenging; however, the application of fourth industrial revolution techniques will prevent ventilation from being cost-prohibitive. The implementation of ventilation--on demand systems can significantly reduce ventilation power consumption by a nominal 23%.

References

Abrahamsson, L., Johansson, B., and Johansson, J. 2009. Future of metal mining: Sixteen predictions. International Journal of Mining and Mineral Engineering, vol. 1, no. 3. pp. 305−311.

Acuna, E. and Allen, C. 2017. Totten mine ventilation control system update: implementation and savings achieved with Level 1 user control and future plans. Colorado School of Mines.

Bluhm, S. and Smit, H. 2014. Planning ventilation and refrigeration requirements. Ventilation and Occupational Environment Engineering in Mines. 3rd edn. Mine Ventilation Society of South Africa, Johannesburg. pp. 773−804.

Cawood, F. 2019. Beyond 2020: The future of mining in a world of technology. Mining Review Africa. https://www.miningreview.com/central-africa/futuremining-technology/[accessed 23 May 2020]

Cawood, F. 2021. uMining's year ahead will demand deep innovation. https://www. bizcommunity.com /Article/ 196/723/211911.html [accessed 1 March 2021]

Creamer, M. 2018. Exciting new mining research thrust. https://www engineeringnews.co.za/article/exciting-new-mining-researchthrust-2018-04-27 [accessed 15 October 2020]

De Souza, E. 2018. Cost-saving strategies in mine ventilation. CIM Bulletin, vol. 9, no. 2. pp. 1−7.

Develo, E., Pillalamarry, M., and Garab, E. 2016. Improving the ventilation system. Journal of the Southern African Institute of Mining and Metallurgy, vol. 116, no. 4. pp. 301−305.

Hardcastle, S.G. and Kocsis, C.A. 2001. Ventilation designs for an automated underground metal mine. Proceedings of the 7th International Mine Ventilation Congress. pp. 779−786.

Kumar, S., Tiwari, P., and Zymbler, M. 2019. Internet of Things is a revolutionary approach for future technology enhancement: A review. https:/ journalofbigdata.springeropen.com/articles/10.1186/s40537-019-0268-2 [accessed 23 October 2020]

Matthews, C. 2020. Zimbabwe’s Chitando says country’s mining sector has entered new heights. https://www.miningmx.com/news/markets/40120zimbabwes-chitando-says-countrys-mining-sector-has-entered-new-heights/ [accessed 14 January 2021]

Nie, X.X. and Wei, X. 2017. Optimization and practice on the reform schemes of ventilation system in the Jinqu Gold Mine. Mining Research and Development, vol. 37, no. 8. pp. 86−89.

Tran-Valade, T. and Allen, C. 2013. Ventilation-On-Demand key consideration for the business case. CIM, Toronto.

Wang, H.N., Peng, B., and Peng J.L 2014. Analysis of commonly existing ventilation problems and the optimal approach to deal with them in large-size mines. Journal of Safety and Environment, vol. 14, no. 3. pp. 24−27.

Zimbabwe. 1989. Explosives regulations. Statutory Instrument 72 of 1989. u

Putting digital technologies to work

Whatever terminology you wish to use, it is obvious the world of work is changing rapidly.

The Mining Industry, along the Mining Value Chain, is a part of this; seeking to take advantage of digital opportunities in the quest for competitiveness, sustainability and Zero Harm.

Mining businesses in Africa, as globally, are on this journey purposefully or by default. This event adds to purpose by being a showcase and learning experience for everyone associated with the Mining Industry. We will learn about Global Best Practices, network with global leaders in mining and other businesses, and do so in an exciting and interactive format.

Be prepared to be challenged and informed and to leave excited and better equipped for today’s digital journey.

E-mail: gugu@saimm.co.za Tel: +27 11 538-0237, Web: www.saimm.co.za

Simulation of production processes and associated costs in mining using the Monte Carlo method

by M. Mathey1

Affiliation:

1Visiting Adjunct Professor, Wits Mining Institute, University of the Witwatersrand, Johannesburg, South Africa.

Correspondence to: M. Mathey

Email: Markus_Mathey@web.de

Dates: Received: 13 Apr. 2022 Revised: 18 Aug. 2022 Accepted: 17 Oct. 2022 Published: December 20223

How to cite: Mathey, M. 2022

Simulation of production processes and associated costs in mining using the Monte Carlo method.

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 697–704

DOI ID: http://dx.doi.org/10.17159/24119717/2079/2022

Synopsis

The application of the Monte Carlo technique to production planning and everyday economic decisionmaking in mine production management is demonstrated. The logic is detailed using an example of underground production with continuous miners (CMs) and truck haulage. It is argued that availability of equipment and personnel are the predominant variables influencing mine output and productivity and that those availabilities may be well represented by binomial probability distributions. The probabilistic model is implemented in a standard Excel® spreadsheet with Palisade’s @Risk add-on to facilitate simulations. Starting from model calibration against data obtained from a mine’s annual reports, some general interdependencies of availability, utilization, productivity, and costs of production processes are outlined. Finally, several possible options and their consequences as regards production improvements are explored.

Keywords

simulation, production processes, costs, Monte Carlo method.

Introduction

The Monte Carlo method is typically used to simulate the interaction of input variables within a problem logic, in order to identify possible outcomes and associated probabilities. As such it is frequently used in financial analysis of mining projects. Heuberger (2005) provides a general introduction to risk analysis with the Monte Carlo method.

The method is just as well suited to simulating success, risk, and opportunities in technical production processes. For example, Brzychczy (2018) makes use of stochastic networks combined with Monte Carlo analysis to simulate and optimize the performance of longwall operations in coal mining. Jung, Baek, and Choi (2021) propose a discrete event simulation of production in an underground limestone mine. Upadhyay and Askari-Nasab (2018) likewise suggest a discrete event simulation for a shovel-truck production system in opencast mining. Common to those publications is the ‘microscopic’ focus on the production process itself, where uncertainty is linked to variables such as equipment travel times, the degree of filling of buckets, and productivity rates in general.

The modelling approach selected in the present paper is ‘macroscopic’, presuming that production outputs in underground mining are predominantly driven by availabilities of equipment and personnel, once equipment types and number of units as well as section layouts and travel distances are decided. Following this argument, the production process may be divided into a number of independent variables, such as the availability of equipment or workforce, and dependent variables, e.g. equipment staffing ratios and productivity. On each given production shift, those variables ‘meet’ and result into a specific production output with associated costs. Through simulation one may therefore predict the most likely production outcome for a particular business year or find ways to optimize KPIs such as specific cost of production.

This paper showcases an equipment and personnel availability-based Monte Carlo simulation using underground production with continuous miners (CMs) and truck haulage as an example. The technical process design, logic, and associated costs can be implemented in a standard Excel® spreadsheet application. The generation of random input parameters, as required by the Monte Carlo method, may also be accomplished using standard functions provided in Excel. However, for complex simulations, it is advised to use add-on software such as the commercially available software @Risk by Palisade, which provides extensive modelling features (e.g. random number generators, goal seek analysis by adjusting values of cells, and sensitivity analyses).

Simulation of production processes and associated costs in mining using the Monte Carlo method

The probabilistic Monte Carlo approach demands that the model logic is built around probability distributions of input variables, which are specified by the user. A fundamental argument proposed in this paper is that most aspects of availabilities in mining production processes can be adequately represented by binomial probability distributions, as discussed in the following section.

Binomial distribution

The term ‘availability’ refers to a binary condition of equipment and personnel, which can be either available or unavailable for production on a particular operating shift. It is argued (and later demonstrated in a case study) that if the average availability of personnel and equipment units in a given business year is known from experience or by assumption, then the probability of having a given number of equipment units or personnel available on a random operating shift can be predicted by a binomial probability function.

In its general definition, the density function of the binomial probability distribution is expressed as

where n is the number of trials, p is the probability of success for each trial, k is the number of successes, and b(k,n,p) is the probability of having exactly k successes out of n trials.

Translated to the context of the production logic proposed here, the binomial density function provides an estimate of the probability of having exactly k equipment units available on a random operating shift from a total fleet of n units with average fleet availability of p

[1]

According to the binomial distribution for 70% truck availability, one easily calculates the chance of having at least six trucks available on a given shift at only 33% (calculated as the sum of the relative availability of exactly six and seven trucks in Figure 1). This is a very low probability. One could now surmise that the production process is either underequipped and requires additional trucks, or that average truck availability requires major improvement, or both. For proper economic decision-making, however, one must consider that the three CMs themselves will not be always available. The question then is: how often will enough trucks be available for the individual number of available CMs on a given shift?

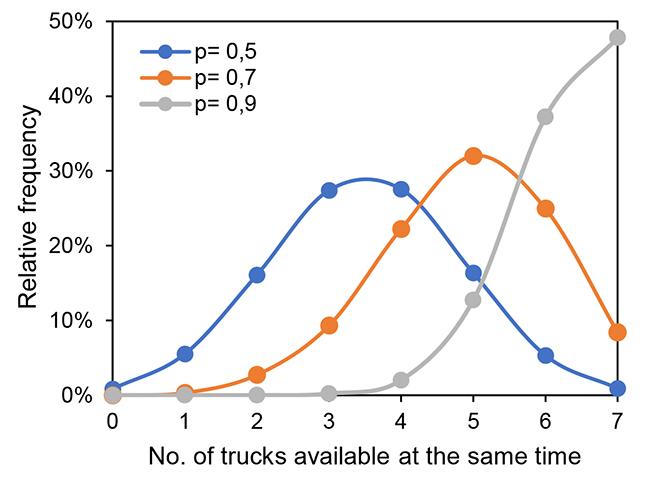
The problem of group availability – or, in general, matching of two or more independent variables with individual probability distributions at a given point in time – may still be computed using standard spreadsheet applications. Using two separate columns, create equally large binomially distributed random numbers for available CMs in one column and trucks in the other. Then, row-by-row, check how often the criterion is met that at least two trucks are available for each available CM.

The results may be charted as shown in Figure 2. In the given example, a fleet of seven trucks with average 70% availability and a fleet of three CMs with 70% availability can be expected to have 72% group availability. The production situation therefore is already much better than initially estimated based on the availability distribution of the trucks alone. Yet it might still not be good enough.

Example: Assume a mine operating a fleet of n = 7 trucks with average fleet availability of p = 50%, 70%, or 90% on a shift basis. The probability (here expressed as relative frequency) of having exactly k = 0, 1, 2, 3 … 7 trucks available on a given working shift may then be calculated from the binomial probability function with corresponding curves presented in Figure 1. For example, if the average fleet availability is 70%, one can expect to have exactly five trucks available on 32% of all shifts within a business year.

More often, however, the production planner requires to know how much equipment from his fleet will at least be available on a given working shift. Assume for instance that the fleet of seven trucks is supposed to serve three CMs for in-section haulage. For the process to work most productively, each CM requires two trucks for haulage. Hence, if all CMs are supposed to work simultaneously, at least six trucks are required to be available at the same time.

Figure 2 also shows how group availability is expected to improve as more trucks are added to the fleet. The diagram highlights an important point: for all practical purposes, the group availability increases near-linearly in the range of investigation up to a level of approximately 80% group availability. Beyond this level, the binomial distribution curves predict that an increasingly disproportional effort is required to reach as high as 100% group availability, hence questioning the economic meaningfulness of this approach.

So far, we have only considered the results of two independent and binomially distributed variables meeting in the production process. There are, of course, many others. For instance, if a mine requires systematic roof support in conjunction with face advance, the availability of roofbolting equipment may be added to the logic. Likewise, the availability of conveyor belts and processing units might become a focus of investigation as well, and the availability of personnel to operate the available units of equipment .

All relevant factors pertaining to the logic of production with CMs are addressed in the following section.

1–Binomial

The Journal of the Southern African Institute of Mining and Metallurgy

Figure

distribution of truck availability with average 50%, 70%, and 90% fleet availability

Figure 2–Predicted group availability of CMs and trucks for three CMs with 70% average availability and various average truck fleet sizes and availabilities

Simulation of production processes and associated costs in mining using the Monte Carlo method

Production modelling

Input variables

A full probabilistic production model must consider all relevant factors pertaining to the production process. To stick with the example of a CM and in-section haulage with trucks, those factors are (compare with Figure 3):

➤ Production time: Planned production shifts per year and hours per shift.

➤ Equipment capacity: Number of relevant units of equipment with payload and their respective implementation in the process, e.g. optimum travel distance to the section conveyor and auxiliary (unproductive) work necessary for the process, such as transport from shaft to section, work break, pick change, fresh air extension, equipment relocation etc.

➤ Equipment availability for groups of equipment, e.g. the fleet of CMs, trucks, and (if applicable) drill rigs or other machines. If the simulation targets optimizing the maintenance strategy, the average fleet availability may be subdivided into further aspects such as frequency of breakdowns, mean time-to-repair, or the share of planned and unplanned maintenance that is expected.

➤ Boundary conditions: All external impacts on the production system, such as bad ground conditions, additional safety precautions, or limitations pertaining to mineral processing such as demand or availability problems. Such factors can also be implemented (combined with an expected probability of occurrence) in the process logic.

➤ Workforce capacity: Number of full-time equivalent (FTE) workers allocated to the production team and their distribution across the planned production shifts per day and per week, as well as work hours per shift (i.e. ‘hot’ or ‘cold’ seat change).

➤ Workforce availability: The expected average sick days, share of annual leave, and share of time that is allocated for ‘unproductive’ (in terms of no tonnage produced) safety induction, training, and the like, resulting in an effective workforce availability for productive work.

➤ Workforce qualification is another important factor, which can result in higher or lower levels of productivity. For instance, a mine operating with well-rehearsed teams or piecework reimbursement contracts may see higher productivities,

and others which operate with a large proportion of unskilled miners or contract workers may perhaps see lower productivities. All such influences, if relevant to the analysis, may be implemented accordingly.

The idea of the Monte Carlo simulation is to simulate a large variety of probable constellations of the above-listed variables per shift and to process the variables using the individual production logic to result in tonnage output, which is then extrapolated to a full business year.

For each simulated shift the production logic needs to check the number of available units of equipment (with minimum staffing requirements) against the available personnel. This step determines if any bottlenecks exist on the technical side (see truck vs. CM problem) and how much equipment can be effectively utilized for production.

In a more refined production logic, the key decision of utilization must also consider all options available to the team leader, such as: is it possible to substitute a missing truck by using an available LHD or another load-carrying unit and by how much will this reduce the overall process capacity? Are there further boundary conditions related to the mineral processing side which prohibit full utilization? How do I distribute the available personnel most effectively across the equipment to result in maximum tonnage?

In fact, the problem of utilization is one of optimal resource allocation under varying boundary conditions and directly affects the productivity (i.e. the specific tonnage output) of the simulated shift. This fact must already be accounted for in the process design and workforce planning. For example, one can easily imagine that allocating an increasing number of employees to a CM section may result in an increase in tonnage output, at least up to a certain level. However, the specific labour productivity (tons per manhour) will decrease from some point.

Figure 4 shows such a staffing-productivity relationship for a typical CM section. The labour productivity curve peaks at around 3.2 workers per section (that is, three workers to operate the CM and two trucks plus 0.2 worker to compensate for work breaks, during which, if not accounted for, the process would either stop entirely or at least decrease in productivity). If more personnel are allocated to the section, auxiliary work such as a pick change or extension of layflats for fresh air supply may be completed more quickly and hence contribute to more production time per shift

Southern African Institute of Mining and Metallurgy

Figure 3–Schematic summary of probabilistic production model

Simulation of production processes and associated costs in mining using the Monte Carlo method

Step 3: Define the desired staffing ratio between available personnel and available CM-truck systems with corresponding productivities (such as suggested in Figure 4) in a table.

Step 4: For a random working shift within a business year, generate a random number of available items of equipment kCM, kTr and random number of available staff kSt from the binomial probability distributions defined in steps 1 and 2.

and tonnage output. However, the tonnage output cannot increase in proportion to the additional man-hours and hence labour productivity in terms of tons per man-hour declines.

Such information is vital to the quality of a production model and, if available, the respective relationships can be easily tabulated and implemented in the Excel-based simulation.

More variables may be added as required as outlined above. For example, if there is a 20% probability that tough geological conditions reduce a shift’s output by, say, 10% (e.g. because a CM’s cutting speed is limited by the strength of rock), then this can be simulated accordingly. However, as the number of variables in the model increases, so does the level of complexity by a disproportional amount and care must be taken that the relationships and causalities of the production process are still programmed in the correct way. It is therefore advisable to set out a clear scope of analysis and include only a minimum number of parameters identified as truly essential to the problem.

Simplified simulation procedure

In a simplified CM-truck production system that is free from limiting boundary conditions (e.g. tonnage demand limitations, limitations from auxiliary processes, geological limitations etc.) the sequence of the Monte Carlo process simulation is as follows (see also Figure 5):

Step 1: For both equipment categories (trucks and CMs), define the total number of units nCM, nTr with respective average availabilities pCM and pTr to create the binomial availability distribution for both categories.

Step 2: For the workforce, define the total number of staff nSt with average availability pSt

Step 5: Compare CM vs truck availability from step 4 and calculate the technically utilizable number of CMs uT,CM based on process requirement, e.g. as the minimum number of trucks that need to be available for one CM to be utilizable.

Step 6: Calculate the number of CMs uST,CM that can possibly be utilized based on the number of available personnel and the table defined in step 3.

Step 7: Select the number of items of equipment to be utilized on shift UCM, which equals the minimum value of either uT,CM or uSt,CM, and the corresponding staffing ratio per utilized CM.

Step 8: Calculate tonnage output and tons per man-hour on shift from the table (step 3).

Step 9: Iterate through steps 4–7 repeatedly, preferably >10 000 times for full representative sample (Monte Carlo method).

This simulation procedure will result in a variety of production outputs per shift which need to be multiplied with the number of planned operating shifts per year to derive annual results.

Case study

The outlined Monte Carlo simulation logic is applied to a real mining situation to showcase how such a model may be calibrated, what the interdependencies of process parameters with effect on tonnage output and costs are, and how the model can be applied to find ways to optimize production.

The selected case study is an underground room-and-pillar mine in a soft rock environment, which produces about 4 Mt ROM per annum from both conventional drill-and-blast-sections and CM sections (the latter being the focus of the case study). The mine operates three CMs with a fleet of seven trucks for in-section haulage, as discussed before. A full set of data (technical data, shift

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 5–Simplified example of CM-truck production model using the Monte Carlo method

Figure 4–Relationship between number of operators, productivity, and total output for continuous miners and truck haulage

Simulation of production processes and associated costs in mining using the Monte Carlo method

reports, KPI reports, and others) from a given business year is available for evaluation and serves as a basis for model calibration. The productivity diagram in Figure 4 has been derived from this empirical data and is implemented in the model.

Equipment availability

The first step in applying the model is to check if the underlying assumption of binomial probability distributions for equipment availability is correct. In the particular business year, the average availability of the truck fleet was 70.4% and the related histogram of truck availability as derived from shift reports is plotted in Figure 6, together with a binomial model of truck availability using the identical input data (n = 7, p = 0.7). The same comparison is made for the fleet of CMs in Figure 7, where n = 3, p = 0.61 as obtained from the mine’s reports. One observes an overall acceptable match between the assumed binomial distributions and reality.

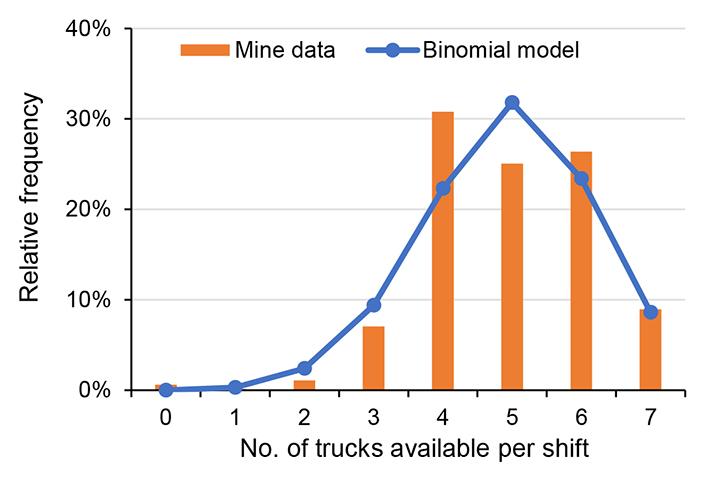
The next step is to implement all remaining input variables based on the actual mine data and the process logic as described above, and to test the model. Some key input factors and model results are summarized in Table I.

Group availability

A group availability of 89% was established from the mine’s reports, compared to only 77% predicted by the model, as shown in Table I. The positive discrepancy of 12% is appreciable and may be due to two reasons. The first is on the side of theory: obviously, the fitted binomial distributions of truck and CM availabilities match the real data well, as seen in Figures 6 and 7, but there is no 100% fit. Hence, through error propagation, a combination of the two distributions will produce (possibly larger) mismatches. The second reason is on the practical side: the mine had successfully prioritized its maintenance efforts to make sure that (as often as possible) enough trucks were available at the time they were required for a given number of CMs. That is, through correct resource allocation the mine was able to ‘beat’ the average statistic. Such effects do not question the principle of modelling but must be borne in mind when interpreting and making decisions based on models.

The mine’s report also revealed that if a truck was missing in the production chain, it could frequently be substituted by an LHD with only slightly smaller payload from the adjacent drill-and-blast sections. Consequently, this improvement was introduced as a general rule in the production simulation (i.e. every missing truck can be substituted by an LHD), so that the lower CM-truck group availability does not influence the predicted utilization, productivity, and tonnage output too much, as can be seen in the following section.

Utilization, productivity and tonnage output

Next, one introduces the variable of workforce availability, allowing for the 33% of time that workers were evidently not available for utilization of available equipment due to annual leave, training, or sickness. The model computes an equipment utilization of 85% on a shift basis, which compares favourably with the 83% utilization in the business year. Also, the simulated annual tonnage and the related tons per employee stand the reality check very well, as shown in Table I.

Note that the results are probabilistic. Figure 8 provides a detailed plot of the simulated annual tonnage output from the mine. The bar chart features three main peaks:

➤ The first peak is at zero tonnage and indicates that at around 6% of the annual production time, there will be zero tonnage output. This point corresponds to the binomial model for CMs (Figure 7) which predicts a 6% chance that none of the CMs will be available during the business year.

➤ The next peak occurs at around 1.3–1.5 Mt and represents the productivity during all those situations in which only one CM will be available, scaled up for a whole business year.

➤ Finally, a third peak at around 2.7 Mt, which is accompanied by a larger scatter to its left and right. This interval represents all those situations in which 2–3 CMs are available for production in a range of sub-optimal (i.e. insufficient number of workers or trucks available) to optimal combinations. Again, the productivity of those situations is scaled up for the whole business year.

Table I

Example of input and output data from the model compared to the mine’s data

Input Mine’s data Simulation

Shifts per day 3 3

Number of CMs- 3 3 Availability of CMs 61% 61% Number of trucks 7 7 Availability of trucks 70% 70% Number of employees (FTE) 38 38 Annual leave 20.3% 20.3% Sick leave 10.2 % 10.2% Induction, training, etc. 2.5% 2.5%

Results

Group availability CM-truck 89% 77% Δ -12% Utilization 83% 85% Δ +2% Productivity (t/FTE) 56 154 55 789 Δ –1% Annual tonnage (Mt) 2.19 2.12 Δ –3%

Figure 6–Comparison of truck availability as observed at the mine and as predicted by the assumed binomial probability distribution

Figure 7–Comparison of CM availability as observed at the mine and as predicted by the assumed binomial probability distribution

Southern African Institute of Mining and Metallurgy

Simulation of production processes and associated costs in mining using the Monte Carlo method

Note that, due to the scaling logic, the most probable production output is determined from the average simulation result, i.e. 2.12 Mt in this case study.

Analysis of production and associated costs

Based on the calibrated model some fundamental relationships and principles of the production process can be examined. For instance, consider the relationship between average CM availability and planned utilization. In the given example, three CMs operating in a three-shift-per-day system allow for utilization of up to nine machine-shifts per day (see Figure 9).

Evidently, there can be a straight-line relationship between planned-utilization and annual output only if the CM availability was 100%. For all availabilities < 100%, output only increases regressively with an increase of planned production shifts.

Consider the curve for 60% average CM availability: the chance of having at least one CM available on each shift is relatively large (93%, calculated as the cumulative probability of having exactly 1, 2, and 3 CMs available using the binomial distribution with k = 1, 2, 3 respectively; n = 3, p = 0.6 as described in the section ‘Binomial distribution’), so that the gradient of output from the first three planned machine-shifts per day is relatively steep. The next 4–6 planned machine-shifts per day require that at least one additional CM is available, the chance of which is already less (65%). Finally, machine-shifts 7–9 require that three CMs are available simultaneously on one to three shifts per day, the chance of which is the lowest (22%).

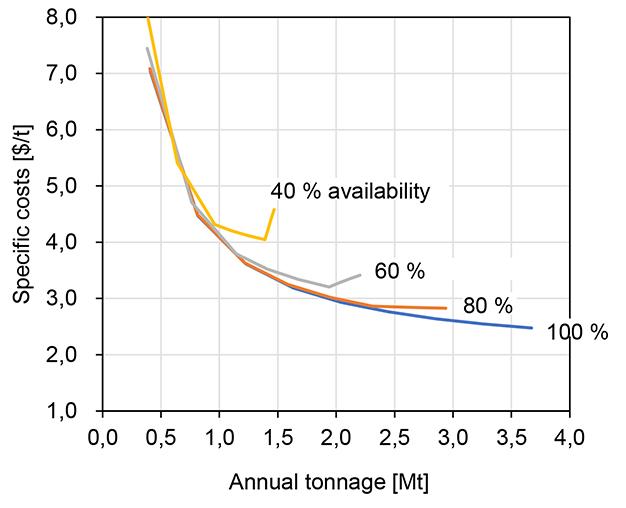
At the same time, each additional planned machine-shift per day requires that a proportional number of workers is permanently employed (since one can rarely foresee when a machine will be available or not), whose specific output in terms of tonnage per employee reduces since the absolute tonnage output increases at a slower rate. Equipment availability and workforce productivity are obviously interlinked.

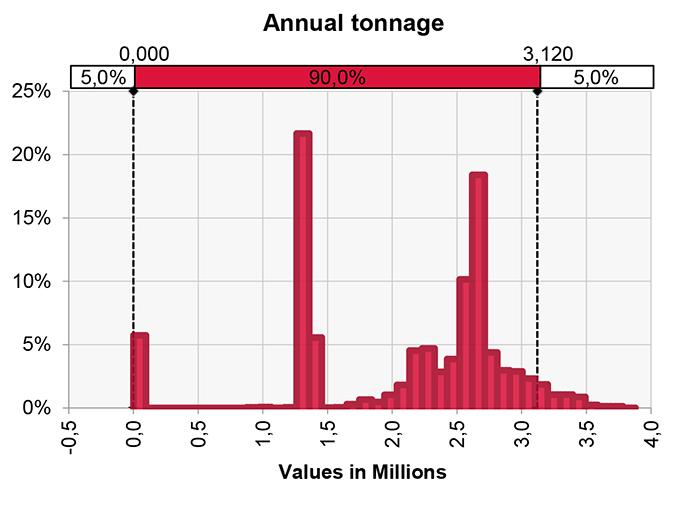
Next, a full set of production costs may be added to the model. From an accounting point of view, there will be fixed costs, such as annual depreciation of equipment and cost of labour for a given number of planned utilization shifts. Other costs are variable, i.e in some ways proportional to operating hours and tonnage output, such as energy and consumables. Some mines may also find that the cost of maintenance is – at least from a long-term average perspective – proportional to the operating hours of equipment and therefore to tonnage.

The above-named cost categories have been implemented in the model assuming realistic values. Figure 10 shows the computed relationship between annual output and expected specific cost of production. At first, all cost curves show the

same regressively decreasing trend. If this trend was to continue for very large production outputs, the fixed part of the cost would become negligibly small and the overall specific costs would tend towards the value of the variable costs. Clearly, this cannot be the case in a real production process, as marginal costs come into effect as well: from a certain point onwards, the cost curves reverse, as every additional tonnage output requires a disproportional amount of effort.

In the example shown in Figure 10 this marginal effect is only due to the inefficient low availability compared to high staffing. However, other factors such as extending production to overtime (surcharge), adding additional equipment to ensure higher output, or increasing the staffing ratio towards a production maximum such as shown in Figure 4 may work to the same effect.

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 9–Relationship between availability, utilization, and tonnage produced

Figure 10–Costs per ton of production (in-section) versus total output at different equipment availabilities

Figure 8–Model output for total tonnage produced in a business year

Simulation of production processes and associated costs in mining using the Monte Carlo method

The relationship in Figure 10 clearly indicates that, depending on the level of equipment availability, there might be an optimal point of production in terms of minimum specific costs. However, there might be at least two good reasons why production should perhaps be extended beyond this point:

➤ Underground mines are typically associated with a very large portion of fixed costs (e.g. shafts, conveyors, processing units), so that a sub-optimal cost increase within the production sections may become irrelevantly small in overall terms.

➤

Sub-optimal costs of production may be over-compensated by exceptionally good selling prices.

Nevertheless, if the company’s focus is on optimizing internal costs of production, or at least to increase production while incurring minimum additional costs, the Monte Carlo simulation can assist in negotiating the various possible approaches. Some examples are provided in the following section.

Optimization

Returning to the case study and the calibrated model, one may now ask several questions as to possible production improvements. The iterative process of querying various parameter combinations is greatly facilitated in @Risk by using the built-in simulation and optimization tool. Some examples:

➤ How does the addition of an eighth truck to the fleet enhance the annual production, assuming the average availability of the fleet does not change?

Answer: An extra 30 000 t of production. Note that this result must be interpreted with care, since the model makes use of the simplified rule that every missing truck can be substituted with an LHD. If this is not the case, the benefit from purchasing an eighth truck is larger than 30 000 t.

➤ Alternatively, what must the average availability of the seven-truck fleet be to achieve the same increase of 30 000 t/a in perhaps a cheaper way?

Answer: 79.6% (a 7.6% increase).

These two alternatives must be negotiated from a cost and reliability point of view. On the one hand, the purchase of an additional truck provides a certain reliability but comes at the disadvantage of additional costs. On the other hand, attempting to improve the availability of the existing fleet may come – through optimization of internal processes – at lesser cost, but may be more difficult to achieve. Other examples:

➤ How does an increase of 5% in equipment availability for both trucks and CMs compare to a 5% improvement in the health of the workforce (i.e. personnel availability)?

Answer: An increase of approximately 160 000 t/a versus 73 000 t/a.

This comparison demonstrates that for the given case study, equipment availability is a more effectful lever than worforce availability. The more so as workforce health is to a large extent dependent on aspects outside of the employer’s realm of influence. Final example:

➤ At the given average equipment and workforce availability, what is the optimal number of workers employed within a business year, in terms of maximum tons mined per employee?

Answer: Reduce planned utilization to two CMs per shift at 3.2 workers per section, totalling about 65 000 t per employee and year (a 16% increase). Note that the mine’s annual output from CM sections will reduce to 1.6 Mt only (a drop of -26%).

The examples showcase the strength of the model in providing quick guidance through the economic decision-making process.

Conclusion

Successful mining is strongly dependent on the availabilities of equipment and workforce. Since those availabilities are highly variable throughout a business year, resulting in wide ranges of favourable to unfavourable conditions for production output and related productivity, a probabilistic approach to production modelling that makes use of the Monte Carlo method has been proposed.

A fundamental finding in this paper is that availabilities can be modelled with binomial probability distributions and input parameters as obtainable from a mine’s report (or from estimation). It has been argued that those binomial distributions, together with a specific process logic, can be implemented into standard spreadsheet application to create a production model which conclusively explains technical and economical relationships of production, such as the occurrence of marginal costs.

The model has been applied to a case study of a selected underground mine, where it was able to accurately predict the mine’s performance in terms of tonnages and productivities in a given business year. Against that background, various relationships between the number of units of equipment, equipment availabilities, and number of staff with respective availabilities have been explored to improve the mine’s production on a system level.

It is tempting to simulate ‘ultimate’ questions that pertain to production optimization, e.g. how a mine can produce a maximum tonnage at minimum unit cost, or at least a maximum tonnage with the given resources at hand. The model will indeed produce several outputs with suitable suggestions.

However, it must be borne in mind that the variable nature of equipment and personnel availabilities, as discussed in this paper, is testament to the fact that it takes much effort to manage, allocate, and develop the resources at hand and to lead production towards its goals. In this context, the presented Monte Carlo production model is best understood as a tool which assists mine planners and management in negotiating different strategic decisions. For the strategic decision to become a success, continuous improvement and controlling is required.

References

Brzychczy, E. 2018. Probabilistic modeling of mining production in an underground coal mine. Proceedings of the International Conference of Intelligent Systems in Production Engineering and Maintenance Advances in Intelligent Systems and Computing, vol. 835. https://doi.org/10.1007/978-3-319-97490-3 62

Heuberger, R . 2005. Risk analysis in the mining industry. Journal of the South African Institute of Mining and Metallurgy, vol. 105, no. 2. pp. 75−79

Jung, D., Baek, J., and Choi, Y. 2021. Stochastic predictions of ore production in an underground limestone mine using different probability density functions: A comparative study using big data from ICT System. Applied Sciences, vol. 11, no. 9. 4301 p. https://doi.org/10.3390/app11094301

Upadhyay, S.P. and Askari-Nasab, H. 2018. Simulation and optimization approach for uncertainty-based short-term planning in open pit mines. International Journal of Mining Science and Technology, vol. 28. pp. 153−66. u

Diamonds Source to Use 2023 Conference

New Beginnings A brave new (diamond) world

CONFERENCE

DATE: 25-26 JULY 2023

VENUE BIRCHWOOD HOTEL AND OR TAMBO CONFERENCE CENTRE, BOKSBURG, JOHANNESBURG

OBJECTIVE

The objective of the conference is to provide a forum for the dissemination of information relating to the latest tools and techniques applicable to all stages of the diamond industry, from exploration through mine design, processing, to cutting, marketing, and sales.

WHO SHOULD ATTEND

 Geologists  Mineral (diamond) resource managers  Mining engineers  Process engineers  Consultants  Suppliers  Sales/marketing  Diamantaires

CALL FOR PAPERS/PRESENTATIONS

Abstract submission 20 February 2023

Abstract acceptance 6 March 2023

Paper submission (if applicable) 3 April 2023

 Mine managers  Mining companies  Students

ECSA, GSSA, and SACNASP CPD points will be allocated to all attending delegates

TOPICS  COVID-19 and impact on diamond sales  Geology and exploration  Mine expansion projects  Mining, metallurgy, and processing technology  Rough diamond sales and marketing  Cutting, polishing, and retail  Project Management  Financial services and industry analysis  Industry governance, beneficiation, and legislation  Mine-specific case-studies.

Prospective authors may choose to submit full (peer-reviewed) papers/presentations or standalone presentations only.

In person presentations will be preferred, although virtual presentations may be streamed live or prerecorded.

Prospective authors are invited to submit titles and abstracts of their papers and/or presentations in English.

• Authors must note whether they wish to submit a peer reviewed paper or a standalone presentation.

• Authors must note whether they plan to attend in person or whether they would deliver a livestreamed or recorded virtual presentation.

• Abstracts should be no longer than 500 words and should be submitted to: Camielah Jardine, Head of Conferencing, E-mail: camielah@saimm.co.za

The complete Proceedings volume will be made available on the internet for public access after the conference.

Limited sponsorship (registration only) may be available to students presenting full, refereed papers.

Applications for such sponsorship will be considered only on the acceptance of a full paper.

For further information contact: Camielah Jardine, Head of Conferencing E-mail: camielah@saimm.co.za Tel: +27 11 538-0237, Web: www.saimm.co.za

Affiliation:

1School of Mechanical Engineering and Automation, Shenyang Institute of Technology, China.

2Liaoning Key Laboratory of Information Physics Fusion and Intelligent Manufacturing for CNC Machine, Shenyang Institute of Technology, China.

Correspondence to: L. Zhang Email: zhanglina1204@126.com

Dates: Received: 23 May 2021 Revised: 1 Sep. 2022 Accepted: 23 Oct. 2022 Published: December 2022

How to cite: Zhang, L., Zhou, Y., Wang, H., and Mo, C. 2022

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 705–714

DOI ID: http://dx.doi.org/10.17159/24119717/1639/2022

ORCID: Y. Zhou https://orcid.org/0000-00019537-9938

Studies on fluorination of Fe₃O₄ (magnetite) by NH₄HF₂

by L. Zhang1,2, Y. Zhou1,2, H. Wang,1,2, and C. Mo1,2

Synopsis

Fluorination of magnetite (Fe₃O₄) by NH₄HF₂ was investigated using simultaneous thermogravimetry and differential thermal analysis (TG-DTA), and observing the morphology and phase changes using scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM-EDS) and X-ray diffractometry (XRD). The results indicate that fluorination with the involvement of oxygen begins at room temperature, peaks at 178.40C, and is completed at 2000C with the formation of only (NH₄)₃FeF₆. On heating, (NH₄)₃FeF₆ gradually releases NH₄F by the formation of NH₄FeF₄ at 2590C, then (NH₄)0.18FeF₃ at 3270C, and finally FeF₃ with minor FeF₂ at 4000C due to the partial reduction of Fe (III) to Fe (II). At 5500C, FeF₃ is oxidized to FeOF/Fe₂O₃.

Keywords

Ammonium bifluoride; fluorination; thermal decomposition; FeF₃; XRD.

Introduction

Transitional metal fluorides such as FeF₃ have gained growing attentions due to their potential for use as electrode materials in lithium ion batteries owing to their low cost and high specific capacities (Ignatiev et al., 2020; Shimoda et al., 2020; Zhou et al., 2017; Zhou et al., 2018). Fe is the fourth most abundant element in the Earth’s crust and the cheapest metal in the market. In particular, the theoretical capacity of FeF₃ is up to 712 mA h g−1 because of its unique reaction mechanism during the charge and discharge processes. However, FeF₃ prepared by hydrometallurgical processes always contains crystal water such as FeF₃·3H₂O. During the dehydraion process, iron oxides form (Sophronov et al., 2016) because Fe fluorides are unstable in the presence of water vapour. The formation of iron oxides significantly decreased the capacity. FeF₃ can also be prepared via thermal process using anhydrous HF or F₂ gas at high temperature in special corrosion-resistant equipment (Johnson., 1981). NH₄F and NH₄HF₂ are recognized as cheaper and versatile fluorinating agent used at low temperatures (<240°C) (Andreev, 2008; Claux et al., 2016; Gordienko et al., 2017; Juneja et al., 1995; Laptash and Maslennikova, 2012; Laptash and Polyshchuk, 1995; Mukherjee et al., 2011; Pourroy and Poix, 1989; Sophronov et al., 2016). However, excess NH₄F should be added in order to produce oxygen-free fluorides due to the highly hygroscopic nature of NH₄F (Mukherjee et al., 2011; Pourroy and Poix, 1989; Sophronov et al., 2016). Fluorination of different oxides by NH₄HF₂ therefore appears to be the most convenient method for obtaining oxygen-free fluorides.

The melting and boiling point of NH₄HF₂ are 126.8°C and 238.8°C, respectively. It is known that that NH₄HF₂ can react with Fe₂O₃ or FeTiO₃ (Andreev, 2008; Gordienko et al., 2017; Juneja et al., 1995; Laptash and Maslennikova, 2012; Laptash and Polyshchuk, 1995) below 230°C to form (NH₄)₃FeF₆ and/or NH₄FeF₃ according to follow reaction:

[1] [2]

Thus, for Fe₃O₄, the reactions can be written as: [3]

On heating, NH₄FeF₃ decomposes to form FeF₂ in ammonium media at 350°C (Andreev., 2008); while (NH₄)₃FeF₆ gradually releases NH₄F to form FeF₃ via two or three steps (Alexeiko et al., 2008; Juneja et

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

al., 1995; Kraidenko, 2008; Laptash and Polyshchuk, 1995; Pourroy and Poix, 1989; Shinn et al., 1966; Sophronov et al., 2016), as listed in Table I. According to Alexeiko et al. (2008), Juneja et al.1(995), Pourroy and Poix (1989), Shinn, Crocket, and Haendler (1966); and Sophronov et al. (2016) the reaction proceeds in two stages:

(NH₄)3FeF₆ → NH₄FeF₄ → FeF₃

However, Laptash and Polyshchuk (1995) and Kraidenko (2008) indicated that there exists an intermediate phase between (NH₄)₃FeF₆ and NH₄FeF₄, comprising (NH₄)₂.₅FeF₅.₅ at 235°C and (NH₄)₂FeF₅ at 255°C. Wang et al. (2021) indicated that (NH₄)0.18FeF3 forms at 320°C between NH4FeF4 and FeF3. With further temperature increase up to 400°C, FeF3 with minor FeF2 forms due to the reduction of Fe (III) (Alexeiko et al., 2008; Laptash and Polyshchuk, 1995; Pourroy and Poix, 1989). Furthermore, FeF₃ is oxidized due to the destruction of NH₄F (Alexeiko et al., 2008; Juneja et al., 1995; Sophronov et al., 2016). Therefore, the reaction pathways between NH₄HF₂ and Fe₃O₄ are complicated. However, to authors’ knowledge, there are no reports about the fluorination of Fe₃O₄ by NH₄HF₂. In the present work, the possible reaction pathways involved during the fluorination of Fe₃O₄ by NH₄HF₂ were simultaneously determined by TGDTA. The fluorides in each stage were prepared by direct thermal treatment and analysed using SEM-EDS and XRD. The results of this work may be useful for studies of the fluorination of Fecontaining minerals and the production of oxygen-free fluorides.

Experimental

Commercial analytical grade magnetite (Fe₃O₄, 99.8 wt.%) and ammonium bifluoride (99.5 wt.%) were supplied by Sinopharm Group (China). To ensure complete fluorination, the theoretical mass ratio of NH₄HF₂:Fe₃O₄ is 1.8450 according to Equation [3]. In order to investigate the reaction progress, two mass ratios of 2.5 and 3.5 (higher than the theoretical value) were chosen for investigation.

TG-DTA runs with pure NH₄HF₂ and Fe₂O₃/NH₄HF₂ mixtures were carried out in a Shimadzu DTG-60 unit at a rate of 5°C/min from 25°C to 600°C under 20 mL/min N₂ gas. Derivative thermogravimetry (DTG) curves were obtained as the first derivative of the TG curves. Based on TG-DTG-DTA

results, the critical reaction temperatures of DTA curves were determined. In order to analyses the composition and determine the morphologies and phases of products before and after each reaction stage, Fe₃O₄ was first mixed with NH₄HF₂ at different mass ratios (NH₄HF₂: Fe₃O₄ = 2.5 or 3.5), put into a pure nickel crucible, then placed in a furnace for the assays. Heating was carried out at a rate of 5°C/min. Once the selected temperature was reached, the samples remained isothermal for 1 hour, and then allowed to cool to room temperature for further characterization. In order to increase repeatability, each test was repeated three times using 100 g Fe₃O₄.

The phases, morphologies, and composition of Fe₃O₄ powder, NH₄HF₂ agent, and fluorides produced were determined by XRD (D/Max-2500 pc type X-ray diffractometer) and scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM-EDS) (Oxford Instruments, INCA)

Results

Properties of Fe₃O₄ powder and NH₄HF₂ agent

Figure 1 shows a SEM image and the corresponding EDS trace of Fe₃O₄ particles. Fe₃O₄ particles exhibit a spherical morphology with particle size less than 500 nm. EDS results in Figure 1b indicated that only Fe and O were detected. The atomic ratio of Fe to O is close to 3:4, which coincides well with the chemical formula of Fe₃O₄. The XRD results indicate that this phase is Fe₃O₄ (#19-0629) (magnetite). Figure 2 shows the XRD spectrum of NH₄HF₂ agent (#12-0302). Clearly, NH₄HF₂ agent has a crystalline nature.

Thermal analysis of NH4HF2

Figure 3 shows the TG-DTG-DTA curve of NH4HF2 between 25 and 600°C. A weak endothermic peak is observed at 126.8°C due to the melting of NH4HF2 (Carling and Westrum, 1976; House and Rippon, 1981; Resentera et al., 2020; White and Pistorius, 1972). The second well-defined endothermic peak overlaps the previous peak, having a maximum at 160.2°CThis peak corresponds to the decomposition and total removal of NH₄HF₂ (Carling and Westrum, 1976; House and Rippon, 1981; Resentera et al., 2020; White and Pistorius, 1972), as observed on the TGA-DTG curve.

al

Shinn et al., 1966 (NH₄)₃FeF₆

350°C

Juneja et al., 1995 (NH₄)₃FeF₆ → NH₄FeF₄ → FeF₃ 250°C 350°C 400°C

Pourroy and Poix, 1989 (NH₄)₃FeF₆ → NH₄FeF₄ → FeF₃ → FeF₃+ FeF₂ 35°C 330°C 400°C 445-490°C

Three-step Laptash and Polyshchuk, 1995 (NH₄)₃FeF₆ → (NH₄)₂ ₅FeF₅ ₅ → NH₄FeF₄ → FeF₃ → FeF₂ 235°C 330°C 400°C

Kraidenkos, 2008 (NH₄)₃FeF₆ → (NH₄)₂FeF₅ → NH₄FeF₄ → FeF₃

The Journal of the Southern African Institute of Mining and Metallurgy

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Figure 3—TGA-DTG-DTA analysis of NH₄HF₂ at 5°C/min

Furthermore, the mass loss of NH₄HF₂ reagent begins from room temperature, as found in previous investigations (Carling and Westrum, 1976; House and Rippon, 1981; Resentera et al., 2020; White and Pistorius, 1972).

Thermal analysis of the fluorination of Fe₃O₄ with NH₄HF₂ Figure 4 shows the TG-DTG-DTA curves of Fe3O4/NH4HF2 mixtures between 25 and 600°C at different mass ratios. Clearly, two endothermic peaks are observed for a mass ratio of 2.5: 144.9°C and 259.9°C as seen in Figure 4a. Moreover, a weak endothermic peak appears at 327°C. For a mass ratio of 3.5, two new endothermic peaks appear at 126.8°C and 178.4°C, as seen in Figure 4b. However, the peak at 144.9°Cdisappears or is overlapped by the peaks at 126.8°C and 178.4°C; while the peak at 327°C increases significantly. From Figure 4a, it can also be seen that the mass loss of about 2-3% begins at room temperature for a

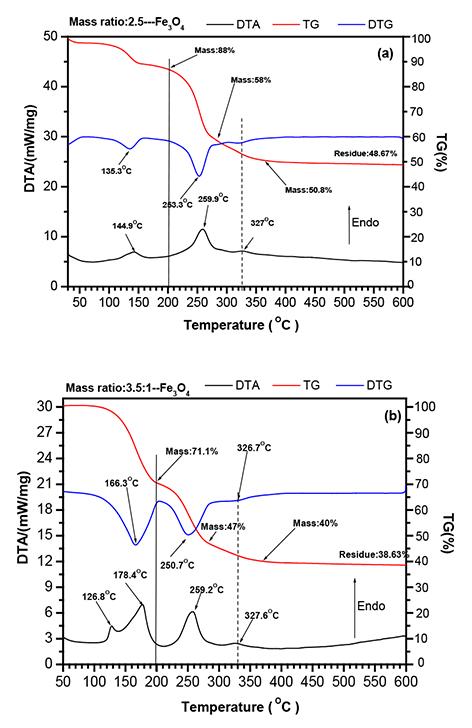
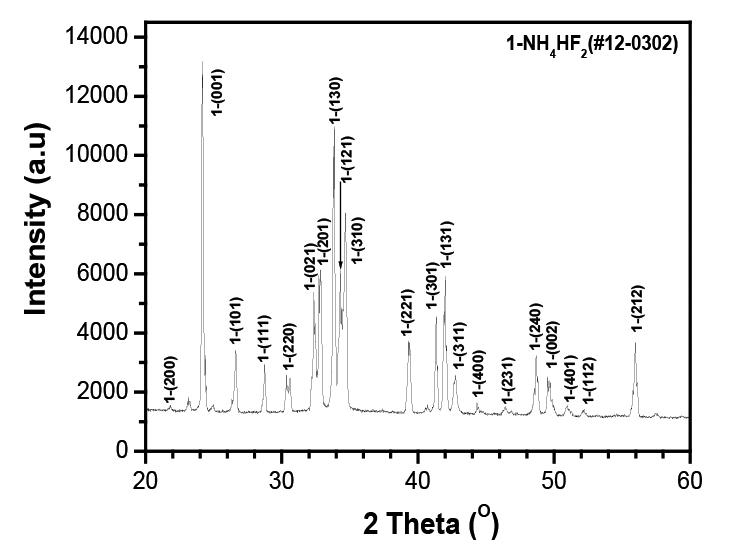
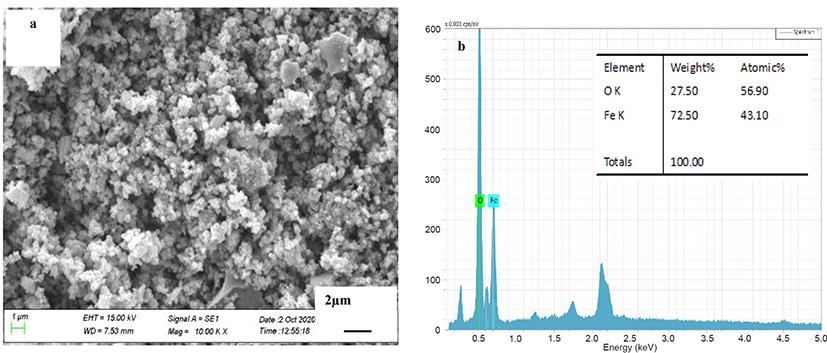
mass ratio of 2.5, the same as for pure NH₄HF₂ (Figure 3); while a minor mass gain (less than 1%) is observed for a mass ratio of 3.5 before 100°C (Figure 4b). With increasing temperature, a mass loss of about 10% is observed between 100 and 150°C for a mass ratio of 2.5; after which a levelling off occurs between 150 and 200°C. However, significant mass loss (approx. 28.9%) is observed between 100 and 200°C for a mass ratio of 3.5 without the curve flattening. By comparison, there are at least three endothermic peaks, which coincide well with the peaks in the DTG curves with large mass loss at 178.4°C, 259.2−259.9°C,and 327−327.6°C. The masses of residues for different temperatures are listed in Table II. In this temperature range, Fe₃O₄ is stable even at ambient condition (Ouertani et al., 2020). These results indicate that the formation of the above three peaks may be due to chemical reactions.

Figure 4—TGA-DTG-DTA analysis of Fe₃O₄/NH₄HF₂ mixtures between 25 and 600°C at heating rates of 5°C/min with different mass ratios of NH₄HF₂ to Fe₃O₄: (a) 2.5:1 and (b) 3.5:1

Figure 1—(a) SEM image and (b) the corresponding EDS of Fe₃O₄ powder

Figure 2—SEM image, EDS trace, and XRD spectrum of NH4HF2 powder

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Theoretical phases, calculated (Mc) and measured (Mm) residue massesat different temperatures with different mass ratios of NH₄HF₂ to Fe₃O₄

Temperature Mass ratio: 2.5

Mass ratio: 3.5 Phase Mc Mm Phase Mc Mm

200°C (NH4)3FeF6+NH4HF₂ 90% 88% (NH₄)₃FeF₆+NH₄HF₂ 92.23% 71.1% (NH₄)₃FeF₆ 81.77% (NH₄)₃FeF₆ 55.42% 280°C NH₄FeF₄ 55.45% 58% NH₄FeF₄ 43.13% 47% 330°C (NH₄)₀ ₁₈FeF₃ 42.96% 52% (NH₄)₀ ₁₈FeF₃ 33.42% 41% 600°C FeF3+FeF2 41.46% 48.67% FeF₃+FeF₂ 32.08% 38.63%

Figure 5—XRD spectra of Fe₃O₄/NH₄HF₂ mixtures after thermal treatment at different temperature for 1 hour with different mass ratios of NH₄HF₂ to Fe₃O₄: (a) 2.5:1 and (b) 3.5:1

Characterization of the fluorination products of Fe₃O₄

In order to identify and analyse the products involved in TGDTG-DTA curves of Figure 4, samples were prepared by direct thermal treatment at different temperatures for 1 hour and then analysed using XRD. The results are shown in Figure 5. Clearly, the products between 135 and 180°C at both mass ratios consist chiefly of (NH₄)₃FeF₆ (#22-1040) with minor NH₄HF₂ (#12-0302) and Fe₃O₄ (#19-0629); the peak intensity of NH₄HF₂ decreases with increasing temperature and disappears at 270°C; the peak of Fe₃O₄ appeared between 135 and 180°C disappears at 270°C; only NH₄FeF₄ (#20-0503) is detected at 270°C at both mass ratios. These results indicate that the mass ratio of NH₄HF₂ to Fe₃O₄ has no influence on the fluoride phases between 135 and 270°C. In this case, only the fluorides with the mass ratio of 2.5 after direct thermal treatment were chosen for analysis.

Macroscopic morphology investigation showed that the fluorides formed between 135 and 180°C exhibit a similar grey color with increasing temperature: light grey, grey, and dark grey. Figure 6 shows the SEM images and the corresponding EDS data for fluorides produced between 135 and 270°C. Clearly, the fluorides formed between 135 and 180°C exhibit a similar large, faceted-grain morphology, as seen in Figures 6a, 6c, and6e. Furthermore, the particle size increases with increasing temperature, although, the average grain size at 180°C is still less than 1 μm. The corresponding EDS results in Figures 6b, 6d, and.6f indicate that the fluorides consist of Fe, F, and N, with minor O. Hydrogen was below the detection limit. In order to obtain more precise results for Fe and F, O is omitted during the quantitative analysis. From Figure 6, it can be seen that the content of Fe and

N increases while the content of F decreases with increasing temperature. The atomic ratios of F:Fe of the fluorides at 135°C, 150°C, and 180°C are 6.4, 6.2, and 6.0, respectively. These results suggest that NH₄HF₂ is lost between 135 and 180°C, which is corroborated by the decreasing peak of NH₄HF₂ in Figure 5.

The fluorides at 270°C become white (Figure 6g). Clearly, the faceted particles formed between 135 and 180°C disappear while finer spherical particles with average size less than 100 nm appear. The EDS results in Figure 6h indicate that the fluorides consist of Fe, F, and N without O, and the atomic ratio of F:Fe further decreases to 4.0.

The fluorides become green at 330°C. The size of the spherical particles slightly increases to larger than 150 nm and significant agglomeration occurs, as seen in Figure 7a. The EDS results in Figure 7b indicate that the fluorides at 330°C also consist of Fe and F with minor N. However, the atomic ratio of F:Fe further decreases to 3.0, which is close to the formula of FeF3. However, the XRD results in Figure 8a indicate that this is not FeF₃ but a new phase comprising (NH₄)0.₁₈FeF₃ (#47-0646). The results suggest that an intermediate phase, (NH₄)0.₁₈FeF₃ (#47-0646), forms between NH₄FeF₄ and FeF₃. In other words, a new chemical reaction occurs between 270 and 330°C.

The fluorides formed at 400°C (Figure 7c) are also green. Clearly, the particle size is the same as that formed at 330°C. However, the EDS results in Figure 7d indicate that the fluorides at 400°C consist of Fe and F without N. The atomic ratio of F:Fe is close to 3, the formula ratio of FeF₃. However, the XRD results in Figure 8b indicate that this is FeF₃ (#33-0647) with minor FeF₂ (#45-1062).

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

The fluorides become red at 550°C (Figure 9a). Clearly, the average particle size increases up to 500 nm. The EDS results in Figure 9b indicate that the fluorides consist of Fe and O with minor F. The atomic ratio of O:Fe is close to 3:2 of the formula ratio of Fe₂O₃. The XRD results in Figure 9c indicate that the fluorides consist mostly of Fe₂O₃ (#33-0664) with minor FeF₃(#330647) and FeF₂ (#45-1062).

Discussion

The melting of NH₄HF₂ at 126.8°C (Carling and Westrum, 1976; House and Rippon, 1981; Resentera et al., 2020; White and

Pistorius, 1972) leads to an endothermic peak in the DTA curve, as found in this work (Figure 3). This is why a clear peak is observed at 126.8°C for a mass ratio of 3.5 (Figure 4b). Even before the melting of NH₄HF₂, a minor mass loss occurs due to the decomposition of NH₄HF₂, as seen in Figures 3 and 4a. With the melting of NH₄HF₂ at 126.8°C, the mass loss increases sharply and a well-defined endothermic peak with large mass loss occurs at 178.4°C due to the fluorination of Fe₃O₄. According to Equations [1], [2], and [3], the fluorination of Fe₃O₄ should form (NH₄)₃FeF₆ and NH₄FeF₃. However, the results in Figures 5 and 6 indicate that only (NH₄)₃FeF₆ (#22-1040) with a comparable coarse faceted-

Figure 6—(a), (c), (e), (g) SEM images and (b), (d), (f), (h) the corresponding EDS data for Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment at different temperature for 1 hour. (a, b) 135°C; (c, d) 150°C, (e, f) 180°C; (g, h) 270°C°

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Figure 7—(a, c) SEM images and (b, d) the corresponding EDS data for Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment at different temperature for 1 hour: (a, b) 330°C and (c, d) 400°C

grain morphology forms between 135 and 180°C. No NH₄FeF₃ was detected. The results suggest that divalent iron becomes trivalent through the oxidation of Fe₃O₄ or the involvement of oxygen during the fluorination progress (Laptash et al., 2000). In a word, oxygen is involved in the fluorination reaction according to the reaction:

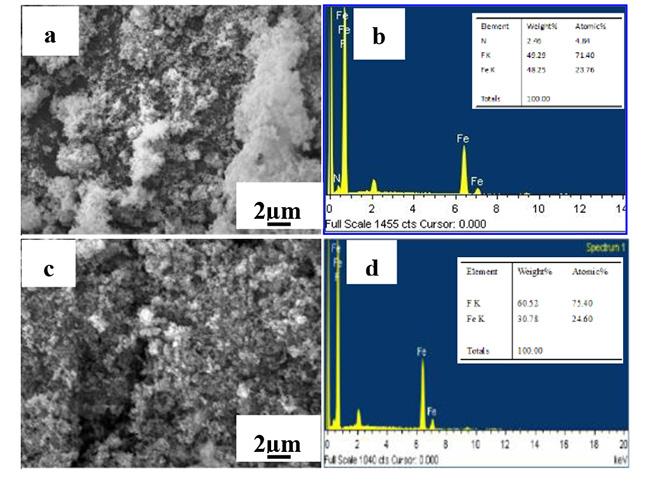
Figure 8–XRD spectra of Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment for 1hour at (a) 330°C and (b) 400°C

In this case, a minor mass gain should be observed. Figure 4b indicates that a minor mass gain occurs even at room temperature, suggesting fluorination may start at room temperature. To confirm this assumption, a Fe₃O₄/NH₄HF₂ mixture with mass ratio of 2.5 was prepared and kept for one week at room temperature, then analysed using XRD (Figure 10). Clearly, only (NH₄)₃FeF₆,

Figure 9—(a) SEM image, (b) EDS data, and (c) XRD spectrum of Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment at 550°C for 1 hour

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Theoretical calculation show that NH4FeF₄ residues at 280°C for mass ratios of 2.5 and 3.5 are 55.45% and 43.13%, in fair agreement with the measured values of 58% and 47% from the TG curve after consideration of the measurement error, as listed in Table II.

Figure 10—XRD spectra of Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) held at room temperature for one week

and no NH₄FeF₃, was detected, the same as at 135-180°C (Figure 5). Furthermore, the samples became warm during mixing, and a smell of ammonia was observed. The results suggest that the fluorination of Fe₃O₄ by NH₄HF₂ really begins at room temperature, the same as Fe₂O₃ (Wang et al., 2021).

According to Equation [4], the fluorination of Fe₃O₄ at room temperature also causes the formation of H₂O, which is absorbed by the fluorides. The loss of absorbed H₂O between 100 and 150°C (Wang et al., 2020) plus the decomposition and removal of NH₄HF₂ between 126.8 and 160.2°C (Mukherjee et al., 2011; Resentera et al., 2020; White and Pistorius, 1972) might cause the formation of another weak peak at 144.9°C, as seen in Figure 4a. The peak at 144.9°C will be overlapped by the fluorination of Fe₃O₄ at 178.4°C at a high mass ratio of 3.5, as seen in Figure 4b.

With the melting of NH₄HF₂ at 126.8°C, the reaction rate increases sharply due to the faster liquid-solid reaction rate compared to the slower solid-solid reaction rate. Based on the above analysis, the peak at 178.4°C at mass ratio 3.5 is mainly due to the fluorination of Fe₃O₄ according to Equation [4]. However, according to Equation [4], the mass ratio of NH₄HF₂ to Fe₃O₄ for complete fluorination is 2.2140. Therefore, fluorination should be completed for both mass ratios. However, results in Figures 5a and 5b indicate that minor Fe₂O₃ and NH₄HF₂ are still detected between 135 and 180°C even after 1 hour, suggesting a slow fluorination rate of Fe₃O₄.

With increasing temperature, the further fluorination of unreacted Fe₃O₄ plus the decomposition/sublimation of NH₄HF₂ will consume all or part of the NH₄HF₂.In this case, the products at 200°Cshould consist of (NH₄)₃FeF₆, possibly with minor NH₄HF₂. Theoretical calculation indicates that the product masses at 200°C for mass ratios of 2.5 and 3.5 are 81.77–90% and 55.42–92.23%, in fair agreement with the measured values of 88% and 71.1% from TG curves, as listed in Table II. In other words, the products at 200°C contain major (NH4)3FeF6 with minor NH₄HF₂ residue. That is reasonable because the boiling point of NH₄HF₂ (238.8°C) is higher than 200°C. At 238.8°C, all NH₄HF₂ sublimes. Therefore, either no NH₄HF₂ will be present or it will be below the detection limit of XRD, as seen in Figure 5.

Figure 4 indicates that a new peak appears at 259.2−259.9°C in the DTA curves, accompanied by a large mass loss. The value coincides well with the values in the literature (Juneja et al., 1995; Pourroy and Poix, 1989). The XRD results in Figure 5 indicate that a new phase of NH₄FeF₄ (#20-0503) forms at 270°C. Furthermore, NH₄FeF₄ (#20-0503) becomes white, and the morphology changes to fine spherical (Figure 6g). From these results, it may be concluded that (NH₄)₃FeF₆ releases NH₄F to form NH₄FeF₄ at 259.2−259.9°C according to the following reaction:

With increasing temperature, NH₄FeF₄ (#20-0503) will lose NH₄F to form FeF₃ at temperature above 330°C (Alexeiko et al., 2008; Juneja et al., 1995; Kraidenko, 2008; Laptash and Polyshchu., 1995; Pourroy and Poix, 1989; Shinn, Crosket, and Haemdler, 1966; Sophronov et al., 2016). However, Figure 4 shows that there exists an another peak at 327-327.6°C. Figures 7a and 8a suggest that the fluoride at 330°C is not FeF3 but (NH4)0.₁₈FeF3 (#470646) with minor N (Bentrup and Menz, 1990). The fluoride of (NH4)0.₁₈FeF₃ is a different colour (green) to that formed at 270°C (white). Furthermore, the particle size increases up to 150 nm. with significant agglomeration (Figure 7a). From the above results, it could be concluded that NH₄FeF₄ lost only part of its NH₄F to form a new intermediate phase of (NH₄)0.₁₈FeF₃ at 327°C. According to theoretical calculation, the residue masses at 330°C for mass ratios of 2.5 and 3.5 are 49.26% and 33.42%. These values are lower than the measured values of 52% and 41%, as seen in Table II. There are three reasons for this. The first is the measurement error, as seen in Table II. The second is the release of NH4F at 327°C, which results in the further fluorination of Fe₃O₄ residues according to follow reaction:

There is no direct evidence for this. However, the XRD results in Figure 5 indicate that the complete fluorination of Fe₃O₄ is a lengthy process Therefore, the assumption that fluorination of Fe₃O₄ is incomplete before 327°Cduring TG-DTA analysis is reasonable (Wang et al, 2021). The third reason is the slower release rate of NH4F from NH4FeF4 at 327°C during TG-DTA analysis. To confirm this assumption, a Fe3O4/NH4HF2 mixture with mass ratio of 2.5 was prepared and heated at 330°C for 10 minutes, then analysed using SEM/EDS and XRD. The results are shown in Figure 11. Clearly, only minor (NH4)0.₁₈FeF₃ (#470646) was detected, with major NH₄FeF₄ (#20-0503). The results indicate that the complete release of NH₄F from NH₄FeF₄ (#200503) takes a long time, even at 327°C.

With a further increase in temperature, (NH₄)0.₁₈FeF₃ will gradually lose all its NH4F to form FeF₃ with minor FeF₂ due to the partial reduction of Fe (II) to Fe (III) by ammonia at 400°C (Alexeiko et al., 2008; Bentrup and Men., 1990; Pourroy and Poix, 1989; Laptash and Polyshchuk, 1995; Laptash et al., 2000; Wang et al., 2021), as seen in Figure 8b. After 400°C, the mass loss is negligible, as seen in Figure 4. Therefore, the measured residue at 600°C is closed to the theoretical value after consideration the measurement error and the adsorption of F, N, and NH₃ by FeF₃ during TG-DTA analysis.

At 550°Cwithout gas protection, Fe oxides (Figure 9) form due to the oxidation of FeF₃ (Alexeiko et al., 2008; Juneja et al., 1995; Sophronov et al., 2016). In order to analyse the oxidation progress, a Fe₃O₄/NH₄HF₂ mixture with mass ratio of 2.5 was prepared and heated at 550°C for 10 minutes, then analysed using SEM/EDS and XRD. The results are shown in Figure 12. Clearly, the fluorides contain a major component of FeF₃ with minor FeOF (#18-0648). FeF₂ is either absent or below the detection limit of XRD. Combined with the results in Figure 9, it can be concluded

Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

that oxidation proceeds through the follow stages: FeF3 → FeOF → Fe2O3. Furthermore, oxidation is faster than reduction under these conditions, which is why no FeF2 is detected (Figure 12), and the fluorides after 1 hour consist of a major proportion of Fe₂O₃ and only minor FeF₂ (Figure 9).

Conclusions

The thermal and microstructural analysis of the fluorination of magnetite (Fe₃O₄) with NH₄HF₂ at different mass ratios of NH₄HF₂ to Fe₃O₄ (2.5 and 3.5) was carried out by means of TGDTG-DTA, SEM/EDS, and XRD. The results indicate that the mass

ratio of NH₄HF₂ to Fe₃O₄ has no influence on the fluorination reaction progress and the corresponding temperature. The fluorination of Fe₃O₄ starts at room temperature, dominates at 178.4°C, and is completed at 200°C with the formation of (NH₄)₃FeF₆. No NH₄FeF₄ forms due to the involvement of oxygen. As the temperature increases above 180°Cthe unreacted NH₄HF₂ decomposes and is removed from the system. Furthermore, (NH₄)₃FeF₆ decomposes sequentially through a three-step reaction by the formation of NH₄FeF₄ at 259.2-259.9°C, then (NH₄)0.₁₈FeF₃ at 320°C, and finally FeF₃ with minor FeF₂ at 400°C. At 550°C in air, FeF₃ is oxidized to FeOF/Fe₂O₃.

Journal of the Southern African Institute of Mining and Metallurgy

Figure 11—(a) SEM image, (b) EDS data, and (c) XRD spectrum of Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment at 330°C for 10 minutes

Figure 12—(a) SEM image, (b) EDS data, and (c) XRD spectrum of Fe₃O₄/NH₄HF₂ mixtures (mass ratio: 2.5) after thermal treatment at 550°C for 10 minutes

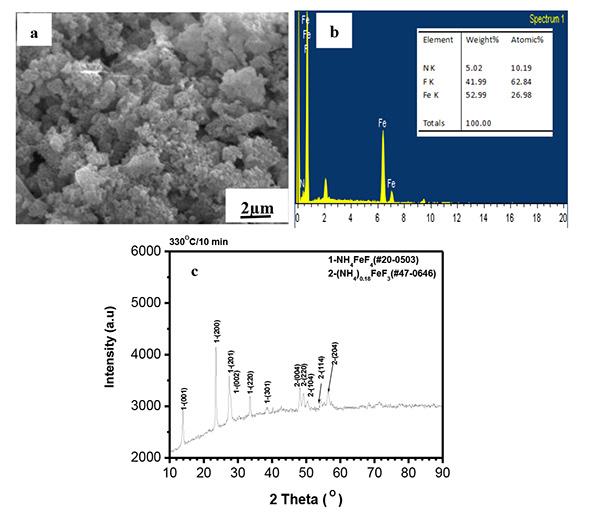
Studies on fluorination of Fe3O4 (magnetite) by NH4HF2

Acknowledgment

This research was supported by Scientific Research Fund of Liaoning Provincial Education Department (No. LJKZ1337) and Doctoral Research Startup Foundation of Shenyang Institute of Technology (BS202202).

References

Alexeiko, L.N., Maslennikova, I.G., Goncharuk, V.K., and Merkulov, E.B. 2008. Kinetics of thermal decomposition of fluorinated ilmenite. Pacific Science Review, vol. 10. pp. 325−328.

Andreev, A. A. 2008. Design of fluorination technology for pigment grade titanium dioxide synthesis from ilmenite Abstract, PhD thesis, Tomsk Politechnical University. p. 22.

Bentrup, U. and Menz, D.H. 1990. Zur thermischen Zersetzung vom (NH4)2[FeF5(H2O)] unter quasi-isobaren Bedingungen. Zeitschrift für anorganische und allgemeine Chemie, vol. 591. pp. 230−236.

Carling, R.W. and Westrum, E.F. 1976. Thermodynamics of the monohydrogen difluorides V. Melting thermodynamics of NH4HF2 Journal of Chemical Thermodynamics, vol. 8. pp. 269−276.

Claux, B., Bene, O., Capelli, E., Soucek, P., and Roland, M. 2016. On the fluorination of plutonium dioxide by ammonium hydrogen fluoride. Journal of Fluorine Chemistry, vol. 183. pp. 10−13.

Gordienko, P.S., Yarusova, S.B., Pashnina, E.V., and Zhevtun, I.G. 2017. Hydrofluoride method of complex processing of titanium-containing raw materials. Process Engineering Journal, vol. 1. pp. 31−34.

House, J.E. and Rippon, C.S. A TG study of the decomposition of ammonium fluoride and ammonium bifluoride. Thermochimica Acta, vol. 47. pp. 213−216.

Ignatiev, L.N., Savchenko, N.N., Marchenko, Yu. V., Mashchenko, V.A., and Tkachenko, I.A . 2020. Glasses in the MnNbOF5-BaF2-FeF3 system: Synthesis, structure and crystallization. Ceramics International, vol. 46B. pp. 16210−16216.

Johnson, G.K. 1981. The enthalpy of formation of FeF3 by fluorine bomb calorimetry. Journal of Chemical Thermodynamics, vol. 13. pp. 465−469.-

Juneja, J.M., Singh, S., Adhyapak, S.V., and Rao, U.R . 1995. Preparation of anhydrous FeF3 by solid state reaction of iron oxide with ammonium hydrogen fluoride. India Journal of Engineering and Materials Science, vol. 2. pp. 136−138.

Karelin, V.A., Strashko, A.N., Dubrovin, A.V., and Sazonov, A.V. 2014. Research of fluorination process of rutile concentrate. Procedia Chemistry, vol. 11. pp. 56−62.

Kraidenko, R.I. 2008. Fluorine-ammonium division of multi-component silicate systems to individual oxides PhD thesis [abstract], Tomsk Politechnical University.

Laptash, N.M. and Maslennikova, I.G. 2012. Fluoride processing of titaniumcontaining minerals. Advances in Materials Physics and Chemistry, vol. 2. pp. 21−24.

Laptash, N.M. and Polyshchuk, S.A . 1995. Thermal decomposition of ammonium fluoroferrates (NH4)xFeF2x (2≤x≤3). Journal of Thermal Analysis, vol. 44. pp. 877−883.

Laptash, N.M., Nikolenko, Y.M., Kurilenko, L.N., Polyshchuk, S.A., and Kalacheva, T.A. 2000. Fluorination of sulfide minerals with ammonium hydrogen difluoride. Journal of Fluorine Chemistry, vol. 105. pp. 53−58.

Mukherjee, A., Awasthi, A., Mishra, S., and Krishnamurthy, N. 2011. Studies on fluorination of Y₂O₃ by NH₄HF₂. Thermochimica Acta, vol. 520. pp. 145−152.

Ouertani, B., Bidouk, G., Ouertani, R., Theys, B., and Ezzaouia, H. 2020. Effect of the ruthenium incorporation on iron oxide phases synthesis, Fe₂O₃ and Fe₃O₄ , at low annealing temperature. Materials Chemistry and Physics, vol. 242. 122272.

Pourroy, G. and Poix, P. 1989. New synthesis routes for difluorides MF2 (M=Fe, Mn, Zn and Ni). Journal of Fluorine Chemistry, vol. 42. pp. 257−263.

Resentera, A.C., Rosales, G.D., Esquivel, M.R., and Rodriguez, M.H. 2020. Thermal and structural analysis of the reaction pathways of α-spodumene with NH₄HF₂. Thermochimica Acta, vol. 689. 178609.

Shimoda, K., Shikano, M., Murakami, M., and Sakaebe, H. 2020. Capacity fading mechanism of conversion-type FeF3 electrode: Investigation by electrochemical operando nuclear magnetic resonance spectroscopy. Journal of Power Sources, vol. 477. pp. 228722.

Shinn, D.B., Crocket, D.S., and Haendler, H.M. 1966. The thermal decomposition of ammonium hexafluoroferrates and ammonium hexafluoroaluminate: A new crystalline form of aluminum fluoride. Inorganic Chemistry, vol. 5. pp. 1927−1933.

Sophronov, V. L., Kalaev, M.E., Makaseev, Yu. N., Sachkov, V., and Verkhoturova, V.V. 2016. Study on the process of Fe (III) oxide fluorination. Materials Science and Engineering, vol. 110. 012069.

Wang, H, Zhou, Y. and B., Mo, C.G., Zhang, L.N., and Cui, J.J. 2021. Fluoridation of α-Fe₂O₃ by NH₄HF₂ to produce FeF₃. Russian Journal of Inorganic Chemistry, vol. 66. pp. 2017–2026.

Wang, Y.D., Zhang, Y.P., Liang, G., and Zhao, X. 2020. Fabrication and properties of amorphous silica particles by fluorination of zircon using ammonium bifluoride. Journal of Fluorine Chemistry, vol. 232. 109467.

White, A.J.C. and Pistorius, C.W.F.T. 1972. Melting curve and high-pressure polymorphism of NH₄HF₂. Journal of Solid State Chemistry, vol. 4. pp. 195−198.

Zhou, X.Y., Sun, H.X., Zhou, H.C., Ding, J., Xu, Z.L., Bin, W.J.J., Tang, J.J., and Yang, J. 2018. Enhancing the lithium storage capacity of FeF3 cathode material by introducing CaLiF additive. Journal of Electroanalytical Chemistry, vol. 810. pp. 41−47.

Zhou, X.Y., Sun, H.X., Zhou, H.C., Xu, Z.L., and Yang, J. 2017. Enhancing cycling performance of FeF3 cathode by introducing a lightweight high conductive adsorbable interlayer. Journal of Alloys and Compounds, vol. 723. pp. 317−326.u

ABOUT THE EVENT

The SAIMM through its committee for Diversity and Inclusion in the Minerals Industry (DIMI) and in collaboration with Women in Mining South Africa (WiMSA) is excited to announce its DIMI Dialogue 2023 focusing on the issues of diversity and inclusion in the mining and minerals industry.

The Southern African minerals industry, just like the global minerals industry, still faces challenges when it comes to diversity and inclusivity in the workplace. While landscape might be changing due to various of companies embracing the need for a more representative and diverse workforce, there is still a lot to be done. Beside issues of gender disparity in the industry, safe spaces in the workplace, protective equipment, sanitation facilities,

pregnancy and childcare facilities are some of the challenges that continue to plague the sector. The industry also needs to go beyond workforce diversity to inclusion, by identifying individuals from different geographic, gender, economic and cultural groups, creating safe spaces for them, providing support for them to grow into their roles. Creating conditions that promote inclusion on a daily basis can go a long way in retaining and advancing the careers of workforce and hence contribute to the long term growth of the minerals industry. DIMI provides a platform for discussion that can lead to the development of strategies for advancing and encouraging decisions that are in the best interest of a diverse workforce.

Stochastic analysis of dig limit optimization using simulated annealing

by J.R. van Duijvenbode1 and M.S. Shishvan1

Affiliation:

1Resource Engineering, Department of Geosciences and Engineering, Delft University of Technology, Netherlands.

Correspondence to: J.R. van Duijvenbode

Email: j.r.vanduijvenbode@tudelft.nl

Dates: Received: 29 Nov. 2019 Revised: 23 Sep. 2022 Accepted: 26 Oct. 2022 Published: December 2022

How to cite: van Duijvenbode, J.R. and Shishvan, M.S. 2022 Stochastic analysis of dig limit optimization using simulated annealing. Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 715–724

DOI ID: http://dx.doi.org/10.17159/24119717/1036/2022

ORCID: J.R. van Duijvenbode https://orcid.org/0000-00016723-0167

M. Soleymani https://orcid.org/0000-00020780-8841

Synopsis

The results of dig limit delineation in open pit mining are never truly optimized due to gaps in the underlying data, such as insufficient sampling. Aside from the data uncertainty, there is also an influence on the final dig limit by either humans or by the heuristic character of an optimization method like simulated annealing. Several dig limit optimizers have been published, which can replace the manual dig-limits designing process. However, these dig limit designs are generally not adapted to account for this heuristic character. In this paper we present a stochastic analysis tool that can be used with the results of heuristic dig-limit optimization to increase confidence in the obtained results. First, an enhanced simulated annealing algorithm for dig limit optimization is presented. Then, this algorithm is tested on ten different blasts at the Marigold mine, Nevada, USA, as a case study. Finally, the results are analysed with a destination-based ensemble probability map and an analysis conducted of the final solution data distribution. The generated dig-limit designs of the algorithm include high revenue areas that are excluded in comparable manual designs and show improved objective and revenue values. The analysis tool provides block destination probabilities and box plots with the distribution of opportunity value for the dig limit. Furthermore, with the analysis tool, it is possible to make well-informed design decisions in areas of uncertainty.

Keywords

open-pit mining, dig-limit optimization, simulated annealing, grade control.

Introduction

Hard rock open-pit mining involves the blasting of mining benches, after which the blasted material is sent to an assigned destination. Making decisions concerning the different material types from a bench and their destinations is commonly known as grade control (Dimitrakopoulos and Godoy, 2014; Kumral, 2013; Verly, 2005). Grade control often relies on the results of grade analysis from blast-hole sampling (or dedicated grade control sampling). Modelling the spatial distribution of these grades results in a high-resolution grade control model, which helps with assigning an appropriate destination to a group of blocks. This approach, known as dig -limit delineation, aims to correctly cluster a group of blocks, which should be mineable, and outline and separate various ore types and waste material (Richmond and Beasley, 2004).

Recently various researchers have developed algorithms to automate and optimize the dig limit delineation process, which rely on heuristics and metaheuristic algorithms. The techniques used include greedy algorithm-based methods (Richmond and Beasley, 2004; Vasylchuk and Deutsch, 2019), mixed integer programming (MIP) (Hmoud and Kumral, 2022; Nelis and Morales, 2021; Nelis, and Meunier, 2022; Sari and Kumral, 2017; Tabesh and Askari-Nasab, 2011), genetic algorithms (Ruiseco, 2016; Ruiseco, Williams, and Kumral, 2016; Ruiseco and Kumral, 2017; Williams et al., 2021), simulated annealing (Deutsch, 2017; Hanemaaijer, 2018; Isaaks, Treloar, and Elenbaas 2014; Kumral, 2013; Neufeld, Norrena, and Deutsch, 2003; Norrena and Deutsch, 2001), block aggregation by clustering (Salman et al., 2021) and convolutional neural networks (Williams et al., 2021), or a combination of techniques. With these algorithms, the definition of ‘mineability’ or ‘digability’ varied greatly between different investigators. The mineability of a dig limit is a quantitative measure that expresses how well a given item of equipment can extract the material without incurring dilution or ore loss. Earlier research methodologies used polygons and circles for dig limit designs (e.g., Neufeld, Norrena, and Deutsch, 2003), whereas currently blocks are often considered.

Stochastic analysis of dig limit optimization using simulated annealing

An example of a greedy dig-limit delineation algorithm can be found in Richmond and Beasley (2004). They used a floating circle-based perturbation mechanism to satisfy the mining equipment constraints. To delineate ore zones, the method uses a floating circle, which moves over the grade control model and expands until the average grade of the covered blocks is below the cut-off grade. This process is repeated multiple times, and the results are stored and evaluated by a mean-downside risk efficiency model that evaluates their dig limit solutions considering the financial risk for the dig limit design. Wilde and Deutsch (2007) used a feasibility grade control (FGC) method to optimize the dig limit profit, which iteratively recalculates the objective value by amalgamating blocks into mining units. Two constraints applied to the mining unit are that all blocks must have an adjacent block with the same destination, and the shape must be easily extractable. Vasylchuk and Deutsch (2019) used a method where dig limits are subject to site-specific rectangular excavating constraints. To satisfy the constraint, the method uses a floating (rectangular) frame that moves over the grade control model. The frame was analysed for its optimal destination, and this destination was assigned to the blocks. Finally, their model adapted problematic locations by reconsidering the neighbouring blocks and their destinations and performed a hill climbing step to improve the solution iteratively. Williams et al. (2021) recently explored GA solutions using a CNN to assess the dig limit cluster quality. The algorithm was very fast but could not well distinguish different clustering penalties (position- and-orientation-related).

More frequently applied optimization methods for solving dig limit problems include SA, GA, and MIP. SA is a metaheuristic, stochastic search algorithm used to approximate the global optimum of a given function (Aarts, Korst, and van Laarhoven, 1997; Kirkpatrick, Gelatt, and Vecchi, 1983; Rutenbar, 1989). The algorithm moves towards a final (optimum) solution by accepting or rejecting solutions based on an acceptance probability (Kirkpatrick, Gelatt, and Vecchi, 1983). SA has been used widely in the mining industry for various optimization problems, for example, for resource modelling (Deutsch, 1992), optimization of blasting costs (Bakhshandeh Amnieh et al., 2019), strategic openpit mine production scheduling (Dimitrakopoulos, 2011; Kumral and Dowd, 2005) for multiple destinations (Jamshidi and Osanloo, 2018) with and without stockpile considerations (Danish et al., 2021) or blast movements (Hmoud and Kumral, 2022). These applications focus on maximizing the profit for mining of each mining block by considering revenues, penalties, dilution factors, or mining constraints. Typically, the results are used in short-term planning, as input for blast design or grade control, surveying, and for field markup of mining benches (Maptek Vulcan, 2016).

In this paper we focus on the application of SA to the dig limit problem, as in Isaaks, Treloar, and Elenbaas (2014) and Hanemaaijer (2018). They used an optimization function that minimizes revenue loss due to wrong block assignments but limited their outcomes to only one near-optimal solution. Their constraints focused explicitly on creating dig limits that account for equipment constraints. For this constraint, they assigned a minimal mining width (MMW) that prevented the individual selection of blocks. Similarly, Ruiseco (2016) and Ruiseco and Kumral (2017) used a GA algorithm for the dig limit selection problem. In addition, they assigned a penalty, when blocks deviated from the correct clustering size. The correct clustering size is related to the mineability and how well a block of material can be extracted. Finally, the algorithm accepted a final solution

with the highest objective value. Ruiseco’s work also showed a distribution from the solution’s objective value after multiple runs and indicated the reliability of this non-optimal solution method. Sari and Kumral (2017) indicated that the dig limit selection problem was not solved using an exact method and therefore used MIP. Their approach complies with an MMW constraint by ensuring each block is connected to an ore or waste zone at least as big as the MMW.

Various commercial implementations of dig limit or grade control-related optimizers are available, which provide polygon outlines as a result (Deswik, 2019; Isaaks, Treloar, and Elenbaas, 2014, Maptek Vulcan, 2016; Orica, 2021). However, only from the mineable shape optimization tool, it is known that it uses a SA and/or a branch and bound algorithm (Deutsch, 2017; Maptek Vulcan, 2016). Furthermore, these applications have limited flexibility and provide few insight into details of the algorithms for solving the dig limit optimization problem, or the probability or quality of any of the solutions. This substantiates the need for an improved SA application methodology which runs multiple diglimit optimizations and gives a stochastic probability insight into the quality of the solutions.

In this paper we investigate the stochasticity of dig limit optimization through SA using an enhanced framework that uses similar frame and MMW constraint ideas as mentioned above. However, the heuristic character of SA implies that the final solution could vary for each realiztion and motivates the use of multiple dig-limit realizations to reduce algorithm uncertainty and increase confidence in the results. The work does not use an interpolated (kriged) grade control model to better show the stochastic influences of dig limit optimization rather than stochastic influences by interpolation. This is also supported by the continuity of the case study orebody and spatially dense dataset of grades due to the small spacing between blast-holes. The SA algorithm is tested on a case study with ten blasts and dig limit designs. We explore the stochastic and metaheuristic effects of SA and dig limit optimization and describe a new tool for making conclusions regarding the dig limit design. The paper concludes with a discussion of the stochastic analysis tool and potential improvements.

Methodology

The following steps were performed to prepare the data-set for the SA algorithm, summarized in Figure 1a. First, a regular grid was fitted to the blast-holes that best represent these original data-points. The blast-hole coordinates were snapped onto the nearest point in this regular east-north grid. As mentioned, the approach’s rationale was to avoid the commonly used kriging method because the initial assumption was that the blast-holes were planned at an (almost) regular densely spaced pattern, and y a high-resolution spatial model is not necessary as long as the average grade of the dig block can be estimated correctly. Finally, the assay results from multiple blast-holes were averaged to determine the metal grades at the grouped blast-holes. At this stage, the data-set was represented by regularized blast-holes with their corresponding attributes. It should be noted that no vertical dimension was used, as the assay results were averaged over the entire blast-hole, which removes the vertical dimension. No blast movement adjustments were made.

The following two concepts were used in the SA algorithm: ➤ Frames (Figure 1b) indicate the area around a blast-hole (node) that must comply with the MMW. Each blast is

The Journal of the Southern African Institute of Mining and Metallurgy

Stochastic analysis of dig limit optimization using simulated annealing

Figure 1–SA algorithm design concepts. (a) (1) grid fitting (rotation and shifting), (2) blast-hole snapping, and (3) assay averaging. (b) Each node represents a block. Frames with a 2 x 2 dimension result in 4 frames per node and are used to indicate the equipment excavation constraints. (c) Frame misfit and node misfit values

divided into frames that contain fx × fy number of nodes, where fx,fy are the frame dimensions in the east and north direction, respectively. Thus, for each node fx × fy possible frames exist.

➤ A misfit value is assigned when the destination of a node is not optimal in relation to the surrounding area, as shown in Figure 1c. The misfit value is defined as the number of nodes in any possible frame not assigned to the same destination as the largest group of nodes in the frame. It is independent of the destination of the misfits, and the value only indicates how many blocks in the frame are not sent to the largest destination group (Hanemaaijer, 2018). Objectives 2 and 3 from the objective function explain how the algorithm uses a node and frame misfit value to indicate the solution quality.

Simulated annealing framework

The presented algorithm uses all the steps of a normal SA algorithm (Kirkpatrick,Gelatt, and Vecchi 1983) to find an optimized solution regarding dig limit shape and revenue by minimizing switching between ore and waste and minimizing the MMW penalty. Normally, the solution is not guaranteed to be the optimal one, especially not during the first run and, therefore, it is proposed to run multiple SA optimizations and define a destination-based ensemble average for the dig limit. The SA framework (Figure 2) was previously described by Hanemaaijer (2018), but is adapted for this study to also produce the ensemble average maps. The algorithm is initialized with a dig limit design (initial solution) and maximized towards a final optimum by iterating over the following steps: penalty calculation, objective value calculation, accept/reject decision, temperature adjustment, perturbation of the solution, and stop criteria check. For each step of the algorithm, different variations were tested before the algorithm as presented was chosen. The reader is referred to Hanemaaijer (2018) and Villalba Matamoros and Kumral (2018) for more details. Each step of the SA framework (Figure 2) is explained in the following sections.

Initial solution

The SA algorithm automatically generates an initial solution from the regularized node data-set. For each non-overlapping frame, the best destination was chosen by determining the revenues for the nodes in the frame by setting all destinations to ore or waste. The highest revenue value determined the initial destination for the nodes in the frame. This procedure also accounted for frames that occurred at bench boundaries. Tests with a free selection or random initial solution provided similar results but entailed a longer computation time.

Objective function

The dig limit delineation problem is expressed as a maximization problem of the revenue by assigning the best destination to each node (a grade control block) and penalizing it due to constraint violations. Penalty weights are used to balance the importance and effect of the corresponding constraint on the dig limit design. The problem is solved by a multi-objective SA function, which consists of three components:

1. Maximize the blast revenue

2. Minimize witching between material types (frame misfit

3. Minimize the MMW penalty (minimal node misfit).

The objective function that determines the objective value is: [1]

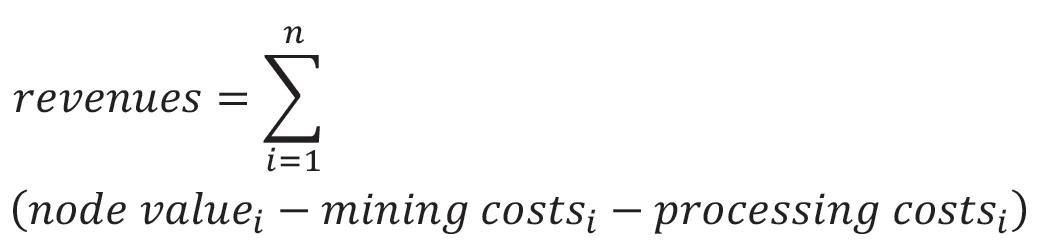
Objective 1. Selecting the right node destination will increase the revenue from extraction. If the ore is sent to the waste dump, there is opportunity loss, but when waste is classified as ore, the extra processing costs outweigh the value recovered. The objective, to get high revenue for a blast, is expressed as follows: Maximize [2] where [3] [4] [5]

where n is the total number of nodes and i the index number of each node (i=1,…,n). Each i also represents a unique ix and i y position of the node along the corresponding axis (x=1,…,nx and y=1,…,n y), where nx and n y are the number of nodes in the east and north directions, p is the metal price, ri the recovery related to node i, gi is the metal grade for node i, desti is the destination indication for node i, which is generally ore or waste, and

Stochastic analysis of dig limit optimization using simulated annealing

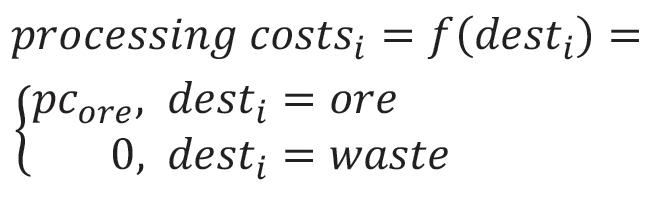
mcwaste,mcore, and pcore are the mining and processing costs for waste and ore, respectively. No node mass was used in the optimization algorithm.

Objective 2. A frame misfit value is assigned to all possible frames in the blast grid (Figure 1c). Minimizing the frame misfit values helps the algorithm with the discouragement of switching between destinations. This is done with a higher frame misfit value which occurs when there are boundaries between destinations. This objective is defined as: Minimize [6] where [7]

where fn is the total number of frames in the grid and f the index number of each frame (f=1,…,fn), misfitf is the misfit value from frame f, fx and fy are the frame dimensions in the east and north directions, and max is the value of the largest group of node destinations in the frame (Figure 1c), wpF is the frame penalty weight. A high wpF will discourage frequent destination switching in a frame and results in bigger zones of one destination. However, a poorly selected value would result in too much ore loss and dilution.

Objective 3. A node misfit is assigned to each node of the blast grid (Figure 1c). The node misfit is the minimum of all frame misfits from the frames that contain the given node. This misfit value helps to indicate whether a node is in at least one frame where all destinations are the same. Satisfying this ensures

compliance with the MMW constraint of the equipment. This objective is expressed as: Minimize [8] where [9]

where misfiti is the misfit value from node i, min{misfitf} is the value of the smallest frame misfit value from all frames where the node corresponds to (Figure 1c), and wpN is the node penalty weight. Similar to the frame penalty weight, the value of wpN should be carefully selected. A small value will result in a highly selective dig-limit design, which is an infeasible solution.

Perturbation mechanism

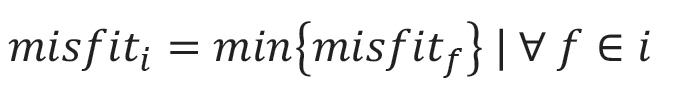
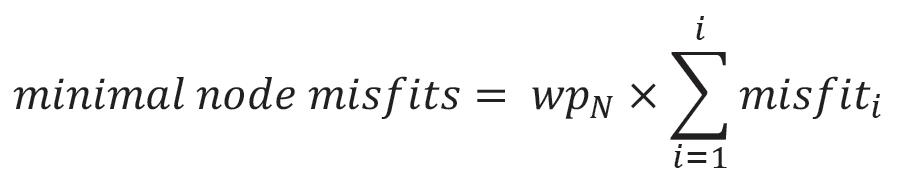
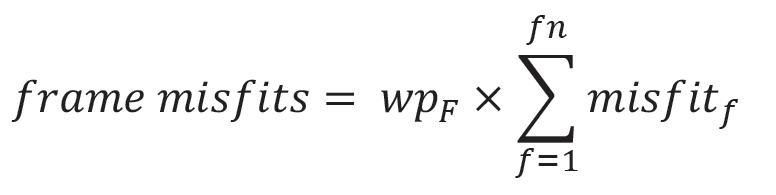
The perturbation step generates new solutions by changing the destination of the nodes in one frame to a randomly chosen destination. The frame choice was either by selecting a frame with a misfitf > 0 or by a random frame. The first selection method helps to specifically induce changes at locations in the grid that have boundaries (for instance, a single waste node in an ore region). After perturbation, the minimal node and frame misfits were updated to accommodate the changes in node destination.

Acceptance criterion

The model uses a metropolis algorithm in order to have a stochastic criterion of acceptance of worse solutions. The Boltzmann probability P(accept)=e-dE/T defines the probability of acceptance of a worse solution, where dE is the absolute objective value difference between the new and old solution

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 2–Overview of the simulated annealing optimization framework (modified after Hanemaaijer, 2018)

Stochastic analysis of dig limit optimization using simulated annealing

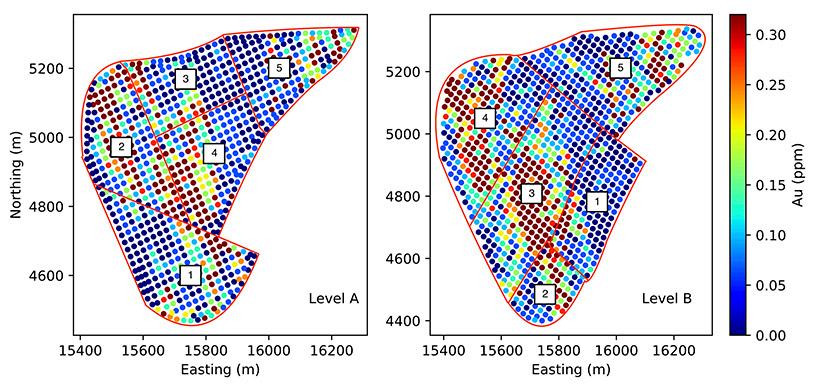
and T is the current temperature. The temperature is analogous with the model progress (cooling down). When the model cools down (progresses), then the changes in solutions become less sporadic. If the Boltzmann probability is greater than a random number between 0 and 1, then the new solution is accepted as the current solution and becomes the old solution. Conversely, if the probability is less than the random number, the algorithm rejects the new solution, and the old solution stays the same for comparison in the next iteration (Martín and Sierra, 2009).

Temperature decrement and termination rule

An epoch is a state of the algorithm where the temperature variable is not changed over a fixed number of iterations. After each epoch, the system cools by a quadratic additive cooling function which uses the total number of epochs and fixed final temperature:

function and speed has a direct bearing on the near-optimality of the SA.

Marigold mine case study

A case study was carried out to demonstrate the performance of the proposed SA algorithm for dig limit optimization. Two benches (A and- B), with five different blasts on each, were studied (Figure 3).

[10]

where Tk is the temperature at epoch number k, T0 the initial temperature, T n the final temperature, and n the total cooling epochs (Martín and Sierra, 2009). The initial temperature ensures an initial acceptance ratio of approximately 0.5 and that the advantage of having a guided initial solution remains. When the system temperature reached T n, it was kept running until the predefined total number of epochs, which was one of the stop criteria. The second stop criterion stops the algorithm earlier when a certain number of non-improving consecutive perturbations (iterations) is reached. This number was chosen to be greater than the total number of nodes in the grid, to ensure that at least every node could be randomly assigned once for perturbation.

Hanemaaijer (2018) tested four different temperature schedules, from which the quadratic additive cooling function was selected as the preferred function. It counteracts the exponential decay (see the Boltzmann probability) in the acceptance criterion with decreasing temperatures. This ensures that no major worse solutions are accepted any more (relatively fast), and that the cooling schedule, or T n, becomes the termination criterion of the SA algorithm. Furthermore, it is fairly unlikely that new solutions will be found if T n is reached and thus the choice of cooling

The Marigold mine (MG), in northern Nevada, USA, is owned and operated by Marigold Mining Company, a wholly owned subsidiary of SSR Mining Inc. A typical drill and blast, truck and shovel technique is used to extract the ore from several open pits. The ore is processed using heap leaching. An ore bench has a height of 7.6 m (25 ft) or 15.2 m (50 ft). The blast patterns are 7.3 m by 6.4 m for the waste benches and 7.6 m by 6.7 m for ore benches. The mine uses three shovels (2 × 28.7 m³ and 1× 52.8 m³ bucket capacity), and the bucket widths define the typical minimal mining width (MMW) of 12.2–15.2 m or two blast-holes. Blast-hole sampling is done to define ore zones. One sample per blast-hole is assayed for gold in an on-site laboratory to obtain a cyanidesoluble and a fire-assay grade, which together determine the total gold value (Aui) contained in each blast-hole (Marigold Mine, 2017).

The traditional dig limit procedure involves entering fire equivalent grades associated with each blast-hole into the grade control model. The blast pattern is then converted to a new block model with block sizes of 3.05 m × 3.05 m × 7.6 m. Next, the blast-hole assay data is kriged using ordinary kriging in two dimensions on the bench. If there are enough blocks above the cut-off grade to constitute a mineable body of ore, this is manually blocked out and marked in the pit to be sent to the leach pad for processing (Marigold Mine, 2017). The data-set used in this paper was obtained in the way described above, except that the data was not kriged.

Design and parameter selection

The selected SA parameters were chosen after testing and parameter tuning (Table I), following procedures similar to those described by Hanemaaijer (2018). Table II displays th case study parameters corresponding with the MG operation. The algorithm is written in the Python programming language according to

Southern African Institute of Mining and Metallurgy

Figure 3–Input grade control model of benches A and B for dig limit delineation, each consisting of five blasts

Stochastic analysis of dig limit optimization using simulated annealing

Table I

Simulated annealing initialization parameters

Parameter Value

Initial and end temperature 10 J 0 Iterations per epoch 15 Consecutive non-improving perturbations before termination 1500 (iterations) Total epochs 2000

Table II

Case study parameters (Marigold mine, 2017)

Parameter

Definition Value

p Gold price $1250 per ounce nx,ny,nz Number of nodes Bench-specific fx,fy Frame dimension 2.2 nodes ri Recovery

Cyanide–soluble grade ×0.92a Fire–assay grade

Mining costs $2.134 per ton, $1.865 per ton pcore Processing costs $1.459 per ton wpF, wpN Penalty weight 10 0.1

mcore, mcwaste

aMarigold Mine (2017)

established geostatistical conventions (GSLIB convention), for example, with the east direction as the x-axis and the north direction as the y-axis (Deutsch and Journel, 1997).

Results

Objective value

For each of the ten blasts, 25 SA runs were conducted to perform a stochastic analysis on dig limit optimization using SA. Each run reached 1500 consecutive non-improving perturbations and caused the algorithm to stop. This shows that each run is converged to an optimum. The average run time was 160 seconds. For example, Figure 4 shows two solutions from level B blast 3, one with the highest objective value (a) and one with the highest revenue (b) from the 25 runs. The difference can be found in the lower left corner, where solution (a) selected a larger ore region. This raised the objective value by 0.57% because a lower penalty was assigned due to the switching between material types. The revenue difference between the two solutions is only 0.58%.

The black outlined area in Figure 4 indicates the ore zone from MG’s dig limit solution. There is a big difference in the selected number of blocks and the associated loss in objective value and revenue. A 16% higher objective value and 5% higher revenue were found compared to MG’s solutions. However, the solutions do not always comply with the MMW constraint (Figure 4a at node (6,1)). In these cases, the penalty for not complying with the constraint was lower than the benefit gained while complying. The penalty weights, wpF and wpN, were chosen such that destination switching was discouraged and the algorithm was forced to comply with the mining constraints (Hanemaaijer, 2018). That the outcome in terms of objective value (and revenue) is better than the manually created dig limit design is promising, despite the fact that SA does not guarantee optimality.

Revenue

The revenues corresponding with the objective values were compared with the manual designed dig limit solutions from MG. Comparing the revenues could be misleading since optimization was done regarding the objective value. However, revenue is still one of the most important factors for the mine. The revenue differences between the MG dig limit and all blast optimization runs (25 each) are shown as box plots in Figure 5. The box extends from the lower to upper quartile values of the data, with a line at the median and the length of the whiskers being within 1.5 times the box length. The algorithm shows that it can improve revenue compared to the MG solution from mining the bench, whether it is in the loss, transition, or profit revenue zone. The boundary between the profit and loss revenue zones is where the total bench revenue moves from positive to negative. Generally, the loss zone

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 4–Best objective value and revenue dig-limit solutions of level B – blast 3 with projected dig limits of MG (black outline)

Stochastic analysis of dig limit optimization using simulated annealing

The whiskers are within 1.5 times the box length

corresponds with mining a lot of waste material (level A – blast 3). An improved dig limit reduces the mining costs, and less potential value ends up at the waste pile. Within the revenue transition zone, a potential loss is converted to a profit (dotted loss-profit boundary). It can be concluded that improvements in the profit region are beneficial for the mining company because small details could be improved during the manual designing process.

In nine out of ten cases the SA’s mean was higher than the MG dig limit revenue (Figure 5). This indicates that the SA optimization performed well. The set of solutions with a small revenue improvement, in the range up to $15 per ton, suggests that MG’s dig -limit solution was already reasonably good. Two solutions outperformed the MG solution with a difference of $22 and $50 per ton, respectively (level A – blast 5 and level B – blast 3). In these cases, the solution missed or included one or several regions rich in ore or waste. Finally, there was one solution that, on average, did not lead to any improvement (lA – blast 2). The main reason for this was that the grid preparation tool had difficulties in constructing the grid correctly. However, it is promising that better revenue solutions were found, and thus future improvements may also improve these difficult blasts.

Stochastic analysis

SA is a metaheuristic optimization method whereby accepting a solution does not guarantee an optimized result. Therefore, we analysed the probabilistic chance for achieving a good solution. Generally, the best solution from the solution distribution should be selected as the final solution. However, the quality of this solution depends on the number of runs. Increasing the number of runs costs more in computational time while not always giving a better result. An alternative consideration is to use a destinationbased ensemble probability map which shows the areas the algorithm is struggling with.

Destination-based ensemble average

Figure 6 shows a revenue box plot and node (mining blocks) destination probability map for 25 SA runs of level A - blasts 1 and 5. The displayed node destination is the destination’s ensemble average from the 25 runs. This ensemble average can be linked with the confidence of the algorithm and the probability that a

node should be assigned to a destination. For instance, nodes with a destination probability of approximately 0.5 indicate uncertainty regarding the best destination of the node. Therefore, a single run from the algorithm could be misleading and insufficient.

When a node’s destination probability is higher, it suggests that this node causes the objective value to increase because the node reduces ore loss and dilution. Ore loss is decreased when nodes of good grade are inside the dig limit, and dilution is reduced when waste material is removed from the dig-limit. However, depending on the economics, it can be worthwhile to include a few waste nodes so that the dig limit can include a higher-grade ore node.

For example, if for a node with a destination probability of approximately 0.5 from level A – blast 1 it was decided to designate the material as waste, then no additional dilution and revenue was created. Thus, most likely, the revenue value of the resulting solution will be in the 25-50% quartile. Two additional factors should be considered when this node is designated as ore. First, when this node is included in the dig limit there is potential that the solution’s revenue will increase due to reduced ore loss. Probably, the final solution’s revenue will be in the 50-75% quartile. Conversely, the node can also be of low grade, causing the mining constraints to fail, including dilution, and reducing the revenue value. In addition, analysing the quartile ranges suggests that the potential revenue gain is smaller than the potential loss. Secondly, assigning this node as ore implies a neighbouring higher-grade ore node that is worthwhile to include in the dig limit. It should be checked whether this is applicable. For level A - blast 5, the 0.5 destination probability node (lower-right) can be better designated as waste since the added revenue value is relatively small. Additionally, selecting this node as waste ensures that the remaining dig limit is less diluted. Similar considerations could be made for the other blasts.

Distribution of final solution data

Analysing the variance of the objective value or revenue from all found solutions could be a measure for the final dig limit acceptance and how close the outcome of SA is to optimality. Hereby, no distinction is made whether the objective value or revenue distribution is considered. While doing multiple runs, an

Southern African Institute of Mining and Metallurgy

Figure 5–Box plot of all blasts with the difference between SA and MG revenue ($ per ton). The blasts are separated into loss, transition, or profit revenue zones.

Stochastic analysis of dig limit optimization using simulated annealing

objective value or revenue boxplot could show the distribution of the final solution data at that moment. When enough of the solution space is explored, one approach is to accept the solution with the highest objective value at that moment and to consider the destination-based ensemble probability map. For example, Figure 7 displays the revenue distribution of 5, 10, 25, 50, and 100 consecutive runs for level A – blast 2. For this example, monitoring the data distribution change could already suggest that after ten runs, enough of the solution space is explored and that the corresponding highest objective value solution should be accepted as the final dig limit.

Analysing the revenue box plot while conducting multiple runs together with the associated destination-based ensemble average helps to inform a final decision regarding the dig limit design. The highest objective value solution provides the so-far best result, and the ensemble average gives more insight into potential interesting areas, which could be included in a final dig limit design.

It is known that the SA solutions are not guaranteed to be the global optimal solutions and they are optimized in terms of

objective value and not revenue. However, from the distribution of solutions in Figure 7 and the associated objective values it is possible to estimate how close most of the solutions are to optimality in terms of objective value. The highest revenue solution ($875 per ton) was only found once (1% chance), but did not have the highest objective value due to its higher penalty. In contrast, the solutions with the highest objective value had a revenue of $863 per ton and would, therefore, better represent the near-optimal solution. The significant effect of the applied penalties is shown in the 100-run box plot in Figure 7 because most solutions are grouped at a revenue of $863 per ton (28 runs) and $869 per ton (45 runs). That implies that the highest revenue is not the global optimal solution, but that it is more likely to be related to the 73 solutions with a revenue between $863 and $869 per ton.

Discussion

The dig limit analysis tool gives insight into the existing variability of the dig limit results. This variability is due to the stochastic influences from the metaheuristic optimization method of

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 6–Revenue box plot and the destination-based ensemble probability map of level A - blasts 1 and 5

Figure 7–The revenue distribution of level A – blast 2 is explored after 10 of the 100 runs of the model

Stochastic analysis of dig limit optimization using simulated annealing

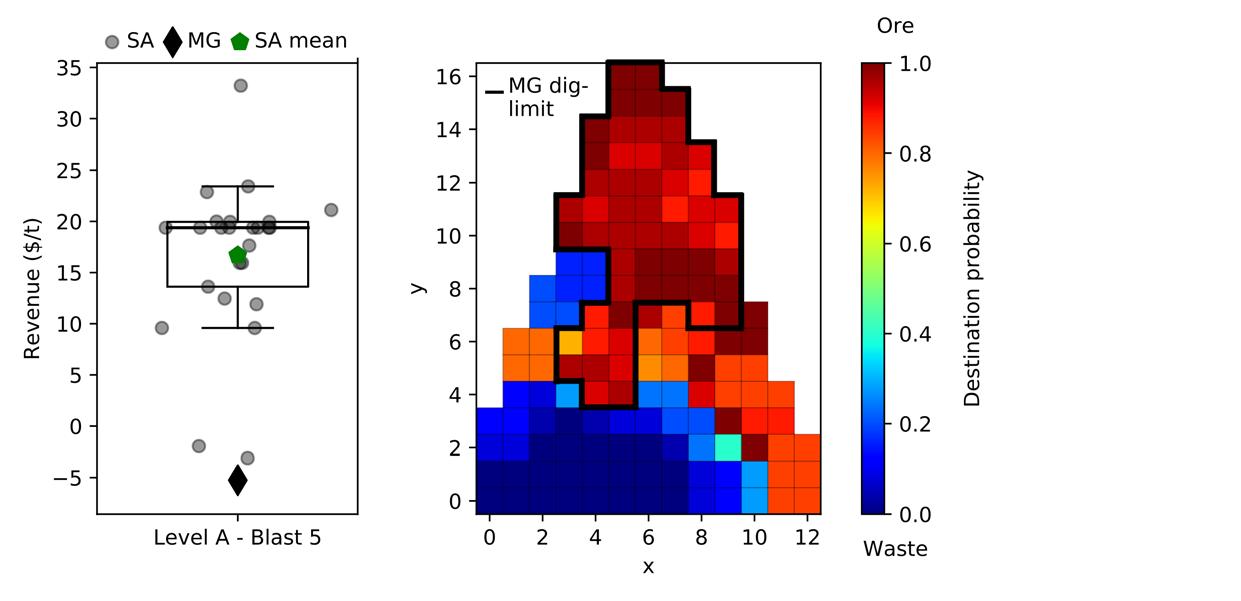
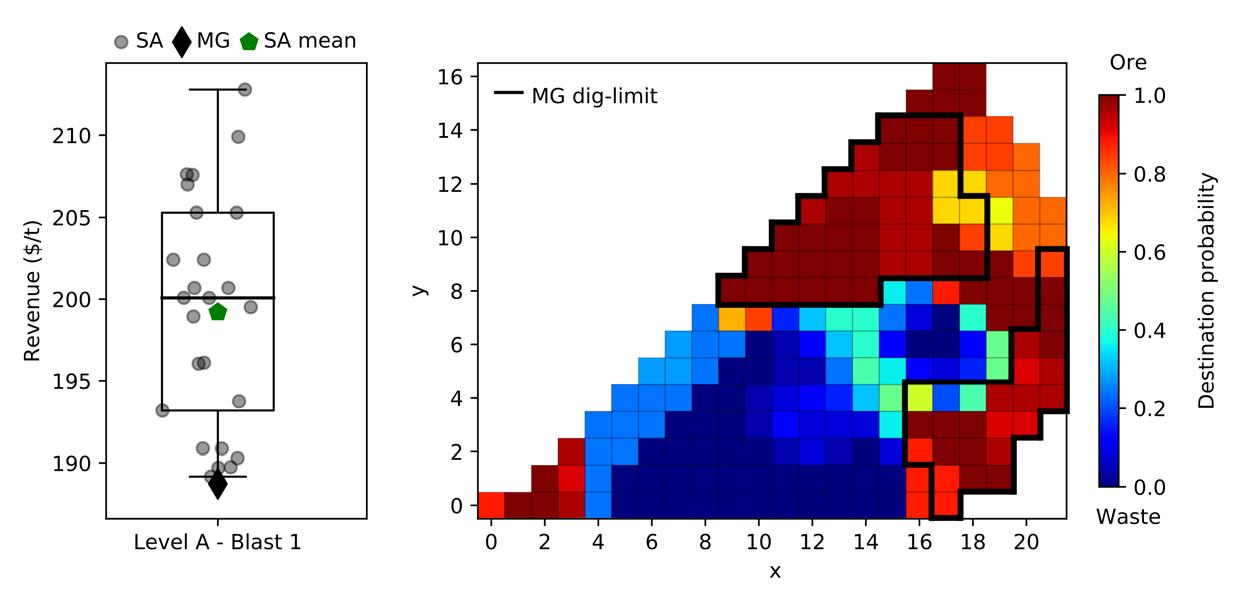
simulated annealing. As opposed to using a single result, the destination-based ensemble averages and box plots were combined as a new data-set to show these stochastic influences. A sequential manual decision could directly incorporate this stochasticity into a final dig limit design. The destination-based ensemble average approach can also be used for dig limit results derived from GA or CNN approaches. These algorithms also provide near-optimal solutions, and running them multiple times will similarly give a distribution of opportunity values and designs for the dig limit. However, these approaches require a large population of solutions, for all of which the objective value needs to be evaluated. This makes SA easier to implement and less computationally intensive. The approach would not work for MIP because this will always give the same optimal solution if the problem is feasible. The computation time of the algorithm is also much longer than SA, GA, or CNN and likely not practical for real mining operations.

Normally, uncertainty in grade control is due to unknown (or interpolated) grades and to-be-included mining constraints. For example, for the areas with much uncertainty, the final (manual) destination decisions can be made by knowing what the impact of the decision will be. This way, for example, it is possible that a single high-grade pocket in a waste area is still classified as ore because there is confidence that the ore will pay for the waste material. Additionally, the blast design’s best practice includes locating the blast boundaries at pre-indicated ore and waste boundaries. The result of this is that the material at the boundary could be assigned to different material classes (due to a grade gradient) and may be indicated as an uncertain region. With human interaction, it is possible to give a final correct classification due to the acquired knowledge while being confident in the decision due to the optimizer.

Some of the conclusions in this research were made based on the revenue, while the optimization was done regarding the objective value. This is because the objective value was mainly considered to facilitate the induced mining constraints, whereas revenue is often the more important factor in the dig limit design for a mine. A balanced mix (adapting the penalty weights) of these two useful insights will improve the grade control procedures.

This study used non-interpolated grade control models and destination ensemble averages to analyse the stochasticity of grade control. The geostatistical interpolation method in similar studies is often not mentioned (Ruiseco, 2016; Sari and Kumral, 2017), and the studies that do mention the method use simulation and kriging (Richmond and Beasley, 2004; Vasylchuk and Deutsch, 2019). Moreover, these studies often do not discuss the stochastic effects and their impact on the methodology used. This research was not focused on giving attention to the stochastic or metaheuristic behaviour of the SA algorithm itself. Induced stochastic effects by dig limit optimization and SA (Deutsch, 1992; Gu, 2008) could be considered in further studies.

Conclusions

A simulated annealing (SA) algorithm for dig limit optimization has been presented and tested on ten blasts on two mining benches. The aim was to investigate the stochasticity of dig limit optimization through SA. The algorithm used a blast-hole data-set which was optimized regarding the dig limit shape and revenue. This was managed by minimizing switching between ore and waste and minimizing the MMW penalty. Compliance with these constraints was achieved by the use of a frame concept. The SA

algorithm results showed that positive revenue improvements ($0-15 per ton) could be obtained. However, the results also contained solutions with substantially higher improvements because they included high revenue areas that were excluded in the manual designs. An improved grid preparing tool could potentially increase the lower limit of the improvement range. The solutions were further explored by an ensemble average destination analysis tool, which gave more insight into the dig limit design and its uncertainty. The destination probability indicated the areas with high and low destination confidence, and the box plot gave evidence for the to-be-made decision regarding the final dig limit design. Additionally, the distribution -of the solution space motivated the acceptance of the best solution so far and further analyse of it together with the destination-based ensemble average.

Future research could focus on including stochastic grades at ore-waste boundaries to accommodate the transition between ore and waste. Stochastic grades are not necessary for larger waste or ore regions since, for these regions, the destination probability and decision are straightforward.

Acknowledgements

The authors wish to acknowledge SSR Mining Inc. for their support in this study. Especially Andrew Smith and Karthik Rathman from the Marigold Mining Company are gratefully acknowledged for their insights into the case study data. Thijs Hanemaaijer is thanked for his contribution in the early stages of this research. The authors also thank Tom Wambeke for his substantial contribution during his employment at the Resource Engineering section of Delft University of Technology. Finally, the anonymous reviewers are thanked for their constructive reviews, which improved the paper.

Contributions

Jeroen van Duijvenbode programmed the algorithms, carried out the experimental work and drafted the written work. Masoud Soleymani Shishvan supervised the study, contributed by interpreting the concept and results and revised the paper.

References

Aarts, E.H.L., Korst, J.H.M., and van Laarhoven, P.J.M. 1997. Simulated annealing. Local Search in Combinatorial Optimization. Wiley-Interscience, Chichester, UK. Bakhshandeh Amnieh, H., Hakimiyan Bidgoli, M., Mokhtari, H., and Aghajani Bazzazi, A . 2019. Application of simulated annealing for optimization of blasting costs due to air overpressure constraints in open-pit mines. Journal of Mining and Environment, vol. 10. pp. 903−916. doi: 10.22044/jme.2019.8084.1675

Danish, A.A.K., Khan, A., Muhammad, K., Ahmad, W., and Salman, S. 2021. A simulated annealing based approach for open pit mine production scheduling with stockpiling option. Resources Policy, vol. 71. doi:10.1016/j. resourpol.2021.102016

Deswik. 2019. Deswik.DO - Dig optimizer. https://www.deswik.com/wp-content/ uploads/2019/07/Deswik.DO-Module-Summary.pd, [accessed 15 September 2022]

Deutsch, C.V. 1992. Annealing techniques applied to reservoir modeling and the integration of geological and engineering (well test) data. PhD thesis, Stanford University, USA.

Deutsch, C V. and Journel, A.G. 1997. GSLIB Geostatistical Software Library and User’s Guide. Oxford University Press, New York, USA.

Stochastic analysis of dig limit optimization using simulated annealing

Deutsch, M. 2017. A branch and bound algorithm for open pit grade control polygon optimization. Proceedings of the 19th Symposium on Application of Computers and Operations Research in the Mineral Industry (APCOM), State College, PA. http://matthewdeutsch.com/publications/ deutsch2017gradecontrol.pdf

Dimitrakopoulos, R . 2011. Stochastic optimization for strategic mine planning: a decade of developments. Journal of Mining Science, vol. 47. pp. 138−150. doi: 10.1134/s1062739147020018

Dimitrakopoulos, R. and Nx Godoy, M. 2014. Grade control based on economic ore/waste classification functions and stochastic simulations: examples, comparisons and applications. Mining Technology, vol. 123. pp. 90−106. doi: 10.1179/1743286314y.0000000062

Gu, X.G. 2008. The behavior of simulated annealing in stochastic optimization. Master's thesis, Iowa State University, USA.

Hanemaaijer, T. 2018. Automated dig-limit optimization through simulated annealing. Master's thesis, Delft University of Technology, the Netherlands.

Hmoud, S. and Kumral, M. 2022. Effect of blast movement uncertainty on diglimits optimization in open-pit mines. Natural Resources Research, vol. 31. pp. 163−178. doi: 10.1007/s11053-021-09998-z

Isaaks, E., Treloar, I., and Elenbaas, T. 2014. Optimum dig lines for open pit grade control. https://www.isaaks.com/files/Optimum%20Dig%20Lines%20for%20 Open%20Pit%20Grade%20Control.pdf [accessed 20 March 2018]

Jamshidi, M. and Osanloo, M. 2018. Optimizing mine production scheduling for multiple destinations of ore blocks. Bangladesh Journal of Scientific and Industrial Research, vol. 53. pp. 99−110. doi: 10.3329/bjsir.v53i2.36670

Kirkpatrick, S., Gelatt, C.D., and Vecchi, M.P. 1983. Optimization by simulated annealing. Science, vol. 220. pp. 671−680.

Kumral, M. 2013. Optimizing ore–waste discrimination and block sequencing through simulated annealing. Applied Soft Computing, vol. 13. pp. 3737−3744. doi: 10.1016/j.asoc.2013.03.005

Kumral, M. and Dowd, P. A. 2005. A simulated annealing approach to mine production scheduling. Journal of the Operational Research Society, vol. 56. pp. 922−930. doi: 10.1057/palgrave.jors.2601902

Maptek Vulcan. 2016. Vulcan geology modules - Grade control optimiser. https:// www.maptek.com/pdf/vulcan/bundles/Maptek_Vulcan_Module_Overview_ Geology.pdf [accessed 15 September 2022]

Marigold Mine. 2017. NI 43-101 technical report on the Marigold mine. SSR Mining.

Martín, J.F.D. and Sierra, J. 2009. A comparison of cooling schedules for simulated annealing. Encyclopedia of Artificial Intelligence. IGI Global, Hershey, USA.

Nelis, G., Meunier, F., and Morales, N. 2022. Column generation for mining cut definition with geometallurgical interactions. Natural Resources Research, vol. 31. pp. 131−148. doi: 10.1007/s11053-021-09976-5

Nelis, G. and Morales, N. 2021. A mathematical model for the scheduling and definition of mining cuts in short-term mine planning. Optimization and Engineering, vol. 23. pp. 233−257. doi: 10.1007/s11081-020-09580-1

Neufeld, C.T., Norrena, K.P., and Deutsch, C.V. 2003. Semi-automatic dig limit generation. Proceedings of the 5th CCG Annual Conference, Alberta, Canada. https://www.ccgalberta.com/ccgresources/report05/2003-115-diglim.pdf

Norrena, K.P. and Deutsch, C.V. 2001. Automatic determination of dig limits subject to geostatistical, economic, and equipment constraints. Proceedings of the SME Annual Conference and Exhibition, Denver, USA. pp. 113−148.

Orica. 2021. Orepro 3D - Blast movement modelling and grade control optimiser. https://www.orica.com/ArticleDocuments/2605/Orica_OrePro%203D%20 Flyer_WEB_New.pdf.aspx [accessed 15 September 2022]

Richmond, A.J. and Beasley, J.E. 2004. Financially efficient dig-line delineation incorporating equipment constraints and grade uncertainty. International Journal of Surface Mining, Reclamation and Environment, vol. 18. pp. 99−121. doi: 10.1080/13895260412331295376

Ruiseco, J.R . 2016. Dig-limit optimization in open pit mines through genetic algorithms. Master's thesis, McGill University, Canada.

Ruiseco, J.R. and Kumral, M. 2017. A practical approach to mine equipment sizing in relation to dig-limit optimization in complex orebodies: multi-rock type, multi-process, and multi-metal case. Natural Resources Research, vol. 26. pp. 23−35. doi: 10.1007/s11053-016-9301-8

Ruiseco, J.R., Williams, J., and Kumral, M. 2016. Optimizing ore-waste dig-limits as part of operational mine planning through genetic algorithms. Natural Resources Research, vol. 25. pp. 473−485. doi: 10.1007/s11053-016-9296-1

Rutenbar, R.A . 1989. Simulated annealing algorithms: an overview. IEEE Circuits and Devices Magazine, vol. 5. pp. 19−26. doi: 10.1109/101.17235

Salman, S., Khan, A., and Muhammad, K., and Glass, H.J. 2021. A block aggregation method for short-term planning of open pit mining with multiple processing destinations. Minerals, vol. 11. doi: 10.3390/min11030288

Sari, Y.A. and Kumral, M. 2017. Dig-limits optimization through mixed-integer linear programming in open-pit mines. Journal of the Operational Research Society, vol. 69. pp. 171−182. doi: 10.1057/s41274-017-0201-z

Tabesh, M. and Askari-Nasab, H. 2011. Two-stage clustering algorithm for block aggregation in open pit mines. Mining Technology, vol. 120. pp. 158-169. doi: 10.1179/1743286311y.0000000009

Vasylchuk, Y.V. and Deutsch, C.V. 2019. Optimization of surface mining dig limits with a practical heuristic algorithm. Mining, Metallurgy & Exploration, vol. 36. pp. 773−784. doi: 10.1007/s42461-019-0072-8

Verly, G. 2005. Grade control classification of ore and waste: a critical review of estimation and simulation based procedures. Mathematical Geology, vol. 37. pp. 451−475. doi: 10.1007/s11004-005-6660-9

Villalba Matamoros, M.E. and Kumral, M. 2018. Calibration of genetic algorithm parameters for mining-related optimization problems. Natural Resources Research, vol. 28. pp. 443−456. doi: 10.1007/s11053-018-9395-2

Wilde, B.J. and Deutsch, C.V. 2007. Feasibility grade control (FGC): Simulation of grade control on geostatistical realizations. Proceedings of the 9th CCG Annual Conference, Alberta, Canada. https://ccg-server.engineering.ualberta. ca/CCG%20Publications/CCG%20Annual%20Reports/Report%209%20-%20 2007/301%20Feasibility%20Grade%20Control.pdf

Williams, J., Singh, J., Kumral, M., and Ramirez Ruiseco, J. 2021. Exploring deep learning for dig-limit optimization in open-pit mines. Natural Resources Research, vol. 30. pp. 2085−2101. doi: 10.1007/s11053-021-09864-y u

The Journal of the Southern African Institute of Mining and Metallurgy

Affiliation:

1Dynamic Physics Consultant, Johannesburg, South Africa.

2AECI Mining Explosives, Johannesburg, South Africa.

Correspondence to: T. Szendrei

Email: szendrei@icon.co.za

Dates: Received: 26 Oct. 2021 Revised: 3 Mar. 2022 Accepted: 2 Nov. 2022 Published: December 2022

How to cite: Szendrei, T. and Tose, S. 2022

Flyrock in surface mining –Limitations of current predictive models and a better alterative through modelling the aerodynamics of flyrock trajectory.

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 725–732

DOI ID: http://dx.doi.org/10.17159/24119717/1873/2022

ORCID: T. Szendrei https://orcid.org/0000-00025693-7850

S. Tose https://orcid.org/0000-00022514-5308

Flyrock in surface mining – Limitations of current predictive models and a better alterative through modelling the aerodynamics of flyrock trajectory

by T. Szendrei1 and S. Tose2

Synopsis

Historical approaches to the problem of flyrock based on correlation studies and regression analysis, including artificial neural networks and similar techniques, are inherently incapable of addressing two core issues – root causes of flyrock and projection velocity. A further shortcoming of correlation techniques is that they give no information on the influence of rock size and shape on the flight distance. The scaled depth of burial model for crater blasting in the collar zone and bench face does not specifically address the question of flyrock velocity. A third approach, based on flight trajectory calculations, often neglects the very significant effects of air resistance on the trajectory. Some trajectory models incorporate air resistance but use an implausible fragment velocity model that cannot propel sizeable rocks to distances much beyond 150 m.

Nonetheless, trajectory calculation incorporating the effects of air drag affords the most promising approach to the prediction of flyrock range. A unique and insightful feature of the proposed realistic flight modelling is that it collapses all suspected causes of flyrock, many of which are not well understood, to just a single parameter – the launch velocity. This indicates that the root causes of flyrock lie in the mechanisms of momentum transfer to broken rock and suggests new avenues of study.

Keywords

flyrock, flyrock velocity, throw distance, scaled depth of burial, airblast, trajectory, air drag.

Introduction

In comparison to the propagation and attenuation of ground and airborne vibrations, flyrock is a much less well understood phenomenon. Yet flyrock is often considered to be the most hazardous of the adverse effects of rock blasting in surface mines and construction works. It can damage machinery, property, and industrial structures, as well as cause serious injuries at distances where ground and air vibrations are not significant.

Following Little (2007), three types of flyrock can be recognized in mining works based on bench blasting:

➤ Burden throw – blast-driven movement of broken rock to form the muckpile, which generally does not extend to more than ten bench heights and falls within the blast zone

➤ Normal flyrock – the propulsion of rock beyond the blast zone but falling within the exclusion or clearance zone.

➤ Wild flyrock – rock fragments propelled outside the clearance zone, often onto private and public areas. A particularly troublesome aspect of wild flyrock is that large fragments can be thrown unexpected distances. For example, Stojadinovic, Pantovic, and Zikic (2011) noted a sizeable rock punching a hole through the brick wall of a double-storey residence located 360 m from the bench. Lundborg (1981) published a photograph of a 3 t boulder that landed 300 m from and 40 m above its source. There have been scattered reports in mining literature of flyrocks thrown up to 1000 m. Many attempts have been made to understand the generation of flyrock and predict its throw distance. In this study we review various historical methods of understanding the flyrock problem, point out their shortcomings, and propose a new way of looking at the problem. Although the concept – trajectory modelling – is not new, its full potential has not been explored in mining literature. Often, it has been simplified to a kinematic (drag-free) approach, or coupled to a defective model of flyrock velocity, resulting in erroneous predictions of maximum range. We demonstrate through calculations how the trajectory approach can deliver useful answers to a range of questions frequently encountered in the field, and point out that it opens a new avenue for the study of the root causes of flyrock.

Flyrock in surface mining – Limitations of current predictive models

Literature overview of flyrock models

Historical correlation studies

Historically, empirical correlations led to predictions of flyrock throw based on readily available blast parameters, such as burden, stemming depth, quantity of charge, and blast-hole diameter (Adhikari, 1999; Aghajani-Bazzazi, Osanloo, and Azimi, 2010).

In recent years, empirical correlations have greatly increased in complexity through the use of multiple regression analysis (Ghasemi, Sari, and Ataei 2012) and RSA (response surface analysis), which is the analysis of variance or ANOVA (Raina and Murthy, 2016a). Artificial intelligence (AI) has been increasingly applied in the form of artificial neural networks (ANNs) and fuzzy logic (Tivedi et al., 2014). Such routines have been used with up to 21 parameters describing the blast and to some degree, the properties of the rock mass to be blasted (Raina and Murthy, 2016b). The independent parameters may be combined in linear arrays, or raised to various powers, or included in various mathematical functions such as logarithms and exponentials.

This increased sophistication of statistical algorithms has not resulted in any better understanding of the problem of flyrock. Empirical correlations, however precise, contain certain inherent limitations as indicated below.

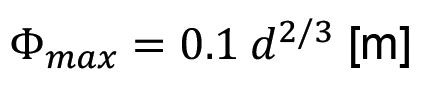
A distinct disadvantage is that predictions of range require a large amount of field data, including measured values of throw distance, before a correlation can be found. A second disadvantage is that the predicted throw distance is site-specific and cannot be used to predict throw distances under any other conditions of blasting. As for multiple regression and neural network analyses, other than indicating the relative importance (sensitivities) of burden, stemming, and some other parameters under site-specific blasting conditions, these techniques do not offer practical guidance for adjusting and controlling the blast plan. The authors of such studies themselves point out that their elaborate predictive equations for flyrock range cannot be applied at mines other than those where they gathered their input data.

The greatest inherent deficiency of empirical correlations is that they do not identify the root causes of flyrock, nor the physical mechanisms resulting in flyrock projection from the bench. A further distinct disadvantage is that correlation equations do not provide any information on the size of rocks being thrown or on the influence of size on the distance travelled. Studies that considered the sizes of projected rocks were done in the context of ballistic flight modelling, as discussed below. It is well known that air drag is a significant factor in calculating the range of various projectiles from bullets to volcanic ejecta and debris thrown out in surface explosions. It is unlikely that any model of flyrock projection that does not consider one of the most important determinants of the distance travelled – air resistance, and hence rock shape and size – can provide reliable estimates of flyrock range.

Lundborg model of flyrock throw

In two often-cited studies Lundborg presented a new method for predicting flyrock range (Lundborg, 1974; Lundborg et al., 1975). The Lundborg model has gained wide recognition because it combined measurements of flyrock throw distance and blasthole diameter with some theoretical considerations of explosion blast impulse and momentum transfer to rocks, together with the use of a realistic trajectory model incorporating air drag. In essence, the Lunborg model derives rock velocities based on the

transfer of impulse from the blast wave to a rock fragment. An empirical correlation is used to define the maximum velocity thus imparted to rocks of various sizes (diameters). A more detailed analysis of the Lundborg impulse-rock velocity model is given in the Appendix. The work of Lundborg et al. (1975) is encapsulated in a family of graphs depicting the variation of range with rock size. Together with these graphs, Lundborg defined the maximum range L max attainable for a given borehole diameter d:

[1]

These maxima are attained at a stone size specific to each hole diameter:

[2]

where L max is the maximum range in metres at hole diameter d inches, and Φ max is the ‘optimal’ rock size in metres at which the maximum range is attained. These equations are not based on independent field observations, but are based directly on the coordinates of maximum points in the calculated trajectories. These trajectories were calculated with launch velocities (m/s) assigned by the following equation:

[3]

In this equation, the borehole diameter ‘dhole’ is in inches. ρ is rock density normalized to granite, and j is rock diameter in metres. The factor 10 is an empirically-based upper bound. Although acknowledged as a comprehensive approach to the problem of flyrock throw, Lundborg’s model has been questioned in the engineering literature for being overly conservative. In fact, it should be noted that the predictions of range according Equations [1-3] and the accompanying graphs are applicable only under some explicit and implicit assumptions. These are: ➤ Predicted throw distances are applicable only to spherically shaped fragments of a very specific size given by Equation [2] pertaining to each hole diameter ➤ For the same mass, other rock shapes would yield significantly less throw distance at the same velocity for the reason that a sphere has the least surface area per unit mass. Thus for flyrock of the same mass, all non-spherical shapes would expose larger surface areas to drag forces and suffer greater deceleration in flight. (An example of this is shown in Figure 1 where a 19% reduction in range is calculated on changing the flyrock shape from spherical to slab-like ➤ Predictions of L max for all rock sizes, j, are ultimately based on velocities defined by Equation [3]. This equation is a direct consequence of an airblast momentum model that Lundborg created in 1974. When updated to reflected current knowledge of blast wave properties, the model yields significantly lower estimates of flyrock velocity than the original model and hence significantly shorter flight distances. The updates to the model relate to the calculation of blast wave impulse acting on rocks in the vicinity of an explosive charge. The details of this re-analysis are given in the Appendix.

A number of other – and simpler – models have been proposed by various authors for the prediction of flyrock throw distance.

Kinematic calculations of throw distance

Various workers have attempted to estimate flyrock projection range using simpler kinematic equations to describe the trajectory

The Journal of the Southern African Institute of Mining and Metallurgy

Flyrock in surface mining – Limitations of current predictive models

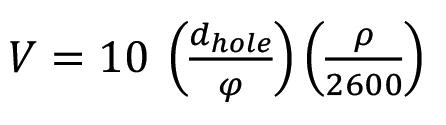
(Roth, 1979; Chiapetta et al., 1983; Workman and Calder, 1994; Richards and Moore, 2005). The kinematic approach considers the motion of a point mass in free flight under the influence of gravity only. Hence it does not consider drag forces and because of this, the shapes and sizes of flyrocks and their masses have no influence on the predicted trajectory path. This is made evident by the kinematic equation for the maximum range, which can be formulated simply as:

[4]

where V o is the projection velocity (m/s) at 45° to the horizontal for maximum range and g the gravitational constant (9.84 m/s²). Clearly, for a given velocity, all rock shapes and sizes are predicted to travel the same distance. It has been argued that the kinematic approach is acceptable since the effects of drag forces are not significant at ‘typical’ flyrock velocities, perhaps even up to the sonic limit (approx. 340 m/s).

This view is mistaken. McKenzie (2009) showed that the difference between the predictions of a drag-free model of a point mass and a realistic model for flyrock possessing a particular shape, surface area, and mass can be a factor of 2 to 5. He considered 50 mm and 250 mm rocks with initial velocities of 70 m/s. At velocities of 100 m/s and above, the discrepancy between kinematic and realistic trajectory distances would become progressively larger.

More recently, Stojadinovic and co-workers (2011, 2013, 2016) attempted to apply drag-inclusive trajectory calculations to the interpretation of a serious flyrock incident at a quarry. These attempts ultimately foundered on two issues – the uncertainty of what drag coefficient to use coupled with the inability to measure it, and the inability to measure launch velocity and the lack of a credible universally applicable predictive model for it.

Various workers have attempted to produce field-calibrated, empirical formulae for predicting throw velocity based on the concept that the velocity is related to confinement conditions, specifically the scaled burden, as described by Workman and Calder (1994), Bauer, Burchell, and Crosby (1982), and St George and Gibson (2001). Defining the ‘scaled burden’ as the burden (or length of stemming) divided by the square root of the explosive weight per metre in a fully coupled hole, Richards and Moore (2002) presented a power-law equation for ejection velocities from the face and from bench-top cratering. The calibration constant in their equation depends on rock strength and specific energy of the charge.

Similarly to Richards and Moore (2002), Chiapetta (2009) found a power law relationship between face velocity and the burden scaled by the charge/mass per unit length, albeit with somewhat different constants for the power law formula. His analysis was based on high-speed cinematography of face movement from large diameter boreholes in dolomite, granite, and iron ore.

The scaled burden (and stemming) approach appears to have been replaced by the scaled depth of burial concept discussed in the following section.

St George and Gibson (2001) and Raina, Murthy, and Soni (2015) attempted to calculate rock velocity from the explosion pressure and its duration of action on rocks, either in the borehole or through the burden respectively. The borehole pressure is not a well-defined concept for commercial blasting agents (Cunningham, 2006) and it is not the appropriate parameter for calculating the external effects of a borehole explosion. The

chemical energy of an explosion resides in the high-temperature and high-pressure gases in the borehole prior to any movement of the rock. The conversion of this energy to work on the external environment can be modelled by the well-known concept of Gurney energy. Attempts to link flyrock velocities, particularly those characterizing normal and wild flyrock, to pressure (or more accurately, stress) pulses propagating through the rock mass can be considered very speculative. Similarly, Roth (1979) attempted to relate flyrock velocity to the ratio of charge mass to rock mass when averaged over the whole bench face. This again neglects the influence that the quality of rock mass as well as the presence of localized under- and overburdened areas in the face may have on the generation of flyrock.

Scaled depth of burial model (SDOB)

McKenzie (2009) presented a detailed model for calculating the velocity and range of non-spherical flyrock on the basis of the scaled depth of burial approach that considers flyrock from the collar zone and from the bench face as examples of crater blasting. The scaling factor is the cube root of the explosive weight.

Numerous studies in the areas of military ballistics and civil engineering have shown that cube-root scaling is appropriate for estimating all linear features of buried explosions, such as crater diameter, depth, extent of mounding, and range of debris throw.

In a comprehensive review of post-2011 flyrock literature, van der Walt and Spite-ri (2020) deemed the scaled depth of burial approach to be currently the most effective model for estimating the throw distance. McKenzie’s equations are reproduced in the ISEE Blasters’ Handbook 2011 and used to calculate range and safety distances. Van der Walt and Spiteri (2020) argued that all methods of flyrock analysis could be improved by using an objective and scientific method for the accurate measurements of flyrock distances.

McKenzie (2018) presented a comparison of surveyed flyrock (range and size) with his SDOB model by overlaying the field observations with the calculated ‘footprint’ of range versus flyrock size calculated at the appropriate SDOB for each blast. The measured values are considerably less than those calculated. They are on average 4.8-fold less and vary from 1.4 to 10. More importantly, the absolute maximum measured range – which is more relevant to flyrock prediction – was 56% of predicted values.

Seeing that McKenzie (2018) calculated flyrock range using a ballistics model that incorporated air drag, the error is clearly associated with the calculated velocity values. This is not surprising. McKenzie (2009) based his model on Lundborg’s velocity values. At a SDOB equal to 0.596 m/kg¹/³ (which is considered by McKenzie to be the equivalent to ‘normal’ bench blasting), the combinations of rock sizes and rock velocities predicted by the McKenzie (2009) model are exactly the same as those predicted by Lundborg. Since those values are questionable for reasons already pointed out, McKenzie’s predictions of projection velocity and the resultant range are also questionable.

Chiapetta (2009) used the concept of cube-root scaled depth of burial to address the problem of collar zone oversize through the design of appropriate column lengths and weights of charges for top stemming, stem charges, stab charges, air decks, and decoupled charges. Appropriate values are those that yield a scaled depth between 0.4 m/kg¹/³ and 1.2 m/kg¹/³. The application of this model to flyrock is incidental. Other than pointing out the likely occurrence of severe flyrock (and airblast) at <0.4 m/kg¹/³ and its absence at >1.2 m/kg¹/³, the model does not make specific predictions of flyrock velocity.

Flyrock in surface mining – Limitations of current predictive models

It is evident that there is no proven and reliable method for predicting flyrock velocity and throw range. The generally accepted methods of Lundborg and Mackenzie for calculating flyrock velocity can be shown to be defective, and hence their throw distance predictions are also unreliable and err on the side of being too conservative when setting safety distances.

Trajectory models incorporating air resistance

Both problematic aspects of flyrock modelling – prediction of velocity and range based on first principles – become far more tractable to quantitative analysis when considered in reverse. Instead of trying to analyse all the multiple blast-related factors that influence flyrock projection from the bench – many of which are not well understood or are difficult to quantify – it is easier to analyse the flight of the flyrock to its eventual landing point. A great deal of simplification arises because the details of the blast and the rock mass blasted have an influence on the range only to the degree that those details contribute to the projection velocity of flyrock.

Once airborne, a flyrock is free of any further influence from the blast and travels a ballistic trajectory determined by the equations of motion (EOM) for free bodies moving under the influence of gravity and air resistance. The solutions of these equations are well known and have been reported in technical literature by, for example, Chernigovskii (1985), Stojadinovic, Pantovic, and Zikic (2011), and Saunderson (2008).

The particular algorithm that we use for trajectory calculations in this study is based on the following formulation of the EOM. The two aerodynamic forces acting on a flyrock are the force of gravity Mg (M being flyrock mass and g the gravitational acceleration), and the force of air resistance (FD), which is defined by the following equation:

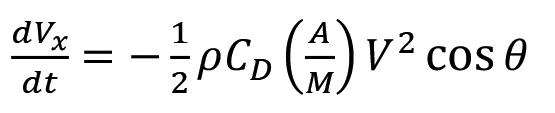
[5]

where CD denotes the drag constant, ρ the density of air, V is the instantaneous velocity, and A the presented area of the flyrock. A is always measured in the plane perpendicular to the direction of flight. By Newton’s Second Law, the resultant of the two aeroballistic forces changes the momentum of the flyrock both in direction and in magnitude. The time (t) rate of this change can be expressed as follows:

[6] [7]

where (x,y) denote the horizontal and vertical directions respectively. θ is the angle above the horizontal defined by the direction of the instantaneous velocity V; initial values (at t = 0) are V o and θo.

Equations [6] and [7] are coupled, nonlinear differential equations that cannot be solved explicitly. It is not possible to derive the solution as an algebraic expression that links the flyrock distance to the input parameters. The equations must be solved by numerical methods that trace the ballistic path of the flyrock in small increments of time. Even in the absence of a detailed numerical solution, some features of the ballistic path can be deduced from the rate equations.

1. Calculation of the maximum travel distance requires only six parameters: ρ, CD, A, M, V o, and θo

2. The deceleration in both x- and y-directions is proportional to the ratio of flyrock surface area to its mass (A/M). This identifies the important effect that rock shape has on the throw distance – the higher the area per unit mass the greater the drag force on all rocks of the same mass.

3. Flyrock shape also defines the applicable drag constant. CD is a dimensionless number that depends solely on shape – it is insignificantly affected by atmospheric conditions (temperature, pressure, precipitation, wind) as well as the velocity of the flyrock (up to the sonic limit).

The six parameters that are required for the calculation of flyrock range are discussed and plausible values for them are identified below.

Air density: The density of air at standard temperature and pressure (1.24 kg/m³) can readily be adjusted to the ambient conditions at the blast site.

Presented area: For regular shapes such as spheres, cubes, rods. slabs, plates, and discs the surface areas are readily calculated. The surface areas of irregular fragments produced by blasting have been considered in the technical literature, e.g. Chernigovskii (1985), McCleskey (1988), Kljuna and Catovic (2019). The rectangular parallelepipedic shape is an acceptable approximation for the calculation of the surface areas of such fragments. Fragment mass is related to the surface areas by the shape factor (SF). This factor is the ratio of the surface area averaged over all orientations of an irregular fragment of a given mass to the presented area of a sphere of equal mass.

For spheres, SF equals 1.00; for compact shapes it is 1.1–1.25; 1.34 for short slabs and about 2.0 for long, slender shapes.

Drag coefficient: Typical values are listed in Kinney and Graham (1995) and NASA (2021). The following general values are relevant to flyrock analysis: rough spheres 0.5–0.8; compact shapes about 1.0; structural shapes (flat and round bar, plate, angles, and channels) 1.2–1.8; large ungainly shapes 1.8–2.5. A key point to note is that drag coefficients that are likely to occur in flyrock analysis cover a relatively small range from about 0.6 to 1.8.

Velocity: Indicative flyrock velocities are listed in Table I and cover the range from about 10 m/s to greater than 100 m/s. In running a trajectory model it is convenient to consider flyrock velocity as a free parameter and derive predictions of flyrock distances for a range of velocities, thereby establishing the link between velocity, mass, and range.

The use of high-speed cameras, with frame rates >1000 frames per second, is well established in the blasting environment for assessing such factors as initiation system timing and face movement. Placing an object of known size and/or surveying the face coupled to a known frame rate of the high-speed camera enables an object to be tracked, the distance measured, and velocity to be calculated. Table I illustrates a range of values measured during blast monitoring conducted by AECI Mining Explosives in many different mining and blasting applications.

Launch angle: Flyrock analyses are generally made to establish the upper limit to expected throw distances. In vacuum, maximum range occurs at 45° launch angle; in air, the maximum is attained at 30° to 60°. Launch angle is not an important determinant of the range of a given mass of flyrock – at any given velocity, maximum range changes less than 10% over a broad range of angles.

Three worked examples are given below with calculations of ballistic trajectories to illustrate the potential uses of the

The Journal of the Southern African Institute of Mining and Metallurgy

Flyrock in surface mining – Limitations of current predictive models

Table I

Blasted rock velocities

Burden throw velocity

5–25 m/s

Normal flyrock 30-50 m/s

Excessive flyrock 50–70 m/s

Falls within blast zone

Falls within exclusion zone

Falls outside exclusions zone

Wild flyrock 100 m/s and above Range up to 500 m or more

trajectory model. The first is the analysis of the distance of throw of the optimal-sized rock from a 5-inch (127 mm) blast-hole (Lundborg et al., 1975) calculated with a more realistic, nonspherical rock shape. The second example examines the variation of throw distance with rock size for a range of velocities and determines the screening effect of air resistance on the range attained by different sizes of rock. The third example examines he effect of flyrock velocity on throw distance in the presence of air drag.

Trajectory calculations

Example 1. Effect of rock shape on range

The ballistic properties of the optimal-sized fragment from a 5-inch. (127 mm) blast-hole as defined by Lundborg’s equations (Equations [1-3]) are:

Shape factor 1.00 Diameter 293 mm

Presented area 0.0674 m² Mass 34.243 kg

Velocity 170.6 m/s

Maximum range 761 m

It should be noted that in the Lunborg model flyrock mass and presented area are calculated from the diameter of ball-shaped rocks. The range of the above optimal rock size as a function of velocity calculated with the air-drag trajectory model as described above in Equations [1–3] is shown in Figure 1 as curve A (spherical rock).

It is seen that the calculated range for spherical rocks is very close to 760 m, as predicted by Equation [1]. It is reached at a launch velocity of about 171 m/s, as predicted by Equation [3]. When the shape factor is changed from 1.0 to 1.34 to reflect a non-spheroidal shape – a parallelepiped fragment with side ratios of 1.6:1.0:0.6 – the trajectory calculations yield curve B. The range attained with this shape at 170 m/s is less than the predicted value by Equation [1], being 618 m in place of 760 m. The velocity

required to attain the predicted range of 761 m increases from 170 m/s to 250 m/s. Both effects can be understood as resulting from the larger presented area of the flyrock compared to a ball shape (of equal mass), and the larger drag force acting on it.

The above example illustrates that the Lundborg family of graphs should not be used for any fragment shape other than spheroidal. In the example, the substitution of a more realistic shape for the optimal fragment size resulted in a decrease of the range by 19% and an increase of 46% in the velocity required to attain the maximum range predicted by the Lundborg equation (Equation [1]). This decrease in range was obtained with an increase of the shape factor from 1.00 (ball) to 1.34 (parallelepipedic). Similar effects would be obtained for any other choice of fragment shape, since in all cases the shape factor would be larger than 1.00.

In conclusion, it is not an acceptable approximation to substitute some representative flyrock size, such as the average length, for the diameter of a ball shape and assume the equivalence of that length with the diameter of a sphere in order to predict the range using the Lundborg curves.

Example 2. Effect of rock mass on throw distance

Figure 2 presents the results for the maximum range attained with rocks from 0.1 kg to 50 kg and shape factor 1.34. Launch velocities from 15 m/s to 250 m/s are considered, which probably covers the full range of velocities encountered in bench blasting operations. To generate Figure 2, the trajectory algorithm was run in parametric mode: at each given rock mass, and the velocity was varied over its full range of values. Each data-point in Figure 2 is the result of one run.

By inspection, it is evident that at a given velocity, the throw distances increase monotonically with fragment mass. In the range of mass and velocity values investigated, there is no optimum fragment size which attains the farthest throw distance.

The upper curve labelled 250 m/s traces the throw distance that cannot be exceeded with the range of rock masses and

Figure 1—Trajectory calculations with air drag for spherical (A) and non-spherical rock (B) of mass 34.2 kg compared to Lundborg’s predicted range

Flyrock in surface mining – Limitations of current predictive models

➤ Rock throw in excess of 500 m requires large stones (>50 kg) at velocities of at least about 100 m/s, or velocities higher than 200 m/s for stones larger than 10 kg.

Figure 3 offers an explanation for a common observation that wild flyrock is often associated with surprisingly heavy rocks. At the highest flyrock velocity assumed in this study (250 m/s), only rocks larger than about 7 kg can attain distances exceeding 500 m. With the information encapsulated in Figures 1, 2, and 3, and even in the absence of an accurate predictive model for velocity, trajectory calculations made by numerically solving the flyrock equations of motion can already to a large extent provide useful answers to many of the questions a flyrock model should be able to address, such as:

➤ Give realistic estimates of expected maximum throw distances, incorporating the effects of rock size, and help to establish appropriate exclusion and other safety zones.

1.34

Figure 3—Flyrock range as a function of projection velocity with rock mass as parameter and shape factor of 1.34

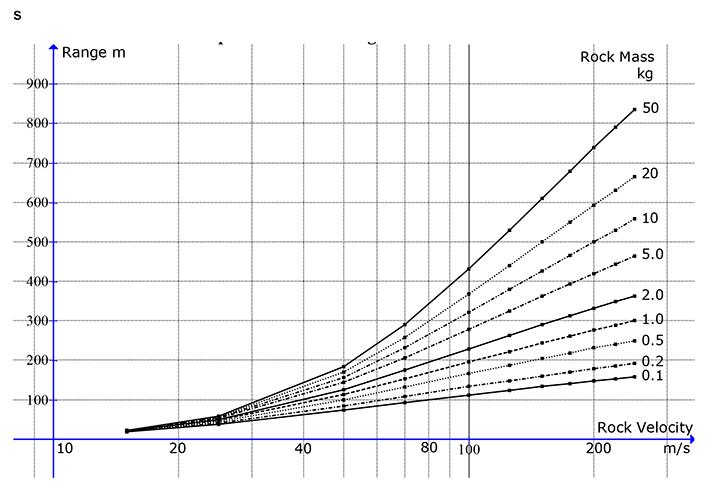
velocities listed in Figure 2. Some general trends are evident.

Rocks under 1 kg all fall to the ground within 300 m; 0.5 kg rocks within 250 m, and 0.2 kg rocks within 200 m. Conversely, distances exceeding 500 m can be attained only by rocks larger than about 6 or 7 kg. Distances of 700–800 m would require rocks larger than 25 kg and possessing velocities higher than 225 m/s.

Example 3. Effect of velocity on throw distance

Figure 3 examines the effect of projection velocity from 15 m/s to 250 m/s on the throw distance for rock sizes from 0.1 kg to 50 kg. Again, the trajectory model was run in parametric mode, where for each selected velocity the rock mass was varied from 0.1 kg to 50 kg.

Some notable features of Figure 3 are:

➤ Under 50 m/s, throw distances increase relatively slowly with velocity and all sizes of rock are spread in a tight group: 5 m wide at 15 m/s, 20 m at 25 m/s, and 100 m at 50 m/s.

➤ Above 50 m/s, the spread of distances fans out as the range difference between low and high rock masses becomes increasingly divergent with increasing velocity.

➤ Under 30 m/s, all sizes of rock are contained within 100 m; within 200 m at 50 m/s, 300 m at 70 m/s; 500 m at 115 m/s, and within 700 m at 180 m/s.

➤ Indicate control measures and restrictions to be imposed on the blast in order to restrict flyrock thrown in the vicinity of vulnerable infrastructure and public areas.

➤ Yield reliable estimates of the influence of rock mass and rock velocity on maximum range and determine the screening effect of air on the dispersion of various sized rocks.

➤ Forensic analysis of flyrock incidents where detailed knowledge of the trajectory would assist in understanding the source of the flyrock. Such details would include the effect of an elevation change between source and landing point, terminal velocity, angle of fall, and rock sizes that are capable of reaching the location of the observed damage. Numerical calculations of trajectories would also yield values for terminal momentum and energy at impact, both of which are useful for assessing the observed damage.

Flyrock projection velocity and sources of momentum

The unrealistic blasting conditions required to propel rocks to velocities of the order of 100 m/s, as derived in the Appendix, suggest that the blast wave propagating through air is not an efficient mechanism for the transfer of momentum to external objects. Yet sizeable rocks have been observed falling 500–600 m from the bench, which would require launch velocities well in excess of 100 m/s, as shown by trajectory calculations in example 3 above. Clearly, short-duration pressure pulses in air cannot be the only, or perhaps even the primary, mechanism for flyrock projection.

The modelling of rock flight ballistics has indicted that significant sources of flyrock projection are those that provide a mechanism for the transfer of momentum, and hence velocity, to rock. It is generally acknowledged that rock fragmentation and throw occur through the combined influence of stress wave action and gas pressure action. While it is possible to conceptualize rock throw along these lines, the details of mechanisms that allow for the transfer of momentum to rock have not been established and will form the subject of further studies by the authors.

Conclusions

➤ A historical review has been given of flyrock prediction models in three broad categories: correlation studies and regression analyses using artificial neural networks (ANNs) and similar approaches; scaled burden and scaled depth of burial; and trajectory calculations with and without air resistance.

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 2—Flyrock range as a function of rock mass with shape factor of

Flyrock in surface mining – Limitations of current predictive models

➤ An inherent deficiency of correlation and regression studies is that they do not address the root causes of flyrock nor the physical mechanisms resulting in its projection. Furthermore, without knowing how long-range flyrock can be generated, it is unlikely that its occurrence can be prevented or at least largely suppressed.

➤ Trajectory calculations without taking air drag into account are highly deficient in two respects. They do not consider the influence of rock shape and size on the range and they overestimate the range by factors of 2 to 8.

➤ The predictions of the Lundborg et al. (1975) model for maximum throw distance are applicable only to ballshaped rock fragments and are underpinned by a model of momentum transfer to rocks that is not supported by present-day knowledge of the properties of blast waves. It is concluded that the Lundborg model significantly overestimates the expected range.

➤ The McKenzie (2009) model of flyrock projection based on the scaled epth of burial appears to have replaced previous correlation approaches based on scaled burden. McKenzie calibrated the velocity calculations of his model against the Lunborg values and this renders his predictions of range based on rock velocity and shape questionable.

➤ The results presented in this study affirm that trajectory calculation incorporating air drag affords the most insightful approach to the analysis of flyrock. It permits the formulation of a scientifically sound, quantitative physical model for the prediction of throw distance, and reduces all the multiple (and often little understood) causes of flyrock generation to a single parameter – the launch velocity.

➤ It has been pointed out that even without a proven and generally applicable velocity model, trajectory calculations can yield useful information in a number of important areas of flyrock analysis, such as realistic estimates of maximum range, appropriate safety distances, degree of control required to limit the range of flyrock in the vicinity of public areas and infrastructure, and investigations of flyrock incidents.

➤ Analysis of the transfer of momentum to rocks (see Appendix) suggests that the pressure impulse of a blast wave is not the primary cause of flyrock propulsion. It is proposed that alternative sources of flyrock velocity reside in the action of stress waves and gas pressure on broken rock. Future work in flyrock generation and projection should focus on elucidating the mechanisms that mediate the transfer of momentum from these sources to rock.

Appendix

A re-examination of Lundborg’s blast impulse rock velocity model

The mechanism proposed by Lundborg et al. (1975) for the transfer of momentum to rocks is based on considerations of a quantity of charge W (kg) surrounded by a number of loose rocks and exposed to the blast wave spreading away from the borehole after detonation of the charge. A blast wave from a single, concentrated source is a steep-fronted, short-duration pressure pulse travelling at supersonic speed in the ambient atmosphere. The interaction between the blast wave and rocks can be modelled through the concept of blast wave impulse by the following equation:

[8]

where I s is the specific impulse of the blast wave (per unit area of the wave front) with units of Pa-s A r is the surface area of a rock exposed to the blast wave, M r its mass, and V r is the velocity that the rock acquires impulsively. The physical significance of impulse intensity in flyrock modelling is that it is a measure of the force per unit area exerted on a surface by the pressure pulse of the blast wave.

The properties of blast waves have been well studied, in particular, the impulse intensity as it is directly connected to the damage causing capacity of airblast. Charts and tabulations of specific impulse intensity may be found in various sources, e.g. Baker (1973), Kinney and Graham (1995), Smith and Hetherington (1994), and Held (1983). A distinction must be made between incident and reflected pressure waves and the corresponding incident and reflected impulse values.

The specific impulse of a blast wave at a distance R (m) from a charge W (kg) can be written as a functional relationship: [9]

where Z is the scaled distance R W1/3 and f is a function of the scaled distance such that for each value of Z, it yields the corresponding value of scaled impulse I s. The shape of this function must be determined empirically. In many applications, and over a limited range, it can be adequately represented by a power law equation.

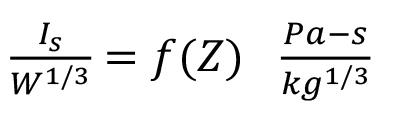
Equation [9] can be applied to derive the blast wave impulse acting on the optimal-sized flyrock from a 5-inch hole (127 mm) in order to propel it to Lundborg’s predicted velocity. The properties of this optimal rock are listed above under example 1. The properties required to evaluate momentum transfer are the mass (34.2 kg), velocity (170.6 m/s), and the surface area A r

Substituting Equation [8] for I s in Equation [9], the impulse momentum-equation becomes:

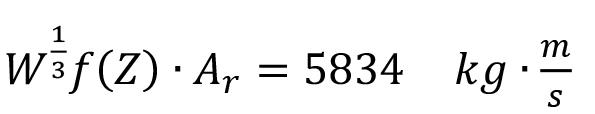
since A r = 0.0674 m2

[10]

Equation [10] defines the charge mass W (as W1/3) required to project the 5-inch hole, optimum-sized rock to a velocity of 170.6 m/s, at which it is predicted to attain its maximum range. Charge quantities required to achieve this at various scaled distances from the charge are listed in Table II.

The values of charge mass listed in Table II (and considered to be concentrated as one lump charge) indicate that unless a rock is within a very short distance of the charge – within two charge diameters – it will not be driven to the predicted velocity (Lundborg et al., 1975) with charge sizes that can reasonably be associated with quarry and open pit bench blasting and hence will not attain the predicted maximum range. A serious conceptual difficulty in the application of the Lundborg model is that it considers the whole borehole charge as one lumped mass (of spherical shape) as the source of the blast wave.

References

Adhikari, G.R . 1999. Studies of flyrock at limestone quarries. Rock Mechanics and Rock Engineering, vol. 32, no. 4. pp. 291−301.

Aghajani-Bazzazi, A., Osanloo, M., and Azimi, Y. 2010. Flyrock prediction by multiple regression analysis in Esfordi phosphate mine of Iran. Rock Fragmentation by Blasting. Sanchidrian, J.A. (ed.). Taylor & Francis, London. pp. 649–657.

Flyrock in surface mining – Limitations of current predictive models

Table II

Charge mass required in a 5-inch hole for 170 m/s velocity of an optimal rock

Scaled distance (m/kg¹/³)

Reflected specific impulse (Pa-s/kg¹/³)

Charge mass W¹/³ (kg¹/³) W (kg)

0.1* 20 000 4.3 80 0.2 6 000 14.4 279 0.3 3 000 28.9 2 400 0.4 2 000 43.3 81 200 0.6** 1 000 86.6 649 500

* The surface of a spherical charge is at Z ≈ 0.05 ** The face of a 3 m burden with a 100 kg charge load would be located at about Z = 0.65

Baker, W.E. 1973. Explosions in Air. University of Texas Press, Austin, TX,. Bauer, A., Burchell, S.L., and Crosby, W.A. 1982. Use of high speed photography in open pit blasting. Mining Resource Engineering Ltd, Kingston, Ontario, Canada.

Chiappetta, F. 2009. Combining electronic detonators with stem charges and air decks. Proceedings of the 9th Symposium on Rock Fragmentation by Blasting (FRAGBLAST9), Granada, Spain, 14–17 September 2009. CRC Press.

Chiapetta, R.F., Bauer A., Dailey, O.J., and Burchell, S.J. 1983. The use of high speed motion picture photography in blast evaluation and design. Proceedings of the 9th Annual Conference on Explosives and Blasting Technique. International Society of Explosives Engineers. pp. 258–309.

Chiapetta, R.F., Treleaven, T., Nixon, E., and Smith, J.D. 1998. History and expansion of the Panama Canal. Fragblast, vol. 2, no. 3. pp. 312–340.

Chernigovskii, A. 1985. Movement of rock subject to air drag. Application of Directional Blasting in Mining and Civil Engineering. Oxonian Press, New Delhi.

Cunningham, C. 2006. Blast hole pressure: What it really means and how we should use it. Fragblast, vol. 10, no. 1. pp. 33–45.

Ghasemi, E., Sari, M., and Ataei, M. 2012. Development of an empirical model for predicting the effects of controllable blasting parameters on flyrock distance in surface mines. International Journal of Rock Mechanics and Mining Sciences, vol. 52. pp. 1631–1670.

Held, M. 1983. Blast waves in free air. Propellants, Explosives, Pyrotechnics, vol. 8. pp. 1–7.

ISEE. 2011. Flyrock. Blasters’ Handbook. Stiehr, J.F. (ed.) Chapter 15. International Society of Explosives Engineers, Cleveland, OH. pp. 385–410.

Kinney, G.F. and Graham, J. 1995. Explosive Shocks In Air. 2nd edn. SpringerVerlag, New York.

Kljuno, E. and Catovic, A . 2019. Estimation of projected surface area of irregularly shaped fragments. Defence Technology, vol. 15. pp. 198–209.

Little, T.N. 2007. Flyrock risk. Proceedings of EXPLO 2007 Blasting: Techniques and Technology, Wollongong, NSW Australia, 3-14 September 2007. Australasian Institute of Mining and Metallurgy, Carlton, Vic. pp. 35–43.

Lundborg, N. 1981. The probability of flyrock damage. Report DS 1981:5. Swedish Detonic Foundation (SveDeFo), Stockholm, Sweden.

Lundborg, N. 1974. The hazards of fly rock when blasting. Report DS 1974:12. Swedish Detonic Foundation (SveDeFo), Stockholm, Sweden.

Lundborg, N., Persson, A., Ladegaard-Pedersen, A., and Holmberg, R . 1975. Keeping the lid on flyrock in open-pit blasting. Engineering and Mining Journal, May 1975. pp. 95–100.

McCleskey, F. 1988. Drag coefficients for irregular fragments. Report NSWC TR 87-78, Naval Surface Weapon Warfare Center, Dahlgren, VA.

McKenzie, C.K. 2009. Flyrock range and fragment size prediction. Proceedings of the 35th Annual Conference on Explosives and Blasting Technique, Denver, CO, 8-11 February 2009, vol. 2. International Society of Explosives Engineers, Cleveland, OH. pp. 17–33.

McKenzie, C. 2018. Flyrock model validation. Proceedings of the ISEE Australia 4th Annual Conference, Fremantle, WA, 8-9 November 2018. International Society of Explosives Engineers Australian Chapter., Australia, https://iseeaustralia. org/wp-content/uploads/2022/08/1_2McKenzie_FlyrockModelValidation-1.pdf

NASA. Shape effects on drag. Hall, N. (ed.). Glenn Research Centre. https://www. grc.nasa.gov/www/k-12/airplane/shaped.html [accessed 3 October 2021]

Raina, A.K. and Murthy, V.M.S.R . 2016a. Prediction of flyrock distance in open pit blasting using surface response analysis. Geotechnical and Geological Engineering, vol. 34. pp. 15–28.

Raina, A.K. and Murthy, V.M.S.R . 2016b. Importance and sensitivity of variables defining throw and flyrock in surface blasting by artificial neural network method. Current Science, vol. 111, no. 9. pp. 1524–1531.

Raina., A.K., Murthy, V.M.S.R., and Soni, A.K. 2015. Estimating flyrock distance in bench blasting through blast induced pressure measurements in rock. International Journal of Rock Mechanics and Mining Sciences, vol. 76. pp. 209–216.

Richards, A.B. and Moore, A.J. 2002. Flyrock control—By chance or design. Proceedings of the 30th ISEE Conference on Explosives and Blasting Technique, New Orleans, LA. International Society of Explosives Engineers, Cleveland, OH.

Richards, A.B. and Moore, A.J. 2005. Golden Pike cut-back flyrock control and calibration of a predictive model. Report no. KCG-0503. Terrock Consulting Engineers, Victoria, Australia.

Roth, J.A . 1979. Model for the determination of flyrock range as a function of shot conditions. Report no. NTIS PB81-222358. U S Department of Commerce. 97 pp.

Saunderson, H.C. 2008. Equations of motion and ballistic paths of volcanic ejecta. Computers and Geosciences, vol. 34, no. 7. pp. 802–814.

Smith, P.D. and Hetherington, J.D. 1994. Blast and Ballistic Loading of Structures. Taylor & Francis, Chichester, UK.

Stojadinovic, S., Lilic N., Obradovic, I., and Pantovic, R . 2016. Prediction of flyrock launch velocity using artificial neural networks. Neural Computing and Applications, vol. 27. pp. 515–524.

Stojadinovic, S., Pantovic, R., and Zikic, M. 2011. Prediction of flyrock trajectories for forensic applications using ballistic flight equations. International Journal of Rock Mechanics and Mining Sciences, vol. 48. pp. 1086–1094.

Stojadinovic, S., Lilic, N., Pantovic, R., Zikic, M., Denic, M., Cokorilo, V., Svrkota, I., and Petrovic, D. 2013. A new model for determining flyrock drag coefficient. International Journal of Rock Mechanics and Mining Sciences, vol. 62. pp. 68–73.

St George, J.D. and Gibson, M.F. 2001. Estimation of flyrock travel distances. A probabilistic approach. Proceedings of the EXPLO 2001 Conference, Hunter Valley. Australasian Institute of Mining and Metallurgy, Melbourne. pp. 245–248.

Trivedi, R., Singh, T.N., Mudgal, K., and Gupta, N. 2014. Application of artificial neural network for blast performance evaluation. International Journal of Engineering Research and Technology, vol. 3, no. 5. pp. 5645–5674.

Van der Walt, J. and Spiteri, W.A. 2020. A critical analysis of recent research into the prediction of flyrock and related issues in surface blasting activities, Journal of the Southern African Institute of Mining and Metallurgy, vol. 120, no. 12. pp. 701–714.

Workman, J.L. and Calder, P.N. 1994. Flyrock prediction and control in surface mine blasting. Proceedings of the ISEE 20th Annual Conference of Explosives and Blasting Technique, Austin, TX, 30 January-3 February 1994. International Society of Explosives Engineers, Cleveland, OH. pp. 59–74. u

The Journal of the Southern African Institute of Mining and Metallurgy

Affiliation:

1Department of Materials Science and Metallurgical Engineering, University of Pretoria, Pretoria, South Africa

2Advanced Materials Engineering, Manufacturing Cluster, Council for Industrial and Scientific Research, Pretoria, South Africa.

Correspondence to: S. Fazluddin

Email: S. Fazluddin@csir.co.za

Dates: Received: 10 May 2022 Revised: 6 Nov. 2022 Accepted: 7 Nov. 2022 Published: December 2022

How to cite:

Serwale, M.R., Coetsee, T., Sole, K.C., and Fazluddin, S. 2022

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride: Effect of leaching conditions. Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 733–740

DOI ID: http://dx.doi.org/10.17159/24119717/2117/2022

ORCID: M.R. Serwale https://orcid.org/0000-00023183-5196

T. Coetsee https://orcid.org/0000-00032028-5755

K.C. Sole https://orcid.org/0000-00034707-1060

S. Fazluddin https://orcid.org/0000-00018364-7974

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride: Effect of leaching conditions

by M.R. Serwale1,2, T. Coetsee1, K.C. Sole1, and S. Fazluddin2

Synopsis

The CSIR-Ti process employs lithiothermic reduction of titanium tetrachloride feedstock to produce titanium sponge. The product is therefore contaminated by a range of lithium and chloride species. In this study we examine the effects of particle size, temperature, and HCl concentration as input leaching variables on the removal of chlorides from the crude titanium sponge. A review of the aqueous chloride chemistry of Li and Ti provided initial conditions for leaching of impurity species from the sponge. Experimental results confirm that the effectiveness of leaching and removal of dissolved impurities from the sponge are dependent on leaching kinetics, which are influenced by temperature, particle size, and morphology. Of the variables tested, reaction temperature had the strongest influence on the oxygen content of the leached product. The HCl lixiviant concentration had a negligible effect under the conditions tested. Leaching of crude titanium sponge (−10 mm size fraction after crushing) at 14°C in either 1 M or 0.032 M HCl yielded a titanium sponge product that met the ASTM standard specification for commercially pure Grade 1 titanium, i.e., oxygen content < 0.18 mass% and chloride content < 0.15 mass%.

Keywords

titanium sponge, titanium tetrachloride, lithiothermic reduction, purification, leaching, CSIR-Ti process.

Introduction

A low-cost titanium manufacturing process, which is aimed at producing particulate titanium by the metallothermic reduction of titanium tetrachloride (TiCl₄) with lithium, is under development at the Council for Industrial and Scientific Research (CSIR), South Africa. The process yields a crude product encapsulated in LiCl and, depending on whether the metallothermic reduction is completed with a stoichiometric excess of Li or TiCl₄, may also contain traces of excess Li, TiCl₃, and TiCl₂. These residual reaction byproducts are detrimental to the mechanical characteristics of manufactured products (Peter et al., 2012): chlorides are volatile at high temperature, resulting in macro-porosity, which degrades fatigue properties (Yan, Tang, and Qian, 2015), while oxygen changes phase selection and microstructure, which increases the elastic modulus and yield strength, but reduces ductility (Baril, Lefebvre, and Thomas, 2011). The challenge encountered in most alternative methods to produce titanium powder is the economic removal of byproducts to achieve the target titanium specification (Liang et al., 2018; Peter et al., 2012).

Leaching is successfully used for impurity removal in the Hunter process (Gambogi and Gerdemann, 1999) and has the advantages of low energy intensity and removal of large quantities of salt at relatively low cost due to the simple equipment required (McKinley, 1955). Drawbacks include the low solution concentrations of byproducts for recycle due to water dilution and product contamination by the leach liquor (Hansen and Gerdemann, 1998). Initial experiments (van Vuuren, Oosthuizen, and Heydenrych, 2011; Serwale, Coetsee, and Fazluddin, 2020) showed promising results for use of this approach in treating the product of the CSIR-Ti process.

This follow-up study investigated the aqueous chemistry of titanium using the selected lixiviant to remove impurities from the sponge, followed by evaluation of selected experimental leaching conditions aimed at achieving a commercially pure (CP) Grade 1 product with respect to oxygen (0.18 mass%) and chloride (0.15 mass%) (ASTM, 2002). The aqueous chemistry behaviour of titanium and lithium salt compounds in the HCl leaching of the crude Ti product were explored. Experimental leaching testwork results were used to identify optimum process conditions.

Aqueous chemistry of titanium

Leaching of titanium sponge is complicated by a series of side reactions between the byproducts and

water, which result in the formation of insoluble hydrolysis products. These precipitate and concentrate on the metal surface and in pores, contaminating the product with oxides and oxychlorides (Garmata et al., 1970; Jamrack, 1963). Dissolution reactions of Li and sub-chlorides (TiCl₂, TiCl₃) in water are exothermic; the resulting heat generation favours rapid precipitation of hydrolysis products and oxidation of titanium (Garmata et al., 1970).

The boundary conditions should be selected such that the titanium metal sponge or powder product is not dissolved or contaminated during acid leaching of the byproducts. In contrast to the high chemical stability of compact titanium, the sponge and powder forms are soluble in HCl solution due to their high specific surface areas (Garmata et al., 1970). Titanium solubility is more prominent in HCl concentrations above 1 M, where the titanous (Ti³⁺; violet) ion predominates, as demonstrated in the Pourbaix diagram of Figure 1 (Sole, 1999; Zhu, Zhang, and Cheng, 2011); however, Straumanis and Chen (1951) stated that dissolution of titanium metal in dilute HCl occurs with difficulty, solubility is extremely low, and is affected by impurities. Garmata et al. (1970) reported that only 0.5% titanium sponge dissolved in 0.16–0.33 M HCl at 100°C.

The slow dissolution is attributed to stable passivated TiO₂·H₂O that forms in aqueous media in the absence of a complexing agent (Figure 1). The stability range of this dominant aqueous species can be expanded in the presence of reducing acidic media (pH 6.0–2.5) (Pourbaix, 1974). Titanium metal dissolution and TiO₂·H₂O formation are minimized in the range of 0 ≤ pH ≤ 1.5, which is consistent with the recommendation by Seon and Nataf (1988) to use pH 1.5 for leaching of metallothermically produced crude titanium.

Although titanium sub-chlorides in the crude product are likely present as complex salts, Garmata et al. (1970) reported that these react with aqueous solutions just like the individual sub-chlorides; in contrast, however, the reaction is perceived to be slow. The aqueous chemistry of TiCl₂ present in the CSIR-Ti crude product is reviewed from that perspective. The aqueous titanium(II) cation (Ti²⁺(aq)) oxidizes rapidly, even at low pH (Gould, 2011), so its chemistry is not well known. It is reported to exist for some time in ice-cold HCl solution; further support for its existence is provided by the electrode potential of Ti²⁺/ Ti³⁺ = −0.37 V vs. standard hydrogen electrode, which appears in

most resources and the Pourbaix diagram in Figure 1 (Kölle and Kölle, 2003). What is known about Ti²⁺(aq) was notably reported by Kölle and Kölle (2003), Park et al. (2012), and Yang and Gould (2005). Gould (2011) concluded that in all reports confirming the existence of Ti²⁺(aq), the samples contained both HF and Ti⁴⁺ in highly acidic conditions, indicating that these contaminants might have stabilized the Ti²⁺ ion. The implication is that, under different conditions, the transients might be short-lived. However, it must be noted that Sekimoto et al. (2010) based their H₂ volumetric analysis and titration procedure on the premise that TiCl₂ reacts with 1 M HCl solution in a standard redox reaction to form Ti³⁺ ions and evolve H₂ in the absence of an oxidizing agent, according to Equation [1] (Richens, 1997; Sekimoto et al., 2010; Wang et al., 2013):

TiCl₃ impurity has more severe consequences for final product properties, so the speciation and stability of Ti³⁺ in HCl have direct implications for the probability of recovering the ion in its soluble state, and consequently the selection of the leaching parameters and scheme. According to Figure 1, Ti³⁺ predominates under reducing conditions and pH ≤ 1. It can, however, be easily oxidized in air to form tetravalent titanium(IV) TiO²⁺, as shown by Equation [2]:

The rate of autoxidation in HCl is dependent on the volume of absorbed oxygen and solution pH (Mackenzie and Tompkins, 1942; Yakovleva et al., 1973), so autoxidation is significantly retarded in highly concentrated acidic solutions (Ashton, 1977).

The existence of the free Ti³⁺ ion in aqueous solutions remains controversial, with some postulates that it cannot exist due to its relatively high ionic potential: instead, it either oxidizes, hydrolyses, or forms hydrolysed polymeric species or complexes with various ligands, such as Cl⁻, OH⁻, CN⁻, SO₄²⁻, and F− (Ashton, 1977; Nabivanets, 1965). Some reports suggest that Ti³⁺ ion dominates only in HCl solution at pH ≤ 0.5 and that the main Ti³⁺ ionic species in dilute HCl solution (pH ≥ 1) is the hexaquotitanium ion [Ti(H₂O)₆]³⁺ (pale reddish-purple) (Cassaignon, Koelsch, and Jolivet, 2007; Pecsok and Fletcher, 1962). [Ti(H₂O)₆]³⁺ has a measured pK a value between 1.8 and 2.5 (Cassaignon, Koelsch, and Jolivet, 2007; Clark, 1973; Richens, 1997). Ti³⁺ is appreciably hydrolysed at pH ≥ 0.7 (Sole, 1999). Hydrolysis reactions can be minimized or inhibited in acidified solution because the precipitation reactions are slow under these conditions (Jamrack, 1963; Kelly, 1963).

Methodology

Selection of experimental input variables

Figure 1—Pourbaix (Eh–pH) diagram for the Ti–H2O system (adapted from Pourbaix, 1974)

Based on the literature and the results of preliminary experimental work (Serwale, Coetsee, and Fazluddin, 2020), the leaching variables selected for experimental investigation were pH, feed material particle size, and temperature. The variable ranges were based on a two-level factorial experimental design, which only considers extremities (minima and maxima) in the test parameters (Free, 2022; Montgomery, 2017). This approach has the advantage that several variables, their interactions, and the effect of each factor on the response output are simultaneously investigated, thereby minimizing the number of experiments

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

The Journal of the Southern African Institute of Mining and Metallurgy

without sacrificing precision (Montgomery, 2017). Table I illustrates the experimental design matrix and interactions investigated in each test.

Material preparation and analyses

The crude titanium product for this study was produced at the CSIR titanium pilot plant (Pretoria, South Africa) using a batch process. The metallothermic reduction batch was run with 2% stoichiometric excess of TiCl4. Samples for this testwork were prepared from a 1500 g sample of crude titanium by crushing under argon gas at 20 mm jaw-crusher gap setting then screening at sieve sizes of 20 mm, 10 mm, and 630 mm. The materials retained on the 10 mm and 630 mm sieves were used in this work and are labelled as the +10 mm and −10 mm size fractions, respectively (Table I). Each size fraction was blended and split into 20 g samples using the cone-and-quartering method. Each 20 g sample was transferred to a glass bottle with a screw-on lid and stored prior to use in a sealed grade 304 stainless-steel vessel flushed with argon.

A composite head sample was analysed for total chloride content by gravimetry at the Nuclear Energy Corporation of South Africa (NECSA), following the ASTM E-120 standard test method for chemical analysis of Ti and Ti alloys. Oxygen content was determined by combustion (ASTM E-1409-97) using an Eltra ONH-2000 instrument. Lithium content was measured by inductively coupled plasma optical emission spectrometry (Optima 5300DV, Perkin Elmer, USA).

Experimental procedure

Batch leaching experiments were conducted in a 250 mL cylindrical glass reactor equipped with four ports on the glass lid, as illustrated in Figure 2. The central port was fitted with a stirrer shaft. One port was used for pH measurements; the other two accommodated an argon gas sparge pipe, a thermocouple inlet, and an argon vent pipe that was connected to a gas trap.

The experimental procedure was initiated by transferring 200 mL of the required dilute acid solution (1 M or 0.032 M HCl) into the leaching vessel, clamping the lid in position, then heating the vessel on a heating mantle to an initial solution temperature of 30°C. The temperature was continuously measured for the duration of the experiment with a K-type thermocouple that was submerged in the solution and recorded using a multi-channel data logger. The solution was agitated at 400 r/min with a polytetrafluoroethylene-coated anchor propeller impeller fitted to an overhead stirrer. Argon gas was sparged through a pipe with an internal diameter of 25 mm at a flow rate of 0.05 L/min, for approximately 10 minutes before leaching commenced, to ensure a non-oxidative environment. The argon flow was controlled and measured with a rotameter.

The heating mantle was switched off when the solution reached the set temperature because the leaching reactions are exothermic (Garmata et al., 1970). A 20 g solid sample was then slowly added into the leaching vessel while agitating vigorously (400 r/min) to dissipate the heat into the bulk solution and prevent the temperature from exceeding 60°C. The solution pH was measured and recorded with a portable pH meter fitted with a glass body pH electrode (Orion 8172 Ross, Thermo Scientific, USA) and stainless-steel temperature-compensation electrode (Orion 917004) to achieve automatic temperature compensation. The measurements intervals were 5, 10, 15, 30, and 60 minutes.

On completion of leaching, the sample was filtered (Munktell no. 1 filter paper, Ahlstrom, Sweden). The solid residue was subjected to four cycles of agitated washing in 200 mL of deionized water at 30°C to neutralize the acid and dissolve the salt from the metal. The deionized water was heated following the same process steps as described for heating the dilute HCl solution. The durations of the four sequential washing cycles were 120, 180, 120, and 60 minutes. The initial and final conductivities of the wash waters were measured with a portable conductivity meter (EC60 Waterproof EC/TDS/C, Martini Instruments, USA). On completing the washing cycles (i.e., when the conductivity reached 14–16 μs), the residue was filtered then dried in a vacuum oven (VO400, Memmert, Germany) at 60°C for 6 hours.

To mitigate the safety risks posed by the pyrophoric behaviour of fine titanium (Bolivar and Friedrich, 2019), the solid residue was not washed with alcohol or acetone to evaporate soluble phases, despite the advantages associated with this process step with regard to the total oxygen content in the final product.

The same experimental procedure was used for the 14–30°C temperature range, except that the leach solution was precooled to 14°C by submersion in a 1000 mL beaker filled with ice blocks before being transferred to the leaching vessel. No external heating was provided. The deionized water washing steps were conducted at room temperature.

Figure 2—Schematic diagram of experimental leaching set-up

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

Southern African Institute of Mining and Metallurgy

Results and discussion

Impurity content of crude titanium sponge

Analyses of the major impurities in a composite sample of the titanium sponge feed are shown in Table II. It was assumed that the impurity concentrations were consistent across both size fractions employed in this testwork. Owing to the low molecular mass of lithium, it is a very significant component when calculated on a molar basis. The chloride content is an order of magnitude lower. The results suggest that only a small proportion of the lithium was present as LiCl, and that most lithium occurred in the titanium sponge in metallic form. The lithiothermic reduction was carried out using excess TiCl₄, so this result indicates that the reaction did not go to completion. Lithium is also present in the feed material as Li₂O. Chlorides in this material were identified as LiCl, TiCl₂, Ti(OH)Cl₂, and Ti(OH)Cl.

Variation in solution pH with reaction duration

Typical pH behaviour observed during tests 1 to 8 is shown in Figure 3. For both initial acid concentrations (Table I), the pH increased rapidly within the first 5 minutes in all experiments, then dropped and stabilized at a constant value after 10 minutes.

These observations are attributed to the increase in OH⁻ concentration, as represented by the Li and Li₂O neutralization reaction steps that take place near or on the exposed titanium surface, in which the weakly basic LiOH(aq) ion pair is formed via Equation [3]. Li also reacts with HCl(aq) to form LiCl(aq) according to Equation [4]. TiCl2 dissolves in water and HCl according to Equations [5] and [6].

Table II

Impurity contents in titanium sponge feed material

Units Units O Li

mass% 0.30 0.02 3.07 mol%* 0.34 0.05 17.9

*Calculated assuming that the balance is Ti

[3a] [3b] [4] [5] [6]

The thermodynamic values for Equations [3] to [6]) were calculated using HSC Chemistry 7 (Chemistry Software, Finland). These reactions all exhibit negative Gibbs free energies (ΔG) in the applied temperature range, indicating that there are no thermodynamic restrictions to these reactions. Enthalpy of reaction (ΔH) was negative, confirming their exothermic nature.

Figure 3 shows that the cumulative acid consumption declined significantly after 5 minutes, suggesting that all exposed excess Li metal and Li2O on the particle surfaces were consumed and

Table III

Figure 3—Variation of pH as a function of reaction time for initial HCl concentrations of (a) 0.032 M and (b) 1 M

that hydrolysis of Ti(III) occurred in the presence of Cl⁻. The pH therefore decreased due to the resulting H₃O⁺ (Equation [7]). The presence of HCl retards hydrolysis by converting the pHdependent hydrolysis product Ti(OH)²⁺ to TiCl²⁺, in proportion to the acid concentration (Mackenzie and Tompkins, 1942). These authors postulated that the reaction proceeds via two mechanisms that involve pH-dependent hydrolysis (Equation [7]) and complex formation (Equation [8]). If these reversible reactions were simultaneously established, the resulting equilibria would correspond to Equation [9] (Mackenzie and Tompkins, 1942; Shuvalov, Solov’ev, and Lebedev, 1978): [7] [8]

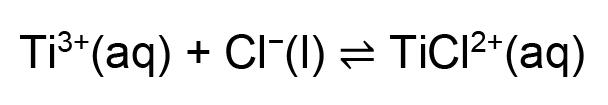
(kJ)

G (kJ)

H (kJ)

G (kJ) 10 -397.0 -403.2 -530.9 -576.5 -41.5 -135.4 -58.9 -120.5 20 -397.8 -403.5 -532.0 -578.0 -42.3 -138.7 -60.7 -122.6 30 -398.5 -403.6 -532.9 -579.6 -43.1 -142.0 -62.3 -124.7 40 -399.2 -403.8 -533.8 -581.1 -43.9 -145.2 -63.8 -126.8 50 -399.9 -403.9 -534.7 -582.6 -44.7 -148.5 -65.3 -128.8 60 -400.6 -404.1 -535.6 -584.1 -45.4 -151.6 -66.7 -130.7

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

The Journal of the Southern African Institute of Mining

[9]

Chloride complexes of Ti³⁺ do not form to any appreciable extent; chloro-complex formation depends on the acid concentration (Nicholls, 2017). Acidic solutions of Ti(III) salts in inert atmospheres (nitrogen and argon) are relatively stable (Ashton, 1977). Therefore, the recovery of pH to lower levels, at 5 to 10 minutes (Figure 3), can be explained by the dominance of Equation [7].

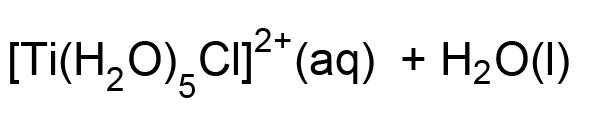
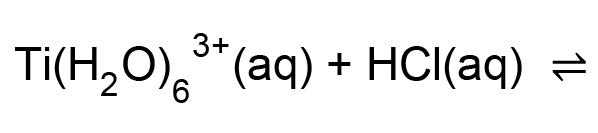
The various aqueous titanium hydroxide and watercoordinated species are thermodynamically unstable at low pH. Hence, it is postulated that the ions continue to react by a bridging reaction or co-ordination re-arrangement to form stable species and water. For instance, it is postulated that a [Ti(H₂O)₆]³⁺ bridging reaction forms [Ti(H₂O)₅Cl]²⁺ according to Equations [10]–[13], which accounts for the stabilization in pH observed after 10 minutes. Despite an order of magnitude difference in initial pH, all test conditions showed similar trends, indicating that the first 5 minutes of the experiments are the most critical. It can be concluded that the concentration of the complexing ligand and the pH of the media are key to stabilizing the ions in solution.

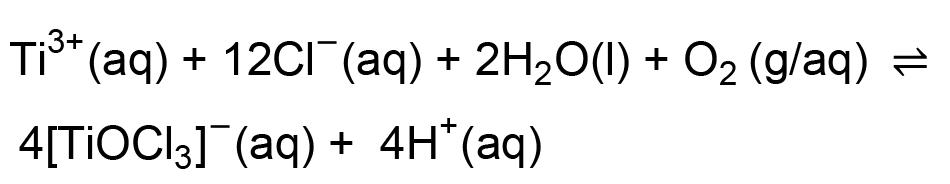
[10] [11] [12] [13]

Variation in solution temperature with reaction duration

Examination of the temperature profile as a function of reaction time (Figure 4) shows that the temperature increased sharply within 5 minutes of adding the crude sample into the leaching vessel and then decreased, suggesting that most exposed and accessible by-products were dissolved during the initial temperature increase. This phenomenon was observed in all tests, despite the precautionary measures implemented to prevent localized overheating at the reaction-mass–solution interface. This effect was also reported in the leaching of sponge produced in the Hunter process, which uses Na as reducing agent (Garmata et al., 1970). Metallic Li, like metallic Na, has a low standard reduction potential and reacts with water to release heat and hydrogen gas, as displayed in Equation [3a], and thereby increases the solution pH (Schweitzer and Pesterfield, 2010).

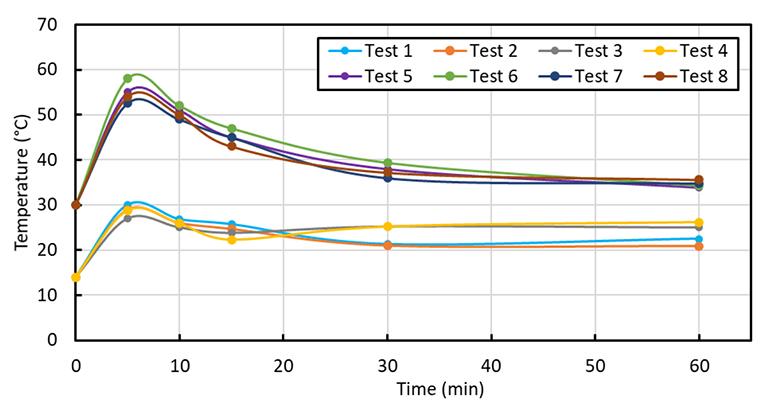
The temperature profiles in Figure 4 suggest that after the initial consumption of the excess reagents on the exposed titanium surface, the reaction changed from activation to masstransfer control due to the formation of a TiH₂ layer on the surface of the titanium particles owing to the incorporation of released hydrogen gas. At this point, the reaction was dependent on the stirring rate, which governs the diffusion rate through the TiH₂ layer.

The observed temperature response indicates that reactivity is related to the rate at which heat is liberated during the initial chemical reaction, rather than the total amount of heat evolved over a prolonged period.

Figure 4—Variation in temperature of leaching solution as a function of time

Figure 5—Final oxygen contents of CSIR-TI products leached under conditions given in Table I

Product quality

Oxygen content

The initial oxygen content of the crude titanium was 0.02 mass%. Assays of the final products (Figure 5) show that the oxygen content increased as a consequence of the leaching process. Nevertheless, the oxygen content was within ASTM standard specifications of 0.18 mass% for CP Grade 1 to 0.4 mass % for CP Grade 4 titanium for tests 1–4 and 7–8. The markedly higher oxygen contents recorded for tests 5 and 6 correspond to the smaller particle size and higher reaction temperature. The oxygen contents for tests 7 and 8 approached the upper limit of the specification, which suggests that the higher reaction temperature was responsible for this effect, rather than the particle size (see Table I).

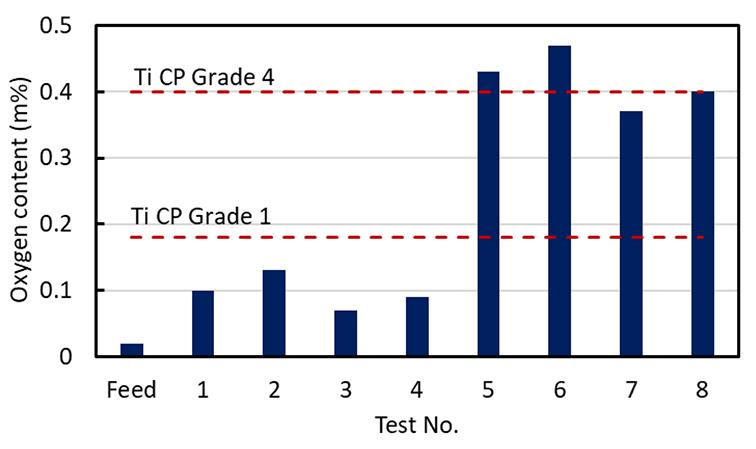
Statistical analysis of the experimental data with respect to oxygen content of the product is presented in Table IV. Inspection of the P-values shows that the experimental parameters with a significant effect at the 0.05 validity boundary level were particle size, temperature, and concentration. The F-values reveal that temperature and particle size had the most significant effect on the final oxygen content.

The strong effect of temperature on the oxygen content is in reasonable agreement with the prediction that the rate of oxidation of titanium in water increases with increasing temperature. No interaction between temperature and pH (HCl concentration) was detected, although these two factors cannot be considered in isolation in actual practice. Hydrolysis of Ti(III) ions occurs at approximately pH 0.6, so any localized overheating may lead to the formation of TiO₂.

As noted in Table I, the two temperature variables considered both involved a wide temperature range, up to 30°C, rather than a defined temperature, owing to the high exothermicity of the leaching reactions and despite efforts to experimentally limit this temperature range. This wide experimental temperature range limits data interpretation. This effect will likely be exacerbated at larger- and commercial-scale operations, so future work should

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

Table IV

Analysis of variance with respect to oxygen content in the leached product

Source

Sum of squares df

Mean square F-value P-value

Model 0.2116 4 0.0529 317.48 0.0003

A: [HCl] 0.0018 1 0.0018 10.80 0.0462

B: Particle size 0.0050 1 0.005 30.00 0.0120

C: Temperature 0.2048 1 0.2048 1228.80 < 0.0001

A × C 0.0000 1 0.0005 0.3000 0.0622

R² = 99.8%, R² (predicted) = 98.3%, R² (adjusted) = 99.5%

consider how to improve control of this parameter, particularly as a higher temperature is shown to exert the strongest detrimental influence on oxygen content of the product.

The increase in oxygen content during leaching is attributed to an increase in surface area owing to particle attrition by the vigorous agitation, combined with the inherent tendency of titanium to form an oxide monolayer (TiO₂) on its surface in both air and water. Hansen and Gerdemann (1998) demonstrated the strong effect of particle size on final oxygen content during leaching of a titanium powder that initially assayed 0.82 mass%. Individual assays of various size fractions, ranging from 0.01–4760 μm, showed that the finest fraction contained 8.38 mass% O, but the coarsest fraction contained only 0.00002 mass% O. Oxygen contamination may also be attributed to the presence of water, which can increase passivation of oxygen on titanium particles (Kelly, 1982; Liang et al., 2020), from precipitation of hydrolysis products due to localized overheating on particle–particle surface contact owing to the exothermicity of leaching, or from surface oxidation of the titanium metal.

Chloride content

The maximum chloride specification for CP Grade 1 titanium sponge is 0.12–0.15 mass% (Nechaev and Polezhaev, 2016; Yan, Tang, and Qian, 2015; Yu and Jones, 2013). The efficiency of chloride removal (ηe) was calculated using Equation [14] (Nechaev and Polezhaev, 2016): [14]

where C₀ and C are the initial and final total chloride contents in the titanium sponge, respectively. The data are summarized in Table V and Figure 6. Statistical analysis of the experimental data is presented in Table VI.

Table V and Figure 6 show that the total residual chloride content in the purified product decreased with increasing temperature and particle size. This trend is opposite to that of the oxygen content. Residual chlorides were significantly

Table VI

Table V

Chloride removal efficiency

Test no. Cl (mass%) Cl removal efficiency,ηe (%)

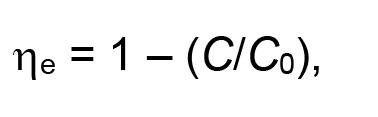
Crude feed 0.301 0.13 57 2 0.12 60 3 0.22 27 4 0.21 30 5 0.04 87 6 0.09 70 7 0.14 53 8 0.10 67

Figure 6—Total residual chloride contents of CSIR-Ti products leached under conditions given in Table I

lower in the samples washed with deionized water at an average temperature of 30°C (tests 5–8) than those washed at 14°C (tests 3 and 4), which could be attributed to the correlation of higher solubility (and hence driving force for dissolution) and higher diffusion coefficient with higher temperature (Richardson et al., 2002). The results for tests 1 and 2 were similar to that of test 7, although the samples were leached at lower temperature. This is attributed to the smaller particle size (−10 mm) of the former and associated larger surface area, resulting in an increased extent of leaching. Test 8 also presented lower chloride content, despite

Analysis of variance with respect to chloride content in the leached product

Source* Sum of squares df

Mean square F-value P-value

Model 0.0231 3 0.0077 14.35 0.0132

B: Particle size 0.0105 1 0.0105 19.56 0.0115

C: Temperature 0.0120 1 0.0120 22.35 0.0091

B × C 0.0006 1 0.0006 1.14 0.345

R² = 90%, R² (predicted) = 70%, R² (adjusted) = 90% *ABC was not included in the model due to the significant error introduced by not considering factor A (HCl concentration) because it lies on the normal distribution line.

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

The Journal of the Southern African Institute of Mining and Metallurgy

the larger particle size, due to the higher leaching temperature. The combination of small particle size (−10 mm), high exothermic temperature, and deionized water washing at 30°C (tests 5 and 6) enhanced chloride removal. These observations suggest that both particle size and temperature exhibit considerable influence on chloride removal.

The results in Table VI show that the individual effects of both temperature and particle size on the extent of chloride removal were statistically significant at the 0.05 boundary level; however, their interaction was not statistically significant, as evidenced by the large P-value (0.3459 > 0.05). The effect of temperature was more significant than all factors and interactions.

Effect of particle size

The interfacial area of a solid–liquid interface increases with decreasing particle size, which is beneficial to the leaching rate owing to the reduced distance within the porous structure of the solid through which the solute needs to diffuse. In this work, both particle-size variables considered covered a wide range: the +10 mm material ranged from 10–20 mm; the −10 mm class ranged from 0.63–10 mm, which exceeds one order of magnitude. Nevertheless, general conclusions can be drawn from the experimental results. As shown by the data in Table V and Figure 6, the lowest residual chloride contents were measured for the −10 mm size fractions. The combination of −10 mm size fraction and 30°C washing temperature gave the highest chloride removal efficiency (tests 5 and 6); oxygen contents of the product were, however, adversely affected by the higher temperature (Figure 5). Particle size selection is therefore a balance between achieving adequate leaching efficiency of chlorides from the crude titanium, favoured by smaller particles sizes, and limiting the amount of oxygen contamination due to leaching in aqueous solution, which is countered by using large particles with low surface area exposed to oxygen adsorption reactions.

Effect of particle morphology

In addition to temperature and particle size, morphology of the titanium sponge is also a key factor that determines the extent of chloride removal. Secondary-electron scanning electron microscopy analysis of the purified products (Figure 7a) showed that the CSIR product had an irregular coral-like porous structure,

akin to a sponge or agglomerate. Higher magnification observation revealed that during crushing to −10 mm, in addition to cracks propagating and isolated pores opening, some particles were flattened (as seen at locations A and B marked on Figure 7b). Formation of sintered and flattened agglomerates with semiclosed voids or closed pores would impede LiCl and TiCl₂ removal during leaching. Sintered grains and dendritic particulates were also detected (Figure 7c). The sintering is attributed to prolonged contact between titanium particles and overheating on the metal surface during metallothermic reduction. Salt that is entrapped in closed pores of the powder by sintering cannot be completely removed by this acid leaching purification process, even if the residence time is increased. Salt entrapment in the microstructure has also been reported in titanium powders produced via the hydride–dihydride and Armstrong processes (Peter et al., 2012).

Conclusions

This study examined the effects of particle size, temperature, and HCl concentration on the leaching removal of chloride from crude titanium sponge produced in the CSIR-Ti batch process, with the aim of achieving target specifications for oxygen and chlorides in the purified product. The experimental results confirm that the effectiveness of leaching and removal of dissolved impurities from the sponge is dependent on temperature, particle size, and morphology. Reaction temperature had the strongest influence on the oxygen content of the leached product. There was negligible difference in the results using HCl concentrations of 1 M and 0.032 M. The low final pH values of the leach solutions indicated that hydroxy/oxychloride formation was unlikely. The chloride impurities likely originated from undissolved LiCl and TiCl2 salts that were physically trapped in the crude sponge by sintering.

Leaching of −10 mm crude titanium sponge at an initial solution temperature of 14°C in 1 M and 0.032 M HCl (tests 1 and 2) followed by washing with deionized water yielded a product that met the ASTM standard specification for CP Grade 1 oxygen content (< 0.18 mass%) and the general specification for chloride content (< 0.15 mass%). These values nevertheless exceed the maximum specification of 0.08 mass% for hydride–dehydride (HDH) process powder (Yan, Tang, and Qian, 2015), the highly recommended value of 0.05 mass% Cl, and are significantly

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

Southern African Institute of Mining

Metallurgy

Figure 7—Scanning electron micrographs of leached product from test no. 6: (a) at 1000× magnification, showing (b) flattened area due to crushing and (c) sintered area due to high- temperature exposure in preceding metallothermic reduction step

higher than the ideal 0.01 mass% Cl required for premium metal powders (van Vuuren, Oosthuizen, and Heydenrych, 2011; Withers et al., 2013). Unfortunately, the conditions that gave the lowest chloride content (tests 5 and 6) correlated with the highest oxygen content, which gave a product that did not even meet the Grade 4 specification. The original premise of this work should perhaps be questioned: whether leaching is, in fact, the best route to achieving product purity in this particular system. The average chloride removal for all tests was only 56%. Options for better chloride separation or improvement in reduction efficiency in the pyrometallurgical parts of the process could be considered.

Acknowledgements

The authors thank the CSIR and South African Department of Science and Innovation for funding, the CSIR-Titanium Centre of Competence production team for advice—specifically Mr Jabu Skosana, and the laboratory team for analysing samples, without whom this study would not have been possible. We are also most grateful for the insights and useful comments of anonymous reviewers of earlier drafts of this manuscript.

CRediT author statement

MRS: Methodology, Investigation, Data analysis, Writing - original draft preparation; TC: Supervision, Writing - review and editing; KCS: Supervision, Writing - review and editing; SF: Project administration, Funding, Supervision, Writing - review and editing.

References

ASTM. 2002. Standard specification for titanium sponge. Designation B 299-01. American Society for Testing and Materials, West Conshohocken, PA. Ashton, J.F. 1977. Some aspects of the solution chemistry of titanium (III). Master‘s thesis, University of Tasmania. https://eprints.utas.edu.au/19394/1/ whole_AshtonJohnFrederick1977_thesis.pdf

Baril, E., Lefebvre, L.P., and Thomas, Y. 2011. Interstitial elements in titanium powder metallurgy: Sources and control. Powder Metallurgy, vol. 54, no. 3. pp. 183–186. https://doi.org/10.1179/ 174329011X 13045076771759

Bolivar, R. and Friedrich, B. 2019. Magnesiothermic reduction from titanium dioxide to produce titanium powder. Journal of Sustainable Metallurgy, vol. 5, no. 2. pp. 219–229. https://doi.org/10.1007/s40831-019-00215-z

Cassaignon, S., Koelsch, M., and Jolivet, J.P. 2007. From TiCl3 to TiO2 nanoparticles (anatase, brookite and rutile): Thermohydrolysis and oxidation in aqueous medium. Journal of Physics and Chemistry of Solids, vol. 68, no. 5-6. pp. 695–700. https://doi.org/10.1016/j.jpcs.2007.02.020

Clark, R.J.H. 1973. The chemistry of titanium. Comprehensive Inorganic Chemistry Bailer Jr., J.C., Emeleus., H.J., Nyholm. R., and Trotman-Dickenson, A.F. (eds), Pergamon Press, Oxford, UK. pp. 355–417.

Free, M.L. 2022. Hydrometallurgy: Fundamentals and Applications. 2nd edn. Wiley, Hoboken, NJ:

Gambogi, J. and Gerdemann, S.J. 1999. Titanium metal: extraction to application. Review of extraction, processing, properties & applications of reactive metals. Proceedings of the Minerals, Metals & Materials Society Annual Meeting, San Diego, CA. Mishra, B. (ed.), Wiley, New York.

Garmata, V.A., Gulyanitskii, B.S., Lipkes, Y.M., Seryakov, G.V., and Kramnik, V.Y. 1970. The Metallurgy of Titanium. National Technical Information Service (1st edn). Springfield, IL: Wright Patterson Air Force Base, OH.

Gould, E.S. 2011. Redox chemistry of aquatitanium(II), Ti²⁺(aq). Coordination Chemistry Reviews, vol. 255, no. 23–24. pp. 2882–2891. https://doi.org/10.1016/j. ccr.2011.06.006

Hansen, D.A. and Gerdemann, S.J. 1998. Producing titanium powder by continuous vapor-phase reduction. JOM, vol. 50, no. 11. pp. 56–58. https://doi. org/10.1007/s11837-998-0289-3

Jamrack, WD. 1963. Rare Metal Extraction by Chemical Engineering Techniques Pergamon, Oxford, UK.

Kelly, E.J. 1982. Electrochemical behaviour of titanium. Modern Aspects of Electrochemistry: No. 14. Bockris, J., Conway, B., and White, R. (eds). Plenum Press, New York. pp. 319–417. https://doi.org/10.1136/bmj.1.3567.930-a

Kelly, J.T. 1963. Metal purification process. US patent 3085874.

Kölle, U. and Kölle, P. 2003. Aqueous chemistry of titanium(II) species. Angewandte Chemie International Edition, vol. 42, no. 37. pp. 4540–4542. https:// oi.org/10.1002/anie.200351280

Liang, L., Dachun, L., Heli, W., Kaihua, L., Juhai, D., and Wenlong, J. 2018. Removal of chloride impurities from titanium sponge by vacuum distillation. Vacuum, vol. 152. pp. 166–172. https://doi.org/10.1016/j.vacuum.2018.02.030

Liang, L., Zhu, F., Deng, P., Jia, Y., Kong, L., Deng, B., Li, K., and Liu, D. 2020.

Separation and recycling of chloride salts from electrolytic titanium powders by vacuum distillation. Separation and Purification Technology, vol. 236. 116282. https://doi.org/10.1016/j.seppur.2019.116282

Mackenzie, H.A.E. and Tompkins, F.C. 1942. The kinetics of the autoxidation of inorganic reducing agents. Part I.—Titanous chloride. Transactions of the Faraday Society, vol. 38. pp. 465−473. https://doi.org/10.1039/tf9423800465

McKinley, T.D. 1955. Recovery of titanium metal. US patent 2707149.

Montgomery, D.C. 2017. Design and Analysis of Experiments. 9th edn.. Wiley, Hoboken, NJ.

Nabivanets, B.I. 1965. The use of ion-exchange chromatography for studying the state of ions of high-valency elements in solution. Russian Chemical Reviews, vol. 34, no. 5. pp. 392–402. https://doi.org/10.1070/rc1965v034n05abeh001452

Nechaev, N.P. and Polezhaev, E.V. 2016. Effect of physicochemical treatment on titanium porous powder quality. Metallurgist, vol. 60, no. 3–4. pp. 339–341. https://doi.org/10.1007/s11015-016-0296-5

Nicholls, D. 2017. Complexes and First-Row Transition Elements. Macmillan, London, UK.

Park, S.H., Batchelor, B., Lee, C., Han, D.S., and Abdel-Wahab, A . 2012. Perchlorate degradation using aqueous titanium ions produced by oxidative dissolution of zero-valent titanium. Chemical Engineering Journal, vol. 192. pp. 301–307. https://doi.org/10.1016/j.cej.2012.04.013

Pecsok, R.L. and Fletcher, A.N. 1962. Hydrolysis of titanium (III). Inorganic Chemistry, vol. 1, no. 1. pp. 155–159. https:/ doi.org/10.1021/ic50001a031

Peter, W.H., Chen, W., Yamamoto, Y., Dehoff, R., Muth, T., Nunn, S.D., Kiggans, J.O., Clark, M.B., Sabau, A.S., Gorti, S., Blue, C.A., and Williams, J.C 2012. Current status of Ti-PM: Progress, opportunities and challenges. Key Engineering Materials, vol. 520. pp. 1–7. https://doi.org/10.4028/www.scientific. net/kem.520.1

Pourbaix, M.J.N. 1974. Atlas of Electrochemical Equilibria in Aqueous Solutions: Translated from the French except sections I, III 5, III 6 which were originally written in English. Franklin, J. (trans.). National Association of Corrosion Engineers, Houston, TX.

Richardson, J.F., Harker, J.H., Backhurst, J.R., and Coulson, J.M. 2002. Coulson and Richardson's Chemical Engineering. Vol 2. Butterworth-Heinemann, Oxford, UK.

Richens, D.T. 1997. The Chemistry of Aqua Ions. Wiley, Chichester, UK.

Sekimoto, H., Nose, Y., Uda, T., and Sugimura, H. 2010. Quantitative analysis of titanium ions in the equilibrium with metallic titanium in NaCl-KCl equimolar molten salt. Materials Transactions, vol. 51, no. 11. pp. 2121–2124. https://doi. org/10.2320/matertrans.M2010238

Seon, F. and Nataf, P. 1988. Production of metals by metallothermia. US patent 4725312.

Serwale, M.R., Coetsee, T., and Fazluddin, S. 2020. Purification of crude titanium powder produced by metallothermic reduction by acid leaching. Journal of the Southern African Institute of Mining and Metallurgy, vol. 120, no. 5. pp. 349–354.

Shuvalov, V.F., Solov’ev, S.L., and Lebedev, Y.S. 1978. ESR investigation of the hydrolysis of titanium(III) in aqueous hydrochloric acid solutions. Bulletin of the Academy of Sciences of the USSR Division of Chemical Science, vol. 27, no. 1. pp. 5–9. https://doi.org/10.1007/bf01153196

Sole, K.C. 1999. Recovery of titanium from the leach liquors of titaniferous magnetites by solvent extraction: Part 1. Review of the literature and aqueous thermodynamics. Hydrometallurgy, vol. 51, no. 2. pp. 239–253. https:/ doi. org/10.1016/s0304-386x(98)00081-4

Straumanis, M.E. and Chen, P.C. 1951. The corrosion of titanium in acids—The rate of dissolution in sulfuric, hydrochloric, hydrobromic and hydroiodic acids. Corrosion, vol. 7, no. 7. pp. 229–237. https://doi.org/10.5006/0010-93127.7.229

Schweitzer, GK. and Pesterfield, L.L. 2010. The Aqueous Chemistry of the Elements. Oxford University Press, New York.

Van Vuuren, D.S., Oosthuizen, S.J., and Heydenrych, M.D. 2011. Titanium production via metallothermic reduction of TiCl₄ in molten salt: Problems and products. Journal of the South African Institute of Mining and Metallurgy, vol. 111, no. 3. pp. 141–147.

Wang, Q., Song, J., Hu, G., Zhu, X., Hou, J., Jiao, S., and Zhu, H. 2013. The equilibrium between titanium ions and titanium metal in NaCl-KCl equimolar molten salt. Metallurgical and Materials Transactions B, vol. 44, no. 4. pp. 906–913. https:// doi.org/10.1007/s11663-013-9853-5

Withers, J.C., Shapovalov, V., Storm, R., and Loutfy, R.O. 2013. The production of titanium alloy powder. Key Engineering Materials, vol. 551. pp. 32–36. https:// doi.org/10.4028/www.scientific.net/KEM.551.32

Yakovleva, E.G., Pechurova, N.I., Martynenko, L.I., and Spitsyn, V.I. 1973. Study of the complex formation of Ti(III) with nitrilotriacetic and diethylenetriaminepentaacetic acids in aqueous solution. Bulletin of the Academy of Sciences of the USSR Division of Chemical Science, vol. 22, no. 8. pp. 1655−1657. https:// doi.org/10.1007/bf00932086

Yan, M., Tang, H.P., and Qian, M. 2015. Scavenging of oxygen and chlorine from powder metallurgy (PM) titanium and titanium alloys. Titanium Powder Metallurgy. Qian, M.A. and Froes, F.H. (eds). Butterworth-Heinemann, Oxford, UK. pp. 253–276. https:// doi.org/10.1016/B978-0-12-800054-0.00015-0

Yang, Z. and Gould, E.S. 2005. Reductions by aquatitanium(II). Dalton Transactions, vol. 10. pp. 1781–1784. https://doi.org/10.1039/b416975c

Yu, C.Z. and Jones, M.I. 2013. Investigation of chloride impurities in hydrogenated–dehydrogenated Kroll processed titanium powders. Powder Metallurgy, vol. 56, no. 4. pp. 304–309. https://doi.org/10.1179/1743290113y.0000000055

Zhu, Z., Zhang, W., and Cheng, C.Y. 2011. A literature review of titanium solvent extraction in chloride media. Hydrometallurgy, vol. 105, no. 3–4. pp. 304–313. https://doi.org/10.1016/j.hydromet.2010.11.006 u

Purification of titanium sponge produced by lithiothermic reduction of titanium tetrachloride

The Journal of the Southern African Institute of Mining and Metallurgy

Affiliation:

1School of Civil, Mining and Environmental Engineering, University of Wollongong, Australia.

2Jilin University of Finance and Economics, China.

Correspondence to: W. Zeng

Email: wz999@uowmail.edu.au

Dates: Received: 30 Apr. 2022 Revised: 8 Oct. 2022 Accepted: 18 Oct. 2022 Published: December 2022

How to cite: Zeng, W., Baafi, E.Y., and Fan, H. 2022

A simulation model to study truck-allocation options.

Journal of the Southern African Institute of Mining and Metallurgy, vol. 122, no. 12, pp. 741–750

DOI ID: http://dx.doi.org/10.17159/24119717/2100/2022

ORCID: W. Zeng https://orcid.org/0000-00034689-003X

A simulation model to study truckallocation options

by W. Zeng1, E.Y. Baafi1, and H. Fan2

Synopsis

We present a discrete event simulator, TSJSim (Truck-Shovel JaamSim Simulator), for evaluating the stochastic and dynamic operational variables in a truck-shovel system. TSJSim offers four truck allocation strategies: Fixed truck assignment (FTA), Minimizing shovel production requirement (MSPR), Minimizing truck waiting time (MTWT), and Minimizing truck semi-cycle time (MTSCT) including the genetic algorithm (GA) optimization and the frozen dispatching algorithm (FDA) optimization rules. Multiple decision points along the haul routes for all the trucks close to the decision points were included in the model. The simulation results indicate that the trends associated with production tons and queuing time utilizing the four truck allocation strategies (MSPR, MTWT, FDA, and GA) all demonstrated similar patterns as the fleet size varied. As the system fleet size increased, the system production tons under these strategies at first increased significantly and then remained relatively constant; the queuing time relating to these strategies showed a positive relationship with the system fleet size. The bunching time decreased when the truck allocation strategies were applied in the model. In the simulated truck-shovel network system with multiple traffic intersections, by assigning the trucks at the intersections, both productivity and fleet utilization increased.

Keywords

truck-shovel system, simulation.,truck allocation strategy, optimization.

Introduction

For a truck-shovel system in an open pit mine, the truck haulage costs have been reported to exceed half of the total direct operating costs (Lizotte and Bonates, 1987). Truck allocation strategies have been applied to improve productivity and/or reduce operating cost by considering alternative truck-shovel assignments in real time in order to increase utilization of system resources (Alarie and Gamache, 2002). By allocating the optimal number of trucks to shovels, the waiting times of trucks in an over-trucked system as well as the idle times for shovels in an under-trucked system can be minimized (Baafi and Ataeepour, 1998). Furthermore, by re-routing trucks when traffic congestion occurs, costs associated with various delays can be minimized (Jaoua, Gamache, and Riopel, 2012b).

According to Alarie and Gamache (2002), the main forms of truck allocation are single stage and multistage systems. The single stage approach assigns trucks to shovels based on one or several criteria without considering any specific production targets or constraints. These criteria are usually heuristic methods based on rules of thumb (Alarie and Gamache, 2002), including fixed truck assignment (Lizotte and Bonates, 1987), minimizing truck waiting time (Baafi and Ataeepour, 1998), minimizing shovel idle time, maximizing truck momentary productivity, and minimizing shovel saturation (Kolonja, Kalasky, and Mutmansky, 1993). The multistage approach, on the other hand, consists of several stages or subproblems (Afrapoli and Askari-Nasab, 2017), which can be usually reduced to an upper stage (i.e., a production optimization problem) and a lower stage (i.e., a real-time dispatching problem). The upper stage aims to set production targets for every shovel according to specific operational constraints, while the lower stage assigns trucks to shovels to minimize the deviation from the production targets set by the upper stage.

The approaches used to solve the production optimization problem in the truck-shovel dispatching models include linear programming (LP) (White and Olson, 1986; Lizotte and Bonates, 1987; Li, 1990; Gurgur, Dagdelen, and Artittong, 2011; Ta, Ingolfsson, and Doucette, 2013; Mena et al., 2013), nonlinear programming (NLP) (Soumis, Ethier, and Elbrond, 1990), goal programming (GP) (Temeng, 1997), and stochastic programming (Ta et al., 2005).

A simulation model to study truck-allocation options

For the real-time dispatching problem, the model developed by White and Olson (1986) assigns trucks to shovels to minimize the deviation between the current path flow rate and the optimal path flow rate specified by the LP model. They created two assignment lists: the first for the trucks and the second for the paths. The dispatching is achieved by matching the ‘best truck’ from the truck list with the ‘neediest path’ from the path list considering the truck capacity, shovel digging rate, expected truck waiting time and travel time, and expected shovel idle time, etc. Elbrond and Soumis (1987) proposed a dispatching procedure that minimizes the sum of squared differences between the average waiting time of trucks and shovels as calculated from the haulage allocation plan and the forecast waiting times based on the current status of the mine operation. However, they did not consider the possibility of assigning more than one truck to a shovel in one decision-making step, and they also assumed that the truck fleet is homogeneous. Bonates and Lizotte (1988) proposed a dispatching method which takes the results from their developed simulator and compares these with an optimal production plan obtained from their LP model. The dispatching criterion with the smallest deviation of results from the optimum production target is chosen as the optimum dispatching rule. Li (1990) proposed a truck dispatching algorithm based on the difference between the actual truck interval time and the optimal truck interval time on a path to a destination. However, a significant disadvantage of this real-time dispatching model is that the truck waiting times at the destinations, especially at the shovels, are ignored. Temeng (1997) proposed a real-time dispatching model based on the transportation problem. In this model, needy shovels are defined as those shovels with current cumulative productions below the target obtained from their GP model. The number of trucks required by each needy shovel is determined by comparing the tonnage for each route required to maintain ore quality and stripping ratios with appropriate truck capacity. However, the model is not able to account for the truck waiting time, which depends on the previously allocated trucks, especially in an overtrucked system.

Ouelhadj and Petrovic (2009) suggested that the intelligent metaheuristic searching methods, including the genetic algorithm, Tabu search (Wu and García de Soto, 2020), and simulated annealing, are more powerful and appropriate for complex system scheduling/control optimization than the simple heuristic rules. Pfeiffer, Kadar, and Monostori (2007) also demonstrated the performance improvement using a dynamic scheduling method based on a genetic algorithm. Jaoua, Gamache, and Riopel (2012a) proposed a metaheuristic model, using the simulated annealing (SA) algorithm to compute the near-optimal assignment in a truck-shovel dispatching system.

Discrete event simulation techniques have been widely used in the mining industry to `evaluate and analyse mining operations (Dindarloo, Osanloo, and Frimpong, 2015; Afrapoli and Askari-Nasab, 2017; Yilmaz and Erkayaoglu, 2021. AskariNasab, Frimpong, and Szymanski (2007) developed an open pit production simulator to represent dynamic expansion of an open pit mine. Fioroni et al. (2008) developed a discrete event simulator that works with an optimization model to implement the short-term production plan. Ebrahim et al. (2015) used GPSS/ H® to develop a discrete event system simulation for a truckshovel system to investigate the environmental impact, taking into account mining haulage performance and production targets. Hashemi and Sattarvand (2015) developed a discrete event

simulation model using Arena simulation software to evaluate the transportation system of a copper mine. Their model is able to monitor the material excavated from different operating benches and considers the -ore grade requirement. Upadhyay and Askari-Nasab (2017) developed a simulation optimization tool that interacts with a GP-based optimization model to generate an uncertainty-based short-term plan.

As identified by Afrapoli and Askari-Nasab (2017), there are still many shortfalls in the existing real-time dispatching algorithms and models. Two major limitations are how to model close to reality and how to determine dynamic best path. For large open-pit mines, there is a large fleet of heterogeneous trucks hauling on a vast network of haul roads in the operation area. Most previous work on simulation of a truck-shovel system (Lizotte and Bonates, 1987; Kolonja, Kalasky, and Mutmansky, 1993; Temeng, 1997; Baafi and Ataeepour, 1998; Hashemi and Sattarvand, 2015; Sofranko, Wittenberger, and Skvarekova, 2015; Que, Anani, and Awuah-Offei, 2016) failed to capture the interaction between the individual vehicles as well as the influence of the dynamic traffic network environment on the real-time truck allocation.

In this paper we present a discrete event simulation model, TSJSim (Truck-Shovel JaamSim Simulator) with the capabilities of evaluating the key performance indicators (KPIs) of a truckshovel system under the influence of truck allocation strategies. TSJSim considers not only the stochastic and dynamic operational elements of the network system, but also the interaction between the individual trucks in the traffic network environment.

Main components of TSJSim

TSJSim was developed using an open source simulation software package, JaamSim (JaamSim, 2018). JaamSim provides the capability of developing new objects in the standard Java programming language. New objects can be programmed with 3D graphics along with the Input Editor and Output Viewer, and can be dragged-and-dropped for direct usage. Twelve new objects were developed for modelling a typical truck-shovel mining network system. The main simulation model objects are OreGenerator, OreSink, OreEntity, Truck, Loader, Dump, Queue, Route, RouteIntersection, RouteSafeZone, Truck-allocationStrategy, and LoaderOperator. Further details about these model objects are provided in Zeng et al. (2016).,

In TSJSim, the dynamic interactions between the haul trucks (i.e., bunching) and between the trucks and the traffic environment (i.e., traffic intersection area and main route priority management) are implemented by the truck velocity module, the truck bunching module, and the intersection management module. Further details about these modules are provided in Zeng, Baafi,and Walker (2019 ).

TSJSim truck allocation approach

In this paper, a truck-allocation decision point is defined as the time or the spatial position at which a truck driver needs to make a decision as to what route to select so as get to a particular destination. This decision may occur before and after loading, before and after dumping, or when a truck arrives at an intersection.

Most of the previous simulation models assume one or two decision points in one truck cycle, either at the loading site or at the dump site or at both. For example, in DISPATCH (White and Olson, 1993), the trucks in the real-time dispatching list are those

The Journal of the Southern African Institute of Mining

A simulation model to study truck-allocation options

that have completed or are about to complete dumping; Hauck (1973) assumed the unloading point to be the decision point for real-time truck dispatching; Jaoua, Gamache, and Riopel (2012a) used a specified regular time interval (the control horizon) to manage the time for dispatching instead of using a decision point.

In the TSJSim simulation model, multiple decision points in the haulage network system within a one truck cycle were considered to handle the complexity of the traffic network and the dynamic operational variables of a surface mine. The RouteIntersection object handles the assignment of the Truck on Route objects. Referring to a typical truck-shovel network system shown in Figure 1, an assignment is generated by the Truckallocation Strategy object to send the Truck to a loading site. This scenario applies as a loaded Truck completes dumping at Dump 2. Moreover, this depends on the system status, e.g., the traffic conditions on the various Routes, the availabilities of the Shovels, the lengths of the Queues at the loading sites and the performance of the LoaderOperators

After hauling for a period of time, the Truck arrives at RouteIntersection a, which provides an opportunity for the Truck to make a decision either to turn left for Shovel 1 or to turn right towards other Shovels {Si, i = 2,3,4,5}. The system status when the Truck arrives at RouteIntersection a may be different from when the Truck was leaving Dump 2. If the Truck-allocation Strategy object regenerates a new truck-allocation solution at that moment, the assignment for the Truck may be different but could be more productive than the assignment when the Truck was leaving Dump 2. After hauling from RouteIntersection a to b, the Truck then makes a further choice between Shovel 2, 3, 4 or 5. A similar decision is made when the Truck arrives at RouteIntersection c, which is the last intersection on the haul route. Thus, it is clear that in a truckshovel network system where the operational variables change continuously, the truck assignment decisions could be made at the decision points on the haulage network to optimize productivity.

In the TSJSim simulation model, the truck-allocation approach is implemented mainly by two objects: the RouteIntersection object and the Truck-allocation Strategy object. The RouteIntersection object specifies all the decision points on Routes as well as the associated possible truck-allocation paths at each decision point. The Truck-allocation Strategy object assigns a Truck object to a destination based on the specified truck-allocation strategy.

Truck allocation paths development

The total possible truck-allocation paths for the trucks to travel from the traffic intersections to all the loading sites or dump sites are specified and stored in a list referred to as the RoutePool list in the RouteIntersection object. For instance, Figure 2 shows an ideal truck-shovel haulage network layout with the decision points for the loaded trucks and the possible paths at the RouteIntersection objects.

The RoutePool list at decision point D has two possible truckallocation paths, i.e., D – Dump 3 and D – Dump 4; the RoutePool list at decision point C contains three possible paths, i.e., C –Dump 2, C –D – Dump 3, and C –D – Dump 4; the RoutePool list at decision point B includes four possible paths, i.e., B – Dump 1, B – C – Dump 2, B – C – D – Dump 3, and B – C – D – Dump 4; the RoutePool list at decision point A has six possible paths, i.e., A – B – Dump 1, A – B – C – Dump 2, A – B – C – D – Dump 3, A – B –C –D – Dump 4, A –D – Dump 3, and A –D – Dump 4. To determine all the possible paths at each RouteIntersection, the route network is a tree structure that consists of the decision points and the destinations being the tree nodes, as shown in Figure 3. The decision points at the lowest level provide the direct routes to the destinations, e.g., decision point D relates to Dump 3 and Dump 4. The decision points at the upper levels provide the routes to both other decision points and the final destinations. For instance, decision point C connects with Dump 2 and another decision point, i.e., D; decision point B connects with Dump 1, and another decision point, i.e., C; decision point A is connected with other decision points, namely B and D.

In TSJSim, the decision points are located with the spatial points on the Route objects, with each decision point at the RouteIntersection having its own RoutePool list. A recursive algorithm which consists of three embedded for-loops and one defined function was developed for generating all the possible truck-allocation paths at the various decision points. The function, named MethodofRoutePool with the three input parameters, calls itself recursively to determine the RoutePool lists.

[1] where

inter = RouteIntersection object which contains the intersecting Route objects route = Route object which consists of various spatial points droute = Truck-allocation path to which the Truck is assigned, consisting of various spatial points.

The starting point of the path is at the RouteIntersection, and the ending point is at the Loader or the Dump or the next RouteIntersection.

Figure 4 illustrates the flow chart for the algorithm. The main aim is to check all the nodes and the associated Route objects of the tree structure from the top to the bottom.

Figure 1—Decision points at intersections in a truck-shovel network system

Figure 2—RoutePool and decision points

Southern African Institute of Mining and Metallurgy

A simulation model to study truck-allocation options

replaced by droute. After that, the third for-loop function loops through all the points on Route (j) to check whether to add point (n) to droute (j) or to implement another MethodofRoutePool for inter (i+1) (the next intersection). Depending on the location of point (n) on Route (j), the following three conditional statements are executed to control the recursion:

➤ If the decision point at inter (i) is connected with a destination, and point (n) is located between inter (i) and the destination, then point (n) is added to droute (j).

Figure 3—Tree structure of decision points on haul routes

The outermost for-loop function loops through all the RouteIntersection objects in the truck-shovel network system. For the ith RouteIntersection object, i.e., inter (i), the MethodofRoutePool (inter, route, droute) is implemented to determine RoutePool (i), which is the RoutePool list at inter (i). The parameter route temporarily saves the Route object that was passed from the previous MethodofRoutePool function (if any), and the parameter droute temporarily saves the paths already generated by all the previous MethodofRoutePool functions (if any). For example, consider the RoutePool list at RouteIntersection A in Figure 2. Suppose the MethodofRoutePool function is used for RouteIntersection C. Then the current route parameter would be Route 2 and the current droute parameter would be the path A-B-C (Figure 3). The initial values of route and droute are set to null, since the starting point of the truck-allocation path at the RouteIntersection contains no previous Route objects or paths (e.g., Node A in Figure 3). The MethodofRoutePool (inter, route, droute) has an inner for-loop function which loops through all the Route objects at inter (i), i.e., all the intersecting routes at the intersection. Within this for-loop, route (j) is compared with the route to check for new branches at the intersection. If route (j) and the route input parameter are two different Route objects, then a new truck-allocation path, i.e., droute (j), is initiated and

➤ If the decision point at inter (i) is connected with another decision point, and point (n) is located between inter (i) and inter (i+1) on route (j), then point (n) is added to droute (j).

➤ If point (n) is the decision point at inter (i+1) on route (j), then the MethodofRoutePool is implemented with inter (i+1), route (j) and droute (j) as the input parameters.

In the case where multiple decision points exist in the system, the spatial points between inter (i) and inter (i+1) are first added to droute (j) at inter (i). Then the second MethodofRoutePool for the next decision point at inter (i+1) is implemented. This process continues until the last MethodofRoutePool function is implemented for the last decision point at the bottom of the tree structure. In the implementation of this last MethodofRoutePool, if the spatial points of the droute (j) are between the last decision point and the destination, then the droute (j) for the Route object at inter (size of inters -1), i.e., the last RouteIntersection object, is added to RoutePool (i). After that, the algorithm executes the second last MethodofRoutePool for inter (size of inters -2), i.e., the second last RouteIntersection object. This process continues until the first MethodofRoutePool is executed, thus solving RoutePool (i) at inter (i) by examining all the decision points from the top to the bottom of the tree structure. By following the above recursive process, all the RoutePool lists of the RouteIntersection objects are generated.

A simulation model to study truck-allocation options

Truck allocation strategy

In TSJSim, the truck allocation decision is made by applying the multi-trucks-at-a-time approach, i.e., the trucks close to the decision points at the loading sites, dump sites, and traffic intersections are all considered in the truck allocation process. For modelling purposes, the truck-shovel haulage system is divided into the following three areas:

➤ Load Area is an area near the loader. Empty trucks haul toward the loader within this area. Trucks forming a queue at the loader and those trucks being loaded are all considered.

➤ Dump Area is an area near the dump. Loaded trucks haul towards the dump within this area. The queuing trucks at the dump and the trucks dumping are all considered.

➤ Intersection Area is an area near the intersection. Trucks hauling inside an intersection area and those trucks waiting outside the intersection area are all considered.

An example is shown, in Figure 5. When Truck 1 finishes loading and is ready for an assignment, in Load Area 1, Truck 2 is waiting, and Truck 3 is travelling empty to Loader 1. In Load Area 2, Truck 4 also travels empty to Loader 2. In the Intersection Area, Truck 5 is hauling a load to Dump 1 and Truck 6 is waiting outside the intersection area according to the passing priority rule (Zeng, Baafi, and Walker, 2019). These trucks are all close to the decision points. Hence Trucks 2, 3, 4, 5, and 6 as well as any other trucks that have already been assigned to respective dump sites could potentially influence the assignment of Truck 1 to a designated dump site.

Four truck-allocation strategies are developed as part of TSJSim model:

➤ Fixed truck assignment (FTA) — each truck is assigned to a fixed shovel and dump at all times. This truck-allocation rule serves as a baseline for comparing and evaluating the effectiveness of other truck-allocation strategies.

➤ Minimizing truck waiting time (MTWT) — the truck is assigned to the shovel or dump that is expected to generate the least amount of expected truck waiting time. The truck

being loaded or dumping and the trucks in the queue are considered when estimating the total expected truck waiting time.

➤ Minimizing shovel production requirement (MSPR) — the shovels have predefined production targets and the trucks are assigned to the shovel with the maximum shortfall between the planned production and the ongoing simulated production.

➤ Minimizing truck semi-cycle time (MTSCT) — two optimization methods, i.e., the genetic algorithm (GA) and the frozen dispatching algorithm (FDA), were developed to implement MTSCT.

Definition of the truck semi-cycle time

One of the measures of the productivity and efficiency of a truckshovel mining system is the truck cycle time. In a complete truck cycle, the truck departs from a loader toward a dump site and then returns from this area back to a loader. The complete truck cycle time includes the loading time, hauling time from the loader to the dump site, queuing time at the dump site, dumping time, hauling time from the dump site to the same loading site or to another one, and queuing time at the loading site. One complete truck cycle includes two destinations:

➤ The departure destination, which is the planned destination of a truck when departing. If a truck is leaving a dump site, then a loading site would be the departure destination; if a truck is leaving a loading site, then a dump site would be the destination for the departing truck.

➤ The returning destination, which is the destination that a truck will return to after arriving at the departure destination. If a truck is leaving a dump site, then a dump site would be the destination for the returning truck. If a truck is leaving a loading site, then a loading site would be the destination.

Due to the influence of the ongoing truck allocations within the entire system, the further the truck travels, the more time the truck will spend on the route, and the more difficult it is to

Southern African Institute of Mining and Metallurgy

A simulation model to study truck-allocation options

estimate the complete truck cycle time. The estimated queuing times at returning destinations vary more than those at departure destinations. If the complete truck cycle time is considered, the varying estimated queuing times at the return destinations may bias the truck allocation decision-making process for the departure destination.

In the TSJSim simulation model, a truck semi-cycle time is defined as the sum of the time durations for a truck travelling from the origin (i.e., a loader, dump or intersection) to its destination (i.e., a dump or loader site) plus the time for queuing and loading or dumping at the departure destination. The influence of the returning destination is not included in the truck semi-cycle time. The objective of the truck allocation algorithm is to obtain the assignment with the minimum estimated truck semi-cycle time.

Components of truck semi-cycle time

The estimated semi-cycle time for a truck at the decision point is expressed as: [2] where etab = estimated semi-cycle time for a truck to travel from origin a, i.e., a loader, dump, or intersection, to destination b, i.e., a dump site or loading site ethb = estimated hauling time to arrive at destination b etqb = estimated initial queuing time at destination b etpb = estimated processing time (loading time or dumping time) at destination b

For the ‘potential truck’ close to a decision point, which is hauling to or waiting at a loader, dump, or intersection, the estimated semi-cycle time is: [3] where etha = estimated hauling time to arrive at origin a, if the truck is still hauling et qa = estimated initial queuing time at origin a, if the truck needs to queue et pa = estimated processing time (loading time or dumping time) at origin a

Suppose one truck just finishes dumping and is ready to be assigned to a loader. There could be n shovels in the network system, i.e., {s1, s2, s3, … , sn} and m trucks that need to be allocated in this assignment, i.e., {t1, t2, t3, … , tm}. The estimated semi-cycle time for each truck to reach the next decision point at a loader (when the truck finishes loading) can be expressed by Equation [4]: [4] where ET = matrix of estimated semi-cycle times for assigning m trucks to n shovels etsjti = estimated semi-cycle time for truck ti to arrive at shovel sj and to finish loading

If the estimated semi-cycle time of each truck is independent of all others, then the solution for ti equals the minimum estimated semi-cycle time in {ets1ti, ets2ti, ets3ti,…, etsnti}, i.e., min{ets1ti, ets2ti, ets3ti,…, etsnti}. However, the estimated semi-cycle times are not independent of one another because the trucks interact with each other in the truck-shovel mining network system. The interaction between the trucks includes the bunching effect on the haul route, the passing priority in the intersection area, and most importantly, queuing at the loader or dump site.

The estimated queuing time expressed in Equations [2] and [3] is an initial value which is the combined result of the present queue length at a loader or dump and the estimated hauling time. However, the actual estimated queuing time is not only influenced by the queue length, but also varies according to the truckallocation. In TSJSim, optimization, methods were designed to change the estimated queuing time to reflect the influence of truck allocation decisions. As more trucks are assigned to the same loader or dump, the estimated queuing time increases, and the resultant increase in the estimated semi-cycle time is considered in the truck assignment.

Optimization methods for searching for the optimum destination with MTSCT

The genetic algorithm (GA) seeks the near-optimal solution by selecting the best solution and its neighbour, and then replacing the worst solution by the selected neighbour until the end of iterations (Gosavi, 2015). The general process structure of the GA is suitable for solving computationally complex problems (Alipour et al., 2017) and it has been used to tackle complex open-pit production scheduling problems due to its ability of producing near-optimal solutions within a short timeframe (Muke, Nhleko, and Musingwini, 2021).

In this paper, the GA and a newly designed algorithm based on the general structure of the GA, i.e, the frozen dispatching algorithm (FDA), were developed to solve the truck allocation problem, respectively.

Genetic algorithm (GA)

In TSJSim, the decision variables (Trucks) are stored in a list named truckListDV, {t1, t2, t3, … , tm}, and their values or destinations, (at shovels or dump sites) are stored in a list named DVV, {s1, s2, s3, … , sn}. The size of the solutionList is set to the number of destinations in the system, {SL1, SL2, SL3,…, SLj,…,SLn}. A solution, SLj, consists of m elements for all the decision variables. The element value is the estimated truck semi-cycle time:

where SLj = jth solution, j ∈ [1,n] etsjti = estimated truck semi-cycle time ti to destination point sj, i ∈ [1,m]

Let r denote the iteration number of the algorithm and r max the maximum number of iterations to be performed. Set r = 1 and r max = a constant value depending on the size of the model. There is no rule to determine an optimal iteration number and it is usually set by the permissible amount of computer time. The GA steps are as follows:

➤ Calculate the function value for each solution, i.e., f(SLj), which is the accumulated estimated semi-cycle times for all the trucks. The steps for calculating f(SLj) are as follows:

The Journal of the Southern African Institute of Mining and Metallurgy

A simulation model to study truck-allocation options

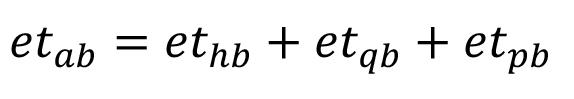
Rank etsjti in SLj in ascending order. In the new SLj, t1 will be the first truck to arrive at destination sj, t2 the second truck, and ti the ith truck. Modify the estimated queuing time of each semi-cycle time element. When ti arrives at sj, if the shovel is still loading ti-1, i.e., the expected arrival time of ti is less than the expected departure time of ti-1, then the queuing time is added to etsjti. Sum all the modified semi-cycle time elements in SLj, namely, [6]

➤ Compare and rank SLj in solutionList according to f(SLj). Denote the minimum by SLmin and the maximum by SLmax Randomly select a neighbour of SLmin, and call it SLnew, i.e., new = min + a random integer{-1,1}. Replace SLmax by SLnew, in other words, SLmax = SLnew. Referring to Figure 6, suppose SLmin is SL2 and SLmax is SL4. Initiate SLnew by reproducing SLmin, and then replace all the elements in SLnew with the elements in the neighbouring solution list. For instance, the replacement for ets2t1 can be either ets1t1 or ets3t1, depending on the generated random number.

➤ Increment r by 1. If r = r max, return SLmin as the optimum solution and STOP. Otherwise, go back to step 1.

Frozen dispatching algorithm (FDA)

The FDA module was originally designed for the TSJSim model based on the actual behaviour of a truck-shovel mining system. The FDA’s basic steps are summarized below:

➤ Select the element with a minimum value or element in list ETti = {ets1ti ets2ti ets3ti etsnti}, i ∈[1,m], and store the element(s) of which the destination is sj in list ETsj, j ∈ [1,n]. For example in Figure 7, suppose ets1ti is the minimum element in ETti = {ets1t1 ets2t1 ets3t1 etsnt1}, and ets1t2 is the minimum element in ETt2 = {ets1t2 ets2t2 ets3t2 etsnt2}. Then ets1t1 and ets1t2 are stored in ET s1 . If ets3t3 ets2t1 is the minimum element in ETt3 = {ets1t3 ets2t3 ets3t3 ... etsnt3}, then ets3t3 is stored in ET s3.

➤ Compare and rank the elements stored in ET sj, j ∈ [1, n]. If the minimum element in ET sj, j ∈ [1, n], is etsjtx, meaning the truck tx is supposed to be the first truck to arrive at sj and there will be no increase in queuing time for tx at sj, then the value of etsjtx will not be changed. This assignment is ‘frozen’ and tx will be assigned to sj. For example, in Figure 7, the two elements, ets1t1 and ets1t2 in ET s1, are compared and ranked. If ets1t2 is the minimum element, then ets1t2 is ‘frozen’ (shaded block) and t2 will be assigned to s1 ET s3 contains only one

element, ets3t3. Thus, ets3t3 is ‘frozen’ (shaded block) and t3 will be assigned to s3. ➤ Consider the elements in ET sj, j ∈ [1, n], that are not ‘frozen’. The truck with the minimum estimated time duration should arrive at the destination first and cause other ‘unfrozen’ trucks in ET sj to wait on the condition that they arrive at the destination before the already assigned truck finishes loading or dumping. Therefore, the expected queuing time is added to other elements in ET sj. To add the queuing time, first add the queuing time to the second minimum element (e.g., ets1t1 in Figure 7) and then repeat steps 1 and 2. If: ets1t1 is still the minimum element in ETt1, this element would be ‘frozen’.

ets2t1 is the minimum element in ETt1, since it is the only element in ET s2, it would be ‘frozen’.

ets3t1 is the minimum element in ETt1, it would be compared with other ‘unfrozen’ elements in ET s3 to decide whether it is the second minimum element in ET s3 .

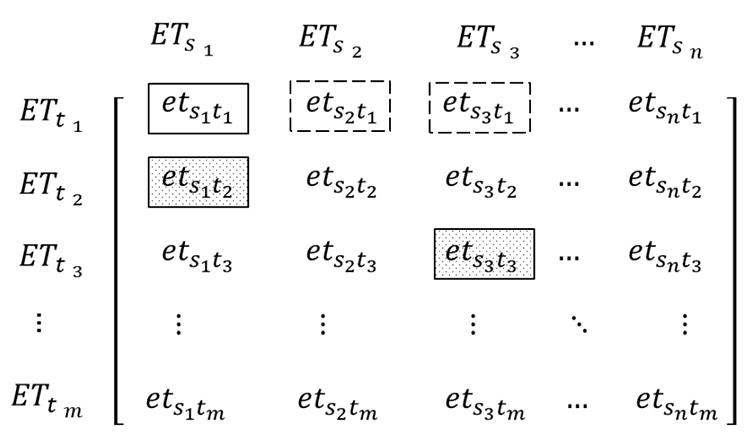
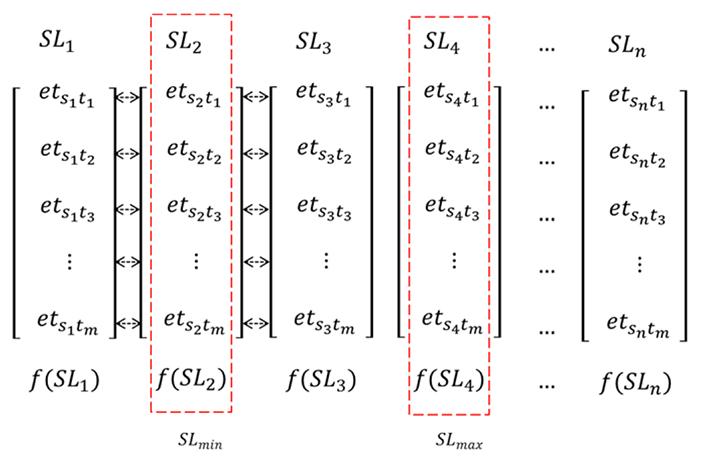
After the second minimum element is ‘frozen’, the third minimum element in ET sj is considered. This process continues until all the elements in ET sj are all ‘frozen’.

Comparison of truck allocation strategies

The following two sensitivity analyses were evaluated using the TSJSim model.

➤ The influence of the truck allocation strategies on the KPIs in the case where the truck-shovel matches varied.

➤ The influence of multiple truck-allocation decision points on the KPIs of the truck-shovel system.

Truck allocation strategies where the truck-shovel matches change

A simplified simulation model was established using TSJSim. This model was validated using field data collected by Shaw (2012) at a truck-shovel mining operation in Western Australia. The mining operation, known as Easter Ridge OB23/25, consists of four loading sites, named S4C, P3WC, P3EC, and P4, and four dumping sites, P1ED, P3WD, P4WD and ROM dump (Figure 8). The routes between P3WC, S4C, and the ROM dump were selected for this sensitivity analysis. The fleet in the system comprises Shovel 1 working at P3WC with associated trucks (named fleet 1, made up of CAT 785Cs) and Shovel 2 serving S4C with associated trucks (named fleet 2, made up of Komatsu 860Es). The main operational inputs are shown in Table I.

Four truck allocation strategies were considered. They are Fixed Truck Assignment (FTA), Minimizing Shovel Production Requirement (MSPR), Minimizing Truck Waiting Time (MTWT,

Southern African Institute of Mining and Metallurgy

Figure 6—The genetic algorithm (GA) method

Figure 7—The frozen dispatching algorithm (FDA) method

A simulation model to study truck-allocation options

Figure 8—Layout of haul routes for the validated model

Table I

eight Komatsu 860Es in the system, the shift production tonnages remained stable.

Operational

input parameters for truck-allocation evaluation

Parameter Value

Material density (kg/m³) 2 788

Material swell factor 1.05

Shovel bucket fill factor 0.9

Shovel bucket capacity (m³) 15

Shovel operater work cycle time (s) Normal (25, 10)

Shift duration (h) 8

Truck type CAT 785C, Komatsu 860E

Safe bunching distance (m) 25

Dumping time (s) Normal (35, 11) for CAT 785C, Normal (46, 12) for Komatsu 860E

and Minimizing Truck Semi-cycle Time (MTSCT), which included GA and FDA optimization. The simulation results included system production, truck queuing time, and bunching time.

The total fleet size varied from 10 to 19 so that the truckshovel match changed from both shovels under-trucked, to one shovel under-trucked and the other over-trucked, and then to both shovels over-trucked.

The assumptions for the model implementation are as follows: ➤ The trucks are not allowed to overtake each other along the routes

➤ The simulation model performs eight hours per shift during one simulation run, using a hot seat shift changeover, without considering other operational delays in the system ➤ Each design experiment is implemented with 100 simulation replications.

The simulation results are as follows.

System production tons

Figure 9 shows the relationship between the system shift production tons and the system fleet size using the four truckallocation rules, i.e., MSPR, MTWT, GA, and FDA.

The MSPR, MTWT, GA, and FDA rules demonstrated similar increasing trends in shift production tonnages. Production using FDA remained higher compared with other rules. The trends can be divided into the following stages:

➤ Fleet size ∈ [10,11]: When both Shovel 1 and Shovel 2 were under-trucked, as the fleet size increased from 10 to 11, the shift production tonnages increased.

➤ Fleet size ∈ [12,16]: When Shovel 1 was under-trucked and Shovel 2 was over-trucked, as the fleet size increased from 12 to 14, the shift production tonnages continued to increase. When the total fleet size exceeded 14, i.e., six CAT 785Cs and

➤ Fleet size ∈ [17,19]: When both Shovel 1 and Shovel 2 were over-trucked, all the shift production tonnages remained stable as the total fleet size increased from 17 to 19.

Queuing time

Figure 10 shows the trends of total queuing time (includes times at shovel and dump) versus the system fleet size using the truck allocation rules. The MSPR, MTWT, GA, and FDA rules all resulted in similar trends with respect to the queuing times. The queuing times showed a stable increasing trend as the fleet size increased. When the fleet size increased from 12 to 16 (when Shovel 1 is under-trucked and Shovel 2 is over-trucked), the queuing times had similar increasing rates as when fleet size increased from 17 to 19 (when both shovels are over-trucked). The queuing time using the FDA rule remained lower than queuing times generated using other rules.

Bunching time

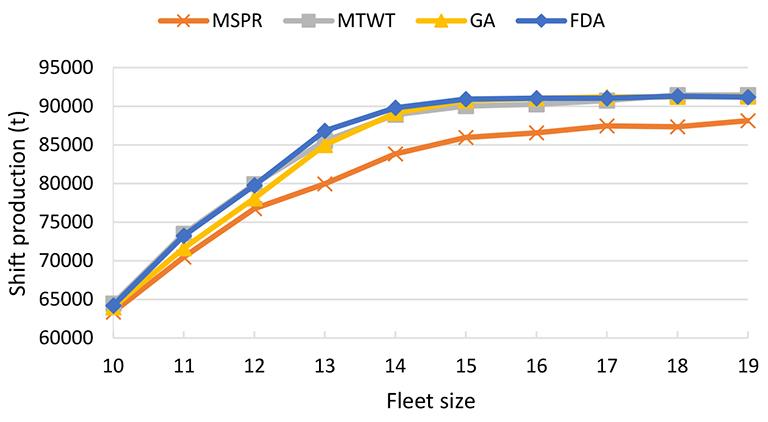
Figure 11 illustrates the trends of bunching times versus the fleet size using the truck allocation rules, ,., FTA, MSPR, MTWT, GA, and FDA. The bunching times using the MSPR, MTWT, GA. and FDA rules were all less than the bunching time when using the FTA rule, meaning that the bunching effect in the model was reduced when the truck allocation rules were applied.

Figure 10—Relationship between queuing time and fleet size relative to truck-allocation rules

The Journal of the Southern African Institute of Mining and Metallurgy

Figure 9—Relationship between production tons and fleet size relative to truck-allocation rules

A simulation model to study truck-allocation options

Multiple decision points effect

A truck-shovel haulage network system with multiple traffic intersections was constructed. Figure 12 illustrates the model layout, which consists of three loading areas, three dumps, and four traffic intersections along with the associated routes. There are 21 trucks (11 CAT 785Cs and 10 Komatsu 860Es) and three shovels of the same type in the system. The main operational inputs are shown in Table II .

Two cases were considered in the sensitivity analysis:

➤ Trucks were assigned only at loading areas and dumping areas and the decision points at traffic intersections were not considered.

➤ Trucks were also assigned at the decision points located at traffic intersections.

The Minimizing Shovel Production Requirement (MSPR), the Minimizing Truck Waiting Time (MTWT), and the Frozen Dispatching Algorithm (FDA) were considered for the sensitivity analysis. The simulation outputs included the system shift production tons and the total lost time, i.e., the sum of total queuing time and total bunching time.

Figure 13 illustrates the system shift production tons using the MSPR, MTWT, and FDA rules. If the decision points at the intersections were not considered, the system shift production tons using the MSPR, MTWT, and FDA rules were 63 114 t, 79 684 t, and 80 577 t, respectively. If the decision points at the intersections were considered, the system shift production tons using the MSPR, MTWT, and FDA rules increased to 70 196 t, 82 090 t, and 85940 t, respectively.

Figure 14 illustrates the total lost times using the MSPR, MTWT, and FDA rules. If the decision points at the intersections were not considered, the total lost time using the MSPR, MTWT and FDA rules was 3 271 minutes (54.5 hours), 2 147 minutes (35.8 hours), and 1 679 minutes (28.9 hours), respectively. If the decision points at the intersections were considered, the total lost time using the MSPR, MTWT, and FDA rules decreased to 2 781 minutes (46.4 hours), 1 513 minutes (25.2 hours), and 1 168 minutes (19.5 hours), respectively.

By considering the decision points at the intersections in the simulation model, both the system productivity and the fleet utilization significantly improve. According to the observation, the intersection decision points should be considered in the truck allocation decision-making process.

Conclusions

A realistic discrete event truck-shovel JaamSim simulator

Figure 11—Relationship between bunching time and fleet size relative to truck-allocation rules

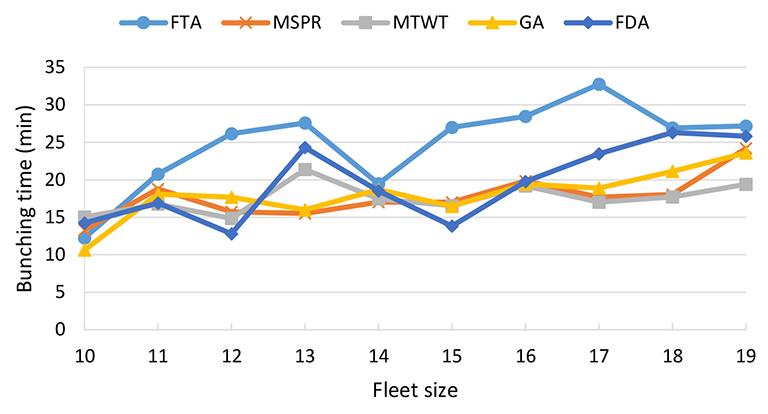
(TSJSim) was developed and integrated with the traffic module and the truck allocation module. The truck allocation module considers multi-trucks-at-a-time and multi-decision-points in the truck allocation strategy. The frozen dispatching algorithm and genetic algorithm were developed for the truck allocation optimization. The sensitivity analyses were designed and implemented based on the TSJSim simulation model. The inferences drawn from the truck-allocation evaluation models are summarized as follows.

➤ In the simulated truck-shovel system with two fleets: the changing trends for the production and queuing times utilizing the four truck-allocation strategies (MSPR, MTWT, FDA, and GA) all demonstrated similar patterns as the fleet size varied. As the system fleet size increased, the system production tons under these truck-allocation strategies at first increased significantly and then remained stable. The queuing time under these truck allocation strategies showed a positive relationship with the system fleet size. The bunching time decreased when the truck allocation strategies were applied in the model.

➤ In the simulated truck-shovel network system with multiple traffic intersections, both productivity and fleet utilization increased by assigning the trucks at the intersections. Thus, the multiple decision points along the haul routes should be considered in the truck allocation decision-making process.

Generally, the optimum fleet size for a truck-shovel system is determined using the MF (s) of the loader(s). Yet, when truck allocation strategies are applied, the number of trucks assigned to the loaders, the loader cycle times, and the truck cycle times may vary owing to flexible truck assignments. This issue is remedied with TSJSim, which can evaluate the influence of the truck allocation strategies on KPIs when the system fleet size is changed.

Figure 12—Layout for the multiple decision points model

Southern African Institute of Mining and Metallurgy

A simulation model to study truck-allocation options

simulation-based real time control architecture: Application to truck control system. Computers in Industry, vol. 63, no. 9. pp. 882−894.

Jaoua, A., Riopel, D., and Gamache, M. 2012b. A simulation framework for realtime fleet management in internal transport systems. Simulation Modelling Practice and Theory, vol. 21, no. 1. pp. 78−90.

Kolonja, B., Kalasky, D.R., and Mutmansky, J.M. 1993. Optimization of dispatching criteria for open-pit truck haulage system design using multiple comparisons with the best and common random numbers. Proceeding of the 1993 Winter Simulation Conference, Piscataway, NJ. IEEE, New York. pp. 393−401.

Li, Z. 1990. A methodology for the optimum control of shovel and truck operations in open-pit mining. Mining Science and Technology, vol. 10, no. 3. pp. 337−340.

Lizotte, Y. and Bonates, E. 1987. Truck and shovel dispatching rules assessment using simulation. Mining Science and Technology, vol. 5, no. 1. pp. 45−58.

Mena, R., Enrico, Z., Fredy, K., and Adolfo, A . 2013. Availability-based simulation and optimization modeling framework for open-pit mine truck allocation under dynamic constraints. International Journal of Mining Science and Technology, vol. 23, no.1. pp. 113−119.

Muke, P.M., Nhleko, A.S., and Musingwini, C. 2021. A genetic algorithm model for optimising long-term open-pit mine production scheduling. APCOM 2021. Proceedingsof Minerals Industry 4,0, 29 August 2 September. Southern African Institute of Mining and Metallurgy, Johannesburg.

Ouelhadj, D. and Petrovic, S. 2009. A survey of dynamic scheduling in manufacturing systems. Journal of Scheduling, vol. 12, no. 4. pp. 417−431.

Pfeiffer, A., Kadar, B., and Monostori, L. 2007. Stability-oriented evaluation of rescheduling strategies, by using simulation. Computers in Industry, vol. 58, no. 7. pp. 630−643.

Figure 14—Total lost times with and without decision points

References

Afrapoli, A.M. and Askari-Nasab, H. 2017. Mining fleet management systems: A review of models and algorithms. International Journal of Surface Mining, Reclamation and Environment, vol. 33, no. 1. pp. 42−60. doi: 10.1080/17480930.2017.1336607

Alarie, S. and Gamache, M. 2002. Overview of solution strategies used in truck dispatching systems for open pit mines. International Journal of Surface Mining, Reclamation and Environment, vol. 16, no. 1. pp. 59−76.

Alipour, A., Khodaiari, A.A., Jafari, A., and Moghaddam, R.T. 2017. A genetic algorithm approach for open-pit mine production scheduling. International Journal of Mining and Geo-Engineering, vol. 1, no. 51. pp. 47−52.

Askari-Nasab, H., Frimpong, S., and Szymanski, J. 2007. Modelling open pit dynamics using discrete simulation. International Journal of Surface Mining, Reclamation and Environment, vol. 21, no. 1. pp. 35−49.

Baafi, E. Y. and Ataeepour, M. 1998. Using ARENA® to simulate truck-shovel operation. Mineral Resources Engineering, vol. 7, no. 3. pp. 253−266.

Bonates, E. and Lizotte, Y. 1988. A computer simulation model to evaluate the effect of dispatching. International Journal of Surface Mining, Reclamation and Environment, vol. 2, no. 2. pp. 99−104.

Dindarloo, S.R., Osanloo, M., and Frimpong, S. 2015. A stochastic simulation framework for truck and shovel selection and sizing in open pit mines. Journal of The Southern African Institute of Mining and Metallurgy, vol. 115, no. 3. pp. 209−219.

Ebrahim, T., John, S., Virginia, I., and Danny, T. 2015. Simulation and animation model to boost mining efficiency and enviro-friendly in multi-pit operations, International Journal of Mining Science and Technology, vol. 25, no. 4. pp. 671−674.

Elbrond, J. and Soumis, F. 1987. Towards integrated production planning and truck dispatching in open pit mines. International Journal of Surface Mining, Reclamation and Environment, vol. 1, no. 1. pp. 1−6.

Fioroni, M.M., Franzese, L.A.G., Bianchi, T.J., Ezawa, L.R.P., and Miranda, G. 2008. Concurrent simulation and optimization models for mining planning. Proceedings of the 2008 Winter Simulation Conference, Miami, FL, 7-10 December 2008.. IEEE, New York. doi: 10.1109/WSC.2008.4736138

Gosavi, A . 2015. Simulation-based Optimization: Parametric Optimization Techniques and Reinforcement Learning. Springer, New York.

Gurgur, C.Z., Dagdelen, K., and Artittong, S. 2011. Optimisation of a real-time multi-period truck dispatching system in mining operations. International Journal of Applied Decision Sciences, vol. 4, no. 1. pp. 57−79.

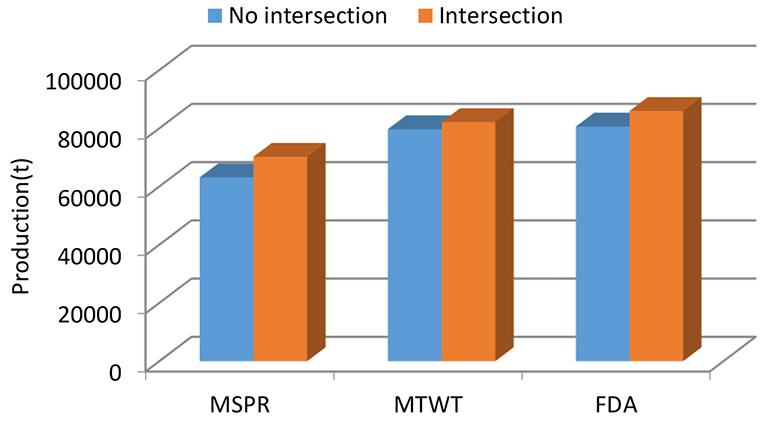
Hashemi, A. S. and Sattarvand, J. 2015. Simulation based investigation of different fleet management paradigms in open pit mines - A case study of Sungun copper mine. Archives of Mining Sciences, vol. 60, no. 1. pp. 195−208.

Hauck, R.F. 1973. A real-time dispatching algorithm for maximizing open-pit mine production under processing and blending requirements. Proceedings of the Seminar on Scheduling in Mining, Smelting and Metallurgy, Montreal, Canada. CIM, Montreal.

JaamSim. 2022. JaamSim software. http://jaamsim.com/ [accessed 1 April 2022].

Jaoua, A., Gamache, M., and Riopel, D. 2012a. Specification of an intelligent

Que, S., Anani, A., and Awuah-Offei, K. 2016. Effect of ignoring input correlation on truck–shovel simulation. International Journal of Mining, Reclamation and Environment, vol. 30, no. 5-6. pp. 405−421.

Shaw, G. 2012. Proactive production estimation and fleet management of a surface mining operation. BE (Mining) thesis, University of Wollongong.

Sofranko, M., Wittenberger, G., and Skvarekova, E. 2015. Optimisation of technological transport in quarries using application software. International Journal of Mining and Mineral Engineering, vol. 6. pp. 1−13.

Soumis, F., Ethier, J., and Elbrond, J. 1990. Evaluation of the new truck dispatching in open pit mines. Proceedings of the 21st International Symposium on the Application of Computers and Operations Research In the Minerals Industry pp. 674-682.

Ta, C.H., Kresta, J.V., Forbes, J.F., and Marquez, H.J. 2005. A stochastic optimization approach to mine truck allocation. International Journal of Surface Mining, Reclamation and Environment, vol. 19, no. 3. pp. 162−175.

Ta, C.H., Ingolfsson, A., and Doucette, J. 2013. A linear model for surface mining haul truck allocation incorporating shovel idle probabilities. European Journal of Operational Research, vol. 231, no. 3. pp. 770−778.

Temeng, V.A . 1997. A computerized model for truck dispatching in open pit mines. PhD thesis, Michigan Technological University.

Upadhyay, S.P. and Askari-Nasab, H. 2017. Dynamic shovel allocation approach to short-term production planning in open-pit mines. International Journal of Mining, Reclamation and Environment, vol. 33, no. 1. pp. 1−20. doi: 10.1080/17480930.2017.1315524

White, J.W. and Olson, J.P. 1986. Computer-based dispatching in mines with concurrent operating objectives. Mining Engineering, vol. 38, no.11. pp. 1045−1054.

White, J. W. and Olson, J.P. 1993. On improving truck/shovel productivity in open pit mines. CIM Bulletin, vol. 86, no. 973. pp. 43−49.

Wu, K. and García de Soto, B. 2020. Spatiotemporal modelling of lifting task scheduling for tower cranes with a tabu search and 4-D simulation. Frontiers in Built Environment, vol. 6, no. 79. doi: 10.3389/fbuil.2020.00079

Yilmaz, E. and Erkayaoglu, M. 2021. A discrete event simulation and data-based framework for equipment performance evaluation in underground coal mining. Mining, Metallurgy & Exploration, vol. 38. pp. 1877–1891.

Zeng, W., Baafi, E.Y., Walker, D., and Cai, D. 2016. A 3D discrete event simulation model of a truck-shovel network system. Proceedings of the Ninth AUSIMM Open Pit Operators' Conference, Kalgoorlie, Australia. Australasian Institute of Mining and Metallurgy, Melbourne. pp. 265−273.

Zeng, W., Baafi, E.Y., and Walker, D. 2019. A simulation model to study bunching effect of a truck-shovel system. International Journal of Mining, Reclamation and Environment, vol. 33, no. 2. pp. 1−16. doi: 10.1080/17480930.2017.1348284

CRediT author statement

Weiguo Zeng: Conceptualization, Methodology, Software, Investigation, Validation, Formal analysis, Writing, Visualization; Ernest Baafi: Resources, Writing- Reviewing and Editing, Supervision, Project administration; Haiying Fan: Software, Investigation, Validation. u

Figure 13—System shift production tons with and without decision points

NATIONAL & INTERNATIONAL ACTIVITIES

11-13 January 2023 — GSSA Geocongress

University of Stellenbosch Campus, Stellenbosch, South Africa

Tel: 021 910 1913

E-mail: geocongress@allevents.co.za Website: https://allevents.eventsair.com/geocongress/ 13-17 February 2023 — Principles of diamond processing

University of the Witwatersrand, Johannesburg, South Africa Website: https://wits-enterprise.co.za/c/principles-ofdiamond-processing/contact

22-23 February 2023 — Drilling and Blasting Online Short Course 2023

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za

13-16 March 2023 — 8TH Sulphur and Sulphuric Acid Conference 2023

The Vineyard Hotel, Newlands, Cape Town, South Africa

Contact: Gugu Charlie Tel: 011 538-0238

E-mail: gugu@saimm.co.za Website: http://www.saimm.co.za

24-25 April 2023 — Southern African Hydrogen and Fuel Cell Conference 2023

From fundamentals to accelerated integration Hazendal Wine Estate, Stellenbosch, Cape Town

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za

11-14 June 2023 — European Metallurgical Conference 2023

Abstracts are to be completed online on https://bit.ly/ Enter2021YPLCfinals

13-15 June 2023 — Copper Cobalt Africa in association with the 10TH Southern African Base Metals Conference 2023

Avani Victoria Falls Resort, Livingstone, Zambia

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za

19-22 June 2023 — Introduction to Multiple-Point Statistics Online Course

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za

25-28 June 2023 — SME APCOM 2023

Intelligent Mining: Innovation, Vision, and Value Rapid City, South Dakota, USA E-mail: Andrea.Brickey@sdsmt.edu

Website: https://www.smenet.org/Conferences/SMEAPCOM

26-29 June 2023 — 26th World Mining Congress 2023 Brisbane Australia Website: https://www.wmc2023.org/ 28-29 June 2023 — Digital Transformation in Mining 2023

Putting digital technologies to work

The Canvas, Riversands, Fourways

Contact: Gugu Charlie Tel: 011 538-0238

E-mail: gugu@saimm.co.za Website: http://www.saimm.co.za

July 2023 — 10th World Gold Conference Xiamen, China E-mail: world@china-gold.org Website: http://world.china-gold.org/# 25-26 July 2023 — Diamonds Source to Use 2023 Conference

New Beginnings A brave new (diamond) world Birchwood Hotel and OR Tambo Conference Centre, Boksburg, Johannesburg

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za 4-7 September 2023 — Geometallurgy Conference 2023

Geomet meets Big Data Hazendal Wine Estate, Stellenbosch, Western Cape Contact: Gugu Charlie Tel: 011 538-0238

E-mail: gugu@saimm.co.za Website: http://www.saimm.co.za

12-14 September 2023 — 10th International Conference on Ground Support in Mining and Underground Construction Perth, Western Australia Website: https://www.acggroundsupport.com/ 27-28 September 2023 — SAIMM Diversity and Inclusion Dialogue 2023 (DIMI)

Intersectionality in the Minerals Industry From Awareness to Action Avianto, Muldersdrift, Johannesburg

Contact: Camielah Jardine Tel: 011 538-0237

E-mail: camielah@saimm.co.za Website: http://www.saimm.co.za

11-13 October 2023 — 11th International Ground Freezing Symposium

London

E-mail: events@iom3.org Website: https://www.iom3.org/events-awards/11thinternational-symposium-on-ground-freezing.html

Company affiliates

The following organizations have been admitted to the Institute as Company Affiliates

3M South Africa (Pty) Limited

acQuire Technology Solutions

AECOM SA (Pty) Ltd

AEL Mining Services Limited

African Pegmatite (Pty) Ltd

Air Liquide (Pty) Ltd

Alexander Proudfoot Africa (Pty) Ltd

Allied Furnace Consultants

AMEC Foster Wheeler

AMIRA International Africa (Pty) Ltd

ANDRITZ Delkor (Pty) Ltd

ANGLO Operations Proprietary

Anglogold Ashanti Ltd

Arcus Gibb (Pty) Ltd

ASPASA

Aurecon South Africa (Pty) Ltd

Aveng Engineering

Aveng Mining Shafts and Underground

Axiom Chemlab Supplies (Pty) Ltd

Axis House Pty Ltd

Bafokeng Rasimone Platinum Mine

Barloworld Equipment -Mining

BASF Holdings SA (Pty) Ltd

BCL Limited

Becker Mining (Pty) Ltd

BedRock Mining Support Pty Ltd

BHP Billiton Energy Coal SA Ltd

Blue Cube Systems (Pty) Ltd

Bluhm Burton Engineering Pty Ltd

Bond Equipment (Pty) Ltd

BOUYGUES Travaux Publics

Caledonia Mining South Africa Plc

Castle Lead Works

CDM Group

CGG Services SA

Coalmin Process Technologies CC

Concor Opencast Mining

Concor Technicrete

Council for Geoscience Library

CRONIMET Mining Processing SA Pty Ltd

CSIR Natural Resources and the Environment (NRE)

Data Mine SA

Digby Wells and Associates

DRA Mineral Projects (Pty) Ltd

DTP Mining - Bouygues Construction

Duraset

EHL Consulting Engineers (Pty) Ltd

Elbroc Mining Products (Pty) Ltd

eThekwini Municipality

Ex Mente Technologies (Pty) Ltd

Expectra 2004 (Pty) Ltd

Exxaro Coal (Pty) Ltd

Exxaro Resources Limited

Filtaquip (Pty) Ltd

FLSmidth Minerals (Pty) Ltd

Fluor Daniel SA (Pty) Ltd

Franki Africa (Pty) Ltd-JHB Fraser Alexander (Pty) Ltd

G H H Mining Machines (Pty) Ltd

Geobrugg Southern Africa (Pty) Ltd

Glencore

Gravitas Minerals (Pty) Ltd

Hall Core Drilling (Pty) Ltd Hatch (Pty) Ltd

Herrenknecht AG

HPE Hydro Power Equipment (Pty) Ltd

Huawei Technologies Africa (Pty) Ltd

Immersive Technologies

IMS Engineering (Pty) Ltd

Ingwenya Mineral Processing (Pty) Ltd

Ivanhoe Mines SA

Kudumane Manganese Resources Leica Geosystems (Pty) Ltd

Loesche South Africa (Pty) Ltd

Longyear South Africa (Pty) Ltd

Lull Storm Trading (Pty) Ltd Maccaferri SA (Pty) Ltd Magnetech (Pty) Ltd

MAGOTTEAUX (Pty) LTD

Malvern Panalytical (Pty) Ltd Maptek (Pty) Ltd

Maxam Dantex (Pty) Ltd

MBE Minerals SA Pty Ltd

MCC Contracts (Pty) Ltd

MD Mineral Technologies SA (Pty) Ltd

MDM Technical Africa (Pty) Ltd

Metalock Engineering RSA (Pty)Ltd

Metorex Limited

Metso Minerals (South Africa) Pty Ltd

Micromine Africa (Pty) Ltd MineARC South Africa (Pty) Ltd

Minerals Council of South Africa

Minerals Operations Executive (Pty) Ltd MineRP Holding (Pty) Ltd Mining Projections Concepts Mintek

MIP Process Technologies (Pty) Limited

MLB Investment CC

Modular Mining Systems Africa (Pty) Ltd

MSA Group (Pty) Ltd

Multotec (Pty) Ltd

Murray and Roberts Cementation

Nalco Africa (Pty) Ltd

Namakwa Sands(Pty) Ltd

Ncamiso Trading (Pty) Ltd

Northam Platinum Ltd - Zondereinde Opermin Operational Excellence

OPTRON (Pty) Ltd

Paterson & Cooke Consulting Engineers (Pty) Ltd

Perkinelmer

Polysius A Division Of Thyssenkrupp Industrial Sol

Precious Metals Refiners

Rams Mining Technologies Rand Refinery Limited

Redpath Mining (South Africa) (Pty) Ltd

Rocbolt Technologies

Rosond (Pty) Ltd

Royal Bafokeng Platinum

Roytec Global (Pty) Ltd

RungePincockMinarco Limited

Rustenburg Platinum Mines Limited Salene Mining (Pty) Ltd

Sandvik Mining and Construction Delmas (Pty) Ltd

Sandvik Mining and Construction RSA(Pty) Ltd

SANIRE

Schauenburg (Pty) Ltd

Sebilo Resources (Pty) Ltd

SENET (Pty) Ltd

Senmin International (Pty) Ltd

SISA Inspection (Pty) Ltd

Smec South Africa

Sound Mining Solution (Pty) Ltd

SRK Consulting SA (Pty) Ltd

Time Mining and Processing (Pty) Ltd

Timrite Pty Ltd

Tomra (Pty) Ltd

Traka Africa (Pty) Ltd

Ukwazi Mining Solutions (Pty) Ltd

Umgeni Water

Webber Wentzel

Weir Minerals Africa

Welding Alloys South Africa Worley

The Southern African Institute of Mining and Metallurgy in collaboration with the Zululand Branch are organising:

2023

TWELFTH INTERNATIONAL HEAVY MINERALS CONFERENCE

21-22 AUGUST 2023 THE CAPITAL ZIMBALI, BALLITO, KWAZULU-NATAL

Countering risks in an evolving future for heavy minerals

CONFERENCE THEME

The HMC series of conferences has previously been focused on mining and processing of heavy minerals. Whilst this conference will still focus on these important issues, there is a shift in focus to include some of the more strategic risks affecting this industry. With the recent global changes such as climate change and its effect on operations close to sea level, the energy crisis and its effect on the economics of smelting and geopolitical risk and its effect on supply chains dependent on unfriendly countries. The future of the industry is now at risk from such changes which are outside of its immediate control. Failure to recognise these significant risks could impact the entire future of the heavy minerals industry. There are also time constraints on finding solutions to such issues. This conference will attempt to high light some of those risks and to suggest possible mitigation measures.

CONFERENCE OBJECTIVE

This series of conferences was started in 1997 and has run since that date. The Conference alternates between South Africa and other heavy mineral producing countries. It provides a forum for an exchange of knowledge in all aspects of heavy minerals, from exploration through processing and product applications. This is a strictly technical conference, and efforts by the Organizing Committee are aimed at preserving its technical nature. The benefit of this focus is that it allows the operators of businesses within this sector to discuss topics not normally covered in such forums. The focus on heavy minerals includes the more obvious minerals such as ilmenite, rutile and zircon; and also other heavy minerals such as garnet, andalusite, and sillimanite.

ABOUT THE VENUE

Located in a luxury eco estate with insanely beautiful Indian Ocean views, less than 15 minutes from King Shaka International Airport. SET IN A TROPICAL FOREST that unfurls into the ocean, the resort blends organically into a lush natural landscape. A magnet for fun seekers, families, couples, solo explorers and business travellers; the resort is far enough removed to allow you to step back and take time to enjoy the tranquil surroundings.

FOR FURTHER INFORMATION, CONTACT:

Gugu Charlie, Conference co-ordinator

WHO SHOULD ATTEND

Professionals specialising or working in the areas of:

• Renewable energy

• Water purification

• Infrastructure

• Desalination plants

As well as the following industry professionals are invited to participate:

• Academics

• Business development managers

• Concentrator managers

• Consultants

• Engineers

• Exploration managers

• Geologists

• Hydrogeologists

• Innovation managers

• Mechanical engineers

• Metallurgical managers

• Metallurgical consultants

• Metallurgists

• Mine managers

• Mining engineers

• New business development managers

• Planning managers

• Process engineers

• Product developers

• Production managers

• Project managers

• Pyrometallurgists

• Researchers

• Scientists

CALL FOR PAPERS AND KEY DATES

Prospective authors are invited to submit abstracts of not more 500 words, in English. Please email abstracts and requests to be added to the conference mailing list to Gugu Charlie: Conference Co-ordinator, SAIMM at gugu@saimm.co.za

27 March 2023 – Submission of abstracts

10 April 2023 – Acceptance of abstracts

15 May 2023 – Submission of papers 21-22 August 2023 – Conference

E-mail: gugu@saimm.co.za Tel: +27 11 538-0237, Web: www.saimm.co.za

Geometallurgy Conference 2023

Geomet meets Big Data

BACKGROUND

The theme of this second geometallurgy conference ‘Geomet meets Big Data’ is inspired by the growing interest and focus on big datasets, machine learning, novel sensors, digital twins and 4IR in the mining industry. The concept of Geometallurgy goes back to some of the earliest mining activities when mineral recognition, mining, separation, and concentration were undertaken simultaneously. Over time, changes in operational structures, product expansion and specialisation ultimately led to the diminishment and breakdown of this holistic approach. In the last two decades, Geometallurgy has become a sophisticated yet entirely logical return to this integrated approach to mine planning. In a world of exponentially increasing ore heterogeneity and metallurgical complexity coupled with a demand for improved sustainability, Geometallurgy is effectively a highly structured, integrated multi-disciplinary collaboration for optimizing the value of an ore deposit. This conference provides a platform for the discussion of some of the newest developments in the field of geometallurgy and a celebration of the success of Geometallurgy integration and value-add.

FOR FURTHER INFORMATION CONTACT: Gugu Charlie, Conference Co-ordinator

4 September 2023 Technical Workshop

5-6 September 2023 Conference

7 September 2023 Technical Visit

Hazendal Wine Estate, Stellenbosch, Western Cape

E-mail: gugu@saimm.co.za Tel: +27 11 538-0237, Web: www.saimm.co.za

SUPPORTED BY