Carrément Math - Livre-cahier 5B

Livre-cahier A Livre-cahier B

Carrément MATH

Composition de Carrément math 4

Pour l’élève : 2 livres-cahiers A et B

Pour l’enseignant : Deux livres de l’enseignant (comprenant le corrigé des livres-cahiers)

Sa version numérique disponible sur www.Myvanin.be

Les annexes, des exercices supplémentaires et des évaluations disponibles sur www.Myvanin.be

Les manuels numériques (A et B) téléchargeables sur www.Myvanin.be

Carrément math 4 – Livre-cahier B

Carrément math 5 – r A

Auteur : Gabriel Heyvaert

Illustrations : M-A IZU (Marie-Anne Gueguen)

Conception graphique : Octopus Creative Communication

Mise en page : NORDCOMPO

Couverture : Steurs

L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.

L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.

Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.

Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.

1re édition : 2019

© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2019

ISBN 978-90-306-8602-6

D/2018/0078/294

Art. 579160/01

Chapitre

Table des matières

5.

Chapitre

Chapitre 11

1.

1.

9

1. Tracer des rectangles et des carrés Vive la fancyfair !

Pour la fancyfair de l’école, il faudrait commander un chapiteau pour que les invités puissent se mettre à l’abri en cas de pluie. Le directeur de l’école, M. Charlier, téléphone à Chapiloc, qui loue des chapiteaux de toutes les grandeurs, pour commander son chapiteau.

Regarde attentivement le plan à la page suivante. Choisis l’endroit et les dimensions qui conviennent le mieux à ce chapiteau et trace celui-ci sur le plan.

Voici les quatre propositions de dimensions.

 12 m sur 30 m

 20 m sur 24 m

 20 m sur 16 m

 24 m sur 14 m

Zone de recherche

Pour l’activité du samedi soir, il faudrait construire un terrain de pétanque dont voici les dimensions : 8 m sur 4 m. Trouve l’endroit où le terrain sera installé et trace-le sur le plan.

Le terrain de pétanque ne peut rien toucher.

Plan de la cour de récréation

Complète les figures suivantes en t’aidant du quadrillage.

– Un carré EFGH de 3 cm de côté.

– Un rectangle ABCD de 6 cm de longueur et de 3 cm de largeur.

Trace un rectangle qui aura le même périmètre que celui du carré.

Construis le carré QRST. [QR] est un de ses côtés.

Je me souviens

Pour tracer des côtés perpendiculaires et parallèles, il faut placer avec précision l’équerre Aristo. Trace une droite parallèle et une droite perpendiculaire à celle qui est donnée. Compare et discutes-en avec ton (ta) voisin(e).

Voici une chaise et un banc.

Dans la classe de Mme Marie-Ève, pour le spectacle de sa classe, il manque 4 bancs et 5 chaises.

Aide-la en traçant ce qui manque.

Pense à bien laisser un passage tout autour des bancs et des chaises pour que les gens puissent se déplacer.

Construis un rectangle XYWZ dont la largeur vaut 4 cm et dont la longueur mesurera le double de la largeur.

Construis un rectangle dont la longueur vaut 6 cm et la largeur vaut  3 5 de la longueur.

2. Tracer des médianes dans les quadrilatères

Parmi ces trois définitions, coche celle qui correspond au dessin.

 Les médianes sont des segments de droite joignant des sommets opposés.

 Les médianes sont des segments de droite joignant les milieux des côtés opposés.

 Les médianes sont des segments de droite joignant un sommet avec le milieu d’un côté opposé.

Trace les médianes pour chacune de ces figures.

Complète le

Nom de la figure

Les médianes… sont isométriques. se coupent en leur milieu. sont perpendiculaires.

tableau par vrai ou faux.

Je retiens

Les médianes

Ce sont des joignant les  de deux côtés opposés.

Sur le plan de la cour de récréation (p. 6), trace les médianes pour chaque quadrilatère que tu trouveras.

Trace les formes demandées.

Le carré STUV dont [AP] est une médiane.

Le parallélogramme ABCD dont [XY] est la grande médiane.

Trace la deuxième médiane pour chacune de ces figures et nomme-les.

Qui suis-je ? Écris le nom du quadrilatère.

? ? ?

Je suis un quadrilatère. Mes médianes se croisent en leur milieu.

Elles sont perpendiculaires. Elles n’ont pas la même longueur.

Je suis

Trace cette figure.

?

4. 5. 6.

3. L’aire du carré et du rectangle

Je me souviens

Quelle est l’aire de ce carré ?

1.

Quelle est l’aire en cm² de ces rectangles tachés ?

2.

Comment dois-je m’y prendre pour trouver l’aire d’un rectangle ?

J’explique avec mes mots

Observe le plan du chapiteau.

Echelle : ENTRÉE

Réponds aux questions.

a) Quelle est l’échelle de ce plan ? Indique-la.

Aide-toi du plan de la cour de récréation de la page 6 pour trouver la réponse.

b) Quelle est la superficie du chapiteau sur le plan ?

c) Que représente 1 cm² dans la réalité ?

d) Quelle est la superficie du chapiteau dans la réalité ?

Zone de recherche

Maintenant que le chapiteau est monté, il convient, à présent, de le préparer pour les festivités. Il faudrait dessiner sur le plan ci-avant :

– une scène rectangulaire de 40 m² (en rouge);

– une zone carrée de 4 m² devant la scène pour mettre la table de mixage (en vert);

– le bar de 33 m² en forme de rectangle (en bleu);

– un espace rectangulaire de 60 m² pour mettre des chaises et des tables (en orange).

Trace chaque espace en tenant compte des informations données ci-dessus et de celles du plan (en effet, tu ne peux rien mettre devant les issues de secours).

Trouve d’autres espaces à placer dans le chapiteau. Trace-les et indique leur superficie à l’intérieur de ceux-ci.

Je retiens

4.

5.

Trouve l’aire de ces rectangles.

Aire : Aire :

Aire :

Attention ! Pour calculer l’aire, il faut que les dimensions soient dans la même unité.

Aire : Aire :

Calcule le périmètre de chaque figure et, dans chacune, inscris le résultat.

Calcule l’aire de ce polygone.

Zone de recherche

6.

7.

Résous ces trois problèmes.

a) Une prairie carrée a une superficie de 9 ares. Quelle est la longueur d’un de ses côtés en m ?

Zone de recherche

Côté :

b) Une photo de 10 cm sur 15 cm a été agrandie en poster de 120 cm sur 180 cm. Quelle est l’aire de ce poster ?

Zone de recherche  :

c) Une table, qui mesure 2,2 m de longueur, a une aire de 3,3 m². Quelle est sa largeur ?

Zone de recherche  :

Trouve la longueur d’une table si la largeur est exactement la même et si la superficie est de 4,2 m².

Pour trouver une dimension manquante…

Rectangle : Aire :

Complète ce tableau.

FiguresLongueur ou côtéLargeur ou côté Aire

Rectangle 24 cm 8 cm cm²

Carré m m81 dam²

Rectangle ........................................ m60 dm 4 800 dm²

Carré 12 cm 120 mm cm²

Rectangle 90 dm cm36 m²

Zone de recherche

Résous ce problème.

Sur un terrain carré de 50 m de côté, la commune a décidé de construire un nouveau hall omnisport de 42 m sur 23 m. Quelle surface du terrain reste-t-il ?

Sur une feuille, trace :

– un rectangle dont l’aire sera de 18 cm² et la largeur vaudra la moitié de la longueur ; – un carré dont l’aire est égale à 25 cm².

Calcule le périmètre de chaque figure.

Périmètre du rectangle :

Périmètre du carré :

1.

4. Les fractions

Voici la salle de gym où des stands doivent être installés pour le plus grand bonheur des enfants. Aide Mme Julie à les répartir grâce aux informations qu’elle va te donner.

ENTRÉE

Zone de recherche

Coupe la salle en 12 morceaux identiques.

Quelle fraction représente l’allée en orange par rapport a la salle de gym ?

5

Je retiens

Une fraction est un rapport entre deux nombres entiers.

Le exprime le nombre de parts égales faites.

Le exprime le nombre de parts prises.

Détermine quelle fraction est représentée pour chacune de ces figures.

Sur le plan de la page précédente, colorie les fractions dans les couleurs demandées pour représenter les différents stands.

a) En rouge : 1 6 de la salle est nécessaire pour le stand du tir à la carabine.

b) En vert : 1 12 de la salle sera réservé à la pêche aux canards.

c) En bleu : on a décidé de réunir le stand du fakir et les lots qui occuperont ensemble 1 4 de la surface de la salle.

d) En mauve : 2 12 de la salle seront occupés par le stand de grimage.

e) En brun : 1 12 sera pour le jeu de massacre.

Trouve une fraction équivalente à celle de l’allée.

Je dépose mes idées

Qu’est-ce qu’une fraction équivalente ?

Classe les fractions de l’exercice précédent dans l’ordre décroissant. > > > >

Trouve la fraction équivalente de chaque fraction. Attention, elles doivent toutes avoir le même dénominateur.

=

=

Classe les fractions de l’exercice précédent dans l’ordre croissant. <

Classe ces fractions dans l’ordre décroissant.

Zone de recherche

Qu’a-t-on fait ?

On a ces fractions pour les rendre .

En t’inspirant de l’exercice, invente des égalités. Simplifie au maximum ces fractions.

Voici une droite des nombres. Combien de parts y a-t-il entre 0 et 1 ?

Entre 0 et 1, il y a  parts.

Donc, quelle fraction vaut une part ? Une part vaut

Quelle fraction représente chaque lettre ?

Place E = 4 5 et F = 3 2 .

Relie ces fractions sur la droite des nombres.

Entre 0 et 1, il y a  parts.

Donc, quelle fraction vaut une part ? Une part vaut

Conseil Utilise la zone de recherche pour t’aider dans tes recherches…

Détermine le nombre de canards que chaque enfant a réussi à pêcher et colorie-les.

Théo en a pêché 5 24  : canards

Romane en a pêché 3 12  : canards

Mehdi en a pêché 1 6  : canards

Combien de canards ont été pêchés par Julia ?

Quelle fraction irréductible cela représente-t-il ?

Zone de recherche

J’explique avec mes mots

5. Tracer un plan

Grâce à l’argent récolté lors des différentes éditions de la fancyfair et grâce à d’autres actions et évènements qui ont été organisés, l’école va pouvoir enfin commencer les travaux d’aménagement d’un bâtiment qu’elle possède.

– 2 classes de 40 m²

– Un loca l polyva lent de 35 m²

– Des toile ttes pour les garçons de 12 m²

– Des toile ttes pour les filles de 16 m²

– Un loca l de rangement de 16 m²

– Attention : pr évoir un couloir d’une la rgeur de 3 m pour pe rmettre une circulation aisé e.

Échelle : 1 : 100

Aménage une des classes en respectant l’échelle.

Voici l’enveloppe du bâtiment. À toi, à présent, de l’aménager en respectant le cahier des charges.

J’explique avec mes mots

a) Quelle est la superficie réelle de ce bâtiment ?

b) Quelle est la superficie du couloir sur le plan ? Zone de recherche

Complète le tableau en fonction des indications données.

Je retiens

Pour tracer un plan, il faut déterminer .

Plus elle sera grande et plus la représentation sur le plan sera .

Plus elle sera petite et plus la représentation sur le plan sera .

3.

Voici le plan d’un terrain sur lequel la famille Dagosti a fait construire sa maison. Aide-les à aménager le terrain tout autour sur la base de la liste donnée. Chaque aménagement que tu vas faire doit être rectangulaire ou carré.

Légende :fenêtres portes

Liste

– Trace l’allée de garage qui aura une largeur de 6 m.

– Trace également l’allée pour se rendre à la porte d’entrée, qui aura une largeur de 2 m. Ces deux allées rejoignent la route.

– Il faut : une terrasse de 40 m², une piscine de 18 m², un potager de 96 m², un abri de jardin carré de 4 m².

Aménage une deuxième terrasse de 30 m2 en forme de « L », un bac à sable de 2 m sur 2 m et une pergola de 24 m².

a) Quelle est la superficie réelle de ce terrain ?

Zone de recherche

b) Dans le potager, colorie :

• 1 3 pour la culture des pommes de terre en jaune;

• 1 6 pour les salades en vert;

c) Quelle fraction reste-t-il ?

• 1 12 pour les tomates en rouge;

• 1 4 pour les aubergines en mauve.

d) Trouve trois possibilités pour tracer un étang de forme rectangulaire qui aurait une surface de 12 m² à l’échelle 1 : 200.

Zone de recherche

1.

Un parc d’attractions de « ouf »

1. Les nombres décimaux (calcul mental + et –)

La famille Guichard a décidé, en ce beau samedi de mai, de se rendre dans le parc d’attractions Wazibi. Une fois la voiture garée dans le parking, les parents et leurs enfants se dirigent vers les caisses pour payer les entrées. Peux-tu les aider à calculer le prix total que cela leur coutera ?

Caisse

TICKET ADULTE

TICKET ENFANT

TICKET ENFANT

TICKET SÉNIOR

TICKET MOINS-VALIDE

TICKET FEMME ENCEINTE sur présentation du certificat médical

Zone de recherche

Calcule le prix pour la famille Bertin composée du papa (1 m 88) et de la maman (1 m 70). Ils ont deux jumeaux, Sidjy et Neven, qui ont la même taille (1 m 35). Jean-Marie, le papy (67 ans), les accompagne.

J’explique avec mes mots

Comment procèdes-tu pour additionner des nombres décimaux ?

Voici différents calculs à réaliser pour déterminer le prix des entrées.

Jeretiens

Pour additionner des nombres décimaux – Je peux additionner les parties qui vont ensemble en commençant par les parties décimales.

Trouve deux étiquettes qui, ensemble, donnent une des sommes proposées également dans une étiquette et colorie les 3 étiquettes de la même couleur.

4.

Résous ces calculs et écris ton développement.

45,56 + 48,70 =

348,7 + 56,8 =

88,7 + 102,71 =

511,4 + 110,870 =

165,735 + 45,25 =

5.

Astuce…

Ajoute un ou des 0 aux parties décimales pour avoir le même nombre de chiffres après la virgule pour chaque terme.

La famille Vasseur a, quant à elle, payé à la caisse : 141,20 €. Le papa a donné 3 billets de 50 €.

Combien d’euros recevra-t-il en retour ?

Zone de recherche

Gérard prend 5 places adultes et donne 200 €.

Combien d’euros lui rendra-t-on en retour ?

J’explique avec mes mots

Comment procèdes-tu pour soustraire des nombres décimaux ?

Voici différentes situations où de l’argent doit être rendu.

Je retiens

2. Tracer des trapèzes, des parallélogrammes et des losanges

Une des attractions qui fonctionnent le mieux dans le parc est la maison fantôme. En effet, les enfants sont friands de sensations fortes et ils n’hésitent pas à aller de pièce en pièce pour découvrir tout ce qu’elles recèlent.

1.

Observe le plan de la maison fantôme.

2.

Sortie

Les potions de la sorcière Belleflamma

Les monstres poilus, c’est par ici !

Bienvenue chez les Monstros !

Les reptiles sont à la fête!

Entrée

Casper, mon ami fantôme ?

Une araignée en cache une autre…

Fais le moins de bruit possible…

Colorie les trapèzes en rouge, les losanges en orange et les parallélogrammes en vert.

Qu’est-ce qu’un trapèze ? qu’un

Reproduis ce trapèze quelconque.

a) Repasse la grande base en vert, la petite base en bleu et les côtés obliques en rouge.

b) Trace la hauteur du trapèze en brun.

La hauteur est un segment de droite rejoignant perpendiculairement les deux bases.

J’explique avec mes mots

Comment as-tu procédé pour reproduire le trapèze ?

Il existe différentes sortes de trapèzes. Écris le nom de chaque trapèze en t’aidant des propositions.

trapèze isocèle – trapèze quelconque – trapèze rectangle

Trace la hauteur de chacun de ces trapèzes.

3.

4.

Trace les trapèzes demandés.

1 Un trapèze quelconque BCDE à partir de cette petite base

B : 6 cm

h : 3 cm

3 Un trapèze rectangle IJKL dont la petite base mesure 3 cm et la grande 7 cm

2 Un trapèze isocèle RSTU à partir de cette grande base

b : 4 cm

h : 4 cm

4 Un trapèze quelconque MNOP dont la hauteur mesure 3,5 cm et dont le point P est donné

Trace, pour chaque trapèze, ce qui est demandé.

1 une hauteur

3 les médianes

2 les diagonales

4 un trapèze isocèle avec la même hauteur

Vrai ou faux ? Entoure la bonne proposition et justifie ta réponse.

Un trapèze est un parallélogramme.VRAI – FAUX

Pourquoi ?

Un polygone est un trapèze. VRAI – FAUX

Pourquoi ?

Je définis

Qu’est-ce qu’un parallélogramme ?

Reproduis ce parallélogramme à l’identique.

a) Repasse les bases en vert.

b) Trace la hauteur du parallélogramme en brun.

Trace un parallélogramme ABCD. Rédige la manière à suivre pour que ton (ta) voisin(e) puisse tracer exactement le même parallélogramme sans avoir vu ton modèle.

7.

8.

Vrai ou faux ? Entoure la bonne proposition et justifie ta réponse. Un parallélogramme est un trapèze.VRAI – FAUX

Pourquoi ?

Complète ces parallélogrammes à l’aide de ton équerre.

Trace la hauteur de ces parallélogrammes.

Trace un parallélogramme de 3 cm de hauteur, ayant une base de 6 cm et dont l’angle à la base a une amplitude de 50°.

Trace un parallélogramme dont la base mesure 6,5 cm, ayant des côtés obliques de 3,5 cm chacun et dont l’angle à la base a une amplitude de 130°.

Trace aussi sa hauteur et mesure-la.

Colorie la proposition correcte. sont supplémentaires.

Les angles opposés du parallélogrammeont la même amplitude deux à deux. sont complémentaires.

ont la même amplitude.

Les angles consécutifs dans un parallélogramme sont complémentaires. sont supplémentaires.

Je définis

Reproduis exactement ce losange.

a) Repasse les côtés en vert.

b) Trace la grande diagonale (D) en mauve.

c) Trace la petite diagonale (d) en orange.

J’explique avec mes mots

Comment as-tu procédé pour reproduire le losange ?

Qu’est-ce qu’un losange ?

Colorie la (les) proposition(s) correcte(s). parallèles.

Les diagonales du losange sontisométriques. perpendiculaires.

des côtés parallèles deux à deux.

Le losange aquatre côtés de même longueur. quatre angles de même amplitude.

Achève le tracé de ces losanges.

Trace les losanges demandés.

Un losange EFGH dont la grande diagonale mesurera 6 cm et la petite 3 cm

Un losange PTDR dont les côtés mesureront 3 cm chacun

Trace les médianes des deux losanges.

17. 18. 19.

Vrai ou faux ? Entoure la bonne proposition et justifie ta réponse.

Un trapèze est un losange. VRAI – FAUX

Pourquoi ?

Un losange est un parallélogramme.VRAI – FAUX

Pourquoi ?

Un losange est un carré. VRAI – FAUX

Pourquoi ?

Trace une croix dans les trapèzes. Colorie les parallélogrammes.

Place le numéro de chaque forme dans l’ensemble qui convient.

Trapèzes Losanges

3.

1.

L’aire du parallélogramme, du losange et du trapèze

Voici le plan du parc avec les différentes zones.

Bienvenue au parc Wazibi

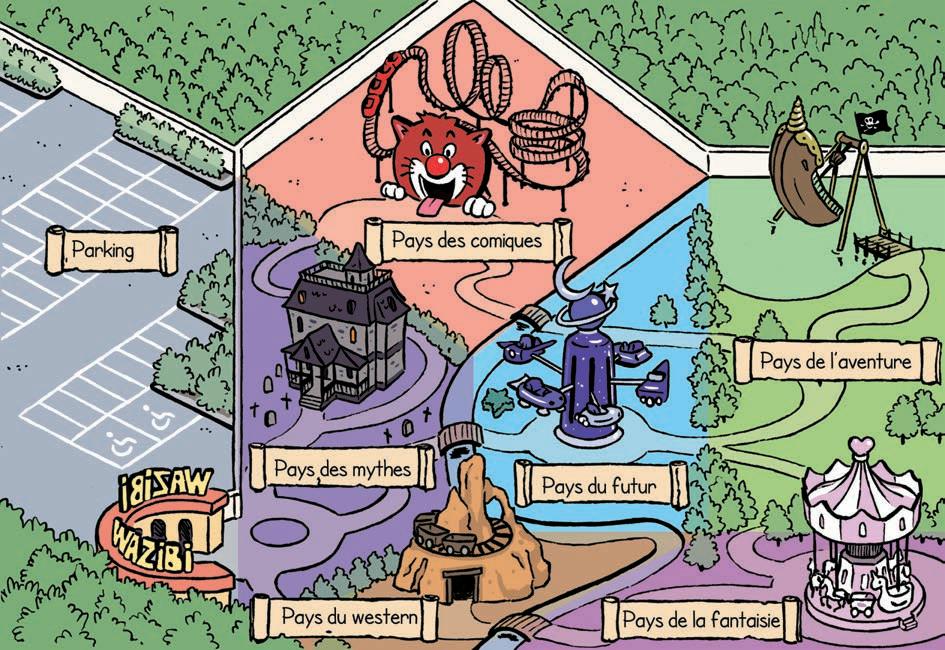
Échelle : 1/10 000

J’observe

Quelles sont les différentes formes géométriques qui composent ce plan ?

Calcule l’aire de la zone « Pays de l’aventure » sur le plan.

Quelles seront les dimensions réelles pour cette zone ? Calcule sa superficie réelle.

Découpe le rectangle (figure no 1) de l’annexe 1. Quelle est l’aire de ce rectangle ?

Transforme ce rectangle pour recouvrir exactement le parallélogramme ci-dessous. Attention, tu ne peux donner qu’un seul coup de ciseau.

Rectangle de départ Parallélogramme

J’observe

Que constates-tu ?

5.

Repasse et/ou trace si nécessaire ce qu’il faut pour calculer l’aire de ce parallélogramme. Prouve ta réponse par un calcul.

Zone de recherche

Je retiens

Aire du parallélogramme

6.

Aire :

B = h =

Hauteur (h)

Calcule l’aire de chacun de ces parallélogrammes. Repasse et trace, si cela est nécessaire, les dimensions dont tu as besoin en rouge.

Trace deux parallélogrammes différents de 15 cm². La base de chacun mesure 5 cm. 7.

8. 9.

Trace, sur une feuille, 3 parallélogrammes de 12 cm² ayant respectivement comme hauteurs : 2 cm, 3 cm et 4 cm. Indique les dimensions.

Découpe le rectangle (figure no 2) de l’annexe 1. Quelle est l’aire de ce rectangle ?

Transforme ce rectangle pour recouvrir exactement le losange ci-dessous. Attention, tu ne peux donner que quatre coups de ciseau.

Rectangle de départ Losange

Que constates-tu ?

Repasse et/ou trace si nécessaire ce qu’il faut pour calculer l’aire de ce losange. Prouve ta réponse par un calcul.

Zone de recherche

Trace deux losanges différents qui auront chacun la même aire que le rectangle donné. Repasse les grandes diagonales en vert et les petites diagonales en bleu.

Je retiens

Aire du losange

Aire :

D = d =

Petite diagonale (d)

Grande diagonale (D)

Calcule l’aire de chacun de ces losanges. Repasse et/ou trace, si cela est nécessaire, les dimensions dont tu as besoin en vert.

La grande diagonale d’un pré mesure 150 m. La petite diagonale mesure les 3 5 de la grande diagonale.

Calcule l’aire de ce pré.

Zone de recherche

L’aire d’un losange vaut 16 cm². La petite diagonale mesure 4 cm. Que vaut la grande diagonale ?

Zone de recherche

Trace ce losange sur une feuille.

Calcule l’aire du parking sur le plan.

Quelles seront les dimensions réelles du parking ? Calcule sa superficie réelle.

Découpe le parallélogramme (figure n° 3) de l’annexe 1. Quelle est l’aire de ce parallélogramme ?

Transforme ce parallélogramme pour obtenir deux trapèzes identiques. Attention, tu ne peux donner qu’un seul coup de ciseau.

Parallélogramme de départ

a) Repasse en bleu les bases de ce parallélogramme.

b) Trace en rouge la hauteur.

Trapèzes identiques

c) Repasse en bleu les bases de chaque trapèze.

d) Trace en rouge leur hauteur.

18.

Repasse et/ou trace si nécessaire ce qu’il faut pour calculer l’aire de ce trapèze. Prouve ta réponse par un calcul.

Zone de recherche

Je retiens

Aire du trapèze

Petite base (b)

Aire :

b =

B =

h =

h

Grande base (B)

Calcule l’aire de ces trapèzes. Repasse et trace, si cela est nécessaire, les dimensions dont tu as besoin en vert. 19.

Le parc Wazibi a racheté trois terrains pour pouvoir agrandir le parc dans le futur. Le prix au centiare est de 40 €. Calcule la somme que le parc a versée aux trois propriétaires.

35 m

30 m

Zone de recherche

30 m 35 m 45 m

Calcule la superficie de ces zones.

Calcule la superficie totale et réelle du parc Wazibi.

Le directeur du parc Wazibi aimerait ajouter 2 zones :

– la zone jaune qui sera un parallélogramme de 18 cm² ;

– la zone rose qui sera un trapèze rectangle de 20 cm².

Trace ces deux zones sur le plan en respectant les couleurs.

Calcule la surface réelle de ces deux zones ensemble.Trouve-leur un nom.

4.

Additionner et soustraire des nombres décimaux (calcul écrit)

À la fin de cette journée du 14 avril, c’est l’heure de faire les comptes. Chacun des responsables du parc Wazibi vient avec la recette de la journée pour la mettre dans le coffre-fort.

Estime la recette de la journée.

Zone de recherche

Peux-tu calculer de manière précise la recette totale ?

Zone de recherche

Calcule la recette d’hier.

Je me souviens

Pour réaliser une addition écrite, je passe par 4 étapes.

2.

Estime, puis effectue les additions écrites.

48 758,913 + 5 674,82 =

Estimation :

Aligne bien tes chiffres en faisant correspondre chaque rang.

329 431,042 + 47 654,91 =

Estimation :

56 004,38 + 907 048,056 =

Estimation :

237 088,909 + 456 708,14 =

Estimation :

Vérifie si tu as bien indiqué la virgule.

Effectue ces additions sur une feuille.

Que représente le report ?

 un millième

 un centième

 un dixième

 une unité

 une dizaine

Que représente le report ?  un millième  un centième

Voici la recette des boutiques de souvenirs pour les trois derniers jours. Calcule

Zone de recherche

Calcule la moyenne pour un jour.

Le jour précédent, le 13 avril, la recette du parc était de 492 124,9 €.

Quelle est la différence par rapport à la recette du 14 avril ?

Estime la différence.

Zone de recherche

Calcule de manière précise cette différence.

Zone de recherche

Je me souviens

Il existe deux méthodes pour effectuer une soustraction écrite :

Pour réaliser une soustraction écrite, je passe par 4 étapes.

Que

Estime et effectue ces calculs en choisissant la méthode de ton choix.

Ajoute un ou des « 0 » dans la partie décimale pour que la résolution soit plus facile.