Relaciones y funciones
FUNCIONES
¿qué es RELACIÓN?
Correspondencia entre elementos de dos conjuntos y dentro de esas relaciones de correspondencia le corresponde mas de un valor a un elemento
¿qué es FUNCIÓN?
Una función es una relación en donde a cada elemento de un conjunto (A) le corresponde uno y sólo un elemento de otro conjunto (B).
A cada niño le toca una zanahoria
Es importante conocer la diferencia entre una relación y una función:
Tiene varios valores para x Un
solo valor para x
DOMINIO Y RANGO DE UNA FUNCIÓN
Todas
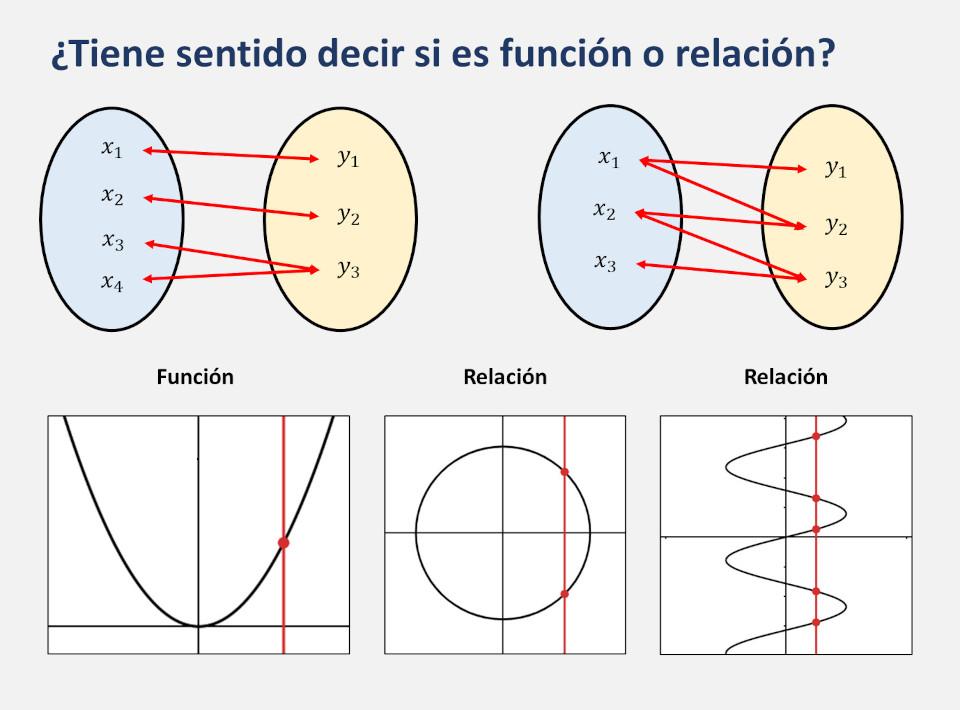
las funciones tienen un dominio y un Rango
Dominio: conjunto de los elementos que definen la función, es decir, los elementos que se van a asociar con otro conjunto (los que sólo pueden asociarse una vez)
Rango: es el conjunto de elementos que son el resultado de la asociación del dominio bajo la relación.
DOMINIO Y RANGO DE UNA FUNCIÓN
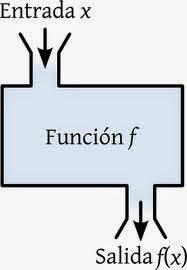
Para comprender de manera apropiada estos elementos, utilicemos la analogía de una maquina, a esta entran los valores del dominio; como x=3; dentro de ella ocurre un proceso en que la función, f(x)=2x2, sustituye los valores entrantes en la variable independiente salen los valores del rango (variable dependiente), que en este ejemplo seria f(x)=18, valor que resulta al trabajar la maquina en el proceso de sustituir x en la función
Función f(x)=2x2 f(x)= 2(3)2 f(x)=18
x=3
-3 -2 -1 0 1 2 3 Ejemplo: 0 1 2 3 4 5 6 7 8 9 Dominio{-3,-2,-1,0,1,2,3} Rango{0, 1, 4, 9} Función f(x)=x2 Serian solo los valores resultantes, al sustituir en la función (- 3)2 = 9 (- 2)2 = 4 (- 1)2 = 1 ( 0 )2 = 0 ( 1)2 = 1 ( 2)2 = 4 ( 3)2 = 9
Ejemplo:
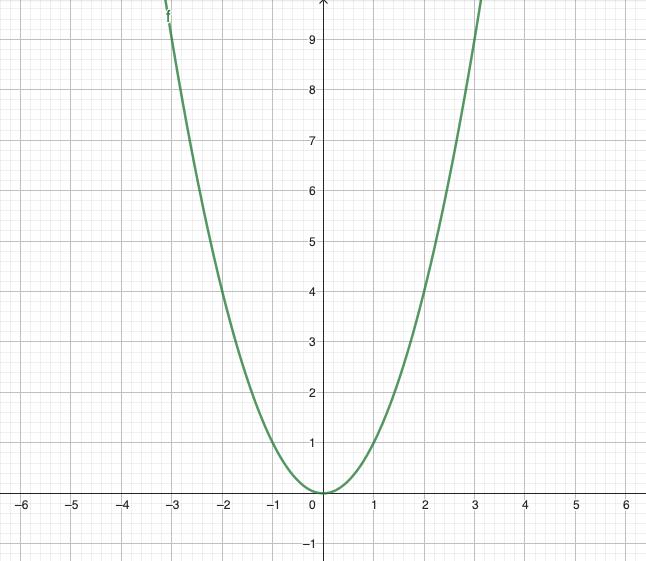
Ahora ¿cómo encontrar el dominio si es una gráfica? Seguiremos trabajando con la función anterior, en la imagen puedes ver la grafica
Función f(x)=x2
Dominio
se refiere a los valores que puede tomar como x, al ser la variable independiente x puede tomar cualquier valor por lo tanto el dominio serian todos los números reales D = R
Ejemplo:
Ahora ¿cómo encontrar el rango si es una gráfica?
Seguiremos trabajando con la función anterior, en la imagen puedes ver la grafica
Función f(x)=x2
Rango en este caso el vértice de la parábola nos indica el inicio del rango, el cual esta en el eje y, es cero y a partir de ahí puede tomar cualquier valor hacia arriba, (infinito) por lo tanto el rango quedaría así:
R = [0,∞)
GRAFICACIÓN DE UNA FUNCIÓN
Una manera de resolver funciones es Graficándolas, para poder realizar este método necesitaremos una tabla de valores y un plano cartesiano que previamente hemos estudiado
La tabla de valores es como la siguiente, donde tendremos dos columnas que pertenecen a la variable independiente (x) que se refiere a que puede tomar cualquier valor y a la variable dependiente (y) que es el resultado de sustituir en la función
x y
Ejemplo: 1. comencemos realizando una tabla de valores Función f(x)=x2 Continuemos trabajando con la x y= x2 y -3 (- 3)2 9 -2 (- 2)2 4 -1 (- 1)2 1 0 ( 0 )2 0 1 ( 1 )2 1 2 ( 2 )2 4 3 ( 3 )2 9 x le asigno los valores que prefiera sustituyo x en la función el resultado
y
de la sustitución me arroja los valores de
Ejemplo:
Función f(x)=x2 Continuemos trabajando con la
2. Graficaremos utilizando los resultados de la tabla de valores
a los valores de (X,Y) se les conoce como par ordenado, y a partir de estos podemos graficar en el plano cortesía
x y -3 9 -2 4 -1 1 0 0 1 1 2 4 3 9
BIBLIOGRAFIA
MEXICO:
Style Citation
MATEMATICAS SIMPLIFICADAS (4.a ed.). (2015). PEARSON/ CONAMAT. GRANVILLE, W. A. (1998). CALCULO DIFERENCIAL E INTEGRAL (1a. ed., 27a. reimp.).
LIMUSA/NORIEGA. Chicago