LA RECTA
PENDIENTE Y ECUACIONES DE LA RECTA
LA RECTA
La línea recta es el lugar geométrico de los puntos del plano, de los cuales al tomar dos cualesquiera, el valor de la pendiente m siempre es constante.
GEOMETRIA
Inclinación de una recta
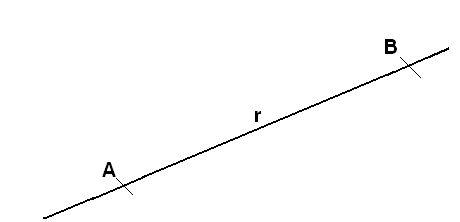
Es el ángulo que una recta forma con el eje X positivo, el cual se representa con a, este ángulo se mide a partir del eje X y girando en sentido opuesto a las manecillas del reloj.
GEOMETRIA
PENDIENTE DE UNA RECTA
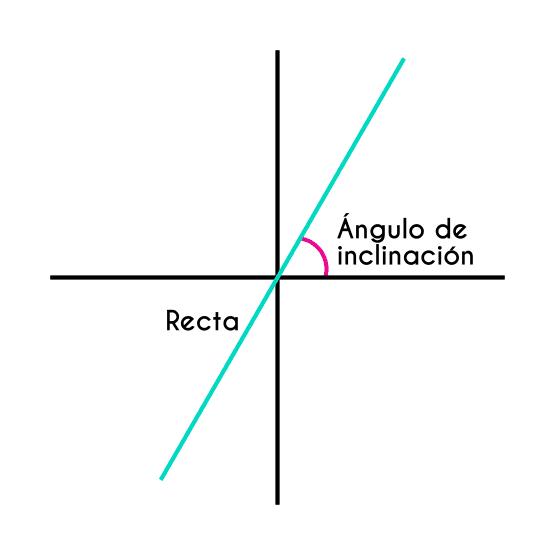
inclinación de la recta con respecto al eje de las abscisas
m = tan a
PENDIENTE DE UNA RECTA a
Donde: a = arc tan (m) si m > 0 a = arc tan (m) + 180º si m < 0
GEOMETRIA
Determinar la grafica de la recta y la
es 120ª EJERCICIO C/ SOLUCIÓN m = tan m = tan m = − 1.73 a = tan − a = − 59.97 a = − 59.97 a = 120 120º 1.73
pendiente si la inclinación
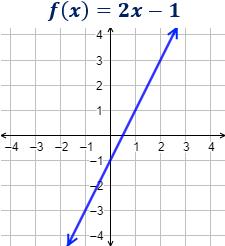
Determinar la grafica de la recta y la pendiente si la inclinación es 70ª
2.14
EJERCICIO C/ SOLUCIÓN m = tan m = tan m = 2.14 a = tan − a = 70 70º
PENDIENTE DE UNA RECTA QUE PASA POR DOS PUNTOS
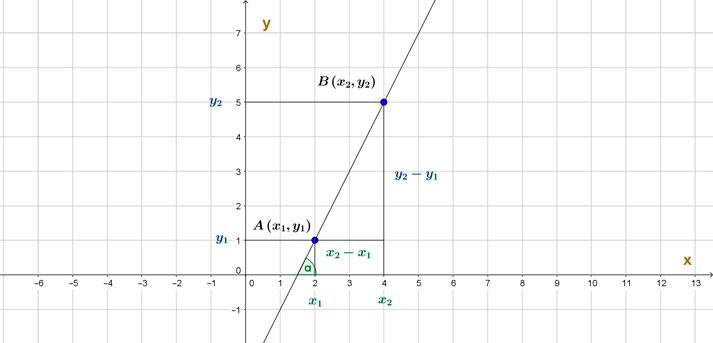
Sea la recta / que pasa por los puntos P1 y P2, entonces su pendiente se define como:
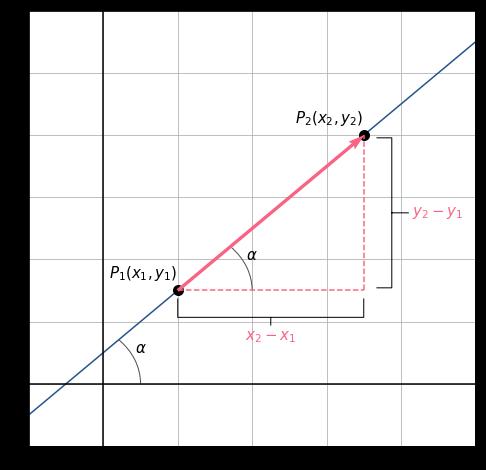
PENDIENTE DE UNA RECTA CONOCIENDO DOS PUNTOS
m = Yb
Ya Xb
Xa
GEOMETRIA
−
−
EJERCICIO C/ SOLUCIÓN
Determinar la pendiente de la siguiente recta y graficar
1. Reconocer valores, acorde a la nomenclatura de formula
2. Sustituir en formula y realizar operaciones m = y x
A(xa, ya) B(xb, yb) m = 3 − 7 2 − 5 m = − 4 − 3
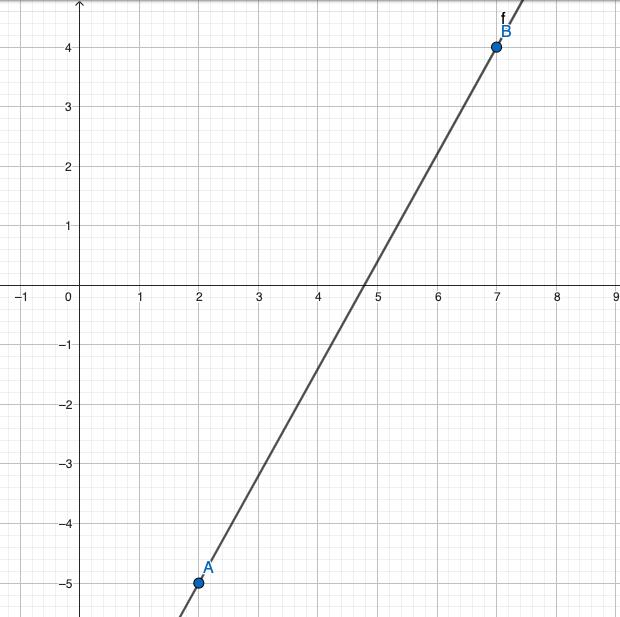
3. Para graficar, graficamos el punto A
A (5,7) (2,3) m = Y b − Ya Xb − Xa
4. para graficar la pendiente, iniciamos con el numerador que corresponde a Y, si es positivo graficamos hacia arriba y si es negativo graficamos hacia abajo
4. Continuamos con el Denominador que corresponde a x, si es positivo graficamos hacia la derecha y si es negativo graficamos hacia izquierda
Xb-Xa
Yb-Ya
GEOMETRIA
TIPOS DE PENDIENTES Y ANGULOS DE INCLINACIÓN
Los casos que se presentan para el valor de la pendiente y su ángulo de inclinación, son los siguientes:
Si m > 0 (positiva) Si m < 0 (negativa) Si m = c/0 Si m = 0
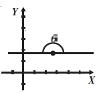
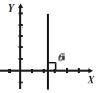
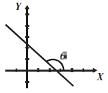
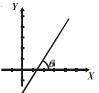
ángulo agudo. ángulo obtuso. ángulo recto. ángulo llano.
GEOMETRIA
ECUACIONES DE LA RECTA
Para determinar la ecuación de una recta en función de las condiciones dadas, se emplean las siguientes ecuaciones, según corresponda.
ECUACIÓN GENERAL
PUNTO – PENDIENTE ECUACIÓN QUE PASA POR DOS PUNTOS
ECUACIÓN
y − ya = m(x − xa) A x + By + C = 0 Y − Ya = Y b − Ya Xb − Xa (X − Xa)
Donde: A,B y C son constantes Dado el punto P(xa, ya) de la recta de pendiente m Dados los puntos A (Xa, Ya) B (Xb, Yb) de la recta.
GEOMETRIA
ECUACIÓN GENERAL DE LA RECTA
Esta forma es la que considera todos los casos de las rectas: horizontales, verticales e inclinadas, y se representa de la siguiente manera: A partir de esta ecuación podemos encontrar la pendiente y la intersección en el eje y Sea la recta si B ≠0 podemos despejar y con lo que obtenemos A x + By + C = 0 Y = − A B x − C B Que tiene la forma de la ecuación donde m es la pendiente y b la intersección y = m x + b m = − A B b = − C B Si B=0, la recta es vertical y la pendiente no esta definida
Ax + By + C = 0
GEOMETRIA
SOLUCIÓN
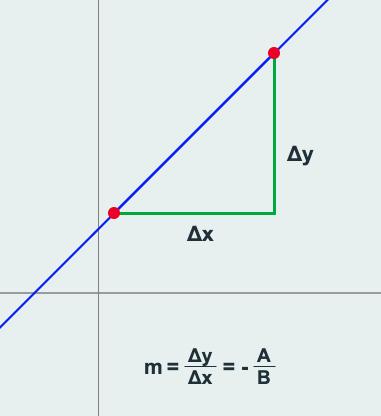
Determine la pendiente (m) y la intersección con el eje y (b) de la ecuación general dada.
y
1. sustituimos valores
2. aplicamos ley de signos en caso de ser requerido, en este ejemplo tenemos dos signos de menos ( — ) al multiplicarlos resulta positivo y = 0.75x + 2 m = 0.75 b = 2
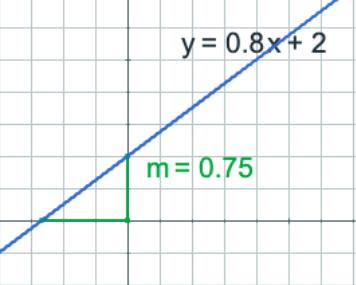
3. puedes realizar la división
GEOMETRIA
EJERCICIO C/
m = − A B b = − C B 3x − 4
+ 8 = 0 m = − 3 − 4 m = 3 4 b = − 8 − 4 b = 8 4
ECUACIÓN PUNTO – PENDIENTE
Punto-pendiente es la forma general para ecuaciones lineales. Hace énfasis en la pendiente de la recta y un punto en esta (que no sea la ordenada al origen). Su representación es la siguiente:
y − ya = m(x − xa)
GEOMETRIA
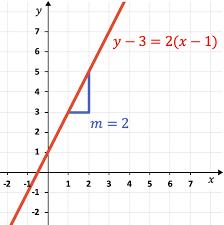
(-2,3)
2. sustituir valores
3 4 GEOMETRIA EJERCICIO
y
3
y
−
A
A
y − 3 = 3(x −
Determine la ecuación de la recta que pasa por el punto A (-2,3) y m = (4) 4y − 12 = 3x + 6 4y = 3x + 6 + 12 4y = 3x + 18 y = 3x 4 + 18 4
C/ SOLUCIÓN
−
= 3 4 (x − (− 2))
− ya = m(x
xa)
1. emplear formula correspondiente 3. si hay denominadores (en este caso es 4) lo cambiaremos al extremo opuesto con su operación inversa, para resolver mi ecuación 4. realizamos operaciones
(xa,ya)
(− 2))
Determine la ecuación de la recta que pasa por el punto A (-2,3) y
EJERCICIO C/ SOLUCIÓN (grafico) A (-2,3) A m = 3 4
ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS
Una recta queda perfectamente determinada con tan solo conocer las coordenadas de dos cualesquiera de sus puntos.
GEOMETRIA (
−
−
X
Xa) Yb − Ya Xb
Xa = Y
Determine la ecuación de la recta que pasa por los punto A (2,-5) y B(7,4) GEOMETRIA EJERCICIO C/ SOLUCIÓN (X − Xa) Y b − Ya Xb − Xa = Y − Ya 1.
formula correspondiente 3.
correspondientes
2.
(X − 2)9 = (Y + 5)(5) Encontramos valores correspondientes A (2 , -5) A (xa,ya) B (7, 4) B (xb,yb) (X − Xa)(Y b − Ya) = Y − Ya(Xb − Xa) (X − 2)(4 − (− 5)) = (Y − (− 5))(7 − 2) 9X − 18 = 5Y + 25 9X − 5Y − 18 − 25 = 0 9X − 5Y − 43 = 0
emplear
Realizamos operaciones
igualamos a cero, y realizamos la operación de las constantes
sustituir valores
ECUACIÓN DE LA RECTA DE LA FORMA PENDIENTE ORDENADA
Una vez que se conoce la pendiente de una recta y su ordenada al origen (intersección con el eje Y), se determina la siguiente ecuación:
y = m x + b m = pendiente b= intersección con el eje y x= variable independiente f(x) ò y = variable dependiente
Esta forma de la ecuación de la recta, también se conoce como forma simplificada o reducida.
GEOMETRIA
¿QUÉ ES LA INTERSECCIÓN CON EL EJE Y (b)?
Es El Punto Donde Intersectan Al Eje De Las Ordenadas
GEOMETRIA b= 3 b= 2 b= 1
Determine la pendiente (m) y la intersección con el eje y (b) de las siguientes ecuaciones reducidas
y = 6 3 x y = 2x
m=2 b=3
f (x) = 2x + 3 3y = 6x y = 5x + 7 f (x) = m x + b y = 2x + 3 y = 2x + 3 m=2 b=0 m=5 b=7
GEOMETRIA
EJERCICIO C/ SOLUCIÓN
BIBLIOGRAFIA
MATEMATICAS SIMPLIFICADAS (4.a ed.). (2015). PEARSON/ CONAMAT.
GEOMETRIA