Triangulo Oblicuángulo
Ley de Senos y Cosenos
Arq. Areli González Ramos
Triangulo Oblicuángulo
Un triángulo es oblicuángulo cuando sus tres ángulos son oblicuos, es decir, no tiene un ángulo recto. Este tipo de triángulos se resuelven mediante la ley de senos de cosenos.
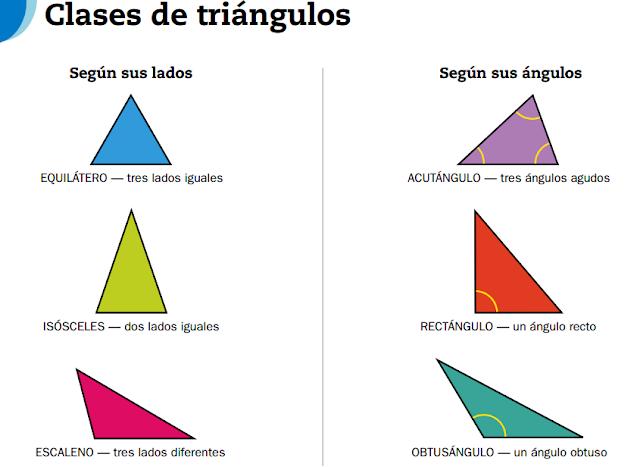
NINGUNO DE SUS ANGULOS MIDE 90º
C
nomenclatura de lados y ángulos
Ley de Senos
formula y casos en que se usa
La razón que existe entre un lado de un triángulo oblicuángulo y el seno del ángulo opuesto a dicho lado es proporcional a la misma razón entre los lados y ángulos restantes.
La ley de senos se aplica conforme a los datos conocidos
a sen A = b senB = c senC
α c
UN LADO Y LOS ANGULOS ADYACENTES
a
DOS LADOS Y UN ANGULO OPUESTO
Ejercicio c/solución:
• Analice la siguiente figura ¿Cuál es el valor del lado a? A. 35.1 B. 30.6 C. 24.5 D. 36.7 a= ?
C 45º 60º A B c=30m
para solucionar este triangulo es importante saber que datos tengo A = 60º a = ? C =45º c= 30
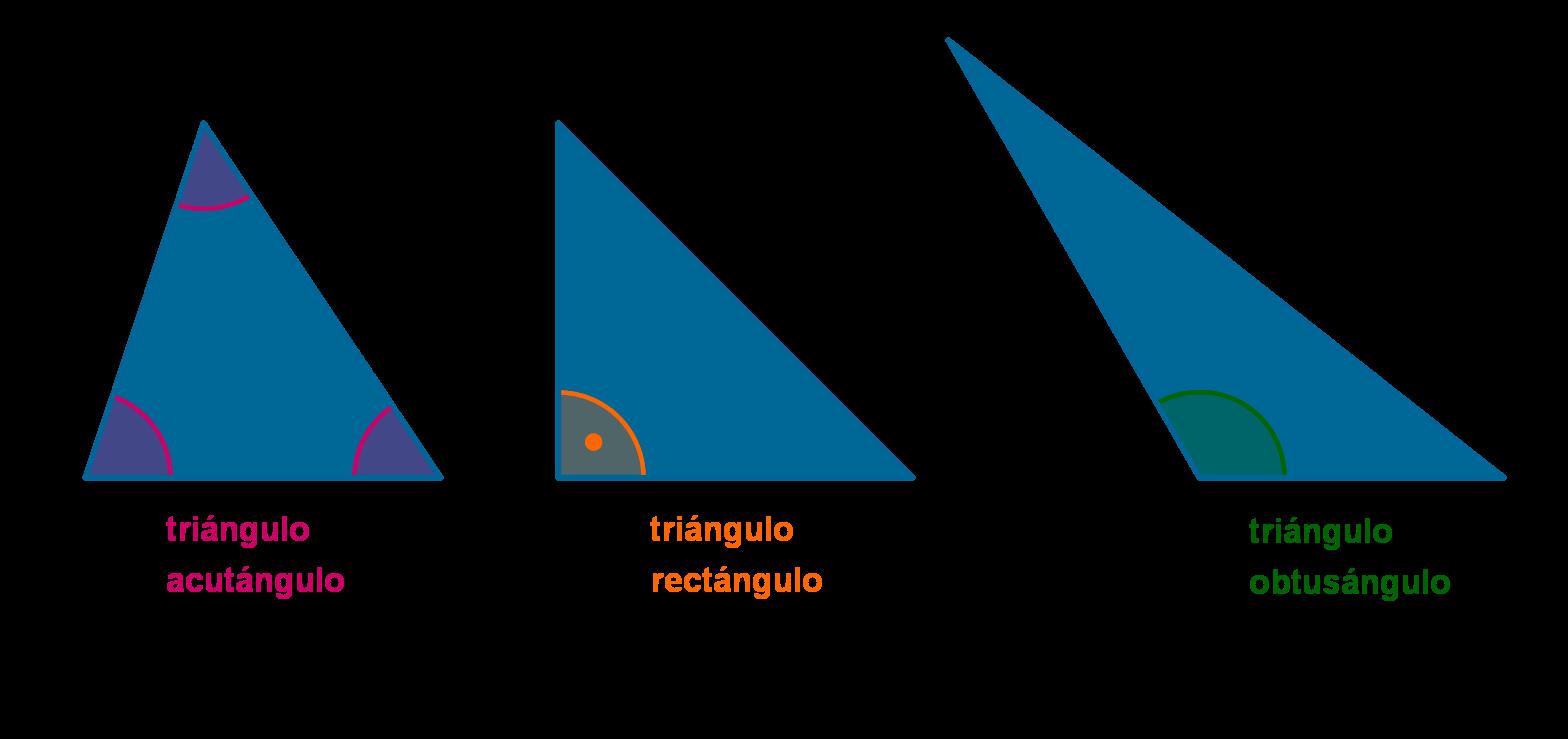
a partir de los datos tomo dos secciones de la ley de senos (en este caso sección a y c), despejo y sustituyo valores
a sen A = c senC a = c senC (sen A) a = 30 sen45 (sen60) a = 30 0.7071 (0.8660) a = (42.4268)(0.8660) a = 36.7
El cuadrado de un lado de un triángulo oblicuángulo es igual a la suma de los cuadrados de los lados restantes, menos el doble producto de dichos lados por el coseno del ángulo opuesto al lado buscado.
Ley de Cosenos
formula y casos en que se usa
PARA CALCULAR LADOS: PARA CALCULAR ANGULOS
a 2 = b 2 + c 2 − 2bc ⋅ CosA b 2 = a 2 + c 2 − 2ac ⋅ CosB c 2 = b 2 + a 2 − 2ba ⋅ CosC cos A = b 2 + c 2 − a 2 2bc cos B = c 2 + a 2 − b 2 2ca cos C = a 2 + b 2 − c 2 2ab
DOS LADOS Y EL ANGULO COMPRENDIDO ENTRE ELLOS
TRES LADOS
Ejercicio c/solución:
• Un terreno cuyo perímetro tiene una forma triangular mide 40m en su lado mayor, 15 m en el otro y 50º en ángulo que forma entre ambos. En el lado faltante se pondrá una cerca de alambre ¿Cuánto medira dicho lado faltante • a. 28.4 para solucionar este triangulo es importante saber que datos tengo a = 15 b = 40 C =50º c= ?
a partir de los datos aplico la formula para encontrar el valor faltante y/o solicitado b = 40 a = 15 50º B
A C
c 2 = b 2 + a 2 − 2ba ⋅ CosC c 2 = 402 + 152 − 2(40)(15) ⋅ Cos50 c 2 = 1600 + 225 − 80(15) ⋅ 0.6427 c 2 = 1825 − 1200 ⋅ 0.6427 c 2 = 1825 − 8771.24 c 2 = 1053.76 c = 1053.76 c = 32.46
BIBLIOGRAFIA
MATEMATICAS SIMPLIFICADAS (4.a ed.). (2015). PEARSON/ CONAMAT.
VIDEOS LEY DE SENOS Y COSENOS https://youtu.be/kavX6gWg3fg