Triángulos
Semejanza y Teorema de Tales
Arq. Areli González Ramos
TRIANGULO
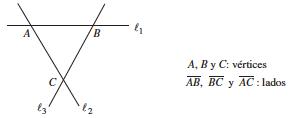
Porción del plano limitada por 3 rectas que se intersectan una a una en puntos llamados vértices.
Elementos de un triangulo
La mediana: Es el segmento que une un vértice y el punto medio del lado opuesto al vértice. Las tres medianas de un triángulo se cortan en un punto G llamado baricentro o centro de gravedad del triángulo.
El baricentro de un triángulo está a doble distancia del vértice que del punto medio del lado opuesto.
Elementos de un triangulo
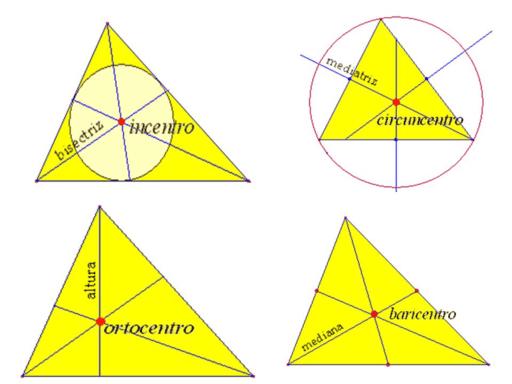
La bisectriz: Es la recta que pasa por el vértice que forman dos lados y divide por la mitad el ángulo que forman los mismos lados. Las tres bisectrices de un triángulo se cortan en un punto que se llama incentro, que tiene la propiedad de ser el centro de la circunferencia inscrita al triángulo
Elementos de un triangulo
La mediatriz: Es la recta que pasa por el punto medio de cada lado y es perpendicular al lado. Las 3 mediatrices de un triángulo se cortan en un punto que se llama circuncentro, que tiene la propiedad de ser el centro de la circunferencia circunscrita al triángulo
Elementos de un triangulo
La altura: Es la recta que pasa por un vértice y es perpendicular al lado opuesto. Las tres alturas de un triángulo se cortan en un punto que se llama ortocentro. Normalmente consideramos la altura de un triángulo como el segmento de la recta punto del lado opuesto, CHc,
•
•
Propiedades
La suma de dos lados es mayor que el otro lado
La suma de los ángulos de un triangulo mide 180º
Para indicar que 2 triángulos son semejantes se escribe Δ ABC ~
Δ A’B’C’, donde el símbolo ( ~ ) se lee: es semejante.
A B C E D
~ DE AB = EF BC = DF AC 6 4 = 4.5 3 = 9 6 = 1.5 6u 4u 3u 9u 4.5u 6u
Propiedad que tienen dos figuras de ser proporcionales con sus correspondientes lados. SEMEJANZA
F
CRITERIOS AA ángulo — ángulo
∆ABC ~ ∆DEF A
D
B C
E F a a Dos triángulos son semejantes si tienen 2 ángulos homólogos.
CRITERIOS LAL lado-ángulo-lado ∆ABC ~ ∆DEF A B C D E F 3u 2u 6u 4u DE AB = EF BC 6 3 = 4 2 Dos triángulos son semejantes si tienen un ángulo igual y los lados que los forman son proporcionales.
CRITERIOS LLL ∆ABC ~ ∆DEF lado-lado-lado A B C E D F DE AB = EF BC = DF AC 6 4 = 4.5 3 = 9 6 = 1.5 6u 4u 3u 9u 4.5u 6u Dos triángulos son semejantes si sus 3 lados son proporcionales.
TEOREMA DE THALES
Cuando en un triángulo se traza una recta paralela a uno de los lados, el triángulo que se forma es semejante al primero.
entonces ∆ACB ~ ∆A’CB’ (teorema de semejanza) A A’ C Si A′B′| | AB
B
B’
EJERCICIO
Para resolver este tipo de ejercicios es necesario hacer una regla de tres con los homólogos para encontrar el valor desconocido Como se muestra en la siguiente pagina
• Calcula el valor de X en las siguiente figura 12 x 14 28 A B C D E
EJERCICIO
• Calcula el valor de X en las siguiente figura 12 x 14 28 = = x 12 * 28 14 = x 336 . 14 = x 24 = 12 x 14 28 A B C D E segmento AD =12 esta en el lado izquierdo y segmento AE= 14 en el derecho; de esta manera seguimos la semejanza; DB= X y EC=28
EJERCICIO
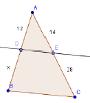
• Un hombre de 1.80 m. de estatura proyecta una sombra de 3.05 m. de largo; al mismo tiempo que un edificio proyecta una sombra de 26.3 m. ¿Cuál es la altura del edificio?
A pesar tener diferente planteamiento el esquema de solución es el mismo
1.80 3.05
x 26.3
EJERCICIO
• Un hombre de 1.80 m. de estatura proyecta una sombra de 3.05 m. de largo; al mismo tiempo que un edificio proyecta una sombra de 26.3 m. ¿Cuál es la altura del edificio? 1.80 3.05
x 26.3
1.80 = 3.05 x = 26.3 x = 1.80 * 26.3 3.05
x = 15.52 m R. LA ALTURA DEL EDIFICIO ES DE 15.51 M
BIBLIOGRAFIA
• MATEMATICAS SIMPLIFICADAS (4.a ed.). (2015). PEARSON/ CONAMAT.
• TRIANGULOS SEMEJANZA Y CONGRUENCIA https://youtu.be/9-AhOQjpKdk