Función lineal
Esta función tiene la forma f(x)=mx+b y representa una recta en el plano cartesiano, en donde m es la pendiente b la ordenada al origen
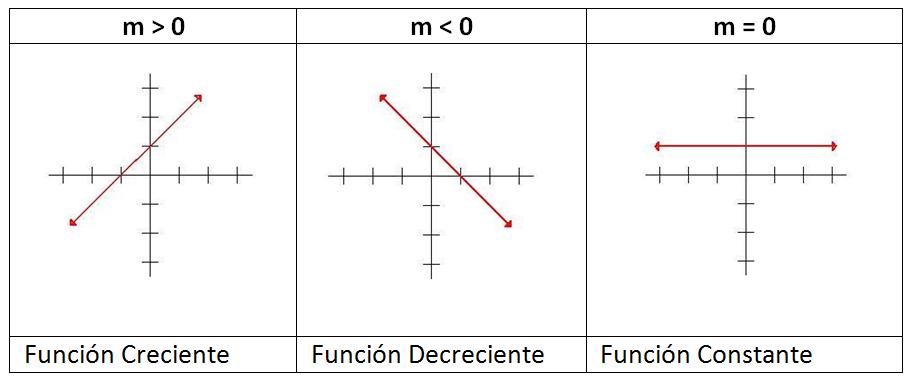
(“x” puede tomar cualquier valor del eje x)
nio : Df = (− ∞, ∞) go : Rf = (− ∞, ∞)
(“y” puede tomar cualquier valor del eje x)
El dominio y rango de la función lineal serán siempre todos los números reales, al ser infinito el los valores posibles de los números reales el dominio y rango se expresa del modo anterior
Para graficar
1. Se localiza la ordena al origen, es decir (0,b)
2. a partir de ese punto, se localiza otro llamado pendiente como el incremento o decremento vertical sobre el incremento horizontal
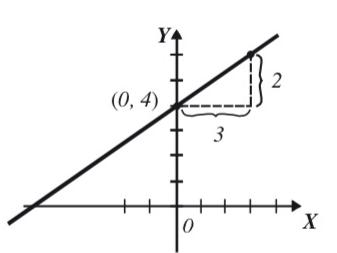
y= ⅔x + 4
la pendiente y la ordena al origen de la función Por lo tanto el dominio y rango quedaría así: Df = (− ∞, ∞) Rf = (− ∞, ∞) m = 2 3 m = 2 incremento ver tical 3 incremento hor izontal b = 4 representa el punto (0,4) Grafica de la función Metodo analitico
Grafica la función
ejemplo: SOLUCIÓN:

Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 Para comenzar a resolver la función, despejaremos Y para tenerla en la forma de base Metodo Grafico


Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 x y -2 0 2 4 ASIGNAR VALORES Para calcular los valores de “y” sustituiremos el valor de “x” en la función como se muestra a continuación:


Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 ASIGNAR VALORES x y -2 0 2 4 y = 2x − 3 y = 2(− 2) − 3 y = − 4 − 3 y = − 7


Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 ASIGNAR VALORES x y -2 -7 0 2 4 y = 2x − 3 y = 2(0) − 3 y = − 3


Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 ASIGNAR VALORES x y -2 -7 0 -3 2 4 y = 2x − 3 y = 2(2) − 3 y = 4 − 3 y = 1


Graficar la función 6 = 4x − 2y ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 ASIGNAR VALORES x y -2 -7 0 -3 2 1 4 y = 2x − 3 y = 2(4) − 3 y = 8 − 3 y = 5



Graficar la función ejemplo: TENER LA FUNCION EN LA FORMA y=mx+b 1 6 = 4x − 2y 2y = 4x − 6 y = 4x − 6 2 y = 2x − 3 2 ASIGNAR VALORES x y -2 -7 0 -3 2 1 4 5 GRAFICAR EN EL PLANO CARTESIANO Para graficar recordaremos los principios básicos de plano cartesianos estudiados en la unidad anterior Al ser una función lineal el dominio y rango queda así: Df = (− ∞, ∞) Rf = (− ∞, ∞)
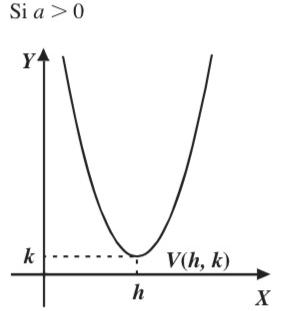
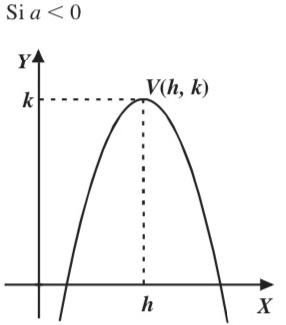
Aquella que puede escribirse de la forma cuya representación grafica es una parábola f (x) = a x 2 + bx + c Función Cuadrática CASO I x2 es positiva Dominio : Df = (− ∞, ∞) Rango : Rf = [f ( − b 2a ), ∞] Dominio : Df = (− ∞, ∞) Rango : Rf = [− ∞, f ( − b 2a )] Concava Convexa CASO II x2 es negativa El dominio y rango queda representado así:
Metodo analitico
Para resolver por método analitico, tentarmos que encontrar los valores del vértice.
Utilizaremos los valores para a, b y c como los trabajamos en las ecuaciones de segundo grado Comenzando con el eje de simetria o h
CALCULAR el vertice para el metodo analitico x = − b 2a
V(h,k) son las coordenadas del vértice. Para obtener las coordenas (h,k) del vértice se aplican las siguientes formulas

k = f ( − b 2a ) h = − b 2a
sustituimos el valor de x en la función
−
Grafica la función y = 2x 2 − 4x
1 ejemplo:
CALCULAR 1 a= 2 b= - 4 c= - 1 x = − (− 4) 2(2) x = 4 4 x = 1


Grafica la función y = 2x 2 − 4x − 1 ejemplo: CALCULAR 1 x = − b 2a a= 2 b= - 4 c= - 1 x = − (− 4) 2(2) x = 4 4 x = 1 CALCULAR EL Valor de k sustituyendo en la función 2 y = 2(1)2 − 4(1) − 1 y = 2 − 4 − 1 y = − 3 Metodo analitico
ya que calculamos h, este valor lo vamos a sustituir en la función inicial como se muestra es en ejemplo



Grafica la función y = 2x 2 − 4x − 1 ejemplo: CALCULAR 1 x = − b 2a a= 2 b= - 4 c= - 1 x = − (− 4) 2(2) x = 4 4 x = 1 CALCULAR EL Valor de k sustituyendo en la función 2 y = 2(1)2 − 4(1) − 1 y = 2 − 4 − 1 y = − 3 Metodo analitico 3 x= -b ± √ b2 - 4ac 2a x= -(-4) ± √ 42 - 4(2)(-1) 2(2) x= 4 ± √ 16 +8 4 x= 4 ± √ 24 4 x1= 4 + 4.89 4 x2= 4 - 4.89 4 = 8 . 89 4 = 2 . 22 = - 0 . 89 4 = — 0 . 22 Recordemos que las funciones cuadraticas su representación es una parábola, por lo tanto calcularemos las raíces para saber en que punto corta al eje x; utilizaremos la formula general para ecuaciones de 2º grado
Para graficar sigue las siguientes recomendaciones 1. para saber si la parabola en concava o convexa revisemos el valor de x2 si es positiva la grafica es convexa 2. Grafica el eje de simetria que son los valores resultantes del punto 1 y 2 en este caso (1,-3)
Grafica el eje X los valores de las raíces que calculaste 4. traza la parabola Para el Dominio recordemos que X puede tomar cualquier valor El Rango se limita a los valores del eje Y en este caso inicia en -3 y hacia arriba puede tomar cualquier valor
Df = (− ∞, ∞)




Grafica
y =
2 − 4x − 1 ejemplo: CALCULAR 1 a= 2 b= - 4 c= - 1 x =
2 y = −
Metodo analitico 4 3 x1= 4 + 4.89 4 x2= 4 - 4.89 4 = 8 . 89 4 = 2 . 22 = - 0 . 89 4 = — 0 . 22
la función
2x
1 CALCULAR EL Valor de k sustituyendo en la función
3
3.
Rf = [− 3,∞]
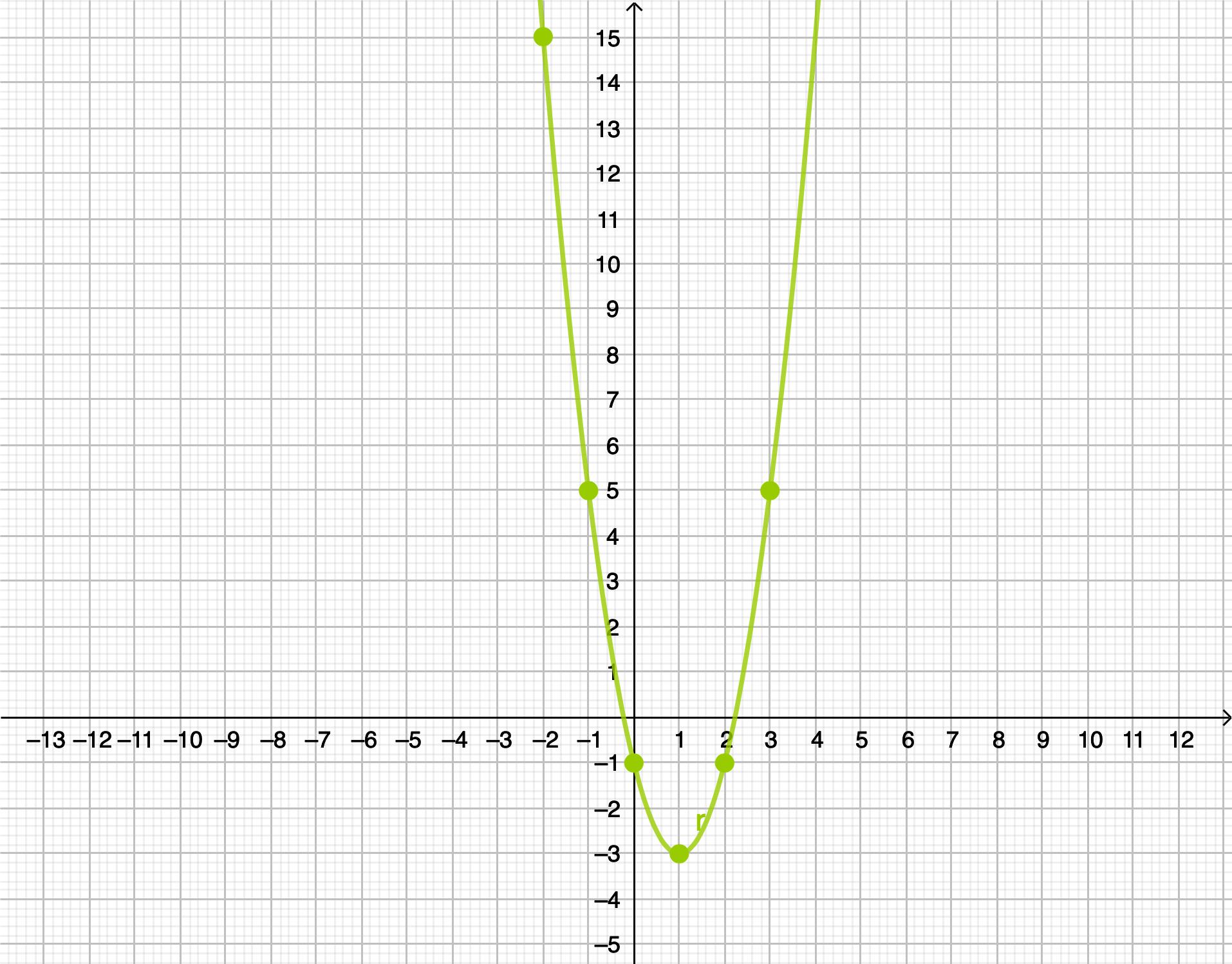
Grafica la función y = 2x 2 − 4x − 1 ejemplo: y= x y 3 5 2 -1 1 -3 0 -1 -1 5 -2 15 -3 29 Metodo grafico se realiza la tabla de valores como en la función lineal Df = (− ∞, ∞) Rf = (− 3,∞)




































