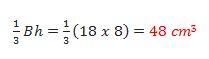Poliedros
Poliedros regulares y Prismas
Arq. Areli González Ramos
Volumen
Al recordar las figuras en tres dimensiones es importante repasar el calculo de volúmenes. Fíjate en el siguiente prisma rectangular:
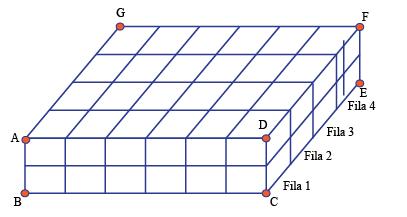
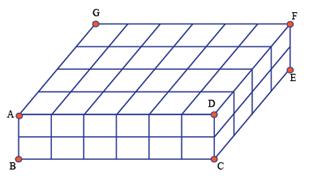
Si consideramos la cara frontal (el rectángulo ABCD) como la base, ésta tendrá un área de 12 unidades cuadradas. Esta cara tiene cuatro filas, cada una con 12 cubos.
Si multiplicamos el área de la cara (12) por las 4 filas, tenemos 48 cubos o un volumen de 48 unidades cúbicas.
Tenemos diferentes figuras en 3D que veremos a continuación
Poliedros
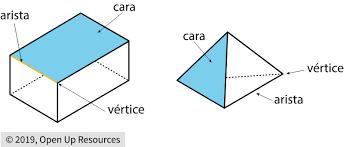
Son aquellos limitados por polígonos regulares iguales, sus ángulos poliedros son iguales y sus ángulos diedros iguales.
TETRAEDRO
Clasificación
Sus caras son cuatro triángulos equiláteros.
HEXAEDRO O CUBO
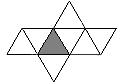
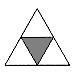
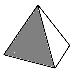
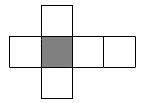
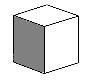
Sus caras son seis cuadrados.
OCTAEDRO
Sus caras son OCHO triángulos equiláteros.
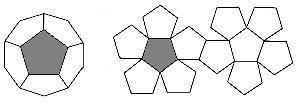
DODECAEDRO
Sus caras son doce pentágonos regulares
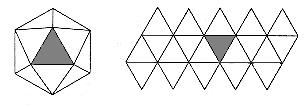
ICOSAEDRO
Sus caras son veinte triángulos equiláteros
AREAS Y VOLUMENES
L Vt
Vt
Vt
L h L L L L L L h L L L L
TETRAEDRO OCTAEDRO HEXAEDRO O CUBO ICOSAEDRO
= 2 12 * L 3 Donde: L=longitud de cara h= altura del cuerpo At = 3 L 2
= 2 3 * L 3 L= longitud de la cara h= altura de todo el cuerpo At = 2 3 L 2
= L 3 Donde: L= longitud de cara At = 6L 2 Vt = 15 + 5 5 12 * L 3 L= longitud de la cara At = 5 3 * L 2 DODECAEDRO Vt = 15 + 7 5 4 * L 3 L= longitud de la cara A = 3 25 + 10 5 * L 2
Cuerpos Redondos
Esfera
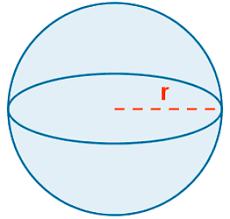
Es un sólido geométrico al que limita una superficie esférica, cuyos puntos equidistan de un punto fijo que se conoce como centro de la esfera.
PRISMA
AREAS Y VOLUMENES
PIRAMIDES Y CONOS CILINDRO
r h
h L h h
ESFERA
Vt = area debase * alt ura Vt = 1 3 b * h
Donde: área de base (verificar formulario de reas y perímetros) h = altura de todo el cuerpo
Vt = π * r 2 * h
Donde: π = 3.1416 r = radio h = altura de todo el cuerpo
Donde: b= área de base h= altura de todo el cuerpo
Vt = 4 3 π * r 3
Donde: π = 3.1416 r = radio
Volumen
Ejemplo
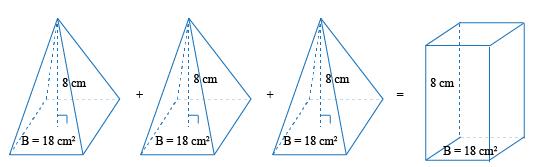
• ¿cuales son volúmenes de las imágenes mostradas a continuación?
Solución
• El volumen de cada pirámide es igual a
• Si sumamos las tres pirámides tenemos un volumen de 144 cm3.
El volumen del prisma es igual a Bh = 18 × 8 = 144 cm3
BIBLIOGRAFIA
MATEMATICAS SIMPLIFICADAS (4.a ed.). (2015). PEARSON/ CONAMAT.