1.2.3 Centrummaten

maximum bij abscis nul, en symmetrisch t.o.v. de y- as. Men kan ook de intervallen op de x- as kleiner maken zodanig dat het frequentiediagram een groter aantal zijden krijgt. Uiteindelijk zal de veelhoek overgaan in een vloeiende kromme: de verdelingskromme of frequentiekromme (fig. 2).

fig. 2

Opmerkingen:

1. De ordinaat Y x van de frequentiekromme geeft voor de abscis x het aantal afwijkingen n x van de waarde x. Y x .dx geeft het aantal afwijkingen waarvan de waarde begrepen ligt tussen x en   b a x x dx y dx geeft dan het aantal afwijkingen waarvan de waarde ligt tussen a en b.   x y dx geeft dus het totaal aantal waarnemingen N. Deze uitdrukkingen worden grafisch voorgesteld door de oppervlakten tussen de kromme en de x- as. 2. Bij de grote N en n x zal de weergave van de kromme moeilijkheden opleveren omdat de ordinaten te groot worden. Voor elk getal N zal een aparte frequentiekromme getekend moeten worden. Men zal daarom niet de absolute frequenties n x voorstellen maar wel de percentages 100nx ., ofwel de relatieve frequenties nx N N

3. Bij weergave van de relatieve frequenties noemt men de verdelingskromme de foutenkromme van Gauss, of waarschijnlijkheidskromme, omdat bij zeer grote N de relatieve frequentie van x gelijk te stellen is met de kans voor het voorkomen van x bij één enkele waarneming.

De oppervlakte tussen de foutenkromme en de x- as wordt = 1.

1.2.3 Centrummaten

= een getal waar rond de waarnemingen zich situeren

2,6 2,8 3,3 3,6 3,8 3,9 4,1 4,4 4,8 5 5,3 5,4 5,6 5,7 5,9 5,9 5,9 6,2 6,2 6,3 6,3 6,3 6,3 6,4 6,4 6,6 6,6 6,8 6,8 6,9 7,1 7,3 7,5 8,1 8,4 8,6 8,7 8,8 9,2 9,4 9,6 9,7 10,3 10,4 10,8 10,9 11,4 11,8

Centrummaten / spreidingsmaten

modus: mediaan: eerste kwartiel: derde kartiel:

 Modus

getal met grootste absolute frequentie In dit voorbeeld ………………………………………………

 mediaan

waarneming sorteren van klein naargroot en de middelste nemen Opgepast met een even aantal waarnemingen!!! In dit voorbeeld ………………………………………………

 Eerste kwartiel

 Derde kwartiel mediaan van getallen ≤ de mediaan 25% van de waarnemingen<eerst kwartiel In dit voorbeeld ………………………………………………

mediaan van getallen ≥ de mediaan 25% van de waarnemingen >derde kwartiel

 Gemiddelde gemiddelde van de populatie μ = gemiddelde van alle metingen???? Gemiddelde van de steekproef x

BOXPLOT

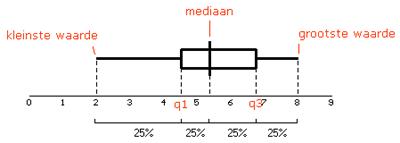
Opgepast met outliers. Outliers zijn waarden die mogelijk zijn maar zijn wel abnormaal en worden niet in een boxplot opgenomen. Bv. De grootte van volwassen mannen  2.45m is mogelijk maar wel abnormaal, we spreken dan van een outlier.