8 MATEMÁTICA
NOS DIAS DE HOJE
8o

MATEMÁTICA
ENSINO FUNDAMENTAL ANOS FINAIS
8 MATEMÁTICA NOS DIAS DE HOJE
8o MATEMÁTICA
Jefferson Cevada
Licenciado em Matemática pela Universidade Federal de Mato Grosso (UFMT). Foi professor e coordenador da rede pública de São Paulo. Editor e elaborador de conteúdos didáticos.
Daniel Romão da Silva
Doutor e Mestre em Educação pela Universidade de São Paulo (USP). Licenciado em Matemática pela Universidade de São Paulo (USP). Foi coordenador e professor da rede pública e particular de São Paulo. Autor de materiais didáticos.
Matemática nos dias de hoje
© 2022 Editora Sei
Direção editorial
Sandro Aloísio
Produção gráfica
Reinaldo Correale
Giliard Andrade
Equipe M10 Editorial
Coordenação pedagógica
Alessandra Corá
Coordenação editorial
Fernanda Azevedo
Edição
Angela Leite
Assistência editorial
Gabriel Santos Novaes
Carolina Tsuda
Conceição Longo
Rui de Melo Neves Neto
Preparação e revisão de textos
Brenda Gomes
Caroline Ponzi
Thais Sanchez
Marina Bueno
Projeto gráfico de capa e miolo
Arte/M10
Coordenação de editoração eletrônica
Eduardo Enoki
Editoração eletrônica
Fanny Sosa
Nathalia Scala
Ricardo Coelho
Iconografia M10 Editorial
Licenciamento de texto e imagens
Tempo Composto
Imagens gerais, de projeto gráfico e ilustrações técnicas
Arte/ M10
Shutterstock.com
Freepik
Impressão e acabamento
Oceano Indústria Gráfica e Editora Ltda.
Rua Osasco, 644 – Rod. Anhanguera, km 33
CEP 07750‑020 – Cajamar – SP
CNPJ: 67.795.906/0001‑10
Tel.: (11) 4446‑7000
Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.
ISBN 978‑85‑54226‑81‑7 (Aluno)

ISBN 978‑85‑54226‑78‑7 (Professor)
Todos os direitos reservados:
Editora Sei
Av. Profa. Ida Kolb, 551 – Jardim das Laranjeiras
São Paulo – SP
CEP 02518‑050
Fone: 55 11 3855‑2100
www.editorasei.com.br
contato@editorasei.com.br
INTRODUÇÃO
Ensinar e aprender dizem respeito às experiências diversas ao longo da trajetória de uma pessoa, uma comunidade, um povo. É na trajetó ria que se manifestam as diversas experiências enriquecedoras para o ensino e a aprendizagem. Sendo ela um elemento fundamental do processo de transformação, quais seriam, então, seus significados?
Como parte de sua essência, destacamos: trajeto, ou seja, um curso a ser percorrido entre uma paisagem material ou imaterial de determi nado espaço; sequência de acontecimentos, como um tecido temporal entrelaçado de fatos diversos, sejam concretos ou não; esboço de um caminho – a órbita desenhada por algo em movimento. Juntos, esses sentidos se complementam, se mesclam e favorecem a construção de uma metáfora para a relação complexa que é ensinar e aprender Aqueles que se colocaram a caminho perceberam o quanto de es tratégias conhecidas e de originalidade para o imprevisível se fizeram necessários. Assim é como se sente um professor, com os materiais que tem em mãos, diante de sua sala de aula, sujeito à diversidade de tempo de aprendizagem de seus alunos. Conhecer esses elementos e ter aptidão para os imprevistos favorecem a construção de estratégias necessárias à sua própria trajetória. Convide seus pares a compartilhar impressões, reflexões, pontos de vista e possibilidades de adaptações tanto no livro do estudante quanto nas propostas do manual do professor, entre outras ações, todas em favor de ressignificações para o melhor uso do material em suas mãos. Esperamos que esses materiais se tornem um aliado para envolver os alunos em aprendizagens significativas.
# SUMÁRIO
EM FOCO: O LIVRO DO ESTUDANTE, VI
EM FOCO: O MANUAL DO PROFESSOR , VIII
PRONTOS PARA COMEÇAR!, X
TRAJETÓRIA 1 – NORTEADORES: PARA TODOS OS VOLUMES , XIV
1. Visão geral da nossa proposta, XV
Como aproveitar ao máximo os recursos apresentados nesta coleção?, XV
• Check‑in, XV
• Salas de aula e realidades diferentes, XVI
• Estrutura da coleção e a prática docente, XVI
Avaliação: informada × assistida, XVI
• As fases da trajetória de aprendizagens, XVII
• A aprendizagem autorregulada, XVIII
• Ciclos de aprendizagens e ciclos avaliativos, XX
Avaliação diagnóstica, XX
Avaliação de processo ou formativa, XX
Avaliação de resultado, XX
• Avaliação a serviço da aprendizagem, XX
1. Para efeitos de avaliação diagnóstica, usos possíveis, XX
2. Para efeitos de avaliação em processo, usos possíveis, XXII
3. Para efeitos de avaliação de resultados, usos possíveis, XXIV
• Autoavaliação e autoconhecimento como aprendiz, XXVI
Como ajustar a prática docente para melhorar o processo de ensino-aprendizagem?, XXVII


• Check‑in, XXVII
• Identidade do professor, ambientes de aprendizagem e ava liação, XXVIII
• Cenários de proposição, XXVIII
• Avaliação formativa, XXX
Avaliação na prática pedagógica, XXX
Verbos da ação avaliativa, XXXI
Aprendizagem assistida por avaliação, XXXI
3. Articulações entre os materiais, XXXII
Articulações entre objetivos, justificativas desses objetivos, competências e habilidades, XLII

• Trajetória 1 do LE, XLII
• Trajetória 2 do LE, XLV
• Trajetória 3 do LE, XLVII
• Trajetória 4 do LE, L
Subsídios para trabalhar a interdisciplinaridade, LIII
Como estabelecer vínculos entre os materiais voltados para o estudante e os que são voltados para o professor?, XXXII
• Check‑in, XXXII
• Vínculo entre a estrutura da obra e as ações docentes vol tadas para a avaliação, XXXIII
• Letramento matemático, XXXIII
A BNCC e o letramento matemático, XXXV
Os processo matemáticos, XXXVI
• Flexibilização curricular da coleção, XXXVIII
Aspectos envolvidos na avaliação, nos problemas e nos exer cícios, XXXVIII
Aspectos envolvidos nas perguntas norteadoras, nos TCTs e na interdisciplinaridade, XXXVIII
• Mapa dos Temas Contemporâneos Transversais na BNCC, XXXIX
• Trajetória 1 do LE, LIII
• Trajetória 2 do LE, LIV
• Trajetória 3 do LE, LV
• Trajetória 4 do LE, LVI
Justificativa e pertinência dos objetivos e propostas de avaliação, LVII
• Trajetória 1 do LE, LVII
• Trajetória 2 do LE, LVIII
• Trajetória 3 do LE, LIX
• Trajetória 4 do LE, LX
BIBLIOGRAFIA, XL
TRAJETÓRIA 2 – ESSENCIAIS: PARA ESTE

VOLUME, XLI
Sugestão de cronograma, LXI
HABILIDADES DE MATEMÁTICA E DE OUTRAS DISCIPLINAS, LXII
• Quadros de habilidades do 8º ano – Matemática, LXII
• Quadros de habilidades do 8º ano – outras disciplinas, LXIII
• Check‑in, XLI
LIGHTSPRING/SHUTTERSTOCK WHITEMOCCA/SHUTTERSTOCKO livro do estudante tem uma estrutura gráfico‑editorial com intencionalidade didática voltada para o processo de mediação da aprendizagem.
ESTRUTURA DA OBRA: MEDIAÇÃO DA APRENDIZAGEM
ALEXANDRE R. / M10
PRÉ-MEDIAÇÃO
Seções especiais para declarar as intenções e os objetivos de aprendizagem, fazer diagnósticos e levantar conhecimentos prévios, ler mapas norteadores, instigar e convidar o aluno a percorrer um novo passeio e se envolver com o conhecimento que está por vir.
PASSEIO 1 NÚMEROS NATURAIS COMO INTERPRETAMOS O MUNDO À NOSSA VOLTA E NOS EXPRESSAMOS POR MEIO DOS NÚMEROS?
de ver as formas no mundo Você gosta de observar a forma dos objetos em lugares diversos?
mil quilômetros quadrados de sua extensão. Texto elaborado com finalidade didática. Informações obtidas em: www.wwf.org.br e https://educacao.uol.com.br. Escreva com algarismos os números destacados no texto, em ordem crescente, utilizando o símbolo de menor (<). 220 < 2 000 2 018 4 617 < 12 028 < 23 102 < 30 000 < 152 706 2. Represente estes números em uma reta numérica: 0 4 0 3 2 2 25 3. Observe as figuras (considere o círculo como o inteiro): Escreva a fração que corresponde às partes pintadas em relação ao todo em cada figura e, em seguida, represente essas frações em uma reta numérica. para doação. Considerando essa
4 4 5. Foi desenhado um plano cartesiano sobre o mapa de certa cidade: 12 11 9
Formas geométricas no design de ambientes. Sabe dar nome, perceber características ou pensar em relações entre algumas figuras geométricas? Veja o que o olhar de Armandinho descobriu:
ALEXANDRE BECK/

pessoa correspond) Se 25% dos livros são de poesia, então há ■ livros de poesia na caixa. 25
Qual das alternativas a correta em cada item? a) O ponto de coordenadas (1, 3) representa um local do mapa: com água área verde b) Um ponto situado em uma área verde do mapa é: 6 0 0 9
Diversidade, quantidade qualidade no mundo ao nosso redor. Ao olhar o mundo ao redor, percebemos uma grande diversidade de objetos, pessoas e seres vivos. Além de serem diversos, também existem em grandes quantidades. Há situações em que nos interessa contar com exatidão essas quantidades e, em outras, gostaríamos somente de ter uma ideia aproximada, ou seja, estimar essas quantidades.

CHECK-IN Observe a imagem e responda: Respostas pessoais. a) Quantas pedras, aproximadamente, existem na imagem? b) Em grupos, elaborem uma estratégia para estimar a quantidade de pedras. Em seguida, compartilhem com a turma. c) É possível organizar as pedras da imagem por cores? Que cores você identifica? Conte ou estime a quantidade de cada uma delas. Compartilhe sua resposta com os colegas.

A Neste passeio, você buscará atingir os seguintes objetivos: Ler, escrever, comparar e ordenar números naturais. Reconhecer o Sistema de Numeração Decimal que prevaleceu no mundo ocidental. Identificar as principais características do Sistema de Numeração Decimal, como valor posicional e função do zero. Compor e decompor números naturais. Localizar números naturais na reta numérica. Fazer estimativas de quantidades. Reconhecer diversos sistemas de numeração de distintos povos e épocas.
ARMANDINHO, VI | MANUAL DO PROFESSOR
quadrilátero.
EM FOCO: O MANUAL DO PROFESSOR
O manual do professor é um livro de múltiplas funcionalidades que impactam diretamente o professor, indiretamente o aluno e, de modo circundante, a comunidade escolar.
O manual do professor tem o caráter de inspirar o professor para a reflexão, a compreensão e a transformação, levando‑o a refletir sobre si mesmo, os conhecimentos, os estudantes e os recursos materiais.

ESTRUTURA DA OBRA × INSPIRAÇÃO PARA O ENSINO
Livro do professor: páginas com teor pedagógico abrangente que antecedem o livro do estudante anotado.
Livro do estudante anotado: livro do estudante em formato reduzido com respostas, orientações e resoluções nas bordas.
Há conteúdos no manual do professor indicados para o trabalho inicial do ano letivo e outros para os trabalhos no decurso do ano letivo.

Trabalhos iniciais do ano letivo
A seção Prontos para começar! – no manual do professor – traz, a cada volume, um diálogo sobre a prática docente e que incentiva a reflexão do professor antes ou durante os primeiros dias do ano letivo. São temas que têm por objetivo favorecer o pla nejamento das unidades didáticas e das aulas, considerando as necessidades reais do contexto local.
#PRONTOSPARACOMEÇAR! 1. O texto a seguir pode ser discutido no momento de trabalho coletivo dos professores. Comece pelo fim Avance do planejamento da unidade para planejamento da aula. Defina objetivo, decida como irá avaliá-lo depois escolha atividades apropriadas para a aula. Quando comecei a lecionar, eu me perguntava enquanto planejava: “O que vou fazer amanhã?”. A pergunta por si só já revelava falhas no meu método de planejamento em pelo menos dois aspectos essenciais – sem contar as minhas respostas algumas vezes dúbias. A primeira falha era que eu estava pensando em uma atividade para as minhas aulas no dia seguinte, e não em um objetivo – que queria que meus alunos soubessem ou fossem capazes de fazer quando a aula tivesse terminado. É muito melhor fazer o contrário e Começar pelo fim – o objetivo. Ao estruturar primeiro um objetivo, você substitui a pergunta: “De que atividades os meus alunos vão participar hoje?” por “O que meus alunos serão capazes de fazer quando minha aula tiver terminado?”. A segunda dessas perguntas é mensurável de uma forma significativa. A primeira não é. O sucesso de uma atividade não determinado pelo fato de você realizá-la ou não os alunos parecerem ter vontade de participar, mas sim se você atingiu um objetivo que possa ser avaliado. Em vez de pensar sobre uma atividade – talvez: “Vamos ler O sol para todos –, estruturar seu objetivo força você se perguntar o que seus alunos vão ganhar com leitura do livro. Eles vão entender e descrever natureza da coragem conforme demonstrado em O sol é para todos? Eles vão entender por que a injustiça algumas vezes prevalece, como mostra o livro O sol para todos O sol é para todos para descrever como autor constrói personagens importantes por meio de suas palavras ações. Em suma, há muitas coisas valiosas que você pode fazer em aula e muitas maneiras de abordar cada uma delas. Sua primeira tarefa escolher lógica mais produtiva: por que você está ensinando esse conteúdo? Qual o resultado que você espera? Como esse resultado se relaciona com o que você vai ensinar amanhã com o que seus alunos precisam para estarem preparados para os anos subsequentes? A segunda falha que minha pergunta revelava tinha ver com o fato de que eu geralmente formulava na noite anterior aula. Além de ser um sinal óbvio de procrastinação, também demonstra que eu estava planejando minhas aulas de forma isolada. Cada aula estava talvez vagamente relacionada com a anterior, porém, não refletia uma progressão intencional no seu propósito. Das duas falhas, esta era na verdade mais censurável. Eu poderia solucionar problema da procrastinação planejando todas as minhas aulas na sexta-feira anterior, por exemplo. Mas até que começasse pensar nas minhas aulas como partes de uma unidade maior, desenvolvendo as ideias com intencionalidade lentamente em direção ao domínio de conceitos maiores, eu estava certo de que estava andando deriva. Na verdade, estaria em melhor situação se planejasse com antecedência todos os meus objetivos (apenas eles) para trimestre e, depois, deixasse o planejamento de cada aula para última hora, do que se tivesse planejado devidamente na semana anterior todo um lote de aulas, porém centradas apenas em atividades. LEMOV, Doug. 62 técnicas para melhorar a gestão da sala de aula. Porto Alegre: Penso, 2017.



Trabalhos no decurso do ano letivo
2. avaliação de chegada dos alunos ao novo ano letivo uma etapa fundamental para nortear as práticas subsequentes. avaliação de chegada ajuda a identificar os conhecimentos que os alunos trazem consigo quais são as melhores estratégias para os diferentes perfis de estudantes. Antes de aplicar a avaliação, é de suma importância planejá-la. Um dos itens desse planejamento



A Trajetória 1 traz a visão geral da proposta, reflexões sobre a prática docente, a organização da obra, as possíveis articulações entre o livro do estudante e o manual do professor para todos os volumes.
A Trajetória 2 apresenta os temas essenciais de cada volume, reforçando seus aspectos específicos e as possibilidades de trabalho para os conteúdos que dizem respeito àquele volume.
Desta forma, o manual do professor busca apoiar o trabalho de formação continuada na escola, e o trabalho coletivo, colaborativo e entre pares, na busca por um ensino com mais sentido.

Compartilhamento de estratégias de ensino.

1. Nas suas práticas de aula, como você se prepara para trabalhar as competências gerais, as competências específicas de Matemática e as habilidades? Há diversas possibilidades. Leia o texto que preparamos para você e seus pares. No ambiente escolar, são muitas as oportunidades para o trabalho com as competências gerais, as competências específicas de Matemática e as habilidades. A articulação entre elas pressupõe “arranjos” que deem clareza às ações docentes, facilitando a definição de focos, a escolha de percursos, a mobilização de ferramentas etc. Uma possibilidade de arranjo é o conceito de cenários de proposição

Ideias criativas, trabalho em equipe, solução de problemas, análises críticas e sugestões de inovação resultam de um ambiente favorável à apresentação de propostas.
Os cenários de proposição são um conjunto de ações impulsionadas para favorecer a problematização, a inovação e a sociali zação em sala de aula. Essas ações articulam três competências essenciais em quatro dimensões de processos: questionamento, imaginação, ação e reflexão.
CENÁRIOS DE PROPOSIÇÃO
CRITICIDADE
CRIATIVIDADE
INTERATIVIDADE
Caráter Racional científico Emocional imaginativo Social tecnológico Ação dominante Questionar e avaliar ideias e soluções
• Observar e descrever experiências.
Dimensão 1:
QUESTIONAMENTO
• Selecionar e analisar conhecimentos e informações relevantes.
• Estabelecer relações entre conceitos e ideias.
• Integrar diferentes perspectivas disciplinares.
• Exercitar a curiosidade intelectual.
• Buscar e criar ideias.
Dimensão 2: IMAGINAÇÃO
• Experimentar ou ampliar ideias incomuns, arriscadas ou radicais.

Apresentar novas ideias e soluções
• Compreender as oportunidades do contexto/cenário e os limites do problema.
• Identificar e questionar premissas.
• Verificar a precisão dos dados, fatos, informações e interpretações. Analisar lacunas no conhecimento.
• Revisar teorias e opiniões estabelecidas e imaginar diferentes perspectivas sobre o problema.
• Identificar pontos fortes e fracos de evidências, argumentos, alegações e opiniões.
Envolver-se socialmente em projetos e soluções
• Apreciar criticamente diversas formas de interações.
• Sentir e expressar empatia.
• Debater e problematizar as práticas de intolerância, discriminação e violência contra indivíduos, grupos sociais ou povos com vistas à tomada de consciência e ao exercício da paz social.
• Idealizar soluções mediadoras de conflitos para produzir entendimento mútuo.
• Conceber projetos que visem ao acolhimento das diversidades na perspectiva dos direitos humanos e da cultura de paz.
Dimensão 3: AÇÃO
CRITICIDADE CRIATIVIDADE INTERATIVIDADE
• Realizar prognóstico de um fato; prever, inferir.
• Produzir, criar protótipos de um produto.
• Propor uma solução ou uma apresentação própria, pessoal, algo novo.
• Considerar e avaliar a novidade da solução escolhida e suas possíveis consequências.
Dimensão 4: REFLEXÃO
• Considerar e avaliar a relevância da solução escolhida e suas possíveis consequências.
• Justificar uma solução ou um produto proposto por meio de critérios/raciocínios lógicos, éticos ou estéticos.
• Aderir ao bem comum propondo ações que incentivem o respeito às diferenças entre pessoas e povos.
• Construir coletivamente, procedimentos e normas de convívio que viabilizem a participação de todos em diferentes espaços.
• Avaliar e reconhecer a incerteza ou os limites da solução ou posição defendida.
• Refletir sobre o possível viés da perspectiva pessoal em comparação com outras perspectivas.
• Julgar sua própria aptidão para respeitar regras básicas de convívio social nas interações.
• Considerar aspectos relativos à qualidade do convívio social no grupo do qual faz parte em favor de propor superação de conflitos ou melhorias nas socializações.
Observação: essa tabela se encontra reproduzida mais adiante, porém, para facilitar a consulta, foi também apresentada aqui.
As competências gerais e as competências específicas de Matemática podem ser ordenadas segundo a ênfase de cada uma, como a seguir.
Competências essenciais no cenário de proposição
Criticidade Criatividade Interatividade
Ação dominante
Questionar e avaliar ideias e soluções.
Apresentar novas ideias e soluções.
Envolver se socialmente em projetos e soluções.
Esse “arranjo” favorece a melhor definição do alvo que você deseja alcançar com determinadas explorações no decurso das aulas. Favorece também a seleção das melhores ações previamente pensadas e que possam se alinhar com esta ou aquela aptidão essencial. Não estamos afirmando que a abordagem de situações didáticas envolvendo, por exemplo, as competências gerais 8 e 9 junto com as competências específicas de Matemática 7 e 8 são exclusivamente voltadas à interatividade e totalmente desprovidas de criticidade e criatividade, até porque, na enunciação de cada uma, já percebemos que essas aptidões essenciais se mesclam pelas articulações internas entre elas. O que nossa proposta pretende é dar a você a possibilidade de pensar em encaminhamentos dire cionando a ênfase a um conjunto de aulas com intencionalidades mais claras para você e para seus alunos.
Nessa coleção há diversos momentos favoráveis ao trabalho articulado entre as competências gerais, específicas e as habili dades. Um exemplo é a seção Barcos e portos e, especialmente, sua subseção Proponha, em que pode ocorrer uma síntese dos significados explorados com as competências e as habilidades, mas também como possibilidade de novas descobertas em direção a outros portos.
No manual do professor, na Trajetória 2: Essenciais para este volume, você encontra diversos quadros relacionando compe tências gerais, competências específicas e habilidades, como no exemplo a seguir.
Trajetória 3 do LE
PASSEIO 1
Competência geral
8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
Competência específica
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Habilidades EF06MA07 e EF06MA09.
Objetivos
• Representar números em forma de fração.
• Reconhecer diferentes significados e interpretações para as frações: parte/todo, fração de uma quantidade, fração como quociente.
• Resolver problemas envolvendo diferentes significados para as frações.
Articulações e justificativas
Ao longo desse passeio, há oportunidades de explorar as competências e as habilidades previstas no material voltadas aos nú meros naturais e aos sistemas de numeração.
No passeio 1 da Trajetória 1 do livro 6, por exemplo, a competência geral 1 e a competência específica 1 são propícias para questionar e avaliar ideias e soluções, pois favorecem a busca de proposições críticas. Nesse exemplo, utilizando a dimensão 1: questionamento, uma possibilidade é incentivar os alunos a:
• observar e descrever experiências de pessoas com deficiência auditiva na aprendizagem dos números e do sistema de numeração decimal;
• selecionar e analisar informações relevantes, experiências reais de alguém conhecido, seja ouvinte ou com deficiência auditiva, em uma interação de aprendizagem de conhecimentos de Matemática;
• estabelecer relações entre conceitos e ideias de modo a favorecer melhores estratégias de interação entre pessoas com defi ciência auditiva e ouvintes;
• integrar diferentes perspectivas e ideias usando conhecimentos matemáticos ou não que possam trazer benefícios para as re lações entre as pessoas.
Esse exemplo mostra possíveis relações entre as competências gerais ou específicas, as habilidades e os conteúdos de Matemática e outras disciplinas.
LUPAS E LUNETAS
a) Reúna se com seus pares e selecione, inicialmente, um passeio de algum volume desta coleção. Depois, identifique as referidas competências gerais, as específicas e as habilidades esperadas do passeio e busque identificar, com apoio do quadro Competências essenciais no cenário de proposição, se a competência essencial é de criticidade, criatividade ou interatividade.
b) Em seguida, com base nos conteúdos a serem mobilizados no passeio, avalie qual dimensão (questionamento, imaginação, ação, reflexão) dos cenários de proposição é a mais conveniente a ser reforçada neste momento.
c) Apresente propostas para ação docente no intuito de desenvolver, ao mesmo tempo, as habilidades esperadas e as competências específicas e gerais correspondentes no passeio de sua escolha.
d) Ao final, compartilhe as propostas.
2. Na reflexão anterior, você explorou algumas possibilidades de articulações entre as competências e habilidade da BNCC, favo recidas pelos cenários de proposição. Veremos agora outro modo de trabalhar essas mesmas competências, reconhecendo as inter relações complexas que envolvem conhecimentos (c), habilidades (h), atitudes (a) e valores (v). As competências da BNCC podem ser compreendidas como um conjunto dotado de muitas relações envolvendo seus elementos, conforme exposto neste quadro:
COMPETÊNCIAS
CONHECIMENTOS HABILIDADES ATITUDES VALORES
Conceituais
Factuais
Procedimentais
Para aprender a conviver
Para aprender a ser
Sensibilidade e alteridade
Cuidado e respeito
Compreensão
Solidariedade e amor
Cabe ao professor identificar o tipo de conhecimento, a categoria de habilidade adequada para desenvolver as atitudes desejadas e para conscientizar os alunos dos valores propostos.
LUPAS E LUNETAS
Pesquise para descobrir o significado dos elementos desse quadro. Por exemplo: o que é cada tipo de conhecimento (conceitual, factual e procedimental)? Busque definições apresentadas, por exemplo, por Antoni Zabala. Faça o mesmo para os demais elementos do quadro. Se preferir, combine com outros professores que pesquisem elementos diferentes dos seus e depois se reúnam para trocar as descobertas e compartilhar os entendimentos.
Articulações e justificativas
Entre as diversas possibilidades de uso de tecnologias digitais, cabe destacar as relacionadas à geometria e a construções geométricas. A partir, por exemplo, de softwares de geometria dinâmica, é possível explorar não somente os procedimentos de construção de ângulos e polígonos, como também suas características e propriedades. Além disso, é possível explorar diferentes resoluções para problemas e testar diversas hipóteses a partir das tecnologias digitais. Dessa maneira, espera-se contribuir para o desenvolvimento da compreensão e criação de tecnologias digitais, bem como seu uso de maneira crítica, significativa, reflexiva e ética.
3. Vamos analisar um exemplo. Na Trajetória 1, passeio 3, do livro 6, consta o seguinte quadro no manual do professor:
PASSEIO 3
Competência geral
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Habilidades EF06MA12, EF06MA14, EF06MA18, EF06MA19 e EF06MA20.
Objetivos
• Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os seus dois membros por um mesmo número e utilizar essa noção para determinar valores desconhecidos na resolução de problemas.
Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.
Identificar características dos triângulos e classificá-los em relação às medidas dos lados e dos ângulos.
Identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles.
Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e classificá-los em regulares e não regulares, tanto em suas representações no plano como em faces de poliedros.
Articulações e justificativas

Considere também a abertura desse passeio no livro do estudante:
A Matemática pode ser interpretada como uma maneira de ler e de agir sobre o mundo. A partir dessa premissa, é possível partir da Matemática em direção ao desenvolvimento de projetos que foquem em questões de urgência social, assumindo, em sua concepção, princípios éticos, democráticos, sustentáveis e solidários. Considerando esse contexto, é possível desenvolver diversas habilidades matemáticas. Por exemplo, a partir da consideração sobre diferentes significados para a igualdade matemática, assim como da análise de semelhanças entre figuras geométricas, é possível extrapolar para discussões mais gerais sobre igualdade, identidade, diferença etc. Possuindo tais discussões como ponto de partida, é possível “exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação”, por exemplo.
PASSEIO 3 – RELAÇÃO DE IGUALDADE E POLÍGONOS
NO ESPAÇO VIRTUAL, SOMOS IGUAIS OU DIFERENTES?
Interatividade e comunicação.
As tecnologias digitais de informação e comunicação abrem possibilidades de nos relacionarmos com várias pessoas ao mesmo tempo sem sair de casa. Essa nova maneira de comunicação permite que possamos estar ligados coletivamente, cada um com suas diferenças, mas também movidos por um interesse em comum.
CHECK-IN
a) Pela imagem, é possível ver quantas crianças na tela do tablet? b) Elas são iguais? Comparando-as, que característica você consideraria comum a todas elas?

c) Cada criança tem a imagem do seu rosto em um pequeno retângulo. Por que não poderiam ser círculos ou triângulos? Argumente em favor da sua ideia e ouça atentamente as ideias dos colegas, valorizando a forma de pensar de cada um, incentivando o outro a expor de modo diferente aquilo que para você ainda não está claro
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os dois membros da igualdade por um mesmo número e utilizar essa noção para determinar valores desconhecidos na resolução de problemas. Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.
Identificar características dos triângulos e classificá-los em relação às medidas dos lados e dos ângulos. Identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles. Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e classificá-los em regulares e não regulares tanto em suas representações no plano como em faces de poliedros.
Desde a abertura do passeio é possível estruturar um roteiro de aula, cujo processo vai reforçando a aprendizagem informada e mediada entre professor e aluno.
LUPAS E LUNETAS
Considere o passeio mencionado acima, analise o e reflita sobre as questões a seguir.
a) Dentre os 5 objetivos matemáticos previstos quanto ao conhecimento mobilizado em cada um deles, quais são conceituais, factuais e procedimentais?
b) Analise as atividades e o que se espera com a competência geral 9 e com as competências específicas 7 e 8. Do ponto de vista das atitudes, o enunciado dessas três competências reforça mais o desenvolvimento de atitudes para aprender a conviver ou aprender a ser? As atividades que constam nesse passeio e que “tocam” nessas competências favorecem, de algum modo, as experiências voltadas às finalidades apontadas por elas? Comente.
c) Em que medida valores como sensibilidade e alteridade podem ser incentivados nas práticas em sala de aula, levando em conta as experiências proporcionadas por esse passeio? Compartilhe com os pares.
TRAJETÓRIA 1 – NORTEADORES: PARA TODOS OS VOLUMES
1. Visão geral da nossa proposta.


Nesta Trajetória:
2. A prática docente
3. Articulação entre os materiais.
Alunos no pátio de escola pública em Santo Antônio de Jesus, Bahia, Brasil. Sala de aula de escola municipal de Dias D’Ávila, Bahia, Brasil. JOA SOUZA/SHUTTERSTOCK1. VISÃO GERAL DA NOSSA PROPOSTA
A Matemática desenvolve um papel fundamental nas atividades do dia a dia, relacionando diferentes áreas das ciências, tecno logias, artes e outras linguagens.
Os conhecimentos matemáticos estabelecidos pela Base Nacional Comum Curricular (BNCC) são entrelaçados nesta coleção por meio de situações apresentadas em contextos diversos do cotidiano e de outras áreas do conhecimento.
Para conhecer as particularidades desta coleção, seja em relação aos materiais do estudante ou do professor, este manual fa vorece, por meio de explorações gradativas, uma forma de conhecê‑lo por sucessivas aproximações no decorrer do ano letivo, em momentos de horário pedagógico coletivo, por exemplo, também entre duplas, trios ou outras pequenas formações. Assim, os pro fessores podem encontrar as melhores formas de construir parcerias por meio desta obra, desde a exploração inicial deste material até o seu uso efetivo em sala de aula.
Como aproveitar ao máximo os recursos apresentados nesta coleção?
A excelência da aula depende do professor, todavia, vai além das suas ações e dos materiais que ele utiliza: há uma rede complexa de fatores que implica a necessidade de competências diversas a todos os envolvidos.

CHECK‑IN
• De que maneira você utiliza o livro didático em sala de aula?
• Além de constituir um suporte de conteúdos sobre matemática e didática, que outras possibilidades quanto à prática docente você enxerga para o livro didático?
• Considerando a noção de avaliação formativa, de que maneira o livro didático pode subsidiar a prática docente?
de aula e realidades diferentes
Existem diversas maneiras de utilizar os mesmos materiais didáticos, todas elas com possibilidades de desencadear aulas exce lentes. Cada turma é diferente: em algumas os alunos são participativos, em outras, eles necessitam de mais estímulos para a par ticipação; algumas são eficientes em diversidade de assuntos e curiosidades e outras não correm os riscos da curiosidade. Também cada professor excelente é diferente: alguns são enérgicos, outros são brandos; alguns são acadêmicos, outros, mais informais. Cada um utiliza melhor seu repertório de técnicas adequadas a cada um dos diversos momentos da aula.
As salas de aula de alta produtividade estão sempre acolhidas por professores que se esforçam para criar os melhores cenários de aprendizagem, buscando cada vez mais um rigor nas suas ações para o ensino, nas atitudes de aprendizagem de seus alunos e na melhoria das formas de interações entre ele, os alunos e os conhecimentos, para que todos possam ter oportunidades de ampliar seu horizonte acadêmico e aprimorar a própria reflexão crítica no convívio pacífico em sala de aula.
Há diversos caminhos para ensinar os diferentes alunos, cada um com suas potencialidades e seus obstáculos.
Conhecer a fundo os recursos materiais, a diversidade de perfis de alunos, os possíveis obstáculos de cada um, as estratégias mais satisfatórias para a maioria – ou as estratégias específicas para determinado aluno –, identificar modos de estimular aqueles que sempre dizem “eu não sei”, entre outras análises profundas, são parte da rotina diária dos excelentes professores. Um bom início para essas análises profundas é conhecer o material que está em suas mãos.

Estrutura da coleção e a prática docente
Avaliação: informada assistida
Vamos apresentar a estrutura padrão de cada volume por meio do processo avaliativo.

Cada volume é assim composto:
Páginas iniciais: avaliação de chegada
Prontos para começar!
Unidades bimestrais Páginas finais: revisão e exames de larga escala
Trajetória (de 1 a 4)
Retornos e Suplemente sua aprendizagem
Cada Trajetória é dividida em três passeios. Os passeios se inter‑relacionam por meio de uma pergunta norteadora abrangente que desencadeia o contexto central da Trajetória. Essa pergunta abrangente, por sua vez, desencadeia outras três perguntas, uma para cada passeio.
Veja o esquema detalhado da estrutura padrão de uma Trajetória.
A avaliação, que ocorre na interação entre professor e aluno, no decorrer de cada passeio é:
• informada, pois cabe ao professor evidenciar as expectativas de aprendizagem, os propósitos das práticas em sala e a qualidade dos resultados; e cabe ao aluno expor suas primeiras noções, informar a percepção sobre sua própria aprendizagem, os possíveis efeitos das práticas em sala e comunicar os resultados obtidos;
• assistida, pois cabe ao professor observar e analisar os movimentos de aprendizagem do aluno; e cabe a este expor e sinalizar os efeitos de todas as práticas de ensino ofertadas pelo professor.
As fases da trajetória de aprendizagens
Chamamos de trajetória de aprendizagens um conjunto de ações didáticas estruturadas em três fases: chegada, núcleo e desfecho, de modo que cada fase seja, ao mesmo tempo, informada e assistida. As fases de uma trajetória de aprendizagens são nomeadas por: mapa de estudos, percurso e porto de chegada
Quais são as diferentes possibilidades para o professor em suas práticas? E como tirar o melhor proveito do processo avaliativo? Como essas questões podem ser contempladas em uma Trajetória no livro do estudante?

O quadro mostra algumas possibilidades oferecidas pela estrutura de uma Trajetória no livro do estudante, segundo as três fases: o mapa, o percurso e o porto.
Fases de uma trajetória de aprendizagens
QUESTÕES REFLEXIVAS
Da parte do aluno
• Onde estou?
Da parte do professor
• Onde o aluno está?
Mapa de estudos
Check‑in; Arredores; Bússola.
Textos e teorias; Atividades; Lupas e lunetas.
• Para onde vou?
• A que precisarei estar atento para ver corretamente?
O foco do olhar:
• O que vejo e o que não vejo?
• O que preciso ver ainda?
• Do que necessita para se colocar a caminho?
• O que ele tem e o que não tem na bagagem?
• O que o aluno é capaz de ver?
• Do que ele precisa para ver aquilo que ainda não consegue?
Percurso
Porto de chegada
Diálogo em aula por meio das atividades.
Levo na bagagem; Barcos e portos; Vistorias.
A crítica do olhar:
• Como vejo?
• O que fazer para ver melhor?
• Para que vejo?
• Consegui chegar?
• Vi tudo que era para ser visto?
• Como poderia ter visto melhor?
• Por que motivos o aluno aprendeu/não aprendeu?
• Para quais ações ele já está apto e em quais ainda precisa de apoio?
• Sob quais pontos de vista o aluno chegou ao objetivo?
• Como poderia ter navegado melhor?
Ao longo de toda a trajetória de aprendizagens, aluno e professor, em um trabalho complementar de esforços, desenvolvem estra tégias para identificar aquilo que representa um obstáculo na aprendizagem e, juntos, podem verificar formas possíveis de superá‑lo.
LUPAS E LUNETAS
Para esta reflexão, tenha em mãos um volume desta coleção, de sua escolha. Abra uma dupla de páginas que contenha as seções Check-in, Arredores e Bússola
Considere a situação de entrada, as informações, os conteúdos, o contexto, o mapa de vínculos e ênfases, que se encontra na seção Arredores, e a lista dos objetivos, que se encontra na seção Bússola
a) Que estratégias você planejaria para o trabalho com essa dupla de páginas, antes de entrar em sala de aula?
b) Segundo seu olhar, que eficácia o uso dessas páginas proporciona à avaliação informada e assistida?
c) Como você utilizaria essa dupla de páginas em sala de aula, levando em conta as reflexões que você acabou de fazer?
A aprendizagem autorregulada
A estrutura da obra oferece ao aluno oportunidades variadas para que, gradativamente, desenvolva autonomia para monitorar sua aprendizagem, organizar seus conhecimentos, desenvolver estratégias de estudo e autoavaliar‑se.
É possível criar condições em sala que o incentivem a vivenciar experiências de aprendizagem voltadas para reflexões, tanto da ordem cognitiva quanto da metacognitiva.
Cuidar da mente, desenvolver bons hábitos de estudos, monitorar e regular o próprio pensamento são habilidades e atitudes que envolvem a aprendizagem autorregulada.
A principal função de uma estratégia cognitiva é lhe ajudar a alcançar o objetivo de qualquer iniciativa cognitiva em que você esteja envolvido. Em contraste, a principal função de uma estratégia metacognitiva é lhe oferecer infor mações sobre a iniciativa ou seu progresso nela. Podemos dizer que as estratégias cognitivas são evocadas para fazer o progresso cognitivo, e as estratégias metacognitivas para monitorá‑lo. (FLAVELL; MILLER; MILLER, 1999, p. 129)


As pesquisas voltadas para aprendizagem autorregulada, metacognição, autoaprendizagem e outros temas desse campo têm se intensificado nos últimos anos.
Barry Zimmerman e outros pesquisadores apresentaram a perspectiva do aprendizado autorregulado ou self regulated learning (SRL). Nesta visão, o aluno autorregulado é consciente e controla o seu processo de aprendizagem; seleciona os métodos e as estratégias que utiliza, revelando um grande sentido de autoeficácia; e organiza e estrutura quer o seu contexto de estudo quer o trabalho a realizar, identificando as situações em que precisa de ajuda e adaptando as estratégias de aprendizagem aos seus objetivos acadêmicos (ZIMMERMAN, 1986).
Estas são as seções do livro que oferecem oportunidades de desenvolver um trabalho com essas finalidades:
• Bússola: seção que apresenta ao aluno, a cada início de passeio, o que se espera que ele aprenda. Uma vez informado da expec tativa quanto à sua aprendizagem, ele próprio deve ficar atento, no decorrer do passeio, ao que é esperado dele.
• Levo na bagagem: boxe que aparece no fechamento do passeio, que é um momento reflexivo individual do aluno quanto à qua lidade do seu aprendizado. As perguntas estão em acordo com as expectativas de aprendizagem declaradas na seção descrita anteriormente.
• Organize (da seção Barcos e portos): há sempre uma proposta de retomada, por parte do aluno, dos conhecimentos e habilida des explorados no passeio, para que ele possa atribuir significados novos ou reorganizar mentalmente os conteúdos explorados.
EAMESBOT/SHUTTERSTOCK• Vistorias: ao final da Trajetória (que equivale a um bimestre), o aluno tem mais um conjunto de atividades representativas das habi lidades essenciais daquela Trajetória. Ele próprio pode verificar quais habilidades desenvolveu em melhores condições e quais não.
• Dicas de estudos: ao final de cada Trajetória, o aluno é convidado a refletir, descobrir modos de estudar e tentar colocar em prática os bons hábitos de estudo individual.
• Suplemente sua aprendizagem: ao final de cada volume, há uma coletânea de questões de exames de larga escala que pode ser utilizada como instrumento de avaliação (ou autoavaliação, uma vez que há o gabarito disponível para o aluno).
• Retornos: para os alunos que demonstrarem dificuldades de compreensão dos conhecimentos essenciais no decorrer do passeio, ou para alunos que desejarem reforçar seus conhecimentos, há uma síntese dos conteúdos explorados em cada Trajetória. A leitura e a construção dos próprios resumos, esquemas, fichamentos de conteúdos devem ser incentivadas na rotina de estudos dos alunos.
O quadro expõe exemplos de perguntas que podem ser ensinadas aos alunos para exercitarem o pensamento metacognitivo.
Possíveis questões com ênfase nas estratégias metacognitivas
SOBRE OS DESEMPENHOS
Das ferramentas
• Eu sei fazer cálculos mentais?
QUESTÕES
• Aprendo melhor registrando no papel ou só mentalizando as etapas de cálculo?
• Eu sei usar diferentes representações para um mesmo cálculo?
• Sei usar cálculo mental em situações do cotidiano?
Do uso das tarefas
Sobre os efeitos do uso das ferramentas
• Como uso as ideias e as propriedades das operações ao registrar no papel ou mentalizar as etapas da realização de uma conta?
• Eu reconheço as diferentes estratégias de cálculo de uma mesma operação em situações do cotidiano, em uma compra de supermercado, por exemplo?
• O que preciso fazer para aprender a calcular mentalmente?
• Como devo agir na hora de registrar mentalmente uma conta para que cada vez eu possa calcular melhor?
• Como posso eliminar a insegurança e o medo de aprender mais de uma estratégia de cálculo para uma mesma operação?
• Para que devo fazer uso do cálculo mental no cotidiano?
Sobre as finalidades de uso das ferramentas
• Por que aprendo melhor (ou é indiferente) as propriedades das operações ao fazer uma conta “de cabeça”, por exemplo, no supermercado?
• Como escolher a melhor estratégia de cálculo para uma conta em uma situação do cotidiano (em uma compra de supermercado, por exemplo)?
Com base nessas questões em que o próprio aluno refletiu, autorregulou seu pensamento e autoavaliou‑se é, agora, a vez de o professor verificar a qualidade dos desempenhos metacognitivos do aluno:
Verificação dos efeitos dos processos metacognitivos
• Descreva os processos de cálculo em uma situação real em que você utilizou cálculo mental.
• Relate um fato que você aprendeu durante um registro por escrito de um cálculo ou de um processo mental de resolução de uma operação.
• Invente uma conta e escreva pelo menos duas maneiras de determinar seu resultado.
LUPAS E LUNETAS
Escolha uma página que contenha o boxe Levo na bagagem. Considere os conhecimentos, as atitudes e a exploração dos contextos aos quais essa seção se refere para realizar o que se segue.
a) Que orientações você daria para a turma quanto ao momento em que cada aluno for refletir sobre sua aprendizagem? Como você monitoraria e validaria a atitude dos alunos na realização dessa autoavaliação?
b) Que outras questões autoavaliativas você acrescentaria às que estão sugeridas no livro do estudante?
c) Com essa página, escolhida por você, roteirize um caminho de trabalho a ser aplicado em aula, escolhendo sempre uma linguagem clara e sucinta.
Ciclos de aprendizagens e ciclos avaliativos
A prática docente é permeada pela atividade avaliativa em suas diversas modalidades.
Avaliação diagnóstica
É aplicada no início de cada ciclo de aprendizagem. Possibilita a identificação de conceitos, procedimentos, fatos e atitudes que os alunos já têm estabelecidos em momentos anteriores ao novo ciclo prestes a começar. Por meio dos feedbacks dos alunos, é possível captar o alcance do que têm já efetivado para, com essas informações, o professor construir as estratégias das novas aprendizagens. Tem a função de ajuste bilateral, aluno/programa de estudos: seja modificando o programa de estudos para adequá‑lo aos alunos, seja orientando as aprendizagens dos alunos para que percorram com sucesso o programa estabelecido.
Avaliação de processo ou formativa

Dentro da atividade avaliativa está a avaliação de processo, que se traduz como o acompanhamento da aprendizagem, de maneira que seja possível monitorar avanços, dificuldades, possíveis obstáculos que envolvem a aprendizagem dos alunos e fazer interven ções em “tempo real”, oferecendo oportunidades que satisfaçam às necessidades diversas que ocorrerem no decurso do ciclo de aprendizagem. Essa avaliação interfere em toda a atividade de ensino‑aprendizagem. É preciso levantar informações úteis e criar modificações eficazes para a regulação do processo de ensino‑aprendizagem. Tem caráter formativo.
Avaliação de resultado
Esta ocorre ao final de um ciclo de aprendizagem. Sua função é verificar quais aquisições foram feitas ao longo do ciclo de aprendizagem com vistas a expedir ou não um “certificado”, ou seja, tem caráter certificativo. Essa avaliação mensura a eficácia do processo de ensino‑aprendizagem.
Avaliação a serviço da aprendizagem
Ao longo do livro do estudante, é possível verificar possibilidades para o trabalho docente que, por vezes, extrapolam a esfera estrita da Matemática e, por outras, complementam‑na a partir do convite à utilização de diversas maneiras de se expressar mate maticamente: oralmente, artisticamente, ludicamente etc.
Levando em conta as três modalidades de avaliação, apresentamos os potenciais das diversas seções do livro quanto a cada uma dessas modalidades avaliativas:
1. Para efeitos de avaliação diagnóstica, usos possíveis:
Prontos para começar!, Check-in, Arredores, Bússola, Atmosfera
Todas essas seções indicam as possibilidades preparatórias para as ações diagnósticas, ou seja, levantamento de indícios e, em seguida, favorecer a condução influenciada por expectativas de aprendizagem específicas a serem monitoradas mediante as produções dos alunos. Tais produções serão desenvolvidas ao longo do processo de ensino‑aprendizagem. Assim, podem ser utili zadas como levantamento de indícios as seções Prontos para começar!, Check-in e Atmosfera
#PRONTOSPARACOMEÇAR!
1. Leia o texto: O Brasil é um país de dimensões continentais, vinte três mil, cento e dois quilômetros de fronteiras, terrestres e marítimas. Esse tamanho abriga uma biodiversidade de doze mil e vinte oito espécies de animais e quatro mil seiscentos e dezessete espécies de plantas. Um animal símbolo dessa biodiversidade é tamanduá-bandeira, que chega a medir duzentos vinte centímetros
de comprimento e consegue comer até trinta mil formigas em um só dia! Mas precisamos cuidar dos biomas brasileiros que abrigam tal biodiversidade. Entre os anos de o Cerrado, bioma que abriga boa parte dos tamanduás-bandeira, teve uma perda de cento cinquenta e dois mil setecentos e seis quilômetros quadrados de sua Texto elaborado com finalidade didática. Informações obtidas em: www.wwf.org.br e https://educacao.uol.com.br. Acessos em: 17 maio 2022. Escreva com algarismos os números destacados no texto, em ordem crescente, utilizando o símbolo de menor (<). 220 < 2 000 < 2 018 < 4 617 < 12 028 < 23 102 < 30 000 < 152 706
2. Represente estes números em uma reta numérica:
0 3 4 0 3 5 2 2 25
3. Observe as figuras (considere o círculo como o inteiro): Escreva a fração que corresponde às partes pintadas em relação ao todo em cada figura e, em seguida, represente essas frações em uma reta numérica.
4. Em uma caixa há 100 livros destinados para doação. Considerando essa informação, substitua cada ■ pelo número correto: a) Se há 75 livros usados, então ■% dos livros são usados. 75 b) Se a décima parte dos livros é de ficção científica, então ■% dos livros são de ficção científica. 10 c) Sabendo que metade dos livros foi doada por uma única pessoa, as doações dessa pessoa correspondem a ■% do
A seção Prontos para começar! é uma ótima ferramenta para realizar um diagnóstico na chegada dos
nas primeiras aulas do ano letivo.
FREEPIK/ ARTE/ M10

PASSEIO 1 – NÚMEROS DECIMAIS
O QUE OS NÚMEROS INDICAM SOBRE O MEIO AMBIENTE?
Observe este infográfico. Levando em conta os números que aparecem nele, responda às questões.
Os países que geram mais e menos lixo eletrônico (kg por pessoa)
ATMOSFERA
[...]
As “contas” do meio ambiente Nossa civilização, assim como todas as demais que já existiram sobre a Terra, possui forte dependência do meio ambiente. Embora muitas vezes a gente se esqueça disso, os recursos naturais estão presentes nas mais elementares atividades humanas, como comer, beber e respirar. Mesmo nas sociedades mais complexas, essa dependência se mantém. Continuamos a precisar de água e de
energia, por exemplo, que são elementos básicos para quase todas as atividades humanas, especialmente as econômicas. Além de prover nossa subsistência, a natureza nos propicia lazer e prazer estético, cultural e espiritual e é também responsável pela reciclagem dos resíduos gerados pelas ações humanas.
[...] CONTAS econômicas ambientais: o que são? Projeto TEEB regional-local Brasília/DF: Ministério do Meio Ambiente, 2019. Disponível em: www.giz.de/en/downloads_els/Cartilha%20Contas%20Econ%C3%B4micas%20Ambientais_09_05_2019.pdf. Acesso em: 12 jul. 2022.
Água: participação das atividades econômicas no consumo total (em %)

Agricultura, pecuária, produção florestal, pesca
e aquicultura 97,4
Indústrias extrativas 0,1
Indústrias de transformação e construção 1,0

Eletricidade e gás 0,0
Água e esgoto 0,8
Demais atividades 0,1
Participação das famílias no consumo total 0,6 Consumo total 100,0
Instituto Brasileiro de Geografia e Estatística (IBGE) e a Agência Nacional de Águas (ANA). Contas Econômicas Ambientais da Água Divulgação em 2020, dados de 2017.
1. Lazer, prazer estético, cultural, espiritual e também reciclagem dos resíduos gerados pelas ações humanas.
ATIVIDADES
CHECK-IN
a) Quantos números há nesse infográfico? 10 números.
b) Pense em alguém que pese 28 kg. Considere essa pessoa e imagine o que significa a quantidade de lixo eletrônico que uma pessoa, sozinha, gera na Noruega. Que conclusões você pode propor com essa comparação? Resposta pessoal.
c) Observe os números: 5, 1 2 10%, 50%, 5 10 50. Quais deles você relacionaria ao número 0,5? Converse com os colegas a esse respeito.
c) 1 2 50% e 5 10 pois são os únicos que equivalem ao número 0,5.
238 TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.
1. Segundo o texto, atividades elementares como comer, beber e respirar são sinais da nossa forte dependência do meio ambiente. A natureza provê nossa subsistência. Além desses, que outros elementos da atividade humana são também a natureza que nos propicia?
2. Quais são os dois elementos que o texto afirma serem básicos para quase todas as atividades humanas? Água e energia.
Agricultura, pecuária, produção florestal, pesca e aquicultura.
3. Qual atividade econômica é a que mais consome água do total de participação?
4. Quanto consomem, juntas, as indústrias extrativas e as de transformação e construção?
5. A soma de quais duas atividades econômicas resulta em 1,5%?
6. Quem consome mais água: as famílias ou as indústrias de construção?
7. Qual dessas atividades econômicas você acha que deveria economizar mais água?
1,1%. Água e esgoto e demais atividades. As indústrias de construção.
Como acredita que isso seria possível? Apresente uma proposta para que essa atividade econômica citada por você possa economizar água. Respostas pessoais.
As seções Check-in e Atmosfera são adequadas para realizar um diagnóstico dos conhecimentos e atitudes dos alunos quanto à Matemática e aos contextos diversos no início de cada novo passeio – que pode durar de 15 a 20 dias.
Para o monitoramento das expectativas de aprendizagem, são adequadas as seções Arredores e Bússola
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
Reconhecer números decimais em situações cotidianas.
Reconhecer a correspondência entre as representações decimal e fracionária de um mesmo número e estabelecer relações entre essas representações, passando de uma representação para outra.
Compreender a representação de números decimais segundo o sistema de numeração decimal.
Compor e decompor números decimais.
• Comparar e ordenar números decimais, representando-os na reta numérica.
Justificar em charges o efeito de humor, ironia ou crítica pelo uso ambíguo de palavras, expressões ou imagens.
Associar a produção de materiais sintéticos ao desenvolvimento científico e tecnológico, reconhecendo benefícios, mas também avaliando impactos ambientais.
O mapa de vínculos e ênfase apresenta uma possibilidade de conexões entre os diferentes conteúdos matemáticos e, logo abaixo, as expectativas de aprendizagem, que podem ser previamente ajustadas pelo professor, de acordo com seu planejamento.
2. Para efeitos de avaliação em processo, usos possíveis: Atividades, Nuvens, Travessias, Lupas e lunetas e Retornos
A seção Atividades fornece as principais ações cotidianas da sala de aula para o olhar da avaliação mediadora. Nesse momen to, o aluno enfrenta uma tarefa, registra um processo, demonstra o produto de uma atividade e, a partir de então, são expostos os elementos observáveis que passam a ser informações para a avaliação em processo. Essa seção tem um duplo papel na avaliação em processo: avaliar a atividade do aluno (sua postura acadêmica no ato de aprender, que vai além de destrezas mentais com os conhecimentos matemáticos, como sua autoestima e perseverança na busca de soluções) e avaliar o resultado da sua produção ou o seu produto (nesse caso, é possível fazer uma observação indireta do aluno como produtor, levando em conta os traços de seu produto).
20. b) Problema possível: Maria comprou cinco bandejas com seis ovos cada uma. Um ovo ela consumiu. Qual fração de meia-dúzia de ovos ainda restam?
19. Escreva uma fração imprópria e a forma mista de modo que sejam representadas as partes pintadas das figuras em relação a um inteiro:
b) A partir dessa situação, elabore um problema e, depois, troque-o com um colega na hora de resolver.
21. Observe as divisões de cada círculo e de cada maçã.
20. Observe esta imagem, considerando meia-dúzia de ovos como o inteiro:
a) Represente a soma dessas quantidades de ovos por uma fração imprópria e, depois, na forma mista.


a) Se as fatias de cada círculo, a partir do segundo, fossem divididas ao meio, a qual fração do todo cada nova fatia corresponderia?
b) Imagine que as quatro maçãs estivessem divididas, cada uma, em três fatias iguais. Quanto representariam sete fatias em relação ao todo (no caso, uma maçã)?
Represente de duas maneiras diferentes.
c) Elabore uma pergunta em que a resposta seja uma fração imprópria ou uma representação mista. Resposta pessoal.
22. Neste labirinto o sapo só pula sobre uma vitória-régia com fração própria. Escreva no caderno a sequência de frações em que
A seção Atividades favorece a exposição, por parte do aluno, de informações observáveis para a avaliação em processo, demonstrando se de fato ele compreendeu as situações, os conceitos, os fatos e os procedimentos explorados anteriormente.
O boxe Lupas e lunetas propõe reflexões sobre os objetos de conhecimento estudados em relação aos diferentes contextos, matemáticos ou não. Além do apelo ao desenvolvimento de um espírito investigativo por parte dos alunos, a marca desse boxe é justamente convidar o aluno para uma reflexão a respeito de um detalhe ou um olhar amplo sobre um conhecimento de modo imediato, no decurso da aula.
#Um mesmo sinal, diferentes significados

Em situações do cotidiano envolvendo noções de igualdade, essa palavra também pode estar associada à noção de equilíbrio, especialmente em situações com balanças e gangorras. Acompanhe o experimento de Carol, em que ela utiliza pequenos pesos de metal, cuja massa é em gramas, e uma balança de dois pratos.


LUPAS E LUNETAS
a) Ao final, o que Carol verificou? Que a maçã pesa 150 g.
b) Escreva uma sentença que represente a síntese da verificação feita por Carol. Utilize algum símbolo de Matemática nessa sentença. Compartilhe sua escrita com os colegas. Resposta pessoal.

A igualdade na Matemática
Exemplo de boxe Lupas e lunetas no qual o aluno é levado a refletir sobre uma situação que é o fio condutor da explanação da aula.
Observe cada situação e sua correspondente sentença matemática.
Mundos imaginados.
A Matemática é uma produção humana. Ao longo da história, diversos povos, culturas e civilizações elaboraram suas maneiras de interpretar e explicar o mundo a partir de sua própria linguagem matemática. Mais do que somente uma maneira de compreender, a Matemática se constituiu como uma maneira de estar e de agir sobre o mundo.
A coleção considera essencial o enfrentamento e a elaboração de perguntas, sejam elas matemáticas ou não, convidando o aluno a ler, entender e reelaborar as perguntas problematizadoras, como ocorre no boxe da abertura de cada Trajetória:
LUPAS E LUNETAS
Reflita sobre as questões expostas anteriormente e considere-as para elaborar outras perguntas de sua própria autoria.

Publique suas perguntas no mural da sala de aula e aprecie as perguntas dos colegas.
Boxe recorrente, que convida o aluno a reelaborar as questões norteadoras, apresentadas a cada abertura de Trajetória.
A coleção também valoriza o desenvolvimento de habilidades e competências relacionadas ao letramento matemático, ou numeramento: representar, comunicar e argumentar matematicamente. As situações descritas anteriormente contemplam tais habilidades; além disso, é também comum verificar problemas e atividades que convidam os alunos a expor suas ideias, hipóteses, argumentações e justificativas.
Além de esses momentos se constituírem em locais privilegiados para a avaliação formativa, cria‑se também nos alunos o senti mento de pertencimento. Em outras palavras, ao investigar um problema matemático coletivamente, argumentar matematicamente e justificar suas estratégias para a resolução, o aluno toma para si o problema e, a partir de então, não se trata mais de um problema “inventado pelo livro”, mas um problema em que todos se envolvem para resolver.
NUVEN S
Ampliar e reduzir figuras utilizando aplicativos de geometria dinâmica
Ao iniciar o aplicativo, será exibido um plano cartesiano e uma barra de ferramentas com diversas opções. Aqui, utilizaremos a função “novo ponto”.
Agora, ampliaremos essa figura de modo que cada lado tenha o triplo do comprimento dos lados da figura original. Para isso, podemos selecionar um dos pontos da lista. Ao abrir o teclado virtual, digitaremos “× 3”.
TRAVESSIAS
As diversas “facetas” do ângulo São diversos os pintores cubistas. Caso tenha interesse, pesquise na internet as obras de alguns deles, como Pablo Picasso (1881-1973), Juan Gris (1887-1927), Georges Braque (1882-1963) e a brasileira Tarsila do Amaral (1886-1973).

A 1 obra é de Juan Gris, intitulada Retrato de Pablo Picasso, 1912. Óleo sobre tela, 93 cm × 74 cm School of the Art Institute of Chicago. As duas outras imagens são criações artísticas contemporâneas no estilo cubista, utilizando softwares especializados.

Em seguida, marcaremos no plano cartesiano os pontos A B C e D Note que, ao marcarmos os pontos no plano, aparece uma lista com as coordenadas dos pontos.
Faremos isso para cada um dos pontos A B C e D. Veja como ficou a figura final, ampliada com o triplo do tamanho da original:
Assim como as obras cubistas, que chamam a atenção por possibilitar diferentes facetas de um mesmo retrato, o ângulo, essa figura geométrica, também é multifacetado. Ao longo da história da Matemática e, em particular, entre os diferentes livros didáticos, é possível encontrar algumas distintas definições de ângulo.

O mais comum atualmente, por um lado, é que um mesmo material didático de Matemática assuma uma das definições possíveis. Por outro, constatar que há distintas definições contribui para ampliar o campo de significados associado ao conceito de ângulo. Pensar nas consequências que cada definição traz também é uma boa reflexão. Veja cinco possíveis definições de ângulo, vindas de materiais escolares brasileiros ao longo dos tempos.
I. Duas retas distintas que se cortam em um ponto, formando quatro aberturas. Cada abertura recebe o nome de ângulo.
II. Ângulo é cada uma das regiões em que o plano fica dividido por duas retas que têm um único ponto comum.
III. Um ângulo é a figura geométrica formada por duas semirretas com uma extremidade comum.

IV. Ângulo é o nome de cada uma das regiões em que o plano fica dividido por duas de suas retas que tenham um só ponto comum.
Em seguida, utilizaremos a função “Reta (Dois Pontos)” para criarmos os lados do polígono que terá seus vértices nos pontos A B C e D. Para fazer isso, é necessário clicar nos pontos até que todos os lados tenham sido desenhados.
ATIVIDADES
Respostas pessoais.
10. Elabore outras figuras e experimente ampliá-las com um aplicativo de geometria dinâmica. Compartilhe sua produção com os colegas.
11. Como faríamos para reduzir uma figura geométrica utilizando esse aplicativo? Compartilhe com os colegas a sua estratégia.


V. Ângulo é uma rotação que transforma uma semirreta em outra semirreta com a mesma origem.
ATIVIDADES
12. Forme dupla ou trio. Leia as questões para realizar essa investigação. Respostas pessoais.
a) Compare as cinco definições com a definição apresentada na página anterior. A qual delas aquela definição corresponde? Explique.
b) Represente cada uma das cinco definições por meio de um desenho. Você pode utilizar lápis de cor para os casos em que for necessário colorir. Compartilhe com os demais colegas as descobertas que vocês fizeram.
As seções Nuvens e Travessias convidam o aluno a se envolver com variadas situações que promovem o letramento matemático.
Finalmente, como parte necessária aos hábitos de estudo do aluno para revisar, reorganizar e construir novas conexões, há a seção Vistorias, que oferece possibilidades de revisão dos conhecimentos. É uma etapa importante para o aluno resgatar as infor mações da memória de longa duração, manipulá‑las na memória de trabalho e também o inverso, o aprendizado que recém‑chegou à memória de trabalho poder ser levado para a memória de longa duração, sempre que o conteúdo for repassado no mesmo dia.
NÃO ESCREVA NO SEU LIVRO. 19 |RETORNOS TRAJETÓRIA 1
Sistemas de numeração
O sistema de numeração que utilizamos –o indo-arábico – tem como características ter base 10 e ser posicional além da existência do zero
Ao longo da história, outros sistemas de numeração foram substituídos pelo indo-arábico (como os sistemas chinês e egípcio antigos); outros ainda têm alguns usos no cotidiano, como o sistema de numeração romano.
Números naturais
O conjunto dos números naturais é representado pela letra N
N {0 1 2 3 4 5 6 7 8 9 10 11
Na reta numérica:
Adicionando 1 a um número natural qualquer, obtemos o seu sucessor Subtraindo 1 de um número natural, diferente de 0, obtemos o seu antecessor
Operações com números naturais
A operação de adição está relacionada a diversas ações: juntar, acrescentar, adicionar, totalizar etc.
• Propriedades da adição
I. Pela propriedade comutativa é possível alterar a ordem das parcelas sem que isso altere o resultado.
II. Pela propriedade associativa em uma adição com três ou mais parcelas, é possível associar parcelas para decidir a ordem em que serão realizadas as adições.
III. Pela propriedade do elemento neutro todo número adicionado a zero resulta nele mesmo.
A operação de subtração está relacionada a diversas ações: tirar, subtrair, descontar, perder, completar etc.
A adição e a subtração são operações inversas Por exemplo, se 3 + 5 = 8 então
8 – 5 3 e 8 – 3 5
A operação de multiplicação está relacionada a significados como contagem, adição de parcelas iguais, proporcionalidade, configuração retangular etc.
• Propriedades da multiplicação
I. Pela propriedade comutativa a ordem dos fatores não altera o produto da multiplicação.
II. A propriedade associativa possibilita associar os fatores de uma multiplicação para realizar os cálculos em uma ordem conveniente.
III. Pela propriedade do elemento neutro, o produto da multiplicação de um número natural por um 1 é sempre ele mesmo.
IV. Pela propriedade distributiva podemos relacionar a operação de multiplicação com as operações de adição e subtração. Por exemplo: 3 (2 + 5) 3 2 + 3 5 6 + 15 21
A operação de divisão está relacionada a significados como repartir, agrupar, separar, partilhar etc.
Podemos escrever a divisão como:
Dividendo Resto Divisor Quociente
E a relação fundamental da divisão é: Div dendo Quoc ente × D visor + Resto
Em expressões numéricas envolvendo as quatro operações fundamentais, deve-se respeitar a seguinte ordem para as operações:
• 1 multiplicação e divisão, na ordem em que aparecem;


• 2 adição e subtração, na ordem em que aparecem.
A multiplicação de fatores iguais recebe o nome de potenciação O produto
2 2 2 2 2 por exemplo, pode ser representado por 25
• Qualquer número a diferente de zero, elevado a 0 é igual a 1: a0 1 para a ≠ 0
• Qualquer número a elevado a 1 é ele mesmo: a = a Sólidos geométricos Sólidos geométricos podem ser classificados em corpos redondos e poliedros Os corpos redondos são sólidos geométricos com superfícies curvas, mas podem ter superfícies planas.
Os poliedros são sólidos geométricos formados somente por superfícies planas.
A superfície dos poliedros é composta de porções de planos. Cada uma dessas porções de superfícies planas é chamada de face do poliedro.
Veja exemplos:
A intersecção de 2 faces de um poliedro é denominada aresta
A intersecção de duas ou mais arestas de um poliedro é denominada vértice Os prismas apresentam duas bases que são polígonos idênticos. Face Vértice
Aresta
As pirâmides têm somente uma base e, externo ao polígono da base, há um único vértice, que é comum a todas as faces laterais triangulares.
A superfície do cubo é composta somente por superfícies planas.
Um metro cúbico (1 m3) corresponde ao volume ocupado por um cubo de arestas com medida 1 m.
A superfície da esfera é composta por uma superfície curva.
A superfície do cilindro é composta por duas
A seção Retornos representa uma oportunidade de revisar, por meio de uma síntese, os conteúdos explorados pelo aluno.
3. Para efeitos de avaliação de resultados, usos possíveis:

303
Levo na bagagem, Barcos e portos, Vistorias e Suplemente sua aprendizagem Todo o processo de avaliação, no contexto escolar, é dotado de uma dimensão de comunicação, ou seja, o professor envia “mensagens” ao aluno pronunciando o modo como ele foi avaliado. A informação deve ser útil e clara de modo que faça sentido na mente do aluno e ele possa reconhecer por quais mudanças devem passar suas posturas durante a aprendizagem e igualmente suas estratégias de estudo em prol do alcance da totalidade da aprendizagem. Especialmente nessa etapa da comunicação de resultados, essa dimensão comunicativa da avaliação ganha um caráter conclusivo.
BARCOS E PORTOS
▶ Organize
Acompanhe o post de Eduarda sobre o modo de ela organizar seus estudos.
Eduarda_Sexto_Ano @Duda_
Eu sempre copio o mapa mental que está no início do passeio. Daí, quando chegamos ao final do passeio, eu pinto de azul o que aprendi bem e de amarelo o que ainda tenho alguma dúvida.
Isso vai me ajudar a enxergar onde estão minhas dificuldades e posso pedir ajuda para o professor, colegas, um adulto que saiba esses conteúdos ou, ainda, fazer pesquisas na internet
Mas sua decomposição está errada. Corrija a decomposição dela e elabore uma justificativa que fundamente a decomposição correta.
▶ Proponha
A pergunta inicial deste passeio é: O que os números indicam sobre o meio ambiente?
Ao longo deste passeio, você identificou diversos números ou índices relacionados a algum fato sobre o meio ambiente. Continue aplicando o que aprendeu. Observe a charge.
Composição e decomposição Comparação de números decimais Reta numérica
Relação entre d, c e m
73 15
Sistema de numeração decima
Milésimos m
Fracionária
Centésimos c Decima
Décimos d
Números decimais Representação de número
a) O que você achou da ideia de Eduarda? Você acredita que isso pode ajudar a organizar seu aprendizado? b) Olhando o esquema de Eduarda, o que você afirmaria sobre a aprendizagem dela?
c) Você sempre toma nota de palavras, termos matemáticos, procedimentos de cálculo, modos de resolver problemas ou algum outro fato matemático que não compreendeu bem para, em seguida, buscar estratégias para superá-los? O que costuma fazer quando não consegue aprender algum conceito?
b) Resposta possível: Ela aprendeu tudo sobre sistema de numeração decimal, mas tem dificuldades com os números decimais.
▶ Elabore Eduarda escreveu no caderno a decomposição de um número decimal.
Pesquise os números relacionados ao meio ambiente em sua cidade. Por exemplo, qual é a quantidade de pneus enviados para o descarte? Quantos são encaminhados aos descartes adequados? Quais locais existem em sua cidade para a reciclagem?
As pessoas sabem dessa informação? Apresente uma proposta que possa melhorar o cenário da qualidade do meio ambiente em sua cidade. Anote os números que você for descobrindo. Escreva-os corretamente. Faça a leitura de cada número corretamente. Destaque aqueles que estão em notação decimal.
Tire fotos da sua produção e poste no mural da sala.
NÃO ESCREVA NO SEU LIVRO.VISTORIAS
Você chegou ao final desta Trajetória. Reflita sobre tudo o que aprendeu e verifique a qualidade da sua aprendizagem. Resolva todos os exercícios no caderno.
CHECK-OUT
4. b) Não equivalentes. Sugestões de frações equivalentes a 2 4 : 4 10 6 15 20 50 etc. Sugestões de frações equivalentes a 4 9 : 8 18 12 27 40 90 etc.

1. Tainá e Aisha são nutricionistas que sempre realizam eventos sobre boa alimentação. O evento criado por Tainá ocorre a cada 5 meses e o de Aisha, a cada 8 meses. Os eventos coincidiram em maio de 2022. Quando serão realizados juntos de novo?
Em setembro de 2025.
2. Lúcia está organizando um dia de games para entretenimento com os amigos.
Ela fez uma votação para saber quais são os estilos de games preferidos de cada um.
Games preferidos Esporte

5. Dois bolos, um de morango e outro de laranja, de mesmo tamanho, foram divididos conforme mostram as figuras.
Do bolo de morango foi comida 3 4 Do bolo de laranja foi consumida uma fração equivalente a essa.
2 fatias.
Quantas fatias do bolo de laranja sobraram?
Na atividade 6 a ideia é parte de um todo. Na atividade 7, é fração de uma quantidade.
8. Nas atividades 6 e 7, qual ideia de fração está associada a cada situação?
Menina
Ação
Estratégia
Para organizar os times para as partidas de cada estilo de jogo, determine qual a quantidade máxima de pessoas em um time de modo que todos os times, de todos os estilos de games, tenham a mesma quantidade de membros. 4 pessoas.
3. São dados os números 10, 15 e 25. Com esses números, em dupla, produzam, revisem e editem dois problemas: um de mmc e outro de mdc. Respostas pessoais.
a) Resolvam os problemas e descrevam a estratégia de resolução para cada um deles por meio de um fluxograma.
b) Quais são as regularidades em termos de construção e composição nos textos dos problemas?
4. Verifique se os pares de frações são equivalentes; se não forem, escreva uma fração equivalente para cada uma no par.
a) 21 36 84 144
b) 2 5 4 9
SUPLEMENTE SUA APRENDIZAGEM
Trajetória 1
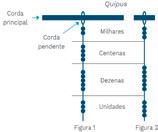
1. (Enem) Os incas desenvolveram uma maneira de registrar quantidades e representar números utilizando um sistema de numeração decimal posicional: um conjunto de cordas com nós denominado quipus O quipus era feito de uma corda matriz, ou principal (mais grossa que as demais), na qual eram penduradas outras cordas, mais finas, de diferentes tamanhos e cores (cordas pendentes). De acordo com sua posição, os nós significavam unidades, dezenas, centenas e milhares. Na Figura 1, o quipus representa o número decimal 2 453. Para representar o “zero” em qualquer posição, não se coloca nenhum nó.


Equivalentes.
atendente e anotou o número 13 98207 sendo que o espaço vazio é o do algarismo que João não entendeu. De acordo com essas informações, a posição ocupada pelo algarismo que falta no número de protocolo é a de
Alternativa b As outras alternativas dispõem as faces numa organização que não é possível a partir da planificação indicada.
a) centena.
b) dezena de milhar.
c) centena de milhar.
d) milhão.
e) centena de milhão.
3. (OBMEP) Cinco dados foram lançados e a soma dos pontos obtidos nas faces de cima foi 19. Em cada um desses dados, a soma dos pontos da face de cima com os pontos da face de baixo é sempre 7. Qual foi a soma dos pontos obtidos nas faces de baixo?
a) 10
b) 12
c) 16
Disponível em: www.culturaperuana.com.br. Acesso em: 13 dez. 2012.
O número da representação do quipus da Figura 2, em base decimal, é a) 364.
b) 463. c) 3 064. d) 3 640. e) 4 603.
2. (Enem) João decidiu contratar os serviços de uma empresa por telefone através do SAC (Serviço de Atendimento ao Consumidor).
O atendente ditou para João o número de protocolo de atendimento da ligação e pediu que ele anotasse. Entretanto, João não entendeu um dos algarismos ditados pelo
d) 18 e) 20
4. (Enem) Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas, estão as planificações dessas caixas.
Alternativa e Nas outras alternativas há contato entre faces que não podem acontecer a partir da planificação apresentada.
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?

a) Cilindro, prisma de base pentagonal e pirâmide.
b) Cone, prisma de base pentagonal e pirâmide.

c) Cone, tronco de pirâmide e prisma.
d) Cilindro, tronco de pirâmide e prisma.
e) Cilindro, prisma e tronco de cone.
6. Rui e Laís compraram uma fazenda em que farão um celeiro usando 1 10 de todo o terreno.

Para a casa principal, vão construir em 2 15 de todo o terreno.
Jovens empreendedores do agronegócio.
a) Determine a fração correspondente à parte de toda a fazenda que será ocupada pelo celeiro e a casa principal.
b) Qual é a diferença entre os tamanhos dos terrenos usados para a casa e para o celeiro?
1 30 de toda a fazenda.
7. Lana recebeu 8 000 reais pela produção anual de seus vídeos. Ela investiu 6 15 desse valor, presenteou seu irmão Fernando com 1 8 e o restante depositou para uma obra de caridade. Determine a quantia que foi para a obra de caridade. R$ 3.800,00.
a) 7 30 de toda a fazenda.
5. (OBMEP) Para montar um cubo, Guilherme recortou um pedaço de cartolina branca e pintou de cinza algumas partes, como na figura.
9. Isabela doou um saco contendo 5 kg de arroz. A instituição vai dividir sacos como esse em outros menores de 1 2 kg e 1 4 kg Determine quantos sacos de cada tipo podem ser feitos a partir de um saco de 5 kg.
10. Calcule as potências: a) 1 2 ⎛ ⎝ ⎞ ⎠ b) 2 5 ⎛ ⎝ ⎞ ⎠
c) 3 10 ⎛ ⎝ ⎞ ⎠ d) 9 10 ⎛ ⎝ ⎞ ⎠
11. Lucas faturou R$ 4.000,00 com sua empresa no mês de fevereiro. Em março seu faturamento aumentou 20%.
a) De quanto foi o aumento do faturamento de Lucas?
b) Quanto foi o faturamento do mês de março?
c) Utilize outro procedimento para resolver esse problema.
a) b) c)
Qual das figuras abaixo representa o cubo construído por Guilherme?
d) e)
6. (FATEC-SP) A figura mostra a planificação de um cubo, que apresenta imagens em suas faces.
7. (OBMEP) Numa reunião da comunidade do bairro, cada uma das 125 pessoas presentes recebeu um número diferente, a partir do número 1 até o 125. Em dado momento, foi feita uma lista das pessoas com número par e das pessoas com número múltiplo de 3, que deveriam participar de um projeto. Algumas pessoas reclamaram, dizendo que o seu nome aparecia duas vezes na lista. Quantas pessoas apareceram duas vezes na lista?
a) 2 b) 6 c) 20
d) 41 e) 62
8. (Enem) A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.
O cubo montado a partir dessa planificação é:
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
1ª mudança: 135 no sentido anti-horário;
2ª mudança: 60 no sentido horário;
3ª mudança: 45o no sentido anti-horário. Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
As seções Barcos e portos, Vistorias e Suplemente sua aprendizagem oferecem possibilidades para a avaliação de resultados e podem ser utilizadas como atividades cotidianas ou na avaliação em processo, a depender das estratégias docentes.


Outro aspecto importante da avaliação de resultados é o aluno desenvolver, aos poucos, a capacidade de ele próprio reconhecer sua lógica de pensamento equivocada ou procedimentos e regras que ele mesmo criou sem fundamentos com os conhecimentos que foram até então explorados. Ou seja, o processo de autoavaliação é, antes de tudo, uma possibilidade de “abrir os olhos” do próprio aluno para não só enxergar seus equívocos, como também enxergar os modos de superá‑los.
LEVO NA BAGAGEM Recupere em sua memória fatos relacionados às suas experiências de estudos sobre os assuntos deste passeio. Tente relembrar aquilo que mais aprendeu e o que você julga necessário estudar um pouco mais. Considere os seguintes aspectos:
▶ Matemática Você sabe resolver e elaborar problemas com números na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos, com e sem uso de calculadora?
Sabe escrever números utilizando múltiplos de potências de 10?
Você sabe resolver e elaborar problemas que envolvam porcentagens, relacionada à ideia de proporcionalidade, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos diversos?


Calcula a probabilidade de um evento aleatório, expressando-a na forma fracionária, decimal e percentual?
Consegue realizar experimentos sucessivos para determinar a probabilidade de um evento?
Resolve problemas que envolvam a grandeza massa inseridos em contextos diversos?
▶ Outras disciplinas
Geografia Sabe analisar interações com a natureza de diferentes povos ou grupos sociais, observando transformações da biodiversidade local ou do mundo?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
MATEMÁTICA
OUTRAS ÁREAS
Ao aluno é oferecida a oportunidade de atribuir a si mesmo uma qualificação a respeito do resultado dos seus próprios trabalhos escolares, segundo os objetivos que lhe foram declarados desde o início do passeio.
Autoavaliação e autoconhecimento como aprendiz
A autoavaliação, a autoestima e o autocuidado são processos que se mesclam e se entrelaçam no desenvolvimento do autoconhecimento como aprendiz.
Pensar sobre a própria aprendizagem, reconhecer os desafios a serem superados e, ao mesmo tempo, ter noção das conquistas realizadas no decurso escolar são ferramentas importantes a serem desenvolvidas pelos jovens estudantes que, gradativamente, se permitem ao monitoramento das suas aprendizagens e assumem para si as responsabilidades dos hábitos acadêmicos. Desenvolver a autoestima e a perseverança na busca por soluções e conhecer‑se como aprendiz de modo crítico e criativo no ambiente escolar são atitudes cada vez mais valorizadas não somente na escola, como também em toda a sociedade contempo rânea. Por exemplo, tomar consciência sobre aquilo em que possui facilidades para aprender e explorar seu potencial na realização dessas atividades ou, por outro lado, reconhecer as limitações momentâneas e as dificuldades a elas associadas, encorajando‑se a buscar formas de superá‑las, são atitudes que tornam o estudante um cidadão mais consciente das suas competências para a vida em sociedade e o faz reconhecer‑se em um processo constante de desenvolvimento pessoal.
Como ajustar a prática docente para melhorar o processo de ensino‑aprendizagem?
Os alunos aprendem de formas diferentes. Muitos deles sentem mais facilidade ao agir ativamente fazendo coisas, manipulando objetos e interagindo com o espaço e com as pessoas em vez de somente estudar de forma abstrata os assuntos apresentados. Todavia, há diversos momentos no decurso da aprendizagem de um aluno. A história construída da aprendizagem individual é mesclada de estratégias e de diversas experiências, sejam individuais, em grupo, coletivamente, concretamente, abstratamente, afetivamente etc.
Os alunos aprendem de formas diferentes nos diversos momentos das experiências de aprendizagem e o olhar atento do professor e a familiaridade quanto aos materiais disponíveis para o melhor desempenho de suas práticas potencializa a realização de excelen tes aulas. Isso torna a prática docente um exercício cotidiano desafiador mas, ao mesmo tempo, satisfatório pelos bons resultados.

Há diversos modos de acompanhar e monitorar a aprendizagem. Desde as formas de expressões do próprio aluno sobre aquilo que aprende até as formas críticas e investigativas do professor com base na observação da atividade do aluno.
CHECK‑IN
• Você ajusta sua prática docente de modo a contemplar a diversidade de interesses, necessidades e dificuldades dos alunos?
• Como você identifica e registra os conhecimentos prévios dos alunos antes de um novo ciclo de aprendizagens?
• De que modo a compreensão desses conhecimentos prévios ajuda no planejamento de sua ação didática?
• Você deixa as suas intenções de aprendizagem claras para os alunos?
Identidade do professor, ambientes de aprendizagem e avaliação
A identidade do professor é construída a partir de sua própria ação docente. É um processo que se situa no dia a dia, nas inte rações com os alunos, com os colegas e com o próprio objeto de conhecimento que é ensinado. A contínua ação docente interfere no processo de delinear a identidade do professor de tal modo que adaptações e ajustes na ação docente demandam reajustes nos esquemas de reconhecimento da própria identidade. Ao assumir a dinâmica da sala de aula, o professor leva consigo suas experiên cias e um conjunto de esquemas práticos que se torna um meio para mobilizar sua ação, conforme cada uma das necessidades que emergem do ambiente de aprendizagem
O ambiente de aprendizagem escolar é compreendido como um lugar previamente organizado para promover oportunidades de aprendizagem e se constitui de forma única, na medida em que é socialmente construído por estu dantes e professores, a partir das interações estabelecidas entre si e com as demais fontes materiais e simbólicas do ambiente. Lugar, nessa conceituação, deve ser entendido em sentido amplo e não reduzido a espaço físico. É o locus do acontecimento, é síntese de múltiplas condições, é o solo, mas, mais ainda, a cultura e a sociedade. (MOREIRA; PEDROSA; PONTELO, 2011).
A avaliação assume um papel fundamental na constituição do ambiente de aprendizagem. É a partir das opções feitas sobre o ato de avaliar que se torna possível a compreensão do que o aluno já sabe e de que maneira se apropriou dos conhecimentos. Mais ainda, é a partir da avaliação que professor e instituição de ensino podem refletir sobre suas práticas e replanejar suas ações caso seja necessário. “Avaliar é informar‑se para julgar. Remediar é ajustar a ação, apoiando‑se no feedback” (HADJI, 2001, p. 123). Observar os diversos modos de aprender nas diferentes situações de aprendizagem é uma das tarefas do professor em sua prá tica docente. Os alunos são diferentes – em seus tempos de aprendizagem, em suas experiências, em suas histórias de vida –, de maneira que os mesmos estímulos geram efeitos diversos no ambiente da sala de aula. Para que todos os alunos tenham chances de aprender, é esperado que a prática docente venha seguida de possibilidades de modificações, situadas em relação a um feedback e encaminhadas em relação ao objetivo.
LUPAS E LUNETAS
Para esta reflexão, aproveite o momento de trabalho coletivo na escola e reúna‑se com outros colegas. Tenham em mãos o livro do estudante deste volume. Escolham uma atividade que, segundo o julgamento do grupo, tenha possibilidade de gerar na aprendizagem dos alunos desempenhos diversos, variando desde alunos que compreenderão com certa facilidade até alunos que demonstrarão dificuldades extremas para realizá‑la.
a) Estipulem qual é a expectativa de aprendizagem com essa atividade, ou seja, aquilo que se espera que o aluno aprenda.
b) Roteirizem um trajeto para a realização dessa atividade em aula, com uma turma real (se possível, especifiquem inclusive o nome da turma).
c) Planejem possibilidades de ajuste na condução da aula no intento de atender a todos os alunos com suas dificuldades específicas. Se for necessário, prevejam atividades preparatórias, atividades complementares, adaptações da mesma atividade alterando a linguagem, o contexto ou a forma de se relacionar (se individual, em grupo, no coletivo) etc.
d) Com o planejamento dos ajustes necessários às diversas demandas de aprendizagem, vocês acreditam que essas intervenções pedagógicas vão favorecer o progresso individual e da turma como um todo?
• Troquem suas impressões e analisem como potencializar o uso do material.
Cenários de proposição
Sabemos que o processo de ensino‑aprendizagem é amplo e complexo. Isso nos leva a buscar meios de aprimorar esse proces so, seja no âmbito da escola, seja da prática docente, mas, especialmente, no âmbito das experiências proporcionadas aos alunos. Nessa busca tomaremos, a nosso favor, a interação entre o professor, os alunos e os conhecimentos como um conjunto chamado de cenários de proposição
As experiências de aprendizagem vivenciadas pelos alunos têm seu contexto a partir de cenários de proposição que, por sua vez, demandam vivências que incentivem a existência de competências que podem ser classificadas deste modo:
CENÁRIO DE PROPOSIÇÃO Criatividade
CARÁTER Emocional‑imaginativo
AÇÃO DOMINANTE Apresentar novas ideias e soluções.
Criticidade
Racional‑científico
Questionar e avaliar ideias e soluções.
Interatividade
Social‑tecnológico
Envolver‑se socialmente em projetos e soluções.
Os cenários de proposição são um conjunto de ações impulsionadas para favorecer a problematização, a inovação e a socia lização em sala de aula. Essas ações articulam três competências essenciais (criticidade, criatividade e interatividade) em quatro dimensões de processos.
CENÁRIO DE PROPOSIÇÃO Criticidade Criatividade Interatividade
CARÁTER Racional‑científico Emocional‑imaginativo
AÇÃO DOMINANTE Questionar e avaliar ideias e soluções.
Observar e descrever experiências.
DIMENSÃO 1:
QUESTIONAMENTO
Selecionar e analisar conhecimentos e informações relevantes.
Estabelecer relações entre conceitos e ideias.
Integrar diferentes perspectivas disciplinares.
Exercitar a curiosidade intelectual.
DIMENSÃO 2:
IMAGINAÇÃO
Buscar e criar ideias.
Experimentar ou ampliar ideias incomuns, arriscadas ou radicais.
Realizar prognóstico de um fato; prever, inferir.
DIMENSÃO 3: AÇÃO
Produzir, criar protótipos de um produto.
Propor uma solução ou uma apresentação de maneira pessoalmente nova.
Apresentar novas ideias e soluções.
Compreender as oportunidades do contexto/cenário e os limites do problema.
Identificar e questionar premissas.
Verificar a precisão de dados, fatos, informações e interpretações.
Analisar lacunas no conhecimento.
Revisar teorias e opiniões estabelecidas e imaginar diferentes perspectivas sobre o problema.
Identificar pontos fortes e fracos de evidências, argumentos, alegações e opiniões.
Social‑tecnológico
Envolver‑se socialmente em projetos e soluções.
Apreciar criticamente diversas formas de interações.
Ter empatia.
Debater e problematizar as práticas de intolerância, discriminação e violência contra indivíduos, grupos sociais ou povos com vistas à tomada de consciência e ao exercício da paz social.
Idealizar soluções mediadoras de conflitos em favor de produzir entendimento mútuo.
Conceber projetos que visam ao acolhimento das diversidades na perspectiva dos direitos humanos e da cultura de paz.
Justificar uma solução ou um produto proposto por meio de critérios/raciocínios lógicos, éticos ou estéticos.
Aderir ao bem comum propondo ações que incentivem o respeito às diferenças entre pessoas e povos.
Construir coletivamente procedimentos e normas de convívio que viabilizem a participação de todos em diferentes espaços.
DIMENSÃO 4: REFLEXÃO
Considerar e avaliar a novidade da solução escolhida e de suas possíveis consequências.
Considerar e avaliar a relevância da solução escolhida e de suas possíveis consequências.
Avaliar e reconhecer a incerteza ou os limites da solução ou posição defendida.
Refletir sobre o possível viés da perspectiva pessoal em comparação com outras perspectivas.
Julgar sua própria aptidão para respeitar regras básicas de convívio social nas interações.
Considerar aspectos relativos à qualidade do convívio social no grupo do qual faz parte em favor de propor superação de conflitos ou melhorias nas socializações.
Quais são os ganhos da prática docente quando transita por diferentes cenários? Uma das respostas está na mudança de pers pectiva, quando professor e alunos se defrontam com questões não previstas ou pouco usuais dentro dos “limites” da Matemática.
Aliás, os limites podem se tornar cada vez mais tênues à medida que mobilizamos conhecimentos por diversos cenários.
De acordo com a Organização para Cooperação e Desenvolvimento Econômico (OCDE):
Embora criatividade e pensamento crítico sejam fundamentais para a inovação e as necessidades do mercado de trabalho, outras competências complementares são igualmente importantes. A estrutura conceitual do projeto dife rencia três categorias sobrepostas de “competências para a inovação”:
1) competências técnicas (know‑what [saber o quê] e know‑how [saber como]);
2) competências de criatividade e de pensamento crítico (pensamento crítico, imaginação, criatividade); e
3) competências socioemocionais (persistência, conscienciosidade, autoestima, comunicação, colaboração).
Essas três categorias de competências precisam ser desenvolvidas em conjunto.
INSTITUTO AYRTON SENNA. OCDE (2020). Desenvolvimento da criatividade e do pensamento crítico dos estudantes: o que significa na escola. Tradução Carbajal Traduções. São Paulo: Fundação Santillana, 2020. p. 52.
LUPAS E LUNETAS
Leia esta frase e, se possível, discuta depois com os outros colegas professores. O conhecimento pode ser explorado pelo aluno em diferentes perspectivas, de uma forma crítica e criativa.
a) Procurem no livro do estudante exemplos de atividades que favoreçam o que está dito nessa frase.
b) Como vocês explorariam essa atividade em sala de aula por meio de cenários de proposição? Quais categorias de cenário e de proposição seriam mais enfáticas nessa atividade? Como a aula seria conduzida para obter o melhor proveito?
c) Converse com seus pares a respeito da proposta didática de exploração dessa atividade e tentem implementá‑la nas aulas. Depois, compartilhem como foi a experiência e os resultados em um mural da sala dos professores ou no espaço virtual de troca de informações dos professores.
Avaliação formativa
Avaliação na prática pedagógica
A atividade de avaliação é contínua porque as aprendizagens estão sempre em andamento. No centro da relação ensino ‑aprendizagem estão dois importantes atores: professor e aluno, impactados reciprocamente – o que favorece, de modo contínuo, a reestruturação sociocognitiva.
A avaliação formativa, decorrente da interação entre professor e aluno, propaga estes efeitos: informativa, verificativa e corretiva. Esses efeitos impactam ambos de modos distintos, mas que se complementam.
EFEITOS DA AVALIAÇÃO FORMATIVA
Informativa
As intenções com a proposta da atividade e as expectativas devem ser informadas antes de efetuar julgamentos.
Por meios indiretos (atividade do aluno) ou diretos (autoavaliação), o aluno comunica seu desempenho.
Verificativa
Por meio da observação da atividade do aluno, o professor será informado dos efeitos reais da ação de ensino e poderá submetê‑la a ajustes.

Por meio de convite à tomada de consciência sobre suas dificuldades, poderá cada vez mais se tornar apto a reconhecer e a corrigir, ele mesmo, seus erros.
Corretiva Professor e aluno, em parceria, corrigem sua ação, modificando seus modos na busca de obter os melhores efeitos.
Verbos da ação avaliativa
Em um cenário de avaliação formativa, o fio condutor das ações essenciais ao professor é composto de, basicamente, um conjunto de seis ou sete verbos:
• Desencadear: situação de ensino, por meio de exercícios, problemas, provas, questões etc.
• Observar: os comportamentos no instante da atividade do aluno;
• Coletar/registrar: informações referentes ao progresso e às dificuldades de aprendizagem;
• Interpretar: os registros desses comportamentos;
• Comunicar: os resultados da análise e apreciação final;
• Remediar: as dificuldades diagnosticadas e analisadas.
O modo como é apresentada a atividade de avaliação não pode ser separado da atividade de ensino. É verdade que a ava liação deve ser tomada como um momento autônomo (caráter de evento), mas será mais útil se, na maior parte do tempo, for concebida como um projeto educativo (caráter de processo).
Aprendizagem assistida por avaliação
O processo de aprendizagem leva, em sua complexa trama, as diversas modalidades de avaliação que, para longe de classificar, estão a serviço de estabelecer, firmar e expandir toda a estrutura de aprendizagem dos alunos. O papel da avaliação – que é o de observar, aferir e julgar – é também o que justifica sua presença no processo de aprendizagem, uma vez que, por meio dela, é pos sível favorecer aos alunos seguirem na progressão do que aprendem.
Avaliar os alunos para fazer com que evoluam melhor (rumo ao êxito), esta é a ideia central do que designamos pela expressão “aprendizagem assistida por avaliação”. Uma avaliação capaz de compreender tanto a situação do alu no quanto de “medir” seu desempenho; capaz de fornecer‑lhe indicações esclarecedoras, mais do que oprimi‑lo com recriminações; capaz de preparar a operacionalização das ferramentas do êxito, mais do que se resignar a ser apenas um termômetro (até mesmo um instrumento) do fracasso, não seria o mais belo auxiliar, e o primeiro meio, de uma pedagogia enfim eficaz? (HADJI, 2001)
A avaliação permeada no trabalho pedagógico eficaz é composta de redes ou camadas que se entrecortam em momentos diversos, na aula e fora dela, e nem sempre sincronizada entre o grupo de alunos. Por ser assistida, entende‑se que há um trabalho de obser vação e “leitura” quanto às produções do aluno, que exigirá, para ser apreciado, uma interpretação que leve em conta um alinhamento entre o que se espera alcançar, como alcançar e o que fazer se, em dado momento, o aluno não alcançar. Esse alinhamento compõe um código favorável para a análise, a interpretação e o julgamento de ações possíveis na remediação da aprendizagem do aluno.
LUPAS E LUNETAS
Sozinho ou junto com outro professor (de Matemática ou de outra área), escolham uma atividade do livro do estudante. Listem duas ou três dificuldades possíveis de ocorrer no momento da aula envolvendo essa atividade. Para cada uma dessas dificuldades, levem em conta perfis de “alunos possíveis” (alunos do contexto real da escola e que valem a pena ser considerados neste exercício de prática docente). Considerem o modo como cada um aprende, sob quais estímulos eles costumam dar melhores respostas, se têm melhor desempenho individualmente ou em grupo, se só resolvem situações contextualizadas ou não etc. (o ideal para essa reflexão seria ter em mãos o registro do desempenho de dois ou três alunos reais do contexto escolar local).
Considerando essas dificuldades e o perfil desses alunos, proponham decisões favoráveis ao avanço de cada um deles. Criem uma estratégia pedagógica voltada para ações de apoio tanto intelectual quanto de caráter afetivo e que sejam favoráveis à continuidade da aprendizagem de cada um desses alunos.

Ao final, publiquem em um mural, na sala dos professores ou na sala virtual, tanto o exercício do livro do estudante, como as análises, a descrição do perfil dos alunos e as propostas de intervenção pedagógica sugeridas para cada um. O ideal é que, na publicação, os nomes dos alunos não sejam citados, para preservar suas identidades e, em vez disso, o foco sejam as estratégias consideradas e os resultados obtidos.
Aproveite para apreciar as soluções apresentadas pelos outros colegas, em outras situações consideradas por eles.
3. ARTICULAÇÕES ENTRE OS MATERIAIS
Como estabelecer os vínculos entre os materiais voltados para o estudante e os que são voltados para o professor?
Concepções artísticas sobre o ato de estabelecer vínculos entre pessoas, objeto e ideias.

CHECK‑IN
• Compare essas duas imagens: a construção de vínculos entre pessoas ou ideias ocorre por acaso? Por tentativa e erro? Por uma busca intencional? O que essas imagens mostram, segundo sua interpretação?
• Como você vê a construção de vínculos entre professor e aluno a partir de diferentes materiais didáticos?
• Em que medida os materiais didáticos favorecem o processo de construção desses vínculos?

• E quanto aos materiais: que vínculos você espera encontrar entre eles próprios no sentido de trazer contribuições para a prática docente?
• Você deixa claro para os alunos as suas intenções de aprendizagem?
Vínculo entre a estrutura da obra e as ações docentes voltadas para a avaliação
As estratégias de ensino e aprendizagem e suas diversas modalidades de avaliação, na etapa do Ensino Fundamental – Anos Finais, da área e do componente de Matemática, podem ser assim representadas:

Ter, de certa forma, a preocupação de informar antes de julgar. Fazer tudo para pôr a avaliação nas mãos do aluno (avaliação em primeira pessoa). Isso não leva a pensar, finalmente, que o momento próprio da avaliação é bastante secundário? Que o essencial é esclarecer, ajudar e remediar? Que, se a avaliação cumulativa é um mal necessário, a avaliação formativa só tem interesse pelo que precede ou pelo que segue o julgamento de avaliação propriamente dito: pela coleta e análise dos dados; por todo o trabalho pedagógico que tem a ambição de permitir ao aluno que progrida (o que será chamado de remediação)? Em última hipótese, a melhor maneira de pôr a avaliação a serviço das aprendi zagens não seria, senão fazê‑la desaparecer totalmente, pelo menos consagrar‑lhe muito menos tempo e energia, para se dedicar ao trabalho pedagógico de facilitação das aprendizagens?
HADJI, Charles. Avaliação desmistificada. Porto Alegre: Artmed, 2001. p. 66.
Assumimos a palavra remediação com triplo sentido:
• Ajuste da ação ao objetivo, ou seja, no sentido de “re‑mediar”, mediar de novo e de outro modo;
• Busca por responsabilidade dupla, entre professor e aluno, na melhoria da aprendizagem.
• Vínculo construído em uma via de mão dupla, envolvendo diagnóstico e ação corretiva eficaz.
Serão apresentadas a seguir algumas noções amplas que se relacionam com o campo da educação, ou da educação matemática, para favorecer a construção de vínculos entre as ofertas de conteúdos no livro do estudante e as possibilidades teóricas norteadoras das ações docentes.
Letramento matemático
O letramento matemático remete ao conceito de letramento, próprio da área de ensino de linguagem. Este, por sua vez, se apresentou como uma resposta à noção de que o aprendizado da língua se resumia à aquisição dos códigos convencionais relacio nados à leitura e à escrita. Nesse sentido, é possível compreender letramento como algo além da alfabetização, estendendo‑se aos contextos de usos da linguagem.
Implícita nesse conceito [de letramento] está a ideia de que a escrita traz consequências sociais, culturais, políti cas, econômicas, cognitivas, linguísticas, quer para o grupo social em que seja introduzida, quer para o indivíduo que aprenda a usá‑la1.
No ensino de Matemática, a noção de letramento (matemático) também considera a diversidade de usos, de contextos sociais e culturais nos quais a Matemática está inserida. Assim como o termo letramento teve sua origem na palavra inglesa literacy, as pri meiras noções envolvendo o letramento matemático tiveram sua origem na palavra inglesa numeracy. No entanto, a tradução direta do termo para a língua portuguesa – numeramento – enfrentou uma série de críticas, uma vez que podia apontar ao entendimento de que o aprendizado de Matemática se resumiria aos conhecimentos sobre os números e suas operações.
Buscando um conceito mais amplo, o PISA define o conceito de letramento matemático como “a capacidade individual de for mular, empregar e interpretar a Matemática em uma variedade de contextos”.
Dados certo contexto e os contornos e as possibilidades por ele apresentados, são mobilizados variados processos matemáticos, como: formular situações matematicamente, aplicar conceitos, procedimentos e raciocínios matemáticos, avaliar e interpretar re sultados matemáticos, assim como planejar ações a partir de resultados matemáticos. Os conteúdos matemáticos, por sua vez, podem ser entendidos como a sistematização desses processos. São exemplos de conteúdos as ideias de variação e relação, espaço e formas, quantidade etc.



A BNCC parte dessas mesmas concepções para definir letramento matemático: […] competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente […]. É o letramento matemático que assegura aos alunos reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo e perceber o caráter de jogo intelectual da matemática, como aspecto que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso (fruição).
De modo a desenvolver o raciocínio matemático, é necessário mobilizar competências e habilidades relacionadas à representação, comunicação e argumentação. Ou seja, é fundamental que alunos e professores interajam em situações de problemas reais, ex pressem suas ideias, produzam argumentações e justifiquem matematicamente as estratégias além do raciocínio empregado. É justamente na “interação com os pares e com adultos que as crianças vão constituindo um modo próprio de agir, sentir e pensar e vão descobrindo que existem outros modos de vida, pessoas diferentes, com outros pontos de vista”2
Representar Comunicar
Argumentar
• Representar
Aprender Matemática implica também aprender a escrever e se expressar matematicamente. Isso significa conhecer e utilizar símbolos, escrever sentenças matemáticas, gráficos e esquemas, assim como utilizar e manipular diferentes representações para os objetos matemáticos. Por exemplo, compreender que é possível descrever uma função a partir de sua expressão algébrica e a partir do gráfico correspondente.
• Comunicar
O ato de comunicar implica a existência de um interlocutor. Desse modo, o desenvolvimento do raciocínio matemático passa pela relação estabelecida entre os indivíduos. Esse ato revela também uma preocupação com o outro, com aquele que vai receber a mensagem. Assim, ao tornar comunicáveis conhecimentos, estratégias e raciocínios matemáticos, é importante também conhecer o outro e saber articular diferentes maneiras de representação. Nesse sentido, representar e comunicar são duas habilidades que não devem ser tomadas isoladamente.
• Argumentar
O desenvolvimento da habilidade de argumentar pressupõe “a formulação e a testagem de conjecturas, com a apresentação de justificativas, além dos aspectos já citados anteriormente em relação às competências de raciocinar e representar” 3. Assim como representar e comunicar são habilidades inter‑relacionadas, argumentar matematicamente perpassa ambas.
A BNCC e o letramento matemático
As Competências Específicas de Matemática para o Ensino Fundamental propostas pela Base Nacional Comum Curricular (BNCC), cada qual a partir de uma perspectiva, têm como maior objetivo o desenvolvimento do letramento matemático:
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e cultu rais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá ‑las e avaliá‑las crítica e eticamente, produzindo argumentos convincentes.
5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
6. Enfrentar situações‑problema em múltiplos contextos, incluindo ‑se situações imaginadas, não diretamente relacionadas com o aspecto prático‑utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas e dados).
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
O desenvolvimento dessas competências ao longo dos nove anos do Ensino Fundamental é gradual, apesar de as habilidades relacionadas a raciocinar, representar, comunicar e argumentar matematicamente serem trabalhadas desde o primeiro ano. De modo geral, nos anos iniciais são retomadas as experiências e vivências cotidianas da Educação Infantil, orientando‑se sempre pela ideia de que compreender a Matemática significa a apreensão dos significados dos objetos matemáticos, assim como as suas aplicações. Desse modo, nos anos iniciais são mais nítidas as relações entre os objetos matemáticos e a realidade concreta, assim como com diferentes áreas do conhecimento. Isso não significa que nos anos finais tal relação com a realidade concreta desapareça. Pelo contrário, continua sendo um elemento que motiva a investigação, que proporciona situações‑problema, que confere sentido e sig nificado para processos e conteúdos matemáticos. No entanto, em muitos casos, será a própria Matemática o contexto em que tais
movimentos ocorrem. Nesse sentido, há um mergulho na própria Matemática, um aprofundamento nos conceitos e procedimentos cujos sentido e significado se posicionam dentro da própria Matemática.
Assim, é possível considerar um desenvolvimento horizontal das habilidades e competências, estabelecendo relações com diversas áreas do conhecimento, da própria Matemática e da realidade concreta, mas também momentos de desenvolvimento vertical, no qual se aprofunda em determinado conteúdo matemático. Vale ressaltar que há complexidade nesse tipo de processo, havendo, ao longo desse desenvolvimento vertical, variadas situações de pausa e desenvolvimento horizontal, das quais se apresen tam novas oportunidades para desenvolvimentos verticais e assim por diante.
O diagrama a seguir ilustra como esse movimento pode ocorrer. A título de exemplo, destacam ‑se dois grupos de habilidades da BNCC: o primeiro trata da noção de números inteiros (EF07MA03 e EF07MA04), enquanto o segundo trata da noção de transfor mações geométricas (EF07MA20 e EF07MA21). Nota‑se um desenvolvimento vertical entre as habilidades de cada grupo. Em ambos os casos se explora o conteúdo matemático de modo a aprofundar discussões ou aprender novos detalhes desse conteúdo. É pos sível verificar também que, particularmente no desenvolvimento de habilidades como EF07MA03 e EF07MA21, ocorre também um movimento horizontal ao relacionar objetos matemáticos a diferentes contextos e significados. De modo geral, o desenvolvimento de cada grupo segue de maneira relativamente desconectada entre si. No entanto, é possível verificar como a habilidade EF07MA19 promove, ao mesmo tempo, um avanço vertical em cada grupo, além de os conectar em um movimento horizontal.
(EF07MA03) Comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, associá-los a pontos da reta numérica e utilizá-los em situações que envolvam adições e subtração.
(EF07MA21) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho ou softwares de geometria dinâmica e vincular esse estudo a representações planas de obras de arte, elementos arquitetônicos, entre outros.
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.
(EF07MA20) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem.
(EF07MA19) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro.
Os processos
matemáticos
Os conhecimentos explorados com os alunos fluem de forma planificada por meio de Trajetórias que entrelaçam contextos e recursos matemáticos de modo a contemplar todos os conteúdos previstos na BNCC para o Ensino Fundamental dos anos finais. Os recursos matemáticos são entendidos como os processos de investigação, a construção de modelos e a resolução de problemas
a) Sobre os processos de investigação:
[…] a atividade investigativa em sala de aula constitui‑se da observação de uma situação; a partir daí começam a surgir conjecturas que vão sendo testadas. Por meio desses testes, elas poderão ser refutadas e estabelecer novas con jecturas ou, então, quando confirmadas pelos testes, vão sendo melhor definidas. Se validadas através da demonstração, podem adquirir o status de uma propriedade estabelecida pelo método matemático.
VARIZO, Zaíra da Cunha Melo; ROCHA, Luciana Parente; MAGALHÃES, Ana Paula de A. S. A Investigação matemática como es tratégia de ensino e aprendizagem da Matemática. XII Encontro Nacional de Educação Matemática. Educação Matemática na Contemporaneidade: desafios e possibilidades. SBEM, São Paulo, 13 a 15 de julho de 2016.
b) Sobre a construção de modelos:
A criação de modelos matemáticos constitui uma ferramenta importante e adequada ao ensino: a modelagem matemática busca sempre um “retorno” ao problema original, ou seja, responder à realidade, evitando se perder na pura discussão abstrata.
Ao tentar resolver um problema, explicar uma situação da realidade ou tomar ações sobre ela, é preciso mobilizar ferramentas necessárias e adequadas. Em outras palavras, um modelo que explique a situação e forneça os meios para agir sobre ela. No caso
de um modelo matemático, as ferramentas são os símbolos e as relações que representam o objeto ou a situação em questão. Trata‑se de construção mental e abstrata para representar a realidade (ainda que somente uma parte específica). Segundo Bassanezi (2002), “a importância do modelo matemático consiste em se ter uma linguagem concisa que expressa nossas ideias de maneira clara e sem ambiguidades, além de proporcionar um arsenal enorme de resultados (teoremas) que propiciam o uso de métodos computacionais para calcular suas soluções numéricas”.
Entretanto, para o desenvolvimento de atividades de modelagem matemática, é fundamental que sejam criados ambientes de aprendizagem que possibilitem a mobilização dos conhecimentos matemáticos dos alunos, sejam prévios, aprendidos na escola ou em outras experiências, sejam os que estão sendo aprendidos no momento. Nesse sentido, tais ambientes de aprendizagem devem convidar os alunos a “indagar e a investigar, por meio da Matemática, situações oriundas de outras áreas da realidade”4
c) Sobre a resolução de problemas:
A resolução de problemas se configura em um elemento privilegiado para o desenvolvimento de habilidades relacionadas ao letra mento matemático, estando também associada aos processos de investigação e construção de modelos. Isso porque um problema apresenta certa questão matemática (oriunda de uma situação imaginada ou da própria realidade), cujos métodos ou estratégias de resolução não estão dados explicitamente ou não são reconhecidos imediatamente pelos alunos. Essa é uma das características que diferencia os problemas dos exercícios. No cotidiano da sala de aula é esperado que haja uma mescla entre problemas e exercícios. A resolução de um exercício costuma demandar menos tempo que de um problema. Isso não significa que se deva optar por um ou outro tipo somente, uma vez que cada um tem objetivos pedagógicos diferentes e, de certo modo, complementares. Nesse sentido, a construção de boas situações‑problema deve:
• contemplar conteúdos diversos que necessitem ou estimulem a mobilização não só de conhecimentos matemáticos, como também de outras áreas e de experiências vivenciadas;
• evitar cenários que admitam uma única estratégia de resolução;
• fomentar a interação e a cooperação entre os alunos;
• valorizar o pensamento reflexivo e crítico, tanto sobre o processo de resolução quanto sobre as soluções obtidas. De modo geral, é possível pensar o processo de resolução de problemas segundo as etapas propostas por Polya5:

Compreender o problema.
Estabelecer um plano para resolver o problema. Executar o plano.
Verificar e avaliar a solução.
Cabe ressaltar que, ao longo dessas etapas, é importante conversar com os alunos sobre o processo de resolução de problemas, de modo a refletir sobre a própria experiência e aplicá‑la em outras situações e contextos. É parte desse processo o ato de elaborar problemas, uma vez que o aluno precisa antecipar possíveis estratégias de resolução.
Os processos de investigação, a modelagem e a linguagem matemática e as estratégias de resolução de problemas compõem um campo abrangente e propício para a aprendizagem em Matemática.
4 ROSA, M.; OREY, D. C. A modelagem como um ambiente de aprendizagem para a conversão do conhecimento matemático. Bolema, Rio Claro (SP), v. 26, n. 42A, p. 261‑290, abr. 2012.
5 POLYA, G. A arte de resolver problemas. Rio de Janeiro: Interciência, 2006.
Flexibilização curricular da coleção
Consideramos o currículo uma estrutura dinâmica e em constante construção e transformação. Não é estático ou cristalizado no tempo, mas aberto às experiências e vivências da comunidade escolar, assim como às discussões mais atuais no âmbito das ciências, da cultura e das transformações sociais. Mais ainda, uma educação pensada segundo ideias de interdisciplinaridade e de valorização da diversidade deve considerar o currículo de maneira ampla e flexível, garantindo a participação ativa dos alunos e da comunidade escolar como um todo, o desenvolvimento de projetos interdisciplinares, assim como fomentar a autonomia dos professores para construir um “currículo” adequado às possibilidades e necessidades apresentadas pelo ambiente em que estão inseridos.
Organizamos cada volume em quatro Trajetórias, que, por sua vez, estão subdivididas em três passeios cada uma. Estimamos que a duração média de trabalho com cada passeio seja de três semanas, considerando um ano letivo de aproximadamente 40 semanas. Entretanto, essa é apenas uma sugestão de organização do cronograma, cabendo ao professor adaptá‑lo a seu ritmo e sua realidade. Para além do fator tempo, há diferentes maneiras de “ler e acompanhar o livro”. Se, por um lado, uma leitura mais linear expressa a organização lógica e a visão pedagógica dos autores, foi também objeto do nosso cuidado garantir que você, professor, pudesse se apropriar das referidas lógica e visão e transformá‑las, de modo que expressasse seus próprios valores, o conhecimento dos seus alunos e famílias, as características da instituição escolar e da comunidade em que se inserem. Nesse sentido, apresentaremos algumas sugestões de outras maneiras de “ler e acompanhar o livro” para servir de inspiração ao professor.
Se o projeto didático do professor reforça os aspectos envolvidos na avaliação, nos problemas e nos exercícios, então as maneiras de flexibilizar o currículo proposto serão de um tal modo; se, por outro lado, o projeto do professor reforça os aspectos envolvidos nas perguntas norteadoras, nos TCTs e na interdisciplinaridade, então as maneiras de flexibilizar serão de outra forma.
Aspectos envolvidos na avaliação, nos problemas e nos exercícios
A seção Prontos para começar! inicia cada livro e tem como objetivo realizar uma avaliação diagnóstica. Os problemas apre sentados na seção apontam para habilidades essenciais de cada unidade temática da Matemática, tal qual pressupostas pela BNCC. É interessante que o professor, a partir do próprio conhecimento sobre os alunos e a escola, avalie a pertinência das atividades propostas e realize adequações, caso sejam necessárias.
Após Prontos para começar!, a estrutura do livro – quanto a avaliações, atividades, exercícios e problemas – segue uma lógica na qual, depois da discussão de certos pontos teóricos e da apresentação de exemplos em meio a contextos diversos, abrem‑se seções de Atividades, com caráter de desenvolvimento ou verificação de conhecimentos, apresentando, em muitos casos, contex tos diferentes daqueles utilizados na discussão teórica. Ao longo dessa discussão, estão os boxes Lupas e lunetas, que conduzem o estudante a uma reflexão mais aprofundada sobre algum aspecto matemático, sobre o contexto geral, ou, ainda, propondo uma articulação entre ambos. Caso julgue que os estudantes ainda não estão preparados para desenvolver satisfatoriamente as propostas de Lupas e lunetas, o professor pode antecipar alguns dos problemas e exercícios de Atividades, tanto para servir, neste momento, como diagnóstico, quanto para tirar eventuais dúvidas ou superar dificuldades pontuais. O mesmo pode ocorrer com seções como Travessias, que conduz os alunos por investigações de caráter matemático, e Nuvens, que apresenta possíveis relações entre o contexto, a Matemática e as tecnologias digitais.
Ao final de cada Trajetória, a seção Vistorias (em especial a subseção Check-out) propõe outros problemas e exercícios rela cionados às discussões realizadas, porém, a partir de outros contextos e apresentando diferentes graus de dificuldade e níveis de complexidade dos problemas e exercícios presentes em Atividades. Para finalizar o livro de cada ano, é apresentada também a seção Suplemente sua aprendizagem, com problemas de diversos tipos de exames, desde concursos, macroavaliações até ves tibulares ou vestibulinhos. Tais problemas, de modo geral, têm graus de dificuldade e níveis de complexidade maiores que os até então apresentados aos estudantes. Uma possibilidade de adaptação desses diferentes momentos de resolução de problemas ou desenvolvimento de atividades é justamente incorporar às Atividades os problemas das seções Check-out e Suplemente sua aprendizagem, construindo, dessa maneira, um conjunto mais amplo de exercícios e problemas. Para estruturar esse movimento, sugerimos a análise dos objetivos de aprendizagem apresentados em Bússola e Levo na bagagem
Aspectos envolvidos nas perguntas norteadoras, nos TCTs e na interdisciplinaridade
Cada Trajetória apresenta uma pergunta norteadora, que, por sua vez, se desdobra em outras três, estabelecendo‑se como os fios condutores de cada passeio. Tais perguntas também se articulam com os Temas Contemporâneos Transversais (TCTs) propos tos para cada passeio. Consideramos, ao longo da coleção, o desenvolvimento de um trabalho interdisciplinar no qual, em certos momentos, são os contextos, os TCTs ou as habilidades e competências de outras áreas do conhecimento que dão significado, ou mesmo ressignificam, os conhecimentos matemáticos, enquanto em outros momentos é justamente a Matemática que se apresenta “a serviço” de outras áreas ou do contexto. Esse tipo de conexão é ocasionado não somente pelas perguntas norteadoras no início dos passeios, mas também pelas seções Atmosfera e Check-in, pelas situações apresentadas, pelos temas desenvolvidos nos boxes Lupas e lunetas e, especialmente, pela seção Barcos e portos, que propõe um olhar integrador para as perguntas norteadoras, os TCTs, a Matemática e as demais áreas do conhecimento.
Dessa maneira, a ênfase dada a tais seções pode transformar o caráter das aulas, desde uma situação na qual os contextos apresentam os sentidos e significados para os conhecimentos matemáticos, atividades que se assemelham a projetos ou sequências didáticas, até aquelas em que variados conhecimentos e saberes são mobilizados, sem dissociar qual é a área do conhecimento predominante.
Caso o professor deseje, é possível enriquecer a experiência dos estudantes aprofundando as discussões sobre as perguntas norteadoras e os TCTs, trazendo convidados ou professores de outras áreas, novos textos, fotografias, vídeos, realizando visitas, passeios de campo etc. Dessa maneira, considere utilizar boxes e seções em diferentes momentos, à luz das alterações pensadas
para as aulas. A seção Barcos e portos, por exemplo, foi idealizada para fechar os passeios, porém muitas delas contêm elementos e discussões que podem ser trazidos para outros momentos do desenvolvimento dos passeios Da mesma maneira, os textos de Atmosfera foram pensados de modo a ambientar os estudantes no início do passeio. Entretanto, o professor tem a liberdade de substituí‑los ou pensar em outras opções, como a apresentação de um vídeo, utilizando o texto em outra ocasião.
Como anunciado anteriormente, as sugestões feitas não são únicas: visam apenas inspirar os professores a considerar “outras leituras” para os livros da coleção, de modo a exercer sua autonomia docente e adaptar as ideias apresentadas às diferentes reali dades em que atuam, ampliando o escopo do trabalho dos autores. Esperamos que este material possa auxiliar o trabalho docente, sendo subsídio e inspiração para os professores.
Mapa dos Temas Contemporâneos Transversais na BNCC
Nesta coleção, os Temas Contemporâneos Transversais (TCTs) são referenciados pelos contextos apresentados nas diversas si tuações didáticas propostas ao longo de cada volume. As perguntas motivadoras, em grande parte, servem de gatilho para propiciar reflexões, ampliar a visão de mundo do aluno e, ao mesmo tempo, atender as demandas sociais contemporâneas.
Na BNCC, os TCTs totalizam quinze temas, distribuídos em seis macroáreas, conforme mostra esta imagem:
MEIO AMBIENTE
Educação Ambiental Educação para o Consumo
CIÊNCIA E TECNOLOGIA
Ciência e Tecnologia
MULTICULTURALISMO
Diversidade Cultural Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras
Temas Contemporâneos
Transversais na BNCC
ECONOMIA
Trabalho
Educação Financeira
Educação Fiscal
SAÚDE
Saúde
Educação Alimentar e Nutricional
CIDADANIA E CIVISMO
Vida Familiar e Social Educação para o Trânsito Educação em Direitos Humanos Direitos da Criança e do Adolescente Processo de envelhecimento, respeito e valorização do Idoso
Fonte: BRASIL. Disponível em: https://www.google.com/url?sa=t&source=web&rct=j&url=http://basenacionalcomum.mec.gov. br/images/implementacao/contextualizacao_temas_contemporaneos.pdf&ved=2ahUKEwjik46_m4P6AhX7ppUCHWngCskQF noECAkQAQ&usg=AOvVaw3cfX9DlW6gGGB2GIXLzRqH. Acesso em: 7. set. 2022
BIBLIOGRAFIA
CARVALHO, Cicefran S. de. A aprendizagem cooperativa no ensino da Matemática Curitiba: Appris, 2019. Relato de uma experiência pedagógica focada na metodologia da aprendizagem cooperativa em uma cidade do Ceará, com o intuito de motivar e inspirar professores a aproveitar elementos dessa metodologia em sua sala de aula.
COHEN, Elizabeth G.; LOTAN, Rachel A. Planejando o trabalho em grupo: estratégias para salas de aula heterogêneas. 3. ed. Porto Alegre: Penso, 2017. O livro contém pesquisas e resultados mais recentes sobre a estratégia do trabalho em grupo na sala de aula, com o objetivo de alcançar uma dinâmica equilibrada e adequada para a aprendizagem de todos os alunos.
HADJI, Charles. Avaliação desmistificada. Porto Alegre: Artmed, 2001. Uma visita aos últimos 30 anos do ensino e as análises, pesquisas e debates sobre o tópico polêmico da avaliação, com o objetivo de fornecer ao docente todos os elementos para implementar um sistema mais justo e adequado em sua sala de aula.
HOFFMANN, Jussara. Avaliação mediadora 35. ed. Porto Alegre: Mediação, 2019. A avaliação mediadora é um instrumento poderoso para legitimar o professor como aquele que encaminha a aprendizagem de forma mais orgânica e fluida. Neste livro, tal prática é aprofundada para tanto.
HOFFMANN, Jussara. O jogo do contrário em avaliação 10. ed. Porto Alegre: Mediação, 2018. E se a melhor avaliação possível fosse exatamente o contrário do que é praticado nas salas de aula até hoje? É o que propõe a autora, com exemplos e ideias que certamente levarão o docente a repensar suas práticas.
LEMOV, Doug. Aula nota 10 2.0: 62 técnicas para melhorar a gestão da sala de aula. 2. ed. Porto Alegre: Penso, 2018. Uma coletânea de diferentes e inusitados relatos de professores em sala de aula por todo o globo, com técnicas e estratégias diferenciadas para aprimorar a experiência em sala de aula.
MOREIRA, Adelson F.; PEDROSA, José Geraldo; PONTELO, Ivan. O conceito de atividade e suas possibilidades na interpretação de práticas educativas. Ensaio: pesquisa em educação em ciências. v. 13, n. 3, p. 13‑29. Belo Horizonte: UFMG, 2011. Elaborações sobre a prática escolar com diálogos entre novas ideias e reflexões sobre o que já é proposto e consolidado por autores como Vygotsky e Leontiev.
SCHÖN, Donald A. Educando o profissional reflexivo: um novo design para o ensino e a aprendizagem. Porto Alegre: Artmed, 2000. Livro com a proposta de trazer uma formação profissional diferenciada para o leitor, focando na “reflexão‑na‑ação”, baseando o ensino muito mais na ação do que no modelo clássico de ouvir e ver.
VILLAS BOAS, Benigna M. de F. (org.). Avaliação: interações com o trabalho pedagógico. Campinas: Papirus, 2017. Análise da avaliação como estratégia que ocorre em três camadas diferentes do ambiente da educação: em todas as ações da escola, especificamente na sala de aula, e no diálogo entre cursos de licenciatura e o ensino básico.
VILLAS BOAS, Benigna M. de F. Portfólio, avaliação e trabalho pedagógico 8. ed. Campinas: Papirus, 2012. A utilização do portfólio como método avaliativo é muito presente em algumas disciplinas e cursos superiores, mas subaproveitado em outros casos. Ao explorar todos os pontos positivos do portfólio, o autor convida o leitor a refletir sobre a possibilidade da inclusão do método em suas avaliações.
ZABALA, Antoni; ARNAU, Laia. Como aprender e ensinar competências. Porto Alegre: Artmed, 2010. A BNCC trouxe à tona a discussão sobre as habilidades e competências, e essa discussão fortaleceu e engrandeceu muito o ensino em geral. Mas... como ensinar as competências?
ZASLAVSKY, Alexandre. Ação pedagógica, ação comunicativa e didática. Conjectura: filosofia e educação. v. 22, n. 1, p. 69‑81. jan./ abr. Caxias do Sul: EDUCS, 2017. Artigo da revista Conjectura, que traz uma reflexão aprofundada sobre o papel da comunicação na didática.
TRAJETÓRIA 2 – ESSENCIAIS: PARA ESTE VOLUME
A noção de pensamento computacional muitas vezes está associada à ideia de algoritmo. Entretanto, elaborar ou seguir algoritmos é apenas um dos elementos constitutivos do pensamento computacional, que pode ser entendido como uma maneira mais ampla de resolver problemas.
CHECK‑IN
• A noção de pensamento computacional se refere à decomposição de um problema em partes menores ou mais simples; ao reconhecimento de padrões, regularidades e tendências; à busca de soluções mais abrangentes e gerais, ou seja, à abstração de detalhes e especificidades de contexto original; e, por fim, aos algoritmos que possam determinar passos ou etapas necessá rios para resolver esse problema. Considerando esse significado, de que maneira você acha possível desenvolver o pensamento computacional nas aulas de Matemática?
• A noção de pensamento computacional como uma maneira de resolver problemas não se restringe à Matemática. Você consegue imaginar situações interdisciplinares que possam desenvolver o pensamento computacional?

ARTICULAÇÕES ENTRE OBJETIVOS, JUSTIFICATIVAS DESSES OBJETIVOS, COMPETÊNCIAS E HABILIDADES
A BNCC se articula em torno de habilidades, competências gerais e específicas. Entretanto, cabem aos sistemas ou redes de ensino e instituições escolares as decisões que objetivem a adequação de tais habilidades e competências às realidades locais, aos contextos e características dos estudantes e suas famílias. Parte dessas decisões se referem às “formas de organização interdisci plinar dos componentes curriculares” (BNCC, 2018, p. 16).
Na concepção desta obra são consideradas fundamentais as concepções de pedagogia por competências e habilidades, assim como a de interdisciplinaridade. Consideramos que uma competência se constitui pelos conhecimentos, atitudes e habilidades mobilizados. Nesse sentido, é importante considerar que os conhecimentos não são estáticos (ou acabados), mas algo em constante condição de revisão, avaliação e aprendizado. As habilidades, por sua vez, situam‑se no âmbito da utilização dos conhecimentos para resolver problemas, desenvolver estratégias, lidar com situações e agir em relação a elas etc. Por fim, as atitudes se enquadram no âmbito das maneiras de se posicionar nas diversas situações de mobilização dos conhecimentos e habilidades.
Já a concepção de interdisciplinaridade pode ser entendida pela proposição de variadas disciplinas mobilizadas simultaneamente, com relações claras entre si. Tais relações pressupõem a existência de coordenação e organização entre elas, além da decisão sobre qual disciplina terá mais ou menos peso dentro de tal organização.
Ambas as concepções se articulam, por sua vez, com o desenvolvimento do letramento matemático ao longo dos anos do Ensino Fundamental, uma vez que a ideia de letramento matemático considera a diversidade de usos, de contextos sociais e culturais nas quais a Matemática está inserida. Segundo a BNCC, o letramento matemático se refere justamente a:
[…] competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente […]. É o letramento matemático que assegura aos alunos reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo e perceber o caráter de jogo intelectual da matemática, como aspecto que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso (fruição).
(BNCC, 2018, p. 266)
É possível verificar que as competências gerais propostas pela BNCC para a Educação Básica se traduzem nas diferentes Competências Específicas de Matemática que, por sua vez, se desdobram em habilidades de diversas áreas: Números, Álgebra, Geometria, Grandezas e Medidas, Probabilidade e Estatística
Apresentamos a seguir como estão articulados os principais objetivos de aprendizagem, as competências e as habilidades de acordo com a concepção desta obra.
Trajetória 1 do LE
PASSEIO 1
Competência geral Competência específica
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
Habilidades
EF08MA01, EF08MA02, EF08MA04 e EF08MA05.
Objetivos
• Resolver e elaborar problemas envolvendo cálculo de porcentagens.
• Reconhecer e utilizar procedimentos para obtenção de uma fração geratriz para uma dízima periódica.
• Efetuar cálculos com potências de expoentes inteiros.
• Utilizar a representação de números em notação científica para escrever números muito grandes ou muito pequenos.
• Resolver e elaborar problemas usando a relação entre potenciação e radiciação para representar uma raiz como potência de expoente fracionário.
Articulações e justificativas
Conforme os anos de escolaridade avançam em direção ao fim do Ensino Fundamental, nota‑se cada vez mais a presença de conteúdos relacionados à álgebra. Apesar de a maioria das situações partir de um problema real ou que simula a realidade, há situações nas quais o próprio contexto é a Matemática. Assim, apresentamos aprofundamento em certos conteúdos, como o caso de potenciação e radiciação. Esse movimento, no entanto, deve ser compreendido como um esforço da inventividade, criatividade e curiosidade humana em aprender cada vez mais e desenvolver a Matemática. Nesse sentido, é interessante pontuar que, quando determinado conteúdo matemático se origina em um contexto real ou concreto, o referido aprofundamento em termos teóricos muitas vezes pode ser interpretado como um caminho rumo à abstração. Entretanto, é fundamental que o movimento de “retorno ao concreto” também ocorra, inclusive ao aplicar os conhecimentos obtidos em contextos diferentes do original. Abre‑se, dessa maneira, espaço para a valorização dos conhecimentos construídos pelas pessoas. Mais ainda, deve‑se utilizar tal movimento de modo a atuar em prol da construção de uma sociedade mais justa, democrática e inclusiva.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
Habilidades
EF08MA03 e EF08MA22.
Objetivos
2
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
• Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
• Calcular a probabilidade de eventos com base na construção do espaço amostral, utilizando o princípio multiplicativo.
• Reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Articulações e justificativas
Existem diferentes maneiras de utilizar o conhecimento matemático para compreender e atuar sobre o mundo. Entre elas, está o desenvolvimento de raciocínio mais relacionado às probabilidades. Trata‑se de um modo de raciocinar que leva em conta a ideia de incerteza. As decisões sobre como atuar frente aos problemas são fundamentadas nas chances de ocorrência ou não de eventos. De certo modo, esse é o tipo de raciocínio que mais mobilizamos no cotidiano, ainda que não explicitamente. Por exemplo, costumamos avaliar se devemos ou não sair com guarda‑chuva analisando as chances de chover ou não naquele dia, seja após ouvir informações de serviços meteorológicos, seja por análise e experiência pessoal das condições climáticas por nós percebidas.
Competência geral
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
Competência específica
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
Habilidades
EF08MA10 e EF08MA11.
Objetivos
• Identificar a regularidade de uma sequência numérica ou figural não recursiva.
• Identificar a regularidade de uma sequência numérica recursiva.
• Construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências recursivas.
• Construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências não recursivas.
Articulações e justificativas
Explorar regularidades em sequências, numéricas ou figurais, contribui para o desenvolvimento do raciocínio lógico. Reconhecer tais regularidades e identificar seus próximos elementos é parte do desenvolvimento do pensamento computacional. Associado a isso, cria‑se uma segunda camada de conhecimentos e habilidades relacionadas ao desenvolvimento de algoritmos e fluxogramas que permitam obter termos em sequência. O trabalho pedagógico desenvolvido com base nesses conceitos contribui não somente para a produção de significado em diversos conteúdos (especialmente os relacionados à álgebra), mas também estimula a curiosidade intelectual e a busca de outras estratégias para a resolução de problemas.
PASSEIO 1
Competência geral Competência específica
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
Habilidade EF08MA06.
Objetivos
• Identificar situações‑problema que podem ser descritas por expressões algébricas.
• Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas.
• Compreender a noção de polinômio.
• Utilizar as propriedades das operações para resolver cálculos envolvendo adição, subtração, multiplicação e divisão entre polinômios.
• Resolver e elaborar problemas que envolvam medidas de área de superfície de figuras geométricas utilizando expressões de cálculo de área.
Articulações e justificativas
No 8o ano do Ensino Fundamental, ao explorar o conteúdo de expressões algébricas, o estudante pode experimentar tanto um movimento “horizontal” ao utilizar a Matemática para descrever e atuar sobre a realidade cotidiana e outras disciplinas, quanto um movimento “vertical” ao se aprofundar teoricamente sobre tal conteúdo, explorando, por exemplo, a ideia de polinômio. Cabe ressaltar que tais movimentos não são estáticos, intercalam‑se e dialogam entre si. Isso porque é possível partir de um problema cotidiano, utilizar conhecimentos algébricos para descrevê‑lo e tomar decisões. Entretanto, em diversos casos, é necessário que haja a apropriação de novos conhecimentos algébricos para agir sobre tal problema. Dessa maneira, é possível compreender o fato de que a Matemática é uma produção humana, além de valorizar e utilizar conhecimentos histórica, social e culturalmente construídos.
Competência geral
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico‑cultural.
Competência específica
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Habilidades
EF08MA07 e EF08MA08.
Objetivos
• Obter diferentes soluções para equação linear de 1º grau com duas incógnitas.
• Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.
• Resolver e elaborar problemas que possam ser representados por sistemas de equações lineares.
• Resolver sistemas de equações lineares utilizando o plano cartesiano como recurso.
Articulações e justificativas
A busca por soluções de equações e o desenvolvimento de diferentes estratégias para isso são maneiras de compreender e agir matematicamente sobre o mundo. Esse processo torna‑se mais interessante quando realizado coletivamente. É por meio da troca de ideias, hipóteses e estratégias com seus pares que os estudantes têm a oportunidade de se aprofundar tanto nos conteúdos matemáticos quanto nos contextos dos quais emanaram. Exercitam‑se também habilidades de argumentação e respeito às ideias dos demais.
3
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo‑se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Habilidade
EF08MA09
Objetivos
• Resolver e elaborar problemas envolvendo equações polinomiais de 2º grau do tipo ax2 + c = 0, a ≠ 0.
• Resolver equações polinomiais de 2º grau do tipo ax2 + c = 0, a ≠ 0 a partir de diferentes estratégias.
• Resolver sistemas de equações de 1º grau com duas incógnitas.
Articulações e justificativas
O estudo de equações polinomiais do tipo ax2 = b pode ser compreendido como um fechamento do estudo de equações e expressões algébricas no 8o ano. Nesse sentido, todo o caráter de desenvolvimento do pensamento computacional e de situações de “matematização da realidade” é mobilizado também neste momento. Entretanto, novas situações e contextos são trazidos para a experiência do estudante, inspirados em questões de urgência social. Espera‑se, dessa maneira, que os estudantes possam se relacionar com os problemas e contextos propostos interagindo cooperativamente entre si, desenvolvendo não somente habilidades de argumentação, comunicação e expressão, mas exercitando também a empatia e o respeito aos demais. Trajetória 3 do LE
4. Utilizar diferentes linguagens – verbal (oral ou visual‑motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
4. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
6. Enfrentar situações‑problema em múltiplos contextos, incluindo‑se situações imaginadas, não diretamente relacionadas com o aspecto prático‑utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Habilidades
EF08MA14 e EF08MA18.
Objetivos
• Reconhecer transformações geométricas isométricas (translação, reflexão e rotação).
• Construir, por composições de transformações geométricas, figuras isométricas, utilizando ou não software de geometria dinâmica.
• Reconhecer o conceito e casos de congruência de triângulos.
• Demonstrar e reconhecer algumas propriedades de quadriláteros e suas relações com a congruência de triângulos.
Articulações e justificativas
O reconhecimento de transformações geométricas pode fundamentar‑se na observação de elementos da natureza e de variadas formas de expressão artística, desde desenhos, fotografias, pinturas e esculturas até obras arquitetônicas. Mais que a identificação das transformações geométricas, espera‑se dos estudantes a produção de figuras pela composição de transformações geométricas. Nesse sentido, eles exercitam uma maneira sensível de olhar o mundo ao redor, ao mesmo tempo que se expressam de variadas formas, movimentos esses mediados pelos conceitos matemáticos de translação, reflexão e rotação. Envolvida nessa exploração, porém não restrita a ela, são exploradas figuras geométricas como quadriláteros e triângulos, incluindo suas características e propriedades. Novamente, os estudantes são encorajados e convidados a interagir com os colegas colaborativamente, compartilhando ideias, hipóteses, estratégias e as produções artísticas e visuais que porventura sejam realizadas.
5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá‑las e avaliá‑las crítica e eticamente, produzindo argumentos convincentes.
5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
Habilidades
EF08MA15, EF08MA16 e EF08MA17.
Objetivos
• Reconhecer o conceito de Lugar Geométrico.
• Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
• Aplicar os conceitos de mediatriz e bissetriz na resolução de problemas.
• Construir hexágono regular de qualquer área usando a medida do ângulo central, esquadro e compasso.
• Descrever, por escrito e em um fluxograma, um algoritmo para a construção de um hexágono regular.
Articulações e justificativas
Construções geométricas são fundamentais para a compreensão da geometria. Por um lado, podem ser tratadas como uma sequência de procedimentos para a resolução de determinado problema. Por outro, esses mesmos procedimentos são baseados não somente nas características e propriedades geométricas do que se constrói, mas das próprias limitações dos instrumentos utilizados. Desse conjunto de fatores é possível discutir tais propriedades e a própria noção de Lugar Geométrico. Ao utilizar softwares de geometria dinâmica, por exemplo, o estudante precisa lidar com as características de instrumentos como régua e compasso (aqui tratados “virtualmente”), ao passo que são apresentadas a ele diversas outras ferramentas e possibilidades, ampliando conhecimentos e experiências quanto a estratégias de resolução de problemas. Nesse sentido, o uso de tecnologias contribui não somente para a resolução de problemas, mas também apresenta outras oportunidades para o estudante se expressar e se comunicar matematicamente.
PASSEIO 3
Competência geral
4. Utilizar diferentes linguagens – verbal (oral ou visual ‑motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
Competência específica
6. Enfrentar situações‑problema em múltiplos contextos, incluindo‑se situações imaginadas, não diretamente relacionadas com o aspecto prático‑utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Habilidades
EF08MA12 e EF08MA13.
Objetivos
• Identificar a natureza da variação de duas grandezas diretamente, inversamente proporcionais ou não proporcionais.
• Expressar a relação entre duas grandezas por meio de sentença algébrica.
• Representar relação de proporcionalidade entre duas grandezas no plano cartesiano.
• Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais por meio de estratégias variadas.
Articulações e justificativas
A habilidade de identificar relações entre duas grandezas é fundamental não somente para modelar matematicamente e resolver problemas em diversos contextos, mas também para desenvolver futuramente a noção de função. Nesta etapa da escolaridade, entretanto, o foco é nas relações de proporcionalidade entre grandezas. Esse tipo de estudo cria oportunidades para os estudantes consolidarem ou ressignificarem uma série de conhecimentos sobre o campo multiplicativo, ao passo que apresenta desafios relacionados a estrutura e escrita algébricas. Dessa maneira, o estudante é convidado a utilizar diferentes maneiras de representação para resolver problemas de variados contextos, além de produzir justificativas e argumentos matemáticos.
7. Argumentar com base em fatos, dados e informações confiáveis para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Habilidades
EF08MA19, EF08MA20 e EF08MA21.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
Objetivos
• Determinar, utilizando expressões de cálculo, áreas das superfícies de figuras geométricas (quadriláteros, triângulos e círculos).
• Resolver e elaborar problemas que envolvam medidas de áreas de superfícies em situações diversas.
• Reconhecer unidade de medida de volume e de capacidade e suas relações.
• Resolver e elaborar problemas que envolvam cálculo de volume e de capacidade de recipientes com formato de bloco retangular.
Articulações e justificativas
A exploração de medidas de superfície e volume envolve trabalhar com uma série de conhecimentos construídos ao longo dos anos de escolarização, assim como com as experiências vivenciadas em diversos contextos, dentro ou fora da escola. Dessa maneira, cria‑se a oportunidade de consolidar e aprofundar tais conhecimentos. Ao propor situações ‑problema envolvendo esse assunto, os alunos são convidados a refletir sobre diferentes contextos cotidianos ou relacionados a outras disciplinas, produzindo argumentos claros e objetivos para justificar ideias ou pontos de vista.
Competência geral
6. Valorizar a diversidade de saberes e vivências culturais e apropriar‑se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
Habilidades
EF08MA23, EF08MA24 e EF08MA25.
Objetivos
PASSEIO 2
Competência específica
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá‑las e avaliá‑las crítica e eticamente, produzindo argumentos convincentes.
• Avaliar a adequação de diferentes tipos de gráficos para representar o conjunto de dados de uma pesquisa.
• Reconhecer a organização de variáveis contínuas cujos dados agrupados em classes favoreçam a análise de informações e a tomada de decisões.
• Determinar média aritmética (simples e ponderada), moda e mediana.
• Compreender os significados de média aritmética (simples e ponderada), moda e mediana relacionando‑os com a dispersão de dados indicada pela amplitude.
Articulações e
justificativas
Coletar dados, organizar em tabelas e expressar graficamente são habilidades fundamentais para o desenvolvimento do letramento matemático. No 8o ano do Ensino Fundamental, essas habilidades ganham novas camadas de complexidade: é necessário tomar decisões sobre a maneira de agrupar dados, de trabalhar com intervalos para variáveis contínuas, compreender e utilizar medidas de tendência central (média, moda e mediana), reconhecer a dispersão de dados, assim como decidir qual tipo de gráfico é mais adequado para cada situação, seja em termos de análise, seja de comunicação dos dados. Um elemento importante de ser trabalhado no desenvolvimento dessas habilidades refere‑se ao cuidado tanto com a veracidade e adequação das informações apresentadas, quanto com o respeito aos envolvidos na pesquisa, sempre à luz de princípios éticos. Ao contextualizar tais aspectos em situações de relevância para os estudantes, desenvolve‑se também o olhar crítico, alinhado ao exercício da cidadania e da democracia.
Competência geral Competência específica
6. Valorizar a diversidade de saberes e vivências culturais e apropriar‑se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
Habilidades
EF08MA26 e EF08MA27.
Objetivos
• Reconhecer, por meio de ideias matemáticas, fatos noticiados e comentados pelos meios de comunicação, averiguando e avaliando a credibilidade da informação usando critérios objetivos.
• Identificar motivos de aspectos físicos, éticos ou econômicos que justifiquem a realização de pesquisas amostrais.
• Identificar diferentes maneiras de selecionar amostras: casual simples, sistemática e estratificada.
• Planejar pesquisa amostral desde a etapa da seleção da amostra até a escrita do relatório (contendo gráficos, análises estatísticas por meio das medidas de posição e da amplitude e registros das conclusões).
Articulações e justificativas
A realização de pesquisas estatísticas deve estar focada em assuntos relevantes ao estudante de modo que promova o protagonismo do jovem ao agir sobre uma questão que lhe é importante. Além do tratamento dos dados e da informação, é fundamental considerar a maneira como serão apresentadas, desde a adequação de gráficos e tabelas, até a elaboração de textos que sintetizem os resultados da pesquisa realizada. Esse tipo de situação favorece o desenvolvimento do pensamento crítico, o sentimento de pertencimento e a tomada de atitude na comunidade à qual pertence, promove valores democráticos e o exercício da cidadania.
LUPAS E LUNETAS
O 8o ano do Ensino Fundamental, de maneira geral, apresenta boas oportunidades para o desenvolvimento do pensamento computacional: modelagem de situações cotidianas a partir de expressões algébricas e equações; estudo de padrões e regularidades em sequências; elaboração de procedimentos e algoritmos para construções geométricas etc. Retome a noção de pensamento computacional apresentada anteriormente e converse com os colegas sobre como potencializar seu desenvolvimento em sala de aula à luz das articulações e justificativas apresentadas.
SUBSÍDIOS PARA TRABALHAR A INTERDISCIPLINARIDADE
Os quadros a seguir explicitam as possibilidades de trabalho com outras disciplinas.
TRAJETÓRIA 1 DO LE
TCTs: Educação Ambiental e Ciência e Tecnologia
Quadro de interdisciplinaridade
DISCIPLINA HABILIDADE JUSTIFICATIVA
(EF08CI07) Comparar diferentes processos reprodutivos em plantas e animais em relação aos mecanismos adaptativos e evolutivos.
Habilidades relacionadas à realização de cálculos e representação de números utilizando potenciação e notação científica podem contribuir para a compreensão de diversos temas relacionados às Ciências, como a análise de populações ou de características de certos indivíduos ou espécies. Da mesma maneira, trazer tais assuntos para as aulas de Matemática possibilita a produção de significados para tais conteúdos, relacionados especialmente às unidades temáticas de números e álgebra. Especialmente quanto à noção de potenciação, a ideia de divisão binária como processo de reprodução assexuada é um tema que contribui para tal produção de significado. No caso específico das aulas de Ciências, tal conhecimento matemático colabora para a compreensão de aspectos relacionados, por exemplo, ao crescimento de uma população ou à obtenção de elementos para discutir as vantagens adaptativas de diferentes processos reprodutivos.
Ciências
(EF08CI12) Justificar, por meio da construção de modelos e da observação da Lua no céu, a ocorrência das fases da Lua e dos eclipses, com base nas posições relativas entre Sol, Terra e Lua.
A construção de modelos relacionados à Astronomia cria uma série de oportunidades para o trabalho pedagógico. No sentido das relações entre Ciências e Matemática, é interessante o aspecto de lidar com as grandezas e medidas envolvidas, as noções de escala e proporcionalidade. Outra possibilidade de trabalho interdisciplinar reside na observação e análise de fenômenos periódicos, como as fases da Lua, com a discussão de seus padrões e regularidades.
(EF08CI15) Identificar as principais variáveis envolvidas na previsão do tempo e simular situações nas quais elas possam ser medidas.
Trabalhar com o contexto de observações meteorológicas favorece as discussões em diversas unidades temáticas da Matemática. A mais evidente é a de grandezas e medidas, desde o trabalho com temperatura até unidades relacionadas à velocidade dos ventos, visibilidade, precipitação etc. Diferentes representações numéricas também podem ser trabalhadas ao se considerar situações com medidas “muito grandes” ou “muito pequenas”. A unidade temática de probabilidade e estatística também tem grande aderência a esse tipo de discussão, tanto no contexto de análise e elaboração de tabelas e gráficos envolvendo dados relacionados ao clima, quanto na discussão sobre as chances de ocorrência de fenômenos em certo período, por exemplo, a chuva.
TCTs: Cidadania e Civismo
Quadro de interdisciplinaridade
DISCIPLINA HABILIDADE JUSTIFICATIVA
(EF69LP15) Apresentar argumentos e contra‑argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
(EF89LP04) Identificar e avaliar teses/ opiniões/posicionamentos explícitos e implícitos, argumentos e contra ‑argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando‑se frente à questão controversa de forma sustentada.
Habilidades relacionadas à argumentação, comunicação e expressão são fundamentais, cada uma com suas respectivas particularidades, para as noções de letramento e de letramento matemático. São diversas as possibilidades de construção de argumentações ou contra‑argumentações utilizando conhecimentos matemáticos. Uma delas é a modelagem algébrica de situações cotidianas, de modo a resolver um problema ou permitir tomar decisões adequadas. Tais modelos podem ser utilizados como fundamentos para o posicionamento frente a dada questão.
Geografia
(EF09GE15) Comparar e classificar diferentes regiões do mundo com base em informações populacionais, econômicas e socioambientais representadas em mapas temáticos e com diferentes projeções cartográficas.
(EF09GE16) Identificar e comparar diferentes domínios morfoclimáticos da Europa, da Ásia e da Oceania.
Com um “olhar matemático” é possível analisar e compreender diferentes aspectos da Geografia global: o uso de várias unidades de medida e de diferentes representações numéricas ao se discutir populações, distâncias, território, relevo etc.; organização, análise e representação de dados a partir de tabelas e gráficos; escalas e trajetos em mapas cartográficos etc.
TRAJETÓRIA 3 DO LE
TCTs: Ciência e Tecnologia; Processo de envelhecimento, respeito e valorização do idoso; Diversidade Cultural; Direitos da Criança e do Adolescente; Vida Familiar e Social e Trabalho
Quadro de interdisciplinaridade
DISCIPLINA HABILIDADE JUSTIFICATIVA
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
Ensino Religioso
Arte
Língua Portuguesa
(EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
Diversos assuntos nas aulas de Matemática podem disparar discussões que contribuam para a promoção da liberdade de pensamento. De maneira geral, criar um espaço no qual os estudantes possam se expressar, defender opiniões pessoais e conviver respeitosamente já configura um exercício para o desenvolvimento dessa habilidade. No entanto, é possível tornar o próprio tema “liberdade de expressão, crenças e convicções” o objeto de discussão. Nesse sentido, devem ser trazidos argumentos racionais, objetivos e claros para a discussão, com uso de dados estatísticos, informações de relatórios de pessoas ou entidades confiáveis etc.
A geometria pode ser considerada uma das interfaces mais evidentes da relação entre Matemática e práticas artísticas. O uso de figuras geométricas e padrões faz‑se presente em diferentes povos e culturas com base em motivações diversas, desde estéticas até ritualísticas. No entanto, é possível fazer também o movimento inverso, ou seja, em vez de observar como a “Arte incorpora a geometria”, podemos utilizar a geometria para explicar ou justificar a Arte. Um exemplo é tentar compreender porque os movimentos de bailarinos e bailarinas parecem tão harmoniosos.
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
O contato com diferentes gêneros da cultura digital é uma prática rotineira para quase todo indivíduo atualmente, especialmente os jovens. Nesse sentido, é possível trazer esses elementos para as aulas de Matemática segundo um duplo movimento: utilizar memes, gifs, charges digitais etc. que tenham conteúdo ou temas matemáticos como ponto de partida ou forma de enriquecer discussões; ou começar com os conteúdos matemáticos trabalhados em aula e produzir tais elementos.
TRAJETÓRIA 4 DO LE
TCTs: Saúde; Vida Familiar e Social e Direitos Humanos
Quadro de interdisciplinaridade
DISCIPLINA HABILIDADE JUSTIFICATIVA
Educação
Física
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem‑estar e cuidado consigo mesmo.
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático –infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
(EF08LP01) Identificar e comparar as várias editoras de jornais impressos e digitais e de sites noticiosos, de forma a refletir sobre os tipos de fato que são noticiados e comentados, as escolhas sobre o que noticiar e o que não noticiar e o destaque/enfoque dado e a fidedignidade da informação.
LUPAS E LUNETAS
Práticas esportivas diversas possibilitam ao indivíduo relacionar‑se com o espaço ao redor. Nesse sentido é possível compreender as próprias dimensões, medidas e formatos dos espaços, tomando como base o próprio corpo. Questões como “Em quanto tempo atravesso o pátio?”, “Se girar os braços, posso bater em algum objeto ao redor?” e “Com que força devo arremessar a bola para ela chegar ao teto?” podem ser tratadas também de maneira quantitativa, ampliando as noções sobre os limites e capacidades do próprio corpo.
É fundamental para o desenvolvimento do letramento matemático saber não somente se expressar e comunicar ‑se oralmente, mas também elaborar textos que sintetizem ideias e explicitem de maneira clara e coerente diferentes argumentos para defender ou refutar determinadas ideias e hipóteses. Nesse sentido, é importante saber incorporar outros elementos ao texto, desde imagens até esquemas visuais, tabelas, gráficos etc. Mais ainda, é fundamental que todos os elementos possam se articular de modo a compor uma argumentação coerente.
Ao trabalhar com a elaboração de pesquisas estatísticas ou a análise de dados apresentados em relatórios, tabelas e gráficos, é fundamental que o estudante tome contato com diferentes referências. Nesse sentido, é possível discutir não somente a presença de erros, informações equivocadas e fake news, mas as opções de cada referência quanto à maneira de tratar ou representar dados e informações.
Os quadros anteriores sugerem possíveis articulações entre habilidades de outras disciplinas e as da Matemática, assim como com alguns TCT.
Considerando que a noção de pensamento computacional essencialmente foca em maneiras de resolver problemas e pode ser considerada de modo interdisciplinar, converse com os colegas sobre possibilidades de desenvolver o pensamento computacional em atividades interdisciplinares.
Língua PortuguesaJUSTIFICATIVA E PERTINÊNCIA DOS OBJETIVOS E PROPOSTAS DE AVALIAÇÃO
TRAJETÓRIA 1 DO LE
O início do 8º ano do Ensino Fundamental resgata e aprofunda alguns conteúdos dos anos anteriores: são discutidas as noções de potenciação e radiciação, as relações entre elas e as possibilidades de representação de números “muito grandes” e “muito pequenos” utilizando notação científica. É apresentada também uma reflexão sobre o conjunto dos números racionais, com a discussão de procedimentos para obtenção da fração geratriz de uma dízima periódica. Na sequência, são retomados aspectos do campo multiplicativo, especialmente os relacionados à ideia de contagem e cálculo de probabilidades. Por fim, a álgebra se apresenta no âmbito da discussão de regularidades em sequências recursivas e não recursivas.
Quadro: objetivos e avaliações
Ao longo da Trajetória são propostas atividades individuais e coletivas, situações de reflexão, de investigação e uso de tecnologias digitais. Utilize‑as para acompanhar a aprendizagem dos estudantes durante a Trajetória. Sugerimos avaliar a aprendizagem na seção Vistorias, ao final da Trajetória, assim como o boxe Levo na bagagem ao fim de cada passeio para promover momentos de autoavaliação. A ficha favorece o registro e o monitoramento da aprendizagem para cada objetivo durante e ao fim da Trajetória.
I. Ficha de monitoramento da aprendizagem – individual
Nome do(a) estudante: ________________ Turma: _______
Objetivos
Durante a Trajetória Ao fim da Trajetória
O(a) estudante está apto(a) a... S N P S N P
Resolver e elaborar problemas envolvendo cálculo de porcentagens.
Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Efetuar cálculos com potências de expoentes inteiros.
Utilizar a representação de números em notação científica para escrever números muito grandes ou muito pequenos.
Resolver e elaborar problemas usando a relação entre potenciação e radiciação para representar uma raiz como potência de expoente fracionário.
Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Calcular a probabilidade de eventos com base na construção do espaço amostral, utilizando o princípio multiplicativo.
Reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Identificar a regularidade de uma sequência numérica ou figural não recursiva.
Identificar a regularidade de uma sequência numérica recursiva.
Construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências recursivas.
Construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências não recursivas.
Legenda: Sim (S), Não (N), Parcialmente (P).
TRAJETÓRIA 2 DO LE
Nesta Trajetória são apresentadas variadas situações que podem ser descritas por expressões algébricas. Ao aprofundar o tema, é discutida a noção de polinômio, bem como suas operações. Em seguida, retomamos algumas estratégias de resolução de equações e apresentamos a ideia de sistema de equações lineares, incluindo estratégias de resolução de representações gráficas e uso de tecnologias digitais. A Trajetória encerra‑se com a discussão de situações‑problema que envolvem equações polinomiais de 2º grau do tipo ax2 = b
Quadro: objetivos e avaliações
Ao longo da Trajetória são propostas atividades individuais e coletivas, situações de reflexão, de investigação e uso de tecno logias digitais. Utilize‑as para acompanhar a aprendizagem dos estudantes durante a Trajetória. Sugerimos avaliar a aprendizagem na seção Vistorias, ao final da Trajetória, assim como o boxe Levo na bagagem ao fim de cada passeio para promover momentos de autoavaliação. A ficha favorece o registro e o monitoramento da aprendizagem para cada objetivo durante e ao fim da Trajetória.
I. Ficha de monitoramento da aprendizagem – individual
Nome do(a) estudante: ________________ Turma: _______
Objetivos Durante a Trajetória Ao fim da Trajetória
O(a) estudante está apto(a) a... S N P S N P
Identificar situações‑problema que podem ser descritas por expressões algébricas.
Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas.
Compreender a noção de polinômio.
Utilizar as propriedades das operações para resolver cálculos envolvendo adição, subtração, multiplicação e divisão entre polinômios.
Resolver e elaborar problemas que envolvam medidas de área de superfícies de figuras geométricas utilizando expressões de cálculo de área.
Obter diferentes soluções para equação linear de 1º grau com duas incógnitas.
Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.
Resolver e elaborar problemas que possam ser representados por sistemas de equações lineares.
Resolver sistemas de equações lineares utilizando o plano cartesiano como recurso.
Resolver e elaborar problemas envolvendo equações polinomiais de 2º grau do tipo ax2 = b.
Resolver equações polinomiais de 2º grau do tipo ax2 = b com diferentes estratégias.
Resolver sistemas de equações de 1º grau com duas incógnitas.
Legenda: Sim (S), Não (N), Parcialmente (P).
TRAJETÓRIA 3 DO LE
A geometria assume boa parte das discussões desta Trajetória, desde o reconhecimento de transformações geométricas como reflexão, translação e rotação, passando pela análise de características e propriedades de quadriláteros e triângulos (incluindo noções de congruência e lugar geométrico), chegando à apresentação de diferentes procedimentos para construções geométricas, incluindo o uso de softwares de geometria dinâmica. A álgebra se apresenta na Trajetória em uma discussão sobre as relações entre duas grandezas de noções de proporcionalidade (direta e inversa).
Quadro: objetivos e avaliações
Ao longo da Trajetória são propostas atividades individuais e coletivas, situações de reflexão, investigação e utilização de tecno logias digitais. Utilize‑as para acompanhar a aprendizagem dos estudantes durante a Trajetória. Sugerimos avaliar a aprendizagem na seção Vistorias, ao final da Trajetória, assim como o boxe Levo na bagagem ao fim de cada passeio para promover momentos de autoavaliação. A ficha favorece o registro e o monitoramento da aprendizagem para cada objetivo durante e ao fim da Trajetória.
I. Ficha de monitoramento da aprendizagem – individual
Nome do(a) estudante: ________________ Turma: _______
Objetivos Durante a Trajetória Ao fim da Trajetória
O(a) estudante está apto(a) a... S N P S N P
Reconhecer transformações geométricas isométricas (translação, reflexão e rotação).
Construir, por composições de transformações geométricas, figuras isométricas, utilizando ou não software de geometria dinâmica.
Reconhecer o conceito e casos de congruência de triângulos.
Demonstrar e reconhecer algumas propriedades de quadriláteros e suas relações com a congruência de triângulos.
Reconhecer o conceito de Lugar Geométrico.
Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.
Aplicar os conceitos de mediatriz e bissetriz na resolução de problemas.
Construir hexágono regular de qualquer área usando a medida do ângulo central, esquadros e compasso.
Descrever por escrito, em um fluxograma, um algoritmo para a construção de um hexágono regular.
Identificar a natureza da variação de duas grandezas diretamente proporcionais, inversamente proporcionais ou não proporcionais.
Expressar a relação entre duas grandezas por meio de sentença algébrica.
Representar relação de proporcionalidade entre duas grandezas no plano cartesiano.
Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais por meio de estratégias variadas.
Legenda: Sim (S), Não (N), Parcialmente (P).
TRAJETÓRIA 4 DO LE
Esta Trajetória se inicia trazendo a discussão das estratégias para o cálculo de áreas de superfícies de figuras geométricas e de volume de blocos retangulares. São exploradas também diferentes unidades de medida de superfície, volume e capacidade. Outra unidade temática trabalhada na Trajetória é Probabilidade e Estatística, com a discussão sobre maneiras de planejar uma pesquisa estatística e estratégias para organizar os dados, analisá‑los e comunicar os resultados da pesquisa.
Quadro: objetivos e avaliações
Ao longo da Trajetória são propostas atividades individuais e coletivas, situações de reflexão, de investigação e de utilização de tecnologias digitais. Utilize‑as para acompanhar a aprendizagem dos estudantes durante a Trajetória. Sugerimos avaliar a aprendizagem na seção Suplemente sua aprendizagem, ao final da Trajetória, assim como o boxe Levo na bagagem ao fim de cada passeio para promover momentos de autoavaliação. A ficha favorece o registro e o monitoramento da aprendizagem para cada objetivo durante e ao fim da Trajetória.
I. Ficha de monitoramento da aprendizagem – individual
Nome do(a) estudante: ________________ Turma: _______
Objetivos
Durante a Trajetória Ao fim da Trajetória
O(a) estudante está apto(a) a... S N P S N P
Determinar, utilizando expressões de cálculo, áreas das superfícies de figuras geométricas (quadriláteros, triângulos e círculos).
Resolver e elaborar problemas que envolvam medidas de áreas de superfícies em situações diversas.
Reconhecer unidade de medida de volume e de capacidade e suas relações.
Resolver e elaborar problemas que envolvam cálculo de volume e de capacidade de recipientes com formato de bloco retangular.
Avaliar a adequação de diferentes tipos de gráficos para representar o conjunto de dados de uma pesquisa.
Reconhecer a organização de variáveis contínuas cujos dados agrupados em classes favoreçam a análise de informações e a tomada de decisões.
Determinar média aritmética (simples e ponderada), moda e mediana.
Compreender os significados de média aritmética (simples e ponderada), moda e mediana relacionando‑os com a dispersão de dados, indicada pela amplitude.
Reconhecer, por meio de ideias matemáticas, fatos noticiados e comentados pelos meios de comunicação, averiguando e avaliando a credibilidade da informação por meio de critérios objetivos.
Identificar motivos de aspectos físicos, éticos ou econômicos que justifiquem a realização de pesquisas amostrais.
Identificar diferentes maneiras de selecionar amostras: casual simples, sistemática e estratificada.
Planejar pesquisa amostral desde a etapa da seleção da amostra até a escrita do relatório (contendo gráficos, análises estatísticas por meio das medidas de posição e da amplitude e registros das conclusões).
Legenda: Sim (S), Não (N), Parcialmente (P).
SUGESTÃO DE CRONOGRAMA
Sugerimos o cronograma a seguir, fundamentado na estrutura de Trajetórias e passeios apresentada neste livro. Entretanto, é importante ressaltar que você pode adaptar este cronograma de acordo com a realidade da turma e o contexto escolar.
PERÍODO TRAJETÓRIA PASSEIO
1. Números racionais, potenciação e radiciação
1º bimestre 1
2. Contagem e probabilidade
3. Sequências
1. Expressões algébricas
2º bimestre 2
2. Equações de 1º grau com duas incógnitas e sistemas lineares
3. Equações polinomiais de 2º grau
1. Isometria e congruência de triângulos
3º bimestre 3
2. Construção geométrica e lugar geométrico
3. Proporcionalidade e plano cartesiano
1. Superfície, volume e capacidade
4º bimestre 4
2. Gráficos e medidas de posição
3. Pesquisa estatística e credibilidade da informação
HABILIDADES DE MATEMÁTICA E OUTRAS DISCIPLINAS
Estas são as competências e habilidades trabalhadas neste volume.
QUADRO DE HABILIDADES DO 8 O ANO
Matemática
NÚMEROS
(EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
ÁLGEBRA
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b
(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
(EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
GEOMETRIA
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA16) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
(EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
GRANDEZAS E MEDIDAS
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
PROBABILIDADE E ESTATÍSTICA
(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
(EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Outras disciplinas
LÍNGUA PORTUGUESA
(EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático – infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
(EF89LP04) Identificar e avaliar teses/opiniões/posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando-se frente à questão controversa de forma sustentada.
(EF08LP01) Identificar e comparar as várias editorias de jornais impressos e digitais e de sites noticiosos, de forma a refletir sobre os tipos de fato que são noticiados e comentados, as escolhas sobre o que noticiar e o que não noticiar e o destaque/enfoque dado e a fidedignidade da informação.
As propostas do material do aluno oferecem oportunidades para o trabalho em parceria com professores de outras disciplinas. O quadro a seguir apresenta as habilidades que, em algum momento, foram tocadas.
ARTE
(EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
GEOGRAFIA
(EF08GE15) Analisar a importância dos principais recursos hídricos da America Latina (Aquífero Guarani, Bacias do rio da Prata, do Amazonas e do Orinoco, sistemas de nuvens na Amazônia e nos Andes, entre outros) e discutir os desafios relacionados à gestão e comercialização da água.
(EF08GE16) Analisar as principais problemáticas comuns às grandes cidades latino-americanas, particularmente aquelas relacionadas à distribuição, estrutura e dinâmica da população e às condições de vida e trabalho.
CIÊNCIAS
(EF08CI07) Comparar diferentes processos reprodutivos em plantas e animais em relação aos mecanismos adaptativos e evolutivos.
(EF08CI12) Justificar, por meio da construção de modelos e da observação da Lua no céu, a ocorrência das fases da Lua e dos eclipses, com base nas posições relativas entre Sol, Terra e Lua.
(EF08CI15) Identificar as principais variáveis envolvidas na previsão do tempo e simular situações nas quais elas possam ser medidas.
ENSINO RELIGIOSO
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
EDUCAÇÃO FÍSICA
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
8o MATEMÁTICA
NOS DIAS DE HOJE
Jefferson Cevada
8 MATEMÁTICA
Licenciado em Matemática pela Universidade Federal de Mato Grosso (UFMT). Foi professor e coordenador da rede pública de São Paulo. Editor e elaborador de conteúdos didáticos.
Daniel Romão da Silva
Doutor e Mestre em Educação pela Universidade de São Paulo (USP). Licenciado em Matemática pela Universidade de São Paulo (USP). Foi coordenador e professor da rede pública e particular de São Paulo. Autor de materiais didáticos.
Matemática nos dias de hoje
© 2022 Editora Sei
Direção editorial
Sandro Aloísio
Produção gráfica
Reinaldo Correale
Giliard Andrade
Equipe M10 Editorial
Coordenação pedagógica
Alessandra Corá
Coordenação editorial
Fernanda Azevedo
Edição
Angela Leite
Assistência editorial
Gabriel Santos Novaes
Preparação e revisão de textos
Brenda Gomes
Caroline Ponzi
Thais Sanchez
Marina Bueno
Projeto gráfico de capa e miolo
Arte/M10
Coordenação de editoração eletrônica
Eduardo Enoki
Editoração eletrônica
Fanny Sosa
Nathalia Scala
Ricardo Coelho
Iconografia
M10 Editorial
Licenciamento de texto e imagens
Tempo Composto
Imagens gerais, de projeto gráfico e ilustrações técnicas
Arte/ M10
Shutterstock.com
Freepik
Impressão e acabamento
Oceano Indústria Gráfica e Editora Ltda.
Rua Osasco, 644 – Rod. Anhanguera, km 33
CEP 07750-020 – Cajamar – SP

CNPJ: 67.795.906/0001-10
Tel.: (11) 4446-7000
Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.
ISBN 978-85-54226-81-7 (Aluno)
ISBN 978-85-54226-78-7 (Professor)
Todos os direitos reservados:
Editora Sei
Av. Profa. Ida Kolb, 551 – Jardim das Laranjeiras
São Paulo – SP
CEP: 02518-050
Fone: 55 11 3855-2100
www.editorasei.com.br contato@editorasei.com.br
#APRESENTAÇÃO
Como você se reconhece, em seu dia a dia, com mais frequência:
• muito interativo?
Sabia que, em qualquer desses casos, você pode exercitar seu talento – e desenvolver outros – por meio de qualquer conhecimento, inclusive matemático? Tudo depende das suas ideias e do que você tem para propor aos que estão em seu entorno.
• muito criativo?
Este livro vai convidá-lo a expor ideias por meio de ferramentas conhecidas por você e incentivá-lo a buscar outras que podem ser novas para você, em atividades que o levarão a questionar, imaginar, analisar e elaborar situações diversas.
Você vai mobilizar conhecimentos, atitudes, afetos e talentos essenciais para formar a pessoa que você vem se tornando. O pensamento matemático, sua linguagem própria, seus objetos de conhecimento, seus processos e produtos no cotidiano escolar geram oportunidades únicas para que você possa apresentar propostas críticas, criativas e de caráter interativo
• muito crítico?
Envolva-se nessa jornada que, certamente, pode ser percorrida do seu jeito, mas sem perder de vista as contribuições da Matemática para a sua formação e as possibilidades que ela oferece para transformar o pensamento e os modos de conviver.



Venha conosco diversificar seu modo de pensar e de apresentar suas propostas!
Os autores
PRONTOS PARA COMEÇAR!
Seja bem-vindo ao novo ano escolar! Comece mostrando o que você já sabe. Leia e resolva sozinho algumas questões do ano anterior.
TRAJETÓRIA
Que tal começar uma Trajetória com per guntas instigantes? Fazer boas perguntas é uma maneira de iniciar novos caminhos.
PASSEIO
Cada Trajetória é composta de três passeios. Cada passeio é norteado por uma pergunta. Inicie seu passeio resgatando os conhecimentos que você já tem, matemáticos ou não, sobre o tema da pergunta. Depois, consulte o mapa mental e os objetivos esperados para o passeio.

CHECK ‑IN
Reflita sobre o tema interdisciplinar do passeio e resgate conhecimentos de Matemática.
ATMOSFERA
Entre no clima! O passeio já começou. Envolva-se com as primeiras reflexões junto aos colegas.
TRAVESSIAS
Investigar, resolver problemas, modelar, atravessar outros conhecimentos: adquira novas ferramentas para prosseguir em seu passeio.
NUVENS
Alcance ferramentas do mundo tecnológico digital e também do pensamento computacional.
Seu livro está organizado em quatro TRAJETÓRIAS, uma para cada bimestre. Cada Trajetória é composta de três PASSEIOS.
LUPAS E LUNETAS
Para “enxergar” melhor – de perto ou de longe –, venha refletir sobre questões que detalham ou que ampliam os temas explorados na página.
LEVO NA BAGAGEM
Pausa para reorganizar conhecimentos e checar se, de fato, os objetivos declarados no início do passeio vieram para sua bagagem.
BARCOS E PORTOS
Selo que indica Encontro com outras disciplinas.
Conclua o seu passeio: organize seus conhecimentos, elabore uma questão e proponha ideias – de modo crítico, criativo e interativo – relacionadas à pergunta norteadora que abriu seu passeio.

VISTORIAS
Depois de três passeios, é hora de encerrar a Trajetória! Resolva exercícios essenciais da Trajetória para verificar quais conhecimentos você adquiriu. Prossiga interagindo com os conhecimentos e desenvolvendo cada vez mais autonomia para monitorar sua própria aprendizagem.


RETORNOS
Aqui, você tem acesso rápido aos principais objetos matemáticos explorados ao longo de cada Trajetória para que possa ir ao encontro da síntese do que aprendeu. Use ao máximo os recursos que o livro oferece para superar todos os obstáculos da sua aprendizagem.

SUPLEMENTE SUA APRENDIZAGEM
Ao final do livro, você encontra questões de concursos organizadas por Trajetória para você continuar aprimorando sua aprendizagem.
TEMAS BÚSSOLA
1 Quais são os extremos da natureza? 18 Como descrever o “muito pequeno” e o “muito grande” na natureza? 20
TRAJETÓRIA
Os fenômenos da natureza são aleatórios ou determinísticos? 44
Quais fenômenos da natureza são periódicos? 58
Como se desenvolvem as diferentes relações sociais no ambiente urbano? 76
2
TRAJETÓRIA
Como criar relações de igualdade e de equidade no convívio social?
78
Passeio 1 21
EF08MA01, EF08MA02, EF08MA04, EF08MA05
Passeio 2 45
EF08MA03, EF08MA22
Passeio 3 59
EF08MA10, EF08MA11
Passeio 1 79
EF08MA06
Passeio 2 93
EF08MA07, EF08MA08
Passeio 3 111
EF07MA09
PASSEIO 1
Números racionais, potenciação e radiciação 20

Muito grande, muito pequeno • Porcentagens • Dízimas periódicas • Potenciação • Notação científica • Radiciação e potenciação
Expressões algébricas 78

Expressões algébricas no cotidiano • Expressões algébricas com mais de uma variável • Polinômios • Operações com polinômios
3
TRAJETÓRIA
Quais relações existem entre os diferentes atores da sociedade? 92
Como lidar com os diferentes recursos disponíveis no ambiente urbano? 110
Como as tecnologias impactam a vida social? 126
Quais transformações as tecnologias digitais podem trazer?
128
Qual lugar ocupam as tecnologias nas relações culturais? 152
Que impactos as tecnologias da comunicação podem trazer à vida familiar e ao mundo do trabalho?
168
4 Quais são as dimensões do bem-estar? 192
TRAJETÓRIA
O que quer dizer bem-estar físico?
194
Como manter o bem-estar mental? 218
Como desenvolver o bem-estar social? 234
Passeio 1 129
EF08MA14, EF08MA18
Passeio 2 153
EF08MA15, EF08MA16, EF08MA17
Passeio 3 169
EF08MA12, EF08MA13
Passeio 1 195
EF08MA19, EF08MA20, EF08MA21
Passeio 2 219
EF08MA23, EF08MA24, EF08MA25
Passeio 3 235
EF08MA26, EF08MA27
Isometria e congruência de triângulos 128 Transformações geométricas • Transformações isométricas • Congruência de triângulos • Propriedades de quadriláteros e congruências de triângulos
Superfície, volume e capacidade 194
Superfícies de retângulos e quadrados • Superfícies de paralelogramos e triângulos • Superfícies de losangos e trapézios • Superfície do círculo • A medida do conteúdo: o volume • O volume de blocos retangulares • Capacidade e volume
Equações polinomiais de 1o grau com duas incógnitas e sistemas lineares 92
Equações polinomiais de 1o grau • Equações polinomiais de 1o grau com duas incógnitas • Sistemas de equações polinomiais de 1o grau • Estratégias de resolução de sistemas de equações • Álgebra: a linguagem da Matemática
PASSEIO 3
Sequências 58
Matemática e fenômenos periódicos • Sequências
BARCOS E PORTOS E VISTORIAS
Passeio 1 43
Mural sobre extremos da natureza.
Passeio 2 57
Pesquisa sobre radiação adaptativa.
Passeio 3 72
Estudo do movimento do Sol e sombras.
Vistorias 73
Construção geométrica e lugar geométrico 152
Lugar geométrico • Construção de polígonos regulares
Equações polinomiais de 2o grau 110
Área da superfície de retângulos representados por equações • Equações polinomiais do tipo ax 2 = b, com a ≠ 0 • Escrevendo álgebra com símbolos
Proporcionalidade e plano cartesiano 168
Grandeza • Razão: uma relação entre grandezas • Proporção • Não proporcionalidade • Proporção e plano cartesiano
Passeio 1 91
Conversa sobre igualdade e equidade.
Passeio 2 109
Estudo das relações sociais na escola.
Passeio 3 120
Estudo sobre recursos e relações sociais.
Vistorias 122
Passeio 1 150
Painel digital sobre sabedoria e cultura que os idosos podem produzir e divulgar.
Passeio 2 166
Reflexão sobre as ferramentas digitais utilizadas para fins artísticos e os efeitos da arte em si próprios.
Passeio 3 186
Mural virtual sobre os impactos das tecnologias da comunicação na sociedade.
Vistorias 188
Gráficos e medidas de posição 218

Tipos e adequação de gráficos • Tabela de frequências a partir dos dados brutos • Dados agrupados em classes • Mediana, moda e média
Pesquisa estatística e credibilidade da informação 234 Notícias e credibilidade • Gestão da credibilidade • Etapas da pesquisa estatística • A problematização em Estatística • População e amostra • Planejamento da pesquisa • A realização, o relatório e a análise estatística • A tomada de decisão
Passeio 1 216
Reflexão sobre as próprias rotinas, a prática de atividades físicas e o bem-estar físico, mental e social.
Passeio 2 232
Grupo virtual para compartilhar informações sobre saúde mental.
Passeio 3 254
Reflexão e pesquisa sobre bem-estar social.
Vistorias 256
A META E O MOTIVO COMO SINALIZADORES DO ENSINO E DA APRENDIZAGEM
A cada volume desta coleção, as competências gerais da educação básica são exploradas por meio de temas diversos do cotidiano, das tecnologias, das ciências, da história etc. Cada competência, de modo geral, sinaliza o que é esperado que o aluno mobilize (conhecimentos, habilidades, atitudes e valores), de maneira que haja um para que correspondente, ou seja, há uma justificativa voltada para as demandas da vida cotidiana, do convívio social, do exercício da cidadania e do mundo do trabalho e consumo.
As competências gerais se interrelacionam e se desdobram ao longo de toda a educação básica; sendo assim, o conjunto composto por sua totalidade é retomado, ampliado e complementado a cada nova oportunidade, fluindo, por meio de diferentes situações, no tratamento didático proposto a cada volume.
Nestas duas páginas é dado ao aluno conhecer as expectativas de aprendizagens amplas e complexas apresentadas de tal modo que se aproximam, a cada ano, das intenções declaradas nas competências gerais da BNCC. Observe que a meta (“o quê”) a ser alcançada está didatica e visualmente separada do motivo (“para quê”) que justifica alcançála. Tanto a meta como o motivo se ajustam a cada ano escolar segundo os conteúdos e os contextos de cada volume.
COMPETÊNCIAS GERAIS DA EDUCAÇÃO BÁSICA
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências,
#O QUÊ
1
Conhecimento: utilizar os conhecimentos historicamente construídos sobre o mundo físico...
2
Pensamento científico, crítico e criativo: exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências...
3
Repertório cultural: valorizar expressões culturais diversas, das locais às mundiais...
4
Comunicação: utilizar diferentes práticas da comunicação (compartilhar, comentar, curtir etc.)...

5
Cultura digital: utilizar tecnologias digitais de informação e comunicação de forma reflexiva e ética...
Propostas críticas
Propostas criativas
Propostas interativas
incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artísticocultural.
6
Projeto de vida: apropriar se de conhecimentos e experiências que lhe possibilitem reconhecer melhores formas de cuidar de si e da própria saúde...
7
Argumentação: argumentar com base em fatos, dados e informações confiáveis...
8
Autoconhecimento e autocuidado: conhecer se e cuidar de sua saúde física, compreendendo se na diversidade humana e interagindo com seus pares de forma cooperativa...
9
Empatia, cooperação e cidadania: exercitar a empatia, o diálogo e a cooperação promovendo o respeito ao outro...
10
Responsabilidade e cidadania: agir pessoal e coletivamente, levando em conta os recursos disponíveis no ambiente urbano, refletindo com responsabilidade, flexibilidade e determinação...
4. Utilizar diferentes linguagens – verbal (oral ou visualmotora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas
...para levar adiante seu projeto de vida com consciência crítica e responsabilidade.
1
# PARA QUÊ?
...para entender e explicar a realidade matematicamente.
2
...para investigar e resolver problemas com base nos conhecimentos das diferentes áreas.
3
...para refletir sobre suas próprias experiências criativas inseridas nas práticas da produção cultural.
4 ...para se expressar e partilhar informações, experiências e ideias de modo a produzir sentidos que levem ao entendimento mútuo.
5
...para disseminar ideias e informações que valorizem o encontro intergeracional provendo o respeito na vida pessoal e coletiva.
7
...para discutir ideias e pontos de vista sobre relações sociais de igualdade e equidade.
8
...para desenvolver a autoestima e a perseverança na busca de soluções.
9
...para valorizar os saberes, as identidades e potencialidades diversas, sem preconceito de qualquer natureza.
10 ...para tomar posicionamentos críticos, sustentáveis, democráticos e solidários.
8. Conhecerse, apreciarse e cuidar de sua saúde física e emocional, compreendendose na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendose respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
6. Valorizar a diversidade de saberes e vivências culturais e apropriarse de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e

ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Prontos para começar!, 14
TRAJETÓRIA 1
Quais são os extremos da natureza?, 18
Passeio 1: Números racionais, potenciação e radiciação, 20
Passeio 2: Contagem e probabilidade, 44
• Check-in, 44
• Arredores e Bússola, 45
• Atmosfera: Nem tão aleatório assim..., 46

• Princípio multiplicativo, 47
• Travessias: Agrupamentos e contagens, 50

• Experimentos aleatórios, 51
• Probabilidades, 52
• Levo na bagagem, 56
• Barcos e portos, 57
Passeio 3: Sequências, 58
• Check-in, 20
• Arredores e Bússola, 21
• Atmosfera: Infinitamente grande e muito pequeno, 22
• Muito grande, muito pequeno, 23
• Porcentagens, 25
• Nuvens: Cálculo de porcentagem na calculadora, 28
• Dízimas periódicas, 30
• Travessias: Experimentos com dízimas periódicas, 31
• Potenciação, 34
• Notação científica, 37

• Radiciação e potenciação, 39
• Levo na bagagem, 42
• Barcos e portos, 43
• Check-in, 58
• Arredores e Bússola, 59
• Atmosfera: Como a ciência aprendeu a prever eclipses solares com precisão, 60
• Matemática e fenômenos periódicos, 61
• Sequências, 62
• Travessias: Sequências e fluxogramas, 70
• Levo na bagagem, 71
• Barcos e portos, 72
• Vistorias, 73
TRAJETÓRIA 2
Como se desenvolvem as diferentes relações sociais
• Check-in, 92
• Arredores e Bússola, 93
• Atmosfera: A importância dos jovens para a sociedade, 94
• Equações polinomiais de 1o grau, 95
• Equações polinomiais de 1o grau com duas incógnitas, 96
• Sistemas de equações polinomiais de 1o grau, 101
• Estratégias de resolução de sistemas de equações, 103
• Nuvens: Sistema de equações e representação no plano cartesiano, 105
• Travessias: Interpretação geométrica de um sistema de equações, 106
• Álgebra: a linguagem da Matemática, 107
• Levo na bagagem, 108
• Barcos e portos, 109
• Check-in, 78
• Arredores e Bússola, 79
• Atmosfera: Qual a diferença entre igualdade e equidade?, 80



• Expressões algébricas no cotidiano, 81
• Expressões algébricas com mais de uma variável, 82
• Polinômios, 85
• Travessias: Variáveis envolvendo perímetro e área de um terreno, 87
• Operações com polinômios, 88
• Levo na bagagem, 90
• Barcos e portos, 91
Passeio 2: Equações polinomiais de 1o grau com duas incógnitas e sistemas lineares, 92
Passeio 3: Equações polinomiais de 2o grau, 110
• Check-in, 110
• Arredores e Bússola, 111
• Atmosfera: Mapa indica locais com mais chances de haver disputas por água no mundo, 112
• Área da superfície de retângulos representados por equações, 113
• Equações polinomiais do tipo ax 2 = b, com a ≠ 0, 114
• Travessias: Geometria, medidas e álgebra, 117
• Escrevendo álgebra com símbolos, 118
• Levo na bagagem, 119
• Barcos e portos, 120
• Vistorias, 122
FRANCESCO SCATENA/ SHUTTERSTOCK BATSHEVS /SHUTTERSTOCKTRAJETÓRIA 3
Como as tecnologias impactam a vida social?, 126


Passeio 1: Isometria e congruência de triângulos, 128
• Check-in, 152
• Arredores e Bússola, 153
• Atmosfera: Crianças e adolescentes se expressam em arte, 154
• Lugar geométrico, 155
• Nuvens: Construção de polígono com software, 160
• Construção de polígonos regulares, 161
• Travessias: A construção do triângulo regular inscrito na circunferência, 163
• Levo na bagagem, 165
• Barcos e portos, 166
Passeio 3: Proporcionalidade e plano cartesiano, 168
• Check-in, 128
• Arredores e Bússola, 129
• Atmosfera: 5 exemplos do impacto das tecnologias na sociedade, 130
• Transformações geométricas, 131
• Transformações isométricas, 132
• Nuvens: Isometrias com software, 138
• Congruência de triângulos, 139
• Propriedades de quadriláteros e congruências de triângulos, 144
• Levo na bagagem, 149
• Barcos e portos, 150
Passeio 2: Construção geométrica e lugar geométrico, 152
• Check-in, 168
• Arredores e Bússola, 169
• Atmosfera: A comunicação e os modos de reagir, 170
• Grandeza, 171
• Razão: uma relação entre grandezas, 172
• Proporção, 175
• Travessias: Proporcionalidade: uma propriedade, 177

• Não proporcionalidade, 180
• Proporção e plano cartesiano, 182
• Levo na bagagem, 185
• Barcos e portos, 186
• Vistorias, 188
MASTER1305/ SHUTTERSTOCK SERHII BOBYK/ SHUTTERSTOCKTRAJETÓRIA 4
Quais são as dimensões do bem estar?, 192

Passeio 1: Superfície, volume e capacidade, 194
• Check-in, 218
• Arredores e Bússola, 219
• Atmosfera: Dicas para controlar a ansiedade, 220
• Tipos e adequação de gráficos, 221
• Nuvens: A organização das informações em tabela de dados brutos, 224
• Tabela de frequências a partir dos dados brutos, 225
• Dados agrupados em classes, 226
• Mediana, moda e média, 228
• Levo na bagagem, 231
• Barcos e portos, 232
Passeio 3: Pesquisa estatística e credibilidade da informação, 234
• Check-in, 194
• Arredores e Bússola, 195
• Atmosfera: Ginástica artística para crianças, 196

• Superfícies de retângulos e quadrados, 197
• Superfícies de paralelogramos e triângulos, 198
• Superfícies de losangos e trapézios, 202
• Superfície do círculo, 204
• A medida do conteúdo: o volume, 205
• O volume de blocos retangulares, 208
• Travessias: Relações entre unidades: cm³, dm³, m³, 210
• Capacidade e volume, 212
• Levo na bagagem, 215
• Barcos e portos, 216
Passeio 2: Gráficos e medidas de posição, 218
• Check-in, 234
• Arredores e Bússola, 235
• Atmosfera: Fake news, 236
• Notícias e credibilidade, 237
• Gestão da credibilidade, 238
• Etapas da pesquisa estatística, 241
• A problematização em Estatística, 241
• População e amostra, 242
• Planejamento da pesquisa, 247
• A realização, o relatório e a análise estatística, 249

• A tomada de decisão, 251
• Levo na bagagem, 253
• Barcos e portos, 254
• Vistorias, 256
Retornos, 261
Quadro de habilidades do 8o ano, 267 Suplemente sua aprendizagem, 270
Leituras para o aluno, 277 Referências bibliográficas, 278
MILAN ILIC PHOTOGRAPHER/ SHUTTERSTOCK1. Observe as estratégias de resolução de problemas envolvendo as operações com números racionais (positivos ou negativos).
a) 8 682,45 + 2 317,55 = 11 000,00
b) 11 000
1 463,38 = 9 536,62
c) O saldo final é –R$ 1 298,98
Ela gastou um total de R$ 11 000,00 + R$ 1 298,98 = R$ 12.298,98.
2. Observe as estratégias de resolução de problemas envolvendo operações com números racionais (naturais).
a) Considerando os 5 tipos de docinhos, temos:
1 500 ÷ 5 = 300
São 300 doces de cada tipo.
b) Se cada convidado come 2 docinhos de cada tipo e há 5 tipos de docinhos, cada convidado comerá 10 docinhos ao todo.
1 500 ÷ 10 = 150
São esperados 150 convidados.
c) Sendo 80 g de bolo por convidado:
80 150 = 12 000 Para converter gramas para quilogramas, dividimos por 1 000:
12 000 ÷ 1 000 = 12 Fabrício fará um bolo de 12 kg.
2. Para a determinação das potências, trabalhe estratégias de cálculo mental:
1. Luiza economizou R$ 8.682,45 na sua conta bancária e recebeu uma bonificação de R$ 2.317,55 da empresa em que trabalha. Com o dinheiro, ela vai realizar uma viagem em suas férias.
de avelã. Dividindo igualmente, qual é a quantia de doces de cada tipo?
b) Foi feita uma estimativa de que cada convidado come 2 docinhos de cada tipo. Quantos convidados há para esse casamento?
300 doces de cada tipo. 150 convidados.
c) Sabendo que cada fatia de bolo servida por pessoa pesa 80 gramas, quanto pesará o bolo que Fabrício irá fazer? 12 kg.
3. Calcule as potências:
a) –3 2 ⎛ ⎝ ⎞ ⎠ 3
b) 103 + 9 102 + 8 102 2 700
c) 26 64
d) 53 125
4. Resolva os problemas usando mmc ou mdc.
a) Qual é o valor total de que Luiza dispõe para a viagem? R$ 11.000,00.

b) Sabendo que a passagem de ida e volta custará R$ 1.463,38, quanto Luiza terá disponível para gastar durante seu trajeto? R$ 9.536,62.
–R$ 1.298,98. Ele gastou um total de R$ 12.298,98.
c) Já tendo gastado todo o dinheiro que havia economizado, Luiza ainda gastou R$ 1.298,98 com o limite especial. Qual é o saldo final da conta bancária de Luiza e quanto ela gastou em sua viagem?
2. Fabrício vende doces e bolos por encomenda. Ele recebeu uma encomenda de 1 500 docinhos e um bolo para uma festa de bodas.
a) Os doces encomendados foram: brigadeiro, beijinho, cajuzinho, bicho-de-pé e leite em pó com creme
Divisores naturais de 54: {1, 2, 3, 6, 9, 18, 27, 54}.
125
4. Avalie a compreensão e a distinção dos conceitos de múltiplo e divisor naturais.
a) Divisores naturais de 24:
{1, 2, 3, 4, 6, 8, 12, 24};
Divisores naturais de 30:
{1, 2, 3, 5, 6, 10, 15, 30};
Divisores naturais de 42: {1, 2, 3, 6, 7, 14, 21, 42};
mdc(24, 30, 42, 54) = 6 Serão dispostos 6 livros de cada gênero por prateleira.
a) Na campanha de doação de livros da escola, as obras foram separadas em 4 gêneros literários: literatura infantojuvenil, com 24 livros; poemas, com 30; divulgação científica, com 42; e biografias, com 54. Para organizar as prateleiras entre os gêneros, determine o maior divisor comum das quantidades de livros de cada gênero.
b) Carla e Fernando correm em uma pista partindo juntos de um mesmo ponto, no mesmo instante. Carla completa uma volta em 84 segundos, enquanto Fernando completa uma volta em 72 segundos. Qual será o primeiro instante em que Carla e Fernando passarão juntos novamente pelo ponto de partida?
b) O instante será 504 segundos depois do início da corrida porque:
M(84) = {0, 84, 168, 252, 336, 420, 504 }
M(72) = {0, 72, 144, 216, 288, 360, 432, 504 }
mmc(84, 72) = 504
6. Veja o anúncio que uma loja virtual fez:
Porcentagem dos brasileiros que praticaram esportes ou atividades físicas (2015)
Televisão 3D 42 polegadas
À vista R$ 1.800,00 ou em 6x de R$ 350,00
a) Qual é o valor do televisor se o pagamento for feito a prazo? Qual foi a taxa de juros para o pagamento a prazo?
R$ 2.100,00. Aproximadamente 16,7%.
Tabela de frequências
Porcentagem dos que praticaram esportes ou atividades físicas, por faixa etária (Brasil - 2015)
b) Um mês após esse anúncio, a televisão teve um desconto de 15% no seu valor à vista. Qual é o novo valor para essa televisão? Mantendo a quantidade de parcelas e a taxa de juros, calcule o valor da nova parcela para o pagamento a prazo.
R$ 1.530,00. O valor da nova parcela será R$ 297,50. 7. a)
7. Uma prova pré-vestibular foi aplicada com 50 adolescentes de 12 a 15 anos. Veja os dados coletados que representam as notas obtidas de 0 a 10.
Fonte: IBGE, Suplemento “Prática de Esporte e Atividade Física” da Pesquisa Nacional por Amostra de Domicílios (PNAD) 2015.
Gráfico de setores e de colunas.
a) Quais são os tipos de gráficos presentes nesse infográfico?
b) Qual é a faixa etária que tem um índice mais alto de praticantes de esportes ou atividades físicas? E a que menos pratica?
c) Escreva um texto sintetizando as informações presentes no infográfico.
Resposta pessoal.
a) Construa uma tabela de frequências com três colunas: Nota, Frequência absoluta e Frequência relativa.
b) Qual nota tem a maior frequência? Essa nota corresponde a que índice percentual do total de notas? 9; 26%.
c) Qual nota tem a menor frequência? Essa nota corresponde a que índice percentual do total de notas?
1, 2 e 4. 2% cada.
d) Construa um gráfico de setores que represente esses dados.
e) Calcule a média aritmética das notas.
5. b) De 15 a 17 anos é a faixa etária com maior índice de praticantes. De 60 anos ou mais é o menor índice.
5. Avalie a qualidade da leitura do infográfico pelos estudantes e orienteos na identificação dos tipos e na compreensão dos dados em cada gráfico de acordo o texto apresentado por eles.
6. Antes da resolução, esclareça, se necessário, os termos “à vista” e “a prazo”.
a) São 6 parcelas de R$ 350,00 cada:
R$2.100,00. Aproximadamente 16,7%.
b) Um desconto de 15% corresponde ao pagamen
c) 1, 2 e 4. 2% cada. d) Se possível, utilize uma planilha eletrônica para a construção do gráfico de setores.
Somandose os valores das notas,
esse valor pelo número de alunos, temos:
8.
a) A taxa de juros é prevista e divulgada (D).
b) Não é possível determinar com exatidão quantos frutos uma árvore produzirá por ano (A).
c) Não é possível determinar com exatidão o índice de precipitação de chuva (A).
d) O horário de entrada no serviço é, em geral, estabelecido; ele não se altera aleatoriamente (D).
9. Para a face com o número 8 só há uma possibilidade em 12.
1
12 ou, aproximadamente, 8,3%.
Para os números pares, as possibilidades das faces voltadas para cima são 2, 4, 6, 8, 10 ou 12, ou seja, 6 faces em 12.
6
12 ou 50%.
10.Considerando os ângulos suplementares em r:
3 x + 5 + 145 = 180
3x = 30
x = 10
Considerando os ângulos colaterais externos também suplementares:
y + 145 = 180 y = 35
x = 10o e y = 35o
11. O triângulo CDE é equilátero e y é a medida de um ângulo externo. Assim:
y = 60 + 60 = 120
Como x e y são suplementares:
x + y = 180
x + 120 = 180
x = 60
x = 60o e y = 120o
12.Sabemos que o diâmetro de uma circunferência é o dobro do raio e o comprimento da circunferência é o produto do dobro do raio, por π Então, o comprimento da circunferência é o produto do diâmetro por π: 30 π ≅ 94 2 cm
9. 1 12 ou aproximadamente 8,3% 6 12 ou 50%
8. Classifique as situações em determinística (D) ou aleatória (A).
a) Juros cobrados em um pagamento a prazo. D
b) Quantidade de frutos que uma árvore produzirá no ano. A
c) Precipitação de chuva à noite. A
d) Horário de entrar no serviço. D
9. Ao lançar um dado honesto de 12 faces, numeradas de 1 a 12, em um jogo de RPG, qual é a probabilidade de sair, na face voltada para cima, o número 8? E qual é a probabilidade de sair, na face voltada para cima, um número par?
10. As retas r e s são cortadas por uma transversal t. Determine os valores de x e de y
e y = 35o
11. Sabendo que o triângulo ABC é equilátero e os segmentos AB e DE são paralelos, determine os valores de x e de y.
60o e y = 120o
12. Calcule o comprimento de uma circunferência que tem diâmetro igual a 30 cm. Considere π ≅ 3,14 94,2 cm.
16 |
13.
I) Rotação, pois o hexágono foi rotacionado em torno de um ponto no sentido horário com ângulo de medida 90o
II) Há um deslocamento com sentido, direção e distância estabelecidos, logo, é uma simetria de translação.
III) A simetria ocorre em relação a uma reta e (eixo de simetria), logo, é uma simetria de reflexão ou axial.
13. Classifique as simetrias em reflexão, rotação ou translação.
I. Rotação.
II. Translação.
III. Reflexão.
14.Converse com os alunos a respeito das sentenças falsas argumentando matematicamente que:
Classifique as expressões algébricas como verdadeiras ou falsas.
I. 5 2 = 2,5
II. 83 ≠ 81
III. 103 > 8 102 + 9 102
IV. (6 + 8) 4 = (7 4) + 27
15. Para estes problemas, determine a equação que modela a situação e a sua solução.
a) Para pagar uma dívida, Adilson vai vender seus dois aparelhos de videogame pelo mesmo valor. Ele já tem R$ 850,00 e a dívida está em R$ 4.500,00. Qual deve ser o preço de cada videogame para ele obter exatamente o valor da sua dívida?
b) Bruno fez 16,5 litros de suco. Ele usou 3 litros de suco de limão e suco de abacaxi, laranja e maçã em mesma quantidade. Qual foi a quantidade de suco de abacaxi na receita?
16. Calcule a área da superfície de cada termo da sequência de polígonos, o volume de cada termo da sequência de blocos retangulares e determine as sequências numéricas correspondentes.
17. Sem riscar seu livro, observe e descubra quantos eixos de simetria há em cada “floco de neve”.
com esse padrão, a sequência é: (6, 12, 18, 24, 30...).
II. O volume do paralelepípedo é: V p = 2 2 4 = 16, logo, o 1o termo dessa sequência é 16.
O 2 o termo será o dobro, portanto, 32. O 3o termo é o triplo do primeiro, portanto, 48. Prosseguindo com esse padrão, a sequência é (16, 32, 48, 64, 80...).
17.
15.
a) Seja x o valor de venda de cada videogame A equação é 2 x + 850 = 4 500
2 x = 4 500 – 850
2x = 3 650 x = 1 825
Cada videogame deve ser vendido por R$ 1.825,00.
b) Seja x a quantidade de suco de abacaxi. A equa
ção é 3 x + 3 = 16,5
3 x = 16,5 – 3
3x = 13,5
x = 4,5
A quantidade de suco foi de 4,5 L.
16.
I A área do tria ^ ngulo é: At = 4 3 2 = 12 2 = 6, logo, o 1o termo dessa sequência é igual a 6. O 2o termo será o dobro, portanto, 12. O 3o termo é o triplo do primeiro, portanto, 18. Prosseguindo
O quadro a seguir apresenta o código alfanumérico das habilidades do 7o ano exploradas nessa proposta de Avaliação Diagnóstica
17
TRAJETÓRIA 1
PANORAMA DA TRAJETÓRIA
Competências gerais: 1, 2. Competências específicas: 1, 2, 3.
Habilidades de Matemática: EF08MA01, EF08MA02, EF08MA03, EF08MA04, EF08MA05, EF08MA10, EF08MA11, EF08MA22
Habilidades de outras disciplinas:
Ciências: EF08CI07, EF08CI12, EF08CI15
Temas Contemporâneos
Transversais: Ciência e Tecnologia

Educação Ambiental
Sugestão de atividade
Esta Trajetória tem ligação estreita com a disciplina de Ciências. Há nela diversas oportunidades para incentivar os estudantes a uma atitude de investigação, buscando ampliar a visão de mundo deles para além da “escala mediana” e explorar outros mundos e fenômenos envolvidos nas dimensões macroscópicas ou microscópicas.
Inicie com uma roda de conversa a respeito da pergunta motivadora desta Trajetória: Quais são os extremos da natureza?
A abrangência dessa pergunta é proposital. Ela foi formulada assim para instigar a curiosidade e incentivar os estudantes a buscar estratégias de investigação. Essas estratégias vão, aos poucos, delineando os propósitos didáticos envolvidos, como: valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital, reconhecer que a Matemática é uma ciência humana e é uma ciência viva, entre outros.
Aproveite para explorar com questionamentos como: o que vocês imaginam que sejam os extremos da natureza? Quais fenômenos podemos observar a olho nu? Para além do que enxergamos, será que ocorrem fenômenos parecidos ou muito diferentes daqueles da

natureza que podemos ver a olho nu? Como será, por exemplo, o “mundo ínfimo” das moléculas? E oque acontece lá? E no “mundo gigantesco“ do espaço sideral, por exemplo, como será? Que coisas acontecem lá? Como será que os cientistas fazem para descobrir os fenômenos, as dimensões e as relações entre elementos como as moléculas no mundo do “muito pequeno” ou os corpos celestes no mundo do “muito grande”?
Essas questões iniciais têm valor primordial para despertar nos estudantes curiosidades e interesse pelos processos variados de descobertas.
QUAIS SÃO OS EXTREMOS DA NATUREZA?
• Como descrever o “muito pequeno” e o “muito grande” na natureza?
• Os fenômenos da natureza são aleatórios ou determinísticos?

• Quais fenômenos da natureza são periódicos?
De modo sucinto, vamos apresentar uma possibilidade de metodologia de investigação dividida em cinco etapas. É importante lembrar que essas etapas não são excludentes e que suas ações não se encerram em si mesmas. Elas são abertas a reavaliações, ajustes, desafios e, por vezes, até à reformulação da pergunta motivadora.
Convide professores de outras disciplinas para fazer parcerias e, assim, os estudantes podem ter experiências em Ciências, Física, Química, Astronomia etc.
Gotas d’água em uma planta: pequenos detalhes, às vezes não perceptíveis a olho nu. Imagem capturada por lentes que proporcionam um desempenho óptico perfeito na focagem de objetos muito próximos.
LUPAS E LUNETAS Respostas pessoais.
Reflita sobre as questões propostas e considere-as para criar outras perguntas de sua própria autoria. Publique suas perguntas no mural da sala e aprecie as perguntas dos colegas.
CONTEÚDOS DA TRAJETÓRIA
Passeio 1:
Números racionais, potenciação e radiciação
• Porcentagens
• Acréscimos e decréscimos usando porcentagem


• Dízimas periódicas e fração geratriz
• Potenciação e radiciação
• Notação científica
Passeio 2:
Contagem e probabilidade
• Princípio multiplicativo
• Experimentos aleatórios
• Probabilidade e espaço amostral
Passeio 3:
Sequências
• Matemática e fenômenos periódicos
• Sequências recursivas
• Sequências não recursivas
• Sequências e fluxogramas
LUPAS E LUNETAS
Neste momento da Trajetória, procure motivar os estudantes em torno das questões norteadoras: certifique-se de que compreenderam as questões e se apropriaram delas, além de agregar novas questões ao percurso que se inicia. Você pode perguntar-lhes o que entendem por “muito grande” e “muito pequeno” no contexto da natureza e do Universo.
1. Problematização e levantamento de hipóteses
É necessário que após as reflexões iniciais sobre a temática dos fenômenos do “muito pequeno” ou do “muito grande”, haja um acordo coletivo a respeito de qual será a pergunta motivadora, que pode ser a que já está colocada na abertura da Trajetória ou pode ser formulada outra, em conjunto, desde que seja mantida a proposta.
Auxilie os estudantes na clareza da formulação da questão motivadora e nas perguntas que representam desdobramentos dela.
2. Atividades investigativas
Para que os estudantes possam se lançar a formulações de variadas hipóteses sobre as perguntas que motivarão as investigações, auxilie-os nas consultas de fontes diversas, levando-os a avaliar se as fontes de consulta são confiáveis, se requerem mais aprofundamento e se será necessário buscar conhecimento em alguma instituição (universidade, por exemplo) ou convidar algum especialista. Texto continua na página seguinte.
3. Conclusões
Reforce com os estudantes que as respostas às perguntas devem vir de conclusões a que eles chegarem por meios das diversas informações coletadas. Auxilie-os a reunir as diversas informações e monitore o modo como eles elaboram as relações entre duas ou mais informações para gerar uma nova, ou seja, uma conclusão. Incentive-os a apresentar em grupos os resultados.
4. Sistematização e registros
Utilize os registros individuais ou feitos em grupo pelos próprios estudantes, que podem ser por escrito, em fotos, em áudios ou por meio de filmagens. A partir de então, auxilie os estudantes a, coletivamente, listar uma síntese dos fatos essenciais que descobriram, das consequências desses fatos e das possíveis respostas. É possível também formular novas questões, pois pode ser que alguma pergunta tenha sido respondida apenas parcialmente.
Não deixe de realizar seu próprio registro, especialmente da evolução da turma nesse processo de descobertas.
5. Divulgação

Combine com a turma a melhor forma de divulgar os resultados para a escola toda ou no bairro. Auxilie-os a respeito das melhores formas de estruturar as informações e as maneiras de comunicá-las. Se julgar possível, faça parcerias com professores de Língua Portuguesa, Arte, Informática, Educação Física ou outros professores dispostos a contribuir com a comunicação, apresentação e divulgação dos resultados.
CHECK-IN
Após a pesquisa dos estudantes, façam uma curadoria das fotos e dos textos pesquisados e exponham no mural da sala, presencial ou virtual. Destaquem os números encontrados relacionados ao mundo do “muito grande” e do “muito pequeno”.
Dados sobre dinossauros
PASSEIO 1
NÚMEROS RACIONAIS, POTENCIAÇÃO E RADICIAÇÃO
COMO DESCREVER O “MUITO PEQUENO” E O “MUITO GRANDE” NA NATUREZA?
CHECK-IN
a) Incentive os alunos ao levantamento de hipóteses. A imagem é a ampliação extrema de uma foto do olho de uma mosca-de-cavalo. Cada unidade é denominada omatídeo.
Em duplas ou trios, observem a imagem e respondam às questões:
a) Sabendo que a figura representa uma ampliação em 50 vezes de algo da natureza, o que você imagina que é?
b) Há fenômenos na natureza que são macroscópicos e outros que são microscópicos. Cite exemplos desses dois tipos de fenômenos. Você pode fazer uma rápida pesquisa.

Possíveis respostas: o movimento das partículas de um corpo quando aquecido; o movimento dos corpos celestes.
20 | TRAJETÓRIA 1 NÃO ESCREVA NO SEU LIVRO.
(medidas de comprimento, tempo em que viveram etc.), insetos (medidas de massa, por exemplo), informações do mundo marinho ou do espaço sideral podem ser de interesse dos estudantes dessa faixa etária.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Resolver e elaborar problemas, envolvendo cálculo de porcentagens.
• Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz de uma dízima periódica.
• Efetuar cálculos com potências de expoentes inteiros.
• Utilizar a representação de números em notação científica para escrever números muito grandes ou muito pequenos.
• Resolver e elaborar problemas usando a relação entre potenciação e radiciação para representar uma raiz como potência de expoente fracionário.
• Comparar diferentes processos reprodutivos de animais marinhos em relação aos mecanismos adaptativos e evolutivos.
ATMOSFERA
Atividade 1
Com base na leitura do texto, conversem sobre as medidas “muito grandes” ou “muito pequenas”, além das medidas relacionadas à distância entre as estrelas e planetas. Comente sobre números que representam a quantidade de moléculas, grãos de areia, velocidade da luz etc. e também sobre os números que podem expressar o tamanho de um átomo, uma bactéria etc. Os instrumentos adequados a grandes e pequenos valores podem incluir telescópios, lupas, lunetas, microscópios etc. Essa discussão pode ser relacionada ao Tema Contemporâneo Transversal (TCT) Ciência e Tecnologia
Atividade 2
Os estudantes podem apresentar exemplos relacionados à ideia da imensidão do Universo ou à ideia de células, vírus ou bactérias serem muito pequenos.
Atividade 3
Os instrumentos para ver objetos muito grandes ou muito pequenos são, por exemplo, o telescópio e o microscópio.
LUPAS E LUNETAS
Esta pesquisa relaciona-se com o estudo dos processos reprodutivos de plantas e animais. Proponha que confeccionem materiais diversos com o resultado de sua pesquisa e divulguem na sala de aula. Exibir a produção feita em sala de aula é uma etapa importante da aprendizagem. Nesse tipo de atividade, o trabalho dos estudantes será valorizado, o que é importante para a construção da identidade de cada um. Se julgar necessário, proponha, em discussão com a turma, se a exposição ficará restrita à própria sala ou se será em um local que permitirá a apreciação de toda a comunidade escolar.
ATMOSFERA
Infinitamente grande e muito pequeno
As estrelas, enormes e distantes, quando vistas da Terra, aparentam ser minúsculas. As fibras de um tecido, vistas de muito perto, aparentam ter estruturas grandes.
Muito provavelmente você já se perguntou, à noite olhando para o céu, quantas estrelas existem. Você já imaginou a distância que elas estão? Sabemos que existem o sol, os planetas, as estrelas, as galáxias, todos bem distantes de nós. A contemplação do céu desperta muitas questões. Ficamos imaginando qual a fronteira do “infinitamente grande”. Até onde podemos imaginar? Até onde o mundo do “muito longe” vai?

O mais interessante é que tem outra direção que nos leva a outro mundo igualmente fascinante: o do “muito pequeno”. Imagine que você pudesse mergulhar numa gota d’agua sobre uma folha e fosse diminuindo cada vez mais de tamanho... Você
veria um mundo igualmente interessante, repleto de bactérias, vírus, moléculas, átomos, cada um deles menor do que o outro e numa sucessão que parece não ter fim.
Embora os nossos olhos sejam ferramentas excelentes, não podemos obter detalhes dos dois mundos que discutimos apenas com os olhos. Precisamos de aparelhos que aumentem o poder da nossa visão. Os cientistas conseguem ver o “muito longe” com os telescópios e o “muito pequeno” com os microscópios. Além desses dois extremos, temos tudo o que nos rodeia e o que nos é mais familiar: carros, computadores, luz elétrica, geladeira...

RIO DE JANEIRO (estado). Nova EJA: Ciências da Natureza e suas tecnologias. Fundação CECIERJ. Disponível em: http://projetoseeduc.cecierj.edu.br/eja/recurso-multimidia-professor/fisica/index.html. Acesso em: 11 ago. 2022.
ATIVIDADES
Respostas pessoais.
1. O texto convida o leitor a imaginar “até onde o mundo do muito longe vai”. Compartilhe com os colegas o que você imagina sobre isso.
2. Você já havia refletido sobre esses mundos do “muito grande” e do “muito pequeno”? Cite exemplos de coisas que considera muito grandes e muito pequenas.
3. O texto cita instrumentos que permitem contemplar os mundos do “muito pequeno e do muito grande”. Que instrumentos são esses? Você conhece outros?
#Muito grande, muito pequeno
O grupo dos mamíferos inclui animais com características bastante variadas. As fotografias a seguir apresentam três mamíferos: cachorro, golfinho e morcego. Observe como eles são diferentes entre si.

Encontro com outras disciplinas
(EF08CI07) Comparar diferentes processos reprodutivos em plantas e animais em relação aos mecanismos adaptativos e evolutivos.
gestação e se a espécie está ameaçada de extinção. Reforce a importância desse tipo de conhecimento para a preservação do meio e do planeta Terra como um todo, tratando assim o TCT Educação Ambiental
Muito grande
A baleia-azul é o maior mamífero do planeta, atingindo o comprimento de 33 m e uma massa corporal de 130 toneladas.
Lembre-se de registrar os diversos momentos da visitação e incentive-os a tirar fotos no decorrer do estudo para ilustrar os trabalhos. No retorno da visita, os estudantes poderão confeccionar páginas com as informações descobertas sobre cada animal organizando as informações em um blog ou uma rede social. Organize algumas perguntas em parceria com o professor de Ciências sobre os resultados dessa pesquisa, como: qual animal tem o menor e qual tem o maior período gestacional?
Desenvolvendo assim a habilidade EF08CI07
Comparação entre uma baleia-azul e um humano.
LUPAS E LUNETAS Respostas pessoais.
Junte-se a um colega e pesquisem sobre as baleias e os golfinhos. Identifique as características adaptativas que essas espécies de mamíferos aquáticos desenvolveram para sobreviver e se reproduzir na água.

Quais são as espécies que estão ameaçadas de extinção? Quais as causas desse risco e quais ações estão sendo realizadas para reverter esses casos?
Para finalizar esse trabalho, exponha no mural (presencial ou virtual) da escola os textos e as fotos dos estudantes das diversas etapas desse trabalho.
CONVÍVIO E BEM-ESTAR SOCIAL

A execução desta atividade tem a intenção de desenvolver o convívio social na comunidade escolar por meio da interação entre os alunos e professores em espaços não formais.
Planeje com antecedência a execução dessa atividade, para mitigar eventuais riscos garantindo a integridade física de todos.
Verifique com a gestão escolar a possibilidade de realizarem um estudo do meio em um aquário ou zoológico da região. Sendo possível,
converse com o professor de Ciências para organizarem uma visita orientada. Como sugestão, organize os estudantes em grupos: cada grupo receberá uma lista com alguns animais que deverão observar e pesquisar informações sobre eles. Algumas informações estarão no local da visitação, porém podem consultar outras fontes para complementar a pesquisa. Aponte as informações que são importantes apresentarem, como nome popular, nome científico, hábitat, expectativa de vida, altura, massa, período de
 O cachorro é um mamífero que se locomove sobre o solo, o golfinho nada e o morcego voa.
O cachorro é um mamífero que se locomove sobre o solo, o golfinho nada e o morcego voa.
LUPAS E LUNETAS
Proponha que reproduzam a imagem da baleia-azul e do humano no caderno. Os mamíferos musaranho-pigmeu e o morcego-nariz-de-porco-de-kitti podem ser representados por um ponto. Proponha que reflitam e investiguem sobre qual a melhor forma de representar a comparação do muito pequeno com o muito grande. Sugira a possibilidade utilizar a matemática para isso, representando as medidas por meio dos números, desenvolvendo, assim, o espírito de investigação e recorrendo à matemática para compreender e atuar no mundo.
Atividade 4
a) A baleia-azul tem em torno de 130 toneladas. Para comparar a baleia com a massa corporal, é preciso dividir a massa de um pela do outro. Essa atividade pode ter diversas respostas possíveis, como: para um estudante de 40 kg, a massa corporal da baleia corresponde à de 3 250 pessoas, pois 130 000 kg ÷ 40 kg = 3 250 Explique aos estudantes que há diferentes unidades de medida – como toneladas, quilogramas e gramas –, e que, para comparar as massas, é preciso considerar a mesma unidade de medida.
b) O morcego-nariz-de-porco pesa 2 g. A massa corporal de uma pessoa de 50 kg, por exemplo, equivale a 25 000 morcegos, pois 50 000 ÷ 2 = 25 000

Atividade 5
a) A massa corporal da baleia corresponde a 2 600 pessoas, pois 130 toneladas correspondem a 130 000 kg. Com isso, 130 000 kg ÷ 50 kg = 2 600 pessoas pessoas.
b) A massa corporal de uma pessoa de 50 kg equivale a 25 000 morcegos, pois 50 kg equivalem a 50 000 g e 50 000 g ÷ 2 g = 25 000
c) A baleia-azul pesa 130 toneladas, e o morcego, 2 g.
Muito pequeno
Se a baleia-azul é indiscutivelmente o maior mamífero do planeta, a disputa pelo título de menor mamífero é bastante acirrada. O musaranho-pigmeu é considerado um dos menores mamíferos, com aproximadamente 5 cm de comprimento (sendo que aproximadamente metade desse comprimento corresponde à sua cauda!) e massa corporal entre 1 e 3 gramas. Outro mamífero minúsculo é o morcego nariz-de-porco-de-kitti, com cerca de 3 cm de envergadura e massa corporal de aproximadamente 2 g.
LUPAS E LUNETAS Respostas pessoais.
Organizem-se em duplas ou trios. Considerando as medidas aproximadas de comprimento ou envergadura do musaranho-pigmeu e do morcego nariz-de-porco-de-kitti, como vocês representariam, no caderno, o tamanho desses animais em comparação com a baleia-azul?
ATIVIDADES 5. c) 65 000 000 morcegos nariz-de-porco-de-kitti.

4. Em duplas ou trios, façam estas estimativas e, em seguida, compartilhem com os demais colegas (lembrando que 1 tonelada equivale a 1 000 kg e que 1 kg equivale a 1 000 g).
a) Quantas pessoas do seu tamanho equivalem a uma baleia-azul em termos de massa corporal?
b) Quantos morcegos nariz-de-porco-de-kitti equivalem a uma pessoa do seu tamanho em termos de massa corporal?
4. a) Sugestão de resposta: por volta de 3 000 pessoas. Sugestão de resposta: 25 000 morcegos.
5. Considere uma pessoa com massa corporal de 50 kg. Em termos de massa corporal, responda:
a) Quantas pessoas como essa equivalem a uma baleia-azul? 2 600 pessoas.
b) Quantos morcegos nariz-de-porco-de-kitti equivalem a essa pessoa?
25 000 morcegos nariz-de-porco-de-kitti.
c) Quantos morcegos nariz-de-porco-de-kitti equivalem a uma baleia-azul?
Para converter toneladas em gramas, precisamos multiplicar 130 por 1 000 000. Assim, 130 000 000 g ÷ 2 g = 65 000 000
Musaranho-pigmeu (Suncus etruscus). Morcego nariz-de-porco-de-kitti (Craseonycteris thonglongyai). 24 | TRAJETÓRIA 1 NÃO ESCREVA NO SEU LIVRO. ANTONIO PETRONE/SHUTTERSTOCK CORINA DANIELA OBERTAS/SHUTTERSTOCK#Porcentagens
O Sistema Solar corresponde ao conjunto de diversos corpos celestes que orbitam o Sol. Além dos oito planetas (Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano, Netuno), outros componentes fazem parte do Sistema Solar, como o planeta anão Plutão, as diversas luas dos planetas e os asteroides.

Habilidade
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
Converse com os estudantes sobre momentos em que usaram porcentagem para que verbalizem sobre seu conhecimento prévio. Apresente as ideias de proporcionalidade e de razão para que compreendam que podem escrever uma porcentagem como uma razão. Apresente alguns exemplos como a porcentagem de:
• meninos e de meninas na turma;
• colegas que têm animais de estimação etc.
Sistema solar representado em cores artificiais. As distâncias entre o Sol e cada planeta não estão representadas em proporção. As linhas curvas representam as órbitas dos planetas ao redor do Sol. Medidas
Eles podem calcular essas porcentagens com o uso de uma calculadora.
Fonte: A escala do Universo. Instituto de Física da Universidade Federal do Rio Grande do Sul. Disponível em: www.if.ufrgs.br/oei/cgu/sca/sca.htm. Acesso em: 11 ago. 2022.
Habilidade (EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
LUPAS E LUNETAS
Essa comparação sobre o diâmetro da Lua e da Terra acontece após os estudantes observarem o cálculo da porcentagem e a imagem que representa que são necessários 3,6 vezes o diâmetro da Lua para obter a medida do diâmetro da Terra. Espera-se que os estudantes apresentem uma destas respostas: o cálculo da porcentagem ou a análise da imagem com a informação das medidas, expressando sua compreensão sobre “partes que superam o todo” (frações impróprias ou porcentagens maiores do que 100%).

Índice porcentual e relação entre duas grandezas
Vamos investigar a relação entre os diâmetros (em km) da Terra e da Lua? Para saber “quantas vezes o diâmetro da Lua cabe no diâmetro da Terra”, podemos dividir o diâmetro da Terra pelo diâmetro da Lua:
Visualmente:
12 742 ÷ 3 475 ≅ 3,6
Assim, podemos dizer que:
• o diâmetro da Terra é aproximadamente 3,6 vezes maior que o diâmetro da Lua;
• o diâmetro da Lua é aproximadamente 3,6 vezes menor que o diâmetro da Terra.
Considerando a razão entre o diâmetro da Terra e o diâmetro da Lua, ou seja:
12 742
3 475 ≅ 3,6
Podemos escrever que: 3,6
Ou seja, podemos dizer que o diâmetro da Terra é, aproximadamente, 360% do diâmetro da Lua.
Se considerarmos a razão entre o diâmetro da Lua e o diâmetro da Terra, ou seja:
3 475 12 742 ≅ 0,27 = 27%
Podemos dizer que o diâmetro da Lua é, aproximadamente, 27% do diâmetro da Terra.
LUPAS E LUNETAS Resposta pessoal.
É comum interpretar porcentagens como “partes em relação a uma centena”. Por exemplo, 27% pode ser interpretado como 27 partes de um total de 100 partes.
No caso da razão entre os diâmetros da Lua e da Terra, imaginando que a Terra tivesse um diâmetro de 100 unidades de comprimento, então, o da Lua seria 27 unidades de comprimento.
E no caso da afirmação “o diâmetro da Terra é, aproximadamente, 360% do diâmetro da Lua”? Explique como interpretar esse valor em porcentagem. Compartilhe com os colegas.
Acréscimos e decréscimos usando porcentagens
No ano de 2006, Plutão deixou de ser classificado como planeta e passou para o status de planeta anão. Dentre outros aspectos, está o seu tamanho em relação aos outros planetas do Sistema Solar. Para se ter uma ideia, Plutão possui diâmetro menor que o da própria Lua terrestre.
Considerando a razão entre o diâmetro de Plutão e o diâmetro da Lua, temos que:
2 274 3 475 ≅ 0,65 = 65%
Nesse caso, podemos dizer que o diâmetro de Plutão corresponde a 65% do diâmetro da Lua. Dos oito planetas do Sistema Solar, Mercúrio é o que apresenta o menor diâmetro: 4 880 km. A diferença entre seu diâmetro e o diâmetro de Plutão, em km, pode ser expressa por:

4 880 – 2 274 = 2 606 km
Em outras palavras, o diâmetro de Plutão precisaria de um acréscimo de 2 606 km para chegar ao diâmetro de Mercúrio. Calculando a razão entre esse valor e o diâmetro de Plutão, temos que:
2 606
2 274 ≅ 1,146 = 114,6%
Ou seja, o diâmetro de Plutão precisaria ser acrescido de aproximadamente 114,6% de seu próprio valor para atingir o diâmetro de Mercúrio, o menor planeta do Sistema Solar:
! + 114,6% de 2 274 acréscimo de # $ & ≅ 4 880 diametro de Mercúrio
! Note que: 2 274 + 114,6% de 2 274 = 2 274 + 1,146 2 274 = propriedade distr butiva
! (1 + 1,146) 2 274
Agora, vamos comparar: quanto precisaria ser reduzido o diâmetro da Terra para que chegasse à medida do diâmetro de Plutão? Calculando a diferença entre os diâmetros da Terra e de Plutão, em km:
12 742 – 2 274 = 10 468
10 468 12 742 ≅ 0,8215 = 82,15%
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
Explore a situação apresentada no livro sobre os planetas usando as informações “Medidas do muito grande”, que apresenta o diâmetro (em km) de corpos celestes. Permita que usem calculadora de modo que os estudantes analisem a diferença entre o diâmetro da Terra e o de Marte, por exemplo.
• Qual é a razão entre o diâmetro da Terra e o de Marte?
• E a razão entre Marte e Terra?
• Em qual situação usamos um acréscimo para comparar esses valores?
• E um decréscimo?
27 |
Nuvens
O símbolo de “porcentagem” das calculadoras simples (comerciais ou não científicas/ financeiras) possibilita calcular acréscimos ou decréscimos diretamente. Por exemplo, para calcular uma redução em 10% de 300 reais, tecle “3 0 0 – 1 0 % = ” e o resultado “270” será apresentado.
Avalie a possibilidade de realizar os cálculos dessa seção com os estudantes também em uma planilha eletrônica.
Atividades 6 a 11
As orientações de uso da calculadora para o cálculo de porcentagem estão na seção Nuvens. Proponha que, usando uma calculadora, os estudantes resolvam os exercícios escolhendo se preferem multiplicar pelo decimal ou pela fração e justificando essa escolha. Também questione se optaram por usar o símbolo “%” nos cálculos de acréscimo ou decréscimo.
Na resolução das situações-problema, façam a leitura coletiva e conversem sobre o enunciado para que perguntem o significado de palavras desconhecidas. Retome com eles que a resolução de problemas, segundo Polya (1978), tem quatro etapas: compreensão do enunciado, elaboração da estratégia, execução da estratégia e verificação do resultado. As estratégias de resolução de problemas podem incluir a organização das informações em listas ou quadros.
Atividade 6
O estudante pode realizar o cálculo da porcentagem usando diferentes estratégias. Uma delas pode ser pela multiplicação da porcentagem na forma decimal.
a) 0,2 450 = 90
b) 0,32 3 500 = 1 120
28 | MANUAL DO PROFESSOR
Cálculo de porcentagem na calculadora
Calculadora virtual simples em smartphone. Calculadora convencional simples.

O uso de calculadoras para resolver problemas envolvendo porcentagens pode ser bastante útil. Porém, isso não significa que a resolução é automática. Pelo contrário, precisamos mobilizar algumas estratégias e até um pouco de cálculo mental!

• Por exemplo, como obter 25% de 351 na calculadora? Uma possibilidade é inserir:
Porém, sabendo que 25% 25% = 25 100 = 0,25 0,25, podemos escrever diretamente:
• Considerando o valor 177, como calcular um acréscimo de 15% sobre esse valor? Novamente, podemos realizar na calculadora cada um dos passos:
I. Calcular 15% de 177.
II. Adicionar o resultado a 177. Porém, sabendo que um acréscimo de 15% sobre 177 significa:
Na calculadora, podemos escrever diretamente:
• Considerando o mesmo valor 177, como calcular um desconto de 15% sobre esse valor?
Novamente, podemos realizar na calculadora cada um dos passos:
I. Calcular 15% de 177.
II. Subtrair o resultado de 177. Porém, sabendo que um desconto de 15% sobre 177 significa:
Nesse momento, comente que, ao se reduzir 15%, restam 85%.
TRAJETÓRIA
c) 0,78 42 100 = 32 838
d) 1,12 15 000 = 16 800
Atividade 7
a) É possível multiplicar pela porcentagem na forma decimal, 0,34 ⋅ 205 = 69,7
b) O acréscimo de 8% corresponde a 108% do valor inicial (cálculo que pode ser realizado mentalmente). Multiplicando pela porcentagem na forma decimal, 1,08 436 = 470,88
c) O desconto de 12% equivale a 88% do valor, pois 100% – 12% = 88% Com a multiplicação
pela porcentagem na forma decimal, temos: 0,88 731 = 643,28
Atividade 8
a) Segundo o enunciado, 22% de 4 500 habitantes foram internados: 0,22 4500=990 habitantes.
ATIVIDADES
6. Determine:
a) 20% de 450 90
b) 32% de 3 500 1 120
c) 78% de 42 100 32 838
d) 112% de 15 000 16 800
7. Digitando apenas uma operação na calculadora, descreva uma sequência de teclas para calcular:
a) 34% de 205.
b) Um acréscimo de 8% sobre 436.
c) Um desconto de 12% sobre 731.
8. Um município de 4 500 habitantes foi afetado por um surto de cólera, em que 22% dos habitantes necessitaram de internação médica. Desses, 10% tiveram que se internar em UTI.
a) Quantos habitantes foram internados? 990 habitantes.
b) Quantos foram para a UTI? 99 habitantes.
Habilidade (EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
diferenc , a populac , a ~ o do Uruguai = 3 700 00 3 400 00 diferenc , a populac , ao do Uruguai = 3 700 000 3 400 000 = 1,088 = 108,8%
d) A diferença entre o número de habitantes do Brasil e da Argentina é
9. Atualmente, as populações aproximadas dos membros ativos do Mercosul (Mercado Comum do Sul) são:
• Argentina: 46 000 000 de habitantes
• Brasil: 212 000 000 de habitantes
• Paraguai: 7 100 000 de habitantes
• Uruguai: 3 400 000 de habitantes
a) A população do Brasil corresponde percentualmente a quanto da população do Uruguai? 6 235,3%.
b) A população paraguaia equivale a qual porcentagem da população argentina? 15,43%.
c) Qual deve ser o acréscimo percentual da população do Uruguai para se igualar à população paraguaia? 108,8%.
que tenham o mesmo número de habitantes, o Brasil precisa reduzir sua população em 166 000 000 habitantes, ou seja: diferenc , a populac , ao do Brasil = 166 000 00 212 000 00 diferenc , a populac , ao do Brasil = 166 000 000 212 000 000 = 0,7830 = 78,30%
d) Qual deve ser o decréscimo percentual da população brasileira para atingir a população da Argentina? 78,30%.
10. Em uma floresta, vivem leopardos e lebres. Quando há o aumento da população de leopardos, há uma consequente diminuição na população de lebres, pois essas são presas dos leopardos. Em determinado período observado, a população de leopardos era de 1 000 e passou para 1 200. No mesmo período, as lebres eram 3 000 e passaram para 2 100. Determine o percentual de aumento e de diminuição que cada espécie sofreu. População de leopardos: aumento de 20%; população de lebres: diminuição de 30%.

Atividade 10
Considerando que são 200 leopardos a mais (1 200 – 1 000 = 200), o aumento percentual foi de:
200 1 000 = 0,20 = 20%
As lebres sofreram uma redução de 900 animais, (3 000 – 2 100 = 900) O decréscimo foi de: 900 3 000 = 0,30 = 30%

11. Em duplas, criem situações-problema envolvendo porcentagens. Troquem-nas entre si. Conversem sobre as estratégias de resolução e compartilhem as situações com os demais colegas da turma. Respostas pessoais.
Atividade 9
a) Na relação entre a população do Brasil e a do Uruguai, a “parte” observada é a população do Brasil, enquanto o total é do Uruguai. Desse modo, temos:
do Paraguai, enquanto o total é da Argentina. Desse modo, temos: populac , ao do Paraguai populac , a ~ o da Argentina = 7 100 000 46 000 000 = 0,1543 = 15,43%
populac , ao do Paraguai populac , ao da Argentina = 7 100 000 46 000 000 = 0,1543 = 15,43%
populac , ao do Brasil populac , a ~ o do Uruguai = 212 000 000 3 400 000 = 62,353 = 6 235,3% opulac , ao do Brasil pulac , ao do Uruguai = 212 000 000 3 400 000 = 62,353 = 6 235,3%
b) Na relação entre a população do Paraguai e da Argentina, a “parte” observada é a população
c) A diferença entre as populações do Paraguai e do Uruguai é 7 100 000 – 3 400 000 = 3 700 000 7 100 000 – 3 400 000 = 3 700 000 Para que tenham o mesmo número de habitantes, 7 100 000, o Uruguai precisa de mais 3 700 000 habitantes, ou seja:
Veja a resolução comentada da atividade 11 na página seguinte.
Habilidade
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Atividade 11
Os estudantes apresentarão diversos problemas que abordam porcentagem; como inspiração leia este enunciado: Marcos decidiu fazer seu testamento para deixar sua fortuna R$ 12.000.000,00 dividida entre sua esposa, dois filhos e quatro netos. Para sua esposa quer deixar R$ 4.000.000,00; para cada um de seus filhos, R$ 3.000.000,00; e o restante deverá ser dividido igualmente entre seus netos. Qual porcentagem da fortuna cada um receberá?
Resposta:
• Esposa
4 000 000
12 000 000 = 33,3%
• Filhos
3 000 000
12 000 000 = 0,25 = 25% (cada filho)
= 25% (cada filho) Com o pagamento do 4 milhões para a esposa e 6 milhões para os filhos, pois cada um receberá 3 milhões, o valor que será dividido entre os netos, em milhões, corresponde a 12 – (4 + 6) = 12 – 10 = 2 Por serem quatro netos, cada um receberá 500 mil.
• Netos
500 000
12 000 000 = 4,16% (cada neto)
LUPAS E LUNETAS
Nesta situação, não foi adequado o uso de fração. Os estudantes podem argumentar que esperavam como resposta um número natural. Algumas respostas possíveis são:
• “O inverno chegou! Aproximadamente três dias...” ou
• “O inverno chegou! Cerca de dois dias...”.
Reforce a importância da matemática na apresentação
#Dízimas periódicas
“O inverno chegou! Um terço dos dias desta semana terá temperaturas extremamente baixas!”
Ao ler essa manchete, uma pessoa quis saber exatamente quantos dias registrariam temperaturas “extremamente baixas”. Como a
LUPAS E LUNETAS Respostas pessoais.
semana possui 7 dias, ela decidiu calcular 1 3 de 7, ou seja, 7 3 . Utilizando o algoritmo da divisão:
Você considera o resultado obtido adequado à informação que a manchete gostaria de transmitir ou à expectativa da pessoa que efetuou o cálculo? Por quê? Como você reelaboraria essa manchete de modo a torná-la mais adequada à informação que se deseja transmitir?
Uma pessoa notou que, ao continuar dividindo o resto, os algarismos das ordens decimais eram sempre iguais e o processo se repetiria indefinidamente.
Números racionais como 2,333... são representados por dízimas periódicas.
Chamamos de dízima periódica a representação decimal de um número racional com uma quantidade infinita de casas decimais de modo que sempre há uma parte que se repete, que é chamada de período ou parte periódica
Podemos representar a dízima periódica com “...” após repetir os algarismos do período ou utilizar uma barra sobre o algarismo que se repete: 2,3
LUPAS E LUNETAS Respostas pessoais.
Como as dízimas periódicas podem ser escritas em forma de fração ou razão entre inteiros, podemos afirmar que são representações de números racionais. Converse com seus colegas sobre essa afirmação. Em grupo, utilizem uma calculadora para investigar outras frações cujo quociente entre numerador e denominador seja uma dízima periódica.
de informações presentes no cotidiano e como ao apresentar dados numéricos a informação fica mais precisa, dando mais credibilidade às informações que são disseminadas para a população em geral.
LUPAS E LUNETAS
explorem frações com, por exemplo, os denominadores 9, 99 ou 999.
Exemplos: 5 9 = 0,5, 12 99 = 0,12 ou 23 999 = 0,0230 5 9 = 0,5, 12 99 = 0,12 ou 23 999 = 0,0230
O uso da calculadora possibilita a exploração dos números racionais. Deixe-os fazer tentativas livremente e, depois de algum tempo, sugira que
Dízimas periódicas simples e dízimas periódicas compostas
As dízimas periódicas podem ser simples, ou seja, o período inicia-se logo após a vírgula:
• 0,555 ou 0,5 (o período é 5);
• 9,131313 ou 9,13 (o período é 13);
• 100,600600600 ou 100,600 (o período é 600).
Mas também podem ser compostas, ou seja, após a vírgula há uma parte que não se repete (denominada antiperíodo), seguida pelo período:
• 1,1555 ou 0,15 (o período é 5 e o antiperíodo é 1);
• 9,960212121 ou 9,96021 (o período é 21 e o antiperíodo é 960);
• 40,123995599559955 ou 40,1239955 (o período é 9955 e o antiperíodo é 123).
TRAVESSIAS
Experimentos com dízimas periódicas
Junte-se a um colega para realizar esses experimentos utilizando uma calculadora.
ATIVIDADES
12. Considere estas frações irredutíveis cujos numeradores são iguais a 1 e os denominadores são números primos: 1 2 , 1 3 , 1 5 , 1 7 , 1 11 , 1 13
a) Obtenha a representação decimal de cada fração.
b) Quais dessas representações são dízimas periódicas?
c) Obtenha outras frações irredutíveis que tenham os mesmos denominadores das frações anteriores.
d) Obtenha a representação decimal de cada fração.
e) Quais dessas representações são dízimas periódicas?
13. Obtenha três frações irredutíveis de modo que seus denominadores sejam:
I. múltiplos de 2 e não de 5;
II. múltiplos de 5 e não de 2;
III. múltiplos de 2 e de 5.
a) Utilizando uma calculadora, obtenha a representação decimal de cada fração.
b) Quais dessas representações são dízimas periódicas?
14. Obtenha quatro frações irredutíveis de modo que seus denominadores sejam:
I. múltiplos de 3;
II. múltiplos de 7;
III. múltiplos de 11;
IV. múltiplos de 13.
a) Utilizando uma calculadora, obtenha a representação decimal de cada fração.
b) Quais dessas representações são dízimas periódicas?
15. Em pequenos grupos, conversem sobre todos os resultados obtidos. Expliquem, com suas palavras, as possíveis relações entre denominadores de frações irredutíveis e a formação de dízimas periódicas. Respostas pessoais.
Habilidade (EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Atividade 14
Com a proposta de apresentar um denominador múltiplo de 3, 7, 11 ou 13 em frações irredutíveis, os numeradores escolhidos não devem ser múltiplos de 3, 7, 11 ou 13, respectivamente.
Atividade 15
Oriente os estudantes na organização das conclusões sobre o tema , perguntando-lhes sobre denominadores com fatores primos, divisores de potências de 10 etc.
TRAVESSIAS
Neste estudo, retome que os números racionais podem ser expressos na forma de fração e que as dízimas periódicas são números racionais, assim como os naturais e os inteiros (como exemplos,
temos: 15 3 = 5 ou –20 4 = –5) Observem os resultados obtidos, proponha a socialização e valide as respostas coletivamente. Um apontamento possível é que as dízimas periódicas são representações decimais de frações cujos denominadores não são formados por divisores de potências de 10. Isso
ocorre porque frações decimais com representação decimal finita originam-se de frações que têm denominadores 10, 100, 1 000 etc.
Atividade 13
Nesta atividade, os estudantes precisam perceber que os múltiplos de 2 e 5 simultaneamente são múltiplos de 10. Assim, para ser múltiplo de 2 e não de 5, odeverá ser um número par diferente de 0. Sendo múltiplo de 5 e não de 2, o número deverá terminar em 5.
Habilidade (EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
LUPAS E LUNETAS
Na realização dessa atividade, sugira que façam o cálculo do seguinte modo:
Fração geratriz de uma dízima periódica
Tendo em mente um número representado em uma forma fracionária, podemos buscar sua representação decimal e verificar se ela é uma dízima periódica ou não.
Por exemplo:
2
3 = 0,666
Nesse caso, dizemos que 2 3 é a fração geratriz da dízima periódica 0,666...
Porém, partindo de uma dízima periódica qualquer, como podemos obter a sua fração geratriz?
Veja estratégias para obter a fração geratriz de uma dízima periódica qualquer.
Exemplo 1
Seja a dízima periódica simples 0,444...
Desejamos saber qual é a sua fração geratriz, ou seja, que fração equivale a 0,444...
Chamando de x a fração que gostaríamos de obter, temos que:
x = 0,444 (I)
Se multiplicarmos ambos os membros dessa equação por 10, teremos:
10x = 4,444 (II)
Em caso de dificuldades, proponha aos estudantes que se organizem em grupos e discutam sobre as diferentes estratégias de resolução. Dê outros exemplos, se necessário.
Note que, como temos infinitas casas decimais iguais a 4, ao multiplicar 0,444... por múltiplos de 10, a parte decimal se mantém inalterada.
Se subtrairmos a primeira equação (I) da segunda equação (II):
Assim, 4 9 é a fração geratriz da dízima periódica 0,444..., ou seja:
4 9 = 0,444 = 0,4
LUPAS E LUNETAS
Podemos representar 4,444 – 0,444 como:
Como o período de cada dízima periódica é igual, ao subtrair uma da outra, todas as infinitas casas decimais da diferença resultam em 0. A partir dessa informação, calcule:
Exemplo 2
Considere a dízima periódica simples
2,191919...
Seja x a fração geratriz dessa dízima periódica, então:
x = 2,191919
10x = 21,9191919
100x = 219,191919
Nesse caso, multiplicamos até 100 porque precisamos obter duas dízimas periódicas com o mesmo período, de modo que, quando subtrairmos uma da outra, obteremos um número cujas casas decimais são iguais a 0. Note que em 21,9191919... o período é 19, mas há um antiperíodo igual a 9. Já em 2,191919... e 219,191919... o período é 19 e não há antiperíodo.
Subtraindo a primeira equação da última equação:
100x – x = 219,191919 – 2,191919 99x = 217
x = 217 99
Assim, 217 99 é a fração geratriz da dízima
ATIVIDADES
16. Verifique quais das frações são dízimas periódicas e classifique-as
a) 1 6
b) 2 5
Apenas 2 5 não é uma dízima periódica.
c) 5 13 d) 5 9
periódica 2,191919..., ou seja:
217
99 = 2,191919 = 2,19
Habilidade
Exemplo 3
Considere a dízima periódica composta 1,45888...
Seja x a fração geratriz dessa dízima periódica, então:
x = 1,45888
10x = 14,5888
100x = 145,888
1 000x = 1 458,888
De modo a obter um número cujas casas decimais sejam iguais a 0, vamos subtrair:
1000x –
100x = 1 458,888 – 145,888
900x = 1 313
x = 1 313 900
Assim, 1 313 900 é a fração geratriz da dízima periódica 1,45888..., ou seja:
1 313 900 = 1,45888 = 1,458
Composta: a Simples: c e d
17. Diga qual é o período e o antiperíodo (quando houver) das dízimas periódicas:
a) 2 3
b) 2 15
Período: 6.
Período: 3, antiperíodo: 1.
18. Obtenha a fração geratriz das dízimas periódicas:
19. Resolva as operações. Dica: obtenha primeiro as frações geratrizes de cada dízima periódica.
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Assim, 2 121 999 = 707 333 é a fração geratriz da dízima periódica 2,123
LUPAS E LUNETAS
A fração geratriz da dízima periódica 0,999... é 9 9 = 1
Observe:
x = 0,999
10x = 9,999
10x – x = 9,999 – 0,999
9x = 9
x = 1
Uma maneira de entender, intuitivamente, é por uma investigação com subtrações dos decimais exatos, 0,9; 0,99; 0,999; 0,9999 etc., de 1. As diferenças são 0,1; 0,01; 0,001; 0,0001 etc., de maneira que cada 9 a mais na parte decimal torna o novo número cada vez mais próximo de 1.
c) 4 33 d) 577 2 475
Período: 12.
Período: 313, antiperíodo: 23.
LUPAS E LUNETAS Respostas pessoais.
Obtenha a fração geratriz da dízima periódica 0,999... Compartilhe com os colegas o resultado que você obteve.
Atividades 16 a 19
O uso da calculadora facilita a resolução das atividades 16 e 17; na atividade 18, sugira que retomem a atividade exploratória que realizaram para identificar algumas dízimas periódicas, e eles poderão determinar mentalmente a solução ou usar o processo descrito anteriormente.
Veja a resolução do item d (atividade 18):
Considere a dízima periódica simples 2,123123...
Seja x a fração geratriz dessa dízima periódica.
Subtraindo
– 2,123123
999 x = 2121
x = 2 121 999
Alguns estudantes ficam perplexos quando nas aulas afirmamos que 0,999... é igual a 1 (e, portanto, 1,999 = 2; –7,999 = –8; 0,1 1,999 = 2; –7,999 = –8; 0,13999 = 0,14) A maioria dos estudantes, quando questionados, afirmam que 0,999... é uma aproximação de 1 e não exatamente o número 1. Veja que 0,999... representa o resultado da adição 0,9 + 0,09 + 0,009 + 0,0009 0,9 + 0,09 + 0,009 + 0,0009 + 0,00009 + , que converge para o valor 1. Para os estudantes, dizemos que 0,9 é uma aproximação de 1. Outra aproximação melhor é 0,99, e ainda mais próximo é 0,999. Conforme aumenta a quantidade de noves depois da vírgula nos aproximamos mais ainda de 1. Então, 0,999... (com uma infinidade de algarismos 9 após a vírgula) é exatamente 1 e não uma aproximação. Se os termos da sequência (0,9; 0,99; 0,999; 0,999...) se aproximam cada vez mais de 1, mas não o superam, então, igualam-se a 1.
Habilidade
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário. Encontro com outras disciplinas
(EF08CI07) Comparar diferentes processos reprodutivos em plantas e animais em relação aos mecanismos adaptativos e evolutivos.
LUPAS E LUNETAS
Esta pesquisa pode ser realizada em aula ou extraclasse. Proponha que os estudantes se organizem em pequenos grupos e determinem a melhor maneira de expor suas descobertas. Isso pode facilitar sua observação de como interagem entre si e em relação ao conhecimento, no ato de aprender.
Promova conversas dentro do grupo, auxiliando-os a localizar as próprias dificuldades e incentivando que eles mesmos sugiram as melhores alternativas para que possam superá-las. Além disso, essas observações podem contribuir com a avaliação em curso.
#Potenciação
As bactérias são microrganismos unicelulares, ou seja, constituídos de uma única célula. Só conseguimos visualizar as bactérias por meio de microscópios, já que seu tamanho varia entre 0,001 e 0,005 milímetro.
O processo mais comum de reprodução das bactérias é chamado de bipartição. Nele, uma bactéria duplica-se em duas iguais entre si e idênticas à célula-mãe. Cada uma dessas bactérias irá se duplicar e assim por diante:
Partindo de uma bactéria original, podemos acompanhar o número de bactérias após cada bipartição:

Antes de ocorrer a 1a bipartição, só há a bactéria original
A potenciação é uma operação matemática que corresponde à multiplicação de fatores iguais. Sejam a um número inteiro e m um número natural não nulo, então:
a m = a a a m vezes ! " $ em que a é a base e m, o expoente dessa potenciação.
LUPAS E LUNETAS Respostas pessoais.
Algumas bactérias podem causar uma série de doenças, como tétano, coqueluche, tuberculose, cólera e disenteria. Entretanto, esses seres microscópicos também podem ser benéficos. É o caso das bactérias que vivem em nosso intestino compondo a flora intestinal. Elas auxiliam no processo de digestão e ajudam inclusive em nossa imunidade.
Pesquise sobre as bactérias que causam as doenças citadas e as que constituem a nossa flora intestinal. Compartilhe com os colegas.
Sugestão de atividade
Antecipadamente, converse com o professor de Ciências, conte o conteúdo que está trabalhando e proponha realizarem uma atividade interdisciplinar, abordando a habilidade de Ciências EF08CI07. Uma possibilidade é apresentar alguma animação disponível na internet sobre a reprodução bacteriana, para que compreendam os tipos de reprodução e como acontece a bipartição no processo reprodutivo. É possível organizar um cartaz (ou animação em flip book) a ser confeccionado coletivamente
relacionando a imagem, as bipartições e a quantidade de bactérias. Exponha o cartaz (ou o flip book) na sala de aula, valorizando a produção dos estudantes.
Nesse passeio, há outras atividades que usam como exemplos a reprodução de mamíferos e plantas. Caso considerem pertinente, podem abordar esses processos reprodutivos interdisciplinarmente também.
Propriedades da potenciação
Vamos investigar algumas propriedades envolvendo potenciação? Considere a e b números inteiros e m e n números naturais não nulos, tais que:
Habilidade (EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
Ao multiplicar potências de mesma base, a potência resultante tem a mesma base e seu expoente corresponde à soma dos expoentes das potências multiplicadas.
• Divisão de potências de mesma base Seja
Ao dividir potências de mesma base, a potência resultante tem a mesma base e seu expoente corresponde à diferença dos expoentes das potências divididas.
Depois da leitura coletiva, crie uma situação para que conversem sobre a propriedade “multiplicar potências de mesma base”: escreva na lousa uma multiplicação de potências de mesma base e peça que resolvam sem usar a propriedade e usando a propriedade. Com isso, alguns registros, por exemplo, de 36 ⋅ 37 , podem ser feitos:
• Com a escrita de todos os fatores e a contagem da quantidade de fatores, pois 36 37 = (3 3 3 3 3) (3 3 36 37 = (3 3 3 3 3) (3 3 3 3 3 3) = 3 13
• Usando a propriedade: 36 37 = 36+ 7 = 313
Questione-os: Qual dessas estratégias consideram mais prática? Qual tem menor chance de erro? Qual método usariam para calcular 315 325 320 ? De modo similar, sugira que os estudantes utilizem essas duas estratégias para as propriedades da divisão de potências de mesma base e potência de um produto, de um quociente e de outra potência.
A potência de um produto, segundo certo expoente, resulta na multiplicação de potências desse mesmo expoente cujas bases são os fatores da multiplicação.
Habilidade (EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
LUPAS E LUNETAS
• Potência de um quociente (ou de fração)
A potência de um número em representação fracionária, segundo certo expoente, resulta em uma fração cujos numerador e denominador são elevados a esse mesmo expoente.
• Potência de potência
b) Auxilie os alunos, caso eles não recordem da propriedade do neutro da multiplicação. c)
A potência de uma potência resulta em uma potência de mesma base cujo expoente é o produto dos expoentes iniciais.
LUPAS E LUNETAS
Considerando a ≠ 0 e m um número natural, em duplas ou trios, utilizem as propriedades apresentadas para:
Atividade 20
Como a intenção é utilizar as propriedades das potências, solicite que expressem o resultado como uma única potência e, depois, calculem. Se considerar adequado, escolha um dos itens para que façam todas as multiplicações e usem as propriedades simultaneamente. Assim, poderão comparar qual estratégia requer menos cálculos para chegar ao resultado. Você pode pedir também que calculem o resultado final utilizando uma calculadora.
a) Calcular a m ÷ a m
b) Concluir que a0 = 1, ou seja, qualquer número a ≠ 0 elevado a 0 resulta em 1.
c) Calcular a n a n
d)
b) Do item a sabemos que: a0 = a m ÷ a m =
do inverso da multiplicação, sabemos que um número (a m ) dividido por ele mesmo (a m ) resulta em
20. Utilize propriedades da potenciação para calcular:
científica
Números muito grandes
Quantos grãos de areia há em uma praia? Apesar de sua enorme quantidade, há uma quantidade finita de areia em uma praia (ou em todo o planeta!). Portanto, existe um número que poderia representar o total de grãos de areia. No entanto, obter esse número com precisão é algo bastante difícil, senão impossível, de calcular.
LUPAS E LUNETAS
Em duplas ou trios, estimem quantos grãos de areia:
a) caberiam em sua mão.
b) há em uma praia.
a) Estimativa possível: em torno de 1 milhão de grãos.
b) Estimativa possível: em torno de 1 trilhão de grãos.
c) há em todo o planeta.
c) Cerca de 1064 grãos.
Esse problema, no entanto, já ocupou a cabeça de grandes matemáticos ao longo da história. Arquimedes, matemático da Grécia Antiga, se propôs não somente a calcular os grãos de areia de uma praia, como também o total de grãos de areia de todo o Universo! Em sua época, os gregos conheciam números grandes, mas só nomeavam até o número 10 000, chamado de murious pelos gregos e, mais tarde, de “miríades” pelos romanos.
Para realizar o cálculo dos grãos de areia, Arquimedes precisava agrupar “miríades”. Por exemplo, uma miríade de miríades corresponde a 10 000 10 000 ou, como representamos hoje: 10 000 10 000 = 10 0002 Uma “miríade de miríades de miríades” seria 10 0003 e assim por diante!
Arquimedes não obteve um número exato para resolver esse problema, mas concluiu que esse número seria da ordem de 10 00016. Note que podemos escrever 10 000 = 10 10 10 10 = 104 Assim, 10 00016 = (104 )16 = 104 16 = 1064 Isso significa que, para representar esse número, precisaríamos escrever o algarismo 1 seguido por 64 “zeros”!
Essa maneira de representar os números utilizando potências de 10 é conhecida como notação científica. Veja alguns exemplos:
• 10 000 = 10 10 10 10 = 104
• 8 000 000 = 8 10 10 10 10 10 10 = 8 106
• 40 000 000 = 4 10 10 10 10 10 10 10 = 4 107
Ao representar um número em notação científica, o fator que multiplica a potência de 10 é sempre um número entre 1 e 9, esses inclusos.
Por exemplo, como representaríamos o número 29 000 000 em notação científica?
Sabemos que: 29 000 000 = 29 10 10 10 10 10 10 = 29 106 Note que podemos representar 29 como 2,9 10 Assim, substituindo 29 por 2,9 ⋅ 10, temos que: 29 106 =
=
Habilidade (EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.
LUPAS E LUNETAS
Com a leitura do texto, poderão compreender a estratégia que Arquimedes utilizou para estimar que há 1064 grãos de areia no Universo. Para que tenham uma ideia da quantidade a ser representada, é preciso estimar que o diâmetro de um grão de areia varia de 0,1 a 2 mm. Proponha aos estudantes que calculem a quantidade de grãos de areia da praia de Copacabana, por exemplo, ou de alguma outra praia conhecida por eles. Os estudantes precisarão levantar alguns dados e hipóteses, como a extensão da orla, a faixa de areia, a profundidade média e a quantidade de areia por m3
Habilidade
(EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
Atividade 21
Observe este modo de contar as ordens decimais para representar o número em notação
ATIVIDADES
21. Represente os números em notação científica:
a) 7 000 000
b) 15 000 000 000
c) 5 230 000
22. Observe uma estratégia para realizar a seguinte operação:
b) Utilize a estratégia apresentada anteriormente para calcular:
• 2 104 + 1,3 105 150 000
• 7 108 – 4 102 699 999 600
23. Utilize as propriedades das potências para efetuar as operações. Represente as respostas em notação científica:
a) 8 1010 7 105
b) 12 1080 4 1034
5,6 1016 3 1046
a) Com suas palavras, explique por que, nesse caso, foi interessante fazer 107 = 105 102
24. Elabore uma situação-problema envolvendo números muito grandes e notação científica. Compartilhe com os colegas. Resposta pessoal.
22. a) Foi interessante para deixar os dois números na forma a a 105 e poder colocar 105 em evidência para adicioná-los.
Números muito pequenos
Assim como a notação científica auxilia na representação de números muito grandes, ela também pode ser utilizada quando consideramos números muito pequenos.
Agora, vamos pensar, não na quantidade de grãos de areia, mas na espessura de um único grão. Existem diversos tipos de grãos de areia, variando desde areias mais grossas até algumas bastante finas. A espessura do grão de uma areia fina é de, aproximadamente, 125 µm (lê-se “micrômetros”). Essa unidade de medida equivale a 1 metro dividido em 1 milhão de partes iguais. Assim, 125 µm pode ser representado, em metros, por:
125 µm = 125 1 000 000 m = 125 106 m
Atividade 22
Outro modo de representar a adição é:
Como dividir por um número equivale a multiplicar pelo seu inverso, podemos escrever: 125
Realizando a divisão entre as potências de 10, temos:
Lembrando que, para representar esse número em notação científica, precisamos considerar
Atividade 23
Para que percebam o uso das propriedades das potências, proponha que organizem assim a multiplicação:
a)
Há muitas possibilidades de criação. Veja uma possível resposta:
A distância da Terra à Lua é de cerca de 384 000 km. Uma barata mede cerca de 4 cm. Quantas baratas podem ser enfileiradas da Terra até à Lua?
Como 384 000 km equivalem a 38 400 000 000 cm:
LUPAS E LUNETAS
a)Sugestão de resposta: um número elevado a um expoente negativo é igual a 1 sobre o número elevado ao oposto do expoente.
Considere o número 1 106 Expressando 1 como 100, temos:
1 106 = 100 106 = 100–6 = 10–6
Ou seja: 1 106 = 10–6
b)O procedimento indicado na teoria mostra que sim:
para a ≠ 0.
a) Com suas palavras, escreva uma afirmação que relacione potências com expoentes inteiros negativos e representações fracionárias.
b) Em duplas ou trios, investiguem se esse fato se verifica para potências com bases diferentes de 10.Compartilhem suas observações com os demais colegas.
ATIVIDADES
25. Escreva em notação científica:



a) 0,006
6 10–3
b) 0,0000023
c) 0,3454
d) 0,000000000003
2,3 10–6 3,454 10–1 3 10–12
26. Calcule:
a) 2 10–2 + 3 10–3
b) 9 10–8 – 2 10–9
b)
c)
d)
27. Elabore uma situação-problema envolvendo números muito pequenos e notação científica. Compartilhe com os colegas. Resposta pessoal.
#Radiciação e potenciação
A natureza apresenta um equilíbrio interessante e também bastante delicado entre extremos, do muito grande ao muito pequeno, seja em quantidades, seja em tamanhos e distâncias, por exemplo.
Habilidades
(EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
LUPAS E LUNETAS
Proponha aos estudantes que usem a calculadora para verificar qual é o número racional na forma decimal correspondente à fração com denominador na forma de potência de base 10, efetuando a divisão de 1 pela potência. Peça
Atividade 25
As estratégias podem ser, por exemplo:
Há muitos enunciados possíveis, como: o vírus da gripe tem a forma aproximada de uma esfera de diâmetro 0,00011 mm (1 mm = 10 3 m). Um grão de areia, conforme o texto, tem diâmetro 125 mm. Quantos vírus são necessários para igualar o diâmetro de um grão de areia?
Caso considere adequado, apresente o cálculo com o número decimal para que os estudantes
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
LUPAS E LUNETAS
De modo simplificado, a regra é: a raiz de um quociente é o quociente das raízes.
Representar números com potências ajuda a lidar com esses valores extremos, desde o muito grande, como 1064, até o muito pequeno, como 10–6
Ao longo da história, diversos povos de diferentes culturas buscaram lidar com os desafios de medir, calcular, contar e, por fim, compreender esses extremos existentes na natureza e na vida cotidiana.
Vimos que, na Antiguidade, Arquimedes teve grande influência no desenvolvimento do que hoje denominamos potenciação. No século IX, os matemáticos árabes também estudaram esse assunto. Em produtos de fatores iguais como:
3 3 3 3 3 3 3
Os árabes denominavam cada um desses fatores pela palavra jadhr. Essa palavra foi traduzida pelos matemáticos europeus como radix. Daí vem a palavra raiz, que utilizamos atualmente na álgebra. Por exemplo, considere o produto:
5 5 = 52 = 25
Dizemos que a raiz quadrada de 25 é 5. Representamos a raiz pelo símbolo 2 ou somente , no caso de raízes quadradas. Assim: 25 = 52 = 5
Agora, considere este outro produto: 10 10 10 = 103 = 1 000
Nesse caso, podemos associar a raiz cúbica de 1 000, que é 10.
1 000 3 = 103 3 = 10
De modo geral (e sob certas condições) a radiciação é a operação matemática inversa da potenciação
Podemos escrever que, sendo a um número racional positivo ou nulo e n um número natural diferente de 0, então:
an = xa = x n
40 | MANUAL DO PROFESSOR
Por exemplo:
• Se 62 = 36, então 36 2 = 6
• Se 210 = 1 024, então 1 024 10 = 2
• Se 75 = 16 807, então 16 807 5 = 7
LUPAS E LUNETAS
Analogamente aos exemplos anteriores:
Partindo desse exemplo, faça o que se pede:
a) Com suas próprias palavras, estabeleça uma regra para calcular radiciação de números em representação fracionária.
A raiz enésima de uma fração é o quociente entre a raiz enésima do numerador e a raiz enésima do denominador da fração original.
| TRAJETÓRIA 1 NÃO ESCREVA
ATIVIDADES
28. Calcule o resultado das radiciações:
a) 49 7
b) 81 4 3
29. Calcule o resultado das radiciações:
a) 32 5 , sabendo que 25 = 32 2
b) 625 4 , sabendo que 54 = 625 5
c) 64 3 , sabendo que 43 = 64 4
16 100
30. Elabore uma situação-problema com a operação de radiciação. Compartilhe com os colegas.
Representando radiciação como potenciação
Considerando que, sob algumas condições, a potenciação e a radiciação são operações inversas, temos:
x ( )2 = x , x, para um x positivo ou nulo
Pensando na propriedade de potência de potência, para um x positivo ou nulo, qual número substituiria a interrogação (?) de modo a obter x?
Habilidade
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
Atividades 28 a 30 Especialmente na atividade 29, para que compreendam as potenciações e radiciações como operações inversas, proponha que escrevam os radicandos na forma de potências. Espera-se que percebam que a base é o resultado.
Uma possível resposta para a resolução de problemas na atividade 30 é:
Qual deve ser a medida da aresta de uma caixa cúbica cujo volume é 343 cm3?
Resposta: a aresta da caixa cúbica deve medir 343 3 = 7 cm, pois 7 3 = 343
É possível representar a radiciação utilizando expoentes fracionários. Por exemplo:
Nesses casos, podemos também representar 36 e 1 000 como potências. Assim:
De modo geral, sendo a e m números racionais e n um número natural diferente de 0, então:
LUPAS E LUNETAS
Em duplas ou trios, escrevam uma regra para representar raízes em forma de potências com expoentes fracionários. Respostas pessoais.
LUPAS E LUNETAS
Os estudantes apresentarão muitas estratégias diferentes dispondo em palavras uma regra sobre as raízes. Valide-as coletivamente. Uma possibilidade de escrita pode ser: a raiz enésima de um número com um expoente m é o número elevado à fração cujo numerador é m e o denominador é o índice n da raiz.
Habilidade (EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
Atividade 31
Apresente alguns exercícios para que percebam que na representação de raízes como potências:
• o expoente do radicando tem o mesmo valor que o numerador do expoente na potência;
• o índice tem o mesmo valor que o denominador do expoente na potência.
Nesse momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
ATIVIDADES
31. Represente as radiciações como potenciação e vice-versa:
a) 43
b) 2 5 6
LEVO NA BAGAGEM
c) 34 7
d) 5 6 11
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática



• Consegue resolver e elaborar problemas envolvendo cálculo de porcentagens?
• Sabe reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz de uma dízima periódica?
• Efetua cálculos com potências de expoentes inteiros?

• Sabe utilizar a representação de números em notação científica para escrever números muito grandes ou muito pequenos?
• Consegue resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário?
▶ Outras disciplinas
Ciências
• Consegue comparar diferentes processos reprodutivos de animais marinhos em relação aos mecanismos adaptativos e evolutivos?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
suficiente Satisfatório Plenamente satisfatório
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
▶ Organize
Neste passeio, você relembrou e aprofundou conhecimentos dos anos anteriores: porcentagem, dízimas periódicas, potenciação, radiciação e notação científica. Repasse as páginas deste passeio e elabore um esquema dos conhecimentos explorados, dividindo-os entre aqueles que já conhecia e aqueles que foram novidade.
▶ Elabore
Considere o esquema que você criou no tópico anterior. Elabore uma questão sobre cada conhecimento que descreveu. Na elaboração dessa questão, procure utilizar o contexto das relações entre o “muito pequeno” e o “muito grande” na natureza. Em seguida, compartilhe com os colegas e apresente algumas possíveis estratégias para a resolução dessas questões.
▶ Proponha
A pergunta inicial deste passeio é: Como descrever o “muito pequeno” e o “muito grande” na natureza?
Pesquise na internet ou em livros sobre “extremos da natureza”, ou seja, busque elementos, coisas ou situações que apresentem números muito grandes (como a distância entre planetas) ou muito pequenos (como o diâmetro de uma gota d’água). Utilize o que você aprendeu neste passeio para interpretar numericamente os dados obtidos.

Proponha uma roda de conversa para que todos possam compartilhar os dados obtidos. Em seguida, montem um mural que resuma esses dados. Agreguem a ele outras informações, curiosidades, fotos, ilustrações etc.
BARCOS E PORTOS
Organize
Os estudantes podem realizar essa atividade em duplas para que conversem sobre os conteúdos que aprenderam e aqueles em que tiveram mais dificuldade. A realização de atividades em duplas permite que os estudantes se conheçam melhor e desenvolvam habilidades como a liderança, a cooperação e a colaboração. Durante as atividades em duplas, os estudantes são expostos à construção do conhecimento por meio da troca de experiências entre seus pares e do contato com opiniões diferentes das suas.
Elabore
Avalie a produção dos estudantes, acompanhando o processo e compartilhando dúvidas e conhecimentos entre as duplas.
Proponha
Na pesquisa sobre números muito grandes, apresente outras situações, como a quantidade de água nos oceanos, a área da superfície ou a quantidade de habitantes do planeta Terra. Na pesquisa sobre números muito pequenos, além das bactérias, podem pesquisar sobre o menor inseto, o menor animal ou a menor planta do mundo.


CHECK-IN
Proponha que observem, inicialmente, as imagens e solicite que associem as palavras possível, improvável e impossível a cada uma.

Depois que classificarem as frases, explore outras interpretações para elas, por exemplo: com certeza uma macieira produzirá maçãs, mas se essa macieira não for regada o suficiente durante o ano ou o solo for pobre em nutrientes, haverá produção de maçãs?

OS FENÔMENOS DA NATUREZA SÃO ALEATÓRIOS OU DETERMINÍSTICOS?

Possível, improvável, impossível... Os fenômenos do acaso podem ser analisados por meio da Matemática.
CHECK-IN
(I)Impossível; (II) com certeza acontecerá; (III) provável; (IV)pouco provável; (V) muito provável.

Classifique cada evento como impossível, pouco provável, provável, muito provável e com certeza acontecerá.

I. Um coqueiro produzir figos.
II. Uma macieira saudável produzir maçãs.
III. Um carneiro e uma ovelha malhada gerarem como filhote uma ovelha malhada.
IV. Chover todos os dias do ano em um mesmo local.
V. Uma roseira florescer pelo menos uma vez no ano.
• Compartilhe suas respostas com os colegas.
CONTAGEM
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
• Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo.
• Reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
• Reconhecer as principais variáveis envolvidas na previsão do tempo e saber citar exemplos de situações nas quais elas possam ser medidas.
CONVÍVIO E BEM-ESTAR SOCIAL

Faça um desafio aos estudantes: jogando dois dados e observando a soma de pontos, você, professor, terá sua aposta fixa no 4 e no 7 e um estudante ganha se obtiver os demais resultados. Use pontos para registrar as vitórias: na 1a rodada, 1 ponto; na 2 a, 10 pontos; na 3a, 20 pontos, e assim sucessivamente.
A cada etapa pergunte: vai jogar ou vai parar? Se jogar e errar vai perder tudo! Quando não sair o resultado que favorece o estudante ele perde todos os pontos e troca-se o voluntário. Continue o estudo desse passeio e, durante o estudo sobre probabilidades, mostre aos estudantes que o número 7 tem a maior probabilidade de sair no sorteio apresentando o raciocínio na tabela de soma dos pontos em dois dados. Apesar de a probabilidade apontar que a chance de sair 7 é maior, esse fato não garante a vitória de quem aposta no 7. A escolha de outro número é para que não percebam o motivo da escolha do 7.
Quando os estudantes conhecerem como usar o estudo da probabilidade para prever o resultado, podem realizar esse mesmo experimento no intervalo com colegas de outras turmas e anotar os resultados obtidos. Com os resultados obtidos, discutam e analisem se o conhecimento sobre probabilidades interfere na escolha do melhor momento de parar o jogo.
Após o jogo, promova uma discussão com os estudantes para que percebam que os jogos ou brincadeiras também se constituem em situações de aprendizagem. Discutir as regras, os momentos do jogo e as estratégias usadas estimula a criticidade e criatividade dos estudantes, promovendo avanços em seus comportamentos, tanto no que diz respeito ao relacionamento com os demais colegas, como também com relação a questões que envolvem desinibição, oralidade, psicomotricidade, entre outros.

ATMOSFER A
Nem tão aleatório assim...
O que você pensa quando falamos em algo aleatório? Um dado? Um jogo de cara ou coroa? Algo totalmente imprevisível?
Até pouco mais de 100 anos atrás, a grande maioria dos cientistas acreditava que a física era completamente determinística, ou seja, que se você for capaz de considerar a força com que o dado é jogado, o vento, a temperatura, a rugosidade da superfície em que ele bate e todos os mínimos detalhes que podem influenciar na sua trajetória, você pode prever, sem nenhuma dúvida, qual face estará voltada para cima quando o dado parar. Da mesma forma, você poderia prever qualquer fenômeno da natureza, contanto que você tivesse informações o suficiente.
Essa ideia mudou após o surgimento da mecânica quântica, com a Interpretação de Copenhague, que diz que um estado quântico só pode ser determinado no momento em que ele for medido, e que até então ele pode ser qualquer um. Nesse sentido, o spin de um átomo pode estar apontando para cima ou para baixo no momento em que você mede, mas isso não é determinado até que a
NEM
medida seja feita, ou seja, é algo “completamente” aleatório. As condições do ambiente ao redor não podem determinar se esse spin será para cima ou para baixo, apenas alterar a probabilidade de se medir uma delas (pode ser mais provável medir o spin para cima do que para baixo, assim como em um dado viciado).
Hoje nós utilizamos 3 conceitos diferentes para falar sobre a determinação de um evento: (i) se nós podemos determinar facilmente o resultado de um evento, conhecendo as condições iniciais, nós chamamos o evento de “previsível” ou “determinístico”, por exemplo, a trajetória de uma bala, disparada por uma arma; (ii) se um sistema depende tanto das condições iniciais, que é impossível prever com exatidão o resultado final, nós dizemos que o sistema é caótico, o clima, por exemplo, que pode ser previsto com bastante precisão para amanhã, mas certamente não para o mês que vem; (iii) por último temos os sistemas aleatórios, cujo resultado pode depender das condições iniciais, mas não pode ser determinado por elas.

#Princípio multiplicativo
Uma estação meteorológica avalia a possibilidade de haver ventos fortes ou moderados; umidade relativa do ar baixa, normal ou alta; e o céu encoberto, parcialmente encoberto ou ensolarado.

Considerando, hipoteticamente, que em certo dia só pode ser verificado um tipo de vento, um de umidade relativa do ar e um estado de encobrimento do céu, o diagrama de árvore ilustra todas as possibilidades para o tempo nesse dia:
Habilidade
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo. Encontro com outras disciplinas
Por exemplo, uma possibilidade é “ventos moderados, umidade relativa do ar baixa e céu encoberto”. Para obtê-la, é possível seguir um ramo do diagrama:

LUPAS E LUNETAS
a) A partir do diagrama, descreva todas as possibilidades para as características do tempo do dia nesse lugar.
b) Pesquise sobre as principais variáveis envolvidas na previsão do tempo e cite exemplos de situações nas quais elas possam ser medidas. Resposta pessoal.
LUPAS E LUNETAS
Oriente os estudantes na observação do diagrama de árvore: para a lista com as possibilidades, precisam fazer o registro de modo organizado, pois se anotarem sem um método poderão fazer registros duplicados ou esquecer de fazer alguns registros.

(EF08CI15) Identificar as principais variáveis envolvidas na previsão do tempo e simular situações nas quais elas possam ser medidas.
Ventos moderados, baixa umidade do ar, ensolarado.
Ventos moderados, baixa umidade do ar, parcialmente encoberto.
Ventos moderados, baixa umidade do ar, encoberto.
Sugestão de atividade
Ventos moderados, umidade do ar normal, ensolarado.
Ventos moderados, umidade do ar normal, parcialmente encoberto.
Ventos moderados, umidade do ar normal, encoberto.
Ventos moderados, alta umidade do ar, ensolarado.
Ventos moderados, alta umidade do ar, parcialmente encoberto.
Ventos moderados, alta umidade do ar, encoberto.
Ventos fortes, baixa umidade do ar, ensolarado.
Ventos fortes, baixa umidade do ar, parcialmente encoberto.
Ventos fortes, baixa umidade do ar, encoberto.
Ventos fortes, umidade do ar normal, ensolarado.
Ventos fortes, umidade do ar normal, parcialmente encoberto.
Ventos fortes, umidade do ar normal, encoberto.
Ventos fortes, alta umidade do ar, ensolarado.
Ventos fortes, alta umidade do ar, parcialmente encoberto.
Ventos fortes, alta umidade do ar, encoberto.
Converse com o professor de Ciências para realizarem uma atividade interdisciplinar sobre a previsão do tempo. Costumamos consultar a previsão do tempo, inclusive nos momentos de viagens, para nos organizarmos antecipadamente. Com a intenção de envolver os estudantes com o tema, indague-os sobre a frequência com que consultam a previsão do tempo e qual fonte utilizam. Com a leitura do texto, pergunte quais são as principais variáveis envolvidas na previsão do tempo. Para ilustrar a situação, pesquise vídeos na internet sobre o “tempescope” – uma caixa transparente que faz uma simulação por meio de informações, compartilhadas com o equipamento por um computador, sobre o clima em determinada cidade. Essa atividade contempla a habilidade de Ciências EF08CI15. Com as discussões sobre o assunto, espera-se que o estudante consiga verbalizar quais são os principais fatores que influenciam o clima.
Habilidade
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Apresente outros exemplos para estudarem as ocorrências usando a árvore de possibilidades para elaborar uma lista de possibilidades e, em seguida, efetuar a contagem das possibilidades de cada etapa do evento. Como sugestão, apresente as situações para combinarem alguns tipos de saladas, pratos quentes e sobremesas ou a escolha de uma fantasia que combine peruca, óculos e chapéu ou outra que considere adequada. Os estudantes podem verificar a quantidade de possibilidades escolhendo um de cada tipo de salada, prato quente, sobremesa ou peruca, óculos e chapéu.
Situações-problema envolvendo contagem
Ao analisar o diagrama, podemos notar que, para cada duas possibilidades para o vento, existem três possibilidades para a umidade relativa do ar. Portanto, o número de possibilidades de combinar vento e umidade pode ser obtido pelo produto 2 3 = 6. Note também que, para cada uma dessas seis, há três possibilidades para o estado de encobrimento do céu. Assim, o total de possibilidades para o clima desse dia pode ser calculado por 6 3 = 18, ou seja: 2 possibilidades para o vento
! 3 possibilidades para a umidade do ar
! 3 possibilidades para o encobrimento do céu
! = 18 total de possibilidades
!
Essa estratégia é conhecida como princípio fundamental da contagem ou princípio multiplicativo
Vamos explorar situações-problema envolvendo o princípio multiplicativo.
Situação 1
Os patos costumam nadar em fila, sendo comum observar a mãe liderando a fila com seus filhotes atrás.

Patinhos acompanhando a mãe pata na lagoa.
Essa organização tem uma explicação física: a água apresenta uma resistência ao movimento; quando a mãe move a água à sua frente, cria ondulações que não somente reduzem a resistência da água para o filhote atrás dela como também ajuda a impulsioná-lo para frente. Os filhotes no restante da fila se beneficiam não somente da movimentação da mãe, como de todos os filhotes à sua frente.
Imagine uma situação em que há três filhotes de pata nadando em fila. Utilizando um diagrama de árvore, podemos verificar as possibilidades de organizar esses filhotes na fila:

A partir do diagrama, podemos verificar que há 6 possibilidades de filas distintas. Pelo princípio multiplicativo:
3 possibilidades para o 1 filhote
! 2 possibilidades para o 2 filhote
! 1 possibilidades para o 3 filhote
Situação 2
Em um bando de patos há os seguintes filhotes:

Habilidade
!
! = 6 total de possibilidades
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Vamos verificar de quantas maneiras diferentes podemos organizar esses filhotes, em fila, dois a dois:
Pelo princípio multiplicativo, serão 7 6 = 42 maneiras de combinar as blusas e saias.
Atividade 2
Pelo princípio multiplicativo:
4 possibilidades para o 1 filhote
! 3 possibilidades para o 2 filhote
ATIVIDADES
1. Uma moça tem 7 blusas e 6 saias. Quantas são as maneiras de ela se vestir com cada uma dessas peças? 42 maneiras.
2. De quantas maneiras diferentes uma pessoa poderá entrar e sair de um edifício por uma porta diferente da que usou para entrar, sendo que o edifício tem 9 portas? 72 maneiras.
3. Um teste é composto de 13 questões cuja resposta pode ser verdadeiro ou falso. Quantos são os gabaritos possíveis para uma prova dessa? 213 = 8 192 gabaritos possíveis.
! = 12 total de possibilidades
Nessa situação, são 9 possibilidades de escolha da porta de entrada e, como a pessoa não poderá retornar pelo mesmo lugar, serão 8 portas para a saída. Assim, 9 8 = 72, ou seja, serão 72 maneiras de entrada e saída.
Assim, há 12 possibilidades de organizar os 4 filhotes, dois a dois, em fila. Note que, nesse caso, pares como e são diferentes, apesar de contarem com os mesmos elementos. Isso porque estamos falando da ordem em um fila. Ou seja, é necessário diferenciar o filhote que é o primeiro do que é o segundo.
!
48 maneiras. 720 pódios distintos. ARTE/ M10
Atividade 3
Como cada questão apresenta duas possibilidades de resposta, existem 213 gabaritos possíveis.
Atividade 4
Pelo princípio multiplicativo, serão 6 8 = 48 maneiras de viajar de uma cidade para a outra passando pela cidade .
4. Existem 6 estradas ligando a cidade P à cidade Q e 8 estradas ligando a cidade Q à cidade R. De quantas maneiras pode-se viajar da cidade P à cidade R, passando-se pela cidade Q?
| ARTE/ M10
Atividade 5
Nessa situação, serão 10 possibilidades para o 1o lugar no pódio, seguidos de 9 e 8 corredores que poderão conquistar o 2o e o 3o lugares do pódio. Assim, as possibilidades de pódio serão: 10 9 8 = 720, ou seja, 720 modos diferentes de compor o pódio dessa corrida.
49 |
4 3)
Habilidade
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
TRAVESSIAS
Apresente o quadro com a combinação dos patinhos e aponte que, em cada quadro, há o mesmo grupo, ou seja, seis grupos serão formados.
No caso dos quatro patinhos que serão organizados em grupos de três, não importando a ordem, usando o princípio multiplicativo também haverá um mesmo grupo contado diversas vezes.
Atividade 6
Após a escolha do 1 o gerente, diminui um candidato para a 2a vaga. Na escolha do 3o gerente, serão dois candidatos a menos disponíveis. Por isso, as possibilidades serão:
8 7 6 = 336
Mas, note que, escolhidos 3 gerentes para compor a comissão, temos sequências como estas:
G1, G2, G3;
G1, G3, G2; G2, G1, G3;
G2, G3, G1;
G3, G1, G2;
G3, G2, G1
Elas formam um único grupo porque, para uma comissão (conjunto), não importa a ordem em que dispomos os gerentes (diferentemente da situação do pódio, por exemplo).
Para eliminar as comissões repetidas, o resultado deve ser dividido por 6. Assim, 336 ÷ 6 = 56 Ou seja, 56 comissões diferentes podem ser formadas.
Atividade 7
Como serão 5 chocolates escolhidos dentre 7 marcas diferentes, são:
Agrupamentos e contagens
Considere novamente o mesmo bando de patos e os seguintes filhotes:

Vamos verificar de quantas maneiras diferentes podemos organizar esses patos, em grupos, dois a dois. Seguiremos uma estratégia similar à da situação anterior. Note que, nesse caso, não estamos falando de uma fila, mas de um grupo: não importa a ordem dos filhotes nesse agrupamento. Portanto, podemos considerar como iguais as possibilidades:
Assim, há 6 possibilidades para organizar os 4 filhotes, dois a dois, em grupos.
ATIVIDADES
÷ 120 = 21 possibilidades
Do mesmo modo, escolhidos os 5 chocolates dentre as 7 marcas, sequências como
! 3 possibil dades para o 2 f lhote
! = 12 total de possibilidades
!
Pelo princípio multiplicativo: 4 poss bil dades para o 1 filhote
Como, nesse caso, há “possibilidades duplicadas”, então precisamos dividir esse resultado por 2:
12 ÷ 2 = 6
• Considere o mesmo bando de filhotes de pata. Vamos calcular quantas maneiras diferentes são possíveis de agrupar esses filhotes, três a três?
a) Descreva todas as possibilidades de realizar esse agrupamento. Note que, nesse caso, possibilidades como:
são consideradas iguais. Assim, agrupe todas as possibilidades consideradas iguais.
b) No caso dos agrupamentos de 4 filhotes 2 a 2, nós dividimos o total de possibilidades por 2, de modo a eliminar as possibilidades “duplicadas”. Como você faria para eliminar as possibilidades repetidas na situação do agrupamento 3 a 3? Respostas pessoais.
6. Uma comissão de 3 gerentes de uma empresa será formada a partir de um grupo de 8 executivos. Quantas comissões poderão ser formadas? 56 comissões.
7. Quantas caixas diferentes contendo 5 barras de chocolate podem ser feitas a partir de barras de 7 marcas diferentes de chocolate? 21 caixas.
8. Um fabricante vende um automóvel com 8 opções de cores, 3 opções de estofamento e 4 tipos de motores. Quantos tipos de automóveis são oferecidos aos clientes? 96 tipos.
9. Uma bolsa de estudos será concedida aos 3 alunos com melhor desempenho em uma prova aplicada a uma classe com 9 alunos. Qual é a quantidade de grupos de 3 alunos dessa classe que pode concorrer à bolsa? 84 grupos.
10. Certa pessoa adotou 4 gatos de um grupo de 7 gatos. Quantas eram as possibilidades de grupos de gatos que a pessoa tinha para escolher? 35 grupos.
(M1, M2, M4, M5, M7) ou (M4, M5, M1, M2, M7) formam o mesmo conjunto {M1, M2, M4, M5, M7}, porque a ordem das marcas não importa nesse caso. São 120 as sequências formadas que geram conjuntos a considerar e, por isso, dividimos por 120.
Atividade 8
(7 6 5 4 3) ÷ 120 = 21 possibilidades
Pelo princípio multiplicativo, ao combinar cor, estofado e motor teremos, 8 3 4 = 96, ou seja, a fábrica oferece 96 tipos de carros diferentes aos clientes.
Atividade 9
Na escolha dos alunos, haverá 84 grupos possíveis a concorrer pela bolsa de estudo, pois (9 8 7) ÷ 6 = 84
Note que, novamente, quaisquer 3 alunos poderão ter melhor desempenho, pois teremos sequências como estas:
A1, A2, A3 ou A1, A3, A2
Elas formam o mesmo grupo de alunos a quem serão concedidas bolsas de estudos. Por isso, dividimos por 6.
#Experimentos aleatórios

Um pomar tem macieiras que produzem três tipos de maçãs: verde, amarela e vermelha.
Um agricultor colocou uma maçã de cada tipo em uma sacola de modo que não fosse possível ver seu interior e as maçãs estivessem muito bem misturadas no interior da sacola. Então, sem olhar, ele retirou uma maçã qualquer da sacola:
Habilidade (EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Após verificar que a maçã era vermelha, o agricultor devolveu-a à sacola e misturou novamente as maçãs em seu interior. Repetiu esse mesmo procedimento outras 4 vezes:
Assim, mesmo repetindo esse experimento em condições idênticas, os resultados foram diferentes. Ou seja, apesar de sabermos que só haveria três possibilidades para o tipo de maçã que poderia ser retirado da sacola, não podemos afirmar com certeza qual será o tipo que será retirado.


Quando um experimento é repetido em condições idênticas e seus resultados não podem ser previstos com certeza, esse experimento é chamado de aleatório
São exemplos de experimentos aleatórios:
• Lançar um dado e observar o número da face superior.
• De uma caixa de papelão, retirar uma bolinha e verificar sua cor.
• Retirar uma carta qualquer de um baralho e verificar seu naipe. No experimento aleatório apresentado anteriormente, os resultados possíveis são: uma maçã verde, uma amarela ou uma vermelha.
Esse conjunto formado por todos os resultados possíveis de um experimento aleatório é chamado de espaço amostral
Atividade 10
Ao escolher 4 de um grupo de 7 gatos, haverá 35 grupos que podem ser formados, pois (7 6 5 4) ÷ 24 = 35
Dividimos por 24 porque essa é a quantidade de sequências de 4 gatos que formam um mesmo grupo de gatos: G1, G2, G3, G4 ou G3, G4, G1, G2, por exemplo, formam o mesmo grupo de gatos, porque a ordem não importa nesse caso.
Conversando sobre experimentos aleatórios, retome a atividade realizada com a soma dos pontos em dois dados. Questione os estudantes: esse experimento é aleatório? Como eles têm conhecimento de que o número 7 tem uma probabilidade maior de ocorrência, podem verbalizar (equivocadamente) que não é um experimento aleatório. A partir da participação dos estudantes, discuta eventos aleatórios equiprováveis e não equiprováveis. Como podemos calcular a probabilidade sem nunca ter realizado o experimento antes?
Habilidade (EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
LUPAS E LUNETAS
O espaço amostral é o conjunto de todas as possíveis combinações diante do que está sendo observado: a combinação de 2 maçãs, de um total de 3 maçãs. O espaço amostral seria formado por estas 6 combinações (3 2):
Por exemplo, seja o experimento aleatório de lançar um dado e observar o número da face de cima. O espaço amostral desse experimento é o conjunto formado pelas possíveis faces numeradas do dado: 1, 2, 3, 4, 5 ou 6.
Outro exemplo: o experimento aleatório de lançar uma moeda e observar sua face. O espaço amostral desse experimento é o conjunto das possíveis faces da moeda: cara ou coroa.
LUPAS E LUNETAS
Considere que o agricultor deseja retirar, ao acaso, duas maçãs da sacola ao mesmo tempo e observar seus tipos. Assim, um dos resultados possíveis é o par “maçã verde, maçã vermelha”. Sabendo disso, descreva o espaço amostral desse experimento aleatório.
{{maçã verde, maçã amarela}, {maçã verde, maçã vermelha}, {maçã amarela, maçã vermelha}}
Considere o experimento aleatório: “retirar ao acaso uma maçã da sacola e verificar seu tipo”. Existe uma variedade de eventos que podemos considerar:
• retirar uma maçã verde;

• retirar uma maçã vermelha;
• retirar uma maçã amarela;
• retirar uma maçã amarela ou verde;
• retirar uma maçã que não seja vermelha.
Em um experimento aleatório, um evento corresponde a um subconjunto do espaço amostral.
ATIVIDADES
Início Mas o agricultor vai retirar, nesse caso, 2 maçãs ao mesmo tempo (e não em sequência) da sacola. Então, as possibilidades maçã verde, maçã vermelha ou maçã vermelha, maçã verde, por exemplo, são indistintas.
Este é o espaço amostral:
{{maçã verde,maçã amarela },{ maçã verde,maçã vermelha},{maçã amarela,maçã vermelha}}
Atividade 11
Os estudantes apresentarão diversas soluções; alguns experimentos possíveis são:
• Lançamento de uma moeda não viciada. Espaço amostral: {cara, coroa}
• Lançamento de um dado honesto. Espaço amostral: {1, 2, 3, 4, 5, 6};
• Sortear um número de uma loteria. Espaço amostral: {1, 2, 3 ... 59, 60};
• Abrir um livro de 1 000 páginas em uma página ao acaso. Espaço amostral: {1, 2, 3 ... 999, 1 000};
11. Cite três exemplos de experimento aleatório e seus respectivos espaços amostrais. Compartilhe com os colegas.
Respostas pessoais.
12. Considere o experimento aleatório: “lançar um dado de seis faces e verificar o valor da face que cair para cima”. Em duplas ou trios, respondam às questões:
a) É mais provável sair 1 ou sair 6 no dado?
b) É possível sair 7 no dado? Não.
c) É mais provável sair 2 ou um número ímpar no dado?
Os resultados são igualmente prováveis. Sair um número ímpar.
#Probabilidades
Se o agricultor colheu 5 maçãs verdes, 3 amarelas e 2 vermelhas e colocou todas em uma sacola, de modo que não fosse possível ver seu interior e que as maçãs estivessem muito bem misturadas, vamos considerar o experimento aleatório de retirar uma maçã da sacola, ao acaso, e verificar seu tipo. Nessa sacola há, ao todo, 10 maçãs:
• Adivinhar o gênero biológico de um bebê que ainda não foi determinado. Espaço amostral: {masculino, feminino};
• Resultado de uma partida de futebol a priori. Espaço amostral: {vitória, empate, derrota}.
Atividade 12 Nessa situação-problema, o espaço amostral é {1, 2, 3, 4, 5, 6}. Assim:
a) A probabilidade de sair 1 ou 6 é 1 6 cada, ou seja, esses resultados são equiprováveis.
b) Como não há face com o número 7 no dado, não é possível obter esse resultado.
c) A probabilidade de sair o número 2 é 1 6 , enquanto de sair um número ímpar é 3 6 ou 1 2 Ou seja, é mais provável sair um número ímpar.
52 | TRAJETÓRIA 1 NÃO ESCREVA NO SEU LIVRO. SHUTTERSTOCK/ ARTE M10Podemos afirmar que:
• a chance de ocorrer o evento “retirar uma maçã verde” é de 5 em 10, pois há 5 maçãs verdes dentre um total de 10 maçãs;
• a chance de ocorrer o evento “retirar uma maçã amarela” é de 3 em 10, pois há 3 maçãs amarelas dentre um total de 10 maçãs;
• a chance de ocorrer o evento “retirar uma maçã vermelha” é de 2 em 10, pois há 2 maçãs vermelhas dentre um total de 10 maçãs.
Chamamos de probabilidade de ocorrer um evento o número que corresponde à razão entre a quantidade de elementos que constitui o evento e a quantidade de elementos do espaço amostral.
Assim, a probabilidade de:
• “retirar uma maçã verde” é 5
quant dade de mac as verdes ! 10
total de mac as !
Podemos escrever também com uma representação
decimal: 0,50, ou como porcentagem: 50%;
• “retirar uma maçã amarela” é
• “retirar uma maçã vermelha” é
quantidade de macas amarelas 3 10
total de mac as ! = 0,30 = 30%;
quant dade de macas vermelhas 2 10
tota de mac as ! = 0,20 = 20%
Podemos representar a probabilidade de ocorrência desses eventos como:
P(retirar uma mac , a verde) = 5 10 ou 0,50 ou 50%
P(retirar uma mac , a amarela) = 3 10 ou 0, 30 ou 30%
P
ATIVIDADES
13. Determine a probabilidade dos eventos relativos ao espaço amostral do texto:
a) Retirar uma maçã verde ou amarela.
b) Retirar uma maçã verde ou vermelha.
c) Retirar uma maçã vermelha ou amarela.
d) Não retirar uma maçã vermelha.
e) Não retirar uma maçã amarela.
f) Não retirar uma maçã verde.
g) Retirar uma maçã roxa.
h) Tirar uma maçã que não é branca.
Habilidades
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Atividade 13
O espaço amostral é formado por 5 maçãs verdes, 3 amarelas e 2 vermelhas.
Os estudantes precisam verificar quais são as possibilidades de ocorrer um evento (além de compará-los), por exemplo:
• retirar uma maçã verde ou amarela (item a ), são 5 e 3 maçãs, respectivamente.
Assim:
P (retirar uma maçã verde ou amarela) = 5 + 3 10 = 8 10 ou 0,80 ou 80%, que equivale a não ser uma maçã vermelha (item d).
• não retirar uma maçã amarela (item e), são 5 e 2 maçãs, verde ou vermelha (item b) respectivamente. Assim: P(retirar uma maçã verde ou vermelha) = 5 + 2 10 = 7 10 ou 0,70 ou 70%.
Habilidades
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
LUPAS E LUNETAS
Espera-se que os estudantes criem problemas que utilizem o princípio multiplicativo no cálculo de probabilidades.
Leia um problema para que os estudantes usem como inspiração. Por exemplo:
Qual é a probabilidade de jogar um dado e uma moeda simultaneamente e obter o resultado “número par” e “cara”?
Na resposta, precisam calcular o total de combinações possíveis ao lançar o dado e a moeda. Pelo princípio multiplicativo, são 12 resultados possíveis no total.
Apenas 2-cara, 4-cara e 6-cara são as combinações que atendem ao evento “número par” e “cara”. Ou seja, a probabilidade de ocorrência de lançar uma moeda e um dado simultaneamente e obter a face “cara” e o número 2, 4 ou 6 é
ou 1
Utilizando o princípio multiplicativo no cálculo de probabilidades
Um biólogo está catalogando as espécies de aves em sua região utilizando um código alfanumérico, ou seja, composto por letras e algarismos. Ele utilizará as vogais e os algarismos de 1 a 9. Cada código terá uma vogal na primeira posição e um algarismo na segunda posição. Por exemplo:
A vogal ! – 9 algarismo !
Esse biólogo imprimiu uma etiqueta com cada código possível. Como saber quantos são os códigos, ou seja, quantas etiquetas ele imprimiu?
Sabendo que há cinco vogais (A, E, I, O U) e nove algarismos de 1 a 9 (1, 2, 3, 4, 5, 6, 7, 8, 9), podemos utilizar o princípio multiplicativo para obter o total de possibilidades de códigos distintos:
!
5 voga s ! 9 algarismos ! = 45 total de cód gos
Considere agora o experimento aleatório: escolher, ao acaso, uma etiqueta e verificar seu código. Vamos calcular probabilidades de alguns eventos relacionados a esse experimento.
• Qual é a probabilidade de que esse código tenha a letra A?
Sabemos que há 45 possibilidades de códigos. Gostaríamos de saber, desses, quais iniciam com a letra A. Nesse caso, só há uma possibilidade de letra (a própria letra A) e 9 possibilidades de algarismos (1, 2, 3, 4, 5, 6, 7, 8, 9). Utilizando o princípio multiplicativo:
Ou seja, há 9 códigos com a letra A (A-1, A-2, A-3, A-4, A-5, A-6, A-7, A-8 e A-9). Assim, a probabilidade de escolher um código iniciado pela letra A pode ser calculada por:
P(A) probab l dade de cód go com letra A
! = 9
número de cód gos com A ! 45 número total de cód gos
= 1 5 = 0,20 = 20%
!
• Qual é a probabilidade de que esse código tenha um número ímpar?
Nesse caso, há 5 possibilidades de letras (A, E, I, O U) e 5 possibilidades de números ímpares (1, 3, 5, 7, 9). Utilizando o princípio multiplicativo para calcular a quantidade de códigos com número ímpar:
5 letras possíveis ! 5 números possíveis ! = 25 códigos com ímpar
!
A probabilidade de escolher um código que possua número ímpar pode ser calculada por:
! " $ = 25 número de cód gos com ímpar !
P(ímpar ) probab l dade de código com ímpar
! = 5 9 ≅ 0,56 = 56%
45 número total de cód gos
LUPAS E LUNETAS Respostas pessoais.
Em duplas, elaborem um problema similar aos anteriores. Compartilhem com os demais colegas da turma e proponham que solucionem o problema que vocês elaboraram.
ATIVIDADES
14. A senha do cartão de crédito de uma pessoa consiste em uma sequência de 5 dígitos. Qual é a probabilidade de a senha terminar com um algarismo par?
5 10 = 0,5 = 50%
15. Ao se preparar lanches para uma saída de campo de uma escola, as opções eram pão francês, pão de forma ou pão integral e queijo, presunto ou salame. Os lanches
foram distribuídos aleatoriamente. Qual é a probabilidade de um estudante ter pego um lanche com salame?
16. As placas de carros no padrão Mercosul são compostas por quatro letras e 3 algarismos (por exemplo, AAA0A00). Determine a probabilidade de uma placa começar por ABC.
Soma de probabilidades e espaço amostral
Vamos considerar o experimento aleatório: lançar uma moeda e verificar o resultado em sua face. O espaço amostral desse experimento é o conjunto dos valores possíveis: {cara, coroa}. Vejamos as probabilidades de saírem as faces “cara” e “coroa” no lançamento de uma moeda:
i P(cara ) = 1 2 = 0,50 = 50%
i P(coroa ) = 1 2 = 0,50 = 50%
Qual seria a probabilidade de sair “cara ou coroa” nesse lançamento? Como só existem essas duas possibilidades, trata-se de um evento certo, ou seja, a probabilidade é 100%.
P(cara ou coroa ) = P(cara ) + P(coroa ) = 0,5 + 0,5 = 1
Vamos considerar agora o experimento aleatório: lançar um dado de seis faces e verificar o resultado em sua face superior. O espaço amostral desse experimento é o conjunto {1, 2, 3, 4, 5, 6}. A probabilidade de sair cada uma das faces desse dado é:
Habilidades
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Como são 3 tipos de lanches com salame, de um total de 9 tipos de lanches, a probabilidade é de 3 9 = 1 3 ou 33,3%
Atividade 16
Calcula-se a quantidade de combinações possíveis para todas as placas, sendo 26 possibilidades por letra e 10 possibilidades por número:
26 26 26 10 26 10 10 = 264 103
E qual é a probabilidade de sair “qualquer uma das faces do dado”? Esse é um evento certo, ou seja, sua probabilidade de ocorrer é 100%.
Calcula-se a quantidade de combinações possíveis para placas começadas em ABC, sabendo que, para as três primeiras letras, há somente uma possibilidade de escolha:
1 1? 1? 10? 26? 10? 10 = 26? 103
A soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Atividade 14
O total de senhas possíveis é 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10
As senhas pares possíveis são 10 10 10 10 5
P (pares) = 50 000 100 000 = 1 2 ou 50%
Atividade 15
Proponha que organizem um quadro como este para combinar os ingredientes:
Pão francês Pão de forma Pão integral
Queijo pão francês, queijo pão de forma, queijo pão integral, queijo
Presunto pão francês, presunto pão de forma, presunto pão integral, presunto
Salame pão francês, salame pão de forma, salame pão integral, salame
Para calcular a probabilidade, divide-se a quantidade de combinações possíveis para placas começadas em ABC pela quantidade de combinações possíveis para todas as placas:
Habilidade (EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Atividade 17
a) Considerando que um dado apresenta 6 eventos possíveis (resultados nas faces), a probabilidade de sair 3 é:
P(A) = 1 6
b) Os números pares no dado são: 2, 4 e 6. Então, a probabilidade de obter um número par é:

P(B ) = 3 6 = 1 2
c) Considere que o evento “sair o número 3 ou um número par” tenha este espaço amostral: {2, 3, 4, 6}. A probabilidade de esse evento ocorrer é 4 6 = 2 3
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
ATIVIDADES
17. Considere o experimento: lançamento de um dado com seis faces. Considere também os seguintes eventos:



A = {sair o número 3} B = {sair número par}
a) Calcule P(A).
LEVO NA BAGAGEM
b) Calcule P(B).
Respostas pessoais.
c) Calcule P(A ou B).
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática
• Sabe resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo?
Consegue calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo?
• Reconhece que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1?
▶ Outras disciplinas
Ciências
Reconhece as principais variáveis envolvidas na previsão do tempo e sabe citar exemplos de situações nas quais elas possam ser medidas?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
BARCOS E PORTOS
▶ Organize
Respostas pessoais.
Neste passeio, você explorou conceitos relacionados a fundamentos da contagem e da probabilidade. Faça um resumo dos principais conceitos abordados.
▶ Elabore
A partir das situações-problema exploradas ao longo deste passeio, elabore problemas envolvendo conceitos relacionados à contagem e à probabilidade. Compartilhe com os demais colegas da turma e conversem sobre as estratégias de resolução e as interpretações dadas às situações e aos contextos.

▶ Proponha
A pergunta inicial deste passeio é: Os fenômenos da natureza são aleatórios ou determinísticos? Durante suas expedições pelas ilhas Galápagos, no século XIX, o cientista e naturalista Charles Darwin (1809-1882) notou que diferentes tipos de aves de uma mesma espécie, chamadas de tentilhões, tinham bicos de tamanhos e formatos variados, adaptados a diferentes tipos de alimentação. Essa característica, por sua vez, estava estreitamente relacionada aos diferentes locais, condições e especificidades de cada região das ilhas.
Tentilhão-cantor Tentilhão-dos-cactos
Tentilhão-carpinteiro ou pica-pau
Tentilhão-das-árvores de bico pequeno
Tentilhão-das-árvores de bico grande
Tentilhão-vegetariano
T e n t i l hõesdasárvores
Tentilhão-da-terra de bico agudo
B icos que agarram
iBoc dicerap o
BARCOS E PORTOS
Organize
Peça ao estudante que retome os principais conceitos estudados no decorrer do passeio para que identifique suas dificuldades.
Elabore
Na elaboração dos problemas, podem reler as atividades realizadas e criar uma situação inédita, como a combinação ao ir até o “barbeiro” e escolher um de 3 tipos de corte de cabelo e 4 modos diferentes de aparar a barba, por exemplo.
Na elaboração das situações, fique atento à compreensão dos estudantes quanto a problemas em que a ordem dos elementos selecionados importa (sequências) e quanto àqueles em que a ordem não importa (conjuntos).
Proponha
-cantores
Comem insetos (insetívoros)
TentilhõesTentilhõesd aterra
Comemplantas
cactos
Comem sementes Comem
Bicos exploradores Bicos que esmagam moc o d e agapap o
Tentilhão-da-terra de bico pequeno
Tentilhão-da-terra de bico médio
Tentilhão-da-terra de bico grande
Na Biologia, esse processo recebe o nome de radiação adaptativa, um fenômeno evolutivo caracterizado pela formação de novas espécies ou de características de uma certa espécie em um curto período, a partir da mesma espécie ancestral.
a) Pesquise mais sobre esse assunto e compartilhe com os colegas as informações obtidas.
b) Identifique as aves típicas de sua região. Pesquise sobre elas, observando características físicas e hábitos.
c) Estabeleça relações entre essas características e os hábitos das aves com as particularidades da sua região.
Retome a pergunta inicial do passeio, organize a leitura sobre o processo Radiação adaptativa, proponha a realização da pesquisa e auxilie-os a relacionar as características das aves com as condições da região. Verifique a disponibilidade do professor de Ciências para compartilhar a atividade.
Peça que pesquisem sobre a importância da matemática para a área da biologia e como ela foi utilizada por outras áreas do conhecimento em diferentes momentos históricos para alicerçar descobertas e solucionar problemas científicos.
Habilidade (EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.

CHECK-IN
Proponha aos estudantes que observem as imagens das estações do ano, das fases da Lua e do fenômeno das marés e questione-os: Esses são fenômenos periódicos? Qual é a periodicidade?
a) Observando as imagens das estações do ano, eles perceberão diferentes regularidades (que nos permitem identificar o lugar como o mesmo em todas as fotos), como a disposição ou o distanciamento entre as árvores, que não se altera com as mudanças climáticas ou em decorrência da mudança de estação.
b) Na pesquisa, proponha as questões:
• O que provoca as estações do ano?
• Quais as características de cada estação?
• As datas oficiais correspondem às mudanças climáticas características da estação?
QUAIS FENÔMENOS DA NATUREZA SÃO PERIÓDICOS?
Exemplos de fenômenos periódicos: as quatro estações no hemisfério norte, as fases da Lua no hemisfério sul e uma sequência de ondas sendo quebradas em uma praia.


CHECK-IN
A primeira imagem representa as diferentes estações do ano em uma mesma paisagem. Respostas pessoais.

a) Que tipo de regularidade você pode identificar?
b) Em duplas ou trios, pesquisem mais sobre as estações do ano e como elas ocorrem no local do planeta onde você vive. Compartilhem com os demais colegas.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Identificar a regularidade de uma sequência numérica ou figural não recursiva.
• Identificar a regularidade de uma sequência numérica recursiva.
• Construir um algoritmo, por meio de um fluxograma, que permita indicar os próximos termos em sequências recursivas.
• Construir um algoritmo, por meio de um fluxograma, que permita indicar os próximos termos em sequências não recursivas.
• Explicar, por meio da descrição de modelos, a ocorrência das fases da Lua, com base nas posições relativas entre Sol, Terra e Lua.
Habilidade
(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
Para preparar os estudantes para as atividades apresentadas a seguir, peça que pesquisem sobre os fenômenos periódicos na natureza, exercitando a curiosidade intelectual.
Nesta pesquisa também solicite uma investigação a respeito das relações entre a matemática e as áreas que pesquisaram, buscando gerar segurança nos estudantes para construir e aplicar os conhecimentos matemáticos que serão estudados nesse passeio.
ATMOSFERA
Proponha a leitura coletiva do texto e instigue os estudantes a verbalizar as informações que desconheciam ou consideraram mais relevantes.
Atividades 1 e 2
A realização destas atividades está relacionada ao texto da seção Atmosfera; ao discutir a importância do Sol para a existência humana e a produção agrícola, se considerar adequado, faça relações com o meio ambiente, de modo que os estudantes percebam que o uso da energia solar contribui com a redução de poluição por gases do efeito estufa e diminui o desmatamento.
ATMOSFERA
Como a ciência aprendeu a prever eclipses solares com precisão

As civilizações antigas dependiam tanto do Sol que era preciso calcular com exatidão quando haveria luz solar. Os povos estudavam os ciclos do Sol para saber a época adequada para plantar, preparar-se para o inverno, e planejar cerimônias relacionadas a mudanças de estação. Não é uma surpresa que eles também temessem eclipses solares.
Embora o Sol fosse considerado um deus poderoso ou um herói cósmico em diversas culturas, ele tinha alguns inimigos para combater. Assim, o eclipse representava demônios da escuridão que escondiam o nosso astro. Considerando a importância da estrela para a vida humana e a falta de conhecimento científico, era compreensível imaginar que o eclipse seria um sinal de fúria divina, ou a ação de algum espírito maligno.
Hoje sabemos que eclipses solares acontecem quando a Lua se posiciona entre o Sol e a Terra de maneira a ocultar a estrela total ou parcialmente. Para isso, é necessário que o Sol, a Lua e a Terra estejam alinhados no mesmo plano, o que não acontece sempre que a Lua está entre a estrela e nosso planeta. [...]
Hoje, somos capazes de compreender o movimento de corpos celestes e calcular as forças atuando sobre eles com grande precisão. Temos até mesmo programas de computador com todo esse conhecimento em suas bases de dados, capazes de calcular rapidamente a data de futuros eclipses.
Prever um eclipse é importante sob vários aspectos, e um deles é a divulgação científica. É que este tipo de evento atrai tanto a atenção da população em geral que escolas e divulgadores científicos aproveitam para ensinar como observá-lo corretamente, aproveitando para explicar como funcionam os movimentos dos corpos celestes do Sistema Solar. [...]
Além disso, cientistas usaram e ainda usam eclipses para novas descobertas. Por exemplo, durante o eclipse solar de 16 de agosto de 1868, Joseph Lockyer e Pierre Janssen descobriram, de forma independente, intrigantes sinais de hélio na corona solar. O hélio tornou-se assim o primeiro elemento químico descoberto fora da Terra [...].
CAVALCANTE, Daniele. Como a ciência aprendeu a prever eclipses solares com precisão. Canal Tech, 28 fev. 2020. Disponível em: https://canaltech.com.br/espaco/como-a-ciencia-aprendeu-a-prever-eclipses-solares-comprecisao-160893. Acesso em: 19 ago. 2022.
2. Os eclipses solares ocorrem quando a Lua se posiciona entre o Sol e a Terra de maneira a ocultar a estrela, total ou parcialmente. Para isso, é necessário que o Sol, a Lua e a Terra estejam alinhados.
ATIVIDADES
1. Conforme o texto, por que as civilizações antigas buscavam compreender os ciclos do Sol? Para calcular quando haveria luz solar e, desse modo, saber a época adequada para plantar, preparar-se para o inverno e planejar cerimônias relacionadas a mudanças de estação.
2. Explique, com suas palavras, como ocorre um eclipse solar.
Cena de uma paisagem e uma luneta em um dia de eclipse solar.#Matemática e fenômenos periódicos
A humanidade sempre esteve atenta aos fenômenos da natureza. É possível que os primeiros fenômenos a despertar a curiosidade dos humanos tenham sido aqueles que apresentam uma regularidade ou padrão, ou seja, apresentam eventos que se repetem, que são periódicos ou cíclicos. É o caso do dia e da noite e das estações do ano.
A imagem representa a sucessão de alguns eventos ao longo do dia e da noite:
Habilidade
(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
Encontro com outras disciplinas
A B C D
Sabemos, a partir do que observamos no dia a dia, que essa sucessão de eventos é periódica ou cíclica.
(EF08CI12) Justificar, por meio da construção de modelos e da observação da Lua no céu, a ocorrência das fases da Lua e dos eclipses, com base nas posições relativas entre Sol, Terra e Lua.
LUPAS E LUNETAS
Note que, independentemente da figura que escolhermos para iniciar essa sucessão, sabemos quais são as imagens anteriores e posteriores a ela. Assim, podemos inclusive reorganizar essa sequência de imagens sem que ela perca sua coerência. Por exemplo, observe a sequência iniciando pela imagem E:

Alguns fenômenos periódicos da natureza são os movimentos de rotação e translação da Terra, que têm a periodicidade de um dia (24 horas) e um ano (365 dias mais 5 horas, 48 minutos e 46 segundos), respectivamente, e as fases da Lua, com duração de aproximadamente 28 dias cada uma.
LUPAS E LUNETAS Respostas pessoais.
Que outros fenômenos periódicos ou cíclicos você identifica na natureza? Cite dois exemplos, sendo um deles as fases da Lua. Depois descreva a sequência de eventos desses dois fenômenos e compartilhe com os colegas.


Habilidade
(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.

Encontro com outras disciplinas
(EF08CI12) Justificar, por meio da construção de modelos e da observação da Lua no céu, a ocorrência das fases da Lua e dos eclipses, com base nas posições relativas entre Sol, Terra e Lua.
LUPAS E LUNETAS
Proponha que, na pesquisa, apresentem as 8 fases da lua: lua nova, crescente, quarto crescente, crescente gibosa, lua cheia, minguante gibosa, quarto minguante, minguante e façam os esboços das posições entre a Terra, Lua e Sol em cada fase.

#Sequências
Por causa dos movimentos de rotação da Terra e da Lua e do movimento desses corpos celestes em torno do Sol (translação), podemos identificar no céu noturno que a aparência da Lua muda todas as noites, ou seja, a Lua passa por diversas fases ao longo de um mês:
A palavra “gibosa” significa que tem giba, ou seja, tem forma convexa. Refere-se à fase de transição da Lua Crescente para a Cheia e da Cheia para a Minguante.
LUPAS E LUNETAS Respostas pessoais.
Sabemos que a Lua não emite luz própria. Por que, então, podemos vê-la no céu e identificar as suas fases? Em duplas ou trios, pesquisem respostas para essa questão. Procurem também explicar por que tais fases ocorrem.
Inspirados nas fases da Lua, vamos considerar a sucessão de figuras:
É possível identificar uma regularidade nessa sequência de figuras. Dessa maneira, sabemos que as próximas figuras dessa sucessão serão:
Matematicamente, podemos descrever essa sucessão de figuras como uma sequência Vamos relembrar a definição de sequência:
Uma sequência é um conjunto de elementos dispostos em uma determinada ordem. Chamamos cada um dos elementos de uma sequência de termo da sequência e, de maneira geral, representamos uma sequência por:
Podemos descrever a sequência figural anterior como:
Note que cada termo dessa sequência se repete a cada quatro termos, ou figuras. Ou seja:
Sugestão de atividade
Converse com o professor de Ciências para realizarem uma atividade interdisciplinar sobre os movimentos da Lua em relação à Terra e ao Sol. Organize os estudantes em grupos para que façam uma maquete que represente os movimentos da Lua – de rotação, revolução e translação – e para que percebam as diferentes fases da Lua.
Podem consultar vídeos na internet com o passo a passo para usarem como inspiração e construírem suas maquetes. Esta atividade contempla a
habilidade de Ciências EF08CI12. Os estudantes podem explicar oralmente a ocorrência de cada fase da Lua e dos eclipses demonstrando que compreenderam os conceitos.
LUPAS E LUNETAS
a) Represente essa sequência até o 15o termo.
Note que essa é uma sequência infinita, ou seja, as figuras se repetirão infinitamente seguindo a mesma regularidade. Existem também sequências finitas, ou seja, que têm um número finito de termos.
b) Elabore uma sequência finita de 5 termos. Compartilhe com os colegas e proponha que eles identifiquem a regularidade da sequência que você elaborou. Respostas pessoais.
Observe que, para obter os termos dessa sequência, utilizamos uma regra: “cada termo dessa sequência se repete a cada quatro termos”. Denominamos regras como essa de lei de formação da sequência
Sequências recursivas
Considere a situação hipotética a seguir. Uma pessoa tem um casal de coelhos recém-nascidos. Eles levam certo tempo para atingir a maturidade e procriar. Esse casal de coelhos produz então, ao final de cada período, um novo casal de coelhos. Após passar o tempo até a maturidade, esse novo casal produz um novo casal (e o casal anterior também produz outro). Veja um esquema com a quantidade de casais de coelhos após cada período:
Habilidade
(EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
LUPAS E LUNETAS
A sequência elaborada pelos estudantes no item b pode ser de figuras ou numérica. Proponha a socialização das sequências e peça que os colegas observem a lei de formação dessas (se houver). Em seguida, proponha a realização da atividade em pequenos grupos. Elaborar sequências pelos estudantes estimula o levantamento de hipóteses sobre as regras que as formam. Discutir essas regras é importante para perceber como os estudantes conseguem verbalizar e abstrair as leis que formam essas sequências. Para avaliar se eles conseguem identificar as regularidades, pergunte-lhes quais seriam os próximos termos das sequências elaboradas, se quisessem aumentá-la para 10 termos.
Assim:
• No início, havia 1 casal de coelhos filhotes.
• Ao fim de 1 período, havia 1 casal de coelhos maduros.
• Ao fim de 2 períodos, havia 1 casal de coelhos maduros e 1 de filhotes, ou seja, 2 casais
• Ao fim de 3 períodos, havia 2 casais de coelhos maduros e 1 de filhotes, ou seja, 3 casais
• Ao fim de 4 períodos, havia 3 casais de coelhos maduros e 2 de filhotes, ou seja, 5 casais

AFRICA STUDIO/ SHUTTERSTOCK
Habilidade
(EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
LUPAS E LUNETAS
a) Observe alguns exemplos que poderão ser apresentados pelos estudantes:
Podemos notar que a quantidade de casais de coelhos ao final de cada período corresponde à soma da quantidade de casais ao final dos dois períodos anteriores. Por exemplo: ao final do 4º período, a quantidade de casais é 5 = 3 + 2, que é a soma das quantidades de casais dos dois períodos anteriores.
Escrevendo uma sequência com as quantidades de casais de coelhos ao final de cada período, temos:
Podemos então identificar que a lei de formação dessa sequência é descrita por:
Desse modo, obtemos os próximos termos dessa sequência adicionando os dois termos anteriores:
E assim por diante.
Nesse caso, notamos que os próximos termos da sequência dependem dos termos anteriores.
Uma sequência na qual os termos seguintes podem ser calculados a partir dos termos anteriores é denominada recursiva
As espirais na concha do mar.
LUPAS E LUNETAS
Esse problema foi apresentado pelo matemático italiano conhecido como Fibonacci, no início do século XIII. Essa sequência ficou conhecida como sequência de Fibonacci, embora ela já tivesse sido descrita por gregos e indianos. Uma curiosidade é que a partir dessa sequência é possível construir uma espiral que pode ser observada em diversas situações na natureza.

A razão áurea no miolo da flor.
A razão áurea na natureza: a espiral na planta e na concha do Nautilus.



a) Pesquise sobre as relações entre a natureza e a sequência de Fibonacci.
• Compartilhe com os colegas.
b) Crie uma sequência recursiva, explicitando sua lei de formação, e compartilhe com os demais colegas.
Fluxogramas e sequências recursivas

Considere a sequência recursiva infinita: (1, 3, 7, 15 )
Nesse caso, com exceção do 1o termo, os seguintes são obtidos multiplicando o termo anterior por 2 e adicionando 1. Ou seja, a lei de formação dessa sequência pode ser escrita como:
Podemos elaborar um fluxograma para representar um algoritmo que obtém os termos dessa sequência após o 2o termo:
Habilidade (EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
Note que o fluxograma apresenta um “laço”, uma recursão ou looping
LUPAS E LUNETAS
Utilize esse algoritmo para obter os próximos três termos daquela sequência. 31, 63, 127
Vamos considerar agora uma sequência de números naturais cujo termo inicial é 10 e cada termo seguinte corresponde ao termo anterior subtraído de 2.
Assim, podemos descrever sua lei de formação:
os termos da sequência devem ser números naturais, eles não podem ser menores do que zero:
Se n = 7, então a7 = a6 – 2 = 0 – 2 = –2, o que não pode ocorrer, pois os termos da sequência devem ser números naturais. Assim, essa sequência é recursiva e finita:
8, 6, 4, 2, 0)
Proponha que utilizem um quadro para organizar as informações do fluxograma: Multiplique por 2
Habilidade (EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
Atividade 3
Caso perceba dificuldade por grande parte dos estudantes, proponha que usem uma lista para organizar os elementos:
a) Subtrair 1 do elemento anterior a1 → 1
a2 → (1 1) = 0
a3 → (0 1) = 1
b) Multiplicar o elemento anterior por 10 a1 → 1
a2 → 1 1 0 = 10
a3 → 10 1 0 = 1 00
c) Adicionar o elemento anterior ao número que indica a posição (índice) a1 → 1

a2 → (1 + 2) = 3
a3 → (3 + 3) = 6
d) Adicionar ao dobro da última posição, o triplo da penúltima posição a1 → 1 a2 → 2
a3 → (2 2 + 3 1) = 7
Atividade 4
Considerando o fluxograma:
Podemos elaborar um fluxograma para representar um algoritmo que obtém os termos dessa sequência após o 2º termo:
Note que esse fluxograma também apresenta um “laço”, uma recursão ou looping, mas há uma condição de parada.
ATIVIDADES
3. Considere estas leis de formação e obtenha, a partir delas, os três primeiros termos de cada sequência (n ∈ |N, n ≥ 2, ou seja, n = 2, 3, ):
4. O fluxograma representa um algoritmo para calcular os próximos termos de uma sequência recursiva:
a) A sequência obtida a partir desse algoritmo é finita ou infinita? Por quê?
b) Obtenha todos os termos dessa sequência. (0, 1, 3, 7)
Adicione 1
Seja a1 = 0 Multiplique por 2 É menor que 12?
Parar algoritmo
Esse é o próximo termo da sequência
5. Em duplas ou trios, escrevam uma sequência recursiva, explicitando sua lei de formação. Em seguida, desenhem um fluxograma para representar um algoritmo que calcule seus termos.

• Compartilhem com os demais colegas.
Multiplique por 2
Adicione 1 É menor que 12?
Esse é o próximo termo da sequência
a) É finita, pois assim que um termo iguala ou ultrapassa 12, o algoritmo para. Respostas pessoais.
Atividade 5
O pensamento computacional está relacionado ao uso do fluxograma na representação da sequência recursiva. Organize a exposição das sequências e seus respectivos fluxogramas na sala de aula.
Sequências não recursivas
Ao plantar algumas flores, um agricultor semeou a terra com espaços iguais, porém em dias distintos. Desse modo, as flores também brotaram em dias diferentes:
Habilidade (EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
CONVÍVIO E BEM-ESTAR SOCIAL
Assim, o total de flores a cada dia pode ser descrito por:
• dia 1: 1 flor;
• dia 2: 4 flores;
• dia 3: 9 flores;
• dia 4: 16 flores.
Note que esses valores correspondem a quadrados perfeitos: 1 = 12 ; 4 = 22 ; 9 = 32 ; 16 = 42
Escrevendo uma sequência com a quantidade de flores dia após dia, temos: (12 , 22 , 32 , 42 )


E podemos escrever a lei de formação dessa sequência: a n = n2 , sendo n = 1, 2, 3, 4
LUPAS E LUNETAS
Suponha que essa lei de formação se mantenha e que nenhuma flor morra. Qual seria a quantidade de flores no 10o dia? 102 = 100 flores
Superfície aquática com nenúfares.
LUPAS E LUNETAS
Observe que essa sequência é a dos quadrados dos números naturais não nulos (quadrados perfeitos) e cada termo pode ser calculado conhecendo-se sua posição na sequência. Desse modo:
a10 = 102 = 100 flores
Caso grande parte dos estudantes tenha dificuldade em compreender essa sequência, proponha que representem os termos em malha quadriculada, sendo cada flor representada por um quadradinho da malha.
Verifique com a gestão escolar se, na escola, há algum espaço que possa ser destinado ao plantio de um jardim. Proponha parceria com o professor de Ciências para que essa atividade seja interdisciplinar, com os estudantes participando ativamente do planejamento e da construção desse espaço que pode ter formas geométricas em seu design. Pesquisem as flores que se adaptariam melhor ao local, verifique se recebe sol intenso ou sombra e se há disponibilidade de água para facilitar a rega das plantas. Organize os estudantes em grupos para realizarem a manutenção, uma vez por semana, retirando folhas e galhos secos e ervas daninhas que possam ter surgido e, depois, molhando as plantas e flores. Se possível, coloquem bancos para que seja um espaço de convívio dos estudantes. Registre os momentos de planejamento, preparação e colocação das plantas e, quando finalizarem, exponham no mural da escola como foi todo o processo de construção usando fotos e cartazes confeccionados pelos estudantes.
67 | NÃO ESCREVA NO SEU LIVRO.Habilidade (EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
LUPAS E LUNETAS
No momento da escrita da lei de formação das sequências não recursivas, proponha que o estudante construa um quadro e observe qual é a variável, qual é o número substituído a cada posição e substitua-o na variável.
• Sequência dos números naturais ímpares.
Podemos obter cada termo dessa sequência por meio de um algoritmo:
Diferentemente das sequências recursivas, nesse caso não é necessário saber o termo anterior para calcular o próximo termo dessa sequência.
Uma sequência na qual os termos seguintes não dependem dos termos anteriores é denominada não recursiva
Veja outros exemplos de sequências não recursivas:
• sequência dos números ímpares: (1, 3, 5 );
• sequência dos múltiplos negativos de 5: (–5, –10, –15 );
• sequência das frações unitárias com denominadores naturais maiores do que
LUPAS E LUNETAS
Escreva uma lei de formação para cada sequência não recursiva dos exemplos anteriores.
• Compartilhe com os colegas.
ATIVIDADES
6. Considere as leis de formação e obtenha, a partir delas, os três primeiros termos de cada sequência:
a) a n = n + 2, sendo n = 1, 2, 3 (3, 4, 5)
b) a n = 3n – 1, sendo n = 1, 2, 3 (2, 5, 8)
c)
7. Observe cada sequência e identifique sua lei de formação.
a) (1, 2, 3, 4...)
b) (2, 4, 6, 8...)
c) (1, 3, 5, 7...)
d) (–3, –6, –9, –12 )
8. Elabore uma sequência não recursiva, explicitando sua lei de formação. Respostas pessoais.
• Compartilhe com os demais colegas.
Fluxogramas e sequências não recursivas
1 5 1 5
2 5 2 –10 a3 5 3 –15
4 5 4 –20 a5 5 5 –25
Ao escrever a lei de formação, temos: a n = 5n n ∈ N* ; a n = 5n n ∈ N*

• Sequência das frações unitárias com denominadores naturais maiores do que 1.
Considere a sequência dos números múltiplos de 10, a partir de 10: ( 10 a1 ! , 20 a2 ! , 30 a3 ! ) Podemos verificar que:
Portanto, é possível afirmar que:
O fluxograma representa um algoritmo para obter os termos de uma sequência infinita de múltiplos de 10 a partir de um número. Lembrando que, para ser múltiplo de 10, o número precisa ser múltiplo de 2 e de 5, simultaneamente.
Habilidade (EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
Atividades 7 e 8
Nesse algoritmo, escolhe-se um número. Verifica-se se ele é múltiplo de 10; se não for, utiliza-se seu sucessor. Verifica-se novamente se é múltiplo de 10. E assim sucessivamente, até que se obtenha um número que é múltiplo de 10. Então esse número torna-se um termo da sequência e utiliza-se o sucessor desse número para reiniciar todo o processo.
LUPAS E LUNETAS
Para que os estudantes façam a atividade 7 com autonomia, proponha que observem a posição do elemento na sequência e como o próximo elemento é formado. Podem comparar a atividade com os colegas.
Atividade 9
a) Escolha um número qualquer e siga esse algoritmo até obter pelo menos dois termos da sequência.
b) Esse não é o único fluxograma que permite obter termos dessa sequência. Em duplas ou trios, elaborem um fluxograma diferente. Resposta pessoal.
ATIVIDADES
9. Observe o fluxograma:
a) Que tipo de número será guardado na etapa “guarde esse número”? Múltiplos inteiros de 5.
b) Escolhendo números 1, 2, 3, 4..., nessa ordem, descreva os quatro primeiros termos de uma sequência formada pelos três números “guardados”. 5, 10, 15.
10. Observe a lei de formação de uma sequência: a n = 2 n + 3, sendo n = 1, 2, 3, 4

Elabore um fluxograma para obter o próximo termo dessa sequência.
LUPAS E LUNETAS
a) 10, 20. Sugestão:
a) Note que a escolha inicial é de um número inteiro qualquer. Portanto, o fluxograma pode selecionar múltiplos inteiros de 5.
b) Estes são os primeiros múltiplos naturais não nulos de 5:
Número escolhido Divisão por 5
1 Não exata
2 Não exata
3 Não exata
4 Não exata
Guardar o número
5 Exata 5
6 Não exata
7 Não exata
8 Não exata
9 Não exata
10 Exata 10
11 Não exata
12 Não exata
13 Não exata
14 Não exata
15 Exata 15
Múltiplo de 2 Múltiplo de 5 Próximo termo da sequência 2 Sim Não 3 Não Não 4 Sim Não 5 Não Não 6 Sim Não 7 Não Não 8 Sim Não 9 Não Não 10 Sim Sim 10 11 Não Não 19 Não Não 20 Sim Sim 20

Esse é o próximo termo da sequência.
69 |
Habilidade (EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
Atividade 10
Considerando n um número natural não nulo, temos aqui uma etapa que será repetida reiteradas vezes para gerar a sequência: Escolha o número n Multiplique n por 2 Adicione 3 ao resultado anterior Esse é o próximo termo da sequência

TRAVESSIAS
Sequências e fluxogramas
Você já reparou que, em certos anos, o mês de fevereiro tem 28 dias e, em outros, tem 29 dias? Por que isso ocorre?
Da observação das regularidades do planeta Terra, por exemplo, a periodicidade de dias e noites e das estações do ano, foi elaborado um calendário que considerava que um ano correspondia a 365 dias. Ou seja, o planeta Terra leva 365 dias para completar uma volta completa ao redor do Sol.
No entanto, esse número não é preciso, uma vez que se descobriu
ATIVIDADES
11. Em duplas ou trios, responda:
que a Terra leva, na verdade, 365,2425 dias para dar a volta completa ao redor do Sol. Esse pequeno erro foi corrigido pela criação do calendário gregoriano, em 1582. Nesse calendário, alguns anos teriam 1 dia a mais para compensar o erro de 0,2425 dias no cálculo de um ano. Esses anos são denominados anos bissextos.
Para saber quais anos deveriam ser bissextos, foram estipuladas algumas regras. Um ano é bissexto se:
• for divisível por 4, mas não por 100;
• for divisível por 400.
a) Considere o ano atual. Ele é bissexto? Resposta conforme o ano corrente.
b) Qual será o próximo ano bissexto? Resposta conforme o ano corrente.
c) Verifique se estes anos são (ou foram) ou não bissextos:
• 2100 Não.
• 1996 Sim. Podemos construir um fluxograma para verificar se certo ano é bissexto:
• 2000 Sim.
d) Em duplas ou trios, elaborem um fluxograma para gerar a sequência de anos bissextos a partir de determinado ano. Resposta pessoal.
e) Utilizem esse fluxograma para obter a sequência dos próximos 2 anos bissextos a partir do ano atual. Resposta conforme o ano corrente.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática


• Consegue identificar a regularidade de uma sequência numérica ou figural não recursiva?
• Identifica a regularidade de uma sequência numérica recursiva?
• Sabe construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências recursivas?
• Sabe construir um algoritmo por meio de um fluxograma que permita indicar os próximos termos em sequências não recursivas?
▶ Outras disciplinas
Ciências
• Consegue explicar, por meio da descrição de modelos, a ocorrência das fases da Lua, com base nas posições relativas entre Sol, Terra e Lua?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
TRAVESSIAS
Atividade 11
Na resolução dessa atividade, os estudantes precisam retomar o critério de divisibilidade por 4 e usar outras regras: ser divisível por 400 (e, consequentemente, por 4 e por 100 ao mesmo tempo) para a construção do fluxograma.
A sequência dos anos bissextos é:
(…2000, 2004, 2008, 2012, 2016, 2020, 2024, 2028, 2032, 2036...)


Início
Leia (ano)
MATEMÁTICA OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
Ano divisível por 4? Sim Sim
Não Escreva “Não é bissexto.”
Não Escreva “É bissexto.”
Não
Ano divisível por 400?
Ano divisível por 100? Sim
Escreva “É bissexto.”
Escreva “Não é bissexto.”
Fim
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
BARCOS E PORTOS
Organize
O mapa da seção Arredores pode ser retomado para auxiliar os estudantes na elaboração de seus resumos.
Elabore
Comente com os estudantes que a sequência do item a está expressa por uma lei de formação não recursiva: obtemos um termo a partir da posição em que ocupa na sequência. Tratase da sequência do cubo dos números naturais não nulos.
Verbalizar a lei de formação da sequência contribui para a compreensão da representação algébrica e a elaboração do algoritmo/fluxograma.
A sequência do item b está expressa por uma lei de formação recursiva: obtemos o próximo termo (a partir do segundo) recorrendo ao termo anterior na sequência. Trata-se da sequência dos múltiplos naturais de 5. Verbalizar a lei de formação da sequência contribui para a compreensão de que se trata de uma recursão. Solicite aos estudantes uma lei de formação para essa sequência que não seja recursiva (a n = 5n 5, n ∈ N*, por exemplo).
Proponha
Retome a questão inicial deste passeio: Quais fenômenos da natureza são periódicos? Depois, solicite que comentem sobre suas descobertas diante dos fenômenos periódicos.
▶ Organize
Respostas pessoais.
Neste passeio, você explorou as noções de sequências recursivas ou não recursivas, além de interpretar e criar algoritmos, em forma de fluxograma, para calcular os próximos elementos das sequências. Faça um resumo dos principais tópicos desses assuntos.
▶ Elabore
Estão apresentadas duas leis de formação de sequências. Para cada uma delas, elabore um algoritmo, em forma de fluxograma, que calcule seus termos.
Respostas pessoais.
a) a n = n3 , sendo n = 1, 2, 3
b) a n = a n–1 + 5, em que a1 = 0 e n = 2, 3
▶ Proponha
A pergunta inicial deste passeio é: Quais fenômenos da natureza são periódicos?
Ao longo deste passeio você explorou diversas situações relacionadas a fenômenos periódicos da natureza.
a) Faça uma lista dessas situações.
b) Com suas palavras, explique cada fenômeno da lista. Se necessário, consulte livros, a internet, colegas ou professores para compreender melhor esses fenômenos. Um dos fenômenos mais simples de se observar é o movimento aparente do Sol no céu, ao longo do dia. Vamos observar a posição do Sol no céu e as sombras formadas por objetos de seu cotidiano.
a) Escolha um ou mais locais com bastante incidência de raios solares.
b) Anote as horas e verifique as sombras projetadas por objetos ou estruturas do local (se possível, fotografe as sombras, sempre de uma mesma posição). Repita esse procedimento a cada hora.
c) Escreva um texto descrevendo as suas observações e algumas conclusões que você obteve a partir delas.
Proponha que observem a sombra de algum objeto a cada hora no decorrer de um dia e registrem a medida. Organize uma roda de conversa para discutirem os resultados desse experimento. Atividade 1
• Proponha uma roda de conversa com os colegas e apresente as observações que você realizou e as conclusões a que você chegou.
Atividade 2

Para resolver cálculos de porcentagem, os estudantes podem usar várias estratégias, dentre elas: calcular a redução de 5% e subtrair ou multiplicar pela porcentagem “complementar” na forma decimal (0,95 42 000 = 39 900); com a redução, o carro passa a custar R$ 39.900,00, e com o aumento de 2% (1,02 ⋅ 39 900 = 40 698), seu valor final é de R$ 40.698,00.
O estudante pode usar seu conhecimento para escrever a fração geratriz de cada dízima periódica e realizar os cálculos:
Você chegou ao final da Trajetória. Reflita sobre tudo o que aprendeu e verifique a qualidade da sua aprendizagem. Resolva todos os exercícios no caderno.
CHECK-OUT
1. Um automóvel que custava R$ 42.000,00 sofreu uma redução de 5% e, em seguida, um aumento de 2%. Determine o preço final do automóvel. R$ 40.698,00

5. O volume de uma caixa-d’água de forma cúbica é de 16 m3. Calcule a medida da aresta da caixa.
VISTORIAS
Habilidades
EF08MA01, EF08MA02, EF08MA03, EF08MA04, EF08MA05, EF08MA10, EF08MA11, EF08MA22
ser calculada por 24 3 = 2 4 3 m Com o auxílio de uma calculadora científica (do celular ou do computador, usando a tecla xy , é possível aproximar esse valor para 2,5 m.
Atividade 6
6. A bandeira de um clube tem quatro listras verticais. Quantas são as possibilidades de colori-la sabendo que se dispõe de 7 cores e não se deseja pintar duas listras consecutivas com a mesma cor?
2. Em uma prova de concurso, havia uma questão que pedia o resultado de (0,666 + 0,454545 ) ÷ 0,090909 Encontre o resultado dessa conta.
3. Calcule: 20 +
4. A massa da Terra é de cerca de 6 000 000 000 000 000 000 000 000 kg e do Sol é em torno de 2 000 000 000 000 000 000 000 000 000 000 kg. Quantas vezes, aproximadamente, a massa do Sol é maior que a da Terra?







7. Ao lançar dois dados honestos, um azul e um vermelho, qual é a probabilidade:


a) de se obter um número par no dado azul e um número ímpar no dado vermelho?
b) de não se obter par no dado azul ou não se obter ímpar no dado vermelho?
Pode-se usar o princípio multiplicativo. Na escolha da cor da 1a listra, todas as cores podem ser usadas; para que não ocorra listras consecutivas com a mesma cor, ao escolher a 2a cor, a anterior deve ser excluída, e assim sucessivamente. Com isso, as possibilidades são: 7 ⋅ 6 ⋅ 6 ⋅ 6 = 1 512 possibilidades.
Atividade 7
8. Escreva ou desenhe os próximos três termos das sequências:
9. Dadas as sequências:
a) Os quatro primeiros termos da 1ª sequência e os próximos quatro termos na 2a sequência.
A probabilidade de ocorrência de um número par é 3 6 = 1 2 e a de um número ímpar é 3 6 = 1 2 A probabilidade de sair par em um dado e ímpar em outro é 1 2 1 2 = 1 4
Atividade 8
a) Temos que cada termo a n (n ≥ 2) pode ser calculado fazendo 3 (n – 1) Assim, 3 (2 – 1) = 3, 3(3 – 1) = 6, 3(4
Atividade 3
Observe se o estudante conhece as propriedades da potenciação e efetua cálculos de potências com expoentes inteiros:
b) Para cada uma, construa um fluxograma que permita determinar seus termos.
a) Primeira sequência: 0, 1, 3, 7; segunda sequência: 1, –1, 0, 1.
b) Respostas pessoais. 73 |
–
=
–
=
–
=
e
–
=
Atividade 4
Utilizando notação científica, a massa da Terra é 6 1024 kg, a massa do Sol é 2 1030 kg Usando as propriedades da potenciação, temos 2 1030 6 1024 = 1 3 106 ≅ 3,3 105 , ou seja, o Sol é, aproximadamente, 330 000 vezes maior que a Terra.
Atividade 5
Essa atividade relaciona raiz com potência de expoente fracionário. Como o volume pode ser representado por 16 = 24 , sabemos que a aresta pode
b) A sequência de figuras apresenta quatro termos que se repetem, |, /, –, \. Como a última imagem é |, a sequência deve apresentar estes próximos termos: /, –, \.
Atividade 9
a) Os termos da 1a sequência são determinados pela adição entre o dobro do termo antecessor e uma unidade:
• a1 = 0;
• a2 = 2 0 + 1 = 1;
• a3 = 2 ⋅ 1 + 1 = 3;
• a4 = 2 3 + 1 = 7 ou seja, os termos são: 0, 1, 3, 7.
Os termos da 2a sequência apenas se repetem (a cada três): 1, –1, 0, 1
b) Fluxograma para a 1a sequência:
Considere o 1o termo da sequência
Multiplique por 2
Adicione 1
O resultado é o próximo termo da sequência
Fluxograma para a 2 a sequência (sendo n a posição de um termo):
Divida n por 3
Escolha n = 3
Se o resto da divisão é 1, o termo é 1
Se o resto da divisão é 2, o termo é –1
Se o resto da divisão é 0, o termo é 0
DE OLHO NA BÚSSOLA
Após resolver os exercícios da seção Check-out, você pôde checar se de fato aprendeu a:
Tome o sucessor de n
Acompanhe o resultado do Check-out e verifique quais objetivos do quadro De olho na bússola os estudantes atingiram. Os resultados positivos demonstram que você conseguiu desenvolver as habilidades associadas e os negativos podem ser utilizados como um parâmetro para que verifique para quais assuntos podem ser retomados os estudos e a compreensão dos conceitos envolvidos.
Considerando os exercícios que você resolveu, como julga seu desempenho: insuficiente, parcialmente suficiente, satisfatório, plenamente satisfatório?
Prossiga ▶
Continue estudando! Retome esta Trajetória buscando, com professores e colegas, alternativas para superar os obstáculos de sua aprendizagem. Estude a seção Retornos e resolva novos exercícios referentes à Trajetória 1 que estão na seção Suplemente sua aprendizagem, ao final do livro.
Respostas pessoais. 74 |
Você tem o hábito de organizar seus materiais, o espaço e o tempo de estudo?
Dicas de estudo
O estudo percorre todo o processo de ensino aprendizagem dos estudantes. Em diversos outros momentos, pudemos avaliar o desempenho a cada conceito trabalhado. Novamente, aproveitamos este momento de reflexão para analisar quais estratégias os estudantes usaram para organizar o tempo e a rotina de estudos, seguindo a atividade proposta nesta seção. Motive-os a replanejar suas atitudes para um melhor desempenho posteriormente.
Materiais escolares e outros objetos típicos de estudante.

Caso não tenha, que tal buscar maneiras que o ajudem a desenvolver bons hábitos de estudo fora da sala de aula? Para começar, você pode refletir sobre como são atualmente suas atitudes e comportamentos para com seus estudos. Leia cada pergunta e busque para si mesmo respostas que sejam verdadeiras
a) Seus materiais (cadernos, livros, portfólios, trabalhos etc.) estão sempre atualizados, organizados e acessíveis para consultas imediatas?
b) Você realiza todas as atividades propostas e procura eliminar as dúvidas imediatamente?
c) O local do seu estudo é tranquilo, iluminado, arejado e o estimula à concentração?
d) Você reserva um tempo todos os dias, em um mesmo horário, para estudar, ainda que não tenha lição de casa?
e) Considerando as respostas anteriores, o que você julga urgente e necessário ser mudado nas suas atitudes em relação aos estudos? Tome nota de quais recursos e quais novas atitudes podem melhorar seus hábitos de estudo e teste-os nos próximos dias.
TRAJETÓRIA 2
PANORAMA DA TRAJETÓRIA
Competências gerais: 7, 9, 10
Competências específicas: 2, 7, 8
Habilidades de Matemática:
EF08MA06, EF08MA07, EF08MA08, EF08MA09
Habilidades de outras
disciplinas:
Língua Portuguesa:
EF69LP15, EF89LP04
Geografia: EF08GE15, EF08GE16
Temas Contemporâneos
Transversais: Cidadania e Civismo
Sugestão de atividade
Para esta segunda Trajetória, antecipadamente, solicite aos estudantes que levem para a aula pesquisas realizadas em fontes diversas a respeito de dois temas: relações sociais e ambiente urbano. No dia previsto para a aula, forme uma grande roda e, com base nas pesquisas que fizeram, proponha que conversem a respeito do seguinte questionamento: Como se desenvolvem as diferentes relações sociais no ambiente urbano?
Explore com os estudantes, especialmente, os termos equidade e igualdade. E, se ainda for necessário, encaminhe novas pesquisas a respeito desses outros dois termos. A palavra igualdade deve ser explorada em seus diferentes significados, matemáticos ou não. Até porque um problema, quando despertado no mundo real, não é identificado como um problema de Matemática ou um problema de Sociologia, mas simplesmente se coloca como um problema. Seu aspecto no mundo real é “mesclado”, necessitando de recursos, ferramentas e processos de várias áreas do conhecimento. Ainda que a maioria de seus aspectos não sejam aprofundados, a compreensão mínima de cada um deles certamente trará novas “tonalidades” à compreensão do problema como um todo.
As questões envolvendo os fenômenos naturais ou sociais demandam variados processos da ciência e do saber que levam aqueles com desejos de descobertas a explorar diversos métodos científicos, buscar relações de causa e efeito, utilizar raciocínios de indução e dedução, formular argumentações etc. Nesse processo abrangente, não faz sentido classificar se aquilo que o estudante conheceu, descobriu, aprendeu é mérito da Matemática ou de outra área do conhecimento. Quem poderá retirar ou invalidar o ganho que teve o estudante por meio dos caminhos investigativos?
COMO SE DESENVOLVEM AS DIFERENTES RELAÇÕES SOCIAIS NO AMBIENTE URBANO?
• Como criar relações de igualdade e de equidade no convívio social?

• Quais relações existem entre os diferentes atores da sociedade?

• Como lidar com diferentes recursos disponíveis no ambiente urbano?
Por essa razão, os trabalhos desenvolvidos em parceria com professores de diferentes disciplinas e, no caso desta Trajetória, especialmente com professores de Ciências Humanas e Sociais, tem um valor inestimável na formação global do estudante. Esta Trajetória é uma excelente oportunidade para que, em vez de fechar, possam se abrir horizontes de pensamento e modos de conhecer dos estudantes.
Praia de Copacabana na cidade do Rio de Janeiro. Ponte Octávio Frias de Oliveira é uma ponte estaiada, na cidade de São Paulo.

O espaço urbano é rico e diversificado em possibilidades de relações sociais. As práticas dos seus habitantes transformam não apenas o espaço mas também as formas de se relacionarem entre si.
LUPAS E LUNETAS Respostas pessoais.
Reflita sobre as questões expostas no início desta Trajetória e considere-as para elaborar outras perguntas de sua própria autoria.
Publique suas perguntas no mural da sala e aprecie as perguntas dos colegas.
CONTEÚDOS DA TRAJETÓRIA
Passeio 1 – Expressões algébricas
• Expressões algébricas fracionárias
• Valor numérico
• Polinômios
• Monômios, binômios, trinômios
• Operações com polinômios
Passeio 2 – Equações de 1o grau com duas incógnitas e sistemas lineares

• Equações polinomiais de 1o grau
• Equações polinomiais de 1o grau com duas incógnitas
• Equações com duas incógnitas no plano cartesiano
• Resoluções de sistemas de equações
• Método da substituição
• Método da adição
Passeio 3 – Equações polinomiais de 2o grau
• Análise de situações-problema
• Área da superfície de quadrados e retângulos
• Equações polinomiais de 2o grau
LUPAS E LUNETAS
Neste momento da Trajetória, procure motivar os estudantes em torno das questões norteadoras: certifique-se de que compreenderam as questões e se apropriaram delas, além de agregar novas questões ao percurso que se inicia.
77 | NÃO ESCREVA NO SEU LIVRO.Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Encontro com outras disciplinas
(EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
CHECK-IN
A discussão sobre igualdade e equidade permite que o estudante elabore reflexões sobre o Tema Contemporâneo Transversal (TCT) Cidadania e Civismo nas relações familiares e sociais. Discutindo esses termos, eles podem relatar suas vivências e fazer uma reflexão crítica diante dos significados de equidade ou igualdade, com uma postura respeitosa e ética que compreenda as diferenças e, por respeitá-las, podem elaborar estratégias para que outras pessoas possam atingir os mesmos objetivos.
Nas discussões sobre igualdade e equidade, crie um ambiente no qual o estudante consiga verbalizar situações em que percebeu que, tendo as mesmas condições de outras pessoas, não conseguiu atingir o mesmo objetivo. Diante das vivências apresentadas faça perguntas para expressarem como compreendem equidade e igualdade. Ainda entrelace o debate com os conteúdos matemáticos: a ideia de igualdade pode ser atrelada às equações de 1 o grau (como 2x + 3 = 11) ou a expressões numéricas (como 2 + 5 3 = 17)

CHECK-IN
COMO CRIAR RELAÇÕES DE IGUALDADE E DE EQUIDADE NO CONVÍVIO SOCIAL?
Em duplas ou trios, observem a figura e respondam às questões: Respostas pessoais.
a) Notaram os tamanhos dos caixotes sobre os quais as pessoas estão? Converse com os colegas sobre como essa representação pode ser utilizada para compreender as noções de equidade e igualdade

b) Elaborem, com suas palavras, uma interpretação para as noções de equidade e igualdade
c) Na Matemática, que significados são possíveis atribuir à ideia de igualdade? Dê alguns exemplos.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Identificar situações-problema que possam ser descritas por expressões algébricas.
• Resolver e elaborar problemas que envolvam o cálculo do valor numérico de expressões algébricas.
• Compreender a noção de polinômio.
• Utilizar as propriedades das operações para resolver cálculos envolvendo adição, subtração, multiplicação e divisão de polinômios.
• Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala na participação em discussões sobre temas controversos ou polêmicos.
Encontro com outras disciplinas (EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
ATMOSFERA
Atividades 1 e 2
Organize a leitura coletiva do texto para que compreendam as diferenças entre igualdade e equidade. Segundo o texto, igualdade significa que todos têm os mesmo direitos e deveres enquanto equidade relaciona a igualdade com justiça social para equilibrar as diferenças.
Sugestão de atividade Após a discussão sobre igualdade e equidade peça aos estudantes que pensem sobre as atividades da rotina escolar e analisar se há pessoas que enfrentam dificuldades para realizá-las. Questione quais são as dificuldades e incentive-os a pensar em propostas para que essas pessoas sejam tratadas com equidade. Caso não identifiquem as dificuldades na escola, ampliem a discussão para as pessoas da família ou da comunidade.
A intenção desta atividade é promover a argumentação de forma respeitosa, contemplando a habilidade de Língua Portuguesa EF69LP15
CONVÍVIO E BEM-ESTAR SOCIAL
Procure informações sobre um grupo de voluntariado que considere interessante. Para que os estudantes conheçam o trabalho que realizam, organize uma visita ou uma roda de conversa com as pessoas que participam do grupo sobre o projeto. Ao final, oriente que registrem em papéis coloridos suas reflexões ou apontem o que consideraram mais
Qual a diferença entre igualdade e equidade?
Pode parecer, mas equidade não é sinônimo de igualdade. Apesar dos conceitos se confundirem, é essencial entender as diferenças.
A igualdade está baseada na ideia de que todos são regidos pelas mesmas regras, com os mesmos direitos e deveres, sem levar em conta as diferenças entre os indivíduos. Dessa forma, não há discriminação.
Por sua vez, a equidade traz o fundamento da igualdade aliado ao senso de justiça social, conceito que se baseia no equilíbrio dos desiguais, ao reconhecer as características e necessidades individuais de cada um ou de um determinado grupo de pessoas. Assim sendo, ela fomenta oportunidades iguais,
considerando as diferenças entre os indivíduos. Imagine duas pessoas, uma baixa e outra alta, tentando alcançar livros em uma estante. Se ambas usassem escadas do mesmo tamanho, a mais alta conseguiria alcançar os livros enquanto a mais baixa não. As políticas equitativas visam corrigir esta desigualdade ao entregar “escadas” de tamanhos diferentes para cada um, de acordo com a necessidade destes, e de forma que todos fiquem na mesma altura. A escada seria, então, uma medida reparadora da situação.
QUAL a diferença entre igualdade e equidade? Fundação Telefônica Vivo, 2 jun. 2021. Disponível em: https://fundacaotelefonicavivo.org.br/noticias/qual-a-diferenca-entre-igualdade-e-equidade. Acesso em: 15 ago. 2022.

ATIVIDADES
1. A igualdade está baseada na ideia de que todos são regidos pelas mesmas regras, com os mesmos direitos e deveres, sem levar em conta as diferenças entre os indivíduos. A equidade traz o fundamento da igualdade aliado ao senso de justiça social, conceito que se baseia no equilíbrio dos desiguais, ao reconhecer as características e necessidades individuais de cada um ou de um determinado grupo de pessoas.
1. Segundo o texto, qual é a diferença entre equidade e igualdade?
2. As concepções de equidade e igualdade apresentadas no texto coincidem com as respostas dadas na seção Check-in? Respostas pessoais.
relevante, emocionante ou motivador. Organize um painel e exponha as fotos com um resumo do evento e com as frases dos estudantes.
Sugestão de atividade
Proponha a discussão sobre a situação-problema: uma empresa está organizando uma confraternização com despesas divididas entre eles os participantes. Os salários variam de 1 a 50 salários mínimos. É justo que todos paguem igualmente? Como esse valor pode impactar sobre
as despesas mensais de cada um? Supondo que o valor seja de R$ 100,00 para cada pessoa, comentem diversos casos possíveis. Espera-se que os estudantes sugiram uma situação que promova a equidade, como: a confraternização paga com uma cota diretamente proporcional ao salário.
#Expressões algébricas no cotidiano
Duas pessoas vão trabalhar em certo projeto. Pelo trabalho, elas receberão uma quantia fixa mais uma quantia que varia de acordo com o número de horas dedicadas ao projeto. Entretanto, os valores dessas quantias fixas e variáveis não serão os mesmos para as duas pessoas:
Habilidade
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Encontro com outras disciplinas
Considerando que nesse projeto a Pessoa A vai trabalhar x horas e a Pessoa B vai trabalhar y horas, podemos representar a quantia total que cada uma deverá receber por uma expressão algébrica:
• Quantia total (em reais) da Pessoa A: 500 + 10x
• Quantia total (em reais) da Pessoa B: 750 + 5y
Expressões matemáticas envolvendo letras, números e os sinais das operações são denominadas expressões algébricas
As letras podem assumir diferentes valores e são denominadas variáveis
Supondo que ambas as pessoas tenham trabalhado 30 horas no projeto, então cada uma deverá receber, em reais:
• Pessoa A: 500 + 10 x 30 horas ! ⇒ 500 + 10 30 = 500 + 300 = 800 reais
• Pessoa B: 750 + 5 y 30 horas ! ⇒ 750 + 5 30 = 750 + 150 = 900 reais
Em uma expressão algébrica, quando substituímos as variáveis por certo valor e realizamos as operações, obtemos o valor numérico da expressão algébrica
LUPAS E LUNETAS
Podemos afirmar que duas expressões algébricas são equivalentes quando apresentam o mesmo valor numérico para quaisquer valores assumidos por suas variáveis.
a) As expressões algébricas que representam as quantias recebidas pelas pessoas da situação-problema são equivalentes? Não.
b) Em grupos, conversem se é justa essa maneira de remunerar pessoas trabalhando no mesmo projeto. Que critérios poderiam justificar a diferença entre os ganhos das duas pessoas? Respostas pessoais.
LUPAS E LUNETAS
a) As expressões algébricas não são equivalentes: cada uma apresenta um valor fixo diferente e um valor para a hora de trabalhada diferente também. Construa tabelas para que percebam como os valores aumentam de acordo com a quantidade de horas trabalhadas.
(EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
Construa também, se julgar adequado, gráficos que representem os salários de acordo com o número de horas trabalhadas.
b) Não há uma única resposta para essa questão. Para alguns, a noção de justiça está exatamente na igualdade, ou seja, defendem que, como ambos trabalharam no mesmo projeto pelo mesmo tempo, deveriam receber a mesma quantia. Para outros, a noção de justiça repousa na ideia, por exemplo, de mérito. Podemos imaginar que, nesse cálculo, foram considerados fatores como “tempo de experiência”, “formação específica” etc.
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.


Antes de iniciar este conteúdo verifique se os estudantes sabem como determinar o valor de uma incógnita. Se considerar conveniente, retome a linguagem algébrica e algumas situações-problema simples que envolvam equações do 1o grau, com o objetivo de rever a identificação de uma incógnita.
Com a leitura do texto, indague: o que representam as incógnitas x e y na situação-problema? Espera-se que os estudantes percebam que representam as dimensões de um espaço retangular.
#Expressões algébricas com mais de uma variável

A prefeitura de uma cidade vai promover um evento e quer calcular o espaço adequado para as necessidades de cada atração. A atração principal ocupará um espaço de formato retangular, com dimensões em metros ainda não definidas:
Podemos calcular a área da superfície dessa figura como: x y ou xy
Uma segunda atração deverá ocupar um espaço como representado nesta imagem, com dimensões também dadas em metros:
Assim, podemos representar a área destinada à segunda atração por: x 10 ou 10x
A área total ocupada pelas duas atrações pode ser calculada pela adição das áreas: xy + 10x
Note que podemos calcular essa área considerando a região retangular formada pelas duas atrações:
x ( y + 10)
Utilizando a propriedade distributiva da multiplicação com relação à adição:
x y
x ( y + 10) = xy + 10x
x 10
Será também destinado um espaço livre, representado a seguir, com dimensões dadas em metros:
A área desse espaço livre pode ser representada por:
15 ( y + 10) = 15y + 150
Analogamente à situação anterior, podemos calcular a área total da superfície adicionando as áreas dos três espaços:
xy + 10x + 15y + 150
Ou podemos calcular a área da região retangular total formada pelas atrações:
(x + 15) ( y + 10)
Para esse cálculo, vamos novamente utilizar a propriedade distributiva, mas, nesse caso, é preciso lembrar de utilizar essa propriedade para cada parcela:
x y x 10
( x + 15) (y + 10) = xy + 10x + 15y + 150
15 y 15 10
Supondo, por exemplo, que x = 50 m e y = 25 m, a área total ocupada por esse evento pode ser calculada por:
LUPAS E LUNETAS Respostas pessoais.
Note que, nas expressões algébricas obtidas, não é possível obter uma forma reduzida, ou seja, continuar realizando as operações de adição e subtração. Por exemplo, considere a expressão algébrica:
5
Dizemos que os termos –7ab e 4ab são semelhantes, pois o número multiplica exatamente as “mesmas letras” (variáveis). O mesmo vale para os termos 5a e –2a Mas, por exemplo, os termos 5a e 4ab não são semelhantes, pois no primeiro há apenas a variável a, enquanto no segundo há uma multiplicação das variáveis ab
Assim, para obter a forma reduzida de uma expressão, devemos realizar as operações de adição e subtração entre os termos semelhantes. Para os demais, deve ser deixada somente a indicação das operações. Em nosso exemplo, pelas propriedades comutativa e associativa da adição, podemos escrever aquela expressão como:
Portanto:
3a – 3ab + 8b + 1 é a forma reduzida de 5a – 7ab + 8b + 4ab – 2a + 1
• Com suas palavras, explique o que é a forma reduzida da expressão algébrica e o que são termos semelhantes. Compartilhe com os colegas.
Habilidade
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
LUPAS E LUNETAS
Os estudantes precisam identificar termos semelhantes. Como sugestão de atividade, ofereça cartões e solicite que escolham e registrem termos algébricos envolvendo algumas das partes literais: a, b, ab, a2 , a2b ou ab2. Depois, recolha os cartões e embaralhe. Coloque alguns cartões na lousa, com fita adesiva, para que avaliem quais termos são semelhantes. Reorganize-os colocando os termos semelhantes lado a lado. Converse sobre o coeficiente preceder a parte literal e apresente o agrupamento dos termos semelhantes, como os cartões “a”, “a”, “a” representarem 3a
Com essa atividade espera-se que os estudantes identifiquem os termos semelhantes e deixem a expressão algébrica em sua forma reduzida, ou seja, que adicionem ou subtraiam os termos semelhantes (aqueles com a mesma parte literal).
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Atividade 3
Caso perceba que os estudantes estão com dificuldade em utilizar a propriedade distributiva, peça que façam exercícios de cálculo de área usando a propriedade distributiva, mas com as medidas dos lados sendo números naturais, para que, compreendendo a parte operatória, consigam realizar a distributiva algebricamente.
a) (x + 3) y = xy + 3y
b) (2x + 9) x = 2x 2 + 9x


c) (5 + y ) (z – 2) = 5z – 10 + zy – 2y y ) (z –

= 5z – 10 + zy – 2y

ATIVIDADES
3. Obtenha expressões algébricas para representar as áreas das superfícies dos retângulos:
4. Considere a figura composta de retângulos:
d) (w – 3)(w – 3) = w 2 – 3w – 3w + 9 = w 2 – 6w + 9 3)(w – 3) = w 2 – 3w – 3w + 9 = w 2 – 6w + 9

3w + 9 = w 2 – 6w + 9
Atividade 4
Para que os estudantes compreendam a decomposição e o cálculo da área da superfície, apresente esta figura (com os ângulos retos), organize-os em duplas e proponha que calculem a área por decomposição:
7 cm
Obtenha uma expressão algébrica que represente a área total dessa figura. Considere que todas as medidas estejam na mesma unidade
5. Obtenha o perímetro da figura. Considere que todas as medidas estejam na mesma unidade.
6. Obtenha a forma reduzida das expressões algébricas:
11 cm
5 cm
7. Elabore um problema envolvendo a área da superfície de uma figura retangular e expressões algébricas. Compartilhe com os colegas
12 cm
Caso os estudantes não consigam decompor a figura, proponha esta decomposição:
7 cm
Agora, use a mesma figura com medidas expressas por variáveis:
Com esse estudo, espera-se que o estudante resolva com autonomia a atividade.
11 cm
5 cm
11 cm
12 cm
Faça perguntas para que completem as medidas que estão faltando e calculem as áreas.
y
(12 – y)
A = 11y x
A = x(12 – y)

12 cm
Há duas formas de resolução possíveis: na socialização proponha que apontem as regiões associadas a wy + 2y 2 + xy – y 2 e também y 2 + wy + xy
Atividade 5
y + (2x – 5) + (y + 10) + (x + 10) = = y + y + x + 2x – 5 + 10 + 10 = = 2y + 3x + 15
#Polinômios
Vamos estudar um caso particular de expressão algébrica: os polinômios
Um polinômio é uma expressão algébrica que apresenta letras (variáveis) e números (coeficientes). Em um polinômio, entre as variáveis, há somente operações de adição, subtração e multiplicação e as variáveis têm apenas números naturais como expoentes.
Veja alguns exemplos de polinômios:
• a – b + 2
• x 3 – x 2 + x 1 – 1
• qp – q 2
• xy + z + 2 5 (apesar de a fração poder representar uma divisão, essa operação não ocorre entre as variáveis, mas entre os números 2 e 5).
• 3 + k 10 (embora a fração corresponda a uma divisão, essa operação não ocorre entre as variáveis, mas entre a variável k e 10. Podemos interpretar também como kk 1 10 ).
• 10 (podemos considerar 10 como um polinômio. Sendo, por exemplo, uma variável y, podemos afirmar que 10 = 10 y 0, porque y 0 = 1, para y ≠ 0)
Veja alguns exemplos de expressões que não são polinômios:
• 5 + 1 x , com x ≠ 0: não é polinômio porque 1 x = x –1 e, em um polinômio, os expoentes das variáveis devem ser números naturais, ou seja, (0, 1, 2, 3...), ou porque temos uma divisão por variável
• wx y , com y ≠ 0: não é polinômio porque em um polinômio não é possível realizar operações de divisão entre as variáveis. Essa limitação pode ser explicada também pelo fato de que 1 y = y –1 , análogo ao caso anterior.
• a : não é polinômio porque a = a 1 2 e, em um polinômio, os expoentes das variáveis devem ser números naturais.
LUPAS E LUNETAS Respostas pessoais.
Chamamos de monômios os polinômios que possuem apenas multiplicação entre números e variáveis. Por exemplo: 5a2b
Ao adicionar ou subtrair dois monômios, obtemos um binômio. Por exemplo: x + 3xy ou k 3 – 2k Se adicionarmos ou subtrairmos três monômios, obteremos um trinômio. Por exemplo: 6 – 2y + x
As adições ou subtrações de quatro ou mais monômios recebem simplesmente o nome de polinômio Escreva um exemplo de monômio, um de binômio e um de trinômio.
Compartilhe com os colegas.
Lembre-se: monômios, binômios e trinômios são todos polinômios!
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
LUPAS E LUNETAS
Para que os estudantes possam compartilhar seus exemplos, faça na lousa um quadro com um exemplo possível de resposta, como:
POLINÔMIOS
Monômio Binômio Trinômio ab
Avalie conjuntamente a pertinência dos exemplos apresentados pelos estudantes.
Atividade 7
Para que os estudantes possam se inspirar leia este problema:
a ser (4 + x )2 = 16 + 8x + x 2 ; com quantidades diferentes, a área passa a ser: (4 + x ) = (4 + y ) = 16 + 4y + 4x + xy ; (4 + x ) = (4 + y ) = 16 + 4y + 4x + xy ;e aumentando apenas um lado,
A escola tem um tanque de areia demarcado no chão por um quadrado de 4m de lado e pretende aumentar esse espaço. Como podemos calcular a nova área se aumentarmos igualmente os lados? E se aumentarmos de quantidades diferentes cada lado? E se aumentarmos apenas um lado?
As respostas esperadas são que, se aumentarmos igualmente os lados, a nova área passa
a nova área seria de 4(4 + x ) = 16 + 4x
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
LUPAS E LUNETAS
Para complementar a atividade, apresente alguns monômios semelhantes com a parte literal registrada em ordem diferente. Por exemplo, x 3 y , –2x 3 y e 2 5 x 3 y pode ser apresentado desta maneira:
x 3 y y , 2 x 3 e 5 x 3 2 y Espera-se que os estudantes notem que a parte literal é a mesma.
Atividade 8
Peça aos estudantes que expliquem por que os itens b e e não são polinômios, indicando quais operações não fazem parte da definição.
A passagem da linguagem natural para a linguagem simbólica pode ser uma grande dificuldade para os estudantes. Nesse caso, verifique a capacidade de abstração e generalização desses estudantes e proponha atividades que desenvolvam as capacidades relacionadas ao pensamento algébrico, como o trabalho com sequências e regularidades.
Vamos considerar o polinômio:
2x 3 – xy + 5
Perceba que ele é composto pela adição ou subtração de três monômios: 2x 3 , –xy e 5 (esses monômios são também chamados de termos do polinômio).
Podemos identificar em cada monômio partes literais, que correspondem às variáveis, e partes numéricas, denominadas coeficientes:
!
i 2 coeficiente ! x 3 parte l teral
i –xy = –1
i 5
coeficiente !
!
coeficiente ! xy parte l teral
LUPAS E LUNETAS Respostas pessoais.
No estudo das expressões algébricas, falamos em termos semelhantes. Podemos descrever esse mesmo conceito utilizando as noções de monômio, coeficiente e parte literal: “dois monômios são semelhantes quando suas partes literais são iguais”.
A partir dessa afirmação, escreva três monômios semelhantes.
ATIVIDADES
8. Verifique quais das expressões algébricas são polinômios. Justifique suas respostas e compartilhe com os colegas:
a) –3x + 4
b) a + b 3
c) y 4 + 3x 5w 2 d) –6
Problemas envolvendo polinômios
e) 5 2w + w y
A figura representa um terreno de forma retangular de 390 m por 170 m. Uma parte desse terreno será concedida à população para criar um parque para as crianças, com dimensões x e y – ainda a definir –, conforme a figura. Considere todas as medidas em metros:
Será construída uma cerca para delimitar o espaço que restou do terreno original, então é necessário calcular os perímetros das figuras que representam as partes do terreno.
O perímetro do retângulo que representa o terreno do parque pode ser representado pelo polinômio:
2 x + 2y
Já o perímetro da figura que representa o terreno que restou é expresso pelo polinômio: 170 + 390 + (170 – y ) + x + y + (390 – x )

TRAVESSIAS
a) Nesta discussão, os estudantes podem relacionar as informações usando um quadro como este:
perceber que não podemos ter
Para efetuar essas operações, vamos utilizar as propriedades comutativa e associativa da adição:
Dessa maneira, independentemente dos valores que possam ser atribuídos a x e y, y
Vamos calcular as áreas das superfícies (em m2) das figuras que representam cada terreno. No caso do terreno destinado ao parque, sua área pode ser representada pelo polinômio:
Para calcular a área do terreno que restou, podemos utilizar como estratégia subtrair da área do terreno original a área do terreno destinada ao parque:
TRAVESSIAS
Variáveis envolvendo perímetro e área de um terreno
Vamos refletir um pouco mais sobre essa situação-problema? Em pequenos grupos, respondam às questões:
b) Verdadeiro. Porque no cálculo do perímetro dessa figura as variáveis x e y se anulam.
a) Considerando as medidas do terreno original, é possível atribuir valores maiores que 390 para a variável x? É possível atribuir valores maiores do que 170 para a variável y? Justifique suas respostas.
b) Independentemente dos valores atribuídos às variáveis x e y, o perímetro da figura que representa o terreno que restou será sempre o mesmo. Verifique se esse fato é verdadeiro e justifique sua resposta.
c) A população do bairro gostaria que as áreas destinadas ao parque e ao que restou do terreno original fossem iguais. Qual seria então a medida, em metros quadrados, da área do parque? Que possíveis valores podem ser atribuídos às variáveis x e y para que as áreas destinadas ao parque e ao que restou do terreno original sejam iguais? Veja uma possível solução:
c) 66 300 ÷ 2 = 33 150 m2
a) Não. Porque se x > 390, entao 390 – x será um número negativo. O mesmo ocorre se y > 170

Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
d) Como a área da superfície do terreno destinado ao parque é representada pelo polinômio xy , então precisamos obter dois números (x e y) de modo que seu produto seja 33 150. No entanto, é também preciso lembrar que x ≤ 390 e y ≤ 170 e É possível utilizar uma estratégia de “tentativa e erro” (o uso de calculadora é recomendável). Outra estratégia é decompor 33 150 em números primos: 33 150 = 2 3 52 33 150 = 2 3 52 13 17 A partir disso, é possível testar produtos de valores naturais que satisfaçam as condições x ≤ 390 e y ≤ 170 Auxilie os estudantes na organização do quadro para fazer as tentativas e descartar os erros. Eles podem determinar um valor para x e calcular o valor que corresponde a y (33 150 ÷ x = y )
Ou seja, se x = 390 e y = 85, pois xy = 390 85 = 33 150.
d) Utilizando um raciocínio semelhante, obtenha outros dois valores que possam ser atribuídos a x e y de modo que as áreas destinadas ao parque e ao que restou do terreno original sejam iguais. x = 195 e y = 170.
e) Obtenha outros possíveis valores que possam ser atribuídos às variáveis x e y para que as áreas destinadas ao parque e ao que restou do terreno original sejam iguais. Use uma calculadora, se necessário
valores negativos para representar medidas de comprimento.
b) É possível utilizar o polinômio obtido no cálculo do perímetro da figura que representa o terreno que restou, 170 + 390 + (170 – y ) + x + y + (390 – x ), (170
y ) + x + y + (390 – x ), para justificar esse fato. Simplificando esse polinômio, cancelamos x e y e o perímetro do terreno que restou é:
c) A área total da superfície do terreno é 66 300 m2 (390 170) A metade dessa medida é 33 150 m2
Note que, como estamos lidando com medidas, os valores podem ser racionais não inteiros. e) Apesar de ser evidente que a multiplicação entre x e y resulta sempre no mesmo valor, proponha que os estudantes percebam essas relações pelas operações inversas da multiplicação e divisão.
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Apresente outro modo de realizar a adição e a subtração de polinômios.
Usando o mesmo exemplo:
#Operações com polinômios
As operações envolvendo polinômios utilizam as mesmas propriedades das operações envolvendo expressões algébricas.
Adição e subtração
Sejam P e Q dois polinômios de modo que:
• Vamos calcular P + Q:
(b2 + ab)
Q ! " $
P ! " $ + (–3b2 + 2ab – 4)
Uma estratégia alternativa para determinar P + Q, parecida com o algoritmo de adição com números quando dispomos ordem sob ordem decimal, é escrever os monômios semelhantes alinhados um com o outro, desta maneira:
b2 ab +
+ –3b2 2ab –4 +
–2b2 3ab –4 + No caso da subtração, temos
P – Q :
(b2 + ab) P ! " $ – (–3b2 + 2ab – 4) Q ! " $
Escrevendo os monômios semelhantes alinhados um com o outro:
b2 ab +
– –3b2 2ab –4 +
–4b2 ab +4 –Isso é o mesmo que P + (–Q ):
b2 ab + ++3b2 2ab +4 –4b2 ab +4 –
LUPAS E LUNETAS
a) Considerando o oposto de P – Q já calculado, temos
Q – P:
–4b2 + ab – 4
b) Para – P – Q, escrevendo os monômios semelhantes de –P e Q alinhados um com o outro, temos:
–b2 ab –3b2 2ab –4 + 2b2 3ab +4 –
Assim como no caso das expressões algébricas, vamos obter a forma reduzida desse polinômio.
Utilizando as propriedades comutativa e associativa da adição de modo a agrupar os monômios semelhantes:
Portanto, o resultado de
• Vamos calcular P – Q:
" $ – (–3b2 + 2ab – 4) Q ! " $
Lembrando que –(–3b2 + 2ab – 4) = +(–1) (–3b2 + 2ab – 4) , então, utilizando a propriedade distributiva:
(b2 + ab) + (–1) (–3b2 + 2ab – 4) =
= (b2 + ab) + (–1)(–3b2 ) + (–1)(2ab) + (–1)(–4) = = b2 + ab + 3b2 – 2ab + 4
Utilizando as propriedades comutativa e associativa da adição:
b2 + 3b2 monomios seme hantes
! " $ + ab – 2ab monomios seme hantes
! " $ + 4 = 4b2 – ab + 4
Portanto, o resultado de P – Q é o polinômio 4b2 – ab + 4
LUPAS E LUNETAS
Utilize estratégias análogas às anteriormente usadas e calcule:
a) Q – P
b) –P – Q
Multiplicação
Sejam P e Q dois polinômios de modo que: P: ab e Q: 4b + a 2 b3
Vamos calcular P Q :
Pela propriedade distributiva:
(ab) ⋅ (4b + a 2 b3 )
(ab) (4b + a 2 b3 ) = (ab)(4b) + (ab)(a 2 b3 ) = a b 4 b + a b a 2 b3
Pela propriedade comutativa da multiplicação: a b 4 b + a b a 2 b3 = a 4 b b + a a 2 b3 b
Lembrando que, pelas propriedades da potenciação:
Pela propriedade comutativa da multiplicação:
Portanto, o resultado de P Q é o polinômio 4
LUPAS E LUNETAS
Utilize estratégias análogas à anteriormente usada e calcule:
a) 5 P 5ab
b) Q2
c) P 2 Q
d) (–P ) Q
e) P (P + Q )
Divisão
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
LUPAS E LUNETAS
Retome os significados das operações com números e estabeleça as analogias com os polinômios:
• a multiplicação por um número (5 P ) como uma adição de parcelas iguais (P + P + P + P + P );
Sejam P e Q dois polinômios, de modo que:
considerando que o polinômio Q representa um valor diferente de 0.
Vamos representar P ÷ Q da seguinte forma:
10a 2 b3 + 3a 4 b2 5a 2 b
Expressões algébricas nas quais há variáveis no denominador são denominadas expressões algébricas fracionárias. Nesse caso, ainda não sabemos se o resultado da divisão P ÷ Q será um polinômio. Lembrando que, para ser um polinômio, em sua forma reduzida não pode haver divisões entre variáveis (ou seja, uma variável cujo expoente é negativo). Vamos prosseguir com os cálculos e verificar se o resultado será um polinômio ou uma expressão algébrica fracionária.
Podemos escrever essa expressão como uma adição de expressões fracionárias com mesmo denominador:
Vamos utilizar a ideia de multiplicação de frações e as propriedades da potenciação para simplificar essas expressões:
• a potenciação (P2) como um produto de fatores iguais (P ⋅ P );
• o oposto (–P ) como o produto de –1 pelo polinômio (–1 ⋅ P )
Retomando a multiplicação apresentada no exemplo, é possível realizar uma etapa intermediária, antes da utilização das propriedades da potenciação (e para retomá-las e compreendê-las):
Uma estratégia alternativa para determinar P ⋅ Q, parecida com o algoritmo da multiplicação com números, é dispor os polinômios deste modo:
Habilidade (EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Atividade 9
Utilizando a ideia de multiplicação de frações e as propriedades da potenciação, temos: 15ab3
que não é um polinômio, mas uma expressão algébrica fracionária.
Portanto, o resultado de R ÷ Q é a expressão algébrica fracionária 3b
ATIVIDADES
9. Considere os polinômios, com a ≠ 0 e b ≠ 0:




a , sendo a ≠ 0
Efetue as divisões entre os polinômios e verifique se o resultado é um polinômio ou uma expressão algébrica fracionária.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática
a) Q ÷ S a2 b + b2a a2 = a a b + b b a a a = a a b a a + b b a a a = b + b b a a2 b + b2a a2 = a a b + b b a a a = a a b a a + b b a a a = b + b b a b b a a = a a b a a + b b a a a = b + b b a b a + b b a a a = b + b b a b + b2 a , com a ≠ 0 É uma expressão algébrica fracionária.
b) P ÷ S
É uma expressão algébrica fracionária.
c) R ÷ S
–9ab a 2 = –9ab a a = –9b a –9b a , com a ≠ 0 É uma expressão algébrica fracionária.
• Identifica situações-problema que podem ser descritas por expressões algébricas? Consegue resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas?
• Compreende a noção de polinômio?
• Utiliza as propriedades das operações para resolver cálculos envolvendo adição, subtração, multiplicação e divisão de polinômios?
▶ Outras disciplinas
Língua Portuguesa
Sabe apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos ou polêmicos?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
MATEMÁTICA OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
▶ Organize
Respostas pessoais.
Neste passeio, você explorou expressões algébricas e, mais especificamente, polinômios. Faça um resumo dos principais tópicos discutidos. Em cada tópico, procure utilizar exemplos diferentes dos já apresentados.

▶ Elabore
De modo geral, aprender sobre expressões algébricas é importante para poder modelar situações-problema cotidianas, analisá-las e propor soluções. Elabore uma situação-problema que possa ser resolvida utilizando expressões algébricas ou polinômios. Compartilhe com os colegas.

▶ Proponha
A pergunta inicial deste passeio é: Como criar relações de igualdade e de equidade no convívio social?
Em diferentes momentos deste passeio foram discutidas as diferenças entre as noções de igualdade e equidade.
a) Retome essas noções e elabore, com suas palavras, uma definição para cada uma.
b) Observe a imagem:
Representação em 3D de dois atores da sociedade.
Ela expressa uma situação de igualdade ou equidade? Justifique sua resposta.
c) Em grupos, compartilhem as definições elaboradas anteriormente e conversem sobre em que momentos do convívio social vocês consideram que é importante se pautar pela igualdade e em quais é importante se pautar pela equidade.
• Compartilhem com a turma os principais argumentos da conversa realizada por seu grupo.
NÃO
b) Equidade, pois a forma de acessar o segundo nível é adaptada às necessidades ou às diferenças de cada um. Se fosse uma situação de igualdade, só haveria uma escada, por exemplo. 91 |
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com
o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
Encontro com outras disciplinas
(EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
BARCOS E PORTOS
Organize
Peça aos estudantes que façam um mapa mental com os conteúdos apresentados neste passeio, incluindo exemplos. Esse material pode ser usado para estudos de revisão em outros momentos.
Elabore
Acompanhe a construção de situações-problema pelos estudantes, orientando sobre os contextos, as restrições, as operações com as expressões algébricas ou polinômios etc. Socialize o material produzido em uma lista coletiva de atividades produzidas pela turma.
Proponha
Retome a questão inicial deste passeio: Como criar relações de igualdade e de equidade no convívio social? Comente alguns pontos específicos que foram discutidos anteriormente nas aulas. Proponha que reflitam sobre o convívio e apontem quando julgam adequado uma situação de igualdade ou equidade.
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.

(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
Encontro com outras disciplinas
(EF89LP04) Identificar e avaliar teses/opiniões/ posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando-se frente à questão controversa de forma sustentada.
CHECK-IN
Proponha que observem a imagem que representa que as relações na sociedade precisam de equilíbrio. Os estudantes podem verbalizar como percebem as igualdades ou as diferenças nas relações humanas.

a) Possivelmente essa imagem promoverá uma discussão em torno de concordar ou não como percebem as relações na sociedade. Em uma situação ideal, há uma busca por uma situação de igualdade ou equidade nas relações de trabalho ou nas relações familiares, em que diferentes pessoas atuam, cada qual à sua maneira, para construir uma sociedade mais igualitária.
b) Considerando o enunciado, a pessoa A trabalhou 10 horas e 30 minutos (a) no mês
PASSEIO
POLINOMIAIS DE 1 O GRAU COM DUAS INCÓGNITAS E SISTEMAS LINEARES
QUAIS RELAÇÕES EXISTEM ENTRE OS DIFERENTES ATORES DA SOCIEDADE?
Equilíbrio é necessário nas relações em sociedade.
CHECK- IN
Observe a imagem e, em pequenos grupos, respondam às seguintes questões:
a) Pensando na participação de diferentes pessoas e grupos na sociedade, que interpretações vocês podem fazer a partir da situação apresentada na imagem?
b) Considere o contexto: duas pessoas A e B participam de um projeto de uma mesma comunidade. Em certo mês, a pessoa A destinou ao projeto o dobro de horas que havia destinado no mês anterior. Por sua vez, a pessoa B destinou ao projeto o triplo de horas que havia destinado no mês anterior. Se a e b representam o tempo que A e B, respectivamente, destinaram ao projeto no mês anterior, então podemos representar o tempo destinado no mês atual por 2a e 3b. Observe as equações e elabore uma possível interpretação para cada uma delas:
• 2a = 21 No mês atual, a pessoa A destinou 21 horas ao projeto.
• 3b = 47 No mês atual, a pessoa B destinou 47 horas ao projeto.
• 2a + 3b = 68 No mês atual, as pessoas A e B destinaram juntas 68 horas ao projeto.
anterior e 21 horas (2a) no mês atual, enquanto a pessoa B trabalhou 15 horas e 40 minutos (b) no mês anterior e 47 horas no mês atual (3b). No mês atual, as pessoas A e B trabalharam juntas (2a + 3b) 68 horas (21 + 47) no projeto.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Obter diferentes soluções para uma equação polinomial de 1o grau com duas incógnitas.
• Associar as soluções de uma equação polinomial de 1o grau com duas incógnitas a uma reta no plano cartesiano.
• Resolver e elaborar problemas que possam ser representados por sistemas lineares.
• Resolver sistemas lineares utilizando o plano cartesiano como recurso.
• Identificar teses/opiniões/posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos, posicionando-se frente à questão controversa de forma sustentada.
Encontro com outras disciplinas
(EF89LP04) Identificar e avaliar teses/opiniões/ posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando-se frente à questão controversa de forma sustentada.
ATMOSFERA
Atividade 1
Organize uma roda de conversa: a leitura coletiva desse texto contribui para as reflexões no próximo tema. O texto aborda a participação dos jovens na construção da sociedade e apresenta que eles são o grupo de maior vulnerabilidade social. Faça um entrelaçamento dessa discussão com o TCT Cidadania e Civismo – Vida Familiar e Social.
1. a) Os jovens exercem papel importante nos movimentos sociais, assumindo postos de liderança em protestos mundo afora, organizando manifestações e ocupando o espaço público com demandas sociais, políticas, econômicas e culturais.
ATMOSFERA
1. b) Segundo o texto, “por estarem na linha de frente do ativismo, da cobrança de líderes locais e globais por um mundo mais justo e solidário e por serem a voz do inconformismo na sociedade, os jovens também estão entre os que mais sofrem com a violência”.

A importância dos jovens para a sociedade
Jovem afrodescendente em protesto antirracismo. Jovens ativistas em marcha pelo meio ambiente.
[...]
Os jovens sempre desempenharam papel importante nos movimentos sociais, assumindo postos de liderança em protestos mundo afora, organizando manifestações e ocupando o espaço público com demandas sociais, políticas, econômicas e culturais. Nas ruas, nas comunidades, nas redes sociais e internet em geral!

Mas justamente por estarem na linha de frente do ativismo, da cobrança de líderes locais e globais por um mundo mais justo e solidário e por serem a voz do inconformismo na sociedade, os jovens também estão entre os que mais sofrem com a violência.
Os jovens e, principalmente, os jovens negros estão entre os grupos de maior vulnerabilidade social, no Brasil e no mundo. E essa vulnerabilidade é facilmente constatada pelos altos índices de mortalidade — no Brasil, a morte violenta atinge principalmente jovens negros entre 15 e 18 anos.
[...]
Segundo dados da Unicef, morrem 16 jovens
por dia no Brasil vítimas de homicídio. Já o DataSus revela que, enquanto a taxa de mortalidade por homicídios de adolescentes está em torno de 35 por 100 mil habitantes, a da população em geral encontra-se em 27 por 100 mil.
Há quem diga, equivocamente, que os altos índices de morte entre jovens se devem ao envolvimento desses em crimes. Tal afirmação não poderia estar mais longe da verdade.
Segundo dados do Instituto Latino-Americano das Nações Unidas para a Prevenção do Delito e Tratamento do Delinquente (Ilanud), o percentual de jovens com idade inferior a 18 anos que comete atos infracionais no Brasil é de menos de 1% da população brasileira nessa faixa etária. No universo de crimes praticados, os delitos cometidos por adolescentes não chegam a 10%.
Ainda assim, mais da metade das mortes por homicídios no Brasil em 2017 (54,54% do total de 65 602), por exemplo, foram de jovens entre 15 e 29 anos, segundo dados do Atlas da Violência. [...]
DIA da Juventude: entenda a importância dos jovens para a sociedade. Oxfam Brasil, 11 ago. 2020. Disponível em: www.oxfam.org.br/blog/dia-internacional-da-juventude. Acesso em: 15 ago. 2022.
c) O equívoco é acreditar que os altos índices de mortalidade se devem ao fato de os jovens estarem mais envolvidos com a criminalidade. Segundo o texto “o percentual de jovens com idade inferior a 18 anos que cometem atos infracionais no Brasil é de menos de 1% da população brasileira nessa faixa etária”.
ATIVIDADES
1. A sociedade é formada, entre outros elementos, por diferentes grupos e pessoas que se relacionam com o mundo e entre si. O texto traz informações sobre situações envolvendo a atuação dos jovens na sociedade.
a) Segundo o texto, quais papéis os jovens assumem na sociedade?
b) O texto cita um aspecto negativo relacionado a esses papéis. Qual?
c) Há um equívoco, segundo o texto, na interpretação feita por algumas pessoas quanto aos índices de mortalidade em relação aos jovens. Qual seria esse equívoco e qual é o argumento do texto para justificar esse fato?
Sugestão de atividade
Sugira ao professor de Língua Portuguesa que trabalhem a discussão desse texto com a intenção de desenvolver a habilidade EF89LP04. Assim, os estudantes desenvolverão argumentos para analisar as informações que recebem constantemente dos diversos meios de comunicação.
Organize uma aula em que os estudantes simulem uma situação de debate sobre um tema escolhido por eles. Oriente que, em um debate, não há o objetivo de apenas estabelecer um embate
ideológico, pois ele é uma forma de propor soluções para possíveis problemas que atingem uma sociedade. O debate é uma importante ferramenta para a formação dos estudantes, pois estimula o desenvolvimento do pensamento crítico e a prática da elocução.
Evidencie o uso de dados e análises estatísticas para combater vieses e preconceitos na argumentação.
#Equações polinomiais de 1o grau
Certa comunidade está planejando melhorias para o espaço do entorno. Os moradores propuseram algumas assembleias e reuniões para discutir os problemas encontrados e pensar em soluções. Pessoas de diferentes faixas etárias se engajaram nesse movimento. Em uma das assembleias compareceram 28 adultos e o dobro de adolescentes que haviam comparecido na reunião anterior.
Vamos investigar algebricamente essa situação?
Como não sabemos o número de adolescentes que compareceu à assembleia anterior, vamos representar tal quantidade pela letra x Assim, podemos representar o total de participantes dessa assembleia pela expressão algébrica:
Agora a letra x não representa mais uma variável, mas uma incógnita. Resolver essa equação significa obter um valor para x que torne a igualdade verdadeira.
A solução de uma equação é denominada raiz dessa equação. Nesse caso, significa descobrir o número de adolescentes que participaram da assembleia anterior (x).
Equações que podem ser reduzidas à forma ax + b = c, com a ≠ 0, são denominadas equações polinomiais de 1o grau
De modo a preservar a relação de igualdade, vamos subtrair 28 de ambos os membros da equação:
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
28 adultos ! + 2 x dobro de adolescentes da assemble a anter or
!
Supondo que na reunião anterior participaram 10 adolescentes, então nessa reunião participou um total de pessoas igual a:
28 + 2 10 = 28 + 20 = 48
Atribuindo valores para x, obteremos diferentes valores para o total de participantes da assembleia. Assim, nesse caso, x é uma variável
Porém, sabe-se que o total de participantes dessa assembleia foi de 62 pessoas. Desse modo, podemos descrever essa situação com uma equação:
28 + 2x ! 62
!
total de partic pantes
LUPAS E LUNETAS
Respostas pessoais.
Assim,
Novamente, de modo a preservar a relação de igualdade e isolar x, vamos dividir ambos os membros da equação por 2:
2 x 2 = 34 2
Portanto, x = 17
Isso significa que, na assembleia anterior, participaram 17 adolescentes. Como na assembleia mais recente esteve presente o dobro dessa quantidade, então, participaram 2 17 = 34 adolescentes.
Você participa ou é convidado a participar de decisões sobre seu ambiente familiar, escolar ou de sua comunidade? O que pensa sobre a participação de crianças e adolescentes nessas situações?
A situação apresentada no texto foi representada por uma expressão algébrica. Procure elaborar outras expressões algébricas que representem situações reais ou fictícias para que os estudantes relembrem a linguagem algébrica.
LUPAS E LUNETAS
Na discussão sobre a participação dos estudantes em decisões em diversos âmbitos, eles podem conhecer e conversar um pouco mais sobre cidadania e civismo, além de apresentar ideias sobre como podem se posicionar para que tenham voz ativa na sociedade.
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
#Equações polinomiais de 1o grau com duas incógnitas
A sociedade é composta de pessoas de diferentes culturas, visões de mundo, interesses, idades, etnias etc. Ao tomar decisões coletivamente na sociedade, é importante que, de alguma maneira, toda essa diversidade esteja representada.
Representação de diversidade de gênero, etnia e cultura.
O centro cultural de certa região organizou um evento para discutir soluções para diferentes problemas e questões locais. A ideia foi criar rodas de conversa entre distintos grupos sociais para debater tais problemas e questões.
Na primeira roda de conversa, participou pelo menos uma pessoa pertencente a cada grupo social X e Y. Considerando x o número de pessoas do grupo X e y o número de pessoas do grupo Y e sabendo que o total de participantes nessa roda foi de 15 pessoas, podemos descrever o total de participantes pela equação: x + y = 15
Como saber quantas pessoas de cada grupo participaram dessa roda de conversa?
Note que essa equação apresenta duas incógnitas. Resolvê-la significa descobrir que valores de x e y tornam a igualdade verdadeira. Nesse caso, existem várias possibilidades, por exemplo:
• Se x = 1 e y = 14, então 1 + 14 = 15
• Se x = 10 e y = 5, então 10 + 5 = 15
• Se x = 9 e y = 6, então 9 + 6 = 15
Assim, quaisquer dessas possibilidades tornam a igualdade verdadeira, ou seja, essa equação admite várias soluções.
Matematicamente, há outros valores que também tornam essa igualdade verdadeira. Por exemplo:
• Se x = –5 e y = 20, então –5 + 20 = 15
• Se x = 12,5 e y = 2,5, então 12,5 + 2,5 = 15
Porém, no contexto a que essa equação faz referência, x e y representam quantidades de pessoas. Assim, essas soluções negativas ou fracionárias não podem ser consideradas.
Veja outras soluções interessantes:
• Se x = 0 e y = 15, então 0 + 15 = 15
• Se x = 15 e y = 0, então 15 + 0 = 15 Podemos interpretar valores como x = 0 ou y = 0 no sentido de que não participaram pessoas dos grupos X ou Y, respectivamente. No entanto, a situação-problema afirma que pelo menos uma pessoa de cada grupo participou dessa roda de conversa. Assim, essas soluções também não podem ser consideradas nesse contexto.
96 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.
CONVÍVIO E BEM-ESTAR SOCIAL

Organize um debate com os estudantes sobre um problema social. Peça que escolham um tema: educação insuficiente, desemprego, escassez de moradia, saúde precária, falta de saneamento etc. O objetivo do debate é conhecer o que gerou o problema e ações que podem contribuir para minimizá-lo, promovendo o bem-estar social. Elabore previamente perguntas sobre o tema e, para que tenham argumentos no debate, procure textos jornalísticos e deixe cada grupo responsável pela
leitura e pelo compartilhamento das principais informações. No início do debate, combine regras para que possam participar da discussão e escolha um estudante para elaborar um relatório sobre os pontos principais discutidos. Coloque uma questão aberta para envolver a turma. Esta atividade pode ser encerrada com a leitura do relatório sobre esse evento.
MELITAS/SHUTTERSTOCKLUPAS E LUNETAS
b) São as situações em que
Reúnam-se em pequenos grupos e façam o que se pede.
a) Obtenham todas as soluções dessa equação que sejam adequadas ao contexto apresentado. Uma possível estratégia é organizar as incógnitas e seus possíveis valores em um quadro como este:
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
b) Considerando que a ideia dessas rodas de conversa foi justamente ouvir diferentes grupos de maneira mais igualitária, quais soluções parecem mais próximas a esse fim? Justifiquem suas respostas e compartilhem com os demais colegas.
c) Considerando a equação x + y = 15 isolada do contexto apresentado, x e y podem ser quaisquer números. O que podemos dizer sobre a quantidade de soluções dessa equação?
Há infinitas soluções.
2. b) Há diversas possibilidades, por exemplo: x
ATIVIDADES
2. Duas pessoas subiram juntas em uma balança. O visor da balança indicou 124 kg.
a) Escreva uma equação que represente o total medido pela balança e as massas corporais das duas pessoas.
b) Sabendo que nenhuma das duas pessoas possui massa corporal menor que 40 kg nem maior que 100 kg, obtenha 3 possíveis valores para as massas corporais de cada uma dessas pessoas.
3. Em uma viagem, duas amigas se revezaram na condução do veículo, de modo que cada uma dirigiu um trecho do percurso. Sabe-se que o total do percurso foi 628 km.

a) Escreva uma equação que represente o total percorrido e quanto cada uma das amigas dirigiu.
x + y = 124 x + y =
b) Obtenha três possíveis pares de valores para os trechos percorridos pelas amigas, em km.
4. Pensei em dois números distintos. Subtraí o menor do maior e obtive resultado igual a 6. Em quais números eu posso ter pensado? Dê 3 respostas diferentes. Compartilhe com os colegas.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
partes literais diferentes e os estudantes podem responder a + b = 124, r + s = 124, k + t = 124 etc.
b) Escolhendo um valor 40 ≤ x ≤ 100, y é calculado por 124 – x Por exemplo: x = 54,5; y = 124 x = 54,5; y = 124 – 54,5 → y = 69,5
Atividade 3
a) Cada amiga percorreu uma distância representada por uma incógnita diferente. Como o total do percurso é de 628 km, x + y = 628
5. Resolva as equações. Dê pelo menos duas soluções distintas de cada uma.
b) Supondo que uma das amigas dirigiu 100, 300 ou 500 km, a outra dirigiu 528, 328 ou 128 km, respectivamente, pois 628 – 100 = 528; 628
628 – 100 = 528; 628 – 300 = 328; 628 – 500 = 128 km 628 – 100 = 528; 628 – 300 = 328; 628 – 500 = 128 km
Atividade 4
3
3. b) Há diversas possibilidades, por exemplo:
LUPAS E LUNETAS
a) Como, no contexto apresentado, x e y representam o número de pessoas de cada grupo, devem ser números naturais não nulos. Observando os valores de x e de y que resultam na soma 15, podemos perceber que se x aumenta uma unidade, o valor de y diminui uma unidade.
b) Como x + y representa um número ímpar, não há uma solução em que ambas as quantidades sejam iguais.
Como a representatividade de cada grupo é importante para o contexto apresentado, as quantidades de participantes de cada grupo devem ser o mais próximas possível.
c) Se, em x + y = 15, pudermos ter qualquer valor para x e y, haverá infinitos valores possíveis para x e o mesmo para y, ou seja, infinitas soluções para a equação.
Atividade 2
para x =
a) Na linguagem algébrica, a massa de cada pessoa pode ser representada por
Sabendo que um número é maior que o outro em 6 unidades, o estudante pode escolher o maior número e subtrair 6 unidades ou escolher o menor número e adicionar 6 unidades.

Atividade 5
Nessa atividade, o estudante pode escolher o valor de uma incógnita e calcular o valor da outra que mantenha a relação de igualdade. Por exemplo, no item a:
a) 3 x 2y = 1; para x = 1 teremos: 2y
2y =
1 y =
Habilidades

(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
LUPAS E LUNETAS
Espera-se que os estudantes busquem por valores que não satisfaçam a situação de contexto ainda que satisfaçam a equação, como x = 2,5 e y = 17, pois, assim, a associação X teria retirado por duas vezes 2,5 cestas, e a associação Y, doado 17 cestas, sobrando 12 cestas básicas, mas o número de cestas a cada doação ou retirada deve ser um número natural.
Equações com duas incógnitas no plano cartesiano
Uma associação de moradores é uma instituição que reúne pessoas moradoras de um mesmo loteamento, bairro ou comunidade para atuarem como mediadores entre os próprios moradores e também com os órgãos públicos, a fim de melhorar a infraestrutura da região, reivindicando direitos e mantendo o local onde moram o mais agradável e organizado possível.
Mulher participando de reunião do bairro no centro comunitário, pronta para fazer uma pergunta. Pacote de arroz, feijão e óleo de soja – itens de uma cesta básica.
Duas associações de moradores X e Y criaram um “banco de cestas básicas” para ajudar pessoas da região. A ideia é que, sempre que possível, as associações doem cestas básicas a esse “banco” e, quando for necessário, retirem cestas básicas para distribuir a quem precisa.
Vamos considerar x o número de cestas básicas doadas ou retiradas pela associação X e y o número de cestas básicas doadas ou retiradas pela associação Y
Em certo mês, não havia cestas básicas no “banco”. Então, a associação Y doou certa quantidade, mas a associação X retirou por duas vezes uma mesma quantidade, diferente da depositada pela associação Y. Após essas doações e retiradas, sabe-se que no banco ainda restaram 12 cestas básicas.

Veja uma equação que representa o total de cestas básicas restantes após as doações e retiradas:
y doac ao da associac ao Y
! –2x ret rada da associac ao X
! = 12 cestas básicas restantes
!
Uma solução para essa equação é y = 14 e x = 1, ou seja, a associação Y doou 14 cestas básicas e a associação X realizou duas retiradas iguais a uma cesta básica. Outra possível solução é y = 20 e x = 4
Podemos atribuir infinitos valores a x e y que tornem verdadeira a relação de igualdade expressa pela equação.
Vamos considerar a equação y – 2x = 12 e suas possíveis soluções desligadas do contexto da situação-problema original. Ou seja, as incógnitas x e y podem representar quaisquer números que tornem essa igualdade verdadeira.
LUPAS E LUNETAS Respostas pessoais.
Afirmar que “as incógnitas x e y podem representar quaisquer números que tornem essa igualdade verdadeira” significa que podemos apresentar soluções que não necessariamente fariam sentido ou seriam adequadas ao contexto da situação-problema.
Em pequenos grupos, investiguem uma possível solução para essa equação que não seria adequada ao contexto original. Justifiquem sua resposta e compartilhem com os demais colegas.
Interpretando algebricamente
Podemos representar as soluções de uma equação por pares ordenados:
( x va ores de x que tornam a gualdade verdadeira
! , y va ores de y que tornam a gualdade verdade ra
! )
Dessa maneira, as duas soluções obtidas para a equação y – 2x = 12 podem ser representadas por:
( 1 x ! , 14 y ! ) e ( 4 x ! , 20 y ! )
Note que a ordem em que se escrevem os valores de x e y importa.
Vejamos, por exemplo, a solução ( 4 x ! , 20 y ! ) Substituindo os valores de x e y na equação: y – 2x = 12 ⇒ 20 – 2 4 = 12 ⇒ 20 – 8 = 12 ⇒ 12 = 12 que é uma afirmação verdadeira.


Porém, se utilizarmos como solução o par ( 20 x ! , 4 y ! ):
Habilidade (EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
y
2 x = 12 ⇒ 4 – 2 20 = 12 ⇒ –36 = 12 que é uma afirmação falsa. Ou seja, (20, 4) não é uma solução para a equação y – 2x = 12 Portanto, (4, 20) ≠ (20, 4)
Nesse sentido, o par (x, y) que representa uma solução de certa equação cujas incógnitas são x e y é um par ordenado e podemos representá-lo no plano cartesiano.
Vamos representar as duas soluções (1, 14) e (4, 20) da equação y – 2x = 12 no plano cartesiano:
Verifique o conhecimento prévio dos estudantes sobre plano cartesiano e localização de pares ordenados. Caso considere adequado, retome esse conteúdo e inclua números racionais nas formas decimal e fracionária como exemplos. Com esse conhecimento, eles podem representar os possíveis pares ordenados por meio de um gráfico e verificar que há infinitas soluções para a equação
Lembrando que dois pontos distintos no plano definem uma única reta que passa por eles, podemos traçar a reta que passa pelos pontos (1, 14) e (4, 20) que correspondem a duas possíveis soluções da equação y – 2x = 12:
Habilidade (EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
LUPAS E LUNETAS
Nas discussões sobre as possíveis soluções da situação-problema, os estudantes perceberão que a reta corresponde a infinitos pontos dados por suas coordenadas em pares ordenados, porém, as soluções do problema sobre as cestas básicas são representadas por pontos com coordenadas no conjunto dos números naturais.
A reta representa a solução da equação de 1o grau (números inteiros negativos, racionais na forma decimal ou fracionária são soluções possíveis), mas não representa a solução da situação-problema discutida. Por se tratar de cestas básicas, as soluções devem ser números naturais, ou seja, serão alguns dos pontos no 1o quadrante do plano cartesiano pertencentes à reta.
Qualquer ponto contido nessa reta também é uma solução dessa equação! Veja alguns exemplos:
Vamos testar se esses pontos de fato são soluções da equação y
De fato, todos esses pontos da reta são soluções da equação.
LUPAS E LUNETAS
Considerando que x e y podem representar quaisquer números que tornem a igualdade verdadeira e que todas as soluções possíveis da equação podem ser representadas por pontos dessa reta, o que se pode dizer sobre o número de soluções daquela equação?
Em duplas ou trios, conversem sobre essa questão e elaborem uma argumentação matemática para justificar sua resposta. Compartilhem com os demais colegas. Respostas pessoais.

Habilidades
#Sistemas de equações polinomiais de 1o grau
Considere as equações de 1o grau com as incógnitas x e y: x
y = –1 e –2x + y = –4
Como já sabemos, resolver cada uma delas significa obter valores para x e y de modo que tornem as igualdades verdadeiras. Sabemos também que equações de 1o grau podem apresentar muitas ou até mesmo infinitas soluções.
Mas e se desejássemos obter valores para x e y de modo que tornem ambas as igualdades verdadeiras simultaneamente?
Por exemplo, (–1, 0) é uma solução da equação x – y = –1, pois: (–1, 0) subst tuindo na equacao x – y –1
→ –1 – 0 = –1 ⇒ –1 = –1 (verdadeira)
Porém, (–1, 0) não é uma solução da equação –2 x + y = –4, veja: (–1, 0) subst tu ndo na equacao –2 x + y = –4
→ –2(–1) + 0 = –4 ⇒ 2 = –4 (falsa)
Para obter valores de x e y que sejam simultaneamente soluções de ambas as equações, utilizaremos um sistema de equações de 1o grau:
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
x – y = –1
–2x + y = –4 ⎧ ⎨ ⎩
Representa-se um sistema de equações com uma chave à esquerda das equações, agrupando o conjunto de equações que serão resolvidas simultaneamente.
Resolver um sistema de equações significa obter valores de x e y que sejam soluções das equações de 1o grau ao mesmo tempo.
Dizemos que sistemas desse tipo são sistemas lineares de duas equações e duas incógnitas
Sistema de equações no plano cartesiano
Vamos representar no plano cartesiano as retas que contêm pontos do plano cujos pares ordenados representam todas as soluções de cada equação. Precisamos obter pelo menos duas soluções diferentes para cada equação.
Veja uma estratégia:
• Seja a equação x – y = –1
Se x = 0, entao: 0 – y = –1 ⇒ y = 1 Portanto, (0, 1) é uma solução.
Se y = 0, entao: x – 0 = –1 ⇒ x = –1 Portanto, (–1, 0) é uma solução.
• Seja a equação –2 x + y = –4
Se x = 0, então: –2 0 + y = –4 ⇒ y = –4 Portanto, (0, –4) é uma solução.
Se y = 0, então: –2x + 0 = –4 ⇒ x = 2 Portanto, (2, 0) é uma solução.
Representando esses pontos e as retas que os contêm no plano cartesiano:
Sugestão de atividade
Antes de iniciar a leitura desta página, peça que, por tentativa, descubram as soluções da situação. A soma de dois números é 10 e a diferença entre eles é 6. Quais são esses números? Os estudantes podem fazer tentativas ou organizar as possíveis soluções para a soma dos números e, depois, identificar as soluções para a diferença de dois números. E podem, finalmente, localizar a solução que satisfaz as duas condições: x + y = 10 x – y
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
Atividade 6
Organize um quadro para facilitar a compreensão sobre as possíveis soluções do sistema linear. Apenas dois pontos determinam a reta, por isso os estudantes podem escolher apenas dois valores para substituir x na equação. Veja alguns exemplos de pares ordenados:
Cada reta contém os infinitos pontos associados às infinitas soluções de cada equação de 1º grau. Note que essas retas se cruzam em um único ponto: (5, 6). Esse ponto em comum representa uma solução comum para ambas as equações.
Vamos testar se (5, 6) é uma solução para ambas as equações:
• Seja a equação x – y = –1
Se x = 5 e y = 6, então: 5 – 6 = –1 (verdadeira).
Portanto, (5, 6) é uma solução de x – y = –1
• Seja a equação –2x + y = –4

Se x = 5 e y = 6, então: –2 5 + 6 = –10 + 6 = –4 (verdadeira).
Portanto, (5, 6) é uma solução de –2x + y = –4
Desse modo, a intersecção entre as duas retas, nesse caso o ponto (5, 6), é solução de ambas as equações. Ou seja, (5, 6) é a solução do sistema linear:
x – y = –1
–2 x + y = –4
ATIVIDADES
6. Considere o sistema linear:
0 0 – y = 4 y = –4 –4 (0, –4)
1 1 – y = 4 y = –3 –3 (1, –3)
2 2 – y = 4 y = –2 –2 (2, –2)
3 3 – y = 4 y = –1 –1 (3, –1)
Espera-se que, construindo as retas em um mesmo plano cartesiano, os estudantes percebam que o ponto comum é a solução do sistema linear.
a) Há diversas possibilidades, por exemplo: para x + y = 2, são soluções x = 0, y = 2 e x = 2, y = 0 Para x – y = 4, são soluções x = 0, y = –4 e x = 4, y = 0 que contenha pontos relacionados às soluções de uma mesma equação.
x + y = 2
x – y = 4
a) Obtenha duas soluções distintas para cada equação do sistema.
b) Represente essas soluções como pontos no sistema cartesiano e trace uma reta
c) A intersecção entre as duas retas ocorre no ponto (3, –1) Portanto, essa é a solução do sistema linear, ou seja, x = 3 e y = –1
c) A partir da análise das retas no plano cartesiano, obtenha a solução desse sistema linear.
d) Elabore um problema que possa ser resolvido utilizando esse sistema linear. Compartilhe com os colegas.
d) Sugestão: “Pensei em dois números inteiros. Adicionando esses números obtive 2 e subtraindo obtive 4. Em que números eu pensei?”.
102 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.
Caso alguns estudantes apresentem dificuldade, proponha construir o quadro com todos os valores de x sugeridos. Eles perceberão que o par ordenado (3, –1)é solução das duas equações simultaneamente.
#Estratégias de resolução de sistemas de equações
Já sabemos como obter a solução de um sistema de equações lineares utilizando a representação das soluções de cada equação do sistema em um plano cartesiano. Vamos apresentar outras estratégias ou métodos para resolver sistemas lineares.
Método da substituição
Considere o sistema linear de equações:
Para resolver esse sistema, será necessário isolar alguma das variáveis em uma das equações. Nesse caso, vamos escolher isolar y na
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
LUPAS E LUNETAS
Pode-se sugerir que os estudantes encontrem uma equação equivalente a 2x + y = 7 isolando tanto a incógnita x quando a y, obtendo: y 2 ou = 5 2 y) (5
Sabendo o valor de x, podemos substituí-lo em qualquer equação e obter o valor de y Substituindo x = 1 na equação 5 x – y =
Portanto, a solução desse sistema é x = 1 e y = 3
LUPAS E LUNETAS
Nesse exemplo, manipulamos a equação 5 x – y = 2 até obter y = –2 + 5x Como todas as operações realizadas sempre preservaram a relação de igualdade entre os membros, essas duas equações são equivalentes. Ou seja, independentemente da sua representação, apresentam as mesmas soluções. Por esse motivo, dizemos que os sistemas:
• Resolva o sistema
pelo método da substituição utilizando uma equação equivalente a 2x + y = 5 x = 1, y = 3 103 |
Ao aplicarem o método da substituição na equação y = 2 5x , devem obter o mesmo resultado anterior, x = 1 e y = 3
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
LUPAS E LUNETAS
Ao adicionar uma equação aos membros da outra, obtém-se uma nova equação em que uma das incógnitas foi eliminada e resta somente a outra, cujo valor determina-se pela resolução de uma equação do 1o grau. Ao se determinar o valor de uma incógnita, basta substituí-la em uma das duas equações originais e determinar o valor da outra incógnita.
Note que o processo descrito no texto justifica o método da adição: o porquê de adicionarmos uma equação a outra e obtermos ainda uma relação de igualdade.
Método da adição
Considere o sistema linear de equações:
Uma maneira de resolver esse sistema é obter um sistema equivalente a partir da adição das duas equações. Por exemplo, vamos manter a 1a equação e produzir uma equação equivalente à 2a adicionando a 1a equação a ela:
Note que agora a 2a equação possui somente uma incógnita. Essa é uma das vantagens de utilizar esse método! Assim:
Sabendo o valor de x, podemos substituí-lo em qualquer uma das equações e obter o valor de y. Substituindo x = 4
LUPAS E LUNETAS
Dada a equação 2 x – y = 3, se adicionarmos o mesmo valor a ambos os membros, a relação de igualdade se mantém.
Assim, se adicionarmos a expressão 3 x + y a ambos os membros, a relação de igualdade será preservada. Mas sabemos que 3 x + y = 1 Ou seja, podemos substituir essa expressão por 1: (2 x – y ) + (3x + y ) = 3 + (3x + y ) equ vale a 1 ! " $
Assim, temos: (2 x – y ) + (3x + y ) = 3 + 1 Converse com os colegas sobre esse método e explique, com suas palavras, o seu funcionamento.
Sistema de equações e representação no plano cartesiano
Utilizando softwares ou aplicativos de geometria dinâmica (alguns disponíveis gratuitamente na internet), podemos obter as soluções de um sistema linear utilizando o plano cartesiano. Como exemplo, considere o sistema linear de equações:
x + 2y = 2
–2x – 10y = 8

No campo “entrada”, escrevemos cada uma das equações desse sistema:
sobre o ponto que representa essa intersecção, serão exibidas na tela as suas coordenadas:
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
Atividades 8 e 9
Você poderá notar que, automaticamente, são desenhadas as retas que representam as soluções de cada uma dessas equações. Sabemos que a intersecção das retas é a solução do sistema. Ao clicar com o mouse
ATIVIDADES
7. Resolva os sistemas lineares utilizando o método da substituição:
Portanto, a solução desse sistema é (6, –2), ou seja, x = 6 e y = –2.

• Retome os exemplos de sistemas lineares explorados anteriormente e resolva-os utilizando um software ou aplicativo de geometria dinâmica.
Converse sobre a eliminação de uma das incógnitas pela adição de coeficientes opostos nesse método.
• Por exemplo, no caso do item a da atividade 9, temos:
8. Considere o sistema linear:
a) Explique por que realizar essa etapa é necessário para resolver o sistema pelo método da adição.
b) Continue resolvendo o sistema pelo método da adição.
9. Resolva os sistemas lineares utilizando o método da adição:
de utilizar o método da adição. Mas, para eliminar a incógnita y na 2a equação, precisamos primeiramente multiplicar ambos os seus membros por 2:
8. a) Porque o intuito de adicionar duas equações é eliminar uma das incógnitas e isso é possível se seus coeficientes forem, em cada equação, números opostos.
NUVENS
Verifique a possibilidade de realizar a atividade na sala de informática utilizando um software de geometria dinâmica.
Atividade 7
Retome as etapas para isolar uma das incógnitas. Mostre que podem escolher qual delas isolar, como no item a:
Já no caso da atividade 8 e dos itens c e d, para empregar o método da adição, é necessário encontrarmos equações equivalentes, que permitam a adição de coeficientes opostos. Por exemplo, ao multiplicar-se ambos os membros de y = 3 3x por 2, obtém-se uma equação equivalente. Ao somar-se y + (5x + 2y) = 6 + 0, 2 6x eliminamos a incógnita y, pelo método da adição.
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
TRAVESSIAS
Na discussão sobre as retas paralelas, questione se há pontos comuns ou de intersecção. Esse sistema é chamado de impossível
Considere o sistema linear:
x + y = 1
x + y = 3
Mostre que, nas duas equações, os 1os membros são iguais; como os 2os membros são diferentes, o sistema não poderia ter solução. A soma de dois números não pode ter dois resultados diferentes, 1 ou 3.
Veja outro sistema impossível:
TRAVESSIAS
Interpretação geométrica de um sistema de equações
Sabemos que as soluções de uma equação de 1o grau com duas incógnitas podem ser representadas por uma reta no plano cartesiano. E também que o ponto de intersecção de duas dessas retas representa a solução de um sistema linear.
• As retas no plano cartesiano representam as soluções de duas equações de 1o grau:
a) O que se pode dizer da posição relativa entre essas duas retas (paralelas, concorrentes ou coincidentes)? São paralelas.
b) O que isso significa quanto à solução do sistema linear formado pelas duas equações de 1o grau que originaram essas retas? Não há solução, pois não há intersecção.
c) O sistema linear que deu origem a essa representação é:
x + y = 1
x + y = 3
Teste valores para x e y que ajudem a explicar a sua resposta ao item b
d) Elabore outro sistema linear que represente situações análogas a essa.
• Considere o sistema linear:
x + y = 1
3 x + 3y = 3
Respostas pessoais. Resposta pessoal.
a) Represente todas as soluções de cada equação em um plano cartesiano.
2x – 3y = 4
4x – 6y = 7 ⎧ ⎨ ⎩
No entanto, ao manter a proporcionalidade dos termos das equações, as retas que as representam neste outro sistema serão coincidentes e há infinitas soluções:
b) O que se pode dizer da posição relativa entre essas duas retas (paralelas, concorrentes ou coincidentes)? São coincidentes.
c) O que isso significa quanto à(às) solução(ões) desse sistema linear?
• Em duplas ou trios, elaborem um texto que relacione as posições relativas das retas que representam as soluções das equações de um sistema linear ao número de soluções que esse sistema pode apresentar. Respostas pessoais.
c) Infinitas soluções, pois as retas têm todos os pontos coincidentes.
2x – 3y = 4

4x – 6y = 8 ⎧ ⎨ ⎩
Ao avaliar as soluções dos sistemas de equações e as posições relativas das retas, temos:
• retas concorrentes, em que há uma única solução, o ponto de interseção;
• retas paralelas, em que não há soluções; e
• retas coincidentes, em que são infinitas as soluções.
#Álgebra: a linguagem da Matemática
Arte analítica de François Viète
Em 1591, Viète publica aquela que viria a se tornar sua obra principal: In artem analyticem isagoge, ou Introdução à arte analítica, muitas vezes chamada apenas de Isagoge. Estranhamente, não é pelos teoremas ou pelas demonstrações matemáticas nela desenvolvidas que a Isagoge marcará época, mas pela maneira como esses resultados são formulados. Viète seria o principal instigador da nova álgebra que, em questão de algumas décadas, daria origem a uma linguagem matemática completamente inovadora.
[...]
Até que, aos poucos, começam a florescer por toda parte, desorganizadamente, símbolos novos que hoje em dia, no entanto, nos parecem tão conhecidos.
[...] Naturalmente, tudo isso não ocorre de maneira linear e ordenada. Ao longo desse período, uma infinidade de outros símbolos nasce e morre. Alguns são usados apenas uma vez. Outros se desenvolvem e concorrem entre si. Entre a primeira utilização de um sinal e sua adoção definitiva pela comunidade matemática, muitas vezes se passam dezenas de anos. Assim, um século depois de introduzidos, os sinais + e – ainda não eram universalmente adotados, e muitos matemáticos ainda utilizavam as letras P e M, iniciais das palavras latinas plus e
minus, para designar a adição e a subtração.
E o que tem Viète a ver com tudo isso? O Cientista francês seria um dos catalizadores desse vasto movimento. Na Isagoge, ele lança um vasto programa de modernização da álgebra e deposita sua pedra angular ao introduzir o cálculo literal, ou seja, o cálculo com letras do alfabeto. Sua proposta é tão simples quanto desconcertante: denotar as incógnitas das equações com vogais, e os números conhecidos, com as consoantes.
Mas essa repartição entre vogais e consoantes seria rapidamente abandonada em proveito de uma sugestão ligeiramente diferente de René Descartes: as primeiras letras do alfabeto (a, b, c...) designarão as quantidades conhecidas, e as últimas (x, y e z) serão as incógnitas. Essa convenção ainda hoje é usada pela maioria dos matemáticos, e a letra “x” tornou-se símbolo de desconhecido e mistério até na linguagem corrente.
Para entender bem de que maneira a álgebra é transformada por essa nova linguagem, lembremos da seguinte equação:
Buscamos um número que, multiplicado por 5, dê 30.
Graças ao novo simbolismo, essa equação pode agora ser escrita com um pequeno número de sinais: 5 × x = 30
Temos de reconhecer que é bem mais sucinto!
107 |
Habilidade
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
Conhecendo um pouco da história da matemática, os estudantes podem percebê-la como um elemento cultural. Com a leitura desse texto, podem ampliar seu interesse pelo estudo da álgebra por compreender a matemática como uma herança cultural.
Nesse movimento de acompanhar as mudanças que ocorreram no estudo de Matemática, podemos concluir que o conhecimento matemático está em construção, ou seja, é inacabado, em constante aprimoração.
 François Viète, matemático francês responsável pela introdução da primeira notação algébrica sistematizada, além de contribuir para a teoria das equações.
LAUNAY, Mickaël. A fascinante história da Matemática: da pré-história aos dias de hoje. 1. ed. Rio de Janeiro: Bertrand Brasil, 2019. p. 162, 166 e 167.
NÃO ESCREVA NO SEU LIVRO.
GERMAN VIZULIS/SHUTTERSTOCK
François Viète, matemático francês responsável pela introdução da primeira notação algébrica sistematizada, além de contribuir para a teoria das equações.
LAUNAY, Mickaël. A fascinante história da Matemática: da pré-história aos dias de hoje. 1. ed. Rio de Janeiro: Bertrand Brasil, 2019. p. 162, 166 e 167.
NÃO ESCREVA NO SEU LIVRO.
GERMAN VIZULIS/SHUTTERSTOCK
Habilidades
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
LUPAS E LUNETAS
a) Nessa atividade, o estudante utiliza os símbolos apresentados no texto para compreender como foram as mudanças na linguagem algébrica.
b) Como exemplo, é possível ler o problema: a soma de dois números distintos é 11 a e diferença entre eles é 1. Que números são esses?
c) O sistema descrito, considerando x = número de carros e y = número de motos, é: x + y = 20 (I)
4x + 2y = 54 (II)
Pelo método da substituição, temos de (I): y = 20 – x Em (II):




4 x + 2(20 – x ) = 54
4x + 4 – 2x = 54
2x = 14 x = 7 carros Substituindo em y = 20 – x : y = 20 – 7 y = 13 motos
LUPAS E LUNETAS
a) Resposta possível: 7 P 15 = 22 e 37 M 21 = 16.
a) Escreva uma adição e uma subtração sem utilizar + e –, mas utilizando P e M, nessa ordem. Dê para um colega resolver. O que você achou dessa notação?
b) Escreva uma equação de 1º grau com duas incógnitas em linguagem natural e dê para um colega representá-la utilizando o simbolismo matemático
Resposta pessoal.
c) Leia o seguinte problema escrito em linguagem natural: em uma rua há, entre carros e motos, 20 veículos estacionados. Alguém realizou uma contagem e conseguiu determinar 54 rodas. Há quantos carros e motos estacionados nessa rua? Represente esse problema utilizando o simbolismo matemático e depois resolva-o
x + y = 20 e 4x + 2y = 54, tal que x é o número de carros e y é o número de motos.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática
• Consegue obter diferentes soluções para uma equação polinomial de 1º grau com duas incógnitas?
• Associa uma equação polinomial de 1º grau com duas incógnitas a uma reta no plano cartesiano?
• Sabe resolver e elaborar problemas que possam ser representados por sistemas lineares? Resolve sistemas lineares utilizando o plano cartesiano como recurso?
▶ Outras disciplinas
Língua Portuguesa
• Consegue identificar teses/opiniões/posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos, posicionando-se frente à questão controversa de forma sustentada?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
MATEMÁTICA
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar
suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
OUTRAS ÁREAS 108 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.BARCOS E PORTOS
▶ Organize
Neste passeio, você explorou equações e sistemas de equações de 1o grau com duas incógnitas. Organize um esquema com as diferentes estratégias exploradas para resolver as equações e os sistemas lineares. Para cada uma delas, elabore uma situação-problema que possa ser resolvida a partir das equações e dos sistemas criados.

▶ Elabore
No início deste passeio, você explorou equações polinomiais de 1o grau com duas incógnitas. O estudo desse tipo de equação foi muito importante na história da Matemática. Um dos matemáticos célebres que estudou equações desse tipo foi Diofanto de Alexandria. Pouco se sabe sobre a vida desse matemático grego, mas alguns historiadores apontam que ele pode ter vivido durante o século III. Um de seus principais estudos refere-se ao que ficou conhecido como equações diofantinas. Uma equação diofantina é uma equação de 1o grau que apresenta duas ou mais incógnitas que representam somente números inteiros. Veja um exemplo: 4x + 2y = 8
Uma solução possível para essa equação é: x = 1 e y = 2.
a) Elabore outras equações diofantinas e compartilhe com os colegas.
b) Em grupos, escolham algumas delas e elaborem possíveis situações-problema que elas possam representar.
▶ Proponha
A pergunta inicial deste passeio é: Quais relações existem entre os diferentes atores da sociedade?
Podemos entender a escola que você frequenta como um recorte da sociedade, com seus atores sociais próprios: alunos de diversas idades e anos escolares, professores de diversas áreas do conhecimento, funcionários que desempenham diferentes funções etc.
• Em grupos, conversem sobre as diferentes pessoas que participam do cotidiano em sua escola. Imaginem há quanto tempo estão na escola, o que pensam dela, como se relacionam com o espaço e com os colegas, que experiências trazem de fora da escola, quais suas perspectivas de futuro, projetos etc.
Reconhecer quem são as pessoas que convivem em seu ambiente é importante. Porém, mais importante é ouvir delas próprias as respostas para os questionamentos que vocês realizaram anteriormente.
• Escolham algumas delas e proponham conversas de modo a conhecer seus pontos de vista e ideias sobre essas questões. Lembre-se de que algumas dessas questões podem ser mais pessoais e não precisam ser obrigatoriamente respondidas!
O que importa é estabelecer o diálogo e compreender melhor como cada pessoa se relaciona com essa “microssociedade” que é a escola.
Encontro com outras disciplinas (EF89LP04) Identificar e avaliar teses/opiniões/ posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando-se frente à questão controversa de forma sustentada.
BARCOS E PORTOS
Organize
Incentive o estudante a organizar, usando exemplos, um passo a passo que possa consultar para resolver sistemas de equações quando considerar conveniente relembrar esse conteúdo.
Elabore
Uma sugestão é ler este problema: Tenho várias notas de R$ 2,00 e de R$ 5,00. Usando essas cédulas, como posso ter R$ 23,00? Uma resposta possível é “4 notas de R$ 2,00 e 3 notas de R$ 5,00” ou “9 notas de R$ 2,00 e uma nota de R$ 5,00”.
Proponha
Revisite a pergunta inicial deste passeio: Quais relações existem entre os diferentes atores da sociedade? Durante essa reflexão, conversem sobre as relações entre as pessoas que participam da vida escolar e pergunte sobre o protagonismo estudantil: os estudantes participam das ações ou decisões na escola? O que pode ser feito para que as relações entre professores, estudantes e funcionários valorizem o papel de cada um na sociedade? Com essas reflexões, os estudantes poderão avaliar sua postura diante das mais diversas situações escolares.
Respostas pessoais. 109 | NÃO ESCREVA NO SEU LIVRO.Encontro com outras disciplinas
(EF08GE15) Analisar a importância dos principais recursos hídricos da América Latina (Aquífero Guarani, Bacias do rio da Prata, do Amazonas e do Orinoco, sistemas de nuvens na Amazônia e nos Andes, entre outros) e discutir os desafios relacionados à gestão e comercialização da água.
CHECK-IN
a) Solicite que observem a imagem e conversem sobre as medidas adequadas para comparar terrenos: o que representa o esboço de um terreno? Que tipo de espaço pode ser a representação da imagem? De acordo com a vivência, os estudantes poderão relatar sobre a área do terreno da casa onde moram ou de lugares que frequentam.
b) A área da superfície de um retângulo pode ser calculada multiplicando as medidas de sua largura e seu comprimento.
PASSEIO 3 – EQUAÇÕES POLINOMIAIS DE 2 O GRAU
COMO LIDAR COM OS DIFERENTES RECURSOS DISPONÍVEIS NO AMBIENTE URBANO?

CHECK-IN
Podemos entender por “recursos” tudo que pode ser utilizado para produzir o necessário para uma sociedade. Nesse sentido, a terra é um recurso importante que pode ser utilizado na agricultura, na pecuária, para construção de indústrias, moradias, área de lazer ou até mesmo bairros e cidades.
a) A imagem sugere que há um planejamento de como utilizar o terreno. Observando a extensão de terra da imagem, estime o que poderia ocupar tal superfície.
b) Você já estudou áreas das superfícies de diversas figuras geométricas. Relembre como calcular a área de uma figura retangular. Compartilhe com os colegas. Respostas pessoais.
Sugestão de atividade
Converse com o professor de Geografia para organizarem uma atividade interdisciplinar sobre a importância dos recursos hídricos. Organize os estudantes em duplas para a leitura do texto “Fatos incríveis sobre o Aquífero Guarani, um dos maiores do mundo” (disponível em: https://www.aguasustentavel.org.br/blog/91-fatos-incriveis-sobre-o-aquifero-guarani-um-dos-maiores-do-mundo; acesso em: 12 ago. 2022) para que conversem sobre o que sabem desse assunto. Depois, peça que verbalizem o que compreenderam do texto.
Oriente que façam uma pesquisa com pessoas de sua convivência sobre fatos que vivenciaram relacionados à falta de água e registrem para comunicar aos colegas. Ainda solicite uma pesquisa na internet sobre como ocorre a captação, o tratamento, a distribuição e a comercialização da água para continuarem a discussão sobre a importância da água. Esta atividade contempla parte da habilidade de Geografia EF08GE15. Espera-se que o estudante tenha conhecimento sobre as reservas hídricas e a importância da água.
 Mapa de projeto de transformação de área verde para futuras instalações de construções.
110 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.
FRANCESCO SCATENA/SHUTTERSTOCK
Mapa de projeto de transformação de área verde para futuras instalações de construções.
110 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.
FRANCESCO SCATENA/SHUTTERSTOCK
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Resolver e elaborar problemas envolvendo equações polinomiais de 2o grau do tipo ax 2 + c = 0, a ≠ 0
• Resolver equações polinomiais de 2o grau do tipo ax 2 + c = 0, a ≠ 0 a partir de diferentes estratégias.
• Analisar a importância dos principais recursos hídricos e discutir os desafios relacionados à gestão desses recursos.
• Analisar as principais problemáticas comuns às grandes cidades, particularmente aquelas relacionadas a distribuição, estrutura e dinâmica da população e às condições de vida e trabalho.
Habilidade
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b. Encontro com outras disciplinas
(EF08GE15) Analisar a importância dos principais recursos hídricos da America
Latina (Aquífero Guarani, Bacias do rio da Prata, do Amazonas e do Orinoco, sistemas de nuvens na Amazônia e nos Andes, entre outros) e discutir os desafios relacionados à gestão e comercialização da água.
ATMOSFERA
Atividades 1 a 3
Organize uma roda de conversa, façam a leitura do texto e conversem sobre as situações de falta de água no mundo. Proponha que complementem as informações com uma pesquisa.
Pautados na discussão sobre o texto, conversem também sobre a falta de água na cidade onde moram ou, se não for o caso, de alguma outra cidade do Brasil:
• Quais foram os anos de maior escassez?
• Quais medidas foram tomadas?
• Como está a situação atual? Essa discussão contribui para a formação crítica do estudante.
Mapa indica locais com mais chances de haver disputas por água no mundo
[...]
A demanda global por água, que deve superar o abastecimento em 40% até 2030, já é ameaça real à vida nos grandes centros urbanos. É o que cravou uma pesquisa de 2014, ao analisar as 500 maiores cidades do mundo: uma em cada quatro se encontra em situação de “estresse hídrico”, quando o abastecimento anual fica abaixo dos 1,7 mil m3 por pessoa.
Na Cidade do México, capital mexicana, 20% dos habitantes só recebe água potável algumas horas por semana. Na Cidade do Cabo, África do Sul, os banhos não podem durar mais de 90 segundos e há um limite de água que cada pessoa pode consumir – 50 litros diários. 600 milhões de pessoas sofrem com escassez na Índia, incluindo a capital, Nova Délhi. No país, 21 cidades devem
esgotar seus lençóis freáticos em um período de dois anos.
Com o esgotamento das reservas hídricas pelo mundo, a gestão dos recursos passa a preocupar tanto quanto seu uso consciente. O que especialistas temem, agora, é que essa desigualdade na distribuição possa motivar conflitos diplomáticos entre os países.
“Ainda que o uso de recursos hídricos ainda não tenha, por si só, motivado guerras até hoje, problemas quanto ao uso e gestão da água podem dinamizar tensões que já existem, aumentando a instabilidade em certas regiões”, diz um artigo científico, recém-publicado na revista científica Global Environmental Change [...]
MAPA indica locais com mais chances de haver disputas por água no mundo. Federação nacional dos urbanitários (FNU), 23 out. 2018. Disponível em: www.fnucut.org.br/14349/mapa-indica-locais-com-mais-chances-dehaver-disputas-por-agua-no-mundo. Acesso em: 15 ago. 2022.
ATIVIDADES
1. Das 500 cidades avaliadas, 1 em cada 4 já sofre com estresse hídrico (125 cidades).
1. A água é um recurso valioso tanto para a própria vida dos seres humanos quanto das plantas, animais e para a produção de diversos recursos. Entretanto, algumas das principais cidades do mundo vêm enfrentando uma situação na qual a demanda por água já é maior que a quantidade que se consegue oferecer. É o denominado estresse hídrico. Segundo estudo citado pelo texto, quantas cidades já sofrem com o estresse hídrico?

2. Segundo o texto, quais problemas podem ocorrer com o esgotamento das reservas hídricas do mundo?
A desigualdade na distribuição de água pode ocasionar conflitos entre países.
3. Reflita sobre a região em que vive: você considera que possa sofrer com o estresse hídrico atualmente ou nos próximos anos? Pesquise sobre esse assunto e compartilhe com os colegas. Respostas pessoais.
Habilidade
#Área da superfície de retângulos representados por equações
A população de certa cidade gostaria de destinar um grande terreno vazio para a construção de moradias populares. Uma das possibilidades é utilizar um terreno de formato retangular representado a seguir:
Como as áreas dos dois terrenos são iguais, então:
x 2 = 160 000
Outra possibilidade é utilizar um terreno de formato quadrado que possui a mesma área do terreno retangular. Porém, não se sabe exatamente quais são as medidas dos lados do quadrado que representa esse terreno. Assim, as medidas foram representadas pela letra x, considerada em metros:
Obtivemos uma equação com uma incógnita. Para resolvê-la, precisamos identificar valores de x que tornem a igualdade verdadeira. Sabemos que elevar um número ao quadrado equivale a multiplicar esse número por ele mesmo. Assim, podemos resolver essa equação nos questionando: que número multiplicado por ele mesmo resulta em 160 000?
Uma estratégia é representar 160 000 como um produto de dois fatores iguais. Primeiramente, podemos representar 160 000 como:
16 10 000
Continuando essa decomposição:
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b.
LUPAS E LUNETAS
Na discussão da situação-problema, apenas o valor positivo é válido para expressar as medidas de comprimento. Porém, ao responder à questão “Que número multiplicado por ele mesmo resulta em ...?”, teremos como resultados tanto os números positivos quanto os negativos.
Observe:
a) 52 = 25 e (–5)2 = 25
b) 102 = 100 e (–10)2 = 100
Como saber a medida x? Sabendo que as áreas dos dois terrenos são iguais, vamos calcular a área do terreno retangular:
200 800 = 160 000 m2
A área do terreno de forma quadrada pode ser representada pela expressão algébrica:
x x = x 2
LUPAS E LUNETAS
Pelas propriedades comutativa e associativa da multiplicação: 4
c) 7002 = 490 000 e (–700)2 = 490 000 7002 = 490 000 e (–700)2 = 490 000
d) 12 = 1 e (–1)2 = 1
Assim, podemos dizer que 400 é uma solução da equação x 2 = 160 000 Portanto, os lados do terreno de formato quadrado possuem medida igual a 400 m.
Nesse contexto, x = 400 é, de fato, uma solução para a equação x 2 = 160 000 Entretanto, há outra solução para essa equação! Lembrando que o produto de dois números negativos é um número positivo, o número –400 também responde à questão: que número multiplicado por ele mesmo resulta em 160 000?

Considerando esse fato, responda: que números inteiros multiplicados por eles mesmos resultam em:

a) 25?
b) 100?
c) 490 000?
d) 1?
5 ou – 5 10 ou – 10 700 ou – 700 1 ou – 1
113 |
Habilidade
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b.
Você já ouviu falar em hortas urbanas? São hortas criadas e mantidas coletivamente pela população de regiões em algumas cidades e centros urbanos. Nelas, geralmente são cultivados frutas, vegetais e hortaliças que podem ser coletados livremente pelas pessoas. Além de contribuir para o bem-estar e reforçar a coletividade, as hortas urbanas representam uma ótima maneira de utilização dos espaços urbanos.

Nas hortas urbanas, todos são responsáveis e todos se beneficiam do cuidado com a terra.
Deseja-se construir uma horta urbana em um terreno de formato retangular. Sabe-se que a área desse terreno é 1 690 m2. As pessoas da comunidade decidiram dividir esse terreno em dez partes iguais de formato quadrado, com medida x, dada em metros:
A área de cada superfície quadrada desse terreno pode ser representada pela expressão algébrica:
x x = x 2
Como há dez partes quadradas com áreas iguais, então a área total da superfície pode ser calculada pela expressão:

10x2
Sabendo que a área total corresponde a 1 690 m2, então:
10x 2 = 1 690
114 | TRAJETÓRIA 2 NÃO ESCREVA NO SEU LIVRO.
CONVÍVIO E BEM-ESTAR SOCIAL
Converse com a gestão escolar, colegas e estudantes e verifique se há, na região, uma horta urbana. Caso exista esse espaço, solicite uma visita, de modo a incentivar os estudantes a conhecer os objetivos e o funcionamento das hortas urbanas. Uma sugestão é conhecerem o projeto “Cidades sem fome” (disponível em: https://www.cidadessemfome.org/; acesso em: 16 ago. 2022), que inclui a horta urbana como uma oportunidade de oferecer trabalho temporário para pessoas com
pouca qualificação enquanto estão desempregadas e dando-lhes uma oportunidade de viver com dignidade. Os estudantes estarão diante de uma situação que podem analisar com criticidade e conhecer meios de trabalho e alimentação para as pessoas que estão em situação de vulnerabilidade.
Equações que apresentam apenas uma incógnita com expoente 2 e podem ser escritas como ax 2 + bx + c = 0, com a ≠ 0, recebem o nome de equações polinomiais de 2o grau
No caso de b = 0 ou c = 0, chamamos de equação polinomial de 2o grau incompleta
Para resolver aquela equação, vamos primeiramente dividir ambos os membros por 10:
Para solucionar essa equação, devemos identificar quais números multiplicados por eles mesmos resultam em 169. Sabemos que 169 = 13 13 e que 169 = (–13) (–13) Portanto, as soluções para essa equação são: –13 e 13 Podemos escrever da seguinte maneira: x = ±13
Como no contexto utilizado falar em medidas de comprimento negativas não faz sentido, utilizaremos somente a solução positiva: os lados de cada quadrado medem 13 m.
Como potenciação e radiciação, sob certas condições, são operações inversas, poderíamos resolver a equação x 2 = 169 fazendo x = 169 2
Porém, lembrando que a raiz quadrada de um número positivo é sempre um número positivo, obteríamos somente a solução x = 13 Calcular 169 2 nos possibilita saber quais números positivos multiplicados por eles mesmos resultam em 169. Desse modo, não podemos esquecer que resolver a equação x 2 = 169 significa responder “que números multiplicados por eles mesmos resultam em 169”. Assim, devemos escrever:
x 2 = 169 ⇒ x = ± 169 2 ⇒ x = ± 13
LUPAS E LUNETAS
Esse fato é bastante útil se não conhecermos de memória “dois números que multiplicados por eles mesmos resultam em (...)” ou se a obtenção desses números for muito difícil. Utilizando uma calculadora simples, podemos obter a raiz quadrada, lembrando de considerar também as soluções negativas.
Por exemplo, vamos resolver a equação x 2 = 2 601 Como a radiciação é a operação inversa da potenciação, então: x 2 = 2 601 ⇒ x = ± 2 601 Utilizando a tecla de uma calculadora, obtemos 2 601 = 51 e, então, x = ± 51
Utilize uma calculadora para resolver as equações:
a) x 2 = 20 164
b) x 2 = 729
ATIVIDADES
x = ± 142 x = ± 27
4. Resolva as equações:
x 2 = 4
x 2 = 9
5. Resolva as equações:
x 2 = 25
x 2 = 49
6. Um artista vai compor uma obra com 9 figuras idênticas em formato quadrado que cobrirão uma área de 36 m2. Determine a medida do lado de cada quadrado. 2 m.
Habilidade (EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b.
Atividade 5
Para essa atividade, o estudante precisa aplicar as operações inversas para isolar o termo em “x2”. Por exemplo, no item a: a) 2 x 2 = 32
x 2 = 32 2
x 2 = 16
x = ± 4
Atividade 6
A situação-problema pode ser resolvida por esta equação de 2o grau, sendo x a medida do lado do quadrado:
9 x 2 = 36
x 2 = 36 9
x 2 = 4
x = 2m
Note que, embora a equação tenha duas soluções – uma positiva e outra negativa, x é uma medida de comprimento e o contexto impõe a restrição para a resposta única positiva.
Sugestão de atividade
Complemente essa atividade solicitando que multipliquem um número por ele mesmo; escreva na lousa a expressão x 2 = b, sendo b o resultado da multiplicação, assim produziremos exercícios como:
x 2 = 3 969
LUPAS E LUNETAS
O objetivo dessa atividade é o estudante aprender a realizar o cálculo de raiz quadrada com o auxílio de uma calculadora e também analisar o resultado.
O resultado da raiz quadrada de um número (positivo ou nulo) é positivo ou nulo. Porém, quando pensamos em qual número elevado ao quadrado resulta em outro, teremos um número positivo e um número negativo como respostas:
• x , para x ≥ 0, tem um único resultado positivo ou nulo;
• x 2 = a, sendo a ≥ 0, tem duas soluções:
x = + a e x = – a
Atividade 4
Essas atividades podem ser realizadas sem o uso da calculadora. O estudante deve perceber a importância de registrar ambas as respostas: valor positivo e valor negativo.
Depois proponha que, usando a calculadora elaborem expressões do tipo ax 2 = k para isso multiplicam um número por ele mesmo e por outro número, representa por “a”. Por exemplo, 75 75 3 = 16 875, ou seja, produziremos equações como 3 x 2 = 16 875
Sugira que elaborem suas equações “ao contrário” (partindo da solução) e peça aos colegas que as resolvam.
Habilidade
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b. Encontro com outras disciplinas
(EF08GE16) Analisar as principais problemáticas comuns às grandes cidades latino-americanas, particularmente aquelas relacionadas à distribuição, estrutura e dinâmica da população e às condições de vida e trabalho.
Atividade 7
Na resolução dos itens, proponha que façam, inicialmente, os registros calculando mentalmente:
a) (x + 3) (x + 3) = 121
Sabemos que 11 11 = 121
Como 8 + 3 = 11:
(8 + 3) (8 + 3) = 121
x = 8
Mas também é verdade que (–11) (–11) = 121 Como
–14 + 3 = –11:
(–14 + 3) (–14 + 3) = 121
x = –14
Logo, x = 8 ou x = –14
Apresente, na sequência, a resolução utilizando as operações inversas:
b) (x + 10)2 = 100
x + 10 = 10 → x = 0 ou
x + 10 = –10 → x = –20

Para os itens c e d, note que o cálculo mental precisará ser mais elaborado e a resolução utilizando as operações inversas pode ser mais eficaz.
Outras situações envolvendo equações polinomiais de 2o grau
No dia a dia, utilizamos inúmeros utensílios e objetos feitos de alumínio. Especialmente nos grandes centros urbanos, é produzido muito lixo composto de alumínio, por exemplo, as latinhas de bebidas. Por isso, é muito importante a reciclagem de produtos feitos desse tipo de material.
Na natureza, obtém-se o alumínio a partir da extração de um mineral chamado bauxita. Na indústria de mineração, o alumínio é produzido a partir da bauxita e transformado em chapas.
No caso da reciclagem, latas e outros objetos de alumínio são limpos, compactados, derretidos e processados até serem transformados novamente em chapas.
Sucata de alumínio.
Uma fábrica de reciclagem de alumínio costumava produzir chapas de formato quadrado com algumas dimensões específicas. Essa fábrica decidiu então aumentar o tamanho da chapa em 1 metro na largura e 1 metro no comprimento, obtendo uma chapa de área igual a 16 m2 Como saber as dimensões originais das chapas produzidas por essa fábrica?

Sendo x (em metros) a medida da largura e do comprimento das chapas quadradas originais, podemos representar a chapa atual por:
Como a chapa atual possui área igual a 16 m2 então: (x + 1)2 = 16
Como calcular o valor de x, nesse caso?
Novamente, devemos nos perguntar: que números multiplicados por eles mesmos resultam em 16? Nesse caso, há duas possibilidades: –4 ou 4 Assim: (
Nesse contexto, falar em medidas de comprimento negativas não faz sentido, então utilizaremos somente a solução positiva: os lados da chapa quadrada original mediam 3 m.
ATIVIDADES
TRAVESSIAS
Geometria, medidas e álgebra
Considere um quadrado com medida de lado igual a x, em metros.
Habilidade
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b.
TRAVESSIAS
Sabemos que, ao aumentarmos as medidas de cada lado em y metros, o novo quadrado terá uma área igual a 25 m2. Porém, se diminuirmos as medidas de cada lado em y metros, o novo quadrado terá uma área igual a 9 m2:
Atividade 8
ATIVIDADES
8. Considerando a situação acima, realize as seguintes investigações.
a) Escreva uma equação que represente a área em cada uma das situações utilizando as incógnitas x e y Para calcular os valores de x e y, vamos considerar cada equação isoladamente.


b) A partir dessas equações, obtenha os valores de x + y e x – y Para calcular os valores de x e y, vamos escrever sistemas lineares. Porém, note que devemos considerar todas as possibilidades de solução:
c) Resolva cada sistema. Vamos identificar quais soluções são adequadas ao contexto do problema apresentado.
Responda:
Os estudantes podem utilizar o cálculo mental para resolver esse exercício, pois os valores para (x + y )2 = 25 e (x – y )2 = 9 serão uma combinação de dois números cuja soma resulta em +5 ou –5 e a diferença resulta +3 ou 3 Algumas possíveis soluções para a soma seriam (1 + 4 = 5), (4 + 1 = 5), (–1 – 4 (1 + 4 = 5), (4 + 1 = 5), (–1 – 4 = –5) ou (–4 – 1 = –5) Descartando as combinações de valores negativos (porque x e y são medidas), há duas possibilidades de (x, y): (1, 4) ou (4, 1), que também satisfazem a diferença; mas, com x > y , o par (4, 1) será a solução.
d) Lembrando que x e y representam medidas de comprimento, devem ser valores positivos. Quais das soluções se adequam a esse critério? (4, 1); (1, 4).
e) Considere agora as soluções obtidas no item anterior. Pela figura, x > y Qual das soluções se adequa a esse critério? (4, 1).
Habilidade
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b.
LUPAS E LUNETAS
Essa leitura procura mostrar a importância de compreender a linguagem algébrica. A parte operatória para descobrir os valores das incógnitas é importante, mas a intenção é mostrar que saber o significado dos símbolos ou dos gráficos pode tornar o problema compreensível para o estudante.
#Escrevendo álgebra com símbolos
Quando uma “coisa” é desconhecida em um problema
Quando você pensa em álgebra, o que vem à mente primeiro? Você pensa em equações ou fórmulas com x’s, y’s e outras letras, amarradas por números e símbolos aritméticos? Muitas pessoas pensam. Na realidade, muitos consideram a álgebra simplesmente como uma coleção de regras para manipular símbolos que têm relação com números.
Há alguma verdade nisso. Mas descrever a álgebra apenas em termos de seus símbolos é como descrever um carro por sua pintura ou pelo estilo da carroceria. O que você vê não é tudo que você obtém. De fato, como um carro, a maior parte do que faz a álgebra funcionar está “sob o capô” de sua aparência simbólica. Entretanto, da mesma maneira como o estilo da carroceria de um automóvel pode afetar seu desempenho e seu valor, também a representação simbólica da álgebra afeta seu poder e utilidade.
Um problema algébrico, independentemente de como é escrito, é uma questão sobre operações numéricas e relações nas quais uma quantidade desconhecida deve ser deduzida de quantidades conhecidas. Aqui está um exemplo simples:
Duas vezes o quadrado de uma coisa é igual a cinco a mais de que três vezes a coisa. O que é a coisa?
LUPAS E LUNETAS
Apesar da ausência de símbolos, essa é claramente uma questão algébrica. Além disso, a palavra “coisa” foi termo algébrico respeitável por um tempo muito longo. No século IX, Al-Khwarizmi (autor do livro cujo título, Al-jabr w’al muqabala, é a fonte da palavra “álgebra”) usou a palavra shai para representar uma quantidade desconhecida. Quando seu livro foi traduzido para o latim, essa palavra se tornou res, que significa “coisa”.

a) Converse com os colegas: o que você entende que seja a álgebra? Você concorda com a metáfora do autor, quando compara a álgebra a um carro? Comente.
Resposta pessoal.
b) Você viu que um problema pode ser representado geometricamente e algebricamente. O autor afirma algo sobre a representação simbólica da álgebra e seu poder e utilidade. Que inferência ou que conclusão você pode obter a respeito das diferentes formas de representar um problema na Matemática?
c) Leia novamente esse problema: duas vezes o quadrado de uma coisa é igual a cinco a mais de que três vezes a coisa. O que é a coisa? Represente-a utilizando a simbologia algébrica. Compartilhe sua representação com os colegas.
Resposta possível: 2x2 = 5 + 3x
b) Resposta possível: as diferentes representações devem comunicar claramente a mesma ideia matemática presente no foco do problema.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte, em seu caderno, os trabalhos que você desenvolveu, suas anotações de estudos e reflita sobre o que aprendeu até agora neste passeio.
▶ Matemática


Sabe resolver e elaborar problemas envolvendo equações polinomiais de 2o grau do tipo ax 2 + c = 0, a ≠ 0?
• Resolve equações polinomiais de 2o grau do tipo ax 2 + c = 0, a ≠ 0 a partir de diferentes estratégias?

▶ Outras disciplinas
Geografia

• Consegue analisar a importância dos principais recursos hídricos e discutir os desafios relacionados à gestão desses recursos?
• Analisa as principais problemáticas comuns às grandes cidades, particularmente aquelas relacionadas a distribuição, estrutura e dinâmica da população e às condições de vida e trabalho?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
MATEMÁTICA
OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
BARCOS E PORTOS
Organize
Incentive os estudantes a elaborar um mapa mental com exemplos. Esse registro pode conter as equações polinomiais de 2o grau e outros conteúdos que foram utilizados e precisam ser relembrados nos momentos de estudos de revisão.
Elabore
Os problemas envolvendo área da superfície de quadrados elaborados pelos estudantes, a serem resolvidos mentalmente, podem ter valores quadrados perfeitos. Por exemplo: qual é a medida do lado de um quadrado de área 2 500 m2? Nesse caso, é 50 m. Mas ressalte que tanto as medidas de comprimento como as de superfície podem ser números racionais não inteiros (desde que positivos ou nulos).
BARCOS E PORTOS
▶ Organize
Respostas pessoais.
Neste passeio, você explorou equações polinomiais de 2o grau, bem como estratégias para resolvê-las. Elabore um esquema de modo a comparar as estratégias utilizadas com aquelas estratégias para resolver equações polinomiais de 1o grau com 1 ou 2 incógnitas.

Junte-se a um ou dois colegas e, após elaborar individualmente o seu esquema, compartilhe e compare o que há de diferente e o que há de parecido entre os esquemas criados por vocês.
Alunos de escolas do Rio de Janeiro estudando juntos e dividindo o que aprendem.


▶ Elabore
Muitas das situações-problema apresentadas neste passeio utilizaram a noção de área da superfície de quadrados ou retângulos.
• Resolva mentalmente os problemas:
a) Qual é a medida do lado de um quadrado de área 25? 5
b) Qual é a medida do lado de um quadrado de área 4? 2
• Elabore problemas similares a esses e que possam ser resolvidos mentalmente. Proponha a seus colegas. Tente resolver os problemas propostos a você também!
Proponha
A pergunta inicial deste passeio é: Como lidar com os diferentes recursos disponíveis no ambiente urbano?
Ao longo deste passeio, citamos apenas alguns exemplos de “recursos” e como é possível lidar com eles em ambientes urbanos.
• Pesquise mais recursos e identifique problemas ou questões importantes relacionadas a seu uso. Compartilhe com os colegas.
Por um lado, certos recursos podem ficar escassos e isso pode causar uma série de problemas, especialmente em centros urbanos que concentram grandes populações. Por outro lado, um problema bastante evidente é que, mesmo quando não há escassez de alguns recursos, eles são mal distribuídos entre as pessoas.
Leia a charge e converse com os colegas sobre ela e as afirmações feitas anteriormente.

Encontro com outras disciplinas (EF08GE16) Analisar as principais problemáticas comuns às grandes cidades latino-americanas, particularmente aquelas relacionadas à distribuição, estrutura e dinâmica da população e às condições de vida e trabalho.
Proponha
A charge apresenta a problemática da desigualdade na distribuição de renda, que, por consequência, leva as pessoas a viverem em situação de falta de saneamento básico e em condições precárias de educação, saúde, alimentação, moradia etc. Faça uma pesquisa sobre pessoas em risco social, vulnerabilidade ou extrema pobreza em reportagens escritas ou disponibilizadas pela internet e selecione algumas para debater com os estudantes. Essa atividade mobiliza a habilidade de Geografia EF08GE16. Os estudantes reunirão informações da região onde vivem, podendo construir reflexões sobre quais fatores influenciaram para os recursos serem mal distribuídos para a população.
VISTORIAS
Habilidades
EF08MA06, EF08MA07, EF08MA08, EF08MA09
Atividade 1
Os estudantes devem identificar que estas situações podem ser expressas algebricamente:
b) 400 m = 50 000; d) 10d = p;
f) v = d + 20; g) 1f + 0,5l
Atividade 2
Você chegou ao final da Trajetória. Reflita sobre tudo o que aprendeu e verifique a qualidade da sua aprendizagem. Resolva todos os exercícios a seguir no caderno.
CHECK-OUT
15y , com y ≠ 0 É uma expressa ! o algébrica fracionária
1. Identifique quais situações podem ser descritas por expressões algébricas e, se a situação puder ser expressa algebricamente, faça-o. Respostas pessoais.
a) Desejo de viajar para o interior.
b) Comprar um carro que custa R$ 50.000,00 economizando R$ 400,00 por mês.
Efetue as divisões entre os polinômios e verifique se o resultado é um polinômio ou uma expressão algébrica fracionária.
a) Q ÷ S
b) P ÷ S
c) R ÷ S
+ y
d) S ÷ R
e) Q ÷ R
É um polino ! mio veterinário e a masPossíveis soluções:
6 kg, y = 4 kg ou x = 55,4 kg, y = 4,6 kg
a) Por decomposição, a área pode ser calculada por 300 400 + 200 100 = 120 000 + 20 000 = 140 000 m2
200 ⋅ 100 = 120 000 + 20 000 = 140 000 m2 + 20 000 = 140 000 m2
b) Sabendo que a área total é de 240 000 m 2 e um dos lados mede 300 m, o outro lado mede 800 m (240 000 ÷ 300 = 800)
Assim, x + 600 = 800 ⇒ x = 200 m, 00 = 800 ⇒ x = 200 m, enquanto y + 400 = 800 ⇒ y = 400 m A área restante pode ser calculada por:
c) Compor uma canção.
d) Ler 10 páginas por dia de um livro.
e) Cuidar da família.
f) Visitar os avós a cada 20 dias.
g) Utilizar 1 xícara de farinha e 1 2 xícara de leite para fazer um bolo.
2. Uma fábrica vai alugar uma parte de um terreno; a parte a ser locada está representada pela cor cinza na figura:
4. Muitas vezes, para pesar um gato, o veterinário sobe na balança carregando-o e subtrai sua massa. Suponhamos que as massas do veterinário e do gato sejam, juntas, 60 kg. Determine uma equação algébrica que represente essa situação e dê ao menos três soluções. Tenha cuidado ao avaliar a massa do gato.
5. Em um jogo de basquete há arremessos de 2 pontos e de 3 pontos. Desconsiderando arremessos livres que valem 1 ponto, um time marcou 110 pontos só com arremessos de 2 e 3 pontos.
a) Escreva a equação que representa o número de pontos do time.
Sabendo que o terreno todo tem 240 000 m2 , calcule:
a) A área locada pela empresa. 140 000 m2
b) A área restante, calculando os valores de x e y
c) Verifique esse resultado pela área da figura cinza.
240 000 – 140 000 = 100 000 m2
b) Dê 3 possíveis soluções dessa equação e determine que tipo de número pode ser solução.
c) Esboce um gráfico com as soluções dessa equação no plano cartesiano.
6. Resolva os sistemas lineares:
= 30 ou x = 25, y = 20 Nessa sipodem ser números naturais.
3. Considere os polinômios, com x ≠ 0 e y ≠ 0: P: 4x 2 – 2, Q: x 3 y + y 3 x , R: –15xy , S: x 3 , sendo que P, Q, R e S representam polinômios diferentes do polinômio nulo.
Atividade 4
A equação é x + y = 60 ou y = 60 – x , considerando x a massa do veterinário e y a massa do gato. Caso o veterinário pese 55 kg, o gato pesa 60 – 55 = 5 kg; para um veterinário que pese 57 kg, o gato pesa 60 – 57 = 3 kg; e se o veterinário pesar 52 kg, o gato pesará 60 – 52 = 8 kg;
Atividade 5
Uma possibilidade é acertar 25 cestas de 2 pontos e 20 cestas de 3 pontos,
7. Resolva estes sistemas lineares:
2 25 + 3 20 = 50 + 60 = 110; Como as variáveis indicam a quantidade de cestas convertidas, devemos considerar o conjunto dos números naturais.
8. Considere o sistema linear:
a) Represente as soluções de cada equação do sistema como uma reta no plano cartesiano.
b) Paralelas distintas.
b) Qual é a posição relativa dessas retas?
c) Qual é a solução desse sistema linear?
9. Qual é a medida do lado de um quadrado de área 144? 12
DE OLHO NA BÚSSOLA
Após resolver os exercícios da seção Check-out, você pôde checar se de fato aprendeu a:
que podem ser descritas por expressões algébricas.
Considerando os exercícios que você resolveu, como julga seu desempenho: insuficiente, parcialmente suficiente, satisfatório, plenamente satisfatório?
Prossiga ▶
Continue estudando! Retome esta Trajetória buscando, com professores e colegas, alternativas para superar os obstáculos de sua aprendizagem. Estude a seção Retornos e resolva novos exercícios referentes à Trajetória 2 que estão na seção Suplemente sua aprendizagem, ao final do livro.
Atividade 6
Avalie se o estudante consegue resolver os sistemas lineares pelos métodos estudados:
a 2a equação por 2:
Atividade 7
Avalie se os estudantes sabem resolver os sistemas lineares pelos métodos estudados:
a) 2 x – y = 2 x + y = 4 ⎧
Pelo Método da Adição:
x em
Note que, se multiplicarmos a 2a equação por –3 ela fica igual à 1a equação. Teremos então uma única equação em duas incógnitas e há infinitas soluções
Uma delas é x = –1 e y = 2
Atividade 8
Arepresentação das soluções no plano cartesiano corresponde a duas retas paralelas distintas e, por não terem pontos comuns, o sistema linear não tem solução. y
Atividade 9
Sabendo que um quadrado tem lados de mesma medida (positiva), sua área resulta do cálculo l 2 = 144 Então, l = 144 ou l =
(comentário da atividade 10 na
Atividade 10
Para resolver as equações polinomiais de 2o grau incompletas, os estudantes precisam aplicar as operações inversas.
a) 2 x 2 = 162 x 2 = 81
x = ± 81 x = ± 9
b) x = ± 121 x 2 = 121
x = ± 11
c) 3 x 2 = 1 200 x 2 = 400
x = ± 400 x = ± 20
d) 7 x 2 = 252 x 2 = 36
x = ± 36 x = ± 6
e) x 2 = 144
DICAS DE ESTUDO
Nosso cérebro foi feito para aprender, mas também para esquecer! Você vai ter uma prova amanhã à tarde e vai deixar para estudar somente na manhã do mesmo dia? Saiba que muitos estudantes fazem isso. Por isso é muito comum ouvir alguém dizer que na hora da prova “deu um branco”!

Imagem representando e expressão “deu branco” na memória, como uma peça que falta no quebra-cabeça do cérebro.
O pesquisador alemão Hermann Ebbinghaus (1850-1909) estudou os processos de memória e de esquecimento. Ele fez experimentos com a sua própria capacidade de memorização entre 1880 e 1885. Com base em seus estudos, surgiu o conceito de curva do esquecimento
Dicas de estudo
Com a leitura deste texto, incentive os estudantes a manterem o estudo diário; podem consultar os mapas e resumos que elaboraram no decorrer de cada passeio. Há várias atitudes que contribuem para o estudo ser eficaz, mas cada pessoa tem características próprias que influenciam seu modo de aprender. Questione quais atitudes eles sabem que favorecem sua aprendizagem e a memorização e quais ações pretendem implementar para ter um melhor desempenho.
Curva do esquecimento de Hermann Ebbinghaus*.
horas1 semana1 mês
*As porcentagens indicadas na teoria de Ebbinghaus não são universais. Estudos mais recentes mostraram que a curva do esquecimento varia de acordo com o indivíduo e o tipo de informação que ele necessita reter. 124 | VISTORIAS NÃO ESCREVA NO SEU LIVRO.
Os motivos do esquecimento são completamente naturais, não é por nenhum problema no cérebro ou por falha no aprendizado, mas por fazer parte das atividades habituais do cérebro, que necessita jogar fora aquilo que ele não considera importante para não se sobrecarregar de informações.
Observe que, segundo a teoria de Ebbinghaus, nas primeiras 24 horas, os assuntos que você aprendeu na aula de hoje, se não forem revisados em seguida, serão esquecidos por volta de 60% a 70% em relação à sua totalidade.
Se o assunto for revisado antes de 24 horas, a memória volta praticamente a 100%. Cada vez que você faz mais uma revisão dos conteúdos, as relações em seu cérebro vão ficando mais conectadas e, portanto, mais fixas. Esses conhecimentos revisados passam a fazer parte da memória de longo prazo.
Observe ainda, no gráfico, que se um assunto não for revisado em uma semana seu cérebro vai esquecer aproximadamente 80% dele.
Quanto ao processo de armazenamento das informações pelo nosso cérebro, há três subprocessos: aquisição, consolidação e evocação
a) A aquisição se dá no momento em que a informação chega até nosso sistema nervoso por meio de estruturas que transportam a informação recebida até o cérebro.
b) A consolidação corresponde ao momento de armazenar a informação. É quando as informações armazenadas anteriormente em regiões difusas do cérebro – que envolvem redes complexas de neurônios – se modificam para armazenar as novas informações.
c) Por último, após o processo de retenção da informação, o cérebro está apto a nos dar as respostas sempre que as evocarmos ou as recuperarmos da memória. Esse retorno se dá de modo espontâneo ou voluntário. A recuperação pode ocorrer por meio do reconhecimento ou da recordação. Por isso, realizar revisões regulares é de suma importância.
Saiba de uma coisa: não haverá bom aprendizado se você não fizer revisões!
Dicas de estudo
Há várias estratégias de estudo diário: fazer resumos, mapas mentais, esquemas, resolver exercícios, reler os textos etc. Dê sugestões aos estudantes para que transformem o estudo diário em um hábito.
TRAJETÓRIA 3
PANORAMA DA TRAJETÓRIA
Competências gerais: 3, 4, 5. Competências específicas: 4, 5, 6.
Habilidades de Matemática: EF08MA12, EF08MA13, EF08MA14, EF08MA15, EF08MA16, EF08MA17, EF08MA18
Habilidades de outras disciplinas:
Ensino Religioso: EF08ER06
Arte: EF69AR31
Língua Portuguesa: EF89LP02
Temas Contemporâneos
Transversais: Ciência e Tecnologia
Processo de Envelhecimento, respeito e valorização do Idoso
Diversidade Cultural Direitos da Criança e do Adolescente
Vida Familiar e Social Trabalho
As transformações isométricas no plano, as congruências de triângulos, a noção de lugar geométrico e as ideias de proporcionalidade representadas no plano cartesiano desenvolvidas nesta Trajetória podem servir de inspiração para transitar por entre significados amplos de palavras como: transformação (não só as do plano), congruência (ser idêntico, não somente entre triângulos), lugar (outros que não o geométrico) e proporcionalidade (não só por meio da representação no plano). Os significados abrangentes e complexos dessas palavras –que dizem respeito a conceitos fundamentais do “interior” da Matemática, mas que também encontram ressonâncias com outros significados “para fora” da Matemática – favorecerão, em muito, a busca por caminhos envolvidos na pergunta: Como as tecnologias impactam a vida social?
Conectar tanto situações-problema quanto conceitos matemáticos com a realidade pode promover um aprendizado mais significativo para estudantes. Trata-se de uma maneira de desmistificar ideias abstratas e materializar a resolução de problemas.

Você pode pedir aos estudantes que falem todas as palavras que lhes vem à mente quando pensam em “transformação”, “lugar” etc. Pode também perdi-lhes que definam “problema”. Dessa forma, poderá identificar se eles fazem conexões
COMO AS TECNOLOGIAS IMPACTAM A VIDA SOCIAL?


• Quais transformações as tecnologias digitais podem trazer?
• Que lugar ocupam as tecnologias nas relações culturais?
• Que impactos as tecnologias da comunicação podem trazer à vida familiar e ao mundo do trabalho?
imediatas com a Matemática ou com o cotidiano. Peça que anotem suas respostas e as dos colegas em um esquema ou mapa conceitual, para consolidar as conexões feitas por eles.
Espera-se que, por meio da questão motivadora, os estudantes desenvolvam um olhar amplo sobre oentorno, compreendendo o mundo a partir da Matemática e, ao mesmo tempo, ressignificando seus conhecimentos matemáticos.
Jovem empreendedora operando tecnologias digitais no seu local de trabalho e moradia. Adolescente blogueiro compartilhando opinião com o seu público, em momento de gravação, na sala de sua residência.


LUPAS E LUNETAS
Reflita sobre as questões apresentadas anteriormente e considere-as para elaborar outras perguntas de sua própria autoria.
• Publique suas perguntas no mural da sala de aula e aprecie as perguntas dos colegas. Respostas pessoais.
CONTEÚDOS DA TRAJETÓRIA
Passeio 1 – Isometria e congruência de triângulos
• Transformações geométricas
• Translação, rotação e reflexão
• Congruência de triângulos
• Casos de congruência
• Propriedades dos quadriláteros
Passeio 2 – Construção geométrica e lugar geométrico
• Lugar geométrico
• Circunferência como lugar geométrico
• Bissetriz como lugar geométrico
• Mediatriz como lugar geométrico
• Construção da bissetriz e da mediatriz
• Construção de ângulos
• Construção de polígonos regulares
Passeio 3 –Proporcionalidade e plano cartesiano
• Proporção direta
• Proporção inversa
• Não proporcionalidade
• Proporção e plano cartesiano
LUPAS E LUNETAS
Converse com os estudantes sobre as questões iniciais desta Trajetória e proponha que elaborem outras questões. Incentive-os a verbalizar suas experiências para que, a partir delas, criem novas perguntas. Oriente-os sobre a organização e a exposição das questões na sala de aula.
|
Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com ouso de instrumentos de desenho ou de softwares de geometria dinâmica. Encontro com outras disciplinas
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
CHECK-IN
a) É esperado que os estudantes apresentem práticas que favoreçam trocas de opiniões, sentimentos e impressões de forma intergeracional, valorizando conhecimentos que os idosos trazem e fruindo também os conceitos em pauta nas juventudes. Alguns exemplos de práticas intergeracionais: narrar e escrever histórias, apresentar brincadeiras relativas a cada geração, fruir músicas, assistir a filmes e conversar sobre as obras com que tiveram contato.
b) Espera-se que os estudantes reconheçam que há alguma similaridade entre o antes e depois. Todavia, não é possível afirmar que medidas ou formas foram preservadas integralmente.
CONVÍVIO E BEM-ESTAR SOCIAL
Quanto à liberdade de expressão dos idosos, proponha uma roda de conversa e, para incentivar o debate, leia para os estudantes o trecho a seguir do art. 2o da lei n. 10 741, de 1o de outubro de 2003:
O idoso goza de todos os direitos fundamentais inerentes à pessoa humana, sem prejuízo da
E CONGRUÊNCIA DE TRIÂNGULOS
QUAIS TRANSFORMAÇÕES AS TECNOLOGIAS
DIGITAIS PODEM TRAZER?
CHECK-IN
Respostas pessoais.
a) As campanhas publicitárias, os produtos de entretenimento, entre outros, reforçam a busca e a manutenção constantes da juventude. Em muitos casos, a liberdade de envelhecer naturalmente, embora com saúde, parece impedida de se mostrar, levando algumas pessoas a mascarar sua idade. Que práticas do cotidiano você reconhece como abertas à promoção da liberdade de expressão dos idosos, seja pela presença física, seja por seus conhecimentos e convicções? Converse com os colegas.
b) As transformações do tipo antes e depois, mostradas na imagem, preservam a forma e as medidas de cada elemento dos rostos?


proteção integral de que trata esta Lei, assegurando-se-lhe, por lei ou por outros meios, todas as oportunidades e facilidades, para preservação de sua saúde física e mental e seu aperfeiçoamento moral, intelectual, espiritual e social, em condições de liberdade e dignidade.

Espera-se que esse trecho favoreça a construção de diversas argumentações e possibilitem conclusões por parte dos estudantes em favor
da liberdade de expressão dos idosos. Peça aos estudantes que pesquisem o termo “etarismo”, que se refere ao preconceito baseado na idade. Ao final, proponha que selecionem os argumentos e as conclusões que mais apreciaram, julgando quais entre elas são possíveis no cotidiano em que estão inseridos. Desenvolveremos, assim, a habilidade EF08ER06 e o Tema Contemporâneo Transversal (TCT) Processo de Envelhecimento, respeito e valorização do Idoso
Rotação
Ângulo-lado-ângulo (ALA) Lado-lado-lado (LLL)
Lado-ângulo-lado (LAL)
Lado-ângulo-ângulo oposto (LAAo)
Translação
Reflexão
Casos de congruência
ISOMETRIA CONGRUÊNCIA DE TRIÂNGULOS
Transformações geométricas
BÚSSOLA
Homotetia
Propriedades dos quadriláteros
Neste passeio, você buscará atingir os seguintes objetivos:
• Reconhecer transformações geométricas (isometrias: translação, reflexão e rotação).
• Construir, por composições de transformações geométricas, figuras isométricas, utilizando ou não um software de geometria dinâmica.
• Reconhecer o conceito e casos de congruência de triângulos.
• Demonstrar e reconhecer algumas propriedades de quadriláteros e suas relações com a congruência de triângulos.
• Identificar práticas públicas que contribuem para a promoção da liberdade de pensamento e convicções.
ATMOSFERA
Atividade 1
Respostas possíveis:
• Educação: materiais interativos e jogos educativos;
• Trabalho: análise de mercado;
• Social: liberdade de opinião digital;
• Comunicação: e-mail;
• Produção: aperfeiçoamento de processos.
Atividade 2
A resposta vai depender de quão presente está o acesso à tecnologia no cotidiano do estudante e de quanto ele é estimulado a utilizar a tecnologia em favor da educação.
ATMOSFERA
5 exemplos do impacto das tecnologias na sociedade Observe um infográfico que mostra os principais impactos das tecnologias na sociedade atual.

130 | MANUAL DO PROFESSOR
Infográfico sobre os cinco grandes impactos das tecnologias na sociedade, enumerados alguns recursos e serviços.
ATIVIDADES
Respostas pessoais.
1. Escolha duas ou três daquelas cinco categorias e cite mais um recurso ou serviço oferecido nos dias atuais e que você considera importante.
130 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.
Fonte: https://weni.ai/blog/impacto-tecnologia-sociedade. Acesso em: 15 ago. 2022.#Transformações geométricas
A palavra transformação carrega em seu significado a noção de “antes” e “depois” ou, ainda, um estado inicial e um estado final no qual algo ou alguém foi sujeito de uma mudança. No campo da Geometria, uma figura passa de um estado inicial para um estado final por uma transformação geométrica. Na prática, é como se uma figura fosse levada a se corresponder com outra, de modo a observarmos as características da alteração da primeira em relação à segunda quanto a sua posição, forma ou medida.
Uma transformação geométrica é uma correspondência entre duas figuras de modo que, partindo da primeira, obtém-se a segunda preservando a sua forma ou as suas medidas (ou ambas) ou, ainda, suas propriedades.
Quando uma transformação geométrica preserva a forma e também as medidas, dizemos que é uma transformação isométrica ou, simplesmente, isometria (do grego isos = mesma; métron = medida).

Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Atividade 3
Dê um tempo para que façam uma investigação no ambiente e reúnam pares de objetos ou ainda representações que considerem ser resultado de alguma transformação geométrica. Depois, escolha alguns para avaliar em conjunto com a turma e sistematize os resultados que foram obtidos intuitivamente. Você pode pedir que observem elementos da arquitetura e do design interior da sala, padrões nos objetos escolares etc.
Se as medidas da segunda figura não forem mantidas, a transformação geométrica resultará em uma ampliação ou em uma redução em relação à primeira. Nesse caso, falamos em transformação homotética ou, simplesmente, homotetia Neste passeio, vamos estudar as transformações isométricas.
ATIVIDADES
Atividade 4
3. Observe o seu entorno: onde você identifica transformações geométricas? Respostas pessoais.
4. A mesma figura O sofreu três transformações gerando as imagens A, B, C. Quais delas representam transformações homotéticas ou isométricas? A e C.

Resposta possível: o polígono que representa o casco do barco antes tinha 2 ângulos retos, 1 agudo e 1 obtuso, após a transformação passou a ter 2 ângulos agudos e 2 obtusos, conforme vemos na representação da figura B. B
Descreva a(s) característica(s) da figura que a impede(m) de ser uma transformação homotética ou isométrica.
Note que o polígono que representa o casco do barco na figura O tinha, aparentemente, 2 ângulos retos, 1 agudo e 1 obtuso; após a deformação que gerou a figura B, passou a ter 2 ângulos agudos e 2 obtusos, conforme vemos na representação.
131 | NÃO ESCREVA NO SEU LIVRO.Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
LUPAS E LUNETAS
Se possível, reproduza as imagens por meios digitais (fotos, por exemplo) e realize os movimentos sugeridos pelas transformações (com aplicativos de edição de imagens dos próprios celulares), levando partes das figuras em outras partes.
a) Na primeira imagem, parece haver um movimento de “ir para frente ou para cima”; na segunda, um movimento de “giro em torno de alguns pontos”.
b) Na primeira imagem, a mudança ocorrida é de posição sempre em linha reta. Na segunda imagem, a mudança também é de posição, mas de giro em torno de um ponto.
#Transformações isométricas
Observe algumas curiosidades nos padrões de ladrilhamento do plano mostrados nas imagens a seguir.
Duas imagens de ladrilhamento do plano. Uma com figuras amarelas e azuis que lembram peixes e pássaros e outra com figura que lembra um rosto humano de perfil, replicada diversas vezes, em dois tons de mesma cor.
LUPAS E LUNETAS
a) Resposta possível: na primeira, movimento de “ir para frente ou para cima”; na segunda, movimento de “giro em torno de alguns pontos”.
Essas composições no plano, criadas por designers gráficos, foram inspiradas nas obras do artista Maurits Cornelis Escher (1898-1972). Você já ouviu falar dele? Pesquise para saber mais.


a) Você tem a sensação de que tipo de movimento ao observar cada uma dessas imagens? Comente.
b) Sem levar em conta as cores e imaginando que uma figura (de “saída”) vai se sobrepor a outra idêntica sua (de “chegada”), que mudança ocorre na chegada em relação à saída? Comente.
b) Na primeira imagem, a mudança ocorrida é de posição sempre em linha reta. Na segunda imagem, a mudança
Os movimentos associados às posições de figuras geométricas não estão presentes apenas em pavimentações (ou ladrilhamentos) do plano. Em comparações entre duas figuras geométricas também é possível observar qual movimento ocorreu de uma para outra. Vão nos interessar os movimentos que não deformam as figuras, ou seja, elas mudam de posição, mas mantêm sua aparência quanto à forma e às suas medidas.
As isometrias são transformações geométricas que preservam as distâncias entre pontos e as aberturas de ângulos, fazendo com que uma figura seja transformada em outra “geometricamente igual”.
Cada segmento de reta da figura transformada tem a mesma medida do segmento correspondente na figura original, podendo variar a direção ou o sentido. O mesmo vale para cada ângulo transformado, mantendo sua abertura inicial.
também é de posição, mas de giro em torno de um ponto.Tipos de isometrias
As isometrias podem ser do tipo translação, rotação e reflexão
Duas situações de isometrias: uma com um “peixe” e outra com um triângulo retângulo.
Em cada situação, a transformação A representa uma translação da figura original O; B representa uma reflexão da original O e C é uma rotação de O
Translação
Vamos observar com mais detalhes as translações
Translação da figura original, a seta cinza, para sua imagem transformada, a seta azul.
Nas translações, observamos as seguintes características:

• Qualquer segmento de reta é transformado em um segmento de reta paralelo e com mesma medida de comprimento.
• Qualquer ângulo é transformado em um ângulo congruente.
• Todos os pontos da figura inicial e os respectivos pontos na imagem definem a mesma direção, o mesmo sentido e estão à mesma distância entre si.
Observe que, para definir uma translação, são necessárias as condições:
I. Fixar uma distância d
II. Indicar uma direção e um sentido.
Observe que na figura anterior a direção é horizontal e o sentido é para a direita.
Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Rotação
Vamos agora observar alguns detalhes das rotações
Rotação da figura original, a seta cinza, em torno do ponto laranja, para gerar sua imagem transformada, a seta azul.
Nas rotações, observamos as seguintes características:
• Qualquer segmento de reta é transformado em um segmento com mesma medida de comprimento, não necessariamente paralelo.
• Qualquer ângulo é transformado em um ângulo congruente.
Observe que, para definir uma rotação, são necessárias as condições:
I. Fixar um ponto do plano no qual está contida a figura como centro de rotação; na figura anterior é o ponto P
II. Indicar um ângulo orientado segundo o qual será feita a rotação.
Na figura anterior, o ângulo é de 90o no sentido dos ponteiros do relógio (horário).
Feito isso, todos os pontos da figura inicial rodam em torno do ponto fixado, de acordo com um ângulo de medida conhecida e sentido determinado. O sentido da rotação pode ser negativo (horário: o mesmo dos ponteiros de um relógio) ou positivo (anti-horário: sentido contrário ao dos ponteiros do relógio).
Reflexão
Por fim, vamos observar melhor as reflexões
Reflexão da figura original, a seta cinza, na reta laranja, que gera sua imagem transformada, a seta azul.
Nas reflexões, observamos as seguintes características:


• Qualquer segmento de reta é transformado em um segmento com mesma medida de comprimento, não necessariamente paralelo.
• Qualquer ângulo é transformado em um ângulo congruente. Observe que, para definir uma reflexão axial (em relação a uma reta ou eixo), é necessária a condição:
I. Fixar uma reta no plano como eixo de simetria; na figura anterior é a reta e 134 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.
Atividade 5
a) Todos os pontos da figura original têm pontos correspondentes na figura transformada por translação que estão a uma mesma distância dos originais.
b) A distância entre O e O’ é 8u. A figura transformada foi obtida transladando os pontos da figura original 8u na direção horizontal, sentido para a esquerda.
c) Sim, existem infinitos pares de pontos correspondentes, dentre eles B e B’, C e C’.
d) Ambos medem 5u: essa transformação preserva medidas de comprimento (isometria).
e) Sim, existem infinitos segmentos homólogos, dentre eles BO e B'O' , OC e O'C'
f) Saindo de B há dois lados que formam, cada um, 45o com o segmento BO, pois são diagonais de quadrados. Adicionando esses dois ângulos compõe-se o ângulo B ! e pode-se concluir que ele mede 90o. Analogamente, B ! ' também mede 90o (essa transformação preserva medidas de ângulos – isometria).
horizontal, no sentido da direita para a esquerda.
Feito isso, cada ponto da figura inicial corresponde a um único ponto da figura transformada. Dado um ponto P da figura original, há um único ponto P' seu correspondente na imagem transformada. Dizemos que P e P' são simétricos em relação a uma reta fixa (na figura anterior é a reta e), pois o ponto P' é a imagem espelhada do ponto P em relação a essa reta fixa. Essa reta é chamada de eixo de simetria. O segmento PP' é cortado ao meio pelo eixo de simetria.
5. g) Resposta possível: um dos ângulos agudos situados na “cauda do peixinho”.
ATIVIDADES
5. Observe, na malha quadriculada, a figura original na cor amarela e sua imagem transformada na cor azul.
6. Considere o plano cartesiano e as figuras dispostas e responda.
a) Translação de 7 unidades na horizontal para a esquerda (coordenada x do ponto P menos 7 unidades).
a) Qual transformação isométrica podemos observar? Translação.
b) Qual é a distância de O até O' ? Descreva como foi obtida a figura transformada em relação à original.
c) Os pontos O e O' são chamados de pontos correspondentes, pois ambos, cada um em relação à sua própria figura, estão na mesma posição. Existem outros pares de pontos correspondentes entre essas duas figuras? Quais?
d) Qual é a medida dos segmentos BC e B'C' ? ?
e) Os segmentos BC e B'C' são chamados de segmentos homólogos, pois ambos, cada um em relação à sua própria figura, estão na mesma posição. Existem outros pares de segmentos homólogos entre elas? Quais?
f) Qual é a medida dos ângulos internos B ! e B' ! ? Ambos medem 90o
g) Os ângulos internos B ! e B' ! estão situados nos vértices correspondentes B e B' Existem outros pares de ângulos internos situados em vértices correspondentes?
Cite oralmente outro exemplo. Ouça os exemplos citados pelos colegas.
b) Translação de 9 unidades na vertical para baixo (coordenada y menos 9 unidades).
c) Translação de 11 unidades na horizontal para a direita (coordenada x mais 11 unidades).
a) Que transformação leva a figura P a P'?
b) Que transformação leva P' a P"?
c) Que transformação leva P" a P"'?
d) Que transformação leva P a P"'?
7. Considere as figuras dispostas no plano cartesiano e o ponto C como o centro de rotação.
g) É esperado que concluam que cada vértice da figura original tem seu correspondente na figura transladada e os ângulos nesses vértices são congruentes.
Atividade 6
a) Translação de 7 unidades na horizontal para a esquerda (coordenada x do ponto P menos 7 unidades, pois 2 – (–5) = 2 + 5 = 7).
a) Descreva a transformação que leva o ponto A ao A'. O que aconteceu com as coordenadas de A?
b) Descreva a transformação que leva A ao A"
c) Descreva a transformação que leva A ao A'"
d) Existem pontos que não se alteram nessas isometrias? Quantos eles são?
b) Translação de 9 unidades na vertical para baixo (coordenada y do ponto P’ menos 9 unidades, pois 3 – (–6) = 3 + 6 = 9).


c) Translação de 11 unidades na horizontal para a direita (coordenada x do ponto P” mais 11 unidades, pois 6 – (–5) = 6 + 5 = 11).
d) Translação de 4 unidades na horizontal para a direita e 9 unidades na vertical para baixo (coordenada x do ponto P mais 4 unidades e coordenada y do ponto P menos 9 unidades, pois 6 – 2 = 4 e 3 – (–6) = 9).

5. c) Existem. Todos os pontos da figura original mantêm a mesma distância em relação ao seu correspondente na figura transformada (B e B', por exemplo).
Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
5. e) Existem. Todos os segmentos possíveis da figura original têm um homólogo seu correspondente na figura transformada (OB e O'B' , por exemplo).
É esperado que os estudantes consigam, a partir dos itens anteriores, perceber que é necessário realizar a composição de transformações (nas direções vertical e horizontal) para descrever essa última translação. Questione-os sobre qual translação levaria P em P”’ (uma única translação na direção da “diagonal” para baixo).
Atividade 7
6. d) Translação de 9 unidades na vertical para baixo seguida de uma translação de 4 unidades na horizontal para a direita (coordenada x mais 4 unidades e coordenada y menos 9 unidades).
Você pode pedir que reproduzam a imagem no caderno e tracem os segmentos OA, OA’ , OA” e OA’” Dessa maneira, podem visualizar melhor as rotações sobre O.
a) Rotação de 90 o de centro C, no sentido anti-horário. A coordenada do eixo Ox (abscissa) de A foi levada na coordenada do eixo Oy (ordenada) de A’; e a coordenada do eixo Oy de A foi levada na coordenada negativa do eixo Ox de A ’. A(5,2) → A'(–2, 5)
7. a) Giro de 90o de centro C, no sentido anti-horário. A coordenada do eixo Ox (abscissa) de A foi levada na coordenada do eixo Oy (ordenada) de A'; e a coordenada do eixo Oy (ordenada) de A foi levada na coordenada negativa do eixo Ox (abscissa) de A' A (5, 2) → A' (–2, 5)
7. b) Giro de 180o de centro C, sentido anti-horário. A (5, 2) → A" (–5, –2)
b) Rotação de 180 o de centro C, sentido anti-horário. A(5,2) → A''(–5, –2)
7. c) Giro de 270o de centro C, sentido anti-horário. A (5, 2) → A'" (2, –5)
c) Rotação de 270 o de centro C, sentido anti-horário. A(5,2) → A'''(2, –5)
d) Apenas o centro de rotação C não se altera.
d) Ambos medem 5uHabilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

Atividade 8
a) Reflexão pelo eixo Oy. A abscissa foi levada no seu oposto e a ordenada foi preservada: B(5, 7) → B'(–5, 7)
b) Reflexão pelo eixo Ox . A abscissa de B' foi levada na abscissa de B" e a ordenada de B ' foi levada no seu oposto como ordenada de B": B(–5, 7) → B''(–5, –7)
c) Reflexão pelo eixo Oy. A abscissa de B" foi levada no seu oposto como abscissa de B'"; e a ordenada de B" foi preservada como a ordenada de B'". B''(–5, –7) → B'"(5, –7)
d) Todos os pontos pertencentes ao eixo Ox. Todo ponto pertencente ao eixo Oy
Atividade 9
Observe que existem diferentes tipos de interpretações das simetrias.
a) Reflexão axial.
b) Rotação de 120o e 240o no sentido horário ou no anti-horário ou rotação da imagem por um ponto central..
c) Podemos interpretar a imagem como uma rotação do “J” de 180o no sentido horário em relação a um ponto acima da imagem e translação na vertical para baixo. Também é possível pensar no logo como um todo, considerando uma rotação de 180º do “JP” em torno de um ponto central na imagem.

d) Translação no “M” na horizontal para a esquerda e reflexão axial nas asas.
e) Rotação de 180o em relação a um ponto central entre os dedões das duas mãos.
f) Rotação de 720o no sentido anti-horário em torno do centro da imagem.
8. Considere o plano, as figuras dispostas e os eixos de simetria como sendo os eixos cartesianos Ox e Oy
a) Reflexão pelo eixo Oy. A abscissa foi levada no seu oposto e a ordenada foi preservada. B (5, 7) → B' (–5, 7)
c) Reflexão pelo eixo Oy. A abscissa de B" foi levada no seu oposto como abscissa de B"'; e a ordenada de B" foi preservada como a ordenada de B"' B" (–5, –7) → B'" (5, –7)
b) Reflexão pelo eixo Ox. A abscissa de B' foi levada na abscissa de B" e a ordenada de B' foi levada no seu oposto como ordenada de B" B' (–5, 7) → B" (–5, –7)
a) Descreva a transformação que leva o ponto B a B'. O que aconteceu com as coordenadas de B?
b) Descreva a transformação que leva B' a B". O que aconteceu com as coordenadas?
c) Descreva a transformação que leva B" a B"'. O que aconteceu com as coordenadas?
d) Quais são os pontos que ficam fixos por reflexão no eixo Ox? E no eixo Oy?
Todos os pontos pertencentes ao eixo Ox; todo ponto pertencente ao eixo Oy
Translação no “M” na horizontal para a esquerda e reflexão axial nas asas.
Reflexão axial.
Rotação de 120o e 240o no sentido horário ou no anti-horário.
9. Nos logotipos, identifique os tipos de isometria. Respostas possíveis: a) b)




Rotação de 180o no sentido horário em relação a um ponto acima da imagem e translação na vertical para baixo.
f) Dica: há logotipos com mais de um tipo de isometria.

Rotação de 180° em relação a um ponto central entre os dedões das duas mãos.
Rotação de 72o no sentido anti-horário em torno do centro da imagem.
Composição de transformações isométricas
Algumas adolescentes estão testando como transformar a letra p em outras letras. Agora, por exemplo, estão transformando o p em b
Habilidade (EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Três adolescentes mostrando suas transformações isométricas de p em b.
A letra em preto é a figura original (de saída) e a letra em azul é a imagem transformada (de chegada). As letras em cinza são passos intermediários.
LUPAS E LUNETAS
a) Sim. Não. Sim. Que há mais de uma maneira de transformar uma figura em outra congruente a ela fazendo composições com transformações isométricas.
Junte-se a um colega para interpretar e responder:
a) Os três adolescentes transformaram, de fato, a letra p em b? Os procedimentos usados por eles foram iguais? Os resultados foram iguais? Que conclusões vocês podem tirar?
b) Identifique quais transformações isométricas cada um utilizou.
c) Qual dos três utilizou mais etapas? E qual deles utilizou menos? Ana. Clis.
b) Ana: utilizou três reflexões; Bil: utilizou uma rotação e uma reflexão; Clis: utilizou apenas uma reflexão.
ATIVIDADES
10. Descreva as transformações isométricas para as figuras a seguir, utilizando somente reflexões em torno de retas. Utilize P e P" e B e B" como referências e determine pontos de transformações intermediárias P' e B'
LUPAS E LUNETAS
Observe com os estudantes que há mais de uma maneira de transformar uma figura em outra congruente a ela fazendo, por exemplo, composições com transformações isométricas.
Atividade 10
Reflexão pelo eixo Oy, levando B(–8, 10) em B'(8, 10) Depois, reflexão pela reta paralela ao eixo Ox que passa pelo ponto (0, 2), levando B'(8, 10) em B''(8, –6)
Reflexão pela reta paralela ao eixo Ox que passa pelo ponto (0, 5) levando P(13, 7) em P’(13, 3). Depois, translação na horizontal para a esquerda, subtraindo 12 unidades da coordenada x, levando P’(13, 3) em P(1, 3). Considere também que as transformações podem ser realizadas por B’(-8,-10) e P’(1,7).
Reflexão pelo eixo Oy, levando
B (–8, 10) em B' (8, 10) Depois, reflexão pela reta paralela ao eixo Ox que passa pelo ponto (0, 2), levando B' (8, 10) em

B" (8, –6)
Reflexão pela reta paralela ao eixo Ox que passa pelo ponto (0, 5) levando P (13, 7) em P' (13, 3). Depois, translação na horizontal para a esquerda, subtraindo 12 unidades da coordenada x, levando P' (13, 3) em P (1, 3).
Habilidade
(EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
NUVENS
O nome da ferramenta nos softwares de geometria dinâmica é “translação por um vetor”. Mesmo que o estudante não tenha estudado ainda o conceito de “vetor”, explique de modo intuitivo que um vetor é um segmento de reta orientado: com comprimento, direção e sentido e é representado por uma seta.
Atividades 11 a 13
Se algum estudante escolher uma reta s coincidente com r, então a figura A'"B'"C'"D'"E'"F'"G'" estará na mesma posição da figura inicial ABCDEFG . Caso nenhum escolha essa opção, apresente a possibilidade.
Após realizarem a construção, faça uma investigação para que estudem qual o resultado da composição de duas reflexões por retas paralelas. Após concluírem que é uma translação, solicite que determinem qual a translação que leva diretamente a figura ABCDEFG à figura A'"B'"C'"D'"E'"F'"G'" que produziram.
NUVENS
Isometrias com software
Para estas atividades, formem grupos e utilizem as tecnologias digitais e suas ferramentas.

Para estudar as isometrias, Beatriz utilizou um software de geometria dinâmica. Veja a composição final dela.
Utilizando a ferramenta polígono ( ), ela traçou a figura ABCDEFG Com a ferramenta reflexão em relação a uma reta ( ), o polígono A'B'C'D'E'F'G' foi gerado.
Por fim, com a ferramenta rotação em torno de um ponto ( ), rotacionou a figura A'B'C'D'E'F'G' em torno de P, no sentido horário e com um ângulo de 60o e obteve A"B"C"D"E"F"G".
ATIVIDADES
11. É possível utilizar somente a ferramenta translação por um vetor ( ) para obter a figura A"B"C"D"E"F"G" a partir da ABCDEFG?
Não, pois composições de translações não podem gerar uma rotação.
12. Faça uma reflexão da figura A'B'C'D'E'F'G' por uma reta s paralela a r, obtendo-se a figura A'"B'"C'"D'"E'"F"G'" Construção pessoal.
13. É possível partir da figura ABCDEFG e chegar à figura A'"B'"C'"D'"E'"F"G'" usando a ferramenta rotação uma única vez? E utilizando a ferramenta translação uma única vez?

Não é possível utilizando a rotação, mas a translação sim.
O nome da ferramenta é “translação por um vetor”. Mesmo que o aluno não tenha visto ainda o conceito de “vetor”, explique de modo intuitivo que o vetor é um segmento de reta que tem comprimento, direção e sentido e é representado por uma seta.
#Congruência de triângulos
Vamos imaginar a seguinte situação: Adele é uma artista plástica. Ela se inspira em padrões ornamentais de culturas diversas para fazer suas criações em estamparia de tapetes. Ela faz seus projetos utilizando softwares específicos para seus trabalhos artísticos.
Habilidade
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Encontro com outras disciplinas
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
Artista plástica idosa e seu projeto desenvolvido em ferramentas digitais.
LUPAS E LUNETAS
Como você vê a produção manual ou intelectual dos idosos? Como interage com eles? Por meio de que atitudes você demonstra valorizar o envelhecimento e as formas de expressão dos idosos? Converse com os colegas. Respostas pessoais.

Veja detalhes deste novo projeto que ela está desenvolvendo, inspirado na cultura asteca:
O triângulo com esse padrão aparece no projeto dela quatro vezes. Seriam os quatro triângulos iguais? Seriam três deles transformações isométricas de um deles?
A igualdade de triângulos é uma noção geométrica associada à ideia ampla de congruência de figuras. De modo intuitivo, podemos dizer que dois triângulos são congruentes se é possível sobrepô-los utilizando movimentos de isometrias, ou seja, movimentos que mudam um triângulo de lugar, sem deformá-lo, para um “cobrir” o outro sem que um deles deixe qualquer parte sua para fora da borda do outro.

O triângulo ABC é congruente ao triângulo A'B'C' quando é possível estabelecer uma correspondência entre seus vértices de modo que:
I. Os vértices correspondentes determinam ângulos internos com medidas iguais.
II. Os lados homólogos tenham medidas de comprimento iguais.
Escrevemos: △ABC ≡ △A'B'C' (lê-se: triângulo ABC é congruente ao triângulo A'B'C').

LUPAS E LUNETAS
Retome o diálogo realizado no início do passeio para que os estudantes novamente reflitam sobre como interagem com os idosos na comunidade em que estão inseridos e como podem ampliar suas perspectivas de interação com outras gerações.
Sugestão de atividade Organize com os estudantes um evento intergeracional artístico em que eles possam convidar adultos e idosos da comunidade escolar para expressar seus pensamentos, suas crenças e suas opiniões por meio de artes diversas. Deixe clara qual é a intenção, instruindo sobre respeito e sujeição, para haver o fortalecimento dos laços entre gerações e a quebra de paradigmas e preconceitos, explicando que nenhuma forma de discriminação entre pessoas é aceitável. Caso possível, deixe uma equipe responsável para realizar registros por meio de fotos ou vídeos que poderão ser utilizados na produção futura da subseção Proponha da seção Barcos e portos
Habilidade (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Comente com os estudantes que o triângulo A ' B ' C ' no início desta página é resultante de uma composição de transformações isométricas sobre o triângulo ABC. Ao aplicar no triângulo ABC uma rotação em torno de um ponto O e, em seguida, aplicar uma reflexão em relação a um eixo e, obtém-se o triângulo A'B'C'. Retome as notações para ângulos de medidas iguais e lados de polígonos de medidas iguais.
Observação: os lados homólogos são formados por vértices correspondentes.
A figura mostra dois triângulos congruentes, ou seja: △ABC ≡ △A'B'C'
Temos: A é correspondente a A', B é correspondente a B' e C é correspondente a C' (ou, representado simbolicamente: A ↔ A' , B ↔ B' e C ↔ C' )
Conforme os itens I e II da definição de congruência de triângulos, temos:
A ! ≡ A' ! , B ! ≡ B' ! e C ! ≡ C' ! e
AB ≡ A'B' , BC ≡ B'C' e CA ≡ C'A'
Para determinar se dois triângulos são congruentes, é necessário verificar as seis congruências: os três pares de ângulos correspondentes e os três pares de lados correspondentes. Mas existem “condições mínimas” – critérios específicos – para que dois triângulos sejam congruentes, evitando assim checar as seis congruências.
Vamos enunciar quatro critérios que são chamados de casos de congruência de triângulos
1o caso: LAL (lado – ângulo – lado)
Se dois triângulos têm, na devida ordem, congruentes dois lados e o ângulo formado por esses dois lados, eles são congruentes.
Exemplo:
A correspondência de vértices é A ↔ A' , B ↔ B' e C ↔ C'


Observe que os lados AB e A'B' são congruentes de medida 3, os lados AC e A'C' são congruentes de medida 5 e os ângulos A ! e A' ! são congruentes de medida 60o
Assim, o caso LAL fornece as congruências adicionais que são: BC ≡ B'C' , B ! ≡ B' ! e C ! ≡ C' !
140 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.
ATIVIDADES
Congruência LAL: lado 3, ângulo de 80o, lado 4,8.
Congruência LAL: lado 5, ângulo de 36o, lado 8,5.
14. Em cada item, aponte quais são os triângulos congruentes. Confirme se a congruência é do tipo LAL. a) b)
Habilidade (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Atividade 14
2o caso: ALA (ângulo – lado – ângulo)
Se dois triângulos têm, na devida ordem, congruentes dois ângulos e o lado adjacente a esses ângulos, eles são congruentes.
Exemplo:
A correspondência de vértices é A ↔ A' , B ↔ B' e C ↔ C'


Observe que os lados BC e B'C' são congruentes de medida 8, os ângulos B ! e B' ! são congruentes de medida 70o e os ângulos C ! e C' ! são congruentes de medida 30o
Assim, o caso ALA fornece as congruências adicionais que são: BA ≡ B'A' , AC ≡ A'C' e A ! ≡ A' !
3o caso: LLL (lado – lado – lado)
Se dois triângulos têm, na devida ordem, congruentes os três lados, eles são congruentes.
Exemplo:
A correspondência de vértices é A ↔ A' , B ↔ B' e C ↔ C' Observe que os pares de lados AB e A'B' , BC e B'C' , CA e C'A' são congruentes e, na devida ordem, medem 4, 6, 5.


Como os estudantes já sabem qual o caso de congruência a ser verificado, é esperado que o utilizem como critério eliminatório na verificação. Caso haja dificuldade, mostre que o triângulo que não satisfaz a relação tem disposição de ângulos e lados diferentes dos outros (o ângulo não está entre os lados correspondentes de medidas iguais ou não é formado por eles).
a) São congruentes os triângulos T1 e T3. Não é possível verificar a congruência destes com T2
b) São congruentes os triângulos T1 e T2. Não é possível verificar a congruência destes com T3
Habilidade
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Atividades 15 a 18
Chame a atenção dos estudantes para a importância da ordem em que escrevem os vértices nomeando os lados e os ângulos correspondentes em triângulos congruentes. Por exemplo, na atividade 15, os triângulos RPQ e MWV não estariam corretamente identificados porque não têm, nessa ordem, lados ou ângulos correspondentes congruentes. A escrita na ordem correta dos vértices facilita a identificação de ângulos congruentes e lados homólogos.
16. Não são congruentes, pois, embora tenham em comum dois ângulos de mesma medida e um lado de mesma medida, essas medidas não correspondem, na devida ordem, a ângulos em vértices correspondentes e a lados homólogos.
WM , por exemplo, corresponde a QR porque são ambos lados de medida 2 e com vértices indicados no sentido do ângulo de 100o para o outro ângulo correspondente de medida não dada.
Da mesma maneira, na atividade 17, para identificar os ângulos correspondentes é preciso notar que eles são formados por lados homólogos de medidas iguais (indicadas pela mesma quantidade de tracinhos em cada triângulo).
Atividade 16
Não são congruentes, pois, embora tenham em comum dois ângulos de mesma medida e um lado de mesma medida, essas medidas não correspondem, na devida ordem, a ângulos em vértices correspondentes e a lados homólogos.
Atividade 17
Você pode orientar os estudantes a reproduzirem os triângulos no caderno, nomeando vértices e ângulos, para auxiliar no processo de identificação.
Assim, o caso LLL fornece as congruências adicionais que são: A ! ≡ A' ! , B ! ≡ B' ! e C ! ≡ C' !
4o caso: LAAo (lado – ângulo – ângulo oposto)
Se dois triângulos têm, na devida ordem, congruentes um lado e um ângulo e o ângulo oposto a esse lado, eles são congruentes.
Exemplo:
A correspondência de vértices é A ↔ A' , B ↔ B' e C ↔ C'




Observe que o par de lados AB e A'B' (de medida 4) e os ângulos B ! ≡ B' ! e C ! ≡ C' ! são congruentes (de medidas 55o e 40o, respectivamente).
Assim, o caso LAAo fornece as congruências adicionais que são: BC ≡ B'C' , CA ≡ C'A' e A ! ≡ A' !
ATIVIDADES
15. a) Lados homólogos QR ≡ WM , QP ≡ WV , PR ≡ VM Vértices correspondentes: Q ↔ W , P ↔ V , R ↔ M
15. Os triângulos RPQ e MVW são congruentes.
a) Determine os lados homólogos e os vértices correspondentes dessa congruência.
b) Qual é o caso de congruência desses dois triângulos? LAL.

16. Os triângulos representados são congruentes? Explique.
18. Identifique os casos de congruência nos pares de triângulos.
17. Calcule os ângulos internos dos triângulos, sabendo que são congruentes:

LAAo.
e VII; II e V; III e VI; IV e VIII.
Habilidade (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.










Atividade 19
I e VII: LAL; II e V: LLL; III e VI: ALA; IV e VIII: LAAo.
Atividade 20
Retome a definição de congruência entre triângulos, para que estudantes identifiquem as relações de igualdade entre medidas de ângulos e lados correspondentes.


30
25
Habilidade (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
#Propriedades de quadriláteros e congruências de triângulos
A ciência e a tecnologia andam em parceria. A ciência busca compreender os fenômenos que acontecem na natureza, e a tecnologia procura por soluções práticas. A engenharia, por exemplo, faz uso frequente da tecnologia. Os conhecimentos sobre triângulos (sua rigidez, as congruências, as isometrias etc.) e quadriláteros (suas propriedades envolvendo medidas de lados e de diagonais), por exemplo, são muito utilizados na engenharia.

Estruturas de pontes aplicando os conhecimentos a respeito de triângulos e quadriláteros.
Arquiteta utilizando tecnologia de realidade virtual na modelagem de problemas da construção civil. Microscopia para análise de material composto para futuros usos na construção de estradas. Muitas estruturas levam em sua composição figuras geométricas básicas como triângulos e quadriláteros.

Esboço da estrutura de uma ponte. É possível reconhecer triângulos e quadriláteros nessa composição esquemática.


144 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.

LUPAS E LUNETAS Respostas pessoais.
Recupere mentalmente os lugares por onde você passa em seus trajetos. Também considere o entorno nesses trajetos: as edificações, a paisagem urbana etc.
a) Que processos e ferramentas matemáticas você é capaz de identificar como aplicações dadas pela tecnologia nos diferentes aspectos da paisagem urbana?

b) Que conhecimentos específicos do amplo campo da Matemática você identifica?
• Converse com os colegas e o professor.
Um uso que podemos fazer dos conhecimentos de congruência de triângulos é aquele que
Habilidade
Esquema matemático mostrando uma propriedade do retângulo: as diagonais são congruentes.
Existem diversas propriedades dos quadriláteros: as que enunciam fatos relacionados aos ângulos (opostos congruentes; medem 90o), aos lados (paralelismos e comprimento) e às diagonais (como se intersectam, comprimento, existência de perpendicularidade).
Vamos estudar três propriedades, dentre várias, que observam as diagonais de alguns quadriláteros.
Propriedade
1: diagonais do paralelogramo

Em todo paralelogramo, as diagonais cortam-se nos correspondentes pontos médios.
LUPAS E LUNETAS
Realize com os estudantes uma discussão ampla sobre como a Matemática está inserida no contexto das tecnologias exploradas e conhecidas pelas juventudes. Todavia, chame atenção para os quadriláteros presentes nas imagens vistas na leitura do texto. Além de engenharia, arquitetura e biologia, há outras áreas de conhecimento que podem ser citadas pelos estudantes. Procure mediar a conversa de modo a destacar as formas dos quadriláteros nos diversos ambientes em que convivem, inclusive o virtual.
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Habilidade
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.




Sugestão de leitura
Relembre com os estudantes as classificações dos quadriláteros e as classificações inclusivas. Esse conhecimento foi explorado no 7o ano.
Este texto pode auxiliar no resgate de conhecimentos prévios.
1. Paralelogramos especiais
Dentre os quadriláteros notáveis, os losangos, retângulos e quadrados são os que têm mais propriedades interessantes. Eles serão objetos de estudo neste tópico. Um quadrilátero convexo é um losango se todos os seus lados são congruentes. Uma vez que, em um losango, os pares de lados opostos são formados por segmentos congruentes, concluímos que todo losango é, em particular, um paralelogramo.
Vamos considerar um paralelogramo ABCD
A C
Um quadrilátero convexo é um retângulo se todos os seus ângulos são retos. Dessa forma, todo retângulo possui ângulos consecutivos (ou opostos) suplementares; assim, todo retângulo também é um exemplo particular de paralelogramo.
Fatos que temos: ABCD é um paralelogramo; M é comum a AC e BC
Fatos que queremos demonstrar: AM ≡ CM e BM ≡ DM
Demonstração: o fato que queremos demonstrar é equivalente a mostrar que: △ ABM ≡ △CDM
Sendo ABCD um paralelogramo, temos duas consequências diretas:
AB ≡ CD (1)
AB ! " ! CD ! "
De AB ! " ! CD ! " (feixe de paralelas cortada por transversal) vem:
• B A ! C ≡ DC ! A (2), pois são alternos internos.
• AB D ≡ C DB (3) , pois são alternos internos.
Juntas, as condições (2), (1) e (3) satisfazem o critério de congruência ALA.
Portanto, △ ABM ≡ △CDM , ou seja: AM ≡ CM e BM ≡ DM
Propriedade 2: diagonais do losango
Todo losango tem diagonais perpendiculares.
Vamos tomar um losango ABCD
Fato que temos: ABCD é losango.
146 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.
Disponível em: https://cdnportaldaobmep.impa.br/portaldaobmep/uploads/ material_teorico/bq7pvlrqqlckc.pdf. Acesso em: 26 abr. 2022.
Fato que queremos demonstrar: AC ⊥ BD
Demonstração: o fato que queremos demonstrar é equivalente a mostrar que as medidas dos quatro ângulos em torno de M são iguais. Vamos mostrar que os quatro triângulos são congruentes, ou seja:
△ AMB ≡ △ AMD ≡ △CMB ≡ △CMD
Sendo ABCD um losango, podemos afirmar que é também um paralelogramo. Desses dois fatos decorrem:
• AB ≡ AD ≡ CB ≡ CD (da definição de losango)
• AM ≡ CM , BM ≡ DM (propriedade 1, demonstrada anteriormente)
Esses fatos, juntos, satisfazem o caso LLL de congruência de triângulos.
Portanto, △ AMB ≡ △ AMD ≡ △CMB ≡ △CMD, ou seja, os ângulos de vértice M são congruentes e suplementares. Logo, AC ⊥ BD
Propriedade 3: diagonais do retângulo
Em todo retângulo as diagonais são congruentes.
Vamos considerar um retângulo ABCD
Fato que temos: ABCD é um retângulo.
Fato que queremos demonstrar: AC ≡ DB
Demonstração: o fato que queremos demonstrar é equivalente a mostrar que:
△BAD ≡ △CDA
Como ABCD é um retângulo, podemos afirmar que é também um paralelogramo. Por definição de paralelogramo, temos: BA ≡ CD
Assim, listamos as seguintes condições:
• BA ≡ CD ;
• A ! ≡ D ! ;
• AD é lado comum aos dois triângulos.

Juntas, essas três condições satisfazem o caso LAL de congruência de triângulos.
Portanto, △BAD ≡ △CDA e, então, AC ≡ DB
147 |
NÃO ESCREVA NO SEU LIVRO.Habilidade (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Atividades 21 e 22
Retome o conceito de rigidez dos triângulos, para complementar a visão geométrica das estruturas.
Atividade 21
Considere essa atividade uma extensão das observações do meio propostas no último boxe Lupas e lunetas
Atividade 22
Se possível, e com cuidado ao manipular os materiais envolvidos na estrutura, realize com os estudantes a construção e investiguem a propriedade associada.
Atividade 23
Apresente exemplos e contraexemplos para esclarecer as relações de inclusão e as propriedades dos quadriláteros nessa atividade.
Atividade 24
D B A C
Decorrente dessa congruência de triângulos, obtemos:

B A ! C ≡ D C ! A ⇒ AB || CD (1)
BC ! A ≡ DA ! C ⇒ AD || BC (2)
ATIVIDADES
21. Observe as imagens de grades de madeira e responda.
22. Um adolescente fez esta estrutura com palitos de sorvete e tachinhas.
148 | MANUAL DO PROFESSOR
Estruturas de madeira para sustentação de plantas ornamentais de escalada em paredes.

São compostas de figuras que lembram quadrados.
a) Quanto à forma, o que há em comum nessas estruturas de madeira?
b) Para qual delas podemos afirmar, com certeza, que não vai desmoronar? Argumente apresentando algum conhecimento geométrico.
Ao utilizar mais dois palitos, com as devidas medidas, a estrutura dele ficou rígida.
a) Desenhe como ficou a nova estrutura.
b) Cite uma propriedade dos quadriláteros que é possível observar no desenho feito no item anterior.

23. Classifique cada sentença em verdadeira (V) ou falsa (F). V, F, V, V, V, V, F.
a) Todo losango é um paralelogramo.
b) Todo losango é um quadrado.
c) Todo quadrado é um losango.
d) As diagonais do losango cortam-se nos correspondentes pontos médios.
e) Todo quadrado tem diagonais perpendiculares.
f) As diagonais do quadrado são congruentes.
g) Se as diagonais de um quadrilátero se cortam nos correspondentes pontos médios, então esse quadrilátero é um losango.
Demonstração.
24. Demonstre o seguinte fato: Todo quadrilátero convexo que tem lados opostos congruentes é paralelogramo.
A estrutura que tem madeira na cor natural, pois, no cruzamento de duas ripas, há uma amarração em forma de X, que, por sua vez, compõe triângulos. Veja o esquema:
a) As diagonais do retângulo cortam-se ao meio.LEVO NA BAGAGEM
LEVO NA BAGAGEM
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado e reflita sobre as perguntas a seguir.

▶ Matemática


Você reconhece transformações geométricas (translação, reflexão e rotação)?
• Constrói, por composições de transformações geométricas, figuras isométricas, utilizando ou não software de geometria dinâmica?
• Reconhece o conceito e os casos de congruência de triângulos?
• Reconhece algumas propriedades de quadriláteros e suas relações com a congruência de triângulos?
▶ Outras disciplinas
Ensino religioso
Identifica práticas públicas que contribuem para a promoção da liberdade de pensamento e convicções?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
MATEMÁTICA
OUTRAS ÁREAS
Insuficiente
QUADRO DE AVALIAÇÃO
Parcialmente suficiente Satisfatório Plenamente satisfatório
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
Respostas pessoais. 149 |
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.

PORTOS
Organize
Caso seja viável, programe essa produção utilizando um software de geometria dinâmica para que os estudantes consigam também revisitar os conteúdos ligados a tecnologias estudados neste passeio.
Elabore
Auxilie os estudantes na reprodução e manipulação das peças pelo aplicativo e exponha as imagens criadas.
▶ Organize
Respostas pessoais.
Desenhe em um plano cartesiano quatro triângulos (use malha quadriculada): para cada um deles imagine outro congruente, contemplando os quatro casos de congruência estudados neste passeio.
Dica: aplique alguma transformação isométrica em cada um dos quatro triângulos para obter seus respectivos congruentes.
Fazendo desse modo você revisita, organiza e reintegra os principais conhecimentos explorados neste passeio.
Compartilhe sua produção com os colegas.
▶ Elabore
a) Leia a frase:
Simetria é uma invariância na propriedade de certo objeto matemático que tem sua estrutura preservada independentemente das transformações isométricas que se apliquem sobre esse objeto.
Procure em dicionários as palavras que você não reconheceu.
Elabore um desenho e represente simétricos a ele, utilizando as três formas de simetria que aprendeu neste passeio.
Apresente seus desenhos para a turma.
b) Usando modelos de peças A e B, André criou estas composições.
Respostas possíveis:

Figura 1 — peça A: reflexão e translação; peça B: translação.

Figura 2 — peça A: rotação e translação; peça B: rotação e translação. Figura 3 — peça A: reflexão; peça B: reflexão.
• Em cada figura, compare os modelos da mesma peça e descreva que tipo de isometria ocorreu.
• Compare as suas descrições com as dos colegas. Resposta pessoal.
• Digitalize as peças A e B. Utilizando um aplicativo de edição de imagens, crie uma composição usando duas vezes cada peça. Poste em uma rede social e descreva que tipo de isometria você utilizou para o modelo das peças A e B.
A pergunta inicial deste passeio é: Quais transformações as tecnologias digitais podem trazer?
Imagens mostrando a diversidade da dinâmica social dos idosos: um grupo de idosos interagindo com dispositivo móvel, um idoso ensinando a adolescentes as tecnologias de engenharia; uma menina acompanhando seu avô em videoconferência; e uma mãe aprendendo com o filho a manusear o celular.
Uma das possibilidades das tecnologias atuais são as mudanças de comportamento não apenas de jovens, mas também de idosos. Você viu que os grandes impactos das tecnologias estão em cinco grandes campos da atuação humana: educação, trabalho, social, comunicação e produção.


Considerando cada um desses campos, pesquise imagens de idosos participando em todos eles. Aproveite e procure identificar quais práticas públicas em sua cidade ou no seu estado existem para contribuir com a promoção da expressão do pensamento e da produção ativa dos idosos.
Você pode montar um painel digital com imagens que podem ser replicadas e transformadas isometricamente para compor uma mostra das diversas atividades dos idosos nos dias atuais para a promoção e valorização da sabedoria dos idosos e na divulgação da cultura pessoal que todos eles trazem consigo.
Inclua no seu painel um ou mais idosos da família e apresente coisas curiosas que ele/ela já fez ou que faz nos dias de hoje e, em uma grande roda de conversa, compartilhe essas experiências, mostrando a todos, por meio de algum aplicativo, o painel que montou.

NÃO ESCREVA NO SEU LIVRO.
Encontro com outras disciplinas
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
Proponha
O objetivo dessa atividade é despertar nos estudantes o valor da presença dos idosos na sociedade. Por meio da utilização das tecnologias digitais, os estudantes podem se envolver em situações reflexivas de questões de ética para disseminar ideias e informações que valorizem o encontro intergeracional, promovendo o acolhimento e orespeito das diversas formas de envelhecer e das diferentes sabedorias e culturas próprias da história de cada idoso, seja de alguém próximo do círculo social, seja alguma personalidade conhecida do público amplo.

Os estudantes podem também buscar práticas ou políticas públicas de valorização e de respeito aos idosos no município ou no estado onde residem.
Retome os conteúdos de mídia produzidos anteriormente, na sugestão do evento artístico intergeracional, para servir de base de dados para a elaboração desse conteúdo.
151 |
Habilidade
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
Encontro com outras disciplinas
(EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
CHECK-IN
a) O desenvolvimento de habilidades e a utilização de processos matemáticos auxiliam na análise de situações-problema, na modelagem da realidade e na algoritmização de atividades, além de ajudar nas etapas de interpretações das produções e na validação dos resultados. Você pode falar sobre as relações entre as áreas da STEAM (acrônimo em inglês para Ciência, Tecnologia, Engenharia, Arte e Matemática).
b) Não há medida para relacionar a Matemática com processos criativos, mas as opiniões podem ser diversas e os argumentos favoráveis à proposta de relacionar a Matemática com outros campos podem gerar mais interesse dos estudantes e a utilização dela em outros campos de atuação.
c) Superfície da esfera no espaço e circunferência no plano.
QUAL LUGAR OCUPAM AS TECNOLOGIAS NAS RELAÇÕES CULTURAIS?
Crianças em processos criativos: criando protótipo de brinquedo por meio de tecnologias dos materiais, fazendo composições coloridas com papéis na aula virtual de Arte, construindo robô com peças de montar e compondo estrutura com palitos e massa de modelar.




CHECK-IN
a) Se a pessoa gosta de Matemática e aprecia usá-la em diversas situações, que impactos isso pode ter em seus processos criativos, sejam artísticos ou não?
b) Em que medida você acha que alguém pode utilizar a Matemática com criatividade em produções diversas (manuais, intelectuais, culturais, sociais etc.)?
c) Imagine que essas crianças utilizaram, em suas criações, conhecimentos a respeito de uma figura em que todos os pontos estão a uma mesma distância de um único ponto dado. Que figura é essa? Respostas pessoais.

Sugestão de leitura
A seção apresenta uma relação entre os processos criativos e os processos matemáticos. Você pode iniciar sua pesquisa para abordar esse tema lendo oartigo “Modelagem Matemática e Criatividade: algumas confluências”, da Revista de Ensino de Ciências e Matemática, da Universidade Cruzeiro do Sul, volume 12, de 2021. Disponível em: http:// portal.amelica.org/ameli/jatsRepo/509/5092221001/ html/. Acesso em: 24 ago. 2022.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Reconhecer o conceito de lugar geométrico.
• Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
• Aplicar os conceitos de mediatriz e bissetriz na resolução de problemas.
• Construir hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.
• Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular.
• Relacionar práticas artísticas locais às diferentes dimensões da vida social, cultural e estética.
Habilidade
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
Encontro com outras disciplinas
(EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
ATMOSFERA
Atividade 1
Inicie perguntando quais são as atividades que realizam em casa. Sugira respostas como “ajudo a arrumar a cama”, “leio revistas em quadrinhos”, “jogo bola no quintal”, “cuido da horta”, “alimento os animais”. Peça que comparem as diferenças entre eles. Depois, pergunte sobre os ambientes que frequentam quando não estão na escola –por exemplo, centros culturais, teatros, lagoas, feiras, parques etc.
É esperado que compreendam então que as crenças, os costumes e as relações sociais são alguns elementos que fazem parte do conjunto de valores culturais.
Atividade 2
Uma resposta possível é que digam que as crianças que desenharam situações do campo estão inseridas nesse ambiente, enquanto as outras estão inseridas em contexto urbano. Outra possibilidade é observar que dois desenhos procuram retratar a realidade enquanto os outros dois têm caráter mais imaginário.
Atividade 3
É esperado que concordem com a afirmação. Proponha que relembre suas produções e como as dimensões da cultura e sociedade influem sobre seus pensamentos.
ATMOSFERA
Crianças e adolescentes se expressam em arte São apresentados a seguir um artigo do Estatuto da Criança e do Adolescente (ECA) e a produção artística de algumas crianças e adolescentes anônimos.
Art. 58. No processo educacional respeitar-se-ão os valores culturais, artísticos e históricos próprios do contexto social da criança e do adolescente,




garantindo-se a estes a liberdade da criação e o acesso às fontes de cultura.
BRASIL. Ministério da Casa Civil. Lei no 8.069, de 13 de julho de 1990, que dispõe sobre o Estatuto da Criança e do Adolescente. Disponível em: www.jusbrasil.com.br/legislacao/91764/ECA-Lei-n-8.069-de-13-de-Julho-de-1990#art-58. Acesso em: 16 ago. 2022.
ATIVIDADES
Respostas pessoais.
1. Após a leitura do artigo 58 do ECA, o que você entende por “valores culturais, artísticos e históricos próprios do contexto social da criança e do adolescente”? Troque ideias com os colegas.
2. Observe essas quatro produções artísticas de diferentes crianças. Como imagina que seja cada uma dessas crianças? Onde elas moram, o que fazem, qual é a história e qual é o contexto social de cada uma delas?
3. Você acha que a dimensão da vida social e cultural dessas crianças impactaram as suas expressões artísticas e estéticas? Exponha sua opinião.
Quatro produções artísticas de crianças em diferentes contextos.Habilidade
#Lugar geométrico
Os primeiros desenhos que João fez, quando menor, foram resultado de algum movimento circular da mão segurando lápis ou pincel sobre uma folha de papel.
Da realidade artística de uma criança pintando figura circular colorida para o modelo matemático composto por circunferências concêntricas.


Depois que João cresceu, começou a entender que havia figuras circulares muito especiais, não só para a arte, mas também para a Geometria.
Ele se lembra de um dia que uma professora chegou na sala e até inventou uma charada.
Charada: Que conjunto é?
Se você tem O um ponto de um plano α , que conjunto é formado por todos os pontos P de α que estão à mesma distância de 5 cm de O?
Resposta:
O conjunto de pontos que formam uma circunferência pode facilmente ser obtido utilizando uma regra ou propriedade.
A circunferência é um exemplo simples do que é um lugar geométrico. Nesse exemplo, todos os pontos dessa circunferência têm esta propriedade: distar 5 cm do ponto O e nenhum outro ponto fora dela tem essa propriedade.

Fixado um plano α, um conjunto de pontos L é o lugar geométrico que tem uma propriedade p cumprindo duas condições:
I. todos os pontos de L usufruem da propriedade p;
II. nenhum outro ponto do plano α que esteja fora de L usufrui da propriedade p
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
Atividade 4
Para essa atividade, sugira aos estudantes que façam um glossário em que possam escrever suas sistematizações e significados de palavras e conceitos matemáticos que surgirem no decorrer dos estudos deste ano letivo e dos demais. Peça que compartilhem as respostas com colegas, para completarem ou melhorarem as definições.
Atividade 5
Verifique se os estudantes de fato demarcaram o interior da circunferência como pertencente ao lugar geométrico, ou seja, L é um círculo de raio 3 cm.

ATIVIDADES
4. Pesquise, em fontes diversas, informações para ampliar seus conhecimentos a respeito dos termos:
Respostas pessoais.
a) Modelo matemático;
b) Circunferências concêntricas;
c) Propriedade e usufruir;
Mediatriz
d) Distar e equidistantes (essa palavra aparecerá logo mais adiante).
5. Desenhe o lugar geométrico L: o conjunto dos pontos que estão a uma distância menor do que ou igual a 3 cm de um ponto A em um plano qualquer.
Em uma história de fantasia um rei e uma rainha, posicionados um de frente para o outro, aguardam na entrada do salão as dezenas de convidados da grande festa passarem por entre eles em linha reta, um por um, para as boas-vindas. Qual é o caminho que os convidados devem fazer?

Esse é um problema clássico de encontrar a mediatriz, que é o caminho exatamente à igual distância entre o rei e a rainha.
Mediatriz é o lugar geométrico dos pontos do plano que equidistam de dois pontos A e B distintos.
A construção da mediatriz
O algoritmo da construção da mediatriz está a seguir. Lembrando que os dois pontos, A e B, são dados.
1. Traçar um segmento que una A e B
2. Posicionar a ponta-seca do compasso em A e, com uma abertura maior do que AB, traçar um arco de circunferência acima e outro abaixo do segmento.
3. Fazer o mesmo com centro em B
4. Nomear os pontos de encontro dos arcos de P e Q
5. Traçar a reta por P e Q. Essa reta é a mediatriz.
Vamos pensar na justificativa dessa construção. Por que a reta PQ ! " corta AB ao meio?
Pela construção feita, o quadrilátero APBQ é um losango e, pelas propriedades do losango, sabemos que suas diagonais se cortam ao meio e são perpendiculares.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
Observação: sempre que for necessário traçar uma reta perpendicular a um segmento passando por seu ponto médio, estaremos traçando a mediatriz.

ATIVIDADES
6. Uma exposição de arte, para mostrar suas obras com segurança, deseja organizar um pavilhão construindo paredes que distam 2 m das bordas de um corredor central, em linha reta. Como seria a planta desse pavilhão?
a) Essa situação é uma aplicação de um problema matemático enunciado do seguinte modo: qual é o lugar geométrico dos pontos do plano que distam d de uma reta s? Construa com régua e compasso esse lugar geométrico. Construção geométrica.

b) Agora, faça o esboço de uma planta do pavilhão. parede
Bissetriz
Uma equipe de jovens está fazendo um projeto de pintura do muro da escola. A composição artística foi inspirada em formas geométricas.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
5. Traçar a mediatriz do segmento EG , determinando a reta x
6. Medir com o compasso na régua a distância d Posicionar a ponta seca em C, marcando os pontos M e I em z
7. Medir com o compasso na régua a distância d Posicionar a ponta seca em F, marcando os pontos J e H em x
8. Ligar os pontos H e I traçando a reta p. Ligar os pontos M e J traçando a reta p' Obs.: a distância d é uma generalização, uma representação de qualquer distância.
No processo de edição do projeto, alguém quis dividir um dos ângulos para que o novo ângulo tivesse a metade da abertura. Isso pode ser feito de diversas maneiras, mas algumas são mais práticas do que outras.
Atividade 6

Construção geométrica do par de paralelas a uma reta dada
Roteiro:
1. Escolher dois pontos quaisquer, o ponto C e o ponto F na reta s dada.
2. Com a ponta seca do compasso posicionada no ponto C e com uma abertura qualquer, marcar os pontos A e B em s
3. Com a ponta seca do compasso posicionada no ponto F e com uma abertura qualquer, marcar os pontos E e G em s
4. Traçar a mediatriz do segmento AB, determinando a reta z
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
LUPAS E LUNETAS
Espera-se que os estudantes façam testes e sugestões para a disposição da bissetriz com relação ao ângulo e terminem compreendendo intuitivamente a ideia da bissetriz.
Utilize ângulos “de papel” e dobraduras para localizarem a bissetriz no vinco formado quando se sobrepõe, por dobra, um lado ao outro do ângulo.
LUPAS E LUNETAS Respostas pessoais.
Junte-se a um colega. Se vocês tivessem que “dividir” um ângulo ao meio, para alterar algum detalhe em um projeto, como fariam isso? Como imaginam que seja “dividir ao meio” um ângulo?
Façam o desenho de um ângulo e mostrem como fariam isso. Compartilhem com os demais colegas.
A distância de um ponto a uma reta
Muitos problemas de lugares geométricos envolvem a noção de distância. Sabemos, por exemplo, que a distância entre dois pontos do plano é o comprimento do menor segmento de reta que liga esses dois pontos.


E se precisarmos determinar a distância de um ponto P a uma reta r? Para isso, tomamos o ponto P' da reta que nos dê a menor distância entre P e P'. Intuitivamente, o ponto P' que nos dá a menor distância é aquele em que o segmento PP' é perpendicular à reta r
A distância de um ponto P a uma reta r é a medida de comprimento do segmento PP' , traçado perpendicularmente a r, com P' pertencente a r
A construção de uma bissetriz
É dado um ângulo O ! com medida de abertura qualquer.
Vamos traçar o conjunto de pontos em que, um a um, todos ficam à mesma distância de cada um dos lados do ângulo O !
1. Posicionar a ponta-seca do compasso em O e, com abertura qualquer, determinar sobre os lados do ângulo os pontos A e B
2. Posicionar a ponta-seca do compasso em A e, com abertura não muito pequena, traçar um arco de circunferência.
3. Manter a abertura e fazer o mesmo com a ponta-seca em B
4. Nomear de C o ponto de intersecção dos arcos.
5. Traçar a reta por O e C. Essa reta é a bissetriz.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
A bissetriz divide o ângulo AO ! B ao meio: AO ! C ≡ BO ! C
Bissetriz é o lugar geométrico dos pontos do plano que equidistam dos lados de um ângulo dado.
9. O perímetro da cerca pode ser calculado adicionando o comprimento de uma circunferência de raio 5 com o perímetro da construção.

5 2π + 2 35 + 2 15 = 100 + 10π Aproximando π para 3,14, o comprimento da cerca é de 131,4 metros.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
Atividade 7
A bissetriz divide o ângulo ao meio. Então:
39 ÷ 2 = 30 ÷ 2 + 9 ÷ 2 = 15 + 4,5 39 ÷ 2 = 30 ÷ 2 + 9 ÷ 2 = 15 + 4,5 = 19,5
O ângulo entre um lado e a bissetriz mede 19,5o ou 19o30’.
ATIVIDADES
7. Sabendo que o ângulo representado na imagem mede 39o, qual é a medida dos ângulos formados pela bissetriz e os lados desse ângulo? 19,5o
9. Uma construção está sendo realizada em um terreno de 35 metros de comprimento e 15 metros de largura. Para a segurança da população foi colocada uma cerca que dista 5 metros da área construída. Qual é o perímetro dessa cerca?
Atividade 8
No triângulo ACD, temos: 40o + 62o + 3x = 180o
3 x = 180o – 102o

3 x = 78o x = 26o
No triângulo BCD, considerando CD " bissetriz e o ângulo BD ! C ângulo externo (ou suplementar a 3x), temos:
4 y = m BD ! C ( ) + m DC ! B ( )
4y = 102o + 40o
8. Dado o triângulo ABC e CD " sendo a bissetriz do ângulo no vértice C, determine os valores de x e y x = 26o e y = 35,5o = 35o 30'


4 y = 142o y = 35,5o
Atividade 9
O perímetro da cerca pode ser calculado adicionando o comprimento de uma circunferência de raio 5 m (formada pelos 4 quartos de circunferência) com o perímetro da construção.
5 2π + 2 35 + 2 15 = 100 + 10π
5 2π + 2 35 + 2 15 = 100 + 10π
Aproximando π para 3,14, o comprimento da cerca é de 131,4 metros.

Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares. (EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
NUVENS
Atividade 10
É esperado que se note que, se a circunferência está no interior do pentágono, então as “pontas” do polígono estrelado serão os vértices do pentágono. Caso a circunferência seja tangente aos lados do pentágono, então os dois polígonos coincidirão. E se o pentágono estiver no interior da circunferência, então as pontas do polígono estrelado serão as intersecções entre a circunferência e as mediatrizes do lado do pentágono.
Atividade 11
Utilizando um software de geometria dinâmica:
I. Escolhemos a ferramenta polígono regular e determinamos o número de vértices igual a 6, para criar um hexágono.
II. Selecionamos a ferramenta mediatriz e traçamos uma para cada um dos lados do hexágono.
III. Usando a ferramenta círculo, construímos a circunferência cujo centro é o encontro das mediatrizes e o ponto dado pode ser um qualquer do interior do hexágono.
Construção de polígono com software
Veja o passo a passo para a construção de um polígono estrelado a partir de um pentágono regular em um software de geometria dinâmica.

I. Para criar o pentágono, usamos a ferramenta polígono regular ( ) e determinamos o número de vértices igual a 5.
II. Usamos a ferramenta mediatriz ( ) e traçamos uma para cada um dos lados do pentágono.
III. Usando a ferramenta círculo, dados um centro e um de seus pontos ( ), construímos a circunferência cujo centro é o encontro das mediatrizes e o ponto dado pode ser um qualquer do interior do pentágono.
IV. Agora utilizando a ferramenta polígono ( ), selecione primeiramente um vértice do pentágono e, em seguida, o ponto mais próximo dele que é comum à circunferência e a uma mediatriz, e prossiga assim sucessivamente, até chegar ao ponto inicial.
ATIVIDADES
Construção e resposta pessoais.
10. Utilizando a ferramenta mover ( ), altere o raio da circunferência para analisar o efeito que isso produz na configuração do polígono estrelado. Escreva suas conclusões.
11. Faça uma construção semelhante a essa, agora usando como referência um hexágono regular.
Após a construção, descreva um passo a passo indicando o processo de construção desse hexágono estrelado.
• Compartilhe com os colegas a descrição da sua construção.
IV. Agora com a ferramenta polígono, selecione primeiro um vértice do hexágono e, em seguida, o ponto mais próximo dele que é comum à circunferência e a uma mediatriz, e prossiga assim sucessivamente, até chegar ao ponto inicial.
Veja um exemplo dessa construção que os estudantes realizarão:
#Construção de polígonos regulares
Vamos acompanhar os processos de construção de alguns polígonos regulares. Antes, porém, vamos relembrar o que é um polígono regular
Um polígono é regular se todos os seus lados são congruentes e todos os seus ângulos internos são congruentes.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

Polígonos regulares inscritos na circunferência.
Em cada polígono, todos os vértices estão ligados ao centro da circunferência por um segmento de reta, determinando, a cada dois segmentos consecutivos, ângulos com vértice no centro da circunferência. Cada um desses é chamado de ângulo central. Nos polígonos regulares inscritos na circunferência, dois ângulos centrais adjacentes têm medidas iguais.
Um ângulo central relativo a uma circunferência é o ângulo que tem o vértice no centro da circunferência.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares. (EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
LUPAS E LUNETAS
Verifique quais produções e estratégias podem ser apresentadas para toda a turma de modo que concluam quais construções têm boa fundamentação matemática nos seus processos.
Em uma circunferência de centro O, com um ângulo central determinado por um arco AB ! , dizemos que AB ! é o arco correspondente ao ângulo central AO ! B
Arco AB correspondente ao ângulo AO ! B
O triângulo regular

Um escritório de design foi contratado pela empresa de engenharia Construfirme para que criasse o logo da empresa. Veja as opções de logos que os designers produziram.

a) Qual desses logos você achou mais interessante? Comente.
b) Na prancheta dos designers, que tipo de figura geométrica foi fundamental para todos esses logos? Como imagina que seja a construção dessa figura?
c) Faça um esboço (à mão livre) mostrando como será o resultado final da construção. Troque ideias com os colegas.
LUPAS E LUNETAS Respostas pessoais.TRAVESSIAS
A construção do triângulo regular inscrito na circunferência
Com régua e compasso, acompanhe as etapas, executando a construção de um triângulo regular.
Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA16) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
C
12. c) O primeiro mede o dobro do segundo e o segundo, a metade do primeiro. Ou o ângulo inscrito na circunferência mede a metade do ângulo central correspondente.
ATIVIDADES
12. Leia as questões e reflita com um colega.
a) Após a marcação dos três pontos sobre a circunferência (que viriam a ser os vértices do triângulo), qual é a medida de cada ângulo central correspondente a cada arco BC ! , CD ! e DB ! ? 120o

b) Considere cada par de ângulos: BO ! C e BD ! C ; CO ! D e C B ! D; DO ! B e DC ! B . Qual é o arco correspondente de cada par?
c) Compare as medidas de cada par de ângulos: BO ! C e B D ! C; CO ! D e C BD; DO ! B e DC ! B Que relação você observa em cada par?
13. Copie as frases trocando as pelas medidas ou termos corretos.
a) inscrito na circunferência; central
a) A medida de um ângulo é a metade da medida do ângulo correspondente.
b) A bissetriz de um ângulo de 60o determina dois ângulos congruentes de medida
14. Levando em conta a construção do triângulo regular, construa agora um hexágono regular. Construção pessoal.
Depois, descreva – por escrito ou por meio de um fluxograma – o passo a passo dessa construção. Resposta pessoal.
III. Com centro em B e mesma abertura, trace um arco que corte a circunferência no ponto C, diferente de A
IV. Repita o processo até marcar o sexto ponto (ponto F, seguindo a ordem alfabética) nessa circunferência.
V. Trace o polígono que tenha esses pontos como vértices.
TRAVESSIAS
Atividades 12 e 13
Observe que os ângulos BD ! C , CB ! D, DC ! B têm vértices na circunferência e pares de lados que cortam a circunferência. Esses ângulos são chamados ângulos inscritos e, nesse caso, são ângulos de 60o
Atividade 14
Traçando as mediatrizes dos lados do triângulo regular, determinam-se pontos de intersecção delas com a circunferência que serão os outros 3 vértices do hexágono regular (além de B, C e D). Considere apresentar esta construção alternativa do hexágono regular:
I. Trace uma circunferência de centro O e marque o ponto A pertencente a ela.
II. Com centro em A e abertura OA, trace um arco que corte a circunferência no ponto B
1. Construir, com o compasso, uma circunferência de centro O e raio qualquer. 2. Destacar um ponto A na circunferência. Com a ponta-seca em A e mesma abertura do raio, trace uma semicircunferência passando pelo centro O e cortando a circunferência em B e 3. Com centro em B (ou C) e abertura BC, trace um arco de circunferência que corte a circunferência em um ponto D. 4. Trace os segmentos BC, CD e DB A figura obtida é o triângulo regular ou triângulo equilátero. Na devida ordem: BC ! , CD ! e DB !Habilidades
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA16) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.



(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
LUPAS E LUNETAS
Construção possível:
Construção do quadrado
Leia o fluxograma da construção de um quadrado inscrito em uma circunferência
Atividade 15
I. Traçar uma circunferência.
II. Traçar um diâmetro que corte a circunferência em dois pontos.
III. Traçar a mediatriz do diâmetro que corta a circunferência em dois pontos.
IV. Traçar as bissetrizes dos ângulos formados pelo diâmetro e sua mediatriz, que cortam a circunferência em quatro pontos.
LUPAS E LUNETAS
Forme uma dupla e juntos esbocem, à mão livre, cada etapa desse fluxograma. Depois, construam rigorosamente cada etapa utilizando apenas régua e compasso. Compartilhem as suas produções com a turma.
ATIVIDADES
15. Levando em conta essa construção do quadrado, construa um octógono regular.
Construção pessoal.
16. Considerando o que aprendeu até agora, construa ângulos de 30o, 45o, 60o e 90o, sem o uso de transferidor. Construção pessoal.
17. Construa um quadrado cuja diagonal meça 5 cm. Construção pessoal.
18. Um instituto de pesquisas biológicas construiu tanques para comportar as serpentes utilizadas na produção de soros antiofídicos. De tempos em tempos, elas são levadas para
V. Traçar o polígono ligando todos os pontos de intersecção com a circunferência.
a visitação do público em geral e ficam em um poço triangular. Para manter a segurança do público, há duas cercas separadas entre si por 3 m de distância, seja qual for o ponto da cerca interna.
Calcule o perímetro da cerca externa sabendo que a cerca interna, com o formato de um triângulo regular, tem 10 m de lado. Utilizando π = 3,14, o perímetro resulta em, aproximadamente, 48,84 m.
Atividade 16
Apresente as construções dos ângulos com régua e compasso:
Imagem sugerindo que cada etapa, sendo clara e encadeada, de uma tarefa é um cubo, que, juntos, levam a um conjunto organizado de cubos.LEVO NA BAGAGEM
Respostas pessoais.
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado e reflita sobre as perguntas a seguir.


▶ Matemática


• Você reconhece o conceito de lugar geométrico?
• Sabe construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares?
• Sabe aplicar os conceitos de mediatriz e bissetriz na resolução de problemas?
Constrói um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadro e compasso?
Descreve, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular?
▶ Outras disciplinas
Arte
• Relaciona práticas artísticas locais às diferentes dimensões da vida social, cultural e estética?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
MATEMÁTICA
OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
O ângulo com medida igual a 60o é obtida da construção de um triângulo equilátero. Por fim, o ângulo com medida de 30o é obtido ao formar-se um triângulo retângulo com um dos ângulos agudos medindo 60o
Atividade 18
O perímetro da cerca externa resulta em:
+
= 48,84
BARCOS E PORTOS
Organize
Auxilie os estudantes na classificação dos diferentes conhecimentos em conceituais, procedimentais ou factuais
Elabore
Modere as discussões fomentadas pela afirmação do item b, organizando as falas e pontuando novas reflexões.
Apresente produções artísticas associadas a temas da Matemática, como as que podem ser feitas com espirógrafos, por exemplo.
▶ Organize
Respostas pessoais.
Considere os registros que você fez levando em conta as questões da seção Levo na bagagem. Atente aos itens do seu registro que sinalizam ainda haver alguma ou muitas dúvidas. Organize seus estudos para esses tópicos. Separe-os em três categorias e registre, em cada categoria, os conhecimentos corretos, que podem ser resgatados deste livro ou de outras fontes. Veja um exemplo de esquema.
Diferentes conhecimentos
CONHECIMENTO CONCEITUAL (CONHECER)
Ângulo central tem o vértice no centro da circunferência.
▶ Elabore Leia a tirinha:
CONHECIMENTO PROCEDIMENTAL (FAZER)
Construir ângulo central relativo a um arco da circunferência com extremidades nos vértices de um triângulo regular inscrito: basta dividir a circunferência em três arcos de mesma medida.
CONHECIMENTO FACTUAL (EXPERIMENTAR)
Relação entre ângulo central e ângulo inscrito na circunferência: a medida de um ângulo inscrito na circunferência é a metade da medida do ângulo central.
BECK, Alexandre. Armandinho. Disponível em: https://pt-br.facebook.com/tirasarmandinho/ posts/2807923772586244. Acesso em: 16 ago. 2022.

a) Nessa tirinha, a palavra arte foi explorada com dois significados. Explique quais.
b) Uma pessoa que goste muito de Matemática, especialmente de Geometria, não será boa com arte nem conseguirá se expressar por meio dela. Você concorda? Comente.

c) Produza uma arte abstrata inspirando-se nas construções geométricas que aprendeu neste passeio. Depois, compartilhe no mural da sala virtual.
a) Arte no sentido de manifestação humana ligada à estética e no sentido de travessura.
A pergunta inicial deste passeio é: Qual lugar ocupam as tecnologias nas relações culturais?
Ao decidir lançar um trabalho criativo artístico é possível, nos dias de hoje, contar com ferramentas úteis para as diferentes dimensões da arte: criação, crítica, expressão, fruição etc. Na etapa de criação, as ferramentas digitais podem ser meio, ou seja, apoio à criação. Elas podem ser também fim: a própria ferramenta digital ser a arte e possibilitar uma experiência diferente de fruição ao se mostrar para o público em uma apresentação digital ou virtual.
Seja como for, a arte é um modo de conhecer, entender e se expressar que faz parte da experiência humana.
Encontro com outras disciplinas (EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
Proponha
O objetivo dessa atividade é incentivar os estudantes a refletir sobre o possível viés da perspectiva pessoal em comparação com outras perspectivas relacionadas às artes e a aspectos culturais de modo geral, desde as locais até as mundiais.
Exposição imersiva de Van Gogh, na cidade de Nova York, que transformou a visão desse artista em uma experiência sensorial virtual única para o público apreciador da arte. Junho de 2021.

a) Você já apreciou obras artísticas virtuais? E já as apreciou em espaços físicos, como museus, exposições ou mostras? Se ainda não, conte como imagina que seja; se já, conte como foi.
b) Reflita sobre os efeitos que a arte lhe causa e compare com o que os colegas afirmam sobre como a arte os impacta.
c) Compare suas experiências com as ferramentas digitais na construção de figuras geométricas ao uso delas para finalidade estética e artística.
• Exponha suas ideias em uma roda de conversa com a turma toda. 167 |

Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
CHECK-IN
Retoma-se o conceito de razão, essencial para o trabalho com proporcionalidade.
Ressalte a importância da ordem em que se mencionam as grandezas para o estabelecimento das razões. Por exemplo:
• a razão entre o número de pessoas on-line e o de pessoas presencialmente é 1 : 4, mas a razão entre o número de pessoas presencialmente e o de pessoas on-line é 4 : 1;
• a razão entre o número de crianças e o de adultos é 2 : 3, mas a razão entre o número adultos e o de crianças é 3 : 2
QUE IMPACTOS AS TECNOLOGIAS DA COMUNICAÇÃO PODEM TRAZER À VIDA FAMILIAR E AO MUNDO DO TRABALHO?
Chamada de

de
família com parentes residindo em outro país. Motivadas pela pandemia da Covid-19, as possibilidades de encontros e reuniões virtuais foram amplamente exploradas por diversos grupos: familiares, escolares, profissionais etc. Nesse novo cenário, as pessoas necessitaram se envolver com as tecnologias e suas ferramentas, que por muitas vezes foram alvo de resistência. Ao mesmo tempo, esse período mostrou como é importante valorizar o contato entre as pessoas.

CHECK-I N
a) Quantas pessoas há na imagem? Quantas estão presencialmente e quantas estão on-line? 5 pessoas: 4 presencialmente e uma on-line
b) Considerando esse grupo, qual é a razão entre o número de pessoas on-line e o de pessoas presencialmente? 1 : 4
c) Qual é a razão entre o número de crianças e o de adultos? 2 : 3
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Identificar a natureza da variação de duas grandezas: diretamente proporcionais, inversamente proporcionais ou não proporcionais.
• Expressar a relação entre duas grandezas por meio de sentença algébrica.
• Representar a relação de proporcionalidade entre duas grandezas no plano cartesiano.
• Resolver e elaborar problemas que envolvam grandezas direta ou inversamente proporcionais, por meio de estratégias variadas.
• Analisar diferentes práticas (curtir, compartilhar, comentar etc.) da cultura digital envolvidas no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Encontro com outras disciplinas
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
ATMOSFERA
Atividades 1 a 3
Chame a atenção dos estudantes para o tipo de linguagem mais informal utilizada, a repetição de palavras, as abreviações usadas, os termos da língua inglesa incorporados ao nosso vocabulário, outros símbolos presentes, os erros de língua portuguesa, as diferenças entre o texto principal e os dos comentários, a fonte etc. Proponha a eles a reescrita (com as devidas correções). Avalie, se possível em conjunto com o professor de Língua Portuguesa, os efeitos das correções e alterações na reescrita quanto a clareza e compreensão ou informalidade do texto.
CONVÍVIO E BEM-ESTAR SOCIAL
Que tal aproveitar esse momento para uma conversa sobre o que é fake news e o que é fato? Esse trabalho pode ser realizado em conjunto com o professor de Língua Portuguesa:
ATMOSFER A
A comunicação e os modos de reagir Leia parte do conteúdo de um site
www.infornet.com.br/blog/a-importancia-da-tecnologia-no-nosso-cotidiano
Impactos gerados pela tecnologia
Essas mudanças impactam também o comportamento do ser humano, que tem que aprender a acompanhar essa evolução e conviver com novas tecnologias. Essa adaptação traz consigo uma série de benefícios, como melhora na qualidade de vida, acesso rápido e fácil ao conhecimento, simplificação da troca de informações e a quebra de várias barreiras da comunicação. Outro fator de destaque é a inclusão social. Constantemente surgem novas tecnologias que auxiliam na rotina de pessoas com deficiências físicas e cognitivas, ajudando que essas pessoas tenham mais facilidade para se inserir na sociedade e tenham um padrão de vida melhor.
Sara Wanessa disse: 19 de setembro de 2024 às 19:56
Eu também amei o post. Então a tecnologia ajudou muito para mim principalmente para se comunica tirar dúvidas que temos me ajuda muito até hoje principalmente nós estudos e muito mais
Responder
Infornet disse:
20 de setembro de 2024 às 08:15
Olá Sara! Ficamos felizes que tenha gostado, agradecemos o comentário e contribuição Abraços! Att. Equipe Infornet
Responder
A IMPORTÂNCIA da tecnologia no nosso cotidiano. Infornet, 16 dez. 2020. Disponível em: www.infornet.com.br/ blog/a-importancia-da-tecnologia-no-nosso-cotidiano. Acesso em: 1 jul. 2022.
ATIVIDADES
1. O que você achou do post? O que ele lhe trouxe de informação nova? Respostas pessoais.
2. Leia os comentários. Há algo que chama a sua atenção? O quê?
3. Quando posta um comentário, você revisa? Edita? Melhora as ideias antes de, definitivamente, publicar?
juntos, é possível promover uma campanha educativa com a checagem de notícias que são falsas ou verdadeiras publicadas na internet Parte da habilidade EF89LP02 poderá ser desenvolvida com essa atividade. Motive os estudantes a responder oralmente a algumas questões, como:
• Você sabe o que são fake news?
• Costuma compartilhar conteúdos recebidos sem checar antes se são falsos ou verdadeiros?
• Você já compartilhou alguma informação e depois descobriu que era falsa?
• Como é possível identificar fake news?
Peça aos estudantes que se reúnam em duplas e selecionem uma notícia verdadeira e uma falsa. Colete todo o material e, na aula seguinte, promova a brincadeira “é fake ou é fato?”.
Finalize a aula com algumas dicas para verificar se uma notícia é verdadeira ou falsa. Por exemplo:
• confira a data da notícia;
• verifique se o veículo de comunicação que divulgou a notícia é confiável;
• verifique o autor da notícia;
• compare a notícia com outras fontes.
No cotidiano, vivenciamos situações envolvidas com as noções de grandeza – a maioria das vezes sem saber disso!
Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Três imagens de crianças em situações envolvendo noções de grandeza: uma criança pequena medindo sua altura; o irmão fazendo força para empurrar a irmã no balanço; uma garota treinando sua velocidade de corrida ao se preparar para um campeonato.

Você tem pressa de crescer? Diverte-se no balanço? Gosta de correr? Saiba então que altura, força e velocidade são grandezas, nessa ordem, envolvidas nas situações das imagens. Mas, afinal, o que é uma grandeza?

Leia o que informa o Instituto de Pesos e Medidas do Estado de São Paulo (Ipem-SP):
Grandeza. O conceito de grandeza é fundamental para se efetuar uma medição. Grandeza pode ser definida, resumidamente, como sendo o atributo físico de um corpo que pode ser qualitativamente distinguido e quantitativamente determinado.
Disponível em: www.ipem.sp.gov.br/index.php/cidadao/conceitos-metrologia-e-qualidade#:~:text=Grandeza%20 pode%20ser%20definida%2C%20resumidamente,qualitativamente%20distinguido%20e%20quantitativamente%20 determinado. Acesso em: 16 ago. 2022. Segundo o Ipem, a grandeza é uma característica de algo que pode ser medido. Vamos acrescentar ainda que algo que pode ser quantificado por uma contagem, por exemplo, também é uma grandeza.

Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Atividade 4
Caso algum estudante não seja capaz de realizar essa atividade, retome o conceito de grandeza como tudo aquilo que pode ser medido e dê exemplos de situações envolvendo grandezas no cotidiano em que estão inseridos.
Atividade 5
Utilize essa atividade para avaliar a compreensão do conceito retomado na atividade anterior.
ATIVIDADES
4. Observe as coisas à sua volta. Preste atenção a alguns atributos ou características como tamanho, cor, tipo de material, textura, temperatura etc. Respostas pessoais.
a) Registre duas ou três coisas que você observou no entorno e os atributos que vai destacar de cada uma delas.
b) Quais dos atributos destacados são grandezas? Pinte de azul.
c) Quais dos atributos destacados não são grandezas? Pinte de vermelho.
5. Observe os dados que uma aluna preencheu em uma ficha de enquete:
DADOS PESSOAIS NOME: Sofia Nogueira dos Reis
IDADE: 13 anos

COR DOS OLHOS: Castanhos
ALTURA: 164 cm
HOBBY: Escrever histórias
MASSA CORPORAL: 51 kg
a) Das informações dessa ficha, selecione as que dizem respeito a grandezas.
b) Crie uma ficha com alguns de seus dados. Os que são grandezas escreva em azul, os que não são, em vermelho.
• Compartilhe sua ficha com os colegas.
a) Idade, altura e massa corporal. Respostas pessoais.
#Razão: uma relação entre grandezas
O conhecimento matemático busca reconhecer características da realidade que possam ser medidas ou quantificadas. Lembrando que às grandezas estão associadas unidades de medida; e às quantidades, números do sistema de numeração decimal.
Situação 1
Andreia trabalha com tecnologia da informação (TI). A cada três meses ela oferece, com muito bom grado, um trabalho de manutenção preventiva dos dispositivos móveis que há em sua casa, para toda a família.
Jovem especialista em tecnologia da informação em seu ambiente de trabalho.

As grandezas envolvidas nessa situação são: tempo (em meses) e quantidade de manutenção preventiva (em unidades). Há uma (1) manutenção a cada 3 meses, ou seja, temos a razão
para
Uma pesquisa a respeito da quantidade de filhos por famílias foi feita em um bairro. Este foi o resultado:
Quantidade de filhos por família
Fonte: dados fictícios.
As grandezas envolvidas são: quantidade de famílias (em porcentagem) e quantidade de filhos (em unidades). Os dados foram agrupados pela quantidade de filhos. Assim, por exemplo, há 40 famílias, de cada 100, que têm apenas um filho, ou seja, a razão entre o número de famílias com apenas um filho e o total de famílias pesquisadas é “40 para 100”, ou “40 : 100”, ou 40 : 100” ou “ 40 100 ” , ou 0,40, ou 40%.
LUPAS E LUNETAS
Respostas pessoais.
a) O que você acha da atitude de Andreia, da situação 1, de oferecer para a família uma ajuda profissional que é a especialidade dela?
b) Considere o gráfico da situação 2. Em sua opinião, quão parecidos são os dados desse gráfico com a realidade do seu bairro? Expresse sua opinião com base no convívio que tem com as diferentes famílias do seu bairro. Ouça atentamente a opinião dos colegas.
Uma “medida” relativa
A razão expressa uma relação entre duas grandezas. Vamos destacar dois fatos importantes sobre as razões.
Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
LUPAS E LUNETAS
Proponha uma roda de conversa sobre os benefícios das boas ações no ambiente familiar. Entre as muitas ações que beneficiam as relações familiares estão: passar tempo realizando atividades em família; realizar refeições juntos; desenvolver a educação financeira familiar; fortalecer o diálogo e o planejamento da rotina e dos deveres domésticos de cada membro.
O que acontece, por exemplo, quando afirmamos que, em uma sala de aula A, a razão entre o número de alunos que possuem celular e dos que não possuem é de 3 : 4 3 : 4 ou 3 4
?
I. Observe que essa razão não nos dá a quantidade de alunos que possuem nem os que não possuem celular, mas significa que, se representarmos essas quantidades por uma fração na qual o numerador é o número dos alunos que possuem celular e o denominador é o número dos que não possuem, então essa fração será equivalente à fração 3 4 De acordo com essa fração, uma possibilidade seria: 12 alunos possuem e 16 não possuem celular. Então, representando essa fração e simplificando, temos:
12
16 = 2 2 3
2 2 2 2 = 3 4
II. Observe também que caso haja outra turma de alunos (B, por exemplo), com mesma razão da turma A entre os que possuem e os que não possuem celular, não quer dizer que ambas tenham iguais números de alunos. Essa turma B poderia, por exemplo, ter 15 e 20 entre os que, nessa ordem, possuem e os que não possuem celular. O que nos dá:
15
20 = 3 5
2 ⋅ 2 ⋅ 5 = 3 4
Esses dois fatos despertam nossa atenção para o seguinte: uma razão é uma “medida” (um índice) relativa, ou seja, não é absoluta
173 |
Habilidade
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Encontro com outras disciplinas
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
Atividade 6
Essa atividade pretende incentivar o estudante a fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a interpretar informações relevantes, para avaliá-las crítica e eticamente, produzindo argumentos convincentes.
Essa é também uma excelente oportunidade de fazer um trabalho em parceria com professores de Língua Portuguesa, uma vez que essa atividade possibilita ao estudante analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) da cultura digital envolvidos no trato com a informação, de modo a possibilitar uma presença mais crítica e ética nas redes.
As diferentes formas de expressar e organizar o conteúdo do texto – a tabela, a linguagem algébrica – também podem ser objeto de análise.
ATIVIDADES
6. Um adolescente postou este problema em uma rede de estudos e, em seguida, uma usuária dessa rede resolveu para ele:
valter teixeira 02.12.2024 •Matemática• Ensino fundamental (básico)
respondido Olá, todos! Alguém pode resolver esse problema para mim, por favor?
Resposta
LouiseSG 13 respostas • 3,4 mil pessoas receberam ajuda
I. Construo uma tabela:
4,8/5 7
Para oferecer maiores oportunidades às mulheres no campo de trabalho, uma empresa tem a política de sempre manter em seu quadro de funcionários a razão entre homens e mulheres de 2 : 3. Atualmente, há na empresa 80 funcionários. Quantos deles são mulheres? Eu resolvi para você organizado em um passo a passo. Bom proveito!
II. Com a regularidade da tabela, escrevo uma equação:
III. Descoberto o valor de x, calculo a quantidade de mulheres (3x): 3
16 = 48
IV. Escrevo a resposta do problema: Atualmente, na empresa, há 48 mulheres.
e mais 12 usuários acharam essa resposta útil
(5 votos)
a) O que você achou desse problema e da resolução dele? Avalie e comente com os colegas e o professor.
b) Você achou correta a atitude desse aluno? E como avalia a resposta dada pela usuária dessa rede? Qual teria sido sua atitude no lugar dela?
c) Junte-se a um colega, elaborem um problema parecido com esse e o resolvam com uma estratégia parecida à da usuária dessa rede. Respostas pessoais.
#Proporção
Vimos que, em uma situação envolvendo razão, duas frações podem representar o mesmo número. Se duas frações, ambas dotadas do significado de razão, são iguais, isso nos leva à ideia de proporção
Duas razões com termos não nulos, a : b e c : d, determinam uma proporção quando as frações a b e c d são equivalentes, ou seja:
a b = c d
Essa proporção pode ser escrita assim: a : b = c : d . Lê-se: a está para b assim como c está para d
Exemplos:
• As razões 2 : 5 e 6 : 15 formam uma proporção, pois 2
• As razões 2 : 5 e 10 : 20 não formam uma proporção, pois
Regra prática da multiplicação em “xis”
Um método prático para descobrir se duas razões formam uma proporção é aplicar a regra da multiplicação em xis (x).
a b = c d é equivalente a ad bd = bc bd (bd é múltiplo, ao mesmo tempo, de b e d, tornando a igualdade de duas frações com denominadores múltiplos comuns). Lembrando que a, b, c e d são todos não nulos.
Assim, podemos afirmar que as razões a b e c d formarão uma proporção se ad = bc Ou, ainda, pela regra prática: a b c d =
Exemplo: são dadas três razões: 9 : 12, 6 : 9, 12 : 16. Quais delas são proporcionais à razão 3 : 4? Vamos fazer, em cada caso, o teste da multiplicação em xis:
9 12 3 4 e ⇒ 9 4 = 36 = 12 3 Portanto, 9 : 12 e 3 : 4 são proporcionais.
6 9 3 4 e ⇒ 6 4 = 24 ≠ 27 = 9 3 Portanto, 6 : 9 e 3 : 4 não são proporcionais.
12 16 3 4 e ⇒ 12 4 = 48 = 16 3 Portanto, 12 : 16 e 3 : 4 são proporcionais.
175 |
Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Habilidade (EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Atividade 7
É esperado que escrevam as razões em forma de fração e verifiquem quais são equivalentes a 2 9 : 2 9 = 4 18 = 6 27
Para identificar as que não são equivalentes a 2 9 é possível escrevê-las na sua forma irredutível: 12 21 = 4 7 e 6 18 = 1 3
Atividade 8
É esperado que os estudantes transformem as quádruplas ordenadas em frações e verifiquem a relação de proporcionalidade encontrando a fração irredutível a elas associadas ou compreendendo que são frações diferentes.

a) 4 6 = 6 9 = 2 3
b) 4 5 ≠ 6 7
c) 3 6 = 4 8 = 1 2
d) 2 3 ≠ 5 6
Atividade 9
Devido à quádrupla proporcional (40, 120, 28, x), afirmamos que se 120 é o triplo de 40, então x é também o triplo de 28, ou seja, o valor de x é 84 cm.
Atividade 10
Pode-se utilizar a regra prática da multiplicação em x, dispondo as frações da seguinte forma exemplificada pelo item a: 4
6 = 8 x
x = 12
ATIVIDADES
7. Indique quais destas razões são proporcionais a 2 : 9:

a) 4 : 18 Sim.
b) 12 : 21 Não.
c) 6 : 18 Não.
d) 6 : 27 Sim.
• A razão 8 : 36 é proporcional à razão 2 : 9. Nesse caso, indicamos essa proporção por uma quádrupla ordenada (8, 36, 2, 9). Indique na forma de quádrupla ordenada as razões acima que são proporcionais a 2 : 9. (2, 9, 4, 18) e (2, 9, 6, 27).
8. Verifique, em cada item, se os quatro números, na ordem em que aparecem, são proporcionais.
a) (4, 6, 6, 9) Sim.
b) (4, 5, 6, 7) Não.
c) (3, 6, 4, 8) Sim.
d) (2, 3, 5, 6) Não.
9. Alexandre trabalha com decoração, gosta de mudar os ambientes de sua casa e se interessou por um quadro que tem as medidas indicadas na figura.
10. As quádruplas (sequências ordenadas de 4 números) representam proporções. Determine o valor de x em cada item.
a) (4, 6, 8, x) 12
b) (3, 5, x, 10) 6
c) (6, x, 9, 3) 2
d) (x, 4, 9, 12) 3
11. Uma comissão escolar formada por 7 professores e 3 funcionários foi escolhida para representar uma escola em uma convenção. Dois dias antes, a escola recebeu um comunicado de que deveria aumentar o número de representantes das duas categorias. Para manter a mesma razão anterior, o número de professores passou a ser de 21. Qual deve ser o novo número de funcionários?
Ele pretende fazer uma ampliação desse quadro, sempre mantendo as proporções. Sabendo que a altura da ampliação será de 120 cm, avalie qual deve ser a medida da largura: 80 cm, 84 cm ou 92 cm? Explique sua resposta.

12. Leia, resolva, elabore.
a) Janine percorreu 400 km em 5 horas. Sua amiga Aline percorreu, na mesma velocidade, uma distância de 200 km. Quanto tempo durou o percurso de Aline? 2,5 h.
b) Romão empacotou 120 produtos em 4 horas. Seu amigo João empacotou, na mesma proporção, 180 produtos. Quanto tempo João levou para embalá-los? 6 h.
c) Elabore um problema semelhante utilizando a ideia de proporção envolvendo uma quádrupla de números. Resposta pessoal.
Atividade 11
A razão entre o número de professores e o de funcionários é 7 3 Para manter a proporcionalidade, determina-se o valor de x na quádrupla (7, 3, 21, x). Escrevendo a proporção e desenvolvendo:
7 3 = 21 x
7 x = 21 3
x = 9
Serão 9 funcionários.
Atividade 12
a) 400 5 = 200 t 400t = 200 5
t = 1 000 400 = 2,5 h
b) 120
9 funcionários.TRAVESSIA S
Proporcionalidade: uma propriedade
Um aplicativo de monitoramento de usuários da internet de uma grande empresa gera quantidades constantes de relatórios em certo tempo. Observe a tabela que relaciona essas grandezas: Aplicativo de monitoramento
Observe que há duas sequências nessa tabela: uma formada pela grandeza tempo e outra pela grandeza quantidade de relatórios. Ambas são crescentes e, além disso, podemos observar que:
0,5 10 = 1 20 = 3 60 = 5 100
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
ATIVIDADES
13. Reúna-se com um colega e, juntos, utilizem uma calculadora para resolver as atividades.
a) Calcule o quociente decimal que resulta do numerador dividido pelo denominador em cada fração daquelas. 0,05 para todas.
b) O que aconteceu com os valores dos quocientes para cada uma?
c) Qual seria o denominador de uma fração equivalente àquelas na qual o numerador fosse 2? 40
14. Com o mesmo colega, analise os fatos que se seguem.
a) Verifiquem se são verdadeiras as proporções: São verdadeiras. 0,5 10 = 0,5 + 1 10 + 20 = k 1 20 = 1 + 3 20 + 60 = k 5 100 = 0,5 + 1 + 3 10 + 20 + 60 = k
b) Que curiosidade vocês podem observar nessas sentenças? Qual é o valor da constante k?
Respostas pessoais. k = 0,05
c) Suponha que a quádrupla (a, b, v, w) forme uma proporção. Será que é válida a sentença? É válida.
a b = v w = a + v b + w
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
c) A sentença a b = v w = a + v b + w é válida. Espera-se que os estudantes cheguem a essa conclusão, nesse item, pela observação dos exemplos numéricos do item a
d) A sentença é uma proposição (afirmação matemática sobre alguns objetos matemáticos) envolvendo proporções. Esse fato pode ser demonstrado matematicamente. A seguir, a demonstração foi iniciada. Com seu colega, complete-a Demonstração
Supondo que a primeira igualdade seja verdadeira, ou seja: a b = v w temos que a w = b v
Adicionando a b a ambos os membros dessa equação e fatorando:
a b + a w = a b + b v
a b + w ( ) = b a + v ( )
A partir daqui, prossiga com a demonstração.
Demonstração.
d) Supondo que a primeira igualdade seja verdadeira, ou seja, a b = v w , temos que a w = b v Adicionando a b a ambos os membros dessa equação e fatorando, temos a b + a w = a b + b v a (b + w ) = b (a + v ) a b = (a + v ) (b + w ) Então: a b = v w = (a + v ) (b + w )
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
LUPAS E LUNETAS
Sabe-se que x 1 y 1
= k
Multiplicando ambos os membros dessa igualdade por y1 e desenvolvendo, temos: x 1 y 1 y 1 = k y 1
x 1 = ky 1
Fazemos de forma análoga para os demais: x 2 = ky 2 , x 3 = ky 3 x n = ky n ky 2 , x 3 = ky 3 x n = ky n
Atividade 15
Observe que estamos considerando que essa é a capacidade da máquina (7 ovos por vez).
Primeiro, convertemos a quantidade de horas para minutos: 2 h = 120 min
Agora, escrevemos a proporção e desenvolvemos: 10
7 = 120 x
10x = 120 7
x = 12 ⋅ 7
x = 84 ovos
Atividade 16
O pedreiro, no mesmo ritmo, levaria 36 h ou um dia e meio, porque: 12 3 = x 9 3x = 12 ⋅ 9 x = 36
Proporcionalidade direta
Você deve ter observado que, quanto mais o tempo passa, a quantidade de relatórios aumenta na mesma proporção. Por exemplo, se triplicarmos as horas, então, triplica do mesmo modo a quantidade de relatórios; e todas as frações equivalentes estão sujeitas a uma mesma constante k que, nesse caso, vale 0,05.
sequências de números não nulos. As sequências são diretamente proporcionais se existe um número k tal que
de modo que k é chamado de constante de proporcionalidade
Note que se, por exemplo, dobrarmos o valor de uma das grandezas em uma proporcionalidade direta, o valor da outra também dobra; se o valor de uma for dividido por 3, o valor da outra também será dividido por 3, de modo a manter a constante k de proporcionalidade:
LUPAS E LUNETAS
Considerando as sequências de números não nulos diretamente proporcionais, verifique que vale também:
ATIVIDADES
15. A máquina de cozinhar ovos de um restaurante leva 10 minutos para cozinhar 7 ovos. Funcionando continuamente, em 2 horas, quantos ovos ela terá cozido?
Atenção: só resolva após transformar as unidades de medida de tempo. 84 ovos.
16. Um pedreiro leva 12 horas para construir um muro de 3 metros de comprimento. Quanto tempo ele levaria para construir um muro de 9 metros no mesmo ritmo? 36 h ou 1,5 dia.
17. Uma mangueira, com sua torneira aberta em fluxo constante, foi colocada dentro de uma piscina vazia. A tabela apresenta o aumento do nível de água na piscina no decorrer do tempo, a partir do instante em que a torneira foi aberta.
Atividade 17
Sabendo que 1 m = 100 cm, escrevemos as proporções e desenvolvemos:
Nível de água na piscina
12 cm 15 min
24 cm 30 min
48 cm 1 h
Quando o nível de água chegar a 1 metro, quanto tempo terá transcorrido desde que a torneira foi aberta? 125 min ou 2h05 min.
18. Leia o problema que a professora Solange passou para os alunos: Aldo, Elson e Irton são irmãos e as idades deles são diretamente proporcionais a 2, 3 e 4 anos. Sabendo que a soma das idades dos três é igual a 36, qual é a idade de cada irmão?
O nível da água chegará a 1 m em 125 minutos ou 2 horas e 5 minutos.
Atividade 18
Acompanhe cada dupla na criação dos problemas: oriente sobre a clareza na escrita do enunciado, as informações necessárias e suficientes, a escolha dos contextos, as unidades de medida envolvidas e a resolução para identificação de possíveis equívocos. Socialize os problemas criados com a turma toda.
Vamos indicar por A, E e I as idades, nessa ordem, de cada um dos três irmãos. Sabemos que as idades são proporcionais a 2, 3 e 4, nessa ordem; assim, temos:
Pela propriedade da proporção, temos:
Como queremos a idade de cada um, basta fazer:
Assim, as idades dos irmãos são: Aldo, 8 anos; Elson, 12 anos; Irton, 16 anos.
a) Converse com os colegas sobre a resolução e o que compreenderam.
Respostas pessoais.
b) Junto com um colega, elabore um problema parecido sobre as idades dos três irmãos.
19. As medidas dos ângulos internos de um triângulo são diretamente proporcionais aos números
5, 8 e 7. Calcule a medida de cada um dos ângulos desse triângulo. 45o; 72o; 63o
Proporcionalidade inversa
Um drone, do instante em que foi colocado em movimento, desloca-se uma distância fixa, com velocidade conforme mostra a tabela.
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
= 9 5
A tecnologia tem impactado cada vez mais o trabalho no campo: agricultor controla drone em campo para monitoramento da plantação.

Observe que há duas sequências nessa tabela: uma formada pelos valores da grandeza velocidade e a outra pelos da grandeza tempo
Observe também que:
LUPAS E LUNETAS
6 ⋅ 150 = 10 ⋅ 90 = 12 ⋅ 75 = 15 ⋅ 60 = 900
Forme dupla ou trio para fazer a análise final dessa situação.
a) Conforme a velocidade aumenta, o tempo correspondente para percorrer a distância fixa diminui ou aumenta?
Diminui.
b) Por exemplo, ao dobrar a velocidade de 6 m/s para 12 m/s, o que aconteceu com os tempos correspondentes? Caíram pela metade: de 150 s para 75 s.
Atividade 19
Realizamos a adição dos números apresentados para determinar qual é o número proporcional à soma das medidas dos ângulos internos do triângulo, que é 180o: 5 + 8 + 7 = 20
Assim, sabemos que 20 está para 180 20 180 =
assim como 5, 8 e 7 estão para as medidas desconhecidas dos ângulos internos do triângulo
= 45
9 = 8 x
= 8 9
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
= 7 z
= 7 9
= 63 As medidas são 45o, 72o e 63o
LUPAS E LUNETAS
a) Conforme a velocidade aumenta, o tempo para percorrer o mesmo trecho diminui.
b) Ao dobrar a velocidade, o tempo parar percorrer o mesmo trecho caiu pela metade.
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
LUPAS E LUNETAS
Sabe-se que
x 1 1 y 1
= k
As sequências são inversamente proporcionais se existe um número k tal que
caso,
Note que se, por exemplo, dobrarmos o valor de uma das grandezas em uma proporcionalidade inversa, o valor da outra passa a ser metade do que era; se o valor de uma for dividido por 3, o valor da outra triplicará, de modo a manter a constante k de proporcionalidade inversa:
LUPAS E LUNETAS
Considerando as sequências de números não nulos inversamente proporcionais, verifique que vale também:
ATIVIDADES
20. As quádruplas representam proporções inversas. Determine o valor desconhecido em cada
1 y 1
= k 1 y 1
Multiplicando ambos os membros da igualdade por 1 y 1 e desenvolvendo, temos: x 1 1 y 1
x 1 = k y 1
Agora, multiplicando ambos os membros por y1:
x 1 y 1 = k y 1 y 1
x 1 y 1 = k Fazemos de forma análoga para os demais: x 2 ⋅ y
y n = k
21. Qual dos quadros representa uma relação de proporcionalidade inversa entre as grandezas a e b?
#Não proporcionalidade
22. Um pedreiro levou um dia de trabalho para construir um muro de 3 metros de comprimento. Se ele tivesse um ajudante que trabalhasse no mesmo ritmo que ele, em quanto tempo ele teria construído esse muro? 0,5 dia de trabalho.
Atividade 20
a) 10 9 = 15 w
w = 10 9 5 3
w = 2 3 = 6
b) 3 ⋅ 5 = y ⋅ 10 y = 15 10 = 1,5
c) 6 x = 8 3
x = 24 6 = 4
d) z 6 = 9 12
z = 9 12 6 = 18
Atividade 21 Comente com os estudantes que, para mostrar que
Alguns problemas aparentam ter uma relação de proporcionalidade, por causa da relação entre duas sequências, mas as grandezas não são nem direta nem inversamente proporcionais Vamos observar esta situação: dois irmãos saíram ao mesmo tempo de casa para o mesmo destino. Cada tabela mostra o deslocamento de um irmão. 180 | TRAJETÓRIA 3 NÃO ESCREVA NO SEU LIVRO.
duas grandezas são inversamente proporcionais (ou que são diretamente proporcionais também), deve ser válida a propriedade para todos os pares apresentados, dois a dois. Para mostrar que não são, basta mostrar que dois pares não satisfazem a propriedade.
a) 5 25 ≠ 10 20
b) 5 6 = 10 3 = 15 2 = 20 1,5
c) 5 15 ≠ 10 30
d) 5 20 ≠ 10 20
Atividade 22
A quantidade de pedreiros (com mesmo desempenho) e o tempo gasto para construir um muro são grandezas inversamente proporcionais:
um pedreiro, 1 dia ! = 2 ⋅ x
dois pedreiros, x dias !
1 ⋅ 1
x = 1 2
Dois pedreiros levariam 0,5 dia para construir o mesmo muro.
LUPAS E LUNETAS
Forme uma dupla para analisar a seguinte situação.
a) Aumenta. Que a distância total percorrida está variando. Ele está em movimento. Não há relação de proporcionalidade direta e nem de proporcionalidade inversa.
a) Na tabela de Lucas, conforme o tempo passa, a distância total percorrida aumenta ou diminui?
O que isso significa? O que está acontecendo com Lucas? Há uma relação de proporcionalidade entre a distância e o tempo? Como você pode justificar sua resposta?


b) Na tabela de Flávio, conforme o tempo passa, a distância total percorrida aumenta ou diminui?
O que isso significa? O que está acontecendo com Flávio? Há uma relação de proporcionalidade entre a distância e o tempo? Como pode justificar sua resposta?
parado.
de
ATIVIDADES
23. Observe cada quadro que exibe a relação entre duas grandezas a e b. Classifique as grandezas em cada item em diretamente proporcionais (DP), inversamente proporcionais (IP) e não proporcionais (NP).
8
b 5 10 15 20 DP
a 2 4 6 8
proporcionalidade direta e o segundo de proporcionalidade inversa.
I. Tadeu está cortando fatias de bolo de aniversário para servir na festa. Ele cortou 6 fatias que pesavam juntas 300 g, depois cortou mais 8 fatias pesando juntas 320 g. Quanto pesarão juntas 10 fatias?
c)
b 60 30 20 15 IP
a 2 4 6 8
d)
b 8 16 32 64 NP
24. Os dois problemas a seguir relacionam grandezas que são não proporcionais. Faça ajustes em alguns valores (ou em todos) de cada problema para que o primeiro seja de
II. Uma vaquinha será feita por alguns jovens para arrecadar um valor a ser revertido em benefício para uma instituição de menores. Se houver 5 pessoas na vaquinha, cada uma contribuirá com R$ 120,00; se houver 8 pessoas, o valor será de R$ 90,00 por pessoa. Qual será o valor por pessoa se na vaquinha entrarem 10 pessoas?
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
Lupas: b) Nem aumenta nem diminui: fica constante após a meia hora inicial. Que a distância total percorrida está constante. Ele está parado depois da meia hora inicial, ou seja, na meia hora inicial andou 2 km e estacionou. Não há relação de proporcionalidade direta, pois:
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
Não há relação de proporcionalidade direta, pois:
de proporcionalidade inversa, pois:
75,00.
Tempo e distância, por si só, podem ou não ser diretamente proporcionais. Se a variação do movimento for uniforme, ou seja, a uma velocidade constante, então tempo e distância serão diretamente proporcionais.
LUPAS E LUNETAS
a) A distância aumenta, ou seja, a distância total percorrida está variando. Lucas está em movimento.
Não há relação de proporcionalidade direta, pois:
Atividade 24
I. Alterando 320 g para 400 g, teremos:
400 = 10 x
A resposta do problema de proporcionalidade direta será: 500 g.
b) A distância nem aumenta, nem diminui, fica constante após a meia hora inicial. A distância total percorrida é constante. Flávio está parado depois da meia hora inicial, ou seja, na meia hora inicial andou 2 km e estacionou.
II. Alterando R$ 90,00 para R$ 75,00:
5 120 = 8 75 = 10 y
A resposta do problema de proporcionalidade inversa será: R$ 60,00.
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

#Proporção e plano cartesiano
Vamos agora analisar situações de proporcionalidade, direta e inversa, segundo a representação dessas situações em um plano cartesiano.
Situação 1
Suelen sempre compra pão na mesma padaria. Ela já decorou o preço que pagará a depender da quantidade de pão francês que comprar.
Ela sabe que, conforme x (quantidade de pães) aumenta, y (preço total) aumenta na mesma proporção, pois há uma proporcionalidade direta entre essas grandezas.
Observe que y é produto da quantidade x de pães pelo valor fixo 1,25 – preço unitário. Isso pode ser escrito algebricamente assim: y = x 1,25 ou y = 1,25x Do primeiro quadro, obtemos os pares ordenados:
Cada um desses pares corresponde a pontos que podem ser representados no plano cartesiano:
Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

Situação 2
Uma piscina, totalmente vazia, será enchida com água. Dependendo da vazão (quantidade de água por unidade de tempo), a piscina encherá menos ou mais rapidamente. Um jato “muito grosso” de água vai encher a piscina de modo mais rápido do que um jato “mais fino” de água.
A tabela mostra a relação da vazão com o tempo:

Habilidades
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
Observe que, conforme x (vazão) aumenta, y (tempo) diminui na mesma proporção, pois há uma relação de proporcionalidade inversa entre essas grandezas.
Sendo assim, sabemos que:
1 000 10 = 800 12,5 = 625 16 = 500 20 = 400 25 = 10 000
Um valor de x multiplicado por seu correspondente valor de y vai gerar 10 000 no produto, ou seja:
x y = 10 000 ou y x = 10 000 ou ainda: y = 10 000 x

Vamos considerar os pares ordenados representados na tabela: (1 000; 10), (800; 12,5), (625; 16), (500; 20), (400; 25) e representar os pontos correspondentes no plano cartesiano.
ATIVIDADES
25. Observe cada quadro que exibe a relação entre os valores de duas grandezas, x e y
a) Represente os pares ordenados de cada quadro em um plano cartesiano. Dica: se preferir, para representar cada conjunto de pontos no plano cartesiano, utilize uma ferramenta digital de geometria dinâmica.
b) Classifique as grandezas em diretamente proporcionais (DP), inversamente proporcionais (IP) e não proporcionais (NP).
I) DP; II) IP; III) NP; IV) IP.
c) Observe o “comportamento” dos pontos em cada representação no plano cartesiano. A organização dos pontos no gráfico lembra que tipo de linhas?
26. A duração da colheita de café em uma fazenda depende da quantidade de trabalhadores, conforme mostra a tabela.
Colheita de café
n (NÚMERO DE TRABALHADORES) 120 60 30 15 10
t (TEMPO EM DIAS) 1 2 4 8 12
Fonte: Administração.
c) II e IV uma curva (hipérbole); I, uma reta inclinada; III, uma reta horizontal. t = 120 n
a) Escreva uma expressão algébrica que relacione n e t
b) Represente os pares ordenados (n, t) por pontos em um plano cartesiano.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado e reflita sobre as perguntas a seguir.
▶ Matemática

Você identifica a natureza da variação de duas grandezas: se diretamente ou inversamente proporcionais ou não proporcionais?
• Expressa a relação entre duas grandezas por meio de sentença algébrica?
• Representa uma relação de proporcionalidade entre duas grandezas no plano cartesiano?
• Resolve e elabora problemas que envolvam grandezas diretamente ou inversamente proporcionais?
▶ Outras disciplinas
Língua Portuguesa
Analisa diferentes práticas (curtir, compartilhar, comentar etc.) da cultura digital envolvidas no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
MATEMÁTICA
OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
Levo na bagagem
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
a) I: DP; II: IP; III: NP; IV: IP.



c) II e IV lembram uma curva (hipérbole); I lembra uma reta inclinada; III lembra uma reta horizontal.
Atividade 26
a) O número de trabalhadores n é inversamente proporcional ao tempo t de trabalho na colheita.
Encontro
com outras
disciplinas
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
BARCOS E PORTOS
Organize
Solicite que façam primeiro um esboço para essa atividade e, só depois das atividades resolvidas e das resoluções devidamente verificadas, produzam um resumo bem organizado e visual, utilizando cores para representar as etapas.
Peça também que retomem os estudos de plano cartesiano e construam representações gráficas das relações entre as grandezas dos problemas resolvidos.
Elabore
a) Considerando-se constante a razão de aproveitamento das ideias:
▶ Organize
Respostas pessoais.
Considere os conhecimentos que você explorou neste passeio. Organize seu aprendizado em três ações:
• Conhecer. Selecione dois ou mais problemas para cada uma das três categorias de relações de proporcionalidade.
• Fazer. Resolva os problemas que selecionou na etapa anterior.
• Experimentar. Elabore um problema para cada uma das categorias de relações de proporcionalidade. Em seguida, resolva-os. Depois, mostre a um colega para ele ler e avaliar se está tudo correto. Faça o mesmo com os problemas elaborados e resolvidos por ele.
▶ Elabore Leia a tirinha:
Disponível em: http://meninomaluquinho.educacional.com.br/paginatirinha/paginaanterior.asp?da=07102015.
Acesso em: 16 ago. 2022.
a) Você acha que os personagens dessa tirinha são criativos? Explique.
b) Imagine que, nessa “campanha de doação de ideias”, de cada cinco ideias doadas apenas duas sejam aproveitadas pelo Menino Maluquinho e seu amigo Bocão. Quantas ideias serão aproveitadas por eles se na campanha forem doadas 25 ideias?
c) Elabore uma estratégia para avaliar ideias que são publicadas o tempo todo na rede. Pense em como melhorar sua forma de verificar a precisão, os fatos, as opiniões e as interpretações que o impactam e as pessoas do seu entorno.
▶ Proponha
2
5 = x 25
x = 50 5 = 10 ideias

b) Oriente os estudantes quanto às ideias deles sugerindo múltiplas fontes, autores que sejam autoridades nos assuntos que abordam, fontes com credibilidade etc.
A pergunta inicial deste passeio é: Que impactos as tecnologias da comunicação podem trazer à vida familiar e ao mundo do trabalho?
Os impactos das tecnologias da comunicação na vida familiar ou no mundo do trabalho podem ser positivos ou negativos. Por isso, deve-se promover o bom uso das tecnologias da comunicação e informação, mas também dedicar atenção aos riscos de seu mau uso.

Impactos positivos das tecnologias da comunicação: um drone com câmera térmica monitora o início do incêndio e envia informações aos profissionais do meio ambiente para as devidas providências; o distanciamento social foi reduzido pela possibilidade das videochamadas.

Proponha
Retome a questão norteadora da Trajetória e, depois de realizada a pesquisa solicitada, estabeleça um debate sobre os impactos positivos e os negativos das tecnologias para as vivências na família, na escola e no mundo do trabalho.
Impactos negativos das tecnologias da comunicação e informação: amigos e familiares reunidos para uma refeição, mas cada um interagindo virtualmente em separado do real; as informações confidenciais no mundo do trabalho estão sujeitas a ataques de hackers.



Pesquise na internet outros possíveis impactos positivos e negativos na vida familiar e no campo do trabalho (e dos estudos, caso você queira ampliar sua pesquisa).
Verifique a precisão das informações que encontrar na internet, reflita sobre elas, busque outras fontes e procure “confrontar” as informações de diferentes fontes, para melhorar seu poder de julgamento da credibilidade do que é disponibilizado na internet.
Exponha suas descobertas no mural virtual da sala.
VISTORIAS
Habilidades
EF08MA12, EF08MA13, EF08MA14, EF08MA15, EF08MA16, EF08MA17, EF08MA18
Atividade 1
a) Translação: coordenada x menos 13 e coordenada y menos 10.
b) Reflexão pelo eixo Ox
c) Resposta possível.
Translação de C (4, 3) para C'(4, –2) e rotação de centro na origem e ângulo de 180o no sentido horário.
Atividade 2
O caso de congruência pode
Você chegou ao final desta Trajetória. Reflita sobre tudo o que aprendeu e verifique a qualidade da sua aprendizagem. Resolva todos os exercícios a seguir no caderno.
CHECK-OUT
1. Considere as figuras e o plano cartesiano.
y
c) Translação de C (4, 3) para C' (4, –2). E rotação de centro na origem e ângulo de 180o no sentido horário.
V. Todo retângulo tem diagonais perpendiculares.
VI. As diagonais do quadrado não são congruentes. F, V, F, F, F, F.
4. Para a exposição de uma escultura, foi delimitada uma região à distância de 1 metro do pedestal da escultura que tem formato hexagonal. O perímetro do pedestal é de 6 m. Descreva uma maneira de calcular o perímetro da região.


Atividade 3
I. (F) Apenas os paralelogramos com lados congruentes são losangos.
II. (V) Todo quadrado tem lados opostos paralelos, então é um paralelogramo.
III. (F) Apenas losangos com os quatro ângulos retos são quadrados.
IV. (F) As diagonais dos trapézios isósceles cortam-se nos correspondentes pontos médios.
V. (F) Os quadrados são retângulos com diagonais perpendiculares.
VI. (F) As diagonais do quadrado são congruentes.
Atividade 5
A mediatriz passa pelo ponto médio M de AB formando um ângulo de 90o que é a mesma inclinação (em relação a AB ) da bissetriz do ângulo raso AM ! B Como as duas retas passam por um mesmo ponto M com a mesma inclinação, são coincidentes.
a) Qual é a transformação que leva o ponto A a A'?
Translação: coordenada x menos 13 e coordenada y menos 10.
b) Qual é a transformação que leva o ponto B a B'? Reflexão pelo eixo Ox
c) Do C até o C" foram aplicadas duas isometrias; determine quais isometrias foram feitas, sendo o ponto C' resultado da primeira isometria.
2. Determine um caso de congruência na figura e calcule os valores de x e y
O caso de congruência pode ser LAL ou ALA. x = 7 e y = 20 3
3. Classifique cada sentença em verdadeira (V) ou falsa (F).
I. Todo paralelogramo é um losango.
II. Todo quadrado é um paralelogramo.
III. Todo losango é um quadrado.
IV. As diagonais do trapézio cortam-se nos correspondentes pontos médios.
O perímetro da região pode ser calculado adicionando o comprimento de uma circunferência de raio 1 m mais o perímetro do hexágono:
2π + 6 ≅ 12,28 m Construções geométricas.
5. Dados os pontos A e B quaisquer no plano:
a) Trace a mediatriz do segmento com extremidades nesses dois pontos.
b) Trace agora a bissetriz do ângulo AM ! B, sendo M o ponto médio do segmento AB
c) Qual é a relação entre essas duas retas? Explique
Atividade 6
O ângulo BD ! C é externo ao triângulo ABD. Então: 7 y = 90 + 15 ⇒ y = 105 7 ⇒ y = 15°

Atividade 7
5. c) São duas retas coincidentes, pois a mediatriz passa pelo ponto médio de AB formando um ângulo de 90o, que é a mesma inclinação (em relação a AB ) da bissetriz do ângulo AM ! B, que é raso. Como as duas retas passam pelo mesmo ponto com a mesma inclinação, com relação a AB, elas são coincidentes.
a) A construção na figura II divide a circunferência em 3 arcos congruentes, o que permitirá a construção do triângulo equilátero e, na sequência, do hexágono regular.
No triângulo BDC e sendo BD " uma bissetriz , temos:
b) Resposta possível:
I. Desenhe uma circunferência de centro O e marque o ponto A pertencente a ela.
II. Com centro em A e abertura OA, trace um arco que corte a circunferência nos pontos B e C
6. Dados o triângulo ABC e BD " a bissetriz do ângulo no vértice B, determine o valor de x + y
500 doadores, cada um contribuirá com R$ 140,00; se houver 1 000 doadores, o valor será de R$ 70,00 por pessoa. Qual será o valor por pessoa se, na arrecadação de fundos, entrarem 70 000 pessoas?
a) Classifique, em cada problema, a natureza da variação das duas grandezas em: DP, IP ou NP.
7. Veja duas construções geométricas diferentes.
b) Reescreva o problema em que não há proporcionalidade, alterando qualquer um dos seus dados numéricos para que seja um problema de proporcionalidade, direta ou inversa, conforme a possibilidade

c) Resolva cada um dos problemas.
d) Represente, por meio de sentença algébrica, a relação entre as grandezas de cada um desses três problemas, inclusive a nova versão do problema que teve seu enunciado reescrito.
9. Observe cada quadro que exibe a relação entre os valores de duas grandezas, x e y, e represente os pares ordenados de cada item em um plano cartesiano. Observe o “comportamento” dos pontos em cada representação no plano cartesiano, classificando as grandezas em diretamente proporcionais (DP) ou inversamente proporcionais (IP).
a) Qual das duas figuras pode representar uma etapa da construção de um hexágono regular?
b) Utilizando a figura correta, termine a construção do hexágono e descreva, por meio de um fluxograma, sua construção.
8. Leia os problemas.
I. Em um atacadista, 10 cadernos custam R$ 125,00 e 12 cadernos custam R$ 138,00. Quanto custará um pacote com 15 cadernos?
II. Uma granja familiar produz 1 100 ovos em dois dias. Mantendo essa relação, quantos ovos serão produzidos em 15 dias?
III. Uma campanha para reflorestamento está arrecadando fundos. Se houver
10. Observe os pontos no plano cartesiano. Considere-os e elabore um problema de proporcionalidade.
8. b) Resposta possível: alterar R$ 138,00 para R$ 150,00 (proporcionalidade direta).
III. Com centro em B e abertura de medida OB, trace um arco que corte a circunferência no ponto D
IV. Trace os segmentos BC , BD e CD
V. Construa as mediatrizes desses segmentos, determinando mais 3 pontos na circunferência (incluindo A).
VI. Trace o polígono que tenha esses pontos como vértices.
Atividade 8
a) I. NP; II. DP; III. IP.
b) Resposta possível: Alterar R$ 138,00 para R$ 150,00 (proporcionalidade direta).
c) Resolvendo cada problema:
R$ 187,50.
Respostas possíveis:
“Uma loja vende um docinho por R$ 0,50 e 4 docinhos por R$ 2,00. Qual será o preço de 6 docinhos?” ou
“Uma loja cobra R$ 1,50 para escanear 3 documentos e R$ 2,00 por 4 documentos. Qual será o preço para escanear 8 documentos?”
DE OLHO NA BÚSSOLA
Após
os
da seção Check-out, verifique se você aprendeu a:
Considerando os exercícios que você resolveu, como julga seu desempenho: insuficiente, parcialmente suficiente, satisfatório, plenamente satisfatório?
pessoal.
Prossiga ▶
Continue estudando! Retome esta Trajetória buscando, com professores e colegas, alternativas para superar os obstáculos de sua aprendizagem. Estude a seção Retornos e resolva novos exercícios referentes à Trajetória 3 que estão na seção Suplemente sua aprendizagem, ao final do livro.
DICAS DE ESTUDO
Descubra o “verbo de aprendizagem” que lhe ensina melhor.
Há conteúdos que envolvem o verbo conhecer: são os conhecimentos conceituais, as nomenclaturas, os termos matemáticos.
Há ainda conteúdos que envolvem o verbo fazer, que são os conhecimentos procedimentais: construções geométricas, descrições de passo a passo, cálculo do resultado de uma operação, resolução de um problema etc.
E, além desses, há também os conteúdos que envolvem o verbo experimentar, que são os conhecimentos factuais: as demonstrações matemáticas, as investigações a partir de regularidades, formulação de conjecturas, pesquisas estatísticas etc.
Procure observar por quais dessas ações você aprende melhor e aquelas em que tem mais fragilidades; comece a pensar em estratégias para superá-las.
Para pensar em estratégias que sejam favoráveis à superação das suas dificuldades, invista em diferentes métodos de aprendizagem: leia, ouça, assista, converse, pratique e, principalmente, ensine! Isso mesmo, ensine.
Veja o que mostra o gráfico, resultado de pesquisas feitas por William Glasser (1925-2013), psiquiatra estadunidense.
COMO APRENDEMOS Pirâmide de aprendizagem de William Glasser
Aprendemos...
10% quando lemos;
20% quando ouvimos;
30% quando observamos;
50% quando vemos e ouvimos;
70% quando conversamos com outros;
80% quando praticamos;
95% quando ensinamos alguém;
Ler
Escutar
Ver
Ver e ouvir
Conversar, perguntar, repetir, relatar, numerar, reproduzir, debater, definir, nomear Escrever, interpretar, traduzir, expressar, revisar, identificar, comunicar, utilizar, demonstrar, praticar, diferenciar, catalogar Explicar, resumir, estruturar, definir, generalizar, elaborar, ilustrar
De acordo com esse psiquiatra, somos prontos a aprender por diversos canais que estão presentes dentro de nós pela liberdade pessoal diante do ato de estudar.
Uma sugestão é: vá aumentando sua frequência em estudos em grupos e individualmente a fim de se tornar mais ativo no seu próprio processo de aprendizagem. Segundo esse estudioso, quanto mais interativo, maior a retenção do seu conhecimento. Faça bom proveito de todas as camadas dessa pirâmide!
Dicas de estudo
Leia o texto com a turma e, em seguida, reunidos em duplas ou trios, os estudantes podem debater sobre as informações do texto e da pirâmide e seu próprio modo de aprender, compartilhando estratégias e métodos que tenham se mostrado eficazes.
4
PANORAMA DA TRAJETÓRIA
Competências gerais: 6, 7
Competências específicas: 2, 4, 7
Habilidades de Matemática: EF08MA19, EF08MA20, EF08MA21, EF08MA23, EF08MA24, EF08MA25, EF08MA26, EF08MA27
Habilidades de outras disciplinas:
Língua Portuguesa: EF69LP33, EF08LP01
Educação Física: EF89EF11
Temas Contemporâneos
Transversais:
Saúde
Educação Alimentar e Nutricional

Vida Familiar e Social
Direitos Humanos
Nesta Trajetória, teremos conteúdos de geometria e de estatística, permeados pela pergunta motivadora: Quais são as dimensões do bem-estar?
A noção de bem-estar deve ser levada às dimensões mais amplas, para além do bem-estar pessoal (centrado em si mesmo), e alcançar noções mais elevadas, como o bem-estar coletivo. É fato que buscar a paz de espírito de caráter interno e desenvolver relações pacíficas de caráter externo fazem parte do processo complexo que é conceber, desejar e difundir ideias envolvendo o bem-estar. Por meio de reflexões e atividades de convívio social, é possível incentivar a construção de projetos de vida, não apenas quanto à vida afetiva, familiar ou do trabalho, mas também quanto ao meio ambiente, aos espaços e tempos para lazer e práticas corporais ou práticas culturais, à participação social, às fontes e formas de difusão de informação etc., seja com foco em transformações locais, seja em transformações globais.

Envolvendo essas noções podemos citar como exemplo as propostas de combate à propagação de fake news
As redes sociais, tão utilizadas
192 | MANUAL DO PROFESSOR
atualmente, têm enorme influência para ampliar o alcance da desinformação, especialmente quanto aos adolescentes que estão mergulhados nesse oceano de compartilhamento de conteúdo nas suas diversas formas e fontes. Em muitos casos, as notícias são compartilhadas sem que se possa, minimamente perguntar: É verdade? É mentira? É uma montagem? Dá para ver que foi editado? Qual foi a intenção da edição? O que posso fazer para descobrir?

Rejeitar a propagação de fake news é um modo de pensar o bem-estar social. Uma boa maneira de
QUAIS SÃO AS DIMENSÕES DO BEM-ESTAR?
• O que quer dizer bem-estar físico?
• Como manter o bem-estar mental?
• Como desenvolver o bem-estar social?
diminuir a desinformação e o combate à informação incorreta é ela ser debatida em sala de aula. E certamente os alunos estarão exercitando um aspecto do bem-estar que é cada vez mais urgente, que é ter senso crítico para realizar filtros quando se navega no oceano de informações.
Jovem em contato com a natureza demonstrando sensação de bem-estar.

CONTEÚDOS DA TRAJETÓRIA
Passeio 1 – Superfície, volume e capacidade
• Área de superfície (cm2, dm2, m2)
• Círculos, triângulos e quadriláteros
• Volume (cm3, dm3, m3)
• Cubo e blocos retangulares
• Capacidade (L, mL)
Passeio 2 – Gráficos e medidas de posição
• Gráficos e adequação (barras ou colunas, setores e linhas)
• Tabela de frequências com dados agrupados em classes
• Média aritmética
• Média aritmética ponderada
• Moda
• Mediana
Passeio 3 – Pesquisa estatística e credibilidade da informação
• Critérios para avaliar a credibilidade da informação
• Etapas da pesquisa estatística
• Técnicas de amostragem
• Relatório da pesquisa
LUPAS E LUNETAS
Pela própria vivência, os estudantes têm uma expectativa do que seja bem-estar físico, mental e social. Ajude-os a organizar como pensam a esse respeito e expressar em um mural físico ou virtual.

LUPAS E LUNETAS
Respostas pessoais.
Reflita sobre as questões apresentadas anteriormente e considere-as para elaborar outras perguntas de sua própria autoria.
Publique suas perguntas no mural da sala de aula e aprecie as perguntas dos colegas.
Mãe e filha em abraço amoroso: sensação de afeto e bem-estar para corpo, mente e espírito.Habilidades
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
Encontro com outras disciplinas
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
CHECK IN
a) Organize a conversa sobre o tema registrando as atividades físicas mencionadas e solicitando breves relatos que incluam os porquês de gostarem mais dessa ou daquela atividade e como se sentem quando a praticam.
b) A ginástica de conscientização corporal (pilates, yoga, ginástica holística, eutonia, tai chi chuan, dança etc.) ajuda a conhecer os movimentos, os limites e as capacidades do nosso corpo, enquanto a ginástica de condicionamento físico (musculação, hidroginástica, alongamento, aeróbica) auxilia a manter a boa forma e o bom desempenho das funções orgânicas.


PASSEIO 1 – SUPERFÍCIE, VOLUME E CAPACIDADE
O QUE QUER DIZER BEM-ESTAR FÍSICO?
Duas modalidades de ginástica: uma de conscientização corporal (yoga, por exemplo) e outra de condicionamento físico (ginástica rítmica, por exemplo), ambas com potencial para melhoria das condições de saúde.
CHECK-IN
Respostas pessoais.
a) Que atividade física você aprecia?
c) Tapete: superfície e volume (se a espessura for conhecida); bola: volume, capacidade e superfície.
b) Pesquise a diferença entre ginástica de conscientização corporal e ginástica de condicionamento físico.
c) Há dois acessórios nas imagens: um tapete de yoga e uma bola de ginástica. Quais das grandezas superfície, volume e capacidade você associa a cada um deles?
d) Converse com os colegas e aponte a estimativa correta para:
I. a área da superfície do tapete: 1 cm2, 1 m2 ou 4 m2;
II. o volume da bola: 2 m3, 0,2 m3 ou 0,02 m3. Tapete: 1 m2; bola: 0,02 m3

c) Avalie a compreensão dos estudantes em relação aos conceitos de superfície, volume e capacidade e às dimensões envolvidas nessa distinção.
d) Desenvolver a capacidade de estimativas de medidas permitirá ao estudante melhorar sua relação com o ambiente que o cerca.
CONVÍVIO E BEM-ESTAR SOCIAL
Aproveite esse momento e converse com os estudantes sobre atividades físicas: em uma roda de conversa, pergunte quais são as atividades físicas praticadas por eles dentro e fora da escola. Pergunte com que periodicidade e se eles sabem quais benefícios essas práticas promovem. Em seguida, realize uma avaliação da aptidão física de cada um, mensurando indicadores como o índice de massa corporal (IMC) (consulte os estudantes e a família se estão de acordo em realizar esse cálculo).
• Reconhecer unidades de medida de volume e de capacidade e suas relações.
• Resolver e elaborar problemas que envolvam cálculos de volume e de capacidade de recipientes com formato de bloco retangular.
• Identificar as qualidades tanto das ginásticas de conscientização corporal como das de condicionamento físico para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
195 | NÃO ESCREVA NO SEU LIVRO.
O IMC é um indicador da composição corporal recomendado pela Organização Mundial da Saúde (OMS) para classificação do estado nutricional. O IMC relaciona massa e altura e os resultados são magreza, normalidade, sobrepeso e obesidade
As faixas de classificação pelo IMC são diferentes para crianças, adolescentes, adultos e idosos.
IMC da turma. A coleta de dados pode ser realizada de forma anônima, se preferirem. Finalize a atividade com uma discussão coletiva sobre os resultados indicados nos gráficos. Conversar e conscientizar sobre temas como esse é também um modo de combater a desinformação, os preconceitos e, em particular, o bullying
195 |
Habilidades
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
Encontro com outras disciplinas
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
ATMOSFERA
Atividades 1 a 4
A prática de atividade física é indicada para todas as idades. Até mesmo para bebês, que podem praticar natação, por exemplo, para prevenir doenças respiratórias, ajudar a engatinhar, a se equilibrar melhor, a reduzir a ansiedade, melhorar o sono etc. As crianças que praticam ginástica podem desenvolver uma boa coordenação motora, equilíbrio, agilidade, concentração, ritmo e força.
Ginástica artística para crianças
[...]
É uma modalidade que através de um conjunto de exercícios e movimentos corporais, realizados no chão ou com auxílio de aparelhos, desenvolve habilidades como coragem, domínio do corpo, agilidade de movimentos com objetivos educativos, terapêuticos, competitivos etc.
A criança pode iniciar aos 2 anos de idade com uma proposta mais lúdica; as aulas de ginástica
artística nessa fase devem durar no máximo 30 minutos. Os exercícios incluem saltos, corridas, rolamentos, escadas tudo como se fosse uma brincadeira.
Conforme a criança vai crescendo, vai evoluindo também a intensidade e o grau de dificuldade dos exercícios.
[...]
GINÁSTICA infantil. Blog Pratique em casa, 4 dez. 2020. Disponível em: https://pratiqueemcasa.com.br/blog/ ginastica-infantil. Acesso em: 31 maio 2022.

ATIVIDADES
1. O que você acha da prática de ginástica para crianças? Respostas pessoais.
2. Que benefícios as práticas de ginástica podem trazer para as crianças?
3. A ginástica artística é uma prática corporal de conscientização do corpo ou de condicionamento físico?
2. Alguns exemplos, conforme o texto: desenvolvem habilidades como coragem, domínio do corpo, agilidade de movimentos. De condicionamento físico. Informações com base na pesquisa realizada pelo aluno na seção Check-in
4. Que atitudes você costuma ter para cuidar de sua própria saúde? Respostas pessoais.
#Superfícies de retângulos e quadrados
O tapete de ginástica é retangular e geralmente mede 1,70 m de comprimento por 0,60 m de largura.
Habilidade (EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

Converse com os estudantes sobre área de uma superfície para avaliar o conhecimento prévio. Use como exemplos a medida de terrenos ou espaços como a própria sala de aula.

SUGESTÃO DE ATIVIDADE
Crianças em atividades de ginástica, alongando-se em tapetes de ginástica.
A medida da superfície desse tapete pode ser determinada pelo cálculo da área da superfície de um retângulo
Mas, antes disso, vamos considerar como ponto de partida para cálculos de áreas de superfícies a noção de quadrado unitário:
Quadrado unitário é a área da superfície de um quadrado de 1 unidade de medida de comprimento (u) de lado e é igual a 1 u2 (lê-se: uma unidade quadrada).
Daqui em diante utilizaremos essa definição para determinar o cálculo da área da superfície de terrenos, de objetos, de espaços, entre outros, com formatos possíveis de serem associados às figuras geométricas planas.
NÃO ESCREVA NO SEU LIVRO.
Para iniciar o estudo de área de uma superfície faça um quadrado de jornal com lados de 1 m e mostre para o estudante a superfície com área 1 m2. Peça aos estudantes que observem e estimem o tamanho do piso da sala de aula deixando alguns registros na lousa. Depois, calculem a área da superfície da sala de aula utilizando o metro quadrado de jornal como unidade de medida e, posteriormente, meçam os lados com uma trena, multiplicando essas dimensões e comparando os resultados.
197 |
LIGHTFIELD STUDIOS/SHUTTERSTOCKHabilidade (EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
LUPAS E LUNETAS
a) É esperado que os estudantes percebam que enquanto a figura A tem medidas de lado com números inteiros, a figura B tem medidas de lado com números racionais não inteiros (na forma fracionária). Além disso, devem avaliar como as áreas seriam comparadas com unidades de medida diferentes e não padrão (quadradinhos maiores ou quadradinhos menores) e, então, concluir pela necessidade da padronização da unidade de medida.
b) Para determinar a medida do lado de cada quadradinho, basta dividir a medida de um dos lados da figura A pelo número de quadradinhos dispostos:
lado: 5 cm 5 = 1 cm; área da superfície: 1 cm2
c) Para a figura B, temos:
lado: 7 3 cm 7 =
= 7 3 1 7 cm = 1 3 cm; área da superfície:
1 3 1 3 = 1 9 cm2
d) Figura A: 5 2 = 10 quadradinhos de 1 cm de lado; figura B: 7 4 = 28 quadradinhos de 1 3 de lado.
e) Figura A: 10 1 cm2 = 10 cm2 ; figura B:
1 9 cm2 = 28 9 cm2
LUPAS E LUNETAS
Junte-se a um colega e, juntos, calculem as áreas das superfícies de cada figura. 2 cm
cm
Figura A Figura B
a) Que diferenças mais chamam a atenção nas duas figuras? Respostas pessoais.
b) Qual é a medida do lado do menor quadradinho na Figura A? E qual é a área dele? 1 cm; 1 cm2
c) Qual é a medida do lado do menor quadradinho na Figura B? E qual é a área dele?
d) Qual é a área de cada figura considerando os quadradinhos unitários em cada uma como as respectivas unidades de medida?
e) Qual é a área de cada figura em centímetros quadrados (cm2)?
Podemos generalizar da seguinte maneira:
Dado um retângulo com medidas de lados a e b, a área de sua superfície é igual a ab a
b
Como o quadrado é um retângulo em que a = b = ℓ , a área da superfície do quadrado é igual a ℓ 2
ATIVIDADES
5. Calcule a área da superfície do tapete de ginástica retangular de medidas indicadas no texto anterior. 1,02 m2
#Superfícies de paralelogramos e triângulos
Considerando as áreas das superfícies do quadrado e do retângulo, podemos deduzir as áreas das superfícies de outros polígonos.
Atividade 5
Caso os estudantes apresentem dificuldades, sugira que decomponham 1,70 m em
+ 0,70) m
Área da superfície do paralelogramo
Em muitos exercícios de Pilates podemos reconhecer ângulos formados entre as partes do corpo. Algumas posições até lembram formas geométricas.
Habilidade
O paralelogramo é, por definição, o quadrilátero que tem os lados opostos paralelos Desejamos deduzir a expressão da área da superfície do paralelogramo. Para isso, precisamos demonstrar que △ AHD ≡ △BEC
Do paralelogramo ABCD, temos:
• AB ≡ CD (propriedade dos paralelogramos)
Do retângulo HECD, temos:
• HE ≡ CD (propriedade dos paralelogramos, e o retângulo é um paralelogramo)
Com essas duas congruências, chegamos à seguinte afirmação:
• AB ≡ CD ≡ HE
Assim: AB ≡ HE e AB = HE
Mas AB = AH + HB e HE = HB + BE e, então, AH = BE
Resumindo, temos:
• AH ≡ BE (lado)
• AH ! D ≡ BE ! C (a ! ngulo)
• DH ≡ CE (lado) (a distância entre os lados opostos paralelos é constante)
Logo, pelo caso LAL de congruência de triângulos, △ AHD ≡ △BEC
Portanto, a área da superfície do paralelogramo ABCD é equivalente à área do retângulo HECD, que, por sua vez, tem área igual a b h
A área A p da superfície de um paralelogramo de base de medida b e altura h é dada por AP = b h
Área da superfície do triângulo
Em algumas modalidades de ginástica, alguns exercícios compõem no corpo humano formas que lembram triângulos.
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

Observe que D é um ponto tal que ABCD é um paralelogramo e, sendo assim, sua área é igual a bh. Observe também que o paralelogramo ABCD é composto por dois triângulos: ABC e DCB

Sugestão de atividade
Para que os estudantes compreendam o cálculo de área da superfície dos paralelogramos, faça uma demonstração usando papel sulfite. Forneça dois paralelogramos congruentes e, em um deles, deixe em tracejado sua altura. Solicite que recortem e colem um deles no caderno; o outro, devem recortar no tracejado. Observando a imagem do livro, devem posicionar o triângulo de modo que forme um retângulo e colar no caderno. Agora,
usando uma régua, devem comparar as medidas da base e da altura do paralelogramo com os lados do retângulo. Com essas observações, espera-se que os estudantes percebam que a área de um paralelogramo pode ser calculada pela multiplicação da medida da base pela da altura. Para a área da superfície do triângulo, proponha que os estudantes elaborem modelo similar com o papel sulfite.
Habilidade
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
Atividade 6
Cada quadrado da malha pontilhada com medidas de lado igual a 1 cm corresponde a uma área de 1 cm2. Portanto, para encontrar a área dessa superfície, deve-se contar os quadrados sombreados: 14 quadrados, portanto, 14 cm2

Atividade 7
Para resolver essa atividade é esperado que os estudantes utilizem as ideias de área de uma superfície de maneira intuitiva e por estimativas.
Comparando a área da região sombreada da figura D com a da figura F, pode-se concluir que têm a mesma área, pois são triângulos de mesma base e mesma altura. E ambas equivalem à metade da área do quadrado.
Comparando a área sombreada da figura B com a da figura F ou da figura D, pode-se concluir que a área da figura B é menor que a de ambas as figuras (menos da metade da área de um quadrado).
Comparando a área sombreada da figura A com a da figura F, pode-se concluir que a área da figura A equivale a aproximadamente 3 4 da área do quadrado.
Por fim, tanto a figura E quanto a figura C têm área equivalente a toda a área do quadrado.
Assim, a ordem é: B, D, F, A, C, E.
Desejamos deduzir a expressão da área da superfície do triângulo, conhecida a área do paralelogramo. Para isso, precisamos demonstrar que △ABC ≡ △DCB
Do paralelogramo ABCD, temos:
• AB ≡ DC (por serem pares de lados opostos de um paralelogramo)
• AC ≡ DB (por serem pares de lados opostos de um paralelogramo)
• BC (lado comum)
Logo, pelo caso de congruência de triângulos LLL, △ ABC ≡ △DCB Portanto, a área da superfície de um dos triângulos que compõem o paralelogramo ABCD é a metade da área do paralelogramo ABDC, ou seja, a área de um desses triângulos é b h 2
A área AT da superfície de um triângulo de base com medida b e altura h é dada por AT = b h 2
ATIVIDADES
6. Na figura, os segmentos horizontais e verticais com extremidades em dois pontos consecutivos têm comprimentos de medida 1 cm. Calcule a área da figura sombreada. 14 cm2
8. Determine a área de cada quadrado e cada retângulo. 11 cm2, 9 cm2, 16 cm2, 12,6 cm2
7. Todos os quadrados a seguir são congruentes. Escreva o nome das figuras em ordem crescente de área de cada região pintada.
Atividade 8
a) 4 2,75 = 11 cm2 ;

b) 3 3 = 9 cm2 ;
c) 4 4 = 16 cm2 ;
d) 2,4 5,25 = 12 5 21 4 = 252 20 = 126 10 = 12,6 cm2
Atividade 9
Como 4 = 2 e 81 = 9, os lados dos quadrados serão, respectivamente, 2 m e 9 cm. Chame atenção para as unidades de medida para que não
9. Determine a medida do lado de um quadrado em que a área é:
a) 4 m2 2 m
b) 81 cm2 9 cm
mantenham a unidade de medida de superfície na medida de comprimento.
Atividade 10
Construa os retângulos que os estudantes sugerirem para que possam comparar suas soluções visualmente. Destaque soluções não inteiras como 4,8 m 5 m = 24 m2 ou 5 cm 7,2 cm = 36 cm2


Atividade 11
Comparando os lados dos quadrados, sendo x a área da superfície do quadrado médio, temos:
10. Determine as medidas dos lados de um retângulo (não quadrado) em que a área seja:
a) 24 m2
b) 36 cm2
• Compare sua solução com a dos colegas. Respostas possíveis: 6 m e 4 m; 3 cm e 12 cm.
11. Um terreno é composto de três quadrados que se “tocam” por, pelo menos, um de seus lados. A área do maior é 36 m2 e a do menor é 4 m2. Qual é a área total desse terreno? 56 m2
14. Determine a área da superfície de cada triângulo. 7,5 m2; 150 cm2; 20 dm2

14. a) 5 3 2 = 7 5 m2 ;
12. A área do quadrado maior é igual a 16 cm2 Quanto mede a superfície do quadrado menor, sabendo que seus vértices dividem os lados do quadrado maior ao meio? 8 cm2
13. Determine a área da superfície de cada paralelogramo. 24 cm2; 12 m2; 11,7 dm2
6 4 = 24 cm2 ;
15. Na figura, M é ponto médio de AB A medida de AB é igual a 8 cm. A área da região amarela é 24 cm2
busca de diferentes soluções. Vamos apresentar mais de um modo de resolver esse problema.
1 o modo: a superfície da região amarela, composta por 4 triângulos retângulos congruentes, mede 24 cm2, logo, a área da superfície de cada triângulo é 6 cm2. Sendo M o ponto médio de AB, cada lado do triângulo que forma um ângulo reto mede 8 cm. Seja x a medida do outro lado que compreende o ângulo reto. Assim:
4 x
a) Calcule a área de um dos paralelogramos azuis. 12 cm2
b) Resolva essa situação-problema de pelo menos duas maneiras diferentes. Depois, compare suas maneiras de resolver com as dos colegas.
• Você acha que foi perseverante em buscar mais de um modo de resolver esse problema? Reflita sobre sua atitude ao enfrentar desafios na busca de soluções.
Resposta pessoal. Resposta pessoal.
; c) 8 5 2 = 20 dm2 ; 201 | NÃO ESCREVA NO SEU LIVRO.
36 = 4 + x ⇒ x = 6 – 2 ⇒ ⇒ x = 4 ⇒ x =
16
As partes do quadrado colorido equivalem a metade das partes do quadrado maior. Logo, a área do quadrado colorido equivale a metade da área do quadrado maior. Assim, 16 2 = 8 cm2
2 = 6 ⇒ x = 3 cm Essa é também a altura do paralelogramo de base 4 cm. Portanto a área da superfície do paralelogramo será: 3 4 = 12 cm2

2 o modo: Traçamos uma perpendicular a AB passando por M
AB M
Observamos que há 8 triângulos retângulos congruentes com área igual a 6 cm2 cada um. Dois desses triângulos compõem o paralelogramo. Logo a área do paralelogramo é o dobro da área de um triângulo retângulo: 2 6 = 12 cm2


Atividade 16
Atividade 12
Pode-se decompor a superfície em 4 partes congruentes:
Atividade 15
Acompanhe e oriente os estudantes na elaboração da situação problema, desafiando-os a utilizar medidas lineares não inteiras.
201 |
Habilidade
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
Sugestão de atividade
Para que os estudantes compreendam a fórmula de cálculo da área da superfície do losango, forneça papel sulfite com dois retângulos desenhados e peça que recortem e dobrem pela metade na horizontal e na vertical para marcar a metade. Com a régua, devem traçar os segmentos conforme indicado na figura e colorir o losango:
#Superfícies de losangos e trapézios
Levando em conta a área do triângulo podemos, a partir de agora, determinar a área da superfície de losangos e trapézios
Área da superfície do losango
Observe a figura de um losango e suas diagonais.
Podemos considerar os seguintes fatos:
I. uma das propriedades dos losangos é que as diagonais se cortam ao meio;
II. a definição de losango estabelece que seus quatro lados são congruentes.
Com base nesses dois fatos, concluímos, pelo caso LLL de congruência de triângulos, que os quatro triângulos retângulos são congruentes.
Sendo assim, a área de um desses triângulos retângulos é:
Mostre que a área do retângulo é a multiplicação da medida da base pela da altura. Pela figura, podem observar que a base tem a mesma medida da diagonal maior e a altura, da diagonal menor do losango.
Os estudantes podem colar um retângulo com o losango inscrito no caderno, e o outro podem dividir ao meio, colar metade e sobrepor a área do losango como indicado:
Por fim, efetuando a adição das áreas dos quatro triângulos, obtemos:
A área AL da superfície de um losango de diagonais com medidas D e d é dada por AL = D d 2
Área da superfície do trapézio
Observe um trapézio de bases paralelas de medidas B e b e altura h
O traçado de uma das diagonais do trapézio divide-o em dois triângulos: um de base medindo B e outro de base b, ambos com altura h



202 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.
Em ambas as representações, temos metade da área do retângulo. Como a área do retângulo pode ser calculada por D d , considerando que a área do losango é metade dessa área, concluímos que a área da superfície do losango é calculada por D d 2
Para a área da superfície do trapézio, proponha que os estudantes elaborem modelo similar com o papel sulfite.
Atividade 17
Para a área da superfície dos trapézios, temos:
A trapéz o laran a = (8 + 5) 2 4 = 26 m2
Atrapézio azul = (3 + 6) 2 9 = 40,5 m2
Para a área da superfície dos losangos, temos:
A losango cinza = (6 ⋅ 8) 2 = 24 m2
A osango azul = (16 12) 2 = 96 m2
Portanto, a área da superfície do trapézio é dada por:
ATrap = Bh 2 + bh 2 = Bh + bh 2 = (B + b) h 2
A área ATrap da superfície de um trapézio de bases medindo B e b e altura h é calculada por ATrap = (B + b) h 2

ATIVIDADES
26 m2, 24 m2, 40,5 m2, 96 m2
17. Calcule a área de cada figura.
Postura de yoga e um trapézio.

20. Dois irmãos herdaram um terreno com formato de trapézio e estas medidas:
Habilidade (EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.


com os estudantes e calcule a medida da diagonal maior: D = x + 18 = 6 + 18 = 24 m Proponha que façam o cálculo da área usando as medidas das diagonais para comprovarem se a área é 120 m2
Atividade 20
a) Calcule a área total do terreno. 286 m2
18. É dada a área de cada trapézio.
b) Sabendo que ambos receberão a mesma porção do terreno, quanto de área caberá a cada irmão? 143 m2
c) Elabore uma situação-problema parecida com essa. Dê para um colega resolver.
Trapézio 1: 12,5 m2

Trapézio 2: 24 m2
Calcule o valor de x em cada um deles.
Trapézio 1: x = 1,125 m; trapézio 2: x = 5,6 m
19. É dada a área da superfície de cada losango.
Losango 1: 120 m2
x = 6 m; x = 3 m
Losango 2: 64 m2
Calcule o valor de x em cada um deles.
a) Observando o desenho, temos as medidas do trapézio:
B = 14 m, b = 8 m e h = 26 m
A = (B + b) 2 h = (14 + 8) 2 26 = 11 2
A = (B + b) 2 h = (14 + 8) 2 26 = 11 26 = 286 m2
Resposta pessoal.
21. Um terreno com formato “irregular” tem as seguintes medidas:
b) Basta dividir a área encontrada por 2, pois a cada irmão caberá a mesma porção de terra: 286 ÷ 2 = 143 m2
c) A formulação de problemas auxilia os estudantes a compreenderem a linguagem dos enunciados e a estabelecer a relação com o conteúdo matemático. Explore os diferentes problemas elaborados e peça que resolvam os problemas uns dos outros.
Atividade 21
Calcule a área de sua superfície. 57 m2
Essa superfície pode ser decomposta em três figuras: um quadrado, um triângulo retângulo e um trapézio:
Atividade 18
Substitua os valores mostrados na figura na fórmula da área do trapézio. Por exemplo, no trapézio 1: 12,5 = 5 + 3 2 (x + 2)
Resolva a equação:
12,5 = 4 (x + 2) ⇒ 12,5 = 4x + 8 ⇒ 4x = 4,5
x = 1,125 m
Proponha aos estudantes que substituam o valor de x e encontrem a altura do trapézio. Em seguida, peça que confiram que, para esse x, a área do trapézio é 12,5 m2
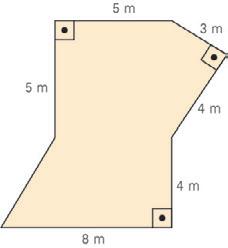
Atividade 19
Substitua os valores mostrados na figura na fórmula da área do losango: A = D d 2 Como, por exemplo, no Losango 1:
120 = (x + 18) 10 2
240 = 10x + 180
10x = 60 x = 6 m
Encontrado o valor de x, retome o problema
área total do terreno será:
Habilidade
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

Atividade 22
a) Basta utilizar a fórmula da área do círculo: A = π r 2
A = π 32
A = π 9
A = 9π m2
b) A figura é um semicírculo, então, calculamos a área do círculo e dividimos por 2. Sabemos que o diâmetro é 8 m, logo, o raio mede 4 m:

A = π 42 = π 16
Asemicírculo = 16π : 2 = 8π m2
c) Temos um semicírculo e um quadrado. O diâmetro do semicírculo é igual à medida do lado do quadrado, 4 m. A área total é a soma das duas áreas.
• Área do semicírculo: 4π m2

• Área do quadrado: 16 m2 Área total: (4π + 16) m2
Atividade 23
Observe que o lado do quadrado é também o diâmetro do círculo.
• Área do quadrado: 102 = 100 cm2
• Área do círculo:
π 52 = 25π cm2
• Área sombreada: (100 – 25π ) cm2
Atividade 24
A área de um círculo de raio 6 cm é:
A = π 62
A = π 36
A = 36π cm2
Observando a imagem, podemos considerar que os três semicírculos correspondem a 1,5 círculo. Assim, 1,5 ⋅ 36π resulta em 54 π cm2



#Superfície do círculo
Para encontrarmos a expressão da área da superfície do círculo, vamos utilizar um método intuitivo. Considere um círculo de raio r dividido em vários setores circulares congruentes (lembrando que o perímetro da circunferência é igual a 2πr).
Cada setor circular tem o formato aproximado de um triângulo com altura r, também aproximada. Ao serem dispostos de certo modo, geram uma figura que se aproxima de um paralelogramo, que tem altura r e base πr (a metade do perímetro da circunferência).
Nota-se que a disposição geométrica dos setores vai se aproximando cada vez mais do formato exato de um paralelogramo na medida em que o número de setores aumenta infinitamente, enquanto suas aberturas assumem medidas cada vez menores. Assim, a base do paralelogramo, composta pela metade dos infinitos setores, se aproxima cada vez mais da medida πr Desse raciocínio intuitivo, resulta que a área da superfície do círculo é igual a
22. Calcule a área
superfície de cada figura.
23. Calcule a área sombreada, sabendo que o lado do quadrado mede 10 cm.
24. Determine a área da região sombreada.
25. Duas circunferências têm o mesmo centro O, o raio da circunferência maior (R) é 6 cm e mede o dobro do raio da circunferência menor (r). Calcule a diferença de área dos dois círculos.

26. Um campo de beisebol está compreendido no interior de um quarto de circunferência. Sabendo que de onde acontece a rebatida (home plate) até a borda do campo há uma distância de 91 metros, calcule sua área.

#A medida do conteúdo: o volume
Há diversas maneiras de buscar o bem-estar físico por meio das práticas corporais, sejam elas individuais ou coletivas. As opções são diversas e é sempre possível encontrar uma atividade que seja do seu agrado. Nadar, pedalar e jogar bola estão entre as práticas preferidas de muitos adolescentes.


Habilidades
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
Atividade 25
Temos:
• Raio da circunferência maior: R = 6 cm
• Raio da circunferência menor: r = 3 cm
Área total = π 62 – π 32 = = 36π – 9π = 27π cm2
Atividade 26
A figura corresponde à área limitada em um quarto de círculo (A). Logo, calculamos a área do círculo (Acírculo) de raio 91 m e dividimos por 4.
Acírculo = π r 2
Acírculo = π 912
Acírculo = π 8 281
A = 8 281 π : 4 = 2 070,25 π m2
Adolescentes em aula de natação. Garoto se preparando para pedalar. Garota praticando embaixadinhas em campo de futebol.
Cada esporte tem seus movimentos, seus itens de segurança, seus aparelhos e equipamentos.

Habilidades

(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
LUPAS E LUNETAS
Comente com os estudantes que o volume de uma figura (um corpo, um objeto etc.) é uma medida do espaço que essa figura ocupa. Intuitivamente, podemos pensar que é a medida do conteúdo de um corpo. Todo sólido geométrico tem volume e ocupa espaço.
As piscinas, por exemplo, são necessárias para a prática da natação. Às vezes, mesmo em uma piscina curta é possível treinar. Você já ouviu falar em nado estático?
Esquema apresentando as condições mínimas para utilizar cinto de natação elástico, necessário para praticar natação estática.
Na natação estática há um cabo c preso a um ponto fixo próximo da piscina. Seu comprimento pode ser regulado para o alcance correto até a borda. A partir do cabo, começa a parte elástica e que se conecta à cintura do nadador, mantendo-o a uma distância segura da borda. Esse equipamento é ideal para treinos em piscinas de curto comprimento, a partir de 4 m. Observe o esquema de uma piscina de pequeno porte.

LUPAS E LUNETAS

Quais são as dimensões dessa piscina? Qual é o volume de água necessário para deixá-la completamente cheia? 4 m; 2 m e 1,5 m; 12 m3 ou 12 000 L.
• Explique para um colega o procedimento de cálculo do volume dessa piscina. Resposta pessoal.

O volume unitário
As medidas de água na piscina, de ar na bola e de concreto no pódio estão todas relacionadas à ideia de volume.
O volume de um corpo pode ser calculado. Mas, antes disso, vamos considerar como ponto de partida, para cálculos de volume, a noção de cubo unitário:
Cubo unitário é o volume de um cubo de 1 unidade de comprimento (u) de aresta e é igual a 1 u3 (lê-se: uma unidade cúbica).

Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
Daqui por diante, utilizaremos essa definição para determinar o cálculo do volume de figuras, de objetos, de espaços, entre outros, com formatos possíveis de serem associados às figuras geométricas com a forma de blocos retangulares.
LUPAS E LUNETAS
Reúna-se com um colega e, juntos, calculem os volumes de cada bloco retangular.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
LUPAS E LUNETAS
Espera-se que o estudante, ao responder a essa sequência de perguntas, compreenda que, no cálculo de volume, as medidas das arestas devem estar na mesma unidade e o volume será essa unidade ao cubo. Assim, se as medidas das arestas estiverem em cm, dm, m, o volume estará em cm3, dm3 e m3, respectivamente.
a) Ambas têm seu volume determinado pelo produto das medidas de suas correspondentes três dimensões: largura, comprimento e altura.
a) O que há em comum no procedimento do cálculo de volume dessas duas figuras? Explique.
b) Quais são as dimensões do menor cubo da figura A? E da figura B?
c) Qual é o volume da figura A considerando o menor cubo em que ela está dividida como unidade de medida? 60 cubinhos (de 1 cm3 cada um).
d) Qual é o volume da figura B considerando o menor cubo em que ela está dividida como unidade de medida?
e) Qual é o volume de cada figura em centímetros cúbicos?
f) Se as medidas das arestas de um desses blocos retangulares fossem x cm, y cm e z cm, números positivos, qual seria seu volume? A que conclusão vocês podem chegar?
Além disso, os estudantes poderão avaliar como os volumes seriam comparados com unidades de medida diferentes e não padrão (cubinhos maiores ou cubinhos menores) e, então, concluir pela necessidade da padronização da unidade de medida.
Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Atividade 27
O volume V do pódio é a soma dos volumes destes três blocos: 20 + 18 + 16
#O volume de blocos retangulares
Podemos generalizar o cálculo do volume de blocos retangulares da seguinte maneira:
Dado um bloco retangular, com medidas de arestas a, b e c (em uma mesma unidade), o seu volume é igual a abc, para quaisquer unidades de medida.
Como o cubo é um caso particular de bloco retangular em que a = b = c, vem que o volume do cubo é igual a a3


ATIVIDADES
27. Leia a situação-problema e resolva-a.
A partir de três blocos retangulares, o senhor João construiu um pódio para a premiação da maratona que será realizada na escola de seu filho. Qual é o volume do sólido resultante da construção?
PROBLEMA para ajudar na escola: O volume de um pódio. Clubes de matemática da OBMEP. Disponível em: http://clubes.obmep.org.br/blog/problema-para-ajudar-na-escola-o-volume-de-um-podio. Acesso em: 31 maio 2022.
28. Determine o volume de cada caixa (em cubinhos unitários). Escreva o número que corresponde a cada uma segundo a ordem crescente dos volumes.
29. a) A quantidade de espaço que ocupa ou pode ser ocupado por qualquer entidade “mensurável”.
VOLUME
A palavra Volume deriva do latim volūmen, e descreve a quantidade de espaço que ocupa ou pode ser ocupado por qualquer entidade ‘mensurável’. Geralmente é medido em metros cúbicos (m3) ou litros (L).
30. Observe as duas figuras. Elas são compostas cada uma por um cubo grande vazado, preenchidas por alguns cubos médios e alguns cubos pequenos. Cada cubo médio tem 20 cm de aresta. Cada cubo pequeno tem 6 cm de aresta.
Habilidade
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Atividade 30
O metro cúbico (m3) é a unidade padrão de volume no Sistema Internacional de Unidades (SI). As unidades derivadas do metro cúbico são: quilômetros cúbicos (km3), hectômetros cúbicos (hm3), decâmetros cúbicos (dam3), decímetros cúbicos (dm3), centímetros cúbicos (cm3), milímetros cúbicos (mm3). Uma das unidades de volume mais utilizada é o litro.
O conceito de volume permite referir-se ao conteúdo de algo. Por isso, refere-se à magnitude (ou grandeza) física que expressa a extensão de um corpo em três dimensões (comprimento, largura e altura). Sendo que 1 m3 corresponde ao espaço ocupado por um cubo de 1 m de aresta. Assim, podemos encontrar o volume multiplicando altura, largura e comprimento desse cubo. CONVERSOR de unidades. Instituto de Pesos e Medidas do Estado de São Paulo (IPEM). Disponível em: www.ipem.sp.gov.br/index.php/servicos/conv-uni. Acesso em: 22 ago. 2022.
a) O que significa a palavra volume?
b) Qual é a unidade padrão de volume no SI? E quais são suas unidades derivadas?
c) Ao medir o volume de um corpo, quais são as três dimensões que devem ser consideradas?
Comprimento, largura e altura.
a) Qual é o volume, em cm3, que falta no cubo grande da figura 1 para que ele seja completamente ocupado por cubos médios?

b) Qual volume, em cm3, falta no cubo grande da figura 2 para que ele seja completamente ocupado por cubos pequenos?
b) O metro cúbico. O quilômetro cúbico, o hectômetro cúbico, o decâmetro cúbico, o decímetro cúbico, o centímetro cúbico e o milímetro cúbico.
Atividade 29
a) Proponha que busquem pela palavra volume em dicionários ou em outros livros de Matemática.
Escreva na lousa as observações dos estudantes. A ideia é que concluam que volume é a quantidade de espaço que ocupa ou pode ser ocupado por qualquer objeto “mensurável”.
b) Pelo Sistema Internacional de Unidades (SI), a unidade-padrão de volume é o metro cúbico. Além do metro cúbico, existem seus múltiplos (decâmetro cúbico, hectômetro cúbico e
A aresta do cubo grande tem medida igual a de 3 arestas do cubo médio ou 10 arestas do cubo pequeno, isto é, de 60 cm.

O volume do cubo grande é:
V1 = 60 ⋅ 60 ⋅ 60 = 216 000 cm3
O volume de um cubo
médio é: V2 = 20 20 20 = 8 000 c
V2 = 20 20 20 = 8 000 cm3
O volume de um cubo
pequeno é: V3 = 6 6 6 = 216 cm
V3 = 6 6 6 = 216 cm3
a) O volume do cubo grande é V1 = 216 000 cm3
Temos 11 cubos médios:
11 8 000 = 88 000 cm3
O volume dos cubos que faltam na figura 1 é:
216 000 – 88 000 = 128 000 cm3
Outra maneira de resolver é calcular a quantidade de cubos médios que faltam. Nesse caso, são:
27 – 11 = 16
16 8 000 = 128 000 cm3
b) Também é possível resolver este item de mais de uma maneira. Veja uma delas. Volume dos cubos que faltam na figura 2: para completar a figura faltam
1 000 – 109 = 891 cubinhos
quilômetro cúbico) e submúltiplos (decímetro cúbico, centímetro cúbico e milímetro cúbico).
É importante relacionar as unidades de medida de volume com as de capacidade, litro, seus múltiplos e submúltiplos (1 m3 corresponde a 1 000 litros).

c) Utilizamos uma unidade cúbica porque o volume é tridimensional, ou seja, sua determinação envolve três dimensões: comprimento, largura e altura.
de volume 216 cm3 cada um.
Logo, 891 216 = 192 456 cm3
Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
TRAVESSIAS
Acompanhe de perto a execução dessa atividade orientando os estudantes na manipulação dos instrumentos necessários de modo que façam uso correto e seguro deles.
A construção e a manipulação desses cubos desenvolvem o senso de medida (de comprimento, de superfície e de volume) e a capacidade de estimar volumes e capacidades.


TRAVESSIA S
Relações entre unidades: cm3, dm3, m3
Não há prática esportiva sem suor. E a quantidade de suor liberada por uma pessoa depende de muitas condições: sua idade, sexo, duração e intensidade do exercício, se está ao ar livre, a umidade relativa do ar etc.


Durante a prática de atividade física, a taxa de transpiração pode chegar a patamares muito elevados e, dependendo das condições, atingir de 1 a 2 dm3 por hora de exercício praticado.
Será muito: 2 dm3 de suor? Vamos tentar compreender. Antes, relembre as relações entre essas unidades de medida.
Junte-se a um ou dois colegas para fazer esta atividade.
Vocês vão construir uma caixinha utilizando papel-cartão, tesoura de pontas arredondadas, régua, lápis e fita adesiva. Recortem 6 quadrados de 10 cm por 10 cm, ou seja, de 1 dm por 1 dm.

Com cinco desses quadrados, procedam conforme mostra o passo a passo (o sexto quadrado servirá de tampa e será móvel).
Quadricule, em 10 cm × 10 cm, a face colorida do papel-cartão.
Junte, com fita adesiva, os quadrados para compor uma caixa.
Sua caixa aberta está pronta!
Homem finalizando, com corpo muito suado, sua prática esportiva de corrida de rua. Mulher com pele suada flexionando músculos.Com a caixinha montada, observem-na e respondam às questões.
a) Qual é o volume dessa caixinha? 1 dm3
b) Imagine que caiba nela todo o suor de uma hora de prática esportiva. O que essa ideia lhe parece: é muito ou pouco? Explique para os colegas. Resposta pessoal.
c) Localize nessa caixa o espaço de 1 cm3. Imagine caixinhas com esse volume. Quantas dessas caixinhas seriam necessárias para preencher o cubo que vocês construíram?
c) 1 000 caixinhas.
d) Tampem sua caixa com o sexto quadrado. Colem, com suavidade, uma ou duas fitas transversalmente às duas bordas opostas da caixa, só para mantê-la fechada momentaneamente. Agora, imaginem uma caixa de 1 m3. Juntando todas as caixas que construíram na sala de aula e empilhando de modo organizado, seria possível preencher um cubo de 1 m3? Quantos cubos desses há na sala toda? Quantos cubos ainda faltam para gerar 1 m3? Respostas pessoais.
e) Você sabia que o volume de 1 decímetro cúbico corresponde a 1 litro? Coloque um saquinho plástico, seguramente sem furos, dentro do seu cubo, sem tampa. Acomode o saco plástico de modo que não fiquem vãos entre a parede de papel-cartão e o saco plástico. Preencha com água até a borda da caixa. Qual é o volume de água que você acabou de medir? 1 dm3 ou 1 L de água.
• Escrevam, em uma folha avulsa, algumas frases sintetizando conclusões e descobertas que fizeram e afixem no mural da sala de aula.
ATIVIDADES
31. A área da superfície da face de um cubo é 25 cm2. Qual é a medida a de sua aresta e a medida V de seu volume?
a = 5 cm e V = 125 cm3

32. São dadas as medidas de uma aresta e das áreas de três faces de um bloco retangular.
Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Atividade 31
Sabemos que a área da face do cubo é 25 cm2. Logo, sua aresta mede 5 cm. Seu volume é: V = 5 5 5 = 125 cm3
Atividade 32
a) Podemos observar as faces desse bloco retangular. A superfície desse bloco retangular é formada por retângulos de áreas 18 m2, 12 m2 e 24 m2 Uma das arestas mede 3 m. O retângulo cujo lado coincide com a aresta que mede 3 m tem superfície 18 m 2 Logo, a medida da outra aresta do bloco é 6 m. Com a aresta encontrada de 6 m, podemos calcular a outra aresta da face do bloco com superfície 24 m2. A medida dessa outra aresta é 4 m.
a) Quais são as medidas das três dimensões desse bloco retangular?
b) Qual é a área da superfície desse bloco retangular?
c) Qual é o seu volume? 72 m3
3 m, 4 m 6 m.
2 (18 + 24 + 12) = 108 m2 211 |
As arestas medem: 3 m, 4 m e 6 m.
b) Basta adicionar a medida das áreas das superfícies das 6 faces: 2 (18 + 24 + 12) = 108 m2
2 (18 + 24 + 12) = 108 m2
c) Para calcular o volume do bloco retangular fazemos: V = 3 4 6 = 72 m3

Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Encontro com outras disciplinas
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
LUPAS E LUNETAS
O acqua spin é realizado de modo semelhante ao spinning tradicional, mas o corpo fica metade dentro da água e metade fora. A bicicleta é mais leve, presa no fundo da piscina e não tem banco, deixando o aluno suspenso apenas com o movimento da água. Devido à pressão da água, o exercício trabalha muito mais o condicionamento cardiovascular e o sistema muscular, com ênfase em glúteos e pernas. A aeróbica aquática ou hidroginástica é um conjunto de exercícios corporais realizados em uma piscina com objetivo da manutenção profilática da saúde. Visa o fortalecimento muscular, o condicionamento físico geral, cardiovascular e respiratório. A hidroginástica é um esporte recomendado para pessoas que sofrem de artrite, fibromialgia, osteoporose etc. Em ambas as modalidades, a vantagem é o
#Capacidade e volume
Há diversas modalidades de ginásticas aquáticas.
Instrutor e alunos em modalidade de aeróbica aquática. Pessoas treinando acqua spin, nome dado ao ciclismo aquático.


LUPAS E LUNETAS Respostas pessoais.
Pesquise sobre as diversas modalidades de ginásticas aquáticas. Escolha duas ou três delas que chamem sua atenção e destaque suas qualidades para a melhoria das condições de vida, saúde e bem-estar. Escreva um parágrafo descrevendo por que você acredita que uma delas lhe faria bem, caso pudesse praticá-la.
• Compartilhe com os colegas suas descobertas.
Relação entre litro e metro cúbico
Para a prática de hidroginástica, com um número pequeno de pessoas, é possível uma piscina com as seguintes dimensões: 6 m × 3 m × 1,40 m Qual é a capacidade dessa piscina, em litros?
Vamos calcular o volume dessa piscina em m3. Depois, convertemos em dm3, o que torna já imediata a correspondência em L.
• Passo 1: volume da piscina: 6 m × 3 m × 1,4 m = 25,2 m3

• Passo 2: 1 m3 = 1 000 dm3 , logo 25,2 1 000 = 25 200 , ou seja, o volume da piscina é de 25 200 dm3
• Passo 3: 1 dm3 = 1 L, logo 25 200 dm3 equivale a 25 200 L. Assim, essa piscina com dimensões de 6 m × 3 m × 1,4 m tem capacidade para 25 200 L de água.
IMAGEM ESQUEMÁTICA, SUJEITA A REPRESENTAÇÃO APROXIMADA DAS PROPORÇÕES ENTRE AS DIMENSÕES LINEARES.Relação entre litro e mililitro
Esse esquema apresenta relações entre algumas unidades de medida de volume e de capacidade comuns no cotidiano.
Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
1 dm3 = 1 L
1 L = 1 000 mL
O mililitro (mL) é um submúltiplo do litro (L), ideal para porções menores do que o litro. É muito usado em produtos das prateleiras dos supermercados.
ATIVIDADES
33. Copie, substituindo a pelo valor correto em cada item.
a) Um metro cúbico corresponde a litros (m3 = L) 1 000; 1; 1 000.
b) Um decímetro cúbico corresponde a litro (dm3 = L) 1; 1; 1.

c) Um centímetro cúbico corresponde a mililitro (cm3 = mL) 1; 1; 1.
d) Um decímetro cúbico corresponde a centímetros cúbicos ( dm3 = cm3)
35. Considere o recipiente contendo exatamente esta capacidade de líquido.
1000; 1; 1000.
e) Um metro cúbico corresponde a decímetros cúbicos ( m3 = dm3). 1000; 1; 1000.
34. Observe a imagem:

(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Atividade 34
A atividade propõe que os cálculos sejam feitos mentalmente:
50 + 100 + 150 + 200 + 250 + 300 = 1 50 + 100 + 150 + 200 + 250 + 300 = 1 050 mL
Discuta quais estratégias de cálculo mental podem ser usadas. Uma delas pode ser a de formar centenas exatas:
(50 + 150) + 250 + (100 + 200 + 300) =
= 200 + 250 + 600 =
= 800 + 250 = 1 050 mL
Outra estratégia pode ser notar que nessa sequência há três somas de mesmo valor:
50 + 100 + 150 + 200 + 250 + 300
Sem lápis e papel, apenas fazendo cálculos “de cabeça”, responda: se os conteúdos de todos esses recipientes fossem despejados em um outro com capacidade máxima de 1 L, o líquido transbordaria ou faltaria? Quanto?

Transbordaria 50 mL.
Se existissem, ao todo, 5 recipientes iguais a esse, com mesmo conteúdo em iguais quantidades, qual seria o volume total?
Responda fazendo um cálculo mental. 900 mL.
Respostas pessoais.
• Depois de fazer o cálculo, converse com os colegas para ouvir como cada um pensou.
• Você julga que fez muito esforço para alcançar a resposta correta? Reflita sobre sua maneira de buscar soluções em diferentes situações. Resposta pessoal.
Então 3 350 mL = 1 050 mL
Como 1 L = 1 000 mL, transbordariam 50 mL.



Atividade 35
A atividade propõe que os cálculos sejam feitos mentalmente:
5 ⋅ 180 = 5 ⋅ (100 + 80) = 500 + 400
5 180 = 5 (100 + 80) = 500 + 400 = 900 mL
Discuta as estratégias de cálculo mental usadas pelos estudantes. Compare os procedimentos e as respostas.
Atividade 33
Construa com os estudantes a tabela de conversões e deixe visível para a resolução dessa atividade.
Submúltiplos
Unidade fundamental
Múltiplos
Milímetro cúbico mm3
Centímetro cúbico cm3
Decímetro cúbico dm3
Metro cúbico m3
Decâmetro cúbico dam3
Hectômetro cúbico hm3
Quilômetro cúbico km3
Habilidades
Capacidade, volume e outras grandezas
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
LUPAS E LUNETAS
⋅
40 = 3 360 ⇒ 3 360 mL = 3,36 L
L
3,6 L = 3 600 mL, temos que
3 600 ÷ 300 = 12 copos.
Ou, considerando que 300 mL = 0,3 L, o cálculo será 3,6 ÷ 0,3 = 12 copos
b) Se cada pessoa bebeu 2 copos de suco, temos que 6 pessoas beberam suco, pois 12 ÷ 2 = 6 pessoas. Essas pessoas são o filho e seus 5 amigos.
Atividade 37
Supondo que eles bebem a mesma quantidade de água todos os dias, Cecília consome 2,4 L por dia e 876 L (365 ⋅ 2,4 = 876) de água por ano. O consumo nesse período será de aproximadamente 44 galões (876 ÷ 20 ≅ 44) No caso de Gustavo, o consumo diário é de 3,36 L e 1 226,4 L por ano (365 3,36 = 1 226,4) A quantidade de galões de água consumidos será aproximadamente 61 galões (1226,4 ÷ 20 ≅ 61)
Atividade 38
O volume do corpo de Aristeu corresponde à quantidade de água que derramou, que pode ser calculada pelo volume que diminuiu na caixa. Para que as unidades de medida sejam
214 | MANUAL DO PROFESSOR
A quantidade de água que cada pessoa deve ingerir pode variar conforme a massa corporal.
= CAST OF THOUSANDS/SHUTTERSTOCK AIRCAM.PRO/SHUTTERSTOCK
Jovens praticantes de atividade física se hidratando com água mineral.
Segundo o Colégio Americano de Medicina do Esporte, os praticantes de atividade física devem ingerir, em média, 40 mL/kg de água nas 24 horas antes da realização do exercício. Cecília e Gustavo são praticantes de atividade física. Ela pesa 60 kg e ele, 84 kg. Quantos litros de água ela precisa consumir nas 24 horas que antecedem o treino?
A cada 1 kg de massa corporal correspondem 40 mL de água. Assim, o volume de água necessário para ela é 60 40 = 2 400, ou seja:
2 400 mL = 2,4 L
LUPAS E LUNETAS
Junte-se a um colega e respondam: quantos litros de água Gustavo deve consumir 24 horas antes do treino?


3,36 L
ATIVIDADES
36. O senhor José fez sucos para os amigos do filho que vieram estudar juntos. Há na jarra 3,6 L e cada copo tem capacidade de 300 mL.
a) Quantos copos cheios ele conseguiu servir para o filho e os amigos?
b) Sabendo que cada um deles bebeu dois copos cheios e que o conteúdo da jarra acabou, quantos amigos vieram estudar junto com seu filho?
70 L corresponde ao volume do corpo de Aristeu. 16 L.
12 : 2 = 6, porém 1 é o filho, logo, vieram 5 amigos.
37. Retorne ao problema de Cecília e Gustavo. Supondo que os valores encontrados sejam os que eles bebem de água todos os dias, em um ano quantos galões de 20 L eles terão bebido?
Cecília: 44 galões. Gustavo: 61 galões.
38. Aristeu fez o seguinte experimento: entrou em uma caixa cúbica com 1 m de aresta, completamente cheia de água. Ele se imergiu totalmente na água, sendo que parte dela
derramou. Quando ele saiu da caixa, percebeu que o nível de água havia diminuído 7 cm. Qual é o volume do corpo de Aristeu?
39. Um aquário em formato de paralelepípedo tem as seguintes medidas: 40 cm × 20 cm × 25 cm O volume de água dentro dele corresponde a 4 5 de sua capacidade total. Calcule quantos litros de água há nele
40. Solange precisa tomar 5 mL a cada 8 horas de um suplemento alimentar líquido que vem com um copinho dosador. Se o frasco possui 240 mL, quantos dias vai durar um frasco?
41. Elabore um problema, envolvendo volume, em que um recipiente tenha o formato de paralelepípedo. Compartilhe seu problema com os colegas. Resposta pessoal.
214 | TRAJETÓRIA 4 NÃO ESCREVA
iguais, temos que 1 m = 100 cm Assim, o volume que diminuiu foi 100 100 7 = 70 000 cm3 Como 1 cm3 = 1 mL são 70 000 mL, o mesmo que 70 L, outro modo é considerar 7 cm = 0,07 m
37. Cecília: em um ano serão 365 2,4 = 876 L que equivalem a
Assim, serão 1 1 0,07 = 0,07 m3 Como 1 m3 = 1 000 L, temos 0,07 ⋅ 1 000 = 70 L
cm ⋅
cm ⋅
1 226,4 L que equivalem a
A quantidade de doses de 5 mL no frasco de 240 mL é 48 (240 ÷ 5 = 48 doses) Como serão 3 doses por dia (24 h ÷ 8 h), o frasco durará 16 dias (48 ÷ 3 = 16 dias)
42. Considere a imagem e os dados que constam nela. Elabore um problema e dê para um colega resolver. Receba-o de volta, corrija a resolução dele e exponha o problema corrigido no mural da sala. Respostas pessoais.
43. Uma piscina tem 10 m de largura, 20 m de comprimento e 2 m de altura. Quantos litros de água serão necessários para encher completamente essa piscina?
Habilidades
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
LEVO NA BAGAGEM
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado sobre:
▶ Matemática


• Determina, utilizando expressões de cálculo, áreas das superfícies de figuras geométricas (quadriláteros, triângulos e círculos)?

Resolve e elabora problemas que envolvem medidas de superfícies em situações diversas?
Reconhece unidades de medida de volume e de capacidade e suas relações?
• Sabe resolver e elaborar problemas que envolvam cálculo de volume e de capacidade de recipientes com formato de bloco retangular?
▶ Outras disciplinas
Educação Física
Identifica as qualidades tanto das ginásticas de conscientização corporal como das de condicionamento físico para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
Atividade 42
Verifique se nos problemas elaborados pelos estudantes eles usaram corretamente os dados presentes nas imagens da garrafa (capacidade de 1 L) e da caixa em formato cúbico com aresta de medida 15 cm.
Atividade 43
Sabemos que a piscina tem estas dimensões:
• Largura: 10 m
• Comprimento: 20 m
• Profundidade: 2 m


Para calcular o volume, basta multiplicar as medidas:
V = 10 20 2 = 400 m3
Como cada 1 m 3 contém 1 000 L de água, temos: 400 1 000 = 400 000 L
LEVO NA BAGAGEM
MATEMÁTICA OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
Atividade 41
Leia um problema que seja inspiração para os estudantes:
Uma piscina retangular tem estas dimensões: de largura, 10 m de comprimento e 2 m de profundidade. Qual é a quantidade de água necessária para encher essa piscina?
Resposta: (V = 4 ⋅ 10 ⋅ 2 = 80 m3 )
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
Garrafa com água. Caixa de plástico em formato cúbico.BARCOS E PORTOS
Organize
Observe os registros dos estudantes para avaliar como compreenderam o conteúdo desenvolvido neste passeio. Conversando sobre os pontos fortes e fracos, você pode aplicar atividades de remediação.
Elabore

Leia alguns problemas que envolvem superfície, volume ou capacidade que foram resolvidos nos estudos deste conteúdo para os estudantes usarem como inspiração.
BARCOS E PORTOS
▶ Organize
Respostas pessoais.
Recupere seus registros feitos na seção Levo na bagagem Liste os conteúdos deste passeio que você classificou como insuficiente, parcialmente suficiente e satisfatório. Para cada conteúdo envolvendo uma dessas três categorias, reescreva um problema que você estudou neste passeio e, junto com um colega, procure explicar o que compreende de cada passo em sua resolução. Permita que seu colega faça contribuições, apontando detalhes que ele percebeu ou em que teve uma ideia muito diferente da sua para resolver. Assim, procure repassar todos os conteúdos que não foram classificados como plenamente satisfatórios
▶ Elabore

Observe as imagens:



Piscina com superfície retangular e piscina com superfície circular.


Escolha uma delas, imagine e crie dados para que possa gerar dois problemas: um envolvendo a ideia de área da superfície e outro, a ideia de volume ou capacidade. Troque seus problemas com um colega: um edita e resolve os problemas do outro. Ao final, exponham no mural da sala de aula.

A pergunta inicial deste passeio é: O que quer dizer bem-estar físico?
a) Leia o texto. Enquanto você lê, esteja atento se o conteúdo pode ajudá-lo a responder à pergunta deste passeio.
Atividade física aumenta disposição e autoestima
A prática de atividade física regularmente tem grande influência positiva na disposição de cada pessoa e pode ajudar a elevar a autoestima. O professor do Programa de Pós Graduação em Educação Física da Universidade de Brasília (UnB), Amilton Vieira, explica como a atividade física contribui para o bem-estar: “Do ponto de vista emocional, quem está ativo diminui a ansiedade e o estresse e aumenta a autoestima e a disposição para fazer tudo no dia a dia. A definição de boa saúde, segundo a Organização Mundial de Saúde (OMS), não fala apenas dos aspectos físicos, mas também do bem-estar mental e social.”
[...]
O exercício físico faz muito mais do que colocar o corpo em forma. “Quando nos exercitamos, nosso corpo responde liberando uma série de hormônios.

Isso influencia de forma positiva em todos os nossos órgãos. Uma pessoa que pratica exercícios físicos regularmente tem mais disposição porque tem maior aptidão cardiorrespiratória e muscular. É alguém que prepara melhor o corpo para qualquer outra atividade”, explica.
BRASIL. Ministério da Saúde. Atividade física aumenta disposição e autoestima. Portal Eu quero me exercitar, 8 dez. 2017. Disponível em: https://saudebrasil.saude.gov.br/eu-quero-me-exercitar-mais/atividade-fisica-aumenta-a-
Encontro com outras disciplinas
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
Proponha
Organize-se em um grupo com 5 integrantes. Juntos, reflitam sobre as questões:
a) A prática de atividade física traz benefícios não apenas para o físico. Sobre quais outros aspectos da experiência humana a atividade física pode proporcionar bem-estar?
b) Você se considera ansioso, estressado, disperso ou com problemas de autoestima? Em que medida acredita que a atividade física pode amenizar ou reverter essas características nos adolescentes?
c) Se for necessário cumprir uma rotina envolvendo a prática de atividade física, você se julga perseverante e com capacidade para superar os obstáculos que possam impedir o sucesso das suas tarefas? Troque ideias com os colegas.
d) Que propostas de melhorias na rotina dos adolescentes escolares vocês teriam para fortalecer tanto o aspecto físico quanto o mental e social do seu grupo?
Combine com o professor de Educação Física para realizar uma aula no pátio da escola. Programe a vinda de um mestre ou grupo de capoeira para dialogar com a turma. Antes, verifique se na comunidade escolar algum dos estudantes, familiares ou amigos praticam a capoeira. Parte da habilidade EF89EF11 poderá ser trabalhada, pois essa manifestação é uma excelente atividade física com possibilidades de desenvolvimento motor, afetivo e cognitivo. Apresente algumas fotografias ou vídeos de pessoas praticando capoeira e pergunte aos estudantes o que as imagens representam para eles. A atividade pode ser realizada antes do dia em que o convidado fará sua apresentação. Combine com o convidado para conversar com a turma sobre a capoeira como uma manifestação cultural e que faça uma contextualização dessa manifestação em nosso país. É importante que o convidado fale sobre alguns fundamentos da luta. Após a apresentação do mestre de capoeira, proponha aos estudantes que sistematizem a atividade por meio de fotos ou vídeos com depoimentos dos estudantes sobre a atividade realizada.
Habilidade

(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
CHECK-IN
Os estudantes estão analisando gráficos em diversas situações do cotidiano, como na leitura de notícias, jornal impresso ou falado, textos de livros didáticos de outras disciplinas. Com essas questões, avalie o conhecimento prévio do estudante. Explique quais gráficos são adequados a cada tipo de informação – por exemplo, os gráficos de setores expressam dados que representam “partes” de um total.

COMO MANTER O BEM-ESTAR MENTAL?
Praticar atividades físicas, desfrutar de um tempo com amigos, ter uma boa noite de sono ou dedicar-se a um momento de leitura são maneiras de cuidar do bem-estar mental.
CHECK-IN
Os gráficos mostram o resultado de uma pesquisa sobre momentos preferidos de bem-estar.

Respostas pessoais.
Preferência de momentos de bem-estar
Fonte: dados fictícios.


a) Quais são os dois tipos de gráficos apresentados? Gráfico de setores e gráfico de colunas.
b) Qual foi o maior índice de preferência? E o menor? 52% e 7%.

BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
• Reconhecer a organização de variáveis contínuas cujos dados agrupados em classes favoreçam a análise de informações e a tomada de decisões.
• Determinar média, moda e mediana.
• Compreender os significados de média, moda e mediana relacionando-os com a dispersão de dados, indicada pela amplitude.
• Transformar conteúdo verbal em não verbal (tabelas, esquemas, gráficos, infográficos), do discursivo para o esquemático e vice-versa, na (re)construção dos sentidos dos textos de divulgação científica como forma de ampliar as possibilidades de compreensão desses textos.
Encontro com outras disciplinas
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático –infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
ATMOSFERA
Atividades 1, 2 e 3
Converse com os estudantes sobre o que eles consideram situações de ansiedade, como o nervosismo diante de uma prova ou de uma lista de atividades. Algumas atitudes podem ser tomadas quando se identificam casos de ansiedade em sala de aula, como o uso de mensagens positivas e motivadoras; estabelecer uma atmosfera agradável; convidar ao quadro apenas os estudantes que manifestarem o desejo; procurar rever o tempo limite em avaliações; entre outras.
Atividade 1
De acordo com o texto, a ansiedade pode ser controlada identificando gatilhos, deixando os materiais organizados e sabendo o que deve ser realizado, controlando a respiração e praticando atividade física.
Atividade 2
A meditação foi efetiva apenas para a garota; o rapaz não conseguiu ficar mais tranquilo.
220 | MANUAL DO PROFESSOR
ATMOSFERA
Dicas para controlar a ansiedade Leia a tirinha e o texto a seguir.
Dicas para controlar a ansiedade
[...]
A ansiedade, como sentimento, pode ser controlada se incorporamos alguns hábitos na nossa rotina, identificando alguns gatilhos que a desencadeiam e lidando com eles de forma a mitigar os danos do estado ansioso prolongado.
[...] A organização é a maior inimiga da ansiedade. Quando deixamos tudo organizado, sabendo exatamente o que temos de executar e onde procurar, tudo fica mais tranquilo.
[...] A respiração é um dos pontos mais importantes quando falamos de ansiedade. O controle da respiração tem a capacidade de induzir ou acabar com uma crise de ansiedade, de tão poderosa que é.
Portanto, ao sentir que está em um ritmo respiratório muito acelerado, procure reduzir a intensidade da respiração, puxando-a para o abdômen e tirando aquela pressão de ar do peito.
[...] Encontre a sua atividade física preferida e pratique-a para aumentar a saúde do seu corpo e o seu bem-estar. Os exercícios ajudam no controle da ansiedade, pois auxiliam na liberação da tensão acumulada, proporcionando mais relaxamento e ritmos cardíacos mais brandos na hora de repouso.
[...] A meditação ajuda muito no controle da ansiedade. Antes que você ache que é impossível para você, tente, pois muitas pessoas têm uma ideia equivocada do que é meditação. [...]

17 DICAS de como controlar a ansiedade. Instituto de Psiquiatria Paulista, 20 fev. 2021. Disponível em: https:// psiquiatriapaulista.com.br/17-dicas-de-como-controlar-a-ansiedade. Acesso em: 17 ago. 2022.
ATIVIDADES
Respostas pessoais. MARCELLO S./ M10
1. Como é possível controlar a ansiedade?
2. Na tirinha, a meditação foi efetiva? Seguir dicas ou cumprir recomendações automáticas são suficientes para alcançar o bem-estar? Como você compreende a busca pelo bem-estar mental?
CONVÍVIO E BEM-ESTAR SOCIAL
Pergunte aos estudantes se eles já ouviram ou conhecem alguma música clássica. Proponha uma pesquisa sobre grandes compositores, como Antonio Vivaldi, Johann Sebastian Bach, Wolfgang Amadeus Mozart, Ludwig van Beethoven e Frédéric Chopin. Converse sobre em que esse estilo musical difere de outros. O vídeo “O Que Você Precisa Saber Antes de Ouvir Música Clássica” (disponível em: https:// www.youtube.com/watch?v=TTsHI73XK3o; acesso em: 26 ago. 2022) pode ser exibido aos estudantes
e discutido em uma roda de conversa. A música clássica no ambiente escolar pode colaborar significativamente para induzir o relaxamento e a redução da ansiedade.
Só no fim você se sentirá menos ansioso Sim. Contei até dois pra chegar logo no fim Já fez?! ... expire pela boca contando até quatro e pause contando até quatro. Repita por cinco vezes. Inspire lentamente pelo nariz contando até quatro, pause contando até quatro Tirinha elaborada pelos autores.#Tipos e adequação de gráficos


Para conhecer melhor os hábitos dos alunos do 8o ano, é feita uma pesquisa anual sobre quais são as atividades de lazer preferidas deles. Com as respostas obtidas no ano 2023, foi construída uma tabela apresentando a distribuição de frequências:
Atividades de lazer preferidas
Fonte: dados fictícios. Adiante vamos estudar com mais detalhes o que são a frequência absoluta e a frequência relativa
A partir desses dados, podemos construir alguns gráficos; vamos analisar qual é o gráfico mais adequado para cada tipo de situação.
Gráfico de setores e gráfico de colunas (ou de barras)
Quando a variável for qualitativa (por exemplo, valores como “sim/não”, “gosto/não gosto) ou quantitativa discreta (assumem valores em um conjunto finito ou enumerável), podemos representar os dados de diferentes formas, como: o gráfico de setores ou o gráfico de colunas/ barras
Para decidir entre os dois, é necessário levar em conta o contexto, seus significados e a intenção daquilo que se deseja comunicar:
• quando a intenção é relacionar a parte com o todo, em geral, a melhor opção é o gráfico de setores;
• quando a intenção é comparar as partes entre si, a análise é favorecida, quase sempre, pelo gráfico de colunas/barras.
Habilidade (EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
Apresente o gráfico de rosca: esse tipo de gráfico têm a mesma função do gráfico de setores, comparar partes com o todo. Acidentes
Os gráficos de barras e de colunas são usados para fazer comparativos. Este gráfico de barras duplas compara dados de anos diferentes:
Habilidade
(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
Encontro com outras disciplinas
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático –infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
LUPAS E LUNETAS
a) Observando o gráfico com dados fictícios, percebemos que, enquanto o uso das redes sociais aumenta, a leitura e a prática de atividades físicas diminuem. Essas atividades podem estar relacionadas: algumas pessoas passaram a dedicar mais horas ao uso das redes sociais e, consequentemente, vêm diminuindo o tempo da leitura ou da prática de atividade física. Ou essas atividades podem não se relacionar: a leitura que acontecia em material impresso começou a acontecer por meio digital e as práticas de atividades físicas terem diminuído por aumentar o número de pessoas que não gostam da prática de atividades físicas. Encorage os alunos a pesquisar dados reais sobre os tópicos.
Gráfico de linhas
Observe o gráfico de linhas que representa a alteração da frequência absoluta de alguns valores obtidos na pesquisa entre os anos 2014 e 2024.
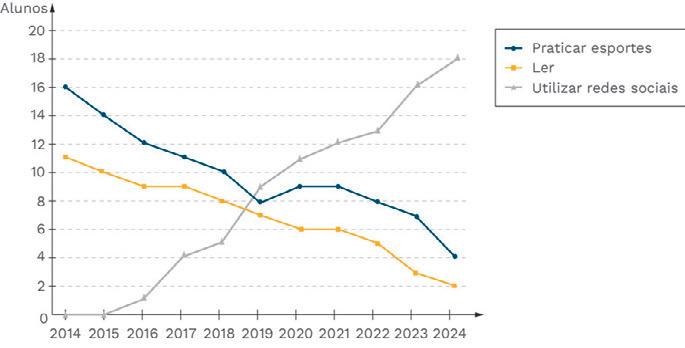
Preferências entre 2014 e 2024
Nesses gráficos, as linhas ligam os pontos que representam as frequências dos valores de uma variável, a fim de facilitar a visualização das alterações ao longo do período estudado. Essas alterações podem ser crescimentos, decrescimentos ou até mesmo não ocorrerem alterações, mantendo-se os valores estáveis.
Observe que, no eixo horizontal, representam-se os anos e no eixo vertical, o número de alunos. Seguindo as linhas, podemos observar que, ao longo dos anos, houve uma queda no número de alunos que preferem ler ou praticar esportes e um aumento no de alunos que preferem utilizar as redes sociais nos momentos de lazer.
LUPAS E LUNETAS
a) Considere os dados apresentados no gráfico de linhas e discorra sobre os possíveis motivos que geraram o crescimento do uso das redes sociais e o decrescimento da prática de atividade física e leitura entre esses jovens pesquisados. Apresente sua opinião aos colegas.
b) Para aprofundar sua opinião, realize duas pesquisas: uma sobre os benefícios que a leitura e a atividade física trazem para o bem-estar mental e outra sobre os malefícios que o uso excessivo das redes sociais pode trazer para a mente.
c) Escreva um texto resumindo as principais descobertas feitas por você nessas pesquisas. Depois, use os dados da sua pesquisa para fundamentar criticamente a situação apresentada nesses gráficos.
b) Os benefícios da prática de atividades físicas podem ser: fortalecimento do sistema imunológico; diminuição da pressão arterial e melhora da circulação sanguínea; controle da glicemia e complicações da diabetes; diminuição da perda óssea; emagrecimento e controle do peso; melhora do sono e do humor; promoção do bem-estar físico e mental. Os benefícios da leitura podem ser: redução do estresse; melhoria do conhecimento geral; expansão do vocabulário; melhoria da escrita; melhoria da memória, foco e concentração; desenvolvimento do
pensamento analítico; estímulo à criatividade. Por outro lado, o uso exagerado das redes sociais pode prejudicar a autoidentidade, aumentar a dificuldade em criar e manter relacionamentos, provocar desestímulos, sensações de exclusão, desânimo, ansiedade etc.
c) A interpretação do gráfico é acompanhada do texto que aponta as principais informações contidas no próprio gráfico e inclui outras informações que podem estar relacionadas com elas.
Fonte: dados fictícios. Respostas pessoais. 222 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.4. Taís fez uma pesquisa sobre a preferência de sobremesas dos seus colegas de turma. Observe a tabela de frequências que ela obteve.
Habilidade
(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
a) Qual é o tipo de variável dessa pesquisa?
b) Quantos valores essa variável assume? Quais são eles?
c) Construa o gráfico que você julgar mais adequado para essa situação. Justifique sua escolha
5 valores: sorvete, brigadeiro, gelatina, pudim e salada de frutas. Resposta pessoal.
5. Israel está organizando uma confraternização para rever seus amigos. Ao perguntar quem iria ao evento, ele obteve 8 respostas “sim”, 4 respostas “talvez” e 3 respostas “não”. Respostas pessoais.
a) Construa o melhor gráfico para Israel visualizar essa informação.
b) Considerando o total de pessoas convidadas e as respostas obtidas, Israel deveria optar por adiar o evento?
6. Tito e Timóteo são irmãos e registraram as quantidades de viagens que fizeram juntos por ano. Nossas viagens

Atividade 5
a) Algumas possibilidades de gráficos são:
a) Construa o gráfico mais adequado para essa situação. Justifique sua escolha.
Resposta pessoal.
b) Em quais anos consecutivos a quantidade de viagens aumentou?
c) Dê uma possível explicação para a não ocorrência de viagens nos anos de 2020 e 2021.
Pandemia de Covid-19.
b) De 2017 para 2018; de 2021 para 2022; de 2022 para 2023; de 2023 para 2024.
Atividade 4
a) Para que os estudantes relembrem os tipos de variáveis, apresente alguns exemplos, como:
• variável qualitativa nominal: profissão, gênero ou religião;
• variável qualitativa ordinal: classe social, nível de escolaridade;
• variável quantitativa discreta: quantidade de filhos ou acessos à plataforma;
• variável quantitativa contínua: altura, massa.
b) A variável é a sobremesa e temos 5 valores: sorvete, brigadeiro, gelatina, pudim e salada de frutas.
c) Os estudantes podem apresentar os gráficos:
b) Há diferentes modos de interpretar essas informações. Uma possibilidade é considerar que mais da metade das pessoas confirmaram presença; considerando que as pessoas que responderam talvez podem também decidir por ir, deve manter a data. Mas, por desejar, a presença de todas as pessoas talvez prefira adiar.
Veja a resolução comentada da atividade 6 na página seguinte.
Habilidade
(EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
Atividade 6
O gráfico de linhas indica a variação do número de viagens (crescimento, decrescimento ou estabilidade) conforme o tempo se passou:

NUVENS
A organização das informações em tabela de dados brutos
Joel fez uma pesquisa com seus colegas de serviço. Ele obteve respostas sobre nome, altura (em m), massa (em kg), idade (em anos completos), alimentação (ruim, regular ou boa) e prática de atividade física (não pratica, raramente, regularmente). Ele construiu a tabela de dados brutos em um editor de planilhas eletrônicas.
LUPAS E LUNETAS
a) Classifique as variáveis da pesquisa em: qualitativa nominal ou ordinal; e quantitativa discreta ou contínua.
b) Reproduza esses dados em uma planilha eletrônica e pense em quais variáveis podem ser relacionadas entre si
a) Qualitativa nominal: nome; qualitativa ordinal: alimentação, atividade física; quantitativa discreta: idade (em anos completos); quantitativa contínua: altura, massa. Respostas pessoais.
• Ao longo das demais atividades deste passeio retome essa planilha para manipular os dados e realizar análises.
LUPAS E LUNETAS
a) Caso considere adequado, apresente este esquema sobre os tipos de variáveis e peça aos estudantes que acrescentem exemplos de cada tipo de variável.
#Tabela de frequências a partir dos dados brutos
Veja a lista de dados retirada da tabela de dados brutos para a variável idade, organizados em ordem crescente:
20 – 20 – 20 – 21 – 21 – 21 – 21 – 21 – 22 – 22 – 22 – 23 – 23 – 24 – 24 – 24 – 24 – 25 – 25 – 25
Essa lista é chamada de rol
Para aprofundar o estudo dessa variável, vamos construir a tabela de frequências Tabela
Habilidade
(EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
LUPAS E LUNETAS
a) A variável “nome” é qualitativa nominal e por isso não é possível ordenar seus valores. É possível fazer a contagem para registrar a frequência de cada nome.
b)
Fonte: dados elaborados para a pesquisa de Joel.
A frequência absoluta (FA) de um valor é a quantidade de vezes que esse valor ocorreu para determinada variável.
No caso apresentado, os valores que ocorreram para a variável idade foram 20, 21, 22, 23, 24 e 25.
A frequência relativa (FR) de um valor é a razão entre a frequência absoluta e a frequência total.
Observação: a frequência relativa pode ser expressa em porcentagem, fração ou decimal e a soma das frequências relativas é 100% = 1,0
Por exemplo:
• A frequência relativa da idade 22 é 3 em 20, ou seja, 3 20 = 15 100 = 15%
• A frequência relativa da idade 24 é 4 em 20, ou seja, 4 20 = 20 100 = 20%
LUPAS E LUNETAS
Respostas pessoais.
a) É viável organizar o rol ou a tabela de frequências para a variável nome?
Alimentação FA FR
(%)
Atividade física FA F
R(%)
225 |
Habilidade (EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
LUPAS E LUNETAS
#Dados agrupados em classes
Analisando as variáveis altura e massa, percebemos que há muitos valores diferentes. Para variáveis quantitativas contínuas, agrupamos os valores em intervalos de classes
Vamos construir a tabela de frequências com dados agrupados em classes da variável massa Começamos representando o rol dessa variável.
59,9 – 60,1 – 60,1 – 60,8 – 62,6 – 63,4 – 63,4 – 64,3 – 67,1 – 68,2 – 71,2 – 72,20 – 72,3 – 73,1 –
75,6 – 77,5 – 78,5 – 80,0 – 88,9 – 95,9
Para saber em quantas classes vamos dividir nossos dados, calculamos a amplitude, fazendo a diferença entre o maior valor e o menor valor. No caso da variável massa, o maior valor é 95,9 kg e o menor é 59,9 kg, assim:
A = 95,9 – 59,9 = 36 kg
Para esse caso, os dados serão organizados em 10 classes, cada classe correspondendo a um intervalo de 4 kg.
Fonte: dados elaborados para a pesquisa de Joel.
Fonte: dados elaborados para a pesquisa de Joel.
b) e c)
Auxilie os estudantes na construção dos gráficos em planilhas eletrônicas e elabore algumas perguntas para auxiliá-los com o relatório:
• O estudante de menor altura é o de menor massa?
• E o de maior altura é o de maior massa?
• O IMC deles é considerado normal?
• Os estudantes com o IMC normal praticam esportes?
• Os estudantes com o IMC normal têm uma alimentação saudável?
• Os que tem sobrepeso ou obesidade praticam esporte ou tem uma boa alimentação?
• O estudante menor é o mais jovem?
• E o mais alto é o mais velho?
LUPAS E LUNETAS
a) Construa a tabela de frequências com dados agrupados por classes da variável altura Tabela de
b) Agora, com todas as tabelas de frequências construídas, use um editor de planilhas para construir os gráficos relativos a cada variável. Se for um usuário mais experiente, pode relacionar duas variáveis para ter dados mais significativos. Respostas pessoais.
c) Produza um relatório com análise crítica, interpretando os gráficos produzidos. Respostas pessoais.
ATIVIDADES
7. Para estudar o desempenho bimestral de alguns alunos, foi realizada uma pesquisa coletando dados sobre a rotina e a nota bimestral. As respostas foram registradas em uma tabela de dados brutos.
a) Quais são os tipos de cada variável presente na tabela?
b) Construa as tabelas de frequências para cada variável. Para “nota”, construa a tabela de frequências com dados agrupados em 10 classes, cada classe correspondendo a um intervalo de 1,0.
c) A partir das tabelas de frequência, selecione e construa os gráficos adequados para cada situação.
d) Escreva um relatório analisando os gráficos. Destaque alguns dados – por exemplo, notas muito baixas ou poucas horas de estudo – e avalie essa situação comparando com o todo.
a) Nome: qualitativa nominal; horas de estudo, horas livres e horas de sono: quantitativa discreta; tarefas de casa: qualitativa ordinal; nota: quantitativa contínua. Respostas pessoais.
Habilidade (EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
Atividade 7
As variáveis são: nome , horas de estudo, horas livres, tarefas de casa, horas de sono e nota. Podemos classificá-las como:

• Nome – variável qualitativa nominal;
• Tarefas de casa – variável qualitativa ordinal;
• Horas de estudo, livres ou de sono – variável quantitativa discreta;
• Nota – variável quantitativa contínua.
Se possível, realize os demais itens em uma sala de informática.
Habilidade
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
LUPAS E LUNETAS
Quando o conjunto de dados tem uma quantidade par de elementos e os dois elementos centrais são diferentes, a mediana é calculada pela média aritmética dos valores. Como os valores são diferentes, a média é um valor entre os dois elementos e não consta do rol.
Por exemplo: As notas de um grupo de seis estudantes são: 4 – 4 – 5 – 7 – 7 – 9
A mediana é a média aritmética dos dois valores centrais.
Md = 5 + 7 2 = 12 2 = 6
A mediana é 6 e esse valor não está no rol.
#Mediana, moda e média
Uma empresa está avaliando a quantidade de horas trabalhadas de seus funcionários e percebeu que há uma grande quantidade deles fazendo horas extras, pela alta demanda de serviços. Veja o rol que essa empresa coletou a respeito das horas trabalhadas semanalmente pelos seus funcionários.
Desejando preservar o bem-estar mental de seus funcionários, essa empresa vai realizar um estudo estatístico para tomar a melhor decisão de como reorganizar as horas trabalhadas. Para a análise de um conjunto de dados, muitas vezes é necessário sintetizar as informações por meio de medidas-resumo. Existe mais de uma modalidade de medidas-resumo. Neste passeio, vamos estudar as medidas de posição (ou medidas de tendência central).
Mediana
Quando procuramos o valor que divide um conjunto de dados em dois subgrupos de mesmo tamanho, estamos querendo determinar a mediana
Veja a mediana das horas trabalhadas semanalmente.
O total de respostas obtidas foi 41. Assim, a mediana (Md) é igual ao valor 48 (horas) destacado, que está na posição central e divide o conjunto de respostas em dois subgrupos iguais com 20 elementos cada.
Suponhamos que a quantidade de respostas fosse par, eliminando o primeiro elemento do rol.
Quando a quantidade de respostas for par, a mediana será a média aritmética dos dois valores centrais:
LUPAS E LUNETAS Respostas pessoais.
Nem sempre a mediana assume valores que aparecem no rol apresentado.
Dê exemplos que verifiquem essa afirmação.
Moda
A moda (Mo) é o valor com maior frequência. No rol de horas trabalhadas fica fácil ver:
As horas trabalhadas semanalmente têm moda igual a 48 h.
LUPAS E LUNETAS Respostas pessoais.
Pode ocorrer de um conjunto de dados ter dois valores com maior frequência. Quando isso acontece, chamamos esse conjunto de bimodal
Também pode acontecer de nenhum valor se repetir; assim, esse conjunto de valores é chamado de amodal
Dê exemplos de conjuntos de dados considerando essas afirmações.
Média aritmética
Para calcular a média aritmética x ( ), vamos utilizar a tabela de frequências da variável estudada.
Habilidade (EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
LUPAS E LUNETAS
Há muitas possibilidades de criação dos estudantes. Veja alguns exemplos: Observe este conjunto de dados com o número do sapato de um grupo de pessoas:
33 – 35 – 35 – 36 – 36 –36 – 36 – 37 – 37 – 37 –37 – 38 – 40
Ele é bimodal, pois as maiores frequências (iguais a 4) são dos números 36 e 37.
Observe o conjunto de dados de uma maternidade com o tempo de vida de cada bebê nascido naquele dia:
1h – 2h – 2h15 – 3h – 5h 5h30 – 10h
Ele é amodal, pois todos os bebês têm quantidades de horas de vida diferentes.
Fonte: dados elaborados pela empresa.
Para calcular a média aritmética, multiplicamos os valores obtidos por suas respectivas frequências e dividimos pelo total de respostas.
Dependendo da amplitude, a média pode não ser o melhor valor representativo dos dados. A análise das medidas de posição pode facilitar as tomadas de decisão.
|
Habilidade
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
LUPAS E LUNETAS
Se possível, realize essa atividade em uma sala de informática para que os estudantes possam alterar muitas vezes os dados e avaliar os efeitos nas medidas de tendência central. Pode-se sugerir uma diminuição da carga horária e contratação de novas pessoas, por exemplo.
Atividade 8
a) A amplitude é a diferença entre o maior e menor valor, 12 – 5 = 7 km
b) Esse conjunto tem 30 valores, sendo os centrais 8 e 9. Assim, a mediana é 8,5 km, pois Md = 8 + 9 2 = 8,5
c) O conjunto é bimodal, pois os valores 8 e 9 aparecem 7 vezes cada um.
d) A frequência relativa é calculada por:
freque ! ncia absoluta
de rua
LUPAS E LUNETAS Respostas pessoais.
A partir das medidas de posição e da amplitude, o que é preciso fazer para reduzir as horas trabalhadas para, no máximo, 47 horas entre todos os funcionários (ou seja, 3 horas extras além das 44 horas semanais asseguradas por lei)?
Altere os dados, mantendo apenas a quantidade de horas totais trabalhadas.
• Determine a mediana, a moda e a média desse novo conjunto de dados.
ATIVIDADES
8. Fernando faz corridas de rua diariamente. Veja o rol dos quilômetros percorridos em um determinado período de tempo.
9. Uma empresa construiu a tabela de frequências dos salários de seus funcionários.
a) Calcule a amplitude dos dados.
b) Qual é o valor da mediana? 8,5 km
c) Determine a(s) moda(s).
d) Copie e complete a tabela de frequências.
dados elaborados pela empresa.
33 400,00;
a) Calcule a amplitude, a mediana e a moda.
b) Para anunciar uma vaga, essa empresa fez a seguinte publicação:
Venha trabalhar conosco! Média salarial de R$ 3.218,00.
e) A partir da tabela de frequências, calcule a média. Aproximadamente 8,5 km.
e) É determinada a soma dos produtos das frequências absolutas pelos respectivos valores de quilômetros:
20 + 12 + 14 + 56 + 63 + 20 + 33 + 36 = 254 km
Então, a média é 254 30 ≅ 8,5 km
Atividade 9
Fonte: dados elaborados por Fernando.
a) A amplitude é a diferença entre o maior e menor valor: R$ 35 000 – R$ 1 600,00 = R$ 33 400,00
A moda é o valor de maior frequência absoluta: R$ 1.600,00. A mediana são os valores centrais
O valor apresentado corresponde à realidade da maioria dos funcionários dessa empresa?
c) Escreva um texto analisando as medidas de posição com relação à amplitude dos dados.
Não, pois 80% dos funcionários recebe menos da metade do que o anunciado. Resposta pessoal.
– como são 50 valores, o 25o e o 26o termos estão entre os primeiros 40 elementos de R$ 1.600,00.
b) De fato, a média salarial é R$ 3.218,00, mas 80% dos funcionários recebe menos da metade do que o anunciado.
x = 40 1 600 + 5 2 500 + 3 4 800 + 2 35 000 50 = 3 218
c) Devido à enorme amplitude, a média não é a melhor medida para representar o conjunto de dados. Os dois salários muito altos causam uma distorção na realidade salarial da empresa.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado sobre:


▶ Matemática


• Avalia a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa?
Reconhece a organização de variáveis contínuas cujos dados agrupados em classes favorecem a análise de informações e a tomada de decisões?
• Calcula média aritmética, moda e mediana?
• Compreende os significados de média, moda e mediana relacionando-os com a dispersão de dados indicada pela amplitude?
▶ Outras disciplinas
Língua Portuguesa
• Sabe transformar um conteúdo verbal em não verbal (tabelas, esquemas, gráficos, infográficos), indo do discursivo para o esquemático e vice-versa, na (re)construção dos sentidos dos textos de divulgação científica como forma de ampliar as possibilidades de compreensão desses textos?
Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
MATEMÁTICA
OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
Encontro com outras disciplinas
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático –infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
BARCOS E PORTOS
Organize
Os estudantes podem realizar essa atividade em duplas para que conversem sobre os conteúdos que aprenderam e aqueles em que tiveram mais dificuldades. A realização de atividades em duplas permite que os estudantes se conheçam melhor e desenvolvam habilidades como a liderança, a cooperação e a colaboração. Durante as atividades em duplas, os estudantes são expostos à construção do conhecimento por meio da troca de experiências entre seus pares e o contato com opiniões diferentes das suas.
Elabore
Reúna os estudantes em pequenos grupos e solicite que escrevam um texto conclusivo escolhendo um dos gráficos estudados ou que selecionem um gráfico publicado em um jornal, uma revista ou um site. Oriente a escrita do texto pontuando alguns elementos importantes que o texto deverá conter, como:
▶ Organize
Respostas pessoais.
Retome suas anotações feitas na seção Levo na bagagem deste passeio. Siga as etapas para os conteúdos (conceitos, procedimentos e fatos matemáticos) que considerou insuficientes e parcialmente suficientes.
I. Reescreva com suas palavras esses conteúdos.
II. Explique para um colega cada conceito, procedimento ou fato. Verifique se seu colega compreendeu suas explicações.
III. Elabore um problema (e a sua solução) para cada tópico que rememorou. Troque esse problema com um colega: ele corrige o seu e você o dele – tanto o enunciado quanto a resolução.
IV. Verifiquem se, feito tudo isso, ainda restaram dúvidas e, só então, apresente-as ao professor.
Organize, por meio de um texto, características de seus estudos no resgate de conhecimentos, destacando os procedimentos que foram mais eficazes nessa etapa de superação das suas dificuldades.
▶ Elabore
Escolha uma das três categorias de gráficos que estudou neste passeio (barras/ colunas, setores e linhas).
a) Colete – de jornais, revistas, sites e outros meios de comunicação – exemplos dessa categoria de gráfico escolhida.
b) Verifique a adequação desses gráficos que coletou quanto ao contexto dos dados apresentados neles. Por exemplo, se as variáveis apresentadas em todos os gráficos são do mesmo tipo.
c) Produza uma análise crítica a respeito das informações que cada um dos gráficos apresenta e destaque semelhanças e diferenças que eles têm entre si.
Ícones representando conjunto com diversas modalidades de gráficos.
• se o gráfico está adequado para o tipo de informação que ele traz;
• se apenas o gráfico dá conta de informar todos os dados importantes para a produção do texto;
• se o título é ideal para esse gráfico;
• se as legendas contribuem para a escrita do texto.

Explique que o texto precisa ser claro sobre as conclusões escritas a partir dos gráficos. Com essa produção, a habilidade de Língua Portuguesa EF69LP33 será desenvolvida em parte. Então, se
possível, combine essa aula com o professor dessa disciplina. Para a socialização do texto produzido, organize uma roda de conversa e peça que os grupos exponham o gráfico escolhido e leiam o texto conclusivo. No momento da apresentação de um grupo, solicite aos demais grupos que observem a apresentação dos colegas e façam anotações de pontos positivos e pontos a melhorar.
A pergunta inicial deste passeio é: Como manter o bem-estar mental?
Muitas pessoas expressam seus sentimentos nas redes sociais esperando encontrar consolo e ajuda para lidar com os problemas. Nem sempre as opiniões que se obtêm como respostas são bem fundamentadas ou eficazes.
Tenho andado tão chateado e desanimado. Não sei o que fazer para melhorar minha disposição. Alguém pode me ajudar?
Proponha
Retome a questão norteadora do passeio (Como manter o bem-estar mental?) e promova as conversas sugeridas, escutando e acolhendo, tanto quanto possível, os estudantes em suas demandas. Busque auxílio de profissionais que possam também lhe acolher e orientar em suas dúvidas para dar o suporte adequado aos seus alunos.
Faça uma pesquisa para descobrir como conversar com uma pessoa que se mostra desestimulada e sem motivação. Descubra também quais são os profissionais dessa área. Se possível, leia e analise o que esses profissionais recomendam nesses casos. Elabore uma terceira resposta para esse post, organizando as informações que você pesquisou (por se tratar de um texto informal e uma situação de fragilidade emocional, procure ter afetuosidade no que escreve).
Proponha um grupo virtual para compartilhar informações sobre saúde mental e mensagens reconfortantes.

Habilidade
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Encontro com outras disciplinas
(EF08LP01) Identificar e comparar as várias editorias de jornais impressos e digitais e de sites noticiosos, de forma a refletir sobre os tipos de fato que são noticiados e comentados, as escolhas sobre o que noticiar e o que não noticiar e o destaque/enfoque dado e a fidedignidade da informação.
CHECK-IN
a) As categorias estão apresentadas no infográfico: cuidados pessoais e beleza; alimentação saudável, nutrição e perda de peso; atividades físicas; turismo de bem-estar; medicina tradicional e complementar; saúde pública, prevenção e medicina personalizada; bem-estar imobiliário; saúde mental; spas; bem-estar no ambiente de trabalho; fontes termais e minerais
b) Os maiores segmentos perfazem: 955 + 946 + 738 = 2 639 946 + 738 = 2 639 Esses segmentos correspondem a 2 639 bilhões, o mesmo que 2,639 trilhões de dólares.

c) O gráfico tem um aspecto de rede de vínculos e ênfase de informações, muito semelhante aos gráficos apresentados na seção Arredores
d) Peça aos estudantes que apresentem suas opiniões com argumentos que
PASSEIO 3 – PESQUISA ESTATÍSTICA E CREDIBILIDADE DA INFORMAÇÃO
COMO DESENVOLVER O BEM-ESTAR SOCIAL?
Receita gerada pela economia global de bem-estar em 2020: total de US$ 4,4 trilhões
Fonte: Global Wellness Institute. CRESCIMENTO do mercado de bem-estar no mundo. CBI Magazine. IHRSA, 22 fev. 2022. Disponível em: https://hub.ihrsa.org/brasil/crescimento-do-mercado-de-bem-estar-no-mundo. Acesso em: 17 ago. 2022. Gráfico mostrando o alcance de onze diferentes segmentos do mercado mundial voltado para produtos e serviços de bem-estar.
CHECK-IN
a) Cuidados pessoais e beleza; alimentação saudável, nutrição e perda de peso; atividades físicas; turismo de bem-estar; medicina tradicional e complementar; saúde pública, prevenção e medicina personalizada; bem-estar imobiliário; saúde mental; spas; bem-estar no ambiente de trabalho; fontes termais e minerais.
a) Quais são as onze categorias de produtos e serviços voltados para a economia em bem-estar?
b) Ao todo, o mercado mundial movimentou 4,4 trilhões de dólares com oferta de produtos e serviços em bem-estar. Desse volume, quanto corresponde aos três maiores segmentos juntos? US$ 2,639 trilhões.
c) O que você achou desse gráfico? Que tipo de fato está sendo noticiado por meio dele? Comente.
d) Em sua opinião, o bem-estar é para ser transformado em mercadoria?
O fato narrado é a receita global gerada por setores de bem-estar no ano de 2020. Respostas pessoais.
e) Que relação há entre os três segmentos que mais movimentaram a economia do bem-estar? Por que você imagina que foram esses os três que mais faturaram? Você tem alguma hipótese? Respostas pessoais.
defendam sua escolha. Explique aos alunos que o sentimento de bem-estar é individual: alguns o atrelam a bens materiais, outros a bens sociais etc. Deixe que dialoguem a respeito do bem-estar também relacionado a boas ações para com o próximo.
e) Os três segmentos mais rentáveis estão relacionados a cuidados pessoais e beleza. Uma possível opinião é dizer que a sensação de bem-estar tem sido moldada pelos grandes veículos de comunicação como existente somente
quando a pessoa se sente bonita. A hipótese é que isso, em longo prazo, traz uma sensação de incapacidade, inadequação e tristeza, pois não é possível se manter nos padrões de beleza perpetuamente.
BÚSSOLA
Neste passeio, você buscará atingir os seguintes objetivos:
• Reconhecer, por meio de ideias matemáticas, fatos noticiados e comentados pelos meios de comunicação, averiguando e avaliando a credibilidade da informação por meio de critérios objetivos.
• Identificar motivos de aspectos físicos, éticos ou econômicos que justifiquem a realização de pesquisas amostrais.
• Identificar diferentes maneiras de selecionar amostras: casual simples, sistemática e estratificada.
• Compreender os significados de média aritmética, moda e mediana relacionando-os com a dispersão de dados, indicada pela amplitude.
• Planejar e realizar pesquisa amostral desde a etapa da seleção da amostra até a escrita do relatório (este contendo gráficos, análises estatísticas por meio das medidas de posição e da amplitude e registro das conclusões).
• Identificar e comparar notícias em suportes e fontes diversas, de modo a refletir sobre os tipos de fatos noticiados e comentados, evitando a disseminação de notícias falsas e desenvolvendo estratégias para reconhecê-las, a partir da verificação/ avaliação da credibilidade da informação; além de escolher o que noticiar e o que não noticiar, orientando-se pela fidedignidade da informação.
Habilidade
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Encontro com outras disciplinas
(EF08LP01) Identificar e comparar as várias editorias de jornais impressos e digitais e de sites noticiosos, de forma a refletir sobre os tipos de fato que são noticiados e comentados, as escolhas sobre o que noticiar e o que não noticiar e o destaque/enfoque dado e a fidedignidade da informação.
ATMOSFERA
Atividade 1
É esperado que os estudantes produzam um entendimento baseado no texto ou em conhecimentos prévios, podendo mencionar, por exemplo, que o termo se popularizou na época das eleições e tinha cunho político, mas atualmente abrange todos os tipos de informações.
Atividade 2
O objetivo das fake news é divulgar notícias falsas com a intenção de obter alguma vantagem financeira ou política.
Atividade 3
Porque, em geral, são provocativas, focadas na reação emocional do leitor diante de temas considerados polêmicos ou tabus.
Atividade 4
Pode-se verificar quem são os autores e comparar com outros transmissores de
Notícias falsas propagadas por meio das redes sociais em suporte como smartphone. Informações reproduzidas pela TV com intenção de manipular o espectador.

O termo fake news pode ser entendido pela sua tradução direta do inglês para notícias falsas, mas outros autores dão uma maior profundidade ao fenômeno associado ao termo, assim define-se fake news não somente como notícias com conteúdo cujos fatos estão incorretos, mas que também têm a intenção de manipular o leitor. Distinguindo-as assim de notícias com caráter jornalístico, mas com fatos incorretos devido a erros na verificação das informações sendo transmitidas [...].

Nesse contexto, é determinado que as fake news são escritas buscando causar uma reação emotiva forte que ressoe com o público ou, mais comumente, com um grupo alvo específico de leitores, dificultando que o destinatário desse conteúdo tenha uma reação racional sobre aquilo que acaba de ler. A reação emocional do leitor também ajuda a explicar o alto índice de compartilhamento dessas notícias em relação às notícias com conteúdo
puramente jornalístico. A chance de uma notícia falsa se tornar viral na internet é muito maior do que uma com conteúdo verdadeiro, como demonstrado por pesquisas em plataformas sociais, notícias de cunho falso tem 70% mais chance de serem compartilhadas do que notícias verdadeiras.
O mesmo estudo também aponta que, apesar de bots nas redes sociais agilizarem a propagação de fake news, eles não são os responsáveis pela diferença entre a velocidade de propagação entre notícias falsas e verdadeiras. O conteúdo verdadeiro quando espalhado por bots mostrou o mesmo crescimento proporcional de propagação que o de notícias falsas. Atribuindo assim que o maior compartilhamento de fake news quando comparado a notícias verdadeiras tem raízes no comportamento humano e não no uso de bots (VOSOUGHI; ROY; ARAL, 2018).
GUARISE, L Detecção de notícias falsas usando técnicas de deep learning. 2019. 49 f. Monografia (Graduação) –Instituto de Ciências Matemáticas e de Computação (ICMC/USP), São Carlos – SP.
2. Conforme o texto, causar uma reação emotiva forte que ressoe com o público ou, mais comumente, com um grupo alvo específico de leitores, dificultando que o destinatário desse conteúdo tenha uma reação racional sobre aquilo que acaba de ler.
ATIVIDADES
1. O que você entende por fake news? Comente. Respostas pessoais.
2. Qual é a intenção das fake news?
3. Por que as fake news são mais compartilhadas do que as notícias verdadeiras?
4. Como você verifica/avalia a credibilidade de uma informação? E como se comporta diante dela? Respostas pessoais.
3. Porque as fake news têm raízes no comportamento humano e são focadas na reação emocional do leitor.
informação. Pode acontecer de a maioria dos estudantes não conhecer nenhum critério para avaliar uma informação. Nesse caso, solicite como tarefa de casa que façam uma pesquisa e elaborem uma lista para avaliar a credibilidade de informações. Alguns critérios que você pode ter como parâmetro avaliativo são: autoria, originalidade, estrutura textual, atualidade e comparação com outras fontes.
Sugestão de atividade
Para contemplar parte da habilidade EF08LP01, da disciplina de Língua Portuguesa, defina um tema
com os estudantes e proponha que pesquisem e levem para a aula seguinte uma cópia de uma reportagem sobre ele. Reúna os estudantes em pequenos grupos e peça para que leiam e analisem as notícias. Dentre as notícias de todos do grupo, eles devem escolher uma para ser apresentada aos demais colegas de classe. Conduza a discussão para que os estudantes percebam que, em reportagens, o mesmo assunto pode ser abordado de diferentes maneiras.
#Notícias e credibilidade
Os meios de comunicação utilizam diversos recursos para transmitir uma notícia. No entanto, na era da informação em que vivemos, tem sido frequente confundir notícia com opinião Além disso, outro fenômeno favorece a propagação de conteúdos duvidosos: o ato acrítico de compartilhar.
Tio, não compartilhe essa notícia, ela é falsa!
As fake news são informações fabricadas, geralmente com intenção de causar dano, que imitam conteúdo noticioso e concorrem com os fatos originais. Essas notícias falsas geram desarranjos da informação como:
I. informação incompleta dos fatos originais ou fatos reconectados de modo simplesmente equivocado. Nesse caso, a intencionalidade danosa é enfática no processo da informação
II. informação construída com fatos equivocados ou incorretos e intenção de manipular e de enganar. Nesse caso, a intencionalidade danosa é enfática no propósito da informação
A era da informação nos expõe aos mais diversos fatos noticiados. As notícias induzem o receptor (leitor ou espectador) a diversas reações. Ter criticidade a respeito de uma notícia é uma atitude cautelosa que evita dar credibilidade a conteúdos aos quais falta rigor de informação e fontes confiáveis.
LUPAS E LUNETAS Respostas pessoais.
Reúna-se com dois ou três colegas.
a) Pesquisem uma notícia qualquer recente. Analisem a fonte (site, blog, portal, jornal etc.) na qual foi publicada.
b) Comparem essa versão com a mesma notícia publicada em outras fontes ou outros veículos de comunicação (TV, rádio, jornal impresso etc.).
c) Analisem os principais fatos noticiados em todas as fontes e veículos de informação. Quais se confirmam entre todos e quais se contradizem? Quais fatos surgem incompletos, quais estão estruturados de modo falho, truncado ou distorcido?
d) Anotem todas as análises e as descobertas feitas por vocês e apresentem para a sala, destacando quais estratégias utilizaram para comparar e investigar se os fatos noticiados eram fiéis aos originais.
Habilidade
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
LUPAS E LUNETAS
Selecione você também previamente notícias e avalie-as segundo seus critérios. Em seguida, apresente as suas notícias para os alunos avaliarem. Por fim, formalize esses conceitos com o quadro:
Critérios Atributos
Autoria
Identificação da origem intelectual do conteúdo.
Originalidade Avaliação da fonte primária do conteúdo e da sua rede de referências.
Estrutura
Análise da estrutura e organização do conteúdo.
Identificação do autor. Credenciais. Disponibilidade de contatos.
Indicação de referências confiáveis. Imagens com crédito, local e data. Comentários positivos sobre o conteúdo.
Organização do conteúdo. Coerência entre as diferentes informações. Rigor dos conceitos. Ausência de erros gramaticais ou ortográficos.
Critérios Atributos
Atualidade
Verificação da qualidade das informações recentes e das duradouras.
Data da criação do conteúdo. Conexões entre informações recentes e conhecimentos de “longa duração”. Atualização das informações.
Comparação

Confronto com outras fontes semelhantes ou complementares
Comparação de rigor conceitual. Reconhecimento de diferentes pontos de vista.
Abrangência do conteúdo a respeito do tema analisado em comparação com outras fontes.
Baseado em: TERRA, Ana Lúcia; SÁ, Salvina. Op. cit. Disponível em: http://hdl.handle.net/10400.22/6098. Acesso em: 26 ago. 2020.
Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Com a leitura desse texto, espera-se que os estudantes percebam que é importante que as notícias que circulam sejam verdadeiras e, para isso, precisam desenvolver hábitos relacionados à gestão da credibilidade ao ler, produzir e fazer circular informações.
#Gestão da credibilidade
O excesso de informação – as formas de receber e enviar instantaneamente mensagens, fotos e vídeos – traz novas necessidades aos jovens que podem ser desenvolvidas com hábitos cotidianos, diretamente relacionados à gestão da credibilidade da informação

Pessoa usando serviços de notícias e informação pela web. Adolescentes empolgados, diante de smartphone, com notícias que receberam via rede social.

A gestão da credibilidade das informações é um conjunto de ações voltadas para a análise crítica da qualidade da informação acessada em diversas fontes, nos mais diversos suportes (digitais ou impressos).
Aplicar critérios de avaliação da qualidade da informação pode trazer benefícios para todos.
Infográfico elaborado pelos autores. Com informações adaptadas de: LEITE, Leonardo Ripoll Tavares. Confiabilidade informacional: a Filosofia da Informação e o desenvolvimento da leitura crítica no ambiente virtual. Universidade do Estado de Santa Catarina, Centro de Ciências Humanas e da Educação, Programa de Pós-Graduação em Gestão da Informação, Florianópolis, 2018.

ATIVIDADES
5. Leia a fala de três influenciadores digitais (fictícios) de uma conhecida plataforma de compartilhamento de vídeos.
Jorge_cinema @cinemacomjorge
A gente está numa expectativa de que esse novo filme do Homem-Aranha vai estourar mais do que o outro!
101 0
Carlos_assiste @carlos_assiste_tudo
Os jornais noticiaram que a bilheteria dos cinemas caiu bastante por conta das plataformas de streaming.
101 0
Tadeu_ama_Cinema @tadeueocinema
Entrevistamos fãs adolescentes desse personagem e eles garantiram que preferem assistir no cinema esse novo filme.
101 0
Reúna-se com um ou dois colegas para realizar esta atividade.
a) A frase 1 é originária (quem está anunciando é o autor dela) e não tem fundamentação em nenhuma pesquisa. A frase 2 é repassada de outra fonte sugerida (jornais), mas não especificada.
a) Considere as frases dos influenciadores 1 e 2. Qual delas é uma informação originária? E qual é uma informação repassada? A informação originária tem fundamentação em alguma pesquisa?
b) Na frase do influencer 2 aparece a palavra “bastante”. Isso é preciso? Em vez dessa palavra, que elemento matemático poderia estar nessa frase para que pudesse ter mais credibilidade? Além disso, a fonte citada – jornais – não foi específica. Reescreva essa frase em uma versão que favoreça a credibilidade.
c) O número de fãs entrevistados torna-se significativo quando cresce, comparado ao total de fãs adolescentes desse personagem.
c) Na fala do influencer 3, não fica clara a quantidade de fãs entrevistados. Há diferença no valor dessa frase se forem 5, se forem 500 ou, ainda, 5 mil fãs? E se fossem 10 mil, sabendo que esse número representa 5% dos fãs adolescentes desse personagem?
• Compartilhem com a turma as suas conclusões.
b) A palavra “bastante” não dá precisão. Poderia haver um índice percentual. Sugestão de reescrita: “Segundo o jornal A Notícia de São Paulo, a bilheteria dos cinemas caiu 25% por conta das plataformas de streaming”
Habilidade
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Atividade 5
A atividade trabalha a análise de comentários corriqueiros em redes sociais, despertando no estudante um senso crítico nesse meio em que a maioria dos jovens estão inseridos. Ao compartilhar as conclusões elaboradas, os estudantes podem também criar seus próprios comentários para uma rede social utilizando os conceitos trabalhados até o momento.
Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Atividade 6
Essa atividade pode ser utilizada com caráter avaliativo a respeito dos conceitos estudados até o momento. Utilize os critérios de avaliação coletiva ao realizar essa tarefa.
Critérios para a avaliação crítica da informação
Já sabemos que as informações causam impactos nas pessoas. Os impactos danosos da informação sobre os espectadores podem ser amenizados, e até evitados, se forem utilizados critérios adequados para a avaliação crítica da informação
Uma mesma informação pode ser submetida a um conjunto formado por diversos critérios de julgamento da qualidade da informação, e eles se complementam. O uso desses critérios estabelece uma atitude crítica em favor de contribuir com o bem-estar social, sejam pessoas no entorno imediato, sejam pessoas distantes e desconhecidas.
ATIVIDADES
6. Considere o infográfico com os Critérios para avaliação crítica da informação e responda:

a) Quais desses critérios você aplica no seu dia a dia?
Respostas pessoais.
b) Recupere a última notícia que leu. Aplique esses seis critérios de avaliação da informação. Registre os resultados avaliativos dessa notícia em um quadro com seis linhas, uma para cada critério.
• Compartilhe sua avaliação com os colegas. Observe como eles aplicaram os critérios de avaliação na notícia que selecionaram.
• Faça uma roda de conversa coletiva e exponha como você pode evitar a disseminação de notícias falsas e como orientaria outras pessoas a fazerem o mesmo. Sinalize também se agora vocês se sentem seguros para avaliar o que propagar e o que não propagar, orientando-se pela fidedignidade da informação.
Infográfico elaborado pelos autores. 240 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO. SHUTTERSTOCK/ ARTE M10#Etapas da pesquisa estatística
Outra maneira de não propagar informações falsas é utilizar informações geradas por métodos de pesquisa confiáveis. Um deles é o método de pesquisa estatística. Esse método segue uma trajetória composta de etapas que têm, cada uma, sua característica própria. Há diversos modelos esquemáticos para representar essas etapas. Apresentamos um deles a seguir.
#A problematização em Estatística


Observe um post em favor do bem-estar do planeta.
Habilidade
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Infográfico elaborado pelos autores.Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
LUPAS E LUNETAS
a) Sim, tem potencial para uma problematização estatística, levando em conta que há na pergunta um caráter quantitativo (quantas pessoas da minha rede de contatos) e também qualitativo de caráter social (acolhem bem essa ideia e qual é o perfil delas).
Além disso, há uma população para a qual a pesquisa está direcionada: as pessoas da rede de contatos de Iago.
b) As opiniões entre os estudantes podem ser divergentes, entretanto, espera-se que reconheçam que a “insatisfação” com a opinião de alguém precisa ser colocada sob o ponto de vista ético, por meio de perguntas semelhantes a: Fiquei insatisfeito com a opinião do outro porque ele não está sendo ético ou sou eu quem não está sendo ético? Essas reflexões favorecem o desenvolvimento da consciência crítica e autocrítica.
LUPAS E LUNETAS
Imagine que esse post tenha sido feito por Iago, um aluno do 8o ano. Ele desejava pesquisar o impacto de uma campanha que fizesse as pessoas refletirem sobre os benefícios de uma atividade física e ao mesmo tempo os benefícios da redução de CO2 para o bem-estar do planeta.
Ele tinha em mente a seguinte problematização: Quantas pessoas da minha rede de contatos acolhem bem essa ideia e qual é o perfil social delas?

No entanto, essa ideia incomodou mais da metade das pessoas de sua rede, que tem 600 seguidores que residem no mesmo município que ele.
Reúna-se com um ou dois colegas para realizar esta atividade. Respostas pessoais.
a) A pergunta feita por Iago tem potencial para uma problematização estatística? Por quê?
b) Iago estava agindo de modo antiético, já que ele causou descontentamento em muitas pessoas com esse post? Explique.
c) Leia o artigo 19 da Declaração Universal dos Direitos Humanos (DUDH):
Todo ser humano tem direito à liberdade de opinião e expressão: esse direito inclui a liberdade de, sem interferência, ter opiniões e de procurar, receber e transmitir informações e ideias por quaisquer meios e independentemente de fronteiras.
BRASIL. Governo Federal. A Declaração Universal dos Direitos Humanos e os Objetivos de Desenvolvimento Sustentável: avanços e desafios. Ministério dos Direitos Humanos: Brasília, 2018. p. 6. Considere esse artigo e avalie a atitude de Iago levando em conta a intenção da pesquisa dele e a qualidade de seu post.
A pergunta em Estatística
Os motivos, ou razões, que levam a uma pesquisa estatística podem ser de caráter físico, ético ou econômico. Esses motivos podem ser “traduzidos” em forma de questões, todas voltadas para a realidade, no intento de levantar dados estatísticos, por meio dos quais se dará o processamento e a análise. As respostas às questões virão por parte das pessoas contempladas na amostra.
#População e amostra
O trabalho de coleta de dados pode se tornar imenso e muito caro se, em uma pesquisa estatística, for pesquisada toda a população. Por isso, muitas vezes, é necessário saber selecionar uma amostra que seja representativa de uma população.
Esquema ilustrativo simbolizando o fato de que a população é um conjunto amplo, enquanto a amostra é, de seus subconjuntos, o que melhor representa o todo.
c) A atitude de Iago, segundo o artigo 19 da DUDH, foi amparada pelo direito à “liberdade de opinião e expressão” e ainda à liberdade de “transmitir informações e ideias por quaisquer meios e independentemente de fronteiras”, que é a intenção da pesquisa dele: incentivar as pessoas a refletir sofre os benefícios de uma atividade física e, ao mesmo tempo, da redução das emissões de CO2 para o bem-estar do planeta.
A amostragem em Estatística consiste em selecionar indivíduos da população para compor um único conjunto de modo que, tanto quanto possível, todos os indivíduos da população tenham a mesma chance de serem contemplados nas devidas pesquisas, seja por meio de questionário, entrevista ou observação.
Essa seleção só será válida se, como amostra, de fato representar a população, uma vez que, para alcançar os objetivos da pesquisa, as conclusões que foram tiradas com base na amostra serão generalizadas para toda essa população.
Técnicas de amostragem
Há diferentes técnicas de amostragem. As três principais são: aleatória simples, estratificada e sistemática
Vamos analisar exemplos de cada uma delas.
Amostragem aleatória simples
Nessa técnica os elementos da população são enumerados um a um. Sendo P o número de elementos da população e a o número de elementos da amostra, cada elemento da população tem probabilidade a P de ser sorteado, sem reposição no conjunto da população, para participar da pesquisa. Nessa situação, existem a possíveis amostras igualmente prováveis de serem selecionadas.
Essa técnica lembra um sorteio lotérico, podendo inclusive ser utilizado um globo giratório com bolinhas numeradas de 1 até P, sendo que cada a sorteado pertence ao intervalo 1 < a < P
Se o número de elementos da amostra for grande (o que pode tornar essa tarefa trabalhosa), a escolha da amostra pode ser feita utilizando-se um quadro de números aleatórios ou um software

Exemplo
Iago assustou-se com a reação dos seus 600 seguidores e tentou entender isso melhor, mudando a forma de apresentar o problema. Por isso criou um post com a pergunta: No centro urbano, você é a favor da bicicleta ou do carro?
Ele numerou de 1 a 600 os nomes dos seus seguidores e, utilizando um site sorteador de números aleatórios, sorteou 60 números, ou seja, 10% dos seus seguidores. Os números sorteados foram estes:
Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Comente com os alunos que existem fórmulas matemáticas sofisticadas para o cálculo da quantidade de elementos a serem selecionados para uma amostra, em relação ao número de elementos de sua população correspondente. Para facilitar os cálculos e tornar mais didática a compreensão desse método, vamos, por vezes, assumir que a amostra seja em torno de 10% da população estudada.
Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Após a leitura do texto, converse com os estudantes para verificar como compreenderam a amostragem. É possível usar como exemplo a pesquisa estatística realizada para acompanhar as intenções de voto nas eleições:
• É adequado entrevistar todos os brasileiros?
• Qual faixa etária não deve participar da pesquisa sobre intenções de voto?
Comente que o voto é obrigatório entre 18 e 70 anos e facultativo entre 16 e 18 anos e para maiores de 70 anos.
Feito isso, ele disparou para cada pessoa que correspondia a um desses números o seguinte post:
Amostragem estratificada
Esse tipo de amostragem é adequada quando a população está dividida em subpopulações, ou estratos, definidos por diferentes categorias e com suas correspondentes quantidades de elementos.
Exemplo
Vamos imaginar agora que, desses 600 seguidores de Iago, 60 moram na periferia, 420 moram em bairros e 120 moram no centro da cidade. Para melhorar os resultados da pesquisa, é mais adequado selecionar uma amostra que represente exatamente as proporções observadas no conjunto do total de seguidores, ou seja, as mesmas proporções da população original. Vamos determinar a proporção necessária na amostra de Iago: há 3 subpopulações na pesquisa dele, ou seja, 3 estratos (moradores de periferia, moradores de bairro, moradores do centro), cada qual com uma quantidade diferente de elementos.
Como construir essa amostra? Vamos acompanhar o passo a passo:

1. Determinar o tamanho de cada estrato. Como a amostra selecionada corresponde a 10% do total da população, então consideraremos 10% de cada estrato.
Distribuição dos seguidores conforme a situação residencial
2. Numerar cada elemento, separados por estratos. Feito o cálculo do tamanho de cada estrato, agora devem-se numerar assim os seguidores:
• 01 a 60 – moradores da periferia;
• 61 a 480 – moradores do bairro;
• 481 a 600 – moradores do centro.
3. Sortear os números dentro de cada intervalo numérico. Nesse caso, devem ser sorteados 6 números que estão no intervalo de 01 a 60, 42 números que estão no intervalo de 61 a 480 e 12 números que estão no intervalo de 481 a 600. 244 | TRAJETÓRIA 4
Amostragem sistemática
Esse tipo de amostragem é parecida com a aleatória simples: é usada quando não há necessidade de levar em conta estratos. Também é utilizada quando os elementos da população já estão naturalmente ordenados. O pesquisador determina o número de elementos da amostra e descobre um intervalo que o auxiliará a determinar quais elementos farão parte da amostra.
Exemplo
Vamos imaginar que os seguidores de Iago estão em ordem alfabética e numerados de 1 a 600. Ele escolheu para a amostra uma quantidade de 60 elementos. Então, ele calcula o intervalo assim: 600 60 = 10 . Esse número indica que a cada 10 nomes (do primeiro até o último da lista) será selecionado um nome, ou seja, para cada grupo de dez, o décimo será selecionado e outros nove serão ignorados.
Assim, os números selecionados são: 10, 20, 30 ... 590, 600.
ATIVIDADES
7. No exemplo dado da amostragem estratificada, faltou fazer os sorteios dos números dentro de cada intervalo, conforme a seguir:
• 6 números que estão no intervalo de 01 a 60;
• 42 números que estão no intervalo de 61 a 480;
• 12 números que estão no intervalo de 481 a 600.
Utilize um aplicativo ou um site sorteador de números aleatórios e indique quais números farão parte dessa amostra. Respostas pessoais.
8. Levando em conta as populações, indique para cada uma o tipo de amostragem (ou toda a população) que melhor se adeque para a coleta de dados.
I. Os estudantes de uma mesma sala.
II. Os estudantes de um município.
III. Os alunos ouvintes e os surdos das escolas de um município.
IV. Os carros nas vagas do estacionamento de um condomínio.
9. Um estudo sobre o bem-estar social no ambiente escolar (livre de violência e de manifestações hostis como bullying) será feito por uma equipe de pesquisadores dentro de uma escola pública muito grande. Para isso, será selecionada uma amostra de alunos dessa escola. Considere as técnicas
de Amostragem Aleatória Simples (AAS), Amostragem Estratificada (AE) e Amostragem Sistemática (AS), e classifique a fala de cada pesquisador quanto ao plano que eles têm para selecionar a amostra
Reinaldo_matematica @reinaldo_matematica
Vou pegar todas as listas, uma sala após a outra, dos nomes de todos os alunos dessa escola e vou numerá-los do 1 até o último aluno do último ano e selecionar aqueles que ocupam posições múltiplas de 15, ou seja, o 15o, 30o, 45o, 60o etc.
119 18
Matilda @matildamarina
Em cada sala vou identificar todos os alunos (lista de chamada). Selecionarei aleatoriamente k alunos de cada sala de aula, de modo que k seja um número inteiro proporcional à quantidade de alunos existentes nessa sala em relação a toda a escola.
27
Isabela @professora_isa#
Vou recolher as listas de chamadas de todas as salas e selecionar ao acaso N alunos.
41
• Que sugestão você daria a esses pesquisadores para combater o bullying e fazer prevalecer os direitos humanos?
Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Atividade 9
Para a sugestão de combate ao bullying leia para os alunos este parágrafo de artigo que menciona a cultura de paz no ambiente escolar (espaço de acesso à instrução):
Artigo 26
2. A instrução será orientada no sentido do pleno desenvolvimento da personalidade humana e do fortalecimento do respeito pelos direitos do ser humano e pelas liberdades fundamentais. A instrução promoverá a compreensão, a tolerância e a amizade entre todas as nações e grupos raciais ou religiosos e coadjuvará as atividades das Nações Unidas em prol da manutenção da paz.
GOVERNO Federal. A Declaração Universal dos Direitos Humanos e os Objetivos de Desenvolvimento Sustentável: avanços e desafios.
Brasília: Ministério dos Direitos Humanos, 2018. p. 14.
Atividade 7
Para essa atividade, utilize um mecanismo de busca pela internet para localizar sites sorteadores de números. Selecione o mais simples e deixe os alunos conduzirem o sorteio.

Atividade 8
É esperado que os alunos façam comparações das populações apresentadas nos exemplos e as que estão dispostas na atividade. Se houver
dificuldade, faça perguntas que contribuam para notarem as semelhanças, como:
• A população de uma sala de aula é pequena?
• É possível realizar a pesquisa com toda a turma sem ter custos elevados?
• Será uma amostra correta se houver uma representatividade maior dos alunos ouvintes do que dos alunos surdos?
• Como são organizadas as vagas de um estacionamento?
8. (I) Toda a população; (II) Aleatória simples; (III) Estratificada; (IV) Sistemática.Habilidade (EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Atividade 10
a) 20% de 150: 20 100 ⋅ 150 = 30 A amostra será de 30 números sorteados. Os números podem ser bastante diferentes, pois não é uma amostra sistemática.
b) 20% de 15: 20 100 15 = 3 Serão sorteadas 3 pessoas da primeira linha e 27 pessoas das demais.
c) É possível que observem que 50 cabe 3 vezes no todo da amostra. Assim, uma possível estratégia seria selecionar uma pessoa a cada três.
10. Uma escola pública do interior do Mato Grosso tem 150 alunos no Ensino Fundamental, anos finais. Como parte de uma campanha que rejeita o bullying na escola, será feita uma pesquisa para ouvir sugestões dos alunos em favor de evitar manifestações hostis entre eles.
Cada aluno dessa população recebeu uma ficha com um número diferente, variando de 1 a 150:
a) Obtenha uma amostra composta de 20% dessa população. Compare sua amostra com a dos colegas. Os números selecionados foram iguais ou foram bastante diferentes? Isso pode ocorrer? Explique.

b) Imagine que a primeira linha desse quadro de números represente pessoas com deficiência. Mantenha a mesma quantidade de elementos da amostra estabelecida no item anterior, mas agora faça uma amostragem estratificada levando em conta as pessoas com deficiência.
c) Apresente uma proposta de como você faria para selecionar uma amostra sistemática contendo 50 elementos. Respostas pessoais.
 246 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.
ARTE/ M10 ARTE/ M10
246 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.
ARTE/ M10 ARTE/ M10
Sofia faz parte da associação pacífica de jovens do seu bairro que é – tal como uma associação comunitária – aberta aos moradores do bairro, porém voltada para os interesses comuns dos jovens. Ela quis fazer parte da associação por diversos motivos. Inclusive motivada por este artigo que ela leu em um livro de Matemática:

Artigo 20 Todo ser humano tem direito à liberdade de reunião e associação pacífica. Ninguém pode ser obrigado a fazer parte de uma associação.
BRASIL. Governo Federal. A Declaração Universal dos Direitos Humanos e os Objetivos de Desenvolvimento Sustentável: avanços e desafios. Ministério dos Direitos Humanos: Brasília, 2018. p. 11.
Ela sentiu-se tão útil fazendo parte da associação que teve vontade de saber se, exceto pelos que já fazem parte da associação, os jovens do bairro dela gostariam de conhecer e participar também.
Então, pensou na seguinte pergunta para fazer um levantamento estatístico:
Por quais motivos você teria interesse em participar de uma associação pacífica de jovens?

Determinar as variáveis de interesse a partir da pergunta
Para o bom planejamento da pesquisa é preciso descobrir quais variáveis de interesse (ou seja, as características de interesse que devem ser medidas nos elementos da amostra) serão observadas, tendo em mente a pergunta da pesquisa.
Na pergunta de Sofia há algumas palavras que têm papel-chave para indicar as variáveis: motivos, interesse, participação, jovens. Assim, Sofia precisa compreender melhor:
• Quais seriam os motivos?
• Qual é o grau do interesse?
• Que tipo de participação?
• Qual é o perfil de jovem?
Embora as quatro perguntas estejam separadas, elas estão estreitamente relacionadas. Por outro lado, ao serem abordadas uma por vez, a pesquisa de Sofia trará boas relações e dará clareza às variáveis que ela pretende medir.
Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Observe que as quatro categorias de palavras na pergunta formulada por Sofia indicam razões, de diferentes naturezas (ética, social, econômica), que levam ao desejo de realizar uma pesquisa amostral. Faça um exercício com os estudantes a respeito de que, mantendo as palavras-chave motivos, interesse, participação e jovem, poderiam ainda ser elaboradas perguntas diferentes da que foi feita por Sofia.
Outras possibilidades de perguntas envolvendo essas quatro palavras poderiam ser:
• Quantos motivos?
• Qual é seu interesse?
• O que você entende por participação?
• Sendo jovem, qual é sua idade?
Se julgar oportuno, confronte essas questões com as elaboradas por Sofia ou proponha que eles próprios elaborem outras questões, mantendo essas mesmas quatro palavras, sempre alertando para o fato de que cada pergunta deve compor, no todo, o interesse da pesquisa, ou seja, não se trata de elaborar perguntas aleatórias.
Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
LUPAS E LUNETAS
Peça que retomem os conceitos trabalhados no passeio de gráficos e medidas de posição. Auxilie os estudantes a tabular as respostas em um software editor de planilhas para, então, elaborar os gráficos e analisar os dados. Os conteúdos dessa pesquisa são de grande valor para o desenvolvimento pessoal, podendo motivar os estudantes a criar uma associação de jovens com interesses relevantes para a comunidade. Você pode ajudá-los nesse projeto.
Para cada uma dessas quatro variáveis, Sofia atribuiu os valores indicados de a a d:
Pesquisa: Por quais motivos você teria interesse em participar de uma associação pacífica de jovens?
DADOS PESSOAIS
NOME: IDADE: anos.
ESCOLARIDADE: 1. EF ( ) 2. EM ( ) 3. ES ( )
GÊNERO: 1. Feminino ( ) 2. Masculino ( ) 3. Outros ( )
HÁ QUANTO TEMPO RESIDE NO BAIRRO? anos
QUESTÕES
Escolha somente uma alternativa para cada questão, exceto a primeira, em que é permitido escolher até duas.
1. Quais motivos fariam você participar de uma associação pacífica de jovens?
a) Pertencer a um movimento que possa transformar nosso futuro.
b) Fazer parte de um grupo que busca junto os mesmos interesses.
c) Desenvolver melhor meu lado social e político.
d) Superar minha dificuldade de expressar minhas ideias no coletivo.
2. Qual é o seu grau de interesse em participar de uma associação?
a) Muito interessado.
b) Interessado, mas receoso por desconhecer como funciona.
c) Tenho curiosidade.
d) Sem interesse.
3. Em que tipo de participação social você gostaria de se envolver?
a) De caráter político.
b) De caráter econômico.
c) De caráter social e cultural.
d) Outros.
4. Você se considera um jovem com que perfil?
a) Muito interativo e ativo socialmente.
b) Bastante interativo, mas apenas virtualmente.
c) Pouco interativo, dependendo do grupo sou mais interativo.
d) Muito tímido e pouco ativo.
LUPAS E LUNETAS Respostas pessoais.
Imagine que você seja um dos jovens selecionados na amostra de Sofia. Responda, em uma folha avulsa, a cada uma das questões elaboradas por ela. Depois que toda a sala tiver respondido, construam, coletivamente, gráficos para cada uma dessas perguntas.
Analisando os gráficos, que conclusão puderam tirar a respeito do grupo como um todo? Façam uma roda de conversa para expor todas as ideias.
248 | TRAJETÓRIA 4 NÃO ESCREVA NO SEU LIVRO.Sofia leu este infográfico a respeito das etapas do planejamento de uma pesquisa:
#A realização, o relatório e a análise estatística
Com o questionário em mãos, Sofia poderia dar continuidade às etapas da sua pesquisa.
A realização da pesquisa
Um pesquisador estatístico deve realizar seu trabalho de pesquisa no local do fenômeno social para coletar e registrar os dados ou pode utilizar os meios digitais, como formulários virtuais, videochamadas etc.

Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Os estudantes podem conversar em grupos para discutir sobre as etapas de planejamento de uma pesquisa de opinião com questões de seu próprio interesse. Nessas etapas de planejamento, precisam decidir como pretendem aplicar o questionário e a melhor maneira de organizar as respostas para a tabulação dos dados e posterior análise das informações e construção dos gráficos.

 Infográfico elaborado pelos autores.
Infográfico elaborado pelos autores.
Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Atividade 11
No item c os alunos devem localizar de que modo os conceitos de amostragem se encaixam nas etapas da pesquisa estatística. Caso haja dificuldade, retome o infográfico das etapas de uma pesquisa e localize em qual etapa está a seleção da amostra. Solicite que apresentem argumentos para validar essa posição.
Atividade 12
a) Retome os conteúdos trabalhados no passeio anterior e localize-os nas etapas da pesquisa estatística.
b) A moda é a idade mais frequente: 14 anos com FA = 7 Como são 30 idades coletadas, a mediana é a média entre a 15 a e a 16 a idades. Adicionando
1 + 2 + 6 + 7 = 16, concluímos que tanto a 15a quanto a 16a idades valem 14. Então Md = 14 anos
O relatório de uma pesquisa estatística precisa ser organizado. Por meio dele é possível identificar as questões investigadas, os dados coletados, as etapas da pesquisa, as análises realizadas, as interpretações despertadas e apontamentos das possíveis soluções.
Os principais elementos de um relatório são: título; objetivo; resumo do trabalho; introdução, apresentando a problemática; descrição dos procedimentos da pesquisa; resultados obtidos; análise e discussão dos resultados; conclusão; e referências bibliográficas.
As possibilidades de intervenção ou de apresentação de propostas de solução podem ser mais bem estudadas pela equipe de pesquisadores amparados nas análises feitas sobre o relatório.
a) Aleatória simples.
11. Sofia utilizou sua rede social, que é ampla e diversificada. Nela há, entre muitos seguidores de outras localidades, uma população de 300 jovens que residem no seu bairro. Um aplicativo numerou-os de 1 a 300 e selecionou 10% desses jovens ao acaso.
a) Que técnica de amostragem ela utilizou?
b) Quantos jovens foram selecionados?
c) Em que etapa do planejamento ela determinou a amostra? Na segunda etapa.
b) 30 jovens.
12. Observe os dados, relativos à variável idade, organizados por Sofia na tabela de frequência.
a) Em que etapa ela organizou essa tabela de frequência? Na quarta etapa.
b) Calcule a média, a moda e a mediana.
c) Considerando o valor mínimo e o valor máximo da variável idade, a média está mais próxima de qual deles? E a moda?
d) Veja o segmento de reta que representa a amplitude dos dados para a variável idade
Qual é o “pedaço” desse segmento em que estão concentrados os valores menores do que ou iguais à mediana?
13. Há dois aspectos importantes da informação: seus processos de produção e seus propósitos na disseminação. Levando em conta a experiência de Sofia referente ao desenvolvimento de sua pesquisa estatística, você julga ético o processo utilizado por ela?


E o propósito é genuíno e franco? Os motivos que a conduziram a desenvolver essa pesquisa podem gerar quais transformações na vida dela e na vida dos jovens que foram pesquisados?
• Elabore com seus colegas algumas conjecturas e exponham no mural da sala.
#A tomada de decisão
Sofia fez várias análises das informações para facilitar suas tomadas de decisão. Observe, por exemplo, um quadro que ela organizou com os dados que coletou. Nesse quadro ela “cruzou” duas informações:
Em que tipo de participação social você gostaria de se envolver?
Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
Fonte: dados da pesquisa de Sofia. Por meio desse quadro, ela pôde perceber alguns fatos:
• A maioria dos jovens estão no Ensino Fundamental (EF) e no Ensino Médio (EM) e correspondem a 83% da amostra.
• A maioria dos jovens que estão no Ensino Superior (ES) tem interesse em questões políticas e correspondem a 10% da amostra.
Considerando essas informações, Sofia pretende tomar estas decisões:
• Propor à diretoria da associação uma campanha voltada para os jovens do EF e EM atraindo-os para contribuírem com ideias de eventos sociais e culturais favoráveis aos jovens do bairro.
• Propor à diretoria que crie uma pauta de conferências – com temática em questões políticas – para enviar pelas redes sociais a jovens ingressantes nas universidades, convidando-os a participarem de uma reflexão coletiva.
LUPAS E LUNETAS Respostas pessoais.
Converse com a turma: o que vocês acharam da estratégia de Sofia de “cruzar” duas informações? E o que acharam das conclusões e das propostas de soluções que ela apresentou?
• Comentem e apontem novas tomadas de decisões com base naquelas informações.
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
LUPAS E LUNETAS
São apresentadas as tabelas de dupla entrada e os estudantes são convidados a construir, em conjunto, novas possibilidades de tomada de decisões, como: “Elaborar um novo projeto voltado para jovens dos Ensinos Fundamental e Médio que não tiveram interesse em temas de política, economia e social/ cultural”.
Atividade 13
É esperado que discutam a respeito da ética na pesquisa, deixando claro que não há obrigatoriedade de resposta ao questionário. O propósito é genuíno, pois é amparado pelo artigo 20 da Declaração Universal dos Direitos Humanos. As transformações podem ser diversas e benéficas e, entre elas, estão diversas competências relacionadas ao desenvolvimento pessoal, social e profissional, como trabalhar em grupo, compreender, utilizar e criar tecnologias digitais de informação, formular ideias,
negociar e defender pontos de vista amparados pelos direitos humanos, pela consciência ambiental e pelo consumo responsável.
Você pode discutir com eles sobre a Lei Geral de Proteção de Dados e sua relação com a coleta de dados em pesquisas estatísticas.
Habilidades
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Atividade 14
São diversas as conclusões (item b) que podem ser elaboradas. Dentre elas estão:
• “Os jovens que residem há mais tempo no bairro são os mais interativos e ativos socialmente (61% de toda amostra moram no bairro entre 10 e 20 anos e são dos perfis A e B)”;
• “Os que moram há menos tempo no bairro são os mais introspectivos (21% de toda a amostra moram no bairro entre 0 e 10 anos e são do perfil C e D)”;
• “Os jovens que moram há mais tempo no bairro são a maioria entre os que responderam à pesquisa (73% de toda amostra mora no bairro entre 10 e 20 anos, enquanto 27% mora entre 0 e 10 anos)”.
As tomadas de decisões (item c ) dependem das conclusões escritas no item anterior. Seguem possíveis exemplos:
ATIVIDADES
14. Observe este outro quadro, elaborado por Sofia, com valores de duas variáveis que se inter-relacionam. Você se considera um jovem com que perfil?
Legendas: A. Muito interativo e ativo socialmente; B. Bastante interativo, mas apenas virtualmente; C. Pouco interativo, dependendo do grupo sou mais interativo; D. Muito tímido e pouco ativo.

a) O tempo de residência no bairro, em anos, e o perfil do jovem (que está na 4a questão do formulário de Sofia).
a) Quais são as duas variáveis que se relacionam nesse quadro?
Fonte: dados da pesquisa de Sofia.
Respostas pessoais.
b) Observando esse quadro, escreva conclusões possíveis de relacionar as duas variáveis.
c) Elabore propostas de tomada de decisão conforme essas conclusões. Respostas pessoais.
15. Forme um grupo composto por 4 ou 5 integrantes.
Jovens desenvolvendo pesquisa estatística.
a) Elaborem uma questão do interesse de vocês com a qual seja possível desenvolver uma pesquisa estatística.
b) Percorram todas as etapas do desenvolvimento da pesquisa estatística (retomem as etapas), observando como fazer o planejamento dessa pesquisa (veja páginas anteriores).
c) Ao fim, publiquem o relatório do seu grupo na rede social da sala. Não se esqueçam de apresentar as propostas de decisão e possibilidades de intervenção no real. Respostas pessoais.
• “Com as duas primeiras conclusões pode-se criar uma campanha para desenvolver a interação entre os jovens do bairro.”;
• “Com a última conclusão é possível criar uma campanha para atrair jovens que moram há poucos anos no bairro”.
Atividade 15
Essa atividade deve ser planejada previamente e avaliada por etapas, estabelecendo prazos de entrega e apresentando feedbacks para que possam melhorar sua produção. Ela mobiliza todas as habilidades desenvolvidas neste passeio e no passeio anterior.
LEVO NA BAGAGEM
Respostas pessoais.
Consulte todas as suas produções até agora neste passeio. Avalie seu aprendizado sobre:
▶ Matemática


• Reconhece, por meio de ideias matemáticas, fatos noticiados e comentados pelos meios de comunicação, averiguando e avaliando a credibilidade da informação por meio de critérios objetivos?
• Identifica motivos de aspectos físicos, éticos ou econômicos que justifiquem a realização de pesquisas amostrais?
• Identifica diferentes maneiras de selecionar amostras: casual simples, sistemática e estratificada?
Compreende os significados de média, moda e mediana relacionando-os com a dispersão de dados, indicada pela amplitude?
• Sabe planejar e realizar pesquisa amostral desde a etapa da seleção da amostra até a escrita do relatório (incluindo gráficos, análises estatísticas por meio das medidas de posição e da amplitude e registros das conclusões)?
▶ Outras disciplinas
Língua Portuguesa
• Identifica e compara notícias em suportes e fontes diversas, de modo a refletir sobre os tipos de fatos noticiados e comentados, evitando a disseminação de notícias falsas e desenvolvendo estratégias para reconhecê-las, a partir da verificação/avaliação da credibilidade da informação e escolhendo o que noticiar e o que não noticiar, orientando-se pela fidedignidade da informação?


Anote no caderno seu parecer para essas questões e, ao final, analise como você julgaria sua aprendizagem em Matemática e em outras disciplinas. Copie e complete este quadro no caderno.
QUADRO DE AVALIAÇÃO
Insuficiente Parcialmente suficiente Satisfatório Plenamente satisfatório
LEVO NA BAGAGEM
Neste momento do passeio, organize a leitura coletiva do texto para que, respondendo às questões propostas, os estudantes reflitam sobre seu próprio aprendizado enquanto escutam ativamente as dificuldades encontradas pelos colegas. Com o preenchimento do quadro, classificarão seu desempenho em Matemática ou nas disciplinas presentes nas atividades interdisciplinares. Diante dessas informações, poderão conversar com professores, familiares ou amigos para compartilhar suas estratégias e repensar em novas atitudes que contribuam para minimizar as dificuldades.
MATEMÁTICA
OUTRAS ÁREAS
Converse com professores e colegas buscando alternativas para superar as dificuldades que autodiagnosticou.
BARCOS E PORTOS
Organize
Nesse momento, leve seus registros avaliativos individuais, compare com os esquemas visuais dos estudantes com a turma, detectem quais habilidades precisam ser melhor trabalhadas antes do fim do passeio.
Elabore
O intuito é utilizar os conhecimentos trabalhados para propor questões que favoreçam a comunidade. Com isso em mente, você pode sugerir que elejam a melhor produção e levem adiante para um projeto na comunidade.



▶ Organize
Respostas pessoais.
Este passeio é rico em conteúdos procedimentais, ou seja, conteúdos que demandam uma ação para “fazer algo”: selecionar amostra, coletar dados, realizar pesquisa, construir gráficos etc. Recupere seus registros feitos na seção Levo na bagagem e, considerando os procedimentos que você não está tão seguro para desenvolver, represente-os em um esquema visual, mostrando, em um passo a passo, quais deles precisa recuperar, buscar exemplos, fazer pesquisas ou consultar outros livros para que sua aprendizagem possa continuar. Compartilhe com os colegas seu esquema e ouça o que eles têm a dizer sobre o que de melhor vocês aprenderam e quais “inseguranças” ainda demonstram ter.
▶ Elabore
Observe as imagens.
Escolha uma imagem e, a partir dela, crie uma pergunta por meio da qual seja possível realizar uma pesquisa estatística envolvendo o tema bem-estar social ou a participação social juvenil.
Compare suas perguntas com as de outros colegas: cada um vai melhorar –amadurecer a forma de perguntar – de modo a facilitar e determinar quais serão as variáveis pesquisadas. Ou seja, utilize os critérios que você aprendeu para elaborar boas perguntas estatísticas, facilitando a percepção das variáveis estatísticas. Use esses critérios para justificar se a qualidade da pergunta está boa ou de quais tipos de melhorias necessita.
▶ Proponha
A pergunta inicial deste passeio é: Como desenvolver o bem-estar social? Leia o texto. Enquanto você lê, esteja atento se o conteúdo pode ajudá-lo a responder à pergunta deste passeio.
Como você pode construir uma sociedade melhor?
Você está satisfeito com a cidade onde mora? Ela oferece boas condições de mobilidade e lazer? A prefeitura realiza o trabalho de zeladoria de forma eficiente? Sabemos que toda cidade tem seus problemas, principalmente as grandes metrópoles, mas a solução mais escolhida acaba sendo calar e deixar as coisas acontecerem. Muitos apenas reclamam nas redes sociais e pronto. Acham que fizeram sua parte.
Separamos 5 dicas para mostrar como você pode ajudar a construir uma cidade melhor.
1. Seja um cidadão ativo.
2. Manifeste-se por causas que atendem à maioria.
3. Utilize os canais à disposição.

4. Agrupe-se.
5. Ofereça soluções. [...]

COMO VOCÊ pode construir uma sociedade melhor? Blog Colab, 16 abr. 2015. Disponível em: www.colab.re/conteudo/como-voce-pode-construir-uma-sociedade-melhor. Acesso em: 31 maio 2022.
Após a leitura desse texto, organize-se em um grupo com 3 integrantes. Juntos reflitam sobre as questões:
a) Para se preocupar e querer contribuir com o bem-estar social você não precisa ser um político eleito: suas atitudes podem fazer a diferença. Quais das cinco ações listadas você reconhece como a mais necessária para os jovens do seu entorno social?
b) Uma das dicas diz para os jovens se agruparem. A finalidade é a construção de ideias e de propostas de impacto social benéficas para todos. Observe as duas imagens e crie para elas legendas que despertem o olhar dos jovens para a ideia de “agrupe-se”.
Proponha
a) A resposta é pessoal e depende de como cada estudante enxerga a realidade.
b) Ao comparar os fios organizados em tramas e os fios dispostos sem organização, é esperado que os alunos concluam que o agrupamento deve ser feito o mais organizadamente possível, em que cada membro tem sua função definida e a executa com zelo.
c) Como a execução da tarefa é em grupo, solicite que se organizem para pesquisar e submeter o texto aos critérios de gestão da informação.
d) Oriente-os no compartilhamento de informações verificadas e relevantes.
c) Procure na internet outro texto que fale sobre como é possível contribuir para a construção de uma sociedade melhor. Submeta-o aos critérios de gestão da credibilidade da informação estudados neste passeio. Compartilhe com os colegas o que vocês descobriram.
d) Selecionem informações, inclusive com dados estatísticos, sobre o tema do bem-estar social e compartilhem essas informações com os contatos de suas redes sociais.
VISTORIAS
Habilidades de Matemática: EF08MA19, EF08MA20, EF08MA21, EF08MA23, EF08MA24, EF08MA25, EF08MA26, EF08MA27
Atividade 1
a) Pode-se utilizar as fórmulas da área do trapézio e do quadrado:
2 ⋅ 15 + 5 ( ) ⋅ 5 2 + 52 =
= 100 + 25 = 125 cm2
Por decomposição, a área corresponde a 5 52 = 5 25 = 125 cm2
5 52 = 5 25 = 125 cm2
5 cm
5 cm 5 cm 5 cm
5 cm
5 cm
b) Por decomposição, temos a área de um círculo de diâmetro 2 m (raio 1 m), outro de diâmetro 4 m (raio 2 m) e um retângulo com lados 2 m e 4 m.
• A c rculo 1 = π r 2 = π 12 = π
• A c rculo 2 = π r 2 = π 22 = 4π
• A ret angulo = base altura = 2 4 = 8 e altura = 2 4 = 8
Área total = (8 + 5 π ) m2
Atividade 2
Sugestões de cálculo:
• primeira maneira:
Duas vezes a área do triângulo retângulo de catetos 2, mais duas vezes a área do triângulo retângulo de catetos 3, mais a área do retângulo de lados 3 e 2.
• segunda maneira:
Área do paralelogramo de base 5 (3 + 2) e altura 3, mais a área do quadrado de lado 2 (composto pelos 2 triângulos retângulos).
VISTORIAS
Você chegou ao final da Trajetória. Reflita sobre tudo o que aprendeu e verifique a qualidade da sua aprendizagem. Resolva todos os exercícios a seguir no caderno.
CHECK-OUT
1. Calcule a área da superfície de cada figura.
3. Um terreno em forma de trapézio tem seu perímetro igual a 90 m. Veja sua representação:
a) Sabendo que AECD é um quadrado, AD mede 15 m e EB mede 20 m, calcule a área desse terreno.
b) Quanto mede BC? 25 m.
4. São dadas as medidas de uma aresta e das áreas das superfícies de três faces de um bloco retangular.
2.
a) Quais são as medidas das três dimensões desse bloco retangular?
b) Qual é a área da superfície desse bloco retangular?
c) Qual é o seu volume? 4 500 cm3
d) Um pequeno aquário com essas medidas teria qual capacidade, em litros? 4,5 litros.
Atividade 3
a) 152 + 15 20 2 = 225 + 150 = 375 m2
b) Considerando o perímetro, temos: BC + CD + DA + AE + EB = 90
BC + 15 + 15 + 15 + 20 = 90
BC + 65 = 90
BC = 90 – 65 = 25 m


Atividade 4
a) Considerando a face de aresta conhecida: 225 ÷ 15 = 15 cm Assim, sabemos que duas das faces são quadradas, restando descobrir a última medida: 300 ÷ 15 = 20 cm
b) Adicionado as áreas das faces:
2 ⋅ (300 + 300 + 225) = 1 650 cm2
c) V = 15 15 20 = 4 500 cm3
d) 4 500 ÷ 1 000 = 4,5 dm3 = 4,5 L

5. Laura tem uma loja e envia um formulário de satisfação para todos os clientes que atende. Veja as respostas obtidas durante um dia.
Insatisfeito Satisfeito Muito satisfeito
26 32
a) Qual é o tipo da variável apresentada?
b) Construa a tabela de frequências com FA e FR
c) Qual é o gráfico mais adequado para a situação de Laura? Justifique sua escolha e construa-o.
d) Escreva uma avaliação dos resultados, propondo soluções para os possíveis problemas que você encontrou.
7. Leia as informações que já foram publicadas um dia em algum meio de comunicação.
I. O susto faz o soluço parar.
II. Desodorante causa câncer de mama.
III. Água fervida com alho serve como tratamento para o coronavírus.
IV. Chá de erva-cidreira ajuda a dormir.
V. Comer mais de três ovos por dia faz mal.
Qualitativa ordinal. Gráfico de setores ou de barras. Resposta pessoal.
6. Um treinador pessoal de ginástica fez uma pesquisa sobre a idade e a massa corporal dos seus clientes. Veja os rols obtidos:
b)
Resposta pessoal.
a) Construa a tabela de frequências para a variável idade e a tabela de frequências com dados agrupados em classes para a variável massa corporal
b) Calcule a amplitude, a mediana, a moda e a média para a variável idade
c) O que seria necessário acontecer com a moda para que ela fosse igual a 33 anos? Calcule a média e a mediana para esses novos dados.
Pesquise sobre cada uma dessas notícias e descubra quais são fake news
São fake news: II, III e V.
• Compartilhe suas descobertas com os colegas e o professor.
8. Três amigos elaboraram cada um uma pergunta que será referência de uma pesquisa estatística.
INSTA_PHOTOS/SHUTTERSTOCK
• Pergunta do Luca: por que os adolescentes do Ensino Fundamental acreditam em fake news?

• Pergunta do Yudi: qual é a numeração dos calçados dos adolescentes do nosso bairro?
a) Luca: ético; Yudi: físico; Olívia: econômico.
• Pergunta da Olívia: quanto gastam com lanches, por mês, os adolescentes estudantes da nossa cidade?
a) Quanto ao motivo da pesquisa, classifique a pergunta de cada amigo, por seu aspecto físico, econômico ou ético.
b) Qual é a população de cada pergunta?
Satisfação FA FR Insatisfeito 2 5% Satisfeito 6 15% Muito satisfeito 32 80% TOTAL 40 100% Fonte: clientes da loja de Laura. Atividade 6 a) Tabela de frequências Idade FA FR 22 3 12% 23 3 12% 24 5 20% 25 2 8% 26 3 12% 27 1 4% 28 1 4% 29 1 4% 30 2 8% 31 1 4% 32 1 4% 33 1 4% 34 1 4% TOTAL 25 100% Tabela de frequências Massa corporal FA FR 60 |- 61 1 4% 61 |- 62 4 16% 62 |- 63 3 12% 63 |- 64 2 8% 64 |- 65 5 20% 65 |- 66 3 12% 66 |- 67 1 4% 67 |- 68 2 8% 68 |- 69 1 4% 69 |- 70 3 12% TOTAL 25 100% b) A = 34 – 22 = 12 anos; Md = 25 ano A = 34 – 22 = 12 anos; Md = 25 anos; Mo = 24 anos; x ≅ 2 A = 34 – 22 = 12 anos; Md = 25 anos; Mo = 24 anos; x ≅ 26,3 anos A = 34 – 22 = 12 anos; Md = 25 anos; Mo = 24 anos; x ≅ 26,3 anos c) Para que a moda fosse 33, uma possibilidade seria o treinador ter mais 5 alunos com idade de 33 anos.
Resposta possível: Pesquisa de satisfação Insatisfeito Satisfeito Muito satisfeito 80% 15% 5% Fonte: clientes da loja de Laura. 257 |
Atividade 9
Observando e organizando os dados, os estudantes podem determinar as medidas de tendência central e analisar as informações pautados nesses parâmetros.
c) Quanto ao modo de determinar a amostra, leia o que disse cada amigo.
Luca Yudi Olívia— Vou selecionar aleatoriamente adolescentes da minha rede e das redes dos meus dois melhores amigos.
— Como nosso bairro é formado por quarteirões organizados, vou selecionar um de cada quatro quarteirões e deixar um formulário na caixa de correio nas casas dos quarteirões selecionados.
— De cada escola da nossa cidade, vou pegar um número proporcional ao número de todos os alunos daquela escola.
Com base no que disseram, classifique a técnica de amostragem de cada um em: AAS (Aleatória simples), AE (Estratificada) ou AS (Sistemática). Luca: AAS; Yudi: AS; Olívia: AE.
9. Observe os dados relativos à variável tempo de residência que Sofia organizou em uma tabela de frequência.
a) Resposta possível: “Há a tendência da miscigenação, ou seja, que a população se misture e o grupo pardo cresça. no caso do aumento da autodeclaração de pretos, tem um fator a mais: reconhecimento da população negra em relação à própria cor, que faz mais pessoas se identificarem como pretas”. Observação: essa frase está no próprio site citado anteriormente.
a) Calcule a média, a moda e mediana.
b) Considerando o valor mínimo e o valor máximo da variável tempo de residência, a média está mais próxima de qual deles? E a moda? Ambas do valor máximo.
c) Qual é a faixa de anos em que estão concentrados os valores maiores do que ou iguais à mediana? Entre 14 e 20 anos.
10. Escreva as etapas do planejamento de uma pesquisa estatística. Respostas pessoais.
11. Leia o texto e o gráfico.
Entre 2012 e 2016, enquanto a população brasileira cresceu 3,4%, chegando a 205,5 milhões, o número dos que se declaravam brancos teve uma redução de 1,8%, totalizando 90,9 milhões. Já o número de pardos autodeclarados cresceu 6,6% e o de pretos, 14,9%, chegando a 95,9 milhões e 16,8 milhões, respectivamente. É o que mostram os dados sobre moradores da Pesquisa Nacional por Amostra de Domicílios Contínua 2016, divulgados hoje pelo IBGE.
Nas pesquisas domiciliares do IBGE, a cor dos moradores é definida por autodeclaração, ou seja, o próprio entrevistado escolhe uma das cinco opções do questionário: branco, pardo, preto, amarelo ou indígena.
PNAD-C | Distribuição da população, por cor ou raça BRASIL - 2012-2016
10
Peça que, depois de registrarem as etapas da pesquisa de opinião, os estudantes compartilhem para complementar as informações que possam ter esquecido.
1. Identificar as variáveis de interesse e a população do estudo.
2. Desenvolver um plano de coleta de dados (certificando-se de que a amostra é representativa da população) e os instrumentos de pesquisa.
3. Realizar a coleta de dados por meios digitais ou diretamente no local.
4. Processar os dados usando técnicas estatísticas.
5. Interpretar as dados utilizando, por exemplo, medidas-resumo.
Fonte: IBGE - Diretoria de Pesquisas, DPE. Disponível em: https://agenciadenoticias.ibge.gov.br/ agencia-noticias/2012-agencia-de-noticias/noticias/ 18282-populacao-chega-a-205-5-milhoes-com-menos-brancos-e-mais-pardos-e-pretos. Acesso em: 17 ago. 2022.
6. Decidir o que fazer sobre a população, levando em conta as informações obtidas pela amostra.
a) Pesquise sobre a tendência do aumento da autodeclaração da população preta e parda no Brasil.
b) Levando em conta que o gráfico não mostra dados sobre as populações amarela e indígena, esse gráfico poderia ser um gráfico de setores para os dados de 2012 e outro para os dados de 2015? Explique.
Poderia, desde que fossem conhecidos os dados dessas duas populações para cada ano; em cada gráfico de setor a totalidade dos índices deve perfazer 100%.
DE OLHO NA BÚSSOLA
Após resolver os exercícios da seção Check-out, verifique se você aprendeu a:
OBJETIVOS
Determinar, utilizando expressões de cálculo, áreas das superfícies de figuras geométricas (quadriláteros, triângulos e círculos).
Resolver e elaborar problemas que envolvam medidas de superfícies em situações diversas.
Reconhecer unidade de medida de volume e de capacidade e suas relações.
Resolver e elaborar problemas que envolvam cálculo de volume e de capacidade de recipientes com formato de bloco retangular.
Avaliar a adequação de
EXERCÍCIOS
1, 2, 3
3
4
4
Atividade 11
Poderia, desde que fossem conhecidos os dados dessas duas populações para cada ano; no gráfico de setores, a totalidade dos índices deve perfazer 100%.
Com a verificação do desempenho dos estudantes, planeje as atividades de remediação para que possam ter outras oportunidades de compreender os conteúdos em que apresentaram dificuldades no decorrer do processo de ensino e aprendizagem.
8 Identificar diferentes maneiras de selecionar amostras: casual simples, sistemática e estratificada.
Planejar pesquisa amostral desde a etapa da seleção da amostra até a escrita do relatório (este contendo gráficos, análises estatísticas por meio das medidas de posição e da amplitude e registros das conclusões).
8
10
Considerando os exercícios que resolveu, como você julga seu desempenho: insuficiente, parcialmente suficiente, satisfatório, plenamente satisfatório?
Prossiga ▶
Continue estudando! Retome esta Trajetória buscando, com professores e colegas, alternativas para superar os obstáculos de sua aprendizagem. Estude a seção Retornos e resolva novos exercícios referentes à Trajetória 4 que estão na seção Suplemente sua aprendizagem, ao final do livro.
Resposta pessoal. 259 |
Dicas de estudo
Há várias estratégias de estudo diário: fazer resumos, mapas mentais, esquemas, resolver exercícios, reler a teoria etc. Há também dicas de bem-estar apresentadas no texto Dê sugestões aos estudantes para que mantenham o estudo diário em um local calmo, silencioso, arejado e façam pausas para descanso.
DICAS DE ESTUDO
Aprendemos melhor quando nos sentimos bem! O bem-estar do seu corpo físico (alimentação correta e práticas corporais, por exemplo), da sua mente (ter uma boa noite de sono, ler bons livros, por exemplo) e do seu convívio social (ambiente pacífico, livre de bullying, por exemplo) pode, e muito, interferir na sua aprendizagem. O espaço por onde seu corpo circula, a qualidade das informações com as quais sua mente entra em contato e o afeto que você oferece e recebe devem ser levados em conta quando seu objetivo é aprender.
Compreender a ligação entre razão e emoção é cada vez mais presente nas pesquisas científicas, envolvendo a filosofia, a psicologia e, mais recentemente, os avanços da neurociência.
Atualmente existem estudos, envolvendo adolescentes, no intuito de compreender “as relações entre indicadores do bem-estar subjetivo (afeto positivo e negativo, satisfação com a vida e autoestima) e desempenho acadêmico (adequado e baixo) e comportamental (problemas de comportamento ou não).”
Os resultados têm mostrado que a satisfação com a vida, a autoestima e os afetos positivos trazem efeitos benéficos na aprendizagem de estudantes adolescentes, impactando o desenvolvimento humano em sua globalidade cognitiva, afetiva, social e moral. Os resultados das pesquisas reforçam a importância do desenvolvimento afetivo na escola e sua relação com a aprendizagem.
Pode ocorrer de que sua dificuldade nem seja o conteúdo em si e você nem esteja percebendo isso! Talvez seja a ausência de bem-estar em algum desses “espaços”: físico, mental ou emocional. Procure observá-los enquanto estuda e aprende, assim poderá perceber qual é o real impacto das condições oferecidas por eles no resultado da sua aprendizagem.
Baseado em: DELL'AGLI, Betânia Alves Veiga et. al. Indicadores de bem-estar subjetivo e a relação com o desempenho e comportamental em adolescentes. Notandum, ano XXV, n. 58, jan./abr.2022. CEMOrOC-Feusp/GTSEAM. Disponível em: https://periodicos.uem.br/ojs/index.php/notandum/article/view/58473/751375153343. Acesso em: 29 ago. 2022.
TRAJETÓRIA 1
Porcentagem
É possível interpretar um percentual como uma fração de denominador igual a 100. Por exemplo, 30% 30% = 30 100
Para calcular uma porcentagem de uma quantidade, multiplicamos a fração que representa o percentual pela quantidade. Por exemplo, 20% de 50 pode ser calculado por 20 100 50 = 1 000 100 = 10
Dízima periódica
Uma dízima periódica é uma representação decimal de um número racional com algarismos em sua parte decimal que se repetem infinitamente. Chamamos de período a parte que se repete:
8 parte inteira ! , 4 período ! 44 parte decimal ! " $ ou 8,4
A representação fracionária correspondente a uma dízima periódica é denominada fração geratriz dessa dízima periódica: 76
9 é a fração geratriz da dízima periódica 8,444 ...
Potenciação
Sendo a e b números inteiros, e m e n números naturais não nulos, então:
i a m = a a a m vezes ! " $ e a n = a a a n vezes ! " $
i a m a n = a m + n
i a m ÷ a n = a m – n , sendo a ≠ 0
i (a b)m = a m bm
i a b ⎛ ⎝ ⎞ ⎠ m = a m bm , sendo b ≠ 0
i (a m )n = a m n
Notação científica
A notação científica é uma forma de representar números utilizando potências de 10. Ao representar um número em notação científica, o fator que multiplica a potência de 10 é sempre um número entre 1 e 9. Por exemplo, 32 000 000 = 3,2 107 ou 0,002902 = 2,902 10–3
Radiciação
A radiciação é a operação matemática inversa (sob certas condições) da potenciação. De modo geral, podemos escrever que, sendo a um número racional não negativo e n um número natural diferente de 0, então:
A raiz quadrada de um número não negativo será sempre positiva ou nula.
É possível representar a radiciação utilizando expoentes fracionários:
Princípio multiplicativo
Utiliza-se o princípio fundamental da contagem, ou princípio multiplicativo, para calcular o total de possibilidades de combinações de certo evento. Por exemplo, quantos números de três algarismos distintos iniciados por 3 podem ser formados com os números 1, 2, 3 e 4?
Utilizando o princípio multiplicativo:
RETORNOS
Suplemente sua aprendizagem
As seções Retornos e Suplemente sua aprendizagem têm o objetivo de contribuir com o aprendizado e a autonomia do estudante.

Esta obra foi organizada em quatro Trajetórias, mas, nesta etapa, os estudantes são convidados a percorrer uma outra trilha diante das atividades exploradas nas aulas.
A proposta inicial – em Retornos – é revisitar os principais conteúdos discutidos em cada Trajetória com a leitura de um novo texto explicativo, mais enxuto, visto que ocorreu uma abordagem aprofundada anteriormente. Diante dessa leitura, o estudante pode usar diferentes estratégias para retomar os conteúdos em que percebeu a necessidade de aprimoramento ou aprofundamento, tais como: observar seus registros, elencar possíveis dúvidas e selecionar outros materiais de estudo.
Com a expectativa de verificação de seu próprio desempenho, os estudantes podem responder às questões selecionadas – em Suplemente sua aprendizagem – e fazer uma autoavaliação conforme o resultado alcançado.
Essa trilha pode ser percorrida ao final de cada Trajetória ou ao final do conjunto das quatro Trajetórias. Ambas as propostas enriquecem e contribuem com o processo de ensino e aprendizagem de Matemática.
É possível representar as possibilidades e obter esse total por meio de um diagrama de árvore:

A probabilidade de ocorrer um evento corresponde ao número que representa a razão entre a quantidade de elementos desse evento e a quantidade de elementos do espaço amostral.
A soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Sequência
Probabilidade
Quando um experimento é repetido em condições idênticas e seus resultados não podem ser previstos com certeza, esse experimento é dito aleatório
O conjunto formado por todos os resultados possíveis de um experimento aleatório é chamado de espaço amostral
Em um experimento aleatório, um evento corresponde a um subconjunto do espaço amostral.
TRAJETÓRIA 2
Expressões algébricas
Expressões matemáticas envolvendo letras, números e os sinais das operações são denominadas expressões algébricas. Nesse caso, as letras podem assumir diferentes valores e são denominadas variáveis. Por exemplo: xy + 5x – 3 é uma expressão algébrica com variáveis x e y
Em uma expressão algébrica, quando substituímos as variáveis por certo valor e realizamos as operações, obtemos o valor numérico da expressão algébrica. Por exemplo, em xy + 5x – 3, se x = 1 e y = 2, então:
xy + 5x – 3 ⇒ 1 2 + 5 1 – 3 = 4
Quando não é possível continuar realizando as operações de adição e subtração (não há mais termos semelhantes), essa expressão algébrica está em sua forma reduzida
Uma sequência é uma lista de elementos em uma determinada ordem. Cada um dos elementos é um termo da sequência
Uma sequência pode ser representada por: ( a1 1o termo ! , a2 2o termo ! , a3 3 o termo ! a n enés mo termo ! )
Uma sequência na qual os próximos termos dependem dos termos anteriores é denominada recursiva. Quando os termos seguintes não dependem dos termos anteriores é denominada não recursiva
Por exemplo, q + 2p – pq 4 está em sua forma reduzida.
Polinômio
Um polinômio é uma expressão algébrica que apresenta letras (variáveis) e números. Em um polinômio somente são permitidas operações de adição, subtração e multiplicação entre as variáveis. As variáveis também devem possuir números naturais como expoentes. Por exemplo, x 3 – x 2 + x 1 – 1 é um polinômio; wx y e m + m não são polinômios.
Um monômio é um polinômio que tem apenas multiplicação entre números e variáveis. Por exemplo: 3 x 2 y 4 é um monômio. Ao adicionar ou subtrair dois monômios, obtemos um binômio e, ao adicionar ou subtrair três monômios, obtemos um trinômio
Um monômio possui uma parte literal e uma parte numérica denominada coeficiente
Por exemplo:
Sistema de equações polinomiais de 1o grau
Dadas duas equações polinomiais de 1o grau, podemos construir um sistema linear de equações polinomiais de 1o grau. Por exemplo:
!
5 coefic ente ! k 2 parte literal
As propriedades das operações podem ser utilizadas para operações entre polinômios.
Ao adicionar ou subtrair polinômios, deve-se operar apenas entre monômios que possuem partes literais iguais (monômios semelhantes).
Ao multiplicar ou dividir polinômios, podem-se utilizar propriedades das potências.
É possível que o resultado da divisão entre polinômios não seja um polinômio, mas uma expressão algébrica fracionária
Equações polinomiais de 1o grau
Equações que podem ser reduzidas à forma ax + b = c , com a ≠ 0 , são denominadas equações polinomiais de 1o grau
Existem equações polinomiais de 1o grau com mais de uma incógnita. Resolver a equação significa descobrir os valores de cada incógnita que, simultaneamente, tornam a equação verdadeira.
Em uma equação polinomial de 1o grau com duas incógnitas a e b, podemos associar a cada solução um par ordenado (x, y) e representá-lo no plano cartesiano.
O conjunto de todos os pares ordenados soluções de uma equação polinomial de 1o grau com duas variáveis pode ser representado por uma reta no plano cartesiano
TRAJETÓRIA 3
Transformações geométricas
Uma transformação geométrica é uma correspondência entre duas figuras de modo que, partindo da primeira, obtém-se a segunda preservando sua forma ou suas medidas (ou ambas).
Uma transformação geométrica que preserva a forma e as medidas é chamada de transformação isométrica. Se preserva a forma, mas não preserva as medidas (ocorre uma ampliação ou redução), então a transformação é homotética
2 x – y = 5
4x + 3y = –4
Resolver o sistema significa obter valores de x e y que sejam, simultaneamente, soluções de ambas as equações.
Representando as soluções de cada equação de um sistema linear como uma reta no plano cartesiano, a única solução do sistema linear corresponde ao ponto de intersecção entre as duas retas, se elas forem concorrentes
Quando as retas que representam as soluções de cada equação de um sistema linear são paralelas distintas, o sistema não tem solução. Quando as retas são coincidentes, o sistema possui infinitas soluções
A solução de um sistema de equações pode ser obtida tanto graficamente como pelos métodos da adição e da substituição
Equações polinomiais de 2o grau
Estudamos equações que apresentam apenas uma incógnita com expoente 2 e podem ser escritas como ax 2 + bx + c = 0, com a ≠ 0 ; elas recebem o nome de equações polinomiais de 2o grau. No caso de b = 0 ou c = 0, chamamos de equação polinomial de 2o grau incompleta
As isometrias são transformações geométricas que preservam as distâncias entre pontos e as aberturas de ângulos Podem ser de: translação, rotação e reflexão (ou composições delas).
Congruência de triângulos
Um triângulo ABC é congruente ao triângulo
A’ B’ C’ quando é possível estabelecer uma correspondência entre seus vértices de modo que:
I. Os vértices correspondentes determinem ângulos internos com medidas iguais.
II. Os lados homólogos tenham medidas de comprimento iguais.
Escrevemos: △ ABC ≡ △ A’B’C’ (lê-se: triângulo ABC é congruente ao triângulo A’B’C ’ ).
Se dois triângulos têm, na devida ordem, congruentes:
• dois lados e o ângulo formado por esses dois lados (caso LAL);
• dois ângulos e o lado adjacente a esses ângulos (caso ALA);
• os três lados (caso LLL);
• um lado, o ângulo adjacente a ele e o ângulo oposto a ele (caso LAAo); então, os triângulos são congruentes.
Quadriláteros
Em todo paralelogramo, as diagonais cortam-se nos correspondentes pontos médios.
Todo losango tem diagonais perpendiculares.
Em todo retângulo as diagonais são congruentes.
Lugar geométrico
Fixado um plano α , um conjunto de pontos L é o lugar geométrico que tem uma propriedade p cumprindo duas condições:
I. Todos os pontos de L usufruem da propriedade p
II. Nenhum outro ponto do plano α que esteja fora de L usufrui da propriedade p Circunferência é o lugar geométrico dos pontos do plano que distam r de um ponto C Mediatriz é o lugar geométrico dos pontos do plano que equidistam de dois pontos A e B distintos.


Bissetriz é o lugar geométrico dos pontos do plano que equidistam dos lados de um ângulo dado.
Construção de polígonos regulares
Um polígono é regular se todos os seus lados são congruentes e todos os seus ângulos internos são congruentes.
Um ângulo central relativo a uma circunferência é o ângulo que tem o vértice no centro da circunferência.
Para construir um triângulo regular inscrito em uma circunferência, deve-se:
I. Construir, com o compasso, uma circunferência de centro O e um raio qualquer.
II. Destacar um ponto A na circunferência. Com a ponta-seca em A e abertura do raio, traçar uma semicircunferência passando pelo centro O e cortando a circunferência em B e C
III. Com centro em B (ou C) e abertura BC, traçar um arco de circunferência que corte a circunferência em um ponto D
IV. Traçar os segmentos BC , CD e DB. A figura obtida é o triângulo regular.
Para construir um quadrado inscrito em uma circunferência, deve-se:
I. Construir, com o compasso, uma circunferência de centro O e um raio qualquer.
II. Traçar o diâmetro de extremidades A e B. Considerando esse diâmetro, traçar sua mediatriz que corta a circunferência em C e D
III. Traçar os segmentos AC , CB, BD e DA A figura obtida é o quadrado.
Razão e proporção
Grandeza pode ser definida como o atributo físico de um corpo que pode ser qualitativamente distinguido e quantitativamente determinado.
Duas razões com termos não nulos, a ! b e c ! d, determinam uma proporção quando as frações a b e c d são equivalentes, ou seja:
a b = c d
Essa proporção pode ser escrita assim: a : b = c : d . Lê-se: a está para b assim como c está para d
TRAJETÓRIA 4
Superfície
Volume e capacidade
O volume de uma figura geométrica é a medida do espaço que essa figura ocupa.
O volume de um bloco retangular de arestas medindo a, b e c é dado por V = a b c
Sejam
) duas sequências de números não nulos:
• as sequências são diretamente proporcionais se existe um número k tal que
• as sequências são inversamente proporcionais se existe um número k tal
e k é chamado de constante de proporcionalidade
Pode haver outras relações entre duas sequências de modo que as grandezas não sejam nem direta, nem inversamente proporcionais
Calculamos a área da superfície destas figuras geométricas planas pelas expressões algébricas (fórmulas):




Algumas unidades de medida de volume e suas relações:

A capacidade, geralmente associada a fluidos, é o volume interno de um recipiente.
A relação fundamental entre unidades de medida de volume e de capacidade é:
1 dm3 = 1 L

Notícias e credibilidade
Fake news é a informação fabricada, geralmente com intenção de causar dano, que imita conteúdo noticioso e concorre com os fatos.
A gestão da credibilidade das informações é um conjunto de ações voltadas para a análise crítica da qualidade da informação.
Pesquisa estatística
Gráficos
A escolha por um tipo de gráfico para representar determinado conjunto de dados deve levar em consideração a intenção daquilo que se deseja comunicar: se é relacionar a parte com o todo, a melhor opção é o gráfico de setores; se é comparar as partes entre si, o gráfico de colunas ou o de barras pode ser mais adequado; se é acompanhar a evolução dos dados ao longo do tempo, então pode ser interessante utilizar o gráfico de linhas
Frequências
A frequência absoluta (FA) de um valor é a quantidade de vezes que esse valor ocorreu para determinada variável.
A frequência relativa (FR) de um valor é a razão entre a frequência absoluta e a frequência total.
Medidas de posição
Dado um conjunto de dados:
• o valor que o divide em 2 subconjuntos de mesmo tamanho é denominado mediana (Md);
• a moda (Mo) é o valor com maior frequência;
• a média aritmética ( x ) corresponde à soma de todos os valores desse conjunto dividida pelo número de elementos do conjunto.
A pesquisa estatística é composta pelas etapas: compreensão do problema, planejamento da pesquisa, amostragem, coleta de dados, tratamento dos dados, análise dos dados e tomada de decisão.
A população é o conjunto de todos os elementos de uma pesquisa e a amostra é um subconjunto da população. Cada um dos elementos de uma pesquisa estatística é denominado indivíduo. Na amostragem:
• aleatória simples, os elementos da população são enumerados um a um. São sorteados aleatoriamente indivíduos para participar da pesquisa;
• estratificada, a população é dividida em “estratos” – subconjuntos organizados de acordo com determinadas características e quantidade de elementos;
• sistemática, o pesquisador determina o número de elementos da amostra e descobre um intervalo que o auxiliará a determinar quais elementos farão parte da amostra.
As variáveis de interesse de uma pesquisa correspondem às características de interesse a serem medidas nos elementos da amostra.
O relatório de pesquisa deve compreender elementos como título; objetivo; resumo do trabalho; introdução apresentando a problemática; descrição dos procedimentos da pesquisa; resultados obtidos; análise e discussão dos resultados; conclusão; e referências bibliográficas.
A tomada de decisão deve levar em conta os dados coletados e as análises realizadas sobre eles.
Matemática
NÚMEROS
(EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.
(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.
(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
ÁLGEBRA
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax 2 = b
(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
(EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.
(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.
GEOMETRIA
(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90o, 60o, 45o e 30o e polígonos regulares.
(EF08MA16) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.
(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.
(EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
NÃO ESCREVA NO SEU LIVRO.
GRANDEZAS E MEDIDAS
(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.
(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
PROBABILIDADE E ESTATÍSTICA
(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
(EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).
(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.
Outras disciplinas
LÍNGUA PORTUGUESA
(EF69LP15) Apresentar argumentos e contra-argumentos coerentes, respeitando os turnos de fala, na participação em discussões sobre temas controversos e/ou polêmicos.
(EF69LP33) Articular o verbal com os esquemas, infográficos, imagens variadas etc. na (re)construção dos sentidos dos textos de divulgação científica e retextualizar do discursivo para o esquemático – infográfico, esquema, tabela, gráfico, ilustração etc. – e, ao contrário, transformar o conteúdo das tabelas, esquemas, infográficos, ilustrações etc. em texto discursivo, como forma de ampliar as possibilidades de compreensão desses textos e analisar as características das multissemioses e dos gêneros em questão.
(EF89LP02) Analisar diferentes práticas (curtir, compartilhar, comentar, curar etc.) e textos pertencentes a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etc.) envolvidos no trato com a informação e opinião, de forma a possibilitar uma presença mais crítica e ética nas redes.
(EF89LP04) Identificar e avaliar teses/opiniões/posicionamentos explícitos e implícitos, argumentos e contra-argumentos em textos argumentativos do campo (carta de leitor, comentário, artigo de opinião, resenha crítica etc.), posicionando-se frente à questão controversa de forma sustentada.
(EF08LP01) Identificar e comparar as várias editorias de jornais impressos e digitais e de sites noticiosos, de forma a refletir sobre os tipos de fato que são noticiados e comentados, as escolhas sobre o que noticiar e o que não noticiar e o destaque/enfoque dado e a fidedignidade da informação.
NÃO ESCREVA NO SEU LIVRO.ARTE
(EF69AR31) Relacionar as práticas artísticas às diferentes dimensões da vida social, cultural, política, histórica, econômica, estética e ética.
GEOGRAFIA
(EF08GE15) Analisar a importância dos principais recursos hídricos da America Latina (Aquífero Guarani, Bacias do rio da Prata, do Amazonas e do Orinoco, sistemas de nuvens na Amazônia e nos Andes, entre outros) e discutir os desafios relacionados à gestão e comercialização da água.
(EF08GE16) Analisar as principais problemáticas comuns às grandes cidades latino-americanas, particularmente aquelas relacionadas à distribuição, estrutura e dinâmica da população e às condições de vida e trabalho.
CIÊNCIAS
(EF08CI07) Comparar diferentes processos reprodutivos em plantas e animais em relação aos mecanismos adaptativos e evolutivos.
(EF08CI12) Justificar, por meio da construção de modelos e da observação da Lua no céu, a ocorrência das fases da Lua e dos eclipses, com base nas posições relativas entre Sol, Terra e Lua.
(EF08CI15) Identificar as principais variáveis envolvidas na previsão do tempo e simular situações nas quais elas possam ser medidas.
ENSINO RELIGIOSO
(EF08ER06) Analisar práticas, projetos e políticas públicas que contribuem para a promoção da liberdade de pensamento, crenças e convicções.
EDUCAÇÃO FÍSICA
(EF89EF11) Identificar as diferenças e semelhanças entre a ginástica de conscientização corporal e as de condicionamento físico e discutir como a prática de cada uma dessas manifestações pode contribuir para a melhoria das condições de vida, saúde, bem-estar e cuidado consigo mesmo.
25
Trajetória 1
1. (Enem) Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, tem uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são:
IMC = massa (kg) [altura (m)]2 RIP = altura (cm) massa (kg) 3
ARAÚJO, C. G. S.; RICARDO, D. R. Índice de Massa Corporal: um questionamento científico baseado em evidências. Arq. Bras. Cardiol., v. 79, n. 1, 2002 (adaptado). Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m2, então ela possui RIP igual a,
a) 0,4 cm/kg 1 3
b) 2,5 cm/kg 1 3
c) 8 cm/kg 1 3
d) 20 cm/kg 1 3
e) 40 cm/kg 1 3
atingiu o índice máximo. Qual desses países obteve o maior IDH?
a) O primeiro.
b) O segundo.
c) O terceiro.
d) O quarto.
e) O quinto.
3. (UNICAMP) O projeto PRODES – Monitoramento do desmatamento das formações florestais na Amazônia Legal –, do INPE (Instituto Nacional de Pesquisas Espaciais), monitora as áreas desmatadas da Amazônia legal e mantém um registro da área desmatada por ano. Um levantamento sobre esses dados a partir de 2016 mostrou que em 2019 houve um acréscimo de 35% da área desmatada em relação a 2018, de 45% em relação a 2017 e de 28% em relação a 2016.
(Fonte: http://terrabrasilis.dpi.inpe.br. Acessado em: 12/12/2020.)
Sabendo que a soma das áreas desmatadas nos anos de 2017, 2018 e 2019 foi de 24 600 km2, a área desmatada no ano de 2019 está entre
a) 8 601 km2 e 9 200 km2
b) 9 201 km2 e 9 800 km2
= x ⇒ y =
4. 75% de 900 é igual a 675, ou seja, compareceram 675 especialistas.
675 – n = 50 100 900
–
n = 450
n = 225
270 | MANUAL DO PROFESSOR
2. (Enem) O Índice de Desenvolvimento Humano (IDH) é uma medida usada para classificar os países pelo seu grau de desenvolvimento. Para seu cálculo, são levados em consideração a expectativa de vida ao nascer, tempo de escolaridade e renda per capita, entre outros. O menor valor deste índice é zero e o maior é um. Cinco países foram avaliados e obtiveram os seguintes índices de desenvolvimento humano: o primeiro país recebeu um valor X, o segundo X , o terceiro X 1 3 , o quarto X 2 e o último X 3. Nenhum desses países zerou ou

c) 8 801 km2 e 10 400 km2
d) 10 401 km2 e 11 200 km2
4. (UNB) Participando de um Congresso, compareceram 900 profissionais da Área, sendo 75% constituído de especialistas. Se n especialistas se retirassem, o percentual deles, em relação ao total de profissionais, inicialmente presentes, cairia para 50%, então pode-se concluir que o valor preciso de n é
a) 225
b) 275
d) 450 e) 675
| SUPLEMENTE SUA APRENDIZAGEM NÃO ESCREVA NO SEU LIVRO.
Assim, o valor preciso de n é 225.
Alternativa a
5. Para as sequências aleatórias de três letras que o macaco digita, há 5 possibilidades de escolha de letras e 3 letras digitadas, ou seja 53, que é igual a 125 possibilidades.
A sequência “SER” é uma única possibilidade nesse universo.
Assim, a probabilidade pode ser calculada:
P = casos favoráveis
total de possibilidades = 1 125
Alternativa d
6. Como a produção de arroz tem um aumento constante, podemos expressá-la algebricamente por meio de uma sequência, com cada ano de produção correspondendo a um termo.
5. (UFPR) Uma adaptação do Teorema do Macaco afirma que um macaco digitando aleatoriamente num teclado de computador, mais cedo ou mais tarde, escreverá a obra “Os Sertões” de Euclides da Cunha. Imagine que um macaco digite sequências aleatórias de 3 letras em um teclado que tem apenas as seguintes letras: S, E, R, T, O. Qual é a probabilidade de esse macaco escrever a palavra “SER” na primeira tentativa?
a) 1 5
b) 1 15
c) 1 75
d) 1 125 e) 1 225
6. (Enem) As projeções para a produção de arroz no período de 2012 – 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
Então, a soma de todos os números ímpares menores do que 100 é:
a) 422
b) 492
c) 502
d) 992
e) 1002
8. (UEMA) Os planetas do sistema solar do qual nosso planeta Terra faz parte realizam órbitas em torno do Sol, mantendo determinada distância, conforme mostra a figura a seguir.
7. Se observarmos a sequência:
• para o primeiro número ímpar (1), a soma é igual a 12;
• para os dois primeiros números ímpares, a soma é igual a 22;
• para os três primeiros números ímpares, a soma é igual a 32; e assim por diante. Como existem 50 números ímpares partindo do 1 até 100, então a soma é igual a 502 Alternativa c
8. A distância indicada entre a Terra e o Sol é 149 600 000 km; em metros são 149 600 000 000 m. Expressando esse valor em notação
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de:
a) 497,25.
b) 500,85.
c) 502,87.
d) 558,75.
e) 563,25.
7. (UFRGS) Desde a Grécia Antiga, sabe-se que a soma dos números ímpares consecutivos, a partir do 1, é sempre um quadrado perfeito. Como exemplo, tem-se
Fonte: Disponível em: http://webciencia.com. Acesso em: 27 ago. 2014. (adaptado)

O valor, em metros, da distância da Terra ao Sol em potência é
a) 14,96 × 10–11
b) 1,496 × 1010
c) 14,96 × 10–10
d) 1,496 × 1011
e) 14,96 × 1011
9. (UNICAMP) Em uma família, cada filha tem o mesmo número de irmãs e irmãos, e cada filho tem um número de irmãs igual ao dobro do número de irmãos. O número total de filhos e filhas dessa família é igual a
a) 11.
b) 9.
c) 7.
d) 5.
ou seja, nessa sequência, com exceção do 1º termo, os seguintes são obtidos adicionando 1,25 ao termo anterior. A lei de formação é:
a1 = 50,25
a n = a n–1 + 1,25, n ≥ 2
Para calcular a quantidade produzida durante o ano de 2012 até 2021, determinamos os dez primeiros termos dessa sequência e fazemos a somatória deles. Os termos são:
a1 = 50,25
a2 = 50,25 + 1,25 = 51,5
a3 = 51,5 + 1,25 = 52,75
a4 = 52,75 + 1,25 = 54
a5 = 54 +1,25 = 55,25
a6 = 55,25 + 1,25 = 56,5
a7 = 56,5 + 1,25 = 57,75
a8 = 57,75 + 1,25 = 59
a9 = 59 + 1,25 = 60,25
a10 = 60,25 + 1,25 = 61,5
9. Do ponto de vista de uma filha, ela tem o mesmo número de irmãs e irmãos, logo, há um homem a menos do que a quantidade total de mulheres. Por outro lado, se cada filho tem um número de irmãs igual ao dobro do número de irmãos, o número de mulheres é igual ao número de homens, menos um. Sendo m o número de mulheres e h o número de homens,
Trajetória 2
10.Sejam x, y e z, respectivamente, o número de mesas de 4, 5 e 6 lugares, tem-se que:
Trajetória 2
10. (UECE) Na sala de reuniões de um condomínio, há mesas de 4, 5 e 6 lugares, perfazendo o total de 22 mesas. Na última reunião que houve, compareceram 113 pessoas, que foram acomodadas nessas mesas, ocupando todos os lugares. Se o número de mesas com 6 lugares era o dobro do número de mesas com 5 lugares, então, o número de mesas com 4 lugares era
a) 10.
b) 7.
c) 4.
d) 13.
Alternativa b
11. Sejam A, B, C e D as quantidades de figurinhas de Abel, Bruno, Caio e Daniel, respectivamente. Do enunciado, sabemos que D = 60 e A = B. Além disso, temos a seguinte equação:

11. (CFSd PM-ES) Quatro amigos, Abel, Bruno, Caio e Daniel, são colecionadores de figurinhas. Sabe-se que Abel possui metade da quantidade de figurinhas de Daniel mais um terço da quantidade de figurinhas de Caio; que Bruno possui o dobro da quantidade de figurinhas de Caio mais a quarta parte da quantidade de figurinhas de Daniel; que Daniel tem 60 figurinhas, e que Abel e Bruno possuem a mesma quantidade de figurinhas. Os quatro amigos possuem, juntos:
a) 125 figurinhas.
b) 128 figurinhas.
c) 130 figurinhas.
d) 132 figurinhas.
e) 135 figurinhas.
12. (EAM – Aprendiz de Marinheiro) Analise a figura a seguir:
y e z. A expressão algébrica que representa o perímetro desse terreno é:
a) 2 x + 3y + z
b) 3 x + 4y + 2 z
c) 3 x + 3y + z
d) 3 x + 2y + 3z
e) 4 x + 3y + 2 z
13. (Enem) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x ) (3 – y )
C = 9
Sabendo que C é igual a 9, calculamos A e B: A = 30 + 9 3 = 33 = B
Determinando o total:
33 + 33 + 9 + 60 = 135 figurinhas
Alternativa e
12. Determinando o perímetro pela soma das medidas dos lados do terreno:
Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis x,
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:
a) 2xy
b) 15 – 3x
c) 15 – 5y
d) –5y – 3x
e) 5 y + 3 x – xy
14. (UERJ) Os números inteiros x e y satisfazem às seguintes equações:
⎧ ⎨ ⎪
⎧ ⎨ ⎪ ⎩ ⎪
3 y
2
5 x + 3 5 y = 37 x – y = 30
Logo, x + y é igual a:
a) 85
b) 90 c) 95 d) 80
2 x 5 + 3 y 5 = 37
x – y = 30
Isolando x na 2a eq e substituindo na 1a →
⎧ ⎨ ⎪ ⎩ ⎪ ⇒
15. (Enem) Um posto de combustível vende 10 000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10 200 litros.
2(30 + y ) 5 + 3 y 5 = 37
x = 30 + y
12 + 2 y 5 + 3 y 5 = 37
⎧ ⎨ ⎪ ⎩ ⎪ ⇒
x = 30 + y
5 y 5 = 25
⎧ ⎨ ⎪ ⎩ ⎪ ⇒ y = 25
x = 30 + y ⎧ ⎨ ⎩
x = 30 + y
y = 25
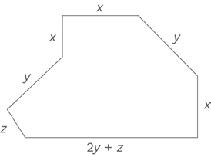
x = 55 ⎧ ⎨ ⎩
x = 30 + 25 ⎧ ⎨ ⎩ ⇒ y = 25
Assim, x + y = 55 + 25 = 80
Alternativa d
Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é:
a) V = 10 000 + 50x – x 2
b) V = 10 000 + 50x + x 2
c) V = 15 000 – 50x – x 2
d) V = 15 000 + 50x – x 2
e) V = 15 000 – 50x + x 2
16. (VUNESP) Uma sala quadrada, com 36 m² de área, foi reformada, tornando-se uma sala retangular, de modo que sua largura
Trajetória 3
17. (Enem/PPL) Isometria é uma transformação geométrica que, aplicada a uma figura, mantém as distâncias entre pontos. Duas das transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:


permaneceu a mesma, mas seu comprimento foi aumentado, conforme mostra a figura. x x
2y = 28 12 = 16
1a) Reflexão no eixo x;
2a) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4a) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5a) Reflexão no eixo x; Disponível em: www.pucsp.br. Acesso em: 2 ago. 2012.
15. Escrevendo uma expressão para litros vendidos (l) com relação ao desconto dado, em centavos (x):
l = 10 000 + 100x
e uma expressão para o preço do litro (p) com relação ao desconto dado (x), desconto esse que devemos multiplicar por 0,01 para converter de centavos para reais:
p = 1,5 – 0,01x
O valor arrecadado é o produto dos litros vendidos por preço do litro; assim temos:
x ?
Antes da reforma Depois da reforma Figuras fora de escala.
Se após a reforma o perímetro da sala aumentou 4 m, então sua área aumentou
a) 6 m²
b) 8 m²
c) 10 m²

d) 12 m²
e) 14 m²
y = 8 m
Portanto, a nova medida da área é de 6m × 8m = 48 m2 , 12 m2 a mais do que a área original.
Alternativa d
Trajetória 3
17. Basta realizar as transformações em sequência:
1a transformação:
Após as cinco transformações, qual é a posição final da figura?
2
3a transformação:
V = (10 000 + 100x ) (1,5 – 0,01x )
V = 15 000 + 150x – 100x – x 2
V = 15 000 + 50x – x 2
Alternativa d
16.Sabemos, pelos dados do enunciado, que x2 = 36, logo, x = 6 m .



O perímetro anterior era de 6 + 6 + 6 + 6 = 24 m.
Seja y a medida do novo comprimento, como o perímetro aumentou 4 m, temos:
4a transformação:
y
5a transformação:
18. Observando a figura, para retornar à posição original, girando-a no sentido horário, o ângulo será de:
45o + 90o = 135o Alternativa b
18. (Enem) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B. Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45o com a linha do horizonte.


figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O
A imagem que representa a nova figura é:
a)
1o quadrante


b)
2o quadrante
19.A nova figura deve apresentar simetria em relação ao ponto O, ou seja, as distâncias de todos os pontos de uma parte da figura ao ponto O devem ser as mesmas dos pontos simétricos da outra figura em relação a esse mesmo ponto O. Podemos verificar a simetria da imagem da alternativa E, dividindo-a em quadrantes: O 4o quadrante
3o quadrante
Alternativa e
c)
d)
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360o
A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de
a) 90o no sentido horário.
b) 135o no sentido horário.
c) 180o no sentido anti-horário.
d) 270o no sentido anti-horário.
e) 315o no sentido horário.
19. (Enem) Um programa de edição de imagens possibilita transformar figuras em outras mais complexas. Deseja-se construir uma nova


e)

20. (UEA) Em uma madrugada, a razão entre o número de adultos e o número de crianças atendidas em um pronto-socorro foi igual
a 2 5 . Se o total de pessoas atendidas nessa madrugada foi igual a 84, o número de crianças atendidas foi
21. (IESES) Três pedreiros constroem uma casa em 15 dias. Se for acrescentando mais dois pedreiros a uma obra igual em quantos dias essa casa ficará pronta?
a) 9 dias
b) 12 dias
22.A figura é formada por um trapézio e um semicírculo.
a) 50.
b) 55. c) 60. d) 65. e) 70.
Trajetória 4
22. (Avança SP) Observe a figura abaixo: Considere π = 3
8 cm 8 cm
A CD
E B
8 cm 6 cm
A área da figura, em cm², é de:
a) 88 cm2
b) 96 cm2
c) 112 cm2
d) 184 cm2 e) 208 cm2
23. (Enem) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a

a) 5 cm.
b) 6 cm.
c) 12 cm.
d) 24 cm.
e) 25 cm.
c) 25 dias
d) 21 dias
24. (OBMEP) O quadrado abaixo está dividido em nove quadradinhos iguais. A área pintada de vermelho mede 6 cm2. Quanto mede a área pintada de azul?
23.Sendo VP e VC os volumes das barras de chocolate de formatos como o do “paralelepípedo” e do “cubo”, respectivamente, e sendo a a medida da aresta do cubo,
a) 10 cm2
b) 12 cm2
c) 14 cm2
d) 16 cm2
e) 18 cm2
25. (Enem) A Comissão Interna de Prevenção de Acidentes (CIPA) de uma empresa, observando os altos custos com os frequentes acidentes de trabalho ocorridos, fez, a pedido da diretoria, uma pesquisa do número de acidentes sofridos por funcionários. Essa pesquisa, realizada com uma amostra de 100 funcionários, norteará as ações da empresa na política de segurança no trabalho. Os resultados obtidos estão no quadro.
20.Sejam x o número de adultos atendidos e y o número de crianças. Do enunciado, sabemos que:
21. Há uma relação de proporcionalidade inversa entre a quantidade de pedreiros e os dias de trabalho para a construção de uma casa. Temos:
24.A parte vermelha é formada por um quadradinho mais 4 metades de quadradinhos. Essas 4 metades juntas têm a mesma área que a de 2 quadradinhos. Assim, a área total da parte vermelha é igual a 3 quadradinhos. Como essa área mede 6 cm 2 , cada quadradinho tem uma área de 2 cm2 O quadrado inteiro é formado por 9 quadradinhos. Assim, a área em azul equivale à área de 6 quadradinhos, que é igual a 12 cm2 Alternativa b
A média do número de acidentes por funcionário na amostra que a CIPA apresentará à diretoria da empresa é
27. (Prefeitura de Nova Hartz-RS) Em uma urna, há 7 bolas azuis, 8 bolas amarelas, 6 bolas verdes e 9 bolas brancas. Sorteando-se, ao acaso, uma das bolas dessa urna, a probabilidade de, na primeira retirada, ela sair verde é de:
a) 1 6
b) 1 5
c) 1 4
d) 1 2
28. (Avança SP) Raquel deseja comprar 15 litros de uma bebida vendida na seguinte embalagem: 5 cm
26. (UFPR) O gráfico abaixo representa a quantidade aproximada de animais adotados ao longo de cinco anos em uma determinada cidade. Qual foi a média anual de animais adotados, ao longo dos cinco anos nessa cidade?

Quantas embalagens iguais a essa, no mínimo, devem ser adquiridas?
a) 15 embalagens
b) 30 embalagens
c) 34 embalagens
d) 45 embalagens
e) 53 embalagens
29. (VUNESP) A figura a seguir ilustra o canal de acesso ao porto de Cabedelo que possui extensão total de aproximadamente 6 km, largura aproximada de 120 m e profundidade aproximada de 9 m.
9 m
120 m
6 km
Figura fora de escala Supondo que essas medidas fossem as medidas de um paralelepípedo reto, o volume de água, em milhões de m3, que ele poderia conter é
25.O total de acidentes é: x
x = 1,11
Dividindo esse número pelo número de funcionários, obtemos a média:
111 100 = 1,11
Alternativa d
b) 6,12 c) 5,94 d) 5,88 e) 5,76
a) 6,48
26.Basta calcular uma média aritmética simples:
x = 300 + 400 + 400 + 450 + 500 5
x = 2 050 5
x = 410
Alternativa d
27. São 6 bolas verdes de um total de 7 + 8 + 6 + 9 = 30 bolas, logo:
P(verde) = 6 30 = 1 5
Alternativa b
Leituras para o aluno
O livro da Matemática, de vários autores, tradução de Maria da Anunciação Rodrigues Nada melhor que uma boa visualização gráfica para entender melhor a Matemática. Neste livro, o famoso “desenha para eu entender melhor, por favor?” ganha vida e potencializa imensamente a aprendizagem matemática.
Desbravadores da Matemática: da alavanca de Arquimedes aos fractais de Mandelbrot, por Ian Stewart
A Matemática não é algo que já existia e foi apenas descoberto pelos seres humanos. Ela foi criada pela mente humana, e sua evolução contém diversas figuras importantes que muito contribuíram para que ela se tornasse o que é hoje. Neste livro, mais de 20 biografias são exploradas em uma jornada para compreender a essência da Matemática e sua construção.
Quem mexeu na minha bagunça?, por Celi Piernikarz

Gastar dinheiro exageradamente é algo que a Matemática pode nos ajudar a controlar. Mas será que isso tem a ver só com a Matemática? Organizar nossa vida será que não ajuda também? Combinar as habilidades matemáticas com uma nova forma de trabalhar os hábitos do dia a dia pode trazer mudanças inesperadas e positivas.
A vizinha antipática que sabia Matemática, por Eliana Martins
O que uma vizinha chata pode nos ensinar sobre a Matemática? Que, muito diferente do que se imagina, ela tem muitas coisas interessantes e que, por meio de desafios, é possível aprender muito bem! Uma leitura leve e agradável, com desafios que farão até os adultos pararem para pensar.
Matemática mortífera, por Kjartan Poskitt
Um gângster chamado Jimmy Dedão e seus amigos mafiosos precisam de Matemática? Sim! E você poderá acompanhar a história deles e todos os percalços por que passam ao terem que enfrentar os números em meio a uma vida de muitas aventuras.
O mistério do caderninho preto, por Ruth Rocha
Imagine escrever um livro sobre mistérios e aventuras e, no meio do caminho, tudo que acontece no livro começa a acontecer de verdade? As relações entre as realidades começam a se entrelaçar, e entender a lógica disso pode ser a única forma de solucionar o caso!
28.
V = 5 5 5 18 = 450 cm3
Sabemos que 450 cm3 equivale a 0,45 L, logo, cada embalagem ocupa 0,45 L.
Calculando a quantidade de embalagens necessárias para totalizar 15 L:
15 ÷ 0,45 = 33,3
Serão necessárias, no mínimo, 34 embalagens. Alternativa c
29.
V = 6 000 9 120 = 6 480 000 m3
Ou seja, 6,48 milhões de metros cúbicos. Alternativa a
Referências bibliográficas
17 DICAS de como controlar a ansiedade. Instituto de Psiquiatria Paulista Disponível em: https://psiquiatriapaulista.com. br/17-dicas-de-como-controlar-a-ansiedade. Acesso em: 11 ago. 2022. Conjunto de dicas explicativas para auxiliar no combate à ansiedade, incluindo exercícios de respiração, meditação, prática de exercícios físicos e alguns outros.
A IMPORTÂNCIA da tecnologia no nosso cotidiano. Infornet, 16 dez. 2020. Disponível em: www.infornet.com.br/blog/a-importancia-da-tecnologia-no-nosso-cotidiano. Acesso em: 1 jul. 2022. Recorte visual de página da web na qual usuários postam comentários sobre uma discussão a respeito da importância e dos impactos da tecnologia em nosso cotidiano, com destaques positivos como a inclusão social e acesso rápido ao conhecimento.
ATIVIDADE física aumenta disposição e autoestima. Portal Saúde Brasil Disponível em: https://saudebrasil.saude.gov.br/eu-quero-me-exercitar-mais/atividade-fisica-aumenta-a-autoestima-e-a-disposicao-no-dia-a-dia. Acesso em: 11 ago. 2022. Explicação sobre os benefícios da prática de atividades físicas, incluindo autoestima, disposição e suas explicações biológicas para tal.
BERLINGHOFF, William P. Matemática através dos tempos: um guia fácil e prático para professores e entusiastas. São Paulo: Blucher, 2010. p. 117.
Explicação sobre a utilização da álgebra e a lógica matemática que existe por trás de tal raciocínio, e como muitas vezes não se percebe toda a complexidade que há ao elaborar uma situação que envolva uma abstração algébrica.
BRASIL. Ministério da Casa Civil. Lei no 8.069, de 13 de julho de 1990, que dispõe sobre o Estatuto da Criança e do Adolescente. Disponível em: www.jusbrasil.com.br/legislacao/91764/ECA-Lei-n-8.069-de-13-de-Julho-de-1990#art-58. Acesso em: 22 ago. 2022.
Trecho da lei que regulamenta o Estatuto da Criança e do Adolescente (ECA), com foco no artigo 58, que trata do acesso à cultura, à arte e o respeito ao passado cultural e histórico.
CAVALCANTE, Daniele. Como a ciência aprendeu a prever eclipses solares com precisão. Canal Tech, 28 fev. 2020. Disponível em: https://canaltech.com.br/espaco/como-a-ciencia-aprendeu-a-prever-eclipses-solares-com-precisao-160893. Acesso em: 22 ago. 2022.
Comparação entre a utilização do Sol como referência nas civilizações antigas e os conhecimentos que possuímos atualmente sobre esse corpo celeste, e sua importância para os estudos astronômicos.
COMO você pode construir uma sociedade melhor? Blog Colab, 16 abr. 2015. Disponível em: www.colab.re/conteudo/comovoce-pode-construir-uma-sociedade-melhor. Acesso em: 22 ago. 2022.
Sugestões de atividades que melhoram a cidadania e auxiliam na construção de um coletivo mais saudável por parte do indivíduo.
DIA da Juventude: entenda a importância dos jovens para a sociedade. Oxfam Brasil, 11 ago. 2020. Disponível em: www. oxfam.org.br/blog/dia-internacional-da-juventude. Acesso em: 22 ago. 2022.
Ponderação sobre a importância dos jovens na operação de mudanças na sociedade e os riscos de exposição à violência que eles sofrem com isso, incluindo algumas pesquisas e estatísticas relevantes.
GINÁSTICA infantil. Blog Pratique em casa Disponível em: https://pratiqueemcasa.com.br/blog/ginastica-infantil. Acesso em: 22 ago. 2022.
Texto sobre a prática da ginástica artística por crianças, seus objetivos, idade inicial e outros detalhes.
GRANDEZA. Disponível em: www.ipem.sp.gov.br/index.php/cidadao/conceitos-metrologia-e-qualidade#:~:text=Grandeza%20 pode%20ser%20definida%2C%20resumidamente,qualitativamente%20distinguido%20e%20quantitativamente%20 determinado. Acesso em: 22 ago. 2022
Definição de grandeza disponível em página do IPEM-SP.
LAUNAY, Mickaël. A fascinante história da Matemática: da pré-história aos dias de hoje. 1. ed. Rio de Janeiro: Bertrand Brasil, 2019. p. 162, 166-167.
A origem da notação atual da Matemática e o processo de adoção de símbolos como + e – para adição e subtração, assim como a utilização de letras para as variáveis e incógnitas na álgebra.
NÃO ESCREVA NO SEU LIVRO.
MAPA indica locais com mais chances de haver disputas por água no mundo. Federação Nacional dos Urbanitários (FNU), 23 out. 2018. Disponível em: www.fnucut.org.br/14349/mapa-indica-locais-com-mais-chances-de-haver-disputas-por-agua-no-mundo. Acesso em: 22 ago. 2022.
Texto sobre o estresse hídrico que deve surgir nos próximos anos, incluindo algumas grandes cidades e centros urbanos mundiais que devem sofrer particularmente mais por conta das mudanças climáticas que devem complicar a distribuição de água no planeta.
NEM TÃO aleatório assim... Let’s Code Disponível em: https://letscode.com.br/blog/nem-tao-aleatorio-assim. Acesso em: 22 ago. 2022.
Texto sobre a introdução da aleatoriedade na ciência, em particular na física, e como isso alterou as concepções sobre o universo e o determinismo que reinava nas exatas, além de noções básicas de como a aleatoriedade aparece nessas ciências.
NEVES, Leandro. Qual é o impacto da tecnologia na sociedade? Veja 8 exemplos. Weni, 14 jun. 2021. Disponível em: https:// weni.ai/blog/impacto-tecnologia-sociedade. Acesso em: 22 ago. 2022.
Texto sobre o impacto de algumas tecnologias, recursos e serviços na sociedade.
QUAL a diferença entre igualdade e equidade? Fundação Telefônica Vivo, 2 jun. 2021. Disponível em: https://fundacaotelefonicavivo.org.br/noticias/qual-a-diferenca-entre-igualdade-e-equidade. Acesso em: 11 ago. 2022.
Diferença entre os termos igualdade e equidade, deixando claro que a equidade busca a justiça social, dando maior oportunidade para os mais desfavorecidos, ao passo que a igualdade, por vezes, pode deixar a desejar.
RIO DE JANEIRO (estado). Nova EJA: Ciências da Natureza e suas tecnologias. O que é ciência, notação científica e unidades.

Fundação CECIERJ. Disponível em: http://projetoseeduc.cecierj.edu.br/eja/recurso-multimidia-professor/fisica/novaeja/ m1u01/mat_didatico_fis_v1_unidade6.pdf. Acesso em: 30 ago. 2022.
Texto indagando sobre as noções de tamanho na realidade, convidando o leitor a pensar sobre o muito pequeno e o muito grande e as ferramentas que precisamos para olhar para tais elementos na natureza.
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL (UFRGS). Instituto de Física. A escala do Universo. Disponível em: www. if.ufrgs.br/oei/cgu/sca/sca.htm. Acesso em: 22 ago. 2022.
Tabela com os diâmetros dos principais corpos celestes do nosso sistema solar.
VOLUME. Disponível em: www.ipem.sp.gov.br/index.php/servicos/conv-uni. Acesso em: 22 ago. 2022. Definição de volume, além de um breve comentário sobre seu conceito e origens, de acordo com o site do IPEM-SP.
279 | NÃO ESCREVA NO SEU LIVRO.
