PRIMARIA INCLUYE LICENCIA 12 MESES PROYECTO DIGITAL
MATEMÁTICAS 4
MÉTODO ABN

4 1 Las decenas de millar
20 2 Las centenas de millar
Las decenas de millar. Composiciones y descomposiciones de números de cinco cifras. Composición de números a partir de sus OOMM. Diferencia entre número de y cifra de.
Lectura y escritura de números de seis cifras. Composición de números a partir de órdenes de magnitud. Completar números por orden de magnitud. Descubrimiento de números a partir de pistas.
34 3 Las fracciones Tipos de fracciones. Fracciones decimales y fracciones equivalentes. Ordenación de fracciones: con el mismo denominador y con el mismo numerador.
Las décimas e iniciación a las centésimas. Equivalencias entre OOMM. Composición y descomposición de decimales. Comparación, ordenación y redondeo de decimales. Intercalación de números decimales.
Sumas y restas con números de cinco cifras. Productos con multiplicando hasta cinco cifras. División con dividendo hasta cinco cifras.
Sumas y restas de OOMM a números grandes. Crecientes del producto de menor a mayor y de mayor a menor. Patrones en el producto. Aproximación del multiplicando.
Suma y resta de fracciones con el mismo denominador. Fracción de una cantidad. Cantidad de una fracción.
Los productos con céntimos. Multiplicación inversa. Del producto a la división. Producto de una cifra con y sin decimales. Cálculo mental con productos por una cifra.
repaso trimestre 1 steam: Maria Montessori REPASO UNIDADES 1 a 4
Producto por dos cifras descompuesto. Producto por dos cifras rápido. Productos de dos cifras con decimales. Patrones en el producto con decimales. Crecientes del producto.
División con decimales en el dividendo. División con extracción de decimales en el resto. Crecientes de la división de mayor a menor y de menor a mayor. Patrones de la división. Divisiones con el dividendo menor que el divisor. División inversa. Establecimiento del número de cifras que va a tener el cociente. Cálculo mental de divisiones por una cifra. División aproximando el dividendo.
División aproximando el dividendo.
repaso trimestre 1 steam: Maria Montessori REPASO UNIDADES 5 a 8
Producto posicional de una cifra, de una cifra con decimales y de dos cifras.
Cálculo mental por aplicación de patrones. Productos por cinco. Cálculo mental por aplicación de la propiedad distributiva del producto. Productos en los que los factores se acerquen a cien. Cálculo mental por aplicación de la propiedad distributiva del producto. Productos en los que los factores se acerquen a mil.
Operaciones con letras sin referencias. La división posicional de una cifra con y sin decimales. Jerarquía de operaciones.
repaso trimestre 1 steam: Maria Montessori REPASO UNIDADES 9 a 12
Números Operaciones Índice
86 6 La división con decimales
102 La división por redondeo y las unidades de tiempo 7
138 9 Rectas, ángulos y simetrías 170 11 Operaciones posicionales y álgebra
186 12 Jerarquía de las operaciones. Estadística
70 5 El producto por dos cifras
206 A Anexo El cálculo tradicional. 154 10 Las figuras planas 118 8 Las unidades de medida 50 4 Las décimas y las centésimas
Fracciones y equivalencias entre las unidades de tiempo. Sumas y restas con unidades de tiempo. Restas en escalera y dobles restas con unidades de tiempo.
Unidades de longitud, capacidad y masa. Múltiplos y submúltiplos. Equivalencias. Expresiones en forma compleja e incompleja. La tonelada.
Repaso de categorías aditivas: cambio, comparación e igualación.
Problemas de escala creciente.
Problemas de escala decreciente.
Repaso de la categoría de escala creciente y decreciente.
REPASO UNIDADES 1 a 4
Relato y preguntas intermedias del producto. Problemas de producto cartesiano I: PC1.
Problemas de reparto igualatorio: RI2 - RI3RI5 - RI6 - RI9 - RI12
Problemas con muchas preguntas.
Relato y preguntas intermedias de la división. Problemas con el dividendo menor que el divisor. Problemas difusos.
Problemas con unidades de tiempo. Introducción de los PAEV2. De dos PAEV1 hacemos un PAEV2. Problemas con pregunta oculta. De un PAEV2 hacemos dos PAEV1.
Problemas con unidades de longitud, capacidad y masa.
REPASO UNIDADES 5 a 8
Origen de los ángulos. Representación de rectas y ángulos. Tipos de rectas. Amplitud de ángulos y medidas. Construcción de ángulos. Ángulos originados por un giro. Simetrías y traslaciones.
Elementos y tipos de polígonos. Clasificación de polígonos según sus lados. Perímetro y área de los polígonos. Tipos de triángulos y de cuadriláteros. Circunferencia y círculo. Recogida de datos y tablas de frecuencias.
Punto medio y mediatriz de un segmento.
Problemas con pregunta oculta. Diferenciamos problemas de una y de dos operaciones.
Numeración en base 2. Unidades de medida de la información.
Diagramas de líneas. Diagramas de líneas dobles.
Problemas de velocidad. Problemas encadenados.
Resolución de problemas de ecuaciones. Problemas de producto cartesiano II: PC2. Convertir una situación en un problema. Problemas en bloque.
Inventamos PAEV2. Repaso general de PAEV1 y PAEV2.
REPASO UNIDADES 9 a 12
El signo igual. Ecuaciones tipo 1 y 2.
Orientación en el plano: líneas del metro.
Medida Geometría y tratamiento de la información Problemas Pensamiento computacional y álgebra
LAS DECENAS DE MILLAR 1
Los números de cinco cifras se leen así:

10 000 8 diez mil 40 000 8 cuarenta mil 70 000 8 setenta mil
59 326 8 cincuenta y nueve mil trescientos veintiséis
El número siguiente al 99 999 es 100 000, y se lee cien mil.
1 Escribe con palabras los siguientes números:
2 Escribe con cifras en tu cuaderno los siguientes números.
a) Veintitrés mil doscientos catorce.
b) Treinta y dos mil seiscientos cinco.
c) Setecientos cuatro mil ocho.
d) Treinta y dos mil seiscientos cinco.

3 Copia en tu cuaderno y escribe los signos >, < o =.
a) 74 568 ? 9 968 c) 82 301 ? 85 812 e) 23 368 ? 23 368
b) 43 C ? 8 568 d) 76 080 ? 8 UM f) 23 UM ? 238 C
4
1 DM = 10 UM = 100 C = 1 000 D = 10 000 U
1 DM = 10 UM
1 UM = 10 C
1 C = 10 D
1
1 D = 10 U DM UM C D U
0 0 0 0
Descubre los números de cinco cifras.
20 000 30 000 50 000 60 000 80 000 90 000 12 328 22 481 34 123 44 528 56 666 67 777 78 880 88 540 90 009
6 Escribe en tu cuaderno dos números que estén entre estos y que cumplan las condiciones indicadas.

a) Entre 34 567 y 34 757 y que la centena sea par.
b) Entre 28 466 y 24 495 y que la unidad de millar sea impar.
c) Entre 71 513 y 13 573 y que todas las cifras sean pares.
d) Entre 68 402 y 26 680 y que todas las cifras sean impares.
7 Completa lo que falta en tu cuaderno:

5 Unidad 1 4 Ordena de mayor a menor. 45 789 31 786 12 683 50 212 31 796 5 Ordena de menor a mayor. 45 789 31 786 12 683 50 212 31 796
suman 100 000 faltan… hasta 100 000 90 000 + 10 000 80 000 + ? 70 000 + 30 000 60 000 + ? 50 000 + ? 40 000 + ? 30 000 + ? 20 000 + ? 10 000 + ? 30 000 + ? = 100 000 90 000 + ? = 100 000 60 000 + ? = 100 000 10 000 + ? = 100 000 80 000 + ? = 100 000 50 000 + ? = 100 000 20 000 + ? = 100 000 70 000 + ? = 100 000 40 000 + ? = 100 000 desde 100 000 quedan… 100 000 − 30 000 = ? 100 000 − 60 000 = ? 100 000 − 50 000 = ? 100 000 − 40 000 = ? 100 000 − 70 000 = ? 100 000 − 10 000 = ? 100 000 − 80 000 = ? 100 000 − 20 000 = ? 100 000 − 90 000 = ?
Descomposiciones de números de cinco cifras



1 Fíjate en el ejemplo y escribe en tu cuaderno seis descomposiciones distintas para cada número de la derecha.
2 Modifica en tu cuaderno los números en rojo para obtener, en cada caso, una descomposición del número 26 578.
3 Copia y completa en tu cuaderno estos triángulos numéricos sabiendo que cada número se obtiene sumando los dos que tiene debajo:
6
DM UM C D U 5 7 2 3 6 0 0 572 3 6 4 17 2 0 36 2 36 12 3 6 1 1 461 13 6 0 57 1 0 136 57 236 73 028 23 254 18 905 DM UM C D U 1 6 5 7 8 0 20 0 0 578 1 4 120 0 378 0 26 3 24 28 0 0 263 0 55 26 578 ? ? ? ? ? ? ? ? 2 000 ? 650 500 1 500 700 ? ? ? ? ? ? 1 100 ? ? 1 500 250 ? 700 ? 900
Composición de números a partir de órdenes de magnitud
Vamos a componer números a partir de órdenes de magnitud en varios niveles de com plejidad.


Recuerda que cuando llegamos a 10 unidades de un orden de magnitud concreto, formamos un orden de magnitud superior.
Observa estos ejemplos:
Sin formar nuevos órdenes de magnitud.
2 DM 3 UM 1 C 5 D 4 U + 4 DM 1 UM 2 C 3 D 5 U
= 6 DM 4 UM 3 C 8 D 9 U = 64 389
Formando nuevo orden de magnitud.
5 DM 3 C 5 U + 2 DM 9 C 8 D 9 U = 7 DM 12 C 8 D 14 U
= 7 DM 1 UM 2 C 9 D 4 U = 71 294
Formando nuevos órdenes de magnitud.
4 UM 7 C 8 U + 4 D 354 U = 7 DM 12 C 8 D 12 U
= 7 DM 1 UM 2 C 9 D 2 U = 71 292
Ahora vamos a hacerlo nosotros poco a poco.
1 Compón el número con estos órdenes de magnitud en los que no se forman nuevos órdenes de magnitud.
a) 7 DM 2 UM 4 C 6 D 1 U + 1 DM 6 UM 3 C 2 D 7 U = ?
b) 5 DM 2 UM 4 D 5 U + 2 DM 5 UM 8 C 3 D 2 U = ?
c) 4 DM 2 UM 1 C 3 D 2 U + 4 DM 5 UM 7 C 4 D 6 U = ?
d) 6 DM 4 UM 1 D 3 U + 2 DM 3 UM 6 D 5 U = ?
2 Compón el número con estos órdenes de magnitud en los que se forman nuevos órdenes de magnitud.
a) 3 DM 4 UM 3 C 9 D 5 U + 2 DM 2 UM 3 C 9 D 4 U = ?
b) 4 DM 9 UM 3 D 2 U + 4 DM 9 UM 7 C 3 D 3 U = ?
c) 1 DM 9 UM 3
d)
?
7 Unidad 1
C
D 2 U
C 3
3
+ 2 DM 5 UM 2
D 4 U =
C 5 U + 1 DM 5 UM 8 C 9 D
U
1 DM 4 UM 1
8
= ?
Descubrimiento de números a partir de pistas
Vamos a dar algunas pistas sobre un número concreto y a partir de esas pistas debes encontrar el número del que se trata entre las opciones. En cada ejercicio tienes un ejemplo.
1
¿Qué número es? Elígelo entre los siguientes números.
Ejemplo: tiene 9 DM 7 C 2 D 3 U. a) 9 723 b) 90 723 c) 97 230
El número que buscamos es el 90 723, ya que dicho número no tiene UM.
Ahora tú:
2 ¿Qué número es? Elígelo entre los siguientes números.
Ejemplo: tiene 4 DM 12 C 6 D. a) 41 260 b) 40 126 c) 40 126
El número que buscamos es el 41 260, porque 12 C son 1 UM y 2 C.
1 UM y 2 C + 4 DM = 4 DM 1 UM 2 C 6 D 0 U
Ahora vosotros:
3 ¿Qué número es? Elígelo entre los siguientes números.
Ejemplo: tiene al menos 5 UM y 3 D. a) 11 289 b) 3 564 c) 4 789
El número que buscamos es el 11 289, que tiene 11 UM, 6 UM más que las indicadas.
Ahora vosotros:
8
núMero opCiones 3 UM 4 C 5 D 6 U 34 560 3 456 30 456 8 DM 2 UM 7 C 4 U 80 274 82 074 82 704 5 DM 6 UM 3 D 2 U 56 032 5 832 56 832
núMero opCiones 4 UM 23 C 5 D 3 U 42 353 6 353 40 235 7 DM 6 UM 14 C 6 U 77 406 7 746 76 146 3 DM 16 UM 53 U 31 653 31 650 46 053
núMero opCiones Tiene al menos 6 C y la cifra de las UM es par 4 567 5 704 4 629 Tiene al menos 2 DM y 3 C 2 370 5 306 30 000 Tiene al menos 3 UM y 25 D 1 256 3 250 6 009
Diferencia entre «número de» y «orden de magnitud»
No es lo mismo el lugar de posición de una cifra dentro de un número que la cantidad de unidades, decenas, centenas… que tenga dicho número.
El número 7 239:
• ¿Cuántas centenas tiene? 8 72 centenas





• ¿Cuál es la cifra de las centenas? 8 2
Observa en el siguiente sol cómo se diferencia entre «número de…» y «orden de magnitud» que ocupa. CIFRA
1 Haz lo mismo en tu cuaderno con todos los órdenes de magnitud de estas cantidades.

a) 2 593 b) 15 678 c) 247 689
2 ¿Qué número se forma?

9 Unidad 1
U 7 842 UM
CIFRA DE D 4 CIFRA DE UM 7 CIFRA DE C 8 D 784 C 78 3 UM + 1 C + 2 D + 4 U 3 UM + 25 C + 34 U 2 UM + 7 C + 12 D 11 UM + 11 D 62 C + 62 D + 62 U 3 U 8 3 + + 14 C 8 1 400 + + 21 D 8 210 Se forma el 1 613 7 842 A C B D e F
DE U 2
7
Sumas y restas con números de cinco cifras

1 ¿Cuál de estos dos vikingos bajará antes del barco? Será aquel que consiga más resultados mayores que 5 DM.


2 En el granero de Erik el Rojo se guardan 32 138 kg de trigo, y en el de Olaf el Tuerto, 12 952 kg. ¿Cuántos kilos hay que pasar de un granero al otro para que en ambos haya la misma cantidad?
3 Magnus guarda en su cabaña 36 206 monedas de oro, y Mikael, 18 680. ¿Cuántas monedas tiene que dar Magnus a Mikael para que los dos tengan la misma cantidad?
10
4 926,45 + 73,55 64 555 − 14 232,9 67,89 + 673,11 75 000,35 + 34 000,45 51 222 − 3 950 66 187 − 9 881 66 234 − 35 123 − 2 058 3 258 + 22 105 − 10 689 78 912 − 34 666 43 238 + 50 036
Recordamos cómo hacemos el producto con este problema y resolvemos algunas preguntas que podemos hacer una vez realizada la operación.
En una fábrica de hielo hay 6 máquinas que hacen 15 235 cubitos al día cada una. ¿Cuántos cubitos de hielo hacen todas las máquinas juntas?

• ¿Cuántos cubitos de hielo hacen todas las máquinas juntas? Hacen 91 410 cubitos.

• ¿Y si cada máquina hiciera solo 15 230? Harían 91 380 cubitos.
• ¿Y si cada máquina hiciera solo 15 200? Harían 91 200 cubitos.
• ¿Y si cada máquina hiciera solo 5 200? Harían 31 200 cubitos.
• ¿Y si cada máquina hiciera solo 235? Harían 1 410 cubitos.
• ¿Y si cada máquina hiciera solo 10 200? Harían 61 200 cubitos.
1 En el ejemplo anterior podríamos seguir haciendo más preguntas. Piensa alguna más y
2 Calcula el producto de estas cuatro multiplicaciones, elige una de ellas e inventa un problema. Luego haz cuatro preguntas intermedias de esa operación.
a) 25 082 × 4 b) 12 731 × 6 c) 13 892 × 7 d) 46 249 × 2
11 Unidad 1
6 10
30
200 1
30 180
Repaso de productos con multiplicando de cinco cifras por una cifra
×
000 60 000 5 000
000 90 000
200 91 200
91 380 5 30 91 420
Repaso de divisiones con dividendo hasta DM y divisor de una cifra
Recordamos cómo hacemos la división con este problema y resolvemos algunas preguntas que podemos hacer una vez realizada la operación.
Se han empaquetado 47 637 globos en 8 cajas. ¿Cuántos globos van en cada caja? ¿Han sobrado globos? ¿Cuántos?
Ten en cuenta que podemos realizar el reparto o división de muchas formas. Vamos a mostrar una de ellas como ejemplo.
: 8
47 637 40 000 5 000
7 637 4 000 500
3 637 3 200 400 437 400 50 37 32 4 5 5 954
Buscamos una cantidad sencilla para poner en cada caja. Hemos optado por 5 000. Quedan por repartir 7 637.
Ahora ponemos 500 globos más, y quedan por repartir 3 637 globos.
Ponemos 400 más y quedan 437 globos.
De esos, ponemos 50 más y quedan 37, de los que solo podemos repartir 4 en cada caja, y sobran 5 globos.
• Si repartimos 5 500 globos en cada caja, ¿cuántos quedan por repartir? 3 637 globos.
• Si en cada caja había ya 5 500 globos, ¿cuántos había en las 8 cajas? 44 000 globos.
• Cuando quedaban aún por repartir 437 globos, ¿cuántos había en cada caja? ¿Y en las 8 cajas? 5 900 en cada caja y 47 200 en las 8 cajas.
• Si hubiéramos repartido solo 3 637 globos, ¿cuántos habría en cada caja? 454, y R = 5.
• ¿Cuántos globos más necesitaríamos para que el reparto hubiera sido exacto? 3 globos.

1 En el ejemplo anterior podríamos seguir haciendo más preguntas. Piensa alguna más y halla la solución.
2 Calcula la división de estas cuatro operaciones, elige una de ellas e inventa un problema. Luego haz cuatro preguntas intermedias de esa operación. a) 1 812 : 4
12
b) 5
c)
6 d) 31
400 : 8
51 252 :
149 : 9
Problemas aditivos
Recuerda I Recuerda II
Elviajedeida
Sofía recoge sus clips en esta cajita. Pablo tiene una bonita colección de peonzas.
Añade los 3 últimos. Se le rompen 3.
Ahora la caja tiene 12. Ahora tiene 8.
¿Cuántos clips había antes de que metiese los últimos?













Resuelvo problemas
¿Cuántas peonzas tenía su colección antes de que se le rompiese ninguna?
1 Un tren con destino a Valencia realiza su primera parada y se bajan 56 pasajeros y 2 perros. Ahora viajan en el tren 143 viajeros. ¿Cuántas personas viajaban en el tren antes de que se realizara la primera parada?

2 Una televisión que costaba 626 €, en las rebajas puede comprarse por 578 €. Una lavadora costaba 350 € y, después de subirle el precio, ahora cuesta 378 €. ¿Cuánto dinero han rebajado la televisión? ¿Cuánto dinero han subido la lavadora?
3 Daniel ha conseguido 178 puntos jugando a su videojuego favorito. Ahora mismo ya tiene 256 puntos acumulados. ¿Cuántos puntos tenía antes de conseguir los últimos 178?
4 Después de la merienda, a Patricia le quedaban 250 g de jamón y 325 g de fruta. Si se comió 125 g de fruta y 100 g de jamón. ¿Cuántos gramos de fruta tenía antes de merendar? ¿Y de jamón?
5 En una botellita había 18 cL de agua. Mario decide llenarla un poco y ahora tiene 330 mL. ¿Cuántos mL de agua ha metido en la botellita?

Invento, creo y razono
6 Inventa un problema similar al del ejercicio 1 cuyo resultado sea:
Al principio había 350 sellos.

13
RESUELVO PROBLEMAS Unidad 1
Problemas de comparar
Recuerda I Recuerda II
Tiene 3 más que Iván.
Tiene 4 menos que Ari.
Raúl tiene 8 chapas.
piensa: ¿Quién tiene más?
Si Raúl tiene 3 más, Iván tiene ?
resuelve: ¿Cuántas chapas tiene Iván?
Comprendo el problema
Carlota tiene 9 galletas.
piensa: ¿Quién tiene más?
Si Carlota tiene 4 menos, Ari tiene ?
resuelve: ¿Cuántas galletas tiene Ari?









1 Completa la tabla siguiente y aprende lo que implican los conceptos «más que» y «menos que».
ChApAs De rAúl rAúl tiene… por tAnto, iván tiene… ChApAs De iván








15 4 más que Iván Iván tiene 4 menos 15 − 4 = 11

27 9 más que Iván ? ?
51 23 menos que Iván ? ?
Resuelvo problemas
2 En una tienda de informática hay 175 ordenadores portátiles y 65 cámaras a la venta. En el almacén hay otros 287 portátiles y 29 cámaras. ¿Cuántos portátiles más hay en el almacén? ¿Y cuántas cámaras menos?
3 En un autobús de línea viajan 36 hombres y 27 mujeres. Viajan 112 hombres y 77 mujeres menos de las que transporta un tren de cercanías. ¿Cuántos hombres y cuántas mujeres viajan en el tren?
4 El alumnado de 4.º de primaria ha recolectado 1 kg 750 g de almendras del huerto escolar. Han recolectado 175 g más que el alumnado de 3.º. ¿Cuántos gramos han recolectado los de 3.º?
Invento, creo y
razono
5 Inventa un enunciado similar al del ejercicio 4 para la siguiente pregunta y operación.
¿Cuántos metros ha recorrido Javier?
380 − 175 = 209 metros
14 RESUELVO PROBLEMAS
Elviajedeida
Construimos todos los problemas de comparación
Observo
Observa todos los problemas de comparar que podemos crear a partir de una situación. Fíjate en los datos que tienes y qué preguntamos cada vez.
Carlos ha metido 8 canastas e Irene 12. La diferencia entre ellos es de 4.
Canastas Carlos: 8 Canastas Irene: 12 Diferencia: ¿? Sentido (más)
Carlos ha metido 8 canastas e Irene 12. ¿Cuántas canastas más ha metido Irene?
Canastas Carlos: 8 Canastas Irene: 12 Diferencia: ¿? Sentido (menos)
Carlos ha metido 8 canastas e Irene 12. ¿Cuántas canastas menos ha metido Carlos?
Canastas Carlos: 8 Canastas: Irene ¿? Diferencia: 4 Sentido (más)
Carlos ha metido 8 canastas. Irene ha metido 4 más. ¿Cuántas canastas ha metido Irene?
Canastas Carlos: ¿? Canastas Irene: 12 Diferencia: 4 Sentido (menos)
Irene ha metido 12 canastas. Carlos ha metido 4 menos. ¿Cuántas canastas ha metido Carlos?
Canastas Carlos: ¿? Canastas Irene: 12 Diferencia: 4 Sentido (más)
Irene ha metido 12 canastas, 4 más que Carlos. ¿Cuántas canastas ha metido Carlos?
Canastas Carlos: 8 Canastas Irene: ¿? Diferencia: 4 Sentido (más)
Carlos ha metido 8 canastas, 4 menos que Irene. ¿Cuántas canastas ha metido Irene?
Invento, creo y razono
1 Un gato pesa 8 kg y un perro 15 kg. La diferencia entre ellos es de 7 kg.
Gato: 8 kg Perro: 15 kg Diferencia: ¿? Sentido (más) ?
Gato: 8 kg Perro: 15 kg Diferencia: ¿? Sentido (menos) ?
Gato: 8 kg Perro: ¿? Diferencia: 7 kg Sentido (más) ?
Gato: ¿? Perro: 15 kg Diferencia: 7 kg Sentido (menos) ?
Gato: ¿? Perro: 15 kg
Diferencia: 7 kg Sentido (más) ?
Gato: 8 kg Perro: ¿? Diferencia: 7 kg Sentido (menos) ?
15 Unidad 1
¡Os toca vosotros!a
Problemas de igualar
Recuerda I Recuerda II
Miguel ha recogido 9 hojas. Vega ha recogido 7 piedras.
Si Marco recogiera 5 hojas más, recogería las mismas hojas que Miguel.
piensa: ¿Quién ha recogido más hojas?
resuelve: ¿Cuántas hojas ha recogido Marco?
Comprendo el problema
1 ?????????????????????????????

Completa la tabla en tu cuaderno.
Si Nuria recogiera 6 piedras menos, recogería las mismas piedras que Vega.
piensa: ¿Quién ha recogido menos piedras?

resuelve: ¿Cuántas piedras ha recogido Nuria?

45 Si Nuria recogiera 9 menos Ha recogido 9 más 45 + 9 = 54
55 Si Nuria recogiera 17 menos ? ?
37 Si Nuria recogiera 19 más ? ?
Resuelvo problemas
Resuelvo problemas
2 Una ardilla ha comido 35 bellotas y 28 castañas. Si un jabalí hubiese comido 75 bellotas menos, habría comido la misma cantidad que la ardilla. ¿Cuántas bellotas comió el jabalí?









3 En la ladera este de una montaña hay plantados 235 árboles. Si en la ladera oeste hubiese plantados 78 árboles más, habría la misma cantidad que en la zona este. ¿Cuántos árboles hay en la ladera oeste?
Invento, creo y razono
5 Inventa un problema similar a alguno de esta página. Selecciona los dos datos que necesites. Comprueba que tiene sentido y resuélvelo.
43 conchas
Invento, creo y razono
4 En una carrera han participado 126 atletas. Íker lleva recorridos 5 400 metros. Si Alba hubiese recorrido 1 km 350 metros más, llevaría recorrida la misma distancia que Íker.
¿Cuántos metros ha recorrido Alba?
28 saltos
Si Aitana diese 14 más
Si Lucía tuviese 34 menos
16
????????????????
RESUELVO PROBLEMAS Elviajedeida
pieDrAs De vegA si nUriA reCogierA… tenDríA lAs MisMAs qUe vegA por tAnto, hA reCogiDo… pieDrAs De nUriA
Investigando y reciclando

El alumnado de 4.º de primaria se ha propuesto realizar un pequeño trabajo de investigación sobre la cantidad (en toneladas) de material que se ha reciclado en su ciudad en los últimos años.
Han recogido la información que han encontrado en esta tabla, pero su estudio está incompleto. Ayúdales a terminarlo.
pApel y CArtón viDrio envAses pilAs y BAteríAs
Año 01 48 000 t 38 000 t 50 000 t 6 000 t
Año 02 44 000 t 40 000 t 60 000 t 8 000 t
Comprendo el problema
Año 03 52 000 t ? ? ?
1 ?????????????????????????????
1 Su trabajo debe contener el número de toneladas de papel y cartón recicladas cada año ordenadas de mayor a menor. ¿Qué opción deberán elegir?
a) Papel y cartón del año 03-año 02-año 01
b) Papel y cartón del año 01-año 02-año 03
c) Papel y cartón del año 03-año 01-año 02
d) Papel y cartón del año 02-año 03-año 01
2 Como habrás podido comprobar, les faltan algunos datos del año 03. Investigando en Internet han encontrado que en su ciudad se reciclaron 6 000 t menos de vidrio en el año 02 que en el año 03. ¿Cuántas toneladas de vidrio se reciclaron en el año 03?
Resuelvo problemas
a) 46 000 toneladas de vidrio.
2 ??????????????????????????????
b) 38 000 toneladas de vidrio.
c) 48 000 toneladas de vidrio.
d) 34 000 toneladas de vidrio.
3 Siguiendo con su búsqueda por Internet, han encontrado las toneladas de pilas y baterías que se reciclaron en el año 03, pero la cantidad exacta viene expresada en órdenes de magnitud: 2 UM 60 C 100 D. ¿Qué cantidad de pilas y baterías se han reciclado?
Invento, creo y razono
4 ?????????????????????????????????????
a) 2 600 t c) 8 800 t
b) 9 000 t d) 13 000 t
17 ??????
????????????????
Unidad 1
TAREA COMPETENCIAL
4 Finalmente, la última información que han encontrado dice que en el año 01 se reciclaron 5 000 toneladas más de envases que en el año 03. ¿Cuántas toneladas de envases reciclaron en el año 03?
a) 55 000 t b) 52 000 t c) 65 000 t d) 45 000 t
5 Ahora que ya tienen toda la información recogida, se han dividido en pequeños grupos de trabajo. Cada grupo debe escoger un material reciclado de la tabla y elaborar un sencillo gráfico de barras que recoja la cantidad de residuos reciclados en los años que ahí aparecen. Escoged el que más os guste y elaborad el gráfico correspondiente.

6 Siempre que se termina cualquier trabajo, hay que revisarlo. Releyéndolo, se han dado cuenta de que en las conclusiones han añadido varias informaciones que son falsas. Señala en tu cuaderno de cuáles se trata para no incluirlas.
En el año 01 se reciclaron aproximadamente 40 000 t de vidrio. En el año 02 se reciclaron mas pilas y baterías que en el año 01. El material más reciclado en el año 02 fue el papel y el cartón.
El material más reciclado en el año 01 fueron las pilas y baterías. Se recicló menos vidrio en el año 02 que en el año 01.
El año que más papel y cartón se recicló fue el año 03.
7 A través del trabajo de investigación realizado por la clase de 4.º, todo su alumnado se ha concienciado de la importancia del reciclaje para crear un mundo más sostenible. Este trabajo ha supuesto una nueva motivación para poner en marcha acciones encaminadas a implicarse más en el reciclaje de materiales. Todos juntos realizad diversas propuestas relacionadas con el reciclaje en vuestro aula y vuestro colegio e intentad poner en práctica algunas de ellas en este nuevo curso.
18 TAREA COMPETENCIAL
1 Completa en tu cuaderno con el número o el nombre.
a) 84 765 8 ? c) Veinticinco mil seiscientos noventa y ocho. 8 ?
b) 70 906 8 ? d) Setenta mil novecientos cuarenta y tres.
2 Descompón de cuatro formas distintas estos números.
a) 34 501 b) 59 476
3 Compón el número con estos órdenes de magnitud.
a) 5 DM 3 UM 2 C 4 D 6 U + 2 DM 4 UM 5 C 2 D 1 U =
b) 3 DM 2 UM 4 D 5 U + 2 DM 4 UM 5 C 2 D 3 U =

c) 3 DM 2 UM 5 C 4 D + 3 UM 25 C = ?
d) 4 DM 5 UM 6 C 3 D 7 U + 422 D = ?
4 Elige entre los siguientes números el número que estamos buscando en cada caso.
5 Completa la tabla en tu cuaderno con la cifra y la cantidad total del orden de magnitud indicado.
6 Calcula estas sumas.
7 Calcula en la rejilla ABN, inventa un problema y haz 4 preguntas intermedias. 24 903 × 4
19 Unidad 1
núMero opCiones 6 UM 3 C 8 D 2 U 63 820 60 382 6 382 3 UM 34 C 6 D 2 U 33 462 33 460 6 462 Tiene 6 C y la cifra de las UM es par 5 680 10 680 23 604 Tiene al menos 14 C y la cifra de las UM es impar 28 250 1 545 6 475
núMero CiFrA De… núMero De… 25 679 Las centenas ? Centenas ? 89 452 Las decenas ? Decenas ? 90 576 Las unidades de millar ? Unidades de millar ? 76 208 Las decenas de millar ? Decenas de millar ?
+ 250 350 270 370 4 326 ? ? ? ?
REPASO
1
2 Completa en tu cuaderno lo que falta.
3

20 LAS CENTENAS DE MILLAR 2
Lee
voz
siguientes números: a) 300 000 c) 400 000 e) 700 000 g) 800 000 i) 112 328 b) 444 528 d) 556 666 f) 667 777 h) 990 009 j) 992 155
en
alta los
suman 1 000 000 faltan… hasta 1 000 000 desde 1 000 000 quedan… 900 000 + 100 000 700 000 + ? 500 000 + ? 200 000 + ? 400 000 + ? 100 000 + 900 000 = 1 000 000 600 000 + ? = 1 000 000 800 000 + ? = 1 000 000 700 000 + ? = 1 000 000 300 000 + ? = 1 000 000 1 000 000 − 100 000 = 900 000 1 000 000 − 300 000 = ? 1 000 000 − 200 000 = ? 1 000 000 − 500 000 = ? 1 000 000 − 900 000 = ? 99 999 + 1 = 100 000 1 CM = 10 DM = 100 UM = 1 000 C = 10 000 D = 100 000 U Los números de seis cifras se leen así: 100 000 8 Cien mil 500 000 8 Quinientos mil 384 103 8 Trescientos ochenta y cuatro mil ciento tres El número siguiente al 999 999 es 1 000 000, y se lee un millón. Setecientos setenta y siete mil setecientos setenta y siete Setecientos setenta y siete mil setenta y siete Setecientos setenta y siete mil setecientos siete Setecientos setenta y siete mil siete Setecientos setenta y siete mil setecientos Cm dm um C d u 1 0 0 0 0 0 a B C d e
Escribe con cifras estos números.
Suma de unidades, decenas, centenas…

1
y completa en tu cuaderno estas tablas. ¡Presta atención!
2 Y
21 Unidad 2
Copia
ahora,
mismo
cantidades
número añado oBtengo 9 1 centena 109 9 1 unidad ? 9 1 decena ? 99 ? 100 99 ? 199 99 ? 109 999 1 decena ? 999 1 unidad de millar ? número añado oBtengo 19 1 unidad 20 29 1 decena ? 39 1 centena ? 499 ? 500 599 ? 699 699 ? 709 7 999 1 decena ? 8 999 1 unidad de millar ? número añado oBtengo 9 999 1 unidad 10 000 9 999 ? 19 999 9 999 ? 10 009 9 999 ? 10 099 99 999 1 decena de millar ? 99 999 1 millón ? 99 999 1 unidad ? 99 999 1 centena ? número añado oB 199 1 unidad 949 ? 899 ? 099 ? 949 1 decena 499 1 centena 9 909 1 unidad 9 959 1 centena ?
haz lo
con
en las que no solo hay nueves. Copia y completa en tu cuaderno.
Resta de unidades, decenas, centenas…

Ahora, restas. Tienes que fijarte bien para no equivocarte. Aun así, te costará menos, porque ya has practicado con la suma.
1 Copia y completa en tu cuaderno estas tablas. ¡Presta atención!
número quito
oBtengo
1 000 000 1 unidad de millar ?
100 000 1 decena de millar ?
220 000 2 centenas de millar ?
1 888 88 decenas ?
número quito oBtengo
4 444 44 decenas 4 004
4 444 404 unidades ?
10 000 3 centenas ?
10 000 60 centenas ?
10 000 50 unidades ?
55 555 55 centenas ?
55 555 55 decenas ?
1 010 000 1 unidad de millar ?
200 000 1 decena de millar ?
200 000 10 decenas de millar ?
2 500 10 decenas ?
3 000 10 centenas ?
40 000 10 unidades de millar ?
5 000 1 decena ?
número quito oBtengo 6 400 1 decena 6 390 7 400 1 unidad ?
8
22
109
55 555 55 unidades ? 9
1 centena
100 000 1 decena ?
1 000 000 1 centena ?
000 1 centena ?
090 1 centena ?
500 1 unidad ?
500 1 unidad de millar ?
500 1 decena ?
1 unidad ?
1 decena ?
2 000 20 decenas ?
9
10
100
100
550 000
550
1 decena de millar 495
quito oBtengo 209 1 centena 109
505 000
000 número
100 100 1 decena ?
1 001 000 1 centena ?
Componemos un número a partir de órdenes de magnitud
Observamos cada orden de magnitud para saber exactamente lo que representan:
• En 524 UM 8 hay 5 CM 2 DM y 4 UM y también 524
• En 1 605 C 8 hay 1 CM 6 DM y 5 C y también 160 500 U.
• En 4 D 8 hay 4 D y también 40 U.
• En 38 U 8 hay 3 D y 8 U y también 38 U.
Fíjate en este otro ejemplo: 24 UM 65 C 4 D 38 U
Si componemos todos los órdenes de magnitud, tendremos:
2 DM y 4 UM + 6 UM y 5 C + 4 D + 3 D y 8 U = 2 DM 10 UM 5 C 7 D 8 U = 30 578
Si componemos sumando todas las unidades, tendremos: 24 000 + 6 500 + 40 + 38 = 30 578
1 Compón a partir de los órdenes de magnitud que se presentan.
a) 345 UM 23 C 6 D 9 U = ?
c) 7 UM 42 C 54 D 3 U = ?
b) 8 DM 5 UM 38 C 2 D 68 U = ? d) 3 DM 62 UM 9 C 14 D 7 U = ?
Cuando se trata de una suma o una resta, podemos operar por órdenes de magnitud. Observa este ejemplo con sumas:
36 UM y 45 C + 3 UM y 23 D = 36 UM +
= 43 UM 8 C 3 D = 43 730
2 Resuelve estas operaciones a partir de los órdenes de magnitud.
a) 5 UM 3 C + 43 D 5 U = ?
+
+
+
c) 2 UM 82 C + 33 D 8 U = ?
b) 2 DM 3 UM 21 C + 38 D 6 U = ? d) 4 DM 15 UM + 3 CM 24 C 87 U = ?
Restas:
y
3 Resuelve estas operaciones a partir de los órdenes de magnitud.

a) 5 UM 3 C − 42 C = ?
c) 9 UM 52 C − 10 UM = ?
b) 4 DM 2 UM − 25 C = ? d) 6 DM 24 UM − 300 C = ?
23 Unidad 2
3 UM + 4 UM
5 C
2 C
3 D
C
36 UM
45 C − 3 UM 23 C = 36 UM − 3 UM + 45 C − 23
= 33 UM + 22 C = 35 200
Composición de números a partir de órdenes de magnitud
Completar números por orden de magnitud
Fíjate cómo puedes obtener números partiendo de otro número.
En a , coinciden centenas, decenas y unidades, necesitas añadir 6 UM a 3 157 para obtener 9 157.
En B , las decenas y unidades coinciden necesitas añadir 13 C a 2 289 para obtener 3 589.
En C , las unidades coinciden, necesitas añadir 314 D a 3 117 para obtener 6 257.
1 Ahora tú. Busca en qué órdenes de unidad coinciden y…
a) …añade las UM que faltan en cada caso.
b) …añade las C que faltan en los siguientes números.

2 Fíjate en el ejemplo. Copia y completa en tu cuaderno.

24
UM C D U tienes 3 1 5 7 UM C D U tienes 2 2 8 9 UM C D U tienes 3 1 1 7 quieres 9 157 15 258 80 025 84 084 6 154 quieres 3 589 quieres 6 257
DM UM C D U 1 0 2 5 8 DM UM C D U 5 0 0 2 5 DM UM C D U 0 53 0 8 4 DM UM C D U 0 0 0 305 4 número añado oBtengo 3 UM 4 C 2 U 5 D 3 452 3 UM 4 C 12 U 5 D 3 462 1 CM 3 DM 4 C 2 D 6U 6 UM ? 1 CM 3 DM 4 C 2 D 6 U 26 UM ? 4 DM 2 UM 10 C ? 4 DM 2 UM 100 C ? a B C
Descubrimiento de números a partir de pistas
1 Averigua de qué número se trata en cada caso.
• Soy un número de cuatro cifras.
• La cifra de las D es 0.
• La cifra de las C es el doble que la de las UM, y la de las U el doble que las UM.
• La cifra de las UM es impar y mayor que uno.
• Soy un número de tres cifras.
• Empezando por la izquierda, la tercera cifra es cuatro veces la segunda.
• La tercera cifra es menor que 5.
• La primera cifra es tres veces la segunda.
• Soy un número de cuatro cifras, todas diferentes y distintas de cero.
• La suma de mis cifras es 10.
• La cifra de UM es 3.
• Las cifras de C y U son pares.





• La cifra de U es el doble de la de C.
• Soy un número de cuatro cifras.
• Empezando por la izquierda, la primera y la tercera cifras son iguales, y la segunda y la cuarta, también.

• La primera cifra es la mitad de la segunda.
• La suma de las cuatro cifras es 12.
2 Fíjate en el ejemplo. Copia en tu cuaderno y completa las siguientes igualdades.

25 Unidad 2
igualdad ComproBaCión 30 D 24 U = 20 D 124 U 300 + 24 = 200 + 124 8 324 = 324 19 C 46 U = 1 UM 9 C 2 D ? U ? 2 184 U = 1 UM ? C 6 D ? U ? 4 UM 7 D = 30 C ? D ? 364 D = 33 C 32 D ? U ?
Crecientes del producto

Creciente del producto de menor a mayor
Vamos a multiplicar 452 × 6 poco a poco, empezando por 2 × 6 y haciéndolo crecer hasta el resultado final. Fíjate cómo lo hacemos.
Multiplicamos 2 × 6 = 12.
2 × 6 = 12
52 × 6 = 312
452 × 6 = 2 712
Ahora, multiplicamos 50 × 6 = 300; y sumamos: 300 + 12 = 312.
Multiplicamos 400 × 6 = 2 400, y sumamos: 2 400 + 312 = 2 712.
El resultado de multiplicar 452 × 6 es 2 712.
1 Ahora tú. Practica estos crecientes del producto de menor a mayor:
Creciente del producto de mayor a menor
Ahora lo vamos a hacer con 367 × 4 poco a poco, empezando por 300 × 4 y haciéndolo decrecer hasta el resultado final.
Multiplicamos 300 × 4 = 1 200.
300 × 4 = 1 200
360 × 4 = 1 440
367 × 4 = 1 468
Ahora, multiplicamos 60 × 4 = 240, y sumamos: 240 + 1200 = 1 440.
Multiplicamos 7 × 4 = 28, y sumamos 28 + 1 440 = 1 468.
El resultado de multiplicar 367 × 4 es 1 468.
2 Ahora tú. Practica estos crecientes del producto de mayor a menor:

6 000 × 2 = 12 000
6 400 × 2 = 12 800
6 460 × 2 = 12 920
6 467 × 2 = 12 934
3 000 × 6 8 ?
3 330 × 6 8 ?
3 333 × 6 8 ?
26
8
48
348
348
× 3
× 3
× 3 2
× 3
1 × 7 61 × 7 261 × 7 1 261 × 7 4 × 8 44 × 8 444 × 8 4 444 × 8
2 000 × 4 8 ?
2 300 × 4 8 ?
2 350 × 4 8 ?
2 358 × 4 8 ?
3 300 × 6 8 ?
a
B
C C
a
B
Patrones en la multiplicación
Observa con estos patrones los siguientes productos:

1 000 × 3 = 3 000
× 3= 300 10 × 3= 30
× 3= 3
× 3= 0,3
× 3= 0,03
3 000 × 3 = 9 000 300 × 3= 900 30 × 3= 90 3 × 3= 9


× 3= 0,9
12 000 × 3 = 36 000
2
por qué número hemos multiplicado en cada caso.
3 Resuelve y observa lo que ocurre con la coma decimal.
4 Una botella de agua vale 0,30 €. ¿Cuánto valen estas botellas?
5 Un cuaderno cuesta 1,25 €. ¿Cuántos cuadernos se pueden comprar con estas cantidades?
2,50 € 25 € 5 € 50 € 250 € 500 €
27 Unidad 2
1 000 × 6 100 ×
10 × 6 1 × 6 0,1 × 6 0,01 × 6
1 Resuelve y observa lo que ocurre con la coma decimal.
6
? × 8 = 8 ? × 8 = 0,8 ? × 8 = 0,08
Averigua
? × 8 = 8 000 ? × 8 = 800 ? × 8 = 80
2 000 ×
200 ×
20 × 7 2 × 7 0,2 × 7 0,02 × 7
7
7
2
4 8 10 20 400
0,1
100
1
0,01
0,3
0,03
× 3= 0,09
0,12
1 200 × 3= 3 600 120 × 3= 360 12 × 3= 36 1,2 × 3= 3,6
× 3= 0,36
Aproximación del multiplicando
Otra forma de multiplicar es sustituir el multiplicando por un número mayor y, después, restar la cantidad añadida.
Vamos a multiplicar 2 988 × 7:


1. Aproximamos 2 988 a la siguiente unidad de millar completa, a 3 000.
2 988 + 12 = 3 000
2. Ahora hay que multiplicar tanto el redondeo como lo que hemos añadido:
(3 000 − 12) × 7, que es lo mismo que (3 000 × 7) − (12 × 7)
3. Multiplicamos primero el redondeo:
3 000 × 7 = 21 000
4. Multiplicamos el añadido: 12 × 7 = 84
5. Quitamos el producto de lo que hemos añadido: 21 000 − 84 = 20 916
2 988 × 7 = (3 000 − 12) × 7 = (3 000 × 7) − (12 × 7) = 21 000 − 84 = 20 916
1 Empezamos con el producto por decenas:
a) 98 × 3 = (100 − 2 ) × 3 = (100 × 3) − (2 × 3) = 300 − 6 = 294

b) 79 × 8
c) 59 × 6

d) 87 × 9
2 Seguimos con el producto por centenas:
a) 198 × 3 = (200 − 2 ) × 3 = (200 × 3) − (2 × 3) = 600 − 6 = 594
b) 490 × 6
c) 689 × 5
d) 895 × 8
3 Y por último, con el producto por millares:
a) 1 994 × 6 = (2 000 − 6 ) × 6 = (2 000 × 6) − (6 × 6) = 12 000 − 36 = 11 964
b) 3 889 × 2
c) 5 980 × 5
d) 9 993 × 9
28
Escala creciente I
Experimento
Coge 4 tizas.
Coge de nuevo 4 tizas.
Comprendo el enunciado
Ahora tu compañero o compañera va a coger tres tizas más que tú.
¿Cuántas tizas tiene tu compañero o compañera? 3 + 3 ×
Ahora tu compañero o compañera va a coger tres veces más tizas que tú.
¿Cuántas tizas tiene tu compañero o compañera?
1 Completa la tabla con símbolos y con números. Aprende la diferencia entre «veces más» y «más». Un concepto implica multiplicar y el otro sumar. Cantidad




30
Resuelvo problemas
2 La bisabuela de Rubén tiene 9 veces más años que él. Si Rubén tiene 9 años, ¿cuántos años tiene su bisabuela?

3 El mes pasado, Ramón tenía 60 puntos verdes y 12 rojos. Este mes tiene 47 puntos verdes más y 3 veces más puntos rojos. ¿Cuántos puntos verdes y cuántos rojos tiene ahora Ramón?
4 Hemos estado jugando a un juego de mesa muy divertido. Vega ha terminado con 200 puntos y Carlos con 4 veces más. ¿Cuántos puntos ha conseguido Carlos? ¿Cuántos puntos tienen entre los dos?
Invento, creo y razono
5 Inventa un problema de «veces más» cuyo resultado sea 56.
29 RESUELVO PROBLEMAS Unidad 2
Elviajedeida
iniCial 4 más + 4 4 veCes más × 4 11 OI OI IIII 15 OI OI OI OI 44 12 ? ? ? ? ? Cantidad iniCial 5 más + 5 5 veCes más × 5
OO ? ? ? ?
20
? ? ? ? ?
Escala creciente II Elviajedeida
Experimento
Coge 8 lápices.
Tú tienes cuatro veces más lápices de los que tiene que coger tu compañero o compañera.
piensa: ¿Quién tiene más lápices, tú o tu compañero o compañera?
Si tú tienes 4 veces más lápices, tu compañero o compañera tendrá 4 veces ? .
resuelve: ¿Cuántos lápices tendrá tu compañero o compañera?
Comprendo el enunciado
1 Izan se ha leído este curso 15 libros, 3 veces más de los que se ha leído Paula. ¿Cuántos libros se ha leído Paula?
Piensa: ¿Quién ha leído más libros?
Si Izan ha leído 3 veces más, Paula ha leído 3 veces ?
Haz tres grupos con los libros de Izan y sabrás los que ha leído Paula
¿Cómo lo hemos resuelto?
Resuelvo problemas
2 La abuela de Emma tiene 72 años. Tiene 8 veces más años que Emma. ¿Cuántos años tiene Emma?
3 Iratxe es fotógrafa y ha hecho hoy 150 fotos, 5 veces más fotos de las que hizo ayer. ¿Cuántos fotos hizo ayer? ¿Cuántas fotos ha hecho entre los dos días?
4 Una motocicleta ha recorrido hoy 65 km y un automóvil 5 veces más. ¿Cuántos km ha recorrido el automóvil? ¿Cuántos km más ha recorrido el automóvil que la motocicleta?
5 Inventa un problema similar al ejercicio 2 y que se resuelva con la siguiente expresión.
36 : 6 = 6 puntos tiene Rafa

30 RESUELVO PROBLEMAS
¿ ?
? ? ? Paula ha leído ? 15 × 3 = 45 15 − 3 = 12 15 : 3 = 5
Invento, creo y razono
Matemágicas I
Hola, querido/a matemago/a:
La malvada Malicia quiere acabar con las matemáticas divertidas y convertirlas en un aburrimiento. Estás entre los preseleccionados para luchar con el fin de impedírselo. Deberás demostrar tu valía resolviendo acertijos. Apresúrate y coge el tren que viaja a la escuela.
El tren súper rápido, que circula a 319 km/h, cuenta con 82 asientos en cada uno de sus 12 vagones. Para subir en él de bes recibir una invitación de la escuela de matemagia que repar ten las palomas mensajeras. Cada paloma reparte 129 cartas. Suelen ir unos 1 000 alumnos a la escuela.
1 ACERTIJO. Centenares de niños y niñas acuden a dicha escuela, pero otros no lo consiguen. ¿Habrá espacio para todos en el tren?
¿Cuántos asientos habrá en total en los 12 vagones?
a) 4 466 asientos c) 1 092 asientos
b) 984 asientos d) 14 000 asientos
2 ACERTIJO. Muchísimos niños y niñas quieren ser matemagos, pero solo pueden serlo los que reciben la invitación. Hay 30 palomas que harán el reparto. Calcula cuántas invitaciones repartirán para saber si habrá bastantes para todos.
a) 14 292 invitaciones c) 36 000 invitaciones
b) 2 808 invitaciones d) 3 870 invitaciones
3 HECHIZO. Empieza a hacer magia y resuelve los siguientes productos aproximando a la centena más próxima.


198 × 4 289 × 6
4 HECHIZO. Cada alumno de matemagia realiza al año 7 145 hechizos. Muestra tus dotes de cálculo mágico y resuelve mediante este creciente de la multiplicación cuántos trucos hacen entre 3 alumnos.
7 000 × 3
7 100 × 3
7 140 × 3
7 145 × 3
31 Unidad 2
TAREA COMPETENCIAL
Unidad
5 ACERTIJO. Usa tu varita y descubre los números que se esconden detrás de estas descomposiciones.
a) 23 UM 133 D 4 440 U b) 12 DM 7 433 C 12 U
Con tanto hechizo, seguro que te ha entrado hambre. Tienes suerte porque en el tren súper rápido venden dulces mágicos. ¡Prepara tus monedas! 125 grageas/caja

6 ACERTIJO. Fíjate bien en las grageas que hay en una caja. Responde:
a) ¿Cuántas grageas habrá en 8 cajas?


b) Si en una caja hubiese 25 grageas, ¿cuántas grageas habría en 8 cajas?
c) Si en una caja hubiese 105 grageas, ¿cuántas grageas habría en 8 cajas?
d) Si hubiese 960 grageas en 8 cajas, ¿cuántas grageas habría en una caja?
e) Si hubiese 200 grageas en 8 cajas, ¿cuántas grageas habría en una caja?
7 ACERTIJO. Calcula cuánto costarán estas lagartijas. A ver si tienes suficiente dinero para comprar más de una.
32 TAREA COMPETENCIAL
QUE HAYAS SUPERADO LA PRUEBA!
¡ESPERO
1
de regalo lagartija de ChoColate 1 2 4 40 8 20 Coste ? ? ? ? ? ? 0,50 � 2,30 � 2,85 � 125 × 28 100 2 800 20 560 3 360 5 140 3 500
cromo
1 Copia y completa en tu cuaderno.
número añado oBtengo
39 1 unidad ?
589 1 decena ?
2 999 1 centena ?
2 Completa estas tablas en tu cuaderno:


número quito oBtengo 909 1 decena ?
9 100 1 unidad ?
9 000 1 centena ? número añado oBtengo
3 Copia en tu cuaderno estas tablas y complétalas:
número añado oBtengo
número
9 179 ? 9 180
9 009 ? 9 010
9 099 1 decena ?
número quito oBtengo
6 400 ? 6 300
7 400 ?
7 399

9 000 1 decena ?
número añado oBtengo
5 UM 7 C 9 D 12 C ?
5 C 27 D 1 U 350 U ?
4 Practica los crecientes del producto de menor a mayor.
5 Practica los crecientes del producto de mayor a menor.
6 Calcula aproximando el producto por unidades de millar. a)
b)
33 Unidad 2
REPASO
5 × 3 25 × 3 325 × 3 6 × 8 36 × 8 236 × 8
4 000 × 2 4 200 × 2 4 210 × 2 4 215 × 2 1 000 × 6 1 300 × 6 1 350 × 6 1 354 × 6
1 896 × 6 = (2 000 − 104) × 6 = (2 000 × 6 ) − (104 × 6) = 12 000 − 624 = 11 376
2 990 × 4 = ? c) 3 988 × 5 = ? d) 4 995 × 7 = ?
7 CM 2 DM 6 U 8 UM ? 4 UM 5 D 35 U 35 C ?
2 6 Numerador 8 Número de partes que se toman. Denominador 8 Número de partes iguales en las que se divide un todo.
propia
Vamos a recordar los tipos de fracciones.
El numerador es menor que el denominador. La fracción es menor que 1.
2 6 es una fracción propia porque 2 6 < 1
impropia
El numerador es mayor que el denominador. La fracción es mayor que 1.
7 6 es una fracción impropia porque 7 6 > 1 fracción igual a la unidad
El numerador y el denominador son iguales. La fracción 6 6 es una fracción unitaria, 6 6 = 1 mixta o número mixto
Formada por un número entero y una fracción. Las fracciones impropias se pueden convertir en mixtas y al revés. Mira el ejemplo.
7

= 1 1
El 1 significa que lo hemos tomado todo: 6 trozos, de los 6 trozos en que hemos dividido el círculo.
1 Clasifica estas fracciones en propias, impropias o igual a la unidad. Pasa a número mixto las que sean impropias.
2 Fíjate y completa esta serie:
34
3 LAS FRACCIONES
6 1 5 ? 5 ? ? 5 5 = 1 6 5 ? ? ? 10 5 = 2 2 7 A 3 2 B 6 6 C 8 5 D 3 3 E 7 5 F
6
Lectura de fracciones y fracciones más habituales
Para leer una fracción, primero nombramos el cardinal del número del numerador y, a continuación, el número del denominador de la siguiente forma:
• Si el denominador es 2, se indica medio . Por ejemplo, 1 2 se nombra «un medio».
• Si el denominador es 3, se indica tercio. Por ejemplo,
• A partir del 4 se lee el número como ordinal. Ejemplos:
1
4 se nombra «un cuarto» o «una cuarta».
1

5 se nombra «un quinto» o «una quinta».
1 10 se nombra «un décimo» o «una décima».
1 18 se nombra «un dieciochoavo» o «una dieciochoava».
En la vida ordinaria usamos algunas fracciones que son muy habituales. Así, decimos «un medio» para cuando queremos la mitad de algo, «un cuarto» cuando pedimos cantidades en kilos o litros, y «tercios» y «quintos» cuando queremos pedir capacidades.
1 Juan tiene 6 años y su hermana tiene la mitad de años. ¿Qué edad tiene su hermana?
Cuando Juan tenga 8 años, ¿qué edad tendrá su hermana?
2 En una clase hay 20 personas, de las cuales la cuarta parte son niñas. ¿Cuántas niñas hay en la clase? ¿Y niños?
3 En un depósito de gasolina de 50 litros de capacidad la aguja señala 5 partes. ¿Cuántos litros quedan en el depósito?
4 Observa esta tabla y completa en tu cuaderno con la cantidad correcta.

35 Unidad 3
nomBrE
1 2 ? 500 g ? ? 1 3 ? ? 333,33 mL ? 1 4 ? ? ? 250 m 1 5 Un quinto ? ? ?
DE 1 kilogrAmo son… DE 1 litro son… DE 1 kilómEtro son…
Fracciones decimales
Una fracción decimal es la que tiene por denominador 10, 100, 1 000…



3 10 es una fracción decimal. Se puede expresar, como número decimal, así: 3 10 = 0,3

Tres décimos Tres décimas
1 Fíjate en los ejemplos y pasa las siguientes fracciones decimales a números decimales.


a) 13 10 = 1,3 b) 2 10 = ? c) 7 10 = ? d) 10 10 = ? e) 4 100 = 0,04 f) 19 100 = ?
2 Y ahora, al revés. Pasa los siguientes números a fracciones decimales.
a) 0,05 = 19 100 = ? b) 0,7 = ? c) 1 = ? d) 1,2 = 12 10 o también 1 2 10 = ? e) 1,5= ?
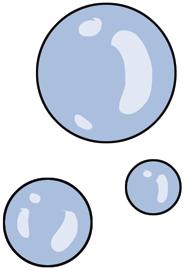
3 ¿Qué fracción representa cada uno de estos grupos de dedos respecto a los dedos de las dos manos?
Somos 7.
Somos 3.
4 ¿Qué fracción de billete de 10 € representan estas cantidades?

36
B A C
Fracciones equivalentes
¿Es lo mismo 1 3 de tableta, que 2 6 o que 8 24 ?
Las fracciones que representan la misma cantidad son equivalentes. Para obtener fracciones equivalentes a una dada, basta con multiplicar o dividir el numerador y el denominador por un mismo número.
1 Busca cuatro fracciones equivalentes, por amplificación, para la fracción de esta frase: «Me he bebido los 3 5 de una jarra de chocolate».
2 Mi hermano se va a enfadar cuando sepa que me he comido los 24 48 de una tarta de chocolate. Ayúdame a buscar cuatro fracciones equivalentes por simplificación, para que parezca que he comido menos.




3 Halla, en cada pareja, fracciones equivalentes con el mismo denominador.
4 ¿Cuál de las dos fracciones de cada pareja es mayor? Halla fracciones equivalentes y verás qué fácil es saberlo.

37 Unidad 3
1 3 2 6 8 24 1 2 = 2 4 = 4 8 = 12 24 10 20 = 5 10 = 1 2 ×2 ×2 ×2 ×3 ×2 ×3 :2 :2 :5 :5 AmpliFiCACión simpliFiCACión
2 3 10 15 3 5 9 15 y A 2 5 7 15 A 1 2 2 6 B 2 3 4 5 C 4 6 3 5 D 4 5 7 10 B 1 4 3 12 E 1 2 1 4 C 1 5 4 10 F 1 2 3 5 D 4 6 4 12 g
Comparar fracciones y ordenarlas según sean mayores o menores dependerá del número de trozos que tengamos (denominador) y de la cantidad de ellos que cojamos (numerador). Mira cómo se hace.




En dos o más fracciones con el mismo denominador (una cantidad que hemos dividido en partes iguales), es mayor la que tenga el numerador más grande (cantidad que tomamos del total).
Observa en estas fracciones como al coger cada vez más fichas rojas (numerador), al ser todas del mismo tamaño (denominador), cada vez la fracción es mayor.





En dos o más fracciones con el mismo numerador (tomamos siempre la misma cantidad), es mayor la que tenga el denominador más pequeño (número de partes que hemos hecho de una misma cantidad).
Observa en estas fracciones cómo el aumento del denominador afecta al tamaño de las fichas. Aunque cojas siempre la misma cantidad de fichas rojas, cada vez menores.

38
Orden de fracciones
4 12 12 12 2 12 7 12 5 12 21 12
1 Ordena de mayor a menor estas fracciones.
a) 1 9 , 3 9 , ? , ? b) 3 9 , 3 7 , ? , ?
3 Continúa la serie con dos fracciones más que sean consecutivamente mayores.
1 7 < 3 7 < 5 7 < 7 7 2 2 > 2 4 > 2 8
7 2 7 6 7 11 7 7 7 4 7 14
2 Y ahora, al revés, ordena estas de menor a mayor.
Suma y resta de fracciones con el mismo denominador
De una tableta con 24 onzas, Gema se come 2 onzas y, más tarde, otras 6 onzas. ¿Qué fracción de la tableta se ha comido en total? 16 24 − 4 24 = 12 24
Para sumar o restar fracciones con el mismo denominador, suma o resta los numeradores, el denominador no cambia.
De la tableta anterior quedan aún 16 24 Si ahora me como 4 onzas, ¿qué fracción queda?

Para sumar o restar fracciones con distinto denominador, conviértelas en fracciones equivalentes con el mismo denominador y luego opera como en el caso anterior.
1 Realiza estas sumas de fracciones con el mismo denominador.
2 Realiza estas restas de fracciones con el mismo denominador.
3 Me como 2 6 de una bolsa de caramelos y luego 1 6 . ¿Qué fracción de la bolsa me he comido?


4 Me he bebido 5 7 de una jarra de limonada y luego 2 7 más. ¿Qué fracción de limonada me queda en la jarra?

39 Unidad 3
2 5 + 3 10 = 4 10 + 3 10 = 7 10 2 3 − 1 6 = 4 6 − 1 6 = 3 6 + = 2 24 6 24 8 24 + = 3 5 + 1 5 = 4 5 6 8 + 3 8 4 7 + 5 7 3 6 + 1 6 7 12 + 5 12
2 3 − 1 3 5 6 − 1 6 7 10 − 5 10 7 7 − 2 7 B C D E A A B C D
Fracción de una cantidad
Para fraccionar una cantidad numérica, divide dicha cantidad en el número de partes iguales que indica el denominador de la fracción y toma tantas partes de ese valor como nos muestra el numerador. Observa un ejemplo:
En un huerto tienen un depósito de agua de 4 000 litros. Con las 4 8 partes del depósito han regado las verduras y con 3 8 han regado los árboles frutales.
¿Cuántos litros han echado en las verduras? ¿Y en los árboles? ¿Cuánta agua ha sobrado?

4 8 implica repartir en 8 partes los 4 000 litros y tomar 4 partes. De la misma manera, 3 8 es tomar 3 partes de esas 8.
Por tanto, cada parte es 4 000 : 8 = 500 litros Como han regado las verduras con 4 partes del depósito, eso son: 500 × 4 = 2 000 litros.
Y como han regado los árboles con 3 partes del depósito, eso son: 500 × 3 = 1 500 litros.
Para saber los litros que han sobrado, lo podemos hacer de dos formas:
1. Del total de litros, restamos los que hemos gastado: 4 000 − 2 000 − 1 500 = 500 litros sobran.
2. Calculamos la cantidad de la fracción que sobra ( 1 8 ): 4 000 : 8 = 500. Sobran 500 litros.
1 Calcula mentalmente las fracciones siguientes.
a) 1 2 de 1 000 b) 1 4 de 1 000 c) 3 4 de 1 000
2 Calcula las fracciones siguientes.
a) 1 2 de 2 800 b) 1 4 de 3 200 c) 2 5 de 3 500

3 En mi hucha tengo 180 €. Si gasto 2 6 en una entrada al parque de atracciones y 1 6 en recuerdos del parque, ¿cuánto me he gastado en cada cosa? ¿Qué fracción me queda?
¿Cuánto dinero me queda?
40
4 Completa con patrones las fracciones de estas cantidades.

1 2 de 48 = 24
1
2 de 480 = ?
1
2 de 4 800 = ?
1
2 de 4,8 = ?
1 2 de 0,48 = ?
2
3 de 6 = ?
2
3 de 60 = ?
2
3 de 600 = ?
2
3 de 6 000 = ?
2
3 de 0,60 = ?
3
4 de 8 = ?
3
4 de 80 = ?
3
4 de 800 = ?
3
4 de 8 000 = ?
3
4 de 0,8 = ?
5 Mi clase tiene 24 alumnos y alumnas. Se van los 3 4 de la misma. ¿Cuántos se han ido? ¿Cuántos quedamos?
6 En una carrera participaron 186 atletas, de los cuales 1 3 eran mujeres. ¿Cuántos hombres corrieron en la carrera?
7 De los corredores y corredoras de la carrera anterior, 1 6 no pudieron acabar la carrera. ¿Cuántos sí pudieron finalizarla?

41 Unidad 3
A B C
Cantidad de una fracción propia
Conociendo un cantidad (parte) de un total y su fracción podemos conocer el total. Lo entenderás mejor con un ejemplo: Para una fiesta llenamos el frigorífico con refrescos, de los que nos sobraron 16 latas, que son las 2 7 partes del total de las latas del frigorífico. ¿Cuántas latas gastamos?
Averigua cuanto es la cantidad de cada parte. Como el numerador es 2, significa que esa parte son las 16 latas. Por tanto 16 : 2 = 8.
Multiplica el valor de cada parte por el total de partes que se han hecho (denominador). En el frigorífico metimos 8 7 (partes) × 8 (latas en cada parte) = 56 latas.
Si queremos saber cuántas latas gastamos, la respuesta sería 56 − 16 = 40 latas.

¿Qué fracción son esas 40 latas? Es la fracción complementaria de 2 7 , es decir, 5 7

1 Calcula el total o cantidad de las siguientes fracciones.
a) 12 son las 3 8 de un total 8 12 : 3 = 4 cada parte 8 4 (partes) × 8 = 32. El total es 32.
b) 45 son las 3 4 = c) 56 son las 7 9 = d) 250 son las 5 6 =
2 Completa la tabla sabiendo que 24 es la cantidad de cada una de las siguientes fracciones.
Cantidad total 96 ? ? ? ? ?
42
1 4 2 3 4 5 2 6 4 7 4 8
Fracción
1 3 2 4
Cantidad de una fracción impropia
Si la fracción es impropia, es decir, si el numerador es mayor que el numerador, se realiza igual. Observa el ejemplo:
En dos frigoríficos tenemos la misma cantidad de refrescos. Si hemos gastados 250 refrescos, que son las 5 3 de todos los refrescos. ¿Cuántos refrescos había en total? ¿Cuántos refrescos sobraron?
Averigua cuánto es la cantidad de cada parte. Como el numerador es 5, significa que esa parte son los 250 refrescos. Por tanto 250 : 5 = 50.

Multiplica el valor de cada parte por el total de partes que se han hecho (denominador). En el frigorífico metimos 8 3 (partes) × 50 (latas en cada parte) = 150 refrescos.
Si queremos saber cuántos refrescos había en total, la respuesta sería 150 × 2 frigoríficos = 300 refrescos.
¿Cuántos refrescos sobraron?
300 − 250 = 50 refrescos, que son 1 3 parte.
1 Mira cómo se resuelve este ejercicio, y luego resuelve los siguientes en tu cuaderno.
a) 350 son las 5 3 . ¿De qué cantidad total hablamos?
Cada parte es de 350 : 5 = 70, como se han realizado 3 partes 8 3 × 70 = 210
b) 720 son las 8 4 c) 120 son las 6 5 d) 72 son las 3 2
2
2 400 litros son las 4 3 partes de los litros que se han gastado de dos depósitos iguales de agua. ¿Cuántos litros tiene cada depósito? ¿Cuántos litros quedan en el segundo depósito?
43 Unidad 3
1
3
2
4
Escala decreciente I
Experimento
¿Qué significa la expresión «veces menos»?
Coge 8 policubos (o cualquier otro objeto).
Tu compañero o compañera debe coger 4 veces menos. Para ello vamos a repartir los 8 policubos en 4 partes.
piensa: Cualquiera de las partes será el número de objetos que tiene tu compañero o compañera. resuelve: ¿Cuántos objetos tiene tu compañero o compañera?
Comprendo el problema
1 Completa la tabla con símbolos y con números. Aprende la diferencia entre «menos» y «veces menos». Un concepto implica restar y el otro dividir.




Resuelvo problemas
2 El hotel Plaza tiene 320 camas. El hotel Príncipe es más pequeño y tiene 4 veces menos camas que el Plaza. ¿Cuántas camas tiene el hotel Príncipe?
3 En un gran acuario hay 124 peces y 25 algas. Una pecera más pequeña tiene 97 peces menos y 5 veces menos algas. ¿Cuántos peces tiene la pecera pequeña? ¿Y cuántas algas?

4 Patricia tiene ahorrados 264 €, mientras que Sandra tiene 6 veces menos dicha cantidad. ¿Cuánto dinero tiene ahorrado Sandra? ¿Cuánto dinero tienen entre las dos?
Invento, creo y razono

5 Inventa un problema de «veces menos» a partir de la siguiente operación y resuélvelo.
63 : 7
44 RESUELVO PROBLEMAS
Elviajedeida
CAntiDAD iniCiAl 3 mEnos 3 3 vECEs mEnos : 3 12 OII IIIIIIIII 9 I I I I 4 15 ? ? ? ? ? 21 ? ? ? ? ? CAntiDAD iniCiAl 4 mEnos 4 4 vECEs mEnos : 4 16 ? ? ? ? ? 24 ? ? ? ? ?
Elviajedeida
Experimento

Coge 5 fichas (u otros objetos). Tienes tres veces menos fichas de las que tiene que coger tu compañero o compañera.






Piensa: ¿Quién tendrá menos fichas, tú o tu compañero o compañera?
Si tú tienes 3 veces menos fichas, tu compañero o compañera tendrá 3 veces ?
Resuelve: ¿Cuántas fichas tendrá tu compañero o compañera?
1 Marc ha hecho 6 fotos, 4 veces menos fotos que Ona. ¿Cuántas fotos ha hecho Ona?
Piensa: ¿Quién ha hecho menos fotos? ?
Si Marc ha hecho 4 veces menos fotos, Ona ha hecho 4 veces ?
Ona ha hecho ?
¿Cómo lo hemos resuelto?
Resuelvo problemas
2 Hace 7 días tenía 20 puntos, 5 veces menos de los que tengo hoy. ¿Cuántos puntos tengo hoy?
3 Laura se está leyendo un libro que tiene 231 páginas. Juan se está leyendo otro que tiene 7 veces menos páginas. ¿Cuántas páginas tiene el libro que se está leyendo Juan? ¿Cuántas páginas menos tiene el libro de Juan que el de Laura?
4 Al partido de fútbol de Manuel de esta semana han ido 125 espectadores, 3 veces menos espectadores que la semana pasada. ¿Cuántos espectadores fueron al partido de la semana pasada? ¿Cuántos espectadores más fueron la semana pasada que esta?
Invento,
5 Inventa un problema similar al anterior utilizando todos estos datos.

45 Unidad 3 Escala decreciente II
creo y razono
¿ ?
6 × 4 = 24 6 − 4 = 2 6 : 4 = 1 R = 2
el problema 45 4 9
Comprendo
Escala decreciente III Elviajedeida
Experimento
Coge 9 clips (u otros objetos). Ahora tu compañero o compañera coge 3 clips.








piensa: Para saber cuántas veces menos tiene uno que otro observa cuántas veces se repite la cantidad menor en la mayor.
resuelve: ¿Cuántas veces menos objetos tendrá tu compañero o compañera?
¿Cuántas veces más objetos tendrás tú?
Comprendo el problema
1 Completa y aprende cómo lo resolvemos.
Cromos soniA Cromos álvAro soniA tiEnE vECEs mEnos ¿Cómo lo hEmos sABiDo? álvAro tiEnE … vECEs más ? ? ? ? ? ? ? ? ?

Resuelvo problemas
2 Una mochila cuesta 24 € y un estuche 6 €. ¿Cuántas veces menos dinero cuesta el estuche? ¿Cuántas veces más dinero cuesta la mochila?
3 35 atletas han participado en una carrera de 10 km, 2 veces menos distancia que la media maratón. ¿Cuántos kilómetros tiene una media maratón?
4 Somos 78 alumnos y alumnas en 4.º y vamos a ir de excursión al teatro. Los 2 autocares que nos llevarán nos costarán un total de 1 200 €. Además, en las entradas al teatro nos gastaremos 4 veces menos. ¿Cuánto nos gastaremos en las entradas al teatro?
5 Cinco amigos han estado jugando a un juego. Al terminar, María tiene 250 puntos y Noelia tan solo 50. ¿Cuántas veces menos puntos tiene Noelia? ¿Cuántos puntos menos tiene Noelia?

Invento, creo y razono
6 Inventa un problema que se corresponda con la pregunta y la solución dadas eligiendo entre los datos propuestos.
7 48 54
6
¿Cuántas veces menos saltos dio Victoria? solución: 8 veces menos.
46 RESUELVO PROBLEMAS
TAREA COMPETENCIAL
La fiesta de cumpleaños


A continuación, te planteamos una situación a partir de la cual tendrás que responder varias preguntas (con una respuesta correcta). Escribe en tu cuaderno la letra que se encuentre junto a ella.
Como todos los años Alejandra ha celebrado su fiesta de cumpleaños con sus amigos. Este año ha invitado a Sara, Ainara y Javier. Esta es la cantidad de tarta que ha tomado cada uno.
Alejandra Sara Ainara Javier
1
Al terminar de comerse la tarta, la madre de Alejandra quiere saber cuánto ha comido cada uno. Alejandra pregunta a sus amigos, pero no todos dicen la verdad. Escribe en tu cuaderno las afirmaciones falsas.
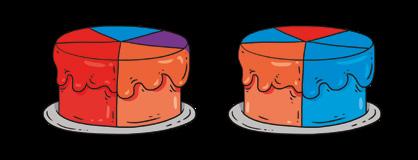
a) Sara dice que comió cuatro décimos.
b) Ainara asegura que comió 3 5
c) Por su parte, Javier dice que comió dos quintos.
d) Sara dice que entre ella y Javier comieron seis décimos.
e) Javier dice que entre él y Sara comieron una fracción impropia.
f) Alejandra afirma que comió una fracción propia.
2 Se ha creado un poco de confusión al respecto. Por ello, Alejandra decide ordenar de mayor a menor las fracciones que han comido todos. Selecciona qué opción lo indica.
a) Sara 4 5 , Ainara 3 5 , Javier 2 5 , Alejandra 1 5 .
b) Sara 4 10 , Ainara 3 10 , Javier 2 10 , Alejandra 1 10 .
c) Alejandra 1 5 , Javier 2 5 , Ainara 3 5 , Sara 4 5 .
d) Alejandra 1 10 , Javier 2 10 , Ainara 3 10 , Sara 4 10 .
47 Unidad 3
3 Alejandra solo ha comido un trozo de tarta. Se le ha ocurrido la brillante idea de representar la porción que ha comido con una fracción equivalente obtenida por amplificación para que «parezca» que ha comido más. Selecciónala.
a) 1 5 b) 2 10 c) 3 4 d) 2 5
Javier, Ainara y Sara han puesto dinero para comprarle un regalo a Alejandra. Además, recogieron el dinero de Mario y Sergio, que por motivos de salud no pudieron acudir a la fiesta. A la hora de hacer las cuentas, no tienen muy claro cuánto pagó cada uno. Ayúdales a averiguarlo.
4 Mario y Sergio pagaron dos quintos del precio del regalo. ¿Cuánto dinero pusieron entre los dos?


a) 14 euros. c) 7 euros.
b) 6 euros. d) 12 euros.
5 Sara puso 3 euros, 3 veces menos que Javier. ¿Cuánto dinero puso Javier?
a) 8 euros. c) 12 euros.
b) 9 euros. d) 6 euros.
6 El regalo costó 30 euros. Si Ainara puso 5 veces menos de lo que costó el regalo, ¿cuánto dinero puso Ainara?
a) 6 euros. c) 150 euros.
b) 12 euros. d) 7 euros.
48 TAREA COMPETENCIAL
30 �
1 Pasa cada número a lo que se indica u opera. Busca los resultados en las claves y descubrirás un mensaje que deberás responder.


2 Observa estos círculos donde aparecen representadas fracciones. Fíjate en el ejemplo y opera.

49 Unidad 3 Claves
REPASO
5 10 a decimal 12 10 a decimal 4 10 a decimal 15 10 a decimal 3,5 a fracción 0,3 a fracción 2,5 a fracción 1 3 + 1 3 5 6 + 2 6 4 8 + 2 8 4 5 − 1 5 3 4 − 1 4 6 8 − 3 8 2 3 + 1 3 2 3 de 9 3 5 de 15 1 4 de 12 ¡Cuidado!, quizá no necesites todas las palabras. la 0,4 ¿Cuál 0,5 es 1,2 mentira 1,5 de 9 cada 3 de 40 % Tres 6 esta 3 10 el 2 6 las 3 8 dos 2 3 problemas 3 5 tienen 6 8 con 2 4 1 fracciones. personas 7 6 frase? 25 10 en 35 10 por 45 10 1 A + L 8 3 6 + 1 6 = 4 6 2 F − D 3 C + K 4 E + D 5 J + K 6 I − B A g B h C i D J E k F l 1 5 9 14 2 6 10 15 3 7 11 16 12 13 17 4 8