

ASSISTENZA AL VOLO

Focus
L’importanza della standardizzazione nel servizio ATC

ASSISTENZA AL VOLO
Pubblicazione trimestrale
Organo ufficiale di ANACNA
Associazione Nazionale Assistenti e Controllori della Navigazione Aerea
Anno XLIX nr. 187 - trimestre 3/2024
Direzione Editoriale: Commissione Comunicazione e Stampa - Giuseppe Marino
Progetto grafico: Sara Manca
Hanno collaborato a questo numero:
Gianluca del Pinto
Marco Riccato
Alessandra Cola
La rivista è aperta alla collaborazione di professionisti, studiosi ed esperti del controllo del traffico aereo e dell’assistenza al volo.
Gli articoli, pubblicati come contributi indipendenti di documentazione e critica, possono non esprimere il punto di vista di ANACNA.
Direzione, redazione e pubblicità:
Via Camilla 39 00181 Roma, tel. 067842963 www.anacna.it
Geometria del vettoramento radar
STORIE FUORI CONTROLLO
Singapore 2024
IFATCA ANNUAL CONFERENCE
FOCUS
L'importanza della standar-
dizzazione nel servizio ATC
L'utilizzo della striscia
cartacea per i veicoli






Editoriale

Nel giugno del 2006 si svolse presso l’Accademia dei Lincei un importante convegno durante il quale, per la prima volta dalla caduta del Muro di Berlino e dopo 15 anni di privatizzazioni selvagge, si sollevò il problema della dismissione dei beni pubblici di carattere strategico. Ovvero di quelle aziende necessarie a che il Sistema Paese potesse sempre e comunque sopravvivere a sé stesso (si pensi al periodo del COVID quando si andava in torre e in sala radar sempre e comunque a garantire la continuità delle operazioni).
Da quel convegno, e dalla successiva commissione Rodotà creata per riformare le parti di Diritto relative alle alienazioni Statuali, venne fuori un disegno di legge che creava tassonomicamente i cosiddetti beni ad appartenenza pubblica necessaria, o beni pubblici sovrani.
Queste tipologie di beni pubblici, presenti ancora e più adesso, rispondono a interessi generali fondamentali la cui cura discende dalle prerogative dello Stato e degli enti pubblici territoriali. Si tratta di interessi quali ad esempio la sicurezza, l’ordine pubblico, la libera circolazione… per essi è prevista una disciplina rafforzata. Venne scritto che questi beni dovevano essere caratterizzati da forme di inalienabilità sostanziale.
In pratica si diceva che in caso di seri problemi alla società italiana alcune aziende sarebbero state chiamate a salvaguardare libertà di movimento, diritto alla sussistenza, tutela dei diritti
civili, etc.
Alla fine non se ne fece niente e il disegno di legge fu affossato.
Questo permise negli anni seguenti la vendita di pezzi pregiati di altrettante pregiate aziende italiane, seguendo la falsariga delle privatizzazioni liberiste, vendendo ciò che meglio funzionava ai privati. Il rischio imprenditoriale azzerato dallo stesso Stato che vendeva.
Anche ENAV anni addietro è entrata nel risiko delle grandi privatizzazioni così che adesso il provider italiano dei servizi della navigazione aerea, unico caso la mondo, quota in borsa corrispondendo i dovuti dividendi a chi ha investito sulle attività ATC.

Da qui è notizia recente del possibile e ulteriore passo di lato dello Stato, che intenderebbe vendere un ulteriore 20% del provider per trovare, nella sommatoria che si verrebbe a creare con altre aziende a partecipazione pubblica, circa 6 miliardi entro il 2025.
Da questa cessione lo Stato potrebbe incassare circa 400 milioni. Forse però l’idea di ravvedere nell’introito di breve periodo un giusto contrappeso alla voce sempre più minuta dello Stato nelle attività strategiche del sistema Paese non è priva di rischio. Perché nel lungo periodo altre nazioni stanno investendo nelle loro aziende, tutelandole dalle spinte dei mercati, sapendo per certo che la differenza fondamentale con quei mondi che cercano di farsi spazio a spallate la può fare solo il possedere un determinato know how accumulato per decenni. E sul quale occorre ancor più investire adesso.
Noi invece ce lo vendiamo.
Gianluca Del Pinto Presidente Anacna





COMAIR FLIGHT 5191

Di Gianluca del Pinto

Il 27 agosto 2006 il volo Comair 5191, in partenza dall’aeroporto di Lexington in Kentucky e diretto ad Atlanta in Georgia, effettuato con un CJR100ER, si schiantò al suolo subito dopo essersi alzato in volo. All’a/m era stata correttamente assegnata la pista 22, lunga 2135 metri, ma i piloti utilizzarono la pista 26 avendo così a disposizione solo 1100 metri per il decollo. Morirono tutti i 47 passeggeri e dei tre membri di equipaggio sopravvisse solo il primo ufficiale. Quella mattina, presso la Torre di Controllo aeroportuale, era presente un solo CTA. Quest’ultimo, oltre ad ottemperare alla fornitura dei servizi ATC unificati di controllo di aeroporto e di radar di avvicinamento, era impegnato nello svolgimento di altre funzioni, quali la registrazione dell’ATIS e la compilazione amministrativa del volato.
La successiva analisi è volutamente breve sì da evidenziare solo la funzione che riassume in se l’intera risonanza del sistema. Nel caso in oggetto si analizza < Il CTA rilascia l’autorizzazione al decollo > evidenziando, graficamente, gli aspetti che maggiormente hanno contribuito all’emersione dell’evento. Le risultanze raccolte ed elaborate basano sull’investigazione della NTSB 1 .
< Il CTA rilascia l’autorizzazione al decollo >
L’analisi può partire dalla disamina dell’input che, come funzione upstream, canalizza la risonanza facendola giungere presso le “coordinate” di tempo e spazio che poi si palesano come evento: < (Il CTA) rilascia la clearance per il rullaggio >. Questa funzione, input a che < Il CTA rilasci l’autorizzazione al decollo > ha come peculiarità, non solo nel caso in oggetto, il fatto che sull’area di manovra aeroportuale essa assume forte preponderanza rispetto alle altre funzioni per il fatto che diviene catalizzatore della variabilità di molte altre funzioni. Date cioè le necessarie premesse essa immette nel sistema quella risonanza stocastica determinante a che l’emersione dell’evento possa avvenire. 1. NTSB, Attempted takeoff from wrong runway Comair Flight 5191 Bombardier CL-600-2B19, N431CA Lexington, Kentucky August 27, 2006

Nome della funzione
Descrizione
Aspetti
Input
Output
Precondizioni
Risorse
Controlli
Tempo
(Il CTA) rilascia la clearance per il rullaggio
Il CTA autorizza l’a/m a raggiungere il punto attesa della pista in uso tramite la comunicazione del percorso da effettuare
Descrizione dell’aspetto
Startup e pushback completati
Clearance ATC rilasciata
Clearance per il rullaggio rilasciata
Esperienza
Addestramento
Osservazione visiva
Supervisore
Procedure locali (IPI, LoA)
Fare il prima possibile
Per quanto riguarda le risorse della funzione < (Il CTA) rilascia la clearance per il rullaggio > qui individuate esse evidenziano l’importanza tanto del livello di sharp end (strip marking ed esperienza) che del livello di blunt end (considerando addestramento, turnazioni, layout operativo, come organizzati e diffusi dal management aziendale). Un’ulteriore risorsa, solo apparentemente “evidente”, è la presenza in numero necessario e sufficiente di Controllori del Traffico Aereo. A questa componente numerica è direttamente collegato il principio della variabilità della Performance.
L’evidenza di tale variabilità, da indicare anche come una zona di emersione dell’evento (vedi il piccolo dizionario ragionato), venne considerata dalla NTSB come concausa dell’evento. Perché in questo caso la Performance influenzò negativamente lo scenario operativo.

Aquesta componente numerica è direttamente collegato il principio della variabilità della Performance
[Controllo]
[L’osservazione visiva] è qui preponderante. Il modello FRAM non ritiene di indicare qualsivoglia funzione come “centrale” nell’analisi dell’evento ché è il sistema nella sua interezza ad aumentare di magnitudine. Ma è altrettanto necessario ritenere tale aspetto come fenomeno stocastico per l’unicità e non ripetibilità dello scenario operativo oggetto della presente analisi. In altro contesto [l’osservazione visiva] può non essere riconoscibile o rappresentare un’importante criticità. Qui è preponderante.
Sempre dal rapporto della NTSB:
1.18 Additional Information
1.18.1 Witness Information
The Safety Board interviewed the two eyewitnesses to this accident. One eyewitness was an American Eagle station agent who was on a ramp by a gate when the accident airplane taxied past his location at a normal taxi speed.
The station agent stated that he saw the airplane make a sharp, instead of a slight, turn to the left. He thought the flight crew might have made this turn so that the airplane could return to the gate. The station agent was not paying attention to the airplane when its engine power increased, but he then realized that the airplane was taking off from runway 26.
He saw the airplane continue down the runway but did not notice if the nose of the airplane rose. The station agent then saw and heard an explosion followed by some “pops” and three or four smaller explosions. In addition, he stated that the runway 22 lights and taxiway lights were illuminated.
Ora, giunti al punto attesa della pista erroneamente ritenuta quella valida e necessaria all’involo, il sistema, per tramite delle sue funzioni, ha accumulato una quantità di energia tale da generare un’enorme risonanza. Ed è qui che < (Il CTA) rilascia l’autorizzazione al decollo >.
Nell’immagine che segue in rosso vengono evidenziati gli aspetti che non hanno permesso all’eccesso di variabilità di rientrare nei parametri dell’accettabilità. Quando cioè ancora il sistema può notare che l’a/m è allineato e pronto al decollo dalla pista sbagliata. Analizziamoli attraverso la funzione a cui appartengono.


Nome della
funzione
Descrizione
(Il CTA) rilascia l’autorizzazione al decollo
Il CTA rilascia l’autorizzazione al decollo dopo aver accertato con ragionevole certezza che le prescritte separazioni, necessarie a consentire che l’a/m si involi in totale sicurezza, esisteranno anteriormente al momento in cui l’aeromobile inizierà il decollo.
Aspetti
Descrizione dell’aspetto
Input
Clearance per il rullaggio rilasciata
Output
Pista occupata
Autorizzazione al decollo rilasciata
Precondizioni
Punto attesa della pista in uso raggiunto
Clearance ATC rilasciata; quando possibile farlo prima del rullaggio della/m
Pista libera
Risorse
Esperienza
Addestramento
Controlli
Osservazione visiva
Supervisore
Procedure locali (IPI, LoA)
Fare il prima possibile
Come precondizione al decollo, che nel caso specifico concorre all’evento, abbiamo che < (il pilota deve) rulla(re) al punto attesa > di modo che il [punto attesa della pista in uso (sia) raggiunto]. La variabilità di tale funzione eccede il range ottimale in ragione del non soddisfacimento di alcuni dei suoi aspetti. Vediamo nello specifico quali. Da notare come anche per il pilota sia il rullaggio sull’area di manovra a catalizzare, fisicamente, l’eccesso di risonanza.


< (il pilota) rulla al punto attesa >
Descrizione
Aspetti
Input
Output
Precondizioni
Risorse
Controlli
Tempo
Il pilota pone in essere quelle azioni che permettono all’a/m di uscire dall’apron e di raggiungere il punto attesa della pista in uso. Si parla di vera e propria navigazione a terra (surface navigation), che impegna i piloti tanto quanto il volo vero e proprio.
Descrizione dell’aspetto
Clearance per il rullaggio
Punto attesa della pista in uso raggiunto
Clearance per il rullaggio ottenuta
Clearance per il rullaggio rilasciata
Esperienza Carte aeronautiche
Briefing per il rullaggio completato
Segnaletica orizzontale e verticale
Flight deck sterile
Tempo sufficiente per comunicare correttamente i dati
Basandosi sul rapporto dell’NTSB in particolare modo si può notare come la variabilità ecceda significativamente nei seguenti aspetti:
[Controlli]
• Il [il briefing per il rullaggio] non viene effettuato in maniera conforme agli standard della compagnia. Come primo volo della giornata occorre effettuare un briefing per il rullaggio rispondente al Comair standard taxi information nella sua interezza. Si riporta infatti che i piloti should have the appropriate diagrams out and available and that traversing the runways required extra diligence. Il comandante effettua un normale briefing omettendo il necessario attraversamento della pista 26 per raggiungere la pista 22.
• La [segnaletica orizzontale e verticale] era adeguata? Dopo l’incidente la Comair informò i piloti che published airport diagrams may not accurately reflect actual airport signage and markings.
• Non si ottempera al [flight deck sterile]. Il data recorder riporta comunicazioni non standard oltre a far supporre che i piloti non utilizzino adeguata diligenza nello svolgimento delle azioni necessarie all’involo. È il caso dell’eccessiva esperienza calata in scenari routinari e ripetitivi. All’eccessiva stabilità segue la stagnazione delle procedure che non considerano più lo scorrere dello scenario operativo, il suo continuo mutamento, ma solo l’equilibrio risultante.
[Risorse]
• L’[esperienza] viene ad essere travisata e compromessa dall’eccessiva ripetitività delle azioni. Le interviste della NTSB ai piloti che operano su LEX concordano sul fatto che la brevità del rullaggio e l’utilizzo di una sola taxiway per raggiungere il punto attesa della pista 22 porta ad omettere la comunicazione/condivisione dell’attraversamento della pista 26.
• Le [carte aeronautiche] non hanno giusta corrispondenza con lo scenario operativo della mattina del 27 agosto 2006. La Jeppesen giustifica tale mancanza con un bug nel software preposto all’elaborazione dei cambiamenti da apportare alla cartografia. Nello specifico la comunicazione dei lavori è giunta di venerdì dopo l’orario di chiusura degli uffici! L’incidente è avvenuto la domenica mattina.
L’output della funzione, cioè il [punto attesa della pista in uso raggiunto], immette nel sistema un ulteriore eccesso di variabilità che porta il valore di magnitudine dell’intero sistema in prossimità della soglia dell’emersione.


azioni ed inazioni del CTA.
Torniamo alle azioni ed inazioni del CTA.
I controlli a che il < (Il CTA) rilasci l’autorizzazione al decollo >, nel caso in analisi, sommano i propri output al valore finale della variabilità dell’istanziazione. Da evidenziare allora abbiamo:
• [L’osservazione visiva] dello scenario operativo. Per quanto esso riguarda dalle evidenze raccolte dalla NTSB si evidenzia che: If the controller had been looking out the tower cab window and monitoring the flight, he could have addressed this situation by alerting the flight crewmembers that the airplane was on the wrong runway or, later, by instructing them to reject the takeoff. The controller did not take any such actions. The controller indicated that he did not see the airplane align with runway 26 or begin its takeoff roll because he had turned around to perform the traffic count, which is an administrative record-keeping task. The Safety Board concludes that the controller did not detect the flight crew’s attempt to take off on the wrong runway because, instead of monitoring the airplane’s departure, he performed a lower-priority administrative task that could have waited until he transferred responsibility for the airplane to the next ATC facility .
Il Controllore aggiunge che it might have been possible for him to detect that the accident airplane was on the wrong runway if he had been looking out the tower cab window. Inoltre che when aircraft separation was not a factor, his decision to watch airplanes taxi and take off depended on whether he had other tasks to perform.
• < L’organizzazione strategica delle operazioni >, intesa come funzione di background che rilascia output sotto forma di controlli e risorse, aggiunge come controlli la figura del [supervisore] e le [procedure locali].
La prima non è presente e ad aumentare la variabilità concorre il fatto che di notte a LEX si lavora in single man operation. Solo dopo l’evento vengono assunti 4 ulteriori Controllori dispiegandone due per lo spezzone operativo notturno. Le [procedure locali] più che essere disattese vengono “a patti” con la quotidiana ripetitività delle azioni per far sì che il sistema venga ritenuto stabile agli occhi e per conto della funzione organizzativa (che poi è il modo distruttivo di operare nel sistema). Ciò ha impedito di osservare l’a/m al punto attesa, soltanto perché occorreva assolvere a compiti burocratici in orario operativo. Il Controllore riporta nelle sue dichiarazioni che: He normally accumulated flight progress strips throughout the night and performed the traffic count once toward the end of the shift.
Le [risorse] necessarie a che < (Il CTA) rilasci l’autorizzazione al decollo > nel caso possono essere identificate in due funzioni di background che tuttavia prevaricano la contingenza del momento. E tanto [l’esperienza] che [l’addestramento] non vengono indicate come possibili catalizzatori in quanto appaiono essere, al contrario, smorzatori di variabilità. Il CTA la-
vora da 17 anni a LEX ed è in regola con le procedure di accertamento psico-fisiche ed operative. Ma si deve riportare che tutto ciò riduce, se non elimina completamente, quella tensione operativa sempre necessaria a che si possa essere in grado di identificare la possibile emersione di un evento. Tanto vale anche per un eventuale modello di analisi da applicare ai piloti.
Riproduzione delle registrazioni CVR, FDR, e B/T.
0604:33 FDR: airplane stops
0605:06 CVR: takeoff checklist completed
0605:15 F/O: “Comair one twenty-one ready to go.”
0605:18 ATC: “Comair one ninety-one cleared for takeoff.”
FDR: airplane resumes taxi
0605:24 Captain: “line-up check.”
0605:41 FDR: airplane begins turning onto runway 26
0605:46 F/O: “line-up check's complete”
0606:05 CVR: recorded a sound similar to an increase in engine rpm.
0606:16 F/O: “[that] is weird with no lights”
0606:31.2 Captain: “V one, rotate”
0606:31.8 Captain: “whooaa”
0606:33 CVR: sound of impact
0606:36 CVR: end of recording
0607:17 ATC: the crash phone activated

Vecchio e nuovo layout aeroportuale
Il disastro del Comair 5191 ha portato una radicale ristrutturazione del layout aeroportuale di LEX. Prima dell’evento la pista 22/04 e la pista 26/08 si intersecavano in corrispondenza delle testate pista 22 e 26; dal 2010 la 26/08 è stata cancellata per far posto alla 27/09. Quest’ultima RWY non interseca più la pista principale ma è posizionata oltre la 22/04 e collegata all’apron principale attraverso una TWY che, questa sì, attraversa la pista principale.
Risulta difficile analizzare e dare un giudizio su tale nuovo scenario operativo soprattutto perché lo studio di fattibilità ha avuto origine da un evento disastroso.
Ma modificare lo scenario operativo può veramente sempre migliorare le operazioni? Può evitare il ripetersi di tali accadimenti?
Certamente non si potrà più realizzare un nuovo Comair 5191 perché è stato eliminato l’eccesso di variabilità di alcune funzioni e risonanze che però sono risultate tali solo per quel particolare scenario verificatosi il 27 agosto 2006.
Tanto vero è che, sempre dal rapporto della NTSB, successivamente al caso del Comair, si sono verificati due scenari all’interno dei quali si sarebbe potuto ricreare l’evento qui analizzato. Il 9 novembre 2006 un Piper PA-32 e il 1 gennaio 2007 un Lear jet 45 in procinto di partire dalla pista principale 22 hanno avuto, o ad essi sono stati richiesti, chiarimenti dalla TWR sulla posizione tenuta all’atto dell’attraversamento della pista 27 per portarsi al punto attesa 22. La variabilità è stata tenuta all’interno dei parametri accettabili.

Volendo cinicamente dare un giudizio si può dire che difficilmente un a/m sarebbe potuto decollare nuovamente dalla pista sbagliata ed è altrettanto vero che così ristrutturato il layout aeroportuale è maggiormente prono alla fattibilità di una RI-VAP. Questo perché l’attraversamento necessario a raggiungere la pista 27/09 si trova a 630 metri dalla THR 22 della pista appunto 22/04.

Occorre imparare dagli eventi, fare in modo che essi non si realizzino e ripetano, ma l’ottica da utilizzare deve essere sempre quella sistemica e l’analisi deve basare sui principi della Safety II che guarda a ciò che funziona, non a ciò che va, o potrebbe, andare male.



FLIGHT LE VEL


Geometria del vettoramento radar
Di Marco Riccato
Se vi chiedessi quali siano i criteri con cui scegliere una prua per un vettoramento radar, molti di voi risponderebbero come il manuale: vento, spazi aerei, orografia, meteo, ecc. Risposta corretta: il vettoramento radar è condizionato da numerosi fattori, al punto che la scelta della soluzione più
appropriata sembra quasi che sia solamente una questione di esperienza, molto difficile da spiegare. Però, se ci limitiamo all’ambito puramente geometrico, il vettoramento può essere affrontato come un problema di analisi matematica, la cui soluzione porta a dei risultati in perfetta armonia

con la pratica quotidiana.
Questo articolo, dedicato a chi già conosce la tecnica radar per il controllo del traffico aereo, si basa su appunti presi molti anni fa, per intenderci, in un periodo in cui gli schermi radar erano a tubo catodico, ed ha l’obiettivo di giustificare alcune semplici regole pratiche della tecnica radar attraverso un po' di calcoli matematici. Chi non ama particolarmente la matematica può tranquillamente saltare le formule e confrontare con la propria esperienza le regole pratiche che ne derivano. Chi invece vorrà affrontare tutti i passaggi del calcolo avrà in premio l’oppor-
tunità di fare un’ottima figura con un figlio o un nipote liceale.
In realtà c’è un altro ottimo motivo per rispolverare oggi questi vecchi risultati: l’attuale disponibilità di sistemi di comunicazione (es. Datalink) e tool di calcolo (es. TCT), che ci permettono di assegnare prue precise senza fatica di valutare graficamente la separazione tra aeromobili, talvolta porta a risultati non in linea con le nostre aspettative: in quei casi la matematica ci può aiutare a migliorare la comprensione dei valori che ci vengono proposti e a lavorare con maggiore serenità.
vettoramento radar

La regola
“1 in 60”
Questa è forse la regola più famosa tra quelle presentate, e permette, in assenza di vento, di calcolare l'angolo di vettoramento per mandare un aeroplano verso un dato punto. La regola recita quanto segue:
Su una distanza di 60NM, un vettore produce una deviazione in NM pari all'angolo di virata in gradi.
Come si vede dalla figura seguente, il rapporto tra la deviazione D e la distanza S è pari alla tangente dell'angolo di vettoramento a.

Il rapporto tra la deviazione D e la distanza S è pari alla tangente dell'angolo di vettoramento a.
Se indichiamo con x un angolo in radianti, lo sviluppo 2 della funzione tangente è: tan x = x + x³/3 + …
Per trasformare l'angolo da radianti a gradi bisogna moltiplicare per π/180 = 3,14/180 = 0,0174. Quindi la deviazione D, con lo sviluppo in serie, si può esprimere nel modo seguente:
D = S tana = S * (0,0174a + 0,0174³a³/3 + …)
Il termine 0,0174³ vale circa 0,00000527. Calcolatrice alla mano si vede facilmente che per valori di a fino a 20 gradi (a³/3 = 4000/3 = 1333) il secondo termine della somma è trascurabile rispetto al primo (0,007 contro 0,348, un valore 50 volte più piccolo). Quindi è possibile approssimare la formula nel modo seguente:
D = S * 0,0174*a
Sostituendo S = 60 NM e a = 1 grado:
D = S * 0,0174*a = 60 * 0,0174 * 1 = 1,044 NM = 1 NM
Che ci conferma che:
Su una distanza di 60 miglia, si crea una deviazione dalla rotta di 1 miglio ogni 1 grado di angolo di vettoramento.
2. Sviluppo in serie di Mac Laurin
Cosa succede se la distanza non è di 60 NM?
Se la distanza S non è di 60 NM allora la deviazione D varia proporzionalmente ad S, quindi si può rendere questa formula più generale. È il caso più comune, in cui un controllore ha la necessità di vettorare un aeromobile ad una data distanza da un punto, per conseguire una deviazione da tale punto di un certo numero di miglia.
Basta prendere la formula individuata precedentemente e “rovesciarla”:
D = S * 0,0174*a diventa
a = (1/0,0174)*D/S = 60 * D/S
Cioè:
l’angolo di vettoramento è pari a 60 volte il rapporto tra la deviazione da conseguire e la distanza.
Attenzione: questa cosa non è vera sempre; bisogna tener presenti i limiti sugli angoli per cui questa formula è valida, abbiamo detto circa 20 gradi. In verità, con un po’ di attenzione, si può usare anche per angoli maggiori, come vedremo nell’esempio seguente.
A una distanza di 40 NM si vuol far deviare un aeromobile di 20 NM. Qual è l’angolo di vettoramento? Applicando la formula: a = 60 * 20/40 = 30 gradi. In realtà non siamo all’interno del campo di validità della formula; perciò, un controllino usando la trigonometria è opportuno: tana = 20/40 => a = 27 gradi. Un errore di 3 gradi è comunque accettabile! Vediamo un altro esempio. Ad una distanza di 80 NM si vuole
conseguire una deviazione di 10 NM. Qual è l’angolo di vettoramento? Applichiamo la formula: a = 60 * 10/80 = 7,5 gradi. Questo aeromobile prenderà una prua di 8 gradi!
Distanza minima di traffici che si incrociano senza
vettoramento
Il problema di calcolare la minima distanza tra due traffici che si incrociano è ormai superato con l’introduzione del tool TCT (Tactical Controller Tool) il quale mostra graficamente la separazione minima. Ad ogni modo, come facevamo prima?
Prima di iniziare un vettoramento, si deve valutare la minima distanza tra due traffici che si incrociano, cioè la distanza tra essi quando si trovano al cosiddetto CPA (Closest Point of Approach), per stabilire se è già sufficiente a garantirne la separazione. L’unica possibilità che avevamo era misurare la distanza dal punto d’incrocio di entrambi gli aeromobili e calcolare la differenza. Il valore così ottenuto non era la distanza minima, perché la distanza tra i voli continua a decrescere, fino al CPA, fino a circa il 70% della distanza così misurata. Nei paragrafi seguenti vedremo una semplice regola pratica per stimare la separazione al CPA.
Consideriamo due aeromobili di ugual velocità le cui rotte si incrociano con un angolo di 90 gradi e costruiamo un modello matematico che descriva questa situazione. Ad esempio, si veda la figura seguente:





I due aeromobili distano rispettivamente dal punto d’incrocio D1 e D2. La distanza S tra loro si può calcolare con il teorema di Pitagora:
S = √[D1²+D2²]
Il modello matematico che stavamo cercando è questo. Ora, come spesso si fa in questi casi, lavoriamo sulle variabili in gioco al fine di semplificare i calcoli: la differenza delle distanze dei due aeromobili dal punto d’incrocio, dato che procedono alla stessa velocità, si mantiene costante, perciò scriviamo:
D1 – D2 = k
Ora se chiamiamo una delle due distanze, ad esempio D2, con x, possiamo scrivere:
D2 = x; D1 = x + k
Fin qui non abbiamo fatto altro che cambiare i nomi alle cose. Vediamo ora come diventa il nostro modello matematico con le sostituzioni fatte:
S = √[D1²+D2²] = √[(x + k)²+x²]= √[2x²+2kx+k²]
Abbiamo quindi espresso la distanza S tra i due aeromobili come una funzione della variabile x e della costante k.
Ci aspettiamo che il valore di S, man mano che gli aeromobili proseguono lungo la rotta (cioè man mano che x diminuisce e poi diventa negativa), dapprima scenda, poi, raggiunto il minimo quando gli aeromobili sono più vicini, tenda poi a salire all’infinito. Facendo il classico “studio di funzione”3 si trova conferma di ciò ed il punto di minima distanza tra gli aeromobili si ha quando x = -k/2. Se andiamo a sostituire questo valore per trovare il corrispondente valore di S troviamo:
S = k/√2
Ma il valore di k, ricordiamo, era pari a D1-D2, cioé alla differenza delle distanze dei due aeromobili dal punto d’incrocio, mentre il termine 1/√2, calcolatrice alla mano, vale circa 0,7.
Perciò:
S = 0,7(D1-D2)
La minima distanza tra due aeromobili le cui rotte si incrociano a 90 gradi è pari al 70% della differenza delle distanze dal punto d’incrocio.
3. Per brevità si omettono i passaggi intermedi e si riportano solo i risultati. La derivata prima dS(x)/dx = (2x+k)/√[2x²+2kx+k²], si annulla per x = -k/2 che è quindi un possibile punto di minimo assoluto. La derivata seconda d²S(x)/dx =k²/[2x²+2kx+k²]^1,5 è sempre positiva, quindi la funzione S è concava verso l’alto ed effettivamente x = -k/2 è un punto di minimo assoluto.
Dati due aeromobili con le rotte che si incrociano a 90 gradi, la loro minima distanza si ottiene misurando la differenza delle distanze dal punto d’incrocio e riducendola del 30%.
Vediamo un esempio pratico: supponiamo che un aeromobile sia a 30 NM dal punto di incrocio, mentre l’altro sia a 20 NM. La distanza sul punto d’incrocio k è pari a 30 – 20 = 10 NM. Quando un aeroplano sarà a D2 = x = -k/2 = -5 NM, cioè 5 NM dopo il punto d’incrocio, e l’altro sarà a D1 = k + D2 = 10 – 5 = 5 NM prima del punto d’incrocio, essi saranno alla distanza minima, che con il teorema di Pitagora ritroviamo essere pari a √(5²+5²) = √50 = 7 NM, a conferma del risultato precedentemente ottenuto.
Cosa succede se
l’angolo
d’incrocio non è 90 gradi?
Intuitivamente viene da pensare che, man mano che l’angolo tra le rotte si riduce, la minima distanza tra i due aeromobili si avvicini sempre più alla differenza delle distanze dal punto d’incrocio, fino a diventarne uguale nel caso della stessa rotta (angolo 0).
Naturalmente la matematica conferma questo fatto, ma il modello matematico si complica un po’ perché bisogna ricorrere alla trigonometria. Il modello è analogo a quello dei paragrafi precedenti, con la definizione dell’angolo a con cui si incrociano le due rotte:




a a a
La distanza tra i due aeromobili, sempre attraverso il teorema di Pitagora, si può esprimere nel modo seguente:
S = √[(x + k-x cos a)²+x²sen²a]= √[2(1-cos a)x²+2(1cos a)kx + k²]
Anche in questo caso ci aspettiamo un andamento prima decrescente e poi crescente, con un punto di minimo assoluto corrispondente alla minima distanza tra i due aeromobili. Facendo lo “studio di funzione”4 si ottiene che, analogamente al caso precedente, il punto di minima distanza si ha per x = -k/2. Il valore di S corrispondente è:
S = k √[(1 + cos a)/2] = (D1-D2) cos(a/2) I lettori più attenti nel passaggio precedente riconosceranno la “formula di bisezione”. Per ricavare una regola utilizzabile nella pratica operativa si veda la seguente tabella, contenente i valori che la formula assume al variare dell’angolo di incrocio a.

I valori riportati si possono riassumere in un’unica regola pratica:
La distanza minima tra due aeromobili che si incrociano si riduce del 3% ogni 10 gradi rispetto alla differenza delle distanze misurata dal punto d’incrocio.
Esempio pratico: due aeroplani convergono con un angolo di 40 gradi e distano dal punto d’incrocio rispettivamente 64 e 50 NM. Quale sarà la loro minima distanza? La differenza sul punto d’incrocio è 64 – 50 = 14 NM. La riduzione è del 40/10*3 = 12% quindi la distanza minima è di 14*0,88 = 10,5 NM
4. Per brevità si omettono i passaggi intermedi e si riportano solo i risultati. La derivata prima dS(x)/dx = (2x+k) (1-cosa)/√[2(1-cosa)x²+2(1-cosa)kx+k²], si annulla per x = -k/2 che è quindi un possibile punto di minimo assoluto. La derivata seconda d²S(x)/dx =(1-cosa)²k²/[2(1-cosa)x²+2(1-cosa)kx+k²]^1,5 è sempre positiva, quindi la funzione S è concava verso l’alto ed effettivamente x = -k/2 è un punto di minimo assoluto.
Cosa succede se gli aeromobili non hanno velocità uguale?
Questa parte, tra l’altro, spiega perché a volte i risultati del TCT non sono attendibili, quindi è ancora interessante. Per avvicinarsi ancora di più al caso realistico, vediamo cosa succede quando i due aeromobili che si incrociano volano a velocità differenti. In questo caso, continuando ad usare la notazione del punto precedente, la distanza dal punto d’incrocio, è:
k’ = (D2-D1)+(V1-V2)*t1, dove:
k’ è la distanza dei due aeromobili al punto di incrocio;
D1 è la distanza del primo aeromobile dal punto di incrocio;
D2 è la distanza del secondo aeromobile dal punto di incrocio;
V1 è la velocità (ground speed) del primo aeromobile in NM/min; V2 è la velocità (ground speed) del secondo aeromobile in NM/min; e, t1 è il tempo in minuti che il primo aeromobile impiega a raggiungere il punto d’incrocio.
Questa formula significa che, rispetto ai casi precedenti, la differenza sul punto d’incrocio va corretta del fattore (V1-V2)*t1, che tiene conto del fatto che uno dei due aeromobili è più veloce. Se il primo aeromobile è più veloce del secondo, questa correzione è positiva e lo spaziamento che si ottiene è maggiore (il primo aeromobile “scappa via” dal secondo). Se il primo aeromobile è più lento del secondo, la correzione è negativa e lo spaziamento che si ottiene è minore (il secondo aeromobile tende a raggiungere il primo).
Regole pratiche (nel caso del secondo aeromobile più veloce del primo):
• una differenza di velocità di 6 nodi (0.01 M) comporta una riduzione di 1 NM ogni 10 minuti;
• una differenza di velocità di 30 nodi (0.05 M) comporta una riduzione di 1 NM ogni 2 minuti;
• una differenza di velocità di 60 nodi (0.09 M) comporta una riduzione di 1 NM ogni 1 minuto.
Le riduzioni indicate si riferiscono alla differenza delle distanze dal punto d’incrocio, non alla minima separazione. Però, come abbiamo visto in precedenza, la minima separazione (al CPA) è proporzionale alla differenza delle distanze dal punto d’incrocio con un fattore che dipende dall’angolo d’incrocio (es.: 90° => 70%) che quindi, ai fini del calcolo della separazione minima va tenuto in considerazione.
Riguardo l’uso del TCT, allora, perché a volte troviamo dei risultati non attendibili? Il TCT non è attendibile in due situazioni: se uno dei due aeromobili è in virata (ovviamente) oppure se cambia la velocità (ad es. quando è in salita, quando cambia il vento, ecc.). Questo secondo caso è facilmente spiegabile per quanto abbiamo appena visto, tenendo presente che la correzione per differenza di velocità è ovviamente già compresa nel calcolo del TCT, purché le velocità rimangano costanti. Quindi il fattore che può invalidare il calcolo, a cui dobbiamo prestare molta attenzione, sono le variazioni di velocità.
A differenza della posizione dell’aeromobile, che viene misurata direttamente dal sensore radar e subito presentata sullo schermo, la velocità

(ground speed) è un valore calcolato, ad esempio, considerando gli ultimi n valori di posizione misurati, con la nota formula velocità=spazio/tempo, e poi facendo la media. Ciò comporta che eventuali variazioni di velocità (ground speed) non entrino immediatamente nel calcolo del TCT, ma che debbano passare diverse decine di secondi perché il TCT si trovi la velocità aggiornata e ricalcoli la separazione tra i traffici.
Minima distanza su rotte
Il vettoramento su rotte incrociate è una delle azioni di controllo più difficili
incrociate, vettorando entrambi gli aeromobili
Nell’ambito del controllo del traffico aereo, il vettoramento su rotte incrociate è una delle azioni di controllo più difficili, perché bisogna saper valutare bene diversi parametri contemporaneamente. Lo studio del vettoramento su rotte incrociate si divide in due casi: questo è quello in cui entrambi gli aeromobili sono su vettore, tipico delle situazioni in cui lo spazio a disposizione per conseguire la separazione non è molto.
Ai fini dell’analisi matematica del problema assumiamo le seguenti ipotesi: assenza di vento, rotte che si incrociano a 90 gradi, aeroplani con la stessa velocità ed equidistanti dal punto d’incrocio, ad entrambi viene data una prua nello stesso verso, gli aeroplani si assumono stabilizzati sulla prua entro una distanza prefissata D dal punto d’incrocio.

Analizziamo l’evoluzione della distanza S tra gli aeromobili che si muovono verso il punto d’incrocio, prendendo come variabile la distanza L percorsa dagli aeromobili su prua.


La distanza S tra gli aeromobili si trova con il teorema di Pitagora:
S = √(x2-x1)²+(y2-y1)²
Mentre le coordinate si possono esprimere in funzione di L e dell’angolo a usando la trigonometria:
x1 = L cosa y1 = L sena
x2 = D + L sena y2 = D - L cosa
Sostituiamo le coordinate nella formula della distanza S per esprimerla in funzione di D, L e dell’angolo a:
S = √(x2-x1)²+(y2-y1)²= √(D + L sena - L cosa)²+(D - L cosa - L sena)²= = √[D² + L²(1-2senacosa) - 2DL(cosa-sena) + D² + L²(1+2senacosa)2DL(cosa+sena)] = = S = √[2(D² + L² - 2DLcosa)]
Per studiare il comportamento di questa funzione al variare di L, è necessario calcolarne la derivata prima e le successive. Con alcuni passaggi5 si trova che il punto di minima distanza si ha quando L = D cosa.
Per angoli di vettoramento piccoli (fino a 20 gradi) il coseno è quasi pari a 1, quindi L = D:
Per piccoli angoli di vettoramento la distanza minima si ha quando gli aeromobili hanno percorso su prua un percorso pari alla distanza dal punto d’incrocio dell’inizio del vettore.
La distanza minima, sostituendo il valore di L trovato nella formula di S, risulta: S = D sena √2
Introduciamo alcune approssimazioni per rendere la formula più leggibile: per angoli di vettoramento fino a 45 gradi il seno dell’angolo è praticamente pari all’angolo espresso in radianti. Perciò risulta, con l’angolo espresso in gradi:
S = 0,0247 D*a da cui si può riscontrare un risultato che tutti i controllori del traffico aereo conoscono: per conseguire una minima distanza S, se la distanza dal punto d’incrocio D si riduce allora l’angolo di vet-
5. dS/dL = 1/2√… * 2(2L-2Dcosa) = (2L-2Dcosa)/√… = 0 Considerando che il termine sotto radice è sempre positivo abbiamo trovato un candidato punto di minimo della funzione che è L = Dcosa. La derivata seconda è: D²(1+ cos²a)/(D² + L² - 2DLcosa)^(1,5) che è costituito dal prodotto e dal rapporto di termini positivi è essa stessa positiva ed il punto trovato è di minimo assoluto.
toramento a deve proporzionalmente aumentare, cioè
Avvicinandosi al punto d’incrocio è necessario un angolo di vettoramento sempre maggiore per conseguire la medesima minima distanza. Meno fatalmente si può dire che:
La minima distanza tra gli aeromobili è direttamente proporzionale all’angolo di vettoramento.
Vediamo degli esempi pratici.
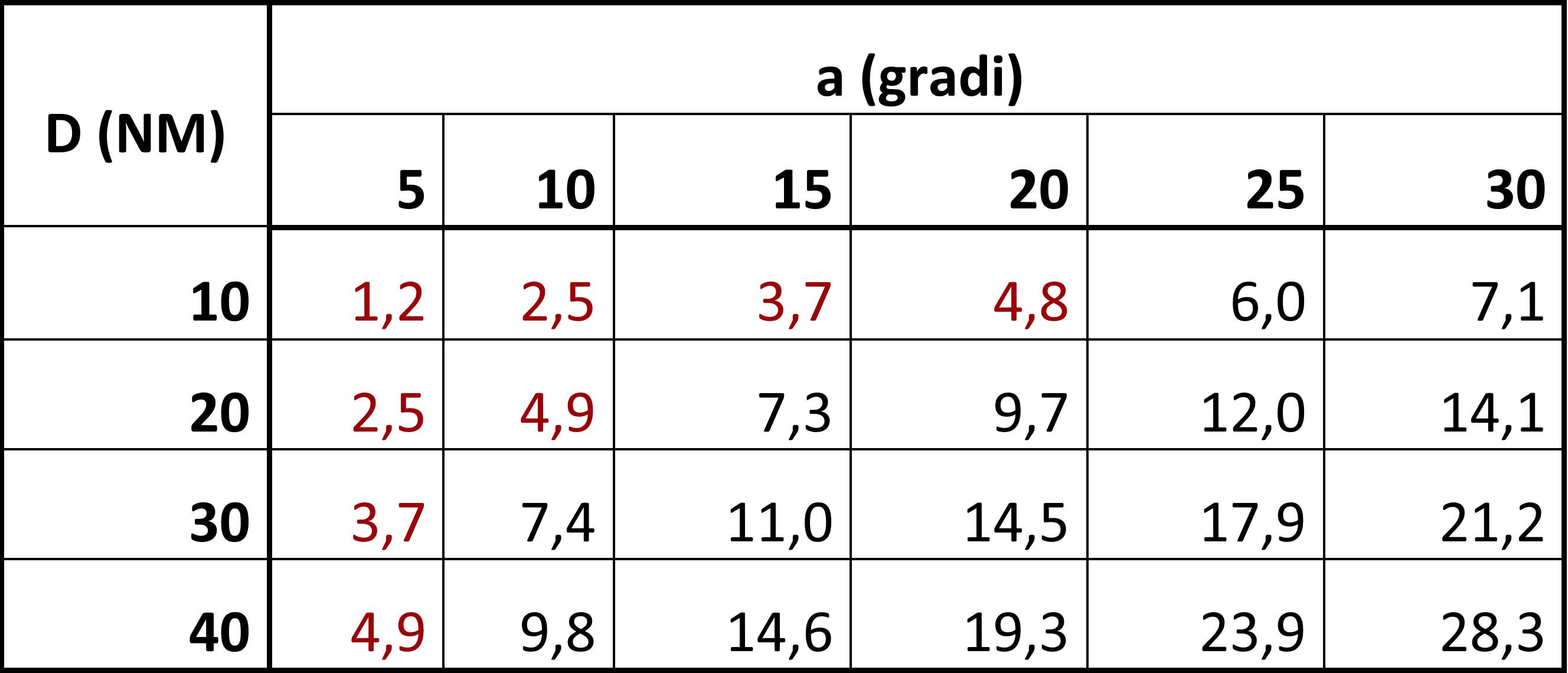
Nella tabella sono riportati alcuni valori di minima distanza S che si ottengono con la formula presentata. I valori inferiori alla minima separazione standard di 5 NM sono riportati in rosso. Si noti che, a 30 NM dal punto d’incrocio l’angolo di vettoramento minimo per rispettare la separazione standard è 10 gradi. Se la distanza scende a 20 NM l’angolo di vettoramento minimo sale a 15 gradi. Se a 30 NM voglio applicare una separazione di 10 NM l’angolo di vettoramento minimo sarà 15 gradi.
Naturalmente ad una distanza dal punto d’incrocio di 10 NM o meno questi risultati cominciano a non valere più, perché gli angoli necessari al conseguimento di una minima distanza sufficiente sono molto elevati ed è molto più sicuro mettere in campo una separazione di tipo diverso, ad esempio quella verticale.
Cosa succede se l’angolo d’incrocio non è 90 gradi?
In base a quanto visto nei capitoli precedenti, se l’angolo d’incrocio è inferiore a 90 gradi, l’angolo di vettoramento va proporzionalmente aumentato. Ad esempio, se l’angolo d’incrocio è di 60 gradi, cioè il 30% in meno di 90 gradi, la separazione che avremmo ottenuto con una prua di 10 gradi, la otterremo con una prua di 13, o meglio 15 gradi. Per lo stesso principio con un angolo d’incrocio di 30 gradi (60% in meno) è richiesto un angolo di 20 gradi.
In generale per angoli inferiori a 90 gradi ci vuole più spazio per completare la separazione, gli aeromobili stanno vicini per più tempo, ma in compenso non deviano molto dal punto d’incrocio ed è più facile concludere la separazione all’interno del buffer laterale dell’aerovia.
Per angoli inferiori a 30 gradi gli aeromobili sono praticamente sulla stessa rotta, perciò è più semplice ricorrere ad una separazione di tipo diverso (verticale).
Minima distanza su rotte incrociate, vettorando uno solo aeromobile
Questo è il caso forse più frequente perché la tecnica operativa è più semplice. Purtroppo, contrariamente a quanto si potrebbe pensare, ha una espressione analitica molto più complessa del caso precedente.


La distanza S tra gli aeromobili si trova sempre con il teorema di Pitagora:
S = √(x2-x1)²+(y2-y1)²
Mentre le coordinate si possono esprimere in funzione di L e dell’angolo a usando la trigonometria:
x1 = L cosa y1 = L sena
x2 = D y2 = D - L
Sostituiamo le coordinate nella formula della distanza S per esprimerla in funzione di D, L e dell’angolo a:
S = √[(x2-x1)²+(y2-y1)²]= √[(D - L cosa)²+(D – L(1+sena))²]= = √[D² + L²cos²a - 2DLcosa + D² + L²(1+sena)² - 2DL(1+sena)] = = S = √[2(D² + L²(1+sena) - DL(1+sena+cosa)]
Per studiare il comportamento di questa funzione al variare di L, è necessario calcolarne la derivata prima e le successive. Con alcuni passaggi6 si trova che il punto di minima distanza si ha quando
L = D(1+sena+cosa)/[2(1+sena)].
Sostituendo questo valore nella formula precedente si ottiene, con un po' di passaggi che omettiamo, la minima separazione tra gli aeromobili in funzione della distanza dal punto d’incrocio D e dell’angolo a.
S=D*√2*√(1-(1+sena+cosa)²/[4(1+sena)]}
Purtroppo non c’è una forma più semplice per questa formula, quindi passiamo direttamente agli esempi pratici, riportando in tabella i valori di S per alcune combinazioni di angoli e distanze dal punto d’incrocio.

6. Per trovare il minimo rispetto a L, eliminiamo la radice quadrata elevando l'espressione al quadrato e togliamo il fattore 2, per semplificare i calcoli. L'obiettivo è quindi minimizzare rispetto a L la funzione f(L)=D² + L²(1+sena)DL(1+sena+cosa). La derivata rispetto a L è: f′(L)=2L(1+sena)−D(1+sena+cosa) che si annulla per L=D(1+sena+cosa)/ [2*(1+sena)], che è un punto di minimo assoluto perché la derivata seconda f’’(L)= 4(1+sena) è sempre positiva per angoli a>0.
I valori inferiori alla minima separazione standard di 5 NM sono riportati in rosso. Si noti che, a 30 NM dal punto d’incrocio l’angolo di vettoramento minimo per rispettare la separazione standard è 15 gradi, a 20 NM servono almeno 25 gradi. Come ci aspettavamo, vettorando un solo aeromobile, la tecnica operativa è più semplice, ma gli angoli e le distanze dal punto d’incrocio necessarie per conseguire la separazione standard sono molto maggiori rispetto al caso precedente.

Con questo esempio si conclude questa panoramica nella geometria del vettoramento.
Non poteva essere altrimenti, i risultati ottenuti sono tutti perfettamente in linea con la tecnica operativa.
Spero che questi appunti dell’epoca in cui lo schermo radar era a tubo catodico rimangano nella memoria di qualche CTA del futuro, confido che non servano mai a nessuno per scegliere la prua giusta, ma che ogni tanto ritornino fuori quali esercizio affascinante ed inutile di geometria applicata al vettoramento.

STORIE FUORI CONTROLLO


SINGAPORE 2024 IFATCA ANNUAL CONFERENCE
Di Alessandra Cola
“Un’ esperienza che tutti dovrebbero fare!”
Partecipare ad una conferenza mondiale di IFATCA in rappresentanza di ANACNA, dopo 26 anni di professione come CTA, è coronare un sogno. Un ‘occasione unica per incontrare, conoscere e comprendere questo nostro mondo al di fuori dei confini europei. Perchè noi controllori del traffico aereo siamo una “specie” rara anche nel resto del mondo. Ma partiamo dall’inizio.
Quando mi chiesero di partecipare mancava un mese alla partenza: bisognava essere veloci nel coordinare le ferie (difficile) e prenotare l’aereo con tariffe economiche. Quindi cominciai a ragionare su come prepararmi tecnicamente. I giorni volarono tra un turno e l’altro e di colpo mi ritrovai in aeroporto per partire. Ma Singapore è lontana, dove esattamente? Tra la Malesia e l’Indonesia, praticamente all’ equatore. Clima caldo umido, flora lussureggiante, spiagge bianchissime...
E’ una città stato con il doppio degli abitanti del comune di Roma in circa la metà della superficie ( isole artificiali comprese): centinaia di grattacieli tra viali alberati e fiori. Ha uno degli aeroporti più belli del mondo che fa transitare più di 60 milioni di passeggeri l’anno (il nono in Asia per passeggeri transitati nel 2019). L’espressione di una realtà ricca, efficiente e moderna. Certo applicano la pena di morte per 33 reati quali omicidio, traffico di droga e terrorismo ecc : uno stato meno garantista del nostro. Non si può fumare per strada per esempio.
Per poter visitare Singapore bisogna trattenersi oltre i giorni programmati per la conferenza poiché sarebbe impegnativo nei cinque giorni fitti di attività.
La location scelta per l’evento era un moderno e grande hotel lungo il canale principale della città che sfocia nella suggestiva Marina, cuore della city.
I partecipanti erano tantissimi, IFATCA stabili nell’occasione il record di organizzazioni presenti, si respirava un’atmosfera mondiale.
Iniziammo il lunedì mattina con un incontro della regione Europa dopo il rituale della registrazione: ANACNA fu subito protagonista con la presentazione del nostro documento con le Policies sugli Unit Endorsement in ambito ACC. L’argomento attirò interesse, il documento venne condiviso con diversi delegati e successivamente fu ripreso nelle discussioni nei giorni a seguire.
EGATS presentò una problematica circa la recente implementazione di un nuovo ausilio per il CTA d’area e chiese alla platea un ragionamento sulle implicazioni professionali/penali per i controllori.
ANACNA presentò anche un video sulla location dell’ERM (Europe Regional Meeting) 2025 a Bologna.

La cerimonia di apertura avvenne nella sala centrale allestita per l’occasione con danze asiatiche molto suggestive, che accompagnarono l’ingresso della ministra del Trasporto (e di altri tre o quattro ministeri) del Singapore.
Nei giorni successivi le attività furono molteplici: ci divisero in tre gruppi secondo esperienze e preferenze, i risultati vennero poi esposti alla platea riunita per il progetto IFATCA 2030+.
Arrivò il momento della presentazione dello stato dei lavori presso ICAO e prese la parola una componente di origine coreana dell’ICAO per la parte ATM per illustrare i temi attualmente in valutazione e come il contributo IFATCA e IFALPA (piloti di linea) siano fondamentali nelle consultazioni precedenti alle decisioni del Board.
Le tre diverse commissioni rappresentate da TOC (Technical and Operational Committee) , PLC (Professional & Legal Committee) e un’ unione tra CAC (Constitution and Administration Committee) e FIC (Fi-
“Partecipare ad una conferenza mondiale di IFATCA in rappresentanza di ANACNA, dopo 26 anni di professione come CTA, è coronare un sogno.
nance Committee) presentarono gli studi effettuati su input delle associazioni, si approvarono eventuali policies.

Tra i lavori di maggiore interesse all’interno del congresso si evidenziano :
• uno studio sull’interazione dei piloti da remoto e l’ATC
• un ‘analisi sulle aree di degradazione del segnale GPS
• alcune considerazioni sull’impatto di un eventuale lavoro per diverse remote TWR in modalità simultanea
• un’ informativa circa l’uso di contributi in testo o immagini dal web (plagiarism, copyright infringement and intellectual property)
• un ‘analisi sulle implicazioni dell’uso di nominativi non corrispondenti alla livrea del velivolo (proposta ANACNA)
• uno studio sull’impatto dei voli VFR sul carico di lavoro e una proposta di metodo per il calcolo dello stesso (lavoro ANACNA)
• ecc
Alla fine del convegno si è proceduto all’elezione dei componenti. Anacna ha ottenuto un posto sia nel TOC con Mauro Barduani che nel PLC con Andrea Poti; inoltre Oliviero Barsanti è rappresentante del FLIGHT OPERATIONS PANEL (FLTOPSP) mentre Eugenio Diotalevi è rappresentante del REMOTELY PILOTED AIRCRAFT SYSTEMS PANEL (RPASP).
Nella terza commissione si sono discusse le problematiche maggiormente legate
alla vita stessa di IFATCA in termini di bilanci, affiliazioni e calcellazioni.
E’ stata confermata l’uscita della Russia e della Bielorussia dalla federazione.
La presentazione di Abu Dhabi per la location del prossimo mondiale, mentre Bucarest si è candidata per ospitare quello del 2026.
È stato eletto il nuovo presidente di IFATCA , la svedese Helena Sjostrom che sostituisce l’australiano Duncan Auld dopo sei anni di presidenza.
Si ringrazia l’organizzazione ospitante di Singapore, con passaggio di consegne alla prossima degli Emirati Arabi presso Abu Dhabi.
Arrivato il momento di rientrare in Italia è d’obbligo una tappa nell’aeroporto menzionato come uno dei più belli ed efficienti del mondo e che vale la pena visitare.
Al centro dei vari terminal è posizionato un vero centro commerciale aperto ai non viaggiatori di forma futuristica circolare. All’interno si trova un enorme ambiente equatoriale con cascata circolare centrale dal soffitto, tutto intorno terrazze a scalare di piante, acqua e luci.
Vicino al soffitto un percorso di tree climbing a pagamento mentre al centro corre un treno che collega i vari terminal (vi si accede solo dall’area di imbarco dopo i controlli di sicurezza). I negozi sono alle spalle delle terrazze.
Una meraviglia.

Nella zona partenze del terminal principale è presente una parete curvilinea di 15 metri circa piena di leds e riproduce un video di una cascata naturale. Per finire, nel percorso che porta ai gates, si trovano diversi giardini interni con un numero impressionante di orchidee di ogni tipo. Insomma Singapore rimane nel cuore per la sua bellezza.
Grazie ANACNA

FOCUS


L’IMPORTANZA DELLA STANDARDIZZAZIONE

Considerata la sempre maggior mobilità di CTA tra diverse realtà aeroportuali, in particolar modo considerando il grande flusso dagli aeroporti “regional” a quelli “strategici”, è fondamentale che le tecniche base del lavoro di torre siano il più possibile standardizzate a livello nazionale. La standardizzazione delle procedure “base” consente di agevolare gli addestramenti di transizione permettendo al CTA in ingresso di porre tutta l’attenzione al nuovo layout senza doversi “riformare” o “riadattare” a quelle che dovrebbero essere delle procedure acquisite e che fan parte del normale knowhow di un CTA.
Da quanto è emerso attraverso contatti ed incontri tra colleghi sembra che questa standardizzazione venga a cadere relativamen-
entrata in vigore.
Le informazioni che possiamo ottenere sull’uso della striscia cartacea veicoli le possiamo ricavare nel MO-ATS, A3.140 al par. A3.10.2.11.
In particolar modo nella lista di descrizione dei campi da compilare al punto “f” si parla dell’uso delle caselle IN/OUT: 6 caselle “spacchettate” in alto a destra. È indicato che tali caselle sono da utilizzare per il tracciamento di uscite temporanee dall’area di interesse seguite da un rientro dopo un breve lasso di tempo. Nel manuale non è presente un esempio di utilizzo della striscia arancione e questo ha portato con il tempo a utilizzi locali differenti. In alcuni posti nella metà superiore viene riportato l’orario di uscita dall’area e nella metà inferiore l’orario di rientro nell’area interessata e la strip viene poi chiusa nella

casella “out” a sinistra al termine di tutta l’operazione.
In altre sale l’uso è esattamente opposto, ossia l’orario di ingresso in alto e l’orario di uscita in basso, ricalcando lo stesso ordine delle due caselle spacchettate a sinistra (in – out).
Infine in altre torri è possibile trovare in alto l’area in cui il veicolo libera l’area di interesse principale e in basso l’orario in cui si porta in tale zona. In questi casi però non è indicato il momento di rioccupazione dell’area iniziale.
Si è trovata un’interpretazione al corretto utilizzo della strip su EAPPRI. All’interno del documento non è presente la descrizione testuale della compilazione ma l’immagine riportata ne illustra le modalità di utilizzo:

Come si può notare nell’esempio riportato in alto le 6 caselle a destra sono da utilizzare per riporti di orari e in questa compilazione è chiaro come la corretta sequenza degli eventi sia:
1 – safety entra sulla RWY 05 con 1 mezzo alle ore 0957 stimando 10’ di occupazione ed essendo in grado di liberare la pista in 2’.
2 – safety libera la pista alle ore 1002.
3 – safety occupa nuovamente la RWY05 alle ore 1004.
4 – safety libera definitivamente la RWY05 alle ore 1007.
Non è dato sapere dove si trova Safety tra le 1002 e le 1004; andrà ad occupare un’altra area che può trovarsi anch’essa in area di manovra.
E’ da intendersi però che l’utilizzo delle uscite/entrate temporanee non comporti un allontanamento del mezzo dall’area di interesse per lunghi periodi di tempo ma semplicemente per il tempo necessario al rullaggio/ atterraggio/decollo di uno o più velivoli; un allontanamento temporaneo tale da non dover considerare interrotta l’operazione e di una durata tale da non generare verosimilmente la possibile dimenticanza del mezzo in un’area “unsafe” o in conflitto con altre movimentazioni sull’area di manovra.
Va ricordato che per ogni attività conclusasi (ispezione safety, ispezione BCU, manutenzione AVL) o nel caso di uscita per lunghi periodi è necessario chiudere la strip arancione con l’orario di out in basso a sx e predisporre successivamente una nuova striscia veicoli al successivo ingresso.
La standardizzazione anche di queste semplici procedure consente un miglioramento della safety e della situation awareness all’interno delle sale.
Fly High We Care!

Fly High We Care!
al terreno

AVVICINAMENTO A VISTA Traffico che segue A380 a cura di ANACNA
Riferimenti normativi:
MO-ATS Ed. 4.3 – 6.5.3 Avvicinamento a vista
ANACNA, Scheda informativa A380-800
FAAO JO 7110.65, Para 7-2-1
Per Avvicinamento a vista si intende quell’avvicinamento effettuato da un volo IFR quando la totalità o parte di una procedura di avvicinamento strumentale non viene completata e l’avvicinamento viene effettuato con riferimento visivo al terreno. Anche in ragione di condizioni meteorologiche espresse in termini di visibilità, distanza dalle nubi e ceiling, uguali o superiori a minime specificate, che ne permettono l’esecuzione.
L’avvicinamento a vista non può essere autorizzato prima che sia stato perfezionato il relativo coordinamento ATC fra APP e TWR o il relativo coordinamento FIS/ALRS fra APP e AFIU.
Il controllore può autorizzare un volo IFR ad effettuare un avvicinamento a vista alle seguenti condizioni:
• L’aeromobile è il primo della sequenza di avvicinamento; oppure
• L’aeromobile è il secondo della sequenza di avvicinamento e:
• Riporta di avere il contatto visivo con l’aeromobile che lo precede e di potersi separare dallo stesso;
• Al momento del rilascio dell’autorizzazione all’avvicinamento a vista, l’aeromobile che precede si trova nelle ultime 8 NM della rotta di avvicinamento finale.
Nel caso in cui l’aeromobile autorizzato all’avvicinamento a vista sia il secondo della sequenza di avvicinamento, il controllore deve istruire l’aeromobile che effettua l’avvicinamento a vista a seguire l’aeromobile che lo precede, mantenendo la propria separazione dallo stesso, e fornire avvisi di precauzione per possibile turbolenza di scia. L’aeromobile autorizzato all’avvicinamento a vista assumerà la responsabilità di garantire la separazione dal precedente anche ai fini degli effetti della turbolenza di scia.
Quest’ultimo aspetto appare essere di particolare rilevanza quando gli aeromobili interessati differiscono sensibilmente per le turbolenze generate e, nel caso, l’A380 rappresenta un unicum in tal senso.
Studi condotti da FAA, EUROCONTROL, AIRBUS e EASA hanno dimostrato che i vortici generati dall’A380-800 sono più forti di quelli prodotti da aeroplani di categorie HEAVY. Così che per tale aeromobile deve essere utilizzata l’espressione SUPER.
Dal punto di vista ATC, la sua gestione necessita di una particolare attenzione per la grossa mole e l’enorme peso. In particolare, l’ATC deve tenere in debita considerazione la grande energia inerziale della macchina durante l’avvicinamento per l’atterraggio e i considerevoli effetti della turbolenza di scia quando in volo.
In ragione di ciò appare utile ritenere necessario un ulteriore barriera tra le normali operazioni e l’evento, ovvero l’utilizzo del best judgment necessario a che un CTA ritenga la variabilità della performance ricadente nel range ritenuto accettabile.
La separazione da mantenere da parte del pilota non è infatti un valore statico, ma dinamico così che velocità, inerzia, reazione dello stesso pilota, vento in finale e al suolo, scenario operativo in divenire possono rapidamente mutare le condizioni presenti.
Il CTA allora interpreterà le variabili presenti e deciderà in accordo alla sua esperienza e giudizio.

Negli USA in ogni caso è vietato autorizzare l’avvicinamento a vista quando il numero 1 è l’A380.



Pubblicazione trimestrale
Organo ufficiale di ANACNA
Associazione Nazionale Assistenti e Controllori della Navigazione Aerea
Anno XLIX nr. 187 - trimestre 3/2024
CONTATTI
Mail: info@anacna.it
Sito: www.ANACNA.it
Sede: Via Camilla 32 Roma Telefono: 06 7842963


