IL CURIOSO CASO DEI CONIGLI

… L'importanza della matematica è incrementata e con essa anche l'importanza delle relative scoperte, comprese quelle già note durante la tua vita terrena, come ad esempio la successione di Fibonacci…

Rif. Scientificast.it

La Matematica è una pura invenzione umana, oppure esiste realmente in Natura e i matematici non fanno altro che scoprirla? In tutto ciò che ci circonda non è difficile rilevare forme e strutture di grande armonia che obbediscono a precise leggi matematiche. Una di queste è la successione di Fibonacci, inventata per risolvere un problema proposto al matematico pisano dall’imperatore Federico II di Svevia, che gli domandò:

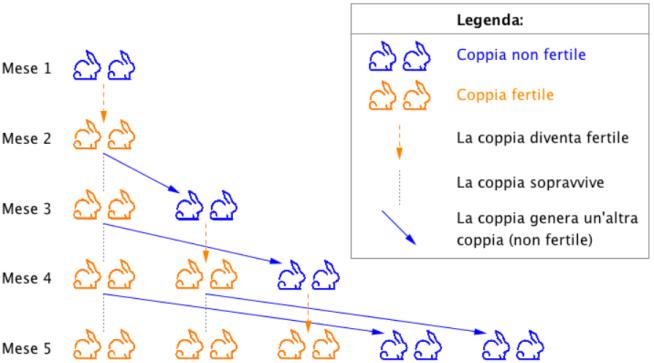
“Quante sono le coppie di conigli che in capo di un anno vengono generate da una coppia, se si suppone che ogni mese ogni coppia genera una nuova coppia, che dal secondo mese in avanti diventa produttiva?”

Rif. Oilproject-WeSchool

Fibonacci risolse il problema ipotizzando che per natura ogni coppia di conigli genera in un mese un’altra coppia, e comincia a procreare a partire dal secondo mese di vita. Il primo mese c’è solo una coppia di conigli, il secondo mese 2, di cui una fertile, il terzo mese 3, di cui 2 fertili e

così via. Nasce quindi la successione di Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55... in cui ogni elemento è dato dalla somma dei due termini che lo precedono. La formula ricorsiva che consente di generare la successione infinita è la seguente:

fn = f n-1 + f n-2 (n > 2)

Rif. Scientificast.it

La caratteristica principale della successione è che il rapporto tra qualunque numero e quello precedente nella serie tende ad avvicinarsi sempre più al numero aureo: 1,618… (ϕ = Phi).

Rif. Flickr

Anche in natura non si contano le occorrenze dei numeri di Fibonacci, dai petali di fiori (Iris, 3 petali; Rosa canina, 5 petali; Hepatica nobilis, 8 petali) alle spirali del cavolfiore romano, che ripresentano la stessa forma in ogni broccolo più piccolo.

Le spirali disegnate in rosso sono in senso orario, le altre in nero. Si scopre che le linee rosse sono 8, quelle nere 13: proprio due numeri consecutivi della successione di Fibonacci!

Questi sono solo alcuni tra i moltissimi casi in cui questa successione si presenta in natura. Vi piacerebbe diventare dei piccoli Fibonacci? Basta osservare la natura.

Alessio Mormando 4BM Claudia Paterino 4CS Martina Perrone 4CS Marta Vizziello 4CS