Tradução e generalização da linguagem natural para

TRADUÇÃO E GENERALIZAÇÃO: da linguagem natural para linguagem algébrica por meio da engenharia didática

Viviane Muniz Oliveira dos Santos Wallace Vallory Nunes

Resumo

Este trabalho relata o desenvolvimento do pensamento algébrico, de uma turma de nono ano do ensino fundamental da rede estadual de educação do Rio de Janeiro. A motivação desse trabalho foi a experiência vivida pela pesquisadora em seu primeiro contato com a sala de aula no projeto “Mais Educação” da Secretaria Estadual de Educação do Rio de Janeiro (SEEDUC/ RJ) onde foi percebido que os alunos não tinham um pensamento algébrico desenvolvido. A partir daí procurou-se investigar novas metodologias que pudessem contribuir na solução desse problema. O objetivo geral desse trabalho foi identificar os obstáculos encontrados pelos alunos na transição da linguagem aritmética, natural, para a linguagem algébrica apontando as prováveis causas e consequências desses obstáculos, propondo um caminho pedagógico para o desenvolvimento do pensamento algébrico. A metodologia usada nesse trabalho foi a Engenharia Didática, onde no primeiro momento foi aplicado um pré-teste, logo após uma sequência didática, composta por cinco atividades, e finalizando com o pós-teste onde foi percebido a evolução do pensamento algébrico dos estudantes.

Palavras-chave: aritmética, álgebra, engenharia didática.

Introdução

Este trabalho é fruto do interesse em desenvolver uma proposta metodológica diferenciada para o estudo de Álgebra no segundo segmento do Ensino Fundamental. Durante seu percurso formativo, a pesquisadora, deparou-se com o ensino de Álgebra desassociado do concreto, reprodutivo e engessado. Nessa abordagem os exercícios tinham uma diretriz característica de encontrar a incógnita “x”, quando se tratava do ensino de equações. Os procedimentos apenas tinham o efeito de somar os coeficientes de incógnitas correspondentes e na hora de transferir de um lado da equação para o outro, alterar o sinal sem, entretanto, discutir os conceitos associados a essa estrutura algébrica e tão importantes para construção do conhecimento matemático. Por ter desenvolvido essa habilidade, a pesquisadora era considerada uma aluna diferenciada, o que a fez ter vontade de cursar a Licenciatura em Matemática. Durante o curso, seu desejo de interferir no ensino de álgebra se ampliou, motivando-a na busca de propor uma metodologia de ensino diferente da forma que aprendeu. Nessa atitude, este trabalho propõe uma reflexão sobre possíveis caminhos ou possibilidades pedagógicas que possam favorecer a construção do pensamento algébrico mais significativo para os alunos. Desde o início da graduação a pesquisadora foi impactada de duas maneiras: a primeira, ela teve muitas dificuldades em algumas matérias iniciais por não dominar a álgebra no nível exigido. Pôde perceber que, na verdade, não havia desenvolvido ou construído o pensamento algébrico necessário ao curso de Licenciatura em Matemática. Isso a forçou na busca de corrigir esse déficit de tantos anos; pois o ideal seria ter chegado na graduação pronto receber a álgebra em níveis mais complexos. A segunda, ela se deparou com as ferramentas da didática do ensino da matemática. Ao perceber que a educação matemática era muito mais abrangente do que ela havia presenciado no ensino fundamental, foi encorajada a atuar na construção de metodologias alternativas que permitissem mudar esse quadro. A partir daí a pesquisadora, passou a olhar a sala de aula de uma forma diferente e, ao mesmo tempo, foi influenciada por alguns autores que sugeriam propostas inovadoras para o ensino-aprendizagem de Álgebra. Hoje, depois de participar de alguns projetos de extensão e pesquisa, tais como: “Mais educação”, da Secretaria Estadual de Educação do Rio de Janeiro (SEEDUC/RJ), “Ensino de Ciências e Matemática nas escolas estaduais da 12

Baixada Fluminense”, do Laboratório de Metodologias de Ensino de Ciências e Matemática (LABMET) e no Programa Institucional de Bolsas à Docência (PIBID), onde foram reforçadas a concepção de um ensino mais diferenciado e contextualizado, a pesquisadora pode perceber realmente o que os autores diziam em seus textos, que é possível fazer acontecer em sala de aula de forma simples e eficaz. A motivação para esse trabalho foi a partir do primeiro contato com a sala de aula, no projeto “Mais Educação” da Secretaria Estadual do Estado do Rio de Janeiro (SEEDUC/RJ), onde foi percebido que os alunos tinham a necessidade de atribuir um valor a incógnita sem questionar o significado de suas ações. Basicamente, procuravam encontrar esse valor sem desenvolver o devido raciocínio algébrico inerente ao estudo das equações de primeiro grau. Em todo momento, ignoravam a situação problema e queria substituir a incógnita pelo seu valor, revelando dificuldade no seu raciocínio algébrico. Essa postura, provavelmente, incentivada pela prática pedagógica baseada na mecanização, dificultando o desenvolvimento da construção do conceito, objetivando apenas a simples reprodução das soluções. A partir daí procurouse investigar novas metodologias que pudessem contribuir na solução desse problema. Portanto, o objetivo geral deste trabalho é identificar os obstáculos da transição da linguagem aritmética para linguagem algébrica. E, especificamente apontar as prováveis causas e consequências desses obstáculos e propor um caminho pedagógico para a construção do pensamento algébrico.

Ensino de Álgebra

De acordo com os PCN (Parâmetros Curriculares Nacionais) o estudo da Álgebra constitui um espaço bastante significativo para que o aluno desenvolva e exercite sua capacidade de abstração e generalização, além de possibilitar a aquisição de uma poderosa ferramenta para resolver problemas. Para Falcão (2008), a passagem da linguagem natural para o simbolismo formal, na introdução à álgebra na escola, se constitui um processo complexo. Pois, realmente acontece uma quebra de raciocínio que o aluno vinha tendo até o presente momento. Os alunos não conseguem visualizar que uma letra (símbolo) pode estar representando um número naquele momento. Talvez se os alunos tivessem sidos inseridos no mundo algébrico mais cedo,

essa simbologia não seria tão complexa para os mesmos. Segundo, Falcão (2008) quando cita Lima (1997) onde crianças podem resolver problemas algébricos desde que sejam auxiliados a trabalhar algebricamente. E, muitas vezes os alunos tem a dificuldade na álgebra por ainda herdar dificuldades na aritmética. Piaget e Garcia (1983), sugerem que a apresentação da álgebra ocorra depois que os alunos dominem alguns princípios da aritmética. E, se justificam em dois motivos: um devido a transposição didática, pois os estudantes teriam que conhecer alguns conteúdos e procedimentos aritméticos; e o outro motivo seria ligado a psicologia cognitiva de Piaget, que a aritmética seria de melhor compreensão por ser concreta do que a álgebra com sua generalização. Primeiro, o aluno deve ser familiarizado ao mundo da simbologia, ter essa “pré-álgebra”, essa transição muito bem feita e fundamentada para depois partir para a resolução das equações, o mesmo deve entender qual o papel daquela variável. Assim como nos PCN, Devido à complexidade que caracteriza os conceitos e procedimentos algébricos não é desejável que no terceiro ciclo se desenvolva um trabalho visando ao aprofundamento das operações com as expressões algébricas e as equações. É suficiente nesse ciclo que os alunos compreendam a noção de variável e reconheçam a expressão algébrica como uma forma de traduzir a relação existente entre a variação de duas grandezas. É provável que ao explorar situaçõesproblema que envolvam variação de grandezas o aluno depare com equações, o que possibilita interpretar a letra como incógnita. Nesse caso, o que se recomenda é que os alunos sejam estimulados a construir procedimentos diversos para resolvê-las, deixando as técnicas convencionais para um estudo mais detalhado no quarto ciclo (BRASIL, 1998). Os PCN deixam bem explicito a importância do aluno se ambientar primeiramente com a simbologia, para assim compreender o conceito de variável. E, depois que esse processo esteja concluído, o aluno deve traduzir situações-problemas na forma algébrica, procurando entender o significado do conceito de incógnitas, para a partir desse momento resolver equações. Infelizmente, podemos perceber que os alunos não são inseridos no mundo algébrico corretamente e logo têm que lidar com a simbologia e generalizações de situações problemas. Todo esse percurso não permite o desenvolvimento natural do pensamento algébrico, pois pula etapas.

Fiorentini (1993), destaca que se o processo de ensino-aprendizagem for conduzido sem o devido suporte concreto a uma linguagem simbólica, impedirá o progresso da aprendizagem significativa da álgebra. Além disso, será considerado o currículo mínimo (Figura 1), da Secretaria Estadual de Educação do Rio de Janeiro (SEEDUC), pois esse trabalho foi aplicado em uma escola pública estadual. Segundo o currículo mínimo de matemática, a álgebra é apresentada aos alunos a partir do sétimo ano do ensino fundamental II (ou segundo segmento do ensino fundamental). O currículo mínimo de matemática da SEEDUC/RJ é um documento elaborado em 2011, revisado em 2012 e definitivamente implantado em 2013 (através da Resolução SEEDUC nº 4.866 de 14 de fevereiro de 2013) que estabelece um conjunto de conteúdos bimestrais básicos para todas as escolas da rede estadual. A proposta está vinculada a ideia de que todos os alunos da rede terão uma formação mínima (básica) comum, independente das características da região onde está localizada a escola. É um documento que tem por finalidade apresentar os conteúdos bimestrais da disciplina, bem como as competências e habilidades a serem desenvolvidas nos alunos, e visa estabelecer um ponto de partida mínimo de onde cada escola deve construir seu currículo.

Figura 1 - Extrato do Currículo Mínimo destacando as habilidades e competências para o estudo do campo algébrico simbólico

Fonte: Currículo Mínimo/SEEDUCRJ

De acordo com os PCN, “embora nas séries iniciais já se possa desenvolver alguns aspectos da álgebra, é especialmente nas séries fi nais do ensino fundamental que as atividades algébricas serão ampliadas” (BRASIL, 1998, p. 50). A Figura 2 apresenta, de forma bem simplificada, as diferentes interpretações da álgebra escolar e os múltiplos usos dos símbolos (letras) no ensino fundamental descrito nos PCN.

Figura 2 - Álgebra no ensino fundamental

Dimensões da Álgebra Aritmética Generalizada Funcional Equações Estrutural

Uso das letras Letras como generalizações do modelo aritméticco Letras como variáveis para expressar relações e funções Letras como incógnitas Letras como símbolo abstrato

Conteúdos (conceitos e procedimentos) Propriedades das operações generalizações de padrões aritméticos Variação de grandezas Resolução de equações

Cálculo algébrico Obtenção de expressões equivalentes

Fonte: PCN

Tinoco (2011), destaca quatro tipos de álgebra estudados no ensino fundamental, sendo a álgebra como generalizadora da aritmética; álgebra funcional; álgebra das equações e álgebra estrutural. Em cada uma delas há especificidades. No caso da álgebra como generalizadora da aritmética, o destaque é o papel da álgebra usada para tradução e generalização; na álgebra funcional, o destaque é relação entre grandezas, usada no estudo de funções onde as variáveis assumem três atribuições: variável independente; variável dependente e parâmetro. O destaque para a álgebra das equações é a resolução de equações; e o destaque para a álgebra estrutural é que as letras são símbolos e não incógnitas, onde não devem ter um valor determinado e também não se relacionam a nenhuma variação de grandeza. Ainda segundo de Tinoco, o papel das variáveis está associado a cada concepção apresentada. Ou seja, ao resolver problemas, encontramos relações entre números que desejamos “traduzir” matematicamente, e as variáveis são úteis para essa tradução. Por exemplo, ao traduzir um problema para linguagem algébrica, monta-se uma equação (modelo matemático) que representa a estrutura matemática do mesmo.

O presente trabalho enfatiza somente uma concepção da álgebra: A álgebra como generalizadora da aritmética, traduzindo e generalizando a linguagem natural para linguagem algébrica. Mas, isso não significa excluir o trabalho com outras concepções. Devido a complexidade do tema, cada uma das concepções pode trabalhar em conjunto, pois elas estão correlacionadas. Dessa maneira, Ao resolver problemas, encontramos relações entre números que desejamos “traduzir” matematicamente, e as variáveis são uteis para essa tradução. Por exemplo, ao traduzir um problema para linguagem algébrica, monta-se uma equação (modelo matemático) que representa a estrutura matemática do mesmo. Neste sentido, cada equação é generalizadora, pois, pode modelar muitos problemas distintos, desde que tenham a mesma estrutura matemática (TINOCO, 2011, p. 7).

1.2 Breve histórico

Como breve relato histórico do ensino de álgebra no Brasil, podemos destacar pouca alteração entre os anos (1549-1890), onde prevaleceu o ensino dado pelos Jesuítas até início do período republicano. O republicanismo com seu ideal progressista inseriu a álgebra, definitivamente, no currículo escolar brasileiro; mas não deu o destaque necessário a esse campo da matemática. Somente mais tarde, pós-1930, é que a álgebra passaria a desfrutar de real importância no currículo escolar nacional. No período da vida colonial brasileira, foram priorizados os conteúdos de aritmética e geometria, a álgebra não recebeu maior atenção dos professores; pois a visão religiosa era focada no ensino da teologia, filosofia e letras, num claro destaque ao ensino humanístico em detrimento do estudo científico. Cabe aqui citar que, ao término do período de controle dos jesuítas sobre o ensino português e brasileiro em 1759, ocorreram transformações importantes em Portugal promovidas pelo Marquês de Pombal. E que, apesar dessas mudanças não surtirem o efeito desejado no ensino da álgebra no Brasil, as reformas no ensino promovidas pelo Marquês de Pombal (as reformas pombalinas de 1772) alteram a estrutura do ensino superior português ao criar uma cadeira específica de matemática (pois até então a matemática não possuía lugar entre os cursos superiores na Universidade de Coimbra) o que contribuiu para o aprofundamento no ensino da álgebra 17

e a gradual mudança do foco do ensino português de humanístico para científico. Ainda, conforme Mondini (2013), ao nível colonial, a saída dos jesuítas significou o fechamento de muitas escolas, não havendo fôlego administrativo e financeiro do poder real em solucionar o problema (reabrir escolas, construir novas, manter professores, habilitar professores... principalmente de matemática). Por último, o fim do período de administração pombalina significou uma retomada do foco nas humanidades no que tange ao ensino. No Brasil, o quadro permanece sem significativas alterações no período 1777-1822. A proclamação da independência em 7 de setembro de 1822 trouxe a necessidade de reorganização do sistema de ensino brasileiro (período do Brasil imperial (1822-1889); afinal não mais cabia a nova nação manter um modelo que não fora pensado pelo novo governo. Assim, mudanças foram feitas em 1827 que organizavam o ensino primário; mas o ensino secundário permanecia com foco nas humanidades e na religiosidade. No ano de 1837 o governo cria o colégio D.Pedro II, voltado para o ensino secundário, focado nas ciências e destinado a ser um modelo de escola para as demais províncias brasileiras. Nessa escola, a álgebra passa a ocupar lugar no currículo de aprendizagem da matemática. Em 1854, uma reforma estabelece a obrigatoriedade do ensino de álgebra no curso secundário. No período imperial pode-se dizer que o destaque para o ensino de álgebra vai para as escolas militares que buscam o aprofundamento desse ramo da matemática. É importante lembrar que no final do século XIX e início do século XX os estudos na abordagem da álgebra apresentam avanços consecutivos no mundo; enquanto isso, no mesmo período, as escolas brasileiras parecem não acompanhar tais avanços na importância do ensino da álgebra. A proclamação da república fornece um novo período de atenção ao ensino de álgebra (1889-1930), que pretendeu colocar o país no foco do progresso. Para que, realmente, o país abandonasse o legado de analfabetismo do período imperial ocorreu uma reforma do ensino em 1890, tornando obrigatório o ensino público gratuito. No campo do ensino da álgebra o nível secundarista mantém a obrigatoriedade desse ramo da matemática iniciado em 1854. O início do regime republicano permitiu que em 1890 ocorresse uma importante reforma no ensino (proposta e implementada por Benjamin 18

Constant) que incluiria, em definitivo, a álgebra no currículo nacional, principalmente devido ao currículo ginasial nacional. Também, é importante lembrar que essa reforma foi a primeira a buscar desvincular o ensino religioso (de herança jesuíta) dos interesses da nação, conforme a constituição republicana, de 1891, que estabeleceu um ensino público laico. Após a reforma de Benjamin Constant até o ano 1925 ocorreram quatro reformas no ensino nacional, mas todas mantiveram o ensino de álgebra no currículo nacional. Devido a revolução de 1930 (que encerrou o período inicial republicano) ocorre a reforma liderada por Francisco Campos que, de acordo com Mondini (2013), foi a primeira tentativa de pensar a educação nacional voltada para as questões do país e para seus cidadãos. Pela reforma de Francisco Campos o ensino de matemática passou a englobar três outros ramos, aritmética, álgebra e geometria. Tal mudança, conforme Mondini (2013), estaria em consonância com o pensamento da Comissão Internacional para o Ensino da Matemática (criada em Roma no início do século XX), que no Brasil tinha em Euclides Roxo um dos seus defensores, nessa visão: [...] À luz das modernas ideias pedagógicas, a ciência matemática sob suas três faces numérica, simbólica e gráfica – é uma só e não é conveniente sob o ponto de vista didático separá-las, por divisões estanques ou dogmáticas em aritmética, álgebra e geometria; antes convém, tanto quanto possível, expor os mesmos princípios sob os três pontos de vista, dando a forma concreta ao ensino, procurando, em uma só palavra, fazer entrar a matemática “pelos olhos”, até que o aluno se ache bastante exercitado para tratar as questões de um modo abstrato (ROXO apud MONDINI, 2013, p. 274). Ainda, pela reforma de Francisco Campos, o ensino da álgebra deveria ocorrer gradualmente dos conceitos mais fáceis aos mais difíceis e sempre partindo do concreto. Cabe lembrar que a reforma de Francisco Campos ocorre no contexto de crescimento do movimento escolanovista, que em 1932 divulgou o Manifesto dos Pioneiros pela Escola Nova. No ano de 1942, ocorre uma nova reforma educacional no Brasil que naquele período estava sob o regime do Estado Novo. Essa reforma foi liderada por Gustavo Capanema. Na reforma, de acordo com Mondini (2013), há uma maior preocupação com a formação humanística (devido a criação do Curso Clássico); mas também busca manter a formação científica necessária aos estudos posteriores.

Ainda, a reforma estabelece um ensino de álgebra mais instrumental visando a utilidade para as demais ciências, em detrimento da construção de um saber matemático lógico-formal. O Movimento da Matemática Moderna surge no contexto da guerra fria (disputa pela hegemonia global entre o bloco capitalista, liderado pelos Estados Unidos; e o bloco comunista, liderado pela União Soviética), pois a matemática se destaca por ser considerada base para o desenvolvimento científico. Segundo Silva (2008, p. 34) o objetivo do Movimento da Matemática Moderna é modernizar a matemática, ou seja, romper com o ensino tradicional e preparar os estudantes para a Ciência, para a pesquisa e para trabalhar com computadores. Estes, por sua vez, “dinamizam a matemática possibilitando cálculos antes impossíveis de serem realizados” (apud MONDINI, 2013, p. 363). Ainda, é importante frisar que uma alteração significativa no ensino de álgebra se deu nesse período (através da Portaria nº 1045 de 14 de dezembro de 1951) com o estabelecimento de um conteúdo mínimo curricular para álgebra, bem como exigindo avanço na abstração e no rigor visando desenvolver no estudante capacidades relacionadas a matemática. Na década de 60, o Grupo de Estudos de Ensino da Matemática (GEEM) – surgido em São Paulo – se torna o propulsor do Movimento da Matemática Moderna no Brasil (BURIGO apud MONDINI, 2013, p. 375). O GEEM promove cursos visando preparar os professores para a Matemática Moderna. Em síntese, o GEEM tinha como objetivo a modernização da linguagem matemática a fim de facilitar o aprendizado, retirando o estigma de “bicho papão” da disciplina perante os estudantes; bem como introduzir os avanços e orientações para o ensino estabelecidos nas reuniões internacionais de matemática.

1.3. Dificuldades no Aprendizado de Álgebra no Ensino Fundamental

Segundo Falcão (2008), a passagem da linguagem natural para o simbolismo formal, no contexto da introdução à álgebra na escola se constitui em processo complexo. Concordando com o autor podemos perceber que é muito mais fácil pedir para o aluno achar o valor de “x” do que interpretar uma situação problema, montando uma equação e achar a solução do problema, ter um pensamento algébrico.

Falcão (2008) apresenta diversas dificuldades que estão presentes no estudo dos conceitos de Álgebra. Esses obstáculos estão resumidos e destacados no Quadro 1, a seguir:

TIPO DE DIFICULDADE

Suporte símbolo misto

Distinção entre variáveis e parâmetros

Generalidade da expressão

Caráter sintético da expressão

Gestão da ordem de prioridade das operações indicadas pela expressão

Quadro 1

DESCRIÇÃO

Utilização de elementos de representação simbólica oriundos da linguagem natural e formal.

Dificuldade de diferenciação de variáveis e parâmetros na proposição de fórmulas genéricas ou equações correspondentes a dados empíricos modelizados ou problemas a por em equação.

Dificuldade em trabalhar com entidades literais, propondo-se frequentemente valores numéricos específicos para os parâmetros da expressão.

Dificuldade em propor expressão única, capaz de sumariar todas as relações pertinentes ao problema ou modelo.

Ausência de marcadores formais que auxiliem a explicitação da ordem de prioridade de operações, como, por exemplo, parênteses, colchetes, barras em expressões fracionárias. Fonte: (FALCÃO, 1992, p. 74)

Essas dificuldades apresentadas por Falcão serviram para que identificássemos os obstáculos que os estudantes tiveram durante a sequência didática; pois Machado (2012) cita em seu livro, Educação Matemática, que o obstáculo epistemológico é uma das causas de dificuldades à aprendizagem da Matemática. Também, em Kikuchi (2012) é explicado que Guy Brosseau, inspirado nas teorias de Piaget, aplicou o conceito de obstáculo epistemológico de Bachelard a Didática da Matemática, ele foi o primeiro que aplicou esses conceitos concretamente a Didática da Matemática.

As análises de Bachelard, segundo Kikuch, eram dedicadas à concepção de rupturas entre o conhecimento comum e cientifico ou dentro da sua própria evolução. Ou seja, experiências passadas que impedem, um sujeito ou uma determinada comunidade de cientistas, de prosseguir e compreender um novo conhecimento científico. Dizemos que o obstáculo se apresenta em forma de resistência a aceitar um novo conhecimento, estagnando o progresso do pensamento humano. Para que o progresso aconteça, Kukuchi cita Bachelard, onde afirma que é preciso desenvolver primeiro um espirito científico que se motive a analisar as causas que o impedem de superar o estado de estagnação. Depois, buscar caminhos para entender conceitos mais avançados do que ele adquiriu anteriormente, e quando necessário, até substituir aqueles que foram mal estabelecidos. Desse modo, Bachelard nomeou, esse estado de estagnação que impede o avanço na ciência, de obstáculo epistemológico. A noção de obstáculo epistemológico na obra de Bachelard, La formation de I’espirit scientifique, é caracterizada como tendência do ser humano em estagnar-se em experiências passadas ou de não identificar possíveis obstáculos. E, propõe para que aconteça a superação de um obstáculo epistemológico ser preciso entender que a ciência é diferente do senso comum, por ser construída através da descontinuidade e da transformação dos conhecimentos. Traçando essas características com o ensino, Bachelard sugere que para ocorrer aprendizado, o aluno precisa romper ou desconstruir o senso comum adquirido anteriormente, quando se percebe que esse o impede de compreender uma situação nova a qual ele nunca tenha sido exposto.

2. METODOLOGIA

2.1. Engenharia didática

Segundo Pommer (2013), a Engenharia Didática surgiu no transcorrer das discussões desenvolvidas no IREM (Instituto de Investigação do Ensino de Matemática), na França, ao final da década de 1960. Em seus primórdios, o IREM desenvolvia uma complementação na formação de professores de matemática e na produção de meios materiais de apoio para a sala de aula, destacando-se o desenvolvimento de jogos, brinquedos, problemas, exercícios e experimentos.

De acordo com Machado (2012) o termo engenharia didática é utilizado desde a década de 80 nas pesquisas da Didática da Matemática que incluem uma parte experimental. A referência mais citada desse período é Michèle Artigue (1988) que comparou a metodologia ao trabalho de um engenheiro. [...] um engenheiro que [...] se vê obrigado a trabalhar sobre objetos bem mais complexos que os objetos depurados da ciência e, portanto, a enfrentar praticamente, com todos meios de que dispõe, problemas que a ciência não quer ou não pode levar em conta (ARTIGUE apud MACHADO, 2012, p. 234). No Brasil, a engenharia didática tem sido abordada por pesquisadores como Machado (2012) e Pais (2008). Na visão de Machado (2012), a engenharia didática pode ser compreendida tanto como um produto resultante de uma análise a priori, quanto uma produção para o ensino. Na mesma linha, o nosso entendimento é que a engenharia didática pode ser, também, compreendida como uma metodologia de pesquisa que une atividade experimental com prática pedagógica. E é justamente esse caráter dual que permite ao professor-pesquisador coletar informações; criar uma sequência didática; aplicá-la aos alunos; observar as ações e/ou interações dos alunos (mediante ao que ficou estabelecido no contrato didático firmado entre professor e alunos) e analisar os resultados obtidos a priori e a posteriori, a fim de confrontá-los com a(s) hipótese(s) do início da pesquisa. A metodologia de aplicação da engenharia didática obedece às seguintes etapas ou fases, exposto no esquema da Figura 3: Análises preliminares; Concepção e Análise a priori; Aplicação ou Experimentação e Análise a posteriori e Validação.

Figura 3: Etapas da Engenharia Didática

ANÁLISES PRELIMINARES

CONCEPÇÃO E ANÁLISE A PRIORI PRELIMINARES

ENGENHARIA DIDÁTICA

APLICAÇÃO OU EXPERIMENTAÇÃO

ANÁLISE A POSTERIORI E VALIDAÇÃO

Fonte: (BRUM; SCHUHMACHER, 2013)

Etapa ou Fase 1:

Nas Análises Preliminares, segundo Machado (2012), são coletados e apresentados dados sobre cenário didático mais amplo e também do cenário mais específico sobre o foco da pesquisa; também considerações no campo epistemológico dos conteúdos (aprendizagem); sobre o objeto da pesquisa; sobre o ambiente/universo dos sujeitos envolvidos e os obstáculos (entraves ao aprendizado); a superação destes, a partir dos objetivos da pesquisa.

Etapa ou Fase 2:

Concepção e Análise a priori, nesta fase, conforme Machado (2012), ocorre a delimitação das variáveis do sistema sobre as quais o ensino pode intervir. Tais variáveis podem ser de origem macrodidáticas ou globais (atingem a engenharia didática como um todo) e as de origem microdidáticas ou locais (atingem uma sessão ou fase/etapa da engenharia) e recebem o nome de variáveis de comando. Também, esta fase/etapa, comporta um caráter descritivo e preditivo ligado a situação a-didática elaborada e aplicada aos alunos, que tem por objetivo descrever as variáveis (global ou local ou ambas); a situação a-didática elaborada a partir das variáveis (com os possíveis desafios enfrentados pelos alunos) e gerar previsões testáveis sobre o comportamento (pensamento) matemático dos alunos. Importante frisar que o papel do professor-pesquisador, nesta fase, é estabelecido pelo contrato didático firmado anteriormente com os alunos ou nas situações de institucionalização, cabendo ao aluno o papel principal.

Etapa ou Fase 3:

Aplicação ou Experimentação é, conforme Machado (2012), a fase da realização da engenharia didática com certa população de alunos objeto da investigação. Também, a explicitação dos objetivos e condições de realização da pesquisa aos alunos que participarão da experimentação; o estabelecimento do contrato didático; aplicação dos instrumentos da pesquisa e o registro das observações sobre a experiência. Complementando, é indicado seguir as especificações, orientações e decisões elaboradas durante a etapa/fase de análises a priori, a fim de evitar o insucesso da pesquisa.

Etapa ou Fase 4:

Análise à Posteriori e Validação, de acordo com Machado (2012), consiste na última fase e está apoiada nos dados colhidos durante a experimentação e nas observações feitas pelo pesquisador. Nessa fase ocorre o tratamento dos dados que constam da seleção de dados pertinentes à posteriori.

2.2 Desenvolvimento

O presente trabalho observou o pensamento algébrico de 20 alunos, em uma turma de nono ano do ensino fundamental de uma escola pública situada no estado do Rio de Janeiro, no município Nilópolis e pertencente a rede estadual de ensino. A escolha pelo nono ano foi para verificar como esses alunos estavam saindo do ensino fundamental e como entrariam no ensino médio, em relação ao pensamento algébrico. Sabendo que de acordo com o currículo mínimo da Secretaria Estadual de Educação - SEEDUC/RJ - os alunos são introduzidos no ensino da álgebra a partir do sétimo ano do ensino fundamental. Foi dividido o trabalho em quatro momentos: um pré-teste para analisar a escrita algébrica dos alunos; no segundo momento aplicação de uma sequência didática, composta por cinco questões, onde foi trabalhado a generalização; no terceiro momento o pós–teste onde foi reaplicação do pré-teste; e, o quarto momento foi a análise de dados obtidos durante a sequência didática identificando as dificuldades da generalização dos alunos. Vejamos no quadro 2 os objetivos, habilidades e competências de cada atividade e do pré-teste/pós-teste. No primeiro momento, a pesquisadora se apresentou a turma explicando que era uma aluna da graduação no curso de Licenciatura em Matemática no Instituto Federal do Rio de Janeiro (IFRJ) situado em Nilópolis, que iria precisar da colaboração deles para produzir o trabalho de conclusão do curso, e que o tema do trabalho era sobre o pensamento algébrico. A eles foi feito um pedido para que evitassem faltar nas semanas que se seguiriam, porque se tratava de uma sequência de atividades a serem feitas em sala, e também que as atividades que seriam aplicadas tratavam da construção de raciocínio e do desenvolvimento do pensamento algébrico.

Atividades

Descobrindo os números maias

Quadro 2: Atividades

Objetivo

Identificar uma linguagem simbólica não usual para a escrita dos números naturais.

Competência

Desenvolver a capacidade de operar símbolos e regularidades.

Enigma

Analisar a existência ou não de regularidade em situações diversas; Registrar argumentos que justificam tais regularidades. Reconhecer operações entre símbolos e regularidades.

Peso

Zoológico

Estrutura do trem

Estrutura da ponte

Identificar uma linguagem simbólica não usual para a escrita dos números naturais; Reconhecer lúdica e simbolicamente o fato de que os números naturais são escritos forma única como produto de números naturais.

Escrever de forma generalizada.

Analisar a existência ou não de regularidade em situações diversas; Escrever de forma generalizada. Identificar uma linguagem simbólica não usual para a escrita dos números naturais; Reconhecer lúdica e simbolicamente o fato de que os números naturais são escritos de forma única como produto de números naturais; Registrar regularidades observadas em sequencias de símbolos e sequencias numéricas. Reconhecer operações entre símbolos.

Identificar a ocorrência de generalizações e desenvolver a capacidade de realizálas.

Desenvolver a capacidade de pensar algebricamente

Reconhecer operações entre símbolos e regularidades. Desenvolver a capacidade de operar linguagem simbólica.

Habilidade

Dominar as operações com símbolos e regularidades. Aplicar as capacidades adquiridas sobre operações com generalizações e linguagem simbólica.

Operar linguagem simbólica.

Realizar generalizações.

Aplicar o pensamento algébrico sobre o problema.

Aplicar as capacidades adquiridas sobre operações com generalizações e linguagem simbólica.

Houve inquietação quando foi citado que se tratava de uma sequência de atividades, e eles logo indagaram se as atividades valeriam ponto. Ou seja, estavam preocupados e/ou interessados em nota para o bimestre. Foi explicado que a colaboração e comprometimento deles iriam, em muito, contribuir para a melhora no aprendizado de cada um deles em álgebra e também na percepção da realidade da sala de aula como futura professora. Durante a aplicação do pré-teste os alunos demonstraram certa falta de interesse; percebendo que havia muita insegurança da parte deles, como se estivessem com medo de arriscar uma resposta, e também como se estivessem certos que a sua resposta não seria a correta. Então foi preciso ter um segundo momento de conversa, para deixá-los bem à vontade e tranquilos. Foi lembrado que não se tratava de uma prova, que não estavam sendo avaliados, que não deveriam ter medo do “errado”, que poderiam ser sinceros ao ponto de escreverem que não sabiam, de realmente serem sinceros em responder com firmeza o que era pedido. A atividade que compõe o préteste foi idêntica ao do livro “Álgebra: pensar, calcular, comunicar”; (TINOCO, 2011). O objetivo especifico do pré-teste foi explorar o estado do pensamento algébrico dos alunos. Como cada um deles se apropriou dos conceitos e como eles trabalham com a álgebra. A abordagem sugerida no pré-teste serviu de inspiração para a elaboração e escolha de cada uma das atividades desenvolvidas nesse trabalho sob a proposta da Engenharia didática. As duas primeiras atividades foram aplicadas individualmente, com a turma assumindo uma postura desinteressada em relação à proposta. Com o desenvolvimento das atividades, os estudantes passaram a interagir entre si na solução das atividades e o ambiente tornou-se prazeroso e propício a construção do conhecimento. É importante ressaltar que a pesquisadora na função de pesquisador-participante, atuou como mediadora durante todo processo de aprendizagem incentivando a interação e construção coletiva. A partir da terceira atividade em diante, já estavam bem à vontade ao ponto de sozinhos fazerem grupos e discutirem entre si, até mesmo sanando um a dúvida do outro.

3. Discussão e resultados

Neste capitulo será descrito cada atividade aplicada; o seu objetivo; o desenvolvimento de cada atividade em sala de aula; os resultados encontrados e a sua discussão.

3.1 Pré-teste

O pré-teste consistiu em identificar como estava o pensamento algébrico dos alunos, era esperado que conseguissem perceber as regularidades e generalizações. Também serviu para nortear como trabalhar nas cinco atividades posteriores, a fim de conseguir alcançar o objetivo deste trabalho. Analisando as respostas dadas, os alunos conseguiram responder os itens “a”, “b” e “c”, nenhum dos 20 alunos deixou esses primeiros itens da atividade em branco ou escreveram que não sabiam responder. Como temos a seguir na Figura 4:

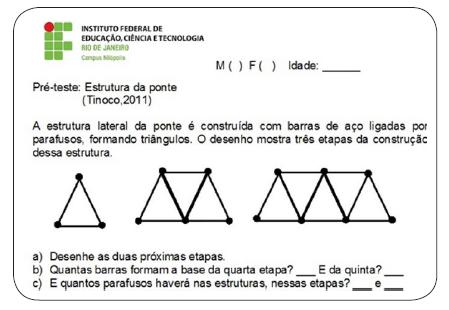
Figura 4 - Extração do Pré-Teste

Figura 5 - Solução aluno 1

Figura 6 - Solução aluno 2

A seguir, descreve-se os resultados da Sequência Didática proposta neste trabalho. Nelas são apresentadas cinco atividades seguintes que foram aplicadas com o intuito de contribuir no desenvolvimento o pensamento algébrico dos estudantes.

Atividade 1

O objetivo da primeira atividade foi trabalhar de forma lúdica a linguagem simbólica, realmente começar a demonstrar para os alunos que podemos escrever os números através de símbolos.

No momento desta atividade os alunos ainda estavam inseguros e com preocupação se valeria ponto, e pode-se observar que muitos não estavam se interessando por não terem feito todos os itens no pré-teste. Mais uma vez, foi preciso dialogar para motivá-los a se dedicarem as atividades. A pesquisadora, pediu que eles não desperdiçassem a oportunidade de estar mais uma vez se deparando, com a álgebra, de forma diferenciada e sem se preocupar com avaliação. Que aquele momento era proveitoso para vida, já que estavam saindo do ensino fundamental e logo iriam se deparar com uma nova realidade que é o ensino médio. Temos na Figura 7, o quadro da primeira atividade.

Figura 7 - números Maia Observe e complete a tabela a seguir com os números correspondentes:

0 1 2 3 4

5

10 — — — — — — 15

● 6 ● — — 11

16 ● ● 7

12

17 ● ● ● 8 ● ● ● — — 13

18 ● ● ● — — — — — — ● ● ● ● 9

14

19

A pesquisadora fez a leitura da atividade com os alunos esclarecendo algumas dúvidas sobre os maias, pois a atividade se inicia com um breve histórico para contextualizar a atividade, e dali iniciou-se um debate que despertou a curiosidade sobre o tema. Nesta atividade, 13 completaram o quadro e 7 alunos deixaram em branco, conseguiram observar a regularidade dos símbolos. Sendo que a última pergunta que seria escrever o número 20, no sistema maia, a maioria deixou em branco e somente 7 alunos arriscaram responder; mas infelizmente ninguém conseguiu escrever 20 no sistema maia. Foi observado nessa atividade, o quanto foi importante a percepção deles em relação a regularidade.

Atividade 2

Na segunda atividade, chamada de enigma, foi iniciada com uma contextualização de uma história sobre uma pesquisa em Marte onde foi encontrado uma pedra inscrita com símbolos, e para decifrar eles teriam que completar a tabela identificando qual operação usada entre os símbolos, que foi a multiplicação.

Figura 8 – Pedra marciana

Agora que completou a tabela anterior, decifre a inscrição registrada na pedra encontrada pelos astronautas.

Os alunos tiveram dificuldade para identificar qual a regularidade usada na tabela e em criar novos símbolos, mas conseguiram completar. E, também mais uma vez foi percebido o quanto é difícil trabalhar com símbolos. Na Figura 8, onde encontramos a Pedra Marciana, não conseguiram decifrar de forma correta a inscrição da pedra, pois não multiplicaram os símbolos e só substituíram, o que nos faz chegar mais uma vez na conclusão do quanto é difícil trabalhar com símbolo. Observe um exemplo de resposta a seguir:

Figura 9 – Solução aluno 3

Agora que completou a tabela anterior, decifre a inscrição registrada na pedra encontrada pelos astronautas.

A Figura 9 representa bem as respostas dada pela maioria dos alunos, não decifraram corretamente, pois só substituíram.

Atividade 3

Como identificado nas atividades anteriores, a dificuldade em fazer operações com símbolos, continuamos na terceira atividade com o mesmo objetivo das atividades anteriores. Chamamos essa atividade de peso, onde os alunos tinham que descobrir quanto valia em quilos cada símbolo na balança. Com essa atividade foi percebido que começaram a entender melhor, por isso foi uma das atividades mais bem proveitosas, e quanto foi gratificante perceber que os alunos estavam finalmente com mais interesse e empenho em aprender. Os itens 1 e 2, os estudantes conseguiram trabalhar com os símbolos e seus respectivos valores. No item 3 foi pedido para não se calcular, e sim só escrever de forma resumida o conteúdo de casa sacola. Sendo que existiram casos de alunos calcularem o peso da sacola, com isso podemos diagnosticar a falta de atenção com enunciado. O próximo item, o quarto, foi para considerar a questão anterior e calcular quantos quilos cada expressão representava, o que foi feito com muito empenho e atenção, ao ponto de todos acertarem todos os itens e demonstrarem claramente o cálculo.

Atividade 4

Nesta atividade o objetivo era trabalhar com os alunos a generalização depois de identificar a regularidade da situação que era a quantidade de medicamento em função do peso do animal. Para iniciar foi oferecido dois exemplos: do papagaio que pesa 400g e recebe 0,8ml de medicamento e do pato que pesa 5Kg e recebe 10ml de medicamento. Então foi proposto qual a quantidade de medicamento que o gavião com o peso de 10Kg receberia. Dos 20 alunos, 7 responderam corretamente, 2 deixaram em branco e 11 não alcançaram o objetivo. Finalizando a atividade foi perguntado como se calcularia a quantidade do medicamento, em ml, para um peso P qualquer, dos 7 que conseguiram resolver com êxito nenhum soube escrever de forma generalizada como foi pedido. Veremos a seguir dois desenvolvimentos:

Figura 10 – Solução aluno 4

Na Figura 10, o aluno teve o raciocínio correto do quantitativo da vacina em função do peso, mas o dobro do peso que seria a quantidade de medicamento em ml. Daí, também podemos diagnosticar a dificuldade de entender o papel da variável, quando ela é dependente ou independente. O que é difícil para alunos de nono ano que não tiveram a possibilidade de construir esses conceitos paulatinamente, habilidade necessária ao estudo de funções.

Figura 11 – Solução aluno 5

Na Figura 11, outro avanço na construção do conceito pode ser percebido. A relação entre o peso e o medicamento o aluno identificou, mas escrever de forma generalizada, usando a variável “P” infelizmente nenhum aluno conseguiu.

Atividade 5

Já nesta fase os alunos estavam bem confiantes e principalmente mais autônomos e participativos. Sendo assim, só um aluno deixou a atividade em branco. A atividade foi contextualizada na estrutura de vagões de trem, para que se diferenciasse dos pré/pós testes a estrutura é de uma ponte formada por triângulos, diferenciando o número de barras por etapas. E, nesta atividade fizemos estrutura de vagões formada por quadrados. O item “a” que era somente para desenhar as outras etapas, foi deixado em branco, o que foi um ponto negativo, pois era um item para facilitar visualmente os dois itens seguintes, “b” e “c”.

Dos 20 alunos que participaram da atividade 5, somente um aluno deixou em branco, um aluno deixou incompleta a tabela. E, o restante da turma, 18 alunos, responderam por completo a atividade. Vamos visualizar algumas atividades:

Figura 12 – Solução aluno 6

Na Figura 12, o aluno 6 calculou corretamente o número total de parafusos e o número total de barras. E, conseguiu generalizar, observando a regularidade, o número total de parafusos e de barras em função de “n”. Figura 13, o aluno 7, calculou corretamente o número total de parafusos e o número total de barras e generalizou corretamente o número total de barras em função de “n”. Mas, não conseguiu alcançar com mesmo êxito a generalização do número total de parafusos.

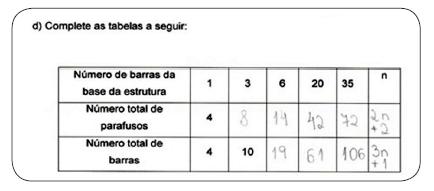
Figura 13 – Solução aluno 7

3.2 Pós-teste

Vamos agora fazer os comparativos com que já apresentamos no início deste capitulo, e perceber a evolução de alguns estudantes.

Comparativo 1: item d

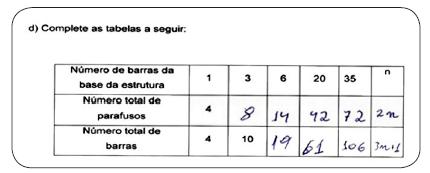
Na Figura 14, podemos destacar o desenvolvimento da questão no pós-teste, a generalização feita pelo aluno 2, pois no pré-teste não feita o que deve ter levado a se equivocar no caso de 15 barras da base da estrutura.

Figura 14 – Pré e Pós-teste aluno 2

Comparativo 2: item d

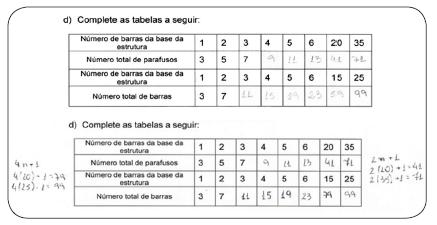
A figura 15 nos mostra a evolução do aluno 3, onde no pré-teste não conseguiu completar a tabela. No pós-teste, depois de ter participado da sequência didática, pode-se perceber a regularidade diagnosticada, até 6 barras da base da estrutura e o total de 6 barras. Mas quando saiu dessa sequência, passando de 6 para 20 e em seguida 35 no número total de parafusos e de 6 para 15 e logo após 25 o número de barras da base da estrutura o aluno 3 respondeu de forma equivocada. Em parte, o aluno 3 conseguiu alcançar a generalização, porém saindo da sequência não alcançou. Os itens “e”, “f”, “g” e “h” foram respondidos pelos 20 alunos, e foi percebido a evolução do pensamento algébrico em cada um, mesmo os cinco desses vinte que responderam de maneira equivocada, nenhum aluno deixou itens em branco ou escreveram que não sabiam ou não entenderam.

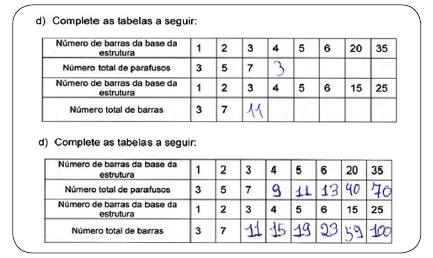
Figura 15 – Pré e Pós-teste aluno 3

Nas Figuras 16 e 17 podemos comparar o que foi apresentado nas Figuras 3 e 4 no pré-teste. É possível verificar o avanço do pensamento algébrico dos alunos 1 e 2, onde no pré-teste os mesmos escreveram: não sei, não entendi e não sei executar a questão, e no pós-teste conseguiram responder todos os itens de forma correta e explicando como calculou.

Figura 16 – Aluno 1

Figura 17 – Aluno 2

Na Figura 18, o aluno 3, que deixou todos os itens em branco no pré-teste, mas alcançou o objetivo no pós-teste, mostrando que houve o desenvolvimento do pensamento algébrico.

Figura 18 – Aluno 3

As dificuldades encontradas pelos alunos, durante as atividades, nos remetem a Falcão (1992), exposto no Quadro 1, que tomamos por base para identificação das dificuldades na utilização de linguagem algébrica pelos alunos. Os primeiros quatro itens, do Quadro 1, evidenciaram as dificuldades encontradas pelos alunos na sequência didática, que foram: Suporte simbólico misto, Distinção entre variáveis e parâmetros, Generalidade da expressão e Caráter sintético da expressão. Foi percebido dificuldades enfrentadas pelos alunos no pré-teste e nas atividades de 1 até 4; no entanto, também foi percebido junto com as dificuldades o desenvolvimento do pensamento e linguagem algébrica. As dificuldades foram percebidas através de questões deixadas em branco e respostas equivocadas. Na quinta atividade as soluções realizadas pelos alunos, pode-se observar o desenvolvimento da linguagem e do pensamento algébrico, uma vez que conseguiram visualizar a regularidade e generalidade da situaçãoproblema, encontrando a solução de forma generalizada, sabendo que a letra “n” serviria para qualquer número. A atividade cinco foi bem proveitosa para os alunos, pois os mesmos chegaram a conclusão que poderiam generalizar. Durante o pós-teste se percebeu a evolução do desenvolvimento do pensamento algébrico que os alunos conseguiram alcançar.

Considerações Finais

Podemos verificar que problemas herdados da aritmética e a interrupção do concreto para o abstrato, travam os estudantes na inicialização do ensino de álgebra. No entanto, os objetivos da pesquisa foram alcançados através da sequência didática, que no decorrer foram evidenciados os obstáculos enfrentados pelos alunos, nas dificuldades em: representar e identificar números com símbolos; distinguir variável de incógnita e dificuldade em generalizar situações-problemas. A experiência da pesquisa utilizando a engenharia didática permitiu verificar que uma abordagem diferenciada do ensino da matemática (menos formal e tradicional) auxiliou no desenvolvimento da abstração dos alunos. Este trabalho também permitiu ampliar a percepção da pesquisadora a respeito da realidade da sala de aula nas escolas da rede pública estadual, salvo raras exceções, o público alvo apresenta carências que tornam o aprendizado 38

da álgebra mais “doloroso” e menos “prazeroso”. Como resultado, o estigma da matemática como “bicho papão”, difícil e chata acaba ganhando força entre os alunos. Há ainda o agravante de que nos dias de hoje, o professor de matemática tem que disputar a atenção do aluno com dispositivos portáteis, a tradicional conversa, a desmotivação, o desinteresse e a crescente prática de incivilidades em sala de aula (violência verbal; física; bullying; depredação...). Todos os efeitos destes fatores em sala de aula são exponencializados quando o número de alunos em sala ultrapassa o aceitável. Não será falado aqui qual seria esse número aceitável, até porque este não foi o foco do trabalho; mas na condição de aluna da graduação em licenciatura e participante de alguns projetos na área da docência, percebeuse que lotar ou superlotar uma sala de aula é, claramente, antipedagógico e contraproducente; uma vez que favorece muito mais a todos os fatores que são contrários a atuação do professor, que ao processo de aprendizagem do aluno. Alunos que já trazem deficiências dos anos anteriores tendem a ter sua capacidade de desenvolvimento das habilidades e competências esperadas em álgebra prejudicadas, some-se a isso os aspectos emocionais e psicológicos que fazem parte do processo de aprendizagem, o resultado disso é que tais alunos tendem a permanecer mais tempo diante do obstáculo didático, até desenvolverem condições de superá-lo. A álgebra solidamente introduzida, primeiramente sendo trabalhado a simbologia, estimulando no aluno o florescimento do pensamento algébrico para a partir daí desenvolver a linguagem algébrica (mostrando aos alunos que o número pode ser representado por símbolos, deixando evidente a diferença de incógnita para variável), permitirá que o aluno avance no aprendizado da álgebra sem maiores dificuldades e desenvolva as competências e habilidades preconizadas nos currículos escolares. É uma expectativa, sem que seja considerada deveras pretenciosa, que este trabalho possa, eventualmente, vir a ser subsídio para outros da mesma linha de pesquisa. Finalizando, a pesquisadora pretende avançar com a temática deste trabalho durante os estudos de pós-graduação a fim de tratá-la em um nível mais aprofundado, pois acredita que a vivência em projetos ligados ao ensino da matemática nas escolas públicas juntamente com todo o embasamento teórico-metodológico e científico adquiridos durante a graduação pavimentam à frente um caminho a ser trilhado. 39

Referências Bibliográficas

ALRO, Helle. Dialogo e Aprendizagem em Educação Matemática; tradução de Orlando Figueiredo – Belo Horizonte: Autentica, 2006. BRUM, Wanderley Pivatto; SCHUHMACHER, Elcio. A engenharia didática como

campo metodológico para o planejamento de aula de matemática: análise de

uma experiência didática para o estudo de geometria esférica. Jornal Internacional de Estudos em Educação Matemática, Santa Catarina, 2013, v. 6 (2), p. 60-84. D’AMBROSIO, Ubiratan. Educação Matemática: da teoria à prática. 23° ed. Campinas, SP: Papirus, 2012. FALCÃO, Jorge Tarcísio da Rocha. Psicologia da Educação Matemática: uma introdução. 1a reimp. Belo Horizonte: Autentica, 2008. KIKUCHI, Luzia Maya. Obstáculos à aprendizagem de conceitos algébricos no

ensino fundamental: uma aproximação entre os obstáculos Epistemológicos e

a Teoria dos Campos Conceituais. Universidade de São Paulo/Programa de PósGraduação, São Paulo, 2012. MACHADO, Silva Dias Alcântara (Org). Educação Matemática: uma (nova) introdução. 3a ed. Revisada, 2a reimp. São Paulo: EDUC, 2012, 254 p.; 18 cm. (Série Trilhas). MEC/SEF. Parâmetros curriculares nacionais: matemática, terceiro e quarto ciclos. MEC/SEF, Brasília, 1998. MONDINI, Fabiane. A presença da álgebra na legislação brasileira. Tese (doutorado Geociências e Ciências Exatas). Universidade Estadual Paulista, São Paulo, 2013. 433 f. PAIS, Luiz Carlos. Didática da Matemática; uma análise da influência francesa. 2a ed., 2a Reimp. Belo Horizonte: Autentica, 2008. POMMER, Wagner Marcelo. A engenharia didática em sala de aula: Elementos básicos e uma ilustração envolvendo as equações Diofantinas lineares, 2013. 72p. ils: Tabs. SCHUBRING, Gert. Desenvolvimento histórico do conceito e do processo de

aprendizage, a partir de recentes concepções matemático-didáticas (erro,

obstáculos, transposição). ZETETIKE-CEPEM-FE/UNICAMP, São Paulo, v. 6, n° 10, p. 9-34, Jul/Dez de 1998. TINOCO, Lucia Arruda Albuquerque, (coord). Álgebra: pensar, calcular, comunicar. 2a ed. Rio de Janeiro: UFRJ/IM, 2011, 111 p.; 29 cm.