Pensa con la Fisica - Ed. Tech

PENSA CON LA

EDIZIONE TECH

PERCORSI DIGITALI INTERATTIVI CON 450 VIDEO

SCHEDE DI EDUCAZIONE CIVICA

ATTIVITÀ DI ORIENTAMENTO STEM

ESERCIZI PENSA CON LA FISICA

PERCORSO DI RIPASSO E RECUPERO

Franco Bocci • Giovanna Malegori • Francesca Toglia

41 Nei centri urbani il limite di velocità è di 50 km/h. Viaggiando a 12 m/s si è passibili di multa?

[No, perché corrispondono a 43 km/h]

42 Negli Stati Uniti il limite di velocità sulle strade è espresso in miglia all’ora (miles per hour: mph o mi/h). Sapendo che 1 mi = 1,609 km, esprimi il limite di 80 mi/h in km/h e in m/s. [130 km/h; 36 m/s]

43 Il 29 luglio 2009 Federica Pellegrini ha stabilito il record mondiale dei 200 m stile libero con il tempo di 1 min 52,98 s diventando la prima donna a scendere sotto al tempo di 1 min 53 s. Qual è stata la sua velocità media sull’intero percorso? E la sua rapidità media?

[0; 1,770 m/s]

44 3 Nella tabella sono riprodotti i dati ottenuti da un sistema Safety Tutor per tre veicoli di-

versi che effettuano un passaggio tra due posizioni distanti tra loro 4,00 km, in un tratto in cui il limite di velocità è 130 km/h.

Targa veicolo Passaggio postazione 1 Passaggio postazione 2

DF343WQ11:24:5611:27:32

OJ243AS11:24:5911:27:11

IH761EW11:25:1511:26:54

Calcola l’intervallo di tempo tra i due passaggi e convertilo nel sistema decimale. Quindi calcola la rapidità media dei tre veicoli. È possibile che anche i veicoli che risultano in regola da questi dati abbiano superato in qualche tratto i limiti di velocità? [92 km/h; 109 km/h; 145 km/h]

45 ESERCIZIO GUIDATO Durante un temporale senti il rumore di un tuono 4,0 s dopo aver visto il lampo. A che distanza ti trovi dal punto in cui è caduto il fulmine? Trascura il tempo che impiega la luce a percorrere la distanza e considera che la velocità del suono è uguale a 340 m/s.

RICONOSCIAMO DATI E INCOGNITE

Intervallo di tempo tra lampo e tuono: Δt = 4 s Velocità del suono: vm = 340 m/s Distanza tra te e il fulmine: ℓ = ?

RISOLVIAMO

Poiché il tuono è un fenomeno sonoro che si scatena non appena si forma un fulmine, il fatto che tu senta il rumore di un tuono dopo 4 s sta a significare che il suono ha percorso:

ℓ = vmΔt = (340 m/s) · (4 s) = .........

46 PROVA TU

Sei in un autobus che viaggia a una rapidità media di 86,4 km/h. Durante i 50 s in cui guardi fuori dal finestrino, che distanza ha percorso l’auto? [1,2 km]

47 Alle olimpiadi di Tokyo 2020, Antonella Palmisano e Massimo Stano hanno vinto la medaglia d’oro nella marcia ed è stata la prima volta che nella stessa olimpiade l’Italia ha conquistato l’oro nella marcia sia maschile che femminile. Stano, con una rapidità media di 4,111 m/s, ha completato la gara in 1 h 21 min 5 s, ossia in 4865 s. Che distanza ha percorso? Palmisano ha impiegato 1 h 29 min 12 s, cioè 5352 s, per percorrere la stessa distanza: qual è stata la sua rapidità media?

[20,00 km; 3,737 m/s]

48 L’1 agosto 2021, alle olimpiadi di Tokyo, Marcell Jacobs è stato il primo atleta italiano a vincere la me-

daglia d’oro nei 100 m piani, percorrendo la distanza con una velocità media di 10,2 m/s. Quanto tempo ha impiegato a completare la gara? [9,80 s]

49 A bowling ball moves from x1 = 3.50 cm to x2 = -4.70 cm during the time interval from t1 = 3.00 s to t2 = 5.50 s. What is the ball’s average speed? [3.28 cm/s]

50 Un autobus scolastico parte da casa tua e impiega 0,700 h a raggiungere la tua scuola. Se la rapidità media dell’autobus è 56,0 km/h, qual è la lunghezza del cammino percorso? [39,2 km]

51 ESERCIZIO RISOLTO Un corpo percorre 100 m in 13,0 s, poi viaggia per altri 15,0 s a 21,0 km/h. Qual è stata la rapidità media su tutto il percorso?

RICONOSCIAMO DATI E INCOGNITE

Indichiamo con Δℓ1 e Δℓ2 gli spazi percorsi nei due intervalli Δt1 e Δ

Rapidità media sull’intero percorso: Δℓ2 = ? vm = ?

con vm1 e vm2 le rispettive rapidità medie:

= 21,0 km/h = 5,83 m/s

RISOLVIAMO

Per calcolare la rapidità media su tutto il percorso abbiamo bisogno di conoscere lo spazio totale percorso e il tempo totale impiegato. Nel secondo intervallo dobbiamo conoscere la lunghezza del cammino percorso:

Lo spazio totale è dunque:

tempo totale è:

rapidità media su tutto il percorso risulta quindi:

52 PROVA TU

Su un tratto rettilineo, Luca percorre 300 m in 5,0 minuti, poi altri 800 m alla velocità media di 5 km/h. Qual è la velocità media di Luca per l’intero percorso? Qual è la rapidità media? [1,3 m/s]

53 Supponi che mentre stai camminando verso la scuola cominci a piovere. Torni indietro di 120 m verso casa correndo per 28,0 s per recuperare il tuo ombrello. Se camminando impieghi 75,0 s per percorrere 120 m, qual è la tua velocità media per i 240 m percorsi? Qual è la tua rapidità media? [0; 2,30 m/s]

La velocità nel grafico posizione-tempo

56 Il grafico descrive il moto di un nuotatore in una piscina olimpica da 50 m.

Calcola la velocità media nella vasca di andata (tratto AB) e nella vasca di ritorno (tratto CD) e nei primi 60 s.

In che posizione si trova al tempo t = 20 s?

[1,25 m/s; -1,00 m/s; 0,667 m/s; 25 m]

54 A man walks at a speed of 1.8 m/s for 750 m and 2.2 m/s for the next 250 m. What is the average speed for the walk of 1 km? [1.9 m/s]

55 Nel passaggio tra due postazioni Safety Tutor, distanti tra loro 5,2 km, un veicolo ha viaggiato a 150 km/h nei primi 3,0 km. Quale velocità dovrà mantenere nei successivi 2,2 km per avere una velocità media di 130 km/h? [110 km/h]

57 Alice e Bianca percorrono un tratto di strada rettilinea, rispettivamente, a velocità 1,2 m/s e 1,6 m/s. Disegna sul quaderno o con un Foglio di calcolo un grafico posizione-tempo in cui siano rappresentate le posizioni delle due ragazze. Dopo 50 s, qual è la distanza che separa le due ragazze? [20 m]

58 Per allenarsi ad una gara di resistenza, Giovanna corre per 15 km e poi cammina a passo veloce per altri 15 km. La tabella riporta i tempi ai passaggi intermedi:

Costruisci sul quaderno o con un Foglio di calcolo il grafico posizione-tempo. Calcola la rapidità media nei primi 15 km, nei secondi 15 km e nell’intero tragitto, esprimendole in km/h.

59 Un allenatore cronometra il suo cavallo da corsa mentre completa un allenamento lungo un percorso rettilineo. In tabella sono riportate le posizioni occupate dal cavallo e l’istante in cui si trova in quella posizione. Disegna sul quaderno o con un Foglio di calcolo il grafico posizione-tempo e calcola la rapidità media del cavallo tra:

a 0 e 10 s; [18 m/s]

b 10 s e 30 s; [16 m/s]

c 0 e 50 s. [14 m/s]

IL MOTO RETTILINEO UNIFORME

Puoi condurre una semplice esperienza con i tuoi compagni per studiare un importante tipo di moto rettilineo, il moto rettilineo uniforme.

PENSA CON LA FISICA

Luca e Paolo fissano un asse di riferimento lungo la linea di un campo di pallavolo con l’origine O in corrispondenza del muro della palestra. Con un nastro adesivo segnano sette traguardi a partire dalla posizione s = 5 m e distanziati di 3 m uno dall’altro. Luca parte dall’origine O e cammina lungo l’asse di riferimento con passo lento e regolare. Paolo misura i tempi di passaggio ai diversi traguardi, facendo partire il cronometro al passaggio da s . Ripetono poi la misura con Luca che cammina con passo più veloce e regolare. Usa i dati raccolti e riportati nella tabella per disegnare sul quaderno o con un Foglio di calcolo il grafico posizione-tempo per entrambe le misure.

1 Come si dispongono i punti su ciascun grafico?

2 Per entrambi i moti, considera lo spostamento dalla posizione iniziale s a ciascun traguardo e calcola la velocità media: che cosa osservi?

Il moto rettilineo uniforme

Il moto rettilineo più semplice è quello di un corpo che si sposta a velocità costante.

Un moto rettilineo si definisce uniforme quando il corpo si muove a velocità costante.

Se rappresentiamo il moto lento dell’attività iniziale in un grafico posizione-tempo, i punti si dispongono con buona approssimazione lungo una retta, come mostrato in figura.

IN ENGLISH

• Moto rettilineo uniforme: uniform linear motion

• Costante di proporzionalità: constant of proportionality

• Legge oraria del moto rettilineo uniforme: equation of uniform linear motion

Il moto è rettilineo perché la traiettoria è rettilinea e, calcolando la velocità media, ci accorgiamo che è costante e, nel nostro esempio, è uguale a 1,3 m/s, qualunque sia l’intervallo di tempo considerato. Possiamo dunque concludere che il moto è uniforme

La velocità istantanea vist in ogni istante assume lo stesso valore e coincide con la velocità media.

In ogni punto la retta tangente al grafico che descrive il moto coincide con la retta stessa.

Usando il simbolo v = vist = vm per la velocità, che è costante, abbiamo che:

un intervallo qualsiasi

In un moto rettilineo uniforme gli spostamenti Δs sono direttamente proporzionali agli intervalli di tempo Δt in cui avvengono. La costante di proporzionalità è la velocità v del corpo.

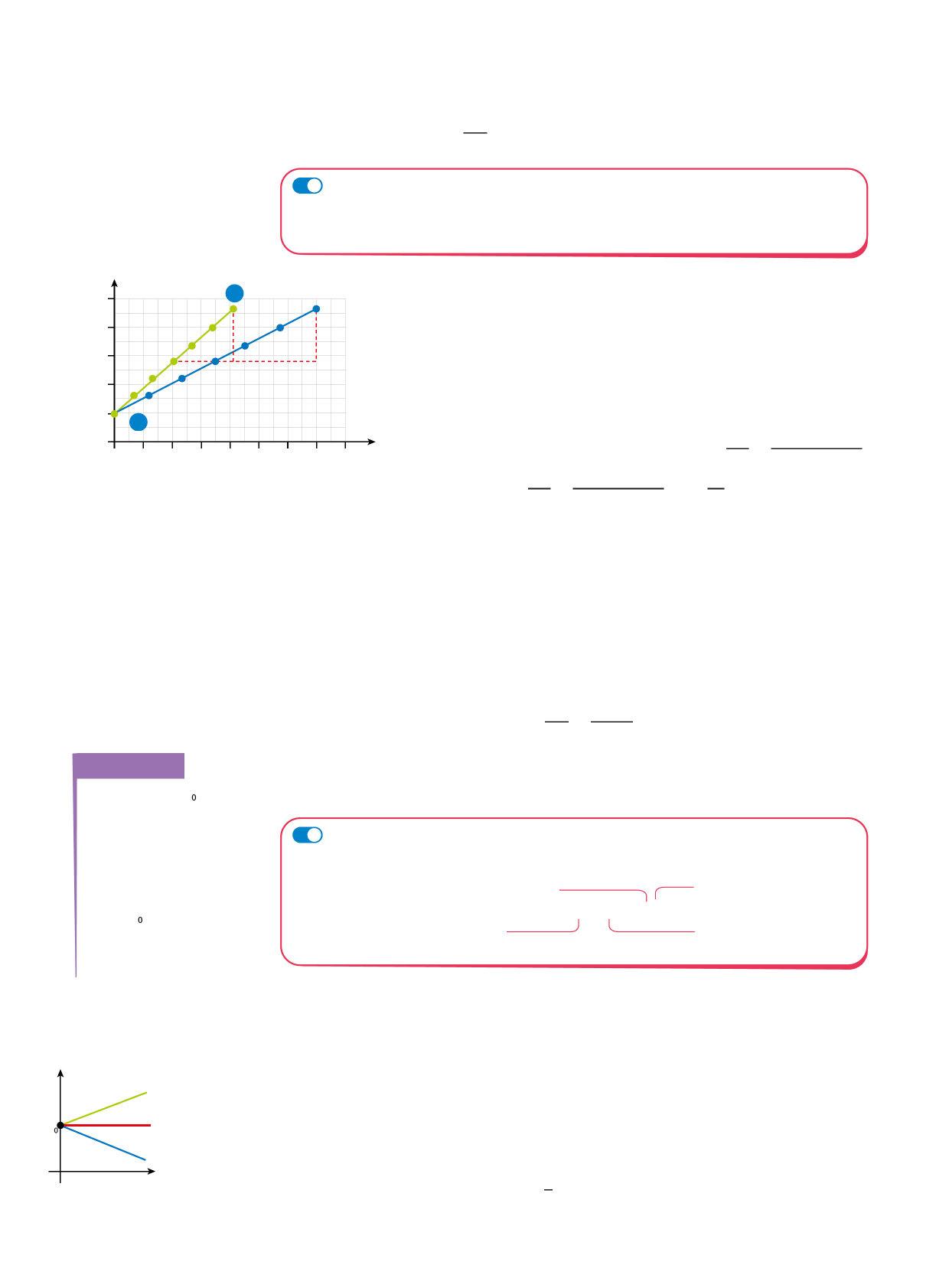
Anche la camminata veloce proposta nell’attività iniziale è un moto rettilineo uniforme, perché il diagramma orario è una retta e gli spostamenti sono direttamente proporzionali agli intervalli di tempo in cui avvengono, come si vede dal grafico.

0246810121614

MATE & FISICA

L’equazione s = s + vt è una relazione lineare del tipo y = mx + q Graficamente m e la velocità v indicano la pendenza della retta mentre q e la posizione iniziale s individuano l’ordinata dell’intersezione con l’asse y

v > 0 nel verso positivo

v = 0 il corpo è fermo

v < 0 nel verso negativo

1. La pendenza della retta verde (camminata veloce) è maggiore rispetto alla pendenza della retta blu (camminata lenta), perché la persona compie gli stessi spostamenti in un tempo minore e la sua velocità è maggiore: vveloce = 2,2 m/s =

t = 23 m - 14 m

s

8,2 s - 4,1 s , mentre vlenta = ∆s ∆t = 23 m - 14 m

13,9 s - 6,9 s = 1,3 m s

2. La posizione iniziale è la stessa perché i cronometri sono stati attivati quando entrambi i camminatori si trovavano in s0 = 5,0 m.

La legge oraria del moto rettilineo uniforme

Scriviamo la relazione della velocità tra l’istante iniziale t = 0 e un generico istante t quando il corpo passa dalla posizione s0 alla posizione s

Considerato che l’intervallo di tempo è Δt = t - 0 = t, abbiamo che:

v = ∆ s ∆t = s s0 t

Con semplici calcoli, ricaviamo l’espressione della posizione s occupata all’istante t: vt = s - s0 ⇒ s = s0 + vt

LEGGE ORARIA DEL MOTO RETTILINEO UNIFORME

La legge oraria o equazione del moto rettilineo uniforme è:

s = s0 + vt velocità (costante) istante di tempo posizione all’istante t posizione iniziale (all’istante t = 0)

Comprendi la legge

• L’equazione oraria consente di conoscere la posizione s del corpo in un qualunque istante di tempo t per l’intero tratto in cui il corpo si muove con velocità costante.

• Tra la posizione e il tempo c’è una relazione lineare che ha come grafico una porzione di retta. La posizione iniziale s0 corrisponde all’ordinata del punto di intersezione con l’asse y, la velocità v indica la pendenza della retta. Un corpo fermo è un caso particolare di moto rettilineo uniforme con v = 0.

• Se la posizione iniziale è s0 = 0, la relazione tra la posizione e il tempo diventa una proporzionalità diretta s = vt ⇒ s t = v . In questo caso il grafico posizione-tempo è un tratto di retta che passa per l’origine.

Applica la legge

Nella camminata lenta, in che posizione si trovava Luca quando il cronometro indicava il tempo t = 3,0 s?

Sostituiamo i valori nella legge oraria e ricaviamo la posizione richiesta:

s = s0 + vt = 5,0 m + 1,3 m/s · 3,0 s = 8,9 m

PROVA TU In quale istante della camminata veloce Luca era nella posizione s = 8,3 m? [1,5 s]

ESERCIZI DI LEZIONE

FISSA I CONCETTI

60 Quale dei seguenti è un moto rettilineo, ma sicuramente non è uniforme?

A Una persona sulla scala mobile

B Un’automobile su un rettilineo che frena e si ferma al semaforo

C Una nave che viaggia in linea retta a velocità di crociera

D Un disco da hockey su ghiaccio diretto in porta

61 Una podista si muove con velocità costante e al tempo t = 2 min la sua velocità è 8,0 km/h. Qual è la sua velocità dopo 3 min?

A e B hanno velocità diverse ma la stessa posizione di partenza

A 4 km/h

D 8,0 m/s

B 16 km/h C 2,2 m/s

62 Nel moto rettilineo uniforme, la relazione tra posizione e tempo è sempre:

A di proporzionalità diretta

B di proporzionalità inversa

C lineare

D quadratica

63 Dopo aver osservato il grafico, scegli l’affermazione corretta:

A B parte da una posizione più lontana dall’origine ed è più veloce di A

B A parte da una posizione più vicina all’origine ed è più veloce di B

C A e B hanno posizioni iniziali diverse, ma stessa velocità

PENSA CON LA FISICA

64 Quale legge oraria corrisponde al grafico in figura?

A s = s0 + vt con s0 = 2 m e v = 3 m/s

B s = vt con v = 3 m/s

C s = s0 + vt con s0 = 2 m e v = 4 m/s

65 INTERPRETA Le immagini, che non sono in scala, riproducono in tre istanti successivi tre auto che si muovono su una strada diritta a velocità costante. Associa a ogni auto la retta del grafico posizione tempo che ne descrive il moto. Individua sul grafico l’istante t2.

66 SPIEGA Con l’attivazione del cruise control un veicolo mantiene una rapidità costante. Spiega perché in genere non si tratta di un moto rettilineo uniforme.

67 TROVA L’ERRORE Il grafico posizione-tempo di un moto rettilineo è un tratto di retta perché la traiettoria è rettilinea.

RISOLVI

69 Una palla da biliardo rimbalza su una sponda e dopo 0,20 s colpisce la sponda adiacente. Nel tratto tra le due sponde la palla si muove con velocità costante di 4,2 m/s. Qual è la distanza percorsa dalla palla tra le due sponde? [84 cm]

70 Un motociclista si muove di moto rettilineo uniforme con una velocità di 80 km/h. Quanto tempo impiega a coprire una distanza di 220 m? [9,9 s]

71 Se un camion viaggia alla velocità di 64 km/h, quanto tempo impiega a percorrere una galleria lunga 2,35 km? Che distanza percorre in 53 s? [132 s; 940 m]

72 Un ragazzo cammina sulla banchina di una stazione ferroviaria con velocità costante. All’istante tA = 2,0 s è nel punto A, al tempo tB = 7,0 s è nel punto B Calcola la velocità del ragazzo e il tempo che impiega ad andare dal punto B al punto C. [-2 m/s; 15 s]

68 CHI HA RAGIONE? Una lumaca si muove di moto rettilineo uniforme con velocità positiva.

Antonio: “La lumaca non può mai passare per l’origine, perché si muove sempre nel verso positivo.”

Manuela: “No, dipende dal sistema di riferimento: se la lumaca partisse da una posizione negativa, mentre si muove potrebbe passare per l’origine.”

73 3 Anche se il codice della strada vieta l’uso del cellulare mentre si guida, il numero di incidenti stradali provocati da questa cattiva abitudine è ancora molto elevato. Per capire la gravità di questo comportamento considera che la lettura di un messaggio anche breve sullo smartphone può richiedere 10 s. Quando la velocità è di 50 km/h, che distanza percorre l’auto in questo intervallo di tempo in cui il conducente è completamente distratto? E se la velocità fosse di 120 km/h? [140 m; 330 m]

74 Il grafico rappresenta il moto rettilineo uniforme di un corpo. Determina:

a la velocità del corpo; [0,4 m/s]

b la posizione iniziale del corpo;

c la legge oraria del moto del corpo;

d dopo quanto tempo si trova a 20 m dall’origine;

e a che distanza si trova dall’origine dopo 40 s.

75 ESERCIZIO GUIDATO In un determinato istante, che consideriamo come iniziale, un podista si trova al kilometro 9,30 di un percorso di gara lungo 16,8 km. Supponi che impieghi 36,0 minuti per terminare il percorso e che la sua velocità sia costante: in quale istante si trova al kilometro 11,8? Tratta il moto come se fosse rettilineo.

RICONOSCIAMO DATI E INCOGNITE

s0 = 9,30 km: posizione al tempo t = 0 s s2 = .......... km: posizione al tempo t2 = 36,0 min

s1 = 11,8 km: posizione al tempo t1 = ?

RISOLVIAMO

La velocità del podista è costante, perciò possiamo calcolarla in un intervallo di tempo del quale abbiamo tutti i dati, cioè

t = t2 - 0 = t2:

Ricaviamo il tempo dalla legge .......................

= 0,208 km/min

Inseriamo i valori numerici: t1 = s1 - s0 v = ........ km - 9,30 km ........ km/min = 12,0 min .

76 PROVA TU

All’istante t = 24,4 min dove si trova il podista? [14,4 km]

77 La legge oraria di un moto rettilineo uniforme è s = vt con v = 2,8 m/s e con s0 = 0. Disegna sul quaderno o con un Foglio di calcolo il grafico posizione tempo. In che posizione si trova il corpo all’istante t = 0? E all’istante t = 3,5 s? In quale istante è nella posizione s = 4,2 m? [0; 9,8 m; 1,5 s]

78 A runner travelling along a straight path maintains a constant velocity of 3.0 m/s east. The positive x – direction along the horizontal axis is defined to be east. At time t = 0, the runner is at x0 = 120 m. At what time is the runner’s position x = 255 m? Where is the runner at time t = 79 s? [45 s; 360 m]

79 Il moto di una bolla d’aria che risale lungo un tubo inclinato è descritto dalla legge oraria: s = s0 + v t con v = 5,0 cm/s e s0 = 4,0 cm. Rappresenta sul quaderno o con un Foglio di calcolo il grafico posizione-tempo. Quanto tempo impiega la bolla a percorrere 37 cm? [7,4 s]

80 All’olimpiade di Tokyo 2020, Federica Cesarini e Valentina Rodini, vincendo la gara del doppio pesi leggeri, hanno conquistato la prima medaglia d’oro olimpica nella storia del canottaggio azzurro femminile.

La tabella riporta i tempi registrati.

a Esprimi i tempi in secondi e costruisci il grafico posizione tempo.

b Verifica che il moto è con ottima approssimazione rettilineo uniforme, con velocità v = 4,9 m/s.

c Quanto tempo hanno impiegato le due atlete a percorrere i primi 250 m? [51 s]

81 I dati in tabella si riferiscono al moto di un corpo che segue una traiettoria rettilinea.

t (s) 01234

s (m) 2,03,24,45,66,8

a Costruisci sul quaderno o con un Foglio di calcolo il grafico spazio-tempo.

b Verifica che il moto è uniforme e calcola la velocità.

c Dove si trova il corpo all’istante t = 2,7 s?

d In quale istante è nella posizione s = 3,9 m?

[b. 1,2 m/s; c. 5,2 m; d. 1,6 s]

82 Un gatto si muove con velocità costante v = -1,4 m/s lungo una linea orientata partendo dalla posizione s0 = 3,5 m.

Dove si trova dopo 4 s? In quale istante passa dall’origine? [-2,1 m; 2,5 s]

83 La tabella fornisce le posizioni di un treno e di una nave. Completala sapendo che entrambi sono moti rettilinei uniformi.

Quale tra i due mezzi ha velocità maggiore? (Miglio nautico: 1 NM = 1852 m)

84 The graph in figure describes the straight-line motion of a student.

a What is his velocity?

b What is the student’s position at 0 s?

c And what is the position at 3.2 s?

85 ESERCIZIO RISOLTO Marco e Anna abitano a 180 m di distanza. Partono dalle loro case contemporaneamente, camminando in linea retta l’uno verso l’altro. Marco ha una velocità costante di 2,00 m/s e Anna di 2,80 m/s. Dopo quanto tempo si incontrano? A che distanza dalla casa di Anna si incontrano?

RICONOSCIAMO DATI E INCOGNITE

Poniamo l’origine in corrispondenza della casa di Marco e orientiamo l’asse nel verso del suo moto. Marco si muove quindi nel verso positivo e ha velocità positiva, Anna si muove in verso opposto e la sua velocità è negativa. Facciamo partire il cronometro quando i due ragazzi escono di casa. Scriviamo i dati che derivano da questa scelta del sistema di riferimento.

Posizione iniziale di Marco: s0M = 0

Velocità di Marco: vM = 2,00 m/s

Posizione iniziale di Anna: s0A = +180 m

Velocità di Anna: vA = -2,80 m/s

Istante dell’incontro: t = ?

Posizione iniziale di Marco: s = 0

di Marco: v = 2,00 m/s

Le equazioni orarie di Marco e di Anna sono rispettivamente:

ragazzi si incontrano quando

quando:

Da questa equazione ricaviamo l’istante t in cui i due ragazzi si incontrano:

Per trovare la posizione in cui si incontrano possiamo sostituire questo valore indifferentemente nell’equazione oraria di Marco o in quella di Anna. Scegliamo la prima perché il calcolo è più rapido essendo solo una moltiplicazione:

sM = vMt = 2,00 m s · 37,5 s = 75,0 m

Verifichiamo che, se avessimo considerato l’equazione oraria di Anna, avremmo ottenuto lo stesso risultato:

sA = s0A + vAt = 180 m - 2,80 m s · 37,5 s = 75,0 m

La distanza dalla casa di Anna è quindi:

d = 180 m - 75,0 m = 105 m

Il problema può essere risolto anche graficamente. Si riportano sullo stesso grafico le due equazioni orarie di Anna e Marco e si deducono l’istante e la posizione dell’incontro (pallino nero).

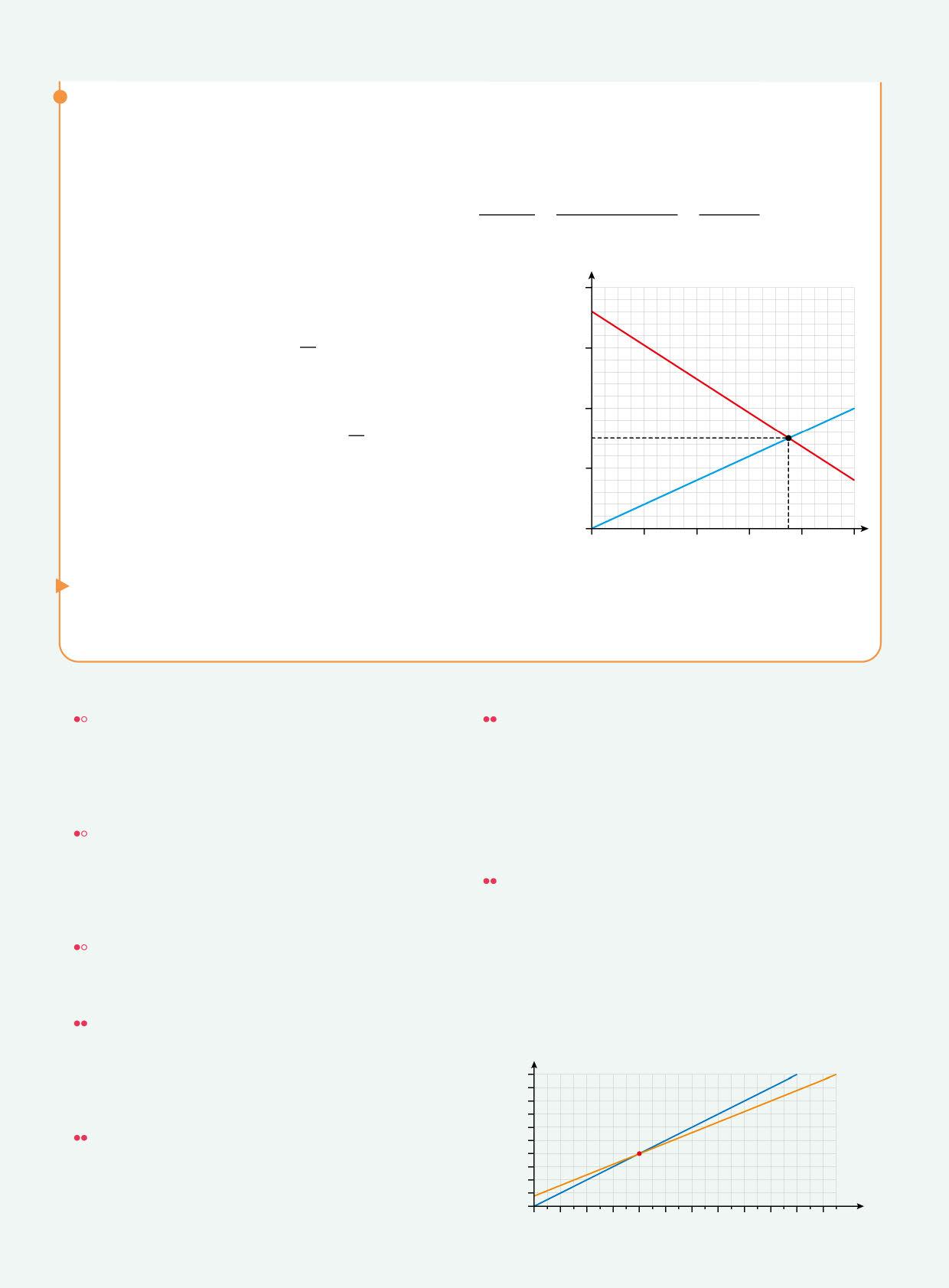
86 PROVA TU

Due amici che abitano a 1,00 km di distanza partono contemporaneamente da casa per incontrarsi. Il primo cammina a piedi a una velocità di 4,00 km/h e il secondo si muove in bicicletta a 12,0 km/h. Dopo quanto tempo si incontrano?

87 Due auto A e B si muovono in verso opposto lungo una strada rettilinea con velocità costante vA = 20 m/s e vB = -25 m/s. L’auto A parte dall’origine mentre l’auto B parte dalla posizione s0B = 1600 m. Qual è la distanza tra le auto al tempo t = 52 s? [740 m]

88 Il traghetto tra Villa San Giovanni (in Calabria) e Messina viaggia alla velocità media di 11,4 km/h. La distanza in linea d’aria tra le due località è 7,6 km. Supponendo che il traghetto parta alle 7:30 da Villa San Giovanni, a che ora arriva a Messina? [8:10]

89 Una gru solleva un carico alla velocità di 28 cm/s. Quanto tempo impiega a portarlo all’altezza di 15 m? [54 s]

90 Un ciclista su una strada rettilinea si muove alla velocità costante di 45 km/h. Se nell’istante t = 6,0 s la sua posizione è s = 60 m, qual era la sua posizione all’istante t = 0? In quale istante si troverà nella posizione 135 m? [-15 m; 12 s]

91 In un fiume una barca riesce a muoversi alla velocità di 6,8 m/s (rispetto alle rive) quando risale la corrente, e alla velocità di 9,2 m/s in senso opposto. Quanto spazio percorre, scendendo lungo la corrente, nello stesso tempo che impiega a percorrere 100 m controcorrente? [135 m]

s]

92 Anna e Barbara si muovono in bicicletta su una strada rettilinea nello stesso verso (che scegliamo essere quello positivo). Barbara ha una velocità di 7,0 m/s. All’istante iniziale, Anna è davanti a Barbara a 100 m di distanza. Qual è la velocità di Anna, se Barbara la raggiunge dopo 50 s? Risolvi il problema sia algebricamente che usando un grafico da disegnare sul quaderno o con un Foglio di calcolo. [5,0 m/s]

93 Il grafico in figura descrive il moto di Andrea e Bruno che fanno una gara in bicicletta. Il traguardo si trova a distanza 500 m dal punto di partenza. Andrea concede un vantaggio di 40 m a Bruno. Determina:

a le velocità dei due amici;

b le leggi orarie dei moti dei due amici;

c chi vince la gara e con quale anticipo arriva al traguardo rispetto al secondo;

d che cosa avviene dopo 80 s dalla partenza.

[a. 9,0 km/h, 7,2 km/h; c. 30 s]

IL MOTO E L’ACCELERAZIONE

Nel linguaggio comune “accelerare” vuol dire aumentare la velocità. In Fisica si parla di accelerazione anche quando la velocità diminuisce, come durante la frenata di un’automobile e, come vedremo nella prossima unità, quando cambia direzione, come quando un’automobile percorre una curva.

PENSA CON LA FISICA

L’airbag è un dispositivo di sicurezza che, insieme alle cinture di sicurezza, protegge i passeggeri delle automobili dagli urti violenti in caso di incidenti stradali.

1 Qual è la grandezza che diminuisce bruscamente durante un urto?

2 Che cosa fa attivare l’airbag?

La variazione di velocità

Consideriamo un’automobile su una strada diritta che riprende velocità dopo un semaforo e poco più avanti rallenta per far passare dei pedoni. La velocità rilevata dal tachimetro non è costante, ma varia nel tempo. Un moto come quello appena descritto, dove il valore della velocità cambia, è un moto vario

Se fissiamo un asse di riferimento orientato verso destra, l’auto ha velocità positiva

1. Dopo il semaforo, quando l’auto va più rapidamente perché riprende velocità, la velocità aumenta, passando da 6 m/s a 12 m/s. La variazione di velocità Δv è positiva e quindi dello stesso segno della velocità.

2. Quando vicino ai pedoni l’auto rallenta, il valore della velocità diminuisce perché la velocità passa da 12 m/s a 2 m/s; Δv è negativo e dunque ha segno opposto alla velocità.

L’accelerazione media

Ogni cambiamento di velocità è sempre associato a un’accelerazione, una grandezza che esprime la variazione di velocità in relazione al tempo.

DEFINIZIONE: ACCELERAZIONE MEDIA

L’accelerazione media di un corpo è il rapporto tra la variazione di velocità Δv e l’intervallo di tempo Δt in cui avviene tale variazione:

Nel moto rettilineo uniforme la velocità non varia (è costante), quindi l’accelerazione è nulla.

Comprendi la definizione

• Dimensionalmente l’accelerazione è il rapporto tra velocità e tempo che si misurano rispettivamente in metri al secondo e in secondi, quindi nel Sistema Internazionale l’unità di misura dell’accelerazione è il metro al secondo quadrato (m/s2).

• Il valore assoluto dell’accelerazione media ci dà un’idea della rapidità con cui sta cambiando la velocità: è piccolo quando la velocità cambia lentamente, è grande se la velocità cambia rapidamente.

• Come la velocità, anche l’accelerazione media è una grandezza vettoriale. La sua direzione e il suo verso coincidono con quelli della variazione di velocità, perché l’intervallo di tempo Δt è sempre positivo. Nel moto rettilineo la direzione è fissata, pertanto possiamo considerare solo il modulo e il verso dell’accelerazione. Il verso dell’accelerazione media è indicato dal segno che coincide sempre con il segno di Δv, perché Δt è sempre positivo.

Il segno dell’accelerazione

Confrontando il segno dell’accelerazione a (o il segno di Δv che è lo stesso) con il segno della velocità v, possiamo dedurre che:

se la velocità e l’accelerazione hanno lo stesso segno il corpo va più rapidamente, se hanno segno opposto il corpo rallenta.

v > 0 e am > 0 v > 0 e am < 0

Se l’accelerazione ha lo stesso segno della velocità (e quindi lo stesso verso), l’auto va più rapidamente am = 12 m/s - 6 m/s 3 s - 0 s =+ 2 m s 2

Applica la definizione

Se l’accelerazione ha segno opposto alla velocità (e quindi verso opposto), l’auto rallenta

am = 2 m/s - 12 m/s 10 s - 6 s = - 2,5 m s 2

Nella fase di atterraggio, una navicella spaziale dispiega il paracadute e passa da 340 km/h a 110 km/h in 30 s. La sua accelerazione media è:

am = ∆v ∆t = 110 km/h - 340 km/h 30s = -64m/s 30s = -2,1 m/s 2

Il segno dell’accelerazione è opposto a quello della velocità e, infatti, la navicella sta rallentando.

PROVA TU Un aereo ha un’accelerazione media di 15 m/s2. In quanto tempo la sua velocità passa da 100 m/s a 160 m/s? [4,0 s]

LA FISICA CHE NON TI ASPETTI!

La lingua può accelerare più di un’auto?

Lo scatto della lingua di un camaleonte che cattura una cavalletta arriva a ben 300 m/s È un valore incredibilmente alto se lo si confronta con lo scatto di circa 2 m/s di un velocista e l’accelerazione di 10 m/s che ha un’auto sportiva quando parte. Vince quindi di gran lunga la lingua del camaleonte.

L’accelerazione istantanea

Anche per l’accelerazione si può introdurre il concetto di accelerazione istantanea.

DEFINIZIONE: ACCELERAZIONE ISTANTANEA

L’accelerazione istantanea è l’accelerazione media calcolata in un intervallo di tempo molto breve, attorno a quell’istante.

L’accelerazione media è riferita a un intervallo di tempo, mentre l’accelerazione istantanea è riferita a un preciso istante di tempo. D’ora in poi, quando parliamo di accelerazione senza aggiungere puntualizzazioni, intendiamo parlare di accelerazione istantanea.

L’accelerazione nei grafici velocità-tempo

Supponiamo di conoscere in ogni istante la velocità di un trenino elettrico su una rotaia diritta. Se riportiamo la velocità sull’asse delle ordinate e il tempo sull’asse delle ascisse, otteniamo il grafico velocità-tempo o grafico v-t (Figura 1):

• consideriamo il valore della velocità. La velocità iniziale è v0 = +2 cm/s e rimane costante per 2 s. Poi inizia ad aumentare fino a raggiungere il valore massimo di +7 cm/s a t = 6 s. Dopodiché la velocità comincia a diminuire;

• consideriamo il verso. Tra 0 e 9 s il treno si muove nel verso positivo perché la velocità è positiva, mentre tra 9 e 10 s si muove nel verso negativo perché la velocità è negativa. Al tempo t = 9 s la velocità si annulla. In questo istante si ha un’inversione del moto perché la velocità cambia segno.

v cambia segno: inversione del moto

IN ENGLISH

• Accelerazione media: average acceleration

• Accelerazione istantanea: instantaneous acceleration

• Grafico velocità-tempo: velocity-time graph

Occorre prestare attenzione alla grandezza riportata sull’asse delle ordinate per non confondere il grafico velocità-tempo (v-t) con il grafico posizione-tempo (s-t)

v > 0: moto nel verso positivo v < 0: moto nel verso negativo

v costante v aumenta v diminuisce

Dal grafico velocità-tempo, si può ricavare il valore dell’accelerazione media. Per esempio, tra gli istanti t1 = 3 s e t2 = 10 s, la velocità passa da v1 = +2,5 cm/s a v2 = 2,5 cm/s.

L’accelerazione media in questo intervallo è negativa:

2,5 - 2,5) ¥ 10-2 m/s (10 - 3)s

Sulla curva velocità-tempo disegniamo il segmento secante che ha per estremi i due punti corrispondenti agli istanti t1 e t2

La differenza tra le ordinate e la differenza tra le ascisse forniscono rispettivamente la variazione della velocità Δv e l’intervallo di tempo Δt. Il rapporto Δv/Δt rappresenta la pendenza del segmento.

Fig. 1

L’“area” di cui parliamo non è la misura della superficie, perché i lati non esprimono delle lunghezze ma le grandezze riportate sugli assi cartesiani, pertanto può assumere anche valori negativi. La sua unità di misura, nel SI, è il metro, non il metro quadrato.

In un grafico velocità-tempo, l’accelerazione media in un dato intervallo di tempo è rappresentata dalla pendenza della retta secante che passa per i punti della curva corrispondenti all’intervallo considerato.

Lo spostamento nei grafici velocità-tempo

Dal grafico velocità-tempo si può ricavare anche lo spostamento compiuto dal corpo in un intervallo di tempo.

L’area sottesa al grafico velocità-tempo in un dato intervallo di tempo fornisce lo spostamento nell’intervallo considerato.

1. Infatti, se consideriamo un corpo in moto rettilineo uniforme, il grafico velocità-tempo è una retta parallela all’asse delle ordinate, perché la velocità è costante. Per questo moto abbiamo visto che la relazione per calcolare lo spostamento in un intervallo di tempo Δt è: Δs = vΔt. Graficamente lo spostamento è uguale all’area del rettangolo che si trova al di sotto della retta che rappresenta la velocità in relazione al tempo e ha per base Δt.

Nota che dal grafico velocità-tempo si può ricavare lo spostamento, ma non la posizione.

2. Analogamente, in un moto qualsiasi, lo spostamento in un intervallo di tempo è dato dall’area delimitata dalla curva che rappresenta la velocità, dall’asse delle ascisse e da due rette verticali corrispondenti agli istanti iniziale e finale dell’intervallo. Per esempio, nel grafico v-t del trenino elettrico di Figura 1, nell’intervallo t1 = 2 s e t2 = 8 s ci sono in totale 11 quadretti, 7 contenuti completamente e 8 contenuti parzialmente che contiamo a metà. Ogni rettangolo ha la base di 1 s e l’altezza di 2,5 cm/s e dunque ha “area” A = 2,5 cm. Quindi l’area totale è di 28 cm e rappresenta lo spostamento Δs.

Area sottesa al grafico (7 + 8/2) quadretti (spostamento: Δs = 28 cm)

ESERCIZI DI LEZIONE

FISSA I CONCETTI

94 L’accelerazione è definita come:

A il rapporto tra l’intervallo di tempo e la variazione di velocità nell’intervallo di tempo stesso

B il prodotto tra la variazione di velocità nell’intervallo di tempo e l’intervallo di tempo stesso

A = 1 s · 2,5 cm/s = 2,5 cm (area di un quadrato)

C il rapporto tra la variazione di velocità nell’intervallo di tempo e l’intervallo di tempo stesso

D il rapporto tra lo spazio percorso nell’intervallo di tempo e l’intervallo di tempo stesso (Scienze Motorie, 2016/17)

95 Un’automobile raggiunge i 72 km/h in 10 s partendo “da ferma”. La sua accelerazione media in m/s2 è:

C la velocità media

D l’accelerazione media

A 2 m/s2

E 3,5 m/s2

D 2,5 m/s2

B 3 m/s2 C 1,5 m/s2

(Scienze e tecnologie agrarie, 2019/20)

96 In un grafico velocità-tempo l’area sottesa al grafico rappresenta:

A la posizione

B lo spostamento

PENSA CON LA FISICA

98 CONFRONTA È maggiore l’accelerazione media di un motociclista che aumenta la sua velocità da 80 km/h a 100 km/h o quella di un ciclista che da fermo passa a 20 km/h nello stesso intervallo di tempo?

99 TROVA L’ERRORE Se un corpo in 10 s rallenta da -2 m/s a -1 m/s, la sua accelerazione media è negativa.

100 CHI HA RAGIONE? Un nuotatore ha in un certo istante la velocità v1 = -1,5 m/s e successivamente la velocità v2 = +1,5 m/s.

Sara: “L’accelerazione media è diversa da zero perché è cambiato il verso della velocità.”

Beatrice: “L’accelerazione media è nulla perché all’inizio e alla fine il nuotatore non va né più rapidamente né più lentamente.”

101 INTERPRETA Nel grafico velocità-tempo in figura individua quando il corpo si muove nel verso positivo, quando nel verso opposto e in quali istanti il corpo inverte il verso del moto.

97 Un ciclista accelera da fermo per 10 s fino alla velocità di 5 m/s. In 5 s un automobilista accelera dalla velocità di 22 m/s alla velocità di 27 m/s. Il rapporto tra l’accelerazione media del ciclista e quella dell’automobilista risulta uguale a:

A 1/4 B 1/2 C 1 D 2 E 4

(Olimpiadi della Fisica, 1° livello, 2021) [Una risposta A, due B e una C]

102 STIMA Le riviste e i siti specializzati nel descrivere le prestazioni delle auto riportano il tempo impiegato a passare da 0 a 100 km/h. Trova il dato per tre modelli diversi e calcola il corrispondente valore dell’accelerazione media.

103 INTERPRETA In figura sono riportati i grafici posizione-tempo e velocità-tempo relativi al moto di tre oggetti.

Associa la lettera di ciascun grafico alla descrizione corrispondente.

Descrizione

L’oggetto rallenta, cambia verso e prosegue sempre più rapidamente in verso opposto.

L’oggetto si muove a velocità costante e poi accelera.

L’oggetto si muove velocemente con velocità costante e poi lentamente con velocità costante.

RISOLVI

La variazione di velocità

104 Un carrello che si muove su una rotaia ha la velocità di 1,0 m/s in un certo istante e successivamente la velocità di 1,3 m/s. Calcola la variazione di velocità. Ripeti il calcolo supponendo che la velocità iniziale sia di 1,0 m/s.

[2,3 m/s; 0,3 m/s]

105 Un corpo ha in un certo istante la velocità di -2,5 m/s. Successivamente, la sua velocità diminuisce di 0,7 m/s. Trova la velocità finale e stabilisci se rallenta o va più rapidamente. [-3,2 m/s; va più rapidamente]

106 Un’auto telecomandata aumenta la sua velocità di 1,8 m/s e alla fine ha una velocità di 3,9 m/s. Calcola la sua velocità iniziale. Nell’intervallo di tempo considerato, l’auto è andata più rapidamente o ha rallentato?

[2,1 m/s; più rapidamente]

L’accelerazione media. L’accelerazione istantanea

107 ESERCIZIO GUIDATO Una palla che parte da ferma e poi si muove a 5,3 m/s subisce un’accelerazione media di

2,4 m/s2. Calcola il tempo che impiega a fermarsi.

RICONOSCIAMO DATI E INCOGNITE

Velocità .............: v1 = 5,3 m/s Velocità ............. (il corpo è fermo): v2 = 0

Accelerazione media: am = 2,4 m/s2 Intervallo di tempo: Δt = ?

RISOLVIAMO

Ricaviamo l’intervallo di tempo dalla definizione di accelerazione media:

108 PROVA TU

Un’auto sportiva ha un’accelerazione media di 8,9 m/s2. Se parte da ferma, quanto tempo impiega a raggiungere i 100 km/h? [3,1 s]

109 Un’automobile sta viaggiando alla velocità di 90 km/h. A un certo punto frena e si ferma in 6,0 s. Calcola l’accelerazione media. [-4,2 m/s ]

110 Il 23 novembre 2014 il razzo Soyuz è partito da Baikonur in Kazakistan diretto verso la Stazione spaziale internazionale. Samantha Cristoforetti, la prima donna italiana a volare nello spazio, era uno dei tre membri dell’equipaggio. Trascorsi 45 s dal lancio, la velocità del razzo era di 1640 km/h. Calcola l’accelerazione media. [10 m/s ]

111 A car speeds up from 4.0 m/s to 16 m/s in 5 s. Calculate the acceleration. [2.4 m/s ]

112 Una pallina da golf rotola con un’accelerazione media di 0,40 m/s2. Calcola il tempo necessario a diminuire la velocità di 5,0 m/s. [12,5 s]

113 Una ciclista, che inizialmente si muove alla velocità di 8,0 m/s, subisce un’accelerazione media di -1,5 m/s2 per 4,0 s. Calcola la velocità finale. [2,0 m/s]

114 Un’automobile frena e si arresta in 4,9 s. La sua accelerazione media durante la frenata è stata -3,8 m/s2 Qual era la sua velocità all’inizio della frenata? [67 km/h]

115 Una pallina viene lanciata su per un piano inclinato con una velocità iniziale di 6,2 m/s. Dopo 3,0 s sta scendendo, e il modulo della sua velocità è 2,8 m/s. Qual è la sua accelerazione media? [-3,0 m/s ]

116 Il treno superveloce, che collega l’aeroporto di Shanghai alla città, da quando parte accelera per 2,0 minuti con accelerazione media di 0,81 m/s2. Calcola la velocità del treno al termine di questo intervallo di tempo. Esprimi il risultato in m/s e km/h. [97 m/s; 350 km/h]

117 Considera un disco da hockey che colpisce perpendicolarmente la sponda e rimbalza all’indietro. Prima dell’impatto la velocità è di 47 km/h, dopo 1,2 s il disco si muove alla velocità di 45 km/h. Calcola l’accelerazione media del disco. [-21 m/s ]

118 Un camion che sta viaggiando a 36 km/h in un certo istante iniza ad accelerare e per 0,50 minuti ha un’accelerazione media di 0,30 m/s2. Calcola la sua velocità finale. [19 m/s]

119 ESERCIZIO RISOLTO Partendo dal grafico posizione-tempo riportato in figura, costruisci sul quaderno o con un Foglio di calcolo il grafico velocità-tempo corrispondente. Calcola la variazione di velocità tra 1 s e 5 s.

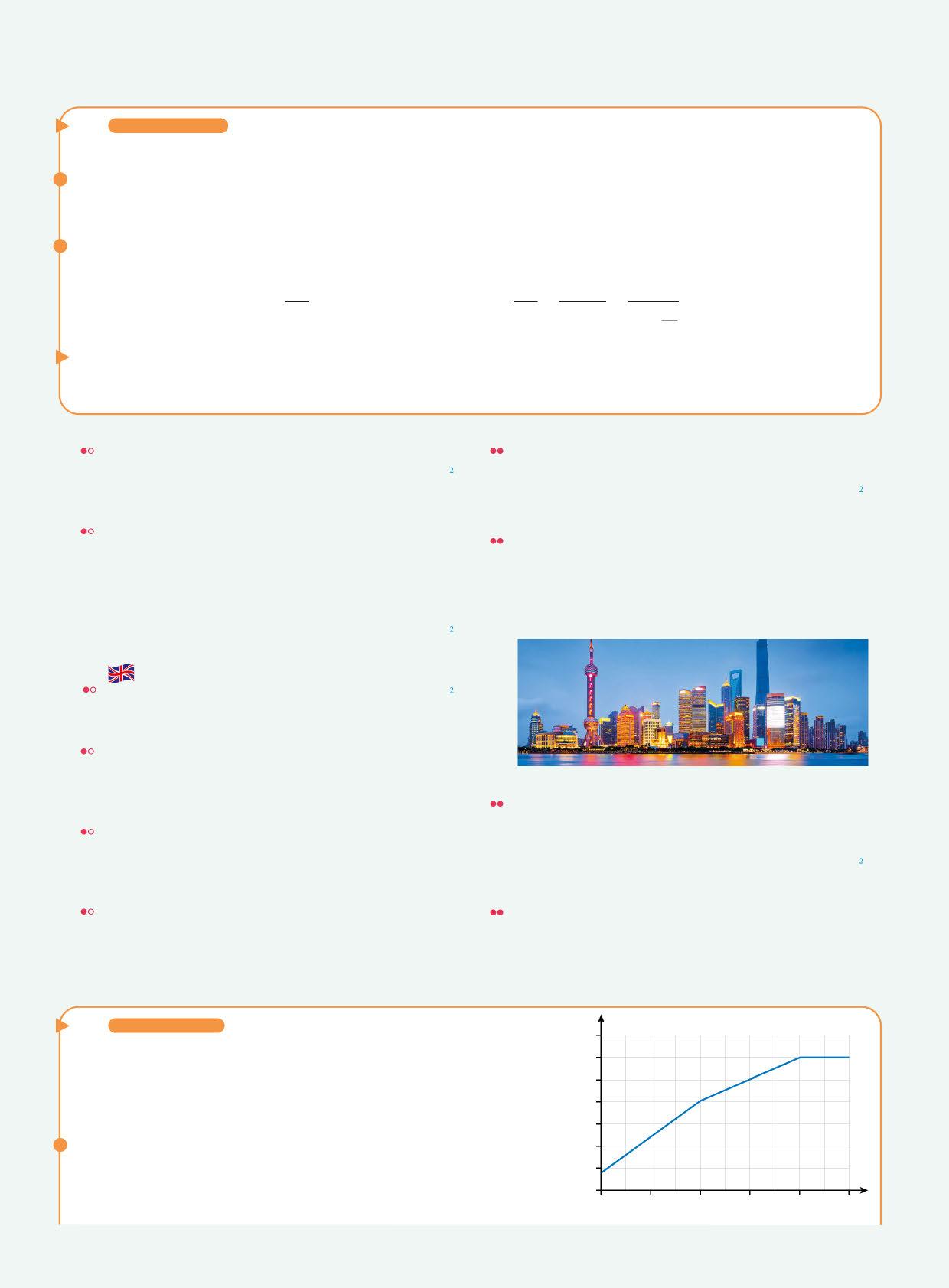
RICONOSCIAMO DATI E INCOGNITE

Istante iniziale: t1 = 1 s Istante finale t2 = 5 s Variazione di velocità: Δv = ?

RISOLVIAMO

Tra 0 e 4 s il grafico posizione-tempo è una retta e quindi la velocità è costante. Il suo valore è:

v = ∆s ∆t = 4,0 m - 0,8 m 4,0 s = 0,80 m s

Analogamente, tra 4 s e 8 s la velocità è costante e uguale a:

v = ∆s

∆t = 6,0 m - 4,0 m 4,0 s = 0,50 m s

Nei secondi finali il corpo non cambia posizione e quindi ha velocità nulla.

Il grafico velocità-tempo è riportato nella figura a lato.

Tra 1 s e 5 s la variazione di velocità è:

Δv = v2 - v1 = 0,5 m/s - 0,8 m/s = -0,3 m/s

Il corpo ha rallentato e infatti la velocità è positiva e la variazione negativa.

120 PROVA TU

Dal grafico velocità-tempo dell’esercizio precedente ricava lo spostamento tra 2 s e 6 s. Confronta poi il risultato con quello che si ricava dal grafico posizione-tempo sovrastante. [2,6 m]

121 Find the acceleration of the object represented by the following velocity-time graph. [0.20 m/s ]

c Deduci dal grafico la velocità dopo che sono trascorsi 20 s dall’istante iniziale. [14 m/s]

124 Su un lungo viale rettilineo, un ciclista parte da fermo, per alcuni secondi aumenta la velocità e poi prosegue a velocità costante. La tabella riporta come varia nel tempo la velocità del ciclista.

t (s) 012345678

v (m/s) 01,42,84,25,67,07,07,07,0

a Costruisci sul quaderno o con un Foglio di calcolo il grafico velocità tempo.

122 La figura mostra il grafico velocità-tempo di un corpo. Calcola l’accelerazione media tra 0 e 4 s e tra 4 s e 8 s. [1,25 m/s ; 0]

b Calcola l’accelerazione media nei primi 5 s. [1,4 m/s ]

c Determina lo spostamento nei primi 2 s e lo spostamento complessivo. [2,8 m; 38,5 m]

125 La figura mostra il grafico velocità-tempo di un carrello che percorre una traiettoria rettilinea.

a Calcola l’accelerazione media nei primi 4 s. [-0,5 m/s ]

b Determina lo spostamento al termine degli 8 s considerati. [20 m]

c Deduci dal grafico la velocità dopo che sono trascorsi 3 s. [2,5 m/s]

123 Giacomo percorre in auto un lungo rettilineo. All’istante iniziale ha una velocità di 16 m/s. Dopo un minuto la sua velocità è di 10 m/s.

a Disegna sul quaderno o con un Foglio di calcolo il grafico velocità-tempo supponendo che in questo intervallo di tempo sia una porzione di retta.

b Determina l’accelerazione media e lo spostamento nell’intervallo considerato. [-0,10 m/s ; 780 m]

Lezione 5

IL MOTO RETTILINEO UNIFORMEMENTE ACCELERATO

Quando l’accelerazione è costante, un moto rettilineo si definisce uniformemente accelerato.

La relazione (1) a = Δv/Δt è valida solo per il moto rettilineo uniformemente accelerato; negli altri casi dobbiamo scrivere a al posto di a.

In questo tipo di moto l’accelerazione media del corpo, calcolata su un intervallo di tempo qualsiasi, è sempre la stessa ed è uguale all’accelerazione istantanea; la indichiamo semplicemente con il simbolo a = aist = am. Per calcolarla possiamo applicare la definizione di accelerazione media in un intervallo di tempo qualsiasi:

Visto che il rapporto al secondo membro è costante, possiamo affermare che: in un moto uniformemente accelerato le variazioni di velocità sono direttamente proporzionali agli intervalli di tempo. L’accelerazione a è la costante di proporzionalità tra le due grandezze.

IN ENGLISH

• Moto rettilineo uniformemente accelerato: linear motion with constant acceleration

• Costante di proporzionalità: constant of proportionality

• Equazione della velocità: velocity equation

• Legge oraria del moto rettilineo uniformemente

Consideriamo ora un intervallo di tempo compreso tra l’istante iniziale t = 0 e un generico istante t: in questo caso abbiamo che Δt = t - 0 = t. Se indichiamo con v0 la velocità iniziale, cioè la velocità che ha il corpo all’istante 0, quando parte il cronometro, e con v la velocità all’istante t, la variazione di velocità è Δv = v - v0. Sostituendo nella (1), otteniamo:

Da qui si ottiene facilmente la relazione che lega la velocità al tempo:

EQUAZIONE DELLA VELOCITÀ DEL MOTO RETTILINEO

UNIFORMEMENTE ACCELERATO

velocità al tempo t

istante di tempo

accelerazione (costante)

v = v0 + at (2) velocità iniziale (all’istante t = 0)

Comprendi la legge

• La relazione scritta consente di conoscere la velocità del corpo in un qualunque istante di tempo t per l’intero tratto in cui il corpo stesso si muove di moto uniformemente accelerato.

• Tra la velocità e il tempo c’è una relazione lineare; se la velocità iniziale è v0 = 0, la relazione diventa una proporzionalità diretta: v = at fi a = v t .

Il grafico velocità-tempo

1. Il grafico della velocità in relazione al tempo è quindi una retta

2. L’intersezione con l’asse delle ordinate indica la velocità iniziale v0. Se nell’istante iniziale il corpo si muove nello stesso verso dell’asse allora v0 è positiva (v0 > 0), se si muove in verso opposto v0 < 0. Se parte da fermo e v0 = 0 la retta passa per l’origine.

3. Il coefficiente angolare (cioè la pendenza) della retta rappresenta l’accelerazione a.

La legge oraria del moto uniformemente accelerato

Nella lezione precedente abbiamo visto che in un grafico velocità-tempo lo spostamento è uguale all’area delimitata dalla curva che descrive l’andamento della velocità. Se sul grafico del moto uniformemente accelerato consideriamo un intervallo di tempo tra l’istante iniziale (t = 0) e un generico istante t, lo spostamento è dato dall’area totale (quadretti arancioni e quadretti rossi) evidenziata in Figura 1:

∆s = s - s0 = v0t + 1 2 at 2

Da questa relazione possiamo ricavare la posizione s in cui si trova il corpo all’istante t.

LEGGE ORARIA DEL MOTO RETTILINEO UNIFORMEMENTE ACCELERATO

posizione iniziale (all’istante t = 0) istante di tempo

s = s0 + v0t + 1 2 at2 posizione all’istante t accelerazione (costante) velocità iniziale

Comprendi la legge

• Il termine v0t (area arancione del rettangolo) rappresenta lo spostamento Δs che avrebbe compiuto il corpo se si fosse mosso con velocità costante v0, seguendo quindi un moto rettilineo uniforme.

• Il termine 1 2 at 2 (area rossa del triangolo) rappresenta lo spostamento Δs compiuto se il corpo si fosse mosso con accelerazione a partendo da fermo.

Il grafico posizione-tempo

Se rappresentiamo il grafico posizione-tempo per un moto uniformemente accelerato otteniamo un arco di parabola

1. La concavità è rivolta verso l’alto se l’accelerazione è positiva.

2. La concavità è rivolta verso il basso se l’accelerazione è negativa.

Quando è presente, il vertice della parabola corrisponde al punto di inversione del moto, quando la velocità cambia segno ed è istantaneamente nulla. L’intersezione con l’asse delle ordinate rappresenta la posizione iniziale s0.

Applica la legge

Supponi che in un parco acquatico un ragazzo parta da fermo e scenda da uno scivolo ad acqua con un’accelerazione costante di 1,4 m/s2. Dopo 2,0 s che velocità ha e di quanto si è spostato? Dal momento che la velocità iniziale è nulla, dopo 2,0 s la velocità del ragazzo è:

lo spostamento è:

PROVA TU In quale istante il ragazzo ha una velocità di 1,7 m/s? Qual è lo spostamento in quell’istante?

ESERCIZI DI LEZIONE

FISSA I CONCETTI

126 Nel moto rettilineo uniformemente accelerato:

a la velocità media non dipende dall’intervallo nel quale la calcoliamo V F

b l’accelerazione è costante V F

c l’accelerazione è sempre positiva V F

d la velocità è sempre direttamente proporzionale al tempo V F

e tra la velocità e il tempo c’è una relazione lineare V F

127 La velocità raggiunta dopo un tempo t in un moto accelerato, con accelerazione costante a e velocità iniziale nulla:

A è uguale a 1/2 at2

B rimane nulla

C è direttamente proporzionale al tempo

D è uguale a 2at

E è inversamente proporzionale al tempo (CISIA, 2016/17)

128 Nel grafico in figura è rappresentata la velocità di un punto materiale in moto.

L’accelerazione è:

A costante e positiva

B costante e negativa

C nulla

D variabile nel tempo

PENSA CON LA FISICA

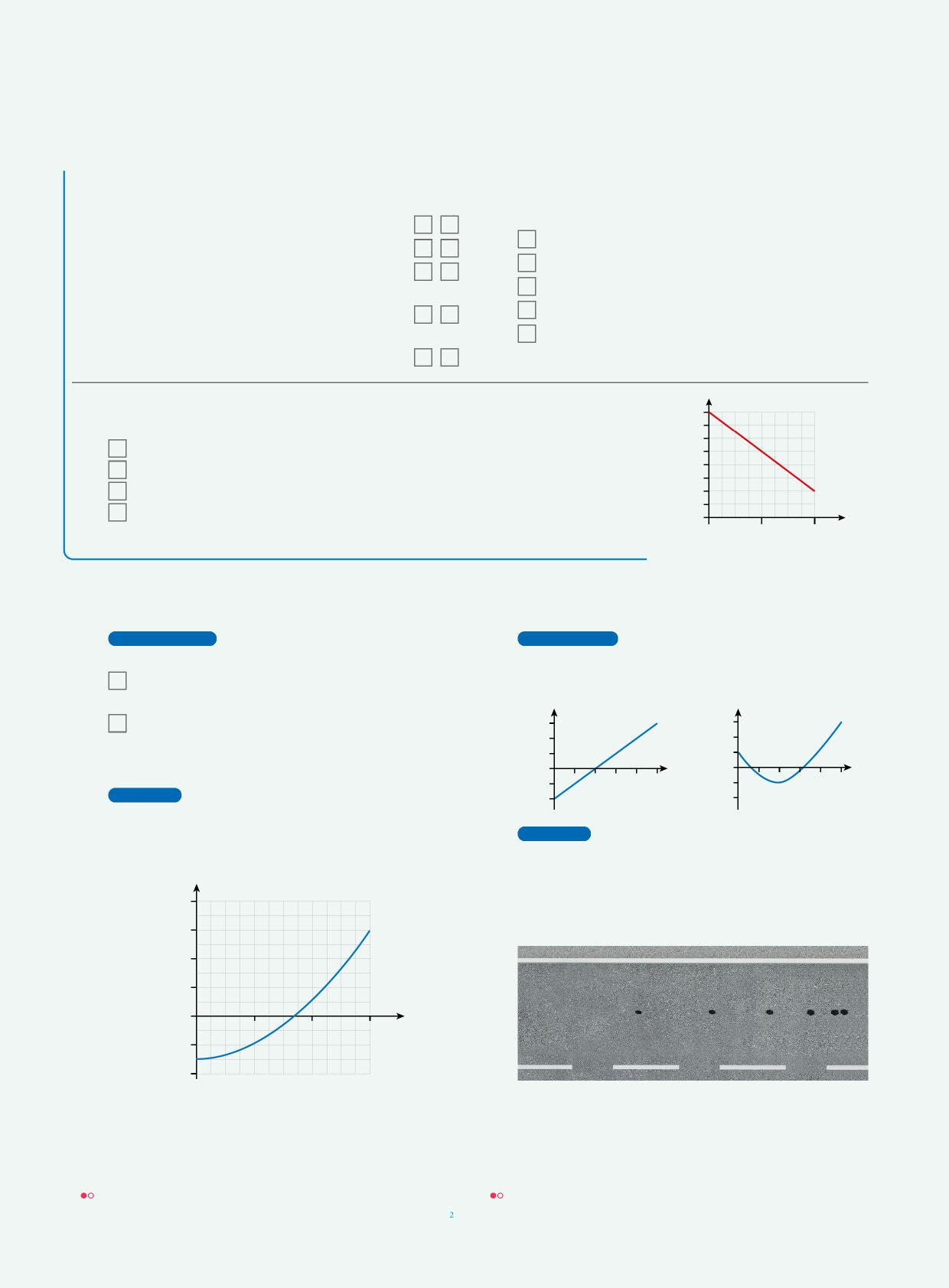
129 CHI HA RAGIONE? Un ciclista frena e si ferma per far attraversare i pedoni.

Giada: “Il moto è uniformemente accelerato con accelerazione negativa perché il ciclista rallenta.”

Mattia: “Non sappiamo se l’accelerazione è costante e quindi non siamo certi che il moto sia uniformemente accelerato.”

130 INTERPRETA Il moto rappresentato in figura è di tipo rettilineo uniformemente accelerato. Descrivi le caratteristiche di questo moto specificando la posizione iniziale, se l’accelerazione è positiva o negativa e se la velocità aumenta o diminuisce.

131 TROVA L’ERRORE Uno studente ha disegnato i grafici posizione-tempo e velocità-tempo per un corpo che si muove con un’accelerazione costante a = 1 m/s2, ma ha commesso un errore: puoi indicare quale?

132 INTERPRETA Federica è ferma a un semaforo con la sua automobile che ha una perdita di olio. Quando l’automobile riparte, le gocce di olio, che cadono a ritmo costante, lasciano sull’asfalto la traccia riprodotta in figura. Nell’immagine il semaforo, che non è rappresentato, si trova nella parte destra o sinistra?

4812 t (s)

RISOLVI

133 Calcola l’accelerazione di un camion che varia la propria velocità da 14 m/s a 5 m/s in 4,3 s con un’accelerazione costante. [-2,1 m/s ]

134 Un pullman procede a 45 km/h quando comincia ad accelerare con un’accelerazione costante di 1,3 m/s2 Qual è la sua velocità dopo 2,5 s? [57 km/h]

[Una risposta B, una C, due V e tre F]

135 Mentre percorre in motorino un viale diritto, Veronica frena per far passare dei pedoni, fermandosi dopo 4,3 s. Se l’accelerazione è stata di -2,85 m/s2, qual era la velocità (in km/h) appena prima della frenata? [44 km/h]

136 Una palla rotola su per un pendio con accelerazione a = -1,7 m/s2. Se la velocità iniziale è di 4,3 m/s, qual è la velocità dopo 2,0 s? In quale istante la pallina si ferma e inverte il moto? [0,9 m/s; 2,5 s]

137 Un ghepardo che parte da fermo raggiunge la velocità di 58 km/h in 2,0 s. Supponi che il moto sia uniformemente accelerato e calcola l’accelerazione. Calcola la velocità in km/h che il ghepardo raggiunge in 3,0 s se mantiene la stessa accelerazione. [87 km/h]

138 A motor cyclist accelerates from 5.0 m/s to 20 m/s at 1.5 m/s2. How long does he take to speed up? [10 s]

139 Il tachimetro di un’auto che viaggia su una strada diritta è stato ripreso con una videocamera. La tabella riporta la velocità rilevata in vari istanti di tempo.

Tempo (s) 02,004,006,008,00

Velocità (m/s) 10,013,0016,0019,0022,00

Disegna sul quaderno o con un Foglio di calcolo il grafico velocità-tempo. Verifica che si tratta di un moto uniformemente accelerato e calcola l’accelerazione. Qual è la velocità dell’auto all’istante t = 2,40 s? In quale istante la sua velocità è di 20,0 m/s? Risolvi il problema algebricamente e graficamente.

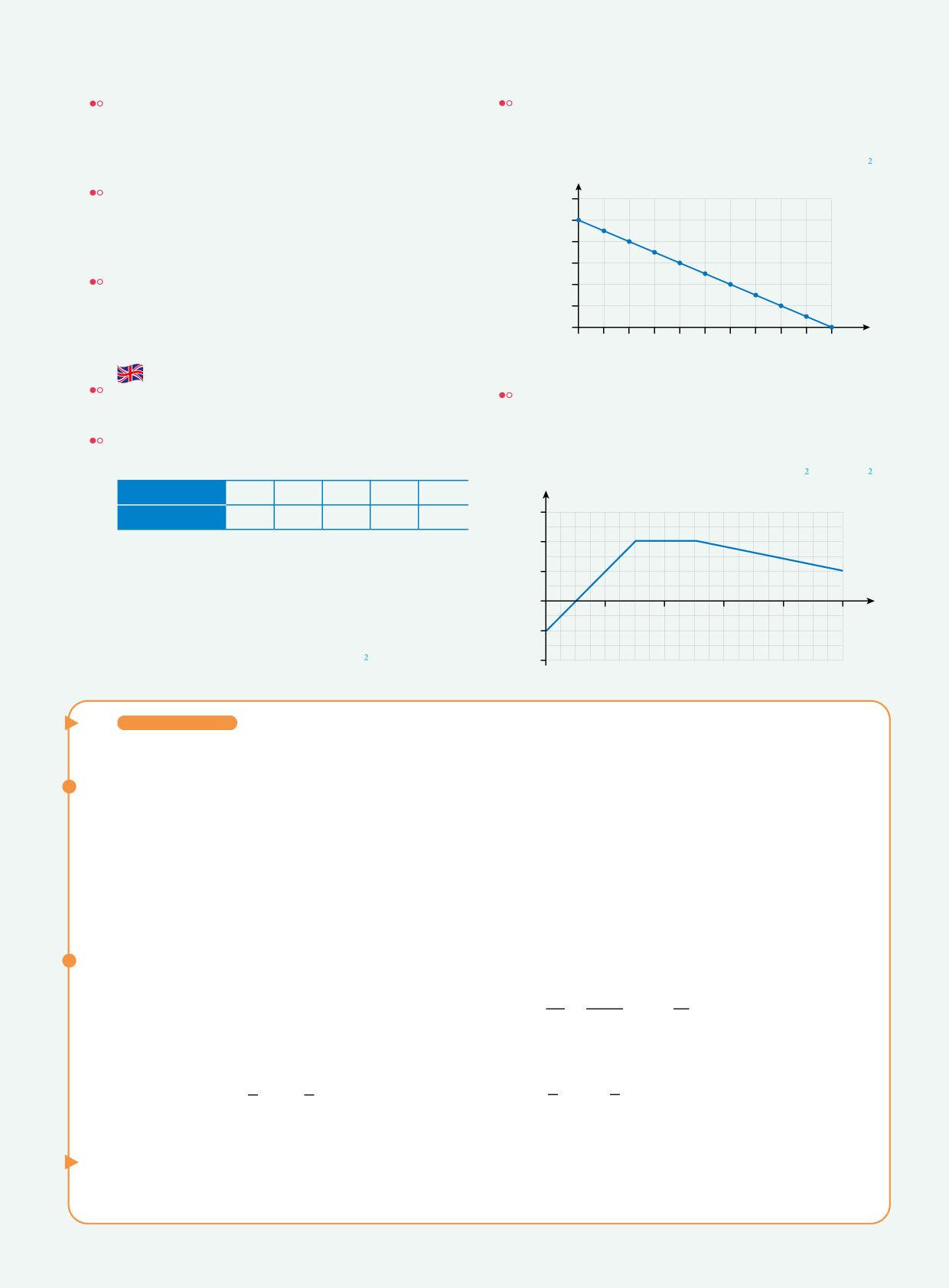
[1,50 m/s ; 13,6 m/s; 6,67 s]

140 In figura è rappresentato il grafico velocità-tempo di un moto rettilineo uniformemente accelerato: calcola l’accelerazione. Il corpo sta aumentando o diminuendo la sua velocità? Che cosa succede all’istante t = 5,0 s? [-2,0 m/s ]

141 La figura descrive il moto di un corpo che si muove su una traiettoria rettilinea. Indica in quali intervalli è un moto uniforme e determina la sua velocità. Individua gli intervalli in cui il moto è uniformemente accelerato e calcola l’accelerazione.

142 ESERCIZIO GUIDATO In una competizione un’auto elettrica ha raggiunto i 100 km/h in 1,8 s. Un’auto di Formula 1 alla partenza ha un’accelerazione di 10,0 m/s2. Se le due auto gareggiassero affiancate, quale delle due sarebbe in testa dopo 1,5 s? Con quale distacco? Considera entrambi i moti uniformemente accelerati.

RICONOSCIAMO DATI E INCOGNITE

Fissiamo l’origine del sistema di riferimento alla partenza, orientato nel senso del moto delle due auto. Facciamo partire il cronometro nel momento in cui avviene la partenza.

Auto elettrica

Posizione iniziale: s0e = 0 m

Velocità iniziale: v0e = 0

Istante t2 = 1,8 s

Velocità al tempo t2: ve = 100 km/h = 27,8 m/s

RISOLVIAMO

Auto di Formula 1

Posizione iniziale: s0F1 = 0 m

Velocità iniziale: v0F1 = 0

Accelerazione: aF1 = 10,0 m/s2

Istante t1 = 1,5 s

Distacco nell’istante t1: d = ?

Dalla legge della velocità ricaviamo l’accelerazione dell’auto elettrica:

Dopo 1,5 s è in testa l’auto elettrica perché ha un’accelerazione maggiore dell’auto di Formula 1.

Calcoliamo la posizione delle due auto dopo 1,5 s.

143 PROVA TU

Un’automobile che sta viaggiando a 17 m/s accelera uniformemente per 3,5 s fino alla velocità di 25 m/s. Qual è lo spostamento dell’auto in questo intervallo di tempo? [74 m]

144 A bus travelling on a straigh road at 12 m/s accelerates uniformily to a speed of 21 m/s in 16 s. Calculate the total distance traveled by the bus. [260 m]

145 Un ciclista che viaggia a 38 km/h frena con accelerazione costante di -3,1 m/s2 fino a fermarsi. Calcola il tempo necessario per fermarsi e lo spazio di frenata. [3,4 s; 18 m]

146 I dragster sono veicoli progettati per gare di accelerazione. Partendo da fermo, un dragster percorre 370 m in 4,9 s. Supponi che l’accelerazione sia costante e calcola la velocità finale espressa in km/h. [540 km/h]

Foglio di calcolo il grafico velocità-tempo e posizione-tempo.

t [s] 0,01,0 2,0 3,04,05,0 v [m/s]

153 Per il moto rappresentato in figura, trova la velocità iniziale e l’accelerazione. Qual è la velocità al tempo t = 7,5 s? Qual è lo spostamento tra l’istante iniziale e l’istante t = 7,5 s? Risolvi il problema algebricamente e graficamente. [1 m/s; 0,2 m/s ; 2,5 m/s; 13 m]

147 Una pallina parte dalla cima di un piano inclinato lungo 51 cm e rotola con un moto uniformemente accelerato descritto dalla legge oraria s = 1 2 at 2 dove a = 2,6 m/s2. Qual è la velocità all’istante iniziale? In che posizione si trova al tempo t = 0,34 s? In quale istante arriva alla base del piano? [0,15 m; 0,63 s]

148 La tabella si riferisce a un moto rettilineo uniformemente accelerato la cui legge oraria è: s = 1 2 at 2 . Calcola l’accelerazione. Completa la tabella e sul quaderno o con un Foglio di calcolo rappresenta in un grafico la posizione in relazione al tempo. [0,4 m/s ] t

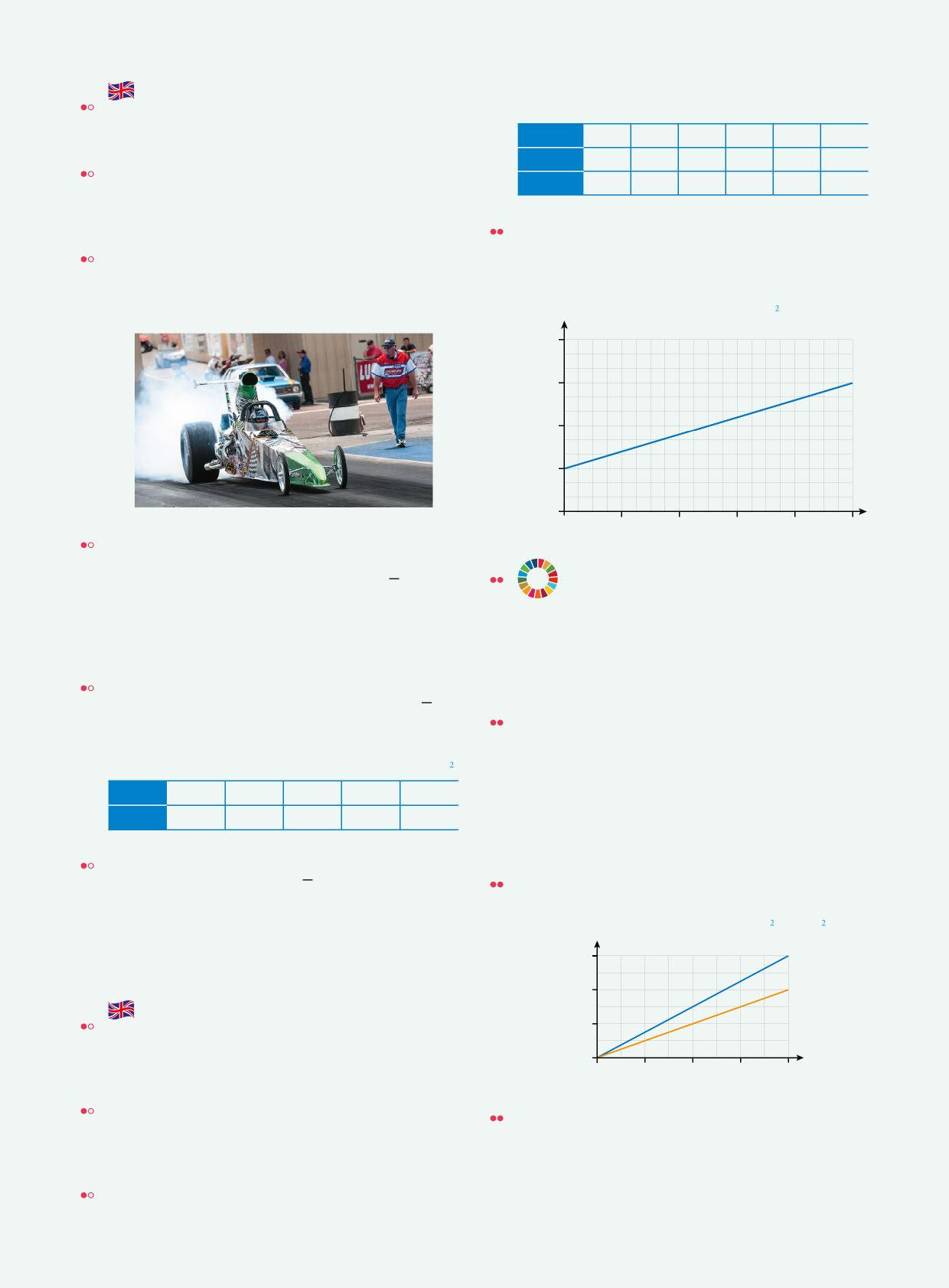
01234

s (m) 1,8

149 La legge oraria di un moto rettilineo uniformemente accelerato è s = s0 + 1 2 at 2 con s0 = 5,0 cm e a = 7,2 cm/s2 Determina le posizioni occupate negli istanti 0,5 s, 1 s, 1,5 s e 2 s e costruisci sul quaderno o con un Foglio di calcolo il grafico posizione-tempo. In quale istante la pallina è nella posizione s = 14 cm?

[1,9 s]

150 A train starts from rest and moves with constant acceleration of 1.00 m/s2 for 30 s. Find the speed attained by the train and the distance travelled.

[30.0 m/s; 450 m]

154 3 Una persona alla guida di un’auto attiva i freni 0,20 s dopo essersi accorta della presenza di un ostacolo (tempo di reazione). L’accelerazione durante la frenata è uguale a -6,3 m/s2. Se sta viaggiando a 90 km/h, qual è la distanza che percorre da quando vede l’ostacolo a quando si ferma? [55 m]

155 Ernesto sta viaggiando sul suo monopattino elettrico a velocità costante, quando supera una moto che ha una velocità di 4,7 m/s e accelera con un’accelerazione costante di 1,3 m/s2. La moto raggiunge Ernesto dopo 2,4 s. Che distanza ha percorso la moto da quando è stata superata dal monopattino a quando la raggiunge? Qual è la velocità (costante) di Ernesto? [15 m; 6,3 m/s]

156 Il grafico riporta la velocità in relazione al tempo di due ciclisti che partono dallo stesso punto lungo una strada diritta. Calcola la loro l’accelerazione e la distanza che li separa dopo 2,4 s. [2,1 m/s ; 1,4 m/s ; 2,0 m]

[12 km/h; 4,9 m]

151 Un pattinatore accelera con un’accelerazione costante di 0,8 m/s2. La sua velocità iniziale è di 6,0 km/h. Qual è la velocità che raggiunge dopo 2,0 s? E che distanza percorre?

152 Un punto materiale parte da fermo con accelerazione costante di 1,8 m/s2. Completa la seguente tabella ponendo s0 = 0 e poi traccia sul quaderno o con un

157 Disegna sul quaderno o con un Foglio di calcolo il grafico posizione-tempo di un corpo A che parte da fermo e si muove con accelerazione di 4 cm/s2 per 5 s e di un corpo B che parte 10 cm più avanti e si muove parallelamente con velocità costante di 5 cm/s. Determina graficamente l’istante in cui il corpo A raggiunge il corpo B. [3,8 s]

LA CADUTA LIBERA

Quali sono le caratteristiche di un corpo che influiscono sul suo moto di caduta? Secondo te è vero che i corpi più pesanti cadono più velocemente di quelli leggeri?

PENSA CON LA FISICA

Lascia cadere contemporaneamente dalla stessa altezza queste coppie di oggetti e annota quale dei due arriva prima o se arrivano contemporaneamente.

1 Due fogli uguali, uno appallottolato, l’altro disteso.

2 Un foglio e un libro con la copertina rigida. Che cosa cambia se appoggi il foglio sopra il libro e lo lasci cadere insieme al libro?

3 Il tappo di una penna e un astuccio pieno di penne.

Alla luce di queste osservazioni, è corretto dire che i corpi più pesanti cadono più velocemente?

La caduta libera

Gli oggetti che si trovano sulla superficie della Terra cadono perché risentono della forza peso che li attrae verso il centro della Terra. La caduta di oggetti leggeri, come le foglie, le piume o i fiocchi di neve, è ostacolata significativamente dalla presenza dell’aria ed è un moto complesso.

In questa lezione analizziamo la situazione più semplice: la caduta di corpi, come i sassi o le monete, che hanno una densità alta e una forma tale da rendere minimo l’effetto della resistenza dell’aria. In questi casi il moto si svolge sotto l’azione della forza peso (caduta) e l’effetto della resistenza dell’aria e di altre forze è trascurabile (libera).

La caduta libera è il moto di un corpo su cui agisce solo la forza peso.

Se non specificato diversamente, assumeremo che nella caduta la resistenza dell’aria sia trascurabile.

IN ENGLISH

• Caduta libera: free fall

• Accelerazione di gravità: gravitational acceleration

La caduta libera si riferisce sia al moto rettilineo verticale degli oggetti che cadono dall’alto verso il basso o sono lanciati verso l’alto 1 sia ai corpi lanciati in altre direzioni (moto di caduta curvilineo) 2 .

In questa lezione analizzeremo la caduta libera lungo la verticale in prossimità della superficie terrestre, nella prossima unità la caduta con traiettoria curvilinea.

Nella tecnica multiflash si fotografa un corpo in movimento illuminandolo con una lampada stroboscopica che emette lampi a intervalli regolari.

L’accelerazione di gravità

La fotografia multiflash mostra una mela che cade.

Durante la caduta, la mela aumenta la propria velocità come si vede dal fatto che la distanza tra due posizioni successive aumenta progressivamente.

Accurate misure mostrano che in prossimità della superficie terrestre, se la resistenza dell’aria è trascurabile, il moto dei corpi in caduta libera è, con ottima approssimazione, uniformemente accelerato e che il valore dell’accelerazione è lo stesso per tutti i corpi indipendentemente dalla loro massa, forma e dimensione.

Questa accelerazione è l’accelerazione di gravità g che abbiamo già incontrato nell’Unità 2

L’accelerazione dei corpi in caduta libera è chiamata accelerazione di gravità ed è indicata con il simbolo g.

Nell’attività iniziale, il libro e il foglio appoggiato sopra il libro, il tappo della penna e l’astuccio cadono con la stessa accelerazione e arrivano a terra insieme perché la resistenza dell’aria è trascurabile. Il moto di questi oggetti è un moto di caduta libera. Numerosi esperimenti hanno dimostrato che nel vuoto, quando l’attrito dell’aria è assente, non solo le monete e le sfere metalliche, ma anche le piume e i ritagli di carta arrivano a terra nello stesso istante perché hanno la stessa accelerazione g Come abbiamo visto nell’Unità 2 nella Lezione 5, il valore di g dipende dalla posizione in cui si trova il corpo: è massimo ai poli, minimo all’equatore e diminuisce all’aumentare dell’altitudine sul livello del mare. Per i nostri esperimenti, le variazioni di g sono molto piccole e possiamo trascurarle useremo sempre il valore di 9,81 m/s2 che si ha a 45° di latitudine.

NELLA STORIA

Fu Galileo Galilei (1564-1642) il primo a capire che, nel vuoto dove non c’è l’attrito dell’aria, tutti i corpi cadono di moto uniformemente accelerato e che l’accelerazione non dipende dalla massa, ma è la stessa per tutti i corpi. Galileo però non realizzò mai l’esperimento di caduta in assenza di aria.

Nel 1971 l’astronauta dell’Apollo 15 David Scott lasciò cadere sul suolo lunare in assenza di atmofera una piuma e un martello contemporaneamente dalla stessa altezza e mostrò che toccavano il suolo nello stesso istante, cadendo con accelerazione costante uguale a un sesto di quella sulla Terra: g = 1,62 m/s . Con un esperimento spettacolare, nel 2014, il fisico inglese Brian Cox verificò la legge di caduta libera nella camera a vuoto della stazione NASA in Ohio, la più grande al mondo. Dopo che la camera fu svuotata dall’aria, una palla da bowling e alcune piume d’oca furono lasciate cadere dalla stessa altezza e, come previsto, cadevano contemporaneamente.

©Ed Hengeveld

Posizione e velocità nel moto di caduta libera

Per descrivere il moto verticale di caduta fissiamo un asse di riferimento verticale orientato verso l’alto con l’origine a livello del terreno.

altezza iniziale velocità iniziale altezza all’istante t

Indichiamo con y l’altezza del corpo, cioè la sua posizione verticale. La legge oraria e l’equazione della velocità sono quelle del moto uniformemente accelerato. L’accelerazione a = -g è negativa perché è rivolta verso il basso nel verso opposto a quello dell’asse di riferimento. y = y 0 + v0t1 2 gt2

1) v = v0 - gt

2) velocità all’istante t accelerazione a = -g

Comprendi la legge

• Se il corpo inizia la caduta da fermo, la sua velocità iniziale v 0 è nulla. Si usa l’espressione “un corpo è lasciato cadere” per indicare che ha velocità iniziale nulla.

• Se il corpo è spinto verso il basso la velocità iniziale è negativa 1 , se è lanciato verso l’alto la velocità iniziale è positiva 2 .

• Il simbolo g indica il modulo dell’accelerazione di gravità ed è sempre positivo: g = +9,81 m/s2. Per questo, per indicare l’accelerazione negativa si deve scrivere a = -g

• Un corpo lanciato verso l’alto, prima sale e poi scende con un’accelerazione che è sempre a = -g, sia durante la salita sia durante la discesa e quindi è sempre negativa

Durante la risalita il corpo rallenta perché l’accelerazione, che è negativa, ha il segno opposto alla velocità che è positiva 3

Durante la discesa il corpo va più rapidamente perché l’accelerazione ha lo stesso segno negativo della velocità 4 .

• Il corpo lanciato verso l’alto, nel punto più alto della sua traiettoria inverte il verso del moto e ha velocità nulla

Un tennista, per effettuare la battuta, lancia la palla in verticale verso l’alto con velocità iniziale v0 = 5,0 m/s da un’altezza y0 = 1,3 m da terra e la colpisce con la racchetta all’istante t = 0,70 s.

Applicando la legge oraria (1) possiamo calcolare la posizione della pallina al momento dell’impatto:

Dall’equazione della velocità (2) determiniamo la velocità della palla immediatamente prima di essere colpita:

v = v0 - gt = 5,0 m s - 9,81 m s 2 0,70 s = -1,9 m s

Il segno negativo indica che in quell’istante la velocità ha verso opposto a quello dell’asse di riferimento e dunque la palla sta scendendo.

PROVA TU Una pallina viene lanciata in verticale verso il basso con velocità di -2,0 m/s. Se impiega 1,5 s a cadere, calcola la velocità che ha un attimo prima di toccare il suolo. [-17 m/s]

ESERCIZI DI LEZIONE

FISSA I CONCETTI

158 Si ha caduta libera quando un oggetto:

A cade verso terra

B è in prossimità della superficie terrestre

C si muove sotto l’effetto della sola forza peso

D è leggero

159 L’accelerazione di gravità:

A dipende dalla massa del corpo

B dipende dalla forma del corpo

C dipende dalla densità del corpo

D è la stessa per tutti i corpi

160 Considera un asse di riferimento verticale orientato verso l’alto. Nel moto di caduta libera, l’accelerazione:

A è sempre negativa

PENSA CON LA FISICA

162 SPERIMENTA Procurati alcuni oggetti di massa e forma differenti (posate, tovaglioli, monete, banconote, mazzi di chiavi…).

Se li lasciassi cadere dalla stessa altezza e nello stesso istante, quali arriverebbero a terra per primi? Ci sono oggetti che puoi considerare in caduta libera e che, quindi, colpiscono il suolo contemporaneamente?

Lasciali cadere e verifica se le tue previsioni sono corrette.

163 E SE… In quale punto della sua traiettoria una palla lanciata in verticale verso l’alto va più lentamente?

164 INTERPRETA Uno studente rappresenta mediante un grafico il moto di un oggetto che cade liberamente nel vuoto, ma si dimentica di indicare quale gran-

B è sempre positiva

C è positiva nella fase di salita e negativa in discesa

D è negativa nella fase di salita e positiva in discesa

161 In una camera a vuoto vengono lasciati cadere, da una distanza di 1 metro dal suolo e nello stesso istante, due oggetti di volume e massa diversi. Si può affermare che l’oggetto di:

A volume minore tocca il suolo per primo

B massa maggiore tocca il suolo per primo

C massa minore tocca il suolo per primo

D volume maggiore tocca il suolo per primo

E i due oggetti toccano il suolo contemporaneamente

(Medicina Veterinaria, 2016/17)

[Una risposta A, una C, una D e una E]

dezza è riportata sull’asse delle ordinate. Di quale grandezza si tratta? Dal grafico puoi ricavare informazioni sulla velocità iniziale?

165 CHI HA RAGIONE? Un giocoliere lancia una pallina verso l’alto.

Umberto: “L’accelerazione è sempre negativa.”

Rebecca: “L’accelerazione è negativa quando la palla sale e rallenta ed è positiva quando la palla scende e va più rapidamente.”

166 INTERPRETA I due grafici si riferiscono ai seguenti moti: a palla lanciata verso l’alto da 10 m di altezza; b moneta lasciata cadere da 10 m di altezza. Associa ciascun grafico al moto corrispondente.

RISOLVI

La caduta libera

167 In campo aerospaziale e automobilistico, l’accelerazione di gravità g è impiegata per esprimere l’accelerazione alla quale sono sottoposti i veicoli, gli astronauti e i piloti. Per esempio, nel resoconto del lancio di una missione spaziale si legge che l’equipaggio ha subito un’accelerazione uguale a 3,5g. Esprimi l’accelerazione nelle unità del Sistema Internazionale. [34,3 m/s ]

168 Quando eseguono le manovre acrobatiche, i piloti degli aerei acrobatici sono sottoposti ad accelerazioni fino a 9g. Per evitare i danni provocati da acce-

Posizione e velocità nel moto di caduta libera

lerazioni così elevate devono indossare speciali tute. Esprimi in unità del SI l’accelerazione di 9g. [88 m/s ]

169 L’accelerazione gravitazionale su Marte è il 38% di quella sulla Terra. Calcola l’accelerazione nelle unità del SI. [3,7 m/s ]

170 Una moto da corsa parte da ferma e raggiunge i 100 km/h in 4,8 s. Calcola l’accelerazione nelle unità del SI. Se usassi g per esprimere l’accelerazione, che valore otterresti? [a = 5,8 m/s ; a = 0,59g]

171 ESERCIZIO RISOLTO Un vaso cade dal davanzale di una finestra al terzo piano a 9,8 m di altezza. Dopo quanto tempo tocca terra? Che velocità ha al momento dell’impatto con il suolo? Esprimi il risultato in km/h e in m/s.

RICONOSCIAMO DATI E INCOGNITE

Scegliamo l’origine a livello del suolo e facciamo partire il cronometro nel momento in cui inizia la caduta.

Accelerazione: a = -g

Velocità iniziale: v0 = 0

Posizione iniziale: y0 = 9,8 m

RISOLVIAMO

Posizione finale: y = 0

Tempo: t = ?

Velocità finale: v = ?

Usiamo la relazione (1) perché contiene i dati y0, y, v0, g e l’incognita t. Attenzione a non confondere la posizione finale, che è nulla, con la posizione iniziale:

Calcoliamo la velocità finale con l’equazione delle velocità (2):

v = v0 - gt = 0 - 9,81 m/s2 1,4 s = -14 m/s = -50,4 km/h

La velocità è negativa perché il corpo sta scendendo e quindi si muove in verso opposto rispetto a quello in cui è orientato l’asse di riferimento.

172 PROVA TU

In un parco dei divertimenti i visitatori entrano in una cabina che, partendo da ferma, è lasciata precipitare in caduta libera verticale per 18,0 m prima di rallentare fino a fermarsi. Quanto tempo dura la caduta libera? Che velocità si raggiunge, espressa in km/h? [1,92 s; -67,8 km/h]

173 Un escursionista attraversa un ponte sospeso a 170 m di altezza quando gli cade di mano un sasso che aveva raccolto. Calcola il tempo di caduta libera del sasso. [5,9 s]

174 Un cestista lancia una palla verso il basso con velocità iniziale di 2,8 m/s. Se la palla tocca terra dopo 0,25 s, da che altezza è partita? [1,0 m]

175 Una palla è lanciata verso l’alto con una velocità di 3,2 m/s. Stabilisci se, trascorsi 0,5 s dal lancio, la palla sta salendo o scendendo.

[v = -1,7 m/s; sta scendendo]

176 Una goccia d’acqua si forma in una nube a 5,0 km dal suolo e inizia la sua caduta. Se non ci fosse l’attrito dell’aria, con quale velocità arriverebbe a terra? Esprimi il risultato in km/h e assumi che l’accelerazione sia costante e pari a g. [1,1 × 10 km/h]

177 Un sasso è lanciato in un pozzo con una velocità iniziale verso il basso di 6,0 m/s. Dopo quanto tempo la velocità è diventata 14 m/s? Quale distanza ha percorso il sasso? [0,82 s; 5,5 m]

178 ESERCIZIO RISOLTO Un mazzo di chiavi viene lanciato verso l’alto da un’altezza di 1,6 m con una velocità di 4,0 m/s. In quale istante si trova nella posizione di altezza massima? Qual è la massima altezza che raggiunge?

RICONOSCIAMO DATI E INCOGNITE

Scegliamo l’origine al suolo e facciamo partire il cronometro nel momento in cui avviene la partenza.

Accelerazione: a = -g

Velocità iniziale: v0 = +4,0 m/s

RISOLVIAMO

Posizione iniziale: y0 = 1,6 m

Altezza massima: ymax = ?

Per prima cosa identifichiamo un dato nascosto nel testo del problema. Alla sommità, il mazzo di chiavi inverte il moto e la sua velocità è nulla, quindi la velocità nel punto di massima altezza è vmax = 0.

Calcoliamo ora l’istante in cui il mazzo di chiavi raggiunge la posizione di altezza massima:

Per calcolare l’altezza massima raggiunta, utilizziamo la legge oraria:

179 PROVA TU

Una palla viene lanciata verso l’alto da un balcone a 8,0 m dal suolo con una velocità di 3,0 m/s. In quale istante si trova nella posizione di altezza massima? Qual è l’altezza massima che raggiunge?

180 A ball is thrown up at a speed of 4.5 m/s. Find the maximun height reached by the ball. [1.0 m]

181 Gianmarco Tamberi all’olimpiade di Tokyo nel 2021 ha saltato 2,39 m. Con quale velocità si è staccato da terra? Tratta l’atleta come se fosse un punto materiale. [6,8 m/s]

182 Un bicchiere si rompe se arriva a terra con una velocità superiore a 2,0 m/s. Qual è la massima altezza da cui lo possiamo far cadere senza romperlo? [20 cm]

183 Una pallavolista in schiacciata si alza di 1,20 m in direzione verticale. Qual è la velocità con cui si stacca da terra? Per quanto tempo resta in volo dall’inizio del salto a quando ricade a terra? [4,85 m/s; 0,490 s]

184 Una moneta è lanciata verso l’alto con una velocità di 3,5 m/s da un’altezza di 75 cm.

Calcola, meglio se utilizzando un Foglio di calcolo, la posizione occupata agli istanti t = 0,20 s, 0,40 s, 0,60 s e 0,80 s.

Disegna sul quaderno o con un Foglio di calcolo il grafico posizione-tempo.

Determina graficamente l’altezza massima raggiunta, l’istante in cui la moneta arriva a terra, la durata della salita e della discesa. [1,4 m; 0,9 s; sale per 0,4 s e scende per 0,5 s]

185 Un vaso cade da un’altezza di 32 m. Con quale velocità tocca terra? Che velocità avrà a un’altezza da terra di 12 m? [25 m/s; 20 m/s]

Autovelox, Safety Tutor e gli incidenti mortali

I sistemi di rilevamento della velocità per i veicoli stradali sono dei dispositivi che si basano sulla relazione fondamentale tra velocità, spazio e tempo. I due sistemi più diffusi nel nostro Paese sono l’Autovelox e il Safety Tutor. Come risultato della misura effettuata, entrambi forniscono la velocità di un veicolo specifico, ma presentano una sostanziale differenza legata al loro funzionamento.

• L’Autovelox è un sistema portatile (o mobile) di rilevamento della velocità, realizzato con due fotocellule posizionate a una distanza nota (tipicamente 40 cm) che attivano e fermano un cronometro al passaggio del profilo del veicolo lungo la strada. Dividendo la distanza nota tra le fotocellule per il tempo intercorso tra attivazione e blocco del cronometro si ottiene la velocità “istantanea” del veicolo.

• Anche il sistema Safety Tutor è realizzato da una coppia di sensori disposti a una distanza nota, ma molto maggiore rispetto al primo caso (tipicamente tra i 10 km e i 25 km). La criticità è quella di abbinare le letture al veicolo: a questo scopo i portali del sistema Tutor sono dotati di un sistema di monitoraggio delle targhe che abbinano l’istante di passaggio del veicolo con la targa per poi accoppiare i tempi rilevati alle diverse postazioni di rilevamento per il calcolo della velocità media.

Per le loro caratteristiche, gli Autovelox risultano più efficaci all’interno dei centri cittadini e nelle tratte urbane come deterrente a una guida pericolosa, mentre il Safety Tutor è impiegato sulla rete autostradale.

Lo scopo di queste tecnologie non è solo quello di sanzionare gli eccessi di velocità, ma anche (e soprattutto) quello di promuovere una guida nei limiti di sicurezza, perché la presenza di sistemi di rilevamento della velocità agisce da deterrente al superamento dei limiti, riducendo significativamente il numero di incidenti con esiti gravi o mortali. In Italia, infatti, secondo i dati riportati dalla Polizia di Stato, nei tratti gestiti con sistemi Safety Tutor si registra una significativa diminuzione degli incidenti mortali.

GUARDA

Per capire nel dettaglio come funzionano questi sistemi, puoi guardare “Polizia Stradale in azione: Tutor e autovelox, miti e leggende da sfatare”.

• https://www.youtube.com/watch?v=0LSpbRSQrT0

• di Moto.it

• del 19 Giugno 2015

• durata: 4ʹ 30ʹʹ

RISOLVI

In una tratta controllata dal Safety Tutor, un veicolo compie un sorpasso di 1,5 km alla velocità di 150 km/h; nel tratto rimanente procede a 129 km/h. Se il limite di velocità è di 130 km/h e i portali sono posti a 12,5 km di distanza, il Safety Tutor rileva una velocità media superiore a quella ammessa? E se ci fosse un Autovelox nella zona del sorpasso verrebbe rilevato un eccesso di velocità?

ORIENTAMENTO

Il controllo della velocità è uno strumento molto utile per la riduzione degli incidenti mortali ma non è l’unico.

• Prendi spunto dalla lettura di questo articolo https://www.europeandatajournalism.eu/ita/Notizie/Data-news/ Gli-autovelox-le-automobili-vecchie-e-il-numero-di-incidenti-mortali e cerca in rete le statistiche europee riguardanti la correlazione tra utilizzo dei sistemi di controllo della velocità e riduzione degli incidenti mortali.

• Valuta quali altri parametri di rischio possono incidere sul numero di incidenti mortali.

• Crea un’infografica che correli i diversi parametri che hai individuato riassumendo i risultati della tua ricerca.

Il moto di una pallina lungo un piano inclinato

In questa esperienza misureremo l’accelerazione di una pallina che rotola lungo un piano inclinato, usando un software di videoanalisi, Tracker. Per le esperienze di questo corso abbiamo utilizzato la versione scaricabile più recente di Tracker, ma tutte le indicazioni riportate sono comunque valide anche per le altre versioni (sia scaricabili che online), anche se possono presentare qualche minima differenza nei nomi dei percorsi da seguire.

Che cosa ti serve?

• Una pallina e un piano inclinato (una tavola un po’ lunga inclinata o un tavolino alzato solo da un lato con due rialzi)

• Uno smartphone dotato di fotocamera

• Un righello

• L’applicativo Tracker Video Analysis and Modeling Tool (https://physlets.org/tracker/) nella versione per computer (https://www.compadre.org/osp/items/detail.cfm?ID=7365) o nella versione on-line

Esegui l’esperimento e raccogli i dati

1. Disponi il set per la ripresa del moto: posiziona il piano inclinato su uno sfondo di colore diverso e ben distinguibile da quello della pallina e inserisci il righello ben visibile in un punto in prossimità della traiettoria della pallina che non interferisca con il moto. Conoscere con precisione una lunghezza all’interno del video serve per la calibrazione del software.

2. Fai rotolare la pallina lungo il piano inclinato e riprendi il moto con lo smartphone.

3. Esporta il video dallo smartphone e importalo all’interno di Tracker (seguendo il percorso “File” → “Importa” → “Video”). Se necessario usa i filtri (che puoi trovare in “Video” → “Filtri”) per migliorare la qualità del video.

4. Seleziona solo i fotogrammi interessanti del video aprendo il menù “Video” → “Impostazioni” → “Clip”: a questo punto si apre una mascherina dove puoi selezionare i frame iniziali e finali del video da analizzare. Per aiutarti in questa fase, puoi anche spostare i cursori a forma di triangolo che si trovano in basso sotto al player del video.

5. Apri il menu “Asta di calibrazione”. Misura con il nastro la lunghezza nota e scrivi il valore corrispondente nella casella “Lunghezza scalata”.

6. Seleziona l’icona ; trascina gli assi cartesiani e posizionali con l’asse delle x orientato lungo la direzione del piano inclinato.

7. Per rilevare la traccia del corpo in movimento (nel nostro caso la pallina) seleziona l’icona “Punto di massa”. Posiziona l’indicatore sulla pallina e premi shift + click (mirino quadrato); ripeti il posizionamento fotogramma per fotogramma.

A questo punto puoi notare che il moto è rettilineo perché, entro l’errore di posizionamento del mirino, la traiettoria corrisponde a una retta.

Analizza i dati

1. Seguendo il moto della pallina, Tracker raccoglie i dati di posizione e tempo e crea automaticamente dei grafici che mostrano “in diretta” l’andamento di alcune delle grandezze che stai misurando. Puoi personalizzare i grafici cliccando sull’etichetta degli assi 1 .

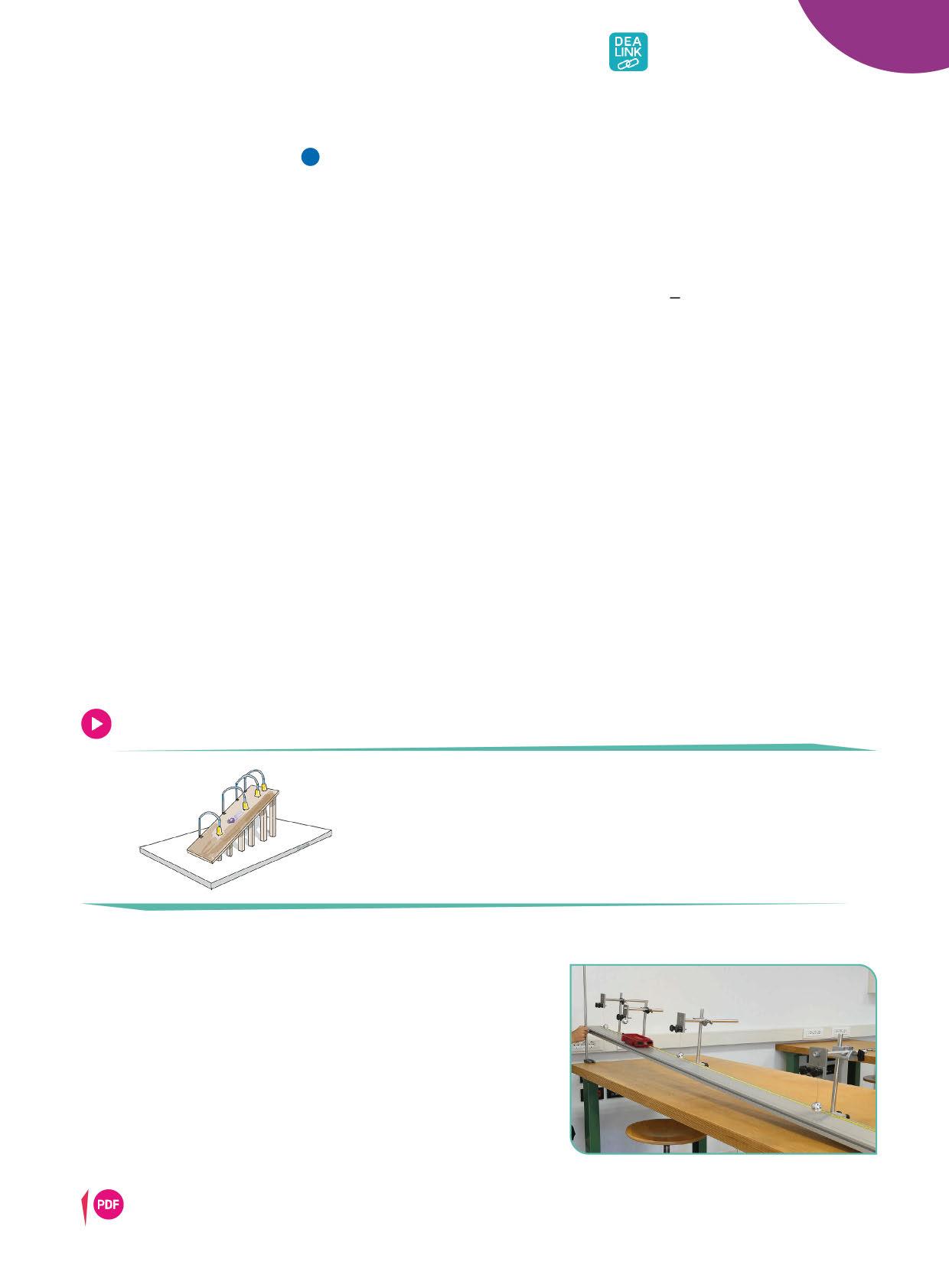
2. Imposta come separatore decimale la virgola o il punto (dal menù “Modifica” → “Numeri” → “Formati”).

3. Esporta col comando “File” → “Esporta” → “File dati” i dati relativi al tempo t, alla posizione x e alla velocità v

4. Disegna il grafico con il Foglio di calcolo mettendo in ascissa il tempo e in ordinata la posizione. I punti inseriti nel grafico dovrebbero disegnare un arco di parabola.

5. Inserisci una linea di tendenza sopra i tuoi punti sperimentali, usando un polinomio di secondo grado; visualizza sul grafico l’equazione e il coefficiente R2. L’equazione oraria è del tipo x = x 0 + v0t + 1 2 at 2 e corrisponde a un moto uniformemente accelerato.

6. x0 è la posizione iniziale e vale: ............................ .

7. v0 è la velocità iniziale e vale: ............................ .

8. a è l’accelerazione, che è costante, e vale: ............................ (per il calcolo di a moltiplica per 2 il coefficiente di t2).

9. Tanto più R2 è vicino a 1, quanto più la relazione quadratica è rispettata.

Osservazioni

Estrapola dal grafico che hai creato con il Foglio di calcolo i valori di x0 e v0 e completa i punti 6. e 7. di Analizza i dati. Calcola a per completare il punto 8. e controlla il coefficiente R2: tanto più il suo valore è vicino a 1, quanto più la relazione quadratica è rispettata.

VIDEOESPERIMENTI DA PROVARE

Il piano inclinato di Galileo

Sperimenta In questo video studieremo il moto di un carrellino che scende lungo un piano inclinato.

Che cosa ti serve?

• Un piano inclinato

• Aste e morsetti

• Campanellini

• Un carrellino

Che cosa devi fare?

1. Con l’aiuto dei morsetti, fissa le aste lungo il piano inclinato a distanze proporzionali ai numeri dispari.

2. Fissa i campanellini alle aste, in modo tale che tutti i campanellini distino egualmente dal piano inclinato e possano essere urtati dal carrellino che farai scendere lungo il piano.

3. Lascia scendere il carrellino lungo il piano inclinato senza imprimergli alcuna velocità iniziale: per far ciò metti la mano davanti al carrello e poi toglila muovendola lungo la discesa, parallelamente al piano.

Che cosa succede?

Scopri che cosa succede nella scheda di laboratorio completa Il piano inclinato di Galileo che trovi online

IL PERCORSO DELLE IDEE

Unità di misura È la linea formata dai punti successivi occupati dal corpo in moto.

IL MOTO RETTILINEO

È un moto che avviene lungo una retta.

Il sistema di riferimento

Il moto è relativo perché dipende dal sistema di riferimento adottato.

La velocità media È il rapporto tra lo spostamento e l’intervallo di tempo impiegato:

L’accelerazione media È il rapporto tra la variazione di velocità e l’intervallo di tempo impiegato:

La velocità istantanea È la velocità media calcolata in un intervallo di tempo molto piccolo.

Il moto rettilineo uniforme È un moto che avviene lungo una retta a velocità costante.

Legge oraria:

s = s0 + vt

Grafico posizione-tempo: s s (m) t (s)

Grafico velocità-tempo:

L’accelerazione istantanea È l’accelerazione media calcolata in un intervallo di tempo molto piccolo.

Il moto rettilineo uniformemente accelerato È un moto che avviene lungo una retta con accelerazione costante.

Legge oraria:

s = s0 + v0 t + 1 2 at 2

Grafico posizione-tempo:

Equazione della velocità:

v = v0 + at

Grafico velocità-tempo:

La caduta libera È il moto di un corpo su cui agisce solo la forza peso.

Equazione oraria: y = y 0 + v0 t 1 2 gt 2

Equazione della velocità: v = v0 gt

Accelerazione di gravità: g = 9,81 m s2

ESERCIZI DI FINE UNITÀ

RISOLVI

1 La seguente tabella (tratta dall’orario di Trenitalia) si riferisce al tragitto percorso da un treno Regionale Veloce.

f Draw on your notebook or on a Spread sheet the velocity-time graph.

a Dove è fissata l’origine del sistema di riferimento? In quale verso è orientato? Quando è fissata l’origine dei tempi?

b Qual è la lunghezza del cammino percorso dal treno tra le stazioni di Orte e Orvieto? Qual è la rapidità media tra Roma Termini e Orvieto? [42 km; 93 km/h]

2 Fulvia entra nell’acqua da una scaletta posta a 5 m dai blocchi di partenza e nuota a rana fino all’estremità più lontana della vasca; dopo la virata percorre a dorso l’intera vasca di ritorno. La corsia è lunga 25 m. Fissa un asse di riferimento con l’origine sui blocchi di partenza e rivolto verso l’altra estremità della vasca. Determina lo spostamento di Fulvia da quando entra in acqua a quando completa la vasca di ritorno. Calcola la lunghezza del cammino percorso. [-5 m; 45 m]

4 Il grafico riportato di seguito descrive il moto del gancio di una gru. L’asse di riferimento è verticale orientato verso l’alto con l’origine sul terreno.

3 The figure shows the space-time graph of a woman.

a When does she move forward and when backward?

b When does she stop?

c What is her total displacement? What distance does she travel? [20 m; 44 m]

d What is the average velocity and the average speed? [0.67 m/s; 1.5 m/s]

e When did she travel fastest? How can you tell it?

a Quale è la posizione del gancio all’istante iniziale e a t = 10 s? Quando è nella posizione s = 6 m? [5,5 m; 0 m; 0,5 s, 3 s]

b Ci sono punti di inversione del moto? In caso di risposta affermativa, in quali istanti e in quali posizioni? [2 s, 7 m]

c In quale intervallo di tempo il gancio si è mosso nel verso positivo? Quando è stato fermo e quando si è mosso verso il basso?

[Da 0 a 2 s; 2 s e da 4 s a 8 s circa; da 2 s a 4 s e da 8 s a 10 s] d Calcola la velocità e la rapidità media nei primi 5 s. [-0,5 m/s; 1,1 m/s]

5 A train, travelling at 10 m/s, starts to accelerate at 1.0 m/s2 for 0.2 min. Find the final velocity. [22 m/s]

6 Una moto supera alla velocità costante di 72 km/h un’auto della polizia che viaggia a 54 km/h. Se al momento del sorpasso l’auto della polizia inizia ad accelerare con accelerazione costante di 2,0 m/s2, che distanza percorre e quanto tempo impiega a raggiunge la moto? Risolvi algebricamente e graficamente disegnando sul quaderno o con un Foglio di calcolo i due moti su un grafico posizione-tempo per un intervallo di tempo di 8 s. [100 m; 5 s]

7 Marco e Luca partecipano a una gara. La figura mostra i grafici dell’andamento delle velocità in relazione al tempo.

11 Un oggetto viene lanciato dalla sommità di un palazzo a una velocità di 54,0 km/h. Colpisce il suolo con una velocità di 126 km/h. Per quanto tempo l’oggetto è rimasto in aria? Quanto è alto l’edificio? [2,04 s; 51,0 m]

12 Un astronauta lancia un sasso sulla Luna, dal basso verso l’alto, e misura la velocità in alcuni istanti di tempo, come illustrato nella tabella.

t (s) 1,002,003,004,005,00

v (m/s) 13,411,810,18,526,90

Descrivi le caratteristiche del moto di ciascuno dei due ragazzi, specificando gli intervalli di tempo in cui l’accelerazione è costante. Qual è l’accelerazione media nei 10 s considerati? Chi è in vantaggio dopo 5 s? Con che distacco? E dopo 10 s? (Suggerimento: calcola lo spostamento come area del sottografico.)

[0,5 m/s ; 0,8 m/s ; Luca, 2,5 m; Marco, 2,5 m]

8 Luca e Fabio si salutano per strada quando distano 50 m e si vanno incontro. Fabio parte da fermo e accelera costantemente di 0,25 m/s2, mentre Luca corre con velocità costante. Se si incontrano dopo 11 s, qual è la velocità di Luca? A quale distanza dal punto di partenza di Fabio si incontrano? [11 km/h; 15 m]

9 Alice lascia cadere in verticale un sassolino in un lago da una scogliera. Il sassolino colpisce la superficie d’acqua dopo un tempo di 3,2 s dopo il lancio. A quale velocità il sassolino ha colpito l’acqua? A quale altezza dal lago si trova la scogliera? [31 m/s; 50 m]

10 SPERIMENTA Con le equazioni della caduta libera si può misurare il tempo di reazione di una persona. Martina tiene nell’estremità superiore una riga da disegno disposta verticalmente. Chiara posiziona il pollice e l’indice vicino all’estremità inferiore, in prossimità della tacca che indica lo zero. Quando Martina lascia la riga, Chiara la afferra in corrispondenza della tacca dei 15 cm. Applica la legge di caduta e deduci il tempo di reazione di Chiara. Ripeti la misura con i tuoi compagni e stabilisci chi ha il minor tempo di reazione. [0,17 s]

Disegna un grafico sul quaderno o con un Foglio di calcolo. Calcola l’accelerazione del sasso e la velocità iniziale con cui è stato lanciato. [1,63 m/s ; 15,0 m/s]

13 In tabella sono riportate le velocità di una sfera che rotola su una guida inclinata. Costruisci sul quaderno o con un Foglio di calcolo il grafico velocità-tempo e verifica che si tratta di un moto rettilineo uniformemente accelerato. Determina l’accelerazione e la velocità iniziale. Calcola la velocità che ha la sfera quando il cronometro segna 1,7 s.

t (s) 00,51,01,52,0

v (m/s) –1,5–0,8–0,10,61,3

Qual è lo spostamento tra gli istanti t = 2,0 s e t = 3,0 s? [1,4 m/s ; -1,5 m/s; 0,9 m/s; 2 m]

14 MEDICINA La velocità con cui si propagano gli impulsi nervosi varia da 5,0 m/s a 120 m/s. Assumendo una velocità media di 50 m/s, se ti pungi un dito, dopo quanto tempo senti dolore? Assumi che l’impulso percorra 1,0 m. [0,02 s]

15 TECNOLOGIA Nell’aprile 2015 in Giappone è stato testato un treno a levitazione magnetica che ha raggiunto la velocità record di 603 km/h. Il test fa parte di un progetto che prevede la costruzione di una linea lunga 286 km per collegare le città di Tokyo e Nagoya in 40 minuti. Calcola la velocità media prevista sulla tratta. [429 km/h]

16 SPORT Il percorso di una gara di canottaggio è lungo 2000 m. In un determinato istante, che consideriamo come iniziale, un equipaggio si trova a 200 m dalla linea di partenza. Dopo 7,5 min giunge al traguardo, viaggiando a velocità costante. Quando si trova a metà del percorso di 200 m? [200 s]

17 SCIENZE Il forapaglie (Acrocephalus schoenobaenus) è un uccello di piccole dimensioni che sverna nelle paludi del Golfo di Guinea. In primavera attraversa le sabbie del Sahara e il Mediterraneo per raggiungere l’Europa, percorrendo circa 4000 km senza fermarsi. Se la sua rapidità media è di 38 km/h, quanto tempo deve volare consecutivamente? [Più di 4 d 9 h]

18 SPORT Alle paraolimpiadi di Tokyo 2020, le atlete Martina Caironi, Monica Contrafatto e Ambra Sabatini hanno realizzato una storica tripletta posizionandosi ai primi tre posti nei 100 m femminili categoria T63. Caironi ha corso in 14,46 s, Contrafatto con una velocità media di 24,44 km/h, Sabatini con una velocità media di 7,087 m/s. Qual è stato l’ordine d’arrivo? E il tempo record del mondo della vincitrice? [14,11 s]

19 3 SICUREZZA L’introduzione sulle autostrade del sistema Safety Tutor per il controllo elettronico della velocità ha portato a una riduzione del numero di incidenti. Per esempio, sulla rete di Strada dei Parchi (A24 Roma-Teramo e A25 Torano-Pescara) l’installazione del Safety Tutor ha prodotto una diminuzione del tasso di mortalità del 50%. La tabella riporta la posizione di due postazioni del sistema Safety Tutor e i tempi di transito di un autoveicolo. Qual è stata la rapidità media del veicolo tra le due postazioni? In base a questi dati, puoi essere sicuro che l’automobile abbia sempre rispettato il limite di velocità di 130 km/h?

termine della corsa, un sistema GPS che aveva con sé fornisce i dati mostrati in figura. Stabilisci in quali istanti Laura ha corso e in quali ha camminato. Qual è lo spazio percorso camminando? E quello percorso correndo? Determina, inoltre, la rapidità media nell’intero percorso. Presta attenzione alle unità di misura. [900 m; 6 km; 2,7 m/s]

no]

20 3 SPORT Laura si allena sul lungomare di Pescara alternando tratti di corsa a tratti di marcia. Al

AUTOVERIFICA

1 Un passeggero sulla banchina osserva un treno che sta arrivando in stazione. Che cosa si può affermare?

A Il macchinista sul treno è fermo

B Il macchinista è in moto

C Il passeggero è in moto rispetto al treno

D Il passeggero è fermo

Punteggio ....../5

2 Il vincitore di una gara di Ultratrail ha percorso i 40 km di salita a una velocità media di 8 km/h, i 30 km di discesa in media a 15 km/h e i 30 km di falsopiano a 10 km/h. Quale è stata la sua velocità media sull’intero percorso?

A 12 km/h

B 11,5 km/h

C 11 km/h

D 10 km/h

E 9,5 km/h

(Design del prodotto e della nautica, 2018/19)

Punteggio ....../5

3 Alle ore 15:30 il contachilometri di un’autovettura segna 22.715. Se alle ore 17:00 il contachilometri segna 22.865, qual è stata la sua velocità media?

A 10 km/h

B 150 km/h

C 50 km/h

D 100 km/h

E 200 km/h

(Architettura, 2016/17)

Punteggio ....../5

21 3 SICUREZZA Per garantire la sicurezza della circolazione, il codice della strada fissa a 50 km/h il limite di velocità nei centri abitati. Mentre viaggia a 50 km/h, un automobilista preme il freno perché vede un pedone che sta attraversando la strada a 15 m di distanza. Per un certo tipo di asfalto asciutto l’auto al massimo può avere un’accelerazione di -7,2 m/s2. L’auto si fermerà in tempo per evitare l’incidente? E se la velocità dell’auto fosse superiore al limite e uguale a 60 km/h? In caso di pioggia è consigliabile guidare con prudenza e ridurre la velocità. Rispondi alle domande precedenti sapendo che in caso di asfalto bagnato l’accelerazione massima si riduce a -5,8 m/s2. [13 m; 19 m; 17 m; 24 m]

4 In un grafico velocità-tempo, l’accelerazione media in un certo intervallo di tempo (t1, t2) è rappresentata da:

A la pendenza della retta tangente al grafico

B la pendenza della retta secante il grafico nei punti corrispondenti a t1 e t2

C l’area sottesa al grafico tra t1 e t2

D l’area sottesa al grafico tra 0 e t2

5 Che cosa si intende per accelerazione?

Punteggio ....../5

A Una variazione di velocità nell’unità di tempo

B Una determinata variazione di velocità

C Una diminuzione di velocità nell’unità di tempo

D Un aumento di velocità nell’unità di tempo (Scienze della formazione primaria, 2019/20)

Punteggio ....../5

6 Un corpo viene lanciato verticalmente verso l’alto. Nel punto più alto della traiettoria:

A cambiano segno la velocità e l’accelerazione

B cambia segno la velocità ma non l’accelerazione

C cambia segno l’accelerazione ma non la velocità

D non cambia segno né la velocità né l’accelerazione

Punteggio ....../5

7 Laura nuota in una piscina di 50 m di lunghezza, percorrendola da un capo all’altro e ritornando indietro in 1 minuto e 30 s. Determina lo spostamento e la distanza percorsa e calcola la velocità media e la rapidità media.

Punteggio ....../15

8 La figura rappresenta il diagramma di un oggetto in moto rettilineo. In quale intervallo di tempo il corpo è fermo? Qual è lo spostamento tra gli istanti t0 = 1 s e t1 = 7 s? Calcola la velocità negli intervalli di tempo in cui il moto è uniforme.

Punteggio ....../15

9 Un’auto che sta viaggiando alla velocità di 60 km/h accelera per 5,0 s fino alla velocità di 90 km/h. Calcola l’accelerazione. Calcola la distanza percorsa dall’auto nei 5,0 s.

Punteggio ....../20

10 Un vaso cade da un’altezza di 45 m. Trascurando la resistenza dell’aria, qual è la sua accelerazione? Quanto tempo impiega per cadere? Con che velocità tocca terra?

Punteggio ....../20

RIPASSO E RECUPERO anche con la playlist di

COMPLETA LA SINTESI INSERENDO LE PAROLE INDICATE (potresti dover usare alcune parole più volte)

1 legge oraria – posizione – spazio

Fissato un sistema di riferimento, un corpo è in moto se la sua ......................... cambia nel tempo. La ......................... associa a ogni istante di tempo la posizione occupata dal corpo in quell’istante e viene rappresentata in un grafico detto diagramma orario o grafico -tempo.

2 lunghezza – velocità – velocità istantanea

La è il rapporto tra lo spostamento e l’intervallo di tempo necessario per compiere tale spostamento. La rapidità media è il rapporto tra la ......................... del cammino percorso e l’intervallo di tempo. La .........................è la velocità media calcolata in un intervallo di tempo molto breve.

3 istante – pendenza – tangente

In un grafico spazio-tempo la velocità media durante un particolare intervallo di tempo è uguale alla ......................... della retta che passa per il punto iniziale e finale dell’intervallo. La velocità istantanea in un particolare ......................... è uguale alla pendenza della ......................... alla curva in quell’istante.

4 retta – traiettoria – velocità

Un moto è rettilineo uniforme se la è rettilinea e la velocità è costante. Il grafico posizione-tempo è un tratto di la cui pendenza rappresenta la .

5 pendenza – secante – velocità

L’accelerazione media è il rapporto tra la variazione di velocità e l’intervallo in cui essa avviene. In un grafico . -tempo è uguale alla della retta che passa per i punti della curva corrispondenti all’intervallo considerato.

6 costante – parabola – variazioni

In un moto rettilineo uniformemente accelerato le ......................... di velocità sono direttamente proporzionali agli intervalli di tempo in cui avvengono e l’accelerazione è quindi ............................... Il grafico posizione-tempo è un arco di .

7 accelerazione – retta

Per un oggetto che si muove con accelerazione costante il grafico velocità-tempo è una linea …………………………………… . La pendenza della retta rappresenta l’......................... . L’area sotto la retta rappresenta lo spostamento.

8 basso – libera – trascurabile

Se la resistenza dell’aria è , tutti i corpi lasciati cadere o lanciati verticalmente verso l’alto cadono per effetto della forza peso con un moto uniformemente accelerato, detto caduta ......................... . L’accelerazione è sempre rivolta verso il ......................... e vale 9,81 m/s2.

RISOLVI

9 Un’auto si muove lungo l’asse x, come nella figura seguente. La sua posizione iniziale è xA. Quindi si sposta in xB; infine torna indietro e passa per il punto xC. Quali sono lo spostamento e la distanza percorsa tra xA e xB? E tra xA e xC?

10 Giulio cammina 10 km verso est per 2 ore e poi 2,5 km verso ovest per 1 ora. Calcola la velocità media e la rapidità media. [2,5 km/h; 4,2 km/h]

11 Un’auto viaggia alla velocità di 24 m/s. Determina la velocità in km/h e lo spazio percorso in 2 minuti. [2,88 km]

12 ESERCIZIO GUIDATO Il grafico spazio-tempo in figura rappresenta il moto di un uomo lungo un rettilineo. Calcola la velocità in ogni tratto del grafico. In quale tratto l’uomo si è fermato? In quale tratto si è mosso nel verso negativo? [1,8 m/s, 0, -1,2 m/s; CD; DE]

FORMULE UTILI vm = s2 - s1 t2 - t1

PROCEDIMENTO

a In ogni tratto del diagramma spazio-tempo la pendenza è costante, quindi la velocità è costante.

b Calcoliamo la velocità media in ogni tratto.

c Nei tratti orizzontali del grafico, l’uomo è stato fermo, mentre nei tratti in cui la pendenza è negativa il moto è nel verso opposto a quello dell’asse di riferimento.

13 Cammini a velocità costante lungo un rettilineo e percorri 0,80 m ogni secondo. Accendi il cronometro quando ti trovi a 15 m dall’inizio della strada. Scrivi l’equazione del moto e calcola a che distanza ti trovi dall’inizio della strada dopo 5,0 s. [19 m]

14 Gaia viaggia in bicicletta alla rapidità costante di 15 km/h. Dopo quanto tempo avrà percorso 10 km? [40 minuti]

15 In 25 s la velocità di un corpo aumenta da 27 km/h a 81 km/h. Qual è la sua accelerazione media? [0,60 m/s ]

16 ESERCIZIO GUIDATO Un’automobilina telecomandata accelera da ferma con accelerazione uguale a 1,1 m/s2, per 8,0 s su un percorso rettilineo. Quale distanza percorre? [35 m]

FORMULE UTILI s = s0 + v0t + 1 2 at2

PROCEDIMENTO

a Ricorda che quando un corpo parte “da fermo” la sua velocità iniziale è v0 = 0.

b Accelerando su una traiettoria rettilinea, l’automobilina compie un moto rettilineo uniformemente accelerato.

c Scrivi per prima cosa la legge oraria del moto e con essa calcola la distanza.

17 Un’auto si muove con velocità iniziale di 20 m/s e si ferma con accelerazione costante in 6,0 s. Qual è l’accelerazione? Qual è lo spazio percorso dall’auto durante la frenata? [3,3 m/s ; 61 m]

18 ESERCIZIO GUIDATO Un sasso viene lanciato verticalmente verso l’alto con una velocità di 8,0 m/s. In quanto tempo arriva alla massima altezza? [0,82 s]

FORMULE UTILI v = v0 + at

PROCEDIMENTO

a Ricorda che quando un corpo viene lanciato verticalmente verso l’alto, compie un moto rettilineo uniformemente accelerato con accelerazione g = 9,81 m/s2.

b Se stabilisci un asse di riferimento verticale orientato verso l’alto, la velocità ha verso positivo e l’accelerazione ha verso negativo.

c Nella posizione di massima altezza la velocità si annulla.

d Scrivi la legge di variazione della velocità e, con la formula inversa, calcola l’istante di tempo richiesto.

19 Un vaso, che si trova sul parapetto di un balcone a 12 m di altezza, cade a terra. Dopo quanto tempo arriva al suolo? (Suggerimento: la velocità iniziale è nulla.) [1,6 s]

20 Un giocoliere lancia una pallina verso l’alto ed essa raggiunge l’altezza massima in 0,49 s. Con quale velocità il giocoliere ha lanciato la pallina? [4,8 m/s]